The Project Gutenberg eBook of On the relative motion of the Earth and the luminiferous æther, by Albert Abraham Moseley
This eBook is for the use of anyone anywhere in the United States and
most other parts of the world at no cost and with almost no restrictions
whatsoever. You may copy it, give it away or re-use it under the terms
of the Project Gutenberg License included with this eBook or online
at
www.gutenberg.org. If you
are not located in the United States, you will have to check the laws of the
country where you are located before using this eBook.
Title: On the relative motion of the Earth and the luminiferous æther
Authors: Albert Abraham Moseley
Edward Morley
Release Date: June 3, 2023 [eBook #70888]
Language: English
Produced by: Laura Natal Rodrigues (Images generously made available by The Internet Archive.)
*** START OF THE PROJECT GUTENBERG EBOOK ON THE RELATIVE MOTION OF THE EARTH AND THE LUMINIFEROUS ÆTHER ***
THE
LONDON, EDINBURGH and DUBLIN
PHILOSOPHICAL MAGAZINE
AND
JOURNAL OF SCIENCE.
[FIFTH SERIES.]
DECEMBER 1860.
LVIII. On the Relative Motion of the Earth and the
Luminiferous Æther.
By ALBERT A. MICHELSON
and
EDWARD W. MORLEY
[1].
The discovery of the aberration of light was
soon followed by an explanation according to the emission theory. The
effect was attributed to a simple composition of the velocity of light with
the velocity of the earth in its orbit. The difficulties in this apparently
sufficient explanation were overlooked until after an explanation on the
undulatory theory of light was proposed. This new explanation was at first
almost as simple as the former. But it failed to account for the fact
proved by experiment that the aberration was unchanged when observations
were made with a telescope filled with water. For if the tangent of the
angle of aberration is the ratio of the velocity of the earth to the
velocity of light, then, since the latter velocity in water is
three-fourths its velocity in a vacuum, the aberration observed with a
water telescope should be four-thirds of its true value.[2]
On the undulatory theory,
according to Fresnel, first, the æther is supposed to be at rest except
in the interior of transparent media, in which secondly, it is supposed
to move with a velocity less than the velocity of the medium in the ratio
 , where
, where  is the index of refraction. These
two hypotheses give a complete and satisfactory explanation of aberration.
The second hypothesis, notwithstanding its seeming improbability, must
be considered as fully proved, first, by the celebrated experiment of
Fizeau,[3]
and secondly, by the ample confirmation of our own work.[4].
The experimental trial of the first hypothesis forms the subject of the
present paper.
is the index of refraction. These
two hypotheses give a complete and satisfactory explanation of aberration.
The second hypothesis, notwithstanding its seeming improbability, must
be considered as fully proved, first, by the celebrated experiment of
Fizeau,[3]
and secondly, by the ample confirmation of our own work.[4].
The experimental trial of the first hypothesis forms the subject of the
present paper.
If the earth were a transparent body, it might perhaps be conceded, in
view of the experiments just cited, that the inter-molecular æther was
at rest in space, notwithstanding the motion of the earth in its orbit;
but we have no right to extend the conclusion from these experiments to
opaque bodies. But there can hardly be question that the æther can and
does pass through metals. Lorentz cites the illustration of a metallic
barometer tube. When the tube is inclined the æther in the space above
the mercury is certainly forced out, for it is imcompressible.[5].
But again we have no right to assume that it makes its escape with perfect
freedom, and if there be any resistance, however slight, we certainly
could not assume an opaque body such as the whole earth to offer free
passage through its entire mass. But as Lorentz aptly remarks: "Quoi
qu'il en soit, on fera bien, à mon avis, de ne pas se laisser guider,
dans une question aussi importante, par des considérations sur le
degré de probabilité ou de simplicité de l'une ou de l'autre
hypothèse, mais de s'addresser a l'expérience pour apprendre à
connaitre l'état, de repos ou de mouvement, dans lequel se trouve
l'æther à la surface terrestre."[6]
In April, 1881, a method was proposed and carried out for testing the
question experimentally.[7]
In deducing the formula for the quantity to be measured, the effect of
the motion of the earth through the æther on the path of the ray at
right angles to this motion was overlooked.[8]
The discussion of this oversight and of the entire experiment forms the
subject of a very searching analysis by H. A. Lorentz,[9],
who finds that this effect can by no means be disregarded. In consequence,
the quantity to be measured had in fact but one-half the value supposed,
and as it was already barely beyond the limits of errors of experiment, the
conclusion drawn from the result of the experiment might well be
questioned; since, however, the main portion of the theory remains
unquestioned, it was decided to repeat the experiment with such
modifications as would insure a theoretical result much too large to be
masked by experimental errors. The theory of the method may be briefly
stated as follows:—
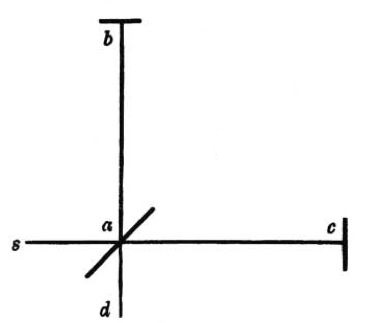
Let  , fig. 1, be a ray of light which is partly reflected in
, fig. 1, be a ray of light which is partly reflected in  ,
and partly transmitted in
,
and partly transmitted in  , being returned by the mirrors
, being returned by the mirrors  and
and
 , along
, along  and
and  .
.  is partly transmitted along
is partly transmitted along  ,
and
,
and  is partly reflected along
is partly reflected along  .
.
If then the paths  and
and  are
equal, the two rays interfere along
are
equal, the two rays interfere along  . Suppose now, the æther being at
rest, that the whole apparatus moves in the direction
. Suppose now, the æther being at
rest, that the whole apparatus moves in the direction  , with the
velocity of the earth in its orbit, the directions and distances
traversed by the rays will be altered thus:—
, with the
velocity of the earth in its orbit, the directions and distances
traversed by the rays will be altered thus:—
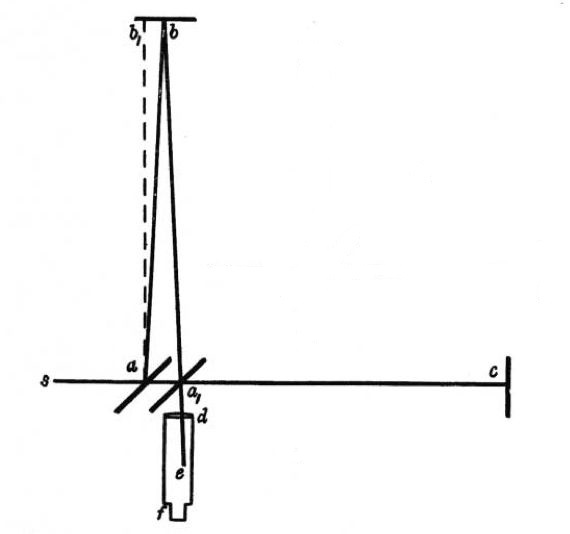
The ray  is reflected along
is reflected along  , fig. 2; the angle
, fig. 2; the angle  , being
equal to the aberration
, being
equal to the aberration  , is returned along
, is returned along  ,
(
,
( ), and goes to the focus of the telescope, whose direction
is unaltered. The transmitted ray goes along
), and goes to the focus of the telescope, whose direction
is unaltered. The transmitted ray goes along  , is returned along
, is returned along
 , and is reflected at
, and is reflected at  , making
, making  equal
equal  ,
and therefore still coinciding with the first ray. It may be remarked
that the rays
,
and therefore still coinciding with the first ray. It may be remarked
that the rays  and
and  , do not now meet exactly in the
same point
, do not now meet exactly in the
same point  , though the difference is of the second order; this
does not affect the validity of the reasoning. Let it now be required to
find the difference in the two paths
, though the difference is of the second order; this
does not affect the validity of the reasoning. Let it now be required to
find the difference in the two paths  , and
, and  .
.
Let  .
.
 .
.
 , fig. 1.
, fig. 1.
 .
.
 ,
(fig. 2.)
,
(fig. 2.)
Then

The whole time of going and coming is
 and the distance traveled in this time is
and the distance traveled in this time is
 neglecting terms of the fourth order. The length of the other path is
evidently
neglecting terms of the fourth order. The length of the other path is
evidently  or to the same degree
of accuracy,
or to the same degree
of accuracy,  . The difference
is therefore
. The difference
is therefore  . If now the whole apparatus be
turned through
. If now the whole apparatus be
turned through  , the difference will be in the opposite
direction, hence the displacement of the interference-fringes should be
, the difference will be in the opposite
direction, hence the displacement of the interference-fringes should be
 . Considering only the velocity of the earth in
its orbit, this would be
. Considering only the velocity of the earth in
its orbit, this would be  . If, as was the case in the
first experiment,
. If, as was the case in the
first experiment,  waves of yellow light, the
displacement to be expected would be
waves of yellow light, the
displacement to be expected would be  of the distance between the
interference fringes.
of the distance between the
interference fringes.
In the first experiment one of the principal difficulties encountered
was that of revolving the apparatus without producing distortion; and
another was its extreme sensitiveness to vibration. This was so great
that it was impossible to see the interference fringes except at brief
intervals when working in the city, even at two o'clock in the morning.
Finally, as before remarked, the quantity to be observed, namely, a
displacement of something less than a twentieth of the distance between
the interference fringes may have been too small to be detected when
masked by experimental errors. The first named difficulties were
entirely overcome by mounting the apparatus on a massive stone floating
on mercury; and the second by increasing, by repeated reflection, the
path of the light to about ten times its former value.
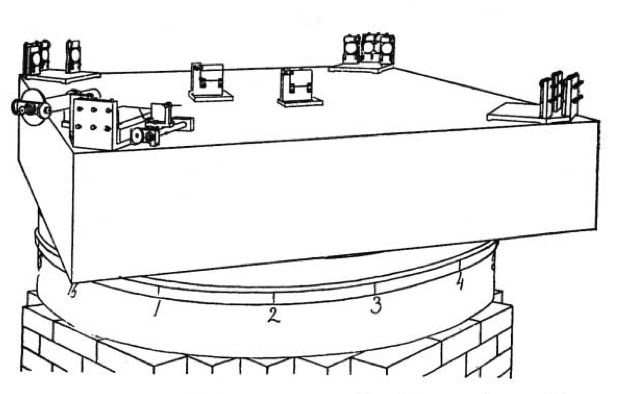
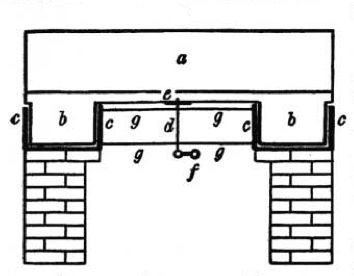
The apparatus is represented in perspective in fig. 3, in plan in fig.
4, and in vertical section in fig. 5.
The stone  (fig. 5) is about
(fig. 5) is about
 and
and  thick.
It rests on an annular wooden float
thick.
It rests on an annular wooden float  ,
,
 outside diameter,
outside diameter,  inside
diameter, and
inside
diameter, and  thick. The float rests on mercury
contained in the cast-iron trough
thick. The float rests on mercury
contained in the cast-iron trough  ,
,  thick, and of such dimensions as to leave a clearance of about one
centimeter around the float. A pin
thick, and of such dimensions as to leave a clearance of about one
centimeter around the float. A pin  , guided by arms
, guided by arms 


 , fits into a socket e attached to the float. The pin may be
pushed into the socket or be withdrawn, by a lever pivoted at
, fits into a socket e attached to the float. The pin may be
pushed into the socket or be withdrawn, by a lever pivoted at  . This
pin keeps the float concentric with the trough, but does not bear any
part of the weight of the stone. The annular iron trough rests on a bed
of cement on a low brick pier built in the form of a hollow octagon.
. This
pin keeps the float concentric with the trough, but does not bear any
part of the weight of the stone. The annular iron trough rests on a bed
of cement on a low brick pier built in the form of a hollow octagon.
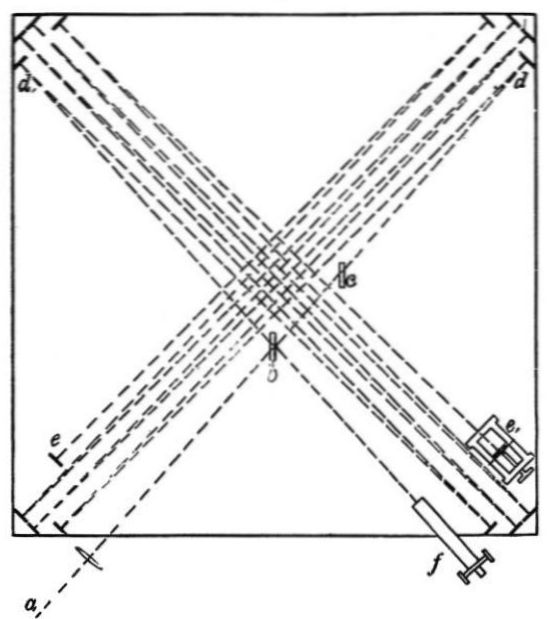
At each corner of the stone were placed four mirrors 
 fig. 4.
Near the center of the stone was a plane-parallel glass
fig. 4.
Near the center of the stone was a plane-parallel glass  . These were
so disposed that light from an argand burner
. These were
so disposed that light from an argand burner  , passing through a lens,
fell on
, passing through a lens,
fell on  so as to be in part reflected to
so as to be in part reflected to  ; the two pencils
followed the paths indicated in the figure,
; the two pencils
followed the paths indicated in the figure, 




 and
and 




 respectively, and
were observed by the telescope
respectively, and
were observed by the telescope  . Both
. Both  and
and  revolved with the
stone. The mirrors were of speculum metal carefully worked to optically
plane surfaces five centimeters in diameter, and the glasses
revolved with the
stone. The mirrors were of speculum metal carefully worked to optically
plane surfaces five centimeters in diameter, and the glasses  and
and
 were plane-parallel and of the same thickness,
were plane-parallel and of the same thickness,
 ; their surfaces measured
; their surfaces measured
 by
by  . The second of these was placed
in the path of one of the pencils to compensate for the passage of the
other through the same thickness of glass. The whole of the optical
portion of the apparatus was kept covered with a wooden cover to prevent
air currents and rapid changes of temperature.
. The second of these was placed
in the path of one of the pencils to compensate for the passage of the
other through the same thickness of glass. The whole of the optical
portion of the apparatus was kept covered with a wooden cover to prevent
air currents and rapid changes of temperature.
The adjustment was effected as follows:—The mirrors having been
adjusted by screws in the castings which held the mirrors, against which
they were pressed by springs, till light from both pencils could be seen
in the telescope, the lengths of the two paths were measured by a light
wooden rod reaching diagonally from mirror to mirror, the distance being
read from a small steel scale to tenths of millimeters. The difference
in the lengths of the two paths was then annulled by moving the mirror
 . This mirror had three adjustments; it had an adjustment in
altitude and one in azimuth, like all the other mirrors, but finer; it
also had an adjustment in the direction of the incident ray, sliding
forward or backward, but keeping very accurately parallel to its former
plane. The three adjustments of this mirror could be made with the
wooden cover in position.
. This mirror had three adjustments; it had an adjustment in
altitude and one in azimuth, like all the other mirrors, but finer; it
also had an adjustment in the direction of the incident ray, sliding
forward or backward, but keeping very accurately parallel to its former
plane. The three adjustments of this mirror could be made with the
wooden cover in position.
The paths being now approximately equal, the two images of the source of
light or of some well-defined object placed in front of the condensing
lens, were made to coincide, the telescope was now adjusted for distinct
vision of the expected interference bands, and sodium light was
substituted for white light, when the interference bands appeared. These
were now made as clear as possible by adjusting the mirror  ;
then white light was restored, the screw altering the length of path was
very slowly moved (one turn of a screw of one hundred threads to the
inch altering the path nearly
;
then white light was restored, the screw altering the length of path was
very slowly moved (one turn of a screw of one hundred threads to the
inch altering the path nearly  till the
colored interference fringes reappeared in white light. These were now
given a convenient width and position, and the apparatus was ready for
observation.
till the
colored interference fringes reappeared in white light. These were now
given a convenient width and position, and the apparatus was ready for
observation.
The observations were conducted as follows:—Around the cast-iron
trough were sixteen equidistant marks. The apparatus was revolved very
slowly (one turn in six minutes) and after a few minutes the cross wire
of the micrometer was set on the clearest of the interference fringes at
the instant of passing one of the marks. The motion was so slow that
this could be done readily and accurately. The reading of the screw-head
on the micrometer was noted, and a very slight and gradual impulse was
given to keep up the motion of the stone; on passing the second mark,
the same process was repeated, and this was continued till the apparatus
had completed six revolutions. It was found that by keeping the
apparatus in slow uniform motion, the results were much more uniform and
consistent than when the stone was brought to rest for every
observation; for the effects of strains could be noted for at least half
a minute after the stone came to rest, and during this time effects of
change of temperature came into action.
The following tables give the means of the six readings; the first, for
observations made near noon, the second, those near six o'clock in the
evening. The readings are divisions of the screw-heads. The width of the
fringes varied from  ,
the mean value being near
,
the mean value being near  , so that one division means
, so that one division means
 . The rotation in the observations at noon
was contrary to, and in the evening observations, with, that of the hands
of a watch.
. The rotation in the observations at noon
was contrary to, and in the evening observations, with, that of the hands
of a watch.
NOON OBSERVATIONS.
| |
16. |
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
| July 8 |
44.7 |
44.0 |
43.5 |
39.7 |
35.2 |
34.7 |
34.3 |
32.5 |
28.2 |
| July 9 |
57.4 |
57.3 |
58.2 |
59.2 |
58.7 |
60.2 |
60.8 |
62.0 |
61.5 |
| July 11 |
27.3 |
23.5 |
22.0 |
19.3 |
19.2 |
19.3 |
18.7 |
18.8 |
16.2 |
| Mean |
43.1 |
41.6 |
41.2 |
39.4 |
37.7 |
38.1 |
37.9 |
37.8 |
35.3 |
| Mean in w. l. |
.862 |
.832 |
.824 |
.788 |
.754 |
.762 |
.758 |
.756 |
.706 |
| |
.706 |
.692 |
.686 |
.688 |
.688 |
.678 |
.672 |
.628 |
.616 |
| Final mean |
.784 |
.762 |
.755 |
.738 |
.721 |
.720 |
.715 |
.692 |
.661 |
| |
9. |
10. |
11. |
12. |
13. |
14. |
15. |
16. |
|
| July 8 |
26.2 |
23.8 |
23.2 |
20.3 |
18.7 |
17.5 |
16.8 |
13.7 |
|
| July 9 |
63.3 |
65.8 |
67.3 |
69.7 |
70.7 |
73.0 |
70.2 |
72.2 |
|
| July 11 |
14.3 |
13.3 |
12.8 |
13.3 |
12.3 |
10.2 |
7.3 |
6.5 |
|
| Mean |
34.6 |
34.3 |
34.4 |
34.4 |
33.9 |
33.6 |
31.4 |
30.8 |
|
| Mean in w. l. |
.692 |
.686 |
.688 |
.688 |
.678 |
.672 |
.628 |
.616 |
|
| |
|
|
|
|
|
|
|
|
|
| Final mean |
... |
... |
... |
... |
... |
... |
... |
... |
|
P.M. OBSERVATIONS.
| |
16. |
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
| July 8 |
61.2 |
63.3 |
63.3 |
68.2 |
67.7 |
69.3 |
70.3 |
69.8 |
69.0 |
| July 9 |
26.0 |
26.0 |
28.2 |
29.2 |
31.5 |
32.0 |
31.3 |
31.7 |
33.0 |
| July 12 |
66.8 |
66.5 |
66.0 |
64.3 |
62.2 |
61.0 |
61.3 |
59.7 |
58.2 |
| Mean |
51.3 |
51.9 |
52.5 |
53.9 |
53.8 |
54.1 |
54.3 |
53.7 |
53.4 |
| Mean in w. l. |
1.026 |
1.038 |
1.050 |
1.078 |
1.076 |
1.082 |
1.086 |
1.074 |
1.068 |
| |
1.068 |
1.086 |
1.076 |
1.084 |
1.100 |
1.136 |
1.144 |
1.154 |
1.172 |
| Final mean |
1.047 |
1.062 |
1.063 |
1.081 |
1.088 |
1.109 |
1.115 |
1.114 |
1.120 |
| |
9. |
10. |
11. |
12. |
13. |
14. |
15. |
16. |
|
| July 8 |
71.3 |
71.3 |
70.5 |
71.2 |
71.2 |
70.5 |
72.5 |
75.7 |
|
| July 9 |
35.8 |
36.5 |
37.3 |
38.8 |
41.0 |
42.7 |
43.7 |
44.0 |
|
| July 12 |
55.7 |
53.7 |
54.7 |
55.0 |
58.2 |
58.5 |
57.0 |
56.0 |
|
| Mean |
54.3 |
53.8 |
54.2 |
55.0 |
56.8 |
57.2 |
57.7 |
58.6 |
|
| Mean in w. l. |
1.086 |
1.076 |
1.084 |
1.100 |
1.136 |
1.144 |
1.154 |
1.172 |
|
| |
|
|
|
|
|
|
|
|
|
| Final mean |
... |
... |
... |
... |
... |
... |
... |
... |
|
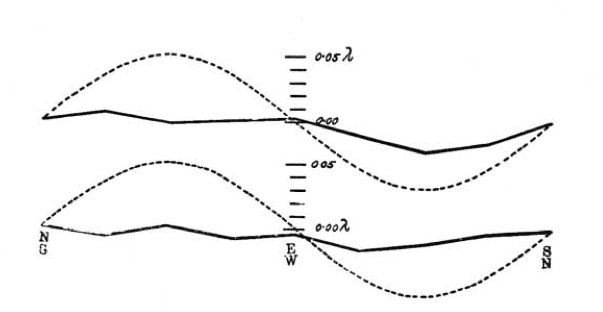
The results of the observations are expressed graphically in fig. 6.
The upper is the curve for the observations at noon, and the lower that
for the evening observations. The dotted curves represent one
eighth of the theoretical displacements. It seems fair to conclude
from the figure that if there is any displacement due to the relative
motion of the earth and the luminiferous æther, this cannot be much
greater than  of the distance between the fringes.
of the distance between the fringes.
Considering the motion of the earth in its orbit only, this displacement
should be
 The distance D was about eleven meters, or
The distance D was about eleven meters, or
 of yellow light; hence the
displacement to be expected was
of yellow light; hence the
displacement to be expected was  . The actual
displacement was certainly less than the twentieth part of this, and
probably less than the fortieth part. But since the displacement is
proportional to the square of the velocity, the relative velocity of the
earth and the æther is probably less than one sixth the earth's orbital
velocity, and certainly less than one-fourth.
. The actual
displacement was certainly less than the twentieth part of this, and
probably less than the fortieth part. But since the displacement is
proportional to the square of the velocity, the relative velocity of the
earth and the æther is probably less than one sixth the earth's orbital
velocity, and certainly less than one-fourth.
In what precedes, only the orbital motion of the earth is considered. If
this is combined with the motion of the solar system, concerning which
but little is known with certainty, the result would have to be
modified; and it is just possible that the resultant velocity at the
time of the observations was small though the chances are much against
it. The experiment will therefore be repeated at intervals of three
months, and thus all uncertainty will be avoided.
It appears, from all that precedes, reasonably certain that if there be
any relative motion between the earth and the luminiferous æther, it
must be small; quite small enough entirely to refute Fresnel's
explanation of aberration. Stokes has given a theory of aberration which
assumes the æther at the earth's surface to be at rest with regard to
the latter, and only requires in addition that the relative velocity
have a potential; but Lorentz shows that these conditions are
incompatible. Lorentz then proposes a modification which combines some
ideas of Stokes and Fresnel, and assumes the existence of a potential,
together with Fresnel's coefficient. If now it were legitimate to
conclude from the present work that the æther is at rest with regard to
the earth's surface, according to Lorentz there could not be a velocity
potential, and his own theory also fails.
Supplement.
It is obvious from what has gone before that it would be hopeless to
attempt to solve the question of the motion of the solar system by
observations of optical phenomena at the surface of the earth. But
it is not impossible that at even moderate distances above the level of the
sea, at the top of an isolated mountain peak, for instance, the relative
motion might be perceptible in an apparatus like that used in these
experiments. Perhaps if the experiment should ever be tried in these
circumstances, the cover should be of glass, or should be removed.
It may be worth while to notice another method for multiplying the
square of the aberration sufficiently to bring it within the range of
observation, which has presented itself during the preparation of this
paper. This is founded on the fact that reflection from surfaces in
motion varies from the ordinary laws of reflection.
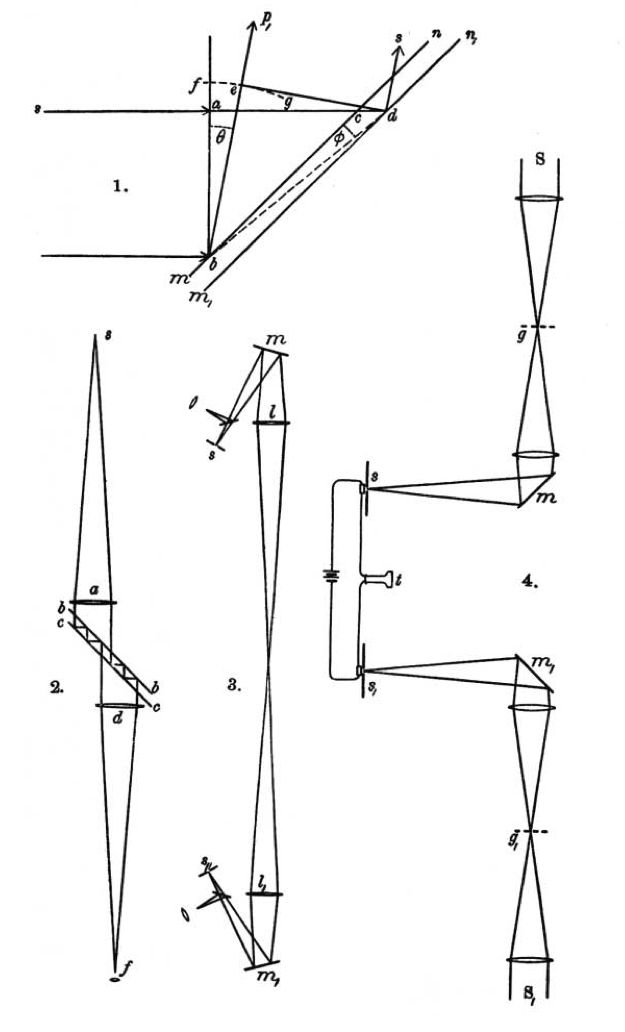
Figures 1, 2, 3 and 4 from Supplement.
Let  (fig. 1 (Figure 07)) be a plane wave
falling on the mirror
(fig. 1 (Figure 07)) be a plane wave
falling on the mirror  at an incidence of
at an incidence of  . If the mirror
is at rest, the wave front after reflection will be
. If the mirror
is at rest, the wave front after reflection will be  .
.
Now suppose the mirror to move in a direction which makes an angle  with its normal, with a velocity
with its normal, with a velocity  . Let
. Let  be the velocity of
light in the æther supposed stationary, and let
be the velocity of
light in the æther supposed stationary, and let  be the increase in
the distance the light has to travel to reach
be the increase in
the distance the light has to travel to reach  . In this time the
mirror will have moved a distance
. In this time the
mirror will have moved a distance  .
.
We have
 which put
which put  , and
, and 
In order to find the new wave front, draw the arc  with
with  as a
center and
as a
center and  as radius; the tangent to this arc from
as radius; the tangent to this arc from  will be the
new wave-front, and the normal to the tangent from
will be the
new wave-front, and the normal to the tangent from  will be the new
direction. This will differ from the direction
will be the new
direction. This will differ from the direction  by the angle
by the angle
 which it is required to find. From the equality of the triangles
which it is required to find. From the equality of the triangles
 and
and  it follows that
it follows that  ,
,  ,
,
 or neglecting terms of the order
or neglecting terms of the order  ,
,

Now let the light fall on a parallel mirror facing the first, we should
then have
 and the total deviation would be
and the total deviation would be
 where
where  is the angle of aberration, if only the orbital motion of
the earth is considered. The maximum displacement obtained by revolving the
whole apparatus through
is the angle of aberration, if only the orbital motion of
the earth is considered. The maximum displacement obtained by revolving the
whole apparatus through  would be
would be
 With fifty such couples the displacement would be
With fifty such couples the displacement would be 
''.
But astronomical observations in circumstances far less favorable than
those in which these may be taken have been made to hundredths of a second;
so that this new method bids fair to be at least as sensitive as the former.
The arrangement of apparatus might be as in fig. 2
(Figure 07);  , in the focus of the lens
, in the focus of the lens  ,
is a slit.
,
is a slit.  are two glass mirrors optically plane and
so silvered as to allow say one twentieth of the light to pass through,
and reflecting say ninety per cent. The intensity of the light falling
on the observing telescope
are two glass mirrors optically plane and
so silvered as to allow say one twentieth of the light to pass through,
and reflecting say ninety per cent. The intensity of the light falling
on the observing telescope  would be about one millionth of the
original intensity, so that if sunlight or the electric arc were used it
could still be readily seen. The mirrors
would be about one millionth of the
original intensity, so that if sunlight or the electric arc were used it
could still be readily seen. The mirrors  and
and  , would
differ from parallelism sufficiently to separate the successive images.
Finally, the apparatus need not be mounted so as to revolve, as the earth's
rotation would be sufficient.
, would
differ from parallelism sufficiently to separate the successive images.
Finally, the apparatus need not be mounted so as to revolve, as the earth's
rotation would be sufficient.
If it were possible to measure with sufficient accuracy the velocity of
light without returning the ray to its starting point, the problem of
measuring the first power of the relative velocity of the earth with
respect to the æther would be solved. This may not be as hopeless as
might appear at first sight, since the difficulties are entirely
mechanical and may possibly be surmounted in the course of time.
For example, suppose (fig. 3 (Figure 07))  and
and
 , two mirrors revolving with equal velocity in opposite
directions. It is evident that light from
, two mirrors revolving with equal velocity in opposite
directions. It is evident that light from  will form a stationary
image at
will form a stationary
image at  and similarly light from
and similarly light from  will form a
stationary image at
will form a
stationary image at  . If now the velocity of the mirrors be increased
sufficiently, their phases still being exactly the same, both images will
be deflected from
. If now the velocity of the mirrors be increased
sufficiently, their phases still being exactly the same, both images will
be deflected from  and
and  , in inverse proportion to the
velocities of light in the two directions; or, if the two deflections are
made equal, and the difference of phase of the mirrors be simultaneously
measured, this will evidently be proportional to the difference of
velocity in the two directions. The only real difficulty lies in this
measurement. The following is perhaps a possible solution.
, in inverse proportion to the
velocities of light in the two directions; or, if the two deflections are
made equal, and the difference of phase of the mirrors be simultaneously
measured, this will evidently be proportional to the difference of
velocity in the two directions. The only real difficulty lies in this
measurement. The following is perhaps a possible solution.
 (fig. 4 (Figure 07)) are two gratings on
which sunlight is concentrated. These are placed so that after falling on
the revolving mirrors
(fig. 4 (Figure 07)) are two gratings on
which sunlight is concentrated. These are placed so that after falling on
the revolving mirrors  and
and  , the light forms images of the
gratings at
, the light forms images of the
gratings at  and
and  , two very sensitive selenium cells in
circuit with a battery and a telephone. If everything be symmetrical,
the sound in the telephone will be a maximum. If now one of the slits
, two very sensitive selenium cells in
circuit with a battery and a telephone. If everything be symmetrical,
the sound in the telephone will be a maximum. If now one of the slits  be displaced through half the distance between the image of the grating
bars, there will be silence. Suppose now that the two deflections having
been made exactly equal, the slit is adjusted for silence. Then if the
experiment be repeated when the earth's rotation has turned the whole
apparatus through
be displaced through half the distance between the image of the grating
bars, there will be silence. Suppose now that the two deflections having
been made exactly equal, the slit is adjusted for silence. Then if the
experiment be repeated when the earth's rotation has turned the whole
apparatus through  , and the deflections are again made equal,
there will no longer be silence, and the angular distance through which
, and the deflections are again made equal,
there will no longer be silence, and the angular distance through which
 must be moved to restore silence will measure the required difference
in phase.
must be moved to restore silence will measure the required difference
in phase.
There remain three other methods, all astronomical, for attacking the
problem of the motion of the solar system through space.
1. The telescopic observation of the proper motions of the stars. This
has given us a highly probably determination of the direction of this
motion, but only a guess as to its amount.
2. The spectroscopic observation of the motion of stars in the line of
sight. This could furnish data for the relative motions only, though it
seems likely that by the immense improvements in the photography of
stellar spectra, the information thus obtained will be far more accurate
than any other.
3. Finally there remains the determination of the velocity of light by
observations of the eclipses of Jupiter's satellites. If the improved
photometric methods practiced at the Harvard observatory make it
possible to observe these with sufficient accuracy, the difference in
the results found for the velocity of light when Jupiter is nearest to
and farthest from the line of motion will give, not merely the motion of
the solar system with reference to the stars, but with reference to the
luminiferous æther itself.
*** END OF THE PROJECT GUTENBERG EBOOK ON THE RELATIVE MOTION OF THE EARTH AND THE LUMINIFEROUS ÆTHER ***
Updated editions will replace the previous one—the old editions will
be renamed.
Creating the works from print editions not protected by U.S. copyright
law means that no one owns a United States copyright in these works,
so the Foundation (and you!) can copy and distribute it in the United
States without permission and without paying copyright
royalties. Special rules, set forth in the General Terms of Use part
of this license, apply to copying and distributing Project
Gutenberg™ electronic works to protect the PROJECT GUTENBERG™
concept and trademark. Project Gutenberg is a registered trademark,
and may not be used if you charge for an eBook, except by following
the terms of the trademark license, including paying royalties for use
of the Project Gutenberg trademark. If you do not charge anything for
copies of this eBook, complying with the trademark license is very
easy. You may use this eBook for nearly any purpose such as creation
of derivative works, reports, performances and research. Project
Gutenberg eBooks may be modified and printed and given away—you may
do practically ANYTHING in the United States with eBooks not protected
by U.S. copyright law. Redistribution is subject to the trademark
license, especially commercial redistribution.
START: FULL LICENSE
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg™ mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase “Project
Gutenberg”), you agree to comply with all the terms of the Full
Project Gutenberg™ License available with this file or online at
www.gutenberg.org/license.
Section 1. General Terms of Use and Redistributing Project Gutenberg™ electronic works
1.A. By reading or using any part of this Project Gutenberg™
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or
destroy all copies of Project Gutenberg™ electronic works in your
possession. If you paid a fee for obtaining a copy of or access to a
Project Gutenberg™ electronic work and you do not agree to be bound
by the terms of this agreement, you may obtain a refund from the person
or entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. “Project Gutenberg” is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg™ electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg™ electronic works if you follow the terms of this
agreement and help preserve free future access to Project Gutenberg™
electronic works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation (“the
Foundation” or PGLAF), owns a compilation copyright in the collection
of Project Gutenberg™ electronic works. Nearly all the individual
works in the collection are in the public domain in the United
States. If an individual work is unprotected by copyright law in the
United States and you are located in the United States, we do not
claim a right to prevent you from copying, distributing, performing,
displaying or creating derivative works based on the work as long as
all references to Project Gutenberg are removed. Of course, we hope
that you will support the Project Gutenberg™ mission of promoting
free access to electronic works by freely sharing Project Gutenberg™
works in compliance with the terms of this agreement for keeping the
Project Gutenberg™ name associated with the work. You can easily
comply with the terms of this agreement by keeping this work in the
same format with its attached full Project Gutenberg™ License when
you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are
in a constant state of change. If you are outside the United States,
check the laws of your country in addition to the terms of this
agreement before downloading, copying, displaying, performing,
distributing or creating derivative works based on this work or any
other Project Gutenberg™ work. The Foundation makes no
representations concerning the copyright status of any work in any
country other than the United States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other
immediate access to, the full Project Gutenberg™ License must appear
prominently whenever any copy of a Project Gutenberg™ work (any work
on which the phrase “Project Gutenberg” appears, or with which the
phrase “Project Gutenberg” is associated) is accessed, displayed,
performed, viewed, copied or distributed:
This eBook is for the use of anyone anywhere in the United States and most
other parts of the world at no cost and with almost no restrictions
whatsoever. You may copy it, give it away or re-use it under the terms
of the Project Gutenberg License included with this eBook or online
at
www.gutenberg.org. If you
are not located in the United States, you will have to check the laws
of the country where you are located before using this eBook.
1.E.2. If an individual Project Gutenberg™ electronic work is
derived from texts not protected by U.S. copyright law (does not
contain a notice indicating that it is posted with permission of the
copyright holder), the work can be copied and distributed to anyone in
the United States without paying any fees or charges. If you are
redistributing or providing access to a work with the phrase “Project
Gutenberg” associated with or appearing on the work, you must comply
either with the requirements of paragraphs 1.E.1 through 1.E.7 or
obtain permission for the use of the work and the Project Gutenberg™
trademark as set forth in paragraphs 1.E.8 or 1.E.9.
1.E.3. If an individual Project Gutenberg™ electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any
additional terms imposed by the copyright holder. Additional terms
will be linked to the Project Gutenberg™ License for all works
posted with the permission of the copyright holder found at the
beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg™
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg™.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg™ License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including
any word processing or hypertext form. However, if you provide access
to or distribute copies of a Project Gutenberg™ work in a format
other than “Plain Vanilla ASCII” or other format used in the official
version posted on the official Project Gutenberg™ website
(www.gutenberg.org), you must, at no additional cost, fee or expense
to the user, provide a copy, a means of exporting a copy, or a means
of obtaining a copy upon request, of the work in its original “Plain
Vanilla ASCII” or other form. Any alternate format must include the
full Project Gutenberg™ License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg™ works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg™ electronic works
provided that:
• You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg™ works calculated using the method
you already use to calculate your applicable taxes. The fee is owed
to the owner of the Project Gutenberg™ trademark, but he has
agreed to donate royalties under this paragraph to the Project
Gutenberg Literary Archive Foundation. Royalty payments must be paid
within 60 days following each date on which you prepare (or are
legally required to prepare) your periodic tax returns. Royalty
payments should be clearly marked as such and sent to the Project
Gutenberg Literary Archive Foundation at the address specified in
Section 4, “Information about donations to the Project Gutenberg
Literary Archive Foundation.”
• You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg™
License. You must require such a user to return or destroy all
copies of the works possessed in a physical medium and discontinue
all use of and all access to other copies of Project Gutenberg™
works.
• You provide, in accordance with paragraph 1.F.3, a full refund of
any money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days of
receipt of the work.
• You comply with all other terms of this agreement for free
distribution of Project Gutenberg™ works.
1.E.9. If you wish to charge a fee or distribute a Project
Gutenberg™ electronic work or group of works on different terms than
are set forth in this agreement, you must obtain permission in writing
from the Project Gutenberg Literary Archive Foundation, the manager of
the Project Gutenberg™ trademark. Contact the Foundation as set
forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
works not protected by U.S. copyright law in creating the Project
Gutenberg™ collection. Despite these efforts, Project Gutenberg™
electronic works, and the medium on which they may be stored, may
contain “Defects,” such as, but not limited to, incomplete, inaccurate
or corrupt data, transcription errors, a copyright or other
intellectual property infringement, a defective or damaged disk or
other medium, a computer virus, or computer codes that damage or
cannot be read by your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the “Right
of Replacement or Refund” described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg™ trademark, and any other party distributing a Project
Gutenberg™ electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium
with your written explanation. The person or entity that provided you
with the defective work may elect to provide a replacement copy in
lieu of a refund. If you received the work electronically, the person
or entity providing it to you may choose to give you a second
opportunity to receive the work electronically in lieu of a refund. If
the second copy is also defective, you may demand a refund in writing
without further opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you ‘AS-IS’, WITH NO
OTHER WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT
LIMITED TO WARRANTIES OF MERCHANTABILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of
damages. If any disclaimer or limitation set forth in this agreement
violates the law of the state applicable to this agreement, the
agreement shall be interpreted to make the maximum disclaimer or
limitation permitted by the applicable state law. The invalidity or
unenforceability of any provision of this agreement shall not void the
remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg™ electronic works in
accordance with this agreement, and any volunteers associated with the
production, promotion and distribution of Project Gutenberg™
electronic works, harmless from all liability, costs and expenses,
including legal fees, that arise directly or indirectly from any of
the following which you do or cause to occur: (a) distribution of this
or any Project Gutenberg™ work, (b) alteration, modification, or
additions or deletions to any Project Gutenberg™ work, and (c) any
Defect you cause.
Section 2. Information about the Mission of Project Gutenberg™
Project Gutenberg™ is synonymous with the free distribution of
electronic works in formats readable by the widest variety of
computers including obsolete, old, middle-aged and new computers. It
exists because of the efforts of hundreds of volunteers and donations
from people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need are critical to reaching Project Gutenberg™’s
goals and ensuring that the Project Gutenberg™ collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg™ and future
generations. To learn more about the Project Gutenberg Literary
Archive Foundation and how your efforts and donations can help, see
Sections 3 and 4 and the Foundation information page at www.gutenberg.org.
Section 3. Information about the Project Gutenberg Literary Archive Foundation
The Project Gutenberg Literary Archive Foundation is a non-profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation’s EIN or federal tax identification
number is 64-6221541. Contributions to the Project Gutenberg Literary
Archive Foundation are tax deductible to the full extent permitted by
U.S. federal laws and your state’s laws.
The Foundation’s business office is located at 809 North 1500 West,
Salt Lake City, UT 84116, (801) 596-1887. Email contact links and up
to date contact information can be found at the Foundation’s website
and official page at www.gutenberg.org/contact
Section 4. Information about Donations to the Project Gutenberg Literary Archive Foundation
Project Gutenberg™ depends upon and cannot survive without widespread
public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine-readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To SEND
DONATIONS or determine the status of compliance for any particular state
visit
www.gutenberg.org/donate.
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including checks, online payments and credit card donations. To
donate, please visit: www.gutenberg.org/donate
Section 5. General Information About Project Gutenberg™ electronic works
Professor Michael S. Hart was the originator of the Project
Gutenberg™ concept of a library of electronic works that could be
freely shared with anyone. For forty years, he produced and
distributed Project Gutenberg™ eBooks with only a loose network of
volunteer support.
Project Gutenberg™ eBooks are often created from several printed
editions, all of which are confirmed as not protected by copyright in
the U.S. unless a copyright notice is included. Thus, we do not
necessarily keep eBooks in compliance with any particular paper
edition.
Most people start at our website which has the main PG search
facility:
www.gutenberg.org.
This website includes information about Project Gutenberg™,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.
, where
is the index of refraction. These
two hypotheses give a complete and satisfactory explanation of aberration.
The second hypothesis, notwithstanding its seeming improbability, must
be considered as fully proved, first, by the celebrated experiment of
Fizeau,[3]
and secondly, by the ample confirmation of our own work.[4].
The experimental trial of the first hypothesis forms the subject of the
present paper.
, fig. 1, be a ray of light which is partly reflected in
,
and partly transmitted in
, being returned by the mirrors
and
, along
and
.
is partly transmitted along
,
and
is partly reflected along
.
and
are
equal, the two rays interfere along
. Suppose now, the æther being at
rest, that the whole apparatus moves in the direction
, with the
velocity of the earth in its orbit, the directions and distances
traversed by the rays will be altered thus:—
is reflected along
, fig. 2; the angle
, being
equal to the aberration
, is returned along
,
(
), and goes to the focus of the telescope, whose direction
is unaltered. The transmitted ray goes along
, is returned along
, and is reflected at
, making
equal
,
and therefore still coinciding with the first ray. It may be remarked
that the rays
and
, do not now meet exactly in the
same point
, though the difference is of the second order; this
does not affect the validity of the reasoning. Let it now be required to
find the difference in the two paths
, and
.
.
.
, fig. 1.
.
,
(fig. 2.)
and the distance traveled in this time is
neglecting terms of the fourth order. The length of the other path is
evidently
or to the same degree
of accuracy,
. The difference
is therefore
. If now the whole apparatus be
turned through
, the difference will be in the opposite
direction, hence the displacement of the interference-fringes should be
. Considering only the velocity of the earth in
its orbit, this would be
. If, as was the case in the
first experiment,
waves of yellow light, the
displacement to be expected would be
of the distance between the
interference fringes.
(fig. 5) is about
and
thick.
It rests on an annular wooden float
,
outside diameter,
inside
diameter, and
thick. The float rests on mercury
contained in the cast-iron trough
,
thick, and of such dimensions as to leave a clearance of about one
centimeter around the float. A pin
, guided by arms
, fits into a socket e attached to the float. The pin may be
pushed into the socket or be withdrawn, by a lever pivoted at
. This
pin keeps the float concentric with the trough, but does not bear any
part of the weight of the stone. The annular iron trough rests on a bed
of cement on a low brick pier built in the form of a hollow octagon.
fig. 4.
Near the center of the stone was a plane-parallel glass
. These were
so disposed that light from an argand burner
, passing through a lens,
fell on
so as to be in part reflected to
; the two pencils
followed the paths indicated in the figure,
and
respectively, and
were observed by the telescope
. Both
and
revolved with the
stone. The mirrors were of speculum metal carefully worked to optically
plane surfaces five centimeters in diameter, and the glasses
and
were plane-parallel and of the same thickness,
; their surfaces measured
by
. The second of these was placed
in the path of one of the pencils to compensate for the passage of the
other through the same thickness of glass. The whole of the optical
portion of the apparatus was kept covered with a wooden cover to prevent
air currents and rapid changes of temperature.
. This mirror had three adjustments; it had an adjustment in
altitude and one in azimuth, like all the other mirrors, but finer; it
also had an adjustment in the direction of the incident ray, sliding
forward or backward, but keeping very accurately parallel to its former
plane. The three adjustments of this mirror could be made with the
wooden cover in position.
;
then white light was restored, the screw altering the length of path was
very slowly moved (one turn of a screw of one hundred threads to the
inch altering the path nearly
till the
colored interference fringes reappeared in white light. These were now
given a convenient width and position, and the apparatus was ready for
observation.
,
the mean value being near
, so that one division means
. The rotation in the observations at noon
was contrary to, and in the evening observations, with, that of the hands
of a watch.