*** START OF THE PROJECT GUTENBERG EBOOK 60619 ***
This book uses a number of astronomical symbols, including signs of the Zodiac (♈, ♉,
♊, ♋, ♌, ♍, ♎, ♏, ♐, ♑, ♒, ♓),
and symbols for planets (☿, ♀, ⊕, ♂, ♃, ♄).
If these characters do not display correctly, you may have to use
an alternative font, such as Arial Unicode MS or DejaVu.
The ORRERY, made by JAMES FERGUSON.

N. 1. The Sun, 2. Mercury, 3. Venus, 4. The Earth, 5. The Moon, 6. The Sydereal Dial plate, 7. The Hour Circle, 8. ye Circle for ye. Moon’s Age,
9. The Moon’s Orbit, 10. ye Pointer, Shewing the Sun’s Place & Day of the Month, 11. The Ecliptic, 12. The Handle for turning ye whole machine
J. Ferguson inv. et delin.
G. Child. Sculp.
ASTRONOMY
EXPLAINED UPON
Sir ISAAC NEWTON’s
PRINCIPLES,
AND MADE EASY
TO THOSE WHO HAVE NOT STUDIED
MATHEMATICS.
By JAMES FERGUSON.
Heb. XI. 3. The Worlds were framed by the Word of GOD.
Job XXVI. 13. By his Spirit he hath garnished the Heavens.
THE SECOND EDITION.
LONDON:
Printed for, and sold by the AUTHOR, at the Globe,
opposite Cecil-Street in the Strand.
MDCCLVII.
TO
THE RIGHT HONOURABLE
GEORGE Earl of Macclesfield,
Viscount PARKER of Ewelme in Oxfordshire,
AND
Baron of Macclesfield in Cheshire;
PRESIDENT of the Royal Society of LONDON,
Member of the Royal Academy of Sciences at PARIS,
OF THE
Imperial Academy of Sciences at Petersburg,
AND ONE OF THE
Trustees of the British MUSEUM;
DISTINGUISHED
By his Generous ZEAL for promoting every
BRANCH of USEFUL KNOWLEDGE;
THIS
Treatise of ASTRONOMY
IS INSCRIBED,
With the Most Profound Respect,
By His LORDSHIP’s
Most Obliged,
And
Most Humble SERVANT,
JAMES FERGUSON.
THE
CONTENTS.
| CHAP. I. |
| |
| Of Astronomy in general |
Page 1 |
| |
| |
| CHAP. II. |
| |
| A brief Description of the Solar System |
5 |
| |
| |
| CHAP. III. |
| |
| The Copernican or Solar System demonstrated to be true |
31 |
| |
| |
| CHAP. IV. |
| |
| The Phenomena of the Heavens as seen from different parts of the Earth |
39 |
| |
| |
| CHAP. V. |
| |
| The Phenomena of the Heavens as seen from different parts of the Solar System |
45 |
| |
| |
| CHAP. VI. |
| |
| The Ptolemean System refuted. The Motions and Phases of Mercury and Venus explained |
50 |
| |
| |
| CHAP. VII. |
| |
| The physical Causes of the Motions of the Planets. The Excentricities of their Orbits. The times in which the Action of Gravity would bring them to the Sun. Archimedes’s ideal Problem for moving the Earth. The world not eternal |
54 |
| |
| |
| CHAP. VIII. |
| |
| Of Light. It’s proportional quantities on the different Planets. It’s Refractions in Water and Air. The Atmosphere, it’s Weight and Properties. The Horizontal Moon |
62 |
| |
| |
| CHAP. IX. |
| |
| The Method of finding the Distances of the Sun, Moon and Planets |
73 |
| |
| |
| CHAP. X. |
| |
| The Circles of the Globe described. The different lengths of days and nights, and the vicissitude of Seasons, explained. The explanation of the Phenomena of Saturn’s Ring concluded |
78 |
| |
| |
| CHAP. XI. |
| |
| The Method of finding the Longitude by the Eclipses of Jupiter’s Satellites: The amazing velocity of Light demonstrated by these Eclipses |
87 |
| |
| |
| CHAP. XII. |
| |
| Of Solar and Sidereal Time |
93 |
| |
| |
| CHAP. XIII. |
| |
| Of the Equation of Time |
97 |
| |
| |
| CHAP. XIV. |
| |
| Of the Precession of the Equinoxes |
108 |
| |
| |
| CHAP. XV. |
| |
| The Moon’s Surface mountainous: Her Phases described: Her Path, and the Paths of Jupiter’s Moons delineated: The proportions of the Diameters of their Orbits, and those of Saturn’s Moons to each other; and to the Diameter of the Sun |
124 |
| |
| |
| CHAP. XVI. |
| |
| The Phenomena of the Harvest-Moon explained by a common Globe: The Years in which the Harvest-Moons are least and most beneficial, from 1751 to 1861. The long duration of Moon-light at the Poles in Winter Page |
136 |
| |
| |
| CHAP. XVII. |
| |
| Of the ebbing and flowing of the Sea |
147 |
| |
| |
| CHAP. XVIII. |
| |
| Of Eclipses: Their Number and Period. A large Catalogue of Ancient and Modern Eclipses |
156 |
| |
| |
| CHAP. XIX. |
| |
| The Calculation of New and Full Moons and Eclipses. The geometrical Construction of Solar and Lunar Eclipses. The examination of ancient Eclipses |
189 |
| |
| |
| CHAP. XX. |
| |
| Of the fixed Stars |
230 |
| |
| |
| CHAP. XXI. |
| |
| Of the Division of Time. A perpetual Table of New Moons. The Times of the Birth and Death of Christ. A Table of remarkable Æras or Events |
248 |
| |
| |
| CHAP. XXII. |
| |
| A Description of the Astronomical Machinery serving to explain and illustrate the foregoing part of this Treatise |
260 |
ERRATA.
In the Table facing Page 31, the Sun’s quantity of matter should be 227500. Page 40,
l. last, for infinite read indefinite. Page 97, l. 20, for this read the next. Page
164, l. 2 from the bottom, for without any acceleration read as above, without any
acceleration. Page 199, l. 16 for XIV read XV. Page 238, l. 16, for 40 read
406. Page 240, l. 15 from the bottom, for Tifri read Tisri, Page 249 l. 13; from
the bottom for XVII read V.
1ASTRONOMY
EXPLAINED UPON
Sir ISAAC NEWTON’s Principles.
CHAP. I.
Of Astronomy in general.
The general use of Astronomy.
1. Of all the sciences cultivated by mankind, Astronomy is acknowledged
to be, and undoubtedly is, the most sublime,
the most interesting, and the most useful. For, by knowledge
derived from this science, not only the bulk of the
Earth is discovered, the situation and extent of the countries and kingdoms
upon it ascertained, trade and commerce carried on to the
remotest parts of the world, and the various products of several countries
distributed for the health, comfort, and conveniency of its inhabitants;
but our very faculties are enlarged with the grandeur of the
ideas it conveys, our minds exalted above the low contracted prejudices
of the vulgar, and our understandings clearly convinced, and
affected with the conviction, of the existence, wisdom, power, goodness,
and superintendency of the SUPREME BEING! So that
without an hyperbole,
“
An undevout Astronomer is mad[1].”
2. From this branch of knowledge we also learn by what means
or laws the Almighty carries on, and continues the admirable harmony,
order, and connexion observable throughout the planetary
system; and are led by very powerful arguments to form the pleasing
deduction, that minds capable of such deep researches not only derive
their origin from that adorable Being, but are also incited to aspire
2after a more perfect knowledge of his nature, and a stricter conformity
to his will.
The Earth but a point as seen from the Sun.
3. By Astronomy we discover that the Earth is at so great a distance
from the Sun, that if seen from thence it would appear no bigger
than a point; although it’s circumference is known to be 25,020 miles.
Yet that distance is so small, compared with the distance of the Fixed
Stars, that if the Orbit in which the Earth moves round the Sun were
solid, and seen from the nearest Star, it would likewise appear no
bigger than a point, although it is at least 162 millions of miles in diameter.
For the Earth in going round the Sun is 162 millions of
miles nearer to some of the Stars at one time of the year than at another;
and yet their apparent magnitudes, situations, and distances
from one another still remain the same; and a telescope which magnifies
above 200 times does not sensibly magnify them: which proves
them to be at least 400 thousand times farther from us than we are
from the Sun.
The Stars are Suns.
4. It is not to be imagined that all the Stars are placed in one concave
surface, so as to be equally distant from us; but that they are
scattered at immense distances from one another through unlimited
space. So that there may be as great a distance between any two
neighbouring Stars, as between our Sun and those which are nearest
to him. Therefore an Observer, who is nearest any fixed Star, will
look upon it alone as a real Sun; and consider the rest as so many
shining points, placed at equal distances from him in the Firmament.
And innumerable.
5. By the help of telescopes we discover thousands of Stars which
are invisible to the naked eye; and the better our glasses are, still the
more become visible: so that we can set no limits either to their
number or their distances. The celebrated Huygens carries his
thoughts so far, as to believe it not impossible that there may be Stars
at such inconceivable distances, that their light has not yet reached
the Earth since it’s creation; although the velocity of light be a million
of times greater than the velocity of a cannon bullet, as shall be demonstrated
afterwards § 197, 216: and, as Mr. Addison very justly
observes, this thought is far from being extravagant, when we consider
that the Universe is the work of infinite power, prompted by infinite
goodness; having an infinite space to exert itself in; so that our imaginations
can set no bounds to it.
Why the Sun appears bigger than the Stars.
6. The Sun appears very bright and large in comparison of the
Fixed Stars, because we keep constantly near the Sun, in comparison
of our immense distance from the Stars. For, a spectator, placed as
near to any Star as we are to the Sun, would see that Star a body as
3large and bright as the Sun appears to us: and a spectator, as far distant
from the Sun as we are from the Stars, would see the Sun as small as
we see a Star, divested of all its circumvolving Planets; and would
reckon it one of the Stars in numbering them.
The Stars are not enlightened by the Sun.
7. The Stars, being at such immense distances from the Sun, cannot
possibly receive from him so strong a light as they seem to have; nor
any brightness sufficient to make them visible to us. For the Sun’s
rays must be so scattered and dissipated before they reach such remote
objects, that they can never be transmitted back to our eyes, so as to
render these objects visible by reflection. The Stars therefore shine
with their own native and unborrowed lustre, as the Sun does; and
since each particular Star, as well as the Sun, is confined to a particular
portion of space, ’tis plain that the Stars are of the same nature with
the Sun.
They are probably surrounded by Planets.
8. It is no ways probable that the Almighty, who always acts
with infinite wisdom and does nothing in vain, should create so many
glorious Suns, fit for so many important purposes, and place them
at such distances from one another, without proper objects near
enough to be benefited by their influences. Whoever imagines they
were created only to give a faint glimmering light to the inhabitants
of this Globe, must have a very superficial knowledge of Astronomy,
and a mean opinion of the Divine Wisdom: since, by an infinitely less
exertion of creating power, the Deity could have given our Earth
much more light by one single additional Moon.
9. Instead then of one Sun and one World only in the Universe,
as the unskilful in Astronomy imagine, that Science discovers to us
such an inconceivable number of Suns, Systems, and Worlds, dispersed
through boundless Space, that if our Sun, with all the Planets,
Moons, and Comets belonging to it were annihilated, they would be
no more missed out of the Creation than a grain of sand from the
sea-shore. The space they possess being comparatively so small, that
it would scarce be a sensible blank in the Universe; although Saturn,
the outermost of our planets, revolves about the Sun in an Orbit of
4884 millions of miles in circumference, and some of our Comets
make excursions upwards of ten thousand millions of miles beyond
Saturn’s Orbit; and yet, at that amazing distance, they are incomparably
nearer to the Sun than to any of the Stars; as is evident from their
keeping clear of the attractive Power of all the Stars, and returning periodically
by virtue of the Sun’s attraction.
The stellar Planets may be habitable.
10. From what we know of our own System it may be reasonably
concluded that all the rest are with equal wisdom contrived, situated,
4and provided with accommodations for rational inhabitants. Let us
therefore take a survey of the System to which we belong; the only
one accessible to us; and from thence we shall be the better enabled
to judge of the nature and end of the other Systems of the Universe.
For although there is almost an infinite variety in all the parts of the
Creation which we have opportunities of examining; yet there is a
general analogy running through and connecting all the parts into one
scheme, one design, one whole!
As our Solar Planets are.
11. And then, to an attentive considerer, it will appear highly
probable, that the Planets of our System, together with their attendants
called Satellites or Moons, are much of the same nature with
our Earth, and destined for the like purposes. For, they are solid
opaque Globes, capable of supporting animals and vegetables. Some
of them are bigger, some less, and some much about the size of our
Earth. They all circulate round the Sun, as the Earth does, in a
shorter or longer time according to their respective distances from
him: and have, where it would not be inconvenient, regular returns
of summer and winter, spring and autumn. They have warmer and
colder climates, as the various productions of our Earth require: and,
in such as afford a possibility of discovering it, we observe a regular
motion round their Axes like that of our Earth, causing an alternate
return of day and night; which is necessary for labour, rest, and
vegetation, and that all parts of their surfaces may be exposed to the
rays of the Sun.
The farthest from the Sun have most Moons to enlighten their nights.
12. Such of the Planets as are farthest from the Sun, and therefore
enjoy least of his light, have that deficiency made up by several
Moons, which constantly accompany, and revolve about them,
as our Moon revolves about the Earth. The remotest Planet has, over
and above, a broad Ring encompassing it; which like a lucid Zone in
the Heavens reflects the Sun’s light very copiously on that Planet: so
that if the remoter Planets have the Sun’s light fainter by day than we,
they have an addition made to it morning and evening by one or more
of their Moons, and a greater quantity of light in the night-time.
Our Moon mountainous like the Earth.
13. On the surface of the Moon, because it is nearer us than any
other of the celestial Bodies are, we discover a nearer resemblance of
our Earth. For, by the assistance of telescopes we observe the Moon
to be full of high mountains, large valleys, and deep cavities. These
similarities leave us no room to doubt but that all the Planets and
Moons in the System are designed as commodious habitations for creatures
endowed with capacities of knowing and adoring their beneficent
Creator.
The Solar System
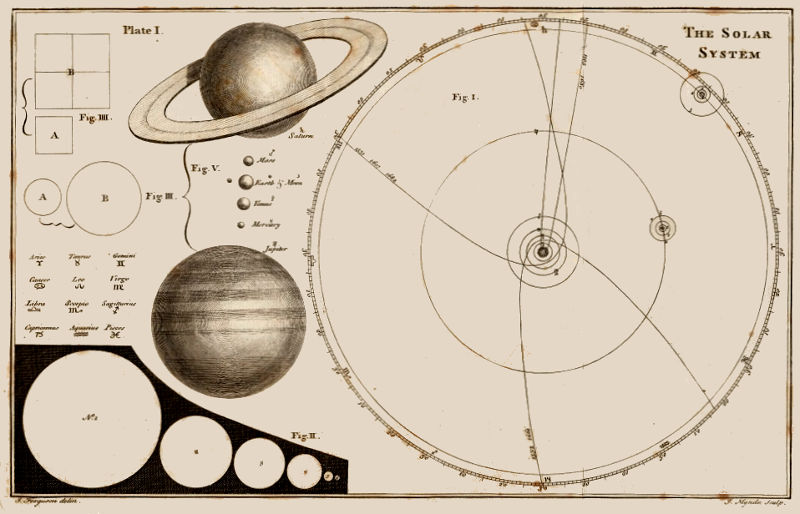
J. Ferguson delin.
J. Mynde Sculp.
514. Since the Fixed Stars are prodigious spheres of fire, like our
Sun, and at inconceivable distances from one another, as well as from
us, it is reasonable to conclude they are made for the same purposes
that the Sun is; each to bestow light, heat, and vegetation on a
certain number of inhabited Planets, kept by gravitation within the
sphere of it’s activity.
Numberless Suns and Worlds.
15. What an august! what an amazing conception, if human imagination
can conceive it, does this give of the works of the Creator!
Thousands of thousands of Suns, multiplied without end, and ranged
all around us, at immense distances from each other, attended by ten
thousand times ten thousand Worlds, all in rapid motion, yet calm,
regular, and harmonious, invariably keeping the paths prescribed them;
and these Worlds peopled with myriads of intelligent beings, formed
for endless progression in perfection and felicity.
16. If so much power, wisdom, goodness, and magnificence is
displayed in the material Creation, which is the least considerable part
of the Universe, how great, how wise, how good must HE be, who
made and governs the Whole!
CHAP. II.
A brief Description of the Solar System.
17. The Planets and Comets which move round the Sun as their
center, constitute the Solar System. Those Planets which
are nearer the Sun not only finish their circuits sooner, but likewise
move faster in their respective Orbits than those which are more remote
from him. Their motions are all performed from west to east,
in Orbits nearly circular. Their names, distances, bulks, and periodical
revolutions, are as follows.
The Sun.
18. The Sun
 , an immense globe of fire, is placed near the
common center, or rather in the lower[2] focus, of the Orbits of all
6the Planets and Comets[3]; and turns round his axis in 25 days 6 hours,
as is evident by the motion of spots seen on his surface. His diameter
is computed to be 763,000 miles; and, by the various attractions
of the circumvolving Planets, he is agitated by a small motion
round the center of gravity of the System. All the Planets, as seen
from him, move the same way, and according to the order of Signs in
the graduated Circle ♈ ♉ ♎ ♋ &c. which represents the great Ecliptic in
the Heavens: but, as seen from any one Planet, the rest appear sometimes
to go backward, sometimes forward, and sometimes to stand
still; not in circles nor ellipses, but in[4] looped curves which never
return into themselves. The Comets come from all parts of the Heavens,
and move in all sorts of directions.
, an immense globe of fire, is placed near the
common center, or rather in the lower[2] focus, of the Orbits of all
6the Planets and Comets[3]; and turns round his axis in 25 days 6 hours,
as is evident by the motion of spots seen on his surface. His diameter
is computed to be 763,000 miles; and, by the various attractions
of the circumvolving Planets, he is agitated by a small motion
round the center of gravity of the System. All the Planets, as seen
from him, move the same way, and according to the order of Signs in
the graduated Circle ♈ ♉ ♎ ♋ &c. which represents the great Ecliptic in
the Heavens: but, as seen from any one Planet, the rest appear sometimes
to go backward, sometimes forward, and sometimes to stand
still; not in circles nor ellipses, but in[4] looped curves which never
return into themselves. The Comets come from all parts of the Heavens,
and move in all sorts of directions.
PLATE I. Fig. I. The Sun.
The Axes of the Planets, what.
19. Having mentioned the Sun’s turning round his axis, and as
there will be frequent occasion to speak of the like motion of the
Earth and other Planets, it is proper here to inform the young Tyro in
Astronomy, that neither the Sun nor Planets have material axes to
turn upon, and support them, as in the little imperfect Machines contrived
to represent them. For the axis of a Planet is a line conceived
to be drawn through it’s center, about which it revolves as on a real
axis. The extremities of this line, terminating in opposite points of
the Planet’s surface, are called its Poles. That which points towards
the northern part of the Heavens is called the North Pole; and the
other, pointing towards the southern part, is called the South Pole. A
bowl whirled from one’s hand into the open air turns round such a line
within itself, whilst it moves forward; and such are the lines we mean,
when we speak of the Axes of the Heavenly bodies.
Their Orbits are not in the same plane with the Ecliptic.
PLATE I.
Their Nodes.
Where situated.
20. Let us suppose the Earth’s Orbit to be a thin, even, solid plane;
cutting the Sun through the center, and extended out as far as the
Starry Heavens, where it will mark the great Circle called the Ecliptic.
This Circle we suppose to be divided into 12 equal parts, called Signs;
each Sign into 30 equal parts, called Degrees; each Degree into
60 equal parts, called Minutes; and every Minute into 60 equal parts,
called Seconds: so that a Second is the 60th part of a Minute; a Minute
7the 60th part of a Degree; and a Degree the 360th part of a Circle,
or 30th part of a Sign. The Planes of the Orbits of all the other
Planets likewise cut the Sun in halves; but extended to the Heavens,
form Circles different from one another, and from the Ecliptic; one
half of each being on the north side, and the other on the south side of
it. Consequently the Orbit of each Planet crosses the Ecliptic in two
opposite points, which are called the Planet’s Nodes. These Nodes are
all in different parts of the Ecliptic; and therefore, if the planetary
Tracks remained visible in the Heavens, they would in some measure
resemble the different rutts of waggon-wheels crossing one another in
different parts, but never going far asunder. That Node, or Intersection
of the Orbit of any Planet with the Earth’s Orbit, from which
the Planet ascends northward above the Ecliptic, is called the Ascending
Node of the Planet; and the other, which is directly opposite thereto,
is called it’s Descending Node. Saturn’s Ascending Node is in 21 deg.
13 min. of Cancer ♋, Jupiter’s in 7 deg. 29 min. of the same Sign,
Mars’s in 17 deg. 17 min. of Taurus ♉, Venus’s in 13 deg. 59 min.
of Gemini ♊, and Mercury’s in 14 deg. 43 min. of Taurus. Here we
consider the Earth’s Orbit as the standard, and the Orbits of all the
other Planets as oblique to it.
The Planets Orbits, what.
21. When we speak of the Planets Orbits, all that is meant is their
Paths through the open and unresisting Space in which they move;
and are kept in, by the attractive power of the Sun, and the projectile
force impressed upon them at first: between which power and force
there is so exact an adjustment, that without any solid Orbits to confine
the Planets, they keep their courses, and at the end of every revolution
find the points from whence they first set out, much more truly than
can be imitated in the best machines made by human art.
Mercury.
Fig. I.
May be inhabited.
PLATE I.
22. Mercury, the nearest Planet to the Sun, goes round him
(as in the circle marked ☿) in 87 days 23 hours of our time nearly;
which is the length of his year. But, being seldom seen, and no
spots appearing on his surface or disc, the time of his rotation on
his axis, or the length of his days and nights, is as yet unknown.
His distance from the Sun is computed to be 32 millions of miles, and
his diameter 2600. In his course, round the Sun, he moves at the
rate of 95 thousand miles every hour. His light and heat from the
Sun are almost seven times as great as ours; and the Sun appears to him
almost seven times as large as to us. The great heat on this Planet is
no argument against it’s being inhabited; since the Almighty could as
easily suit the bodies and constitutions of it’s inhabitants to the heat of
8their dwelling, as he has done ours to the temperature of our Earth.
And it is very probable that the people there have such an opinion of
us, as we have of the inhabitants of Jupiter and Saturn; namely,
that we must be intolerably cold, and have very little light at so great
a distance from the Sun.
Has like phases with the Moon.
23. This Planet appears to us with all the various phases of the
Moon, when viewed at different times by a good telescope; save only
that he never appears quite Full, because his enlightened side is never
turned directly towards us but when he is so near the Sun as to be lost to
our sight in it’s beams. And, as his enlightened side is always toward
the Sun, it is plain that he shines not by any light of his own; for
if he did, he would constantly appear round. That he moves about
the Sun in an Orbit within the Earth’s Orbit is also plain (as will be
more largely shewn by and by, § 141, & seq.) because he is never seen
opposite to the Sun, nor above 56 times the Sun’s breadth from his
center.
His Orbit and Nodes.
24. His Orbit is inclined seven degrees to the Ecliptic; and that
Node § 20, from which he ascends northward above the Ecliptic is
in the 14th degree of Taurus; the opposite, in the 14th degree of
Scorpio. The Earth is in these points on the 5th of November and
4th of May, new style; and when Mercury comes to either of his
Nodes at his[5] inferior Conjunction about these times, he will appear
to pass over the disc or face of the Sun, like a dark round spot. But
in all other parts of his Orbit his Conjunctions are invisible, because
he either goes above or below the Sun.
When he will be seen as if upon the Sun.
25. Mr. Whiston has given us an account of several periods at
which Mercury may be seen on the Sun’s disc, viz. In the year
1782, Nov. 12th, at 3 h. 44 m. in the afternoon: 1786, May 4th,
at 6 h. 57 m. in the forenoon: 1789, Dec. 6th, at 3 h. 55 m. in the
afternoon; and 1799, May 7th, at 2 h. 34 m. in the afternoon. There
will be several intermediate Transits, but none of them visible at
London.
Fig. I.
Venus.
26. Venus, the next Planet in order, is computed to be 59 millions
of miles from the Sun; and by moving at the rate of 69 thousand
miles every hour in her Orbit (as in the circle marked ♀), she goes
round the Sun in 224 days 17 hours of our time nearly; in which,
though it be the full length of her year, she has only
91⁄4
days, according
to Bianchini’s observations; so that in her, every day and
night together is as long as
241⁄3
days and nights with us. This odd
9quarter of a day in every year makes every fourth year a leap-year to
Venus; as the like does to our Earth. Her diameter is 7906 miles;
and by her diurnal motion the inhabitants about her Equator are carried
43 miles every hour: besides the 69,000 above-mentioned.
Her Orbit lies between the Earth and Mercury.
27. Her Orbit includes that of Mercury within it; for at her greatest
Elongation, or apparent distance from the Sun, she is 96 times his
breadth from his centre; which is almost double of Mercury’s. Her
Orbit is included by the Earth’s; for if it were not, she might be seen
as often in Opposition to the Sun as in Conjunction with him; but
she was never seen 90 degrees, or a fourth part of a Circle, from
the Sun.
She is our morning and evening Star by turns.
28. When Venus appears west of the Sun she rises before him in the
morning, and is called the Morning Star: when she appears east of
the Sun she shines in the evening after he sets, and is then called the
Evening Star: being each in it’s turn for 290 days. It may perhaps
be surprising at first, that Venus should keep longer on the east or west
of the Sun than the whole time of her Period round him. But the
difficulty vanishes when we consider that the Earth is all the while
going round the Sun the same way, though not so quick as Venus:
and therefore her relative motion to the Earth must in every Period be
as much slower than her absolute motion in her Orbit, as the Earth
during that time advances forward in the Ecliptic; which is 220 degrees.
To us she appears through a telescope in all the various shapes of the
Moon.
29. The Axis of Venus is inclined 75 degrees to the Axis of her
Orbit; which is
511⁄2
degrees more than our Earth’s Axis is inclined to
the Axis of the Ecliptic: and therefore the variation of her seasons is
much greater than of ours. The North Pole of her Axis inclines toward
the 20th degree of Aquarius, our Earth’s to the beginning of
Cancer; and therefore the northern parts of Venus have summer in
the Signs where those of our Earth have winter, and vice versâ.
Remarkable appearances.
30. The [6]artificial day at each Pole of Venus is as long as
1121⁄2
[7]natural days on our Earth.
Her Tropics and polar Circles, how situated.
31. The Sun’s greatest Declination on each side of her Equator
amounts to 75 degrees; therefore her[8] Tropics are only 15 degrees
10from her Poles; and her [9]Polar Circles as far from her Equator. Consequently,
the Tropics of Venus are between her Polar Circles and her
Poles; contrary to what those of our Earth are.
The Sun’s daily Course.
32. As her annual Revolution contains only
91⁄4
of her days, the
Sun will always appear to go through a Sign, or twelfth Part of her
Orbit, in little more that three quarters of her natural day, or nearly
in
183⁄4
of our days and nights.
And great declination.
33. Because her day is so great a part of her year, the Sun changes
his Declination in one day so much, that if he passes vertically, or
directly over head of any given place on the Tropic, the next day he
will be 26 degrees from it: and whatever place he passes vertically
over when in the Equator, one day’s revolution will remove him
361⁄4
degrees from it. So that the Sun changes his Declination every day in
Venus about 14 degrees more at a mean rate, than he does in a quarter
of a year on our Earth. This appears to be providentially ordered,
for preventing the too great effects of the Sun’s heat (which is twice
as great on Venus as on the Earth) so that he cannot shine perpendicularly
on the same places for two days together; and by that means,
the heated places have time to cool.
To determine the points of the Compass at her Poles.
34. If the inhabitants about the North Pole of Venus fix their South,
or Meridian Line, through that part of the Heavens where the Sun
comes to his greatest Height, or North Declination, and call those
the East and West points of their Horizon, which are 90 degrees on
each side from that point where the Horizon is cut by the Meridian
Line, these inhabitants will have the following remarkables.
Surprising appearances at her Poles;
The Sun will rise
221⁄2
degrees[10] north of the East, and going on
1121⁄2
degrees, as measured on the plane of the [11]Horizon, he will
cross the Meridian at an altitude of
121⁄2
degrees; then making an
entire revolution without setting, he will cross it again at an altitude of
481⁄2
degrees; at the next revolution he will cross the Meridian as he
comes to his greatest height and declination, at the altitude of 75 degrees;
being then only 15 degrees from the Zenith, or that point of
the Heavens which is directly over head: and thence he will descend
in the like spiral manner; crossing the Meridian first at the altitude of
481⁄2
degrees; next at the altitude of
121⁄2
degrees; and going on thence
1121⁄2
degrees, he will set
221⁄2
degrees north of the West; so that, after
11having been
45⁄8
revolutions above the Horizon, he descends below it
to exhibit the like appearances at the South Pole.
35. At each Pole, the Sun continues half a year without setting in
summer, and as long without rising in winter; consequently the polar
inhabitants of Venus have only one day and one night in the year; as
it is at the Poles of our Earth. But the difference between the heat of
summer and cold of winter, or of mid-day and mid-night, on Venus,
is much greater than on the Earth: because in Venus, as the Sun is
for half a year together above the Horizon of each Pole in it’s turn,
so he is for a considerable part of that time near the Zenith; and
during the other half of the year, always below the Horizon, and
for a great part of that time at least 70 degrees from it. Whereas,
at the Poles of our Earth, although the Sun is for half a year together
above the Horizon, yet he never ascends above, nor descends below it,
more than
231⁄2
degrees. When the Sun is in the Equinoctial, or in that
Circle which divides the northern half of the Heavens from the
southern, he is seen with one half of his Disc above the Horizon of
the North Pole, and the other half above the Horizon of the South
Pole; so that his center is in the Horizon of both Poles: and then descending
below the Horizon of one, he ascends gradually above that of
the other. Hence, in a year, each Pole has one spring, one harvest,
a summer as long as them both, and a winter equal in length to the
other three seasons.
At her polar Circles;
36. At the Polar Circles of Venus, the seasons are much the same as
at the Equator, because there are only 15 degrees betwixt them, § 31;
only the winters are not quite so long, nor the summers so short: but
the four seasons come twice round every year.
At her Tropics;
37. At Venus’s Tropics, the Sun continues for about fifteen of our
weeks together without setting in summer; and as long without rising
in winter. Whilst he is more than 15 degrees from the Equator, he
neither rises to the inhabitants of the one Tropic, nor sets to those of
the other: whereas, at our terrestrial Tropics he rises and sets every
day of the year.
38. At Venus’s Tropics, the Seasons are much the same as at her
Poles; only the summers are a little longer, and the winters a little
shorter.
At her Equator.
39. At her Equator, the days and nights are always of the same
length; and yet the diurnal and nocturnal Arches are very different,
especially when the Sun’s declination is about the greatest: for then,
his meridian altitude may sometimes be twice as great as his midnight
depression, and at other times the reverse. When the Sun is at his
12greatest Declination, either North or South, his rays are as oblique at
Venus’s Equator, as they are at London on the shortest day of winter.
Therefore, at her Equator there are two winters, two summers, two
springs, and two autumns every year. But because the Sun stays for
some time near the Tropics, and passes so quickly over the Equator,
every winter there will be almost twice as long as summer: the four
seasons returning twice in that time, which consists only of
91⁄4
days.
40. Those parts of Venus which lie between the Poles and Tropics,
and between the Tropics and Polar Circles, and also between the
Polar Circles and Equator, partake more or less of the Phenomena of
these Circles, as they are more or less distant from them.
Great difference of the Sun’s amplitude at rising and setting.
41. From the quick change of the Sun’s declination it happens,
that when he rises due east on any day, he will not set due west on that
day, as with us; for if the place where he rises due east be on the
Equator, he will set on that day almost west-north-west; or about
181⁄2
degrees north of the west. But if the place be in 45 degrees north
latitude, then on the day that the Sun rises due east he will set north-west
by west, or 33 degrees north of the west. And in 62 degrees
north latitude when he rises in the east, he sets not in that revolution,
but just touches the Horizon 10 degrees to the west of the north point;
and ascends again, continuing for
31⁄4
revolutions above the Horizon
without setting. Therefore, no place has the forenoon and afternoon
of the same day equally long, unless it be on the Equator or at the Poles.
The longitude of places easily found in Venus.
42. The Sun’s altitude at noon, or any other time of the day, and
his amplitude at rising and setting, being so different at places on the
same parallels of latitude, according to the different longitudes of those
places, the longitude will be almost as easily found on Venus as the
latitude is found on the Earth: which is an advantage we can never
enjoy, because the daily change of the Sun’s declination is by much too
small for that purpose.
Her Equinoxes shift a quarter of a day forward every year.
43. On this Planet, wherever the Sun crosses the Equator in any
year, he will have 9 degrees of declination from that place on the same
day and hour next year; and will cross the Equator 90 degrees farther
to the west; which makes the time of the Equinox a quarter of a day
(almost equal to six of our days) later every year. Hence, although the
spiral in which the Sun’s motion is performed, be of the same sort every
year, yet it will not be the very same, because the Sun will not pass
vertically over the same places till four annual revolutions are finished.
Every fourth year a leap-year to Venus.
PLATE I.
44. We may suppose that the inhabitants of Venus will be careful
to add a day to some particular part of every fourth year; which will
keep the same seasons to the same days. For, as the great annual
13change of the Equinoxes and Solstices shifts the seasons a quarter of a
day every year, they would be shifted through all the days of the year
in 36 years. But by means of this intercalary day, every fourth year
will be a leap-year; which will bring her time to an even reckoning,
and keep her Calendar always right.
When she will appear on the Sun.
45. Venus’s Orbit is inclined
31⁄2
degrees to the Earth’s; and crosses
it in the 14th degree of Gemini and of Sagittarius; and therefore,
when the Earth is about these points of the Ecliptic at the time that
Venus is in her inferiour conjunction, she will appear like a spot on the
Sun, and afford a more certain method of finding the distances of all
the Planets from the Sun than any other yet known. But these
appearances happen very seldom; and will only be thrice visible at
London for three hundred years to come. The first time will be in
the year 1761, June the 6th, at 5 hours 55 minutes in the morning.
The second 1996, June the 9th, at 2 hours 13 minutes in the afternoon.
And the third in the year 2004, June the 6th, at 7 hours 18
minutes in the forenoon. Excepting such Transits as these, she shews the
same appearances to us regularly every eight years; her Conjunctions,
Elongations, and Times of rising and setting being very nearly the
same, on the same days, as before.
She may have a Moon although we cannot see it.
46. Venus may have a Satellite or Moon, although it be undiscovered
by us: which will not appear very surprising, if we consider
how inconveniently we are placed for seeing it. For it’s enlightened side
can never be fully turned towards us but when Venus is beyond the
Sun; and then, as Venus appears little bigger than an ordinary
Star, her Moon may be too small to be perceptible at such a distance.
When she is between us and the Sun, her full Moon has it’s dark
side towards us; and then, we cannot see it any more than we can our
own Moon at the time of Change. When Venus is at her greatest
Elongation, we have but one half of the enlightened side of her Full
Moon towards us; and even then it may be too far distant to be seen
by us. But if she has a Moon, it may certainly be seen with her upon
the Sun, in the year 1761, unless it’s Orbit be considerably inclined to
the Ecliptic: for if it should be in conjunction or opposition at that
time, we can hardly imagine that it moves so slow as to be hid by
Venus all the six hours that she will appear on the Sun’s Disc.
The Earth.
Fig. I.
It’s diurnal and annual motion.
47. The Earth is the next Planet above Venus in the System. It
is 81 millions of miles from the Sun, and goes round him (as in the
circle ⊕) in 365 days 5 hours 49 minutes, from any Equinox or Solstice
to the same again: but from any fixed Star to the same again, as
14seen from the Sun, in 365 days 6 hours and 9 minutes; the former
being the length of the Tropical year, and the latter the length of the
Sidereal. It travels at the rate of 58 thousand miles every hour, which
motion, though 120 times swifter than that of a cannon ball, is little
more than half as swift as Mercury’s motion in his Orbit. The Earth’s
diameter is 7970 miles; and by turning round it’s Axis every 24 hours
from West to East, it causes an apparent diurnal motion of all the
heavenly Bodies from East to West. By this rapid motion of the Earth
on it’s Axis, the inhabitants about the Equator are carried 1042 miles
every hour, whilst those on the parallel of London are carried only
about 580, besides the 58 thousand miles by the annual motion above-mentioned,
which is common to all places whatever.
Inclination of it’s Axis.
48. The Earth’s Axis makes an angle of
231⁄2
degrees with the Axis
of it’s Orbit; and keeps always the same oblique direction; inclining
towards the same fixed Stars[12] throughout it’s annual course; which
causes the returns of spring, summer, autumn, and winter; as will be
explained at large in the tenth Chapter.
A proof of it’s being round.
49. The Earth is round like a globe; as appears, 1. from it’s shadow
in Eclipses of the Moon; which shadow is always bounded by a circular
line § 314. 2. From our seeing the masts of a ship whilst the hull is
hid by the convexity of the water. 3. From it’s having been sailed
round by many navigators. The hills take off no more from the roundness
of the Earth in comparison, than grains of dust do from the roundness
of a common Globe.
It’s number of square miles.
50. The seas and unknown parts of the Earth (by a measurement
of the best Maps) contain 160 million 522 thousand and 26 square
miles; the inhabited parts 38 million 990 thousand 569: Europe
4 million 456 thousand and 65; Asia 10 million 768 thousand 823;
Africa 9 million 654 thousand 807; America 14 million 110 thousand
874. In all, 199 million 512 thousand 595; which is the number
of square miles on the whole surface of our Globe.
The proportion of land and sea.
PLATE I.
51. Dr. Long, in the first volume of his Astronomy, pag. 168,
mentions an ingenious and easy method of finding nearly what proportion
the land bears to the sea; which is, to take the papers of a
large terrestrial globe, and after separating the land from the sea with
a pair of scissars, to weigh them carefully in scales. This supposes the
globe to be exactly delineated, and the papers all of equal thickness.
15The Doctor made the experiment on the papers of Mr. Senex’s seventeen
inch globe; and found that the sea papers weighed 349 grains, and the
land only 124: by which it appears that almost three fourth parts of the
surface of our Earth between the Polar Circles are covered with water, and
that little more than one fourth is dry land. The Doctor omitted weighing
all within the Polar Circles; because there is no certain measurement of
the land there, so as to know what proportion it bears to the sea.
The Moon.
52. The Moon is not a Planet, but only a Satellite or Attendant of
the Earth, moving round the Earth from Change to Change in 29 days
12 hours and 44 minutes; and going round the Sun with it every year.
The Moon’s diameter is 2180 miles; and her distance from the Earth
240 thousand. She goes round her Orbit in 27 days 7 hours 43 minutes,
moving about 2290 miles every hour; and turns round her Axis exactly
in the time that she goes round the Earth, which is the reason of her
keeping always the same side towards us, and that her day and night
taken together is as long as our lunar month.
Her Phases.
53. The Moon is an opaque Globe like the Earth, and shines only
by reflecting the light of the Sun: therefore whilst that half of her
which is toward the Sun is enlightened, the other half must be dark
and invisible. Hence, she disappears when she comes between us and
the Sun; because her dark side is then toward us. When she is gone
a little way forward, we see a little of her enlightened side; which still
increases to our view, as she advances forward, until she comes to be
opposite to the Sun; and then her whole enlightened side is towards
the Earth, and she appears with a round, illumined Orb; which we
call the Full Moon: her dark side being then turned away from the
Earth. From the Full she seems to decrease gradually as she goes
through the other half of her course; shewing us less and less of her
enlightened side every day, till her next change or conjunction with
the Sun, and then she disappears as before.
A proof that she shines not by her own light.
Fig. I.
54. The continual changing of the Moon’s phases or shapes demonstrates
that she shines not by any light of her own: for if she did, being
globular, we should always see her with a round full Orb like the Sun.
Her Orbit is represented in the Scheme by the little circle m, upon the
Earth’s Orbit ⊕: but it is drawn fifty times too large in proportion to
the Earth’s; and yet is almost too small to be seen in the Diagram.
One half of her always enlightened.
55. The Moon has scarce any difference of seasons; her Axis being
almost perpendicular to the Ecliptic. What is very singular, one half
of her has no darkness at all; the Earth constantly affording it a strong
light in the Sun’s absence; while the other half has a fortnight’s darkness
and a fortnight’s light by turns.
Our Earth is her Moon.
1656. Our Earth is a Moon to the Moon, waxing and waneing regularly,
but appearing thirteen times as big, and affording her thirteen
times as much light, as she does to us. When she changes to us, the
Earth appears full to her; and when she is in her first quarter to us,
the Earth is in it’s third quarter to her; and vice versâ.
57. But from one half of the Moon, the Earth is never seen at all:
from the middle of the other half, it is always seen over head; turning
round almost thirty times as quick as the Moon does. From the line
which limits our view of the Moon, or all round what we call her
edges, only one half of the Earth’s side next her is seen; the other
half being hid below the Horizon. To her, the Earth seems to be
the biggest Body in the Universe; for it appears thirteen times as big
as she does to us.
A Proof of the Moon’s having no Atmosphere;
58. The Moon has no such Atmosphere, or body of air surrounding
her as we have: for if she had, we could never see her edge so well
defined as it appears; but there would be a sort of a mist or haziness
round her, which would make the Stars look fainter, when they were
seen through it. But observation proves, that the Stars which disappear
behind the Moon retain their full lustre until they seem to touch her very
edge, and then vanish in a moment. This has been often observed by
Astronomers, but particularly by Cassini[13] of the Star γ in the breast
of Virgo, which appears single and round to the bare eye; but through
a refracting Telescope of 16 feet appears to be two Stars so near together,
that the distance between them seems to be but equal to one of
their apparent diameters. The Moon was observed to pass over them
on the 21st of April 1720, N. S. and as her dark edge drew near to
them, it caused no change in their colour or Situation. At 25 min.
14 sec. past 12 at night, the most westerly of these Stars was hid
by the dark edge of the Moon; and in 30 seconds afterward, the most
easterly Star was hid: each of them disappearing behind the Moon in
an instant, without any preceding diminution of magnitude or brightness;
which by no means could have been the case if there were an
Atmosphere round the Moon; for then, one of the Stars falling obliquely
into it before the other, ought by refraction to have suffered some change
in its colour, or in it’s distance from the other Star which was not yet
entered into the Atmosphere. But no such alteration could be perceived
though the observation was performed with the utmost attention to that
particular; and was very proper to have made such a discovery. The
faint light, which has been seen all around the Moon, in total Eclipses
of the Sun, has been observed, during the time of darkness, to
17have it’s center coincident with the center of the Sun; and is therefore
much more likely to arise from the Atmosphere of the Sun than from
that of the Moon; for if it were the latter, it’s center would have gone
along with the Moon’s.
Nor Seas.
She is full of caverns and deep pits.
59. If there were seas in the Moon, she could have no clouds, rains,
nor storms as we have; because she has no such Atmosphere to support
the vapours which occasion them. And every one knows, that
when the Moon is above our Horizon in the night time, she is visible,
unless the clouds of our Atmosphere hide her from our view; and all
parts of her appear constantly with the same clear, serene, and calm
aspect. But those dark parts of the Moon, which were formerly thought
to be seas, are now found to be only vast deep cavities, and places
which reflect not the Sun’s light so strongly as others, having many
caverns and pits whose shadows fall within them, and are always dark
on the sides next the Sun; which demonstrates their being hollow:
and most of these pits have little knobs like hillocks standing within
them, and casting shadows also; which cause these places to appear
darker than others which have fewer, or less remarkable caverns. All
these appearances shew that there are no seas in the Moon; for if there
were any, their surfaces would appear smooth and even, like those on
the Earth.
The Stars always visible to the Moon.
60. There being no Atmosphere about the Moon, the Heavens in
the day time have the appearance of night to a Lunarian who turns his
back toward the Sun; and when he does, the Stars appear as bright
to him as they do in the night to us. For, it is entirely owing to our
Atmosphere that the Heavens are bright about us in the day.
The Earth a Dial to the Moon.
61. As the Earth turns round it’s Axis, the several continents, seas,
and islands appear to the Moon’s inhabitants like so many spots of different
forms and brightness, moving over it’s surface; but much fainter
at some times than others, as our clouds cover them or leave them.
By these spots the Lunarians can determine the time of the Earth’s
diurnal motion, just as we do the motion of the Sun: and perhaps
they measure their time by the motion of the Earth’s spots; for they
cannot have a truer dial.
PLATE I.
How the Lunarians may know the length of their year.
62. The Moon’s Axis is so nearly perpendicular to the Ecliptic, that
the Sun never removes sensibly from her Equator: and the[14] obliquity
of her Orbit, which is next to nothing as seen from the Sun, cannot
cause any sensible declination of the Sun from her Equator. Yet her
18inhabitants are not destitute of means for determining the length of
their year, though their method and ours must differ. For we can
know the length of our year by the return of our Equinoxes; but the
Lunarians, having always equal day and night, must have recourse to
another method; and we may suppose, they measure their year by
observing the Poles of our Earth; as one always begins to be enlightened,
and the other disappears, at our Equinoxes; they being
conveniently situated for observing great tracks of land about our Earth’s
Poles, which are entirely unknown to us. Hence we may conclude,
that the year is of the same absolute length both to the Earth and
Moon, though very different as to the number of days: we having
3651⁄4
natural days, and the Lunarians only
127⁄19;
every day and night
in the Moon being as long as
291⁄2
on the Earth.
And the longitudes of their places.
63. The Moon’s inhabitants on the side next the Earth may as easily
find the longitude of their places as we can find the latitude of ours.
For the Earth keeping constantly, or very nearly so, over one Meridian
of the Moon, the east or west distances of places from that Meridian
are as easily found, as we can find our distance from the Equator by
the Altitude of our celestial Poles.
Mars.
Fig. I.
64. The Planet Mars is next in order, being the first above the
Earth’s Orbit. His distance from the Sun is computed to be 123 millions
of miles; and by travelling at the rate of 47 thousand miles every
hour, as in the circle ♂, he goes round the Sun in 687 of our days and
17 hours; which is the length of his year, and contains
6671⁄4
of his
days; every day and night together being 40 minutes longer than with
us. His diameter is 4444 miles, and by his diurnal rotation the inhabitants
about his Equator are carried 556 miles every hour. His
quantity of light and heat is equal but to one half of ours; and the Sun
appears but half as big to him as to us.
His Atmosphere and Phases.
65. This Planet being but a fifth part so big as the Earth, if any
Moon attends him, she must be very small, and has not yet been discovered
by our best telescopes. He is of a fiery red colour, and by
his Appulses to some of the fixed Stars, seems to be surrounded by a
very gross Atmosphere. He appears sometimes gibbous, but never
horned; which both shews that his Orbit includes the Earth’s within it,
and that he shines not by his own light.
66. To Mars, our Earth and Moon appear like two Moons, a bigger
and a less; changing places with one another, and appearing sometimes
horned, sometimes half or three quarters illuminated, but never full;
nor at most above a quarter of a degree from each other, although they
are 240 thousand miles asunder.
PLATE I.
How the other Planets appear to Mars.
1967. Our Earth appears almost as big to Mars as Venus does to us,
and at Mars it is never seen above 48 degrees from the Sun; sometimes
it appears to pass over the Disc of the Sun, and so do Mercury and
Venus: but Mercury can never be seen from Mars by such eyes as ours,
unassisted by proper instruments; and Venus will be as seldom seen as
we see Mercury. Jupiter and Saturn are as visible to Mars as to us.
His Axis is perpendicular to the Ecliptic, and his Orbit is 2 degrees
inclined to it.
Jupiter.
Fig. I.
68. Jupiter, the biggest of all the Planets, is still higher in the
System, being about 424 millions of miles from the Sun: and going
at the rate of 25 thousand miles every hour in his Orbit, as in the
circle ♃ finishes his annual period in eleven of our years 314 days
and 18 hours. He is above 1000 times as big as the Earth, for his
diameter is 81,000 miles; which is more than ten times the diameter
of the Earth.
The number of days in his year.
69. Jupiter turns round his Axis in 9 hours 56 minutes; so that his
year contains 10 thousand 464 days; and the diurnal velocity of his
equatoreal parts is greater than the swiftness with which he moves in
his annual Orbit; a singular circumstance, as far as we know. By this
prodigious quick Rotation, his equatoreal inhabitants are carried 25
thousand 920 miles every hour (which is 920 miles an hour more than
an inhabitant of our Earth moves in twenty-four hours) besides the
25 thousand above-mentioned, which is common to all parts of his surface,
by his annual motion.
His Belts and spots.
70. Jupiter is surrounded by faint substances, called Belts, in which
so many changes appear, that they are generally thought to be clouds:
for some of them have been first interrupted and broken, and then have
vanished entirely. They have sometimes been observed of different
breadths, and afterwards have all become nearly of the same breadth.
Large spots have been seen in these Belts; and when a Belt vanishes,
the contiguous spots disappear with it. The broken ends of some Belts
have been generally observed to revolve in the same time with the spots;
only those nearer the Equator in somewhat less time than those near
the Poles; perhaps on account of the Sun’s greater heat near the
Equator, which is parallel to the Belts and course of the spots. Several
large spots, which appear round at one time, grow oblong by degrees,
and then divide into two or three round spots. The periodical time of
the spots near the Equator is 9 hours 50 minutes, but of those near the
Poles 9 hours 56 minutes. See Dr. Smith’s Optics, § 1004 & seq.
He has no change of seasons;
2071. The Axis of Jupiter is so nearly perpendicular to his Orbit, that
he has no sensible change of seasons; which is a great advantage, and
wisely ordered by the Author of Nature. For, if the Axis of this
Planet were inclined any considerable number of degrees, just so many
degrees round each Pole would in their turn be almost six of our years
together in darkness. And, as each degree of a great Circle on Jupiter
contains 706 of our miles at a mean rate, it is easy to judge what vast
tracts of land would be rendered uninhabitable by any considerable inclination
of his Axis.
But has four Moons.
72. The Sun appears but
1⁄28
part so big to Jupiter as to us; and his
light and heat are in the same small proportion, but compensated by
the quick returns thereof, and by four Moons (some bigger and some
less than our Earth) which revolve about him: so that there is scarce
any part of this huge Planet but what is during the whole night enlightened
by one or more of these Moons, except his Poles, whence
only the farthest Moons can be seen, and where their light is not
wanted, because the Sun constantly circulates in or near the Horizon,
and is very probably kept in view of both Poles by the Refraction of
Jupiter’s Atmosphere, which, if it be like ours, has certainly refractive
power enough for that purpose.
Their periods round Jupiter.
Their grand period.
73. The Orbits of these Moons are represented in the Scheme of
the Solar System by four small circles marked 1. 2. 3. 4. on Jupiter’s
Orbit ♃; but are drawn fifty times too large in proportion to it. The
first Moon, or that nearest to Jupiter, goes round him in 1 day 18
hours and 36 minutes of our time; and is 229 thousand miles distant
from his center: The second performs it’s revolution in three days
13 hours and 15 minutes, at 364 thousand miles distance: The third
in 7 days three hours and 59 minutes, at the distance of 580 thousand
miles: And the fourth, or outermost, in 16 days 18 hours and 30
minutes, at the distance of one million of miles from his center.
The Periods of these Moons are so incommensurate to one another,
that if ever they were all in a right line between Jupiter and the Sun,
it will require more than 3,000,000,000,000 years from that time
to bring them all into the same right line again, as any one will find
who reduces all their periods into seconds, then multiplies them into one
another, and divides the product by 432; which is the highest number
that will divide the product of all their periodical times, namely
42,085,303,376,931,994,955,904 seconds, without a remainder.
Parallax of their Orbits, and distances from Jupiter.
PLATE I.
How he appears to his nearest Moon.
74. The Angles under which the Orbits of Jupiter’s Moons are seen
from the Earth, at it’s mean distance from Jupiter, are as follow:
The first, 3ʹ 55ʺ; the second, 6ʹ 14ʺ; the third, 9ʹ 58ʺ; and the
21fourth, 17ʹ 30ʺ. And their distances from Jupiter, measured by his
semidiameters, are thus: The first,
52⁄3;
the second, 9; the third.
1423⁄60;
and the fourth,
2518⁄60
[15]. This Planet, seen from it’s nearest
Moon, appears 1000 times as large as our Moon does to us; waxing
and waneing in all her monthly shapes, every
421⁄2
hours.
Two grand discoveries made by the Eclipse of Jupiter’s Moons.
75. Jupiter’s three nearest Moons fall into his shadow, and are
eclipsed in every Revolution: but the Orbit of the fourth Moon is so
much inclined, that it passeth by Jupiter, without falling into his
shadow, two years in every six. By these Eclipses, Astronomers have
not only discovered that the Sun’s light comes to us in eight minutes;
but have also determined the longitudes of places on this Earth with
greater certainty and facility than by any other method yet known;
as shall be explained in the eleventh Chapter.
The great difference between the Equatoreal and Polar diameters
of Jupiter.
The difference little in those of our Earth.
76. The difference between the Equatoreal and Polar diameters of
Jupiter is 6230 miles; for his equatoreal diameter is to his polar as 13
to 12. So that his Poles are 3115 miles nearer his center than his
Equator is. This results from his quick motion round his Axis; for
the fluids, together with the light particles, which they can carry or
wash away with them, recede from the Poles which are at rest, towards
the Equator where the motion is quickest, until there be a sufficient
number accumulated to make up the deficiency of gravity occasioned
by the centrifugal force, which always arises from a quick motion round
an axis: and when the weight is made up so, as that all parts of the
surface press equally heavy toward the center, there is an equilibrium, and
the equatoreal parts rise no higher. Our Earth being but a very small
Planet, compared to Jupiter, and it’s motion on it’s Axis being much
slower, it is less flattened of course; for the difference between it’s
equatoreal and polar diameters is only as 230 to 229, or 35 miles.
Place of his Nodes.
77. Jupiter’s Orbit is 1 degree 20 minutes inclined to the Ecliptic.
His North Node is in the 7th degree of Cancer, and his South Node
in the 7th degree of Capricorn.
Saturn.
Fig. I.
78. Saturn, the remotest of all the Planets, is about 777 millions
of miles from the Sun; and, travelling at the rate of 18 thousand miles
every hour, as in the circle marked ♄, performs his annual circuit in
29 years 167 days and 5 hours of our time; which makes only one
year to that Planet. His diameter is 67,000 miles; and therefore he is
near 600 times as big as the Earth.
79. He is surrounded by a thin broad Ring, as an artificial Globe is
by its Horizon. This Ring appears double when seen through a good
22telescope, and is represented by the figure in such an oblique view as it
is generally seen. It is inclined 30 degrees to the Ecliptic, and is
about 21 thousand miles in breadth; which is equal to it’s distance from
Saturn on all sides. There is reason to believe that the Ring turns
round it’s Axis, because, when it is almost edge-wise to us, it appears
somewhat thicker on one side of the Planet than on the other; and
the thickest edge has been seen on different sides at different times. But
Saturn having no visible spots on his body, whereby to determine the
time of his turning round his Axis, the length of his days and nights,
and the position of his Axis, are unknown to us.
His five Moons.
Fig. I.
80. To Saturn, the Sun appears only
1⁄90th
part so big as to us;
and the light and heat he receives from the Sun are in the same proportion
to ours. But to compensate for the small quantity of sun-light,
he has five Moons, all going round him on the outside of his Ring,
and nearly in the same plane with it. The first, or nearest Moon to
Saturn, goes round him in 1 day 21 hours 19 minutes; and is 140
thousand miles from his center: The second, in two days 17 hours
40 minutes; at the distance of 187 thousand miles: The third, in 4
days 12 hours 25 minutes; at 263 thousand miles distance: The fourth,
in 15 days 22 hours 41 minutes; at the distance of 600 thousand
miles: And the fifth, or outermost, at one million 800 thousand miles
from Saturn’s center, goes round him in 79 days 7 hours 48 minutes.
Their Orbits in the Scheme of the Solar System are represented by
the five small circles, marked 1. 2. 3. 4. 5. on Saturn’s Orbit; but these,
like the Orbits of the other Satellites, are drawn fifty times too large
in proportion to the Orbits of their Primary Planets.
His Axis probably inclined to his Ring.
81. The Sun shines almost fifteen of our years together on one side
of Saturn’s Ring without setting, and as long on the other in it’s
turn. So that the Ring is visible to the inhabitants of that Planet for
almost fifteen of our years, and as long invisible by turns, if it’s
Axis has no Inclination to it’s Ring: but if the Axis of the Planet be
inclined to the Ring, suppose about 30 degrees, the Ring will appear
and disappear once every natural day to all the inhabitants within 30
degrees of the Equator, on both sides, frequently eclipsing the Sun in
a Saturnian day. Moreover, if Saturn’s Axis be so inclined to his
Ring, it is perpendicular to his Orbit; and thereby the inconvenience
of different seasons to that Planet is avoided. For considering the
length of Saturn’s year, which is almost equal to thirty of ours, what
a dreadful condition must the inhabitants of his Polar regions be in,
if they be half of that time deprived of the light and heat of the Sun?
which must not be their case alone, if the Axis of the Planet be perpendicular
23to the Ring, but also the Ring must hide the Sun from vast
tracks of land on each side of the Equator for 13 or 14 of our years
together, on the south side and north side by turns, as the Axis inclines
to or from the Sun: the reverse of which inconvenience is another
good presumptive proof of the Inclination of Saturn’s Axis to
it’s Ring, and also of his Axis being perpendicular to his Orbit.
How the Ring appears to Saturn and to us.
In what Signs Saturn appears to lose his Ring; and in what
Signs it appears most open to us.
82. This Ring, seen from Saturn, appears like a vast luminous Arch
in the Heavens, as if it did not belong to the Planet. When we see
the Ring most open, it’s shadow upon the Planet is broadest; and from
that time the shadow grows narrower, as the Ring appears to do to us;
until, by Saturn’s annual motion, the Sun comes to the plane of the
Ring, or even with it’s edge; which being then directed towards us,
becomes invisible on account of it’s thinness; as shall be explained more
largely in the tenth Chapter, and illustrated by a figure. The Ring
disappears twice in every annual Revolution of Saturn, namely, when he
is in the 19th degree both of Pisces and of Virgo. And when Saturn
is in the middle between these points, or in the 19th degree either of
Gemini or of Sagittarius, his Ring appears most open to us; and then
it’s longest diameter is to it’s shortest as 9 to 4.
No Planet but Saturn can be seen from Jupiter; nor any from Jupiter besides Saturn.
83. To such eyes as ours, unassisted by instruments, Jupiter is the
only Planet that can be seen from Saturn; and Saturn the only Planet
that can be seen from Jupiter. So that the inhabitants of these two
Planets must either see much farther than we do, or have equally good
instruments to carry their sight to remote objects, if they know that
there is such a body as our Earth in the Universe: for the Earth is no
bigger seen from Jupiter than his Moons are seen from the Earth; and
if his large body had not first attracted our sight, and prompted our
curiosity to view him with the telescope, we should never have known
any thing of his Moons; unless by chance we had directed the telescope
toward that small part of the Heavens where they were at the time of
observation. And the like is true of the Moons of Saturn.
Place of Saturn’s Nodes.
84. The Orbit of Saturn is
21⁄2
degrees inclined to the Ecliptic, or
Orbit of our Earth, and intersects it in the 21st degree of Cancer and
of Capricorn; so that Saturn’s Nodes are only 14 degrees from Jupiter’s,
§ 77.
The Sun’s light much stronger on Jupiter and Saturn than is
generally believed.
All our heat depends not on the Sun’s rays.
85. The quantity of light, afforded by the Sun of Jupiter, being
but
1⁄28th
part, and to Saturn only
1⁄90th
part, of what we enjoy; may
at first thought induce us to believe that these two Planets are entirely
unfit for rational beings to dwell upon. But, that their light is not so
weak as we imagine, is evident from their brightness in the night-time;
and also, that when the Sun is so much eclipsed to us as to have
24only the 40th part of his Disc left uncovered by the Moon, the decrease
of light is not very sensible: and just at the end of darkness in Total
Eclipses, when his western limb begins to be visible, and seems no
bigger than a bit of fine silver wire, every one is surprised at the brightness
wherewith that small part of him shines. The Moon when Full
affords travellers light enough to keep them from mistaking their way;
and yet, according to Dr. Smith[16], it is equal to no more than a 90
thousandth part of the light of the Sun: that is, the Sun’s light is 90
thousand times as strong as the light of the Moon when Full. Consequently,
the Sun gives a thousand times as much light to Saturn as
the Full Moon does to us; and above three thousand times as much
to Jupiter. So that these two Planets, even without any Moons,
would be much more enlightened than we at first imagine; and by
having so many, they may be very comfortable places of residence.
Their heat, so far as it depends on the force of the Sun’s rays, is certainly
much less than ours; to which no doubt the bodies of their
inhabitants are as well adapted as ours are to the seasons we enjoy.
And if we consider, that Jupiter never has any winter, even at his
Poles; which probably is also the case with Saturn, the cold cannot
be so intense on these two Planets as is generally imagined. Besides,
there may be something in their nature or soil much warmer than in
that of our Earth: and we find that all our heat depends not on the
rays of the Sun; for if it did, we should always have the same months
equally hot or cold at their annual returns. But it is far otherwise, for
February is sometimes warmer than May, which must be owing to
vapours and exhalations from the Earth.
It is highly probable that all the Planets are inhabited.
PLATE I.
86. Every person who looks upon, and compares the Systems of
Moons together, which belong to Jupiter and Saturn, must be amazed
at the vast magnitude of these two Planets, and the noble attendance
they have in respect of our little Earth: and can never bring himself to
think, that an infinitely wise Creator should dispose of all his animals
and vegetables here, leaving the other Planets bare and destitute of
rational creatures. To suppose that he had any view to our Benefit,
in creating these Moons and giving them their motions round Jupiter
and Saturn; to imagine that he intended these vast Bodies for any advantage
to us, when he well knew that they could never be seen but
by a few Astronomers peeping through telescopes; and that he gave to
the Planets regular returns of days and nights, and different seasons to
all where they would be convenient; but of no manner of service to us,
25except only what immediately regards our own Planet the Earth; to
imagine, I say, that he did all this on our account, would be charging
him impiously with having done much in vain: and as absurd, as to
imagine that he has created a little Sun and a Planetary System within
the shell of our Earth, and intended them for our use. These considerations
amount to little less than a positive proof that all the Planets
are inhabited: for if they are not, why all this care in furnishing them
with so many Moons, to supply those with light which are at the greater
distances from the Sun? Do we not see, that the farther a Planet is
from the Sun, the greater Apparatus it has for that purpose? save only
Mars, which being but a small Planet, may have Moons too small to be
seen by us. We know that the Earth goes round the Sun, and turns
round it’s own Axis, to produce the vicissitudes of summer and winter by
the former, and of day and night by the latter motion, for the benefit
of its inhabitants. May we not then fairly conclude, by parity of reason,
that the end and design of all the other Planets is the same? and is not
this agreeable to that beautiful harmony which reigns over the Universe?
Surely it is: and raises in us the most magnificent ideas of the
SUPREME BEING, who is every where, and at all times present;
displaying his power, wisdom, and goodness among all his creatures!
and distributing happiness to innumerable ranks of various beings!
Fig. II.
How the Sun appears to the different Planets.
87. In Fig. 2d, we have a view of the proportional breadth of the
Sun’s face or disc, as seen from the different Planets. The Sun is
represented No 1, as seen from Mercury; No 2, as seen from Venus;
No 3, as seen from the Earth; No 4, as seen from Mars; No 5, as
seen from Jupiter; and No 6, as seen from Saturn.
Fig. III.
Fig. IV.
Let the circle B be the Sun as seen from any Planet, at a given
distance; to another Planet, at double that distance, the Sun will appear
just of half that breadth, as A; which contains only one fourth part
of the area or surface of B. For, all circles, as well as square surfaces,
are to one another as the squares of their diameters. Thus, the square
A is just half as broad as the square B; and yet it is plain to sight, that
B contains four times as much surface as A. Hence, in round numbers,
the Sun appears 7 times larger to Mercury than to us, 90 times larger
to us than to Saturn, and 630 times as large to Mercury as to Saturn.
Fig. V.
Proportional bulks and distances of the Planets.
PLATE I.
88. In Fig. 5th, we have a view of the bulks of the Planets in proportion
to each other, and to a supposed globe of two foot diameter for
the Sun. The Earth is 27 times as big as Mercury, very little bigger
than Venus, 5 times as big as Mars; but Jupiter is 1049 times as big
as the Earth, Saturn 586 times as big, exclusive of his Ring; and the
26Sun is 877 thousand 650 times as big as the Earth. If the Planets in
this Figure were set at their due distances from a Sun of two feet diameter,
according to their proportional bulks, as in our System, Mercury would
be 28 yards from the Sun’s center; Venus 51 yards 1 foot; the Earth
70 yards 2 feet; Mars 107 yards 2 feet; Jupiter 370 yards 2 feet;
and Saturn 760 yards two feet. The Comet of the year 1680, at it’s
greatest distance, 10 thousand 760 yards. In this proportion, the
Moon’s distance from the center of the Earth would be only
71⁄2
inches.
An idea of their distances.
89. To assist the imagination in conceiving an idea of the vast distances
of the Sun, Planets, and Stars, let us suppose, that a body projected
from the Sun should continue to fly with the swiftness of a cannon ball;
i. e. 480 miles every hour; this body would reach the Orbit of Mercury,
in 7 years 221 days; of Venus, in 14 years 8 days; of the
Earth, in 19 years 91 days; of Mars, in 29 years 85 days; of Jupiter,
in 100 years 280 days; of Saturn, in 184 years 240 days; to the
Comet of 1680, at it’s greatest distance from the Sun, in 2660 years;
and to the nearest fixed Stars in about 7 million 600 thousand years.
Why the Planets appear bigger and less at different times.
90. As the Earth is not the center of the Orbits in which the Planets
move, they come nearer to it and go farther from it and at different
times; on which account they appear bigger and less by turns. Hence,
the apparent magnitudes of the Planets are not always a certain rule to
know them by.
Fig. I.
91. Under Fig. 3, are the names and characters of the twelve Signs
of the Zodiac, which the Reader should be perfectly well acquainted
with; so as to know the characters without seeing the names. Every
Sign contains 30 degrees, as in the Circle bounding the Solar System;
to which the characters of the Signs are set in their proper places.
The Comets.
92. The Comets are solid opaque bodies, with long transparent
trains or tails, issuing from that side which is turned away from the Sun.
They move about the Sun, in very excentric ellipses; and are of a much
greater density than the Earth; for some of them are heated in every
Period to such a degree, as would vitrify or dissipate any substance
known to us. Sir Isaac Newton computed the heat of the Comet
which appeared in the year 1680, when nearest the Sun, to be 2000
times hotter than red-hot iron, and that being thus heated, it must
retain it’s heat until it comes round again, although it’s Period should
be more than twenty thousand years; and it is computed to be only 575.
The method of computing the heat of bodies, keeping at any known
distance from the Sun, so far as their heat depends on the force of the
Sun’s rays, is very easy; and shall be explained in the eighth Chapter.
PLATE I.
Fig. I.
They prove that the Orbits of the Planets are not solid.
The Periods only of three are known.
They prove the Stars to be at immense distances.
2793. Part of the Paths of three Comets are delineated in the Scheme
of the Solar System, and the years marked in which they made their
appearance. It is believed, that there are at least 21 Comets belonging
to our System, moving in all sorts of directions: and all those which
have been observed, have moved through the ethereal Regions and
the Orbits of the Planets without suffering the least sensible resistance
in their motions; which plainly proves that the Planets do not move in
solid Orbs. Of all the Comets, the Periods of the above-mentioned
three only are known with any degree of certainty. The first of these
Comets appeared in the years 1531, 1607, and 1682; and is expected
to appear again in the year 1758, and every 75th year afterwards.
The second of them appeared in 1532 and 1661, and may be
expected to return in 1789 and every 129th year afterwards. The
third, having last appeared in 1680, and it’s Period being no less than
575 years, cannot return until the year 2225. This Comet, at it’s
greatest distance, is about 11 thousand two hundred millions of miles
from the Sun; and at it’s least distance from the Sun’s center, which
is 490,000 miles, is within less than a third part of the Sun’s semi-diameter
from his surface. In that part of it’s Orbit which is nearest
the Sun, it flies with the amazing swiftness of 880,000 miles in an
hour; and the Sun, as seen from it, appears an hundred degrees in
breadth; consequently, 40 thousand times as large as he appears to us.
The astonishing length that this Comet runs out into empty Space,
suggests to our minds an idea of the vast distance between the Sun and
the nearest fixed Stars; of whose Attractions all the Comets must keep
clear, to return periodically, and go round the Sun; and it shews us
also, that the nearest Stars, which are probably those that seem the
largest, are as big as our Sun, and of the same nature with him; otherwise,
they could not appear so large and bright to us as they do at such
an immense distance.
Inferences drawn from the above phenomena.
94. The extreme heat, the dense atmosphere, the gross vapours,
the chaotic state of the Comets, seem at first sight to indicate them
altogether unfit for the purposes of animal life, and a most miserable
habitation for rational beings: and therefore [17]some are of opinion that
they are so many hells for tormenting the damned with perpetual vicissitudes
of heat and cold. But, when we consider, on the other hand,
the infinite power and goodness of the Deity; the latter inclining, and
the former enabling him to make creatures suited to all states and circumstances;
that matter exists only for the sake of intelligence; and
that wherever we find it, we always find it pregnant with life, or
28necessarily subservient thereto; the numberless species, the astonishing
diversity of animals in earth, air, water, and even on other animals;
every blade of grass, every tender leaf, every natural fluid, swarming
with life; and every one of these enjoying such gratifications as the
nature and state of each requires: when we reflect moreover that some
centuries ago, till experience undeceived us, a great part of the Earth
was judged uninhabitable; the Torrid Zone by reason of excessive
heat, and the two Frigid Zones because of their intollerable cold;
it seems highly probable, that such numerous and large masses of durable
matter as the Comets are, however unlike they be to our Earth, are
not destitute of beings capable of contemplating with wonder, and
acknowledging with gratitude the wisdom, symmetry, and beauty of
the Creation; which is more plainly to be observed in their extensive
Tour through the Heavens, than in our more confined Circuit. If
farther conjecture is permitted, may we not suppose them instrumental
in recruiting the expended fuel of the Sun; and supplying the exhausted
moisture of the Planets? However difficult it may be, circumstanced
as we are, to find out their particular destination, this is an undoubted
truth, that wherever the Deity exerts his power, there he also
manifests his wisdom and goodness.
This System very ancient, and demonstrable.
95. THE SOLAR SYSTEM here described is not a late
invention; for it was known and taught by the wise Samian philosopher
Pythagoras, and others among the ancients; but in latter times
was lost, ’till the 15th century, when it was again restored by the
famous Polish philosopher Nicholaus Copernicus, who was born
at Thorn in the year 1473. In this, he was followed by the greatest
mathematicians and philosophers that have since lived; as Kepler,
Galileo, Descartes, Gassendus, and Sir Isaac Newton;
the last of whom has established this System on such an everlasting
foundation of mathematical and physical demonstration, as can never
be shaken: and none who understand him can hesitate about it.
The Ptolemean System absurd.
96. In the Ptolemean System the Earth was supposed to be fixed in
the Center of the Universe; and that the Moon, Mercury, Venus,
the Sun, Mars, Jupiter, and Saturn moved round the Earth: above
the Planets, this Hypothesis placed the Firmament of Stars, and then
the two Crystalline Spheres; all which were included in and received
motion from the Primum Mobile, which constantly revolved about
the Earth in 24 hours, from East to West. But as this rude Scheme
was found incapable to stand the test of art and observation, it was soon
rejected by all true philosophers; notwithstanding the opposition and
violence of blind and zealous bigots.
The Tychonic System, partly true and partly false.
2997. The Tychonic System succeeded the Ptolemean, but was never so
generally received. In this the Earth was supposed to stand still in the
Center of the Universe or Firmament of Stars, and the Sun to revolve
about it every 24 hours; the Planets, Mercury, Venus, Mars, Jupiter,
and Saturn, going round the Sun in the times already mentioned. But
some of Tycho’s disciples supposed the Earth to have a diurnal motion
round it’s Axis, and the Sun with all the above Planets to go round the
Earth in a year; the Planets moving round the Sun in the foresaid
times. This hypothesis, being partly true and partly false, was embraced
by few; and soon gave way to the only true and rational System,
restored by Copernicus and demonstrated by Sir Isaac Newton.
98. To bring the foregoing particulars at once in view, with several
others which follow, concerning the Periods, Distances, Bulks, &c.
of the Planets, the following Table is inserted.
30A TABLE
Of the PERIODS, REVOLUTIONS, MAGNITUDES, &c. of the PLANETS.
| Sun and Planets. |
Annual period round the Sun. |
Diurnal rotation on it’s Axis. |
Diameter in English miles. |
Mean diam. as seen fr. the Sun. |
Mean distance from the Sun in English miles. |
| Sun |
---- |
25d. 6h. |
763000 |
---- |
---- |
| Mercury |
87d 23h |
Unknown. |
2600 |
20ʺ |
32,000,000 |
| Venus |
224d 17h |
24d. 8h. |
7906 |
30ʺ |
59,000,000 |
| Earth |
365d 6h |
1d. 0h. |
7970 |
21ʺ |
81,000,000 |
| Moon |
365d 6h |
29d. 123⁄4h. |
2180 |
6ʺ |
81,000,000 |
| Mars |
686d 23h |
24h. 40m. |
4444 |
11ʺ |
123,000,000 |
| Jupiter |
4332d 12h |
9h. 56m. |
81000 |
37ʺ |
424,000,000 |
| Saturn |
10759d 7h |
Unknown. |
67000 |
16ʺ |
777,000,000 |
| Sun and Planets. |
Excentricity of it’s Orbit in miles. |
Axis inclined to Orbit. |
Orbit inclined to Ecliptic. |
Place of it’s Aphelion. |
Place of it’s Ascending Node. |
Proportion of Diameters. |
| Sun |
---- |
8° 0ʹ |
---- |
---- |
---- |
10000 |
| Mercury |
6,720,000 |
Unkn. |
6° 54ʹ |
♐ 13° 8ʹ |
♉ 14° 43ʹ |
341⁄10 |
| Venus |
413,000 |
75° 0ʹ |
3° 20ʹ |
♒ 4° 20ʹ |
♊ 13° 59ʹ |
1031⁄2 |
| Earth |
1,377,000 |
23° 29ʹ |
0° 0ʹ |
♑ 8° 1ʹ |
---- |
1041⁄2 |
| Moon |
13,000 |
2° 10ʹ |
5° 8ʹ |
---- |
Variable. |
281⁄2 |
| Mars |
11,439,000 |
0° 0ʹ |
1° 52ʹ |
♍ 0° 32ʹ |
♉ 17° 17ʹ |
581⁄6 |
| Jupiter |
20,352,000 |
0° 0ʹ |
1° 20ʹ |
♎ 9° 10ʹ |
♋ 7° 29ʹ |
10612⁄3 |
| Saturn |
42,735,000 |
Unkn. |
2° 30ʹ |
♐ 27° 50ʹ |
♋ 21° 13ʹ |
8781⁄9 |
| Sun and Planets. |
Proportion of Bulk. |
Prop. of Gravity on the surface. |
Proportion of Density. |
Proportion of Light & Heat. |
Propor. quantity of Matter. |
Hourly motion in it’s Orbit. |
Hourly motion of it’s Equator. |
| Sun |
877650 |
24 |
251⁄2 |
45000 |
227500 |
---- |
3818 |
| Mercury |
1⁄27 |
Unkn. |
Unkn. |
61⁄2 |
Unkn. |
95000 |
Unkn. |
| Venus |
1 |
Unkn. |
Unkn. |
13⁄4 |
Unkn. |
69000 |
43 |
| Earth |
1 |
1 |
100 |
1 |
1 |
58000 |
1042 |
| Moon |
1⁄50 |
34⁄100 |
1231⁄2 |
1 ± |
1⁄40 |
2290 |
91⁄2 |
| Mars |
1⁄5 |
Unkn. |
Unkn. |
3⁄7 |
Unkn. |
47000 |
556 |
| Jupiter |
1049 |
2 |
19 |
1⁄28 |
220 |
25000 |
25920 |
| Saturn |
586 |
11⁄2 |
15 |
1⁄90 |
94 |
18000 |
Unkn. |
| Sun and Planets. |
Square miles in surface. |
Cubic miles in solidity. |
Would fall to the Sun in |
| Sun |
1,828,911,000,000 |
232,577,115,137,000,000 |
days h. |
| Mercury |
21,236,800 |
9,195,534,500 |
15 13 |
| Venus |
691,361,300 |
258,507,832,200 |
39 17 |
| Earth |
199,852,860 |
265,404,598,080 |
14 10 |
| Moon |
14,898,750 |
5,408,246,000 |
64 10 |
| Mars |
62,038,240 |
45,969,335,840 |
121 0 |
| Jupiter |
20,603,970,000 |
278,153,595,000,000 |
290 0 |
| Saturn |
14,102,562,000 |
155,128,182,000,000 |
767 0 |
| |
|
|
If the projectile force was destroyed. |
If the Moon’s
projectile force was destroyed, she would fall
to the Earth in 4 days 21 hours.
| Jupiter’s Moons. |
Periods round Jupiter. |
| No |
D. |
H. |
M. |
| 1 |
1 |
18 |
36 |
| 2 |
3 |
13 |
15 |
| 3 |
7 |
3 |
59 |
| 4 |
16 |
18 |
30 |
| Saturn’s Moons. |
Periods round Saturn. |
| No |
D. |
H. |
M. |
| 1 |
1 |
21 |
19 |
| 2 |
2 |
17 |
40 |
| 3 |
4 |
12 |
25 |
| 4 |
15 |
22 |
41 |
| 5 |
79 |
7 |
48 |
31
CHAP. III.
The COPERNICAN SYSTEM demonstrated to be true.
Of matter and motion.
99. Matter is of itself inactive, and indifferent to motion or
rest. A body at rest can never put itself in motion; a body
in motion can never stop nor move slower of itself. Hence, when we
see a body in motion we conclude some other substance must have
given it that motion; when we see a body fall from motion to rest we
conclude some other body or cause stopt it.
100. All motion is naturally rectilineal. A bullet thrown by the
hand, or discharged from a cannon would continue to move in the
same direction it received at first, if no other power diverted its course.
Therefore, when we see a body moving in a curve of whatever kind,
we conclude it must be acted upon by two powers at least: one to put
it in motion, and another drawing it off from the rectilineal course
which it would otherwise have continued to move in.
Gravity demonstrable.
101. The power by which bodies fall towards the Earth is called
Gravity or Attraction. By this power in the Earth it is, that all bodies,
on whatever side, fall in lines perpendicular to it’s surface. On opposite
parts of the Earth bodies fall in opposite directions, all towards the
centre where the force of gravity is as it were accumulated. By this
power constantly acting on bodies near the Earth they are kept from
leaving it altogether; and those on its surface are kept thereto on all
sides, so that they cannot fall from it. Bodies thrown with any obliquity
are drawn by this power from a straight line into a curve, until
they fall to the Ground: the greater the force by which they are
thrown, the greater is the distance they are carried before they fall.
If we suppose a body carried several miles above the Earth, and there
projected in an horizontal direction, with so great a velocity that it
would move more than a semidiameter of the Earth, in the time it
would take to fall to the Earth by gravity; in that case, if there were
no resisting medium in the way, the body would not fall to the Earth
at all; but continue to circulate round the Earth, keeping always the
same path, and returning to the point from whence it was projected,
with the same velocity as at first.
Projectile force demonstrable.
102. We find the Moon moves round the Earth in an Orbit nearly
circular. The Moon therefore must be acted on by two powers or
forces; one which would cause her to move in a right line, another
32bending her motion from that line into a curve. This attractive power
must be seated in the Earth; for there is no other body within the
Moon’s Orbit to draw her. The attractive power of the Earth therefore
extends to the Moon; and, in combination with her projectile force,
causes her to move round the Earth in the same manner as the circulating
body above supposed.
The Sun and Planets attract each other.
103. The Moons of Jupiter and Saturn are observed to move round
their primary Planets: therefore there is such a power as gravity in
these Planets. All the Planets move round the Sun, and respect it for
their centre of motion: therefore the Sun must be endowed with attracting
force, as well as the Earth and Planets. The like may be
proved of the Comets. So that all the bodies or matter in the Solar
System are possessed of this power; and perhaps so is all matter whatsoever.
104. As the Sun attracts the Planets with their Satellites, and the
Earth the Moon, so the Planets and Satellites re-attract the Sun, and
the Moon the Earth: action and re-action being always equal. This
is also confirmed by observation; for the Moon raises tides in the ocean,
the Satellites and Planets disturb one another’s motions.
105. Every particle of matter being possessed of an attracting power,
the effect of the whole must be in proportion to the number of attracting
particles: that is, to the quantity of matter in the body. This is
demonstrated from experiments on pendulums: for, if they are of equal
lengths, whatever their weights be, they always vibrate in equal times.
Now, if one be double the weight of another, the force of gravity
or attraction must be double to make it oscillate with the same celerity:
if one is thrice the weight or quantity of matter of another, it requires
thrice the force of gravity to make it move with the same celerity.
Hence it is certain, that the power of gravity is always proportional to
the quantity of matter in bodies, whatever their bulks or figures are.
106. Gravity also, like all other virtues or emanations issuing from a
centre, decreases as the square of the distance increases: that is, a
body at twice the distance attracts another with only a fourth part of
the force; at four times the distance, with a sixteenth part of the force.
This too is confirmed from observation, by comparing the distance
which the Moon falls in a minute from a right line touching her Orbit,
with the space which bodies near the Earth fall in the same time:
and also by comparing the forces which retain Jupiter’s Moons in
their Orbits. This will be more fully explained in the seventh Chapter.
Gravitation and projection exemplified.
107. The mutual attraction of bodies may be exemplified by a
boat and a ship on the Water, tied by a rope. Let a man either in
33ship or boat pull the rope (it is the same in effect at which end he
pulls, for the rope will be equally stretched throughout,) the ship and
boat will be drawn towards one another; but with this difference,
that the boat will move as much faster than the ship as the ship is
heavier than the boat. Suppose the boat as heavy as the ship, and
they will draw one another equally (setting aside the greater resistance
of the Water on the bigger body) and meet in the middle of the first
distance between them. If the ship is a thousand or ten thousand times
heavier than the boat, the boat will be drawn a thousand or ten thousand
times faster than the ship; and meet proportionably nearer the place from
which the ship set out. Now, whilst one man pulls the rope, endeavouring
to bring the ship and boat together, let another man, in the
boat, endeavour to row her off sidewise, or at right Angles to the rope;
and the former, instead of being able to draw the boat to the ship, will
find it enough for him to keep the boat from going further off; whilst
the latter, endeavouring to row off the boat in a straight line, will, by
means of the other’s pulling it towards the ship, row the boat round
the ship at the rope’s length from her. Here, the power employed
to draw the ship and boat to one another represents the mutual attraction
of the Sun and Planets, by which the Planets would fall freely
towards the Sun with a quick motion; and would also in falling attract
the Sun towards them. And the power employed to row off the boat
represents the projectile force impressed on the Planets at right Angles,
or nearly so, to the Sun’s attraction; by which means the Planets move
round the Sun, and are kept from falling to it. On the other hand,
if it be attempted to make a heavy ship go round a light boat, they
will meet sooner than the ship can get round; or the ship will drag the
boat after it.
108. Let the above principles be applied to the Sun and Earth; and
they will evince, beyond a possibility of doubt, that the Sun, not the
Earth, is the center of the System; and that the Earth moves round
the Sun as the other Planets do.
The absurdity of supposing the Earth at rest.
For, if the Sun moves about the Earth, the Earth’s attractive power
must draw the Sun towards it from the line of projection so, as to bend
it’s motion into a curve; and the Earth being at least 169 thousand
times lighter than the Sun, by being so much less as to it’s quantity
of matter, must move 169 thousand times faster toward the Sun
than the Sun does toward the Earth; and consequently would fall to
the Sun in a short time if it had not a very strong projectile motion
to carry it off. The Earth therefore, as well as every other Planet in
34the System, must have a rectilineal impulse to prevent its falling into
the Sun. To say, that gravitation retains all the other Planets in their
Orbits without affecting the Earth, which is placed between the Orbits
of Mars and Venus, is as absurd as to suppose that six cannon bullets
might be projected upwards to different heights in the Air, and that
five of them should fall down to the ground; but the sixth, which
is neither the highest nor the lowest, should remain suspended in
the Air without falling; and the Earth move round about it.
109. There is no such thing in nature as a heavy body moving
round a light one as its centre of motion. A pebble fastened to a mill-stone
by a string, may by an easy impulse be made to circulate round
the mill-stone: but no impulse can make a mill-stone circulate round
a loose pebble, for the heaviest would undoubtedly carry the lightest
along with it wherever it goes.
110. The Sun is so immensely bigger and heavier than the Earth[18],
that if he was moved out of his place, not only the Earth, but all
the other Planets if they were united into one mass, would be carried
along with the Sun as the pebble would be with the mill-stone.
The harmony of the celestial motions.
The absurdity of supposing the Stars and Planets to move round
the Earth.
111. By considering the law of gravitation, which takes place throughout
the Solar System, in another light, it will be evident that the Earth
moves round the Sun in a year; and not the Sun round the Earth. It
has been shewn (§ 106) that the power of gravity decreases as the
square of the distance increases: and from this it follows with mathematical
certainty, that when two or more bodies move round another
as their centre of motion, the squares of their periodic times will be
to one another in the same proportion as the cubes of their distances
from the central body. This holds precisely with regard to the Planets
round the Sun, and the Satellites round the Planets; the relative distances
of all which, are well known. But, if we suppose the Sun
to move round the Earth, and compare its period with the Moon’s
by the above rule, it will be found that the Sun would take no less
than 173,510 days to move round the Earth, in which case our year
would be 475 times as long as it now is. To this we may add, that
the aspects of increase and decrease of the Planets, the times of their
seeming to stand still, and to move direct and retrograde, answer precisely
to the Earth’s motion; but not at all to the Sun’s without introducing
the most absurd and monstrous suppositions, which would destroy
all harmony, order, and simplicity in the System. Moreover, if
the Earth is supposed to stand still, and the Stars to revolve in free
spaces about the Earth in 24 hours, it is certain that the forces by
35which the Stars revolve in their Orbits are not directed to the Earth,
but to the centres of the several Orbits: that is, of the several parallel
Circles which the Stars on different sides of the Equator describe every
day: and the like inferences may be drawn from the supposed diurnal
motion of the Planets, since they are never in the Equinoctial but
twice, in their courses with regard to the starry Heavens. But, that
forces should be directed to no central body, on which they physically
depend, but to innumerable imaginary points in the axe of the Earth
produced to the Poles of the Heavens, is an hypothesis too absurd to be
allowed of by any rational creature. And it is still more absurd to
imagine that these forces should increase exactly in proportion to the distances
from this axe; for this is an indication of an increase to infinity:
whereas the force of attraction is found to decrease in receding from the
fountain from whence it flows. But, the farther that any Star is from
the quiescent Pole the greater must be the Orbit which it describes; and
yet it appears to go round in the same time as the nearest Star to the
Pole does. And if we take into consideration the two-fold motion observed
in the Stars, one diurnal round the Axis of the Earth in 24 hours,
and the other round the Axis of the Ecliptic in 25920 years § 251, it
would require an explication of such a perplexed composition of forces,
as could by no means be reconciled with any physical Theory.
Objections against the Earth’s motion answered.
112. There is but one objection of any weight that can be made to
the Earth’s motion round the Sun; which is, that in opposite points
of the Earth’s Orbit, it’s Axis which always keeps a parallel direction
would point to different fixed Stars; which is not found to be fact.
But this objection is easily removed by considering the immense distance
of the Stars in respect of the diameter of the Earth’s Orbit; the latter being
no more than a point when compared to the former. If we lay a ruler
on the side of a table, and along the edge of the ruler view the top of a
spire at ten miles distance; then lay the ruler on the opposite side of the
table in a parallel situation to what it had before, and the spire will still
appear along the edge of the ruler; because our eyes, even when assisted by
the best instruments are incapable of distinguishing so small a change.
113. Dr. Bradley, our present Astronomer Royal, has found by
a long series of the most accurate observations, that there is a small
apparent motion of the fixed Stars, occasioned by the aberration of their
light, and so exactly answering to an annual motion of the Earth, as
evinces the same, even to a mathematical demonstration. Those who
are qualified to read the Doctor’s modest Account of this great discovery
may consult the Philosophical Transactions, No 406. Or they may find
36it treated of at large by Drs. Smith[19], Long[20], Desaguliers[21],
Rutherfurth, Mr. Maclaurin[22], and M. de la Caille[23].
Why the Sun appears to change his place.
114. It is true that the Sun seems to change his place daily, so as to
make a tour round the starry Heavens in a year. But whether the
Earth or Sun moves, this appearance will be the same; for, when the
Earth is in any part of the Heavens, the Sun will appear in the opposite.
And therefore, this appearance can be no objection against the motion
of the Earth.
115. It is well known to every person who has sailed on smooth
Water, or been carried by a stream in a calm, that however fast the
vessel goes he does not feel its progressive motion. The motion of
the Earth is incomparably more smooth and uniform than that of a
ship, or any machine made and moved by human art: and therefore
it is not to be imagined that we can feel it’s motion.
The Earth’s motion on it’s Axis demonstrated.
116. We find that the Sun, and those Planets on which there are
visible spots, turn round their Axes: for the spots move regularly over
their Disks[24]. From hence we may reasonably conclude that the
other Planets on which we see no spots, and the Earth which is likewise
a Planet, have such rotations. But being incapable of leaving the
Earth, and viewing it at a distance; and it’s rotation being smooth and
uniform, we can neither see it move on it’s Axis as we do the Planets,
nor feel ourselves affected by it’s motion. Yet there is one effect of
such a motion which will enable us to judge with certainty whether
the Earth revolves on it’s Axis or not. All Globes which do not turn
round their Axes will be perfect spheres, on account of the equality of
the weight of bodies on their surfaces; especially of the fluid parts. But
all Globes which turn on their Axes will be oblate spheroids; that is,
their surfaces will be higher, or farther from the centre, in the equatoreal
than in the polar Regions: for, as the equatoreal parts move
quickest, they will recede farther from the Axis of motion, and enlarge
the equatoreal diameter. That our Earth is really of this figure is
demonstrable from the unequal vibrations of a pendulum, and the
unequal lengths of degrees in different latitudes. Since then, the
Earth is higher at the Equator than at the Poles, the sea, which naturally
runs downward, or towards the places which are nearest the centre,
would run towards the polar Regions, and leave the equatoreal parts
dry, if the centrifugal force of these parts did not raise and carry the
37waters thither. The Earth’s equatoreal diameter is 35 miles longer
than its Axis.
All bodies heavier at the Poles than they would be at the Equator.
117. Bodies near the Poles are heavier than those towards the
Equator, because they are nearer the Earth’s centre, where the whole
force of the Earth’s attraction is accumulated. They are also heavier
because their centrifugal force is less on account of their diurnal motion
being slower. For both these reasons, bodies carried from the Poles
toward the Equator, gradually lose of their weight. Experiments prove
that a pendulum, which vibrates seconds near the Poles vibrates slower
near the Equator, which shews that it is lighter or less attracted there.
To make it oscillate in the same time, ’tis found necessary to diminish
it’s length. By comparing the different lengths of pendulums swinging
seconds at the Equator and at London, it is found that a pendulum
must be
2169⁄1000
lines shorter at the Equator than at the Poles. A line
is a twelfth part of an inch.
How they might lose all their weight.
118. If the Earth turned round it’s Axis in 84 minutes 43 seconds,
the centrifugal force would be equal to the power of gravity at the
Equator; and all bodies there would entirely lose their weight. If
the Earth revolved quicker they would all fly off, and leave it.
The Earth’s motion cannot be felt.
119. One on the Earth can no more be sensible of it’s undisturbed
motion on it’s Axis, than one in the cabin of a ship on smooth Water
can be sensible of her motion when she turns gently and uniformly
round. It is therefore no argument against the Earth’s diurnal motion
that we do not feel it: nor is the apparent revolutions of the celestial
bodies every day a proof of the reality of these motions; for whether
we or they revolve, the appearance is the very same. A person looking
through the cabin windows of a ship as strongly fancies the objects
on land to go round when the ship turns, as if they were actually in
motion.
To the different Planets the Heavens appear to turn round on different Axes.
120. If we could translate ourselves from Planet to Planet, we should
still find that the Stars would appear of the same magnitudes, and at
the same distances from each other, as they do to us here; because
the width of the remotest Planet’s Orbit bears no sensible proportion
to the distance of the Stars. But then, the Heavens would seem to
revolve about very different Axes; and consequently, those quiescent
Points which are our Poles in the Heavens would seem to revolve
about other points, which, though apparently in motion to us on Earth
would be at rest as seen from any other Planet. Thus, the Axis of
Venus, which lies almost at right Angles to the Axis of the Earth,
would have it’s motionless Poles in two opposite points of the Heavens
38lying almost in our Equinoctial, where the motion appears quickest
because it is performed in the greatest Circle. And the very Poles,
which are at rest to us, have the quickest motion of all as seen from
Venus. To Mars and Jupiter the Heavens appear to turn round with
very different velocities on the same Axis, whose Poles are about
231⁄2
degrees from ours. Were we on Jupiter we should be at first amazed
at the rapid motion of the Heavens; the Sun and Stars going round in
9 hours 56 minutes. Could we go from thence to Venus we should
be as much surprised at the slowness of the heavenly motions: the
Sun going but once round in 584 hours, and the Stars in 540. And
could we go from Venus to the Moon we should see the Heavens turn
round with a yet slower motion; the Sun in 708 hours, the Stars in
655. As it is impossible these various circumvolutions in such different
times and on such different Axes can be real, so it is unreasonable to
suppose the Heavens to revolve about our Earth more than it does
about any other Planet. When we reflect on the vast distance of the
fixed Stars, to which 162,000,000 of miles is but a point, we are
filled with amazement at the immensity of their distance. But if we
try to frame an idea of the extreme rapidity with which the Stars must
move, if they move round the Earth in 24 hours, the thought becomes
so much too big for our imagination, that we can no more conceive it
than we do infinity or eternity. If the Sun was to go round the Earth
in a day, he must travel upwards of 300,000 miles in a minute: but
the Stars being at least 10,000 times as far as the Sun from us, those
about the Equator must move 10,000 times as quick. And all this
to serve no other purpose than what can be as fully and much more
simply obtained by the Earth’s turning round eastward as on an Axis,
every 24 hours, causing thereby an apparent diurnal motion of the Sun
westward, and bringing about the alternate returns of day and night.
Pl. II.
Objections against the Earth’s diurnal motion answered.
121. As to the common objections against the Earth’s motion on
it’s Axis, they are all easily answered and set aside. That it may turn
without being seen or felt to do so, has been already shewn, § 119.
But some are apt to imagine that if the Earth turns eastward (as it
certainly does if it turns at all) a ball fired perpendicularly upward in
the air must fall considerably westward of the place it was projected
from. This objection, which at first seems to have some weight, will
be found to have none at all when we consider that the gun and ball
partake of the Earth’s motion; and therefore the ball being carried forward
with the air as quick as the Earth and air turn, must fall down again
on the same place. A stone let fall from the top of a main-mast, if it
39meets with no obstacle, falls on the deck as near the foot of the mast
when the ship sails as when it does not. And if an inverted bottle,
full of liquor, be hung up to the cieling of the cabin, and a small
hole be made in the cork to let the liquor drop through on the floor,
the drops will fall just as far forward on the floor when the ship sails
as when it is at rest. And gnats or flies can as easily dance among
one another in a moving cabin as in a fixed chamber. As for those
scripture expressions which seem to contradict the Earth’s motion, this
general answer may be made to them all, viz. ’tis plain from many
instances that the Scriptures were never intended to instruct us in Philosophy
or Astronomy; and therefore, on those subjects, expressions are
not always to be taken in the strictest sense; but for the most part as
accommodated to the common apprehensions of mankind. Men of
sense in all ages, when not treating of the sciences purposely, have
followed this method: and it would be in vain to follow any other in
addressing ourselves to the vulgar, or bulk of any community. Moses
calls the Moon A GREAT LUMINARY (as it is in the Hebrew)
as well as the Sun: but the Moon is known to be an opaque body,
and the smallest that Astronomers have observed in the Heavens and
shines upon us not by any inherent light of it’s own, but by reflecting
the light of the Sun. If Moses had known this, and told the Israelites
so, they would have stared at him; and considered him rather as a
madman than as a person commissioned by the Almighty to be their
leader.
CHAP. IV.
The Phenomena of the Heavens as seen from different parts of the Earth.
We are kept to the Earth by gravity.
PLATE II. Fig. I.
Antipodes.
Axis of the World. It’s Poles. Fig. II.
122. We are kept to the Earth’s surface on all sides by the power
of it’s central attraction; which, laying hold of all bodies
according to their densities or quantities of matter without regard to
their bulks, constitutes what we call their weight. And having the
sky over our heads, go where we will, and our feet towards the centre
of the Earth, we call it up over our heads, and down under our feet:
although the same right line which is down to us, if continued through
and beyond the opposite side of the Earth, would be up to the inhabitants
on the opposite side. For, the inhabitants n, i, e, m, s, o, q, l
stand with their feet toward the Earth’s centre C; and have the same
40figure of sky N, l, E, M, S, O, Q, L over their heads. Therefore, the
point S is as directly upward to the inhabitant s on the south Pole
as N is to the inhabitant n on the North Pole: so is E to the inhabitant
e, supposed to be on the north end of Peru; and Q to the
opposite inhabitant q on the middle of the island Sumatra. Each of
these observers is surprised that his opposite or Antipode can stand
with his head hanging downwards. But let either go to the
other, and he will tell him that he stood as upright and firm on the
place where he was as he now stands where he is. To all these observers
the Sun, Moon, and Stars seem to turn round the points N and
S as the Poles of the fixed Axis NCS; because the Earth does really
turn round the mathematical line nCs as round an Axis of which n
is the North Pole and s the South Pole. The Inhabitant U (Fig. II.)
affirms that he is on the uppermost side of the Earth, and wonders
how another at L can stand on the undermost side with his head hanging
downwards. But U in the mean time forgets that in twelve hours
time he will be carried half round with the Earth; and then be in the
very situation that L now is, although as far from him as before.
And yet, when U comes there, he will find no difference as to his
manner of standing; only he will see the opposite half of the Heavens,
and imagine the Heavens to have gone half round him.
How our Earth might have an upper and an under side.
123. When we see a globe hung up in a room we cannot help
imagining it to have an upper and an under side, and immediately
form a like idea of the Earth; from whence we conclude, that it is
as impossible for persons to stand on the under side of the Earth as for
pebbles to lie on the under side of a common Globe, which instantly
fall down from it to the ground; and well they may, because the attraction
of the Earth, being too strong for the attraction of the Globe, pulls
them away. Just so would be the case with our Earth, if it were
placed near a Globe much bigger than itself, such as Jupiter: for
then it would really have an upper and an under side with respect to
that large Globe; which, by it’s Attraction, would pull away every
thing from the side of the Earth next to it; and only those on the
top of the opposite or upper side could keep upon it. But there is
no larger Globe near enough our Earth to overcome it’s central attraction;
and therefore it has no such thing as an upper and an under side:
for all bodies on or near it’s surface, even to the Moon, gravitate
towards it’s center.
124. Let any man imagine that the Earth and every thing but
himself is taken away, and he left alone in the midst of indefinite Space;
41he could then have no idea of up or down; and were his pockets full of
gold, he might take the pieces one by one, and throw them away on
all sides of him, without any danger of losing them; for the attraction
of his body would bring them all back by the ways they went, and
he would be down to every one of them. But then, if a Sun or any
other large body were created, and placed in any part of Space several
millions of miles from him, he would be attracted towards it, and could
not save himself from falling down to it.
Fig. I.
One half of the Heavens visible to an inhabitant on any part
of the Earth.
Phenomena at the Poles.
PLATE II.
125. The Earth’s bulk is but a point, as that at C, compared to the
Heavens; and therefore every inhabitant upon it, let him be where he
will, as at n, e, m, s, &c. sees one half of the Heavens. The inhabitant
n, on the North Pole of the Earth, constantly sees the Hemisphere
ENQ; and having the North Pole N of the Heavens just over his head,
his [25]Horizon coincides with the Celestial Equator ECQ. Therefore all
the Stars in the Northern Hemisphere ENC, between the Equator and
North Pole, appear to turn round the line NC, moving parallel to the
Horizon. The Equatoreal Stars keep in the Horizon, and all those in
the Southern Hemisphere ESQ are invisible. The like Phenomena are
seen by the observer s on the South Pole, with respect to the Hemisphere
ESQ; and to him the opposite Hemisphere is always invisible. Hence,
under either Pole, only one half of the Heavens is seen; for those parts
which are once visible never set, and those which are once invisible never
rise. But the Ecliptic YCX or Orbit which the Sun appears to describe
once a year by the Earth’s annual motion, has the half YC constantly
above the Horizon ECQ of the North Pole n; and the other half CX always
below it. Therefore whilst the Sun describes the northern half YC
of the Ecliptic he neither sets to the North Pole nor rises to the South;
and whilst he describes the southern half CX he neither sets to the South
Pole nor rises to the North. The same things are true with respect to the
Moon; only with this difference, that as the Sun describes the Ecliptic
but once a year, he is for half that time visible to each Pole in it’s
turn, and as long invisible; but as the Moon goes round the Ecliptic
in 27 days 8 hours, she is only visible for 13 days 16 hours, and as
long invisible to each Pole by turns. All the Planets likewise rise and
set to the Poles, because their Orbits are cut obliquely in halves by the
Horizon of the Poles. When the Sun (in his apparent way from X)
arrives at C, which is on the 20th of March, he is just rising to an
observer at n on the North Pole, and setting to another at s on the
42South Pole. From C he rises higher and higher in every apparent
Diurnal revolution ’till he comes to the highest point of the Ecliptic y,
on the 21st of June, and then he is at his greatest Altitude, which is
231⁄2
degrees, or the Arc Ey, equal to his greatest North declination;
and from thence he seems to descend gradually in every apparent Circumvolution,
’till he sets at C on the 23d of September; and then he
goes to exhibit the like Appearances at the South Pole for the other
half of the year. Hence the Sun’s apparent motion round the Earth is
not in parallel Circles, but in Spirals; such as might be represented by a
thread wound round a Globe from Tropic to Tropic; the Spirals being
at some distance from one another about the Equator, but gradually
nearer to each other as they approach nearer to the Tropics.
Phenomena at the Equator.
Fig. I.
126. If the observer be any where on the Terrestrial Equator eCq,
as suppose at e, he is in the Plane of the Celestial Equator; or under
the Equinoctial ECQ; and the Axis of the Earth nCs is coincident with
the Plane of his Horizon, extended out to N and S, the North and
South Poles of the Heavens. As the Earth turns round the line NCS,
the whole Heavens MOLl seem to turn round the same line, but the
contrary way. It is plain that this observer has the Poles constantly in
his Horizon, and that his Horizon cuts the Diurnal paths of all the
Celestial bodies perpendicularly and in halves. Therefore the Sun,
Planets, and Stars rise every day, and ascend perpendicularly above the
Horizon for six hours, and passing over the Meridian, descend in the
same manner for the six following hours; then set in the Horizon, and
continue twelve hours below it. Consequently at the Equator the days
and nights are equally long throughout the year. When the observer
is in the situation e, he sees the Hemisphere SEN; but in twelve hours
after, he is carried half round the Earth’s Axis to q, and then the Hemisphere
SQN becomes visible to him; and SEN disappears, being hid
by the Convexity of the Earth. Thus we find that to an observer at
either of the Poles one half of the Sky is always visible, and the other
half never seen; but to an observer on the Equator the whole Sky is
seen every 24 hours.
The Figure here referred to, represents a Celestial globe of glass,
having a Terrestrial globe within it; after the manner of the Glass Sphere
invented by my generous friend Dr. Long, Lowndes’s Professor of
Astronomy in Cambridge.
Remark.
127. If a Globe be held sidewise to the eye, at some distance, and
so that neither of it’s Poles can be seen, the Equator ECQ and all
Circles parallel to it, as DL, yzx, abX, MO, &c. will appear to be
43straight lines, as projected in this Figure; which is requisite to be mentioned
here, because we shall have occasion to call them Circles in the
following Article[26].
Phenomena between the Equator and Poles.
The Circles of perpetual Apparition and Occultation.
128. Let us now suppose that the observer has gone from the Equator
e towards the North Pole n, and that he stops at i, from which
place he then sees the Hemisphere MElNL; his Horizon MCL having
shifted as many [27]Degrees from the Celestial poles N and S as he has
travelled from under the Equinoctial E. And as the Heavens seem
constantly to turn round the line NCS as an Axis, all those Stars
which are as far from the North Pole N as the observer is from under,
the Equinoctial, namely the Stars north of the dotted parallel DL,
never set below the Horizon; and those which are south of the dotted
parallel MO never rise above it. Hence, the former of these two
parallel Circles is called the Circle of perpetual Apparition, and the latter
the Circle of perpetual Occultation: but all the Stars between these two
Circles rise and set every day. Let us imagine many Circles to be drawn
between these two, and parallel to them; those which are on the north
side of the Equinoctial will be unequally cut by the Horizon MCL,
having larger portions above the Horizon than below it; and the more
so, as they are nearer to the Circle of perpetual Apparition; but the
reverse happens to those on the south side of the Equinoctial, whilst
the Equinoctial is divided in two equal parts by the Horizon. Hence,
by the apparent turning of the Heavens, the northern Stars describe
greater Arcs or Portions of Circles above the Horizon than below it;
and the greater as they are farther from the Equinoctial towards the
Circle of perpetual Apparition; whilst the contrary happens to all
Stars south of the Equinoctial: but those upon it describe equal Arcs
both above and below the Horizon, and therefore they are just as long
above as below it.
129. An observer on the Equator has no Circle of perpetual Apparition
or Occultation, because all the Stars, together with the Sun and
Moon, rise and set to him every day. But, as a bare view of the Figure
is sufficient to shew that these two Circles DL and MO are just
as far from the Poles N and S as the observer at i (or one opposite
to him at o) is from the Equator ECQ; it is plain, that if an observer
begins to travel from the Equator towards either Pole, his Circle of
perpetual Apparition rises from that Pole as from a Point, and his Circle
of perpetual Occultation from the other. As the observer advances
44toward the nearer Pole, these two Circles enlarge their diameters, and
come nearer one another, until he comes to the Pole; and then they
meet and coincide in the Equator. On different sides of the Equator,
to observers at equal distances from it, the Circle of perpetual Apparition
to one is the Circle of perpetual Occultation to the other.
Why the Stars always describe the same parallel of motion, and the Sun a different.
130. Because the Stars never vary their distances from the Equinoctial,
so as to be sensible in an age, the lengths of their diurnal and
nocturnal Arcs are always the same to the same places on the Earth. But
as the Earth goes round the Sun every year in the Ecliptic, one half
of which is on the north side of the Equinoctial and the other half
on it’s south side, the Sun appears to change his place every day, so
as to go once round the Circle YCX every year § 114. Therefore
whilst the Sun appears to advance northward, from having described
the Parallel abX touching the Ecliptic in X the days continually
lengthen and the nights shorten, until he comes to y and describes the
Parallel yzx, when the days are at the longest and the nights at the
shortest: for then, as the Sun goes no farther northward, the greatest
portion that is possible of the diurnal Arc yz is above the Horizon of
the inhabitant i; and the smallest portion zx below it. As the Sun
declines southward from y he describes smaller diurnal and greater
nocturnal Arcs, or Portions of Circles, every day; which causeth the
days to shorten and nights to lengthen, until he arrives again at the
Parallel abX; which having only the small part ab above the Horizon
MCL, and the great part bX below it, the days are at the
shortest and the nights at the longest; because the Sun recedes no farther
south, but returns northward as before. It is easy to see that the
Sun must be in the Equinoctial ECQ twice every year, and then the
days and nights are equally long; that is, 12 hours each. These hints
serve at present to give an idea of some of the Appearances resulting
from the motions of the Earth; which will be more particularly described
in the tenth Chapter.
Fig. I.
Parallel, Oblique, and Right sphere, what.
131. To an observer at either Pole, the Horizon and Equinoctial are
coincident; and the Sun and Stars seem to move parallel to the Horizon:
therefore, such an observer is said to have a Parallel position of the
Sphere. To an observer any where between the Poles and Equator, the
Parallels described by the Sun and Stars are cut obliquely by the Horizon,
and therefore he is said to have an Oblique position of the Sphere.
To an observer any where on the Equator, the Parallels of Motion,
described by the Sun and Stars are cut perpendicularly, or at Right angles,
45by the Horizon; and therefore he is said to have a Right position
of the Sphere. And these three are all the different ways that the
Sphere can be posited to all people, on the Earth.
CHAP. V.
The Phenomena of the Heavens as seen from different Parts of the Solar System.
132. So vastly great is the distance of the starry Heavens, that if
viewed from any part of the Solar System, or even many
millions of miles beyond it, its appearance would be the very same to
us. The Sun and Stars would all seem to be fixed on one concave
surface, of which the Spectator’s eye would be the centre. But the
Planets, being much nearer than the Stars, their appearances will vary
considerably with the place from which they are viewed.
133. If the spectator is at rest without their Orbits, the Planets will
seem to be at the same distance as the Stars; but continually changing
their places with respect to the Stars, and to one another: assuming
various phases of increase and decrease like the Moon. And, notwithstanding
their regular motions about the Sun, will sometimes
appear to move quicker, sometimes slower, be as often to the west as
to the east of the Sun; and at their greatest distances seem quite stationary.
The duration, extent, and points in the Heavens where these
digressions begin and end, would be more or less according to the respective
distances of the several Planets from the Sun: but in the same
Planet they would continue invariably the same at all times; like pendulums
of unequal lengths oscillating together, the shorter move quick
and go over a small space, the longer move slow and go over a large
space. If the observer is at rest within the Orbits of the Planets, but
not near the common center, their apparent motions will be irregular,
but less so than in the former case. Each of the several Planets will
appear bigger and less by turns, as they approach nearer or recede farther
from the observer; the nearest varying most in their size. They
will also move quicker or slower with regard to the fixed Stars, but
will never be retrograde or stationary.
134. Next, let a spectator in motion view the Heavens: the same
apparent irregularities will be observed, but with some variation resulting
from his own motion. If he is on a Planet which has a rotation
on it’s Axis, not being sensible of his own motion he will imagine
46the whole Heavens, Sun, Planets, and Stars to revolve about him in the
same time that his Planet turns round, but the contrary way; and will
not be easily convinced of the deception. If his Planet moves round
the Sun, the same irregularities and aspects as above will appear in the
motions of the Planets: only, the times of their being direct, stationary
and retrograde will be accelerated or retarded as they concur with, or
are contrary to his motion: and the Sun will seem to move among the
fixed Stars or Signs, directly opposite to those in which his Planet
moves; changing it’s place every day as he does. In a word, whether
our observer be in motion or at rest, whether within or without the
Orbits of the Planets, their motions will seem irregular, intricate and
perplexed, unless he is in the center of the System; and from thence,
the most beautiful order and harmony will be observed.
The Sun’s center the only point from which the true motions and places of the Planets could be seen.
135. The Sun being the center of all the Planets motions, the only
place from which their motions could be truly seen, is the Sun’s center;
where the observer being supposed not to turn round with the Sun
(which, in this case, we must imagine to be a transparent body) would
see all the Stars at rest, and seemingly equidistant from him. To such
an observer the Planets would appear to move among the fixed Stars,
in a simple, regular, and uniform manner; only, that as in equal times
they describe equal Areas, they would describe spaces somewhat unequal,
because they move in elliptic Orbits § 155. Their motions would also
appear to be what they are in fact, the same way round the Heavens;
in paths which cross at small Angles in different parts of the Heavens,
and then separate a little from one another § 20. So that, if the solar
Astronomer should make the Path or Orbit of any one Planet a standard,
and consider it as having no obliquity § 201, he would judge the
paths of all the rest to be inclined to it; each Planet having one half
of it’s path on one side, and the other half on the opposite side of the
standard Path or Orbit. And if he should ever see all the Planets start
from a conjunction with each other[28]; Mercury would move so much
faster than Venus as to overtake her again (though not in the same
point of the Heavens) in a quantity of time almost equal to 145 of
our days and nights; or, as we commonly call them, Natural Days,
which include both the days and nights: Venus would move so much
faster than the Earth as to overtake it again in 585 natural days: the
Earth so much faster than Mars as to overtake him again in 778 such
47days: Mars is much faster than Jupiter as to overtake him again in
817 such days: and Jupiter so much faster than Saturn as to overtake
him again in 7236 days, all of our time.
The judgment that a solar Astronomer would probably make concerning the distances and bulks of the Planets.
136. But as our solar Astronomer could have no idea of measuring
the courses of the Planets by our days, he would very probably take
the period of Mercury, which is the quickest moving Planet, for a
measure to compare the periods of the others by. As all the Stars
would appear quiescent to him, he would never think that they had
any dependance upon the Sun; but could naturally imagine that the
Planets have, because they move round the Sun. And it is by no
means improbable, that he would conclude those Planets whose
periods are quickest to move in Orbits proportionably less than those do
which make slower circuits. But being destitute of a method for finding
their Parallaxes, or, more properly speaking, as they could have no
Parallax to him, he could never know any thing of their real distances
or magnitudes. Their relative distances he might perhaps guess at by
their periods, and from thence infer something of truth concerning
their relative bulks, by comparing their apparent bulks with one another.
For example, Jupiter appearing bigger to him than Mars, he
would conclude it to be much bigger in fact; because it appears so,
and must be farther from him, on account of it’s longer period.
Mercury would seem bigger than the Earth; but by comparing it’s
period with the Earth’s, he would conclude that the Earth is much
farther from him than Mercury, and consequently that it must be really
bigger though apparently less; and so of the rest. And, as each
Planet would appear somewhat bigger in one part of it’s Orbit than in
the opposite, and to move quickest when it seems biggest, the observer
would be at no loss to determine that all the Planets move in Orbits
of which the Sun is not precisely in the center.
The Planetary motions very irregular as seen from the Earth.
PLATE III.
137. The apparent magnitudes of the Planets continually change as
seen from the Earth, which demonstrates that they approach nearer
to it, and recede farther from it by turns. From these Phenomena,
and their apparent motions among the Stars, they seem to describe
looped curves which never return into themselves, Venus’s path excepted.
And if we were to trace out all their apparent paths, and
put the figures of them together in one diagram, they would appear
so anomalous and confused, that no man in his senses could believe
them to be representations of their real paths; but would immediately
conclude, that such apparent irregularities must be owing to some Optic
illusions. And after a good deal of enquiry, he might perhaps be at a
48loss to find out the true cause of these inequalities; especially if he
were one of those who would rather, with the greatest justice, charge
frail man with ignorance, than the Almighty with being the author
of such confusion.
Those of Mercury and Venus represented.
Fig. I.
138. Dr. Long, in his first volume of Astronomy, has given us
figures of the apparent paths of all the Planets separately from Cassini;
and on seeing them I first thought of attempting to trace some
of them by a machine[29] that shews the motions of the Sun, Mercury,
Venus, the Earth and Moon, according to the Copernican System.
Having taken off the Sun, Mercury, and Venus, I put black-lead
pencils in their places, with the points turned upward; and fixed a
circular sheet of paste-board so, that the Earth kept constantly under
it’s center in going round the Sun; and the paste-board kept its parallelism.
Then, pressing gently with one hand upon the paste-board to
make it touch the three pencils, with the other hand I turned the
winch which moves the whole machinery: and as the Earth, together
with the pencils in the places of Mercury and Venus, had their
proper motions round the Sun’s pencil, which kept at rest in the center
of the machine, all the three pencils described a diagram from which
the first Figure of the third Plate is truly copied in a smaller size.
As the Earth moved round the Sun, the Sun’s pencil described the
dotted Circle of Months, whilst Mercury’s pencil drew the curve with
the greatest number of loops, and Venus’s that with the fewest. In
their inferiour conjunctions they come as much nearer the Earth, or
within the Circle of the Sun’s apparent motion round the Heavens, as
they go beyond it in their superiour conjunctions. On each side of the
loops they appear Stationary; in that part of each loop next the Earth
retrograde; and in all rest of their paths direct.
Plate III.
J. Ferguson delin.
J. Mynde Sc.
If Cassini’s Figures of the paths of the Sun, Mercury and Venus were
put together, the Figure as above traced out, would be exactly like them.
It represents the Sun’s apparent motion round the Ecliptic, which is
the same every year; Mercury’s motion for seven years; and Venus’s
for eight; in which time Mercury’s path makes 23 loops, crossing
itself so many times, and Venus’s only five. In eight years Venus falls
so nearly into the same apparent path again, as to deviate very little
from it in some ages; but in what number of years Mercury and the
rest of the Planets would describe the same visible paths over again,
I cannot at present determine. Having finished the above Figure of
the paths of Mercury and Venus, I put the Ecliptic round them as in
the Doctor’s Book; and added the dotted lines from the Earth to the
49Ecliptic for shewing Mercury’s apparent or geocentric motion therein
for one year; in which time his path makes three loops, and goes on
a little farther; which shews that he has three inferiour, and as many
superiour conjunctions with the Sun in that time, and also that he is
six times Stationary, and thrice Retrograde. Let us now trace out his
motion for one year in the Figure.
Fig. I.
Suppose Mercury to be setting out from A towards B (between
the Earth and left-hand corner of the Plate) and as seen from the Earth
his motion will then be direct, or according to the order of the Signs.
But when he comes to B, he appears to stand still in the 23d degree
of ♏ at F, as shewn by the line BF. Whilst he goes from B
to C, the line BF goes backward from F to E, or contrary to the
order of Signs; and when he is at C he appears Stationary at E;
having gone back
111⁄2
degrees. Now, suppose him Stationary on
the first of January at C, on the tenth thereof he will appear in the
Heavens as at 20, near F; on the 20th he will be seen as at G;
on the 31st at H; on the 10th of February at I; on the 20th at
K; and on the 28th at L; as the dotted lines shew, which are drawn
through every tenth day’s motion in his looped path, and continued
to the Ecliptic. On the 10th of March he appears at M; on the
20th at N; and on the 31st at O. On the 10th of April he appears
Stationary at P; on the 20th he seems to have gone back again to
O; and on the 30th he appears Stationary at Q having gone back
111⁄2
degrees. Thus Mercury seems to go forward 4 Signs 11 Degrees, or
131 Degrees; and to go back only 11 or 12 Degrees, at a mean rate.
From the 30th of April to the 10th of May, he seems to move from
Q to R; and on the 20th he is seen at S, going forward in the
same manner again, according to the order of letters; and backward
when they go back; which, ’tis needless to explain any farther, as the
reader can trace him out so easily through the rest of the year. The
same appearances happen in Venus’s motion; but as she moves slower
than Mercury, there are longer intervals of time between them.
Having already § 120. given some account of the apparent diurnal
motions of the Heavens as seen from the different Planets, we shall not
trouble the reader any more with that subject.
50
CHAP. VI.
The Ptolemean System refuted. The Motions and Phases of Mercury and Venus explained.
139. The Tychonic System § 97, being sufficiently refuted by the
109th Article, we shall say nothing more about it.
140. The Ptolemean System § 96, which asserts the Earth to be at
rest in the Center of the Universe, and all the Planets with the Sun
and Stars to move round it, is evidently false and absurd. For if
this hypothesis were true, Mercury and Venus could never be hid behind
the Sun, as their Orbits are included within the Sun’s: and again,
these two Planets would always move direct, and be as often in
Opposition to the Sun as in Conjunction with him. But the contrary
of all this is true: for they are just as often behind the Sun as before
him, appear as often to move backwards as forwards, and are so far
from being seen at any time in the side of the Heavens opposite to the
Sun, that they were never seen a quarter of a circle in the Heavens
distant from him.
Appearances of Mercury and Venus.
141. These two Planets, when viewed with a good telescope, appear
in all the various shapes of the Moon; which is a plain proof that they
are enlightened by the Sun, and shine not by any light of their own:
for if they did, they would constantly appear round as the Sun does;
and could never be seen like dark spots upon the Sun when they pass
directly between him and us. Their regular Phases demonstrate them
to be Spherical bodies; as may be shewn by the following experiment.
Experiment to prove they are round.
Hang an ivory ball by a thread, and let any Person move it round the
flame of a candle, at two or three yards distance from your Eye: when
the ball is beyond the candle, so as to be almost hid by the flame, it’s
enlightened side will be towards you, and appear round like the Full
Moon: When the ball is between you and the candle, it’s enlightened
side will disappear, as the Moon does at the Change: When it is half
way between these two positions, it will appear half illuminated, like
the Moon in her Quarters: But in every other place between these
positions, it will appear more or less horned or gibbous. If this experiment
be made with a circular plate which has a flat surface, you may
make it appear fully enlightened, or not enlightened at all; but can
never make it seem either horned or gibbous.
PLATE II.
Experiment to represent the motions of Mercury and Venus.
51142. If you remove about six or seven yards from the candle, and
place yourself so that it’s flame may be just about the height of your
eye, and then desire the other person to move the ball slowly round the
candle as before, keeping it as near of an equal height with the flame
as he possibly can, the ball will appear to you not to move in a circle,
but rather to vibrate backward and forward like a pendulum; moving
quickest when it is directly between you and the candle, and when directly
beyond it; and gradually slower as it goes farther to the right or
left side of the flame, until it appears at the greatest distance from the
flame; and then, though it continues to move with the same velocity,
it will seem to stand still for a moment. In every Revolution it will
shew all the above Phases § 141; and if two balls, a smaller and a greater,
be moved in this manner round the candle, the smaller ball being
kept nearest the flame, and carried round almost three times as often
as the greater, you will have a tolerably good representation of the
apparent Motions of Mercury and Venus; especially, if the bigger ball
describes a circle almost twice as large in diameter as the circle described
by the lesser.
Fig. III.
The elongations or digressions of Mercury from the Sun.
PLATE II.
143. Let ABCDE be a part or segment of the visible Heavens, in
which the Sun, Moon, Planets, and Stars appear to move at the same
distance from the Earth E. For there are certain limits, beyond which
the eye cannot judge of different distances; as is plain from the Moon’s
appearing to be no nearer to us than the Sun and Stars are. Let the
circle fghiklmno be the Orbit in which Mercury m moves round the
Sun S, according to the order of the letters. When Mercury is at f,
he disappears to the Earth at E, because his enlightened side is
turned from it; unless he be then in one of his Nodes § 20, 25;
in which case, he will appear like a dark spot upon the Sun. When
he is at g in his Orbit, he appears at B in the Heavens, westward of
the Sun S, which is seen at C: when at h, he appears at A, at his
greatest western elongation or distance from the Sun; and then seems
to stand still. But, as he moves from h to i, he appears to go from
A to B; and seems to be in the same place when at i as when he was
at g, only not near so big: at k he is hid from the Earth E by the Sun
S; being then in his superiour Conjunction. In going from k to l,
he appears to move from C to D; and when he is at n, he appears
stationary at E; being seen as far east from the Sun then, as he was
west from him at A. In going from n to o in his Orbit, he seems to go
back again in the Heavens, from E to D; and is seen in the same
place (with respect to the Sun) at o as when he was at l; but of a
larger diameter at o, because he is then nearer the Earth E: and
52when he comes to f, he again passes by the Sun, and disappears as
before. In going from n to h in his Orbit, he seems to go backward in
the Heavens from E to A; and in going from h to n, he seems
to go forward from A to E. As he goes on from f a little of his enlightened
side at g is seen from E; at h he appears half full, because
half of his enlightened side is seen; at i, gibbous, or more than half
full; and at k he would appear quite full, were he not hid from the
Earth E by the Sun S. At l he appears gibbous again; at n half
decreased, at o horned, and at f new like the Moon at her Change.
He goes sooner from his eastern station at n to his western station at h
than from h to n again; because he goes through less than half his Orbit
in the former case, and more in the latter.
Fig. III.
The Elongations and Phases of Venus.
The greatest Elongations of Mercury and Venus.
144. In the same Figure, let FGHIKLMN be the Orbit in which
Venus v moves round the Sun S, according to the order of the letters:
and let E be the Earth as before. When Venus is at F she is in her
inferiour Conjunction; and disappears like the New Moon because
her dark side is toward the Earth. At G she appears half enlightened
to the Earth, like the Moon in her first quarter: at h she appears
gibbous; at I, almost full; her enlightened side being then nearly
towards the Earth: at K, she would appear quite full to the Earth E;
but is hid from it by the Sun S: at L, she appears upon the decrease,
or gibbous; at M, more so; at N, only half enlightened; and at F
she disappears again. In moving from N to G, she seems to go
backward in the Heavens; and from G to N, forward: but, as she
describes a much greater portion of her Orbit in going from G to N
than from N to G, she appears much longer direct than retrograde in
her motion. At N and G she appears stationary; as Mercury does
at n and h. Mercury, when stationary seems to be only 28 degrees
from the Sun; and Venus when so, 47; which is a demonstration
that Mercury’s Orbit is included within Venus’s, and Venus’s within
the Earth’s.
Morning and Evening Star, what.
145. Venus, from her superiour Conjunction at K to her inferiour
Conjunction at F is seen on the east side of the Sun S from the Earth.
E; and therefore she shines in the Evening after the Sun sets, and is
called the Evening Star: for, the Sun being then to the westward of
Venus, he must set first. From her inferiour Conjunction to her
superiour, she appears on the west side of the Sun; and therefore rises
before him, for which reason she is called the Morning Star. When
she is about N or G, she shines so bright, that bodies cast shadows in
the night-time.
PLATE II.
The stationary places of the Planets variable.
53146. If the Earth kept always at E, it is evident that the Stationary
places of Mercury and Venus would always be in the same points of the
Heavens where they were before. For example; whilst Mercury m
goes from h to n, according to the order of the letters, he appears to
describe the arc ABCDE in the Heavens, direct: and whilst he
goes from n to h, he seems to describe the same arc back again, from
E to A, retrograde: always at n and h he appears stationary at the
same points E and A as before. But Mercury goes round his
Orbit, from f to f again, in 88 days; and yet there are 116 days
from any one of his Conjunctions, or apparent Stations, to the same
again: and the places of these Conjunctions and Stations are found to
be about 114 degrees eastward from the points of the Heavens where
they were last before; which proves, that the Earth has not kept all
that time at E, but has had a progressive motion in it’s Orbit from E
to t. Venus also differs every time in the places of her Conjunctions
and Stations; but much more than Mercury; because, as Venus describes
a much larger Orbit than Mercury does, the Earth advances
so much the farther in it’s annual path before Venus comes round
again.
The Elongations of all Saturn’s inferiour Planets as seen from him.
147. As Mercury and Venus, seen from the Earth, have their respective
Elongations from the Sun, and Stationary places; so has the
Earth, seen from Mars; and Mars, seen from Jupiter; and Jupiter,
seen from Saturn. That is, to every superiour Planet, all the inferiour
ones have their Stations and Elongations; as Venus and Mercury have
to the Earth. As seen from Saturn, Mercury never goes above
21⁄2
degrees from the Sun; Venus
41⁄3;
the Earth 6; Mars
91⁄2;
and Jupiter
331⁄4:
so that Mercury, as seen from the Earth, has almost as
great a Digression or Elongation from the Sun, as Jupiter seen from
Saturn.
A proof of the Earth’s annual motion.
148. Because the Earth’s Orbit is included within the Orbits of
Mars, Jupiter, and Saturn, they are seen on all sides of the Heavens;
and are as often in Opposition to the Sun as in Conjunction with him.
If the Earth stood still, they would always appear direct in their motions,
never retrograde nor stationary. But they seem to go just as often backward
as forward; which, if gravity be allowed to exist, affords a sufficient
proof of the Earth’s annual motion.
Fig. III.
PLATE II.
General Phenomena of a superiour Planet to an inferiour.
149. As Venus and the Earth are superiour Planets to Mercury,
they shew much the same Appearances to him that Mars and Jupiter
do to us. Let Mercury m be at f, Venus v at F, and the Earth at
E; in which situation Venus hides the Earth from Mercury;
but, being in opposition to the Sun, she shines on Mercury with a full
54illumined Orb; though, with respect to the Earth, she is in conjunction
with the Sun and invisible. When Mercury is at f, and Venus
at G, her enlightened side not being directly towards him, she appears
a little gibbous; as Mars does in a like situation to us: but, when
Venus is at I, her enlightened side is so much towards Mercury at f,
that she appears to him almost of a round figure. At K, Venus disappears
to Mercury at f, being then hid by the Sun; as all our superiour
Planets are to us, when in conjunction with the Sun. When
Venus has, as it were, emerged out of the Sun beams, as at L, she
appears almost full to Mercury at f; at M and N, a little gibbous;
quite full at F, and largest of all; being then in opposition to the Sun,
and consequently nearest to Mercury at f; shining strongly on him in
the night, because her distance from him then is somewhat less than a
fifth part of her distance from the Earth, when she appears roundest to
it between I and K, or between K and L, as seen from the Earth E.
Consequently, when Venus is opposite to the Sun as seen from Mercury,
she appears more than 25 times as large to him as she does to us
when at the fullest. Our case is almost similar with respect to Mars,
when he is opposite to the Sun; because he is then so near the Earth,
and has his whole enlightened side towards it. But, because the Orbits
of Jupiter and Saturn are very large in proportion to the Earth’s, these
two Planets appear much less magnified at their Oppositions or diminished
at their Conjunctions than Mars does, in proportion to their
mean apparent Diameters.
CHAP. VII.
The physical Causes of the Motions of the Planets. The Excentricities of their Orbits. The Times in which the Action of Gravity would bring them to the Sun. Archimedes’s ideal Problem for moving the Earth. The World not eternal.
Gravitation and Projection.
Fig. IV.
PLATE II.
Circular Orbits.
Fig. IV.
150. From the uniform projectile motion of bodies in straight
lines, and the universal power of attraction, arises the curvilineal
motions of all the Heavenly bodies. If the body A be projected
along the right line ABX, in open Space, where it meets with
no resistance, and is not drawn aside by any other power, it will for
ever go on with the same velocity, and in the same direction. For,
55the force which moves it from A to B in any given time, will carry
it from B to X in as much more time; and so on, there being nothing
to obstruct or alter it’s motion. But if, when this projectile force
has carried it, suppose to B, the body S begins to attract it, with a
power duly adjusted, and perpendicular to it’s motion at B, it will
then be drawn from the straight line ABX, and forced to revolve about
S in the Circle BYTU. When the body A comes to U, or any other
part of it’s Orbit, if the small body u, within the sphere of U’s attraction,
be projected as in the right line Z, with a force perpendicular to
the attraction of U, then u will go round U in the Orbit W, and accompany
it in it’s whole course round the body S. Here, S may represent
the Sun, U the Earth, and u the Moon.
151. If a Planet at B gravitates, or is attracted, toward the Sun, so
as to fall from B to y in the time that the projectile force would have
carried it from B to X, it will describe the curve BY by the combined
action of these two forces, in the same time that the projectile
force singly would have carried it from B to X, or the gravitating power
singly have caused it to descend from B to y; and these two forces being
duly proportioned, and perpendicular to one another, the Planet
obeying them both, will move in the circle BYTU[30].
152. But if, whilst the projectile force carries the Planet from B to
b, the Sun’s attraction (which constitutes the Planet’s gravitation)
should bring it down from B to I, the gravitating power would then
be too strong for the projectile force; and would cause the Planet to
describe the curve BC. When the Planet comes to C, the gravitating
power (which always increases as the square of the distance from the
Sun S diminishes) will be yet stronger for the projectile force; and by
conspiring in some degree therewith, will accelerate the Planet’s motion
all the way from C to K; causing it to describe the arcs BC, CD,
DE, EF, &c. all in equal times. Having it’s motion thus accelerated,
it gains so much centrifugal force, or tendency to fly off at K in the
line Kk, as overcomes the Sun’s attraction: and the centrifugal force
being too great to allow the Planet to be brought nearer the Sun, or
even to move round him in the Circle Klmn, &c. it goes off, and
ascends in the curve KLMN, &c. it’s motion decreasing as gradually
from K to B as it increased from B to K, because the Sun’s attraction
acts now against the Planet’s projectile motion just as much as it
56acted with it before. When the Planet has got round to B, it’s projectile
force is as much diminished from it’s mean state about G or N,
as it was augmented at K; and so, the Sun’s attraction being more
than sufficient to keep the Planet from going off at B, it describes the
same Orbit over again, by virtue of the same forces or laws.
Fig. IV.
The Planets describe equal Areas in equal times.
153. A double projectile force will always balance a quadruple
power of gravity. Let the Planet at B have twice as great an impulse
from thence towards X, as it had before: that is, in the same length
of time that it was projected from B to b, as in the last example, let it
now be projected from B to c; and it will require four times as much
gravity to retain it in it’s Orbit: that is, it must fall as far as from B
to 4 in the time that the projectile force would carry it from B to c;
otherwise it could not describe the curve BD, as is evident by the
Figure. But, in as much time as the Planet moves from B to C in
the higher part of it’s Orbit, it moves from I to K or from K to L in
the lower part thereof; because, from the joint action of these two
forces, it must always describe equal areas in equal times, throughout
it’s annual course. These Areas are represented by the triangles
BSC, CSD, DSE, ESF, &c. whose contents are equal to one another,
quite round the Figure.
A difficulty removed.
154. As the Planets approach nearer the Sun, and recede farther
from him, in every Revolution; there may be some difficulty in conceiving
the reason why the power of gravity, when it once gets the
better of the projectile force, does not bring the Planets nearer and
nearer the Sun in every Revolution, till they fall upon and unite with
him. Or why the projectile force, when it once gets the better of gravity,
does not carry the Planets farther and farther from the Sun, till
it removes them quite out of the sphere of his attraction, and causes
them to go on in straight lines for ever afterward. But by considering
the effects of these powers as described in the two last Articles, this
difficulty will be removed. Suppose a Planet at B to be carried by
the projectile force as far as from B to b, in the time that gravity would
have brought it down from B to 1: by these two forces it will describe
the curve BC. When the Planet comes down to K, it will be but half
as far from the Sun S as it was at B; and therefore, by gravitating four
times as strongly towards him, it would fall from K to V in the same
length of time that it would have fallen from B to 1 in the higher
part of it’s Orbit, that is, through four times as much space; but it’s
projectile force is then so much increased at K, as would carry it from
K to k in the same time; being double of what it was at B, and is
57therefore too strong for the tendency of the gravitating power, either to
draw the Planet to the Sun, or cause it to go round him in the
circle Klmn, &c. which would require it’s falling from K to w, through
a greater space than gravity can draw it whilst the projectile force is such
as would carry it from K to k: and therefore the Planet ascends in
it’s Orbit KLMN, decreasing in it’s velocity for the cause already assigned
in § 152.
The Planetary Orbits elliptical.
Their Excentricities.
155. The Orbits of all the Planets are Ellipses, very little different
from Circles: but the Orbits of the Comets are very long Ellipses; the
lower focus of them all being in the Sun. If we suppose the mean
distance (or middle between the greatest and least) of every Planet and
Comet from the Sun to be divided into 1000 equal parts, the Excentricities
of their Orbits, both in such parts and in English miles, will
be as follows. Mercury’s, 210 parts, or 6,720,000 miles; Venus’s,
7 parts, or 413,000 miles; the Earth’s, 17 parts, or 1,377,000 miles;
Mars’s, 93 parts, or 11,439,000 miles; Jupiter’s, 48 parts, or
20,352,000 miles; Saturn’s, 55 parts, or 42,735,000 miles. Of
the nearest of the three forementioned Comets, 1,458,000 miles;
of the middlemost, 2,025,000,000 miles; and of the outermost,
6,600,000,000.
The above laws sufficient for motions both in circular and elliptic Orbits.
156. By the above-mentioned laws § 150 & seq. bodies will move
in all kinds of Ellipses, whether long or short, if the spaces they move
in be void of resistance. Only, those which move in the longer
Ellipses, have so much the less projectile force impressed upon them
in the higher parts of their Orbits; and their velocities, in coming
down towards the Sun, are so prodigiously increased by his attraction,
that their centrifugal forces in the lower parts of their Orbits are so great
as to overcome the Sun’s attraction there, and cause them to ascend
again towards the higher parts of their Orbits; during which time, the
Sun’s attraction acting so contrary to the motions of those bodies, causes
them to move slower and slower, until their projectile forces are diminished
almost to nothing; and then they are brought back again by
the Sun’s attraction, as before.
In what times the Planets would fall to the Sun by the power of gravity.
157. If the projectile forces of all the Planets and Comets were
destroyed at their mean distances from the Sun, their gravities would
bring them down so, as that Mercury would fall to the Sun in 15 days
13 hours; Venus in 39 days 17 hours; the Earth or Moon in 64
days 10 hours; Mars in 121 days; Jupiter in 290; and Saturn in
767. The nearest Comet in 13 thousand days; the middlemost in
23 thousand days; and the outermost in 66 thousand days. The
58Moon would fall to the Earth in 4 days 20 hours; Jupiter’s first
Moon would fall to him in 7 hours, his second in 15, his third
in 30, and his fourth in 71 hours. Saturn’s first Moon would fall to
him in 8 hours; his second in 12, his third in 19, his fourth in
68 hours, and the fifth in 336. A stone would fall to the Earth’s
center, if there were an hollow passage, in 21 minutes 9 seconds.
Mr. Whiston gives the following Rule for such Computations.
“[31]It is demonstrable, that half the Period of any Planet, when it is diminished
in the sesquialteral proportion of the number 1 to the number 2,
or nearly in the proportion of 1000 to 2828, is the time that it would
fall to the Center of it’s Orbit.” This proportion is, when a quantity
or number contains another once and a half as much more.
The prodigious attraction of the Sun and Planets.
158. The quick motions of the Moons of Jupiter and Saturn round
their Primaries, demonstrate that these two Planets have stronger attractive
powers than the Earth has. For, the stronger that one body
attracts another, the greater must be the projectile force, and consequently
the quicker must be the motion of that other body, to keep
it from falling to it’s primary or central Planet. Jupiter’s second
Moon is 124 thousand miles farther from Jupiter than our Moon is
from us; and yet this second Moon goes almost eight times round
Jupiter whilst our Moon goes only once round the Earth. What a
prodigious attractive power must the Sun then have, to draw all the
Planets and Satellites of the System towards him; and what an amazing
power must it have required to put all these Planets and Moons
into such rapid motions at first! Amazing indeed to us, because impossible
to be effected by the strength of all the living Creatures in an
unlimited number of Worlds, but no ways hard for the Almighty,
whose Planetarium takes in the whole Universe!
Archimedes’s Problem for raising the Earth.
159. The celebrated Archimedes affirmed he could move the
Earth if he had a place to stand on to manage his machinery[32]. This
assertion is true in Theory, but, upon examination, will be found absolutely
impossible in fact, even though a proper place and materials of
sufficient strength could be had.
The simplest and easiest method of moving a heavy body a little
way is by a lever or crow, where a small weight or power applied to
the long arm will raise a great weight on the short one. But then,
the small weight must move as much quicker than the great weight
59as the latter is heavier than the former; and the length of the long
arm of the lever to the length of the short arm must be in the same
proportion. Now, suppose a man pulls or presses the end of
the long arm with the force of 200 pound weight, and that the
Earth contains in round Numbers 4,000,000,000,000,000,000,000
or 4000 Trillions of cubic feet, each at a mean rate weighing 100
pound; and that the prop or center of motion of the lever is 6000
miles from the Earth’s center: in this case, the length of the lever from
the Fulcrum or center of motion to the moving power or weight ought
to be 12,000,000,000,000,000,000,000,000 or 12 Quadrillions of
miles; and so many miles must the power move, in order to raise the
Earth but one mile, whence ’tis easy to compute, that if Archimedes
or the power applied could move as swift as a cannon bullet, it would
take 27,000,000,000,000 or 27 Billions of years to raise the Earth one
inch.
If any other machine, such as a combination of wheels and screws,
was proposed to move the Earth, the time it would require, and the
space gone through by the hand that turned the machine, would be
the same as before. Hence we may learn, that however boundless our
Imagination and Theory may be, the actual operations of man are
confined within narrow bounds; and more suited to our real wants than
to our desires.
Hard to determine what Gravity is.
160. The Sun and Planets mutually attract each other: the power
by which they do so we call Gravity. But whether this power be
mechanical or no, is very much disputed. We are certain that the
Planets disturb one another’s motions by it, and that it decreases according
to the squares of the distances of the Sun and Planets; as
light, which is known to be material, likewise does. Hence Gravity
should seem to arise from the agency of some subtile matter pressing
towards the Sun and Planets, and acting, like all mechanical causes,
by contact. But on the other hand, when we consider that the degree
or force of Gravity is exactly in proportion to the quantities of matter in
those bodies, without any regard to their bulks or quantity of surface,
acting as freely on their internal as external parts, it seems to surpass
the power of mechanism; and to be either the immediate agency of
the Deity, or effected by a law originally established and imprest on all
matter by him. But some affirm that matter, being altogether inert,
cannot be impressed with any Law, even by almighty Power: and that
the Deity must therefore be constantly impelling the Planets toward
the Sun, and moving them with the same irregularities and disturbances
60which Gravity would cause, if it could be supposed to exist. But, if a
man may venture to publish his own thoughts, (and why should not
one as well as another?) it seems to me no greater absurdity, to suppose
the Deity capable of superadding a Law, or what Laws he pleases,
to matter, than to suppose him capable of giving it existence at first.
The manner of both is equally inconceivable to us; but neither of them
imply a contradiction in our ideas: and what implies no contradiction
is within the power of Omnipotence. Do we not see that a human
creature can prepare a bar of steel so as to make it attract needles and
filings of iron; and that he can put a stop to that power or virtue, and
again call it forth again as often as he pleases? To say that the workman
infuses any new power into the bar, is saying too much; since the needle
and filings, to which he has done nothing, re-attract the bar. And
from this it appears that the power was originally imprest on the matter
of which the bar, needle, and filings are composed; but does not seem
to act until the bar be properly prepared by the artificer: somewhat
like a rope coiled up in a ship, which will never draw a boat or any
other thing towards the ship, unless one end be tied to it, and the
other end to that which is to be hauled up; and then it is no matter
which end of the rope the sailors pull at, for the rope will be equally
stretched throughout, and the ship and boat will move towards one another.
To say that the Almighty has infused no such virtue or power
into the materials which compose the bar, but that he waits till the
operator be pleased to prepare it by due position and friction, and then,
when the needle or filings are brought pretty near the bar, the Deity
presses them towards it, and withdraws his hand whenever the workman
either for use, curiosity or whim, does what appears to him to
destroy the action of the bar, seems quite ridiculous and trifling; as it
supposes God not only to be subservient to our inconstant wills, but
also to do what would be below the dignity of any rational man to be
employed about.
161. That the projectile force was at first given by the Deity is
evident. For, since matter can never put itself into motion, and all
bodies may be moved in any direction whatsoever; and yet all the
Planets both primary and secondary move from west to east, in planes
nearly coincident; whilst the Comets move in all directions, and in
planes so different from one another; these motions can be owing to no
mechanical cause of necessity, but to the free choice and power of an
intelligent Being.
61162. Whatever Gravity be, ’tis plain that it acts every moment of
time: for should it’s action cease, the projectile force would instantly
carry off the Planets in straight lines from those parts of their Orbits
where Gravity left them. But, the Planets being once put into motion,
there is no occasion for any new projectile force, unless they meet with
some resistance in their Orbits; nor for any mending hand, unless they
disturb one another too much by their mutual attractions.
The Planets disturb one another’s motion.
The consequences thereof.
163. It is found that there are disturbances among the Planets in
their motions, arising from their mutual attractions when they are in the
same quarter of the Heavens; and that our years are not always precisely
of the same length[33]. Besides, there is reason to believe that
the Moon is somewhat nearer the Earth now than she was formerly;
her periodical month being shorter than it was in former ages. For,
our Astronomical Tables, which in the present Age shew the times of
Solar and Lunar Eclipses to great precision, do not answer so well for
very ancient Eclipses. Hence it appears, that the Moon does not
move in a medium void of all resistance, § 174; and therefore her
projectile force being a little weakened, whilst there is nothing to diminish
her gravity, she must be gradually approaching nearer the Earth,
describing smaller and smaller Circles round it in every revolution, and
finishing her Period sooner, although her absolute motion with regard to
space be not so quick now as it was formerly: and therefore, she must
come to the Earth at last; unless that Being, which gave her a sufficient
projectile force at the beginning, adds a little more to it in due time.
And, as all the Planets move in spaces full of æther and light, which
are material substances, they too must meet with some resistance.
And therefore, if their gravities are not diminished, nor their projectile
forces increased, they must necessarily approach nearer and nearer the
Sun, and at length fall upon and unite with him.
The World not eternal.
164. Here we have a strong philosophical argument against the eternity
of the World. For, had it existed from eternity, and been left
62by the Deity to be governed by the combined actions of the above
forces or powers, generally called Laws, it had been at an end long
ago. And if it be left to them it must come to an end. But we
may be certain that it will last as long as was intended by it’s Author,
who ought no more to be found fault with for framing so perishable a
work, than for making man mortal.
CHAP. VIII.
Of Light. It’s proportional quantities on the different Planets. It’s Refractions in Water and Air. The Atmosphere; it’s weight and properties. The Horizontal Moon.
The amazing smallness of the particles of light.
165. Light consists of exceeding small particles of matter issuing
from a luminous body; as from a lighted candle
such particles of matter continually flow in all directions. Dr.
Niewentyt[34] computes, that in one second of time there flows
418,660,000,000,000,000,000,000,000,000,000,000,000,000,000
particles of light out of a burning candle; which number contains at
least 6,337,242,000,000 times the number of grains of sand in the
whole Earth; supposing 100 grains of sand to be equal in length to an
inch, and consequently, every cubic inch of the Earth to contain one
million of such grains.
The dreadful effects that would ensue from their being larger.
166. These amazingly small particles, by striking upon our eyes,
excite in our minds the idea of light: and, if they were so large as
the smallest particles of matter discernible by our best microscopes,
instead of being serviceable to us, they would soon deprive us of sight
by the force arising from their immense velocity, which is above 164
thousand miles every second[35], or 1,230,000 times swifter than the
motion of a cannon bullet. And therefore, if the particles of light
were so large, that a million of them were equal in bulk to an ordinary
grain of land, we durst no more open our eyes to the light than
suffer sand to be shot point blank against them.
How objects become visible to us.
PLATE II.
167. When these small particles, flowing from the Sun or from a
candle, fall upon bodies, and are thereby reflected to our eyes, they
excite in us the idea of that body by forming it’s picture on the retina[36].
63And since bodies are visible on all sides, light must be reflected from
them in all directions.
The rays of Light naturally move in straight lines.
A proof that they hinder not one another’s motions.
168. A ray of light is a continued stream of these particles, flowing
from any visible body in straight lines. That they move in straight,
and not in crooked lines, unless they be refracted, is evident from bodies
not being visible if we endeavour to look at them through the bore of a
bended pipe; and from their ceasing to be seen by the interposition of
other bodies, as the fixed Stars by the interposition of the Moon and
Planets, and the Sun wholly or in part by the interposition of the
Moon, Mercury, or Venus. And that these rays do not interfere, or
jostle one another out of their ways, in flowing from different bodies
all around, is plain from the following Experiment. Make a little
hole in a thin plate of metal, and set the plate upright on a table,
facing a row of lighted candles standing by one another; then place a
sheet of paper or pasteboard at a little distance from the other side of
the plate, and the rays of all the candles, flowing through the hole,
will form as many specks of light on the paper as there are candles
before the plate, each speck as distinct and large, as if there were
only one candle to cast one speck; which shews that the rays are no
hinderance to each other in their motions, although they all cross in
the hole.
Fig. XI.
In what proportion light and heat decrease at any given
distance from the Sun.
PLATE II.
169. Light, and therefore heat so far as it depends on the Sun’s rays
(§ 85, towards the end) decreases in proportion to the squares of the
distances of the Planets from the Sun. This is easily demonstrated by
a Figure which, together with it’s description, I have taken from Dr.
Smith’s Optics[37]. Let the light which flows from a point A, and
passes through a square hole B, be received upon a plane C, parallel
to the plane of the hole; or, if you please, let the figure C be the
shadow of the plane B; and when the distance C is double of B, the
length and breadth of the shadow C will be each double of the length
and breadth of the plane B; and treble when AD is treble of AB;
and so on: which may be easily examined by the light of a candle
placed at A. Therefore the surface of the shadow C, at the distance
AC double of AB, is divisible into four squares, and at a treble distance,
into nine squares, severally equal to the square B, as represented
in the Figure. The light then which falls upon the plane B,
being suffered to pass to double that distance, will be uniformly
spread over four times the space, and consequently will be four times
thinner in every part of that space, and at a treble distance it will be
64nine times thinner, and at a quadruple distance sixteen times thinner,
than it was at first; and so on, according to the increase of the square
surfaces B, C, D, E, built upon the distances AB, AC, AD, AE.
Consequently, the quantities of this rarefied light received upon a surface
of any given size and shape whatever, removed successively to
these several distances, will be but one quarter, one ninth, one sixteenth
of the whole quantity received by it at the first distance AB. Or in
general words, the densities and quantities of light, received upon any
given plane, are diminished in the same proportion as the squares of
the distances of that plane, from the luminous body, are increased:
and on the contrary, are increased in the same proportion as these
squares are diminished.
Why the Planets appear dimmer when viewed thro’ telescopes than by the bare eye.
170. The more a telescope magnifies the disks of the Moon and
Planets, they appear so much dimmer than to the bare eye; because
the telescope cannot magnify the quantity of light, as it does the surface;
and, by spreading the same quantity of light over a surface so
much larger than the naked eye beheld, just so much dimmer must it
appear when viewed by a telescope than by the bare eye.
Fig. VIII.
Refraction of the rays of light.
171. When a ray of light passes out of one medium[38] into another,
it is refracted, or turned out of it’s first course, more or less, as it falls
more or less obliquely on the refracting surface which divides the two
mediums. This may be proved by several experiments; of which
we shall only give three for example’s sake. 1. In a bason FGH put
a piece of money as DB, and then retire from it as to A, till the
edge of the bason at E just hides the money from your sight: then,
keeping your head steady, let another person fill the bason gently with
water. As he fills it, you will see more and more of the piece DB;
which will be all in view when the bason is full, and appear as if lifted
up to C. For, the ray AEB, which was straight whilst the bason was
empty, is now bent at the surface of the water in E, and turned out
of it’s rectilineal course into the direction ED. Or, in other words,
the ray DEK, that proceeded in a straight line from the edge D whilst
the bason was empty, and went above the eye at A, is now bent at E;
and instead of going on in the rectilineal direction DEK, goes in the
angled direction DEA, and by entering the eye at A renders the object
DB visible. Or, 2dly, place the bason where the Sun shines obliquely,
and observe where the shadow of the rim E falls on the bottom, as at
65B: then fill it with water, and the shadow will fall at D; which
proves, that the rays of light, falling obliquely on the surface of the
water, are refracted, or bent downwards into it.
172. The less obliquely the rays of light fall upon the surface of
any medium, the less they are refracted; and if they fall perpendicularly
thereon, they are not refracted at all. For, in the last experiment,
the higher the Sun rises, the less will be the difference between the
places where the edge of the shadow falls, in the empty and full bason.
And, 3dly, if a stick be laid over the bason, and the Sun’s rays be reflected
perpendicularly into it from a looking-glass, the shadow of the
stick will fall upon the same place of the bottom, whether the bason
be full or empty.
173. The denser that any medium is, the more is light refracted
in passing through it.
The Atmosphere.
The Air’s compression and rarity at different heights.
174. The Earth is surrounded by a thin fluid mass of matter, called
the Air, or Atmosphere, which gravitates to the Earth, revolves with it
in it’s diurnal motion, and goes round the Sun with it every year.
This fluid is of an elastic or springy nature, and it’s lowermost parts
being pressed by the weight of all the Air above them, are squeezed the
closer together; and are therefore densest of all at the Earth’s surface,
and gradually rarer the higher up. “It is well known[39] that the Air
near the surface of our Earth possesses a space about 1200 times greater
than water of the same weight. And therefore, a cylindric column of
Air 1200 foot high is of equal weight with a cylinder of water of the
same breadth and but one foot high. But a cylinder of Air reaching to
the top of the Atmosphere is of equal weight with a cylinder of water
about 33 foot high[40]; and therefore if from the whole cylinder of Air,
the lower part of 1200 foot high is taken away, the remaining upper
part will be of equal weight with a cylinder of water 32 foot high; wherefore,
at the height of 1200 feet or two furlongs, the weight of the incumbent
Air is less, and consequently the rarity of the compressed Air is
greater than near the Earth’s surface in the ratio of 33 to 32. And
having this ratio we may compute the rarity of the Air at all heights
whatsoever, supposing the expansion thereof to be reciprocally proportional
to its compression; and this proportion has been proved by the experiments
of Dr. Hooke and others. The result of the computation I have set
down in the annexed Table, in the first column of which you have the
height of the Air in miles, whereof 4000 make a semi-diameter of the
66Earth; in the second the compression of the Air or the incumbent weight;
in the third it’s rarity or expansion, supposing gravity to decrease in the duplicate
ratio of the distances from the Earth’s center. And the small
numeral figures are here used to shew what number of cyphers must be
joined to the numbers expressed by the larger figures, as 0.171224 for
0.000000000000000001224, and 2695615 for 26956000000000000000.
| Air’s |
| Height. |
Compression. |
Expansion. |
| 0 |
33 |
1 |
| 5 |
17.8515 |
1.8486 |
| 10 |
9.6717 |
3.4151 |
| 20 |
2.852 |
11.571 |
| 40 |
0.2525 |
136.83 |
| 400 |
0.171224 |
2695615 |
| 4000 |
0.1054465 |
73907102 |
| 40000 |
0.1921628 |
26263189 |
| 400000 |
0.2107895 |
41798207 |
| 4000000 |
0.2129878 |
33414209 |
| Infinite. |
0.2126041 |
54622209 |
From this Table it appears that the
Air in proceeding upwards is rarefied
in such manner, that a sphere of that
Air which is nearest the Earth but of
one inch diameter, if dilated to an
equal rarefaction with that of the Air
at the height of ten semi-diameters of
the Earth, would fill up more space
than is contained in the whole Heavens
on this side the fixed Stars, according to
the preceding computation of their distance[41].”
And it likewise appears that
the Moon does not move in a perfectly
free and un-resisting medium; although the air at a height equal to her
distance, is at least 34000190 times thinner than at the Earth’s surface;
and therefore cannot resist her motion so as to be sensible in many
ages.
175. The weight of the Air, at the Earth’s surface, is found by experiments
made with the air-pump; and also by the quantity of mercury
that the Atmosphere balances in the barometer; in which, at a mean
state; the mercury stands
291⁄2
inches high. And if the tube were a
square inch wide, it would at that height contain
291⁄2
cubic inches of
mercury, which is just 15 pound weight; and so much weight of air every
square inch of the Earth’s surface sustains; and every square foot 144 times
as much, because it contains 144 square inches. Now as the Earth’s surface
contains about 199,409,400 square miles, it must be of no less than
5,559,215,016,960,000 square feet; which, multiplied by 2016, the
number of pounds on every foot, amounts to 11,207,377,474,191,360,000;
or 11 trillion 207 thousand 377 billion 474 thousand 191
million and 360 thousand pounds, for the weight of the whole Atmosphere.
At this rate, a middle sized man, whose surface may be about
14 square feet, is pressed by 28,224 pound weight of Air all round;
for fluids press equally up and down and on all sides. But, because
67this enormous weight is equal on all sides, and counterbalanced by the
spring of the internal Air in our blood vessels, it is not felt.
A common mistake about the weight of the Air.
176. Oftentimes the state of the Air is such that we feel ourselves
languid and dull; which is commonly thought to be occasioned by the
Air’s being foggy and heavy about us. But that the Air is then too
light, is evident from the mercury’s sinking in the barometer, at which
time it is generally found that the Air has not sufficient strength to
bear up the vapours which compose the Clouds: for, when it is otherwise,
the Clouds mount high, the Air is more elastic and weighty about
us, by which means it balances the internal spring of the Air within
us, braces up our blood-vessels and nerves, and makes us brisk and lively.
Without an Atmosphere the Heavens would always appear dark, and we should have no twilight.
177. According to [42]Dr. Keill, and other astronomical writers, it is
entirely owing to the Atmosphere that the Heavens appear bright in the
day-time. For, without an Atmosphere, only that part of the Heavens
would shine in which the Sun was placed: and if an observer could
live without Air, and should turn his back towards the Sun, the whole
Heavens would appear as dark as in the night, and the Stars would be
seen as clear as in the nocturnal sky. In this case, we should have no
twilight; but a sudden transition from the brightest sunshine to the
blackest darkness immediately after sun-set; and from the blackest
darkness to the brightest sun-shine at sun-rising; which would be extremely
inconvenient, if not blinding, to all mortals. But, by means
of the Atmosphere, we enjoy the Sun’s light, reflected from the aerial
particles, before he rises and after he sets. For, when the Earth by
its rotation has withdrawn the Sun from our sight, the Atmosphere
being still higher than we, has his light imparted to it; which gradually
decreases until he has got 18 degrees below the Horizon; and then, all
that part of the Atmosphere which is above us is dark. From the length
of twilight, the Doctor has calculated the height of the Atmosphere (so
far as it is dense enough to reflect any light) to be about 44 miles. But it
is seldom dense enough at two miles height to bear up the Clouds.
It brings the Sun in view before he rises, and keeps him in view after he sets.
178. The Atmosphere refracts the Sun’s rays so, as to bring him in
sight every clear day, before he rises in the Horizon; and to keep him
in view for some minutes after he is really set below it. For, at some
times of the year, we see the Sun ten minutes longer above the Horizon
than he would be if there were no refractions: and about six minutes
every day at a mean rate.
179. To illustrate this, let IEK be a part of the Earth’s surface, covered
with the Atmosphere HGFC; and let HEO be the[43] sensible Horizon
68of an observer at E. When the Sun is at A, really below the Horizon,
a ray of light AC proceeding
from him comes straight to
C, where it falls on the surface
of the Atmosphere, and there entering
a denser medium, it is
turned out of its rectilineal course
ACdG, and bent down to the
observer’s eye at E; who then
sees the Sun in the direction of
the refracted ray edE, which lies
above the Horizon, and being
extended out to the Heavens,
shews the Sun at B § 171.
Fig. IX.
180. The higher the Sun rises,
the less his rays are refracted, because
they fall less obliquely on
the surface of the Atmosphere
§ 172. Thus, when the Sun is in
the direction of the line EfL continued,
he is so nearly perpendicular
to the surface of the Earth
at E, that his rays are but very little
bent from a rectilineal course.
The quantity of refraction.
181. The Sun is about
321⁄4
min. of a deg. in breadth, when
at his mean distance from the
Earth; and the horizontal refraction
of his rays is
333⁄4
min. which
being more than his whole diameter,
brings all his Disc in
view, when his uppermost edge
rises in the Horizon. At ten deg.
height the refraction is not quite
5 min. at 20 deg. only 2 min.
26 sec.; at 30 deg. but 1 min.
32 sec.; between which and the
Zenith, it is scarce sensible: the
quantity throughout, is shewn
by the annexed table, calculated
by Sir Isaac Newton.
182. A Table shewing the Refractions
of the Sun, Moon, and Stars;
adapted to their apparent Altitudes.
| Appar. Alt. |
Refraction. |
|
Ap. Alt. |
Refraction. |
|
Ap. Alt. |
Refraction. |
| D. |
M. |
M. |
S. |
|
D. |
M. |
S. |
|
D. |
M. |
S. |
| 0 |
0 |
33 |
45 |
|
21 |
2 |
18 |
|
56 |
0 |
36 |
| 0 |
15 |
30 |
24 |
|
22 |
2 |
11 |
|
57 |
0 |
35 |
| 0 |
30 |
27 |
35 |
|
23 |
2 |
5 |
|
58 |
0 |
34 |
| 0 |
45 |
25 |
11 |
|
24 |
1 |
59 |
|
59 |
0 |
32 |
| 1 |
0 |
23 |
7 |
|
25 |
1 |
54 |
|
60 |
0 |
31 |
| 1 |
15 |
21 |
20 |
|
26 |
1 |
49 |
|
61 |
0 |
30 |
| 1 |
30 |
19 |
46 |
|
27 |
1 |
44 |
|
62 |
0 |
28 |
| 1 |
45 |
18 |
22 |
|
28 |
1 |
40 |
|
63 |
0 |
27 |
| 2 |
0 |
17 |
8 |
|
29 |
1 |
36 |
|
64 |
0 |
26 |
| 2 |
30 |
15 |
2 |
|
30 |
1 |
32 |
|
65 |
0 |
25 |
| 3 |
0 |
13 |
20 |
|
31 |
1 |
28 |
|
66 |
0 |
24 |
| 3 |
30 |
11 |
57 |
|
32 |
1 |
25 |
|
67 |
0 |
23 |
| 4 |
0 |
10 |
48 |
|
33 |
1 |
22 |
|
68 |
0 |
22 |
| 4 |
30 |
9 |
50 |
|
34 |
1 |
19 |
|
69 |
0 |
21 |
| 5 |
0 |
9 |
2 |
|
35 |
1 |
16 |
|
70 |
0 |
20 |
| 5 |
30 |
8 |
21 |
|
36 |
1 |
13 |
|
71 |
0 |
19 |
| 6 |
0 |
7 |
45 |
|
37 |
1 |
11 |
|
72 |
0 |
18 |
| 6 |
30 |
7 |
14 |
|
38 |
1 |
8 |
|
73 |
0 |
17 |
| 7 |
0 |
6 |
47 |
|
39 |
1 |
6 |
|
74 |
0 |
16 |
| 7 |
30 |
6 |
22 |
|
40 |
1 |
4 |
|
75 |
0 |
15 |
| 8 |
0 |
6 |
0 |
|
41 |
1 |
2 |
|
76 |
0 |
14 |
| 8 |
30 |
5 |
40 |
|
42 |
1 |
0 |
|
77 |
0 |
13 |
| 9 |
0 |
5 |
22 |
|
43 |
0 |
58 |
|
78 |
0 |
12 |
| 9 |
30 |
5 |
6 |
|
44 |
0 |
56 |
|
79 |
0 |
11 |
| 10 |
0 |
4 |
52 |
|
45 |
0 |
54 |
|
80 |
0 |
10 |
| 11 |
0 |
4 |
27 |
|
46 |
0 |
52 |
|
81 |
0 |
9 |
| 12 |
0 |
4 |
5 |
|
47 |
0 |
50 |
|
82 |
0 |
8 |
| 13 |
0 |
3 |
47 |
|
48 |
0 |
48 |
|
83 |
0 |
7 |
| 14 |
0 |
3 |
31 |
|
49 |
0 |
47 |
|
84 |
0 |
6 |
| 15 |
0 |
3 |
17 |
|
50 |
0 |
45 |
|
85 |
0 |
5 |
| 16 |
0 |
3 |
4 |
|
51 |
0 |
44 |
|
86 |
0 |
4 |
| 17 |
0 |
2 |
53 |
|
52 |
0 |
42 |
|
87 |
0 |
3 |
| 18 |
0 |
2 |
43 |
|
53 |
0 |
40 |
|
88 |
0 |
2 |
| 19 |
0 |
2 |
34 |
|
54 |
0 |
39 |
|
89 |
1 |
1 |
| 20 |
0 |
2 |
26 |
|
55 |
0 |
38 |
|
90 |
0 |
0 |
PLATE II.
The inconstancy of Refractions.
A very remarkable case concerning refraction.
69183. In all observations, to have the true altitude of the Sun, Moon,
or Stars, the refraction must be subtracted from the observed altitude.
But the quantity of refraction is not always the same at the same altitude;
because heat diminishes the air’s refractive power and density,
and cold increases both; and therefore no one table can serve precisely
for the same place at all seasons, nor even at all times of the same day;
much less for different climates: it having been observed that the
horizontal refractions are near a third part less at the Equator than at
Paris, as mentioned by Dr. Smith in the 370th remark on his Optics,
where the following account is given of an extraordinary refraction
of the sun-beams by cold. “There is a famous observation of
this kind made by some Hollanders that wintered in Nova Zembla in
the year 1596, who were surprised to find, that after a continual night
of three months, the Sun began to rise seventeen days sooner than according
to computation, deduced from the Altitude of the Pole observed
to be 76°: which cannot otherwise be accounted for, than by
an extraordinary quantity of refraction of the Sun’s rays, passing thro’
the cold dense air in that climate. Kepler computes that the Sun
was almost five degrees below the Horizon when he first appeared;
and consequently the refraction of his rays was about nine times greater
than it is with us.”
184. The Sun and Moon appear of an oval figure as FCGD, just
after their rising, and before their setting: the reason is, that the refraction
being greater in the Horizon than at any distance above it, the
lowermost limb G appears more elevated than the uppermost. But
although the refraction shortens the vertical Diameter FG, it has no
sensible effect on the horizontal Diameter CD, which is all equally
elevated. When the refraction is so small as to be imperceptible, the
Sun and Moon appear perfectly round, as AEBF.
Our imagination cannot judge rightly of the distance of inaccessible objects.
185. We daily observe, that the objects which appear most distinct
are generally those which are nearest to us; and consequently, when
we have nothing but our imagination to assist us in estimating of distances,
bright objects seem nearer to us than those which are less bright,
or than the same objects do when they appear less bright and worse
defined, even though their distance in both cases be the same. And
as in both cases they are seen under the same angle[44], our imagination
70naturally suggests an idea of a greater distance between us and those
objects which appear fainter and worse defined than those which appear
brighter under the same Angles; especially if they be such objects as
we were never near to, and of whose real Magnitudes we can be no
judges by sight.
Nor always of those which are accessible.
186. But, it is not only in judging of the different apparent Magnitudes
of the same objects, which are better or worse defined by their
being more or less bright, that we may be deceived: for we may make
a wrong conclusion even when we view them under equal degrees of
brightness, and under equal Angles; although they be objects whose
bulks we are generally acquainted with, such as houses or trees: for
proof of which, the two following instances may suffice.
First, When a house is seen over a very broad river by a person standing
on low ground, who sees nothing of the river, nor knows of it
beforehand; the breadth of the river being hid from him, because the
banks seem contiguous, he loses the idea of a distance equal to that
breadth; and the house seems small, because he refers it to a less distance
than it really is at. But, if he goes to a place from which the river
and interjacent ground can be seen, though no farther from the house,
he then perceives the house to be at a greater distance than he imagined;
and therefore fancies it to be bigger than he did at first; although in
both cases it appears under the same Angle, and consequently makes no
71bigger picture on the retina of his eye in the latter case than it did in
the former. Many have been deceived, by taking a red coat of arms,
fixed upon the iron gate in Clare-Hall walks at Cambridge, for a brick
house at a much greater distance[45].
Fig. XII.
Secondly, In foggy weather, at first sight, we generally imagine a
small house, which is just at hand, to be a great castle at a distance;
because it appears so dull and ill defined when seen through the Mist,
that we refer it to a much greater distance than it really is at; and
therefore, under the same Angle, we judge it to be much bigger. For,
the near object FE, seen by the eye ABD, appears under the same
Angle GCH, that the remote object GHI does: and the rays GFCN
and HECM crossing one another at C in the pupil of the eye, limit the size
of the picture MN on the retina; which is the picture of the object
FE, and if FE were taken away, would be the picture of the object
GHI, only worse defined; because GHI, being farther off, appears
duller and fainter than FE did. But if a Fog, as KL, comes between
the eye and the object FE, it appears dull and ill defined like GHI;
which causes our imagination to refer FE to the greater distance CH,
instead of the small distance CE which it really is at. And consequently,
as mis-judging the distance does not in the least diminish the
Angle under which the object appears, the small hay-rick FE seems to
be as big as GHI.
Fig. IX.
Why the Sun and Moon appear biggest in the Horizon.
187. The Sun and Moon appear bigger in the Horizon than at any
considerable height above it. These Luminaries, although at great distances
from the Earth, appear floating, as it were, on the surface of
our Atmosphere HGFfeC, a little way beyond the Clouds; of which,
those about F, directly over our heads at E, are nearer us than those
about H or e in the Horizon HEe. Therefore, when the Sun or Moon
appear in the Horizon at e, they are not only seen in a part of the Sky
which is really farther from us than if they were at any considerable
72Altitude, as about f; but they are also seen through a greater quantity
of Air and Vapours at e than at f. Here we have two concurring appearances
which deceive our imagination, and cause us to refer the Sun
and Moon to a greater distance at their rising or setting about e, than
when they are considerably high as at f: first, their seeming to be on
a part of the Atmosphere at e, which is really farther than f from a
spectator at E; and secondly, their being seen through a grosser medium
when at e than when at f; which, by rendering them dimmer, causes
us to imagine them to be at a yet greater distance. And as, in both cases,
they are seen[46] much under the same Angle, we naturally judge them
to be biggest when they seem farthest from us; like the above-mentioned
house § 186, seen from a higher ground, which shewed it to
be farther off than it appeared from low ground; or the hay-rick,
which appeared at a greater distance by means of an interposing Fog.
Their Diameters are not less on the Meridian than in the Horizon.
188. Any one may satisfy himself that the Moon appears under no
greater Angle in the Horizon than on the Meridian, by taking a large
sheet of paper, and rolling it up in the form of a Tube, of such a
width, that observing the Moon through it when she rises, she may,
as it were, just fill the Tube; then tie a thread round it to keep it
of that size; and when the Moon comes to the Meridian, and appears
much less to the eye, look at her again through the same Tube,
and she will fill it just as much, if not more, than she did at her
rising.
189. When the full Moon is in perigeo, or at her least distance from
the Earth, she is seen under a larger Angle, and must therefore appear
bigger than when she is Full at other times: and if that part of
the Atmosphere where she rises be more replete with vapours than
usual, she appears so much the dimmer; and therefore we fancy her
to be still the bigger, by referring her to an unusually great distance;
knowing that no objects which are very far distant can appear big unless
they be really so.
Plate IIII.
J. Ferguson delin.
J. Mynde Sculp.
73
CHAP. IX.
The Method of finding the Distances of the Sun, Moon, and Planets.
190. Those who have not learnt how to take the [47]Altitude of
any Celestial Phenomenon by a common Quadrant, nor
know any thing of Plain Trigonometry, may pass over the first Article
of this short Chapter, and take the Astronomer’s word for it, that the
distances of the Sun and Planets are as stated in the first Chapter of this
Book. But, to every one who knows how to take the Altitude of the
Sun, the Moon, or a Star, and can solve a plain right-angled Triangle,
the following method of finding the distances of the Sun and Moon
will be easily understood.
Fig I.
Let BAG be one half of the Earth, AC it’s semi-diameter, S the
Sun, m the Moon, and EKOL a quarter of the Circle described by
the Moon in revolving from the Meridian to the Meridian again.
Let CRS be the rational Horizon of an observer at A, extended to the
74Sun in the Heavens, and HAO his sensible Horizon; extended to
the Moon’s Orbit. ALC is the Angle under which the Earth’s semi-diameter
AC is seen from the Moon at L, which is equal to the
Angle OAL, because the right lines AO and CL which include both
these Angles are parallel. ASC is the Angle under which the Earth’s
semi-diameter AC is seen from the Sun at S, and is equal to the Angle
OAf because the lines AO and CRS are parallel. Now, it is found
by observation, that the Angle OAL is much greater than the Angle
OAf; but OAL is equal to ALC, and OAf is equal to ASC. Now,
as ASC is much less than ALC, it proves that the Earth’s semi-diameter
AC appears much greater as seen from the Moon at L than
from the Sun at S: and therefore the Earth is much farther from the
Sun than from the Moon[48]. The Quantities of these Angles are determined
by observation in the following manner.
The Moon’s horizontal Parallax, what.
The Moon’s distance determined.
Let a graduated instrument as DAE, (the larger the better) having
a moveable Index and Sight-holes, be fixed in such a manner, that it’s
plane surface may be parallel to the Plan of the Equator, and it’s edge
AD in the Meridian: so that when the Moon is in the Equinoctial,
and on the Meridian at E, she may be seen through the sight-holes
when the edge of the moveable index cuts the beginning of the divisions
at o, on the graduated limb DE; and when she is so seen, let
the precise time be noted. Now, as the Moon revolves about the
Earth from the Meridian to the Meridian again in 24 hours 48 minutes,
she will go a fourth part round it in a fourth part of that time, viz.
in 6 hours 12 minutes, as seen from C, that is, from the Earth’s
center or Pole. But as seen from A, the observer’s place on the Earth’s
surface, the Moon will seem to have gone a quarter round the Earth
when she comes to the sensible Horizon at O; for the Index through
the sights of which she is then viewed will be at d, 90 degrees from D,
where it was when she was seen at E. Now, let the exact moment when
the Moon is seen at O (which will be when she is in or near the sensible
Horizon) be carefully noted[49], that it may be known in what time
she has gone from E to O; which time subtracted from 6 hours
12 minutes (the time of her going from E to L) leaves the time of
her going from O to L, and affords an easy method for finding the
Angle OAL (called the Moon’s horizontal Parallax, which is equal to
the Angle ALC) by the following Analogy: As the time of the Moon’s
75describing the arc EO is to 90 degrees, so is 6 hours 12 minutes to
the degrees of the Arc DdE, which measures the Angle EAL; from
which subtract 90 degrees, and there remains the Angle OAL, equal
to the Angle ALC, under which the Earth’s Semi-diameter AC is
seen from the Moon. Now, since all the Angles of a right-lined
Triangle are equal to 180 degrees, or to two right Angles, and the
sides of a Triangle are always proportional to the Sines of the opposite
Angles, say, by the Rule of Three, as the Sine of the Angle ALC at the
Moon L is to it’s opposite side AC the Earth’s Semi-diameter, which is
known to be 3985 miles, so is Radius, viz. the Sine of 90 degrees, or of
the right Angle ACL to it’s opposite side AL, which is the Moon’s
distance at L from the observer’s place at A on the Earth’s surface;
or, so is the Sine of the Angle CAL to its opposite side CL, which is
the Moon’s distance from the Earth’s centre, and comes out at a mean
rate to be 240,000 miles. The Angle CAL is equal to what OAL
wants of 90 degrees.
The Sun’s distance cannot be yet so exactly determined as the
Moon’s;
How near the truth it may soon be determined.
191. The Sun’s distance from the Earth is found the same way,
but with much greater difficulty; because his horizontal Parallax, or
the Angle OAS equal to the Angle ASC, is so small as, to be hardly
perceptible, being only 10 seconds of a minute, or the 360th part of
a degree. But the Moon’s horizontal Parallax, or Angle OAL equal
to the Angle ALC, is very discernible; being 57ʹ 49ʺ, or 3469ʺ at it’s
mean state; which is more than 340 times as great as the Sun’s: and
therefore, the distances of the heavenly bodies being inversely as the
Tangents of their horizontal Parallaxes, the Sun’s distance from the
Earth is at least 340 times as great as the Moon’s; and is rather understated
at 81 millions of miles, when the Moon’s distance is certainly
known to be 240 thousand. But because, according to some Astronomers,
the Sun’s horizontal Parallax is 11 seconds, and according to
others only 10, the former Parallax making the Sun’s distance to be
about 75,000,000 of miles, and the latter 82,000,000; we may take
it for granted, that the Sun’s distance is not less than as deduced from
the former, nor more than as shewn by the latter: and every one who
is accustomed to make such observations, knows how hard it is, if
not impossible, to avoid an error of a second; especially on account of
the inconstancy of horizontal Refractions. And here, the error of one
second, in so small an Angle, will make an error of 7 millions of
miles in so great a distance as that of the Sun’s; and much more in
the distances of the superiour Planets. But Dr. Halley has shewn us
how the Sun’s distance from the Earth, and consequently the distances
of all the Planets from the Sun, may be known to within a 500th part
76of the whole, by a Transit of Venus over the Sun’s Disc, which will
happen on the 6th of June, in the year 1761; till which time we must
content ourselves with allowing the Sun’s distance to be about 81 millions
of miles, as commonly stated by Astronomers.
The Sun proved to be much bigger than the Moon.
192. The Sun and Moon appear much about the same bulk: And
every one who understands Geometry knows how their true bulks may
be deduced from the apparent, when their real distances are known.
Spheres are to one another as the Cubes of their Diameters; whence, if
the Sun be 81 millions of miles from the Earth, to appear as big as the
Moon, whose distance does not exceed 240 thousand miles, he must, in
solid bulk, be 42 millions 875 thousand times as big as the Moon.
193. The horizontal Parallaxes are best observed at the Equator;
1. Because the heat is so nearly equal every day, that the Refractions are
almost constantly the same. 2. Because the parallactic Angle is greater
there as at A (the distance from thence to the Earth’s Axis being greater,)
than upon any parallel of Latitude, as a or b.
The relative distances of the Planets from the Sun are known to great precision, though their real distances are not well known.
194. The Earth’s distance from the Sun being determined, the distances
of all the other Planets from him are easily found by the following
analogy, their periods round him being ascertained by observation.
As the square of the Earth’s period round the Sun is to the cube of it’s
distance from him, so is the square of the period of any other Planet to
the cube of it’s distance, in such parts or measures as the Earth’s distance
was taken; see § 111. This proportion gives us the relative mean distances
of the Planets from the Sun to the greatest degree of exactness;
and they are as follows, having been deduced from their periodical
times, according to the law just mentioned, which was discovered by
Kepler and demonstrated by Sir Isaac Newton.
Periodical Revolution to the same fixed Star in days and decimal parts of a day.
| Of Mercury |
Venus |
The Earth |
Mars |
Jupiter |
Saturn |
| |
| 87.9692 |
224.6176 |
365.2564 |
686.9785 |
4332.514 |
10759.275 |
| |
| Relative mean distances from the Sun. |
| |
| 38710 |
72333 |
100000 |
152369 |
520096 |
954006 |
| |
| From these numbers we deduce, that if the Sun’s horizontal Parallax be 10ʺ, the real mean distances of the Planets from the Sun in English miles are |
| |
| 31,742,200 |
59,313,060 |
82,000,000 |
124,942,580 |
426,478,720 |
782,284,920 |
| |
| But if the Sun’s Parallax be 11ʺ their distances are no more than |
| |
| 29,032,500 |
54,238,570 |
75,000,000 |
114,276,750 |
390,034,500 |
715,504,500 |
| |
| Errors in distance a rising from the mistake of 1ʺ in the Sun’s Parallax |
| |
| 2,709,700 |
5,074,490 |
7,000,000 |
10,665,830 |
36,444,220 |
66,780,420 |
77195. These last numbers shew, that although we have the relative
distances of the Planets from the Sun to the greatest nicety, yet the best
observers have not hitherto been able to ascertain their true distances
to within less than a twelfth part of what they really are. And therefore,
we must wait with patience till the 6th of June, A. D. 1761;
wishing that the Sky may then be clear to all places where there are
good Astronomers and accurate instruments for observing the Transit
of Venus over the Sun’s Disc at that time: as it will not happen again,
so as to be visible in Europe, in less than 235 years after.
Why the celestial Poles seem to keep still in the same points of the Heavens, notwithstanding the Earth’s motion round the Sun.
196. The Earth’s Axis produced to the Stars, being carried [50]parallel
to itself during the Earth’s annual revolution, describes a circle in the
Sphere of the fixed Stars equal to the Orbit of the Earth. But this
Orbit, though very large in itself, if viewed from the Stars, would
appear no bigger than a point; and consequently, the circle described
in the Sphere of the Stars by the Axis of the Earth produced, if
viewed from the Earth, must appear but as a point; that is, it’s diameter
appears too little to be measured by observation: for Dr.
Bradley has assured us, that if it had amounted to a single second,
or two at most, he should have perceived it in the great number of
observations he has made, especially upon γ Dragonis; and that it
seemed to him very probable that the annual Parallax of this Star is
not so great as a single second: and consequently, that it is above
400 thousand times farther from us than the Sun. Hence the celestial
poles seem to continue in the same points of the Heavens throughout
the year; which by no means disproves the Earth’s annual motion, but
plainly proves the distance of the Stars to be exceeding great.
197. The small apparent motion of the Stars § 113, discovered by
that great Astronomer, he found to be no ways owing to their annual
Parallax (for it came out contrary thereto) but to the Aberration of
their light, which can result from no known cause besides that of the
Earth’s annual motion; and as it agrees so exactly therewith, it proves
beyond dispute that the Earth has such a motion: for this Aberration
compleats all it’s various Phenomena every year; and proves
that the velocity of star-light is such as carries it through a space
equal to the Sun’s distance from us in 8 minutes 13 seconds of
time. Hence, the velocity of light is [51]10 thousand 210 times as
78great as the Earth’s velocity in it’s Orbit; which velocity (from what
we know already of the Earth’s distance from the Sun) may be affected
to be at least between 57 and 58 thousand miles every hour:
and supposing it to be 58000, this number multiplied by the above
10210, gives 592 million 180 thousand miles for the hourly motion of
light: which last number divided by 3600, the number of seconds in
an hour, shews that light flies at the rate of more than 164 thousand
miles every second of time, or swing of a common clock pendulum.
CHAP. X.
The Circles of the Globe described. The different lengths of days and nights, and the vicissitudes of seasons, explained. The explanation of the Phenomena of Saturn’s Ring concluded. (See § 81 and 82.)
Circles of the Sphere.
Fig. II
Equator, Tropics, Polar Circles, and Poles.
Fig. II.
Earth’s Axis.
PLATE IV.
Meridians.
198. If the reader be hitherto unacquainted with the principal circles
of the Globe, he should now learn to know them; which he
may do sufficiently for his present purpose in a quarter of an hour, if
he sets the ball of a terrestrial Globe before him, or looks at the Figure
of it, wherein these circles are drawn and named. The Equator is
that great circle which divides the northern half of the Earth from
the southern. The Tropics are lesser circles parallel to the Equator,
and each of them is
231⁄2
degrees from it; a degree in this sense being
the 360th part of any great circle which divides the Earth into two
equal parts. The Tropic of Cancer lies on the north side of the Equator,
and the Tropic of Capricorn on the south. The Arctic Circle has the
North Pole for it’s center, and is just as far from the north Pole as the
Tropics are from the Equator: and the Antarctic Circle (hid by the
supposed convexity of the Figure) is just as far from the South Pole,
every way round it. These Poles are the very north and south points
of the Globe: and all other places are denominated northward or southward
according to the side of the Equator they lie on, and the Pole
to which they are nearest. The Earth’s Axis is a straight line passing
through the center of the Earth, perpendicular to the Equator, and
terminating in the Poles at it’s surface. This, in the real Earth and
Planets is only an imaginary line; but in artificial Globes or Planets it
is a wire by which they are supported, and turned round in Orreries,
79or such like machines, by wheel-work. The circles 12. 1. 2. 3. 4,
&c. are Meridians to all places they pass through; and we must suppose
thousands more to be drawn, because every place that is ever so
little to the east or west of any other place, has a different Meridian
from that other place. All the Meridians meet in the Poles; and
whenever the Sun’s center is passing over any Meridian, in his apparent
motion round the Earth, it is mid-day or noon to all places on that
Meridian.
Zones.
199. The broad Space lying between the Tropics, like a girdle surrounding
the Globe, is called the torrid Zone, of which the Equator is
in the middle, all around. The Space between the Tropic of Cancer
and Arctic Circle is called the North temperate Zone. That between
the Tropic of Capricorn and the Antarctic Circle, the South temperate
Zone. And the two circular Spaces bounded by the Polar Circles are
the two Frigid Zones; denominated north or south, from that Pole which
is in the center of the one or the other of them.
200. Having acquired this easy branch of knowledge, the learner
may proceed to make the following experiment with his terrestrial
ball; which will give him a plain idea of the diurnal and annual
motions of the Earth, together with the different lengths of days and
nights, and all the beautiful variety of seasons, depending on those
motions.
Fig. III.
A pleasant experiment shewing the different lengths of days
and nights, and the variety of seasons.
Summer Solstice.
Take about seven feet of strong wire, and bend it into a circular
form, as abcd, which being viewed obliquely, appears elliptical as in
the Figure. Place a lighted candle on a table, and having fixed one
end of a silk thread K, to the north pole of a small terrestrial Globe
H, about three inches diameter, cause another person to hold the wire
circle so that it may be parallel to the table, and as high as the flame
of the candle I, which should be in or near the center. Then, having
twisted the thread as towards the left hand, that by untwisting it may
turn the Globe round eastward, or contrary to the way that the hands
of a watch move; hang the Globe by the thread within this circle,
almost contiguous to it; and as the thread untwists, the Globe (which
is enlightened half round by the candle as the Earth is by the Sun)
will turn round it’s Axis, and the different places upon it will be
carried through the light and dark Hemispheres, and have the appearance
of a regular succession of days and nights, as our Earth has
in reality by such a motion. As the Globe turns, move your hand
slowly so as to carry the Globe round the candle according to the order
of the letters abcd, keeping it’s center even with the wire circle; and
80you will perceive, that the candle being still perpendicular to the Equator
will enlighten the Globe from pole to pole in it’s motion round
the circle; and that every place on the Globe goes equally through
the light and the dark, as it turns round by the untwisting of the
thread, and therefore has a perpetual Equinox. The Globe thus turning
round represents the Earth turning round it’s Axis; and the motion
of the Globe round the candle represents the Earth’s annual motion
round the Sun, and shews, that if the Earth’s Orbit had no inclination
to it’s Axis, all the days and nights of the year would be equally long,
and there would be no different seasons. But now, desire the person
who holds the wire to hold it obliquely in the position ABCD,
raising the side ♋ just as much as he depresses the side ♑, that the
flame may be still in the plane of the circle; and twisting the thread
as before, that the Globe may turn round it’s Axis the same way as
you carry it round the candle; that is, from west to east, let the Globe
down into the lowermost part of the wire circle at ♑, and if the circles
be properly inclined, the candle will shine perpendicularly on the Tropic
of Cancer, and the frigid Zone, lying within the arctic or north
polar Circle, will be all in the light, as in the Figure; and will keep
in the light let the Globe turn round it’s Axis ever so often. From the
Equator to the north polar Circle all the places have longer days and
shorter nights; but from the Equator to the south polar Circle just the
reverse. The Sun does not set to any part of the north frigid Zone,
as shewn by the candle’s shining on it so that the motion of the Globe
can carry no place of that Zone into the dark: and at the same time the
south frigid Zone is involved in darkness, and the turning of the Globe
brings none of it’s places into the light. If the Earth were to continue
in the like part of it’s Orbit, the Sun would never set to the inhabitants
of the north frigid Zone, nor rise to those of the south. At the
Equator it would be always equal day and night; and as the places
are gradually more and more distant from the Equator, towards the
arctic Circle, they would have longer days and shorter nights, whilst
those on the south side of the Equator would have their nights longer
than their days. In this case there would be continual summer on the
north side of the Equator, and continual winter on the south side of it.
Plate V.

J. Ferguson delin.
J. Mynde Sc.
But as the Globe turns round it’s Axis, move your hand slowly forward
so as to carry the Globe from H towards E, and the boundary of
light and darkness will approach towards the north Pole, and recede
towards the south Pole; the northern places will go through less and
less of the light, and the southern places through more and more of
it; shewing how the northern days decrease in length, and the southern
81days increase, whilst the Globe proceeds from H to F. When the
Globe is at E, it is at a mean state between the lowest and highest
parts of it’s Orbit; the candle is directly over the Equator, the boundary
of light and darkness just reaches to both the Poles, and all places on
the Globe go equally through the light and dark Hemispheres, shewing
that the days and nights are then equal at all places of the Earth,
the Poles only excepted; for the Sun is then setting to the north Pole,
and rising to the south Pole.
Winter Solstice.
Continue moving the Globe forward, and as it goes through the
quarter A, the north Pole recedes still farther into the dark Hemisphere,
and the south Pole advances more into the light, as the Globe comes
nearer to ♋; and when it comes there at F, the candle is directly
over the Tropic of Capricorn, the days are at the shortest, and nights
at the longest, in the northern Hemisphere, all the way from the
Equator to the arctic Circle; and the reverse in the southern Hemisphere
from the antarctic Circle; within which Circles it is dark to the
north frigid Zone and light to the south.
Vernal Equinox.
Continue both motions, and as the Globe moves through the quarter
B, the north Pole advances toward the light, and the south Pole
recedes as fast from it; the days lengthen in the northern Hemisphere,
and shorten in the southern; and when the Globe comes to G the
candle will be again over the Equator (as when the Globe was at E)
and the days and nights will again be equal as formerly: and the
north Pole will be just coming into the light, the south Pole going out
of it.
Thus we see the reason why the days lengthen and shorten from
the Equator to the polar Circles every year; why there is no day or
night for several turnings of the Earth, within the polar Circles; why
there is but one day and one night in the whole year at the Poles; and
why the days and nights are equally long all the year round at the
Equator, which is always equally cut by the circle bounding light and
darkness.
201. The inclination of an Axis or Orbit is merely relative, because
we compare it with some other Axis or Orbit which we consider
as not inclined at all. Thus, our Horizon being level to us whatever
place of the Earth we are upon, we consider it as having no
inclination; and yet, if we travel 90 degrees from that place, we
shall then have an Horizon perpendicular to the former; but it
will still be level to us. And, if this Book be held so that the
82[52]Circle ABCD be parallel to the Horizon, both the Circle abcd, and
the Thread or Axis K will be inclined to it. But if Book or Plate be
held, so that the Thread be perpendicular to the Horizon, then the Orbit
ABCD will be inclined to the Thread, and the Orbit abcd perpendicular
to it, and parallel to the Horizon. We generally consider the
Earth’s annual Orbit as having no inclination, and the Orbits of all the
other Planets as inclined to it § 20.
202. Let us now take a view of the Earth in it’s annual course round
the Sun, considering it’s Orbit as having no inclination; and it’s Axis
as inclining
231⁄2
degrees from a line perpendicular to it’s Orbit, and
keeping the same oblique direction in all parts of it’s annual course; or,
as commonly termed, keeping always parallel to itself § 196.
Fig. I.
A concise view of the seasons.
Let a, b, c, d, e, f, g, h be the Earth in eight different parts of it’s Orbit,
equidistant from one another; Ns it’s Axis, N the north Pole, s the
south Pole, and S the Sun nearly in the center of the Earth’s Orbit
§ 18. As the Earth goes round the Sun according to the order of the
letters abcd, &c. it’s Axis Ns keeps the same obliquity, and is still
parallel to the line MNs. When the Earth is at a, it’s north Pole
inclines toward the Sun, and brings all the northern places more into
the light than at any other time of the year. But when the Earth is
at e in the opposite time of the year, the north Pole declines from the
Sun, which occasions the northern places to be more in the dark than
in the light; and the reverse at the southern places, as is evident by
the Figure, which I have taken from Dr. Long’s Astronomy. When
the Earth is either at c or g, it’s Axis inclines not either to or from
the Sun, but lies sidewise to him; and then the Poles are in the
boundary of light and darkness; and the Sun, being directly over the
Equator, makes equal day and night at all places. When the Earth
is at b it is half way between the Summer Solstice and Harvest Equinox;
when it is at d it is half way from the Harvest Equinox to the Winter
Solstice; at f half way from the Winter Solstice to the Spring Equinox:
and at h half way from the Spring Equinox to the Summer Solstice.
Fig. II.
PLATE V.
The Ecliptic.
The seasons shewn in another view of the Earth, and it’s Orbit.
203. From this oblique view of the Earth’s Orbit, let us suppose
ourselves to be raised far above it, and placed just over it’s center S,
looking down upon it from it’s north pole; and as the Earth’s Orbit
differs but very little from a Circle, we shall have it’s figure in such a
83view represented by the Circle ABCDEFGH. Let us suppose this
Circle to be divided into 12 equal parts called Signs, having their
names affixed to them; and each Sign into 30 equal parts called
Degrees, numbered 10, 20, 30, as in the outermost Circle of the
Figure, which represents the great Ecliptic in the Heavens. The
Earth is shewn in eight different positions in this Circle, and in each
position Æ is the Equator, T the Tropic of Cancer, the dotted Circle
the parallel of London, U the arctic or north polar Circle, and P the
north Pole where all the Meridians or hour Circles meet § 198. As
the Earth goes round the Sun the north Pole keeps constantly towards
one part of the Heavens, as it keeps in the Figure towards the right
hand side of the Plate.
Vernal Equinox.
When the Earth is at the beginning of Libra, namely on the 20th of
March, in this Figure (as at g in Fig. I.) the Sun S as seen from
the Earth appears at the beginning of Aries in the opposite part of
the Heavens[53], the north Pole is just coming into the light, the Sun
is vertical to the Equator; which, together with the Tropic of Cancer,
parallel of London, and arctic Circle, are all equally cut by the Circle
bounding light and darkness, coinciding with the six o’clock hour
Circle, and therefore the days and nights are equally long at all
places: for every part of the Meridian ÆTLa comes into the light at
six in the morning, and revolving with the Earth according to the order
of the hour-letters, goes into the dark at six in the evening. There are
24 Meridians or hour-Circles drawn on the Earth in this Figure, to shew
the time of Sun rising and setting at different Seasons of the Year.
Fig. II.
As the Earth moves in the Ecliptic according to the order of the
letters ABCD, &c. through the Signs Libra, Scorpio, and Sagittarius,
the north Pole comes more and more into the light; the days increase
as the nights decrease in length, at all places north of the Equator Æ;
which is plain by viewing the Earth at b on the 5th of May, when it
is in the 15th degree of Scorpio[54], and the Sun as seen from the Earth
appears in the 15th degree of Taurus. For then, the Tropic of Cancer
T is in the light from a little after five in the morning till almost
seven in the evening; the parallel of London from half an hour past
four till half an hour past seven; the polar Circle U from three till
nine; and a large track round the north Pole P has day all the 24
hours, for many rotations of the Earth on it’s Axis.
Summer Solstice.
84When the Earth comes to c, at the beginning of Capricorn, and the
Sun as seen from the Earth appears at the beginning of Cancer, on
the 21st of June, as in this Figure, it is in the position a in Fig. I;
and it’s north Pole inclines toward the Sun, so as to bring all the north
frigid Zone into the light, and the northern parallels of Latitude more
into the light than the dark from the Equator to the polar Circles;
and the more so as they are farther from the Equator. The Tropic
of Cancer is in the light from five in the morning till seven at night,
the parallel of London from a quarter before four till a quarter after
eight; and the polar Circle just touches the dark, so that the Sun
has only the lower half of his Disc hid from the inhabitants on that
Circle for a few minutes about midnight, supposing no inequalities in
the Horizon and no Refractions.
Autumnal Equinox.
Winter Solstice.
A bare view of the Figure is enough to shew, that as the Earth
advances from Capricorn toward Aries, and the Sun appears to move from
Cancer toward Libra, the north Pole recedes toward the dark, which
causes the days to decrease, and the nights to increase in length, till
the Earth comes to Aries, and then they are equal as before; for the
boundary of light and darkness cut the Equator and all it’s parallels
equally, or in halves. The north pole then goes into the dark, and
continues therein until the Earth goes half way round it’s Orbit; or,
from the 23d of September till the 20th of March. In the middle
between these times, viz. on the 22d of December, the north Pole is
as far as it can be in the dark, which is
231⁄2
degrees, equal to the
inclination of the Earth’s Axis from a perpendicular to it’s Orbit: and
then, the northern parallels are as much in the dark as they were in
the light on the 21 of June; the winter nights being as long as the
summer days, and the winter days as short as the summer nights.
It is needless to multiply words on this subject, as we shall have occasion
to mention the seasons again in describing the Orrery, § 439.
Only this must be noted, that all that has been said of the northern
Hemisphere, the contrary must be understood of the southern; for
on different sides of the Equator the seasons are contrary, because,
when the northern Hemisphere inclines toward the Sun the southern
declines from him.
The Phenomena of Saturn’s Ring.
PLATE V.
204. As Saturn goes round the Sun, his obliquely posited ring, like
our Earth’s Axis, keeps parallel to itself, and is therefore turned edgewise
to the Sun twice in a Saturnian year, which is almost as long
as 30 of our years § 81. But the ring, though considerably broad,
is too thin to be seen when it is turned round edgewise to the Sun, at
85which time it is also edgewise to the Earth; and therefore it disappears
once in every fifteen years to us. As the Sun shines half a year
on the north pole of our earth, then disappears to it, and shines as
long on the south pole; so, during one half of Saturn’s year the Sun
shines on the north side of his ring, then disappears to it, and shines
as long on it’s south side. When the Earth’s Axis inclines neither to
nor from the Sun, but sidewise to him, he instantly ceases to shine
on one pole, and begins to enlighten the other; and when Saturn’s
Ring inclines neither to nor from the Sun, but sidewise to him, he
ceases to shine on the one side of it, and begins to shine upon the
other.
Fig. III.
Let S be the Sun, ABCDEFGH Saturn’s Orbit, and IKLMNO
the Earth’s Orbit. Both Saturn and the Earth move according to the
order of the letters, and when Saturn is at A his ring is turned edgewise
to the Sun S, and he is then seen from the Earth as if he had lost
his ring, let the Earth be in any part of it’s Orbit whatever, except between
N and O; for whilst it describes that space, Saturn is apparently so
near the Sun as to be hid in his beams. As Saturn goes from A to
C his ring appears more and more open to the Earth: at C the ring appears
most open of all; and seems to grow narrower and narrower as Saturn
goes from C to E; and when he comes to E, the ring is again
turned edgewise both to the Sun and Earth: and as neither of it’s
sides are illuminated, it is invisible to us, because it’s edge is too thin
to be perceptible: and Saturn appears again as if he had lost his ring.
But as he goes from E to G, his ring opens more and more to our
view on the under side; and seems just as open at G as it was at C;
and may be seen in the night-time from the Earth in any part of it’s
Orbit, except about M, when the Sun hides the Planet from our view.
As Saturn goes from G to A his ring turns more and more edgewise
to us, and therefore it seems to grow narrower and narrower; and at
A it disappears as before. Hence, while Saturn goes from A to E
the Sun shines on the upper side of his ring, and the under side is
dark; but whilst he goes from E to A the Sun shines on the under
side of his ring, and the upper side is dark.
Fig. I and III.
It may perhaps be imagined that this Article might have been placed
more properly after § 81 than here: but when the candid reader considers
that all the various Phenomena of Saturn’s Ring depend upon
a cause similar to that of our Earth’s seasons, he will readily allow
that they are best explained together; and that the two Figures serve
to illustrate each other.
PLATE VI.
The Earth nearer the Sun in winter than in summer.
Why the weather is coldest when the Earth is nearest the Sun.
86205. The Earth’s Orbit being elliptical, and the Sun constantly
keeping in it’s lower Focus, which is 1,377,000 miles from the middle
point of the longer Axis, the Earth comes twice so much, or
2,754,000 miles nearer the Sun at one time of the year than at another:
for the Sun appearing under a larger Angle in our winter
than summer, proves that the Earth is nearer the Sun in winter, (see
the Note on Art. 185.) But here, this natural question will arise,
Why have we not the hottest weather when the Earth is nearest the
Sun? In answer it must be observed, that the excentricity of the
Earth’s Orbit, or 1 million 377 miles bears no greater proportion
to the Earth’s mean distance from the Sun than 17 does to 1000;
and therefore, this small difference of distance cannot occasion any
great difference of heat or cold. But the principal cause of this difference
is, that in winter the Sun’s rays fall so obliquely upon us,
that any given number of them is spread over a much greater portion
of the Earth’s surface where we live; and therefore each point
must then have fewer rays than in summer. Moreover, there
comes a greater degree of cold in the long winter nights, than there
can return of heat in so short days; and on both these accounts the
cold must increase. But in summer the Sun’s rays fall more perpendicularly
upon us, and therefore come with greater force, and in
greater numbers on the same place; and by their long continuance,
a much greater degree of heat is imparted by day than can fly off by
night.
Fig. II.
206. That a greater number of rays fall on the same place, when
they come perpendicularly, than when they come obliquely on it,
will appear by the Figure. For, let AB be a certain number of the
Sun’s rays falling on CD (which, let us suppose to be London) on
the 22d of June: but, on the 22d of December, the line CD, or
London; has the oblique position Cd to the same rays; and therefore
scarce a third part of them falls upon it, or only those between A and
e; all the rest eB being expended on the space dP, which is more
than double the length of CD or Cd. Besides, those parts which are
once heated, retain the heat for some time; which, with the additional
heat daily imparted, makes it continue to increase, though the
Sun declines toward the south: and this is the reason why July is
hotter than June, although the Sun has withdrawn from the summer
Tropic; as we find it is generally hotter at three in the afternoon,
when the Sun has gone toward the west, than at noon when he is
on the Meridian. Likewise, those places which are well cooled require
time to be heated again; for the Sun’s rays do not heat even
87the surface of any body till they have been some time upon it.
And therefore we find January for the most part colder than December,
although the Sun has withdrawn from the winter Tropic, and
begins to dart his beams more perpendicularly upon us, when we
have the position CF. An iron bar is not heated immediately upon
being put into the fire, nor grows cold till some time after it has
been taken out.
CHAP. XI.
The Method of finding the Longitude by the Eclipses of Jupiter’s Satellites: The amazing Velocity of Light demonstrated by these Eclipses.
First Meridian, and Longitude of places, what.
207. Geographers arbitrarily choose to call the Meridian of some
remarkable place the first Meridian. There they begin
their reckoning; and just so many degrees and minutes as any other
place is to the eastward or westward of that Meridian, so much east or west
Longitude they say it has. A degree is the 360th part of a Circle, be
it great or small; and a minute the 60th part of a degree. The English
Geographers reckon the Longitude from the Meridian of the Royal
Observatory at Greenwich, and the French from the Meridian of Paris.
PLATE V.
Fig. II.
Hour Circles.
An hour of time equal to 15 degrees of motion.
208. If we imagine twelve great Circles, one of which is the
Meridian of any given place, to intersect each other in the two Poles
of the Earth, and to cut the Equator Æ at every 15th degree, they
will be divided by the Poles into 24 Semicircles which divide the
Equator into 24 equal parts; and as the Earth turns on it’s Axis,
the planes of these Semicircles come successively after one another every
hour to the Sun. As in an hour of time there is a revolution of
15 degrees of the Equator, in a minute of time there will be a revolution
of 15 minutes of the Equator, and in a second of time a revolution
of 15 seconds. There are two tables annexed to this Chapter, for
reducing mean solar time into degrees and minutes of the terrestrial
Equator; and also for converting degrees and parts of the Equator into
mean solar time.
209. Because the Sun enlightens only one half of the Earth at once,
as it turns round it’s Axis he rises to some places at the same moments
of absolute Time that he sets to others; and when it is mid-day to
some places, it is mid-night to others. The XII on the middle of the
Earth’s enlightened side, next the Sun, stands for mid-day; and the
88opposite XII on the middle of the dark side, for mid-night. If we
suppose this Circle of hours to be fixed in the plane of the Equinoctial,
and the Earth to turn round within it, any particular Meridian will
come to the different hours so, as to shew the true time of the day or
night at all places on that Meridian. Therefore,
And consequently to 15 degrees of Longitude.
Lunar Eclipses useful in finding the Longitude.
210. To every place 15 degrees eastward from any given Meridian,
it is noon an hour sooner than on that Meridian; because their Meridian
comes to the Sun an hour sooner: and to all places 15 degrees
westward it is noon an hour later § 208, because their Meridian comes
an hour later to the Sun; and so on: every 15 degrees of motion
causing an hour’s difference in time. Therefore they who have noon
an hour later than we, have their Meridian, that is, their Longitude
15 degrees westward from us; and they who have noon an hour sooner
than we, have their Meridian 15 degrees eastward from ours: and so
for every hour’s difference of time 15 degrees difference of Longitude.
Consequently, if the beginning or ending of a Lunar Eclipse be observed,
suppose at London, to be exactly at mid-night, and in some
other place at 11 at night, that place is 15 degrees westward from the
Meridian of London: if the same Eclipse be observed at one in the
morning at another place, that place is 15 degrees eastward from the
said Meridian.
Eclipses of Jupiter’s Satellites much better for that purpose.
211. But as it is not easy to determine the exact moment either of
the beginning or ending of a Lunar Eclipse, because the Earth’s
shadow through which the Moon passes is faint and ill defined about
the edges; we have recourse to the Eclipses of Jupiter’s Satellites,
which disappear so instantaneously as they enter into Jupiter’s shadow,
and emerge so suddenly out of it, that we may fix the phenomenon
to half a second of time. The first or nearest Satellite to Jupiter is the
most advantageous for this purpose, because it’s motion is quicker than
the motion of any of the rest, and therefore it’s immersions and emersions
are more frequent.
How to solve this important problem.
PLATE V.
212. The English Astronomers have made Tables for shewing the
times of the Eclipses of Jupiter’s Satellites to great precision, for the
Meridian of Greenwich. Now, let an observer, who has these Tables
with a good Telescope and a well-regulated Clock at any other place
of the Earth, observe the beginning or ending of an Eclipse of one
of Jupiter’s Satellites, and note the precise moment of time that he
saw the Satellite either immerge into, or emerge out of the shadow,
and compare that time with the time shewn by the Tables for Greenwich;
then, 15 degrees difference of Longitude being allowed for every
89hour’s difference of time, will give the Longitude of that place from
Greenwich, as above § 210; and if there be any odd minutes of time,
for every minute a quarter of a degree, east or west must be allowed,
as the time of observation is before or after the time shewn by the
Tables. Such Eclipses are very convenient for this purpose at land,
because they happen almost every day; but are of no use at sea, because
the rolling of the ship hinders all nice telescopical observations.
Fig. II.
Illustrated by an example.
213. To explain this by a Figure, let J be Jupiter, K, L, M, N
his four Satellites in their respective Orbits 1, 2, 3, 4; and let the
Earth be at f (suppose in November, although that month is no otherways
material than to find the Earth readily in this scheme, where it
is shewn in eight different parts of it’s Orbit.) Let Q be a place on
the Meridian of Greenwich, and R a place on some other Meridian.
Let a person at R observe the instantaneous vanishing of the first Satellite
K into Jupiter’s shadow, suppose at three o’clock in the morning;
but by the Tables he finds the immersion of that Satellite to be at midnight
at Greenwich: he can then immediately determine, that as there
are three hours difference of time between Q and R, and that R is
three hours forwarder in reckoning than Q, it must be 45 degrees of
east Longitude from the Meridian of Q. Were this method as practicable
at sea as at land, any sailor might almost as easily, and with
equal certainty, find the Longitude as the Latitude.
Fig. II.
We seldom see the beginning and end of the same Eclipse of
any of Jupiter’s Moons.
214. Whilst the Earth is going from C to F in it’s Orbit, only the
immersions of Jupiter’s Satellites into his shadow are generally seen;
and their emersions out of it while the Earth goes from G to B. Indeed,
both these appearances may be seen of the second, third, and
fourth Satellite when eclipsed, whilst the Earth is between D and E,
or between G and A; but never of the first Satellite, on account of the
smallness of it’s Orbit and the bulk of Jupiter; except only when Jupiter
is directly opposite to the Sun; that is, when the Earth is at g:
and even then, strictly speaking, we cannot see either the immersions
or emersions of any of his Satellites, because his body being directly between
us and his conical shadow, his Satellites are hid by his body a few
moments before they touch his shadow; and are quite emerged from
thence before we can see them, as it were, just dropping from him.
And when the Earth is at c, the Sun being between it and Jupiter hides
both him and his Moons from us.
In this Diagram, the Orbits of Jupiter’s Moons are drawn in true
proportion to his diameter; but, in proportion to the Earth’s Orbit they
are drawn 81 times too large.
PLATE VI.
Jupiter’s conjunctions with the Sun, or oppositions to him,
are every year in different parts of the Heavens.
90215. In whatever month of the year Jupiter is in conjunction with
the Sun, or in opposition to him, in the next year it will be a month
later at least. For whilst the Earth goes once round the Sun, Jupiter
describes a twelfth part of his Orbit. And therefore, when the Earth
has finished it’s annual period from being in a line with the Sun and
Jupiter, it must go as much forwarder as Jupiter has moved in that
time, to overtake him again: just like the minute hand of a watch, which
must, from any conjunction with the hour hand, go once round the
dial-plate and somewhat above a twelfth part more, to overtake the
hour hand again.
The surprising velocity of light.
216. It is found by observation, that when the Earth is between the
Sun and Jupiter, as at g, his Satellites are eclipsed about 8 minutes
sooner than they should be according to the Tables: and when the
Earth is at B or C, these Eclipses happen about 8 minutes later than
the Tables predict them. Hence it is undeniably certain, that the
motion of light is not instantaneous, since it takes about
161⁄2
minutes
of time to go through a space equal to the diameter of the Earth’s
Orbit, which is 162 millions of miles in length: and consequently
the particles of light fly about 164 thousand 494 miles every second of
time, which is above a million of times swifter than the motion of a
cannon bullet. And as light is
161⁄2
minutes in travelling across the
Earth’s Orbit, it must be
81⁄4
minutes in coming from the Sun to us:
therefore, if the Sun were annihilated we should see him for
81⁄4
minutes
after; and if he were again created he would be
81⁄4
minutes old
before we could see him.
Fig. V.
Illustrated by a Figure.
217. To illustrate this progressive motion of light, let A and B be
the Earth in two different parts of it’s Orbit, whose distance is 81
millions of miles, equal to the Earth’s distance from the Sun S. It
is plain, that if the motion of light were instantaneous, the Satellite 1
would appear to enter into Jupiter’s shadow FF at the same moment
of time to a spectator in A as to another in B. But by many years
observations it has been found, that the immersion of the Satellite into
the shadow is seen
81⁄4
minutes sooner when the Earth is at B, than
when it is at A. And so, as Mr. Romer first discovered, the motion
of light is thereby proved to be progressive, and not instantaneous,
as was formerly believed. It is easy to compute in what time the
Earth moves from A to B; for the chord of 60 degrees of any Circle
is equal to the Semidiameter of that Circle; and as the Earth goes
through all the 360 degrees of it’s Orbit in a year, it goes through
60 of those degrees in about 61 days. Therefore, if on any given
91day, suppose the first of June, the Earth is at A, on the first of
August it will be at B: the chord, or straight line AB, being equal to
DS the Radius of the Earth’s Orbit, the same with AS it’s distance
from the Sun.
218. As the Earth moves from D to C, through the side AB of
it’s Orbit, it is constantly meeting the light of Jupiter’s Satellites sooner,
which occasions an apparent acceleration of their Eclipses: and as it
moves through the other half H of it’s Orbit, from C to D, it is
receding from their light, which occasions an apparent retardation
of their Eclipses, because their light is then longer ere it overtakes
the Earth.
219. That these accelerations of the immersions of Jupiter’s Satellites
into his shadow, as the Earth approaches towards Jupiter, and
the retardations of their emersions out of his shadow, as the Earth
is going from him, are not occasioned by any inequality arising from
the motions of the Satellites in excentric Orbits, is plain, because it
affects them all alike, in whatever parts of their Orbits they are eclipsed.
Besides, they go often round their Orbits every year, and their motions
are no way commensurate to the Earth’s. Therefore, a Phenomenon
not to be accounted for from the real motions of the Satellites, but so
easily deducible from the Earth’s motion, and so answerable thereto,
must be allowed to result from it. This affords one very good proof
of the Earth’s annual motion.
92220. TABLES for converting mean solar Time into Degrees and
Parts of the terrestrial Equator; and also for converting Degrees
and Parts of the Equator into mean solar Time.
Table I. For converting Time into
Degrees and Parts of the Equator.
| Hours |
Degrees |
*Min. |
Deg. |
Min. |
*Min. |
Deg. |
Min. |
| Sec. |
Min. |
Sec. |
Sec. |
Min. |
Sec. |
| Thirds |
Sec. |
Thirds |
Thirds |
Sec. |
Thirds |
| 1 |
15 |
1 |
0 |
15 |
31 |
7 |
45 |
| 2 |
30 |
2 |
0 |
30 |
32 |
8 |
0 |
| 3 |
45 |
3 |
0 |
45 |
33 |
8 |
15 |
| 4 |
60 |
4 |
1 |
0 |
34 |
8 |
30 |
| 5 |
75 |
5 |
1 |
15 |
35 |
8 |
45 |
| 6 |
90 |
6 |
1 |
30 |
36 |
9 |
0 |
| 7 |
105 |
7 |
1 |
45 |
37 |
9 |
15 |
| 8 |
120 |
8 |
2 |
0 |
38 |
9 |
30 |
| 9 |
135 |
9 |
2 |
15 |
39 |
9 |
45 |
| 10 |
150 |
10 |
2 |
30 |
40 |
10 |
0 |
| 11 |
165 |
11 |
2 |
45 |
41 |
10 |
15 |
| 12 |
180 |
12 |
3 |
0 |
42 |
10 |
30 |
| 13 |
195 |
13 |
3 |
15 |
43 |
10 |
45 |
| 14 |
210 |
14 |
3 |
30 |
44 |
11 |
0 |
| 15 |
225 |
15 |
3 |
45 |
45 |
11 |
15 |
| 16 |
240 |
16 |
4 |
0 |
46 |
11 |
30 |
| 17 |
255 |
17 |
4 |
15 |
47 |
11 |
45 |
| 18 |
270 |
18 |
4 |
30 |
48 |
12 |
0 |
| 19 |
285 |
19 |
4 |
45 |
49 |
12 |
15 |
| 20 |
300 |
20 |
5 |
0 |
50 |
12 |
30 |
| 21 |
315 |
21 |
5 |
15 |
51 |
12 |
45 |
| 22 |
330 |
22 |
5 |
30 |
52 |
13 |
0 |
| 23 |
345 |
23 |
5 |
45 |
53 |
13 |
15 |
| 24 |
360 |
24 |
6 |
0 |
54 |
13 |
30 |
| 25 |
375 |
25 |
6 |
15 |
55 |
13 |
45 |
| 26 |
390 |
26 |
6 |
30 |
56 |
14 |
0 |
| 27 |
405 |
27 |
6 |
45 |
57 |
14 |
15 |
| 28 |
420 |
28 |
7 |
0 |
58 |
14 |
30 |
| 29 |
435 |
29 |
7 |
15 |
59 |
14 |
45 |
| 30 |
450 |
30 |
7 |
30 |
60 |
15 |
0 |
Table II. For converting Degrees and Parts of the Equator into Time.
| *Deg. |
Hours |
Min. |
*Deg. |
Hours |
Min. |
Degrees |
Hours |
Minutes |
| Min. |
Min. |
Sec. |
Min. |
Min. |
Sec. |
| Sec. |
Sec. |
Thirds |
Sec. |
Sec. |
Thirds |
| 1 |
0 |
4 |
31 |
2 |
4 |
70 |
4 |
40 |
| 2 |
0 |
8 |
32 |
2 |
8 |
80 |
5 |
20 |
| 3 |
0 |
12 |
33 |
2 |
12 |
90 |
6 |
0 |
| 4 |
0 |
16 |
34 |
2 |
16 |
100 |
6 |
40 |
| 5 |
0 |
20 |
35 |
2 |
20 |
110 |
7 |
20 |
| 6 |
0 |
24 |
36 |
2 |
24 |
120 |
8 |
0 |
| 7 |
0 |
28 |
37 |
2 |
28 |
130 |
8 |
40 |
| 8 |
0 |
32 |
38 |
2 |
32 |
140 |
9 |
20 |
| 9 |
0 |
36 |
39 |
2 |
36 |
150 |
10 |
0 |
| 10 |
0 |
40 |
40 |
2 |
40 |
160 |
10 |
40 |
| 11 |
0 |
44 |
41 |
2 |
44 |
170 |
11 |
20 |
| 12 |
0 |
48 |
42 |
2 |
48 |
180 |
12 |
0 |
| 13 |
0 |
52 |
43 |
2 |
52 |
190 |
12 |
40 |
| 14 |
0 |
56 |
44 |
2 |
56 |
200 |
13 |
20 |
| 15 |
1 |
0 |
45 |
3 |
0 |
210 |
14 |
0 |
| 16 |
1 |
4 |
46 |
3 |
4 |
220 |
14 |
40 |
| 17 |
1 |
8 |
47 |
3 |
8 |
230 |
15 |
20 |
| 18 |
1 |
12 |
48 |
3 |
12 |
240 |
16 |
0 |
| 19 |
1 |
16 |
49 |
3 |
16 |
250 |
16 |
40 |
| 20 |
1 |
20 |
50 |
3 |
20 |
260 |
17 |
20 |
| 21 |
1 |
24 |
51 |
3 |
24 |
270 |
18 |
0 |
| 22 |
1 |
28 |
52 |
3 |
28 |
280 |
18 |
40 |
| 23 |
1 |
32 |
53 |
3 |
32 |
290 |
19 |
20 |
| 24 |
1 |
36 |
54 |
3 |
36 |
300 |
20 |
0 |
| 25 |
1 |
40 |
55 |
3 |
40 |
310 |
20 |
40 |
| 26 |
1 |
44 |
56 |
3 |
44 |
320 |
21 |
20 |
| 27 |
1 |
48 |
57 |
3 |
48 |
330 |
22 |
0 |
| 28 |
1 |
52 |
58 |
3 |
52 |
340 |
22 |
40 |
| 29 |
1 |
56 |
59 |
3 |
56 |
350 |
23 |
20 |
| 30 |
2 |
0 |
60 |
4 |
0 |
360 |
24 |
0 |
93These are the Tables mentioned in the 208th Article, and are so easy
that they scarce require any farther explanation than to inform the reader,
that if, in Table I. he reckons the columns marked with Asterisks to
be minutes of time, the other columns give the equatoreal parts or
motion in degrees and minutes; if he reckons the Asterisk columns to
be seconds, the others give the motion in minutes and seconds of the
Equator; if thirds, in seconds and thirds: And if in Table II. he
reckons the Asterisk columns to be degrees of motion, the others give
the time answering thereto in hours and minutes; if minutes of motion,
the time is minutes and seconds; if seconds of motion, the corresponding
time is given in seconds and thirds. An example in each
case will make the whole very plain.
In 10 hours 15 minutes 24
seconds 20 thirds, Qu. How
much of the Equator revolves
through the Meridian?
| |
Deg. |
M. |
S. |
| Hours |
10 |
150 |
0 |
0 |
| Min. |
15 |
3 |
45 |
0 |
| Sec. |
24 |
|
6 |
0 |
| Thirds |
20 |
|
|
5 |
| Answer |
153 |
51 |
5 |
In what time will 153 degrees
51 minutes 5 seconds of the
Equator revolve through the
Meridian?
| |
H. |
M. |
S. |
T. |
| Deg. |
150 |
10 |
0 |
0 |
0 |
| 3 |
|
12 |
0 |
0 |
| Min. |
51 |
|
3 |
24 |
0 |
| Sec. |
5 |
|
20 |
| Answer |
10 |
15 |
24 |
20 |
CHAP. XII.
Of Solar and Sidereal Time.
Sidereal days shorter than solar days, and why.
221. The fixed Stars appear to go round the Earth in 23 hours
56 minutes 4 seconds, and the Sun in 24 hours: so that
the Stars gain three minutes 56 seconds upon the Sun every day, which
amounts to one diurnal revolution in a year; and therefore, in 365
days as measured by the returns of the Sun to the Meridian, there are
366 days as measured by the Stars returning to it: the former are called
Solar Days, and the latter Sidereal.
The diameter of the Earth’s Orbit is but a physical point in proportion
to the distance of the Stars; for which reason, and the Earth’s uniform
motion on it’s Axis, any given Meridian will revolve from any
94Star to the same Star again in every absolute turn of the Earth on it’s
Axis, without the least perceptible difference of time shewn by a
clock which goes exactly true.
If the Earth had only a diurnal motion, without an annual, any
given Meridian would revolve from the Sun to the Sun again in the
same quantity of time as from any Star to the same Star again; because
the Sun would never change his place with respect to the Stars. But,
as the Earth advances almost a degree eastward in it’s Orbit in the
time that it turns eastward round its Axis, whatever Star passes over
the Meridian on any day with the Sun, will pass over the same Meridian
on the next day when the Sun is almost a degree short of it; that
is, 3 minutes 56 seconds sooner. If the year contained only 360 days
as the Ecliptic does 360 degrees, the Sun’s apparent place, so far as
his motion is equable, would change a degree every day; and then the
sidereal days would be just four minutes shorter than the solar.
Fig. II.
Let ABCDEFGHIKLM be the Earth’s Orbit, in which it goes
round the Sun every year, according to the order of the letters, that
is, from west to east, and turns round it’s Axis the same way from the
Sun to the Sun again every 24 hours. Let S be the Sun, and R a
fixed Star at such an immense distance that the diameter of the
Earth’s Orbit bears no sensible proportion to that distance. Let Nm be
any particular Meridian of the Earth, and N a given point or place
upon that Meridian. When the Earth is at A, the Sun S hides the
Star R, which would always be hid if the Earth never removed from
A; and consequently, as the Earth turns round it’s Axis, the point N
would always come round to the Sun and Star at the same time. But
when the Earth has advanced, suppose a twelfth part of it’s Orbit from
A to B, it’s motion round it’s Axis will bring the point N a twelfth
part of a day or two hours sooner to the Star than to the Sun; for the
Angle NBn is equal to the Angle ASB: and therefore, any Star which
comes to the Meridian at noon with the Sun when the Earth is at A,
will come to the Meridian at 10 in the forenoon when the Earth is at
B. When the Earth comes to C the point N will have the Star on
it’s Meridian at 8 in the morning, or four hours sooner than it comes
round to the Sun; for it must revolve from N to n, before it has the Sun
in it’s Meridian. When the Earth comes to D, the point N will have
the Star on it’s Meridian at six in the morning, but that point must
revolve six hours more from N to n, before it has mid-day by the Sun:
for now the Angle ASD is a right Angle, and so is NDn; that is, the
Earth has advanced 90 degrees in it’s Orbit, and must turn 90 degrees
on its Axis to carry the point N from the Star to the Sun: for the
95Star always comes
to the Meridian
when Nm is parallel
to RSA; because
DS is but a
point in respect of
RS. When the
Earth is at E, the
Star comes to the
Meridian at 4 in
the morning; at
F, at two in the
morning; and at
G, the Earth having
gone half
round it’s Orbit,
N points to the
Star R at midnight,
being then
directly opposite
to the Sun; and
therefore, by the
Earth’s diurnal
motion the Star
comes to the Meridian
12 hours
before the Sun.
When the Earth
is at H, the Star
comes to the Meridian
at 10 in the
evening; at I it
comes to the Meridian
at 8, that is,
16 hours before
the Sun; at K 18
hours before him;
at L 20 hours;
at M 22; and at
A equally with
the Sun again.
A Table, shewing how much of the Celestial Equator passes over the
Meridian in any part of a mean Solar Day; and how much the Fixed
Stars gain upon the mean Solar Time every Day, for a Month.
| Time |
Motion. |
Time |
Motion. |
Time |
Motion. |
| Hours |
Degrees |
Minutes |
Seconds |
*Min. |
Deg. |
Min. |
Sec. |
*Min. |
Deg. |
Min. |
Sec. |
| Sec. |
Min. |
Sec. |
Th. |
Sec. |
Min. |
Sec. |
Th. |
| Th. |
Sec. |
Th. |
ʺʺ |
Th. |
Sec. |
Th. |
ʺʺ |
| 1 |
15 |
2 |
28 |
1 |
0 |
15 |
2 |
31 |
7 |
46 |
16 |
| 2 |
30 |
4 |
56 |
2 |
0 |
30 |
5 |
32 |
8 |
1 |
19 |
| 3 |
45 |
7 |
24 |
3 |
0 |
45 |
7 |
33 |
8 |
16 |
21 |
| 4 |
60 |
9 |
51 |
4 |
1 |
0 |
10 |
34 |
8 |
31 |
24 |
| 5 |
75 |
12 |
19 |
5 |
1 |
15 |
12 |
35 |
8 |
46 |
26 |
| 6 |
90 |
14 |
47 |
6 |
1 |
30 |
15 |
36 |
9 |
1 |
29 |
| 7 |
105 |
17 |
15 |
7 |
1 |
45 |
17 |
37 |
9 |
16 |
31 |
| 8 |
120 |
19 |
43 |
8 |
2 |
0 |
20 |
38 |
9 |
31 |
34 |
| 9 |
135 |
22 |
11 |
9 |
2 |
15 |
22 |
39 |
9 |
46 |
36 |
| 10 |
150 |
24 |
38 |
10 |
2 |
30 |
25 |
40 |
10 |
1 |
39 |
| 11 |
165 |
27 |
6 |
11 |
2 |
45 |
27 |
41 |
10 |
16 |
41 |
| 12 |
180 |
29 |
34 |
12 |
3 |
0 |
30 |
42 |
10 |
31 |
43 |
| 13 |
195 |
32 |
2 |
13 |
3 |
15 |
32 |
43 |
10 |
46 |
46 |
| 14 |
210 |
34 |
30 |
14 |
3 |
30 |
34 |
44 |
11 |
1 |
48 |
| 15 |
225 |
36 |
58 |
15 |
3 |
45 |
37 |
45 |
11 |
16 |
51 |
| 16 |
240 |
39 |
26 |
16 |
4 |
0 |
39 |
46 |
11 |
31 |
53 |
| 17 |
255 |
41 |
53 |
17 |
4 |
15 |
41 |
47 |
11 |
46 |
56 |
| 18 |
270 |
44 |
21 |
18 |
4 |
30 |
44 |
48 |
12 |
1 |
58 |
| 19 |
285 |
46 |
49 |
19 |
4 |
45 |
47 |
49 |
12 |
17 |
1 |
| 20 |
300 |
49 |
17 |
20 |
5 |
0 |
49 |
50 |
12 |
32 |
3 |
| 21 |
315 |
51 |
45 |
21 |
5 |
15 |
52 |
51 |
12 |
47 |
6 |
| 22 |
330 |
54 |
13 |
22 |
5 |
30 |
54 |
52 |
13 |
2 |
8 |
| 23 |
345 |
56 |
40 |
23 |
5 |
45 |
57 |
53 |
13 |
17 |
11 |
| 24 |
360 |
59 |
8 |
24 |
6 |
0 |
59 |
54 |
13 |
32 |
13 |
| 25 |
376 |
1 |
36 |
25 |
6 |
16 |
2 |
55 |
13 |
47 |
16 |
| 26 |
391 |
4 |
4 |
26 |
6 |
31 |
4 |
56 |
14 |
2 |
18 |
| 27 |
406 |
6 |
32 |
27 |
6 |
46 |
7 |
57 |
14 |
17 |
21 |
| 28 |
421 |
9 |
0 |
28 |
7 |
1 |
9 |
58 |
14 |
32 |
23 |
| 29 |
436 |
11 |
28 |
29 |
7 |
16 |
11 |
59 |
14 |
47 |
26 |
| 30 |
451 |
13 |
56 |
30 |
7 |
31 |
14 |
60 |
15 |
2 |
28 |
Accelerations of the Fixed Stars.
| D. |
H. |
M. |
S. |
| 1 |
0 |
3 |
56 |
| 2 |
0 |
7 |
52 |
| 3 |
0 |
11 |
48 |
| 4 |
0 |
15 |
44 |
| 5 |
0 |
19 |
39 |
| 6 |
0 |
23 |
35 |
| 7 |
0 |
27 |
31 |
| 8 |
0 |
31 |
27 |
| 9 |
0 |
35 |
23 |
| 10 |
0 |
39 |
19 |
| 11 |
0 |
43 |
15 |
| 12 |
0 |
47 |
11 |
| 13 |
0 |
51 |
7 |
| 14 |
0 |
55 |
3 |
| 15 |
0 |
58 |
58 |
| 16 |
1 |
2 |
54 |
| 17 |
1 |
6 |
50 |
| 18 |
1 |
10 |
46 |
| 19 |
1 |
14 |
42 |
| 20 |
1 |
18 |
38 |
| 21 |
1 |
22 |
34 |
| 22 |
1 |
26 |
30 |
| 23 |
1 |
30 |
26 |
| 24 |
1 |
34 |
22 |
| 25 |
1 |
38 |
17 |
| 26 |
1 |
42 |
13 |
| 27 |
1 |
46 |
9 |
| 28 |
1 |
50 |
5 |
| 29 |
1 |
54 |
1 |
| 30 |
1 |
57 |
57 |
PLATE III.
An absolute Turn of the Earth on it’s Axis never finishes a
solar day.
Fig. II.
96222. Thus it is plain, that an absolute turn of the Earth on it’s Axis
(which is always completed when the same Meridian comes to be parallel
to it’s situation at any time of the day before) never brings the same
Meridian round from the Sun to the Sun again; but that the Earth
requires as much more than one turn on it’s Axis to finish a natural
day, as it has gone forward in that time; which, at a mean state is a
365th part of a Circle. Hence, in 365 days the Earth turns 366
times round it’s Axis; and therefore, as a turn of the Earth on it’s
Axis compleats a sidereal day, there must be one sidereal day more in
a year than the number of solar days, be the number what it will, on
the Earth, or any other Planet. One turn being lost with respect
to the number of solar days in a year, by the Planet’s going round
the Sun; just as it would be lost to a traveller, who, in going round
the Earth, would lose one day by following the apparent diurnal motion
of the Sun: and consequently, would reckon one day less at his
return (let him take what time he would to go round the Earth) than
those who remained all the while at the place from which he set
out. So, if there were two Earths revolving equably on their Axes, and
if one remained at A until the other travelled round the Sun from A
to A again, that Earth which kept it’s place at A would have it’s solar
and sidereal days always of the same length; and so, would have one
solar day more than the other at it’s return. Hence, if the Earth
turned but once round it’s Axis in a year, and if that turn was made
the same way as the Earth goes round the Sun, there would be continual
day on one side of the Earth, and continual night on the other.
To know by the Stars whether a Clock goes true or not.
223. The first part of the preceding Table shews how much of the
celestial Equator passes over the Meridian in any given part of a mean
solar day, and is to be understood the same way as the Table in the
220th article. The latter part, intitled, Accelerations of the fixed Stars,
affords us an easy method of knowing whether or no our clocks and
watches go true: For if, through a small hole in a window-shutter,
or in a thin plate of metal fixed to a window, we observe at what
time any Star disappears behind a chimney, or corner of a house, at a
little distance; and if the same Star disappears the next night 3 minutes
56 seconds sooner by the clock or watch; and on the second night, 7
minutes 52 seconds sooner; the third night 11 minutes 48 seconds
sooner; and so on, every night, as in the Table, which shews this difference
for 30 natural days, it is an infallible Sign that the machine
goes true; otherwise it does not go true; and must be regulated accordingly:
and as the disappearing of a Star is instantaneous, we may
depend on this information to half a second.
Pl. VI.
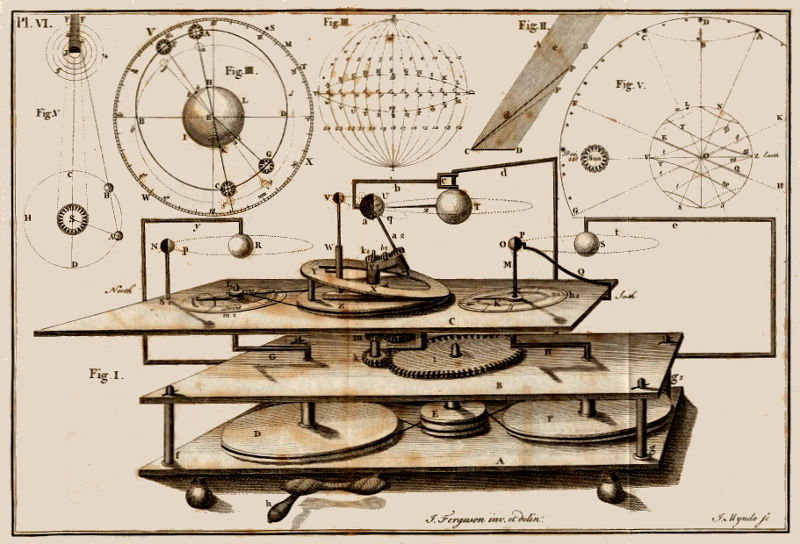
J. Ferguson inv. et delin.
J. Mynde Sc.
97
CHAP. XIII.
Of the Equation of Time.
The Sun and Clocks equal only on four days of the year.
224. The Earth’s motion on it’s Axis being perfectly uniform, and
equal at all times of the year, the sidereal days are always
precisely of the same length; and so would the solar or natural days be,
if the Earth’s orbit were a perfect Circle, and it’s Axis perpendicular
to it’s orbit. But the Earth’s diurnal motion on an inclined Axis, and
it’s annual motion in an elliptic orbit, cause the Sun’s apparent motion
in the Heavens to be unequal: for sometimes he revolves from the
Meridian to the Meridian again in somewhat less than 24 hours, shewn
by a well regulated clock; and at other times in somewhat more: so
that the time shewn by an equal going clock and a true Sun-dial is
never the same but on the 15th of April, the 16th of June, the 31st
of August, and the 24th of December. The clock, if it goes equally
and true all the year round, will be before the Sun from the 24th of
December till the 15th of April; from that time till the 16th of June
the Sun will be before the clock; from the 16th of June till the 31st
of August the clock will be again before the Sun; and from thence to
the 24th of December the Sun will be faster than the clock.
Use of the Equation Table.
225. The Tables of the Equation of natural days, at the end of the next
Chapter, shew the time that ought to be pointed out by a well regulated
clock or watch every day of the year at the precise moment of
solar noon; that is, when the Sun’s centre is on the Meridian, or
when a true Sun-dial shews it to be precisely Twelve. Thus, on the
5th of January in Leap-year, when the Sun is on the Meridian, it
ought to be 5 minutes 51 seconds past twelve by the clock; and on the
15th of May, when the Sun is on the Meridian, the time by the clock
should be but 55 minutes 57 seconds past eleven; in the former case,
the clock is 5 minutes 51 seconds beforehand with the Sun; and in
the latter case, the Sun is 4 minutes 3 seconds faster than the clock.
The column at the right hand of each month shews the daily difference
of this equation, as it increases or decreases. But without a
Meridian Line, or a Transit-Instrument fixed in the plane of the Meridian,
we cannot set a Sun-dial true.
How to draw a Meridian Line.
226. The easiest and most expeditious way of drawing a Meridian
Line is this: Make four or five concentric Circles, about a quarter of
98an inch from one another, on a flat board about a foot in breadth;
and let the outmost Circle be but little less than the board will contain.
Fix a pin perpendicularly in the center, and of such a length
that it’s whole shadow may fall within the innermost Circle for at least
four hours in the middle of the day. The pin ought to be about an
eighth part of an inch thick, with a round blunt point. The board
being set exactly level in a place where the Sun shines, suppose from
eight in the morning till four in the afternoon, about which hours the
end of the shadow should fall without all the Circles; watch the times
in the forenoon, when the extremity of the shortening shadow just
touches the several Circles, and there make marks. Then, in the
afternoon of the same day, watch the lengthening shadow, and where
it’s end touches the several Circles in going over them, make marks
also. Lastly, with a pair of compasses, find exactly the middle point
between the two marks on any Circle, and draw a straight line from the
center to that point; which Line will be covered at noon by the shadow
of a small upright wire, which should be put in the place of the pin.
The reason for drawing several Circles is, that in case one part of the
day should prove clear, and the other part somewhat cloudy, if you
miss the time when the point of the shadow should touch one Circle,
you may perhaps catch it in touching another. The best time for drawing
a Meridian Line in this manner is about the middle of summer;
because the Sun changes his Declination slowest and his Altitude
fastest in the longest days.
If the casement of a window on which the Sun shines at noon be
quite upright, you may draw a line along the edge of it’s shadow on
the floor, when the shadow of the pin is exactly on the Meridian Line
of the board: and as the motion of the shadow of the casement will be
much more sensible on the Floor, than that of the shadow of the pin
on the board, you may know to a few seconds when it touches the
Meridian Line on the floor, and so regulate your clock for the day of
observation by that line and the Equation Tables above-mentioned
§ 225.
Equation of natural days explained.
227. As the Equation of time, or difference between the time
shewn by a well regulated Clock and a true Sun-dial, depends upon
two causes, namely, the obliquity of the Ecliptic, and the unequal
motion of the Earth in it, we shall first explain the effects of these
causes separately considered, and then the united effects resulting from
their combination.
PLATE VI.
The first part of the Equation of time.
99228. The Earth’s motion on it’s Axis being perfectly equable, or
always at the same rate, and the [55]plane of the Equator being perpendicular
to it’s Axis, ’tis evident that in equal times equal portions
of the Equator pass over the Meridian; and so would equal
portions of the Ecliptic if it were parallel to or coincident with the
Equator. But, as the Ecliptic is oblique to the Equator, the equable
motion of the Earth carries unequal portions of the Ecliptic over the
Meridian in equal times, the difference being proportionate to the
obliquity; and as some parts of the Ecliptic are much more oblique
than others, those differences are unequal among themselves. Therefore,
if two Suns should start either from the beginning of Aries or
Libra, and continue to move through equal arcs in equal times, one
in the Equator, and the other in the Ecliptic, the equatoreal Sun
would always return to the Meridian in 24 hours time, as measured
by a well regulated clock; but the Sun in the Ecliptic would return
to the Meridian sometimes sooner, and sometimes later than the
equatoreal Sun; and only at the same moments with him on four
days of the year; namely, the 20th of March, when the Sun enters
Aries; the 21st of June, when he enters Cancer; the 23d of
September, when he enters Libra; and the 21st of December, when
he enters Capricorn. But, as there is only one Sun, and his apparent
motion is always in the Ecliptic, let us henceforth call him the
real Sun, and the other which is supposed to move in the Equator
the fictitious; to which last, the motion of a well regulated clock
always answers.
Fig. III.
Let Z♈z♎ be the Earth, ZFRz it’s Axis, abcde &c. the Equator,
ABCDE &c. the northern half of the Ecliptic from ♈ to ♎ on
the side of the Globe next the eye, and MNOP &c. the southern
half on the opposite side from ♎ to ♈. Let the points at A, B,
C, D, E, F, &c. quite round from ♈ to ♈ again bound equal portions
of the Ecliptic, gone through in equal times by the real Sun;
and those at a, b, c, d, e, f, &c. equal portions of the Equator
described in equal times by the fictitious Sun; and let Z♈z be the
Meridian.
As the real Sun moves obliquely in the Ecliptic, and the fictitious
Sun directly in the Equator, with respect to the Meridian, a degree,
or any number of degrees, between ♈ and F on the Ecliptic, must
100be nearer the Meridian Z♈z, than a degree, or any corresponding
number of degrees on the Equator from ♈ to f; and the more so,
as they are the more oblique: and therefore the true Sun comes
sooner to the Meridian whilst he is in the quadrant ♈ F, than the
fictitious Sun does in the quadrant ♈ f; for which reason, the
solar noon precedes noon by the Clock, until the real Sun comes
to F, and the fictitious to f; which two points, being equidistant
from the Meridian, both Suns will come to it precisely at noon by the
Clock.
Whilst the real Sun describes the second quadrant of the Ecliptic
FGHIKL from ♋ to ♎; he comes later to the Meridian every
day, than the fictitious Sun moving through the second quadrant of
the Equator from f to ♎; for the points at G, H, I, K, and L
being farther from the Meridian than their corresponding points at
g, h, i, k, and l, they must be later of coming to it: and as both
Suns come at the same moment to the point ♎, they come to the
Meridian at the moment of noon by the Clock.
In departing from Libra, through the third quadrant, the real Sun
going through MNOPQ towards ♑ at R, and the fictitious Sun
through mnopq towards r, the former comes to the Meridian every day
sooner than the latter, until the real Sun comes to ♑, and the fictitious
to r, and then they both come to the Meridian at the same time.
Lastly, as the real Sun moves equably through STUVW, from
♑ towards ♈; and the fictitious Sun through stuvw, from r
towards ♈, the former comes later every day to the Meridian than the
latter, until they both arrive at the point ♈, and then they make
noon at the same time with the clock.
A Table of the Equation of Time depending on the Sun’s place
in the Ecliptic.
PLATE VI.
229. The annexed Table shews how much the Sun is faster or slower
than the clock ought to be, so far as the difference depends upon the
obliquity of the Ecliptic; of which the Signs of the first and third quadrants
are at the head of the Table, and their Degrees at the left hand;
and in these the Sun is faster than the Clock: the Signs of the second
and fourth quadrants are at the foot of the Table, and their degrees at
the right hand; in all which the Sun is slower than the Clock: so
that entering the Table with the given Sign of the Sun’s place at the
head of the Table, and the Degree of his place in that Sign at the
left hand; or with the given Sign at the foot of the Table, and Degree
at the right hand; in the Angle of meeting is the number of minutes
and seconds that the Sun is faster or slower than the clock: or in other
words, the quantity of time in which the real Sun, when in that
101part of the Ecliptic, comes sooner or
later to the Meridian than the fictitious
Sun in the Equator. Thus, when the
Sun’s place is ♉ Taurus 12 degrees,
he is 9 minutes 49 seconds faster than
the clock; and when his place is ♋
Cancer 18 degrees, he is 6 minutes 2
seconds slower.
| Sun faster than the Clock in |
| Degrees |
♈ |
♉ |
♊ |
1st Q. |
| ♎ |
♏ |
♐ |
3d Q. |
| ʹ |
ʺ |
ʹ |
ʺ |
ʹ |
ʺ |
Deg. |
| 0 |
0 |
0 |
8 |
24 |
8 |
46 |
30 |
| 1 |
0 |
20 |
8 |
35 |
8 |
36 |
29 |
| 2 |
0 |
40 |
8 |
45 |
8 |
25 |
28 |
| 3 |
1 |
0 |
8 |
54 |
8 |
14 |
27 |
| 4 |
1 |
19 |
9 |
3 |
8 |
1 |
26 |
| 5 |
1 |
39 |
9 |
11 |
7 |
49 |
25 |
| 6 |
1 |
59 |
9 |
18 |
7 |
35 |
24 |
| 7 |
2 |
18 |
9 |
24 |
7 |
21 |
23 |
| 8 |
2 |
37 |
9 |
31 |
7 |
6 |
22 |
| 9 |
2 |
56 |
9 |
36 |
6 |
51 |
21 |
| 10 |
3 |
16 |
9 |
41 |
6 |
35 |
20 |
| 11 |
3 |
34 |
9 |
45 |
6 |
19 |
19 |
| 12 |
3 |
53 |
9 |
49 |
6 |
2 |
18 |
| 13 |
4 |
11 |
9 |
51 |
5 |
45 |
17 |
| 14 |
4 |
29 |
9 |
53 |
5 |
27 |
16 |
| 15 |
4 |
47 |
9 |
54 |
5 |
9 |
15 |
| 16 |
5 |
4 |
9 |
55 |
4 |
50 |
14 |
| 17 |
5 |
21 |
9 |
55 |
4 |
31 |
13 |
| 18 |
5 |
38 |
9 |
54 |
4 |
12 |
12 |
| 19 |
5 |
54 |
9 |
52 |
3 |
52 |
11 |
| 20 |
6 |
10 |
9 |
50 |
3 |
32 |
10 |
| 21 |
6 |
26 |
9 |
47 |
3 |
12 |
9 |
| 22 |
6 |
41 |
9 |
43 |
2 |
51 |
8 |
| 23 |
6 |
55 |
9 |
38 |
2 |
30 |
7 |
| 24 |
7 |
9 |
9 |
33 |
2 |
9 |
6 |
| 25 |
7 |
23 |
9 |
27 |
1 |
48 |
5 |
| 26 |
7 |
36 |
9 |
20 |
1 |
27 |
4 |
| 27 |
7 |
49 |
9 |
13 |
1 |
5 |
3 |
| 28 |
8 |
1 |
9 |
5 |
0 |
43 |
2 |
| 29 |
8 |
13 |
8 |
56 |
0 |
22 |
1 |
| 30 |
8 |
24 |
8 |
46 |
0 |
0 |
0 |
| 2d Q. |
♍ |
♌ |
♋ |
Deg. |
| 4th Q. |
♓ |
♒ |
♑ |
| Sun slower than the Clock in |
Fig. III.
230. This part of the Equation of
time may perhaps be somewhat difficult
to understand by a Figure, because both
halves of the Ecliptic seem to be on
the same side of the Globe; but it may
be made very easy to any person who
has a real Globe before him, by putting
small patches on every tenth or fifteenth
degree both of the Equator and Ecliptic;
and then, turning the ball slowly
round westward, he will see all the
patches from Aries to Cancer come to
the brazen Meridian sooner than the
corresponding patches on the Equator;
all those from Cancer to Libra will come
later to the Meridian than their corresponding
patches on the Equator;
those from Libra to Capricorn sooner,
and those from Capricorn to Aries later:
and the patches at the beginnings of
Aries, Cancer, Libra, and Capricorn,
being also on the Equator, shew that
the two Suns meet there, and come to
the Meridian together.
A machine for shewing the sidereal, the equal, and the solar
Time.
PLATE VI.
231. Let us suppose that there are two little balls moving equably
round a celestial Globe by clock-work, one always keeping in the
Ecliptic, and gilt with gold, to represent the real Sun; and the other
keeping in the Equator, and silvered, to represent the fictitious Sun:
and that whilst these balls move once, round the Globe according to
the order of Signs, the Clock turns the Globe 366 times round it’s
Axis westward. The Stars will make 366 diurnal revolutions from
the brasen Meridian to it again; and the two balls representing the real
and fictitious Sun always going farther eastward from any given Star,
102will come later than it to the Meridian every following day; and each
ball will make 365 revolutions to the Meridian; coming equally to
it at the beginnings of Aries, Cancer, Libra, and Capricorn: but
in every other point of the Ecliptic, the gilt ball will come either sooner
or later to the Meridian than the silvered ball, like the patches above-mentioned.
This would be a pretty-enough way of shewing the
reason why any given Star, which, on a certain day of the year,
comes to the Meridian with the Sun, passes over it so much sooner
every following day, as on that day twelvemonth to come to the Meridian
with the Sun again; and also to shew the reason why the real
Sun comes to the Meridian sometimes sooner, sometimes later, than
it is noon by the clock; and, on four days of the year, at the same
time; whilst the fictitious Sun always comes to the Meridian when
it is twelve at noon by the clock. This would be no difficult task
for an artist to perform; for the gold ball might be carried round
the Ecliptic by a wire from it’s north Pole, and the silver ball round
the Equator by a wire from it’s south Pole, with a few wheels to
each; which might be easily added to my improvement of the celestial
Globe, described in No 483 of the Philosophical Transactions; and of
which I shall give a description in the latter part of this Book, from
the 3d Figure of the 3d plate.
Fig. III.
232. ’Tis plain that if the Ecliptic were more obliquely posited to
the Equator, as the dotted Circle ♈x♎, the equal divisions from ♈
to x would come still sooner to the Meridian Z0♈ than those
marked A, B, C, D, and E do: for two divisions containing 30 degrees,
from ♈ to the second dott, a little short of the figure 1, come
sooner to the Meridian than one division containing only 15 degrees
from ♈ to A does, as the Ecliptic now stands; and those of the
second quadrant from x to ♎ would be so much later. The third
quadrant would be as the first, and the fourth as the second. And
it is likewise plain, that where the Ecliptic is most oblique, namely
about Aries and Libra, the difference would be greatest: and least
about Cancer and Capricorn, where the obliquity is least.
The second part of the Equation of Time.
PLATE VI.
234. Having explained one cause of the difference of time shewn by
a well-regulated Clock and a true Sun-dial; and considered the Sun,
not the Earth, as moving in the Ecliptic; we now proceed to explain
the other cause of this difference, namely, the inequality of the Sun’s
apparent motion § 205, which is slowest in summer, when the Sun is
farthest from the Earth, and swiftest in winter when he is nearest to
it. But the Earth’s motion on it’s Axis is equable all the year round,
103and is performed from west to east; which is the way that the Sun
appears to change his place in the Ecliptic.
235. If the Sun’s motion were equable in the Ecliptic, the whole
difference between the equal time as shewn by a Clock, and the unequal
time as shewn by the Sun, would arise from the obliquity of the
Ecliptic. But the Sun’s motion sometimes exceeds a degree in 24
hours, though generally it is less: and when his motion is slowest
any particular Meridian will revolve sooner to him than when his
motion is quickest; for it will overtake him in less time when he
advances a less space than when he moves through a larger.
236. Now, if there were two Suns moving in the plane of the
Ecliptic, so as to go round it in a year; the one describing an equal
arc every 24 hours, and the other describing sometimes a less arc in
24 hours, and at other times a larger; gaining at one time of the
year what it lost at the opposite; ’tis evident that either of these Suns
would come sooner or later to the Meridian than the other as it happened
to be behind or before the other: and when they were both in
conjunction they would come to the Meridian at the same moment.
Fig. IV.
237. As the real Sun moves unequably in the Ecliptic, let us suppose
a fictitious Sun to move equably in it. Let ABCD be the Ecliptic
or Orbit in which the real Sun moves, and the dotted Circle abcd
the imaginary Orbit of the fictitious Sun; each going round in a year
according to the order of letters, or from west to east. Let HIKL
be the Earth turning round it’s Axis the same way every 24 hours;
and suppose both Suns to start from A and a, in a right line with the
plane of the Meridian EH, at the same moment: the real Sun at A,
being then at his greatest distance from the Earth, at which time his
motion is slowest; and the fictitious Sun at a, whose motion is always
equable because his distance from the Earth is supposed to be always
the same. In the time that the Meridian revolves from H to H again,
according to the order of the letters HIKL, the real Sun has moved
from A to F; and the fictitious with a quicker motion from a to f,
through a larger arc: therefore, the Meridian EH will revolve sooner
from H to h under the real Sun at F, than from H to k under the fictitious
Sun at f; and consequently it will be noon by the Sun-dial
sooner than by the Clock.
As the real Sun moves from A towards C, the swiftness of his
motion increases all the way to C, where it is at the quickest. But
notwithstanding this, the fictitious Sun gains so much upon the real,
soon after his departing from A, that the increasing velocity of the real
Sun does not bring him up with the equally moving fictitious Sun till
104the former comes to C, and the latter to c, when each has gone half
round it’s respective orbit; and then being in conjunction, the Meridian
EH revolving to EK comes to both Suns at the same time, and therefore
it is noon by them both at the same moment.
But the increased velocity of the real Sun, now being at the quickest,
carries him before the fictitious; and therefore, the same Meridian will
come to the fictitious Sun sooner than to the real: for whilst the fictitious
Sun moves from c to g, the real Sun moves through a greater arc
from C to G: consequently the point K has it’s fictitious noon when it
comes to k, but not it’s real noon till it comes to l. And although
the velocity of the real Sun diminishes all the way from C to A, and
the fictitious Sun by an equable motion is still coming nearer to the
real Sun, yet they are not in conjunction till the one comes to A and the
other to a; and then it is noon by them both at the same moment.
And thus it appears, that the real noon by the Sun is always later
than the fictitious noon by the clock whilst the Sun goes from C to A,
sooner whilst he goes from A to C, and at these two points the Sun
and Clock being equal, it is noon by them both at the same moment.
Apogee, Perigee, and Apsides, what.
Fig. IV.
238. The point A is called the Sun’s Apogee, because when he is
there he is at his greatest distance from the Earth; the point C his
Perigee, because when in it he is at his least distance from the Earth:
and a right line, as AEC, drawn through the Earth’s center, from
one of these points to the other, is called the line of the Apsides.
Mean Anomaly, what.
239. The distance that the Sun has gone in any time from his
Apogee (not the distance he has to go to it though ever so little) is
called his mean Anomaly, and is reckoned in Signs and Degrees,
allowing 30 Degrees to a Sign. Thus, when the Sun has gone suppose
174 degrees from his Apogee at A, he is said to be 5 Signs 24
Degrees from it, which is his mean Anomaly: and when he is gone
suppose 355 degrees from his Apogee, he is said to be 11 Signs 25
Degrees from it, although he be but 5 Degrees short of A in coming
round to it again.
240. From what was said above it appears, that when the Sun’s
Anomaly is less than 6 Signs, that is, when he is any where between
A and C, in the half ABC of his orbit, the true noon precedes the
fictitious; but when his Anomaly is more than 6 Signs, that is, when
he is any where between C and A, in the half CDA of his Orbit,
the fictitious noon precedes the true. When his Anomaly is 0 Signs 0
Degrees, that is, when he is in his Apogee at A; or 6 Signs 0
Degrees, which is when he is in his Perigee at C; he comes to the
105Meridian at the moment that the fictitious Sun does, and then it is
noon by them both at the same instant.
| Sun faster than the Clock if his Anomaly be |
| D. |
0 Signs |
1 |
2 |
3 |
4 |
5 |
|
| ʹ |
ʺ |
ʹ |
ʺ |
ʹ |
ʺ |
ʹ |
ʺ |
ʹ |
ʺ |
ʹ |
ʺ |
| 0 |
0 |
0 |
3 |
48 |
6 |
39 |
7 |
45 |
6 |
47 |
3 |
57 |
30 |
| 1 |
0 |
8 |
3 |
55 |
6 |
43 |
7 |
45 |
6 |
43 |
3 |
50 |
29 |
| 2 |
0 |
16 |
3 |
2 |
6 |
47 |
7 |
45 |
6 |
39 |
3 |
43 |
28 |
| 3 |
0 |
24 |
4 |
9 |
6 |
51 |
7 |
45 |
6 |
35 |
3 |
35 |
27 |
| 4 |
0 |
32 |
4 |
16 |
6 |
54 |
7 |
45 |
6 |
30 |
3 |
28 |
26 |
| 5 |
0 |
40 |
4 |
22 |
6 |
58 |
7 |
44 |
6 |
26 |
3 |
20 |
25 |
| 6 |
0 |
48 |
4 |
29 |
7 |
1 |
7 |
44 |
6 |
21 |
3 |
13 |
24 |
| 7 |
0 |
56 |
4 |
35 |
7 |
5 |
7 |
43 |
6 |
16 |
3 |
5 |
23 |
| 8 |
1 |
3 |
4 |
42 |
7 |
8 |
7 |
42 |
6 |
11 |
2 |
58 |
22 |
| 9 |
1 |
11 |
4 |
48 |
7 |
11 |
7 |
41 |
6 |
6 |
2 |
50 |
21 |
| 10 |
1 |
19 |
4 |
54 |
7 |
14 |
7 |
40 |
6 |
1 |
2 |
42 |
20 |
| 11 |
1 |
27 |
5 |
0 |
7 |
17 |
7 |
38 |
5 |
56 |
2 |
35 |
19 |
| 12 |
1 |
35 |
5 |
6 |
7 |
20 |
7 |
37 |
5 |
51 |
2 |
27 |
18 |
| 13 |
1 |
43 |
5 |
12 |
7 |
22 |
7 |
35 |
5 |
45 |
2 |
19 |
17 |
| 14 |
1 |
50 |
5 |
18 |
7 |
25 |
7 |
34 |
5 |
40 |
2 |
11 |
16 |
| 15 |
1 |
58 |
5 |
24 |
7 |
27 |
7 |
32 |
5 |
34 |
2 |
3 |
15 |
| 16 |
2 |
6 |
5 |
30 |
7 |
29 |
7 |
30 |
5 |
28 |
1 |
55 |
14 |
| 17 |
2 |
13 |
5 |
35 |
7 |
31 |
7 |
28 |
5 |
22 |
1 |
47 |
13 |
| 18 |
2 |
21 |
5 |
41 |
7 |
33 |
7 |
25 |
5 |
16 |
1 |
39 |
12 |
| 19 |
2 |
28 |
5 |
46 |
7 |
35 |
7 |
23 |
5 |
10 |
1 |
31 |
11 |
| 20 |
2 |
36 |
5 |
52 |
7 |
36 |
7 |
20 |
5 |
4 |
1 |
22 |
10 |
| 21 |
2 |
43 |
5 |
57 |
7 |
38 |
7 |
18 |
4 |
58 |
1 |
14 |
9 |
| 22 |
2 |
51 |
6 |
2 |
7 |
39 |
7 |
15 |
4 |
51 |
1 |
6 |
8 |
| 23 |
2 |
58 |
6 |
7 |
7 |
41 |
7 |
12 |
4 |
45 |
0 |
58 |
7 |
| 24 |
3 |
6 |
6 |
12 |
7 |
42 |
7 |
9 |
4 |
38 |
0 |
50 |
6 |
| 25 |
3 |
13 |
6 |
16 |
7 |
43 |
7 |
5 |
4 |
31 |
0 |
41 |
5 |
| 26 |
3 |
20 |
6 |
21 |
7 |
43 |
7 |
2 |
4 |
25 |
0 |
33 |
4 |
| 27 |
3 |
27 |
6 |
26 |
7 |
44 |
6 |
58 |
4 |
18 |
0 |
25 |
3 |
| 28 |
3 |
34 |
6 |
30 |
7 |
44 |
6 |
55 |
4 |
11 |
0 |
17 |
2 |
| 29 |
3 |
41 |
6 |
34 |
7 |
45 |
6 |
51 |
4 |
4 |
0 |
8 |
1 |
| 30 |
3 |
48 |
6 |
39 |
7 |
45 |
6 |
47 |
3 |
57 |
0 |
0 |
0 |
| |
11 Signs |
10 |
9 |
8 |
7 |
6 |
D. |
| Sun slower than the Clock if his Anomaly be |
A Table of the Equation of Time, depending on the Sun’s Anomaly.
241. The annexed Table shews the Variation, or Equation of time
depending on the Sun’s Anomaly, and arising from his unequal motion
in the Ecliptic; as the former Table § 229 shews the Variation
depending on the Sun’s place, and resulting from the obliquity of the
Ecliptic: this is to be understood the same way as the other, namely,
that when the Signs are at the head of the Table, the Degrees are at
the left hand; but
when the Signs are at
the foot of the Table
the respective Degrees
are at the right
hand; and in both
cases the Equation is
in the Angle of meeting.
When both the
above-mentioned Equations
are either
faster or slower, their
sum is the absolute Equation
of Time; but
when the one is faster,
and the other slower,
it is their difference.
Thus, suppose the Equation
depending on
the Sun’s place, be 6
minutes 41 seconds
too slow, and the Equation
depending on
the Sun’s Anomaly, be
4 minutes 20 seconds
too slow, their Sun is
11 minutes 1 second
too slow. But if the
one had been 6 minutes
41 seconds too
fast, and the other 4
minutes 20 seconds too slow, their difference had been 2 minutes 21
seconds too fast, because the greater quantity is too fast.
106242. The obliquity of the Ecliptic to the Equator, which is the first
mentioned cause of the Equation of Time, would make the Sun and
Clocks agree on four days of the year; which are, when the Sun enters
Aries, Cancer, Libra, and Capricorn: but the other cause, now
explained, would make the Sun and Clocks equal only twice in a
year; that is, when the Sun is in his Apogee and Perigee. Consequently,
when these two points fall in the beginnings of Cancer and
Capricorn, or of Aries and Libra, they concur in making the Sun and
Clocks equal in these points. But the Apogee at present is in the 9th
degree of Cancer, and the Perigee in the 9th degree of Capricorn;
and therefore the Sun and Clocks cannot be equal about the beginning
of these Signs, nor at any time of the year, except when the swiftness
or slowness of Equation resulting from one cause just balances the
slowness or swiftness arising from the other.
243. The last Table but one, at the end of this Chapter, shews
the Sun’s place in the Ecliptic at the noon of every day by the clock,
for the second year after leap-year; and also the Sun’s Anomaly to
the nearest degree, neglecting the odd minutes of a degree. Their
use is only to assist in shewing the method of making a general Equation
Table from the two fore-mentioned Tables of Equation depending
on the Sun’s Place and Anomaly § 229, 241; concerning which
method we shall give a few examples presently. The following Tables
are such as might be made from these two; and shew the absolute
Equation of Time resulting from the combination of both it’s causes;
in which the minutes, as well as degrees, both of the Sun’s Place
and Anomaly are considered. The use of these Tables is already explained,
§ 225; and they serve for every day in leap-year, and the
first, second, and third years after: For on most of the same days
of all these years the Equation differs, because of the odd six hours
more than the 365 days of which the year consists.
Examples for making Equation Tables.
Example I. On the 15th of April the Sun is in the 25th degree
of ♈ Aries, and his Anomaly is 9 Signs 15 Degrees; the Equation
resulting from the former is 7 minutes 23 seconds of time too fast
§ 229; and from the latter, 7 minutes 27 seconds too slow, § 241;
the difference is 4 seconds that the Sun is too slow at the noon of
that day; taking it in gross for the degrees of the Sun’s Place and
Anomaly, without making proportionable allowance for the odd minutes.
Hence, at noon the swiftness of the one Equation balancing so
nearly the slowness of the other, makes the Sun and Clocks equal on
some part of that day.
107Example II. On the 16th of June, the Sun is in the 25th
degree of ♊ Gemini, and his Anomaly is 11 Signs 16 Degrees; the
Equation arising from the former is 1 minute 48 seconds too fast;
and from the latter 1 minute 50 seconds too slow; which balancing
one another at noon to 2 seconds, the Sun and Clocks are again equal
on that day.
Example III. On the 31st of August the Sun’s place is 7 degrees
52 minutes of ♍ Virgo (which we shall call the 8th degree, as it is
so near) and his Anomaly is 2 Signs 0 Degrees; the Equation arising
from the former is 6 minutes 41 seconds too slow; and from the latter
6 minutes 39 seconds too fast; the difference being only 2 seconds
too slow at noon, and decreasing towards an equality will make the
Sun and Clocks equal in the afternoon of that day.
Example. IV. On the 23d of December the Sun’s place is 1 degree
41 minutes (call it 2 degrees) of ♑ Capricorn, and his Anomaly
is 5 Signs 23 Degrees; the Equation for the former is 43 seconds
too slow, and for the latter 58 seconds too fast; the difference is
15 seconds too fast at noon; which decreasing will come to an
equality, and so make the Sun and Clocks equal in the evening of
that day.
And thus we find, that on some part of each of the above-mentioned
four days, the Sun and Clocks are equal; but if we work examples
for all other days of the year we shall find them different. And,
Remark.
244. On those days which are equidistant from any Equinox or
Solstice, we do not find that the Equation is as much too fast or too
slow, on the one side, as it is too slow or too fast on the other.
The reason is, that the line of the Apsides § 238, does not, at present,
fall either into the Equinoctial or Solsticial points § 242.
The reason why Equation Tables are but temporary.
245. If the line of the Apsides, together with the Equinoctial and
Solsticial points, were immoveable, a general Equation Table might
be made from the preceding Equation Tables, which would always
keep true, because these Tables themselves are permanent. But, with
respect to the fixed Stars, the line of the Apsides moves forwards 12
seconds of a degree every year, and the above points 50 seconds
backward. So that if in any given year, the Equinoctial points, and
line of the Apsides were coincident, in 100 years afterward they
would be separated 1 degree 43 minutes 20 seconds; and consequently
108in 5225.8 years they would be separated 90 degrees, and
could not meet again, so that the same Equinoctial point should fall
again into the Apogee in less than 20,903 years: and this is the shortest
Period in which the Equation of Time can be restored to the same
state again, with respect to the same seasons of the year.
CHAP. XIV.
Of the Precession of the Equinoxes.
246. It has been already observed, § 116, that by the Earth’s motion
on it’s Axis, there is more matter accumulated all round the
equatoreal parts than any where else on the Earth.
The Sun and Moon, by attracting this redundancy of matter, bring
the Equator sooner under them in every return towards it than if there
was no such accumulation. Therefore, if the Sun sets out, as from
any Star, or other fixed point in the Heavens, the moment he is departing
from the Equinoctial or either Tropic, he will come to the same
again before he compleats his annual course, so as to arrive at the same
fixed Star or Point from whence he set out.
When the Sun arrives at the same [56]Equinoctial or Solstitial Point,
he finishes what we call the Tropical Year, which, by long observation,
is found to contain 365 days 5 hours 48 minutes 57 seconds:
and when he arrives at the same fixed Star again, as seen from the
Earth, he compleats the Sidereal Year; which is found to contain 365
days 6 hours 9 minutes
141⁄2
seconds. The Sidereal Year is therefore
20 minutes
171⁄2
seconds longer than the Solar or Tropical year, and
9 minutes
141⁄2
seconds longer than the Julian or Civil year, which we
state at 365 days 6 hours: so that the Civil year is almost a mean
betwixt the Sidereal and Tropical.
247. As the Sun describes the whole Ecliptic, or 360 degrees, in
a Tropical year, he moves 59ʹ 8ʺ of a degree every day; and consequently
50ʺ of a degree in 20 minutes
171⁄2
seconds of time: therefore,
he will arrive at the same Equinox or Solstice when he is 50ʺ of a
degree short of the same Star or fixed point in the Heavens from which
he set out in the year before. So that, with respect to the fixed Stars,
109the Sun and Equinoctial
points fall
back (as it were)
30 degrees in 2160
years; which will
make the Stars appear
to have gone
30 deg. forward,
with respect to the
Signs of the Ecliptic
in that time:
for the same Signs
always keep in the
same points of the
Ecliptic, without
regard to the constellations.
| A Table shewing the Precession of the Equinoctial
Points in the Heavens, both in Motion and Time;
and the Anticipation of the Equinoxes on Earth. |
| Julian years. |
Precession of the Equinoctial Points in the Heavens. |
|
Anticipation of the Equinoxes on the Earth. |
| Motion. |
Time. |
| S. |
° |
ʹ |
ʺ |
Days |
H. |
M. |
S. |
D. |
H. |
M. |
S. |
| 1 |
0 |
0 |
0 |
50 |
0 |
0 |
20 |
171⁄2 |
0 |
0 |
11 |
3 |
| 2 |
0 |
0 |
1 |
40 |
0 |
0 |
40 |
35 |
0 |
0 |
22 |
6 |
| 3 |
0 |
0 |
2 |
30 |
0 |
1 |
0 |
521⁄2 |
0 |
0 |
33 |
9 |
| 4 |
0 |
0 |
3 |
20 |
0 |
1 |
21 |
10 |
0 |
0 |
44 |
12 |
| 5 |
0 |
0 |
4 |
10 |
0 |
1 |
41 |
271⁄2 |
0 |
0 |
55 |
15 |
| 6 |
0 |
0 |
5 |
0 |
0 |
2 |
1 |
45 |
0 |
1 |
6 |
18 |
| 7 |
0 |
0 |
5 |
50 |
0 |
2 |
22 |
21⁄2 |
0 |
1 |
17 |
21 |
| 8 |
0 |
0 |
6 |
40 |
0 |
2 |
42 |
20 |
0 |
1 |
28 |
24 |
| 9 |
0 |
0 |
7 |
30 |
0 |
3 |
2 |
371⁄2 |
0 |
1 |
39 |
27 |
| 10 |
0 |
0 |
8 |
20 |
0 |
3 |
22 |
55 |
0 |
1 |
50 |
30 |
| 20 |
0 |
0 |
16 |
40 |
0 |
6 |
45 |
50 |
0 |
3 |
41 |
0 |
| 30 |
0 |
0 |
25 |
0 |
0 |
10 |
8 |
45 |
0 |
5 |
31 |
30 |
| 40 |
0 |
0 |
33 |
20 |
0 |
13 |
31 |
40 |
0 |
7 |
22 |
0 |
| 50 |
0 |
0 |
41 |
40 |
0 |
16 |
54 |
35 |
0 |
9 |
12 |
30 |
| 60 |
0 |
0 |
50 |
0 |
0 |
20 |
17 |
30 |
0 |
11 |
3 |
0 |
| 70 |
0 |
0 |
58 |
20 |
0 |
23 |
40 |
25 |
0 |
12 |
53 |
30 |
| 80 |
0 |
1 |
6 |
40 |
1 |
3 |
3 |
20 |
0 |
14 |
44 |
0 |
| 90 |
0 |
1 |
15 |
0 |
1 |
6 |
26 |
15 |
0 |
16 |
34 |
30 |
| 100 |
0 |
1 |
23 |
20 |
1 |
9 |
49 |
10 |
0 |
18 |
25 |
0 |
| 200 |
0 |
2 |
46 |
40 |
2 |
19 |
38 |
20 |
1 |
12 |
50 |
0 |
| 300 |
0 |
4 |
10 |
0 |
4 |
5 |
27 |
30 |
2 |
7 |
15 |
0 |
| 400 |
0 |
5 |
33 |
20 |
5 |
15 |
16 |
40 |
3 |
1 |
40 |
0 |
| 500 |
0 |
6 |
56 |
40 |
7 |
1 |
5 |
50 |
3 |
20 |
5 |
0 |
| 600 |
0 |
8 |
20 |
0 |
8 |
10 |
55 |
0 |
4 |
14 |
30 |
0 |
| 700 |
0 |
9 |
43 |
20 |
9 |
20 |
44 |
10 |
5 |
8 |
55 |
0 |
| 800 |
0 |
11 |
6 |
40 |
11 |
6 |
33 |
20 |
6 |
3 |
20 |
0 |
| 900 |
0 |
12 |
29 |
0 |
12 |
16 |
22 |
30 |
6 |
21 |
45 |
0 |
| 1000 |
0 |
13 |
53 |
20 |
14 |
2 |
11 |
40 |
7 |
16 |
10 |
0 |
| 2000 |
0 |
27 |
46 |
40 |
28 |
4 |
23 |
20 |
15 |
8 |
20 |
0 |
| 3000 |
1 |
11 |
40 |
0 |
42 |
6 |
35 |
0 |
23 |
0 |
30 |
0 |
| 4000 |
1 |
25 |
33 |
20 |
56 |
8 |
46 |
40 |
30 |
16 |
40 |
0 |
| 5000 |
2 |
9 |
26 |
40 |
70 |
10 |
58 |
20 |
38 |
8 |
50 |
0 |
| 6000 |
2 |
23 |
20 |
0 |
84 |
13 |
10 |
0 |
46 |
1 |
0 |
0 |
| 7000 |
3 |
7 |
13 |
20 |
98 |
15 |
21 |
40 |
53 |
17 |
10 |
0 |
| 8000 |
3 |
21 |
6 |
40 |
112 |
17 |
33 |
20 |
61 |
9 |
20 |
0 |
| 9000 |
4 |
5 |
0 |
0 |
126 |
19 |
45 |
0 |
69 |
1 |
30 |
0 |
| 10000 |
4 |
18 |
53 |
20 |
140 |
21 |
56 |
40 |
76 |
17 |
40 |
0 |
| 20000 |
9 |
7 |
46 |
40 |
281 |
19 |
53 |
20 |
153 |
11 |
20 |
0 |
| 25920 |
12 |
0 |
0 |
0 |
365 |
6 |
0 |
0 |
198 |
21 |
36 |
0 |
Fig. IV.
To explain this
by a Figure, let
the Sun be in conjunction
with a fixed
Star at S, suppose
in the 30th degree
of ♉, on the
20th day of May
1756. Then, making
2160 revolutions
through the
Ecliptic VWX, at
the end of so many
Sidereal years,
he will be found
again at S: but at
the end of so many
Julian years, he
will be found at M,
short of S: and at
the end of so many
Tropical years,
he will be found
short of M, in the
30th deg. of Taurus
110at T, which has receded back from S to T in that time, by the
Precession of the Equinoctial points ♈ Aries and ♎ Libra. The Arc
ST will be equal to the amount of the Precession of the Equinox in
2160 years, at the rate of 50ʺ of a degree, or 20 min.
171⁄2
sec. of
time, annually: this, in so many years, makes 30 days,
101⁄2
hours;
which is the difference between 2160 Sidereal and Tropical years:
And the Arc MT will be equal to the space moved through by the Sun
in 2160 times 11 min. 3 sec. or 16 days, 13 hours 48 minutes, which
is the difference between 2160 Julian and Tropical years.
248. From the shifting of the Equinoctial points, and with them all
the Signs of the Ecliptic, it follows that those Stars which in the infancy
of astronomy were in Aries are now got into Taurus; those of
Taurus into Gemini, &c. Hence likewise it is, that the Stars which rose or
set at any particular season of the year, in the time of Hesiod, Eudoxus,
Virgil, Pliny, &c. by no means answer at this time to their descriptions.
The preceding table shews the quantity of this shifting both in
the heavens and on the earth, for any number of years to 25,920;
which compleats the grand celestial period: within which any number
and its quantity is easily found; as in the following example, for 5763
years; which at the Autumnal Equinox, A. D. 1756, is thought to be
the age of the world. So that with regard to the fixed Stars, the Equinoctial
points in the
heavens, have receded
2s 20° 2ʹ 30ʺ
since the creation;
which is as much as
the Sun moves in
81d 5h 0m 52s. And
since that time, or
in 5763 years, the
Equinoxes with us
have fallen back
44d 5h 21m 9s; hence, reckoning from the time of the Julian Equinox,
A. D. 1756, viz. Sept. 12th, it appears that the Autumnal
Equinox at the creation was on the 26th of October.
| Julian years. |
Precession of the Equinoctial Points in the Heavens. |
|
Anticipation of the Equinoxes on the Earth. |
| Motion. |
Time. |
| S. |
° |
ʹ |
ʺ |
D. |
H. |
M. |
S. |
D. |
H. |
M. |
S. |
| 5000 |
2 |
9 |
26 |
40 |
70 |
10 |
58 |
20 |
38 |
8 |
50 |
0 |
| 700 |
0 |
9 |
43 |
20 |
9 |
20 |
44 |
10 |
5 |
8 |
55 |
0 |
| 60 |
0 |
0 |
50 |
0 |
0 |
20 |
17 |
30 |
0 |
11 |
3 |
0 |
| 3 |
0 |
0 |
2 |
30 |
0 |
1 |
0 |
52 |
0 |
0 |
33 |
9 |
| 5763 |
2 |
20 |
2 |
30 |
81 |
5 |
0 |
52 |
44 |
5 |
21 |
9 |
The anticipation of the Equinoxes and Seasons.
PLATE VI.
249. The anticipation of the Equinoxes, and consequently of the
seasons, is by no means owing to the Precession of the Equinoctial
and Solsticial points in the Heavens, (which can only affect the apparent
motions, places and declinations of the fixed Stars) but to the difference
between the Civil and Solar year, which is 11 minutes 3 seconds;
111the Civil year containing 365 days 6 hours, and the Solar
year 365 days 5 hours 48 minutes 57 seconds. The following table
shews the length, and consequently the difference of any number of Sidereal,
Civil, and Solar years from 1 to 10,000.
The reason for altering the Style.
250. The above 11 minutes 3 seconds, by which the Civil or Julian
year exceeds the Solar, amounts to 11 days in 1433 years: and so much
our seasons have fallen back with respect to the days of the months,
since the time of the Nicene Council in A.D. 325, and therefore in order
to bring back all the Fasts and Festivals to the days then settled, it
was requisite to suppress 11 nominal days. And that the same seasons
might be kept to the same times of the year for the future, to leave
out the Bissextile day in February at the end of every century of years
not divisible by 4; reckoning them only common years, as the 17th,
18th and 19th centuries, viz. the years 1700, 1800, 1900, &c. because
a day intercalated every fourth year was too much, and retaining
the Bissextile-day at the end of those Centuries of years which are
divisible by 4, as the 16th, 20th and 24th Centuries; viz. the years
1600, 2000, 2400, &c. Otherwise, in length of time the seasons
would have been quite reversed with regard to the months of the years;
though it would have required near 23,783 years to have brought
about such a total change. If the Earth had made exactly
3651⁄4
diurnal
rotations on its axis, whilst it revolved from any Equinoctial or
Solstitial point to the same again, the Civil and Solar years would always
have kept pace together; and the style would never have needed
any alteration.
The Precession of the Equinoctial Points.
251. Having already mentioned the cause of the Precession of the
Equinoctial points in the heavens, § 246, which occasions a flow deviation
of the earth’s axis from its parallelism, and thereby a change
of the declination of the Stars from the Equator, together with a slow
apparent motion of the Stars forward with respect to the Signs of
the Ecliptic; we shall now describe the Phenomena by a Diagram.
Fig. V.
Let NZSVL be the Earth, SONA its Axis produced to the starry
Heavens, and terminating in A, the present north Pole of the Heavens,
which is vertical to N the north Pole of the Earth. Let EOQ
be the Equator, T♋Z the Tropic of Cancer, and VT♑ the Tropic
of Capricorn: VOZ the Ecliptic, and BO its Axis, both which are
immoveable among the Stars. But, as [57]the Equinoctial points recede
112in the Ecliptic, the Earth’s Axis SON is in motion upon the
Earth’s center O, in such a manner as to describe the double Cone
NOn and SOs, round the Axis of the Ecliptic BO, in the time that
the Equinoctial points move quite round the Ecliptic, which is 25,920
years; and in that length of time, the north Pole of the Earth’s Axis
produced, describes the Circle ABCDA in the starry Heavens, round
the Pole of the Ecliptic, which keeps immoveable in the center of that
Circle. The Earth’s Axis being
231⁄2
degrees inclined to the Axis of
the Ecliptic, the Circle ABCDA, described by the north Pole of
the Earth’s Axis produced to A, is 47 degrees in diameter, or
double the inclination of the Earth’s Axis. In consequence of this,
the point A, which at present is the North Pole of the Heavens, and
near to a Star of the second magnitude in the tail of the constellation
called the Little Bear, must be deserted by the Earth’s Axis; which
moving backwards a degree every 72 years, will be directed towards
the Star or Point B in 6480 years hence: and in double of that time,
or 12,960 years, it will be directed towards the Star or Point C;
which will then be the North Pole of the Heavens, although it is at
present
81⁄2
degrees south of the Zenith of London L. The present position
of the Equator EOQ will then be changed into eOq, the Tropic
of Cancer T♋Z into Vt♋, and the Tropic of Capricorn VT♑
into t♑Z; as is evident by the Figure. And the Sun, in the same part of
the Heavens where he is now over the earthly Tropic of Capricorn, and
makes the shortest days and longest nights in the Northern Hemisphere,
will then be over the earthly Tropic of Cancer, and make the days longest,
and nights shortest. So that it will require 12,960 years yet more, or
25,920 from the present time, to bring the North Pole N quite round,
so as to be directed toward that point of the Heavens which is vertical
to it at present. And then, and not till then, the same Stars which at
present describe the Equator, Tropics, polar Circles, and Poles, by the
Earth’s diurnal motion, will describe them over again.
113A TABLE shewing the Time contained in any number of Sidereal, Julian, and Solar Years, from 1 to 10000.
| Sidereal Years. |
|
Julian Years. |
|
Solar Years. |
| Years |
Days |
H. |
M. |
S. |
Days |
H. |
Days |
H. |
M. |
S. |
| 1 |
Contain 365 |
6 |
9 |
141⁄2 |
Contain 365 |
6 |
Contain 365 |
5 |
48 |
57 |
| 2 |
730 |
12 |
18 |
29 |
730 |
12 |
370 |
11 |
37 |
54 |
| 3 |
1095 |
18 |
27 |
431⁄2 |
1095 |
18 |
1095 |
17 |
26 |
51 |
| 4 |
1461 |
0 |
36 |
58 |
1461 |
0 |
1460 |
23 |
15 |
48 |
| 5 |
1826 |
6 |
46 |
121⁄2 |
1826 |
6 |
1826 |
5 |
4 |
45 |
| 6 |
2191 |
12 |
55 |
27 |
2191 |
12 |
2191 |
10 |
53 |
42 |
| 7 |
2556 |
19 |
5 |
411⁄2 |
2556 |
18 |
2556 |
16 |
42 |
39 |
| 8 |
2922 |
1 |
13 |
56 |
2922 |
0 |
2921 |
22 |
31 |
36 |
| 9 |
3287 |
7 |
23 |
101⁄2 |
3287 |
6 |
3287 |
4 |
20 |
33 |
| 10 |
3652 |
13 |
32 |
25 |
3652 |
12 |
3652 |
10 |
9 |
30 |
| 20 |
7305 |
3 |
4 |
50 |
7305 |
0 |
7304 |
20 |
19 |
0 |
| 30 |
10957 |
16 |
37 |
15 |
10957 |
12 |
10957 |
6 |
28 |
30 |
| 40 |
14610 |
6 |
9 |
40 |
14610 |
0 |
14609 |
16 |
38 |
0 |
| 50 |
18262 |
19 |
42 |
5 |
18262 |
12 |
18262 |
2 |
47 |
30 |
| 60 |
21915 |
9 |
14 |
30 |
21915 |
0 |
21914 |
12 |
57 |
0 |
| 70 |
25567 |
22 |
46 |
55 |
25567 |
12 |
25566 |
23 |
6 |
30 |
| 80 |
29220 |
12 |
19 |
20 |
25220 |
0 |
29219 |
9 |
16 |
0 |
| 90 |
32873 |
1 |
51 |
45 |
32872 |
12 |
32871 |
19 |
25 |
30 |
| 100 |
36525 |
15 |
24 |
10 |
36525 |
|
36524 |
5 |
35 |
|
| 200 |
73051 |
6 |
48 |
20 |
73050 |
|
73048 |
11 |
10 |
|
| 300 |
109576 |
22 |
12 |
30 |
109575 |
|
109572 |
16 |
45 |
|
| 400 |
146102 |
13 |
36 |
40 |
146100 |
|
146096 |
22 |
20 |
|
| 500 |
182628 |
5 |
0 |
50 |
182625 |
|
182621 |
3 |
55 |
|
| 600 |
219153 |
20 |
25 |
|
219150 |
|
219145 |
9 |
30 |
|
| 700 |
255679 |
11 |
49 |
10 |
255675 |
|
255669 |
15 |
5 |
|
| 800 |
292205 |
3 |
13 |
20 |
292200 |
|
292193 |
20 |
10 |
|
| 900 |
328730 |
18 |
37 |
30 |
328725 |
|
328718 |
2 |
15 |
|
| 1000 |
365256 |
10 |
1 |
40 |
365250 |
|
365242 |
7 |
50 |
|
| 2000 |
730512 |
20 |
3 |
20 |
730500 |
|
730484 |
15 |
40 |
|
| 3000 |
1095769 |
6 |
5 |
|
1095750 |
|
1095726 |
23 |
30 |
|
| 4000 |
1461025 |
16 |
6 |
40 |
1461000 |
|
1460969 |
7 |
20 |
|
| 5000 |
1826282 |
2 |
8 |
20 |
1826250 |
|
1826211 |
15 |
10 |
|
| 6000 |
2191538 |
12 |
10 |
|
2191500 |
|
2191453 |
14 |
40 |
|
| 7000 |
2556794 |
22 |
11 |
40 |
2556750 |
|
2556696 |
6 |
50 |
|
| 8000 |
2922051 |
8 |
13 |
20 |
2922000 |
|
2921938 |
14 |
40 |
|
| 9000 |
3287037 |
18 |
15 |
|
3287250 |
|
3287180 |
22 |
30 |
|
| 10000 |
3652564 |
4 |
16 |
40 |
3652500 |
|
3652423 |
6 |
20 |
|
114
| A TABLE shewing the Sun’s true Place, and Distance from his Apogee,
for the second Year after Leap-year. |
| Days |
January |
February |
March |
April |
May |
June |
| Sun’s Place. |
Sun’s Anom. |
Sun’s Place. |
Sun’s Anom. |
Sun’s Place. |
Sun’s Anom. |
Sun’s Place. |
Sun’s Anom. |
Sun’s Place. |
Sun’s Anom. |
Sun’s Place. |
Sun’s Anom. |
| D. |
M. |
S. |
D. |
D. |
M. |
S. |
D. |
D. |
M. |
S. |
D. |
D. |
M. |
S. |
D. |
D. |
M. |
S. |
D. |
D. |
M. |
S. |
D. |
| 1 |
11♑ |
7 |
6 |
2 |
12♒ |
39 |
7 |
3 |
10♓ |
53 |
8 |
0 |
11♈ |
40 |
9 |
1 |
10♉ |
57 |
10 |
0 |
10♊ |
46 |
11 |
1 |
| 2 |
12 |
8 |
6 |
3 |
13 |
40 |
7 |
4 |
11 |
53 |
8 |
1 |
12 |
39 |
9 |
2 |
11 |
55 |
10 |
1 |
11 |
44 |
11 |
2 |
| 3 |
13 |
9 |
6 |
4 |
14 |
41 |
7 |
5 |
12 |
53 |
8 |
2 |
13 |
38 |
9 |
3 |
12 |
53 |
10 |
2 |
12 |
41 |
11 |
3 |
| 4 |
14 |
10 |
6 |
5 |
15 |
42 |
7 |
6 |
13 |
53 |
8 |
3 |
14 |
37 |
9 |
4 |
13 |
51 |
10 |
3 |
13 |
38 |
11 |
4 |
| 5 |
15 |
11 |
6 |
6 |
16 |
43 |
7 |
7 |
14 |
53 |
8 |
4 |
15 |
36 |
9 |
5 |
14 |
49 |
10 |
4 |
14 |
35 |
11 |
5 |
| 6 |
16 |
12 |
6 |
7 |
17 |
43 |
7 |
8 |
5 |
53 |
8 |
5 |
16 |
35 |
9 |
6 |
15 |
47 |
10 |
5 |
15 |
33 |
11 |
6 |
| 7 |
17 |
14 |
6 |
8 |
18 |
44 |
7 |
9 |
16 |
53 |
8 |
6 |
17 |
34 |
9 |
7 |
16 |
45 |
10 |
6 |
16 |
30 |
11 |
7 |
| 8 |
18 |
15 |
6 |
9 |
19 |
45 |
7 |
10 |
17 |
53 |
8 |
7 |
18 |
33 |
9 |
8 |
17 |
43 |
10 |
7 |
17 |
28 |
11 |
8 |
| 9 |
19 |
16 |
6 |
10 |
20 |
46 |
7 |
11 |
18 |
53 |
8 |
8 |
19 |
32 |
9 |
9 |
18 |
41 |
10 |
8 |
18 |
25 |
11 |
9 |
| 10 |
20 |
17 |
6 |
11 |
21 |
46 |
7 |
12 |
19 |
53 |
8 |
9 |
20 |
30 |
9 |
10 |
19 |
39 |
10 |
9 |
19 |
22 |
11 |
10 |
| 11 |
21 |
18 |
6 |
12 |
22 |
47 |
7 |
13 |
20 |
52 |
8 |
10 |
21 |
29 |
9 |
11 |
20 |
37 |
10 |
10 |
20 |
20 |
11 |
11 |
| 12 |
22 |
19 |
6 |
13 |
23 |
47 |
7 |
14 |
21 |
52 |
8 |
11 |
22 |
28 |
9 |
12 |
21 |
34 |
10 |
11 |
21 |
17 |
11 |
12 |
| 13 |
23 |
21 |
6 |
14 |
24 |
48 |
7 |
15 |
22 |
52 |
8 |
12 |
23 |
26 |
9 |
13 |
22 |
32 |
10 |
12 |
22 |
14 |
11 |
13 |
| 14 |
24 |
22 |
6 |
15 |
25 |
48 |
7 |
16 |
23 |
52 |
8 |
13 |
24 |
25 |
9 |
14 |
23 |
30 |
10 |
13 |
23 |
11 |
11 |
14 |
| 15 |
25 |
23 |
6 |
16 |
26 |
49 |
7 |
17 |
24 |
51 |
8 |
14 |
25 |
24 |
9 |
15 |
24 |
28 |
10 |
14 |
24 |
8 |
11 |
15 |
| 16 |
26 |
24 |
6 |
17 |
27 |
49 |
7 |
18 |
25 |
51 |
8 |
15 |
26 |
22 |
9 |
16 |
25 |
26 |
10 |
15 |
25 |
6 |
11 |
16 |
| 17 |
27 |
25 |
6 |
18 |
28 |
50 |
7 |
19 |
26 |
51 |
8 |
16 |
27 |
21 |
9 |
17 |
26 |
23 |
10 |
16 |
26 |
3 |
11 |
17 |
| 18 |
28 |
26 |
6 |
19 |
29 |
50 |
7 |
20 |
27 |
50 |
8 |
17 |
28 |
19 |
9 |
18 |
27 |
21 |
10 |
17 |
27 |
0 |
11 |
18 |
| 19 |
29 |
27 |
6 |
20 |
♓ |
51 |
7 |
21 |
28 |
50 |
8 |
18 |
29 |
18 |
9 |
19 |
28 |
19 |
10 |
18 |
27 |
58 |
11 |
18 |
| 20 |
♒ |
28 |
6 |
21 |
1 |
51 |
7 |
22 |
29 |
49 |
8 |
19 |
♉ |
16 |
9 |
20 |
29 |
16 |
10 |
19 |
28 |
55 |
11 |
19 |
| 21 |
1 |
29 |
6 |
22 |
2 |
51 |
7 |
23 |
♈ |
49 |
8 |
20 |
1 |
15 |
9 |
21 |
♊ |
15 |
10 |
20 |
29 |
52 |
11 |
20 |
| 22 |
2 |
30 |
6 |
23 |
3 |
52 |
7 |
24 |
1 |
48 |
8 |
21 |
2 |
13 |
9 |
22 |
1 |
11 |
10 |
21 |
♋ |
49 |
11 |
21 |
| 23 |
3 |
31 |
6 |
24 |
4 |
52 |
7 |
25 |
2 |
47 |
8 |
22 |
3 |
11 |
9 |
23 |
2 |
9 |
10 |
22 |
1 |
46 |
11 |
22 |
| 24 |
4 |
32 |
6 |
25 |
5 |
52 |
7 |
26 |
3 |
47 |
8 |
23 |
4 |
10 |
9 |
24 |
3 |
6 |
10 |
23 |
2 |
44 |
11 |
23 |
| 25 |
5 |
33 |
6 |
26 |
6 |
52 |
7 |
27 |
4 |
46 |
8 |
24 |
5 |
8 |
9 |
25 |
4 |
4 |
10 |
24 |
3 |
41 |
11 |
24 |
| 26 |
6 |
34 |
6 |
27 |
7 |
53 |
7 |
28 |
5 |
45 |
8 |
25 |
6 |
6 |
9 |
26 |
5 |
2 |
10 |
25 |
4 |
38 |
11 |
25 |
| 27 |
7 |
35 |
6 |
28 |
8 |
53 |
7 |
29 |
6 |
45 |
8 |
26 |
7 |
4 |
9 |
27 |
5 |
59 |
10 |
26 |
5 |
35 |
11 |
26 |
| 28 |
8 |
36 |
6 |
29 |
9 |
53 |
8 |
0 |
7 |
44 |
8 |
27 |
8 |
3 |
9 |
28 |
6 |
56 |
10 |
27 |
6 |
32 |
11 |
27 |
| 29 |
9 |
37 |
7 |
0 |
|
|
|
|
8 |
43 |
8 |
28 |
9 |
1 |
9 |
29 |
7 |
54 |
10 |
28 |
7 |
30 |
11 |
28 |
| 30 |
10 |
38 |
7 |
1 |
|
|
|
|
9 |
42 |
8 |
29 |
9 |
59 |
9 |
29 |
8 |
51 |
10 |
29 |
8 |
27 |
11 |
29 |
| 31 |
11 |
39 |
7 |
2 |
|
|
|
|
10 |
41 |
9 |
0 |
|
|
|
|
9 |
48 |
11 |
0 |
|
|
|
|
115
| A TABLE shewing the Sun’s true Place, and Distance from his Apogee,
for the second Year after Leap-year. |
| Days |
July |
August |
September |
October |
November |
December |
| Sun’s Place. |
Sun’s Anom. |
Sun’s Place. |
Sun’s Anom. |
Sun’s Place. |
Sun’s Anom. |
Sun’s Place. |
Sun’s Anom. |
Sun’s Place. |
Sun’s Anom. |
Sun’s Place. |
Sun’s Anom. |
| D. |
M. |
S. |
D. |
D. |
M. |
S. |
D. |
D. |
M. |
S. |
D. |
D. |
M. |
S. |
D. |
D. |
M. |
S. |
D. |
D. |
M. |
S. |
D. |
| 1 |
9♋ |
24 |
0 |
0 |
8♌ |
59 |
1 |
0 |
8♍ |
51 |
2 |
1 |
8♎ |
10 |
3 |
1 |
9♏ |
0 |
4 |
2 |
9♐ |
18 |
5 |
1 |
| 2 |
10 |
21 |
0 |
1 |
9 |
57 |
1 |
1 |
9 |
49 |
2 |
2 |
9 |
9 |
3 |
2 |
10 |
0 |
4 |
3 |
10 |
19 |
5 |
2 |
| 3 |
11 |
18 |
0 |
2 |
10 |
54 |
1 |
2 |
10 |
47 |
2 |
3 |
10 |
8 |
3 |
3 |
11 |
0 |
4 |
4 |
11 |
20 |
5 |
3 |
| 4 |
12 |
15 |
0 |
3 |
11 |
52 |
1 |
3 |
11 |
45 |
2 |
4 |
11 |
8 |
3 |
4 |
12 |
1 |
4 |
5 |
12 |
21 |
5 |
4 |
| 5 |
13 |
13 |
0 |
4 |
12 |
49 |
1 |
4 |
12 |
43 |
2 |
5 |
12 |
7 |
3 |
5 |
13 |
1 |
4 |
6 |
13 |
22 |
5 |
5 |
| 6 |
14 |
10 |
0 |
5 |
13 |
47 |
1 |
5 |
13 |
42 |
2 |
6 |
13 |
6 |
3 |
6 |
14 |
1 |
4 |
7 |
14 |
23 |
5 |
6 |
| 7 |
15 |
7 |
0 |
6 |
14 |
44 |
1 |
6 |
14 |
40 |
2 |
7 |
14 |
6 |
3 |
7 |
15 |
2 |
4 |
8 |
15 |
24 |
5 |
7 |
| 8 |
16 |
4 |
0 |
7 |
15 |
42 |
1 |
7 |
15 |
39 |
2 |
8 |
15 |
5 |
3 |
8 |
16 |
2 |
4 |
9 |
16 |
25 |
5 |
8 |
| 9 |
17 |
1 |
0 |
8 |
16 |
39 |
1 |
8 |
16 |
37 |
2 |
9 |
16 |
4 |
3 |
9 |
17 |
2 |
4 |
10 |
17 |
26 |
5 |
9 |
| 10 |
17 |
59 |
0 |
8 |
17 |
37 |
1 |
9 |
17 |
35 |
2 |
10 |
17 |
4 |
3 |
10 |
18 |
3 |
4 |
11 |
18 |
27 |
5 |
10 |
| 11 |
18 |
56 |
0 |
9 |
18 |
35 |
1 |
10 |
18 |
34 |
2 |
11 |
18 |
3 |
3 |
11 |
19 |
3 |
4 |
12 |
19 |
28 |
5 |
11 |
| 12 |
19 |
53 |
0 |
10 |
19 |
32 |
1 |
11 |
19 |
32 |
2 |
12 |
19 |
3 |
3 |
12 |
20 |
4 |
4 |
13 |
20 |
29 |
5 |
12 |
| 13 |
20 |
50 |
0 |
11 |
20 |
30 |
1 |
12 |
20 |
31 |
2 |
13 |
20 |
2 |
3 |
13 |
21 |
4 |
4 |
14 |
21 |
30 |
5 |
13 |
| 14 |
21 |
47 |
0 |
12 |
21 |
28 |
1 |
13 |
21 |
29 |
2 |
14 |
21 |
2 |
3 |
14 |
22 |
5 |
4 |
15 |
22 |
31 |
5 |
14 |
| 15 |
22 |
45 |
0 |
13 |
22 |
25 |
1 |
14 |
22 |
28 |
2 |
15 |
22 |
2 |
3 |
15 |
23 |
5 |
4 |
16 |
23 |
32 |
5 |
15 |
| 16 |
23 |
42 |
0 |
14 |
23 |
23 |
1 |
15 |
23 |
27 |
2 |
16 |
23 |
1 |
3 |
16 |
24 |
6 |
4 |
17 |
24 |
33 |
5 |
16 |
| 17 |
24 |
39 |
0 |
15 |
24 |
21 |
1 |
16 |
24 |
25 |
2 |
17 |
24 |
1 |
3 |
17 |
25 |
7 |
4 |
18 |
25 |
34 |
5 |
17 |
| 18 |
25 |
36 |
0 |
16 |
25 |
19 |
1 |
17 |
25 |
24 |
2 |
18 |
25 |
1 |
3 |
18 |
26 |
7 |
4 |
19 |
26 |
35 |
5 |
18 |
| 19 |
26 |
34 |
0 |
17 |
26 |
17 |
1 |
18 |
26 |
23 |
2 |
19 |
26 |
0 |
3 |
19 |
27 |
8 |
4 |
20 |
27 |
36 |
5 |
19 |
| 20 |
27 |
31 |
0 |
18 |
27 |
14 |
1 |
19 |
27 |
21 |
2 |
20 |
27 |
0 |
3 |
20 |
28 |
9 |
4 |
21 |
28 |
38 |
5 |
20 |
| 21 |
28 |
28 |
0 |
19 |
28 |
12 |
1 |
20 |
28 |
20 |
2 |
21 |
28 |
0 |
3 |
21 |
29 |
9 |
4 |
22 |
29 |
39 |
5 |
21 |
| 22 |
29 |
26 |
0 |
20 |
29 |
10 |
1 |
21 |
29 |
19 |
2 |
22 |
29 |
0 |
3 |
22 |
♐ |
10 |
4 |
23 |
♑ |
40 |
5 |
22 |
| 23 |
♌ |
23 |
0 |
21 |
♍ |
8 |
1 |
22 |
♎ |
18 |
2 |
23 |
♏ |
0 |
3 |
23 |
1 |
11 |
4 |
24 |
1 |
41 |
5 |
23 |
| 24 |
1 |
20 |
0 |
22 |
1 |
6 |
1 |
23 |
1 |
17 |
2 |
24 |
1 |
0 |
3 |
24 |
2 |
12 |
4 |
25 |
2 |
42 |
5 |
24 |
| 25 |
2 |
18 |
0 |
23 |
2 |
4 |
1 |
24 |
2 |
16 |
2 |
25 |
2 |
0 |
3 |
25 |
3 |
12 |
4 |
26 |
3 |
44 |
5 |
25 |
| 26 |
3 |
15 |
0 |
24 |
3 |
2 |
1 |
25 |
3 |
15 |
2 |
26 |
3 |
0 |
3 |
26 |
4 |
13 |
4 |
27 |
4 |
45 |
5 |
26 |
| 27 |
4 |
12 |
0 |
25 |
4 |
0 |
1 |
26 |
4 |
14 |
2 |
27 |
4 |
0 |
3 |
27 |
5 |
14 |
4 |
28 |
5 |
46 |
5 |
27 |
| 28 |
5 |
10 |
0 |
26 |
4 |
58 |
1 |
27 |
5 |
13 |
2 |
28 |
5 |
0 |
3 |
28 |
6 |
15 |
4 |
29 |
6 |
47 |
5 |
28 |
| 29 |
6 |
7 |
0 |
27 |
5 |
56 |
1 |
28 |
6 |
12 |
2 |
29 |
6 |
0 |
3 |
29 |
7 |
16 |
4 |
29 |
7 |
48 |
5 |
29 |
| 30 |
7 |
5 |
0 |
28 |
6 |
54 |
1 |
29 |
7 |
11 |
3 |
0 |
7 |
0 |
4 |
0 |
8 |
17 |
5 |
0 |
8 |
49 |
6 |
0 |
| 31 |
8 |
2 |
0 |
29 |
7 |
52 |
2 |
0 |
|
|
|
|
8 |
0 |
4 |
1 |
|
|
|
|
9 |
51 |
6 |
1 |
116
| A TABLE of the Equation of natural Days, shewing what Time it ought to
be by the Clock when the Sun is on the Meridian. |
| The Bissextile, or Leap-year. |
| Days |
January |
Dif. |
February |
Dif. |
March |
Dif. |
April |
Dif. |
May |
Dif. |
June |
Dif. |
| H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
| |
|
Inc. |
|
Inc. |
|
Dec. |
|
Dec. |
|
Dec. |
|
Inc. |
| 1 |
12 |
4 |
0 |
|
12 |
14 |
5 |
|
12 |
12 |
36 |
|
12 |
3 |
48 |
|
11 |
56 |
47 |
|
11 |
57 |
22 |
|
| |
|
28 |
|
7 |
|
13 |
|
18 |
|
7 |
|
9 |
| 2 |
12 |
4 |
28 |
|
12 |
14 |
12 |
|
12 |
12 |
23 |
|
12 |
3 |
30 |
|
11 |
56 |
40 |
|
11 |
57 |
31 |
|
| |
|
28 |
|
7 |
|
13 |
|
19 |
|
7 |
|
9 |
| 3 |
12 |
4 |
56 |
|
12 |
14 |
19 |
|
12 |
12 |
10 |
|
12 |
3 |
11 |
|
11 |
56 |
33 |
|
11 |
57 |
40 |
|
| |
|
28 |
|
6 |
|
14 |
|
18 |
|
6 |
|
10 |
| 4 |
12 |
5 |
24 |
|
12 |
14 |
25 |
|
12 |
11 |
56 |
|
12 |
2 |
53 |
|
11 |
56 |
27 |
|
11 |
57 |
50 |
|
| |
|
27 |
|
5 |
|
14 |
|
18 |
|
6 |
|
10 |
| 5 |
12 |
5 |
51 |
|
12 |
14 |
30 |
|
12 |
11 |
42 |
|
12 |
2 |
35 |
|
11 |
56 |
21 |
|
11 |
58 |
0 |
|
| |
|
27 |
|
4 |
|
14 |
|
18 |
|
5 |
|
11 |
| |
|
|
|
|
|
| 6 |
12 |
6 |
18 |
|
12 |
14 |
34 |
|
12 |
11 |
28 |
|
12 |
2 |
17 |
|
11 |
56 |
16 |
|
11 |
58 |
11 |
|
| |
|
26 |
|
3 |
|
15 |
|
17 |
|
4 |
|
11 |
| 7 |
12 |
6 |
44 |
|
12 |
14 |
37 |
|
12 |
11 |
13 |
|
12 |
2 |
0 |
|
11 |
56 |
12 |
|
11 |
58 |
22 |
|
| |
|
26 |
|
3 |
|
15 |
|
17 |
|
4 |
|
11 |
| 8 |
12 |
7 |
10 |
|
12 |
14 |
40 |
|
12 |
10 |
58 |
|
12 |
1 |
43 |
|
11 |
56 |
8 |
|
11 |
58 |
33 |
|
| |
|
25 |
|
2 |
|
16 |
|
17 |
|
4 |
|
11 |
| 9 |
12 |
7 |
35 |
|
12 |
14 |
42 |
|
12 |
10 |
42 |
|
12 |
1 |
26 |
|
11 |
56 |
4 |
|
11 |
58 |
44 |
|
| |
|
25 |
|
1 |
|
16 |
|
17 |
|
3 |
|
12 |
| 10 |
12 |
8 |
0 |
|
12 |
14 |
43 |
|
12 |
10 |
46 |
|
12 |
1 |
9 |
|
11 |
56 |
1 |
|
11 |
58 |
56 |
|
| |
|
24 |
|
Dec. |
|
16 |
|
16 |
|
2 |
|
12 |
| |
|
|
|
|
|
| 11 |
12 |
8 |
24 |
|
12 |
14 |
44 |
|
12 |
10 |
10 |
|
12 |
0 |
53 |
|
11 |
55 |
59 |
|
11 |
59 |
8 |
|
| |
|
23 |
|
1 |
|
17 |
|
16 |
|
1 |
|
12 |
| 12 |
12 |
8 |
47 |
|
12 |
14 |
43 |
|
12 |
9 |
53 |
|
12 |
0 |
37 |
|
11 |
55 |
58 |
|
11 |
59 |
20 |
|
| |
|
23 |
|
1 |
|
17 |
|
16 |
|
1 |
|
12 |
| 13 |
12 |
9 |
10 |
|
12 |
14 |
42 |
|
12 |
9 |
36 |
|
12 |
0 |
21 |
|
11 |
55 |
57 |
|
11 |
59 |
32 |
|
| |
|
22 |
|
2 |
|
17 |
|
15 |
|
Inc. |
|
12 |
| 14 |
12 |
9 |
32 |
|
12 |
14 |
40 |
|
12 |
9 |
19 |
|
12 |
0 |
6 |
|
11 |
55 |
56 |
|
11 |
59 |
44 |
|
| |
|
22 |
|
3 |
|
17 |
|
15 |
|
1 |
|
13 |
| 15 |
12 |
9 |
54 |
|
12 |
14 |
37 |
|
12 |
9 |
2 |
|
11 |
59 |
51 |
|
11 |
55 |
57 |
|
11 |
59 |
57 |
|
| |
|
21 |
|
4 |
|
18 |
|
15 |
|
1 |
|
13 |
| |
|
|
|
|
|
| 16 |
12 |
10 |
15 |
|
12 |
14 |
33 |
|
12 |
8 |
44 |
|
11 |
59 |
36 |
|
11 |
55 |
58 |
|
12 |
0 |
10 |
|
| |
|
20 |
|
4 |
|
18 |
|
15 |
|
1 |
|
13 |
| 17 |
12 |
10 |
35 |
|
12 |
14 |
29 |
|
12 |
8 |
26 |
|
11 |
59 |
21 |
|
11 |
55 |
59 |
|
12 |
0 |
23 |
|
| |
|
19 |
|
5 |
|
18 |
|
14 |
|
2 |
|
12 |
| 18 |
12 |
10 |
54 |
|
12 |
14 |
24 |
|
12 |
8 |
8 |
|
11 |
59 |
7 |
|
11 |
56 |
1 |
|
12 |
0 |
35 |
|
| |
|
19 |
|
5 |
|
18 |
|
13 |
|
2 |
|
13 |
| 19 |
12 |
10 |
13 |
|
12 |
14 |
19 |
|
12 |
7 |
50 |
|
11 |
58 |
54 |
|
11 |
56 |
3 |
|
12 |
0 |
48 |
|
| |
|
18 |
|
6 |
|
18 |
|
13 |
|
3 |
|
13 |
| 20 |
12 |
10 |
31 |
|
12 |
14 |
13 |
|
12 |
7 |
32 |
|
11 |
58 |
41 |
|
11 |
56 |
6 |
|
12 |
1 |
1 |
|
| |
|
17 |
|
7 |
|
18 |
|
13 |
|
3 |
|
13 |
| |
|
|
|
|
|
| 21 |
12 |
11 |
48 |
|
12 |
14 |
6 |
|
12 |
7 |
14 |
|
11 |
58 |
28 |
|
11 |
56 |
9 |
|
12 |
1 |
14 |
|
| |
|
17 |
|
8 |
|
19 |
|
12 |
|
4 |
|
13 |
| 22 |
12 |
12 |
5 |
|
12 |
13 |
58 |
|
12 |
6 |
55 |
|
11 |
58 |
16 |
|
11 |
56 |
13 |
|
12 |
1 |
27 |
|
| |
|
16 |
|
8 |
|
19 |
|
12 |
|
5 |
|
13 |
| 23 |
12 |
12 |
21 |
|
12 |
13 |
50 |
|
12 |
6 |
36 |
|
11 |
58 |
4 |
|
11 |
56 |
18 |
|
12 |
1 |
40 |
|
| |
|
15 |
|
9 |
|
19 |
|
12 |
|
5 |
|
13 |
| 24 |
12 |
12 |
36 |
|
12 |
13 |
41 |
|
12 |
6 |
17 |
|
11 |
57 |
52 |
|
11 |
56 |
23 |
|
12 |
1 |
53 |
|
| |
|
14 |
|
9 |
|
19 |
|
11 |
|
6 |
|
13 |
| 25 |
12 |
12 |
50 |
|
12 |
13 |
32 |
|
12 |
5 |
58 |
|
11 |
57 |
41 |
|
11 |
56 |
29 |
|
12 |
2 |
6 |
|
| |
|
13 |
|
10 |
|
18 |
|
10 |
|
6 |
|
12 |
| |
|
|
|
|
|
| 26 |
12 |
13 |
3 |
|
12 |
13 |
22 |
|
12 |
5 |
40 |
|
11 |
57 |
31 |
|
11 |
56 |
35 |
|
12 |
2 |
18 |
|
| |
|
12 |
|
11 |
|
19 |
|
10 |
|
7 |
|
13 |
| 27 |
12 |
13 |
15 |
|
12 |
13 |
11 |
|
12 |
5 |
21 |
|
11 |
57 |
21 |
|
11 |
56 |
42 |
|
12 |
2 |
31 |
|
| |
|
12 |
|
11 |
|
19 |
|
9 |
|
7 |
|
12 |
| 28 |
12 |
13 |
27 |
|
12 |
13 |
0 |
|
12 |
5 |
2 |
|
11 |
57 |
12 |
|
11 |
56 |
49 |
|
12 |
2 |
43 |
|
| |
|
11 |
|
12 |
|
18 |
|
9 |
|
7 |
|
12 |
| |
|
|
|
|
|
| 29 |
12 |
13 |
38 |
|
12 |
12 |
48 |
|
12 |
4 |
44 |
|
11 |
57 |
3 |
|
11 |
56 |
56 |
|
12 |
2 |
55 |
|
| |
|
10 |
|
12 |
|
19 |
|
8 |
|
8 |
|
12 |
| 30 |
12 |
13 |
48 |
|
|
|
|
|
12 |
4 |
25 |
|
11 |
56 |
55 |
|
11 |
57 |
4 |
|
12 |
3 |
7 |
|
| |
|
9 |
|
|
|
19 |
|
8 |
|
9 |
|
11 |
| |
|
|
|
|
|
|
| 31 |
12 |
13 |
57 |
|
|
|
|
|
12 |
4 |
6 |
|
|
|
|
|
11 |
57 |
13 |
|
|
|
|
|
| |
|
8 |
|
|
|
18 |
|
|
|
9 |
|
|
| |
Incr. 9ʹ 57ʺ |
Incr. 0ʹ 39ʺ |
Decr. 8ʹ 30ʺ |
Decr. 6ʹ 53ʺ |
Decr. 0ʹ 50ʺ |
Incr. 5ʹ 45ʺ |
| |
Decr. 1 56 |
|
Incr. 1 17 |
|
118
| A TABLE of the Equation of natural Days, shewing what Time it ought to
be by the Clock when the Sun is on the Meridian. |
| The first after Leap-year. |
| Days |
January |
Dif. |
February |
Dif. |
March |
Dif. |
April |
Dif. |
May |
Dif. |
June |
Dif. |
| H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
| |
|
Inc. |
|
Inc. |
|
Dec. |
|
Dec. |
|
Dec. |
|
Inc. |
| 1 |
12 |
4 |
21 |
|
12 |
14 |
11 |
|
12 |
12 |
39 |
|
12 |
3 |
52 |
|
11 |
56 |
49 |
|
11 |
57 |
18 |
|
| |
|
28 |
|
7 |
|
13 |
|
18 |
|
8 |
|
9 |
| 2 |
12 |
4 |
49 |
|
12 |
14 |
18 |
|
12 |
12 |
26 |
|
12 |
3 |
34 |
|
11 |
56 |
41 |
|
11 |
57 |
27 |
|
| |
|
27 |
|
6 |
|
13 |
|
18 |
|
7 |
|
9 |
| 3 |
12 |
5 |
16 |
|
12 |
14 |
24 |
|
12 |
12 |
13 |
|
12 |
3 |
16 |
|
11 |
56 |
34 |
|
11 |
57 |
36 |
|
| |
|
27 |
|
5 |
|
13 |
|
18 |
|
6 |
|
10 |
| 4 |
12 |
5 |
43 |
|
12 |
14 |
29 |
|
12 |
12 |
0 |
|
12 |
2 |
58 |
|
11 |
56 |
28 |
|
11 |
57 |
46 |
|
| |
|
27 |
|
5 |
|
14 |
|
18 |
|
6 |
|
10 |
| 5 |
12 |
6 |
10 |
|
12 |
14 |
34 |
|
12 |
11 |
46 |
|
12 |
2 |
40 |
|
11 |
56 |
22 |
|
11 |
57 |
56 |
|
| |
|
27 |
|
4 |
|
14 |
|
18 |
|
5 |
|
10 |
| |
|
|
|
|
|
| 6 |
12 |
6 |
37 |
|
12 |
14 |
38 |
|
12 |
11 |
32 |
|
12 |
2 |
22 |
|
11 |
56 |
17 |
|
11 |
58 |
6 |
|
| |
|
26 |
|
3 |
|
15 |
|
18 |
|
4 |
|
11 |
| 7 |
12 |
7 |
3 |
|
12 |
14 |
41 |
|
12 |
11 |
17 |
|
12 |
2 |
4 |
|
11 |
56 |
13 |
|
11 |
58 |
17 |
|
| |
|
25 |
|
2 |
|
15 |
|
17 |
|
4 |
|
11 |
| 8 |
12 |
7 |
28 |
|
12 |
14 |
43 |
|
12 |
11 |
2 |
|
12 |
1 |
47 |
|
11 |
56 |
9 |
|
11 |
58 |
28 |
|
| |
|
25 |
|
1 |
|
16 |
|
17 |
|
4 |
|
12 |
| 9 |
12 |
7 |
53 |
|
12 |
14 |
44 |
|
12 |
10 |
46 |
|
12 |
1 |
30 |
|
11 |
56 |
5 |
|
11 |
58 |
40 |
|
| |
|
24 |
|
0 |
|
16 |
|
17 |
|
3 |
|
12 |
| 10 |
12 |
8 |
17 |
|
12 |
14 |
44 |
|
12 |
10 |
30 |
|
12 |
1 |
13 |
|
11 |
56 |
2 |
|
11 |
58 |
52 |
|
| |
|
24 |
|
Dec. |
|
16 |
|
16 |
|
2 |
|
12 |
| 11 |
12 |
8 |
41 |
|
12 |
14 |
44 |
|
12 |
10 |
14 |
|
12 |
0 |
57 |
|
11 |
56 |
0 |
|
11 |
59 |
4 |
|
| |
|
23 |
|
1 |
|
17 |
|
16 |
|
2 |
|
12 |
| 12 |
12 |
9 |
4 |
|
12 |
14 |
43 |
|
12 |
9 |
57 |
|
12 |
0 |
41 |
|
11 |
55 |
58 |
|
11 |
59 |
16 |
|
| |
|
22 |
|
2 |
|
17 |
|
16 |
|
1 |
|
12 |
| 13 |
12 |
9 |
26 |
|
12 |
14 |
41 |
|
12 |
9 |
40 |
|
12 |
0 |
25 |
|
11 |
55 |
57 |
|
11 |
59 |
28 |
|
| |
|
22 |
|
3 |
|
17 |
|
16 |
|
1 |
|
12 |
| 14 |
12 |
9 |
48 |
|
12 |
14 |
38 |
|
12 |
9 |
23 |
|
12 |
0 |
9 |
|
11 |
55 |
56 |
|
11 |
59 |
40 |
|
| |
|
21 |
|
3 |
|
17 |
|
15 |
|
Inc. |
|
13 |
| 15 |
12 |
10 |
9 |
|
12 |
14 |
35 |
|
12 |
9 |
6 |
|
11 |
59 |
54 |
|
11 |
55 |
56 |
|
11 |
59 |
53 |
|
| |
|
21 |
|
4 |
|
18 |
|
15 |
|
1 |
|
13 |
| |
|
|
|
|
|
| 16 |
12 |
10 |
30 |
|
12 |
14 |
31 |
|
12 |
8 |
48 |
|
11 |
59 |
39 |
|
11 |
55 |
57 |
|
12 |
0 |
6 |
|
| |
|
20 |
|
5 |
|
18 |
|
14 |
|
1 |
|
13 |
| 17 |
12 |
10 |
50 |
|
12 |
14 |
26 |
|
12 |
8 |
30 |
|
11 |
59 |
25 |
|
11 |
55 |
58 |
|
12 |
0 |
19 |
|
| |
|
19 |
|
6 |
|
18 |
|
14 |
|
2 |
|
13 |
| 18 |
12 |
11 |
9 |
|
12 |
14 |
20 |
|
12 |
8 |
12 |
|
11 |
59 |
11 |
|
11 |
56 |
0 |
|
12 |
0 |
32 |
|
| |
|
18 |
|
6 |
|
18 |
|
14 |
|
2 |
|
13 |
| 19 |
12 |
11 |
27 |
|
12 |
14 |
14 |
|
12 |
7 |
54 |
|
11 |
58 |
57 |
|
11 |
56 |
2 |
|
12 |
0 |
45 |
|
| |
|
17 |
|
7 |
|
18 |
|
13 |
|
3 |
|
13 |
| 20 |
12 |
11 |
44 |
|
12 |
14 |
7 |
|
12 |
7 |
36 |
|
11 |
58 |
44 |
|
11 |
56 |
5 |
|
12 |
0 |
58 |
|
| |
|
17 |
|
7 |
|
18 |
|
13 |
|
3 |
|
13 |
| 21 |
12 |
12 |
1 |
|
12 |
14 |
0 |
|
12 |
7 |
18 |
|
11 |
58 |
31 |
|
11 |
56 |
8 |
|
12 |
1 |
11 |
|
| |
|
16 |
|
8 |
|
19 |
|
12 |
|
4 |
|
13 |
| 22 |
12 |
12 |
17 |
|
12 |
13 |
52 |
|
12 |
6 |
59 |
|
11 |
58 |
19 |
|
11 |
56 |
12 |
|
12 |
1 |
24 |
|
| |
|
15 |
|
9 |
|
19 |
|
12 |
|
4 |
|
13 |
| 23 |
12 |
12 |
32 |
|
12 |
13 |
43 |
|
12 |
6 |
40 |
|
11 |
58 |
7 |
|
11 |
56 |
16 |
|
12 |
1 |
37 |
|
| |
|
14 |
|
9 |
|
19 |
|
12 |
|
5 |
|
13 |
| 24 |
12 |
12 |
46 |
|
12 |
13 |
34 |
|
12 |
6 |
21 |
|
11 |
57 |
55 |
|
11 |
56 |
21 |
|
12 |
1 |
50 |
|
| |
|
13 |
|
10 |
|
19 |
|
11 |
|
6 |
|
13 |
| 25 |
12 |
12 |
59 |
|
12 |
13 |
24 |
|
12 |
6 |
2 |
|
11 |
57 |
44 |
|
11 |
56 |
27 |
|
12 |
2 |
3 |
|
| |
|
13 |
|
10 |
|
19 |
|
10 |
|
6 |
|
13 |
| |
|
|
|
|
|
| 26 |
12 |
13 |
12 |
|
12 |
13 |
14 |
|
12 |
5 |
43 |
|
11 |
57 |
34 |
|
11 |
56 |
33 |
|
12 |
2 |
16 |
|
| |
|
12 |
|
11 |
|
19 |
|
10 |
|
6 |
|
12 |
| 27 |
12 |
13 |
24 |
|
12 |
13 |
3 |
|
12 |
5 |
24 |
|
11 |
57 |
24 |
|
11 |
56 |
39 |
|
12 |
2 |
28 |
|
| |
|
11 |
|
12 |
|
19 |
|
10 |
|
7 |
|
12 |
| 28 |
12 |
13 |
35 |
|
12 |
12 |
51 |
|
12 |
5 |
5 |
|
11 |
57 |
14 |
|
11 |
56 |
46 |
|
12 |
2 |
40 |
|
| |
|
10 |
|
12 |
|
19 |
|
9 |
|
7 |
|
12 |
| 29 |
12 |
13 |
45 |
|
|
|
|
|
12 |
4 |
46 |
|
11 |
57 |
5 |
|
11 |
56 |
53 |
|
12 |
2 |
52 |
|
| |
|
|
|
9 |
|
18 |
|
8 |
|
8 |
|
12 |
| 30 |
12 |
13 |
54 |
|
|
|
|
|
12 |
4 |
28 |
|
11 |
56 |
57 |
|
11 |
57 |
1 |
|
12 |
3 |
4 |
|
| |
|
|
|
9 |
|
18 |
|
8 |
|
8 |
|
11 |
| |
|
|
|
|
|
|
| 31 |
12 |
14 |
3 |
|
|
|
|
|
12 |
4 |
10 |
|
|
|
|
|
11 |
57 |
9 |
|
|
|
|
|
| |
|
8 |
|
|
|
18 |
|
|
|
9 |
|
|
| |
Incr. 9ʹ 42ʺ |
Incr. 0ʹ 33ʺ |
Decr. 8ʹ 29ʺ |
Decr. 6ʹ 55ʺ |
Decr. 0ʹ 53ʺ |
Incr. 5ʹ 46ʺ |
| |
Decr. 1 53 |
|
Incr. 1 12 |
|
119
| A TABLE of the Equation of natural Days, shewing what Time it ought to
be by the Clock when the Sun is on the Meridian. |
| The first after Leap-year. |
| Days |
July |
Dif. |
August |
Dif. |
September |
Dif. |
October |
Dif. |
November |
Dif. |
December |
Dif. |
| H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
| |
|
Inc. |
|
Dec. |
|
Dec. |
|
Dec. |
|
Dec. |
|
Inc. |
| 1 |
12 |
3 |
15 |
|
12 |
5 |
48 |
|
11 |
59 |
38 |
|
11 |
49 |
33 |
|
11 |
43 |
49 |
|
11 |
49 |
36 |
|
| |
|
12 |
|
4 |
|
19 |
|
19 |
|
0 |
|
24 |
| 2 |
12 |
3 |
27 |
|
12 |
5 |
44 |
|
11 |
59 |
19 |
|
11 |
49 |
14 |
|
11 |
43 |
49 |
|
11 |
50 |
0 |
|
| |
|
11 |
|
5 |
|
19 |
|
19 |
|
Inc. |
|
24 |
| 3 |
12 |
3 |
38 |
|
12 |
5 |
39 |
|
11 |
59 |
0 |
|
11 |
48 |
55 |
|
11 |
43 |
49 |
|
11 |
50 |
24 |
|
| |
|
11 |
|
5 |
|
19 |
|
18 |
|
1 |
|
25 |
| 4 |
12 |
3 |
49 |
|
12 |
5 |
34 |
|
11 |
58 |
41 |
|
11 |
48 |
37 |
|
11 |
43 |
50 |
|
11 |
50 |
49 |
|
| |
|
10 |
|
6 |
|
20 |
|
17 |
|
2 |
|
25 |
| 5 |
12 |
3 |
59 |
|
12 |
5 |
28 |
|
11 |
58 |
21 |
|
11 |
48 |
20 |
|
11 |
43 |
52 |
|
11 |
51 |
14 |
|
| |
|
10 |
|
6 |
|
20 |
|
17 |
|
3 |
|
26 |
| |
|
|
|
|
|
| 6 |
12 |
4 |
9 |
|
12 |
5 |
22 |
|
11 |
58 |
1 |
|
11 |
48 |
3 |
|
11 |
43 |
55 |
|
11 |
51 |
40 |
|
| |
|
10 |
|
7 |
|
20 |
|
17 |
|
3 |
|
26 |
| 7 |
12 |
4 |
19 |
|
12 |
5 |
15 |
|
11 |
57 |
41 |
|
11 |
47 |
46 |
|
11 |
43 |
58 |
|
11 |
52 |
6 |
|
| |
|
10 |
|
7 |
|
20 |
|
17 |
|
4 |
|
27 |
| 8 |
12 |
4 |
29 |
|
12 |
5 |
8 |
|
11 |
57 |
21 |
|
11 |
47 |
29 |
|
11 |
44 |
2 |
|
11 |
52 |
33 |
|
| |
|
9 |
|
8 |
|
20 |
|
16 |
|
5 |
|
27 |
| 9 |
12 |
4 |
38 |
|
12 |
5 |
0 |
|
11 |
57 |
1 |
|
11 |
47 |
13 |
|
11 |
44 |
7 |
|
11 |
53 |
0 |
|
| |
|
8 |
|
9 |
|
20 |
|
15 |
|
6 |
|
27 |
| 10 |
12 |
4 |
46 |
|
12 |
4 |
51 |
|
11 |
56 |
41 |
|
11 |
46 |
58 |
|
11 |
44 |
13 |
|
11 |
53 |
27 |
|
| |
|
8 |
|
9 |
|
20 |
|
15 |
|
7 |
|
28 |
| |
|
|
|
|
|
| 11 |
12 |
4 |
54 |
|
12 |
4 |
42 |
|
11 |
56 |
21 |
|
11 |
46 |
43 |
|
11 |
44 |
20 |
|
11 |
53 |
35 |
|
| |
|
8 |
|
10 |
|
21 |
|
14 |
|
8 |
|
28 |
| 12 |
12 |
5 |
2 |
|
12 |
4 |
32 |
|
11 |
56 |
0 |
|
11 |
46 |
29 |
|
11 |
44 |
28 |
|
11 |
54 |
23 |
|
| |
|
8 |
|
10 |
|
21 |
|
13 |
|
9 |
|
29 |
| 13 |
12 |
5 |
10 |
|
12 |
4 |
22 |
|
11 |
55 |
39 |
|
11 |
46 |
16 |
|
11 |
44 |
37 |
|
11 |
54 |
52 |
|
| |
|
7 |
|
11 |
|
21 |
|
13 |
|
10 |
|
29 |
| 14 |
12 |
5 |
17 |
|
12 |
4 |
11 |
|
11 |
55 |
18 |
|
11 |
46 |
3 |
|
11 |
44 |
47 |
|
11 |
55 |
21 |
|
| |
|
6 |
|
11 |
|
21 |
|
13 |
|
11 |
|
29 |
| 15 |
12 |
5 |
23 |
|
12 |
4 |
0 |
|
11 |
54 |
57 |
|
11 |
45 |
50 |
|
11 |
44 |
58 |
|
11 |
55 |
50 |
|
| |
|
6 |
|
12 |
|
21 |
|
13 |
|
12 |
|
30 |
| |
|
|
|
|
|
| 16 |
12 |
5 |
29 |
|
12 |
3 |
48 |
|
11 |
54 |
36 |
|
11 |
45 |
37 |
|
11 |
45 |
10 |
|
11 |
56 |
19 |
|
| |
|
5 |
|
12 |
|
21 |
|
12 |
|
13 |
|
30 |
| 17 |
12 |
5 |
34 |
|
12 |
3 |
36 |
|
11 |
54 |
15 |
|
11 |
45 |
25 |
|
11 |
45 |
23 |
|
11 |
56 |
49 |
|
| |
|
5 |
|
13 |
|
21 |
|
11 |
|
13 |
|
30 |
| 18 |
12 |
5 |
39 |
|
12 |
3 |
23 |
|
11 |
53 |
54 |
|
11 |
45 |
14 |
|
11 |
45 |
36 |
|
11 |
57 |
19 |
|
| |
|
4 |
|
13 |
|
21 |
|
11 |
|
14 |
|
30 |
| 19 |
12 |
5 |
43 |
|
12 |
3 |
10 |
|
11 |
53 |
33 |
|
11 |
45 |
3 |
|
33 |
45 |
50 |
|
11 |
57 |
49 |
|
| |
|
4 |
|
14 |
|
21 |
|
10 |
|
14 |
|
30 |
| 20 |
12 |
5 |
47 |
|
12 |
2 |
56 |
|
11 |
53 |
12 |
|
11 |
44 |
53 |
|
11 |
46 |
4 |
|
11 |
58 |
19 |
|
| |
|
4 |
|
14 |
|
21 |
|
10 |
|
15 |
|
30 |
| |
|
|
|
|
|
| 21 |
12 |
5 |
51 |
|
12 |
2 |
42 |
|
11 |
52 |
51 |
|
11 |
44 |
43 |
|
11 |
46 |
19 |
|
11 |
58 |
49 |
|
| |
|
3 |
|
15 |
|
20 |
|
9 |
|
16 |
|
30 |
| 22 |
12 |
5 |
54 |
|
12 |
2 |
17 |
|
11 |
52 |
31 |
|
11 |
44 |
34 |
|
11 |
46 |
35 |
|
11 |
59 |
19 |
|
| |
|
2 |
|
15 |
|
20 |
|
8 |
|
17 |
|
30 |
| 23 |
12 |
5 |
56 |
|
12 |
2 |
12 |
|
11 |
52 |
11 |
|
11 |
44 |
26 |
|
11 |
46 |
52 |
|
11 |
59 |
49 |
|
| |
|
1 |
|
16 |
|
21 |
|
7 |
|
18 |
|
30 |
| 24 |
12 |
5 |
57 |
|
12 |
1 |
56 |
|
11 |
51 |
50 |
|
11 |
44 |
19 |
|
11 |
47 |
10 |
|
12 |
0 |
19 |
|
| |
|
1 |
|
16 |
|
21 |
|
6 |
|
19 |
|
30 |
| 25 |
12 |
5 |
58 |
|
12 |
1 |
40 |
|
11 |
51 |
29 |
|
11 |
44 |
13 |
|
11 |
47 |
29 |
|
12 |
0 |
49 |
|
| |
|
Dec. |
|
16 |
|
20 |
|
6 |
|
19 |
|
30 |
| |
|
|
|
|
|
| 26 |
12 |
5 |
59 |
|
12 |
1 |
24 |
|
11 |
51 |
9 |
|
11 |
44 |
7 |
|
11 |
47 |
48 |
|
12 |
1 |
19 |
|
| |
|
1 |
|
17 |
|
20 |
|
5 |
|
20 |
|
30 |
| 27 |
12 |
5 |
58 |
|
12 |
1 |
7 |
|
11 |
50 |
40 |
|
11 |
44 |
2 |
|
11 |
48 |
8 |
|
12 |
1 |
49 |
|
| |
|
1 |
|
17 |
|
19 |
|
4 |
|
21 |
|
29 |
| 28 |
12 |
5 |
57 |
|
12 |
1 |
50 |
|
11 |
50 |
30 |
|
11 |
43 |
58 |
|
11 |
48 |
29 |
|
12 |
2 |
18 |
|
| |
|
2 |
|
18 |
|
19 |
|
3 |
|
22 |
|
29 |
| 29 |
12 |
5 |
55 |
|
12 |
1 |
32 |
|
11 |
50 |
11 |
|
11 |
43 |
55 |
|
11 |
48 |
51 |
|
12 |
2 |
47 |
|
| |
|
2 |
|
18 |
|
19 |
|
3 |
|
22 |
|
29 |
| 30 |
12 |
5 |
53 |
|
12 |
0 |
14 |
|
11 |
49 |
52 |
|
11 |
43 |
52 |
|
11 |
49 |
13 |
|
12 |
3 |
16 |
|
| |
|
2 |
|
18 |
|
19 |
|
2 |
|
23 |
|
29 |
| |
|
|
|
|
|
| 31 |
12 |
5 |
51 |
|
11 |
59 |
56 |
|
|
|
|
|
11 |
43 |
50 |
|
|
|
|
|
12 |
3 |
45 |
|
| |
|
3 |
|
18 |
|
|
|
1 |
|
|
|
29 |
| |
Incr. 2ʹ 43ʺ |
Decr. 5ʹ 52ʺ |
Decr. 9ʹ 46ʺ |
Decr. 5ʹ 43ʺ |
Decr. 0ʹ 0ʺ |
Incr. 14ʹ 9ʺ |
| |
Decr. 0 8 |
|
Incr. 5 24 |
|
120
| A TABLE of the Equation of natural Days, shewing what Time it ought to
be by the Clock when the Sun is on the Meridian. |
| The second after Leap-year. |
| Days |
January |
Dif. |
February |
Dif. |
March |
Dif. |
April |
Dif. |
May |
Dif. |
June |
Dif. |
| H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
| |
|
Inc. |
|
Dec. |
|
Inc. |
|
Dec. |
|
Dec. |
|
Inc. |
| 1 |
12 |
4 |
14 |
|
12 |
14 |
9 |
|
12 |
12 |
42 |
|
12 |
3 |
56 |
|
11 |
56 |
50 |
|
11 |
57 |
16 |
|
| |
|
28 |
|
7 |
|
13 |
|
18 |
|
8 |
|
9 |
| 2 |
12 |
4 |
42 |
|
12 |
14 |
16 |
|
12 |
12 |
20 |
|
12 |
3 |
38 |
|
11 |
56 |
42 |
|
11 |
57 |
25 |
|
| |
|
28 |
|
6 |
|
13 |
|
18 |
|
7 |
|
10 |
| 3 |
12 |
5 |
10 |
|
12 |
14 |
22 |
|
12 |
12 |
16 |
|
12 |
3 |
20 |
|
11 |
56 |
35 |
|
11 |
57 |
35 |
|
| |
|
27 |
|
5 |
|
13 |
|
18 |
|
6 |
|
10 |
| 4 |
12 |
5 |
37 |
|
12 |
14 |
27 |
|
12 |
12 |
3 |
|
12 |
3 |
2 |
|
11 |
56 |
29 |
|
11 |
57 |
45 |
|
| |
|
27 |
|
5 |
|
14 |
|
18 |
|
6 |
|
10 |
| 5 |
12 |
6 |
4 |
|
12 |
14 |
32 |
|
12 |
11 |
49 |
|
12 |
2 |
44 |
|
11 |
56 |
23 |
|
11 |
57 |
55 |
|
| |
|
27 |
|
4 |
|
14 |
|
18 |
|
5 |
|
10 |
| |
|
|
|
|
|
| 6 |
12 |
6 |
30 |
|
12 |
14 |
36 |
|
12 |
11 |
35 |
|
12 |
2 |
26 |
|
11 |
56 |
18 |
|
11 |
58 |
5 |
|
| |
|
26 |
|
3 |
|
15 |
|
17 |
|
5 |
|
11 |
| 7 |
12 |
6 |
56 |
|
12 |
14 |
39 |
|
12 |
11 |
20 |
|
12 |
2 |
9 |
|
11 |
56 |
23 |
|
11 |
58 |
16 |
|
| |
|
26 |
|
2 |
|
15 |
|
17 |
|
4 |
|
11 |
| 8 |
12 |
7 |
22 |
|
12 |
14 |
41 |
|
12 |
11 |
5 |
|
12 |
1 |
52 |
|
11 |
56 |
9 |
|
11 |
58 |
27 |
|
| |
|
25 |
|
2 |
|
15 |
|
17 |
|
3 |
|
11 |
| 9 |
12 |
7 |
47 |
|
12 |
14 |
43 |
|
12 |
10 |
50 |
|
12 |
1 |
35 |
|
11 |
56 |
6 |
|
11 |
58 |
38 |
|
| |
|
24 |
|
1 |
|
16 |
|
17 |
|
3 |
|
12 |
| 10 |
12 |
8 |
11 |
|
12 |
14 |
44 |
|
12 |
10 |
34 |
|
12 |
1 |
18 |
|
11 |
56 |
3 |
|
11 |
58 |
50 |
|
| |
|
24 |
|
Dec. |
|
16 |
|
17 |
|
2 |
|
12 |
| |
|
|
|
|
|
| 11 |
12 |
8 |
35 |
|
12 |
14 |
44 |
|
12 |
10 |
18 |
|
12 |
1 |
1 |
|
11 |
56 |
1 |
|
11 |
59 |
2 |
|
| |
|
23 |
|
1 |
|
17 |
|
16 |
|
2 |
|
12 |
| 12 |
12 |
8 |
58 |
|
12 |
14 |
43 |
|
12 |
10 |
1 |
|
12 |
0 |
45 |
|
11 |
55 |
59 |
|
11 |
59 |
14 |
|
| |
|
22 |
|
2 |
|
17 |
|
16 |
|
2 |
|
12 |
| 13 |
12 |
9 |
20 |
|
12 |
14 |
41 |
|
12 |
9 |
44 |
|
12 |
0 |
29 |
|
11 |
55 |
57 |
|
11 |
59 |
26 |
|
| |
|
22 |
|
3 |
|
17 |
|
16 |
|
1 |
|
12 |
| 14 |
12 |
9 |
42 |
|
12 |
14 |
38 |
|
12 |
9 |
27 |
|
12 |
0 |
13 |
|
11 |
55 |
56 |
|
11 |
59 |
38 |
|
| |
|
21 |
|
3 |
|
17 |
|
15 |
|
Inc. |
|
12 |
| 15 |
12 |
10 |
3 |
|
12 |
14 |
35 |
|
12 |
9 |
10 |
|
11 |
59 |
58 |
|
11 |
55 |
56 |
|
11 |
59 |
50 |
|
| |
|
21 |
|
4 |
|
18 |
|
15 |
|
1 |
|
13 |
| |
|
|
|
|
|
| 16 |
12 |
10 |
24 |
|
12 |
14 |
31 |
|
12 |
8 |
52 |
|
11 |
59 |
43 |
|
11 |
55 |
57 |
|
12 |
0 |
3 |
|
| |
|
20 |
|
4 |
|
18 |
|
14 |
|
1 |
|
13 |
| 17 |
12 |
10 |
44 |
|
12 |
14 |
27 |
|
12 |
8 |
34 |
|
11 |
59 |
29 |
|
11 |
55 |
58 |
|
12 |
0 |
16 |
|
| |
|
19 |
|
5 |
|
18 |
|
14 |
|
2 |
|
13 |
| 18 |
12 |
11 |
3 |
|
12 |
14 |
22 |
|
12 |
8 |
16 |
|
11 |
59 |
15 |
|
11 |
56 |
0 |
|
12 |
0 |
29 |
|
| |
|
18 |
|
6 |
|
18 |
|
14 |
|
2 |
|
13 |
| 19 |
12 |
11 |
21 |
|
12 |
14 |
16 |
|
12 |
7 |
58 |
|
11 |
59 |
1 |
|
11 |
56 |
2 |
|
12 |
0 |
42 |
|
| |
|
18 |
|
7 |
|
18 |
|
14 |
|
3 |
|
13 |
| 20 |
12 |
11 |
39 |
|
12 |
14 |
9 |
|
12 |
7 |
40 |
|
11 |
58 |
47 |
|
11 |
56 |
5 |
|
12 |
0 |
55 |
|
| |
|
17 |
|
7 |
|
18 |
|
13 |
|
3 |
|
13 |
| |
|
|
|
|
|
| 21 |
12 |
11 |
56 |
|
12 |
14 |
2 |
|
12 |
7 |
22 |
|
11 |
58 |
34 |
|
11 |
56 |
8 |
|
12 |
1 |
8 |
|
| |
|
16 |
|
8 |
|
18 |
|
12 |
|
3 |
|
13 |
| 22 |
12 |
12 |
12 |
|
12 |
13 |
54 |
|
12 |
7 |
4 |
|
11 |
58 |
22 |
|
11 |
56 |
11 |
|
12 |
1 |
21 |
|
| |
|
15 |
|
9 |
|
19 |
|
12 |
|
4 |
|
13 |
| 23 |
12 |
12 |
27 |
|
12 |
13 |
45 |
|
12 |
6 |
45 |
|
11 |
58 |
10 |
|
11 |
56 |
15 |
|
12 |
1 |
34 |
|
| |
|
15 |
|
9 |
|
19 |
|
12 |
|
5 |
|
13 |
| 24 |
12 |
12 |
42 |
|
12 |
13 |
36 |
|
12 |
6 |
26 |
|
11 |
57 |
58 |
|
11 |
56 |
20 |
|
12 |
1 |
47 |
|
| |
|
14 |
|
10 |
|
19 |
|
11 |
|
6 |
|
12 |
| 25 |
12 |
12 |
56 |
|
12 |
13 |
26 |
|
12 |
6 |
7 |
|
11 |
57 |
47 |
|
11 |
56 |
26 |
|
12 |
1 |
59 |
|
| |
|
13 |
|
10 |
|
19 |
|
11 |
|
6 |
|
13 |
| |
|
|
|
|
|
| 26 |
12 |
13 |
9 |
|
12 |
13 |
16 |
|
12 |
5 |
48 |
|
11 |
57 |
36 |
|
11 |
56 |
32 |
|
12 |
2 |
12 |
|
| |
|
12 |
|
11 |
|
19 |
|
10 |
|
6 |
|
13 |
| 27 |
12 |
13 |
21 |
|
12 |
13 |
5 |
|
12 |
5 |
29 |
|
11 |
57 |
26 |
|
11 |
56 |
38 |
|
12 |
2 |
25 |
|
| |
|
11 |
|
11 |
|
19 |
|
10 |
|
7 |
|
12 |
| 28 |
12 |
13 |
32 |
|
12 |
12 |
54 |
|
12 |
5 |
10 |
|
11 |
57 |
16 |
|
11 |
56 |
45 |
|
12 |
2 |
37 |
|
| |
|
10 |
|
12 |
|
19 |
|
9 |
|
7 |
|
12 |
| 29 |
12 |
13 |
42 |
|
|
|
|
|
12 |
4 |
51 |
|
11 |
57 |
7 |
|
11 |
56 |
52 |
|
12 |
2 |
49 |
|
| |
|
10 |
|
|
|
18 |
|
9 |
|
8 |
|
12 |
| 30 |
12 |
13 |
52 |
|
|
|
|
|
12 |
4 |
33 |
|
11 |
56 |
58 |
|
11 |
57 |
0 |
|
12 |
3 |
1 |
|
| |
|
9 |
|
|
|
18 |
|
8 |
|
8 |
|
11 |
| |
|
|
|
|
|
|
| 31 |
12 |
14 |
1 |
|
|
|
|
|
12 |
4 |
15 |
|
|
|
|
|
11 |
57 |
8 |
|
|
|
|
|
| |
|
8 |
|
|
|
18 |
|
|
|
8 |
|
|
| |
Incr. 9ʹ 47ʺ |
Incr. 0ʹ 35ʺ |
Decr. 8ʹ 27ʺ |
Decr. 6ʹ 58ʺ |
Decr. 0ʹ 54ʺ |
Incr. 5ʹ 45ʺ |
| |
Decr. 1 50 |
|
Incr. 1 12 |
|
121
| A TABLE of the Equation of natural Days, shewing what Time it ought to
be by the Clock when the Sun is on the Meridian. |
| The second after Leap-year. |
| Days |
July |
Dif. |
August |
Dif. |
September |
Dif. |
October |
Dif. |
November |
Dif. |
December |
Dif. |
| H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
| |
|
Inc. |
|
Dec. |
|
Dec. |
|
Dec. |
|
Dec. |
|
Inc. |
| 1 |
12 |
3 |
12 |
|
12 |
5 |
48 |
|
11 |
59 |
43 |
|
11 |
49 |
37 |
|
11 |
43 |
49 |
|
11 |
49 |
30 |
|
| |
|
12 |
|
4 |
|
19 |
|
19 |
|
1 |
|
23 |
| 2 |
12 |
3 |
24 |
|
12 |
5 |
44 |
|
11 |
59 |
24 |
|
11 |
49 |
18 |
|
11 |
43 |
48 |
|
11 |
49 |
53 |
|
| |
|
11 |
|
4 |
|
19 |
|
18 |
|
Inc. |
|
24 |
| 3 |
12 |
3 |
35 |
|
12 |
5 |
40 |
|
11 |
59 |
5 |
|
11 |
49 |
0 |
|
11 |
43 |
49 |
|
11 |
50 |
17 |
|
| |
|
11 |
|
5 |
|
19 |
|
18 |
|
1 |
|
25 |
| 4 |
12 |
3 |
46 |
|
12 |
5 |
35 |
|
11 |
58 |
46 |
|
11 |
48 |
42 |
|
11 |
43 |
50 |
|
11 |
50 |
42 |
|
| |
|
11 |
|
5 |
|
20 |
|
18 |
|
2 |
|
25 |
| 5 |
12 |
3 |
57 |
|
12 |
5 |
30 |
|
11 |
58 |
26 |
|
11 |
48 |
24 |
|
11 |
43 |
52 |
|
11 |
51 |
7 |
|
| |
|
10 |
|
6 |
|
20 |
|
17 |
|
3 |
|
26 |
| |
|
|
|
|
|
| 6 |
12 |
4 |
7 |
|
12 |
5 |
24 |
|
11 |
58 |
6 |
|
11 |
48 |
7 |
|
11 |
43 |
55 |
|
11 |
51 |
33 |
|
| |
|
10 |
|
7 |
|
20 |
|
17 |
|
3 |
|
26 |
| 7 |
12 |
4 |
17 |
|
12 |
5 |
17 |
|
11 |
57 |
46 |
|
11 |
47 |
50 |
|
11 |
43 |
58 |
|
11 |
51 |
59 |
|
| |
|
9 |
|
7 |
|
20 |
|
17 |
|
4 |
|
26 |
| 8 |
12 |
4 |
26 |
|
12 |
5 |
10 |
|
11 |
57 |
26 |
|
11 |
47 |
33 |
|
11 |
44 |
2 |
|
11 |
52 |
25 |
|
| |
|
9 |
|
8 |
|
21 |
|
16 |
|
5 |
|
27 |
| 9 |
12 |
4 |
35 |
|
12 |
5 |
2 |
|
11 |
57 |
5 |
|
11 |
47 |
17 |
|
11 |
44 |
7 |
|
11 |
52 |
52 |
|
| |
|
9 |
|
9 |
|
20 |
|
16 |
|
6 |
|
28 |
| 10 |
12 |
4 |
44 |
|
12 |
4 |
53 |
|
11 |
56 |
45 |
|
11 |
47 |
1 |
|
11 |
44 |
13 |
|
11 |
53 |
20 |
|
| |
|
8 |
|
9 |
|
21 |
|
15 |
|
7 |
|
28 |
| |
|
|
|
|
|
| 11 |
12 |
4 |
52 |
|
12 |
4 |
44 |
|
11 |
56 |
24 |
|
11 |
46 |
46 |
|
11 |
44 |
20 |
|
11 |
53 |
48 |
|
| |
|
8 |
|
9 |
|
21 |
|
14 |
|
8 |
|
28 |
| 12 |
12 |
5 |
0 |
|
12 |
4 |
35 |
|
11 |
56 |
3 |
|
11 |
46 |
32 |
|
11 |
44 |
28 |
|
11 |
54 |
16 |
|
| |
|
8 |
|
10 |
|
21 |
|
14 |
|
9 |
|
28 |
| 13 |
12 |
5 |
8 |
|
12 |
4 |
25 |
|
11 |
55 |
42 |
|
11 |
46 |
18 |
|
11 |
44 |
37 |
|
11 |
54 |
44 |
|
| |
|
7 |
|
11 |
|
20 |
|
13 |
|
9 |
|
29 |
| 14 |
12 |
5 |
15 |
|
12 |
4 |
13 |
|
11 |
55 |
22 |
|
11 |
46 |
5 |
|
11 |
44 |
46 |
|
11 |
54 |
13 |
|
| |
|
6 |
|
11 |
|
20 |
|
13 |
|
10 |
|
29 |
| 15 |
12 |
5 |
21 |
|
12 |
4 |
3 |
|
11 |
55 |
2 |
|
11 |
45 |
52 |
|
11 |
44 |
56 |
|
11 |
55 |
42 |
|
| |
|
6 |
|
12 |
|
21 |
|
13 |
|
11 |
|
29 |
| |
|
|
|
|
|
| 16 |
12 |
5 |
27 |
|
12 |
3 |
51 |
|
|11 |
54 |
41 |
|
11 |
45 |
39 |
|
11 |
45 |
7 |
|
11 |
56 |
11 |
|
| |
|
6 |
|
12 |
|
21 |
|
12 |
|
12 |
|
30 |
| 17 |
12 |
5 |
33 |
|
12 |
3 |
39 |
|
11 |
54 |
20 |
|
11 |
45 |
27 |
|
11 |
45 |
19 |
|
11 |
56 |
41 |
|
| |
|
5 |
|
12 |
|
21 |
|
11 |
|
13 |
|
30 |
| 18 |
12 |
5 |
38 |
|
12 |
3 |
27 |
|
11 |
53 |
59 |
|
11 |
45 |
16 |
|
11 |
45 |
32 |
|
11 |
57 |
11 |
|
| |
|
4 |
|
13 |
|
20 |
|
10 |
|
14 |
|
30 |
| 19 |
12 |
5 |
42 |
|
12 |
3 |
14 |
|
11 |
53 |
39 |
|
11 |
45 |
6 |
|
11 |
45 |
46 |
|
11 |
57 |
41 |
|
| |
|
4 |
|
14 |
|
21 |
|
10 |
|
15 |
|
30 |
| 20 |
12 |
5 |
46 |
|
12 |
3 |
0 |
|
11 |
53 |
18 |
|
11 |
44 |
56 |
|
11 |
46 |
1 |
|
11 |
58 |
11 |
|
| |
|
3 |
|
14 |
|
21 |
|
10 |
|
15 |
|
30 |
| |
|
|
|
|
|
| 21 |
12 |
5 |
49 |
|
12 |
2 |
46 |
|
11 |
52 |
57 |
|
11 |
44 |
46 |
|
11 |
46 |
16 |
|
11 |
58 |
41 |
|
| |
|
3 |
|
15 |
|
20 |
|
9 |
|
16 |
|
30 |
| 22 |
12 |
5 |
52 |
|
12 |
2 |
31 |
|
11 |
52 |
37 |
|
11 |
44 |
37 |
|
11 |
46 |
32 |
|
11 |
59 |
11 |
|
| |
|
2 |
|
15 |
|
21 |
|
8 |
|
17 |
|
30 |
| 23 |
12 |
5 |
54 |
|
12 |
2 |
16 |
|
11 |
52 |
16 |
|
11 |
44 |
29 |
|
11 |
46 |
49 |
|
11 |
59 |
41 |
|
| |
|
2 |
|
15 |
|
21 |
|
7 |
|
18 |
|
30 |
| 24 |
12 |
5 |
56 |
|
12 |
2 |
1 |
|
11 |
51 |
55 |
|
11 |
44 |
22 |
|
11 |
47 |
7 |
|
12 |
0 |
11 |
|
| |
|
2 |
|
16 |
|
21 |
|
7 |
|
18 |
|
30 |
| 25 |
12 |
5 |
58 |
|
12 |
1 |
45 |
|
11 |
51 |
34 |
|
11 |
44 |
15 |
|
11 |
47 |
25 |
|
12 |
0 |
41 |
|
| |
|
1 |
|
16 |
|
20 |
|
6 |
|
19 |
|
30 |
| |
|
|
|
|
|
| 26 |
12 |
5 |
59 |
|
12 |
1 |
29 |
|
11 |
51 |
14 |
|
11 |
44 |
9 |
|
11 |
47 |
44 |
|
12 |
1 |
11 |
|
| |
|
Dec. |
|
17 |
|
20 |
|
5 |
|
20 |
|
30 |
| 27 |
12 |
5 |
58 |
|
12 |
1 |
12 |
|
11 |
50 |
54 |
|
11 |
44 |
4 |
|
11 |
48 |
4 |
|
12 |
1 |
41 |
|
| |
|
1 |
|
17 |
|
20 |
|
5 |
|
21 |
|
30 |
| 28 |
12 |
5 |
57 |
|
12 |
0 |
55 |
|
11 |
50 |
34 |
|
11 |
43 |
59 |
|
11 |
48 |
25 |
|
12 |
2 |
11 |
|
| |
|
1 |
|
18 |
|
19 |
|
4 |
|
21 |
|
29 |
| 29 |
12 |
5 |
56 |
|
12 |
0 |
37 |
|
11 |
50 |
15 |
|
11 |
43 |
55 |
|
11 |
48 |
46 |
|
12 |
2 |
40 |
|
| |
|
2 |
|
18 |
|
19 |
|
3 |
|
22 |
|
29 |
| 30 |
12 |
5 |
54 |
|
12 |
0 |
19 |
|
11 |
49 |
56 |
|
11 |
43 |
52 |
|
11 |
49 |
8 |
|
12 |
3 |
9 |
|
| |
|
3 |
|
18 |
|
19 |
|
2 |
|
22 |
|
29 |
| |
|
|
|
|
|
| 31 |
12 |
5 |
51 |
|
12 |
0 |
1 |
|
|
|
|
|
11 |
43 |
50 |
|
|
|
|
|
12 |
3 |
38 |
|
| |
|
3 |
|
18 |
|
|
|
1 |
|
|
|
29 |
| |
Incr. 2ʹ 46ʺ |
Decr. 5ʹ 47ʺ |
Decr. 9ʹ 47ʺ |
Decr. 5ʹ 47ʺ |
Decr. 0ʹ 1ʺ |
Incr. 14ʹ 8ʺ |
| |
Decr. 0 8 |
|
Incr. 5 19 |
|
122
| A TABLE of the Equation of natural Days, shewing what Time it ought to
be by the Clock when the Sun is on the Meridian. |
| The third after Leap-year. |
| Days |
January |
Dif. |
February |
Dif. |
March |
Dif. |
April |
Dif. |
May |
Dif. |
June |
Dif. |
| H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
| |
|
Inc. |
|
Inc. |
|
Dec. |
|
Dec. |
|
Dec. |
|
Inc. |
| 1 |
12 |
4 |
7 |
|
12 |
14 |
6 |
|
12 |
12 |
44 |
|
12 |
4 |
1 |
|
11 |
56 |
52 |
|
11 |
57 |
15 |
|
| |
|
28 |
|
7 |
|
12 |
|
18 |
|
8 |
|
9 |
| 2 |
12 |
4 |
35 |
|
12 |
14 |
13 |
|
12 |
12 |
32 |
|
12 |
3 |
43 |
|
11 |
56 |
44 |
|
11 |
57 |
24 |
|
| |
|
28 |
|
7 |
|
13 |
|
18 |
|
7 |
|
9 |
| 3 |
12 |
5 |
3 |
|
12 |
14 |
20 |
|
12 |
12 |
19 |
|
12 |
3 |
25 |
|
11 |
56 |
37 |
|
11 |
57 |
33 |
|
| |
|
27 |
|
6 |
|
13 |
|
18 |
|
7 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
12 |
5 |
30 |
|
12 |
14 |
26 |
|
12 |
12 |
6 |
|
12 |
3 |
7 |
|
11 |
56 |
30 |
|
11 |
57 |
42 |
|
| |
|
27 |
|
5 |
|
14 |
|
18 |
|
6 |
|
10 |
| 5 |
12 |
5 |
57 |
|
12 |
14 |
31 |
|
12 |
11 |
52 |
|
12 |
2 |
49 |
|
11 |
56 |
24 |
|
11 |
57 |
52 |
|
| |
|
27 |
|
4 |
|
14 |
|
18 |
|
5 |
|
10 |
| |
|
|
|
|
|
| 6 |
12 |
6 |
24 |
|
12 |
14 |
35 |
|
12 |
11 |
38 |
|
12 |
2 |
31 |
|
11 |
56 |
19 |
|
11 |
58 |
2 |
|
| |
|
26 |
|
3 |
|
14 |
|
18 |
|
5 |
|
11 |
| 7 |
12 |
6 |
50 |
|
12 |
14 |
38 |
|
12 |
11 |
24 |
|
12 |
2 |
13 |
|
11 |
56 |
14 |
|
11 |
58 |
13 |
|
| |
|
25 |
|
2 |
|
15 |
|
18 |
|
4 |
|
11 |
| 8 |
12 |
7 |
15 |
|
12 |
14 |
41 |
|
12 |
11 |
9 |
|
12 |
1 |
55 |
|
11 |
56 |
10 |
|
11 |
58 |
24 |
|
| |
|
25 |
|
1 |
|
16 |
|
17 |
|
4 |
|
11 |
| 9 |
12 |
7 |
40 |
|
12 |
14 |
43 |
|
12 |
10 |
53 |
|
12 |
1 |
38 |
|
11 |
56 |
6 |
|
11 |
58 |
35 |
|
| |
|
25 |
|
1 |
|
16 |
|
17 |
|
3 |
|
11 |
| 10 |
12 |
8 |
5 |
|
12 |
14 |
44 |
|
12 |
10 |
37 |
|
12 |
1 |
21 |
|
11 |
56 |
3 |
|
11 |
58 |
46 |
|
| |
|
24 |
|
Dec. |
|
16 |
|
16 |
|
2 |
|
12 |
| |
|
|
|
|
|
| 11 |
12 |
8 |
29 |
|
12 |
14 |
44 |
|
12 |
10 |
21 |
|
12 |
1 |
5 |
|
11 |
56 |
1 |
|
11 |
58 |
58 |
|
| |
|
23 |
|
1 |
|
16 |
|
16 |
|
2 |
|
12 |
| 12 |
12 |
8 |
52 |
|
12 |
14 |
43 |
|
12 |
10 |
5 |
|
12 |
0 |
49 |
|
11 |
55 |
59 |
|
11 |
59 |
10 |
|
| |
|
23 |
|
2 |
|
17 |
|
16 |
|
2 |
|
12 |
| 13 |
12 |
9 |
15 |
|
12 |
14 |
41 |
|
12 |
10 |
48 |
|
12 |
0 |
33 |
|
11 |
55 |
57 |
|
11 |
59 |
22 |
|
| |
|
22 |
|
2 |
|
17 |
|
16 |
|
1 |
|
12 |
| 14 |
12 |
9 |
37 |
|
12 |
14 |
39 |
|
12 |
9 |
31 |
|
12 |
0 |
17 |
|
11 |
55 |
56 |
|
11 |
59 |
34 |
|
| |
|
21 |
|
3 |
|
17 |
|
15 |
|
Inc. |
|
13 |
| 15 |
12 |
9 |
58 |
|
12 |
14 |
36 |
|
12 |
9 |
14 |
|
12 |
0 |
2 |
|
11 |
55 |
56 |
|
11 |
59 |
47 |
|
| |
|
21 |
|
4 |
|
17 |
|
15 |
|
1 |
|
13 |
| |
|
|
|
|
|
| 16 |
12 |
10 |
19 |
|
12 |
14 |
32 |
|
12 |
8 |
57 |
|
11 |
59 |
47 |
|
11 |
55 |
57 |
|
12 |
0 |
0 |
|
| |
|
20 |
|
4 |
|
18 |
|
15 |
|
1 |
|
13 |
| 17 |
12 |
10 |
39 |
|
12 |
14 |
28 |
|
12 |
8 |
39 |
|
11 |
59 |
32 |
|
11 |
55 |
58 |
|
12 |
0 |
13 |
|
| |
|
19 |
|
5 |
|
18 |
|
14 |
|
1 |
|
13 |
| 18 |
12 |
10 |
58 |
|
12 |
14 |
23 |
|
12 |
8 |
21 |
|
11 |
59 |
18 |
|
11 |
55 |
59 |
|
12 |
0 |
26 |
|
| |
|
18 |
|
6 |
|
18 |
|
14 |
|
2 |
|
13 |
| 19 |
12 |
11 |
16 |
|
12 |
14 |
17 |
|
12 |
8 |
3 |
|
11 |
59 |
4 |
|
11 |
56 |
1 |
|
12 |
0 |
39 |
|
| |
|
18 |
|
7 |
|
18 |
|
14 |
|
2 |
|
13 |
| 20 |
12 |
11 |
34 |
|
12 |
14 |
10 |
|
12 |
7 |
45 |
|
11 |
58 |
50 |
|
11 |
56 |
3 |
|
12 |
0 |
52 |
|
| |
|
17 |
|
7 |
|
18 |
|
13 |
|
3 |
|
13 |
| |
|
|
|
|
|
| 21 |
12 |
11 |
51 |
|
12 |
14 |
3 |
|
12 |
7 |
27 |
|
11 |
58 |
37 |
|
11 |
56 |
6 |
|
12 |
1 |
5 |
|
| |
|
16 |
|
8 |
|
19 |
|
13 |
|
4 |
|
12 |
| 22 |
12 |
12 |
7 |
|
12 |
13 |
55 |
|
12 |
7 |
8 |
|
11 |
58 |
24 |
|
11 |
56 |
10 |
|
12 |
1 |
17 |
|
| |
|
16 |
|
8 |
|
19 |
|
12 |
|
4 |
|
13 |
| 23 |
12 |
12 |
23 |
|
12 |
13 |
47 |
|
12 |
6 |
49 |
|
11 |
58 |
12 |
|
11 |
56 |
14 |
|
12 |
1 |
30 |
|
| |
|
15 |
|
9 |
|
19 |
|
12 |
|
5 |
|
13 |
| 24 |
12 |
12 |
38 |
|
12 |
13 |
38 |
|
12 |
6 |
30 |
|
11 |
58 |
0 |
|
11 |
56 |
19 |
|
12 |
1 |
43 |
|
| |
|
14 |
|
9 |
|
19 |
|
11 |
|
5 |
|
13 |
| 25 |
12 |
12 |
52 |
|
12 |
13 |
29 |
|
12 |
6 |
11 |
|
11 |
57 |
49 |
|
11 |
56 |
24 |
|
12 |
1 |
56 |
|
| |
|
13 |
|
10 |
|
18 |
|
11 |
|
6 |
|
13 |
| |
|
|
|
|
|
| 26 |
12 |
13 |
5 |
|
12 |
13 |
19 |
|
12 |
5 |
53 |
|
11 |
57 |
38 |
|
11 |
56 |
30 |
|
12 |
2 |
9 |
|
| |
|
12 |
|
11 |
|
19 |
|
10 |
|
6 |
|
13 |
| 27 |
12 |
13 |
17 |
|
12 |
13 |
8 |
|
12 |
5 |
34 |
|
11 |
57 |
28 |
|
11 |
56 |
36 |
|
12 |
2 |
22 |
|
| |
|
11 |
|
12 |
|
19 |
|
10 |
|
7 |
|
12 |
| 28 |
12 |
13 |
28 |
|
12 |
12 |
56 |
|
12 |
5 |
15 |
|
11 |
57 |
18 |
|
11 |
56 |
43 |
|
12 |
2 |
34 |
|
| |
|
11 |
|
12 |
|
18 |
|
9 |
|
7 |
|
12 |
| 29 |
12 |
13 |
39 |
|
|
|
|
|
12 |
4 |
57 |
|
11 |
57 |
9 |
|
11 |
56 |
50 |
|
12 |
2 |
46 |
|
| |
|
10 |
|
|
|
19 |
|
9 |
|
8 |
|
12 |
| 30 |
12 |
13 |
49 |
|
|
|
|
|
12 |
4 |
38 |
|
11 |
57 |
0 |
|
11 |
56 |
58 |
|
12 |
2 |
58 |
|
| |
|
9 |
|
|
|
19 |
|
8 |
|
8 |
|
12 |
| |
|
|
|
|
|
|
| 31 |
12 |
13 |
58 |
|
|
|
|
|
12 |
4 |
19 |
|
|
|
|
|
11 |
57 |
6 |
|
|
|
|
|
| |
|
8 |
|
|
|
18 |
|
|
|
9 |
|
|
| |
Incr. 9ʹ 51ʺ |
Incr. 0ʹ 38ʺ |
Decr. 8ʹ 25ʺ |
Decr. 7ʹ 1ʺ |
Decr. 0ʹ 56ʺ |
Incr. 5ʹ 43ʺ |
| |
Decr. 1 48 |
|
Incr. 1 10 |
|
123
| A TABLE of the Equation of natural Days, shewing what Time it ought to
be by the Clock when the Sun is on the Meridian. |
| The third after Leap-year. |
| Days |
July |
Dif. |
August |
Dif. |
September |
Dif. |
October |
Dif. |
November |
Dif. |
December |
Dif. |
| H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
H. |
M. |
S. |
S. |
| |
&nbps; |
Inc. |
&nbps; |
Dec. |
&nbps; |
Dec. |
&nbps; |
Dec. |
&nbps; |
Dec. |
&nbps; |
Inc. |
| 1 |
12 |
3 |
10 |
|
12 |
5 |
49 |
|
11 |
59 |
47 |
|
11 |
49 |
42 |
|
11 |
43 |
49 |
|
11 |
49 |
25 |
|
| |
|
11 |
|
4 |
|
19 |
|
18 |
|
1 |
|
23 |
| 2 |
12 |
3 |
21 |
|
12 |
5 |
45 |
|
11 |
59 |
28 |
|
11 |
49 |
24 |
|
11 |
43 |
48 |
|
11 |
49 |
48 |
|
| |
|
11 |
|
4 |
|
19 |
|
18 |
|
Inc. |
|
24 |
| 3 |
12 |
3 |
32 |
|
12 |
5 |
41 |
|
11 |
59 |
9 |
|
11 |
49 |
6 |
|
11 |
43 |
48 |
|
11 |
50 |
12 |
|
| |
|
11 |
|
5 |
|
19 |
|
18 |
|
1 |
|
24 |
| 4 |
12 |
3 |
43 |
|
12 |
5 |
36 |
|
11 |
58 |
50 |
|
11 |
48 |
48 |
|
11 |
43 |
49 |
|
11 |
50 |
36 |
|
| |
|
11 |
|
5 |
|
19 |
|
18 |
|
2 |
|
25 |
| 5 |
12 |
3 |
54 |
|
12 |
5 |
31 |
|
11 |
58 |
31 |
|
11 |
48 |
30 |
|
11 |
43 |
51 |
|
11 |
51 |
1 |
|
| |
|
10 |
|
6 |
|
20 |
|
18 |
|
2 |
|
25 |
| |
|
|
|
|
|
| 6 |
12 |
4 |
4 |
|
12 |
5 |
25 |
|
11 |
58 |
11 |
|
11 |
48 |
12 |
|
11 |
43 |
53 |
|
11 |
51 |
26 |
|
| |
|
10 |
|
7 |
|
20 |
|
17 |
|
3 |
|
26 |
| 7 |
12 |
4 |
14 |
|
12 |
5 |
18 |
|
11 |
57 |
51 |
|
11 |
47 |
55 |
|
11 |
43 |
56 |
|
11 |
52 |
52 |
|
| |
|
10 |
|
7 |
|
20 |
|
16 |
|
4 |
|
27 |
| 8 |
12 |
4 |
24 |
|
12 |
5 |
11 |
|
11 |
57 |
31 |
|
11 |
47 |
39 |
|
11 |
44 |
0 |
|
11 |
52 |
19 |
|
| |
|
9 |
|
7 |
|
20 |
|
16 |
|
5 |
|
27 |
| 9 |
12 |
4 |
33 |
|
12 |
5 |
4 |
|
11 |
57 |
11 |
|
11 |
47 |
23 |
|
11 |
44 |
5 |
|
11 |
52 |
46 |
|
| |
|
9 |
|
8 |
|
20 |
|
16 |
|
6 |
|
27 |
| 10 |
12 |
4 |
42 |
|
12 |
4 |
56 |
|
11 |
56 |
51 |
|
11 |
47 |
7 |
|
11 |
44 |
11 |
|
11 |
53 |
13 |
|
| |
|
8 |
|
8 |
|
20 |
|
15 |
|
7 |
|
28 |
| |
|
|
|
|
|
| 11 |
12 |
4 |
50 |
|
12 |
4 |
48 |
|
11 |
56 |
31 |
|
11 |
46 |
52 |
|
11 |
44 |
18 |
|
11 |
53 |
41 |
|
| |
|
8 |
|
9 |
|
21 |
|
15 |
|
8 |
|
28 |
| 12 |
12 |
4 |
58 |
|
12 |
4 |
37 |
|
11 |
56 |
10 |
|
11 |
46 |
37 |
|
11 |
44 |
26 |
|
11 |
54 |
9 |
|
| |
|
8 |
|
10 |
|
21 |
|
14 |
|
8 |
|
28 |
| 13 |
12 |
5 |
6 |
|
12 |
4 |
27 |
|
11 |
55 |
49 |
|
11 |
46 |
23 |
|
11 |
44 |
34 |
|
11 |
54 |
37 |
|
| |
|
7 |
|
10 |
|
21 |
|
14 |
|
9 |
|
29 |
| 14 |
12 |
5 |
13 |
|
12 |
4 |
17 |
|
11 |
55 |
28 |
|
11 |
46 |
9 |
|
11 |
44 |
43 |
|
11 |
55 |
6 |
|
| |
|
6 |
|
11 |
|
21 |
|
13 |
|
10 |
|
30 |
| 15 |
12 |
5 |
19 |
|
12 |
4 |
6 |
|
11 |
55 |
7 |
|
11 |
45 |
56 |
|
11 |
44 |
53 |
|
11 |
55 |
36 |
|
| |
|
6 |
|
12 |
|
20 |
|
12 |
|
11 |
|
29 |
| |
|
|
|
|
|
| 16 |
12 |
5 |
25 |
|
12 |
3 |
54 |
|
11 |
54 |
47 |
|
11 |
45 |
44 |
|
11 |
45 |
4 |
|
11 |
56 |
6 |
|
| |
|
6 |
|
12 |
|
21 |
|
12 |
|
12 |
|
30 |
| 17 |
12 |
5 |
31 |
|
12 |
3 |
42 |
|
11 |
54 |
26 |
|
11 |
45 |
32 |
|
11 |
45 |
16 |
|
11 |
56 |
36 |
|
| |
|
5 |
|
13 |
|
21 |
|
12 |
|
13 |
|
30 |
| 18 |
12 |
5 |
36 |
|
12 |
3 |
29 |
|
11 |
54 |
5 |
|
11 |
45 |
20 |
|
11 |
45 |
29 |
|
11 |
57 |
6 |
|
| |
|
5 |
|
13 |
|
21 |
|
11 |
|
14 |
|
29 |
| 19 |
12 |
5 |
41 |
|
12 |
3 |
16 |
|
11 |
53 |
44 |
|
11 |
45 |
9 |
|
11 |
45 |
43 |
|
11 |
57 |
35 |
|
| |
|
4 |
|
13 |
|
21 |
|
10 |
|
14 |
|
30 |
| 20 |
12 |
5 |
45 |
|
12 |
3 |
3 |
|
11 |
53 |
23 |
|
11 |
44 |
59 |
|
11 |
45 |
57 |
|
11 |
58 |
5 |
|
| |
|
4 |
|
14 |
|
20 |
|
9 |
|
15 |
|
30 |
| |
|
|
|
|
|
| 21 |
12 |
5 |
49 |
|
12 |
2 |
49 |
|
11 |
53 |
3 |
|
11 |
44 |
50 |
|
11 |
46 |
12 |
|
11 |
58 |
34 |
|
| |
|
3 |
|
15 |
|
21 |
|
9 |
|
16 |
|
30 |
| 22 |
12 |
5 |
52 |
|
13 |
2 |
34 |
|
11 |
52 |
42 |
|
11 |
44 |
41 |
|
11 |
46 |
28 |
|
11 |
59 |
4 |
|
| |
|
3 |
|
15 |
|
21 |
|
9 |
|
17 |
|
30 |
| 23 |
12 |
5 |
55 |
|
12 |
2 |
19 |
|
11 |
52 |
21 |
|
11 |
44 |
32 |
|
11 |
46 |
45 |
|
11 |
59 |
34 |
|
| |
|
2 |
|
15 |
|
20 |
|
8 |
|
17 |
|
30 |
| 24 |
12 |
5 |
57 |
|
12 |
2 |
4 |
|
11 |
52 |
1 |
|
11 |
44 |
24 |
|
11 |
47 |
2 |
|
12 |
0 |
4 |
|
| |
|
1 |
|
16 |
|
21 |
|
7 |
|
18 |
|
30 |
| 25 |
12 |
5 |
58 |
|
12 |
1 |
48 |
|
11 |
51 |
40 |
|
11 |
44 |
17 |
|
11 |
47 |
20 |
|
12 |
0 |
34 |
|
| |
|
1 |
|
16 |
|
20 |
|
6 |
|
19 |
|
30 |
| |
|
|
|
|
|
| 26 |
12 |
5 |
59 |
|
12 |
1 |
32 |
|
11 |
51 |
20 |
|
11 |
44 |
11 |
|
11 |
47 |
39 |
|
12 |
1 |
4 |
|
| |
|
Dec. |
|
16 |
|
20 |
|
5 |
|
20 |
|
30 |
| 27 |
12 |
5 |
58 |
|
12 |
1 |
16 |
|
11 |
51 |
0 |
|
11 |
44 |
6 |
|
11 |
47 |
59 |
|
12 |
1 |
34 |
|
| |
|
1 |
|
17 |
|
20 |
|
5 |
|
20 |
|
30 |
| 28 |
12 |
5 |
57 |
|
12 |
0 |
59 |
|
11 |
50 |
40 |
|
11 |
44 |
1 |
|
11 |
48 |
19 |
|
12 |
2 |
4 |
|
| |
|
1 |
|
17 |
|
20 |
|
4 |
|
21 |
|
29 |
| 29 |
12 |
5 |
56 |
|
12 |
0 |
42 |
|
11 |
50 |
20 |
|
11 |
43 |
57 |
|
11 |
48 |
40 |
|
12 |
2 |
33 |
|
| |
|
2 |
|
18 |
|
19 |
|
3 |
|
22 |
|
29 |
| 30 |
12 |
5 |
54 |
|
12 |
0 |
24 |
|
11 |
50 |
1 |
|
11 |
43 |
54 |
|
11 |
49 |
2 |
|
12 |
3 |
2 |
|
| |
|
2 |
|
18 |
|
19 |
|
3 |
|
23 |
|
29 |
| |
|
|
|
|
|
| 31 |
12 |
5 |
52 |
|
12 |
0 |
6 |
|
|
|
|
|
11 |
43 |
51 |
|
|
|
|
|
12 |
3 |
31 |
|
| |
|
3 |
|
19 |
|
|
|
2 |
|
|
|
29 |
| |
Incr. 2ʹ 48ʺ |
Decr. 5ʹ 43ʺ |
Decr. 9ʹ 46ʺ |
Decr. 5ʹ 51ʺ |
Decr. 0ʹ 1ʺ |
Incr. 14ʹ 6ʺ |
| |
Decr. 0 7 |
|
|
|
Incr. 5 14 |
|
124
CHAP. XV.
The Moon’s surface mountainous: Her Phases described: Her path, and the paths of Jupiter’s Moons delineated: The proportions of the Diameters of their Orbits, and those of Saturn’s Moons, to each other; and to the Diameter of the Sun.
252. By looking at the Moon with an ordinary telescope we perceive
that her surface is diversified with long tracts of prodigious
high mountains and deep cavities. Some of her mountains, by
comparing their height with her diameter (which is 2180 miles) are
found to be three times higher than the highest hills on our Earth.
This ruggedness of the Moon’s surface is of great use to us, by
reflecting the Sun’s light to all sides: for if the Moon were smooth
and polished like a looking-glass, or covered with water, she could
never distribute the Sun’s light all round; only in some positions she
would shew us his image, no bigger than a point, but with such a
lustre as would be hurtful to our eyes.
Why no hills appear on her edge.
253. The Moon’s surface being so uneven, many have wondered
why her edge appears not jagged, as well as the curve bounding the
light and dark places. But if we consider, that what we call the edge
of the Moon’s Disc is not a single line set round with mountains, in
which case it would appear irregularly indented, but a large Zone
having many mountains lying behind one another from the observer’s
eye, we shall find that the mountains in some rows will be opposite to
the vales in others; and so fill up the inequalities as to make her appear
quite round: just as when one looks at an orange, although it’s roughness
be very discernible on the side next the eye, especially if the Sun
or a Candle shines obliquely on that side, yet the line terminating the
visible part still appears smooth and even.
Plate VII.
J. Ferguson delin.
J. Mynde Sculp.
The Moon has no twilight.
Fig. I.
254. As the Sun can only enlighten that half of the Earth which
is at any moment turned towards him, and being withdrawn from
the opposite half leaves it in darkness; so he likewise doth to the
Moon: only with this difference, that the Earth being surrounded by
an Atmosphere, and the Moon having none, we have twilight after the
Sun sets; but the Lunar Inhabitants have an immediate transition from
the brightest Sun-shine to the blackest darkness § 177. For, let tkrsw
125be the Earth, and A, B, C, D, E, F, G, H the Moon in eight different parts
of her Orbit. As the Earth turns round its Axis, from west to east,
when any place comes to t the twilight begins there, and when it
revolves from thence to r the Sun S rises; when the place comes to s the
Sun sets, and when it comes to w the twilight ends. But as the Moon
turns round her Axis, which is only once a month, the moment that
any point of her surface comes to r (see the Moon at G) the Sun rises
there without any previous warning by twilight; and when the same
point comes to s the Sun sets, and that point goes into darkness as
black as at midnight.
The Moon’s Phases.
255. The Moon being an opaque spherical body, (for her hills
take off no more from her roundness than the inequalities on the surface
of an orange takes off from its roundness) we can only see that
part of the enlightened half of her which is towards the Earth. And
therefore, when the Moon is at A, in conjunction with the Sun S, her
dark half is towards the Earth, and she disappears as at a, there being no
light on that half to render it visible. When she comes to her first
Octant at B, or has gone an eighth part of her orbit from her Conjunction,
a quarter of her enlightened side is towards the Earth, and
she appears horned as at b. When she has gone a quarter of her orbit
from between the Earth and Sun to C, she shews us one half of her
enlightened side as at c, and we say, she is a quarter old. At D she is
in her second Octant, and by shewing us more of her enlightened side
she appears gibbous as at d. At E her whole enlightened side is towards
the Earth, and therefore she appears round as at e, when we say, it
is Full Moon. In her third Octant at F, part of her dark side being
towards the Earth, she again appears gibbous, and is on the decrease,
as at f. At G we see just one half of her enlightened side, and she
appears half decreased, or in her third Quarter, as at g. At H we
only see a quarter of her enlightened side, being in her fourth Octant,
where she appears horned as at h. And at A, having compleated her
course from the Sun to the Sun again, she disappears; and we say, it
is New Moon. Thus in going from A to E the Moon seems continually
to increase; and in going from E to A, to decrease in the
same proportion; having like Phases at equal distances from A or E,
but as seen from the Sun S, she is always Full.
The Moon’s Disc not always quite round when full.
256. The Moon appears not perfectly round when she is Full in
the highest or lowest part of her Orbit, because we have not a direct
view of her enlightened side at that time. When Full in the highest
part of her orbit, a small deficiency appears on her lower edge; and
the contrary when Full in the lowest part of her Orbit.
The Phases of the Earth and Moon contrary.
126257. ’Tis plain by the Figure, that when the Moon changes to the
Earth, the Earth appears Full to the Moon; and vice versâ. For
when the Moon is at A, New to the Earth, the whole enlightened
side of the Earth is towards the Moon: and when the Moon is at E,
Full to the Earth, it’s dark side is towards her. Hence a New Moon
answers to a Full Earth, and a Full Moon to a New Earth. The
Quarters are also reversed to each other.
An agreeable Phenomenon.
258. Between the third Quarter and Change, the Moon is frequently
visible in the forenoon, even when the Sun shines; and then
she affords us an opportunity of seeing a very agreeable appearance,
wherever we find a globular stone above the level of the eye, as suppose
on the top of a gate. For, if the Sun shines on the stone, and
we place ourselves so as the upper part of the stone may just seem
to touch the point of the Moon’s lowermost horn, we shall then see
the enlightened part of the stone exactly of the same shape with the
Moon; horned as she is, and inclining the same way to the Horizon.
The reason is plain; for the Sun enlightens the stone the same way as
he does the Moon: and both being Globes, when we put ourselves
into the above situation, the Moon and stone have the same position
to our eyes; and therefore we must see as much of the illuminated
part of the one as of the other.
The nonagesimal Degree, what.
259. The position of the Moon’s Cusps, or a right line touching
the points of her horns, is very differently inclined to the Horizon at
different hours of the same days of her age. Sometimes she stands, as
it were, upright on her lower horn, and then such a line is perpendicular
to the Horizon: when this, happens, she is in what the Astronomers
call the Nonagesimal Degree; which is the highest point of the
Ecliptic above the Horizon at that time, and is 90 degrees from both
sides of the Horizon where it is then cut by the Ecliptic. But this
never happens when the Moon is on the Meridian, except when she
is at the very beginning of Cancer or Capricorn.
How the inclination of the Ecliptic may be found by the
position of the Moon horns.
PL. VII.260. The inclination of that part of the Ecliptic to the Horizon in
which the Moon is at any time when horned, may be known by the
position of her horns; for a right line touching their points is perpendicular
to the Ecliptic. And as the Angle that the Moon’s orbit
makes with the Ecliptic can never raise her above, nor depress her
below the Ecliptic, more than two minutes of a degree, as seen from
the Sun; it can have no sensible effect upon the position of her horns.
Therefore, if a Quadrant be held up, so as one of it’s edges may seem
to touch the Moon’s horns, the graduated side being kept towards
the eye, and as far from the eye as it can be conveniently held, the
127arc between the Plumb-line and that edge of the Quadrant which
seems to touch the Moon’s horns will shew the inclination of that
part of the Ecliptic to the Horizon. And the arc between the other
edge of the Quadrant and Plumb-line will shew the inclination of the
Moon’s horns to the Horizon at that time also.
Fig. I.
Why the Moon appears as big as the Sun.
261. The Moon generally appears as large as the Sun; for the
Angle vkA, under which the Moon is seen from the Earth, is the
same with the Angle LkM, under which the Sun is seen from it.
And therefore the Moon may hide the Sun’s whole Disc from us, as
she sometimes does in solar Eclipses. The reason why she does
not eclipse the Sun at every Change shall be explained afterwards.
If the Moon were farther from the Earth as at a, she could never
hide the whole of the Sun from us; for then she would appear under
the Angle NkO, eclipsing only that part of the Sun which lies between
N and O: were she still further from the Earth, as at X, she would
appear under the small Angle TkW, like a spot on the Sun, hiding
only the part TW from our sight.
A proof of the Moon’s turning round her Axis.
262. The Moon turns round her Axis in the time that she goes
round her orbit; which is evident from hence, that a spectator at
rest, without the periphery of the Moon’s orbit, would see all her
sides turned regularly towards him in that time. She turns round
her Axis from any Star to the same Star again in 27 days 8 hours;
from the Sun to the Sun again in
291⁄2
days: the former is the length
of her sidereal day, and the latter the length of her solar day. A
body moving round the Sun would have a solar day in every revolution,
without turning on it’s Axis; the same as if it had kept all the
while at rest, and the Sun moved round it: but without turning round
it’s Axis it could never have one sidereal day, because it would always
keep the same side towards any given Star.
Her periodical and synodical Revolution.
263. If the Earth had no annual motion, the Moon would go
round it so as to compleat a Lunation, a sidereal, and a solar day,
all in the same time. But, because the Earth goes forward in
it’s orbit while the Moon goes round the Earth in her orbit, the
Moon must go as much more than round her orbit from Change
to Change in compleating a solar day as the Earth has gone forward
in it’s orbit during that time, i. e. almost a twelfth part of a
Circle.
Familiarly represented.
A Table shewing the times that the hour and minute hands of a
watch are in conjunction.
A machine for shewing the motions of the Sun and Moon.
PL. VII.264. The Moon’s periodical and synodical revolution may be familiarly
represented by the motions of the hour and minute hands of a
watch round it’s dial-plate, which is divided into 12 equal parts or
128hours, as the Ecliptic is divided into 12 Signs, and the year into 12
months. Let us suppose
these 12 hours to be 12
months, the hour hand the
Sun, and the minute hand
the Moon; then will the
former go round once in a
year, and the latter once in
a month; but the Moon,
or minute hand must go
more than round from any
point of the Circle where
it was last conjoined with
the Sun, or hour hand, to
overtake it again: for the
hour hand being in motion, can never be overtaken by the minute
hand at that point from which they started at their last conjunction.
The first column of the annexed Table shews the number of conjunctions
which the hour and minute hand make whilst the hour hand
goes once round the dial-plate; and the other columns shew the times
when the two hands meet at every conjunction. Thus, suppose the
two hands to be in conjunction at XII, as they always are; then, at
the first following conjunction it is 5 minutes 27 seconds 16 thirds
21 fourths
491⁄11
fifths past I where they meet; at the second conjunction
it is 10 minutes 54 seconds 32 thirds 43 fourths
381⁄2
fifths
past II; and so on. This, though an easy illustration of the motions
of the Sun and Moon, is not precise as to the times of their conjunctions;
because, while the Sun goes round the Ecliptic, the Moon
makes
121⁄3
conjunctions with him; but the minute hand of a watch
or clock makes only 11 conjunctions with the hour hand in one period
round the dial-plate. But if, instead of the common wheel-work
at the back of the dial-plate, the Axis of the minute hand had a
pinion of 6 leaves turning a wheel of 40, and this last turning the
hour hand, in every revolution it makes round the dial-plate the minute
hand would make
121⁄3
conjunctions with it; and so would be a pretty
device for shewing the motions of the Sun and Moon; especially, as
the slowest moving hand might have a little Sun fixed on it’s point,
and the quickest a little Moon. Besides, the plate, instead of hours
and quarters, might have a Circle of months, with the 12 Signs and
their Degrees; and if a plate of
291⁄2
equal parts for the days of the
Moon’s age were fixed to the Axis of the Sun-hand, and below it, so
129as the Sun always kept at the
1⁄2
day of that plate, the Moon-hand
would shew the Moon’s age upon that plate for every day pointed out
by the Sun-hand in the Circle of months; and both Sun and Moon
would shew their places in the Ecliptic: for the Sun would go round
the Ecliptic in 365 Days and the Moon in
271⁄3
days, which is her
periodical revolution; but from the Sun to the Sun again, or from
Change to Change, in
291⁄2
days, which is her synodical revolution.
| Conj. |
H. |
M. |
S. |
ʺʹ |
ʺʺ |
v pts. |
| 1 |
I |
5 |
27 |
16 |
21 |
491⁄11 |
| 2 |
II |
10 |
54 |
32 |
43 |
382⁄11 |
| 3 |
III |
16 |
21 |
49 |
5 |
273⁄11 |
| 4 |
IIII |
21 |
49 |
5 |
27 |
164⁄11 |
| 5 |
V |
27 |
16 |
21 |
49 |
55⁄11 |
| 6 |
VI |
32 |
43 |
38 |
10 |
546⁄11 |
| 7 |
VII |
38 |
10 |
54 |
32 |
437⁄11 |
| 8 |
VIII |
43 |
38 |
10 |
54 |
328⁄11 |
| 9 |
IX |
49 |
5 |
27 |
16 |
219⁄11 |
| 10 |
X |
54 |
32 |
43 |
38 |
1010⁄11 |
| 11 |
XII |
0 |
0 |
0 |
0 |
0 |
The Moon’s motion thro’ open space described.
265. If the Earth had no annual motion, the Moon’s motion round
the Earth, and her track in absolute space, would be always the
same[58]. But as the Earth and Moon move round the Sun, the Moon’s
real path in the Heavens is very different from her path round the
Earth: the latter being in a progressive Circle, and the former in a
curve of different degrees of concavity, which would always be the
same in the same parts of the Heavens, if the Moon performed a compleat
number of Lunations in a year.
An idea of the Earth’s path and the Moon’s.
266. Let a nail in the end of the axle of a chariot-wheel represent
the Earth, and a pin in the nave the Moon; if the body of the
chariot be propped up so as to keep that wheel from touching the
ground, and the wheel be then turned round by hand, the pin will
describe a Circle both round the nail and in the space it moves through.
But if the props be taken away, the horses put to, and the chariot
driven over a piece of ground which is circularly convex; the nail in
the axle will describe a circular curve, and the pin in the nave will still
describe a circle round the progressive nail in the axle, but not in the
space through which it moves. In this case, the curve described by the
nail will resemble in miniature as much of the Earth’s annual path round
the Sun, as it describes whilst the Moon goes as often round the Earth
as the pin does round the nail: and the curve described by the nail will
have some resemblance of the Moon’s path during so many Lunations.
Let us now suppose that the Radius of the circular curve described
by the nail in the axle is to the Radius of the Circle which the pin in
the nave describes round the axle as
3371⁄2
to 1; which is the proportion
of the Radius or Semidiameter of the Earth’s Orbit to that of the
Moon’s; or of the circular curve A 1 2 3 4 5 6 7 B &c. to the little
Circle a; and then, whilst the progressive nail describes the said curve
from A to E, the pin will go once round the nail with regard to the
center of it’s path, and in doing so, will describe the curve abcde. The
130former will be a true representation of the Earth’s path for one Lunation,
and the latter of the Moon’s for that time. Here we may set
aside the inequalities of the Moon’s Moon, and also the Earth’s moving
round it’s common center of gravity and the Moon’s: all which, if
they were truly copied in this experiment, would not sensibly alter the
figure of the paths described by the nail and pin, even though they should
rub against a plain upright surface all the way, and leave their tracks visible.
And if the chariot should be driven forward on such a convex
piece of ground, so as to turn the wheel several times round, the track
of the pin in the nave would still be concave toward the center of the
circular curve described by the pin in the Axle; as the Moon’s path is
always concave to the Sun in the center of the Earth’s annual Orbit.
Proportion of the Moon’s Orbit to the Earth’s.
In this Diagram, the thickest curve line ABCD, with the numeral figures
set to it, represents as much of the Earth’s annual Orbit as it describes
in 32 days from west to east; the little Circles at a, b, c, d, e shew the
Moon’s Orbit in due proportion to the Earth’s; and the smallest curve
abcdef represents the line of the Moon’s path in the Heavens for 32
days, accounted from any particular New Moon at a. The machine,
Fig. 5th is for delineating the Moon’s path, and will be described,
with the rest of my Astronomical machinery, in the last Chapter. The
Sun is supposed to be in the center of the curve A 1 2 3 4 5 6 7 B
&c. and the small dotted Circles upon it represent the Moon’s Orbit, of
which the Radius is in the same proportion to the Earth’s path in this
scheme, that the Radius of the Moon’s Orbit in the Heavens bears
to the Radius of the Earth’s annual path round the Sun; that is, as
240,000 to 81,000,000, or as 1 to
3371⁄2.
Fig. II.
When the Earth is at A the New Moon is at a; and in the seven
days that the Earth describes the curve 1 2 3 4 5 6 7, the Moon in
accompanying the Earth describes the curve ab; and is in her first
Quarter at b when the Earth is at B. As the Earth describes the
curve B 8 9 10 11 12 13 14 the Moon describes the curve bc; and
is opposite to the Sun at c, when the Earth is at C. Whilst the Earth
describes the curve C 15 16 17 18 19 20 21 22 the Moon describes
the curve cd; and is in her third Quarter at d when the Earth is at D.
Once more, whilst the Earth describes the curve D 23 24 25 26 27 28 29
the Moon describes the curve de; and is again in conjunction at e with
the Sun when the Earth is at E, between the 29th and 30th day of the
Moon’s age, accounted by the numeral Figures from the New Moon at
A. In describing the curve abcde, the Moon goes round the progressive
Earth as really as if she had kept in the dotted Circle A, and the Earth
continued immoveable in the center of that Circle.
The Moon’s motion always concave towards the Sun.
131And thus we see, that although the Moon goes round the Earth in
a Circle, with respect to the Earth’s center, her real path in the
Heavens is not very different in appearance from the Earth’s path.
To shew that the Moon’s path is concave to the Sun, even at the time
of Change, it is carried on a little farther into a second Lunation,
as to f.
How her motion is alternately retarded and accelerated.
267. The Moon’s absolute motion from her Change to her first
Quarter, or from a to b, is so much slower than the Earth’s, that she
falls 240 thousand miles (equal to the Semidiameter of her Orbit)
behind the Earth at her first Quarter in b, when the Earth is in B;
that is, she falls back a space equal to her distance from the Earth.
From that time her motion is gradually accelerated to her Opposition
or Full at c, and then she is come up as far as the Earth, having
regained what she lost in her first Quarter from a to b. From the
Full to the last Quarter at d her motion continues accelerated, so as
to be just as far before the Earth at D, as she was behind it at her
first Quarter in b. But, from d to e her motion is retarded so, that
she loses as much with respect to the Earth as is equal to her distance
from it, or to the Semidiameter of her Orbit; and by that means she
comes to e, and is then in conjunction with the Sun as seen from the
Earth at E. Hence we find, that the Moon’s absolute motion is slower
than the Earth’s from her third Quarter to her first; and swifter than
the Earth’s from her first Quarter to her third: her path being less
curved than the Earth’s in the former case, and more in the latter.
Yet it is still bent the same way towards the Sun; for if we imagine
the concavity of the Earth’s Orbit to be measured by the length of a
perpendicular line Cg, let down from the Earth’s place upon the
straight line bgd at the Full of the Moon, and connecting the places
of the Earth at the end of the Moon’s first and third Quarters,
that length will be about 640 thousand miles; and the Moon when
New only approaching nearer to the Sun by 240 thousand miles
than the Earth is, the length of the perpendicular let down from
her place at that time upon the same straight line, and which shews
the concavity of that part of her path, will be about 400 thousand
miles.
268. The Moon’s path being concave to the Sun throughout, demonstrates
that her gravity towards the Sun, at her conjunction, exceeds
her gravity towards the Earth. And if we consider that the
quantity of matter in the Sun is almost 230 thousand times as great
as the quantity of matter in the Earth, and that the attraction
132of each body diminishes as the square of the distance from it increases,
we shall soon find, that the point of equal attraction where these two
powers would be equally strong, is about 70 thousand miles nearer the
Earth than the Moon is at her Change. It may now appear surprising
that the Moon does not abandon the Earth when she is between it and
the Sun, because she is considerably more attracted by the Sun than by
the Earth at that time. But this difficulty vanishes when we consider,
that the Moon is so near the Earth in proportion to the Earth’s distance
from the Sun, that she is but very little more attracted by the Sun at that
time than the Earth is; and whilst the Earth’s attraction is greater upon
the Moon than the difference of the Sun’s attraction upon the Earth and
her (and that it is always much greater is demonstrable) there is no
danger of the Moon’s leaving the Earth; for if she should fall towards the
Sun, the Earth would follow her almost with equal speed. The absolute
attraction of the Earth upon a drop of falling rain is much greater than
the absolute attraction of the particles of that drop upon each other, or
of it’s center upon all parts of it’s circumference; but then the side of
the drop next the Earth is attracted with so very little more force than
it’s center, or even it’s opposite side; that the attraction of the center of
the drop upon it’s side next the Earth is much greater than the difference
of force by which the Earth attracts it’s nearer surface and center: on
which account the drop preserves it’s round figure, and might be projected
about the Earth by a strong circulating wind so as to be kept
from falling to the Earth. It is much the same with the Earth and
Moon in respect to the Sun; for if we should suppose the Moon’s
Orbit to be filled with a fluid Globe, of which all the parts would
be attracted towards the Earth in it’s center, but the whole of it
much more attracted by the Sun; one part of it could not fall to the
Sun without the other, and a sufficient projectile force would carry the
whole fluid Globe round the Sun. A ship, at the distance of the
Moon, sailing round the Earth on the surface of the fluid Globe, could
no more be taken away by the Sun when it is on the side next him,
than the Earth could be taken away from it when it is on the opposite
side; which could never happen unless the Earth’s projectile motion
were stopt; and if it were stopt, the Ship with the whole fluid Globe,
Earth and all together, would as naturally fall to the Sun as a drop
of rain in calm air falls to the Earth. Hence we may see, that the
Earth is in no more danger of being left by the Moon at the Change,
than the Moon is of being left by the Earth at the Full: the diameter of
the Moon’s Orbit being so small in comparison of the Sun’s distance,
that the Moon is but little more or less attracted than the Earth at any
133time. And as the Moon’s projectile force keeps her from falling to the
Earth, so the Earth’s projectile force keeps it from falling to the Sun.
Fig. III.
269. All the curves which Jupiter’s Satellites describe, are different
from the path described by our Moon, although these Satellites go
round Jupiter, as the Moon goes round the Earth. Let ABCDE &c.
be as much of Jupiter’s Orbit as he describes in 18 days from A to T;
and the curves a, b, c, d will be the paths of his four Moons going
round him in his progressive motion.
The absolute Path of Jupiter and his Satellites delineated.
Fig. III.
Now let us suppose all these Moons to set out from a conjunction
with the Sun, as seen from Jupiter. When Jupiter is at A his first
or nearest Moon will be at a, his second at b, his third at c, and his fourth
at d. At the end of 24 terrestrial hours after this conjunction, Jupiter
has moved to B, his first Moon or Satellite has described the curve
a1, his second the curve b1, his third c1, and his fourth d1. The
next day when Jupiter is at C, his first Satellite has described the curve a2
from its conjunction, his second the curve b2, his third the curve c2,
and his fourth the curve d2, and so on. The numeral Figures under
the capital letters shew Jupiter’s place in his path every day for
18 days, accounted from A to T; and the like Figures set to the
paths of his Satellites, shew where they are at the like times. The
first Satellite, almost under C, is stationary at + as seen from the
Sun; and retrograde from + to 2: at 2 it appears stationary again, and
thence it moves forward until it has past 3, being twice stationary,
and once retrograde between 3 and 4. The path of this Satellite
intersects itself every
421⁄2
hours of our time, making such loops as in
the Diagram at 2. 3. 5. 7. 9. 10. 12. 14. 16. 18, a little after every
Conjunction. The second Satellite b, moving slower, barely crosses it’s
path every 3 days 13 hours; as at 4. 7. 11. 14. 18, making only five
loops and as many conjunctions in the time that the first makes ten.
The third Satellite c moving still slower, and having described the
curve c 1. 2. 3. 4. 5. 6. 7, comes to an Angle at 7 in conjunction with
the Sun at the end of 7 days 4 hours; and so goes on to describe
such another curve 7. 8. 9. 10. 11. 12. 13. 14, and is at 14 in it’s next
conjunction. The fourth Satellite d is always progressive, making
neither loops nor angles in the Heavens; but comes to it’s next conjunction
at e between the numeral figures 16 and 17, or in 16 days
18 hours. In order to have a tolerably good figure of the paths of
these Satellites, I took the following method.
Fig. IV.
PL. VII.How to delineate the paths of Jupiter’s Moons.
And Saturn’s.
Having drawn their Orbits on a Card, in proportion to their relative
distances from Jupiter, I measured the radius of the Orbit of the
134fourth Satellite, which was an inch and a tenth part; then multiplied
this by 424 for the radius of Jupiter’s Orbit, because Jupiter is 424
times as far from the Sun’s center as his fourth Satellite is from his center;
and the product thence arising was
4664⁄10
inches. Then taking
a small cord of this length, and fixing one end of it to the floor of
a long room by a nail, with a black lead pencil at the other end I
drew the curve ABCD &c. and set off a degree and an half thereon,
from A to T; because Jupiter moves only so much, whilst his outermost
Satellite goes once round him, and somewhat more; so that this
small portion of so large a circle differs but very little from a straight
line. This done, I divided the space AT into 18 equal parts, as
AB, BC, &c. for the daily progress of Jupiter; and each part into
24 for his hourly progress. The Orbit of each Satellite was also divided
into as many equal parts as the Satellite is hours in finishing it’s
synodical period round Jupiter. Then drawing a right line through
the center of the Card, as a diameter to all the 4 Orbits upon it, I
put the card upon the line of Jupiter’s motion, and transferred it to
every horary division thereon, keeping always the said diameter-line on
the line of Jupiter’s path; and running a pin through each horary division
in the Orbit of each Satellite as the card was gradually transferred
along the Line ABCD etc. of Jupiter’s motion, I marked points for
every hour through the Card for the Curves described by the Satellites
as the primary planet in the center of the Card was carried forward
on the line: and so finished the Figure, by drawing the lines of
each Satellite’s motion, through those (almost innumerable) points:
by which means, this is perhaps as true a Figure of the paths of these
Satellites as can be desired. And in the same manner might those for
Saturn’s Satellites be delineated.
The grand Period of Jupiter’s Moons.
270. It appears by the scheme, that the three first Satellites come
almost into the same line or position every seventh day; the first being
only a little behind with the second, and the second behind with the
third. But the period of the fourth Satellite is so incommensurate to
the periods of the other three, that it cannot be guessed at by the diagram
when it would fall again into a line of conjunction with them,
between Jupiter and the Sun. And no wonder; for supposing them
all to have been once in conjunction, it will require 3,087,043,493,260
years to bring them in a conjunction again: See § 73.
Fig. IV. The proportions of the Orbits of the Planets and Satellites.
271. In Fig. 4th we have the proportions of the Orbits of Saturn’s
five Satellites, and of Jupiter’s four, to one another, to our Moon’s
Orbit, and to the Disc of the Sun. S is the Sun; M m the Moon’s
Orbit (the Earth supposed to be at E;) J Jupiter; 1. 2. 3. 4 the Orbits
135of his four Moons or Satellites; Sat Saturn; and 1. 2. 3. 4. 5 the
Orbits of his five Moons. Hence it appears, that the Sun would much
more than fill the whole Orbit of the Moon; for the Sun’s diameter is
763,000 miles, and the diameter of the Moon’s Orbit only 480,000. In
proportion to all these Orbits of the Satellites, the Radius of Saturn’s
annual Orbit would be
211⁄4
yards, of Jupiter’s orbit
112⁄3,
and of the
Earth’s
21⁄4,
taking them in round numbers.
272. The
annexed table
shews at once
what proportion
the Orbits,
Revolutions,
and Velocities,
of all
the Satellites
bear to those
of their primary
Planets,
and what sort
of curves the
several Satellites
describe.
For, those Satellites
whose
velocities round
their primaries are greater than the velocities of their primaries in open
space, make loops at their conjunctions § 269; appearing retrograde
as seen from the Sun whilst they describe the inferior parts of their
Orbits, and direct whilst they describe the superior. This is the case
with Jupiter’s first and second Satellites, and with Saturn’s first. But
those Satellites whose velocities are less than the velocities of their primary
planets move direct in their whole circumvolutions; which is
the case of the third and fourth Satellites of Jupiter, and of the second,
third, fourth, and fifth Satellites of Saturn, as well as of our Satellite
the Moon: But the Moon is the only Satellite whose motion
is always concave to the Sun. There is a table of this sort in
De la Caile’s Astronomy, but it is very different from the above, which
I have computed from our English accounts of the periods and distances
of these Planets and Satellites.
| The Satellites |
Proportion of the Radius of
the Planet’s Orbit to the Radius of the Orbit of each Satellite. |
Proportion of the Time of the Planet’s
Revolution to the Revolution of each Satellite. |
Proportion of the Velocity of
each Satellite to the Velocity of its primary Planet. |
| of Saturn |
1 |
As 5322 |
to 1 |
As 5738 |
to 1 |
As 5738 |
to 5322 |
| 2 |
4155 |
1 |
3912 |
1 |
3912 |
4155 |
| 3 |
2954 |
1 |
2347 |
1 |
2347 |
2954 |
| 4 |
1295 |
1 |
674 |
1 |
674 |
1295 |
| 5 |
432 |
1 |
134 |
1 |
134 |
432 |
| of Jupiter |
1 |
As 1851 |
to 1 |
As 2445 |
to 1 |
As 2445 |
to 1851 |
| 2 |
1165 |
1 |
1219 |
1 |
1219 |
1165 |
| 3 |
731 |
1 |
604 |
1 |
604 |
731 |
| 4 |
424 |
1 |
258 |
1 |
258 |
424 |
| The Moon |
As 3371⁄2 |
to 1 |
As 121⁄3 |
to 1 |
As 121⁄3 |
to 3371⁄2 |
136
CHAP. XVI.
The Phenomena of the Harvest-Moon explained by a common Globe: The years in which the Harvest-Moons are least and most beneficial from 1751, to 1861. The long duration of Moon-light at the Poles in winter.
No Harvest-Moon at the Equator.
273. It is generally believed that the Moon rises about 48 minutes
later every day than on the preceding; but this is true only
with regard to places on the Equator. In places of considerable Latitude
there is a remarkable difference, especially in the harvest time;
with which Farmers were better acquainted than Astronomers till of
late; and gratefully ascribed the early rising of the Full Moon at that
time of the year to the goodness of God, not doubting that he had
ordered it so on purpose to give them an immediate supply of moon-light
after sun-set for their greater conveniency in reaping the fruits of
the earth.
But remarkable according to the distance of places from it.
In this instance of the harvest-moon, as in many others discoverable
by Astronomy, the wisdom and beneficence of the Deity is conspicuous,
who really ordered the course of the Moon so, as to bestow
more or less light on all parts of the earth as their several circumstances
and seasons render it more or less serviceable. About the Equator,
where there is no variety of seasons, and the weather changes
seldom, and at stated times, Moon-light is not necessary for gathering
in the produce of the ground; and there the moon rises about 48 minutes
later every day or night than on the former. At considerable
distances from the Equator, where the weather and seasons are more
uncertain, the autumnal Full Moons rise very soon after sun-set for several
evenings together. At the polar circles, where the mild season
is of very short duration, the autumnal Full Moon rises at Sun-set from
the first to the third quarter. And at the Poles, where the Sun is for
half a year absent, the winter Full moons shine constantly without
setting from the first to the third quarter.
It is soon said that all these Phenomena are owing to the different
Angles made by the Horizon and different parts of the Moon’s orbit;
and that the Moon can be full but once or twice in a year in those
parts of her orbit which rise with the least angles. But to explain this
subject intelligibly we must dwell much longer upon it.
137274. The [59]plane of the Equinoctial is perpendicular to the Earth’s
Axis: and therefore, as the Earth turns round its Axis, all parts of
the Equinoctial make equal Angles with the Horizon both at rising
and setting; so that equal portions of it always rise or set in equal
times. Consequently, if the Moon’s motion were equable, and in the
Equinoctial, at the rate of 12 degrees from the Sun every day, as it is
in her orbit, she would rise and set 48 minutes later every day than
on the preceding: for 12 degrees of the Equinoctial rise or set in 48
minutes of time in all Latitudes.
Fig. III.
275. But the Moon’s motion is so nearly in the Ecliptic that we
may consider her at present as moving in it. Now the different parts
of the Ecliptic, on account of its obliquity to the Earth’s Axis, make
very different Angles with the Horizon as they rise or set. Those
parts or Signs which rise with the smallest Angles set with the greatest,
and vice versâ. In equal times, whenever this Angle is least, a greater
portion of the Ecliptic rises than when the Angle is larger; as may be
seen by elevating the pole of a Globe to any considerable Latitude, and
then turning it round its Axis in the Horizon. Consequently, when the
Moon is in those Signs which rise or set with the smallest Angles, she
rises or sets with the least difference of time; and with the greatest
difference in those Signs which rise or set with the greatest Angles.
Fig. III.
The different Angles made by the Ecliptic and Horizon.
But, because all who read this Treatise may not be provided with
Globes, though in this case it is requisite to know how to use them, we
shall substitute the Figure of a Globe; in which FUP is the Axis, ♋TR
the Tropic of Cancer, LT♑ the Tropic of Capricorn, ♋EU♑
the Ecliptic touching both the Tropics which are 47 degrees from
each other, and AB the Horizon. The Equator, being in the middle
between the Tropics, is cut by the Ecliptic in two opposite
points, which are the beginnings of ♈ Aries and ♎ Libra. K is the
Hour circle with its Index, F the North pole of the Globe elevated
to the Latitude of London[60], namely
511⁄2
degrees above the Horizon;
and P the South Pole depressed as much below it. Because
of the oblique position of the Sphere in this Latitude, the Ecliptic has
the high elevation N♋ above the Horizon, making the Angle NU♋
of 62 degrees with it when ♋ Cancer is on the Meridian, at which
time ♎ Libra rises in the East. But let the Globe be turned half
round its Axis, till ♑ Capricorn comes to the Meridian and ♈ Aries
rises in the East, and then the Ecliptic will have the low elevation
138NL above the Horizon making only an Angle NUL of 15 degrees,
with it; which is 47 degrees less than the former Angle, equal
to the distance between the Tropics.
Least and greatest, when.
276. The smallest Angle made by the Ecliptic and Horizon is
when Aries rises, at which time Libra sets: the greatest when Libra
rises, at which time Aries sets. From the rising of Aries to the rising
of Libra (which is twelve [61]Sidereal hours) the angle increases; and
from the rising of Libra to the rising of Aries it decreases in the same
proportion. By this article and the preceding, it appears that the
Ecliptic rises fastest about Aries and slowest about Libra.
| Days |
Signs |
Degrees |
Rising Diff. |
Setting Diff. |
| H. |
M. |
H. |
M. |
| 1 |
♋ |
13 |
1 |
5 |
0 |
50 |
| 2 |
|
26 |
1 |
10 |
0 |
43 |
| 3 |
♌ |
10 |
1 |
14 |
0 |
37 |
| 4 |
|
23 |
1 |
17 |
0 |
32 |
| 5 |
♍ |
6 |
1 |
16 |
0 |
28 |
| 6 |
|
19 |
1 |
15 |
0 |
24 |
| 7 |
♎ |
2 |
1 |
15 |
0 |
20 |
| 8 |
|
15 |
1 |
15 |
0 |
18 |
| 9 |
|
28 |
1 |
15 |
0 |
17 |
| 10 |
♏ |
12 |
1 |
15 |
0 |
22 |
| 11 |
|
25 |
1 |
14 |
0 |
30 |
| 12 |
♐ |
8 |
1 |
13 |
0 |
39 |
| 13 |
|
21 |
1 |
10 |
0 |
47 |
| 14 |
♑ |
4 |
1 |
4 |
0 |
56 |
| 15 |
|
17 |
0 |
46 |
1 |
5 |
| 16 |
♒ |
1 |
0 |
40 |
1 |
8 |
| 17 |
|
14 |
0 |
35 |
1 |
12 |
| 18 |
|
27 |
0 |
30 |
1 |
15 |
| 19 |
♓ |
10 |
0 |
25 |
1 |
16 |
| 20 |
|
23 |
0 |
20 |
1 |
17 |
| 21 |
♈ |
7 |
0 |
17 |
1 |
16 |
| 22 |
|
20 |
0 |
17 |
1 |
15 |
| 23 |
♉ |
3 |
0 |
20 |
1 |
15 |
| 24 |
|
16 |
0 |
24 |
1 |
15 |
| 25 |
|
29 |
0 |
30 |
1 |
14 |
| 26 |
♊ |
13 |
0 |
40 |
1 |
13 |
| 27 |
|
26 |
0 |
50 |
1 |
7 |
| 28 |
♋ |
9 |
1 |
0 |
1 |
58 |
Quantity of this Angle at London.
277. On the Parallel of London, as much of the Ecliptic rises about
Pisces and Aries in two hours as the Moon
goes through in six days: and therefore
whilst the Moon is in these Signs, she differs
but two hours in rising for six days together;
that is, 20 minutes later every day
or night than on the preceding. But in
fourteen days afterwards, the Moon comes
to Virgo and Libra; which are the opposite
Signs to Pisces and Aries; and then she differs
almost four times as much in rising;
namely, one hour and about fifteen minutes
later every day or night than the former,
whilst she is in these Signs; for by § 275
their rising Angle is at least four times as
great as that of Pisces and Aries. The annexed
Table shews the daily mean difference
of the Moon’s rising and setting on the
Parallel of London, for 28 days; in which
time the Moon finishes her period round
the Ecliptic, and gets 9 degrees into the same
Sign from the beginning of which she set out.
So it appears by the Table, that while the
Moon is in ♍ and ♎ she rises an hour and
a quarter later every day than the former;
and differs only 24, 20, 18 or 17 minutes
139in setting. But, when she comes to ♓ and ♈, she is only 20 or
17 minutes later of rising; and an hour and a quarter later in setting.
278. All these things will be made plain by putting small patches
on the Ecliptic of a Globe, as far from one another as the Moon moves
from any Point of the celestial Ecliptic in 24 hours, which at a mean
rate is [62]
131⁄6
degrees; and then in turning the globe round, observe the
rising and setting of the patches in the Horizon, as the Index points out
the different times in the hour circle. A few of these patches are represented
by dots at 0 1 2 3 &c. on the Ecliptic, which has the position
LUI when Aries rises in the East; and by the dots 0 1 2 3, &c.
when Libra rises in the East, at which time the Ecliptic has the position
EU♑: making an angle of 62 degrees with the Horizon in the
latter case, and an angle of no more than 15 degrees with it in the
former; supposing the Globe rectified to the Latitude of London.
279. Having rectified the Globe, turn it until the patch at 0, about
the beginning of ♓ Pisces on the half LUI of the Ecliptic, comes to
the Eastern side of the Horizon; and then keeping the ball steady, set
the hour Index to XII, because that hour may perhaps be more easily
remembred than any other. Then, turn the Globe round westward,
and in that time, suppose the patch 0 to have moved thence to 1,
131⁄6
degrees, whilst the Earth turns once round its Axis, and you will
see that 1 rises only about 20 minutes later than 0 did on the day before.
Turn the Globe round again, and in that time suppose the same
patch to have moved from 1 to 2; and it will rise only 20 minutes
later by the hour-index than it did at 1 on the day or turn before.
At the end of the next turn, suppose the patch to have gone from 2
to 3 at U, and it will rise 20 minutes later than it did at 2. And
so on for six turns, in which time there will scarce be two hours
difference: Nor would there have been so much if the 6 degrees of
the Sun’s motion in that time had been allowed for. At the first
Turn the patch rises south of the East, at the middle Turn due East,
and at the last Turn north of the East. But these patches will be 9
hours of setting on the western side of the Horizon, which shews that
the Moon will be so much later of setting in that week in which she
moves through these two Signs. The cause of this difference is evident;
for Pisces and Aries make only an Angle of 15 degrees with
the Horizon when they rise; but they make an Angle of 62 degrees
with it when they set § 275. As the Signs Taurus, Gemini,
140Cancer, Leo, Virgo, and Libra rise successively, the Angle increases
gradually which they make with the Horizon; and decreases in the
same proportion as they set. And for that reason, the Moon differs
gradually more in the time of her rising every day whilst she is in these
Signs, and less in her setting: After which, through the other six Signs,
viz. Scorpio, Sagittary, Capricorn, Aquarius, Pisces, and Aries, the
rising difference becomes less every day, until it be at the least of all,
namely, in Pisces and Aries.
280. The Moon goes round the Ecliptic in 27 days 8 hours; but
not from Change to Change in less than 29 days 12 hours: so that
she is in Pisces and Aries at least once in every Lunation, and in some
Lunations twice.
Why the Moon is always Full in different Signs.
Her periodical and synodical Revolution exemplified.
281. If the Earth had no annual motion, the Sun would never
appear to shift his place in the Ecliptic. And then every New Moon
would fall in the same Sign and degree of the Ecliptic, and every
Full Moon in the opposite: for the Moon would go precisely round the
Ecliptic from Change to Change. So that if the Moon was once Full
in Pisces, or Aries, she would always be Full when she came round
to the same Sign and Degree again. And as the Full Moon rises
at Sun-set (because when any point of the Ecliptic sets the opposite
point rises) she would constantly rise within two hours of Sun-set
during the week in which she were Full. But in the time that the
Moon goes round the Ecliptic from any conjunction or opposition,
the Earth goes almost a Sign forward; and therefore the Sun will
seem to go as far forward in that time, namely
271⁄2
degrees: so
that the Moon must go
271⁄2
degrees more than round; and as much
farther as the Sun advances in that interval, which is
21⁄15
degrees,
before she can be in conjunction with, or opposite to the Sun again.
Hence it is evident, that there can be but one conjunction or
opposition of the Sun and Moon in a year in any particular part
of the Ecliptic. This may be familiarly exemplified by the hour
and minute hands of a watch, which are never in conjunction or
opposition in that part of the dial-plate where they were so last
before. And indeed if we compare the twelve hours on the dial-plate
to the twelve Signs of the Ecliptic, the hour-hand to the
Sun and the minute-hand to the Moon, we shall have a tolerably
near resemblance in miniature to the motions of our great celestial
Luminaries. The only difference is, that whilst the Sun goes
once round the Ecliptic the Moon makes
121⁄3
conjunctions with
him: but whilst the hour-hand goes round the dial-plate the minute-hand
makes only 11 conjunctions with it; because the minute hand
141moves slower in respect of the hour-hand than the Moon does
with regard to the Sun.
The Harvest
and Hunter’s Moon.
282. As the Moon can never be full but when she is opposite to the
Sun, and the Sun is never in Virgo and Libra but in our autumnal
months, ’tis plain that the Moon is never full in the opposite Signs,
Pisces and Aries, but in these two months. And therefore we can
have only two Full Moons in the year, which rise so near the time of
Sun-set for a week together as above-mentioned. The former of these
is called the Harvest Moon, and the latter the Hunter’s Moon.
Why the Moon’s regular rising is never perceived but in Harvest.
283. Here it will probably be asked, why we never observe this remarkable
rising of the Moon but in harvest, since she is in Pisces and
Aries at least twelve times in the year besides; and must then rise
with as little difference of time as in harvest? The answer is plain:
for in winter these Signs rise at noon; and being then only a Quarter
of a Circle distant from the Sun, the Moon in them is in her first Quarter:
but when the Sun is above the Horizon the Moon’s rising is
neither regarded nor perceived. In spring these Signs rise with the Sun
because he is then in them; and as the Moon changeth in them at
that time of the year, she is quite invisible. In summer they rise
about mid-night, and the Sun being then three Signs, or a Quarter
of a Circle before them, the Moon is in them about her third Quarter;
when rising so late, and giving but very little light, her rising passes
unobserved. And in autumn, these Signs being opposite to the Sun,
rise when he sets, with the Moon in opposition, or at the Full, which
makes her rising very conspicuous.
284. At the Equator, the North and South Poles lie in the Horizon;
and therefore the Ecliptic makes the same Angle southward with the
Horizon when Aries rises as it does northward when Libra rises. Consequently,
as the Moon at all the fore-mentioned patches rises and sets
nearly at equal Angles with the Horizon all the year round; and about
48 minutes later every day or night than on the preceding, there can
be no particular Harvest Moon at the Equator.
285. The farther that any place is from the Equator, if it be not
beyond the Polar Circle, the Angle gradually diminishes which the
Ecliptic and Horizon make when Pisces and Aries rise; and therefore
when the Moon is in these Signs she rises with a nearly proportionable
difference later every day than on the former; and is for that reason
the more remarkable about the Full, until we come to the Polar
Circles, or 66 degrees from the Equator; in which Latitude the
Ecliptic and Horizon become coincident, every day for a moment,
142at the same sidereal hour (or 3 minutes 56 seconds sooner every day
than the former) and the very next moment one half of the Ecliptic
containing Capricorn, Aquarius, Pisces, Aries, Taurus, and Gemini
rises, and the opposite half sets. Therefore, whilst the Moon is going
from the beginning of Capricorn to the beginning of Cancer,
which is almost 14 days, she rises at the same sidereal hour; and in
autumn just at Sun-set, because all that half of the Ecliptic in which
the Sun is at that time sets at the same sidereal hour, and the opposite
half rises: that is, 3 minutes 56 seconds, of mean solar time, sooner
every day than on the day before. So whilst the Moon is going from
Capricorn to Cancer she rises earlier every day than on the preceding;
contrary to what she does at all places between the polar Circles. But
during the above fourteen days, the Moon is 24 sidereal hours later in
setting; for the six Signs which rise all at once on the eastern side of
the Horizon are 24 hours in setting on the western side of it: as any
one may see by making chalk-marks at the beginning of Capricorn and
of Cancer, and then, having elevated the Pole
661⁄2
degrees, turn the
Globe slowly round it’s Axis, and observe the rising and setting of the
Ecliptic. As the beginning of Aries is equally distant from the beginning
of Cancer and of Capricorn, it is in the middle of that half of
the Ecliptic which rises all at once. And when the Sun is at the beginning
of Libra, he is in the middle of the other half. Therefore, when
the Sun is in Libra and the Moon in Capricorn, the Moon is a Quarter
of a Circle before the Sun; opposite to him, and consequently full in
Aries, and a Quarter of a Circle behind him when in Cancer. But
when Libra rises Aries sets, and all that half of the Ecliptic of which
Aries is the middle. And therefore, at that time of the year the Moon
rises at Sun-set from her first to her third Quarter.
The Harvest Moons regular on both sides of the Equator.
286. In northern Latitudes, the autumnal Full Moons are in Pisces
and Aries; and the vernal Full Moons in Virgo and Libra: in southern
Latitudes just the reverse because the seasons are contrary. But
Virgo and Libra rise at as small Angles with the Horizon in southern
Latitudes as Pisces and Aries do in the northern; and therefore
the Harvest Moons are just as regular on one side of the Equator as on
the other.
287. As these Signs which rise with the least Angles set with the
greatest, the vernal Full Moons differ as much in their times of rising
every night as the autumnal Full Moons differ in their times of setting;
and set with as little difference as the autumnal Full Moons rise:
the one being in all cases the reverse of the other.
The Moon’s Nodes.
143288. Hitherto, for the sake of plainness, we have supposed the Moon
to move in the Ecliptic, from which the Sun never deviates. But the
orbit in which the Moon really moves is different from the Ecliptic:
one half being elevated
51⁄3
degrees above it, and the other half as much
depressed below it. The Moon’s orbit therefore intersects the Ecliptic
in two points diametrically opposite to each other: and these intersections
are called the Moon’s Nodes. So the Moon can never be in the
Ecliptic but when she is in either of her Nodes, which is at least
twice in every course from Change to Change, and sometimes thrice.
For, as the Moon goes almost a whole Sign more than round her Orbit
from Change to Change; if she passes by either Node about the
time of Change, she will pass by the other in about fourteen days after, and
come round to the former Node two days again before the next Change.
That Node from which the Moon begins to ascend northward, or
above the Ecliptic, in northern Latitudes, is called the Ascending Node;
and the other the Descending Node, because the Moon, when she passes
by it, descends below the Ecliptic southward.
289. The Moon’s oblique motion with regard to the Ecliptic causes
some difference in the times of her rising and setting from what is
already mentioned. For whilst she is northward of the Ecliptic, she rises
sooner and sets later than if she moved in the Ecliptic: and when she is
southward of the Ecliptic she rises later and sets sooner. This difference
is variable even in the same Signs, because the Nodes shift backward
about
192⁄3
degrees in the Ecliptic every year; and so go round it contrary
to the order of Signs in 18 years 225 days.
290. When the Ascending Node is in Aries, the southern half of the
Moon’s Orbit makes an Angle of
51⁄3
degrees less with the Horizon than
the Ecliptic does, when Aries rises in northern Latitudes: for which
reason the Moon rises with less difference of time whilst she is in Pisces
and Aries than there would be if she kept in the Ecliptic. But in 9 years
and 112 days afterward, the Descending Node comes to Aries; and then
the Moon’s Orbit makes an Angle
51⁄3
degrees greater with the Horizon
when Aries rises, than the Ecliptic does at that time; which causes the
Moon to rise with greater difference of time in Pisces and Aries than
if she moved in the Ecliptic.
291. To be a little more particular, when the Ascending Node is in
Aries, the Angle is only
92⁄3
degrees on the parallel of London when
Aries rises. But when the Descending Node comes to Aries, the Angle
is
201⁄3
degrees; this occasions as great a difference of the Moon’s rising
in the same Signs every 9 years, on the parallel of London, as there would
be on two parallels
102⁄3
degrees from one another, if the Moon’s course
144were in the Ecliptic. The following Table shews how much the
obliquity of the Moon’s Orbit affects her rising and setting on the parallel
of London from the 12th to the 18th day of her age; supposing her to be
Full at the autumnal Equinox; and then, either in the Ascending Node,
highest part of her Orbit, Descending Node, or lowest part of her
Orbit. M signifies morning, A afternoon; and the line at the foot of
the Table shews a week’s difference in rising and setting.
| Moon’s Age |
Full in her Ascending node. |
In the highest part of her Orbit. |
Full in her Descending node. |
In the lowest part of her Orbit. |
| Rises at |
Sets at |
Rises at |
Sets at |
Rises at |
Sets at |
Rises at |
Sets at |
| H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
| 12 |
5 |
A15 |
3 |
M20 |
4 |
A30 |
3 |
M15 |
4 |
A32 |
3 |
M40 |
5 |
A16 |
3 |
M0 |
| 13 |
5 |
32 |
4 |
25 |
4 |
50 |
4 |
45 |
5 |
15 |
4 |
20 |
6 |
0 |
4 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 14 |
5 |
48 |
5 |
30 |
5 |
15 |
6 |
0 |
5 |
45 |
5 |
40 |
6 |
20 |
5 |
28 |
| 15 |
6 |
5 |
7 |
0 |
5 |
42 |
7 |
20 |
6 |
15 |
6 |
56 |
6 |
45 |
6 |
32 |
| 16 |
6 |
20 |
8 |
15 |
6 |
2 |
8 |
35 |
6 |
46 |
8 |
0 |
7 |
8 |
7 |
45 |
| 17 |
6 |
36 |
9 |
12 |
6 |
26 |
9 |
45 |
7 |
18 |
9 |
15 |
7 |
30 |
9 |
15 |
| 18 |
6 |
54 |
10 |
30 |
7 |
0 |
10 |
40 |
8 |
0 |
10 |
20 |
7 |
52 |
10 |
0 |
| Dif. |
1 |
39 |
7 |
10 |
2 |
30 |
7 |
25 |
3 |
28 |
6 |
40 |
2 |
36 |
7 |
0 |
This Table was not computed, but only estimated as near as could
be done from a common Globe, on which the Moon’s Orbit was delineated
with a black lead pencil. It may at first sight appear erroneous;
since as we have supposed the Moon to be full in either Node at the
autumnal Equinox, she ought by the Table to rise just at six o’clock,
or at Sun-set, on the 15th day of her age; being in the Ecliptic
at that time. But it must be considered, that the Moon is only
141⁄4
days old when she is Full; and therefore in both cases she is a
little past the Node on the 15th day, being above it at one time, and
below it at the other.
The period of the Harvest Moons.
292. As there is a compleat revolution of the Nodes in
182⁄3
years,
there must be a regular period of all the Varieties which can happen
in the rising and setting of the Moon during that time. But this shifting
of the Nodes never affects the Moon’s rising so much, even in her
quickest descending Latitude, as not to allow us still the benefit of her
rising nearer the time of Sun-set for a few days together about the Full
in Harvest, than when she is Full at any other time of the year. The
following Table shews in what years the Harvest-Moons are least beneficial
as to the times of their rising, and in what years most, from 1751
to 1861. The column of years under the letter L are those in which
the Harvest-Moons are least of all beneficial, because they fall about
the Descending Node: and those under M are the most of all beneficial,
145because they fall about the Ascending Node. In all the columns
from N to S the Harvest-Moons descend gradually in the Lunar
Orbit, and rise to less heights above the Horizon. From S to N they
ascend in the same proportion, and rise to greater heights above the
Horizon. In both the columns under S the Harvest-Moons are in the
lowest part of the Moon’s Orbit, that is, farthest South of the Ecliptic;
and therefore stay shortest of all above the Horizon: in the columns
under N just the reverse. And in both cases, their rising, though not
at the same times, are nearly the same with regard to difference of
time, as if the Moon’s Orbit were coincident with the Ecliptic.
Years in which the Harvest-Moons are least beneficial.
| N |
|
|
|
L |
|
|
|
S |
|
| 1751 |
1752 |
1753 |
1754 |
1755 |
1756 |
1757 |
1758 |
1759 |
|
| 1770 |
1771 |
1772 |
1773 |
1774 |
1775 |
1776 |
1777 |
1778 |
|
| 1788 |
1789 |
1790 |
1791 |
1792 |
1793 |
1794 |
1795 |
1796 |
1797 |
| 1807 |
1808 |
1809 |
1810 |
1811 |
1812 |
1813 |
1814 |
1815 |
|
| 1826 |
1827 |
1828 |
1829 |
1830 |
1831 |
1832 |
1833 |
1834 |
|
| 1844 |
1845 |
1846 |
1847 |
1848 |
1849 |
1850 |
1851 |
1852 |
|
Years in which they are most beneficial.
| S |
|
|
|
M |
|
|
|
N |
|
| 1760 |
1761 |
1762 |
1763 |
1764 |
1765 |
1766 |
1767 |
1768 |
1769 |
| 1779 |
1780 |
1781 |
1782 |
1783 |
1784 |
1785 |
1786 |
1787 |
|
| 1798 |
1799 |
1800 |
1801 |
1802 |
1803 |
1804 |
1805 |
1806 |
|
| 1816 |
1817 |
1818 |
1819 |
1820 |
1821 |
1822 |
1823 |
1824 |
1825 |
| 1835 |
1836 |
1837 |
1838 |
1839 |
1840 |
1841 |
1842 |
1843 |
|
| 1853 |
1854 |
1855 |
1856 |
1857 |
1858 |
1859 |
1860 |
1861 |
|
293. At the Polar Circles, when the Sun touches the Summer Tropic,
he continues 24 hours above the Horizon; and 24 hours below it
when he touches the Winter Tropic. For the same reason the Full
Moon neither rises in Summer, nor sets in Winter, considering her as
moving in the Ecliptic. For the Winter Full Moon being as high in
the Ecliptic as the Summer Sun, must therefore continue as long
above the Horizon; and the Summer Full Moon being as low in the
Ecliptic as the Winter Sun, can no more rise than he does. But
these are only the two Full Moons which happen about the Tropics,
for all the others rise and set. In Summer the Full Moons are low,
and their stay is short above the Horizon, when the nights are short,
and we have least occasion for Moon-light: in Winter they go high,
146and stay long, above the Horizon when the nights are long, and we
want the greatest quantity of Moon-light.
The long continuance of Moon-light at the Poles.
Fig. V.
294. At the Poles, one half of the Ecliptic never sets, and the other
half never rises: and therefore, as the Sun is always half a year in
describing one half of the Ecliptic, and as long in going through the
other half, ’tis natural to imagine that the Sun continues half a year
together above the Horizon of each Pole in it’s turn, and as long
below it; rising to one Pole when he sets to the other. This would
be exactly the case if there were no refraction: but by the Atmosphere’s
refracting the Sun’s rays, he becomes visible some days
sooner § 183, and continues some days longer in sight than he would
otherwise do: so that he appears above the Horizon of either Pole
before he has got below the Horizon of the other. And, as he never
goes more than
231⁄2
degrees below the Horizon of the Poles, they
have very little dark night: it being twilight there as well as at all
other places till the Sun be 18 degrees below the Horizon, § 177.
The Full Moon being always opposite to the Sun, can never be seen
while the Sun is above the Horizon, except when the Moon falls in
the northern half of her Orbit; for whenever any point of the Ecliptic
rises the opposite point sets. Therefore, as the Sun is above the Horizon
of the north Pole from the 20th of March till the 23d of September,
it is plain that the Moon, when Full, being opposite to the Sun, must
be below the Horizon during that half of the year. But when the
Sun is in the southern half of the Ecliptic he never rises to the
north Pole, during which half of the year, every Full Moon happens
in some part of the northern half of the Ecliptic, which never sets.
Consequently, as the polar Inhabitants never see the Full Moon in
Summer, they have her always in the Winter, before, at, and after
the Full, shining for 14 of our days and nights. And when the Sun
is at his greatest depression below the Horizon, being then in Capricorn,
the Moon is at her First Quarter in Aries, Full in Cancer, and
at her Third Quarter in Libra. And as the beginning of Aries is the
rising point of the Ecliptic, Cancer the highest, and Libra the setting
point, the Moon rises at her First Quarter in Aries, is most elevated
above the Horizon, and Full in Cancer, and sets at the beginning of
Libra in her Third Quarter, having continued visible for 14 diurnal
rotations of the Earth. Thus the Poles are supplied one half of the
winter time with constant Moon-light in the Sun’s absence; and only
lose sight of the Moon from her Third to her First Quarter, while she
gives but very little light; and could be but of little, and sometimes of no
service to them. A bare view of the Figure will make this plain; in
147which let S be the Sun, e the Earth in Summer when it’s north Pole
n inclines toward the Sun, and E the Earth in Winter, when it’s north
Pole declines from him. SEN and NWS is the Horizon of the north
Pole, which is coincident with the Equator; and, in both these positions
of the Earth, ♈♋♎♑ is the Moon’s Orbit, in which she goes
round the Earth, according to the order of the letters abcd, ABCD.
When the Moon is at a she is in her Third Quarter to the Earth at e,
and just rising to the north Pole n; at b she changes, and is at the
greatest height above the Horizon, as the Sun likewise is; at c she is
in her First Quarter, setting below the Horizon; and is lowest of all
under it at d, when opposite to the Sun, and her enlightened side toward
the Earth. But then she is full in view to the south Pole p;
which is as much turned from the Sun as the north Pole inclines towards
him. Thus in our Summer, the Moon is above the Horizon
of the north Pole whilst she describes the northern half of the Ecliptic
♈♋♎, or from her Third Quarter to her First; and below the
Horizon during the progress through the southern half ♎♑♈; highest
at the Change, most depressed at the Full. But in winter, when
the Earth is at E, and it’s north Pole declines from the Sun, the New
Moon at D is at her greatest depression below the Horizon NWS, and
the Full Moon at B at her greatest height above it; rising at her First
Quarter A, and keeping above the Horizon till she comes to her Third
Quarter C. At a mean state she is
231⁄2
degrees above the Horizon
at B and b, and as much below it at D and d, equal to the inclination
of the Earth’s Axis F. S♋ and S♑ are, as it were, a ray of
light proceeding from the Sun to the Earth; and shews that when the
Earth is at e, the Sun is above the Horizon, vertical to the Tropic of
Cancer; and when the Earth is at E, he is below the Horizon, vertical
to the Tropic of Capricorn.
Plate VIII.
J. Ferguson delin.
J. Mynde Sculp.
Plate IX.

J. Ferguson delin.
J. Mynde Sculp.
CHAP. XVII.
Of the ebbing and flowing of the Sea.
The cause of the Tides discovered by
Kepler.
PLATE IX.
Their Theory improved by Sir
Isaac Newton.
295. The cause of the Tides was discovered by Kepler, who,
in his Introduction to the Physics of the Heavens, thus explains
it: “The Orb of the attracting power, which is in the Moon,
is extended as far as the Earth; and draws the waters under the torrid
Zone, acting upon places where it is vertical, insensibly on confined
seas and bays, but sensibly on the ocean whose beds are large, and the
148waters have the liberty of reciprocation; that is, of rising and falling.”
And in the 70th page of his Lunar Astronomy——“But the cause of
the Tides of the Sea appears to be the bodies of the Sun and Moon
drawing the waters of the Sea.” This hint being given, the immortal Sir
Isaac Newton improved it, and wrote so amply on the subject, as
to make the Theory of the Tides in a manner quite his own; by
discovering the cause of their rising on the side of the Earth opposite
to the Moon. For Kepler believed that the presence of the Moon
occasioned an impulse which caused another in her absence.
Explained on the Newtonian principles.
Fig. I.
Fig. I.
296. It has been already shewn § 106, that the power of gravity
diminishes as the square of the distance increases; and therefore the
waters at Z on the side of the Earth ABCDEFGH next the Moon
M are more attracted than the central parts of the Earth O by the
Moon, and the central parts are more attracted by her than the waters
on the opposite side of the Earth at n: and therefore the distance between
the Earth’s center and the waters on it’s surface under and opposite
to the Moon will be increased. For, let there be three bodies at
H, O, and D: if they are all equally attracted by the body M, they
will all move equally fast toward it, their mutual distances from each
other continuing the same. If the attraction of M is unequal, then
that body which is most strongly attracted will move fastest, and this
will increase it’s distance from the other body. Therefore, by the law
of gravitation, M will attract H more strongly than it does O, by which,
the distance between H and O will be increased: and a spectator on O
will perceive H rising higher toward Z. In like manner, O being
more strongly attracted than D, it will move farther towards M than
D does: consequently, the distance between O and D will be increased;
and a spectator on O, not perceiving his own motion, will see
D receding farther from him towards n: all effects and appearances
being the same whether D recedes from O or O from D.
297. Suppose now there is a number of bodies, as A, B, C, D, E, F, G, H
placed round O, so as to form a flexible or fluid ring: then, as the
whole is attracted towards M, the parts at H and D will have their
distance from O increased; whilst the parts at B and F, being nearly
at the same distance from M as O is, these parts will not recede from one
another; but rather, by the oblique attraction of M, they will approach
nearer to O. Hence, the fluid ring will form itself into an ellipse
ZIBLnKFNZ, whose longer Axis nOZ produced will pass through M,
and it’s shorter Axis BOF will terminate in B and F. Let the ring be
filled with bodies, so as to form a flexible or fluid sphere round O;
then, as the whole moves toward M, the fluid sphere being lengthned
149at Z and n, will assume an oblong or oval form. If M is the Moon,
O the Earth’s center, ABCDEFGH the Sea covering the Earth’s surface,
’tis evident by the above reasoning, that whilst the Earth by it’s
gravity falls toward the Moon, the Water directly below her at B
will swell and rise gradually towards her: also, the Water at D will
recede from the center [strictly speaking, the center recedes from D] and
rise on the opposite side of the Earth: whilst the Water at B and F is
depressed, and falls below the former level. Hence, as the Earth
turns round it’s Axis from the Moon to the Moon again in
243⁄4
hours,
there will be two tides of flood and two of ebb in that time, as we
find by experience.
Fig. II.
298. As this explanation of the ebbing and flowing of the Sea
is deduced from the Earth’s constantly falling toward the Moon
by the power of gravity, some may find a difficulty in conceiving
how this is possible when the Moon is Full, or in opposition to
the Sun; since the Earth revolves about the Sun, and must continually
fall towards it, and therefore cannot fall contrary ways at the
same time: or if the Earth is constantly falling towards the Moon,
they must come together at last. To remove this difficulty, let it be
considered, that it is not the center of the Earth that describes the
annual orbit round the Sun; but the [63]common center of gravity of
the Earth and Moon together: and that whilst the Earth is moving
round the Sun, it also describes a Circle round that centre of gravity;
going as many times round it in one revolution about the Sun as there
are Lunations or courses of the Moon round the Earth in a year: and
therefore, the Earth is constantly falling towards the Moon from a
tangent to the Circle it describes round the said common center of gravity.
Let M be the Moon, TW part of the Moon’s Orbit, and C
the center of gravity of the Earth and Moon: whilst the Moon goes
round her Orbit, the center of the Earth describes the Circle ged round
C, to which Circle gak is a tangent: and therefore, when the Moon
has gone from M to a little past W, the Earth has moved from g to
e; and in that time has fallen towards the Moon, from the tangent at
a to e; and so round the whole Circle.
150299. The Sun’s influence in raising the Tides is but small in comparison
of the Moon’s: For though the Earth’s diameter bears a considerable
proportion to it’s distance from the Moon, it is next to nothing
when compared with the distance of the Sun. And therefore,
the difference of the Sun’s attraction on the sides of the Earth under
and opposite to him, is much less than the difference of the Moon’s
attraction on the sides of the Earth under and opposite to her: and
therefore the Moon must raise the Tides much higher than they can be
raised by the Sun.
Why the Tides are not highest when the Moon is on the Meridian.
Fig. I.
300. On this Theory so far as we have explained it, the Tides ought
to be highest directly under and opposite to the Moon; that is, when
the Moon is due north and south. But we find, that in open Seas,
where the water flows freely, the Moon M is generally past the north
and south Meridian as at p when it is high water at Z and at n. The
reason is obvious; for though the Moon’s attraction was to cease altogether
when she was past the Meridian, yet the motion of ascent communicated
to the water before that time would make it continue to
rise for some time after; much more must it do so when the attraction
is only diminished: as a little impulse given to a moving ball will
cause it still move farther than otherwise it could have done. And as
experience shews, that the day is hotter about three in the afternoon,
than when the Sun is on the Meridian, because of the increment made
to the heat already imparted.
Nor always answer to her being at the same distance from it.
301. The Tides answer not always to the same distance of the Moon
from the Meridian at the same places; but are variously affected by
the action of the Sun, which brings them on sooner when the Moon
is in her first and third Quarters, and keeps them back later when she
is in her second and fourth: because, in the former case, the Tide
raised by the Sun alone would be earlier than the Tide raised by the
Moon; and in the latter case later.
302. The Moon goes round the Earth in an elliptic Orbit, and
therefore she approaches nearer to the Earth than her mean distance,
and recedes farther from it, in every Lunar Month. When she is nearest:
she attracts strongest, and so rises the Tides most; the contrary happens
when she is farthest, because of her weaker attraction. When both
Luminaries are in the Equator, and the Moon in Perigeo, or at her
least distance from the Earth, she raises the Tides highest of all,
especially at her Conjunction and opposition; both because the equatoreal
parts have the greatest centrifugal force from their describing the
151largest Circle, and from the concurring actions of the Sun and Moon.
At the Change, the attractive forces of the Sun and Moon being united,
they diminish the gravity of the waters under the Moon, which
is also diminished on the other side, by means of a greater centrifugal
force. At the full, whilst the Moon raises the Tide under and opposite
to her, the Sun acting in the same line, raises the Tide under and
opposite to him; whence their conjoint effect is the same as at the
Change; and in both cases, occasion what we call the Spring Tides.
But at the Quarters the Sun’s action on the waters at O and H diminishes
the Moon’s action on the waters at Z and N; so that they rise a little
under and opposite to the Sun at O and H, and fall as much under and
opposite to the Moon at Z and N; making what we call the Neap
Tides, because the Sun and Moon then act cross-wise to each other.
But, strictly speaking, these Tides happen not till some time after; because
in this, as in other cases, § 300, the actions do not produce the
greatest effect when they are at the strongest, but some time afterward.
Not greatest at the Equinoxes, and why.
303. The Sun being nearer the Earth in Winter than in Summer,
§ 205, is of course nearer to it in February and October than in March
and September: and therefore the greatest Tides happen not till some
time after the autumnal Equinox, and return a little before the vernal.
The Tides would not immediately cease upon the annihilation of the Sun and Moon.
The Sea being thus put in motion, would continue to ebb and
flow for several times, even though the Sun and Moon were annihilated,
or their influence should cease: as if a bason of water were
agitated, the water would continue to move for some time after the
bason was left to stand still. Or like a Pendulum, which having been
put in motion by the hand, continues to make several vibrations without
any new impulse.
The lunar day, what.
The Tides rise to unequal heights in the same day, and why.
PLATE IX.
Fig. III, IV, V.
Fig. III.
Fig. IV.
Fig. V.
304. When the Moon is in the Equator, the Tides are equally
high in both parts of the lunar day, or time of the Moon’s revolving
from the Meridian to the Meridian again, which is 24 hours 48
minutes. But as the Moon declines from the Equator towards either
Pole, the Tides are alternately higher and lower at places having north
or south Latitude. For one of the highest elevations, which is that
under the Moon, follows her towards the same Pole, and the other
declines towards the opposite; each describing parallels as far distant
from the Equator, on opposite sides, as the Moon declines from it to
either side; and consequently, the parallels described by these elevations
of the water are twice as many degrees from one another, as
the Moon is from the Equator; increasing their distance as the Moon
increases her declination, till it be at the greatest, when the said parallels
152are, at a mean state, 47 degrees from one another: and on that
day, the Tides are most unequal in their heights. As the Moon
returns toward the Equator, the parallels described by the opposite
elevations approach towards each other, until the Moon comes to the
Equator, and then they coincide. As the Moon declines toward the
opposite Pole, at equal distances, each elevation describes the same
parallel in the other part of the lunar day, which it’s opposite elevation
described before. Whilst the Moon has north declination, the greatest
Tides in the northern Hemisphere are when she is above the Horizon;
and the reverse whilst her declination is south. Let NESQ be the
Earth, NCS it’s Axis, EQ the Equator, T♋ the Tropic of Cancer,
t♑ the Tropic of Capricorn, ab the arctic Circle, cd the Antarctic, N
the north Pole, S the south Pole, M the Moon, F and G the two
eminences of water, whose lowest parts are at a and d (Fig. III.) at
N and S (Fig. IV.) and at b and c (Fig. V.) always 90 degrees from
the highest. Now when the Moon is in her greatest north declination
at M, the highest elevation G under her, is on the Tropic of Cancer
T♋, and the opposite elevation F on the Tropic of Capricorn t♑; and
these two elevations describe the Tropics by the Earth’s diurnal rotation.
All places in the northern Hemisphere ENQ have the highest Tides
when they come into the position b♋Q, under the Moon; and the
lowest Tides when the Earth’s diurnal rotation carries them into the
position aTE, on the side opposite to the Moon; the reverse happens
at the same time in the southern Hemisphere ESQ, as is evident to
sight. The Axis of the Tides aCd has now it’s Poles a and d (being
always 90 degrees from the highest elevations) in the arctic and
antarctic Circles; and therefore ’tis plain, that at these Circles there is
but one Tide of Flood, and one of Ebb, in the lunar day. For,
when the point a revolves half round to b, in 12 lunar hours, it has
a Tide of Flood; but when it comes to the same point a again in
12 hours more, it has the lowest ebb. In seven days afterward, the
Moon M comes to the equinoctial Circle, and is over the Equator EQ,
when both Elevations describe the Equator; and in both Hemispheres,
at equal distances from the Equator, the Tides are equally high in both
parts of the lunar day. The whole Phenomena being reversed when
the Moon has south declination to what they were when her declination
was north, require no farther description.
Fig. VI.
When both Tides are equally high in the same day, they arrive
at unequal intervals of Time; and vice versa.
305. In the three last-mentioned Figures, the Earth is orthographically
projected on the plane of the Meridian; but in order to describe
a particular Phenomenon we now project it on the plane of the
Ecliptic. Let HZON be the Earth and Sea, FED the Equator, T
153the Tropic of Cancer, C the arctic Circle, P the north Pole, and the
Curves 1, 2, 3, &c. 24 Meridians, or hour Circles, intersecting each
other in the Poles; AGM is the Moon’s orbit, S the Sun, M the
Moon, Z the Water elevated under the Moon, and N the opposite
equal Elevation. As the lowest parts of the Water are always 90 degrees
from the highest, when the Moon is in either of the Tropics (as
at M) the Elevation Z is on the Tropic of Capricorn, and the opposite
Elevation N on the Tropic of Cancer, the low-water Circle HCO
touches the polar Circles at C; and the high-water Circle ETP6 goes
over the Poles at P, and divides every parallel of Latitude into two
equal segments. In this case the Tides upon every parallel are alternately
higher and lower; but they return in equal times: the point T,
for example, on the Tropic of Cancer (where the depth of the Tide
is represented by the breadth of the dark shade) has a shallower Tide
of Flood at T than when it revolves half round from thence to 6,
according to the order of the numeral Figures; but it revolves as
soon from 6 to T as it did from T to 6. When the Moon is in the
Equinoctial, the Elevations Z and N are transferred to the Equator
at O and H, and the high and low-water Circles are got into each
other’s former places; in which case the Tides return in unequal times,
but are equally high in both parts of the lunar day: for a place at 1
(under D) revolving as formerly, goes sooner from 1 to 11 (under F)
than from 11 to 1, because the parallel it describes is cut into unequal
segments by the high-water Circle HCO: but the points 1 and 11 being
equidistant from the Pole of the Tides at C, which is directly under
the Pole of the Moon’s orbit MGA, the Elevations are equally high
in both parts of the day.
306. And thus it appears, that as the Tides are governed by the
Moon, they must turn on the Axis of the Moon’s orbit, which is
inclined
231⁄2
degrees to the Earth’s Axis at a mean state: and therefore
the Poles of the Tides must be so many degrees from the Poles
of the Earth, or in opposite points of the polar Circles, going round
these Circles in every lunar day. ’Tis true that according to Fig. IV.
when the Moon is vertical to the Equator ECQ, the Poles of the
Tides seem to fall in with the Poles of the World N and S: but
when we consider that FHG is under the Moon’s orbit, it will appear,
that when the Moon is over H, in the Tropic of Capricorn, the
north Pole of the Tides, (which can be no more than 90 degrees
from under the Moon) must be at c in the arctic Circle, not at N;
the north Pole of the Earth; and as the Moon ascends from H to
154G in her orbit, the north Pole of the Tides must shift from c to a
in the arctic Circle; and the South Pole as much in the antarctic.
It is not to be doubted, but that the Earth’s quick rotation brings
the poles of the Tides nearer to the Poles of the World, than they
would be if the Earth were at rest, and the Moon revolved about
it only once a month; for otherwise the Tides would be more unequal
in their heights, and times of their returns, than we find they
are. But how near the Earth’s rotation may bring the Poles of
it’s Axis and those of the Tides together, or how far the preceding
Tides may affect those which follow, so as to make them keep up nearly
to the same heights, and times of ebbing and flowing, is a problem
more fit to be solved by observation than by theory.
To know at what times we may expect the greatest and least Tides.
307. Those who have opportunity to make observations, and choose
to satisfy themselves whether the Tides are really affected in the above
manner by the different positions of the Moon; especially as to the
unequal times of their returns, may take this general rule for knowing,
when they ought to be so affected. When the Earth’s Axis inclines
to the Moon, the northern Tides, if not retarded in their passage
through Shoals and Channels, nor affected by the Winds, ought to be
greatest when the Moon is above the Horizon, least when she is below
it; and quite the reverse when the Earth’s Axis declines from her:
but in both cases, at equal intervals of time. When the Earth’s Axis
inclines sidewise to the Moon, both Tides are equally high, but they
happen at unequal intervals of time. In every Lunation the Earth’s
Axis inclines once to the Moon, once from her, and twice sidewise
to her, as it does to the Sun every year; because the Moon goes
round the Ecliptic every month, and the Sun but once in a year. In
Summer, the Earth’s Axis inclines towards the Moon when New;
and therefore the day-tides in the north ought to be highest, and
night-tides lowest about the Change: at the Full the reverse. At
the Quarters they ought to be equally high, but unequal in their
returns; because the Earth’s Axis then inclines sidewise to the Moon.
In winter the Phenomena are the same at Full-Moon as in Summer
at New. In Autumn the Earth’s Axis inclines sidewise to the Moon
when New and Full; therefore the Tides ought to be equally high,
and unequal in their returns at these times. At the first Quarter the
Tides of Flood should be least when the Moon is above the Horizon,
greatest when she is below it; and the reverse at her third Quarter.
In Spring, Phenomena of the first Quarter answer to those of the third
155Quarter in Autumn; and vice versa. The nearer any time is to either
of these seasons, the more the Tides partake of the Phenomena
of these seasons; and in the middle between any two of them the
Tides are at a mean state between those of both.
Why the Tides rise higher in Rivers than in the Sea.
308. In open Seas, the Tides rise but to very small heights in proportion
to what they do in wide-mouthed rivers, opening in the
Direction of the Stream of Tide. For, in Channels growing narrower
gradually, the water is accumulated by the opposition of the
contracting Bank. Like a gentle wind, little felt on an open plain,
but strong and brisk in a street; especially if the wider end of the
street be next the plain, and in the way of the wind.
The Tides happen at all distances of the Moon from the Meridian at different places, and why.
309. The Tides are so retarded in their passage through different
Shoals and Channels, and otherwise so variously affected by striking
against Capes and Headlands, that to different places they happen
at all distances of the Moon from the Meridian; consequently at all
hours of the lunar day. The Tide propagated by the Moon in the
German ocean, when she is three hours past the Meridian, takes 12
hours to come from thence to London bridge; where it arrives by the
time that a new Tide is raised in the ocean. And therefore when
the Moon has north declination, and we should expect the Tide at
London to be greatest when the Moon is above the Horizon, we find
it is least; and the contrary when she has south declination. At several
places ’tis high water three hours before the Moon comes to the
Meridian; but that Tide which the Moon pushes as it were before
her, is only the Tide opposite to that which was raised by her when
she was nine hours past the opposite Meridian.
The Water never rises in Lakes.
310. There are no Tides in Lakes, because they are generally so
small that when the Moon is vertical she attracts every part of them
alike, and therefore by rendering all the water equally light, no
part of it can be raised higher than another. The Mediterranean and
Baltic Seas suffer very small elevations, because the Inlets by which
they communicate with the ocean are so narrow, that they cannot, in
so short a time, receive or discharge enough to raise or sink their surfaces
sensibly.
The Moon raises Tides in the Air.
Why the Mercury in the Barometer is not affected by the
aerial
Tides.
311. Air being lighter than Water, and the surface of the Atmosphere
being nearer to the Moon than the surface of the Sea, it cannot
be doubted that the Moon raises much higher Tides in the Air
than in the Sea. And therefore many have wondered why the Mercury
does not sink in the Barometer when the Moon’s action on the
particles of Air makes them lighter as she passes over the Meridian.
156But we must consider, that as these particles are rendered lighter, a
greater number of them is accumulated, until the deficiency of gravity
be made up by the height of the column; and then there is an
equilibrium, and consequently an equal pressure upon the Mercury as
before; so that it cannot be affected by the aerial Tides.
CHAP. XVIII.
Of Eclipses: Their Number and Periods. A large Catalogue of Ancient and Modern Eclipses.
A shadow, what.
312. Every Planet and Satellite is illuminated by the Sun;
and casts a shadow towards that point of the Heavens
which is opposite to the Sun. This shadow is nothing but a privation
of light in the space hid from the Sun by the opake body that intercepts
his rays.
Eclipses of the Sun and Moon, what.
313. When the Sun’s light is so intercepted by the Moon, that
to any place of the Earth the Sun appears partly or wholly covered,
he is said to undergo an Eclipse; though properly speaking, ’tis only
an Eclipse of that part of the Earth where the Moon’s shadow or
[64]Penumbra falls. When the Earth comes between the Sun and
Moon, the Moon falls into the Earth’s shadow; and having no light
of her own, she suffers a real Eclipse from the interception of the
Sun’s rays. When the Sun is eclipsed to us, the Moon’s Inhabitants
on the side next the Earth (if any such there be) see her shadow like
a dark spot travelling over the Earth, about twice as fast as its equatoreal
parts move, and the same way as they move. When the Moon
is in an Eclipse, the Sun appears eclipsed to her, total to all those parts
on which the Earth’s shadow falls, and of as long continuance as they
are in the shadow.
Plate X.
J. Ferguson delin.
J. Mynde Sculp.
A proof that the Earth and Moon are globular bodies.
314. That the Earth is spherical (for the hills take off no more
from the roundness of the Earth, than grains of dust do from the
roundness of a common Globe) is evident from the figure of its
shadow on the Moon; which is always bounded by a circular line,
although the Earth is incessantly turning its different sides to the
Moon, and very seldom shews the same side to her in different
157Eclipses, because they seldom happen at the same hours. Were the
Earth shaped like a round flat plate, its shadow would only be circular
when either of its sides directly faced the Moon; and more
or less elliptical as the Earth happened to be turned more or less obliquely
towards the Moon when she is eclipsed. The Moon’s different
Phases prove her to be round § 254; for, as she keeps still the
same side towards the earth, if that side were flat, as it appears to be,
she would never be visible from the third Quarter to the first; and
from the first Quarter to the third, she would appear as round as
when we say she is Full: because at the end of her first Quarter the
Sun’s light would come as suddenly on all her side next the Earth,
as it does on a flat wall, and go off as abruptly at the end of her
third Quarter.
And that the Sun is much bigger than the Earth, and the Moon much less.
315. If the Earth and Sun were equally big, the Earth’s shadow would
be infinitely extended, and all of the same breadth; and the Planet
Mars, in either of its nodes and opposite to the Sun, would be eclipsed
in the Earth’s shadow. Were the Earth bigger than the Sun, it’s
shadow would increase in breadth the farther it was extended, and
would eclipse the great Planets Jupiter and Saturn, with all their
Moons, when they were opposite to the Sun. But as Mars in opposition
never falls into the Earth’s shadow, although he is not then above
42 millions of miles from the Earth, ’tis plain that the Earth is much
less than the Sun; for otherwise it’s shadow could not end in a point
at so small a distance. If the Sun and Moon were equally big, the
Moon’s shadow would go on to the Earth with an equal breadth, and
cover a portion of the Earth’s surface more than 2000 miles broad,
even if it fell directly against the Earth’s center, as seen from the
Moon: and much more if it fell obliquely on the Earth: but the
Moon’s shadow is seldom 150 miles broad at the Earth, unless when
it falls very obliquely on the Earth, in total Eclipses of the Sun. In
annular Eclipses, the Moon’s real shadow ends in a point at some
distance from the Earth. The Moon’s small distance from the Earth,
and the shortness of her shadow, prove her to be less than the Sun.
And, as the Earth’s shadow is large enough to cover the Moon, if her
diameter was three times as large as it is (which is evident from her
long continuance in the shadow when she goes through it’s center) ’tis
plain, that the Earth is much bigger than the Moon.
The primary Planets never eclipse one another.
PLATE X.
316. Though all opake bodies on which the Sun shines have their
shadows, yet such is the bulk of the Sun, and the distances of the
Planets, that the primary Planets can never eclipse one another. A
Primary can eclipse only it’s secondary, or be eclipsed by it; and never
158but when in opposition or conjunction with the Sun. The primary
Planets are very seldom in these positions, but the Sun and Moon are
so every month: whence one may imagine that these two Luminaries
should be eclipsed every month. But there are few Eclipses in respect
of the number of New and Full Moons; the reason of which
we shall now explain.
Why there are so few Eclipses.
The Moon’s Nodes.
Limits of Eclipses.
317. If the Moon’s Orbit were coincident with the Plane of the
Ecliptic, in which the Earth always moves and the Sun appears to
move, the Moon’s shadow would fall upon the Earth at every Change,
and eclipse the Sun to some parts of the Earth. In like manner the
Moon would go through the middle of the Earth’s shadow, and be
eclipsed at every Full; but with this difference, that she would be totally
darkened for above an hour and half; whereas the Sun never was
above four minutes totally eclipsed by the interposition of the Moon.
But one half of the Moon’s Orbit, is elevated
51⁄3
degrees above the
Ecliptic, and the other half as much depressed below it: consequently,
the Moon’s Orbit intersects the Ecliptic in two opposite points called
the Moon’s Nodes, as has been already taken notice of § 288. When
these points are in a right line with the center of the Sun at New
or Full Moon, the Sun, Moon, and Earth are all in a right line;
and if the Moon be then New, her shadow falls upon the Earth; if
Full the Earth’s shadow falls upon her. When the Sun and Moon
are more than 17 degrees from either of the Nodes at the time of
Conjunction, the Moon is then too high or too low in her Orbit
to cast any part of her shadow upon the Earth. And when the
Sun is more than 12 degrees from either of the Nodes at the time
of Full Moon, the Moon is too high or too low in her Orbit to
go through any part of the Earth’s shadow: and in both these cases
there will be no Eclipse. But when the Moon is less than 17 degrees
from either Node at the time of Conjunction, her shadow or Penumbra
falls more or less upon the Earth, as she is more or less within this
limit. And when she is less than 12 degrees from either Node at the
time of opposition, she goes through a greater or less portion of the
Earth’s shadow, as she is more or less within this limit. Her Orbit
contains 360 degrees; of which 17, the limit of solar Eclipses on either
side of the Nodes, and 12 the limit of lunar Eclipses, are but
small portions: and as the Sun commonly passes by the Nodes but
twice in a year, it is no wonder that we have so many New and Full
Moons without Eclipses.
To illustrate this, let ABCD be the Ecliptic, RSTU a Circle lying
in the same Plane with the Ecliptic, and VWXY the Moon’s Orbit,
159all thrown into an oblique view, which gives them an elliptical shape
to the eye. One half of the Moon’s Orbit, as VWX, is always below
the Ecliptic, and the other half XYV above it. The points V and X,
where the Moon’s Orbit intersects the Circle RSTU, which lies even
with the Ecliptic, are the Moon’s Nodes; and a right line as XEV
drawn from one to the other, through the Earth’s center, is the Line of
the Nodes, which is carried almost parallel to itself round the Sun in a
year.
If the Moon moved round the Earth in the Orbit RSTU, which is
coincident with the Plane of the Ecliptic, her shadow would fall upon
the Earth every time she is in conjunction with the Sun; and at every
opposition she would go through the Earth’s shadow. Were this the
case, the Sun would be eclipsed at every Change, and the Moon at
every Full, as already mentioned.
But although the Moon’s shadow N must fall upon the Earth at a,
when the Earth is at E, and the Moon in conjunction with the Sun at i,
because she is then very near one of her Nodes; and at her opposition n
she must go through the Earth’s shadow I, because she is then near the
other Node; yet, in the time that she goes round the Earth to her
next Change, according to the order of the letters XYVW, the Earth
advances from E to e, according to the order of the letters EFGH,
and the line of the Nodes VEX being carried nearly parallel to itself,
brings the point f of the Moon’s Orbit in conjunction with the Sun at
that next Change; and then the Moon being at f is too high above
the Ecliptic to cast her shadow on the Earth: and as the Earth is still
moving forward, the Moon at her next opposition will be at g, too
far below the Ecliptic to go through any part of the Earth’s shadow;
for by that time the point g will be at a considerable distance from the
Earth as seen from the Sun.
Fig. I and II.
When the Earth comes to F, the Moon in conjunction with the
Sun Z is not at k, in a Plane coincident with the Ecliptic, but above
it at Y in the highest part of her Orbit: and then the point b of her
shadow O goes far above the Earth (as in Fig. II, which is an edge
view of Fig. I.) The Moon at her next opposition is not at o (Fig I)
but at W where the Earth’s shadow goes far above her, (as in Fig. II.)
In both these cases the line of the Nodes VFX (Fig. I.) is about 90
degrees from the Sun, and both Luminaries as far as possible from
the limits of Eclipses.
When the Earth has gone half round the Ecliptic from E to G, the
line of the Nodes VGX is nearly, if not exactly, directed towards the
Sun at Z; and then the New Moon l casts her shadow P on the
160Earth G; and the Full Moon p goes through the Earth’s shadow L;
which brings on Eclipses again, as when the Earth was at E.
When the Earth comes to H the New Moon falls not at m in a
plane coincident with the Ecliptic CD, but at W in her Orbit below
it: and then her shadow Q (see Fig. II) goes far below the Earth.
At the next Full she is not at q (Fig. I) but at Y in her orbit
51⁄3
degrees
above q, and at her greatest height above the Ecliptic CD; being
then as far as possible, at any opposition, from the Earth’s shadow M
(as in Fig. II.)
So, when the Earth is at E and G, the Moon is about her Nodes at
New and Full; and in her greatest North and South Declination, (or
Latitude as it is generally called) from the Ecliptic at her Quarters:
but when the Earth is at F or H, the Moon is in her greatest North
and South Declination from the Ecliptic at New and Full, and in the
Nodes about her Quarters.
The Moon’s ascending and descending Node.
Her North and South Latitude.
318. The point X where the Moon’s Orbit crosses the Ecliptic is
called the Ascending Node, because the Moon ascends from it above
the Ecliptic: and the opposite point of intersection V is called the Descending
Node, because the Moon descends from it below the Ecliptic.
When the Moon is at Y in the highest point of her Orbit, she is in
her greatest North Latitude; and when she is at W in the lowest point
of her Orbit, she is in her greatest South Latitude.
The Nodes have a retrograde motion.
Fig. I.
Which brings on the Eclipses sooner every year than they would
be if the Nodes had not such a motion.
319. If the line of the Nodes, like the Earth’s Axis, was carried
parallel to itself round the Sun, there would be just half a year between
the conjunctions of the Sun and Nodes. But the Nodes shift
backward, or contrary to the Earth’s annual motion,
191⁄3
degrees every
year; and therefore the same Node comes round to the Sun 19 days sooner
every year than on the year before. Consequently, from the time that
the ascending Node X (when the Earth is at E) passes by the Sun as
seen from the Earth, it is only 173 days (not half a year) till the descending
Node V passes by him. Therefore, in whatever time of the
year we have Eclipses of the Luminaries about either Node, we may
be sure that in 173 days afterward we shall have Eclipses about the
other Node. And when at any time of the year the line of the Nodes is in
the situation VGX, at the same time next year it will be in the situation
rGs; the ascending Node having gone backward, that is, contrary to
the order of Signs from X to s, and the descending Node from V to r;
each
191⁄3
degrees. At this rate the Nodes shift through all the Signs
and degrees of the Ecliptic in 18 years and 225 days; in which time
there would always be a regular period of Eclipses, if any compleat
number of Lunations were finished without a fraction. But this never
161happens, for if the Sun and Moon should start from a conjunction with
either of the Nodes in any point of the Ecliptic, whilst the same Node
is going round to that point again the Earth performs 18 annual revolutions
about the Sun and 222 Degrees (or 7 Signs 12 Degrees) over;
and the Moon 230 Lunations or Courses from Change to Change and
85 Degrees (or 2 Signs 25 Degrees) over; so that the Sun will be
138 Degrees from the same Node when it comes round, and the Moon
85 Degrees from the Sun. Hence, the period of Eclipses and revolution
of the Nodes are completed in different times.
A period of Eclipses.
The defects of it.
320. In 18 years 10 days 7 hours 43 minutes after the Sun Moon
and Nodes have been in a line of conjunction, they come very
near to a conjunction again: only, if the conjunction from which you
reckon falls in a leap-year, the return of the conjunction will be one
day later. Therefore, if to the [65]mean time of any Eclipse of the
Sun or Moon in leap-year, you add 18 years 11 days 7 hours 43
minutes; or in a common year a day less, you will have the mean
time of that Eclipse returned again for some ages; though not always
visible, because the 7 hours 43 minutes may shift a solar Eclipse into
the night, and a lunar Eclipse into the day. In this period there are
just 223 Lunations, and the Sun is again within half a degree of the
same Node, but short of it. Therefore, although this period will serve
tolerably well for some ages to examine Eclipses by, it cannot hold
long; because half a degree from the Node sets the Moon
21⁄2
minutes
of a degree from the Ecliptic. And as the Moon’s mean distance from
the Earth is equal to 60 Semidiameters of the Earth, every minute of
a degree at that distance is equal to 60 geographical miles, or one
degree on the Earth; consequently
21⁄2
minutes of declination from the
Ecliptic in the Moon’s Orbit, is equal to 150 such miles, or
21⁄2
degrees
on the Earth. Consequently, if the Moon be passing by her ascending
Node at the end of this period, her shadow will go 150 miles
more southward on the Earth than it did at the beginning thereof. If
the Moon be passing by her descending Node, her shadow will go 150
miles more northward: and in either case, in 500 years the shadow
will have too great a Latitude to touch the Earth. So that any Eclipse
of the Sun, which begins (for example) to touch the Earth at the
south Pole (and that must be when the Moon is 17 degrees past her
descending Node) will advance gradually northward in every return
for about a thousand years, and then go off at the north Pole; and
cannot take such another course again in less than 11,683 years.
162This falling back of the Sun and Moon in every period, with respect
to the Nodes, will occasion those Eclipses which happen about
the ascending Node to go more southerly in each return; and those
which happen about the descending Node to go more northerly: for
the farther the Moon is short of the ascending Node, within the limits
of Eclipses, the farther she is south of the Ecliptic; and on the contrary,
the more she is short of the descending Node, the farther she is
northward of the Ecliptic.
From Mr. G. Smith’s dissertation on Eclipses, printed at London, by E. Cave, in the year 1748.
321. “To illustrate this a little farther, we shall examine some of
the most remarkable circumstances of the returns of the Eclipse
which happened July 14, 1748, about noon: This Eclipse, after
traversing the voids of space from the Creation, at last began to enter
the Terra Australis Incognita, about 88 years after the Conquest,
which was the last of King Stephen’s reign; every [66]Chaldean
period it has crept more northerly, but was still invisible in Britain
before the year 1622; when on the 30th of April it began to touch
the south parts of England about 2 in the afternoon; its central appearance
rising in the American South Seas, and traversing Peru and
the Amazon’s country, through the Atlantic ocean into Africa, and
setting in the Æthiopian continent, not far from the beginning of
the Red Sea.
“Its next visible period was after three Chaldean revolutions in 1676,
on the first of June, rising central in the Atlantic ocean, passing us
about 9 in the morning, with four [67]Digits eclipsed on the under
limb; and setting in the gulf of Cochinchina in the East-Indies.
“It being now near the Solstice, this Eclipse was visible the very
next return in 1694, in the evening; and in two periods more,
which was in 1730, on the 4th of July, was seen above half eclipsed
just after Sun-rise, and observed both at Wirtemberg in Germany, and
Pekin in China, soon after which it went off.
“Eighteen years more afforded us the Eclipse which fell on the 14th
of July 1748.
“The next visible return will happen on July 25, 1766, in the
evening, about four Digits eclipsed; and after two periods more, on
August 16th, 1802, early in the morning, about five Digits, the
center coming from the north frozen continent, by the capes of Norway,
through Tartary, China, and Japan, to the Ladrone islands,
where it goes off.
163“Again, in 1820, August 26, betwixt one and two, there will be
another great Eclipse at London, about 10 Digits; but happening so
near the Equinox, the center will leave every part of Britain to the
West, and enter Germany at Embden, passing by Venice, Naples,
Grand Cairo, and set in the gulf of Bassora near that city.
“It will be no more visible till 1874, when five Digits will be
obscured, the center being now about to leave the Earth on September
28. In 1892 the Sun will go down eclipsed at London,
and again in 1928 the passage of the center will be in the expansum,
though there will be two Digits eclipsed at London, October the 31st
of that year; and about the year 2090 the whole Penumbra will
be wore off; whence no more returns of this Eclipse can happen
till after a revolution of 10 thousand years.
“From these remarks on the intire revolution of this Eclipse, we
may gather, that a thousand years, more or less (for there are
some irregularities that may protract or lengthen this period 100
years) complete the whole terrestrial Phenomena of any single
Eclipse: and since 20 periods of 54 years each, and about 33 days,
comprehend the intire extent of their revolution, ’tis evident that
the times of the returns will pass through a circuit of one year and
ten months, every Chaldean period being ten or eleven days later,
and of the equable appearances about 32 or 33 days. Thus,
though this Eclipse happens about the middle of July, no other
subsequent Eclipse of this period will return to the middle of the
same month again; but wear constantly each period 10 or 11
days forward, and at last appear in Winter, but then it begins to
cease from affecting us.
“Another conclusion from this revolution may be drawn, that there
will seldom be any more than two great Eclipses of the Sun in the
interval of this period, and these follow sometimes next return, and
often at greater distances. That of 1715 returned again in 1733
very great; but this present Eclipse will not be great till the arrival
of 1820, which is a revolution of four Chaldean periods: so that the
irregularities of their circuits must undergo new computations to
assign them exactly.
“Nor do all Eclipses come in at the south Pole: that depends altogether
on the position of the lunar Nodes, which will bring in as
many from the expansum one way as the other; and such Eclipses
will wear more southerly by degrees, contrary to what happens in
the present case.
164“The Eclipse, for example, of 1736, in September, had its center
in the expansum, and set about the middle of its obscurity in Britain;
it will wear in at the north Pole, and in the year 2600, or thereabouts,
go off into the expansum on the south side of the Earth.
“The Eclipses therefore which happened about the Creation are
little more than half way yet of their etherial circuit; and will
be 4000 years before they enter the Earth any more. This grand
revolution seems to have been entirely unknown to the antients.
Why our present Tables agree not with antient observations.
“322. It is particularly to be noted, that Eclipses which have happened
many centuries ago, will not be found by our present Tables
to agree exactly with antient observations, by reason of the great
Anomalies in the lunar motions; which appears an incontestable
demonstration of the non-eternity of the Universe. For it seems
confirmed by undeniable proofs, that the Moon now finishes her
period in less time than formerly, and will continue by the centripetal
law to approach nearer and nearer the Earth, and to go sooner
and sooner round it: nor will the centrifugal power be sufficient to
compensate the different gravitations of such an assemblage of bodies
as constitute the solar system, which would come to ruin of itself,
without some new regulation and adjustment of their original motions[68].
Thales’s Eclipse.
“323. We are credibly informed from the testimony of the antients,
that there was a total Eclipse of the Sun predicted by
165Thales to happen in the fourth year of the 48th [69]Olympiad, either
at Sardis or Miletus in Asia, where Thales then resided. That
year corresponds to the 585th year before Christ; when accordingly
there happened a very signal Eclipse of the Sun, on the 28th of May,
answering to the present 10th of that month[70], central through
North America, the south parts of France, Italy, &c. as far as Athens,
or the Isles in the Ægean Sea; which is the farthest that even the
Caroline Tables carry it; and consequently make it invisible to any
part of Asia, in the total character; though I have good reasons to
believe that it extended to Babylon, and went down central over that
city. We are not however to imagine, that it was set before it past
Sardis and the Asiatic towns, where the predictor lived; because an
invisible Eclipse could have been of no service to demonstrate his
ability in Astronomical Sciences to his countrymen, as it could give
no proof of its reality.
Thucydides’s Eclipse.
“324. For a farther illustration, Thucydides relates, that a solar
Eclipse happened on a Summer’s day in the afternoon, in the first
year of the Peloponnesian war, so great that the Stars appeared.
Rhodius was victor in the Olympic games the fourth year of the
said war, being also the fourth of the 87th Olympiad, on the 428th
166year before Christ. So that the Eclipse must have happened in
the 431st year before Christ; and by computation it appears, that
on the 3d of August there was a signal Eclipse which would have past
over Athens, central about 6 in the evening, but which our present
Tables bring no farther than the antient Syrtes on the African coast,
above 400 miles from Athens; which suffering in that case but 9
Digits, could by no means exhibit the remarkable darkness recited by
this historian; the center therefore seems to have past Athens about
6 in the evening, and probably might go down about Jerusalem, or
near it, contrary to the construction of the present Tables. I have
only obviated these things by way of caution to the present Astronomers,
in re-computing antient Eclipses; and refer them to examine
the Eclipse of Nicias, so fatal to the Athenian fleet[71]; that which
overthrew the Macedonian Army[72] &c.” So far Mr. Smith.
The number of Eclipses.
325. In any year, the number of Eclipses of both Luminaries cannot
be less than two, nor more than seven; the most usual number is four,
and it is very rare to have more than six. For the Sun passes by both
the Nodes but once a year, unless he passes by one of them in the
beginning of the year; and if he does, he will pass by the same Node
again a little before the year be finished; because, as these points move
19 degrees backward every year, the Sun will come to either of them
173 days after the other § 319. And when either Node is within 17
degrees of the Sun at the time of New Moon, the Sun will be eclipsed.
At the subsequent opposition the Moon will be eclipsed in the other
Node; and come round to the next conjunction again ere the former
Node be 17 degrees past the Sun, and will therefore eclipse him again.
When three Eclipses fall about either Node, the like number generally
falls about the opposite; as the Sun comes to it in 173 days afterward:
and six Lunations contain but four days more. Thus, there may be
two Eclipses of the Sun and one of the Moon about each of her
Nodes. But when the Moon changes in either of the Nodes, she
cannot be near enough the other Node at the next Full to be eclipsed;
and in six lunar months afterward she will change near the other Node:
in these cases there can be but two Eclipses in a year, and they are
both of the Sun.
Two periods of Eclipses.
326. A longer, and consequently more exact period than the above-mentioned
§ 320, for comparing and examining Eclipses which happen
at long intervals of time, is 57 Julian years 324 days 21 hours 41
minutes and 35 seconds; in which time there are just 716 mean Lunations,
167and the Sun is again within 5 minutes of the same Node as
before. But a still better period is 557 years 21 days 18 hours 30
minutes 12 seconds; in which time there are 6890 mean Lunations;
and the Sun and Node meet again so nearly as to be but 11 seconds
distant.
An account of the following catalogue of Eclipses.
327. We shall subjoin a catalogue of Eclipses recorded in history,
from 721 years before Christ to A. D. 1485; of computed Eclipses
from 1485 to 1700; and of all the Eclipses visible in Europe from 1700
to 1800. From the beginning of the catalogue to A.D. 1485 the
Eclipses are taken from Struyk’s Introduction to universal Geography,
as that indefatigable author has, with much labour, collected them
from Ptolemy, Thucydides, Plutarch, Calvisius, Xenophon, Diodorus
Siculus, Justin, Polybius, Titus Livius, Cicero, Lucanus, Theophanes,
Dion Cassius, and many others. From 1485 to 1700 the Eclipses are
taken from Ricciolus’s Almagest: and from 1700 to 1800 from L’art de
verifier les Dates[73]. Those from Struyk have all the places mentioned
where they were observed: Those from the French authors, viz. the
religious Benedictines of the Congregation of St. Maur, are fitted to the
Meridian of Paris: And concerning those from Ricciolus, that author
gives the following account.
Because it is of great use for fixing the Cycles or Revolutions of
Eclipses, to have at hand, without the trouble of calculation, a list of
successive Eclipses for many years, computed by authors of Ephemerides,
although from Tables not perfect in all respects, I shall for the benefit of
Astronomers give a summary collection of such. The authors I extract
from are, an anonymous one who published Ephemerides from 1484
to 1506 inclusive; Jacobus Pflaumen and Jo. Stæflerinus, to the Meridian
of Ulm, from 1507 to 1534: Lucas Gauricus, to the Latitude of
45 degrees, from 1534 to 1551: Peter Appian, to the Meridian of
Leysing, from 1538 to 1578: Jo. Stæflerus to the Meridian of Tubing,
from 1543 to 1554: Petrus Pitatus, to the Meridian of Venice from
1544 to 1556: Georgius-Joachimus Rheticus, for the year 1551: Nicholaus
Simus, to the Meridian of Bologna, from 1552 to 1568: Michael
Mæstlin, to the Meridian of Tubing, from 1557 to 1590: Jo.
Stadius, to the Meridian of Antwerp, from 1554 to 1574: Jo. Antoninus
Maginus, to the Meridian of Venice, from 1581 to 1630: David
Origan, to the Meridian of Franckfort on the Oder, from 1595 to 1664:
Andrew Argol, to the Meridian of Rome, from 1630 to 1700: Franciscus
Montebrunus, to the Meridian of Bologna, from 1461 to 1660:
168Among which, Stadius, Mæstlin, and Maginus, used the Prutenic
Tables; Origan the Prutenic and Tychonic; Montebrunus the Lansbergian,
as likewise those of Duret. Almost all the rest the Alphonsine.
But, that the places may readily be known for which these Eclipses
were computed, and from what Tables, consult the following list, in
which the years inclusive are also set down.
| From 1485 |
to |
1506 |
The place and author unknown. |
| 1507 |
|
1553 |
Ulm in Suabia, from the Alphonsine. |
| 1554 |
|
1576 |
Antwerp, from the Prutenic. |
| 1577 |
|
1585 |
Tubing, from the Prutenic. |
| 1586 |
|
1594 |
Venice, from the Prutenic. |
| 1595 |
|
1600 |
Franckfort on Oder, from the Prutenic. |
| 1601 |
|
1640 |
Franckfort on Oder, from the Tychonic. |
| 1641 |
|
1660 |
Bologna, from the Lansbergian. |
| 1661 |
|
1700 |
Rome, from the Tychonic. |
So far Ricciolus.
N. B. The Eclipses marked with an Asterisk are not in Ricciolus’s
catalogue; but are supplied from L’art de verifier les Dates.
From the beginning of the catalogue to A. D. 1700, the time is
reckoned from the noon of the day mentioned to the noon of the following
day; but from 1700 to 1800 the time is set down according to
our common way of reckoning. Those marked Pekin and Canton are
Eclipses from the Chinese chronology according to Struyk; and
throughout the Table this mark
 signifies Sun, and this
signifies Sun, and this
 Moon.
Moon.
169Struyk’s Catalogue of ECLIPSES.
| Bef. Chr. |
Eclipses of the Sun and Moon seen at |
|
M. & D. |
Middle |
Digits eclipsed |
| H. |
M. |
| 721 |
Babylon |
 |
Mar. 19 |
10 |
34 |
Total |
| 720 |
Babylon |
 |
Mar. 8 |
11 |
56 |
1 |
5 |
| 720 |
Babylon |
 |
Sept. 1 |
10 |
18 |
5 |
4 |
| 621 |
Babylon |
 |
Apr. 21 |
18 |
22 |
2 |
36 |
| 523 |
Babylon |
 |
July 16 |
12 |
47 |
7 |
24 |
| 502 |
Babylon |
 |
Nov. 19 |
12 |
21 |
1 |
52 |
| 491 |
Babylon |
 |
Apr. 25 |
12 |
12 |
1 |
44 |
| 431 |
Athens |
 |
Aug. 3 |
6 |
35 |
11 |
0 |
| 425 |
Athens |
 |
Oct. 9 |
6 |
45 |
Total |
| 424 |
Athens |
 |
Mar. 20 |
20 |
17 |
9 |
0 |
| 413 |
Athens |
 |
Aug. 27 |
10 |
15 |
Total |
| 406 |
Athens |
 |
Apr. 15 |
8 |
50 |
Total |
| 404 |
Athens |
 |
Sept. 2 |
21 |
12 |
8 |
40 |
| 403 |
Pekin |
 |
Aug. 28 |
5 |
53 |
10 |
40 |
| 394 |
Gnide |
 |
Aug. 13 |
22 |
17 |
11 |
0 |
| 383 |
Athens |
 |
Dec. 22 |
19 |
6 |
2 |
1 |
| 382 |
Athens |
 |
June 18 |
8 |
54 |
6 |
15 |
| 382 |
Athens |
 |
Dec. 12 |
10 |
21 |
Total |
| 364 |
Thebes |
 |
July 12 |
23 |
51 |
6 |
10 |
| 357 |
Syracuse |
 |
Feb. 28 |
22 |
-- |
3 |
33 |
| 357 |
Zant |
 |
Aug. 29 |
7 |
29 |
4 |
21 |
| 340 |
Zant |
 |
Sept. 14 |
18 |
-- |
9 |
0 |
| 331 |
Arbela |
 |
Sept. 20 |
10 |
9 |
Total |
| 310 |
Sicily Island |
 |
Aug. 14 |
20 |
5 |
10 |
22 |
| 219 |
Mysia |
 |
Mar. 19 |
14 |
5 |
Total |
| 218 |
Pergamos |
 |
Sept. 1 |
rising |
Total |
| 217 |
Sardinia |
 |
Feb. 11 |
1 |
57 |
9 |
6 |
| 203 |
Frusini |
 |
May 6 |
2 |
52 |
5 |
40 |
| 202 |
Cumis |
 |
Oct. 18 |
22 |
24 |
1 |
0 |
| 201 |
Athens |
 |
Sept. 22 |
7 |
14 |
8 |
58 |
| 200 |
Athens |
 |
Mar. 19 |
13 |
9 |
Total |
| 200 |
Athens |
 |
Sept. 11 |
14 |
48 |
Total |
| 198 |
Rome |
 |
Aug. 6 |
---- |
---- |
| 190 |
Rome |
 |
Mar. 13 |
18 |
-- |
11 |
0 |
| 188 |
Rome |
 |
July 16 |
20 |
38 |
10 |
48 |
| 174 |
Athens |
 |
Apr. 30 |
14 |
33 |
7 |
1 |
| 168 |
Macedonia |
 |
June 21 |
8 |
2 |
Total |
| 141 |
Rhodes |
 |
Jan. 27 |
10 |
8 |
3 |
26 |
| 104 |
Rome |
 |
July 18 |
22 |
0 |
11 |
52 |
| 63 |
Rome |
 |
Oct. 27 |
6 |
22 |
Total |
| 60 |
Gibralter |
 |
Mar. 16 |
setting |
Central |
| 54 |
Canton |
 |
May 9 |
3 |
41 |
Total |
| 51 |
Rome |
 |
Mar. 7 |
2 |
12 |
9 |
0 |
| 48 |
Rome |
 |
Jan. 18 |
10 |
0 |
Total |
| 45 |
Rome |
 |
Nov. 6 |
14 |
-- |
Total |
| 36 |
Rome |
 |
May 19 |
3 |
52 |
6 |
47 |
| 31 |
Rome |
 |
Aug. 20 |
setting |
Gr. Ecl. |
| 29 |
Canton |
 |
Jan. 5 |
4 |
2 |
11 |
0 |
| 28 |
Pekin |
 |
June 18 |
23 |
48 |
Total |
| 26 |
Canton |
 |
Oct. 23 |
4 |
16 |
11 |
15 |
| 24 |
Pekin |
 |
April 7 |
4 |
11 |
2 |
0 |
| 16 |
Pekin |
 |
Nov. 1 |
5 |
13 |
2 |
8 |
| 2 |
Canton |
 |
Feb. 1 |
20 |
8 |
11 |
42 |
| Aft. Chr. |
Eclipses of the Sun and Moon seen at |
|
M. & D. |
Middle |
Digits eclipsed |
| H. |
M. |
| 1 |
Pekin |
 |
June 10 |
1 |
10 |
11 |
43 |
| 5 |
Rome |
 |
Mar. 28 |
4 |
13 |
4 |
45 |
| 14 |
Panonia |
 |
Sept. 26 |
17 |
15 |
Total |
| 27 |
Canton |
 |
July 22 |
8 |
56 |
Total |
| 30 |
Canton |
 |
Nov. 13 |
19 |
20 |
10 |
30 |
| 40 |
Pekin |
 |
Apr. 30 |
5 |
50 |
7 |
34 |
| 45 |
Rome |
 |
July 31 |
22 |
1 |
5 |
17 |
| 46 |
Pekin |
 |
July 21 |
22 |
25 |
2 |
10 |
| 46 |
Rome |
 |
Dec. 31 |
9 |
52 |
Total |
| 49 |
Pekin |
 |
May 20 |
7 |
16 |
10 |
8 |
| 53 |
Canton |
 |
Mar. 8 |
20 |
42 |
11 |
6 |
| 55 |
Pekin |
 |
July 12 |
21 |
50 |
6 |
40 |
| 56 |
Canton |
 |
Dec. 25 |
0 |
28 |
9 |
20 |
| 59 |
Rome |
 |
Apr. 30 |
3 |
8 |
10 |
38 |
| 60 |
Canton |
 |
Oct. 13 |
3 |
31 |
10 |
30 |
| 65 |
Canton |
 |
Dec. 15 |
21 |
50 |
10 |
23 |
| 69 |
Rome |
 |
Oct. 18 |
10 |
43 |
10 |
49 |
| 70 |
Canton |
 |
Sept. 22 |
21 |
13 |
8 |
26 |
| 71 |
Rome |
 |
Mar. 4 |
8 |
32 |
6 |
0 |
| 95 |
Ephesus |
 |
May 21 |
---- |
1 |
0 |
| 125 |
Alexandria |
 |
April 5 |
9 |
16 |
1 |
44 |
| 133 |
Alexandria |
 |
May 6 |
11 |
44 |
Total |
| 134 |
Alexandria |
 |
Oct. 20 |
11 |
5 |
10 |
19 |
| 136 |
Alexandria |
 |
Mar. 5 |
15 |
56 |
5 |
17 |
| 237 |
Bologna |
 |
Apr. 12 |
---- |
Total |
| 238 |
Rome |
 |
April 1 |
20 |
20 |
8 |
45 |
| 290 |
Carthage |
 |
May 15 |
3 |
20 |
11 |
20 |
| 304 |
Rome |
 |
Aug. 31 |
9 |
36 |
Total |
| 316 |
Constantinople |
 |
Dec. 30 |
19 |
53 |
2 |
18 |
| 334 |
Toledo |
 |
July 17 |
at noon |
Central |
| 348 |
Constantinople |
 |
Oct. 8 |
19 |
24 |
8 |
0 |
| 360 |
Ispahan |
 |
Aug. 27 |
18 |
0 |
Central |
| 364 |
Alexandria |
 |
Nov. 25 |
15 |
24 |
Total |
| 401 |
Rome |
 |
June 11 |
---- |
Total |
| 401 |
Rome |
 |
Dec. 6 |
12 |
15 |
Total |
| 402 |
Rome |
 |
June 1 |
8 |
43 |
10 |
2 |
| 402 |
Rome |
 |
Nov. 10 |
20 |
33 |
10 |
30 |
| 447 |
Compostello |
 |
Dec. 23 |
0 |
46 |
1 |
-- |
| 451 |
Compostello |
 |
April 1 |
16 |
34 |
19 |
52 |
| 451 |
Compostello |
 |
Sept. 26 |
6 |
30 |
0 |
2 |
| 458 |
Chaves |
 |
May 27 |
23 |
16 |
18 |
53 |
| 462 |
Compostello |
 |
Mar. 1 |
13 |
2 |
11 |
11 |
| 464 |
Chaves |
 |
July 19 |
19 |
1 |
10 |
15 |
| 484 |
Constantinople |
 |
Jan. 13 |
19 |
53 |
0 |
0 |
| 486 |
Constantinople |
 |
May 19 |
1 |
10 |
5 |
15 |
| 497 |
Constantinople |
 |
Apr. 18 |
6 |
5 |
17 |
57 |
| 512 |
Constantinople |
 |
June 28 |
23 |
8 |
1 |
50 |
| 538 |
England |
 |
Feb. 14 |
19 |
-- |
8 |
23 |
| 540 |
London |
 |
June 19 |
20 |
15 |
8 |
-- |
| 577 |
Tours |
 |
Dec. 10 |
17 |
28 |
6 |
46 |
| 581 |
Paris |
 |
April 4 |
13 |
33 |
6 |
42 |
| 582 |
Paris |
 |
Sept. 17 |
12 |
41 |
Total |
| 590 |
Paris |
 |
Oct. 18 |
6 |
30 |
9 |
25 |
| 170592 |
Constantinople |
 |
Mar. 18 |
22 |
6 |
10 |
0 |
| 603 |
Paris |
 |
Aug. 12 |
3 |
3 |
11 |
20 |
| 622 |
Constantinople |
 |
Febr. 1 |
11 |
28 |
Total |
| 644 |
Paris |
 |
Nov. 5 |
0 |
30 |
9 |
53 |
| 680 |
Paris |
 |
June 17 |
12 |
30 |
Total |
| 683 |
Paris |
 |
April 16 |
11 |
30 |
Total |
| 693 |
Constantinople |
 |
Oct. 4 |
23 |
54 |
11 |
54 |
| 716 |
Constantinople |
 |
Jan. 13 |
7 |
-- |
Total |
| 718 |
Constantinople |
 |
June 3 |
1 |
15 |
Total |
| 733 |
England |
 |
Aug. 13 |
20 |
-- |
11 |
1 |
| 734 |
England |
 |
Jan. 23 |
14 |
-- |
Total |
| 752 |
England |
 |
July 30 |
13 |
-- |
Total |
| 753 |
England |
 |
June 8 |
22 |
-- |
10 |
35 |
| 753 |
England |
 |
Jan. 23 |
13 |
-- |
Total |
| 760 |
England |
 |
Aug. 15 |
4 |
-- |
8 |
15 |
| 760 |
London |
 |
Aug. 30 |
5 |
50 |
10 |
40 |
| 764 |
England |
 |
June 4 |
at noon |
7 |
15 |
| 770 |
London |
 |
Feb. 14 |
7 |
12 |
Total |
| 774 |
Rome |
 |
Nov. 22 |
14 |
37 |
11 |
58 |
| 784 |
London |
 |
Nov. 1 |
14 |
2 |
Total |
| 787 |
Constantinople |
 |
Sept. 14 |
20 |
43 |
9 |
47 |
| 796 |
Constantinople |
 |
Mar. 27 |
16 |
22 |
Total |
| 800 |
Rome |
 |
Jan. 15 |
9 |
0 |
10 |
17 |
| 807 |
Angoulesme |
 |
Feb. 10 |
21 |
24 |
9 |
42 |
| 807 |
Paris |
 |
Feb. 25 |
13 |
43 |
Total |
| 807 |
Paris |
 |
Aug. 21 |
10 |
20 |
Total |
| 809 |
Paris |
 |
July 15 |
21 |
33 |
8 |
8 |
| 809 |
Paris |
 |
Dec. 25 |
8 |
-- |
Total |
| 810 |
Paris |
 |
June 20 |
8 |
-- |
Total |
| 810 |
Paris |
 |
Nov. 30 |
0 |
12 |
Total |
| 810 |
Paris |
 |
Dec. 14 |
8 |
-- |
Total |
| 812 |
Constantinople |
 |
May 14 |
2 |
13 |
9 |
-- |
| 813 |
Cappadocia |
 |
May 3 |
17 |
5 |
10 |
35 |
| 817 |
Paris |
 |
Feb. 5 |
5 |
42 |
Total |
| 818 |
Paris |
 |
July 6 |
18 |
-- |
6 |
55 |
| 820 |
Paris |
 |
Nov. 23 |
6 |
26 |
Total |
| 824 |
Paris |
 |
Mar. 18 |
7 |
55 |
Total |
| 828 |
Paris |
 |
June 30 |
15 |
-- |
Total |
| 828 |
Paris |
 |
Dec. 24 |
13 |
45 |
Total |
| 831 |
Paris |
 |
April 30 |
6 |
19 |
11 |
8 |
| 831 |
Paris |
 |
May 15 |
23 |
-- |
4 |
24 |
| 831 |
Paris |
 |
Oct. 24 |
11 |
18 |
Total |
| 832 |
Fulda |
 |
Apr. 18 |
9 |
0 |
Total |
| 840 |
Paris |
 |
May 4 |
23 |
22 |
9 |
20 |
| 841 |
Paris |
 |
Oct. 17 |
18 |
58 |
5 |
24 |
| 842 |
Paris |
 |
Mar. 29 |
14 |
38 |
Total |
| 843 |
Paris |
 |
Mar. 19 |
7 |
1 |
Total |
| 861 |
Paris |
 |
Mar. 29 |
15 |
7 |
Total |
| 878 |
Paris |
 |
Oct. 14 |
16 |
-- |
Total |
| 878 |
Paris |
 |
Oct. 29 |
1 |
-- |
11 |
14 |
| 883 |
Arracta |
 |
July 23 |
7 |
44 |
11 |
-- |
| 889 |
Constantinople |
 |
April 3 |
17 |
52 |
9 |
23 |
| 891 |
Constantinople |
 |
Aug. 7 |
23 |
48 |
10 |
30 |
| 901 |
Arracta |
 |
Aug. 2 |
15 |
7 |
Total |
| 904 |
London |
 |
May 31 |
11 |
47 |
Total |
| 904 |
London |
 |
Nov. 25 |
9 |
0 |
Total |
| 912 |
London |
 |
Jan. 6 |
15 |
12 |
Total |
| 926 |
Paris |
 |
Mar. 31 |
15 |
17 |
Total |
| 934 |
Paris |
 |
Apr. 16 |
4 |
30 |
11 |
36 |
| 939 |
Paris |
 |
July 18 |
19 |
45 |
10 |
7 |
| 955 |
Paris |
 |
Sept. 4 |
11 |
18 |
Total |
| 961 |
R pl prhemes |
 |
May 16 |
20 |
13 |
9 |
18 |
| 970 |
Constantinople |
 |
May 7 |
18 |
38 |
11 |
22 |
| 976 |
London |
 |
July 13 |
15 |
7 |
Total |
| 985 |
Messina |
 |
July 20 |
3 |
52 |
4 |
10 |
| 989 |
Constantinople |
 |
May 28 |
6 |
54 |
8 |
40 |
| 990 |
Fulda |
 |
Apr. 12 |
10 |
22 |
9 |
5 |
| 990 |
Fulda |
 |
Oct. 6 |
15 |
4 |
11 |
10 |
| 990 |
Constantinople |
 |
Oct. 21 |
0 |
45 |
10 |
5 |
| 995 |
Augsburgh |
 |
July 14 |
11 |
27 |
Total |
| 1009 |
Ferrara |
 |
Oct. 6 |
11 |
38 |
Total |
| 1010 |
Messina |
 |
Mar. 18 |
5 |
41 |
9 |
12 |
| 1016 |
Nimeguen |
 |
Nov. 16 |
16 |
39 |
Total |
| 1017 |
Nimeguen |
 |
Oct. 22 |
2 |
8 |
6 |
-- |
| 1020 |
Cologne |
 |
Sept. 4 |
11 |
38 |
Total |
| 1023 |
London |
 |
Jan. 23 |
23 |
29 |
11 |
-- |
| 1030 |
Rome |
 |
Feb. 20 |
11 |
43 |
Total |
| 1031 |
Paris |
 |
Feb. 9 |
11 |
51 |
Total |
| 1033 |
Paris |
 |
Dec. 8 |
11 |
11 |
9 |
17 |
| 1034 |
Milan |
 |
June 4 |
9 |
8 |
Total |
| 1037 |
Paris |
 |
Apr. 17 |
20 |
45 |
10 |
45 |
| 1039 |
Auxerre |
 |
Aug. 21 |
23 |
40 |
11 |
5 |
| 1042 |
Rome |
 |
Jan. 8 |
16 |
39 |
Total |
| 1044 |
Auxerre |
 |
Nov. 7 |
16 |
12 |
10 |
1 |
| 1044 |
Cluny |
 |
Nov. 21 |
22 |
12 |
11 |
-- |
| 1056 |
Nuremburg |
 |
April 2 |
12 |
9 |
Total |
| 1063 |
Rome |
 |
Nov. 8 |
12 |
16 |
Total |
| 1074 |
Augsburgh |
 |
Oct. 7 |
10 |
13 |
Total |
| 1080 |
Constantinople |
 |
Nov. 29 |
11 |
12 |
9 |
36 |
| 1082 |
London |
 |
May 14 |
10 |
32 |
10 |
2 |
| 1086 |
Constantinople |
 |
Feb. 16 |
4 |
7 |
Total |
| 1089 |
Naples |
 |
June 25 |
6 |
6 |
Total |
| 1093 |
Augsburgh |
 |
Sept. 22 |
22 |
35 |
10 |
12 |
| 1096 |
Gemblours |
 |
Feb. 10 |
16 |
4 |
Total |
| 1096 |
Augsburgh |
 |
Aug. 6 |
8 |
21 |
Total |
| 1098 |
Augsburgh |
 |
Dec. 25 |
1 |
25 |
10 |
12 |
| 1099 |
Naples |
 |
Nov. 30 |
4 |
58 |
Total |
| 1103 |
Rome |
 |
Sept. 17 |
10 |
18 |
Total |
| 1106 |
Erfurd |
 |
July 17 |
11 |
28 |
11 |
54 |
| 1107 |
Naples |
 |
Jan. 10 |
13 |
16 |
Total |
| 1109 |
Erfurd |
 |
May 31 |
1 |
30 |
10 |
20 |
| 1110 |
London |
 |
May 5 |
10 |
51 |
Total |
| 1113 |
Jerusalem |
 |
Mar. 18 |
19 |
0 |
9 |
12 |
| 1114 |
London |
 |
Aug. 17 |
15 |
5 |
Total |
| 1117 |
Trier |
 |
June 15 |
13 |
26 |
Total |
| 1117 |
Trier |
 |
Dec. 10 |
12 |
51 |
Total |
| 1711118 |
Naples |
 |
Nov. 29 |
15 |
46 |
4 |
11 |
| 1121 |
Trier |
 |
Sept. 27 |
16 |
47 |
Total |
| 1122 |
Prague |
 |
Mar. 24 |
11 |
20 |
3 |
49 |
| 1124 |
Erfurd |
 |
Feb. 1 |
6 |
43 |
8 |
39 |
| 1124 |
London |
 |
Aug. 10 |
23 |
29 |
9 |
58 |
| 1132 |
Erfurd |
 |
March 3 |
8 |
14 |
Total |
| 1133 |
Prague |
 |
Feb. 20 |
16 |
41 |
3 |
23 |
| 1135 |
London |
 |
Dec. 22 |
20 |
11 |
Total |
| 1142 |
Rome |
 |
Feb. 11 |
14 |
17 |
8 |
30 |
| 1143 |
Rome |
 |
Feb. 1 |
6 |
36 |
Total |
| 1147 |
Auranches |
 |
Oct. 25 |
22 |
38 |
7 |
20 |
| 1149 |
Bary |
 |
Mar. 25 |
13 |
54 |
5 |
29 |
| 1151 |
Eimbeck |
 |
Aug. 28 |
12 |
4 |
4 |
29 |
| 1153 |
Augsburgh |
 |
Jan. 26 |
0 |
42 |
11 |
-- |
| 1154 |
Paris |
 |
June 26 |
16 |
1 |
Total |
| 1154 |
Paris |
 |
Dec. 21 |
8 |
30 |
4 |
42 |
| 1155 |
Auranches |
 |
June 10 |
8 |
45 |
0 |
53 |
| 1160 |
Rome |
 |
Aug. 18 |
7 |
53 |
6 |
49 |
| 1161 |
Rome |
 |
Aug. 7 |
8 |
15 |
Total |
| 1162 |
Erfurd |
 |
Feb. 1 |
6 |
40 |
5 |
56 |
| 1162 |
Erfurd |
 |
July 27 |
12 |
30 |
4 |
11 |
| 1163 |
Mont Cassin. |
 |
July 3 |
7 |
40 |
2 |
0 |
| 1164 |
Milan |
 |
June 6 |
10 |
0 |
Total |
| 1168 |
London |
 |
Sept. 18 |
14 |
0 |
Total |
| 1172 |
Cologne |
 |
Jan. 11 |
13 |
31 |
Total |
| 1176 |
Auranches |
 |
April 25 |
7 |
2 |
8 |
6 |
| 1176 |
Auranches |
 |
Oct. 19 |
11 |
20 |
8 |
53 |
| 1178 |
Cologne |
 |
March 5 |
setting |
7 |
52 |
| 1178 |
Auranches |
 |
Aug. 29 |
13 |
52 |
5 |
31 |
| 1178 |
Cologne |
 |
Sept. 12 |
-- |
-- |
10 |
51 |
| 1179 |
Cologne |
 |
Aug. 18 |
14 |
28 |
Total |
| 1180 |
Auranches |
 |
Jan. 28 |
4 |
14 |
10 |
34 |
| 1181 |
Auranches |
 |
July 13 |
3 |
15 |
3 |
48 |
| 1181 |
Auranches |
 |
Dec. 22 |
8 |
58 |
4 |
40 |
| 1185 |
Rhemes |
 |
May 1 |
1 |
53 |
9 |
0 |
| 1186 |
Cologne |
 |
April 5 |
6 |
-- |
Total |
| 1186 |
Franckfort |
 |
April 20 |
7 |
19 |
4 |
0 |
| 1187 |
Paris |
 |
Mar. 25 |
16 |
17 |
8 |
42 |
| 1187 |
England |
 |
Sept. 3 |
21 |
54 |
8 |
6 |
| 1189 |
England |
 |
Feb. 2 |
10 |
-- |
9 |
-- |
| 1191 |
England |
 |
June 23 |
0 |
20 |
11 |
32 |
| 1192 |
France |
 |
Nov. 20 |
14 |
-- |
6 |
-- |
| 1193 |
France |
 |
Nov. 10 |
5 |
27 |
Total |
| 1194 |
London |
 |
April 22 |
2 |
15 |
6 |
49 |
| 1200 |
London |
 |
Jan. 2 |
17 |
2 |
4 |
35 |
| 1201 |
London |
 |
June 17 |
15 |
4 |
Total |
| 1204 |
England |
 |
April 15 |
12 |
39 |
Total |
| 1204 |
Saltzburg |
 |
Oct. 10 |
6 |
32 |
Total |
| 1207 |
Rhemes |
 |
Feb. 27 |
10 |
50 |
10 |
20 |
| 1208 |
Rhemes |
 |
Feb. 2 |
5 |
10 |
Total |
| 1211 |
Vienna |
 |
Nov. 21 |
13 |
57 |
Total |
| 1215 |
Cologne |
 |
Mar. 16 |
15 |
35 |
Total |
| 1216 |
Acre |
 |
Feb. 18 |
21 |
15 |
11 |
36 |
| 1216 |
Acre |
 |
March 5 |
9 |
38 |
7 |
4 |
| 1218 |
Damietta |
 |
July 9 |
9 |
46 |
11 |
31 |
| 1222 |
Rome |
 |
Oct. 22 |
14 |
28 |
Total |
| 1223 |
Colmar |
 |
April 16 |
8 |
13 |
11 |
0 |
| 1228 |
Naples |
 |
Dec. 27 |
9 |
55 |
9 |
19 |
| 1230 |
Naples |
 |
May 13 |
17 |
-- |
Total |
| 1230 |
London |
 |
Nov. 21 |
13 |
21 |
9 |
34 |
| 1232 |
Rhemes |
 |
Oct. 15 |
4 |
29 |
4 |
25 |
| 1245 |
Rhemes |
 |
July 24 |
17 |
47 |
6 |
-- |
| 1248 |
London |
 |
June 7 |
8 |
49 |
Total |
| 1255 |
London |
 |
July 20 |
9 |
47 |
Total |
| 1255 |
Constantinople |
 |
Dec. 30 |
2 |
52 |
Annul. |
| 1258 |
Augsburgh |
 |
May 18 |
11 |
17 |
Total |
| 1261 |
Vienna |
 |
Mar. 31 |
22 |
40 |
9 |
8 |
| 1262 |
Vienna |
 |
March 7 |
5 |
50 |
Total |
| 1262 |
Vienna |
 |
Aug. 30 |
14 |
39 |
Total |
| 1263 |
Vienna |
 |
Feb. 24 |
6 |
52 |
6 |
29 |
| 1263 |
Augsburgh |
 |
Aug. 5 |
3 |
24 |
11 |
17 |
| 1263 |
Vienna |
 |
Aug. 20 |
7 |
35 |
9 |
7 |
| 1265 |
Vienna |
 |
Dec. 23 |
16 |
25 |
Total |
| 1267 |
Constantinople |
 |
May 24 |
23 |
11 |
11 |
40 |
| 1270 |
Vienna |
 |
Mar. 22 |
18 |
47 |
10 |
40 |
| 1272 |
Vienna |
 |
Aug. 10 |
7 |
27 |
8 |
53 |
| 1274 |
Vienna |
 |
Jan. 23 |
10 |
39 |
9 |
25 |
| 1275 |
Lauben |
 |
Dec. 4 |
6 |
20 |
4 |
29 |
| 1276 |
Vienna |
 |
Nov. 22 |
15 |
-- |
Total |
| 1277 |
Vienna |
 |
May 18 |
-- |
-- |
Total |
| 1279 |
Franckfort |
 |
Apr. 12 |
6 |
55 |
10 |
6 |
| 1280 |
London |
 |
Mar. 17 |
12 |
12 |
Total |
| 1284 |
Reggio |
 |
Dec. 23 |
16 |
11 |
9 |
13 |
| 1290 |
Wittemburg |
 |
Sept. 4 |
19 |
37 |
10 |
30 |
| 1291 |
London |
 |
Feb. 14 |
10 |
2 |
Total |
| 1302 |
Constantinople |
 |
Jan. 14 |
10 |
25 |
Total |
| 1307 |
Ferrara |
 |
April 2 |
22 |
18 |
0 |
54 |
| 1309 |
London |
 |
Feb. 24 |
17 |
44 |
Total |
| 1309 |
Lucca |
 |
Aug. 21 |
10 |
32 |
Total |
| 1310 |
Wittemburg |
 |
Jan. 31 |
2 |
2 |
10 |
10 |
| 1310 |
Torcello |
 |
Feb. 14 |
4 |
8 |
10 |
20 |
| 1310 |
Torcello |
 |
Aug. 10 |
15 |
33 |
7 |
16 |
| 1312 |
Wittemburg |
 |
July 4 |
19 |
49 |
3 |
23 |
| 1312 |
Plaisance |
 |
Dec. 14 |
7 |
19 |
Total |
| 1313 |
Torcello |
 |
Dec. 3 |
8 |
58 |
9 |
34 |
| 1316 |
Modena |
 |
Oct. 1 |
14 |
55 |
Total |
| 1321 |
Wittemburg |
 |
June 25 |
18 |
1 |
11 |
17 |
| 1323 |
Florence |
 |
May 20 |
15 |
24 |
Total |
| 1324 |
Florence |
 |
May 9 |
6 |
3 |
Total |
| 1324 |
Wittemburg |
 |
Apr. 23 |
6 |
35 |
8 |
8 |
| 1327 |
Constantinople |
 |
Aug. 31 |
18 |
26 |
Total |
| 1328 |
Constantinople |
 |
Feb. 25 |
13 |
47 |
11 |
-- |
| 1330 |
Florence |
 |
June 30 |
15 |
10 |
7 |
34 |
| 1330 |
Constantinople |
 |
July 16 |
4 |
5 |
10 |
43 |
| 1330 |
Prague |
 |
Dec. 25 |
15 |
49 |
Total |
| 1331 |
Prague |
 |
Nov. 29 |
20 |
26 |
7 |
41 |
| 1721331 |
Prague |
 |
Dec. 14 |
18 |
-- |
11 |
-- |
| 1333 |
Wittemburg |
 |
May 14 |
3 |
-- |
10 |
18 |
| 1334 |
Cesena |
 |
Apr. 19 |
10 |
33 |
Total |
| 1341 |
Constantinople |
 |
Nov. 23 |
12 |
23 |
Total |
| 1341 |
Constantinople |
 |
Dec. 8 |
22 |
15 |
6 |
30 |
| 1342 |
Constantinople |
 |
May 20 |
14 |
27 |
Total |
| 1344 |
Alexandria |
 |
Oct. 6 |
18 |
40 |
8 |
55 |
| 1349 |
Wittemburg |
 |
June 30 |
12 |
20 |
Total |
| 1354 |
Wittemburg |
 |
Sept. 16 |
20 |
45 |
8 |
43 |
| 1356 |
Florence |
 |
Feb. 16 |
11 |
43 |
Total |
| 1361 |
Constantinople |
 |
May 4 |
22 |
15 |
8 |
54 |
| 1367 |
In China |
 |
Jan. 16 |
8 |
27 |
Total |
| 1389 |
Eugibin |
 |
Nov. 3 |
17 |
5 |
Total |
| 1396 |
Augsburg |
 |
Jan. 11 |
0 |
16 |
6 |
22 |
| 1396 |
Augsburg |
 |
June 21 |
11 |
10 |
Total |
| 1399 |
Forli |
 |
Oct. 29 |
0 |
43 |
9 |
-- |
| 1406 |
Constantinople |
 |
June 1 |
13 |
-- |
10 |
31 |
| 1406 |
Constantinople |
 |
June 15 |
18 |
1 |
11 |
38 |
| 1408 |
Forli |
 |
Oct. 18 |
21 |
47 |
9 |
32 |
| 1409 |
Constantinople |
 |
Apr. 15 |
3 |
1 |
10 |
48 |
| 1410 |
Vienna |
 |
Mar. 20 |
13 |
13 |
Total |
| 1415 |
Wittemburg |
 |
June 6 |
6 |
43 |
Total |
| 1419 |
Franckfort |
 |
Mar. 25 |
22 |
5 |
1 |
45 |
| 1421 |
Forli |
 |
Feb. 17 |
8 |
2 |
Total |
| 1422 |
Forli |
 |
Feb. 6 |
8 |
26 |
11 |
7 |
| 1424 |
Wittemburg |
 |
June 26 |
3 |
57 |
11 |
20 |
| 1431 |
Forli |
 |
Feb. 12 |
2 |
4 |
1 |
39 |
| 1433 |
Wittemburg |
 |
June 17 |
5 |
-- |
Total |
| 1438 |
Wittemburg |
 |
Sept. 18 |
20 |
59 |
8 |
7 |
| 1442 |
Rome |
 |
Dec. 17 |
3 |
56 |
Total |
| 1448 |
Tubing |
 |
Aug. 28 |
22 |
23 |
8 |
53 |
| 1450 |
Constantinople |
 |
July 24 |
7 |
19 |
Total |
| 1457 |
Vienna |
 |
Sept. 3 |
11 |
17 |
Total |
| 1460 |
Austria |
 |
July 3 |
7 |
31 |
5 |
23 |
| 1460 |
Austria |
 |
July 17 |
17 |
32 |
11 |
19 |
| 1460 |
Vienna |
 |
Dec. 27 |
13 |
30 |
Total |
| 1461 |
Vienna |
 |
June 22 |
11 |
50 |
Total |
| 1461 |
Rome |
 |
Dec. 17 |
-- |
-- |
Total |
| 1462 |
Viterbo |
 |
June 11 |
15 |
-- |
7 |
38 |
| 1462 |
Viterbo |
 |
Nov. 21 |
0 |
10 |
2 |
6 |
| 1464 |
Padua |
 |
Apr. 21 |
12 |
43 |
Total |
| 1465 |
Rome |
 |
Sept. 20 |
5 |
15 |
8 |
46 |
| 1465 |
Rome |
 |
Oct. 4 |
5 |
12 |
Total |
| 1469 |
Rome |
 |
Jan. 27 |
7 |
9 |
Total |
| 1485 |
Norimburg |
 |
Mar. 16 |
3 |
53 |
11 |
-- |
The following ECLIPSES are all taken from Ricciolus, except those marked
with an Asterisk, which are from L’Art de verifier les Dates.
| Aft. Chr. |
|
M. & D. |
Middle |
Digits eclipsed |
| H. |
M. |
| 1486 |
 |
Feb. 18 |
5 |
41 |
Total |
| 1486 |
 |
Mar. 5 |
17 |
43 |
9 |
0 |
| 1487 |
 |
Feb. 7 |
15 |
49 |
Total |
| 1487 |
 |
July 20 |
2 |
6 |
7 |
0 |
| 1488 |
 |
Jan. 28 |
6 |
-- |
* |
| 1488 |
 |
July 8 |
17 |
30 |
4 |
0 |
| 1489 |
 |
Dec. 7 |
17 |
41 |
Total |
| 1490 |
 |
May 19 |
Noon |
* |
| 1490 |
 |
June 2 |
10 |
6 |
Total |
| 1490 |
 |
Nov. 26 |
18 |
25 |
Total |
| 1491 |
 |
May 8 |
2 |
19 |
9 |
0 |
| 1491 |
 |
Nov. 15 |
18 |
-- |
* |
| 1492 |
 |
Apr. 26 |
7 |
-- |
* |
| 1492 |
 |
Oct. 20 |
23 |
-- |
* |
| 1493 |
 |
April 1 |
14 |
0 |
Total |
| 1493 |
 |
Oct. 10 |
2 |
40 |
8 |
0 |
| 1494 |
 |
Mar. 7 |
4 |
12 |
4 |
0 |
| 1494 |
 |
Mar. 21 |
14 |
38 |
Total |
| 1494 |
 |
Sept. 14 |
19 |
45 |
Total |
| 1495 |
 |
Mar. 10 |
16 |
-- |
* |
| 1495 |
 |
Aug. 19 |
17 |
-- |
* |
| 1496 |
 |
Jan. 29 |
14 |
-- |
* |
| 1497 |
 |
Jan. 18 |
6 |
38 |
Total |
| 1497 |
 |
July 29 |
3 |
2 |
3 |
0 |
| 1499 |
 |
June 22 |
17 |
-- |
* |
| 1499 |
 |
Aug. 23 |
18 |
-- |
* |
| 1499 |
 |
Nov. 17 |
10 |
-- |
* |
| 1500 |
 |
Mar. 27 |
In the Night |
| 1500 |
 |
Apr. 11 |
At Noon |
| 1500 |
 |
Oct. 5 |
14 |
2 |
10 |
0 |
| 1501 |
 |
May 2 |
17 |
49 |
Total |
| 1502 |
 |
Sept. 30 |
19 |
45 |
10 |
0 |
| 1502 |
 |
Oct. 15 |
12 |
20 |
2 |
0 |
| 1503 |
 |
Mar. 12 |
9 |
-- |
* |
| 1503 |
 |
Sept. 19 |
22 |
-- |
* |
| 1504 |
 |
Feb. 29 |
13 |
36 |
Total |
| 1504 |
 |
Mar. 16 |
3 |
-- |
* |
| 1505 |
 |
Aug. 14 |
8 |
18 |
Total |
| 1506 |
 |
Feb. 7 |
15 |
-- |
* |
| 1506 |
 |
July 20 |
3 |
11 |
2 |
0 |
| 1506 |
 |
Aug. 3 |
10 |
-- |
* |
| 1507 |
 |
Jan. 12 |
19 |
-- |
* |
| 1508 |
 |
Jan. 2 |
4 |
-- |
* |
| 1508 |
 |
May 29 |
6 |
-- |
* |
| 1508 |
 |
June 12 |
17 |
40 |
Total |
| 1509 |
 |
June 2 |
11 |
11 |
7 |
0 |
| 1509 |
 |
Nov. 11 |
22 |
-- |
* |
| 1510 |
 |
Oct. 16 |
19 |
-- |
* |
| 1511 |
 |
Oct. 6 |
11 |
50 |
Total |
| 1512 |
 |
Sept. 25 |
3 |
56 |
Total |
| 1513 |
 |
Mar. 7 |
0 |
30 |
6 |
0 |
| 1513 |
 |
Aug. 30 |
1 |
-- |
* |
| 1515 |
 |
Jan. 29 |
15 |
18 |
Total |
| 1516 |
 |
Jan. 19 |
6 |
0 |
Total |
| 1516 |
 |
July 13 |
11 |
37 |
Total |
| 1516 |
 |
Dec. 23 |
3 |
47 |
3 |
0 |
| 1517 |
 |
June 18 |
16 |
-- |
* |
| 1731517 |
 |
Nov. 27 |
19 |
-- |
* |
| 1518 |
 |
May 24 |
11 |
19 |
9 |
11 |
| 1518 |
 |
June 7 |
17 |
56 |
11 |
0 |
| 1519 |
 |
May 28 |
1 |
-- |
* |
| 1519 |
 |
Oct. 23 |
4 |
33 |
6 |
0 |
| 1519 |
 |
Nov. 6 |
6 |
24 |
Total |
| 1520 |
 |
May 2 |
7 |
-- |
* |
| 1520 |
 |
Oct. 11 |
5 |
22 |
3 |
| 1520 |
 |
Oct. 25 |
19 |
-- |
* |
| 1520 |
 |
Mar. 21 |
17 |
-- |
* |
| 1521 |
 |
April 6 |
19 |
-- |
* |
| 1521 |
 |
Sept. 30 |
3 |
-- |
* |
| 1522 |
 |
Sept. 5 |
12 |
17 |
Total |
| 1523 |
 |
Mar. 1 |
8 |
26 |
Total |
| 1523 |
 |
Aug. 25 |
15 |
24 |
Total |
| 1524 |
 |
Feb. 4 |
1 |
-- |
* |
| 1524 |
 |
Aug. 16 |
16 |
-- |
* |
| 1525 |
 |
Jan. 23 |
4 |
-- |
* |
| 1525 |
 |
July 4 |
10 |
10 |
Total |
| 1525 |
 |
Dec. 29 |
10 |
46 |
Total |
| 1526 |
 |
Dec. 18 |
10 |
30 |
Total |
| 1527 |
 |
Jan. 2 |
3 |
-- |
* |
| 1527 |
 |
Dec. 7 |
10 |
-- |
* |
| 1528 |
 |
May 17 |
20 |
-- |
* |
| 1529 |
 |
Oct. 16 |
20 |
23 |
11 |
55 |
| 1530 |
 |
Mar. 28 |
18 |
23 |
8 |
24 |
| 1530 |
 |
Oct. 6 |
12 |
11 |
Total |
| 1531 |
 |
April 1 |
7 |
-- |
* |
| 1532 |
 |
Aug. 30 |
0 |
49 |
3 |
35 |
| 1533 |
 |
Aug. 4 |
11 |
50 |
Total |
| 1533 |
 |
Aug. 19 |
17 |
-- |
* |
| 1534 |
 |
Jan. 14 |
1 |
42 |
5 |
45 |
| 1534 |
 |
Jan. 29 |
14 |
25 |
Total |
| 1535 |
 |
June 30 |
Noon |
* |
| 1535 |
 |
July 14 |
8 |
-- |
* |
| 1535 |
 |
Dec. 24 |
2 |
-- |
* |
| 1536 |
 |
June 18 |
2 |
2 |
8 |
0 |
| 1536 |
 |
Nov. 27 |
6 |
21 |
10 |
15 |
| 1537 |
 |
May 24 |
8 |
3 |
Total |
| 1537 |
 |
June 7 |
7 |
-- |
* |
| 1537 |
 |
Nov. 16 |
14 |
56 |
Total |
| 1538 |
 |
May 13 |
14 |
24 |
3 |
0 |
| 1538 |
 |
Nov. 6 |
5 |
31 |
3 |
37 |
| 1539 |
 |
Apr. 18 |
4 |
33 |
9 |
0 |
| 1540 |
 |
April 6 |
17 |
15 |
Total |
| 1541 |
 |
Mar. 11 |
16 |
34 |
Total |
| 1541 |
 |
Aug. 21 |
0 |
56 |
3 |
0 |
| 1542 |
 |
Mar. 1 |
8 |
46 |
1 |
38 |
| 1542 |
 |
Aug. 10 |
17 |
-- |
* |
| 1543 |
 |
July 15 |
16 |
-- |
* |
| 1544 |
 |
Jan. 9 |
18 |
13 |
Total |
| 1544 |
 |
Jan. 23 |
21 |
16 |
11 |
17 |
| 1544 |
 |
July 4 |
8 |
31 |
Total |
| 1544 |
 |
Dec. 28 |
18 |
27 |
Total |
| 1545 |
 |
June 8 |
20 |
48 |
3 |
45 |
| 1545 |
 |
Dec. 17 |
18 |
-- |
* |
| 1546 |
 |
May 30 |
5 |
-- |
* |
| 1546 |
 |
Nov. 22 |
23 |
-- |
* |
| 1547 |
 |
May 4 |
10 |
27 |
8 |
0 |
| 1547 |
 |
Oct. 28 |
4 |
56 |
11 |
34 |
| 1547 |
 |
Nov. 12 |
2 |
9 |
9 |
30 |
| 1548 |
 |
April 8 |
3 |
-- |
* |
| 1548 |
 |
Apr. 22 |
11 |
24 |
Total |
| 1549 |
 |
Apr. 11 |
15 |
19 |
2 |
0 |
| 1549 |
 |
Oct. 6 |
6 |
-- |
* |
| 1550 |
 |
Mar. 16 |
20 |
-- |
* |
| 1551 |
 |
Feb. 20 |
8 |
21 |
Total |
| 1551 |
 |
Aug. 31 |
2 |
0 |
1 |
52 |
| 1553 |
 |
Jan. 12 |
22 |
54 |
1 |
22 |
| 1553 |
 |
July 10 |
7 |
-- |
* |
| 1553 |
 |
July 24 |
16 |
0 |
0 |
31 |
| 1554 |
 |
June 29 |
6 |
-- |
* |
| 1554 |
 |
Dec. 8 |
13 |
7 |
10 |
12 |
| 1555 |
 |
June 4 |
15 |
0 |
Total |
| 1555 |
 |
Nov. 13 |
19 |
-- |
* |
| 1556 |
 |
Nov. 1 |
18 |
0 |
9 |
41 |
| 1556 |
 |
Nov. 16 |
12 |
44 |
6 |
55 |
| 1557 |
 |
Oct. 20 |
20 |
-- |
* |
| 1558 |
 |
April 2 |
11 |
0 |
9 |
50 |
| 1558 |
 |
Apr. 18 |
1 |
-- |
* |
| 1559 |
 |
Apr. 16 |
4 |
50 |
Total |
| 1560 |
 |
Mar. 11 |
15 |
40 |
4 |
13 |
| 1560 |
 |
Aug. 21 |
1 |
0 |
6 |
22 |
| 1560 |
 |
Sept. 4 |
7 |
-- |
* |
| 1561 |
 |
Feb. 13 |
19 |
-- |
* |
| 1562 |
 |
Feb. 3 |
5 |
-- |
* |
| 1562 |
 |
July 15 |
15 |
50 |
Total |
| 1563 |
 |
Jan. 22 |
19 |
-- |
* |
| 1563 |
 |
June 20 |
4 |
50 |
8 |
38 |
| 1563 |
 |
July 5 |
8 |
4 |
11 |
34 |
| 1565 |
 |
Mar. 7 |
12 |
53 |
------ |
| 1565 |
 |
May 14 |
16 |
-- |
* |
| 1565 |
 |
Nov. 7 |
12 |
46 |
11 |
46 |
| 1566 |
 |
Oct. 28 |
5 |
38 |
Total |
| 1567 |
 |
April 8 |
23 |
4 |
9 |
34 |
| 1567 |
 |
Oct. 17 |
13 |
43 |
2 |
40 |
| 1568 |
 |
Mar. 28 |
5 |
-- |
* |
| 1569 |
 |
Mar. 2 |
15 |
18 |
Total |
| 1570 |
 |
Feb. 20 |
5 |
46 |
Total |
| 1570 |
 |
Aug. 15 |
9 |
17 |
Total |
| 1571 |
 |
Jan. 25 |
4 |
-- |
* |
| 1572 |
 |
Jan. 14 |
19 |
-- |
* |
| 1572 |
 |
June 25 |
9 |
0 |
5 |
26 |
| 1573 |
 |
June 28 |
18 |
-- |
* |
| 1573 |
 |
Nov. 24 |
4 |
-- |
* |
| 1573 |
 |
Dec. 8 |
6 |
51 |
Total |
| 1574 |
 |
Nov. 13 |
3 |
50 |
5 |
21 |
| 1575 |
 |
May 19 |
8 |
-- |
* |
| 1575 |
 |
Nov. 2 |
5 |
-- |
* |
| 1576 |
 |
Oct. 7 |
9 |
45 |
------ |
| 1577 |
 |
April 2 |
8 |
33 |
Total |
| 1577 |
 |
Sept. 26 |
13 |
4 |
Total |
| 1578 |
 |
Sept. 15 |
13 |
4 |
2 |
20 |
| 1579 |
 |
Feb. 15 |
5 |
41 |
8 |
36 |
| 1579 |
 |
Aug. 20 |
19 |
0 |
* |
| 1580 |
 |
Jan. 31 |
10 |
7 |
Total |
| 1581 |
 |
Jan. 19 |
9 |
22 |
Total |
| 1581 |
 |
July 15 |
17 |
51 |
Total |
| 1582 |
 |
Jan. 8 |
10 |
29 |
0 |
53 |
| 1582 |
 |
June 19 |
17 |
5 |
7 |
5 |
| 1583 |
 |
Nov. 28 |
21 |
51 |
Total |
| 1584 |
 |
May 9 |
18 |
20 |
3 |
36 |
| 1584 |
 |
Nov. 17 |
14 |
15 |
Total |
| 1585 |
 |
Apr. 29 |
7 |
53 |
11 |
7 |
| 1585 |
 |
May 13 |
5 |
2 |
6 |
54 |
| 1586 |
 |
Sept. 27 |
8 |
-- |
* |
| 1586 |
 |
Oct. 12 |
Noon |
* |
| 1587 |
 |
Sept. 16 |
9 |
28 |
10 |
2 |
| 1588 |
 |
Feb. 26 |
1 |
23 |
1 |
3 |
| 1588 |
 |
Mar. 12 |
14 |
14 |
Total |
| 1588 |
 |
Sept. 4 |
17 |
30 |
Total |
| 1589 |
 |
Aug. 10 |
18 |
-- |
* |
| 1589 |
 |
Aug. 25 |
8 |
1 |
3 |
54 |
| 1590 |
 |
Feb. 4 |
5 |
-- |
* |
| 1590 |
 |
July 16 |
17 |
4 |
3 |
54 |
| 1590 |
 |
July 30 |
19 |
57 |
10 |
27 |
| 1591 |
 |
Jan. 9 |
6 |
21 |
9 |
40 |
| 1591 |
 |
July 6 |
5 |
8 |
Total |
| 1591 |
 |
July 20 |
4 |
2 |
1 |
0 |
| 1591 |
 |
Dec. 29 |
16 |
11 |
Total |
| 1592 |
 |
June 24 |
10 |
13 |
8 |
58 |
| 1592 |
 |
Dec. 18 |
7 |
24 |
5 |
54 |
| 1593 |
 |
May 30 |
2 |
30 |
2 |
38 |
| 1594 |
 |
May 19 |
14 |
58 |
10 |
23 |
| 1594 |
 |
Oct. 28 |
19 |
15 |
9 |
40 |
| 1595 |
 |
April 9 |
Ter. de Fuego |
| 1595 |
 |
Apr. 24 |
4 |
12 |
Total |
| 1595 |
 |
May 7 |
22 |
-- |
* |
| 1595 |
 |
Oct. 3 |
2 |
4 |
5 |
18 |
| 1595 |
 |
Oct. 18 |
20 |
47 |
Total |
| 1596 |
 |
Mar. 28 |
In Chili |
| 1596 |
 |
Apr. 12 |
8 |
52 |
6 |
4 |
| 1596 |
 |
Sept. 21 |
In China |
| 1596 |
 |
Oct. 6 |
21 |
15 |
3 |
33 |
| 1597 |
 |
Mar. 17 |
St. Pet. Isle |
| 1597 |
 |
Sept. 11 |
Picora |
9 |
49 |
| 1598 |
 |
Feb. 20 |
18 |
12 |
10 |
55 |
| 1598 |
 |
Mar. 6 |
22 |
12 |
11 |
57 |
| 1598 |
 |
Aug. 16 |
8 |
15 |
Total |
| 1741598 |
 |
Aug. 31 |
Magel. |
8 |
34 |
| 1599 |
 |
Feb. 10 |
17 |
21 |
Total |
| 1599 |
 |
July 22 |
4 |
31 |
4 |
18 |
| 1599 |
 |
Aug. 6 |
------ |
Total |
| 1600 |
 |
Jan. 15 |
Java |
11 |
48 |
| 1600 |
 |
Jan. 30 |
6 |
40 |
2 |
58 |
| 1600 |
 |
July 10 |
2 |
10 |
5 |
39 |
| 1601 |
 |
Jan. 4 |
Ethiop. |
9 |
40 |
| 1601 |
 |
June 15 |
6 |
18 |
4 |
52 |
| 1601 |
 |
June 29 |
China |
4 |
29 |
| 1601 |
 |
Dec. 9 |
7 |
6 |
10 |
53 |
| 1601 |
 |
Dec. 24 |
2 |
46 |
9 |
52 |
| 1602 |
 |
May 21 |
Greenl. |
2 |
41 |
| 1602 |
 |
June 4 |
7 |
18 |
Total |
| 1602 |
 |
June 19 |
N. Gra. |
5 |
43 |
| 1602 |
 |
Nov. 13 |
Magel. |
3 |
-- |
| 1602 |
 |
Nov. 28 |
10 |
2 |
Total |
| 1603 |
 |
May 10 |
China |
11 |
21 |
| 1603 |
 |
May 24 |
11 |
41 |
7 |
59 |
| 1603 |
 |
Nov. 3 |
Rom. I. |
11 |
17 |
| 1603 |
 |
Nov. 18 |
7 |
31 |
3 |
26 |
| 1604 |
 |
Apr. 29 |
Arabia |
9 |
32 |
| 1604 |
 |
Oct. 22 |
Peru |
6 |
49 |
| 1605 |
 |
April 3 |
9 |
19 |
11 |
49 |
| 1605 |
 |
Apr. 18 |
Madag. |
5 |
31 |
| 1605 |
 |
Sept. 27 |
4 |
27 |
9 |
26 |
| 1605 |
 |
Oct. 12 |
2 |
32 |
9 |
24 |
| 1606 |
 |
Mar. 8 |
Mexico |
6 |
0 |
| 1606 |
 |
Mar. 24 |
11 |
17 |
Total |
| 1606 |
 |
Sept. 2 |
Magel. |
6 |
40 |
| 1606 |
 |
Sept. 16 |
15 |
6 |
Total |
| 1607 |
 |
Feb. 25 |
21 |
48 |
1 |
13 |
| 1607 |
 |
Mar. 13 |
6 |
36 |
1 |
22 |
| 1607 |
 |
Sept. 5 |
15 |
40 |
4 |
7 |
| 1608 |
 |
Feb. 15 |
at the Antipo. |
| 1608 |
 |
July 27 |
0 |
30 |
1 |
53 |
| 1608 |
 |
Aug. 9 |
4 |
39 |
0 |
40 |
| 1609 |
 |
Jan. 19 |
15 |
21 |
10 |
32 |
| 1609 |
 |
Feb. 4 |
Fuego |
5 |
22 |
| 1609 |
 |
July 16 |
12 |
8 |
Total |
| 1609 |
 |
July 30 |
Canada |
4 |
10 |
| 1609 |
 |
Dec. 26 |
19 |
-- |
5 |
50 |
| 1610 |
 |
Jan. 9 |
1 |
31 |
Total |
| 1610 |
 |
June 20 |
Java |
10 |
46 |
| 1610 |
 |
July 5 |
16 |
58 |
11 |
13 |
| 1610 |
 |
Dec. 15 |
Cyprus |
4 |
50 |
| 1610 |
 |
Dec. 29 |
16 |
47 |
4 |
23 |
| 1611 |
 |
June 10 |
Califor. |
11 |
30 |
| 1612 |
 |
May 14 |
10 |
38 |
7 |
22 |
| 1612 |
 |
May 29 |
23 |
38 |
7 |
14 |
| 1612 |
 |
Nov. 8 |
3 |
22 |
9 |
49 |
| 1612 |
 |
Nov. 22 |
Magel. |
9 |
0 |
| 1613 |
 |
Apr. 20 |
Magellanica |
| 1613 |
 |
May 4 |
0 |
35 |
Total |
| 1613 |
 |
May 19 |
East Tartary |
| 1613 |
 |
Oct. 13 |
South Amer. |
| 1613 |
 |
Oct. 28 |
4 |
19 |
Total |
| 1614 |
 |
April 8 |
N. Gui. |
8 |
44 |
| 1614 |
 |
Apr. 23 |
17 |
36 |
5 |
25 |
| 1614 |
 |
Oct. 3 |
0 |
57 |
5 |
2 |
| 1614 |
 |
Oct. 17 |
4 |
38 |
4 |
56 |
| 1615 |
 |
Mar. 29 |
Goa |
10 |
38 |
| 1615 |
 |
Sept. 22 |
Salom Isle |
| 1616 |
 |
Mar. 3 |
1 |
58 |
Total |
| 1616 |
 |
Mar. 17 |
Mexico |
6 |
47 |
| 1616 |
 |
Aug. 26 |
15 |
33 |
Total |
| 1616 |
 |
Sept. 10 |
Magel. |
10 |
33 |
| 1617 |
 |
Feb. 5 |
Magellanica |
| 1617 |
 |
Feb. 20 |
1 |
49 |
Total |
| 1617 |
 |
Mar 6 |
22 |
-- |
* |
| 1617 |
 |
Aug. 1 |
Biarmia |
| 1617 |
 |
Aug. 16 |
8 |
22 |
Total |
| 1618 |
 |
Jan. 26 |
Magellanica |
| 1618 |
 |
Feb. 9 |
3 |
29 |
2 |
57 |
| 1618 |
 |
July 21 |
Mexico |
------ |
| 1619 |
 |
Jan. 15 |
California |
| 1619 |
 |
June 26 |
12 |
40 |
3 |
10 |
| 1619 |
 |
July 11 |
Africa |
11 |
39 |
| 1619 |
 |
Dec. 20 |
15 |
53 |
10 |
47 |
| 1620 |
 |
May 31 |
Arctic Circle |
| 1620 |
 |
June 14 |
13 |
47 |
Total |
| 1620 |
 |
June 29 |
Magel. |
7 |
20 |
| 1620 |
 |
Dec. 9 |
6 |
39 |
Total |
| 1620 |
 |
Dec. 23 |
Magellanica |
| 1621 |
 |
May 20 |
14 |
54 |
10 |
44 |
| 1621 |
 |
June 3 |
19 |
42 |
9 |
53 |
| 1621 |
 |
Nov. 13 |
Magellanica |
| 1621 |
 |
Nov. 28 |
15 |
43 |
3 |
38 |
| 1622 |
 |
May 10 |
C. Verd |
11 |
52 |
| 1622 |
 |
Nov. 2 |
Malacca In. |
| 1623 |
 |
Apr. 14 |
7 |
19 |
10 |
54 |
| 1623 |
 |
Apr. 29 |
------ |
------ |
| 1623 |
 |
Oct. 8 |
0 |
22 |
8 |
35 |
| 1623 |
 |
Oct. 23 |
Califor. |
10 |
46 |
| 1624 |
 |
May 18 |
N. Zem. |
6 |
0 |
| 1624 |
 |
Apr. 3 |
7 |
9 |
Total |
| 1624 |
 |
Apr. 17 |
Antar. Circle |
| 1624 |
 |
Sept. 12 |
Magellanica |
| 1624 |
 |
Sept. 26 |
8 |
55 |
Total |
| 1625 |
 |
Mar. 8 |
Florida |
| 1625 |
 |
Mar. 23 |
14 |
11 |
2 |
11 |
| 1625 |
 |
Sept. 1 |
St. Peter’s Isl. |
| 1625 |
 |
Sept. 16 |
11 |
41 |
5 |
6 |
| 1626 |
 |
Feb. 25 |
Madag. |
8 |
27 |
| 1626 |
 |
Aug. 7 |
7 |
48 |
0 |
25 |
| 1626 |
 |
Aug. 21 |
In | Mexico |
| 1627 |
 |
Jan. 30 |
11 |
38 |
10 |
21 |
| 1627 |
 |
Feb. 15 |
Magellanica |
| 1627 |
 |
July 27 |
9 |
4 |
Total |
| 1627 |
 |
Aug. 11 |
Tenduc |
10 |
0 |
| 1628 |
 |
Jan. 6 |
Tenduc |
5 |
40 |
| 1628 |
 |
Jan. 20 |
10 |
11 |
Total |
| 1628 |
 |
July 1 |
C Good Hope |
| 1628 |
 |
July 16 |
11 |
26 |
Total |
| 1628 |
 |
Dec. 25 |
In England |
| 1629 |
 |
Jan. 9 |
1 |
36 |
4 |
27 |
| 1629 |
 |
June 21 |
Ganges |
11 |
25 |
| 1629 |
 |
Dec. 14 |
Peru |
10 |
14 |
| 1630 |
 |
May 25 |
17 |
56 |
6 |
0 |
| 1630 |
 |
June 10 |
7 |
47 |
9 |
8 |
| 1630 |
 |
Nov. 19 |
11 |
24 |
9 |
27 |
| 1630 |
 |
Dec. 3 |
N. Gui. |
10 |
10 |
| 1631 |
 |
Apr. 30 |
Antar. Circle |
| 1631 |
 |
May 15 |
8 |
15 |
Total |
| 1631 |
 |
Oct. 24 |
C Good Hope |
| 1631 |
 |
Nov. 8 |
12 |
0 |
Total |
| 1632 |
 |
Apr. 19 |
C Good Hope |
| 1632 |
 |
May 4 |
1 |
24 |
6 |
35 |
| 1632 |
 |
Oct. 13 |
Mexico |
8 |
37 |
| 1632 |
 |
Oct. 27 |
12 |
23 |
5 |
31 |
| 1633 |
 |
April 8 |
5 |
14 |
4 |
30 |
| 1633 |
 |
Oct. 3 |
Maldiv. |
Total |
| 1634 |
 |
Mar. 14 |
9 |
35 |
11 |
18 |
| 1634 |
 |
Mar. 28 |
Japan |
10 |
19 |
| 1634 |
 |
Sept. 7 |
5 |
0 |
Total |
| 1634 |
 |
Sept. 22 |
C.G.H. |
9 |
54 |
| 1635 |
 |
Feb. 17 |
Antar. Circle |
| 1635 |
 |
Mar. 3 |
9 |
26 |
Total |
| 1635 |
 |
Mar. 18 |
Mexico |
0 |
16 |
| 1635 |
 |
Aug. 12 |
Iceland |
5 |
0 |
| 1635 |
 |
Aug. 27 |
16 |
4 |
Total |
| 1636 |
 |
Feb. 6 |
In Peru |
| 1636 |
 |
Feb. 20 |
11 |
34 |
3 |
23 |
| 1636 |
 |
Aug. 1 |
Tartary |
11 |
20 |
| 1636 |
 |
Aug. 16 |
4 |
34 |
1 |
25 |
| 1637 |
 |
Jan. 26 |
Camboya |
|
| 1637 |
 |
July 21 |
Jucutan |
|
| 1637 |
 |
Dec. 31 |
0 |
44 |
10 |
45 |
| 1638 |
 |
Jan. 14 |
Persia |
9 |
45 |
| 1638 |
 |
June 25 |
20 |
17 |
Total |
| 1638 |
 |
July 11 |
Magellan |
9 |
5 |
| 1638 |
 |
Dec. 5 |
Magellan |
2 |
10 |
| 1638 |
 |
Dec. 20 |
15 |
16 |
Total |
| 1639 |
 |
Jan. 4 |
Tartary |
0 |
30 |
| 1639 |
 |
June 1 |
5 |
59 |
10 |
40 |
| 1639 |
 |
June 15 |
2 |
41 |
11 |
9 |
| 1639 |
 |
Nov. 24 |
Magel. |
11 |
0 |
| 1639 |
 |
Dec. 9 |
11 |
57 |
3 |
46 |
| 1751640 |
 |
May 20 |
N. Spa. |
10 |
30 |
| 1640 |
 |
Nov. 13 |
Peru |
10 |
36 |
| 1641 |
 |
Apr. 25 |
1 |
2 |
9 |
49 |
| 1641 |
 |
May 9 |
Peru |
10 |
16 |
| 1641 |
 |
Oct. 18 |
8 |
19 |
6 |
31 |
| 1641 |
 |
Nov. 2 |
18 |
46 |
------ |
| 1642 |
 |
Mar. 30 |
Estotl. |
4 |
0 |
| 1642 |
 |
Apr. 14 |
14 |
31 |
Total |
| 1642 |
 |
Sept. 25 |
Magellan |
| 1642 |
 |
Oct. 7 |
16 |
45 |
Total |
| 1643 |
 |
Mar. 19 |
13 |
53 |
------ |
| 1643 |
 |
April 3 |
21 |
10 |
3 |
9 |
| 1643 |
 |
Sept. 12 |
17 |
0 |
------ |
| 1643 |
 |
Sept. 27 |
7 |
38 |
6 |
0 |
| 1644 |
 |
Mar. 8 |
6 |
20 |
------ |
| 1644 |
 |
Aug. 31 |
18 |
10 |
------ |
| 1645 |
 |
Feb. 10 |
7 |
45 |
8 |
52 |
| 1645 |
 |
Feb. 26 |
Rom. I. |
10 |
46 |
| 1645 |
 |
Aug. 7 |
2 |
4 |
Total |
| 1645 |
 |
Aug. 21 |
0 |
35 |
4 |
40 |
| 1646 |
 |
Jan. 16 |
Str. of Anian. |
| 1646 |
 |
Jan. 30 |
18 |
11 |
Total |
| 1646 |
 |
July 12 |
6 |
57 |
------ |
| 1646 |
 |
July 27 |
6 |
2 |
Total |
| 1647 |
 |
Jan. 5 |
12 |
10 |
------ |
| 1647 |
 |
Jan. 20 |
9 |
43 |
4 |
47 |
| 1647 |
 |
July 2 |
0 |
9 |
------ |
| 1647 |
 |
Dec. 25 |
13 |
38 |
------ |
| 1648 |
 |
June 5 |
0 |
55 |
4 |
28 |
| 1648 |
 |
June 20 |
13 |
28 |
------ |
| 1648 |
 |
Nov. 29 |
19 |
17 |
7 |
40 |
| 1648 |
 |
Dec. 13 |
21 |
48 |
------ |
| 1649 |
 |
May 25 |
15 |
20 |
Total |
| 1649 |
 |
June 9 |
Arct. C. |
4 |
0 |
| 1649 |
 |
Nov. 4 |
2 |
10 |
5 |
19 |
| 1649 |
 |
Nov. 18 |
19 |
56 |
Total |
| 1650 |
 |
Apr. 30 |
5 |
54 |
------ |
| 1650 |
 |
May 15 |
8 |
37 |
7 |
57 |
| 1650 |
 |
Oct. 24 |
17 |
17 |
------ |
| 1650 |
 |
Nov. 7 |
20 |
29 |
5 |
3 |
| 1651 |
 |
Apr. 19 |
Tuber. |
------ |
| 1651 |
 |
Oct. 14 |
2 |
15 |
------ |
| 1652 |
 |
Mar. 24 |
16 |
52 |
8 |
50 |
| 1652 |
 |
April 7 |
22 |
40 |
9 |
59 |
| 1652 |
 |
Sept. 17 |
7 |
27 |
9 |
49 |
| 1652 |
 |
Oct. 2 |
5 |
2 |
------ |
| 1653 |
 |
Feb. 27 |
-- |
-- |
------ |
| 1653 |
 |
Mar. 13 |
17 |
9 |
Total |
| 1653 |
 |
Aug. 22 |
-- |
-- |
------ |
| 1653 |
 |
Sept. 6 |
23 |
45 |
Total |
| 1654 |
 |
Feb. 16 |
9 |
10 |
------ |
| 1654 |
 |
Mar. 2 |
19 |
25 |
3 |
14 |
| 1654 |
 |
Aug. 11 |
22 |
24 |
2 |
28 |
| 1654 |
 |
Aug. 27 |
11 |
49 |
1 |
53 |
| 1655 |
 |
Feb. 6 |
2 |
37 |
4 |
20 |
| 1655 |
 |
Aug. 1 |
14 |
19 |
------ |
| 1655 |
 |
Aug. 16 |
16 |
-- |
* |
| 1656 |
 |
Jan. 11 |
9 |
4 |
10 |
0 |
| 1656 |
 |
July 6 |
3 |
17 |
Total |
| 1656 |
 |
July 21 |
11 |
48 |
------ |
| 1656 |
 |
Dec. 30 |
23 |
30 |
Total |
| 1657 |
 |
June 11 |
11 |
20 |
------ |
| 1657 |
 |
June 25 |
9 |
35 |
Total |
| 1657 |
 |
Dec. 4 |
20 |
0 |
------ |
| 1657 |
 |
Dec. 20 |
7 |
47 |
3 |
9 |
| 1658 |
 |
May 31 |
16 |
0 |
------ |
| 1658 |
 |
June 14 |
22 |
58 |
------ |
| 1658 |
 |
Nov. 9 |
13 |
56 |
0 |
10 |
| 1658 |
 |
Nov. 24 |
11 |
36 |
------ |
| 1659 |
 |
May 6 |
8 |
34 |
8 |
5 |
| 1659 |
 |
May 20 |
17 |
4 |
------ |
| 1659 |
 |
Oct. 29 |
16 |
16 |
5 |
52 |
| 1659 |
 |
Nov. 14 |
4 |
25 |
9 |
51 |
| 1660 |
 |
Apr. 24 |
21 |
58 |
Total |
| 1660 |
 |
Oct. 3 |
22 |
34 |
------ |
| 1660 |
 |
Oct. 18 |
0 |
32 |
Total |
| 1660 |
 |
Nov. 2 |
13 |
48 |
------ |
| 1661 |
 |
Mar. 29 |
22 |
32 |
------ |
| 1661 |
 |
Apr. 14 |
4 |
28 |
------ |
| 1661 |
 |
Sept. 23 |
1 |
36 |
11 |
19 |
| 1661 |
 |
Oct. 7 |
14 |
51 |
7 |
4 |
| 1662 |
 |
Mar. 19 |
15 |
8 |
------ |
| 1662 |
 |
Apr. 12 |
1 |
8 |
------ |
| 1663 |
 |
Feb. 21 |
16 |
11 |
3 |
14 |
| 1663 |
 |
Mar. 9 |
5 |
47 |
------ |
| 1663 |
 |
Aug. 18 |
8 |
45 |
Total |
| 1663 |
 |
Sept. 1 |
8 |
8 |
------ |
| 1664 |
 |
Jan. 27 |
20 |
40 |
------ |
| 1664 |
 |
Feb. 11 |
3 |
16 |
------ |
| 1664 |
 |
July 22 |
14 |
48 |
------ |
| 1664 |
 |
Aug. 20 |
22 |
10 |
------ |
| 1665 |
 |
Jan. 30 |
18 |
47 |
4 |
34 |
| 1665 |
 |
July 12 |
7 |
48 |
------ |
| 1665 |
 |
July 26 |
13 |
31 |
0 |
10 |
| 1666 |
 |
Jan. 4 |
21 |
33 |
------ |
| 1666 |
 |
July 1 |
19 |
0 |
11 |
10 |
| 1667 |
 |
June 5 |
Noon |
------ |
| 1667 |
 |
July 21 |
2 |
32 |
------ |
| 1667 |
 |
Nov. 15 |
11 |
30 |
------ |
| 1668 |
 |
May 10 |
Setting |
------ |
| 1668 |
 |
May 25 |
16 |
26 |
9 |
32 |
| 1668 |
 |
Nov. 4 |
2 |
53 |
9 |
50 |
| 1668 |
 |
Nov. 18 |
3 |
54 |
6 |
45 |
| 1669 |
 |
Apr. 29 |
18 |
18 |
------ |
| 1669 |
 |
Oct. 24 |
10 |
13 |
------ |
| 1670 |
 |
Apr. 19 |
7 |
0 |
------ |
| 1670 |
 |
Sept. 10 |
19 |
0 |
------ |
| 1670 |
 |
Sept. 28 |
15 |
43 |
9 |
7 |
| 1670 |
 |
Oct. 13 |
12 |
5 |
------ |
| 1671 |
 |
April 8 |
23 |
29 |
------ |
| 1671 |
 |
Sept. 2 |
21 |
25 |
------ |
| 1671 |
 |
Sept. 18 |
7 |
44 |
Total |
| 1672 |
 |
Feb. 28 |
3 |
38 |
------ |
| 1672 |
 |
Mar. 13 |
3 |
17 |
------ |
| 1672 |
 |
Aug. 22 |
6 |
43 |
------ |
| 1672 |
 |
Sept. 6 |
18 |
54 |
------ |
| 1673 |
 |
Feb. 16 |
7 |
29 |
------ |
| 1673 |
 |
Aug. 11 |
21 |
44 |
------ |
| 1674 |
 |
Jan. 21 |
18 |
22 |
11 |
21 |
| 1674 |
 |
Feb. 5 |
9 |
4 |
------ |
| 1674 |
 |
July 17 |
9 |
40 |
Total |
| 1675 |
 |
Jan. 11 |
8 |
29 |
Total |
| 1675 |
 |
Jan. 25 |
10 |
36 |
------ |
| 1675 |
 |
July 6 |
16 |
31 |
Total |
| 1676 |
 |
June 10 |
21 |
26 |
4 |
34 |
| 1676 |
 |
June 25 |
6 |
26 |
------ |
| 1676 |
 |
Dec. 4 |
20 |
52 |
------ |
| 1677 |
 |
Nov. 24 |
12 |
5 |
------ |
| 1677 |
 |
May 16 |
16 |
25 |
8 |
15 |
| 1678 |
 |
May 6 |
5 |
30 |
------ |
| 1678 |
 |
Oct. 29 |
9 |
17 |
Total |
| 1679 |
 |
Apr. 10 |
21 |
0 |
------ |
| 1679 |
 |
Apr. 25 |
11 |
53 |
5 |
47 |
| 1680 |
 |
Mar. 29 |
23 |
22 |
------ |
| 1680 |
 |
Sept. 22 |
7 |
57 |
------ |
| 1681 |
 |
Mar. 4 |
Noon |
------ |
| 1681 |
 |
Mar. 10 |
13 |
43 |
------ |
| 1681 |
 |
Aug. 28 |
15 |
22 |
10 |
35 |
| 1681 |
 |
Sept. 11 |
15 |
43 |
------ |
| 1682 |
 |
Feb. 21 |
12 |
28 |
Total |
| 1682 |
 |
Aug. 17 |
18 |
56 |
Total |
| 1683 |
 |
Jan. 27 |
1 |
35 |
10 |
30 |
| 1683 |
 |
Feb. 9 |
3 |
39 |
------ |
| 1683 |
 |
Aug. 6 |
20 |
36 |
------ |
| 1684 |
 |
Jan. 16 |
6 |
34 |
------ |
| 1684 |
 |
June 26 |
15 |
18 |
1 |
35 |
| 1684 |
 |
July 12 |
3 |
26 |
Total |
| 1684 |
 |
Dec. 21 |
11 |
18 |
9 |
45 |
| 1685 |
 |
Jan. 4 |
16 |
0 |
------ |
| 1685 |
 |
June 16 |
6 |
0 |
------ |
| 1685 |
 |
Dec. 10 |
11 |
26 |
Total |
| 1686 |
 |
May 21 |
17 |
9 |
------ |
| 1686 |
 |
June 6 |
Noon |
------ |
| 1686 |
 |
Nov. 29 |
12 |
22 |
Total |
| 1687 |
 |
May 11 |
1 |
-- |
* |
| 1687 |
 |
May 26 |
14 |
-- |
* |
| 1687 |
 |
Apr. 15 |
7 |
4 |
6 |
49 |
| 1688 |
 |
Apr. 29 |
16 |
27 |
------ |
| 1688 |
 |
Oct. 9 |
Noon |
------ |
| 1761688 |
 |
Oct. 25 |
19 |
40 |
------ |
| 1689 |
 |
April 4 |
7 |
42 |
Total |
| 1689 |
 |
Sept. 28 |
15 |
46 |
Total |
| 1690 |
 |
Mar. 10 |
-- |
-- |
------ |
| 1690 |
 |
Mar. 24 |
11 |
14 |
5 |
43 |
| 1690 |
 |
Sept. 3 |
-- |
-- |
------ |
| 1690 |
 |
Sept. 18 |
2 |
42 |
------ |
| 1691 |
 |
Feb. 27 |
17 |
30 |
------ |
| 1691 |
 |
Aug. 23 |
5 |
51 |
------ |
| 1692 |
 |
Feb. 2 |
3 |
20 |
------ |
| 1692 |
 |
Feb. 16 |
17 |
31 |
------ |
| 1692 |
 |
July 27 |
16 |
9 |
Total |
| 1693 |
 |
Jan. 21 |
17 |
25 |
Total |
| 1693 |
 |
July 17 |
Noon |
------ |
| 1694 |
 |
Jan. 11 |
Noon |
------ |
| 1694 |
 |
June 22 |
4 |
22 |
6 |
22 |
| 1694 |
 |
July 6 |
13 |
51 |
0 |
47 |
| 1695 |
 |
May 11 |
6 |
3 |
------ |
| 1695 |
 |
May 28 |
Noon |
------ |
| 1695 |
 |
Nov. 20 |
8 |
0 |
6 |
55 |
| 1695 |
 |
Dec. 5 |
17 |
7 |
------ |
| 1696 |
 |
May 16 |
12 |
45 |
Total |
| 1696 |
 |
May 30 |
12 |
56 |
------ |
| 1696 |
 |
Nov. 8 |
17 |
30 |
Total |
| 1696 |
 |
Nov. 23 |
17 |
32 |
------ |
| 1697 |
 |
Apr. 20 |
14 |
32 |
------ |
| 1697 |
 |
May 5 |
18 |
27 |
------ |
| 1697 |
 |
Oct. 29 |
8 |
44 |
8 |
54 |
| 1698 |
 |
Apr. 10 |
9 |
13 |
------ |
| 1698 |
 |
Oct. 3 |
15 |
29 |
------ |
| 1699 |
 |
Mar. 15 |
8 |
14 |
9 |
7 |
| 1699 |
 |
Mar. 30 |
22 |
0 |
------ |
| 1699 |
 |
Sept. 8 |
23 |
22 |
------ |
| 1699 |
 |
Sept. 23 |
22 |
38 |
9 |
58 |
| 1700 |
 |
Mar. 4 |
20 |
11 |
------ |
| 1700 |
 |
Aug. 29 |
1 |
42 |
------ |
The Eclipses from Struyk were observed: those from Ricciolus calculated:
the following from L’Art de verifier les Dates, are only those which
are visible in Europe for the present century: those which are total are marked
with a T; and M signifies Morning, A Afternoon.
Visible ECLIPSES from 1700 to 1800.
| Aft. Chr. |
|
Months and Days. |
Time of the Day or Night. |
| 1701 |
 |
Feb. 22 |
11 A. |
|
| 1703 |
 |
Jan. 3 |
7 M. |
|
| 1703 |
 |
June 29 |
1 M. |
T. |
| 1703 |
 |
Dec. 23 |
7 M. |
T. |
| 1704 |
 |
Dec. 11 |
7 M. |
|
| 1706 |
 |
Apr. 28 |
2 M. |
|
| 1706 |
 |
May 12 |
10 M. |
|
| 1706 |
 |
Oct. 21 |
7 A. |
|
| 1707 |
 |
Apr. 17 |
2 M. |
T. |
| 1708 |
 |
April 5 |
6 M. |
|
| 1708 |
 |
Dec. 14 |
8 M. |
|
| 1708 |
 |
Sept. 29 |
9 A. |
|
| 1709 |
 |
Mar. 11 |
2 A. |
|
| 1710 |
 |
Feb. 13 |
11 A. |
|
| 1710 |
 |
Feb. 28 |
1 A. |
|
| 1711 |
 |
July 15 |
8 A. |
|
| 1711 |
 |
July 29 |
6 A. |
T. |
| 1712 |
 |
Jan. 23 |
8 A. |
|
| 1713 |
 |
June 8 |
6 A. |
|
| 1713 |
 |
Dec. 2 |
4 M. |
|
| 1715 |
 |
May 3 |
9 M. |
T. |
| 1715 |
 |
Nov. 11 |
5 M. |
|
| 1717 |
 |
Mar. 27 |
3 M. |
|
| 1717 |
 |
May 20 |
6 A. |
|
| 1718 |
 |
Sept. 9 |
8 A. |
T. |
| 1719 |
 |
Aug. 29 |
9 A. |
|
| 1721 |
 |
Jan. 13 |
3 A. |
|
| 1722 |
 |
June 29 |
3 M. |
|
| 1722 |
 |
Dec. 8 |
3 A. |
|
| 1722 |
 |
Dec. 22 |
4 A. |
|
| 1724 |
 |
May 22 |
7 A. |
T. |
| 1724 |
 |
Nov. 1 |
4 M. |
|
| 1725 |
 |
Oct. 21 |
7 A. |
|
| 1726 |
 |
Sept. 25 |
6 A. |
|
| 1726 |
 |
Oct. 11 |
5 M. |
|
| 1727 |
 |
Sept. 15 |
7 M. |
|
| 1729 |
 |
Feb. 13 |
9 A. |
T. |
| 1729 |
 |
Aug. 9 |
1 M. |
|
| 1730 |
 |
Feb. 4 |
4 M. |
|
| 1731 |
 |
June 20 |
2 M. |
|
| 1732 |
 |
Dec. 1 |
10 A. |
T. |
| 1733 |
 |
May 13 |
7 A. |
|
| 1733 |
 |
May 28 |
7 A. |
|
| 1735 |
 |
Oct. 2 |
1 M. |
|
| 1736 |
 |
Mar. 26 |
12 A. |
T. |
| 1736 |
 |
Sept. 20 |
3 M. |
T. |
| 1736 |
 |
Oct. 4 |
6 A. |
|
| 1737 |
 |
Mar. 1 |
4 A. |
|
| 1737 |
 |
Sept. 9 |
4 M. |
|
| 1738 |
 |
Aug. 15 |
11 M. |
|
| 1739 |
 |
Jan. 24 |
11 A. |
|
| 1739 |
 |
Aug. 4 |
5 A. |
|
| 1739 |
 |
Dec. 30 |
9 M. |
|
| 1740 |
 |
Jan. 13 |
11 A. |
T. |
| 1741 |
 |
Jan. 1 |
12 A. |
|
| 1743 |
 |
Nov. 2 |
3 M. |
T. |
| 1744 |
 |
Aug. 26 |
9 A. |
|
| 1746 |
 |
Aug. 30 |
12 A. |
|
| 1747 |
 |
Feb. 14 |
5 M. |
T. |
| 1748 |
 |
July 25 |
11 M. |
|
| 1771748 |
 |
Aug. 8 |
12 A. |
|
| 1749 |
 |
Dec. 23 |
8 A. |
|
| 1750 |
 |
Jan. 8 |
9 M. |
|
| 1750 |
 |
June 19 |
9 A. |
T. |
| 1750 |
 |
Dec. 13 |
7 M. |
|
| 1751 |
 |
June 9 |
2 M. |
|
| 1751 |
 |
Dec. 2 |
10 A. |
|
| 1752 |
 |
May 13 |
8 A. |
|
| 1753 |
 |
Apr. 17 |
7 A. |
|
| 1753 |
 |
Oct. 26 |
10 M. |
|
| 1755 |
 |
Mar. 28 |
1 M. |
|
| 1757 |
 |
Feb. 4 |
6 M. |
|
| 1757 |
 |
July 30 |
12 A. |
|
| 1758 |
 |
Jan. 24 |
7 M. |
T. |
| 1758 |
 |
Dec. 30 |
7 M. |
|
| 1759 |
 |
June 24 |
7 A. |
|
| 1759 |
 |
Dec. 19 |
2 A. |
|
| 1760 |
 |
May 29 |
9 A. |
|
| 1760 |
 |
June 13 |
7 M. |
|
| 1760 |
 |
Nov. 22 |
9 A. |
|
| 1761 |
 |
May 18 |
11 A. |
T. |
| 1762 |
 |
May 8 |
4 M. |
|
| 1762 |
 |
Oct. 17 |
8 M. |
|
| 1762 |
 |
Nov. 1 |
8 A. |
|
| 1763 |
 |
Apr. 13 |
8 M. |
|
| 1764 |
 |
Apr. 1 |
10 M. |
|
| 1764 |
 |
Apr. 16 |
1 M. |
|
| 1765 |
 |
Mar. 21 |
2 A. |
|
| 1765 |
 |
Aug. 16 |
5 A. |
|
| 1766 |
 |
Feb. 24 |
7 A. |
|
| 1766 |
 |
Aug. 5 |
7 A. |
|
| 1768 |
 |
Jan. 4 |
5 M. |
|
| 1768 |
 |
June 30 |
4 M. |
T. |
| 1768 |
 |
Dec. 23 |
4 A. |
T. |
| 1769 |
 |
June 4 |
8 M. |
|
| 1769 |
 |
Dec. 13 |
7 M. |
|
| 1770 |
 |
Nov. 17 |
10 M. |
|
| 1771 |
 |
Apr. 28 |
2 M. |
|
| 1771 |
 |
Oct. 23 |
5 A. |
|
| 1772 |
 |
Oct. 11 |
6 A. |
T. |
| 1772 |
 |
Oct. 26 |
10 M. |
|
| 1773 |
 |
Mar. 23 |
5 M. |
|
| 1773 |
 |
Sept. 30 |
7 A. |
|
| 1774 |
 |
Mar. 12 |
10 M. |
|
| 1776 |
 |
July 31 |
1 M. |
T. |
| 1776 |
 |
Aug. 14 |
5 M. |
|
| 1777 |
 |
Jan. 9 |
5 A. |
|
| 1778 |
 |
June 24 |
4 A. |
|
| 1778 |
 |
Dec. 4 |
6 M. |
|
| 1779 |
 |
May 30 |
5 M. |
T. |
| 1779 |
 |
June 14 |
8 M. |
|
| 1779 |
 |
Nov. 23 |
8 A. |
|
| 1780 |
 |
Oct. 27 |
6 A. |
|
| 1780 |
 |
Nov. 12 |
4 M. |
|
| 1781 |
 |
Apr. 23 |
6 A. |
|
| 1781 |
 |
Oct. 17 |
8 M. |
|
| 1782 |
 |
Apr. 12 |
7 A. |
|
| 1783 |
 |
Mar. 18 |
9 A. |
T. |
| 1783 |
 |
Sept. 10 |
11 A. |
T. |
| 1784 |
 |
Mar. 7 |
3 M. |
|
| 1785 |
 |
Feb. 9 |
1 A. |
|
| 1787 |
 |
Jan. 3 |
12 A. |
T. |
| 1787 |
 |
Jan. 19 |
10 M. |
|
| 1787 |
 |
June 15 |
5 A. |
|
| 1787 |
 |
Dec. 24 |
3 A. |
|
| 1788 |
 |
June 4 |
9 M. |
|
| 1789 |
 |
Nov. 2 |
12 A. |
|
| 1790 |
 |
Apr. 28 |
12 A. |
T. |
| 1790 |
 |
Oct. 23 |
1 M. |
T. |
| 1791 |
 |
April 3 |
1 A. |
|
| 1791 |
 |
Oct. 12 |
3 M. |
|
| 1792 |
 |
Sept. 16 |
11 M. |
|
| 1793 |
 |
Feb. 25 |
10 A. |
|
| 1793 |
 |
Sept. 5 |
3 A. |
|
| 1794 |
 |
Jan. 31 |
4 A. |
|
| 1794 |
 |
Feb. 14 |
11 A. |
T. |
| 1794 |
 |
Aug. 25 |
5 A. |
|
| 1795 |
 |
Feb. 4 |
1 M. |
|
| 1795 |
 |
July 16 |
9 M. |
|
| 1795 |
 |
July 31 |
8 A. |
|
| 1797 |
 |
June 25 |
8 A. |
|
| 1797 |
 |
Dec. 4 |
6 M. |
|
| 1798 |
 |
May 27 |
7 A. |
T. |
| 1800 |
 |
Oct. 2 |
11 A. |
|
328.
A List of Eclipses, and historical Events, which happened about the same Times, from Ricciolus.
Historical Eclipses.
| Before Christ. |
| 754 |
July 5 |
But according to an old Calendar this Eclipse of
the Sun was on the 21st of April, on which day the
Foundations of Rome were laid if we may believe Taruntius Firmanus. |
| 721 |
March 19 |
A total Eclipse of the Moon. The Assyrian
Empire at an end; the Babylonian established. |
| 585 |
May 28 |
An Eclipse of the Sun foretold by Thales, by
which a peace was brought about between the Medes and Lydians. |
| 523 |
July 16 |
An Eclipse of the Moon, which was followed
by the death of Cambyses. |
| 178502 |
Nov. 19 |
An Eclipse of the Moon, which was followed
by the slaughter of the Sabines, and death of Valerius Publicola. |
| 463 |
April 30 |
An Eclipse of the Sun. The Persian war, and the
falling off of the Persians from the Egyptians. |
| 431 |
April 25 |
An Eclipse of the Moon, which was followed by a great famine at Rome; and the beginning of
the Peloponnesian war. |
| 431 |
August 3 |
A total Eclipse of the Sun. A Comet and Plague at Athens[74]. |
| 413 |
Aug. 27 |
A total Eclipse of the Moon. Nicias with his
ship destroyed at Syracuse. |
| 394 |
Aug. 14 |
An Eclipse of the Sun. The Persians beat by
Conon in a sea engagement. |
| 168 |
June 21 |
A total Eclipse of the Moon. The next day
Perseus King of Macedonia was conquered by Paulus Emilius. |
| After Christ. |
| 59 |
April 30 |
An Eclipse of the Sun. This is reckoned among
the prodigies, on account of the murther of Agrippinus by Nero. |
| 237 |
April 12 |
A total Eclipse of the Sun. A sign that the reign
of the Gordiani would not continue long. A sixth persecution of the Christians. |
| 306 |
July 27 |
An Eclipse of the Sun. The Stars were seen,
and the Emperor Constantius died. |
| 840 |
May 4 |
A dreadful Eclipse of the Sun. And Lewis the
Pious died within six months after it. |
| 1009 |
---- |
An Eclipse of the Sun. And Jerusalem taken by
the Saracens. |
| 1133 |
Aug. 2 |
A terrible Eclipse of the Sun. The Stars were
seen. A schism in the church, occasioned by there being three Popes at once. |
Plate XI.
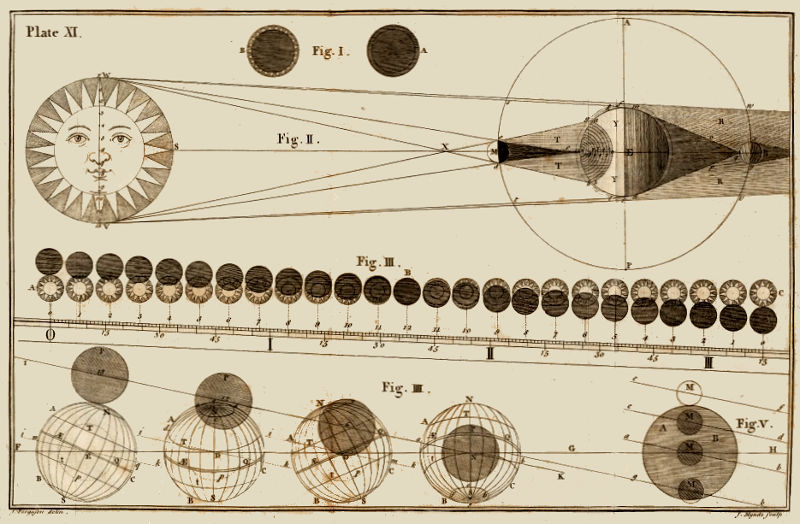
J. Ferguson delin.
J. Mynde Sculp.
The superstitious notions of the antients with regard to
Eclipses.
PLATE XI.
329. I have not cited one half of Ricciolus’s list of potentous
Eclipses; and for the same reason that he declines giving any more
of them than what that list contains: namely, that ’tis most disagreeable
179to dwell any longer on such nonsense, and as much as possible
to avoid tiring the reader: the superstition of the antients may be
seen by the few here copied. My author farther says, that there
were treatises written to shew against what regions the malevolent
effects of any particular Eclipse was aimed: and the writers affirmed,
that the effects of an Eclipse of the Sun continued as many years as the
Eclipse lasted hours; and that of the Moon as many months.
Very fortunate once for Christopher Columbus.
330. Yet such idle notions were once of no small advantage to
Christopher Columbus; who, in the year 1493, was driven on
the island of Jamaica, where he was in the greatest distress for want
of provisions, and was moreover refused any assistance from the inhabitants;
on which he threatened them with a plague, and that in token
of it there should be an Eclipse: which accordingly fell on the day he
had foretold, and so terrified the Barbarians, that they strove who
should be first in bringing him all sorts of provisions; throwing them
at his feet, and imploring his forgiveness. Ricciolus’s Almagest,
Vol. I. 1. v. c. ii.
Why there are more visible Eclipses of the Moon than of the Sun.
331. Eclipses of the Sun are more frequent than of the Moon,
because the Sun’s ecliptic limits are greater than the Moon’s § 317:
yet we have more visible Eclipses of the Moon than of the Sun,
because Eclipses of the Moon are seen from all parts of that Hemisphere
of the Earth which is next her, and equally great to each of
these parts; but the Sun’s Eclipses are visible only to that small portion
of the Hemisphere next him whereon the Moon’s shadow falls; as
shall be explained by and by at large.
Fig. I.
Total and annular Eclipses of the Sun.
PLATE XI.
332. The Moon’s Orbit being elliptical, and the Earth in one of its
focuses, she is once at her least distance from the Earth, and once at
her greatest in every Lunation. When the Moon changes at her
least distance from the Earth, and so near the Node that her dark
shadow falls on the Earth, she appears big enough to cover the whole
[75]Disc of the Sun from that part on which her shadow falls; and the
Sun appears totally eclipsed there, as at A, for some minutes: But
when the Moon changes at her greatest distance from the Earth, and
so near the Node that her dark shadow is directed towards the Earth,
her diameter subtends a less angle than the Sun’s; and therefore she
cannot hide his whole Disc from any part of the Earth, nor does her
shadow reach it at that time; and to the place over which the point of
180her shadow hangs, the Eclipse is annular as at B; the Sun’s edge
appearing like a luminous ring all around the body of the Moon.
When the Change happens within 17 degrees of the Node, and the
Moon at her mean distance from the Earth, the point of her shadow
just touches the Earth, and she eclipseth the Sun totally to that small
spot whereon her shadow falls; but the darkness is not of a moment’s
continuance.
The longest duration of total Eclipses of the Sun.
333. The Moon’s apparent diameter when largest exceeds the Sun’s
when least only 1 minute 38 seconds of a degree: And in the greatest
Eclipse of the Sun that can happen at any time and place, the total
darkness continues no longer than whilst the Moon is going 1 minute
38 seconds from the Sun in her Orbit; which is about 3 minutes and
13 seconds of an hour.
To how much of the Earth the Sun may be totally or partially eclipsed at once.
334. The Moon’s dark shadow covers only a spot on the Earth’s
surface, about 180 English miles broad, when the Moon’s diameter
appears largest and the Sun’s least; and the total darkness can extend
no farther than the dark shadow covers. Yet the Moon’s partial Shadow
or Penumbra may then cover a circular space 4900 miles in diameter,
within all which the Sun is more or less eclipsed as the places are
less or more distant from the Center of the Penumbra. When the
Moon changes exactly in the Node, the Penumbra is circular on the
Earth at the middle of the general Eclipse; because at that time it
falls perpendicularly on the Earth’s surface: But at every other moment
it falls obliquely, and will therefore be elliptical; and the more so, as
the time is longer before or after the middle of the general Eclipse;
and then, much greater portions of the Earth’s surface are involved in
the Penumbra.
Duration of general and particular Eclipses.
The Moon’s dark shadow.
And Penumbra.
335. When the Penumbra first touches the Earth the general
Eclipse begins: when it leaves the Earth the general Eclipse ends:
from the beginning to the end the Sun appears eclipsed in some part
of the Earth or other. When the Penumbra touches any place the
Eclipse begins at that place, and ends when the Penumbra leaves it.
When the Moon changes in the Node, the Penumbra goes over the
center of the Earth’s Disc as seen from the Moon; and consequently,
by describing the longest line possible on the Earth, continues the
longest upon it; namely, at a mean rate, 5 hours 50 minutes: more,
if the Moon be at her greatest distance from the Earth, because she
then moves slowest; less, if she be at her least distance, because of
her quicker motion.
Fig. II.
336. To make the last five articles and several other Phenomena
plainer, let S be the Sun, E the Earth, M the Moon, and AMP the
181Moon’s Orbit. Draw the right line Wc 12 from the western edge of
the Sun at W, touching the western edge of the Moon at c and the
Earth at 12: draw also the right line Vd 12 from the eastern edge of
the Sun at V, touching the eastern edge of the Moon at d and the
Earth at 12: the dark space ce 12 d included between those lines is
the Moon’s shadow, ending in a point at 12 where it touches the
Earth; because in this case the Moon is supposed to change at M in
the middle between A the Apogee, or farthest point of her Orbit from
the Earth, and P the Perigee, or nearest point to it. For, had the
point P been at M, the Moon had been nearer the Earth; and her
dark shadow at e would have covered a space upon it about 180 miles
broad, and the Sun would have been totally darkened as at A (Fig I)
with some continuance: but had the point A (Fig. II) been at M,
the Moon would have been farther from the Earth, and her shadow
would have ended in a point about e, and therefore the Sun would
have appeared as at B (Fig. I) like a luminous ring all around the
Moon. Draw the right lines WXdh and VXcg, touching the contrary
sides of the Sun and Moon, and ending on the Earth at a
and b: draw also the right line SXM 12, from the center of the
Sun’s Disc, through the Moon’s center, to the Earth at 12; and
suppose the two former lines WXdh and VXcg to revolve on the line
SXM 12 as an Axis, and their points a and b will describe the limits
of the Penumbra TT on the Earth’s surface, including the large
space a0b12a; within which the Sun appears more or less eclipsed
as the places are more or less distant from the verge of the Penumbra
a0b.
Digits, what.
Draw the right line y 12 across the Sun’s Disc, and parallel to
the plane of the Moon’s Orbit; divide this line into twelve equal
parts, as in the Figure, for the twelve [76]Digits of the Sun’s diameter:
and at equal distances from the center of the Penumbra TT to its
edge on the Earth, or from 12 to 0, draw twelve concentric Circles,
as marked with the numeral Figures 1 2 3 4 &c. and remember that
the Moon’s motion in her Orbit AMP is from west to east, as from
s to t. Then,
The different phases of a solar Eclipse.
PLATE XI.
Fig. III.
To an observer on the Earth at b, the eastern limb of the Moon at
d seems to touch the western limb of the Sun at W, when the Moon
is at M; and the Sun’s Eclipse begins at b; appearing as at A in
Fig. III at the left hand; but at the same moment of absolute time
to an observer at a in Fig. II the western edge of the Moon at c leaves
182the eastern edge of the Sun at V, and the Eclipse ends, as at the
right hand C of Fig. III. At the very same instant, to all those who
live on the Circle marked 1 on the Earth E in Fig. II, the Moon M
cuts off or darkens a twelfth part of the Sun S, and eclipses him one
Digit, as at 1 in Fig. III: to those who live on the Circle marked 2 in
Fig. II the Moon cuts off two twelfth parts of the Sun, as at 2 in
Fig. III: to those on the Circle 3, three parts; and so on to the center
at 12 in Fig. II, where the Sun is centrally eclipsed as at B in the
middle of Fig. III: under which Figure there is a scale of hours and
minutes, to shew at a mean state how long it is from the beginning to
the end of a central Eclipse of the Sun on the parallel of London; and
how many Digits are eclipsed at any particular time from the beginning
at A to the middle at B, or the end at C. Thus in 16 minutes
from the beginning, the Sun is two Digits eclipsed; in an hour and
five minutes, 8 Digits; and in an hour and thirty-seven minutes, 12
Digits.
Fig. II.
The Velocity of the Moon’s shadow on the Earth.
Fig. IV.
337. By Fig. II it is plain, that the Sun is totally or centrally
eclipsed but to a small part of the Earth at any time; because the dark
conical shadow e of the Moon M falls but on a small part of the Earth:
and that the partial Eclipse is confined at that time to the space included
by the Circle a 0 b, of which only one half can be projected in the
Figure, the other half being supposed to be hid by the convexity of the
Earth E: and likewise, that no part of the Sun is eclipsed to the large
space YY of the Earth, because the Moon is not between the Sun
and that part of the Earth: and therefore to all that part the Eclipse is
invisible. The Earth turns eastward on its Axis, as from g to h,
which is the same way that the Moon’s shadow moves; but the Moon’s
motion is much swifter in her Orbit from s to t: and therefore, altho’
Eclipses of the Sun are of longer duration on account of the Earth’s
motion on its Axis, than they would be if that motion was stopt, yet
in 3 minutes and 13 seconds of time, the Moon’s swifter motion carries
her dark shadow quite over any place that its center touches at the
time of greatest obscuration. The motion of the shadow on the Earth’s
Disc is equal to the Moon’s motion from the Sun, which is about
301⁄2
minutes of a degree every hour at a mean rate; but so much of the
Moon’s Orbit is equal to
301⁄2
degrees of a great Circle on the Earth,
§ 320; and therefore the Moon’s shadow goes
301⁄2
degrees or 1830
geographical miles on the Earth in an hour, or
301⁄2
miles in a
minute, which is almost four times as swift as the motion of a
cannon-ball.
PLATE XI.
Fig. IV.
Phenomena of the Earth as seen from the Sun or New Moon
at different times of the year.
183338. As seen from the Sun or Moon, the Earth’s Axis appears differently
inclined every day of the year, on account of keeping its
parallelism throughout its annual course. Let E, D, O, N, be the
Earth at the two Equinoxes and the two Solstices; N S its Axis, N
the North Pole, S the South Pole, Æ Q the Equator, T the Tropic
of Cancer, t the Tropick of Capricorn, and ABC the Circumference
of the Earth’s enlightened Disc as seen from the Sun or New Moon at
these times. The Earth’s Axis has the position NES at the vernal
Equinox, lying towards the right hand, as seen from the Sun or New
Moon; its Poles N and S being then in the Circumference of the Disc;
and the Equator and all its parallels seem to be straight lines, because
their planes pass through the observer’s eye looking down upon the
Earth from the Sun or Moon directly over E, where the Ecliptic FG
intersects the Equator Æ. At the Summer Solstice, the Earth’s
Axis has the position NDS; and that part of the Ecliptic FG in
which the Moon is then New, touches the Tropic of Cancer T at D.
The North Pole N at that time inclining
231⁄2
degrees towards the Sun,
falls so many degrees within the Earth’s enlightened Disc, because
the Sun is then vertical to D,
231⁄2
degrees north of the Equator ÆQ;
and the Equator with all its parallels seem elliptic curves bending
downward, or towards the South Pole as seen from the Sun: which
Pole, together with
231⁄2
degrees all round it, is hid behind the Disc
in the dark Hemisphere of the Earth. At the autumnal Equinox
the Earth’s Axis has the position NOS, lying to the left hand as seen
from the Sun or New Moon, which are then vertical to O, where the
Ecliptic cuts the Equator ÆQ. Both Poles now lie in the circumference
of the Disc, the North Pole just going to disappear behind it,
and the South Pole just entering into it; and the Equator with all its
parallels seem to be straight lines, because their planes pass through
the observer’s eye, as seen from the Sun, and very nearly so as seen
from the Moon. At the Winter Solstice the Earth’s Axis has the
position NNS; when its South Pole S inclining
231⁄2
degrees toward the
Sun falls
231⁄2
degrees within the enlightened Disc, as seen from the
Sun or New Moon which are then vertical to the Tropic of Capricorn
t,
231⁄2
degrees south of the Equator ÆQ; and the Equator with all
its parallels seem elliptic curves bending upward; the North Pole
being as far hid behind the Disc in the dark Hemisphere, as the
South Pole is come into the light. The nearer that any time of the
year is to the Equinoxes or Solstices, the more it partakes of the
Phenomena relating to them.
PLATE XI.
Various positions of the Earth’s Axis, as seen from the Sun
at different times of the year.
184339. Thus it appears, that from the vernal equinox to the autumnal,
the North Pole is enlightened; and the Equator and all its parallels
appear Semi-ellipses as seen from the Sun, more or less curved as the
time is nearer to or farther from the Summer Solstice; and bending
downwards or towards the South Pole; the reverse of which happens
from the autumnal Equinox to the vernal. A little consideration
will be sufficient to convince the reader, that the Earth’s Axis inclines
towards the Sun at the Summer Solstice; from the Sun at the Winter
Solstice; and sidewise to the Sun at the Equinoxes; but towards the
right hand, as seen from the Sun at the vernal Equinox; and towards
the left hand at the autumnal. From the Winter to the Summer
Solstice, the Earth’s Axis inclines more or less to the right hand, as
seen from the Sun; and the contrary from the Summer to the Winter
Solstice.
How these positions affect solar Eclipses.
340. The different positions of the Earth’s Axis, as seen from the
Sun at different times of the year, affect solar Eclipses greatly with regard
to particular places; yea so far as would make central Eclipses
which fall at one time of the year invisible if they fell at another, even
though the Moon should always change in the Nodes and at the same
hour of the day: of which indefinitely various affections, we shall only
give Examples for the times of the Equinoxes and Solstices.
Fig. IV.
In the same Diagram, let FG be part of the Ecliptic, and IK
ik ik ik part of the Moon’s Orbit; both seen edgewise, and therefore
projected into right lines; and let the intersections N, O, D, E be
one and the same Node at the above times, when the Earth has the
forementioned different positions; and let the spaces included by the
Circles P, p, p, p be the Penumbra at these times, as its center is
passing over the center of the Earth’s Disc. At the Winter Solstice,
when the Earth’s Axis has the position NNS, the center of the Penumbra
P touches the Tropic of Capricorn t in N at the middle
of the general Eclipse; but no part of the Penumbra touches the
Tropic of Cancer T. At the Summer Solstice, when the Earth’s Axis
has the position NDS (iDk being then part of the Moon’s Orbit
whose Node is at D) the Penumbra p has its center on the Tropic
of Cancer T at the middle of the general Eclipse, and then no part
of it touches the Tropic of Capricorn t. At the autumnal Equinox
the Earth’s Axis has the position NOS (iOk being then part of the
Moon’s Orbit) and the Penumbra equally includes part of both Tropics
T and t at the middle of the general Eclipse: at the vernal Equinox
it does the same, because the Earth’s Axis has the position NES:
But, in the former of these two last cases, the Penumbra enters the
185Earth at A, north of the Tropic of Cancer T, and leaves it at m,
south of the Tropic of Capricorn t; having gone over the Earth obliquely
southward, as its center described the line AOm: whereas in the latter
case the Penumbra touches the Earth at n, south of the Equator
ÆQ, and describing the line nEq (similar to the former line AOm in
open space) goes obliquely northward over the Earth, and leaves it at
q, north of the Equator.
In all these circumstances, the Moon has been supposed to change
at noon in her descending Node: had she changed in her ascending
Node, the Phenomena would have been as various the contrary way,
with respect to the Penumbra’s going northward or southward over the
Earth. But because the Moon changes at all hours, as often in one
Node as the other, and at all distances from them both at different
times as it happens, the variety of the Phases of Eclipses are almost
innumerable, even at the same places, considering also how variously
the same places are situated on the enlightened Disc of the Earth, with
respect to the Penumbra’s motion, at the different hours that Eclipses
happen.
How much of the Penumbra falls on the Earth at different distances from the Nodes.
341. When the Moon changes 17 degrees short of her descending
Node, the Penumbra P 18 just touches the northern part of the Earth’s
Disc, near the North Pole N; and, as seen from that place the Moon
appears to touch the Sun, but hides no part of him from sight.
Had the Change been as far short of the ascending Node, the
Penumbra would have touched the southern part of the Disc near
the South Pole S. When the Moon changes 12 degrees short of
the descending Node, more than a third part of the Penumbra P 12
falls on the northern parts of the Earth at the middle of the general
Eclipse: had she changed as far past the same Node, as much of
the other side of the Penumbra about P would have fallen on the
southern part of the Earth; all the rest in the expansum, or open
space. When the Moon changes 6 degrees from the Node, almost
the whole Penumbra P6 falls on the Earth at the middle of the
general Eclipse. And lastly, when the Moon changes in the Node,
the Penumbra PN takes the longest course possible on the Earth’s
Disc; its center falling on the middle thereof, at the middle of the
general Eclipse. The farther the Moon changes from either Node
within 17 degrees of it, the shorter is the Penumbra’s continuance on
the Earth, because it goes over a less portion of the Disc, as is evident
by the Figure.
The Earth’s diurnal motion lengthens the duration of solar Eclipses, which fall without the polar Circles.
342. The nearer that the Penumbra’s center is to the Equator at
the middle of the general Eclipse, the longer is the duration of the
186Eclipse at all those places where it is central; because, the nearer
that any place is to the Equator, the greater is the Circle it describes
by the Earth’s motion on its Axis: and so, the place moving quicker
keeps longer in the Penumbra whose motion is the same way with that
of the place, tho’ faster as has been already mentioned § 337. Thus,
(see the Earth at D and the Penumbra at 12) whilst the point b in
the polar Circle abcd is carried from b to c by the Earth’s diurnal
motion, the point d on the Tropick of Cancer T is carried a much
greater length from d to D: and therefore, if the Penumbra’s center
goes one time over c and another time over D, the Penumbra will be
longer in passing over the moving place d than it was in passing over the
moving place b. Consequently, central Eclipses about the Poles are of
the shortest duration; and about the Equator of the longest.
And shortens the duration of some which fall within these Circles.
343. In the middle of Summer the whole frigid Zone included
by the polar Circle abcd is enlightened; and if it then happens that
the Penumbra’s center goes over the north Pole, the Sun will be
eclipsed much the same number of Digits at a as at c; but whilst the
Penumbra moves eastward over c it moves westward over a, because
with respect to the Penumbra, the motions of a and c are contrary:
for c moves the same way with the Penumbra towards d, but a
moves the contrary way towards b; and therefore the Eclipse will be
of longer duration at c than at a. At a the Eclipse begins on the Sun’s
eastern limb, but at c on his western: at all places lying without the
polar Circles, the Sun’s Eclipses begin on his western limb, or near
it, and end on or near his eastern. At those places where the Penumbra
touches the Earth, the Eclipse begins with the rising Sun, on the top
of his western or uppermost edge; and at those places where the Penumbra
leaves the Earth, the Eclipse ends with the setting Sun, on the
top of his eastern edge which is then the uppermost, just at its disappearing
in the Horizon.
The Moon has no Atmosphere.
344. If the Moon were surrounded by an Atmosphere of any considerable
Density, it would seem to touch the Sun a little before the
Moon made her appulse to his edge, and we should see a little faintness
on that edge before it were eclipsed by the Moon: But as no such
faintness has been observed, at least so far as I ever heard, it seems
plain, that the Moon has no such Atmosphere as that of the Earth.
The faint ring of light surrounding the Sun in total Eclipses, called by
Cassini la Chevelure du Soleil, seems to be the Atmosphere of the
Sun; because it has been observed to move equally with the Sun, not
with the Moon.
187345. Having been so prolix concerning Eclipses of the Sun, we
shall drop that subject at present, and proceed to the doctrine
of lunar Eclipses; which, being more simple, may be explained in less
time.
Eclipses of the Moon.
Fig. II.
That the Moon can never be eclipsed but at the time of her being
Full, and the reason why she is not eclipsed at every Full, have been
shewn already § 316, 317. Let S be the Sun, E the Earth, RR the
Earth’s shadow, and B the Moon in opposition to the Sun: in this
situation the Earth intercepts the Sun’s light in its way to the Moon;
and when the Moon touches the Earth’s shadow at v she begins to be
eclipsed on her eastern limb x, and continues eclipsed until her western
limb y leaves the shadow at w: at B she is in the middle of the
shadow, and consequently in the middle of the Eclipse.
Why the Moon is visible in a total Eclipse.
346. The Moon when totally eclipsed, is not invisible if she be
above the Horizon and the Sky be clear; but appears generally of a
dusky colour like tarnished copper, which some have thought to be
the Moon’s native light. But the true cause of her being visible is the
scattered beams of the Sun, bent into the Earth’s shadow by going
through the Atmosphere; which, being more dense near the Earth
than at considerable heights above it, refracts or bends the Sun’s rays
more inward § 179, the nearer they are passing by the Earth’s surface,
than those rays which go through higher parts of the Atmosphere,
where it is less dense according to its height, until it be so thin or
rare as to lose its refractive power. Let the Circle fghi, concentric to
the Earth, include the Atmosphere whose refractive power vanishes at
the heights f and i; so that the rays Wfw and Viv go on straight
without suffering the least refraction: But all those rays which enter the
Atmosphere between f and k, and between i and l, on opposite sides
of the Earth, are gradually more bent inward as they go through a
greater portion of the Atmosphere, until the rays Wk and Vl, touching the
Earth at m and n, are bent so as to meet at q, a little short of the Moon;
and therefore the dark shadow of the Earth is contained in the space
moqpn where none of the Sun’s rays can enter: all the rest RR, being
mixed by the scattered rays which are refracted as above, is in some
measure enlightened by them; and some of those rays falling on the
Moon give her the colour of tarnished copper, or of iron almost red
hot. So that if the Earth had no Atmosphere, the Moon would be
as invisible in total Eclipses as she is when New. If the Moon were
so near the Earth as to go into its dark shadow, suppose about po,
she would be invisible during her stay in it; but visible before and after
in the fainter shadow RR.
PLATE XI.
Why the Sun and Moon are sometimes visible when the Moon is
totally eclipsed.
188347. When the Moon goes through the center of the Earth’s shadow
she is directly opposite to the Sun: yet the Moon has been often seen
totally eclipsed in the Horizon when the Sun was also visible in the
opposite part of it: for, the horizontal refraction being almost 34
minutes of a degree § 181, and the diameter of the Sun and Moon
being each at a mean state but 32 minutes, the refraction causes
both Luminaries to appear above the Horizon when they are really
below it § 179.
Fig. V.
Duration of central Eclipses of the Moon.
348. When the Moon is Full at 12 degrees from either of her
Nodes, she just touches the Earth’s shadow but enters not into it.
Let GH be the Ecliptic, ef the Moon’s Orbit where she is 12 degrees
from the Node at her Full; cd her Orbit where she is 6 degrees
from the Node, ab her Orbit where she is Full in the Node, AB the
Earth’s shadow, and M the Moon. When the Moon describes the line
ef she just touches the shadow but does not enter into it; when she
describes the line cd she is totally though not centrally immersed in the
shadow; and when she describes the line ab she passes by the Node at
M in the center of the shadow, and takes the longest line possible, which
is a diameter, through it: and such an Eclipse being both total and central
is of the longest duration, namely, 3 hours 57 minutes 6 seconds
from the beginning to the end, if the Moon be at her greatest distance
from the Earth: and 3 hours 37 minutes 26 seconds, if she be at her
least distance. The reason of this difference is, that when the Moon
is farthest from the Earth she moves slowest; and when nearest to it,
quickest.
Digits.
349. The Moon’s diameter, as well as the Sun’s, is supposed to be
divided into twelve equal parts called Digits; and so many of these
parts as are darkened by the Earth’s shadow, so many Digits is the
Moon eclipsed. All that the Moon is eclipsed above 12 Digits, shew
how far the shadow of the Earth is over the body of the Moon, on
that edge to which she is nearest at the middle of the Eclipse.
Why the beginning and end of a lunar Eclipse is so difficult to be determined by observation.
350. It is difficult to observe exactly either the beginning or ending
of a lunar Eclipse, even with a good Telescope; because the Earth’s
shadow is so faint, and ill defined about the edges, that when the Moon
is either just touching or leaving it, the obscuration of her limb is
scarce sensible; and therefore the nicest observers can hardly be certain
to four or five seconds of time. But both the beginning and ending
of solar Eclipses are visibly instantaneous; for the moment that the
edge of the Moon’s Disc touches the Sun’s, his roundness seems a little
broke on that part; and the moment she leaves it he appears perfectly
round again.
The use of Eclipses in Astronomy, Geography, and Chronology.
189351. In Astronomy, Eclipses of the Moon are of great use for
ascertaining the periods of her motions; especially such Eclipses as
are observed to be alike in all circumstances, and have long intervals of
time between them. In Geography, the Longitudes of places are
found by Eclipses, as already shewn in the eleventh chapter: but for
this purpose Eclipses of the Moon are more useful than those of the
Sun, because they are more frequently visible, and the same lunar
Eclipse is of equal largeness and duration at all places where it is seen.
In Chronology, both solar and lunar Eclipses serve to determine exactly
the time of any past event: for there are so many particulars
observable in every Eclipse, with respect to its quantity, the places
where it is visible (if of the Sun) and the time of the day or night;
that ’tis impossible there can be two Eclipses in the course of many
ages which are alike in all circumstances.
The darkness at our Saviour’s crucifixion supernatural.
352. From the above explanation of the doctrine of Eclipses it is
evident, that the darkness at our Saviour’s crucifixion was supernatural.
For he suffered on the next day after eating his last Passover-Supper,
on which day it was impossible that the Moon’s shadow could
fall on the Earth, for the Jews kept the Passover at the time of
Full Moon: nor does the darkness in total Eclipses of the Sun
last four minutes in any place § 333, whereas the darkness at the
crucifixion lasted three hours, Matt. xxviii. 15. and overspread at least
all the land of Judea.
CHAP. XIX.
The Calculation of New and Full Moons and Eclipses. The geometrical Construction of Solar and Lunar Eclipses. The examination of antient Eclipses.
353. To construct an Eclipse of the Sun, we must collect these
ten Elements or Requisites from the following Astronomical
Tables.
Requisites for a solar Eclipse.
I. The true time of conjunction of the Sun and Moon: to know
at what conjunctions the Sun must be eclipsed; and to the times of
those conjunctions,
II. The Moon’s horizontal parallax, or angle which the semi-diameter
of the Earth subtends as seen from the Moon.
III. The Sun’s true place, and distance from the solstitial colure to
which he is then nearest, either in coming to it or going from it.
190IV. The Sun’s declination.
V. The angle of the Moon’s visible path with the Ecliptic.
VI. The Moon’s Latitude or Declination from the Ecliptic.
VII. The Moon’s true hourly motion from the Sun.
VIII. The Angle of the Sun’s semi-diameter as seen from the
Earth.
IX. The Angle of the Moon’s semi-diameter as seen from the
Earth.
X. The semi-diameter of the Penumbra.
And for an Eclipse of the Moon, the following Elements.
Requisites for a lunar Eclipse.
I. The true time of opposition of the Sun and Moon; and for that
time,
II. The Moon’s horizontal parallax.
III. The Sun’s semi-diameter.
IV. The semi-diameter of the Earth’s shadow.
V. The Moon’s semi-diameter.
VI. The Moon’s Latitude.
VII. The Moon’s true hourly motion from the Sun.
VIII. The Angle of the Moon’s visible path with the Ecliptic.
These Elements are easily found from the following Tables and
Precepts, by the common Rules of Arithmetic.
Note, 60 minutes make a Degree, 30 degrees a Sign, and 12 Signs
a Circle. A Sign is marked thus s, a Degree thus °, and a Minute
thus ʹ.
When you exceed 12 Signs, always reject them and set down the
remainder. When the number of Signs to be subtracted is greater
than the number you subtract from, add 12 Signs to that which you
subtract from; and then you will have a remainder to set down.
How the Signs are reckoned.
354. As we fix arbitrarily upon the beginning of the Sign Aries to
reckon from, when we speak of the places of the Sun, Moon, and
Nodes; we call Aries 0 Signs, Taurus 1 Sign, Gemini 2 Signs, Cancer
3 Signs, &c. So, when the Sun is in the 10th degree of Aries,
we say his Place or Longitude is 0 Signs 10 Degrees, because he is
only 10 Degrees from the beginning of Aries: if he is in the 5th,
10th, &c. Degree of Taurus, we say his Place or Longitude is 1
Sign, 5, 10, &c. Degrees: and so on, till he comes quite round
again. But in reckoning the Anomalies of the Sun and Moon, and
their distance from the Nodes, we only consider the number of Signs
191and Degrees the Luminaries are gone past their Apogee or Nodes;
not how far they have to go to these points, were the distance ever so
little. The Sun, Moon, and Apogee move according to the order of
Signs, but the Nodes contrary. We shall now give the Precepts and
Examples for the above Requisites in their due order.
To calculate the time of New and Full Moon.
First Element or Requisite.
355. Precept I. For any proposed year in the 18th Century, take
out the mean time of the New Moon in March from Table I., and
the mean time of Full Moon from Table III., for the Old Stile; or
from Tables II and IV for New Stile; with the mean Anomalies of
the Sun and Moon for these times, and set them by themselves. Then,
from Table VI, take out as many Lunations as the proposed Month is
after March, with the days, hours, and minutes belonging to them;
and also the mean Anomalies of the Sun and Moon for these Lunations.
II. Add the days, hours, and minutes of these Lunations to the
time of New or Full Moon in March, and the Anomalies for the Lunations
to the Anomalies for March: the sums give the hours and
minutes of the mean New or Full Moon required, and the mean Anomalies
of the Sun and Moon for that time.
III. Then, with the number of days enter Table VII, under the
given Month, and right against this number, in the left hand column
you have the day of New or Full Moon; which set before the hours
and minutes above-mentioned.
IV. But, (as it will sometimes happen) if the number of days
fall short of all those under the given Month, add one Lunation with
its Anomalies from Table VI to the foresaid sums; so you will have
a new sum of days wherewith to enter the 7th Table under the given
Month, where you are sure to find that sum the second time, if the
first falls short.
V. With the Signs and Degrees of the Sun’s Anomaly enter Table
VIII, The Moon’s annual Equation, and take out the minutes of time
of that Equation by the Anomaly; remembring, that if the Signs are
at the head of the Table, the degrees are at the left hand, in which
case the Equation found in the Angle of meeting must be subtracted
from the mean time of New or Full Moon, as the title Subtract, at the
head of the Table directs: but if the Signs are at the foot of the
Table their degrees are in the right-hand column, and the Equation
where the Signs and Degrees meet in the Table is to be added to
192the mean time, as the title Add, at the foot of the Table directs;
which Equation, so applied, gives the mean time of New or Full Moon
corrected.
VI. With the Signs and Degrees of the Sun’s Anomaly enter
Table IX, Equation of the Moon’s mean Anomaly, and take out the Equation
thereof; adding it to the mean Anomaly or subtracting it therefrom, as
the titles at the head or foot of the Table direct; and it gives the
mean Anomaly corrected. Then, with the Sun’s Anomaly enter
Table XII, Equation of the Sun’s mean Place, and take out that Equation,
applying it to the Moon’s corrected Anomaly as the titles direct;
and it will give the Moon’s Anomaly equated[77]. N. B. In all these
Equations, care must be taken to make proper allowance for the odd
minutes of Anomaly; the Tables having the Equations only for compleat
Degrees.
VII. With the Moon’s equated Anomaly enter Table X, The
Moon’s elliptic Equation, and take out that Equation in the same
manner as the preceding: adding it to the former corrected time
if the Signs be at the head of the Table, or subtracting it if they
be at the foot, as the Table directs; and this gives the mean time
equated.
VIII. Lastly, enter Table XI, The Sun’s Equation at New and
Full Moon, with the Sun’s Anomaly, and take out the Sun’s Equation
in the same manner as the others; adding it to, or subtracting
it from the former equated time, as the titles direct: and by
this last Equation you have the true time of New or Full Moon,
agreeing with well regulated Clocks and Watches. But to make it
agree with true Sun-Dials, the Equation of time must be applied
as taught § 225.
193
EXAMPLE I.
To find the time of New Moon in April 1764, N. S.
| |
Days |
Hours |
Min. |
Sun’s Anom. |
Moon’s Ano. |
| s |
° |
ʹ |
s |
° |
ʹ |
| Tab. II. Mean time of New Moon in March |
2 |
8 |
57 |
8 |
2 |
23 |
10 |
13 |
32 |
| Add, for Lunation, from Tab. VI. |
29 |
12 |
44 |
0 |
29 |
6 |
0 |
25 |
49 |
| Mean New Moon and Anomaly |
31 |
21 |
41 |
0 |
1 |
29 |
11 |
9 |
21 |
| To which Time add the Moon’s Ann. Equ. Tab. VIII. |
+ |
0 |
22 |
Equ. Moon’s Anom. |
|
- |
20 |
| And it gives the Mean time corrected |
31 |
22 |
3 |
Anom. cor. |
11 |
9 |
1 |
| From which subtract the Moon’s elliptic Equ. Tab. X. |
- |
3 |
10 |
Sun’s Equat. |
+ |
1 |
56 |
| Moon’s Ano. |
11 |
10 |
57 |
| And it gives the Mean time equated |
31 |
18 |
53 |
|
h. |
m. |
|
| To which add the Sun’s Equation, Tab. XI. |
+ |
3 |
32 |
Moon’s ann. Equ. |
0 |
22 |
add |
| |
|
Her ellipt. Equ. |
3 |
10 |
sub. |
| |
| And it gives the true time of Conjunction |
31 |
22 |
25 |
Sun’s Equation |
3 |
32 |
add |
Which true time answers to the first of April, at 25 minutes past 10 in
the forenoon: for, as the Astronomical Day begins at Noon, then 22
hours 25 min. after the Noon of March 31, is April 1, at 10 hours
25 min. in the Forenoon.
EXAMPLE II.
To find the time of Full Moon in May 1761, N. S.
| |
Days |
Hours |
Min. |
Sun’s Anom. |
Moon’s Ano. |
| s |
° |
ʹ |
s |
° |
ʹ |
| Mean time of Full Moon in March |
20 |
12 |
9 |
8 |
20 |
2 |
9 |
1 |
13 |
| Add, for two Lunations |
59 |
1 |
28 |
1 |
28 |
13 |
1 |
21 |
38 |
| The several sums are |
79 |
13 |
37 |
10 |
18 |
15 |
10 |
22 |
51 |
| The days, in Tab. VII, answer to May 18 |
18 |
13 |
37 |
Equ. Moon’s Anom. |
- |
13 |
| Moon’s annual Equation add |
|
+ |
14 |
Anom. cor. |
10 |
22 |
38 |
| Mean time corrected |
18 |
13 |
51 |
Sun’s Equat. |
+ |
1 |
15 |
| Moon’s elliptic Equation subtract |
- |
5 |
38 |
Moon’s Ano. |
10 |
23 |
53 |
| Mean time equated |
18 |
8 |
13 |
|
h. |
m. |
|
| Sun’s Equation add |
+ |
2 |
19 |
Moon’s ann. Equ. |
0 |
14 |
add |
| |
|
Her ellipt. Equ. |
5 |
38 |
sub. |
| |
| True time of Opposition, May |
18 |
10 |
32 |
Sun’s Equation |
2 |
19 |
add |
Namely, the 18th day, at 32 minutes past 10 at night.
The Leap-years are allowed for in the Tables, so as to give no
Trouble in these Calculations.
194To compute the time of New and Full Moon in a given year and month, of
any particular Century, between the Christian Æra[78] and 18th Century.
Precept I. Find the like year of the 18th Century in Table I., for
New Moon, or Table III., for Full Moon; and take out the New or
Full Moon in March for that year, with the Anomalies of the Sun and
Moon.
II. From Table V, take as many compleat Centuries, as when subtracted
from the above year of the 18th Century, will answer to the
given year; and take out the Conjunctions and Anomalies of these
Centuries.
III. Subtract the Conjunctions and Anomalies of these Centuries from
those of the New or Full Moon in March above taken out, and the
remainders will shew the mean time of New or Full Moon in March
the given year, with the Anomalies of the Sun and Moon at that
time. Then, work in all respects for the true time of the proposed
New or Full Moon, as taught by the Precepts already given § 355.
EXAMPLE I.
To find the time of New Moon in July 1581, O. S.
From 1781 subtract 200 years, and there remains 1581.
| |
Days |
Hours |
Min. |
Sun’s Anom. |
Moon’s Ano. |
| s |
° |
ʹ |
s |
° |
ʹ |
| Table I. Mean time of New Moon in March 1781 |
13 |
7 |
52 |
8 |
23 |
37 |
0 |
0 |
53 |
| Tab. V. Conj. and Anom. for 200 years subtract |
8 |
16 |
22 |
0 |
6 |
42 |
5 |
0 |
44 |
| Remain the Conj. and Anom. for March 1581 |
4 |
15 |
30 |
8 |
16 |
55 |
7 |
0 |
9 |
| Tab. VI. Add, for five Lunations, to bring it to July |
147 |
15 |
40 |
4 |
25 |
32 |
4 |
9 |
5 |
| The sums are |
152 |
7 |
10 |
1 |
12 |
27 |
11 |
9 |
14 |
| The Days in Tab. VII. answer to July 30th |
30 |
7 |
10 |
Equ. Moon’s Anom. |
+ |
13 |
| Sum of the three Equations subtract |
- |
7 |
9 |
Anom. cor. |
11 |
9 |
27 |
| |
|
Sun’s Equat. |
- |
1 |
16 |
| |
| True time of Conjunction, July |
30 |
0 |
1 |
Moon’s Ano. |
11 |
8 |
11 |
| Which is the 30th day, at one minute
past noon, as shewn by well regulated Clocks or Watches |
Moon’s ann. Eq. |
0h |
14m |
sub. |
| Her ellipt. Equ. |
3 |
35 |
sub. |
| Sun’s Equation |
3 |
20 |
sub. |
| Sum |
7 |
9 |
sub. |
195EXAMPLE II.
To find the time of Full Moon in April A. D. 30, O. S.
From 1730 subtract 1700, and there remains 30.
| |
Days |
Hours |
Min. |
Sun’s Anom. |
Moon’s Ano. |
| s |
° |
ʹ |
s |
° |
ʹ |
| Tab. III. Mean time of Full Moon in March 1730 |
22 |
6 |
58 |
9 |
2 |
40 |
3 |
13 |
23 |
| Tab. V. Conj. and Anom. for 1700 years subtract |
14 |
17 |
37 |
11 |
28 |
46 |
10 |
29 |
36 |
| Rem. the Opposition and Anom. in March A. D. 30 |
7 |
13 |
21 |
9 |
3 |
54 |
4 |
13 |
47 |
| Tab. V. Add, for one Lunation, to bring it into April |
29 |
12 |
44 |
0 |
29 |
6 |
0 |
25 |
49 |
| The sums are |
37 |
2 |
5 |
10 |
3 |
0 |
5 |
9 |
36 |
| The Days in Tab. VII. answer to April 6 |
6 |
2 |
5 |
Equ. Moon’s Anom. |
- |
17 |
| To which add the sum of the three Equations |
|
6 |
1 |
Anom. cor. |
5 |
9 |
19 |
| |
|
Sun’s Equat. |
+ |
1 |
35 |
| |
| True time of Opposition April A. D. 30 |
6 |
8 |
6 |
Moon’s Ano. |
5 |
10 |
54 |
| Which is the 6th day, at 6 minutes past
8 in the Evening. And thus, the time of New or Full Moon may be found for
any given year and month after the Christian Æra. |
|
Moon’s ann. Eq. |
0h |
18m |
add |
| Her ellipt. Equ. |
2 |
46 |
add |
| Sun’s Equat. |
2 |
57 |
add |
| Sum |
6 |
1 |
add |
Remark.
N. B. Sometimes it happens that the days annexed to the Centuries
in Table V are more in number than the days on which the New or
Full Moon happens in March the year of the 18th Century, with
which the computation begins; as in the third following Example,
viz. for the Full Moon in March the year before Christ 721: in
which case, a Lunation and it’s Anomalies must be added, from Table
VI, to the days and Anomalies of the New or Full Moon in March;
and then, subtraction can be made: and having gained a remainder,
work in all respects as taught in § 355.
To find the time of New or Full Moon in any given year and month before the Christian Æra.
356. Precept I. Find a year of the 18th Century, which added to
the given number of years before Christ, diminished by one, shall
make a number of whole Centuries.
196II. Find this number of Centuries in Table V, and subtract the
Time and Anomalies answering to it from the Time and Anomalies
answering to the mean New or Full Moon in March the year of the 18th
Century thus found; and they will give the mean time of New or Full
Moon in March the given year before Christ, with the Anomalies
answering thereto. Whence the true time of that New or Full Moon
may be had by the Precepts already delivered § 355.
III. The Tables are calculated for the Meridian of London: therefore,
in computing for any place westward of London, four minutes of
time must be subtracted from the time shewn by the Tables, for every
degree the place is westward; and added for every degree it is eastward.
See § 210.
EXAMPLE I.
To find the time of New Moon at London and Athens in March, the year before Christ 424.
The years 423 added to 1777 make 2200, or 22 Centuries.
| |
Days |
Hours |
Min. |
Sun’s Anom. |
Moon’s Ano. |
| s |
° |
ʹ |
s |
° |
ʹ |
| Tab. I. Mean New Moon in March A. D. 1777 |
27 |
7 |
53 |
9 |
7 |
27 |
5 |
25 |
51 |
| From which subtract 2200 years in Tab. V. |
6 |
21 |
47 |
11 |
16 |
26 |
4 |
20 |
37 |
| Mean Conj. and Anom. in March before Chr. 424 |
20 |
10 |
6 |
9 |
21 |
1 |
1 |
5 |
14 |
| Which with, the total of the three Equations added |
|
9 |
20 |
Equ. Moon’s Anom. |
- |
19 |
| |
|
Anom. cor. |
1 |
4 |
55 |
| |
| Gives the true time of Conjunction |
20 |
19 |
26 |
Sun’s Equat. |
+ |
1 |
48 |
| Which was the 21st day of March, at
26 minutes past 7 in the morning at London: and if 1 hour 35 minutes
be added for Athens, which is 23° 52ʹ east of the meridian of London, we
have the time at Athens; namely, 1 minute past 9 in the morning. |
|
Moon’s Ano. |
1 |
6 |
43 |
| Moon’s ann. Eq. |
0h |
20m |
add |
| Her ellipt. Equ. |
5 |
43 |
add |
| Sun’s Equation |
3 |
17 |
add |
| Total |
9 |
20 |
add |
197
EXAMPLE II.
To find the time of Full Moon in October, the year before Christ 4030.
The years 1771 added to 4029 make 5800, or 58 Centuries.
| |
Days |
Hours |
Min. |
Sun’s Anom. |
Moon’s Ano. |
| s |
° |
ʹ |
s |
° |
ʹ |
| Tab. III. From the mean Full Moon in March 1771 |
19 |
7 |
11 |
8 |
29 |
6 |
7 |
22 |
30 |
| Tab. V. Subtr. the numbers for 5800 years |
|
5000 |
10 |
7 |
56 |
10 |
23 |
56 |
0 |
17 |
36 |
| 800 |
5 |
4 |
43 |
11 |
27 |
43 |
7 |
7 |
7 |
| Which collected make |
15 |
12 |
39 |
10 |
21 |
39 |
7 |
24 |
43 |
| Rem. the mean Full Moon &c. March before Chr. 4030 |
3 |
18 |
32 |
10 |
7 |
27 |
11 |
27 |
47 |
| To which add eight Lunations to carry it to October |
236 |
5 |
52 |
7 |
22 |
50 |
6 |
26 |
32 |
| And the several sums will be |
240 |
0 |
24 |
6 |
0 |
17 |
6 |
24 |
19 |
| Which, for Full Moon day, Tab. VII, is October 26 |
26 |
0 |
24 |
|
h. |
m. |
|
| Moon’s ellipt. Equation subtr. there being none besides |
|
3 |
28 |
Moon’s Ann. Eq. |
0 |
0 |
add |
| |
Moon’s ellipt. Eq. |
3 |
28 |
sub. |
| |
| Rem. the true time of Full Moon, October |
25 |
20 |
56 |
Sun’s Equation |
0 |
0 |
add |
| Which is the 26th day, at 8 hours 26 minutes in the forenoon[79]. |
|
Total |
3 |
28 |
sub. |
Age of the world uncertain.
By the method prescribed § 248 it will be found, that the Autumnal
Equinox in the year before Christ 4030, fell on the 26th of October;
as this Example shews the Full Moon to have been on the same day:
and by working as hereafter taught, it will appear that the Dominical
Letter was then G, which shews the 26th of that October to have been on
a Friday; namely our sixth day of the week, but the Ante-Mosaic fifth
day. And as, according to Genesis, chap. i. ver. 14. the Sun and
Moon were created on the fourth day of the week, those who are of
opinion that the world was made at the time of the Autumnal Equinox,
and that the Moon at her first appearance was in full lustre, opposite
to the Sun, or nearly so, may perhaps look upon this as a Criterion
for ascertaining the year of the creation; since it shews the Moon to
have been Full the next day after she was made: and this is only 9
years sooner than Rheinholt makes it, and 11 years later than according
to Lange. Whereas, they who maintain that the world was created
in the 4007th year before Christ, with the Sun on the Autumnal
Equinoctial Point, October 26, and the Moon then Full; will find, if
they compute by the best Tables extant, that the Moon was New,
instead of being Full, on that day.
198If it could be proved from the writings of Moses that the Sun was
created on the point of the Autumnal Equinox, and the Moon in
opposition; as well as it can be proved that these Luminaries were made
(or according to some, did not shine out till) on the fourth day of the
creation-week, there would be Data enough for ascertaining the age
of the world: for supposing the Moon to have been Full on an Equinoctial
Day, which was the fourth day of the week, it would require
many thousands of years to bring these three characters together again.
For, the soonest in which the Moon returns to be New or Full on
the same days of the Months as before, is 19 years wanting an hour
and half, but then the days of the week return not to the same days of
the months in less than 28 years, in which time the Moon has gone
through one Course of Lunations, and 9 years over; therefore a co-incidence
of the Full Moon and day of the Week and Month cannot
happen in that time, and if we multiply 19 by 28, which is the nearest
co-incidence of these three characters, namely 532 years; the Moon’s
falling back an hour and half every 19 years will amount to 42 hours
in so many years; and the Equinox will have anticipated five days.
From all which we may venture to say, that 200000 years would not
be sufficient to bring all these circumstances together again.
EXAMPLE III.
To find the time of Full Moon at Babylon in March, the year before Christ 721.
The years 720 added to 1780 make 2500, or 25 Centuries.
| |
Days |
Hours |
Min. |
Sun’s Anom. |
Moon’s Ano. |
| s |
° |
ʹ |
s |
° |
ʹ |
| Tab. I. To the mean F. Moon and Anom. in Mar. 1780 |
9 |
4 |
41 |
8 |
19 |
48 |
7 |
8 |
10 |
| Add one Lunation and it’s Anomalies from Tab. VI[80] |
29 |
12 |
44 |
0 |
29 |
6 |
0 |
25 |
49 |
| The several sums are |
38 |
17 |
25 |
9 |
18 |
54 |
8 |
3 |
59 |
| Fr. which subt. the Days & Anom. of 2500 years, Tab. V |
19 |
22 |
20 |
11 |
26 |
19 |
6 |
6 |
43 |
| Rem. the mean time and Anom. of F.M. in Mar. b.C. 721 |
18 |
19 |
5 |
9 |
22 |
25 |
1 |
27 |
16 |
| To which add the sum of the three Equations |
+ |
11 |
36 |
Equ. Moon’s Anom. |
- |
18 |
| And it gives the true time of Full Moon, Mar. b.C. 721 |
18 |
6 |
41 |
Anom. cor. |
1 |
26 |
48 |
| |
|
Sun’s Equat. |
+ |
1 |
47 |
| Which was the 19th day, at 41 minutes
past 6 in the evening, at London; to which time, if[81] 2 hours 51
minutes be added, we shall have the time at Babylon, namely,
9 hours 51 minutes. |
|
Moon’s Anom. |
1 |
28 |
35 |
| Moon’s ann. Eq. |
0h |
20m |
add |
| Her ellipt. Equ. |
8 |
1 |
add |
| Sun’s Equation |
3 |
15 |
add |
| Sum |
11 |
36 |
add |
199357. To know whether the Sun will be eclipsed or no, at the
time of any given New Moon; collect the Sun’s distance from the
Node at that time, and if it be less than 17 degrees he will be eclipsed,
otherwise not.
EXAMPLE.
For the time of New Moon in April 1764.
| |
Sun from Node |
| s |
° |
ʹ |
| Table II, mean New Moon in March 1764, New Stile, |
11 |
4 |
57 |
| Table VI, add for 1 Lunation to carry it to April |
1 |
0 |
40 |
| Sun’s distance from the Node at New Moon in April |
0 |
5 |
37 |
Which, being within the above limit, the Sun must be eclipsed: and
therefore, we proceed to find the rest of the Elements for computing
this Eclipse.
To find the Moons Horizontal Parallax, or the Angle of the Earth’s semi-diameter as seen from the Moon.
Second Element.
358. Precept. Having found the Moon’s mean Anomaly for the
above time, by the first and second Precepts of § 355, enter the XVth
Table with the signs and degrees of that Anomaly, and thereby take
out the Moon’s Horizontal Parallax: only note, that this is given but
to every 6th degree of Anomaly in the Table, because it is very easy
to make proper allowance by sight. So the Moon’s Horizontal Parallax
April the 1st 1764, at 10 hours 25 minutes in the Forenoon, answering
to her mean Anomaly at that time (namely 11s 9° 21ʹ) is
55ʹ 7ʺ; which, diminished by 10ʺ, the Sun’s constant Horizontal
Parallax, gives for the semi-diameter of the Earth’s Disc 54ʹ 57ʺ.
To find the Sun’s true Place, and his distance from the nearest Solstice.
Third Element.
359. Precept I. We are to consider, that the beginning of Aries
and of Libra, which are the Equinoctial Points, are equidistant from the
beginning of Cancer and of Capricorn, which are the Solstitial Points.
Hence, when we know in what Sign and Degree the Sun is, we can
easily find his distance from the nearest Solstice. Now, to find the
Sun’s Place, or Longitude from Aries, April the 1st, 1764, at 10 hours
21 minutes in the Forenoon; being the equated time of New Moon.
200Precept II. This being to the time of New Moon, take out the
Sun’s mean Place and Anomaly from Table II. for that time, and the
Equation of his mean Place from Table XII by his Anomaly; adding
the Equation to his mean Place or subtracting it from the same, as the
Table directs, will give his true Place.
EXAMPLE.
| |
Sun’s Long. from Aries. |
Sun’s mean Anomaly. |
| s |
° |
ʹ |
s |
° |
ʹ |
| Table I. To the Sun’s mean Place and Anomaly at the mean time of New Moon in March 1764, N. S. |
11 |
17 |
7 |
8 |
2 |
23 |
| Add the same from Tab. VI. for one Lunation, to carry it to April |
0 |
29 |
6 |
0 |
29 |
6 |
| Mean Place and Anomaly at the time of New Moon in April |
0 |
10 |
13 |
9 |
1 |
29 |
| To which place add the Sun’s Equation from Tab. XII. |
|
1 |
56 |
Equal |
1° |
56ʹ |
| And it gives the Sun’s true place |
0 |
12 |
9 |
Additive. |
Which is Aries 12° 9ʹ; and this, when taken from three Signs, or the
beginning of Cancer, leaves 2 signs 17 deg. 51 min., or 77° 51ʹ for
the Sun’s distance from the then nearest Solstice.
360. But because the Sun’s true Place is often wanted when the
Moon is neither New nor Full, we shall next shew how it may be
found for any given moment of time: though this be digressing from
our present purpose.
In Table XVI find the nearest lesser year to that in which the Sun’s
Place is sought; and take out the Sun’s mean Longitude and Anomaly
answering thereto; to which add his mean motion and Anomaly
for the compleat residue of the years, with the month, day, hour,
and minute, all taken from the same Table, and you have the Sun’s
mean Longitude and Anomaly for the given time. Then, from
Table XII take out the Sun’s Equation by means of his Anomaly
(making proportions for the odd minutes of Anomaly) which Equation
being added to or subtracted from the Sun’s mean Longitude
from Aries, as the titles in the Table direct, gives his true Place, or
Longitude from the beginning of Aries, reckoned according to the
order of the Signs § 354.
201
EXAMPLE.
To find the Sun’s true Place April 30th, A. D. 1757, at 18 minutes 40 seconds past 10 in the morning.
| |
Sun’s Long. |
Sun’s Anom. |
| s |
° |
ʹ |
ʺ |
s |
° |
ʹ |
| The year next less than 1757 in the Table is 1753, at the beginning of which, the
Sun’s mean Longitude from the beginning of Aries, and his mean Anomaly, is |
9 |
10 |
16 |
52 |
6 |
1 |
38 |
| To which add his mean Mot. and Anom. for four years to make 1757 |
0 |
0 |
1 |
49 |
11 |
29 |
58 |
| And likewise his mean Mot. and Anom. for |
|
April |
2 |
28 |
42 |
30 |
2 |
28 |
42 |
| days |
29 |
0 |
28 |
35 |
2 |
0 |
28 |
35 |
| hours |
22 |
|
0 |
54 |
13 |
|
0 |
54 |
| min. |
18 |
|
|
0 |
44 |
|
|
1 |
| sec. |
49 |
|
|
|
2 |
|
|
0 |
| Sun’s mean Longitude and Anomaly for the given time is |
1 |
8 |
31 |
12 |
9 |
29 |
48 |
| To which add the Equation of the Sun’s mean Place |
|
1 |
40 |
14 |
Sun’s Eq. |
| And it gives his true Place, viz. ♉ Taurus 10° 11ʹ 26ʺ |
1 |
10 |
11 |
26 |
1° |
40ʹ |
14ʺ |
N. B. In leap-years after February, the Sun’s mean Motion and Anomaly must be taken
out for the day next after the given one.
361. To calculate the Sun’s true Place for any time in a given year before
the first year of Christ: subtract the mean Motions and Anomalies for
the compleat hundreds next above the given year; to the remainder add
those for the residue of years, months, &c. and then work in all respects
as above taught.
EXAMPLE.
To find the Suns true Place May the 28th at 4 hours 3 min. 42 sec. in the afternoon, the year before Christ 585, which was a Leap year[82].
| |
Sun’s Long. |
Sun’s Anom. |
| s |
° |
ʹ |
ʺ |
s |
° |
ʹ |
| From the Sun’s mean Longitude and Anomaly
at the beginning of the year Christ 1 |
9 |
7 |
53 |
10 |
6 |
29 |
54 |
| Subtract his mean Motion and Anomaly for
600 years |
0 |
4 |
32 |
0 |
11 |
24 |
2 |
| And the remainder, or radix, is |
9 |
3 |
21 |
10 |
7 |
5 |
52 |
| To which add what 585 wants of 600, viz. 15 years |
11 |
29 |
22 |
27 |
11 |
29 |
7 |
| And also those of |
|
May |
3 |
28 |
16 |
40 |
3 |
28 |
17 |
| days |
28 |
Bissextile |
0 |
28 |
35 |
2 |
0 |
28 |
35 |
| hours |
4 |
|
0 |
9 |
51 |
|
0 |
10 |
| min. |
3 |
|
|
0 |
7 |
|
| |
| sec. |
42 |
|
|
|
2 |
0 |
2 |
1 |
| |
|
Sun’s Anom. |
| |
| Sun’s mean Long. May 28th, at 4 hour
3 min. 24 sec. afternoon |
1 |
29 |
45 |
19 |
|
| |
| Equation of the Sun’s mean Place subtract |
|
|
2 |
2 |
2ʹ 22ʺ |
| |
|
Sun’s Equat. |
| |
| Rem. his true Place for the same time, viz. ♉ Taurus 29° 43ʹ 17ʺ |
1 |
29 |
43 |
17 |
subtract. |
202N. B. As the Longitudes or Places of all the visible Stars in the
Heavens are well known, we have an easy method of finding the
Sun’s true Place in the Ecliptic: for the Sun is directly opposite to that
Point of the Ecliptic which comes to the Meridian at mid-night.
To find the Sun’s Declination.
Fourth Element.
362. Precept. Enter Table XVII with the Signs and Degrees of
the Sun’s Place; and making proportions, take out his Declination
answering thereto. If the Signs are at the head of the Table, the
Degrees are at the left hand; but if the Signs are at the foot of the
Table, the Degrees are at the right hand. So, the Sun’s Declination
answering to his true Place (found by § 359 to be 0s 12° 9ʹ) is 4
degrees 48 minutes 54 seconds, making allowance for the 9ʹ that
his Place exceeds 12°.
To find the Angle of the Moon’s visible Path with the Ecliptic.
Fifth Element.
Precept. This we may state at 5 degrees 38 minutes, as near
enough for the purpose; since it is never above 8 minutes of a degree
more or less.
To find the Moon’s Latitude.
Sixth Element.
363. Precept. Having found the Sun’s distance from the Ascending
Node by § 357, at the mean time of New Moon, and his Anomaly
for that time by § 359, find the Equation of the Node in Table
XIII, by the Sun’s Anomaly, and the Equation of the Sun’s mean
Place in Table XII by his Anomaly: these two Equations applied (as
the titles direct) to the Sun’s mean distance from the Ascending Node,
give his true distance from it, and also the Moon’s true distance at the
time of Change: but when the Moon is Full, this distance must be
increased by the addition of 6 Signs, which will then be the Moon’s
true distance from the same Node.
The Moon’s true distance from the Ascending Node is called the
Argument of the Moon’s Latitude; with the Signs of which, at the
head of Table XIV, and Degrees at the left hand, or with the Signs
at the foot of the Table and Degrees at the right hand, take out
the Moon’s Latitude: which is North Ascending, North Descending,
South Ascending, or South Descending, according to the letters NA, ND,
SA or SD, annexed to the Signs of the said Argument.
Plate XII.
The Geometrical Construction of Solar and Lunar Eclipses.
J. Ferguson delin.
J. Mynde Sculp.
203
EXAMPLE.
| |
s |
° |
ʹ |
| Sun’s mean Dist. from the [83]Node at New Moon in April 1764 |
0 |
5 |
37 |
| To which add the Equation of the Node |
|
+ |
10 |
| And it gives the Sun’s corrected Distance from the Node |
0 |
5 |
47 |
| To which cor. Dist. add the Eq. of the Sun’s mean Place |
+ |
1 |
56 |
| And it gives the Sun’s true Distance from the Node |
0 |
7 |
43 |
Which, being at the time of New Moon, is the Argument of
Latitude; and in Table XIV, (making proportions for the 43ʹ) shews
the Moon’s Latitude to be 40ʹ 9ʺ North Ascending[84].
To find the Moon’s true hourly Motion from the Sun.
Seventh Element.
364. Precept. With the Moon’s Anomaly enter Table XV, and
thereby take out her true hourly Motion: then with the Sun’s Anomaly
take out his true hourly Motion from the same Table: which
done, subtract the Sun’s hourly Motion from the Moon’s, and the remainder
will be the Moon’s true hourly Motion from the Sun; which,
for the above time § 359, is 27ʹ 50ʺ.
To find the Semi-diameters of the Sun and Moon as seen from the Earth at the above-mentioned time.
Eighth and Ninth Elements.
365. Precept. Enter the XVth Table with the Sun’s Anomaly,
and thereby take out his Semi-diameter; and in the same manner
take out the Moon’s Semi-diameter by her Anomaly. The former of
which for the above time will be found to be 16ʹ 6ʺ; the latter
14ʹ 58ʺ.
To find the Semi-diameter of the Penumbra.
Tenth Element.
366. Precept. Add the Sun’s semi-diameter to the Moon’s, and
their Sum will be the Semi-diameter of the Penumbra; namely, at the
above time 31ʹ 4ʺ.
204366. Having found the proper Elements or Requisites for the Sun’s
Eclipse April 1, 1764, and intending to project this Eclipse Geometrically,
we shall now collect them under the eye, that they may be the
more readily found as they are wanted in order for the Projection.
The proper Elements collected.
|
D |
H |
M |
| 367. I. The true time of Conj. or New Moon April |
1 |
10 |
25 |
|
° |
ʹ |
ʺ |
| II. The Earth’s Semi-Disc, which is equal to the Moon’s Horizontal Parallax 55ʹ 7ʺ diminished by the Sun’s Horizontal Parallax which is always 10ʺ |
0 |
54 |
57 |
| |
| III. The Sun’s distance from the nearest Solstice, viz. ♋ |
77 |
51 |
0 |
| |
| IV. The Sun’s Declination, North |
4 |
48 |
54 |
| |
| V. The Angle of the Moon’s vis. path with the Eclipt. |
5 |
38 |
0 |
| |
| VI. The Moon’s true Latitude, North Ascending |
|
40 |
9 |
| |
| VII. The Moon’s true Horary Motion from the Sun |
|
27 |
50 |
| |
| VIII. The Sun’s Semi-diameter |
|
16 |
6 |
| |
| IX. The Moon’s Semi-diameter |
|
14 |
58 |
| |
| X. The Semi-diameter of the Penumbra |
|
31 |
4 |
368. Having collected these Elements or Requisites, the following
part of the work may be very much facilitated by means of a good
Sector, with the use of which the reader should be so well acquainted,
as to know how to open it to any given Radius, as far as it will go;
and to take off the Chord or Sine of any Arc of that Radius. This is
done by first taking the extent of the given Radius in your Compasses,
and then opening the Sector so as the distance cross-wise between the
ends of the lines of Sines or Chords at S or C, from Leg to Leg of the
Sector, may be equal to that extent; then, without altering the Sector,
take the Sine or Chord of the given Arc with your Compasses extended
cross-wise from Leg to Leg of the Sector in these lines. But if the operator
has not a Sector, he must construct these lines to such different lengths
as he wants them in the projection. And lest this Treatise should fall
into the hands of any person who would wish to project the Figure of
a solar or lunar Eclipse, and has not a Sector to do it by, we shall
shew how he may make a line of Sines or Chords to any Radius.
Fig. II.
How to make a line of Chords.
Pl. XII.369. Draw the right line BCA at pleasure; and upon C as a Center,
with the distance CA or CB as a Radius, describe the Semi-circle BDA;
and from the Center C draw AC perpendicular to BCA. Then divide the
Quadrants AD and BD each into 90 equal parts or degrees, and join the
right line AD for the Chord of the Quadrant AD. This done, setting
one foot of the Compasses in A, extend the other to the different divisions
of the Quadrant AD; and so transfer them to the right line AD as in
205the Figure, and you have a line of Chords AD to the Radius CA.
N. B. 60 Degrees on the Line of Chords is always equal to the Radius
of the Circle it is made from; as is evident by the Figure, where the
Arch E, whose Center is A, drawn from 60 on the Quadrant AD, cuts
the Chord line in 60 degrees, and terminates in the Center C.
And of Sines.
Then, from the divisions or degrees of the Quadrant BD, draw
lines parallel to CD, which will fall perpendicularly on the Radius BC,
dividing it into a line of Sines; and it will be near enough for the present
purpose, to have them to every fifth Degree, as in the Figure. And
thus the young Tyro may supply himself with Chords and Sines, if he has
not a Sector. But as the Sector greatly shortens the work, we shall describe
the projection as done by it, so far as Signs and Chords are required.
Fig. II.
Earth’s Semi-Disc.
370. Make a Scale of any convenient length (six inches at least) as
AC, and divide it into as many equal parts as the semi-diameter of the
Earth’s Disc contains minutes, which in this construction of the Eclipse
for London in April 1764, is 54 minutes and 57 seconds; but as it
wants only 3ʺ of 55ʹ the Scale may be divided into 55 equal parts,
as in the Figure. Then, with the whole length of the Scale as a
Radius, setting one foot of your Compasses in C as a center, describe the
Semi-circle AMB for the northern Hemisphere or Semi-disc of the
Earth, as seen from the Sun at that time. Had the Place for which
the Construction is made been in South Latitude, this Semi-circle
would have been the Southern Hemisphere of the Earth’s Disc.
Axis of the Ecliptic.
371. Upon the center C raise the straight line CH for the Axis of the
Ecliptic, perpendicular to ACB.
North Pole of the Earth.
372. Make a line of Chords to the Radius AC, and taking from
thence the Chord of
231⁄2
Degrees, set it off from H to g and to h, on
the periphery of the Semi-disc; and draw the straight line gNh, in
which the North Pole of the Disc is always found.
373. While the Sun is in Aries, Taurus, Gemini, Cancer, Leo,
and Virgo, the North Pole of the Disc is illuminated; but while the Sun
is in Libra, Scorpio, Sagittary, Capricorn, and Aquarius, the North
Pole is hid in the obscure part behind the Disc.
374. And, whilst the Sun is in Capricorn, Aquarius, Pisces, Aries,
Taurus, and Gemini, the Earth’s Axis CP lies to the right hand of the
Axis of the Ecliptic CH as seen from the Sun, and to the left hand
while the Sun is in the other six Signs.
Earth’s Axis.
Universal Meridian.
375. Make a line of Sines equal in length to Ng or Nh, and
take off with your Compasses from it the Sine of the Sun’s distance
from the nearest Solstice, which in the present case is 77° 51ʹ § 367,
206and set that distance to the right hand, from N to P, on the line gNh,
because the Sun being in Aries § 359, the Earth’s Axis lies to the right
hand of the Axis of the Ecliptic § 374: then draw the straight line
CXIIP, for the Earth’s Axis and the Universal Meridian; of both
which P is the North Pole.
Path of a given Place on the Disc as seen from the Sun.
376. To draw the parallel of Latitude of any given Place (suppose
London) which parallel is the visible Path of the Place On the Disc, as
seen from the Sun, from the time that the Sun rises till it sets; subtract
the Latitude of the Place (London)
511⁄2
degrees from 90 degrees,
and there remains
381⁄2;
which take from the Line of Chords in your
Compasses, and set it from h (where the Universal Meridian CP
cuts the periphery of the Semi-disc) to VI and VI; and draw the
occult Line VILVI. Then, on the left hand of the Earth’s Axis,
set off the Chord of the Sun’s Declination 4° 48ʹ 5ʺ § 367, from VI
to D and to F; set off the same on the right hand from VI to E and
to G; and draw the occult Lines DsE and FXIIG parallel to VI L VI.
Situation of the Place on the Disk from Sun-rise to Sun-set.
377. Bisect s XII in K, and through the point K draw the black
Line VIKV1 parallel to the occult or dotted Line VILVI. Then,
making AC the Radius or length of a Line of Lines, set off the Sine
of
381⁄2
degrees, the Co-Latitude of London, from K to VI and VI;
and with that extent as a Radius, describe the Semi-Circle VI 7 8 9
&c. and divide it into 12 equal parts, beginning at VI. From these
divisions, draw the occult Lines 7m, 8l, 9k, &c. all to the Line VIKVI,
and parallel to CXIIP. Then, with KXII as a Radius, describe the
Circle abcdef, round the Center K, and divide the Quadrant aXII into
six equal parts, as ab, bc, cd, de, &c. Then, through these points of
division b, c, d, e, and f, draw the occult Lines VIIbV, VIIIcIIII,
IXdIII, &c. intersecting the former Lines 7m, 8l, 9k, 10i, &c. in
the points VII, VIII, IX, X, XI, &c. which points mark the situation
of London on the Earth’s Disc as seen from the Sun at these hours
respectively, from six in the morning till six at night: and if the
elliptic Curve VI, VII, VIII, &c. be drawn through these points, it
will represent the parallel of London, or the path it seems to describe
as viewed from the Sun, from Sun-rise to Sun-set. N.B. When the
Sun’s Declination is North, the said Curve is the diurnal Path of
London; and the opposite part VIsVI is it’s nocturnal Path behind
the Disc, or in the obscure part thereof, § 338, 339. But if the Sun’s
Declination had been South, the Curve VIsVI would have been the
diurnal path of London; in which case the Lines 7m, 8l, &c. must have
been continued thro’ the right Line VIKVI, and their lengths beyond
that line determined by dividing the Quadrant s a of the little Circle
207abcd into six equal parts, and drawing the parallels VIIb, VIIIc &c.
through that division, in the same manner as done on the side K XII;
and the Curve VII, VIII, IX, &c. would have been the nocturnal
Path. It is requisite to divide the hours of the diurnal Path into
quarters, as in the Diagram; and if possible into minutes also.
Axis of the Moon’s Orbit.
378. From the Line of Chords § 372 take the Angle of the Moon’s
visible Path with the Ecliptic, viz. 5° 38ʹ § 367: and note, that when
the Moon’s Latitude is North Ascending, as in the present case, the
Chord of this Angle must be set off to the left hand of the Axis of the
Ecliptic CH, as from H to M, and the right line CM drawn for the
Axis of the Moon’s Orbit: but when the Moon’s Latitude is North
Descending, this Angle and Axis must be set to the right hand, or
from H toward h. When the Moon’s Latitude South Ascending, the Axis
of her Orbit lies the same way as when her Latitude is North Ascending;
and when South Descending, the same way as when North Descending.
Path of the Penumbra’s center over the Earth.
379. Take the Moon’s Latitude, 40ʹ 9ʺ § 367, from the Scale CA,
and set it from C to T on the Axis of the Ecliptic; and through T,
at right Angles to the Axis of the Moon’s Orbit CM, draw the straight
Line RTS; which is the Moon’s Path, or Line that the center of her
shadow and Penumbra describes in going over the Earth’s Disc. The
Point T in the Axis of the Ecliptic is the Place where the true Conjunction
of the Sun and Moon falls, according to the Tables; and the
Point W, in the Axis of the Moon’s Orbit, is that where the center of
the Penumbra approaches nearest to the center of the Earth’s Disc, and
consequently the middle of the general Eclipse.
It’s Place on the Earth’s Disc shewn for every minute of it’s Transit.
380. Take the Moon’s true Horary Motion from the Sun 27ʹ 50ʺ
§ 367, from the Scale CA with your Compasses (every division of the
Scale being a minute of a Degree) and with that extent make marks
in the Line of the Moon’s Path RTS: then divide each of these equal
spaces by dots into 60 equal parts or horary minutes, and set the
hours to every 60th minute, in such a manner that the dot; signifying
the precise minute of New Moon by the Tables, may fall in the
Point T where the Axis of the Ecliptic cuts the Line of the Moon’s
Path; which, in this Eclipse, is the 25th minute past ten in the Forenoon:
and then the other marks will shew the places on the Earth’s
Disc where the center of the Penumbra is, at the hours and minutes
denoted by them, during its transit over the Earth.
Middle of the Eclipse.
It’s Phases.
381. Apply one side of a Square to the Line of the Moon’s Path,
and move the Square backward or forward until the other side cuts the
same hour and minute both in the Path of the Place (London, in this
Construction) and Path of the Moon; and that minute, cut at the same
208time in both Paths, will be the precise minute of visible Conjunction
of the Sun and Moon at London, and therefore the time of greatest
obscuration, or middle of the Eclipse at London; which time, in this
Projection, falls at t, 34 minutes past 10 in the Moon’s Path; and at
u, 34 minutes past 10 in the Path of London. Then, upon the Point
u as a center, describe the Circle zYy whose Radius uy is equal to the
Sun’s semi-diameter 16ʹ 6ʺ § 367, taken from the Scale CA: And
upon the Point t as a center, describe the Circle Hy whose Radius is
equal to the Moon’s semi-diameter 14ʹ 58ʺ § 367, taken from the
same Scale. The Circle zYy represents the Disc of the Sun as seen
from the Earth, and the Circle Hy the Disc of the Moon. The
portion of the Sun’s Disc cut off by the Moon’s shews the Quantity
of the Eclipse at the time of greatest obscuration: and if a right Line
as yz be drawn across the Sun’s Disc through t and u, the minute of
greatest obscuration in both Paths, and divided into 12 equal parts, it
will shew what number of Digits are then eclipsed. If these two
Circles do not touch one another, the Eclipse will not be visible at
the given Place.
It’s beginning and ending.
382. Lastly, take the Semi-diameter of the Penumbra 31ʹ 4ʺ § 367,
from the Scale CA with your Compasses; and setting one foot in
the Moon’s Path, to the left hand of the Axis of the Ecliptic, direct
the other toward the Path of London; and carry this extent backwards
or forwards until both Points of the Compasses fall into the same
instants of time in both Paths: which will denote the time of the beginning
of the Eclipse: then, do the same on the right hand of the Axis
of the Ecliptic, and where both Points mark the same instants in both
Paths, they will shew at what time the Eclipse ends. These trials give
the Points R in the Moon’s Path and r in the Path of London, namely
9 minutes past 9 in the Morning for the beginning of the Eclipse at
London, April 1, 1764: t and u for the middle or greatest obscuration,
at 35 minutes past 10; when the Eclipse will be barely annular on
the Sun’s lower-most edge, and only two thirds of a Digit left free on
his upper-most edge: and for the end of the Eclipse, S in the Moon’s
Path and x in the Path of London, at 4 minutes past 12 at Noon.
In this Construction it is supposed that the Equator, Tropics, Parallel
of London, and Meridians through every 15th degree of Longitude
are projected in visible Lines on the Earth’s Disc, as seen from
the Sun at almost an infinite distance; that the Angle under which
the Moon’s diameter is seen, during the time of the Eclipse, continues
invariably the same; that the Moon’s motion is uniform, and her Path
rectilineal, for that time. But all these suppositions do not exactly agree
209with the truth; and therefore, supposing the Elements § 367, given
by the Tables to be perfectly accurate, yet the time and phases of
the Eclipse deduced from it’s Construction will not answer exactly to
what passeth in the Heavens; but may be two or three minutes wrong
though done with the utmost care. Moreover, the Paths of all Places
of considerable Latitude go nearer the center of the Disc as seen from
the Moon than these Constructions make them; because the Earth’s
Disc is projected as if the Earth were a perfect sphere, although it is
known to be a spheroid. Consequently, the Moon’s shadow will go
farther North in places of northern Latitude, and farther South in places
of southern Latitude than these projections answer to. Hence we may
venture to predict that this Eclipse will be more annular at London
(that is, the annulus will be somewhat broader on the southern Limb
of the Sun) than the Diagram shews it.
383. Having shewn how to compute the times and project the phases
of a Solar Eclipse, we now proceed to those of the Lunar. And it has
been already mentioned § 317, that when the Full Moon is within 12
degrees of either of her Nodes, she must be eclipsed. We shall now
enquire whether or no the Moon will be eclipsed May 18, 1761, N. S.
at 32 minutes past 10 at Night. See page 193.
| |
s |
° |
ʹ |
| Sun from Node at Full Moon in March 1761 |
9 |
25 |
27 |
| Add his distance for two Lunations, to bring it into May |
2 |
1 |
20 |
| And his distance at Full Moon in that month is |
11 |
26 |
47 |
Subtract this from a Circle, or 12 Signs, and there will remain 3° 13ʹ;
which is all that the Sun wants of coming round to the Ascending Node;
and the Moon being then opposite to the Sun, must be just as near the
Descending Node: consequently, far within the limit of an Eclipse.
384. Knowing then that the Moon will be eclipsed in May 1761,
we must find her true distance from the Node at that time, by applying
the proper Equations as taught § 363, and then find her true Latitude
as taught in that article.
| |
s |
° |
ʹ |
| Sun’s mean distance from the Node at F. Moon in May 1761 |
11 |
26 |
47 |
| Add the Equation of the Node, for the Sun’s Anomaly 10s 18° 15ʹ[85] |
|
+ |
6 |
| Sun’s mean distance from the Node corrected |
11 |
26 |
53 |
| Add the Equation of the Sun’s mean Place |
+ |
1 |
15 |
| Sun’s true distance from the Ascending Node |
11 |
28 |
8 |
| To which add 6 Signs, See § 363 |
6 |
|
| The sum is the Moon’s true distance from the same Node |
5 |
28 |
8 |
210Or the Argument of her Latitude; which in Table XIV, gives the
Moon’s true Latitude, viz. 9ʹ 56ʺ North Descending.
385. Having by the foregoing precepts § 355 found the true time
of Opposition of the Sun and Moon in a lunar Eclipse, with the Moon’s
Anomaly enter Table XV and take out her horizontal Parallax, also
her true horary Motion and Semi-diameter: and likewise those of the
Sun by his Anomaly, as already taught § 364 & seq. Then add the
Sun’s horizontal Parallax, which is always 10 Seconds, to the Moon’s
horizontal Parallax, and from their sum subtract the Sun’s Semi-diameter;
the remainder will be the Semi-diameter of that part of the
Earth’s shadow which the Moon goes through.
386. From the Sum of the Semi-diameters of the Moon and Earth’s
Shadow, subtract the Moon’s Latitude; the remainder is the parts deficient.
Then, as the Semi-diameter of the Moon is to 6 Digits, so
are the parts deficient to the Digits eclipsed.
387. If the parts deficient be more than the Moon’s Diameter, the
Eclipse will be total with continuance; if less, it will not be total; if
equal, it will be total, but without continuance.
388. Now collect the Elements for projecting this Eclipse.
|
ʹ |
ʺ |
| Moon’s horizontal Parallax |
55 |
32 |
| Sun’s horizontal Parallax (always) |
|
10 |
| The Sum of both Parallaxes |
55 |
42 |
| From which subtract the Sun’s Semi-diameter |
15 |
54 |
| Remains the Semi-diameter of the Earth’s Shadow |
39 |
48 |
| Semidiameter of the Moon |
15 |
2 |
| Sum of the two last |
54 |
50 |
| Moon’s Latitude subtract |
9 |
56 |
| Remains the parts deficient |
45 |
0 |
| Moon’s horary motion |
30 |
46 |
| Sun’s horary motion subtract |
2 |
24 |
| Remains the Moon’s horary motion from the Sun |
28 |
22 |
To project a lunar Eclipse.
Fig. III.
389. This done, make a Scale of any convenient length as W,
whereof each division is a minute of a degree; and take from it in your
Compasses 54 Minutes 50 Seconds, the Sum of Semi-diameters of the
Moon and Earth’s shadow; and with that extent as a Radius, describe
that Circle OVLG round C as a Center.
From the same Scale take 39 Minutes 48 Seconds, the Semi-diameter
of the Earth’s shadow, and therewith as a Radius, describe the Circle
UUUU for the Earth’s shadow, round C as a Center. Subtract the
211Moon’s Semi-diameter from the Semi-diameter of the Shadow, and
with the difference 24 Minutes 46 seconds as a Radius, taken from the
Scale W, describe the Circle YZ round the Center C.
Draw the right line AB through the Center C for the Ecliptic, and
cross it at right Angles with the line EG for the Axis of the Ecliptic.
Because the Moon’s Latitude in this Eclipse is North Descending,
§ 384, set off the Angle of her visible Path with the Ecliptic 5 Degrees
38 Minutes (Page 202.) from E to V; and draw VCv for the Axis of the
Moon’s Orbit. Had the Moon’s Latitude been North Ascending, this
Angle must have been set off from E to f. N. B. When the Moon’s
Latitude is South Ascending, the Axis of her Orbit lies the same way
as when she has North Ascending Latitude; and when her Latitude is
North Descending, the Axis of her Orbit lies the same way as when
her Latitude is South Descending.
Take the Moon’s true Latitude 9ʹ 56ʺ in your Compasses from the
Scale W, and set it off from C to F on the Axis of the Ecliptic because
the Moon is north of the Ecliptic; (had she been to the South of it,
her Latitude must have been set off the contrary way, as from C towards
v:) and through F, at right Angles to the Axis of the Moon’s
Orbit VCv, draw the right line LMHNO for the Moon’s Orbit, or
her Path through the Earth’s shadow. N. B. When the Moon’s
Latitude is North Ascending, or North Descending, she is above the
Ecliptic: but when her Latitude is South Ascending, or South Descending,
she is below it.
Take the Moon’s true horary motion from the Sun, viz. 28 Minutes
22 Seconds, from the Scale W in your Compasses; and with that
extent make marks in the line of the Moon’s Path LMHNO:
then divide each of these equal spaces into 60 equal parts or minutes
of time: and set the hours to them as in the Figure, in such a
manner that the precise time of Full Moon, as shewn by the Tables,
may fall in the Axis of the Ecliptic at F, where the line of the Moon
Path cuts it.
Lastly, Take the Moon’s Semi-diameter 15 Minutes 2 Seconds
from the Scale W in your Compasses, and therewith as a Radius describe
the Circles P, Q, R, S, and T on the Centers L, M, H, N, and
O; the Circles P and T just touching the Earth’s Shadow UU, but no
part of them within it; the Circles Q and S all within it, but touching
at its edges; and the Circle R in the middle of the Moon’s Path
through the shadow. So the Circle P shall be the Moon touching
the shadow at the moment the Eclipse begins; the Circle Q the Moon
just immersed into the shadow at the moment she is totally eclipsed;
212the Circle R the Moon at the greatest obscuration, in the middle
of the Eclipse; the Circle S the Moon just beginning to be enlightened
on her western limb at the end of total darkness; and the
Circle T the Moon quite clear of the Earth’s shadow at the moment
the Eclipse ends. The moments of time marked at the points L, M, H, N
and O answer to these Phenomena: and according to this small projection
are as follow. The beginning of the Eclipse at 8 Hours 36
Minutes P. M. The total immersion at 9 Hours 42 Minutes. The
middle of the Eclipse at 10 Hours 26 Minutes. The end of total
darkness at 11 Hours 12 Minutes. And the end of the Eclipse at
12 Hours 18 Minutes; but the Figure is too small to admit of precision.
The examination of antient Eclipses.
390. By computing the times of New and Full Moons, together
with the distance of the Sun and Moon from the Nodes; and knowing
that when the Sun is within 17 Degrees of either Node at New
Moon he must be eclipsed; and when the Moon is within 12 Degrees
of either Node at Full she cannot escape an Eclipse; and that there
can be no Eclipses without these limits; ’tis easy to examine whether
the accounts of antient Eclipses recorded in history be true. I shall
take the liberty to examine two of those mentioned in the foregoing
catalogue, namely, that of the Moon at Babylon on the 19th of March
in the 721st year before Christ; and that of the Sun at Athens, on
the 20th of March, in the 424th year before Christ.
The time of Full Moon for the former of these Eclipses is already
calculated, Page 198, and the time of New Moon for the latter,
Page 196, both to the Old Style; so that we have nothing now to do
but find the Sun’s distance from the Nodes the same way as we did
the Anomalies; and if the Full Moon in March 721 years before
Christ was within 12 degrees of either Node, she was then
eclipsed; and if the Sun, at the time of New Moon in March 424
years before Christ was within 17 degrees of either Node, he
must have been eclipsed at that time.
EXAMPLE I.
To find the distance of the Sun and Moon from the Nodes, at the time of Full Moon in March, the year before Christ 721, O. S.
The years 720 added to 1780 make 2500, or 25 Centuries.
213
| |
Sun from Node |
| |
s |
° |
ʹ |
| To the mean time of Full Moon in March 1780, Table III. |
10 |
3 |
1 |
| Add the distance for 1 Lunation [See N. B. Page 195,
and Example III, Page 198] |
1 |
0 |
40 |
| Sum |
11 |
3 |
41 |
| From which subtract the Sun’s distance from the Node
for 2500 years, Table V |
5 |
4 |
11 |
| Remains the Sun’s distance from the Node, March 19,
721 years before Christ |
5 |
29 |
30 |
| To which add 6 Signs for the Moon’s distance, because
she was then in opposition to the Sun |
6 |
0 |
0 |
| The Sum is the Moon’s dist. from the Ascend. Node |
11 |
29 |
30 |
That is, she was within half a degree of coming round to it again; and therefore, being so near, she must have been totally, and almost centrally eclipsed.
EXAMPLE II
To find the Suns distance from the Node at the Time of New Moon in March, the year before Christ 424, O. S.
The years 423 added to 1777 make 2200, or 22 Centuries.
| |
Sun from Node |
| |
s |
° |
ʹ |
| At the mean time of New Moon in March 1777, Tab. I. |
8 |
23 |
33 |
| From which subtract the Sun’s distance from the Node for 2200 years, Table V |
3 |
6 |
0 |
| Remains the Sun’s distance from the Ascending Node,
March 21, 424 years before Christ |
5 |
17 |
33 |
| Which, taken from 6 Signs, the distance of the Nodes from each other |
6 |
0 |
0 |
| Leaves the Sun’s distance at that time from the Descending
Node, Descending viz. |
0 |
12 |
27 |
Which being less than 17 degrees, shews that the Sun was then
eclipsed. And as from these short Calculations we find those two antient
Eclipses taken at a venture, to be truly recorded; it is natural to
imagine that so are all the rest in the catalogue.
Here follow Astronomical Tables, for calculating the Times
of New and Full Moons and Eclipses.
214
Table I. The mean time of New Moon in March, the mean Anomaly of the Sun and Moon, the Sun’s mean Distance from the Ascending Node; with the mean Longitude of the Sun and Node from the beginning of the Sign Aries, at the times of all the New Moons in March for 100 years, Old Style.
| Years of Christ. |
Mean time of New Moon in March. |
The Sun’s mean Anomaly. |
The Moon’s mean Anomaly. |
The Sun’s distance from the Node. |
The Sun’s Longitude from Aries. |
The Node’s Longitude from Aries. |
| D. |
H. |
M. |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
| 1701 |
27 |
13 |
45 |
9 |
8 |
23 |
0 |
28 |
5 |
7 |
23 |
15 |
0 |
16 |
3 |
4 |
22 |
48 |
| 1702 |
16 |
22 |
34 |
8 |
27 |
39 |
11 |
7 |
53 |
8 |
1 |
17 |
0 |
5 |
20 |
4 |
4 |
3 |
| 1703 |
6 |
7 |
23 |
8 |
16 |
55 |
9 |
17 |
41 |
8 |
9 |
20 |
11 |
24 |
37 |
3 |
15 |
17 |
| 1704 |
24 |
4 |
55 |
9 |
4 |
30 |
8 |
23 |
18 |
9 |
18 |
3 |
0 |
13 |
0 |
2 |
24 |
57 |
| 1705 |
13 |
13 |
44 |
8 |
23 |
54 |
7 |
3 |
6 |
9 |
26 |
6 |
0 |
2 |
17 |
2 |
6 |
11 |
| 1706 |
2 |
22 |
32 |
8 |
13 |
48 |
5 |
12 |
54 |
10 |
4 |
9 |
11 |
21 |
34 |
1 |
17 |
25 |
| 1707 |
21 |
20 |
5 |
9 |
2 |
17 |
4 |
18 |
31 |
11 |
12 |
52 |
0 |
9 |
57 |
0 |
27 |
5 |
| 1708 |
10 |
4 |
54 |
8 |
21 |
10 |
2 |
28 |
19 |
11 |
20 |
55 |
11 |
29 |
14 |
0 |
8 |
19 |
| 1709 |
29 |
2 |
26 |
9 |
9 |
48 |
2 |
3 |
56 |
0 |
29 |
38 |
0 |
17 |
37 |
11 |
17 |
59 |
| 1710 |
18 |
11 |
16 |
8 |
28 |
32 |
0 |
13 |
44 |
1 |
7 |
40 |
0 |
6 |
54 |
10 |
29 |
14 |
| 1711 |
7 |
20 |
5 |
8 |
17 |
27 |
10 |
23 |
33 |
1 |
15 |
43 |
11 |
26 |
11 |
10 |
10 |
28 |
| 1712 |
25 |
17 |
36 |
9 |
5 |
8 |
9 |
29 |
10 |
2 |
24 |
26 |
0 |
14 |
34 |
9 |
20 |
8 |
| 1713 |
15 |
2 |
25 |
8 |
25 |
48 |
8 |
8 |
58 |
3 |
2 |
29 |
0 |
3 |
50 |
9 |
1 |
21 |
| 1714 |
4 |
11 |
14 |
8 |
14 |
52 |
6 |
16 |
46 |
3 |
10 |
32 |
11 |
23 |
7 |
8 |
12 |
35 |
| 1715 |
23 |
8 |
46 |
9 |
3 |
37 |
5 |
24 |
22 |
4 |
19 |
15 |
0 |
11 |
30 |
7 |
22 |
15 |
| 1716 |
11 |
17 |
35 |
8 |
21 |
26 |
4 |
4 |
11 |
4 |
27 |
18 |
0 |
0 |
47 |
7 |
3 |
29 |
| 1717 |
1 |
2 |
23 |
8 |
11 |
58 |
2 |
13 |
59 |
5 |
5 |
20 |
11 |
20 |
4 |
6 |
14 |
44 |
| 1718 |
19 |
23 |
56 |
9 |
0 |
31 |
1 |
19 |
36 |
6 |
14 |
3 |
0 |
8 |
27 |
5 |
24 |
24 |
| 1719 |
9 |
8 |
45 |
8 |
19 |
47 |
11 |
29 |
24 |
6 |
22 |
6 |
11 |
27 |
43 |
5 |
5 |
37 |
| 1720 |
27 |
6 |
17 |
9 |
8 |
9 |
11 |
5 |
1 |
8 |
0 |
49 |
0 |
16 |
6 |
4 |
15 |
17 |
| 1721 |
16 |
15 |
6 |
8 |
27 |
25 |
9 |
14 |
49 |
8 |
8 |
52 |
0 |
5 |
23 |
3 |
26 |
31 |
| 1722 |
5 |
23 |
55 |
8 |
16 |
41 |
7 |
24 |
38 |
8 |
16 |
55 |
11 |
24 |
40 |
3 |
7 |
45 |
| 1723 |
24 |
21 |
27 |
9 |
5 |
3 |
7 |
0 |
15 |
9 |
25 |
38 |
0 |
13 |
4 |
2 |
17 |
26 |
| 1724 |
13 |
6 |
16 |
8 |
24 |
19 |
5 |
10 |
3 |
10 |
3 |
41 |
0 |
2 |
22 |
1 |
28 |
41 |
| 1725 |
2 |
15 |
4 |
8 |
13 |
45 |
3 |
19 |
51 |
10 |
11 |
43 |
11 |
21 |
39 |
1 |
9 |
56 |
| 1726 |
21 |
12 |
37 |
9 |
1 |
57 |
2 |
25 |
28 |
11 |
20 |
26 |
0 |
10 |
3 |
0 |
19 |
37 |
| 1727 |
10 |
21 |
26 |
8 |
21 |
13 |
1 |
5 |
16 |
11 |
28 |
29 |
11 |
29 |
20 |
0 |
0 |
51 |
| 1728 |
28 |
18 |
58 |
9 |
9 |
35 |
0 |
10 |
53 |
1 |
7 |
13 |
0 |
17 |
43 |
11 |
10 |
30 |
| 1729 |
18 |
3 |
47 |
8 |
28 |
51 |
10 |
20 |
41 |
1 |
15 |
15 |
0 |
7 |
0 |
10 |
21 |
45 |
| 1730 |
7 |
12 |
36 |
8 |
18 |
7 |
9 |
0 |
29 |
1 |
23 |
18 |
11 |
26 |
17 |
10 |
2 |
59 |
| 1731 |
26 |
10 |
8 |
9 |
6 |
29 |
8 |
6 |
6 |
3 |
2 |
1 |
0 |
14 |
40 |
9 |
12 |
39 |
| 1732 |
14 |
18 |
57 |
8 |
25 |
45 |
6 |
15 |
54 |
3 |
10 |
3 |
0 |
3 |
57 |
8 |
23 |
54 |
| 1733 |
4 |
3 |
45 |
8 |
14 |
49 |
4 |
25 |
43 |
3 |
18 |
6 |
11 |
23 |
14 |
8 |
5 |
7 |
| 1734 |
23 |
1 |
18 |
9 |
3 |
25 |
4 |
1 |
20 |
4 |
26 |
49 |
0 |
11 |
37 |
7 |
14 |
48 |
| 1735 |
12 |
10 |
7 |
8 |
22 |
39 |
2 |
11 |
8 |
5 |
4 |
52 |
0 |
0 |
54 |
6 |
26 |
1 |
| 2151736 |
30 |
7 |
39 |
0 |
11 |
1 |
1 |
16 |
45 |
6 |
13 |
35 |
0 |
19 |
17 |
6 |
5 |
42 |
| 1737 |
19 |
16 |
28 |
9 |
0 |
1 |
11 |
26 |
33 |
6 |
21 |
38 |
0 |
8 |
34 |
5 |
16 |
56 |
| 1738 |
9 |
1 |
17 |
8 |
19 |
33 |
10 |
6 |
21 |
6 |
29 |
42 |
11 |
27 |
51 |
4 |
28 |
9 |
| 1739 |
27 |
22 |
49 |
9 |
7 |
55 |
9 |
11 |
58 |
8 |
8 |
24 |
0 |
16 |
14 |
4 |
7 |
50 |
| 1740 |
16 |
7 |
38 |
8 |
27 |
11 |
7 |
21 |
46 |
8 |
16 |
27 |
0 |
5 |
30 |
3 |
19 |
3 |
| 1741 |
5 |
16 |
26 |
8 |
16 |
27 |
6 |
1 |
34 |
8 |
24 |
30 |
11 |
24 |
47 |
3 |
0 |
16 |
| 1742 |
24 |
13 |
59 |
9 |
4 |
49 |
5 |
7 |
11 |
10 |
3 |
12 |
0 |
13 |
10 |
2 |
9 |
58 |
| 1743 |
13 |
22 |
48 |
8 |
24 |
5 |
3 |
16 |
59 |
10 |
11 |
15 |
0 |
2 |
27 |
1 |
21 |
12 |
| 1744 |
2 |
7 |
36 |
8 |
13 |
21 |
1 |
26 |
48 |
10 |
19 |
18 |
11 |
21 |
44 |
1 |
2 |
25 |
| 1745 |
21 |
5 |
9 |
9 |
1 |
43 |
1 |
2 |
25 |
11 |
28 |
0 |
0 |
10 |
7 |
0 |
12 |
7 |
| 1746 |
10 |
13 |
58 |
8 |
20 |
59 |
11 |
12 |
13 |
0 |
6 |
3 |
11 |
29 |
44 |
11 |
23 |
20 |
| 1747 |
29 |
11 |
30 |
9 |
9 |
21 |
10 |
17 |
50 |
1 |
14 |
45 |
0 |
17 |
47 |
11 |
3 |
2 |
| 1748 |
17 |
20 |
19 |
8 |
28 |
37 |
8 |
27 |
38 |
1 |
22 |
49 |
0 |
7 |
4 |
10 |
14 |
15 |
| 1749 |
7 |
5 |
8 |
8 |
17 |
53 |
7 |
7 |
26 |
2 |
0 |
53 |
11 |
26 |
21 |
9 |
25 |
28 |
| 1750 |
26 |
2 |
40 |
9 |
6 |
15 |
6 |
13 |
3 |
3 |
9 |
35 |
0 |
14 |
44 |
9 |
5 |
9 |
| 1751 |
15 |
11 |
29 |
8 |
25 |
32 |
4 |
22 |
51 |
3 |
17 |
38 |
0 |
4 |
1 |
8 |
16 |
23 |
| 1752 |
3 |
20 |
17 |
8 |
14 |
47 |
3 |
2 |
39 |
3 |
25 |
41 |
11 |
23 |
18 |
7 |
27 |
37 |
| 1753 |
22 |
17 |
50 |
9 |
3 |
10 |
2 |
8 |
16 |
5 |
4 |
24 |
0 |
11 |
41 |
7 |
7 |
17 |
| 1754 |
12 |
2 |
39 |
8 |
22 |
26 |
0 |
18 |
4 |
5 |
12 |
27 |
0 |
0 |
59 |
6 |
18 |
32 |
| 1755 |
1 |
11 |
27 |
8 |
11 |
41 |
10 |
27 |
52 |
5 |
20 |
30 |
11 |
20 |
16 |
5 |
29 |
45 |
| 1756 |
19 |
9 |
0 |
9 |
0 |
4 |
10 |
3 |
30 |
6 |
29 |
13 |
0 |
8 |
39 |
5 |
9 |
27 |
| 1757 |
8 |
17 |
49 |
8 |
19 |
20 |
8 |
13 |
18 |
7 |
10 |
15 |
11 |
27 |
56 |
4 |
20 |
41 |
| 1758 |
27 |
15 |
21 |
9 |
7 |
42 |
7 |
18 |
55 |
8 |
15 |
58 |
0 |
16 |
19 |
4 |
0 |
21 |
| 1759 |
17 |
0 |
10 |
8 |
26 |
58 |
5 |
28 |
43 |
8 |
24 |
1 |
0 |
5 |
36 |
3 |
11 |
36 |
| 1760 |
5 |
8 |
58 |
8 |
16 |
13 |
4 |
8 |
31 |
9 |
2 |
4 |
11 |
24 |
53 |
2 |
22 |
49 |
| 1761 |
24 |
6 |
31 |
9 |
4 |
35 |
3 |
14 |
8 |
10 |
10 |
47 |
0 |
13 |
16 |
2 |
2 |
29 |
| 1762 |
13 |
15 |
19 |
8 |
23 |
52 |
1 |
23 |
56 |
10 |
18 |
51 |
0 |
2 |
33 |
1 |
13 |
44 |
| 1763 |
3 |
0 |
8 |
8 |
13 |
7 |
0 |
3 |
44 |
10 |
26 |
53 |
11 |
21 |
50 |
0 |
24 |
57 |
| 1764 |
20 |
21 |
41 |
9 |
1 |
29 |
11 |
9 |
21 |
0 |
5 |
36 |
0 |
10 |
13 |
0 |
4 |
37 |
| 1765 |
10 |
6 |
30 |
8 |
20 |
46 |
9 |
19 |
9 |
0 |
13 |
38 |
11 |
29 |
30 |
11 |
15 |
52 |
| 1766 |
29 |
4 |
2 |
9 |
9 |
8 |
8 |
24 |
46 |
1 |
22 |
21 |
0 |
17 |
53 |
10 |
25 |
32 |
| 1767 |
18 |
12 |
51 |
8 |
28 |
24 |
7 |
4 |
35 |
2 |
0 |
24 |
0 |
7 |
10 |
10 |
6 |
47 |
| 1768 |
6 |
21 |
39 |
8 |
17 |
39 |
5 |
14 |
23 |
2 |
8 |
27 |
11 |
26 |
27 |
9 |
18 |
1 |
| 1769 |
25 |
19 |
12 |
9 |
6 |
2 |
4 |
20 |
0 |
3 |
17 |
0 |
0 |
14 |
50 |
8 |
27 |
41 |
| 1770 |
15 |
4 |
1 |
8 |
25 |
17 |
2 |
29 |
48 |
3 |
25 |
12 |
0 |
4 |
7 |
8 |
8 |
56 |
| 1771 |
4 |
12 |
49 |
8 |
14 |
33 |
1 |
9 |
36 |
4 |
3 |
16 |
11 |
23 |
24 |
7 |
20 |
8 |
| 1772 |
22 |
10 |
22 |
9 |
2 |
56 |
0 |
15 |
13 |
5 |
11 |
49 |
0 |
11 |
47 |
6 |
29 |
48 |
| 1773 |
11 |
19 |
10 |
8 |
22 |
11 |
10 |
25 |
1 |
5 |
20 |
1 |
0 |
1 |
4 |
6 |
11 |
3 |
| 1774 |
1 |
3 |
59 |
8 |
11 |
27 |
9 |
4 |
49 |
5 |
28 |
4 |
11 |
20 |
21 |
5 |
22 |
17 |
| 1775 |
20 |
1 |
32 |
8 |
29 |
50 |
8 |
10 |
26 |
7 |
6 |
4 |
0 |
8 |
44 |
5 |
1 |
57 |
| 2161776 |
8 |
10 |
20 |
8 |
19 |
5 |
6 |
20 |
14 |
7 |
14 |
50 |
11 |
28 |
1 |
4 |
13 |
12 |
| 1777 |
27 |
7 |
53 |
9 |
7 |
27 |
5 |
25 |
51 |
8 |
23 |
23 |
0 |
16 |
24 |
3 |
22 |
52 |
| 1778 |
16 |
16 |
42 |
8 |
26 |
43 |
4 |
5 |
40 |
9 |
1 |
36 |
0 |
5 |
41 |
3 |
4 |
6 |
| 1779 |
6 |
1 |
30 |
8 |
15 |
59 |
2 |
15 |
28 |
9 |
9 |
39 |
11 |
24 |
58 |
2 |
15 |
19 |
| 1780 |
23 |
23 |
3 |
9 |
4 |
21 |
1 |
21 |
5 |
10 |
18 |
22 |
0 |
13 |
21 |
1 |
24 |
59 |
| 1781 |
13 |
7 |
52 |
8 |
23 |
37 |
0 |
0 |
53 |
10 |
26 |
24 |
0 |
2 |
38 |
1 |
6 |
14 |
| 1782 |
2 |
16 |
40 |
8 |
12 |
53 |
10 |
10 |
41 |
11 |
4 |
27 |
11 |
21 |
54 |
0 |
17 |
27 |
| 1783 |
21 |
14 |
13 |
9 |
1 |
15 |
9 |
16 |
18 |
0 |
13 |
10 |
0 |
10 |
17 |
11 |
27 |
7 |
| 1784 |
9 |
23 |
2 |
8 |
20 |
32 |
7 |
26 |
6 |
0 |
21 |
13 |
11 |
29 |
34 |
11 |
8 |
22 |
| 1785 |
28 |
20 |
35 |
9 |
8 |
54 |
7 |
1 |
43 |
1 |
29 |
56 |
0 |
17 |
57 |
10 |
18 |
2 |
| 1786 |
18 |
5 |
23 |
8 |
28 |
9 |
5 |
11 |
31 |
2 |
7 |
59 |
0 |
7 |
14 |
9 |
29 |
16 |
| 1787 |
7 |
14 |
11 |
8 |
17 |
25 |
3 |
21 |
19 |
2 |
16 |
2 |
11 |
26 |
31 |
9 |
10 |
29 |
| 1788 |
25 |
11 |
44 |
9 |
5 |
47 |
2 |
26 |
56 |
3 |
24 |
45 |
0 |
14 |
54 |
8 |
20 |
9 |
| 1789 |
14 |
20 |
33 |
8 |
25 |
3 |
1 |
6 |
45 |
4 |
2 |
47 |
0 |
4 |
11 |
8 |
1 |
25 |
| 1790 |
4 |
5 |
21 |
8 |
14 |
19 |
11 |
16 |
33 |
4 |
10 |
50 |
11 |
23 |
28 |
7 |
12 |
38 |
| 1791 |
23 |
2 |
54 |
9 |
2 |
41 |
10 |
22 |
10 |
5 |
19 |
33 |
0 |
11 |
51 |
6 |
22 |
18 |
| 1792 |
11 |
11 |
43 |
8 |
21 |
57 |
9 |
1 |
58 |
5 |
27 |
56 |
0 |
1 |
7 |
6 |
3 |
32 |
| 1793 |
0 |
20 |
31 |
8 |
11 |
12 |
7 |
11 |
45 |
6 |
5 |
39 |
11 |
20 |
24 |
5 |
14 |
45 |
| 1794 |
19 |
18 |
4 |
8 |
29 |
35 |
6 |
17 |
23 |
7 |
14 |
22 |
0 |
8 |
48 |
4 |
24 |
27 |
| 1795 |
9 |
2 |
52 |
8 |
18 |
51 |
4 |
27 |
11 |
7 |
22 |
25 |
11 |
28 |
6 |
4 |
5 |
41 |
| 1796 |
27 |
0 |
25 |
9 |
7 |
13 |
4 |
2 |
48 |
9 |
1 |
8 |
0 |
16 |
29 |
3 |
15 |
21 |
| 1797 |
16 |
9 |
14 |
8 |
26 |
29 |
2 |
12 |
36 |
9 |
9 |
10 |
0 |
5 |
46 |
2 |
26 |
36 |
| 1798 |
5 |
18 |
2 |
8 |
15 |
44 |
0 |
22 |
24 |
9 |
17 |
13 |
11 |
25 |
3 |
2 |
7 |
50 |
| 1799 |
24 |
15 |
35 |
9 |
4 |
6 |
11 |
28 |
1 |
10 |
25 |
56 |
0 |
13 |
26 |
1 |
17 |
30 |
| 1800 |
13 |
0 |
24 |
8 |
23 |
23 |
10 |
7 |
49 |
11 |
3 |
59 |
0 |
2 |
43 |
0 |
28 |
44 |
Table II. The mean New Moons, &c. in March to the New Style.
| Years of Christ. |
Mean time of New Moon in March. |
The Sun’s mean Anomaly. |
The Moon’s mean Anomaly. |
The Sun’s distance from the Node. |
The Sun’s Longitude from Aries. |
The Node’s Longitude from Aries. |
| D. |
H. |
M. |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
| 1753 |
4 |
5 |
6 |
7 |
4 |
2 |
1 |
12 |
27 |
4 |
3 |
44 |
11 |
12 |
35 |
7 |
8 |
50 |
| 1754 |
23 |
2 |
39 |
8 |
22 |
26 |
0 |
18 |
4 |
5 |
12 |
27 |
0 |
0 |
59 |
6 |
18 |
32 |
| 1755 |
12 |
11 |
27 |
8 |
11 |
41 |
10 |
27 |
52 |
5 |
20 |
29 |
11 |
20 |
16 |
5 |
29 |
45 |
| 1756 |
30 |
9 |
0 |
9 |
0 |
3 |
10 |
3 |
29 |
6 |
29 |
12 |
0 |
8 |
39 |
5 |
9 |
27 |
| 1757 |
19 |
17 |
49 |
8 |
19 |
19 |
8 |
13 |
17 |
7 |
7 |
15 |
11 |
27 |
56 |
4 |
20 |
41 |
| 1758 |
9 |
2 |
37 |
8 |
8 |
35 |
6 |
23 |
5 |
7 |
15 |
18 |
11 |
17 |
13 |
4 |
1 |
54 |
| 1759 |
28 |
0 |
9 |
8 |
26 |
58 |
5 |
28 |
43 |
8 |
24 |
1 |
0 |
5 |
36 |
3 |
11 |
36 |
| 1760 |
16 |
8 |
58 |
8 |
16 |
14 |
4 |
8 |
31 |
9 |
2 |
4 |
11 |
24 |
53 |
2 |
22 |
49 |
| 2171761 |
5 |
7 |
47 |
8 |
5 |
29 |
2 |
18 |
19 |
9 |
10 |
9 |
11 |
14 |
10 |
2 |
4 |
1 |
| 1762 |
24 |
15 |
19 |
8 |
23 |
52 |
1 |
23 |
56 |
10 |
18 |
51 |
0 |
2 |
33 |
1 |
13 |
44 |
| 1763 |
14 |
0 |
8 |
8 |
13 |
7 |
0 |
3 |
44 |
10 |
26 |
53 |
11 |
21 |
50 |
0 |
24 |
57 |
| 1764 |
2 |
8 |
57 |
8 |
2 |
23 |
10 |
13 |
32 |
11 |
4 |
57 |
11 |
11 |
7 |
0 |
6 |
10 |
| 1765 |
21 |
6 |
30 |
8 |
20 |
46 |
9 |
19 |
9 |
0 |
13 |
38 |
11 |
29 |
30 |
11 |
15 |
52 |
| 1766 |
10 |
15 |
18 |
8 |
10 |
1 |
7 |
28 |
58 |
0 |
21 |
41 |
11 |
18 |
47 |
10 |
27 |
5 |
| 1767 |
29 |
12 |
51 |
8 |
28 |
23 |
7 |
4 |
35 |
2 |
0 |
23 |
0 |
7 |
10 |
10 |
6 |
47 |
| 1768 |
17 |
21 |
39 |
8 |
17 |
39 |
5 |
14 |
23 |
2 |
8 |
26 |
11 |
26 |
27 |
9 |
18 |
1 |
| 1769 |
7 |
6 |
28 |
8 |
6 |
55 |
3 |
24 |
11 |
2 |
16 |
29 |
11 |
15 |
44 |
8 |
29 |
15 |
| 1770 |
26 |
4 |
1 |
8 |
25 |
18 |
2 |
29 |
48 |
3 |
25 |
11 |
0 |
4 |
7 |
8 |
8 |
56 |
| 1771 |
15 |
12 |
49 |
8 |
14 |
33 |
1 |
9 |
36 |
4 |
3 |
16 |
11 |
23 |
24 |
7 |
20 |
8 |
| 1772 |
3 |
21 |
38 |
8 |
3 |
49 |
11 |
19 |
24 |
4 |
11 |
19 |
11 |
12 |
41 |
7 |
1 |
22 |
| 1773 |
22 |
19 |
10 |
8 |
22 |
11 |
10 |
25 |
1 |
5 |
20 |
1 |
0 |
1 |
4 |
6 |
11 |
3 |
| 1774 |
12 |
3 |
59 |
8 |
11 |
27 |
9 |
4 |
49 |
5 |
28 |
4 |
11 |
20 |
21 |
5 |
22 |
17 |
| 1775 |
1 |
12 |
48 |
8 |
0 |
43 |
7 |
14 |
37 |
6 |
6 |
7 |
11 |
9 |
38 |
5 |
3 |
30 |
| 1776 |
19 |
10 |
20 |
8 |
19 |
5 |
6 |
20 |
14 |
7 |
14 |
50 |
11 |
28 |
1 |
4 |
13 |
12 |
| 1777 |
8 |
19 |
9 |
8 |
8 |
21 |
5 |
0 |
2 |
7 |
22 |
53 |
11 |
17 |
18 |
3 |
24 |
25 |
| 1778 |
27 |
16 |
42 |
8 |
26 |
43 |
4 |
5 |
40 |
9 |
1 |
36 |
0 |
5 |
41 |
3 |
4 |
6 |
| 1779 |
17 |
1 |
30 |
8 |
15 |
59 |
2 |
15 |
28 |
9 |
9 |
39 |
11 |
24 |
58 |
2 |
15 |
19 |
| 1780 |
5 |
10 |
19 |
8 |
5 |
15 |
0 |
25 |
16 |
9 |
17 |
42 |
11 |
14 |
15 |
1 |
26 |
32 |
| 1781 |
24 |
7 |
52 |
8 |
23 |
37 |
0 |
0 |
53 |
10 |
26 |
24 |
0 |
2 |
38 |
1 |
6 |
14 |
| 1782 |
13 |
16 |
40 |
8 |
12 |
53 |
10 |
10 |
41 |
11 |
4 |
27 |
11 |
21 |
54 |
0 |
17 |
27 |
| 1783 |
3 |
1 |
29 |
8 |
2 |
8 |
8 |
20 |
29 |
11 |
12 |
30 |
11 |
11 |
11 |
11 |
28 |
40 |
| 1784 |
20 |
23 |
2 |
8 |
20 |
32 |
7 |
26 |
6 |
0 |
21 |
13 |
11 |
29 |
34 |
11 |
8 |
22 |
| 1785 |
10 |
7 |
50 |
8 |
9 |
47 |
6 |
5 |
54 |
0 |
29 |
16 |
11 |
18 |
51 |
10 |
19 |
35 |
| 1786 |
29 |
5 |
23 |
8 |
28 |
9 |
5 |
11 |
31 |
2 |
7 |
59 |
0 |
7 |
14 |
9 |
29 |
16 |
| 1787 |
18 |
14 |
11 |
8 |
17 |
25 |
3 |
21 |
19 |
2 |
16 |
2 |
11 |
26 |
31 |
9 |
10 |
29 |
| 1788 |
6 |
23 |
0 |
8 |
6 |
41 |
2 |
1 |
7 |
2 |
24 |
5 |
11 |
15 |
48 |
8 |
21 |
43 |
| 1789 |
25 |
20 |
33 |
8 |
25 |
3 |
1 |
6 |
45 |
4 |
2 |
47 |
0 |
4 |
11 |
8 |
1 |
25 |
| 1790 |
15 |
5 |
21 |
8 |
14 |
19 |
11 |
16 |
33 |
4 |
10 |
50 |
11 |
23 |
28 |
7 |
12 |
38 |
| 1791 |
4 |
14 |
10 |
8 |
3 |
34 |
9 |
26 |
21 |
4 |
18 |
53 |
11 |
12 |
44 |
6 |
23 |
51 |
| 1792 |
22 |
11 |
43 |
8 |
21 |
57 |
9 |
1 |
58 |
5 |
27 |
36 |
0 |
1 |
7 |
6 |
3 |
32 |
| 1793 |
11 |
20 |
31 |
8 |
11 |
12 |
7 |
11 |
45 |
6 |
5 |
39 |
11 |
20 |
24 |
5 |
14 |
45 |
| 1794 |
1 |
6 |
20 |
8 |
0 |
29 |
5 |
21 |
34 |
6 |
13 |
42 |
11 |
9 |
22 |
4 |
7 |
15 |
| 1795 |
20 |
2 |
52 |
8 |
18 |
51 |
4 |
27 |
11 |
7 |
22 |
25 |
11 |
28 |
6 |
4 |
5 |
41 |
| 1796 |
8 |
11 |
41 |
8 |
8 |
6 |
3 |
6 |
59 |
8 |
0 |
28 |
11 |
17 |
23 |
3 |
16 |
54 |
| 1797 |
27 |
9 |
14 |
8 |
26 |
29 |
2 |
12 |
36 |
9 |
9 |
10 |
0 |
5 |
46 |
2 |
26 |
36 |
| 1798 |
16 |
18 |
2 |
8 |
15 |
44 |
0 |
22 |
24 |
9 |
17 |
13 |
11 |
25 |
3 |
2 |
7 |
50 |
| 1799 |
6 |
2 |
51 |
8 |
5 |
0 |
11 |
2 |
12 |
9 |
25 |
16 |
11 |
14 |
20 |
1 |
19 |
3 |
| 1800 |
25 |
0 |
24 |
8 |
23 |
23 |
10 |
7 |
49 |
11 |
3 |
59 |
0 |
2 |
43 |
0 |
28 |
44 |
218
Table III. The mean time of Full Moon in March, the mean Anomaly of the Sun and Moon, the Sun’s mean Distance from the Ascending Node; with the mean Longitude of the Sun and Node from the beginning of the Sign Aries, at the time of all the Full Moons in March for 100 years, Old Style.
| Years of Christ. |
Mean time of Full Moon in March. |
The Sun’s mean Anomaly. |
The Moon’s mean Anomaly. |
The Sun’s distance from the Node. |
The Sun’s Longitude from Aries. |
The Node’s Longitude from Aries. |
| D. |
H. |
M. |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
| 1701 |
12 |
19 |
23 |
8 |
23 |
56 |
6 |
15 |
11 |
7 |
7 |
55 |
0 |
1 |
30 |
4 |
23 |
35 |
| 1702 |
2 |
4 |
12 |
8 |
13 |
6 |
4 |
24 |
59 |
7 |
15 |
57 |
11 |
20 |
47 |
4 |
4 |
48 |
| 1703 |
21 |
1 |
45 |
9 |
1 |
28 |
4 |
0 |
35 |
8 |
24 |
40 |
0 |
9 |
10 |
3 |
14 |
30 |
| 1704 |
9 |
10 |
33 |
8 |
19 |
57 |
2 |
10 |
24 |
9 |
2 |
43 |
11 |
28 |
27 |
2 |
25 |
43 |
| 1705 |
28 |
8 |
6 |
9 |
8 |
27 |
1 |
16 |
0 |
10 |
11 |
26 |
0 |
16 |
50 |
2 |
5 |
25 |
| 1706 |
17 |
16 |
54 |
8 |
28 |
11 |
11 |
25 |
48 |
10 |
19 |
29 |
0 |
6 |
7 |
1 |
16 |
38s |
| 1707 |
7 |
1 |
43 |
8 |
17 |
44 |
10 |
5 |
37 |
10 |
27 |
32 |
11 |
25 |
24 |
0 |
27 |
51 |
| 1708 |
24 |
23 |
16 |
9 |
5 |
43 |
9 |
11 |
14 |
0 |
6 |
15 |
0 |
13 |
47 |
0 |
7 |
33 |
| 1709 |
14 |
8 |
4 |
8 |
25 |
15 |
7 |
21 |
2 |
0 |
14 |
18 |
0 |
3 |
4 |
11 |
18 |
46 |
| 1710 |
3 |
16 |
54 |
8 |
13 |
59 |
6 |
0 |
50 |
0 |
22 |
21 |
11 |
22 |
21 |
11 |
0 |
0 |
| 1711 |
22 |
14 |
27 |
9 |
2 |
0 |
5 |
6 |
27 |
2 |
1 |
3 |
0 |
10 |
44 |
10 |
9 |
42 |
| 1712 |
10 |
23 |
14 |
8 |
20 |
35 |
3 |
16 |
16 |
2 |
9 |
6 |
0 |
0 |
1 |
9 |
20 |
55 |
| 1713 |
29 |
20 |
47 |
9 |
10 |
21 |
2 |
21 |
52 |
3 |
17 |
48 |
0 |
18 |
23 |
9 |
0 |
35 |
| 1714 |
19 |
5 |
36 |
8 |
29 |
25 |
1 |
1 |
40 |
3 |
25 |
53 |
0 |
7 |
40 |
8 |
11 |
48 |
| 1715 |
8 |
14 |
24 |
8 |
19 |
4 |
11 |
11 |
28 |
4 |
3 |
56 |
11 |
26 |
57 |
7 |
23 |
1 |
| 1716 |
26 |
11 |
57 |
9 |
5 |
59 |
0 |
17 |
5 |
5 |
12 |
38 |
0 |
15 |
20 |
7 |
2 |
43 |
| 1717 |
15 |
20 |
45 |
8 |
26 |
31 |
18 |
26 |
53 |
5 |
20 |
41 |
0 |
4 |
37 |
6 |
13 |
56 |
| 1718 |
5 |
5 |
34 |
8 |
15 |
58 |
7 |
6 |
42 |
5 |
28 |
44 |
11 |
23 |
54 |
5 |
25 |
10 |
| 1719 |
24 |
3 |
7 |
9 |
4 |
20 |
6 |
12 |
18 |
7 |
7 |
26 |
0 |
12 |
17 |
5 |
4 |
52 |
| 1720 |
12 |
11 |
55 |
8 |
23 |
36 |
4 |
22 |
7 |
7 |
15 |
29 |
0 |
1 |
34 |
4 |
16 |
5 |
| 1721 |
1 |
20 |
44 |
8 |
12 |
52 |
3 |
1 |
55 |
7 |
23 |
32 |
11 |
20 |
51 |
3 |
27 |
18 |
| 1722 |
20 |
18 |
17 |
9 |
1 |
14 |
2 |
7 |
32 |
9 |
2 |
15 |
0 |
9 |
14 |
3 |
6 |
59 |
| 1723 |
10 |
3 |
5 |
8 |
20 |
30 |
0 |
17 |
21 |
9 |
10 |
18 |
11 |
28 |
31 |
2 |
18 |
12 |
| 1724 |
28 |
0 |
38 |
9 |
8 |
52 |
11 |
22 |
57 |
10 |
19 |
0 |
0 |
16 |
55 |
1 |
27 |
55 |
| 1725 |
17 |
9 |
26 |
8 |
28 |
18 |
10 |
2 |
45 |
10 |
27 |
3 |
0 |
6 |
12 |
1 |
9 |
9 |
| 1726 |
6 |
18 |
15 |
8 |
17 |
24 |
8 |
12 |
34 |
11 |
5 |
6 |
11 |
25 |
30 |
0 |
20 |
23 |
| 1727 |
25 |
15 |
48 |
9 |
5 |
46 |
7 |
18 |
10 |
0 |
13 |
49 |
0 |
13 |
53 |
0 |
0 |
5 |
| 1728 |
14 |
0 |
36 |
8 |
25 |
2 |
5 |
27 |
59 |
0 |
21 |
52 |
0 |
3 |
10 |
11 |
11 |
18 |
| 1729 |
3 |
9 |
25 |
8 |
14 |
18 |
4 |
7 |
47 |
0 |
29 |
55 |
11 |
22 |
27 |
10 |
22 |
32 |
| 1730 |
22 |
6 |
58 |
9 |
2 |
40 |
3 |
13 |
23 |
2 |
8 |
38 |
0 |
10 |
50 |
10 |
2 |
13 |
| 1731 |
11 |
15 |
46 |
8 |
21 |
56 |
1 |
23 |
12 |
2 |
16 |
41 |
0 |
0 |
7 |
9 |
13 |
26 |
| 1732 |
29 |
13 |
19 |
9 |
10 |
18 |
0 |
28 |
48 |
3 |
25 |
23 |
0 |
18 |
30 |
8 |
23 |
8 |
| 1733 |
18 |
22 |
7 |
8 |
29 |
22 |
11 |
8 |
37 |
4 |
3 |
26 |
0 |
7 |
47 |
8 |
4 |
21 |
| 1734 |
8 |
6 |
56 |
8 |
18 |
50 |
9 |
18 |
26 |
4 |
11 |
29 |
11 |
27 |
4 |
7 |
15 |
34 |
| 1735 |
27 |
4 |
29 |
9 |
7 |
12 |
8 |
24 |
2 |
5 |
20 |
12 |
0 |
15 |
27 |
6 |
25 |
15 |
| 2191736 |
15 |
13 |
17 |
8 |
26 |
29 |
7 |
3 |
51 |
5 |
28 |
15 |
0 |
4 |
44 |
6 |
6 |
29 |
| 1737 |
4 |
22 |
6 |
8 |
15 |
44 |
5 |
13 |
39 |
6 |
6 |
18 |
11 |
24 |
1 |
5 |
17 |
42 |
| 1738 |
23 |
19 |
39 |
9 |
4 |
6 |
4 |
19 |
15 |
7 |
15 |
1 |
0 |
12 |
24 |
4 |
27 |
24 |
| 1739 |
13 |
4 |
27 |
8 |
23 |
22 |
2 |
29 |
4 |
7 |
23 |
4 |
0 |
1 |
41 |
4 |
8 |
37 |
| 1740 |
1 |
13 |
16 |
8 |
12 |
38 |
1 |
8 |
52 |
8 |
1 |
7 |
11 |
20 |
57 |
3 |
19 |
50 |
| 1741 |
20 |
10 |
48 |
9 |
1 |
0 |
0 |
14 |
28 |
9 |
9 |
49 |
0 |
9 |
20 |
2 |
29 |
30 |
| 1742 |
9 |
19 |
37 |
8 |
20 |
16 |
10 |
24 |
17 |
9 |
17 |
52 |
11 |
28 |
37 |
2 |
10 |
44 |
| 1743 |
28 |
17 |
10 |
9 |
8 |
38 |
9 |
29 |
53 |
10 |
26 |
35 |
0 |
17 |
0 |
1 |
20 |
26 |
| 1744 |
17 |
1 |
58 |
8 |
27 |
54 |
8 |
9 |
42 |
11 |
4 |
38 |
0 |
6 |
17 |
1 |
1 |
39 |
| 1745 |
6 |
10 |
47 |
8 |
17 |
10 |
6 |
19 |
31 |
11 |
12 |
41 |
11 |
25 |
34 |
0 |
12 |
52 |
| 1746 |
25 |
8 |
19 |
9 |
5 |
32 |
5 |
25 |
7 |
0 |
21 |
24 |
0 |
13 |
57 |
11 |
22 |
34 |
| 1747 |
14 |
17 |
8 |
8 |
24 |
48 |
4 |
4 |
56 |
0 |
29 |
27 |
0 |
3 |
14 |
11 |
3 |
47 |
| 1748 |
3 |
1 |
57 |
8 |
14 |
4 |
2 |
14 |
44 |
1 |
7 |
30 |
11 |
22 |
31 |
10 |
15 |
0 |
| 1749 |
21 |
23 |
30 |
9 |
2 |
26 |
1 |
20 |
20 |
2 |
16 |
12 |
0 |
10 |
54 |
9 |
24 |
42 |
| 1750 |
11 |
8 |
18 |
8 |
21 |
42 |
0 |
0 |
9 |
2 |
24 |
15 |
0 |
0 |
11 |
9 |
5 |
59 |
| 1751 |
30 |
5 |
51 |
9 |
10 |
5 |
11 |
5 |
45 |
4 |
2 |
58 |
0 |
18 |
34 |
8 |
15 |
37 |
| 1752 |
18 |
14 |
39 |
8 |
29 |
20 |
9 |
15 |
33 |
4 |
11 |
1 |
0 |
7 |
51 |
7 |
26 |
50 |
| 1753 |
7 |
23 |
18 |
7 |
18 |
35 |
7 |
25 |
21 |
4 |
19 |
4 |
11 |
27 |
8 |
7 |
8 |
4 |
| 1754 |
26 |
21 |
1 |
9 |
6 |
59 |
7 |
0 |
58 |
7 |
27 |
47 |
0 |
15 |
32 |
6 |
17 |
45 |
| 1755 |
16 |
5 |
49 |
8 |
26 |
14 |
5 |
10 |
46 |
6 |
5 |
49 |
0 |
4 |
49 |
5 |
29 |
0 |
| 1756 |
4 |
14 |
38 |
8 |
15 |
30 |
3 |
20 |
35 |
6 |
13 |
52 |
11 |
24 |
6 |
5 |
10 |
14 |
| 1757 |
23 |
12 |
11 |
9 |
3 |
53 |
2 |
26 |
12 |
7 |
25 |
35 |
0 |
12 |
29 |
4 |
19 |
54 |
| 1758 |
12 |
20 |
59 |
8 |
23 |
8 |
1 |
5 |
59 |
8 |
0 |
38 |
0 |
1 |
46 |
4 |
1 |
9 |
| 1759 |
2 |
5 |
47 |
8 |
12 |
25 |
11 |
15 |
48 |
8 |
8 |
41 |
11 |
21 |
3 |
3 |
12 |
22 |
| 1760 |
20 |
3 |
20 |
9 |
0 |
46 |
10 |
21 |
25 |
9 |
17 |
24 |
0 |
9 |
26 |
2 |
22 |
2 |
| 1761 |
9 |
12 |
9 |
8 |
20 |
2 |
9 |
1 |
13 |
9 |
25 |
27 |
11 |
28 |
43 |
2 |
3 |
16 |
| 1762 |
28 |
9 |
41 |
9 |
8 |
25 |
8 |
6 |
50 |
11 |
4 |
11 |
0 |
17 |
6 |
1 |
12 |
57 |
| 1763 |
17 |
18 |
30 |
8 |
27 |
40 |
6 |
16 |
38 |
11 |
12 |
13 |
0 |
6 |
23 |
0 |
24 |
11 |
| 1764 |
6 |
3 |
19 |
8 |
16 |
56 |
4 |
26 |
26 |
11 |
20 |
16 |
11 |
25 |
40 |
0 |
5 |
24 |
| 1765 |
25 |
0 |
52 |
9 |
5 |
19 |
4 |
2 |
3 |
0 |
28 |
58 |
0 |
14 |
3 |
11 |
15 |
5 |
| 1766 |
14 |
9 |
40 |
8 |
24 |
34 |
2 |
11 |
52 |
1 |
7 |
1 |
0 |
3 |
20 |
10 |
26 |
20 |
| 1767 |
7 |
18 |
29 |
8 |
13 |
50 |
0 |
21 |
41 |
1 |
15 |
4 |
11 |
22 |
37 |
10 |
7 |
34 |
| 1768 |
21 |
16 |
1 |
9 |
2 |
12 |
11 |
27 |
17 |
2 |
23 |
47 |
0 |
11 |
0 |
9 |
17 |
14 |
| 1769 |
11 |
0 |
50 |
8 |
21 |
28 |
10 |
7 |
9 |
3 |
1 |
49 |
0 |
0 |
17 |
8 |
28 |
28 |
| 1770 |
0 |
9 |
39 |
8 |
10 |
44 |
8 |
16 |
57 |
3 |
9 |
52 |
11 |
19 |
54 |
8 |
9 |
42 |
| 1771 |
19 |
7 |
11 |
8 |
29 |
6 |
7 |
22 |
30 |
4 |
18 |
36 |
0 |
7 |
57 |
7 |
19 |
21 |
| 1772 |
7 |
16 |
0 |
8 |
18 |
22 |
6 |
2 |
18 |
4 |
26 |
39 |
11 |
27 |
14 |
7 |
0 |
35 |
| 1773 |
26 |
13 |
32 |
9 |
6 |
44 |
5 |
7 |
55 |
6 |
5 |
21 |
0 |
15 |
37 |
6 |
10 |
16 |
| 1774 |
15 |
22 |
21 |
8 |
26 |
0 |
3 |
17 |
43 |
6 |
13 |
24 |
0 |
4 |
54 |
5 |
21 |
31 |
| 1775 |
5 |
7 |
10 |
8 |
15 |
16 |
1 |
27 |
31 |
6 |
21 |
27 |
11 |
24 |
11 |
5 |
2 |
44 |
| 2201776 |
23 |
4 |
42 |
9 |
3 |
38 |
1 |
3 |
8 |
8 |
0 |
10 |
0 |
12 |
34 |
4 |
12 |
25 |
| 1777 |
12 |
13 |
31 |
8 |
22 |
54 |
11 |
12 |
56 |
8 |
8 |
13 |
0 |
1 |
51 |
8 |
23 |
30 |
| 1778 |
1 |
22 |
20 |
8 |
12 |
10 |
9 |
22 |
45 |
8 |
16 |
16 |
11 |
21 |
8 |
3 |
4 |
52 |
| 1779 |
20 |
19 |
52 |
9 |
0 |
32 |
8 |
28 |
22 |
9 |
24 |
59 |
0 |
9 |
31 |
2 |
14 |
32 |
| 1780 |
9 |
4 |
41 |
8 |
19 |
48 |
7 |
8 |
10 |
10 |
3 |
1 |
11 |
28 |
48 |
1 |
25 |
47 |
| 1781 |
28 |
2 |
14 |
9 |
8 |
9 |
6 |
13 |
47 |
11 |
11 |
44 |
0 |
17 |
11 |
1 |
5 |
27 |
| 1782 |
19 |
11 |
2 |
8 |
27 |
28 |
4 |
23 |
34 |
11 |
19 |
47 |
0 |
6 |
27 |
0 |
6 |
41 |
| 1783 |
6 |
19 |
51 |
8 |
16 |
44 |
3 |
3 |
23 |
11 |
27 |
50 |
11 |
25 |
44 |
11 |
27 |
54 |
| 1784 |
24 |
17 |
24 |
9 |
5 |
4 |
2 |
9 |
0 |
1 |
6 |
35 |
0 |
14 |
7 |
11 |
7 |
35 |
| 1785 |
14 |
2 |
12 |
8 |
24 |
20 |
0 |
18 |
48 |
1 |
14 |
36 |
0 |
3 |
24 |
10 |
18 |
48 |
| 1786 |
3 |
11 |
1 |
8 |
13 |
36 |
10 |
28 |
37 |
1 |
22 |
39 |
11 |
22 |
41 |
10 |
0 |
2 |
| 1787 |
22 |
8 |
33 |
9 |
1 |
57 |
10 |
4 |
13 |
3 |
1 |
22 |
0 |
11 |
4 |
9 |
9 |
42 |
| 1788 |
10 |
17 |
22 |
8 |
21 |
14 |
8 |
14 |
2 |
3 |
9 |
25 |
0 |
0 |
21 |
8 |
20 |
57 |
| 1789 |
29 |
14 |
55 |
9 |
9 |
36 |
7 |
19 |
39 |
4 |
18 |
7 |
0 |
18 |
44 |
8 |
0 |
38 |
| 1790 |
18 |
23 |
43 |
8 |
28 |
52 |
5 |
29 |
27 |
4 |
26 |
10 |
0 |
8 |
1 |
7 |
11 |
51 |
| 1791 |
8 |
8 |
32 |
8 |
18 |
8 |
4 |
9 |
15 |
5 |
4 |
13 |
11 |
27 |
17 |
6 |
23 |
4 |
| 1792 |
26 |
6 |
5 |
9 |
6 |
20 |
3 |
14 |
52 |
6 |
12 |
56 |
0 |
15 |
40 |
6 |
2 |
45 |
| 1793 |
15 |
14 |
53 |
8 |
25 |
46 |
1 |
24 |
40 |
6 |
20 |
59 |
0 |
4 |
58 |
5 |
13 |
59 |
| 1794 |
4 |
23 |
42 |
8 |
15 |
2 |
0 |
4 |
29 |
6 |
29 |
2 |
11 |
24 |
15 |
4 |
25 |
13 |
| 1795 |
23 |
21 |
14 |
9 |
3 |
14 |
11 |
10 |
5 |
8 |
7 |
45 |
0 |
12 |
39 |
4 |
4 |
54 |
| 1796 |
12 |
6 |
3 |
8 |
22 |
39 |
9 |
19 |
53 |
8 |
15 |
48 |
0 |
1 |
56 |
3 |
16 |
8 |
| 1797 |
1 |
14 |
52 |
8 |
11 |
55 |
7 |
29 |
42 |
8 |
23 |
50 |
11 |
21 |
13 |
2 |
27 |
23 |
| 1798 |
20 |
12 |
24 |
9 |
0 |
7 |
7 |
5 |
18 |
10 |
2 |
33 |
0 |
9 |
36 |
2 |
7 |
3 |
| 1799 |
9 |
21 |
13 |
8 |
19 |
33 |
5 |
15 |
6 |
10 |
10 |
36 |
11 |
28 |
53 |
1 |
18 |
18 |
| 1800 |
27 |
18 |
46 |
9 |
7 |
46 |
4 |
20 |
43 |
11 |
19 |
19 |
0 |
17 |
16 |
0 |
27 |
57 |
Table IV. The mean Full Moons, &c. in March to the New Style.
| Years of Christ. |
Mean time of Full Moon in March. |
The Sun’s mean Anomaly. |
The Moon’s mean Anomaly. |
The Sun’s distance from the Node. |
The Sun’s Longitude from Aries. |
The Node’s Longitude from Aries. |
| D. |
H. |
M. |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
| 1753 |
18 |
23 |
18 |
7 |
18 |
35 |
7 |
25 |
21 |
4 |
19 |
4 |
11 |
27 |
8 |
7 |
8 |
4 |
| 1754 |
8 |
8 |
17 |
7 |
7 |
53 |
6 |
5 |
10 |
4 |
27 |
7 |
11 |
16 |
26 |
6 |
19 |
18 |
| 1755 |
27 |
5 |
49 |
8 |
26 |
14 |
5 |
10 |
46 |
6 |
5 |
49 |
0 |
4 |
49 |
5 |
29 |
0 |
| 1756 |
15 |
14 |
38 |
8 |
15 |
30 |
3 |
20 |
35 |
6 |
13 |
52 |
11 |
24 |
6 |
5 |
10 |
14 |
| 1757 |
4 |
23 |
27 |
8 |
4 |
36 |
2 |
0 |
23 |
6 |
21 |
55 |
11 |
13 |
23 |
4 |
21 |
27 |
| 1758 |
23 |
20 |
59 |
8 |
23 |
8 |
1 |
5 |
59 |
8 |
0 |
38 |
0 |
1 |
46 |
4 |
1 |
9 |
| 1759 |
13 |
5 |
47 |
8 |
12 |
25 |
11 |
15 |
48 |
8 |
8 |
41 |
11 |
21 |
3 |
3 |
12 |
22 |
| 1760 |
1 |
14 |
36 |
8 |
1 |
41 |
9 |
25 |
37 |
8 |
16 |
44 |
11 |
10 |
20 |
2 |
23 |
35 |
| 2211761 |
20 |
12 |
9 |
8 |
20 |
2 |
9 |
1 |
13 |
9 |
25 |
27 |
11 |
28 |
43 |
2 |
3 |
16 |
| 1762 |
9 |
20 |
57 |
8 |
9 |
19 |
7 |
11 |
2 |
10 |
3 |
31 |
11 |
18 |
0 |
1 |
14 |
29 |
| 1763 |
28 |
18 |
30 |
8 |
27 |
40 |
6 |
16 |
38 |
11 |
12 |
13 |
0 |
6 |
23 |
0 |
24 |
11 |
| 1764 |
17 |
3 |
19 |
8 |
16 |
56 |
4 |
26 |
26 |
11 |
20 |
16 |
11 |
25 |
40 |
0 |
5 |
24 |
| 1765 |
6 |
12 |
8 |
8 |
6 |
13 |
3 |
6 |
15 |
11 |
28 |
19 |
11 |
14 |
57 |
11 |
16 |
38 |
| 1766 |
25 |
9 |
40 |
8 |
24 |
34 |
2 |
11 |
52 |
1 |
7 |
1 |
0 |
3 |
20 |
10 |
26 |
20 |
| 1767 |
18 |
18 |
29 |
8 |
13 |
50 |
0 |
21 |
41 |
1 |
15 |
4 |
11 |
22 |
37 |
10 |
7 |
33 |
| 1768 |
3 |
3 |
17 |
8 |
3 |
6 |
11 |
1 |
29 |
1 |
23 |
7 |
11 |
11 |
54 |
9 |
18 |
46 |
| 1769 |
22 |
0 |
50 |
8 |
21 |
28 |
10 |
7 |
5 |
3 |
1 |
49 |
0 |
0 |
17 |
8 |
28 |
28 |
| 1770 |
11 |
9 |
39 |
8 |
15 |
45 |
8 |
16 |
54 |
3 |
9 |
52 |
11 |
19 |
34 |
8 |
9 |
42 |
| 1771 |
30 |
7 |
11 |
8 |
29 |
6 |
7 |
22 |
30 |
4 |
18 |
36 |
0 |
7 |
57 |
7 |
19 |
21 |
| 1772 |
18 |
16 |
0 |
8 |
18 |
22 |
6 |
2 |
18 |
4 |
26 |
39 |
11 |
27 |
14 |
7 |
0 |
35 |
| 1773 |
8 |
0 |
48 |
8 |
7 |
38 |
4 |
12 |
7 |
5 |
4 |
42 |
11 |
16 |
31 |
6 |
11 |
49 |
| 1774 |
26 |
22 |
21 |
8 |
26 |
0 |
3 |
17 |
43 |
6 |
13 |
24 |
0 |
4 |
54 |
5 |
21 |
31 |
| 1775 |
16 |
7 |
10 |
8 |
15 |
16 |
1 |
27 |
31 |
6 |
21 |
27 |
11 |
24 |
11 |
5 |
2 |
44 |
| 1776 |
4 |
15 |
58 |
8 |
4 |
32 |
0 |
7 |
20 |
6 |
29 |
30 |
11 |
13 |
28 |
4 |
13 |
58 |
| 1777 |
23 |
13 |
31 |
8 |
22 |
54 |
11 |
12 |
56 |
8 |
8 |
13 |
0 |
1 |
51 |
3 |
23 |
39 |
| 1778 |
12 |
22 |
20 |
8 |
12 |
10 |
9 |
22 |
45 |
8 |
16 |
16 |
11 |
21 |
8 |
3 |
4 |
52 |
| 1779 |
2 |
7 |
8 |
8 |
1 |
26 |
8 |
2 |
34 |
8 |
24 |
19 |
11 |
10 |
25 |
2 |
16 |
5 |
| 1780 |
20 |
4 |
41 |
8 |
19 |
48 |
7 |
8 |
10 |
10 |
3 |
1 |
11 |
28 |
48 |
1 |
25 |
47 |
| 1781 |
9 |
13 |
30 |
8 |
9 |
4 |
5 |
17 |
59 |
10 |
11 |
4 |
11 |
18 |
5 |
1 |
7 |
0 |
| 1782 |
28 |
11 |
2 |
8 |
27 |
28 |
4 |
23 |
34 |
11 |
19 |
47 |
0 |
6 |
27 |
0 |
16 |
41 |
| 1783 |
17 |
19 |
51 |
8 |
16 |
44 |
3 |
3 |
23 |
11 |
27 |
50 |
11 |
25 |
44 |
11 |
27 |
54 |
| 1784 |
6 |
4 |
40 |
8 |
5 |
59 |
1 |
13 |
12 |
0 |
5 |
53 |
11 |
15 |
1 |
11 |
9 |
7 |
| 1785 |
25 |
2 |
12 |
8 |
24 |
20 |
0 |
18 |
48 |
1 |
14 |
36 |
0 |
3 |
24 |
10 |
18 |
48 |
| 1786 |
14 |
11 |
1 |
8 |
13 |
36 |
10 |
28 |
37 |
1 |
22 |
39 |
11 |
22 |
41 |
10 |
0 |
2 |
| 1787 |
3 |
19 |
49 |
8 |
2 |
52 |
9 |
8 |
25 |
2 |
0 |
42 |
11 |
11 |
58 |
9 |
11 |
15 |
| 1788 |
21 |
17 |
22 |
8 |
21 |
14 |
8 |
14 |
2 |
3 |
9 |
25 |
0 |
0 |
21 |
8 |
20 |
57 |
| 1789 |
11 |
2 |
11 |
8 |
10 |
30 |
6 |
23 |
51 |
3 |
17 |
28 |
11 |
19 |
38 |
8 |
2 |
10 |
| 1790 |
29 |
23 |
43 |
8 |
28 |
52 |
5 |
29 |
27 |
4 |
26 |
10 |
0 |
8 |
1 |
7 |
11 |
51 |
| 1791 |
19 |
8 |
32 |
8 |
18 |
8 |
4 |
9 |
15 |
5 |
4 |
13 |
11 |
27 |
17 |
6 |
23 |
4 |
| 1792 |
7 |
17 |
21 |
8 |
7 |
24 |
2 |
19 |
4 |
5 |
12 |
16 |
11 |
16 |
34 |
6 |
4 |
17 |
| 1793 |
26 |
14 |
53 |
8 |
25 |
46 |
1 |
24 |
40 |
6 |
20 |
59 |
0 |
4 |
58 |
5 |
13 |
59 |
| 1794 |
15 |
23 |
42 |
8 |
15 |
2 |
0 |
4 |
29 |
6 |
29 |
2 |
11 |
24 |
15 |
4 |
25 |
13 |
| 1795 |
5 |
8 |
30 |
8 |
4 |
18 |
10 |
14 |
17 |
7 |
7 |
5 |
0 |
13 |
32 |
4 |
6 |
26 |
| 1796 |
23 |
6 |
3 |
8 |
22 |
39 |
9 |
19 |
53 |
8 |
15 |
48 |
0 |
1 |
56 |
3 |
16 |
8 |
| 1797 |
12 |
14 |
52 |
8 |
11 |
55 |
7 |
29 |
42 |
8 |
23 |
50 |
11 |
21 |
13 |
2 |
27 |
23 |
| 1798 |
1 |
23 |
40 |
8 |
1 |
11 |
6 |
9 |
30 |
9 |
1 |
53 |
11 |
10 |
30 |
2 |
8 |
36 |
| 1799 |
20 |
21 |
13 |
8 |
19 |
33 |
5 |
15 |
6 |
10 |
10 |
36 |
11 |
28 |
53 |
1 |
18 |
18 |
| 1800 |
10 |
6 |
2 |
8 |
8 |
50 |
3 |
24 |
55 |
10 |
18 |
39 |
11 |
18 |
10 |
0 |
29 |
31 |
222
Tab. V. The first mean Conjunction of the Sun and Moon after a compleat Century, beginning with March, for 5000 years 10 days 7 hours 56 minutes (in which time there are just 61843 mean Lunations) with the mean Anomaly of the Sun and Moon, the Sun’s mean distance from the Ascending Node, and the mean Long. of the Sun and Node from the beginning of the sign Aries, at the times of all those mean Conjunctions.
| Centuries of Julian Years. |
First Conjunction after a Century. |
The Sun’s mean Anomaly. |
The Moon’s mean Anomaly. |
The Sun’s distance from the Node. |
The Sun’s Longitude from Aries. |
The Node’s Longitude from Aries. |
| D. |
H. |
M. |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
| 100 |
4 |
8 |
11 |
0 |
3 |
21 |
8 |
15 |
22 |
4 |
19 |
27 |
0 |
5 |
2 |
4 |
14 |
25 |
| 200 |
8 |
16 |
22 |
0 |
6 |
42 |
5 |
0 |
44 |
9 |
8 |
55 |
0 |
10 |
4 |
8 |
28 |
51 |
| 300 |
13 |
0 |
33 |
0 |
10 |
3 |
1 |
16 |
6 |
1 |
28 |
22 |
0 |
15 |
6 |
1 |
13 |
16 |
| 400 |
17 |
8 |
43 |
0 |
13 |
24 |
10 |
1 |
28 |
6 |
17 |
49 |
0 |
20 |
8 |
5 |
27 |
41 |
| 500 |
21 |
16 |
54 |
0 |
16 |
46 |
6 |
16 |
50 |
11 |
7 |
16 |
0 |
25 |
10 |
10 |
12 |
6 |
| 600 |
26 |
1 |
5 |
0 |
20 |
7 |
3 |
2 |
12 |
3 |
26 |
44 |
1 |
0 |
12 |
2 |
26 |
32 |
| 700 |
0 |
20 |
32 |
11 |
24 |
22 |
10 |
21 |
45 |
7 |
15 |
31 |
0 |
6 |
7 |
7 |
9 |
24 |
| 800 |
5 |
4 |
43 |
11 |
27 |
43 |
7 |
7 |
7 |
0 |
4 |
58 |
0 |
11 |
9 |
11 |
23 |
49 |
| 900 |
9 |
12 |
54 |
0 |
1 |
4 |
3 |
22 |
29 |
4 |
24 |
25 |
0 |
16 |
12 |
4 |
8 |
13 |
| 1000 |
13 |
21 |
5 |
0 |
4 |
25 |
0 |
7 |
51 |
9 |
13 |
53 |
0 |
21 |
14 |
8 |
22 |
39 |
| 1100 |
18 |
5 |
16 |
0 |
7 |
46 |
8 |
23 |
13 |
2 |
3 |
20 |
0 |
26 |
16 |
1 |
7 |
4 |
| 1200 |
22 |
13 |
26 |
0 |
11 |
7 |
5 |
8 |
35 |
6 |
22 |
47 |
1 |
1 |
18 |
5 |
21 |
29 |
| 1300 |
26 |
21 |
37 |
0 |
14 |
28 |
1 |
23 |
57 |
11 |
12 |
15 |
1 |
6 |
20 |
10 |
5 |
55 |
| 1400 |
1 |
17 |
4 |
11 |
18 |
43 |
9 |
13 |
30 |
3 |
1 |
2 |
0 |
12 |
15 |
2 |
18 |
47 |
| 1500 |
6 |
1 |
15 |
11 |
22 |
4 |
5 |
28 |
52 |
7 |
20 |
29 |
0 |
17 |
17 |
7 |
3 |
12 |
| 1600 |
10 |
9 |
26 |
11 |
25 |
25 |
2 |
14 |
14 |
0 |
9 |
56 |
0 |
22 |
19 |
11 |
17 |
37 |
| 1700 |
14 |
17 |
37 |
11 |
28 |
46 |
10 |
29 |
36 |
4 |
29 |
23 |
0 |
27 |
22 |
4 |
2 |
2 |
| 1800 |
19 |
1 |
48 |
0 |
2 |
8 |
7 |
14 |
58 |
9 |
18 |
51 |
1 |
2 |
24 |
8 |
16 |
27 |
| 1900 |
23 |
9 |
58 |
0 |
5 |
29 |
4 |
0 |
20 |
2 |
8 |
18 |
1 |
7 |
26 |
1 |
0 |
52 |
| 2000 |
27 |
18 |
9 |
0 |
8 |
50 |
0 |
15 |
42 |
6 |
27 |
45 |
1 |
12 |
28 |
5 |
15 |
17 |
| 2100 |
2 |
13 |
36 |
11 |
13 |
5 |
8 |
5 |
15 |
10 |
16 |
32 |
0 |
18 |
24 |
9 |
28 |
8 |
| 2200 |
6 |
21 |
47 |
11 |
16 |
26 |
4 |
20 |
37 |
3 |
6 |
0 |
0 |
23 |
26 |
2 |
12 |
34 |
| 2300 |
11 |
5 |
58 |
11 |
19 |
47 |
1 |
5 |
59 |
7 |
25 |
27 |
0 |
28 |
28 |
6 |
26 |
59 |
| 2400 |
15 |
14 |
9 |
11 |
23 |
8 |
9 |
21 |
21 |
0 |
14 |
54 |
1 |
3 |
30 |
11 |
11 |
24 |
| 2500 |
19 |
22 |
20 |
11 |
26 |
29 |
6 |
6 |
43 |
5 |
4 |
11 |
1 |
8 |
32 |
3 |
25 |
49 |
| 2600 |
24 |
6 |
31 |
11 |
29 |
50 |
2 |
22 |
4 |
9 |
23 |
49 |
1 |
13 |
35 |
8 |
10 |
14 |
| 2700 |
28 |
14 |
41 |
0 |
3 |
11 |
11 |
17 |
26 |
2 |
13 |
16 |
1 |
18 |
37 |
0 |
24 |
39 |
| 2800 |
3 |
10 |
8 |
11 |
7 |
26 |
6 |
26 |
59 |
6 |
2 |
3 |
0 |
24 |
31 |
5 |
7 |
33 |
| 2900 |
7 |
18 |
19 |
11 |
10 |
47 |
3 |
12 |
21 |
10 |
21 |
30 |
0 |
29 |
33 |
9 |
21 |
58 |
| 3000 |
12 |
2 |
30 |
11 |
14 |
8 |
11 |
27 |
43 |
3 |
10 |
58 |
1 |
4 |
35 |
2 |
6 |
23 |
| 3100 |
16 |
10 |
41 |
11 |
17 |
30 |
8 |
13 |
5 |
8 |
10 |
25 |
1 |
9 |
37 |
6 |
20 |
48 |
| 3200 |
20 |
18 |
52 |
11 |
20 |
51 |
4 |
28 |
27 |
0 |
19 |
52 |
1 |
14 |
39 |
11 |
5 |
13 |
| 3300 |
25 |
3 |
3 |
11 |
24 |
11 |
1 |
13 |
49 |
5 |
9 |
20 |
1 |
19 |
41 |
3 |
19 |
39 |
| 3400 |
29 |
11 |
14 |
11 |
27 |
32 |
9 |
29 |
11 |
9 |
28 |
47 |
1 |
24 |
43 |
8 |
4 |
4 |
| 3500 |
4 |
6 |
41 |
11 |
1 |
47 |
5 |
18 |
44 |
1 |
17 |
34 |
1 |
0 |
41 |
0 |
16 |
53 |
| 2233600 |
8 |
14 |
52 |
11 |
4 |
58 |
2 |
4 |
6 |
6 |
7 |
1 |
1 |
5 |
42 |
5 |
1 |
19 |
| 3700 |
12 |
23 |
3 |
11 |
8 |
9 |
10 |
19 |
28 |
10 |
26 |
28 |
1 |
10 |
43 |
9 |
15 |
45 |
| 3800 |
17 |
7 |
14 |
11 |
11 |
20 |
7 |
4 |
50 |
3 |
15 |
55 |
1 |
15 |
45 |
2 |
0 |
10 |
| 3900 |
21 |
15 |
25 |
11 |
14 |
31 |
4 |
20 |
12 |
8 |
5 |
22 |
1 |
20 |
47 |
6 |
14 |
35 |
| 4000 |
25 |
23 |
36 |
11 |
17 |
42 |
1 |
5 |
34 |
0 |
24 |
49 |
1 |
25 |
49 |
10 |
29 |
0 |
| 4100 |
0 |
19 |
3 |
10 |
22 |
56 |
8 |
25 |
7 |
4 |
13 |
36 |
1 |
0 |
45 |
3 |
12 |
51 |
| 4200 |
5 |
3 |
14 |
10 |
26 |
17 |
5 |
10 |
29 |
9 |
3 |
3 |
1 |
6 |
47 |
7 |
6 |
16 |
| 4300 |
9 |
11 |
25 |
10 |
29 |
37 |
1 |
25 |
51 |
1 |
12 |
30 |
1 |
11 |
48 |
11 |
25 |
39 |
| 4400 |
13 |
19 |
36 |
11 |
2 |
58 |
10 |
11 |
13 |
6 |
1 |
57 |
1 |
16 |
51 |
4 |
10 |
4 |
| 4500 |
18 |
3 |
46 |
11 |
6 |
18 |
6 |
26 |
35 |
10 |
21 |
24 |
1 |
21 |
53 |
8 |
29 |
31 |
| 4600 |
22 |
11 |
57 |
11 |
9 |
39 |
3 |
11 |
15 |
3 |
10 |
51 |
1 |
26 |
55 |
1 |
13 |
56 |
| 4700 |
26 |
20 |
7 |
11 |
12 |
59 |
11 |
27 |
19 |
8 |
0 |
16 |
2 |
1 |
57 |
5 |
28 |
19 |
| 4800 |
1 |
15 |
34 |
10 |
17 |
14 |
7 |
16 |
52 |
11 |
19 |
4 |
1 |
7 |
53 |
10 |
11 |
11 |
| 4900 |
5 |
23 |
45 |
10 |
20 |
35 |
4 |
2 |
14 |
4 |
8 |
30 |
1 |
12 |
55 |
2 |
25 |
35 |
| 5000 |
10 |
7 |
56 |
10 |
23 |
56 |
0 |
17 |
36 |
8 |
27 |
57 |
1 |
17 |
57 |
7 |
10 |
0 |
Table VI. The mean Anomaly of the Sun and Moon, the Sun’s mean distance from the Ascending Node, with the mean Longitude of the Sun and Node from the beginning of the Sign Aries, for 13 mean Lunations.
| Lunations. |
Mean Lunations. |
The Sun’s mean Anomaly. |
The Moon’s mean Anomaly. |
The Sun’s motion from the Node. |
The Sun’s mean Motion. |
The Node’s retrograde Motion. |
| D. |
H. |
M. |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
s |
° |
ʹ |
| 1 |
29 |
12 |
44 |
0 |
29 |
6 |
0 |
25 |
49 |
1 |
0 |
40 |
0 |
29 |
6 |
0 |
1 |
34 |
| 2 |
59 |
1 |
28 |
1 |
28 |
13 |
1 |
21 |
38 |
2 |
1 |
20 |
1 |
28 |
13 |
0 |
3 |
8 |
| 3 |
88 |
14 |
12 |
2 |
27 |
19 |
2 |
17 |
27 |
3 |
2 |
1 |
2 |
27 |
19 |
0 |
4 |
41 |
| 4 |
118 |
2 |
56 |
3 |
26 |
26 |
3 |
13 |
16 |
4 |
2 |
41 |
3 |
26 |
26 |
0 |
6 |
15 |
| 5 |
147 |
15 |
4 |
4 |
25 |
32 |
4 |
9 |
5 |
5 |
3 |
21 |
4 |
25 |
32 |
0 |
7 |
49 |
| 6 |
177 |
4 |
24 |
5 |
24 |
38 |
5 |
4 |
54 |
6 |
4 |
1 |
5 |
24 |
38 |
0 |
9 |
23 |
| 7 |
206 |
17 |
8 |
6 |
23 |
44 |
6 |
0 |
43 |
7 |
4 |
42 |
6 |
23 |
45 |
0 |
10 |
57 |
| 8 |
236 |
5 |
52 |
7 |
22 |
50 |
6 |
26 |
32 |
8 |
5 |
22 |
7 |
22 |
51 |
0 |
12 |
31 |
| 9 |
265 |
18 |
36 |
8 |
21 |
57 |
7 |
22 |
21 |
9 |
6 |
2 |
8 |
21 |
58 |
0 |
14 |
4 |
| 10 |
295 |
7 |
21 |
9 |
21 |
3 |
8 |
18 |
10 |
10 |
6 |
42 |
9 |
21 |
4 |
0 |
15 |
38 |
| 11 |
324 |
20 |
5 |
10 |
20 |
9 |
9 |
13 |
59 |
11 |
7 |
22 |
10 |
20 |
10 |
0 |
17 |
12 |
| 12 |
354 |
8 |
49 |
11 |
19 |
16 |
10 |
9 |
48 |
0 |
8 |
3 |
11 |
19 |
17 |
0 |
18 |
46 |
| 13 |
383 |
21 |
33 |
0 |
18 |
22 |
11 |
5 |
37 |
1 |
8 |
43 |
0 |
18 |
23 |
0 |
20 |
20 |
The first, second, third, and fourth Tables may be continued, by means of the sixth, to any
length of time: for, by adding 12 Lunations to the mean time of the New or Full Moon which
happens next after the 11th day of March, and then, casting out 365 days in common years,
and 366 days in leap-years, we have the mean time of New or Full Moon in March the following
year. But when the mean New or Full Moon happens on or before the 11th of March,
there must be 13 Lunations added to carry it to March again. The Anomalies, Sun’s distance
from the Node, and Longitude of the Sun, are found the same way, by adding them for 12
or 13 Lunations. But the retrograde Motion of the Node for these Lunations must be subtracted
from it’s longitude from Aries in March, to have it’s Longitude or Place in the March following.
224
Table VII. The number of Days, reckoned from the beginning of March, answering to the Days of all the mean New and Full Moons.
| Days. |
March. |
April. |
May. |
June. |
July. |
August. |
September. |
October. |
November. |
December. |
January. |
February. |
| 1 |
1 |
32 |
62 |
93 |
123 |
154 |
185 |
215 |
246 |
276 |
307 |
338 |
| 2 |
2 |
33 |
63 |
94 |
124 |
155 |
186 |
216 |
247 |
277 |
308 |
339 |
| 3 |
3 |
34 |
64 |
95 |
125 |
156 |
187 |
217 |
248 |
278 |
309 |
340 |
| 4 |
4 |
35 |
65 |
96 |
126 |
157 |
188 |
218 |
249 |
279 |
310 |
341 |
| 5 |
5 |
36 |
66 |
97 |
127 |
158 |
189 |
219 |
250 |
280 |
311 |
342 |
| 6 |
6 |
37 |
67 |
98 |
128 |
159 |
190 |
220 |
251 |
281 |
312 |
343 |
| 7 |
7 |
38 |
68 |
99 |
129 |
160 |
191 |
221 |
252 |
282 |
313 |
344 |
| 8 |
8 |
39 |
69 |
100 |
130 |
161 |
192 |
222 |
253 |
283 |
314 |
345 |
| 9 |
9 |
40 |
70 |
101 |
131 |
162 |
193 |
223 |
254 |
284 |
315 |
346 |
| 10 |
10 |
41 |
71 |
102 |
132 |
163 |
194 |
224 |
255 |
285 |
316 |
347 |
| 11 |
11 |
42 |
72 |
103 |
133 |
164 |
195 |
225 |
256 |
286 |
317 |
348 |
| 12 |
12 |
43 |
73 |
104 |
134 |
165 |
196 |
226 |
257 |
287 |
318 |
349 |
| 13 |
13 |
44 |
74 |
105 |
135 |
166 |
197 |
227 |
258 |
288 |
319 |
350 |
| 14 |
14 |
45 |
75 |
106 |
136 |
167 |
198 |
228 |
259 |
289 |
320 |
351 |
| 15 |
15 |
46 |
76 |
107 |
137 |
168 |
199 |
229 |
260 |
290 |
321 |
352 |
| 16 |
16 |
47 |
77 |
108 |
138 |
169 |
200 |
230 |
261 |
291 |
322 |
353 |
| 17 |
17 |
48 |
78 |
109 |
139 |
170 |
201 |
231 |
262 |
292 |
323 |
354 |
| 18 |
18 |
49 |
79 |
110 |
140 |
171 |
202 |
232 |
263 |
293 |
324 |
355 |
| 19 |
19 |
50 |
80 |
111 |
141 |
172 |
203 |
233 |
264 |
294 |
325 |
356 |
| 20 |
20 |
51 |
81 |
112 |
142 |
173 |
204 |
234 |
265 |
295 |
326 |
357 |
| 21 |
21 |
52 |
82 |
113 |
143 |
174 |
205 |
235 |
266 |
296 |
327 |
358 |
| 22 |
22 |
53 |
83 |
114 |
144 |
175 |
206 |
236 |
267 |
297 |
328 |
359 |
| 23 |
23 |
54 |
84 |
115 |
145 |
176 |
207 |
237 |
268 |
298 |
329 |
360 |
| 24 |
24 |
55 |
85 |
116 |
146 |
177 |
208 |
238 |
269 |
299 |
330 |
361 |
| 25 |
25 |
56 |
86 |
117 |
147 |
178 |
209 |
239 |
270 |
300 |
331 |
362 |
| 26 |
26 |
57 |
87 |
118 |
148 |
179 |
210 |
240 |
271 |
301 |
332 |
363 |
| 27 |
27 |
58 |
88 |
119 |
149 |
180 |
211 |
241 |
272 |
302 |
333 |
364 |
| 28 |
28 |
59 |
89 |
120 |
150 |
181 |
212 |
242 |
273 |
303 |
334 |
365 |
| 29 |
29 |
60 |
90 |
121 |
151 |
182 |
213 |
243 |
274 |
304 |
335 |
366 |
| 30 |
30 |
61 |
91 |
122 |
152 |
183 |
214 |
244 |
275 |
305 |
336 |
— |
| 31 |
31 |
— |
92 |
— |
153 |
184 |
— |
245 |
— |
306 |
337 |
— |
Table VIII. The Moon’s annual Equation.
| Sun’s Ano. |
Subtract |
Sun’s Ano. |
| 0 |
1 |
2 |
3 |
4 |
5 |
| S. |
S. |
S. |
S. |
S. |
S. |
| D. |
M. |
M. |
M. |
M. |
M. |
M. |
D. |
| 0 |
0 |
11 |
18 |
22 |
19 |
11 |
30 |
| 1 |
0 |
11 |
19 |
22 |
19 |
11 |
29 |
| 2 |
1 |
11 |
19 |
22 |
18 |
10 |
28 |
| 3 |
1 |
11 |
19 |
22 |
18 |
10 |
27 |
| 4 |
1 |
12 |
19 |
22 |
18 |
10 |
26 |
| 5 |
2 |
12 |
19 |
22 |
18 |
9 |
25 |
| 6 |
2 |
12 |
19 |
21 |
18 |
9 |
24 |
| 7 |
3 |
13 |
20 |
21 |
17 |
9 |
23 |
| 8 |
3 |
13 |
20 |
21 |
17 |
8 |
22 |
| 9 |
3 |
13 |
20 |
21 |
17 |
8 |
21 |
| 10 |
4 |
14 |
20 |
21 |
17 |
8 |
20 |
| 11 |
4 |
14 |
20 |
21 |
16 |
7 |
19 |
| 12 |
4 |
14 |
20 |
21 |
16 |
7 |
18 |
| 13 |
5 |
14 |
20 |
21 |
16 |
6 |
17 |
| 14 |
5 |
15 |
20 |
21 |
16 |
6 |
16 |
| 15 |
5 |
15 |
21 |
21 |
15 |
6 |
15 |
| 16 |
6 |
15 |
21 |
21 |
15 |
5 |
14 |
| 17 |
6 |
15 |
21 |
21 |
15 |
5 |
13 |
| 18 |
6 |
16 |
21 |
21 |
15 |
5 |
12 |
| 19 |
7 |
16 |
21 |
20 |
14 |
4 |
11 |
| 20 |
7 |
16 |
21 |
20 |
14 |
4 |
10 |
| 21 |
7 |
16 |
21 |
20 |
14 |
3 |
9 |
| 22 |
8 |
17 |
21 |
20 |
13 |
3 |
8 |
| 23 |
8 |
17 |
21 |
20 |
13 |
3 |
7 |
| 24 |
9 |
17 |
21 |
20 |
13 |
2 |
6 |
| 25 |
9 |
17 |
21 |
20 |
13 |
2 |
5 |
| 26 |
9 |
18 |
21 |
20 |
12 |
2 |
4 |
| 27 |
10 |
18 |
21 |
19 |
12 |
1 |
3 |
| 28 |
10 |
18 |
21 |
19 |
12 |
1 |
2 |
| 29 |
10 |
18 |
22 |
19 |
11 |
0 |
1 |
| 30 |
11 |
18 |
22 |
19 |
11 |
0 |
0 |
| Sun’s Ano. |
11 |
10 |
9 |
8 |
7 |
6 |
Sun’s Ano. |
| S. |
S. |
S. |
S. |
S. |
S. |
| Add |
225
Table IX. Equation of the Moon’s mean Anomaly.
| Sun’s Anom. |
Add |
Sun’s Anom. |
| 0 |
1 |
2 |
3 |
4 |
5 |
| S. |
S. |
S. |
S. |
S. |
S. |
| ° |
ʹ |
ʹ |
ʹ |
ʹ |
ʹ |
ʹ |
° |
| 0 |
0 |
10 |
17 |
20 |
17 |
10 |
30 |
| 1 |
0 |
10 |
17 |
20 |
17 |
10 |
29 |
| 2 |
1 |
11 |
17 |
20 |
17 |
9 |
28 |
| 3 |
1 |
11 |
18 |
20 |
17 |
9 |
27 |
| 4 |
1 |
11 |
18 |
20 |
17 |
9 |
26 |
| 5 |
2 |
12 |
18 |
20 |
17 |
9 |
25 |
| 6 |
2 |
12 |
18 |
20 |
16 |
8 |
24 |
| 7 |
2 |
12 |
18 |
20 |
16 |
8 |
23 |
| 8 |
3 |
12 |
18 |
20 |
16 |
8 |
22 |
| 9 |
3 |
12 |
19 |
20 |
16 |
7 |
21 |
| 10 |
3 |
13 |
19 |
20 |
16 |
7 |
20 |
| 11 |
4 |
13 |
19 |
20 |
15 |
7 |
19 |
| 12 |
4 |
13 |
19 |
20 |
15 |
6 |
18 |
| 13 |
4 |
13 |
19 |
19 |
15 |
6 |
17 |
| 14 |
5 |
14 |
19 |
19 |
15 |
6 |
16 |
| 15 |
5 |
14 |
19 |
19 |
14 |
5 |
15 |
| 16 |
5 |
14 |
19 |
19 |
14 |
5 |
14 |
| 17 |
6 |
14 |
19 |
19 |
14 |
5 |
13 |
| 18 |
6 |
15 |
19 |
19 |
14 |
4 |
12 |
| 19 |
6 |
15 |
20 |
19 |
13 |
4 |
11 |
| 20 |
7 |
15 |
20 |
19 |
13 |
4 |
10 |
| 21 |
7 |
15 |
20 |
19 |
13 |
3 |
9 |
| 22 |
7 |
16 |
20 |
19 |
13 |
3 |
8 |
| 23 |
8 |
16 |
20 |
19 |
12 |
3 |
7 |
| 24 |
8 |
16 |
20 |
18 |
12 |
2 |
6 |
| 25 |
8 |
16 |
20 |
18 |
12 |
2 |
5 |
| 26 |
9 |
16 |
20 |
18 |
11 |
1 |
4 |
| 27 |
9 |
17 |
20 |
18 |
11 |
1 |
3 |
| 28 |
9 |
17 |
20 |
18 |
11 |
1 |
2 |
| 29 |
10 |
17 |
20 |
18 |
10 |
0 |
1 |
| 30 |
10 |
17 |
20 |
17 |
10 |
0 |
0 |
| Sun’s Anom. |
11 |
10 |
9 |
8 |
7 |
6 |
Sun’s Anom. |
| S. |
S. |
S. |
S. |
S. |
S. |
| Subtract |
Table X. The Moon’s elliptic Equation.
| Moon’s Ano. |
Add |
Moon’s Ano. |
| 0 |
1 |
2 |
3 |
4 |
5 |
| Signs |
Signs |
Signs |
Signs |
Signs |
Signs |
| ° |
H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
° |
| 0 |
0 |
0 |
4 |
49 |
8 |
8 |
9 |
2 |
7 |
32 |
4 |
14 |
30 |
| 1 |
0 |
10 |
4 |
57 |
8 |
12 |
9 |
1 |
7 |
27 |
4 |
6 |
29 |
| 2 |
0 |
20 |
5 |
5 |
8 |
16 |
9 |
0 |
7 |
22 |
3 |
58 |
28 |
| 3 |
0 |
30 |
5 |
13 |
8 |
20 |
8 |
59 |
7 |
17 |
3 |
50 |
27 |
| 4 |
0 |
40 |
5 |
21 |
8 |
24 |
8 |
58 |
7 |
12 |
3 |
42 |
26 |
| 5 |
0 |
50 |
5 |
29 |
8 |
28 |
8 |
57 |
7 |
6 |
3 |
34 |
25 |
| 6 |
1 |
0 |
5 |
37 |
8 |
31 |
8 |
55 |
7 |
0 |
3 |
26 |
24 |
| 7 |
1 |
10 |
5 |
45 |
8 |
34 |
8 |
53 |
6 |
54 |
3 |
18 |
23 |
| 8 |
1 |
20 |
5 |
53 |
8 |
37 |
8 |
51 |
6 |
48 |
3 |
10 |
22 |
| 9 |
1 |
30 |
6 |
1 |
8 |
40 |
8 |
49 |
6 |
42 |
3 |
2 |
21 |
| 10 |
1 |
40 |
6 |
9 |
8 |
43 |
8 |
47 |
6 |
36 |
2 |
53 |
20 |
| 11 |
1 |
50 |
6 |
16 |
8 |
45 |
8 |
44 |
6 |
30 |
2 |
45 |
19 |
| 12 |
2 |
0 |
6 |
23 |
8 |
47 |
8 |
41 |
6 |
24 |
2 |
37 |
18 |
| 13 |
2 |
10 |
6 |
30 |
8 |
49 |
8 |
38 |
6 |
18 |
2 |
29 |
17 |
| 14 |
2 |
20 |
6 |
37 |
8 |
51 |
8 |
35 |
6 |
11 |
2 |
21 |
16 |
| 15 |
2 |
30 |
6 |
44 |
8 |
53 |
8 |
32 |
6 |
4 |
2 |
12 |
15 |
| 16 |
2 |
40 |
6 |
51 |
8 |
55 |
8 |
29 |
5 |
57 |
2 |
3 |
14 |
| 17 |
2 |
50 |
6 |
58 |
8 |
57 |
8 |
26 |
5 |
50 |
1 |
54 |
13 |
| 18 |
3 |
0 |
7 |
4 |
8 |
59 |
8 |
23 |
5 |
43 |
1 |
45 |
12 |
| 19 |
3 |
10 |
7 |
10 |
9 |
0 |
8 |
20 |
5 |
36 |
1 |
36 |
11 |
| 20 |
3 |
19 |
7 |
16 |
9 |
1 |
8 |
16 |
5 |
29 |
1 |
27 |
10 |
| 21 |
3 |
28 |
7 |
22 |
9 |
2 |
8 |
12 |
5 |
22 |
1 |
19 |
9 |
| 22 |
3 |
37 |
7 |
28 |
9 |
2 |
8 |
8 |
5 |
15 |
1 |
11 |
8 |
| 23 |
3 |
46 |
7 |
33 |
9 |
3 |
8 |
4 |
5 |
8 |
1 |
3 |
7 |
| 24 |
3 |
55 |
7 |
38 |
9 |
3 |
8 |
0 |
5 |
1 |
0 |
54 |
6 |
| 25 |
4 |
4 |
7 |
43 |
9 |
4 |
7 |
56 |
4 |
54 |
0 |
45 |
5 |
| 26 |
4 |
13 |
7 |
48 |
9 |
4 |
7 |
52 |
4 |
46 |
0 |
36 |
4 |
| 27 |
4 |
22 |
7 |
53 |
9 |
4 |
7 |
47 |
4 |
38 |
0 |
27 |
3 |
| 28 |
4 |
31 |
7 |
58 |
9 |
3 |
7 |
42 |
4 |
30 |
0 |
18 |
2 |
| 29 |
4 |
40 |
8 |
3 |
9 |
3 |
7 |
37 |
4 |
22 |
0 |
9 |
1 |
| 30 |
4 |
49 |
8 |
8 |
9 |
2 |
7 |
32 |
4 |
14 |
0 |
0 |
0 |
| Moon’s Ano. |
11 |
10 |
9 |
8 |
7 |
6 |
Moon’s Ano. |
| Signs |
Signs |
Signs |
Signs |
Signs |
Signs |
| Subtract |
226
Table XI. The Sun’s Equation at the time of New and Full Moon.
| Sun’s Anom. |
Subtract |
Sun’s Anom. |
| 0 |
1 |
2 |
3 |
4 |
5 |
| Signs |
Signs |
Signs |
Signs |
Signs |
Signs |
| ° |
H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
H. |
M. |
° |
| 0 |
0 |
0 |
1 |
44 |
3 |
2 |
3 |
32 |
3 |
5 |
1 |
48 |
30 |
| 1 |
0 |
4 |
1 |
47 |
3 |
3 |
3 |
32 |
3 |
3 |
1 |
45 |
29 |
| 2 |
0 |
7 |
1 |
50 |
3 |
5 |
3 |
32 |
3 |
2 |
1 |
42 |
28 |
| 3 |
0 |
11 |
1 |
53 |
3 |
7 |
3 |
32 |
3 |
0 |
1 |
38 |
27 |
| 4 |
0 |
14 |
1 |
57 |
3 |
9 |
3 |
32 |
2 |
58 |
1 |
35 |
26 |
| 5 |
0 |
18 |
2 |
0 |
3 |
10 |
3 |
31 |
2 |
56 |
1 |
31 |
25 |
| 6 |
0 |
22 |
2 |
3 |
3 |
12 |
3 |
31 |
2 |
54 |
1 |
28 |
24 |
| 7 |
0 |
25 |
2 |
6 |
3 |
14 |
3 |
31 |
2 |
52 |
1 |
24 |
23 |
| 8 |
0 |
29 |
2 |
8 |
3 |
16 |
3 |
30 |
2 |
50 |
1 |
21 |
22 |
| 9 |
0 |
32 |
2 |
11 |
3 |
17 |
4 |
30 |
2 |
48 |
1 |
17 |
21 |
| 10 |
0 |
36 |
2 |
14 |
3 |
18 |
3 |
30 |
2 |
45 |
1 |
14 |
20 |
| 11 |
0 |
40 |
2 |
17 |
3 |
19 |
3 |
29 |
2 |
43 |
1 |
11 |
19 |
| 12 |
0 |
43 |
2 |
20 |
3 |
20 |
3 |
29 |
2 |
40 |
1 |
7 |
18 |
| 13 |
0 |
47 |
2 |
22 |
3 |
21 |
3 |
28 |
2 |
37 |
1 |
4 |
17 |
| 14 |
0 |
50 |
2 |
25 |
3 |
22 |
3 |
27 |
2 |
35 |
1 |
0 |
16 |
| 15 |
0 |
54 |
2 |
28 |
3 |
23 |
3 |
26 |
2 |
32 |
0 |
56 |
15 |
| 16 |
0 |
57 |
2 |
30 |
3 |
24 |
3 |
25 |
2 |
29 |
0 |
52 |
14 |
| 17 |
1 |
0 |
2 |
32 |
3 |
25 |
3 |
24 |
2 |
26 |
0 |
49 |
13 |
| 18 |
1 |
4 |
2 |
35 |
3 |
26 |
3 |
23 |
2 |
23 |
0 |
45 |
12 |
| 19 |
1 |
7 |
2 |
38 |
3 |
27 |
3 |
22 |
2 |
21 |
0 |
41 |
11 |
| 20 |
1 |
11 |
2 |
40 |
3 |
28 |
3 |
21 |
2 |
18 |
0 |
38 |
10 |
| 21 |
1 |
14 |
2 |
43 |
3 |
28 |
3 |
20 |
2 |
15 |
0 |
34 |
9 |
| 22 |
1 |
17 |
2 |
45 |
3 |
29 |
3 |
19 |
2 |
12 |
0 |
30 |
8 |
| 23 |
1 |
21 |
2 |
47 |
3 |
29 |
3 |
18 |
2 |
10 |
0 |
26 |
7 |
| 24 |
1 |
24 |
2 |
49 |
3 |
30 |
3 |
17 |
2 |
7 |
0 |
23 |
6 |
| 25 |
1 |
28 |
2 |
51 |
3 |
30 |
3 |
15 |
2 |
4 |
0 |
19 |
5 |
| 26 |
1 |
31 |
2 |
54 |
3 |
31 |
3 |
13 |
2 |
1 |
0 |
15 |
4 |
| 27 |
1 |
34 |
2 |
57 |
3 |
31 |
3 |
11 |
1 |
58 |
0 |
11 |
3 |
| 28 |
1 |
38 |
2 |
59 |
3 |
31 |
3 |
9 |
1 |
55 |
0 |
7 |
2 |
| 29 |
1 |
41 |
3 |
1 |
3 |
32 |
3 |
7 |
1 |
52 |
0 |
4 |
1 |
| 30 |
1 |
44 |
3 |
2 |
3 |
32 |
3 |
5 |
1 |
48 |
0 |
0 |
0 |
| Sun’s Anom. |
11 |
10 |
9 |
8 |
7 |
6 |
Sun’s Anom. |
| Signs |
Signs |
Signs |
Signs |
Signs |
Signs |
| Add |
Table XII. Equation of the Sun’s mean Place.
| Sun’s Anom. |
Subtract |
Sun’s Anom. |
| 0 |
1 |
2 |
3 |
4 |
5 |
| Signs |
Signs |
Signs |
Signs |
Signs |
Signs |
| ° |
° |
ʹ |
° |
ʹ |
° |
ʹ |
° |
ʹ |
° |
ʹ |
° |
ʹ |
° |
| 0 |
0 |
0 |
0 |
57 |
1 |
40 |
1 |
56 |
1 |
42 |
0 |
59 |
30 |
| 1 |
0 |
2 |
0 |
59 |
1 |
41 |
1 |
56 |
1 |
41 |
0 |
57 |
29 |
| 2 |
0 |
4 |
1 |
0 |
1 |
42 |
1 |
56 |
1 |
40 |
0 |
56 |
28 |
| 3 |
0 |
6 |
1 |
1 |
1 |
43 |
1 |
56 |
1 |
39 |
0 |
54 |
27 |
| 4 |
0 |
8 |
1 |
2 |
1 |
44 |
1 |
56 |
1 |
38 |
0 |
52 |
26 |
| 5 |
0 |
10 |
1 |
4 |
1 |
45 |
1 |
56 |
1 |
36 |
0 |
50 |
25 |
| 6 |
0 |
12 |
1 |
6 |
1 |
45 |
1 |
56 |
1 |
35 |
0 |
48 |
24 |
| 7 |
0 |
14 |
1 |
7 |
1 |
46 |
1 |
55 |
1 |
34 |
0 |
46 |
23 |
| 8 |
0 |
16 |
1 |
9 |
1 |
47 |
1 |
55 |
1 |
33 |
0 |
44 |
22 |
| 9 |
0 |
18 |
1 |
10 |
1 |
48 |
1 |
55 |
1 |
32 |
0 |
42 |
21 |
| 10 |
0 |
20 |
1 |
12 |
1 |
48 |
1 |
54 |
1 |
30 |
0 |
41 |
20 |
| 11 |
0 |
22 |
1 |
14 |
1 |
49 |
1 |
54 |
1 |
29 |
0 |
39 |
19 |
| 12 |
0 |
24 |
1 |
15 |
1 |
50 |
1 |
54 |
1 |
28 |
0 |
37 |
18 |
| 13 |
0 |
26 |
1 |
17 |
1 |
51 |
1 |
53 |
1 |
26 |
0 |
35 |
17 |
| 14 |
0 |
28 |
1 |
18 |
1 |
51 |
1 |
53 |
1 |
25 |
0 |
33 |
16 |
| 15 |
0 |
30 |
1 |
20 |
1 |
52 |
1 |
52 |
1 |
23 |
0 |
31 |
15 |
| 16 |
0 |
31 |
1 |
21 |
1 |
52 |
1 |
52 |
1 |
22 |
0 |
29 |
14 |
| 17 |
0 |
33 |
1 |
22 |
1 |
53 |
1 |
51 |
1 |
21 |
0 |
27 |
13 |
| 18 |
0 |
35 |
1 |
24 |
1 |
53 |
1 |
51 |
1 |
19 |
0 |
25 |
12 |
| 19 |
0 |
37 |
1 |
25 |
1 |
54 |
1 |
50 |
1 |
18 |
0 |
23 |
11 |
| 20 |
0 |
39 |
1 |
27 |
1 |
54 |
1 |
49 |
1 |
16 |
0 |
21 |
10 |
| 21 |
0 |
41 |
1 |
28 |
1 |
55 |
1 |
49 |
1 |
14 |
0 |
19 |
9 |
| 22 |
0 |
43 |
1 |
29 |
1 |
55 |
1 |
48 |
1 |
13 |
0 |
17 |
8 |
| 23 |
0 |
45 |
1 |
30 |
1 |
55 |
1 |
47 |
1 |
11 |
0 |
14 |
7 |
| 24 |
0 |
46 |
1 |
32 |
1 |
56 |
1 |
46 |
1 |
10 |
0 |
12 |
6 |
| 25 |
0 |
48 |
1 |
33 |
1 |
56 |
1 |
46 |
1 |
8 |
0 |
10 |
5 |
| 26 |
0 |
50 |
1 |
34 |
1 |
56 |
1 |
45 |
1 |
6 |
0 |
8 |
4 |
| 27 |
0 |
52 |
1 |
35 |
1 |
56 |
1 |
45 |
1 |
5 |
0 |
6 |
3 |
| 28 |
0 |
54 |
1 |
36 |
1 |
56 |
1 |
44 |
1 |
3 |
0 |
4 |
2 |
| 29 |
0 |
55 |
1 |
38 |
1 |
56 |
1 |
43 |
1 |
1 |
0 |
2 |
1 |
| 30 |
0 |
57 |
1 |
40 |
1 |
56 |
1 |
42 |
0 |
59 |
0 |
0 |
0 |
| Sun’s Anom. |
11 |
10 |
9 |
8 |
7 |
6 |
Sun’s Anom. |
| Signs |
Signs |
Signs |
Signs |
Signs |
Signs |
| Add |
227
Table XIII. Equation of the Moon’s Nodes.
| Sun’s Ano. |
Subtract |
Sun’s Ano. |
| 0 |
1 |
2 |
3 |
4 |
5 |
| S. |
S. |
S. |
S. |
S. |
S. |
| ° |
ʹ |
ʹ |
ʹ |
ʹ |
ʹ |
ʹ |
° |
| 0 |
0 |
5 |
8 |
10 |
8 |
5 |
30 |
| 1 |
0 |
5 |
8 |
10 |
8 |
5 |
29 |
| 2 |
0 |
5 |
8 |
10 |
8 |
5 |
28 |
| 3 |
0 |
5 |
8 |
10 |
8 |
4 |
27 |
| 4 |
1 |
5 |
8 |
10 |
8 |
4 |
26 |
| 5 |
1 |
5 |
8 |
10 |
8 |
4 |
25 |
| 6 |
1 |
6 |
9 |
10 |
8 |
4 |
24 |
| 7 |
1 |
6 |
9 |
9 |
8 |
4 |
23 |
| 8 |
1 |
6 |
9 |
9 |
8 |
4 |
22 |
| 9 |
1 |
6 |
9 |
9 |
7 |
3 |
21 |
| 10 |
2 |
6 |
9 |
9 |
7 |
3 |
20 |
| 11 |
2 |
6 |
9 |
9 |
7 |
3 |
19 |
| 12 |
2 |
6 |
9 |
9 |
7 |
3 |
18 |
| 13 |
2 |
6 |
9 |
9 |
7 |
3 |
17 |
| 14 |
2 |
7 |
9 |
9 |
7 |
3 |
16 |
| 15 |
2 |
7 |
9 |
9 |
7 |
3 |
15 |
| 16 |
2 |
7 |
9 |
9 |
7 |
2 |
14 |
| 17 |
3 |
7 |
9 |
9 |
7 |
2 |
13 |
| 18 |
3 |
7 |
9 |
9 |
6 |
2 |
12 |
| 19 |
3 |
7 |
9 |
9 |
6 |
2 |
11 |
| 20 |
3 |
7 |
9 |
9 |
6 |
2 |
10 |
| 21 |
3 |
7 |
9 |
9 |
6 |
2 |
9 |
| 22 |
4 |
7 |
9 |
9 |
6 |
1 |
8 |
| 23 |
4 |
8 |
9 |
9 |
6 |
1 |
7 |
| 24 |
4 |
8 |
9 |
9 |
6 |
1 |
6 |
| 25 |
4 |
8 |
9 |
9 |
6 |
1 |
5 |
| 26 |
4 |
8 |
10 |
9 |
5 |
1 |
4 |
| 27 |
4 |
8 |
10 |
9 |
5 |
1 |
3 |
| 28 |
4 |
8 |
10 |
8 |
5 |
0 |
2 |
| 29 |
5 |
8 |
10 |
8 |
5 |
0 |
1 |
| 30 |
5 |
8 |
10 |
8 |
5 |
0 |
0 |
| Sun’s Ano. |
11 |
10 |
9 |
8 |
7 |
6 |
Sun’s Ano. |
| S. |
S. |
S. |
S. |
S. |
S. |
| Add |
The above titles, Add and Subtract,
are right when the Equation is applied
to the Sun’s mean distance from the
Node; but when it is applied to the
mean place of the Node, the titles must
be changed.
Tab. XIV. The Moon’s latitude in Eclipses.
| Argument of Latit. |
| Moon fr. the Node. |
Sig. 0 N. A. |
| Sig. 6 S. D. |
| ° |
° |
ʹ |
ʺ |
° |
| 0 |
0 |
0 |
0 |
30 |
| 1 |
0 |
5 |
15 |
29 |
| 2 |
0 |
10 |
30 |
28 |
| 3 |
0 |
15 |
44 |
27 |
| 4 |
0 |
20 |
59 |
26 |
| 5 |
0 |
26 |
13 |
25 |
| 6 |
0 |
31 |
26 |
24 |
| 7 |
0 |
36 |
39 |
23 |
| 8 |
0 |
41 |
51 |
22 |
| 9 |
0 |
47 |
2 |
21 |
| 10 |
0 |
52 |
13 |
20 |
| 11 |
0 |
57 |
23 |
19 |
| 12 |
1 |
2 |
31 |
18 |
| 13 |
1 |
7 |
38 |
17 |
| 14 |
1 |
12 |
44 |
16 |
| 15 |
1 |
17 |
49 |
15 |
| 16 |
1 |
22 |
52 |
14 |
| 17 |
1 |
27 |
53 |
13 |
| 18 |
1 |
32 |
54 |
12 |
| N. D. Sig. 5 |
Moon fr. the Node. |
| S. A. Sig. 11 |
| Argument of Latit. |
This Table extends
no farther than the
limits of Eclipses.
N. A. signifies North
Ascending Lat. S. A.
South Ascending; N. D.
North Descending;
and S. D. South
Descending.
Table XV. The Moons Horizontal Parallax; the Semidiameters and true Horary motions of the Sun and Moon.
| Anomaly of the Sun and Moon. |
Moon’s Horizontal Parallax. |
Sun’s Semidiameter. |
Moon’s Semidiamet. |
Moon’s horary Mot. |
Sun’s horary Mot. |
Anomaly of the Sun and Moon. |
| s |
° |
ʹ |
ʺ |
ʹ |
ʺ |
ʹ |
ʺ |
ʹ |
ʺ |
ʹ |
ʺ |
s |
° |
| 0 |
0 |
54 |
59 |
15 |
50 |
14 |
54 |
30 |
10 |
2 |
23 |
12 |
0 |
| |
6 |
54 |
59 |
15 |
50 |
14 |
55 |
30 |
12 |
2 |
23 |
|
24 |
| |
12 |
55 |
0 |
15 |
50 |
14 |
56 |
30 |
15 |
2 |
23 |
|
18 |
| |
18 |
55 |
4 |
15 |
51 |
14 |
57 |
30 |
18 |
2 |
23 |
|
12 |
| |
24 |
55 |
11 |
15 |
51 |
14 |
58 |
30 |
26 |
2 |
23 |
|
6 |
| 1 |
0 |
55 |
20 |
15 |
52 |
14 |
59 |
30 |
34 |
2 |
23 |
11 |
0 |
| |
6 |
55 |
30 |
15 |
53 |
15 |
1 |
30 |
44 |
2 |
24 |
|
24 |
| |
12 |
55 |
40 |
13 |
54 |
15 |
4 |
30 |
55 |
2 |
24 |
|
18 |
| |
18 |
55 |
51 |
15 |
55 |
15 |
8 |
31 |
9 |
2 |
24 |
|
12 |
| |
24 |
56 |
0 |
15 |
56 |
15 |
12 |
31 |
23 |
2 |
25 |
|
6 |
| 2 |
0 |
56 |
11 |
15 |
58 |
15 |
17 |
31 |
40 |
2 |
25 |
10 |
0 |
| |
6 |
56 |
24 |
15 |
59 |
15 |
22 |
31 |
58 |
2 |
26 |
|
24 |
| |
12 |
56 |
41 |
16 |
1 |
15 |
26 |
32 |
17 |
2 |
27 |
|
18 |
| |
18 |
57 |
12 |
16 |
2 |
15 |
30 |
32 |
39 |
2 |
27 |
|
12 |
| |
24 |
57 |
30 |
16 |
4 |
15 |
36 |
33 |
11 |
2 |
28 |
|
6 |
| 3 |
0 |
57 |
49 |
16 |
6 |
15 |
41 |
33 |
23 |
2 |
28 |
9 |
0 |
| |
6 |
58 |
10 |
16 |
8 |
15 |
46 |
33 |
47 |
2 |
29 |
|
24 |
| |
12 |
58 |
31 |
16 |
9 |
15 |
52 |
34 |
11 |
2 |
29 |
|
18 |
| |
18 |
58 |
52 |
16 |
11 |
15 |
58 |
34 |
34 |
2 |
29 |
|
12 |
| |
24 |
59 |
11 |
16 |
13 |
16 |
3 |
34 |
58 |
2 |
30 |
|
6 |
| 4 |
0 |
59 |
30 |
16 |
14 |
16 |
9 |
35 |
22 |
2 |
30 |
8 |
0 |
| |
6 |
59 |
52 |
16 |
15 |
16 |
14 |
35 |
45 |
2 |
31 |
|
24 |
| |
12 |
60 |
9 |
16 |
17 |
16 |
19 |
36 |
0 |
2 |
31 |
|
18 |
| |
18 |
60 |
26 |
16 |
19 |
16 |
24 |
36 |
20 |
2 |
32 |
|
12 |
| |
24 |
60 |
40 |
16 |
20 |
16 |
28 |
36 |
40 |
2 |
32 |
|
6 |
| 5 |
0 |
60 |
54 |
16 |
21 |
16 |
31 |
37 |
0 |
2 |
32 |
7 |
0 |
| |
6 |
61 |
4 |
16 |
21 |
16 |
34 |
37 |
10 |
2 |
33 |
|
24 |
| |
12 |
61 |
11 |
16 |
22 |
16 |
37 |
37 |
19 |
2 |
33 |
|
18 |
| |
18 |
61 |
16 |
16 |
22 |
16 |
38 |
37 |
28 |
2 |
33 |
|
12 |
| |
24 |
61 |
20 |
16 |
23 |
16 |
39 |
37 |
36 |
2 |
33 |
|
6 |
| 6 |
0 |
61 |
24 |
16 |
23 |
16 |
39 |
37 |
40 |
2 |
33 |
6 |
0 |
The gradual increase or decrease of the above numbers
being so small, it is sufficient to have them to every
sixth degree; the proportions for the intermediate
degrees being easily made by sight.
228
Table XVI. The Sun’s mean Motion and Anomaly.
| |
Years of Christ beginning |
Sun’s mean Longitude from Aries. |
Sun’s mean Anomaly. |
| s |
° |
ʹ |
ʺ |
s |
° |
ʹ |
| O.S. |
1 |
9 |
7 |
53 |
10 |
6 |
29 |
54 |
| 1301 |
9 |
17 |
42 |
30 |
6 |
16 |
58 |
| 1401 |
9 |
18 |
27 |
50 |
6 |
15 |
59 |
| 1501 |
9 |
19 |
13 |
10 |
6 |
14 |
59 |
| 1601 |
9 |
19 |
58 |
30 |
6 |
13 |
59 |
| 1701 |
9 |
20 |
43 |
50 |
6 |
12 |
59 |
| N.S. |
1753 |
9 |
10 |
16 |
52 |
6 |
1 |
38 |
| 1801 |
9 |
9 |
39 |
39 |
6 |
0 |
10 |
| Old Style to the beginning of A. D. 1753;
then New Style |
Years of Christ compleat |
Sun’s mean Motion. |
Sun’s mean Anomaly. |
| s |
° |
ʹ |
ʺ |
s |
° |
ʹ |
| |
1 |
11 |
29 |
45 |
40 |
11 |
29 |
45 |
| |
2 |
11 |
29 |
31 |
20 |
11 |
29 |
29 |
| |
3 |
11 |
29 |
17 |
0 |
11 |
29 |
14 |
| |
4 |
0 |
0 |
1 |
49 |
11 |
29 |
58 |
| |
5 |
11 |
29 |
47 |
29 |
11 |
29 |
42 |
| |
6 |
11 |
29 |
33 |
9 |
11 |
29 |
27 |
| |
7 |
11 |
29 |
18 |
49 |
11 |
29 |
11 |
| |
8 |
0 |
0 |
3 |
38 |
11 |
29 |
55 |
| |
9 |
11 |
29 |
49 |
18 |
11 |
29 |
40 |
| |
10 |
11 |
29 |
34 |
58 |
11 |
29 |
24 |
| |
11 |
11 |
29 |
20 |
38 |
11 |
29 |
9 |
| |
12 |
0 |
0 |
5 |
26 |
11 |
29 |
53 |
| |
13 |
11 |
29 |
51 |
7 |
11 |
29 |
37 |
| |
14 |
11 |
29 |
36 |
47 |
11 |
29 |
22 |
| |
15 |
11 |
29 |
22 |
27 |
11 |
29 |
7 |
| |
16 |
0 |
0 |
7 |
15 |
11 |
29 |
50 |
| |
17 |
11 |
29 |
52 |
55 |
11 |
29 |
35 |
| |
18 |
11 |
29 |
38 |
35 |
11 |
29 |
20 |
| |
19 |
11 |
29 |
24 |
16 |
11 |
29 |
4 |
| |
20 |
0 |
0 |
9 |
4 |
11 |
29 |
48 |
| |
40 |
0 |
0 |
18 |
8 |
11 |
29 |
36 |
| |
60 |
0 |
0 |
27 |
12 |
11 |
29 |
24 |
| |
80 |
0 |
0 |
36 |
16 |
11 |
29 |
12 |
| |
100 |
0 |
0 |
45 |
20 |
11 |
29 |
0 |
| |
200 |
0 |
1 |
30 |
40 |
11 |
28 |
1 |
| |
300 |
0 |
2 |
16 |
0 |
11 |
27 |
1 |
| |
400 |
0 |
3 |
1 |
20 |
11 |
26 |
1 |
| |
500 |
0 |
3 |
46 |
40 |
11 |
25 |
2 |
| |
600 |
0 |
4 |
32 |
0 |
11 |
24 |
2 |
| |
700 |
0 |
5 |
17 |
20 |
11 |
23 |
2 |
| |
800 |
0 |
6 |
2 |
40 |
11 |
22 |
3 |
| |
900 |
0 |
6 |
48 |
0 |
11 |
21 |
3 |
| |
1000 |
0 |
7 |
33 |
20 |
11 |
20 |
3 |
| |
2000 |
0 |
15 |
6 |
40 |
11 |
10 |
7 |
| |
3000 |
0 |
22 |
40 |
0 |
11 |
0 |
10 |
| |
4000 |
1 |
0 |
13 |
20 |
10 |
20 |
13 |
| |
5000 |
1 |
7 |
46 |
40 |
10 |
10 |
16 |
| |
6000 |
1 |
15 |
20 |
0 |
10 |
0 |
19 |
| |
Months |
Sun’s mean Motion. |
Sun’s mean Anomaly. |
| |
s |
° |
ʹ |
ʺ |
s |
° |
ʹ |
| |
Jan. |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| |
Feb. |
1 |
0 |
33 |
18 |
1 |
0 |
33 |
| |
Mar. |
1 |
28 |
9 |
11 |
1 |
28 |
9 |
| |
Apr. |
2 |
28 |
42 |
30 |
2 |
28 |
42 |
| |
May. |
3 |
28 |
16 |
40 |
3 |
28 |
17 |
| |
June |
4 |
28 |
49 |
58 |
4 |
28 |
50 |
| |
July |
5 |
28 |
24 |
8 |
5 |
28 |
24 |
| |
Aug. |
6 |
28 |
57 |
26 |
6 |
28 |
57 |
| |
Sep. |
7 |
29 |
30 |
44 |
7 |
29 |
30 |
| |
Oct. |
8 |
29 |
4 |
54 |
8 |
29 |
4 |
| |
Nov. |
9 |
29 |
38 |
12 |
9 |
29 |
37 |
| |
Dec. |
10 |
29 |
12 |
22 |
10 |
29 |
11 |
| Days. |
Sun’s mean Motion and Anomaly. |
| s |
° |
ʹ |
ʺ |
| 1 |
0 |
0 |
59 |
8 |
| 2 |
0 |
1 |
58 |
17 |
| 3 |
0 |
2 |
57 |
25 |
| 4 |
0 |
3 |
56 |
33 |
| 5 |
0 |
4 |
55 |
42 |
| 6 |
0 |
5 |
54 |
50 |
| 7 |
0 |
5 |
53 |
58 |
| 8 |
0 |
7 |
53 |
7 |
| 9 |
0 |
8 |
52 |
15 |
| 10 |
0 |
9 |
51 |
23 |
| 11 |
0 |
10 |
50 |
32 |
| 12 |
0 |
11 |
49 |
40 |
| 13 |
0 |
12 |
48 |
48 |
| 14 |
0 |
13 |
47 |
57 |
| 15 |
0 |
14 |
47 |
5 |
| 16 |
0 |
15 |
46 |
13 |
| 17 |
0 |
16 |
45 |
22 |
| 18 |
0 |
17 |
44 |
30 |
| 19 |
0 |
18 |
43 |
38 |
| 20 |
0 |
19 |
42 |
47 |
| 21 |
0 |
20 |
41 |
55 |
| 22 |
0 |
21 |
41 |
3 |
| 23 |
0 |
22 |
40 |
12 |
| 24 |
0 |
23 |
39 |
20 |
| 25 |
0 |
24 |
38 |
28 |
| 26 |
0 |
25 |
37 |
37 |
| 27 |
0 |
26 |
36 |
45 |
| 28 |
0 |
27 |
35 |
53 |
| 29 |
0 |
28 |
35 |
2 |
| 30 |
0 |
29 |
34 |
10 |
| 31 |
1 |
0 |
33 |
18 |
In Leap-years,
after February,
add one Day and
one Day’s motion.
Sun’s mean Motion and Anomaly.
| Hours. |
Mot. & Ano. |
| ° |
ʹ |
ʺ |
| ʹ |
ʹ |
ʺ |
ʺʹ |
| ʺ |
ʺ |
ʺʹ |
ʺʺ |
| 1 |
0 |
2 |
28 |
| 2 |
0 |
4 |
56 |
| 3 |
0 |
7 |
24 |
| 4 |
0 |
9 |
51 |
| 5 |
0 |
12 |
19 |
| 6 |
0 |
14 |
47 |
| 7 |
0 |
17 |
15 |
| 8 |
0 |
19 |
43 |
| 9 |
0 |
22 |
11 |
| 10 |
0 |
24 |
38 |
| 11 |
0 |
27 |
6 |
| 12 |
0 |
29 |
34 |
| 13 |
0 |
32 |
2 |
| 14 |
0 |
34 |
30 |
| 15 |
0 |
36 |
58 |
| 16 |
0 |
39 |
26 |
| 17 |
0 |
41 |
53 |
| 18 |
0 |
44 |
21 |
| 19 |
0 |
46 |
49 |
| 20 |
0 |
49 |
17 |
| 21 |
0 |
51 |
45 |
| 22 |
0 |
54 |
13 |
| 23 |
0 |
56 |
40 |
| 24 |
0 |
59 |
8 |
| 25 |
1 |
1 |
36 |
| 26 |
1 |
4 |
4 |
| 27 |
1 |
6 |
32 |
| 28 |
1 |
9 |
0 |
| 29 |
1 |
11 |
28 |
| 30 |
1 |
13 |
55 |
| 31 |
1 |
16 |
23 |
| 32 |
1 |
18 |
51 |
| 33 |
1 |
21 |
19 |
| 34 |
1 |
23 |
47 |
| 35 |
1 |
26 |
15 |
| 36 |
1 |
28 |
42 |
| 37 |
1 |
31 |
10 |
| 38 |
1 |
33 |
38 |
| 39 |
1 |
36 |
6 |
| 40 |
1 |
38 |
34 |
| 41 |
1 |
41 |
2 |
| 42 |
1 |
43 |
30 |
| 43 |
1 |
45 |
57 |
| 44 |
1 |
48 |
25 |
| 45 |
1 |
50 |
53 |
| 46 |
1 |
53 |
21 |
| 47 |
1 |
55 |
49 |
| 48 |
1 |
58 |
17 |
| 49 |
2 |
0 |
44 |
| 50 |
2 |
3 |
12 |
| 51 |
2 |
5 |
40 |
| 52 |
2 |
8 |
8 |
| 53 |
2 |
10 |
36 |
| 54 |
2 |
13 |
4 |
| 55 |
2 |
15 |
32 |
| 56 |
2 |
17 |
59 |
| 57 |
2 |
20 |
27 |
| 58 |
2 |
22 |
55 |
| 59 |
2 |
25 |
23 |
| 60 |
2 |
27 |
51 |
In Leap-years, after
February, add one
Day and one Day’s
motion.
229
Table XVII. The Sun’s Declination in every Degree of the Ecliptic.
| Signs |
♈ |
|
♎ |
♉ |
|
♏ |
♊ |
|
♐ |
|
| 0 |
6 |
1 |
7 |
2 |
8 |
| Nor. |
Sou. |
Nor. |
Sou. |
Nor. |
Sou. |
| ° |
° |
ʹ |
ʺ |
° |
ʹ |
ʺ |
° |
ʹ |
ʺ |
° |
| 0 |
0 |
0 |
0 |
11 |
29 |
33 |
20 |
11 |
16 |
30 |
| 1 |
0 |
23 |
54 |
11 |
50 |
35 |
20 |
23 |
49 |
29 |
| 2 |
0 |
47 |
48 |
12 |
11 |
26 |
20 |
36 |
0 |
28 |
| 3 |
1 |
11 |
42 |
12 |
32 |
5 |
20 |
47 |
48 |
27 |
| 4 |
1 |
35 |
34 |
12 |
52 |
31 |
20 |
59 |
13 |
26 |
| 5 |
1 |
59 |
25 |
13 |
12 |
44 |
21 |
10 |
15 |
25 |
| 6 |
2 |
23 |
14 |
13 |
32 |
54 |
21 |
20 |
53 |
24 |
| 7 |
2 |
47 |
1 |
13 |
52 |
32 |
21 |
31 |
7 |
23 |
| 8 |
3 |
10 |
45 |
14 |
12 |
5 |
21 |
40 |
58 |
22 |
| 9 |
3 |
34 |
26 |
14 |
31 |
24 |
21 |
50 |
24 |
21 |
| 10 |
3 |
58 |
4 |
14 |
50 |
28 |
21 |
59 |
25 |
20 |
| 11 |
4 |
21 |
38 |
15 |
9 |
17 |
22 |
8 |
2 |
19 |
| 12 |
4 |
45 |
8 |
15 |
27 |
51 |
22 |
16 |
14 |
18 |
| 13 |
5 |
8 |
34 |
15 |
46 |
9 |
22 |
24 |
0 |
17 |
| 14 |
5 |
31 |
55 |
16 |
4 |
11 |
22 |
31 |
21 |
16 |
| 15 |
5 |
55 |
11 |
16 |
21 |
57 |
22 |
38 |
16 |
15 |
| 16 |
6 |
18 |
21 |
16 |
39 |
26 |
22 |
44 |
45 |
14 |
| 17 |
6 |
41 |
25 |
16 |
56 |
37 |
22 |
50 |
49 |
13 |
| 18 |
7 |
4 |
23 |
17 |
13 |
31 |
22 |
56 |
26 |
12 |
| 19 |
7 |
27 |
15 |
17 |
30 |
7 |
23 |
1 |
36 |
11 |
| 20 |
7 |
50 |
0 |
17 |
46 |
15 |
23 |
6 |
20 |
10 |
| 21 |
8 |
12 |
36 |
18 |
2 |
24 |
23 |
10 |
38 |
9 |
| 22 |
8 |
35 |
5 |
18 |
18 |
3 |
23 |
14 |
29 |
8 |
| 23 |
8 |
57 |
26 |
18 |
33 |
24 |
23 |
17 |
52 |
7 |
| 24 |
9 |
19 |
39 |
18 |
48 |
25 |
23 |
20 |
49 |
6 |
| 25 |
9 |
41 |
43 |
19 |
3 |
5 |
23 |
23 |
19 |
5 |
| 26 |
10 |
3 |
37 |
19 |
17 |
26 |
23 |
25 |
22 |
4 |
| 27 |
10 |
25 |
21 |
19 |
31 |
25 |
23 |
26 |
57 |
3 |
| 28 |
10 |
46 |
56 |
19 |
45 |
3 |
23 |
28 |
5 |
2 |
| 29 |
11 |
8 |
20 |
19 |
58 |
20 |
23 |
28 |
46 |
1 |
| 30 |
11 |
29 |
33 |
20 |
11 |
16 |
23 |
29 |
0 |
0 |
| Signs |
♓ |
|
♍ |
♒ |
|
♌ |
♑ |
|
♋ |
|
| 1 |
5 |
10 |
4 |
9 |
3 |
| Sou. |
Nor. |
Sou. |
Nor. |
Sou. |
Nor. |
If the Sun’s place be taken from the Tables
on pag. 114 and 115, his declination may be
had thereby, near enough for common use,
from this Table, by entering it with the
signs at the head and degrees at the left
hand; or with the signs at the foot and
degrees at the right hand. Thus, March
the 5th, the Sun’s place is ♓ 14° 53ʹ
(call it 15°, being so near) to which
answers 5° 55ʹ 11ʺ of the south
declination.
Table XVIII. Lunations from 1 to 100000.
| Lunat. |
Days. |
H. |
M. |
S. |
| 1 |
Contain 29 |
12 |
44 |
3 |
| 2 |
59 |
1 |
28 |
6 |
| 3 |
88 |
14 |
12 |
9 |
| 4 |
118 |
2 |
56 |
13 |
| 5 |
147 |
15 |
40 |
16 |
| 6 |
177 |
4 |
24 |
19 |
| 7 |
206 |
17 |
8 |
22 |
| 8 |
236 |
5 |
52 |
25 |
| 9 |
265 |
18 |
36 |
28 |
| 10 |
295 |
7 |
20 |
31 |
| 20 |
590 |
14 |
41 |
3 |
| 30 |
885 |
22 |
1 |
34 |
| 40 |
1181 |
5 |
22 |
6 |
| 50 |
1476 |
12 |
42 |
37 |
| 60 |
1771 |
20 |
3 |
9 |
| 70 |
2067 |
3 |
23 |
40 |
| 80 |
2362 |
10 |
44 |
12 |
| 90 |
2657 |
18 |
4 |
43 |
| 100 |
2953 |
1 |
25 |
15 |
| 200 |
5906 |
2 |
50 |
30 |
| 300 |
8859 |
4 |
15 |
45 |
| 400 |
11812 |
5 |
41 |
0 |
| 500 |
14765 |
7 |
6 |
15 |
| 600 |
17718 |
8 |
31 |
30 |
| 700 |
20671 |
9 |
56 |
45 |
| 800 |
23624 |
11 |
22 |
0 |
| 900 |
26577 |
12 |
47 |
15 |
| 1000 |
29530 |
14 |
12 |
30 |
| 2000 |
59061 |
4 |
25 |
0 |
| 3000 |
88591 |
18 |
37 |
30 |
| 4000 |
118122 |
8 |
50 |
0 |
| 5000 |
147652 |
23 |
2 |
30 |
| 6000 |
177183 |
13 |
15 |
0 |
| 7000 |
206714 |
3 |
27 |
30 |
| 8000 |
236244 |
17 |
40 |
0 |
| 9000 |
265775 |
7 |
52 |
30 |
| 10000 |
295305 |
22 |
5 |
|
| 20000 |
590611 |
20 |
10 |
|
| 30000 |
885917 |
18 |
15 |
|
| 40000 |
1181223 |
16 |
20 |
|
| 50000 |
1476529 |
14 |
25 |
|
| 60000 |
1771835 |
12 |
30 |
|
| 70000 |
2067141 |
10 |
35 |
|
| 80000 |
2362447 |
8 |
40 |
|
| 90000 |
2657753 |
6 |
45 |
|
| 100000 |
2953059 |
4 |
50 |
|
By comparing this Table with
the Table on page 113, it is
easy to find how many Lunations
are contained in any given
number of Sidereal, Julian, and
Solar years, from 1 to 8000.
230
CHAP. XX.
Of the fixed Stars.
Why the fixed Stars appear bigger when viewed by the bare eye than when seen through a telescope.
391. The Stars are said to be fixed, because they have been generally
observed to keep at the same distance from each other: their
apparent diurnal revolutions being caused solely by the Earth’s turning on
its Axis. They appear of a sensible magnitude to the bare eye, because
the retina is affected not only by the rays of light which are emitted
directly from them, but by many thousands more, which falling upon
our eye-lids, and upon the aerial particles about us, are reflected
into our eyes so strongly as to excite vibrations not only in those points
of the retina where the real images of the Stars are formed, but also
in other points at some distance round about. This makes us imagine
the Stars to be much bigger than they would appear, if we saw them
only by the few rays which come directly from them, so as to enter
our eyes without being intermixed with others. Any one may be sensible
of this, by looking at a Star of the first Magnitude through a long
narrow tube; which, though it takes in as much of the sky as would
hold a thousand such Stars, yet scarce renders that one visible.
A proof that they shine by their own light.
The more a telescope magnifies, the less is the aperture through
which the Star is seen; and consequently the fewer rays it admits into
the eye. Now since the Stars appear less in a telescope which magnifies
200 times than they do to the bare eye, insomuch that they seem
to be only indivisible points, it proves at once both that the Stars are
at immense distances from us, and that they shine by their own proper
light. If they shone by borrowed light they would be as invisible
without telescopes as the Satellites of Jupiter are: for these Satellites
appear bigger when viewed with a good telescope than the largest
fixed Stars do.
Their number much less than is generally imagined.
392. The number of Stars discoverable, in either Hemisphere, by
the naked eye, is not above a thousand. This at first may appear incredible,
because they seem to be without number: But the deception
arises from our looking confusedly upon them, without reducing them
into any order. For look but stedfastly upon a pretty large portion of
the sky, and count the number of Stars in it, you will be surprised to
find them so few. Or, if one considers how seldom the Moon meets
with any Stars in her way, although there are as many about her Path
as in other parts of the Heavens (the Milky way excepted) he will soon
be convinced that the Stars are much thinner sown than he was aware
231of. The British catalogue, which, besides the Stars visible to the bare
eye, includes a great number which cannot be seen without the assistance
of a telescope, contains no more than 3000, in both Hemispheres.
The absurdity of supposing the Stars were made only to enlighten our nights.
393. As we have incomparably more light from the Moon than
from all the Stars together, it were the greatest absurdity to imagine
that the Stars were made for no other purpose than to cast a faint light
upon the Earth: especially since many more require the assistance of a
good telescope to find them out, than are visible without that Instrument.
Our Sun is surrounded by a system of Planets and Comets; all
which would be invisible from the nearest fixed Star. And from what
we already know of the immense distance of the Stars, the nearest
may be computed at 32,000,000,000,000 of miles from us which is
more than a cannon bullet would fly in 7,000,000 of years. Hence
’tis easy to prove, that the Sun seen from such a distance, would appear
no bigger than a Star of the first magnitude. From all this it is highly
probable that each Star is a Sun to a system of worlds moving round
it though unseen by us; especially, as the doctrine of a plurality of
worlds is rational, and greatly manifests the Power, Wisdom, and
Goodness of the great Creator.
Their different Magnitudes.
394. The Stars, on account of their apparently various magnitudes,
have been distributed into several classes or orders. Those which appear
largest are called Stars of the first magnitude; the next to them in lustre,
Stars of the second magnitude, and so on to the sixth, which are the
smallest that are visible to the bare eye. This distribution having
been made long before the invention of telescopes, the Stars which
cannot be seen without the assistance of these instruments are distinguished
by the name of Telescopic Stars.
And division into Constellations.
395. The antients divided the starry Sphere into particular Constellations,
or Systems of Stars, according as they lay near one another,
so as to occupy those spaces which the figures of different sorts of animals
or things would take up, if they were there delineated. And
those Stars which could not be brought into any particular Constellation
were called unformed Stars.
The use of this division.
396. This division of the Stars into different Constellations or Asterisms,
serves to distinguish them from one another, so that any particular Star
may be readily found in the Heavens by means of a Celestial Globe;
on which the Constellations are so delineated as to put the most remarkable
Stars into such parts of the figures as are most easily distinguished.
The number of the antient Constellations is 48, and upon our present
Globes about 70. On Senex’s Globes are inserted Bayer’s Letters; the
232first in the Greek Alphabet being put to the biggest Star in each Constellation,
the second to the next, and so on: by which means, every
Star is as easily found as if a name were given to it. Thus, if the
Star γ in the Constellation of the Ram be mentioned, every Astronomer
knows as well what Star is meant as if it were pointed out to him in
the Heavens.
The Zodiac.
397. There is also a division of the Heavens into three parts.
1. The Zodiac, (ζωδιακὸς) from ζώδιον Zodion an Animal, because
most of the Constellations in it, which are twelve in number, are the
figures of Animals: as Aries the Ram, Taurus the Bull, Gemini the
Twins, Cancer the Crab, Leo the Lion, Virgo the Virgin, Libra the
Balance, Scorpio the Scorpion, Sagittarius the Archer, Capricornus the
Goat, Aquarius the Water-bearer, and Pisces the Fishes. The Zodiac
goes quite round the Heavens: it is about 16 degrees broad, so that it
takes in the Orbits of all the Planets, and likewise the Orbit of the
Moon. Along the middle of this Zone or Belt is the Ecliptic, or
Circle which the Earth describes annually as seen from the Sun; and
which the Sun appears to describe as seen from the Earth. 2. All
that Region of the Heavens, which is on the north side of the Zodiac,
containing 21 Constellations. And 3. that on the south side, containing
15.
The manner of dividing it by the antients.
398. The antients divided the Zodiac into the above 12 Constellations
or Signs in the following manner. They took a vessel with a small
hole in the bottom, and having filled it with water, suffered the same
to distil drop by drop into another Vessel set beneath to receive it; beginning
at the moment when some Star rose, and continuing until it
rose the next following night. The water fallen down into the receiver
they divided into twelve equal parts; and having two other small vessels
in readiness, each of them fit to contain one part, they again poured
all the water into the upper vessel, and strictly observing the rising of
some Star in the Zodiac, they at the same time suffered the water to
drop into one of the small vessels; and as soon as it was full, they
shifted it and set an empty one in it’s place. By this means, when
each vessel was full, they observed what Star of the Zodiac rose; and
though not possible in one night, yet in many, they observed the
rising of twelve Stars, by which they divided the Zodiac into twelve
parts.
399. The names of the Constellations, and the number of Stars
observed in each of them by different Astronomers, are as follows.
233
The antient Constellations.
| |
Ptolemy. |
Tycho. |
Hevelius. |
Flamsteed. |
| Ursa minor |
The Little Bear |
8 |
7 |
12 |
24 |
| Ursa major |
The Great Bear |
35 |
29 |
73 |
87 |
| Draco |
The Dragon |
31 |
32 |
40 |
80 |
| Cepheus |
Cepheus |
13 |
4 |
51 |
35 |
| Bootes, Arctophilax |
|
23 |
18 |
52 |
54 |
| Corona Borealis |
The northern Crown |
8 |
8 |
8 |
21 |
| Hercules, Engonasin |
Hercules kneeling |
29 |
28 |
45 |
113 |
| Lyra |
The Harp |
10 |
11 |
17 |
21 |
| Cygnus, Gallina |
The Swan |
19 |
18 |
47 |
81 |
| Cassiopea |
The Lady in her Chair |
13 |
26 |
37 |
55 |
| Perseus |
Perseus |
29 |
29 |
46 |
59 |
| Auriga |
The Waggoner |
14 |
9 |
40 |
66 |
| Serpentarius, Ophiuchus |
Serpentarius |
29 |
15 |
40 |
74 |
| Serpens |
The Serpent |
18 |
13 |
22 |
64 |
| Sagitta |
The Arrow |
5 |
5 |
5 |
18 |
| Aquila, Vultur |
The Eagle |
|
15 |
12 |
23 |
71 |
| Antinous |
Antinous |
3 |
19 |
| Delphinus |
The Dolphin |
10 |
10 |
14 |
18 |
| Equulus, Equi sectio |
The Horse’s Head |
4 |
4 |
6 |
10 |
| Pegasus, Equus |
The Flying Horse |
20 |
19 |
38 |
89 |
| Andromeda |
Andromeda |
23 |
23 |
47 |
66 |
| Triangulum |
The Triangle |
4 |
4 |
12 |
16 |
| Aries |
The Ram |
18 |
21 |
27 |
66 |
| Taurus |
The Bull |
44 |
43 |
51 |
141 |
| Gemini |
The Twins |
25 |
25 |
38 |
85 |
| Cancer |
The Crab |
23 |
15 |
29 |
83 |
| Leo |
The Lion |
|
35 |
30 |
49 |
95 |
| Coma Berenices |
Berenice’s Hair |
14 |
21 |
43 |
| Virgo |
The Virgin |
32 |
33 |
50 |
110 |
| Libra, Chelæ |
The Scales |
17 |
10 |
20 |
51 |
| Scorpius |
The Scorpion |
24 |
10 |
20 |
44 |
| Sagittarius |
The Archer |
31 |
14 |
22 |
69 |
| Capricornus |
The Goat |
28 |
28 |
29 |
51 |
| Aquarius |
The Water-bearer |
45 |
41 |
47 |
108 |
| Pisces |
The Fishes |
38 |
36 |
39 |
113 |
| Cetus |
The Whale |
22 |
21 |
45 |
97 |
| Orion |
Orion |
38 |
42 |
62 |
78 |
| Eridanus, Fluvius |
Eridanus, the River |
34 |
10 |
27 |
84 |
| Lepus |
The Hare |
12 |
13 |
16 |
19 |
| Canis major |
The Great Dog |
29 |
13 |
21 |
31 |
| Canis minor |
The Little Dog |
2 |
2 |
13 |
14 |
| Argo Navis |
The Ship |
45 |
3 |
4 |
64 |
| Hydra |
The Hydra |
27 |
19 |
31 |
60 |
| Crater |
The Cup |
7 |
3 |
10 |
31 |
| Corvus |
The Crow |
7 |
4 |
|
9 |
| Centaurus |
The Centaur |
37 |
|
|
35 |
| Lupus |
The Wolf |
19 |
|
|
24 |
| Ara |
The Altar |
7 |
|
|
9 |
| Corona Australis |
The southern Crown |
13 |
|
|
12 |
| Pisces Australis |
The southern Fish |
18 |
|
|
24 |
234
The New Southern Constellations.
| Columba Noachi |
Noah’s Dove |
10 |
| Robur Carolinum |
The Royal Oak |
12 |
| Grus |
The Crane |
13 |
| Phœnix |
The Phenix |
13 |
| Indus |
The Indian |
12 |
| Pavo |
The Peacock |
14 |
| Apus, Avis Indica |
The Bird of Paradise |
11 |
| Apis, Musca |
The Bee or Fly |
4 |
| Chamæleon |
The Chameleon |
10 |
| Triangulum Australis |
The South Triangle |
5 |
| Piscis volans, Passer |
The Flying Fish |
8 |
| Dorado, Xiphias |
The Sword Fish |
6 |
| Toucan |
The American Goose |
9 |
| Hydrus |
The Water Snake |
10 |
Hevelius’s Constellations made out of the unformed Stars.
|
|
Hevelius. |
Flamsteed. |
| Lynx |
The Lynx |
19 |
44 |
| Leo minor |
The Little Lion |
|
53 |
| Asterion & Chara |
The Greyhounds |
23 |
25 |
| Cerberus |
Cerberus |
4 |
|
| Vulpecula & Anser |
The Fox and Goose |
27 |
35 |
| Scutum Sobieski |
Sobieski’s Shield |
7 |
|
| Lacerta |
The Lizard |
10 |
16 |
| Camelopardalus |
The Camelopard |
32 |
58 |
| Monoceros |
The Unicorn |
19 |
31 |
| Sextans |
The Sextant |
11 |
41 |
The Milky Way.
400. There is a remarkable track round the Heavens, called the
Milky Way from its peculiar whiteness, which is owing to a great
number of Stars scattered therein; none of which can be distinctly
seen without telescopes. This track appears single in some parts, in
others double.
Lucid Spots.
401. There are several little whitish spots in the Heavens, which
appear magnified, and more luminous when seen through telescopes;
yet without any Stars in them. One of these is in Andromeda’s girdle,
first observed A. D. 1612, by Simon Marius; and which has some
whitish rays near its middle: it is liable to several changes, and is
sometimes invisible. Another is near the Ecliptic, between the head
235and bow of Sagittarius: it is small, but very luminous. A third is on
the back of the Centaur, which is too far South to be seen in Britain.
A fourth, of a smaller size, is before Antinous’s right foot; having a
Star in it, which makes it appear more bright. A fifth is in the Constellation
of Hercules, between the Stars ζ and η, which spot, though
but small, is visible to the bare eye if the sky be clear and the Moon
absent.
Cloudy Stars.
Magellanic Clouds.
402. Cloudy Stars are so called from their misty appearance. They
look like dim Stars to the naked eye; but through a telescope they
appear broad illuminated parts of the sky; in some of which is one
Star, in others more. Five of these are mentioned by Ptolemy.
1. One at the extremity of the right hand of Perseus. 2. One in
the middle of the Crab. 3. One unformed, near the Sting of the
Scorpion. 4. The eye of Sagittarius. 5. One in the head of Orion.
In the first of these appear more Stars through the telescope than in
any of the rest, although 21 have been counted in the head of Orion,
and above 40 in that of the Crab. Two are visible in the eye of Sagittarius
without a telescope, and several more with it. Flamsteed
observed a cloudy Star in the bow of Sagittarius, containing many
small Stars: and the Star d above Sagittary’s right shoulder is encompassed
with several more. Both Cassini and Flamsteed discovered one
between the Great and Little Dog, which is very full of Stars visible
only by the telescope. The two whitish spots near the South Pole,
called the Magellanic Clouds by Sailors, which to the bare eye resemble
part of the Milky-Way, appear through telescopes to be a mixture of
small Clouds and Stars. But the most remarkable of all the cloudy
Stars is that in the middle of Orion’s Sword, where seven Stars (of
which three are very close together) seem to shine through a cloud,
very lucid near the middle, but faint and ill defined about the edges.
It looks like a gap in the sky, through which one may see (as it were)
part of a much brighter region. Although most of these spaces are but
a few minutes of a degree in breadth, yet, since they are among the
fixed Stars, they must be spaces larger than what is occupied by our solar
System; and in which there seems to be a perpetual uninterrupted
day among numberless Worlds which no human art ever can discover.
Changes in the Heavens.
403. Several Stars are mentioned by antient Astronomers, which are
not now to be found; and others are now visible to the bare eye which
are not recorded in the antient catalogues. Hipparchus observed a new
Star about 120 years before Christ; but he has not mentioned in what
part of the Heavens it was seen, although it occasioned his making a
catalogue of the Stars; which is the most antient that we have.
New Stars.
236The first New Star that we have any good account of, was discovered
by Cornelius Gemma on the 8th of November A. D. 1572, in the Chair
of Cassiopea. It surpassed Sirius in brightness and magnitude; and
was seen for 16 months successively. At first it appeared bigger
than Jupiter to some eyes, by which it was seen even at mid-day: afterwards
it decayed gradually both in magnitude and lustre, until March
1573, when it became invisible.
On the 13th of August 1596, David Fabricius observed the Stella
Mira, or wonderful Star, in the Neck of the Whale; which has been
since found to appear and disappear periodically, seven times in six
years, continuing in its greatest lustre for 15 days together; and is
never quite extinguished.
In the year 1600, William Jansenius discovered a changeable Star in
the Neck of the Swan; which, in time became so small as to be
thought to disappear entirely, till the years 1657, 1658, and 1659,
when it recovered its former lustre and magnitude; but soon decayed,
and is now of the smallest size.
In the year 1604 Kepler and several of his friends saw a new Star
near the heel of the right foot of Serpentarius, so bright and sparkling
that it exceeded any thing they had ever seen before; and took notice
that it was every moment changing into some of the colours of the
rainbow, except when it was near the horizon, at which time it was
generally white. It surpassed Jupiter in magnitude, which was near it
all the month of October, but easily distinguished from it by a steady
light. It disappeared between October 1605 and the February following,
and has not been seen since that time.
In the year 1670, July 15, Hevelius discovered a new Star, which
in October was so decayed as to be scarce perceptible. In April following
it regained its lustre, but wholly disappeared in August. In March
1672 it was seen again, but very small; and has not been visible
since.
In the year 1686 a new Star was discovered by Kirch, which returns
periodically in 404 days.
In the year 1672, Cassini saw a Star in the Neck of the Bull, which
he thought was not visible in Tycho’s time; nor when Bayer made his
Figures.
Cannot be Comets.
404. Many Stars, besides those above-mentioned, have been observed
to change their magnitudes: and as none of them could ever
be perceived to have tails, ’tis plain they could not be Comets; especially
as they had no parallax, even when largest and brightest. It
would seem that the periodical Stars have vast clusters of dark spots,
237and very slow rotations on their Axis; by which means, they must
disappear when the side covered with spots is turned towards us.
And as for those which break out all of a sudden with such lustre,
’tis by no means improbable that they are Suns whose Fuel is almost
spent, and again supplied by some of their Comets falling upon them,
and occasioning an uncommon blaze and splendor for some time:
which indeed appears to be the greatest use of the cometary part of
any system[86].
Some Stars change their Places.
Some of the Stars, particularly Arcturus, have been observed to
change their places above a minute of a degree with respect to others.
But whether this be owing to any real motion in the Stars themselves,
must require the observations of many ages to determine. If our solar
System changeth its Place, with regard to absolute space, this must in
process of time occasion an apparent change in the distances of the
Stars from each other: and in such a case, the places of the nearest
Stars to us being more affected than of those which are very remote,
their relative positions must seem to alter, though the Stars themselves
were really immoveable. On the other hand, if our own system be
at rest, and any of the Stars in real motion, this must vary their positions;
and the more so, the nearer they are to us, or the swifter their
motions are; or the more proper the direction of their motion is, for
our perception.
The Ecliptic less oblique now to the Equator than formerly.
405. The obliquity of the Ecliptic to the Equinoctial is found at
present to be above a third part of a degree less than Ptolemy found it.
And most of the observers after him found it to decrease gradually
down to Tycho’s time. If it be objected, that we cannot depend on the
observations of the antients, because of the incorrectness of their Instruments;
we have to answer, that both Tycho and Flamsteed are
allowed to have been very good observers: and yet we find that Flamsteed
makes this obliquely
21⁄2
minutes of a degree less than Tycho did, about
100 years before him: and as Ptolemy was 1324 years before Tycho,
238so the gradual decrease answers nearly to the difference of time between
these three Astronomers. If we consider, that the Earth is not a perfect
sphere, but an oblate spheroid, having its Axis shorter than its
Equatoreal diameter; and that the Sun and Moon are constantly acting
obliquely upon the greater quantity of matter about the Equator, pulling
it, as it were, towards a nearer and nearer co-incidence with the
Ecliptic; it will not appear improbable that these actions should gradually
diminish the Angle between those Planes. Nor is it less probable
that the mutual attractions of all the Planets should have a
tendency to bring the planes of all their Orbits to a co-incidence: but
this change is too small to become sensible in many ages.
CHAP. XXI.
Of the Division of Time. A perpetual Table of New Moons. The Times of the Birth and Death of Christ. A Table of remarkable Æras or Events.
406. The parts of time are Seconds, Minutes, Hours, Days, Years,
Cycles, Ages, and Periods.
A Year.
407. The original standard, or integral measure of Time, is a year;
which is determined by the Revolution of some Celestial Body in
its Orbit, viz. the Sun or Moon.
Tropical Year.
408. The time measured by the Sun’s Revolution in the Ecliptic,
from any Equinox or Solstice to the same again, is called the Solar or
Tropical Year, which contains 365 days 5 hours 48 minutes 57 seconds;
and is the only proper or natural year, because it always keeps
the same seasons to the same months.
Sidereal year.
409. The quantity of time, measured by the Sun’s Revolution, as
from any fixed Star to the same Star again, is called the Sidereal Year;
which contains 365 days 6 hours 9 minutes
141⁄2
seconds; and is 20
minutes
171⁄2
seconds longer than the true Solar Year.
Lunar Year.
410. The time measured by twelve Revolutions of the Moon, from
the Sun to the Sun again, is called the Lunar Year; it contains 354 days
8 hours 48 minutes 37 seconds; and is therefore 10 days 21 hours
0 minutes 20 seconds shorter than the Solar Year. This is the foundation
of the Epact.
Civil Year.
411. The Civil Year is that which is in common use among the
different nations of the world; of which, some reckon by the Lunar,
but most by the Solar. The Civil Solar Year contains 365 days, for
239three years running, which are called Common Years; and then comes
in what is called the Bissextile or Leap-Year, which contains 366
days. This is also called the Julian Year on account of Julius Cæsar,
who appointed the Intercalary-day every fourth year, thinking thereby
to make the Civil and Solar Year keep pace together. And this day,
being added to the 23d of February, which in the Roman Calendar,
was the sixth of the Calends of March, that sixth day was twice reckoned,
or the 23d and 24th were reckoned as one day; and was called Bis sextus dies,
and thence came the name Bissextile for that year. But in
our common Almanacks this day is added at the end of February.
Lunar Year.
412. The Civil Lunar Year is also common or intercalary. The
common Year consists of 12 Lunations, which contain 354 days;
at the end of which, the year begins again. The Intercalary, or
Embolimic Year is that wherein a month was added, to adjust the
Lunar Year to the Solar. This method was used by the Jews, who
kept their account by the Lunar Motions. But by intercalating no
more than a month of 30 days, which they called Ve-Adar, every
third year, they fell
33⁄4
days short of the Solar Year in that time.
Roman Year.
413. The Romans also used the Lunar Embolimic Year at first, as it
was settled by Romulus their first King, who made it to consist only
of ten months or Lunations; which fell 61 days short of the Solar
Year, and so their year became quite vague and unfixed; for which
reason, they were forced to have a Table published by the High Priest,
to inform them when the spring and other seasons began. But Julius
Cæsar, as already mentioned, § 411, taking this troublesome affair
into consideration, reformed the Calendar, by making the year to
consist of 365 days 6 hours.
The original of the Gregorian, or New Style.
414. The year thus settled, is what we still make use of in Britain:
but as it is somewhat more than 11 minutes longer than the Solar
Tropical Year, the times of the Equinoxes go backward, and fall earlier
by one day in about 130 years. In the time of the Nicene Council
(A. D. 325.) which was 1431 years ago, the vernal Equinox fell on
the 21st of March: and, if we divide 1431 by 130, it will quote
11, which is the number of days the Equinox has fallen back since
the Council of Nice. This causing great disturbances, by unfixing the
times of the celebration of Easter, and consequently of all the other
moveable Feasts, Pope Gregory the 13th, in the year 1582 ordered
ten days to be at once struck out of that year; and the next day after
the fourth of October was called the fifteenth. By this means the
vernal Equinox was restored to the 21st of March; and it was endeavoured,
by the omission of three intercalary days in 400 years,
240to make the civil or political year keep pace with the Solar for time
to come. This new form of the year is called the Gregorian Account
or New Style; which is received in all Countries where the Pope’s
Authority is acknowledged, and ought to be in all places where
truth is regarded.
Months.
415. The principal division of the year is into Months, which are
of two sorts, namely Astronomical and Civil. The Astronomical month
is the time in which the Moon runs through the Zodiac, and is
either Periodical or Synodical. The Periodical Month is the time spent
by the Moon in making one compleat Revolution from any point of
the Zodiac to the same again; which is 27d 7h 43m. The Synodical
Month, called a Lunation, is the time contained between the Moon’s
parting with the Sun at a Conjunction, and returning to him again;
which is in 29d 12h 44m. The Civil Months are those which are
framed for the uses of Civil life; and are different as to their names,
number of days, and times of beginning, in several different Countries.
The first month of the Jewish Year fell according to the Moon in
our August and September, Old Style; the second in September and
October, and so on. The first month of the Egyptian Year began on
the 29th of our August. The first month of the Arabic and Turkish
Year began the 16th of July. The first month of the Grecian Year fell
according to the Moon in June and July, the second in July and August,
and so on, as in the following Table.
| No |
The Jewish year. |
Days |
|
No |
The Egyptian year. |
Days |
| 1 |
Tisri |
Aug.-Sept. |
30 |
1 |
Thoth |
August 29 |
30 |
| 2 |
Marchesvan |
Sept.-Oct. |
29 |
2 |
Paophi |
Septemb. 28 |
30 |
| 3 |
Casleu |
Oct.-Nov. |
30 |
3 |
Athir |
October 28 |
30 |
| 4 |
Tebeth |
Nov.-Dec. |
29 |
4 |
Chojac |
Novemb. 27 |
30 |
| 5 |
Shebat |
Dec.-Jan. |
30 |
5 |
Tybi |
Decemb. 27 |
30 |
| 6 |
Adar |
Jan.-Feb. |
29 |
6 |
Mechir |
January 26 |
30 |
| 7 |
Nisan or Abib |
Feb.-Mar. |
30 |
7 |
Phamenoth |
Februar. 25 |
30 |
| 8 |
Jiar |
Mar.-Apr. |
29 |
8 |
Parmuthi |
March 27 |
30 |
| 9 |
Sivan |
April-May |
30 |
9 |
Pachon |
April 26 |
30 |
| 10 |
Tamuz |
May-June |
29 |
10 |
Payni |
May 26 |
30 |
| 11 |
Ab |
June-July |
30 |
11 |
Epiphi |
June 25 |
30 |
| 12 |
Elul |
July-Aug. |
29 |
12 |
Mesori |
July 25 |
30 |
| Days in the year |
354> |
Epagomenæ or days added |
5 |
| In the _Embolimic year after
Adar they added a month called Ve-Adar of 30 days. |
Days in the year |
365 |
241
| No |
The Arabic and Turkish year. |
Days |
|
No |
The ancient Grecian year. |
Days |
| 1 |
Muharram |
July 16 |
30 |
1 |
Hecatombæon |
June-July |
30 |
| 2 |
Saphar |
August 15 |
29 |
2 |
Metagitnion |
July-Aug. |
29 |
| 3 |
Rabia I. |
Septemb. 13 |
30 |
3 |
Boedromion |
Aug.-Sept. |
30 |
| 4 |
Rabia II. |
October 13 |
29 |
4 |
Pyanepsion |
Sept.-Oct. |
29 |
| 5 |
Jomada I. |
Novemb. 11 |
30 |
5 |
Mæmacterion |
Oct.-Nov. |
30 |
| 6 |
Jomada II. |
Decemb. 11 |
29 |
6 |
Posideon |
Nov.-Dec. |
29 |
| 7 |
Rajab |
January 9 |
30 |
7 |
Gamelion |
Dec.-Jan. |
30 |
| 8 |
Shasban |
February 8 |
29 |
8 |
Anthesterion |
Jan.-Feb. |
29 |
| 9 |
Ramadan |
March 9 |
30 |
9 |
Elapheloblion |
Feb.-Mar. |
30 |
| 10 |
Shawal |
April 8 |
29 |
10 |
Munichion |
Mar.-Apr. |
29 |
| 11 |
Dulhaadah |
May 7 |
30 |
11 |
Thargelion |
April-May |
30 |
| 12 |
Dulheggia |
June 5 |
29 |
12 |
Schirrophorion |
May-June |
29 |
| Days in the year |
354 |
Days in the year |
354 |
| The Arabians add 11 days at the end of every year,
which keep the same months to the same seasons. |
Weeks
416. A month is divided into four parts called Weeks, and a Week
into seven parts called Days; so that in a Julian Year there are 13
such Months, or 52 Weeks, and one Day over. The Gentiles gave
the names of the Sun, Moon, and Planets to the Days of the Week.
To the first, the Name of the Sun; to the second, of the Moon; to
the third, of Mars; to the fourth, of Mercury; to the fifth, of Jupiter;
and to the sixth, of Saturn.
Days
417. A Day is either Natural or Artificial. The Natural Day
contains 24 hours; the Artificial the time from Sun-rise to Sun-set.
The Natural Day is either Astronomical or Civil. The Astronomical
Day begins at Noon, because the increase and decrease of Days
terminated by the Horizon are very unequal among themselves;
which inequality is likewise augmented by the inconstancy of the
horizontal Refractions § 183: and therefore the Astronomer takes
the Meridian for the limit of diurnal Revolutions; reckoning Noon,
that is the instant when the Sun’s Center is on the Meridian, for the
beginning of the Day. The British, French, Dutch, Germans, Spaniards,
Portuguese, and Egyptians, begin the Civil Day at mid-night:
the antient Greeks, Jews, Bohemians, Silesians, with the modern Italians,
and Chinese, begin it at Sun-setting: And the antient Babylonians,
Persians, Syrians, with the modern Greeks, at Sun-rising.
Hours
418. An Hour is a certain determinate part of the Day, and is either
equal or unequal. An equal Hour is the 24th part of a mean natural
Day, as shewn by well regulated Clocks and Watches; but those
Hours are not quite equal as measured by the returns of the Sun to the
Meridian, because of the obliquity of the Ecliptic and Sun’s unequal
242motion in it § 224-245. Unequal Hours are those by which the
Artificial Day is divided into twelve Parts, and the Night into as
many.
Minutes, Seconds, Thirds, and Scruples.
419. An Hour is divided into 60 equal parts called Minutes, a minute
into 60 equal parts called Seconds, and these again into 60 equal
parts called Thirds. The Jews, Chaldeans, and Arabians, divide the
Hour into 1080 equal parts called Scruples; which number contains
18 times 60, so that one minute contains 18 Scruples.
Cycles, of the Sun, Moon, and Indiction.
420. A Cycle is a perpetual round, or circulation of the same parts
of time of any sort. The Cycle of the Sun is a revolution of 28 years,
in which time, the days of the months return again to the same days
of the week; the Sun’s Place to the same Signs and Degrees of the
Ecliptic on the same months and days, so as not to differ one degree
in 100 years; and the leap-years begin the same course over again with
respect to the days of the week on which the days of the months fall.
The Cycle of the Moon, commonly called the Golden Number, is a revolution
of 19 years; in which time, the Conjunctions, Oppositions,
and other Aspects of the Moon are within an hour and half of being
the same as they were on the same days of the months 19 years before.
The Indiction is a revolution of 15 years, used only by the Romans
for indicating the times of certain payments made by the subjects to the
republic: It was established by Constantine, A.D. 312.
To find the Years of these Cycles.
421. The year of our Saviour’s Birth, according to the vulgar Æra,
was the 9th year of the Solar Cycle; the first year of the Lunar Cycle;
and the 312th year after his birth was the first year of the Roman Indiction.
Therefore, to find the year of the Solar Cycle, add 9 to any
given year of Christ, and divide the sum by 28, the Quotient is the
number of Cycles elapsed since his birth, and the remainder is the
Cycle for the given year: if nothing remains, the Cycle is 28. To
find the Lunar Cycle, add 1 to the given year of Christ, and divide
the sum by 19; the Quotient is the number of Cycles elapsed in the
interval, and the remainder is the Cycle for the given year: if nothing
remains, the Cycle is 19. Lastly, subtract 312 from the given year
of Christ, and divide the remainder by 15; and what remains after
this division is the Indiction for the given year: if nothing remains, the
Indiction is 15.
The deficiency of the Lunar Cycle, and consequence thereof.
422. Although the above deficiency in the Lunar Cycle of an hour
and half every 19 years be but small, yet in time it becomes so sensible
as to make a whole Natural Day in 310 years. So that, although this
Cycle be of use, when rightly placed against the days of the month
in the Calendar, as in our Common Prayer Books, for finding the days
243of the mean Conjunctions or Oppositions of the Sun and Moon, and
consequently the time of Easter; it will only serve for 310 years Old Style.
For as the New and Full Moons anticipate a day in that time, the
Golden Numbers ought to be placed one day earlier in the Calendar
for the next 310 years to come. These Numbers were rightly placed
against the days of New Moon in the Calendar, by the Council of
Nice, A. D. 325; but the anticipation which has been neglected ever
since, is now grown almost into 5 days: and therefore, all the Golden
Numbers ought now to be placed 5 days higher in the Calendar for the
O.S. than they were at the time of the said Council; or six days lower
for the New Style, because at present it differs 11 days from the Old.
| Days |
|
Jan. |
Feb. |
March |
April |
May |
June |
July |
August |
Sept. |
Octob. |
Nov. |
Dec. |
| 1 |
|
9 |
|
9 |
17 |
17 |
6 |
|
|
|
11 |
|
19 |
| 2 |
|
|
17 |
|
|
6 |
14 |
14 |
3 |
11 |
|
19 |
|
| 3 |
|
17 |
6 |
17 |
6 |
|
|
3 |
11 |
|
19 |
8 |
8 |
| 4 |
|
6 |
|
6 |
14 |
14 |
3 |
|
|
19 |
8 |
|
16 |
| 5 |
|
|
14 |
|
|
3 |
11 |
11 |
19 |
8 |
|
16 |
|
| 6 |
|
14 |
3 |
14 |
3 |
|
|
19 |
|
|
16 |
5 |
5 |
| 7 |
|
3 |
|
3 |
11 |
11 |
19 |
|
8 |
16 |
|
|
13 |
| 8 |
|
|
11 |
|
|
19 |
8 |
8 |
16 |
5 |
5 |
13 |
|
| 9 |
|
11 |
19 |
11 |
19 |
|
|
|
|
|
13 |
|
2 |
| 10 |
|
|
|
19 |
8 |
8 |
16 |
16 |
5 |
13 |
|
2 |
10 |
| 11 |
|
19 |
8 |
|
|
|
|
5 |
13 |
2 |
2 |
10 |
|
| 12 |
|
8 |
16 |
8 |
16 |
16 |
5 |
|
|
|
10 |
|
18 |
| 13 |
|
|
|
|
|
5 |
13 |
13 |
2 |
10 |
|
18 |
7 |
| 14 |
|
16 |
5 |
16 |
5 |
|
|
2 |
10 |
18 |
18 |
7 |
|
| 15 |
|
5 |
|
5 |
13 |
13 |
2 |
|
|
|
7 |
|
15 |
| 16 |
|
|
13 |
|
|
2 |
10 |
10 |
18 |
7 |
|
15 |
|
| 17 |
|
13 |
2 |
13 |
2 |
|
|
18 |
7 |
|
15 |
4 |
4 |
| 18 |
|
2 |
|
2 |
10 |
10 |
18 |
|
|
15 |
|
|
12 |
| 19 |
|
|
10 |
|
|
18 |
7 |
7 |
15 |
4 |
4 |
12 |
|
| 20 |
|
10 |
18 |
10 |
18 |
|
|
15 |
|
|
12 |
1 |
1 |
| 21 |
|
|
|
18 |
7 |
7 |
15 |
|
4 |
12 |
|
|
9 |
| 22 |
|
18 |
7 |
|
|
15 |
4 |
4 |
12 |
1 |
1 |
9 |
|
| 23 |
|
7 |
15 |
7 |
15 |
|
|
12 |
|
|
9 |
17 |
17 |
| 24 |
|
|
|
15 |
4 |
4 |
12 |
|
1 |
9 |
|
|
6 |
| 25 |
|
15 |
4 |
|
|
12 |
|
1 |
9 |
17 |
17 |
6 |
|
| 26 |
|
4 |
|
4 |
12 |
|
1 |
|
|
|
6 |
|
14 |
| 27 |
|
|
12 |
|
1 |
1 |
9 |
9 |
17 |
6 |
|
14 |
|
| 28 |
|
12 |
1 |
12 |
|
9 |
|
17 |
6 |
14 |
14 |
3 |
3 |
| 29 |
|
1 |
|
1 |
9 |
|
17 |
|
|
|
3 |
|
11 |
| 30 |
|
|
|
|
|
17 |
6 |
6 |
14 |
3 |
|
11 |
|
| 31 |
|
9 |
|
9 |
|
|
|
14 |
3 |
|
11 |
|
19 |
How to find the day of the New Moon by the Golden Number.
423. In the annexed Table,
the Golden Numbers under
the months stand against the
days of New Moon in the left
hand column, for the New
Style; adapted chiefly to the
second year after leap-year as
being the nearest mean for all
the four; and will serve till
the year 1900. Therefore,
to find the day of New Moon
in any month of a given year
till that time, look for the
Golden Number of that year
under the desired month, and
against it, you have the day
of New Moon in the left
hand column. Thus, suppose
it were required to find
the day of New Moon in
September 1757; the Golden
Number for that year is 10,
which I look for under September
and right against it in
the left hand column I find
13, which is the day of New
Moon in that month. N. B.
If all the Golden Numbers,
except 17 and 6, were set
one day lower in the Table,
244it would serve from the beginning of the year 1900 till the end of the
year 2199. The first Table after this chapter shews the Golden Number
for 4000 years after the birth of Christ, by looking for the even
hundreds of any given year at the left hand, and for the rest to make
up that year at the head of the Table; and where the columns meet,
you have the Golden Number (which is the same both in Old and New
Style) for the given year. Thus, suppose the Golden Number was
wanted for the year 1757; I look for 1700 at the left hand of the
Table, and for 57 at the top of it; then guiding my eye downward
from 57 to over against 1700, I find 10, which is the Golden Number
for that year.
A perpetual Table of the time of New Moon to the nearest hour, for the Old Style.
424. But because the lunar Cycle of 19 years sometimes includes
five leap-years, and at other times only four, this Table will sometimes
vary a day from the truth in leap-years after February. And
it is impossible to have one more correct, unless we extend it to four
times 19 or 76 years; in which there are 19 leap years without a
remainder. But even then to have it of perpetual use, it must be
adapted to the Old Style, because in every centurial year not divisible by
4, the regular course of leap-years is interrupted in the New; as will
be the case in the year 1800. Therefore, upon the regular Old Style
plan, I have computed the following Table of the mean times of all
the New Moons to the nearest hour for 76 years; beginning with the
year of Christ 1724, and ending with the year 1800.
This Table may be made perpetual, by deducting 6 hours from the
time of New Moon in any given year and month from 1724 to 1800,
in order to have the mean time of New Moon in any year and month
76 years afterward; or deducting 12 hours for 152 years, 18 hours
for 228 years; and 24 hours for 304 years, because in that time the
changes of the Moon anticipate almost a complete natural day. And
if the like number of hours be added for so many years past, we shall
have the mean time of any New Moon already elapsed. Suppose, for
example, the mean time of Change was required for January 1802;
deduct 76 years and there remains 1726, against which in the following
Table under January I find the time of New Moon was on the 21st
day at 11 in the evening: from which take 6 hours and there remains
the 21st day at 5 in the evening for the mean time of Change in January
1802. Or, if the time be required for May, A. D. 1701, add 76
years and it makes 1777, which I look for in the Table, and against it
under May I find the New Moon in that year falls on the 25th day at
9 in the evening; to which add 6 hours, and it gives the 26th day at
3 in the Morning for the time of New Moon in May, A. D. 1701.
245By this addition for time past, or subtraction for time to come, the
Table will not vary 24 hours from the truth in less than 14592 years.
And if, instead of 6 hours for every 76 years, we add or subtract only
5 hours 52 minutes, it will not vary a day in 10 millions of years.
Although this Table is calculated for 76 years only, and according
to the Old Style, yet by means of two easy Equations it may be made
to answer as exactly to the New Style, for any time to come. Thus,
because the year 1724 in this Table is the first year of the Cycle for
which it is made; if from any year of Christ after 1800 you subtract
1723, and divide the overplus by 76, the Quotient will shew how
many entire Cycles of 76 years are elapsed since the beginning of the
Cycle here provided for; and the remainder will shew the year of the
current Cycle answering to the given year of Christ. Hence, if the
remainder be 0, you must instead thereof put 76, and lessen the
Quotient by unity.
Then, look in the left hand column of the Table for the number
in your remainder, and against it you will find the times of all the
mean New Moons in that year of the present Cycle. And whereas
in 76 Julian Years the Moon anticipates 5 hours 52 minutes, if therefore
these 5 hours 52 minutes be multiplied by the above found Quotient,
that is, by the number of entire Cycles past; the product subtracted
from the times in the Table will leave the corrected times
of the New Moons to the Old Style; which may be reduced to the
New Style thus:
Divide the number of entire hundreds in the given year of Christ
by 4, multiply this Quotient by 3, to the product add the remainder,
and from their sum subtract 2: this last remainder denotes the number
of days to be added to the times above corrected, in order to reduce
them to the New Style. The reason of this is, that every 400 years
of the New Style gains 3 days upon the Old Style: one of which it
gains in each of the centurial years succeeding that which is exactly
divisible by 4 without remainder; but then, when you have found
the days so gained, 2 must be subtracted from their number on account
of the rectifications made in the Calendar by the Council of Nice, and
since by Pope Gregory. It must also be observed, that the additional
days found as above directed do not take place in the centurial Years
which are not multiples of 4 till February 29th, O. S. for on that day
begins the difference between the Styles; till which day therefore,
those that were added in the preceding years must be used. The
following Example will make this accommodation plain.
246
Required the mean time of New Moon in June, A.D. 1909, N.S.
| From 1909 take 1723 Years, and there rem. |
|
186 |
|
| Which divided by 76, gives the Quotient 2
and the remainder |
|
34 |
|
| Then, against 34 in the Table is June |
5d |
8h |
0m |
Afternoon. |
| And 5h 52m multiplied by 2 make to be subtr. |
|
11 |
44 |
|
| Remains the mean time according to the Old Style, June |
5d |
9h |
16m |
Morning. |
| Entire hundred in 1909 are 19, which divided by 4, quotes |
|
4 |
|
| And leaves a remainder of |
|
3 |
|
| Which Quotient multiplied by 3 makes 12,
and the remainder added makes |
|
15 |
|
| From which subtract 2, and there remains |
|
13 |
|
| Which number of days added to the above time Old Style, gives June |
18d |
9h |
16m |
Morn.N.S. |
So the mean time of New Moon in June 1909 New Style is the 18th
day at 16 minutes past 9 in the Morning.
If 11 days be added to the time of any New Moon in this Table,
it will give the time thereof according to the New Style till the year
1800. And if 14 days 18 hours 22 minutes be added to the mean
time of New Moon in either Style, it will give the mean time of the
next Full Moon according to that Style.
247
A Table shewing the times of all the mean Changes of the Moon, to the nearest Hour, through four Lunar Periods, or 76 years. M signifies morning, A afternoon.
| Yrs of the Cyc. |
A.D. |
January |
February |
March |
April |
May |
June |
July |
August |
Septemb. |
October |
Novemb. |
Decemb. |
| D. |
H. |
D. |
H. |
D. |
H. |
D. |
H. |
D. |
H. |
D. |
H. |
D. |
H. |
D. |
H. |
D. |
H. |
D. |
H. |
D. |
H. |
D. |
H. |
| 1 |
1724 |
14 |
5A |
13 |
5M |
13 |
6A |
12 |
7M |
11 |
8A |
10 |
8M |
9 |
9A |
8 |
10M |
6 |
10A |
6 |
11M |
4 |
12A |
4 |
1A |
| 2 |
1725 |
3 |
2M |
1 |
2A |
3 |
3M |
1 |
4A |
1 |
4M |
29 |
6M |
28 |
7A |
27 |
8M |
25 |
8A |
25 |
9M |
23 |
10A |
23 |
11M |
| 30 |
5A |
| 3 |
1726 |
21 |
11A |
20 |
11M |
21 |
12A |
20 |
1A |
20 |
1M |
18 |
2A |
18 |
3M |
16 |
4A |
15 |
5M |
14 |
5A |
13 |
6M |
12 |
7A |
| 4 |
1727 |
11 |
8M |
9 |
9A |
11 |
9M |
9 |
10A |
9 |
11M |
7 |
12A |
7 |
0A |
6 |
1M |
4 |
1A |
4 |
2M |
2 |
3A |
2 |
4M |
| 31 |
5A |
| 5 |
1728 |
30 |
6M |
28 |
7A |
29 |
7M |
27 |
8A |
27 |
8M |
25 |
9A |
25 |
10M |
23 |
11A |
22 |
11M |
21 |
12A |
20 |
1A |
20 |
2M |
| 6 |
1729 |
18 |
2A |
17 |
3M |
18 |
4A |
17 |
4M |
16 |
5A |
15 |
6M |
14 |
7A |
12 |
7M |
11 |
8A |
11 |
9M |
9 |
0A |
9 |
11M |
| 7 |
1730 |
7 |
11A |
6 |
0A |
8 |
1M |
6 |
1A |
6 |
2M |
4 |
3A |
4 |
3M |
2 |
4A |
2 |
5M |
30 |
7M |
28 |
8A |
28 |
9M |
| 30 |
6A |
| 8 |
1731 |
26 |
9A |
25 |
10M |
26 |
10A |
25 |
11M |
24 |
11A |
23 |
0A |
23 |
1M |
21 |
2A |
20 |
2M |
19 |
3A |
18 |
4M |
17 |
5A |
| 9 |
1732 |
16 |
5M |
14 |
6A |
15 |
7M |
13 |
8A |
13 |
8M |
11 |
9A |
11 |
10M |
9 |
11A |
8 |
11M |
7 |
12A |
6 |
1A |
6 |
2M |
| 10 |
1733 |
4 |
2A |
3 |
3M |
4 |
4A |
3 |
4M |
2 |
5A |
1 |
6M |
30 |
8M |
28 |
8A |
27 |
9M |
26 |
10A |
25 |
11M |
24 |
11A |
| 30 |
7A |
| 11 |
1734 |
23 |
0A |
22 |
1M |
23 |
1A |
22 |
2M |
21 |
2A |
20 |
3M |
19 |
4A |
18 |
5M |
16 |
5A |
16 |
6M |
14 |
7A |
14 |
8M |
| 12 |
1735 |
12 |
9A |
11 |
9M |
12 |
10A |
11 |
11M |
10 |
11A |
9 |
0A |
9 |
1M |
7 |
2A |
6 |
2M |
5 |
3A |
4 |
4M |
3 |
5A |
| 13 |
1736 |
2 |
5M |
---- |
1 |
7M |
29 |
9M |
28 |
9A |
27 |
10M |
26 |
11A |
25 |
0A |
23 |
12A |
23 |
1A |
22 |
2M |
21 |
3A |
| 31 |
6A |
30 |
8A |
| 14 |
1737 |
20 |
3M |
18 |
4A |
20 |
4M |
18 |
5A |
18 |
5M |
16 |
6A |
16 |
7M |
14 |
8A |
13 |
8M |
12 |
9A |
11 |
10M |
10 |
11A |
| 15 |
1738 |
9 |
11M |
7 |
12A |
9 |
1A |
8 |
1M |
7 |
2A |
6 |
3M |
5 |
4A |
4 |
5M |
2 |
5A |
2 |
6M |
30 |
8M |
29 |
8A |
| 31 |
7A |
| 16 |
1739 |
28 |
9M |
26 |
10A |
28 |
11M |
26 |
12A |
26 |
0A |
25 |
1M |
24 |
2A |
23 |
3M |
21 |
3A |
21 |
4M |
19 |
5A |
19 |
6M |
| 17 |
1740 |
17 |
6A |
16 |
7M |
16 |
8A |
15 |
9M |
14 |
9A |
13 |
10M |
12 |
11A |
11 |
0A |
9 |
12A |
9 |
1A |
8 |
2M |
7 |
3A |
| 18 |
1741 |
6 |
3M |
4 |
4A |
6 |
4M |
4 |
5A |
4 |
5M |
2 |
6A |
2 |
7M |
30 |
8M |
28 |
9A |
28 |
10M |
26 |
11A |
26 |
11M |
| 31 |
7A |
| 19 |
1742 |
24 |
12A |
23 |
1A |
25 |
2M |
23 |
3A |
23 |
3M |
21 |
4A |
21 |
5M |
19 |
6A |
18 |
6M |
17 |
7A |
16 |
8M |
15 |
9A |
| 20 |
1743 |
14 |
9M |
12 |
10A |
14 |
11M |
12 |
12A |
12 |
0A |
11 |
1M |
10 |
2A |
9 |
3M |
7 |
3A |
7 |
4M |
5 |
5A |
5 |
6M |
| 21 |
1744 |
3 |
6A |
2 |
7M |
2 |
8A |
1 |
9M |
30 |
10M |
28 |
11A |
28 |
0A |
26 |
12A |
25 |
1A |
25 |
2M |
23 |
3A |
23 |
3M |
| 30 |
9A |
| 22 |
1745 |
21 |
4A |
20 |
5M |
21 |
5A |
20 |
6M |
19 |
6A |
18 |
7M |
17 |
8A |
16 |
8M |
14 |
9A |
14 |
10M |
12 |
11A |
12 |
0A |
| 23 |
1746 |
10 |
12A |
9 |
1A |
11 |
2M |
9 |
3A |
9 |
3M |
7 |
4A |
7 |
5M |
5 |
6A |
4 |
6M |
3 |
7A |
2 |
8M |
1 |
9A |
| 31 |
10M |
| 24 |
1747 |
29 |
10A |
28 |
11M |
29 |
11A |
28 |
0A |
27 |
12A |
26 |
1A |
26 |
2M |
24 |
3A |
23 |
3M |
22 |
4A |
21 |
5M |
20 |
6A |
| 25 |
1748 |
19 |
6M |
17 |
7A |
18 |
8M |
16 |
9A |
16 |
9M |
14 |
10A |
14 |
11M |
12 |
12A |
11 |
0A |
11 |
1M |
9 |
2A |
9 |
3M |
| 26 |
1749 |
7 |
3A |
6 |
4M |
7 |
5A |
6 |
6M |
5 |
6A |
4 |
7M |
3 |
8A |
2 |
9M |
30 |
10M |
29 |
11A |
28 |
0A |
27 |
12A |
| 31 |
9A |
| 27 |
1750 |
26 |
1A |
25 |
2M |
26 |
3A |
25 |
4M |
24 |
4A |
23 |
5M |
22 |
6A |
21 |
7M |
19 |
7A |
19 |
8M |
17 |
9A |
17 |
10M |
| 28 |
1751 |
15 |
10A |
14 |
11M |
15 |
11A |
14 |
0A |
13 |
12A |
12 |
1A |
12 |
2M |
10 |
3A |
9 |
3M |
8 |
4A |
7 |
5M |
6 |
6A |
| 29 |
1752 |
5 |
6M |
3 |
7A |
4 |
8M |
2 |
9A |
2 |
9M |
30 |
11M |
29 |
12A |
28 |
0A |
27 |
1M |
26 |
2A |
25 |
3M |
24 |
3A |
| 31 |
10A |
| 30 |
1753 |
23 |
4M |
21 |
5A |
23 |
6M |
21 |
7A |
21 |
7M |
19 |
8A |
19 |
9M |
17 |
10A |
16 |
10M |
15 |
11A |
14 |
0A |
14 |
1M |
| 31 |
1754 |
12 |
1A |
11 |
2M |
12 |
3A |
11 |
4M |
10 |
4A |
9 |
5M |
8 |
6A |
7 |
7M |
5 |
7A |
5 |
8M |
3 |
9A |
3 |
10M |
| 32 |
1755 |
1 |
10A |
---- |
1 |
11A |
29 |
12A |
29 |
1A |
28 |
2M |
27 |
3A |
25 |
3M |
24 |
4A |
24 |
5M |
22 |
6A |
22 |
6M |
| 31 |
11M |
31 |
0A |
| 33 |
1756 |
20 |
7A |
19 |
8M |
19 |
9A |
18 |
9M |
17 |
10A |
16 |
11M |
15 |
12A |
14 |
1A |
13 |
1M |
12 |
2A |
11 |
3M |
10 |
4A |
| 34 |
1757 |
9 |
4M |
7 |
5A |
9 |
6M |
7 |
7A |
7 |
7M |
5 |
8A |
5 |
9M |
3 |
10A |
2 |
10M |
1 |
14A |
30 |
1M |
29 |
1A |
| 31 |
0A |
| 35 |
1758 |
28 |
2M |
26 |
3A |
28 |
3M |
26 |
4A |
26 |
4M |
24 |
5A |
24 |
6M |
22 |
7A |
21 |
7M |
20 |
8A |
19 |
9M |
18 |
10A |
| 36 |
1759 |
17 |
10M |
15 |
11A |
17 |
0A |
16 |
1M |
15 |
1A |
14 |
2M |
13 |
3A |
12 |
2M |
10 |
4A |
10 |
5M |
8 |
6A |
8 |
7M |
| 37 |
1760 |
6 |
7A |
5 |
8M |
5 |
9A |
4 |
10M |
3 |
10A |
2 |
11M |
1 |
12A |
30 |
1M |
28 |
2A |
28 |
3M |
26 |
4A |
26 |
4M |
| 31 |
1A |
| 38 |
1761 |
24 |
5A |
23 |
6M |
24 |
7A |
23 |
8M |
22 |
9A |
21 |
10M |
20 |
10A |
19 |
11M |
17 |
11A |
17 |
0A |
16 |
1M |
15 |
2A |
| 39 |
1762 |
14 |
2M |
12 |
3A |
14 |
3M |
12 |
4A |
12 |
4M |
10 |
5A |
10 |
6M |
8 |
7A |
7 |
7M |
6 |
8A |
5 |
9M |
4 |
10A |
| 24840 |
1763 |
3 |
11M |
1 |
12A |
3 |
0A |
2 |
1M |
1 |
1A |
29 |
3A |
29 |
4M |
27 |
4M |
26 |
5M |
25 |
6A |
24 |
7M |
23 |
7A |
| 31 |
2M |
| 41 |
1764 |
22 |
8M |
20 |
9A |
21 |
10M |
19 |
11A |
19 |
11M |
17 |
12A |
17 |
1A |
16 |
2M |
14 |
2A |
14 |
3M |
12 |
4A |
12 |
5M |
| 42 |
1765 |
10 |
5A |
9 |
6M |
10 |
6A |
9 |
7M |
8 |
7A |
7 |
8M |
6 |
9A |
5 |
10M |
3 |
10A |
3 |
11M |
1 |
12A |
1 |
1A |
| 31 |
1M |
| 43 |
1766 |
29 |
2A |
28 |
3M |
29 |
4A |
28 |
5M |
27 |
5A |
26 |
6M |
25 |
7A |
24 |
8M |
22 |
8A |
22 |
9M |
20 |
10A |
20 |
11M |
| 44 |
1767 |
18 |
11A |
17 |
0A |
19 |
1M |
17 |
2A |
17 |
2M |
15 |
3A |
15 |
4M |
13 |
5A |
12 |
6M |
11 |
6A |
10 |
7M |
9 |
8A |
| 45 |
1768 |
8 |
8M |
6 |
9A |
7 |
10M |
5 |
11A |
5 |
11M |
3 |
12A |
3 |
1A |
2 |
2M |
30 |
3M |
29 |
4A |
28 |
5M |
27 |
5A |
| 31 |
2A |
| 46 |
1769 |
26 |
6M |
24 |
7A |
26 |
7M |
24 |
8A |
24 |
8M |
22 |
9A |
22 |
10M |
20 |
11A |
19 |
11M |
18 |
12A |
17 |
1A |
17 |
2M |
| 47 |
1770 |
15 |
2A |
14 |
3M |
15 |
4A |
14 |
5M |
13 |
5A |
12 |
4M |
11 |
7A |
10 |
8M |
8 |
8A |
8 |
9M |
6 |
10A |
6 |
11M |
| 48 |
1771 |
4 |
11M |
3 |
0A |
5 |
1M |
3 |
2A |
3 |
2M |
1 |
3A |
1 |
4M |
29 |
5M |
27 |
6A |
27 |
7M |
25 |
8A |
25 |
9M |
| 30 |
5A |
| 49 |
1772 |
23 |
9A |
22 |
10M |
22 |
10A |
21 |
11M |
20 |
11A |
19 |
0A |
19 |
1M |
17 |
2A |
16 |
2M |
15 |
3A |
14 |
4M |
13 |
5A |
| 50 |
1773 |
12 |
5M |
10 |
6A |
12 |
7M |
10 |
8A |
10 |
8M |
8 |
9A |
8 |
9M |
6 |
10A |
5 |
11M |
4 |
12A |
3 |
1A |
3 |
2M |
| 51 |
1774 |
1 |
2A |
---- |
1 |
4A |
29 |
5A |
29 |
6M |
27 |
7A |
27 |
8M |
25 |
8A |
24 |
9M |
23 |
10A |
22 |
11M |
21 |
11A |
| 31 |
3M |
31 |
5M |
| 52 |
1775 |
20 |
0A |
19 |
1M |
20 |
2A |
19 |
3M |
18 |
3A |
17 |
4M |
16 |
5A |
15 |
6M |
13 |
6A |
13 |
7M |
11 |
8A |
11 |
9M |
| 53 |
1776 |
9 |
9A |
8 |
10M |
8 |
10A |
7 |
11M |
6 |
12A |
5 |
0A |
5 |
1M |
3 |
2A |
2 |
2M |
1 |
3A |
29 |
5A |
29 |
5M |
| 31 |
4M |
| 54 |
1777 |
27 |
6A |
26 |
7M |
27 |
8A |
26 |
9M |
25 |
9A |
24 |
10M |
23 |
11A |
22 |
0A |
20 |
12A |
20 |
1A |
19 |
2M |
18 |
3A |
| 55 |
1778 |
17 |
3M |
15 |
4A |
17 |
5M |
15 |
6A |
15 |
6M |
13 |
7A |
13 |
8M |
11 |
9A |
10 |
9M |
9 |
10A |
8 |
11M |
7 |
12A |
| 56 |
1779 |
6 |
0A |
5 |
1M |
6 |
2A |
5 |
3M |
4 |
3A |
3 |
4M |
2 |
5A |
1 |
6M |
29 |
7M |
28 |
8A |
27 |
9M |
26 |
9A |
| 30 |
6A |
| 57 |
1780 |
25 |
10M |
23 |
11A |
24 |
11M |
22 |
12A |
22 |
0A |
21 |
1M |
20 |
2A |
19 |
3M |
17 |
3A |
17 |
4M |
15 |
5A |
15 |
6M |
| 58 |
1781 |
13 |
6A |
12 |
7M |
13 |
8A |
12 |
9M |
11 |
9A |
10 |
10M |
9 |
11A |
8 |
0A |
6 |
12A |
6 |
1A |
5 |
2M |
4 |
3A |
| 59 |
1782 |
3 |
3M |
1 |
4A |
3 |
5M |
1 |
6A |
1 |
6M |
29 |
8M |
28 |
9A |
27 |
9M |
25 |
10A |
25 |
11M |
23 |
12A |
23 |
0A |
| 30 |
7A |
| 60 |
1783 |
22 |
1M |
20 |
2A |
22 |
2M |
20 |
3A |
20 |
3M |
18 |
4A |
18 |
5M |
16 |
6A |
15 |
6M |
14 |
7A |
13 |
8M |
12 |
9A |
| 61 |
1784 |
11 |
9M |
9 |
10A |
10 |
11M |
8 |
12A |
8 |
0A |
7 |
1M |
6 |
2A |
5 |
3M |
3 |
3A |
3 |
4M |
1 |
5A |
1 |
6M |
| 30 |
6A |
| 62 |
1785 |
29 |
7M |
27 |
8A |
29 |
9M |
27 |
10A |
27 |
10M |
25 |
11A |
25 |
0A |
24 |
1M |
22 |
1A |
22 |
2M |
20 |
3A |
20 |
3M |
| 63 |
1786 |
18 |
4A |
17 |
5M |
18 |
5A |
17 |
6M |
16 |
6A |
15 |
7M |
14 |
8A |
13 |
9M |
11 |
9A |
11 |
10M |
9 |
11A |
9 |
0A |
| 64 |
1787 |
7 |
12A |
6 |
1A |
8 |
2M |
6 |
3A |
6 |
3M |
4 |
4A |
4 |
5M |
2 |
6A |
1 |
6M |
30 |
8M |
28 |
9A |
28 |
9M |
| 30 |
7A |
| 65 |
1788 |
26 |
10A |
25 |
11M |
25 |
12A |
24 |
1A |
24 |
1M |
22 |
2A |
22 |
3M |
20 |
4M |
19 |
4M |
18 |
5A |
17 |
6M |
16 |
7A |
| 66 |
1789 |
15 |
7M |
13 |
8A |
15 |
9M |
13 |
10A |
13 |
10M |
11 |
11A |
11 |
0A |
10 |
1M |
8 |
1A |
8 |
2M |
6 |
3A |
6 |
4M |
| 67 |
1790 |
4 |
4A |
3 |
5M |
4 |
5A |
3 |
6M |
2 |
6A |
1 |
7M |
30 |
9M |
28 |
9A |
27 |
10M |
26 |
11A |
25 |
0A |
24 |
12A |
| 30 |
8A |
| 68 |
1791 |
23 |
1A |
22 |
2M |
23 |
3A |
22 |
4M |
21 |
4A |
20 |
5M |
19 |
6A |
18 |
7M |
16 |
7A |
16 |
8M |
14 |
9A |
14 |
10M |
| 69 |
1792 |
12 |
10A |
11 |
11M |
11 |
12A |
10 |
1A |
10 |
1M |
8 |
2A |
8 |
3M |
6 |
4A |
5 |
4A |
4 |
5A |
3 |
6M |
2 |
7A |
| 70 |
1793 |
1 |
7M |
---- |
1 |
9M |
29 |
10M |
28 |
11A |
27 |
0A |
27 |
1M |
25 |
1A |
24 |
2M |
23 |
3A |
22 |
4M |
21 |
4A |
| 30 |
8A |
30 |
10A |
| 71 |
1794 |
20 |
5M |
18 |
6A |
20 |
6M |
18 |
7A |
18 |
7M |
16 |
8A |
16 |
9M |
14 |
10A |
13 |
10M |
12 |
11A |
11 |
0A |
11 |
1M |
| 72 |
1795 |
9 |
1A |
8 |
2M |
9 |
3A |
8 |
4M |
7 |
4A |
6 |
5M |
5 |
6A |
4 |
7M |
2 |
7A |
2 |
8M |
30 |
10M |
29 |
10A |
| 31 |
9A |
| 73 |
1796 |
28 |
11M |
26 |
12A |
27 |
0A |
26 |
1M |
25 |
1A |
24 |
2M |
23 |
3A |
22 |
4M |
20 |
4A |
20 |
5M |
18 |
6A |
18 |
7M |
| 74 |
1797 |
16 |
7A |
15 |
8M |
16 |
9A |
15 |
10M |
14 |
10A |
13 |
11M |
12 |
12A |
11 |
1A |
10 |
1M |
9 |
2A |
8 |
3M |
7 |
4A |
| 75 |
1798 |
6 |
4M |
4 |
5A |
6 |
6M |
4 |
7A |
4 |
7M |
2 |
8A |
2 |
9M |
30 |
10M |
28 |
11A |
28 |
0A |
27 |
1M |
26 |
1A |
| 31 |
10A |
| 76 |
1799 |
25 |
2M |
23 |
3A |
25 |
4M |
23 |
5A |
23 |
5M |
21 |
6A |
21 |
6M |
19 |
8A |
18 |
8M |
17 |
9A |
16 |
10M |
15 |
11A |
| 1 |
1800 |
14 |
11A |
12 |
12A |
13 |
0A |
12 |
1M |
11 |
1A |
10 |
2M |
9 |
3A |
8 |
4M |
6 |
4A |
6 |
5M |
4 |
6A |
4 |
7M |
The year 1800 begins a new Cycle.
Easter Cycle, deficient.
249425. The Cycle of Easter, also called the Dionysian Period, is a revolution
of 532 years, found by multiplying the Solar Cycle 28 by the
Lunar Cycle 19. If the New Moons did not anticipate upon this
Cycle, Easter-Day would always be the Sunday next after the first
Full Moon which succeeds the 21st of March. But, on account of
the above anticipation § 422, to which no proper regard was had before
the late alteration of the Style, the Ecclesiastic Easter has several
times been a week different from the true Easter within this last Century:
which inconvenience is now remedied by making the Table
which used to find Easter for ever, in the Common Prayer Book, of
no longer use than the Lunar difference from the New Style will admit
of.
Number of Direction.
To find the true Easter.
426. The earliest Easter possible is the 22d of March, the latest the
25th of April. Within these limits are 35 days, and the number belonging
to each of them is called the Number of Direction; because
thereby the time of Easter is found for any given year. To find the
Number of Direction, according to the New Style, enter Table V
following this Chapter, with the compleat hundreds of any given year at
the top, and the years thereof (if any) below an hundred at the left hand;
and where the columns meet is the Dominical Letter for the given
year. Then, enter Table I, with the compleat hundreds of the same
year at the left hand, and the years below an hundred at the top; and
where the columns meet is the Golden Number for the same year.
Lastly, enter Table II with the Dominical Letter at the left hand and
Golden Number at the top; and where the columns meet is the
Number of Direction for that year; which number, added to the 21st
day of March shews on what day either of March or April Easter
Sunday falls in that year. Thus, the Dominical Letter New Style for
the year 1757 is B (Table V) and the Golden Number is 10,
(Table I) by which in Table II, the Number of Direction is found to
be 20; which, reckoned from the 21st of March, ends on the 10th of
April, and that is Easter Sunday in the year 1757. N. B. There are
always two Dominical Letters to the leap-year, the first of which
takes place to the 24th of February, the last for the following part of
the year.
Dominical Letter.
427. The first seven Letters of the Alphabet are commonly placed in
the annual Almanacks to shew on what days of the week the days of
the months fall throughout the year. And because one of those seven
Letters must necessarily stand against Sunday it is printed in a capital
form, and called the Dominical Letter: the other six being inserted in
small characters to denote the other six days of the week. Now,
250since a common Julian Year contains 365 Days, if this number be
divided by 7 (the number of days in a week) there will remain one
day. If there had been no remainder, ’tis plain the year would constantly
begin on the same day of the week. But since one remains,
’tis as plain that the year must begin and end on the same day of
the week; and therefore the next year will begin on the day following.
Hence, when January begins on Sunday, A is the Dominical
or Sunday Letter for that year: then, because the next year
begins on Monday, the Sunday will fall on the seventh day, to
which is annexed the seventh Letter G, which therefore will be the
Dominical Letter for all that year: and as the third year will begin
on Tuesday, the Sunday will fall on the sixth day; therefore F will be
the Sunday Letter for that year. Whence ’tis evident that the Sunday
Letters will go annually in a retrograde order thus, G, F, E, D, C, B, A.
And in the course of seven years, if they were all common ones, the
same days of the week and Dominical Letters would return to the
same days of the months. But because there are 366 days in a leap-year,
if this number be divided by 7, there will remain two days over
and above the 52 weeks of which the year consists. And therefore,
if the leap-year begins on Sunday, it will end on Monday; and the next
year will begin on Tuesday, the first Sunday whereof must fall on the sixth
of January, to which is annexed the Letter F, and not G as in common
years. By this means, the leap-year returning every fourth year,
the order of the Dominical Letters is interrupted; and the Series does
not return to its first state till after four times seven, or 28 years: and
then the same days of the month return in order to the same days of
the week.
To find the Dominical Letter.
428. To find the Dominical Letter for any year either before or after the
Christian Æra[87]: In Table III or IV for Old Style, or V for New
Style, look for the hundreds of years at the head of the Table, and
for the years below an hundred (to make up the given year) at the
left hand: and where the columns meet you have the Dominical
Letter for the year desired. Thus, suppose the Dominical Letter be
required for the year of Christ 1758, New Style, I look for 1700 at
the head of Table V, and for 58 at the left hand of the same Table;
and in the angle of meeting, I find A, which is the Dominical Letter
for that year. If it was wanted for the same year Old Style, it would
be found by Table IV to be D. But to find the Dominical Letter
for any given year before Christ, subtract one from that year and
then proceed in all respects as just now taught, to find it by Table III
251Thus, suppose the Dominical Letter be required for the 585th year
before the first year of Christ, look for 500 at the head of Table III,
and for 84 at the left hand; in the meeting of these columns is FE,
which were the Dominical Letters for that year, and shews that it was
a leap-year; because, leap-year has always two Dominical Letters.
To find the Days of the Months.
429. To find the day of the month answering to any day of the week,
or the day of the week answering to any day of the month; for any year past
or to come: Having found the Dominical Letter for the given year,
enter Table VI, with the Dominical Letter at the head; and under it,
all the days in that column to the right hand are Sundays, in the divisions
of the months; the next column to the right are Mondays; the next,
Tuesdays; and so on to the last column under G, from which go back to
the column under A, and thence proceed towards the right hand
as before. Thus, in the year 1757, the Dominical Letter New Style
is B, in Table V, then in Table VI all the days under B are Sundays
in that year, viz. the 2d, 9th, 16th, 23d, and 30th of January and
October; the 6th, 13th, 20th, and 27th of February, March and
November; the 3d, 10th, and 17th, of April and July, together with
the 31st of July: and so on to the foot of the column. Then, of
course, all the days under C on Mondays, namely the 3d, 10th, &c.
of January and October; and so of all the rest in that column. If the
day of the week answering to any day of the month be required, it is easily
had from the same Table by the Letter that stands at the top of the
column in which the given day of the month is found. Thus, the
Letter that stands over the 28th of May is A; and in the year 585
before Christ the Dominical Letter was found to be FE § 428;
which being a leap-year, and E taking place from the 24th of February
to the end of that year, shews by the Table that the 25th of May was
on a Sunday; and therefore the 28th must have been on a Wednesday:
for when E stands for Sunday, F must stand for Monday, G for Tuesday,
A for Wednesday, B for Thursday, C for Friday, and D for Saturday.
Hence, as it appears that the famous Eclipse of the Sun foretold
by Thales, by which a peace was brought about between the Medes
and Lydians, happened on the 28th of May, in the 585th year before
Christ, it certainly fell on a Wednesday.
Julian Period.
430. From the multiplication of the Solar Cycle of 28 years into
the Lunar Cycle of 19 years, arises the great Julian Period consisting of
7980 years; which had its beginning 764 years before the supposed year
of the creation (when all the three Cycles began together) and is not yet
compleated, and therefore it comprehends all other Cycles, Periods and
Æras. There is but one year in the whole Period which has the same
252numbers for the three Cycles of which it is made up: and therefore, if
historians had remarked in their writings the Cycles of each year, there
had been no dispute about the time of any action recorded by them.
To find the year of this Period.
And the Cycles of that year.
431. The Dionysian or vulgar Æra of Christ’s birth was about the
end of the year of the Julian Period 4713; and consequently the first
year of his age, according to that account, was the 4714th year of
the said Period. Therefore, if to the current year of Christ we add
4713, the Sum will be the year of the Julian Period. So the year
1757 will be found to be the 6470th year of that Period. Or, to
find the year of the Julian Period answering to any given year before
the first year of Christ, subtract the number of that given year from
4714, and the remainder will be the year of the Julian Period. Thus,
the year 585 before the first year of Christ (which was the 584th
before his birth) was the 4129th year of the said Period. Lastly, to
find the Cycles of the Sun, Moon, and Indiction for any given year
of this Period, divide the given year by 28, 19, and 15; the three
remainders will be the Cycles sought, and the Quotients the numbers
of Cycles run since the beginning of the Period. So in the above
4714th year of the Julian Period the Cycle of the Sun was 10, the
Cycle of the Moon 2, and the Cycle of Indiction 4; the Solar Cycle
having run through 168 courses, the Lunar 248, and the Indiction 314.
The true Æra of Christ’s birth.
432. The vulgar Æra of Christ’s birth was never settled till the
year 527; when Dionysius Exiguus, a Roman Abbot, fixed it to the
end of the 4713th year of the Julian Period; which was certainly four
years too late. For, our Saviour was undoubtedly born before the
Death of Herod the Great, who sought to kill him as soon as he heard
of his birth. And, according to the testimony of Josephus (B. xvii.
c. 8.) there was an eclipse of the Moon in the time of Herod’s last
illness: which very eclipse our Astronomical Tables shew to have
been in the year of the Julian Period 4710, March 13th, 3 hours 21
minutes after mid-night, at Jerusalem. Now, as our Saviour must
have been born some months before Herod’s death, since in the interval
he was carried into Ægypt; the latest time in which we can possibly
fix the true Æra of his birth is about the end of the 4709th year of
the Julian Period. And this is four years before the vulgar Æra
thereof.
The time of his crucifixion.
In the former edition of this book, I endeavoured to ascertain the
time of Christ’s death; by shewing in what year, about the reputed
time of the Passion, there was a Passover Full Moon on a Friday: on
which day of the week, and at the time of the Passover, it is evident
253from Mark xv. 42. that our Saviour was crucified. And in computing
the times of all the Passover Full Moons from the 20th to the
40th year of Christ, after the Jewish manner, which was to add 14
days to the time when the New Moon next before the Passover was
first visible at Jerusalem, in order to have their day of the Passover Full
Moon, I found that the only Passover Full Moon which fell on a
Friday, in all that time, was in the year of the Julian Period 4746, on
the third day of April: which year was the 33d year of Christ’s age,
reckoning from the vulgar Æra of his birth, but the 37th counting from
the true Æra thereof: and was also the last year of the 402d Olympiad[88],
in which very year Phlegon an Heathen writer tells us, there was the
most extraordinary Eclipse of the Sun that ever was known, and that it
was night at the sixth hour of the day. Which agrees exactly with the
time that the darkness at the crucifixion began, according to the three
Evangelists who mention it[89]: and therefore must have been the very
same darkness, but mistaken by Phlegon for a natural Eclipse of the
Sun; which was impossible on two accounts, 1. because it was at the
time of Full Moon; and 2. because whoever takes the pains to calculate,
will find that there could be no regular and total Eclipse of the
Sun that year in any part of Judea, nor any where between Jerusalem
and Egypt: so that this darkness must have been quite out of the common
course of nature.
From the co-incidence of these characters, I made no doubt of
having ascertained the true year and day of our Saviour’s death.
But having very lately read what some eminent authors have wrote on
the same subject, of which I was really ignorant before; and heard
the opinions of other candid and ingenious enquirers after truth (which
every honest man will follow wherever it leads him) and who think
they have strong reasons for believing that the time of Christ’s death
was not in the year of the Julian Period 4746, but in the year 4743;
I find difficulties on both sides, not easily got over: and shall therefore
state the case both ways as fairly as I can; leaving the reader to
take which side of the Question he pleases.
Both Dr. Prideaux and Sir Isaac Newton are of opinion that
Daniel’s seventy weeks, consisting of 490 years (Dan. chap. ix. v. 23-26)
began with the time when Ezra received his commission from Artaxerxes
to go to Jerusalem, which was in the seventh year of that King’s
reign (Ezra ch. vii. v. 11-26) and ended with the death of Christ.
For, by joining the accomplishment of that prophecy with the expiation
of Sin, those weeks cannot well be supposed to end at any other
254time. And both these authors agree that this was Artaxerxes Longimanus,
not Artaxerxes Mnemon. The Doctor thinks that the last of
those annual weeks was equally divided between John’s ministry and
Christ’s. And, as to the half week, mentioned by Daniel chap. ix.
v. 27. Sir Isaac thinks it made no part of the above seventy; but only
meant the three years and an half in which the Romans made war
upon the Jews from spring in A.D. 67 to autumn in A.D. 70, when
a final Period was put to their sacrifices and oblations by destroying
their city and sanctuary, on which they were utterly dispersed. Now,
both by the undoubted Canon of Ptolemy, and the famous Æra of
Nabonassar, which is so well verified by Eclipses that it cannot deceive
us, the beginning of these seventy weeks, or the seventh year of the
reign of Artaxerxes Longimanus, is pinned down to the year of the
Julian Period 4256: from which count 490 years to the death of
Christ, and the same will fall in the above year of the Julian Period
4746: which would seem to ascertain the true year beyond dispute.
But as Josephus’s Eclipse of the Moon in a great measure fixes our
Saviour’s birth to the end of the 4713th year of the Julian Period,
and a Friday Passover Full Moon fixes the time of his death to the
third of April in the 4746th year of that Period, the same as above
by Daniel’s weeks, this supposes our Saviour to have been crucified
in the 37th year of his age. And as St. Luke chap. iii. ver. 23. fixes
the time of Christ’s baptism to the beginning of his 30th year, it
would hence seem that his publick ministry, to which his baptism
was the initiation, lasted seven years. But, as it would be very difficult
to find account in all the Evangelists of more than four Passovers
which he kept at Jerusalem during the time of his ministry, others
think that he suffered in the vulgar 30th year of his age, which was
really the 33d; namely in the year of the Julian Period 4743. And
this opinion is farther strengthened by considering that our Saviour
eat his last Paschal Supper on a Thursday evening, the day immediately
before his crucifixion: and that as he subjected himself to the
law, he would not break the law by keeping the Passover on the day
before the law prescribed; neither would the Priests have suffered the
Lamb to be killed for him before the fourteenth day of Nisan when it
was killed for all the people, Exod. xii. ver. 6. And hence they infer
that he kept this Passover at the same time with the rest of the Jews,
in the vulgar 30th year of his age: at which time it is evident by calculation
that there was a Passover Full Moon on Thursday April the 6th.
But this is pressed with two difficulties. 1. It drops the last half
of Daniel’s seventieth week, as of no moment in the prophecy;
255and 2. it sets aside the testimony of Phlegon, as if he had mistaken
almost a whole Olympiad.
Others again endeavour to reconcile the whole difference, by supposing,
that as Christ expressed himself only in round numbers concerning
the time he was to lie in the grave, Matt. xii. 40. so might
St. Luke possibly have done with regard to the year of his baptism:
which would really seem to be the case when we consider, that the
Jews told our Saviour, sometime before his death, Thou art not yet
fifty years old, John vii. 57. which indeed was more likely to be said
to a person near forty than to one but just turned of thirty. And as to
his eating the above Passover on Thursday, which must have been on
the Jewish Full Moon day, they think it may be easily accommodated
to the 37th year of his age; since, as the Jews always began their day
in the evening, their Friday of course began on the evening of our
Thursday. And it is evident, as above-mentioned, that the only Jewish
Friday Full Moon, at the time of their Passover, was in the vulgar
33d, but the real 37th year of Christ’s age; which was the 4746th
year of the Julian Period, and the last year of the 202d Olympiad.
Æras or Epochas.
433. As there are certain fixed points in the Heavens from which
Astronomers begin their computations, so there are certain points of
time from which historians begin to reckon; and these points or roots
of time are called Æras or Epochas. The most remarkable Æras are
those of the Creation, the Greek Olympiads, the building of Rome, the
Æra of Nabonassar, the death of Alexander, the birth of Christ,
the Arabian Hegira, and the Persian Jesdegird: All which, together
with several others of less note, have their beginnings in the following
Table fixed to the years of the Julian Period, to the age of the world
at those times, and to the years before and after the birth of Christ.
| |
Julian Period. |
Y. of the World. |
Before Christ. |
| 1. The creation of the world, according to Strauchius |
764 |
1 |
3949 |
| 2. The Deluge, or Noah’s Flood |
2420 |
1656 |
2293 |
| 3. The Assyrian Monarchy by Nimrod |
2537 |
1773 |
2176 |
| 4. The Birth of Abraham |
2712 |
1948 |
2001 |
| 5. The beginning of the Kingdom of the Argives |
2856 |
2092 |
1857 |
| 6. The begin. of the Kingdom of Athens by Cecrops |
3157 |
2393 |
1556 |
| 7. The departure of the Israelites from Egypt |
3216 |
2452 |
1497 |
| 8. Their entrance into Canaan, or the Jubilee |
3256 |
2492 |
1457 |
| 9. The destruction of Troy |
3529 |
2865 |
1184 |
| 10. The beginning of King David’s reign |
3653 |
2889 |
1060 |
| 11. The foundation of Solomon’s Temple |
3696 |
2932 |
1017 |
| 25612. The Argonautic expedition |
3776 |
3012 |
937 |
| 13. Arbaces, the first King of the Medes |
3838 |
3074 |
175 |
| 14. Mandaucus the second |
3865 |
3101 |
848 |
| 15. Sosarmus the third |
3915 |
3151 |
798 |
| 16. Artica the fourth |
3945 |
3181 |
768 |
| 17. Cardica the fifth |
3996 |
3232 |
718 |
| 18. Phraortes the sixth |
4057 |
3293 |
656 |
| 19. Cyaxares the seventh |
4080 |
3316 |
633 |
| 20. The beginning of the Olympiads |
3938 |
3174 |
775 |
| 21. The Catonian Epocha of the building of Rome |
3961 |
3197 |
752 |
| 22. The Æra of Nabonassar |
3967 |
3202 |
746 |
| 23. The destruction of Samaria |
3990 |
3226 |
723 |
| 24. The Babylonish captivity |
4133 |
3349 |
600 |
| 25. The destruction of Solomon’s Temple |
4124 |
3360 |
589 |
| 26. The Persian monarchy founded by Cyrus |
4154 |
3390 |
559 |
| 27. The battle of Marathon |
4224 |
3460 |
489 |
| 28. The begin. of the reign of Art. Longimanus |
4249 |
3485 |
464 |
| 29. The beginning of Daniel’s 70 weeks |
4256 |
3492 |
457 |
| 30. The beginning of the Peloponnesian war |
4282 |
3518 |
431 |
| 31. The death of Alexander |
4390 |
3626 |
323 |
| 32. The restoration of the Jews |
4548 |
3784 |
129 |
| 33. The corr. of the Calendar by Julius Cæsar |
4669 |
3905 |
44 |
| 34. The beginning of the reign of Herod |
4673 |
3909 |
40 |
| 35. The Spanish Æra |
4675 |
3911 |
38 |
| 36. The battle at Actium |
4683 |
3919 |
30 |
| 37. The taking of Alexandria |
4683 |
3919 |
30 |
| 38. The Epoch of the title of Augustus |
4686 |
3922 |
27 |
| 39. The true Æra of Christ’s birth |
4709 |
3945 |
4 |
| 40. The death of Herod |
4710 |
3946 |
3 |
| 41. The Diony. or vulg. Æra of the birth of Christ |
4713 |
3949 |
AD0 |
| 42. The true year of Christ’s death |
4746 |
3982 |
33 |
| 43. The destruction of Jerusalem |
4783 |
4019 |
70 |
| 44. The Dioclesian persecution |
5015 |
4251 |
302 |
| 45. The Epoch of Constantine the Great |
5019 |
4255 |
306 |
| 46. The Council of Nice |
5038 |
4274 |
325 |
| 47. The Epocha of the Hegira |
5335 |
4571 |
622 |
| 48. The Epoch of Yesdejerd |
5344 |
4580 |
631 |
| 49. The Jellalæan Epocha |
5791 |
5027 |
1078 |
| 50. The Epocha of the reformation |
6230 |
5466 |
1517 |
257
Tab. I. Shewing the Golden Number (which is the same both in the Old and New Style) from the Christian Æra to A.D. 4000.
| Years less than an Hundred. |
| Hundreds of Years. |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
| |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
| |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
| |
57 |
58 |
59 |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
| |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
91 |
92 |
93 |
94 |
| |
95 |
96 |
97 |
98 |
99 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 |
1900 |
3800 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| 100 |
2000 |
3900 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
| 200 |
2100 |
4000 |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 300 |
2200 |
&c. |
|
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 400 |
2300 |
-- |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
| 500 |
2400 |
-- |
|
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
| 600 |
2500 |
-- |
|
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 700 |
2600 |
-- |
|
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 800 |
2700 |
-- |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
| 900 |
2800 |
-- |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1000 |
2900 |
-- |
|
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 1100 |
3000 |
-- |
|
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 1200 |
3100 |
-- |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
| 1300 |
3200 |
-- |
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 1400 |
3300 |
-- |
|
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| 1500 |
3400 |
-- |
|
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
| 1600 |
3500 |
-- |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
| 1700 |
3600 |
-- |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1800 |
3700 |
-- |
|
15 |
16 |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
Tab. II. Shewing the Number of Direction, for finding Easter Sunday by the Golden Number and Dominical Letter.
| G. N. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| A |
26 |
19 |
5 |
26 |
12 |
33 |
19 |
12 |
26 |
19 |
5 |
26 |
12 |
5 |
26 |
12 |
33 |
19 |
12 |
| B |
27 |
13 |
6 |
27 |
13 |
34 |
20 |
13 |
27 |
20 |
6 |
27 |
13 |
6 |
20 |
13 |
34 |
20 |
6 |
| C |
28 |
14 |
7 |
21 |
14 |
35 |
21 |
7 |
28 |
21 |
7 |
28 |
14 |
7 |
21 |
14 |
28 |
21 |
7 |
| D |
29 |
15 |
8 |
22 |
15 |
29 |
22 |
8 |
29 |
15 |
8 |
29 |
15 |
1 |
22 |
15 |
29 |
22 |
8 |
| E |
30 |
16 |
2 |
23 |
16 |
30 |
23 |
9 |
30 |
16 |
9 |
23 |
16 |
2 |
23 |
9 |
30 |
23 |
9 |
| F |
24 |
17 |
3 |
24 |
10 |
31 |
24 |
10 |
31 |
17 |
10 |
24 |
17 |
3 |
24 |
10 |
31 |
17 |
10 |
| G |
25 |
18 |
4 |
25 |
11 |
32 |
18 |
11 |
32 |
18 |
4 |
25 |
18 |
4 |
25 |
11 |
32 |
18 |
11 |
This Table is adapted to the New Style.
258
Tab. III. Shewing the Dominical Letters, Old Style, for 4200 Years before the Christian Æra.
| Before Christ |
Hundreds of Years. |
| Years less than an Hundred. |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
| 700 |
800 |
900 |
1000 |
1100 |
1200 |
1300 |
| 1400 |
1500 |
1600 |
1700 |
1800 |
1900 |
2000 |
| 2100 |
2200 |
2300 |
2400 |
2500 |
2600 |
2700 |
| 2800 |
2900 |
3000 |
3100 |
3200 |
3300 |
3400 |
| 3500 |
3600 |
3700 |
3800 |
3900 |
4000 |
4100 |
| 0 |
28 |
56 |
84 |
D C |
C B |
B A |
A G |
G F |
F E |
E D |
| 1 |
29 |
57 |
85 |
E |
D |
C |
B |
A |
G |
F |
| 2 |
30 |
58 |
86 |
F |
E |
D |
C |
B |
A |
G |
| 3 |
31 |
59 |
87 |
G |
F |
E |
D |
C |
B |
A |
| 4 |
32 |
60 |
88 |
B A |
A G |
G F |
F E |
E D |
D C |
C B |
| 5 |
33 |
61 |
89 |
C |
B |
A |
G |
F |
E |
D |
| 6 |
34 |
62 |
90 |
D |
C |
B |
A |
G |
F |
E |
| 7 |
35 |
63 |
91 |
E |
D |
C |
B |
A |
G |
F |
| 8 |
36 |
64 |
92 |
G F |
F E |
E D |
D C |
C B |
B A |
A G |
| 9 |
37 |
65 |
93 |
A |
G |
F |
E |
D |
C |
B |
| 10 |
38 |
66 |
94 |
B |
A |
G |
F |
E |
D |
C |
| 11 |
39 |
67 |
95 |
C |
B |
A |
G |
F |
E |
D |
| 12 |
40 |
68 |
96 |
E D |
D C |
C B |
B A |
A G |
G F |
F E |
| 13 |
41 |
69 |
97 |
F |
E |
D |
C |
B |
A |
G |
| 14 |
42 |
70 |
98 |
G |
F |
E |
D |
C |
B |
A |
| 15 |
43 |
71 |
99 |
A |
G |
F |
E |
D |
C |
B |
| 16 |
44 |
72 |
|
C B |
B A |
A G |
G F |
F E |
E D |
D C |
| 17 |
45 |
73 |
|
D |
C |
B |
A |
G |
F |
E |
| 18 |
46 |
74 |
|
E |
D |
C |
B |
A |
G |
F |
| 19 |
47 |
75 |
|
F |
E |
D |
C |
B |
A |
G |
| 20 |
48 |
76 |
|
A G |
G F |
F E |
E D |
D C |
C B |
B A |
| 21 |
49 |
77 |
|
B |
A |
G |
F |
E |
D |
C |
| 22 |
50 |
78 |
|
C |
B |
A |
G |
F |
E |
D |
| 23 |
51 |
79 |
|
D |
C |
B |
A |
G |
F |
E |
| 24 |
52 |
80 |
|
F E |
E D |
D C |
C B |
B A |
A G |
G F |
| 25 |
53 |
81 |
|
G |
F |
E |
D |
C |
B |
A |
| 26 |
54 |
82 |
|
A |
G |
F |
E |
D |
C |
B |
| 27 |
55 |
83 |
|
B |
A |
G |
F |
E |
D |
C |
Tab. IV. Shewing the Dominical Letters, Old Style, for 4200 Years after the Christian Æra.
| After Christ |
Hundreds of Years. |
| Years less than an Hundred. |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
| 700 |
800 |
900 |
1000 |
1100 |
1200 |
1300 |
| 1400 |
1500 |
1600 |
1700 |
1800 |
1900 |
2000 |
| 2100 |
2200 |
2300 |
2400 |
2500 |
2600 |
2700 |
| 2800 |
2900 |
3000 |
3100 |
3200 |
3300 |
3400 |
| 3500 |
3600 |
3700 |
3800 |
3900 |
4000 |
4100 |
| 0 |
28 |
56 |
84 |
D C |
E D |
F E |
G F |
A G |
B A |
C B |
| 1 |
29 |
57 |
85 |
B |
C |
D |
E |
F |
G |
A |
| 2 |
30 |
58 |
86 |
A |
B |
C |
D |
E |
F |
G |
| 3 |
31 |
59 |
87 |
G |
A |
B |
C |
D |
E |
F |
| 4 |
32 |
60 |
88 |
F E |
G F |
A G |
B A |
C B |
D C |
E D |
| 5 |
33 |
61 |
89 |
D |
E |
F |
G |
A |
B |
C |
| 6 |
34 |
62 |
90 |
C |
D |
E |
F |
G |
A |
B |
| 7 |
35 |
63 |
91 |
B |
C |
D |
E |
F |
G |
A |
| 8 |
36 |
64 |
92 |
A G |
B A |
C B |
D C |
E D |
F E |
G F |
| 9 |
37 |
65 |
93 |
F |
G |
A |
B |
C |
D |
E |
| 10 |
38 |
66 |
94 |
E |
F |
G |
A |
B |
C |
D |
| 11 |
39 |
67 |
95 |
D |
E |
F |
G |
A |
B |
C |
| 12 |
40 |
68 |
96 |
C B |
D C |
E D |
F E |
G F |
A G |
B A |
| 13 |
41 |
69 |
97 |
A |
B |
C |
D |
E |
F |
G |
| 14 |
42 |
70 |
98 |
G |
A |
B |
C |
D |
E |
F |
| 15 |
43 |
71 |
99 |
F |
G |
A |
B |
C |
D |
E |
| 16 |
44 |
72 |
|
E D |
F E |
G F |
A G |
B A |
C B |
D C |
| 17 |
45 |
73 |
|
C |
D |
E |
F |
G |
A |
B |
| 18 |
46 |
74 |
|
B |
C |
D |
E |
F |
G |
A |
| 19 |
47 |
75 |
|
A |
B |
C |
D |
E |
F |
G |
| 20 |
48 |
76 |
|
G F |
A G |
B A |
C B |
D C |
E D |
F E |
| 21 |
49 |
77 |
|
E |
F |
G |
A |
B |
C |
D |
| 22 |
50 |
78 |
|
D |
E |
F |
G |
A |
B |
C |
| 23 |
51 |
79 |
|
C |
D |
E |
F |
G |
A |
B |
| 24 |
52 |
80 |
|
B A |
C B |
D C |
E D |
F E |
G F |
A G |
| 25 |
53 |
81 |
|
G |
A |
B |
C |
D |
E |
F |
| 26 |
54 |
82 |
|
F |
G |
A |
B |
C |
D |
E |
| 27 |
55 |
83 |
|
E |
F |
G |
A |
B |
C |
D |
259
Tab. V. The Dominical Letter, New Style, for 4000 Years after the Christian Æra.
| After Christ. |
Hundreds of Years. |
| Years less than an Hundred. |
100 |
200 |
300 |
400 |
| 500 |
600 |
700 |
800 |
| 900 |
1000 |
1100 |
1200 |
| 1300 |
1400 |
1500 |
1600 |
| 1700 |
1800 |
1900 |
2000 |
| 2100 |
2200 |
2300 |
2400 |
| 2500 |
2600 |
2700 |
2800 |
| 2900 |
3000 |
3100 |
3200 |
| 3300 |
3400 |
3500 |
3600 |
| 3700 |
3800 |
3900 |
4000 |
| C |
E |
G |
B A |
| 1 |
29 |
57 |
85 |
B |
D |
F |
G |
| 2 |
30 |
58 |
86 |
A |
C |
E |
F |
| 3 |
31 |
59 |
87 |
G |
B |
D |
E |
| 4 |
32 |
60 |
88 |
F E |
A G |
C B |
D C |
| 5 |
33 |
61 |
89 |
D |
F |
A |
B |
| 6 |
34 |
62 |
90 |
C |
E |
G |
A |
| 7 |
35 |
63 |
91 |
B |
D |
F |
G |
| 8 |
36 |
64 |
92 |
A G |
C B |
C D |
F E |
| 9 |
37 |
65 |
93 |
F |
A |
C |
D |
| 10 |
38 |
66 |
94 |
E |
G |
B |
C |
| 11 |
39 |
67 |
95 |
D |
F |
A |
B |
| 12 |
40 |
68 |
96 |
C B |
E D |
G F |
A G |
| 13 |
41 |
69 |
97 |
A |
C |
E |
F |
| 14 |
42 |
70 |
98 |
G |
B |
D |
E |
| 15 |
43 |
71 |
99 |
F |
A |
C |
D |
| 16 |
44 |
72 |
|
E D |
G F |
B A |
C B |
| 17 |
45 |
73 |
|
C |
E |
G |
A |
| 18 |
46 |
74 |
|
B |
D |
F |
G |
| 19 |
47 |
75 |
|
A |
C |
E |
F |
| 20 |
48 |
76 |
|
G F |
B A |
D C |
E D |
| 21 |
49 |
77 |
|
E |
G |
B |
C |
| 22 |
50 |
78 |
|
D |
F |
A |
B |
| 23 |
51 |
79 |
|
C |
E |
G |
A |
| 24 |
52 |
80 |
|
B A |
D C |
F E |
G F |
| 25 |
53 |
81 |
|
G |
B |
D |
E |
| 26 |
54 |
82 |
|
F |
A |
C |
D |
| 27 |
55 |
83 |
|
E |
G |
B |
C |
| 28 |
56 |
84 |
|
D C |
F E |
A G |
B A |
Tab. VI. Shewing the Days of the Months for both Styles by the Dominical Letters.
| Week Day. |
A |
B |
C |
D |
E |
F |
G |
January 31
October 31 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 8 |
9 |
10 |
11 |
12 |
13 |
14 |
| 15 |
16 |
17 |
18 |
19 |
20 |
21 |
| 22 |
23 |
24 |
25 |
26 |
27 |
28 |
| 29 |
30 |
31 |
|
|
|
|
| 1 |
2 |
3 |
4 |
Feb. 28-29
March 31
Nov. 30 |
|
|
|
| 5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 12 |
13 |
14 |
15 |
16 |
17 |
18 |
| 19 |
20 |
21 |
22 |
23 |
24 |
25 |
| 26 |
27 |
28 |
29 |
30 |
31 |
|
| 1 |
April 30
July 31 |
|
|
|
|
|
|
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 16 |
17 |
18 |
19 |
20 |
21 |
22 |
| 23 |
24 |
25 |
26 |
27 |
28 |
29 |
| 30 |
31 |
|
|
|
|
|
| 1 |
2 |
3 |
4 |
5 |
| August 31 |
|
|
| 6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 13 |
14 |
15 |
16 |
17 |
18 |
19 |
| 20 |
21 |
22 |
23 |
24 |
25 |
26 |
| 27 |
28 |
29 |
30 |
31 |
|
|
| 1 |
2 |
Septemb. 30
Decemb. 31 |
|
|
|
|
|
| 3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 17 |
18 |
19 |
20 |
21 |
22 |
23 |
| 24 |
25 |
26 |
27 |
28 |
29 |
30 |
| 31 |
|
|
|
|
|
|
| 1 |
2 |
3 |
4 |
5 |
6 |
| May 31 |
|
| 7 |
8 |
9 |
10 |
11 |
12 |
13 |
| 14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 21 |
22 |
23 |
24 |
25 |
26 |
27 |
| 28 |
29 |
30 |
31 |
|
|
|
| 1 |
2 |
3 |
| June 30 |
|
|
|
|
| 4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 18 |
19 |
20 |
21 |
22 |
23 |
24 |
| 25 |
26 |
27 |
28 |
29 |
30 |
|
260
CHAP. XXII.
A Description of the Astronomical Machinery serving to explain and illustrate the foregoing part of this Treatise.
Fronting the Title Page.
The Orrery.
434. The Orrery. This Machine shews the Motions of the
Sun, Mercury, Venus, Earth, and Moon; and occasionally,
the superior Planets, Mars, Jupiter, and Saturn may be put on; Jupiter’s
four Satellites are moved round him in their proper times by a
small Winch; and Saturn has his five Satellites, and his Ring which
keeps its parallelism round the Sun; and by a Lamp put in the Sun’s
place, the Ring shews all the Phases described in the 204th Article.
The Sun.
The Ecliptic.
In the Center, No 1. represents the Sun, supported by it’s Axis
inclining almost 8 Degrees from the Axis of the Ecliptic; and turning
round in
251⁄4
days on its Axis, of which the North Pole inclines
toward the 8th Degree of Pisces in the great Ecliptic (No. 11.) whereon
the Months and Days are engraven over the Signs and Degrees in
which the Sun appears, as seen from the Earth, on the different days
of the year.
Mercury.
The nearest Planet (No. 2) to the Sun is Mercury, which goes round
him in 87 days 23 hours, or
8723⁄24
diurnal rotations of the Earth; but has
no Motion round its Axis in the Machine, because the time of its
diurnal Motion in the Heavens is not known to us.
Venus.
The next Planet in order is Venus (No. 3) which performs her annual
Course in 224 days 17 hours; and turns round her Axis in 24
days 8 hours, or in
241⁄3
diurnal rotations of the Earth. Her Axis inclines
75 Degrees from the Axis of the Ecliptic, and her North Pole inclines
towards the 20th Degree of Aquarius, according to the observations
of Bianchini. She shews all the Phenomena described from the
30th to the 44th Article in Chap. I.
The Earth.
Next without the Orbit of Venus is the Earth (No. 4) which
turns round its Axis, to any fixed point at a great distance, in 23 hours
56 minutes 4 seconds of mean solar time (221 & seq.) but from the
Sun to the Sun again in 24 hours of the same time. No. 6 is a sidereal
Dial-Plate under the Earth; and No. 7 a solar Dial-Plate on the
cover of the Machine. The Index of the former shews sidereal, and
of the latter, solar time; and hence, the former Index gains one entire
revolution on the latter every year, as 365 solar or natural days
contain 366 sidereal days, or apparent revolutions of the Stars. In
261the time that the Earth makes
3651⁄4
diurnal rotations on its Axis, it
goes once round the Sun in the Plane of the Ecliptic; and always
keeps opposite to a moving Index (No. 10) which shews the Sun’s
daily change of place, and also the days of the months.
The Earth is half covered with a black cap for dividing the apparently
enlightened half next the Sun, from the other half, which when
turned away from him is in the dark. The edge of the cap represents
the Circle bounding Light and Darkness, and shews at what time the
Sun rises and sets to all places throughout the year. The Earth’s
Axis inclines
231⁄2
Degrees from the Axis of the Ecliptic, the North
Pole inclines toward the beginning of Cancer; and keeps its parallelism
throughout its annual Course § 48, 202; so that in Summer the northern
parts of the Earth incline towards the Sun, and in the Winter
from him: by which means, the different lengths of days and nights,
and the cause of the various seasons, are demonstrated to sight.
There is a broad Horizon, to the upper side of which is fixed a
Meridian Semi-circle in the North and South Points, graduated on both
sides from the Horizon to 90° in the Zenith, or vertical Point. The
edge of the Horizon is graduated from the East and West to the South
and North Points, and within these Divisions are the Points of the
Compass. On the lower side of this thin Horizon Plate stand out
four small Wires, to which is fixed a Twilight Circle 18 Degrees from
the graduated side of the Horizon all round. This Horizon may be
put upon the Earth (when the cap is taken away) and rectified to the
Latitude of any place: and then, by a small Wire called the Solar Ray,
which may be put on so as to proceed directly from the Sun’s Center
towards the Earth’s, but to come no farther than almost to touch the
Horizon, the beginning of Twilight, time of Sun-rising, with his
Amplitude, Meridian Altitude, time of Setting, Amplitude, and end
of Twilight, are shewn for every day of the year, at that place to
which the Horizon is rectified.
The Moon.
The Moon (No. 5) goes round the Earth, from between it and
any fixed point at a great distance, in 27 days 7 hours 43 minutes,
or through all the Signs and Degrees of her Orbit; which is called
her Periodical Revolution; but she goes round from the Sun to the Sun
again, or from Change to Change, in 29 days 12 hours 45 minutes,
which is her Synodical Revolution; and in that time she exhibits all the
Phases already described § 255.
When the above-mentioned Horizon is rectified to the Latitude of
any given place, the times of the Moon’s rising and setting, together
with her Amplitude, are shewn to that place as well as the Sun’s;
262and all the various Phenomena of the Harvest Moon § 273 & seq.
made obvious to sight.
The Nodes.
The Moon’s Orbit (No. 9.) is inclined to the Ecliptic, (No. 11.)
one half being above, and the other below it. The Nodes, or Points
at 0 and 0 lie in the Plane of the Ecliptic, as described § 317, 318,
and shift backward through all it’s Signs and Degrees in
182⁄3
years. The Degrees of the Moon’s Latitude, to the highest at NL
(North Latitude) and lowest at SL (South Latitude) are engraven
both ways from her Nodes at 0 and 0; and, as the Moon rises
and falls in her Orbit according to its inclination, her Latitude and
Distance from her Nodes are shewn for every day; having first rectified
her Orbit so as to set the Nodes to their proper places in the
Ecliptic: and then, as they come about at different, and almost opposite
times of the year § 319, and then point towards the Sun, all
the Eclipses may be shewn for hundreds of years (without any new
rectification) by turning the Machinery backward for time past, or
forward for time to come. At 17 Degrees distance from each Node,
on both Sides, is engraved a small Sun; and at 12 Degrees distance, a
small Moon; which shew the limits of solar and lunar Eclipses § 317:
and when, at any change, the Moon falls between either of these
Suns and the Node, the Sun will be eclipsed on the day pointed to by
the annual Index (No. 10,) and as the Moon has then North or South
Latitude, one may easily judge whether that Eclipse will be visible
in the Northern or Southern Hemisphere; especially as the Earth’s
Axis inclines towards the Sun or from him at that time. And
when, at any Full, the Moon falls between either of the little Moon’s
and Node, she will be eclipsed, and the annual Index shews the day
of that Eclipse. There is a Circle of
291⁄2
equal parts (No. 8.) on
the cover of the Machine, on which an Index shews the days of the
Moon’s age.
There are two Semi-circles fixed to an elliptical Ring, which being
put like a cap upon the Earth, and the forked part F upon the
Moon, shews the Tides as the Earth turns round within them, and
they are led round it by the Moon. When the different Places come
to the Semi-circle AaEbB, they have Tides of Flood; and when they
come to the Semicircle CED they have Tides of Ebb § 304, 305;
the Index on the hour Circle (No. 7.) shewing the times of these
Phenomena.
There is a jointed Wire, of which one end being put into a hole
in the upright stem that holds the Earth’s cap, and the Wire laid into
a small forked piece which may be occasionally put upon Venus or
263Mercury, shews the direct and retrograde Motions of these two Planets,
with their stationary Times and Places as seen from the Earth.
The whole Machinery is turned by a winch or handle (No. 12,)
and is so easily moved that a clock might turn it without any danger
of stopping.
To give a Plate of the wheel-work of this Machine, would answer
no purpose, because many of the wheels lie so behind others as to hide
them from sight in any view whatsoever.
435. Another Orrery. In this Machine, which is the simplest I
ever saw, for shewing the diurnal and annual motions of the Earth,
together with the motion of the Moon and her Nodes; A and B are
two oblong square Plates held together by four upright pillars; of
which three appear at f, g, and g2. Under the Plate A is an endless
screw on the Axis of the handle b, which works in a wheel fixed on
the same Axis with the double grooved wheel E; and on the top
of this Axis is fixed the toothed wheel i, which turns the pinion k, on
the top of whose Axis is the pinion k2 which turns another pinion b2,
and that other turns a third, on the Axis a2 of which is the Earth
U turning round; this last Axis inclining
231⁄2
Degrees. The supporter
X2, in which the Axis of the Earth turns, is fixed to the moveable
Plate C.
In the fixed Plate B, beyond H, is fixed the strong wire d, on
which hangs the Sun T so as it may turn round the wire. To this
Sun is fixed the wire or solar ray Z, which (as the Earth U turns
round its Axis) points to all the places that the Sun passes vertically
over, every day of the year. The Earth is half covered with a black
cap a, as in the former Orrery, for dividing the day from the night;
and, as the different places come out from below the edge of the cap,
or go in below it, they shew the times of Sun-rising and setting every
day of the year. This cap is fixed on the wire b, which has a forked
piece C turning round the wire d: and, as the Earth goes round the
Sun, it carries the Cap, Wire, and solar Ray round him; so that the
solar Ray constantly points towards the Earth’s Center.
On the Axis of the pinion k is the pinion m, which turns a
wheel on the cock or supporter n, and on the Axis of this wheel
nearest n is a pinion (hid from view) under the Plate C, which
pinion turns a wheel that carries the Moon V round the Earth U;
the Moon’s Axis rising and falling in the socket W, which is fixed
to the triangular piece above Z; and this piece is fixed to the top
of the Axis of the last mentioned wheel. The socket W is slit on
264the outermost side; and in this slit the two pins near Y, fixed in the
Moon’s Axis, move up and down; one of them being above the
inclined Plane YX, and the other below it. By this mechanism, the
Moon V moves round the Earth T in the inclined Orbit q, parallel
to the Plane of the Ring YX; of which the Descending Node
is at X, and the Ascending Node opposite to it, but hid by the supporter
X2.
The small wheel E turns the large wheels D and F, of equal diameters,
by cat-gut strings crossing between them: and the Axis of
these two wheels are cranked at G and H, above the Plate B. The
upright stems of these cranks going through the Plate C, carry it over
and over the fixed Plate B, with a motion which carries the Earth U
round the Sun T, keeping the Earth’s Axis always parallel to itself; or
still inclining towards the left-hand of the Plate; and shewing the vicissitudes
of seasons, as described in the tenth chapter. As the Earth
goes round the Sun the pinion k goes round the wheel i, for the
Axis of k never touches the fixed Plate B; but turns on a wire fixed
into the Plate C.
On the top of the crank G is an Index L, which goes round the
Circle m2 in the time that the Earth goes round the Sun; and points
to the days of the months; which, together with the names of the
seasons, are marked in this Circle.
This Index has a small grooved wheel L fixed upon it, round
which, and the Plate Z, goes a cat-gut string crossing between them;
and by this means the Moon’s inclined Plane YX with its Nodes
is turned backward, for shewing the times and returns of Eclipses
§ 319, 320.
The following parts of this machine must be considered as distinct
from those already described.
Towards the right hand, let S be the Earth hung on the wire e,
which is fixed into the Plate B; and let O be the Moon fixed on the
Axis M, and turning round within the cap P, in which, and in the
Plate C the crooked wire Q is fixed. On the Axis M is also fixed the
Index K, which goes round a Circle h2, divided into
291⁄2
equal parts,
which are the days of the Moon’s age: but to avoid confusion in the
scheme, it is only marked with the numeral figures 1 2 3 4, for the
Quarters. As the crank H carries this Moon round the Earth S in the
Orbit t, she shews all her Phases by means of the cap P for the different
days of her age, which are shewn by the Index K; this Index,
turning just as the Moon O does, demonstrates her turning round her
Axis as she still keeps the same side towards the Earth S § 262.
265At the other end of the Plate C, a Moon N goes round an Earth R
in the Orbit p; but this Moon’s Axis is stuck fast into the Plate C at
S2; so that neither Moon nor Axis can turn round; and as this Moon
goes round her Earth she shews herself all round to it; which
proves, that if the Moon was seen all round from the Earth in a Lunation,
she could not turn round her Axis.
N. B. If there were only the two wheels D and F, with a cat-gut
string over them, but not crossing between them, the Axis of the
Earth U would keep its parallelism round the Sun T, and shew all the
seasons; as I sometimes make these Machines: and the Moon O
would go round the Earth S, shewing her Phases as above; as likewise
would the Moon N round the Earth R; but then, neither could
the diurnal motion of the Earth U on its Axis be shewn, nor the
motion of the Moon V round that Earth.
The Calculator.
436. In the year 1746 I contrived a very simple Machine, and
described it’s performance in a small treatise upon the Phenomena
of the Harvest Moon, published in the year 1747. I improved it
soon after, by adding another wheel, and called it the Calculator.
It may be easily made by any Gentleman who has a mechanical
Genius.
Fig. I.
The great flat Ring supported by twelve pillars, and on which the
twelve Signs with their respective Degrees are laid down, is the
Ecliptic; nearly in the center of it is the Sun S supported by the
strong crooked Wire I; and from the Sun proceeds a Wire W,
called the Solar Ray, pointing towards the center of the Earth E,
which is furnished with a moveable Horizon H, together with a
brazen Meridian, and Quadrant of Altitude. R is a small Ecliptic,
whose Plane co-incides with that of the great one, and has the like
Signs and Degrees marked upon it; and is supported by two Wires
D and D, which enter into the Plate PP, but may be taken off at
pleasure. As the Earth goes round the Sun, the Signs of this small
Circle keep parallel to themselves, and to those of the great Ecliptic.
When it is taken off, and the solar Ray W drawn farther out,
so as almost to touch the Horizon H, or the Quadrant of Altitude, the
Horizon being rectified to any given Latitude, and the Earth turned
round its Axis by hand, the point of the Wire W shews the Sun’s
Declination in passing over the graduated brass Meridian, and his
height at any given time upon the Quadrant of Altitude, together
with his Azimuth, or point of Bearing upon the Horizon at that time;
and likewise his Amplitude, and time of Rising and Setting by the
266hour Index, for any day of the year that the annual Index U points
to in the Circle of Months below the Sun. M is a solar Index or
Pointer supported by the Wire L which is fixed into the knob K: the
use of this Index is to shew the Sun’s place in the Ecliptic every day
in the year; for it goes over the Signs and Degrees as the Index U
goes over the months and days; or rather as they pass under the
Index U, in moving the cover plate with the Earth and its Furniture
round the Sun; for the Index U is fixed tight on the immoveable Axis
in the Center of the Machine. K is a knob or handle for moving the
Earth round the Sun, and the Moon round the Earth.
As the Earth is carried round the Sun, its Axis constantly keeps
the same oblique direction, or parallel to itself § 48, 202, shewing
thereby the different lengths of days and nights at different times of
the year, with all the various seasons. And, in one annual revolution
of the Earth, the Moon M goes
121⁄3
times round it from
Change to Change, having an occasional provision for shewing her
different Phases. The lower end of the Moon’s Axis bears by a small
friction wheel upon the inclined Plane T, which causes the Moon to
rise above and sink below the Ecliptic R in every Lunation; crossing
it in her Nodes, which shift backward through all the Signs and
Degrees of the said Ecliptic, by the retrograde Motion of the inclined
Plane T, in 18 years and 225 days. On this Plane the Degrees and
Parts of the Moon’s North and South Latitude are laid down from
both the Nodes, one of which, viz. the Descending Node appears
at 0, by DN above B; the other Node being hid from Sight on this
Plane by the plate PP; and from both Nodes, at proper distances,
as in the other Orrery, the limits of Eclipses are marked, and all the
solar and lunar Eclipses are shewn in the same manner, for any given
year, within the limits of 6000, either before or after the Christian
Æra. On the plate that covers the wheel-work, under the Sun S,
and round the knob K are Astronomical Tables, by which the Machine
may be rectified to the beginning of any given year within these
limits, in three or four minutes of time; and when once set right,
may be turned backward for 300 years past, or forward for as many
to come, without requiring any new rectification. There is a method
for its adding up the 29th of February every fourth year, and
allowing only 28 days to that month for every other three: but all
this being performed by a particular manner of cutting the teeth of
the wheels, and dividing the month circle, too long and intricate to
be described here, I shall only shew how these motions may be performed
near enough for common use, by wheels with grooves and
267cat-gut strings round them, only here I must put the Operator in
mind that the grooves are to be made sharp (not round) bottomed to
keep the strings from slipping.
The Moon’s Axis moves up and down in the socket N fixed into
the bar O (which carries her round the Earth) as she rises above or
sinks below the Ecliptic; and immediately below the inclined Plane T
is a flat circular plate (between Y and T) on which the different Excentricities
of the Moon’s Orbit are laid down; and likewise her
mean Anomaly and elliptic Equation by which her true Place may
be very nearly found at any time. Below this Apogee-plate, which
shews the Anomaly, &c. is a Circle Y divided into
291⁄2
equal parts
which are the days of the Moon’s age: and the forked end A of the
Index AB (Fig II) may be put into the Apogee-part of this plate;
there being just such another Index to put into the inclined Plane T
at the Ascending Node; and then the curved points B of these
Indexes shew the direct motion of the Apogee, and retrograde motion
of the Nodes through the Ecliptic R, with their Places in it at any
given time. As the Moon M goes round the Earth E, she shews
her Place every day in the Ecliptic R, and the lower end of her
Axis shews her Latitude and distance from her Node on the inclined
Plane T, also her distance from her Apogee and Perigee, together
with her mean Anomaly, the then Excentricity of her Orbit, and her
elliptic Equation, all on the Apogee Plate, and the day of her age
in the Circle Y of
291⁄2
equal parts; for every day of the year pointed
out by the annual Index U in the Circle of months.
Having rectified the Machine by the Tables for the beginning of
any year, move the Earth and Moon forward by the knob K, until
the annual Index comes to any given day of the month; then stop,
and not only all the above Phenomena may be shewn for that
day, but also, by turning the Earth round its Axis, the Declination,
Azimuth, Amplitude, Altitude of the Moon at any hour, and
the times of her Rising and Setting, are shewn by the Horizon,
Quadrant of Altitude, and hour Index. And in moving the Earth
round the Sun, the days of all the New and Full Moons and
Eclipses in any given year are shewn. The Phenomena of the
Harvest Moon, and those of the Tides, by such a cap as that in
Plate 9 Fig. 10. put upon the Earth and Moon, together with
the solution of many problems not here related, are made conspicuous.
The easiest, though not the best way, that I can instruct any
mechanical person to make the wheel-work of such a machine, is
268as follows; which is the way that I made it, before I thought of
numbers exact enough to make it worth the trouble of cutting teeth
in the wheels.
Fig. III.
Fig. 3d of Plate 8 is a section of this Machine; in which ABCD
is a frame of wood held together by four pillars at the corners,
whereof two appear at AC and BD. In the lower Plate CD of this
Frame are three small friction-wheels, at equal distances from each
other; two of them appearing at e and e. As the frame is moved
round, these wheels run upon the fixed bottom Plate EE which supports
the whole work.
In the Center of this last mentioned Plate is fixed the upright
Axis f FFG, and on the same Axis is fixed the wheel HHH in which
are four grooves I, X, k, L of different Diameters. In these grooves
are cat-gut strings going also round the separate wheels M, N, O
and P.
The wheel M is fixed on a solid Spindle or Axis, the lower
pivot of which turns at R in the under Plate of the moveable
frame ABCD; and on the upper end of this Axis is fixed the
Plate o o (which is PP, under the Earth, in Fig. I.) and to this
Plate is fixed, at an Angle of
231⁄2
Degrees inclination, the Dial-plate
below the Earth T; on the Axis of which, the Index q is
turned round by the Earth. This Axis, together with the
Wheel M, and Plate o o, keep their parallelism in going round the
Sun S.
On the Axis of the wheel M is a moveable socket on which the
small wheel N is fixed, and on the upper end of this socket is put
on tight (but so as it may be occasionally turned by hand) the bar
ZZ (viz. the bar O in Fig. I.) which carries the Moon m round
the Earth T, by the Socket n, fixed into the bar. As the Moon
goes round the Earth her Axis rises and falls in the Socket n;
because, on the lower end of her Axis, which is turned inward, there
is a small friction Wheel s running on the inclined Plane X (which
is T in Fig. I.) and so causes the Moon alternately to rise above
and sink below the little Ecliptic VV (R in Fig. I.) in every Lunation.
On the Socket or hollow Axis of the Wheel N, there is another
Socket on which the Wheel O is fixed; and the Moon’s inclined Plane
X is put tightly on the upper end of this Socket, not on a square, but
on a round, that it may be occasionally set by hand without wrenching
the Wheel or Axle.
269Lastly, on the hollow Axis of the Wheel O is another Socket on
which is fixed the Wheel P, and on the upper end of this Socket
is put on tightly the Apogee-plate Y, (that immediately below T in
Fig. I.) all these Axles turn in the upper Plate of the moveable
frame at Q which Plate is covered with the thin Plate cc (screwed
to it) whereon are the fore-mentioned Tables and month Circle in
Fig. I.
The middle part of the thick fixed Wheel HHH is much broader
than the rest of it, and comes out between the Wheels M and O
almost to the Wheel N. To adjust the diameters of the grooves of
this fixed wheel to the grooves of the separate Wheels M, N, O and
P, so as they may perform their motions in the proper times, the
following method must be observed.
The Groove of the Wheel M, which keeps the parallelism of the
Earth’s Axis, must be precisely of the same Diameter as the lower
Groove I of the fixed Wheel HHH; but, when this Groove is so
well adjusted as to shew, that in ever so many annual revolutions
of the Earth, its Axis keeps its parallelism, as may be observed by
the solar Ray W (Fig. I.) always coming precisely to the same Degree
of the small Ecliptic R at the end of every annual revolution,
when the Index M points to the like Degree in the great Ecliptic;
then, with the edge of a thin File give the Groove of the Wheel M
a small rub all round; and by that means, lessening the Diameter of
the Groove, perhaps about the 20th part of a hair’s breadth, it
will cause the Earth to shew the precession of the Equinoxes;
which, in many annual revolutions will begin to be sensible as the
Earth’s Axis slowly deviates from its parallelism § 246, towards the
antecedent Signs of the Ecliptic.
The Diameter of the Groove of the Wheel N, which carries the
Moon round the Earth, must be to the Diameter of the Groove X as a
Lunation is to a year; that is, as
291⁄2
to
3651⁄4.
The Diameter of the Groove of the Wheel O, which turns the
inclined Plane X with the Moon’s Nodes backward, must be to the
Diameter of the Groove k as 20 to
18225⁄365.
And,
Lastly, the Diameter of the Groove of the Wheel P, which carries
the Moon’s Apogee forward, must be to the Diameter of the Groove
L as 70 to 62.
But, after all this nice adjustment of the Grooves to the proportional
times of their respective Wheels turning round, and which
seems to promise very well in Theory, there will still be found a
necessity of a farther adjustment by hand; because proper allowance
270must be made for the Diameters of the cat-gut strings: and the
Grooves must be so adjusted by hand, as, that in the time the Earth is
moved once round the Sun, the Moon must perform 12 synodical
revolutions round the Earth, and be almost 11 days old in her 13th
revolution. The inclined Plane with its Nodes must go once
round backward through all the Signs and Degrees of the small
Ecliptic in 18 annual revolutions of the Earth and 225 days over.
And the Apogee-plate must go once round forward, so as its
Index may go over all the Signs and Degrees of the small Ecliptic
in eight years (or so many annual revolutions of the Earth) and 312
days over.
N. B. The string which goes round the Grooves X and N for the
Moon’s Motion must cross between these Wheels; but all the rest of
the strings go in their respective Grooves IM, kO, and LP without
crossing.
The Cometarium.
437. The Cometarium. This curious Machine shews the Motion
of a Comet or excentric Body moving round the Sun, describing
equal Areas in equal times § 152, and may be so contrived
as to shew such a Motion for any Degree of Excentricity.
It was invented by the late Dr. Desaguliers.
Fig. IV.
The dark elliptical Groove round the letters abcdefghiklm is the
Orbit of the Comet Y: this Comet is carried round in the Groove
according to the order of letters, by the Wire W, fixed in the Sun S,
and slides on the Wire as it approaches nearer to or recedes farther
from the Sun, being nearest of all in the Perihelion a, and farthest
in the Aphelion g. The Areas aSb, bSc, cSd &c. or contents of
these several Triangles are all equal; and in every turn of the Winch
N the Comet Y is carried over one of these Areas; consequently
in as much time as it moves, from f to g, or from g to h, it
moves from m to a, or from a to b; and so of the rest, being
quickest of all at a, and slowest at g. Thus, the Comet’s velocity
in its Orbit continually decreases from the Perihelion a to the Aphelion
g; and increases in the same proportion from g to a.
The elliptic Orbit is divided into 12 equal Parts or Signs with
their respective Degrees, and so is the Circle n o p q r s t n which
represents a great Circle in the Heavens, and to which all the fixed
Stars in the Comet’s way are referred. Whilst the Comet moves
from f to g in its Orbit it appears to move only about 5 Degrees
in this Circle, as is shewn by the small knob on the end
of the Wire W; but in as short time as the Comet moves from m
271to a, or from a to b, and it appears to describe the large space
tn or no in the Heavens, either of which spaces contains 120
Degrees or four Signs. Were the Excentricity of its Orbit greater, the
greater still would be the difference of its Motion, and vice versâ.
ABCDEFGHIKLMA is a circular Orbit for shewing the equable
Motion of a Body round the Sun S, describing equal Areas ASB,
BSC, &c. in equal times with those of the Body Y in its elliptical
Orbit above mentioned; but with this difference, that the circular
Motion describes the equal Arcs AB, BC, &c. in the same
equal times that the elliptical Motion describes the unequal Arcs
ab, bc, &c.
Now, suppose the two Bodies Y and I to start from the Points
a and A at the same moment of time, and each having gone
round its respective Orbit, to arrive at these Points again at the same
instant, the Body Y will be forwarder in its Orbit than the Body I
all the way from a to g, and from A to G; but I will be forwarder
than Y through all the other half of the Orbit; and the
difference is equal to the Equation of the Body Y in its Orbit.
At the Points a, A, and g, G, that is, in the Perihelion and Aphelion,
they will be equal; and then the Equation vanishes. This
shews why the Equation of a Body moving in an elliptic Orbit,
is added to the mean or supposed circular Motion from the Perihelion
to the Aphelion, and subtracted from the Aphelion to the Perihelion,
in Bodies moving round the Sun, or from the Perigee to the
Apogee, and from the Apogee to the Perigee in the Moon’s Motion
round the Earth, according to the Precepts in the 355th Article;
only we are to consider, that when Motion is turned into Time,
it reverses the titles in the Table of The Moon’s elliptic Equation.
Fig. V.
This curious Motion is performed in the following manner. ABC
is a wooden bar (in the box containing the wheel-work) above which
are the wheels D and E; and below it the elliptic Plates FF and
GG; each Plate being fixed on an Axis in one of its Focuses, at
E and K; and the Wheel E is fixed on the same Axis with the Plate
FF. These Plates have Grooves round their edges precisely of equal
Diameters to one another, and in these Grooves is the cat-gut
string gg, gg crossing between the Plates at h. On H, the Axis of the
handle or winch N in Fig. 4th, is an endless screw in Fig. 5, working
in the Wheels D and E, whose numbers of teeth being equal, and
should be equal to the number of lines aS, bS, cS, &c. in Fig. 4,
they turn round their Axes in equal times to one another, and to the
Motion of the elliptic Plates. For, the Wheels D and E having
272equal numbers of teeth, the Plate FF being fixed on the same Axis
with the Wheel E, and the Plate FF turning the equally big Plate
GG by a cat-gut string round them both, they must all go round
their Axes in as many turns of the handle N as either of the Wheels
has teeth.
’Tis easy to see, that the end h of the elliptical Plate FF being
farther from its Axis E than the opposite end i is, must describe a
Circle so much the larger in proportion; and therefore move through
so much more space in the same time; and for that reason the end
h moves so much faster than the end i, although it goes no sooner
round the Center E. But then, the quick-moving end h of the Plate
FF leads about the short end hK of the Plate GG with the same
velocity; and the slow moving end i of the Plate FF coming half
round as to B, must then lead the long end k of the Plate GG as
slowly about: So that the elliptical Plate FF and it’s Axis E move
uniformly and equally quick in every part of its revolution; but
the elliptical Plate GG, together with its Axis K must move very
unequally in different parts of its revolution; the difference being
always inversely as the distance of any point of the Circumference of
GG from its Axis at K: or in other words, to instance in two points,
if the distance Kk be four, five, or six times as great as the distance
Kh, the Point h will move in that position four, five, or six times as
fast as the Point k does, when the Plate GG has gone half round:
and so on for any other Excentricity or difference of the Distances
Kk and Kh. The tooth i on the Plate FF falls in between the two
teeth at k on the Plate GG, by which means the revolution of the latter
is so adjusted to that of the former, that they can never vary from one
another.
On the top of the Axis of the equally moving Wheel D, in
Fig. 5th, is the Sun S in Fig. 4th; which Sun, by the Wire Z
fixed to it, carries the Ball I round the Circle ABCD, &c. with an
equable Motion according to the order of the letters: and on the
top of the Axis K of the unequally moving Ellipsis GG, in Fig. 5th,
is the Sun S in Fig. 4th, carrying the Ball Y unequably round in the
elliptical Groove a b c d, &c. N.B. This elliptical Groove must be
precisely equal and similar to the verge of the Plate GG, which is
also equal to that of FF.
In this manner, Machines may be made to shew the true Motion
of the Moon about the Earth, or of any Planet about the Sun;
by making the elliptical Plates of the same Excentricities, in proportion
to the Radius, as the Orbits of the Planets are whose Motions
273they represent: and so, their different Equations in different
parts of their Orbits may be made plain to sight; and clearer Ideas
of these Motions and Equations acquired in half an hour, than
could be gained from reading half a day about such Motions and
Equations.
The improved
Celestial Globe.
PLATE III. Fig. III.
438. The Improved Celestial Globe. On the North Pole
of the Axis, above the Hour Circle, is fixed an Arch MKH of
231⁄2
Degrees; and at the end H is fixed an upright pin HG, which
stands directly over the North Pole of the Ecliptic, and perpendicular
to that part of the surface of the Globe. On this pin are two
moveable Collets at D and H, to which are fixed the quadrantal
Wires N and O, having two little Balls on their ends for the Sun
and Moon, as in the Figure. The Collet D is fixed to the circular
Plate F whereon the
291⁄2
days of the Moon’s age are engraven,
beginning just under the Sun’s Wire N; and as this Wire is moved
round the Globe, the Plate F turns round with it. These Wires
are easily turned if the Screw G be slackened; and when they are
set to their proper places, the Screw serves to fix them there so, as
in turning the Ball of the Globe, the Wires with the Sun and
Moon go round with it; and these two little Balls rise and set at
the same times, and on the same points of the Horizon, for the
day to which they are rectified, as the Sun and Moon do in the
Heavens.
Because the Moon keeps not her course in the Ecliptic (as the Sun
appears to do) but has a Declination of
51⁄3
Degrees on each side from
it in every Lunation § 317, her Ball may be screwed as many Degrees
to either side of the Ecliptic as her Latitude or Declination from
the Ecliptic amounts to at any given time; and for this purpose S is
a small piece of pasteboard, of which the curved edge S is to be set
upon the Globe at right Angles to the Ecliptic, and the dark line
over S to stand upright upon it. From this line, on the convex
edge, are drawn the
51⁄3
Degrees of the Moon’s Latitude on both sides
of the Ecliptic; and when this piece is set upright on the Globe, it’s
graduated edge reaches to the Moon on the Wire O, by which
means she is easily adjusted to her Latitude found by an Ephemeris.
The Horizon is supported by two semicircular Arches, because Pillars
would stop the progress of the Balls when they go below the Horizon
in an oblique sphere.
To rectify it.
To rectify the Globe. Elevate the Pole to the Latitude of the Place;
then bring the Sun’s place in the Ecliptic for the given day to the
274brasen Meridian, and set the Hour Index to XII at noon, that is, to
the upper XII on the Hour Circle; keeping the Globe in that situation,
slacken the Screw G, and set the Sun directly over his place on
the Meridian; which done, set the Moon’s Wire under the number
that expresses her age for that day on the Plate F, and she will then
stand over her place in the Ecliptic, and shew what Constellation she
is in. Lastly, fasten the Screw G, and laying the curved edge of
the pasteboard S over the Ecliptic below the Moon, adjust the Moon
to her Latitude over the graduated edge of the pasteboard; and the
Globe will be rectified.
It’s use.
Having thus rectified the Globe, turn it round, and observe on what
points of the Horizon the Sun and Moon Balls rise and set, for these
agree with the points of the Compass on which the Sun and Moon rise
and set in the Heavens on the given day; and the Hour Index shews
the times of their rising and setting; and likewise the time of the Moon’s
passing over the Meridian.
This simple Apparatus shews all the varieties that can happen in
the rising and setting of the Sun and Moon; and makes the forementioned
Phenomena of the Harvest Moon (Chap. xvi.) plain to
the Eye. It is also very useful in reading Lectures on the Globes,
because a large company can see this Sun and Moon going round,
rising above and setting below the Horizon at different times,
according to the seasons of the year; and making their appulses
to different fixed Stars. But, in the usual way, where there is
only the places of the Sun and Moon in the Ecliptic to keep
the Eye upon, they are easily lost sight of, unless covered with
Patches.
439. The Planetary Globe. In this Machine, T is a terrestrial
Globe fixed on its Axis standing upright on the Pedestal CDE,
on which is an Hour Circle, having its Index fixed on the Axis,
which turns somewhat tightly in the Pedestal, so that the Globe may
not be liable to shake; to prevent which, the Pedestal is about two
Inches thick, and the Axis goes quite through it, bearing on a
shoulder. The Globe is hung in a graduated brasen Meridian, much
in the usual way; and the thin Plate N, NE, E, is a moveable
Horizon, graduated round the outer edge, for shewing the Bearings
and Amplitudes of the Sun, Moon, and Planets. The brasen Meridian
is grooved round the outer edge; and in this Groove is a slender
Semi-circle of brass, the ends of which are fixed to the Horizon
in its North and South Points: this Semi-circle slides in the Groove
275as the Horizon is moved in rectifying it for different Latitudes. To
the middle of the Semi-circle is fixed a Pin which always keeps in
the Zenith of the Horizon, and on this Pin the Quadrant of Altitude
q turns; the lower end of which, in all Positions, touches the Horizon
as it is moved round the same. This Quadrant is divided into
90 Degrees from the Horizon to the zenithal Pin on which it is turned,
at 90. The great flat Circle or Plate AB is the Ecliptic, on the
outer edge of which, the Signs and Degrees are laid down; and every
fifth Degree is drawn through the rest of the surface of this Plate towards
its Center. On this Plate are seven Grooves, to which seven little
Balls are adjusted by sliding Wires, so that they are easily moved in
the Grooves, without danger of starting out of them. The Ball next
the terrestrial Globe is the Moon, the next without it is Mercury, the
next Venus, the next the Sun, then Mars, then Jupiter, and lastly
Saturn; and in order to know them, they are separately stampt with
the following Characters; ☽, ☿, ♀,
 , ♂, ♃, ♄. This Plate
or Ecliptic is supported by four strong Wires, having their lower ends
fixed into the Pedestal, at C, D, and E, the fourth being hid by the
Globe. The Ecliptic is inclined
231⁄2
Degrees to the Pedestal, and is
therefore properly inclined to the Axis of the Globe which stands
upright on the Pedestal.
, ♂, ♃, ♄. This Plate
or Ecliptic is supported by four strong Wires, having their lower ends
fixed into the Pedestal, at C, D, and E, the fourth being hid by the
Globe. The Ecliptic is inclined
231⁄2
Degrees to the Pedestal, and is
therefore properly inclined to the Axis of the Globe which stands
upright on the Pedestal.
To rectify it.
To rectify this Machine. Set all the planetary Balls to their geocentric
places in the Ecliptic for any given time by an Ephemeris: then,
set the North Point of the Horizon to the Latitude of your place on
the brasen Meridian, and the Quadrant of Altitude to the South Point
of the Horizon; which done, turn the Globe with its Furniture till
the Quadrant of Altitude comes right against the Sun, viz. to his
place in the Ecliptic; and keeping it there, set the Hour Index to the
XII next the letter C; and the Machine will be rectified, not only for
the following Problems, but for several others, which the Artist may
easily find out.
PROBLEM I.
To find the Amplitudes, Meridian Altitudes, and times of Rising, Culminating, and Setting, of the Sun, Moon, and Planets.
It’s use.
Turn the Globe round eastward, or according to the order of
Signs; and as the eastern edge of the Horizon comes right against
the Sun, Moon, or any Planet, the Hour Index will shew the time
of it’s rising; and the inner edge of the Ecliptic will cut it’s rising
Amplitude in the Horizon. Turn on, and as the Quadrant of Altitude
276comes right against the Sun, Moon, or Planets, the Ecliptic cuts
their meridian Altitudes in the Quadrant, and the Hour Index shews
the times of their coming to the Meridian. Continue turning, and
as the western edge of the Horizon comes right against the Sun,
Moon, or Planets, their setting Amplitudes are cut in the Horizon
by the Ecliptic; and the times of their setting are shewn by the Index
on the Hour Circle.
PROBLEM II.
To find the Altitude and Azimuth of the Sun, Moon, and Planets, at any time of their being above the Horizon.
Turn the Globe till the Index comes to the given time in the Hour
Circle; then keep the Globe steady, and moving the Quadrant of
Altitude to each Planet respectively, the edge of the Ecliptic will cut
the Planet’s mean Altitude on the Quadrant, and the Quadrant will
cut the Planet’s Azimuth, or Point of Bearing on the Horizon.
PROBLEM III.
The Sun’s Altitude being given at any time either before or after Noon, to find the Hour of the Day, and the Variation of the Compass, in any known Latitude.
With one hand hold the edge of the Quadrant right against the Sun;
and, with the other hand, turn the Globe westward, if it be in the
forenoon, or eastward if it be in the afternoon, until the Sun’s place
at the inner edge of the Ecliptic cuts the Quadrant in the Sun’s observed
Altitude; and then the Hour Index will point out the time of
the day, and the Quadrant will cut the true Azimuth, or Bearing of
the Sun for that time: the difference between which, and the Bearing
shewn by the Azimuth Compass, shews the variation of the Compass
in that place of the Earth.
The
Trajectorium Lunare.
PL. VII. Fig. V.
440. The Trajectorium Lunare. This Machine is for delineating
the paths of the Earth and Moon, shewing what sort of
Curves they make in the etherial regions; and was just mentioned in
the 266th Article. S is the Sun, and E the Earth, whose Centers
are 81 Inches distant from each other; every Inch answering to a
Million of Miles § 47. M is the Moon, whose Center is
24⁄100
parts
of an Inch from the Earth’s in this Machine, this being in just proportion
to the Moon’s distance from the Earth § 52. AA is a Bar
277of Wood, to be moved by hand round the Axis g which is fixed in
the Wheel Y. The Circumference of this Wheel is to the Circumference
of the small Wheel L (below the other end of the Bar) as
3651⁄4
days is to
291⁄2;
or as a Year is to a Lunation. The Wheels
are grooved round their edges, and in the Grooves is the cat-gut
string GG crossing between the Wheels at X. On the Axis of the
Wheel L is the Index F, in which is fixed the Moon’s Axis M for
carrying her round the Earth E (fixed on the Axis of the Wheel L)
in the time that the Index goes round a Circle of
291⁄2
equal parts,
which are the days of the Moon’s age. The Wheel Y has the Months
and Days of the year all round it’s Limb; and in the Bar AA is fixed
the Index I, which points out the Days of the Months answering to
the Days of the Moon’s age, shewn by the Index F, in the Circle of
291⁄2
equal parts at the other end of the Bar. On the Axis of the
Wheel L is put the piece D, below the Cock C, in which this Axis
turns round; and in D are put the Pencils e and m, directly under
the Earth E and Moon M; so that m is carried round e as M is
round E.
It’s use.
Lay the Machine on an even Floor, pressing gently on the Wheel
Y to cause its spiked Feet (of which two appear at P and P, the
third being supposed to be hid from sight by the Wheel) enter a little
into the Floor to secure the Wheel from turning. Then lay a
paper about four foot long under the Pencils e and m, cross-wise to
the Bar: which done, move the Bar slowly round the Axis g of the
Wheel Y; and, as the Earth E goes round the Sun S, the Moon
M will go round the Earth with a duly proportioned velocity; and
the friction Wheel W running on the Floor, will keep the Bar from
bearing too heavily on the Pencils e and m, which will delineate the
paths of the Earth and Moon, as in Fig. 2d, already described at large,
§ 266, 267. As the Index I points out the Days of the Months,
the Index F shews the Moon’s age on these Days, in the Circle of
291⁄2
equal parts. And as this last Index points to the different Days
in it’s Circle, the like numeral Figures may be set to those parts of the
Curves of the Earth’s Path and Moon’s, where the Pencils e and m
are at those times respectively, to shew the places of the Earth and
Moon. If the Pencil e be pushed a very little off, as if from the Pencil
m, to about
1⁄40
part of their distance, and the Pencil m pushed as
much towards e, to bring them to the same distances again, though
not to the same points of space; then as m goes round e, e will go
as it were round the Center of Gravity between the Earth e and Moon
m § 298: but this Motion will not sensibly alter the Figure of the
Earth’s Path or the Moon’s.
278If a Pin as p be put through the Pencil m, with its head towards
that of the Pin q in the Pencil e, its head will always keep thereto
as m goes round e, or as the same side of the Moon is still obverted
to the Earth. But the Pin p, which may be considered as an equatoreal
Diameter of the Moon, will turn quite round the Point m,
making all possible Angles with the Line of its progress or line of the
Moon’s Path. This is an ocular proof of the Moon’s turning round
her Axis.
The
Tide Dial.
PLATE IX. Fig. VII.
It’s use.
441. The Tide-Dial. The outside parts of this Machine consist
of, 1. An eight-sided Box, on the top of which at the corner is
shewn the Phases of the Moon at the Octants, Quarters, and Full.
Within these is a Circle of
291⁄2
equal parts, which are the days of
the Moon’s age accounted from the Sun at New Moon round to
the same again. Within this Circle is one of 24 hours divided into
their respective Halves and Quarters. 2. A moving elliptical Plate
painted blue to represent the rising of the Tides under and opposite
to the Moon; and has the words, High Water, Tide falling, Low
Water, Tide rising, marked upon it. To one end of this Plate is
fixed the Moon M by the Wire W, and goes along with it.
3. Above this elliptical Plate is a round one, with the Points of the
Compass upon it, and also the names of above 200 places in the large
Machine (but only 32 in the Figure to avoid confusion) set over
those Points on which the Moon bears when she raises the Tides to
the greatest heights at these Places twice in every lunar day: and
to the North and South Points of this Plate are fixed two Indexes
I and K, which shew the times of High Water in the Hour Circle
at all these places. 4. Below the elliptical Plate are four small Plates,
two of which project out from below its ends at New and Full
Moon; and so, by lengthening the Ellipse shew the Spring Tides,
which are then raised to the greatest heights by the united attractions
of the Sun and Moon § 302. The other two of these small Plates
appear at low water when the Moon is in her Quadratures, or at
the sides of the elliptic Plate, to shew the Nepe Tides; the Sun
and Moon then acting cross-wise to each other. When any two
of these small Plates appear, the other two are hid; and when the
Moon is in her Octants they all disappear, there being neither
Spring nor Nepe Tides at those times. Within the Box are a
few Wheels for performing these Motions by the Handle or
Winch H.
Plate XIII.

J. Ferguson inv. et del.
J. Mynde Sculp.
279Turn the Handle until the Moon M comes to any given day of
her age in the Circle of
291⁄2
equal parts, and the Moon’s Wire W
will cut the time of her coming to the Meridian on that day, in the
Hour Circle; the XII under the Sun being Mid-day, and the opposite
XII Mid-night: then looking for the name of any given place on
the round Plate (which makes
291⁄2
rotations whilst the Moon M
makes only one revolution from the Sun to the Sun again) turn the
Handle till that place comes to the word High Water under the
Moon, and the Index which falls among the Afternoon Hours will
shew the time of high water at that place in the Afternoon of the
given day: then turn the Plate half round, till the same place comes
to the opposite High Water Mark, and the Index will shew the
time of High Water in the Forenoon at that place. And thus, as
all the different places come successively under and opposite to the
Moon, the Indexes shew the times of High Water at them in both
parts of the day: and when the same places come to the Low
Water Marks the Indexes shew the times of Low Water. For
about two days before and after the times of New and Full Moon,
the two small Plates come out a little way from below the High
Water Marks on the elliptical Plate, to shew that the Tides rise
still higher about these times: and about the Quarters, the other two
Plates come out a little from under the Low Water Marks towards
the Sun and on the opposite side, shewing that the Tides of
Flood rise not then so high, nor do the Tides of Ebb fall so low, as at
other times.
By pulling the Handle a little way outward, it is disengaged from
the Wheel-work, and then the upper Plate may be turned round
quickly by hand so, as the Moon may be brought to any given day of
her age in about a quarter of a minute.
The inside work described.
Fig. VIII.
On AB, the Axis of the Handle H, is an endless Screw C which
turns the Wheel FED of 24 teeth round in 24 revolutions of the
Handle: this Wheel turns another ONG of 48 teeth, and on its
Axis is the Pinion PQ of four leaves which turns the Wheel LKI
of 59 teeth round in
291⁄2
turnings or rotations of the Wheel FED,
or in 708 revolutions of the Handle, which is the number of Hours
in a synodical revolution of the Moon. The round Plate with the
names of Places upon it is fixed on the Axis of the Wheel FED;
and the Elliptical or Tide-Plate with the Moon fixed to it is upon
the Axis of the Wheel LKI; consequently, the former makes
291⁄2
revolutions in the time that the latter makes one. The whole Wheel
FED with the endless Screw C, and dotted part of the Axis of the
280Handle AB, together with the dotted part of the Wheel ONG, lie
hid below the large Wheel LKI.
Fig. 9th represents the under side of the Elliptical or Tide-Plate
abcd, with the four small Plates ABCD, EFGH, IKLM, NOPQ
upon it: each of which has two slits as TT, SS, RR, UU sliding
on two Pins as nn, fixed in the elliptical Plate. In the four small
Plates are fixed four Pins at W, X, Y, and Z; all of which work
in an elliptic Groove oooo on the cover of the Box below the elliptical
Plate; the longest Axis of this Groove being in a right line with the
Sun and Full Moon. Consequently, when the Moon is in Conjunction
or Opposition, the Pins W and X thrust out the Plates ABCD
and IKLM a little beyond the ends of the elliptic Plate at d and b,
to f and e; whilst the Pins Y and Z draw in the Plates EFGH
and NOPQ quite under the elliptic Plate to g and h. But, when
the Moon comes to her first or third Quarter, the elliptic Plate lies
across the fixed elliptic Groove in which the Pins work; and therefore
the end Plates ABCD and IKLM are drawn in below the great
Plate, and the other two Plates EFGH and NOPQ are thrust out
beyond it to a and c. When the Moon is in her Octants the Pins
V, X, Y, Z are in the parts o, o, o, o of the elliptic Groove, which
parts are at a mean between the greatest and least distances from the
Center q, and then all the four small Plates disappear below the
great one.
442. The Eclipsareon. This Piece of Mechanism exhibits the
Time, Quantity, Duration, and Progress of solar Eclipses, at all Parts
of the Earth.
The principal parts of this Machine are, 1. A terrestrial Globe A
turned round its Axis B by the Handle or Winch M; the Axis B
inclines
231⁄2
Degrees, and has an Index which goes round the Hour
Circle D in each rotation of the Globe. 2. A circular Plate E on
the Limb of which the Months and Days of the year are inserted.
This Plate supports the Globe, and gives its Axis the same position
to the Sun, or to a candle properly placed, that the Earth’s Axis has
to the Sun upon any day of the year § 338, by turning the Plate
till the given Day of the Month comes to the fixed Pointer or annual
Index G. 3. A crooked Wire F which points towards the middle
of the Earth’s enlightened Disc at all times, and shews to what place
of the Earth the Sun is vertical at any given time. 4. A Penumbra,
or thin circular Plate of brass I divided into 12 Digits by 12 concentric
Circles, which represent a Section of the Moon’s Penumbra,
281and is proportioned to the size of the Globe; so that the shadow of
this Plate, formed by the Sun, or a candle placed at a convenient
distance, with it’s Rays transmitted through a convex Lens to make
them fall parallel on the Globe, covers exactly all those places upon
it that the Moon’s Shadow and Penumbra do on the Earth: so that
the Phenomena of any solar Eclipse may be shewn by this Machine
with candle-light, almost as well as by the light of the Sun. 5. An
upright frame HHHH, on the sides of which are Scales of the Moon’s
Latitude or Declination from the Ecliptic. To these Scales are fitted
two Sliders K and K, with Indexes for adjusting the Penumbra’s
Center to the Moon’s Latitude, as it is North or South Ascending or
Descending. 6. A solar Horizon C, dividing the enlightened Hemisphere
of the Globe from that which is in the dark at any given
time, and shewing at what places the general Eclipse begins and
ends with the rising or setting Sun. 7. A Handle M, which turns the
Globe round it’s Axis by wheel-work, and at the same time moves the
Penumbra across the frame by threads over the Pullies L, L, L,
with the velocity duly proportioned to that of the Moon’s shadow
over the Earth, as the Earth turns on its Axis. And as the Moon’s
Motion is quicker or slower, according to her different distances from
the Earth, the penumbral Motion is easily regulated in the Machine
by changing one of the Pullies.
To rectify it.
To rectify the Machine for use. The true time of New Moon and
her Latitude being known by the foregoing Precepts § 355, 363,
if her Latitude exceeds the number of minutes or divisions on the
Scales (which are on the side of the frame hid from view in the
Figure of the Machine) there can be no Eclipse of the Sun at that
Conjunction; but if it does not, the Sun will be eclipsed to some
places of the Earth; and, to shew the times and various appearances
of the Eclipse at those places, proceed in order as follows.
To rectify the Machine for performing by the Light of the Sun. 1. Move
the Sliders KK till their Indexes point to the Moon’s Latitude on the
Scales, as it is North and South Ascending or Descending, at that
time. 2. Turn the Month Plate E till the day of the given New
Moon comes to the annual Index G. 3. Unscrew the Collar N a
little on the Axis of the Handle, to loosen the contiguous Socket
on which the threads that move the Penumbra are wound; and set
the Penumbra by Hand till its Center comes to the perpendicular
thread in the middle of the frame; which thread represents the
Axis of the Ecliptic § 371. 4. Turn the Handle till the Meridian of
London on the Globe comes just under the point of the crooked
282Wire F; then stop, and turn the Hour Circle D by Hand till XII
at Noon comes to its Index. 5. Turn the Handle till the Hour
Index points to the time of New Moon in the Circle D; and holding
it there, screw fast the Collar N. Lastly, elevate the Machine till
the Sun shines through the Sight-Holes in the small upright Plates
O, O, on the Pedestal; and the whole Machine will be rectified.
To rectify the Machine for shewing the Candle-Light, proceed in every
respect as above, except in that part of the last paragraph where the
Sun is mentioned; instead of which place a Candle before the Machine,
about four yards from it, so as the shadow of Intersection of the cross
threads in the middle of the frame may fall precisely on that part of
the Globe to which the crooked Wire F points: then, with a pair of
Compasses take the distance between the Penumbra’s Center and Intersection
of the threads; and equal to that distance set the Candle
higher or lower as the Penumbra’s Center is above or below the said
Intersection. Lastly, place a large convex Lens between the Machine
and Candle, so as the Candle may be in the Focus of the Lens, and
then the Rays will fall parallel, and cast a strong light on the Globe.
It’s use.
These things done, which may be sooner than expressed, turn the
Handle backward until the Penumbra almost touches the side HF
of the frame; then turning it gradually forward, observe the following
Phenomena. 1. Where the eastern edge of the Shadow of the
penumbral Plate I first touches the Globe at the solar Horizon, those
who inhabit the corresponding part of the Earth see the Eclipse
begin on the uppermost edge of the Sun, just at the time of its
rising. 2. In that place where the Penumbra’s Center first touches the
Globe, the inhabitants have the Sun rising upon them centrally
eclipsed. 3. When the whole Penumbra just falls upon the Globe, its
western edge, at the solar Horizon, touches and leaves the place
where the Eclipse ends at Sun-rise on his lowermost edge. Continue
turning, and, 4. the cross lines in the Center of the Penumbra
will go over all those places on the Globe where the Sun is centrally
eclipsed. 5. When the eastern edge of the Shadow touches
any place of the Globe, the Eclipse begins there: when the vertical
line in the Penumbra comes to any place, then is the greatest obscuration
at that place; and when the western edge of the Penumbra
leaves the place, the Eclipse ends there; the times of all which are
shewn on the Hour Circle: and from the beginning to the end,
the Shadows of the concentric penumbral Circles shew the number
of Digits eclipsed at all the intermediate times. 6. When the eastern
edge of the Penumbra leaves the Globe at the solar Horizon C,
283the inhabitants see the Sun beginning to be eclipsed on his lowermost
edge at its setting. 7. Where the Penumbra’s Center leaves the
Globe, the inhabitants see the Sun set centrally eclipsed. And lastly,
where the Penumbra is wholly departing from the Globe, the inhabitants
see the Eclipse ending on the uppermost part of the Sun’s edge,
at the time of its disappearing in the Horizon § 343.
N.B. If any given day of the year on the Plate E be set to the
annual Index G, and the Handle turned till the Meridian of any place
comes under the point of the crooked Wire, and then the Hour
Circle D set by the hand till XII comes to its Index; in turning the
Globe round by the Handle, when the said place touches the eastern
edge of the Hoop or solar Horizon C, the Index shews the time of
Sun-setting at that place; and when the place is just coming out from
below the other edge of the Hoop C, the Index shews the time that
the evening Twilight ends to it. When the place has gone through
the dark part A, and comes about so to touch under the back of the
Hoop C on the other side, the Index shews the time that the Morning
Twilight begins; and when the same place is just coming out from
below the edge of the Hoop next the frame, the Index points out
the time of Sun-rising. And thus, the times of Sun-rising and setting
are shewn at all places in one rotation of the Globe, for any given day
of the year: and the point of the crooked Wire F shews all the places
that the Sun passes vertically over on that day.
284
INDEX.
The numeral Figures refer to the Articles, and the small n to the Notes on the Articles.
- A.
- Acceleration of the Stars, 221.
- Angle, what, 185.
- Annual Parallax of the Stars, 196.
- Anomaly, what, 239.
- Antients, their superstitious notions of Eclipses, 329.
- Their method of dividing the Zodiac, 398.
- Antipodes, what, 122.
- Apsides, line of, 238.
- Archimedes, his ideal Problem for moving the Earth, 159.
- Areas described by the Planets, equal in times, 153.
- Astronomy, the great advantages arising from it both in our religious and civil concerns, 1 Discovers the laws by which the Planets move, and are retained in their Orbits, 2
- Atmosphere, the higher the thinner, 174.
- It’s prodigious expansion, ib.
- It’s whole weight on the Earth, 175.
- Generally thought to be heaviest when it is lightest, 176.
- Without it the Heavens would appear dark in the day-time, 177.
- Is the cause of twilight, ib.
- It’s height, ib.
- Refracts the Sun’s rays, 178.
- Causeth the Sun and Moon to appear above the Horizon when they are really below it, ib.
- Foggy, deceives us in the bulk and distance of objects, 185.
- Attraction, 101-105.
- Decreases as the square of the distance increases, 106.
- Greater in the larger than in the smaller Planets, 158.
- Greater in the Sun than in all the Planets if put together, ib.
- Axes of the Planets, what, 19.
- Their different positions with respect to one another, 120.
- Axis of the Earth, it’s parallelism, 302.
- It’s position variable as seen from the Sun or Moon, 338.
- the Phenomena thence arising, 340.
- B.
- Bodies, on the Earth, lose of their weight the nearer they are to the Equator, 117.
- How they might lose all their weight, 118,
- How they become visible, 167.
- C.
- Calculator, (an Instrument) described, 436.
- Calendar, how to inscribe the Golden Numbers rightly in it for shewing the days of New Moons, 423.
- Cannon-Ball, it’s swiftness, 89.
- In what times it would fly from the Sun to the different Planets and fixed Stars, ib.
- Cassini, his account of a double Star eclipsed by the Moon, 58.
- His Diagrams of the Paths of the Planets, 138.
- Catalogue of the Eclipses, 327.
- Of the Constellations and Stars, 367.
- Of remarkable Æras and events, 433.
- Celestial Globe improved, 438.
- Centripetal and centrifugal forces, how they alternately overcome each other in the motions of the Planets, 152-154.
- Changes in the Heavens, 403.
- Chords, line of, how to make, 369.
- Circles, of perpetual Apparition and Occultation, 128.
- Of the Sphere, 198.
- Contain 360 Degrees whether they be great or small, 207.
- Civil Year, what, 411.
- Columbus (Christopher) his story concerning an Eclipse, 330.
- Clocks and Watches, an easy method of knowing whether they go true or false, 223.
- Why they seldom agree with the Sun if they go true, 228-245.
- How to regulate them by Equation Tables and a Meridian line, 225, 226.
- Cloudy Stars, 402.
- Cometarium (an Instrument) described, 437.
- Constellations, antient, their number, 396.
- The number of Stars in each, according to different Astronomers, 399.
- Cycle, Solar, Lunar, and Romish, 420.
- D.
- Darkness at our Saviour’s crucifixion supernatural, 352, 432.
- Day, natural and artificial, what, 417.
- And Night, always equally long at the Equator, 126.
- Natural, not compleated in an absolute turn of the Earth on it’s Axis, 222.
- Degree, what, 207.
- Digit, what, 321, n.
- Direction, (Number of) 426.
- Distances of the Planets from the Sun, an idea thereof, 89.
- A Table thereof, 98.
- How found, 190.
- Diurnal and annual Motions of the Earth illustrated, 200, 202.
- Dominical Letter, 427.
- Double projectile force, a balance to a Quadruple Power of Gravity, 153.
- Star covered by the Moon, 58.
- E.
- Earth, it’s bulk but a point as seen from the Sun, 3 It’s Diameter, annual Period, and Distance from the Sun, 47.
- Turns round it’s Axis, ib.
- Velocity of it’s equatoreal Parts, ib.
- Velocity in it’s annual Orbit, ib.
- Inclination of it’s Axis, 48.
- Proof of it’s being globular, or nearly so, 49, 314.
- Measurement of it’s surface, 50, 51.
- Difference between it’s Equatoreal and Polar Diameters, 76.
- It’s motion round the Sun demonstrated by gravity, 108, 111.
- by Dr. Bradley’s observations, 113.
- by the Eclipses of Jupiter’s Satellites, 219.
- It’s diurnal motion highly probable from the absurdity that must follow upon supposing it not to move, 111. 120.
- and demonstrable from it’s figure, 116.
- this motion cannot be felt, 119.
- Objections against it’s motion answered, 112, 121.
- It has no such thing as an upper or under side, 122.
- in what case it might, 123.
- The swiftness of it’s motion in it’s Orbit compared with the velocity of light, 197.
- It’s diurnal and annual motions illustrated by an easy experiment, 200.
- Proved to be less than the Sun and bigger than the Moon, 315.
- Easter Cycle, 425.
- Eclipsareon (an Instrument) described, 442.
- Eclipses, of Jupiter’s Satellites, how the Longitude is found by them, 207-218.
-
- they demonstrate the velocity of light, 216.
- Of the Sun and Moon, 312-327.
- Why they happen not in every month, 316.
- When they must be, 317.
- Their limits, ib.
- Their Period, 320, 326.
- A dissertation on their progress, 321-324.
- A large catalogue of them, 327.
- Historical ones, 328.
- More of the Sun than of the Moon, and why, 331.
- The proper Elements for their calculation and projection, 353-390.
- Ecliptic, it’s Signs, their names and characters, 91.
- Makes different Angles with the Horizon every hour and minute, 275.
- how these Angles may be estimated by the position of the Moon’s horns, 260.
- It’s obliquity to the Equator less now than it was formerly, 405.
- How it’s Signs are numbered, 354.
- Elongations, of the Planets, as seen by an observer at rest on the outside of all their Orbits, 133.
- Of Mercury and Venus as seen from the Earth, illustrated, 142.
- Of Mercury, Venus, the Earth, Mars, and Jupiter; it’s quantity as seen from Saturn, 147.
- Epochas or Æras, 433.
- Equation of time, 224-245.
- Of the Moon’s Place, 355.
- Of the Sun’s Place, ib.
- Of the Nodes, 363.
- Equator, day and night always equal there, 126.
- Makes always the same Angle with the Horizon of the same place; the Ecliptic not, 274, 275.
- Equinoctial Points in the Heavens, their precession, 246,
- a very different thing from the recession or anticipation of the Equinoxes on Earth, the one no ways occasioned by the other, 249.
- Excentricities of the Planets Orbits, 155.
- F.
- Fallacies in judging of the bulk of objects by their apparent distance, 185;
- applied to the solution of the horizontal Moon, 187.
- First Meridian, what, 207.
- Fixed Stars, why they appear of less magnitude when viewed through a telescope than by the bare eye, 391.
- Their number, 392.
- Their division into different Classes and Constellations, 395-399.
- G.
- General Phenomena of a superior Planet as seen from an inferior, 149.
- Gravity, demonstrable, 101-104.
- Keeps all bodies on the Earth to it’s surface, or brings them back when thrown upward; and constitutes their weight, 101, 122.
- Retains all the Planets in their Orbits, 103.
- Decreases as the square of the distance increases, 106.
- Proves the Earth’s annual motion, 108.
- Demonstrated to be greater in the larger Planets than in the smaller; and stronger in the Sun than in all the Planets together, 158.
- Hard to understand what it is, 160.
- Acts every moment, 162.
- Globe, improved celestial, 438.
- Great Year, 251.
- H.
- Harmony of the celestial motions, 111.
- Harvest-Moon, 273-293.
- None at the Equator, 273.
- Remarkable at the Polar Circles, 285.
- In what years most and least advantageous, 292.
- Heat, decreases as the square of the distance from the Sun increases, 169.
- Why not greatest when the Earth is nearest the Sun, 205.
- Why greater about three o’Clock in the afternoon than when the Sun is on the Meridian, 300.
- Heavens, seem to turn round with different velocities as seen from the different Planets; and on different Axes as seen from most of them, 120.
- Only one Hemisphere of them seen at once from any one Planet’s surface, 125.
- The Sun’s Center the only point from which their true Motions could be seen, 135.
- Changes in them, 403.
- Horizon, what, 125, n.
- Horizontal-Moon explained, 187.
- Horizontal Parallax, of the Moon, 190;
- of the Sun, 191;
- best observed at the Equator, 193.
- Hour-Circles, what, 208.
- Hour of time equal to 15 degrees of motion, ib.
- How divided by the Jews, Chaldeans, and Arabians, 419.
- Huygenius, his thoughts concerning the distance of some Stars, 5
- I. J.
- Inclination of Venus’s Axis, 29.
- Of the Earth’s, 48.
- Of the Axis or Orbit of a Planet only relative, 201.
- Inhabitants of the Earth (or any other Planet) stand on opposite sides with their feet toward one another, yet each thinks himself on the upper side, 122.
- Julian Period, 430.
- Jupiter, it’s distance, diameter, diurnal and annual revolutions, 67-69.
- The Phenomena of it’s Belts, 70.
- Has no difference of seasons, 71.
- Has four Moons, 72,
- their grand Period, 73,
- the Angles which their Orbits subtend as seen from the Earth, 74,
- most of them are eclipsed in every revolution, 75.
- The great difference between it’s equatoreal and polar Diameters, 76.
- The inclination of it’s Orbit, and place of it’s Ascending Node, 77.
- The Sun’s light 3000 times as strong on it as Full Moon-light is on the Earth, 85.
- Is probably inhabited, 86.
- The amazing strength required to put it in motion, 158.
- The figures of the Paths described by it’s Satellites, 269.
- L.
- Light, the inconceivable smallness of it’s particles, 165,
-
- and the dreadful mischief they would do if they were larger, 166.
- It’s surprising velocity, 166,
- compared with the swiftness of the Earth’s annual motion, 197.
- Decreases as the square of the distance from the luminous body increases, 169.
- Is refracted in passing through different Mediums, 171-173.
- Affords a proof of the Earth’s annual motion, 197, 219.
- In what time it comes from the Sun to the Earth, 216,
- this explained by a figure, 217.
- Limits of Eclipses, 317.
- Line, of the Nodes, what, 317;
-
- has a retrograde motion, 319.
- Of Sines and Chords, how to make, 369.
- Long (Rev. Dr.) his method of comparing the quantity of the surface of dry land with that of the Sea, 51.
- Longitude, how found, 207-213.
- Lucid Spots in the Heavens, 401.
- Lunar Cycle deficient, 422.
- M.
- Magellanic Clouds, 402.
- Man, of a middle size, how much pressed by the weight of the Atmosphere, 175;
- why this pressure is not felt, ib.
- Mars, it’s Diameter, Period, Distance, and other Phenomena, 64-67.
- Matter, it’s properties, 99.
- Mean Anomaly, what, 239.
- Mercury, it’s Diameter, Period, Distance, &c. 22.
- Appears in all the shapes of the Moon, 23.
- When it will be seen on the Sun, 24.
- The inclination of it’s Orbit and Place of it’s Ascending Node, ib.
- It’s Path delineated, 138.
- Experiment to shew it’s Phases and apparent Motion, 142.
- Mercury (Quicksilver) in the Barometer, why not affected by the Moon’s raising Tides in the Air, 311.
- Meridian, first, 207.
- Line, how to draw one, 226.
- Milky Way, what, 400.
- Months, Jewish, Arabian, Egyptian, and Grecian, 415.
- Moon, her Diameter and Period, 52.
- Her phases, 53, 255.
- Shines not by her own light, 54.
- Has no difference of seasons, 55.
- The Earth is a Moon to her, 56.
- Has no Atmosphere of any visible Density, 58;
- How her inhabitants may be supposed to measure their year, 62.
- Her light compared with day-light, 85.
- The excentricity of her Orbit, 98.
- Is nearer the Earth now than she was formerly, 163.
- Appears bigger in the Horizon than at any considerable height above it, and why, 187;
- yet is seen much under the same Angle in both cases, 188.
- Her surface mountainous, 252:
- if smooth she could give us no light, ib.
- Why no hills appear round her edge, 253.
- Has no Twilight, 254.
- Appears not always quite round when full, 256.
- Her phases agreeably represented by a globular Stone viewed in Sun-shine when she is above the Horizon, and the observer placed as if he saw her on the top of the Stone, 258.
- Turns round her Axis, 262.
- The length of her Solar and Sidereal Day, ib.
- Her periodical and synodical revolution represented by the motions of the hour and minute hands of a Watch, 264.
- Her Path delineated, and shewn to be always concave to the Sun, 265-268.
- Her motion alternately retarded and accelerated, 267.
- Her gravity toward the Sun greater than toward the Earth at her Conjunction, and why she does not then abandon the Earth on that account, 268.
- Rises nearer the time of Sun-set when about the full in harvest for a whole week than when she is about the full at any other time of the year, and why, 273-284:
- this rising goes through a course of increasing and
- decreasing benefit to the farmers every 19 years, 292.
- Continues above the Horizon of the Poles for fourteen of our natural Days together, 293.
- Proved to be globular, 314.
- and to be less than the Earth, 315.
- Her Nodes, 317.
- ascending and descending, 318.
- their retrograde motion, 319.
- Her acceleration proved from antient Eclipses, 322, n.
- Her Apogee and Perigee, 336.
- Not invisible when she is totally eclipsed, and why, 346.
- How to calculate her Conjunctions, Oppositions, and Eclipses, 355-390.
- How to find her age in any Lunation by the Golden Number, 423.
- Morning and Evening Star, what, 145.
- Motion, naturally rectilineal, 100.
- Apparent, of the Planets as seen by a spectator at rest on the outside of all their Orbits, 133;
- and of the Heavens as seen from any Planet, 154.
- N.
- Natural Day, not compleated in the time that the Earth turns round it’s Axis, 222.
- New and Full Moon, to calculate the times of 355.
- New Stars, 403,
- New Style, it’s original, 414.
- Nicias’s Eclipse, 328.
- Nodes, of the Planet’s Orbits, their places in the Ecliptic, 20.
- Of the Moon’s Orbit, 317.
- their retrograde motion, 319.
- Nonagesimal Degree, what, 259.
- Number of Direction, 426.
- O.
- Objects, we often mistake their bulk by mistaking their distance, 185.
- Appear bigger when seen through a fog than through clear Air, and why, ib.
- this applied to the solution of the Horizontal Moon, 187.
- Oblique Sphere, what, 131.
- Olympiads, what, 323. n.
- Orbits of the Planets not solid, 21.
- Orrery described, 434, 435, 436.
- P.
- Parallax, Horizontal, what, 190.
- Parallel Sphere, what, 131.
- Path of the Moon, 265, 266, 267.
- Pendulums, their vibrating slower at the Equator than near the Poles proves that the Earth turns on it’s Axis, 117.
- Penumbra, what, 336.
- It’s velocity on the Earth in Solar Eclipses, 337.
- Period of Eclipses, 320, 326.
- Phases of the Moon, 252-268.
- Planets, much of the same nature with the Earth, 11.
- Some have Moons belonging to them, 12.
- Move all the same way as seen from the Sun, but not as seen from one another, 18.
- Their Moons denote them to be inhabited, 86.
- The proportional breadth of the Sun’s Disc as seen from each of them, 87.
- Their proportional bulks as seen from the Sun, 88.
- An idea of their distances from the Sun, 89.
- Appear bigger and less by turns, and why, 90.
- Are kept in their Orbits by the power of gravity, 101, 150-158.
- Their motions very irregular as seen from the Earth, 137.
- The apparent motions of Mercury and Venus delineated by Pencils in an Orrery, 138.
- Elongations of all the rest as seen from Saturn, 147.
- Describe equal areas in equal times, 153.
- The excentricities of their Orbits, 155.
- In what times they would fall to the Sun by the power of gravity, 157.
- Disturb one another’s motions, the consequence thereof, 163.
- Appear dimmer when seen through telescopes than by the bare eye, the reason of this, 170.
- Planetary Globe described, 439.
- Polar Circles, 198.
- Poles, of the Planets, what, 19.
- Of the world, what, 122.
- Celestial, seem to keep on the same points of the Heavens all the year, and why, 196.
- Projectile Force, 150;
- if doubled would require a quadruple power of gravity to retain the Planets in their Orbits, 153.
- Is evidently an impulse from the hand of the Almighty, 161.
- Precession of the Equinoxes, 246-251.
- Ptolemean System absurd, 96, 140.
- R.
- Rays of Light, if not disturbed, move in straight lines, and hinder not one another’s motions, 168.
- Are refracted in passing through different mediums, 171.
- Reflection of the Atmosphere causes the Twilight, 177.
- Refraction of the Atmosphere bends the rays of light from straight lines, and keeps the Sun and Moon longer in sight than they would otherwise be, 178.
- A surprising instance of this, 183.
- Must be allowed for in taking the Altitudes of the celestial bodies, ib.
- Right Sphere, 131.
- S.
- Satellites; the times of their revolutions round their primary Planets, 52, 73, 80.
- Their Orbits compared with each other, with the Orbits of the primary Planets, and with the Sun’s circumference, 271.
- What sort of Curves they describe, 272.
- Saturn, with his Ring and Moon’s, their Phenomena, 78, 79, 82.
- The Sun’s light 1000 times as strong to him as the light of the Full Moon is to us, 85.
- The Phenomena of his Ring farther explained, 204.
- Our blessed Saviour, the darkness at his crucifixion supernatural, 352.
- The prophetic year of his crucifixion found to agree with an astronomical calculation, 432.
- Seasons, different, illustrated by an easy experiment, 200;
- Shadow, what, 312.
- Sidereal Time, what, 221;
-
- the number of Sidereal Days in a year exceeds the number of Solar Days by one, and why, 222.
- An easy method for regulating Clocks and Watches by it, 223.
- Signs of the Zodiac, their names and characters, 91, 365.
- How they are numbered by Astronomers, 354.
- Sines, line of, how to make, 369.
- Smith, (Rev. Dr.) his companion between Moon-light and Day-light, 85.
- His demonstration that light decreases as the square of the distance from the luminous body increases, 169.
- (Mr. George) his Dissertation on the Progress of a Solar Eclipse, 321-324.
- Solar Astronomer, the judgment he might be supposed to make concerning the Planets and Stars, 135, 136.
- Sphere, parallel, oblique, and right, 131.
- Spring and Neap Tides, 302.
- Stars, their vast distance from the Earth, 3, 196.
- Probably not all at the same distance, 4 Shine by their own light, and are therefore Suns 7,
- probably to other worlds, 8 A demonstration that they do not move round the Earth, 111.
- Have an apparent slow motion round the Poles of the Ecliptic, and why, 251.
- A catalogue of them, 399.
- Cloudy, 402.
- New, 403.
- Some of them change their places, 404.
- Starry Heavens have the same appearance from any part of the Solar System, 132.
- Sun appears bigger than the Stars, and why, 4 Turns round his Axis, 18.
- His proportional breadth as seen from the different Planets, 87.
- Describes unequal arcs above and below the Horizon at different times, and why, 130.
- His Center the only place from which the true motions of the Planets could be seen, 135.
- Is for half a year together visible at each Pole in it’s turn, and as long in visible, 200, 294.
- Is nearer the Earth in Winter than in Summer, 205.
- Why his motion agrees so seldom with the motion of a well regulated Clock, 224-245.
- Would more than fill the Moon’s Orbit, 271.
- Proved to be much bigger than the Earth, and the Earth to be bigger than the Moon, 315.
- To calculate his true place, 360.
- Systems, the Solar, 17-95;
- the Ptolemean, 96;
- the Tychonic, 97.
- T.
- Table, of the Periods, Revolutions, Magnitudes, Distances, &c. of the Planets, facing § 99.
- Of the Air’s rarity, compression, and expansion at different heights, 174.
- Of refractions, 182.
- For converting time into motion, and the reverse, 220.
- For shewing how much of the celestial Equator passes over the Meridian in any part of a mean Solar Day; and how much the Stars accelerate upon the mean Solar time for a month, 221.
- Of the first part of the Equation of time, 229;
- Of the precession of the Equinox, 247.
- Of the length of Sidereal, Julian, and Tropical Years, 251.
- Of the Sun’s place and Anomaly, following 251.
- Of the Equation of natural Days, following 251
- Of the Conjunctions of the hour and minute hands of a Watch, 264.
- Of the Curves described by the Satellites, 272.
- Of the difference of time in the Moon’s rising and setting on the parallel of
- London every day during her course round the Ecliptic, 277.
- Of Eclipses, 327.
- For calculating New and Full Moons and Eclipses, following 390.
- Of the Constellations and number of the Stars, 399.
- Of the Jewish, Egyptian, Arabic, and Grecian months, 415.
- For inserting the Golden Numbers right in the Calendar, 423.
- Of the times of all the New Moons for 76 years, 424.
- Of remarkable Æras or Events, 433.
- Of the Golden Number, Number of Direction, Dominical Letter and Days of the Months, following 433.
- Thales’s Eclipse, 323.
- Thucydides’s Eclipse 324.
- Tides, their Cause and Phenomena, 295-311.
- Tide-Dial described, 441.
- Trajectorium Lunare described, 440.
- Tropics, 198.
- Twilight, none in the Moon, 254.
- Tychonic System absurd, 97.
- U.
- Universe, the Work of Almighty Power, 5, 161.
- Up and down, only relative terms, 122.
- Upper or under side of the Earth no such thing, 123.
- V.
- Velocity of Light compared with the velocity of the Earth in it’s annual Orbit, 197.
- Venus, her bulk, distance, period, length of days and nights, 26.
- Shines not by her own light, ib.
- Is our morning and evening Star, 28.
- Her Axis, how situated, 29.
- Her surprising Phenomena, 29-43.
- The inclination of her Orbit, 45.
- When she will be seen on the Sun, ib.
- How it may probably be soon known if she has a Satellite, 46.
- Appears in all the Shapes of the Moon, 23, 141.
- An experiment to shew her phases and apparent motion, 141.
- Vision, how caused, 167.
- W.
- Weather, not hottest when the Sun is nearest to us, and why, 205.
- Weight, the cause of it, 122.
- World not eternal, 164.
- Y.
- Year, 407,
- Great, 251,
- Tropical, 408,
- Sidereal, 400,
- Lunar, 410,
- Civil, 411,
- Bissextile, ib.
- Roman, 413,
- Jewish, Egyptian, Arabic, and Grecian, 415,
- how long it would be if the Sun moved round the Earth, 111.
- Z.
- Zodiac, what, 397.
- How divided by the antients, 398.
- Zones, what, 199.
DIRECTIONS to the BOOKBINDER.
The Orrery Plate is to front the Title Page.
| Plate I |
fronting Page 5 |
| II |
39 |
| III |
49 |
| IV |
73 |
| V |
81 |
| VI |
97 |
| VII |
125 |
| VIII |
147 |
| IX |
147 |
| X |
157 |
| XI |
179 |
| XII |
203 |
| XIII |
279 |
Footnotes
This book uses inconsistent spelling and hyphenation, which were retained
in the ebook version. Some corrections have been made to the text, including
correcting the errata and normalizing punctuation.
Further corrections are noted below:
Errata: l. 15 from botton -> l. 15 from bottom
p. 9: forward in the Eliptic -> forward in the Ecliptic
p. 31: is at it were -> is as it were
Maclaurin, additionally ‘Isacc Newton’ changed to ‘Isaac Newton’.
Footnote marker on Rutherfurth removed as there was no footnote
associated with it.
p. 38: on the the same Axis -> on the same Axis
p. 69: who were suprised to find -> who were surprised to find
p. 69: than those whch -> than those which
p. 72: than tie a thread -> then tie a thread
p. 74: is is equal to -> is equal to
p. 74: the graduaded limb -> the graduated limb
p. 78: different lenghts -> different lengths
p. 78: from the the Equator -> from the Equator
p. 90: is not instantaneons -> is not instantaneous
p. 92: Degreees and Parts of the Equtor-> Degrees and Parts of the Equator
p. 132: appear supprising -> appear surprising
p. 133: When Jupiter at -> When Jupiter is at
Sidenote
p. 136: The reason of of this -> the reason of this
p. 140 the opposite points rises -> the opposite point rises
Sidenote
p. 141: Harvest aad Hunter’s -> Harvest and Hunter’s
p. 154: espeically as to the -> especially as to the
Sidenote
p. 155: aereal Tides -> aerial Tides
p. 158: the the Earth -> the Earth
p. 160: goes round him 87 days -> goes round him in 87 days
p. 161: Eclipses and revolulution -> Eclipses and revolution
p. 167: Jacobus Ptlaumen -> Jacobus Pflaumen
p. 168: set set down -> set down
p. 172 Table 2, 1st column, 6th row: 1388 -> 1488
p. 174: duplicate entry for 1606 Sept 2. removed
p. 177: foretold by Thalls -> foretold by Thales
p. 180: the Eclipse is annualar -> the Eclipse is annular
p. 193: EAAMPLE II. -> EXAMPLE II
p. 202: these two Fquations -> these two Equations
p. 203: their Sun will be -> their Sum will be
p. 210: the page number was printed as 110 and has been corrected
p. 210: Motion and Semi diameter -> Motion and Semi-diameter
p. 238: oblate spheriod -> oblate spheroid
p. 261 18 Degres -> 18 Degrees
Index Mercury (Quicksiver) -> Mercury (Quicksilver)
*** END OF THE PROJECT GUTENBERG EBOOK 60619 ***
















