
BY
JOHN TYNDALL, D.C.L., LL.D., F.R.S.

NEW YORK
P. F. COLLIER & SON
MCMII
7
SCIENCE
TO THE MEMORY
OF
MY FRIEND RICHARD DAWES
LATE DEAN OF HEREFORD
THIS BOOK IS DEDICATED
J. T.
CHAPTER I |
|
The Nerves and Sensation—Production and Propagation of Sonorous Motion—Experiments on Sounding Bodies placed in Vacuo—Deadening of Sound by Hydrogen—Action of Hydrogen on the Voice—Propagation of Sound through Air of Varying Density—Reflection of Sound—Echoes—Refraction of Sound—Diffraction of Sound; Case of Erith Village and Church—Influence of Temperature on Velocity—Influence of Density on Elasticity—Newton’s Calculation of Velocity—Thermal Changes Produced by the Sonorous Wave—Laplace’s Correction of Newton’s Formula—Ratio of Specific Heats at Constant Pressure and at Constant Volume deduced from Velocities of Sound—Mechanical Equivalent of Heat deduced from this Ratio—Inference that Atmospheric Air Possesses no Sensible Power to Radiate Heat—Velocity of Sound in Different Gases—Velocity in Liquids and Solids—Influence of Molecular Structure on the Velocity of Sound. | 31 |
| Summary of Chapter I | 77 |
CHAPTER II |
|
Physical Distinction between Noise and Music—A Musical Tone Produced by Periodic, Noise Produced by Unperiodic, Impulses—Production of Musical Sounds by Taps—Production of Musical Sounds by Puffs—Definition of Pitch in Music—Vibrations of a Tuning-Fork; their Graphic Representation on Smoked Glass—Optical Expression of the Vibrations of a Tuning-Fork—Description of the Siren—Limits of the Ear; Highest and Deepest Tones—Rapidity of Vibration Determined by the Siren—Determination of the Lengths of Sonorous Waves—Wave-Lengths of the Voice in Man and Woman—Transmission of Musical Sounds through Liquids and Solids. | 82 |
| Summary of Chapter II | 117 |
| 8
CHAPTER III |
|
Vibration of Strings—How employed in Music—Influence of Sound-Boards—Laws of Vibrating String—Combination of Direct and Reflected Pulses—Stationary and Progressive Waves—Nodes and Ventral Segments—Application of Results to the Vibrations of Musical Strings—Experiments of Melde—Springs set in Vibration by Tuning-Forks—Laws of Vibration thus demonstrated—Harmonic Tones of Strings—Definitions of Timbre or Quality, or Overtones and Clang—Abolition of Special Harmonies—Conditions which affect the Intensity of the Harmonic Tones—Optical Examination of the Vibrations of a Piano-Wire | 120 |
| Summary of Chapter III | 161 |
CHAPTER IV |
|
Vibrations of a Rod fixed at Both Ends: its Subdivisions and Corresponding Overtones—Vibrations of a Rod fixed at One End—The Kaleidophone—The Iron Fiddle and Musical Box—Vibrations of a Rod free at Both Ends—The Claque-bois and Glass Harmonica—Vibrations of a Tuning-Fork: its Subdivisions and Overtones—Vibrations of Square Plates—Chladni’s Discoveries—Wheatstone’s Analysis of the Vibrations of Plates—Chladni’s Figures—Vibrations of Disks and Bells—Experiments of Faraday and Strehlke. | 165 |
| Summary of Chapter IV | 196 |
CHAPTER V |
|
Longitudinal Vibrations of a Wire—Relative Velocities of Sound in Brass and Iron—Longitudinal Vibrations of Rods fixed at One End—Of Rods free at Both Ends—Divisions and Overtones of Rods vibrating longitudinally—Examination of Vibrating Bars by Polarized Light—Determination of Velocity of Sound in Solids—Resonance—Vibrations of Stopped Pipes: their Divisions and Overtones—Relation of the Tones of Stopped Pipes to those of Open Pipes—Condition of Column of Air within a Sounding Organ-Pipe—Reeds and Reed-Pipes—The Voice—Overtones of the Vocal Chords—The Vowel Sounds—Kundt’s Experiments—New Methods of determining the Velocity of Sound. | 200 |
| Summary of Chapter V | 254 |
CHAPTER VI |
|
Singing Flames—Influence of the Tube surrounding the Flame—Influence of Size of Flame—Harmonic Notes of Flames—Effect of Unisonant 9 Notes on Singing Flames—Action of Sound on Naked Flames—Experiments with Fish-Tail and Bat’s-Wing Burners—Experiments on Tall Flames—Extraordinary Delicacy of Flames as Acoustic Reagents—The Vowel-Flame—Action of Conversational Tones upon Flames—Action of Musical Sounds on Smoke-Jets—Constitution of Water-Jets—Plateau’s Theory of the Resolution of a Liquid Vein into Drops—Action of Musical Sounds on Water-Jets—A Liquid Vein may compete in Point of Delicacy with the Ear | 260 |
| Summary of Chapter VI | 301 |
CHAPTER VII |
|
PART I |
|
RESEARCHES ON THE ACOUSTIC TRANSPARENCY OF THE ATMOSPHERE IN RELATION TO THE QUESTION OF FOG-SIGNALLING |
|
Introduction—Instruments and Observations—Contradictory Results from the 19th of May to the 1st of July inclusive—Solution of Contradictions—Aërial Reflection and its Causes—Aërial Echoes—Acoustic Clouds—Experimental Demonstration of Stoppage of Sound by Aërial Reflection | 305 |
PART II |
|
INVESTIGATION OF THE CAUSES WHICH HAVE HITHERTO BEEN SUPPOSED EFFECTIVE IN PREVENTING THE TRANSMISSION OF SOUND THROUGH THE ATMOSPHERE |
|
Action of Hail and Rain—Action of Snow—Action of Fog; Observations in London—Experiments on Artificial Fogs—Observations on Fogs at the South Foreland—Action of Wind—Atmospheric Selection—Influence of Sound-Shadow | 341 |
| Summary of Chapter VII | 374 |
CHAPTER VIII |
|
Law of Vibratory Motions in Water and Air—Superposition of Vibrations—Interference of Sonorous Waves—Destruction of Sound by Sound—Combined Action of Two Sounds nearly in Unison with each other—Theory of Beats—Optical Illustration of the Principle of Interference—Augmentation of Intensity by Partial Extinction of Vibrations—Resultant Tones—Conditions of their Production—Experimental Illustrations—Difference-Tones and Summation-Tones—Theories of Young and Helmholtz | 377 |
| Summary of Chapter VIII | 407 |
| 10
CHAPTER IX |
|
Combination of Musical Sounds—The smaller the Two Numbers which express the Ratio of their Rates of Vibration, the more perfect is the Harmony of Two Sounds—Notions of the Pythagoreans regarding Musical Consonance—Euler’s Theory of Consonance—Theory of Helmholtz—Dissonance due to Beats—Interference of Primary Tones and of Overtones—Mechanism of Hearing—Schultze’s Bristles—The Otoliths—Corti’s Fibres—Graphic Representation of Consonance and Dissonance—Musical Chords—The Diatonic Scale—Optical Illustration of Musical Intervals—Lissajous’s Figures—Sympathetic Vibrations—Various Modes of illustrating the Composition of Vibrations | 410 |
| Summary of Chapter IX | 450 |
APPENDIX I |
|
On the Influence of Musical Sounds on the Flame of a Jet of Coal-gas. By John le Conte, M.D. | 454 |
APPENDIX II |
|
| On Acoustic Reversibility | 461 |
| INDEX | 471 |
| ILLUSTRATION—Fog-Siren | Frontispiece |
In preparing this new edition of “Sound,” I have carefully gone over the last one; amended, as far as possible, its defects of style and matter, and paid at the same time respectful attention to the criticisms and suggestions which the former editions called forth.
The cases are few in which I have been content to reproduce what I have read of the works of acousticians. I have sought to make myself experimentally familiar with the ground occupied; trying, in all cases, to present the illustrations in the form and connection most suitable for educational purposes.
Though bearing, it may be, an undue share of the imperfection which cleaves to all human effort, the work has already found its way into the literature of various nations of diverse intellectual standing. Last year, for example, a new German edition was published “under the special supervision” of Helmholtz and Wiedemann. That men so eminent, and so overladen with official duties, should add to these the labor of examining and correcting every proof-sheet of a work like this, shows that they consider it to be what it was meant to be—a serious attempt to improve the public knowledge of science. It is especially gratifying to me to be thus assured that not in England alone has the book met a public want, but also in that learned land to which I owe my scientific education.
Before me, on the other hand, lie two volumes of foolscap size, curiously stitched, and printed in characters the meaning of which I am incompetent to penetrate. Here and there, however, I notice the familiar figures of the former editions of “Sound.” For these volumes I am indebted to Mr. John Fryer, of Shanghai, who, along with them, favored me, a few weeks ago, with a letter from which the following is an extract: “One day,” writes Mr. Fryer, “soon after the first copy of your work on Sound reached Shanghai, I was reading it in my study, when an intelligent official, named Hsii-chung-hu, noticed some of the engravings and asked me to explain them to him. He became so deeply interested in the subject of Acoustics that nothing would satisfy him but to make a translation. Since, however, engineering and other works were then considered to be of more practical importance by the higher authorities, we agreed to translate your work during our leisure time every evening, and publish it separately ourselves. Our translation, however, when completed, and shown to the higher officials, so much interested them, and pleased them, that they at once ordered it to be published at the expense of the Government, and sold at cost price. The price is four hundred and eighty copper cash per copy, or about one shilling and eightpence. This will give you an idea of the cheapness of native printing.”
Mr. Fryer adds that his Chinese friend had no difficulty in grasping every idea in the book.
The new matter of greatest importance which has been introduced into this edition is an account of an investigation which, during the past two years, I have had the13 honor of conducting in connection with the Elder Brethren of the Trinity House. Under the title “Researches on the Acoustic Transparency of the Atmosphere, in Relation to the Question of Fog-signalling,” the subject is treated in Chapter VII. of this volume. It was only by Governmental appliances that such an investigation could have been made; and it gives me pleasure to believe that not only have the practical objects of the inquiry been secured, but that a crowd of scientific errors, which for more than a century and a half have surrounded this subject, have been removed, their place being now taken by the sure and certain truth of Nature. In drawing up the account of this laborious inquiry, I aimed at linking the observations so together that they alone should offer a substantial demonstration of the principles involved. Further labors enabled me to bring the whole inquiry within the firm grasp of experiment; and thus to give it a certainty which, without this final guarantee, it could scarcely have enjoyed.
Immediately after the publication of the first brief abstract of the investigation, it was subjected to criticism. To this I did not deem it necessary to reply, believing that the grounds of it would disappear in presence of the full account. The only opinion to which I thought it right to defer was to some extent a private one, communicated to me by Prof. Stokes. He considered that I had, in some cases, ascribed too exclusive an influence to the mixed currents of aqueous vapor and air, to the neglect of differences of temperature. That differences of temperature, when they come into play, are an efficient cause of acoustic opacity, I never doubted. In fact, aërial reflection arising from this cause is, in the present in14quiry, for the first time made the subject of experimental demonstration. What the relative potency of differences of temperature and differences due to aqueous vapor, in the cases under consideration, may be, I do not venture to state; but as both are active, I have, in Chapter VII., referred to them jointly as concerned in the production of those “acoustic clouds” to which the stoppage of sound in the atmosphere is for the most part due.
Subsequently, however, to the publication of the full investigation another criticism appeared, to which, in consideration of its source, I would willingly pay all respect and attention. In this criticism, which reached me first through the columns of an American newspaper, differences in the amounts of aqueous vapor, and differences of temperature, are alike denied efficiency as causes of acoustic opacity. At a meeting of the Philosophical Society of Washington the emphatic opinion had, it was stated, been expressed that I was wrong in ascribing the opacity of the atmosphere to its flocculence, the really efficient cause being refraction. This view appeared to me so obviously mistaken that I assumed, for a time, the incorrectness of the newspaper account.
Recently, however, I have been favored with the “Report of the United States Lighthouse Board for 1874,” in which the account just referred to is corroborated. A brief reference to the Report will here suffice. Major Elliott, the accomplished officer and gentleman referred to at page 261, had published a record of his visit of inspection to this country, in which he spoke, with a perfectly enlightened appreciation of the facts, of the differences between our system of lighthouse illumination15 and that of the United States. He also embodied in his Report some account of the investigation on fog-signals, the initiation of which he had witnessed, and indeed aided, at the South Foreland.
On this able Report of their own officer the Lighthouse Board at Washington make the following remark: “Although this account is interesting in itself and to the public generally, yet, being addressed to the Lighthouse Board of the United States, it would tend to convey the idea that the facts which it states were new to the Board, and that the latter had obtained no results of a similar kind; while a reference to the appendix to this Report1 will show that the researches of our Lighthouse Board have been much more extensive on this subject than those of the Trinity House, and that the latter has established no facts of practical importance which had not been previously observed and used by the former.”
The “appendix” here referred to is from the pen of the venerable Prof. Joseph Henry, chairman of the Lighthouse Board at Washington. To his credit be it recorded that at a very early period in the history of fog-signalling Prof. Henry reported in favor of Daboll’s trumpet, though he was opposed by one of his colleagues on the ground that “fog-signals were of little importance, since the mariner should know his place by the character of his soundings.” In the appendix, he records the various efforts made in the United States with a view to the establishment of fog-signals. He describes experiments on bells, and on the employment of reflectors to reinforce their sound. These, though effectual close at hand, were found 16to be of no use at a distance. He corrects current errors regarding steam-whistles, which by some inventors were thought to act like ringing bells. He cites the opinion of the Rev. Peter Ferguson, that sound is better heard in fog than in clear air. This opinion is founded on observations of the noise of locomotives; in reference to which it may be said that others have drawn from similar experiments diametrically opposite conclusions. On the authority of Captain Keeney he cites an occurrence, “in the first part of which the captain was led to suppose that fog had a marked influence in deadening sound, though in a subsequent part he came to an opposite conclusion.” Prof. Henry also describes an experiment made during a fog at Washington, in which he employed “a small bell rung by clock-work, the apparatus being the part of a moderator lamp, intended to give warning to the keepers when the supply of oil ceased. The result of the experiment was, he affirms, contrary to the supposition of absorption of the sound by the fog.” This conclusion is not founded on comparative experiments, but on observations made in the fog alone; for, adds Prof. Henry, “the change in the condition of the atmosphere, as to temperature and the motion of the air, before the experiment could be repeated in clear weather, rendered the result not entirely satisfactory.”
This, I may say, is the only experiment on fog which I have found recorded in the appendix.
In 1867 the steam-siren was mounted at Sandy Hook, and examined by Prof. Henry. He compared its action with that of a Daboll trumpet, employing for this purpose a stretched membrane covered with sand, and placed at the small end of a tapering tube which concentrated17 the sonorous motion upon the membrane. The siren proved most powerful. “At a distance of 50, the trumpet produced a decided motion of the sand, while the siren gave a similar result at a distance of 58.” Prof. Henry also varied the pitch of the siren, and found that in association with its trumpet 400 impulses per second yielded the maximum sound; while the best result with the unaided siren was obtained when the impulses were 360 a second. Experiments were also made on the influence of pressure; from which it appeared that when the pressure varied from 100 lbs. to 20 lbs., the distance reached by the sound (as determined by the vibrating membrane) varied only in the ratio of 61 to 51. Prof. Henry also showed the sound of the fog-trumpet to be independent of the material employed in its construction; and he furthermore observed the decay of the sound when the angular distance from the axis of the instrument was increased. Further observations were made by Prof. Henry and his colleagues in August, 1873, and in August, and September, 1874. In the brief but interesting account of these experiments a hypothetical element appears, which is absent from the record of the earlier observations.
It is quite evident from the foregoing that, in regard to the question of fog-signalling, the Lighthouse Board of Washington have not been idle. Add to this the fact that their eminent chairman gives his services gratuitously, conducting without fee or reward experiments and observations of the character here revealed, and I think it will be conceded that he not only deserves well of his own country, but also sets his younger scientific contemporaries, both in his country and ours, an example of high-minded devotion.
I was quite aware, in a general way, that labors like those now for the first time made public had been conducted in the United States, and this knowledge was not without influence upon my conduct. The first instruments mounted at the South Foreland were of English manufacture; and I, on various accounts, entertained a strong sympathy for their able constructor, Mr. Holmes. From the outset, however, I resolved to suppress such feelings, as well as all other extraneous considerations, individual or national; and to aim at obtaining the best instruments, irrespective of the country which produced them. In reporting, accordingly, on the observations of May 19 and 20, 1873 (our first two days at the South Foreland), these were my words to the Elder Brethren of the Trinity House:
“In view of the reported performance of horns and whistles in other places, the question arises whether those mounted at the South Foreland, and to which the foregoing remarks refer, are of the best possible description.... I think our first duty is to make ourselves acquainted with the best instruments hitherto made, no matter where made; and then, if home genius can transcend them, to give it all encouragement. Great and unnecessary expense may be incurred, through our not availing ourselves of the results of existing experience.
“I have always sympathized, and I shall always sympathize, with the desire of the Elder Brethren to encourage the inventor who first made the magneto-electric light available for lighthouse purposes. I regard his aid and counsel as, in many respects, invaluable to the corporation. But, however original he may be, our duty is to demand that his genius shall be expended in making ad19vances on that which has been already achieved elsewhere. If the whistles and horns that we heard on the 19th and 20th be the very best hitherto constructed, my views have been already complied with; but if they be not—and I am strongly inclined to think that they are not—then I would submit that it behooves us to have the best, and to aim at making the South Foreland, both as regards light and sound, a station not excelled by any other in the world.”
On this score it gives me pleasure to say that I never had a difficulty with the Elder Brethren. They agreed with me; and two powerful steam-whistles, the one from Canada, the other from the United States, together with a steam-siren—also an American instrument—were in due time mounted at the South Foreland. It will be seen in Chapter VII. that my strongest recommendation applies to an instrument for which we are indebted to the United States.
In presence of these facts, it will hardly be assumed that I wish to withhold from the Lighthouse Board of Washington any credit that they may fairly claim. My desire is to be strictly just; and this desire compels me to express the opinion that their Report fails to establish the inordinate claim made in its first paragraph. It contains observations, but contradictory observations; while as regards the establishment of any principle which should reconcile the conflicting results, it leaves our condition unimproved.
But I willingly turn aside from the discussion of “claims” to the discussion of science. Inserted, as a kind of intrusive element, into the Report of Prof. Henry, is a second Report by General Duane, founded20 on an extensive series of observations made by him in 1870 and 1871. After stating with distinctness the points requiring decision, the General makes the following remarks:
“Before giving the results of these experiments, some facts will be stated which will explain the difficulties of determining the power of a fog-signal.
“There are six steam fog-whistles on the coast of Maine: these have been frequently heard at a distance of twenty miles, and as frequently cannot be heard at the distance of two miles, and this with no perceptible difference in the state of the atmosphere.
“The signal is often heard at a great distance in one direction, while in another it will be scarcely audible at the distance of a mile. This is not the effect of wind, as the signal is frequently heard much further against the wind than with it.2 For example, the whistle on Cape Elizabeth can always be distinctly heard in Portland, a distance of nine miles, during a heavy northeast snowstorm, the wind blowing a gale directly from Portland toward the whistle.3
“The most perplexing difficulties, however, arise from the fact that the signal often appears to be surrounded by a belt, varying in radius from one mile to one mile and a half, from which the sound appears to be entirely absent. Thus, in moving directly from a station the sound is audible for the distance of a mile, is then lost for 21about the same distance, after which it is again distinctly heard for a long time. This action is common to all ear-signals, and has been at times observed at all the stations, at one of which the signal is situated on a bare rock twenty miles from the mainland, with no surrounding objects to affect the sound.”
It is not necessary to assume here the existence of a “belt,” at some distance from the station. The passage of an acoustic cloud over the station itself would produce the observed phenomenon.
Passing over the record of many other valuable observations in the Report of General Duane, I come to a few very important remarks which have a direct bearing upon the present question:
“From an attentive observation,” writes the General, “during three years, of the fog-signals on this coast, and from the reports received from the captains and pilots of coasting vessels, I am convinced that, in some conditions of the atmosphere, the most powerful signals will be at times unreliable.4
“Now it frequently occurs that a signal which, under ordinary circumstances, would be audible at the distance of fifteen miles, cannot be heard from a vessel at the distance of a single mile. This is probably due to the reflection mentioned by Humboldt.
“The temperature of the air over the land where the fog-signal is located being very different from that over the sea, the sound, in passing from the former to the latter, undergoes reflection at their surface of contact. The 22correctness of this view is rendered more probable by the fact that, when the sound is thus impeded in the direction of the sea, it has been observed to be much stronger inland.
“Experiments and observation lead to the conclusion that these anomalies in the penetration and direction of sound from fog-signals are to be attributed mainly to the want of uniformity in the surrounding atmosphere, and that snow, rain, and fog, and the direction of the wind, have much less influence than has been generally supposed.”
The Report of General Duane is marked throughout by fidelity to facts, rare sagacity, and soberness of speculation. The last three of the paragraphs just quoted exhibit, in my opinion, the only approach to a true explanation of the phenomena which the Washington Report reveals. At this point, however, the eminent Chairman of the Lighthouse Board strikes in with the following criticism:
“In the foregoing I differ entirely in opinion from General Duane as to the cause of extinction of powerful sounds being due to the unequal density of the atmosphere. The velocity of sound is not at all affected by barometric pressure; but if the difference in pressure is caused by a difference in heat, or by the expansive power of vapor mingled with the air, a slight degree of obstruction of sound may be observed. But this effect we think is entirely too minute to produce the results noted by General Duane and Dr. Tyndall, while we shall find in the action of currents above and below a true and efficient cause.”
I have already cited the remarkable observation of23 General Duane, that with a snowstorm from the northeast blowing against the sound, the signal at Cape Elizabeth is always heard at Portland, a distance of nine miles. The observations at the South Foreland, where the sound has-been proved to reach a distance of more than twelve miles against the wind, backed by decisive experiments, reduce to certainty the surmises of General Duane. It has, for example, been proved that a couple of gas-flames placed in a chamber can, in a minute or two, render its air so non-homogeneous as to cut a sound practically off; while the same sound passes without sensible impediment through showers of paper-scraps, seeds, bran, raindrops, and through fumes and fogs of the densest description. The sound also passes through thick layers of calico, silk, serge, flannel, baize, close felt, and through pads of cotton-net impervious to the strongest light.
As long, indeed, as the air on which snow, hail, rain or fog is suspended is homogeneous, so long will sound pass through the air, sensibly heedless of the suspended matter.5 This point is illustrated upon a large scale by my own observations on the Mer de Glace, and by those of General Duane, at Portland, which prove the snow-laden air from the northeast to be a highly homogeneous medium. Prof. Henry thus accounts for the fact that the northeast snow-wind renders the sound of Cape Elizabeth audible at Portland: In the higher regions of the atmosphere he places an ideal wind, blowing in a direction opposed to the real one, which always accompanies the latter, and which more than neutralizes its action. In 24speculating thus he bases himself on the reasoning of Prof. Stokes, according to which a sound-wave moving against the wind is tilted upward. The upper, and opposing wind, is invented for the purpose of tilting again the already lifted sound-wave downward. Prof. Henry does not explain how the sound-wave recrosses the hostile lower current, nor does he give any definite notion of the conditions under which it can be shown that it will reach the observer.
This, so far as I know, is the only theoretic gleam cast by the Washington Report on the conflicting results which have hitherto rendered experiments on fog-signals so bewildering. I fear it is an ignis fatuus, instead of a safe guiding light. Prof. Henry, however, boldly applies the hypothesis in a variety of instances. But he dwells with particular emphasis upon a case of non-reciprocity which he considers absolutely fatal to my views regarding the flocculence of the atmosphere. The observation was made on board the steamer “City of Richmond,” during a thick fog in a night of 1872. “The vessel was approaching Whitehead from the southwestward, when, at a distance of about six miles from the station, the fog-signal, which is a 10-inch steam-whistle, was distinctly perceived, and continued to be heard with increasing intensity of sound until within about three miles, when the sound suddenly ceased to be heard, and was not perceived again until the vessel approached within a quarter of a mile of the station, although from conclusive evidence, furnished by the keeper, it was shown that the signal had been sounding during the whole time.”
But while the 10-inch shore-signal thus failed to make itself heard at sea, a 6-inch whistle on board the steamer25 made itself heard on shore. Prof. Henry thus turns this fact against me. “It is evident,” he writes, “that this result could not be due to any mottled condition or want of acoustic transparency in the atmosphere, since this would absorb the sound equally in both directions.” Had the observation been made in a still atmosphere, this argument would, at one time, have had great force. But the atmosphere was not still, and a sufficient reason for the observed non-reciprocity is to be found in the recorded fact that the wind was blowing against the shore-signal, and in favor of the ship-signal.
But the argument of Prof. Henry, on which he places his main reliance, would be untenable, even had the air been still. By the very aërial reflection which he practically ignores, reciprocity may be destroyed in a calm atmosphere. In proof of this assertion I would refer him to a short paper on “Acoustic Reversibility,” printed at the end of this volume.6 The most remarkable case of non-reciprocity on record, and which, prior to the demonstration of the existence and power of acoustic clouds, remained an insoluble enigma, is there shown to be capable of satisfactory solution. These clouds explain perfectly the “abnormal phenomena” of Prof. Henry. Aware of their existence, the falling off and subsequent recovery of a signal-sound, as noticed by him and General Duane, is no more a mystery than the interception of the solar light by a common cloud, and its restoration after the cloud has moved or melted away.
The clew to all the difficulties and anomalies of this question is to be found in the aërial echoes, the signifi26cance of which has been overlooked by General Duane, and misinterpreted by Prof. Henry. And here a word might be said with regard to the injurious influence still exercised by authority in science. The affirmations of the highest authorities, that from clear air no sensible echo ever comes, were so distinct that my mind for a time refused to entertain the idea. Authority caused me for weeks to depart from the truth, and to seek counsel among delusions. On the day our observations at the South Foreland began I heard the echoes. They perplexed me. I heard them again and again, and listened to the explanations offered by some ingenious persons at the Foreland. They were an “ocean-echo”: this is the very phraseology now used by Prof. Henry. They were echoes “from the crests and slopes of the waves”: these are the words of the hypothesis which he now espouses. Through a portion of the month of May, through the whole of June, and through nearly the whole of July, 1873, I was occupied with these echoes; one of the phases of thought then passed through, one of the solutions then weighed in the balance and found wanting, being identical with that which Prof. Henry now offers for acceptation.
But though it thus deflected me from the proper track, shall I say that authority in science is injurious? Not without some qualification. It is not only injurious, but deadly, when it cows the intellect into fear of questioning it. But the authority which so merits our respect as to compel us to test and overthrow all its supports, before accepting a conclusion opposed to it, is not wholly noxious. On the contrary, the disciplines it imposes may be in the highest degree salutary, though they may end,27 as in the present case, in the ruin of authority. The truth thus established is rendered firmer by our struggles to reach it. I groped day after day, carrying this problem of aërial echoes in my mind; to the weariness, I fear, of some of my colleagues who did not know my object. The ships and boats afloat, the “slopes and crests of the waves,” the visible clouds, the cliffs, the adjacent lighthouses, the objects landward, were all in turn taken into account, and all in turn rejected.
With regard to the particular notion which now finds favor with Prof. Henry, it suggests the thought that his observations, notwithstanding their apparent variety and extent, were really limited as regards the weather. For did they, like ours, embrace weather of all kinds, it is not likely that he would have ascribed to the sea-waves an action which often reaches its maximum intensity when waves are entirely absent. I will not multiply instances, but confine myself to the definite statement that the echoes have often manifested an astonishing strength when the sea was of glassy smoothness. On days when the echoes were powerful, I have seen the southern cumuli mirrored in the waveless ocean, in forms almost as definite as the clouds themselves. By no possible application of the law of incidence and reflection could the echoes from such a sea return to the shore; and if we accept for a moment a statement which Prof. Henry seems to indorse, that sound-waves of great intensity, when they impinge upon a solid or liquid surface, do not obey the law of incidence and reflection, but “roll along the surface like a cloud of smoke,” it only increases the difficulty. Such a “cloud,” instead of returning to the coast of England, would, in our case, have28 rolled toward the coast of France. Nothing that I could say in addition could strengthen the case here presented. I will only add one further remark. When the sun shines uniformly on a smooth sea, thus producing a practically uniform distribution of the aërial currents to which the echoes are due, the direction in which the trumpet-echoes reach the shore is always that in which the axis of the instrument is pointed. At Dungeness this was proved to be the case throughout an arc of 210°—an impossible result, if the direction of reflection were determined by that of the ocean waves.
Rightly interpreted and followed out, these aërial echoes lead to a solution which penetrates and reconciles the phenomena from beginning to end. On this point I would stake the issue of the whole inquiry, and to this point I would, with special earnestness, direct the attention of the Lighthouse Board of Washington. Let them prolong their observations into calm weather: if their atmosphere resembles ours—which I cannot doubt—then I affirm that they will infallibly find the echoes strong on days when all thought of reflection “from the crests and slopes of the waves” must be discarded. The echoes afford the easiest access to the core of this question, and it is for this reason that I dwell upon them thus emphatically. It requires no refined skill or profound knowledge to master the conditions of their production; and these once mastered, the Lighthouse Board of Washington will find themselves in the real current of the phenomena, outside of which—I say it with respect—they are now vainly speculating. The acoustic deportment of the atmosphere in haze, fog, sleet, snow, rain, and hail will be no longer a mystery; even those “abnormal29 phenomena” which are now referred to an imaginary cause, or reserved for future investigation, will be found to fall naturally into place, as illustrations of a principle as simple as it is universal.
“With the instruments now at our disposal wisely established along our coasts, I venture to think that the saving of property, in ten years, will be an exceedingly large multiple of the outlay necessary for the establishment of such signals. The saving of life appeals to the higher motives of humanity.” Such were the words with which I wound up my Report on Fog-Signals.7 One year after their utterance, the “Schiller” goes to pieces on the Scilly rocks. A single calamity covers the predicted multiple, while the sea receives three hundred and thirty-three victims. As regards the establishment of fog-signals, energy has been hitherto paralyzed by their reputed uncertainty. We now know both the reason and the range of their variations; and such knowledge places it within our power to prevent disasters like the recent one. The inefficiency of bells, which caused their exclusion from our inquiry, was sadly illustrated in the case of the “Schiller.”
JOHN TYNDALL.
Royal institution, June, 1875.
In the following pages I have tried to render the science of Acoustics interesting to all intelligent persons, including those who do not possess any special scientific culture.
The subject is treated experimentally throughout, and I have endeavored so to place each experiment before the reader that he should realize it as an actual operation. My desire, indeed, has been to give distinct images of the various phenomena of acoustics, and to cause them to be seen mentally in their true relations.
I have been indebted to the kindness of some of my English friends for a more or less complete examination of the proof-sheets of this work. To my celebrated German friend Clausius, who has given himself the trouble of reading the proofs from beginning to end, my especial thanks are due and tendered.
There is a growing desire for scientific culture throughout the civilized world. The feeling is natural, and, under the circumstances, inevitable. For a power which influences so mightily the intellectual and material action of the age could not fail to arrest attention and challenge examination. In our schools and universities a movement in favor of science has begun which, no doubt, will end in the recognition of its claims, both as a source of knowledge and as a means of discipline. If by showing, however inadequately, the methods and results of physical science to men of influence, who derive their culture from another source, this book should indirectly aid in promoting the movement referred to, it will not have been written in vain.
SOUND
The Nerves and Sensation—Production and Propagation of Sonorous Motion—Experiments on Sounding Bodies placed in Vacuo—Deadening of Sound by Hydrogen—Action of Hydrogen on the Voice—Propagation of Sound through Air of Varying Density—Reflection of Sound—Echoes—Refraction of Sound—Diffraction of Sound; Case of Erith Village and Church—Influence of Temperature on Velocity—Influence of Density on Elasticity—Newton’s Calculation of Velocity—Thermal Changes Produced by the Sonorous Wave—Laplace’s Correction of Newton’s Formula—Ratio of Specific Heats at Constant Pressure and at Constant Volume deduced from Velocities of Sound—Mechanical Equivalent of Heat deduced from this Ratio—Inference that Atmospheric Air Possesses no Sensible Power to Radiate Heat—Velocity of Sound in Different Gases—Velocity in Liquids and Solids—Influence of Molecular Structure on the Velocity of Sound
THE various nerves of the human body have their origin in the brain, which is the seat of sensation. When the finger is wounded, the sensor nerves convey to the brain intelligence of the injury, and if these nerves be severed, however serious the hurt may be, no pain is experienced. We have the strongest reason for believing that what the nerves convey to the brain is in all cases motion. The motion here meant is not, however, that of the nerve as a whole, but of its molecules or smallest particles.8
Different nerves are appropriated to the transmission of different kinds of molecular motion. The nerves of taste, for example, are not competent to transmit the tremors of light, nor is the optic nerve competent to transmit sonorous vibrations. For these a special nerve is necessary, which passes from the brain into one of the cavities of the ear, and there divides into a multitude of filaments. It is the motion imparted to this, the auditory nerve, which, in the brain, is translated into sound.
Applying a flame to a small collodion balloon which contains a mixture of oxygen and hydrogen, the gases explode, and every ear in this room is conscious of a shock, which we name a sound. How was this shock transmitted from the balloon to our organs of hearing? Have the exploding gases shot the air-particles against the auditory nerve as a gun shoots a ball against a target? No doubt, in the neighborhood of the balloon, there is to some extent a propulsion of particles; but no particle of air from the vicinity of the balloon reached the ear of any person here present. The process was this: When the flame touched the mixed gases they combined chemically, and their union was accompanied by the development of intense heat. The heated air expanded suddenly, forcing the surrounding air violently away on all sides. This motion of the air close to the balloon was rapidly imparted to that a little further off, the air first set in motion coming at the same time to rest. The air, at a little distance, passed its motion on to the air at a greater distance, and came also in its turn to rest. Thus each shell of air, if I may use the term, surrounding the balloon took up the motion of the shell next preceding, and transmitted it to the next succeeding33 shell, the motion being thus propagated as a pulse or wave through the air.
The motion of the pulse must not be confounded with the motion of the particles which at any moment constitute the pulse. For while the wave moves forward through considerable distances, each particular particle of air makes only a small excursion to and fro.
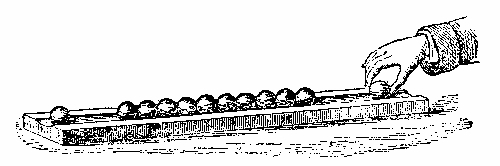
The process may be rudely represented by the propagation of motion through a row of glass balls, such as are employed in the game of solitaire. Placing the balls along a groove thus, Fig. 1, each of them touching its neighbor, and urging one of them against the end of the row: the motion thus imparted to the first ball is delivered up to the second, the motion of the second is delivered up to the third, the motion of the third is imparted to the fourth; each ball, after having given up its motion, returning itself to rest. The last ball only of the row flies away. In a similar way is sound conveyed from particle to particle through the air. The particles which fill the cavity of the ear are finally driven against the tympanic membrane, which is stretched across the passage leading from the external ear toward the brain. This membrane, which closes outwardly the “drum” of the ear, is thrown into vibration, its motion is transmitted34 to the ends of the auditory nerve, and afterward along that nerve to the brain, where the vibrations are translated into sound. How it is that the motion of the nervous matter can thus excite the consciousness of sound is a mystery which the human mind cannot fathom.
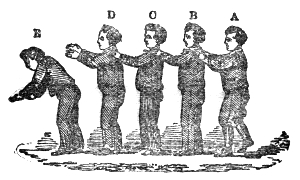
The propagation of sound may be illustrated by another homely but useful illustration. I have here five young assistants, A, B, C, D, and E, Fig. 2, placed in a row, one behind the other, each boy’s hands resting against the back of the boy in front of him. E is now foremost, and A finishes the row behind. I suddenly push A, A pushes B, and regains his upright position; B pushes C; C pushes D; D pushes E; each boy, after the transmission of the push, becoming himself erect. E, having nobody in front, is thrown forward. Had he been standing on the edge of a precipice, he would have fallen over; had he stood in contact with a window, he would have broken the glass; had he been close to a drumhead, he would have shaken the drum. “We could thus transmit a push through a row of a hundred boys, each particular boy, however, only swaying to and fro. Thus, also, we send sound through the air, and shake the drum of a distant ear, while each particular particle of the air35 concerned in the transmission of the pulse makes only a small oscillation.
But we have not yet extracted from our row of boys all that they can teach us. When A is pushed he may yield languidly, and thus tardily deliver up the motion to his neighbor B. B may do the same to C, C to D, and D to E. In this way the motion might be transmitted with comparative slowness along the line. But A, when pushed, may, by a sharp muscular effort and sudden recoil, deliver up promptly his motion to B, and come himself to rest; B may do the same to C, C to D, and D to E, the motion being thus transmitted rapidly along the line. Now this sharp muscular effort and sudden recoil is analogous to the elasticity of the air in the case of sound. In a wave of sound, a lamina of air, when urged against its neighbor lamina, delivers up its motion and recoils, in virtue of the elastic force exerted between them; and the more rapid this delivery and recoil, or in other words the greater the elasticity of the air, the greater is the velocity of the sound.

A very instructive mode of illustrating the transmission of a sound-pulse is furnished by the apparatus represented in Fig. 3, devised by my assistant, Mr. Cottrell. It consists of a series of wooden balls separated from each other by spiral springs. On striking the knob A, a rod attached to it impinges upon the first ball B, which transmits its motion to C, thence it passes to E, and so on through the entire series. The arrival at D is36 announced by the shock of the terminal ball against the wood, or, if we wish, by the ringing of a bell. Here the elasticity of the air is represented by that of the springs. The pulse may be rendered slow enough to be followed by the eye.
Scientific education ought to teach us to see the invisible as well as the visible in nature, to picture with the vision of the mind those operations which entirely elude bodily vision; to look at the very atoms of matter in motion and at rest, and to follow them forth, without ever once losing sight of them, into the world of the senses, and see them there integrating themselves in natural phenomena. With regard to the point now under consideration, we must endeavor to form a definite image of a wave of sound. We ought to see mentally the air-particles, when urged outward by the explosion of our balloon, crowding closely together; but immediately behind this condensation we ought to see the particles separated more widely apart. We must, in short, to be able to seize the conception that a sonorous wave consists of two portions, in the one of which the air is more dense, and in the other of which it is less dense than usual. A condensation and a rarefaction, then, are the two constituents of a wave of sound. This conception shall be rendered more complete in our next lecture.
That air is thus necessary to the propagation of sound
was proved by a celebrated experiment made before the
Royal Society, by a philosopher named Hawksbee, in
1705.9 He so fixed a bell within the receiver of an air-37pump that he could ring the bell when the receiver was
exhausted. Before the air was withdrawn the sound of
the bell was heard within the receiver; after the air was
withdrawn the sound became so faint as to be hardly
perceptible. An arrangement is before you which enables
us to repeat in a very perfect manner the experiment
of Hawksbee. Within this jar, G G′, Fig. 4, resting
on the plate of an air-pump is a
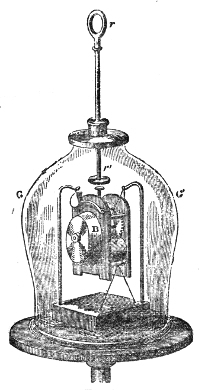 Fig. 4.
bell, B, associated with cloc-kwork.10
After the jar has been exhausted
as perfectly as possible, I release,
by means of a rod, r r′, which
passes air-tight through the top
of the vessel, the detent which
holds the hammer. It strikes,
and you see it striking, but only
those close to the bell can hear
the sound. Hydrogen gas, which
you know is fourteen times lighter
than air, is now allowed to enter
the vessel. The sound of the bell
is not augmented by the presence
of this attenuated gas, though the
receiver is now full of it. By
working the pump, the atmosphere
round the bell is rendered still more attenuated.
In this way we obtain a vacuum more perfect than that
of Hawksbee, and this is important, for it is the last
traces of air that are chiefly effective in this experiment.
You now see the hammer pounding the bell, but you
38hear no sound. Even when the ear is placed against
the exhausted receiver not the faintest tinkle is heard.
Observe also that the bell is suspended by strings, for
if it were allowed to rest upon the plate of the air-pump
the vibrations would be communicated to the plate, and
thence transmitted to the air outside. Permitting the air
to enter the jar with as little noise as possible, you immediately
hear a feeble sound, which grows louder as the
air becomes more dense, until finally every person in this
large assembly distinctly hears the ringing of the bell.11
Fig. 4.
bell, B, associated with cloc-kwork.10
After the jar has been exhausted
as perfectly as possible, I release,
by means of a rod, r r′, which
passes air-tight through the top
of the vessel, the detent which
holds the hammer. It strikes,
and you see it striking, but only
those close to the bell can hear
the sound. Hydrogen gas, which
you know is fourteen times lighter
than air, is now allowed to enter
the vessel. The sound of the bell
is not augmented by the presence
of this attenuated gas, though the
receiver is now full of it. By
working the pump, the atmosphere
round the bell is rendered still more attenuated.
In this way we obtain a vacuum more perfect than that
of Hawksbee, and this is important, for it is the last
traces of air that are chiefly effective in this experiment.
You now see the hammer pounding the bell, but you
38hear no sound. Even when the ear is placed against
the exhausted receiver not the faintest tinkle is heard.
Observe also that the bell is suspended by strings, for
if it were allowed to rest upon the plate of the air-pump
the vibrations would be communicated to the plate, and
thence transmitted to the air outside. Permitting the air
to enter the jar with as little noise as possible, you immediately
hear a feeble sound, which grows louder as the
air becomes more dense, until finally every person in this
large assembly distinctly hears the ringing of the bell.11
Sir John Leslie found hydrogen singularly incompetent to act as the vehicle of the sound of a bell rung in the gas. More than this, he emptied a receiver like that before you of half its air, and plainly heard the ringing of the bell. On permitting hydrogen to enter the half-filled receiver until it was wholly filled, the sound sank until it was scarcely audible. This result remained an enigma until it received a simple and satisfactory explanation at the hands of Prof. Stokes. When a common pendulum oscillates it tends to form a condensation in front and a rarefaction behind. But it is only a tendency; the motion is so slow, and the air is so elastic, that it moves away in front before it is sensibly condensed, and fills the space behind before it can become sensibly dilated. Hence waves or pulses are not generated by the pendulum. It requires a certain sharpness of shock to produce the condensation and rarefaction which constitute a wave of sound in air.
The more elastic and mobile the gas, the more able will it be to move away in front and to fill the space behind, and thus to oppose the formation of rarefactions and condensations by a vibrating body. Now hydrogen is much more mobile than air; and hence the production of sonorous waves in it is attended with greater difficulty than in air. A rate of vibration quite competent to produce sound-waves in the one may be wholly incompetent to produce them in the other. Both calculation and observation prove the correctness of this explanation, to which we shall again refer.
At great elevations in the atmosphere sound is sensibly diminished in loudness. De Saussure thought the explosion of a pistol at the summit of Mont Blanc to be about equal to that of a common cracker below. I have several times repeated this experiment; first, in default of anything better, with a little tin cannon, the torn remnants of which are now before you, and afterward with pistols. What struck me was the absence of that density and sharpness in the sound which characterize it at lower elevations. The pistol-shot resembled the explosion of a champagne bottle, but it was still loud. The withdrawal of half an atmosphere does not very materially affect our ringing bell, and air of the density found at the top of Mont Blanc is still capable of powerfully affecting the auditory nerve. That highly attenuated air is able to convey sound of great intensity is forcibly illustrated by the explosion of meteorites at elevations where the tenuity of the atmosphere must be almost infinite. Here, however, the initial disturbance must be exceedingly great.
The motion of sound, like all other motion, is en40feebled by its transference from a light body to a heavy one. When the receiver which has hitherto covered our bell is removed you hear how much more loudly it rings in the open air. When the bell was covered the aërial vibrations were first communicated to the heavy glass jar, and afterward by the jar to the air outside; a great diminution of intensity being the consequence. The action of hydrogen gas upon the voice is an illustration of the same kind. The voice is formed by urging air from the lungs through an organ called the larynx, where it is thrown into vibration by the vocal chords which thus generate sound. But when the lungs are filled with hydrogen, the vocal chords on speaking produce a vibratory motion in the hydrogen, which then transfers the motion to the outer air. By this transference from a light gas to a heavy one the voice is so weakened as to become a mere squeak.12
The intensity of a sound depends on the density of the air in which the sound is generated, and not on that of the air in which it is heard.13 Supposing the summit of Mont Blanc to be equally distant from the top of the Aiguille Verte and the bridge at Chamouni; and supposing two observers stationed, the one upon the bridge and the other upon the Aiguille: the report of a cannon fired on Mont Blanc would reach both observers with the same intensity, though in the one case the sound would pursue its way through the rare air above, while in the other it would descend though the denser air below. Again, let a straight line equal to that from the bridge 41at Chamouni to the summit of Mont Blanc be measured along the earth’s surface in the valley of Chamouni, and let two observers be stationed, the one on the summit and the other at the end of the line: the report of a cannon fired on the bridge would reach both observers with the same intensity, though in the one case the sound would be propagated through the dense air of the valley, and in the other case would ascend through the rarer air of the mountain. Finally, charge two cannon equally, and fire one of them at Chamouni and the other at the top of Mont Blanc: the one fired in the heavy air below may be heard above, while the one fired in the light air above is unheard below.
In the case of our exploding balloon the wave of sound expands on all sides, the motion produced by the explosion being thus diffused over a continually augmenting mass of air. It is perfectly manifest that this cannot occur without an enfeeblement of the motion. Take the case of a thin shell of air with a radius of one foot, reckoned from the centre of explosion. A shell of air of the same thickness, but of two feet radius, will contain four times the quantity of matter; if its radius be three feet, it will contain nine times the quantity of matter; if four feet, it will contain sixteen times the quantity of matter, and so on. Thus the quantity of matter set in motion augments as the square of the distance from the centre of explosion. The intensity or loudness of sound diminishes in the same proportion. We express this law by saying that the intensity of the sound varies inversely as the square of the distance.
Let us look at the matter in another light. The mechanical effect of a ball striking a target depends on two things—the weight of the ball, and the velocity with which it moves. The effect is proportional to the weight simply; but it is proportional to the square of the velocity. The proof of this is easy, but it belongs to ordinary mechanics rather than to our present subject. Now what is true of the cannon-ball striking a target is also true of an air-particle striking the tympanum of the ear. Fix your attention upon a particle of air as the sound-wave passes over it; it is urged from its position of rest toward a neighbor particle, first with an accelerated motion, and then with a retarded one. The force which first urges it is opposed by the resistance of the air, which finally stops the particle and causes it to recoil. At a certain point of its excursion the velocity of the particle is its maximum. The intensity of the sound is proportional to the square of this maximum velocity.
The distance through which the air-particle moves to and fro, when the sound-wave passes it, is called the amplitude of the vibration. The intensity of the sound is proportional to the square of the amplitude.
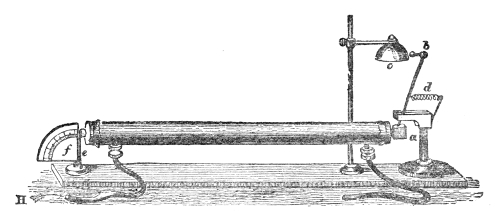
This weakening of the sound, according to the law of inverse squares, would not take place if the sound-wave were so confined as to prevent its lateral diffusion. By sending it through a tube with a smooth interior surface we accomplish this, and the wave thus confined may be transmitted to great distances with very little diminution of intensity. Into one end of this tin tube, fifteen feet long, I whisper in a manner quite inaudible to the peo43ple nearest to me, but a listener at the other end hears me distinctly. If a watch be placed at one end of the tube, a person at the other end hears the ticks, though nobody else does. At the distant end of the tube is now placed a lighted candle, c, Fig. 5. When the hands are clapped at this end, the flame instantly ducks down at the other. It is not quite extinguished, but it is forcibly depressed. When two books, B B′, Fig. 5, are clapped together, the candle is blown out.14 You may here observe, in a rough way, the speed with which the sound-wave is propagated. The instant the clap is heard the flame is extinguished. I do not say that the time required by the sound to travel this tube is immeasurably short, but simply that the interval is too short for your senses to appreciate it.
That it is a pulse and not a puff of air is proved by filling one end of the tube with the smoke of brown paper. On clapping the books together no trace of this smoke is ejected from the other end. The pulse has passed through both smoke and air without carrying either of them along with it.
An effective mode of throwing the propagation of a 44pulse through air has been devised by my assistant. The two ends of a tin tube fifteen feet long are stopped by sheet India-rubber stretched across them. At one end, e, a hammer with a spring handle rests against the India-rubber; at the other end is an arrangement for the striking of a bell, c. Drawing back the hammer e to a distance measured on the graduated circle and liberating it, the generated pulse is propagated through the tube, strikes the other end, drives away the cork termination a of the lever a b, and causes the hammer b to strike the bell. The rapidity of propagation is well illustrated here. When hydrogen (sent through the India-rubber tube H) is substituted for air the bell does not ring.
The celebrated French philosopher, Biot, observed the transmission of sound through the empty water-pipes of Paris, and found that he could hold a conversation in a low voice through an iron tube 3,120 feet in length. The lowest possible whisper, indeed, could be heard at this distance, while the firing of a pistol into one end of the tube quenched a lighted candle at the other.
The action of sound thus illustrated is exactly the same as that of light and radiant heat. They, like sound, are wave-motions. Like sound they diffuse themselves in space, diminishing in intensity according to the same law. Like sound also, light and radiant heat, when sent through a tube with a reflecting interior surface, may be conveyed to great distances with comparatively little loss. In fact, every experiment on the reflection of light has its analogy in the reflection of sound. On yonder gallery stands an electric lamp, placed close to the clock of this lecture-room. An assistant in the gallery ignites the lamp, and directs its powerful beam upon a mirror placed here behind the lecture-table. By the act of reflection the divergent beam is converted into this splendid luminous cone traced out upon the dust of the room. The point of convergence being marked and the lamp extinguished, I place my ear at that point. Here every sound-wave sent forth by the clock and reflected by the mirror is gathered up, and the ticks are heard as if they came, not from the clock, but from the mirror. Let us stop the clock, and place a watch w, Fig. 7, at the place occupied a moment ago by the electric light. At this great distance the ticking of the watch is distinctly heard. The hearing is much aided by introducing the end f of a glass funnel into the ear, the funnel here acting the part of an ear-trumpet. We know, moreover, that in optics the positions of a body and of its image are reversible. When a candle is placed at this lower focus, you see its image on the gallery above, and I have only to turn the mirror on its stand to make the46 image of the flame fall upon any one of the row of persons who occupy the front seat in the gallery. Removing the candle, and putting the watch, w, Fig. 8, in its place, the person on whom the light falls distinctly hears the sound. When the ear is assisted by the glass funnel, the reflected ticks of the clock in our first experiment are so powerful as to suggest the idea of something pounding against the tympanum, while the direct ticks are scarcely if at all, heard.
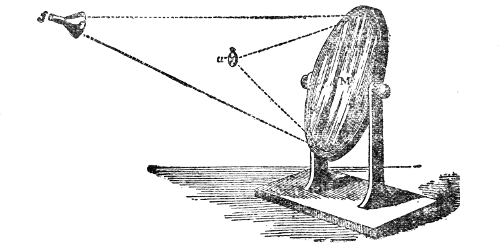
One of these two parabolic mirrors, n n′, Fig. 9, is
placed upon the table, the other, m m′, being drawn up
to the ceiling of this theatre; they are five-and-twenty
feet apart. When the carbon-points of the electric light
are placed in the focus a of the lower mirror and ignited,
a fine luminous cylinder rises like a pillar to the upper
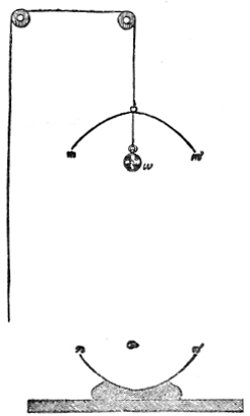 Fig. 9.
mirror, which brings the
parallel beam to a focus.
At that focus is seen a
spot of sunlike brilliancy,
due to the reflection of
the light from the surface
of a watch, w, there
suspended. The watch is
ticking, but in my present
position I do not hear
it. At this lower focus,
a, however, we have the
energy of every sonorous
wave converged. Placing
the ear at a, the ticking
is as audible as if the
watch were at hand; the
sound, as in the former
case, appearing to proceed,
not from the watch itself, but from the lower mirror.15
Fig. 9.
mirror, which brings the
parallel beam to a focus.
At that focus is seen a
spot of sunlike brilliancy,
due to the reflection of
the light from the surface
of a watch, w, there
suspended. The watch is
ticking, but in my present
position I do not hear
it. At this lower focus,
a, however, we have the
energy of every sonorous
wave converged. Placing
the ear at a, the ticking
is as audible as if the
watch were at hand; the
sound, as in the former
case, appearing to proceed,
not from the watch itself, but from the lower mirror.15
Curved roofs and ceilings and bellying sails act as mirrors upon sound. In our old laboratory, for example, 48the singing of a kettle seemed, in certain positions, to come, not from the fire on which it was placed, but from the ceiling. Inconvenient secrets have been thus revealed, an instance of which has been cited by Sir John Herschel.16 In one of the cathedrals in Sicily the confessional was so placed that the whispers of the penitents were reflected by the curved roof, and brought to a focus at a distant part of the edifice. The focus was discovered by accident, and for some time the person who discovered it took pleasure in hearing, and in bringing his friends to hear, utterances intended for the priest alone. One day, it is said, his own wife occupied the penitential stool, and both he and his friends were thus made acquainted with secrets which were the reverse of amusing to one of the party.
When a sufficient interval exists between a direct and a reflected sound, we hear the latter as an echo.
Sound, like light, may be reflected several times in succession, and, as the reflected light under these circumstances becomes gradually feebler to the eye, so the successive echoes become gradually feebler to the ear. In mountain regions this repetition and decay of sound produce wonderful and pleasing effects. Visitors to Killarney will remember the fine echo in the Gap of Dunloe. When a trumpet is sounded in the proper place in the Gap, the sonorous waves reach the ear in succession after one, two, three, or more reflections from the adjacent cliffs, and thus die away in the sweetest cadences. There is a deep cul-de-sac, called the Ochsenthal, formed by the great cliffs of the Engelhörner, near Rosenlaui, in Switzerland, where the echoes warble in a wonderful manner.
The sound of the Alpine horn, echoed from the rocks of the Wetterhorn or the Jungfrau, is in the first instance heard roughly. But by successive reflections the notes are rendered more soft and flute-like, the gradual diminution of intensity giving the impression that the source of sound is retreating further and further into the solitudes of ice and snow. The repetition of echoes is also in part due to the fact that the reflecting surfaces are at different distances from the hearer.
In large, unfurnished rooms the mixture of direct and reflected sound sometimes produces very curious effects. Standing, for example, in the gallery of the Bourse at Paris, you hear the confused vociferation of the excited multitude below. You see all the motions—of their lips as well as of their hands and arms. You know they are speaking—often, indeed, with vehemence—but what they say you know not. The voices mix with their echoes into a chaos of noise, out of which no intelligible utterance can emerge. The echoes of a room are materially damped by its furniture. The presence of an audience may also render intelligible speech possible where, without an audience, the definition of the direct voice is destroyed by its echoes. On the 16th of May, 1865, having to lecture in the Senate House of the University of Cambridge, I first made some experiments as to the loudness of voice necessary to fill the room, and was dismayed to find that a friend, placed at a distant part of the hall, could not follow me because of the echoes. The assembled audience, however, so quenched the sonorous waves that the echoes were practically absent, and my voice was plainly heard in all parts of the Senate House.
Sounds are also said to be reflected from the clouds.50 Arago reports that, when the sky is clear, the report of a cannon on an open plain is short and sharp, while a cloud is sufficient to produce an echo like the rolling of distant thunder. The subject of aërial echoes will be subsequently treated at length, when it will be shown that Arago’s conclusion requires correction.
Sir John Herschel, in his excellent article “Sound,” In the “Encyclopædia Metropolitana,” has collected with others the following instances of echoes. An echo in Woodstock Park repeats seventeen syllables by day and twenty by night; one, on the banks of the Lago del Lupo, above the fall of Terni, repeats fifteen. The tick of a watch may be heard from one end of the abbey church of St. Albans to the other. In Gloucester Cathedral, a gallery of an octagonal form conveys a whisper seventy-five feet across the nave. In the whispering-gallery of St. Paul’s, the faintest sound is conveyed from one side to the other of the dome, but is not heard at any intermediate point. At Carisbrook Castle, in the Isle of Wight, is a well two hundred and ten feet deep and twelve wide. The interior is lined by smooth masonry; when a pin is dropped into the well it is distinctly heard to strike the water. Shouting or coughing into this well produces a resonant ring of some duration.17
Another important analogy between sound and light has been established by M. Sondhauss.18 When a large lens is placed in front of our lamp, the lens compels the rays of light that fall upon it to deviate from their direct and divergent course, and to form a convergent cone behind it. This refraction of the luminous beam is a consequence of the retardation suffered by the light in passing through the glass. Sound may be similarly refracted by causing it to pass through a lens which retards its motion. Such a lens is formed when we fill a thin balloon with some gas heavier than air. A collodion balloon, B, Fig. 10, filled with carbonic-acid gas, the envelope being so thin as to yield readily to the pulses which strike against it, answers the purpose.19 A watch, w, is hung up close to the lens, beyond which, and at a distance of four or five feet from the lens, is placed the ear, assisted by the glass funnel f f′. By moving the head about, a position is soon discovered in which the ticking is particularly loud. This, in fact, is the focus of the 52lens. If the ear be moved from this focus the intensity of the sound falls; if, when the ear is at the focus, the balloon be removed, the ticks are enfeebled; on replacing the balloon their force is restored. The lens, in fact, enables us to hear the ticks distinctly when they are perfectly inaudible to the unaided ear.
How a sound-wave is thus converged may be comprehended
by reference to Fig. 11. Let m o n o″ be a section
of the sound-lens, and a b a portion of a sonorous
wave approaching it from a distance. The middle point,
o, of the wave first touches the lens, and is first retarded
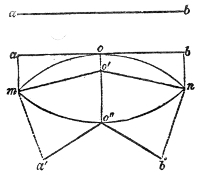 Fig. 11.
by it. By the time the ends
a and b, still moving through
air, reach the balloon, the middle
point o, pursuing its way through
the heavier gas within, will have
only reached o′. The wave is
therefore broken at o; and the
direction of motion being at right
angles to the face of the wave,
the two halves will encroach upon each other. This
convergence of the two halves of the wave is augmented
on quitting the lens. For when o′ has reached o″, the
two ends a and b will have pushed forward to a greater
distance, say to a′ and b′. Soon afterward the two halves
of the wave will cross each other, or in other words
come to a focus, the air at the focus being agitated by
the sum of the motions of the two waves.20
Fig. 11.
by it. By the time the ends
a and b, still moving through
air, reach the balloon, the middle
point o, pursuing its way through
the heavier gas within, will have
only reached o′. The wave is
therefore broken at o; and the
direction of motion being at right
angles to the face of the wave,
the two halves will encroach upon each other. This
convergence of the two halves of the wave is augmented
on quitting the lens. For when o′ has reached o″, the
two ends a and b will have pushed forward to a greater
distance, say to a′ and b′. Soon afterward the two halves
of the wave will cross each other, or in other words
come to a focus, the air at the focus being agitated by
the sum of the motions of the two waves.20
When a long sea-roller meets an isolated rock in its passage, it rises against the rock and embraces it all round. Facts of this nature caused Newton to reject the undulatory theory of light. He contended that if light were a product of wave-motion we could have no shadows, because the waves of light would propagate themselves round opaque bodies as a wave of water round a rock. It has been proved since his time that the waves of light do bend round opaque bodies; but with that we have nothing now to do. A sound-wave certainly bends thus round an obstacle, though as it diffuses itself in the air at the back of the obstacle it is enfeebled in power, the obstacle thus producing a partial shadow of the sound. A railway train passing through cuttings and long embankments exhibits great variations in the intensity of the sound. The interposition of a hill in the Alps suffices to diminish materially the sound of a cataract; it is able sensibly to extinguish the tinkle of the cowbells. Still the sound-shadow is but partial, and the marker at the rifle-butts never fails to hear the explosion, though he is well protected from the ball. A striking example of this diffraction of a sonorous wave was exhibited at Erith after the tremendous explosion of a powder magazine which occurred there in 1864. The village of Erith was some miles distant from the magazine, but in nearly all cases the windows were shattered; and it was noticeable that the windows turned away from the origin of the explosion suffered almost as much as those which faced it. Lead sashes were employed in Erith54 Church, and these, being in some degree flexible, enabled the windows to yield to pressure without much fracture of the glass. As the sound-wave reached the church it separated right and left, and, for a moment, the edifice was clasped by a girdle of intensely compressed air, every window in the church, front and back, being bent inward. After compression, the air within the church no doubt dilated, tending to restore the windows to their first condition. The bending in of the windows, however, produced but a small condensation of the whole mass of air within the church; the recoil was therefore feeble in comparison with the pressure, and insufficient to undo what the latter had accomplished.
Two conditions determine the velocity of propagation of a sonorous wave; namely, the elasticity and the density of the medium through which the wave passes. The elasticity of air is measured by the pressure which it sustains or can hold in equilibrium. At the sea-level this pressure is equal to that of a stratum of mercury about thirty inches high. At the summit of Mont Blanc the barometric column is not much more than half this height; and, consequently, the elasticity of the air upon the summit of the mountain is not much more than half what it is at the sea-level.
If we could augment the elasticity of air, without at the same time augmenting its density, we should augment the velocity of sound. Or, if allowing the elasticity to remain constant we could diminish the density, we should augment the velocity. Now, air in a closed vessel, where55 it cannot expand, has its elasticity augmented by heat, while its density remains unchanged. Through such heated air sound travels more rapidly than through cold air. Again, air free to expand has its density lessened by warming, its elasticity remaining the same, and through such air sound travels more rapidly than through cold air. This is the case with our atmosphere when heated by the sun.
The velocity of sound in air, at the freezing temperature, is 1,090 feet a second.
At all lower temperatures the velocity is less than this, and at all higher temperatures it is greater. The late M. Wertheim has determined the velocity of sound in air of different temperatures, and here are some of his results:
| Temperature of air | Velocity of sound | |
| 0·5° | centigrade | 1,089 feet |
| 2·10 | ” | 1,091 ” |
| 8·5 | ” | 1,109 ” |
| 12·0 | ” | 1,113 ” |
| 26·6 | ” | 1,140 ” |
At a temperature of half a degree above the freezing-point of water the velocity is 1,089 feet a second; at a temperature of 26·6 degrees, it is 1,140 feet a second, or a difference of 51 feet for 26 degrees; that is to say, an augmentation of velocity of nearly two feet for every single degree centigrade.
With the same elasticity the density of hydrogen gas is much less than that of air, and the consequence is that the velocity of sound in hydrogen far exceeds its velocity in air. The reverse holds good for heavy carbonic-acid gas. If density and elasticity vary in the same proportion, as the law of Boyle and Mariotte proves them to56 do in air when the temperature is preserved constant, they neutralize each other’s effects; hence, if the temperature were the same, the velocity of sound upon the summits of the highest Alps would be the same as that at the mouth of the Thames. But, inasmuch as the air above is colder than that below, the actual velocity on the summits of the mountains is less than that at the sea-level. To express this result in stricter language, the velocity is directly proportional to the square root of the elasticity of the air; it is also inversely proportional to the square root of the density of the air. Consequently, as in air of a constant temperature elasticity and density vary in the same proportion, and act oppositely, the velocity of sound is not affected by a change of density, if unaccompanied by a change of temperature.
There is no mistake more common than to suppose the velocity of sound to be augmented by density. The mistake has arisen from a misconception of the fact that in solids and liquids the velocity is greater than in gases. But it is the higher elasticity of those bodies, in relation to their density, that causes sound to pass rapidly through them. Other things remaining the same, an augmentation of density always produces a diminution of velocity. Were the elasticity of water, which is measured by its compressibility, only equal to that of air, the velocity of sound in water, instead of being more than quadruple the velocity in air, would be only a small fraction of that velocity. Both density and elasticity, then, must be always borne in mind; the velocity of sound being determined by neither taken separately, but by the relation of the one to the other. The effect of small density and high elasticity is exemplified in an astonishing57 manner by the luminiferous ether, which transmits the vibrations of light—not at the rate of so many feet, but at the rate of nearly two hundred thousand miles a second.
Those who are unacquainted with the details of scientific investigation have no idea of the amount of labor expended in the determination of those numbers on which important calculations or inferences depend. They have no idea of the patience shown by a Berzelius in determining atomic weights; by a Regnault in determining coefficients of expansion; or by a Joule in determining the mechanical equivalent of heat. There is a morality brought to bear upon such matters which, in point of severity, is probably without a parallel in any other domain of intellectual action. Thus, as regards the determination of the velocity of sound in air, hours might be filled with a simple statement of the efforts made to establish it with precision. The question has occupied the attention of experimenters in England, France, Germany, Italy, and Holland. But to the French and Dutch philosophers we owe the application of the last refinements of experimental skill to the solution of the problem. They neutralized effectually the influence of the wind; they took into account barometric pressure, temperature, and hygrometric condition. Sounds were started at the same moment from two distant stations, and thus caused to travel from station to station through the self-same air. The distance between the stations was determined by exact trigonometrical observations, and means were devised for measuring with the utmost accuracy the time required by the sound to pass from the one station to the other. This time, expressed in sec58onds, divided into the distance expressed in feet, gave 1,090 feet per second as the velocity of sound through air at the temperature of 0° centigrade.
The time required by light to travel over all terrestrial distances is practically zero; and in the experiments just referred to the moment of explosion was marked by the flash of a gun, the time occupied by the sound in passing from station to station being the interval observed between the appearance of the flash and the arrival of the sound. The velocity of sound in air once established, it is plain that we can apply it to the determination of distances. By observing, for example, the interval between the appearance of a flash of lightning and the arrival of the accompanying thunder-peal, we at once determine the distance of the place of discharge. It is only when the interval between the flash and peal is short that danger from lightning is to be apprehended.
We now come to one of the most delicate points in
the whole theory of sound. The velocity through air has
been determined by direct experiment; but knowing the
elasticity and density of the air, it is possible, without
any experiment at all, to calculate the velocity with
which a sound-wave is transmitted through it. Sir Isaac
Newton made this calculation, and found the velocity at
the freezing temperature to be 916 feet a second. This is
about one-sixth less than actual observation had proved
the velocity to be, and the most curious suppositions
were made to account for the discrepancy. Newton himself
threw out the conjecture that it was only in passing59
from particle to particle of the air that sound required
time for its transmission; that it moved instantaneously
through the particles themselves. He then supposed the
line along which sound passes to be occupied by air-particles
for one-sixth of its extent, and thus he sought
to make good the missing velocity. The very art and ingenuity
of this assumption were sufficient to throw doubt
on it; other theories were therefore advanced, but the
great French mathematician Laplace was the first
 Fig. 12.
to completely solve the enigma. I shall now endeavor
to make you thoroughly acquainted with
his solution.
Fig. 12.
to completely solve the enigma. I shall now endeavor
to make you thoroughly acquainted with
his solution.
Into this strong cylinder of glass, T U, Fig. 12, which is accurately bored, and quite smooth within, fits an air-tight piston. By pushing the piston down, I condense the air beneath it, heat being at the same time developed. A scrap of amadou attached to the bottom of the piston is ignited by the heat generated by compression. If a bit of cotton wool dipped into bisulphide of carbon be attached to the piston, when the latter is forced down, a flash of light, due to the ignition of the bisulphide of carbon vapor, is observed within the tube. It is thus proved that when air is compressed heat is generated. By another experiment it may be shown that when air is rarefied cold is developed. This brass box contains a quantity of condensed air. I open the cock, and permit the air to discharge itself against a suitable thermometer; the sinking of the instrument immediately declares the chilling of the air.
All that you have heard regarding the transmission of60 a sonorous pulse through air is, I trust, still fresh in your minds. As the pulse advances it squeezes the particles of air together, and two results follow from this compression. First, its elasticity is augmented through the mere augmentation of its density. Secondly, its elasticity is augmented by the heat of compression. It was the change of elasticity which resulted from a change of density that Newton took into account, and he entirely overlooked the augmentation of elasticity due to the second cause just mentioned. Over and above, then, the elasticity involved in Newton’s calculation, we have an additional elasticity due to changes of temperature produced by the sound-wave itself. When both are taken into account, the calculated and the observed velocities agree perfectly.
But here, without due caution, we may fall into the gravest error. In fact, in dealing with Nature, the mind must be on the alert to seize all her conditions; otherwise we soon learn that our thoughts are not in accordance with her facts. It is to be particularly noted that the augmentation of velocity due to the changes of temperature produced by the sonorous wave itself is totally different from the augmentation arising from the heating of the general mass of the air. The average temperature of the air is unchanged by the waves of sound. We cannot have a condensed pulse without having a rarefied one associated with it. But in the rarefaction, the temperature of the air is as much lowered as it is raised in the condensation. Supposing, then, the atmosphere parcelled out into such condensations and rarefactions, with their respective temperatures, an extraneous sound passing through such an atmosphere would be as much re61tarded in the latter as accelerated in the former, and no variation of the average velocity could result from such a distribution of temperature.
Whence, then, does the augmentation pointed out by Laplace arise? I would ask your best attention while I endeavor to make this knotty point clear to you. If air be compressed it becomes smaller in volume; if the pressure be diminished, the volume expands. The force which resists compression, and which produces expansion, is the elastic force of the air. Thus an external pressure squeezes the air-particles together; their own elastic force holds them asunder, and the particles are in equilibrium when these two forces are in equilibrium. Hence it is that the external pressure is a measure of the elastic force. Let the middle row of dots, Fig. 13, represent a series of air-particles in a state of quiescence between the points a and x. Then, because of the elastic force exerted between the particles, if any one of them be moved from its position of rest, the motion will be transmitted through the entire series. Supposing the particle a to be driven by the prong of a tuning-fork, or some other vibrating body, toward x, so as to be caused finally to occupy the position a′ in the lowest row of particles: at the instant the excursion of a commences, its motion begins62 to be transmitted to b. In the next following moments b transmits the motion to c, c to d, d to e, and so on. So that by the time a has reached the position a′, the motion will have been propagated to some point o′ of the line of particles more or less distant from a′. The entire series of particles between a′ and o′ is then in a state of condensation. The distance a′ o′, over which the motion has travelled during the excursion of a to a′, will depend upon the elastic force exerted between the particles. Fix your attention on any two of the particles, say a and b. The elastic force between them may be figured as a spiral spring, and it is plain that the more flaccid this spring the more sluggish would be the communication of the motion from a to b; while the stiffer the spring the more prompt would be the communication of the motion. What is true of a and b is true for every other pair of particles between a and o. Now the spring between every pair of these particles is suddenly stiffened by the heat developed along the line of condensation, and hence the velocity of propagation is augmented by this heat. Reverting to our old experiment with the row of boys, it is as if, by the very act of pushing his neighbor, the muscular rigidity of each boy’s arm was increased, thus enabling him to deliver his push more promptly than he would have done without this increase of rigidity. The condensed portion of a sonorous wave is propagated in the manner here described, and it is plain that the velocity of propagation is augmented by the heat developed in the condensation.
Let us now turn our thoughts for a moment to the propagation of the rarefaction. Supposing, as before, the middle row a x to represent the particles of air in equi63librium under the pressure of the atmosphere, and suppose the particle a to be suddenly drawn to the right, so as to occupy the position a″ in the highest line of dots: a″ is immediately followed by b″, b″ by c″, c″ by d″, d″ by e″; and thus the rarefaction is propagated backward toward x″, reaching a point o″ in the line of particles by the time a has completed its motion to the right. Now, why does b″ follow a″ when a″ is drawn away from it? Manifestly because the elastic force exerted between b″ and a″ is less than that between b″ and c″. In fact, b″ will be driven after a″ by a force equal to the difference of the two elasticities between a″ and b″ and between b″ and c″. The same remark applies to the motion of c″ after b″, to that of d″ after c″, in fact, to the motion of each succeeding particle when it follows its predecessor. The greater the difference of elasticity on the two sides of any particle the more promptly will it follow its predecessor. And here observe what the cold of rarefaction accomplishes. In addition to the diminution of the elastic force between a″ and b″ by the withdrawal of a″ to a greater distance, there is a further diminution due to the lowering of the temperature. The cold developed augments the difference of elastic force on which the propagation of the rarefaction depends. Thus we see that because the heat developed in the condensation augments the rapidity of the condensation, and because the cold developed in the rarefaction augments the rapidity of the rarefaction, the sonorous wave, which consists of a condensation and a rarefaction, must have its velocity augmented by the heat and the cold which it develops during its own progress.
It is worth while fixing your attention here upon the64 fact that the distance a′ o′, to which the motion has been propagated while a is moving to the position a′, may be vastly greater than that passed over in the same time by the particle itself. The excursion of a′ may not be more than a small fraction of an inch, while the distance to which the motion is transferred during the time required by a′ to perform this small excursion may be many feet, or even many yards. If this point should not appear altogether plain to you now, it will appear so by and by.
Having grasped this, even partially, I will ask you to accompany me to a remote corner of the domain of physics, with the view, however, of showing that remoteness does not imply discontinuity. Let a certain quantity of air at a temperature of 0°, contained in a perfectly inexpansible vessel, have its temperature raised 1°. Let the same quantity of air, placed in a vessel which permits the air to expand when it is heated—the pressure on the air being kept constant during its expansion—also have its temperature raised 1°. The quantities of heat employed in the two cases are different. The one quantity expresses what is called the specific heat of air at constant volume; the other the specific heat of air at constant pressure.21 It is an instance of the manner in which apparently unrelated natural phenomena are bound together, that from the calculated and observed velocities of sound in air we can deduce the ratio of these two specific heats. Squaring Newton’s theoretic velocity and 65 the observed velocity, and dividing the greater square by the less, we obtain the ratio referred to. Calling the specific heat at constant volume Cv, and that at constant pressure Cp; calling, moreover, Newton’s calculated velocity V, and the observed velocity V′, Laplace proved that—
Inserting the values of V and V′ in this equation, and making the calculation, we find—
Thus, without knowing either the specific heat at constant volume or at constant pressure, Laplace found the ratio of the greater of them to the less to be 1·42. It is evident from the foregoing formulæ that the calculated velocity of sound, multiplied by the square root of this ratio, gives the observed velocity.
But there is one assumption connected with the determination of this ratio, which must be here brought clearly forth. It is assumed that the heat developed by compression remains in the condensed portion of the wave, and applies itself there to augment the elasticity; that no portion of it is lost by radiation. If air were a powerful radiator, this assumption could not stand. The heat developed in the condensation could not then remain in the condensation. It would radiate all round, lodging itself for the most part in the chilled and rarefied portion of the wave, which would be gifted with a proportionate power of absorption. Hence the direct tendency of radiation would be to equalize the temperatures of the differ66ent parts of the wave, and thus to abolish the increase of velocity which called forth Laplace’s correction.22
The question, then, of the correctness of this ratio involves the other and apparently incongruous question, whether atmospheric air possesses any sensible radiative power. If the ratio be correct, the practical absence of radiative power on the part of air is demonstrated. How then are we to ascertain whether the ratio is correct or not? By a process of reasoning which illustrates still further how natural agencies are intertwined. It was this ratio, looked at by a man of genius, named Mayer, which helped him to a clearer and a grander conception of the relation and interaction of the forces of inorganic and organic nature than any philosopher up to his time had attained. Mayer was the first to see that the excess 0·42 of the specific heat at constant pressure over that at constant volume was the quantity of heat consumed in the work performed by the expanding gas. Assuming the air to be confined laterally and to expand in a vertical direction, in which direction it would simply have to lift the weight of the atmosphere, he attempted to calculate the precise amount of heat consumed in the raising of this or any other weight. He thus sought to determine the “mechanical equivalent” of heat. In the combination of his data his mind was clear, but for the numerical 67correctness of these data he was obliged to rely upon the experimenters of his age. Their results, though approximately correct, were not so correct as the transcendent experimental ability of Regnault, aided by the last refinements of constructive skill, afterward made them. Without changing in the slightest degree the method of his thought or the structure of his calculation, the simple introduction of the exact numerical data into the formula of Mayer brings out the true mechanical equivalent of heat.
But how are we able to speak thus confidently of the accuracy of this equivalent? We are enabled to do so by the labors of an Englishman, who worked at this subject contemporaneously with Mayer; and who, while animated by the creative genius of his celebrated German brother, enjoyed also the opportunity of bringing the inspirations of that genius to the test of experiment. By the immortal experiments of Mr. Joule, the mutual convertibility of mechanical work and heat was first conclusively established. And “Joule’s equivalent,” as it is rightly called, considering the amount of resolute labor and skill expended in its determination, is almost identical with that derived from the formula of Mayer.
Consider now the ground we have trodden, the curious labyrinth of reasoning and experiment through which we have passed. We started with the observed and calculated velocities of sound in atmospheric air. We found Laplace, by a special assumption, deducing from these velocities the ratio of the specific heat of air at constant pressure to its specific heat at constant volume. We68 found Mayer calculating from this ratio the mechanical equivalent of heat; finally, we found Joule determining the same equivalent by direct experiments on the friction of solids and liquids. And what is the result? Mr. Joule’s experiments prove the result of Mayer to be the true one; they therefore prove the ratio determined by Laplace to be the true ratio; and, because they do this, they prove at the same time the practical absence of radiative power in atmospheric air. It seems a long step from the stirring of water, or the rubbing together of iron plates in Joule’s experiments, to the radiation of the atoms of our atmosphere; both questions are, however, connected by the line of reasoning here followed out.
But the true physical philosopher never rests content with an inference when an experiment to verify or contravene it is possible. The foregoing argument is clinched by bringing the radiative power of atmospheric air to a direct test. When this is done, experiment and reasoning are found to agree; air being proved to be a body sensibly devoid of radiative and absorptive power.23
But here the experimenter on the transmission of sound through gases needs a word of warning. In Laplace’s day, and long subsequently, it was thought that gases of all kinds possessed only an infinitesimal power of radiation; but that this is not the case is now well established. It would be rash to assume that, in the case of such bodies as ammonia, aqueous vapor, sulphurous acid, and olefiant gas, their enormous radiative powers do not interfere with the application of the formula of Laplace. It behooves us to inquire whether the ratio of the two specific heats deduced from the velocity of 69sound in these bodies is the true ratio; and whether, if the true ratio could be found by other methods, its square root, multiplied into the calculated velocity, would give the observed velocity. From the moment heat first appears in the condensation and cold in the rarefaction of a sonorous wave in any of those gases, the radiative power comes into play to abolish the difference of temperature. The condensed part of the wave is on this account rendered more flaccid and the rarefied part less flaccid than it would otherwise be, and with a sufficiently high radiative power the velocity of sound, instead of coinciding with that derived from the formula of Laplace, must approximate to that derived from the more simple formula of Newton.
To complete our knowledge of the transmission of sound through gases, a table is here added from the excellent researches of Dulong, who employed in his experiments a method which shall be subsequently explained:
Velocity of Sound in Gases at the Temperature of 0° C.
| Velocity | ||
| Air | 1,092 | feet |
| Oxygen | 1,040 | ” |
| Hydrogen | 4,164 | ” |
| Carbonic acid | 858 | ” |
| Carbonic oxide | 1,107 | ” |
| Protoxide of nitrogen | 859 | ” |
| Olefiant gas | 1,030 | ” |
According to theory, the velocities of sound in oxygen and hydrogen are inversely proportional to the square roots of the densities of the two gases. We here find this theoretic deduction verified by experiment. Oxygen70 being sixteen times heavier than hydrogen, the velocity of sound in the latter gas ought, according to the above law, to be four times its velocity in the former; hence, the velocity in oxygen being 1,040, in hydrogen calculation would make it 4,160. Experiment, we see, makes it 4,164.
The velocity of sound in liquids may be determined theoretically, as Newton determined its velocity in air; for the density of a liquid is easily determined, and its elasticity can be measured by subjecting it to compression. In the case of water, the calculated and the observed velocities agree so closely as to prove that the changes of temperature produced by a sound-wave in water have no sensible influence upon the velocity. In a series of memorable experiments in the Lake of Geneva, MM. Colladon and Sturm determined the velocity of sound through water, and made it 4,708 feet a second. By a mode of experiment which you will subsequently be able to comprehend, the late M. Wertheim determined the velocity through various liquids, and in the following table I have collected his results:
Transmission of Sound through Liquids
| Name of Liquid | Temperature | Velocity | |
| River-water (Seine) | 15° C. | 4,714 | feet |
| River”water (S” | 30 | 5,013 | ” |
| River”water (S” | 60 | 5,657 | ” |
| Sea-water (artificial) | 20 | 4,768 | ” |
| Solution of common salt | 18 | 5,132 | ” |
| Solution of sulphate of soda | 20 | 5,194 | ” |
| Solution of carbonate of soda | 22 | 5,230 | ” |
| Solution of nitrate of soda | 21 | 5,477 | ” |
| Solution of chloride of calcium | 23 | 6,493 | ” |
| Common alcohol | 20 | 4,218 | ” |
| Absolute alcohol | 23 | 3,804 | ” |
| Spirits of turpentine | 24 | 3,976 | ” |
| Sulphuric ether | 0 | 3,801 | ” |
We learn from this table that sound travels with different velocities through different liquids; that a salt dissolved in water augments the velocity, and that the salt which produces the greatest augmentation is chloride of calcium. The experiments also teach us that in water, as in air, the velocity augments with the temperature. At a temperature of 15° C., for example, the velocity in Seine water is 4,714 feet, at 30° it is 5,013 feet, and at 60° 5,657 feet a second.
I have said that from the compressibility of a liquid, determined by proper measurements, the velocity of sound through the liquid may be deduced. Conversely, from the velocity of sound in a liquid, the compressibility of the liquid may be deduced. Wertheim compared a series of compressibilities deduced from his experiments on sound with a similar series obtained directly by M. Grassi. The agreement of both, exhibited in the following table, is a strong confirmation of the accuracy of the method pursued by Wertheim:
| Cubic compressibility | ||
| ╭———————^———————╮ | ||
| from Wertheim’s velocity of sound | from the direct experiments of M. Grassi | |
| Sea-water | 0·0000467 | 0·0000436 |
| Solution of common salt | 0·0000349 | 0·0000321 |
| ” carbonate of soda | 0·0000337 | 0·0000297 |
| ” nitrate of soda | 0·0000301 | 0·0000295 |
| Absolute alcohol | 0·0000947 | 0·0000991 |
| Sulphuric ether | 0·0001002 | 0·0001110 |
The greater the resistance which a liquid offers to compression, the more promptly and forcibly will it return to its original volume after it has been compressed. The less the compressibility, therefore, the greater is the elasticity, and consequently, other things72 being equal, the greater the velocity of sound through the liquid.
We have now to examine the transmission of sound through solids. Here, as a general rule, the elasticity, as compared with the density, is greater than in liquids, and consequently the propagation of sound is more rapid.
In the following table the velocity of sound through various metals, as determined by Wertheim, is recorded:
Velocity of Sound through Metals
| Name of Metal | At 20° C. | At 100° C. | At 200° C. |
| Lead | 4,030 | 3,951 | ...... |
| Gold | 5,717 | 5,640 | 5,619 |
| Silver | 8,553 | 8,658 | 8,127 |
| Copper | 11,666 | 10,802 | 9,690 |
| Platinum | 8,815 | 8,437 | 8,079 |
| Iron | 16,822 | 17,386 | 15,483 |
| Iron wire (ordinary) | 16,130 | 16,728 | ...... |
| Cast steel | 16,357 | 16,153 | 15,709 |
| Steel wire (English) | 15,470 | 17,201 | 16,394 |
| Steel wire | 16,023 | 16,443 | ...... |
As a general rule, the velocity of sound through metals is diminished by augmented temperature; iron is, however, a striking exception to this rule, but it is only within certain limits an exception. While, for example, a rise of temperature from 20° to 100° C. in the case of copper causes the velocity to fall from 11,666 to 10,802, the same rise produces in the case of iron an increase of velocity from 16,822 to 17,386. Between 100° and 200°, however, we see that iron falls from the last figure to 15,483. In iron, therefore, up to a certain point, the elasticity is augmented by heat; beyond that point it is lowered. Silver is also an example of the same kind.
The difference of velocity in iron and in air may be illustrated by the following instructive experiment: Choose one of the longest horizontal bars employed for fencing in Hyde Park; and let an assistant strike the bar at one end while the ear of the observer is held close to the bar at a considerable distance from the point struck. Two sounds will reach the ear in succession; the first being transmitted through the iron and the second through the air. This effect was obtained by M. Biot, in his experiments on the iron water-pipes of Paris.
The transmission of sound through a solid depends on the manner in which the molecules of the solid are arranged. If the body be homogeneous and without structure, sound is transmitted through it equally well in all directions. But this is not the case when the body, whether inorganic like a crystal or organic like a tree, possesses a definite structure. This is also true of other things than sound. Subjecting, for example, a sphere of wood to the action of a magnet, it is not equally affected in all directions. It is repelled by the pole of the magnet, but it is most strongly repelled when the force acts along the fibre. Heat also is conducted with different facilities in different directions through wood. It is most freely conducted along the fibre, and it passes more freely across the ligneous layers than along them. Wood, therefore, possesses three unequal axes of calorific conduction. These, established by myself, coincide with the axes of elasticity discovered by Savart. MM. Wertheim and Chevandier have determined the velocity of sound along these three axes and obtained the following results:
Velocity of Sound in Wood
| Name of Wood | Along Fibre | Across Rings | Along Rings |
| Acacia | 15,467 | 4,840 | 4,436 |
| Fir | 15,218 | 4,382 | 2,572 |
| Beech | 10,965 | 6,028 | 4,643 |
| Oak | 12,622 | 5,036 | 4,229 |
| Pine | 10,900 | 4,611 | 2,605 |
| Elm | 13,516 | 4,665 | 3,324 |
| Sycamore | 14,639 | 4,916 | 3,728 |
| Ash | 15,314 | 4,567 | 4,142 |
| Alder | 15,306 | 4,491 | 3,423 |
| Aspen | 16,677 | 5,297 | 2,987 |
| Maple | 13,472 | 5,047 | 3,401 |
| Poplar | 14,050 | 4,600 | 3,444 |
Separating a cube from the bark-wood of a good-sized
tree, where the rings for a short distance may be regarded
as straight: then, if A R, Fig. 14, be the section
 Fig. 14.
of the tree, the velocity of the
sound in the direction m n,
through such a cube, is greater
than in the direction a b.
Fig. 14.
of the tree, the velocity of the
sound in the direction m n,
through such a cube, is greater
than in the direction a b.
The foregoing table strikingly illustrates the influence of molecular structure. The great majority of crystals show differences of the same kind. Such bodies, for the most part, have their molecules arranged in different degrees of proximity in different directions, and where this occurs there are sure to be differences in the transmission and manifestation of heat, light, electricity, magnetism, and sound.
I will conclude this lecture on the transmission of sound through gases, liquids, and solids, by a quaint and75 beautiful extract from the writings of that admirable thinker, Dr. Robert Hooke. It will be noticed that the philosophy of the stethoscope is enunciated in the following passage, and another could hardly be found which illustrates so well that action of the scientific imagination which, in all great investigators, is the precursor and associate of experiment:
“There may also be a possibility,” writes Hooke, “of discovering the internal motions and actions of bodies by the sound they make. Who knows but that, as in a watch, we may hear the beating of the balance, and the running of the wheels, and the striking of the hammers, and the grating of the teeth, and multitudes of other noises; who knows, I say, but that it may be possible to discover the motions of the internal parts of bodies, whether animal, vegetable, or mineral, by the sound they make; that one may discover the works performed in the several offices and shops of a man’s body, and thereby discover what instrument or engine is out of order, what works are going on at several times, and lie still at others, and the like; that in plants and vegetables one might discover by the noise the pumps for raising the juice, the valves for stopping it, and the rushing of it out of one passage into another, and the like? I could proceed further, but methinks I can hardly forbear to blush when I consider how the most part of men will look upon this: but, yet again, I have this encouragement, not to think all these things utterly impossible, though never so much derided by the generality of men, and never so seemingly mad, foolish, and fantastic, that as the thinking them impossible cannot much improve my knowledge, so the believing them possible may, per76haps, be an occasion of taking notice of such things as another would pass by without regard as useless. And somewhat more of encouragement I have also from experience, that I have been able to hear very plainly the beating of a man’s heart, and it is common to hear the motion of wind to and fro in the guts, and other small vessels; the stopping of the lungs is easily discovered by the wheezing, the stopping of the head by the humming and whistling noises, the slipping to and fro of the joints, in many cases, by crackling, and the like, as to the working or motion of the parts one among another; methinks I could receive encouragement from hearing the hissing noise made by a corrosive menstruum in its operation, the noise of fire in dissolving, of water in boiling, of the parts of a bell after that its motion is grown quite invisible as to the eye, for to me these motions and the other seem only to differ secundum magis minus, and so to their becoming sensible they require either that their motions be increased, or that the organ be made more nice and powerful to sensate and distinguish them.”
The recent explosion of a powder-laden barge in the Regent’s Park produced effects similar to those mentioned in § 7. The sound-wave bent round houses and broke the windows at the back, the coalescence of different portions of the wave at special points being marked by intensified local action. Close to the place where the explosion occurred the unconsumed gunpowder was in the wave, and, as a consequence, the dismantled gatekeeper’s lodge was girdled all round by a black belt of carbon.
The sound of an explosion is propagated as a wave or pulse through the air.
This wave impinging upon the tympanic membrane causes it to shiver, its tremors are transmitted to the auditory nerve, and along the auditory nerve to the brain, where it announces itself as sound.
A sonorous wave consists of two parts, in one of which the air is condensed, and in the other rarefied.
The motion of the sonorous wave must not be confounded with the motion of the particles which at any moment form the wave. During the passage of the wave every particle concerned in its transmission makes only a small excursion to and fro.
The length of this excursion is called the amplitude of the vibration.
Sound cannot pass through a vacuum.
A certain sharpness of shock, or rapidity of vibration, is needed for the production of sonorous waves in air. It is still more necessary in hydrogen, because the greater mobility of this light gas tends to prevent the formation of condensations and rarefactions.
Sound is in all respects reflected like light; it is also refracted like light; and it may, like light, be condensed by suitable lenses.
Sound is also diffracted, the sonorous wave bending round obstacles; such obstacles, however, in part shade off the sound.
Echoes are produced by the reflected waves of sound.
In regard to sound and the medium through which it passes, four distinct things are to be borne in mind—intensity, velocity, elasticity, and density.
The intensity is proportional to the square of the amplitude as above defined.
It is also proportional to the square of the maximum velocity of the vibrating air-particles.
When sound issues from a small body in free air, the intensity diminishes as the square of the distance from the body increases.
If the wave of sound be confined in a tube with a smooth interior surface, it may be conveyed to great distances without sensible loss of intensity.
The velocity of sound in air depends on the elasticity of the air in relation to its density. The greater the elasticity the swifter is the propagation; the greater the density the slower is the propagation.
The velocity is directly proportional to the square root of the elasticity; it is inversely proportional to the square root of the density.
Hence, if elasticity and density vary in the same proportion, the one will neutralize the other as regards the velocity of sound.
That they do vary in the same proportion is proved by the law of Boyle and Mariotte; hence the velocity of sound in air is independent of the density of the air.
But that this law shall hold good, it is necessary that79 the dense air and the rare air should have the same temperature.
The intensity of a sound depends upon the density of the air in which it is generated, but not on that of the air in which it is heard.
The velocity of sound in air of the temperature 0° C. is 1,090 feet a second; it augments nearly 2 feet for every degree Centigrade added to its temperature.
Hence, given the velocity of sound in air, the temperature of the air may be readily calculated.
The distance of a fired cannon or of a discharge of lightning may be determined by observing the interval which elapses between the flash and the sound.
From the foregoing, it is easy to see that if a row of soldiers form a circle, and discharge their pieces all at the same time, the sound will be heard as a single discharge by a person occupying the centre of the circle.
But if the men form a straight row, and if the observer stand at one end of the row, the simultaneous discharge of the men’s pieces will be prolonged to a kind of roar.
A discharge of lightning along a lengthy cloud may in this way produce the prolonged roll of thunder. The roll of thunder, however, must in part at least be due to echoes from the clouds.
The pupil will find no difficulty in referring many common occurrences to the fact that sound requires a sensible time to pass through any considerable length of air. For example, the fall of the axe of a distant wood-cutter is not simultaneous with the sound of the stroke. A company of soldiers marching to music along a road80 cannot march in time, for the notes do not reach those in front and those behind simultaneously.
In the condensed portion of a sonorous wave the air is above, in the rarefied portion of the wave it is below, its average temperature.
This change of temperature, produced by the passage of the sound-wave itself, virtually augments the elasticity of the air, and makes the velocity of sound about one-sixth greater than it would be if there were no change of temperature.
The velocity found by Newton, who did not take this change of temperature into account, was 916 feet a second.
Laplace proved that by multiplying Newton’s velocity by the square root of the ratio of the specific heat of air at constant pressure to its specific heat at constant volume, the actual or observed velocity is obtained.
Conversely, from a comparison of the calculated and observed velocities, the ratio of the two specific heats may be inferred.
The mechanical equivalent of heat may be deduced from this ratio; it is found to be the same as that established by direct experiment.
This coincidence leads to the conclusion that atmospheric air is devoid of any sensible power to radiate heat. Direct experiments on the radiative power of air establish the same result.
The velocity of sound in water is more than four times its velocity in air.
The velocity of sound in iron is seventeen times its velocity in air.
The velocity of sound along the fibre of pine-wood is ten times its velocity in air.
The cause of this great superiority is that the elasticities of the liquid, the metal, and the wood, as compared with their respective densities, are vastly greater than the elasticity of air in relation to its density.
The velocity of sound is dependent to some extent upon molecular structure. In wood, for example, it is conveyed with different degrees of rapidity in different directions.
Physical Distinction between Noise and Music—A Musical Tone Produced by Periodic, Noise Produced by Unperiodic, Impulses—Production of Musical Sounds by Taps—Production of Musical Sounds by Puffs—Definition of Pitch in Music—Vibrations of a Tuning-Fork; their Graphic Representation on Smoked Glass—Optical Expression of the Vibrations of a Tuning-Fork—Description of the Siren—Limits of the Ear; Highest and Deepest Tones—Rapidity of Vibration Determined by the Siren—Determination of the Lengths of Sonorous Waves—Wave-Lengths of the Voice in Man and Woman—Transmission of Musical Sounds through Liquids and Solids
IN OUR last chapter we considered the propagation through air of a sound of momentary duration. We have to-day to consider continuous sounds, and to make ourselves in the first place acquainted with the physical distinction between noise and music. As far as sensation goes, everybody knows the difference between these two things. But we have now to inquire into the causes of sensation, and to make ourselves acquainted with the condition of the external air which in one case resolves itself into music and in another into noise.
We have already learned that what is loudness in our sensations is outside of us nothing more than width of swing, or amplitude, of the vibrating air-particles. Every other real sonorous impression of which we are conscious has its correlative without, as a mere form or state of the atmosphere. Were our organs sharp enough to see the motions of the air through which an agreeable voice is passing, we might see stamped upon that air the condi83tions of motion on which the sweetness of the voice depends. In ordinary conversation, also, the physical precedes and arouses the psychical; the spoken language, which is to give us pleasure or pain, which is to rouse us to anger or soothe us to peace, existing for a time, between us and the speaker, as a purely mechanical condition of the intervening air.
Noise affects us as an irregular succession of shocks. We are conscious while listening to it of a jolting and jarring of the auditory nerve, while a musical sound flows smoothly and without asperity or irregularity. How is this smoothness secured? By rendering the impulses received by the tympanic membrane perfectly periodic. A periodic motion is one that repeats itself. The motion of a common pendulum, for example, is periodic, but its vibrations are far too sluggish to excite sonorous waves. To produce a musical tone we must have a body which vibrates with the unerring regularity of the pendulum, but which can impart much sharper and quicker shocks to the air.
Imagine the first of a series of pulses following each other at regular intervals, impinging upon the tympanic membrane. It is shaken by the shock; and a body once shaken cannot come instantaneously to rest. The human ear, indeed, is so constructed that the sonorous motion vanishes with extreme rapidity, but its disappearance is not instantaneous; and if the motion imparted to the auditory nerve by each individual pulse of our series continues until the arrival of its successor, the sound will not cease at all. The effect of every shock will be renewed before it vanishes, and the recurrent impulses will link themselves together to a continuous musical sound.84 The pulses, on the contrary, which produce noise, are of irregular strength and recurrence. The action of noise upon the ear has been well compared to that of a flickering light upon the eye, both being painful through the sudden and abrupt changes which they impose upon their respective nerves.
The only condition necessary to the production of a musical sound is that the pulses should succeed each other in the same interval of time. No matter what its origin may be, if this condition be fulfilled the sound becomes musical. If a watch, for example, could be caused to tick with sufficient rapidity—say one hundred times a second—the ticks would lose their individuality and blend to a musical tone. And if the strokes of a pigeon’s wings could be accomplished at the same rate, the progress of the bird through the air would be accompanied by music. In the humming-bird the necessary rapidity is attained; and when we pass on from birds to insects, where the vibrations are more rapid, we have a musical note as the ordinary accompaniment of the insects’ flight.24 The puffs of a locomotive at starting follow each other slowly at first, but they soon increase so rapidly as to be almost incapable of being counted. If this increase could continue up to fifty or sixty puffs a second, the approach of the engine would be heralded by an organ-peal of tremendous power.
Galileo produced a musical sound by passing a knife
over the edge of a piastre. The minute serration of the
85coin indicated the periodic character of the motion, which
consisted of a succession of taps quick enough to produce
sonorous continuity. Every schoolboy knows how
to produce a note with his slate-pencil. I will not call it
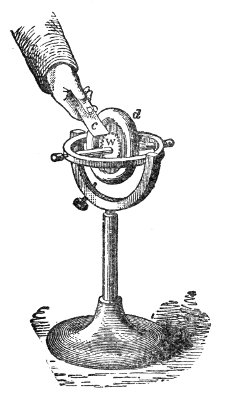 Fig. 15.
musical, because this term is
usually associated with pleasure,
and the sound of the pencil
is not pleasant.
Fig. 15.
musical, because this term is
usually associated with pleasure,
and the sound of the pencil
is not pleasant.
The production of a musical sound by taps is usually effected by causing the teeth of a rotating wheel to strike in quick succession against a card. This was first illustrated by the celebrated Robert Hooke,25 and nearer our own day by the eminent French experimenter Savart. We will confine ourselves to homelier modes of illustration. This gyroscope is an instrument consisting mainly of a heavy brass ring, d, Fig. 15, loading the circumference of a disk, through which and at right angles 86to its surface, passes a steel axis, delicately supported at its two ends. By coiling a string round the axis, and drawing it vigorously out, the ring is caused to spin rapidly; and along with it rotates a small-toothed wheel, w. On touching this wheel with the edge of a card c, a musical sound of exceeding shrillness is produced. I place my thumb for a moment against the ring; the rapidity of its rotation is thereby diminished, and this is instantly announced by a lowering of the pitch of the note. By checking the motion still more, the pitch is lowered still further. We are here made acquainted with the important fact that the pitch of a note depends upon the rapidity of its pulses.26 At the end of the experiment you hear the separate taps of the teeth against the card, their succession not being quick enough to produce that continuous flow of sound which is the essence of music. A screw with a milled head attached to a whirling table, and caused to rotate, produces by its taps against a card a note almost as clear and pure as that obtained from the toothed wheel of the gyroscope.
The production of a musical sound by taps may also be pleasantly illustrated in the following way: In this vise are fixed vertically two pieces of sheet-lead, with their horizontal edges a quarter of an inch apart. I lay a bar of brass across them, permitting it to rest upon the edges, and, tilting the bar a little, set it in oscillation like a see-saw. After a time, if left to itself, it comes to rest. But suppose the bar on touching the lead to be always tilted upward by a force issuing from the lead itself, it 87is plain that the vibrations would then be rendered permanent. Now such a force is brought into play when the bar is heated. On its then touching the lead the heat is communicated, a sudden jutting upward of the lead at the point of contact being the result. Hence an incessant tilting of the bar from side to side, so long as it continues sufficiently hot. Substituting for the brass bar the heated fire-shovel shown in Fig. 16, the same effect is produced.
In its descent upon the lead the bar taps it gently, the taps being so slow that you may readily count them. But a mass of metal differently shaped may be caused to vibrate more briskly, and the taps to succeed each other more rapidly. When such a heated rocker, Fig. 17, is placed upon a block of lead, the taps hasten to a loud rattle. When, with the point of a file, the rocker is pressed against the lead, the vibrations are rendered more rapid, and the taps link themselves together to a deep musical tone. A second rocker, which oscillates more quickly than the last, produces music without any other pressure than that due to its own weight. Pressing it, however, with the file, the pitch rises, until a note of88 singular force and purity fills the room. Relaxing the pressure, the pitch instantly falls; resuming the pressure, it again rises; and thus by the alternation of the pressure we obtain great variations of tone. Nor are such rockers essential. Allowing one face of the clean, square end of a heated poker to rest upon the block of lead, a rattle is heard; causing another face to rest upon the block, a clear musical note is obtained. The two faces have been bevelled differently by a file, so as to secure different rates of vibration.27 This curious effect was discovered by Schwartz and Trevelyan.
Prof. Robison was the first to produce a musical sound by a quick succession of puffs of air. His device was the first form of an instrument which will soon be introduced to you under the name of the siren. Robison describes his experiment in the following words: “A stop-cock was so constructed that it opened and shut the passage of a pipe 720 times in a second. The apparatus was fitted to the pipe of a conduit leading from the bellows to the wind-chest of an organ. The air was simply allowed to pass gently along this pipe by the opening of the cock. When this was repeated 720 times in a second, the sound g in alt was most smoothly uttered, equal in sweetness to a clear female voice. When the frequency was reduced to 360, the sound was that of a clear but rather a harsh man’s voice. The cock was now altered in such a manner that it never shut the hole entirely, but left about one-third of it open. When this was repeated 720 times in a second, the sound was uncommonly smooth and sweet. When reduced to 360, the sound was more mellow than any man’s voice of the same pitch.”
But the difficulty of obtaining the necessary speed renders another form of the experiment preferable. A disk of Bristol board, B, Fig. 18, twelve inches in diameter, is perforated at equal intervals along a circle near its90 circumference. The disk, being strengthened by a backing of tin, can be attached to a whirling table, and caused to rotate rapidly. The individual holes then disappear, blending themselves into a continuous shaded circle. Immediately over this circle is placed a bent tube, m, connected with a pair of acoustic bellows. The disk is now motionless, the lower end of the tube being immediately over one of the perforations of the disk. If, therefore, the bellows be worked, the wind will pass from m through the hole underneath. But if the disk be turned a little, an unperforated portion of the disk comes under the tube, the current of air being then intercepted. As the disk is slowly turned, successive perforations are brought under the tube, and whenever this occurs a puff of air gets through. On rendering the rotation rapid, the puffs succeed each other in very quick succession, producing pulses in the air which blend to a continuous musical note, audible to you all. Mark how the note varies. When the whirling table is turned rapidly the sound is shrill; when its motion is slackened the pitch immediately falls. If instead of a single glass tube there were two of them, as far apart as two of our orifices, so that whenever the one tube stood over an orifice, the other should stand over another, it is plain that if both tubes were blown through, we should, on turning the disk, get a puff through two holes at the same time. The intensity of the sound would be thereby augmented, but the pitch would remain unchanged. The two puffs issuing at the same instant would act in concert, and produce a greater effect than one upon the ear. And if instead of two tubes we had ten of them, or better still, if we had a tube for every orifice in the disk, the puffs91 from the entire series would all issue, and would be all cut off at the same time. These puffs would produce a note of far greater intensity than that obtained by the alternate escape and interruption of the air from a single tube. In the arrangement now before you, Fig. 19, there are nine tubes through which the air is urged—through nine apertures, therefore, puffs escape at once. On turning the whirling table, and alternately increasing and relaxing its speed, the sound rises and falls like the loud wail of a changing wind.
Various other means may be employed to throw the air into a state of periodic motion. A stretched string pulled aside and suddenly liberated imparts vibrations to the air which succeed each other in perfectly regular intervals. A tuning-fork does the same. When a bow is drawn across the prongs of this tuning-fork, Fig. 20, the resin of the bow enables the hairs to grip the prong, which is thus pulled aside. But the resistance of the prong soon becomes too strong, and it starts suddenly back; it is, however, immediately laid hold of again by the bow, to start back once more as soon as its resistance becomes great enough. This rhythmic process, continu92ally repeated during the passage of the bow, finally throws the fork into a state of intense vibration, and the result is a musical note. A person close at hand could see the fork vibrating; a deaf person bringing his hand sufficiently near would feel the shivering of the air. Or causing its vibrating prong to touch a card, taps against the card link themselves, as in the case of the gyroscope, to a musical sound, the fork coming rapidly to rest. What we call silence expresses this absence of motion.
When the tuning-fork is first excited the sound issues from it with maximum loudness, becoming gradually feebler as the fork continues to vibrate. A person close to the fork can notice at the same time that the amplitude, or space through which the prongs oscillate, becomes gradually less and less. But the most expert ear in this assembly can detect no change in the pitch of the note. The lowering of the intensity of a note does not therefore imply the lowering of its pitch. In fact, though the amplitude changes, the rate of vibration remains the same. Pitch and intensity must therefore be held distinctly apart; the latter depends solely upon the amplitude, the former solely upon the rapidity of vibration.
This tuning-fork may be caused to write the story of its own motion. Attached to the side of one of its prongs, F, Fig. 21, is a thin strip of sheet-copper which tapers to a point. When the tuning-fork is excited it vibrates, and the strip of metal accompanies it in its vibration. The point of the strip being brought gently down upon a piece of smoked glass, it moves to and fro over the smoked surface, leaving a clear line behind. As long as the hand is kept motionless, the point merely passes to and fro over the same line; but it is plain that we have only to draw the fork along the glass to produce a sinuous line, Fig. 21.
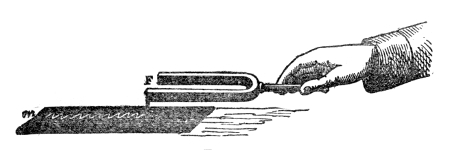
When this process is repeated without exciting the fork afresh, the depth of the indentations diminishes. The sinuous line approximates more and more to a straight one. This is the visual expression of decreasing amplitude. When the sinuosities entirely disappear, the amplitude has become zero, and the sound, which depends upon the amplitude, ceases altogether.
To M. Lissajous we are indebted for a very beautiful method of giving optical expression to the vibrations of a tuning-fork. Attached to one of the prongs of a very large fork is a small metallic mirror, F, Fig. 22, the other prong being loaded with a piece of metal to establish equilibrium. Permitting a slender beam of intense light94 to fall upon the mirror, the beam is thrown back by reflection. In my hands is held a small looking-glass, which receives the reflected beam, and from which it is again reflected to the screen, forming a small luminous disk upon the white surface. The disk is perfectly motionless, but the moment the fork is set in vibration the reflected beam is tilted rapidly up and down, the disk describing a band of light three feet long. The length of the band depends on the amplitude of the vibration, and you see it gradually shorten as the motion of the fork is expended. It remains, however, a straight line as long as the glass is held in a fixed position. But on suddenly turning the glass so as to make the beam travel from left to right over the screen, you observe the straight line instantly resolved into a beautiful luminous ripple m n. A luminous impression once made upon the retina lingers there for the tenth of a second; if then the time required to transfer the elongated image from side to side of the screen be less than the tenth of a second, the wavy line of light will occupy for a moment the whole width of the screen. Instead of permitting the95 beam from the lamp to issue through a single aperture, it may be caused to issue through two apertures, about half an inch asunder, thus projecting two disks of light, one above the other, upon the screen. When the fork is excited and the mirror turned, we have a brilliant double sinuous line running over the dark surface, Fig. 23. turning the diaphragm so as to place the two disks beside each other, on exciting the fork and moving the mirror we obtain a beautiful interlacing of the two sinuous lines, Fig. 24.

How are we to picture to ourselves the condition of the air through which this musical sound is passing? Imagine one of the prongs of the vibrating fork swiftly advancing; it compresses the air immediately in front of it, and when it retreats it leaves a partial vacuum behind, the process being repeated by every subsequent advance and retreat. The whole function of the tuning-fork is to carve the air into these condensations and rarefactions, and they, as they are formed, propagate themselves in succession through the air. A condensation with its associated rarefaction constitutes, as already96 stated, a sonorous wave. In water the length of a wave is measured from crest to crest; while, in the case of sound, the wave-length is the distance between two successive condensations. The condensation of the sound-wave corresponds to the crest, while the rarefaction of the sound-wave corresponds to the sinus, or depression, of the water-wave. Let the dark spaces, a, b, c, d, Fig. 25, represent the condensations, and the light ones, a′, b′, c′, d′, the rarefactions of the waves issuing from the fork a b: the wave-length would then be measured from a to b, from b to c, or from c to d.
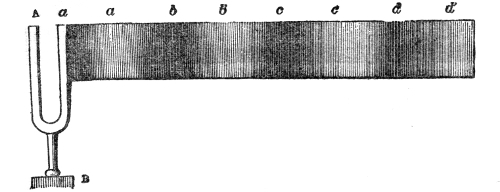
When two notes from two distinct sources are of the same pitch, their rates of vibration are the same. If, for example, a string yield the same note as a tuning-fork, it is because they vibrate with the same rapidity; and if a fork yield the same note as the pipe of an organ or the tongue of a concertina, it is because the vibrations of the fork in the one case are executed in precisely the same time as the vibrations of the column of air, or of the tongue, in the other. The same holds good for the human voice. If a string and a voice yield the same note, it is because the vocal chords of the singer vibrate in97 the same time as the string vibrates. Is there any way of determining the actual number of vibrations corresponding to a musical note? Can we infer from the pitch of a string, of an organ-pipe, of a tuning-fork, or of the human voice, the number of waves which it sends forth in a second? This very beautiful problem is capable of the most complete solution.
By the rotation of a perforated pasteboard disk, it has been proved to you that a musical sound is produced by a quick succession of puffs. Had we any means of registering the number of revolutions accomplished by that disk in a minute, we should have in it a means of determining the number of puffs per minute due to a note of any determinate pitch. The disk, however, is but a cheap substitute for a far more perfect apparatus, which requires no whirling table, and which registers its own rotations with the most perfect accuracy.
I will take the instrument asunder, so that you may see its various parts. A brass tube, t, Fig. 26, leads into a round box, C, closed at the top by a brass plate a b. This plate is perforated with four series of holes, placed along four concentric circles. The innermost series contains 8, the next 10, the next 12, and the outermost 16 orifices. When we blow into the tube t, the air escapes through the orifices, and the problem now before us is to convert these continuous currents into discontinuous puffs. This is accomplished by means of a brass disk d e, also perforated with 8, 10, 12, and 16 holes, at the same distances from the centre and with the same intervals between them as those in the top of the box C. Through98 the centre of the disk passes a steel axis, the two ends of which are smoothly bevelled off to points at p and p′. My object now is to cause this perforated disk to rotate over the perforated top a b of the box C. You will understand how this is done by observing how the instrument is put together.
In the centre of a b, Fig. 26, is a depression x sunk in steel, smoothly polished and intended to receive the99 end p′ of the axis. I place the end p′ in this depression, and, holding the axis upright, bring down upon its upper end p a steel cap, finely polished within, which holds the axis at the top, the pressure both at top and bottom being so gentle, and the polish of the touching surfaces so perfect, that the disk can rotate with an exceedingly small amount of friction. At c, Fig. 27, is the cap which fits on to the upper end of the axis p p′. In this figure the disk d e is shown covering the top of the cylinder C. You may neglect for the present the wheel-work of the figure. Turning the disk d e slowly round, its perforations may be caused to coincide or not coincide with those of the cylinder underneath. As the disk turns, its orifices come alternately over the perforations of the cylinder and over the spaces between the perforations. Hence it is plain that if air were urged into C, and if the disk could be caused to rotate at the same time, we should accomplish our object, and carve into puffs the streams of air. In this beautiful instrument the disk is caused to rotate by the very air currents which it renders intermittent. This is done by the simple device of causing the perforations to pass obliquely through the top of the cylinder C, and also obliquely, but oppositely inclined, through the rotating disk d e. The air is thus caused to issue from C, not vertically, but in side currents, which impinge against the disk and drive it round. In this way, by its passage through the siren, the air is molded into sonorous waves.
Another moment will make you acquainted with the
recording portion of the instrument. At the upper part
of the steel axis p p′, Fig. 27, is a screw s, working into
a pair of toothed wheels (seen when the back of the100
instrument is turned toward you). As the disk and its
axis turn, these wheels rotate. In front you simply
 Fig. 28.
see two graduated dials,
Fig. 28, each furnished
with an index like the
hand of a clock. These
indexes record the number
of revolutions executed by
the disk in any given time.
By pushing the button a
or b the wheel-work is
thrown into or out of action,
thus starting or suspending,
in a moment, the process of recording. Finally,
by the pins m, n, o, p, Fig. 27, any series of orifices
in the top of the cylinder C can be opened or closed
at pleasure. By pressing m, one series is opened; by
pressing n, another. By pressing two keys, two series
of orifices are opened; by pressing three keys, three
series; and by pressing all the keys, puffs are caused to
issue from the four series simultaneously. The perfect
instrument is now before you, and your knowledge of it
is complete.
Fig. 28.
see two graduated dials,
Fig. 28, each furnished
with an index like the
hand of a clock. These
indexes record the number
of revolutions executed by
the disk in any given time.
By pushing the button a
or b the wheel-work is
thrown into or out of action,
thus starting or suspending,
in a moment, the process of recording. Finally,
by the pins m, n, o, p, Fig. 27, any series of orifices
in the top of the cylinder C can be opened or closed
at pleasure. By pressing m, one series is opened; by
pressing n, another. By pressing two keys, two series
of orifices are opened; by pressing three keys, three
series; and by pressing all the keys, puffs are caused to
issue from the four series simultaneously. The perfect
instrument is now before you, and your knowledge of it
is complete.
This instrument received the name of siren from its inventor, Cagniard de la Tour. The one now before you is the siren as greatly improved by Dove. The pasteboard siren, whose performance you have already heard, was devised by Seebeck, who gave the instrument various interesting forms, and executed with it many important experiments. Let us now make the siren sing. By pressing the key m, the outer series of apertures in the cylinder C is opened, and by working the bellows, the101 air is caused to impinge against the disk. It begins to rotate, and you hear a succession of puffs which follow each other so slowly that they may be counted. But as the motion augments, the puffs succeed each other with increasing rapidity, and at length you hear a deep musical note. As the velocity of rotation increases the note rises in pitch; it is now very clear and full, and as the air is urged more vigorously, it becomes so shrill as to be painful. Here we have a further illustration of the dependence of pitch on rapidity of vibration. I touch the side of the disk and lower its speed; the pitch falls instantly. Continuing the pressure the tone continues to sink, ending in the discontinuous puffs with which it began.
Were the blast sufficiently powerful and the siren sufficiently free from friction, it might be urged to higher and higher notes, until finally its sound would become inaudible to human ears. This, however, would not prove the absence of vibratory motion in the air; but would rather show that our auditory apparatus is incompetent to take up and translate into sound vibrations whose rapidity exceeds a certain limit. The ear, as we shall immediately learn, is in this respect similar to the eye.
By means of this siren we can determine with extreme accuracy the rapidity of vibration of any sonorous body. It may be a vibrating string, an organ-pipe, a reed, or the human voice. Operating delicately, we might even determine from the hum of an insect the number of times it flaps its wings in a second. I will illustrate the subject by determining in your presence a tuning-fork’s rapidity of vibration. From the acoustic102 bellows I urge the air through the siren, and, at the same time, draw my bow across the fork. Both now sound together, the tuning-fork yielding at present the highest note. But the pitch of the siren gradually rises, and at length you hear the “beats” so well known to musicians, which indicate that the two notes are not wide apart in pitch. These beats become slower and slower; now they entirely vanish, both notes blending as it were to a single stream of sound.
All this time the clockwork of the siren has remained out of action. As the second-hand of a watch crosses the number 60, the clockwork is set going by pushing the button a. We will allow the disk to continue its rotation for a minute, the tuning-fork being excited from time to time to assure you that the unison is preserved. The second-hand again approaches 60; as it passes that number the clockwork is stopped by pushing the button b; and then, recorded on the dials, we have the exact number of revolutions performed by the disk. The number is 1,440. But the series of holes open during the experiment numbers 16; for every revolution, therefore, we had 16 puffs of air, or 16 waves of sound. Multiplying 1,440 by 16, we obtain 23,040 as the number of vibrations executed by the tuning-fork in a minute. Dividing this by 60, we find the number of vibrations executed in a second to be 384.
Having determined the rapidity of vibration, the length of the corresponding sonorous wave is found with the utmost facility. Imagine a tuning-fork vibrating in free air. At the end of a second from the time it103 commenced its vibrations the foremost wave would have reached a distance of 1,090 feet in air of the freezing temperature. In the air of a room which has a temperature of about 15° C., it would reach a distance of 1,120 in a second. In this distance, therefore, are embraced 384 sonorous waves. Dividing 1,120 by 384, we find the length of each wave to be nearly 3 feet. Determining in this way the rates of vibration of the four tuning-forks now before you, we find them to be 256, 320, 384, and 512; these numbers corresponding to wave-lengths of 4 feet 4 inches, 3 feet 6 inches, 2 feet 11 inches, and 2 feet 2 inches respectively. The waves generated by a man’s voice in common conversation are from 8 to 12 feet, those of a woman’s voice are from 2 to 4 feet in length. Hence a woman’s ordinary pitch in the lower sounds of conversation is more than an octave above a man’s; in the higher sounds it is two octaves.
And here it is important to note that by the term vibrations is meant complete ones; and by the term sonorous wave is meant a condensation and its associated rarefaction. By a vibration an excursion to and fro of the vibrating body is to be understood. Every wave generated by such a vibration bends the tympanic membrane once in and once out. These are the definitions of a vibration and of a sonorous wave employed in England and Germany. In France, however, a vibration consists of an excursion of the vibrating body in one direction, whether to or fro. The French vibrations, therefore, are only the halves of ours, and we therefore call them semi-vibrations. In all cases throughout these chapters, when the word vibration is employed without qualification, it refers to complete vibrations.
During the time required by each of those sonorous waves to pass entirely over a particle of air, that particle accomplishes one complete vibration. It is at one moment pushed forward into the condensation, while at the next moment it is urged back into the rarefaction. The time required by the particle to execute a complete oscillation is, therefore, that required by the sonorous wave to move through a distance equal to its own length. Supposing the length of the wave to be eight feet, and the velocity of sound in air of our present temperature to be 1,120 feet a second, the wave in question will pass over its own length of air in, 1/140th of a second: this is the time required by every air-particle that it passes to complete an oscillation.
In air of a definite density and elasticity a certain length of wave always corresponds to the same pitch. But supposing the density or elasticity not to be uniform; supposing, for example, the sonorous waves from one of our tuning-forks to pass from cold to hot air: an instant augmentation of the wave-length would occur, without any change of pitch, for we should have no change in the rapidity with which the waves would reach the ear. Conversely with the same length of wave the pitch would be higher in hot air than in cold, for the succession of the waves would be quicker. In an atmosphere of hydrogen, waves of a certain length would produce a note nearly two octaves higher than waves of the same length in air; for, in consequence of the greater rapidity of propagation, the number of impulses received in a given time in the one case would be nearly four times the number received in the other.
Opening the innermost and outermost series of the orifices of our siren, and sounding both of them, either together or in succession, the musical ears present at once detect the relationship of the two sounds. They notice immediately that the sound which issues from the circle of sixteen orifices is the octave of that which issues from the circle of eight. But for every wave sent forth by the latter, two waves are sent forth by the former. In this way we prove that the physical meaning of the term “octave” is, that it is a note produced by double the number of vibrations of its fundamental. By multiplying the vibrations of the octave by two, we obtain its octave, and by a continued multiplication of this kind we obtain a series of numbers answering to a series of octaves. Starting, for example, from a fundamental note of 100 vibrations, we should find, by this continual multiplication, that a note five octaves above it would be produced by 3,200 vibrations. Thus:
| 100 | Fundamental note. |
| 2 | |
| —— | |
| 200 | 1st octave. |
| 2 | |
| —— | |
| 400 | 2d octave. |
| 2 | |
| —— | |
| 800 | 3d octave. |
| 2 | |
| —— | |
| 1600 | 4th octave. |
| 2 | |
| —— | |
| 3200 | 5th octave. |
This result is more readily obtained by multiplying the vibrations of the fundamental note by the fifth power of two. In a subsequent chapter we shall return to this106 question of musical intervals. For our present purpose it is only necessary to define an octave.
The ear’s range of hearing is limited in both directions. Savart fixed the lower limit at eight complete vibrations a second; and to cause these slowly recurring vibrations to link themselves together he was obliged to employ shocks of great power. By means of a toothed wheel and an associated counter, he fixed the upper limit of hearing at 24,000 vibrations a second. Helmholtz has recently fixed the lower limit at 16 vibrations, and the higher at 38,000 vibrations, a second. By employing very small tuning-forks, the late M. Depretz showed that a sound corresponding to 38,000 vibrations a second is audible.28 Starting from the note 16, and multiplying continually by 2, or more compendiously raising 2 to the 11th power, and multiplying this by 16, we should find that at 11 octaves above the fundamental note the number of vibrations would be 32,768. Taking, therefore, the limit assigned by Helmholtz, the entire range of the human ear embraces about eleven octaves. But all the notes comprised within these limits cannot be employed in music. The practical range of musical sounds is comprised between 40 and 4,000 vibrations a second, which amounts, in round numbers, to seven octaves.29
The limits of hearing are different in different persons. While endeavoring to estimate the pitch of certain sharp sounds, Dr. Wollaston remarked in a friend a total insensibility to the sound of a small organ-pipe, which, in respect to acuteness, was far within the ordinary limits of hearing. The sense of hearing of this person terminated at a note four octaves above the middle E of the pianoforte. The squeak of the bat, the sound of a cricket, even the chirrup of the common house-sparrow, are unheard by some people who for lower sounds possess a sensitive ear. A difference of a single note is sometimes sufficient to produce the change from sound to silence. “The suddenness of the transition,” writes Wollaston, “from perfect hearing to total want of perception, occasions a degree of surprise which renders an experiment of this kind with a series of small pipes among several persons rather amusing. It is curious to observe the change of feeling manifested by various individuals of the party, in succession, as the sounds approach and pass the limits of their hearing. Those who enjoy a temporary triumph are often compelled, in their turn, to acknowledge to how short a distance their little superiority extends.” “Nothing can be more surprising,” writes Sir John Herschel, “than to see two persons, neither of them deaf, the one complaining of the penetrating shrillness of a sound, while the other maintains there is no sound at108 all. Thus, while one person mentioned by Dr. Wollaston could but just hear a note four octaves above the middle E of the pianoforte, others have a distinct perception of sounds full two octaves higher. The chirrup of the sparrow is about the former limit; the cry of the bat about an octave above it; and that of some insects probably another octave.” In “The Glaciers of the Alps” I have referred to a case of short auditory range, noticed by myself in crossing the Wengern Alps in company with a friend. The grass at each side of the path swarmed with insects, which to me rent the air with their shrill chirruping. My friend heard nothing of this, the insect-music lying beyond his limit of audition.
Behind the tympanic membrane exists a cavity—the drum of the ear—in part crossed by a series of bones, and in part occupied by air. This cavity communicates with the mouth by means of a duct called the Eustachian tube. This tube is generally closed, the air-space behind the tympanic membrane being thus shut off from the external air. If, under these circumstances, the external air becomes denser, it will press the tympanic membrane inward. If, on the other hand, the air outside becomes rarer, while the Eustachian tube remains closed, the membrane will be pressed outward. Pain is felt in both cases, and partial deafness is experienced. I once crossed the Stelvio Pass by night in company with a friend who complained of acute pain in the ears. On swallowing his saliva the pain instantly disappeared. By the act of swallowing, the Eustachian tube is opened, and thus equilibrium is established between the external and internal pressure.
It is possible to quench the sense of hearing of low sounds by stopping the nose and mouth, and trying to expand the chest, as in the act of inspiration. This effort partially exhausts the space behind the tympanic membrane, which is then thrown into a state of tension by the pressure of the outward air. A similar deafness to low sounds is produced when the nose and mouth are stopped, and a strong effort is made to expire. In this case air is forced through the Eustachian tube into the drum of the ear, the tympanic membrane being distended by the pressure of the internal air. The experiment may be made in a railway carriage, when the low rumble will vanish or be greatly enfeebled, while the sharper sounds are heard with undiminished intensity. Dr. Wollaston was expert in closing the Eustachian tube, and leaving the space behind the tympanic membrane occupied by either compressed or rarefied air. He was thus able to cause his deafness to continue for any required time without effort on his part, always, however, abolishing it by the act of swallowing. A sudden concussion may produce deafness by forcing air either into or out of the drum of the ear, and this may account for a fact noticed by myself in one of my Alpine rambles. In the summer of 1858, jumping from a cliff on to what was supposed to be a deep snowdrift, I came into rude collision with a rock which the snow barely covered. The sound of the wind, the rush of the glacier-torrents, and all the other noises which a sunny day awakes upon the mountains, instantly ceased. I could hardly hear the sound of my guide’s voice. This deafness continued for half an hour; at the end of which time the blowing of the nose opened, I suppose, the Eustachian tube, and restored, with the110 quickness of magic, the innumerable murmurs which filled the air around me.
Light, like sound, is excited by pulses or waves; and lights of different colors, like sounds of different pitch, are excited by different rates of vibration. But in its width of perception the ear exceedingly transcends the eye; for while the former ranges over eleven octaves, but little more than a single octave is possible to the latter. The quickest vibrations which strike the eye, as light, have only about twice the rapidity of the slowest;30 whereas the quickest vibrations which strike the ear, as a musical sound, have more than two thousand times the rapidity of the slowest.
Prof. Dove, as we have seen, extended the utility of
the siren of Cagniard de la Tour, by providing it with
four series of orifices instead of one. By doubling all its
parts, Helmholtz has recently added vastly to the power
of the instrument. The double siren, as it is called, is
now before you, Fig. 29 (next page). It is composed of
two of Dove’s sirens, C and C′, one turned upside down.
You will recognize in the lower siren the instrument
with which you are already acquainted. The disks of
the two sirens have a common axis, so that when one
disk rotates the other rotates with it. As in the former
case, the number of revolutions is recorded by clockwork
(omitted in the figure). When air is urged through
the tube t′ the upper siren alone sounds; when urged
111
112through t, the lower one only sounds; when it is urged
simultaneously through t′ and t, both the sirens sound.
With this instrument, therefore, we are able to introduce
much more varied combinations than with the former
one. Helmholtz has also contrived a means by which
not only the disk of the upper siren, but the box C′
above the disk, can be caused to rotate. This is effected
by a toothed wheel and pinion, turned by a handle. Underneath
the handle is a dial with an index, the use of
which will be subsequently illustrated.
Let us direct our attention for the present to the upper siren. By means of an India-rubber tube, the orifice t′ is connected with an acoustic bellows, and air is urged into C′. Its disk turns round, and we obtain with it all the results already obtained with Dove’s siren. The pitch of the note is uniform. Turning the handle above, so as to cause the orifices of the cylinder C′ to meet those of the disk, the two sets of apertures pass each other more rapidly than when the cylinder stood still. An instant rise of pitch is the result. By reversing the motion, the orifices are caused to pass each other more slowly than when C′ is motionless, and in this case you notice an instant fall of pitch when the handle is turned. Thus, by imparting in quick alternation a right-handed and left-handed motion to the handle, we obtain successive rises and falls of pitch. An extremely instructive effect of this kind may be observed at any railway station on the passage of a rapid train. During its approach the sonorous waves emitted by the whistle are virtually shortened, a greater number of them being crowded into the ear in a given time. During its retreat we have a virtual lengthening of the sonorous113 waves. The consequence is, that, when approaching, the whistle sounds a higher note, and when retreating it sounds a lower note, than if the train were still. A fall of pitch, therefore, is perceived as the train passes the station.31 This is the basis of Doppler’s theory of the colored stars. He supposes that all stars are white, but that some of them are rapidly retreating from us, thereby lengthening their luminiferous waves and becoming red. Others are rapidly approaching us, thereby shortening their waves, and becoming green or blue. The ingenuity of this theory is extreme, but its correctness is more than doubtful.
We have thus far occupied ourselves with the transmission
of musical sounds through air. They are also
transmitted by liquids and solids. When a tuning-fork
screwed into a little wooden foot vibrates, nobody, except
the persons closest to it, hears its sound. On dipping the
foot into a glass of water a musical sound is audible:
the vibrations having been transmitted through the water
to the air. The tube M N, Fig. 30, three feet long, is set
upright upon a wooden tray A B. The tube ends in a
funnel at the top, and is now filled with water to the
brim. The fork F is thrown into vibration, and on dipping
its foot into the funnel at the top of the tube, a
musical sound swells out. I must so far forestall matters
as to remark that in this experiment the tray is the real
sounding body. It has been thrown into vibration by
114the fork, but the vibrations have been conveyed to the
tray by the water. Through the same medium vibrations
 Fig. 30.
are communicated to
the auditory nerve,
the terminal filaments
of which are immersed
in a liquid:
substituting mercury
for water, a similar
result is obtained.
Fig. 30.
are communicated to
the auditory nerve,
the terminal filaments
of which are immersed
in a liquid:
substituting mercury
for water, a similar
result is obtained.
The siren has received its name from its capacity to sing under water. A vessel now in front of the table is half filled with water, in which a siren is wholly immersed. When a cock is turned, the water from the pipes which supply the house forces itself through the instrument. Its disk is now rotating, and a sound of rapidly augmenting pitch issues from the vessel. The pitch rises thus rapidly because the heavy and powerfully pressed water soon drives the disk up to its maximum speed of rotation. When the supply is lessened, the motion relaxes and the pitch falls. Thus, by alternately opening and closing the cock, the song of the siren is caused to rise and fall in a wild and melancholy manner. You would not consider such a sound likely to woo mariners to their doom.
The transmission of musical sounds through solid bodies is also capable of easy and agreeable illustration. Before you is a wooden rod, thirty feet long, passing from the table through a window in the ceiling, into the open air above. The lower end of the rod rests upon a wooden tray, to which the musical vibrations of a body applied to the upper end of the rod are to be transferred. An assistant is above, with a tuning-fork in his hand. He strikes the fork against a pad; it vibrates, but you hear nothing. He now applies the stem of the fork to the end of the rod, and instantly the wooden tray upon the table is rendered musical. The pitch of the sound, moreover, is exactly that of the tuning-fork; the wood has been passive as regards pitch, transmitting the precise vibrations imparted to it without any alteration. With another fork a note of another pitch is obtained. Thus fifty forks might be employed instead of two, and 300 feet of wood instead of 30; the rod would transmit the precise vibrations imparted to it, and no other.
We are now prepared to appreciate an extremely beautiful experiment, for which we are indebted to Sir Charles Wheatstone. In a room underneath this, and separated from it by two floors, is a piano. Through the two floors passes a tin tube 2-1/2 inches in diameter, and along the axis of this tube passes a rod of deal, the end of which emerges from the floor in front of the lecture-table. The rod is clasped by India-rubber bands, which entirely close the tin tube. The lower end of the rod rests upon the sound-board of the piano, its upper end being exposed before you. An artist is at this moment engaged at the instrument, but you hear no sound.116 When, however, a violin is placed upon the end of the rod, the instrument becomes instantly musical, not, however, with the vibrations of its own strings, but with those of the piano. When the violin is removed, the sound ceases; putting in its place a guitar, the music revives. For the violin and guitar we may substitute a plain wooden tray, which is also rendered musical. Here, finally, is a harp, against the sound-board of which the end of the deal rod is caused to press; every note of the piano is reproduced before you. On lifting the harp so as to break the connection with the piano, the sound vanishes; but the moment the sound-board is caused to press upon the rod the music is restored. The sound of the piano so far resembles that of the harp that it is hard to resist the impression that the music you hear is that of the latter instrument. An uneducated person might well believe that witchcraft or “spiritualism” is concerned in the production of this music.
What a curious transference of action is here presented to the mind! At the command of the musician’s will, the fingers strike the keys; the hammers strike the strings, by which the rude mechanical shock is converted into tremors. The vibrations are communicated to the sound-board of the piano. Upon that board rests the end of the deal rod, thinned off to a sharp edge to make it fit more easily between the wires. Through the edge, and afterward along the rod, are poured with unfailing precision the entangled pulsations produced by the shocks of those ten agile fingers. To the sound-board of the harp before you the rod faithfully delivers up the vibrations of which it is the vehicle. This second sound-board transfers the motion to the air, carving it and chasing it117 into forms so transcendently complicated that confusion alone could be anticipated from the shock and jostle of the sonorous waves. But the marvellous human ear accepts every feature of the motion, and all the strife and struggle and confusion melt finally into music upon the brain.32
A musical sound is produced by sonorous shocks which follow each other at regular intervals with a sufficient rapidity of succession.
Noise is produced by an irregular succession of sonorous shocks.
A musical sound may be produced by taps which rapidly and regularly succeed each other. The taps of a card against the cogs of a rotating wheel are usually employed to illustrate this point.
A musical sound may also be produced by a succession of puffs. The siren is an instrument by which such puffs are generated.
The pitch of a musical note depends solely on the number of vibrations concerned in its production. The more rapid the vibrations, the higher the pitch.
By means of the siren the rate of vibration of any sounding body may be determined. It is only necessary to render the sound of the siren and that of the body identical in pitch to maintain both sounds in unison for a certain time, and to ascertain, by means of the counter of the siren, how many puffs have issued from, the instrument 118 in that time. This number expresses the number of vibrations executed by the sounding body.
When a body capable of emitting a musical sound—a tuning-fork, for example—vibrates, it molds the surrounding air into sonorous waves, each of which consists of a condensation and a rarefaction.
The length of the sonorous wave is measured from condensation to condensation, or from rarefaction to rarefaction.
The wave-length is found by dividing the velocity of sound per second by the number of vibrations executed by the sounding body in a second.
Thus a tuning-fork which vibrates 256 times in a second produces in air of 15° C., where the velocity is 1,120 feet a second, waves 4 feet 4 inches long. While two other forks, vibrating respectively 320 and 384 times a second, generate waves 3 feet 6 inches, and 2 feet 11 inches long.
A vibration, as defined in England and Germany, comprises a motion to and fro. It is a complete vibration. In France, on the contrary, a vibration comprises a movement to or fro. The French vibrations are with us semi-vibrations.
The time required by a particle of air over which a sonorous wave passes to execute a complete vibration is that required by the wave to move through a distance equal to its own length.
The higher the temperature of the air, the longer is the sonorous wave corresponding to any particular rate of vibration. Given the wave-length and the rate of vibration, we can readily deduce the temperature of the air.
The human ear is limited in its range of hearing mu119sical sounds. If the vibrations number less than 16 a second, we are conscious only of the separate shocks. If they exceed 38,000 a second, the consciousness of sound ceases altogether. The range of the best ear covers about 11 octaves, but an auditory range limited to 6 or 7 octaves is not uncommon.
The sounds available in music are produced by vibrations comprised between the limits of 40 and 4,000 a second. They embrace 7 octaves.
The range of the ear far transcends that of the eye, which hardly exceeds an octave.
By means of the Eustachian tube, which is opened in the act of swallowing, the pressure of the air on both sides of the tympanic membrane is equalized.
By either condensing or rarefying the air behind the tympanic membrane, deafness to sounds of low pitch may be produced.
On the approach of a railway train the pitch of the whistle is higher, on the retreat of the train the pitch is lower, than it would be if the train were at rest.
Musical sounds are transmitted by liquids and solids. Such sounds may be transferred from one room to another; from the ground-floor to the garret of a house of many stories, for example, the sound being unheard in the rooms intervening between both, and rendered audible only when the vibrations are communicated to a suitable sound-board.
Vibration of Strings—How employed in Music—Influence of Sound-Boards—Laws of Vibrating Strings—Combination of Direct and Reflected Pulses—Stationary and Progressive Waves—Nodes and Ventral Segments—Application of Results to the Vibrations of Musical Strings—Experiments of Melde—Strings set in Vibration by Tuning-Forks—Laws of Vibration thus demonstrated—Harmonic Tones of Strings—Definitions of Timbre or Quality, or Overtones and Clang—Abolition of Special Harmonics—Conditions which affect the Intensity of the Harmonic Tones—Optical Examination of the Vibrations of a Piano-Wire.
WE HAVE to begin our studies to-day with the vibrations of strings or wires; to learn how bodies of this form are rendered available as sources of musical sounds, and to investigate the laws of their vibrations.
To enable a musical string to vibrate transversely, or at right angles to its length, it must be stretched between two rigid points. Before you, Fig. 31 (next page), is an instrument employed to stretch strings, and to render their vibrations audible. From the pin p, to which one end of it is firmly attached, a string passes across the two bridges B and B′, being afterward carried over the wheel H, which moves with great freedom. The string is finally stretched by a weight W, of 28 lbs., attached to its extremity. The bridges B and B′, which constitute the real ends of the string, are fastened on to the long121 wooden box M N. The whole instrument is called a monochord, or sonometer.
Taking hold of the stretched string B B′ at its middle and plucking it aside, it springs back to its first position, passes it, returns, and thus vibrates for a time to and fro across its position of equilibrium. You hear a sound, but the sonorous waves which at present strike your ears do not proceed immediately from the string. The amount of wave-motion generated by so thin a body is too small to be sensible at any distance. But the string is drawn tightly over the two bridges B B′; and when it vibrates, its tremors are communicated through these bridges to the entire mass of the box M N, and to the air within the box, which thus become the real sounding bodies.
That the vibrations of the string alone are not sufficient
to produce the sound may be thus experimentally
demonstrated: A B, Fig. 32 (next page), is a piece of
wood placed across an iron bracket C. From each end
of the piece of wood depends a rope ending in a loop,122
while stretching across from loop to loop is an iron bar
m n. From the middle of the iron bar hangs a steel
wire s s′, stretched by a weight W, of 28 lbs. By this
 Fig. 32.
arrangement the wire is detached
from all large surfaces
to which it could impart its
vibrations. Plucking the wire
s s′, it vibrates vigorously, but
even those nearest to it do not
hear any sound. The agitation
imparted to the air is too inconsiderable
to affect the auditory
nerve at any distance. A
second wire t t′, Fig. 33 (next
page), of the same length, thickness,
and material as s s′, has
one of its ends attached to the
wooden tray A B. This wire also
carries a weight W, of 28 lbs.
Finally, passing over the bridges
B B′ of the sonometer, Fig. 31, is
our third wire, in every respect
like the two former, and, like
them, stretched by a weight W,
of 28 lbs. When the wire t t′,
Fig. 33, is caused to vibrate,
you hear its sound distinctly.
Though one end only of the wire
is connected with the tray A B, the vibrations transmitted
to it are sufficient to convert the tray into a sounding
body. Finally, when the wire of the sonometer M N,
Fig. 31, is plucked, the sound is loud and full, because123
the instrument is specially constructed to take up the
vibrations of the wire.
Fig. 32.
arrangement the wire is detached
from all large surfaces
to which it could impart its
vibrations. Plucking the wire
s s′, it vibrates vigorously, but
even those nearest to it do not
hear any sound. The agitation
imparted to the air is too inconsiderable
to affect the auditory
nerve at any distance. A
second wire t t′, Fig. 33 (next
page), of the same length, thickness,
and material as s s′, has
one of its ends attached to the
wooden tray A B. This wire also
carries a weight W, of 28 lbs.
Finally, passing over the bridges
B B′ of the sonometer, Fig. 31, is
our third wire, in every respect
like the two former, and, like
them, stretched by a weight W,
of 28 lbs. When the wire t t′,
Fig. 33, is caused to vibrate,
you hear its sound distinctly.
Though one end only of the wire
is connected with the tray A B, the vibrations transmitted
to it are sufficient to convert the tray into a sounding
body. Finally, when the wire of the sonometer M N,
Fig. 31, is plucked, the sound is loud and full, because123
the instrument is specially constructed to take up the
vibrations of the wire.
The importance of employing proper sounding apparatus
in stringed instruments is rendered manifest by
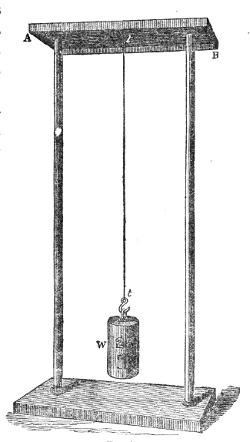 Fig. 33.
these experiments. It
is not the strings of a
harp, or a lute, or a
piano, or a violin, that
throw the air into sonorous
vibrations. It is
the large surfaces with
which the strings are
associated, and the air
inclosed by these surfaces.
The goodness
of such instruments depends
almost wholly
upon the quality and
disposition of their
sound-boards.33
Fig. 33.
these experiments. It
is not the strings of a
harp, or a lute, or a
piano, or a violin, that
throw the air into sonorous
vibrations. It is
the large surfaces with
which the strings are
associated, and the air
inclosed by these surfaces.
The goodness
of such instruments depends
almost wholly
upon the quality and
disposition of their
sound-boards.33
Take the violin as
an example. It is, or
ought to be, formed of
wood of the most perfect
elasticity. Imperfectly
elastic wood expends
the motion imparted
to it in the friction of its own molecules; the
124motion is converted into heat, instead of sound. The
strings of the violin pass from the “tail-piece” of the
instrument over the “bridge,” being thence carried to
the “pegs,” the turning of which regulates the tension
of the strings. The bow is drawn across at a point about
one-tenth of the length of the string from the bridge.
The two “feet” of the bridge rest upon the most yielding
portion of the “belly” of the violin, that is, the portion
that lies between the two f-shaped orifices. One foot is
fixed over a short rod, the “sound post,” which runs
from belly to back through the interior of the violin.
This foot of the bridge is thereby rendered rigid, and it
is mainly through the other foot, which is not thus supported,
that the vibrations are conveyed to the wood of
the instrument, and thence to the air within and without.
The sonorous quality of the wood of a violin is
mellowed by age. The very act of playing also has a
beneficial influence, apparently constraining the molecules
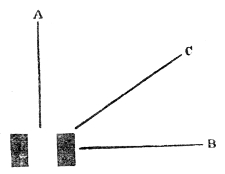 Fig. 34.
of the wood, which in the
first instance might be refractory,
to conform at last to the requirements
of the vibrating strings.
Fig. 34.
of the wood, which in the
first instance might be refractory,
to conform at last to the requirements
of the vibrating strings.
This is the place to make the promised reference (page 38) to Prof. Stokes’s explanation of the action of sound-boards. Although the amplitude of the vibrating board may be very small, still its larger area renders the abolition of the condensations and rarefactions difficult. The air cannot move away in front nor slip in behind before it is sensibly condensed and rarefied. Hence with such vibrating bodies sound-waves may be generated, and loud tones125 produced, while the thin strings that set them in vibration, acting alone, are quite inaudible.
The increase of sound, produced by the stoppage of lateral motion, has been experimentally illustrated by Prof. Stokes. Let the two black rectangles in Fig. 34 represent the section of a tuning-fork. After it has been made to vibrate, place a sheet of paper, or the blade of a broad knife, with its edge parallel to the axis of the fork, and as near to the fork as may be without touching. If the obstacle be so placed that the section of it is A or B, no effect is produced; but if it be placed at C, so as to prevent the reciprocating to-and-fro movement of the air, which tends to abolish the condensations and rarefactions, the sound becomes much stronger.
Having thus learned how the vibrations of strings are rendered available in music, we have next to investigate the laws of such vibrations. I pluck at its middle point the string B B′, Fig. 31. The sound heard is the fundamental or lowest note of the string, to produce which it swings, as a whole, to and fro. By placing a movable bridge under the middle of the string, and pressing the string against the bridge, it is divided into two equal parts. Plucking either of those at its centre, a musical note is obtained, which many of you recognize as the octave of the fundamental note. In all cases, and with all instruments, the octave of a note is produced by doubling the number of its vibrations. It can, moreover, be proved, both by theory and by the siren, that this half string vibrates with exactly twice the rapidity of the whole. In the same way it can be proved that one-third126 of the string vibrates with three times the rapidity, producing a note a fifth above the octave, while one-fourth of the string vibrates with four times the rapidity, producing the double octave of the whole string. In general terms, the number of vibrations is inversely proportional to the length of the string.
Again, the more tightly a string is stretched the more rapid is its vibration. When this comparatively slack string is caused to vibrate, you hear its low fundamental note. By turning a peg, round which one end of it is coiled, the string is tightened, and the pitch rendered higher. Taking hold with my left hand of the weight w, attached to the wire B B′ of our sonometer, and plucking the wire with the fingers of my right, I alternately press upon the weight and lift it. The quick variations of tension are expressed by a varying wailing tone. Now, the number of vibrations executed in the unit of time bears a definite relation to the stretching force. Applying different weights to the end of the wire B B′, and determining in each case the number of vibrations executed in a second, we find the numbers thus obtained to be proportional to the square roots of the stretching weights. A string, for example, stretched by a weight of one pound, executes a certain number of vibrations per second; if we wish to double this number, we must stretch it by a weight of four pounds; if we wish to treble the number, we must apply a weight of nine pounds, and so on.
The vibrations of a string also depend upon its thickness. Preserving the stretching weight, the length, and the material of the string constant, the number of vibrations varies inversely as the thickness of the string. If,127 therefore, of two strings of the same material, equally long and equally stretched, the one has twice the diameter of the other, the thinner string will execute double the number of vibrations of its fellow in the same time. If one string be three times as thick as another, the latter will execute three times the number of vibrations, and so on.
Finally, the vibrations of a string depend upon the density of the matter of which it is composed. A platinum wire and an iron wire, for example, of the same length and thickness, stretched by the same weight, will not vibrate with the same rapidity. For, while the specific gravity of iron, or in other words its density, is 7·8, that of platinum is 21·5. All other conditions remaining the same, the number of vibrations is inversely proportional to the square root of the density of the string. If the density of one string, therefore, be one-fourth that of another of the same length, thickness, and tension, it will execute its vibrations twice as rapidly; if its density be one-ninth that of the other, it will vibrate with three times the rapidity, and so on. The last two laws, taken together, may be expressed thus: The number of vibrations is inversely proportional to the square root of the weight of the string.
In the violin and other stringed instruments we avail ourselves of thickness instead of length to obtain the deeper tones. In the piano we not only augment the thickness of the wires intended to produce the bass notes, but we load them by coiling round them an extraneous substance. They resemble horses heavily jockeyed, and move more slowly on account of the greater weight imposed upon the force of tension.
These, then, are the four laws which regulate the
transverse vibrations of strings. We now turn to certain
allied phenomena, which, though they involve mechanical
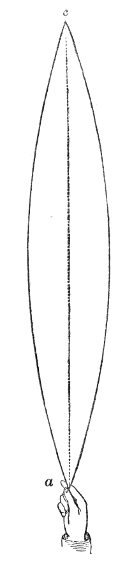 Fig. 35.
considerations of a rather complicated kind, may be completely mastered by an average
Fig. 35.
considerations of a rather complicated kind, may be completely mastered by an average
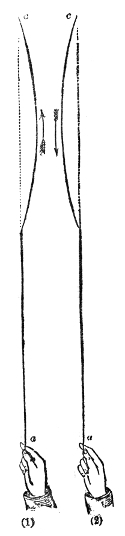 Fig. 36.
amount of attention. And they
must be mastered if we would
thoroughly comprehend the
philosophy of stringed instruments.
Fig. 36.
amount of attention. And they
must be mastered if we would
thoroughly comprehend the
philosophy of stringed instruments.
From the ceiling c, Fig. 35, of this room hangs an India-rubber tube twenty-eight feet long. The tube is filled with sand to render its motions slow and more easily followed by the eye. I take hold of its free end a, stretch the tube a little, and by properly timing my impulses cause it to swing to and fro as a whole, as shown in the figure. It has its definite period of vibration dependent on its length, weight, thickness, and tension, and my impulses must synchronize with that period.
I now stop the motion, and by a sudden jerk raise a hump upon the tube, which runs along it as a pulse129 toward its fixed end; here the hump reverses itself, and runs back to my hand. At the fixed end of the tube, in obedience to the law of reflection, the pulse reversed both its position and the direction of its motion. Supposing c, Fig. 36, to be the fixed end of the tube, and a the end held in the hand: if the pulse on reaching c have the position shown in (1), after reflection it will have the position shown in (2). The arrows mark the direction of progression. The time required for the pulse to pass from the hand to the fixed end and back is exactly that required to accomplish one complete vibration of the tube as a whole. It is indeed the addition of such impulses which causes the tube to continue to vibrate as a whole.
If, instead of a single jerk, a succession of jerks be imparted, thereby sending a series of pulses along the tube, every one of them will be reflected above, and we have now to inquire how the direct and reflected pulses behave toward each other.
Let the time required by the pulse to pass from my hand to the fixed end be one second; at the end of half a second it occupies the position a b (1), Fig. 37, its foremost point having reached the middle of the tube. At the end of a whole second it would have the position b c130 (2), its foremost point having reached the fixed end c of the tube. At the moment when reflection begins at c, let another jerk be imparted at a. The reflected pulse from c moving with the same velocity as this direct one from a, the foremost points of both will arrive at the centre b (3) at the same moment. What must occur? The hump a b wishes to move on to c, and to do so must move the point b to the right. The hump c b wishes to move toward a, and to do so must move the point b to the left. The point b, urged by equal forces in two opposite directions at the same time, will not move in either direction. Under these circumstances, the two halves, a b, b c of the tube will oscillate as if they were independent of each other (4). Thus by the combination of two progressive pulses, the one direct and the other reflected, we produce two stationary pulses on the tube a c.
The vibrating parts a b and b c are called ventral segments; the point of no vibration b is called a node.
The term “pulse” is here used advisedly, instead of the more usual term wave. For a wave embraces two of these pulses. It embraces both the hump and the depression which follows the hump. The length of a wave, therefore, is twice that of a ventral segment.
Supposing the jerks to be so timed as to cause each hump to be one-third of the tube’s length. At the end of one-third of a second from starting the pulse will be in the position a b (1), Fig. 38. In two-thirds of a second it will have reached the position b b′ (2), Fig. 38. At this moment let a new pulse be started at a; after the lapse of an entire second from the commencement we shall have two humps upon the tube, one occupying the position a b (3), the other the position b′ c (3). It is here131 manifest that the end of the reflected pulse from c, and the end of the direct one from a, will reach the point b′ at the same moment. We shall therefore have the state of things represented in (4), where b b′ wishes to move upward, and c b′ to move downward. The action of both upon the point b′ being in opposite directions, that point will remain fixed. And from it, as if it were a fixed point, the pulse b b′ will be reflected, while the segment b′ c will oscillate as an independent string. Supposing that at132 the moment b b′ (4) begins to be reflected at b′ we start another pulse from a, it will reach b at the same moment the pulse reflected from b′ reaches it. The pulses will neutralize each other at b, and we shall have there a second node. Thus, by properly timing our jerks, we divide the rope into three ventral segments, separated from each other by two nodal points. As long as the agitation continues the tube will vibrate as in (6).
There is no theoretic limit to the number of nodes and ventral segments that may be thus produced. By the quickening of the impulses, the tube is divided into four ventral segments separated by three nodes; quickening still more we have five ventral segments and four nodes. With this particular tube the hand may be caused to vibrate sufficiently quick to produce ten ventral segments, as shown in Fig. 38 (7). When the stretching force is constant, the number of ventral segments is proportional to the rapidity of the hand’s vibration. To produce 2, 3, 4, 10 ventral segments requires twice, three times, four times, ten times the rapidity of vibration necessary to make the tube swing as a whole. When the vibration is very rapid the ventral segments appear like a series of shadowy spindles, separated from each other by dark motionless nodes. The experiment is a beautiful one, and it is easily performed.
If, instead of moving the hand to-and fro, it be caused to describe a small circle, the ventral segments become “surfaces of revolution.” Instead of the hand, moreover, we may employ a hook turned by a whirling-table. Before you is a cord more rigid than the India-rubber tube, 25 feet long, with one of its ends attached to a freely-moving swivel fixed in the ceiling of the room.133 By turning the whirling-table to which the other end is attached, this cord may be divided into as many as 20 ventral segments, separated from each other by their appropriate nodes. In another arrangement a string of catgut 12 feet long, with silvered beads strung along it, is stretched horizontally between a vertical wheel and a free swivel fixed in a rigid stand. On turning the wheel, and properly regulating both the tension and the rapidity of rotation, the beaded cord may be caused to rotate as a whole, and to divide itself successively into 2, 3, 4, or 5 ventral segments. When we envelop the cord in a luminous beam, every spot of light on every bead describes a brilliant circle, and a very beautiful experiment is the result.
The subject of stationary waves was first experimentally treated by the Messrs. Weber, in their excellent researches on wave-motion. It is a subject which will well repay your attention by rendering many of the most difficult phenomena of musical strings perfectly intelligible. It will make the connection of both classes of vibrations more obvious if we vary our last experiments. Before you is a piece of India-rubber tubing, 10 or 12 feet long, stretched from c to a, Fig. 39, and made fast to two pins at c and a. The tube is blackened, and behind it is placed a surface of white paper, to render its motions more visible. Encircling the tube at its centre b (1) by the thumb and forefinger of my left hand, and taking the middle of the lower half b a of the tube in my right, I pluck it aside. Not only does the lower half swing,134 but the upper half also is thrown into vibration. Withdrawing the hands wholly from the tube, its two halves a b and b c continue to vibrate, being separated from each other by a node b at the centre (2).
I now encircle the tube at a point b (3) one-third of its length from its lower end a, and, taking hold of a b at its centre, pluck it aside; the length b c above my hand instantly divides into two vibrating segments. Withdrawing the hands wholly, you see the entire tube divided into three ventral segments, separated135 from each other by two motionless nodes, b and b′ (4). I pass on to the point b (5), which marks off one-fourth of the length of the tube, encircle it, and pluck the shorter segment aside. The longer segment above my hand divides itself immediately into three vibrating parts. So that, on withdrawing the hand, the whole tube appears before you divided into four ventral segments, separated from each other by three nodes b b′ b″ (6). In precisely the same way the tube may be divided into five vibrating segments with four nodes.
This sudden division of the long upper segment of the tube, without any apparent cause, is very surprising; but if you grant me your attention for a moment, you will find that these experiments are essentially similar to those which illustrated the coalescence of direct and reflected undulations. Reverting for a moment to the latter, you observed that the to-and-fro motion of the hand through the space of a single inch was sufficient to make the middle points of the ventral segments vibrate through a foot or eighteen inches. By being properly timed the impulses accumulated, until the amplitude of the vibrating segments exceeded immensely that of the hand which produced them. The hand, in fact, constituted a nodal point, so small was its comparative motion. Indeed, it is usual, and correct, to regard the ends of the tube also as nodal points.
Consider now the case represented in (1), Fig. 39, where the tube was encircled at its middle, the lower segment a b being thrown into the vibration corresponding to its length and tension. The circle formed by the finger and thumb permitted the tube to oscillate at the point b through the space of an inch; and the vibrations136 at that point acted upon the upper half b c exactly as my hand acted when it caused the tube suspended from the ceiling to swing as a whole, as in Fig. 35. Instead of the timid vibrations of the hand, we have now the timid vibrations of the lower half of the tube; and these, though narrowed to an inch at the place clasped by the finger and thumb, soon accumulate, and finally produce an amplitude, in the upper half, far exceeding their own. The same reasoning applies to all the other cases of subdivision. If, instead of encircling a point by the finger and thumb, and plucking the portion of the tube below it aside, that same point were taken hold of by the hand and agitated in the period proper to the lower segment of the tube, precisely the same effect would be produced. We thus reduce both effects to one and the same cause; namely, the combination of direct and reflected undulations.
And here let me add that, when the tube was divided by the timid impulses of the hand, not one of its nodes was, strictly speaking, a point of no motion; for were the nodes not capable of vibrating through a very small amplitude, the motion of the various segments of the tube could not be maintained.
What is true of the undulations of an India-rubber tube applies to all undulations whatsoever. Water-waves, for example, obey the same laws, and the coalescence of direct and reflected waves exhibits similar phenomena. This long and narrow vessel with glass sides, Fig. 40, is a copy of the wave-canal of the brothers Weber. It is filled to the level A B with colored water. By tilting the137 end A suddenly, a wave is generated, which moves on to B, and is there reflected. By sending forth fresh waves at the proper intervals, the surface is divided into two stationary undulations. Making the succession of impulses more rapid we can subdivide the surface into three, four (shown in the figure), or more stationary undulations, separated from each other by nodes. The step of a water-carrier is sometimes so timed as to throw the surface of the water in his vessel into stationary waves, which may augment in height until the water splashes over the brim. Practice has taught the water-carrier what to do; he changes his step, alters the period of his impulses, and thus stops the accumulation of the motion.
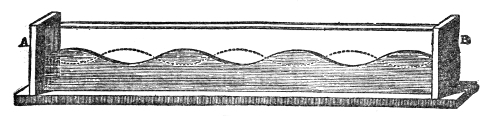
In travelling recently in the coupé of a French railway carriage, I had occasion to place a bottle half filled with water on one of the little coupé tables. It was interesting to observe it. At times it would be quite still; at times it would oscillate violently. To the passenger within the carriage there was no sensible change in the motion of the train to which the difference could be ascribed. But in the one case the tremor of the carriage contained no vibrations synchronous with the oscillating period of the water, while in the other case such vibrations were present. Out of the confused assemblage of tremors the water selected the particular constituent138 which belonged to itself, and declared its presence when the traveller was utterly unconscious of its introduction.
From these comparatively gross, but by no means unbeautiful, mechanical vibrations, we pass to those of a sounding string. In the experiments with our monochord, when the wire was to be shortened, a movable bridge was employed, against which the wire was pressed so as to deprive the point resting on the bridge of all possibility of motion. This strong pressure, however, is not necessary. Placing the feather-end of a goose-quill lightly against the middle of the string, and drawing a violin-bow over one of its halves, the string yields the octave of the note yielded by the whole string. The mere damping of the string at the centre, by the light touch of the feather, is sufficient to cause the string to divide into two vibrating segments. Nor is it necessary to hold the feather there throughout the experiment: after having drawn the bow, the feather may be removed; the string will continue to vibrate, emitting the same note as before. We have here a case exactly analogous to that in which the central point of our stretched India-rubber tube was damped, by encircling it with the finger and thumb as in Fig. 39 (1). Not only did the half plucked aside vibrate, but the other half vibrated also. We can, in fact, reproduce, with the vibrating string, every effect obtained with the tube. This, however, is a point of such importance as to demand full experimental illustration.
To prove that when the centre is damped, and the139 bow drawn across one of the halves of the string, the other half vibrates, I place across the middle of the untouched half a little rider of red paper. Damping the centre and drawing the bow, the string shivers, and the rider is overthrown, Fig. 41.
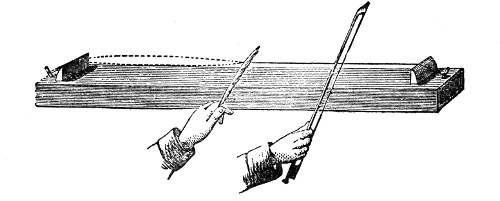
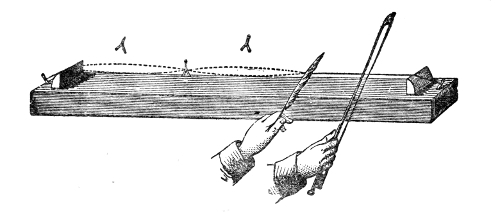
When the string is damped at a point which cuts off one-third of its length, and the bow drawn across the shorter section, not only is this section thereby thrown into vibration, but the longer section divides itself into two ventral segments with a node between them. This is proved by placing small riders of red paper on the ventral segments, and a rider of blue paper at the node. Passing the bow across the short segment you observe a fluttering of the red riders, and now they are completely140 tossed off, while the blue rider which crosses the node is undisturbed, Fig. 42.
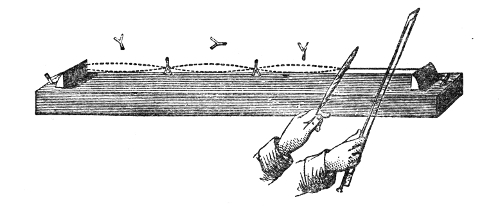
Damping the string at the end of one-fourth of its length, the bow is drawn across the shorter section; the remaining three-fourths divide themselves into three ventral segments, with two nodes between them. This is proved by the unhorsing of the three riders placed astride the ventral segments, the two at the nodes keeping their places undisturbed, Fig. 43.
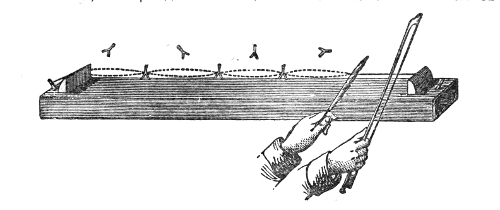
Finally, damping the string at the end of one-fifth of its length, and arranging, as before, the red riders on the ventral segments and the blue ones on the nodes, by a single sweep of the bow the four red riders are unhorsed, and the three blue ones left undisturbed, Fig. 44. In141 this way we perform with a sounding string the same series of experiments that were formerly executed with a stretched India-rubber tube, the results in both cases being identical.34
To make, if possible, this identity still more evident to you, a stout steel wire 28 feet in length is stretched behind the table from side to side of the room. I take the central point of this wire between my finger and thumb, and allow my assistant to pluck one-half of it aside. It vibrates, and the vibrations transmitted to the other half are sufficiently powerful to toss into the air a large sheet of paper placed astride the wire. With this long wire, and with riders not of one-eighth of a square inch, but of 30, 40, or 50 square inches in area, we may repeat all the experiments which you have witnessed with the musical string. The sheets of paper placed across the nodes remain always in their places, while those placed astride the ventral segments are tossed simultaneously into the air when the shorter segment of the wire is set in vibration. In this case, when close to it, you can actually see the division of the wire.
It is now time to introduce to your notice some recent experiments on vibrating strings, which appeal to the eye with a beauty and a delicacy far surpassing anything attainable with our monochord. To M. Melde, of Mar142burg, we are indebted for this new method of exhibiting the vibrations of strings. The scale of the experiments will be here modified so as to suit our circumstances.
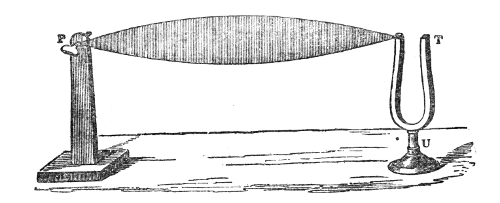
First, then, you observe here a large tuning-fork T, Fig. 45, with a small screw fixed into the top of one of its prongs, by which a silk string can be firmly attached to the prong. From the fork the string passes round a distant peg P, by turning which it may be stretched to any required extent. When the bow is drawn across the fork, an irregular flutter of the string is the only result. On tightening it, however, when at the proper tension it expands into a beautiful gauzy spindle six feet long, more than six inches across at its widest part, and shining with a kind of pearly lustre. The stretching force at the present moment is such that the string swings to and fro as a whole, its vibrations being executed in a vertical plane.
Relaxing the string gradually, when the proper tension has been reached, it suddenly divides into two ventral segments, separated from each other by a sharply-defined and apparently motionless node.
While the fork continues vibrating, if the string be relaxed still further, it divides into three vibrating parts.143 Slackening it still more, it divides into four vibrating parts. And thus we might continue to subdivide the string into ten, or even twenty ventral segments, separated from each other by the appropriate number of nodes.

When white-silk strings vibrate thus, the nodes appear perfectly fixed, while the ventral segments form spindles of the most delicate beauty. Every protuberance of the twisted string, moreover, writes its motion in a more or less luminous line on the surface of the aërial gauze. The four nodes of vibration just illustrated are represented in Fig. 46, 1, 2, 3, 4.35
When the synchronism between fork and string is perfect, the vibrations of the string are steady and long-continued. A slight departure from synchronism, however, introduces unsteadiness, and the ventral segments, though they may show themselves for a time, quickly disappear.
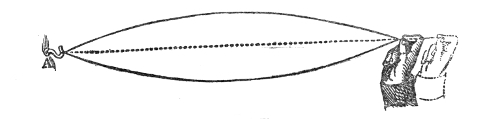
In the experiments just executed the fork vibrated in the direction of the length of the string. Every forward stroke of the fork raised a protuberance, which ran to the fixed end of the string, and was there reflected; so that when the longitudinal impulses were properly timed they produced a transverse vibration. Let us consider this further. One end of this heavy cord is attached to a hook A, Fig. 47, fixed in the wall. Laying hold of the other end I stretch the cord horizontally, and then move my hand to and fro in the direction of the cord. It swings as a whole, and you may notice that always, when the cord is at the limit of its swing, the hand is in its most forward position. If it vibrate in a vertical145 plane, the hand, in order to time the impulses properly, must be at its forward limit at the moment the cord reaches the upper boundary, and also at the moment it reaches the lower boundary of its excursion. A little reflection will make it plain that, in order to accomplish this, the hand must execute a complete vibration while the cord executes a semi-vibration; in other words, the vibrations of the hand must be twice as rapid as those of the cord.
Precisely the same is true of our tuning-fork. When the fork vibrates in the direction of the string, the number of vibrations which it executes in a certain time is twice the number executed by the string itself. And if, while arranged thus, a fork and string vibrate with sufficient rapidity to produce musical notes, the note of the fork will be an octave above that of the string.
But if, instead of the hand being moved to and fro in the direction of this heavy cord, it is moved at right angles to that direction, then every upward movement of the hand coincides with an upward movement of the cord; every downward movement of the hand with a downward movement of the cord. In fact, the vibrations of hand and string, in this case, synchronize perfectly; and if the hand could emit a musical note, the cord would, emit a note of the same pitch. The same holds good when a vibrating fork is substituted for the vibrating hand.
Hence, if the string vibrate as a whole when the vibrations of the fork are along it, it will divide into two ventral segments when the vibrations are across it; or, more generally expressed, preserving the tension constant, whatever be the number of ventral segments pro146duced by the fork when its vibrations are in the direction of the string, twice that number will be produced when the vibrations are transverse to the string. The string A B, for example, Figs. 48 and 49, passing over a pulley B, is stretched by a definite weight (not shown in the figure). When the tuning-fork vibrates along it, as in Fig. 48, the string divides into two equal ventral segments. When the fork is turned so that it shall vibrate at right angles to the string, the number of ventral segments is four, Fig. 49, or double the former number. Attaching two strings of the same length to the same fork, the one parallel and the other perpendicular to the direction of vibration, and stretching both with equal weights, when the fork is caused to vibrate, one of them divides itself into twice the number of ventral segments exhibited by the other.


A number of exquisite effects may be obtained with these vibrating cords. The path described by any point of any one of them may be studied, after the manner of Dr. Young, by illuminating that point, and watching the147 line of light which it describes. This is well illustrated by a flat burnished silver wire, twisted so as to form a spiral surface, from which, at regular intervals, the light flashes when the wire is illuminated. When the vibration is steady, the luminous spots describe straight lines of sunlike brilliancy. On slackening the wire, but not so much as to produce its next higher subdivision, upon the larger motion of the wire are superposed a host of minor motions, the combination of all producing scrolls of marvellous complication and of indescribable splendor.
In reflecting on the best means of rendering these effects visible, the thought occurred to me of employing a fine platinum wire heated to redness by an electric current. Such a wire now stretches from a tuning-fork over a bridge of copper, and then passes round a peg. The copper bridge on the one hand and the tuning-fork on the other are the poles of a voltaic battery, from which a current passes through the wire and causes it to glow. On drawing the bow across the fork, the wire vibrates as a whole; its two ends are brilliant, while its middle is dark, being chilled by its rapid passage through the air. Thus you have a shading off of incandescence from the ends to the centre of the wire. On relaxing the tension, the wire divides itself into two ventral segments; on relaxing still further, we obtain three; still further, and the wire divides into four ventral segments, separated from each other by three brilliant nodes. Right and left from every node the incandescence shades away until it disappears. You notice also, when the wire settles into steady vibration, that the nodes shine out with greater brilliancy than that possessed by the wire before the vibration commenced. The reason is this. Electricity passes more148 freely along a cold wire than along a hot one. When, therefore, the vibrating segments are chilled by their swift passage through the air, their conductivity is improved, more electricity passes through the vibrating than through the motionless wire, and hence the augmented glow of the nodes. If, previous to the agitation of the fork, the wire be at a bright-red heat, when it vibrates its nodes may be raised to the temperature of fusion.
We may extend the experiments of M. Melde to the establishment of all the laws of vibrating strings. Here are four tuning-forks, which we may call a, b, c, d, whose rates of vibration are to each other as the numbers 1, 2, 4, 8. To the largest fork is attached a string, a, stretched by a weight, which causes it to vibrate as a whole. Keeping the stretching weight the same, I determine the lengths of the same string, which, when attached to the other three forks, b, c, d, swing as a whole. The lengths in the four respective cases are as the numbers 8, 4, 2, 1.
From this follows the first law of vibration, already established (p. 126) by another method; viz., the length of the string is inversely proportional to the rapidity of vibration.36
In this case the longest string vibrates as a whole when attached to the fork a. I now transfer the string 149to b, still keeping it stretched by the same weight. It vibrates when b vibrates; but how? By dividing into two equal ventral segments. In this way alone can it accommodate itself to the swifter vibrating period of b. Attached to c, the same string separates into four, while when attached to d, it divides into eight ventral segments. The number of the ventral segments is proportional to the rapidity of vibration. It is evident that we have here, in a more delicate form, a result which we have already established in the case of our India-rubber tube set in motion by the hand. It is also plain that this result might be deduced theoretically from our first law.
We may extend the experiment. Here are two tuning-forks separated from each other by the musical interval called a fifth. Attaching a string to one of the forks, I stretch the string until it divides into two ventral segments: attached to the other fork, and stretched by the same weight, it divides instantly into three segments when the fork is set in vibration. Now, to form the interval of a fifth, the vibrations of the one fork must be to those of the other in the ratio of 2:3. The division of the string, therefore, declares the interval. In, the same way the division of the string in relation to all other musical intervals may be illustrated.37
Again. Here are two tuning-forks, a and b, one of which (a) vibrates twice as rapidly as the other. A string of silk is attached to a, and stretched until it synchronizes with the fork, and vibrates as a whole. Here is a second string of the same length, formed by laying four strands of the first one side by side. I attach this compound thread to b, and, keeping the tension 150the same as in the last experiment, set b in vibration. The compound thread synchronizes with b, and swings as a whole. Hence, as the fork b vibrates with half the rapidity of a, by quadrupling the weight of the string we halved its rapidity of vibration. In the same simple way it might be proved that by augmenting the weight of the string nine times we reduce the number of its vibrations to one-third. We thus demonstrate the law:
The rapidity of vibration is inversely proportional to the square root of the weight of the string.
An instructive confirmation of this result is thus obtained: Attached to this tuning-fork is a silk string six feet long. Two feet of the string are composed of four strands of the single thread, placed side by side; the remaining four feet are a single thread. A stretching force is applied, which causes the string to divide into two ventral segments. But how does it divide? Not at its centre, as is the case when the string is of uniform thickness throughout, but at the precise point where the thick string terminates. This thick segment, two feet long, is now vibrating at the same rate as the thin segment four feet long, a result which follows by direct deduction from the two laws already established.
Here again are two strings of the same length and thickness. One of them is attached to the fork a, the other to the fork b, which vibrates with twice the rapidity of a. Stretched by a weight of 20 grains, the string attached to b vibrates as a whole. Substituting b for a, a weight of 80 grains causes the string to vibrate as a whole. Hence, to double the rapidity of vibration, we must quadruple the stretching weight. In the same way it might be proved that to treble the rapidity of vibra151tion we should have to make the stretching weight ninefold. Hence our third law:
The rapidity of vibration is proportional to the square root of the tension.
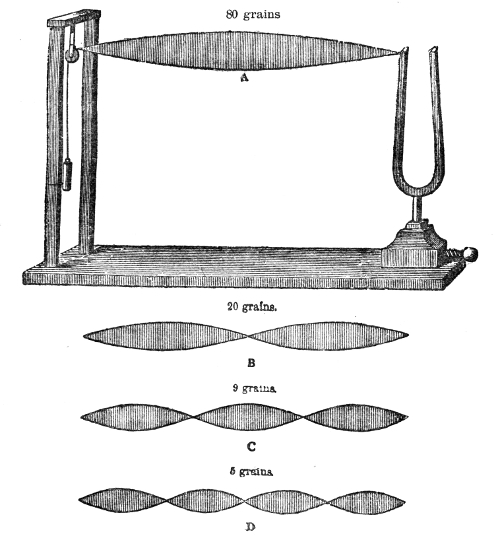
Let us vary this experiment. This silk cord is carried from the tuning-fork over the pulley, and stretched by a weight of 80 grains. The string vibrates as a whole as at A, Fig. 50. By diminishing the weight the string is relaxed, and finally divides sharply into two ventral segments, as at B, Fig. 50. What is now the stretching152 weight?—20 grains, or one-fourth of the first. With a stretching weight of almost exactly 9 grains it divides into three segments, as at C; while with a stretching weight of 5 grains it divides into four segments, as at D. Thus then, a tension of one-fourth doubles, a tension of one-ninth trebles, and a tension of one-sixteenth quadruples the number of ventral segments. In general terms, the number of segments is inversely proportional to the square root of the tension. This result may be deduced by reasoning from our first and third laws, and its realization here confirms their correctness.
Thus, by a series of reasonings and experiments totally different from those formerly employed, we arrive at the self-same laws. In science, different lines of reasoning often converge upon the same truth; and if we only follow them faithfully, we are sure to reach that truth at last. We may emerge, and often do emerge, from our reasoning with a contradiction in our hands; but on retracing our steps, we infallibly find the cause of the contradiction to be due, not to any lack of constancy in Nature, but of accuracy in man. It is the millions of experiences of this kind which science furnishes that give us our present faith in the stability of Nature.
We now approach a portion of our subject which will subsequently prove to be of the very highest importance. It has been shown by the most varied experiments that a stretched string can either vibrate as a whole, or divide itself into a number of equal parts, each of which vi153brates as an independent string. Now it is not possible to sound the string as a whole without at the same time causing, to a greater or less extent, its subdivision; that is to say, superposed upon the vibrations of the whole string we have always, in a greater or less degree, the vibrations of its aliquot parts. The higher notes produced by these latter vibrations are called the harmonics of the string. And so it is with other sounding bodies; we have in all cases a coexistence of vibrations. Higher tones mingle with the fundamental one, and it is their intermixture which determines what, for want of a better term, we call the quality of the sound. The French call it timbre, and the Germans call it Klangfarbe.38 It is this union of high and low tones that enables us to distinguish one musical instrument from another. A clarinet and a violin, for example, though tuned to the same fundamental note, are not confounded; the auxiliary tones of the one are different from those of the other, and these latter tones, uniting themselves to the fundamental tones of the two instruments, destroy the identity of the sounds.
All bodies and instruments, then, employed for producing musical sounds emit, besides their fundamental tones, others due to higher orders of vibration. The Germans embrace all such sounds under the general term Obertöne. I think it will be an advantage if we in England adopt the term overtones as the equivalent of the term employed in Germany. One has occasion to envy the power of the German language to adapt itself to requirements of this nature. The term Klangfarbe, for ex154ample, employed by Helmholtz is exceedingly expressive, and we need its equivalent also. Color depends upon rapidity of vibration, blue light bearing to red the same relation that a high tone does to a low one. A simple color has but one rate of vibration, and it may be regarded as the analogue of a simple tone in music. A tone, then, may be defined as the product of a vibration which cannot be decomposed into more simple ones. A compound color, on the contrary, is produced by the admixture of two or more simple ones, and an assemblage of tones, such as we obtain when the fundamental tone and the harmonics of a string sound together, is called by the Germans a Klang. May we not employ the English word clang to denote the same thing, and thus give the term a precise scientific meaning akin to its popular one? And may we not, like Helmholtz, add the word color or tint, to denote the character of the clang, using the term clang-tint as the equivalent of Klangfarbe?
With your permission I shall henceforth employ these terms; and now it becomes our duty to look a little more closely than we have hitherto done into the subdivision of a string into its harmonic segments. Our monochord with its stretched wire is before you. The scale of the instrument is divided into 100 equal parts. At the middle point of the wire stands the number 50; at a point almost exactly one-third of its length from its end stands the number 33; while at distances equal to one-fourth and one-fifth of its length from its end stand the numbers 25 and 20 respectively. These numbers are sufficient for our present purpose. When the wire is plucked at 50 you hear its clang, rather hollow and dull. When plucked at 33, the clang is different. When plucked at155 25, the clang is different from either of the former. As we retreat from the centre of the string, the clang-tint becomes more “brilliant,” the sound more brisk and sharp. What is the reason of these differences in the sound of the same wire?
The celebrated Thomas Young, once professor in this Institution, enables us to solve the question. He proved that when any point of a string is plucked, all the higher tones which require that point for a node vanish from the clang. Let me illustrate this experimentally. I pluck the point 50, and permit the string to sound. It may be proved that the first overtone, which corresponds to a division of the string into two vibrating parts, is now absent from the clang. If it were present, the damping of the point 50 would not interfere with it, for this point would be its node. But on damping the point 50 the fundamental tone is quenched, and no octave of that tone is heard. Along with the octave its whole progeny of overtones, with rates of vibration four times, six times, eight times—all even numbers of times—the rate of the fundamental tone, disappear from the clang. All these tones require that a node should exist at the centre, where, according to the principle of Young, it cannot now be formed. Let us pluck some other point, say 25, and damp 50 as before. The fundamental tone is now gone, but its octave, clear and full, rings in your ears. The point 50 in this case not being the one plucked, a node can form there; it has formed, and the two halves of the string continue to vibrate after the vibrations of the string as a whole have been extinguished. Plucking the point 33, the second harmonic or overtone is absent from the clang. This is proved by damping the point156 33. If the second harmonic were on the string this would not affect it, for 33 is its node. The fundamental is quenched, but no tone corresponding to a division of the string into three vibrating parts is now heard. The tone is not heard because it was never there.
All the overtones which depend on this division, those with six times, nine times, twelve times the rate of vibration of the fundamental one, are also withdrawn from the clang. Let us now pluck 20, damping 33 as before. The second harmonic is not extinguished, but continues to sound clearly and fully after the extinction of the fundamental tone. In this case the point 33 not being that plucked, a node can form there, and the string can divide itself into three parts accordingly. In like manner, if 25 be plucked and then damped, the third harmonic is not heard; but when a point between 25 and the end of the wire is plucked, and the point 25 damped, the third harmonic is plainly heard. And thus we might proceed, the general rule enunciated by Young, and illustrated by these experiments, being, that when any point of a string is plucked or struck, or, as Helmholtz adds, agitated with a bow, the harmonic which requires that point for a node vanishes from the general clang of the string.
You are now in a condition to estimate the influence which these higher vibrations must have upon the quality of the tone emitted by the string. The sounds which ring in your ears so plainly after the fundamental tone is quenched mingled with that note before it was extin157guished. It seems strange that tones of such power could be so masked by the fundamental one that even the disciplined ear of a musician is unable to separate the one from the other. But Helmholtz has shown that this is due to want of practice and attention. The musician’s faculties were never exercised in this direction. There are numerous effects which the musician can distinguish, because his art demands the habit of distinguishing them. But it is no necessity of his art to resolve the clang of an instrument into its constituent tones. By attention, however, even the unaided ear can accomplish this, particularly if the mind be informed beforehand what the ear has to bend itself to find.
And this reminds me of an occurrence which took place in this room at the beginning of my acquaintance with Faraday. I wished to show him a peculiar action of an electro-magnet upon a crystal. Everything was arranged, when just before the magnet was excited he laid his hand upon my arm and asked, “What am I to look for?” Amid the assemblage of impressions connected with an experiment, even this prince of experimenters felt the advantage of having his attention directed to the special point to be illustrated. Such help is the more needed when we attempt to resolve into its constituent parts an effect so intimately blended as the composite tones of a clang. When we desire to isolate a particular tone, one way of helping the attention is to sound that tone feebly on a string of the proper length. Thus prepared, the ear glides more readily from the single tone to that of the same pitch in a composite clang, and detaches it more readily from its companions. In the experiments executed a moment ago, where our158 aim in each respective case was to bring out the higher tone of the string in all its power, we entirely extinguished its fundamental tone. It may, however, be enfeebled without being destroyed. I pluck this string at 33, and lay the feather lightly for a moment on the string at 50. The fundamental tone is thereby so much lowered that its octave can make itself plainly heard. By again touching the string at 50, the fundamental tone is lowered still more; so that now its first harmonic is more powerful than itself. You hear the sound of both, and you might have heard them in the first instance by a sufficient stretch of attention.
The harmonics of a string may be augmented or subdued within wide limits. They may, as we have seen, be masked by the fundamental tone, and they may also effectually mask it. A stroke with a hard body is favorable, while a stroke with a soft body is unfavorable to their development. They depend, moreover, on the promptness with which the body striking the string retreats after striking. Thus they are influenced by the weight and elasticity of the hammers in the pianoforte. They also depend upon the place at which the shock is imparted. When, for example, a string is struck in the centre, the harmonics are less powerful than when it is struck near one end.
Helmholtz, who is equally eminent as a mathematician and as an experimental philosopher, has calculated the theoretic intensity of the harmonics developed in various ways; that is to say, the actual vis viva or energy of the vibration, irrespective of its effects upon the ear. A single example given by him will suffice to illustrate this subject. Calling the intensity of the fundamental159 tone, in each case, 100, that of the second harmonic, when the string was simply pulled aside at a point one-seventh of its length from its end and then liberated, was found to be 56·1, or a little better than one-half. When the string was struck with the hammer of a pianoforte, whose contact with the string endured for three-sevenths of the period of vibration of the fundamental tone, the intensity of the same tone was 9. In this case the second harmonic was nearly quenched. When, however, the duration of contact was diminished to three-twentieths of the period of the fundamental, the intensity of the harmonic rose to 357; while, when the string was sharply struck with a very hard hammer, the intensity mounted to 505, or to more than quintuple that of the fundamental tone.39 Pianoforte manufacturers have found that the most pleasing tone is excited by the middle strings of their instruments, when the point against which the hammer strikes is from one-seventh to one-ninth of the length of the wire from its extremity.
Why should this be the case? Helmholtz has given the answer. Up to the tones which require these points as nodes the overtones all form chords with the fundamental; but the sixth and eighth overtones of the wire do not enter into such chords; they are dissonant tones, and hence the desirability of doing away with them. This is accomplished by making the point at which a node is required that on which the hammer falls. The possibility of the tone forming is thereby shut out, and its injurious effect is avoided.
The strings of the Æolian harp are divided into harmonic parts by a current of air passing over them. The 160instrument is usually placed in a window between the sash and frame, so as to leave no way open to the entrance of the air except over the strings. Sir Charles Wheatstone recommends the stretching of a first violin-string at the bottom of a door which does not closely fit. When the door is shut, the current of air entering beneath sets the string in vibration, and when a fire is in the room, the vibrations are so intense that a great variety of sounds are simultaneously produced.40 A gentleman in Basel once constructed with iron wires a large instrument which he called the weather-harp or giant-harp, and which, according to its maker, sounded as the weather changed. Its sounds were also said to be evoked by changes of terrestrial magnetism. Chladni pointed out the error of these notions, and reduced the action of the instrument to that of the wind upon its strings.
Finally, with regard to the vibrations of a wire, the experiments of Dr. Young, who was the first to employ optical methods in such experiments, must be mentioned. He allowed a sheet of sunlight to cross a pianoforte-wire, and obtained thus a brilliant dot. Striking the wire he caused it to vibrate, the dot described a luminous line like that produced by the whirling of a burning coal in the air, and the form of this line revealed the character of the vibration. It was rendered manifest by these experiments that the oscillations of the wire were not confined to a single plane, but that it described in its vibra161tions curves of greater or less complexity. Superposed upon the vibration of the whole string were partial vibrations, which revealed themselves as loops and sinuosities. Some of the lines observed by Dr. Young are given in Fig. 51. Every one of these figures corresponds to a distinct impression made by the wire upon the surrounding air. The form of the sonorous wave is affected by these superposed vibrations, and thus they influence the clang-tint or quality of the sound.

The amount of motion communicated by a vibrating string to the air is too small to be perceived as sound, even at a small distance from the string.
When a broad surface vibrates in air, condensations and rarefactions are more readily formed than when the vibrating body is of small dimensions like a string. Hence, when strings are employed as sources of musical sounds, they are associated with surfaces of larger area which take up their vibrations, and transfer them to the surrounding air.
Thus the tone of a harp, a piano, a guitar, or a violin, depends mainly upon the sound-board of the instrument.
The following four laws regulate the vibrations of strings: The rate of vibrations is inversely proportional to the length; it is inversely proportional to the diameter; it is directly proportional to the square root of the stretching weight or tension; and it is inversely proportional to the square root of the density of the string.
When strings of different diameters and densities are compared, the law is, that the rate of vibration is inversely proportional to the square root of the weight of the string.
When a stretched rope, or an India-rubber tube filled with sand, with one of its ends attached to a fixed object, receives a jerk at the other end, the protuberance raised upon the tube runs along it as a pulse to the fixed end, and, being there reflected, returns to the hand by which the jerk was imparted.
The time required for the pulse to travel from the hand to the fixed end of the tube and back is that required by the whole tube to execute a complete vibration.
When a series of pulses are sent in succession along the tube, the direct and reflected pulses meet, and by their coalescence divide the tube into a series of vibrating parts, called ventral segments, which are separated from each other by points of apparent rest called nodes.
The number of ventral segments is directly proportional to the rate of vibration at the free end of the tube.
The hand which produces these vibrations may move through less than an inch of space; while by the accumulation of its impulses the amplitude of the ventral163 segments may amount to several inches, or even to several feet.
If an India-rubber tube, fixed at both ends, be encircled at its centre by the finger and thumb, when either of its halves is pulled aside and liberated, both halves are thrown into a state of vibration.
If the tube be encircled at a point one-third, one-fourth, or one-fifth of its length from one of its ends, on pulling the shorter segment aside and liberating it, the longer segment divides itself into two, three, or four vibrating parts, separated from each other by nodes.
The number of vibrating segments depends upon the rate of vibration at the point encircled by the finger and thumb.
Here also the amplitude of vibration at the place encircled by the finger and thumb may not be more than a fraction of an inch, while the amplitude of the ventral segments may amount to several inches.
A musical string damped by a feather at a point one-half, one-third, one-fourth, one-fifth, etc., of its length from one of its ends, and having its shorter segment agitated, divides itself exactly like the India-rubber tube. Its division may be rendered apparent by placing little paper riders across it. Those placed at the ventral segments are thrown off, while those placed at the nodes retain their places.
The notes corresponding to the division of a string into its aliquot parts are called the harmonics of the string.
When a string vibrates as a whole, it usually divides at the same time into its aliquot parts. Smaller vibrations are superposed upon the larger; the tones corre164sponding to those smaller vibrations, and which we have agreed to call overtones, mingling at the same time with the fundamental tone of the string.
The addition of these overtones to the fundamental tone determines the timbre or quality of the sound, or, as we have agreed to call it, the clang-tint.
It is the addition of such overtones to fundamental tones of the same pitch which enables us to distinguish the sound of a clarionet from that of a flute, and the sound of a violin from both. Could the pure fundamental tones of these instruments be detached, they would be indistinguishable from each other; but the different admixture of overtones in the different instruments renders their clang-tints diverse, and therefore distinguishable.
Instead of the heavy India-rubber tube in the experiment above referred to, we may employ light silk strings, and, instead of the vibrating hand, we may employ vibrating tuning-forks, and cause the strings to swing as a whole, or to divide themselves into any number of ventral segments. Effects of great beauty are thus obtained, and by experiments of this character all the laws of vibrating strings may be demonstrated.
When a stretched string is plucked aside or agitated by a bow, all the overtones which require the agitated point for a node vanish from the clang of the string.
The point struck by the hammer of the piano is from one-seventh to one-ninth of the length of the string from its end: by striking this point, the notes which require it as a node cannot be produced, a source of dissonance being thus avoided.
Vibrations of a Rod fixed at Both Ends: its Subdivisions and Corresponding Overtones—Vibrations of a Rod fixed at One End—The Kaleidophone—The Iron Fiddle and Musical Box—Vibrations of a Rod free at Both Ends—The Claque-bois and Glass Harmonica—Vibrations of a Tuning-Fork: its Subdivisions and Overtones—Vibrations of Square Plates—Chladni’s Discoveries—Wheatstone’s Analysis of the Vibrations of Plates—Chladni’s Figures—Vibrations of Disks and Bells—Experiments of Faraday and Strehlke
OUR last chapter was devoted to the transverse vibrations of strings. This one I propose devoting to the transverse vibrations of rods, plates, and bells, commencing with the case of a rod fixed at both ends. Its modes of vibration are exactly those of a string. It vibrates as a whole, and can also divide itself into two, three, four, or more vibrating parts. But, for a reason to be immediately assigned, the laws which regulate the pitch of the successive notes are entirely different in the two cases. Thus, when a string divides into two equal parts, each of its halves vibrates with twice the rapidity of the whole; while, in the case of the rod, each of its halves vibrates with nearly three times166 the rapidity of the whole. With greater strictness, the ratio of the two rates of vibration is as 9 is to 25, or as the square of 3 to the square of 5. In Fig. 52, a a′, c c′, b b′, d d′, are sketched the first four modes of vibration of a rod fixed at both ends: the successive rates of vibration, in the four cases bear to each other the following relation:
| Number of nodes | 0 | 1 | 2 | 3 |
| Number of vibrations | 9 | 25 | 49 | 81 |
the last row of figures being the squares of the odd numbers 3, 5, 7, 9.
In the case of a string, the vibrations are maintained by a tension externally applied; in the case of a rod, the vibrations are maintained by the elasticity of the rod itself. The modes of division are in both cases the same, but the forces brought into play are different, and hence also the successive rates of vibration.
Let us now pass on to the case of a rod fixed at one end and free at the other. Here also it is the elasticity of the material, and not any external tension, that sustains the vibrations. Approaching, as usual, sonorous vibrations through more grossly mechanical ones, I fix this long rod of iron, n o, Fig. 53, in a vise, draw it aside, and liberate it. To make its vibrations more evident, its shadow is thrown upon a screen. The rod oscillates as a whole to and fro, between the points p p′. But it is capable of other modes of vibration. Damping it at the point a, by holding it gently there between the finger and thumb, and striking it sharply between a and o, the rod divides into two vibrating parts, separated by a node167 as shown in Fig. 54. You see upon the screen a shadowy spindle between a and the vise below, and a shadowy fan above a, with a black node between both. The division may be effected without damping a, by merely imparting a sufficiently sharp shock to the rod between a and o. In this case, however, besides oscillating in parts, the rod oscillates as a whole, the partial oscillations being superposed upon the large one.
Fig. 53.
|
Fig. 54.
|
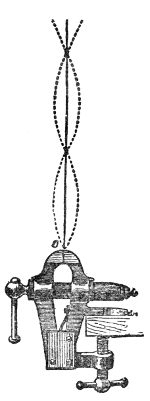
Fig. 55.
|
You notice, moreover, that the amplitude of the partial oscillations depends upon the promptness of the stroke. When the stroke is sluggish, the partial division is but feebly pronounced, the whole oscillation being most marked. But when the shock is sharp and prompt, the whole oscillation is feeble, and the partial oscillations are executed with vigor. If the vibrations of this168 rod were rapid enough to produce a musical sound, the oscillation of the rod as a whole would correspond to its fundamental tone, while the division of the rod into two vibrating parts would correspond to the first of its overtones. If, moreover, the rod vibrated as a whole and as a divided rod at the same time, the fundamental tone and the overtone would be heard simultaneously. By damping the proper point and imparting the proper shock, we can still further subdivide the rod, as shown in Fig. 55.
And now let us shorten our rod, so as to bring its vibrations into proper relation to our ears. When it is about four inches long, it emits a low musical sound. When further shortened, the tone is higher; and, by continuing to shorten the rod, the speed of vibration is augmented, until finally the sound becomes painfully acute. These musical vibrations differ only in rapidity from the grosser oscillations which a moment ago appealed to the eye.
The increase in the rate of vibrations here observed is ruled by a definite law; the number of vibrations executed at a given time is inversely proportional to the square of the length of the vibrating rod. You hear the sound of this strip of brass, two inches long, as the fiddle-bow is passed over its end. Making the length of the strip one inch, the sound is the double octave of the last one; the rate of vibration is augmented four times. Thus, by doubling the length of the vibrating strip, we reduce its rate of vibration to one-fourth; by trebling the length, we reduce the rate of vibration to one-ninth; by quadrupling the length, we reduce the vibrations to one-sixteenth,169 and so on. It is plain that, by proceeding in this way, we should finally reach a length where the vibrations would be sufficiently slow to be counted. Or, it is plain that, beginning with a long strip whose vibrations could be counted, we might, by shortening, not only make the strip sound, but also determine the rates of vibration corresponding to its different tones. Supposing we start with a strip 36 inches long, which vibrates once in a second, the strip reduced to 12 inches would, according to the above law, execute 9 vibrations a second; reduced to 6 inches, it would execute 36, to 3 inches, 144; while, if reduced to 1 inch in length, it would execute 1,296 vibrations in a second. It is easy to fill the spaces between the lengths here given, and thus to determine the rate of vibration corresponding to any particular tone. This method was proposed and carried out by Chladni.
A musical instrument may be formed of short rods. Into this common wooden tray a number of pieces of stout iron wire of different lengths are fixed, being ranged in a semicircle. When the fiddle-bow is passed over the series, we obtain a succession of very pleasing notes. A competent performer could certainly extract very tolerable music from a sufficient number of these iron pins. The iron fiddle (violon de fer) is thus formed. The notes of the ordinary musical box are also produced by the vibrations of tongues of metal fixed at one end. Pins are fixed in a revolving, cylinder, the free ends of the tongues are lifted by these pins and then suddenly let go. The tongues vibrate, their length and strength being so arranged as to produce in each particular case the proper rapidity of vibration.
Sir Charles Wheatstone has devised a simple and ingenious optical method for the study of vibrating rods fixed at one end. Attaching light glass beads, silvered within, to the end of a metal rod, and allowing the light of a lamp or candle to fall upon the bead, he obtained a small spot intensely illuminated. When the rod vibrated, this spot described a brilliant line which showed the character of the vibration. A knitting-needle, fixed in a vise with a small bead stuck on to it by marine glue, answers perfectly as an illustration. In Wheatstone’s more complete instrument, which he calls a kaleidophone, the vibrating rods are firmly screwed into a massive stand. Extremely beautiful figures are obtained by this simple contrivance, some of which may now be projected on a magnified scale upon the screen before you.
Fixing the rod horizontally in the vise, a condensed beam is permitted to fall upon the silvered bead, a spot of sunlike brilliancy being thus obtained. Placing a lens in front of the bead, a bright image of the spot is thrown upon the screen, the needle is then drawn aside, and suddenly liberated. The spot describes a ribbon of light, at first straight, but speedily opening out into an ellipse, passing into a circle, and then again through a second ellipse back to a straight line. This is due to the fact that a rod held thus in a vise vibrates not only in the direction in which it is drawn aside, but also at right angles to this direction. The curve is due to the combination of two rectangular vibrations.41 While the rod 171is thus swinging as a whole, it may also divide itself into vibrating parts. By properly drawing a violin-bow across the needle, this serrated circle, Fig. 56, is obtained, a number of small undulations being superposed upon the large one. You moreover hear a musical tone, which you did not hear when the rod vibrated as a whole only; its oscillations, in fact, were then too slow to excite such a tone. The vibrations which produce these sinuosities, and which correspond to the first division of the rod, are executed with about 6-1/4 times the rapidity of the vibrations of the rod swinging as a whole. Again I draw the bow; the note rises in pitch, the serrations run more closely together, forming on the screen a luminous ripple more minute and, if possible, more beautiful than the last one, Fig. 57. Here we have the second division of the rod, the sinuosities of which correspond to 17-13/36 times its rate of vibration as a whole. Thus every change in the sound of the rod is accompanied by a change of the figure upon the screen.

Fig. 56.
|

Fig. 57.
|
The rate of vibration of the rod, as a whole, is to the rate corresponding to its first division nearly as the square of 2 is to the square of 5, or as 4:25. From the first division onward the rates of vibration are approximately proportional to the squares of the series of odd numbers 3, 5, 7, 9, 11, etc. Supposing the vibrations of172 the rod as a whole to number 36, then the vibrations corresponding to this and to its successive divisions would be expressed approximately by the following series of number’s:
36, 225, 625, 1225, 2025, etc.
In Fig. 58, a, b, c, d, e, are shown the modes of division corresponding to this series of numbers. You will not fail to observe that these overtones of a vibrating rod rise far more rapidly in pitch than the harmonics of a string.
Other forms of vibration may be obtained by smartly striking the rod with the finger near its fixed end. In fact, an almost infinite variety of luminous scrolls can be thus produced, the beauty of which may be inferred from the subjoined figures (see next page) first obtained by Sir C. Wheatstone. They may be produced by illuminating the bead with sunlight, or with the light of a lamp or candle. The scrolls, moreover, may be doubled by employing two candles instead of one. Two spots of light then appear, each of which describes its own luminous line when the knitting-needle is set in vibration. In a173 subsequent lecture we shall become acquainted with Wheatstone’s application of his method to the study of rectangular vibrations.

From a rod or bar fixed at one end, we will now pass to rods or bars free at both ends; for such an arrangement has also been employed in music. By a method174 afterward to be described, Chladni, the father of modern acoustics, determined experimentally the modes of vibration possible to such bars. The simplest mode of division in this case occurs when the rod is divided by two nodes into three vibrating parts. This division is easily illustrated by a flexible box ruler, six feet long. Holding it at about twelve inches from its two ends between the forefinger and thumb of each hand, and shaking it, or causing its centre to be struck, it vibrates, the middle segment forming a shadowy spindle, and the two ends forming fans. The shadow of the ruler on the screen renders the mode of vibration very evident. In this case the distance of each node from the end of the ruler is about one-fourth of the distance between the two nodes. In its second mode of vibration the rod or ruler is divided into four vibrating parts by three nodes. In Fig. 60, 1 and 2, these respective modes of division are shown. Looking at the edge of the ruler 1, the dotted lines cutting a a′, b b′, show the manner in which the segments bend up and down when the first division occurs, while c c′, d d′, show the mode of vibration corresponding to the second division. The deepest tone of a rod free at both ends is higher than the deepest tone of a rod fixed at one end in the proportion of 4:25. Be175ginning with the first two nodes, the rates of vibration of the free bar rise in the following proportion:
| Number of nodes | 2, 3, 4, 5, 6, 7 | |
| Numbers to the squares of which the | } | 3, 5, 7, 9, 11, 13 |
| pitch is approximately proportional |
Here, also, we have a similarly rapid rise of pitch to that noticed in the last two cases.
For musical purposes the first division only of a free rod has been employed. When bars of wood of different lengths, widths, and depths, are strung along a cord which passes through the nodes, we have the claque-bois of the French, an instrument now before you, A B, Fig. 61. Supporting the cord at one end by a hook k and holding it at the other in the left hand, I run the hammer h along the series of bars, and produce an agreeable succession of musical tones. Instead of using the cord, the bars may rest at their nodes on cylinders of twisted straw; hence the name “straw-fiddle,” sometimes applied to this instrument. Chladni informs us that it is introduced as a play of bells (Glockenspiel) into Mozart’s176 opera of “Die Zauberflöte.” If, instead of bars of wood, we employ strips of glass, we have the glass harmonica.
From the vibrations of a bar free at both ends it is easy to pass to the vibrations of a tuning-fork, as analyzed by Chladni. Supposing a a, Fig. 62, to represent a straight steel bar, with the nodal points corresponding to its first mode of division marked by the transverse dots. Let the bar be bent to the form b b; the two nodal points still remain, but they have approached nearer to each other. The tone of the bent bar is also somewhat lower than that of the straight one. Passing through various stages of bending, c c, d d, we at length convert the bar into a tuning-fork e e, with parallel prongs; it still retains its two nodal points, which, however, are much closer together than when the bar was straight.
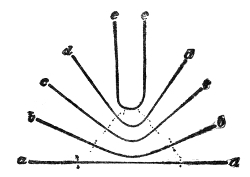

When such a fork sounds its deepest note, its free ends oscillate as in Fig. 63, where the prongs vibrate between the limits b and n, and f and m, and where p and q are the nodes. There is no division of a tuning-fork corresponding to the division of a straight bar by three nodes. In its second mode of division, which cor177responds to the first overtone of the fork, we have a node on each prong, and two at the bottom. The principle of Young, referred to at page 155, extends also to tuning-forks. To free the fundamental tone from an overtone, you draw your bow across the fork at the place where the node is required to form the latter. In the third mode of division there are two nodes on each prong and one at the bottom; in the fourth division there are two nodes on each prong and two at the bottom; while in the fifth division there are three nodes on each prong and one at the bottom. The first overtone of the fork requires, according to Chladni, 6-1/4 times the number of vibrations of the fundamental tone.
It is easy to elicit the overtones of tuning-forks. Here, for example, is our old series, vibrating respectively 256, 320, 384, and 512 times in a second. In passing from the fundamental tone to the first overtone of each you notice that the interval is vastly greater than that between the fundamental tone and the first overtone of a stretched string. From the numbers just mentioned we pass at once to 1,600, 2,000, 2,400, and 3,200 vibrations a second. Chladni’s numbers, however, though approximately correct, are not always rigidly verified by experiment. A pair of forks, for example, may have their fundamental tones in perfect unison and their overtones discordant. Two such forks are now before you. When the fundamental tones of both are sounded, the unison is perfect; but when the first overtones of both are sounded, they are not in unison. You hear rapid “beats,” which grate upon the ear. By loading one of the forks with wax, the two overtones may be brought178 into unison; but now the fundamental tones produce loud beats when sounded together. This could not occur if the first overtone of each fork was produced by a number of vibrations exactly 6-1/4 times the rate of its fundamental. In a series of forks examined by Helmholtz, the number of vibrations of the first overtone varied from 5·6 to 6·6 times that of the fundamental.
Starting from the first overtone, and including it, the rates of vibration of the whole series of overtones are as the squares of the numbers 3, 5, 7, 9, etc. That is to say, in the time required by the first overtone to execute 9 vibrations, the second executes 25, the third 49, the fourth 81, and so on. Thus the overtones of the fork rise with far greater rapidity than those of a string. They also vanish more speedily, and hence adulterate to a less extent the fundamental tone by their admixture.
The device of Chladni for rendering these sonorous vibrations visible has been of immense importance to the science of acoustics. Lichtenberg had made the experiment of scattering an electrified powder over an electrified resin-cake, the arrangement of the powder revealing the electric condition of the surface. This experiment suggested to Chladni the idea of rendering sonorous vibrations visible by means of sand strewed upon the surface of the vibrating body. Chladni’s own account of his discovery is of sufficient interest to justify its introduction here:
“As an admirer of music, the elements of which I had begun to learn rather late, that is, in my nineteenth year, I noticed that the science of acoustics was more neglected179 than most other portions of physics. This excited in me the desire to make good the defect, and by new discovery to render some service to this part of science. In 1785 I had observed that a plate of glass or metal gave different sounds when it was struck at different places, but I could nowhere find any information regarding the corresponding modes of vibration. At this time there appeared in the journals some notices of an instrument made in Italy by the Abbé Mazzochi, consisting of bells, to which one or two violin-bows were applied. This suggested to me the idea of employing a violin-bow to examine the vibrations of different sonorous bodies. When I applied the bow to a round plate of glass fixed at its middle it gave different sounds, which, compared with each other, were (as regards the number of their vibrations) equal to the squares of 2, 3, 4, 5, etc.; but the nature of the motions to which these sounds corresponded, and the means of producing each of them at will, were yet unknown to me. The experiments on the electric figures formed on a plate of resin, discovered and published by Lichtenberg, in the memoirs of the Royal Society of Göttingen, made me presume that the different vibratory motions of a sonorous plate might also present different appearances, if a little sand or some other similar substance were spread over the surface. On employing this means, the first figure that presented itself to my eyes upon the circular plate already mentioned resembled a star with ten or twelve rays, and the very acute sound, in the series alluded to, was that which agreed with the square of the number of diametrical lines.”
I will now illustrate the experiments of Chladni, commencing with a square plate of glass held by a suitable clamp at its centre. The plate might be held with the finger and thumb, if they could only reach far enough. Scattering fine sand over the plate, the middle point of one of its edges is damped by touching it with the finger-nail, and a bow is drawn across the edge of the plate, near one of its corners. The sand is tossed away from certain parts of the surface, and collects along two nodal lines which divide the large square into four smaller ones, as in Fig. 64. This division of the plate corresponds to its deepest tone.
Fig. 64.
|
Fig. 65.
|
Fig. 66.
|
The signs + and - employed in these figures denote that the two squares on which they occur are always moving in opposite directions. When the squares marked + are above the average level of the plate those marked - are below it; and when those marked - are above the average level those marked + are below it. The nodal lines mark the boundaries of these opposing motions. They are the places of transition from the one motion to the other, and are therefore unaffected by either.
Scattering sand once more over its surface, I damp one of the corners of the plate, and excite it by drawing the bow across the middle of one of its sides. The sand181 dances over the surface, and finally ranges itself in two sharply-defined ridges along its diagonals, Fig. 65. The note here produced is a fifth above the last. Again damping two other points, and drawing the bow across the centre of the opposite side of the plate, we obtain a far shriller note than in either of the former cases, and the manner in which the plate vibrates to produce this note is represented in Fig. 66.
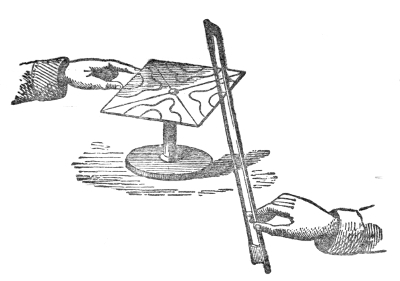
Thus far plates of glass have been employed held by a clamp at the centre. Plates of metal are still more suitable for such experiments. Here is a plate of brass, 12 inches square, and supported on a suitable stand. Damping it with the finger and thumb of my left hand at two points of its edge, and drawing the bow with my right across a vibrating portion of the opposite edge, the complicated pattern represented in Fig. 67 is obtained.

The beautiful series of patterns shown on page 182
were obtained by Chladni, by damping and exciting
square plates in different ways. It is not only interesting
but startling to see the suddenness with which
182
183these sharply-defined figures are formed by the sweep
of the bow of a skilful experimenter.
And now let us look a little more closely into the
mechanism of these vibrations. The manner in which
a bar free at both ends divides itself when it vibrates
transversely has been already explained. Rectangular
pieces of glass or of sheet metal—the glass strips of
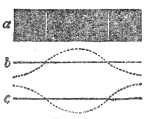 Fig. 69.
the harmonica, for example—also obey
the laws of free rods and bars. In
Fig. 69 is drawn a rectangle a, with
the nodes corresponding to its first
division marked upon it, and underneath
it is placed a figure showing the
manner in which the rectangle, looked at edgewise, bends
up and down when it is set in vibration.42 For the sake
of plainness the bending is greatly exaggerated. The figures
b and c indicate that the vibrating parts of the plate
alternately rise above and fall below the average level
of the plate. At one moment, for example, the centre of
the plate is above the level and its ends below it, as at
b; while at the next moment its centre is below and its
two ends above the average level, as at c. The vibrations
of the plate consist in the quick successive assumption
of these two positions. Similar remarks apply to all
other modes of division.
Fig. 69.
the harmonica, for example—also obey
the laws of free rods and bars. In
Fig. 69 is drawn a rectangle a, with
the nodes corresponding to its first
division marked upon it, and underneath
it is placed a figure showing the
manner in which the rectangle, looked at edgewise, bends
up and down when it is set in vibration.42 For the sake
of plainness the bending is greatly exaggerated. The figures
b and c indicate that the vibrating parts of the plate
alternately rise above and fall below the average level
of the plate. At one moment, for example, the centre of
the plate is above the level and its ends below it, as at
b; while at the next moment its centre is below and its
two ends above the average level, as at c. The vibrations
of the plate consist in the quick successive assumption
of these two positions. Similar remarks apply to all
other modes of division.
Now suppose the rectangle gradually to widen, till it becomes a square. There then would be no reason why the nodal lines should form parallel to one pair of sides rather than to the other. Let us now examine what would be the effect of the coalescence of two such systems of vibrations.
To keep your conceptions clear, take two squares of glass and draw upon each of them the nodal lines belonging to a rectangle. Draw the lines on one plate in white, and on the other in black; this will help you to keep the plates distinct in your mind as you look at them. Now lay one square upon the other so that their nodal lines shall coincide, and then realize with perfect mental clearness both plates in a state of vibration. Let us assume, in the first instance, that the vibrations of the two plates are concurrent; that the middle segment and the end segments of each rise and fall together; and now suppose the vibrations of one plate transferred to the other. What would be the result? Evidently vibrations of a double amplitude on the part of the plate which has received this accession. But suppose the vibrations of the two plates, instead of being concurrent, to be in exact opposition to each other—that when the middle segment of the one rises the middle segment of the other falls—what would be the consequence of adding them together? Evidently a neutralization of all vibration.
Instead of placing the plates so that their nodal lines coincide, set these lines at right angles to each other. That is to say, push A over A′, Fig. 70. In these figures the letter P means positive, indicating, in the section where it occurs, a motion of the plate upward; while N means negative, indicating, where it occurs, a motion185 downward. You have now before you a kind of check pattern, as shown in the third square, consisting of a square s in the middle, a smaller square b at each corner, and four rectangles at the middle portions of the four sides. Let the plates vibrate, and let the vibrations of their corresponding sections be concurrent, as indicated by the letters P and N; and then suppose the vibrations of one of them transferred to the other. What must result? A moment’s reflection will show you that the big middle square s will vibrate with augmented energy; the same is true of the four smaller squares b, b, b, b, at the four corners; but you will at once convince yourselves that the vibrations in the four rectangles are in opposition, and that where their amplitudes are equal they will destroy each other. The middle point of each side of the plate of glass would therefore be a point of rest; the points where the nodal lines of the two plates cross each other would also be points of rest. Draw a line through every three of these points and you will obtain a second square inscribed in the first. The sides of this square are lines of no motion.
We have thus far been theorizing. Let us now clip a square plate of glass at a point near the centre of one of its edges, and draw the bow across the adjacent corner of186 the plate. When the glass is homogeneous, a close approximation to this inscribed square is obtained. The reason is that when the plate is agitated in this manner the two sets of vibrations which we have been considering actually coexist in the plate, and produce the figure due to their combination.
Again, place the squares of glass one upon the other exactly as in the last case; but now, instead of supposing them to concur in their vibrations, let their corresponding sections oppose each other: that is, let A cover A′, Fig. 71. Then it is manifest that on superposing the vibrations the middle point of our middle square must be a point of rest; for here the vibrations are equal and opposite. The intersections of the nodal lines are also points of rest, and so also is every corner of the plate itself, for here the added vibrations are also equal and opposite. We have thus fixed four points of rest on each diagonal of the square. Draw the diagonals, and they will represent the nodal lines consequent on the superposition of the two vibrations.

These two systems actually coexist in the same plate when the centre is clamped and one of the corners touched, while the fiddle-bow is drawn across the middle of one of the sides. In this case the sand which187 marks the lines of rest arranges itself along the diagonals. This, in its simplest possible form, is Sir C. Wheatstone’s analysis of these superposed vibrations.
Passing from square plates to round ones, we also obtain various beautiful effects. This disk of brass is supported horizontally upon an upright stand: it is blackened, and fine white sand is scattered lightly over it. The disk is capable of dividing itself in various ways, and of emitting notes of various pitch. I sound the lowest fundamental note of the disk by touching its edge at a certain point and drawing the bow across the edge at a point 45° distant from the damped one. You hear the note and you see the sand. It quits the four quadrants of the disk, and ranges itself along two of the diameters, Fig. 72, A (next page). When a disk divides itself thus into four vibrating segments, it sounds its deepest note. I stop the vibration, clear the disk, and once more scatter sand over it. Damping its edge, and drawing the bow across it at a point 30° distant from the damped one, the sand immediately arranges itself in a star. We have here six vibrating segments, separated from each other by their appropriate nodal lines, Fig. 72, B. Again I damp a point, and agitate another nearer to the damped one than in the last instance; the disk divides itself into eight vibrating segments with lines of sand between them, Fig. 72, C. In this way the disk may be subdivided into ten, twelve, fourteen, sixteen sectors, the number of sectors being always an even one. As the division becomes more minute the vibrations become more rapid, and the pitch consequently more high. The note emitted188 by the sixteen segments into which the disk is now divided is so acute as to be almost painful to the ear. Here you have Chladni’s first discovery. You can understand his emotion on witnessing this wonderful effect, “which no mortal had previously seen.” By rendering the centre of the disk free, and damping appropriate points of the surface, nodal circles and other curved lines may be obtained.
The rate of vibration of a disk is directly proportional to its thickness, and inversely proportional to the square of its diameter. Of these three disks two have the same diameter, but one is twice as thick as the other; two of them are of the same thickness, but one has half the diameter of the other. According to the law just enunciated, the rules of vibration of the disks are as the numbers 1, 2, 4. When they are sounded in succession, the musical ears present can testify that they really stand to each other in the relation of a note, its octave, and its double octave.
The actual movement of the sand toward the nodal lines may be studied by clogging the sand with a semi-fluid substance. When gum is employed to retard the189 motion of the particles, the curves which they individually describe are very clearly drawn upon the plates. M. Strehlke has sketched these appearances, and from him the patterns A, B, C, Fig. 73, are borrowed.


Fig. 74.
|
Fig. 75.
|
Fig. 76.
|
An effect of vibrating plates which long perplexed experimenters is here to be noticed. When with the sand strewed over a plate a little fine dust is mingled, say the fine seed of lycopodium, this light substance, instead of collecting along the nodal lines, forms little heaps at the places of most violent motion. It is heaped at the four corners of the plate, Fig. 74, at the four sides of the plate, Fig. 75, and lodged between the nodal lines of the plate, Fig. 76. These three figures represent the three states of vibration illustrated in Figs. 64, 65, and 66. The dust chooses in all cases the place of greatest agitation. Various explanations of this effect had been given, but it was reserved for Faraday to assign its extremely190 simple cause. The light powder is entangled by the little whirlwinds of air produced by the vibrations of the plate: it cannot escape from the little cyclones, though the heavier sand particles are readily driven through them. When, therefore, the motion ceases, the light powder settles down at the places where the vibration was a maximum. In vacuo no such effect is observed: here all powders, light and heavy, move to the nodal lines.
The vibrating segments and nodes of a bell are similar
to those of a disk. When a bell sounds its deepest note,
the coalescence of its pulses causes it to divide into four
vibrating segments, separated from each other by four
nodal lines, which run up from the sound-bow to the
 Fig. 77.
crown of the bell. The place
where the hammer strikes is always
the middle of a vibrating
segment; the point diametrically
opposite is also the middle of
such a segment. Ninety degrees
from these points, we have also
vibrating segments, while at 45 degrees
right and left of them we
come upon the nodal lines. Supposing
the strong, dark circle in Fig. 77 to represent
the circumference of the bell in a state of quiescence,
then when the hammer falls on any one of the segments
a, c, b, or d, the sound-bow passes periodically through
the changes indicated by the dotted lines. At one moment
it is an oval, with a b for its longest diameter; at
the next moment it is an oval, with c d for its longest191
diameter. The changes from one oval to the other constitute,
in fact, the vibrations of the bell. The four
points n, n, n, n, where the two ovals intersect each
other, are the nodes. As in the case of a disk, the number
of vibrations executed by a bell in a given time
varies directly as the thickness, and inversely as the
square of the bell’s diameter.
Fig. 77.
crown of the bell. The place
where the hammer strikes is always
the middle of a vibrating
segment; the point diametrically
opposite is also the middle of
such a segment. Ninety degrees
from these points, we have also
vibrating segments, while at 45 degrees
right and left of them we
come upon the nodal lines. Supposing
the strong, dark circle in Fig. 77 to represent
the circumference of the bell in a state of quiescence,
then when the hammer falls on any one of the segments
a, c, b, or d, the sound-bow passes periodically through
the changes indicated by the dotted lines. At one moment
it is an oval, with a b for its longest diameter; at
the next moment it is an oval, with c d for its longest191
diameter. The changes from one oval to the other constitute,
in fact, the vibrations of the bell. The four
points n, n, n, n, where the two ovals intersect each
other, are the nodes. As in the case of a disk, the number
of vibrations executed by a bell in a given time
varies directly as the thickness, and inversely as the
square of the bell’s diameter.
Like a disk, also, a bell can divide itself into any even number of vibrating segments, but not into an odd number. By damping proper points in succession the bell can be caused to divide into 6, 8, 10, and 12 vibrating parts. Beginning with the fundamental note, the number of vibrations corresponding to the respective divisions of a bell, as of a disk, is as follows:
| Number of divisions | 4, 6, 8, 10, 12 | |
| Numbers the squares of which express the | } | 2, 3, 4, 5, 6 |
| rates of vibration |
Thus, if the vibrations of the fundamental tone be 40, that of the next higher tone will be 90, the next 160, the next 250, the next 360, and so on. If the bell be thin, the tendency to subdivision is so great that it is almost impossible to bring out the pure fundamental tone without the admixture of the higher ones.
I will now repeat before you a homely, but an instructive experiment. This common jug, when a fiddle-bow is drawn across its edge, divides into four vibrating segments exactly like a bell. The jug is provided with a handle; and you are to notice the influence of this handle upon the tone. When the fiddle-bow is drawn across the edge at a point diametrically opposite to the handle, a certain note is heard. When it is drawn at a point 90° from the handle, the same note is heard. In192 both these cases the handle occupies the middle of a vibrating segment, loading that segment by its weight. But I now draw the bow at an angular distance of 45° from the handle; the note is sensibly higher than before. The handle in this experiment occupies a node; it no longer loads a vibrating segment, and hence the elastic force, having to cope with less weight, produces a more rapid vibration. Chladni executed with a teacup the experiment here made with a jug. Now bells often exhibit round their sound-bows an absence of uniform thickness tantamount to the want of symmetry in the case of our jug; and we shall learn subsequently that the intermittent sound of many bells, noticed more particularly when their tones are dying out, is produced by the combination of two distinct rates of vibration, which have this absence of uniformity for their origin.
There are no points of absolute rest in a vibrating bell, for the nodes of the higher tones are not those of the fundamental one. But it is easy to show that the various parts of the sound-bow, when the fundamental tone is predominant, vibrate with very different degrees of intensity. Suspending a little ball of sealing-wax a, Fig. 78 (next page), by a string, and allowing it to rest gently against the interior surface of an inverted bell, it is tossed to and fro when the bell is thrown into vibration. But the rattling of the sealing-wax ball is far more violent when it rests against the vibrating segments than when it rests against the nodes. Permitting the ivory bob of a short pendulum to rest in succession against a vibrating segment and against a node of the “Great Bell” of Westminster, I found that in the former position it was driven away five inches, in the latter only193 two inches and three-quarters, when the hammer fell upon the bell.
Could the “Great Bell” be turned upside down and filled with water, on striking it the vibrations would express themselves in beautiful ripples upon the liquid surface. Similar ripples may be obtained with smaller bells, or even with finger and claret glasses, but they would be too minute for our present purpose. Filling a large hemispherical glass with water, and passing the fiddle-bow across its edge, large crispations immediately cover its surface. When the bow is vigorously drawn, the water rises in spray from the four vibrating segments. Projecting, by means of a lens, a magnified image of the illuminated water-surface upon the screen, pass the bow gently across the edge of the glass, or rub the finger gently along the edge. You hear this low sound, and at the same time observe the ripples breaking, as it were, in visible music over the four sectors of the figure.
You know the experiment of Leidenfrost which proves that, if water be poured into a red-hot silver basin, it rolls about upon its own vapor. The same effect is produced if we drop a volatile liquid, like ether, on the surface of warm water. And, if a bell-glass be filled with ether or with alcohol, a sharp sweep of the bow over the edge of the glass detaches the liquid spherules, which, when they fall back, do not mix with the liquid, but are driven over the surface on wheels of vapor to the nodal lines. The warming of the liquid, as might be expected, improves the effect. M. Melde, to whom we are indebted for this beautiful experiment, has given the drawings, Figs. 79 and 80, representing what occurs when the surface is divided into four and into six vibrating parts. With a thin wineglass and strong brandy the effect may also be obtained.43
Fig. 79.
|
Fig. 80.
|
The glass and the liquid within it vibrate here together, and everything that interferes with the perfect continuity of the entire mass disturbs the sonorous effect. 195A crack in the glass passing from the edge downward extinguishes its sounding power. A rupture in the continuity of the liquid has the same effect. When a glass containing a solution of carbonate of soda is struck with a bit of wood, you hear a clear musical sound. But when a little tartaric acid is added to the liquid, it foams, and a dry, unmusical collision takes the place of the musical sound. As the foam disappears, the sonorous power returns, and now that the liquid is once more clear, you hear the musical ring as before.
The ripples of the tide leave their impressions upon the sand over which they pass. The ripples produced by sonorous vibrations have been proved by Faraday competent to do the same. Attaching a plate of glass to a long flexible board, and pouring a thin layer of water over the surface of the glass, on causing the board to vibrate its tremors chase the water into a beautiful mosaic of ripples. A thin stratum of sand strewed upon the plate is acted upon by the water, and carved into patterns, of which Fig. 81 is a reduced specimen.
A rod fixed at both ends and caused to vibrate transversely divides itself in the same manner as a string vibrating transversely.
But the succession of its overtones is not the same as those of a string, for while the series of tones emitted by the string is expressed by the natural numbers 1, 2, 3, 4, 5, etc., the series of tones emitted by the rod is expressed by the squares of the odd numbers 3, 5, 7, 9, etc.
A rod fixed at one end can also vibrate as a whole, or can divide itself into vibrating segments separated from each other by nodes.
In this case the rate of vibration of the fundamental tone is to that of the first overtone as 4:25, or as the square of 2 to the square of 5. From the first division onward the rates of vibration are proportional to the squares of the odd numbers 3, 5, 7, 9, etc.
With rods of different lengths the rate of vibration is inversely proportional to the square of the length of the rod.
Attaching a glass bead silvered within to the free end of the rod, and illuminating the bead, the spot of light reflected from it describes curves of various forms when the rod vibrates. The kaleidophone of Wheatstone is thus constructed.
The iron fiddle and the musical box are instruments whose tones are produced by rods, or tongues, fixed at one end and free at the other.
A rod free at both ends can also be rendered a source of sonorous vibrations. In its simplest mode of division it has two nodes, the subsequent overtones correspond to divisions by 3, 4, 5, etc., nodes. Beginning with its first mode of division, the tones of such a rod are represented by the squares of the odd numbers 3, 5, 7, 9, etc.
The claque-bois, straw-fiddle, and glass harmonica are instruments whose tones are those of rods or bars free at both ends, and supported at their nodes.
When a straight bar, free at both ends, is gradually bent at its centre, the two nodes corresponding to its fundamental tone gradually approach each other. It finally assumes the shape of a timing-fork which, when it sounds its fundamental note, is divided by two nodes near the base of its two prongs into three vibrating parts.
There is no division of a tuning-fork by three nodes.
In its second mode of division, which corresponds to the first overtone of the fork, there is a node on each prong and two others at the bottom of the fork.
The fundamental tone of the fork is to its first overtone approximately as the square of 2 is to the square of 5. The vibrations of the first overtone are, therefore, about 6-1/4 times as rapid as those of the fundamental. From the first overtone onward the successive rates of vibration are as the squares of the odd numbers 3, 5, 7, 9, etc.
We are indebted to Chladni for the experimental investigation of all these points. He was enabled to conduct his inquiries by means of the discovery that, when198 sand is scattered over a vibrating surface, it is driven from the vibrating portions of the surface, and collects along the nodal lines.
Chladni embraced in his investigations plates of various forms. A square plate, for example, clamped at the centre, and caused to emit its fundamental tone, divides itself into four smaller squares by lines parallel to its sides.
The same plate can divide itself into four triangular vibrating parts, the nodal lines coinciding with the diagonals. The note produced in this case is a fifth above the fundamental note of the plate.
The plate may be further subdivided, sand-figures of extreme beauty being produced; the notes rise in pitch as the subdivision of the plate becomes more minute.
These figures may be deduced from the coalescence of different systems of vibration.
When a circular plate clamped at its centre sounds its fundamental tone, it divides into four vibrating parts, separated by four radial nodal lines.
The next note of the plate corresponds to a division into six vibrating sectors, the next note to a division into eight sectors; such a plate can divide into any even number of vibrating sectors, the sand-figures assuming beautiful stellar forms.
The rates of vibration corresponding to the divisions of a disk are represented by the squares of the numbers 2, 3, 4, 5, 6, etc. In other words, the rates of vibration are proportional to the squares of the numbers representing the sectors into which the disk is divided.
When a bell sounds its deepest note it is divided into four vibrating parts separated from each other by nodal199 lines, which run upward from the sound-bow and cross each other at the crown.
It is capable of the same subdivisions as a disk; the succession of its tones being also the same.
The rate of vibration of a disk or bell is directly proportional to the thickness and inversely proportional to the square of the diameter.
Longitudinal Vibrations of a Wire—Relative Velocities of Sound in Brass and Iron—Longitudinal Vibrations of Rods fixed at One End—Of Rods free at Both Ends—Divisions and Overtones of Rods vibrating longitudinally—Examination of Vibrating Bars by Polarized Light—Determination of Velocity of Sound in Solids—Resonance—Vibrations of Stopped Pipes: their Divisions and Overtones—Relation of the Tones of Stopped Pipes to those of Open Pipes—Condition of Column of Air within a Sounding Organ-Pipe—Reeds and Reed-Pipes—The Voice—Overtones of the Vocal Chords—The Vowel Sounds—Kundt’s Experiments—New Methods of determining the Velocity of Sound
WE HAVE thus far occupied ourselves exclusively with transversal vibrations; that is to say, vibrations executed at right angles to the lengths of the strings, rods, plates, and bells subjected to examination. A string is also capable of vibrating in the direction of its length, but here the power which enables it to vibrate is not a tension applied externally, but the elastic force of its own molecules. Now this molecular elasticity is much greater than any that we can ordinarily develop by stretching the string, and the consequence is that the sounds produced by the longitudinal vibrations of a string are, as a general rule, much more acute than those produced by its transverse vibrations. These longitudinal vibrations may be excited by the oblique passage of a fiddle-bow; but they are more easily201 produced by passing briskly along the string a bit of cloth or leather on which powdered resin has been strewed. The resined fingers answer the same purpose.
When the wire of our monochord is plucked aside, you hear the sound produced by its transverse vibrations. When resined leather is rubbed along the wire, a note much more piercing than the last is heard. This is due to the longitudinal vibrations of the wire. Behind the table is stretched a stout iron wire 23 feet long. One end of it is firmly attached to an immovable wooden tray, the other end is coiled round a pin fixed firmly into one of our benches. With a key this pin can be turned, and the wire stretched so as to facilitate the passage of the rubber. Clasping the wire with the resined leather, and passing the hand to and fro along it, a rich, loud musical sound is heard. Halving the wire at its centre, and rubbing one of its halves, the note heard is the octave of the last: the vibrations are twice as rapid. When the wire is clipped at one-third of its length and the shorter segment rubbed, the note is a fifth above the octave. Taking one-fourth of its length and rubbing as before, the note yielded is the double octave of that of the whole wire, being produced by four times the number of vibrations. Thus, in longitudinal as well as in transverse vibrations, the number of vibrations executed in a given time is inversely proportional to the length of the wire.
And notice the surprising power of these sounds when the wire is rubbed vigorously. With a shorter length, the note is so acute, and at the same time so powerful, as to be hardly bearable. It is not the wire itself which produces this intense sound; it is the wooden tray at its202 end to which its vibrations are communicated. And, the vibrations of the wire being longitudinal, those of the tray, which is at right angles to the wire, must be transversal. We have here, indeed, an instructive example of the conversion of longitudinal into transverse vibrations.
Causing the wire to vibrate again longitudinally through its entire length, my assistant shall at the same time turn the key at the end, thus changing the tension. You notice no variation of the note. The longitudinal vibrations of the wire, unlike the transverse ones, are independent of the tension. Beside the iron wire is stretched a second, of brass, of the same length and thickness. I rub them both. Their tones are not the same; that of the iron wire is considerably the higher of the two. Why? Simply because the velocity of the sound-pulse is greater in iron than in brass. The pulses in this case pass to and fro from end to end of the wire. At one moment the wire pushes the tray at its end; at the next moment it pulls the tray, this pushing and pulling being due to the passage of the pulse to and fro along the whole wire. The time required for a pulse to run from one end to the other and back is that of a complete vibration. In that time the wire imparts one push and one pull to the wooden tray at its end; the wooden tray imparts one complete vibration to the air, and the air bends once in and once out the tympanic membrane. It is manifest that the rapidity of vibration, or, in other words, the pitch of the note, depends upon the velocity with which the sound-pulse is transmitted through the wire.
And now the solution of a beautiful problem falls of itself into our hands. By shortening the brass wire we cause it to emit a note of the same pitch as that emitted by the other. You hear both notes now sounding in unison, and the reason is that the sound-pulse travels through these 23 feet of iron wire, and through these 15 feet 6 inches of brass wire, in the same time. These lengths are in the ratio of 11:17, and these two numbers express the relative velocities of sound in brass and iron. In fact, the former velocity is 11,000 feet, and the latter 17,000 feet a second. The same method is of course applicable to many other metals.
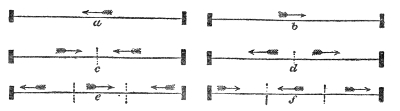
When a wire or string, vibrating longitudinally, emits its lowest note, there is no node whatever upon it; the pulse, as just stated, runs to and fro along the whole length. But, like a string vibrating transversely, it can also subdivide itself into ventral segments separated by nodes. By damping the centre of the wire we make that point a node. The pulses here run from both ends, meet in the centre, recoil from each other, and return to the ends, where they are reflected as before. The note produced is the octave of the fundamental note. The next higher note corresponds to the division of the wire into three vibrating segments, separated from each other by two nodes. The first of these three modes of vibration is shown in Fig. 82, a and b; the second at c and d;204 the third at e and f; the nodes being marked by dotted transverse lines, and the arrows in each case pointing out the direction in which the pulse moves. The rates of vibration follow the order of the numbers 1, 2, 3, 4, 5, etc., just as in the case of a wire vibrating transversely.
A rod or bar of wood or metal, with its two ends fixed, and vibrating longitudinally, divides itself in the same manner as the wire. The succession of tones is also the same in both cases.
Rods and bars with one end fixed are also capable of
vibrating longitudinally. A smooth wooden or metal
rod, for example, with one of its ends fixed in a vise,
yields a musical note, when the resined fingers are passed
along it. When such a note yields its lowest note, it
simply elongates and shortens in quick alternation; there
is, then, no node upon the rod. The pitch of the note is
 Fig. 83.
inversely proportional to the
length of the rod. This follows
necessarily from the fact
that the time of a complete
vibration is the time required
for the sonorous pulse to run
twice to and fro over the
rod. The first overtone of a
rod, fixed at one end, corresponds
to its division by a node at a point one-third of
its length from its free end. Its second overtone corresponds
to a division by two nodes, the highest of which
is at a point one-fifth of the length of the rod from its205
free end, the remainder of the rod being divided into
two equal parts by the second node. In Fig. 83, a and
b, c and d, e and f, are shown the conditions of the rod
answering to its first three modes of vibration: the nodes,
Fig. 83.
inversely proportional to the
length of the rod. This follows
necessarily from the fact
that the time of a complete
vibration is the time required
for the sonorous pulse to run
twice to and fro over the
rod. The first overtone of a
rod, fixed at one end, corresponds
to its division by a node at a point one-third of
its length from its free end. Its second overtone corresponds
to a division by two nodes, the highest of which
is at a point one-fifth of the length of the rod from its205
free end, the remainder of the rod being divided into
two equal parts by the second node. In Fig. 83, a and
b, c and d, e and f, are shown the conditions of the rod
answering to its first three modes of vibration: the nodes,
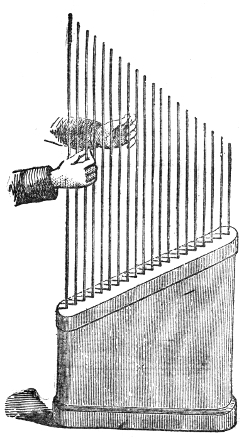 Fig. 84.
as before, are marked by
dotted lines, the arrows in
the respective cases marking
the direction of the pulses.
Fig. 84.
as before, are marked by
dotted lines, the arrows in
the respective cases marking
the direction of the pulses.
The order of the tones of a rod fixed at one end and vibrating longitudinally is that of the odd numbers 1, 3, 5, 7, etc. It is easy to see that this must be the case. For the time of vibration of c or d is that of the segment above the dotted line: and the length of this segment being only one-third that of the whole rod, its vibrations must be three times as rapid. The time of vibration in e or f is also that of its highest segment, and as this segment is one-fifth of the length of the whole rod, its vibrations must be five times as rapid. Thus the order of the tones must be that of the odd numbers.
Before you, Fig. 84, is a musical instrument, the sounds of which are due to the longitudinal vibrations of a number of deal rods of different lengths. Passing the resined fingers over the rods in succession, a series of notes of varying pitch is obtained. An expert per206former might render the tones of this instrument very pleasant to you.
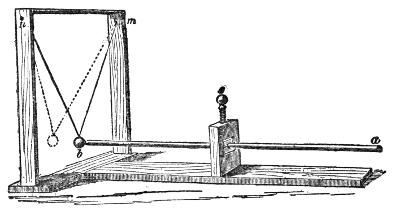
Rods with both ends free are also capable of vibrating longitudinally, and producing musical tones. The investigation of this subject will lead us to exceedingly important results. Clasping a long glass tube exactly at its centre, and passing a wetted cloth over one of its halves, a clear musical sound is the result. A solid glass rod of the same length would yield the same note. In this case the centre of the tube is a node, and the two halves elongate and shorten in quick alternation. M. König, of Paris, has provided us with an instrument which will illustrate this action. A rod of brass, a b, Fig. 85, is held at its centre by the clamp s, while an ivory ball, suspended by two strings from the points, m and n, of a wooden frame, is caused to rest against the end, b, of the brass rod. Drawing gently a bit of resined leather over the rod near a, it is thrown into longitudinal vibration. The centre, s, is a node; but the uneasiness of the207 ivory ball shows you that the end, b, is in a state of tremor. I apply the rubber still more briskly. The ball, b, rattles, and now the vibration is so intense that the ball is rejected with violence whenever it comes into contact with the end of the rod.
When the wetted cloth is passed over the surface of a glass tube the film of liquid left behind by the cloth is seen forming narrow tremulous rings all along the rod. Now this shivering of the liquid is due to the shivering of the glass underneath it, and it is possible so to augment the intensity of the vibration that the glass shall actually go to pieces. Savart was the first to show this. Twice in this place I have repeated this experiment, sacrificing in each case a fine glass tube 6 feet long and 2 inches in diameter. Seizing the tube at its centre C, Fig. 86, I swept my hand vigorously to and fro along C D, until finally the half most distant from my hand was shivered into annular fragments. On examining these it was found that, narrow as they were, many of them were marked by circular cracks indicating a still more minute subdivision.
In this case also the rapidity of vibration is inversely proportional to the length of the rod. A rod of half the length vibrates longitudinally with double the rapidity, a rod of one-third the length with treble the rapidity, and so on. The time of a complete vibration being that required by the pulse to travel to and fro over the rod, and that time being directly proportional to the length of the rod, the rapidity of vibration must, of necessity, be in the inverse proportion.
This division of a rod by a single node at its centre corresponds to the deepest tone produced by its longitudinal vibration. But, as in all other cases hitherto examined, such rods can subdivide themselves further. Holding the long glass rod a e, Fig. 87, at a point b, midway between its centre and one of its ends, and rubbing its short section, a b, with a wet cloth, the point b becomes a node, a second node, d, being formed at the same distance from the opposite end of the rod. Thus we have the rod divided into three vibrating parts, consisting of one whole ventral segment, b d, and two half ones, a b and d e. The sound corresponding to this division of the rod is the octave of its fundamental note.
You have now a means of checking me. For, if the second mode of division just described produces the octave of the fundamental note, and if a rod of half the length produces the same octave, then the whole rod held at a point one-fourth of its length from one of its ends ought to emit the same note as the half rod held209 in the middle. When both notes are sounded together they are heard to be identical in pitch.
Fig. 88, a and b, c and d, e and f, shows the three first divisions of a rod free at both ends and vibrating longitudinally. The nodes, as before, are marked by transverse dots, the direction of the pulses being shown by arrows. The order of the tones is that of the numbers, 1, 3, 4, etc.
When a tube or rod vibrating longitudinally yields its fundamental tone, its two ends are in a state of free vibration, the glass there suffering neither strain nor pressure. The case at the centre is exactly the reverse; here there is no vibration, but a quick alternation of tension and compression. When the sonorous pulses meet at the centre they squeeze the glass; when they recoil they strain it. Thus while at the ends we have the maximum of vibration, but no change of density, at the centre we have the maximum changes of density, but no vibration.
We have now cleared the way for the introduction of a very beautiful experiment made many years ago by Biot, but never, to my knowledge, repeated on the scale here presented to you. The beam from our electric lamp, L, Fig. 89, being sent through a prism, B, of bi-refracting spar, a beam of polarized light is obtained.210 This beam impinges on a second prism of spar, n, but, though both prisms are perfectly transparent, the light which has passed through the first cannot get through the second. By introducing a piece of glass between the two prisms, and subjecting the glass to either strain or pressure, the light is enabled to pass through the entire system.
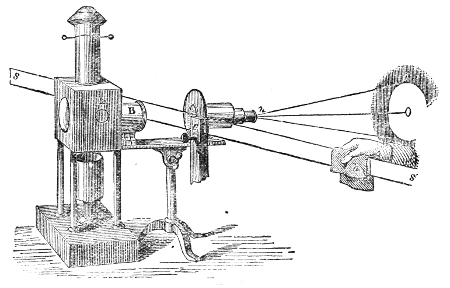
I now introduce between the prisms B and n a rectangle, s s′, of plate glass, 6 feet long, 2 inches wide, and one-third of an inch thick, which is to be thrown into longitudinal vibration. The beam from L passes through the glass at a point near its centre, which is held in a vise, c, so that when a wet cloth is passed over one of the halves, c s′, of the strip, the centre will be a node. During its longitudinal vibration the glass near the centre is, as already explained, alternately strained and compressed; and this successive strain and pressure so changes the condition of the light as to enable it to pass through the second prism. The screen is211 now dark; but on passing the wetted cloth briskly over the glass a brilliant disk of light, three feet in diameter, flashes out upon the screen. The vibration quickly subsides, and the luminous disk as quickly disappears, to be, however, revived at will by the passage of the wetted cloth along the glass.
The light of this disk appears to be continuous, but it is really intermittent, for it is only when the glass is under strain or pressure that the light can get through. In passing from strain to pressure, and from pressure to strain, the glass is for a moment in its natural state, which, if it continued, would leave the screen dark. But the impressions of brightness, due to the strains and pressures, remain far longer upon the retina than is necessary to abolish the intervals of darkness; hence the screen appears illuminated by a continuous light. When the glass rectangle is shifted so as to cause the beam of polarized light to pass through it close to its end, s, the longitudinal vibrations of the glass have no effect whatever upon the polarized beam.
Thus, by means of this subtile investigator, we demonstrate that, while the centre of the glass, where the vibration is nil, is subjected to quick alternations of strain and pressure, the ends of the rectangle, where the vibration is a maximum, suffer neither.44
Rods of wood and metal also yield musical tones when they vibrate longitudinally. Here, however, the rubber 212employed is not a wet cloth, but a piece of leather covered with powdered resin. The resined fingers also elicit the music of the rods. The modes of vibration here are those already indicated, the pitch, however, varying with the velocity of the sonorous pulse in the respective substances. When two rods of the same length, the one of deal, the other of Spanish mahogany, are sounded together, the pitch of the one is much lower than that of the other. Why? Simply because the sonorous pulses pass more slowly through the mahogany than through the deal. Can we find the relative velocity of sound through both? With the greatest ease. We have only to carefully shorten the mahogany rod till it yields the same note as the deal one. The notes, rendered approximate by the first trials, are now identical. Through this rod of mahogany 4 feet long, and through this rod of deal 6 feet long, the sound-pulse passes in the same time, and these numbers express the relative velocities of sound through the two substances.
Modes of investigation, which could only be hinted at in our earlier lectures, are now falling naturally into our hands. When in the first lecture the velocity of sound in air was spoken of, many possible methods of determining this velocity must have occurred to your minds, because here we have miles of space to operate upon. Its velocity through wood or metal, where such distances are out of the question, is determined in the simple manner just indicated. From the notes which they emit when suitably prepared, we may infer with certainty the relative velocities of sound through different solid substances; and determining the ratio of the velocity in any one of them to its velocity in air, we are able to draw up a213 table of absolute velocities. But how is air to be introduced into the series? We shall soon be able to answer this question, approaching it, however, through a number of phenomena with which, at first sight, it appears to have no connection.
The series of tuning-forks now before you have had their rates of vibration determined by the siren. One, you will remember, vibrates 256 times in a second, the length of its sonorous wave being 4 feet 4 inches. It is detached from its case, so that when struck against a pad you hardly hear it. When held over this glass jar, A B, Fig. 90, 18 inches deep, you still fail to hear the sound of the fork. Preserving the fork in its position, I pour water with the least possible noise into the jar. The column of air underneath the fork shortens, the sound augments in intensity, and when the water has reached a certain level it bursts forth with extraordinary power. A greater quantity of water causes the sound to sink, and become finally inaudible, as at first. By pouring the water carefully out, a point is reached where the reinforcement of the sound again occurs. Experimenting thus, we learn that there is one particular length of the column of air which, when the fork is placed above it, produces a maximum augmentation of the sound. This reinforcement of the sound is named resonance.
Operating in the same way with all the forks in succession,
a column of air is found for each, which yields214
a maximum resonance. These columns become shorter as
the rapidity of vibration increases. In Fig. 91 the series
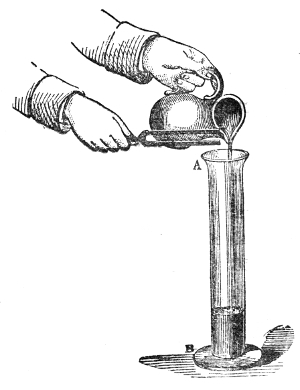 Fig. 90.
of jars is represented, the
number of vibrations to
which each resounds being
placed above it.
Fig. 90.
of jars is represented, the
number of vibrations to
which each resounds being
placed above it.
What is the physical
meaning of this very wonderful
effect? To solve
this question we must revive
our knowledge of the
relation of the motion of
the fork itself to the motion
of the sonorous wave
produced by the fork.
Supposing a prong of this
fork, which executes 256
vibrations in a second, to
vibrate between the points a and b, Fig. 92, in its motion
from a to b the fork generates half a sonorous wave, and
 Fig. 91.
as the length of the whole wave
emitted by this fork is 4 feet 4
inches, at the moment the prong
reaches b the foremost point of the
sonorous wave will be at C, 2 feet
2 inches distant from the fork.
The motion of the wave, then, is
vastly greater than that of the
fork. In fact, the distance a b is,
in this case, not more than one-twentieth of an inch, while
the wave has passed over a distance of 26 inches. With
forks of lower pitch the difference would be still greater.
Fig. 91.
as the length of the whole wave
emitted by this fork is 4 feet 4
inches, at the moment the prong
reaches b the foremost point of the
sonorous wave will be at C, 2 feet
2 inches distant from the fork.
The motion of the wave, then, is
vastly greater than that of the
fork. In fact, the distance a b is,
in this case, not more than one-twentieth of an inch, while
the wave has passed over a distance of 26 inches. With
forks of lower pitch the difference would be still greater.

Our next question is, what is the length of the column of air which resounds to this fork? By measurement with a two-foot rule it is found to be 13 inches. But the length of the wave emitted by the fork is 52 inches; hence the length of the column of air which resounds to the fork is equal to one-fourth of the length of the sound-wave produced by the fork. This rule is general, and might be illustrated by any other of the forks instead of this one.
Let the prong, vibrating between the limits a and b, be placed over its resonant jar, A B, Fig. 93. In the time required by the prong to move from a to b, the condensation it produces runs down to the bottom of the jar, is there reflected, and, as the distance to the bottom and back is 26 inches, the reflected wave will reach the fork at the moment when it is on the point of returning from b to a. The rarefaction of the wave is produced by the retreat of the prong from b to a. This rarefaction will also run to the bottom of the jar and back, overtaking the prong just as it reaches the limit, a, of its excursion. It is plain from this analysis that216 the vibrations of the fork are perfectly synchronous with the vibrations of the aërial column A B; and in virtue of this synchronism the motion accumulates in the jar, spreads abroad in the room, and produces this vast augmentation of the sound.
When we substitute for the air in one of these jars a gas of different elasticity, we find the length of the resounding column to be different. The velocity of sound through coal-gas is to its velocity in air about as 8:5. Hence, to synchronize with our fork, a jar filled with coal-gas must be deeper than one filled with air. I turn this jar, 18 inches long, upside down, and hold close to its open mouth our agitated tuning-fork. It is scarcely audible. The jar, with air in it, is 5 inches too deep for this fork. Let coal-gas now enter the jar. As it ascends the note at a certain point swells out, proving that for the more elastic gas a depth of 18 inches is not too great. In fact, it is not great enough; for if too much gas be allowed to enter the jar the resonance is weakened. By suddenly turning the jar upright, still holding the fork close to its mouth, the gas escapes, and at the point of proper admixture of gas and air the note swells out again.45
This fine, sonorous bell, Fig. 94, is thrown into intense vibration by the passage of a resined bow across its edge. You hear its sound, pure, but not very forcible. When, however, the open mouth of this large tube, which is closed at one end, is brought close to one of the vibrat217ing segments of the bell, the tone swells into a musical roar. As the tube is alternately withdrawn and advanced, the sound sinks and swells in this extraordinary manner.

The second tube, open at both ends, is capable of being lengthened and shortened by a telescopic slider. When brought near the vibrating bell, the resonance is feeble. On lengthening the tube by drawing out the slider at a certain point, the tone swells out as before. If the tube be made longer, the resonance is again enfeebled. Note the fact, which shall be explained presently, that the open tube which gives the maximum resonance is exactly twice the length of the closed one. For these fine experiments we are indebted to Savart.
With the India-rubber tube employed in our third chapter it was found necessary to time the impulses properly, so as to produce the various ventral segments. I could then feel that the muscular work performed, when the impulses were properly timed, was greater than218 when they were irregular. The same truth may be illustrated by a claret-glass half filled with water. Endeavor to move your hand to and fro, in accordance with the oscillating period of the water: when you have thoroughly established synchronism, the work thrown upon the hand apparently augments the weight of the water. So likewise with our tuning-fork; when its impulses are timed to the vibrations of the column of air contained in this jar, its work is greater than when they are not so timed. As a consequence of this the tuning-fork comes sooner to rest when it is placed over the jar than when it is permitted to vibrate either in free air, or over a jar of a depth unsuited to its periods of vibration.46
Reflecting on what we have now learned, you would have little difficulty in solving the following beautiful problem: You are provided with a tuning-fork and a siren, and are required by means of these two instruments to determine the velocity of sound in air. To solve this problem you lack, if anything, the mere power of manipulation which practice imparts. You would first determine, by means of the siren, the number of vibrations executed by the tuning-fork in a second; you would then determine the length of the column of air which resounds to the fork. This length multiplied by 4 would give you, approximately, the wave-length of the fork, and the wave-length multiplied by the number of vibrations in a second would give you the velocity in a second. Without quitting your private room, therefore, you 219could solve this important problem. We will go on, if you please, in this fashion, making our footing sure as we advance.
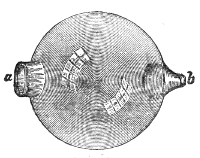
Helmholtz has availed himself of the principle of resonance in analyzing composite sounds. He employs little hollow spheres, called resonators, one of which is shown in Fig. 94a. The small projection b, which has an orifice, is placed in the ear, while the sound-waves enter the hollow sphere through the wide aperture at a. Reinforced by the resonance of such a cavity, and rendered thereby more powerful than its companions, a particular note of a composite clang may be in a measure isolated and studied alone.
Thus disciplined we are prepared to consider the subject of organ-pipes, which is one of great importance. Before me on the table are two resonant jars, and in my right hand and my left are held two tuning-forks. I agitate both, and hold them over this jar. One of them only is heard. Held over the other jar, the other fork alone is heard. Each jar selects that fork whose periods of vibration synchronize with its own. And instead of two forks suppose several of them to be held over the jar; from the confused assemblage of pulses thus gener220ated, the jar would select and reinforce that one which corresponds to its own period of vibration.
When I blow across the open mouth of the jar, or, better still, for the jar is too wide for this experiment, when I blow across the open end of a glass tube, t u, Fig. 95, of the same length as the jar, a fluttering of the air is thereby produced, an assemblage of pulses at the open mouth of the tube being generated. And what is the consequence? The tube selects that pulse of the flutter which is in synchronism with itself, and raises it to a musical sound. The sound, you perceive, is precisely that obtained when the proper tuning-fork is placed over the tube. The column of air within the tube has, in this case, virtually created its own tuning-fork; for by the reaction of its pulses upon the sheet of air issuing from the lips it has compelled that sheet to vibrate in synchronism with itself, and made it thus act the part of the tuning-fork.
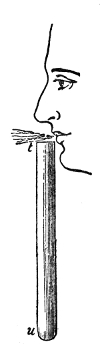
Selecting for each of the other tuning-forks a resonant tube, in every case, on blowing across the open end of the tube, a tone is produced identical in pitch with that obtained through resonance.
When different tubes are compared, the rate of vibration is found to be inversely proportional to the length of the tube. These three tubes are 24, 12, and 6 inches long, respectively. I blow gently across the 24-inch tube, and bring out its fundamental note; similarly treated, the 12-inch tube yields the octave of the note of the 24-inch. In like manner the 6-inch tube yields the octave of the 12-inch. It is plain that this must be the case; for,221 the rate of vibration depending on the distance which the pulse has to travel to complete a vibration, if in one case this distance be twice what it is in another, the rate of vibration must be twice as slow. In general terms, the rate of vibration is inversely proportional to the length of the tube through which the pulse passes.
But that the current of air should be thus able to accommodate itself to the requirements of the tube, it must enjoy a certain amount of flexibility. A little reflection will show you that the power of the reflected pulse over the current must depend to some extent on the force of the current. A stronger current, like a more powerfully stretched string, requires a great force to deflect it, and when deflected vibrates more quickly. Accordingly, to obtain the fundamental note of this 24-inch tube, we must blow very gently across its open end; a rich, full, and forcible musical tone is then produced. With a little stronger blast the sound approaches a mere rustle; blowing stronger still, a tone is obtained of much higher pitch than the fundamental one. This is the first overtone of the tube, to produce which the column of air within it has divided itself into two vibrating parts, with a node between them. With a still stronger blast a still higher note is obtained. The tube is now divided into three vibrating parts, separated from each other by two nodes. Once more I blow with sudden strength; a higher note than any before obtained is the consequence.
In Fig. 96 are represented the divisions of the column222 of air corresponding to the first three notes of a tube stopped at one end. At a and b, which correspond to the fundamental note, the column is undivided; the bottom of the tube is the only node, and the pulse simply moves up and down from top to bottom, as denoted by the arrows. In c and d, which correspond to the first overtone of the tube, we have one nodal surface shown by dots at x, against which the pulses abut, and from which they are reflected as from a fixed surface. This nodal surface is situated at one-third of the length of the tube from its open end. In e and f, which correspond to the second overtone, we have two nodal surfaces, the upper one, x′, of which is at one-fifth of the length of the tube from its open end, the remaining four-fifths being divided into two equal parts by the second nodal surface. The arrows, as before, mark the directions of the pulses.
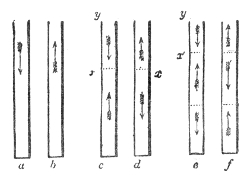
We have now to inquire into the relation of these successive notes to each other. The space from node to node has been called all through “a ventral segment”; hence the space between the middle of a ventral segment and a node is a semi-ventral segment. You will readily bear in mind the law that the number of vibrations is directly proportional to the number of semi-ventral segments into which the column of air within the tube is divided. Thus, when the fundamental note is sounded, we have but a single semi-ventral segment, as at a and b. The bottom here is a node, and the open end of the tube,223 where the air is agitated, is the middle of a ventral segment. The mode of division represented in c and d yields three semi-ventral segments; in e and f we have five. The vibrations, therefore, corresponding to this series of notes, augment in the proportion of the series of odd numbers 1:3:5. Could we obtain still higher notes, their relative rates of vibration would continue to be represented by the odd numbers 7, 9, 11, 13, etc.
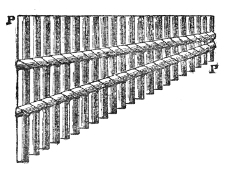
It is evident that this must be the law of succession. For the time of vibration in c or d is that of a stopped tube of the length x y; but this length is one-third of the length of the whole tube, consequently its vibrations must be three times as rapid. The time of vibration in e or f is that of a stopped tube of the length x′ y′, and inasmuch as this length is one-fifth that of the whole tube, its vibrations must be five times as rapid. We thus obtain the succession 1, 3, 5; if we pushed matters further we should obtain the continuation of the series of odd numbers.
And here it is once more in your power to subject my statements to an experimental test. Here are two tubes, one of which is three times the length of the other. I sound the fundamental note of the longest tube, and then the next note above the fundamental. The vibrations of these two notes are stated to be in the ratio of 1:3. This latter note, therefore, ought to be of precisely the same pitch as the fundamental note of the shorter of the two tubes. When both tubes are sounded their notes are identical.
It is only necessary to place a series of such tubes of different lengths thus together to form that ancient instrument, Pan’s pipes, p p′, Fig. 97 (page 223), with which we are so well acquainted.
The successive divisions, and the relation of the overtones of a rod fixed at one end (described in page 205), are plainly identical with those of a column of air in a tube stopped at one end, which we have been here considering.
From tubes closed at one end, and which, for the sake of brevity, may be called stopped tubes, we now pass to tubes open at both ends, which we shall call open tubes. Comparing, in the first instance, a stopped tube with an open one of the same length, we find the note of the latter an octave higher than that of the former. This result is general. To make an open tube yield the same note as a closed one, it must be twice the length of the latter. And, since the length of a closed tube sounding its fundamental note is one-fourth of the length of its sonorous wave, the length of an open tube is one-half that of the sonorous wave that it produces.
It is not easy to obtain a sustained musical note by blowing across the end of an open glass tube; but a mere puff of breath across the end reveals the pitch to the disciplined ear. In each case it is that of a closed tube half the length of the open one.


There are various ways of agitating the air at the ends of pipes and tubes, so as to throw the air-columns within them into vibration. In organ-pipes this is done by blowing a thin sheet of air against a sharp edge.225 You will have no difficulty in understanding the construction of an open organ-pipe, from this model, Fig. 98, one side of which has been removed so that you may see its inner parts. Through the tube t the air passes from the wind-chest into the chamber, C, which is closed at the top, save a narrow slit, e d, through which the compressed air of the chamber issues. This thin air-current breaks against the sharp edge, a b, and there produces a fluttering noise, and the proper pulse of this flutter is converted by the resonance of the pipe above into a musical sound. The open space between the edge, a b, and the slit below it is called the embouchure. Fig. 99 represents a stopped pipe of the same length as that shown in Fig. 98, and hence producing a note an octave lower.
Instead of a fluttering sheet
of air, a tuning-fork whose rate
of vibration synchronizes with
that of the organ-pipe may be226
placed at the embouchure, as at a b, Fig. 100. The
pipe will resound. Here, for example, are four open
pipes of different lengths, and four tuning-forks of
different rates of vibration. Striking the most slowly
vibrating fork, and bringing it near the embouchure of
the longest pipe, the pipe speaks powerfully. When
blown into, the same pipe yields a tone identical with
that of the tuning-fork. Going through all the pipes
in succession, we find in each case that the note obtained
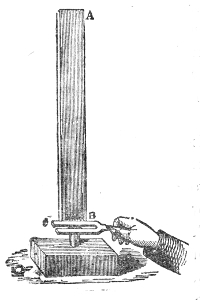 Fig. 100.
by blowing into the pipe
is exactly that produced when
the proper tuning-fork is placed
at the embouchure. Conceive
now the four forks placed together
near the same embouchure;
we should have pulses of
four different periods there excited;
but out of the four the
pipe would select only one.
And if four hundred vibrating
forks could be placed there instead
of four, the pipe would still
make the proper selection. This it
also does when for the pulses of tuning-forks we substitute
the assemblage of pulses created by the current of air
when it strikes against the sharp upper edge of the
embouchure.
Fig. 100.
by blowing into the pipe
is exactly that produced when
the proper tuning-fork is placed
at the embouchure. Conceive
now the four forks placed together
near the same embouchure;
we should have pulses of
four different periods there excited;
but out of the four the
pipe would select only one.
And if four hundred vibrating
forks could be placed there instead
of four, the pipe would still
make the proper selection. This it
also does when for the pulses of tuning-forks we substitute
the assemblage of pulses created by the current of air
when it strikes against the sharp upper edge of the
embouchure.
The heavy vibrating mass of the tuning-fork is practically uninfluenced by the motion of the air within the pipe. But this is not the case when air itself is the vibrating body. Here, as before explained, the pipe creates, as it were, its own tuning-fork, by compelling227 the fluttering stream at its embouchure to vibrate in periods answering to its own.
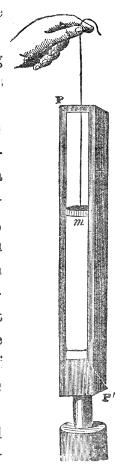
The condition of the air within an open organ-pipe, when its fundamental note is sounded, is that of a rod free at both ends, held at its centre, and caused to vibrate longitudinally. The two ends are places of vibration, the centre is a node. Is there any way of feeling the vibrating air-column so as to determine its nodes and its places of vibration? The late excellent William Hopkins has taught us the following mode of solving this problem: Over a little hoop is stretched a thin membrane, forming a little tambourine. The front of this organ-pipe, P P′, Fig. 101, is of glass, through which you can see the position of any body within it. By means of a string, the little tambourine, m, can be raised or lowered at pleasure through the entire length of the pipe. When held above the upper end of the pipe, you hear the loud buzzing of the membrane. When lowered into the pipe, it continues to buzz for a time; the sound becoming gradually feebler, and finally ceasing totally. It is now in the middle of the pipe, where it cannot vibrate, because the air around it is at rest. On lowering it still further, the buzzing sound instantly recommences, and continues down to the bottom of the pipe. Thus, as the membrane is raised and lowered in quick succession, during every descent and ascent, we have two periods of228 sound separated from each other by one of silence. If sand were strewed upon the membrane, it would dance above and below, but it would be quiescent at the centre. We thus prove experimentally that, when an organ-pipe sounds its fundamental note, it divides itself into two semi-ventral segments separated by a node.
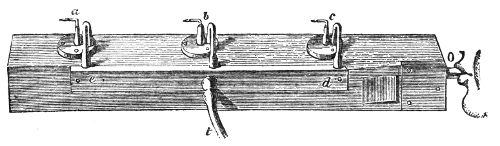
What is the condition of the air at this node? Again, that of the middle of a rod, free at both ends, and yielding the fundamental note of its longitudinal vibration. The pulses reflected from both ends of the rod, or of the column of air, meet in the middle, and produce compression; they then retreat and produce rarefaction. Thus, while there is no vibration in the centre of an organ-pipe, the air there undergoes the greatest changes of density. At the two ends of the pipe, on the other hand, the air-particles merely swing up and down without sensible compression or rarefaction.
If the sounding pipe were pierced at the centre, and the orifice stopped by a membrane, the air, when condensed, would press the membrane outward, and, when rarefied, the external air would press the membrane inward. The membrane would therefore vibrate in unison with the column of air. The organ-pipe, Fig. 102, is so arranged that a small jet of gas, b, can be lighted opposite the centre of the pipe, and there acted upon by the229 vibrations of a membrane. Two other gas-jets, a and c, are placed nearly midway between the centre and the two ends of the pipe. The three burners, a, b, c, are fed in the following manner: through the tube, t, the gas enters the hollow chamber, e d, from which issue three little bent tubes, shown in the figure, each communicating with a capsule closed underneath by the membrane. This is in direct contact with the air of the organ-pipe. From the three capsules issue the three little burners, with their flames, a, b, c.
Blowing into the pipe so as to sound its fundamental note, the three flames are agitated, but the central one is most so. Lowering the flames so as to render them very small, and blowing again, the central flame, b, is extinguished, while the others remain lighted. The experiment may be performed half a dozen times in succession; the sounding of the fundamental note always quenches the middle flame.
By blowing more sharply into the pipe, it is caused to yield its first overtone. The middle node no longer exists. The centre of the pipe is now a place of maximum vibration, while two nodes are formed midway between the centre and the two ends. But if this be the case, and if the flame opposite the node be always blown out, then, when the first overtone of this pipe is sounded, the two flames a and c ought to be extinguished, while the central flame remains lighted. This is the case. When the first harmonic is sounded the two nodal flames are infallibly extinguished, while the flame b in the middle of the ventral segment is not sensibly disturbed.
There is no theoretic limit to the subdivision of an
organ-pipe, either stopped or open. In stopped pipes we230
begin with 1 semi-ventral segment, and pass on to 3, 5,
7, etc., semi-ventral segments, the number of vibrations
of the successive notes augmenting in the same ratio. In
open pipes we begin with 2 semi-ventral segments, and
pass on to 4, 6, 8, 10, etc., the number of vibrations of
the successive notes augmenting in the same ratio; that
is to say, in the ratio 1:2:3:4:5, etc. When, therefore,
we pass from the fundamental tone to the first overtone
in an open pipe, we obtain the octave of the fundamental.
 Fig. 103.
When we make the
same passage in a stopped
pipe, we obtain a note a
fifth above the octave. No
intermediate modes of vibration
are in either case
possible. If the fundamental
tone of a stopped
pipe be produced by 100
vibrations a second, the
first overtone will be produced
by 300 vibrations,
the second by 500, and so
on. Such a pipe, for example,
cannot execute 200 or 400 vibrations in a second.
In like manner the open pipe, whose fundamental note
is produced by 100 vibrations a second, cannot vibrate 150
times in a second, but passes, at a jump, to 200, 300, 400,
and so on.
Fig. 103.
When we make the
same passage in a stopped
pipe, we obtain a note a
fifth above the octave. No
intermediate modes of vibration
are in either case
possible. If the fundamental
tone of a stopped
pipe be produced by 100
vibrations a second, the
first overtone will be produced
by 300 vibrations,
the second by 500, and so
on. Such a pipe, for example,
cannot execute 200 or 400 vibrations in a second.
In like manner the open pipe, whose fundamental note
is produced by 100 vibrations a second, cannot vibrate 150
times in a second, but passes, at a jump, to 200, 300, 400,
and so on.
In open pipes, as in stopped ones, the number of vibrations executed in the unit of time is inversely proportional to the length of the pipe. This follows from the fact, already dwelt upon so often, that the time of a231 vibration is determined by the distance which the sonorous pulse has to travel to complete a vibration.
In Fig. 103, a and b (at the bottom) represent the division of an open pipe corresponding to its fundamental tone; c and d represent the division corresponding to its first, e and f the division corresponding to its second overtone, the dots marking the nodes. The distance m n is one-half, o p is one-fourth, and s t is one-sixth of the whole length of the pipe. But the pitch of a is that of a stopped pipe equal in length to m n; the pitch of c is that of a stopped pipe of the length o p; while the pitch of e is that of a stopped pipe of the length s t. Hence, as these lengths are in the ratio of 1/2:1/4:1/6, or as 1:1/2:1/3, the rates of vibration must be as the reciprocals of these, or as 3:2:1. From the mere inspection, therefore, of the respective modes of vibration, we can draw the inference that the succession of tones of an open pipe must correspond to the series of natural numbers.
The pipe a, Fig. 103, has been purposely drawn twice the length of a, Fig. 93 (p. 215). It is perfectly manifest that to complete a vibration the pulse has to pass over the same distance in both pipes, and hence that the pitch of the two pipes must be the same. The open pipe, a n, consists virtually of two stopped ones, with the central nodal surface at m as their common base. This shows the relation of a stopped pipe to an open one to be that which experiment establishes.
We have already learned that the relative velocities of sound in different solid bodies may be determined from232 the notes which they emit when thrown into longitudinal vibration. It was remarked at the time that to draw up a table of absolute velocities we only required the accurate comparison of the velocity in any one of those solids with the velocity in air. We are now in a condition to supply this comparison. For we have learned that the vibrations of the air in an organ-pipe open at both ends are executed precisely as those of a rod free at both ends. Any difference of rapidity, therefore, between the vibrations of a rod and of an open organ-pipe of the same length must be due solely to the different velocities with which the sonorous pulses are propagated through them. Take therefore an organ-pipe of a certain length, emitting a note of a certain pitch, and find the length of a rod of pine which yields the same note. This length would be ten times that of the organ-pipe, which would prove the velocity of sound in pine to be ten times its velocity in air. But the absolute velocity in air is 1,090 feet a second; hence the absolute velocity in pine is 10,900 feet a second, which is that given in our first chapter (p. 74). To the celebrated Chladni we are indebted for this beautiful mode of determining the velocity of sound in solid bodies.
We had also in our first lecture a table of the velocities of sound in other gases than air. I am persuaded that you could tell me, after due reflection, how this table was constructed. It would only be necessary to find a series of organ-pipes which, when filled with the different gases, yield the same note; the lengths of these pipes would give the relative velocities of sound through the gases. Thus we should find the length of a pipe filled with hydrogen to be four times that of a pipe filled233 with oxygen, yielding the same note, and this would prove the velocity of sound in the former to be four times its velocity in the latter.
But we had also a table of velocities through various liquids. How was it constructed? By forcing the liquids through properly constructed organ-pipes, and comparing their musical tones. Thus, in water it requires a pipe a little better than four feet long to produce the note of an air-pipe one foot long; and this proves the velocity of sound in water to be somewhat more than four times its velocity in air. My object here is to give you a clear notion of the way in which scientific knowledge enables us to cope with these apparently insurmountable problems. It is not necessary to go into the niceties of these measurements. You will, however, readily comprehend that all the experiments with gases might be made with the same organ-pipe, the velocity of sound in each respective gas being immediately deduced from the pitch of its note. With a pipe of constant length the pitch, or, in other words, the number of vibrations, would be directly proportional to the velocity. Thus, comparing oxygen with hydrogen, we should find the note of the latter to be the double octave of that of the former, whence we should infer the velocity of sound in hydrogen to be four times its velocity in oxygen. The same remark applies to experiments with liquids. Here also the same pipe may be employed throughout, the velocities being inferred from the notes produced by the respective liquids.
In fact, the length of an open pipe being, as already explained, one-half the length of its sonorous wave, it is only necessary to determine, by means of the siren, the234 number of vibrations executed by the pipe in a second, and to multiply this number by twice the length of the pipe, in order to obtain the velocity of sound in the gas or liquid within the pipe. Thus, an open pipe 26 inches long and filled with air executes 256 vibrations in a second. The length of its sonorous wave is twice 26 inches, or 4-1/3 feet: multiplying 256 by 4-1/3 we obtain 1,120 feet per second as the velocity of sound through air of this temperature. Were the tube filled with carbonic-acid gas, its vibrations would be slower: were it filled with hydrogen, its vibrations would be quicker; and applying the same principle, we should find the velocity of sound in both these gases.
So likewise the length of a solid rod free at both ends, and sounding its fundamental note, is half that of the sonorous wave in the substance of the solid. Hence we have only to determine the rate of vibration of such a rod, and multiply it by twice the length of the rod, to obtain the velocity of sound in the substance of the rod. You can hardly fail to be impressed by the power which physical science has given us over these problems; nor will you refuse your admiration to that famous old investigator, Chladni, who taught us how to master them experimentally.
The construction of the siren and our experiments with that instrument are, no doubt, fresh in your recollection. Its musical sounds are produced by the cutting up into puffs of a series of air-currents. The same purpose is effected by a vibrating reed, as employed in the accor235dion, the concertina, and the harmonica. In these instruments it is not the vibrations of the reed itself which, imparted to the air, and transmitted through it to our organs of hearing, produce the music; the function of the reed is constructive, not generative; it molds into a series of discontinuous puffs that which without it would be a continuous current of air.
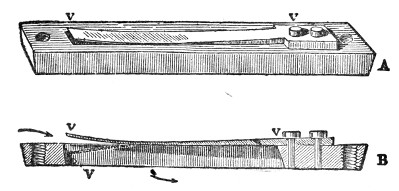
Reeds, if associated with organ-pipes, sometimes command,
and are sometimes commanded by, the vibrations
of the column of air. When they are stiff they rule the
column; when they are flexible the column rules them.
In the former case, to derive any advantage from the air-column,
its length ought to be so regulated that either its
fundamental tone or one of its overtones shall correspond
to the rate of vibration of the reed. The metal reed
commonly employed in organ-pipes is shown in Fig. 104,
A and b, both in perspective and in section. It consists
of a long and flexible strip of metal, V V, placed in a
rectangular orifice, through which the current of air
enters the pipe. The manner in which the reed and pipe
are associated is shown in Fig. 105. The front, b c, of
the space containing the flexible tongue is of glass, so
that you may see the tongue within it. A conical pipe,236
A B, surmounts the reed.47 The wire w i, shown pressing
 Fig. 105.
against the reed, is employed to lengthen or shorten it,
and thus to vary within certain limits its
rate of vibration. At one time in the
practice of music the reed closed the
aperture by simply falling against its
sides; every stroke of the reed produced
a tap, and these linked themselves together
to an unpleasant, screaming sound,
which materially injured that of the associated
organ-pipe. This was mitigated,
but not removed, by permitting the reed
to strike against soft leather; but the
reed now employed is the free reed,
which vibrates to and fro between the
sides of the aperture, almost, but not
quite, filling it. In this way the unpleasantness
referred to is avoided. When
reed and pipe synchronize perfectly, the
sound is most pure and forcible; a certain
latitude, however, is possible on
both sides of perfect synchronism. But
if the discordance be pushed too far, the
pipe ceases to be of any use. We then
obtain the sound due to the vibrations
of the reed alone.
Fig. 105.
against the reed, is employed to lengthen or shorten it,
and thus to vary within certain limits its
rate of vibration. At one time in the
practice of music the reed closed the
aperture by simply falling against its
sides; every stroke of the reed produced
a tap, and these linked themselves together
to an unpleasant, screaming sound,
which materially injured that of the associated
organ-pipe. This was mitigated,
but not removed, by permitting the reed
to strike against soft leather; but the
reed now employed is the free reed,
which vibrates to and fro between the
sides of the aperture, almost, but not
quite, filling it. In this way the unpleasantness
referred to is avoided. When
reed and pipe synchronize perfectly, the
sound is most pure and forcible; a certain
latitude, however, is possible on
both sides of perfect synchronism. But
if the discordance be pushed too far, the
pipe ceases to be of any use. We then
obtain the sound due to the vibrations
of the reed alone.
Flexible wooden reeds, which can accommodate themselves to the requirements of the pipes above them, are also employed in organ-pipes. Perhaps the simplest illus237tration of the action of the reed commanded by its aërial column is furnished by a common wheaten straw. At about an inch from a knot, at r, I bury my penknife in this straw, s r′, Fig. 106, to a depth of about one-fourth of the straw’s diameter, and, turning the blade flat, pass it upward toward the knot, thus raising a strip of the straw nearly an inch in length. This strip, r r′, is to be our reed, and the straw itself is to be our pipe. It is now eight inches long. When blown into, it emits this decidedly musical sound. When cut so as to make its length six inches, the pitch is higher; with a length of four inches, the pitch is higher still; and with a length of two inches, the sound is very shrill indeed. In these experiments the reed was compelled to accommodate itself throughout to the requirements of the vibrating column of air.
The clarinet is a reed-pipe. It has a single broad tongue, with which a long, cylindrical tube is associated. The reed-end of the instrument is grasped by the lips, and by their pressure the slit between the reed and its frame is narrowed to the required extent. The overtones of a clarinet are different from those of a flute. A flute is an open pipe, a clarinet a stopped one, the end at which the reed is placed answering to the closed end of the pipe. The tones of a flute follow the order of the natural numbers 1, 2, 3, 4, etc., or of the even numbers 2, 4, 6, 8, etc.; while the tones of a clarinet follow the order of the odd numbers 1, 3, 5, 7, etc. The inter238mediate notes are supplied by opening the lateral orifices of the instrument. Sir C. Wheatstone was the first to make known this difference between the flute and clarinet, and his results agree with the more thorough investigations of Helmholtz. In the hautboy and bassoon we have two reeds inclined to each other at a sharp angle, with a slit between them, through which the air is urged. The pipe of the hautboy is conical, and its overtones are those of an open pipe—different, therefore, from those of a clarinet. The pulpy end of a straw of green corn may be split by squeezing it, so as to form a double reed of this kind, and such a straw yields a musical tone. In the horn, trumpet, and serpent, the performer’s lips play the part of the reed. These instruments are formed of long, conical tubes, and their overtones are those of an open organ-pipe. The music of the older instruments of this class was limited to their overtones, the particular tone elicited depending on the force of the blast and the tension of the lips. It is now usual to fill the gaps between the successive overtones by means of keys, which enable the performer to vary the length of the vibrating column of air.
The most perfect of reed instruments is the organ of voice. The vocal organ in man is placed at the top of the trachea or wind-pipe, the head of which is adjusted for the attachment of certain elastic bands which almost close the aperture. When the air is forced from the lungs through the slit which separates these vocal chords, they are thrown into vibration; by varying their tension, the rate of vibration is varied, and the sound changed in239 pitch. The vibrations of the vocal chords are practically unaffected by the resonance of the mouth, though we shall afterward learn that this resonance, by reinforcing one or the other of the tones of the vocal chords, influences in a striking manner the quality of the voice. The sweetness and smoothness of the voice depend on the perfect closure of the slit of the glottis at regular intervals during the vibration.
The vocal chords may be illuminated and viewed in a mirror, placed suitably at the back of the mouth. Varied experiments of this kind have been executed by Sig. Garcia.48 I once sought to project the larynx of M. Czermak upon a screen in this room, but with only partial success. The organ may, however, be viewed directly in the laryngoscope; its motions, in singing, speaking, and coughing, being strikingly visible. It is represented at rest in Fig. 107. The roughness of the voice in colds is due, according to Helmholtz, to mucous flocculi, which get into the slit of the glottis, and which are seen by means of the laryngoscope. The squeaking falsetto voice, with which some persons are afflicted, Helmholtz thinks, may be produced by the drawing aside of the mucous layer which ordinarily lies under and loads the vocal chords. Their edges thus become sharper and their weight less; while, their elasticity remaining the same, 240they are shaken into more rapid tremors. The promptness and accuracy with which the vocal chords can change their tension, their form, and the width of the slit between them, to which must be added the elective resonance of the cavity of the mouth, render the voice the most perfect of musical instruments.
The celebrated comparative anatomist, John Müller, imitated the action of the vocal chords by means of bands of India-rubber. He closed the open end of a glass tube by two strips of this substance, leaving a slit between them. On urging air through the slit, the bands were thrown into vibration, and a musical tone produced. Helmholtz recommends the form shown in Fig. 108, where the tube, instead of ending in a section at right angles to its axis, terminates in two oblique sections, over which the bands of India-rubber are drawn. The easiest mode of obtaining sounds from reeds of this character is to roll round the end of a glass tube a strip of thin India-rubber, leaving about an inch of the substance projecting beyond the end of the tube. Taking two opposite portions of the projecting rubber in the fingers, and stretching it, a slit is formed, the blowing through which produces a musical sound, which varies in pitch, as the sides of the slit vary in tension.
The formation of the vowel sounds of the human voice excited long ago philosophic inquiry. We can distinguish one vowel sound from another, while assign241ing to both the same pitch and intensity. What, then, is the quality which renders the distinction possible? In the year 1779 this was made a prize question by the Academy of St. Petersburg, and Kratzenstein gained the prize for the successful manner in which he imitated the vowel sounds by mechanical arrangements. At the same time Von Kempelen, of Vienna, made similar and more elaborate experiments. The question was subsequently taken up by Mr. Willis, who succeeded beyond all his predecessors in the experimental treatment of the subject. The true theory of vowel sounds was first stated by Sir C. Wheatstone, and quite recently they have been made the subject of exhaustive inquiry by Helmholtz. You will find little difficulty in comprehending their origin.
Mounted on the acoustic bellows, without any pipe associated with it, when air is urged through its orifice, a free reed speaks in this forcible manner. When upon the frame of the reed a pyramidal pipe is fixed, you notice a change in the sound; and by pushing my flat hand over the open end of the pipe, the similarity between the sound produced and that of the human voice is unmistakable. Holding the palm of the hand over the end of the pipe so as to close it altogether, and then raising the hand twice in quick succession, the word “mamma” is heard as plainly as if it were uttered by an infant. For this pyramidal tube I now substitute a shorter one, and with it make the same experiment. The “mamma” now heard is exactly such as would be uttered by a child with a stopped nose. Thus, by associating with a vibrating reed a suitable pipe, we can impart to the sound the qualities of the human voice.
In the organ of voice, the reed is formed by the vocal chords, and associated with this reed is the resonant cavity of the mouth, which can so alter its shape as to resound, at will, either to the fundamental tone of the vocal chords or to any of their overtones. With the aid of the mouth, therefore, we can mix together the fundamental tone and the overtones of the voice in different proportions. Different vowel sounds are due to different admixtures of this kind. Striking one of this series of tuning-forks, and placing it before my mouth, I adjust the size of that cavity until it resounds forcibly to the fork. Then, without altering in the least the shape or size of my mouth, I urge air through the glottis. The vowel sound “U” (oo in hoop) is produced, and no other. I strike another fork, and, placing it in front of the mouth, adjust the cavity to resonance. Then removing the fork and urging air through the glottis, the vowel sound “O,” and it only, is heard. I strike a third fork, adjust my mouth to it, and then urge air through the larynx; the vowel sound ah! and no other, is heard. In all these cases the vocal chords have been in the same constant condition. They have generated throughout the same fundamental tone and the same overtones, the changes of sound which you have heard being due solely to the fact that different tones in the different cases were reinforced by the resonance of the mouth. Donders first proved that the mouth resounded differently for the different vowels.
In the formation of the different vowel sounds the resonant cavity of the mouth undergoes, according to Helmholtz, the following changes:
For the production of the sound “U” (oo in hoop),243 the lips must be pushed forward, so as to make the cavity of the mouth as deep as possible, and the orifice of the mouth, by the contraction of the lips, as small as possible. This arrangement corresponds to the deepest resonance of which the mouth is capable. The fundamental tone itself of the vocal chords is here reinforced, while the higher tones retreat.
The vowel “O” requires a somewhat wider opening of the mouth. The overtones which lie in the neighborhood of the middle b of the soprano come out strongly in the case of this vowel.
When “Ah” is sounded, the mouth assumes the shape of a funnel, widening outward. It is thus tuned to a note an octave higher than in the case of the vowel “O.” Hence, in sounding “Ah,” those overtones are most strengthened which lie near the higher b of the soprano. As the mouth is in this case wide open, all the other overtones are also heard, though feebly.
In sounding “A” and “E,” the hinder part of the mouth is deepened, while the front of the tongue rises against the gums and forms a tube; this yields a higher resonance-tone, rising gradually from “A” to “E,” while the hinder hollow space yields a lower resonance-tone, which is deepest when “E” is sounded.
These examples sufficiently illustrate the subject of vowel sounds. We may blend in various ways the elementary tints of the solar spectrum, producing innumerable composite colors by their admixture. Out of violet and red we produce purple, and out of yellow and blue we produce white. Thus also may elementary sounds be blended so as to produce all possible varieties of clang-tint. After having resolved the human voice into its244 constituent tones, Helmholtz was able to imitate these tones by tuning-forks, and, by combining them appropriately together, to produce the sounds of all the vowels.
Unwilling to interrupt the continuity of our reasonings and experiments on the sound of organ-pipes, and their relations to the vibrations of solid rods, I have reserved for the conclusion of this discourse some reflections and experiments which, in strictness, belong to an earlier portion of the chapter. You have already heard the tones, and made yourselves acquainted with the various modes of division of a glass tube, free at both ends, when thrown into longitudinal vibration. When it sounds its fundamental tone, you know that the two halves of such a tube lengthen and shorten in quick alternation. If the tube were stopped at its ends, the closed extremities would throw the air within the tube into a state of vibration; and if the velocity of sound in air were equal to its velocity in glass, the air of the tube would vibrate in synchronism with the tube itself. But the velocity of sound in air is far less than its velocity in glass, and hence, if the column of air is to synchronize with the vibrations of the tube, it can only do so by dividing itself into vibrating segments of a suitable length. In an investigation of great interest, recently published in “Poggendorff’s Annalen,” M. Kundt, of Berlin, has taught us how these segments may be rendered visible. Into this six-foot tube is introduced the light powder of lycopodium, being shaken all over the interior surface. A small quantity of the powder clings to that surface. Stopping245 the ends of the tube, holding its centre by a fixed clamp, and sweeping a wet cloth briskly over one of its halves, instantly the powder, which a moment ago clung to its interior surface, falls to the bottom of the tube in the forms shown in Fig. 109, the arrangement of the lycopodium marking the manner in which the column of air has been divided. Every node here is encircled by a ring of dust, while from node to node the dust arranges itself in transverse streaks along the ventral segments.

You will have little difficulty in seeing that we perform here, with air, substantially the same experiment as that of M. Melde with a vibrating string. When the string was too long to vibrate as a whole, it met the requirements of the tuning-fork to which it was attached by dividing into ventral segments. Now, in all cases, the length from a node to its next neighbor is half that of the sonorous wave: how many such half-waves then have we in our tube in the present instance? Sixteen (the figure shows only four of them). But the length of our glass tube vibrating thus longitudinally is also half that of the sonorous wave in glass. Hence, in the case before us, with the same rate of vibration, the length of the semi-wave in glass is sixteen times the length of the semi-wave in air. In other words, the velocity of sound in glass is sixteen times its velocity in air. Thus, by a single sweep of the wet rubber, we solve a most important problem. But, as M. Kundt has shown, we246 need not confine ourselves to air. Introducing any other gas into the tube, a single stroke of our wet cloth enables us to determine the relative velocity of sound in that gas and in glass. When hydrogen is introduced, the number of ventral segments is less than in air; when carbonic acid is introduced, the number is greater.
From the known velocity of sound in air, coupled with the length of one of these dust segments, we can immediately deduce the number of vibrations executed in a second by the tube itself. Clasping a glass tube at its centre and drawing my wetted cloth over one of its halves, I elicit this shrill note. The length of every dust segment, now within the tube, is 3 inches. Hence the length of the aërial sonorous wave corresponding to this note is 6 inches. But the velocity of sound in air of our present temperature is 1,120 feet per second; a distance which would embrace 2,240 of our sonorous waves. This number, therefore, expresses the number of vibrations per second executed by the glass tube now before us.
Instead of damping the centre of the tube, and making it a nodal point, we may employ any other of its subdivisions. Laying hold of it, for example, at a point midway between its centre and one of its ends, and rubbing it properly, it divides into three vibrating parts, separated by two nodes. We know that in this division the note elicited is the octave of that heard when a single node is formed at the middle of the tube; for the vibrations are twice as rapid. If therefore we divide the tube, having air within it, by two nodes instead of one, the number of ventral segments revealed by the lycopodium dust will be thirty-two instead of sixteen. The same remark applies, of course, to all other gases.
Filling a series of four tubes with air, carbonic acid, coal-gas, and hydrogen, and then rubbing each so as to produce two nodes, M. Kundt found the number of dust segments formed within the tube in the respective cases to be as follows:
| Air | 32 | dust segments |
| Carbonic acid | 40 | ” |
| Coal-gas | 20 | ” |
| Hydrogen | 9 | ” |
Calling the velocity in air unity, the following fractions express the ratio of this velocity to those in the other gases:
| 32 | ||
| Carbonic acid | — | = 0·8 |
| 40 | ||
| 32 | ||
| Coal-gas | — | = 1·6 |
| 20 | ||
| 32 | ||
| Hydrogen | — | = 3·56 |
| 9 |
Referring to a table introduced in our first chapter, we learn that Dulong by a totally different mode of experiment found the velocity in carbonic acid to be 0.86, and in hydrogen 3·8 times the velocity in air. The results of Dulong were deduced from the sounds of organ-pipes filled with the various gases; but here, by a process of the utmost simplicity, we arrive at a close approximation to his results. Dusting the interior surfaces of our tubes, filling them with the proper gases, and sealing their ends, they may be preserved for an indefinite time. By properly shaking one of them at any moment, its inner surface becomes thinly coated with the dust; and afterward a single stroke of the wet cloth produces the division from248 which the velocity of sound in the gas may be immediately inferred. Savart found that a spiral nodal line is formed round a tube or rod when it vibrates longitudinally, and Seebeck showed that this line was produced, not by longitudinal, but by secondary transverse vibrations. Now this spiral nodal line tends to complicate the division of the dust in our present experiments. It is, therefore, desirable to operate in a manner which shall altogether avoid the formation of this line; M. Kundt has accomplished this, by exciting the longitudinal vibrations in one tube, and producing the division into ventral segments in another, into which the first fits like a piston. Before you is a tube of glass, Fig. 110, seven feet long, and two inches internal diameter. One end of this tube is filled by the movable stopper b. The other end, K K, is also stopped by a cork, through the centre of which passes the narrower tube A a, which is firmly clasped at its middle by the cork, K K. The end of the interior tube, A a, is also closed with a projecting stopper, a, almost sufficient to fill the larger tube, but still fitting into it so loosely that the friction of a against the interior surface is too slight to interfere practically with its vibrations. The interior surface between a and b being lightly coated with the lycopodium dust, a wet cloth is passed briskly over A K; instantly the dust between a and b divides into a number of ventral segments. When the length of the column of air, a b, is equal to that of the glass tube, A a, the number of ventral segments is249 sixteen. When, as in the figure, a b is only one-half the length of A a, the number of ventral segments is eight.
But here you must perceive that the method of experiment is capable of great extension. Instead of the glass tube, A a, we may employ a rod of any other solid substance—of wood or metal, for example, and thus determine the relative velocity of sound in the solid and in air. In the place of the glass tube, for example, a rod of brass of equal length may be employed. Rubbing its external half by a resined cloth, it divides the column a b into the number of ventral segments proper to the metal’s rate of vibrations. In this way M. Kundt operated with brass, steel, glass, and copper, and his results prove the method to be capable of great accuracy. Calling, as before, the velocity of sound in air unity, the following numbers expressive of the ratio of the velocity of sound in brass to its velocity in air were obtained in three different series of experiments:
| 1st experiment | 10·87 |
| 2d experiment | 10·87 |
| 3d experiment | 10·86 |
The coincidence is here extraordinary. To illustrate the possible accuracy of the method, the length of the individual dust segments was measured. In a series of twenty-seven experiments, this length was found to vary between 43 and 44 millimètres (each millimètre 1/25th of an inch), never rising so high as the latter and never falling so low as the former. The length of the metal rod, compared with that of one of the segments capable of this accurate measurement, gives us at once the velocity of sound in the metal, as compared with its velocity in air.
Three distinct experiments, performed in the same250 manner on steel, gave the following velocities, the velocity through air, as before, being regarded as unity:
| 1st experiment | 15·34 |
| 2d experiment | 15·33 |
| 3d experiment | 15·34 |
Here the coincidence is quite as perfect as in the case of brass.
In glass, by this new mode of experiment, the velocity was found to be
15·25.49
Finally, in copper the velocity was found to be
11·96.
These results agree extremely well with those obtained by other methods. Wertheim, for example, found the velocity of sound in steel wire to be 15·108; M. Kundt finds it to be 15·34: Wertheim also found the velocity in copper to be 11·17; M. Kundt finds it to be 11·96. The differences are not greater than might be produced by differences in the materials employed by the two experimenters.

The length of the aërial column may or may not be an exact multiple of the wave-length, corresponding to the rod’s rate of vibration. If not, the dust segments usually take the form shown in Fig. 111. But if, by 251means of the stopper, b, the column of air be made an exact multiple of the wave-length, then the dust quits the vibrating segments altogether, and forms, as in Fig. 112, little isolated heaps at the nodes.
And here a difficulty presents itself. The stopped end b of the tube Fig. 110 is, of course, a place of no vibration, where in all cases a nodal dust-heap is formed; but, whenever the column of air was an exact multiple of the wave-length, M. Kundt always found a dust-heap close to the end a of the vibrating rod also. Thus the point from which all the vibration emanated seemed itself to be a place of no vibration.

This difficulty was pointed out by M. Kundt, but he did not attempt its solution. We are now in a condition to explain it. In Lecture III. it was remarked that in strictness a node is not a place of no vibration; that it is a place of minimum vibration; and that, by the addition of the minute pulses which the node permits, vibrations of vast amplitude may be produced. The ends of M. Kundt’s tube are such points of minimum motion, the lengths of the vibrating segments being such that, by the coalescence of direct and reflected pulses, the air at a distance of half a ventral segment from the end of the tube vibrates much more vigorously than that at the end of the tube itself. This addition of impulses is more252 perfect when the aërial column is an exact multiple of the wave-length, and hence it is that, in this case, the vibrations become sufficiently intense to sweep the dust altogether away from the vibrating segments. The same point is illustrated by M. Melde’s tuning-forks, which, though they are the sources of all the motion, are themselves nodes.
An experiment of Helmholtz’s is here capable of instructive application. Upon the string of the sonometer described in our third lecture I place the iron stem of this tuning-fork, which executes 512 complete vibrations in a second. At present you hear no augmentation of the sound of the fork; the string remains quiescent. But on moving the fork along the string, at the number 33, a loud, swelling note issues from the string. At this particular tension the length 33 exactly synchronizes with the vibrations of the fork. By the intermediation of the string, therefore, the fork is enabled to transfer its motion to the sonometer, and through it to the air. The sound continues as long as the fork vibrates, but the least movement to the right or to the left from this point causes a sudden fall of the sound. Tightening the string, the note disappears; for it requires a greater length of this more highly tensioned string to respond to the fork. But, on moving the fork further away, at the number 36 the note again bursts forth. Tightening still more, 40 is found to be the point of maximum power. When the string is slackened, it must, of course, be shortened in order to make it respond to the fork. Moving the fork now toward the end of the string, at the number 25 the note is found as before. Again, shifting the fork to 35, nothing is heard; but, by the cau253tious turning of the key, the point of synchronism, if I may use the term, is moved further from the end of the string. It finally reaches the fork, and at that moment a clear, full note issues from the sonometer. In all cases, before the exact point is attained, and immediately in its vicinity, we hear “beats,” which, as we shall afterward understand, are due to the coalescence of the sound of the fork with that of the string, when they are nearly, but not quite, in unison with each other.
In these experiments, though the fork was the source of all the motion, the point on which it rested was a nodal point. It constituted the comparatively fixed extremity of the wire, whose vibrations synchronized with those of the fork. The case is exactly analogous to that of the hand holding the India-rubber tube, and to the tuning-fork in the experiments of M. Melde. It is also an effect precisely the same in kind as that observed by M. Kundt, where the part of the column of air in contact with the end of his vibrating rod proved to be a node instead of the middle of a ventral segment.
The resonance of caves and of rocky inclosures is well known. Bunsen notices the thunder-like sound produced when one of the steam jets of Iceland breaks out near the mouth of a cavern. Most travellers in Switzerland have noticed the deafening sound produced by the fall of the Reuss at the Devil’s Bridge. The sound heard when a hollow shell is placed close to the ear is a case of resonance. Children think they hear in it the sound254 of the sea. The noise is really due to the reinforcement of the feeble sounds with which even the stillest air is pervaded, and also in part to the noise produced by the pressure of the shell against the ear itself. By using tubes of different lengths, the variation of the resonance with the length of the tube may be studied. The channel of the ear itself is also a resonant cavity. When a poker is held by two strings, and when the fingers of the hands holding the poker are thrust into the ears on striking the poker against a piece of wood, a sound is heard as deep and sonorous as that of a cathedral bell. When open, the channel of the ear resounds to notes whose periods of vibration are about 3,000 per second. This has been shown by Helmholtz, and Madame Seiler has found that dogs which howl to music are particularly sensitive to the same notes. We may expect from Mr. Francis Galton interesting results in connection with this subject.
When a stretched wire is suitably rubbed, in the direction of its length, it is thrown into longitudinal vibrations: the wire can either vibrate as a whole or divide itself into vibrating segments separated from each other by nodes.
The tones of such a wire follow the order of the numbers 1, 2, 3, 4, etc.
The transverse vibrations of a rod fixed at both ends do not follow the same order as the transverse vibrations255 of a stretched wire; for here the forces brought into play, as explained in Lecture IV., are different. But the longitudinal vibrations of a stretched wire do follow the same order as the longitudinal vibrations of a rod fixed at both ends, for here the forces brought into play are the same, being in both cases the elasticity of the material.
A rod fixed at one end vibrates longitudinally as a whole, or it divides into two, three, four, etc., vibrating parts, separated from each other by nodes. The order of the tones of such a rod is that of the odd numbers 1, 3, 5, 7, etc.
A rod free at both ends can also vibrate longitudinally. Its lowest note corresponds to a division of the rod into two vibrating parts by a node at its centre. The overtones of such a rod correspond to its division into three, four, five, etc., vibrating parts, separated from each other by two, three, four, etc., nodes. The order of the tones of such a rod is that of the numbers 1, 2, 3, 4, 5, etc.
We may also express the order by saying that while the tones of a rod fixed at both ends follow the order of the odd numbers 1, 3, 5, 7, etc., the tones of a rod free at both ends follow the order of the even numbers 2, 4, 6, 8, etc.
At the points of maximum vibration the rod suffers no change of density; at the nodes, on the contrary, the changes of density reach a maximum. This may be proved by the action of the rod upon polarized light.
Columns of air of definite length resound to tuning-forks of definite rates of vibration.
The length of a tube filled with air, and closed at one256 end, which resounds to a fork is one-fourth of the length of the sonorous wave produced by the fork.
This resonance is due to the synchronism which exists between the vibrating period of the fork and that of the column of air.
By blowing across the mouth of a tube closed at one end, we produce a flutter of the air, and some pulse of this flutter may be raised by the resonance of the tube to a musical sound.
The sound is the same as that obtained when a tuning-fork, whose rate of vibration is that of the tube, is placed over the mouth of the tube.
When a tube closed at one end—a stopped organ-pipe, for example—sounds its lowest note, the column of air within it is undivided by a node. The overtones of such a column correspond to its division into parts, like those of a rod fixed at one end and vibrating longitudinally. The order of its tones is that of the odd numbers 1, 3, 5, 7, etc. That this must be the order follows from the manner in which the column is divided.
In organ-pipes the air is agitated by causing it to issue from a narrow slit, and to strike upon a cutting edge. Some pulse of the flutter thus produced is raised by the resonance of the pipe to a musical sound.
When, instead of the aërial flutter, a tuning-fork of the proper rate of vibration is placed at the embouchure of an organ-pipe, the pipe speaks in response to the fork. In practice, the organ-pipe virtually creates its own tuning-fork, by compelling the sheet of air at its embouchure to vibrate in periods synchronous with its own.
An open organ-pipe yields a note an octave higher than that of a closed pipe of the same length. This257 relation is a necessary consequence of the respective modes of vibration.
When, for example, a stopped organ-pipe sounds its deepest note, the column of air, as already explained, is undivided. When an open pipe sounds its deepest note, the column is divided by a node at its centre. The open pipe in this case virtually consists of two stopped pipes with a common base. Hence it is plain that the fundamental note of an open pipe must be the same as that of a stopped pipe of half its length.
The length of a stopped pipe is one-fourth that of the sonorous wave which it produces, while the length of an open pipe is one-half that of its sonorous wave.
The order of the tones of an open pipe is that of the even numbers 2, 4, 6, 8, etc., or of the natural numbers 1, 2, 3, 4, etc.
In both stopped and open pipes the number of vibrations executed in a given time is inversely proportional to the length of the pipe.
The places of maximum vibration in organ-pipes are places of minimum changes of density; while at the places of minimum vibration the changes of density reach a maximum.
The velocities of sound in gases, liquids, and solids may be inferred from the tones which equal lengths of them produce; or they may be inferred from the lengths of these substances which yield equal tones.
Reeds, or vibrating tongues, are often associated with vibrating columns of air. They consist of flexible laminæ, which vibrate to and fro in a rectangular orifice, thus rendering intermittent the air-current passing through the orifice.
The action of the reed is the same as that of the siren.
The flexible wooden reeds sometimes associated with organ-pipes are compelled to vibrate in unison with the column of air in the pipe; other reeds are too stiff to be thus controlled by the vibrating air. In this latter case the column of air is taken of such a length that its vibrations synchronize with those of the reed.
By associating suitable pipes with reeds we impart to their tones the qualities of the human voice.
The vocal organ in man is a reed instrument, the vibrating reed in this case being elastic bands placed at the top of the trachea, and capable of various degrees of tension.
The rate of vibration of these vocal chords is practically uninfluenced by the resonance of the mouth; but the mouth, by changing its shape, can be caused to resound to the fundamental tone, or to any of the overtones of the vocal chords.
By the strengthening of particular tones through the resonance of the mouth, the clang-tint of the voice is altered.
The different vowel-sounds are produced by different admixtures of the fundamental tone and the overtones of the vocal chords.
When the solid substance of a tube stopped at one, or at both ends, is caused to vibrate longitudinally, the air within it is also thrown into vibration.
By covering the interior surface of the tube with a light powder, the manner in which the aërial column divides itself may be rendered apparent. From the division of the column the velocity of sound in the substance259 of the tube, compared with its velocity in air, may be inferred.
Other gases may be employed instead of air, and the velocity of sound in these gases, compared with its velocity in the substance of the tube, may be determined.
The end of a rod vibrating longitudinally may be caused to agitate a column of air contained in a tube, compelling the air to divide itself into ventral segments. These segments may be rendered visible by light powders, and from them the velocity of sound in the substance of the vibrating rod, compared with its velocity in air, may be inferred.
In this way the relative velocities of sound in all solid substances capable of being formed into rods, and of vibrating longitudinally, may be determined.
Singing Flames—Influence of the Tube surrounding the Flame—Influence of Size of Flame—Harmonic Notes of Flames—Effect of Unisonant Notes on Singing Flames—-Action of Sound on Naked Flames—Experiments with Fish-Tail and Bat’s-Wing Burners—Experiments on Tall Flames—Extraordinary Delicacy of Flames as Acoustic Reagents—The Vowel-Flame—Action of Conversational Tones upon Flames—Action of Musical Sounds on Smoke-Jets—Constitution of Water-Jets—Plateau’s Theory of the Resolution of a Liquid Vein into Drops—Action of Musical Sounds on Water-Jets—A Liquid Vein may compete in Point of Delicacy with the Ear
FRICTION is always rhythmic. When a resined bow is passed across a string, the tension of the string secures the perfect rhythm of the friction. When the wetted finger is moved round the edge of a glass, the breaking up of the friction into rhythmic pulses expresses itself in music. Savart’s beautiful experiments on the flow of liquids through small orifices bear immediately upon this question. We have here the means of verifying his results. The tube A B, Fig. 113, is filled with water, its extremity, B, being closed by a plate of brass, which is pierced by a circular orifice of a diameter equal to the thickness of the plate. Removing a little peg which stops the orifice, the water issues from it, and as it sinks in the tube a musical note of great sweetness issues from the liquid column. This note is due to the261 intermittent flow of the liquid through the orifice, by which the whole column above it is thrown into vibration. The tendency to this effect shows itself when tea is poured from a teapot, in the circular ripples that cover the falling liquid. The same intermittence is observed in the black, dense smoke which rolls in rhythmic rings from the funnel of a steamer. The unpleasant noise of unoiled machinery is also a declaration of the fact that the friction is not uniform, but is due to the alternate “bite” and release of the rubbing surfaces.
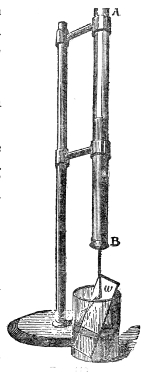
Where gases are concerned, friction is of the same intermittent character. A rifle-bullet sings in its passage through the air; while to the rubbing of the wind against the boles and branches of the trees are to be ascribed the “waterfall tones” of an agitated pine-wood. Pass a steadily-burning candle rapidly through the air; an indented band of light, declaring intermittence, is often the consequence, while the almost musical sound which accompanies the appearance of this band is the audible expression of the rhythm. On the other hand, if you blow gently against a candle-flame, the fluttering noise announces a rhythmic action. We have already learned what can be done when a pipe is associated with such a flutter; we have learned that the pipe selects a special pulse from the flutter, and raises it by resonance to a musical sound. In a similar manner the noise of a flame may be turned to account. The262 blow-pipe flame of our laboratory, for example, when inclosed within an appropriate tube, has its flutter raised to a roar. The special pulse first selected soon reacts upon the flame so as to abolish in a great degree the other pulses, compelling the flame to vibrate in periods answering to the selected one. And this reaction can become so powerful—the timed shock of the reflected pulses may accumulate to such an extent—as to beat the flame, even when very large, into extinction.
Nor is it necessary to produce this flutter by any extraneous means. When a gas-flame is simply inclosed within a tube, the passage of the air over it is usually sufficient to produce the necessary rhythmic action, so as to cause the flame to burst spontaneously into song. This flame-music may be rendered exceedingly intense. Over a flame issuing from a ring burner with twenty-eight orifices, I place a tin tube 5 feet long and 2-1/2 inches in diameter. The flame flutters at first, but it soon chastens its impulses into perfect periodicity, and a deep and clear musical tone is the result. By lowering the gas the note now sounded is caused to cease, but, after a momentary interval of silence, another note, which is the octave of the last, is yielded by the flame. The first note was the fundamental note of the surrounding tube; this second note is its first harmonic. Here, as in the case of open organ-pipes, we have the aërial column dividing itself into vibrating segments, separated from each other by nodes.
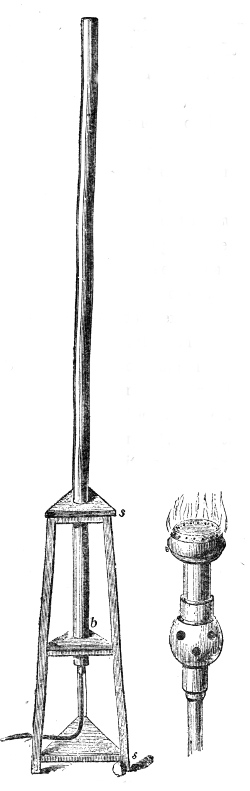 Fig. 114.
A still more striking effect is obtained with this larger
tube, a b, Fig. 114, 15 feet long and 4 inches wide,263
which was made for a totally different
purpose. It is supported by a steady
stand, s s′, and into it is lifted the tall
burner, shown enlarged at B. You hear
the incipient flutter: you now hear the
more powerful sound. As the flame is
lifted higher the action becomes more violent,
until finally a storm of music issues
from the tube. And now all has suddenly
ceased; the reaction of its own
pulses upon the flame has beaten it into
extinction. I relight the flame and make
it very small. When raised within the
tube, the flame again sings, but it is one
of the harmonics of the tube that you
now hear. On turning the gas fully on,
the note ceases—all is silent for a moment;
but the storm is brewing, and soon
it bursts forth, as at first in a kind of
hurricane of sound. By
lowering the flame the fundamental
note is abolished,
and now you hear the first
harmonic of the tube. Making
the flame still smaller,
the first harmonic disappears,
and the second is
heard. Your ears being
disciplined to the apprehension
of these sounds, I turn
the gas once more fully on.
Mingling with the deepest264
note you notice the harmonics, as if struggling to be
heard amid the general uproar of the flame. With a
large Bunsen’s rose burner, the sound of this tube becomes
powerful enough to shake the floor and seats, and
the large audience that occupies the seats of this room,
while the extinction of the flame, by the reaction of the
Fig. 114.
A still more striking effect is obtained with this larger
tube, a b, Fig. 114, 15 feet long and 4 inches wide,263
which was made for a totally different
purpose. It is supported by a steady
stand, s s′, and into it is lifted the tall
burner, shown enlarged at B. You hear
the incipient flutter: you now hear the
more powerful sound. As the flame is
lifted higher the action becomes more violent,
until finally a storm of music issues
from the tube. And now all has suddenly
ceased; the reaction of its own
pulses upon the flame has beaten it into
extinction. I relight the flame and make
it very small. When raised within the
tube, the flame again sings, but it is one
of the harmonics of the tube that you
now hear. On turning the gas fully on,
the note ceases—all is silent for a moment;
but the storm is brewing, and soon
it bursts forth, as at first in a kind of
hurricane of sound. By
lowering the flame the fundamental
note is abolished,
and now you hear the first
harmonic of the tube. Making
the flame still smaller,
the first harmonic disappears,
and the second is
heard. Your ears being
disciplined to the apprehension
of these sounds, I turn
the gas once more fully on.
Mingling with the deepest264
note you notice the harmonics, as if struggling to be
heard amid the general uproar of the flame. With a
large Bunsen’s rose burner, the sound of this tube becomes
powerful enough to shake the floor and seats, and
the large audience that occupies the seats of this room,
while the extinction of the flame, by the reaction of the
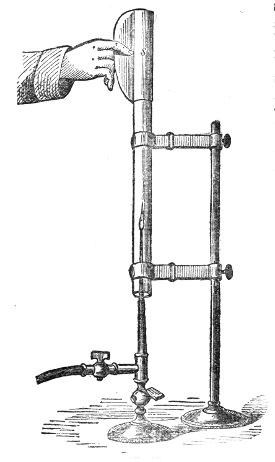 Fig. 115.
sonorous pulses, announces
itself by an explosion almost
as loud as a pistol-shot.
It must occur to
you that a chimney is a
tube of this kind upon
a large scale, and that
the roar of a flame in a
chimney is simply a rough
attempt at music.
Fig. 115.
sonorous pulses, announces
itself by an explosion almost
as loud as a pistol-shot.
It must occur to
you that a chimney is a
tube of this kind upon
a large scale, and that
the roar of a flame in a
chimney is simply a rough
attempt at music.
Let us now pass on to shorter tubes and smaller flames. Placing tubes of different lengths over eight small flames, each of them starts into song, and you notice that as the tubes lengthen the tones deepen. The lengths of these tubes are so chosen that they yield in succession the eight notes of the gamut. Round some of them you observe a paper slider, s, Fig. 115, by which the tube can be lengthened or shortened. If while the flame is sounding the slider be raised, the pitch instantly falls; if lowered, the pitch rises. These experiments prove the flame265 to be governed by the tube. By the reaction of the pulses, reflected back upon the flame, its flutter is rendered perfectly periodic, the length of that period being determined, as in the case of organ-pipes, by the length of the tube.
The fixed stars, especially those near the horizon,
shine with an unsteady light, sometimes changing color
as they twinkle. I have often watched at night, upon
the plateaux of the Alps, the alternate flash of ruby and
emerald in the lower and larger stars. If you place a
piece of looking-glass so that you can see in it the
image of such a star, on tilting the glass quickly to and
 Fig. 116.
fro, the line of light obtained
will not be continuous, but will
form a string of colored beads
of extreme beauty. The same
effect is obtained when an opera-glass
is pointed to the star and
shaken. This experiment shows
that in the act of twinkling the
light of the star is quenched at intervals; the dark spaces
between the bright beads corresponding to the periods of
extinction. Now, our singing flame is a twinkling flame.
When it begins to sing you observe a certain quivering
motion which may be analyzed with a looking-glass, or
an opera-glass, as in the case of the star.50 I can now
see the image of this flame in a small looking-glass. On
tilting the glass, so as to cause the image to form a circle
of light, the luminous band is not seen to be continuous,
as it would be if the flame were perfectly steady;
it is resolved into a beautiful chain of flames, Fig. 116.
Fig. 116.
fro, the line of light obtained
will not be continuous, but will
form a string of colored beads
of extreme beauty. The same
effect is obtained when an opera-glass
is pointed to the star and
shaken. This experiment shows
that in the act of twinkling the
light of the star is quenched at intervals; the dark spaces
between the bright beads corresponding to the periods of
extinction. Now, our singing flame is a twinkling flame.
When it begins to sing you observe a certain quivering
motion which may be analyzed with a looking-glass, or
an opera-glass, as in the case of the star.50 I can now
see the image of this flame in a small looking-glass. On
tilting the glass, so as to cause the image to form a circle
of light, the luminous band is not seen to be continuous,
as it would be if the flame were perfectly steady;
it is resolved into a beautiful chain of flames, Fig. 116.
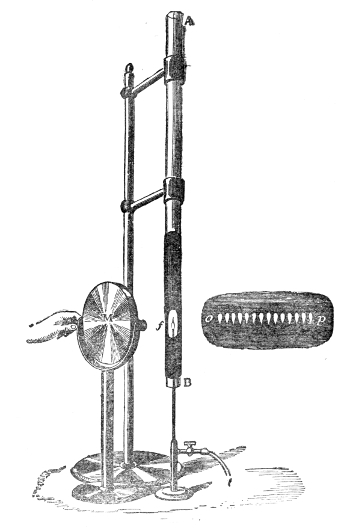
With a larger, brighter, and less rapidly-vibrating flame, you may all see this intermittent action. Over this gas-flame, f, Fig. 117, is placed a glass tube, A B, 6 feet long and 2 inches in diameter. The back of the tube is blackened, so as to prevent the light of the flame from falling directly upon the screen, which it is now desirable to have as dark as possible. In front of the tube is placed a concave mirror, M, which forms upon the267 screen an enlarged image of the flame. I turn the mirror with my hand and cause the image to pass over the screen. Were the flame silent and steady, we should obtain a continuous band of light; but it quivers, and emits at the same time a deep and powerful note. On twirling the mirror, therefore, we obtain, instead of a continuous band, a luminous chain of images. By fast turning, these images are drawn more widely apart; by slow turning, they are caused to close up, the chain of flames passing through the most beautiful variations. Clasping the lower end, B, of the tube with my hand, I so impede the air as to stop the flame’s vibration; a continuous band is the consequence. Observe the suddenness with which this band breaks up into a rippling line of images the moment my hand is removed and the current of air is permitted to pass over the flame.
When a small vibrating coal-gas flame is carefully examined by the rotating mirror, the beaded line is a series of yellow-tipped flames, each resting upon a base of the richest blue. In some cases I have been unable to observe any union of one flame with another; the spaces between the flames being absolutely dark to the eye. But if dark, the flame must have been totally extinguished at intervals, a residue of heat, however, remaining sufficient to reignite the gas. This is at least possible, for gas may be ignited by non-luminous air.51 By means of the siren, we can readily determine the number of times this flame 268extinguishes and relights itself in a second. As the note of the instrument approaches that of the flame, unison is preceded by these well-known beats, which become gradually less rapid, and now the two notes melt into perfect unison. Maintaining the siren at this pitch for a minute, at the end of that time I find recorded upon our dials 1,700 revolutions. But the disk being perforated by 16 holes, it follows that every revolution corresponds to 16 pulses. Multiplying 1,700 by 16, we find the number of pulses in a minute to be 27,200. This number of times did our little flame extinguish and rekindle itself during the continuance of the experiment; that is to say, it was put out and relighted 453 times in a second.
A flash of light, though instantaneous, makes an impression upon the retina which endures for the tenth of a second or more. A flying rifle-bullet, illuminated by a single flash of lightning, would seem to stand still in the air for the tenth of a second. A black disk with radial white strips, when rapidly rotated, causes the white and black to blend to an impure gray; while a spark of electricity, or a flash of lightning, reduces the disk to apparent stillness, the white radial strips being for a time plainly seen. Now, the singing flame is a flashing flame, and M. Toepler has shown that by causing a striped disk to rotate at the proper speed in the presence of such a flame it is brought to apparent stillness, the white stripes being rendered plainly visible. The experiment is both easy and interesting.
A singing flame yields so freely to the pulses falling upon it that it is almost wholly governed by the sur269rounding tube; almost, but not altogether. The pitch of the note depends in some measure upon the size of the flame. This is readily proved, by causing two flames to emit the same note, and then slightly altering the size of either of them. The unison is instantly disturbed by beats. By altering the size of a flame we can also, as already illustrated, draw forth the harmonic overtones of the tube which surrounds it. This experiment is best performed with hydrogen, its combustion being much more vigorous than that of ordinary gas. When a glass tube 7 feet long is placed over a large hydrogen-flame, the fundamental note of the tube is obtained, corresponding to a division of the column of air within it by a single node at the centre. Placing a second tube, 3 feet 6 inches long, over the same flame, no musical sound whatever is obtained; the large flame, in fact, is not able to accommodate itself to the vibrating period of the shorter tube. But, on lessening the flame, it soon bursts into vigorous song, its note being the octave of that yielded by the longer tube. I now remove the shorter tube, and once more cover the flame with the longer one. It no longer sounds its fundamental notes, but the precise note of the shorter tube. To accommodate itself to the vibrating period of the diminished flame, the longer column of air divides itself like an open organ-pipe when it yields its first harmonic. By varying the size of the flame, it is possible, with the tube now before you, to obtain a series of notes whose rates of vibration are in the ratio of the numbers 1:2:3:4:5; that is to say, the fundamental tone and its first four harmonics.
These sounding flames, though probably never before raised to the intensity in which they have been exhibited270 here to-day, are of old standing. In 1777, the sounds of a hydrogen-flame were heard by Dr. Higgins. In 1802, they were investigated to some extent by Chladni, who also refers to an incorrect account of them given by De Luc. Chladni showed that the tones are those of the open tube which surrounds the flame, and he succeeded in obtaining the first two harmonics. In 1802, G. De la Rive experimented on this subject. Placing a little water in the bulb of a thermometer, and heating it, he showed that musical tones of force and sweetness could be produced by the periodic condensation of the vapor in the stem of the thermometer. He accordingly referred the sounds of flames to the alternate expansion and condensation of the aqueous vapor produced by the combustion. We can readily imitate his experiments. Holding, with its stem oblique, a thermometer-bulb containing water in the flame of a spirit-lamp the sounds are heard soon after the water begins to boil. In 1818, however, Faraday showed that the tones are produced when the tube surrounding the flame is placed in air of a temperature higher than 100° C., condensation being then impossible. He also showed that the tones could be obtained from flames of carbonic oxide, where aqueous vapor is entirely out of the question.
After these experiments, the first novel acoustic observation on flames was made in Berlin by the late Count Schaffgotsch, who showed that when an ordinary gas-flame was surmounted by a short tube, a strong falsetto voice pitched to the note of the tube, or to its higher271 octave, caused the flame to quiver. In some cases when the note of the tube was high, the flame could even be extinguished by the voice.
In the spring of 1857, this experiment came to my notice. No directions were given in the short account of the observation published in “Poggendorff’s Annalen”; but, in endeavoring to ascertain the conditions of success, a number of singular effects forced themselves upon my attention. Meanwhile, Count Schaffgotsch also followed up the subject. To a great extent we travelled over the same ground, neither of us knowing how the other was engaged; but, so far as the experiments then executed are common to us both, to Count Schaffgotsch belongs the priority.
Let me here repeat his first observation. Within this tube, 11 inches long, burns a small gas-flame, bright and silent. The note of the tube has been ascertained, and now, standing at some distance from the flame, I sound that note; the flame quivers. To obtain the extinction of the flame it is necessary to employ a burner with a very narrow aperture, from which the gas issues under considerable pressure. On gently sounding the note of the tube surrounding such a flame, it quivers; but on throwing more power into the voice the flame is extinguished.
The cause of the quivering of the flame will be best revealed by an experiment with the siren. As the note of the siren approaches that of the flame you hear beats, and at the same time you observe a dancing of the flame synchronous with the beats. The jumps succeed each other more slowly as unison is approached. They cease when the unison is perfect, and they begin again as soon272 as the siren is urged beyond unison, becoming more rapid as the discordance is increased. The cause of the quiver observed by M. Schaffgotsch was revealed to me. The flame jumped because the note of the tube surrounding it was nearly, but not quite, in unison with the voice of the experimenter.
That the jumping of the flame proceeds in exact accordance with the beats is well shown by a tuning-fork, which yields the same note as the flame. Loading such a fork with a bit of wax, so as to throw it slightly out of unison, and bringing it, when agitated, near the tube in which the flame is singing, the beats and the leaps of the flame occur at the same intervals. When the fork is placed over a resonant jar, all of you can hear the beats, and see at the same time the dancing of the flame. By changing the load upon the tuning-fork, or by slightly altering the size of the flame, the rate at which the beats succeed each other may be altered; but in all cases the jumps address the eye at the moments when the beats address the ear.
While executing these experiments I noticed that, on raising my voice to the proper pitch, a flame which had been burning silently in its tube began to sing. The same observation had, without my knowledge, been made a short time previously by Count Schaffgotsch. A tube, 12 inches long, is placed over this flame, which occupies a position about an inch and a half from the lower end of the tube. When the proper note is sounded the flame trembles, but it does not sing. When the tube is lowered until the flame is three inches from its end, the song is spontaneous. Between these two positions there is a third, at which, if the flame be placed, it will burn273 silently; but if it be excited by the voice it will sing, and continue to sing.
Even when the back is turned toward the flame the sonorous pulses run round the body, reach the tube, and call forth the song. A pitch-pipe, or any other instrument which yields a note of the proper height, produces the same effect. Mounting a series of tubes, capable of emitting all the notes of the gamut, over suitable flames, with an instrument sufficiently powerful, and from a distance of 20 or 30 yards, a musician, by running over the scale, might call forth all the notes in succession, the whole series of flames finally joining in the song.
When a silent flame, capable of being excited in the manner here described, is looked at in a moving mirror,274 it produces there a continuous band of light. Nothing can be more beautiful than the sudden breaking up of this band into a string of richly-luminous pearls at the instant the voice is pitched to the proper note.
One singing flame may be caused to effect the musical ignition of another. Before you are two small flames, f′ and f, Fig. 118 (p. 273), the tube over f′ being 10-1/2 inches, that over f 12 inches long. The shorter tube is clasped by a paper slider, s. The flame f′ is now singing, but the flame f, in the longer tube, is silent. I raise the paper slider which surrounds f′, so as to lengthen the tube, and on approaching the pitch of the tube surrounding f, that flame sings. The experiment may be varied by making f the singing flame and f′ the silent one at starting. Raising the telescopic slider, a point is soon attained where the flame f′ commences its song. In this way one flame may excite another through considerable distances. It is also possible to silence the singing flame by the proper management of the voice.
We have hitherto dealt with flames surrounded by resonant tubes; and none of these flames, if naked, would respond in any way to such noise or music as could be here applied. Still it is possible to make naked flames thus sympathetic. This action of musical sounds upon naked flames was first observed by Prof. Le Conte at a musical party in the United States. His observation is thus described: “Soon after the music commenced, I observed that the flame exhibited pulsations which were275 exactly synchronous with the audible beats. This phenomenon was very striking to every one in the room, and especially so when the strong notes of the violoncello came in. It was exceedingly interesting to observe how perfectly even the trills of this instrument were reflected on the sheet of flame. A deaf man might have seen the harmony. As the evening advanced, and the diminished consumption of gas in the city increased the pressure, the phenomenon became more conspicuous. The jumping of the flame gradually increased, became somewhat irregular, and, finally, it began to flare continuously, emitting the characteristic sound, indicating the escape of a greater amount of gas than could be properly consumed. I then ascertained, by experiment, that the phenomenon did not take place unless the discharge of gas was so regulated that the flame approximated to the condition of flaring. I likewise determined, by experiment, that the effects were not produced by jarring or shaking the floor and walls of the room by means of repeated concussions. Hence it is obvious that the pulsations of the flame were not owing to indirect vibrations propagated through the medium of the walls of the room to the burning-apparatus, but must have been produced by the direct influence of aërial sonorous pulses on the burning jet.”52
The significant remark, that the jumping of the flame was not observed until it was near flaring, suggests the 276means of repeating the experiments of Dr. Le Conte; while a more intimate knowledge of the conditions of success enables us to vary and exalt them in a striking degree. Before you burns a bright candle-flame, but no sound that can be produced here has any effect upon it. Though sonorous waves of great power be sent through the air, the candle-flame remains insensible.
Fig. 119.
|
Fig. 120.
|
But by proper precautions even a candle-flame may be rendered sensitive. Urging from a small blow-pipe a narrow stream of air through such a flame, an incipient flutter is produced. The flame then jumps visibly to the sound of a whistle, or to a chirrup. The experiment may be so arranged that, when the whistle sounds, the flame shall be either restored almost to its pristine brightness, or that the small amount of light it still possesses shall disappear.
The blow-pipe flame of our laboratory is totally unaffected by the sound of the whistle as long as no air is urged through it. By properly tempering the force of the blast, a flame is obtained of the shape shown in Fig. 119. On sounding the whistle the erect portion of the flame277 drops down, and while the sound continues the flame maintains the form shown in Fig. 120.
We now pass on to a thin sheet of flame, issuing from a common fish-tail burner, Fig. 121. You might sing to this flame, varying the pitch of your voice; no shiver of the flame would be visible. You might employ pitch-pipes, tuning-forks, bells, and trumpets, with a like absence of all effect. A barely perceptible motion of the interior of the flame may be noticed when a shrill whistle is blown close to it. But by turning the cock more fully on, the flame is brought to the verge of flaring. And now, when the whistle is blown, the flame thrusts suddenly out seven quivering tongues, Fig. 122. The moment the sound ceases, the tongues disappear, and the flame becomes quiescent.
Fig. 121.
|

Fig. 122.
|
Passing from a fish-tail to a bat’s-wing burner, we obtain a broad, steady flame, Fig. 123. It is quite insen278sible to the loudest sound which would be tolerable here. The flame is fed from a small gas-holder.53 Increasing gradually the pressure, a slight flutter of the edge of the flame at length answers to the sound of the whistle. Turning on the gas until the flame is on the point of roaring, and blowing the whistle, it roars, and suddenly assumes the form shown in Fig. 124.
When a distant anvil is struck with a hammer, the flame instantly responds by thrusting forth its tongues.
Fig. 123.
|
Fig. 124.
|
An essential condition to entire success in these experiments disclosed itself in the following manner: I was operating on two fish-tail flames, one of which jumped to a whistle while the other did not. The gas of the non-sensitive flame was turned off, additional pressure being thereby thrown upon the other flame. It flared, and its cock was turned so as to lower the flame; but it now proved non-sensitive, however close it might be brought to the point of flaring. The narrow orifice of the half-turned cock interfered with the action of the sound. When the gas was turned fully on, the flame 279being lowered by opening the cock of the other burner, it became again sensitive. Up to this time a great number of burners had been tried, but with many of them the action was nil. Acting, however, upon the hint conveyed by this observation, the cocks which fed the flames were more widely opened, and our most refractory burners thus rendered sensitive.
In this way the observation of Dr. Le Conte is easily and strikingly illustrated; in our subsequent, and far more delicate, experiments the precaution just referred to is still more essential.
A long flame may be shortened and a short one lengthened, according to circumstances, by sonorous vibrations. The flame shown in Fig. 125 is long, straight, and smoky; that in Fig. 126 is short, forked, and brilliant. On sounding the whistle, the long flame becomes short, forked, and brilliant, as in Fig. 127; while the forked flame becomes long and smoky, as in Fig. 128. As regards, therefore, their response to the sound of the whistle, one of these flames is the complement of the other.
In Fig. 129 is represented another smoky flame which, when the whistle sounds, breaks up into the form shown in Fig. 130.
When a brilliant sensitive flame illuminates an otherwise dark room, in which a suitable bell is caused to strike, a series of periodic quenchings of the light by the sound occurs. Every stroke of the bell is accompanied by a momentary darkening of the room.
The foregoing experiments illustrate the lengthening280 and shortening of flames by sonorous vibrations. They may also produce rotation. From some of our homemade burners issue flat flames, about ten inches high, and three inches across at their widest part. When the whistle sounds, the plane of each flame turns ninety degrees round, and continues in its new position as long as the sound continues.

Fig. 125.
|

Fig. 126.
|

Fig. 127.
|

Fig. 128.
|

Fig. 129.
|

Fig. 130.
|
A flame of admirable steadiness and brilliancy now burns before you. It issues from a single circular orifice in a common iron nipple. This burner, which requires great pressure to make its flame flare, has been specially chosen for the purpose of enabling you to observe, with distinctness, the gradual change from apathy to sensitiveness. The flame, now 4 inches high, is quite indifferent281 to sound. On increasing the pressure its height becomes 6 inches; but it is still indifferent. When its length is 12 inches, a barely perceptible quiver responds to the whistle. When 16 or 17 inches high, it jumps briskly the moment an anvil is tapped or the whistle sounded. When the flame is 20 inches long you observe a quivering at intervals, which announces that it is near roaring. A slight increase of pressure causes it to roar, and shorten at the same time to 8 inches.
Diminishing the pressure a little, the flame is again 20 inches long, but it is on the point of roaring and shortening. Like the singing flames which were started by the voice, it stands on the brink of a precipice. The proper note pushes it over. It shortens when the whistle sounds, exactly as it did when the pressure is in excess. The action reminds one of the story of the Swiss muleteers, who are said to tie up their bells at certain places lest the tinkle should bring an avalanche down. The snow must be very delicately poised before this could occur. It probably never did occur, but our flame illustrates the principle. We bring it to the verge of falling, and the sonorous pulses precipitate what was already imminent. This is the simple philosophy of all these sensitive flames.
When the flame flares, the gas in the orifice of the burner is in a state of vibration; conversely, when the gas in the orifice is thrown into vibration, the flame, if sufficiently near the flaring point, will flare. Thus the sonorous vibrations, by acting on the gas in the passage of the burner, become equivalent to an augmentation of pressure in the holder. In fact, we have here revealed to us the physical cause of flaring through excess of282 pressure, which, common as it is, has never been hitherto explained. The gas encounters friction in the orifice of the burner, which, when the force of transfer is sufficiently great, throws the issuing stream into the state of vibration that produces flaring. It is because the flaring is thus caused that an infinitesimal amount of energy in the form of vibrations of the proper period can produce an effect equivalent to a considerable increase of pressure.
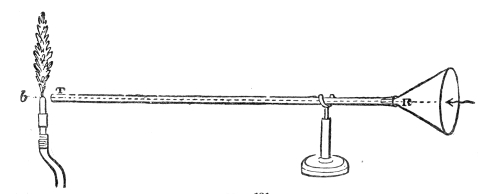
That the external vibrations act upon the gas in the orifice of the burner, and not first upon the burner itself, the tube leading to it, or the flame above it, is thus proved. A glass funnel R, Fig. 131, is attached to a tube 3 feet long and half an inch in diameter. A sensitive flame b is placed at the open end T of the tube, while a small high-pitched reed is placed in the funnel at R. When the sound is converged upon the root of the flame, as in Fig. 131, the action is violent; when converged on a point half an inch above the burner, as in Fig. 132, or at half an inch below the burner, as in Fig. 133, there is no action. The glass tube may be dispensed with and the funnel alone employed, if care be taken to screen off283 all sound, save that which passes through the shank of the funnel.54

Fig. 132.
|

Fig. 133.
|
All sounds are not equally effective on the flame; waves of special periods are required to produce the maximum effect. The effectual periods are those which synchronize with the waves produced by the friction of the gas itself against the sides of its orifice. With some of these flames a low deep whistle is more effective than a shrill one. With others the exciting tremors must be very rapid, and the sound consequently shrill. Not one of these four tuning-forks, which vibrate 256 times, 320 times, 384 times, and 512 times respectively in a second, has any effect upon the flame from our iron nipple. But, besides their fundamental tones, these forks, as you know, can be caused to yield a series of overtones of very high pitch. The vibrations of this series are 1,600, 2,000, 2842,400, and 3,200 per second, respectively. The flame jumps in response to each of these sounds; the response to that of the highest pitch being the most prompt and energetic of all.
To the tap of a hammer upon a board the flame responds; but to the tap of the same hammer upon an anvil the response is much more brisk and animated. The reason is, that the clang of the anvil is rich in the higher tones to which the flame is most sensitive. The powerful tone obtained when our inverted bell is reinforced by its resonant tube has no power over this flame. But when a halfpenny is brought into contact with the vibrating surface the flame instantly shortens, flutters, and roars. I send an assistant with a smaller bell, worked by clockwork, to the most distant part of the gallery. He there detaches the hammer; the strokes follow each other in rhythmic succession, and at every stroke the flame falls from a height of 20 to a height of 8 inches, roaring as it falls.
The rapidity with which sound is propagated through air is well illustrated by these experiments. There is no sensible interval between the stroke of the bell and the ducking of the flame.
When the sound acting on the flame is of very short duration a curious and instructive effect is observed. The sides of the flame half-way down, and lower, are seen suddenly fringed by luminous tongues, the central285 flame remaining apparently undisturbed in both height and thickness. The flame in its normal state is shown in Fig. 134, and with its fringes in Fig. 135. The effect is due to the retention of the impression upon the retina. The flame actually falls as low as the fringes, but its recovery is so quick that to the eye it does not appear to shorten at all.55
A flame of astonishing sensitiveness now burns before you. It issues from the single orifice of a steatite burner, and reaches a height of 24 inches. The slightest tap on a distant anvil reduces its height to 7 inches. When a bunch of keys is shaken the flame is violently agitated, and emits a loud roar. The dropping of a sixpence into a hand already containing coin, at a distance of 20 yards, knocks the flame down. It is not possible to walk across the floor without agitating the flame. The creaking of boots sets it in violent commotion. The crumpling, or tearing of paper, or the rustle of a silk dress, does the same. It is startled by the patter of a rain-drop. I hold a watch near the flame: nobody hears its ticks; but you all see their effect upon the flame. At every tick it falls and roars. The winding up of the watch also produces tumult. The twitter of a distant sparrow shakes the flame; the note of a cricket would do the same. A chirrup from a distance of 30 yards causes it to fall and roar. I repeat a passage from Spenser:

The flame selects from the sounds those to which it can respond. It notices some by the slightest nod, to others it bows more distinctly, to some its obeisance is very profound, while to many sounds it turns an entirely deaf ear.
In Fig. 136, this wonderful flame is represented. On chirruping to it, or on shaking a bunch of keys within a few yards of it, it falls to the size shown in Fig. 137, the whole length, a b, of the flame being suddenly abolished. The light at the same time is practically destroyed, a pale and almost non-luminous residue of it alone remaining. These figures are taken from photographs of the flame.

To distinguish it from the others I have called this the “vowel-flame,” because the different vowel-sounds affect it differently. A loud and sonorous U does not move the flame; on changing the sound to O, the flame quivers; when E is sounded, the flame is strongly affected. I utter the words boot, boat, and beat, in succession. To the first there is no response; to the second, the flame starts; by the third, is thrown into greater commotion; the sound Ah! is still more powerful.287 Did we not know the constitution of vowel-sounds this deportment would be an insoluble enigma. As it is, however, the flame illustrates the theory of vowel-sounds. It is most sensitive to sounds of high pitch; hence we should infer that the sound Ah! contains higher notes than the sound E; that E contains higher notes than O; and O higher notes than U. I need not say that this agrees perfectly with the analysis of Helmholtz.
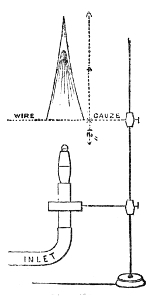
This flame is peculiarly sensitive to the utterance of the letter S. A hiss contains the elements that most forcibly affect the flame. The gas issues from its burner with a hiss, and an external sound of this character is therefore exceedingly effective. From a metal box containing compressed air I allow a puff to escape; the flame instantly ducks down not by any transfer of air from the box to the flame, for the distance between both utterly excludes this idea—it is the sound that affects the flame. From the most distant part of the gallery my assistant permits the compressed air to issue in puffs from the box; at every puff the flame suddenly falls. The hiss of the issuing air at the one orifice precipitates the tumult of the flame at the other.
When a musical-box is placed on the table, and permitted to play, the flame behaves like a sentient and motor creature—bowing slightly to some tones, and courtesying deeply to others.
Mr. Philip Barry has discovered a new and very effective form of sensitive flame, which he thus describes in a letter to myself: “It is the most sensitive of all the flames that I am acquainted with, though from its smaller size it is not so striking as your vowel-flame. It possesses the advantage that the ordinary pressure in the gas-mains is quite sufficient to produce it. The method of producing it consists in igniting the gas (ordinary coal-gas) not at the burner but some inches above it, by interposing between the burner and the flame a piece of wire-gauze.”
I give a sketch of the arrangement adopted in Fig. 138. The space between the burner and gauze was 2 inches. The gauze was about 7 inches square, resting on the ring of a retort-stand. It had 32 meshes to the lineal inch. The burner was Sugg’s steatite pinhole burner, the same as used for the vowel-flame.
The flame is a slender cone about four inches high, the upper portion giving a bright-yellow light, the base being a non-luminous blue flame. At the least noise this flame roars, sinking down to the surface of the gauze, becoming at the same time invisible. It is very active in its responses, and, being rather a noisy flame, its sympathy is apparent to the ear as well as the eye.
“To the vowel-sounds it does not appear to answer so discriminately as the vowel-flame. It is extremely sensitive to A, very slightly to E, more so to I, entirely non-sensitive to O, but slightly sensitive to U.
“It dances in the most perfect manner to a small289 musical snuff-box, and is highly sensitive to most of the sonorous vibrations which affect the vowel-flames.”
It is not to the flame, as such, that we owe the extraordinary phenomena which have been just described. Effects substantially the same are obtained when a jet of unignited gas, of carbonic acid, hydrogen, or even air itself, issues from an orifice under proper pressure. None of these gases, however, can be seen in its passage through air, and, therefore, we must associate with them some substance which, while sharing their motions, will reveal them to the eye. The method employed from time to time in this place of rendering aërial vortices visible is well known to many of you. By tapping a membrane which closes the mouth of a large funnel filled with smoke, we obtain beautiful smoke-rings, which reveal the motion of the air. By associating smoke with our gas-jets, in the present instance, we can also trace their course, and, when this is done, the unignited gas proves as sensitive as the flames. The smoke-jets jump, shorten, split into forks, or lengthen into columns, when the proper notes are sounded.
Underneath this gas-holder are placed two small basins, the one containing hydrochloric acid, and the other ammonia. Fumes of sal-ammoniac are thus copiously formed, and mingle with the gas contained in the holder. We may, as already stated, operate with coal-gas, carbonic acid, air, or hydrogen; each of them yields good effects. From our excellent steatite burner now issues a thin column of smoke. On sounding the whistle, which was so effective with the flames, it is found290 ineffective. When, moreover, the highest notes of a series of Pandean pipes are sounded, they are also ineffective. Nor will the lowest notes answer. But when a certain pipe, which stands about the middle of the series, is sounded, the smoke-column falls, forming a short stem with a thick, bushy head. It is also pressed down, as if by a vertical wind, by a knock upon the table. At every tap it drops. A stroke on an anvil, on the contrary, produces little or no effect. In fact, the notes here effective are of a much lower pitch than those which were most efficient in the case of the flames.
The amount of shrinkage exhibited by some of these smoke-columns, in proportion to their length, is far greater than that of the flames. A tap on the table causes a smoke-jet eighteen inches high to shorten to a bushy bouquet, with a stem not more than an inch in height. The smoke-column, moreover, responds to the voice. A cough knocks it down; and it dances to the tune of a musical-box. Some notes cause the mere top of the smoke-column to gather itself up into a bunch; at other notes the bunch is formed midway down; while notes of more suitable pitch cause the column to contract itself to a cumulus not much more than an inch above the end of the burner. Various forms of the dancing smoke-jet are shown in Fig. 139. As the music con291tinues, the action of the smoke-column consists of a series of rapid leaps from one of these forms to another.
In a perfectly still atmosphere these slender smoke-columns rise sometimes to a height of nearly two feet, apparently vanishing into air at the summit. When this is the case, our most sensitive flames fall far behind them in delicacy; and though less striking than the flames, the smoke-wreaths are often more graceful. Not only special words, but every word, and even every syllable, of the foregoing stanza from Spenser, tumbles a really sensitive smoke-jet into confusion. To produce such effects, a perfectly tranquil atmosphere is necessary. Flame-experiments, in fact, are possible in an atmosphere where smoke-jets are utterly unmanageable.56
We have thus far confined our attention to jets of ignited and unignited coal-gas—of carbonic acid, hydrogen, and air. We will now turn to jets of water. And here a series of experiments, remarkable for their beauty, has long existed, which claim relationship to those just described. These are the experiments of Felix Savart on liquid veins. If the bottom of a vessel containing water be pierced by a circular orifice, the descending liquid vein will exhibit two parts unmistakably distinct. The part of the vein nearest the orifice is steady and limpid, 292presenting the appearance of a solid glass rod. It decreases in diameter as it descends, reaches a point of maximum contraction, from which point downward it appears turbid and unsteady. The course of the vein, moreover, is marked by periodic swellings and contractions. Savart has represented these appearances as in Fig. 140. The part a n nearest the orifice is limpid and steady, while all the part below n is in a state of quivering motion. This lower part of the vein appears continuous to the eye; but the finger can be sometimes passed through it without being wetted. This, of course, could not be the case if the vein were really continuous. The upper portion of the vein, moreover, intercepts vision; the lower portion, even when the liquid is mercury, does not. In fact, the vein resolves itself, at n, into liquid spherules, its apparent continuity being due to the retention of the impressions made by the falling drops upon the retina. If, while looking at the disturbed portion of the vein,293 the head be suddenly lowered, the descending column will be resolved for a moment into separate drops. Perhaps the simplest way of reducing the vein to its constituent spherules is to illuminate the vein, in a dark room, by a succession of electric flashes. Every flash reveals the drops, as if they were perfectly motionless in the air.
Could the appearance of the vein illuminated by a single flash be rendered permanent, it would be that represented in Fig. 141. And here we find revealed the cause of those swellings and contractions which the disturbed portion of the vein exhibits. The drops, as they descend, are continually changing their forms. When first detached from the end of the limpid portion of the vein, the drop is a spheroid with its longest axis vertical. But a liquid cannot retain this shape, if abandoned to the forces of its own molecules. The spheroid seeks to become a sphere—the longer diameter, therefore, shortens; but, like a pendulum which seeks to return to its position of rest, the contraction of the vertical diameter goes too far, and the drop becomes a flattened spheroid. Now, the contractions of the jet are formed at those places where the longest axis of the drop is vertical, while the swellings appear where the longest axis is horizontal. It will be noticed that between every two of the larger drops is a third one of much smaller dimensions. According to Savart, their appearance is invariable.
I wish to make the constitution of a liquid vein evident to you by a simple but beautiful experiment. The condensing lens has been removed from our electric lamp, the light being permitted to pass through a vertical slit294 directly from the carbon-points. The slice of light thus obtained is so divergent that it illuminates, from top to bottom, a liquid vein several feet long, and placed at some distance from the lamp. Immediately in front of the camera is a large disk of zinc with six radial slits, about ten inches long and an inch wide. By the rotation of the disk the light is caused to fall in flashes upon the jet; and, when the suitable speed of rotation has been attained, the vein is resolved into its constituent spherules. Receiving the shadow of the vein upon a white screen, its constitution is rendered clearly visible to all here present.
This breaking-up of a liquid vein into drops has been a subject of frequent experiment and much discussion. Savart traced the pulsations to the orifice, but he did not think that they were produced by friction. They are powerfully influenced by sonorous vibrations. In the midst of a large city it is hardly possible to obtain the requisite tranquillity for the full development of the continuous, portion of the vein; still, Savart was so far able to withdraw his vein from the influence of such irregular vibrations that its limpid portion became elongated to the extent shown in Fig. 142. It will be understood that Fig. 141 represents a vein exposed to the irregular vibrations of the city of Paris, while Fig. 142 represents one produced under precisely the same conditions, but withdrawn from those vibrations.
The drops into which the vein finally resolves itself are incipient even in its limpid portion, announcing themselves there as annular protuberances, which become more and more pronounced, until finally they separate. Their birthplace is near the orifice itself, and under even mod295erate pressure they succeed each other with sufficient rapidity to produce a feeble musical note. By permitting the drops to fall upon a membrane, the pitch of this note may be fixed; and now we come to the point which connects the phenomena of liquid veins with those of sensitive flames and smoke-jets. If a note in unison with that of the vein be sounded near it, the limpid portion instantly shortens; the pitch may vary to some extent, and still cause a shortening; but the unisonant note is the most effectual. Savart’s experiments on vertically-descending veins have been recently repeated in our laboratory with striking effect. From a distance of thirty yards the limpid portion of the vein has been shortened by the sound of an organ-pipe of the proper pitch and of moderate intensity.
I have also recently gone carefully, not merely by reading, but by experiment, over Plateau’s account of the resolution of a liquid vein into drops. In his researches on the figures of equilibrium of bodies withdrawn from the action of gravity, he finds that a liquid cylinder is stable as long as its length does not exceed three times its diameter; or, more accurately, as long as the ratio between them does not exceed that of the diameter of a circle to its circumference, or 3.1416. If this be a little exceeded the cylinder begins to narrow at some point or other of its length; nips itself together, breaks, and forms immediately two spheres. If the ratio of the length of the cylinder to its diameter greatly exceed 3.1416, then, instead of breaking up into two spheres, it breaks up into several.
A liquid cylinder may be obtained by introducing olive-oil into a mixture of alcohol and water, of the296 same density as the oil. The latter forms a sphere. Two disks of smaller diameter than the sphere are brought into contact with it, and then drawn apart; the oil clings to the disks, and the sphere is transformed into a cylinder. If the quantity of oil be insufficient to produce the maximum length of cylinder, more may be added by a pipette. In making this experiment it will be noticed that, when the proper length is exceeded, the nipped portion of the cylinder elongates, and exists for a moment as a very thin liquid cylinder uniting the two incipient spheres; and that, when rupture occurs, the thin cylinder, which has also exceeded its proper length, breaks so as to form a small spherule between the two larger ones. This is a point of considerable significance in relation to our present question.
Now, Plateau contends that the play of the molecular forces in a liquid cylinder is not suspended by its motion of translation. The first portion of a vein of water quitting an orifice is a cylinder, to which the laws which he has established regarding motionless cylinders apply. The moment the descending vein exceeds the proper length it begins to pinch itself so as to form drops; but urged forward as it is by the pressure above it, and by its own gravity, in the time required for the rounding of the drop it reaches a certain distance from the orifice. At this distance, the pressure remaining constant, and the vein being withdrawn from external disturbance, rupture invariably occurs. And the rupture is accompanied by the phenomenon which has just been called significant. Between every two succeeding large drops a small spherule is formed, as shown in Fig. 141.
Permitting a vein of oil to fall from an orifice, not297 through the air, but through a mixture of alcohol and water of the proper density, the continuous portion of the vein, its resolution into drops, and the formation of the small spherule between each liberated drop and the end of the liquid cylinder which it has just quitted, may be watched with the utmost deliberation. The effect of this and other experiments upon the mind will be to produce the conviction that the very beautiful explanation offered by Plateau is also the true one. The various laws established experimentally by Savart all follow immediately from Plateau’s theory.
In a small paper published more than twenty years ago I drew attention to the fact that when a descending vein intersects a liquid surface above the point of rupture, if the pressure be not too great, it enters the liquid silently; but when the surface intersects the vein below the point of rupture a rattle is immediately heard, and bubbles are copiously produced. In the former case, not only is there no violent dashing aside of the liquid, but round the base of the vein, and in opposition to its motion, the liquid collects in a heap, by its surface tension or capillary attraction. This experiment can be combined with two other observations of Savart’s, in a beautiful and instructive manner. In addition to the shortening of the continuous portion by sound, Savart found that, when he permitted his membrane to intersect the vein at one of its protuberances, the sound was louder than when the intersection occurred at the contracted portion.
I permitted a vein to descend, under scarcely any pressure, from a tube three-quarters of an inch in diameter, and to enter silently a basin of water placed nearly 20 inches below the orifice. On sounding vigorously a298 Ut2 tuning-fork the pellucid jet was instantly broken, and as many as three of its swellings were seen above the surface. The rattle of air-bubbles was instantly heard, and the basin was seen to be filled with them. The sound was allowed slowly to die out; the continuous portion of the vein lengthened, and a series of alternations in the production of the bubbles was observed. When the swellings of the vein cut the surface of the water, the bubbles were copious and loud; when the contracted portions crossed the surface, the bubbles were scanty and scarcely audible.
Removing the basin, placing an iron tray in its place, and exciting the fork, the vein, which at first struck silently upon the tray, commenced a rattle which rose and sank with the dying out of the sound, according as the swellings or contractions of the jet impinged upon the surface. This is a simple and beautiful experiment.
Savart also caused his vein to issue horizontally and at various inclinations to the horizon, and found that, in certain cases, sonorous vibrations were competent to cause a jet to divide into two or three branches. In these experiments the liquid was permitted to issue through an orifice in a thin plate. Instead of this, however, we will resort to our favorite steatite burner; for with water also it asserts the same mastery over its fellows that it exhibited with flames and smoke-jets. It will, moreover, reveal to us some entirely novel results. By means of an India-rubber tube the burner is connected with the water-pipes of the Institution, and, by pointing it obliquely upward, we obtain a fine parabolic jet (Fig. 143). At a certain distance from the orifice, the vein resolves itself into beautiful spherules, whose motions are not rapid299 enough to make the vein appear continuous. At the vertex of the parabola the spray of pearls is more than an inch in width, and, further on, the drops are still more widely scattered. On sweeping a fiddle-bow across a tuning-fork which executes 512 vibrations in a second, the scattered drops, as if drawn together by their mutual attractions, instantly close up, and form an apparently continuous liquid arch several feet in height and span (shown in Fig. 144). As long as the proper note is maintained the vein looks like a frozen band, so motionless does it appear. On stopping the fork the arch is shaken asunder, and we have the same play of liquid300 pearls as before. Every sweep of the bow, however, causes the drops to fall into a common line of march.
A pitch-pipe, or an organ-pipe yielding the note of this tuning-fork, also powerfully controls the vein. The voice does the same. On pitching it to a note of moderate intensity, it causes the wandering drops to gather themselves together. At a distance of twenty yards, the voice is, to all appearance, as powerful in curbing the vein, and causing its drops to close up, as it is when close to the issuing jet.
The effect of “beats” upon the vein is also beautiful and instructive. They may be produced either by organ-pipes or by tuning-forks. When two forks vibrate, the one 512 times and the other 508 times in a second, you will learn in our next lecture that they produce four beats in a second. When the forks are sounded the beats are heard, and the liquid vein is seen to gather up its pearls, and scatter them in synchronism with the beats. The sensitiveness of this vein is astounding; it rivals that of the ear itself. Placing the two tuning-forks on a distant table, and permitting the beats to die gradually out, the vein continues its rhythm almost as long as hearing is possible. A more sensitive vein might actually prove superior to the ear—a very surprising result, considering the marvellous delicacy of this organ.57
By introducing a Leyden-jar into the circuit of a powerful induction-coil, a series of dense and dazzling flashes of light, each of momentary duration, is obtained. Every such flash in a darkened room renders the drops distinct, 301each drop being transformed into a little star of intense brilliancy. If the vein be then acted on by a sound of the proper pitch, it instantly gathers its drops together into a necklace of inimitable beauty.
In these experiments the whole vein gathers itself into a single arched band when the proper note is sounded; but, by varying the conditions, it may be caused to divide into two or more such bands, as shown in Fig. 145. Drawings, however, are ineffectual here; for the wonder of these experiments depends mainly on the sudden transition of the vein from one state to the other. In the motion dwells the surprise, and this no drawing can render.58
When a gas-flame is placed in a tube, the air in passing over the flame is thrown into vibration, musical sounds being the consequence.
Making allowance for the high temperature of the column of air associated with the flame, the pitch of the note is that of an open organ-pipe of the length of the tube surrounding the flame.
The vibrations of the flame, while the sound continues, consist of a series of periodic extinctions, total or partial, between every two of which the flame partially recovers its brightness.
The periodicity of the phenomenon may be demonstrated by means of a concave mirror which forms an image of the vibrating flame upon a screen. When the image is sharply defined, the rotation of the mirror reduces the single image to a series of separate images of the flame. The dark spaces between the images correspond to the extinctions of the flame, while the images themselves correspond to its periods of recovery.
Besides the fundamental note of the associated tube, the flame can also be caused to excite the higher overtones of the tube. The successive divisions of the column of air are those of an open organ-pipe when its harmonic tones are sounded.
On sounding a note nearly in unison with a tube containing a silent flame, the flame jumps; and if the position of the flame in the tube be rightly chosen, the extraneous sound will cause the flame to sing.
While the flame is singing, a note nearly in unison with its own produces beats, and the flame is seen to jump in synchronism with the beats. The jumping is also observed when the position of the flame within its tube is not such as to enable it to sing.
When the pressure of the gas which feeds a naked flame is augmented, the flame, up to a certain point, increases in size. But if the pressure be too great, the flame roars or flares.
The roaring or flaring of the flame is caused by the state of vibration into which the gas is thrown in the orifice of the burner, when the pressure which urges it through the orifice is excessive.
If the vibrations in the orifice of the burner be super-induced by an extraneous sound, the flame will flare under a pressure less than that which, of itself, would produce flaring.
The gas under excessive pressure has vibrations of a definite period impressed upon it as it passes through the burner. To operate with a maximum effect upon the flame the external sound must contain vibrations synchronous with those of the issuing gas.
When such a sound is chosen, and when the flame is brought sufficiently near its flaring-point, it furnishes an acoustic reagent of unexampled delicacy.
At a distance of 30 yards, for example, the chirrup of a house-sparrow would be competent to throw the flame into commotion.
It is not to the flame, as such, that we are to ascribe these effects. Effects substantially similar are produced when we employ jets of unignited coal-gas, carbonic acid, hydrogen, or air. These jets may be rendered visible by smoke, and the smoke jets show a sensitiveness to sonorous vibrations even greater than that of the flames.
When a brilliant sensitive flame illuminates an otherwise dark room, in which a suitable bell is caused to strike, a series of periodic quenchings of the light by the sound occurs. Every stroke of the bell is accompanied by a momentary darkening of the room.
A jet of water descending from a circular orifice is composed of two distinct portions, the one pellucid and304 calm; the other in commotion. When properly analyzed the former portion is found continuous; the latter being a succession of drops.
If these drops be received upon a membrane, a musical sound is produced. When an extraneous sound of this particular pitch is produced in the neighborhood of the vein, the continuous portion is seen to shorten.
The continuous portion of the vein presents a series of swellings and contractions, in the former of which the drops are flattened, and in the latter elongated. The sound produced by the flattened drops on striking the membrane is louder than that produced by the elongated ones.
Above its point of rupture a vein of water may be caused to enter water silently; but on sounding a suitable note, the rattle of bubbles is immediately heard; the discontinuous part of the vein rises above the surface, and as the sound dies out the successive swellings and contractions produce alternations of the quantity and sound of the bubbles.
In veins propelled obliquely, the scattered water-drops may be called together by a suitable sound, so as to form an apparently continuous liquid arch.
Liquid veins may be analyzed by the electric spark, or by a succession of flashes illuminating the veins.
RESEARCHES ON THE ACOUSTIC TRANSPARENCY OF THE ATMOSPHERE IN RELATION TO THE QUESTION OF FOG-SIGNALLING
Introduction—Instruments and Observations—Contradictory Results from the 19th of May to the 1st of July inclusive—Solution of Contradictions—Aërial Reflection and its Causes—Aërial Echoes—Acoustic Clouds—Experimental Demonstration of Stoppage of Sound by Aërial Reflection
WE ARE now fully equipped for the investigation of an important practical problem. The cloud produced by the puff of a locomotive can quench the rays of the noonday sun; it is not, therefore, surprising that in dense fogs our most powerful coast-lights, including even the electric light, should become useless to the mariner.
Disastrous shipwrecks are the consequence. During the last ten years no less than two hundred and seventy-three vessels have been reported as totally lost on our own coasts in fog or thick weather. The loss, I believe, has been far greater on the American seaboard, where trade is more eager, and fogs more frequent, than they are here. No wonder, then, that earnest efforts should be made to find a substitute for light in sound-signals, powerful enough to give warning and guidance to mariners while still at a safe distance from the shore.
Such signals have been established to some extent306 upon our own coasts, and to a still greater extent along the coasts of Canada and the United States. But the evidence as to their value and performance is of the most conflicting character, and no investigation sufficiently thorough to clear up the uncertainty has hitherto been made. In fact, while the velocity of sound has formed the subject of refined and repeated experiment by the ablest philosophers, the publication of Dr. Derham’s celebrated paper in the “Philosophical Transactions” for 1708 marks the latest systematic inquiry into the causes which affect the intensity of sound in the atmosphere.
Jointly with the Elder Brethren of the Trinity House, and as their scientific adviser, I have recently had the honor of conducting an inquiry designed to fill the blank here indicated.
One or two brief references will suffice to show the state of the question when this investigation began. “Derham,” says Sir John Herschel, “found that fogs and falling rain, but more especially snow, tend powerfully to obstruct the propagation of sound, and that the same effect was produced by a coating of fresh-fallen snow on the ground, though when glazed and hardened at the surface by freezing it had no such influence.”59
In a very clear and able letter, addressed to the President of the Board of Trade in 1863,60 Dr. Robinson, of Armagh, thus summarizes our knowledge of fog-signals: “Nearly all that is known about fog-signals is to be found in the ‘Report on Lights and Beacons’; and of it 307much is little better than conjecture. Its substance is as follows:
“‘Light is scarcely available for this purpose. Blue lights are used in the Hooghly; but it is not stated at what distance they are visible in fog; their glare may be seen further than their flame.61 It might, however, be desirable to ascertain how far the electric light, or its flash, can be traced.62
“‘Sound is the only known means really effective; but about it testimonies are conflicting, and there is scarcely one fact relating to its use as a signal which can be considered as established. Even the most important of all, the distance at which it ceases to be heard, is undecided.
“‘Up to the present time all signal-sounds have been made in air, though this medium has grave disadvantages: its own currents interfere with the sound-waves, so that a gun or bell which is heard several miles down the wind is inaudible more than a few furlongs up it. A still greater evil is that it is least effective when most needed; for fog is a powerful damper of sound.’”
Dr. Robinson here expresses the universally-prevalent opinion, and he then assigns the theoretic cause. “Fog,” he says, “is a mixture of air and globules of water, and at each of the innumerable surfaces where these two touch, a portion of the vibration is reflected and lost.63 ... Snow produces a similar effect, and one still more injurious.”
Reflection being thus considered to take place at the 308surfaces of the suspended particles, it followed that the greater the number of particles, or, in other words, the denser the fog, the more injurious would be its action upon sound. Hence optic transparency came to be considered a measure of acoustic transparency. On this point Dr. Robinson, in the letter referred to, expresses himself thus: “At the outset, it is obvious that, to make experiments comparable, we must have some measure of the fog’s power of stopping sound, without attending to which the most anomalous results may be expected. It seems probable that this will bear some simple relation to its opacity to light, and that the distance at which a given object, as a flag or pole, disappears may be taken as the measure.” “Still, clear air” was regarded in this letter as the best vehicle of sound, the alleged action of fogs, rain, and snow being ascribed to their rendering the atmosphere “a discontinuous medium.”
Prior to the investigation now to be described, the views here enunciated were those universally entertained. That sound is unable to penetrate fogs was taken to be “a matter of common observation.” The bells and horns of ships were affirmed “not to be heard so far in fogs as in clear weather.” In the fogs of London the noise of the carriage-wheels was reported to be so much diminished that “they seem to be at a distance where really close by.” My knowledge does not inform me of the existence of any other source for these opinions regarding the deadening power of fog than the paper of Derham, published one hundred and sixty-seven years ago. In consequence of their à priori probability, his conclusions seem to have been transmitted unquestioned from generation to generation of scientific men.
On the 19th of May, 1873, this inquiry began. The South Foreland, near Dover, was chosen as the signal-station, steam-power having been already established there to work two powerful magneto-electro lights. The observations for the most part were made afloat, one of the yachts of the Trinity Corporation being usually employed for this purpose. Two stations had been established, the one at the top, the other at the bottom, of the South Foreland Cliff; and at each of them trumpets, air-whistles, and steam-whistles of great size were mounted. The whistles first employed were of English manufacture. To these was afterward added a large United States whistle, and also a Canadian whistle, of great reputed power.
On the 8th of October another instrument, which has played a specially important part in these observations, was introduced. This was a steam-siren, constructed and patented by Mr. Brown of New York, and introduced by Prof. Henry into the lighthouse system of the United States. As an example of international courtesy worthy of imitation, I refer with pleasure to the fact that when informed by Major Elliot of the United States Army that our experiments had begun, the Lighthouse Board at Washington, of their own spontaneous kindness, forwarded to us for trial a very noble instrument of this description, which was immediately mounted at the South Foreland.
In the steam-siren, as in the ordinary one, described in Chapter II., a fixed disk and a rotating disk are employed, but radial slits are used instead of circular apertures. One disk is fixed vertically across the throat of a310 conical trumpet 16-1/2 feet long, 5 inches in diameter where the disk crosses it, and gradually opening out till at the other extremity it reaches a diameter of 2 feet 3 inches. Behind the fixed disk is the rotating one, which is driven by separate mechanism. The trumpet is connected with a boiler. In our experiments steam of 70 lbs. pressure was for the most part employed. Just as in the ordinary siren, when the radial slits of the two disks coincide, and then only, a strong puff of steam escapes. Sound-waves of great intensity are thus sent through the air, the pitch of the note depending on the velocity of rotation. (A drawing of the steam-siren constitutes our frontispiece.)
To the siren, trumpets, and whistles were added three guns—an 18-pounder, a 5-1/2-inch howitzer, and a 13-inch mortar. In our summer experiments all three were fired; but the howitzer having shown itself superior to the other guns it was chosen in our autumn experiments as not only a fair but a favorable representative of this form of signal. The charges fired were for the most part those now employed at Holyhead, Lundy Island, and the Kish light-vessel; namely, 3 lbs. of powder. Gongs and bells were not included in this inquiry, because previous observations had clearly proved their inferiority to the trumpets and whistles.
On the 19th of May the instruments tested were:
On the top of the cliff:
a. Two brass trumpets or horns, 11 feet 2 inches long, 2 inches in diameter at the mouth-piece, and opening out at the other end to a diameter of 22-1/2 inches. They were provided with vibrating steel reeds 9 inches long, 2 inches wide, and 1/4 inch thick, and were sounded by air of 18 lbs. pressure.
b. A whistle, shaped like that of a locomotive, 6 inches in diameter, also sounded by air of 18 lbs. pressure.
c. A steam-whistle, 12 inches in diameter, attached to a boiler, and sounded by steam of 64 lbs. pressure.
At the bottom of the cliff:
d. Two trumpets or horns, of the same size and arrangement as those above, and sounded by air of the same pressure. They were mounted vertically on the reservoir of compressed air; but within about two feet of their extremities they were bent at a right angle, so as to present their mouths to the sea.
e. A 6-inch air-whistle, similar to the one above, and sounded by the same means.
The upper instruments were 235 feet above high-water mark, the lower ones 40 feet. A vertical distance of 195 feet, therefore, separated the instruments. A shaft, provided with a series of twelve ladders, led from the one to the other.
Numerous comparative experiments made at the outset gave a slight advantage to the upper instruments. They, therefore, were for the most part employed throughout the subsequent inquiry.
Our first observations were a preliminary discipline rather than an organized effort at discovery. On May 19th the maximum distance reached by the sound was about three and a half miles.64 The wind, however, was high and the sea rough, so that local noises interfered to some extent with our appreciation of the sound.
Mariners express the strength of the wind by a series of numbers extending from 0 = calm to 12 = a hurricane, 312a little practice in common producing a remarkable unanimity between different observers as regards the force of the wind. Its force on May 19th was 6, and it blew at right angles to the direction of the sound.
The same instruments on May 20th covered a greater range of sound; but not much greater, though the disturbance due to local noises was absent. At 4 miles’ distance in the axes of the horns they were barely heard, the air at the time being calm, the sea smooth, and all other circumstances exactly those which have been hitherto regarded as most favorable to the transmission of sound. We crept a little further away, and by stretched attention managed to hear at intervals, at a distance of 6 miles, the faintest hum of the horns. A little further out we again halted; but though local noises were absent, and though we listened intently, we heard nothing.
This position, clearly beyond the range of whistles and trumpets, was expressly chosen with the view of making what might be considered a decisive comparative experiment between horns and guns as instruments for fog-signalling. The distinct report of the 12 o’clock gun fired at Dover on the 19th suggested this comparison, and through the prompt courtesy of General Sir A. Horsford we were enabled to carry it out. At 12.30 precisely the puff of an 18-pounder, with a 3-lb. charge, was seen at Dover Castle, which was about a mile further off than the South Foreland. Thirty-six seconds afterward the loud report of the gun was heard, its complete superiority over the trumpets being thus, to all appearance, demonstrated.
We clinched this observation by steaming out to a distance of 8-1/2 miles, where the report of a second gun313 was well heard by all of us. At a distance of 10 miles the report of a third gun was heard by some, and at 9·7 miles the report of a fourth gun was heard by all.
The result seemed perfectly decisive. Applying the law of inverse squares, the sound of the gun at a distance of 6 miles from the Foreland must have had more than two and a half times the intensity of the sound of the trumpets. It would not have been rash under the circumstances to have reported without qualification the superiority of the gun as a fog-signal. No single experiment is, to my knowledge, on record to prove that a sound once predominant would not be always predominant, or that the atmosphere on different days would show preferences to different sounds. On many subsequent occasions, however, the sound of the horns proved distinctly superior to that of the gun. This selective power of the atmosphere revealed itself more strikingly in our autumn experiments than in our summer ones; and it was sometimes illustrated within a few hours of the same day: of two sounds, for example, one might have the greatest range at 10 A.M., and the other the greatest range at 2 P.M.
In the experiments on May 19th and 20th the superiority of the trumpets over the whistles was decided; and indeed, with few exceptions, this superiority was maintained throughout the inquiry. But there were exceptions. On June 2d, for example, the whistles rose in several instances to full equality with, and on rare occasions subsequently even surpassed, the horns. The sounds were varied from day to day, and various shiftings of the horns and reeds were resorted to, with a view of bringing out their maximum power. On the date last314 mentioned a single horn was sounded, two were sounded, and three were sounded together; but the utmost range of the loudest sound, even with the paddles stopped, did not exceed 6 miles. With the view of concentrating their power, the axes of the horns had been pointed in the same direction, and, unless stated to the contrary, this in all subsequent experiments was the case.
On June 3d the three guns already referred to were permanently mounted at the South Foreland. They were ably served by gunners from Dover Castle.
On the same day dense clouds quite covered the firmament, some of them particularly black and threatening, but a marked advance was observed in the transmissive power of the air. At a distance of 6 miles the horn-sounds were not quite quenched by the paddle-noises; at 8 miles the whistles were heard, and the horns better heard; while at 9 miles, with the paddles stopped, the horn-sounds alone were fairly audible. During the day’s observations a remarkable and instructive phenomenon was observed. Over us rapidly passed a torrential shower of rain, which, according to Derham, is a potent damper of sound. We could, however, notice no subsidence of intensity as the shower passed. It is even probable that, had our minds been free from bias, we should have noticed an augmentation of the sound, such as occurred with the greatest distinctness on various subsequent occasions during violent rain.
The influence of “beats” was tried on June 3d, by throwing the horns slightly out of unison; but though the beats rendered the sound characteristic, they did not seem to augment the range. At a distance from the station curious fluctuations of intensity were noticed. Not315 only did the different blasts vary in strength, but sudden swellings and fallings off, even of the same blast, were observed. This was not due to any variation on the part of the instruments, but purely to the changes of the medium traversed by the sound. What these changes were shall be indicated subsequently.
The range of our best horns on June 10th was 8-3/4 miles. The guns at this distance were very feeble. That the loudness of the sound depends on the shape of the gun was proved by the fact that thus far the howitzer, with a 3-lb. charge, proved more effective than the other guns.
On June 25th a gradual improvement in the transmissive power of the air was observed from morning to evening; but at the last the maximum range was only moderate. The fluctuations in the strength of the sound were remarkable, sometimes sinking to inaudibility and then rising to loudness. A similar effect, due to a similar cause, is often noticed with church-bells. The acoustic transparency of the air was still further augmented on the 26th: at a distance of 9-1/4 miles from the station the whistles and horns were plainly heard against a wind with a force of 4; while on the 25th, with a favoring wind, the maximum range was only 6-1/2 miles. Plainly, therefore, something else than the wind must be influential in determining the range of the sound.
On Tuesday, July 1st, observations were made on the decay of the sound at various angular distances from the axis of the horn. As might be expected, the sound in the axis was loudest, the decay being gradual on both sides. In the case of the gun, however, the direction of pointing has very little influence.
The day was acoustically clear; at a distance of 10 miles the horn yielded a plain sound, while the American whistle seemed to surpass the horn. Dense haze at this time quite hid the Foreland. At 10-1/2 miles occasional blasts of the horn came to us, but after a time all sound ceased to be audible; it seemed as if the air, after having been exceedingly transparent, had become gradually more opaque to the sound.
At 4.45 P.M. we took the master of the Varne light-ship on board the “Irene.” He and his company had heard the sound at intervals during the day, although he was dead to windward and distant 12-3/4 miles from the source of sound.
Here a word of reflection on our observations may be fitly introduced. It is, as already shown, an opinion entertained in high quarters that the waves of sound are reflected at the limiting surfaces of the minute particles which constitute haze and fog, the alleged waste of sound in fog being thus explained. If, however, this be an efficient practical cause of the stoppage of sound, and if clear calm air be, as alleged, the best vehicle, it would be impossible to understand how to-day, in a thick haze, the sound reached a distance of 12-3/4 miles, while on May 20th, in a calm and hazeless atmosphere, the maximum range was only from 5 to 6 miles. Such facts foreshadow a revolution in our notions regarding the action of haze and fogs upon sound.
An interval of 12 hours sufficed to change in a surprising degree the acoustic transparency of the air. On the 1st of July the sound had a range of nearly 13 miles; on the 2d the range did not exceed 4 miles.
Thus far the investigation proceeded with hardly a gleam of a principle to connect the inconstant results. The distance reached by the sound on the 19th of May was 3-1/2 miles; on the 20th it was 5-1/2 miles; on the 2d of June 6 miles; on the 3d more than 9 miles; on the 10th it was also 9 miles; on the 25th it fell to 6-1/2 miles; on the 26th it rose again to more than 9-1/4 miles; on the 1st of July, as we have just seen, it reached 12-3/4, whereas on the 2d the range shrunk to 4 miles. None of the meteorological agents observed could be singled out as the cause of these fluctuations. The wind exerts an acknowledged power over sound, but it could not account for these phenomena. On the 25th of June, for example, when the range was only 6-1/2 miles, the wind was favorable; on the 26th, when the range exceeded 9-1/4 miles, it was opposed to the sound. Nor could the varying optical clearness of the atmosphere be invoked as an explanation; for on July 1st, when the range was 12-3/4 miles, a thick haze hid the white cliffs of the Foreland, while on many other days, when the acoustic range was not half so great, the atmosphere was optically clear. Up to July 3d all remained enigmatical; but on this date observations were made which seemed to me to displace surmise and perplexity by the clearer light of physical demonstration.
On July 3d we first steamed to a point 2·9 miles S.W. by W. of the signal-station. No sounds, not even the guns, were heard at this distance. At 2 miles they were equally inaudible. But this being a position at318 which the sounds, though strong in the axis of the horn, invariably subsided, we steamed to the exact bearing from which our observations had been made on July 1st. At 2.15 P.M., and at a distance of 3-3/4 miles from the station, with calm, clear air and a smooth sea, the horns and whistle (American) were sounded, but they were inaudible. Surprised at this result, I signalled for the guns. They were all fired, but, though the smoke seemed at hand, no sound whatever reached us. On July 1st, in this bearing, the observed range of both horns and guns was 10-1/2 miles, while on the bearing of the Varne light-vessel it was nearly 13 miles. We steamed in to 3 miles, paused, and listened with all attention; but neither horn nor whistle was heard. The guns were again signalled for; five of them were fired in succession, but not one of them was heard. We steamed on in the same bearing to 2 miles, and had the guns fired pointblank at us. The howitzer and the mortar, with 3-lb. charges, yielded a feeble thud, while the 18-pounder was wholly unheard. Applying the law of inverse squares, it follows that, with the air and sea, according to accepted notions, in a far worse condition, the sound at 2 miles’ distance on July 1st must have had more than forty times the intensity which it possessed at the same distance at 3 P.M. on the 3d.
“On smooth water,” says Sir John Herschel, “sound is propagated with remarkable clearness and strength.” Here was the condition; still, with the Foreland so close to us, the sea so smooth, and the air so transparent, it was difficult to realize that the guns had been fired or the trumpets blown at all. What could be the reason? Had the sound been converted by internal friction into319 heat? or had it been wasted in partial reflections at the limiting surfaces of non-homogeneous masses of air? I ventured, two or three years ago, to say something regarding the function of the Imagination in Science, and, notwithstanding the care then taken, to define and illustrate its real province, some persons, among whom were one or two able men, deemed me loose and illogical. They misunderstood me. The faculty to which I referred was that power of visualizing processes in space, and the relations of space itself, which must be possessed by all great physicists and geometers. Looking, for example, at two pieces of polished steel, we have not a sense, or the rudiment of a sense, to distinguish the inner condition of the one from that of the other. And yet they may differ materially, for one may be a magnet, the other not. What enabled Ampère to surround the atoms of such a magnet with channels in which electric currents ceaselessly run, and to deduce from these pictured currents all the phenomena of ordinary magnetism? What enabled Faraday to visualize his lines of force, and make his mental picture a guide to discoveries which have rendered his name immortal? Assuredly it was the disciplined imagination. Figure the observers on the deck of the “Irene,” with the invisible air stretching between them and the South Foreland, knowing that it contained something which stifled the sound, but not knowing what that something is. Their senses are not of the least use to them; nor could all the philosophical instruments in the world render them any assistance. They could not, in fact, take a single step toward the solution without the formation of a mental image—in other words, without the exercise of the imagination.
Sulphur, in homogeneous crystals, is exceedingly transparent to radiant heat, whereas the ordinary brimstone of commerce is highly impervious to it—the reason being that the brimstone does not possess the molecular continuity of the crystal, but is a mere aggregate of minute grains not in perfect optical contact with each other. Where this is the case, a portion of the heat is always reflected on entering and on quitting a grain; hence, when the grains are minute and numerous, this reflection is so often repeated that the heat is entirely wasted before it can plunge to any depth into the substance. The same remark applies to snow, foam, clouds, and common salt, indeed, to all transparent substances in powder; they are all impervious to light, not through the immediate absorption or extinction of the light, but through repeated internal reflection.
Humboldt, in his observations at the Falls of the Orinoco, is known to have applied these principles to sound. He found the noise of the falls far louder by night than by day, though in that region the night is far noisier than the day. The plain between him and the falls consisted of spaces of grass and rock intermingled. In the heat of the day he found the temperature of the rock to be considerably higher than that of the grass. Over every heated rock, he concluded, rose a column of air rarefied by the heat; its place being supplied by the descent of heavier air. He ascribed the deadening of the sound to the reflections which it endured at the limiting surfaces of the rarer and denser air. This philosophical explanation made it generally known that a non-homogeneous atmosphere is unfavorable to the transmission of sound.
But what on July 3d, not with the variously-heated plain of Antures, but with a calm sea as a basis for the atmosphere, could so destroy its homogeneity as to enable it to quench in so short a distance so vast a body of sound? My course of thought at the time was thus determined: As I stood upon the deck of the “Irene” pondering the question, I became conscious of the exceeding power of the sun beating against my back and heating the objects near me. Beams of equal power were falling on the sea, and must have produced copious evaporation. That the vapor generated should so rise and mingle with the air as to form an absolutely homogeneous medium, was in the highest degree improbable. It would be sure, I thought, to rise in invisible streams, breaking through the superincumbent air now at one point, now at another, thus rendering the air flocculent with wreaths and striæ, charged in different degrees with the buoyant vapor. At the limiting surfaces of these spaces, though invisible, we should have the conditions necessary to the production of partial echoes and the consequent waste of sound. Ascending and descending air-currents, of different temperatures, as far as they existed, would also contribute to the effect.
Curiously enough, the conditions necessary for the testing of this explanation immediately set in. At 3.15 P.M. a solitary cloud threw itself athwart the sun, and shaded the entire space between us and the South Foreland. The heating of the water and the production of vapor- and air-currents were checked by the interposition of this screen; hence the probability of suddenly-improved transmission. To test this inference, the steamer was immediately turned and urged back to our last position of322 inaudibility. The sounds, as I expected, were distinctly though faintly heard. This was at 3 miles’ distance. At 3-3/4 miles, the guns were fired, both pointblank and elevated. The faintest pop was all that we heard; but we did hear a pop, whereas we had previously heard nothing, either here or three-quarters of a mile nearer. We steamed out to 4-1/4 miles, where the sounds were for a moment faintly heard; but they fell away as we waited; and though the greatest quietness reigned on board, and though the sea was without a ripple, we could hear nothing. We could plainly see the steam-puffs which announced the beginning and the end of a series of trumpet-blasts, but the blasts themselves were quite inaudible.
It was now 4 P.M., and my intention at first was to halt at this distance, which was beyond the sound-range, but not far beyond it, and see whether the lowering of the sun would not restore the power of the atmosphere to transmit the sound. But after waiting a little the anchoring of a boat was suggested, so as to liberate the steamer for other work; and though loth to lose the anticipated revival of the sounds myself, I agreed to this arrangement. Two men were placed in the boat and requested to give all attention, so as to hear the sound if possible. With perfect stillness around them they heard nothing. They were then instructed to hoist a signal if they should hear the sounds, and to keep it hoisted as long as the sounds continued.
At 4.45 we quitted them and steamed toward the South Sand Head light-ship. Precisely 15 minutes after we had separated from them the flag was hoisted; the sound had at length succeeded in piercing the body of air between the boat and the shore.
We continued our journey to the light-ship, went on board, heard the report of the lightsmen, and returned to our anchored boat. We then learned that when the flag was hoisted the horn-sounds were heard, that they were succeeded after a little time by the whistle-sounds, and that both increased in intensity as the evening advanced. On our arrival, of course, we heard the sounds ourselves.
We pushed the test further by steaming further out. At 5-3/4 miles we halted and heard the sounds: at 6 miles we heard them distinctly, but so feebly that we thought we had reached the limit of the sound-range; but while we waited the sounds rose in power. We steamed to the Varne buoy, which is 7-3/4 miles from the signal-station, and heard the sounds there better than at 6 miles’ distance. We continued our course outward to 10 miles, halted there for a brief interval, but heard nothing.
Steaming, however, on to the Varne light-ship, which is situated at the other end of the Varne shoal, we hailed the master, and were informed by him that up to 5 p.m. nothing had been heard, but that at that hour the sounds began to be audible. He described one of them as “very gross, resembling the bellowing of a bull,” which very accurately characterizes the sound of the large American steam-whistle. At the Varne light-ship, therefore, the sounds had been heard toward the close of the day; though it is 12-3/4 miles from the signal-station. I think it probable that, at a point 2 miles from the Foreland, the sound at 5 P.M. possessed fifty times the intensity which it possessed at 2 P.M. To such undreamed-of fluctuations is the atmosphere liable. On our return to Dover Bay, at 10 P.M., we heard the sounds, not only distinct but loud, where nothing could be heard in the morning.
In his excellent lecture entitled “Wirkungen aus der Ferne,” Dove has collected some striking cases of the interception of sound. The Duke of Argyll has also favored me with some highly-interesting illustrations; but nothing of this description that I have read equals in point of interest the following account of the battle of Gaines’s Farm, for which I am indebted to the Rector of the University of Virginia:
“Lynchburg, Virginia, March 19, 1874.
“Sir—I have just read with great interest your lecture of January 16th, on the acoustic transparency and opacity of the atmosphere. The remarkable observations you mention induce me to state to you a fact which I have occasionally mentioned, but always, where I am not well known, with the apprehension that my veracity would be questioned. It made a strong impression on me at the time, but was an insoluble mystery until your discourse gave me a possible solution.
“On the afternoon of June 28, 1862, I rode, in company with General G. W. Randolph, then Secretary of War of the Confederate States, to Price’s house, about nine miles from Richmond; the evening before General Lee had begun his attack on McClellan’s army, by crossing the Chickahominy about four miles above Price’s, and driving in McClellan’s right wing. The battle of Gaines’s Farm was fought the afternoon to which I refer. The valley of the Chickahominy is about one mile and a half wide from hilltop to hilltop. Price’s is on one hilltop, that nearest to Richmond; Gaines’s farm, just opposite, is on the other, reaching back in a plateau to Cold Harbor.
“Looking across the valley I saw a good deal of the battle, Lee’s right resting in the valley, the Federal left wing the same. My line of vision was nearly in the line of the lines of battle. I saw the advance of the Confed325erates, their repulse two or three times, and in the gray of the evening the final retreat of the Federal forces.
“I distinctly saw the musket-fire of both lines, the smoke, individual discharges, the flash of the guns. I saw batteries of artillery on both sides come into action and fire rapidly. Several field-batteries on each side were plainly in sight. Many more were hid by the timber which bounded the range of vision.
“Yet looking for nearly two hours, from about 5 to 7 P.M. on a midsummer afternoon, at a battle in which at least 50,000 men were actually engaged, and doubtless at least 100 pieces of field-artillery, through an atmosphere optically as limpid as possible, not a single sound of the battle was audible to General Randolph and myself. I remarked it to him at the time as astonishing.
“Between me and the battle was the deep broad valley of the Chickahominy, partly a swamp shaded from the declining sun by the hills and forest in the west (my side). Part of the valley on each side of the swamp was cleared; some in cultivation, some not. Here were conditions capable of providing several belts of air, varying in the amount of watery vapor (and probably in temperature), arranged like laminæ at right angles to the acoustic waves as they came from the battlefield to me.
“Respectfully,
“Your obedient servant,
“R. G. H. Kean.
“Prof. John Tyndall.”
I learn from a subsequent letter that during the battle the air was still.—J. T.
But both the argument and the phenomena have a complementary side, which we have now to consider. A stratum of air less than 3 miles thick on a calm day has been proved competent to stifle both the cannonade and326 the horn-sounds employed at the South Foreland; while, according to the foregoing explanation, this result was due to the reflection of the sound from invisible acoustic clouds which filled the atmosphere on a day of perfect optical transparency. But, granting this, it is incredible that so great a body of sound could utterly disappear in so short a distance without rendering some account of itself. Supposing, then, instead of placing ourselves behind the acoustic cloud, we were to place ourselves in front of it, might we not, in accordance with the law of conservation, expect to receive by reflection the sound which had failed to reach us by transmission? The case would then be strictly analogous to the reflection of light from an ordinary cloud to an observer between it and the sun.
My first care in the early part of the day in question was to assure myself that our inability to hear the sound did not arise from any derangement of the instruments on shore. Accompanied by the private secretary of the Deputy Master of the Trinity House, at 1 P.M. I was rowed to the shore, and landed at the base of the South Foreland Cliff. The body of air which had already shown such extraordinary power to intercept the sound, and which manifested this power still more impressively later in the day, was now in front of us. On it the sonorous waves impinged, and from it they were sent back with astonishing intensity. The instruments, hidden from view, were on the summit of a cliff 235 feet above us, the sea was smooth and clear of ships, the atmosphere was without a cloud, and there was no object in sight which could possibly produce the observed effect. From the perfectly transparent air the echoes came, at first with327 a strength apparently little less than that of the direct sound, and then dying away. A remark made by my talented companion in his notebook at the time shows how the phenomenon affected him: “Beyond saying that the echoes seemed to come from the expanse of ocean, it did not appear possible to indicate any more definite point of reflection.” Indeed no such point was to be seen; the echoes reached us, as if by magic, from the invisible acoustic clouds with which the optically transparent atmosphere was filled. The existence of such clouds in all weathers, whether optically cloudy or serene, is one of the most important points established by this inquiry.
Here, in my opinion, we have the key to many of the mysteries and discrepancies of evidence which beset this question. The foregoing observations show that there is no need to doubt either the veracity or the ability of the conflicting witnesses, for the variations of the atmosphere are more than sufficient to account for theirs. The mistake, indeed, hitherto has been, not in reporting incorrectly, but in neglecting the monotonous operation of repeating the observations during a sufficient time. I shall have occasion to remark subsequently on the mischief likely to arise from giving instructions to mariners founded on observations of this incomplete character.
It required, however, long pondering and repeated observation before this conclusion took firm root in my mind; for it was opposed to the results of great observers, and to the statements of celebrated writers. In science as elsewhere, a mind of any depth which accepts a doctrine undoubtingly, discards it unwillingly. The328 question of aërial echoes has a historic interest. While cloud-echoes have been accepted as demonstrated by observation, it has been hitherto held as established that audible echoes never occur in optically clear air. We owe this opinion to the admirable report of Arago on the experiments made to determine the velocity of sound at Montlhéry and Villejuif in 1822.65 Arago’s account of the phenomenon observed by him and his colleagues is as follows: “Before ending this note we will only add that the shots fired at Montlhéry were accompanied by a rumbling like that of thunder, which lasted from 20 to 25 seconds. Nothing of this kind occurred at Villejuif. Once we heard two distinct reports, a second apart, of the Montlhéry cannon. In two other cases the report of the same gun was followed by a prolonged rumbling. These phenomena never occurred without clouds. Under a clear sky the sounds were single and instantaneous. May we not, therefore, conclude that the multiple reports of the Montlhéry gun heard at Villejuif were echoes from the clouds, and may we not accept this fact as favorable 329to the explanation given by certain physicists of the rolling of thunder?”
This explanation of the Montlhéry echoes is an inference from observations made at Villejuif. The inference requires qualification. Some hundreds of cannon-shots have been fired at the South Foreland, many of them when the heavens were completely free from clouds, and never in a single case has a roulement similar to that noticed at Montlhéry been absent. It follows, moreover, so hot upon the direct sound as to present hardly a sensible breach of continuity between the sound and the echo. This could not be the case if the clouds were its origin. A reflecting cloud, at the distance of a mile; would leave a silent interval of nearly ten seconds between sound and echo; and had such an interval been observed at Montlhéry, it could hardly have escaped record by the philosophers stationed there; but they have not recorded it.
I think both the fact and the inference need reconsideration. For our observations prove to demonstration that air of perfect visual transparency is competent to produce echoes of great intensity and long duration. The subject is worthy of additional illustration. On the 8th of October, as already stated, the siren was established at the South Foreland. I visited the station on that day, and listened to its echoes. They were far more powerful than those of the horn. Like the others, they were perfectly continuous, and faded, as if into distance, gradually away. The direct sound seemed rendered complex and multitudinous by its echoes, which resembled a band of trumpeters, first responding close at hand, and then retreating rapidly toward the coast of France. The330 siren echoes on that day had 11 seconds’, those of the horn 8 seconds’, duration.
In the case of the siren, moreover, the reinforcement of the direct sound by its echo was distinct. About a second after the commencement of the siren-blast the echo struck in as a new sound. This first echo, therefore, must have been flung back by a body of air not more than 600 or 700 feet in thickness. The few detached clouds visible at the time were many miles away, and could clearly have had nothing to do with the effect.
On the 10th of October I was again at the Foreland listening to the echoes, with results similar to those just described. On the 15th I had an opportunity of remarking something new concerning them at Dungeness, where a horn similar to, but not so powerful as, those at the South Foreland, has been mounted. It rotates automatically through an arc of 210°, halting at four different points on the arc and emitting a blast of 6 seconds’ duration, these blasts being separated from each other by intervals of silence of 20 seconds.
The new point observed was this: as the horn rotated the echoes were always returned along the line in which the axis of the horn pointed. Standing either behind or in front of the lighthouse tower, or closing the eyes so as to exclude all knowledge of the position of the horn, the direction of its axis when sounded could always be inferred from the direction in which the aërial echoes reached the shore. Not only, therefore, is knowledge of direction given by a sound, but it may also be given by the aërial echoes of the sound.
On the 17th of October, at about 5 P.M., the air being perfectly free from clouds, we rowed toward the Foreland,331 landed, and passed over the seaweed to the base of the cliff. As I reached the base the position of the “Galatea” was such that an echo of astonishing intensity was sent back from her side; it came as if from an independent source of sound established on board the steamer. This echo ceased suddenly, leaving the aërial echoes to die gradually into silence.
At the base of the cliff a series of concurrent observations made the duration of the aërial siren-echoes from 13 to 14 seconds.
Lying on the shingle under a projecting roof of chalk, the somewhat enfeebled diffracted sound reached me, and I was able to hear with great distinctness, about a second after the starting of the siren-blast, the echoes striking in and reinforcing the direct sound. The first rush of echoed sound was very powerful, and it came, as usual, from a stratum of air 600 or 700 feet in thickness. On again testing the duration of the echoes, it was found to be from 14 to 15 seconds. The perfect clearness of the afternoon caused me to choose it for the examination of the echoes. It is worth remarking that this was our day of longest echoes, and it was also our day of greatest acoustic transparency, this association suggesting that the duration of the echo is a measure of the atmospheric depths from which it comes. On no day, it is to be remembered, was the atmosphere free from invisible acoustic clouds; and on this day, and when their presence did not prevent the direct sound from reaching to a distance of 15 or 16 nautical miles, they were able to send us echoes of 15 seconds’ duration.
On various occasions, when fully three miles from the shore, the Foreland bearing north, we have had the dis332tinct echoes of the siren sent back to us from the cloudless southern air.
To sum up this question of aërial echoes. The siren sounded three blasts a minute, each of 5 seconds’ duration. From the number of days and the number of hours per day during which the instrument was in action we can infer the number of blasts. They reached nearly twenty thousand. The blasts of the horns exceeded this number, while hundreds of shots were fired from the guns. Whatever might be the state of the weather, cloudy or serene, stormy or calm, the aërial echoes, though varying in strength and duration from day to day, were never absent; and on many days, “under a perfectly clear sky,” they reached, in the case of the siren, an astonishing intensity. It is doubtless to these air-echoes, and not to cloud-echoes, that the rolling of thunder is to be ascribed.
Thus far we have dealt in inference merely, for the interception of sound through aërial reflection has never been experimentally demonstrated; and, indeed, according to Arago’s observation, which has hitherto held undisputed possession of the scientific field, it does not sensibly exist. But the strength of science consists in verification, and I was anxious to submit the question of aërial reflection to an experimental test. The knowledge gained in the last lecture enables us to apply such a test; but, as in most similar cases, it was not the simplest combinations that were first adopted. Two gases of different densities were to be chosen, and I chose carbonic acid and coal-gas. With the aid of my skillful333 assistant, Mr. John Cottrell, a tunnel was formed, across which five-and-twenty layers of carbonic acid were permitted to fall, and five-and-twenty alternate layers of coal-gas to rise. Sound was sent through this tunnel, making fifty passages from medium to medium in its course. These, I thought, would waste in aërial echoes a sensible portion of sound.
To indicate this waste an objective test was found in one of the sensitive flames described in the last chapter. Acquainted with it, we are prepared to understand a drawing and description of the apparatus first employed in the demonstration of aërial reflection. The following clear account of the apparatus was given by a writer in “Nature,” February 5, 1874:
“A tunnel t t′ (Fig. 146), 2 inches square, 4 feet 8
inches long, open at both ends, and having a glass front,
runs through the box a b c d. The spaces above and
below are divided into cells opening into the tunnel by
transverse orifices exactly corresponding vertically. Each
alternate cell of the upper series—the 1st, 3d, 5th, etc.—communicates
by a bent tube (e e e) with a common
upper reservoir (g), its counterpart cell in the lower
series having a free outlet into the air. In like manner
the 2d, 4th, 6th, etc., of the lower series of cells are
connected by bent tubes (n n n) with the lower reservoir
(i), each having its direct passage into the air through the
cell immediately above it. The gas-distributors (g and i)
are filled from both ends at the same time, the upper
with carbonic-acid gas, the lower with coal-gas, by
branches from their respective supply-pipes (f and h).
A well-padded box (P) open to the end of the tunnel
forms a little cavern, whence the sound-waves are sent
334
335forth by an electric bell (dotted in the figure). A few
feet from the other end of the tunnel, and in a direct
line with it, is a sensitive flame (k), provided with a
funnel as sound-collector, and guarded from chance
currents by a shade.
“The bell was set ringing. The flame, with quick response to each blow of the hammer, emitted a sort of musical roar, shortening and lengthening as the successive sound-pulses reached it. The gases were then admitted. Twenty-five flat jets of coal-gas ascended from the tubes below, and twenty-five cascades of carbonic acid fell from the tubes above. That which was a homogeneous medium had now fifty limiting surfaces, from each of which a portion of the sound was thrown back. In a few moments these successive reflections became so effective that no sound having sufficient power to affect the flame could pierce the clear, optically-transparent, but acoustically-opaque, atmosphere in the tunnel. So long as the gases continued to flow the flame remained perfectly tranquil. When the supply was cut off, the gases rapidly diffused into the air. The atmosphere of the tunnel became again homogeneous, and therefore acoustically transparent, and the flame responded to each sound-pulse as before.”
Not only do gases of different densities act thus upon sound, but atmospheric air in layers of different temperatures does the same. Across a tunnel resembling t t′, Fig. 146, sixty-six platinum wires were stretched, all of them being in metallic connection. The bell, in its padded box, was placed at one end of the tunnel, and the sensitive flame k, near its flaring-point, at the other. When the bell rang the flame flared. A current from a336 strong voltaic battery being sent through the platinum wires, they became heated: layers of warm air rose from them through the tunnel, and immediately the agitation of the flame was stilled. On stopping the current, the agitation recommenced. In this experiment the platinum wires had not reached a red heat. Employing half the number and the same battery, they were raised to a red heat, the action in this case upon the sound-waves being also energetic. Employing one-third of the number of wires, and the same strength of battery, the wires were raised to a white heat. Here also the flame was immediately rendered tranquil by the stoppage of the sound.
But not only do gases of different densities, and air of different temperatures, act thus upon sound, but air saturated, in different degrees, with the vapors of volatile liquids can be shown by experiment to produce the same effect. Into the path pursued by the carbonic acid in our first experiment a flask, which I have frequently employed to charge air with vapor, was introduced. Through a volatile liquid, partially filling the flask, air was forced into the tunnel t t′, which was thus divided into spaces of air saturated with the vapor, and other spaces in their ordinary condition. The action of such a medium upon the sound-waves issuing from the bell is very energetic, instantly reducing the violently-agitated flame to stillness and steadiness. The removal of the heterogeneous medium instantly restores the noisy flaring of the flame.
A few illustrations of the action of non-homogeneous atmospheres, produced by the saturation of layers of air with the vapors of volatile liquids, may follow here:
Bisulphide of Carbon.—Flame very sensitive, and noisily responsive to the sound. The action of the non-homogeneous atmosphere was prompt and strong, stilling the agitated flame.
Chloroform.—Flame still very sensitive; action similar to the last.
Iodide of Methyl.—Action prompt and energetic.
Amylene.—Very fine action; a short and violently-agitated flame was immediately rendered tall and quiescent.
Sulphuric Ether.—Action prompt and energetic.
The vapor of water at ordinary temperatures is so small in quantity and so attenuated that it requires special precautions to bring out its action. But with such precautions it was found competent to reduce to quiescence the sensitive flame.
As the skill and knowledge of the experimenter augment he is often able to simplify his experimental combinations. Thus, in the present instance, by the suitable arrangement of the source of sound and the sensitive flame, it was found that not only twenty-five layers, but three or four layers of coal-gas and carbonic acid sufficed to still the agitated flame. Nay, with improved manipulation, the action of a single layer of either gas was rendered perfectly sensible. So also as regards heated layers of air, not only were sixty-six or twenty-two heated platinum wires found sufficient, but the heated air from two or three candle-flames, or even from a single flame, or a heated poker, was found perfectly competent to stop the flame’s agitation. The same remark applies to vapors. Three or four heated layers of air, saturated with the vapor of a volatile liquid, stilled the flame; and, by improved manipulation, the action of a single338 saturated layer could be rendered sensible. In all these cases, moreover, a small, high-pitched reed might be substituted for the bell.
My assistant has devised the simple apparatus sketched in Fig. 147, for showing reflection by gases, vapors, and heated air. At the end A of the square pipe A B is a small vibrating reed of high pitch, the sound of which violently agitates the sensitive flame f. To the horizontal tube g g′ are attached four small burners, and above them four chimneys, through which the heated gases from the flames can ascend into A B. When the coverings of the chimneys are removed and the gas is ignited, the air within A B is rendered rapidly non-homogeneous, and immediately stills the agitated flame.
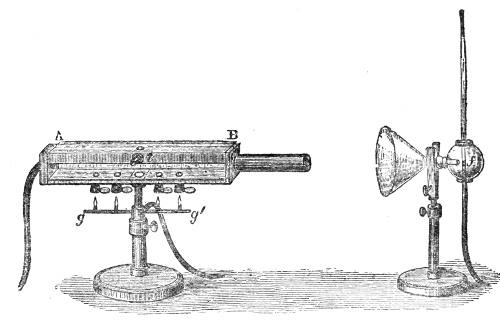
The pipe A B may be turned upside down, an orifice seen between A and B fitting on to the stand which supports the tube. The conduit t leads into a shallow rectangular box, which communicates by a series of trans339verse apertures with A B. When air, saturated with the vapor of a volatile liquid, is forced through these apertures, the atmosphere in A B is immediately rendered heterogeneous, the agitated flame being as rapidly stilled.
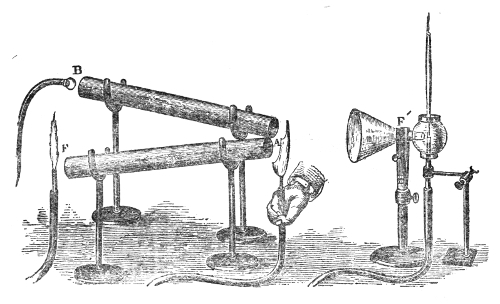
In the experiments at the South Foreland, not only was it proved that the acoustic clouds stopped the sound; but, in the proper position, the sounds which had been refused transmission were received by reflection. I wished very much to render this echoed sound evident experimentally; and stated to my assistant that we ought to be able to accomplish this. Mr. Cottrell met my desire by the following beautiful experiment, which has been thus described before the Royal Society:
A vibrating reed B (Fig. 148) was placed so as to send sound-waves through a tin tube, 38 inches long, and 1-3/4 inch diameter, in the direction B A, the action of the sound being rendered manifest by its causing a sensitive flame placed at F′ to become violently agitated.
“The invisible heated layer immediately above the luminous portion of an ignited coal-gas flame issuing from an ordinary bat’s-wing burner was allowed to stream upward across the end A of the tin tube. A portion of the sound issuing from the tube was reflected at the limiting surfaces of the heated layer; the part transmitted being now only competent to slightly agitate the sensitive flame at F′.
“The heated layer was then placed at such an angle that the reflected portion of the sound was sent through a second tin tube, A F (of the same dimensions as B A). Its action was rendered visible by causing a second sensitive flame placed at the end of the tube at F to become violently affected. This echo continued active as long as the heated layer intervened; but upon its withdrawal the sensitive flame placed at F′, receiving the whole of the direct pulse, became again violently agitated, and at the same moment the sensitive flame at F, ceasing to be affected by the echo, resumed its former tranquillity.
“Exactly the same action takes place when the luminous portion of a gas-flame is made the reflecting layer; but in the experiments above described the invisible layer above the flame only was used. By proper adjustment of the pressure of the gas the flame at F′ can be rendered so moderately sensitive to the direct sound-wave that the portion transmitted through the reflecting layer shall be incompetent to affect the flame. Then by the introduction and withdrawal of the bat’s-wing flame the two sensitive flames can be rendered alternately quiescent and strongly agitated.
“An illustration is here afforded of the perfect analogy between light and sound; for if a beam of light be341 projected from B to F′, and a plate of glass be introduced at A in the exact position of the reflecting layer of gas, the beam will be divided, one portion being reflected in the direction A F, and the other portion transmitted through the glass toward F′, exactly as the sound-wave is divided into a reflected and transmitted portion by the layer of heated gas or flame.”
Thus far, therefore, we have placed our subject in the firm grasp of experiment; nor shall we find this test failing us further on.
INVESTIGATION OF THE CAUSES WHICH HAVE HITHERTO BEEN SUPPOSED EFFECTIVE IN PREVENTING THE TRANSMISSION OF SOUND THROUGH THE ATMOSPHERE
Action of Hail and Rain—Action of Snow—Action of Fog; Observations in London—Experiments on Artificial Fogs—Observations on Fogs at the South Foreland—Action of Wind—Atmospheric Selection—Influence of Sound-Shadow
In the first part of this chapter it was demonstrated that the optic transparency and acoustic transparency of our atmosphere were by no means necessarily coincident; that on days of marvellous optical clearness the atmosphere may be filled with impervious acoustic clouds, while days optically turbid may be acoustically clear. We have now to consider, in detail, the influence of various agents which have hitherto been considered potent in reference to the transmission of sound through the atmosphere.
Derham, and after him all other writers, considered that falling rain tended powerfully to obstruct sound.342 An observation on June 3d has been already referred to as tending to throw doubt on this conclusion. Two other crucial instances will suffice to show its untenability. On the morning of October 8th, at 7.45 A.M., a thunderstorm accompanied by heavy rain broke over Dover. But the clouds subsequently cleared away, and the sun shone strongly on the sea. For a time the optical clearness of the atmosphere was extraordinary, but it was acoustically opaque. At 2.30 P.M. a densely-black scowl again overspread the heavens to the W.S.W. The distance being 6 miles, and all hushed on board, the horn was heard very feebly, the siren more distinctly, while the howitzer was better than either, though not much superior to the siren.
A squall approached us from the west. In the Alps or elsewhere I have rarely seen the heavens blacker. Vast cumuli floated to the N.E. and S.E.; vast streamers of rain descended in the W.N.W.; huge scrolls of cloud hung in the N.; but spaces of blue were to be seen to the N.N.E.
At 7 miles’ distance the siren and horn were both feeble, while the gun sent us a very faint report. A dense shower now enveloped the Foreland.
The rain at length reached us, falling heavily all the way between us and the Foreland; but the sound, instead of being deadened, rose perceptibly in power. Hail was now added to the rain, and the shower reached a tropical violence, the hailstones floating thickly on the flooded deck. In the midst of this furious squall both the horns and the siren were distinctly heard; and as the shower lightened, thus lessening the local pattering, the sounds so rose in power that we heard them at a distance of 7-1/2 miles343 distinctly louder than they had been heard through the rainless atmosphere at 5 miles.
At 4 P.M. the rain had ceased and the sun shone clearly through the calm air. At 9 miles’ distance the horn was heard feebly, the siren clearly, while the howitzer sent us a loud report. All the sounds were better heard at this distance than they had previously been at 5-1/2 miles; from which, by the law of inverse squares, it follows that the intensity of the sound at 5-1/2 miles’ distance must have been augmented at least threefold by the descent of the rain.
On the 23d of October our steamer had forsaken us for shelter, and I sought to turn the weather to account by making other observations on both sides of the fog-signal station. Mr. Douglass, the chief engineer of the Trinity House, was good enough to undertake the observations N.E. of the Foreland; while Mr. Ayers, the assistant engineer, walked in the other direction. At 12.50 P.M. the wind blew a gale, and broke into a thunderstorm with violent rain. Inside and outside the Cornhill Coast-guard Station, a mile from the instruments in the direction of Dover, Mr. Ayers heard the sound of the siren through the storm; and after the rain had ceased, all sounds were heard distinctly louder than before. Mr. Douglass had sent a fly before him to Kingsdown, and the driver had been waiting for fifteen minutes before he arrived. During this time no sound had been heard, though 40 blasts had been blown in the interval; nor had the coast-guard man on duty, a practiced observer, heard any of them throughout the day. During the thunderstorm, and while the rain was actually falling with a violence which Mr. Douglass describes as perfectly344 torrential, the sounds became audible and were heard by all.
To rain, in short, I have never been able to trace the slightest deadening influence upon sound. The reputed barrier offered by “thick weather” to the passage of sound was one of the causes which tended to produce hesitation in establishing sound-signals on our coasts. It is to be hoped that the removal of this error may redound to the advantage of coming generations of seafaring men.
Falling snow, according to Derham, is the most serious obstacle of all to the transmission of sound. We did not extend our observations at the South Foreland into snowy weather; but a previous observation of my own bears directly upon this point. On Christmas night, 1859, I arrived at Chamouni, through snow so deep as to obliterate the road-fences, and to render the labor of reaching the village arduous in the extreme. On the 26th and 27th it fell heavily. On the 27th, during a lull in the storm, I reached the Montavert, sometimes breast deep in snow. On the 28th, with great difficulty, two lines of stakes were set out across the glacier, with the view of determining its winter motion. On the 29th the entry in my journal, written in the morning, is: “Snow, heavy snow; it must have descended through the entire night, the quantity freshly fallen is so great.”
Under these circumstances I planted my theodolite beside the Mer de Glace, having waded to my position through snow, which, being dry, reached nearly to my breast. Assistants were sent across the glacier with instructions to measure the displacement of a transverse345 line of stakes planted previously in the snow. A storm drifted up the valley, darkening the air as it approached. It reached us, the snow falling more heavily than I had ever seen it elsewhere. It soon formed a heap on the theodolite, and thickly covered my own clothes. Here, then, was a combination of snow in the air, and of soft fresh snow on the ground, such as Derham could hardly have enjoyed; still through such an atmosphere I was able to make my instructions audible quite across the glacier, the distance being half a mile, while the experiment was rendered reciprocal by one of my assistants making his voice audible to me.
The flakes here were so thick that it was only at intervals that I was able to pick up the retreating forms of the men. Still the air through which the flakes fell was continuous. Did the flakes merely yield passively to the sonorous waves, swinging like the particles of air themselves to and fro as the sound-waves passed them? Or did the waves bend by diffraction round the flakes, and emerge from them without sensible loss? Experiment will aid us here by showing the astonishing facility with which sound makes its way among obstacles, and passes through tissues, so long as the continuity of the air in their interstices is preserved.
A piece of millboard or of glass, a plank of wood, or the hand, placed across the open end t′ of the tunnel a b c d, Fig. 146 (page 334), intercepts the sound of the bell, placed in the padded box P, and stills the sensitive flame k.
An ordinary cambric pocket-handkerchief, on the other hand, placed across the tunnel-end produced hardly an appreciable effect upon the sound. Through two layers of the handkerchief the flame was strongly agitated; through four layers it was still agitated; while through six layers, though nearly stilled, it was not entirely so.
Dipping the same handkerchief into water, and stretching a single wetted layer across the tunnel-end, it stilled the flame as effectually as the millboard or the wood. Hence the conclusion that the sound-waves in the first instance passed through the interstices of the cambric.
Through a single layer of thin silk the sound passed without sensible interruption; through six layers the flame was strongly agitated; while through twelve layers the agitation was quite perceptible.
A single layer of this silk, when wetted, stilled the flame.
A layer of soft lint produced but little effect upon the sound; a layer of thick flannel was almost equally ineffectual. Through four layers of flannel the flame was perceptibly agitated. Through a single layer of green baize the sound passed almost as freely as through air; through four layers of the baize the action was still sensible. Through a layer of close hard felt, half an inch thick, the sound-waves passed with sufficient energy to sensibly agitate the flame. Through 200 layers of cotton-net the sound passed freely. I did not witness these effects without astonishment.
A single layer of thin oiled silk stopped the sound and stilled the flame. A leaf of common note-paper, or a five-pound note, also stopped the sound.
The sensitive flame is not absolutely necessary to these347 experiments. Let a ticking watch be hung six inches from the ear, a cambric handkerchief dropped between it and the ear scarcely sensibly affects the ticking; a sheet of oil-skin or an intensely heated gas-column cuts it almost wholly off.
But though oiled silk, foreign post, or a banknote, can stop the sound, a film sufficiently thin to yield freely to the aërial pulses transmits it. A thick soap-film produces an obvious effect upon the sensitive flame; a very thin one does not. The augmentation of the transmitted sound may be observed simultaneously with the generation and brightening of the colors which indicate the increasing thinness of the film. A very thin collodion-film acts in the same way.
Acquainted with the foregoing facts regarding the passage of sound through cambric, silk, lint, flannel, baize, felt, and cotton-net, you are prepared for the statement that the sound-waves pass without sensible impediment through heavy artificial showers of rain, hail, and snow. Water-drops, seeds, sand, bran, and flocculi of various kinds, have been employed to form such showers; through all of these, as through the actual rain and hail already described, and through the snow on the Mer de Glace, the sound passes without sensible obstruction.
But the mariner’s greatest enemy, fog, is still to be dealt with; and here for a long time the proper conditions of experiment were absent. Up to the end of November we had had frequent days of haze, sufficiently thick to obscure the white cliffs of the Foreland, but no real fog. Still those cases furnished demonstrative evidence348 that the notions entertained regarding the reflection of sound by suspended particles were wrong; for on many days of the thickest haze the sound covered twice the range attained on other days of perfect optical transparency. Such instances dissolved the association hitherto assumed to exist between acoustic transparency and optic transparency, but they left the action of dense fogs undetermined.
On December 9th a memorable fog settled down on London. I addressed a telegram to the Trinity House suggesting some gun observations. With characteristic promptness came the reply that they would be made in the afternoon at Blackwall. I went to Greenwich in the hope of hearing the guns across the river; but the delay of the train by the fog rendered my arrival too late. Over the river the fog was very dense, and through it came various sounds with great distinctness. The signal-bell of an unseen barge rang clearly out at intervals, and I could plainly hear the hammering at Cubitt’s Town, half a mile away, on the opposite side of the river. No deadening of the sound by the fog was apparent.
Through this fog and various local noises, Captain Atkins and Mr. Edwards heard the report of a 12-pounder carronade with a 1-lb. charge distinctly better than the 18-pounder with a 3-lb. charge, an optically clear atmosphere, and all noises absent, on July 3d.
Anxious to turn to the best account a phenomenon for which we had waited so long, I tried to grapple with the problem by experiments on a small scale. On the 10th, I stationed my assistant with a whistle and organ-pipe on the walk below the southwest end of the bridge dividing Hyde Park from Kensington Gardens. From349 the eastern end of the Serpentine I heard distinctly both the whistle and the pipe, which produced 380 waves a second. On changing places with my assistant, I heard for a time the distinct blast of the whistle only. The deeper note of the organ-pipe at length reached me, rising sometimes to great distinctness, and sometimes falling to inaudibility. The whistle showed the same intermittence as to period, but in an opposite sense; for, when the whistle was faint, the pipe was strong, and vice versa. To obtain the fundamental note of the pipe, it had to be blown gently, and on the whole the whistle proved the most efficient in piercing the fog.
An extraordinary amount of sound filled the air during these experiments. The resonant roar of the Bayswater and Knightsbridge roads; the clangor of the great bell of Westminster; the railway-whistles, which were frequently blown, and the fog-signals exploded at the various metropolitan stations, were all heard with extraordinary intensity. This could by no means be reconciled with the statements so categorically made regarding the acoustic impenetrability of a London fog.
On the 11th of December, the fog being denser than before, I heard every blast of the whistle, and occasional blasts of the pipe, over the distance between the bridge and the eastern end of the Serpentine. On joining my assistant at the bridge, the loud concussion of a gun was heard by both of us. A police-inspector affirmed that it came from Woolwich, and that he had heard several shots about 2 P.M. and previously. The fact, if a fact, was of the highest importance; so I immediately telegraphed to Woolwich for information. Prof. Abel kindly furnished me with the following particulars:
“The firing took place at 1.40 P.M. The guns proved were of comparatively small size—64-pounders, with 10-lb. charges of powder.
“The concussion experienced at my house and office, about three-quarters of a mile from the butt, was decidedly more severe than that experienced when the heaviest guns are proved with charges of 110 to 120 lbs. of powder. There was a dense fog here at the time of firing.”
These were the guns heard by the police-inspector; on subsequent inquiry it was ascertained that two guns were fired about 3 P.M. These were the guns heard by myself.
Prof. Abel also communicated to me the following fact: “Our workman’s bell at the Arsenal Gate, which is of moderate size and anything but clear in tone, is pretty distinctly heard by Prof. Bloxam only when the wind is northeast. During the whole of last week the bell was heard with great distinctness, the wind being southwesterly (opposed to the sound). The distance of the bell from Bloxam’s house is about three-quarters of a mile as the crow flies.”
Assuredly no question of science ever stood so much in need of revision as this of the transmission of sound through the atmosphere. Slowly, but surely, we mastered the question; and the further we advanced, the more plainly it appeared that our reputed knowledge regarding it was erroneous from beginning to end.
On the morning of the 12th the fog attained its maximum density. It was not possible to read at my window, which fronted the open western sky. At 10.30 I sent an assistant to the bridge, and listened for his whistle and pipe at the eastern end of the Serpentine. The whistle351 rose to a shrillness far surpassing anything previously heard, but it sank sometimes almost to inaudibility; proving that, though the air was on the whole highly homogeneous, acoustic clouds still drifted through the fog. A second pipe, which was quite inaudible yesterday, was plainly heard this morning. We were able to discourse across the Serpentine to-day with much greater ease than yesterday.
During our summer observations I had once or twice been able to fix the position of the Foreland in thick haze by the direction of the sound. To-day my assistant, hidden by the fog, walked up to the Watermen’s Boathouse sounding his whistle; and I walked along the opposite side of the Serpentine, clearly appreciating for a time that the line joining us was oblique to the axis of the river. Coming to a point which seemed to be exactly abreast of him, I marked it; and on the following day, when the fog had cleared away, the marked position was found to be perfectly exact. When undisturbed by echoes, the ear, with a little practice, becomes capable of fixing with great precision the direction of a sound.
On reaching the Serpentine this morning, a peal of bells, which then began to ring, seemed so close at hand that it required some reflection to convince me that they were ringing to the north of Hyde Park. The sounds fluctuated wonderfully in power. Prior to the striking of eleven by the great bell of Westminster, a nearer bell struck with loud clangor. The first five strokes of the Westminster bell were afterward heard, one of them being extremely loud; but the last six strokes were inaudible. An assistant was stationed to attend to the 12352 o’clock bells. The clock which had struck so loudly at 11 was unheard at 12, while of the Westminster bell eight strokes out of twelve were inaudible. To such astonishing changes is the atmosphere liable.
At 7 P.M. the Westminster bell, striking seven, was not at all heard from the Serpentine, while the nearer bell already alluded to was heard distinctly. The fog had cleared away, and the lamps on the bridge could be seen from the eastern end of the Serpentine burning brightly; but, instead of the sound sharing the improvement of the light, what might be properly called an acoustic fog took the place of its optical predecessor. Several series of the whistle and organ-pipe were sounded in succession; one series only of the whistle-sounds was heard, all the others being quite inaudible. Three series of the organ-pipe were heard, but very faintly. On reversing the positions and sounding as before, nothing whatever was heard.
At 8 o’clock the chimes and hour-bell of the Westminster clock were both very loud. The “acoustic fog” had shifted its position, or temporarily melted away.
Extraordinary fluctuations were also observed in the case of the church-bells heard in the morning: in a few seconds they would sink from a loudly ringing-peal into utter silence, from which they would rapidly return to loud-tongued audibility. The intermittent drifting of fog over the sun’s disk (by which his light is at times obscured, at times revealed) is the optical analogue of these effects. As regards such changes, the acoustic deportment of the atmosphere is a true transcript of its optical deportment.
At 9 P.M. three strokes only of the Westminster clock353 were heard; the others were inaudible. The air had relapsed in part into its condition at 7 P.M., when all the strokes were unheard. The quiet of the park this evening, as contrasted with the resonant roar which filled the air on the two preceding days, was very remarkable. The sound, in fact, was stifled in the optically clear but acoustically flocculent atmosphere.
On the 13th, the fog being displaced by thin haze, I went again to the Serpentine. The carriage-sounds were damped to an extraordinary degree. The roar of the Knightsbridge and Bayswater roads had subsided, the tread of troops which passed us a little way off was unheard, while at 11 A.M. both the chimes and the hour-bell of the Westminster clock were stifled. Subjectively considered, all was favorable to auditory impressions; but the very cause that damped the local noises extinguished our experimental sounds. The voice across the Serpentine to-day, with my assistant plainly visible in front of me, was distinctly feebler than it had been when each of us was hidden from the other in the densest fog.
Placing the source of sound at the eastern end of the Serpentine I walked along its edge from the bridge toward the end. The distance between these two points is about 1,000 paces. After 500 of them had been stepped, the sound was not so distinct as it had been at the bridge on the day of densest fog; hence, by the law of inverse squares, the optical cleansing of the air through the melting away of the fog had so darkened it acoustically that a sound generated at the eastern end of the Serpentine was lowered to one-fourth of its intensity at a point midway between the end and the bridge.
To these demonstrative observations one or two sub354sequent ones may be added. On several of the moist and warm days, at the beginning of 1874, I stood at noon beside the railing of St. James’s Park, near Buckingham Palace, three-quarters of a mile from the clock-tower, which was clearly visible. Not a single stroke of “Big Ben” was heard. On January 19th fog and drizzling rain obscured the tower; still from the same position I not only heard the strokes of the great bell, but also the chimes of the quarter-bells.
During the exceedingly dense and “dripping” fog of January 22d, from the same railings, I heard every stroke of the bell. At the end of the Serpentine, when the fog was densest, the Westminster bell was heard striking loudly eleven. Toward evening this fog began to melt away, and at 6 o’clock I went to the end of the Serpentine to observe the effect of the optical clearing upon the sound. Not one of the strokes reached me. At 9 o’clock and at 10 o’clock my assistant was in the same position, and on both occasions he failed to hear a single stroke of the bell. It was a case precisely similar to that of December 13th, when the dissolution of the fog was accompanied by a decided acoustic thickening of the air.66
Satisfactory, and indeed conclusive, as these results seemed, I desired exceedingly to confirm them by experiments with the instruments actually employed at the South Foreland. On the 10th of February I had the 355gratification of receiving the following note and inclosure from the Deputy Master of Trinity House:
“My dear Tyndall—The inclosed will show how accurately your views have been verified, and I send them on at once without waiting for the details. I think you will be glad to have them, and as soon as I get the report it shall be sent to you. I made up my mind ten days ago that there would be a chance in the light foggy-disposed weather at home, and therefore sent the ‘Argus’ off at an hour’s notice, and requested the Fog Committee to keep one member on board. On Friday I was so satisfied that the fog would occur that I sent Edwards down to record the observations.
“Very truly yours,
“Fred. Arrow.”
The inclosure referred to was notes from Captain Atkins and Mr. Edwards. Captain Atkins writes thus:
“As arranged, I came down here by the mail express, meeting Mr. Edwards at Cannon Street. We put up at the Dover Castle, and next morning at 7 I was awoke by sounds of the siren. On jumping up I discovered that the long-looked-for fog had arrived, and that the ‘Argus’ had left her moorings.
“However, had I been on board, the instructions I left with Troughton (the master of the ‘Argus’) could not have been better carried out. About noon the fog cleared up, and the ‘Argus’ returned to her moorings, when I learned that they had taken both siren and horn sounds to a distance of 11 miles from the station, where they dropped a buoy. This I knew to be correct, as I have this morning recovered the buoy, and the distances both356 in and out agree with Troughton’s statement. I have also been to the Varne light-ship (12-3/4 miles from the Foreland), and ascertained that during the fog of Saturday forenoon they ‘distinctly’ heard the sounds.”
Mr. Edwards, who was constantly at my side during our summer and autumn observations, and who is thoroughly competent to form a comparative estimate of the strength of the sounds, states that those of the 7th were “extraordinarily loud,” both Captain Atkins and himself being awoke by them. He does not remember ever before hearing the sounds so loud in Dover; it seemed as though the observers were close to the instruments.
Other days of fog preceded this one, and they were all days of acoustic transparency, the day of densest fog being acoustically the clearest of all.
The results here recorded are of the highest importance, for they bring us face to face with a dense fog and an actual fog-signal, and confirm in the most conclusive manner the previous observations. The fact of Captain Atkins and Mr. Edwards being awakened by the siren proves, beyond all our previous experience, its power during this dense fog.
It is exceedingly interesting to compare the transmission of sound on February 7th with its transmission on October 14th. The wind on both days had the same strength and direction. My notes of the observations show the latter to have been throughout a day of extreme optical clearness. The range was 10 miles. During the fog of February 7th the “Argus” heard the sound at 11 miles; and it was also heard at the Varne light-vessel, which is 12-3/4 miles from the Foreland.
It is also worthy of note that through the same fog the sounds were well heard at the South Sand Head light-vessel, which is in the opposite direction from the South Foreland, and was actually behind the siren. For this important circumstance is to be borne in mind: on February 7th the siren happened to be pointed, not toward the “Argus,” but toward Dover. Had the yacht been in the axis of the instrument it is highly probable that the sound would have been heard all the way across to the coast of France.
It is hardly necessary for me to say a word to guard myself against the misconception that I consider sound to be assisted by the fog itself. The fog-particles have no more influence upon the waves of sound than the suspended particles stirred up over the banks of Newfoundland have upon the waves of the Atlantic. A homogeneous air is the usual associate of fog, and hence the acoustic clearness of foggy weather.
These observations are clinched and finished by being brought within the range of laboratory experiment. Here we shall learn incidentally a lesson as to the caution required from an experimenter.
The smoke from smouldering brown paper was allowed to stream upward through its rectangular apertures, into the tunnel a b c d (Fig. 146); the action upon the sound-waves was strong, rendering the short and agitated sensitive flame k tall and quiescent.
Air first passed through ammonia, then through hydrochloric acid, and, thus loaded with thick fumes, was sent into the tunnel; the agitated flame was rendered imme358diately quiescent, indicating a very decided action on the part of the artificial fog.
Air passed through perchloride of tin and sent into the tunnel produced exceedingly dense fumes. The action upon the sound-waves was very strong.
The dense smoke of resin, burned before the open end of the tunnel, and blown into it with a pair of bellows, had also the effect of stopping the sound-waves, so as to still the agitated flame.
The conclusion seems clear, and its perfect harmony with the prevalent à priori notions as to the action of fog upon sound makes it almost irresistible. But caution is here necessary. The smoke of the brown paper was hot; the flask containing the hydrochloric acid was hot; that containing the perchloride of tin was hot; while the resin fumes produced by a red-hot poker were also obviously hot. Were the results, then, due to the fumes or to the differences of temperature? The observations might well have proved a trap to an incautious reasoner.
Instead of the smoke and heated air, the heated air alone from four red-hot pokers was permitted to stream upward into the tunnel; the action on the sound-waves was very decided, though the tunnel was optically empty. The flame of a candle was placed at the upper end, and the hot air just above its tip was blown into the tunnel; the action on the sensitive flame was decided. A similar effect was produced when the air, ascending from a red-hot iron, was blown into the tunnel.
In these latter cases the tunnel remained optically clear, while the same effect as that produced by the resin, smoke, and fumes was observed. Clearly, then, we are not entitled to ascribe, without further investigation, to359 the artificial fog an effect which may have been due to the air which accompanied it.
Having eliminated the fog and proved the non-homogeneous air effective, our reasoning will be completed by eliminating the heat, and proving the fog ineffective.
Instead of the tunnel a b c d, Fig. 146, a cupboard with glass sides, 3 feet long, 2 feet wide, and about 5 feet high, was filled with fumes of various kinds. Here it was thought the fumes might remain long enough for differences of temperature to disappear. Two apertures were made in two opposite panes of glass 3 feet asunder. In front of one aperture was placed the bell in its padded box, and behind the other aperture, and at some distance from it, the sensitive flame.
Phosphorus placed in a cup floating on water was ignited within the closed cupboard. The fumes were so dense that considerably less than the three feet traversed by the sound extinguished totally a bright candle-flame.
At first there was a slight action upon the sound; but this rapidly vanished, the flame being no more affected than if the sound had passed through pure air. The first action was manifestly due to differences of temperature, and it disappeared when the temperature was equalized.
The cupboard was next filled with the dense fumes of gunpowder. At first there was a slight action; but this disappeared even more rapidly than in the case of the phosphorus, the sound passing as if no fumes were there. It required less than half a minute to abolish the action in the case of the phosphorus, but a few seconds sufficed in the case of the gunpowder. These fumes were far more than sufficient to quench the candle-flame.
The dense smoke of resin, when the temperature had become equable, exerted no action on the sound.
The fumes of gum-mastic were equally ineffectual.
The fumes of the perchloride of tin, though of extraordinary density, exerted no sensible effect upon the sound.
Exceedingly dense fumes of chloride of ammonium next filled the cupboard. A fraction of the length of the 3-foot tube sufficed to quench the candle-flame. Soon after the cupboard was filled, the sound passed without the least sensible deterioration. An aperture at the top of the cupboard was opened; but though a dense smoke-column ascended through it, many minutes elapsed before the candle-flame could be seen through the attenuated fog.
Steam from a copper boiler was so copiously admitted into the cupboard as to fill it with a dense cloud. No real cloud was ever so dense; still the sound passed through it without the least sensible diminution. This being the case, cloud-echoes are not a likely phenomenon.
In all of these cases, when a couple of Bunsen’s burners were ignited within the cupboard containing the fumes, less than a minute’s action rendered the air so heterogeneous that the sensitive flame was completely stilled.
These acoustically inactive fogs were subsequently proved competent to cut off the electric light.
Experiment and observation go, therefore, hand in hand in demonstrating that fogs have no sensible action upon sound. The notion of their impenetrability, which so powerfully retarded the introduction of phonic coast-signals, being thus abolished, we have solid ground for361 the hope that disasters due to fogs and thick weather will in the future be materially mitigated.
In stormy weather we were frequently forsaken by our steamer, which had to seek shelter in the Downs or Margate Roads, and on such occasions the opportunity was turned to account to determine the effect of the wind. On October 11th, accompanied by Mr. Douglass and Mr. Edwards, I walked along the cliffs from Dover Castle toward the Foreland, the wind blowing strongly against the sound. About a mile and a half from the Foreland, we first heard the faint but distinct sound of the siren. The horn-sound was inaudible. A gun fired during our halt was also unheard.
As we approached the Foreland we saw the smoke of a gun. Mr. Edwards heard a faint crack, but neither Mr. Douglass nor I heard anything. The sound of the siren was at the same time of piercing intensity. We waited for ten minutes, when another gun was fired. The smoke was at hand, and I thought I heard a faint thud, but could not be certain. My companions heard nothing. On pacing the distance afterward we were found to be only 550 yards from the gun. We were shaded at the time by a slight eminence from both the siren and the gun, but this could not account for the utter extinction of the gun-sound at so short a distance, and at a time when the siren sent to us a note of great power.
Mr. Ayres at my request walked windward along the cliff, while Mr. Douglass proceeded to St. Margaret’s Bay. During their absence I had three guns fired. Mr. Ayres heard only one of them. Favored by the wind, Mr.362 Douglass, at twice the distance, and far more deeply immersed in the sound-shadow, heard all three reports with the utmost distinctness.
Joining Mr. Douglass, we continued our walk to a distance of three-quarters of a mile beyond St. Margaret’s Bay. Here, being dead to leeward, though the wind blew with unabated violence, the sound of the siren was borne to us with extraordinary power.67 In this position we also heard the gun loudly, and two other loud reports at the proper interval of ten minutes, as we returned to the Foreland.
It is within the mark to say that the gun on October 11th was heard five times, and might have been heard fifteen times, as far to leeward as to windward.
In windy weather the shortness of its sound is a serious drawback to the use of the gun as a signal. In the case of the horn and siren, time is given for the attention to be fixed upon the sound; and a single puff, while cutting out a portion of the blast, does not obliterate it wholly. Such a puff, however, may be fatal to the momentary gun-sound.
On the leeward side of the Foreland, on the 23d of October, the sounds were heard at least four times as far as on the windward side, while in both directions the siren possessed the greatest penetrative power.
On the 24th the wind shifted to E.S.E., and the sounds, which, when the wind was W.S.W., failed to reach Dover, were now heard in the streets through thick rain. On the 27th the wind was E.N.E. In our writing-room in the Lord Warden Hotel, in the bed363rooms, and on the staircase, the sound of the siren reached us with surprising power, piercing through the whistling and moaning of the wind, which blew through Dover toward Folkestone. The sounds were heard by Mr. Edwards and myself at 6 miles from the Foreland on the Folkestone road; and had the instruments not then ceased sounding, they might have been heard much further. At the South Sand Head light-vessel, 3-3/4 miles on the opposite side, no sound had been heard throughout the day. On the 28th, the wind being N. by E., the sounds were heard in the middle of Folkestone, 8 miles off, while in the opposite direction they failed to reach 3-3/4 miles. On the 29th the limits of range were Eastware Bay on the one side, and Kingsdown on the other; on the 30th the limits were Kingsdown on the one hand, and Folkestone Pier on the other. With a wind having a force of 4 or 5 it was a very common observation to hear the sound in one direction three times as far as in the other.
This well-known effect of the wind is exceedingly difficult to explain. Indeed, the only explanation worthy of the name is one offered by Prof. Stokes, and suggested by some remarkable observations of De la Roche. In Vol. I. of “Annales de Chimie” for 1816, p. 176, Arago introduces De la Roche’s memoir in these words: “L’auteur arrive à des conclusions, qui d’abord pourront paraître paradoxales, mais ceux qui savent combien il mettait de soins et d’exactitude dans toutes ses recherches se garderont sans doute d’opposer une opinion populaire à des expériences positives.” The strangeness of De la Roche’s results consisted in his establishing, by quantitative measurements, not only that sound has a greater range in the direction of the wind than in the364 opposite direction, but that the range at right angles to the wind is the maximum.
In a short but exceedingly able communication, presented to the British Association in 1857, the eminent physicist above mentioned points out a cause which, if sufficient, would account for the results referred to. The lower atmospheric strata are retarded by friction against the earth, and the upper ones by those immediately below them; the velocity of transition, therefore, in the case of wind, increases from the ground upward. It may be proved that this difference of velocity tilts the sound-wave upward in a direction opposed to, and downward in a direction coincident with, the wind. In this latter case the direct wave is reinforced by the wave reflected from the earth. Now the reinforcement is greatest in the direction in which the direct and reflected waves inclose the smallest angle; and this is at right angles to the direction of the wind. Hence the greater range in this direction. It is not, therefore, according to Prof. Stokes, a stifling of the sound to windward, but a tilting of the sound-wave over the heads of the observers, that defeats the propagation in that direction.
This explanation calls for verification, and I wished much to test it by means of a captive balloon rising high enough to catch the deflected wave; but on communicating with Mr. Coxwell, who has earned for himself so high a reputation as an aeronaut, and who has always shown himself so willing to promote a scientific object, I learned with regret that the experiment was too dangerous to be carried out.68
It has been stated that the atmosphere on different days shows preferences to different sounds. This point is worthy of further illustration.
After the violent shower which passed over us on October 18th, the sounds of all the instruments, as already stated, rose in power; but it was noticed that the horn-sound, which was of lower pitch than that of the siren, improved most, at times not only equalling, but surpassing, the sound of its rival. From this it might be inferred that the atmospheric change produced by the rain favored more especially the transmission of the longer sonorous waves.
But our programme enabled us to go further than mere inference. It had been arranged on the day mentioned that up to 3.30 P.M. the siren should perform 2,400 revolutions a minute, generating 480 waves a second. As long as this rate continued, the horn, after the shower, had the advantage. The rate of rotation was then changed to 2,000 a minute, or 400 waves a second, when the siren-sound immediately surpassed that of the horn. A clear connection was thus established between aërial reflection and the length of the sonorous waves.
The 10-inch Canadian whistle being capable of adjustment so as to produce sounds of different pitch, on the 10th of October I ran through a series of its sounds. The shrillest appeared to possess great intensity and penetrative power. The belief is common that a note of this character (which affects so powerfully, and even painfully, an observer close at hand) has also the greatest range. Mr. A. Gordon, in his examination before the366 Committee on Lighthouses, in 1845, expressed himself thus: “When you get a shrill sound, high in the scale, that sound is carried much further than a lower note in the scale.” I have heard the same opinion expressed by other scientific men.
On the 14th of October the point was submitted to an experimental test. It had been arranged that up to 11.30 A.M. the Canadian whistle, which had been heard with such piercing intensity on the 10th, should sound its shrillest note. At the hour just mentioned we were beside the Varne buoy, 7-3/4 miles from the Foreland. The siren, as we approached the buoy, was heard through the paddle-noises; the horns were also heard, but more feebly than the siren. We paused at the buoy and listened for the 11.30 gun. Its boom was heard by all. Neither before nor during the pause was the shrill-sounding Canadian whistle once heard. At the appointed time it was adjusted to produce its ordinary low-pitched note, which was immediately heard. Further out the low boom of the cannon continued audible after all the other sounds had ceased.
But it was only during the early part of the day that this preference for the longer wave was manifested. At 3 P.M. the case was completely altered, for then the high-pitched siren was heard when all the other sounds were inaudible. On many other days we had illustrations of the varying comparative power of the siren and the gun. On the 9th of October sometimes the one, sometimes the other, was predominant. On the morning of the 13th the siren was clearly heard on Shakespeare’s Cliff, while two guns with their puffs perfectly visible were unheard. On October 16th, 2 miles from the signal-station, the gun367 at 11 o’clock was inferior to the siren, but both were heard. At 12.30, the distance being 6 miles, the gun was quite unheard, while the siren continued faintly audible. Later on in the day the experiment was twice repeated. The puff of the gun was in each case seen, but nothing was heard. In the last experiment, when the gun was quenched, the siren sent forth a sound so strong as to maintain itself through the paddle-noises. The day was clearly hostile to the passage of the longer sonorous waves.
October 17th began with a preference for the shorter waves. At 11.30 A.M. the mastery of the siren over the gun was pronounced; at 12.30 the gun slightly surpassed the siren; at 1, 2, and 2.30 P.M. the gun also asserted its mastery. This preference for the longer waves was continued on October 18th. On October 20th the day began in favor of the gun, then both became equal, and finally the siren gained the mastery; but the day had become stormy, and a storm is always unfavorable to the momentary gun-sound. The same remark applies to the experiments of October 21st. At 11 A.M., distance 6-1/2 miles, when the siren made itself heard through the noises of wind, sea, and paddles, the gun was fired; but, though listened for with all attention, no sound was heard. Half an hour later the result was the same. On October 24th five observers saw the flash of the gun at a distance of 5 miles, but heard nothing; all of them at this distance heard the siren distinctly; a second experiment on the same day yielded the same result. On the 27th also the siren was triumphant; and on three distinct occasions on the 29th its mastery over the gun was very decided.
Such experiments yield new conceptions as to the368 scattering of sound in the atmosphere. No sound here employed is a simple sound; in every case the fundamental note is accompanied by others, and the action of the atmosphere on these different groups of waves has its optical analogue in that scattering of the waves of the luminiferous ether which produces the various shades and colors of the sky.
A few additional remarks and suggestions will fitly wind up this chapter. It has been proved that in some states of the weather the howitzer firing a 3-lb. charge commands a larger range than the whistles, trumpets, or siren. This was the case, for example, on the particular day, October 17th, when the ranges of all the sounds reached their maximum.
On many other days, however, the inferiority of the gun to the siren was demonstrated in the clearest manner. The gun-puffs were seen with the utmost distinctness at the Foreland, but no sound was heard, the note of the siren at the same time reaching us with distinct and considerable power.
The disadvantages of the gun are these:
a. The duration of the sound is so short that, unless the observer is prepared beforehand, the sound, through lack of attention rather than through its own powerlessness, is liable to be unheard.
b. Its liability to be quenched by a local sound is so great that it is sometimes obliterated by a puff of wind taking possession of the ears at the time of its arrival. This point was alluded to by Arago, in his report on the celebrated experiments of 1822. By such a puff a mo369mentary gap is produced in the case of a continuous sound, but not entire extinction.
c. Its liability to be quenched or deflected by an opposing wind, so as to be practically useless at a very short distance to windward, is very remarkable. A case has been cited in which the gun failed to be heard against a violent wind at a distance of 550 yards from the place of firing, the sound of the siren at the same time reaching us with great intensity.
Still, notwithstanding these drawbacks, I think the gun is entitled to rank as a first-class signal. I have had occasion myself to observe its extreme utility at Holyhead and the Kish light-vessel near Kingstown. The commanders of the Holyhead boats, moreover, are unanimous in their commendation of the gun. An important addition in its favor is the fact that in a fog the flash or glare often comes to the aid of the sound. On this point, the evidence is quite conclusive.
There may be cases in which the combination of the gun with one of the other signals may be desirable. Where it is wished to confer an unmistakable individuality on a fog-signal station, such a combination might with advantage be resorted to.
If the gun be retained as one form of fog-signal (and I should be sorry at present to recommend its total abolition), it ought to be of the most suitable description. Our experiments prove the sound of the gun to be dependent on its shape; but we do not know that we have employed the best shape. This suggests the desirability of constructing a gun with special reference to the production of sound.69
An absolutely uniform superiority on all days cannot be conceded to any one of the instruments subjected to examination; still, our observations have been so numerous and long-continued as to enable us to come to the sure conclusion, that, on the whole, the steam-siren is the most powerful fog-signal which has hitherto been tried in England. It is specially powerful when local noises, such as those of wind, rigging, breaking waves, shore-surf, and the rattle of pebbles, have to be overcome. Its density, quality, pitch, and penetration, render it dominant over such noises after all other signal-sounds have succumbed.
I have not, therefore, hesitated to recommend the introduction of the siren as a coast-signal.
It will be desirable in each case to confer upon the instrument a power of rotation, so as to enable the person in charge of it to point its trumpet against the wind or in any other required direction. This arrangement was made at the South Foreland, and it presents no mechanical difficulty. It is also desirable to mount the siren, so as to permit of the depression of its trumpet fifteen or twenty degrees below the horizon.
In selecting the position at which a fog-signal is to be mounted, the possible influence of a sound-shadow, and the possible extinction of the sound by the interference of the direct waves with waves reflected from the shore, must form the subject of the gravest consideration. Preliminary trials may, in most cases, be necessary before fixing on the precise point at which the instrument is to be placed.
The siren which has been long known to scientific men is worked with air; and it would be worth while371 to try how the fog-siren would behave supposing compressed air to be substituted for steam. Compressed air might also be tried with the whistles.
No fog-signal hitherto tried is able to fulfil the condition laid down in a very able letter already referred to, namely, “that all fog-signals should be distinctly audible for at least 4 miles, under every circumstance.” Circumstances may exist to prevent the most powerful sound from being heard at half this distance. What may with certainty be affirmed is, that in almost all cases the siren may certainly be relied on at a distance of 2 miles; in the great majority of cases it may be relied upon at a distance of 3 miles, and in the majority of cases to a distance greater than 3 miles.
Happily the experiments thus far made are perfectly concurrent in indicating that at the particular time when fog-signals are needed, the air holding the fog in suspension is in a highly-homogeneous condition; hence it is in the highest degree probable that in the case of fog we may rely upon the signals being effective at far greater distances than those just mentioned.
I am cautious not to inspire the mariner with a confidence which may prove delusive. When he hears a fog-signal he ought, as a general rule (at all events until extended experience justifies the contrary), to assume the source of sound to be not more than 2 or 3 miles distant, and to heave his lead or to take other necessary precautions. If he errs at all in his estimate of distance, it ought to be on the side of safety.
With the instruments now at our disposal wisely established along our coasts, I venture to think that the saving of property in ten years will be an exceedingly372 large multiple of the outlay necessary for the establishment of such signals. The saving of life appeals to the higher motives of humanity.
In a report written for the Trinity House on the subject of fog-signals, my excellent predecessor, Prof. Faraday, expresses the opinion that a false promise to the mariner would be worse than no promise at all. Casting our eyes back upon the observations here recorded, we find the sound-range on clear, calm days varying from 2-1/2 miles to 16-1/2 miles. It must be evident that an instruction founded on the latter observation would be fraught with peril in weather corresponding to the former. Not the maximum but the minimum sound-range should be impressed upon the mariner. Want of attention to this point may be followed by disastrous consequences.
This remark is not made without cause. I have before me a “Notice to Mariners” regarding a fog-whistle recently mounted at Cape Race, which is reputed to have a range of 20 miles in calm weather, 30 miles with the wind, and in stormy weather or against the wind 7 to 10 miles. Now, considering the distance reached by sound in our observations, I should be willing to concede the possibility, in a more homogeneous atmosphere than ours, of a sound-range on some calm days of 20 miles, and on some light windy days of 30 miles, to a powerful whistle; but I entertain a strong belief that the stating of these distances, or of the distance 7 to 10 miles against a storm, without any qualification, is calculated to inspire the mariner with false confidence. I would venture to affirm that at Cape Race calm days might be found in which the range of the sound will be less than one-fourth373 of what this notice states it to be. Such publications ought to be without a trace of exaggeration, and furnish only data on which the mariner may with perfect confidence rely. My object in extending these observations over so long a period was to make evident to all how fallacious it would be, and how mischievous it might be, to draw general conclusions from observations made in weather of great acoustic transparency.
Thus ends, for the present at all events, an inquiry which I trust will prove of some importance, scientific as well as practical. In conducting it I have had to congratulate myself on the unfailing aid and co-operation of the Elder Brethren of the Trinity House. Captain Drew, Captain Close, Captain Were, Captain Atkins, and the Deputy Master, have all from time to time taken part in the inquiry. To the eminent arctic navigator, Admiral Collinson, who showed throughout unflagging and, I would add, philosophic interest in the investigation, I am indebted for most important practical aid. He was almost always at my side, comparing opinions with me, placing the steamer in the required positions, and making with consummate skill and promptness the necessary sextant observations. I am also deeply sensible of the important services rendered by Mr. Douglass, the able and indefatigable engineer, by Mr. Ayres, the assistant engineer, and by Mr. Price Edwards, the private secretary of the Deputy Master of the Trinity House.
The officers and gunners at the South Foreland also merit my best thanks, as also Mr. Holmes and Mr. Laidlaw, who had charge of the trumpets, whistles, and siren.
In the subsequent experimental treatment of the sub374ject I have been most ably aided by my excellent assistant, Mr. John Cottrell.
NOTE
In the Appendix will be found a brief paper on “Acoustic Reversibility,” in which I offer a solution of a difficulty encountered by the French philosophers in their experiments on the velocity of sound in 1822. The solution is based on the experiments and observations recorded in the foregoing chapter.—J. T.
The paper of Dr. Derham, published in the “Philosophical Transactions” for 1708, has been hitherto the almost exclusive source of our knowledge of the causes which affect the transmission of sound through the atmosphere.
Derham found that fog obstructed sound, that rain and hail obstructed sound, but that above all things falling snow, or a coating of fresh snow upon the ground, tended to check the propagation of sound through the atmosphere.
With a view to the protection of life and property at sea in the years 1873 and 1874, this subject received an exhaustive examination, observational and experimental. The investigation was conducted at the expense of the Government and under the auspices of the Elder Brethren of the Trinity House.
The most conflicting results were at first obtained. On the 19th of May, 1873, the sound range was 3-1/3 miles; on the 20th it was 5-1/2 miles; on the 2d of June, 6 miles; on the 3d, more than 9 miles; on the 10th, 9 miles; on the 25th, 6 miles; on the 26th, 9-1/4 miles; on the 1st of July, 12-3/4 miles; on the 2d, 4 miles; while on the 3d,375 with a clear calm atmosphere and smooth sea, it was less than 3 miles.
These discrepancies were proved to be due to a state of the air which bears the same relation to sound that cloudiness does to light. By streams of air differently heated, or saturated in different degrees with aqueous vapors, the atmosphere is rendered flocculent to sound.
Acoustic clouds, in fact, are incessantly floating or flying through the air. They have nothing whatever to do with ordinary clouds, fogs, or haze. The most transparent atmosphere may be filled with them; converting days of extraordinary optical transparency into days of equally extraordinary acoustic opacity.
The connection hitherto supposed to exist between a clear atmosphere and the transmission of sound is therefore dissolved.
The intercepted sound is wasted by repeated reflections in the acoustic cloud, as light is wasted by repeated reflections in an ordinary cloud. And as from the ordinary cloud the light reflected reaches the eye, so from the perfectly invisible acoustic cloud the reflected sound reaches the ear.
Aërial echoes of extraordinary intensity and of long duration are thus produced. They occur, contrary to the opinion hitherto entertained, in the clearest air.
It is to the wafting of such acoustic clouds through the atmosphere that the fluctuations in the sounds of our public clocks and of church-bells are due.
The existence of these aërial echoes has been proved both by observation and experiment. They may arise either from air-currents differently heated, or from air-currents differently saturated with vapor.
Rain has no sensible power to obstruct sound.
Hail has no sensible power to obstruct sound.
Snow has no sensible power to obstruct sound.
Fog has no sensible power to obstruct sound.
The air associated with fog is, as a general rule, highly homogeneous and favorable to the transmission of sound. The notions hitherto entertained regarding the action of fog are untenable.
Experiments on artificial showers of rain, hail, and snow, and on artificial fogs of extraordinary density, confirm the results of observation.
As long as the air forms a continuous medium the amount of sound scattered by small bodies suspended in it is astonishingly small.
This is illustrated by the ease with which sound traverses layers of calico, cambric, silk, flannel, baize, and felt. It freely passes through all these substances in thicknesses sufficient to intercept the light of the sun.
Through six layers of thin silk, for example, it passes with little obstruction; it finds its way through a layer of close felt half an inch thick, and it is not wholly intercepted by 200 layers of cotton-net.
The atmosphere exercises a selective choice upon the waves of sound which varies from day to day, and even from hour to hour. It is sometimes favorable to the transmission of the longer, and at other times favorable to the transmission of the shorter, sonorous waves.
The recognized action of the wind has been confirmed by this investigation.
Law of Vibratory Motions in Water and Air—Superposition of Vibrations—Interference of Sonorous Waves—Destruction of Sound by Sound—Combined Action of Two Sounds nearly in Unison with each other—Theory of Beats—Optical Illustration of the Principle of Interference—Augmentation of Intensity by Partial Extinction of Vibrations—Resultant Tones—Conditions of their Production—Experimental Illustrations—Difference-Tones and Summation-Tones—Theories of Young and Helmholtz
FROM a boat in Cowes Harbor, in moderate weather, I have often watched the masts and ropes of the ships, as mirrored in the water. The images of the ropes revealed the condition of the surface, indicating by long and wide protuberances the passage of the larger rollers, and, by smaller indentations, the ripples which crept like parasites over the sides of the larger waves. The sea was able to accommodate itself to the requirements of all its undulations, great and small. When the surface was touched with an oar, or when drops were permitted to fall from the oar into the water, there was also room for the tiny wavelets thus generated. This carving of the surface by waves and ripples had its limit only in my powers of observation; every wave and every ripple asserted its right of place, and retained its individual existence, amid the crowd of other motions which agitated the water.
The law that rules this chasing of the sea, this crossing and intermingling of innumerable small waves, is that378 the resultant motion of every particle of water is the sum of the individual motions imparted to it. If a particle be acted on at the same moment by two impulses, both of which tend to raise it, it will be lifted by a force equal to the sum of both. If acted upon by two impulses, one of which tends to raise it, and the other to depress it, it will be acted upon by a force equal to the difference of both. When, therefore, the sum of the motions is spoken of, the algebraic sum is meant—the motions which tend to raise the particle being regarded as positive, and those which tend to depress it as negative.
When two stones are cast into smooth water, 20 or 30 feet apart, round each stone is formed a series of expanding circular waves, every one of which consists of a ridge and a furrow. The waves touch, cross each other, and carve the surface into little eminences and depressions. Where ridge coincides with ridge, we have the water raised to a double height; where furrow coincides with furrow, we have it depressed to a double depth; where ridge coincides with furrow, we have the water reduced to its average level. The resultant motion of the water at every point is, as above stated, the algebraic sum of the motions impressed upon that point. And if, instead of two sources of disturbance, we had ten, or a hundred, or a thousand, the consequence would be the same; the actual result might transcend our powers of observation, but the law above enunciated would still hold good.
Instead of the intersection of waves from two distinct centres of disturbance, we may cause direct and reflected waves, from the same centre, to cross each other. Many of you know the beauty of the effects produced when light is reflected from ripples of water. When mercury379 is employed the effect is more brilliant still. Here, by a proper mode of agitation, direct and reflected waves may be caused to cross and interlace, and by the most wonderful self-analysis to untie their knotted scrolls. The adjacent figure (Fig. 149), which is copied from the excellent “Wellenlehre” of the brothers Weber, will give some idea of the beauty of these effects. It represents the chasing produced by the intersection of direct and reflected water-waves in a circular vessel, the point of disturbance (marked by the smallest circle in the figure) being midway between the centre and the circumference.

This power of water to accept and transmit multitudinous impulses is shared by air, which concedes the right of space and motion to any number of sonorous waves. The same air is competent to accept and transmit the380 vibrations of a thousand instruments at the same time. When we try to visualize the motion of that air—to present to the eye of the mind the battling of the pulses direct and reverberated—the imagination retires baffled from the attempt. Still, amid all the complexity, the law above enunciated holds good, every particle of air being animated by a resultant motion, which is the algebraic sum of all the individual motions imparted to it. And the most wonderful thing of all is, that the human ear, though acted on only by a cylinder of that air, which does not exceed the thickness of a quill, can detect the components of the motion, and, by an act of attention, can even isolate from the aërial entanglement any particular sound.
When two unisonant tuning-forks are sounded together, it is easy to see that the forks may so vibrate that the condensations of the one shall coincide with the condensations of the other, and the rarefactions of the one with the rarefactions of the other. If this be the case, the two forks will assist each other. The condensations will, in fact, become more condensed, the rarefactions more rarefied; and as it is upon the difference of density between the condensations and rarefactions that loudness depends, the two vibrating forks, thus supporting each other, will produce a sound of greater intensity than that of either of them vibrating alone.
It is, however, also easy to see that the two forks may be so related to each other that one of them shall require a condensation at the place where the other requires a rarefaction; that the one fork shall urge the air-particles381 forward, while the other urges them backward. If the opposing forces be equal, particles so solicited will move neither backward nor forward, the aërial rest which corresponds to silence being the result. Thus it is possible, by adding the sound of one fork to that of another, to abolish the sounds of both. We have here a phenomenon which, above all others, characterizes wave-motion. It was this phenomenon, as manifested in optics, that led to the undulatory theory of light, the most cogent proof of that theory being based upon the fact that, by adding light to light, we may produce darkness, just as we can produce silence by adding sound to sound.

During the vibration of a tuning-fork the distance between the two prongs is alternately increased and diminished. Let us call the motion which increases the distance the outward swing, and that which diminishes the distance the inward swing of the fork. And let us suppose that our two forks, A and B, Fig. 150, reach the limits of their outward swing and their inward swing at the same moment. In this case the phases of their motion, to use the technical term, are the same. For the sake of simplicity we will confine our attention to the right-hand prongs, A and B, of the two forks, neglecting the other two prongs; and now let us ask what must be the distance between the prongs A and B, when the condensations and rarefactions of both, indicated respec382tively by the dark and light shading, coincide? A little reflection will make it clear that if the distance from B to A be equal to the length of a whole sonorous wave, coincidence between the two systems of waves must follow. The same would evidently occur were the distance between A and B two wave-lengths, three wave-lengths, four wave-lengths—in short, any number of whole wavelengths. In all such cases we shall have coincidence of the two systems of waves, and consequently a reinforcement of the sound of the one fork by that of the other. Both the condensations and rarefactions between A and C are, in this case, more pronounced than they would be if either of the forks were suppressed.

But if the prong B be only half the length of a wave behind A, what must occur? Manifestly the rarefactions of one of the systems of waves will then coincide with the condensations of the other system, the air to the right of A being reduced to quiescence. This is shown in Fig. 151, where the uniformity of shading indicates an absence both of condensations and rarefactions. When B is two half wave-lengths behind A, the waves, as already explained, support each other; when they are three half wave-lengths apart, they destroy each other. Or expressed generally, we have augmentation or destruction according as the distance between the two prongs amounts to an even or an odd number of semi-undula383tions. Precisely the same is true of the waves of light. If through any cause one system of ethereal waves be any even number of semi-undulations behind another system, the two systems support each other when they coalesce, and we have more light. If the one system be any odd number of semi-undulations behind the other, they oppose each other, and a destruction of light is the result of their coalescence.
The action here referred to, both as regards sound and light is called Interference.
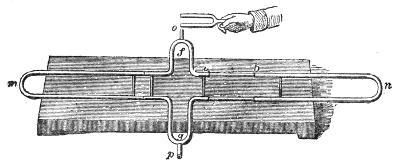
Sir John Herschel was the first to propose to divide a stream of sound into two branches, of different lengths, causing the branches afterward to reunite, and interfere with each other. This idea has been recently followed out with success by M. Quincke; and it has been still further improved upon by M. König. The principle of these experiments will be at once evident from Fig. 152. The tube o f divides into two branches at f, the one branch being carried round n, and the other round m. The two branches are caused to reunite at g, and to end in a common canal, g p. The portion b n of the tube384 which slides over a b can be drawn out as shown in the figure, and thus the sound-waves can be caused to pass over different distances in the two branches. Placing a vibrating tuning-fork at o, and the ear at p, when the two branches are of the same length, the waves through both reach the ear together, and the sound of the fork is heard. Drawing n b out, a point is at length obtained where the sound of the fork is extinguished. This occurs when the distance a b is one-fourth of a wave-length; or, in other words, when the whole right-hand branch is half a wave-length longer than the left-hand one. Drawing b n still further out, the sound is again heard; and when twice the distance a b amounts to a whole wave-length, it reaches a maximum. Thus, according as the difference of both branches amounts to half a wave-length, or to a whole wave-length, we have reinforcement or destruction of the two series of sonorous waves. In practice, the tube o f ought to be prolonged until the direct sound of the fork is unheard, the attention of the ear being then wholly concentrated on the sounds that reach it through the tube.
It is quite plain that the wave-length of any simple tone may be readily found by this instrument. It is only necessary to ascertain the difference of path which produces complete interference. Twice this difference is the wave-length; and if the rate of vibration be at the same time known, we can immediately calculate the velocity of sound in air.
Each of the two forks now before you executes exactly 256 vibrations in a second. Sounded together, they are in unison. Loading one of them with a bit of wax, it vibrates a little more slowly than its neighbor.385 The wax, say, reduces the number of vibrations to 255 in a second; how must their waves affect each other? If they start at the same moment, condensation coinciding with condensation, and rarefaction with rarefaction, it is quite manifest that this state of things cannot continue. At the 128th vibration their phases are in complete opposition, one of them having gained half a vibration on the other. Here the one fork generates a condensation where the other generates a rarefaction; and the consequence is, that the two forks, at this particular point, completely neutralize each other. From this point onward, however, the forks support each other more and more, until, at the end of a second, when the one has completed its 255th, and the other its 256th vibration, condensation again coincides with condensation, and rarefaction with rarefaction, the full effect of both sounds being produced upon the ear.
It is quite manifest that under these circumstances we cannot have the continuous flow of perfect unison. We have, on the contrary, alternate reinforcements and diminutions of the sound. We obtain, in fact, the effect known to musicians by the name of beats, which, as here explained, are a result of interference.
I now load this fork still more heavily, by attaching a fourpenny-piece to the wax; the coincidences and interferences follow each other more rapidly than before; we have a quicker succession of beats. In our last experiment, the one fork accomplished one vibration more than the other in a second, and we had a single beat in the same time. In the present case, one fork vibrates 250 times, while the other vibrates 256 times in a second, and the number of beats per second is 6. A little reflection386 will make it plain that in the interval required by the one fork to execute one vibration more than the other, a beat must occur; and inasmuch as, in the case now before us, there are six such intervals in a second, there must be six beats in the same time. In short, the number of beats per second is always equal to the difference between the two rates of vibration.
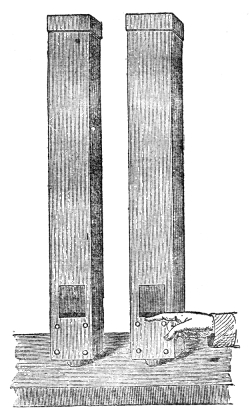
Beats may be produced by all sonorous bodies. These two tall organ-pipes, for example, when sounded together, give powerful beats, one of them being slightly longer than the other. Here are two other pipes, which are now in perfect unison, being exactly of the same length. But it is only necessary to bring the finger near the embouchure of one of the pipes, Fig. 153, to lower its rate of vibration, and produce loud and rapid beats. The placing of the hand over the open top of one of the pipes also lowers its rate of vibration, and produces beats, which follow each other with augmented rapidity as the top of the pipe is closed more and more. By a stronger blast the first two harmonics of the pipes are brought out. These higher notes also interfere, and you have these quicker beats.
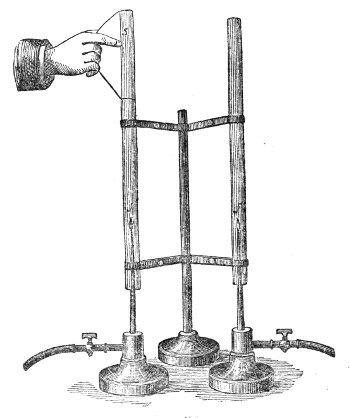
No more beautiful illustration of this phenomenon can387 be adduced than that furnished by two sounding-flames. Two such flames are now before you, the tube surrounding one of them being provided with a telescopic slider, Fig. 154. There are, at present, no beats, because the tubes are not sufficiently near unison. I gradually lengthen the shorter tube by raising its slider. Rapid beats are now heard; now they are slower; now slower still; and now both flames sing together in perfect unison. Continuing the upward motion of the slider, I make the tube too long; the beats begin again, and quicken, until finally their sequence is so rapid as to appeal only as roughness to the ear. The flames, you observe, dance within their tubes in time to the beats. As already stated, these beats cause a silent flame within388 a tube to quiver when the voice is thrown to a proper pitch, and when the position of the flame is rightly chosen, the beats set it singing. With the flames of large rose-burners, and with tin tubes from 3 to 9 feet long, we obtain beats of exceeding power.

You have just heard the beats produced by two tall organ-pipes nearly in unison with each other. Two other pipes are now mounted on our wind-chest, Fig. 155, each of which, however, is provided at its centre with a membrane intended to act upon a flame.70 Two small tubes lead from the spaces closed by the membranes, and unite afterward, the membranes of both the organ-pipes being thus connected with the same flame. By means of the sliders, s s′, near the summits of the pipes, they are 389 either brought into unison or thrown out of it at pleasure. They are not at present in unison, and the beats they produce follow each other with great rapidity. The flame connected with the central membranes dances in time to the beats. When brought nearer to unison, the beats are slower, and the flame at successive intervals withdraws its light and appears to exhale it. A process which reminds you of the inspiration and expiration of the breath is thus carried on by the flame. If the mirror, M, be now turned, the flame produces a luminous band—continuous at certain places, but for the most part broken into distinct images of the flame. The continuous parts correspond to the intervals of interference where the two sets of vibrations abolish each other.
Instead of permitting both pipes to act upon the same flame, we may associate a flame with each of them. The deportment of the flames is then very instructive. Imagine both flames to be in the same vertical line, the one of them being exactly under the other. Bringing the pipes into unison, and turning the mirror, we resolve each flame into a chain of images, but we notice that the images of the one occupy the spaces between the images of the other. The periods of extinction of the one flame, therefore, correspond to the periods of kindling of the other. The experiment proves that, when two unisonant pipes are placed thus close to each other, their vibrations are in opposite phases. The consequence of this is, that the two sets of vibrations permanently neutralize each other, so that at a little distance from the pipes you fail to hear the fundamental tone of either. For this reason we cannot, with any advantage, place close to each other in an organ several pipes of the same pitch.
In the case of beats, the amplitude of the oscillating air reaches a maximum and a minimum periodically. By the beautiful method of M. Lissajous we can illustrate optically this alternate augmentation and diminution of amplitude. Placing a large tuning-fork, T′, Fig. 156, in front of the lamp L, a luminous beam is received upon the mirror attached to the fork. This is reflected back to the mirror of a second fork, T, and by it thrown on to the screen, where it forms a luminous disk. When the bow is drawn over the fork T′, the beam, as in the experiments described in the second chapter, is tilted up and down, the disk upon the screen stretching to a luminous band three feet long. If, in drawing the bow over this second fork, the vibrations of both coincide in phase, the band will be lengthened; if the phases are in opposition, total or partial neutralization of the one fork by the other will be the result. It so happens that in the present instance the second fork adds something to the action391 of the first, the band of light being now four feet long. These forks have been tuned as perfectly as possible. Each of them executes exactly 64 vibrations in a second; the initial relation of their phases remains, therefore, constant, and hence you notice a gradual shortening of the luminous band, like that observed during the subsidence of the vibrations of a single fork. The band at length dwindles to the original disk, which remains motionless upon the screen.
By attaching, with wax, a threepenny-piece to the prong of one of these forks, its rate of vibration is lowered. The phases of the two forks cannot now retain a constant relation to each other. One fork incessantly gains upon the other, and the consequence is that sometimes the phases of both coincide, and at other times they are in opposition. Observe the result. At the present moment the two forks conspire, and we have a luminous band four feet long upon the screen. This slowly contracts, drawing itself up to a mere disk; but the action halts here only during the moment of opposition. That passed, the forks begin again to assist each other, and the disk once more slowly stretches into a band. The action here is very slow; but it may be quickened by attaching a sixpence to the loaded fork. The band of light now stretches and contracts in perfect rhythm. The action, rendered thus optically evident, is impressed upon the air of this room; its particles alternately vibrate and come to rest, and, as a consequence, beats are heard in synchronism with the changes of the figure upon the screen.
The time which elapses from maximum to maximum, or from minimum to minimum, is that required for the392 one fork to perform one vibration more than the other. At present this time is about two seconds. In two seconds, therefore, one beat occurs. When we augment the dissonance by increasing the load, the rhythmic lengthening and shortening of the band is more rapid, while the intermittent hum of the forks is more audible. There are now six elongations and shortenings in the interval taken up a moment ago by one; the beats at the same time being heard at the rate of three a second. By loading the forks still more, the alternations may be caused to succeed each other so rapidly that they can no longer be followed by the eye, while the beats, at the same time, cease to be individually distinct, and appeal as a kind of roughness to the ear.

In the experiments with a single tuning-fork, already described (Fig. 22, Chapter II.), the beam reflected from the fork was received on a looking-glass, and, by turning the glass, the band of light on the screen was caused to stretch out into a long wavy line. It was explained at the time that the loudness of the sound depended on the depth of the indentations. Hence, if the band of light of varying length now before us on the screen be drawn out in a sinuous line, the indentations ought to be at some places deep, while at others they ought to vanish altogether. This is the case. By a little tact the mirror of the fork T (Fig. 156) is caused to turn through a small angle, a sinuous line composed of swellings and contractions (Fig. 157) being drawn upon the screen. The swell393ings correspond to the periods of sound, and the contractions to those of silence.71
Two vibrating bodies, then, each of which separately produces a musical sound, can, when acting together, neutralize each other. Hence, by quenching the vibrations of one of them, we may give sonorous effect to the other. It often happens, for instance, that when two tuning-forks, on their resonant cases, are vibrating in unison, the stoppage of one of them is accompanied by an augmentation of the sound. This point may be further illustrated by the vibrating bell, already described (Fig. 78, Chapter IV.) Placing its resonant tube in front of one of its nodes, a sound is heard, but nothing like what is heard when the tube is opposed to a ventral segment. The reason of this is that the vibrations of a bell on the opposite sides of a nodal line are in opposite directions, and they therefore interfere with each other. By introducing a glass plate between the bell and the tube, the vibrations on one side of the nodal line may be intercepted; an instant augmentation of the sound is the consequence.
In a vibrating disk every two adjacent sectors move at the same time in opposite directions. When the one sector rises the other falls, the nodal line marking the limit between them. Hence, at the moment when any sector produces a condensation in the air above it, the 394adjacent sector produces a rarefaction in the same air. A partial destruction of the sound of one sector by the other is the result. You will now understand the instrument by which the late William Hopkins illustrated the principle of interference. The tube A B, Fig. 158, divides at B into two branches. The end A of the tube is closed by a membrane. Scattering sand upon this membrane, and holding the ends of the branches over adjacent sectors of a vibrating disk, no motion (or, at least, an extremely feeble motion) of the sand is perceived. Placing the ends of the two branches over alternate sectors of the disk, the sand is tossed from the membrane, proving that in this case we have coincidence of vibration on the part of the two sectors.
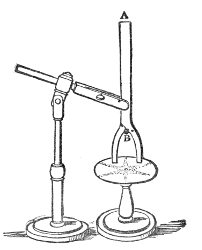
Fig. 158.
|
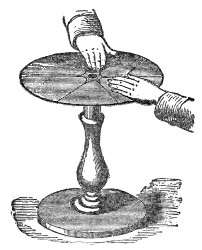
Fig. 159.
|
We are now prepared for a very instructive experiment, which we owe to M. Lissajous. Drawing a bow over the edge of a brass disk, I divide it into six vibrating sectors. When the palm of the hand is brought over any one of them, the sound, instead of being diminished,395 is augmented. When two hands are placed over two adjacent sectors, you notice no increase of the sound; but when they are placed over alternate sectors, as in Fig. 159, a striking augmentation of the sound is the consequence. By simply lowering and raising the hands, marked variations of intensity are produced. By the approach of the hands the vibrations of the two sectors are intercepted; their interference right and left being thus abolished, the remaining sectors sound more loudly. Passing the single hand to and fro along the surface, you also hear a rise and fall of the sound. It rises when the hand is over a vibrating sector; it falls when the hand is over a nodal line. Thus, by sacrificing a portion of the vibrations, we make the residue more effectual. Experiments similar to these may be made with light and radiant heat. If of two beams of the former, which destroy each other by interference, one be removed, light takes the place of darkness; and if of two interfering beams of the latter one be intercepted, heat takes the place of cold.
You have remarked the almost total absence of sound
on the part of a vibrating tuning-fork when held free in
the hand. The feebleness of the fork as a sounding
body arises in part from interference. The prongs always
vibrate in opposite directions, one producing a condensation
where the other produces a rarefaction, a destruction
of sound being the consequence. By simply
passing a pasteboard tube over one of the prongs of the
fork, its vibrations are in part intercepted, and an aug396mentation
of the sound is the result. The single prong
is thus proved to be more effectual than the two prongs.
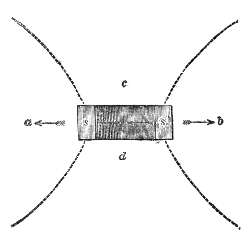 Fig. 160.
There are positions in
which the destruction
of the sound of one
prong by that of the
other is total. These
positions are easily
found by striking the
fork and turning it
round before the ear.
When the back of the
prong is parallel to
the ear, the sound is
heard; when the side
surfaces of both prongs are parallel to the ear, the sound
is also heard; but when the corner of a prong is carefully
presented to the ear, the sound is utterly destroyed.
During one complete rotation of the fork we find four
positions where the sound is thus obliterated.
Fig. 160.
There are positions in
which the destruction
of the sound of one
prong by that of the
other is total. These
positions are easily
found by striking the
fork and turning it
round before the ear.
When the back of the
prong is parallel to
the ear, the sound is
heard; when the side
surfaces of both prongs are parallel to the ear, the sound
is also heard; but when the corner of a prong is carefully
presented to the ear, the sound is utterly destroyed.
During one complete rotation of the fork we find four
positions where the sound is thus obliterated.
Let s s (Fig. 160) represent the two ends of the tuning-fork, looked down upon as it stands upright. When the ear is placed at a or b, or at c or d, the sound is heard. Along the four dotted lines, on the contrary, the waves generated by the two prongs completely neutralize each other, and nothing is there heard. These lines have been proved by Weber to be hyperbolic curves; and this must be their character according to the principle of interference.
This remarkable case of interference, which was first
noticed by Dr. Thomas Young, and thoroughly investigated
by the brothers Weber, may be rendered audible397
by means of resonance. Bringing a vibrating fork over
a jar which resounds to it, and causing the fork to rotate
slowly, in four positions we have a loud resonance; in
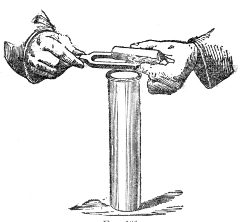 Fig. 161.
four others absolute
silence, alternate risings
and fallings of the sound
accompanying the fork’s
rotation. While the fork
is over the jar with its
corner downward and
the sound entirely extinguished,
let a pasteboard
tube be passed
over one of its prongs,
as in Fig. 161, a loud
resonance announces the withdrawal of the vibrations of
that prong. To obtain this effect, the fork must be held
over the centre of the jar, so that the air shall be symmetrically
distributed on both sides of it. Moving the fork
from the centre toward one of the sides, without altering
its inclination in the least, we obtain a forcible sound.
Interference, however, is also possible near the side of
the jar. Holding the fork, not with its corner downward,
but with both its prongs in the same horizontal plane, a
position is soon found near the side of the jar where the
sound is extinguished. In passing completely from side
to side over the mouth of the jar, two such places of
interference are discoverable.
Fig. 161.
four others absolute
silence, alternate risings
and fallings of the sound
accompanying the fork’s
rotation. While the fork
is over the jar with its
corner downward and
the sound entirely extinguished,
let a pasteboard
tube be passed
over one of its prongs,
as in Fig. 161, a loud
resonance announces the withdrawal of the vibrations of
that prong. To obtain this effect, the fork must be held
over the centre of the jar, so that the air shall be symmetrically
distributed on both sides of it. Moving the fork
from the centre toward one of the sides, without altering
its inclination in the least, we obtain a forcible sound.
Interference, however, is also possible near the side of
the jar. Holding the fork, not with its corner downward,
but with both its prongs in the same horizontal plane, a
position is soon found near the side of the jar where the
sound is extinguished. In passing completely from side
to side over the mouth of the jar, two such places of
interference are discoverable.
A variety of experiments will suggest themselves to the reflecting mind, by which the effect of interference may be illustrated. It is easy, for example, to find a jar which resounds to a vibrating plate. Such a jar, placed398 over a vibrating segment of the plate, produces a powerful resonance. Placed over a nodal line, the resonance is entirely absent; but if a piece of pasteboard be interposed between the jar and plate, so as to cut off the vibrations on one side of the nodal line, the jar instantly resounds to the vibrations of the other. Again, holding two forks, which vibrate with the same rapidity, over two resonant jars, the sound of both flows forth in unison. When a bit of wax is attached to one of the forks, powerful beats are heard. Removing the wax, the unison is restored. When one of these unisonant forks is placed in the flame of a spirit-lamp its elasticity is changed, and it produces long loud beats with its unwarmed fellow.72 If while one of the forks is sounding on its resonant case the other be excited and brought near the mouth of the case, as in Fig. 162, loud beats declare the absence of unison. Dividing a jar by a vertical diaphragm, and bringing one 399of the forks over one of its halves, and the other fork over the other; the two semi-cylinders of air produce beats by their interference. But the diaphragm is not necessary; on removing it, the beats continue as before, one-half of the same column of air interfering with the other.73
The intermittent sound of certain bells, heard more especially when their tones are subsiding, is an effect of interference. The bell, through lack of symmetry, as explained in the fourth chapter, vibrates in one direction a little more rapidly than in the other, and beats are the consequence of the coalescence of the two different rates of vibration.
We have now to turn from this question of interference to the consideration of a new class of musical sounds, of which the beats were long considered to be the progenitors. The sounds here referred to require for their production the union of two distinct musical tones. Where such union is effected, under the proper conditions, resultant tones are generated, which are quite distinct from the primaries concerned in their production. They were discovered, in 1745, by a German organist named Sorge, but the publication of the fact attracted little attention. They were discovered independently, in 1754, by the celebrated Italian violinist Tartini, and after him have been called Tartini’s tones.
To produce them it is desirable, if not necessary, to 400have the two primary tones of considerable intensity. Helmholtz prefers the siren to all other means of exciting them, and with this instrument they are very readily obtained. It requires some attention at first, on the part of the listener, to single out the resultant tone from the general mass of sound; but, with a little practice, this is readily accomplished; and though the unpracticed ear may fail, in the first instance, thus to analyze the sound, the clang-tint is influenced in an unmistakable manner by the admixture of resultant tones. I set Dove’s siren in rotation, and open two series of holes at the same time; with the utmost strain of attention, I am as yet unable to hear the least symptom of a resultant tone. Urging the instrument to greater rapidity, a dull, low droning mingles with the two primary sounds. Raising the speed of rotation, the low, resultant tone rises rapidly in pitch, and now, to those who stand close to the instrument, it is very audible. The two series of holes here open number 8 and 12 respectively. The resultant tone is in this case an octave below the deepest of the two primaries. Opening two other series of orifices, numbering 12 and 16 respectively, the resultant tone is quite audible. Its rate of vibration is one-third of the rate of the deepest of the two primaries. In all cases, the resultant tone is that which corresponds to a rate of vibration equal to the difference of the rates of the two primaries.
The resultant tone here spoken of is that actually heard in the experiment. But with finer methods of experiment other resultant tones are proved to exist. Those on which we have now fixed our attention are, however, the most important. They are called difference-tones by Helmholtz, in consequence of the law just mentioned.
To bring these resultant tones audibly forth, the primaries must, as already stated, be forcible. When they are feeble the resultants are unheard. I am acquainted with no method of exciting these tones more simple and effectual than a pair of suitable singing-flames. Two such flames may be caused to emit powerful notes—self-created, self-sustained, and requiring no muscular effort on the part of the observer to keep them going. Here are two of them. The length of the shorter of the two tubes surrounding these flames is 10-3/8 inches, that of the other is 11·4 inches. I hearken to the sound, and in the midst of the shrillness detect a very deep resultant tone. The reason of its depth is manifest: the two tubes being so nearly alike in length, the difference between their vibrations is small, and the note corresponding to this difference, therefore, low in pitch. Lengthening one of the tubes by means of its slider, the resultant tone rises gradually, and now it swells surprisingly. When the tube is shortened the resultant tone falls, and thus, by alternately raising and lowering the slider, the resultant tone is caused to rise and sink in accordance with the law which makes the number of its vibrations the difference between the number of its two primaries.
We can determine, with ease, the actual number of vibrations corresponding to any one of those resultant tones. The sound of the flame is that of the open tube which surrounds it, and we have already learned (Chapter III.) that the length of such a tube is half that of the sonorous wave it produces. The wave-length, therefore, corresponding to our 10-3/8-inch tube is 20-3/4 inches. The velocity of sound in air of the present temperature is 1,120 feet a second. Bringing these feet to inches, and dividing402 by 20-3/4, we find the number of vibrations corresponding to a length of 10-3/8 inches to be 648 per second.
But it must not be forgotten here that the air in which the vibrations are actually executed is much more elastic than the surrounding air. The flame heats the air of the tube, and the vibrations must, therefore, be executed more rapidly than they would be in an ordinary organ-pipe of the same length. To determine the actual number of vibrations, we must fall back upon our siren; and with this instrument it is found that the air within the 10-3/8 inch tube executes 717 vibrations in a second. The difference of 69 vibrations a second is due to the heating of the aërial column. Carbonic acid and aqueous vapor are, moreover, the product of the flame’s combustion, and their presence must also affect the rapidity of the vibration.
Determining in the same way the rate of vibration of the 11·4-inch tube, we find it to be 667 per second; the difference between this number and 717 is 50, which expresses the rate of vibration corresponding to the first deep resultant tone.
But this number does not mark the limit of audibility. Permitting the 11·4-inch tube to remain as before, and lengthening its neighbor, the resultant tone sinks near the limit of hearing. When the shorter tube measures 11 inches, the deep sound of the resultant tone is still heard. The number of vibrations per second executed in this 11-inch tube is 700. We have already found the number executed in the 11·4-inch tube to be 667; hence 700-667=33, which is the number of vibrations corresponding to the resultant tone now plainly heard when the attention is converged upon it. We here come very403 near the limit which Helmholtz has fixed as that of musical audibility. Combining the sound of a tube 17-3/8 inches in length with that of a 10-3/8-inch tube, we obtain a resultant tone of higher pitch than any previously heard. Now the actual number of vibrations executed in the longer tube is 459; and we have already found the vibrations of our 10-3/8-inch tube to be 717; hence 717-459=258, which is the number corresponding to the resultant tone now audible. This note is almost exactly that of one of our series of tuning-forks, which vibrates 256 times in a second.
And now we will avail ourselves of a beautiful check which this result suggests to us. The well-known fork which vibrates at the rate just mentioned is here, mounted on its case, and I touch it with the bow so lightly that the sound alone could hardly be heard; but it instantly coalesces with the resultant tone, and the beats produced by their combination are clearly audible. By loading the fork, and thus altering its pitch, or by drawing up the paper slider, and thus altering the pitch of the flame, the rate of these beats can be altered, exactly as when we compare two primary tones together. By slightly varying the size of the flame, the same effect is produced. We cannot fail to observe how beautifully these results harmonize with each other.
Standing midway between the siren and a shrill singing-flame, and gradually raising the pitch of the siren, the resultant tone soon makes itself heard, sometimes swelling out with extraordinary power. When a pitch-pipe is blown near the flame, the resultant tone is also heard, seeming, in this case, to originate in the ear itself, or rather in the brain. By gradually drawing out404 the stopper of the pipe, the pitch of the resultant tone is caused to vary in accordance with the law already enunciated.
The resultant tones produced by the combination of the ordinary harmonic intervals74 are given in the following table:
| Interval | Ratio of vibrations | Difference | The resultant tone is deeper than the lowest primary tone by |
| Octave | 2 : 3 | 1 | an octave |
| Fourth | 3 : 4 | 1 | a twelfth |
| Major third | 4 : 5 | 1 | two octaves |
| Minor third | 5 : 6 | 1 | two octaves and a major third |
| Major sixth | 3 : 5 | 2 | a fifth |
| Minor sixth | 5 : 8 | 3 | major sixth |
The celebrated Thomas Young thought that these resultant tones were due to the coalescence of rapid beats, which linked themselves together like the periodic impulses of an ordinary musical note. This explanation harmonized with the fact that the number of the beats, like that of the vibrations of the resultant tone, is equal to the difference between the two sets of vibrations. This explanation, however, is insufficient. The beats tell more forcibly upon the ear than any continuous sound. They can be plainly heard when each of the two sounds that produce them has ceased to be audible. This depends in part upon the sense of hearing, but it also depends upon the fact that when two notes of the same intensity produce beats, the amplitude of the vibrating air-particles is at times destroyed, and at times doubled. But by doubling the amplitude we quadruple the intensity of the sound. Hence, when two notes of the same 405intensity produce beats, the sound incessantly varies between silence and a tone of four times the intensity of either of the interfering ones.
If, therefore, the resultant tones were due to the beats of their primaries, they ought to be heard, even when the primaries are feeble. But they are not heard under these circumstances. When several sounds traverse the same air, each particular sound passes through the air as if it alone were present, each particular element of a composite sound asserting its own individuality. Now, this is in strictness true only when the amplitudes of the oscillating particles are infinitely small. Guided by pure reasoning, the mathematician arrives at this result. The law is also practically true when the disturbances are extremely small; but it is not true after they have passed a certain limit. Vibrations which produce a large amount of disturbance give birth to secondary waves, which appeal to the ear as resultant tones. This has been proved by Helmholtz, and, having proved this, he inferred further that there are also resultant tones formed by the sum of the primaries, as well as by their difference. He thus discovered the summation-tones before he had heard them; and bringing his result to the test of experiment, he found that these tones had a real physical existence. They are not at all to be explained by Young’s theory.
Another consequence of this departure from the law of superposition is, that a single sounding body, which disturbs the air beyond the limits of the law of superposition, also produces secondary waves, which correspond to the harmonic tones of the vibrating body. For example, the rate of vibration of the first overtone of a tuning-fork, as stated in the fourth chapter, is 6-1/4 times406 the rate of the fundamental tone. But Helmholtz shows that a tuning-fork, not excited by a bow, but vigorously struck against a pad, emits the octave of its fundamental note, this octave being due to the secondary waves set up when the limits of the law of superposition have been exceeded.
These considerations make it probably evident to you that a coalescence of musical sounds is a far more complicated dynamical condition than you have hitherto supposed it to be. In the music of an orchestra, not only have we the fundamental tones of every pipe and of every string, but we have the overtones of each, sometimes audible as far as the sixteenth in the series. We have also resultant tones; both difference-tones and summation-tones; all trembling through the same air, all knocking at the self-same tympanic membrane. We have fundamental tone interfering with fundamental tone; overtone with overtone; resultant tone with resultant tone. And, besides this, we have the members of each class interfering with the members of every other class. The imagination retires baffled from any attempt to realize the physical condition of the atmosphere through which these sounds are passing. And, as we shall immediately learn, the aim of music, through the centuries during which it has ministered to the pleasure of man, has been to arrange matters empirically, so that the ear shall not suffer from the discordance produced by this multitudinous interference. The musicians engaged in this work knew nothing of the physical facts and principles involved in their efforts; they knew no more about it than the inventors of gunpowder knew about the law of atomic proportions. They tried and tried till they obtained a satisfactory re407sult; and now, when the scientific mind is brought to bear upon the subject, order is seen rising through the confusion, and the results of pure empiricism are found to be in harmony with natural law.
When several systems of waves proceeding from distinct centres of disturbance pass through water or air, the motion of every particle is the algebraic sum of the several motions impressed upon it.
In the case of water, when the crests of one system of waves coincide with the crests of another system, higher waves will be the result of the coalescence of the two systems. But when the crests of one system coincide with the sinuses, or furrows, of the other system, the two systems, in whole or in part, destroy each other.
This coalescence and destruction of two systems of waves is called interference.
Similar remarks apply to sonorous waves. If in two systems of sonorous waves condensation coincides with condensation, and rarefaction with rarefaction, the sound produced by such coincidence is louder than that produced by either system taken singly. But if the condensations of the one system coincide with the rarefactions of the other, a destruction, total or partial, of both systems is the consequence.
Thus, when two organ-pipes of the same pitch are placed near each other on the same wind-chest and thrown into vibration, they so influence each other that408 as the air enters the embouchure of the one it quits that of the other. At the moment, therefore, the one pipe produces a condensation the other produces a rarefaction. The sounds of two such pipes mutually destroy each other.
When two musical sounds of nearly the same pitch are sounded together the flow of the sound is disturbed by beats.
These beats are due to the alternate coincidence and interference of the two systems of sonorous waves. If the two sounds be of the same intensity, their coincidence produces a sound of four times the intensity of either; while their opposition produces absolute silence.
The effect, then, of two such sounds, in combination, is a series of shocks, which we have called “beats,” separated from each other by a series of “pauses.”
The rate at which the beats succeed each other is equal to the difference between the two rates of vibration.
When a bell or disk sounds, the vibrations on opposite sides of the same nodal line partially neutralize each other; when a tuning-fork sounds, the vibrations of its two prongs in part neutralize each other. By cutting off a portion of the vibrations in these cases the sound may be intensified.
When a luminous beam, reflected on to a screen from two tuning-forks producing beats, is acted upon by the vibrations of both, the intermittence of the sound is announced by the alternate lengthening and shortening of the band of light upon the screen.
The law of the superposition of vibrations above enunciated is strictly true only when the amplitudes are exceedingly small. When the disturbance of the air by a sounding body is so violent that the law no longer409 holds good, secondary waves are formed, which correspond to the harmonic tones of the sounding body.
When two tones are rendered so intense as to exceed the limits of the law of superposition, their secondary waves combine to produce resultant tones.
Resultant tones are of two kinds; the one class corresponding to rates of vibration equal to the difference of the rates of the two primaries; the other class corresponding to rates of vibration equal to the sum of the two primaries. The former are called difference-tones, the latter summation-tones.
Combination of Musical Sounds—The smaller the Two Numbers which express the Ratio of their Rates of Vibration, the more perfect is the Harmony of Two Sounds—Notions of the Pythagoreans regarding Musical Consonance—Euler’s Theory of Consonance—Theory of Helmholtz—Dissonance due to Beats—Interference of Primary Tones and of Over-tones—Mechanism of Hearing—Schultze’s Bristles—The Otoliths—Corti’s Fibres—Graphic Representation of Consonance and Dissonance—Musical Chords—The Diatonic Scale—Optical Illustration of Musical Intervals—Lissajous’s Figures—Sympathetic Vibrations—Various Modes of illustrating the Composition of Vibrations
THE subject of this day’s lecture has two sides, a physical and an æsthetical. We have to-day to study the question of musical consonance—to examine musical sounds in definite combination with each other, and to unfold the reason why some combinations are pleasant and others unpleasant to the ear.
Pythagoras made the first step toward the physical explanation of the musical intervals. This great philosopher stretched a string, and then divided it into three equal parts. At one of its points of division he fixed it firmly, thus converting it into two, one of which was twice the length of the other. He sounded the two sections of the string simultaneously, and found the note emitted by the short section to be the higher octave of that emitted by the long one. He then divided his string into two parts, bearing to each other the proportion of 2:3, and found that the notes were separated by an interval of a fifth. Thus, dividing his string at different411 points, Pythagoras found the so-called consonant intervals in music to correspond with certain lengths of his string; and he made the extremely important discovery that the simpler the ratio of the two parts into which the string was divided, the more perfect was the harmony of the two sounds. Pythagoras went no further than this, and it remained for the investigators of a subsequent age to show that the strings act in this way in virtue of the relation of their lengths to the number of their vibrations. Why simplicity should give pleasure remained long an enigma, the only pretence of a solution being that of Euler, which, briefly expressed, is, that the human soul takes a constitutional delight in simple calculations.
The double siren (Fig. 163) enables us to obtain a great variety of combinations of musical sounds. And this instrument possesses over all others the advantage that, by simply counting the number of orifices corresponding respectively to any two notes, we obtain immediately the ratio of their rates of vibration. Before proceeding to these combinations I will enter a little more fully into the action of the double siren than has been hitherto deemed necessary or desirable.
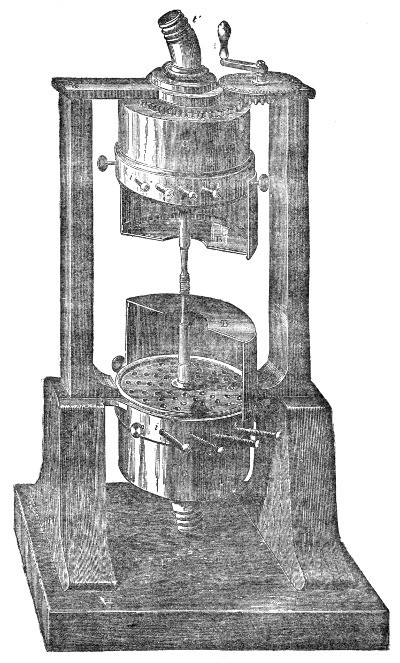
The instrument, as already stated, consists of two of Dove’s sirens, C′ and C, connected by a common axis, the upper one being turned upside down. Each siren is provided with four series of apertures, numbering as follows:
| Upper siren Number of apertures | Lower siren Number of apertures | |
| 1st Series | 16 | 18 |
| 2d Series | 15 | 12 |
| 3d Series | 12 | 10 |
| 4th Series | 9 | 8 |
The number 12, it will be observed, is common to both
sirens. I open the two series of 12 orifices each, and
412
413urge air through the instrument; both sounds flow together
in perfect unison; the unison being maintained,
however the pitch may be exalted. We have, however,
already learned (Chapter II.) that by turning the handle
of the upper siren the orifices in its wind-chest C′ are
caused either to meet those of its rotating disk, or to
retreat from them, the pitch of the upper siren being
thereby raised or lowered. This change of pitch instantly
announces itself by beats. The more rapidly the
handle is turned, the more is the tone of the upper siren
raised above or depressed below that of the lower one,
and, as a consequence, the more rapid are the beats.
Now the rotation of the handle is so related to the rotation of the wind-chest C′ that when the handle turns through half a right angle the wind-chest turns through one-sixth of a right angle, or through the one-twenty-fourth of its whole circumference. But in the case now before us, where the circle is perforated by 12 orifices, the rotation through one-twenty-fourth of its circumference causes the apertures of the upper wind-chest to be closed at the precise moments when those of the lower one are opened, and vice versa. It is plain, therefore, that the intervals between the puffs of the lower siren, which correspond to the rarefactions of its sonorous waves, are here filled by the puffs, or condensations, of the upper siren. In fact, the condensations of the one coincide with the rarefactions of the other, and the absolute extinction of the sounds of both sirens is the consequence.
I may seem to you to have exceeded the truth here; for when the handle is placed in the position which corresponds to absolute extinction, you still hear a distinct sound. And, when the handle is turned continuously,414 though alternate swellings and sinkings of the tone occur, the sinkings by no means amount to absolute silence. The reason is this: The sound of the siren is a highly composite one. By the suddenness and violence of its shocks, not only does it produce waves corresponding to the number of its orifices, but the aërial disturbance breaks up into secondary waves, which associate themselves with the primary waves of the instrument, exactly as the harmonics of a string, or of an open organ-pipe, mix with their fundamental tone. When the siren sounds, therefore, it emits, besides the fundamental tone, its octave, its twelfth, its double octave, and so on. That is to say, it breaks the air up into vibrations which have twice, three times, four times, etc., the rapidity of the fundamental one. Now, by turning the upper siren through one-twenty-fourth of its circumference, we extinguish utterly the fundamental tone. But we do not extinguish its octave.75 Hence, when the handle is in the position which corresponds to the extinction of the fundamental tone, instead of silence we have the full first harmonic of the instrument.
Helmholtz has surrounded both his upper and his lower siren with circular brass boxes, B, B′, each composed of two halves, which can be readily separated (one-half of each box is removed in the figure). These boxes exalt by their resonance the fundamental tone of the instrument, and enable us to follow its variations much more easily than if it were not thus reinforced. It requires a certain rapidity of rotation to reach the maximum resonance of the brass boxes; but when this speed 415is attained, the fundamental tone swells out with greatly augmented force, and, if the handle be then turned, the beats succeed each other with extraordinary power.
Still, as already stated, the pauses between the beats of the fundamental tone are not intervals of absolute silence, but are filled by the higher octave; and this renders caution necessary when the instrument is employed to determine rates of vibration. It is not without reason that I say so. Wishing to determine the rate of vibration of a small singing-flame, I once placed a siren at some distance from it, sounded the instrument, and after a little time observed the flame dancing in synchronism with audible beats. I took it for granted that unison was nearly attained, and, under this assumption, determined the rate of vibration. The number obtained was surprisingly low—indeed not more than half what it ought to be. What was the reason? Simply this: I was dealing, not with the fundamental tone of the siren, but with its higher octave. This octave and the flame produced beats by their coalescence; and hence the counter of the instrument, which recorded the rate, not of the octave, but of the fundamental, gave a number which was only half the true one. The fundamental tone was afterward raised to unison with the flame. On approaching unison beats were again heard, and the jumping of the flame proceeded with an energy greater than that observed in the case of the octave. The counter of the instrument then recorded the accurate rate of the flame’s vibration.
The tones first heard in the case of the siren are always overtones. These attain sonorous continuity sooner than the fundamental, flowing as smooth musical sounds416 while the fundamental tone is still in a state of intermittence. The siren is, however, so delicately constructed that a rate of rotation which raises the fundamental tone above its fellows is almost immediately attained. And if we seek, by making the blast feeble, to keep the speed of rotation low, it is at the expense of intensity. Hence the desirability, if we wish to examine the overtones, of devising some means by which a strong blast and slow rotation shall be possible.
Helmholtz caused a spring to press as a light brake against the disk of the siren. Thus raising by slow degrees the speed of rotation, he was able deliberately to notice the predominance of the overtones at the commencement, and the final triumph of the fundamental tone. He did not trust to the direct observation of pitch, but determined the tone by the number of beats corresponding to one revolution of the handle of the upper siren. Supposing 12 orifices to be opened above and 12 below, the motion of the handle through 45° produces interference, and extinguishes the fundamental tone. The coincidences of that tone occur at the end of every rotation of 90°. Hence, for the fundamental tone, there must be four beats for every complete rotation of the handle. Now Helmholtz, when he made the arrangement just described, found that the first beats numbered, not 4, but 12, for every revolution. They were, in fact, the beats, not of the fundamental tone, not even of the first overtone, but of the second overtone, whose rate of vibration is three times that of the fundamental. These beats continued as long as the number of air-shocks did not exceed 30 or 40 per second. When the shocks were between 40 and 80 per second, the beats fell from 12 to 8417 for every revolution of the handle. Within this interval the first overtone, or the octave of the fundamental tone, was the most powerful, and made the beats its own. Not until the impulses exceeded 80 per second did the beats sink to 4 per revolution. In other words, not until the speed of rotation had passed this limit was the fundamental tone able to assert its superiority over its companions.
This premised, we will combine the tones in definite order, while the cultivated ears here present shall judge of their musical relationship. The flow of perfect unison when the two series of 12 orifices each are opened has been already heard. I now open a series of 8 holes in the upper and of 16 in the lower siren. The interval you judge at once to be an octave. If a series of 9 holes in the upper and of 18 holes in the lower siren be opened, the interval is still an octave. This proves that the interval is not disturbed by altering the absolute rates of vibration, so long as the ratio of the two rates remains the same. The same truth is more strikingly illustrated by commencing with a low speed of rotation, and urging the siren to its highest pitch; as long as the orifices are in the ratio of 1:2, we retain the constant interval of an octave. Opening a series of 10 holes in the upper and of 15 in the lower siren, the ratio is as 2:3, and every musician present knows that this is the interval of a fifth. Opening 12 holes in the upper and 18 in the lower siren does not change the interval. Opening two series of 9 and 12, or of 12 and 16, we obtain an interval of a fourth; the ratio in both these cases being as 3:4. In like manner two series of 8 and 10, or of 12 and 15, give us the interval of a major third; the ratio in this case being as 4:5. Finally, two418 series of 10 and 12, or of 15 and 18, yield the interval of a minor third, which corresponds to the ratio 5:6.
These experiments amply illustrate two things: First, that a musical interval is determined, not by the absolute number of vibrations of the two combining notes, but by the ratio of their vibrations. Secondly, and this is of the utmost significance, that the smaller the two numbers which express the ratio of the two rates of vibration, the more perfect is the consonance of the two sounds. The most perfect consonance is the unison 1:1; next comes the octave 1:2; after that the fifth 2:3; then the fourth 3:4; then the major third 4:5; and finally the minor third 5:6. We can also open two series numbering, respectively, 8 and 9 orifices: this interval corresponds to a tone in music. It is a dissonant combination. Two series which number respectively 15 and 16 orifices make the interval of a semi-tone: it is a very sharp and grating dissonance.
Whence, then, does this arise? Why should the smaller ratio express the more perfect consonance? The ancients attempted to solve this question. The Pythagoreans found intellectual repose in the answer “All is number and harmony.” The numerical relations of the seven notes of the musical scale were also thought by them to express the distances of the planets from their central fire; hence the choral dance of the worlds, the “music of the spheres,” which, according to his followers, Pythagoras alone was privileged to hear. And might we not in passing contrast this glorious superstition with the grov419elling delusion which has taken hold of the fantasy of our day? Were the character which superstition assumes in different ages an indication of man’s advance or retrogression, assuredly the nineteenth century would have no reason to plume itself, in comparison with the sixth B.C. A more earnest attempt to account for the more perfect consonance of the smaller ratios was made by the celebrated mathematician, Euler, and his explanation, if such it could be called, long silenced, if it did not satisfy, inquirers. Euler analyzes the cause of pleasure. We take delight in order; it is pleasant to us to observe means “co-operant to an end.” But then, the effort to discern order must not be so great as to weary us. If the relations to be disentangled are too complicated, though we may see the order, we cannot enjoy it. The simpler the terms in which the order expresses itself, the greater is our delight. Hence the superiority of the simpler ratios in music over the more complex ones. Consonance, then, according to Euler, was the satisfaction derived from the perception of order without weariness of mind.
But in this theory it was overlooked that Pythagoras himself, who first experimented on the musical intervals, knew nothing about rates of vibration. It was forgotten that the vast majority of those who take delight in music, and who have the sharpest ears for the detection of a dissonance, are in the condition of Pythagoras, knowing nothing whatever about rates or ratios. And it may also be added that the scientific man, who is fully informed upon these points, has his pleasure in no way enhanced by his knowledge. Euler’s explanation, therefore, does not satisfy the mind, and it was reserved for an eminent German investigator of our own day, after a pro420found analysis of the entire question, to assign the physical cause of consonance and dissonance—a cause which, when once clearly stated, is so simple and satisfactory as to excite surprise that it remained so long without a discoverer.
Various expressions employed in our previous lectures have already, in part, forestalled Helmholtz’s explanation of consonance and dissonance. Let me here repeat an experiment which will, almost of itself, force this explanation upon your attention. Before you are two jets of burning gas, which can be converted into singing-flames by inclosing them within two tubes (represented in Fig. 118). The tubes are of the same length, and the flames are now singing in unison. By means of a telescopic slider I lengthen slightly one of the tubes; you hear deliberate beats, which succeed each other so slowly that they can readily be counted. I augment still further the length of the tube. The beats are now more rapid than before: they can barely be counted. It is perfectly manifest that the shocks of which you are now sensible differ only in point of rapidity from the slow beats which you heard a moment ago. There is no breach of continuity here. We begin slowly, we gradually increase the rapidity, until finally the succession of the beats is so rapid as to produce that particular grating effect which every musician that hears it would call dissonance. Let us now reverse the process, and pass from these quick beats to slow ones. The same continuity of the phenomenon is noticed. By degrees the beats separate from each other more and more, until finally they are slow enough to be counted. Thus these singing-flames enable us to follow the beats with certainty, until they cease to be beats and are converted into dissonance.
This experiment proves conclusively that dissonance may be produced by a rapid succession of beats; and I imagine this cause of dissonance would have been pointed out earlier, had not men’s minds been thrown off the proper track by the theory of “resultant tones” enunciated by Thomas Young. Young imagined that, when they were quick enough, the beats ran together to form a resultant tone. He imagined the linking together of the beats to be precisely analogous to the linking together of simple musical impulses; and he was strengthened in this notion by the fact already adverted to, that the first difference-tone, that is to say, the loudest resultant tone, corresponded, as the beats do, to a rate of vibration equal to the difference of the rates of the two primaries. The fact, however, is that the effect of beats upon the ear is altogether different from that of the successive impulses of an ordinary musical tone.
But to grasp, in all its fulness, the new theory of musical consonance some preliminary studies will be necessary. And here I would ask you to call to mind the experiments (in Chapter III.) by which the division of a string into its harmonic segments was illustrated. This was done by means of little paper riders, which were unhorsed, or not, according as they occupied a ventral segment or a node upon the string. Before you at present is the sonometer, employed in the experiments just referred to. Along it, instead of one, are stretched two strings, about three inches asunder. By means of a key these strings are brought into unison. And now I place a little paper rider upon the middle of one of422 them, and agitate the other. What occurs? The vibrations of the sounding string are communicated to the bridges on which it rests, and through the bridges to the other string. The individual impulses are very feeble, but, because the two strings are in unison, the impulses can so accumulate as finally to toss the rider off the untouched string.
Every experiment executed with the riders and a single string may be repeated with these two unisonant strings. Damping, for instance, one of the strings, at a point one-fourth of its length from one of its ends, and placing the red and blue riders formerly employed, not on the nodes and ventral segments of the damped string, but at points upon the second string exactly opposite to those nodes and segments, when the bow is passed across the shorter segment of the damped string, the five red riders on the adjacent string are unhorsed, while the four blue ones remain tranquilly in their places. By relaxing one of the strings, it is thrown out of unison with the other, and then all efforts to unhorse the riders are unavailing. That accumulation of impulses, which unison alone renders possible, cannot here take place, and the consequence is that, however great the agitation of the one string may be, it fails to produce any sensible effect upon the other.
The influence of synchronism may be illustrated in a still more striking manner, by means of two tuning-forks which sound the same note. Two such forks mounted on their resonant supports are placed upon the table. I draw the bow vigorously across one of them, permitting the other fork to remain untouched. On stopping the agitated fork, the sound is enfeebled, but by no means423 quenched. Through the air and through the wood the vibrations have been conveyed from fork to fork, and the untouched fork is the one you now hear. When, by means of a morsel of wax, a small coin is attached to one of the forks, its power of influencing the other ceases; the change in the rate of vibration, if not very small, so destroys the sympathy between the two forks as to render a response impossible. On removing the coin the untouched fork responds as before.
This communication of vibrations through wood and air may be obtained when the forks, mounted on their cases, stand several feet apart. But the vibrations may also be communicated through the air alone. Holding the resonant case of a vigorously vibrating fork in my hand, I bring one of its prongs near an unvibrating one, placing the prongs back to back, but allowing a space of air to exist between them. Light as is the vehicle, the accumulation of impulses, secured by the perfect unison of the two forks, enables the one to set the other in vibration. Extinguishing the sound of the agitated fork, that which a moment ago was silent continues sounding, having taken up the vibrations of its neighbor. Removing one of the forks from its resonant case, and striking it against a pad, it is thrown into strong vibration. Held free in the air, its sound is audible. But, on bringing it close to the silent mounted fork, out of the silence rises a full mellow sound, which is due, not to the fork originally agitated, but to its sympathetic neighbor.
Various other examples of the influence of synchronism, already brought forward, will occur to you here; and cases of the kind might be indefinitely multiplied. If two clocks, for example, with pendulums of the same424 period of vibration, be placed against the same wall, and if one of the clocks is set going and the other not, the ticks of the moving clock, transmitted through the wall, will act upon its neighbor. The quiescent pendulum, moved by a single tick, swings through an extremely minute arc; but it returns to the limit of its swing just in time to receive another impulse. By the continuance of this process, the impulses so add themselves together as finally to set the clock a-going. It is by this timing of impulses that a properly-pitched voice can cause a glass to ring, and that the sound of an organ can break a particular window-pane.
If I dwell so fully upon this object, it is for the purpose of rendering intelligible the manner in which sonorous motion is communicated to the auditory nerve. In the organ of hearing, in man, we have first of all the external orifice of the ear, closed at the bottom by the circular tympanic membrane. Behind that membrane is the drum of the ear, this cavity being separated from the space between it and the brain by a bony partition, in which there are two orifices, the one round and the other oval. These orifices are also closed by fine membranes. Across the drum stretches a series of four little bones. The first, called the hammer, is attached to the tympanic membrane; the second, called the anvil, is connected by a joint with the hammer; a third little round bone connects the anvil with the stirrup-bone, the base of which is planted against the membrane of the oval orifice just referred to. This oval membrane is almost covered by the stirrup-bone, a narrow rim only of the membrane425 surrounding the bone being left uncovered. Behind the bony partition, and between it and the brain, we have the extraordinary organ called the labyrinth, filled with water, over the lining membrane of which are distributed the terminal fibres of the auditory nerve. When the tympanic membrane receives a shock, it is transmitted through the series of bones above referred to, being concentrated on the membrane against which the base of the stirrup-bone is fixed. The membrane transfers the shock to the water of the labyrinth, which, in its turn, transfers it to the nerves.
The transmission, however, is not direct. At a certain place within the labyrinth exceedingly fine elastic bristles, terminating in sharp points, grow up between the terminal nerve-fibres. These bristles, discovered by Max Schultze, are eminently calculated to sympathize with such vibrations of the water as correspond to their proper periods. Thrown thus into vibration, the bristles stir the nerve-fibres which lie between their roots. At another place in the labyrinth we have little crystalline particles called otolites—the Hörsteine of the Germans—imbedded among the nervous filaments, which, when they vibrate, exert an intermittent pressure upon the adjacent nerve-fibres. The otolites probably serve a different purpose from that of the bristles of Schultze. They are fitted, by their weight, to accept and prolong the vibrations of evanescent sounds, which might otherwise escape attention, while the bristles of Schultze, because of their extreme lightness, would instantly yield up an evanescent motion. They are, on the other hand, eminently fitted for the transmission of continuous vibrations.
Finally, there is in the labyrinth an organ, discovered426 by the Marchese Corti, which is to all appearance a musical instrument, with its chords so stretched as to accept vibrations of different periods, and transmit them to the nerve-filaments which traverse the organ. Within the ears of men, and without their knowledge or contrivance, this lute of 3,000 strings76 has existed for ages, accepting the music of the outer world and rendering it fit for reception by the brain. Each musical tremor which falls upon this organ selects from the stretched fibres the one appropriate to its own pitch, and throws it into unisonant vibration. And thus, no matter how complicated the motion of the external air may be, these microscopic strings can analyze it and reveal the constituents of which it is composed. Surely, inability to feel the stupendous wonder of what is here revealed would imply incompleteness of mind; and surely those who practically ignore, or fear them, must be ignorant of the ennobling influence which such discoveries may be made to exercise upon both the emotions and the understanding of man.
This view of the use of Corti’s fibres is theoretical; but it comes to us commended by every appearance of truth. It will enable us to tie together many things, whose relations it would be otherwise difficult to discern. When a musical note is sounded its corresponding Corti’s fibre resounds, being moved, as a string is moved by a second unisonant string. And when two sounds coalesce to produce beats, the intermittent motion is transferred to the proper fibre within the ear. But here it is to be 427 noted that, for the same fibre to be affected simultaneously by two different sounds, it must not be far removed in pitch from either of them. Call to mind our repetition of Melde’s experiments (in Chapter III.). You then had frequent occasion to notice that, even before perfect synchronism had been established between the string and the tuning-fork to which it was attached, the string began to respond to the fork. But you also noticed how rapidly the vibrating amplitude of the string increased, as it came close to perfect synchronism with the vibrating fork. On approaching unison the string would open out, say to an amplitude of an inch; and then a slight tightening or slackening, as the case might be, would bring it up to unison, and cause it to open out suddenly to an amplitude of six inches.
So also in reference to the experiment made a moment ago with the sonometer; you noticed that the unhorsing of the paper riders was preceded by a fluttering of the bits of paper; showing that the sympathetic response of the second string had begun, though feebly, prior to perfect synchronism. Instead of two strings, conceive three strings, all nearly of the same pitch, to be stretched upon the sonometer; and suppose the vibrating period of the middle string to lie midway between the periods of its two neighbors, being a little higher than the one and a little lower than the other. Each of the side strings, sounded singly, would cause the middle string to respond. Sounding the two side strings together they would produce beats; the corresponding intermittence would be propagated to the central string, which would beat in synchronism with the beats of its neighbors. In this way we make plain to our minds how428 a Corti’s fibre may, to some extent, take up the vibrations of a note, nearly, but not exactly, in unison with its own; and that when two notes close to the pitch of the fibre act upon it together, their beats are responded to by an intermittent motion on the part of the fibre. This power of sympathetic vibration would fall rapidly on both sides of the perfect unison, so that on increasing the interval between the two notes, a time would soon arrive when the same fibre would refuse to be acted on simultaneously by both. Here the condition of the organ, necessary for the perception of audible beats, would cease.
In the middle region of the pianoforte, with the interval of a semitone, the beats are sharp and distinct, falling indeed upon the ear as a grating dissonance. Extending the interval to a whole tone, the beats become more rapid, but less distinct. With the interval of a minor third between the two notes, the beats in the middle region of the scale cease to be sensible. But this smoothening of the sound is not wholly due to the augmented rapidity of the beats. It is due in part to the fact, for which the foregoing considerations have prepared us, that the two notes here sounded are too far removed from that of the intermediate Corti’s fibre to affect it powerfully. By ascending to the higher regions of the scale we can produce, with a narrower interval than the minor third, the same, or even a greater, number of beats, which are sharply distinguishable because of the closeness of their component notes. In the very highest regions of the scale, however, the beats, when they become very rapid, cease to appeal as roughness to the ear.
Hence both the rapidity of the beats, and the width of the interval, enter into the question of consonance.429 Helmholtz judges that in the middle and higher regions of the musical scale, when the beats reach 33 per second, the dissonance reaches its maximum. Both slower and quicker beats have a less grating or dissonant effect. When the beats are very slow, they may be of advantage to the music; and, when they reach 132 per second, their roughness is no longer discernible.
Thanks to Helmholtz, whose views I have here sought to express in the briefest possible language, we are now in a condition to grapple with the question of musical intervals, and to give the reason why some are consonant and some dissonant to the ear. Circumstanced as we are upon earth, all our feelings and emotions, from the lowest sensation to the highest æsthetic consciousness, have a mechanical cause: though it may be forever denied to us to take the step from cause to effect; or to understand why the agitations of nervous matter can awaken the delights which music imparts. Take, then, the case of a violin. The fundamental tone of every string of this instrument is demonstrably accompanied by a crowd of overtones; so that, when two violins are sounded, we have not only to take into account the consonance or dissonance of the fundamental tones, but also those of the higher tones of both. Supposing two strings sounded whose fundamental tones, and all of whose partial tones, coincide, we have then absolute unison; and this we actually have when the ratio of vibration is 1:1. So also when the ratio of vibration is accurately 1:2, each overtone of the fundamental finds itself in absolute coincidence with either the fundamental tone or some higher tone of the octave. There is no room for beats or dissonance. When we examine the interval of a fifth, with a ratio of430 2:3, we find the coincidence of the partial tones of the two so perfect as almost, though not wholly, to exclude every trace of dissonance. Passing on to the other intervals, we find the coincidence of the partial tones less perfect, as the numbers expressing the ratio of the vibrations become more large. Thus, the dissonance of intervals whose rates of vibration can only be expressed by large numbers, is not to be ascribed to any mystic quality of the numbers themselves, but to the fact that the fundamental tones which require such numbers are inexorably accompanied by partial tones whose coalescence produces beats, these producing the grating effect known as dissonance.
Helmholtz has attempted to represent this result graphically, and from his work I copy, with some modification, the next two diagrams. He assumes, as already stated, the maximum dissonance to correspond to 33 beats per second; and he seeks to express different degrees of dissonance by lines of different lengths. The horizontal line c′ c″, Fig. 164, represents a range of the musical scale in which c″ is our middle C, with 528 vibrations, and c′ the lower octave of c″. The distance from any point of this line to the curve above it represents the dissonance corresponding to that point. The pitch here is supposed to ascend continuously, and not by jumps. Supposing, for example, two performers on the violin to start with the same note c′, and that, while one of them continues to sound that note, the other gradually and continuously shortens his string, thus gradually raising its pitch up to the octave c″. The effect upon the ear would be repre431sented by the irregular curved line in Fig. 164. Soon after the unison, which is represented by contact at c′, is departed from, the curve suddenly rises, showing the dissonance here to be the sharpest of all. At c′, the curve approaches the straight line c′ c″, and this point corresponds to the major third. At f′ the approach, is still nearer, and this point corresponds to the fourth. At g′ the curve almost touches the straight line, indicating that at this point, which corresponds to the fifth, the dissonance almost vanishes. At a′ we have the major sixth; while at c″, where the one note is an octave above the other, the dissonance entirely vanishes. The e s′ and the a s′, of this diagram are the German names of a third and a flat sixth.
Maintaining the same fundamental note c′, and passing through the octave above c″, the various degrees of consonance and dissonance are those shown in Fig. 165. That is to say, beginning with the octave c′-c″, and gradually elevating the pitch of one of the strings till it reaches c″′, the octave of c″, the curved line represents the effect upon the ear. We see, from both these curves, that dissonance is the general rule, and that only at certain definite points does the dissonance vanish, or become so decidedly enfeebled as not to destroy the harmony.432 These points correspond to the places where the numbers expressing the ratio of the two rates of vibration are small whole numbers. It must be remembered that these curves are constructed on the supposition that the beats are the cause of the dissonance; and the agreement between calculation and experience sufficiently demonstrates the truth of the assumption.77
You have thus accompanied me to the verge of the Physical portion of the science of Acoustics, and through the æsthetic portion I have not the knowledge of music necessary to lead you. I will only add that, in comparing three or more sounds together, that is to say, in choosing them for chords, we are guided by the principles just mentioned. We choose sounds which are in harmony with the fundamental sound and with each other. In choosing a series of sounds for combination two by two, the simplicity alone of the ratios would lead us to fix on those expressed by the numbers 1, 5/4, 4/3, 3/2, 5/3, 2; these being the simplest ratios that we can have within an octave. But, when the notes represented by these ratios are sounded in succession, it is found that the intervals between 1 433 and 5/4, and between 5/3 and 2, are wider than the others, and require the interpolation of a note in each case. The notes chosen are such as form chords, not with the fundamental tone, but with the note 3/2 regarded as a fundamental tone. The ratios of these two notes with the fundamental are 9/8 and 15/8. Interpolating these, we have the eight notes of the natural or diatonic scale, expressed by the following names and ratios:
| Names | C. | D. | E. | F. | G. | A. | B. | C′. |
| Intervals | 1st. | 2d. | 3d. | 4th. | 5th. | 6th. | 7th. | 8th. |
| Rates of vibration | 1, | 9/8, | 5/4, | 4/3, | 3/2, | 5/3, | 15/8, | 2. |
Multiplying these ratios by 24, to avoid fractions, we obtain the following series of whole numbers, which express the relative rates of vibration of the notes of the diatonic scale:
24, 27, 30, 32, 36, 40, 45, 48.
The meaning of the terms third, fourth, fifth, etc., which we have so often applied to the musical intervals, is now apparent; the term has reference to the position of the note in the scale.
In our second lecture I referred to, and in part illustrated, a method devised by M. Lissajous for studying musical vibrations. By means of a beam of light reflected from a mirror attached to a tuning-fork, the fork was made to write the story of its own motion. In our last lecture the same method was employed to illustrate optically the phenomenon of beats. I now propose to apply it to the study of the composition of the vibrations which constitute the principal intervals of the diatonic scale. We must, however, prepare ourselves for the434 thorough comprehension of this subject by a brief preliminary examination of the vibrations of a common pendulum.
Such a pendulum hangs before you. It consists of a wire carefully fastened to a plate of iron at the roof of the house, and bearing a copper ball weighing 10 lbs. I draw the pendulum aside and let it go; it oscillates to and fro almost in the same plane.
I say “almost,” because it is practically impossible to suspend a pendulum without some little departure from perfect symmetry around its point of attachment. In consequence of this, the weight deviates sooner or later from a straight line, and describes an oval more or less elongated. Some years ago this circumstance presented a serious difficulty to those who wished to repeat M. Foucault’s celebrated experiment, demonstrating the rotation of the earth.
Nevertheless, in the case now before us, the pendulum is so carefully suspended that its deviation from a straight line is not at first perceptible. Let us suppose the amplitude of its oscillation to be represented by the dotted line a b, Fig. 166. The point d, midway between a and b, is the pendulum’s point of rest. When drawn aside from this point to b, and let go, it will return to d, and in virtue of its momentum will pass on to a. There it comes momentarily to rest, and returns through d to b. And thus it will continue to oscillate until its motion is expended.
The pendulum having first reached the limit of its
swing at b, let us suppose a push in a direction perpendicular
to a b imparted to it; that is to say, in the
direction b c. Supposing the time required by the pen435dulum
to swing from b to a to be one second,78 then the
time required to swing from b to d will be half a second.
 Fig. 166.
Suppose, further, the force applied at b
to be such as would carry the bob, if
free to move in that direction alone, to
c in half a second, and that the distance
b c is equal to b d, the question then
occurs, where will the bob really find
itself at the end of half a second? It
Fig. 166.
Suppose, further, the force applied at b
to be such as would carry the bob, if
free to move in that direction alone, to
c in half a second, and that the distance
b c is equal to b d, the question then
occurs, where will the bob really find
itself at the end of half a second? It
 Fig. 167.
is perfectly manifest that both forces are satisfied
by the pendulum reaching the point e,
exactly opposite the centre d, in half a second.
To reach this point, it can be shown
that it must describe the circular arc b e, and
it will pursue its way along the continuation
of the same arc, to a, and then pass round to b.
Thus, by the rectangular impulse the rectilinear
oscillation is converted into a rotation,
the pendulum describing a circle, as shown in
Fig. 167.
Fig. 167.
is perfectly manifest that both forces are satisfied
by the pendulum reaching the point e,
exactly opposite the centre d, in half a second.
To reach this point, it can be shown
that it must describe the circular arc b e, and
it will pursue its way along the continuation
of the same arc, to a, and then pass round to b.
Thus, by the rectangular impulse the rectilinear
oscillation is converted into a rotation,
the pendulum describing a circle, as shown in
Fig. 167.
If the force applied at b be sufficient to urge the weight in half a second through a greater distance than b c, the pendulum will describe an ellipse, with the lines a b for its smaller axis; if, on the contrary, the force applied at b urge the pendulum in half a second through a distance less than b c, the weight will describe an ellipse, with the line a b for its greater axis.
Let us now inquire what occurs when the rectangular 436impulse is applied at the moment the ball is passing through its position of rest at d.
Supposing the pendulum to be moving from a to b, Fig. 168, and that at d a shock is imparted to it sufficient of itself to carry it in half a second to c; it is here manifest that the resultant motion will be along the straight line d g lying between b d and d c. The pendulum will return along this line to d, and pass on to h. In this case, therefore, the pendulum will describe a straight line, g h, oblique to its original direction of oscillation.
Supposing the direction of motion at the moment the push is applied to be from b to a, instead of from a to b, it is manifest that the resultant here will also be a straight line oblique to the primitive direction of oscillation; but its obliquity will be that shown in Fig. 169.
Fig. 168.
|
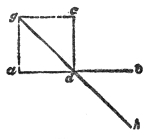
Fig. 169.
|
When the impulse is imparted to the pendulum neither at the centre nor at the limit of its swing, but at some point between both, we obtain neither a circle nor a straight line, but something between both. We have, in fact, a more or less elongated ellipse with its axis oblique to a b, the original direction of vibration. If, for example, the impulse be imparted at d′, Fig. 170, while the pendulum is moving toward b, the position of the ellipse will be that shown in Fig. 170; but if the push at437 d′ be given when the motion is toward a, then the position of the ellipse will be that represented in Fig. 171.
Fig. 170.
|
Fig. 171.
|
By the method of M. Lissajous we can combine the rectangular vibrations of two tuning-forks, a subject which I now wish to illustrate before you. In front of an electric lamp, L, Fig. 172, is placed a large tuning-fork, T′, fixed in a stand horizontally, and provided with a mirror, on which a narrow beam of light, L T′, is permitted to fall. The beam is thrown back, by reflection. In the path of the reflected beam is placed a second upright tuning-fork, T, also furnished with a mirror. By438 the horizontal fork, when it vibrates, the beam is tilted laterally; by the vertical fork, vertically. At the present moment both forks are motionless, the beam of light being reflected from the mirror of the horizontal to that of the vertical fork, and from the latter to the screen, on which it prints a brilliant disk. I now agitate the upright fork, leaving the other motionless. The disk is drawn out into a fine luminous band, 3 feet long. On sounding the second fork, the straight band is instantly transformed into a white ring o p, Fig. 172, 36 inches in diameter. What have we done here? Exactly what we did in our first experiment with the pendulum. We have caused a beam of light to vibrate simultaneously in two directions, and have accidentally hit upon the phase when one fork has just reached the limit of its swing and come momentarily to rest, while the beam is receiving the maximum impulse from the other fork.
That the circle was obtained is, as stated, a mere accident; but it was a fortunate accident, as it enables us to see the exact similarity between the motion of the beam and that of the pendulum. I stop both forks, and, agitating them afresh, obtain an ellipse with its axis oblique. After a few trials we obtain the straight line, indicating that both the forks then pass simultaneously through their positions of equilibrium. In this way, by combining the vibrations of the two forks, we reproduce all the figures obtained with the pendulum.
When the vibrations of the two forks are, in all respects, absolutely alike, whatever the figure may be which is first traced upon the screen, it remains unchanged in form, diminishing only in size as the motion is expended. But the slightest difference in the rates of vibration de439stroys this fixity of the image. I endeavored before the lecture to reader the unison between these two forks as perfect as possible, and hence you have observed very little alteration in the shape of the figure. But by moving a small weight along the prong of either fork, or by attaching to either of them a bit of wax, the unison is impaired. The figure then obtained by the combination of both passes slowly from a straight line into an oblique ellipse, thence into a circle; after which it narrows again to an ellipse with an opposed obliquity, it then passes again into a straight line, the direction of which is at right angles to the first direction. Finally, it passes, in the reverse order, through the same series of figures to the straight line with which we began. The interval between two successive identical figures is the time in which one of the forks succeeds in executing one complete vibration more than the other. Loading the fork still more heavily, we have more rapid changes; the straight line, ellipse, and circle being passed through in quick succession. At times the luminous curve exhibits a stereoscopic depth, which renders it difficult to believe that we are not looking at a solid ring of white-hot metal.

By causing the mirror of the fork, T, to rotate through a small arc, the steady circle first obtained is drawn out into a luminous scroll stretching right across the screen, Fig. 173. The same experiment made with the changing440 figure, obtained by throwing the forks out of unison, gives us a scroll of irregular amplitude, Fig. 174.79

We have next to combine the vibrations of two forks,
one of which oscillates with twice the rapidity of the
other; in other words, to determine the figure corresponding
to the combination of a note and its octave.
 Fig. 175.
To prepare ourselves for the mechanics
of the problem, we must resort once
more to our pendulum; for it also can
be caused to oscillate in one direction
twice as rapidly as in another. By
a complicated mechanical arrangement
this might be done in a very perfect
manner, but at present simplicity is
preferable to completeness. The wire
of our pendulum is therefore permitted
to descend from its point of suspension,
A, Fig. 175, midway between two
horizontal glass rods, a b, a′ b′, supported
firmly at their ends, and about
an inch asunder. The rods cross the
wire at a height of 7 feet above the
bob of the pendulum. The whole
length of the pendulum being 28 feet,
the glass rods intercept one-fourth of
this length. On drawing the pendulum aside in the
441direction of the rods, a b, a′ b′, and letting it go, it
oscillates freely between them. I bring it to rest and
draw it aside in a direction perpendicular to the last; a
length of 7 feet only can now oscillate, and by the laws
of oscillation a pendulum 7 feet long vibrates with twice
the rapidity of a pendulum 28 feet long.
Fig. 175.
To prepare ourselves for the mechanics
of the problem, we must resort once
more to our pendulum; for it also can
be caused to oscillate in one direction
twice as rapidly as in another. By
a complicated mechanical arrangement
this might be done in a very perfect
manner, but at present simplicity is
preferable to completeness. The wire
of our pendulum is therefore permitted
to descend from its point of suspension,
A, Fig. 175, midway between two
horizontal glass rods, a b, a′ b′, supported
firmly at their ends, and about
an inch asunder. The rods cross the
wire at a height of 7 feet above the
bob of the pendulum. The whole
length of the pendulum being 28 feet,
the glass rods intercept one-fourth of
this length. On drawing the pendulum aside in the
441direction of the rods, a b, a′ b′, and letting it go, it
oscillates freely between them. I bring it to rest and
draw it aside in a direction perpendicular to the last; a
length of 7 feet only can now oscillate, and by the laws
of oscillation a pendulum 7 feet long vibrates with twice
the rapidity of a pendulum 28 feet long.
I wish to show you the figure described by the combination of these two rates of vibration. Attached to the copper ball, p, is a camel’s-hair pencil, intended to rub lightly upon a glass plate placed on black paper and over which is strewed white sand. Allowing the pendulum to oscillate as a whole, the sand is rubbed away along a straight line which represents the amplitude of the vibration. Let a b, Fig. 176, represent this line, which, as before, we will assume to be described in one second. When the pendulum is at the limit, b, of its swing, let a rectangular impulse be imparted to it sufficient to carry it to c in one-fourth of a second. If this were the only impulse acting on the pendulum, the bob would reach c and return to b in half a second. But under the actual circumstances it is also urged toward d, which point, through the vibration of the whole pendulum, it ought also to reach in half a second. Both vibrations, therefore, require that the bob shall reach d at the same moment; and to do this it will have to describe the curve b c′ d. Again, in the time required by the long pendulum to pass from d to a, the short pendulum will pass to and fro over the half of its excursion; both vibrations must therefore reach a at the same moment, and to accomplish this the pendulum describes the lower curve between d and a. It is manifest that these two curves will repeat themselves at the opposite sides of a b, the442 combination of both vibrations producing finally a figure of 8, which you now see fairly drawn upon the sand before you.
The same figure is obtained if the rectangular impulse be imparted when the pendulum is passing its position of rest, d.
Fig. 176.
|
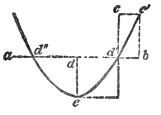
Fig. 177.
|
I have here supposed the time occupied by the pendulum in describing the line a b to be one second. Let us suppose three-fourths of the second exhausted, and the pendulum at d′, Fig. 177, in its excursion toward b; let the rectangular impulse then be imparted to it, sufficient to carry it to c in one-fourth of a second. Now the long pendulum requires that it should move from d′ to b in one-fourth of a second; both impulses are therefore satisfied by the pendulum taking up the position c′ at the end of a quarter of a second. To reach this position it must describe the curve d′ c′. It will manifestly return along the same curve, and at the end of another quarter of a second find itself again at d′. From d′ to d the long pendulum requires a quarter of a second. But at the end of this time the short pendulum must be at the lower limit of its swing: both requirements are satisfied by the pendulum being at e. We thus obtain one arm, c′ e, of a curve, which repeats itself to the left of e; so that the entire curve, due to the combination of the two vibrations, is that represented in Fig. 165. This figure443 is a parabola, whereas the figure of 8 before obtained is a lemniscata.
We have here supposed that, at the moment when the rectangular impulse was applied, the motion of the pendulum was toward b: if it were toward a we should obtain the inverted parabola, as shown in Fig. 178.
Supposing, finally, the impulse to be applied, not when the pendulum is passing through its position of equilibrium, nor when it is passing a point corresponding to three-fourths or one-fourth of the time of its excursion, but at some other point in the line, a b, between its end and centre. Under these circumstances we should have neither the parabola nor the perfectly symmetrical figure of 8, but a distorted 8.
And now we are prepared to witness with profit the combined vibration of our two tuning-forks, one of which sounds the octave of the other. Permitting the vertical fork, T, Fig. 172, to remain undisturbed in front of the lamp, we can oppose to it a horizontal fork, which vibrates with twice the rapidity. The first passage of the bow across the two forks reveals the exact similarity of this combination, and that of our pendulum. A very perfect figure of 8 is described upon the screen. Before the lecture the vibrations of these two forks were fixed as nearly as possible to the ratio of 1:2, and the steadiness of the figure indicates the perfection of the tuning. Stopping both forks, and again agitating them, we have the distorted 8 upon the screen. A few trials enable me to bring out the parabola. In all these cases the figure remains fixed upon the screen. But if a morsel of wax be attached to one of the forks, the figure is steady no longer, but passes from the perfect 8 into the distorted444 one, thence into the parabola, from which it afterward opens out to an 8 once more. By augmenting the discord, we can render those changes as rapid as we please.
When the 8 is steady on the screen, a rotation of the mirror of the fork, T, produces the scroll shown in Fig. 179.

Our next combination will be that of two forks vibrating in the ratio of 2:3. Observe the admirable steadiness of the figure produced by the compounding of these two rates of vibration. On attaching a four-penny-piece with wax to one of the forks the steadiness ceases, and we have an apparent rocking to and fro of the luminous figure. Passing on to intervals of 3:4, 4:5, and 5:6, the figures become more intricate as we proceed. The last combination, 5:6, is so entangled that to see the figure plainly a very narrow band of light must be employed. The distance existing between the forks and the screen also helps us to unravel the complication.

And here it is worth noting that, when the figure is
fully developed, the loops along the vertical and horizontal
edges express the ratio of the combined vibrations.
In the octave, for example, we have two loops
in one direction, and one in another; in the fifth, two
loops in one direction, and three in another. When
the combination is as 1:3, the luminous loops are also
as 1:3. The changes which some of these figures un445
446dergo,
when the tuning is not perfect, are extremely
remarkable. In the case of 1:3, for example, it is
difficult at times not to believe that you are looking
at a solid link of white-hot metal. The figure exhibits
a depth, apparently incompatible with its being traced
upon a plane surface.

Fig. 180 (page 445) is a diagram of these beautiful figures, including combinations from 1:1 to 5:6. In each case, the characteristic phases of the vibration are shown; and through all of these each figure passes when the interval between the two forks is not pure. I also add here, Fig. 181, two phases of the combination 8:9.

Fig. 182. 1:2.
|

Fig. 183. 2:3.
|
To these illustrations of rectangular vibrations I add two others, Figs. 182 and 183, from a very beautiful series obtained by Mr. Herbert Airy with a compound pendulum. The experiments are described in “Nature447” for August 17 and September 7, 1871. As their loops indicate, the figures are those of an octave and a twelfth.

Fig. 184. 2:3
|

Fig. 185. 3:4
|
But the most instructive apparatus for the compounding of rectangular vibrations is that of Mr. Tisley. Figs. 184 and 185 are copies of figures obtained by him through the joint action of two distinct pendulums; the rates of vibration corresponding to these particular figures being 2:3 and 3:4 respectively. The pen which traces the figures is moved simultaneously by two rods attached to the pendulums above their places of suspension. These two rods lie in the two planes of vibration, being at right angles to the pendulums, and to each other. At their place of intersection is the pen. By means of a ball and socket, of a special kind, the rods are enabled to move with a minimum of friction in all directions, while the rates of vibration are altered, in a moment, by the shifting of movable weights. The figures are drawn either with ink on paper, or, when projection on a screen448 is desired, by a sharp point on smoked glass. When the pendulums, having gone through the entire figure, return to their starting-point, they have lost a little in amplitude. The second excursion will, therefore, be smaller than the first, and the third smaller than the second. Hence the series of fine lines, inclosing gradually-diminishing areas, shown in these exquisite figures.80 Mr. Tisley’s apparatus reflects the highest credit upon its able constructor.
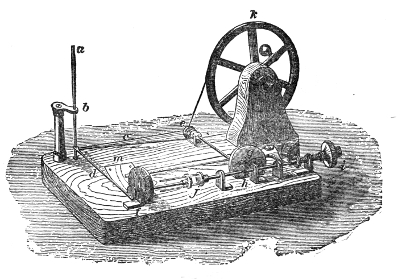
Sir Charles Wheatstone devised, many years ago, a small and very efficient apparatus for the compounding of rectangular vibrations. A drawing, Fig. 186, and a description of this beautiful little instrument, for both of which I am indebted to its eminent inventor, may find a place here: a is a steel rod polished at its upper end so as to reflect a point of light; this rod moves in a ball-449and-socket joint at b, so that it may assume any position. Its lower end is connected with two arms c and d, placed at right angles to each other, the other ends of which are respectively attached to the circumferences of the two circular disks e and f. The axis of the disk e carries at its opposite end another large disk g, which gives motion to the small disk h, placed on the axis which carries the disk f; and, according as this small disk h is placed nearer to or further from the centre of the disk g, it communicates a different relative motion to the disk f. The nut and screw i enable the disk h to be placed in any position between the centre, and circumference of the larger disk g; and by means of the fork j the disk f is caused to revolve, whatever may be the position of the disk h. By this arrangement, while the wheel k is turned regularly, the rod a is moved backward and forward by the disk e in one direction, and by the disk f, with any relative oscillatory motion, in the rectangular direction. The end of the rod is thus made to describe and to exhibit optically all the beautiful acoustical figures produced by the composition of vibrations of different periods in directions rectangular to each other. A lever l, bearing against the nut i, indicates, on a scale m, the numerical ratio of the two vibrations.81
I close these remarks on the combination of rectangular vibrations with a brief reference to an apparatus constructed by Mr. A. E. Donkin, of Exeter College, Oxford, and described in the “Proceedings of the Royal Society,” vol. xxii., p. 196. In its construction great mechanical knowledge is associated with consummate 450skill. I saw the apparatus as a wooden model, before it quitted the hands of its inventor, and was charmed with its performance. It is now constructed by Messrs. Tisley and Spiller.
By the division of a string Pythagoras determined the consonant intervals in music, proving that, the simpler the ratio of the two parts into which the string was divided, the more perfect is the harmony of the sounds emitted by the two parts of the string. Subsequent investigators showed that the strings act thus because of the relation of their lengths to their rates of vibration.
With the double siren this law of consonance is readily illustrated. Here the most perfect harmony is the unison, where the vibrations are in the ratio of 1:1. Next comes the octave, where the vibrations are in the ratio of 1:2. Afterward follow in succession the fifth, with a ratio of 2:3; the fourth, with a ratio of 3:4; the major third, with a ratio of 4:5; and the minor third, with a ratio of 5:6. The interval of a tone, represented by the ratio 8:9, is dissonant, while that of a semitone, with a ratio of 15:16, is a harsh and grating dissonance.
The musical interval is independent of the absolute number of the vibrations of the two notes, depending only on the ratio of the two rates of vibration.
The Pythagoreans referred the pleasing effect of the consonant intervals to number and harmony, and connected them with “the music of the spheres.” Euler explained the consonant intervals by reference to the constitution of the mind, which, he affirmed, took pleas451ure in simple calculations. The mind was fond of order, but of such order as involved no weariness in its contemplation. This pleasure was afforded by the simpler ratios in the case of music.
The researches of Helmholtz prove the rapid succession of beats to be the real cause of dissonance in music.
By means of two singing-flames, the pitch of one of them being changeable by the telescopic lengthening of its tube, beats of any degree of slowness or rapidity may be produced. Commencing with beats slow enough to be counted, and gradually increasing their rapidity, we reach, without breach of continuity, downright dissonance.
But, to grasp this theory in all its completeness, we must refer to the constitution of the human ear. We have first the tympanic membrane, which is the anterior boundary of the drum of the ear. Across the drum stretches a series of little bones, called respectively the hammer, the anvil, and the stirrup-bone; the latter abutting against a second membrane, which forms part of the posterior boundary of the drum. Beyond this membrane is the labyrinth filled with water, and having its lining membrane covered with the filaments of the auditory nerve.
Every shock received by the tympanic membrane is transmitted through the series of bones to the opposite membrane; thence to the water of the labyrinth, and thence to the auditory nerve.
The transmission is not direct. The vibrations are in the first place taken up by certain bodies, which can swing sympathetically with them. These bodies are of three kinds: the otolites, which are little crystalline par452ticles; the bristles of Max Schultze; and the fibres of Corti’s organ. This latter is to all intents and purposes a stringed instrument, of extraordinary complexity and perfection, placed within the ear.
As regards our present subject, the strings of Corti’s organ probably play an especially important part. That one string should respond, in some measure, to another, it is not necessary that the unison should be perfect; a certain degree of response occurs in the immediate neighborhood of unison.
Hence each of two strings, not far removed from each other in pitch, can cause a third string, of intermediate pitch, to respond sympathetically. And if the two strings be sounded together, the beats which they produce are propagated to the intermediate string.
So, as regards Corti’s organ, when single sounds of various pitches, or rather when vibrations of various rapidities, fall upon its strings, the vibrations are responded to by the particular string whose period coincides with theirs. And when two sounds, close to each other in pitch, produce beats, the intermediate Corti’s fibre is acted on by both, and responds to the beats.
In the middle and upper portions of the musical scale the beats are most grating and harsh when they succeed each other at the rate of 33 per second. When they occur at the rate of 132 per second, they cease to be sensible.
The perfect consonance of certain musical intervals is due to the absence of beats. The imperfect consonance of other intervals is due to their existence. And here the overtones play a part of the utmost importance. For, though the primaries may sound together without any453 perceptible roughness, the overtones may be so related to each other as to produce harsh and grating beats. A strict analysis of the subject proves that intervals which require large numbers to express them are invariably accompanied by overtones which produce beats; while in intervals expressed by small numbers the beats are practically absent.
The graphic representation of the consonances and dissonances of the musical scale, by Helmholtz, furnishes a striking proof of this explanation.
The optical illustration of the musical intervals has been effected in a very beautiful manner by Lissajous. Corresponding to each interval is a definite figure, produced by the combination of its vibrations.
The compounding of vibrations has, of late years, been beautifully illustrated by apparatus constructed by Sir C. Wheatstone, Mr. Herbert Airy, and Mr. A. E. Donkin; and by the beautiful pendulum apparatus of Mr. Tisley, of the firm of Tisley and Spiller.
The pressure which, on a former occasion, prevented me from adding a “summary” to this chapter, was also the cause of hastiness, and partial inaccuracy, in its sketch of the theory of Helmholtz. That the sketch needed emendation I have long known, but I did not think it worth while to anticipate the correction here made; as the chapter, imperfect as it was, had been published, without comment, in Germany, by Helmholtz himself.
ON THE INFLUENCE OF MUSICAL SOUNDS ON THE FLAME OF A JET OF COAL-GAS. BY JOHN LE CONTE, M.D.82
A short time after reading Prof. John Tyndall’s excellent article “On the Sounds produced by the Combustion of Gases in Tubes,”83 I happened to be one of a party of eight persons assembled after tea for the purpose of enjoying a private musical entertainment. Three instruments were employed in the performance of several of the grand trios of Beethoven, namely, the piano, violin, and violoncello. Two “fish-tail” gas-burners projected from the brick wall near the piano. Both of them burned with remarkable steadiness, the windows being closed and the air of the room being very calm. Nevertheless, it was evident that one of them was under a pressure nearly sufficient to make it flare.
Soon after the music commenced, I observed that the flame of the last-mentioned burner exhibited pulsations in height which were exactly synchronous with the audible beats. This phenomenon was very striking to every one in the room, and especially so when the strong notes of the violoncello came in. It was exceedingly interesting to observe how perfectly even the trills of this instrument were reflected on the sheet of flame. A deaf man might have seen 455 the harmony. As the evening advanced, and the diminished consumption of gas in the city increased the pressure, the phenomenon became more conspicuous. The jumping of the flame gradually increased, became somewhat irregular, and finally it began to flare continuously, emitting the characteristic sound indicating the escape of a greater amount of gas than could be properly consumed. I then ascertained by experiment that the phenomenon did not take place unless the discharge of gas was so regulated that the flame approximated to the condition of flaring. I likewise determined by experiment that the effects were not produced by jarring or shaking the floor and walls of the room by means of repeated concussions. Hence it is obvious that the pulsations of the flame were not owing to indirect vibrations propagated through the medium of the walls of the room to the burning apparatus, but must have been produced by the direct influence of the aërial sonorous pulses on the burning jet.
In the experiments of M. Schaffgotsch and Prof. J. Tyndall, it is evident that “the shaking of the singing-flame within the glass tube,” produced by the voice or the siren, was a phenomenon perfectly analogous to what took place under my observation without the intervention of a tube. In my case the discharge of gas was so regulated that there was a tendency in the flame to flare, or to emit a “singing-sound.” Under these circumstances, strong aërial pulsations occurring at regular intervals were sufficient to develop synchronous fluctuations in the height of the flame. It is probable that the effects would be more striking when the tones of the musical instrument are nearly in unison with the sounds which would be produced by the flame under the slight increase in the rapidity of discharge of gas required to manifest the phenomenon of flaring. This point might be submitted to an experimental test.
As in Prof. Tyndall’s experiments on the jet of gas burning within a tube, clapping of the hands, shouting, etc., were ineffectual in converting the “silent” into the “singing-flame,”456 so, in the case under consideration, irregular sounds did not produce any perceptible influence. It seems to be necessary that the impulses should accumulate, in order to exercise an appreciable effect.
With regard to the mode in which the sounds are produced by the combustion of gases in tubes, it is universally admitted that the explanation given by Prof. Faraday in 1818 is essentially correct. It is well known that he referred these sounds to the successive explosions produced by the periodic combination of the atmospheric oxygen with the issuing jet of gas. While reading Prof. J. Plateau’s admirable researches (third series) on the “Theory of the Modifications experienced by Jets of Liquid issuing from Circular Orifices when exposed to the Influence of Vibratory Motions,”84 the idea flashed across my mind that the phenomenon which had fallen under my observation was nothing more than a particular case of the effects of sounds on all kinds of fluid jets. Subsequent reflection has only served to fortify this first impression.
The beautiful investigations of Felix Savart, on the influence of sounds on jets of water, afford results presenting so many points of analogy with their effects on the jet of burning gas, that it may be well to inquire whether both of them may be referred to a common cause. In order to place this in a striking light, I shall subjoin some of the results of Savart’s experiments. Vertically-descending jets of water receive the following modifications under the influence of vibrations:
1. The continuous portions become shortened; the vein resolves itself into separate drops nearer the orifice than when not under the influence of vibrations.
2. Each of the masses, as they detach themselves from the extremity of the continuous part, becomes flattened alternately in a vertical and horizontal direction, presenting to the eye, under the influence of their translatory motion, 457 regularly-disposed series of maxima and minima of thickness, or ventral segments and nodes.
3. The foregoing modifications become much more developed and regular when a note, in unison with that which would be produced by the shock of the discontinuous part of the jet against a stretched membrane, is sounded in its neighborhood. The continuous part becomes considerably shortened, and the ventral segments are enlarged.
4. When the note of the instrument is almost in unison, the continuous part of the jet is alternately lengthened and shortened and the beats which coincide with these variations in length can be recognized by the ear.
5. Other tones act with less energy on the jet, and some produce no sensible effect.
When a jet is made to ascend obliquely, so that the discontinuous part appears scattered into a kind of sheaf in the same vertical plane, M. Savart found:
a. That, under the influence of vibrations of a determinate period, this sheaf may form itself into two distinct jets, each possessing regularly-disposed ventral segments and nodes; sometimes with a different node the sheaf becomes replaced by three jets.
b. The note which produces the greatest shortening of the continuous part always reduces the whole to a single jet, presenting a perfectly regular system of ventral segments and nodes.
In the last memoir of M. Savart—a posthumous one, presented to the Academy of Sciences of Paris, by M. Arago, in 185385—several remarkable acoustic phenomena are noticed in relation to the musical tones produced by the efflux of liquids through short tubes. When certain precautions and conditions are observed (which are minutely detailed by this able experimentalist), the discharge of the liquid gives rise to a succession of musical tones of great intensity and of a peculiar quality, somewhat analogous to 458that of the human voice. That these notes were not produced by the descending drops of the liquid vein was proved by permitting it to discharge itself into a vessel of water, while the orifice was below the surface of the latter. In this case the jet of liquid must have been continuous, but nevertheless the notes were produced. These unexpected results have been entirely confirmed by the more recent experiments of Prof. Tyndall.86
According to the researches of M. Plateau, all the phenomena of the influence of vibrations on jets of liquid are referable to the conflict between the vibrations and the forces of figure (“forces figuratrices”). If the physical fact is admitted—and it seems to be indisputable—that a liquid cylinder attains a limit of stability when the proportion between its length and its diameter is in the ratio of twenty-two to seven, it is almost a physical necessity that the jet should assume the constitution indicated by the observations of Savart. It likewise seems highly probable that a liquid jet, while in a transition stage to discontinuous drops, should be exceedingly sensitive to the influence of all kinds of vibrations. It must be confessed, however, that Plateau’s beautiful and coherent theory does not appear to embrace Savart’s last experiment, in which the musical tones were produced by a jet of water issuing under the surface of the same liquid. It is rather difficult to imagine what agency the “forces of figure” could have, under such circumstances, in the production of the phenomenon. This curious experiment tends to corroborate Savart’s original idea, that the vibrations which produce the sounds must take place in the glass reservoir itself, and that the cause must be inherent in the phenomenon of the flow.
To apply the principles of Plateau’s theory to gaseous jets, we are compelled to abandon the idea of the non-existence of molecular cohesion in gases. But is there not abundant evidence to show that cohesion does exist among the particles of gaseous masses? Does not the deviation 459from rigorous accuracy, both in the law of Mariotte and Gay-Lussac—especially in the case of condensable gases, as shown by the admirable experiments of M. Regnault—clearly prove that the hypothesis of the non-existence of cohesion in aëriform bodies is fallacious? Do not the expanding rings which ascend when a bubble of phosphuretted hydrogen takes fire in the air indicate the existence of some cohesive force in the gaseous product of combustion (aqueous vapor), whose outlines are marked by the opaque phosphoric acid? In short, does not the very form of the flame of a “fish-tail” burner demonstrate that cohesion must exist among the particles of the issuing gas? It is well known that in this burner the single jet which issues is formed by the union of two oblique jets immediately before the gas is emitted. The result is a perpendicular sheet of flame. How is such a result produced by the mutual action of two jets, unless the force of cohesion is brought into play? Is it not obvious that such a fanlike flame must be produced by the same causes as those varied and beautiful forms of aqueous sheets, developed by the mutual action of jets of water, so strikingly exhibited in the experiments of Savart and of Magnus?
If it be granted that gases possess molecular cohesion, it seems to be physically certain that jets of gas must be subject to the same laws as those of liquid. Vibratory movements excited in the neighborhood ought, therefore, to produce modifications in them analogous to those recorded by M. Savart in relation to jets of water. Flame or incandescent gas presents gaseous matter in a visible form, admirably adapted for experimental investigation; and, when produced by a jet, should be amenable to the principles of Plateau’s theory. According to this view, the pulsations or beats which I observed in the gas-flame when under the influence of musical sounds, are produced by the conflict between the aërial vibrations and the “forces of figure” (as Plateau calls them) giving origin to periodical fluctuations of intensity, depending on the sonorous pulses.
If this view is correct, will it not be necessary for us to modify our ideas in relation to the agency of tubes in developing musical sounds by means of burning jets of gas? Must we not look upon all burning jets—as in the case of water-jets—as musically inclined; and that the use of tubes merely places them in a condition favorable for developing the tones? It is well known that burning jets frequently emit a singing-sound when they are perfectly free. Are these sounds produced by successive explosions analogous to those which take place in glass tubes? It is very certain that, under the influence of molecular forces, any cause which tends to elongate the flame, without affecting the velocity of discharge, must tend to render it discontinuous, and thus bring about that mixture of gas and air which is essential to the production of the explosions. The influence of tubes, as well as of aërial vibrations, in establishing this condition of things, is sufficiently obvious. Was not the “beaded line” with its succession of “luminous stars,” which Prof. Tyndall observed when a flame of olefiant gas, burning in a tube, was examined by means of a moving mirror, an indication that the flame became discontinuous, precisely as the continuous part of a jet of water becomes shortened, and resolved into isolated drops, under the influence of sonorous pulsations? But I forbear enlarging on this very interesting subject, inasmuch as the accomplished physicist last named has promised to examine it at a future period. In the hands of so sagacious a philosopher, we may anticipate a most searching investigation of the phenomena in all their relations. In the meantime I wish to call the attention of men of science to the view presented in this article, in so far as it groups together several classes of phenomena under one head, and may be considered a partial generalization.—From Silliman’s “American Journal” for January, 1858.
ON ACOUSTIC REVERSIBILITY87
On the 21st and 22d of June, 1822, a commission, appointed by the Bureau des Longitudes of France, executed a celebrated series of experiments on the velocity of sound. Two stations had been chosen, the one at Villejuif, the other at Montlhéry, both lying south of Paris, and 11·6 miles distant from each other. Prony, Mathieu, and Arago were the observers at Villejuif, while Humboldt, Bouvard, and Gay-Lussac were at Montlhéry. Guns, charged sometimes with two pounds and sometimes with three pounds of powder, were fired at both stations, and the velocity was deduced from the interval between the appearance of the flash and the arrival of the sound.
On this memorable occasion an observation was made which, as far as I know, has remained a scientific enigma to the present hour. It was noticed that while every report of the cannon fired at Montlhéry was heard with the greatest distinctness at Villejuif, by far the greater number of the reports from Villejuif failed to reach Montlhéry. Had wind existed, and had it blown from Montlhéry to Villejuif, it would have been recognized as the cause of the observed difference; but the air at the time was calm, the slight motion of translation actually existing being from Villejuif toward Montlhéry, or against the direction in which the sound was best heard.
So marked was the difference in transmissive power between the two directions, that on June 22d, while every shot fired at Montlhéry was heard à merveille at Villejuif, but one shot out of twelve fired at Villejuif was heard, and that feebly, at the other station.
With the caution which characterized him on other occasions, and which has been referred to admiringly by Faraday,88 Arago made no attempt to explain this anomaly. His words are: “Quant aux différences si remarquables d’intensité que le bruit du canon a toujours présentées suivant qu’il se propageait du nord au sud entre Villejuif et Montlhéry, ou du sud au nord entre cette seconde station et la première, nous ne chercherons pas aujourd’hui à l’expliquer, parce que nous ne pourrions offrir au lecteur que des conjectures denuées de preuves.”89
I have tried, after much perplexity of thought, to bring this subject within the range of experiment, and have now to submit the following solution of the enigma: The first step was to ascertain whether the sensitive flame, referred to in my recent paper in the “Philosophical Transactions,” could be safely employed in experiments on the mutual reversibility of a source of sound and an object on which the sound impinges. Now, the sensitive flame usually employed by me measures from eighteen to twenty-four inches in height, while the reed employed as a source of sound is less than a square quarter of an inch in area. If, therefore, the whole flame, or the pipe which fed it, were sensitive to sonorous vibrations, strict experiments on reversibility with the reed and flame might be difficult, if not impossible. Hence my desire to learn whether the seat of sensitiveness was so localized in the flame as to render the contemplated interchange of flame and reed permissible.
The flame being placed behind a cardboard screen, the shank of a funnel passed through a hole in the cardboard was directed upon the middle of the flame. The sound-waves issuing from the vibrating reed, placed within the funnel, produced no sensible effect upon the flame. Shifting the funnel so as to direct its shank upon the root of the flame, the action was violent.
To augment the precision of the experiment, the funnel was connected with a glass tube three feet long and half an inch in diameter, the object being to weaken, by distance, the effect of the waves diffracted round the edge of the funnel, and to permit those only which passed through the glass tube to act upon the flame.
Presenting the end of the tube to the orifice of the burner (b, Fig. 1), or the orifice to the end of the tube, the flame was violently agitated by the sounding-reed, R. On shifting the tube, or the burner, so as to concentrate the sound on a portion of the flame about half an inch above the orifice, the action was nil. Concentrating the sound upon the burner itself, about half an inch below its orifice, there was no action.
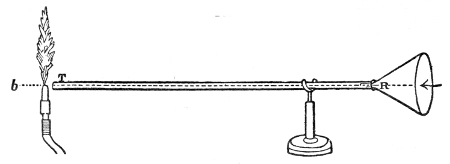
These experiments demonstrate the localization of “the seat of sensitiveness,” and they prove the flame to be an appropriate instrument for the contemplated experiments on reversibility.
The experiments then proceeded thus: The sensitive flame being placed close behind a screen of cardboard 18 inches high by 12 inches wide, a vibrating reed, standing at the same height as the root of the flame, was placed at a distance of 6 feet on the other side of the screen. The sound of the reed, in this position, produced a strong agitation of the flame.
The whole upper half of the flame was here visible from the reed; hence the necessity of the foregoing experiments to prove the action of the sound on the upper portion of the464 flame to be nil, and that the waves had really to bend round the edge of the screen, so as to reach the seat of sensitiveness in the neighborhood of the burner.
The positions of the flame and reed were reversed, the latter being now close behind the screen, and the former at a distance of 6 feet from it. The sonorous vibrations were without sensible action upon the flame.
The experiment was repeated and varied in many ways. Screens of various sizes were employed; and, instead of reversing the positions of the flame and reed, the screen itself was moved, so as to bring in some experiments the flame, and in other experiments the reed, close behind it. Care was also taken that no reflected sound from the walls or ceiling of the laboratory, or from the body of the experimenter, should have anything to do with the effect. In all cases it was shown that the sound was effective when the reed was at a distance from the screen, and the flame close behind it; while the action was insensible when these positions were reversed.

Thus, let s e, Fig. 2, be a vertical section of the screen. When the reed was at A and the flame at B there was no action; when the reed was at B and the flame at A the action was decided. It may be added that the vibrations communicated to the screen itself, and from it to the air beyond it, were without effect; for when the reed, which at B was effectual, was shifted to C, where its action on the screen was greatly augmented, it ceased to have any action on the flame at A.
We are now, I think, prepared to consider the failure of reversibility in the larger experiments of 1822. Happily an incidental observation of great significance comes here465 to our aid. It was observed and recorded at the time that, while the reports of the guns at Villejuif were without echoes, a roll of echoes lasting from 20 to 25 seconds accompanied every shot at Montlhéry, being heard by the observers there. Arago, the writer of the report, referred these echoes to reflection from the clouds, an explanation which I think we are now entitled to regard as problematical. The report says that “tous les coups tirés à Montlhéry y étaient accompagnés d’un roulement semblable à celui du tonnerre.” I have italicized a very significant word—a word which fairly applies to our experiments on gun-sounds at the South Foreland, where there was no sensible interval between explosion and echo, but which could hardly apply to echoes coming from the clouds. For supposing the clouds to be only a mile distant, the sound and its echo would have been separated by an interval of nearly ten seconds. But there is no mention of any interval; and, had such existed, surely the word “followed,” instead of “accompanied,” would have been the one employed. The echoes, moreover, appear to have been continuous, while the clouds observed seem to have been separate. “Ces phénomènes,” says Arago, “n’ont jamais eu lieu qu’au moment de l’apparition de quelques nuages.” But from separate clouds a continuous roll of echoes could hardly come. When to this is added the experimental fact that clouds far denser than any ever formed in the atmosphere are demonstrably incapable of sensibly reflecting sound, while cloudless air, which Arago pronounced echoless, has been proved capable of powerfully reflecting it, I think we have strong reason to question the hypothesis of the illustrious French philosopher.90
And, considering the hundreds of shots fired at the South Foreland, with the attention especially directed to the aërial echoes, when no single case occurred in which echoes of measurable duration did not accompany the report 466of the gun, I think Arago’s statement, that at Villejuif no echoes were heard when the sky was clear, must simply mean that they vanished with great rapidity. Unless the attention was specially directed to the point, a slight prolongation of the cannon-sound might well escape observation; and it would be all the more likely to do so if the echoes were so loud and prompt as to form apparently part and parcel of the direct sound.
I should be very loth to transgress here the limits of fair criticism, or to throw doubt, without good reason, on the recorded observations of illustrious men. Still, taking into account what has been just stated, and remembering that the minds of Arago and his colleagues were occupied by a totally different problem (that the echoes were an incident rather than an object of observation), I think we may justly consider the sound which he called “instantaneous” as one whose aërial echoes did not differentiate themselves from the direct sound by any noticeable fall of intensity, and which rapidly died into silence.
Turning now to the observations at Montlhéry, we are struck by the extraordinary duration of the echoes heard at that station. At the South Foreland the charge habitually fired was equal to the largest of those employed by the French philosophers; but on no occasion did the gun-sounds produce echoes approaching to 20 or 25 seconds’ duration. The time rarely reached half this amount. Even the siren-echoes, which were more remarkable and more long-continued than those of the gun, never reached the duration of the Montlhéry echoes. The nearest approach to it was on October 17, 1873, when the siren-echoes required 15 seconds to subside into silence.
On this same day, moreover (and this is a point of marked significance), the transmitted sound reached its maximum range, the gun-sounds being heard at the Quenocs buoy, 16-1/2 nautical miles from the South Foreland. I have stated in another place that the duration of the air-echoes indicates “the atmospheric depths” from which they467 came. An optical analogy may help us here. Let light fall upon chalk, the light is wholly scattered by the superficial particles; let the chalk be powdered and mixed with water, light reaches the observer from a far greater depth of the turbid liquid. The solid chalk typifies the action of exceedingly dense acoustic clouds; the chalk and water that of clouds of more moderate density. In the one case we have echoes of short, in the other echoes of long, duration. These considerations prepare us for the inference that Montlhéry, on the occasion referred to, must have been surrounded by a highly-diacoustic atmosphere; while the shortness of the echoes at Villejuif shows that the atmosphere surrounding that station must have been, in a high degree, acoustically opaque.
Have we any clew to the cause of the opacity? I think we have. Villejuif is close to Paris, and over it, with the observed light wind, was slowly wafted the air from the city. Thousands of chimneys to windward of Villejuif were discharging their heated currents; so that an exceeding non-homogeneous atmosphere must have surrounded that station.91 At no great height in the atmosphere the equilibrium of temperature would be established. This non-homogeneous air surrounding Villejuif is experimentally typified by our screen, with the source of sound close behind it, the upper edge of the screen representing the place where equilibrium of temperature was established in the atmosphere above the station. In virtue of its proximity to the screen, the echoes from our sounding-reed would, in the case here supposed, so blend with the direct sound as to be practically indistinguishable from it, as the echoes at Villejuif followed the direct sound so hotly, and vanished so rapidly, that they escaped observation. And as our sensitive flame, at a distance, failed to be affected by the sounding body placed close behind the cardboard screen, so, I take it, did the observers at Montlhéry fail to hear the sounds of the Villejuif gun.
Something further may be done toward the experimental elucidation of this subject. The facility with which sounds pass through textile fabrics has been already illustrated,92 a layer of cambric or calico, or even of thick flannel or baize, being found competent to intercept but a small fraction of the sound from a vibrating reed. Such a layer of calico may be taken to represent a layer of air, differentiated from its neighbors by temperature or moisture; while a succession of such sheets of calico may be taken to represent successive layers of non-homogeneous air.

Two tin tubes (M N and O P, Fig. 3) with open ends were placed so as to form an acute angle with each other. At the end of one was the vibrating reed r; opposite the end of the other, and in the prolongation of P O, the sensitive flame f, a second sensitive flame (f′) being placed in the continuation of the axis of M N. On sounding the reed, the direct sound through M N agitated the flame f′. Introducing the square of calico a b at the proper angle, a slight decrease of the action on f′ was noticed, and the feeble echo from a b produced a barely perceptible agitation of the flame f. Adding another square, c d, the sound transmitted by a b impinged on c d; it was partially echoed, returned through a b, passed along P O, and still further agitated the flame f. Adding a third square, e f, the reflected sound was still further augmented, every accession 469to the echo being accompanied by a corresponding withdrawal of the vibrations from f′, and a consequent stilling of that flame.
With thinner calico or cambric it would require a greater number of layers to intercept the entire sound; hence with such cambric we should have echoes returned from a greater distance, and therefore of greater duration. Eight layers of the calico employed in these experiments, stretched on a wire frame and placed close together as a kind of pad, may be taken to represent a dense acoustic cloud. Such a pad, placed at the proper angle beyond N, cuts off the sound, which in its absence reaches f′, to such an extent that the flame f′, when not too sensitive, is thereby stilled, while f is far more powerfully agitated than by the reflection from a single layer. With the source of sound close at hand, the echoes from such a pad would be of insensible duration. Thus close at hand do I suppose the acoustic clouds surrounding Villejuif to have been, a similar shortness of echo being the consequence.
A further step is here taken in the illustration of the analogy between light and sound. Our pad acts chiefly by internal reflection. The sound from the reed is a composite one, made up of partial sounds differing in pitch. If these sounds be ejected from the pad in their pristine proportions, the pad is acoustically white; if they return with their proportions altered, the pad is acoustically colored.
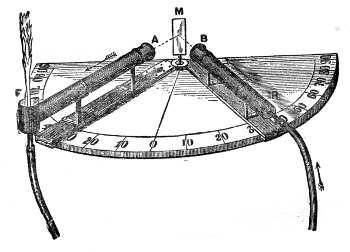
In these experiments my assistant, Mr. Cottrell, has rendered me material assistance.93
Note, June 3d.—I annex here a sketch of an apparatus94 devised by my assistant, Mr. Cottrell, and constructed by 470Tisley and Spiller, for the demonstration of the law of reflection of sound. It consists of two tubes (A F, B R) with a source of sound at the end R of one of them, and a sensitive flame at the end F of the other. The axes of the tube converge upon the mirror, M, and they are capable of being placed so as to inclose any required angle. The angles of incidence and reflection are read off on the graduated semicircle. The mirror M is also movable round a vertical axis.
1 It will be borne in mind that the Washington Appendix was published nearly a year after my Report to the Trinity House.
2 That is to say, homogeneous air with an opposing wind is frequently more favorable to sound than non-homogeneous air with a favoring wind. We had the same experience at the South Foreland.—J. T.
3 Had this observation been published, it could only have given me pleasure to refer to it in my recent writings. It is a striking confirmation of my observations on the Mer de Glace in 1859.
4 Had I been aware of its existence I might have used the language of General Duane to express my views on the point here adverted to. See Chap. VII., pp. 340-341.
5 This does not seem more surprising than the passage of light, or radiant heat, through rock salt.
6 Also “Proceedings of the Royal Society,” vol. xxiii., p. 159, and “Proceedings of the Royal Institution,” vol. vii., p. 344.
8 The rapidity with which an impression is transmitted through the nerves, as first determined by Helmholtz, and confirmed by Du Bois-Reymond, is 93 feet a second.
9 And long previously by Robert Boyle.
10 A very effective instrument, presented to the Royal Institution by Mr. Warren De La Rue.
11 By directing the beam of an electric lamp on glass bulbs filled with a mixture of equal volumes of chlorine and hydrogen, I have caused the bulbs to explode in vacuo and in air. The difference, though not so striking as I at first expected, was perfectly distinct.
12 It may be that the gas fails to throw the vocal chords into sufficiently strong vibration. The laryngoscope might decide this question.
13 Poisson, “Mécanique,” vol. ii., p. 707.
14 To converge the pulse upon the flame, the tube was caused to end in a cone.
15 It is recorded that a bell placed on an eminence in Heligoland failed, on account of its distance, to be heard in the town. A parabolic reflector placed behind the bell, so as to reflect the sound-waves in the direction of the long, sloping street, caused the strokes of the bell to be distinctly heard at all times. This observation needs verification.
16 “Encyclopædia Metropolitana,” art. “Sound.”
17 Placing himself close to the upper part of the wall of the London Colosseum, a circular building one hundred and thirty feet in diameter, Mr. Wheatstone found a word pronounced to be repeated a great many times. A single exclamation appeared like a peal of laughter, while the tearing of a piece of paper was like the patter of hail.
18 “Poggendorff’s Annalen,” vol. lxxxv., p. 378; “Philosophical Magazine,” vol. v., p. 73.
19 Thin India-rubber balloons also form excellent sound lenses.
20 For the sake of simplicity, the wave is shown broken at o′ and its two halves straight. The surface of the wave, however, is really a curve, with its concavity turned in the direction of its propagation.
21 See “Heat as a Mode of Motion,” chap. iii.
22 In fact, the prompt abstraction of the motion of heat from the condensation, and its prompt communication to the rarefaction by the contiguous luminiferous ether, would prevent the former from ever rising so high, or the latter from ever falling so low, in temperature as it would do if the power of radiation was absent.
23 “Heat a Mode of Motion,” chap. x.
24 According to Burmeister, through the injection and ejection of air into and from the cavity of the chest.
25 On July 27, 1681, “Mr. Hooke showed an experiment of making musical and other sounds by the help of teeth of brass wheels; which teeth were made of equal bigness for musical sounds, but of unequal for vocal sounds.”—Birch’s “History of the Royal Society,” p. 96, published in 1757.
The following extract is taken from the “Life of Hooke,” which precedes his “Posthumous Works,” published in 1705, by Richard Waller, Secretary of the Royal Society: “In July the same year he (Dr. Hooke) showed a way of making musical and other sounds by the striking of the teeth of several brass wheels, proportionally cut as to their numbers, and turned very fast round, in which it was observable that the equal or proportional strokes of the teeth, that is, 2 to 1, 4 to 3, etc., made the musical notes, but the unequal strokes of the teeth more answered the sound of the voice in speaking.”
26 Galileo, finding the number of notches on his metal to be great when the pitch of the note was high, inferred that the pitch depended on the rapidity of the impulses.
27 When a rough tide rolls in upon a pebble beach, as at Blackgang Chine or Freshwater Gate in the Isle of Wight the rounded stones are carried up the slope by the impetus of the water and when the wave retreats the pebbles are dragged down. Innumerable collisions thus ensue of irregular intensity and recurrence. The union of these shocks impresses us as a kind of scream. Hence the line in Tennyson’s “Maud”
The height of the note depends in some measure upon the size of the pebble, varying from a kind of roar—heard when the stones are large—to a scream; from a scream to a noise resembling that of frying bacon; and from this, when the pebbles are so small as to approach the state of gravel, to a mere hiss. The roar of the breaking wave itself is mainly due to the explosion of bladders of air.
28 The error of Savart consists, according to Helmholtz, in having adopted an arrangement in which overtones (described in Chapter III.) were mistaken for the fundamental one.
29 “The deepest tone of orchestra instruments is the E of the double-bass, with 41-1/4 vibrations. The new pianos and organs go generally as far as C1, with 33 vibrations; new grand pianos may reach A11, with 27-1/2 vibrations. In large organs a lower octave is introduced, reaching to C11, with 16-1/2 vibrations. But the musical character of all these tones under E is imperfect, because they are near the limit where the power of the ear to unite the vibrations to a tone ceases. In height the pianoforte reaches to aiv, with 3,520 vibrations, or sometimes to cv, with 4,224 vibrations. The highest note of the orchestra is probably the dv of the piccolo flute, with 4,752 vibrations.”—Helmholtz, “Tonempfindungen,” p. 30. In this notation we start from C, with 66 vibrations, calling the first lower octave C1, and the second C11; and calling the first highest octave c, the second c1, the third c11, the fourth c12, etc. In England the deepest tone, Mr. Macfarren informs me, is not E, but A, a fourth above it.
30 It is hardly necessary to remark that the quickest vibrations and shortest waves correspond to the extreme violet, while the slowest vibrations and longest waves correspond to the extreme red, of the spectrum.
31 Experiments on this subject were first made by M. Buys Ballot on the Dutch railway, and subsequently by Mr. Scott Russell in this country. Doppler’s idea is now applied to determine, from changes of wave-length, motions in the sun and fixed stars.
32 An ordinary musical box may be substituted for the piano in this experiment.
33 To show the influence of a large vibrating surface in communicating sonorous motion to the air, Mr. Kilburn incloses a musical box within cases of thick felt. Through the cases a wooden rod, which rests upon the box, issues. When the box plays a tune, it is unheard as long as the rod only emerges; but when a thin disk of wood is fixed on the rod, the music becomes immediately audible.
34 Chladni remarks (“Akustik,” p. 55) that it is usual to ascribe to Sauveur the discovery, in 1701, of the nodes of vibration corresponding to the higher tones of strings; but that Noble and Pigott had made the discovery in Oxford in 1676, and that Sauveur declined the honor of the discovery when he found that others had made the observation before him.
35 The first experiment really made in the lecture was with a bar of steel 62 inches long, 1-1/2 inch wide, and 1/2 an inch thick, bent into the shape of a tuning-fork, with its prongs 2 inches apart, and supported on a heavy stand. The cord attached to it was 9 feet long and a quarter of an inch thick. The prongs were thrown into vibration by striking them briskly with two pieces of lead covered with pads and held one in each hand. The prongs vibrated transversely to the cord. The vibrations produced by a single stroke were sufficient to carry the cord through several of its subdivisions and back to a single ventral segment. That is to say, by striking the prongs and causing the cord to vibrate as a whole, it could, by relaxing the tension, be caused to divide into two, three, or four vibrating segments; and then, by increasing the tension, to pass back through four, three, and two divisions, to one, without renewing the agitation of the prongs. The cord was of such a character that, instead of oscillating to and fro in the same plane, each of its points described a circle. The ventral segments, therefore, instead of being flat surfaces were surfaces of revolution, and were equally well seen from all parts of the room. The tuning-forks employed in the subsequent illustrations were prepared for me by that excellent acoustic mechanician, König, of Paris, being such as are usually employed in the projection of Lissajou’s experiments.
36 A string steeped in a solution of the sulphate of quinine, and illuminated by the violet rays of the electric lamp, exhibits brilliant fluorescence. When the fork to which it is attached vibrates, the string divides itself into a series of spindles, and separated from each other by more intensely luminous nodes, emitting a light of the most delicate greenish-blue.
37 The subject of musical intervals will be treated in a subsequent lecture.
38 “This quality of sound, sometimes called its register, color, or timbre.”—Thomas Young, “Essay on Music.”
39 “Lehre von den Tonempfindungen,” p. 135.
40 The action of such a string is substantially the same as that of the siren. The string renders intermittent the current of air. Its action also resembles that of a reed. See Lecture V.
41 Chladni also observed this compounding of vibrations, and executed a series of experiments, which, in their developed form, are those of the kaleidophone. The composition of vibrations will be studied at some length in a subsequent lecture.
42 I copy this figure from Sir C. Wheatstone’s memoir; the nodes, however, ought to be nearer the ends, and the free terminal portions of the dotted lines ought not to be bent upward or downward. The nodal lines in the next two figures are also drawn too far from the edge of the plates.
43 Under the shoulder of the Wetterhorn I found in 1867 a pool of clear water into which a driblet fell from a brow of overhanging limestone rock. The rebounding water-drops, when they fell back, rolled in myriads over the surface. Almost any fountain, the spray of which falls into a basin, will exhibit the same effect.
44 This experiment succeeds almost equally well with a glass tube.
45 This experiment is more easily executed with hydrogen than with coal-gas.
46 Only an extremely small fraction of the fork’s motion is, however, converted into sound. The remainder is expended in overcoming the internal friction of its own particles. In other words, nearly the whole of the motion is converted into heat.
47 The clear illustrations of organ-pipes and reeds introduced here, and at page 226, have been substantially copied from the excellent work of Helmholtz. Pipes opening with hinges, so as to show their inner parts, were shown in the lecture.
48 I owe it to this eminent artist to direct attention to his experiments communicated to the Royal Society in May, 1855, and recorded in the “Philosophical Magazine” for 1855, vol. x., page 218.
49 The velocity in glass varies with the quality; the result of each experiment has therefore reference only to the particular kind of glass employed in the experiment.
50 This experiment was first made with a hydrogen-flame by Sir C. Wheatstone.
51 A gas-jet, for example, can be ignited five inches above the tip of a visible gas-flame, where platinum-leaf shows no redness.
52 “Philosophical Magazine,” March, 1858, p. 235. In the Appendix Prof. Le Conte’s interesting paper is given in extenso. Some years subsequently Mr. (now Professor) Barrett, while preparing some experiments for my lectures, observed the action of a musical sound upon a flame, and by the selection of suitable burners he afterward succeeded in rendering the flame extremely sensitive. Le Conte, of whose discovery I informed Mr. Barrett, was my own starting-point.
53 A gas-bag properly weighted also answers for these experiments.
54 In the actions described in the case of the blow-pipe and candle-flames, it was the jet of air issuing from the blow-pipe, and not the flame itself, that was directly acted on by the external vibrations.
55 Numerous modifications of these experiments are possible. Other inflammable gases than coal-gas may be employed. Mixtures of gases have also been found to yield beautiful and striking results. An infinitesimal amount of mechanical impurity has been found to exert a powerful influence.
56 Referring to these effects, Helmholtz says: “Die erstaunliche Empfindlichkeit eines mit Rauch imprägnirten cylindrischen Luftstrahls gegen Schall ist von Herrn Tyndall beschrieben worden; ich habe dieselbe bestätigt gefunden. Es ist dies offenbar eine Eigenschaft der Trennungsflächen die für das Anblasen der Pfeifen von grösster Wichtigkeit ist.”—“Discontinuirliche Luftbewegung,” Monatsbericht, April, 1868.
57 When these two tuning-forks were placed in contact with a vessel from which a liquid vein issued, the visible action on the vein continued long after the forks had ceased to be heard.
58 The experiments on sounding flames have been recently considerably extended by my assistant, Mr. Cottrell. By causing flame to rub against flame, various musical sounds can be obtained—some resembling those of a trumpet, others those of a lark. By the friction of unignited gas-jets, similar though less intense effects are produced. When the two flames of a fish-tail burner are permitted to impinge upon a plate of platinum, as in Scholl’s “perfectors,” the sounds are trumpet-like, and very loud. Two ignited gas-jets may be caused to flatten out like Savart’s water-jets. Or they may be caused to roll themselves into two hollow horns, forming a most instructive example of the Wirbelflächen of Helmholtz. The carbon-particles liberated in the flame rise through the horns in continuous red-hot or white-hot spirals, which are extinguished at a height of some inches from their place of generation.
59 “Essay on Sound,” par. 21.
60 “Report of the British Association for 1863,” page 105.
61 A very sagacious remark, as observation proves.
62 Powerful electric lights have since been established and found ineffectual.
63 This is also Sir John Herschel’s way of regarding the subject. “Essay on Sound,” par. 38.
64 In all cases nautical miles are meant.
65 Sir John Herschel gives the following account of Arago’s observation: “The rolling of thunder has been attributed to echoes among the clouds; and, if it is considered that a cloud is a collection of particles of water, however minute, in a liquid state, and therefore each individually capable of reflecting sound, there is no reason why very large sounds should not be reverberated confusedly (like bright lights) from a cloud. And that such is the case has been ascertained by direct observation on the sound of cannon. Messrs. Arago, Matthieu, and Prony, in their experiments on the velocity of sound, observed that under a perfectly clear sky the explosions of their guns were always single and sharp; whereas, when the sky was overcast, and even when a cloud came in sight over any considerable part of the horizon, they were frequently accompanied by a long-continued roll like thunder.”—“Essay on Sound,” par. 38. The distant clouds would imply a long interval between sound and echo, but nothing of the kind is reported.
66 A friend informs me that he has followed a pack of hounds on a clear calm day without hearing a single yelp from the dogs; while on calm foggy days from the same distance the musical uproar of the pack was loudly audible.
67 The horn here was temporarily suspended, but doubtless would have been well heard.
68 Experiments so important as those of De la Roche ought not to be left without verification. I have made arrangements with a view to this object.
69 The Elder Brethren have already had plans of a new signal-gun laid before them by the constructors of the War Department.
70 Described in Chapter V., p. 229.
71 The figure is but a meagre representation of the fact. The band of light was two inches wide, the depth of the sinuosities varying from three feet to zero.
72 In his admirable experiments on tuning, Scheibler found in the beats a test of differences of temperature of exceeding delicacy.
73 Sir John Herschel and Sir C. Wheatstone, I believe, made this experiment independently.
74 A subject to be dealt with in Chapter IX.
75 Nor indeed any of those tones whose rates of vibration are even multiples of the rate of the fundamental.
76 According to Kolliker, this is the number of fibres in Corti’s organ.
77 The comparison employed by Mr. Sedley Taylor appeals with graphic truth to a mountaineer. Considering, the above curve to represent a mountain-chain, he calls the discords peaks, and the concords passes.
78 This supposition is of course made for the sake of simplicity, the real period of oscillation of a pendulum 28 feet long being between two and three seconds.
79 This figure corresponds to the interval 15:16. For it and some other figures, I am indebted to that excellent mechanician, M. König, of Paris.
80 For some beautiful figures of this description I am indebted to Prof. Lyman, of Yale College.
81 Mr. Sang, of Edinburgh, was, I believe, the first to treat this subject analytically.
82 This able paper was the starting-point of the experiments on sensitive flames, recorded in Chapters VI. and VII.; the researches of Thomas Young and Savart being the starting-point of the experiments on smoke-jets and water-jets.—J. T.
83 “Philosophical Magazine,” section 4, vol. xiii., p. 413, 1857.
84 “Philosophical Magazine,” section 4, vol. xiv., p. 1, et seq., July, 1857.
85 “Comptes Rendus” for August, 1853. Also “Philosophical Magazine,” section 4, vol. vii., p. 186, 1854.
86 “Philosophical Magazine,” section 4, vol. viii., p. 74, 1854.
87 “Proceedings of the Royal Institution,” January 15, 1875.
88 “Researches in Chemistry and Physics,” p. 484.
89 “Connaissance des Temps,” 1825, p. 370.
91 The effect of the air of London is sometimes strikingly evident.
92 “Philosophical Transactions,” 1874, Part I., p. 208, and Chapter VII. of this volume.
93 Since this was written I have sent the sound through fifteen layers of calico, and echoed it back through the same layers, in strength sufficient to agitate the flame. Thirty layers were here crossed by the sound. The sound was subsequently found able to penetrate two hundred layers of cotton net; a single layer of wetted calico being competent to stop it.
94 The cut reached me too late for introduction at the proper place.