TRANSCRIBER’S NOTES:
—Obvious print and punctuation errors were corrected.
—The transcriber of this project created the book cover image using the title page of the original book. The image is placed in the public domain.
A
VIEW
OF
Sir ISAAC NEWTON’s
PHILOSOPHY.

LONDON:
Printed by S. Palmer, 1728.

To the Noble and Right Honourable
Sir ROBERT WALPOLE.
SIR,

I Take the liberty to send you this view of Sir Isaac Newton’s philosophy, which, if it were performed suitable to the dignity of the subject, might not be a present unworthy the acceptance of the greatest person. For his philosophy[iv] operations of nature, which for so many ages had imployed the curiosity of mankind; though no one before him was furnished with the strength of mind necessary to go any depth in this difficult search. However, I am encouraged to hope, that this attempt, imperfect as it is, to give our countrymen in general some conception of the labours of a person, who shall always be the boast of this nation, may be received with indulgence by one, under whose influence these kingdoms enjoy so much happiness. Indeed my admiration at the surprizing inventions of this great man, carries me to conceive of him as a person, who not only must raise the glory of the country, which gave him birth; but that he has even done honour to human nature, by having extended the greatest and most noble of our faculties, reason, to subjects, which, till he attempted them, appeared to be wholly beyond the reach of our limited capacities. And what can give us a[v] more pleasing prospect of our own condition, than to see so exalted a proof of the strength of that faculty, whereon the conduct of our lives, and our happiness depends; our passions and all our motives to action being in such manner guided by our opinions, that where these are just, our whole behaviour will be praise-worthy? But why do I presume to detain you, Sir, with such reflections as these, who must have the fullest experience within your own mind, of the effects of right reason? For to what other source can be ascribed that amiable frankness and unreserved condescension among your friends, or that masculine perspicuity and strength of argument, whereby you draw the admiration of the publick, while you are engaged in the most important of all causes, the liberties of mankind?
I humbly crave leave to make the only acknowledgement within my power, for the benefits,[vi] which I receive in common with the rest of my countrymen from these high talents, by subscribing my self
SIR,
Your most faithful,
and
Most humble Servant,
Henry Pemberton.
PREFACE.
I Drew up the following papers many years ago at the desire of some friends, who, upon my taking care of the late edition of Sir Isaac Newton’s Principia, perswaded me to make them publick. I laid hold of that opportunity, when my thoughts were afresh employed on this subject, to revise what I had formerly written. And I now send it abroad not without some hopes of answering these two ends. My first intention was to convey to such, as are not used to mathematical reasoning, some idea of the philosophy of a person, who has acquired an universal reputation, and rendered our nation famous for these speculations in the learned world. To which purpose I have avoided using terms of art as much as possible, and taken care to define such as I was obliged to use. Though this caution was the less necessary at present, since many of them are become familiar words to our language, from the great number of books wrote in it upon philosophical subjects, and the courses of experiments, that have of late years been given by several ingenious men. The other view I had, was to encourage such young gentlemen as have a turn for the mathematical sciences, to pursue those studies the more chearfully, in order to understand in our author himself the demonstrations of the things I here declare. And to facilitate their progress herein, I intend to proceed still farther in the explanation of Sir Isaac Newton’s philosophy. For as I have received very much pleasure from perusing his writings, I hope it is no illaudable ambition to endeavour the rendering them more easily understood, that greater numbers may enjoy the same satisfaction.
It will perhaps be expected, that I should say something particular of a person, to whom I must always acknowledge my self to be much obliged. What I have to declare on this head will be but short; for it was in the very last years of Sir Isaac’s life, that I had the honour[viii] of his acquaintance. This happened on the following occasion. Mr. Polenus, a Professor in the University of Padua, from a new experiment of his, thought the common opinion about the force of moving bodies was overturned, and the truth of Mr. Libnitz’s notion in that matter fully proved. The contrary of what Polenus had asserted I demonstrated in a paper, which Dr. Mead, who takes all opportunities of obliging his friends, was pleased to shew Sir Isaac Newton This was so well approved of by him, that he did me the honour to become a fellow-writer with me, by annexing to what I had written, a demonstration of his own drawn from another consideration. When I printed my discourse in the philosophical transactions, I put what Sir Isaac had written in a scholium by it self, that I might not seem to usurp what did not belong to me. But I concealed his name, not being then sufficiently acquainted with him to ask whether he was willing I might make use of it or not. In a little time after he engaged me to take care of the new edition he was about making if his Principia. This obliged me to be very frequently with him, and as he lived at some distance from me, a great number of letters passed between us on this account. When I had the honour of his conversation, I endeavoured to learn his thoughts upon mathematical subjects, and something historical concerning his inventions, that I had not been before acquainted with. I found, he had read fewer of the modern mathematicians, than one could have expected; but his own prodigious invention readily supplied him with what he might have an occasion for in the pursuit of any subject he undertook. I have often heard him censure the handling geometrical subjects by algebraic calculations; and his book of Algebra he called by the name of Universal Arithmetic, in opposition to the injudicious title of Geometry, which Des Cartes had given to the treatise, wherein he shews, how the geometer may assist his invention by such kind of computations. He frequently praised Slusius, Barrow and Huygens for not being influenced by the false taste, which then began to prevail. He used to commend the laudable attempt of Hugo de Omerique to restore the ancient analysis, and very much esteemed Apollonius’s book De sectione rationis for giving us a clearer notion of that analysis than we had before. Dr. Barrow may be esteemed as having[ix] shewn a compass of invention equal, if not superior to any of the moderns, our author only excepted; but Sir Isaac Newton has several times particularly recommended to me Huygens’s stile and manner. He thought him the most elegant of any mathematical writer of modern times, and the most just imitator of the antients. Of their taste, and form of demonstration Sir Isaac always professed himself a great admirer: I have heard him even censure himself for not following them yet more closely than he did; and speak with regret of his mistake at the beginning of his mathematical studies, in applying himself to the works of Des Cartes and other algebraic writers, before he had considered the elements of Euclide with that attention, which so excellent a writer deserves. As to the history of his inventions, what relates to his discoveries of the methods of series and fluxions, and of his theory of light and colours, the world has been sufficiently informed of already. The first thoughts, which gave rise to his Principia, he had, when he retired from Cambridge in 1666 on account of the plague. As he sat alone in a garden, he fell into a speculation on the power of gravity: that as this power is not found sensibly diminished at the remotest distance from the center of the earth, to which we can rise, neither at the tops of the loftiest buildings, nor even on the summits of the highest mountains; it appeared to him reasonable to conclude, that this power must extend much farther than was usually thought; why not as high as the moon, said he to himself? and if so, her motion must be influenced by it; perhaps she is retained in her orbit thereby. However, though the power of gravity is not sensibly weakened in the little change of distance, at which we can place our selves from the center of the earth; yet it is very possible, that so high as the moon this power may differ much in strength from what it is here. To make an estimate, what might be the degree of this diminution, he considered with himself, that if the moon be retained in her orbit by the force of gravity, no doubt the primary planets are carried round the sun by the like power. And by comparing the periods of the several planets with their distances from the sun, he found, that if any power like gravity held them in their courses, its strength must decrease in the duplicate proportion of the increase of distance. This[x] be concluded by supposing them to move in perfect circles concentrical to the sun, from which the orbits of the greatest part of them do not much differ. Supposing therefore the power of gravity, when extended to the moon, to decrease in the same manner, he computed whether that force would be sufficient to keep the moon in her orbit. In this computation, being absent from books, he took the common estimate in use among geographers and our seamen, before Norwood had measured the earth, that 60 English miles were contained in one degree of latitude on the surface of the earth. But as this is a very faulty supposition, each degree containing about 69½ of our miles, his computation did not answer expectation; whence he concluded, that some other cause must at least join with the action of the power of gravity on the moon. On this account he laid aside for that time any farther thoughts upon this matter. But some years after, a letter which he received from Dr. Hook, put him on inquiring what was the real figure, in which a body let fall from any high place descends, taking the motion of the earth round its axis into consideration. Such a body, having the same motion, which by the revolution of the earth the place has whence it falls, is to be considered as projected forward and at the same time drawn down to the center of the earth. This gave occasion to his resuming his former thoughts concerning the moon; and Picart in France having lately measured the earth, by using his measures the moon appeared to be kept in her orbit purely by the power of gravity; and consequently, that this power decreases as you recede from the center of the earth in the manner our author had formerly conjectured. Upon this principle he found the line described by a falling body to be an ellipsis, the center of the earth being one focus. And the primary planets moving in such orbits round the sun, he had the satisfaction to see, that this inquiry, which he had undertaken merely out of curiosity, could be applied to the greatest purposes. Hereupon he composed near a dozen propositions relating to the motion of the primary planets about the sun. Several years after this, some discourse he had with Dr. Halley, who at Cambridge made him a visit, engaged Sir Isaac Newton to resume again the consideration of this subject; and gave occasion[xi] to his writing the treatise which he published under the title of mathematical principles of natural philosophy. This treatise, full of such a variety of profound inventions, was composed by him from scarce any other materials than the few propositions before mentioned, in the space of one year and an half.
Though his memory was much decayed, I found he perfectly understood his own writings, contrary to what I had frequently heard in discourse from many persons. This opinion of theirs might arise perhaps from his not being always ready at speaking on these subjects, when it might be expected he should. But as to this, it may be observed, that great genius’s are frequently liable to be absent, not only in relation to common life, but with regard to some of the parts of science they are the best informed of. Inventors seem to treasure up in their minds, what they have found out, after another manner than those do the same things, who have not this inventive faculty. The former, when they have occasion to produce their knowledge, are in some measure obliged immediately to investigate part of what they want. For this they are not equally fit at all times: so it has often happened, that such as retain things chiefly by means of a very strong memory, have appeared off hand more expert than the discoverers themselves.
As to the moral endowments of his mind, they were as much to be admired as his other talents. But this is a field I leave others to exspatiate in. I only touch upon what I experienced myself during the few years I was happy in his friendship. But this I immediately discovered in him, which at once both surprized and charmed me: Neither his extreme great age, nor his universal reputation had rendred him stiff in opinion, or in any degree elated. Of this I had occasion to have almost daily experience. The Remarks I continually sent him by letters on his Principia were received with the utmost goodness. These were so far from being any ways displeasing to him, that on the contrary it occasioned him to speak many kind things of me to my friends, and to honour me with a publick testimony of his good opinion. He also approved of the following treatise, a great part of which we read together. As many alterations were[xii] made in the late edition of his Principia, so there would have been many more if there had been a sufficient time. But whatever of this kind may be thought wanting, I shall endeavour to supply in my comment on that book. I had reason to believe he expected such a thing from me, and I intended to have published it in his life time, after I had printed the following discourse, and a mathematical treatise Sir Isaac Newton had written a long while ago, containing the first principles of fluxions, for I had prevailed on him to let that piece go abroad. I had examined all the calculations, and prepared part of the figures; but as the latter part of the treatise had never been finished, he was about letting me have other papers, in order to supply what was wanting. But his death put a stop to that design. As to my comment on the Principia, I intend there to demonstrate whatever Sir Isaac Newton has set down without express proof, and to explain all such expressions in his book, as I shall judge necessary. This comment I shall forthwith put to the press, joined to an english translation of his Principia, which I have had some time by me. A more particular account of my whole design has already been published in the new memoirs of literature for the month of march 1727.
I have presented my readers with a copy of verses on Sir Isaac Newton, which I have just received from a young Gentleman, whom I am proud to reckon among the number of my dearest friends. If I had any apprehension that this piece of poetry stood in need of an apology, I should be desirous the reader might know, that the author is but sixteen years old, and was obliged to finish his composition in a very short space of time. But I shall only take the liberty to observe, that the boldness of the digressions will be best judged of by those who are acquainted with Pindar.
A
POEM
ON
Sir ISAAC NEWTON.
To Newton’s genius, and immortal fame
Th’ advent’rous muse with trembling pinion soars.
Thou, heav’nly truth, from thy seraphick throne
Look favourable down, do thou assist
My lab’ring thought, do thou inspire my song.
Newton, who first th’ almighty’s works display’d,
And smooth’d that mirror, in whose polish’d face
The great creator now conspicuous shines;
Who open’d nature’s adamantine gates,
And to our minds her secret powers expos’d;
Newton demands the muse; his sacred hand
Shall guide her infant steps; his sacred hand
Shall raise her to the Heliconian height,
Where, on its lofty top inthron’d, her head
Shall mingle with the Stars. Hail nature, hail,
O Goddess, handmaid of th’ ethereal power,
Now lift thy head, and to th’ admiring world
Shew thy long hidden beauty. Thee the wise
Of ancient fame, immortal Plato’s self,
[xiv]The Stagyrite, and Syracusian sage,
From black obscurity’s abyss to raise,
(Drooping and mourning o’er thy wondrous works)
With vain inquiry sought. Like meteors these
In their dark age bright sons of wisdom shone:
But at thy Newton all their laurels fade,
They shrink from all the honours of their names.
So glimm’ring stars contract their feeble rays,
When the swift lustre of Aurora’s face
Flows o’er the skies, and wraps the heav’ns in light.
The Deity’s omnipotence, the cause,
Th’ original of things long lay unknown.
Alone the beauties prominent to sight
(Of the celestial power the outward form)
Drew praise and wonder from the gazing world.
As when the deluge overspread the earth,
Whilst yet the mountains only rear’d their heads
Above the surface of the wild expanse,
Whelm’d deep below the great foundations lay,
Till some kind angel at heav’n’s high command
Roul’d back the rising tides, and haughty floods,
And to the ocean thunder’d out his voice:
Quick all the swelling and imperious waves,
The foaming billows and obscuring surge,
Back to their channels and their ancient seats
Recoil affrighted: from the darksome main
Earth raises smiling, as new-born, her head,
And with fresh charms her lovely face arrays.
So his extensive thought accomplish’d first
The mighty task to drive th’ obstructing mists
Of ignorance away, beneath whose gloom
Th’ inshrouded majesty of Nature lay.
He drew the veil and swell’d the spreading scene.
[xv]How had the moon around th’ ethereal void
Rang’d, and eluded lab’ring mortals care,
Till his invention trac’d her secret steps,
While she inconstant with unsteady rein
Through endless mazes and meanders guides
In its unequal course her changing carr:
Whether behind the sun’s superior light
She hides the beauties of her radiant face,
Or, when conspicuous, smiles upon mankind,
Unveiling all her night-rejoicing charms.
When thus the silver-tressed moon dispels
The frowning horrors from the brow of night,
And with her splendors chears the sullen gloom,
While sable-mantled darkness with his veil
The visage of the fair horizon shades,
And over nature spreads his raven wings;
Let me upon some unfrequented green
While sleep sits heavy on the drowsy world,
Seek out some solitary peaceful cell,
Where darksome woods around their gloomy brows
Bow low, and ev’ry hill’s protended shade
Obscures the dusky vale, there silent dwell,
Where contemplation holds its still abode,
There trace the wide and pathless void of heav’n,
And count the stars that sparkle on its robe.
Or else in fancy’s wild’ring mazes lost
Upon the verdure see the fairy elves
Dance o’er their magick circles, or behold,
In thought enraptur’d with the ancient bards,
Medea’s baleful incantations draw
Down from her orb the paly queen of night.
But chiefly Newton let me soar with thee,
And while surveying all yon starry vault
With admiration I attentive gaze,
[xvi]Thou shalt descend from thy celestial seat,
And waft aloft my high-aspiring mind,
Shalt shew me there how nature has ordain’d
Her fundamental laws, shalt lead my thought
Through all the wand’rings of th’ uncertain moon,
And teach me all her operating powers.
She and the sun with influence conjoint
Wield the huge axle of the whirling earth,
And from their just direction turn the poles,
Slow urging on the progress of the years.
The constellations seem to leave their seats,
And o’er the skies with solemn pace to move.
You, splendid rulers of the day and night,
The seas obey, at your resistless sway
Now they contract their waters, and expose
The dreary desart of old ocean’s reign.
The craggy rocks their horrid sides disclose;
Trembling the sailor views the dreadful scene,
And cautiously the threat’ning ruin shuns.
But where the shallow waters hide the sands,
There ravenous destruction lurks conceal’d,
There the ill-guided vessel falls a prey,
And all her numbers gorge his greedy jaws.
But quick returning see th’ impetuous tides
Back to th’ abandon’d shores impell the main.
Again the foaming seas extend their waves,
Again the rouling floods embrace the shoars,
And veil the horrours of the empty deep.
Thus the obsequious seas your power confess,
While from the surface healthful vapours rise
Plenteous throughout the atmosphere diffus’d,
Or to supply the mountain’s heads with springs,
Or fill the hanging clouds with needful rains,
That friendly streams, and kind refreshing show’rs
[xvii]May gently lave the sun-burnt thirsty plains,
Or to replenish all the empty air
With wholsome moisture to increase the fruits
Of earth, and bless the labours of mankind.
O Newton, whether flies thy mighty soul,
How shall the feeble muse pursue through all
The vast extent of thy unbounded thought,
That even seeks th’ unseen recesses dark
To penetrate of providence immense.
And thou the great dispenser of the world
Propitious, who with inspiration taught’st
Our greatest bard to send thy praises forth;
Thou, who gav’st Newton thought; who smil’dst serene,
When to its bounds he stretch’d his swelling soul;
Who still benignant ever blest his toil,
And deign’d to his enlight’ned mind t’ appear
Confess’d around th’ interminated world:
To me O thy divine infusion grant
(O thou in all so infinitely good)
That I may sing thy everlasting works,
Thy inexhausted store of providence,
In thought effulgent and resounding verse.
O could I spread the wond’rous theme around,
Where the wind cools the oriental world,
To the calm breezes of the Zephir’s breath,
To where the frozen hyperborean blasts.
To where the boist’rous tempest-leading south
From their deep hollow caves send forth their storms.
Thou still indulgent parent of mankind,
Left humid emanations should no more
Flow from the ocean, but dissolve away
Through the long series of revolving time;
And left the vital principle decay,
By which the air supplies the springs of life;
[xviii]Thou hast the fiery visag’d comets form’d
With vivifying spirits all replete,
Which they abundant breathe about the void,
Renewing the prolifick soul of things.
No longer now on thee amaz’d we call,
No longer tremble at imagin’d ills,
When comets blaze tremendous from on high,
Or when extending wide their flaming trains
With hideous grasp the skies engirdle round,
And spread the terrors of their burning locks.
For these through orbits in the length’ning space
Of many tedious rouling years compleat
Around the sun move regularly on;
And with the planets in harmonious orbs,
And mystick periods their obeysance pay
To him majestick ruler of the skies
Upon his throne of circled glory fixt.
He or some god conspicuous to the view,
Or else the substitute of nature seems,
Guiding the courses of revolving worlds.
He taught great Newton the all-potent laws
Of gravitation, by whose simple power
The universe exists. Nor here the sage
Big with invention still renewing staid.
But O bright angel of the lamp of day,
How shall the muse display his greatest toil?
Let her plunge deep in Aganippe’s waves,
Or in Castalia’s ever-flowing stream,
That re-inspired she may sing to thee,
How Newton dar’d advent’rous to unbraid
The yellow tresses of thy shining hair.
Or didst thou gracious leave thy radiant sphere,
And to his hand thy lucid splendours give,
[xix]T’ unweave the light-diffusing wreath, and part
The blended glories of thy golden plumes?
He with laborious, and unerring care,
How different and imbodied colours form
Thy piercing light, with just distinction found.
He with quick sight pursu’d thy darting rays,
When penetrating to th’ obscure recess
Of solid matter, there perspicuous saw,
How in the texture of each body lay
The power that separates the different beams.
Hence over nature’s unadorned face
Thy bright diversifying rays dilate
Their various hues: and hence when vernal rains
Descending swift have burst the low’ring clouds,
Thy splendors through the dissipating mists
In its fair vesture of unnumber’d hues
Array the show’ry bow. At thy approach
The morning risen from her pearly couch
With rosy blushes decks her virgin cheek;
The ev’ning on the frontispiece of heav’n
His mantle spreads with many colours gay;
The mid-day skies in radiant azure clad,
The shining clouds, and silver vapours rob’d
In white transparent intermixt with gold,
With bright variety of splendor cloath
All the illuminated face above.
When hoary-headed winter back retires
To the chill’d pole, there solitary sits
Encompass’d round with winds and tempests bleak
In caverns of impenetrable ice,
And from behind the dissipated gloom
Like a new Venus from the parting surge
The gay-apparell’d spring advances on;
When thou in thy meridian brightness sitt’st,
[xx]And from thy throne pure emanations flow
Of glory bursting o’er the radiant skies:
Then let the muse Olympus’ top ascend,
And o’er Thessalia’s plain extend her view,
And count, O Tempe, all thy beauties o’er.
Mountains, whose summits grasp the pendant clouds,
Between their wood-invelop’d slopes embrace
The green-attired vallies. Every flow’r
Here in the pride of bounteous nature clad
Smiles on the bosom of th’ enamell’d meads.
Over the smiling lawn the silver floods
Of fair Peneus gently roul along,
While the reflected colours from the flow’rs,
And verdant borders pierce the lympid waves,
And paint with all their variegated hue
The yellow sands beneath. Smooth gliding on
The waters hasten to the neighbouring sea.
Still the pleas’d eye the floating plain pursues;
At length, in Neptune’s wide dominion lost,
Surveys the shining billows, that arise
Apparell’d each in Phœbus’ bright attire:
Or from a far some tall majestick ship,
Or the long hostile lines of threat’ning fleets,
Which o’er the bright uneven mirror sweep,
In dazling gold and waving purple deckt;
Such as of old, when haughty Athens power
Their hideous front, and terrible array
Against Pallene’s coast extended wide,
And with tremendous war and battel stern
The trembling walls of Potidæa shook.
Crested with pendants curling with the breeze
The upright masts high bristle in the air,
Aloft exalting proud their gilded heads.
The silver waves against the painted prows
[xxi]Raise their resplendent bosoms, and impearl
The fair vermillion with their glist’ring drops:
And from on board the iron-cloathed host
Around the main a gleaming horrour casts;
Each flaming buckler like the mid-day sun,
Each plumed helmet like the silver moon,
Each moving gauntlet like the light’ning’s blaze,
And like a star each brazen pointed spear.
But lo the sacred high-erected fanes,
Fair citadels, and marble-crowned towers,
And sumptuous palaces of stately towns
Magnificent arise, upon their heads
Bearing on high a wreath of silver light.
But see my muse the high Pierian hill,
Behold its shaggy locks and airy top,
Up to the skies th’ imperious mountain heaves
The shining verdure of the nodding woods.
See where the silver Hippocrene flows,
Behold each glitt’ring rivulet, and rill
Through mazes wander down the green descent,
And sparkle through the interwoven trees.
Here rest a while and humble homage pay,
Here, where the sacred genius, that inspir’d
Sublime Mæonides and Pindar’s breast,
His habitation once was fam’d to hold.
Here thou, O Homer, offer’dst up thy vows,
Thee, the kind muse Calliopæa heard,
And led thee to the empyrean feats,
There manifested to thy hallow’d eyes
The deeds of gods; thee wise Minerva taught
The wondrous art of knowing human kind;
Harmonious Phœbus tun’d thy heav’nly mind,
And swell’d to rapture each exalted sense;
Even Mars the dreadful battle-ruling god,
[xxii]Mars taught thee war, and with his bloody hand
Instructed thine, when in thy sounding lines
We hear the rattling of Bellona’s carr,
The yell of discord, and the din of arms.
Pindar, when mounted on his fiery steed,
Soars to the sun, opposing eagle like
His eyes undazled to the fiercest rays.
He firmly seated, not like Glaucus’ son,
Strides his swift-winged and fire-breathing horse,
And born aloft strikes with his ringing hoofs
The brazen vault of heav’n, superior there
Looks down upon the stars, whose radiant light
Illuminates innumerable worlds,
That through eternal orbits roul beneath.
But thou all hail immortalized son
Of harmony, all hail thou Thracian bard,
To whom Apollo gave his tuneful lyre.
O might’st thou, Orpheus, now again revive,
And Newton should inform thy list’ning ear
How the soft notes, and soul-inchanting strains
Of thy own lyre were on the wind convey’d.
He taught the muse, how sound progressive floats
Upon the waving particles of air,
When harmony in ever-pleasing strains,
Melodious melting at each lulling fall,
With soft alluring penetration steals
Through the enraptur’d ear to inmost thought,
And folds the senses in its silken bands.
So the sweet musick, which from Orpheus’ touch
And fam’d Amphion’s, on the sounding string
Arose harmonious, gliding on the air,
Pierc’d the tough-bark’d and knotty-ribbed woods,
Into their saps soft inspiration breath’d
And taught attention to the stubborn oak.
[xxiii]Thus when great Henry, and brave Marlb’rough led
Th’ imbattled numbers of Britannia’s sons,
The trump, that swells th’ expanded cheek of fame,
That adds new vigour to the gen’rous youth,
And rouzes sluggish cowardize it self,
The trumpet with its Mars-inciting voice,
The winds broad breast impetuous sweeping o’er
Fill’d the big note of war. Th’ inspired host
With new-born ardor press the trembling Gaul;
Nor greater throngs had reach’d eternal night,
Not if the fields of Agencourt had yawn’d
Exposing horrible the gulf of fate;
Or roaring Danube spread his arms abroad,
And overwhelm’d their legions with his floods.
But let the wand’ring muse at length return;
Nor yet, angelick genius of the sun,
In worthy lays her high-attempting song
Has blazon’d forth thy venerated name.
Then let her sweep the loud-resounding lyre
Again, again o’er each melodious string
Teach harmony to tremble with thy praise.
And still thine ear O favourable grant,
And she shall tell thee, that whatever charms,
Whatever beauties bloom on nature’s face,
Proceed from thy all-influencing light.
That when arising with tempestuous rage,
The North impetuous rides upon the clouds
Dispersing round the heav’ns obstructive gloom,
And with his dreaded prohibition stays
The kind effusion of thy genial beams;
Pale are the rubies on Aurora’s lips,
No more the roses blush upon her cheeks,
Black are Peneus’ streams and golden sands
In Tempe’s vale dull melancholy sits,
[xxiv]And every flower reclines its languid head.
By what high name shall I invoke thee, say,
Thou life-infusing deity, on thee
I call, and look propitious from on high,
While now to thee I offer up my prayer.
O had great Newton, as he found the cause,
By which sound rouls thro’ th’ undulating air,
O had he, baffling times resistless power,
Discover’d what that subtle spirit is,
Or whatsoe’er diffusive else is spread
Over the wide-extended universe,
Which causes bodies to reflect the light,
And from their straight direction to divert
The rapid beams, that through their surface pierce.
But since embrac’d by th’ icy arms of age,
And his quick thought by times cold hand congeal’d,
Ev’n Newton left unknown this hidden power;
Thou from the race of human kind select
Some other worthy of an angel’s care,
With inspiration animate his breast,
And him instruct in these thy secret laws.
O let not Newton, to whose spacious view,
Now unobstructed, all th’ extensive scenes
Of the ethereal ruler’s works arise;
When he beholds this earth he late adorn’d,
Let him not see philosophy in tears,
Like a fond mother solitary sit,
Lamenting him her dear, and only child.
But as the wise Pythagoras, and he,
Whose birth with pride the fam’d Abdera boasts,
With expectation having long survey’d
This spot their ancient seat, with joy beheld
Divine philosophy at length appear
In all her charms majestically fair,
[xxv]Conducted by immortal Newton’s hand.
So may he see another sage arise,
That shall maintain her empire: then no more
Imperious ignorance with haughty sway
Shall stalk rapacious o’er the ravag’d globe:
Then thou, O Newton, shalt protect these lines.
The humble tribute of the grateful muse;
Ne’er shall the sacrilegious hand despoil
Her laurel’d temples, whom his name preserves:
And were she equal to the mighty theme,
Futurity should wonder at her song;
Time should receive her with extended arms,
Seat her conspicuous in his rouling carr,
And bear her down to his extreamest bound.
Fables with wonder tell how Terra’s sons
With iron force unloos’d the stubborn nerves
Of hills, and on the cloud-inshrouded top
Of Pelion Ossa pil’d. But if the vast
Gigantick deeds of savage strength demand
Astonishment from men, what then shalt thou,
O what expressive rapture of the soul,
When thou before us, Newton, dost display
The labours of thy great excelling mind;
When thou unveilest all the wondrous scene,
The vast idea of th’ eternal king,
Not dreadful bearing in his angry arm
The thunder hanging o’er our trembling heads;
But with th’ effulgency of love replete,
And clad with power, which form’d th’ extensive heavens.
O happy he, whose enterprizing hand
Unbars the golden and relucid gates
Of th’ empyrean dome, where thou enthron’d
Philosophy art seated. Thou sustain’d
[xxvi]By the firm hand of everlasting truth
Despisest all the injuries of time;
Thou never know’st decay when all around,
Antiquity obscures her head. Behold
Th’ Egyptian towers, the Babylonian walls,
And Thebes with all her hundred gates of brass,
Behold them scatter’d like the dust abroad.
Whatever now is flourishing and proud,
Whatever shall, must know devouring age.
Euphrates’ stream, and seven-mouthed Nile,
And Danube, thou that from Germania’s soil
To the black Euxine’s far remoted shore,
O’er the wide bounds of mighty nations sweep’st
In thunder loud thy rapid floods along.
Ev’n you shall feel inexorable time;
To you the fatal day shall come; no more
Your torrents then shall shake the trembling ground,
No longer then to inundations swol’n
Th’ imperious waves the fertile pastures drench,
But shrunk within a narrow channel glide;
Or through the year’s reiterated course
When time himself grows old, your wond’rous streams
Lost ev’n to memory shall lie unknown
Beneath obscurity, and Chaos whelm’d,
But still thou sun illuminatest all
The azure regions round, thou guidest still
The orbits of the planetary spheres;
The moon still wanders o’er her changing course,
And still, O Newton, shall thy name survive:
As long as nature’s hand directs the world,
When ev’ry dark obstruction shall retire,
And ev’ry secret yield its hidden store,
Which thee dim-sighted age forbad to see
Age that alone could stay thy rising soul.
[xxvii]And could mankind among the fixed stars,
E’en to th’ extremest bounds of knowledge reach,
To those unknown innumerable suns,
Whose light but glimmers from those distant worlds,
Ev’n to those utmost boundaries, those bars
That shut the entrance of th’ illumin’d space
Where angels only tread the vast unknown,
Thou ever should’st be seen immortal there:
In each new sphere, each new-appearing sun,
In farthest regions at the very verge
Of the wide universe should’st thou be seen.
And lo, th’ all-potent goddess Nature takes
With her own hand thy great, thy just reward
Of immortality; aloft in air
See she displays, and with eternal grasp
Uprears the trophies of great Newton’s fame.
R. Glover.
THE
CONTENTS.
INTRODUCTION concerning Sir Isaac Newton’s
method of reasoning in philosophy————————pag. 1
Book I.
| Chap. 1. Of the laws of motion | |
| The first law of motion proved | p. 29 |
| The second law of motion proved | p. 29 |
| The third law of motion proved | p. 31 |
| Chap. 2. Further proofs of the laws of motion | |
| The effects of percussion | p. 49 |
| The perpendicular descent of bodies | p. 55 |
| The oblique descent of bodies in a straight line | p. 57 |
| The curvilinear descent of bodies | p. 58 |
| The perpendicular ascent of bodies | ibid. |
| The oblique ascent of bodies | p. 59 |
| The power of gravity proportional to the quantity of matter in each body | p. 60 |
| The centre of gravity of bodies | p. 62 |
| The mechanical powers | p. 69 |
| The lever | p. 71 |
| The wheel and axis | p. 77 |
| The pulley | p. 80 |
| The wedge | p. 83 |
| The screw | ibid. |
| The inclined plain | p. 84 |
| The pendulum[xxix] | p. 86 |
| Vibrating in a circle | ibid. |
| Vibrating in a cycloid | p. 91 |
| The line of swiftest descent | p. 93 |
| The centre of oscillation | p. 94 |
| Experiments upon the percussion of bodies made by pendulums | p. 98 |
| The centre of percussion | p. 100 |
| The motion of projectiles | p. 102 |
| The description of the conic sections | p. 106 |
| The difference between absolute and relative motion, as also between absolute and relative time | p. 112 |
| Chap. 3. Of centripetal forces | p. 117 |
| Chap. 4. Of the resistance of fluids | p. 143 |
| Bodies are resisted in the duplicate proportion of their velocities | p. 147 |
| Of elastic fluids and their resistance | p. 149 |
| How fluids may be rendered elastic | p. 150 |
| The degree of resistance in regard to the proportion between the density of the body and of the fluid | |
| In rare and uncompressed fluids | p. 153 |
| In compressed fluids | p. 155 |
| The degree of resistance as it depends upon the figure of bodies | |
| In rare and uncompressed fluids | p. 155 |
| In compressed fluids | p. 158 |
Book II.
| Chap. 1. That the planets move in a space empty of sensible matter | p. 161 |
| The system of the world described | p. 162 |
| The planets suffer no sensible resistance in their motion | p. 166 |
| They are not kept in motion by a fluid | p. 168 |
| That all space is not full of matter without vacancies | p. 169 |
| [xxx]Chap. 2. Concerning the cause that keeps in motion the primary planets | p. 171 |
| They are influenced by a centripetal power directed to the sun | p. 171 |
| The strength of this power is reciprocally in the duplicate proportion of the distance | ibid. |
| The cause of the irregularities in the motions of the planets | p. 175 |
| A correction of their motions | p. 178 |
| That the frame of the world is not eternal | p. 180 |
| Chap. 3. Of the motion of the moon and the other secondary planets | |
| That they are influenced by a centripetal force directed toward their primary, as the primary are influenced by the sun | p. 182 |
| That the power usually called gravity extends to the moon | p. 189 |
| That the sun acts on the secondary planets | p. 190 |
| The variation of the moon | p. 193 |
| That the circuit of the moons orbit is increased by the sun in the quarters, and diminished in the conjunction and opposition | p. 198 |
| The distance of the moon from the earth in the quarters and in the conjunction and opposition is altered by the sun | p. 200 |
| These irregularities in the moon’s motion varied by the change of distance between the earth and sun | p. 201 |
| The period of the moon round the earth and her distance varied by the same means | ibid. |
| The motion of the nodes and the inclination of the moons orbit | p. 202 |
| The motion of the apogeon and change of the eccentricity | p. 218 |
| [xxxi]The inequalities of the other secondary planets deducible from these of the moon | p. 229 |
| Chap. 4. Of comets | |
| They are not meteors, nor placed totally without the planetary system | p. 230 |
| The sun acts on them in the same manner as on the planets | p. 231 |
| Their orbits are near to parabola’s | p. 233 |
| The comet that appeared at the end of the year 1680, probably performs its period in 575 years, and another comet in 75 years | p. 234 |
| Why the comets move in planes more different from one another than the planets | p. 235 |
| The tails of comets | p. 238 |
| The use of them | p. 243 244 |
| The possible use of the comet it self | p. 245 246 |
| Chap. 5. Of the bodies of the sun and planets | |
| That each of the heavenly bodies is endued with an attractive power, and that the force of the same body on others is proportional to the quantity of matter in the body attracted | p. 247 |
| This proved in the earth | p. 248 |
| In the sun | p. 250 |
| In the rest of the planets | p. 251 |
| That the attractive power is of the same nature in the sun and in all the planets, and therefore is the same with gravity | p. 252 |
| That the attractive power in each of these bodies is proportional to the quantity of matter in the body attracting | ibid. |
| [xxxii]That each particle of which the sun and planets are composed is endued with an attracting power, the strength of which is reciprocally in the duplicate proportion of the distance | p. 257 |
| The power of gravity universally belongs to all matter | p. 259 |
| The different weight of the same body upon the surface of the sun, the earth, Jupiter and Saturn; the respective densities of these bodies, and the proportion between their diameters | p. 261 |
| Chap. 6. Of the fluid parts of the planets | |
| The manner in which fluids press | p. 264 |
| The motion of waves on the surface of water | p. 269 |
| The motion of sound through the air | p. 270 |
| The velocity of sound | p. 282 |
| Concerning the tides | p. 283 |
| The figure of the earth | p. 296 |
| The effect of this figure upon the power of gravity | p. 300 |
| The effect it has upon pendulums | p. 302 |
| Bodies descend perpendicularly to the surface of the earth | p. 304 |
| The axis of the earth changes its direction twice a year, and twice a month | p. 313 |
| The figure of the secondary planets | ibid. |
Book III.
| Chap. 1. Concerning the cause of colours inherent in the light | |
| The sun’s light is composed of rays of different colours | p. 318 |
| The refraction of light | p. 319 320 |
| Bodies appear of different colour by day-light, because some reflect one kind of light more copiously than the rest, and other bodies other kinds of light | p. 329 |
| The effect of mixing rays of different colours | p. 334 |
| [xxxiii]Chap. 2. Of the properties of bodies whereon their colours depend. | |
| Light is not reflected by impinging against the solid parts of bodies | p. 339 |
| The particles which compose bodies are transparent | p. 341 |
| Cause of opacity | p. 342 |
| Why bodies in the open day-light have different colours | p. 344 |
| The great porosity of bodies considered | p. 355 |
| Chap. 3. Of the refraction, reflection, and inflection of light. | |
| Rays of different colours are differently refracted | p. 357 |
| The sine of the angle of incidence in each kind of rays bears a given proportion to the sine of refraction | p. 361 |
| The proportion between the refractive powers in different bodies | p. 366 |
| Unctuous bodies refract most in proportion to their density | p. 368 |
| The action between light and bodies is mutual | p. 369 |
| Light has alternate fits of easy transmission and reflection | p. 371 |
| The fits found to return alternately many thousand times | p. 375 |
| Why bodies reflect part of the light incident upon them and transmit another part | ibid. |
| Sir Isaac Newton’s conjecture concerning the cause of this alternate reflection and transmission of light | p. 376 |
| The inflection of light | p. 377 |
| Chap. 4. Of optic glasses. | |
| How the rays of light are refracted by a spherical surface of glass | p. 378 |
| How they are refracted by two such surfaces | p. 380 |
| How the image of objects is formed by a convex glass | p. 381 |
| Why convex glasses help the sight in old age, and concave glasses assist short-sighted people | p. 383 |
| The manner in which vision is performed by the eye | p. 385 |
| [xxxiv]Of telescopes with two convex glasses | p. 386 |
| Of telescopes with four convex glasses | p. 388 |
| Of telescopes with one convex and one concave glass | ibid. |
| Of microscopes | p. 389 |
| Of the imperfection of telescopes arising from the different refrangibility of the light | p. 390 |
| Of the reflecting telescope | p. 393 |
| Chap. 5. Of the rainbow | |
| Of the inner rainbow | p. 394 395 398 399 |
| Of the outter bow | p. 396 397 400 |
| Of a particular appearance in the inner rainbow | p. 401 |
| Conclusion | p. 405 |
ERRATA.
PAGE 25. line 4. read In these Precepts. p. 40. l. 24. for I read K. p. 53. l. penult. f. Æ. r. F. p. 82. l. ult. f. 40. r. 41. p. 83 l. ult. f. 43. r. 45. p. 91. l. 3. f. 48. r. 50. ibid. l. 25. for 49. r. 51. p. 92. l. 18. f. A G F E. r. H G F C. p. 96. l. 23. dele the comma after {⅓}. p. 140. l. 12. dele and. p. 144. l. 15. f. threefold. r. two-fold. p. 162. l. 25. f. {⅓}. r. {⅞}. p. 193. 1. 2. r. always. p. 199. l. penult. and p. 200. l. 3. 5. f. F. r. C. p. 201. l. 8. f. ascends. r. must ascend. ibid. l. 10. f. it descends. r. descend. p. 208. l. 14. f. W T O. r. N T O. In fig. 110. draw a line from I through T, till it meets the circle A D C B, where place W. p. 216. l. penult. f. action. r. motion. p. 221. l. 23. f. A F. r. A H. p. 232. l. 23. after invention put a full point. p. 253. l. penult. delete the comma after remarkable. p. 255. l. ult. f. D E. r. B E. p. 278. l. 17. f. ξ τ. r. ξ π. p. 299. l. 19 r. the. p. 361. l. 12. f. I. r. t. p. 369. l. 2, 3. r. Pseudo-topaz. p. 378. l. 12. f. that. r. than. p. 379. l. 15. f. converge. r. diverge. p. 384. l. 7. f. optic-glass. r. optic-nerve. p. 391. l. 18. r. as 50 to 78. p. 392. l. 18. after telescope add be about 100 feet long and the. in fig. 161. f. δ put ε. p. 399. l. 8. r. A n, A x. &c. p. 400. 1. 19. r. A π, A ρ. A σ, A τ. A φ. p. 401. l. 14. r. fig. 163. The pages 374, 375, 376 are erroneously numbered 375, 376, 377; and the pages 382, 383 are numbered 381, 382.
A LIST of such of the
SUBSCRIBERS NAMES
As are come to the Hand of the
AUTHOR.
A
MOnseigneur d’Aguesseau, Chancelier de France
Reverend Mr Abbot, of Emanuel Coll. Camb.
Capt. George Abell
The Hon. Sir John Anstruther, Bar.
Thomas Abney, Esq;
Mr. Nathan Abraham
Sir Arthur Acheson, Bart.
Mr William Adair
Rev. Mr John Adams, Fellow of Sidney Coll. Cambridge
Mr William Adams
Mr George Adams
Mr William Adamson, Scholar of Caius Coll. Camb.
Mr Samuel Adee, Fell. of Corp. Chr. Coll. Oxon
Mr Andrew Adlam
Mr John Adlam
Mr Stephen Ainsworth
Mrs Aiscot
Mr Robert Akenhead, Bookseller at Newcastle upon Tyne
S. B. Albinus, M. D. Anatom. and Chirurg in Acad. L. B. Prof.
George Aldridge, M. D.
Mr George Algood
Mr Aliffe
Robert Allen, Esq;
Mr Zach. Allen
Rev. Mr Allerton, Fellow of Sidney Coll. Cambridge
Mr St. Amand
Mr John Anns
Thomas Anson, Esq;
Rev. Dr. Christopher Anstey
Mr Isaac Antrabus
Mr Joshua Appleby
John Arbuthnot, M. D.
William Archer, Esq;
Mr John Archer, Merchant of Amsterdam
Thomas Archer, Esq;
Coll. John Armstrong, Surveyor-General of His Majesty’s Ordnance
Mr Armytage
Mr Street Arnold, Surgeon
Mr Richard Arnold
Mr Ascough
Mr Charles Asgill
Richard Ash, Esq; of Antigua
Mr Ash, Fellow-Commoner of Jesus Coll. Cambridge
William Ashurst, Esq; of Castle Henningham, Essex
Mr Thomas Ashurst
Mr Samuel Ashurst
Mr John Askew, Merchant
Mr Edward Athawes, Merchant
Mr Abraham Atkins
Mr Edward Kensey Atkins
Mr Ayerst
Mr Jonathan Ayleworth, Jun.
Rowland Aynsworth, Esq;
B
His Grace the Duke of Bedford
Right Honourable the Marquis of Bowmont
Right Hon. the Earl of Burlington
Right Honourable Lord Viscount Bateman
Rt. Rev. Ld. Bp. of Bath and Wells
Rt. Rev. Lord Bishop of Bristol
Right Hon. Lord Bathurst
Richard Backwell, Esq;
Mr William Backshell, Merch.
Edmund Backwell, Gent.
Sir Edmund Bacon
Richard Bagshaw, of Oakes, Esq;
Tho. Bagshaw, of Bakewell, Esq;
Rev. Mr. Bagshaw
Sir Robert Baylis
Honourable George Baillie, Esq;
Giles Bailly, M. D. of Bristol
Mr Serjeant Baines
Rev. Mr. Samuel Baker, Residen. of St. Paul’s.
Mr George Baker
Mr Francis Baker
Mr Robert Baker
Mr John Bakewell
Anthony Balam, Esq;
[xxxvi]Charles Bale, M. D.
Mr Atwell, Fellow of Exeter Coll. Oxon
Mr Savage Atwood
Mr John Atwood
Mr James Audley
Sir Robert Austen, Bart.
Sir John Austen
Benjamin Avery, L. L. D.
Mr Balgay
Rev. Mr Tho. Ball, Prebendary of Chichester
Mr Pappillon Ball, Merchant
Mr Levy Ball
Rev. Mr Jacob Ball, of Andover
Rev. Mr Edward Ballad, of Trin. Coll. Cambridge
Mr Baller
John Bamber, M. D.
Rev. Mr Banyer, Fellow of Emanuel Coll. Cambridge
Mr Henry Banyer, of Wisbech, Surgeon
Mr John Barber, Apothecary in Coventry
Henry Steuart Barclay, of Colairny, Esq;
Rev. Mr Barclay, Canon of Windsor
Mr David Barclay
Mr Benjamin Barker, Bookseller in London
—— Barker, Esq;
Mr Francis Barkstead
Rev. Mr Barnard
Thomas Barrett, Esq;
Mr Barrett
Richard Barret, M. D.
Mr Barrow, Apothecary
William Barrowby, M. D.
Edward Barry, M. D. of Corke
Mr Humphrey Bartholomew, of University College, Oxon
Mr Benjamin Bartlett
Mr Henry Bartlett
Mr James Bartlett
Mr Newton Barton, of Trinity College, Cambridge
Rev. Mr. Barton
William Barnsley, Esq;
Mr Samuel Bateman
Mr Thomas Bates
Peter Barhurst, Esq;
Mark Barr, Esq;
Thomas Bast, Esq;
Mr Batley, Bookseller in London
Mr Christopher Batt, jun.
Mr William Batt, Apothecary
Rev. Mr Battely, M. A. Student of Christ Church, Oxon
Mr Edmund Baugh
Rev. Mr. Thomas Bayes
Edward Bayley, M. D. of Havant
John Bayley, M. D. of Chichester
Mr. Alexander Baynes, Professor of Law in the University of Edinburgh
Mr Benjamin Beach
Thomas Beacon, Esq;
Rev. Mr Philip Bearcroft
Mr Thomas Bearcroft
Mr William Beachcroft
Richard Beard, M. D. of Worcester
Mr Joseph Beasley
Rev. Mr Beats, M. A. Fellow of Magdalen College, Cambridge
Sir George Beaumont
John Beaumont, Esq; of Clapham
William Beecher, of Howberry, Esq;
Mr Michael Beecher
Mr Finney Beifield, of the Inner-Temple
Mr Benjamin Bell
Mr Humphrey Bell
Mr Phineas Bell
Leonard Belt, Gent.
William Benbow, Esq;
Mr Martin Bendall
Mr George Bennet, of Cork, Bookseller
Rev. Mr Martin Benson, Archdeacon of Berks
Samuel Benson, Esq;
William Benson, Esq;
Rev. Richard Bently, D. D. Master of Trinity Coll. Cambridge
Thomas Bere, Esq;
The Hon. John Berkley, Esq;
Mr Maurice Berkley, sen. Surgeon
John Bernard, Esq;
Mr Charles Bernard
Hugh Bethell, of Rise in Yorkshire, Esq;
Hugh Bethell, of Swindon in Yorkshire, Esq;
Mr Silvanus Bevan, Apothecary
Mr Calverly Bewick, jun.
Henry Bigg, B. D. Warden of New College, Oxon
Sir William Billers
—— Billers, Esq;
Mr John Billingsley
Mr George Binckes
Rev. Mr Birchinsha, of Exeter College, Oxon
Rev. Mr Richard Biscoe
Mr Hawley Bishop, Fellow of St. John’s College, Oxon
Dr Bird, of Reading
Henry Blaake, Esq;
Mr Henry Blaake
Rev. Mr George Black
Steward Blacker, Esq;
William Blacker, Esq;
Rowland Blackman, Esq;
Rev. Mr Charles Blackmore, of Worcester
Rev Mr Blackwall, of Emanuel College, Cambridge
Jonathan Blackwel, Esq;
James Blackwood, Esq;
Mr Thomas Blandford
Arthur Blaney, Esq;
Mr James Blew
Mr William Blizard
Dr Blomer
Mr Henry Blunt
Mr Elias Bocket
Mr Thomas Bocking
Mr Charles Boehm, Merchant
Mr William Bogdani
Mr John Du Bois, Merchant
Mr Samuel Du Bois
Mr Joseph Bolton, of Londonderry, Esq;
Mr John Bond
John Bonithon, M. A.
Mr James Bonwick, Bookseller in London
Thomas Boone, Esq;
Rev. Mr Pennystone, M. A.
Mrs Judith Booth
Thomas Bootle, Esq;
Thomas Borret, Esq;
Mr Benjamin Boss
Dr Bostock
Henry Bosville, Esq;
Mr John Bosworth
Dr George Boulton
Hon. Bourn M. D. of Chesterfield
Mrs Catherine Bovey
Mr Humphrey Bowen
Mr Bower
John Bowes, Esq;
William Bowles, Esq;
Mr John Bowles
Mr Thomas Bowles
Mr Duvereux Bowly
[xxxvii]Duddington Bradeel, Esq;
Rev. Mr James Bradley, Professor of Astronomy, in Oxford
Mr Job Bradley, Bookseller in Chesterfield
Rev. Mr John Bradley
Rev. Mr Bradshaw, Fellow of Jesus College, Cambridge
Mr Joseph Bradshaw
Mr Thomas Blackshaw
Mr Robert Bragge
Champion Bramfield, Esq;
Joseph Brand, Esq;
Mr Thomas Brancker
Mr Thomas Brand
Mr Braxton
Capt. David Braymer
Rev Mr Charles Brent, of Bristol
Mr William Brent
Mr Edmund Bret
John Brickdale, Esq;
Rev. Mr John Bridgen A. M.
Abraham Bridges, Esq;
George Briggs, Esq;
John Bridges, Esq;
Brook Bridges, Esq;
Orlando Bridgman, Esq;
Mr Charles Bridgman
Mr William Bridgman, of Trinity College, Cambridge
Sir Humphrey Briggs, Bart.
Robert Bristol, Esq;
Mr Joseph Broad
Peter Brooke, of Meer, Esq;
Mr Jacob Brook
Mr Brooke, of Oriel Coll. Oxon
Mr Thomas Brookes
Mr James Brooks
William Brooks, Esq;
Rev. Mr William Brooks
Stamp Brooksbank, Esq;
Mr Murdock Broomer
William Brown, Esq;
Mr Richard Brown, of Norwich
Mr William Brown, of Hull
Mrs Sarah Brown
Mr John Browne
Mr John Browning, of Bristol
Mr John Browning
Noel Broxholme, M. D.
William Bryan, Esq;
Rev. Mr Brydam
Christopher Buckle, Esq;
Samuel Buckley, Esq;
Mr Budgen
Sir John Bull
Josiah Bullock, of Faulkbourn-Hall, Essex, Esq;
Rev. Mr Richard Bullock
Rev. Mr Richard Bundy
Mr Alexander Bunyan
Rev. Mr D. Burges
Ebenezer Burgess, Esq;
Robert Burleston, M. B.
Gilbert Burnet, Esq;
Thomas Burnet, Esq;
Rev. Mr Gilbert Burnet
His Excellency Will. Burnet, Esq; Governour of New-York
Mr Trafford Burnston, of Trin. College, Cambridge
Peter Burrel Esq;
John Burridge, Esq;
James Burrough, Esq; Beadle and Fellow of Caius Coll. Cambr.
Mr Benjamin Burroughs
Jeremiah Burroughs, Esq;
Rev. Mr Joseph Burroughs
Christopher Burrow, Esq;
James Burrow, Esq;
William Burrow, A. M.
Francis Burton, Esq;
John Burton, Esq;
Samuel Burton, of Dublin, Esq;
William Burton, Esq;
Mr Burton.
Richard Burton, Esq;
Dr Simon Burton
Rev. Mr Thomas Burton, M.A. Fellow of Caius College, Cambridge
John Bury, jun. Esq;
Rev. Mr Samuel Bury
Mr William Bush
Rev. Mr Samuel Butler
Mr Joseph Button, of Newcastle upon Tyne
Hon. Edward Byam, Governour of Antigua
Mr Edward Byam, Merchant
Mr John Byrom
Mr Duncumb Bristow, Merch.
Mr William Bradgate
C
His Grace the Archbishop of Canterbury
Right Hon. the Lord Chancellor
His Grace the Duke of Chandois
The Right Hon. the Earl of Carlisle
Right Hon. Earl Cowper
Rt. Rev. Lord Bishop of Carlisle
Rt. Rev. Lord Bishop of Chichester
Rt. Rev. Lord Bish. of Clousert in Ireland
Rt. Rev, Lord Bishop of Cloyne
Rt. Hon. Lord Clinton
Rt. Hon. Lord Chetwynd
Rt. Hon. Lord James Cavendish
The Hon. Lord Cardross
Rt. Hon. Lord Castlemain
Right Hon. Lord St. Clare
Cornelius Callaghan, Esq;
Mr Charles Callaghan
Felix Calvert, of Allbury, Esq;
Peter Calvert, of Hunsdown in Hertfordshire, Esq;
Mr William Calvert of Emanuel College, Cambridge
Reverend Mr John Cambden
John Campbell, of Stackpole-Court, in the County of Pembroke, Esq;
Mrs Campbell, of Stackpole-Court
Mrs. Elizabeth Caper
Mr Dellillers Carbonel
Mr John Carleton
Mr Richard Carlton, of Chesterfield
Mr Nathaniel Carpenter
Henry Carr, Esq;
John Carr, Esq;
John Carruthers, Esq;
Rev. Dr. George Carter, Provost of Oriel College
Mr Samuel Carter
Honourable Edward Carteret, Esq;
Robert Cartes, jun. in Virginia, Esq;
Mr William Cartlich
James Maccartney, Esq;
Mr Cartwright, of Ainho
Mr William Cartwright, of Trinity College, Cambridge
Reverend Mr William Cary, of Bristol
Mr Lyndford Caryl
Mr John Case
Mr John Castle
Reverend Mr Cattle
Hon. William Cayley, Consul at Cadiz, Esq;
William Chambers, Esq;
Mr Nehemiah Champion
Mr Richard Champion
Matthew Chandler, Esq;
Mr George Channel
Mr Channing
Mr Joseph Chappell, Attorney at Bristol
[xxxviii]Mr Rice Charlton, Apothecary at Bristol
St. John Charelton, Esq;
Mr Richard Charelton
Mr Thomas Chase, of Lisbon, Merchant
Robert Chauncey, M. D.
Mr Peter Chauvel
Patricius Chaworth, of Ansley, Esq;
Pole Chaworth of the Inner Temple, Esq;
Mr William Cheselden, Surgeon to her Majesty
James Chetham, Esq;
Mr James Chetham
Charles Child, A. B. of Clare-Hall, in Cambridge, Esq;
Mr Cholmely, Gentleman Commoner of New-College, Oxon
Thomas Church, Esq;
Reverend Mr St. Clair
Reverend Mr Matthew Clarke
Mr William Clark
Bartholomew Clarke, Esq;
Charles Clarke, of Lincolns-Inn, Esq;
George Clarke, Esq;
Samuel Clarke, of the Inner-Temple, Esq;
Reverend Mr Alured Clarke, Prebendary of Winchester
Rev. John Clarke, D. D. Dean of Sarum
Mr John Clark, A. B. of Trinity College, Cambridge
Matthew Clarke, M. D.
Rev. Mr Renb. Clarke, Rector of Norton, Leicestershire
Rev. Mr Robert Clarke, of Bristol
Rev. Samuel Clarke, D. D.
Mr Thomas Clarke, Merchant
Mr Thomas Clarke
Rev. Mr Clarkson, of Peter-House, Cambridge
Mr Richard Clay
William Clayton, of Marden, Esq;
Samuel Clayton, Esq;
Mr William Clayton
Mr John Clayton
Mr Thomas Clegg
Mr Richard Clements, of Oxford, Bookseller
Theophilus Clements, Esq;
Mr George Clifford, jun. of Amsterdam
George Clitherow, Esq;
George Clive, Esq;
Dr. Clopton, of Bury
Stephen Clutterbuck, Esq;
Henry Coape, Esq;
Mr Nathaniel Coatsworth
Rev. Dr. Cobden, Chaplain to the Bishop of London
Hon. Col. John Codrington, of Wraxall, Somersetshire
Right Hon. Marmaduke Coghill, Esq;
Francis Coghlan, Esq;
Sir Thomas Coke
Mr Charles Colborn
Benjamin Cole, Gent.
Dr Edward Cole
Mr Christian Colebrandt
James Colebrooke, Esq;
Mr William Coleman, Merchant
Mr Edward Collet
Mrs Henrietta Collet
Mr John Collet
Mrs Mary Collett
Mr Samuel Collet
Mr Nathaniel Collier
Anthony Collins, Esq;
Thomas Collins, of Greenwich, M. D.
Mr Peter Collinson
Edward Colmore, Fellow of Magdalen College, Oxon
Rev. Mr John Colson
Mrs Margaret Colstock, of Chichester
Capt. John Colvil
Renè de la Combe, Esq;
Rev. Mr John Condor
John Conduit, Esq;
John Coningham, M. D.
His Excellency William Conolly, one of the Lords Justices of Ireland
Mr Edward Constable, of Reading
Rev. Mr Conybeare, M. A.
Rev. Mr James Cook
Mr John Cooke
Mr Benjamin Cook
William Cook, B L. of St. John’s College, Oxon
James Cooke, Esq;
John Cooke, Esq;
Mr Thomas Cooke
Mr William Cooke, Fellow of St. John’s College, Oxon
Rev. Mr Cooper, of North-Hall
Charles Cope, Esq;
Rev. Mr Barclay Cope
Mr John Copeland
John Copland, M. B.
Godfrey Copley, Esq;
Sir Richard Corbet, Bar.
Rev. Mr Francis Corbett
Mr Paul Corbett
Mr Thomas Corbet
Henry Cornelisen, Esq;
Rev. Mr John Cornish
Mrs Elizabeth Cornwall
Library of Corpus Christi College, Cambridge
Mr William Cossley, of Bristol, Bookseller
Mr Solomon du Costa
Dr. Henry Costard
Dr. Cotes, of Pomfret
Caleb Cotesworth, M. D.
Peter Cottingham, Esq;
Mr John Cottington
Sir John Hinde Cotton
Mr James Coulter
George Courthop, of Whiligh in Sussex, Esq;
Mr Peter Courthope
Mr John Coussmaker, jun.
Mr Henry Coward, Merchant
Anthony Ashley Cowper, Esq;
The Hon. Spencer Cowper, Esq; One of the Justices of the Court of Common Pleas
Mr Edward Cowper
Rev. Mr John Cowper
Sir Charles Cox
Samuel Cox, Esq;
Mr Cox, of New Coll. Oxon
Mr Thomas Cox
Mr Thomas Cradock, M. A.
Rev. Mr John Craig
Rev. Mr John Cranston, Archdeacon of Cloghor
John Crafter, Esq;
Mr John Creech
James Creed, Esq;
Rev. Mr William Crery
John Crew, of Crew Hall, in Cheshire, Esq;
Thomas Crisp, Esq;
Mr Richard Crispe
Rev. Mr Samuel Cuswick
Tobias Croft, of Trinity College, Cambridge
Mr John Crook
Rev. Dr Crosse, Master of Katherine Hall
Christopher Crowe, Esq;
George Crowl, Esq;
Hon. Nathaniel Crump, Esq; of Antigua
Mrs Mary Cudworth
[xxxix]Alexander Cunningham, Esq;
Henry Cunningham, Esq;
Mr Cunningham
Dr Curtis of Sevenoak
Mr William Curtis
Henry Curwen, Esq;
Mr John Caswall, of London, Merchant
Dr Jacob de Castro Sarmento
D
His Grace the Duke of Devonshire
His Grace the Duke of Dorset
Right Rev. Ld. Bishop of Durham
Right Rev. Ld. Bishop of St. David
Right Hon. Lord Delaware
Right Hon. Lord Digby
Right Rev. Lord Bishop of Derry
Right Rev. Lord Bishop of Donne
Rt. Rev. Lord Bishop of Dromore
Right Hon. Dalhn, Lord Chief Baron of Ireland
Mr Thomas Dade
Capt. John Dagge
Mr Timothy Dallowe
Mr James Danzey, Surgeon
Rev. Dr Richard Daniel, Dean of Armagh
Mr Danvers
Sir Coniers Darcy, Knight of the Bath
Mr Serjeant Darnel
Mr Joseph Dash
Peter Davall, Esq;
Henry Davenant, Esq;
Davies Davenport, of the Inner-Temple, Esq;
Sir Jermyn Davers, Bart.
Capt. Thomas Davers
Alexander Davie, Esq;
Rev. Dr. Davies, Master of Queen’s College, Cambridge
Mr John Davies, of Christ-Church, Oxon
Mr Davies, Attorney at Law
Mr William Dawkins, Merch.
Rowland Dawkin, of Glamorganshire, Esq;
Mr John Dawson
Edward Dawson, Esq;
Mr Richard Dawson
William Dawsonne, Esq;
Thomas Day, Esq;
Mr John Day
Mr Nathaniel Day
Mr Deacon
Mr William Deane
Mr James Dearden, of Trinity College, Cambridge
Sir Matthew Deckers, Bart.
Edward Deering, Esq;
Simon Degge, Esq;
Mr Staunton Degge, A. B. of Trinity Col. Cambridge
Rev. Dr Patrick Delaney
Mr Delhammon
Rev. Mr Denne
Mr William Denne
Capt. Jonathan Dennis
Daniel Dering, Esq;
Jacob Desboverie, Esq;
Mr James Deverell, Surgeon in Bristol
Rev. Mr John Diaper
Mr Rivers Dickenson
Dr. George Dickens, of Liverpool
Hon. Edward Digby, Esq;
Mr Dillingham
Mr Thomas Dinely
Mr Samuel Disney, of Bennet College, Cambridge
Robert Dixon, Esq;
Pierce Dodd, M. D.
Right Hon. Geo. Doddinton, Esq;
Rev. Sir John Dolben, of Findon, Bart.
Nehemiah Donellan, Esq;
Paul Doranda, Esq;
James Douglas, M. D.
Mr Richard Dovey, A. B. of Wadham College, Oxon
John Dowdal, Esq;
William Mac Dowell, Esq;
Mr Peter Downer
Mr James Downes
Sir Francis Henry Drake, Knt.
William Drake, of Barnoldswick-Cotes, Esq;
Mr Rich. Drewett, of Fareham
Mr Christopher Drisfield, of Christ-Church, Oxon
Edmund Dris, A. M. Fellow of Trinity Coll. Cambridge
George Drummond, Esq; Lord Provost of Edenburgh
Mr Colin Drummond, Professor of Philosophy in the University of Edinburgh
Henry Dry, Esq;
Richard Ducane Esq;
Rev. Dr Paschal Ducasse, Dean of Ferns
George Ducket, Esq;
Mr Daniel Dufresnay
Mr Thomas Dugdale
Mr Humphry Duncalfe, Merchant
Mr James Duncan
John Duncombe, Esq;
Mr William Duncombe
John Dundass, jun. of Duddinstown, Esq;
William Dunstar, Esq;
James Dupont, of Trinity Coll. Cambridge
E
Right Rev. and Right Hon. Lord Erskine
Theophilus, Lord Bishop of Elphin
Mr Thomas Eames
Rev. Mr. Jabez Earle
Mr William East
Sir Peter Eaton
Mr John Eccleston
James Eckerfall, Esq;
—— Edgecumbe, Esq;
Rev. Mr Edgley
Rev. Dr Edmundson, President of St. John’s Coll. Cambridge
Arthur Edwards, Esq;
Thomas Edwards, Esq;
Vigerus Edwards, Esq;
Capt. Arthur Edwards
Mr Edwards
Mr William Elderton
Mrs Elizabeth Elgar
Sir Gilbert Eliot, of Minto, Bart. one of the Lords of Session
Mr John Elliot, Merchant
George Ellis, of Barbadoes, Esq;
Mr John Ellison, of Sheffield
Sir Richard Ellys, Bart.
Library of Emanuel College, Cambridge
Francis Emerson, Gent.
Thomas Emmerson, Esq;
Mr Henry Emmet
Mr John Emmet
Thomas Empson, of the Middle-Temple, Esq;
Mr Thomas Engeir
Mr Robert England
Mr Nathaniel English
Rev. Mr Ensly, Minister of the Scotch Church in Rotterdam
[xl]John Essington, Esq;
Rev. Mr Charles Este, of Christ-Church, Oxon
Mr Hugh Ethersey, Apothecary
Henry Evans, of Surry, Esq;
Isaac Ewer, Esq;
Mr Charles Ewer
Rev. Mr Richard Exton
Sir John Eyles, Bar.
Sir Joseph Eyles
Right Hon. Sir Robert Eyre, Lord Chief Justice of the Common Pleas.
Edward Eyre, Esq;
Henry Samuel Eyre, Esq;
Kingsmill Eyre, Esq;
Mr Eyre
F
Right Rev. Josiah, Lord Bishop of Fernes and Loghlin
Den Heer Fagel
Mr Thomas Fairchild
Thomas Fairfax, of the Middle Temple, Esq;
Mr John Falconer, Merchant
Daniel Falkiner, Esq;
Charles Farewell, Esq;
Mr Thomas Farnaby, of Merton College, Oxon
Mr William Farrel
James Farrel, Esq;
Thomas Farrer, Esq;
Dennis Farrer, Esq;
John Farrington, Esq;
Mr Faukener
Mr Edward Faulkner
Francis Fauquiere, Esq;
Charles De la Fay, Esq;
Thomas De lay Fay, Esq;
Capt. Lewis De la Fay
Nicholas Fazakerly, Esq;
Governour Feake
Mr John Fell, of Attercliffe
Martyn Fellowes, Esq;
Coston Fellows, Esq;
Mr Thomas Fellows
Mr Francis Fennell
Mr Michael Fenwick
John Ferdinand, of the Inner-Temple, Esq;
Mr James Ferne, Surgeon
Mr John Ferrand, of Trinity College, Cambridge
Mr Daniel Mussaphia Fidalgo
Mr Fidler
Hon. Mrs Celia Fiennes
Hon. and Rev. Mr. Finch, Dean of York
Hon. Edward Finch, Esq;
Mr John Finch
Philip Fincher Esq;
Mr Michael Fitch, of Trinity College, Cambridge
Hon. John Fitz-Morris, Esq;
Mr Fletcher
Martin Folkes, Esq;
Dr Foot
Mr Francis Forester
John Forester, Esq;
Mrs Alice Forth
Mr John Forthe
Mr Joseph Foskett
Mr Edward Foster
Mr Peter Foster
Peter Foulkes, D. D. Canon of Christ-Church, Oxon
Rev. Dr. Robert Foulkes
Rev. Mr Robert Foulks, M. A. Fellow of Magdalen College, Cambridge
Mr Abel Founereau, Merchant
Mr Christopher Fowler
Mr John Fowler, of Northamp.
Mr Joseph Fowler
Hon. Sir William Fownes, Bar.
George Fox, Esq;
Edward Foy, Esq;
Rev. Dr. Frankland, Dean of Gloucester
Frederick Frankland, Esq;
Mr Joseph Franklin
Mr Abraham Franks
Thomas Frederick, Esq; Gentleman Commoner of New College, Oxon
Thomas Freeke, Esq;
Mr Joseph Freame
Richard Freeman, Esq;
Mr Francis Freeman, of Bristol
Ralph Freke, Esq;
Patrick French, Esq;
Edward French, M. D.
Dr. Frewin
John Freind, M. D.
Mr Thomas Frost
Thomas Fry, of Hanham, Gloucestershire, Esq;
Mr Rowland Fry, Merchant
Francis Fuljam, Esq;
Rev. Mr Fuller, Fellow of Emanuel College, Cambridge
Mr John Fuller
Thomas Fuller, M. D.
Mr William Fullwood, of Huntingdon
Rev. James Fynney, D. D. Prebendary of Durham
Capt. Fyshe
Mr Francis Fayram, Bookseller in London
G
His Grace the Duke of Grafton
Right Hon. Earl of Godolphin
Right Hon. Lady Betty Germain
Right Hon. Lord Garlet
Right Rev. Bishop of Gloucester
Right Hon. Lord St. George
Rt. Hon. Lord Chief Baron Gilbert
Mr Jonathan Gale, of Jamaica
Roger Gale, Esq;
His Excellency Monsieur Galvao, Envoy of Portugal
James Gambier, Esq;
Mr Joseph Gambol, of Barbadoes
Mr Joseph Gamonson
Mr Henry Garbrand
Rev. Mr Gardiner
Mr Nathaniel Garland
Mr Nathaniel Garland, jun.
Mr Joas Garland
Mr James Garland
Mrs Anne Garland
Mr Edward Garlick
Mr Alexander Garrett
Mr John Gascoygne, Merchant
Rev. Dr Gasketh
Mr Henry Gatham
Mr John Gay
Thomas Gearing, Esq;
Coll. Gee
Mr Edward Gee, of Queen’s College, Cambridge
Mr Joshua Gee, sen.
Mr Joshua Gee, jun.
Richard Fitz-Gerald, of Gray’s-Inn, Esq
Mr Thomas Gerrard
Edward Gibbon, Esq;
John Gibbon, Esq;
Mr Harry Gibbs
Rev. Mr Philip Gibbs
Thomas Gibson, Esq;
Mr John Gibson
Mr Samuel Gideon
Rev. Dr Clandish Gilbert, of Trinity College, Dublin
Mr John Gilbert
John Girardos, Esq;
Mr John Girl, Surgeon
[xli]Rev. Dr. Gilbert, Dean of Exeter, 4 Books
Mr Gisby, Apothecary
Mr Richard Glanville
John Glover, Esq;
Mr John Glover, Merchant
Mr Thomas Glover, Merchant
John Goddard, Merchant, in Rotterdam
Peter Godfrey, Esq;
Mr Joseph Godfrey
Capt. John Godlee
Joseph Godman, Esq;
Capt. Harry Goff
Mr Thomas Goldney
Jonathan Goldsmyth, M. D.
Rev. Mr William Goldwin
—— Gooday, Esq;
John Goodrick, Esq; Fellow Commoner of Trinity Coll. Cambridge
Sir Henry Goodrick, Bart.
Mr Thomas Goodwin
Sir William Gordon, Bar.
Right Hon. Sir Ralph Gore, Bart.
Arthur Gore, Esq;
Mr Francis Gore
Mr John Charles Goris
Rev. Mr William Gosling, M. A.
William Goslin, Esq;
Mr William Gossip, A. B. of Trin. Coll. Cambridge
John Gould, jun. Esq;
Nathaniel Gould, Esq;
Mr Thomas Gould
Rev. Mr Gowan, of Leyden
Richard Graham, jun. Esq;
Mr George Graham
Mr Thomas Grainger
Mr Walter Grainger
Mr John Grant
Monsieur S’ Gravesande, Professor of Astronomy and Experim. Philosophy in Leyden
Dr Gray
Mr Charles Gray of Colchester
Mr John Greaves
Mr Francis Green
Dr Green, Professor of Physick in Cambridge
Samuel Green, Gent.
Mr George Green, B. D.
Mr Peter Green
Mr Matthew Green
Mr Nathaniel Green, Apothecary
Mr Stephen Greenhill, of Jesus College, Cambridge
Mr Arthur Greenhill
Mr Joseph Greenup
Mr Randolph Greenway, of Thavies Inn
Mr Thomas Gregg, of the Middle Temple
Mr Gregory, Profess. of Modern Hist. in Oxon
Mrs Katherine Gregory
Samuel Gray, Esq;
Mr Richard Gray, Merchant in Rotterdam
Thomas Griffiths, M. D.
Mr Stephen Griggman
Mr Renè Grillet
Mr Richard Grimes
Johannes Groeneveld, J. U. & M. D. and Poliater Leidensis
Rev. Mr Grosvenor
Mr Richard Grosvenor
Mr Joseph Grove, Merchant
Mr John Henry Grutzman, Merchant
Mathurin Guiznard, Esq;
Sir John Guise
Rev. Mr John Guise
Mr Ralph Gulston
Matthew Gundry, Esq;
Nathaniel Gundry, Esq;
Mrs Sarah Gunston
Charles Gunter Niccol, Esq;
Thomas Gwillin, Esq;
Marmaduke Gwynne, Esq;
Roderick Gwynne, Esq;
David Gausell, Esq; of Leyton Grange
Samuel Grey, Esq;
Mr J. Grisson
H.
Right Hon. Earl of Hertford
Rt. Hon. Ld. Herbert, of Cherbury
Right Hon. Lord Herbert
Right Hon. Lord Hervey
Right Hon. Lord Hunsdon
John Haddon, M. B. of Christ-Church, Oxon
Mr Haines
Mrs Mary Haines
Edward Haistwell, Esq;
Othniel Haggett, of Barbadoes, Esq;
Robert Hale, Esq;
Mr Philip Hale
Mr Charles Hallied
Abraham Hall, M. B.
Dr. Hall
Mr Henry Hall
Mr Jonathan Hall
Mr Matthew Hall
Francis Hall, Esq; of St. James’s Place
Rev. Mr Hales
William Hallet, of Exeter, M. D.
Edmund Halley, L. L. D. Astro. Reg. & Profess. of Modern Hist. in Ox. Savilian.
Edmund Hallsey, Esq;
Mr John Hamerse
John Hamilton, Esq;
Andrew Hamilton, Esq;
Rev. Andrew Hamilton, D. D. Arch-Deacon of Raphoe
Mr William Hamilton, Professor of Divinity in the University of Edinburgh
Mr John Hamilton
Mr Thomas Hammond, Bookseller in York
Mrs Martha Hammond
Mr John Hand
Rev. Mr Hand, Fellow of Emanuel College, Cambridge
Mr Samuel Handly
Gabriel Hanger, Esq;
James Hannott, of Spittle-Fields, Esq;
Mr Han Hankey
Harbord Harbord, of Gunton in Norfolk, Esq;
Richard Harcourt, Esq;
Mr Thomas Hardey
John Harding, Esq;
Sir William Hardress, Bar.
Peter Hardwick, M. D. of Bristol
Mr Thomas Hardwick, Attorney
Rev. Mr Jonathan Hardey
Henry Hare, Esq;
Mr Hare, of Beckingham in Kent
Mr Mark Harford
Mr Trueman Harford
Hon. Edward Harley, Esq;
Capt. Harlowe
Mr Henry Harmage
Mr Jeremiah Harman
Henry Harrington, Esq;
Barrows Harris, Esq;
James Harris, Esq;
William Harris, of Sarum, Esq;
Rev. Mr Dean Harris
Mr Thomas Harris
Rev. Mr Harris, Professor of Modern History in Cambridge
Mr Richard Harris
Mrs Barbara Harrison
Mr William Harrison
Rev. Mr Henry Hart
[xlii]Mr Moses Hart
Sir John Hartop, Bart.
Mr Peter Harvey
Henry Harwood, Esq;
John Harwood, L. D.
Robert Prose Hassel, Esq;
George Hatley, Esq;
Mr William Havens
Capt. John Hawkins
Mr Mark Hawkins, Surgeon
Mr Walter Hawksworth, Merch.
Mr Francis Hawling
Mr John Huxley, of Sheffield
Mr Richard Hayden, Merchant
Cherry Hayes, M. A.
Mr Thompson Hayne
Mr Samuel Haynes
Mr Thomas Haynes
Mr John Hayward, Surgeon
Mr Joseph Hayward, of Madera, Merchant
Rev. Sir Francis Head, Bart.
James Head, Esq;
Thomas Heames, Esq;
Edmund Heath, Esq;
Thomas Heath, Esq;
Mr Benjamin Heath
Cornelius Heathcote, of Cutthoy, M. D.
Mr James Hamilton, Merchant
Mr Thomas Hasleden
Sir Gilbert Heathcote
John Heathcote, Esq;
William Heathcote, Esq;
Mr Abraham Heaton
Anthony Heck, Esq;
John Hedges, Esq;
Mr Paul Heeger, jun. Merch.
Dr Richard Heisham
Mr Jacob Henriques
Mr John Herbert, Apothecary in Coventry
George Hepburn, M. D. of Lynn-Regis
Mr Samuel Herring
Mr John Hetherington
Mr Richard Hett, Bookseller
Fitz Heugh, Esq;
Hewer Edgley Hewer, Esq;
Robert Heysham, Esq;
Mr Richard Heywood
Mr John Heywood
Mr Samuel Hibberdine
Nathaniel Hickman, M. A.
Mr Samuel Hickman
Rev. Mr Hiffe, Schoolmaster at Kensington
Mr Banger Higgens
Mr Samuel Highland
Mr Joseph Highmore
Rev. Mr John Hildrop. M. A. Master of the Free-School in Marlborough
Mr Francis Hildyard, Bookseller in York
Mr Hilgrove
Mr James Hilhouse
John Hill, Esq;
Mr John Hill
Mr Rowland Hill, of St. John’s College, Cambridge
Samuel Hill, Esq;
Mr Humphrey Hill
Rev. Mr Richard Hill
Mr Peter St. Hill, Surgeon
Mr William Hinchliff, Bookseller
Mr Peter Hind
Benjamin Hinde, of the Inner-Temple, Esq;
Robert Hinde, Esq;
Mr Peter Hinde, jun.
Rev. Mr Dean Hinton
Mr Robert Hirt
Capt. Joseph Hiscox, Merchant
Mr William Hoare
Mr William Hobman
Sir Nathaniel Hodges
Mr Hodges, M. A. of Jesus College, Oxon
Mr Joseph Jory Hodges
Mr Hodgson, Master of the Mathematicks in Christ’s Hospital
Mr Hodson
Edward Hody, M. D.
Mr Thomas Hook
Samuel Holden, Esq;
Mr Adam Holden, of Greenwich
Rogers Holland, Esq;
Mr James Holland, Merchant
Richard Holland M. D.
John Hollings, M. D.
Mr Thomas Hollis
Mr John Hollister
Mr Edward Holloway
Mr Thomas Holmes
Rev. Mr Holmes, Fellow of Emanuel College, Cambridge
Rev. Mr Samuel Holt
Matthew Holworthy, Esq;
Mr John Hook
Mr Le Hook
Mrs Elizabeth Hooke
John Hooker, Esq;
Mr John Hoole
Mr Samuel Hoole
Mr Thomas Hope
Thomas Hopgood, Gent.
Sir Richard Hopkins
Richard Hopwood, M. D.
Mr Henry Horne
Rev. Mr John Horseley
Samuel Horseman, M. D.
Mr Stephen Horseman
Mr Thomas Houghton
Mr Thomas Houlding
James How, Esq;
John How, of Hans Cope, Esq;
Mr John Howe
Mr Richard How
Hon. Edward Howard, Esq;
William Howard, Esq;
Rev. Dean Robert Howard
Thomas Hucks, Esq;
Mr Hudsford, of Trinity Coll. Oxon
Capt. Robert Hudson, jun.
Mr John Hughes
Edward Hulse, M. D.
Sir Gustavus Humes
Rev. Mr David Humphreys, S. T. B. Fellow of Trin. Coll. Cambridge
Maurice Hunt, Esq;
Mr Hunt, of Hart-Hall, Oxon
Mr John Hunt
James Hunter, Esq;
Mr William Hunter
Mr John Hussey, of Sheffield
Ignatius Hussey, Esq;
Rev. Mr Christopher Hussey, M. A. Rector of West-Wickham in Kent
Thomas Hutchinson, Esq; Fellow Commoner of Sidney-College, Cambridge
Rev. Mr Hutchinson, of Hart-Hall, Oxon
Mr Sandys Hutchinson, of Trinity College, Cambridge
Mr Huxley, M. A. of Brazen Nose College, Oxon
Mr Thomas Hyam, Merchant
Mr John Hyde
Mr Hyett, Gent. Commoner of Pembroke College, Oxon
I
Right Hon. the Earl of Ilay
Edward Jackson, Esq;
Mr Stephen Jackson, Merchant
Mr Cuthbert Jackson
Rev. Mr. Peter Jackson
Mr Joshua Jackson
[xliii]John Jacob, Esq;
Mr Jacobens
Joseph Jackson, of London, Goldsmith
Rev. Sir George Jacobs, of Houghton in Norfolk
Mr Henry Jacomb
Mr John Jacques, Apothecary in Coventry
Mr Samuel Jacques, Surgeon at Uxbridge
William James, Esq;
Rev. Mr David James, Rector of Wroughton, Bucks
Mr Benjamin James
Mr Robert James, of St. John’s, Oxon
Sir Theodore Janssen, Bart.
Mr John Jarvis, Surgeon at Dartford in Kent
Mr Edward Jasper
Edward Jauncy, of the Middle-Temple Esq;
Rev. Dr Richard Ibbetson
John Idle, of the Middle Temple, Esq;
Mr Samuel Jeake
Mr Samuel Jebb
Mr David Jefferies
Rev. Mr Joseph Jefferies
Bartholomew Jeffrey, of the Middle Temple, Esq;
Edward Jeffries, Esq;
Lady Jekyll
Ralph Jenison, Esq; 2 Books
David Jenkins, L. L. D. Chancellor of Derry
Mr Jenkins
Mr Samuel Jennings, of Hull
Library of Jesus Coll. Cambridge
John Ingilby, Esq;
Martin Innys, of Bristol, Gent.
Messieurs William and John Innys of London, Booksellers
Thomas Jobber, Esq;
Robert Jocelyn, Esq;
Rev. Mr Samuel Jocham
Oliver St. John, Esq;
George Johnson, Esq;
Hon. James Johnson, Esq;
James Jurin, M. D.
Rev. Mr Rob. Johnson. S. T. B. Fellow of Trinity College,
Cambridge
Mr Isaac Johnson
Mr Michael Johnson, Merchant in Rotterdam
Edward Jones, Esq; Chancellor of the Diocese of St. David’s
Mr Jones, M. A. of Jesus College, Oxon
Mr Jacob Jones
Rev. Mr James Jones, Rector of Cound, Salop
Mr Somerset Jones, A. B. of Christ-Church, Oxon
Mr John Jones, Surgeon
Mr John Jope, Fellow of New College, Oxon
Charles Joy, Esq;
Daniel Ivie, Esq; of Chelsea Hospital
K
His Grace the Duke of Kingston
Right Honourable Gerrard, Lord Viscount Kingsale
Right Reverend Lord Bishop of Killale
Rt. Rev. Lord Bishop of Killdare
Right Reverend Lord Bishop of Killmore
Rev. Mr William Kay, Rector of Wigginton, Yorkshire
Benjamin Keene, Esq;
Hon. Major General Kellum
Mr Thomas Kemp, M. A of St. John’s College, Oxon
Mr Robert Kendall
Mr Clayton Kendrick
John Kendrick, Esq;
John Kemp, of the Middle Temple, Esq;
Mr Chidrock Kent
Samuel Kent, Esq;
Rev Mr Samuel Kerrick, Fellow of Christ Church College,
Cambridge.
Mr Kidbey
Mr Robert Kidd
Library of King’s College, Cambridge
Benjamin King, of Antigua, Esq;
Mr Matthias King
Mrs Jane King
Hon. Colonel Pearcy Kirke
Mr Thomas Knap
Rev. Samuel Knight, D. D. Prebendary of Ely
Mr Robert Knight, jun.
Francis Knowllyes, Esq;
Mr Ralph Knox
L
Rt. Hon. Lord Viscount Lonsdale
Rt. Hon. Ld. Viscount Lymington
Rt. Rev. Lord Bishop of London
Right Rev. Lord Bishop of Landaff
Right Honourable Lord Lyn
John Lade, Esq;
Mr Hugh Langharne
Mr John Langford
Mr William Larkman
Mr William Lambe, of Exeter College, Oxon
Richard Langley, Esq;
Mr Robert Lacy
James Lamb, Esq;
Rev. Mr Thomas Lambert, M. A. Vicar of Ledburgh, Yorkshire
Mr Daniel Lambert
Mr John Lampe
Dr. Lane, of Hitchin in Hertfordshire
Mr Timothy Lane
Rev. Dr. Laney, Master of Pembroke Hall, Cambr. 2 Books
Mr Peter de Langley
Rev. Mr Nathaniel Lardner
Mr Larnoul
Mr Henry Lascelles, of Barbadoes, Merchant
Rev. Mr John Laurence, Rector of Bishop’s Waremouth
Mr Roger Laurence, M. A.
Mr Lavington
Mr William Law, Professor of Moral Philosophy in the University of Edinburgh
Mr John Lawton, of the Excise-Office
Mr Godfrey Laycock, of Hallifax
Mr Charles Leadbetter, Teacher of the Mathematicks
Mr James Leake, Bookseller in Bath
Stephen Martin Leak, Esq;
Rev. Mr Lechmere
William Lee, Esq;
Mr Lee, of Christ Church, Oxon
Rev. Mr John Lee
Mr William Leek
Rev. Mr Leeson
[xliv]Peter Legh, of Lyme in Cheshire, Esq;
Robert Leguarre, of Gray’s-Inn, Esq;
Mr Lehunt
Mr John Lehunt, of Canterbury
Francis Leigh, Esq;
Mr John Leigh
Mr Percival Lewis
Mr Thomas Lewis
New College Library
Sir Henry Liddell, Bar. of St. Peter’s College, Cambridge
Henry Liddell, Esq;
Mr William Limbery
Robert Lindsay, Esq;
Countess of Lippe
Rev. Dr. James Lisle
Rev. Mr Lister
Mr George Livingstone, One of the Clerks of Session
Salisbury Lloyd, Esq;
Rev. Mr John Lloyd, A. B. of Jesus College
Mr Nathaniel Lloyd, Merchant
Mr Samuel Lobb, Bookseller at Chelmsford
William Lock, Esq;
Mr James Lock, 2 Books
Mr Joshua Locke
Charles Lockier, Esq;
Richard Lockwood, Esq;
Mr Bartholom. Loftus, 9 Books
William Logan, M. D.
Mr Moses Loman, jun.
Mr Longley
Mr Benjamin Longuet
Mr Grey Longueville
Mr Robert Lord
Mrs Mary Lord
Mr Benjamin Lorkin
Mr William Loup
Richard Love, of Basing in Hants, Esq;
Mrs Love, in Laurence-Lane
Mr Joshua Lover, of Chichester
William Lowndes, Esq;
Charles Lowndes, Esq;
Mr Cornelius Lloyd
Robert Lucas, Esq;
Coll. Richard Lucas
Sir Bartlet Lucy
Edward Luckin, Esq;
Mr John Ludbey
Mr Luders, Merchant
Lambert Ludlow, Esq;
William Ludlow, Esq;
Peter Ludlow, Esq;
John Lupton, Esq;
Nicholas Luke, Esq;
Lyonel Lyde, Esq;
Dr. George Lynch
Mr Joshua Lyons
M.
His Grace the Duke of Montague
His Grace the Duke of Montrosse
His Grace the Duke of Manchester
The Rt. Hon. Lord Viscount Molesworth
The Rt. Hon. Lord Mansel
The Rt. Hon. Ld. Micklethwait
The Rt. Rev. Ld. Bishop of Meath
Mr Mace
Mr Joseph Macham, Merchant
Mr John Machin, Professor of Astronomy in Gresham College
Mr Mackay
Mr Mackelcan
William Mackinen, of Antigua, Esq;
Mr Colin Mac Laurin, Professor of the Mathematicks in the University of Edinburgh
Galatius Macmahon, Esq;
Mr Madox, Apothecary
Rev. Mr Isaac Madox, Prebendary of Chichester
Henry Mainwaring, of Over-Peover in Cheshire, Esq;
Mr Robert Mainwaring, of London, Merchant
Capt. John Maitland
Mr Cecil Malcher
Sydenham Mallhust, Esq;
Richard Malone, Esq;
Mr Thomas Malyn
Mr John Mann
Mr William Man
Dr. Manaton
Mr John Mande
Dr. Bernard Mandeville
Mr James Mandy
Rev. Mr Bellingham Manleveror, M. A. Rector of Mahera
Isaac Manley, Esq;
Thomas Manley, of the Inner-Temple, Esq;
Mr John Manley
Mr William Manley
Mr Benjamin Manning
Rawleigh Mansel, Esq;
Henry March, Esq;
Mr John Marke
Sir George Markham
Mr John Markham, Apothecary
Mr William Markes
Mr James Markwick
Hon. Thomas Marley, Esq; one of his Majesty’s Sollicitors general of Ireland
Rev. Mr George Marley
Mr Benjamin Marriot, of the Exchequer
John Marsh, Esq;
Mr Samuel Marsh
Robert Marshall, Esq; Recorder of Clonmell
Rev. Mr Henry Marshall
Rev. Nathaniel Marshall, D. D. Canon of Windsor
Matthew Martin, Esq;
Thomas Martin, Esq;
Mr John Martin
Mr James Martin
Mr Josiah Martin
Coll. Samuel Martin, of Antigua
John Mason, Esq;
Mr John Mason, of Greenwich
Mr Charles Mason, M. A. Fell. of Trin. Coll. Cambridge
Mr Cornelius Mason
Dr. Richard Middleton Massey
Mr Masterman
Robert Mather, of the Middle-Temple, Esq;
Mr William Mathews
Rev. Mr Mathew
Mr John Matthews
Mrs Hester Lumbroso de Mattos
Rev. Dr. Peter Maturin, Dean of Killala
William Maubry, Esq;
Mr Gamaliel Maud
Rev. Mr Peter Maurice, Treasurer of the Ch. of Bangor
Henry Maxwell, Esq;
John Maxwell, jun. of Pollock, Esq;
Rev. Dr. Robert Maxwell, of Fellow’s Hall, Ireland
Mr May
Mr Thomas Mayleigh
Thomas Maylin, jun. Esq;
Hon. Charles Maynard, Esq;
Thomas Maynard, Esq;
Dr. Richard Mayo
Mr Samuel Mayo
Samuel Mead, Esq;
Richard Mead, M. D.
Rev. Mr Meadowcourt
Rev. Mr Richard Meadowcourt, Fellow of Merton Coll. Oxon
[xlv]Mr Mearson
Mr George Medcalfe
Mr David Medley, 3 Books
Charles Medlycott, Esq;
Sir Robert Menzies, of Weem, Bart.
Mr Thomas Mercer, Merchant
John Merrill, Esq;
Mr Francis Merrit
Dr. Mertins
Mr John Henry Mertins
Library of Merton College
Mr William Messe, Apothecary
Mr Metcalf
Mr Thomas Metcalf, of Trinity Coll. Cambridge
Mr Abraham Meure, of Leatherhead in Surrey
Mr John Mac Farlane
Dr. John Michel
Dr. Robert Michel, of Blandford
Mr Robert Michell
Nathaniel Micklethwait, Esq;
Mr Jonathan Micklethwait, Merchant
Mr John Midford, Merchant
Mr Midgley
Rev. Mr Miller, 2 Books
Rev. Mr Milling, of the Hague
Rev. Mr Benjamin Mills
Rev. Mr Henry Mills, Rector of Meastham, Head-Master of Croyden-School
Thomas Milner, Esq;
Charles Milner, M. D.
Mr William Mingay
John Misaubin, M. D.
Mrs Frances Mitchel
David Mitchell, Esq;
Mr John Mitton
Mr Abraham de Moivre
John Monchton, Esq;
Mr John Monk, Apothecary
J. Monro, M. D.
Sir William Monson, Bart.
Edward Montagu, Esq;
Colonel John Montagu
Rev. John Montague, Dean of Durham, D. D.
Mr Francis Moor
Mr Jarvis Moore
Mr Richard Moore, of Hull, 3 Books
Mr William Moore
Sir Charles Mordaunt, of Walton, in Warwickshire
Mr Mordant, Gentleman Commoner of New College, Oxon
Charles Morgan, Esq;
Francis Morgan, Esq;
Morgan Morgan, Esq;
Rev. Mr William Morland, Fell. of Trin. Coll. Cambr. 2 Books
Thomas Morgan, M. D.
Mr John Morgan, of Bristol
Mr Benjamin Morgan, High-Master of St. Paul’s-School
Hon. Coll. Val. Morris, of Antigua
Mr Gael Morris
Mr John Morse, of Bristol
Hon. Ducey Morton, Esq;
Mr Motte
Mr William Mount
Coll. Moyser
Dr. Edward Mullins
Mr Joseph Murden
Mr Mustapha
Robert Myddleton, Esq;
Robert Myhil, Esq;
N
His Grace the Duke of Newcastle
Rt. Rev. Ld. Bishop of Norwich
Stephen Napleton, M. D.
Mr Robert Nash, M. A. Fellow of Wadham College, Oxon
Mr Theophilus Firmin Nash
Dr. David Natto
Mr Anthony Neal
Mr Henry Neal, of Bristol
Hampson Nedham, Esq; Gentleman Commoner of Christ Church Oxon
Rev. Dr. Newcome, Senior-Fellow of St. John’s College, Cambridge, 6 Books
Rev. Mr Richard Newcome
Mr Henry Newcome
Mr Newland
Rev. Mr John Newey, Dean of Chichester
Mr Benjamin Newington, M. A.
John Newington, M. B. of Greenwich in Kent
Mr Samuel Newman
Mrs Anne Newnham
Mr Nathaniel Newnham, sen.
Mr Nathaniel Newnham, jun.
Mr Thomas Newnham
Mrs Catherine Newnham
Sir Isaac Newton, 12 Books
Sir Michael Newton
Mr Newton
William Nicholas, Esq;
John Nicholas, Esq;
John Niccol, Esq;
General Nicholson
Mr Samuel Nicholson
John Nicholson, M. A. Rector of Donaghmore
Mr Josias Nicholson, 3 Books
Mr James Nimmo, Merchant of Edinburgh
David Nixon, Esq;
Mr George Noble
Stephen Noquiez, Esq;
Mr Thomas Norman, Bookseller at Lewes
Mr Anthony Norris
Mr Henry Norris
Rev. Mr Edward Norton
Richard Nutley, Esq;
Mr John Nutt, Merchant
O
Right Hon. Lord Orrery
Rev. Mr John Oakes
Mr William Ockenden
Mr Elias Ockenden
Mr Oddie
Crew Offley, Esq;
Joseph Offley, Esq;
William Ogbourne, Esq;
Sir William Ogbourne
James Oglethorp, Esq;
Mr William Okey
John Oldfield, M. D.
Nathaniel Oldham, Esq;
William Oliver, M. D. of Bath
John Olmins, Esq;
Arthur Onslow, Esq;
Paul Orchard, Esq;
Robert Ord, Esq;
John Orlebar, Esq;
Rev. Mr George Osborne
Rev. Mr John Henry Ott
Mr James Ottey
Mr Jan. Oudam, Merchant at Rotterdam
Mr Overall
John Overbury, Esq;
Mr Charles Overing
Mr Thomas Owen
Charles Owsley, Esq;
Mr John Owen
Mr Thomas Oyles
P
Right Hon. Countess of Pembroke, 10 Books
Right Hon. Lord Paisley
[xlvi]Right Hon. Lady Paisley
The Right Hon. Lord Parker
Christopher Pack, M. D.
Mr Samuel Parker, Merchant at Bristol
Mr Thomas Page, Surgeon at Bristol
Sir Gregory Page, Bar.
William Palgrave, M. D, Fellow of Caius Coll. Cambridge
William Pallister, Esq;
Thomas Palmer, Esq;
Samuel Palmer, Esq;
Henry Palmer, Merchant
Mr John Palmer, of Coventry
Mr Samuel Palmer, Surgeon
William Parker, Esq;
Edmund Parker, Gent.
Rev. Mr Henry Parker, M. A.
Mr John Parker
Mr Samuel Parkes, of Fort St. George in East-India
Mr Daniel Parminter
Mr Parolet, Attorney
Rev. Thomas Parn, Fellow of Trin. Coll. Cambr. 2 Books
Rev. Mr Thomas Parne, Fellow of Trin. Coll. Cambridge
Rev. Mr Henry Parratt, M. A. Rector of Holywell in Huntingtonshire
Thomas Parratt, M. D.
Stannier Parrot, Gent.
Right Hon. Benjamin Parry, Esq;
Mr Parry, of Jesus Coll. Oxon B. D.
Robert Paul, of Gray’s-Inn, Esq;
Mr Josiah Paul, Surgeon
Mr Paulin
Robert Paunceforte, Esq;
Edward Pawlet, of Hinton St. George, Esq;
Mr Henry Pawson, of York, Merchant
Mr Payne
Mr Samuel Peach
Mr Marmaduke Peacock, Merchant in Rotterdam
Flavell Peake, Esq;
Capt. Edward Pearce
Rev. Zachary Pearce, D. D.
James Pearse, Esq;
Thomas Pearson, Esq;
John Peers, Esq;
Mr Samuel Pegg, of St. John’s College, Cambridge
Mr Peirce, Surgeon at Bath
Mr Adam Peirce
Harry Pelham, Esq;
James Pelham, Esq;
Jeremy Pemberton, of the Inner-Temple, Esq;
Library of Pembroke-Hall, Camb.
Mr Thomas Penn
Philip Pendock, Esq;
Edward Pennant, Esq;
Capt. Philip Pennington
Mr Thomas Penny
Mr Henry Penton
Mr Francis Penwarne, at Liskead in Cornwall
Rev. Mr Thomas Penwarne
Mr John Percevall
Rev. Mr Edward Percevall
Mr Joseph Percevall
Rev. Dr. Perkins, Prebend. of Ely
Mr Farewell Perry
Mr James Petit
Mr John Petit, of Aldgate
Mr John Petit, of Nicholas Lane
Mr John Petitt, of Thames-Street
Honourable Coll. Pettit, of Eltham in Kent
Mr Henry Peyton, of St. John’s College, Cambridge
Daniel Phillips, M. D.
John Phillips, Esq;
Thomas Phillips, Esq;
Mr Gravet Phillips
William Phillips, of Swanzey, Esq;
Mr Buckley Phillips
John Phillipson, Esq;
William Phipps, L. L. D.
Mr Thomas Phipps, of Trinity College, Cambridge
The Physiological Library in the College of Edinburgh
Mr Pichard
Mr William Pickard
Mr John Pickering
Robert Pigott, of Chesterton, Esq;
Mr Richard Pike
Henry Pinfield, of Hampstead, Esq;
Charles Pinfold, L. L. D.
Rev. Mr. Pit, of Exeter College, Oxon
Mr Andrew Pitt
Mr Francis Place
Thomas Player, Esq;
Rev. Mr Plimly
Mr William Plomer
William Plummer, Esq;
Mr Richard Plumpton
John Plumptre, Esq;
Fitz-Williams Plumptre, M. D.
Henry Plumptre, M. D.
John Pollen, Esq;
Mr Joshua Pocock
Francis Pole, of Park-Hall, Esq;
Mr Isaac Polock
Mr Benjamin Pomfret
Mr Thomas Pool, Apothecary
Alexander Pope, Esq;
Mr Arthur Pond
Mr Thomas Port
Mr John Porter
Mr Joseph Porter
Mr Thomas Potter, of St. John’s College, Oxon
Mr John Powel
—— Powis, Esq;
Mr Daniel Powle
John Prat, Esq;
Mr James Pratt
Mr Joseph Pratt
Mr Samuel Pratt
Mr Preston, City-Remembrancer
Capt. John Price
Rev. Mr Samuel Price
Mr Nathaniel Primat
Dr. John Pringle
Thomas Prior, Esq;
Mr Henry Proctor, Apothecary
Sir John Pryse, of Newton Hill in Montgomeryshire
Mr Thomas Purcas
Mr Robert Purse
Mr John Putland
George Pye, M. D.
Samuel Pye, M. D.
Mr Samuel Pye, Surgeon at Bristol
Mr Edmund Pyle, of Lynn
Mr John Pine, Engraver
Q.
His Grace the Duke of Queenborough
Rev. Mr. Question, M. A. of Exeter College, Oxon
Jeremiah Quare, Merchant
R.
His Grace the Duke of Richmond
The Rt. Rev. Ld. Bishop of Raphoe
The Rt. Hon. Lord John Russel
Rev. Mr Walter Rainstorp, of Bristol
[xlvii]Mr John Ranby, Surgeon
Rev. Mr Rand
Mr Richard Randall
Rev. Mr Herbert Randolph, M.A.
Moses Raper, Esq;
Matthew Raper, Esq;
Mr William Rastrick, of Lynne
Mr Ratcliffe, M. A. of Pembroke College, Oxon
Rev. Mr John Ratcliffe
Anthony Ravell, Esq;
Mr Richard Rawlins
Mr Robert Rawlinson A. B. of Trinity College, Cambr.
Mr Walter Ray
Coll. Hugh Raymond
Rt. Hon. Sir Robert Raymond, Lord Chief Justice of the King’s-Bench
Mr Alexander Raymond
Samuel Read, Esq;
Rev. Mr James Read
Mr John Read, Merchant
Mr William Read, Merchant
Mr Samuel Read
Mrs Mary Reade
Mr Thomas Reddall
Mr Andrew Reid
Felix Renolds, Esq;
John Renton, of Christ-Church, Esq;
Leonard Reresby, Esq;
Thomas Reve, Esq;
Mr Gabriel Reve
William Reeves, Merch. of Bristol
Mr Richard Reynell, Apothecary
Mr John Reynolds
Mr Richard Ricards
John Rich, of Bristol, Esq;
Francis Richards, M. B.
Rev. Mr Escourt Richards, Prebend. of Wells
Rev. Mr Richards, Rector of Llanvyllin, in Montgomeryshire
William Richardson, of Smally in Derbyshire, Esq;
Mr Richard Richardson
Mr Thomas Richardson, Apothecary
Edward Richier, Esq;
Dudley Rider, Esq;
Richard Rigby, M. D.
Edward Riggs, Esq;
Thomas Ripley, Esq. Comptroller of his Majesty’s Works
Sir Thomas Roberts, Bart.
Richard Roberts, Esq;
Capt. John Roberts
Thomas Robinson, Esq;
Matthew Robinson, Esq;
Tancred Robinson, M. D.
Nicholas Robinson, M. D.
Christopher Robinson, of Sheffield, A. M.
Mr Henry Robinson
Mr William Robinson
Mrs Elizabeth Robinson
John Rochfort, Esq;
Mr Rodrigues
Mr Rocke
Sir John Rodes, Bart.
Mr Francis Rogers
Rev. Mr Sam. Rogers, of Bristol
John Rogerson, Esq; his Majesty’s General of Ireland
Edmund Rolfe, Esq;
Henry Roll, Esq; Gent. Comm. of New College, Oxon
Rev. Mr Samuel Rolleston, Fell. of Merton College, Oxon
Lancelot Rolleston, of Wattnal, Esq;
Philip Ronayne, Esq;
Rev. Mr de la Roque
Mr Benjamin Rosewell, jun.
Joseph Rothery, M. A. Arch-Deacon of Derry
Guy Roussignac, M. D.
Mr James Round
Mr William Roundell, of Christ Church, Oxon
Mr Rouse, Merchant
Cuthbert Routh, Esq;
John Rowe, Esq;
Mr John Rowe
Dr. Rowel, of Amsterdam
John Rudge, Esq;
Mr James Ruck
Rev. Dr. Rundle, Prebendary of Durham
Mr John Rust
John Rustatt, Gent.
Mr Zachias Ruth
William Rutty, M. D. Secretary of the Royal Society
Maltis Ryall, Esq;
S
His Grace the Duke of St. Albans
Rt. Hon. Earl of Sunderland
Rt. Hon. Earl of Scarborough
Rt. Rev. Ld. Bp. of Salisbury
Rt. Rev. Lord Bishop of St. Asaph
Rt. Hon. Thomas Lord Southwell
Rt. Hon. Lord Sidney
Rt. Hon. Lord Shaftsbury
The Rt. Hon. Lord Shelburn
His Excellency Baron Sollenthal, Envoy extraordinary from the King of Denmark
Mrs Margarita Sabine
Mr Edward Sadler, 2 Books
Thomas Sadler, of the Pell-Office, Esq;
Rev. Mr Joseph Sager, Canon of the Church of Salisbury
Mr William Salkeld
Mr Robert Salter
Lady Vanaker Sambrooke
Jer. Sambrooke, Esq;
John Sampson, Esq;
Dr. Samuda
Mr John Samwaies
Alexander Sanderland, M. D.
Samuel Sanders, Esq;
William Sanders, Esq;
Rev. Mr Daniel Sanxey
John Sargent, Esq;
Mr Saunderson
Mr Charles Savage, jun.
Mr John Savage
Mrs Mary Savage
Rev. Mr Samuel Savage
Mr William Savage
Jacob Sawbridge, Esq;
John Sawbridge, Esq;
Mr William Sawrey
Humphrey Sayer, Esq;
Exton Sayer, L. L. D. Chanceller of Durham
Rev. Mr George Sayer, Prebendary of Durham
Mr Thomas Sayer
Herm. Osterdyk Schacht, M. D. & M. Theor. & Pratt, in Acad. Lug. Bat. Prof.
Meyer Schamberg, M. D.
Mrs Schepers, of Rotterdam
Dr. Scheutcher
Mr Thomas Scholes
Mr Edward Score, of Exeter, Bookseller
Thomas Scot, of Essex, Esq;
Daniel Scott, L. L. D.
Rev. Mr Scott, Fellow of Winton College
Mr Richard Scrafton, Surgeon
Mr Flight Scurry, Surgeon
Rev. Mr Thomas Seeker
Rev Mr Sedgwick
Mr Selwin
Mr Peter Serjeant
Mr John Serocol, Merchant
[xlviii]Rev. Mr Seward, of Hereford
Mr Joseph Sewel
Mr Thomas Sewell
Mr Lancelot Shadwell
Mr Arthur Shallet
Mr Edmund Shallet, Consul at Barcelona
Mr Archdeacon Sharp
James Sharp, jun. Surgeon
Rev. Mr Thomas Sharp, Arch-Deacon of Northumberland
Mr John Shaw, jun.
Mr Joseph Shaw
Mr Sheafe
Mr Edw. Sheldon, of Winstonly
Mr Shell
Mr Richard Shephard
Mr Shepherd of Trinity Coll. Oxon
Mrs Mary Shepherd
Mr William Sheppard
Rev. Mr William Sherlock, M. A.
William Sherrard, L. L. D.
John Sherwin, Esq;
Mr Thomas Sherwood
Mr Thomas Shewell
Mr John Shipton, Surgeon
Mr John Shipton, sen.
Mr John Shipton, jun.
Francis Shipwith, Esq, Fellow Comm. of Trinity Coll. Camb.
John Shish, of Greenwich in Kent, Esq;
Mr Abraham Shreighly
John Shore, Esq;
Rev. Mr Shove
Bartholomew Shower, Esq;
Mr Thomas Sibley, jun.
Mr Jacob Silver, Bookseller in Sandwich
Robert Simpson, Esq; Beadle and Fellow of Caius Coll. Cambr.
Mr Robert Simpson Professor of the Mathematicks in the University of Glascow
Henry Singleton, Esq; Prime Sergeant of Ireland
Rev. Mr John Singleton
Rev. Mr Rowland Singleton
Mr Singleton, Surgeon
Mr Jonathan Sisson
Francis Sitwell, of Renishaw, Esq;
Ralph Skerret, D. D.
Thomas Skinner, Esq;
Mr John Skinner
Mr Samuel Skinner, jun.
Mr John Skrimpshaw
Frederic Slare, M. D.
Adam Slater, of Chesterfield, Surgeon
Sir Hans Sloane, Bar.
William Sloane, Esq;
William Sloper, Esq;
William Sloper, Esq, Fellow Commoner of Trin. Coll. Cambr.
Dr. Sloper, Chancellor of the Diocese of Bristol
Mr Smart
Mr John Smibart
Robert Smith, L. L. D. Professor of Astronomy in the University of Cambridge, 22 Books
Robert Smith, of Bristol, Esq;
William Smith, of the Middle-Temple, Esq;
James Smith, Esq;
Morgan Smith, Esq;
Rev. Mr Smith, of Stone in the County of Bucks
John Smith, Esq;
Mr John Smith
Mr John Smith, Surgeon in Coventry, 2 Books
Mr John Smith, Surgeon in Chichester
Mr Allyn Smith
Mr Joshua Smith
Mr Joseph Smith
Rev. Mr Elisha Smith, of Tid St. Gyles’s, in the Isle of Ely
Mr Ward Smith
Mr Skinner Smith
Rev. Mr George Smyth
Mr Snablin
Dr. Snell, of Norwich
Mr Samuel Snell
Mr William Snell
William Snelling, Esq;
William Sneyd, Esq;
Mr Ralph Snow
Mr Thomas Snow
Stephen Soame, Esq; Fellow Commoner of Sidney Coll. Cambr.
Cockin Sole, Esq;
Joseph Somers, Esq;
Mr Edwin Sommers, Merchant
Mr Adam Soresby
Thomas Southby, Esq;
Sontley South, Esq;
Mr Sparrow
Mr Speke, of Wadham Coll. Ox.
Rev. Mr Joseph Spence
Mr Abraham Spooner
Sir Conrad Joachim Springel
Mr William Stammers
Mr Charles Stanhope
Mr Thomas Stanhope
Sir John Stanley
George Stanley, Esq;
Rev. Dr. Stanley, Dean of St. Asaph
Mr John Stanly
Eaton Stannard, Esq;
Thomas Stansal, Esq;
Mr Samuel Stanton
Temple Stanyan, Esq;
Mrs Mary Stanyforth
Rev. Mr Thomas Starges, Rector of Hadstock, Essex
Mr Benjamin Steel
Mr John Stebbing, of St. John’s College, Cambridge
Mr John Martis Stehelin, Merch.
Dr. Steigerthal
Mr Stephens, of Gloucester
Mr Joseph Stephens
Sir James Steuart of Gutters, Bar.
Mr Robert Steuart, Professor of Natural Philosophy, in the University of Edinburgh
Rev. Mr Stevens, Fellow of Corp. Chr. Coll. Cambridge
Mr John Stevens, of Trinity College, Oxon
Rev. Mr Bennet Stevenson
Hon. Richard Stewart, Esq;
Major James Stewart
Capt Bartholomew Stibbs
Mr Denham Stiles
Mr Thomas Stiles, sen.
Mr Thomas Stiles, jun.
Rev. Mr Stillingfleet
Mr Edward Stillingfleet
Mr John Stillingfleet
Mr William Stith
Mr Stock, of Rochdall in Lancashire
Mr Stocton, Watch-Maker
Mr Robert Stogdon
Rev. Mr Richard Stonehewer
Thomas Stoner, Esq;
Mr George Story, of Trinity College, Cambridge
Mr Thomas Story
William Strahan, L. L. D.
Mr Thomas Stratfield
Rev. Dr. Stratford, Canon of Christ Church, Oxford
Capt. William Stratton
Rev. Mr Streat
Samuel Strode, Esq;
Mr George Strode
[xlix]Rev. Mr John Strong
Hon. Commodore Stuart
Alexander Stuart, M. D.
Charles Stuart, M. D.
Lewis Stucly
Mr John Sturges, of Bloomsbury
Mr Sturgeon, Surgeon in Bury
Hon. Lady Suasso
Mr Gerrard Suffield
Mr William Sumner, of Windsor
Sir Robert Sutton, Kt. of the Bath
Rev. Mr John Sutton
Mr Gerrard Swartz
Mr Thomas Swayne
William Swinburn, Esq;
Rev. Mr. John Swinton, M. A.
Mr Joshua Symmonds, Surgeon
Rev. Mr Edward Synge
T.
His Grace the Archbishop of Tuam
Right Hon. Earl of Tankerville
Rt. Hon. Ld. Viscount Townshend, One of His Majesty’s Principal Secretaries of State
Right Honourable Lady Viscountess Townshend
Right Hon Ld Viscount Tyrconnel
The Honourable Lord Trevor Charles Talbot, Esq; Solicitor-General.
Francis Talbot, Esq;
John Ivory Talbot, Esq;
Mr George Talbot, M. A.
Mr Talbot
Thomas Tanner, D. D. Chancellor of Norwich
Mr Thomas Tanner
Mr Tateham of Clapham
Mr Henry Tatham
Mr John Tatnall
Mr Arthur Tayldeur
Mr John Tayleur
Arthur Taylor, Esq;
Joseph Taylor, Esq;
Simon Taylor, Esq;
Rev. Mr Abraham Taylor
Brook Taylor, L. L. D.
William Tempest, Esq;
William Tenison, Esq;
Dr. Tenison
Rev. Dr. Terry, Canon of Christ Church, Oxon
Mr Theed, Attorney
Mr Lewis Theobald
James Theobalds, Esq;
Robert Thistlethwayte, D. D. Warden of Wadham Coll. Oxon
Rev. Mr Thomlinson
Richard Thompson Coley, Esq;
Rev. Mr William Thompson
Mr William Thompson, A. B. of Trinity Coll. Cambridge
Mr Thoncas
Mr Thornbury, Vicar of Thame
Sir James Thornhill, 3 Books
Mr Thornhill
William Thornton, Esq;
Mr Catlyn Thorowgood
Mr John Thorpe
William Thorseby, Esq;
Mr William Thurlbourn, Bookseller in Cambridge
Mark Thurston, Esq; Master in Chancery
Rev. Mr William Tiffin, of Lynn
Edmund Tigh, Esq;
Right Hon. Richard Tighe, Esq;
Mr Abraham Tilghman
Mr George Tilson
Rev Mr Tilson
Mr William Tims
Rev. Mr John Tisser
Capt. Joseph Tolson
Mr Tomkins
Mr William Tomlinson
Richard Topham, Esq;
Dr. Torey
George Torriano, of West-Ham, Esq;
Mr John Torriano
Mr James le Touch
Rev. Mr Charles Tough
Mr John Towers
Rev. Mr Nehemiah Towgood
Mr Edward Town
Joseph Townsend, Esq;
Charles Townshend, of Lincoln’s Inn, Esq;
Hon. Thomas Townshend, Esq;
Mr Townson
John Tracey, of Stanway in Gloucester, Esq;
Capt. Richard Tracey
Mr Samuel Traverse, Merchant
Mr Charles Trelawny, Student of Christ Church
Fredric Trench, Esq;
Mr Edmund Trench
Mr Samuel Trench
Richard Trevor, Esq;
Hon. Thomas Trevor, Esq;
Hon. Mr John Trevor
Mr Trimble, Merch. in Rotterd.
Rev. Dr. Trimnell, Dean of Winchester
Thomas Trotter, L. L. D.
John Trubshaw, Esq;
Mr Thomas Truman
Dr. Daniel Turner
Rev. Mr. Robert Turner, of Colchester
Mr John Turton
Mr William Turton
John Twistleton, near the City of York, Esq;
Col. Tyrrell
Mr William Tyson
Mr Samuel Tyssen
Capt. Edward Tyzack
V
Rt. Hon. Lord Viscount Vane
Rev. Mr Thomas Valentine
Mr Vallack, of Plymouth
Mr John Vanderbank
Mr Daniel Vandewall
Mr John Vandewall, Merchant
Mr Edward Vaus
Hon. John Verney, Esq;
William Vesey, Esq;
Rev. Mr John Vesey
William Vigor, of Westbury College near Bristol
Mr George Virgoe
Mr Frederick Voguel, Merchant
Mr Thomas Vickers
Robert Viner, Esq;
W
Rt. Hon. the Earl of Winchelsea
Rt. Rev. Lord Bishop of Winchester
Rev. Mr Wade
Sir Charles Wager
Rev. Mr Wagstaffe
Rev. Dr. Edward Wake
Mr Jasper Wakefield
Mr Samuel Walbank
Mr Walbridge
Mr Waldron
Edmund Waldrond. M. A.
Mr Walford, of Wadham Coll. Oxon
Rev. Mr Edward Walker
Mr Samuel Walker, of Trinity College, Cambridge
Mr Thomas Walker
Henry Waller, Esq;
William Waller, Esq;
Mrs Waller
Mr John Waller, of Lincoln’s-Inn
Mr George Wallis
[l]Rev. Mr William Wallis
Mr Edward Walmsley, 2 Books
Edward Walpole, Esq;
Mr Peter Walter
John Walton, Esq;
Peter Warburton of Ford in Cheshire, Esq;
Richard Warburton, Esq;
John Ward, jun. Esq;
Michael Ward, Esq;
Edward Ward, Esq;
Knox Ward, Esq;
Mr John Ward, Professor of Rhetoric in Gresham College
William Ward, L. L. D.
Mr Richard Warring
Mr Jacob Warneck
Mr Richard Warner
Mr Robert Warner
William Wasey, M. D.
Rev. Mr Washington, Fellow of Peterhouse, Cambridge
Mr Edward Wastfield
Mr Watkins
Rev. Mr Thomas Watkis, of Knutsford
Robert Watley, Esq;
Mr Joel Watson
Mr John Watson
Mr Thomas Watson
Richard Watts, M. D. 2 Books
Mr Thomas Watts
Rev. Mr Isaac Watts
Mr William Weamen
Mr Thomas Wear
Mr William Weathers
Edward Weaver, Esq;
Anthony Weaver, M. D.
Mr Webb
Mr Willam Webb, A. B. of Trinity College, Cambridge
Mr Humphrey Webb, M. A.
Rt. Hon. Edward Webster, Esq;
William Wenman, of Edwinstowe, Esq;
Mr Samuel Wesley, jun.
Gilbert West, Esq;
Rt. Hon Richard West, Esq; late Lord high Chancellor of Ireland
Thomas West, Esq;
Dr. Thomas West
Mrs Anne West
Daniel Westcomb, Esq;
Herbert Westfaling, Esq;
Messieurs Werstein and Smith, Booksellers in Amsterdam
Mr Western, in Dover-Street
Mr Matthew Westly
Mr Tho. Weston, of Greenwich
Matthew Weymondefold, Esq;
Mr Edward Wharton
Mr Stephen Whatley
Mr James Whatman
Granville Wheler, Esq;
Rev. Mr William Whiston
Dr. William Whitaker
Taylor White, Esq;
Mr Charles White
Mr Edward White, Scholar of Caius College, Cambridge
Mr John White
Mr Joseph White
Mr Nicholas White
Mr William Whitehead
Rev. Mr Whitehead, Fellow of Emanuel College, Cambridge 6 Books
John Whitfield, D. D. Rector of Dickleburgh
Rev. Mr Whitfield
Mr Nathaniel Whitlock
Mr John Whittering
Robert Wild, Esq;
Mr William Wildman
Rev. Mr Wilkes, Prebendary of Westminster
Dr. Wilkin
Mr Wilkins, Bookseller
Mr Abel Wilkinson
Mr William Wilks
John Willes, Esq;
John Willet, Esq; of the Island of St. Christophers
John Williams, Esq;
William Peer Williams, jun. Esq;
Rev. Mr Philip Williams, B. D.
Mr Williams, B. A. of Jesus College, Oxon
Mr Francis Williams
Hon. Coll. Adam Williamson
Mr Robert Willimott
John Willis, Esq;
Edward Wilmot, M. D.
Mr Robert Willmott
Mr Joseph Willoughby
William Willys, Esq;
Mr John Wilmer, Merchant
Mr John Wilmer, Apothecary
Mr Wilmott, Bookseller in Oxford
Richard Wilson, of Leeds, Esq;
Rev. Mr Daniel Wilson, Prebendary of the Church of Hereford
William Winde, Esq;
Mr Samuel Winder, jun.
Sir William Windham Bar.
Mr John Windsor
Library of Windsor College
Mr Winnington
Mr Winnock
Mr Abraham Winterbottom
Will. Withers, of Gray’s-Inn, Esq;
Mr Conway Withorne, of the Inner-Temple
Rev. Mr John Witter
Jacobus Wittichius, Phil. D. & in Acad. Lugd. Bat. Prof.
Mr John Wittingham
Rev. Mr John Witton, Rector of Howton Witton, Cambridge
Mr Thomas Wood
Thomas Woodcock, Esq;
Thomas Woodford, Esq;
William Woodford, M. D.
John Woodhouse, M. D.
Mr J. Woods, of Bramshot, Merch.
Rev. Mr Benjamin Woodroof, Prebendary of Worcester
Mr Joseph Woodward
Josiah Woolaston, Esq;
Mr Woolball, Merchant
Francis Woollaston, Esq;
Charlton Woollaston, Esq;
Mr William Woollaston
Wight Woolly, Esq;
Library of the Cathed. of Worcester
Josias Wordsworth, jun. Esq;
Mr John Worster, Merchant
Rev. Dr. William Wotton
Mr John Wowen
Edward Wright, of the Middle-Temple, Esq;
Henry Wright, of Molberly, in Cheshire, Esq;
Samual Wright, Esq;
William Wright, of Offerton, in Cheshire, Esq;
Mr Wright
Mr William Wright, of Baldock, Hertfordshire
Rev. Mr Wrigley, Fellow of St. John’s College, Cambridge
Rt. Hon. Thomas Wyndham, Ld. Chief Justice of the Common Pleas, of Ireland
Mr Joseph Wyeth
Thomas Wyndham, Esq;
Rev. Mr John Wynne
Y
Mr John Yardley, Surg. in Coven.
Mr Thomas Yates
Mrs Yeo, of Exeter, Bookseller
Sir William Yonge
Lady York
Nicholas Young, of the Inner-Temple, Esq;
Hitch Young, Esq;
Rev. Edward Young, L. L. D.

INTRODUCTION.

THE manner, in which Sir Isaac Newton has published his philosophical discoveries, occasions them to lie very much concealed from all, who have not made the mathematics particularly their study. He once, indeed, intended to deliver, in a more familiar way, that part of his inventions, which relates to the system of the world; but upon farther consideration he altered his design. For as the nature of those discoveries made it impossible to prove them upon any other than geometrical principles; he apprehended, that those, who should not fully perceive the force of his arguments, would hardly be prevailed on to exchange their former sentiments for new opinions, so very different from[2] what were commonly received[1]. He therefore chose rather to explain himself only to mathematical readers; and declined the attempting to instruct such in any of his principles, who, by not comprehending his method of reasoning, could not, at the first appearance of his discoveries, have been persuaded of their truth. But now, since Sir Isaac Newton’s doctrine has been fully established by the unanimous approbation of all, who are qualified to understand the same; it is without doubt to be wished, that the whole of his improvements in philosophy might be universally known. For this purpose therefore I drew up the following papers, to give a general notion of our great philosopher’s inventions to such, as are not prepared to read his own works, and yet might desire to be informed of the progress, he has made in natural knowledge; not doubting but there were many, besides those, whose turn of mind had led them into a course of mathematical studies, that would take great pleasure in tasting of this delightful fountain of science.
2. It is a just remark, which has been made upon the human mind, that nothing is more suitable to it, than the contemplation of truth; and that all men are moved with a strong desire after knowledge; esteeming it honourable to excel therein; and holding it, on the contrary, disgraceful to mistake, err, or be in any way deceived. And this sentiment is by nothing more fully illustrated, than by the inclination of men to gain an acquaintance with the operations of nature; which disposition to enquire after the causes of things is[3] so general, that all men of letters, I believe, find themselves influenced by it. Nor is it difficult to assign a reason for this, if we consider only, that our desire after knowledge is an effect of that taste for the sublime and the beautiful in things, which chiefly constitutes the difference between the human life, and the life of brutes. These inferior animals partake with us of the pleasures, that immediately flow from the bodily senses and appetites; but our minds are furnished with a superior sense, by which we are capable of receiving various degrees of delight, where the creatures below us perceive no difference. Hence arises that pursuit of grace and elegance in our thoughts and actions, and in all things belonging to us, which principally creates imployment for the active mind of man. The thoughts of the human mind are too extensive to be confined only to the providing and enjoying of what is necessary for the support of our being. It is this taste, which has given rise to poetry, oratory, and every branch of literature and science. From hence we feel great pleasure in conceiving strongly, and in apprehending clearly, even where the passions are not concerned. Perspicuous reasoning appears not only beautiful; but, when set forth in its full strength and dignity, it partakes of the sublime, and not only pleases, but warms and elevates the soul. This is the source of our strong desire of knowledge; and the same taste for the sublime and the beautiful directs us to chuse particularly the productions of nature for the subject of our contemplation: our creator having so adapted our minds to the condition, wherein he has placed us, that all his visible[4] works, before we inquire into their make, strike us with the most lively ideas of beauty and magnificence.
3. But if there be so strong a passion in contemplative minds for natural philosophy; all such must certainly receive a particular pleasure in being informed of Sir Isaac Newton’s discoveries, who alone has been able to make any great advancements in the true course leading to natural knowledge: whereas this important subject had before been usually attempted with that negligence, as cannot be reflected on without surprize. Excepting a very few, who, by pursuing a more rational method, had gained a little true knowledge in some particular parts of nature; the writers in this science had generally treated of it after such a manner, as if they thought, that no degree of certainty was ever to be hoped for. The custom was to frame conjectures; and if upon comparing them with things, there appeared some kind of agreement, though very imperfect, it was held sufficient. Yet at the same time nothing less was undertaken than intire systems, and fathoming at once the greatest depths of nature; as if the secret causes of natural effects, contrived and framed by infinite wisdom, could be searched out by the slightest endeavours of our weak understandings. Whereas the only method, that can afford us any prospect of success in this difficult work, is to make our enquiries with the utmost caution, and by very slow degrees. And after our most diligent labour, the greatest part of nature will, no doubt, for ever remain beyond our reach.
4. This neglect of the proper means to enlarge our knowledge, joined with the presumption to attempt, what was quite out of the power of our limited faculties, the Lord Bacon judiciously observes to be the great obstruction to the progress of science[2]. Indeed that excellent person was the first, who expresly writ against this way of philosophizing; and he has laid open at large the absurdity of it in his admirable treatise, intitled Novum organon scientiarum; and has there likewise described the true method, which ought to be followed.
5. There are, saith he, but two methods, that can be taken in the pursuit of natural knowledge. One is to make a hasty transition from our first and slight observations on things to general axioms, and then to proceed upon those axioms, as certain and uncontestable principles, without farther examination. The other method; (which he observes to be the only true one, but to his time unattempted;) is to proceed cautiously, to advance step by step, reserving the most general principles for the last result of our inquiries[3]. Concerning the first of these two methods; where objections, which happen to appear against any such axioms taken up in haste, are evaded by some frivolous distinction, when the axiom it self ought rather to be corrected[4]; he affirms, that the united endeavours of all ages cannot make it successful; because this original error in the first digestion of the mind (as he expresses himself) cannot afterwards be remedied[5]: whereby he would signify to us, that if we set out in a[6] wrong way; no diligence or art, we can use, while we follow so erroneous a course, will ever bring us to our designed end. And doubtless it cannot prove otherwise; for in this spacious field of nature, if once we forsake the true path, we shall immediately lose our selves, and must for ever wander with uncertainty.
6. The impossibility of succeeding in so faulty a method of philosophizing his Lordship endeavours to prove from the many false notions and prejudices, to which the mind of man is exposed[6]. And since this judicious writer apprehends, that men are so exceeding liable to fall into these wrong tracts of thinking, as to incur great danger of being misled by them, even while they enter on the true course in pursuit of nature[7]; I trust, I shall be excused, if, by insisting a little particularly upon this argument, I endeavour to remove whatever prejudice of this kind, might possibly entangle the mind of any of my readers.
7. His Lordship has reduced these prejudices and false modes of conception under four distinct heads[8].
8. The first head contains such, as we are subject to from the very condition of humanity, through the weakness both of our senses, and of the faculties of the mind[9]; seeing, as this author well observes, the subtilty of nature far exceeds the greatest subtilty of our senses or acutest reasonings[10]. One[7] of the false modes of conception, which he mentions under this head, is the forming to our selves a fanciful simplicity and regularity in natural things. This he illustrates by the following instances; the conceiving the planets to move in perfect circles; the adding an orb of fire to the other three elements, and the supposing each of these to exceed the other in rarity, just in a decuple proportion[11]. And of the same nature is the assertion of Des Cartes, without any proof, that all things are made up of three kinds of matter only[12]. As also this opinion of another philosopher; that light, in passing through different mediums, was refracted, so as to proceed by that way, through which it would move more speedily, than through any other[13]. The second erroneous turn of mind, taken notice of by his Lordship under this head, is, that all men are in some degree prone to a fondness for any notions, which they have once imbibed; whereby they often wrest things to reconcile them to those notions, and neglect the consideration of whatever will not be brought to an agreement with them; just as those do, who are addicted to judicial astrology, to the observation of dreams, and to such-like superstitions; who carefully preserve the memory of every incident, which serves to confirm their prejudices, and let slip out of their minds all instances, that make against them[14]. There is also a farther impediment to true knowledge, mentioned under the same head by this noble writer, which is; that whereas, through the weakness and imperfection of our senses, many things are concealed.[8] from us, which have the greatest effect in producing natural appearances; our minds are ordinarily most affected by that, which makes the strongest impression on our organs of sense; whereby we are apt to judge of the real importance of things in nature by a wrong measure[15]. So, because the figuration and the motion of bodies strike our senses more immediately than most of their other properties, Des Cartes and his followers will not allow any other explication of natural appearances, than from the figure and motion of the parts of matter. By which example we see how justly his Lordship observes this cause of error to be the greatest of any[16]; since it has given rise to a fundamental principle in a system of philosophy, that not long ago obtained almost an universal reputation.
9. These are the chief branches of those obstructions to knowledge, which this author has reduced under his first head of false conceptions. The second head contains the errors, to which particular persons are more especially obnoxious[17]. One of these is the consequence of a preceding observation: that as we are exposed to be captivated by any opinions, which have once taken possession of our minds; so in particular, natural knowledge has been much corrupted by the strong attachment of men to some one part of science, of which they reputed themselves the inventers, or about which they have spent much of their time; and hence have been apt to conceive it to be of greater use in the study of natural[9] philosophy than it was: like Aristotle, who reduced his physics to logical disputations; and the chymists, who thought, that nature could be laid open only by the force of their fires[18]. Some again are wholly carried away by an excessive veneration for antiquity; others, by too great fondness for the moderns; few having their minds so well balanced, as neither to depreciate the merit of the ancients, nor yet to despise the real improvements of later times[19]. To this is added by his Lordship a difference in the genius of men, that some are most fitted to observe the similitude, there is in things, while others are more qualified to discern the particulars, wherein they disagree; both which dispositions of mind are useful: but to the prejudice of philosophy men are apt to run into excess in each; while one sort of genius dwells too much upon the gross and sum of things, and the other upon trifling minutenesses and shadowy distinctions[20].
10. Under the third head of prejudices and false notions this writer considers such, as follow from the lax and indefinite use of words in ordinary discourse; which occasions great ambiguities and uncertainties in philosophical debates (as another eminent philosopher has since shewn more at large[21];) insomuch that this our author thinks a strict defining of terms to be scarce an infallible remedy against this inconvenience[22]. And perhaps he has no small reason on his side: for the common inaccurate sense of words, notwithstanding the limitations given them by definitions, will offer it self so constantly to[10] the mind, as to require great caution and circumspection for us not to be deceived thereby. Of this we have a very eminent instance in the great disputes, that have been raised about the use of the word attraction in philosophy; of which we shall be obliged hereafter to make particular mention[23]. Words thus to be guarded against are of two kinds. Some are names of things, that are only imaginary[24]; such words are wholly to be rejected. But there are other terms, that allude to what is real, though their signification is confused[25]. And these latter must of necessity be continued in use; but their sense cleared up, and freed, as much as possible, from obscurity.
11. The last general head of these errors comprehends such, as follow from the various sects of false philosophies; which this author divides into three sorts, the sophistical, empirical, and superstitious[26]. By the first of these he means a philosophy built upon speculations only without experiments[27]; by the second, where experiments are blindly adhered to, without proper reasoning upon them[28]; and by the third, wrong opinions of nature fixed in mens minds either through false religions, or from misunderstanding the declarations of the true[29].
12. These are the four principal canals, by which this judicious author thinks, that philosophical errors have flowed in upon us. And he rightly observes, that the faulty method of[11] proceeding in philosophy, against which he writes[30], is so far from assisting us towards overcoming these prejudices; that he apprehends it rather suited to rivet them more firmly to the mind[31]. How great reason then has his Lordship to call this way of philosophizing the parent of error, and the bane of all knowledge[32]? For, indeed, what else but mistakes can so bold and presumptuous a treatment of nature produce? have we the wisdom necessary to frame a world, that we should think so easily, and with so slight a search to enter into the most secret springs of nature, and discover the original causes of things? what chimeras, what monsters has not this preposterous method brought forth? what schemes, or what hypothesis’s of the subtilest wits has not a stricter enquiry into nature not only overthrown, but manifested to be ridiculous and absurd? Every new improvement, which we make in this science, lets us see more and more the weakness of our guesses. Dr. Harvey, by that one discovery of the circulation of the blood, has dissipated all the speculations and reasonings of many ages upon the animal oeconomy. Asellius, by detecting the lacteal veins, shewed how little ground all physicians and philosophers had in conjecturing, that the nutritive part of the aliment was absorbed by the mouths of the veins spread upon the bowels: and then Pecquet, by finding out the thoracic duct, as evidently proved the vanity of the opinion, which was persisted in after the lacteal vessels were known, that the alimental juice was conveyed immediately to the liver, and there converted into blood.
13. As these things set forth the great absurdity of proceeding in philosophy on conjectures, by informing us how far the operations of nature are above our low conceptions; so on the other hand, such instances of success from a more judicious method shew us, that our bountiful maker has not left us wholly without means of delighting our selves in the contemplation of his wisdom. That by a just way of inquiry into nature, we could not fail of arriving at discoveries very remote from our apprehensions; the Lord Bacon himself argues from the experience of mankind. If, says he, the force of guns should be described to any one ignorant of them, by their effects only, he might reasonably suppose, that those engines of destruction were only a more artificial composition, than he knew, of wheels and other mechanical powers: but it could never enter his thoughts, that their immense force should be owing to a peculiar substance, which would enkindle into so violent an explosion, as we experience in gunpowder: since he would no where see the least example of any such operation; except perhaps in earthquakes and thunder, which he would doubtless look upon as exalted powers of nature, greatly surpassing any art of man to imitate. In the same manner, if a stranger to the original of silk were shewn a garment made of it, he would be very far from imagining so strong a substance to be spun out of the bowels of a small worm; but must certainly believe it either a vegetable substance, like flax or cotton; or the natural covering of some animal, as wool is of sheep. Or had we been told, before the invention of the magnetic needle among us, that another people was in possession of a certain[13] contrivance, by which they were inabled to discover the position of the heavens, with vastly more ease, than we could do; what could have been imagined more, than that they were provided with some fitter astronomical instrument for this purpose than we? That any stone should have so amazing a property, as we find in the magnet, must have been the remotest from our thoughts[33].
14. But what surprizing advancements in the knowledge of nature may be made by pursuing the true course in philosophical inquiries; when those searches are conducted by a genius equal to so divine a work, will be best understood by considering Sir Isaac Newton discoveries. That my’s reader may apprehend as just a notion of these, as can be conveyed to him, by the brief account, which I intend to lay before him; I have set apart this introduction for explaining, in the fullest manner I am able, the principles, whereon Sir Isaac Newton proceeds. For without a clear conception of these, it is impossible to form any true idea of the singular excellence of the inventions of this great philosopher.
15. The principles then of this philosophy are; upon no consideration to indulge conjectures concerning the powers and laws of nature, but to make it our endeavour with all diligence to search out the real and true laws, by which the constitution of things is regulated. The philosopher’s first care must be to distinguish, what he sees to be within his power, from what[14] is beyond his reach; to assume no greater degree of knowledge, than what he finds himself possessed of; but to advance by slow and cautious steps; to search gradually into natural causes; to secure to himself the knowledge of the most immediate cause of each appearance, before he extends his views farther to causes more remote. This is the method, in which philosophy ought to be cultivated; which does not pretend to so great things, as the more airy speculations; but will perform abundantly more: we shall not perhaps seem to the unskilful to know so much, but our real knowledge will be greater. And certainly it is no objection against this method, that some others promise, what is nearer to the extent of our wishes: since this, if it will not teach us all we could desire to be informed of, will however give us some true light into nature; which no other can do. Nor has the philosopher any reason to think his labour lost, when he finds himself stopt at the cause first discovered by him, or at any other more remote cause, short of the original: for if he has but sufficiently proved any one cause, he has entered so far into the real constitution of things, has laid a safe foundation for others to work upon, and has facilitated their endeavours in the search after yet more distant causes; and besides, in the mean time he may apply the knowledge of these intermediate causes to many useful purposes. Indeed the being able to make practical deductions from natural causes, constitutes the great distinction between the true philosophy and the false. Causes assumed upon conjecture, must be so loose and undefined, that nothing particular can be collected from them. But those causes, which are brought to light by a strict examination[15] of things, will be more distinct. Hence it appears to have been no unuseful discovery, that the ascent of water in pumps is owing to the pressure of the air by its weight or spring; though the causes, which make the air gravitate, and render it elastic, be unknown: for notwithstanding we are ignorant of the original, whence these powers of the air are derived; yet we may receive much advantage from the bare knowledge of these powers. If we are but certain of the degree of force, wherewith they act, we shall know the extent of what is to be expected from them; we shall know the greatest height, to which it is possible by pumps to raise water; and shall thereby be prevented from making any useless efforts towards improving these instruments beyond the limits prescribed to them by nature; whereas without so much knowledge as this, we might probably have wasted in attempts of this kind much time and labour. How long did philosophers busy themselves to no purpose in endeavouring to perfect telescopes, by forming the glasses into some new figure; till Sir Isaac Newton demonstrated, that the effects of telescopes were limited from another cause, than was supposed; which no alteration in the figure of the glasses could remedy? What method Sir Isaac Newton himself has found for the improvement of telescopes shall be explained hereafter[34]. But at present I shall proceed to illustrate, by some farther instances, this distinguishing character of the true philosophy, which we have now under consideration. It was no trifling discovery, that the contraction of the muscles of animals puts their limbs in motion, though the original cause of that contraction[16] remains a secret, and perhaps may always do so; for the knowledge of thus much only has given rise to many speculations upon the force and artificial disposition of the muscles, and has opened no narrow prospect into the animal fabrick. The finding out, that the nerves are great agents in this action, leads us yet nearer to the original cause, and yields us a wider view of the subject. And each of these steps affords us assistance towards restoring this animal motion, when impaired in our selves, by pointing out the seats of the injuries, to which it is obnoxious. To neglect all this, because we can hitherto advance no farther, is plainly ridiculous. It is confessed by all, that Galileo greatly improved philosophy, by shewing, as we shall relate hereafter, that the power in bodies, which we call gravity, occasions them to move downwards with a velocity equably accelerated[35]; and that when any body is thrown forwards, the same power obliges it to describe in its motion that line, which is called by geometers a parabola[36]: yet we are ignorant of the cause, which makes bodies gravitate. But although we are unacquainted with the spring, whence this power in nature is derived, nevertheless we can estimate its effects. When a body falls perpendicularly, it is known, how long time it takes in descending from any height whatever: and if it be thrown forwards, we know the real path, which it describes; we can determine in what direction, and with what degree of swiftness it must be projected, in order to its striking against any object desired; and we can also ascertain the very force, wherewith it will strike.[17] Sir Isaac Newton has farther taught, that this power of gravitation extends up to the moon, and causes that planet to gravitate as much towards the earth, as any of the bodies, which are familiar to us, would, if placed at the same distance[37]: he has proved likewise, that all the planets gravitate towards the sun, and towards one another; and that their respective motions follow from this gravitation. All this he has demonstrated upon indisputable geometrical principles, which cannot be rendered precarious for want of knowing what it is, which causes these bodies thus mutually to gravitate: any more than we can doubt of the propensity in all the bodies about us, to descend towards the earth; or can call in question the forementioned propositions of Galileo, which are built upon that principle. And as Galileo has shewn more fully, than was known before, what effects were produced in the motion of bodies by their gravitation towards the earth; so Sir Isaac Newton, by this his invention, has much advanced our knowledge in the celestial motions. By discovering that the moon gravitates towards the sun, as well as towards the earth; he has laid open those intricacies in the moon’s motion, which no astronomer, from observations only, could ever find out[38]: and one kind of heavenly bodies, the comets, have their motion now clearly ascertained; whereof we had before no true knowledge at all[39].
16. Doubtless it might be expected, that such surprizing success should have silenced, at once, every cavil. But we[18] have seen the contrary. For because this philosophy professes modestly to keep within the extent of our faculties, and is ready to confess its imperfections, rather than to make any fruitless attempts to conceal them, by seeking to cover the defects in our knowledge with the vain ostentation of rash and groundless conjectures; hence has been taken an occasion to insinuate that we are led to miraculous causes, and the occult qualities of the schools.
17. But the first of these accusations is very extraordinary. If by calling these causes miraculous nothing more is meant than only, that they often appear to us wonderful and surprizing, it is not easy to see what difficulty can be raised from thence; for the works of nature discover every where such proofs of the unbounded power, and the consummate wisdom of their author, that the more they are known, the more they will excite our admiration: and it is too manifest to be insisted on, that the common sense of the word miraculous can have no place here, when it implies what is above the ordinary course of things. The other imputation, that these causes are occult upon the account of our not perceiving what produces them, contains in it great ambiguity. That something relating to them lies hid, the followers of this philosophy are ready to acknowledge, nay desire it should be carefully remarked, as pointing out proper subjects for future inquiry. But this is very different from the proceeding of the schoolmen in the causes called by them occult. For as their occult qualities were understood to operate in a manner occult, and not apprehended by us; so they were obtruded[19] upon us for such original and essential properties in bodies, as made it vain to seek any farther cause; and a greater power was attributed to them, than any natural appearances authorized. For instance, the rise of water in pumps was ascribed to a certain abhorrence of a vacuum, which they thought fit to assign to nature. And this was so far a true observation, that the water does move, contrary to its usual course, into the space, which otherwise would be left void of any sensible matter; and, that the procuring such a vacuity was the apparent cause of the water’s ascent. But while we were not in the least informed how this power, called an abhorrence of a vacuum, produced the visible effects; instead of making any advancement in the knowledge of nature, we only gave an artificial name to one of her operations: and when the speculation was pushed so beyond what any appearances required, as to have it concluded, that this abhorrence of a vacuum was a power inherent in all matter, and so unlimited as to render it impossible for a vacuum to exist at all; it then became a much greater absurdity, in being made the foundation of a most ridiculous manner of reasoning; as at length evidently appeared, when it came to be discovered, that this rise of the water followed only from the pressure of the air, and extended it self no farther, than the power of that cause. The scholastic stile in discoursing of these occult qualities, as if they were essential differences in the very substances, of which bodies consisted, was certainly very absurd; by reason it tended to discourage all farther inquiry. But no such ill consequences can follow from the considering of any natural causes, which confessedly are not traced up to[20] their first original. How shall we ever come to the knowledge of the several original causes of things, otherwise than by storing up all intermediate causes which we can discover? Are all the original and essential properties of matter so very obvious, that none of them can escape our first view? This is not probable. It is much more likely, that, if some of the essential properties are discovered by our first observations, a stricter examination should bring more to light.
18. But in order to clear up this point concerning the essential properties of matter, let us consider the subject a little distinctly. We are to conceive, that the matter, out of which the universe of things is formed, is furnished with certain qualities and powers, whereby it is rendered fit to answer the purposes, for which it was created. But every property, of which any particle of this matter is in it self possessed, and which is not barely the consequence of the union of this particle with other portions of matter, we may call an essential property: whereas all other qualities or attributes belonging to bodies, which depend on their particular frame and composition, are not essential to the matter, whereof such bodies are made; because the matter of these bodies will be deprived of those qualities, only by the dissolution of the body, without working any change in the original constitution of one single particle of this mass of matter. Extension we apprehend to be one of these essential properties, and impenetrability another. These two belong universally to all matter; and are the principal ingredients in the idea, which this word matter usually excites in the mind. Yet as the idea, marked[21] by this name, is not purely the creature of our own understandings, but is taken for the representation of a certain substance without us; if we should discover, that every part of the substance, in which we find these two properties, should likewise be endowed universally with any other essential qualities; all these, from the time they come to our notice, must be united under our general idea of matter. How many such properties there are actually in all matter we know not; those, of which we are at present apprized, have been found out only by our observations on things; how many more a farther search may bring to light, no one can say; nor are we certain, that we are provided with sufficient methods of perception to discern them all. Therefore, since we have no other way of making discoveries in nature, but by gradual inquiries into the properties of bodies; our first step must be to admit without distinction all the properties, which we observe; and afterwards we must endeavour, as far as we are able, to distinguish between the qualities, wherewith the very substances themselves are indued, and those appearances, which result from the structure only of compound bodies. Some of the properties, which we observe in things, are the attributes of particular bodies only; others universally belong to all, that fall under our notice. Whether some of the qualities and powers of particular bodies, be derived from different kinds of matter entring their composition, cannot, in the present imperfect state of our knowledge, absolutely be decided; though we have not yet any reason to conclude, but that all the bodies, with which we converse, are framed out of the very same kind of matter, and that their distinct[22] qualities are occasioned only by their structure; through the variety whereof the general powers of matter are caused to produce different effects. On the other hand, we should not hastily conclude, that whatever is found to appertain to all matter, which falls under our examination, must for that reason only be an essential property thereof, and not be derived from some unseen disposition in the frame of nature. Sir Isaac Newton has found reason to conclude, that gravity is a property universally belonging to all the perceptible bodies in the universe, and to every particle of matter, whereof they are composed. But yet he no where asserts this property to be essential to matter. And he was so far from having any design of establishing it as such, that, on the contrary, he has given some hints worthy of himself at a cause for it[40]; and expresly says, that he proposed those hints to shew, that he had no such intention[41].
19. It appears from hence, that it is not easy to determine, what properties of bodies are essentially inherent in the matter, out of which they are made, and what depend upon their frame and composition. But certainly whatever properties are found to belong either to any particular systems of matter, or universally to all, must be considered in philosophy; because philosophy will be otherwise imperfect. Whether those properties can be deduced from some other appertaining to matter, either among those, which are already known, or among such as can be discovered by us, is afterwards to be sought for the farther improvement of our knowledge. But this[23] inquiry cannot properly have place in the deliberation about admitting any property of matter or bodies into philosophy; for that purpose it is only to be considered, whether the existence of such a property has been justly proved or not. Therefore to decide what causes of things are rightly received into natural philosophy, requires only a distinct and clear conception of what kind of reasoning is to be allowed of as convincing, when we argue upon the works of nature.
20. The proofs in natural philosophy cannot be so absolutely conclusive, as in the mathematics. For the subjects of that science are purely the ideas of our own minds. They may be represented to our senses by material objects, but they are themselves the arbitrary productions of our own thoughts; so that as the mind can have a full and adequate knowledge of its own ideas, the reasoning in geometry can be rendered perfect. But in natural knowledge the subject of our contemplation is without us, and not so compleatly to be known: therefore our method of arguing must fall a little short of absolute perfection. It is only here required to steer a just course between the conjectural method of proceeding, against which I have so largely spoke; and demanding so rigorous a proof, as will reduce all philosophy to mere scepticism, and exclude all prospect of making any progress in the knowledge of nature.
21. The concessions, which are to be allowed in this science, are by Sir Isaac Newton included under a very few simple precepts.
22. The first is, that more causes are not to be received into philosophy, than are sufficient to explain the appearances of nature. That this rule is approved of unanimously, is evident from those expressions so frequent among all philosophers, that nature does nothing in vain; and that a variety of means, where fewer would suffice, is needless. And certainly there is the highest reason for complying with this rule. For should we indulge the liberty of multiplying, without necessity, the causes of things, it would reduce all philosophy to mere uncertainty; since the only proof, which we can have, of the existence of a cause, is the necessity of it for producing known effects. Therefore where one cause is sufficient, if there really should in nature be two, which is in the last degree improbable, we can have no possible means of knowing it, and consequently ought not to take the liberty of imagining, that there are more than one.
23. The second precept is the direct consequence of the first, that to like effects are to be ascribed the same causes. For instance, that respiration in men and in brutes is brought about by the same means; that bodies descend to the earth here in Europe, and in America from the same principle; that the light of a culinary fire, and of the sun have the same manner of production; that the reflection of light is effected in the earth, and in the planets by the same power; and the like.
24. The third of these precepts has equally evident reason for it. It is only, that those qualities, which in the same body can neither be lessened nor increased, and which belong[25] to all bodies that are in our power to make trial upon, ought to be accounted the universal properties of all bodies whatever.
25. In this precept is founded that method of arguing by induction, without which no progress could be made in natural philosophy. For as the qualities of bodies become known to us by experiments only; we have no other way of finding the properties of such bodies, as are out of our reach to experiment upon, but by drawing conclusions from those which fall under our examination. The only caution here required is, that the observations and experiments, we argue upon, be numerous enough, and that due regard be paid to all objections, that occur, as the Lord Bacon very judiciously directs[42]. And this admonition is sufficiently complied with, when by virtue of this rule we ascribe impenetrability and extension to all bodies, though we have no sensible experiment, that affords a direct proof of any of the celestial bodies being impenetrable; nor that the fixed stars are so much as extended. For the more perfect our instruments are, whereby we attempt to find their visible magnitude, the less they appear; insomuch that all the sensible magnitude, which we observe in them, seems only to be an optical deception by the scattering of their light. However, I suppose no one will imagine they are without any magnitude, though their immense distance makes it undiscernable by us. After the same manner, if it can be proved, that all[26] bodies here gravitate towards the earth, in proportion to the quantity of solid matter in each; and that the moon gravitates to the earth likewise, in proportion to the quantity of matter in it; and that the sea gravitates towards the moon, and all the planets towards each other; and that the very comets have the same gravitating faculty; we shall have as great reason to conclude by this rule, that all bodies gravitate towards each other. For indeed this rule will more strongly hold in this case, than in that of the impenetrability of bodies; because there will more instances be had of bodies gravitating, than of their being impenetrable.
25. This is that method of induction, whereon all philosophy is founded; which our author farther inforces by this additional precept, that whatever is collected from this induction, ought to be received, notwithstanding any conjectural hypothesis to the contrary, till such times as it shall be contradicted or limited by farther observations on nature.


BOOK I.
Concerning the
MOTION of BODIES
IN GENERAL.
Chap. I.
Of the LAWS of MOTION.

HAVING thus explained Sir Isaac Newton’s method of reasoning in philosophy, I shall now proceed to my intended account of his discoveries. These are contained in two treatises. In one of them, the Mathematical principles of natural philosophy, his chief design is to shew by what laws the heavenly[28] motions are regulated; in the other, his Optics, he discourses of the nature of light and colours, and of the action between light and bodies. This second treatise is wholly confined to the subject of light: except some conjectures proposed at the end concerning other parts of nature, which lie hitherto more concealed. In the other treatise our author was obliged to smooth the way to his principal intention, by explaining many things of a more general nature: for even some of the most simple properties of matter were scarce well established at that time. We may therefore reduce Sir Isaac Newton’s doctrine under three general heads; and I shall accordingly divide my account into three books. In the first I shall speak of what he has delivered concerning the motion of bodies, without regard to any particular system of matter; in the second I shall treat of the heavenly motions; and the third shall be employed upon light.
2. In the first part of my design, we must begin with an account of the general laws of motion.
3. These laws are some universal affections and properties of matter drawn from experience, which are made use of as axioms and evident principles in all our arguings upon the motion of bodies. For as it is the custom of geometers to assume in their demonstrations some propositions, without exhibiting the proof of them; so in philosophy, all our reasoning must be built upon some properties of matter, first admitted as principles whereon to argue. In geometry these axioms are thus assumed, on account of their being so evident[29] as to make any proof in form needless. But in philosophy no properties of bodies can be in this manner received for self-evident; since it has been observed above, that we can conclude nothing concerning matter by any reasonings upon its nature and essence, but that we owe all the knowledge, we have thereof, to experience. Yet when our observations on matter have inform’d us of some of its properties, we may securely reason upon them in our farther inquiries into nature. And these laws of motion, of which I am here to speak, are found so universally to belong to bodies, that there is no motion known, which is not regulated by them. These are by Sir Isaac Newton reduced to three[43].
4. The first law is, that all bodies have such an indifference to rest, or motion, that if once at rest they remain so, till disturbed by some power acting upon them: but if once put in motion, they persist in it; continuing to move right forwards perpetually, after the power, which gave the motion, is removed; and also preserving the same degree of velocity or quickness, as was first communicated, not stopping or remitting their course, till interrupted or otherwise disturbed by some new power impressed.
5. The second law of motion is, that the alteration of the state of any body, whether from rest to motion, or from motion to rest, or from one degree of motion to another, is always proportional to the force impressed. A body at rest, when[30] acted upon by any power, yields to that power, moving in the same line, in which the power applied is directed; and moves with a less or greater degree of velocity, according to the degree of the power; so that twice the power shall communicate a double velocity, and three times the power a threefold velocity. If the body be moving, and the power impressed act upon the body in the direction of its motion, the body shall receive an addition to its motion, as great as the motion, into which that power would have put it from a state of rest; but if the power impressed upon a moving body act directly opposite to its former motion, that power shall then take away from the body’s motion, as much as in the other case it would have added to it. Lastly, if the power be impressed obliquely, there will arise an oblique motion differing more or less from the former direction, according as the new impression is greater or less. For example, if the body A (in fig. 1.) be moving in the direction A B, and when it is at the point A, a power be impressed upon it in the direction A C, the body shall from henceforth neither move in its first direction A B, nor in the direction of the adventitious power, but shall take a course as A D between them: and if the power last impressed be just equal to that, which first gave to the body its motion; the line A D shall pass in the middle between A B and A C, dividing the angle under B A C into two equal parts; but if the power last impressed be greater than the first, the line A D shall incline most to A C; whereas if the last impression be less than the first, the line A D shall incline most to A B. To be more particular, the situation of[31] the line A D is always to be determined after this manner. Let A E be the space, which the body would have moved through in the line A B during any certain portion of time; provided that body, when at A, had received no second impulse. Suppose likewise, that A F is the part of the line A C, through which the body would have moved during an equal portion of time, if it had been at rest in A, when it received the impulse in the direction A C: then if from E be drawn a line parallel to, or equidistant from A C, and from F another line parallel to A B, those two lines will meet in the line A D.
6. The third and last of these laws of motion is, that when any body acts upon another, the action of that body upon the other is equalled by the contrary reaction of that other body upon the first.
7. These laws of motion are abundantly confirmed by this, that all the deductions made from them, in relation to the motion of bodies, how complicated soever, are found to agree perfectly with observation. This shall be shewn more at large in the next chapter. But before we proceed to so diffusive a proof; I chuse here to point out those appearances of bodies, whereby the laws of motion are first suggested to us.
8. Daily observation makes it appear to us, that any body, which we once see at rest, never puts it self into fresh[32] motion; but continues always in the same place, till removed by some power applied to it.
9. Again, whenever a body is once in motion, it continues in that motion some time after the moving power has quitted it, and it is left to it self. Now if the body continue to move but a single moment, after the moving power has left it, there can no reason be assigned, why it should ever stop without some external force. For it is plain, that this continuance of the motion is caused only by the body’s having already moved, the sole operation of the power upon the body being the putting it in motion; therefore that motion continued will equally be the cause of its farther motion, and so on without end. The only doubt that can remain, is, whether this motion communicated continues intire, after the power, that caused it, ceases to act; or whether it does not gradually languish and decrease. And this suspicion cannot be removed by a transient and slight observation on bodies, but will be fully cleared up by those more accurate proofs of the laws of motion, which are to be considered in the next chapter.
10. Lastly, bodies in motion appear to affect a straight course without any deviation, unless when disturbed by some adventitious power acting upon them. If a body be thrown perpendicularly upwards or downwards, it appears to continue in the same straight line during the whole time of its motion. If a body be thrown in any other direction, it is found to deviate from the line, in which it began to move, more and[33] more continually towards the earth, whither it is directed by its weight: but since, when the weight of a body does not alter the direction of its motion, it always moves in a straight line, without doubt in this other case the body’s, declining from its first course is no more, than what is caused by its weight alone. As this appears at first sight to be unquestionable, so we shall have a very distinct proof thereof in the next chapter, where the oblique motion of bodies will be particularly considered.
11. Thus we see how the first of the laws of motion agrees with what appears to us in moving bodies. But here occurs this farther consideration, that the real and absolute motion of any body is not visible to us: for we are our selves also in constant motion along with the earth whereon we dwell; insomuch that we perceive bodies to move so far only, as their motion is different from our own. When a body appears to us to lie at rest, in reality it only continues the motion, it has received, without putting forth any power to change that motion. If we throw a body in the course or direction, wherein we are carried our selves; so much motion as we seem to have given to the body, so much we have truly added to the motion, it had, while it appeared to us to be at rest. But if we impel a body the contrary way, although the body appears to us to have received by such an impulse as much motion, as when impelled the other way; yet in this case we have taken from the body so much real motion, as we seem to have given it. Thus the motion, which we see in bodies,[34] is not their real motion, but only relative with respect to us; and the forementioned observations only shew us, that this first law of motion has place in this relative or apparent motion. However, though we cannot make any observation immediately on the absolute motion of bodies, yet by reasoning upon what we observe in visible motion, we can discover the properties and effects of real motion.
12. With regard to this first law of motion, which is now under consideration, we may from the foregoing observations most truly collect, that bodies are disposed to continue in the absolute motion, which they have once received, without increasing or diminishing their velocity. When a body appears to us to lie at rest, it really preserves without change the motion, which it has in common with our selves: and when we put it into visible motion, and we see it continue that motion; this proves, that the body retains that degree of its absolute motion, into which it is put by our acting upon it: if we give it such an apparent motion, which adds to its real motion, it preserves that addition; and if our acting on the body takes off from its real motion, it continues afterwards to move with no more real motion, than we have left it.
13. Again, we do not observe in bodies any disposition or power within themselves to change the direction of their motion; and if they had any such power, it would easily be discovered. For suppose a body by the structure or disposition of its parts, or by any other circumstance in its make, was indued[35] with a power of moving it self; this self-moving principle, which should be thus inherent in the body, and not depend on any thing external, must change the direction wherein it would act, as often as the position of the body was changed: so that for instance, if a body was lying before me in such a position, that the direction, wherein this principle disposes the body to move, was pointed directly from me; if I then gradually turned the body about, the direction of this self-moving principle would no longer be pointed directly from me, but would turn about along with the body. Now if any body, which appears to us at rest, were furnished with any such self-moving principle; from the body’s appearing without motion we must conclude, that this self-moving principle lies directed the same way as the earth is carrying the body; and such a body might immediately be put into visible motion only by turning it about in any degree, that this self-moving principle might receive a different direction.
14. From these considerations it very plainly follows, that if a body were once absolutely at rest; not being furnished with any principle, whereby it could put it self into motion, it must for ever continue in the same place, till acted upon by something external: and also that when a body is put into motion, it has no power within it self to make any change in the direction of that motion; and consequently that the body must move on straight forward without declining any way whatever. But it has before been shewn, that bodies do not appear to have in themselves any power to[36] change the velocity of their motion: therefore this first law of motion has been illustrated and confirmed, as much as can be from the transient observations, which have here been discoursed upon; and in the next chapter all this will be farther established by more correct observations.
15. But I shall now pass to the second law of motion; wherein, when it is asserted, that the velocity, with which any body is moved by the action of a power upon it, is proportional to that power; the degree of power is supposed to be measured by the greatness of the body, which it can move with a given celerity. So that the sense of this law is, that if any body were put into motion with that degree of swiftness, as to pass in one hour the length of a thousand yards; the power, which would give the same degree of velocity to a body twice as great, would give this lesser body twice the velocity, causing it to describe in the same space of an hour two thousand yards. But by a body twice as great as another, I do not here mean simply of twice the bulk, but one that contains a double quantity of solid matter.
16. Why the power, which can move a body twice as great as another with the same degree of velocity, should be called twice as great as the power, which can give the lesser body the same velocity, is evident. For if we should suppose the greater body to be divided into two equal parts, each equal to the lesser body, each of these halves will require the same degree of power to move them with the velocity of the lesser body, as the lesser body it self requires; and therefore both[37] those halves, or the whole greater body, will require the moving power to be doubled.
17. That the moving power being in this sense doubled, should just double likewise the velocity of the same body, seems near as evident, if we consider, that the effect of the power applied must needs be the same, whether that power be applied to the body at once, or in parts. Suppose then the double power not applied to the body at once, but half of it first, and afterwards the other half; it is not conceivable for what reason the half last applied should come to have a different effect upon the body, from that which is applied first; as it must have, if the velocity of the body was not just doubled by the application of it. So far as experience can determine, we see nothing to favour such a supposition. We cannot indeed (by reason of the constant motion of the earth) make trial upon any body perfectly at rest, whereby to see whether a power applied in that case would have a different effect, from what it has, when the body is already moving; but we find no alteration in the effect of the same power on account of any difference there may be in the motion of the body, when the power is applied. The earth does not always carry bodies with the same degree of velocity; yet we find the visible effects of any power applied to the same body to be, at all times the very same: and a bale of goods, or other moveable body lying in a ship is as easily removed from place to place, while the ship is under sail, if its motion be steady, as when it is fixed at anchor.
18. Now this experience is alone sufficient to shew to us the whole of this law of motion.
19. Since we find, that the same power will always produce the same change in the motion of any body, whether that body were before moving with a swifter or slower motion; the change wrought in the motion of a body depends only on the power applied to it, without any regard to the body’s former motion: and therefore the degree of motion, which the body already possesses, having no influence on the power applied to disturb its operation, the effects of the same power will not only be the same in all degrees of motion of the body; but we have likewise no reason to doubt, but that a body perfectly at rest would receive from any power as much motion, as would be equivalent to the effect of the same power applied to that body already in motion.
20. Again, suppose a body being at rest, any number of equal powers should be successively applied to it; pushing it forward from time to time in the same course or direction. Upon the application of the first power the body would begin to move; when the second power was applied, it appears from what has been said, that the motion of the body would become double; the third power would treble the motion of the body; and so on, till after the operation of the last power the motion of the body would be as many times the motion, which the first power gave it, as there are powers in number. and the effect of this number of powers will be always the[39] same, without any regard to the space of time taken up in applying them: so that greater or lesser intervals between the application of each of these powers will produce no difference at all in their effects. Since therefore the distance of time between the action of each power is of no consequence; without doubt the effect will still be the same, though the powers should all be applied at the very same instant; or although a single power should be applied equal in strength to the collective force of all these powers. Hence it plainly follows, that the degree of motion, into which any body will be put out of a state of rest by any power, will be proportional to that power. A double power will give twice the velocity, a treble power three times the velocity, and so on. The foregoing reasoning will equally take place, though the body were not supposed to be at rest, when the powers began to be applied to it; provided the direction, in which the powers were applied, either conspired with the action of the body, or was directly opposite to it. Therefore if any power be applied to a moving body, and act upon the body either in the direction wherewith the body moves, so as to accelerate the body; or if it act directly opposite to the motion of the body, so as to retard it: in both these cases the change of motion will be proportional to the power applied; nay, the augmentation of the motion in one case, and the diminution thereof in the other, will be equal to that degree of motion, into which the same power would put the body, had it been at rest, when the power was applied.
21. Farther, a power may be so applied to a moving body, as to act obliquely to the motion of the body. And the effects of such an oblique motion may be deduced from this observation; that as all bodies are continually moving along with the earth, we see that the visible effects of the same power are always the same, in whatever direction the power acts: and therefore the visible effects of any power upon a body, which seems only to be at rest, is always to appearance the same as the real effect would be upon a body truly at rest. Now suppose a body were moving along the line A B (in fig. 2.) and the eye accompanied it with an equal motion in the line C D equidistant from A B; so that when the body is at A, the eye shall be at C, and when the body is advanced to E in the line A B, the eye shall be advanced to F in the line C D, the distances A E and C F being equal. It is evident, that here the body will appear to the eye to be at rest; and the line F E G drawn from the eye through the body shall seem to the eye to be immoveable; though as the body and eye move forward together, this line shall really also move; so that when the body shall be advanced to H and the eye to K, the line F E G shall be transferred into the situation K H L, this line K H L being equidistant from F E G. Now if the body when at E were to receive an impulse in the direction of the line F E G; while the eye is moving on from F to K and carrying along with it the line F E G, the body will appear to the eye to move along this line F E G: for this is what has just now been said; that while bodies are moving along with the earth, and the spectator’s eye partakes of the same motion, the effect of any power upon the body will appear to be what[41] it would really have been, had the body been truly at rest, when the power was applied. From hence it follows, that when the eye is advanced to K, the body will appear somewhere in the line K H L. Suppose it appear in M; then it is manifest, from what has been premised at the beginning of this paragraph, that the distance H M is equal to what the body would have run upon the line E G, during the time, wherein the eye has passed from F to K, provided that the body had been at rest, when acted upon in E. If it be farther asked, after what manner the body has moved from E to M? I answer, through a straight line; for it has been shewn above in the explication of the first law of motion, that a moving body, from the time it is left to it self, will proceed on in one continued straight line.
22. If E N be taken equal to H M and N M be drawn; since H M is equidistant from E N, N M will be equidistant from E H. Therefore the effect of any power upon a moving body, when that power acts obliquely to the motion of the body, is to be determined in this manner. Suppose the body is moving along the straight line A E B, if when the body is come to E, a power gives it an impulse in the direction of the line E G, to find what course the body will afterwards take we must proceed thus. Take in E B any length E H, and in E G take such a length E N, that if the body had been at rest in E, the power applied to it would have caused it to move over E N in the same space of time, as it would have employed in passing over E H, if the power had not acted at all upon it. Then draw H L equidistant from E G, and N M equidistant[42] from E B. After this, if a line be drawn from E to the point M, where these two lines meet, the line E M will be the course into which the body will be put by the action of the power upon it at E.
23. A mathematical reader would here expect in some particulars more regular demonstrations; but as I do not at present address my self to such, so I hope, what I have now written will render my meaning evident enough to those, who are unacquainted with that kind of reasoning.
24. Now as we have been shewing, that some actual force is necessary either to put bodies out of a state of rest into motion, or to change the motion, which they have once received; it is proper here to observe, that this quality in bodies, whereby they preserve their present state, with regard to motion or rest, till some active force disturb them, is called the vis inertiae of matter: and by this property, matter, sluggish and unactive of it self, retains all the power impressed upon it, and cannot be made to cease from action, but by the opposition of as great a power, as that which first moved it. By the degree of this vis inertiae, or power of inactivity, as we shall henceforth call it, we primarily judge of the quantity of solid matter in each body; for as this quality is inherent in all the bodies, upon which we can make any trial, we conclude it to be a property essential to all matter; and as we yet know no reason to suppose, that bodies are composed of different kinds of matter, we rather presume, that the matter of all bodies is the same; and that the degree of[43] this power of inactivity is in every body proportional to the quantity of the solid matter in it. But although we have no absolute proof, that all the matter in the universe is uniform, and possesses this power of inactivity in the same degree; yet we can with certainty compare together the different degrees of this power of inactivity in different bodies. Particularly this power is proportional to the weight of bodies, as Sir Isaac Newton has demonstrated[44]. However, notwithstanding that this power of inactivity in any body can be more certainly known, than the quantity of solid matter in it; yet since there is no reason to suspect that one is not proportional to the other, we shall hereafter speak without hesitation of the quantity of matter in bodies, as the measure of the degree of their power of inactivity.
25. This being established, we may now compare the effects of the same power upon different bodies, as hitherto we have shewn the effects of different powers upon the same body. And here if we limit the word motion to the peculiar sense given to it in philosophy, we may comprehend all that is to be said upon this head under one short precept; that the same power, to whatever body it is applied, will always produce the same degree of motion. But here motion does not signify the degree of celerity or velocity with which a body moves, in which sense only we have hitherto used it; but it is made use of particularly in philosophy to signify the force with which a body moves: as if two bodies A and B being[44] in motion, twice the force would be required to stop A as to stop B, the motion of A would be esteemed double the motion of B. In moving bodies, these two things are carefully to be distinguished; their velocity or celerity, which is measured by the space they pass through during any determinate portion of time; and the quantity of their motion, or the force, with which they will press against any resistance. Which force, when different bodies move with the same velocity, is proportional to the quantity of solid matter in the bodies; but if the bodies are equal, this force is proportional to their respective velocities, and in other cases it is proportional both to the quantity of solid matter in the body, and also to its velocity. To instance in two bodies A and B: if A be twice as great as B, and they have both the same velocity, the motion of A shall be double the motion of B; and if the bodies be equal, and the velocity of A be twice that of B, the motion of A shall likewise be double that of B; but if A be twice as large as B, and move twice as swift, the motion of A will be four times the motion of B; and lastly, if A be twice as large as B, and move but half as fast, the degree of their motion shall be the same.
26. This is the particular sense given to the word motion by philosophers, and in this sense of the word the same power always produces the same quantity or degree of motion. If the same power act upon two bodies A and B, the velocities, it shall give to each of them, shall be so adjusted to the respective bodies, that the same degree of motion shall be produced in each. If A be twice as great as B, its velocity shall be half[45] that of B; if A has three times as much solid matter as B, the velocity of A shall be one third of the velocity of B; and generally the velocity given to A shall bear the same proportion to the velocity given to B, as the quantity of solid matter contained in the body B bears to the quantity of solid matter contained in A.
27. The reason of all this is evident from what has gone before. If a power were applied to B, which should bear the same proportion to the power applied to A, as the body B bears to A, the bodies B and A would both receive the same velocity; and the velocity, which B will receive from this power, will bear the same proportion to the velocity, which it would receive from the action of the power applied to A, as the former of these powers bears to the latter: that is, the velocity, which A receives from the power applied to it, will bear to the velocity, which B would receive from the same power, the same proportion as the body B bears to A.
28. From hence we may now pass to the third law of motion, where this distinction between the velocity of a body and its whole motion is farther necessary to be regarded, as shall immediately be shewn; after having first illustrated the meaning of this law by a familiar instance. If a stone or other load be drawn by a horse; the load re-acts upon the horse, as much as the horse acts upon the load; for the harness, which is strained between them, presses against the horse as much as against the load; and the progressive motion of the[46] horse forward is hindred as much by the load, as the motion of the load is promoted by the endeavour of the horse: that is, if the horse put forth the same strength, when loosened from the load, he would move himself forwards with greater swiftness in proportion to the difference between the weight of his own body and the weight of himself and load together.
29. This instance will afford some general notion of the meaning of this law. But to proceed to a more philosophical explication: if a body in motion strike against another at rest, let the body striking be ever so small, yet shall it communicate some degree of motion to the body it strikes against, though the less that body be in comparison of that it impinges upon, and the less the velocity is, with which it moves, the smaller will be the motion communicated. But whatever degree of motion it gives to the resting body, the same it shall lose it self. This is the necessary consequence of the forementioned power of inactivity in matter. For suppose the two bodies equal, it is evident from the time they meet, both the bodies are to be moved by the single motion of the first; therefore the body in motion by means of its power of inactivity retaining the motion first given it, strikes upon the other with the same force, wherewith it was acted upon it self: but now both the bodies being to be moved by that force, which before moved one only, the ensuing velocity will be the same, as if the power, which was applied to one of the bodies, and put it into motion, had been applied to both; whence it appears, that they will proceed forwards,[47] with half the velocity, which the body first in motion had: that is, the body first moved will have lost half its motion, and the other will have gained exactly as much. This rule is just, provided the bodies keep contiguous after meeting; as they would always do, if it were not for a certain cause that often intervenes, and which must now be explained. Bodies upon striking against each other, suffer an alteration in their figure, having their parts pressed inwards by the stroke, which for the most part recoil again afterwards, the bodies endeavouring to recover their former shape. This power, whereby bodies are inabled to regain their first figure, is usually called their elasticity, and when it acts, it forces the bodies from each other, and causes them to separate. Now the effect of this elasticity in the present case is such, that if the bodies are perfectly elastic, so as to recoil with as great a force as they are bent with, that they recover their figure in the same space of time, as has been taken up in the alteration made in it by their compression together; then this power will separate the bodies as swiftly, as they before approached, and acting upon both equally, upon the body first in motion contrary to the direction in which it moves, and upon the other as much in the direction of its motion, it will take from the first, and add to the other equal degrees of velocity: so that the power being strong enough to separate them with as great a velocity, as they approached with, the first will be quite stopt, and that which was at rest, will receive all the motion of the other. If the bodies are elastic in a less degree, the first will not lose all its motion, nor will the other acquire the motion of the first, but fall as much short of it, as the other retains.[48] For this rule is never deviated from, that though the degree of elasticity determines how much more than half its velocity the body first in motion shall lose; yet in every case the loss in the motion of this body shall be transferred to the other, that other body always receiving by the stroke as much motion, as is taken from the first.
30. This is the case of a body striking directly against an equal body at rest, and the reasoning here used is fully confirmed by experience. There are many other cases of bodies impinging against one another: but the mention of these shall be reserved to the next chapter, where we intend to be more particular and diffusive in the proof of these laws of motion, than we have been here.
Chap. II.
Farther proofs of the Laws of Motion.
HAVING in the preceding chapter deduced the three laws of motion, delivered by our great philosopher, from the most obvious observations, that suggest them to us; I now intend to give more particular proofs of them, by recounting some of the discoveries which have been made in philosophy before Sir Isaac Newton. For as they were all collected by reasoning upon those laws; so the conformity of these discoveries to experience makes them so many proofs of the truth of the principles, from which they were derived.
2. Let us begin with the subject, which concluded the last chapter. Although the body in motion be not equal to the body at rest, on which it strikes; yet the motion after the stroke is to be estimated in the same manner as above. Let A (in fig. 3.) be a body in motion towards another body B lying at rest. When A is arrived at B, it cannot proceed farther without putting B into motion; and what motion it gives to B, it must lose it self, that the whole degree of motion of A and B together, if neither of the bodies be elastic, shall be equal, after the meeting of the bodies, to the single motion of A before the stroke. Therefore, from what has been said above, it is manifest, that as soon as the two bodies are met, they will move on together with a velocity, which will bear the same proportion to the original velocity of A, as the body A bears to the sum of both the bodies.
3. If the bodies are elastic, so that they shall separate after the stroke, A must lose a greater part of its motion, and the subsequent motion of B will be augmented by this elasticity, as much as the motion of A is diminished by it. The elasticity acting equally between both the bodies, it will communicate to each the same degree of motion; that is, it will separate the bodies by taking from the body A and adding to the body B different degrees of velocity, so proportioned to their respective quantities of matter, that the degree of motion, wherewith A separates from B, shall be equal to the degree of motion, wherewith B separates from A. It follows therefore, that the velocity taken from A by the elasticity bears to the velocity, which the same elasticity adds to B, the[50] same proportion, as B bears to A: consequently the velocity, which the elasticity takes from A, will bear the same proportion to the whole velocity, wherewith this elasticity causes the two bodies to separate from each other, as the body B bears to the sum of the two bodies A and B; and the velocity, which is added to B by the elasticity, bears to the velocity, wherewith the bodies separate, the same proportion, as the body A bears to the sum of the two bodies A and B. Thus is found, how much the elasticity takes from the velocity of A, and adds to the velocity of B; provided the degree of elasticity be known, whereby to determine the whole velocity wherewith the bodies separate from each other after the stroke[45].
4. After this manner is determined in every case the result of a body in motion striking against another at rest. The same principles will also determine the effects, when both bodies are in motion.
5. Let two equal bodies move against each other with equal swiftness. Then the force, with which each of them presses forwards, being equal when they strike; each pressing in its own direction with the same energy, neither shall surmount the other, but both be stopt, if they be not elastic: for if they be elastic, they shall from thence recover new motion, and recede from each other, as swiftly as they met, if they be perfectly elastic; but more slowly, if less so. In the same manner, if two bodies of unequal bigness strike against each other, and their velocities be so related, that the velocity[51] of the lesser body shall exceed the velocity of the greater in the same proportion, as the greater body exceeds the lesser (for instance, if one body contains twice the solid matter as the other, and moves but half as fast) two such bodies will entirely suppress each other’s motion, and remain from the time of their meeting fixed; if, as before, they are not elastic: but, if they are so in the highest degree, they shall recede again, each with the same velocity, wherewith they met. For this elastic power, as in the preceding case, shall renew their motion, and pressing equally upon both, shall give the same motion to both; that is, shall cause the velocity, which the lesser body receives, to bear the same proportion to the velocity, which the greater receives, as the greater body bears to the lesser: so that the velocities shall bear the same proportion to each other after the stroke, as before. Therefore if the bodies, by being perfectly elastic, have the sum of their velocities after the stroke equal to the sum of their velocities before the stroke, each body after the stroke will receive its first velocity. And the same proportion will hold likewise between the velocities, wherewith they go off, though they are elastic but in a less degree; only then the velocity of each will be less in proportion to the defect of elasticity.
6. If the velocities, wherewith the bodies meet, are not in the proportion here supposed; but if one of the bodies, as A, has a swifter velocity in comparison to the velocity of the other; then the effect of this excess of velocity in the body A must be joined to the effect now mentioned, after the manner of this following example. Let A be twice as great as B, and[52] move with the same swiftness as B. Here A moves with twice that degree of swiftness, which would answer to the forementioned proportion. For A being double to B, if it moved but with half the swiftness, wherewith B advances, it has been just now shewn, that the two bodies upon meeting would stop, if they were not elastic; and if they were elastic, that they would each recoil, so as to cause A to return with half the velocity, wherewith B would return. But it is evident from hence, that B by encountring A will annul half its velocity, if the bodies be not elastic; and the future motion of the bodies will be the same, as if A had advanced against B at rest with half the velocity here assigned to it. If the bodies be elastic, the velocity of A and B after the stroke may be thus discovered. As the two bodies advance against each other, the velocity, with which they meet, is made up of the velocities of both bodies added together. After the stroke their elasticity will separate them again. The degree of elasticity will determine what proportion the velocity, wherewith they separate, must bear to that, wherewith they meet. Divide this velocity, with which the bodies separate into two parts, that one of the parts bear to the other the same proportion, as the body A bears to B; and ascribe the lesser part to the greater body A, and the greater part of the velocity to the lesser body B. Then take the part ascribed to A from the common velocity, which A and B would have had after the stroke, if they had not been elastic; and add the part ascribed to B to the same common velocity. By this means the true velocities of A and B after the stroke will be made known.
7. If the bodies are perfectly elastic, the great Huygens has laid down this rule for finding their motion after concourse[46]. Any straight line C D (in fig. 4, 5.) being drawn, let it be divided in E, that C E bear the same proportion to E D, as the swiftness of A bore to the swiftness of B before the stroke. Let the same line C D be also divided in F, that C F bear the same proportion to F D, as the body B bears to the body A. Then F G being taken equal to F E, if the point G falls within the line C D, both the bodies shall recoil after the stroke, and the velocity, wherewith the body A shall return, will bear the same proportion to the velocity, wherewith B shall return, as G C bears to G D; but if the point G falls without the line C D, then the bodies after their concourse shall both proceed to move the same way, and the velocity of A shall bear to the velocity of B the same proportion, that G C bears to G D, as before.
8. If the body B had stood still, and received the impulse of the other body A upon it; the effect has been already explained in the case, when the bodies are not elastic. And when they are elastic, the result of their collision is found by combining the effect of the elasticity with the other effect, in the same manner as in the last case.
9. When the bodies are perfectly elastic, the rule of Huygens[47] here is to divide the line C D (fig. 6.) in E as before, and to take E G equal to E D. And by these points[54] thus found, the motion of each body after the stroke is determined, as before.
10. In the next place, suppose the bodies A and B were both moving the same way, but A with a swifter motion, so as to overtake B, and strike against it. The effect of the percussion or stroke, when the bodies are not elastic, is discovered by finding the common motion, which the two bodies would have after the stroke, if B were at rest, and A were to advance against it with a velocity equal to the excess of the present velocity of A above the velocity of B; and by adding to this common velocity thus found the velocity of B.
11. If the bodies are elastic, the effect of the elasticity is to be united with this other, as in the former cases.
12. When the bodies are perfectly elastic, the rule of Huygens[48] in this case is to prolong C D (fig. 7.) and to take in it thus prolonged C E in the same proportion to E D, as the greater velocity of A bears to the lesser velocity of B; after which F G being taken equal to F E, the velocities of the two bodies after the stroke will be determined, as in the two preceding cases.
13. Thus I have given the sum of what has been written concerning the effects of percussion, when two bodies freely in motion strike directly against each other; and the results here set down, as the consequence of our reasoning[55] from the laws of motion, answer most exactly to experience. A particular set of experiments has been invented to make trial of these effects of percussion with the greatest exactness. But I must defer these experiments, till I have explained the nature of pendulums[49]. I shall therefore now proceed to describe some of the appearances, which are caused in bodies from the influence of the power of gravity united with the general laws of motion; among which the motion of the pendulum will be included.
14. The most simple of these appearances is, when bodies fall down merely by their weight. In this case the body increases continually its velocity, during the whole time of its fall, and that in the very same proportion as the time increases. For the power of gravity acts constantly on the body with the same degree of strength: and it has been observed above in the first law of motion, that a body being once in motion will perpetually preserve that motion without the continuance of any external influence upon it: therefore, after a body has been once put in motion by the force of gravity, the body would continue that motion, though the power of gravity should cease to act any farther upon it; but, if the power of gravity continues still to draw the body down, fresh degrees of motion must continually be added to the body; and the power of gravity acting at all times with the same strength, equal degrees of motion will constantly be added in equal portions of time.
15. This conclusion is not indeed absolutely true: for we shall find hereafter[50], that the power of gravity is not of the same strength at all distances from the center of the earth. But nothing of this is in the least sensible in any distance, to which we can convey bodies. The weight of bodies is the very same to sense upon the highest towers or mountains, as upon the level ground; so that in all the observations we can make, the forementioned proportion between the velocity of a falling body and the time, in which it has been descending, obtains without any the least perceptible difference.
16. From hence it follows, that the space, through which a body falls, is not proportional to the time of the fall; for since the body increases its velocity, a greater space will be passed over in the same portion of time at the latter part of the fall, than at the beginning. Suppose a body let fall from the point A (in fig. 8.) were to descend from A to B in any portion of time; then if in an equal portion of time it were to proceed from B to C; I say, the space B C is greater than A B; so that the time of the fall from A to C being double the time of the fall from A to B, A C shall be more than double of A B.
17. The geometers have proved, that the spaces, through which bodies fall thus by their weight, are just in a duplicate or two-fold proportion of the times, in which the body has been falling. That is, if we were to take the line D E in the same proportion to A B, as the time, which the body has imployed in falling from A to C, bears to the time of the fall[57] from A to B; then A C will be to D E in the same proportion. In particular, if the time of the fall through A C be twice the time of the fall through A B; then D E will be twice A B, and A C twice D E; or A C four times A B. But if the time of the fall through A C had been thrice the time of the fall through A B; D E would have been treble of A B, and A C treble of D E; that is, A C would have been equal to nine times A B.
18. If a body fall obliquely, it will approach the ground by slower degrees, than when it falls perpendicularly. Suppose two lines A B, A C (in fig. 9.) were drawn, one perpendicular, and the other oblique to the ground D E: then if a body were to descend in the slanting line A C; because the power of gravity draws the body directly downwards, if the line A C supports the body from falling in that manner, it must take off part of the effect of the power of gravity; so that in the time, which would have been sufficient for the body to have fallen through the whole perpendicular line A B, the body shall not have passed in the line A C a length equal to A B; consequently the line A C being longer than A B, the body shall most certainly take up more time in passing through A C, than it would have done in falling perpendicularly down through A B.
19. The geometers demonstrate, that the time, in which the body will descend through the oblique straight line A C, bears the same proportion to the time of its descent through the perpendicular A B, as the line it self A C bears to A B. And in respect to the velocity, which the body will have acquired[58] in the point C, they likewise prove, that the length of the time imployed in the descent through A C so compensates the diminution of the influence of gravity from the obliquity of this line, that though the force of the power of gravity on the body is opposed by the obliquity of the line A C, yet the time of the body’s descent shall be so much prolonged, that the body shall acquire the very same velocity in the point C, as it would have got at the point B by falling perpendicularly down.
20. If a body were to descend in a crooked line, the time of its descent cannot be determined in so simple a manner; but the same property, in relation to the velocity, is demonstrated to take place in all cases: that is, in whatever line the body descends, the velocity will always be answerable to the perpendicular height, from which the body has fell. For instance, suppose the body A (in fig. 10.) were hung by a string to the pin B. If this body were let fall, till it came to the point C perpendicularly under B, it will have moved from A to C in the arch of a circle. Then the horizontal line A D being drawn, the velocity of the body in C will be the same, as if it had fallen from the point D directly down to C.
21. If a body be thrown perpendicularly upward with any force, the velocity, wherewith the body ascends, shall continually diminish, till at length it be wholly taken away; and from that time the body will begin to fall down again, and pass over a second time in its descent the line, wherein it ascended; falling through this line with an increasing velocity in such a manner, that in every point thereof, through[59] which it falls, it shall have the very same velocity, as it had in the same place, when it ascended; and consequently shall come down into the place, whence it first ascended, with the velocity which was at first given to it. Thus if a body were thrown perpendicularly up in the line A B (in fig. II.) with such a force, as that it should stop at the point B, and there begin to fall again; when it shall have arrived in its descent to any point as C in this line, it shall there have the same velocity, as that wherewith it passed by this point C in its ascent; and at the point A it shall have gained as great a velocity, as that wherewith it was first thrown upwards. As this is demonstrated by the geometrical writers; so, I think, it will appear evident, by considering only, that while the body descends, the power of gravity must act over again, in an inverted order, all the influence it had on the body in its ascent; so as to give again to the body the same degrees of velocity, which it had taken away before.
22. After the same manner, if the body were thrown upwards in the oblique straight line C A (in fig. 9.) from the point C, with such a degree of velocity as just to reach the point A; it shall by its own weight return again through the line A C by the same degrees, as it ascended.
23. And lastly, if a body were thrown with any velocity in a line continually incurvated upwards, the like effect will be produced upon its return to the point, whence it was thrown. Suppose for instance, the body A (in fig. 12.) were hung by a string A B. Then if this body be impelled any[60] way, it must move in the arch of a circle. Let it receive such an impulse, as shall cause it to move in the arch A C; and let this impulse be of such strength, that the body may be carried from A as far as D, before its motion is overcome by its weight: I say here, that the body forthwith returning from D, shall come again into the point A with the same velocity, as that wherewith it began to move.
24. It will be proper in this place to observe concerning the power of gravity, that its force upon any body does not at all depend upon the shape of the body; but that it continues constantly the same without any variation in the same body, whatever change be made in the figure of the body: and if the body be divided into any number of pieces, all those pieces shall weigh just the same, as they did, when united together in one body: and if the body be of a uniform contexture, the weight of each piece will be proportional to its bulk. This has given reason to conclude, that the power of gravity acts upon bodies in proportion to the quantity of matter in them. Whence it should follow, that all bodies must fall from equal heights in the same space of time. And as we evidently see the contrary in feathers and such like substances, which fall very slowly in comparison of more solid bodies; it is reasonable to suppose, that some other cause concurs to make so manifest a difference. This cause has been found by particular experiments to be the air. The experiments for this purpose are made thus. They set up a very tall hollow glass; within which near the top they lodge a feather and some very ponderous body, usually a piece of gold,[61] this metal being the most weighty of any body known to us. This glass they empty of the air contained within it, and by moving a wire, which passes through the top of the glass, they let the feather and the heavy body fall together; and it is always found, that as the two bodies begin to descend at the same time, so they accompany each other in the fall, and come to the bottom at the very same instant, as near as the eye can judge. Thus, as far as this experiment can be depended on, it is certain, that the effect of the power of gravity upon each body is proportional to the quantity of solid matter, or to the power of inactivity in each body. For in the limited sense, which we have given above to the word motion, it has been shown, that the same force gives to all bodies the same degree of motion, and different forces communicate different degrees of motion proportional to the respective powers[51]. In this case, if the power of gravity were to act equally upon the feather, and upon the more solid body, the solid body would descend so much slower than the feather, as to have no greater degree of motion than the feather: but as both bodies descend with equal swiftness, the degree of motion in the solid body is greater than in the feather, bearing the same proportion to it, as the quantity of matter in the solid body to the quantity of matter in the feather. Therefore the effect of gravity on the solid body is greater than on the feather, in proportion to the greater degree of motion communicated; that is, the effect of the power of gravity on the solid body bears the same proportion to its effect on the feather, as the quantity[62] of matter in the solid body bears to the quantity of matter in the feather. Thus it is the proper deduction from this experiment, that the power of gravity acts not on the surface of bodies only, but penetrates the bodies themselves most intimately, and operates alike on every particle of matter in them. But as the great quickness, with which the bodies fall, leaves it something uncertain, whether they do descend absolutely in the same time, or only so nearly together, that the difference in their swift motion is not discernable to the eye; this property of the power of gravity, which has here been deduced from this experiment, is farther confirmed by pendulums, whose motion is such, that a very minute difference would become sufficiently sensible. This will be farther discoursed on in another place[52]; but here I shall make use of the principle now laid down to explain the nature of what is called the center of gravity in bodies.
25. The center of gravity is that point, by which if a body be suspended, it shall hang at rest in any situation. In a globe of a uniform texture the center of gravity is the same with the center of the globe; for as the parts of the globe on every side of its center are similarly disposed, and the power of gravity acts alike on every part; it is evident, that the parts of the globe on each side of the center are drawn with equal force, and therefore neither side can yield to the other; but the globe, if supported at its center, must of necessity hang at rest. In like manner, if two equal bodies A and B (in[63] fig. 13.) be hung at the extremities of an inflexible rod C D, which should have no weight; these bodies, if the rod be supported at its middle E, shall equiponderate; and the rod remain without motion. For the bodies being equal and at the same distance from the point of support E, the power of gravity will act upon each with equal strength, and in all respects under the same circumstances; therefore the weight of one cannot overcome the weight of the other. The weight of A can no more surmount the weight of B, than the weight of B can surmount the weight of A. Again, suppose a body as A B (in fig. 14.) of a uniform texture in the form of a roller, or as it is more usually called a cylinder, lying horizontally. If a straight line be drawn between C and D, the centers of the extreme circles of this cylinder; and if this straight line, commonly called the axis of the cylinder, be divided into two equal parts in E: this point E will be the center of gravity of the cylinder. The cylinder being a uniform figure, the parts on each side of the point E are equal, and situated in a perfectly similar manner; therefore this cylinder, if supported at the point E, must hang at rest, for the same reason as the inflexible rod above-mentioned will remain without motion, when suspended at its middle point. And it is evident, that the force applied to the point E, which would uphold the cylinder, must be equal to the cylinder’s weight. Now suppose two cylinders of equal thickness A B and C D to be joined together at C B, so that the two axis’s E F, and F G lie in one straight line. Let the axis E F be divided into two equal parts at H, and the axis F G into two[64] equal parts at I. Then because the cylinder A B would be upheld at rest by a power applied in H equal to the weight of this cylinder, and the cylinder C D would likewise be upheld by a power applied in I equal to the weight of this cylinder; the whole cylinder A D will be supported by these two powers: but the whole cylinder may likewise be supported by a power applied to K, the middle point of the whole axis E G, provided that power be equal to the weight of the whole cylinder. It is evident therefore, that this power applied in K will produce the same effect, as the two other powers applied in H and I. It is farther to be observed, that H K is equal to half F G, and K I equal to half E F; for E K being equal to half E G, and E H equal to half E F, the remainder H K must be equal to half the remainder F G; so likewise G K being equal to half G E, and G I equal to half G F, the remainder I K must be equal to half the remainder E F. It follows therefore, that H K bears the same proportion to K I, as F G bears to E F. Besides, I believe, my readers will perceive, and it is demonstrated in form by the geometers, that the whole body of the cylinder C D bears the same proportion to the whole body of the cylinder A B, as the axis F G bears to the axis E F[53]. But hence it follows, that in the two powers applied at H and I, the power applied at H bears the same proportion to the power applied at I, as K I bears to K H. Now suppose two strings H L and I M extended upwards, one from the point H and the other from I, and to be laid hold on by two powers, one strong enough to hold up the cylinder A B, and the other of[65] strength sufficient to support the cylinder C D. Here as these two powers uphold the whole cylinder, and therefore produce an effect, equal to what would have been produced by a power applied to the point K of sufficient force to sustain the whole cylinder: it is manifest, that if the cylinder be taken away, the axis only being left, and from the point K a string, as K N, be extended, which shall be drawn down by a power equivalent to the weight of the cylinder, this power shall act against the other two powers, as much as the cylinder acted against them; and consequently these three powers shall be upon a balance, and hold the axis H I fixed between them. But if these three powers preserve a mutual balance, the two powers applied to the strings H L and I M are a balance to each other; the power applied to the string H L bearing the same proportion to the power applied to the string I M, as the distance I K bears to the distance K H. Hence it farther appears, that if an inflexible rod A B (in fig. 15.) be suspended by any point C not in the middle thereof; and if at A the end of the shorter arm be hung a weight, and at B the end of the longer arm be also hung a weight less than the other, and that the greater of these weights bears to the lesser the same proportion, as the longer arm of the rod bears to the shorter; then these two weights will equiponderate: for a power applied at C equal to both these weights will support without motion the rod thus charged; since here nothing is changed from the preceding case but the situation of the powers, which are now placed on the contrary sides of the line, to which they are fixed. Also for the[66] same reason, if two weights A and B (in fig. 16.) were connected together by an inflexible rod C D, drawn from C the center of gravity of A to D the center of gravity of B; and if the rod C D were to be so divided in E, that the part D E bear the same proportion to the other part C E, as the weight A bears to the weight B: then this rod being supported at E will uphold the weights, and keep them at rest without motion. This point E, by which the two bodies A and B will be supported, is called their common center of gravity. And if a greater number of bodies were joined together, the point, by which they could all be supported, is called the common center of gravity of them all. Suppose (in fig. 17.) there were three bodies A, B, C, whose respective centers of gravity were joined by the three lines D E, D F, E F: the line D E being so divided in G, that D G bear the same proportion to G E, as B bears to A; G is the center of gravity common to the two bodies A and B; that is, a power equal to the weight of both the bodies applied to G would support them, and the point G is pressed as much by the two weights A and B, as it would be, if they were both hung together at that point. Therefore, if a line be drawn from G to F, and divided in H, so that G H bear the same proportion to H F, as the weight C bears to both the weights A and B, the point H will be the common center of gravity of all the three weights; for H would be their common center of gravity, if both the weights A and B were hung together at G, and the point G is pressed as much by them in their present situation, as it would be in that case. In the same manner from the common center of these three[67] weights, you might proceed to find the common center, if a fourth weight were added, and by a gradual progress might find the common center of gravity belonging to any number of weights whatever.
26. As all this is the obvious consequence of the proposition laid down for assigning the common center of gravity of any two weights, by the same proposition the center of gravity of all figures is found. In a triangle, as A B C (in fig. 18.) the center of gravity lies in the line drawn from the middle point of any one of the sides to the opposite angle, as the line B D is drawn from D the middle of the line A C to the opposite angle B[54]; so that if from the middle of either of the other sides, as from the point E in the side A B, a line be drawn, as E C, to the opposite angle; the point F, where this line crosses the other line B D, will be the center of gravity of the triangle[55]. Likewise D F is equal to half F B, and E F equal to half F C[56]. In a hemisphere, as A B C (fig. 19.) if from D the center of the base the line D B be erected perpendicular to that base, and this line be so divided in E, that D E be equal to three fifths of B E, the point E is the center of gravity of the hemisphere[57].
27. It will be of use to observe concerning the center of gravity of bodies; that since a power applied to this center alone can support a body against the power of gravity, and[68] hold it fixed at rest; the effect of the power of gravity on a body is the same, as if that whole power were to exert itself on the center of gravity only. Whence it follows, that, when the power of gravity acts on a body suspended by any point, if the body is so suspended, that the center of gravity of the body can descend; the power of gravity will give motion to that body, otherwise not: or if a number of bodies are so connected together, that, when any one is put into motion, the rest shall, by the manner of their being joined, receive such motion, as shall keep their common center of gravity at rest; then the power of gravity shall not be able to produce any motion in these bodies, but in all other cases it will. Thus, if the body A B (in fig. 20, 21.) whose center of gravity is C, be hung on the point A, and the center C be perpendicularly under A (as in fig. 20.) the weight of the body will hold it still without motion, because the center C cannot descend any lower. But if the body be removed into any other situation, where the center C is not perpendicularly under A (as in fig. 21.) the body by its weight will be put into motion towards the perpendicular situation of its center of gravity. Also if two bodies A, B (in fig. 22.) be joined together by the rod C D lying in an horizontal situation, and be supported at the point E; if this point be the center of gravity common to the two bodies, their weight will not put them into motion; but if this point E is not their common center of gravity, the bodies will move; that part of the rod C D descending, in which the common center of gravity is found. So in like manner, if these two bodies were connected together by any more complex contrivance; yet[69] if one of the bodies cannot move without so moving the other, that their common center of gravity shall rest, the weight of the bodies will not put them in motion, otherwise it will.
28. I shall proceed in the next place to speak of the mechanical powers. These are certain instruments or machines, contrived for the moving great weights with small force; and their effects are all deducible from the observation we have just been making. They are usually reckoned in number five; the lever, the wheel and axis, the pulley, the wedge, and the screw; to which some add the inclined plane. As these instruments have been of very ancient use, so the celebrated Archimedes seems to have been the first, who discovered the true reason of their effects. This, I think, may be collected from what is related of him, that some expressions, which he used to denote the unlimited force of these instruments, were received as very extraordinary paradoxes: whereas to those, who had understood the cause of their great force, no expressions of that kind could have appeared surprizing.
29. All the effects of these powers may be judged of by this one rule, that, when two weights are applied to any of these instruments, the weights will equiponderate, if, when put into motion, their velocities will be reciprocally proportional to their respective weights. And what is said of weights, must of necessity be equally understood of any other forces[70] equivalent to weights, such as the force of a man’s arm, a stream of water, or the like.
30. But to comprehend the meaning of this rule, the reader must know, what is to be understood by reciprocal proportion; which I shall now endeavour to explain, as distinctly as I can; for I shall be obliged very frequently to make use of this term. When any two things are so related, that one increases in the same proportion as the other, they are directly proportional. So if any number of men can perform in a determined space of time a certain quantity of any work, suppose drain a fish-pond, or the like; and twice the number of men can perform twice the quantity of the same work, in the same time; and three times the number of men can perform as soon thrice the work; here the number of men and the quantity of the work are directly proportional. On the other hand, when two things are so related, that one decreases in the same proportion, as the other increases, they are said to be reciprocally proportional. Thus if twice the number of men can perform the same work in half the time, and three times the number of men can finish the same in a third part of the time; then the number of men and the time are reciprocally proportional. We shewed above[58] how to find the common center of gravity of two bodies, there the distances of that common center from the centers of gravity of the two bodies are reciprocally proportional to the respective bodies. For C E in fig. 16. being in the same proportion[71] to E D, as B bears to A; C E is so much greater in proportion than E D, as A is less in proportion than B.
31. Now this being understood, the reason of the rule here stated will easily appear. For if these two bodies were put in motion, while the point E rested, the velocity, wherewith A would move, would bear the same proportion to the velocity, wherewith B would move, as E C bears to E D. The velocity therefore of each body, when the common center of gravity rests, is reciprocally proportional to the body. But we have shewn above[59], that if two bodies are so connected together, that the putting them in motion will not move their common center of gravity; the weight of those bodies will not produce in them any motion. Therefore in any of these mechanical engines, if, when the bodies are put into motion, their velocities are reciprocally proportional to their respective weights, whereby the common center of gravity would remain at rest; the bodies will not receive any motion from their weight, that is, they will equiponderate. But this perhaps will be yet more clearly conceived by the particular description of each mechanical power.
32. The lever was first named above. This is a bar made use of to sustain and move great weights. The bar is applied in one part to some strong support; as the bar A B (in fig. 23, 24.) is applied at the point C to the support D. In some other part of the bar, as E, is applied the weight to be sustained or moved; and in a third place, as F, is applied another weight or equivalent force, which is to sustain or move[72] the weight at E. Now here, if, when the level should be put in motion, and turned upon the point C, the velocity, wherewith the point F would move, bears the same proportion to the velocity, wherewith the point E would move, as the weight at E bears to the weight or force at F; then the lever thus charged will have no propensity to move either way. If the weight or other force at F be not so great as to bear this proportion, the weight at E will not be sustained; but if the force at F be greater than this, the weight at E will be surmounted. This is evident from what has been said above[60], when the forces at E and F are placed (as in fig. 23.) on different sides of the support D. It will appear also equally manifest in the other case, by continuing the bar B C in fig. 24. on the other side of the support D, till C G be equal to C F, and by hanging at G a weight equivalent to the power at F; for then, if the power at F were removed, the two weights at G and E would counterpoize each other, as in the former case: and it is evident, that the point F will be lifted up by the weight at G with the same degree of force, as by the other power applied to F; since, if the weight at E were removed, a weight hung at F equal to that at G would balance the lever, the distances C G and C F being equal.
33. If the two weights, or other powers, applied to the lever do not counterbalance each other; a third power may be applied in any place proposed of the lever, which shall[73] hold the whole in a just counterpoize. Suppose (in fig. 25.) the two powers at E and F did not equiponderate, and it were required to apply a third power to the point G, that might be sufficient to balance the lever. Find what power in F would just counterbalance the power in E; then if the difference between this power and that, which is actually applied at F, bear the same proportion to the third power to be applied at G, as the distance C G bears to C F; the lever will be counterpoized by the help of this third power, if it be so applied as to act the same way with the power in F, when that power is too small to counterbalance the power in E; but otherwise the power in G must be so applied, as to act against the power in F. In like manner, if a lever were charged with three, or any greater number of weights or other powers, which did not counterpoize each other, another power might be applied in any place proposed, which should bring the whole to a just balance. And what is here said concerning a plurality of powers, may be equally applied to all the following cases.
34. If the lever should consist of two arms making an angle at the point C (as in fig. 26.) yet if the forces are applied perpendicularly to each arm, the same proportion will hold between the forces applied, and the distances of the center, whereon the lever rests, from the points to which they are applied. That is, the weight at E will be to the force in F in the same proportion, as C F bears to C E.
35. But whenever the forces applied to the lever act obliquely to the arm, to which they are applied (as in fig. 27.)[74] then the strength of the forces is to be estimated by lines let fall from the center of the lever to the directions, wherein the forces act. To balance the levers in fig. 27, the weight or other force at F will bear the same proportion to the weight at E, as the distance C E bears to C G the perpendicular let fall from the point C upon the line, which denotes the direction wherein the force applied to F acts: for here, if the lever be put into motion, the power applied to F will begin to move in the direction of the line F G; and therefore its first motion will be the same, as the motion of the point G.
36. When two weights hang upon a lever, and the point, by which the lever is supported, is placed in the middle between the two weights, that the arms of the lever are both of equal length; then this lever is particularly called a balance; and equal weights equiponderate as in common scales. When the point of support is not equally distant from both weights, it constitutes that instrument for weighing, which is called a steelyard. Though both in common scales, and the steelyard, the point, on which the beam is hung, is not usually placed just in the same straight line with the points, that hold the weights, but rather a little above (as in fig. 28.) where the lines drawn from the point C, whereon the beam is suspended, to the points E and F, on which the weights are hung, do not make absolutely one continued line. If the three points E, C, and F were in one straight line, those weights, which equiponderated, when the beam hung horizontally, would also equiponderate in any other situation.
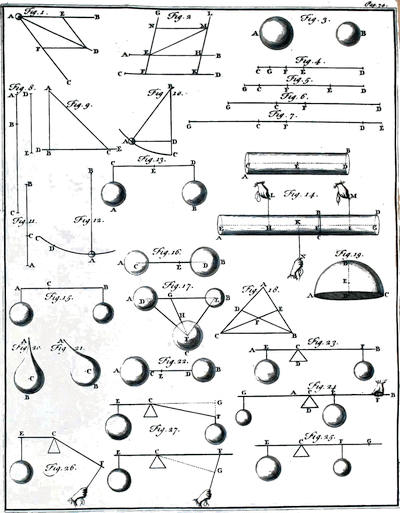
But we see in these instruments, when they are charged with weights, [75]which equiponderate with the beam hanging horizontally; that, if the beam be inclined either way, the weight most elevated surmounts the other, and descends, causing the beam to swing, till by degrees it recovers its horizontal position. This effect arises from the forementioned structure: for by this structure these instruments are levers composed of two arms, which make an angle at the point of support (as in fig. 29, 30.) the first of which represents the case of the common balance, the second the case of the steelyard. In the first, where C E and C F are equal, equal weights hung at E and F will equiponderate, when the points E and F are in an horizontal situation. Suppose the lines E G and F H to be perpendicular to the horizon, then they will denote the directions, wherein the forces applied to E and F act. Therefore the proportion between the weights at E and F, which shall equiponderate, are to be judged of by perpendiculars, as C I, C K, let fall from C upon E G and F H: so that the weights being equal, the lines C I, C K, must be equal also, when the weights equiponderate. But I believe my readers will easily see, that since C E and C F are equal, the lines C I and C K will be equal, when the points E and F are horizontally situated.
37. If this lever be set into any other position (as in fig. 31.) then the weight, which is raised highest, will outweigh the other. Here, if the point F be raised higher than E, the perpendicular C K will be longer than C I: and therefore the weights would equiponderate, if the weight at F[76] were less than the weight at E. But the weight at F is equal to that at E; therefore is greater, than is necessary to counterbalance the weight at E, and consequently will outweigh it, and draw the beam of the lever down.
38. In like manner in the case of the steelyard (fig. 32.) if the weights at E and F are so proportioned, as to equiponderate, when the points E and F are horizontally situated; then in any other situation of this lever the weight, which is raised highest, will preponderate. That is, if in the horizontal situation of the points E and F the weight at F bears the same proportion to the weight at E, as C I bears to C K; then, if the point F be raised higher than E (as in fig. 32.) the weight at F shall bear a greater proportion to the weight at E, than C I bears to C K.
39. Farther a lever may be hung upon an axis, and then the two arms of the lever need not be continuous, but fixed to different parts of this axis; as in fig. 33, where the axis A B is supported by its two extremities A and B. To this axis one arm of the lever is fixed at the point C, the other at the point D. Now here, if a weight be hung at E, the extremity of that arm, which is fixed to the axis at the point C; and another weight be hung at F, the extremity of the arm, which is fixed on the axis at D; then these weights will equiponderate, when the weight at E bears the same proportion to the weight at F, as the arm D F bears to C E.
40. This is the case, if both the arms are perpendicular to the axis, and lie (as the geometers express themselves) in the same plane; or, in other words, if the arms are so fixed perpendicularly upon the axis, that, when one of them lies horizontally, the other shall also be horizontal. If either arm stand not perpendicular to the axis; then, in determining the proportion between the weights, instead of the length of that arm, you must use the perpendicular let fall upon the axis from the extremity of that arm. If the arms are not so fixed as to become horizontal, at the same time; the method of assigning the proportion between the weights is analogous to that made use of above in levers, which make an angle at the point, whereon they are supported.
41. From this case of the lever hung on an axis, it is easy to make a transition to another mechanical power, the wheel and axis.
42. This instrument is a wheel fixed on a roller, the roller being supported at each extremity so as to turn round freely with the wheel, in the manner represented in fig. 34, where A B is the wheel, C D the roller, and E F its two supports. Now suppose a weight G hung by a cord wound round the roller, and another weight H hung by a cord wound about the wheel the contrary way: that these weights may support each other, the weight H must bear the same proportion to the weight G, as the thickness of the roller bears to the diameter of the wheel.
43. Suppose the line k l to be drawn through the middle of the roller; and from the place of the roller, where the cord, on which the weight G hangs, begins to leave the roller, as at m, let the line m n be drawn perpendicularly to k l; and from the point, where the cord holding the weight H begins to leave the wheel, as at o, let the line o p be drawn perpendicular to k l. This being done, the two lines o p and m n represent two arms of a lever fixed on the axis k l; consequently the weight H will bear to the weight G the same proportion, as m n bears to o p. But m n bears the same proportion to o p, as the thickness of the roller bears to the diameter of the wheel; for m n is half the thickness of the roller, and o p half the diameter of the wheel.
44. If the wheel be put into motion, and turned once round, that the cord, on which the weight G hangs, be wound once more round the axis; then at the same time the cord, whereon the weight H hangs, will be wound off from the wheel one circuit. Therefore the velocity of the weight G will bear the same proportion to the velocity of the weight H, as the circumference of the roller to the circumference of the wheel. But the circumference of the roller bears the same proportion to the circumference of the wheel, as the thickness of the roller bears to the diameter of the wheel, consequently the velocity of the weight G bears to the velocity of the weight H the same proportion, as the thickness of the roller bears to the diameter of the wheel, which is the proportion that the weight H bears to the weight G. Therefore as before in the lever, so here also the general rule laid[79] down above is verified, that the weights equiponderate, when their velocities would be reciprocally proportional to their respective weights.
45. In like manner, if on the same axis two wheels of different sizes are fixed (as in fig. 35.) and a weight hung on each; the weights will equiponderate, if the weight hung on the greater wheel bear the same proportion to the weight hung on the lesser, as the diameter of the lesser wheel bears to the diameter of the greater.
46. It is usual to join many wheels together in the same frame, which by the means of certain teeth, formed in the circumference of each wheel, shall communicate motion to each other. A machine of this nature is represented in fig. 36. Here A B C is a winch, upon which is fixed a small wheel D indented with teeth, which move in the like teeth of a larger wheel E F fixed on the axis G H. Let this axis carry another wheel I, which shall move in like manner a greater wheel K L fixed on the axis M N. Let this axis carry another small wheel O, which after the same manner shall turn about a larger wheel P Q fixed on the roller R S, on which a cord shall be wound, that holds a weight, as T. Now the proportion required between the weight T and a power applied to the winch at A sufficient to support the weight, will most easily be estimated, by computing the proportion, which the velocity of the point A would bear to the velocity of the weight. If the winch be turned round, the point A will describe a circle as A V. Suppose the wheel E F to have ten times the number of teeth, as[80] the wheel D; then the winch must turn round ten times to carry the wheel E F once round. If wheel K L has also ten times the number of teeth, as I, the wheel I must turn round ten times to carry the wheel K L once round; and consequently the winch A B C must turn round an hundred times to turn the wheel K L once round. Lastly, if the wheel P Q has ten times the number of teeth, as the wheel O, the winch must turn about one thousand times in order to turn the wheel P Q, or the roller R S once round. Therefore here the point A must have gone over the circle A V a thousand times, in order to lift the weight T through a space equal to the circumference of the roller R S: whence it follows, that the power applied at A will balance the weight T, if it bear the same proportion to it, as the circumference of the roller to one thousand times the circle A V; or the same proportion as half the thickness of the roller bears to one thousand times A B.
47. I shall now explain the effect of the pulley. Let a weight hang by a pulley, as in fig. 37. Here it is evident, that the power A, by which the weight B is supported, must be equal to the weight; for the cord C D is equally strained between them; and if the weight B move, the power A must move with equal velocity. The pulley E has no other effect, than to permit the power A to act in another direction, than it must have done, if it had been directly applied to support the weight without the intervention of any such instrument.
48. Again, let a weight be supported, as in fig. 38; where the weight A is fixed to the pulley B, and the cord, by[81] which the weight is upheld, is annexed by one extremity to a hook C, and at the other end is held by the power D. Here the weight is supported by a cord doubled; insomuch that although the cord were not strong enough to hold the weight single, yet being thus doubled it might support it. If the end of the cord held by the power D were hung on the hook C, as well as the other end; then, when both ends of the cord were tied to the hook, it is evident, that the hook would bear the whole weight; and each end of the string would bear against the hook with the force of half the weight only, seeing both ends together bear with the force of the whole. Hence it is evident, that, when the power D holds one end of the weight, the force, which it must exert to support the weight, must be equal to just half the weight. And the same proportion between the weight and power might be collected from comparing the respective velocities, with which they would move; for it is evident, that the power must move through a space equal to twice the distance of the pulley from the hook, in order to lift the pulley up to the hook.
49. It is equally easy to estimate the effect, when many pulleys are combined together, as in fig. 39, 40; in the first of which the under set of pulleys, and consequently the weight is held by six strings; and in the latter figure by five: therefore in the first of these figures the power to support the weight, must be one sixth part only of the weight, and in the latter figure the power must be one fifth part.
50. There are two other ways of supporting a weight by pulleys, which I shall particularly consider.
51. One of these ways is represented in fig. 41. Here the weight being connected to the pulley B, a power equal to half the weight A would support the pulley C, if applied immediately to it. Therefore the pulley C is drawn down with a force equal to half the weight A. But if the pulley D were to be immediately supported by half the force, with which the pulley C is drawn down, this pulley D will uphold the pulley C; so that if the pulley D be upheld with a force equal to one fourth part of the weight A, that force will support the weight. But, for the same reason as before, if the power in E be equal to half the force necessary to uphold the pulley D; this pulley, and consequently the weight A, will be upheld: therefore, if the power in E be one eighth part of the weight A, it will support the weight.
52. Another way of applying pulleys to a weight is represented in fig. 42. To explain the effect of pulleys thus applied, it will be proper to consider different weights hanging, as in fig. 43. Here, if the power and weights balance each other, the power A is equal to the weight B; the weight C is equal to twice the power A, or the weight B; and for the same reason the weight D is equal to twice the weight C, or equal to four times the power A. It is evident therefore, that all the three weights B, C, D together are equal to seven times the power A. But if these three weights were joined in one, they would produce the case of fig. 40: so that in that figure the[83] weight A, where there are three pulleys, is seven times the power B. If there had been but two pulleys, the weight would have been three times the power; and if there had been four pulleys, the weight would have been fifteen times the power.
53. The wedge is next to be considered. The form of this instrument is sufficiently known. When it is put under any weight (as in fig. 44.) the force, with which the wedge will lift the weight, when drove under it by a blow upon the end A B, will bear the same proportion to the force, wherewith the blow would act on the weight, if directly applied to it; as the velocity, which the wedge receives from the blow, bears to the velocity, wherewith the weight is lifted by the wedge.
54. The screw is the fifth mechanical power. There are two ways of applying this instrument. Sometimes it is screwed into a hole, as in fig. 45, where the screw A B is screwed through the plank C D. Sometimes the screw is applied to the teeth of a wheel, as in fig. 46, where the thread of the screw A B turns in the teeth of a wheel C D. In both these cases, if a bar, as A E, be fixed to the end A of the screw; the force, wherewith the end B of the screw in fig. 45 is forced down, and the force, wherewith the teeth of the wheel C D in fig. 44 are held, bears the same proportion to the power applied to the end E of the bar; as the velocity, wherewith the end E will move, when the screw is turned, bears to the velocity, wherewith the end B of the screw in fig. 43, or the teeth of the wheel C D in fig. 46, will be moved.
55. The inclined plane affords also a means of raising a weight with less force, than what is equal to the weight it self. Suppose it were required to raise the globe A (in fig. 47.) from the ground B C up to the point, whose perpendicular height from the ground is E D. If this globe be drawn along the slant D F, less force will be required to raise it, than if it were lifted directly up. Here if the force applied to the globe bear the same proportion only to its weight, as E D bears to F D, it will be sufficient to hold up the globe; and therefore any addition to that force will put it in motion, and draw it up; unless the globe, by pressing against the plane, whereon it lies, adhere in some degree to the plane. This indeed it must always do more or less, since no plane can be made so absolutely smooth as to have no inequalities at all; nor yet so infinitely hard, as not to yield in the least to the pressure of the weight. Therefore the globe cannot be laid on such a plane, whereon it will slide with perfect freedom, but they must in some measure rub against each other; and this friction will make it necessary to imploy a certain degree of force more, than what is necessary to support the globe, in order to give it any motion. But as all the mechanical powers are subject in some degree or other to the like impediment from friction; I shall here only shew what force would be necessary to sustain the globe, if it could lie upon the plane without causing any friction at all. And I say, that if the globe were drawn by the cord G H, lying parallel to the plane D F; and the force, wherewith the cord is pulled, bear the same proportion to the weight of the globe, as E D bears to D F;[85] this force will sustain the globe. In order to the making proof of this, let the cord G H be continued on, and turned over the pulley I, and let the weight K be hung to it. Now I say, if this weight bears the same proportion to the globe A, as D E bears to D F, the weight will support the globe. I think it is very manifest, that the center of the globe A will lie in one continued line with the cord H G. Let L be the center of the globe, and M the center of gravity of the weight K. In the first place let the weight hang so, that a line drawn from L to M shall lie horizontally; and I say, if the globe be moved either up or down the plane D F, the weight will so move along with it, that the center of gravity common to both the weights shall continue in this line L M, and therefore shall in no case descend. To prove this more fully, I shall depart a little from the method of this treatise, and make use of a mathematical proportion or two: but they are such, as any person, who has read Euclid’s Elements, will fully comprehend; and are in themselves so evident, that, I believe, my readers, who are wholly strangers to geometrical writings, will make no difficulty of admitting them. This being premised, let the globe be moved up, till its center be at G, then will M the center of gravity of the weight K be sunk to N; so that M N shall be equal to G L. Draw N G crossing the line M L in O; then I say, that O is the common center of gravity of the two weights in this their new situation. Let G P be drawn perpendicular to M L; then G L will bear the same proportion to G P, as D F bears to D E; and M N being equal to G L, M N will bear the same proportion[86] to G P, as D F bears to D E. But N O bears the same proportion to O G, as M N bears to G P; consequently N O will bear the same proportion to O G, as D F bears to D E. In the last place, the weight of the globe A bears the same proportion to the other weight K, as D F bears to D E; therefore N O bears the same proportion to O G, as the weight of the globe A bears to the weight K. Whence it follows, that, when the center of the globe A is in G, and the center of gravity of the weight K is in N, O will be the center of gravity common to both the weights. After the same manner, if the globe had been caused to descend, the common center of gravity would have been found in this line M L. Since therefore no motion of the globe either way will make the common center of gravity descend, it is manifest, from what has been said above, that the weights A and K counterpoize each other.
56. I shall now consider the case of pendulums. A pendulum is made by hanging a weight to a line, so that it may swing backwards and forwards. This motion the geometers have very carefully considered, because it is the most commodious instrument of any for the exact measurement of time.
57. I have observed already[61], that if a body hanging perpendicularly by a string, as the body A (in fig. 48.) hangs by the string A B, be put so into motion, as to be made to ascend up the circular arch A C; then as soon as it has arrived[87] at the highest point, to which the motion, that the body has received, will carry it; it will immediately begin to descend, and at A will receive again as great a degree of motion, as it had at first. This motion therefore will carry the body up the arch A D, as high as it ascended before in the arch A C. Consequently in its return through the arch D A it will acquire again at A its original velocity, and advance a second time up the arch A C as high as at first; by this means continuing without end its reciprocal motion. It is true indeed, that in fact every pendulum, which we can put in motion, will gradually lessen its swing, and at length stop, unless there be some power constantly applied to it, whereby its motion shall be renewed; but this arises from the resistance, which the body meets with both from the air, and the string by which it is hung: for as the air will give some obstruction to the progress of the body moving through it; so also the string, whereon the body hangs, will be a farther impediment; for this string must either slide on the pin, whereon it hangs, or it must bend to the motion of the weight; in the first there must be some degree of friction, and in the latter the string will make some resistance to its inflection. However, if all resistance could be removed, the motion of a pendulum would be perpetual.
58. But to proceed, the first property, I shall take notice of in this motion, is, that the greater arch the pendulous body moves through, the greater time it takes up: though the length of time does not increase in so great a proportion as the arch. Thus if C D be a greater arch, and E F a lesser, where C A is equal to A D, and E A equal to A F; the body,[88] when it swings through the greater arch C D, shall take up in its swing from C to D a longer time than in swinging from E to F, when it moves only in that lesser arch; or the time in which the body let fall from C will descend through the arch C A is greater than the time, in which it will descend through the arch E A, when let fall from E. But the first of these times will not hold the same proportion to the latter, as the first arch C A bears to the other arch E A; which will appear thus. Let C G and E H be two horizontal lines. It has been remarked above[62], that the body in falling through the arch C A will acquire as great a velocity at the point A, as it would have gained by falling directly down through G A; and in falling through the arch E A it will acquire in the point A only that velocity, which it would have got in falling through H A. Therefore, when the body descends through the greater arch C A, it shall gain a greater velocity, than when it passes only through the lesser; so that this greater velocity will in some degree compensate the greater length of the arch.
59. The increase of velocity, which the body acquires in falling from a greater height, has such an effect, that, if straight lines be drawn from A to C and E, the body would fall through the longer straight line C A just in the same time, as through the shorter straight line E A. This is demonstrated by the geometers, who prove, that if any circle, as A B C D (fig. 49.) be placed in a perpendicular situation; a body shall fall obliquely through every line, as A B drawn from the lowest point A in the circle to any other point in the circumference[89] just in the same time, as would be imployed by the body in falling perpendicularly down through the diameter C A. But the time in which the body will descend through the arch, is different from the time, which it would take up in falling through the line A B.
60. It has been thought by some, that because in very small arches this correspondent straight line differs but little from the arch itself; therefore the descent through this straight line would be performed in such small arches nearly in the same time as through the arches themselves: so that if a pendulum were to swing in small arches, half the time of a single swing would be nearly equal to the time, in which a body would fall perpendicularly through twice the length of the pendulum. That is, the whole time of the swing, according to this opinion, will be four fold the time required for the body to fall through half the length of the pendulum; because the time of the body’s falling down twice the length of the pendulum is half the time required for the fall through one quarter of this space, that is through half the pendulum’s length. However there is here a mistake; for the whole time of the swing, when the pendulum moves through small arches, bears to the time required for a body to fall down through half the length of the pendulum very nearly the same proportion, as the circumference of a circle bears to its diameter; that is very nearly the proportion of 355 to 113, or little more than the proportion of 3 to 1. If the pendulum takes so great a swing, as to pass over an arch equal to one sixth part of the whole circumference of the[90] circle, it will swing 115 times, while it ought according to this proportion to have swung 117 times; so that, when it swings in so large an arch, it loses something less than two swings in an hundred. If it swing through 1/10 only of the circle, it shall not lose above one vibration in 160. If it swing in 1/20 of the circle, it shall lose about one vibration in 690. If its swing be confined to 1/40 of the whole circle, it shall lose very little more than one swing in 2600. And if it take no greater a swing than through 1/60 of the whole circle, it shall not lose one swing in 5800.
61. Now it follows from hence, that, when pendulums swing in small arches, there is very nearly a constant proportion observed between the time of their swing, and the time, in which a body would fall perpendicularly down through half their length. And we have declared above, that the spaces, through which bodies fall, are in a two fold proportion of the times, which they take up in falling[63]. Therefore in pendulums of different lengths, swinging through small arches, the lengths of the pendulums are in a two fold or duplicate proportion of the times, they take in swinging; so that a pendulum of four times the length of another shall take up twice the time in each swing, one of nine times the length will make one swing only for three swings of the shorter, and so on.
62. This proportion in the swings of different pendulums not only holds in small arches; but in large ones also,[91] provided they be such, as the geometers call similar; that is, if the arches bear the same proportion to the whole circumferences of their respective circles. Suppose (in fig. 48.) A B, C D to be two pendulums. Let the arch E F be described by the motion of the pendulum A B, and the arch G H be described by the pendulum C D; and let the arch E F bear the same proportion to the whole circumference, which would be formed by turning the pendulum A B quite round about the point A, as the arch G H bears to the whole circumference, that would be formed by turning the pendulum C D quite round the point C. Then I say, the proportion, which the length of the pendulum A B bears to the length of the pendulum C D, will be two fold of the proportion, which the time taken up in the description of the arch E F bears to the time employed in the description of the arch G H.
63. Thus pendulums, which swing in very small arches, are nearly an equal measure of time. But as they are not such an equal measure to geometrical exactness; the mathematicians have found out a method of causing a pendulum so to swing, that, if its motion were not obstructed by any resistance, it would always perform each swing in the same time, whether it moved through a greater, or a lesser space. This was first discovered by the great Huygens, and is as follows. Upon the straight line A B (in fig. 49.) let the circle C D E be so placed, as to touch the straight line in the point C. Then let this circle roll along upon the straight line A B, as a coach-wheel rolls along upon the ground. It is evident, that, as[92] soon as ever the circle begins to move, the point C in the circle will be lifted off from the straight line A B; and in the motion of the circle will describe a crooked course, which is represented by the line C F G H. Here the part C H of the straight line included between the two extremities C and H of the line C F G H will be equal to the whole circumference of the circle C D E; and if C H be divided into two equal parts at the point I, and the straight line I K be drawn perpendicular to C H, this line I K will be equal to the diameter of the circle C D E. Now in this line if a body were to be let fall from the point H, and were to be carried by its weight down the line H G K, as far as the point K, which is the lowest point of the line C F G H; and if from any other point G a body were to be let fall in the same manner; this body, which falls from G, will take just the same time in coming to K, as the body takes up, which falls from H. Therefore if a pendulum can be so hung, that the ball shall move in the line A G F E, all its swings, whether long or short, will be performed in the same time; for the time, in which the ball will descend to the point K, is always half the time of the whole swing. But the ball of a pendulum will be made to swing in this line by the following means. Let K I (in fig. 52.) be prolonged upwards to L, till I L is equal to I K. Then let the line L M H equal and like to K H be applied, as in the figure between the points L and H, so that the point which in this line L M H answers to the point H in the line K H shall be applied to the point L, and the point answering to the point K shall be applied to the point H. Also let such another line L N C be applied between L and C in the same[93] manner. This preparation being made; if a pendulum be hung at the point L of such a length, that the ball thereof shall reach to K; and if the string shall continually bend against the lines H M L and L N C, as the pendulum swings to and fro; by this means the ball shall constantly keep in the line C K H.
64. Now in this pendulum, as all the swings, whether long or short, will be performed in the same time; so the time of each will exactly bear the same proportion to the time required for a body to fall perpendicularly down, through half the length of the pendulum, that is from I to K, as the circumference of a circle bears to its diameter.
65. It may from hence be understood in some measure, why, when pendulums swing in circular arches, the times of their swings are nearly equal, if the arches are small, though those arches be of very unequal lengths; for if with the semidiameter L K the circular arch O K P be described, this arch in the lower part of it will differ very little from the line C K H.
66. It may not be amiss here to remark, that a body will fall in this line C K H (fig. 53.) from C to any other point, as Q or R in a shorter space of time, than if it moved through the straight line drawn from C to the other point; or through any other line whatever, that can be drawn between these two points.
67. But as I have observed, that the time, which a pendulum takes in swinging, depends upon its length; I shall now say something concerning the way, in which this length of the pendulum is to be estimated. If the whole ball of the pendulum could be crouded into one point, this length, by which the motion of the pendulum is to be computed, would be the length of the string or rod. But the ball of the pendulum must have a sensible magnitude, and the several parts of this ball will not move with the same degree of swiftness; for those parts, which are farthest from the point, whereon the pendulum is suspended, must move with the greatest velocity. Therefore to know the time in which the pendulum swings, it is necessary to find that point of the ball, which moves with the same degree of velocity, as if the whole ball were to be contracted into that point.
68. This point is not the center of gravity, as I shall now endeavour to shew. Suppose the pendulum A B (in fig. 54.) composed of an inflexible rod A C and ball C B, to be fixed on the point A, and lifted up into an horizontal situation. Here if the rod were not fixed to the point A, the body C B would descend directly with the whole force of its weight; and each part of the body would move down with the same degree of swiftness. But when the rod is fixed at the point A, the body must fall after another manner; for the parts of the body must move with different degrees of velocity, the parts more remote from A descending with a swifter motion, than the parts nearer to A; so that the body will receive a kind of rolling motion while it descends. But it has been observed above, that the effect of gravity upon any body is the same, as if the whole force were exerted on the body’s center of gravity[64].
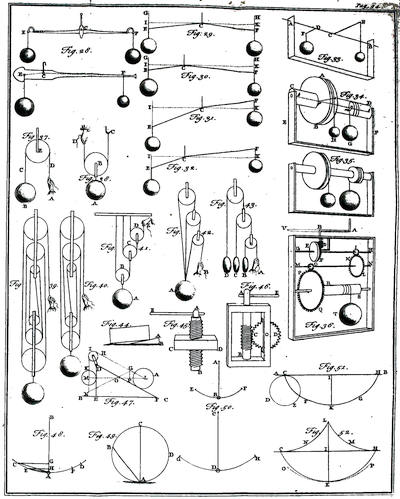
Since therefore the power of gravity in drawing down the body must also communicate to it the rolling motion just described; it seems evident, that the center of gravity of the body cannot be drawn down as swiftly, as when the power of gravity has no other effect to produce on the body, than merely to draw it downward. If therefore the whole matter of the body C B could be crouded into its center of gravity, so that being united into one point, this rolling motion here mentioned might give no hindrance to its descent; this center would descend faster, than it can now do. And the point, which now descends as fast, as if the whole matter or the body C B were crouded into it, will be farther removed from the point A, than the center of gravity of the body C B.
69. Again, suppose the pendulum A B (in fig. 55.) to hang obliquely. Here the power of gravity will operate less upon the ball of the pendulum, than before: but the line D E being drawn so, as to stand perpendicular to the rod A C of the pendulum; the force of gravity upon the body C B, now it is in this situation, will produce the same effect, as if the body were to glide down an inclined plane in the position of D E. But here the motion of the body, when the rod is fixed to the point A, will not be equal to the uninterrupted descent of the body down this plane; for the body[96] will here also receive the same kind of rotation in its motion, as before; so that the motion of the center of gravity will in like manner be retarded; and the point, which here descends with that degree of swiftness, which the body would have, if not hindered by being fixed to the point A; that is, the point, which descends as fast, as if the whole body were crouded into it, will be as far removed from the point A, as before.
70. This point, by which the length of the pendulum is to be estimated, is called the center of oscillation. And the mathematicians have laid down general directions, whereby to find this center in all bodies. If the globe A B (in fig. 56.) be hung by the string C D, whose weight need not be regarded, the center of oscillation is found thus. Let the straight line drawn from C to D be continued through the globe to F. That it will pass through the center of the globe is evident. Suppose E to be this center of the globe; and take the line G of such a length, that it shall bear the same proportion to E D, as E D bears to E C. Then E H being made equal to ⅖ of G, the point H shall be the center of oscillation[65]. If the weight of the rod C D is too considerable to be neglected, divide C D (fig. 57) in I, that D I be equal to ⅓, part of C D; and take K in the same proportion to C I, as the weight of the globe A B to the weight of the rod C D. Then having found H, the center of oscillation of the globe, as before, divide I K in I, so that I L shall bear the same proportion[97] to L H, as the line C H bears to K; and L shall be the center of oscillation of the whole pendulum.
71. This computation is made upon supposition, that the center of oscillation of the rod C D, if that were to swing alone without any other weight annexed, would be the point I. And this point would be the true center of oscillation, so far as the thickness of the rod is not to be regarded. If any one chuses to take into consideration the thickness of the rod, he must place the center of oscillation thereof so much below the point I, that eight times the distance of the center from the point I shall bear the same proportion to the thickness of the rod, as the thickness of the rod bears to its length C D[66].
72. It has been observed above, that when a pendulum swings in an arch of a circle, as here in fig. 58, the pendulum A B swings in the circular arch C D; if you draw an horizontal line, as E F, from the place whence the pendulum is let fall, to the line A G, which is perpendicular to the horizon: then the velocity, which the pendulum will acquire in coming to the point G, will be the same, as any body would acquire in falling directly down from F to G. Now this is to be understood of the circular arch, which is described by the center of oscillation of the pendulum. I shall here farther observe, that if the straight line E G be drawn from the point, whence the pendulum falls, to the lowest point of the arch; in the same or in equal pendulums the velocity, which the[98] pendulum acquires in G, is proportional to this line: that is, if the pendulum, after it has descended from E to G, be taken back to H, and let fall from thence, and the line H G be drawn; the velocity, which the pendulum shall acquire in G by its descent from H, shall bear the same proportion to the velocity, which it acquires in falling from E to G, as the straight line H G bears to the straight line E G.
73. We may now proceed to those experiments upon the percussion of bodies, which I observed above might be made with pendulums. This expedient for examining the effects of percussion was first proposed by our late great architect Sir Christopher Wren. And it is as follows. Two balls, as A and B (in fig. 59.) either equal or unequal, are hung by two strings from two points C and D, so that, when the balls hang down without motion, they shall just touch each other, and the strings be parallel. Here if one of these balls be removed to any distance from its perpendicular situation, and then let fall to descend and strike against the other; by the last preceding paragraph it will be known, with what velocity this ball shall return into its first perpendicular situation, and consequently with what force it shall strike against the other ball; and by the height to which this other ball ascends after the stroke, the velocity communicated to this ball will be discovered. For instance, let the ball A be taken up to E, and from thence be let fall to strike against B, passing over in its descent the circular arch E F. By this impulse let B fly up to G, moving through the circular arch H G. Then E I and G K being drawn horizontally,[99] the ball A will strike against B with the velocity, which it would acquire in falling directly down from I; and the ball B has received a velocity, wherewith, if it had been thrown directly upward, it would have ascended up to K. Likewise if straight lines be drawn from E to F and from H to G, the velocity of A, wherewith it strikes, will bear the same proportion to the velocity, which B has received by the blow, as the straight line E F bears to the straight line H G. In the same manner by noting the place to which A ascends after the stroke, its remaining velocity may be compared with that, wherewith it struck against B. Thus may be experimented the effects of the body A striking against B at rest. If both the bodies are lifted up, and so let fall as to meet and impinge against each other just upon the coming of both into their perpendicular situation; by observing the places into which they move after the stroke, the effects of their percussion in all these cases may be found in the same manner as before.
74. Sir Isaac Newton has described these experiments; and has shewn how to improve them to a greater exactness by making allowance for the resistance, which the air gives to the motion of the balls[67]. But as this resistance is exceeding small, and the manner of allowing for it is delivered by himself in very plain terms, I need not enlarge upon it here. I shall rather speak to a discovery, which he made by these experiments upon the elasticity of bodies. It has been explained above[68], that when two bodies strike, if they be not elastic,[100] they remain contiguous after the stroke; but that if they are elastic, they separate, and that the degree of their elasticity determines the proportion between the celerity wherewith they separate, and the celerity wherewith they meet. Now our author found, that the degree of elasticity appeared in the same bodies always the same, with whatever degree of force they struck; that is, the celerity wherewith they separated, always bore the same proportion to the celerity wherewith they met: so that the elastic power in all the bodies, he made trial upon, exerted it self in one constant proportion to the compressing force. Our author made trial with balls of wool bound up very compact, and found the celerity with which they receded, to bear about the proportion of 5 to 9 to the celerity wherewith they met; and in steel he found nearly the same proportion; in cork the elasticity was something less; but in glass much greater; for the celerity, wherewith balls of that material separated after percussion, he found to bear the proportion of 15 to 16 to the celerity wherewith they met[69].
75. I shall finish my discourse on pendulums, with this farther observation only, that the center of oscillation is also the center of another force. If a body be fixed to any point, and being put in motion turns round it; the body, if uninterrupted by the power of gravity or any other means, will continue perpetually to move about with the same equable motion. Now the force, with which such a body[101] moves, is all united in the point, which in relation to the power of gravity is called the center of oscillation. Let the cylinder A B C D (in fig. 60.) whose axis is E F, be fixed to the point E. And supposing the point E to be that on which the cylinder is suspended, let the center of oscillation be found in the axis E F, as has been explained above[70]. Let G be that center: then I say, that the force, wherewith this cylinder turns round the point E, is so united in the point G, that a sufficient force applied in that point shall stop the motion of the cylinder, in such a manner, that the cylinder should immediately remain without motion, though it were to be loosened from the point E at the same instant, that the impediment was applied to G: whereas, if this impediment had been applied to any other point of the axis, the cylinder would turn upon the point, where the impediment was applied. If the impediment had been applied between E and G, the cylinder would so turn on the point, where the impediment was applied, that the end B C would continue to move on the same way it moved before along with the whole cylinder; but if the impediment were applied to the axis farther off from E than G, the end A D of the cylinder would start out of its present place that way in which the cylinder moved. From this property of the center of oscillation, it is also called the center of percussion. That excellent mathematician, Dr. Brook Taylor, has farther improved this doctrine concerning the center of percussion, by shewing, that if through this point G a line, as G H I, be drawn perpendicular to E F, and lying[102] in the course of the body’s motion; a sufficient power applied to any point of this line will have the same effect, as the like power applied to G[71]: so that as we before shewed the center of percussion within the body on its axis; by this means we may find this center on the surface of the body also, for it will be where this line H I crosses that surface.
76. I shall now proceed to the last kind of motion, to be treated on in this place, and shew what line the power of gravity will cause a body to describe, when it is thrown forwards by any force. This was first discovered by the great Galileo, and is the principle, upon which engineers should direct the shot of great guns. But as in this case bodies describe in their motion one of those lines, which in geometry are called conic sections; it is necessary here to premise a description of those lines. In which I shall be the more particular, because the knowledge of them is not only necessary for the present purpose, but will be also required hereafter in some of the principal parts of this treatise.
77. The first lines considered by the ancient geometers were the straight line and the circle. Of these they composed various figures, of which they demonstrated many properties, and resolved divers problems concerning them. These problems they attempted always to resolve by the describing straight lines and circles. For instance, let a square A B C D (fig. 61.) be proposed, and let it be required to make another[103] square in any assigned proportion to this. Prolong one side, as D A, of this square to E, till A E bear the same proportion to A D, as the new square is to bear to the square A C. If the opposite side B C of the square A C be also prolonged to F, till B F be equal to A E, and E F be afterwards drawn, I suppose my readers will easily conceive, that the figure A B F E will bear to the square A B C D the same proportion, as the line A E bears to the line A D. Therefore the figure A B F E will be equal to the new square, which is to be found, but is not it self a square, because the side A E is not of the same length with the side E F. But to find a square equal to the figure A B F E you must proceed thus. Divide the line D E into two equal parts in the point G, and to the center G with the interval G D describe the circle D H E I; then prolong the line A B, till it meets the circle in K; and make the square A K L M, which square will be equal to the figure A B F E, and bear to the square A B C D the same proportion, as the line A E bears to A D.
78. I shall not proceed to the proof of this, having only here set it down as a specimen of the method of resolving geometrical problems by the description of straight lines and circles. But there are some problems, which cannot be resolved by drawing straight lines or circles upon a plane. For the management therefore of these they took into consideration solid figures, and of the solid figures they found that, which is called a cone, to be the most useful.
79. A cone is thus defined by Euclide in his elements of geometry[72]. If to the straight line A B (in fig. 62.) another straight line, as A C, be drawn perpendicular, and the two extremities B and C be joined by a third straight line composing the triangle A C B (for so every figure is called, which is included under three straight lines) then the two points A and B being held fixed, as two centers, and the triangle A C B being turned round upon the line A B, as on an axis; the line A C will describe a circle, and the figure A C B will describe a cone, of the form represented by the figure B C D E F (fig. 63.) in which the circle C D E F is usually called the base of the cone, and B the vertex.
80. Now by this figure may several problems be resolved, which cannot by the simple description of straight lines and circles upon a plane. Suppose for instance, it were required to make a cube, which should bear any assigned proportion to some other cube named. I need not here inform my readers, that a cube is the figure of a dye. This problem was much celebrated among the ancients, and was once inforced by the command of an oracle. This problem may be performed by a cone thus. First make a cone from a triangle, whose side A C shall be half the length of the side B C Then on the plane A B C D (fig. 64.) let the line E F be exhibited equal in length to the side of the cube proposed; and let the line F G be drawn perpendicular to E F, and of such a length, that it bear the same proportion to E F, as the[105] cube to be sought is required to bear to the cube proposed. Through the points E, F, and G let the circle F H I be described. Then let the line E F be prolonged beyond F to K, that F K be equal to F E, and let the triangle F K L, having all its sides F K, K L, L F equal to each other, be hung down perpendicularly from the plane A B C D. After this, let another plane M N O P be extended through the point L, so as to be equidistant from the former plane A B C D, and in this plane let the line Q L R be drawn so, as to be equidistant from the line E F K. All this being thus prepared, let such a cone, as was above directed to be made, be so applied to the plane M N O P, that it touch this plane upon the line Q R, and that the vertex of the cone be applied to the point L. This cone, by cutting through the first plane A B C D, will cross the circle F H I before described. And if from the point S, where the surface of this cone intersects the circle, the line S T be drawn so, as to be equidistant from the line E F; the line F T will be equal to the side of the cube sought: that is, if there be two cubes or dyes formed, the side of one being equal to E F, and the side of the other equal to F T; the former of these cubes shall bear the same proportion to the latter, as the line E F bears to F G.
81. Indeed this placing a cone to cut through a plane is not a practicable method of resolving problems. But when the geometers had discovered this use of the cone, they applied themselves to consider the nature of the lines, which will be produced by the intersection of the surface of a cone[106] and a plane; whereby they might be enabled both to reduce these kinds of solutions to practice, and also to render their demonstrations concise and elegant.
82. Whenever the plane, which cuts the cone, is equidistant from another plane, that touches the cone on the side; (which is the case of the present figure;) the line, wherein the plane cuts the surface of the cone, is called a parabola. But if the plane, which cuts the cone, be so inclined to this other, that it will pass quite through the cone (as in fig. 65.) such a plane by cutting the cone produces the figure called an ellipsis, in which we shall hereafter shew the earth and other planets to move round the sun. If the plane, which cuts the cone, recline the other way (as in fig. 66.) so as not to be parallel to any plane, whereon the cone can lie, nor yet to cut quite through the cone; such a plane shall produce in the cone a third kind of line, which is called an hyperbola. But it is the first of these lines named the parabola, wherein bodies, that are thrown obliquely, will be carried by the force of gravity; as I shall here proceed to shew, after having first directed my readers how to describe this sort of line upon a plane, by which the form of it may be seen.
83. To any straight line A B (fig. 67.) let a straight ruler C D be so applied, as to stand against it perpendicularly. Upon the edge of this ruler let another ruler E F be so placed, as to move along upon the edge of the first ruler C D, and keep always perpendicular to it. This being so disposed, let any point, as G, be taken in the line A B, and let a string equal[107] in length to the ruler E F be fastened by one end to the point G, and by the other to the extremity F of the ruler E F. Then if the string be held down to the ruler E F by a pin H, as is represented in the figure; the point of this pin, while the ruler E F moves on the ruler C D, shall describe the line I K L, which will be one part of the curve line, whose description we were here to teach: and by applying the rulers in the like manner on the other side of the line A B, we may describe the other part I M of this line. If the distance C G be equal to half the line E F in fig. 64, the line M I L will be that very line, wherein the plane A B C D in that figure cuts the cone.
84. The line A I is called the axis of the parabola M I L, and the point G is called the focus.
85. Now by comparing the effects of gravity upon falling bodies, with what is demonstrated of this figure by the geometers, it is proved, that every body thrown obliquely is carried forward in one of these lines, the axis whereof is perpendicular to the horizon.
86. The geometers demonstrate, that if a line be drawn to touch a parabola in any point, as the line A B (in fig. 68.) touches the parabola C D, whose axis is Y Z, in the point E; and several lines F G, H I, K L be drawn parallel to the axis of the parabola: then the line F G will be to H I in the duplicate proportion of E F to E H, and F G to K L in the duplicate proportion of E F to E K; likewise H I to K L in the duplicate proportion of E H to E K. What is to be understood by duplicate or two-fold[108] proportion, has been already explained[73]. Accordingly I mean here, that if the line M be taken to bear the same proportion to E H, as E H bears to E F, H I will bear the same proportion to F G, as M bears to E F; and if the line N bears the same proportion to E K, as E K bears to E F, K L will bear the same proportion to F G, as N bears to E F; or if the line O bear the same proportion to E K, as E K bears to E H, K L will bear the same proportion to H I, as O bears to E H.
87. This property is essential to the parabola, being so connected with the nature of the figure, that every line possessing this property is to be called by this name.
88. Now suppose a body to be thrown from the point A (in fig. 69.) towards B in the direction of the line A B. This body, if left to it self, would move on with a uniform motion through this line A B. Suppose the eye of a spectator to be placed at the point C just under the point A; and let us imagine the earth to be so put into motion along with the body, as to carry the spectator’s eye along the line C D parallel to A B; and that the eye would move on with the same velocity, wherewith the body would proceed in the line A B, if it were to be left to move without any disturbance from its gravitation towards the earth. In this case if the body moved on without being drawn towards the earth, it would appear to the spectator to be at rest. But if the power of gravity exerted it self on the body, it would appear to the spectator[109] to fall directly down. Suppose at the distance of time, wherein the body by its own progressive motion would have moved from A to E, it should appear to the spectator to have fallen through a length equal to E F: then the body at the end of this time will actually have arrived at the point F. If in the space of time, wherein the body would have moved by its progressive motion from A to G, it would have appeared to the spectator to have fallen down the space G H: then the body at the end of this greater interval of time will be arrived at the point H. Now if the line A F H I be that, through which the body actually passes; from what has here been said, it will follow, that this line is one of those, which I have been describing under the name of the parabola. For the distances E F, G H, through which the body is seen to fall, will increase in the duplicate proportion of the times[74]; but the lines A E, A G will be proportional to the times wherein they would have been described by the single progressive motion of the body: therefore the lines E F, G H will be in the duplicate proportion of the lines A F, A G; and the line A F H I possesses the property of the parabola.
89. If the earth be not supposed to move along with the body, the case will be a little different. For the body being constantly drawn directly towards the center of the earth, the body in its motion will be drawn in a direction a little oblique to that, wherein it would be drawn by the earth in motion, as before supposed. But the distance to the center of the[110] earth bears so vast a proportion to the greatest length, to which we can throw bodies, that this obliquity does not merit any regard. From the sequel of this discourse it may indeed be collected, what line the body being thrown thus would be found to describe, allowance being made for this obliquity of the earth’s action[75]. This is the discovery of Sir Is. Newton; but has no use in this place. Here it is abundantly sufficient to consider the body as moving in a parabola.
90. The line, which a projected body describes, being thus known, practical methods have been deduced from hence for directing the shot of great guns to strike any object desired. This work was first attempted by Galileo, and soon after farther improved by his scholar Torricelli; but has lately been rendred more complete by the great Mr. Cotes, whose immature death is an unspeakable loss to mathematical learning. If it be required to throw a body from the point A (in fig. 70.) so as to strike the point B; through the points A, B draw the straight line C D, and erect the line A E perpendicular to the horizon, and of four times the height, from which a body must fall to acquire the velocity, wherewith the body is intended to be thrown. Through the points A and E describe a circle, that shall touch the line C D in the point A. Then from the point B draw the line B F perpendicular to the horizon, intersecting the circle in the points G and H. This being done, if the body be projected directly towards either of these points G or H, it shall fall upon the point B; but with this difference, that, if it be thrown[111] in the direction A G, it shall sooner arrive at B, than if it were projected in the direction A H. When the body is projected in the direction A G; the time, it will take up in arriving at B, will bear the same proportion to the time, wherein it would fall down through one fourth part of A E, as A G bears to half A E. But when the body is thrown in the direction of A H, the time of its passing to B will bear the same proportion to the time, wherein it would fall through one fourth part of A E, as A H bears to half A E.
91. If the line A I be drawn so as to divide the angle under E A D in the middle, and the line I K be drawn perpendicular to the horizon; this line will touch the circle in the point I, and if the body be thrown in the direction A I, it will fall upon the point K: and this point K is the farthest point in the line A D, which the body can be made to strike, without increasing its velocity.
92. The velocity, wherewith the body every where moves, may be found thus. Suppose the body to move in the parabola A B (fig. 71.) Erect A C perpendicular to the horizon, and equal to the height, from which a body must fall to acquire the velocity, wherewith the body sets out from A. If you take any points as D and E in the parabola, and draw D F and E G parallel to the horizon; the velocity of the body in D will be equal to what a body will acquire in falling down by its own weight through C F, and in E the velocity will be the same, as would be acquired in falling through C G. Thus the body moves slowest at the highest point H of the parabola; and at equal distances from this point will[112] move with equal swiftness, and descend from that highest point through the line H B altogether like to the line A H in which it ascended; abating only the resistance of the air, which is not here considered. If the line H I be drawn from the highest point H parallel to the horizon, A I will be equal to ¼ of B G in fig. 70, when the body is projected in the direction A G, and equal to ¼ of B H, when the body is thrown in the direction A H provided A D be drawn horizontally.
93. Thus I have recounted the principal discoveries, which had been made concerning the motion of bodies by Sir Isaac Newton’s predecessors; all these discoveries, by being found to agree with experience, contributing to establish the laws of motion, from whence they were deduced. I shall therefore here finish what I had to say upon those laws; and conclude this chapter with a few words concerning the distinction which ought to be made between absolute and relative motion. For some have thought fit to confound them together; because they observe the laws of motion to take place here on the earth, which is in motion, after the same manner as if it were at rest. But Sir Isaac Newton has been careful to distinguish between the relative and absolute consideration both of motion and time[76]. The astronomers anciently found it necessary to make this distinction in time. Time considered in it self passes on equably without relation to any thing external, being the proper measure of the continuance and duration of all things. But it is most frequently conceived of by us under a relative view to some succession in[113] sensible things, of which we take cognizance. The succession of the thoughts in our own minds is that, from whence we receive our first idea of time, but is a very uncertain measure thereof; for the thoughts of some men flow on much more swiftly, than the thoughts of others; nor does the same person think equally quick at all times. The motions of the heavenly bodies are more regular; and the eminent division of time into night and day, made by the sun, leads us to measure our time by the motion of that luminary: nor do we in the affairs of life concern our selves with any inequality, which there may be in that motion; but the space of time which comprehends a day and night is rather supposed to be always the same. However astronomers anciently found these spaces of time not to be always of the same length, and have taught how to compute their differences. Now the time, when so equated as to be rendered perfectly equal, is the true measure of duration, the other not. And therefore this latter, which is absolutely true time, differs from the other, which is only apparent. And as we ordinarily make no distinction between apparent time, as measured by the sun, and the true; so we often do not distinguish in our usual discourse between the real, and the apparent or relative motion of bodies; but use the same words for one, as we should for the other. Though all things about us are really in motion with the earth; as this motion is not visible, we speak of the motion of every thing we see, as if our selves and the earth stood still. And even in other cases, where we discern the motion of bodies, we often speak of them not in relation to the whole motion we see, but with regard to other[114] bodies, to which they are contiguous. If any body were lying on a table; when that table shall be carried along, we say the body rests upon the table, or perhaps absolutely, that the body is at rest. However philosophers must not reject all distinction between true and apparent motions, any more than astronomers do the distinction between true and vulgar time; for there is as real a difference between them, as will appear by the following consideration. Suppose all the bodies of the universe to have their courses stopped, and reduced to perfect rest. Then suppose their present motions to be again restored; this cannot be done without an actual impression made upon some of them at least. If any of them be left untouched, they will retain their former state, that is, still remain at rest; but the other bodies, which are wrought upon, will have changed their former state of rest, for the contrary state of motion. Let us now suppose the bodies left at rest to be annihilated, this will make no alteration in the state of the moving bodies; but the effect of the impression, which was made upon them, will still subsist. This shews the motion they received to be an absolute thing, and to have no necessary dependence upon the relation which the body said to be in motion has to any other body[77].
94. Besides absolute and relative motion are distinguishable by their Effects. One effect of motion is, that bodies, when moved round any center or axis, acquire a certain[115] power, by which they forcibly press themselves from that center or axis of motion. As when a body is whirled about in a sling, the body presses against the sling, and is ready to fly out as soon as liberty is given it. And this power is proportional to the true, not relative motion of the body round such a center or axis. Of this Sir Isaac Newton gives the following instance[78]. If a pail or such like vessel near full of water be suspended by a string of sufficient length, and be turned about till the string be hard twisted. If then as soon as the vessel and water in it are become still and at rest, the vessel be nimbly turned about the contrary way the string was twisted, the vessel by the strings untwisting it self shall continue its motion a long time. And when the vessel first begins to turn, the water in it shall receive little or nothing of the motion of the vessel, but by degrees shall receive a communication of motion, till at last it shall move round as swiftly as the vessel it self. Now the definition of motion, which Des Cartes has given us upon this principle of making all motion meerly relative, is this: that motion, is a removal of any body from its vicinity to other bodies, which were in immediate contact with it, and are considered as at rest[79]. And if this be compared with what he soon after says, that there is nothing real or positive in the body moved, for the sake of which we ascribe motion to it, which is not to be found as well in the contiguous bodies, which are considered as at rest[80]; it will follow from thence, that we may consider the vessel as at rest[116] and the water as moving in it: and the water in respect of the vessel has the greatest motion, when the vessel first begins to turn, and loses this relative motion more and more, till at length it quite ceases. But now, when the vessel first begins to turn, the surface of the water remains smooth and flat, as before the vessel began to move; but as the motion of the vessel communicates by degrees motion to the water, the surface of the water will be observed to change, the water subsiding in the middle and rising at the edges: which elevation of the water is caused by the parts of it pressing from the axis, they move about; and therefore this force of receding from the axis of motion depends not upon the relative motion of the water within the vessel, but on its absolute motion; for it is least, when that relative motion is greatest, and greatest, when that relative motion is least, or none at all.
95. Thus the true cause of what appears in the surface of this water cannot be assigned, without considering the water’s motion within the vessel. So also in the system of the world, in order to find out the cause of the planetary motions, we must know more of the real motions, which belong to each planet, than is absolutely necessary for the uses of astronomy. If the astronomer should suppose the earth to stand still, he could ascribe such motions to the celestial bodies, as should answer all the appearances; though he would not account for them in so simple a manner, as by attributing motion to the earth. But the motion of the earth must of necessity be considered, before the real causes, which actuate the planetary system, can be discovered.
Chap. III.
Of CENTRIPETAL FORCES.
WE have just been describing in the preceding chapter the effects produced on a body in motion, from its being continually acted upon by a power always equal in strength, and operating in parallel directions[81]. But bodies may be acted upon by powers, which in different places shall have different degrees of force, and whose several directions shall be variously inclined to each other. The most simple of these in respect to direction is, when the power is pointed constantly to one center. This is truly the case of that power, whose effects we described in the foregoing chapter; though the center of that power is so far removed, that the subject then before us is most conveniently to be considered in the light, wherein we have placed it: But Sir Isaac Newton has considered very particularly this other case of powers, which are constantly directed to the same center. It is upon this foundation, that all his discoveries in the system of the world are raised. And therefore, as this subject bears so very great a share in the philosophy, of which I am discoursing, I think it proper in this place to take a short view of some of the general effects of these powers, before we come to apply them particularly to the system of the world.
2. These powers or forces are by Sir Isaac Newton called centripetal; and their first effect is to cause the body, on which they act, to quit the straight course, wherein it would proceed if undisturbed, and to describe an incurvated line, which shall always be bent towards the center of the force. It is not necessary, that such a power should cause the body to approach that center. The body may continue to recede from the center of the power, notwithstanding its being drawn by the power; but this property must always belong to its motion, that the line, in which it moves, will continually be concave towards the center, to which the power is directed. Suppose A (in fig. 72.) to be the center of a force. Let a body in B be moving in the direction of the straight line B C, in which line it would continue to move, if undisturbed; but being attracted by the centripetal force towards A, the body must necessarily depart from this line B C, and being drawn into the curve line B D, must pass between the lines A B and B C. It is evident therefore, that the body in B being gradually turned off from the straight line B C, it will at first be convex toward the line B C, and consequently concave towards the point A: for these centripetal powers are supposed to be in strength proportional to the power of gravity, and, like that, not to be able after the manner of an impulse to turn the body sensibly out of its course into a different one in an instant, but to take up some space of time in producing a visible effect. That the curve will always continue to have its concavity towards A may thus appear. In the line B C near to B take any point as E, from which the line E F G may be so[119] drawn, as to touch the curve line B D in some point as F. Now when the body is come to F, if the centripetal power were immediately to be suspended, the body would no longer continue to move in a curve line, but being left to it self would forthwith reassume a straight course; and that straight course would be in the line F G: for that line is in the direction of the body’s motion at the point F. But the centripetal force continuing its energy, the body will be gradually drawn from this line F G so as to keep in the line F D, and make that line near the point F to be convex toward F G, and concave toward A. After the same manner the body may be followed on in its course through the line B D, and every part of that line be shewn to be concave toward the point A.
3. This then is the constant character belonging to those motions, which are carried on by centripetal forces; that the line, wherein the body moves, is throughout concave towards the center of the force. In respect to the successive distances of the body from the center there is no general rule to be laid down; for the distance of the body from the center may either increase, or decrease, or even keep always the same. The point A (in fig. 73.) being the center of a centripetal force, let a body at B set out in the direction of the straight line B C perpendicular to the line A B drawn from A to B. It will be easily conceived, that there is no other point in the line B C so near to A, as the point B; that A B is the shortest of all the lines, which can be drawn from A to any part of the line B C; all other lines, as A D, or A E, drawn from A to the line B C being longer than A B. Hence it follows, that the body setting[120] out from B, if it moved in the line B C, it would recede more and more from the point A. Now as the operation of a centripetal force is to draw a body towards the center of the force: if such a force act upon a resting body, it must necessarily put that body so into motion, as to cause it to move towards the center of the force: if the body were of it self moving towards that center, the centripetal force would accelerate that motion, and cause it to move faster down: but if the body were in such a motion, as being left to itself it would recede from this center, it is not necessary, that the action of a centripetal power upon it should immediately compel the body to approach the center, from which it would otherwise have receded; the centripetal power is not without effect, if it cause the body to recede more slowly from that center, than otherwise it would have done. Thus in the case before us, the smallest centripetal power, if it act on the body, will force it out of the line B C, and cause it to pass in a bent line between B C and the point A, as has been before explained. When the body, for instance, has advanced to the line A D, the effect of the centripetal force discovers it self by having removed the body out of the line B C, and brought it to cross the line A D somewhere between A and D: suppose at F. Now A D being longer than A B, A F may also be longer than A B. The centripetal power may indeed be so strong, that A F shall be shorter than A B; or it may be so evenly balanced with the progressive motion of the body, that A F and A B shall be just equal: and in this last case, when the centripetal force is of that strength, as constantly to draw the body as much toward[121] the center, as the progressive motion would carry it off, the body will describe a circle about the center A, this center of the force being also the center of the circle.
4. If the body, instead of setting out in the line B C perpendicular to A B, had set out in another line B G more inclined towards the line A B, moving in the curve line B H; then as the body, if it were to continue its motion in the line B G, would for some time approach the center A; the centripetal force would cause it to make greater advances toward that center. But if the body were to set out in the line B I reclined the other way from the perpendicular B C, and were to be drawn by the centripetal force into the curve line B K; the body, notwithstanding any centripetal force, would for some time recede from the center; since some part at least of the curve line B K lies between the line B I and the perpendicular B C.
5. Thus far we have explained such effects, as attend every centripetal force. But as these forces may be very different in regard to the different degrees of strength, wherewith they act upon bodies in different places; I shall now proceed to make mention in general of some of the differences attending these centripetal motions.
6. To reassume the consideration of the last mentioned case. Suppose a centripetal power directed toward the point A (in fig. 74.) to act on a body in B, which is moving in the direction of the straight line B C, the line B C reclining off from A B. If from A the straight lines A D, A E, A F are[122] drawn at pleasure to the line C B; the line C B being prolonged beyond B to G, it appears that A D is inclined to the line G C more obliquely, than A B is inclined to it, A E is inclined more obliquely than A D, and A F more than A E. To speak more correctly, the angle under A D G is less than that under A B G, the angle under A E G less than that under A D G, and the angle under A F G less than that under A E G. Now suppose the body to move in the curve line B H I K. Then it is here likewise evident, that the line B H I K being concave towards A, and convex towards the line B C, it is more and more turned off from the line B C; so that in the point H the line A H will be less obliquely inclined to the curve line B H I K, than the same line A H D is inclined to B C at the point D; at the point I the inclination of the line A I to the curve line will be more different from the inclination of the same line A I E to the line B C, at the point E; and in the points K and F the difference of inclination will be still greater; and in both the inclination at the curve will be less oblique, than at the straight line B C. But the straight line A B is less obliquely inclined to B G, than A D is inclined towards D G: therefore although the line A H be less obliquely inclined towards the curve H B, than the same line A H D is inclined towards D G; yet it is possible, that the inclination at H may be more oblique, than the inclination at B. The inclination at H may indeed be less oblique than the other, or they may be both the same. This depends upon the degree of strength, wherewith the centripetal force exerts it self, during the passage of the body from B to H. After the same manner the inclinations at I and K depend entirely on the degree[123] of strength, wherewith the centripetal force acts on the body in its passage from H to K: if the centripetal force be weak enough, the lines A H and A I drawn from the center A to the body at H and at I shall be more obliquely inclined to the curve, than the line A B is inclined towards B G. The centripetal force may be of that strength as to render all these inclinations equal, or if stronger, the inclinations at I and K will be less oblique than at B. Sir Isaac Newton has particularly shewn, that if the centripetal power decreases after a certain manner with the increase of distance, a body may describe such a curve line, that all the lines drawn from the center to the body shall be equally inclined to that curve line.[82] But I do not here enter into any particulars, my present intention being only to shew, that it is possible for a body to be acted upon by a force continually drawing it down towards a center, and yet that the body shall continue to recede from that center; for here as long as the lines A H, A I, &c drawn from the center A to the body do not become less oblique to the curve, in which the body moves; so long shall those lines perpetually increase, and consequently the body shall more and more recede from the center.
7. But we may observe farther, that if the centripetal power, while the body increases its distance from the center, retain sufficient strength to make the lines drawn from the center to the body to become at length less oblique to the curve; then if this diminution of the obliquity continue, till[124] at last the line drawn from the center to the body shall cease to be obliquely inclined to the curve, and shall become perpendicular thereto; from this instant the body shall no longer recede from the center, but in its following motion it shall again descend, and shall describe a curve line in all respects like to that, which it has described already; provided the centripetal power, every where at the same distance from the center, acts with the same strength. So we observed in the preceding chapter, that, when the motion of a projectile became parallel to the horizon, the projectile no longer ascended, but forthwith directed its course downwards, descending in a line altogether like that, wherein it had before ascended[83].
8. This return of the body may be proved by the following proposition: that if the body in any place, suppose at I, were to be stopt, and be thrown directly backward with the velocity, wherewith it was moving forward in that point I; then the body, by the action of the centripetal force upon it, would move back again over the path I H B, in which it had before advanced forward, and would arrive again at the point B in the same space of time, as was taken up in its passage from B to I; the velocity of the body at its return to the point B being the same, as that wherewith it first set out from that point. To give a full demonstration of this proposition, would require that use of mathematics, which I here purpose to avoid; but, I believe, it will appear in great measure evident from the following considerations.
9. Suppose (in fig. 75.) that a body were carried after the following manner through the bent figure A B C D E F, composed of the straight lines A B, B C, C D, D E, E F. First let it be moving in the line A B, from A towards B, with any uniform velocity. At B let the body receive an impulse directed toward some point, as G, taken within the concavity of the figure. Now whereas this body, when once moving in the straight line A B, will continue to move on in this line, so long as it shall be left to it self; but being disturbed at the point B in its motion by the impulse, which there acts upon it, it will be turned out of this line A B into some other straight line, wherein it will afterwards continue to move, as long as it shall be left to itself. Therefore let this impulse have strength sufficient to turn the body into the line B C. Then let the body move on undisturbed from B to C, but at C let it receive another impulse pointed toward the same point G, and of sufficient strength to turn the body into the line C D. At D let a third impulse, directed like the rest to the point G, turn the body into the line D E. And at E let another impulse, directed likewise to the point G, turn the body into the line E F. Now, I say, if the body while moving in the line E F be stopt, and turned back again in this line with the same velocity, as that wherewith it was moving forward in this line; then by the repetition of the former impulse at E the body will be turned into the line E D, and move in it from E to D with the same velocity as before it moved with from D to E; by the repetition of the impulse at D, when the body shall have returned to that point, it will be turned into the line D C; and by the repetition of the other impulses at C and B[126] the body will be brought back again into the line B A, with the velocity, wherewith it first moved in that line.
10. This I prove as follows. Let D E and F E be continued beyond E. In D E thus continued take at pleasure the length E H, and let H I be so drawn, as to be equidistant from the line G E. Then, by what has been written upon the second law of motion[84], it follows, that after the impulse on the body in E it will move through E I in the same time, as it would have imployed in moving from E to H, with the velocity which it had in the line D E. In F E prolonged take E K equal to E I, and draw K L equidistant from G E. Then, because the body is thrown back in the line F E with the same velocity as that wherewith it went forward in that line; if, when the body was returned to E, it were permitted to go straight on, it would pass through E K in the same time, as it took up in passing through E I, when it went forward in the line E F. But, if at the body’s return to the point E, such an impulse directed toward the point D were to be given it, whereby it should be turned into the line D E; I say, that the impulse necessary to produce this effect must be equal to that, which turned the body out of the line D E into E F; and that the velocity, with which the body will return into the line E D, is the same, as that wherewith it before moved through this line from D to E. Because E K is equal to E I, and K L and H I, being each equidistant from G E, are by consequence equidistant from each other; it follows, that the two[127] triangular figures I E H and K E L are altogether like and equal to each other. If I were writing to mathematicians, I might refer them to some proportions in the elements of Euclid for the proof of this[85] but as I do not here address my self to such, so I think this assertion will be evident enough without a proof in form; at least I must desire my readers to receive it as a proposition true in geometry. But these two triangular figures being altogether like each other and equal; as E K is equal to E I, so E L is equal to E H, and K L equal to H I. Now the body after its return to E being turned out of the line F E into E D by an impulse acting upon it in E, after the manner above expressed; the body will receive such a velocity by this impulse, as will carry it through E L in the same time, as it would have imployed in passing through E K, if it had gone on in that line undisturbed. And it has already been observed, that the time, in which the body would pass over E K with the velocity wherewith it returns, is equal to the time it took up in going forward from E to I; that is, equal to the time, in which it would have gone through E H with the velocity, wherewith it moved from D to E. Therefore the time, in which the body will pass through E L after its return into the line E D, is the same, as would have been taken up by the body in passing through E H with the velocity, wherewith the body first moved in the line D E. Since therefore E L and E H are equal, the body returns into the line D E with the velocity, which it had before in that line. Again I say, the second impulse in E is equal to the first. By what has[128] been said on the second law of motion concerning the effect of oblique impulses[86], it will be understood, that the impulse in E, whereby the body was turned out of the line D E into the line E F, is of such strength, that if the body had been at rest, when this impulse had acted upon it, this impulse would have communicated so much motion to the body, as would have carried it through a length equal to H I, in the time wherein the body would have passed from E to H, or in the time wherein it passed from E to I. In the same manner, on the return of the body, the impulse in E, whereby the body is turned out of the line F E into E D, is of such strength, that if it had acted on the body at rest, it would have caused the body to move through a length equal to K L, in the same time, as the body would imploy in passing through E K with the velocity, wherewith it returns in the line F E. Therefore the second impulse, had it acted on the body at rest, would have caused it to move through a length equal to K L in the same space of time, as would be taken up by the body in passing through a length equal to H I, were the first impulse to act on the body when at rest. That is, the effects of the first and second impulse on the body when at rest would be the same; for K L and H I are equal: consequently the second impulse is equal to the first.
11. Thus if the body be returned through F E with the velocity, wherewith it moved forward; we have shewn how by the repetition of the impulse, which acted on it at E, the[129] body will return again into the line D E with the velocity, which it had before in that line. By the same process of reasoning it may be proved, that, when the body is returned back to D, the impulse, which before acted on the body at that point, will throw the body into the line D C with the velocity, which it first had in that line; and the other impulses being successively repeated, the body will at length be brought back again into the line B A with the velocity, wherewith it set out in that line.
12. Thus these impulses, by acting over again in an inverted order all their operation on the body, bring it back again through the path, in which it had proceeded forward. And this obtains equally, whatever be the number of the straight lines, whereof this curve figure is composed. Now by a method of reasoning, which Sir Isaac Newton makes great use of, and which he introduced into geometry, thereby greatly inriching that science[87]; we might make a transition from this figure composed of a number of straight lines to a figure of one continued curvature, and from a number of separate impulses repeated at distinct intervals to a continual centripetal force, and shew, that, because what has been here advanced holds universally true, whatever be the number of straight lines, whereof the curve figure A C F is composed, and howsoever frequently the impulses at the angles of this figure are repeated; therefore the same will still remain true, although this figure should be converted into one of a continued curvature, and these distinct impulses should be[130] changed into a continual centripetal force. But as the explaining this method of reasoning is foreign to my present design; so I hope my readers, after what has been said, will find no difficulty in receiving the proposition laid down above: that, if the body, which has moved through the curve line B H I (in fig. 74.) from B to I, when it is come to I, be thrown directly back with the same velocity as that, wherewith it proceeded forward, the centripetal force, by acting over again all its operation on the body, shall bring the body back again in the line I H B: and as the motion of the body in its course from B to I was every where in such a manner oblique to the line drawn from the center to the body, that the centripetal power acted in some degree against the body’s motion, and gradually diminished it; so in the return of the body, the centripetal power will every where draw the body forward, and accelerate its motion by the same degrees, as before it retarded it.
13. This being agreed, suppose the body in K to have the line A K no longer obliquely inclined to its motion. In this case, if the body be turned back, in the manner we have been considering, it must be directed back perpendicularly to A K. But if it had proceeded forward, it would likewise have moved in a direction perpendicular to A K; consequently, whether it move from this point K backward or forward, it must describe the same kind of course. Therefore since by being turned back it will go over again the line K I H B; if it be permitted to go forward, the line K L, which it shall describe, will be altogether similar to the line K H B.
14. In like manner we may determine the nature of the motion, if the line, wherein the body sets out, be inclined (as in fig. 76.) down toward the line B A drawn between the body and the center. If the centripetal power so much increases in strength, as the body approaches, that it can bend the path, in which the body moves, to that degree, as to cause all the lines as A H, A I, A K to remain no less oblique to the motion of the body, than A B is oblique to B C; the body shall continually more and more approach the center. But if the centripetal power increases in so much less a degree, as to permit the line drawn from the center to the body, as it accompanies the body in its motion, at length to become more and more erect to the curve wherein the body moves, and in the end, suppose at K, to become perpendicular thereto; from that time the body shall rise again. This is evident from what has been said above; because for the very same reason here also the body shall proceed from the point K to describe a line altogether similar to the line, in which it has moved from B to K. Thus, as it was observed of the pendulum in the preceding chapter[88], that all the time it approaches towards being perpendicular to the horizon, it more and more descends; but, as soon as it is come into that perpendicular situation, it immediately rises again by the same degrees, as it descended by before: so here the body more and more approaches the center all the time it is moving from B to K; but thence forward it rises from the center again by the same degrees, as it approached by before.
15. If (in fig. 77.) the line B C be perpendicular to A B; then it has been observed above[89], that the centripetal power may be so balanced with the progressive motion of the body, that the body may keep moving round the center A constantly at the same distance; as a body does, when whirled about any point, to which it is tyed by a string. If the centripetal power be too weak to produce this effect, the motion of the body will presently become oblique to the line drawn from itself to the center, after the manner of the first of the two cases, which we have been considering. If the centripetal power be stronger, than what is required to carry the body in a circle, the motion of the body will presently fall in with the second of the cases, we have been considering.
16. If the centripetal power so change with the change of distance, that the body, after its motion has become oblique to the line drawn from itself to the center, shall again become perpendicular thereto; which we have shewn to be possible in both the cases treated of above; then the body shall in its subsequent motion return again to the distance of A B, and from that distance take a course similar to the former: and thus, if the body move in a space free from all resistance, which has been here all along supposed; it shall continue in a perpetual motion about the center, descending and ascending alternately therefrom. If the body setting out from B (in fig. 78.) in the line B C perpendicular to A B, describe the line B D E, which in D shall be oblique to the line A D, but in E shall again become erect to A E drawn from the body in E to the center A; then from this point E the body shall describe the line E F G altogether like to the line B D E, and at G shall be at the same distance from A, as it was at B. But likewise the line A G shall be erect to the body’s motion. Therefore the body shall proceed to describe from G the line G H I altogether similar to the line G F E, and at I have the same distance from the center, as it had at E; and also have the line A I erect to its motion: so that its following motion must be in the line I K L similar to I H G, and the distance A L equal to A G. Thus the body will go on in a perpetual round without ceasing, alternately inlarging and contracting its distance from the center.
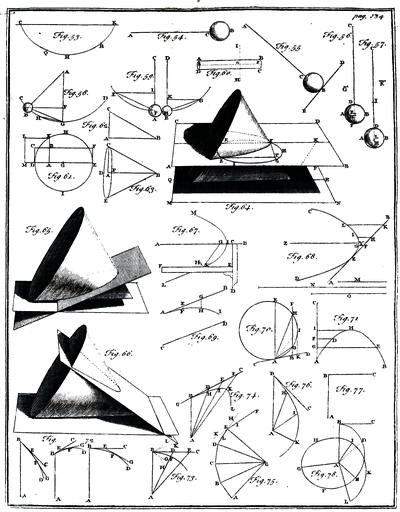
17. If it so happen, that the point E fall upon the line B A continued beyond A; then the point G will fall on B, I on E, and L also on B; so that the body will describe in this case a simple curve line round the center A, like the line B D E F in fig. 79, in which it will continually revolve from B to E and from E to B without end.
18. If A E in fig. 78 should happen to be perpendicular to A B, in this case also a simple line will be described; for the point G will fall on the line B A prolonged beyond A, the point I on the line A E prolonged beyond A, and the point L on B: so that the body will describe a line like the curve line B E G I in fig. 80, in which the opposite points B and G are equally distant from A, and the opposite points E and I are also equally distant from the same point A.
19. In other cases the line described will have a more complex figure.
20. Thus we have endeavoured to shew how a body, while it is constantly attracted towards a center, may notwithstanding by its progressive motion keep it self from falling down to that center; but describe about it an endless circuit, sometimes approaching toward that center, and at other times as much receding from the same.
21. But here we have supposed, that the centripetal power is of equal strength every where at the same distance from the center. And this is the case of that centripetal power, which will hereafter be shewn to be the cause, that keeps the planets in their courses. But a body may be kept on in a perpetual circuit round a center, although the centripetal power have not this property. Indeed a body may by a centripetal force be kept moving in any curve line whatever, that shall have its concavity turned every where towards the center of the force.
22. To make this evident I shall first propose the case of a body moving through the incurvated figure A B C D E (in fig. 81.) which is composed of the straight lines A B, B C, C D, D E, and E A; the motion being carried on in the following manner. Let the body first move in the line A B with any uniform velocity. When it is arrived at the point B, let it receive an impulse directed toward any point F taken within the figure; and let the impulse be of that strength as to turn the body out[135] of the line A B into the line B C. The body after this impulse, while left to itself, will continue moving in the line B C. At C let the body receive another impulse directed towards the same point F, of such strength, as to turn the body from the line B C into the line C D. At D let the body by another impulse, directed likewise to the point F, be turned out of the line C D into D E. And at E let another impulse, directed toward the point F, turn the body from the line D E into E A. Thus we see how a body may be carried through the figure A B C D E by certain impulses directed always toward the same center, only by their acting on the body at proper intervals, and with due degrees of strength.
23. But farther, when the body is come to the point A, if it there receive another impulse directed like the rest toward the point F, and of such a degree of strength as to turn the body into the line A B, wherein it first moved; I say that the body shall return into this line with the same velocity, as it had at first.
24. Let A B be prolonged beyond B at pleasure, suppose to G; and from G let G H be drawn, which if produced should always continue equidistant from B F, or, according to the more usual phrase, let G H be drawn parallel to B F. Then it appears, from what has been said upon the second law of motion[90], that in the time, wherein the body would have moved from B to G, had it not received a new impulse in B, by the means of that impulse it will have acquired a velocity, which will carry it from B to H. After the same manner, if C I be[136] taken equal to B H, and I K be drawn equidistant from or parallel to C F; the body will have moved from C to K with the velocity, which it has in the line C D, in the same time, as it would have employed in moving from C to I with the velocity, it had in the line B C. Therefore since C I and B H are equal, the body will move through C K in the same time, as it would have taken up in moving from B to G with the original velocity, wherewith it moved through the line A B. Again, D L being taken equal to C K and L M drawn parallel to D F; for the same reason as before the body will move through D M with the velocity, which it has in the line D E, in the same time, as it would imploy in moving through B G with its original velocity. In the last place, if E N be taken equal to D M, and N O be drawn parallel to E F; likewise if A P be taken equal to E O, and P Q be drawn parallel to A F: then the body with the velocity, wherewith it returns into the line A B, will pass through A Q in the same time, as it would have imployed in passing through B G with its original velocity. Now as all this follows directly from what has above been delivered, concerning the effect of oblique impulses impressed upon bodies in motion; so we must here observe farther, that it can be proved by geometry, that A Q will always be equal to E G. The proof of this I am obliged, from the nature of my present design, to omit; but this geometrical proportion being granted, it follows, that the body has returned into the line A B with the velocity, which it had, when it first moved in that line; for the velocity, with which it returns into the line A B, will carry it over the line A Q in the same time, as would[137] have been taken up in its passing over an equal line B G with the original velocity.
25. Thus we have found, how a body may be carried round the figure A B C D E by the action of certain impulses upon it which should all be pointed toward one center. And we likewise see, that when the body is brought back again to the point, whence it first set out; if it there meet with an impulse sufficient to turn it again into the line, wherein it moved at first, its original velocity will be again restored; and by the repetition of the same impulses, the body will be carried again in the same round. Therefore if these impulses, which act on the body at the points B, C, D, E, and A, continue always the same, the body will make round this figure innumerable revolutions.
26. The proof, which we have here made use of, holds the same in any number of straight lines, whereof the figure A B D should be composed; and therefore by the method of reasoning referred to above[91] we are to conclude, that what has here been said upon this rectilinear figure, will remain true, if this figure were changed into one of a continued curvature, and instead of distinct impulses acting by intervals at the angles of this figure, we had a continual centripetal force. We have therefore shewn, that a body may be carried round in any curve figure A B C ( fig. 82.) which shall every where be concave towards any one point as D, by the continual action[138] of a centripetal power directed to that point, and when it is returned to the point, from whence it set out, it shall recover again the velocity, with which it departed from that point. It is not indeed always necessary, that it should return again into its first course; for the curve line may have some such figure as the line A B C D B E in fig. 83. In this curve line, if the body set out from B in the direction B F, and moved through the line B C D, till it returned to B; here the body would not enter again into the line B C D, because the two parts B D and B C of the curve line make an angle at the point B: so that the centripetal power, which at the point B could turn the body from the line B F into the curve, will not be able to turn the body into the line B C from the direction, in which it returns to the point B; a forceable impulse must be given the body in the point B to produce that effect.
27. If at the point B, whence the body sets out, the curve line return into it self (as in fig. 82;) then the body, upon its arrival again at B, may return into its former course, and thus make an endless circuit about the center of the centripetal power.
28. What has here been said, I hope, will in some measure enable my readers to form a just idea of the nature of these centripetal motions.
29. I have not attempted to shew, how to find particularly, what kind of centripetal force is necessary to carry a body in any curve line proposed. This is to be deduced from the degree[139] of curvature, which the figure has in each point of it, and requires a long and complex mathematical reasoning. However I shall speak a little to the first proportion, which Sir Isaac Newton lays down for this purpose. By this proposition, when a body is found moving in a curve line, it may be known, whether the body be kept in its course by a power always pointed toward the same center; and if it be so, where that center is placed. The proposition is this: that if a line be drawn from some fixed point to the body, and remaining by one extream united to that point, it be carried round along with the body; then, if the power, whereby the body is kept in its course, be always pointed to this fixed point as a center, this line will move over equal spaces in equal portions of time. Suppose a body were moving through the curve line A B C D (in fig. 84.) and passed over the arches A B, B C, C D in equal portions of time; then if a point, as E, can be found, from whence the line E A being drawn to the body in A, and accompanying the body in its motion, it shall make the spaces E A B, E B C, and E C D equal, over which it passes, while the body describes the arches A B, B C, and C D: and if this hold the same in all other arches, both great and small, of the curve line A B C D, that these spaces are always equal, where the times are equal; then is the body kept in this line by a power always pointed to E as a center.
30. The principle, upon which Sir Isaac Newton has demonstrated this, requires but small skill in geometry to comprehend. I shall therefore take the liberty to close the present[140] chapter with an explication of it; because such an example will give the clearest notion of our author’s method of applying mathematical reasoning to these philosophical subjects.
31. He reasons thus. Suppose a body set out from the point A (in fig. 85.) to move in the straight line A B; and after it had moved for some time in that line, it were to receive an impulse directed to some point as C. Let it receive that impulse at D; and thereby be turned into the line D E; and let the body after this impulse take the same length of time in passing from D to E, as it imployed in the passing from A to D. Then the straight lines C A, C D, and C E being drawn, Sir Isaac Newton proves, that the and triangular spaces C A D and C D E are equal. This he does in the following manner.
32. Let E F be drawn parallel to C D. Then, from what has been said upon the second law of motion[92], it is evident, that since the body was moving in the line A B, when it received the impulse in the direction D C; it will have moved after that impulse through the line D E in the same time, as it would have taken up in moving through D F, provided it had received no disturbance in D. But the time of the body’s moving from D to E is supposed to be equal to the time of its moving through A D; therefore the time, which the body would have imployed in moving through D F, had it not been disturbed in D, is equal to the time, wherein it moved through A D: consequently D F is equal in length to A D; for if the[141] body had gone on to move through the line A B without interruption, it would have moved through all parts thereof with the same velocity, and have passed over equal parts of that line in equal portions of time. Now C F being drawn, since A D and D F are equal, the triangular space C D F is equal to the triangular space C A D. Farther, the line E F being parallel to C D, it is proved by Euclid, that the triangle C E D is equal to the triangle C F D[93]: therefore the triangle C E D is equal to the triangle C A D.
33. After the same manner, if the body receive at E another impulse directed toward the point C, and be turned by that impulse into the line E G; if it move afterwards from E to G in the same space of time, as was taken up by its motion from D to E, or from A to D; then C G being drawn, the triangle C E G is equal to C D E. A third impulse at G directed as the two former to C, whereby the body shall be turned into the line G H, will have also the like effect with the rest. If the body move over G H in the same time, as it took up in moving over E G, the triangle C G H will be equal to the triangle C E G. Lastly, if the body at H be turned by a fresh impulse directed toward C into the line H I, and at I by another impulse directed also to C be turned into the line I K; and if the body move over each of the lines H I, and I K in the same time, as it imployed in moving over each of the preceding lines A D, D E, E G, and G H: then each of the triangles C H I, and C I K will be equal to each of the preceding. Likewise[142] as the time, in which the body moves over A D E, is equal to the time of its moving over E G H, and to the time of its moving over H I K; the space C A D E will be equal to the space C E G H, and to the space C H I K. In the same manner as the time, in which the body moved over A D E G is equal to the time of its moving over G H I K, so the space C A D E G will be equal to the space C G H I K.
34. From this principle Sir Isaac Newton demonstrates the proposition mentioned above, by that method of arguing introduced by him into geometry, whereof we have before taken notice[94], by making according to the principles of that method a transition from this incurvated figure composed of straight lines, to a figure of continued curvature; and by shewing, that since equal spaces are described in equal times in this present figure composed of straight lines, the same relation between the spaces described and the times of their description will also have place in a figure of one continued curvature. He also deduces from this proposition the reverse of it; and proves, that whenever equal spaces are continually described; the body is acted upon by a centripetal force directed to the center, at which the spaces terminate.
Chap. IV.
Of the RESISTANCE of FLUIDS.
BEFORE the cause can be discovered, which keeps the planets in motion, it is necessary first to know, whether the space, wherein they move, is empty and void, or filled with any quantity of matter. It has been a prevailing opinion, that all space contains in it matter of some kind or other; so that where no sensible matter is found, there was yet a subtle fluid substance by which the space was filled up; even so as to make an absolute plenitude. In order to examine this opinion, Sir Isaac Newton has largely considered the effects of fluids upon bodies moving in them.
2. These effects he has reduced under these three heads. In the first place he shews how to determine in what manner the resistance, which bodies suffer, when moving in a fluid, gradually increases in proportion to the space, they describe in any fluid; to the velocity, with which they describe it; and to the time they have been in motion. Under the second head he considers what degree of resistance different bodies moving in the same fluid undergo, according to the different proportion between the density of the fluid and the density of the body. The densities of bodies, whether fluid or solid, are measured by the quantity of matter, which is comprehended under the same magnitude; that body being[144] the most dense or compact, which under the same bulk contains the greatest quantity of solid matter, or which weighs most, the weight of every body being observed above to be proportional to the quantity of matter in it[95]. Thus water is more dense than cork or wood, iron more dense than water, and gold than iron. The third particular Sir Is. Newton considers concerning the resistance of fluids is the influence, which the diversity of figure in the resisted body has upon its resistance.
3. For the more perfect illustration of the first of these heads, he distinctly shews the relation between all the particulars specified upon three different suppositions. The first is, that the same body be resisted more or less in the simple proportion to its velocity; so that if its velocity be doubled, its resistance shall become threefold. The second is of the resistance increasing in the duplicate proportion of the velocity; so that, if the velocity of a body be doubled, its resistance shall be rendered four times; and if the velocity be trebled, nine times as great as at first. But what is to be understood by duplicate proportion has been already explained[96]. The third supposition is, that the resistance increases partly in the single proportion of the velocity, and partly in the duplicate proportion thereof.
4. In all these suppositions, bodies are considered under two respects, either as moving, and opposing themselves[145] against the fluid by that power alone, which is essential to them, of resisting to the change of their state from rest to motion, or from motion to rest, which we have above called their power of inactivity; or else, as descending or ascending, and so having the power of gravity combined with that other power. Thus our author has shewn in all those three suppositions, in what manner bodies are resisted in an uniform fluid, when they move with the aforesaid progressive motion[97]; and what the resistance is, when they ascend or descend perpendicularly[98]. And if a body ascend or descend obliquely, and the resistance be singly proportional to the velocity, it is shewn how the body is resisted in a fluid of an uniform density, and what line it will describe[99], which is determined by the measurement of the hyperbola, and appears to be no other than that line, first considered in particular by Dr. Barrow[100], which is now commonly known by the name of the logarithmical curve. In the supposition that the resistance increases in the duplicate proportion of the velocity, our author has not given us the line which would be described in an uniform fluid; but has instead thereof discussed a problem, which is in some sort the reverse; to find the density of the fluid at all altitudes, by which any given curve line may be described; which problem is so treated by him, as to be applicable to any kind of resistance whatever[101]. But here not unmindful of practice, he shews that a body in a fluid of uniform density, like the[146] air, will describe a line, which approaches towards an hyperbola; that is, its motion will be nearer to that curve line than to the parabola. And consequent upon this remark, he shews how to determine this hyperbola by experiment, and briefly resolves the chief of those problems relating to projectiles, which are in use in the art of gunnery, in this curve[102]; as Torricelli and others have done in the parabola[103], whose inventions have been explained at large above[104].
5. Our author has also handled distinctly that particular sort of motion, which is described by pendulums[105]; and has likewise considered some few cases of bodies moving in resisting fluids round a center, to which they are impelled by a centripetal force, in order to give an idea of those kinds of motions[106].
6. The treating of the resistance of pendulums has given him an opportunity of inserting into another part of his work some speculations upon the motions of them without resistance, which have a very peculiar elegance; where in he treats of them as moved by a gravitation acting in the law, which he shews to belong to the earth below its surface[107]; performing in this kind of gravitation, where the force is proportional to the distance from the center, all that Huygens had before done in the common supposition of its being uniform, and acting in parallel lines[108].
7. Huygens at the end of his treatise of the cause of gravity[109] informs us, that he likewise had carried his speculations on the first of these suppositions, of the resistance in fluids being proportional to the velocity of the body, as far as our author. But finding by experiment that the second was more conformable to nature, he afterwards made some progress in that, till he was stopt, by not being able to execute to his wish what related to the perpendicular descent of bodies; not observing that the measurement of the curve line, he made use of to explain it by, depended on the hyperbola. Which oversight may well be pardoned in that great man, considering that our author had not been pleased at that time to communicate to the publick his admirable discourse of the quadrature or measurement of curve lines, with which he has since obliged the world: for without the use of that treatise, it is I think no injury even to our author’s unparalleled abilities to believe, it would not have been easy for himself to have succeeded so happily in this and many other parts of his writings.
8. What Huygens found by experiment, that bodies were in reality resisted in the duplicate proportion of their velocity, agrees with the reasoning of our author[110], who distinguishes the resistance, which fluids give to bodies by the tenacity of their parts, and the friction between them and the body, from that, which arises from the power of inactivity, with which the constituent particles of fluids are endued like all[148] other portions of matter, by which power the particles of fluids like other bodies make resistance against being put into motion.
9. The resistance, which arises from the friction of the body against the parts of the fluid, must be very inconsiderable; and the resistance, which follows from the tenacity of the parts of fluids, is not usually very great, and does not depend much upon the velocity of the body in the fluid; for as the parts of the fluid adhere together with a certain degree of force, the resistance, which the body receives from thence, cannot much depend upon the velocity, with which the body moves; but like the power of gravity, its effect must be proportional to the time of its acting. This the reader may find farther explained by Sir Isaac Newton himself in the postscript to a discourse published by me in the philosophical transactions, No 371. The principal resistance, which most fluids give to bodies, arises from the power of inactivity in the parts of the fluids, and this depends upon the velocity, with which the body moves, on a double account. In the first place, the quantity of the fluid moved out of place by the moving body in any determinate space of time is proportional to the velocity, wherewith the body moves; and in the next place, the velocity with which each particle of the fluid is moved, will also be proportional to the velocity of the body: therefore since the resistance, which any body makes against being put into motion, is proportional both to the quantity of matter moved and the velocity it is moved with; the resistance, which a fluid gives on this account, will be doubly increased with the increase of the velocity in the moving body;[149] that is, the resistance will be in a two-fold or duplicate proportion of the velocity, wherewith the body moves through the fluid.
10. Farther it is most manifest, that this latter kind of resistance increasing with the increase of velocity, even in a greater degree than the velocity it self increases, the swifter the body moves, the less proportion the other species of resistance will bear to this: nay that this part of the resistance may be so much augmented by a due increase of velocity, till the former resistances shall bear a less proportion to this, than any that might be assigned. And indeed experience shews, that no other resistance, than what arises from the power of inactivity in the parts of the fluid, is of moment, when the body moves with any considerable swiftness.
11. There is besides these yet another species of resistance, found only in such fluids, as, like our air, are elastic. Elasticity belongs to no fluid known to us beside the air. By this property any quantity of air may be contracted into a less space by a forcible pressure, and as soon as the compressing power is removed, it will spring out again to its former dimensions. The air we breath is held to its present density by the weight of the air above us. And as this incumbent weight, by the motion of the winds, or other causes, is frequently varied (which appears by the barometer;) so when this weight is greatest, we breath a more dense air than at other times. To what degree the air would expand it self by its spring, if all pressure were removed, is not[150] known, nor yet into how narrow a compass it is capable of being compressed. Mr. Boyle found it by experiment capable both of expansion and compression to such a degree, that he could cause a quantity of air to expand it self over a space some hundred thousand times greater, than the space to which he could confine the same quantity[111]. But I shall treat more fully of this spring in the air hereafter[112]. I am now only to consider what resistance to the motion of bodies arises from it.
12. But before our author shews in what manner this cause of resistance operates, he proposes a method, by which fluids may be rendered elastic, demonstrating that if their particles be provided with a power of repelling each other, which shall exert it self with degrees of strength reciprocally proportional to the distances between the centers of the particles; that then such fluids will observe the same rule in being compressed, as our air does, which is this, that the space, into which it yields upon compression, is reciprocally proportional to the compressing weight[113]. The term reciprocally proportional has been explained above[114]. And if the centrifugal force of the particles acted by other laws, such fluids would yield in a different manner to compression[115].
13. Whether the particles of the air be endued with such a power, by which they can act upon each other out of contact, our author does not determine, but leaves that[151] to future examination, and to be discussed by philosophers. Only he takes occasion from hence to consider the resistance in elastic fluids, under this notion; making remarks, as he passes along, upon the differences, which will arise, if their elasticity be derived from any other fountain[116]. And this, I think, must be confessed to be done by him with great judgment; for this is far the most reasonable account, which has been given of this surprizing power, as must without doubt be freely acknowledged by any one, who in the least considers the insufficiency of all the other conjectures, which have been framed; and also how little reason there is to deny to bodies other powers, by which they may act upon each other at a distance, as well as that of gravity; which we shall hereafter shew to be a property universally belonging to all the bodies of the universe, and to all their parts[117]. Nay we actually find in the loadstone a very apparent repelling, as well as an attractive power. But of this more in the conclusion of this discourse.
14. By these steps our author leads the way to explain the resistance, which the air and such like fluids will give to bodies by their elasticity; which resistance he explains thus. If the elastic power of the fluid were to be varied so, as to be always in the duplicate proportion of the velocity of the resisted body, it is shewn that then the resistance derived from the elasticity, would increase in the duplicate proportion of the velocity; in so much that the[152] whole resistance would be in that proportion, excepting only that small part, which arises from the friction between the body and the parts of the fluid. From whence it follows, that because the elastic power of the same fluid does in truth continue the same, if the velocity of the moving body be diminished, the resistance from the elasticity, and therefore the whole resistance, will decrease in a less proportion, than the duplicate of the velocity; and if the velocity be increased, the resistance from the elasticity will increase in a less proportion, than the duplicate of the velocity, that is in a less proportion, than the resistance made by the power of inactivity of the parts of the fluid. And from this foundation is raised the proof of a property of this resistance, given by the elasticity in common with the others from the tenacity and friction of the parts of the fluid; that the velocity may be increased, till this resistance from the fluid’s elasticity shall bear no considerable proportion to that, which is produced by the power of inactivity thereof[118]. From whence our author draws this conclusion; that the resistance of a body, which moves very swiftly in an elastic fluid, is near the same, as if the fluid were not elastic; provided the elasticity arises from the centrifugal power of the parts of the medium, as before explained, especially if the velocity be so great, that this centrifugal power shall want time to exert it self[119]. But it is to be observed, that in the proof of all this our author proceeds upon the supposition of this centrifugal power in the parts of the fluid; but if the elasticity be caused by the expansion of the parts in the[153] manner of wool compressed, and such like bodies, by which the parts of the fluid will be in some measure entangled together, and their motion be obstructed, the fluid will be in a manner tenacious, and give a resistance upon that account over and above what depends upon its elasticity only[120]; and the resistance derived from that cause is to be judged of in the manner before set down.
15. It is now time to pass to the second part of this theory; which is to assign the measure of resistance, according to the proportion between the density of the body and the density of the fluid. What is here to be understood by the word density has been explained above[121]. For this purpose as our author before considered two distinct cases of bodies moving in mediums; one when they opposed themselves to the fluid by their power of inactivity only, and another when by ascending or descending their weight was combined with that other power: so likewise, the fluids themselves are to be regarded under a double capacity; either as having their parts at rest, and disposed freely without restraint, or as being compressed together by their own weight, or any other cause.
16. In the first case, if the parts of the fluid be wholly disingaged from one another, so that each particle is at liberty to move all ways without any impediment, it is shewn, that if a globe move in such a fluid, and the globe and particles[154] of the fluid are endued with perfect elasticity; so that as the globe impinges upon the particles of it, they shall bound off and separate themselves from the globe, with the same velocity, with which the globe strikes upon them; then the resistance, which the globe moving with any known velocity suffers, is to be thus determined. From the velocity of the globe, the time, wherein it would move over two third parts of its own diameter with that velocity, will be known. And such proportion as the density of the fluid bears to the density of the globe, the same the resistance given to the globe will bear to the force, which acting, like the power of gravity, on the globe without intermission during the space of time now mentioned, would generate in the globe the same degree of motion, as that wherewith it moves in the fluid[122]. But if neither the globe nor the particles of the fluid be elastic, so that the particles, when the globe strikes against them, do not rebound from it, then the resistance will be but half so much[123]. Again, if the particles of the fluid and the globe are imperfectly elastic, so that the particles will spring from the globe with part only of that velocity wherewith the globe impinges upon them; then the resistance will be a mean between the two preceding cases, approaching nearer to the first or second, according as the elasticity is more or less[124].
17. The elasticity, which is here ascribed to the particles of the fluid, is not that power of repelling one another,[155] when out of contact, by which, as has before been mentioned, the whole fluid may be rendred elastic; but such an elasticity only, as many solid bodies have of recovering their figure, whenever any forcible change is made in it, by the impulse of another body or otherwise. Which elasticity has been explained above at large[125].
18. This is the case of discontinued fluids, where the body, by pressing against their particles, drives them before itself, while the space behind the body is left empty. But in fluids which are compressed, so that the parts of them removed out of place by the body resisted immediately retire behind the body, and fill that space, which in the other case is left vacant, the resistance is still less; for a globe in such a fluid which shall be free from all elasticity, will be resisted but half as much as the least resistance in the former case[126]. But by elasticity I now mean that power, which renders the whole fluid so; of which if the compressed fluid be possessed, in the manner of the air, then the resistance will be greater than by the foregoing rule; for the fluid being capable in some degree of condensation, it will resemble so far the case of uncompressed fluids[127]. But, as has been before related, this difference is most considerable in slow motions.
19. In the next place our author is particular in determining the degrees of resistance accompanying bodies of different figures; which is the last of the three heads, we[156] divided the whole discourse of resistance into. And in this disquisition he finds a very surprizing and unthought of difference, between free and compressed fluids. He proves, that in the former kind, a globe suffers but half the resistance, which the cylinder, that circumscribes the globe, will do, if it move in the direction of its axis[128]. But in the latter he proves, that the globe and cylinder are resisted alike[129]. And in general, that let the shape of bodies be ever so different, yet if the greatest sections of the bodies perpendicular to the axis of their motion be equal, the bodies will be resisted equally[130].
20. Pursuant to the difference found between the resistance of the globe and cylinder in rare and uncompressed fluids, our author gives us the result of some other inquiries of the same nature. Thus of all the frustums of a cone, that can be described upon the same base and with the same altitude, he shews how to find that, which of all others will be the least resisted, when moving in the direction of its axis[131]. And from hence he draws an easy method of altering the figure of any spheroidical solid, so that its capacity may be enlarged, and yet the resistance of it diminished[132]: a note which he thinks may not be useless to ship-wrights. He concludes with determining the solid, which will be resisted the least that is possible, in these discontinued fluids[133].
21. That I may here be understood by readers unacquainted with mathematical terms, I shall explain what I mean by a frustum of a cone, and a spheroidical solid. A cone has been defined above. A frustum is what remains, when part of the cone next the vertex is cut away by a section parallel to the base of the cone, as in fig. 86. A spheroid is produced from an ellipsis, as a sphere or globe is made from a circle. If a circle turn round on its diameter, it describes by its motion a sphere; so if an ellipsis (which figure has been defined above, and will be more fully explained hereafter[134]) be turned round either upon the longest or shortest line, that can be drawn through the middle of it, there will be described a kind of oblong or flat sphere, as in fig. 87. Both these figures are called spheroids, and any solid resembling these I here call spheroidical.
22. If it should be asked, how the method of altering spheroidical bodies, here mentioned, can contribute to the facilitating a ship’s motion, when I just above affirmed, that the figure of bodies, which move in a compressed fluid not elastic, has no relation to the augmentation or diminution of the resistance; the reply is, that what was there spoken relates to bodies deep immerged into such fluids, but not of those, which swim upon the surface of them; for in this latter case the fluid, by the appulse of the anterior parts of the body, is raised above the level of the surface, and behind the body is sunk somewhat below; so[158] that by this inequality in the superficies of the fluid, that part of it, which at the head of the body is higher than the fluid behind, will resist in some measure after the manner of discontinued fluids[135], analogous to what was before observed to happen in the air through its elasticity, though the body be surrounded on every side by it[136]. And as far as the power of these causes extends, the figure of the moving body affects its resistance; for it is evident, that the figure, which presses least directly against the parts of the fluid, and so raises least the surface of a fluid not elastic, and least compresses one that is elastic, will be least resisted.
23. The way of collecting the difference of the resistance in rare fluids, which arises from the diversity of figure, is by considering the different effect of the particles of the fluid upon the body moving against them, according to the different obliquity of the several parts of the body upon which they respectively strike; as it is known, that any body impinging against a plane obliquely, strikes with a less force, than if it fell upon it perpendicularly; and the greater the obliquity is, the weaker is the force. And it is the same thing, if the body be at rest, and the plane move against it[137].
24. That there is no connexion between the figure of a body and its resistance in compressed fluids, is proved thus. Suppose A B C D (in fig. 88.) to be a canal, having such a fluid, water for instance, running through it with an equable[159] velocity; and let any body E, by being placed in the axis of the canal, hinder the passage of the water. It is evident, that the figure of the fore part of this body will have little influence in obstructing the water’s motion, but the whole impediment will arise from the space taken up by the body, by which it diminishes the bore of the canal, and straightens the passage of the water[138]. But proportional to the obstruction of the water’s motion, will be the force of the water upon the body E[139]. Now suppose both orifices of the canal to be closed, and the water in it to remain at rest; the body E to move, so that the parts of the water may pass by it with the same degree of velocity, as they did before; it is beyond contradiction, that the pressure of the water upon the body, that is, the resistance it gives to its motion, will remain the same; and therefore will have little connexion with the figure of the body[140].
25. By a method of reasoning drawn from the same fountain is determined the measure of resistance these compressed fluids give to bodies, in reference to the proportion between the density of the body and that of the fluid. This shall be explained particularly in my comment on Sir Is. Newton’s mathematical principles of natural philosophy; but is not a proper subject to be insisted on farther in this place.
26. We have now gone through all the parts of this theory. There remains nothing more, but in few words to mention the experiments, which our author has made, both[160] with bodies falling perpendicularly through water, and the air[141], and with pendulums[142]: all which agree with the theory. In the case of falling bodies, the times of their fall determined by the theory come out the same, as by observation, to a surprizing exactness; in the pendulums, the rod, by which the ball of the pendulum hangs, suffers resistance as well as the ball, and the motion of the ball being reciprocal, it communicates such a motion to the fluid, as increases the resistance, but the deviation from the theory is no more, than what may reasonably follow from these causes.
27. By this theory of the resistance of fluids, and these experiments, our author decides the question so long agitated among natural philosophers, whether all space is absolutely full of matter. The Aristotelians and Cartesians both assert this plenitude; the Atomists have maintained the contrary. Our author has chose to determine this question by his theory of resistance, as shall be explained in the following chapter.


BOOK II.
Concerning the
SYSTEM of the WORLD.
Chap. I.
That the Planets move in a space empty of
all sensible matter.

I HAVE now gone through the first part of my design, and have explained, as far as the nature of my undertaking would permit, what Sir Isaac Newton has delivered in general concerning the motion of bodies. It follows now to speak of the discoveries, he has made in the system of the world;[162] and to shew from him what cause keeps the heavenly bodies in their courses. But it will be necessary for the use of such, as are not skilled in astronomy, to premise a brief description of the planetary system.
2. This system is disposed in the following manner. In the middle is placed the sun. About him six globes continually roll. These are the primary planets; that which is nearest to the sun is called Mercury, the next Venus, next to this is our earth, the next beyond is Mars, after him Jupiter, and the outermost of all Saturn. Besides these there are discovered in this system ten other bodies, which move about some of these primary planets in the same manner, as they move round the sun. These are called secondary planets. The most conspicuous of them is the moon, which moves round our earth; four bodies move in like manner round Jupiter; and five round Saturn. Those which move about Jupiter and Saturn, are usually called satellites; and cannot any of them be seen without a telescope. It is not impossible, but there may be more secondary planets, beside these; though our instruments have not yet discovered any other. This disposition of the planetary or solar system is represented in fig. 89.
3. The same planet is not always equally distant from the sun. But the middle distance of Mercury is between ⅕ and ⅖ of the distance of the earth from the sun; Venus is distant from the sun almost ¾ of the distance of the earth; the middle distance of Mars is something more than half as much again, as the distance of the earth; Jupiter’s middle distance exceeds five times the distance of the earth, by between ⅕ and 1/6 part of this distance; Saturn’s middle distance is scarce more than 9½ times the distance between the earth and sun; but the middle distance between the earth and sun is about 217⅛ times the sun’s semidiameter.
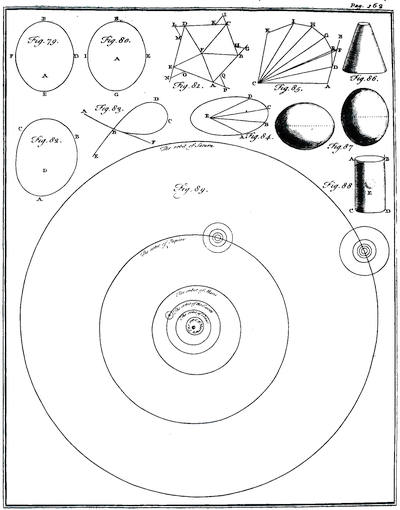
4. All these planets move one way, from west to east; and of the primary planets the most remote is longest in finishing its course round the sun. The period of Saturn falls short only sixteen days of 29 years and a half. The period of Jupiter is twelve years wanting about 50 days. The period of Mars falls short of two years by about 43 days. The revolution of the earth constitutes the year. Venus performs her period in about 224½ days, and Mercury in about 88 days.
5. The course of each planet lies throughout in one plane or flat surface, in which the sun is placed; but they do not all move in the same plane, though the different planes, in which they move, cross each other in very small angles. They all cross each other in lines, which pass through the sun; because the sun lies in the plane of each orbit. This inclination of the several orbits to each other is represented in fig. 90. The line, in which the plane of any orbit crosses the plane of the earth’s motion, is called the line of the nodes of that orbit.
6. Each planet moves round the sun in the line, which we have mentioned above[143] under the name of ellipsis; which I shall here shew more particularly how to describe. I have there said how it is produced in the cone. I shall now shew how to form it upon a plane. Fix upon any plane two pins, as at A and B in fig. 91. To these tye a string A C B of any length. Then apply a third pin D so to the string, as to hold it strained; and in that manner carrying this pin about, the point of it will describe an ellipsis. If through the points A, B the straight line E A B F be drawn, to be terminated at the ellipsis in the points E and F, this is the longest line of any, that can be drawn within the figure, and is called the greater axis of the ellipsis. The line G H, drawn perpendicular to this axis E F, so as to pass through the middle of it, is called the lesser axis. The two points A and B are called focus’s. Now each planet moves round the sun in a line of this kind, so that the sun is found in one focus. Suppose A to be the place of the sun. Then E is the point, wherein the planet will be nearest of all to the sun, and at F it will be most remote. The point E is called the perihelion of the planet, and F the aphelion. In G and H the planet is said to be in its middle or mean distance; because the distance A G or A H is truly the middle between A E the least, and A F the greatest distance. In fig. 92. is represented how the greater axis of each orbit is situated in respect of the rest. The proportion between the greatest and least distances of the planet from the sun is very different in the different planets.
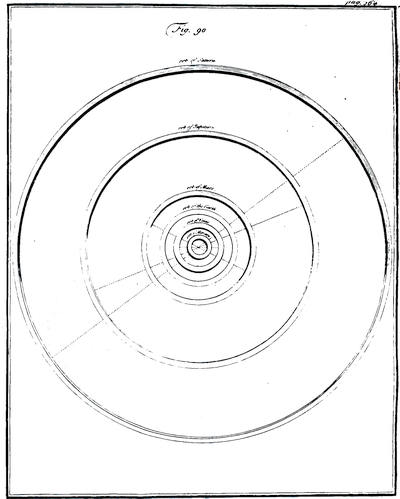
In Saturn the proportion of the [165]greatest distance to the least is something less, than the proportion of 9 to 8, but much nearer to this, than to the proportion of 10 to 9. In Jupiter this proportion is a little greater, than that of 11 to 10. In Mars it exceeds the proportion of 6 to 5. In the earth it is about the proportion of 30 to 29. In Venus it is near to that of 70 to 69. And in Mercury it comes not a great deal short of the proportion of 3 to 2.

7. Each of these planets so moves through its ellipsis, that the line drawn from the sun to the planet, by accompanying the planet in its motion, will describe about the sun equal spaces in equal times, after the manner spoke of in the chapter of centripetal forces[144]. There is also a certain relation between the greater axis’s of these ellipsis’s, and the times, in which the planets perform their revolutions through them. Which relation may be expressed thus. Let the period of one planet be denoted by the letter A, the greater axis of its orbit by D; let the period of another planet be denoted by B, and the greater axis of this planet’s orbit by E. Then if C be taken to bear the same proportion to B, as B bears to A; likewise if F be taken to bear the same proportion to E, as E bears to D; and G taken to bear the same proportion likewise to F, as E bears to D; then A shall bear the same proportion to C, as D bears to G.
8. The secondary planets move round their respective primary, much in the same manner as the primary do round[166] the sun. But the motions of these shall be more fully explained hereafter[145]. And there is, besides the planets, another sort of bodies, which in all probability move round the sun; I mean the comets. The farther description of which bodies I also leave to the place, where they are to be particularly treated on[146].
9. Far without this system the fixed stars are placed. These are all so remote from us, that we seem almost incapable of contriving any means to estimate their distance. Their number is exceeding great. Besides two or three thousand, which we see with the naked eye, telescopes open to our view vast numbers; and the farther improved these instruments are, we still discover more and more. Without doubt these are luminous globes, like our sun, and ranged through the wide extent of space; each of which, it is to be supposed, perform the same office, as our sun, affording light and heat to certain planets moving about them. But these conjectures are not to be pursued in this place.
10. I shall therefore now proceed to the particular design of this chapter, and shew, that there is no sensible matter lodged in the space where the planets move.
11. That they suffer no sensible resistance from any such matter, is evident from the agreement between the observations of astronomers in different ages, with regard to the time, in which the planets have been found to perform their[167] periods. But it was the opinion of Des Cartes[147], that the planets might be kept in their courses by the means of a fluid matter, which continually circulating round should carry the planets along with it. There is one appearance that may seem to favour this opinion; which is, that the sun turns round its own axis the same way, as the planets move. The earth also turns round its axis the same way, as the moon moves round the earth. And the planet Jupiter turns upon its axis the same way, as his satellites revolve round him. It might therefore be supposed, that if the whole planetary region were filled with a fluid matter, the sun, by turning round on its own axis, might communicate motion first to that part of the fluid, which was contiguous, and by degrees propagate the like motion to the parts more remote. After the same manner the earth might communicate motion to this fluid, to a distance sufficient to carry round the moon, and Jupiter communicate the like to the distance of its satellites. Sir Isaac Newton has particularly examined what might be the result of such a motion as this[148]; and he finds, that the velocities, with which the parts of this fluid will move in different distances from the center of the motion, will not agree with the motion observed in different planets: for instance, that the time of one intire circulation of the fluid, wherein Jupiter should swim, would bear a greater proportion to the time of one intire circulation of the fluid, where the earth is; than the period of Jupiter bears to the period of the earth. But he also proves[149], that the planet cannot circulate in such a fluid,[168] so as to keep long in the same course, unless the planet and the contiguous fluid are of the same density, and the planet be carried along with the same degree of motion, as the fluid. There is also another remark made upon this motion by our author; which is, that some vivifying force will be continually necessary at the center of the motion[150]. The sun in particular, by communicating motion to the ambient fluid, will lose from it self as much motion, as it imparts to the fluid; unless some acting principle reside in the sun to renew its motion continually. If the fluid be infinite, this gradual loss of motion would continue till the whole should stop[151]; and if the fluid were limited, this loss of motion would continue, till there would remain no swifter a revolution in the sun, than in the utmost part of the fluid; so that the whole would turn together about the axis of the sun, like one solid globe[152].
12. It is farther to be observed, that as the planets do not move in perfect circles round the sun; there is a greater distance between their orbits in some places, than in others. For instance, the distance between the orbit of Mars and Venus is near half as great again in one part of their orbits, as in the opposite place. Now here the fluid, in which the earth should swim, must move with a less rapid motion, where there is this greater interval between the contiguous orbits; but on the contrary, where the space is straitest, the earth moves more slowly, than where it is widest[153].
13. Farther, if this our globe of earth swam in a fluid of equal density with the earth it self, that is, in a fluid more dense than water; all bodies put in motion here upon the earth’s surface must suffer a great resistance from it; where as, by Sir Isaac Newton’s experiments mentioned in the preceding chapter, bodies, that fell perpendicularly down through the air, felt about 1/860 part only of the resistance, which bodies suffered that fell in like manner through water.
14. Sir Isaac Newton applies these experiments yet farther, and examines by them the general question concerning the absolute plenitude of space. According to the Aristotelians, all space was full without any the least vacuities whatever. DesCartes embraced the same opinion, and therefore supposed a subtile fluid matter, which should pervade all bodies, and adequately fill up their pores. The Atomical philosophers, who suppose all bodies both fluid and solid to be composed of very minute but solid atoms, assert that no fluid, how subtile soever the particles or atoms whereof it is composed should be, can ever cause an absolute plenitude; because it is impossible that any body can pass through the fluid without putting the particles of it into such a motion, as to separate them, at least in part, from one another, and so perpetually to cause small vacuities; by which these Atomists endeavour to prove, that a vacuum, or some space empty of all matter, is absolutely necessary to be in nature. Sir Isaac Newton objects against the filling of space with such a subtile fluid, that all bodies in motion must be unmeasurably resisted[170] by a fluid so dense, as absolutely to fill up all the space, through which it is spread. And lest it should be thought, that this objection might be evaded by ascribing to this fluid such very minute and smooth parts, as might remove all adhesion or friction between them, whereby all resistance would be lost, which this fluid might otherwise give to bodies moving in it; Sir Isaac Newton proves, in the manner above related, that fluids resist from the power of inactivity of their particles; and that water and the air resist almost entirely on this account: so that in this subtile fluid, however minute and lubricated the particles, which compose it, might be; yet if the whole fluid was as dense as water, it would resist very near as much as water does; and whereas such a fluid, whose parts are absolutely close together without any intervening spaces, must be a great deal more dense than water, it must resist more than water in proportion to its greater density; unless we will suppose the matter, of which this fluid is composed, not to be endued with the same degree of inactivity as other matter. But if you deprive any substance of the property so universally belonging to all other matter, without impropriety of speech it can scarce be called by this name.
15. Sir Isaac Newton made also an experiment to try in particular, whether the internal parts of bodies suffered any resistance. And the result did indeed appear to favour some small degree of resistance; but so very little, as to leave it doubtful, whether the effect did not arise from some other latent cause[154].
Chap. II.
Concerning the cause, which keeps in motion
the primary planets.
SINCE the planets move in a void space and are free from resistance; they, like all other bodies, when once in motion, would move on in a straight line without end, if left to themselves. And it is now to be explained what kind of action upon them carries them round the sun. Here I shall treat of the primary planets only, and discourse of the secondary apart in the next chapter. It has been just now declared, that these primary planets move so about the sun, that a line extended from the sun to the planet, will, by accompanying the planet in its motion, pass over equal spaces in equal portions of time[155]. And this one property in the motion of the planets proves, that they are continually acted on by a power directed perpetually to the sun as a center. This therefore is one property of the cause, which keeps the planets in their courses, that it is a centripetal power, whose center is the sun.
2. Again, in the chapter upon centripetal forces[156] it was observ’d, that if the strength of the centripetal power was suitably accommodated every where to the motion of any body round a center, the body might be carried in[172] any bent line whatever, whose concavity should be every where turned towards the center of the force. It was farther remarked, that the strength of the centripetal force, in each place, was to be collected from the nature of the line, wherein the body moved[157]. Now since each planet moves in an ellipsis, and the sun is placed in one focus; Sir Isaac Newton deduces from hence, that the strength of this power is reciprocally in the duplicate proportion of the distance from the sun. This is deduced from the properties, which the geometers have discovered in the ellipsis. The process of the reasoning is not proper to be enlarged upon here; but I shall endeavour to explain what is meant by the reciprocal duplicate proportion. Each of the terms reciprocal proportion, and duplicate proportion, has been already defined[158]. Their sense when thus united is as follows. Suppose the planet moved in the orbit A B C (in fig. 93.) about the sun in S. Then, when it is said, that the centripetal power, which acts on the planet in A, bears to the power acting on it in B a proportion, which is the reciprocal of the duplicate proportion of the distance S A to the distance S B; it is meant that the power in A bears to the power in B the duplicate of the proportion of the distance S B to the distance S A. The reciprocal duplicate proportion may be explained also by numbers as follows. Suppose several distances to bear to each other proportions expressed by the numbers 1, 2, 3, 4, 5; that is, let the second distance be double the first, the third be three times, the fourth four times, and the fifth five times as great as the[173] first. Multiply each of these numbers by it self, and 1 multiplied by 1 produces still 1, 2 multiplied by 2 produces 4, 3 by 3 makes 9, 4 by 4 makes 16, and 5 by 5 gives 25. This being done, the fractions ¼, 1/9, 1/16, 1/25, will respectively express the proportion, which the centripetal power in each of the following distances bears to the power at the first distance: for in the second distance, which is double the first, the centripetal power will be one fourth part only of the power at the first distance; at the third distance the power will be one ninth part only of the first power; at the fourth distance, the power will be but one sixteenth part of the first; and at the fifth distance, one twenty fifth part of the first power.
3. Thus is found the proportion, in which this centripetal power decreases, as the distance from the sun increases, within the compass of one planet’s motion. How it comes to pass, that the planet can be carried about the sun by this centripetal power in a continual round, sometimes rising from the sun, then descending again as low, and from thence be carried up again as far remote as before, alternately rising and falling without end; appears from what has been written above concerning centripetal forces: for the orbits of the planets resemble in shape the curve line proposed in § 17 of the chapter on these forces[159].
4. But farther, in order to know whether this centripetal force extends in the same proportion throughout, and consequently whether all the planets are influenced by the very same[174] power, our author proceeds thus. He inquires what relation there ought to be between the periods of the different planets, provided they were acted upon by the same power decreasing throughout in the forementioned proportion; and he finds, that the period of each in this case would have that very relation to the greater axis of its orbit, as I have declared above[160] to be found in the planets by the observations of astronomers. And this puts it beyond question, that the different planets are pressed towards the sun, in the same proportion to their distances, as one planet is in its several distances. And thence in the last place it is justly concluded, that there is such a power acting towards the sun in the foresaid proportion at all distances from it.
5. This power, when referred to the planets, our author calls centripetal, when to the sun attractive; he gives it likewise the name of gravity, because he finds it to be of the same nature with that power of gravity, which is observed in our earth, as will appear hereafter[161]. By all these names he designs only to signify a power endued with the properties before mentioned; but by no means would he have it understood, as if these names referred any way to the cause of it. In particular in one place where he uses the name of attraction, he cautions us expressly against implying any thing but a power directing a body to a center without any reference to the cause of it, whether residing in that center, or arising from any external impulse[162].
6. But now, in these demonstrations some very minute inequalities in the motion of the planets are neglected; which is done with a great deal of judgment; for whatever be their cause, the effects are very inconsiderable, they being so exceeding small, that some astronomers have thought fit wholly to pass them by[163]. However the excellency of this philosophy, when in the hands of so great a geometer as our author, is such, that it is able to trace the least variations of things up to their causes. The only inequalities, which have been observed common to all the planets, are the motion of the aphelion and the nodes. The transverse axis of each orbit does not always remain fixed, but moves about the sun with a very slow progressive motion: nor do the planets keep constantly the same plane, but change them, and the lines in which those planes intersect each other by insensible degrees. The first of these inequalities, which is the motion of the aphelion, may be accounted for, by supposing the gravitation of the planets towards the sun to differ a little from the forementioned reciprocal duplicate proportion of the distances; but the second, which is the motion of the nodes, cannot be accounted for by any power directed towards the sun; for no such can give the planet any lateral impulse to divert it from the plane of its motion into any new plane, but of necessity must be derived from some other center. Where that power is lodged, remains to be discovered. Now it is proved, as shall be explained in the following chapter, that the three primary planets Saturn, Jupiter, and the earth, which have satellites revolving about them, are endued with a power of[176] causing bodies, in particular those satellites, to gravitate towards them with a force, which is reciprocally in the duplicate proportion of their distances; and the planets are in all respects, in which they come under our examination, so similar and alike, that there is no reason to question, but they have all the same property. Though it be sufficient for the present purpose to have it proved of Jupiter and Saturn only; for these planets contain much greater quantities of matter than the rest, and proportionally exceed the others in power[164]. But the influence of these two planets being allowed, it is evident how the planets come to shift continually their planes: for each of the planets moving in a different plane, the action of Jupiter and Saturn upon the rest will be oblique to the planes of their motion; and therefore will gradually draw them into new ones. The same action of these two planets upon the rest will cause likewise a progressive motion of the aphelion; so that there will be no necessity of having recourse to the other cause for this motion, which was before hinted at[165]; viz, the gravitation of the planets towards the sun differing from the exact reciprocal duplicate proportion of the distances. And in the last place, the action of Jupiter and Saturn upon each other will produce in their motions the same inequalities, as their joint action produces in the rest. All this is effected in the same manner, as the sun produces the same kind of inequalities and many others in the motion of the moon and the other secondary planets; and therefore will be best apprehended by what shall be said in the next chapter.[177] Those other irregularities in the motion of the secondary planets have place likewise here; but are too minute to be observable: because they are produced and rectified alternately, for the most part in the time of a single revolution; whereas the motion of the aphelion and nodes, which continually increase, become sensible in a long series of years. Yet some of these other inequalities are discernible in Jupiter and Saturn, in Saturn chiefly; for when Jupiter, who moves faster than Saturn, approaches near to a conjunction with him, his action upon Saturn will a little retard the motion of that planet, and by the reciprocal action of Saturn he will himself be accelerated. After conjunction, Jupiter will again accelerate Saturn, and be likewise retarded in the same degree, as before the first was retarded and the latter accelerated. Whatever inequalities besides are produced in the motion of Saturn by the action of Jupiter upon that planet, will be sufficiently rectified, by placing the focus of Saturn’s ellipsis, which should otherwise be in the sun, in the common center of gravity of the sun and Jupiter. And all the inequalities in the motion of Jupiter, caused by Saturn’s action upon him, are much less considerable than the irregularities of Saturn’s motion[166].
7. This one principle therefore of the planets having a power, as well as the sun, to cause bodies to gravitate towards them, which is proved by the motion of the secondary planets to obtain in fact, explains all the irregularities relating to the planets ever observed by astronomers.
8. Sir Isaac Newton after this proceeds to make an improvement in astronomy by applying this theory to the farther correction of their motions. For as we have here observed the planets to possess a principle of gravitation, as well as the sun; so it will be explained at large hereafter, that the third law of motion, which makes action and reaction equal, is to be applied in this case[167]; and that the sun does not only attract each planet, but is it self also attracted by them; the force, wherewith the planet is acted on, bearing to the force, wherewith the sun it self is acted on at the same time, the proportion, which the quantity of matter in the sun bears to the quantity of matter in the planet. From the action between the sun and planet being thus mutual Sir Isaac Newton proves that the sun and planet will describe about their common center of gravity similar ellipsis’s; and then that the transverse axis of the ellipsis described thus about the moveable sun, will bear to the transverse axis of the ellipsis, which would be described about the sun at rest in the same time, the same proportion as the quantity of solid matter in the sun and planet together bears to the first of two mean proportionals between this quantity and the quantity of matter in the sun only[168].
9. Above, where I shewed how to find a cube, that should bear any proportion to another cube[169], the lines F T and T S are two mean proportionals between E F and F G; and counting from E F, F T is called the first, and F S the second of those means. In numbers these mean proportionals[179] are thus found.

Suppose A and B two numbers, and it be required to find C the first, and D the second of the two mean proportionals between them. First multiply A by it self, and the product multiply by B; then C will be the number which in arithmetic is called the cubic root of this last product; that is, the number C being multiplied by it self, and the product again multiplied by the same number C, will produce the product above mentioned. In like manner D is the cubic root of the product of B multiplied by it self, and the produce of that multiplication multiplied again by A.
10. It will be asked, perhaps, how this correction can be admitted, when the cause of the motions of the planets was before found by supposing the sun the center of the power, which acted upon them: for according to the present correction this power appears rather to be directed to their common center of gravity. But whereas the sun was at first concluded to be the center, to which the power acting on the planets was directed, because the spaces described round the sun in equal times were found to be equal; so Sir Isaac Newton proves, that if the sun and planet move round their common center of gravity, yet to an eye placed in the planet, the spaces, which will appear to be described about the sun, will have the same relation to the times of their description, as the real spaces would have, if the sun were at rest[170]. I farther asserted, that, supposing the planets to move round the sun at rest,[180] and to be attracted by a power, which every where should act with degrees of strength reciprocally in the duplicate proportion of the distances; then the periods of the planets must observe the same relation to their distances, as astronomers find them to do. But here it must not be supposed, that the observations of astronomers absolutely agree without any the least difference; and the present correction will not cause a deviation from any one astronomer’s observations, so much as they differ from one another. For in Jupiter, where this correction is greatest, it hardly amounts to the 3000th part of the whole axis.
11. Upon this head I think it not improper to mention a reflection made by our excellent author upon these small inequalities in the planets motions; which contains under it a very strong philosophical argument against the eternity of the world. It is this, that these inequalities must continually increase by slow degrees, till they render at length the present frame of nature unfit for the purposes, it now serves[171]. And a more convincing proof cannot be desired against the present constitution’s having existed from eternity than this, that a certain period of years will bring it to an end. I am aware this thought of our author has been represented even as impious, and as no less than casting a reflection upon the wisdom of the author of nature, for framing a perishable work. But I think so bold an assertion ought to have been made with singular caution. For if this remark upon the increasing irregularities of the heavenly motions[181] be true in fact, as it really is, the imputation must return upon the asserter, that this does detract from the divine wisdom. Certainly we cannot pretend to know all the omniscient Creator’s purposes in making this world, and therefore cannot undertake to determine how long he designed it should last. And it is sufficient, if it endure the time intended by the author. The body of every animal shews the unlimited wisdom of its author no less, nay in many respects more, than the larger frame of nature; and yet we see, they are all designed to last but a small space of time.
12. There need nothing more be said of the primary planets; the motions of the secondary shall be next considered.
Chap. III.
Of the motion of the MOON and the other
SECONDARY PLANETS.
THE excellency of this philosophy sufficiently appears from its extending in the manner, which has been related, to the minutest circumstances of the primary planets motions; which nevertheless bears no proportion to the vast success of it in the motions of the secondary; for it not only accounts for all the irregularities, by which their motions were known to be disturbed, but has discovered others so complicated, that astronomers were never able to distinguish them, and reduce them under proper heads; but these were only to be[182] found out from their causes, which this philosophy has brought to light, and has shewn the dependence of these inequalities upon such causes in so perfect a manner, that we not only learn from thence in general, what those inequalities are, but are able to compute the degree of them. Of this Sir Is. Newton has given several specimens, and has moreover found means to reduce the moon’s motion so completely to rule, that he has framed a theory, from which the place of that planet may at all times be computed, very nearly or altogether as exactly, as the places of the primary planets themselves, which is much beyond what the greatest astronomers could ever effect.
2. The first thing demonstrated of these secondary planets is, that they are drawn towards their respective primary in the same manner as the primary planets are attracted by the sun. That each secondary planet is kept in its orbit by a power pointed towards the center of the primary planet, about which the secondary revolves; and that the power, by which the secondaries of the same primary are influenced, bears the same relation to the distance from the primary, as the power, by which the primary planets are guided, does in regard to the distance from the sun[172]. This is proved in the satellites of Jupiter and Saturn, because they move in circles, as far as we can observe, about their respective primary with an equable course, the respective primary being the center of each orbit: and by comparing the times, in which the different satellites of the same primary perform their periods, they are[183] found to observe the same relation to the distances from their primary, as the primary planets observe in respect of their mean distances from the sun[173]. Here these bodies moving in circles with an equable motion, each satellite passes over equal parts of its orbit in equal portions of time; consequently the line drawn from the center of the orbit, that is, from the primary planet, to the satellite, will pass over equal spaces along with the satellite in equal portions of time; which proves the power, by which each satellite is held in its orbit, to be pointed towards the primary as a center[174]. It is also manifest that the centripetal power, which carries a body in a circle concentrical with the power, acts upon the body at all times with the same strength. But Sir Isaac Newton demonstrates that, when bodies are carried in different circles by centripetal powers directed to the centers of those circles, then, the degrees of strength of those powers are to be compared by considering the relation between the times, in which the bodies perform their periods through those circles[175]; and in particular he shews, that if the periodical times bear that relation, which I have just now asserted the satellites of the same primary to observe; then the centripetal powers are reciprocally in the duplicate proportion of the semidiameters of the circles, or in that proportion to the distances of the bodies from the centers[176]. Hence it follows that in the planets Jupiter and Saturn, the centripetal power in each decreases with the increase of distance, in the same proportion as the centripetal[184] power appertaining to the sun decreases with the increase of distance. I do not here mean that this proportion of the centripetal powers holds between the power of Jupiter at any distance compared with the power of Saturn at any other distance; but only in the change of strength of the power belonging to the same planet at different distances from him. Moreover what is here discovered of the planets Jupiter and Saturn by means of the different satellites, which revolve round each of them, appears in the earth by the moon alone; because she is found to move round the earth in an ellipsis after the same manner as the primary planets do about the sun; excepting only some small irregularities in her motion, the cause of which will be particularly explained in what follows, whereby it will appear, that they are no objection against the earth’s acting on the moon in the same manner as the sun acts on the primary planets; that is, as the other primary planets Jupiter and Saturn act upon their satellites. Certainly since these irregularities can be otherwise accounted for, we ought not to depart from that rule of induction so necessary in philosophy, that to like bodies like properties are to be attributed, where no reason to the contrary appears. We cannot therefore but ascribe to the earth the same kind of action upon the moon, as the other primary planets Jupiter and Saturn have upon their satellites; which is known to be very exactly in the proportion assigned by the method of comparing the periodical times and distances of all the satellites which move about the same planet; this abundantly compensating our not being near enough to observe the exact figure of their orbits. For if the little deviation of the moon’s orbit[185] orbit from a true permanent ellipsis arose from the action of the earth upon the moon not being in the exact reciprocal duplicate proportion of the distance, were another moon to revolve about the earth, the proportion between the periodical times of this new moon, and the present, would discover the deviation from the mentioned proportion much more manifestly.
3. By the number of satellites, which move round Jupiter and Saturn, the power of each of these planets is measured in a great diversity of distance; for the distance of the outermost satellite in each of these planets exceeds several times the distance of the innermost. In Jupiter the astronomers have usually placed the innermost satellite at a distance from the center of that planet equal to about 5⅔ of the semidiameters of Jupiter’s body, and this satellite performs its revolution in about 1 day 18½ hours. The next satellite, which revolves round Jupiter in about 3 days 13⅕ hours, they place at the distance from Jupiter of about 9 of that planet’s semidiameters. To the third satellite, which performs its period nearly in 7 days 3¾ hours, they assign the distance of about 14⅖ semidiameters. But the outermost satellite they remove to 25⅓ semidiameters, and this satellite makes its period in about 16 days 16½ hours[177]. In Saturn there is still a greater diversity in the distance of the several satellites. By the observations of the late Cassini, a celebrated astronomer in France, who first discovered all these satellites, except one known before, the innermost is distant about 4½ of Saturn’s semidiameters from his center, and revolves[186] round in about 1 day 21⅓ hours. The next satellite is distant about 5¾ semidiameters, and makes its period in about 2 days 17⅔ hours. The third is removed to the distance of about 8 semidiameters, and performs its revolution in near 4 days 12½ hours. The fourth satellite discovered first by the great Huygens, is near 18⅔ semidiameters, and moves round Saturn in about 15 days 22⅔ hours. The outermost is distant 56 semidiameters, and makes its revolution in about 79 days 7⅘ hours[178]. Besides these satellites, there belongs to the planet Saturn another body of a very singular kind. This is a shining, broad, and flat ring, which encompasses the planet round. The diameter of the outermost verge of this ring is more than double the diameter of Saturn. Huygens, who first described this ring, makes the whole diameter thereof to bear to the diameter of Saturn the proportion of 9 to 4. The late reverend Mr. Pound makes the proportion something greater, viz. that of 7 to 3. The distances of the satellites of this planet Saturn are compared by Cassini to the diameter of the ring. His numbers I have reduced to those above, according to Mr. Pound’s proportion between the diameters of Saturn and of his ring. As this ring appears to adhere no where to Saturn, so the distance of Saturn from the inner edge of the ring seems rather greater than the breadth of the ring. The distances, which have here been given, of the several satellites, both for Jupiter and Saturn, may be more depended on in relation to the proportion, which those belonging to the same primary planet[187] bear one to another, than in respect to the very numbers, that have been here set down, by reason of the difficulty there is in measuring to the greatest exactness the diameters of the primary planets; as will be explained hereafter, when we come to treat of telescopes[179]. By the observations of the forementioned Mr. Pound, in Jupiter the distance of the innermost satellite should rather be about 6 semidiameters, of the second 9-½, of the third 15, and of the outermost 26⅔[180]; and in Saturn the distance of the innermost satellite 4 semidiameters, of the next 6¼, of the third 8¾, of the fourth 20⅓, and of the fifth 59[181]. However the proportion between the distances of the satellites in the same primary is the only thing necessary to the point we are here upon.
4. But moreover the force, wherewith the earth acts in different distances, is confirmed from the following consideration, yet more expresly than by the preceding analogical reasoning. It will appear, that if the power of the earth, by which it retains the moon in her orbit, be supposed to act at all distances between the earth and moon, according to the forementioned rule; this power will be sufficient to produce upon bodies, near the surface of the earth, all the effects ascribed to the principle of gravity. This is discovered by the following method. Let A (in fig. 94.) represent the earth, B the moon, B C D the moon’s orbit, which differs little from a circle, of which A is the center. If the moon in B were left to it self to move with the velocity, it has in the point B, it[188] would leave the orbit, and proceed right forward in the line B E, which touches the orbit in B. Suppose the moon would upon this condition move from B to E in the space of one minute of time. By the action of the earth upon the moon, whereby it is retained in its orbit, the moon will really be found at the end of this minute in the point F, from whence a straight line drawn to A shall make the space B F A in the circle equal to the triangular space B E A; so that the moon in the time wherein it would have moved from B to E, if left to it self, has been impelled towards the earth from E to F. And when the time of the moon’s passing from B to F is small, as here it is only one minute, the distance between E and F scarce differs from the space, through which the moon would descend in the same time, if it were to fall directly down from B toward A without any other motion. A B the distance of the earth and moon is about 60 of the earth’s semidiameters, and the moon completes her revolution round the earth in about 27 days 7 hours and 43 minutes: therefore the space E F will here be found by computation to be about 16⅛ feet. Consequently, if the power, by which the moon is retained in its orbit, be near the surface of the earth greater, than at the distance of the moon in the duplicate proportion of that distance; the number of feet, a body would descend near the surface of the earth by the action of this power upon it in one minute of time, would be equal to 16⅛ multiplied twice into the number 60, that is, equal to 58050. But how fast bodies fall near the surface of the earth may be known by the pendulum[182]; and[189] by the exactest experiments they are found to descend the space of 16⅛ feet in a second of time; and the spaces described by falling bodies being in the duplicate proportion of the times of their fall[183], the number of feet, a body would describe in its fall near the surface of the earth in one minute of time, will be equal to 16⅛ twice multiplied by 60, the same as would be caused by the power which acts upon the moon.
5. In this computation the earth is supposed to be at rest, whereas it would have been more exact to have supposed it to move, as well as the moon, about their common center of gravity; as will easily be understood, by what has been said in the preceding chapter, where it was shewn, that the sun is subjected to the like motion about the common center of gravity of it self and the planets. The action of the sun upon the moon, which is to be explain’d in what follows, is likewise here neglected: and Sir Isaac Newton shews, if you take in both these considerations, the present computation will best agree to a somewhat greater distance of the moon and earth, viz. to 60½ semidiameters of the earth, which distance is more conformable to astronomical observations.
6. These computations afford an additional proof, that the action of the earth observes the same proportion to the distance, which is here contended for. Before I said, it was reasonable to conclude so by induction from the planets[190] Jupiter and Saturn; because they act in that manner. But now the same thing will be evident by drawing no other consequence from what is seen in those planets, than that the power, by which the primary planets act on their secondary, is extended from the primary through the whole interval between, so that it would act in every part of the intermediate space. In Jupiter and Saturn this power is so far from being confined to a small extent of distance, that it not only reaches to several satellites at very different distances, but also from one planet to the other, nay even through the whole planetary system[184]. Consequently there is no appearance of reason, why this power should not act at all distances, even at the very surfaces of these planets as well as farther off. But from hence it follows, that the power, which retains the moon in her orbit, is the same, as causes bodies near the surface of the earth to gravitate. For since the power, by which the earth acts on the moon, will cause bodies near the surface of the earth to descend with all the velocity they are found to do, it is certain no other power can act upon them besides; because if it did, they must of necessity descend swifter. Now from all this it is at length very evident, that the power in the earth, which we call gravity, extends up to the moon, and decreases in the duplicate proportion of the increase of the distance from the earth.
7. This finishes the discoveries made in the action of the primary planets upon their secondary. The next thing[191] to be shewn is, that the sun acts upon them likewise: for this purpose it is to be observed, that if to the motion of the satellite, whereby it would be carried round its primary at rest, be superadded the same motion both in regard to velocity and direction, as the primary it self has, it will describe about the primary the same orbit, with as great regularity, as if the primary was indeed at rest. The cause of this is that law of motion, which makes a body near the surface of the earth, when let fall, to descend perpendicularly, though the earth be in so swift a motion, that if the falling body did not partake of it, its descent would be remarkably oblique; and that a body projected describes in the most regular manner the same parabola, whether projected in the direction, in which the earth moves, or in the opposite direction, if the projecting force be the same[185]. From this we learn, that if the satellite moved about its primary with perfect regularity, besides its motion about the primary, it would participate of all the motion of its primary; have the same progressive velocity, with which the primary is carried about the sun; and be impelled with the same velocity as the primary towards the sun, in a direction parallel to that impulse of its primary. And on the contrary, the want of either of these, in particular of the impulse towards the sun, will occasion great inequalities in the motion of the secondary planet. The inequalities, which would arise from the absence of this impulse towards the sun are[192] so great, that by the regularity, which appears in the motion of the secondary planets, it is proved, that the sun communicates, the same velocity to them by its action, as it gives to their primary at the same distance. For Sir Isaac Newton informs us, that upon examination he found, that if any of the satellites of Jupiter were attracted by the sun more or less, than Jupiter himself at the same distance, the orbit of that satellite, instead of being concentrical to Jupiter, must have its center at a greater or less distance, than the center of Jupiter from the sun, nearly in the subduplicate proportion of the difference between the sun’s action upon the satellite, and upon Jupiter; and therefore if any satellite were attracted by the sun but 1/1000 part more or less, than Jupiter is at the same distance, the center of the orbit of that satellite would be distant from the center of Jupiter no less than a fifth part of the distance of the outermost satellite from Jupiter[186]; which is almost the whole distance of the innermost satellite. By the like argument the satellites of Saturn gravitate towards the sun, as much as Saturn it self at the same distance; and the moon as much as the earth.
8. Thus is proved, that the sun acts upon the secondary planets, as much as upon the primary at the same distance: but it was found in the last chapter, that the action of the sun upon bodies is reciprocally in the duplicate proportion of the distance; therefore the secondary[193] planets being sometimes nearer to the sun than the primary, and sometimes more remote, they are not alway acted upon in the same degree with their primary, but when nearer to the sun, are attracted more, and when farther distant, are attracted less. Hence arise various inequalities in the motion of the secondary planets[187].
9. Some of these inequalities would take place, though the moon, if undisturbed by the sun, would have moved in a circle concentrical to the earth, and in the plane of the earth’s motion; others depend on the elliptical figure, and the oblique situation of the moon’s orbit. One of the first kind is, that the moon is caused so to move, as not to describe equal spaces in equal times, but is continually accelerated, as she passes from the quarter to the new or full, and is retarded again by the like degrees in returning from the new and full to the next quarter. Here we consider not so much the absolute, as the apparent motion of the moon in respect to us.
10. The principles of astronomy teach how to distinguish these two motions. Let S (in fig. 95.) represent the sun, A the earth moving in its orbit B C, D E F G the moon’s orbit, the place of the moon H. Suppose the earth to have moved from A to I. Because it has been shewn, that the moon partakes of all the progressive motion of the earth; and likewise that the sun attracts both the earth and moon equally, when they are at the same distance from it, or that the mean action of the sun upon the moon is equal to its action[194] upon the earth: we must therefore consider the earth as carrying about with it the moon’s orbit; so that when the earth is removed from A to I, the moon’s orbit shall likewise be removed from its former situation into that denoted by K L M N. But now the earth being in I, if the moon were found in O, so that O I should be parallel to H A, though the moon would really have moved from H to O, yet it would not have appeared to a spectator upon the earth to have moved at all, because the earth has moved as much it self; so that the moon would still appear in the same place with respect to the fixed stars. But if the moon be observed in P, it will then appear to have moved, its apparent motion being measured by the angle under O I P. And if the angle under P I S be less than the angle under H A S, the moon will have approached nearer to its conjunction with the sun.
11. To come now to the explication of the mentioned inequality in the moon’s motion: let S (in fig. 96.) represent the sun, A the earth, B C D E the moon’s orbit, C the place of the moon, when in the latter quarter. Here it will be nearly at the same distance from the sun, as the earth is. In this case therefore they will both be equally attracted, the earth in the direction A S, and the moon in the direction C S. Whence as the earth in moving round the sun is continually descending toward it, so the moon in this situation must in any equal portion of time descend as much; and therefore the position of the line A C in respect of A S, and the change, which the moon’s motion produces in the angle under C A S, will not be altered by the sun.
12. But now as soon as ever the moon is advanced from the quarter toward the new or conjunction, suppose to G, the action of the sun upon it will have a different effect. Here, were the sun’s action upon the moon to be applied in the direction G H parallel to A S, if its action on the moon were equal to its action on the earth, no change would be wrought by the sun on the apparent motion of the moon round the earth. But the moon receiving a greater impulse in G than the earth receives in A, were the sun to act in the direction G H, yet it would accelerate the description of the space D A G, and cause the angle under G A D to decrease faster, than otherwise it would. The sun’s action will have this effect upon account of the obliquity of its direction to that, in which the earth attracts the moon. For the moon by this means is drawn by two forces oblique to each other, one drawing from G toward A, the other from G toward H, therefore the moon must necessarily be impelled toward D. Again, because the sun does not act in the direction G H parallel to S A, but in the direction G S oblique to it, the sun’s action on the moon will by reason of this obliquity farther contribute to the moon’s acceleration. Suppose the earth in any short space of time would have moved from A to I, if not attracted by the sun; the point I being in the straight line C E, which touches the earth’s orbit in A. Suppose the moon in the same time would have moved in her orbit from G to K, and besides have partook of all the progressive motion of the earth. Then if K L be drawn parallel to A I, and taken equal to it, the moon, if not attracted by the sun, would be found[196] in L. But the earth by the sun’s action is removed from I. Suppose it were moved down to M in the line I M N parallel to S A, and if the moon were attracted but as much, and in the same direction, as the earth is here supposed to be attracted, so as to have descended during the same time in the line L O, parallel also to A S, down as far as P, till L P were equal to I M; the angle under P M N would be equal to that under L I N, that is, the moon will appear advanced no farther forward, than if neither it nor the earth had been subject to the sun’s action. But this is upon the supposition, that the action of the sun upon the moon and earth were equal; whereas the moon being acted upon more than the earth, did the sun’s action draw the moon in the line L O parallel to A S, it would draw it down so far as to make L P greater than I M; whereby the angle under P M N will be rendred less, than that under L I N. But moreover, as the sun draws the earth in a direction oblique to I N, the earth will be found in its orbit somewhat short of the point M; however the moon is attracted by the sun still more out of the line L O, than the earth is out of the line I N; therefore this obliquity of the sun’s action will yet farther diminish the angle under P M N.
13. Thus the moon at the point G receives an impulse from the sun, whereby her motion is accelerated. And the sun producing this effect in every place between the quarter and the conjunction, the moon will move from the quarter with a motion continually more and more accelerated; and therefore by acquiring from time to time additional degrees[197] of velocity in its orbit, the spaces, which are described in equal times by the line drawn from the earth to the moon, will not be every where equal, but those toward the conjunction will be greater, than those toward the quarter. But now in the moon’s passage from the conjunction D to the next quarter the sun’s action will again retard the moon, till at the next quarter in E it be restored to the first velocity, which it had in C.
14. Again as the moon moves from E to the full or opposition to the sun in B, it is again accelerated, the deficiency of the sun’s action upon the moon, from what it has upon the earth, producing here the same effect as before the excess of its action. Consider the moon in Q, moving from E towards B. Here if the moon were attracted by the sun in a direction parallel to A S, yet being acted on less than the earth, as the earth descends toward the sun, the moon will in some measure be left behind. Therefore Q F being drawn parallel to S B, a spectator on the earth would see the moon move, as if attracted from the point Q in the direction Q F with a degree of force equal to that, whereby the sun’s action on the moon falls short of its action on the earth. But the obliquity of the sun’s action has also here an effect. In the time the earth would have moved from A to I without the influence of the sun, let the moon have moved in its orbit from Q to R. Drawing therefore R T parallel to A I, and equal to the same, for the like reason as before, the moon by the motion of its orbit, if not at all attracted by the sun, must be found in T; and therefore, if attracted in a direction parallel to S A, would[198] be in the line T V parallel to A S; suppose in W. But the moon in Q being farther off the sun than the earth, it will be less attracted, that is, T W will be less than I M, and if the line S M be prolonged toward X, the angle under X M W will be less than that under X I T. Thus by the sun’s action the moon’s passage from the quarter to the full would be accelerated, if the sun were to act on the earth and moon in a direction parallel to A S: and the obliquity of the sun’s action will still more increase this acceleration. For the action of the sun on the moon is oblique to the line S A the whole time of the moon’s passage from Q to T, and will carry the moon out of the line T V toward the earth. Here I suppose the time of the moon’s passage from Q to T so short, that it shall not pass beyond the line S A. The earth also will come a little short of the line I N, as was said before. From these causes the angle under X M W will be still farther lessened.
15. The moon in passing from the opposition B to the next quarter will be retarded again by the same degrees, as it is accelerated before its appulse to the opposition. Because this action of the sun, which in the moon’s passage from the quarter to the opposition causes it to be extraordinarily accelerated, and diminishes the angle, which measures its distance from the opposition; will make the moon slacken its pace afterwards, and retard the augmentation of the same angle in its passage from the opposition to the following quarter; that is, will prevent that angle from increasing so fast, as otherwise it would. And thus the moon, by the sun’s action upon it, is twice accelerated and twice restored to its first velocity, every[199] circuit it makes round the earth. This inequality of the moon’s motion about the earth is called by astronomers its variation.
16. The next effect of the sun upon the moon is, that it gives the orbit of the moon in the quarters a greater degree of curvature, than it would receive from the action of the earth alone; and on the contrary in the conjunction and opposition the orbit is less inflected.
17. When the moon is in conjunction with the sun in the point D, the sun attracting the moon more forcibly than it does the earth, the moon by that means is impelled less toward the earth, than otherwise it would be, and so the orbit is less incurvated; for the power, by which the moon is impelled toward the earth, being that, by which it is inflected from a rectilinear course, the less that power is, the less it will be inflected. Again, when the moon is in the opposition in B, farther removed from the sun than the earth is; it follows then, though the earth and moon are both continually descending to the sun, that is, are drawn by the sun toward it self out of the place they would otherwise move into, yet the moon descends with less velocity than the earth; insomuch that the moon in any given space of time from its passing the point of opposition will have less approached the earth, than otherwise it would have done, that is, its orbit in respect of the earth will approach nearer to a straight line. In the last place, when the moon is in the quarter in F, and equally distant from the sun as the earth, we observed before, that[200] the earth and moon would descend with equal pace toward the sun, so as to make no change by that descent in the angle under F A S; but the length of the line F A must of necessity be shortned. Therefore the moon in moving from F toward the conjunction with the sun will be impelled more toward the earth by the sun’s action, than it would have been by the earth alone, if neither the earth nor moon had been acted on by the sun; so that by this additional impulse the orbit is rendred more curve, than it would otherwise be. The same effect will also be produced in the other quarter.
18. Another effect of the sun’s action, consequent upon this we have now explained, is, that though the moon undisturbed by the sun might move in a circle having the earth for its center; by the sun’s action, if the earth were to be in the very middle or center of the moon’s orbit, yet the moon would be nearer the earth at the new and full, than in the quarters. In this probably will at first appear some difficulty, that the moon should come nearest to the earth, where it is least attracted to it, and be farthest off when most attracted. Which yet will appear evidently to follow from that very cause, by considering what was last shewn, that the orbit of the moon in the conjunction and opposition is rendred less curve; for the less curve the orbit of the moon is, the less will the moon have descended from the place it would move into, without the action of the earth. Now if the moon were to move from any place without farther disturbance from that action, since it would proceed in the line, which would touch its orbit in that place, it would[201] recede continually from the earth; and therefore if the power of the earth upon the moon, be sufficient to retain it at the same distance, this diminution of that power will cause the distance to increase, though in a less degree. But on the other hand in the quarters, the moon, being pressed more towards the earth than by the earth’s single action, will be made to approach it; so that in passing from the conjunction or opposition to the quarters the moon ascends from the earth, and in passing from the quarters to the conjunction and opposition it descends again, becoming nearer in these last mentioned places than in the other.
19. All these forementioned inequalities are of different degrees, according as the sun is more or less distant from the earth; greater when the earth is nearest the sun, and less when it is farthest off. For in the quarters, the nearer the moon is to the sun, the greater is the addition to the earth’s action upon it by the power of the sun; and in the conjunction and opposition, the difference between the sun’s action upon the earth and upon the moon is likewise so much the greater.
20. This difference in the distance between the earth and the sun produces a farther effect upon the moon’s motion; causing the orbit to dilate when less remote from the sun, and become greater, than when at a farther distance. For it is proved by Sir Isaac Newton, that the action of the sun, by which it diminishes the earth’s power over the moon, in the conjunction or opposition, is about twice as[202] great, as the addition to the earth’s action by the sun in the quarters[188]; so that upon the whole, the power of the earth upon the moon is diminished by the sun, and therefore is most diminished, when the action of the sun is strongest: but as the earth by its approach to the sun has its influence lessened, the moon being less attracted will gradually recede from the earth; and as the earth in its recess from the sun recovers by degrees its former power, the orbit of the moon must again contract. Two consequences follow from hence: the moon will be most remote from the earth, when the earth is nearest the sun; and also will take up a longer time in performing its revolution through the dilated orbit, than through the more contracted.
21. These irregularities the sun would produce in the moon, if the moon, without being acted on unequally by the sun, would describe a perfect circle about the earth, and in the plane of the earth’s motion; but though neither of these suppositions obtain in the motion of the moon, yet the forementioned inequalities will take place, only with some difference in respect to the degree of them; but the moon by not moving in this manner is subject to some other inequalities also. For as the moon describes, instead of a circle concentrical to the earth, an ellipsis, with the earth in one focus, that ellipsis will be subjected to various changes. It can neither preserve constantly the same position, nor yet the same figure; and because the plane of this ellipsis is not the same[203] with that of the earth’s orbit, the situation of the plane, wherein the moon moves, will continually change; neither the line in which it intersects the plane of the earth’s orbit, nor the inclination of the planes to each other, will remain for any time the same. All these alterations offer themselves now to be explained.
22. I shall first consider the changes which are made in the plane of the moon’s orbit. The moon not moving in the same plane with the earth, the sun is seldom in the plane of the moon’s orbit, viz. only when the line made by the common intersection of the two planes, if produced, will pass through the sun, as is represented in fig. 97. where S denotes the sun; T the earth; A T B the earth’s orbit described upon the plane of this scheme; C D E F the moon’s orbit, the part C D E being raised above, and the part C F E depressed under the plane of this scheme. Here the line C E, in which the plane of this scheme, that is, the plane of the earth’s orbit and the plane of the moon’s orbit intersect each other, being continued passes through the sun in S. When this happens, the action of the sun is directed in the plane of the moon’s orbit, and cannot draw the moon out of this plane, as will evidently appear to any one that shall consider the present scheme: for suppose the moon in G, and let a straight line be drawn from G to S, the sun draws the moon in the direction of this line from G toward S: but this line lies in the plane of the orbit; and if it be prolonged from S beyond G, the continuation of it will lie on the plane C D E; for the plane itself, if sufficiently extended, will pass through the sun.[204] But in other cases the obliquity of the sun’s action to the plane of the orbit will cause this plane continually to change.
23. Suppose in the first place, the line, in which the two planes intersect each other, to be perpendicular to the line which joins the earth and sun. Let T (in fig. 98, 99, 100, 101.) represent the earth; S the sun; the plane of this scheme the plane of the earth’s motion, in which both the sun and earth are placed. Let A C be perpendicular to S T, which joins the earth and sun; and let the line A C be that, in which the plane of the moon’s orbit intersects the plane of the earth’s motion. To the center T describe in the plane of the earth’s motion the circle A B C D. And in the plane of the moon’s orbit describe the circle A E C F, one half of which A E C will be elevated above the plane of this scheme, the other half A F C as much depressed below it.
24. Now suppose the moon to set forth from the point A (in fig. 98.) in the direction of the plane A E C. Here she will be continually drawn out of this plane by the action of the sun: for this plane A E C, if extended, will not pass through the sun, but above it; so that the sun, by drawing the moon directly toward it self, will force it continually more and more from that plane towards the plane of the earth’s motion, in which it self is; causing it to describe the line A K G H I, which will be convex to the plane A E C, and concave to the plane of the earth’s motion. But here this power of the sun, which is said to draw the moon toward the plane of the earth’s motion, must be understood principally of so much only of the sun’s action upon the moon, as it exceeds the action of the same upon the earth. For suppose the preceding figure to be viewed by the eye, placed in the plane of that scheme, and in the line C T A on the side of A, the plane A B C D will appear as the straight line D T B, (in fig. 102.) and the plane A E C F as another straight line F E; and the curve line A K G H I under the form of the line T K G H I.
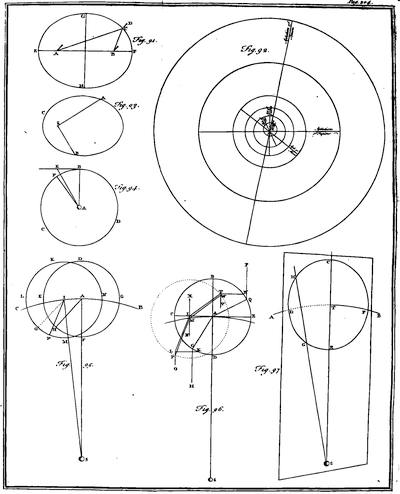
Now it is plain, that the earth and moon being both attracted by the sun, if the sun’s action upon both was equally strong, the earth T, and with it the plane A E C F or line F T E in this scheme, would be carried toward the sun with as great a pace as the moon, and therefore the moon not drawn out of it by the sun’s action, excepting only from the small obliquity of the direction of this action upon the moon to that of the sun’s action upon the earth, which arises from the moon’s being out of the plane of the earth’s motion, and is not very considerable; but the action of the sun upon the moon being greater than upon the earth, all the time the moon is nearer to the sun than the earth is, it will be drawn from the plane A E C or the line T E by that excess, and made to describe the curve line A G I or T G I. But it is the custom of astronomers, instead of considering the moon as moving in such a curve line, to refer its motion continually to the plane, which touches the true line wherein it moves, at the point where at any time the moon is. Thus when the moon is in the point A, its motion is considered as being in the plane A E C, in whose direction it then essaies to move; and when in the point K (in fig. 99.) its motion is referred to the plane, which passes through the earth, and touches the line A K G H I in the point K. Thus[206] the moon in passing from A to I will continually change the plane of her motion. In what manner this change proceeds, I shall now particularly explain.
25. Let the plane, which touches the line A K I in the point K (in fig. 99.) intersect the plane of the earth’s orbit in the line L T M. Then, because the line A K I is concave to the plane A B C, it falls wholly between that plane, and the plane which touches it in K; so that the plane M K L will cut the plane A E C, before it meets with the plane of the earth’s motion; suppose in the line Y T, and the point A will fall between K and L. With a semidiameter equal to T Y or T L describe the semicircle L Y M. Now to a spectator on the earth the moon, when in A, will appear to move in the circle A E C F, and, when in K, will appear to be moving in the semicircle L Y M. The earth’s motion is performed in the plane of this scheme, and to a spectator on the earth the sun will appear always moving in that plane. We may therefore refer the apparent motion of the sun to the circle A B C D, described in this plane about the earth. But the points where this circle, in which the sun seems to move, intersects the circle in which the moon is seen at any time to move, are called the nodes of the moon’s orbit at that time. When the moon is seen moving in the circle A E C D, the points A and C are the nodes of the orbit; when she appears in the semicircle L Y M, then L and M are the nodes. Now here it appears, from what has been said, that while the moon has moved from A to K, one of the nodes has been carried from A to L, and the other as much from C to M. But the motion from A to L, and from C to[207] M, is backward in regard to the motion of the moon, which is the other way from A to K, and from thence toward C.
26. Farther the angle, which the plane, wherein the moon at any time appears, makes with the plane of the earth’s motion, is called the inclination of the moon’s orbit at that time. And I shall now proceed to shew, that this inclination of the orbit, when the moon is in K, is less than when she was in A; or, that the plane L Y M, which touches the line of the moon’s motion in K, makes a less angle with the plane of the earth’s motion or with the circle A B C D, than the plane A E C makes with the same. The semicircle L Y M intersects the semicircle A E C in Y; and the arch A Y is less than L Y, and both together less than half a circle. But it is demonstrated by the writers on that part of astronomy, which is called the doctrine of the sphere, that when a triangle is made, as here, by three arches of circles A L, A Y, and Y L, the angle under Y A B without the triangle is greater than the angle under Y L A within, if the two arches A Y, Y L taken together do not amount to a semicircle; if the two arches make a complete semicircle, the two angles will be equal; but if the two arches taken together exceed a semicircle, the inner angle under Y L A is greater than the other[189]. Here therefore the two arches A Y and L Y together being less than a semicircle, the angle under A L Y is less, than the angle under B A E. But from the doctrine of the sphere it is also evident, that the angle under A L Y is equal to that, in which the plane of the[208] circle L Y K M, that is, the plane which touches the line A K G H I in K, is inclined to the plane of the earth’s motion A B C; and the angle under B A E is equal to that, in which the plane A E C is inclined to the same plane. Therefore the inclination of the former plane is less than the inclination of the latter.
27. Suppose now the moon to be advanced to the point G (in fig. 100.) and in this point to be distant from its node a quarter part of the whole circle; or in other words, to be in the midway between its two nodes. And in this case the nodes will have receded yet more, and the inclination of the orbit be still more diminished: for suppose the line A K G H I to be touched in the point G by a plane passing through the earth T: let the intersection of this plane with the plane of the earth’s motion be the line W T O, and the line T P its intersection with the plane L K M. In this plane let the circle N G O be described with the semidiameter T P or N T cutting the other circle L K M in P. Now the line A K G I is convex to the plane L K M, which touches it in K; and therefore the plane N G O, which touches it in G, will intersect the other touching plane between G and K; that is, the point P will fall between those two points, and the plane continued to the plane of the earth’s motion will pass beyond L; so that the points N and O, or the places of the nodes, when the moon is in G, will be farther from A and C than L and M, that is, will have moved farther backward. Besides, the inclination of the plane N G O to the plane of the earth’s motion A B C is less, than the inclination of the plane L K M to the same; for here also the two arches L P and N P taken together are less[209] than a semicircle, each of these arches being less than a quarter of a circle; as appears, because G N, the distance of the moon in G from its node N, is here supposed to be a quarter part of a circle.
28. After the moon is passed beyond G, the case is altered; for then these arches will be greater than quarters of the circle, by which means the inclination will be again increased, tho’ the nodes still go on to move the same way. Suppose the moon in H, (in fig. 101.) and that the plane, which touches the line A K G I in H, intersects the plane of the earth’s motion in the line Q T R, and the plane N G O in the line T V, and besides that the circle Q H R be described in that plane; then, for the same reason as before, the point V will fall between H and G, and the plane R V Q will pass beyond the last plane O V N, causing the points Q and R to fall farther from A and C than N and O. But the arches N V, V Q are each greater than a quarter of a circle, N V the least of them being greater than G N, which is a quarter of a circle; and therefore the two arches N V and V Q together exceed a semicircle; consequently the angle under B Q V will be greater, than that under B N V.
29. In the last place, when the moon is by this attraction of the sun, drawn at length into the plane of the earth’s motion, the node will have receded yet more, and the inclination be so much increased, as to become somewhat more than at first: for the line A K G H I being convex to all the planes, which touch it, the part H I will wholly fall between[210] the plane Q V R and the plane A B C; so that the point I will fall between B and R; and drawing I T W, the point W will be farther remov’d from A than Q. But it is evident, that the plane, which passes through the earth T, and touches the line A G I in the point I, will cut the plane of the earth’s motion A B C D in the line I T W, and be inclined to the same in the angle under H I B; so that the node, which was first in A, after having passed into L, N and Q, comes at last into the point W; as the node which was at first in C has passed successively from thence through the points M, O and R to I: but the angle under H I B, which is now the inclination of the orbit to the plane of the ecliptic, is manifestly not less than the angle under E C B or E A B, but rather something greater.
30. Thus the moon in the case before us, while it passes from the plane of the earth’s motion in the quarter, till it comes again into the same plane, has the nodes of its orbit continually moved backward, and the inclination of its orbit is at first diminished, viz. till it comes to G in fig. 100, which is near to its conjunction with the sun, but afterwards is increased again almost by the same degrees, till upon the moon’s arrival again to the plane of the earth’s motion, the inclination of the orbit is restored to something more than its first magnitude, though the difference is not very great, because the points I and C are not far distant from each other[190].
31. After the same manner, if the moon had departed from the quarter in C, it should have described the curve line C X W (in fig. 98.) between the planes A F C and A D C, which would be convex to the former of those planes, and concave to the latter; so that, here also, the nodes should continually recede, and the inclination of the orbit gradually diminish more and more, till the moon arrived near its opposition to the sun in X; but from that time the inclination should again increase, till it became a little greater than at first. This will easily appear, by considering, that as the action of the sun upon the moon, by exceeding its action upon the earth, drew it out of the plane A E C towards the sun, while the moon passed from A to I; so, during its passage from C to W, the moon being all that time farther from the sun than the earth, it will be attracted less; and the earth, together with the plane A E C F, will as it were be drawn from the moon, in such sort, that the path the moon describes shall appear from the earth, as it did in the former case by the moon’s being drawn away.
32. These are the changes, which the nodes and the inclination of the moon’s orbit undergo, when the nodes are in the quarters; but when the nodes by their motion, and the motion of the sun together, come to be situated between the quarter and conjunction or opposition, their motion and the change made in the inclination of the orbit are somewhat different.
33. Let A G C H (in fig. 103.) be a circle described in the plane of the earth’s motion, having the earth in T for its center. Let the point opposite to the sun be A, and the point G a fourth part of the circle distant from A. Let the nodes of the moon’s orbit be situated in the line B T D, and B the node, falling between A, the place where the moon would be in the full, and G the place where the moon would be in the quarter. Suppose B E D F to be the plane, in which the moon essays to move, when it proceeds from the point B. Because the moon in B is more distant from the sun than the earth, it shall be less attracted by the sun, and shall not descend towards the sun so fast as the earth: consequently it shall quit the plane B E D F, which we suppose to accompany the earth, and describe the line B I K convex thereto, till such time as it comes to the point K, where it will be in the quarter: but from thenceforth being more attracted than the earth, the moon shall change its course, and the following part of the path it describes shall be concave to the plane B E D or B G D, and shall continue concave to the plane B G D, till it crosses that plane in L, just as in the preceding case. Now I say, while the moon is passing from B to K, the nodes, contrary to what was found in the foregoing case, will proceed forward, or move the same way with the moon[191]; and at the same time the inclination of the orbit will increase[192].
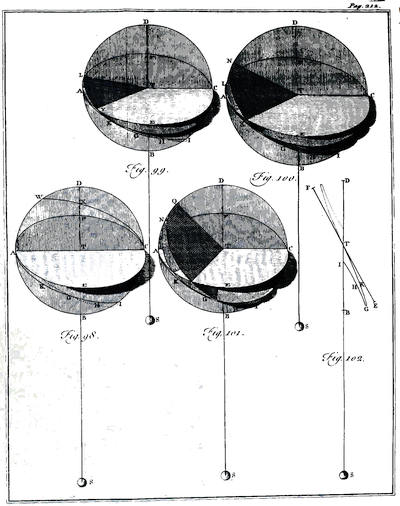
34. When the moon is in the point I, let the plane M I N pass through the earth T, and touch the path of the moon in I, cutting the plane of the earth’s motion, in the line M T N, and the plane B E D in the line T O. Because the line B I K is convex to the plane B E D, which touches it in B, the plane N I M must cross the plane D E B, before it meets the plane C G B; and therefore the point M will fall from B towards G, and the node of the moon’s orbit being translated from B to M is moved forward.
35. I say farther, the angle under O M G, which the plane M O N makes with the plane B G C, is greater than the angle under O B G, which the plane B O D makes with the same. This appears from what has been already explained; because the arches B O, O M are each less than the quarter of a circle, and therefore taken both together are less than a semicircle.
36. Again, when the moon is come to the point K in its quarter, the nodes will be advanced yet farther forward, and the inclination of the orbit also more augmented. Hitherto the moon’s motion has been referred to the plane, which passing through the earth touches the path of the moon in the point, where the moon is, according to what was asserted at the beginning of this discourse upon the nodes, that it is the custom of astronomers so to do. But here in the point K no such plane can be found; on the contrary, seeing the line of the moon’s motion on one side the point K is convex to the plane B E D, and on the other side concave to the same, no plane can pass through the points T and K but will cut the line B K L in that point. Therefore instead[214] of such a touching plane, we must here make use of what is equivalent, the plane P K Q, with which the line B K L shall make a less angle than with any other plane; for this plane does as it were touch the line B K in the point K, since it so cuts it, that no other plane can be drawn so, as to pass between the line B K and the plane P K Q. But now it is evident, that the point P, or the node, is removed from M towards G, that is, has moved yet farther forward; and it is likewise as manifest, that the angle under K P G, or the inclination of the moon’s orbit in the point K, is greater than the angle under I M G, for the reason so often assigned.
37. After the moon has passed the quarter, the path of the moon being concave to the plane A G C H, the nodes, as in the preceding case, shall recede, till the moon arrives at the point L; which shews, that considering the whole time of the moon’s passing from B to L, at the end of that time the nodes shall be found to have receded, or to be placed backwarder, when the moon is in L, than when it was in B. For the moon takes a longer time in passing from K to L, than in passing from B to K; and therefore the nodes continue to recede a longer time, than they moved forwards; so that their recess must surmount their advance.
38. In the same manner, while the moon is in its passage from K to L, the inclination of the orbit shall diminish, till the moon comes to the point, in which it is one quarter part of a circle distant from its node; suppose in the point R; and from that time the inclination shall again increase.[215] Since therefore the inclination of the orbit increases, while the moon is passing from B to K, and diminishes itself again only, while the moon is passing from K to R, and then augments again, till the moon arrive in L; while the moon is passing from B to L, the inclination of the orbit is much more increased than diminished, and will be distinguishably greater, when the moon is come to L, than when it set out from B.
39. In like manner, while the moon is passing from L on the other side the plane A G C H, the node shall advance forward, as long as the moon is between the point L and the next quarter; but afterwards it shall recede, till the moon come to pass the plane A G C H again in the point V, between B and A: and because the time between the moon’s passing from L to the next quarter is less, than the time between that quarter and the moon’s coming to the point V, the node shall have more receded than advanced; so that the point V will be nearer to A, than L is to C. So also the inclination of the orbit, when the moon is in V, will be greater, than when the moon was at L; for this inclination increases all the time the moon is between L and the next quarter; it decreases only while the moon is passing from this quarter to the mid way between the two nodes, and from thence increases again during the whole passage through the other half of the way to the next node.
40. Thus we have traced the moon from her node in the quarter, and shewn, that at every period of the moon the nodes will have receded, and thereby will have approached[216] toward a conjunction with the sun. But this conjunction will be much forwarded by the visible motion of the sun itself. In the last scheme the sun will appear to move from S toward W. Suppose it appeared to have moved from S to W, while the moon’s node has receded from B to V, then drawing the line W T X, the arch V X will represent the distance of the line drawn between the nodes from the sun, when the moon is in V; whereas the arch B A represented that distance, when the moon was in B. This visible motion of the sun is much greater, than that of the node; for the sun appears to revolve quite round each year, and the node is near 19 years in making one revolution. We have also seen, that when the node was in the quadrature, the inclination of the moon’s orbit decreased, till the moon came to the conjunction, or opposition, according to which node it set out from; but that afterwards it again increased, till it became at the next node rather greater than at the former. When the node is once removed from the quarter nearer to a conjunction with the sun, the inclination of the moon’s orbit, when the moon comes into the node, is more sensibly greater, than it was in the node preceding; the inclination of the orbit by this means more and more increasing till the node comes into conjunction with the sun; at which time it has been shewn above, that the sun has no power to change the plane of the moon’s motion; and consequently has no effect either on the nodes, or on the inclination of the orbit.
41. As soon as the nodes, by the action of the sun, are got out of conjunction toward the other quarters, they begin[217] again to recede as before; but the inclination of the orbit in the appulse of the moon to each succeeding node is less than at the preceding, till the nodes come again into the quarters. This will appear as follows. Let A (in fig. 104.) represent one of the moon’s nodes placed between the point of opposition B and the quarter C. Let the plane A D E pass through the earth T, and touch the path of the moon in A. Let the line A F G H be the path of the moon in her passage from A to H, where she crosses again the plane of the earth’s motion. This line will be convex toward the plane A D E, till the moon comes to G, where she is in the quarter; and after this, between G and H, the same line will be concave toward this plane. All the time this line is convex toward the plane A D E, the nodes will recede; and on the contrary proceed, while it is concave to that plane. All this will easily be conceived from what has been before so largely explained. But the moon is longer in passing from A to G, than from G to H; therefore the nodes recede a longer time, than they proceed; consequently upon the whole, when the moon is arrived at H, the nodes will have receded, that is, the point H will fall between B and E. The inclination of the orbit will decrease, till the moon is arrived to the point F, in the middle between A and H. Through the passage between F and G the inclination will increase, but decrease again in the remaining part of the passage from G to H, and consequently at H must be less than at A. The like effects, both in respect to the nodes and inclination of the orbit, will take place in the following passage of the moon on the other side of the plane A B E C, from H, till it comes over that plane again in I.
42. Thus the inclination of the orbit is greatest, when the line drawn between the moon’s nodes will pass through the sun; and least, when this line lies in the quarters, especially if the moon at the same time be in conjunction with the sun, or in the opposition. In the first of these cases the nodes have no motion, in all others, the nodes will each month have receded: and this regressive motion will be greatest, when the nodes are in the quarters; for in that case the nodes have no progressive motion during the whole month, but in all other cases the nodes do at some times proceed forward, viz. whenever the moon is between either quarter, and the node which is less distant from that quarter than a fourth part of a circle.
43. It now remains only to explain the irregularities in the moon’s motion, which follow from the elliptical figure of the orbit. By what has been said at the beginning of this chapter it appears, that the power of the earth on the moon acts in the reciprocal duplicate proportion of the distance: therefore the moon, if undisturbed by the sun, would move round the earth in a true ellipsis, and the line drawn from the earth to the moon would pass over equal spaces in equal portions of time. That this description of the spaces is altered by the sun, has been already declared. It has also been shown, that the figure of the orbit is changed each month; that the moon is nearer the earth at the new and full, and more remote in the quarters, than it would be without the sun. Now we must pass by these monthly changes, and consider the effect, which the sun will have in the different[219] situations of the axis of the orbit in respect of that luminary.
44. The action of the sun varies the force, wherewith the moon is drawn toward the earth; in the quarters the force of the earth is directly increased by the sun; at the new and full the same is diminished; and in the intermediate places the influence of the earth is sometimes aided, and sometimes lessened by the sun. In these intermediate places between the quarters and the conjunction or opposition, the sun’s action is so oblique to the action of the earth on the moon, as to produce that alternate acceleration and retardment of the moon’s motion, which I observed above to be stiled the variation. But besides this effect, the power, by which the earth attracts the moon toward itself, will not be at full liberty to act with the same force, as if the sun acted not at all on the moon. And this effect of the sun’s action, whereby it corroborates or weakens the action of the earth, is here only to be considered. And by this influence of the sun it comes to pass, that the power, by which the moon is impelled toward the earth, is not perfectly in the reciprocal duplicate proportion of the distance. Consequently the moon will not describe a perfect ellipsis. One particular, wherein the moon’s orbit will differ from an ellipsis, consists in the places, where the motion of the moon is perpendicular to the line drawn from itself to the earth. In an ellipsis, after the moon should have set out in the direction perpendicular to this line drawn from itself to the earth, and at its greatest distance from the earth, its motion would[220] again become perpendicular to this line drawn between itself and the earth, and the moon be at its nearest distance from the earth, when it should have performed half its period; after performing the other half of its period its motion would again become perpendicular to the forementioned line, and the moon return into the place whence it set out, and have recovered again its greatest distance. But the moon in its real motion, after setting out as before, sometimes makes more than half a revolution, before its motion comes again to be perpendicular to the line drawn from itself to the earth, and the moon is at its nearest distance; and then performs more than another half of an intire revolution before its motion can a second time recover its perpendicular direction to the line drawn from the moon to the earth, and the moon arrive again to its greatest distance from the earth. At other times the moon will descend to its nearest distance, before it has made half a revolution, and recover again its greatest distance, before it has made an intire revolution. The place, where the moon is at its greatest distance from the earth, is called the moon’s apogeon, and the place of the least distance the perigeon. This change of the place, where the moon successively comes to its greatest distance from the earth, is called the motion of the apogeon. In what manner the sun causes the apogeon to move, I shall now endeavour to explain.
45. Our author shews, that if the moon were attracted toward the earth by a composition of two powers, one of which were reciprocally in the duplicate proportion of the distance from the earth, and the other reciprocally[221] in the triplicate proportion of the same distance; then, though the line described by the moon would not be in reality an ellipsis, yet the moon’s motion might be perfectly explained by an ellipsis, whose axis should be made to move round the earth; this motion being in consequence, as astronomers express themselves, that is, the same way as the moon itself moves, if the moon be attracted by the sum of the two powers; but the axis must move in antecedence, or the contrary way, if the moon be acted on by the difference of these powers. What is meant by duplicate proportion has been often explained; namely, that if three magnitudes, as A, B, and C, are so related, that the second B bears the same proportion to the third C, as the first A bears to the second B, then the proportion of the first A to the third C, is the duplicate of the proportion of the first A to the second B. Now if a fourth magnitude, as D, be assumed, to which C shall bear the same proportion as A bears to B, and B to C, then the proportion of A to D is the triplicate of the proportion of A to B.
46. The way of representing the moon’s motion in this case is thus. T denoting the earth (in fig. 105, 106.) suppose the moon in the point A, its apogeon, or greatest distance from the earth, moving in the direction A F perpendicular to A B, and acted upon from the earth by two such forces as have been named. By that power alone, which is reciprocally in the duplicate proportion of the distance, if the moon let out from the point A with a proper degree of velocity, the ellipsis A M B may be described.[222] But if the moon be acted upon by the sum of the forementioned powers, and the velocity of the moon in the point A be augmented in a certain proportion[193]; or if that velocity be diminished in a certain proportion, and the moon be acted upon by the difference of those powers; in both these cases the line A E, which shall be described by the moon, is thus to be determined. Let the point M be that, into which the moon would have arrived in any given space of time, had it moved in the ellipsis A M B. Draw M T, and likewise C T D in such sort, that the angle under A T M shall bear the same proportion to the angle under A T C, as the velocity, with which the ellipsis A M B must have been described, bears to the difference between this velocity, and the velocity, with which the moon must set out from the point A in order to describe the path A E. Let the angle A T C be taken toward the moon (as in fig. 105.) if the moon be attracted by the sum of the powers; but the contrary way (as in fig. 106.) if by their difference. Then let the line A B be moved into the position C D, and the ellipsis A M B into the situation C N D, so that the point M be translated to L: then the point L shall fall upon the path of the moon A E.
47. The angular motion of the line A T, wereby it is removed into the situation C T, represents the motion of the apogeon; by the means of which the motion of the moon might be fully explicated by the ellipsis A M B, if the action of the sun upon it was directed to the center of the earth, and[223] reciprocally in the triplicate proportion of the moon’s distance from it. But that not being so, the apogeon will not move in the regular manner now described. However, it is to be observed here, that in the first of the two preceding cases, where the apogeon moves forward, the whole centripetal power increases faster, with the decrease of distance, than if the intire power were reciprocally in the duplicate proportion of the distance; because one part only is in that proportion, and the other part, which is added to this to make up the whole power, increases faster with the decrease of distance. On the other hand, when the centripetal power is the difference between these two, it increases less with the decrease of the distance, than if it were simply in the reciprocal duplicate proportion of the distance. Therefore if we chuse to explain the moon’s motion by an ellipsis (as is most convenient for astronomical uses to be done, and by reason of the small effect of the sun’s power, the doing so will not be attended with any sensible error;) we may collect in general, that when the power, by which the moon is attracted to the earth, by varying the distance, increases in a greater than in the duplicate proportion of the distance diminished, a motion in consequence must be ascribed to the apogeon; but that when the attraction increases in a less proportion than that named, the apogeon must have given to it a motion in antecedence[194]. It is then observed by Sir Is. Newton, that the first of these cases obtains, when the moon is in the conjunction and opposition; and the latter, when the moon is in the quarters: so that in the first the apogeon moves according to the order of the[224] signs; in the other, the contrary way[195]. But, as was said before, the disturbance given to the action of the earth by the sun in the conjunction and opposition being near twice as great as in the quarters[196], the apogeon will advance with a greater velocity than recede, and in the compass of a whole revolution of the moon will be carried in consequence[197].
48. It is shewn in the next place by our author, that when the line A B coincides with that, which joins the earth and the sun, the progressive motion of the apogeon, when the moon is in the conjunction or opposition, exceeds the regressive in the quadratures more than in any other situation of the line A B[198]. On the contrary, when the line A B makes right angles with that, which joins the earth and sun, the retrograde motion will be more considerable[199], nay is found so great as to exceed the progressive; so that in this case the apogeon in the compass of an intire revolution of the moon is carried in antecedence. Yet from the considerations in the last paragraph the progressive motion exceeds the other; so that in the whole the mean motion of the apogeon is in consequence, according as astronomers find. Moreover, the line A B changes its situation with that, which joins the earth and sun, by such slow degrees, that the inequalities in the motion of the apogeon arising from this last consideration, are much greater than what arises from the other[200].
49. Farther, this unsteady motion in the apogeon is attended with another inequality in the motion of the moon, that it cannot be explained at all times by the same ellipsis. The ellipsis in general is called by astronomers an eccentric orbit. The point, in which the two axis’s cross, is called the center of the figure; because all lines drawn through this point within the ellipsis, from side to side, are divided in the middle by this point. But the center, about which the heavenly bodies revolve, lying out of this center of the figure in one focus, these orbits are said to be eccentric; and where the distance of the focus from this center bears the greatest proportion to the whole axis, that orbit is called the most eccentric: and in such an orbit the distance from the focus to the remoter extremity of the axis bears the greatest proportion to the distance of the nearer extremity. Now whenever the apogeon of the moon moves in consequence, the moon’s motion must be referred to an orbit more eccentric, than what the moon would describe, if the whole power, by which the moon was acted on in its passing from the apogeon, changed according to the reciprocal duplicate proportion of the distance from the earth, and by that means the moon did describe an immoveable ellipsis; and when the apogeon moves in antecedence, the moon’s motion must be referred to an orbit less eccentric. In the first of the two figures last referred to, the true place of the moon L falls without the orbit A M B, to which its motion is referred: whence the orbit A L E, truly described by the moon, is less incurvated in the point A, than is the orbit A M B; therefore the orbit A M B is more oblong, and differs farther from a circle, than the ellipsis would,[226] whose curvature in A were equal to that of the line A L B, that is, the proportion of the distance of the earth T from the center of the ellipsis to its axis will be greater in the ellipsis A M B, than in the other; but that other is the ellipsis, which the moon would describe, if the power acting upon it in the point A were altered in the reciprocal duplicate proportion of the distance. In the second figure, when the apogeon recedes, the place of the moon L falls within the orbit A M B, and therefore that orbit is less eccentric, than the immoveable orbit which the moon should describe. The truth of this is evident; for, when the apogeon moves forward, the power, by which the moon is influenced in its descent from the apogeon, increases faster with the decrease of distance, than in the duplicate proportion of the distance; and consequently the moon being drawn more forcibly toward the earth, it will descend nearer to it. On the other hand, when the apogeon recedes, the power acting on the moon increases with the decrease of distance in less than the duplicate proportion of the distance; and therefore the moon is less impelled toward the earth, and will not descend so low.
50. Now suppose in the first of these figures, that the apogeon A is in the situation, where it is approaching toward the conjunction or opposition of the sun. In this case the progressive motion of the apogeon is more and more accelerated. Here suppose that the moon, after having descended from A through the orbit A E as far as F, where it is come to its nearest distance from the earth, ascends again up the line F G. Because the motion of the apogeon is here continually more and[227] more accelerating, the cause of its motion is constantly upon the increase; that is, the power, whereby the moon is drawn to the earth, will decrease with the increase of distance, in the moon’s ascent from F, in a greater proportion than that wherewith it increased with the decrease of distance in the moon’s descent to F. Consequently the moon will ascend higher than to the distance A T, from whence it descended; therefore the proportion of the greatest distance of the moon to the least is increased. And when the moon descends again, the power will yet more increase with the decrease of distance, than in the last ascent it decreased with the augmentation of distance; the moon therefore must descend nearer to the earth than it did before, and the proportion of the greatest distance to the least yet be more increased. Thus as long as the apogeon is advancing toward the conjunction or opposition, the proportion of the greatest distance of the moon from the earth to the least will continually increase; and the elliptical orbit, to which the moon’s motion is referred, will be rendered more and more eccentric.
51. As soon as the apogeon is passed the conjunction with the sun or the opposition, the progressive motion thereof abates, and with it the proportion of the greatest distance of the moon from the earth to the least distance will also diminish; and when the apogeon becomes regressive, the diminution of this proportion will be still farther continued on, till the apogeon comes into the quarter; from thence this proportion, and the eccentricity of the orbit will increase again. Thus the orbit of the moon is most eccentric, when the apogeon[228] is in conjunction with the sun, or in opposition to it, and least of all when the apogeon is in the quarters.
52. These changes in the nodes, in the inclination of the orbit to the plane of the earth’s motion, in the apogeon, and in the eccentricity, are varied like the other inequalities in the motion of the moon, by the different distance of the earth from the sun; being greatest, when their cause is greatest, that is, when the earth is nearest to the sun.
53. I said at the beginning of this chapter, that Sir Isaac Newton has computed the very quantity of many of the moon’s inequalities. That acceleration of the moon’s motion, which is called the variation, when greatest, removes the moon out of the place, in which it would otherwise be found, something more than half a degree[201]. In the phrase of astronomers, a degree is 1/360 part of the whole circuit of the moon or any planet. If the moon, without disturbance from the sun, would have described a circle concentrical to the earth, the sun will cause the moon to approach nearer to the earth in the conjunction and opposition, than in the quarters, nearly in the proportion of 69 to 70[202]. We had occasion to mention above, that the nodes perform their period in almost 19 years. This the astronomers found by observation; and our author’s computations assign to them the same period[203]. The inclination of the moon’s orbit when least, is an angle about 1/18 part of that angle, which constitutes[229] a perpendicular; and the difference between the greatest and least inclination of the orbit is determined by our author’s computation to be about 1/18 of the least inclination[204]. And this also is agreeable to the observations of astronomers. The motion of the apogeon, and the changes in the eccentricity, Sir Isaac Newton has not computed. The apogeon performs its revolution in about eight years and ten months. When the moon’s orbit is most eccentric, the greatest distance of the moon from the earth bears to the least distance nearly the proportion of 8 to 7; when the orbit is least eccentric, this proportion is hardly so great as that of 12 to 11.
54. Sir Isaac Newton shews farther, how, by comparing the periods of the motion of the satellites, which revolve round Jupiter and Saturn, with the period of our moon round the earth, and the periods of those planets round the sun with the period of our earth’s motion, the inequalities in the motion of those satellites may be derived from the inequalities in the moon’s motion; excepting only in regard to that motion of the axis of the orbit, which in the moon makes the motion of the apogeon; for the orbits of those satellites, as far as can be discerned by us at this distance, appearing little or nothing eccentric, this motion, as deduced from the moon, must be diminished.
Chap. IV.
Of Comets.
IN the former of the two preceding chapters the powers have been explained, which keep in motion those celestial bodies, whose courses had been well determined by the astronomers. In the last chapter we have shewn, how those powers have been applied by our author to the making a more perfect discovery of the motion of those bodies, the courses of which were but imperfectly understood; for some of the inequalities, which we have been describing in the moon’s motion, were unknown to the astronomers. In this chapter we are to treat of a third species of the heavenly bodies, the true motion of which was not at all apprehended before our author writ; in so much, that here Sir Isaac Newton has not only explained the causes of the motion of these bodies, but has performed also the part of an astronomer, by discovering what their motions are.
2. That these bodies are not meteors in our air, is manifest; because they rise and set in the same manner, as the sun and stars. The astronomers had gone so far in their inquiries concerning them, as to prove by their observations, that they moved in the etherial spaces far beyond the moon; but they had no true notion at all of the path, which they described. The most prevailing opinion before[231] our author was, that they moved in straight lines; but in what part of the heavens was not determined. DesCartes[205] removed them far beyond the sphere of Saturn, as finding the straight motion attributed to them, inconsistent with the vortical fluid, by which he explains the motions of the planets, as we have above related[206]. But Sir Isaac Newton distinctly proves from astronomical observation, that the comets pass through the region of the planets, and are mostly invisible at a less distance, than that of Jupiter[207].
3. And from hence finding the comets to be evidently within the sphere of the sun’s action, he concludes they must, necessarily move about the sun, as the planets do[208]. The planets move in ellipsis’s; but it is not necessary that every body, which is influenced by the sun, should move in that particular kind of line. However our author proves, that the power of the sun being reciprocally in the duplicate proportion of the distance, every body acted on by the sun must either fall directly down, or move in some conic section; of which lines I have above observed, that there are three species, the ellipsis, parabola, and hyperbola[209]. If a body, which descends toward the sun as low as the orbit of any planet, move with a swifter motion than the planet does, that body will describe an orbit of a more oblong figure, than that of the planet, and have a longer axis at least. The velocity of the body may be so great, that it[232] shall move in a parabola, and having once passed about the sun, shall ascend for ever without returning any more: but the sun will be placed in the focus of this parabola. With a velocity still greater the body will move in an hyperbola. But it is most probable, that the comets move in elliptical orbits, though of a very oblong, or in the phrase of astronomers, of a very eccentric form, such as is represented in fig. 107, where S is the sun, C the comet, and A B D E its orbit, wherein the distance of S and D far exceeds that of S and A. Whence it is, that they sometimes are found at a moderate distance from the sun, and appear within the planetary regions; at other times they ascend to vast distances, far beyond the very orbit of Saturn, and so become invisible. That the comets do move in this manner is proved by our author, from computations built upon the observations, which astronomers had made on many comets. These computations were performed by Sir Isaac Newton himself upon the comet, which appeared toward the latter end of the year 1680, and at the beginning of the year following[210]; but the learned Dr. Halley prosecuted the like computations more at large in this, and also in many other comets[211]. Which computations are made upon propositions highly worthy of our author’s unparallel’d genius, such as could scarce have been discovered by any one not possessed of the utmost force of invention;
4. Those computations depend upon this principle, that the eccentricity of the orbits of the comets is so great, that if they are really elliptical, yet they approach so near to parabolas in that part of them, where they come under our view, that they may be taken for such without sensible error[212]: as in the preceding figure the parabola F A G differs in the lower part of it about A very little from the ellipsis D E A B. Upon which ground our great author teaches a method of finding by three observations made upon any comet the parabola, which nearest agrees with its orbit[213].
5. Now what confirms this whole theory beyond the least room for doubt is, that the places of the comets computed in the orbits, which the method here mentioned assigns them, agree to the observations of astronomers with the same degree of exactness, as the computations of the primary planets places usually do; and this in comets, whose motions are very extraordinary[214].
6. Our author afterwards shews how to make use of any small deviation from the parabola, that shall be observed, to determine whether the orbits of the comets are elliptical or not, and so to discover if the same comet returns at certain periods[215]. And upon examining the comet in 1680, by the rule laid down for this purpose, he finds its orbit to agree more exactly to an ellipsis than[234] to a parabola, though the ellipsis be so very eccentric, that the comet cannot perform its period through it in the space of 500 years[216]. Upon this Dr. Halley observed, that mention is made in history of a comet, with the like eminent tail as this, having appeared three several times before; the first of which appearances was at the death of Julius Cesar, and each appearance was at the distance of 575 years from the next preceding. He therefore computed the motion of this comet in such an elliptic orbit, as would require this number of years for the body to revolve through it; and these computations agree yet more perfectly with the observations made on this comet, than any parabolical orbit will do[217].
7. The comparing together different appearances of the same comet, is the only way to discover certainly the true form of the orbit: for it is impossible to determine with exactness the figure of an orbit so exceedingly eccentric, from single observations taken in one part of it; and therefore Sir Isaac Newton[218] proposes to compare the orbits, upon the supposition that they are parabolical, of such comets as appear at different times; for if the same orbit be found to be described by a comet at different times, in all probability it will be the same comet which describes it. And here he remarks from Dr. Halley, that the same orbit very nearly agrees to two appearances of a comet about the space of 75 years distance[219]; so that[235] if those two appearances were really of the same comet, the transverse axis of the orbit of the comet would be near 18 times the axis of the earth’s orbit; and the comet, when at its greatest distance from the sun, will be removed not less than 35 times as far as the middle distance of the earth.
8. And this seems to be the shortest period of any of the comets. But it will be farther confirmed, if the same comet should return a third time after another period of 75 years. However it is not to be expected, that comets should preserve the same regularity in their periods, as the planets; because the great eccentricity of their orbits makes them liable to suffer very considerable alterations from the action of the planets, and other comets, upon them.
9. It is therefore to prevent too great disturbances in their motions from these causes, as our author observes, that while the planets revolve all of them nearly in the same plane, the comets are disposed in very different ones; and distributed over all parts of the heavens; that, when in their greatest distance from the sun, and moving slowest, they might be removed as far as possible out of the reach of each other’s action[220]. The same end is likewise farther answered in those comets, which by moving slowest in the aphelion, or remotest distance from the sun, descend nearest to it, by placing the aphelion of these at the greatest height from the sun[221].
10. Our philosopher being led by his principles to explain the motions of the comets, in the manner now related, takes occasion from thence to give us his thoughts upon their nature and use. For which end he proves in the first place, that they must necessarily be solid and compact bodies, and by no means any sort of vapour or light substance exhaled from the planets or stars: because at the near distance, to which some comets approach the sun, it could not be, but the immense heat, to which they are exposed, should instantaneously disperse and scatter any such light volatile substance[222]. In particular the forementioned comet of 1680 descended so near the sun, as to come within a sixth part of the sun’s diameter from the surface of it. In which situation it must have been exposed, as appears by computation, to a degree of heat exceeding the heat of the sun upon our earth no less than 28000 times; and therefore might have contracted a degree of heat 2000 times greater, than that of red hot iron[223]. Now a substance, which could endure so intense a heat, without being dispersed in vapor, must needs be firm and solid.
11. It is shewn likewise, that the comets are opake substances, shining by a reflected light, borrowed from the sun[224]. This is proved from the observation, that comets, though they are approaching the earth, yet diminish in lustre, if at the same time they recede from[237] the sun; and on the contrary, are found to encrease daily in brightness, when they advance towards the sun, though at the same time they move from the earth[225].
12. The comets therefore in these respects resemble the planets; that both are durable opake bodies, and both revolve about the sun in conic sections. But farther the comets, like our earth, are surrounded by an atmosphere. The air we breath is called the earth’s atmosphere; and it is most probable, that all the other planets are invested with the like fluid. Indeed here a difference is found between the planets and comets. The atmospheres of the planets are of so fine and subtile a substance, as hardly to be discerned at any distance, by reason of the small quantity of light which they reflect, except only in the planet Mars. In him there is some little appearance of such a substance surrounding him, as stars which have been covered by him are said to look somewhat dim a small space before his body comes under them, as if their light, when he is near, were obstructed by his atmosphere. But the atmospheres which surround the comets are so gross and thick, as to reflect light very copiously. They are also much greater in proportion to the body they surround, than those of the planets, if we may judge of the rest from our air; for it has been observed of comets, that the bright light appearing in the middle of them, which[238] is reflected from the solid body, is scarce a ninth or tenth part of the whole comet,
13. I speak only of the heads of the comets, the most lucid part of which is surrounded by a fainter light, the most lucid part being usually not above a ninth or tenth part of the whole in breadth[226]. Their tails are an appearance very peculiar, nothing of the same nature appertaining in the least degree to any other of the celestial bodies. Of that appearance there are several opinions; our author reduces them to three[227]. The two first, which he proposes, are rejected by him; but the third he approves. The first is, that they arise from a beam of light transmitted through the head of the comet, in like manner as a stream of light is discerned, when the sun shines into a darkened room through a small hole. This opinion, as Sir Isaac Newton observes, implies the authors of it wholly unskilled in the principles of optics; for that stream of light, seen in a darkened room, arises from the reflection of the sun beams by the dust and motes floating in the air: for the rays of light themselves are not seen, but by their being reflected to the eye from some substance, upon which they fall[228]. The next opinion examined by our author is that of the celebrated DesCartes, who imagins these tails to be the light of the comet refracted in its passage to us, and thence affording an oblong representation; as the light of the sun does, when refracted[239] by the prism in that noted experiment, which will have a great share in the third book of this discourse[229]. But this opinion is at once overturned from this consideration only, that the planets could be no more free from this refraction than the comets; nay ought to have larger or brighter tails, than they, because the light of the planets is strongest. However our author has thought proper to add some farther objections against this opinion: for instance, that these tails are not variegated with colours, as is the image produced by the prism, and which is inseparable from that unequal refraction, which produces that disproportioned length of the image. And besides, when the light in its passage from different comets to the earth describes the same path through the heavens, the refraction of it should of necessity be in all respects the same. But this is contrary to observation; for the comet in 1680, the 28th day of December, and a former comet in the year 1577, the 29th day of December, appear’d in the same place of the heavens, that is, were seen adjacent to the same fixed stars, the earth likewise being in the same place at both times; yet the tail of the latter comet deviated from the opposition to the sun a little to the northward, and the tail of the former comet declined from the opposition of the sun five times as much southward[230].
14. There are some other false opinions, though less regarded than these, which have been advanced upon this[240] argument. These our excellent author passes over, hastening to explain, what he takes to be the true cause of this appearance. He thinks it is certainly owing to steams and vapours exhaled from the body, and gross atmosphere of the comets, by the heat of the sun; because all the appearances agree perfectly to this sentiment. The tails are but small, while the comet is descending to the sun, but enlarge themselves to an immense degree, as soon as ever the comet has passed its perihelion; which shews the tail to depend upon the degree of heat, which the comet receives from the sun. And that the intense heat to which comets, when nearest the sun, are exposed, should exhale from them a very copious vapour, is a most reasonable supposition; especially if we consider, that in those free and empty regions steams will more easily ascend, than here upon the surface of the earth, where they are suppressed and hindered from rising by the weight of the incumbent air: as we find by experiments made in vessels exhausted of the air, where upon removal of the air several substances will fume and discharge steams plentifully, which emit none in the open air. The tails of comets, like such a vapour, are always in the plane of the comet’s orbit, and opposite to the sun, except that the upper part thereof inclines towards the parts, which the comet has left by its motion; resembling perfectly the smoak of a burning coal, which, if the coal remain fixed, ascends from it perpendicularly; but, if the coal be in motion, ascends obliquely, inclining from the motion of the coal. And besides, the tails of comets may be compared to this smoak in another[241] respect, that both of them are denser and more compact on the convex side, than on the concave. The different appearance of the head of the comet, after it has past its perihelion, from what it had before, confirms greatly this opinion of their tails: for smoke raised by a strong heat is blacker and grosser, than when raised by a less; and accordingly the heads of comets, at the same distance from the sun, are observed less bright and shining after the perihelion, than before, as if obscured by such a gross smoke.
15. The observations of Hevelius upon the atmospheres of comets still farther illustrate the same; who relates, that the atmospheres, especially that part of them next the sun, are remarkably contracted when near the sun, and dilated again afterwards.
16. To give a more full idea of these tails, a rule is laid down by our author, whereby to determine at any time, when the vapour in the extremity of the tail first rose from the head of the comet. By this rule it is found, that the tail does not consist of a fleeting vapour, dissipated soon after it is raised, but is of long continuance; that almost all the vapour, which rose about the time of the perihelion from the comet of 1680, continued to accompany it, ascending by degrees, being succeeded constantly by fresh matter, which rendered the tail contiguous to the comet. From this computation the tails are found to participate of another property of ascending vapours, that, when they ascend with the greatest velocity, they are least incurvated.
17. The only objection that can be made against this opinion is the difficulty of explaining, how a sufficient quantity of vapour can be raised from the atmosphere of a comet to fill those vast spaces, through which their tails are sometimes extended. This our author removes by the following computation: our air being an elastic fluid, as has been said before[231], is more dense here near the surface of the earth, where it is pressed upon by the whole air above; than it is at a distance from the earth, where it has a less weight incumbent. I have observed, that the density of the air is reciprocally proportional to the compressing weight. From hence our author computes to what degree of rarity the air must be expanded, according to this rule, at an height equal to a semidiameter of the earth: and he finds, that a globe of such air, as we breath here on the surface of the earth, which shall be one inch only in diameter, if it were expanded to the degree of rarity, which the air must have at the height now mentioned, would fill all the planetary regions even to the very sphere of Saturn, and far beyond. Now since the air at a greater height will be still immensly more rarified, and the surface of the atmospheres of comets is usually about ten times the distance from the center of the comet, as the surface of the comet it self, and the tails are yet vastly farther removed from the center of the comet; the vapour, which composes those tails, may very well be allowed to be so expanded, as that a moderate quantity of matter may fill all that space, they are seen to take up. Though indeed the atmospheres of comets being[243] very gross, they will hardly be rarified in their tails to so great a degree, as our air under the same circumstances; especially since they may be something condensed, as well by their gravitation to the sun, as that the parts will gravitate to one another; which will hereafter be shewn to be the universal property of all matter[232]. The only scruple left is, how so much light can be reflected from a vapour so rare, as this computation implies. For the removal of which our author observes, that the most refulgent of these tails hardly appear brighter, than a beam of the sun’s light transmitted into a darkened room through a hole of a single inch diameter; and that the smallest fixed stars are visible through them without any sensible diminution of their lustre.
18. All these considerations put it beyond doubt, what is the true nature of the tails of comets. There has indeed nothing been said, which will account for the irregular figures, in which those tails are sometimes reported to have appeared; but since none of those appearances have ever been recorded by astronomers, who on the contrary ascribe the same likeness to the tails of all comets, our author with great judgment refers all those to accidental refractions by intervening clouds, or to parts of the milky way contiguous to the comets[233].
19. The discussion of this appearance in comets has led Sir Isaac Newton into some speculations relating to their use, which I cannot but extreamly admire, as[244] representing in the strongest light imaginable the extensive providence of the great author of nature, who, besides the furnishing this globe of earth, and without doubt the rest of the planets, so abundantly with every thing necessary for the support and continuance of the numerous races of plants and animals, they are stocked with, has over and above provided a numerous train of comets, far exceeding the number of the planets, to rectify continually, and restore their gradual decay, which is our author’s opinion concerning them[234]. For since the comets are subject to such unequal degrees of heat, being sometimes burnt with the most intense degree of it, at other times scarce receiving any sensible influence from the sun; it can hardly be supposed, they are designed for any such constant use, as the planets. Now the tails, which they emit, like all other kinds of vapour, dilate themselves as they ascend, and by consequence are gradually dispersed and scattered through all the planetary regions, and thence cannot but be gathered up by the planets, as they pass through their orbs: for the planets having a power to cause all bodies to gravitate towards them, as will in the sequel of this discourse be shewn[235]; these vapours will be drawn in process of time into this or the other planet, which happens to act strongest upon them. And by entering the atmospheres of the earth and other planets, they may well be supposed to contribute to the renovation of the face of things, in particular to supply the diminution caused in the humid parts[245] by vegetation and putrefaction. For vegetables are nourished by moisture, and by putrefaction are turned in great part into dry earth; and an earthy substance always subsides in fermenting liquors; by which means the dry parts of the planets must continually increase, and the fluids diminish, nay in a sufficient length of time be exhausted, if not supplied by some such means. It is farther our great author’s opinion, that the most subtile and active parts of our air, upon which the life of things chiefly depends, is derived to us, and supplied by the comets. So far are they from portending any hurt or mischief to us, which the natural fears of men are so apt to suggest from the appearance of any thing uncommon and astonishing.
20. That the tails of comets have some such important use seems reasonable, if we consider, that those bodies do not send out those fumes merely by their near approach to the sun; but are framed of a texture, which disposes them in a particular manner to fume in that sort: for the earth, without emitting any such steam, is more than half the year at a less distance from the sun, than the comet of 1664 and 1665 approached it, when nearest; likewise the comets of 1682 and 1683 never approached the sun much above a seventh part nearer than Venus, and were more than half as far again from the sun as Mercury; yet all these emitted tails.
21. From the very near approach of the comet of 1680 our author draws another speculation; for if the[246] sun have an atmosphere about it, the comet mentioned seems to have descended near enough to the sun to enter within it. If so, it must have been something retarded by the resistance it would meet with, and consequently in its next descent to the sun will fall nearer than now; by which means it will meet with a greater resistance, and be again more retarded. The event of which must be, that at length it will impinge upon the sun’s surface, and thereby supply any decrease, which may have happened by so long an emission of light, or otherwise. And something like this our author conjectures may be the case of those fixed stars which by an additional increase of their lustre have for a certain time become visible to us, though usually they are out of sight. There is indeed a kind of fixed stars, which appear and disappear at regular and equal intervals: here some more steady cause must be sought for; perhaps these stars turn round their own axis’s, as our sun does[236], and have some part of their body more luminous than the other, whereby they are seen, when the most lucid part is next to us, and when the darker part is turned toward us, they vanish out of sight.
22. Whether the sun does really diminish, as has been here suggested, is difficult to prove; yet that it either does so, or that the earth increases, if not both, is rendered probable from Dr. Halley’s observation[237], that by comparing[247] the proportion, which the periodical time of the moon bore to that of the sun in former times, with the proportion between them at present, the moon is found to be something accelerated in respect of the sun. But if the sun diminish, the periods of the primary planets will be lengthened; and if the earth be encreased, the period of the moon will be shortened: as will appear by the next chapter, wherein it shall be shewn, that the power of the sun and earth is the result of the same power being lodg’d in all their parts, and that this principle of producing gravitation in other bodies is proportional to the solid matter in each body.
Chap. V.
Of the BODIES of the SUN and PLANETS.
OUR author, after having discovered that the celestial motions are performed by a force extended from the sun and primary planets, follows this power into the deepest recesses of those bodies themselves, and proves the same to accompany the smallest particle, of which they are composed.
2. Preparative hereto he shews first, that each of the heavenly bodies attracts the rest, and all bodies, with such different degrees of force, as that the force of the same attracting[248] body is exerted on others exactly in proportion to the quantity of matter in the body attracted[238].
3. Of this the first proof he brings is from experiments made here upon the earth. The power by which the moon is influenced was above shewn to be the same, with that power here on the surface of the earth, which we call gravity[239]. Now one of the effects of the principle of gravity is, that all bodies descend by this force from the same height in equal times. Which has been long taken notice of; particular methods having been invented to shew that the only cause, why some bodies were observed to fall from the same height sooner than others, was the resistance of the air. This we have above related[240]; and proved from hence, that since bodies resist to any change of their state from rest to motion, or from motion to rest, in proportion to the quantity of matter contained in them; the power that can move different quantities of matter equally, must be proportional to the quantity. The only objection here is, that it can hardly be made certain, whether this proportion in the effect of gravity on different bodies holds perfectly exact or not from these experiments; by reason that the great swiftness, with which bodies fall, prevents our being able to determine the times of their descent with all the exactness requisite. Therefore to remedy this inconvenience, our author substitutes another more certain experiment in the room of these made upon falling bodies. Pendulums[249] are caused to vibrate by the same principle, as makes bodies descend; the power of gravity putting them in motion, as well as the other. But if the ball of any pendulum, of the same length with another, were more or less attracted in proportion to the quantity of solid matter in the ball, that pendulum must accordingly move faster or slower than the other. Now the vibrations of pendulums continue for a great length of time, and the number of vibrations they make may easily be determined without suspicion of error; so that this experiment may be extended to what exactness one pleases: and our author assures us, that he examined in this way several substances, as gold, silver, lead, glass, sand, common salt, wood, water, and wheat; in all which he found not the least deviation from the proportion mentioned, though he made the experiment in such a manner, that in bodies of the same weight a difference in the quantity of their matter less than a thousandth part of the whole would have discovered it self[241]. It appears therefore, that all bodies are made to descend by the power of gravity here, near the surface of the earth, with the same degree of swiftness. We have above observed this descent to be after the rate of 16⅛ feet in the first second of time from the beginning of their fall. Moreover it was also observed, that if any body, which fell here at the surface of the earth after this rate, were to be conveyed up to the height of the moon, it would[250] descend from thence just with the same degree of velocity, as that with which the moon is attracted toward the earth; and therefore the power of the earth upon the moon bears the same proportion to the power it would have upon those bodies at the same distance, as the quantity of matter in the moon bears to the quantity in those bodies.
4. Thus the assertion laid down is proved in the earth, that the power of the earth on every body it attracts is, at the same distance from the earth, proportional to the quantity of solid matter in the body acted on. As to the sun, it has been shewn, that the power of the sun’s action upon the same primary planet is reciprocally in the duplicate proportion of the distance; and that the power of the sun decreases throughout in the same proportion, the motion of comets traversing the whole planetary region testifies. This proves, that if any planet were removed from the sun to any other distance whatever, the degree of its acceleration toward the sun would yet remain reciprocally in the duplicate proportion of its distance. But it has likewise been shewn, that the degree of acceleration, which the sun gives to every one of the planets, is reciprocally in the duplicate proportion of their respective distances. All which compared together puts it out of doubt, that the power of the sun upon any planet, removed into the place of any ether, would give it the same velocity of descent, as it gives that other; and consequently, that the sun’s action upon different planets at the same distance would be proportional to the quantity of matter in each. It has farther[251] been shewn, that the sun attracts the primary planets, and their respective secondary, when at the same distance, so as to communicate to both the same degree of velocity; and therefore the force, wherewith the sun acts on the secondary planet, bears the same proportion to the force, wherewith at the same distance it attracts the primary, as the quantity of solid matter in the secondary planet bears to the quantity of matter in the primary.
5. This property therefore is proved of both kinds of planets, in respect of the sun. Therefore the sun possesses the quality found in the earth, of acting on bodies with a degree of force proportional to the quantity of matter in the body, which receives the influence.
6. That the power of attraction, with which the other planets are endued, should differ from that of the earth, can hardly be supposed, if we consider the similitude between those bodies; and that it does not in this respect, is farther proved from the satellites of Saturn and Jupiter, which are attracted by their respective primary according to the same law, that is, in the same proportion to their distances, as the primary are attracted by the sun: so that what has been concluded of the sun in relation to the primary planets, may be justly concluded of these primary in respect of their secondary, and in consequence of that, in regard likewise to all other bodies, viz. that they will attract every body in proportion to the quantity of solid matter it contains.
7. Hence it follows, that this attraction extends itself to every particle of matter in the attracted body: and that no portion of matter whatever is exempted from the influence of those bodies, to which we have proved this attractive power to belong.
8. Before we proceed farther, we may here remark, that this attractive power both of the sun and planets now appears to be quite of the same nature in all; for it acts in each in the same proportion to the distance, and in the same manner acts alike upon every particle of matter. This power therefore in the sun and other planets is not of a different nature from this power in the earth; which has been already shewn to be the same with that, which we call gravity[242].
9. And this lays open the way to prove, that the attracting power lodged in the sun and planets, belongs likewise to every part of them: and that their respective powers upon the same body are proportional to the quantity of matter, of which they are composed; for instance, that the force with which the earth attracts the moon, is to the force, with which the sun would attract it at the same distance, as the quantity of solid matter contained in the earth, to the quantity contained in the sun[243].
10. The first of these assertions is a very evident consequence from the latter. And before we proceed to the proof,[253] it must first be shewn, that the third law of motion, which makes action and reaction equal, holds in these attractive powers. The most remarkable attractive force, next to the power of gravity, is that, by which the loadstone attracts iron. Now if a loadstone were laid upon water, and supported by some proper substance, as wood or cork, so that it might swim; and if a piece of iron were caused to swim upon the water in like manner: as soon as the loadstone begins to attract the iron, the iron shall move toward the stone, and the stone shall also move toward the iron; when they meet, they shall stop each other, and remain fixed together without any motion. This shews, that the velocities, wherewith they meet, are reciprocally proportional to the quantities of solid matter in each; and that by the stone’s attracting the iron, the stone itself receives as much motion, in the strict philosophic sense of that word[244], as it communicates to the iron: for it has been declared above to be an effect of the percussion of two bodies, that if they meet with velocities reciprocally proportional to the respective bodies, they shall be stopped by the concourse, unless their elasticity put them into fresh motion; but if they meet with any other velocities, they shall retain some motion after meeting[245]. Amber, glass, sealing-wax, and many other substances acquire by rubbing a power, which from its having been remarkable, particularly in amber, is called electrical. By this power they will for some time after[254] rubbing attract light bodies, that shall be brought within the sphere of their activity. On the other hand Mr. Boyle found, that if a piece of amber be hung in a perpendicular position by a string, it shall be drawn itself toward the body whereon it was rubbed, if that body be brought near it. Both in the loadstone and in electrical bodies we usually ascribe the power to the particular body, whose presence we find necessary for producing the effect. The loadstone and any piece of iron will draw each other, but in two pieces of iron no such effect is ordinarily observed; therefore we call this attractive power the power of the loadstone: though near a loadstone two pieces of iron will also draw each other. In like manner the rubbing of amber, glass, or any such body, till it is grown warm, being necessary to cause any action between those bodies and other substances, we ascribe the electrical power to those bodies. But in all these cases if we would speak more correctly, and not extend the sense of our expressions beyond what we see; we can only say that the neighbourhood of a loadstone and a piece of iron is attended with a power, whereby the loadstone and the iron are drawn toward each other; and the rubbing of electrical bodies gives rise to a power, whereby those bodies and other substances are mutually attracted. Thus we must also understand in the power of gravity, that the two bodies are mutually made to approach by the action of that power. When the sun draws any planet, that planet also draws the sun; and the motion, which the planet receives from the sun, bears the same proportion to the motion, which the sun it self receives, as[255] the quantity of solid matter in the sun bears to the quantity of solid matter in the planet. Hitherto, for brevity sake in speaking of these forces, we have generally ascribed them to the body, which is least moved; as when we called the power, which exerts itself between the sun and any planet, the attractive power of the sun; but to speak more correctly, we should rather call this power in any case the force, which acts between the sun and earth, between the sun and Jupiter, between the earth and moon, &c. for both the bodies are moved by the power acting between them, in the same manner, as when two bodies are tied together by a rope, if that rope shrink by being wet, or otherwise, and thereby cause the bodies to approach, by drawing both, it will communicate to both the same degree of motion, and cause them to approach with velocities reciprocally proportional to the respective bodies. From this mutual action between the sun and planet it follows, as has been observed above[246], that the sun and planet do each move about their common center of gravity. Let A (in fig. 108.) represent the sun, B a planet, C their common center of gravity. If these bodies were once at rest, by their mutual attraction they would directly approach each other with such velocities, that their common center of gravity would remain at rest, and the two bodies would at length meet in that point. If the planet B were to receive an impulse, as in the direction of the line D E, this would prevent the two bodies from falling together;[256] but their common center of gravity would be put into motion in the direction of the line C F equidistant from B E. In this case Sir Isaac Newton proves[247], that the sun and planet would describe round their common center of gravity similar orbits, while that center would proceed with an uniform motion in the line C F; and so the system of the two bodies would move on with the center of gravity without end. In order to keep the system in the same place, it is necessary, that when the planet received its impulse in the direction B E, the sun should also receive such an impulse the contrary way, as might keep the center of gravity C without motion; for if these began once to move without giving any motion to their common center of gravity, that center would always remain fixed.
11. By this may be understood in what manner the action between the sun and planets is mutual. But farther, we have shewn above[248], that the power, which acts between the sun and primary planets, is altogether of the same nature with that, which acts between the earth and the bodies at its surface, or between the earth and its parts, and with that which acts between the primary planets and their secondary; therefore all these actions must be ascribed to the same cause[249]. Again, it has been already proved, that in different planets the force of the sun’s action upon each at the same distance would be proportional to the quantity of solid matter in the planet[250]; therefore the reaction of each planet on the sun at the same distance, or the motion, which the sun would receive from each planet, would also be proportional to the quantity of matter in the planet; that is, these planets at the same distance would act on the same body with degrees of strength proportional to the quantity of solid matter in each.
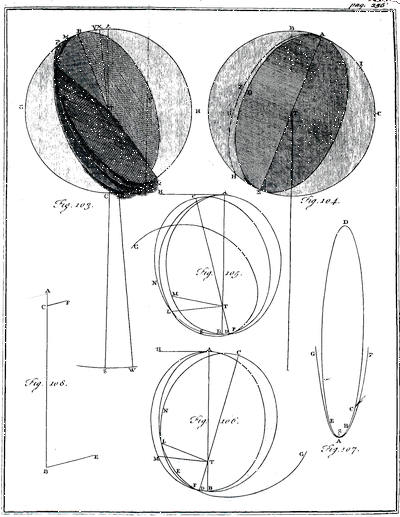
12. In the next place, from what has been now proved, our great author has deduced this farther consequence, no less surprizing than elegant; that each of the particles, out of which the bodies of the sun and planets are framed, exert their power of gravitation by the same law, and in the same proportion to the distance, as the great bodies which they compose. For this purpose he first demonstrates, that if a globe were compounded of particles, which will attract the particles of any other body reciprocally in the duplicate proportion of their distances, the whole globe will attract the same in the reciprocal duplicate proportion of their distances from the center of the globe; provided the globe be of uniform density throughout[251]. And from this our author deduces the reverse, that if a globe acts upon distant bodies by the law just now specified, and the power of the globe is derived from its being composed of attractive particles; each of those particles will attract after the same proportion[252]. The manner of deducing this is not set down at large by our author, but is as follows. The globe is[258] supposed to act upon the particles of a body without it constantly in the reciprocal duplicate proportion of their distances from its center; and therefore at the same distance from the globe, on which side soever the body be placed, the globe will act equally upon it. Now because, if the particles, of which the globe is composed, acted upon those without in the reciprocal duplicate proportion of their distances, the whole globe would act upon them in the same manner as it does; therefore, if the particles of the globe have not all of them that property, some must act stronger than in that proportion, while others act weaker: and if this be the condition of the globe, it is plain, that when the body attracted is in such a situation in respect of the globe, that the greater number of the strongest particles are nearest to it, the body will be more forcibly attracted; than when by turning the globe about, the greater quantity of weak particles should be nearest, though the distance of the body should remain the same from the center of the globe. Which is contrary to what was at first remarked, that the globe on all sides of it acts with the same strength at the same distance. Whence it appears, that no other constitution of the globe can agree to it.
13. From these propositions it is farther collected, that if all the particles of one globe attract all the particles of another in the proportion so often mentioned, the attracting globe will act upon the other in the same proportion to the distance between the center of the globe which attracts, and the center of that which is attracted[253]: and farther, that this[259] proportion holds true, though either or both the globes be composed of dissimilar parts, some rarer and some more dense; provided only, that all the parts in the same globe equally distant from the center be homogeneous[254]. And also, if both the globes attract each other[255]. All which place it beyond contradiction, that this proportion obtains with as much exactness near and contiguous to the surface of attracting globes, as at greater distances from them.
14. Thus our author, without the pompous pretence of explaining the cause of gravity, has made one very important step toward it, by shewing that this power in the great bodies of the universe, is derived from the same power being lodged in every particle of the matter which composes them: and consequently, that this property is no less than universal to all matter whatever, though the power be too minute to produce any visible effects on the small bodies, wherewith we converse, by their action on each other[256]. In the fixed stars indeed we have no particular proof that they have this power; for we find no apperance to demonstrate that they either act, or are acted upon by it. But since this power is found to belong to all bodies, whereon we can make observation; and we see that it is not to be altered by any change in the form of bodies, but always accompanies them in every shape without diminution, remaining ever proportional to the quantity of solid matter in each; such a power must without doubt belong universally to all matter.
15. This therefore is the universal law of matter; which recommends it self no less for its great plainness and simplicity, than for the surprizing discoveries it leads us to. By this principle we learn the different weight, which the same body will have upon the surfaces of the sun and of diverse planets; and by the same we can judge of the composition of those celestial bodies, and know the density of each; which is formed of the most compact, and which of the most rare substance. Let the adversaries of this philosophy reflect here, whether loading this principle with the appellation of an occult quality, or perpetual miracle, or any other reproachful name, be sufficient to dissuade us from cultivating it; since this quality, which they call occult, leads to the knowledge of such things, that it would have been reputed no less than madness for any one, before they had been discovered, even to have conjectured that our faculties should ever have reached so far.
16. See how all this naturally follows from the foregoing principles in those planets, which have satellites moving about them. By the times, in which these satellites perform their revolutions, compared with their distances from their respective primary, the proportion between the power, with which one primary attracts his satellites, and the force with which any other attracts his will be known; and the proportion of the power with which any planet attracts its secondary, to the power with which it attracts a body at its surface is found, by comparing the distance of the secondary planet from the center of the primary, to[261] the distance of the primary planet’s surface from the same: and from hence is deduced the proportion between the power of gravity upon the surface of one planet, to the gravity upon the surface of another. By the like method of comparing the periodical time of a primary planet about the sun, with the revolution of a satellite about its primary, may be found the proportion of gravity, or of the weight of any body upon the surface of the sun, to the gravity, or to the weight of the same body upon the surface of the planet, which carries about the satellite.
17. By these kinds of computation it is found, that the weight of the same body upon the surface of the sun will be about 23 times as great, as here upon the surface of the earth; about 10⅗ times as great, as upon the surface of Jupiter; and near 19 times as great, as upon the surface of Saturn[257].
18. The quantity of matter, which composes each of these bodies, is proportional to the power it has upon a body at a given distance. By this means it is found, that the sun contains 1067 times as much matter as Jupiter; Jupiter 158⅔ times as much as the earth, and 2-5/6 times as much as Saturn[258]. The diameter of the sun is about 92 times, that of Jupiter about 9 times, and that of Saturn about 7 times the diameter of the earth.
19. By making a comparison between the quantity of matter in these bodies and their magnitudes, to be found from their diameters, their respective densities are readily deduced; the density of every body being measured by the quantity of matter contained under the same bulk, as has been above remarked[259]. Thus the earth is found 4¼ times more dense than Jupiter; Saturn has between ⅔ and ¾ of the density of Jupiter; but the sun has one fourth part only of the density of the earth[260]. From which this observation is drawn by our author; that the sun is rarified by its great heat, and that of the three planets named, the more dense is nearer the sun than the more rare; as was highly reasonable to expect, the densest bodies requiring the greatest heat to agitate and put their parts in motion; as on the contrary, the planets which are more rare, would be rendered unfit for their office, by the intense heat to which the denser are exposed. Thus the waters of our seas, if removed to the distance of Saturn from the sun, would remain perpetually frozen; and if as near the sun as Mercury, would constantly boil[261].
20. The densities of the three planets Mercury, Venus, and Mars, which have no satellites, cannot be expresly assigned; but from what is found in the others, it is very probable, that they also are of such different degrees of density, that universally the planet which is nearest to the sun, is formed of the most compact substance.
Chap. VI.
Of the FLUID PARTS of the PLANETS.
THIS globe, that we inhabit, is composed of two parts; the solid earth, which affords us a foundation to dwell upon; and the seas and other waters, that furnish rains and vapours necessary to render the earth fruitful, and productive of what is requisite for the support of life. And that the moon, though but a secondary planet, is composed in like manner, is generally thought, from the different degrees of light which appear on its surface; the parts of that planet, which reflect a dim light, being supposed to be fluid, and to imbibe the sun’s rays, while the solid parts reflect them more copiously. Some indeed do not allow this to be a conclusive argument: but whether we can distinguish the fluid part of the moon’s surface from the rest or not; yet it is most probable that there are two such different parts, and with still greater reason we may ascribe the like to the other primary planets, which yet more nearly resemble our earth. The earth is also encompassed by another fluid the air, and we have before remarked, that probably the rest of the planets are surrounded by the like. These fluid parts in particular engage our author’s attention, both by reason of some remarkable appearances peculiar to them, and likewise of some effects they have upon the whole bodies to which they belong.
2. Fluids have been already treated of in general, with respect to the effect they have upon solid bodies moving in them[262]; now we must consider them in reference to the operation of the power of gravity upon them. By this power they are rendered weighty, like all other bodies, in proportion to the quantity of matter, which is contained in them. And in any quantity of a fluid the upper parts press upon the lower as much, as any solid body would press on another, whereon it should lie. But there is an effect of the pressure of fluids on the bottom of the vessel, wherein they are contained, which I shall particularly explain. The force supported by the bottom of such a vessel is not simply the weight of the quantity of the fluid in the vessel, but is equal to the weight of that quantity of the fluid, which would be contained in a vessel of the same bottom and of equal width throughout, when this vessel is filled up to the same height, as that to which the vessel proposed is filled. Suppose water were contained in the vessel A B C D (in fig. 109.) filled up to E F. Here it is evident, that if a part of the bottom, as G H, which is directly under any part of the space E F, be considered separately; it will appear at once, that this part sustains the weight of as much of the fluid, as stands perpendicularly over it up to the height of E F; that is, the two perpendiculars G I and H K being drawn, the part G H of the bottom will sustain the whole weight of the fluid included between these two perpendiculars. Again, I say, every other part of the bottom equally broad with this, will sustain as great a pressure. Let the part L M be of the[265] same breadth with G H. Here the perpendiculars L O and M N being drawn, the quantity of water contained between these perpendiculars is not so great, as that contained between the perpendiculars G I and H K; yet, I say, the pressure on L M will be equal to that on G H. This will appear by the following considerations. It is evident, that if the part of the vessel between O and N were removed, the water would immediately flow out, and the surface E F would subside; for all parts of the water being equally heavy, it must soon form itself to a level surface, if the form of the vessel, which contains it, does not prevent. Therefore since the water is prevented from rising by the side N O of the vessel, it is manifest, that it must press against N O with some degree of force. In other words, the water between the perpendiculars L O and M N endeavours to extend itself with a certain degree of force; or more correctly, the ambient water presses upon this, and endeavours to force this pillar or column of water into a greater length. But since this column of water is sustained between N O and L M, each of these parts of the vessel will be equally pressed against by the power, wherewith this column endeavours to extend. Consequently L M bears this force over and above the weight of the column of water between L O and M N. To know what this expansive force is, let the part O N of the vessel be removed, and the perpendiculars L O and M N be prolonged; then by means of some pipe fixed over N O let water be filled between these perpendiculars up to P Q an equal height with E F. Here the water between the perpendiculars L P and M Q is of an equal height with the highest part of the water in the vessel; therefore the water in the[266] vessel cannot by its pressure force it up higher, nor can the water in this column subside; because, if it should, it would raise the water in the vessel to a greater height than itself. But it follows from hence, that the weight of water contained between P O and Q N is a just balance to the force, wherewith the column between L O and M N endeavours to extend. So the part L M of the bottom, which sustains both this force and the weight of the water between L O and M N, is pressed upon by a force equal to the united weight of the water between L O and M N, and the weight of the water between P O and Q N; that is, it is pressed on by a force equal to the weight of all the water contained between L P and M Q. And this weight is equal to that of the water contained between G I and H K, which is the weight sustained by the part G H of the bottom. Now this being true of every part of the bottom B C, it is evident, that if another vessel R S T V be formed with a bottom R V equal to the bottom B C, and be throughout its whole height of one and the same breadth; when this vessel is filled with water to the same height, as the vessel A B C D is filled, the bottoms of these two vessels shall be pressed upon with equal force. If the vessel be broader at the top than at the bottom, it is evident, that the bottom will bear the pressure of so much of the fluid, as is perpendicularly over it, and the sides of the vessel will support the rest. This property of fluids is a corollary from a proposition of our author[263]; from whence also he deduces the effects of the pressure of fluids on bodies resting in them.[267] These are, that any body heavier than a fluid will sink to the bottom of the vessel, wherein the fluid is contained, and in the fluid will weigh as much as its own weight exceeds the weight of an equal quantity of the fluid; any body uncompressible of the same density with the fluid, will rest any where in the fluid without suffering the least change either in its place or figure from the pressure of such a fluid, but will remain as undisturbed as the parts of the fluid themselves; but every body of less density than the fluid will swim on its surface, a part only being received within the fluid. Which part will be equal in bulk to a quantity of the fluid, whose weight is equal to the weight of the whole body; for by this means the parts of the fluid under the body will suffer as great a pressure as any other parts of the fluid as much below the surface as these.
3. In the next place, in relation to the air, we have above made mention, that the air surrounding the earth being an elastic fluid, the power of gravity will have this effect on it, to make the lower parts near the surface of the earth more compact and compressed together by the weight of the air incumbent, than the higher parts, which are pressed upon by a less quantity of the air, and therefore sustain a less weight[264]. It has been also observed, that our author has laid down a rule for computing the exact degree of density in the air at all heights from the earth[265]. But there is a farther effect from the air’s being compressed by[268] the power of gravity, which he has distinctly considered. The air being elastic and in a state of compression, any tremulous body will propagate its motion to the air, and excite therein vibrations, which will spread from the body that occasions them to a great distance. This is the efficient cause of sound: for that sensation is produced by the air, which, as it vibrates, strikes against the organ of hearing. As this subject was extremely difficult, so our great author’s success is surprizing.
4. Our author’s doctrine upon this head I shall endeavour to explain somewhat at large. But preliminary thereto must be shewn, what he has delivered in general of pressure propagated through fluids; and also what he has set down relating to that wave-like motion, which appears upon the surface of water, when agitated by throwing any thing into it, or by the reciprocal motion of the finger, &c.
5. Concerning the first, it is proved, that pressure is spread through fluids, not only right forward in a streight line, but also laterally, with almost the same ease and force. Of which a very obvious exemplification by experiment is proposed: that is, to agitate the surface of water by the reciprocal motion of the finger forwards and backwards only; for though the finger have no circular motion given it, yet the waves excited in the water will diffuse themselves on each hand of the direction of the motion, and soon surround the finger. Nor is what we observe in sounds unlike to this, which do not proceed in straight lines only, but are heard though a[269] mountain intervene, and when they enter a room in any part of it, they spread themselves into every corner; not by reflection from the walls, as some have imagined, but as far as the sense can judge, directly from the place where they enter.
6. How the waves are excited in the surface of stagnant water, may be thus conceived. Suppose in any place, the water raised above the rest in form of a small hillock; that water will immediately subside, and raise the circumambient water above the level of the parts more remote, to which the motion cannot be communicated under longer time. And again, the water in subsiding will acquire, like all falling bodies, a force, which will carry it below the level surface, till at length the pressure of the ambient water prevailing, it will rise again, and even with a force like to that wherewith it descended, which will carry it again above the level. But in the mean time the ambient water before raised will subside, as this did, sinking below the level; and in so doing, will not only raise the water, which first subsided, but also the water next without itself. So that now beside the first hillock, we shall have a ring investing it, at some distance raised above the plain surface likewise; and between them the water will be sunk below the rest of the surface. After this, the first hillock, and the new made annular rising, will descend; raising the water between them, which was before depressed, and likewise the adjacent part of the surface without. Thus will these annular waves be successively spread more and more. For, as the hillock subsiding produces one ring, and that ring subsiding[270] raises again the hillock, and a second ring; so the hillock and second ring subsiding together raise the first ring, and a third; then this first and third ring subsiding together raise the first hillock, the second ring, and a fourth; and so on continually, till the motion by degrees ceases. Now it is demonstrated, that these rings ascend and descend in the manner of a pendulum; descending with a motion continually accelerated, till they become even with the plain surface of the fluid, which is half the space they descend; and then being retarded again by the same degrees as those, whereby they were accelerated, till they are depressed below the plain surface, as much as they were before raised above it: and that this augmentation and diminution of their velocity proceeds by the same degrees, as that of a pendulum vibrating in a cycloid, and whose length should be a fourth part of the distance between any two adjacent waves: and farther, that a new ring is produced every time a pendulum, whose length is four times the former, that is, equal to the interval between the summits of two waves, makes one oscillation or swing[266].
7. This now opens the way for understanding the motion consequent upon the tremors of the air, excited by the vibrations of sonorous bodies: which we must conceive to be performed in the following manner.
8. Let A, B, C, D, E, F, G, H (in fig. 110.) represent a series of the particles of the air, at equal distances from each other. I K L a musical chord, which I shall use for the tremulous[271] and sonorous body, to make the conception as simple as may be. Suppose this chord stretched upon the points I and L, and forcibly drawn into the situation I K L, so that it become contiguous to the particle A in its middle point K: and let the chord from this situation begin to recoil, pressing against the particle A, which will thereby be put into motion towards B: but the particles A, B, C being equidistant, the elastic power, by which B avoids A, is equal to, and balanced by the power, by which it avoids C; therefore the elastic force, by which B is repelled from A, will not put B into any degree of motion, till A is by the motion of the chord brought nearer to B, than B is to C: but as soon as that is done, the particle B will be moved towards C; and being made to approach C, will in the next place move that; which will upon that advance, put D likewise into motion, and so on: therefore the particle A being moved by the chord, the following particles of the air B, C, D, &c. will successively be moved. Farther, if the point K of the chord moves forward with an accelerated velocity, so that the particle A shall move against B with an advancing pace, and gain ground of it, approaching nearer and nearer continually; A by approaching will press more upon B, and give it a greater velocity likewise, by reason that as the distance between the particles diminishes, the elastic power, by which they fly each other, increases. Hence the particle B, as well as A, will have its motion gradually accelerated, and by that means will more and more approach to C. And from the same cause C will more and more approach D; and so of the rest. Suppose now, since the agitation of these particles has been shewn to[272] be successive, and to follow one another, that E be the remotest particle moved, while the chord is moving from its curve situation I K L into that of a streight line, as I k L; and F the first which remains unaffected, though just upon the point of being put into motion. Then shall the particles A, B, C, D, E, F, G, when the point K is moved into k, have acquired the rangement represented by the adjacent points a, b, c, d, e, f, g: in which a is nearer to b than b to c, and b nearer to c than c to d, and c nearer to d than d to e and d nearer to e than e to f, and lastly e nearer to f than f to g.
9. But now the chord having recovered its rectilinear situation I k L, the following motion will be changed, for the point K, which before advanced with a motion more and more accelerated, though by the force it has acquired it will go on to move the same way as before, till it has advanced near as far forwards, as it was at first drawn backwards; yet the motion of it will henceforth be gradually lessened. The effect of which upon the particles a, b, c, d, e, f, g will be, that by the time the chord has made its utmost advance, and is upon the return, these particles will be put into a contrary rangement; so that f shall be nearer to g, than e to f, and e nearer to f than d to e; and the like of the rest, till you come to the first particles a, b, whose distance will then be nearly or quite what it was at first. All which will appear as follows. The present distance between a and b is such, that the elastic power, by which a repels b, is strong enough to maintain that distance, though a advance with the velocity, with which the string resumes its rectilinear figure; and the[273] motion of the particle a being afterwards slower, the present elasticity between a and b will be more than sufficient to preserve the distance between them. Therefore while it accelerates b it will retard a. The distance b c will still diminish, till b come about as near to c, as it is from a at present; for after the distances a b and b c are become equal, the particle b will continue its velocity superior to that of c by its own power of inactivity, till such time as the increase of elasticity between b and c more than shall be between a and b shall suppress its motion: for as the power of inactivity in b made a greater elasticity necessary on the side of a than on the side of c to push b forward, so what motion b has acquired it will retain by the same power of inactivity, till it be suppressed by a greater elasticity on the side of c, than on the side of a. But as soon as b begins to slacken its pace the distance of b from c will widen as the distance a b has already done. Now as a acts on b, so will b on c, c on d, &c. so that the distances between all the particles b, c, d, e, f, g will be successively contracted into the distance of a from b, and then dilated again. Now because the time, in which the chord describes this present half of its vibration, is about equal to that it took up in describing the former; the particles a, b will be as long in dilating their distance, as before in contracting it, and will return nearly to their original distance. And farther, the particles b, c, which did not begin to approach so soon as a, b, are now about as much longer, before they begin to recede; and likewise the particles c, d, which began to approach after b, c, begin to separate later. Whence it appears that the particles, whose distance began to be lessened, when[274] that of a, b was first enlarged, viz. the particles f, g, should be about their nearest distance, when a and b have recovered their prime interval. Thus will the particles a, b, c, d, e, f, g have changed their situation in the manner asserted. But farther, as the particles f, g or F, G gradually approach each other, they will move by degrees the succeeding particles to as great a length, as the particles A, B did by a like approach. So that, when the chord has made its greatest advance, being arrived into the situation I ϰ L, the particles moved by it will have the rangement noted by the points α, β, γ, δ, ε, ζ, η, θ, λ, μ, ν, χ. Where α, β are at the original distance of the particles in the line A H; ζ, η are the nearest of all, and the distance ν χ is equal to that between α and β.
10. By this time the chord I ϰ L begins to return, and the
distance between the particles α and β being enlarged to its
original magnitude, α has lost all that force it had acquired
by its motion, being now at rest; and therefore will
return with the chord, making the distance between α and
β greater than the natural; for β will not return so soon,
because its motion forward is not yet quite suppressed, the
distance β γ not being already enlarged to its prime dimension:
but the recess of α, by diminishing the pressure upon
β by its elasticity, will occasion the motion of β to be
stopt in a little time by the action of γ, and then shall
β begin to return: at which time the distance between γ
and δ shall by the superior action of δ above β be enlarged
to the dimension of the distance β γ, and therefore
soon after to that of α β. Thus it appears, that each of
these particles goes on to move forward, till its distance from[275]
the preceding one be equal to its original distance; the
whole chain α, β, γ, δ, ε, ζ, η, having an undulating motion
forward, which is stopt gradually by the excess of the expansive
power of the preceding parts above that of the
hinder. Thus are these parts successively stopt, as before
they were moved; so that when the chord has regained its
rectilinear situation, the expansion of the parts of the air
will have advanced so far, that the interval between ζ η,
which at present is most contracted, will then be restored
to its natural size: the distances between η and θ, θ and λ, λ
and μ, μ and ν, ν and χ, being successively contracted into
the present distance of ζ from η, and again enlarged; so
that the same effect shall be produced upon the parts beyond
ζ η, by the enlargement of the distance between those two
particles, as was occasioned upon the particles α, β, γ, δ, ε,
ζ, η, θ, λ, μ, ν, χ, by the enlargement of the distance α β to
its natural extent. And therefore the motion in the air
will be extended half as much farther as at present, and
the distance between ν and χ contracted into that, which
is at present between ζ and η, all the particles of the air
in motion taking the rangement expressed in figure
111. by the points α, β, γ, δ, ε, ζ, η, θ, λ, μ, ν, χ, ϰ, ρ, σ, τ, φ
wherein the particles from α to χ have their distances from
each other gradually diminished, the distances between the
particles ν, χ being contracted the most from the natural distance
between those particles, and the distance between α, β as
much augmented, and the distance between the middle particles
ζ, η becoming equal to the natural. The particles π, ρ, ω
[276]τ, φ which follow χ, have their distances gradually greater
and greater, the particles ν, χ, π, ρ, σ, τ, φ being ranged like
the particles a, b, c, d, e, f, g, or like the particles ζ, η, θ, λ,
μ, ν, χ in the former figure. Here it will be understood, by what
has been before explained, that the particles ζ, η being at
their natural distance from each other, the particle ζ is at
rest, the particles ε, δ, λ, β, ϰ between them and the string
being in motion backward, and the rest of the particles
η, θ, λ, μ, ν, χ, π, ρ, σ, τ in motion forward: each of the particles
between η and χ moving faster than that, which immediately
follows it; but of the particles from χ to φ, on
the contrary, those behind moving on faster than those,
which precede.
11. But now the string having recovered its rectilinear figure, though it shall go on recoiling, till it return near to its first situation I K L, yet there will be a change in its motion; so that whereas it returned from the situation I ϰ L with an accelerated motion, its motion shall from hence be retarded again by the same degrees, as accelerated before. The effect of which change upon the particles of the air will be this. As by the accelerated motion of the chord α contiguous to it moved faster than β, γ, so as to make the interval α β greater than the interval β γ, and from thence β was made likewise to move faster than γ, and the distance between β and γ rendered greater than the distance between γ and δ, and so of the rest; now the motion of α being diminished, β shall overtake it, and the distance between α and β be reduced into that, which is at present between β and γ, the interval between β and γ being inlarged into the present[277] distance between α and β; but when the interval β γ is increased to that, which is at present between α and β γ the distance between γ and δ shall be enlarged to the present distance between γ and β, and the distance between δ and ι inlarged into the present distance between γ and δ; and the same of the rest. But the chord more and more slackening its pace, the distance between α and β shall be more and more diminished; and in consequence of that the distance between β and γ shall be again contracted, first into its present dimension, and afterwards into a narrower space; while the interval γ δ shall dilate into that at present between α and β, and as soon as it is so much enlarged, it shall contract again. Thus by the reciprocal expansion and contraction of the air between α and ζ, by that time the chord is got into the situation I K L, the interval ζ η shall be expanded into the present distance between α and β; and by that time likewise the present distance of α from β will be contracted into their natural interval: for this distance will be about the same time in contracting it self, as has been taken up in its dilatation; seeing the string will be as long in returning from its rectilinear figure, as it has been in recovering it from its situation I ϰ L. This is the change which will be made in the particles between α and ζ. As for those between ζ and χ, because each preceding particle advances faster than that, which immediately follows it, their distances will successively be dilated into that, which is at present between ζ and η. And as soon as any two particles are arrived at their natural distance, the hindermost of them shall be stopt, and immediately after return,[278] the distances between the returning particles being greater than the natural. And this dilatation of these distances shall extend so far, by that time the chord is returned into its first situation I K L, that the particles ι χ shall be removed to their natural distance. But the dilatation of ν χ shall contract the interval τ φ into that at present between ν and χ, and the contraction of the distance between those two particles τ and φ will agitate a part of the air beyond; so that when the chord is returned into the situation I K L, having made an intire vibration, the moved particles of the air will take the rangement expressed by the points, l, m, n, o, p, q, r, s, t, u, w, x, y, z, 1, 2, 3, 4, 5, 6, 7, 8: in which l m, are at the natural distance of the particles, the distance m n greater than l m and n o greater than m n, and so on, till you come to q r, the widest of all: and then the distances gradually diminish not only to the natural distance, as w x, but till they are contracted as much as χ τ was before; which falls out in the points 2, 3, from whence the distances augment again, till you come to the part of the air untouched.
12. This is the motion, into which the air is put, while the chord makes one vibration, and the whole length of air thus agitated in the time of one vibration of the chord our author calls the length of one pulse. When the chord goes on to make another vibration, it will not only continue to agitate the air at present in motion, but spread the pulsation of the air as much farther, and by the same degrees, as before. For when the chord returns into its rectilinear situation I k L, l m shall be brought into its most contracted[279] state, q r now in the state of greatest dilatation shall be reduced to its natural distance, the points w, x now at their natural distance shall be at their greatest distance, the points 2, 3 now most contracted enlarged to their natural distance, and the points 7, 8 reduced to their most contracted state: and the contraction of them will carry the agitation of the air as far beyond them, as that motion was carried from the chord, when it first moved out of the situation I K L into its rectilinear figure. When the chord is got into the situation I ϰ L, l m shall recover its natural dimensions, q r be reduced to its state of greatest contraction, w x brought to its natural dimension, the distance 2 3 enlarged to the utmost, and the points 7, 8 shall have recovered their natural distance; and by thus recovering themselves they shall agitate the air to as great a length beyond them, as it was moved beyond the chord, when it first came into the situation I ϰ L. When the chord is returned back again into its rectilinear situation, l m shall be in its utmost dilatation, q r restored again to its natural distance, w x reduced into its state of greatest contraction, 2 3 shall recover its natural dimension, and 7 8 be in its state of greatest dilatation. By which means the air shall be moved as far beyond the points 7, 8, as it was moved beyond the chord, when it before made its return back to its rectilinear situation; for the particles 7, 8 have been changed from their state of rest and their natural distance into a state of contraction, and then have proceeded to the recovery of their natural distance, and after that to a dilatation of it, in the same manner as the particles contiguous to the chord were agitated before. In[280] the last place, when the chord is returned into the situation I K L, the particles of air from l to δ shall acquire their present rangement, and the motion of the air be extended as much farther. And the like will happen after every compleat vibration of the string.
13. Concerning this motion of sound, our author shews how to compute the velocity thereof, or in what time it will reach to any proposed distance from the sonorous body. For this he requires to know the height of air, having the same density with the parts here at the surface of the earth, which we breath, that would be equivalent in weight to the whole incumbent atmosphere. This is to be found by the barometer, or common weatherglass. In that instrument quicksilver is included in a hollow glass cane firmly closed at the top. The bottom is open, but immerged into quicksilver contained in a vessel open to the air. Care is taken when the lower end of the cane is immerged, that the whole cane be full of quicksilver, and that no air insinuate itself. When the instrument is thus fixed, the quicksilver in the cane being higher than that in the vessel, if the top of the cane were open, the fluid would soon sink out of the glass cane, till it came to a level with that in the vessel. But the top of the cane being closed up, so that the air, which has free liberty to press on the quicksilver in the vessel, cannot bear at all on that, which is within the cane, the quicksilver in the cane will be suspended to such a height, as to balance the pressure of the air on the quicksilver in the vessel. Here it is evident, that the[281] weight of the quicksilver in the glass cane is equivalent to the pressure of so much of the air, as is perpendicularly over the hollow of the cane; for if the cane be opened that the air may enter, there will be no farther use of the quicksilver to sustain the pressure of the air without; for the quicksilver in the cane, as has already been observed, will then subside to a level with that without. Hence therefore if the proportion between the density of quicksilver and of the air we breath be known, we may know what height of such air would form a column equal in weight to the column of quicksilver within the glass cane. When the quicksilver is sustained in the barometer at the height of 30 inches, the height of such a column of air will be about 29725 feet; for in this case the air has about 1/870 of the density of water, and the density of quicksilver exceeds that of water about 13⅔ times, so that the density of quicksilver exceeds that of the air about 11890 times; and so many times 30 inches make 29725 feet. Now Sir Isaac Newton determines, that while a pendulum of the length of this column should make one vibration or swing, the space, which any sound will have moved, shall bear to this length the same proportion, as the circumference of a circle bears to the diameter thereof; that is, about the proportion of 355 to 113[267]. Only our author here considers singly the gradual progress of sound in the air from particle to particle in the manner we have explained, without taking into consideration the magnitude of those particles. And though there requires time for the motion to be propagated from one particle[282] to another, yet it is communicated to the whole of the same particle in an instant: therefore whatever proportion the thickness of these particles bears to their distance from each other, in the same proportion will the motion of sound be swifter. Again the air we breath is not simply composed of the elastic part, by which sound is conveyed, but partly of vapours, which are of a different nature; and in the computation of the motion of sound we ought to find the height of a column of this pure air only, whose weight should be equal to the weight of the quicksilver in the cane of the barometer, and this pure air being a part only of that we breath, the column of this pure air will be higher than 29725 feet. On both these accounts the motion of sound is found to be about 1142 feet in one second of time, or near 13 miles in a minute, whereas by the computation proposed above, it should move but 979 feet in one second.
14. We may observe here, that from these demonstrations of our author it follows, that all sounds whether acute or grave move equally swift, and that sound is swiftest, when the quicksilver stands highest in the barometer.
15. Thus much of the appearances, which are caused in these fluids from their gravitation toward the earth. They also gravitate toward the moon; for in the last chapter it has been proved, that the gravitation between the earth and moon is mutual, and that this gravitation of the whole bodies arises from that power acting in all their parts; so that[283] every particle of the moon gravitates toward the earth, and every particle of the earth toward the moon. But this gravitation of these fluids toward the moon produces no sensible effect, except only in the sea, where it causes the tides.
16. That the tides depend upon the influence of the moon has been the receiv’d opinion of all antiquity; nor is there indeed the least shadow of reason to suppose otherwise, considering how steadily they accompany the moon’s course. Though how the moon caused them, and by what principle it was enabled to produce so distinguish’d an appearance, was a secret left for this philosophy to unfold: which teaches, that the moon is not here alone concerned, but that the sun likewise has a considerable share in their production; though they have been generally ascribed to the other luminary, because its effect is greatest, and by that means the tides more immediately suit themselves to its motion; the sun discovering its influence more by enlarging or restraining the moon’s power, than by any distinct effects. Our author finds the power of the moon to bear to the power of the sun about the proportion of 4½ to 1. This he deduces from the observations made at the mouth of the river Avon, three miles from Bristol, by Captain Sturmey, and at Plymouth by Mr. Colepresse, of the height to which the water is raised in the conjunction and opposition of the luminaries, compared with the elevation of it, when the moon is in either quarter; the first being caused[284] by the united actions of the sun and moon, and the other by the difference of them, as shall hereafter be shewn.
17. That the sun should have a like effect on the sea, as the moon, is very manifest; since the sun likewise attracts every single particle, of which this earth is composed. And in both luminaries since the power of gravity is reciprocally in the duplicate proportion of the distance, they will not draw all the parts of the waters in the same manner; but must act upon the nearest parts stronger, than upon the remotest, producing by this inequality an irregular motion. We shall now attempt to shew how the actions of the sun and moon on the waters, by being combined together, produce all the appearances observed in the tides.
18. To begin therefore, the reader will remember what has been said above, that if the moon without the sun would have described an orbit concentrical to the earth, the action of the sun would make the orbit oval, and bring the moon nearer to the earth at the new and full, than at the quarters[268]. Now our excellent author observes, that if instead of one moon, we suppose a ring of moons, contiguous and occupying the whole orbit of the moon, his demonstration would still take place, and prove that the parts of this ring in passing from the quarter to the conjunction or opposition would be accelerated, and be retarded again in passing from the conjunction or opposition to the next quarter. And as this effect does not depend[285] on the magnitude of the bodies, whereof the ring is composed, the same would hold, though the magnitude of these moons were so far to be diminished, and their number increased, till they should form a fluid[269]. Now the earth turns round continually upon its own center, causing thereby the alternate change of day and night, while by this revolution each part of the earth is successively brought toward the sun, and carried off again in the space of 24 hours. And as the sea revolves round along with the earth itself in this diurnal motion, it will represent in some sort such a fluid ring.
19. But as the water of the sea does not move round with so much swiftness, as would carry it about the center of the earth in the circle it now describes, without being supported by the body of the earth; it will be necessary to consider the water under three distinct cases. The first case shall suppose the water to move with the degree of swiftness, required to carry a body round the center of the earth disingaged from it in a circle at the distance of the earth’s semidiameter, like another moon. The second case is, that the waters make but one turn about the axis of the earth in the space of a month, keeping pace with the moon; so that all parts of the water should preserve continually the same situation in respect of the moon. The third case shall be the real one of the waters moving with a velocity between these two, neither so swift as the first case requires, nor so slow as the second.
20. In the first case the waters, like the body which they equalled in velocity, by the action of the moon would be brought nearer the center under and opposite to the moon, than in the parts in the middle between these eastward or westward. That such a body would so alter its distance by the moon’s action upon it, is clear from what has been mentioned of the like changes in the moon’s motion caused by the sun[270]. And computation shews, that the difference between the greatest and least distance of such a body would not be much above 4½ feet. But in the second case, where all the parts of the water preserve the same situation continually in respect of the moon, the weight of those parts under and opposite to the moon will be diminished by the moon’s action, and the parts in the middle between these will have their weight increased: this being effected just in the same manner, as the sun diminishes the attraction of the moon towards the earth in the conjunction and opposition, but increases that attraction in the quarters. For as the first of these consequences from the sun’s action on the moon is occasioned by the moon’s being attracted by the sun in the conjunction more than the earth, and in the opposition less than it, and therefore in the common motion of the earth and moon, the moon is made to advance toward the sun in one case too fast, and in the other is left as it were behind; so the earth will not have its middle parts drawn towards the moon so strongly as the nearer parts, and yet more forcibly than the remotest: and therefore since the earth and moon move each[287] month round their common center of gravity[271], while the earth moves round this center, the same effect will be produced, on the parts of the water nearest to that center or to the moon, as the moon feels from the sun when in conjunction, and the water on the contrary side of the earth will be affected by the moon, as the moon is by the sun, when in opposition[272]; that is, in both cases the weight of the water, or its propensity towards the center of the earth, will be diminished. The parts in the middle between these will have their weight increased, by being pressed towards the center of the earth through the obliquity of the moon’s action upon them to its action upon the earth’s center, just as the sun increases the gravitation of the moon in the quarters from the same cause[273]. But now it is manifest, that where the weight of the same quantity of water is least, there it will be accumulated; while the parts, which have the greatest weight, will subside. Therefore in this case there would be no tide or alternate rising and falling of the water, but the water would form it self into an oblong figure, whose axis prolonged would pass through the moon. By Sir Isaac Newton’s computation the excess of this axis above the diameters perpendicular to it, that is, the height of the waters under and opposite to the moon above their height in the middle between these places eastward or westward caused by the moon, is about 8⅔ feet.
21. Thus the difference of height in this latter supposition is little short of twice that difference in the preceding. But the case of the sea is a middle between these two: for a body, which should revolve round the center of the earth at the distance of a semidiameter without pressing on the earth’s surface, must perform its period in less than an hour and half, whereas the earth turns round but once in a day; and in the case of the waters keeping pace with the moon it should turn round but once in a month: so that the real motion of the water is between the motions required in these two cases. Again, if the waters moved round as swiftly as the first case required, their weight would be wholly taken off by their motion; for this case supposes the body to move so, as to be kept revolving in a circle round the earth by the power of gravity without pressing on the earth at all, so that its motion just supports its weight. But if the power of gravity had been only 1/289 part of what it is, the body could have moved thus without pressing on the earth, and have been as long in moving round, as the earth it self is. Consequently the motion of the earth takes off from the weight of the water in the middle between the poles, where its motion is swiftest, 1/289 part of its weight and no more. Since therefore in the first case the weight of the waters must be intirely taken off by their motion, and by the real motion of the earth they lose only 1/289 part thereof, the motion of the water will so little diminish their weight, that their figure will much nearer resemble the case of their keeping pace with the moon than the other. Upon the whole, if the waters moved with the[289] velocity necessary to carry a body round the center of the earth at the distance of the earth’s semidiameter without bearing on its surface, the water would be lowest under the moon, and rise gradually as it moved on with the earth eastward, till it came half way toward the place opposite to the moon; from thence it would subside again, till it came to the opposition, where it would become as low as at first; afterwards it would rise again, till it came half way to the place under the moon; and from hence it would subside, till it came a second time under the moon. But in case the water kept pace with the moon, it would be highest where in the other case it is lowest, and lowest where in the other it is highest; therefore the diurnal motion of the earth being between the motions of these two cases, it will cause the highest place of the water to fall between the places of the greatest height in these two cases. The water as it passes from under the moon shall for some time rise, but descend again before it arrives half way to the opposite place, and shall come to its least height before it becomes opposite to the moon; then it shall rise again, continuing so to do till it has passed the place opposite to the moon, but subside before it comes to the middle between the places opposite to and under the moon; and lastly it shall come to its lowest, before it comes a second time under the moon. If A (in fig. 112, 113, 114.) represent the moon, B the center of the earth, the oval C D E F in fig. 112. will represent the situation of the water in the first case; but if the water kept pace with the moon, the line C D E F in fig. 113. would represent the situation[290] of the water; but the line C D E F in fig. 114. will represent the same in the real motion of the water, as it accompanies the earth in its diurnal rotation: in all these figures C and E being the places where the water is lowest, and D and F the places where it is highest. Pursuant to this determination it is found, that on the shores, which lie exposed to the open sea, the high water usually falls out about three hours after the moon has passed the meridian of each place.
22. Let this suffice in general for explaining the manner, in which the moon acts upon the seas. It is farther to be noted, that these effects are greatest, when the moon is over the earth’s equator[274], that is, when it shines perpendicularly upon the parts of the earth in the middle between the poles. For if the moon were placed over either of the poles, it could have no effect upon the water to make it ascend and descend. So that when the moon declines from the equator toward either pole, it’s action must be something diminished, and that the more, the farther it declines. The tides likewise will be greatest, when the moon is nearest to the earth, it’s action being then the strongest.
23. Thus much of the action of the moon. That the sun should produce the very same effects, though in a less degree, is too obvious to require a particular explanation: but as was remarked before, this action of the[291] sun being weaker than that of the moon, will cause the tides to follow more nearly the moon’s course, and principally shew it self by heightening or diminishing the effects of the other luminary. Which is the occasion, that the highest tides are found about the conjunction and opposition of the luminaries, being then produced by their united action, and the weakest tides about the quarters of the moon; because the moon in this case raising the water where the sun depresses it, and depressing it where the sun raises it, the stronger action of the moon is in part retunded and weakened by that of the sun. Our author computes that the sun will add near two feet to the height of the water in the first case, and in the other take from it as much. However the tides in both comply with the same hour of the moon. But at other times, between the conjunction or opposition and quarters, the time deviates from that forementioned, towards the hour in which the sun would make high water, though still it keeps much nearer to the moon’s hour than to the sun’s.
24. Again the tides have some farther varieties from the situation of the places where they happen northward or southward. Let p P (in fig. 115.) represent the axis, on which the earth daily revolves, let h p H P represent the figure of the water, and let n B N D be a globe inscribed within this figure. Suppose the moon to be advanced from the equator toward the north pole, so that h H the axis of the figure of the water p A H P E h shall decline towards the north pole N; take any place G nearer to[292] the north pole than to the south, and from the center of the earth C draw C G F; then will G F denote the altitude to which the water is raised by the tide, when the moon is above the horizon: in the space of twelve hours, the earth having turned half round its axis, the place G will be removed to g; but the axis h H will have kept its place preserving its situation in respect of the moon, at least will have moved no more than the moon has done in that time, which it is not necessary here to take into consideration. Now in this case the height of the water will be equal to g f, which is not so great as G F. But whereas G F is the altitude at high water, when the moon is above the horizon, g f will be the altitude of the same, when the moon is under the horizon. The contrary happens toward the south pole, for K L is less than k l. Hence is proved, that when the moon declines from the equator, in those places, which are on the same side of the equator as the moon, the tides are greater, when the moon is above the horizon, than when under it; and the contrary happens on the other side of the equator.
25. Now from these principles may be explained all the known appearances in the tides; only by the assistance of this additional remark, that the fluctuating motion, which the water has in flowing and ebbing, is of a durable nature, and would continue for some time, though the action of the luminaries should cease; for this prevents the difference between the tide when the moon is above[293] the horizon, and the tide when the moon is below it from being so great, as the rule laid down requires. This likewise makes the greatest tides not exactly upon the new and full moon, but to be a tide or two after; as at Bristol and Plymouth they are found the third after.
26. This doctrine farther shews us, why not only the spring tides fall out about the new and full moon, and the neap tides about the quarters; but likewise how it comes to pass, that the greatest spring tides happen about the equinoxes; because the luminaries are then one of them over the equator, and the other not far from it. It appears too, why the neap tides, which accompany these, are the least of all, for the sun still continuing over the equator continues to have the greatest power of lessening the moon’s action, and the moon in the quarters being far removed toward one of the poles, has its power thereby weakned.
27. Moreover the action of the moon being stronger, when near the earth, than when more remote; if the moon, when new suppose, be at its nearest distance from the earth, it shall when at the full be farthest off; whence it is, that two of the very largest spring tides do never immediately succeed each other.
28. Because the sun in its passage from the winter solstice to the summer recedes from the earth, and passing from the summer solstice to the winter approaches it, and is therefore nearer the earth before the vernal equinox than[294] after, but nearer after the autumnal equinox than before; the greatest tides oftner precede the vernal equinox than follow it, and in the autumnal equinox on the contrary they oftner follow it than come before it.
29. The altitude, to which the water is raised in the open ocean, corresponds very well to the forementioned calculations; for as it was shewn, that the water in spring tides should rise to the height of 10 or 11 feet, and the neap tides to 6 or 7; accordingly in the Pacific, Atlantic and Ethiopic oceans in the parts without the tropics, the water is observed to rise about 6, 9, 12 or 15 feet. In the Pacific ocean this elevation is said to be greater than in the other, as it ought to be by reason of the wide extent of that sea. For the same reason in the Ethiopic ocean between the tropics the ascent of the water is less than without, by reason of the narrowness of the sea between the coasts of Africa and the southern parts of America. And islands in such narrow seas, if far from shore, have less tides than the coasts. But now in those ports where the water flows in with great violence upon fords and shoals, the force it acquires by that means will carry it to a much greater height, so as to make it ascend and descend to 30, 40 or even 50 feet and more; instances of which we have at Plymouth, and in the Severn near Chepstow; at St. Michael’s and Auranches in Normandy; at Cambay and Pegu in the East Indies.
30. Again the tides take a considerable time in passing through long straits, and shallow places. Thus the tide,[295] which is made on the west coast of Ireland and on the coast of Spain at the third hour after the moon’s coming to the meridian, in the ports eastward toward the British channel falls out later, and as the flood passes up that channel still later and later, so that the tide takes up full twelve hours in coming up to London bridge.
31. In the last place tides may come to the same port from different seas, and as they may interfere with each other, they will produce particular effects. Suppose the tide from one sea come to a port at the third hour after the moon’s passing the meridian of the place, but from another sea to take up six hours more in its passage. Here one tide will make high water, when by the other it should be lowest; so that when the moon is over the equator, and the two tides are equal, there will be no rising and falling of the water at all; for as much as the water is carried off by one tide, it will be supplied by the other. But when the moon declines from the equator, the same way as the port is situated, we have shewn that of the two tides of the ocean, which are made each day, that tide, which is made when the moon is above the horizon, is greater than the other. Therefore in this case, as four tides come to this port each day the two greatest will come on the third, and on the ninth hour after the moon’s passing the meridian, and the two least at the fifteenth and at the twenty first hour. Thus from the third to the ninth hour more water will be in this port by the two greatest tides than from the ninth to the fifteenth, or from the twenty first to the[296] following third hour, where the water is brought by one great and one small tide; but yet there will be more water brought by these tides, than what will be found between the two least tides, that is, between the fifteenth and twenty first hour. Therefore in the middle between the third and ninth hour, or about the moon’s setting, the water will be at its greatest height; in the middle between the ninth and fifteenth, as also between the twenty first and following third hour it will have its mean height; and be lowest in the middle between the fifteenth and twenty first hour, that is, at the moon’s rising. Thus here the water will have but one flood and one ebb each day. When the moon is on the other side of the equator, the flood will be turned into ebb, and the ebb into flood; the high water falling out at the rising of the moon, and the low water at the setting. Now this is the case of the port of Batsham in the kingdom of Tunquin in the East Indies; to which port there are two inlets, one between the continent and the islands which are called the Manillas, and the other between the continent and Borneo.
32. The next thing to be considered is the effect, which these fluids of the planets have upon the solid part of the bodies to which they belong. And in the first place I shall shew, that it was necessary upon account of these fluid parts to form the bodies of the planets into a figure something different from that of a perfect globe. Because the diurnal rotation, which our earth performs about its axis, and the like motion we see in some of the other planets,[297] (which is an ample conviction that they all do the like) will diminish the force, with which bodies are attracted upon all the parts of their surfaces, except at the very poles, upon which they turn. Thus a stone or other weighty substance resting upon the surface of the earth, by the force which it receives from the motion communicated to it by the earth, if its weight prevented not, would continue that motion in a straight line from the point where it received it, and according to the direction, in which it was given, that is, in a line which touches the surface at that point; insomuch that it would move off from the earth in the same manner, as a weight fasten’d to a string and whirled about endeavours continually to recede from the center of motion, and would forthwith remove it self to a greater distance from it, if loosed from the string which retains it. And farther, as the centrifugal force, with which such a weight presses from the center of its motion, is greater, by how much greater the velocity is, with which it moves; so such a body, as I have been supposing to lie on the earth, would recede from it with the greater force, the greater the velocity is, with which the part of the earth’s surface it rests upon is moved, that is, the farther distant it is from the poles. But now the power of gravity is great enough to prevent bodies in any part of the earth from being carried off from it by this means; however it is plain that bodies having an effort contrary to that of gravity, though much weaker than it, their weight, that is, the degree of force, with which they are pressed to the earth, will be diminished thereby, and be the more diminished,[298] the greater this contrary effort is; or in other words, the same body will weigh heavier at either of the poles, than upon any other part of the earth; and if any body be removed from the pole towards the equator, it will lose of its weight more and more, and be lightest of all at the equator, that is, in the middle between the poles.
33. This now is easily applied to the waters of the seas, and shews that the water under the poles will press more forcibly to the earth, than at or near the equator: and consequently that which presses least, must give place, till by ascending it makes room for receiving a greater quantity, which by its additional weight may place the whole upon a ballance. To illustrate this more particularly I shall make use of fig. 116 In which let A C B D be a circle, by whose revolution about the diameter A B a globe should be formed, representing a globe of solid earth. Suppose this globe covered on all sides with water to the same height, suppose that of E A or B F, at which distance the circle E G F H surrounds the circle A C B D; then it is evident, if the globe of earth be at rest, the water which surrounds it will rest in that situation. But if the globe be turned incessantly about its axis A B, and the water have likewise the same motion, it is also evident, from what has been explained, that the water between the circles E H F G and A D B C will remain no longer in the present situation, the parts of it between H and D, and between G and C being by this rotation become lighter, than the parts between E and A and between B and F; so that the water over the poles A and B must of necessity subside, and the[299] water be accumulated over D and C, till the greater quantity in these latter places supply the defect of its weight. This would be the case, were the globe all covered with water. And the same figure of the surface would also be preserved, if some part of the water adjoining to the globe in any part of it were turned into solid earth, as is too evident to need any proof; because the parts of the water remaining at rest, it is the same thing, whether they continue in the state of being easily separable, which denominates them fluid, or were to be consolidated together, so as to make a hard body: and this, though the water should in some places be thus consolidated, even to the surface of it. Which shews that the form of the solid part of the earth makes no alteration in the figure the water will take: and by consequence in order to the preventing some parts of the earth from being entirely overflowed, and other parts quite deserted, the solid parts of the earth must have given them much the same figure, as if the whole earth were covered on all sides with water.
34. Farther, I say, this figure of the earth is the same, as it would receive, were it entirely a globe of water, provided that water were of the same density as the substance of the globe. For suppose the globe A C B D to be liquified, and that the globe E H F G, now entirely water, by its rotation about its axis should receive such a figure as we have been describing, and then the globe A C B D should be consolidated again, the figure of the water would plainly not be altered, by such a consolidation.
35. But from this last observation our author is enabled to determine the proportion between the axis of the earth drawn from pole to pole, and the diameter of the equator, upon the supposition that all the parts of the earth are of equal density; which he does by computing in the first place the proportion of the centrifugal force of the parts under the equator to the power of gravity; and then by considering the earth as a spheroid, made by the revolution of an ellipsis about its lesser axis, that is, supposing the line M I L K to be an exact ellipsis, from which it can differ but little, by reason that the difference between the lesser axis M L and the greater I K is but very small. From this supposition, and what was proved before, that all the particles which compose the earth have the attracting power explained in the preceding chapter, he finds at what distance the parts under the equator ought to be removed from the center, that the force, with which they shall be attracted to the center, diminished by their centrifugal force, shall be sufficient to keep those parts in a ballance with those which lie under the poles. And upon the supposition of all the parts of the earth having the same degree of density, the earth’s surface at the equator must be above 17 miles more distant from the center, than at the poles[275].
36. After this it is shewn, from the proportion of the equatorial diameter of the earth to its axis, how the same may be determined of any other planet, whose density in[301] comparison of the density of the earth, and the time of its revolution about its axis, are known. And by the rule delivered for this, it is found, that the diameter of the equator in Jupiter should bear to its axis about the proportion of 10 to 9[276], and accordingly this planet appears of an oval form to the astronomers. The most considerable effects of this spheroidical figure our author takes likewise into consideration; one of which is that bodies are not equally heavy in all distances from the poles; but near the equator, where the distance from the center is greatest, they are lighter than towards the poles: and nearly in this proportion, that the actual power, by which they are drawn to the center, resulting from the difference between their absolute gravity and centrifugal force, is reciprocally as the distance from the center. That this may not appear to contradict what has before been said of the alteration of the power of gravity, in proportion to the change of the distance from the center, it is proper carefully to remark, that our author has demonstrated three things relating hereto: the first is, that decrease of the power of gravity as we recede from the center, which has been fully explained in the last chapter, upon supposition that the earth and planets are perfect spheres, from which their difference is by many degrees too little to require notice for the purposes there intended: the next is, that whether they be perfect spheres, or exactly such spheroids as have now been mentioned, the power of gravity, as we descend in the same line to the center, is at all distances as the distance from the center, the parts of the[302] earth above the body by drawing the body towards them lessening its gravitation towards the center[277]; and both these assertions relate to gravity alone: the third is what we mentioned in this place, that the actual force on different parts of the surface, with which bodies are drawn to the center, is in the proportion here assigned[278].
38. The next effect of this figure of the earth is an obvious consequence of the former: that pendulums of the same length do not in different distances from the pole make their vibrations in the same time; but towards the poles, where the gravity is strongest, they move quicker than near the equator, where they are less impelled to the center; and accordingly pendulums, that measure the same time by their vibrations, must be shorter near the poles than at a greater distance. Both which deductions are found true in fact; of which our author has recounted particularly several experiments, in which it was found, that clocks exactly adjusted to the true measure of time at Paris, when transported nearer to the equator, became erroneous and moved too slow, but were reduced to their true motion by contracting their pendulums. Our author is particular in remarking, how much they lost of their motion, while the pendulums remained unaltered; and what length the observers are said to have shortened them, to bring them to time. And the experiments, which appear to be most carefully made, shew the earth to be raised in the middle between the poles, as much as our author found it by his computation[279].
39. These experiments on the pendulum our author has been very exact in examining, inquiring particularly how much the extension of the rod of the pendulum by the great heats in the torrid zone might make it necessary to shorten it. For by an experiment made by Picart, and another made by De la Hire, heat, though not very intense, was found to increase the length of rods of iron. The experiment of Picart was made with a rod one foot long, which in winter, at the time of frost, was found to increase in length by being heated at the fire. In the experiment of De la Hire a rod of six foot in length was found, when heated by the summer sun only, to grow to a greater length, than it had in the aforesaid cold season. From which observations a doubt has been raised, whether the rod of the pendulums in the aforementioned experiments was not extended by the heat of those warm climates to all that excess of length, the observers found themselves obliged to lessen them by. But the experiments now mentioned shew the contrary. For in the first of them the rod of a foot long was lengthened no more than 1/9 part of what the pendulum under the equator must be diminished; and therefore a rod of the length of the pendulum would not have been extended above ⅓ of that length. In the experiment of De la Hire, where the heat was less, the rod of six foot long was extended no more than 3/10 of what the pendulum must be shortened; so that a rod of the length of the pendulum would not have gained above 3/20 or 1/7 of that length. And the heat in this latter experiment, though less than in the former, was yet greater than the rod of a pendulum can ordinarily[304] contract in the hottest country; for metals receive a great heat when exposed to the open sun, certainly much greater than that of a human body. But pendulums are not usually so exposed, and without doubt in these experiments were kept cool enough to appear so to the touch; which they would do in the hottest place, if lodged in the shade. Our author therefore thinks it enough to allow about 1/10 of the difference observed upon account of the greater warmth of the pendulum.
40. There is a third effect, which the water has on the earth by changing its figure, that is taken notice of by our author; for the explaining of which we shall first prove, that bodies descend perpendicularly to the surface of the earth in all places. The manner of collecting this from observation, is as follows. The surfaces of all fluids rest parallel to that part of the surface of the sea, which is in the same place with them, to the figure of which, as has been particularly shewn, the figure of the whole earth is formed. For if any hollow vessel, open at the bottom, be immersed into the sea; it is evident, that the surface of the sea within the vessel will retain the same figure it had, before the vessel inclosed it; since its communication with the external water is not cut off by the vessel. But all the parts of the water being at rest, it is as clear, that if the bottom of the vessel were closed, the figure of the water could receive no change thereby, even though the vessel were raised out of the sea; any more than from the insensible alteration of the power of gravity, consequent upon the augmentation of[305] the distance from the center. But now it is clear, that bodies descend in lines perpendicular to the surfaces of quiescent fluids; for if the power of gravity did not act perpendicularly to the surface of fluids, bodies which swim on them could not rest, as they are seen to do; because, if the power of gravity drew such bodies in a direction oblique to the surface whereon they lay, they would certainly be put in motion, and be carried to the side of the vessel, in which the fluid was contained, that way the action of gravity inclined.
41. Hence it follows, that as we stand, our bodies are perpendicular to the surface of the earth. Therefore in going from north to south our bodies do not keep in a parallel direction. Now in all distances from the pole the same length gone on the earth will not make the same change in the position of our bodies, but the nearer we are to the poles, we must go greater length to cause the same variation herein. Let M I L K (in fig. 117) represent the figure of the earth, M, L the poles, I, K two opposite points in the middle between these poles. Let T V and P O be two arches, T V being most remote from the pole L; draw T W, V X, P Q, O R, each perpendicular to the surface of the earth, and let T W, V X meet in Y, and P Q, O R in S. Here it is evident, that in passing from V to T the position of a man’s body would be changed by the angle under T Y V, for at V he would stand in the line Y V continued upward, and at T in the line Y T; but in passing from O to P the position of his body would be changed by[306] the angle under O S P. Now I say, if these two angles are equal the arch O P is longer than T V: for the figure M I L K being oblong, and I K longer than M L, the figure will be more incurvated toward I than toward L; so that the lines T W and V X will meet in Y before they are drawn out to so great a length as the lines P Q and O R must be continued to, before they will meet in S. Since therefore Y T and Y V are shorter than P S and S V, T V must be less than O P. If these angles under T Y V and O S P are each 1/90 part of the angle made by a perpendicular line, they are said each to contain one degree. And the unequal length of these arches O P and V T gives occasion to the assertion, that in passing from north to south the degrees on the earth’s surface are not of an equal length, but those near the pole longer than those toward the equator. For the length of the arch on the earth lying between the two perpendiculars, which make an angle of a degree with each other, is called the length of a degree on the earth’s surface.
42. This figure of the earth has some effect on eclipses. It has been observed above, that sometimes the nodes of the moon’s orbit lie in a straight line drawn from the sun to the earth; in which case the moon will cross the plane of the earth’s motion at the new and full. But whenever the moon passes near the plane at the full, some part of the earth will intercept the sun’s light, and the moon shining only with light borrow’d from the sun, when that light is prevented from falling on any part of the moon, so much of her body will be darkened. Also when the moon at the[307] new is near the plane of the earth’s motion, the inhabitants on some part of the earth will see the moon come under the sun, and the sun thereby be covered from them either wholly or in part. Now the figure, which we have shewn to belong to the earth, will occasion the shadow of the earth on the moon not to be perfectly round, but cause the diameter from east to west to be somewhat longer than the diameter from north to south. In eclipse of the sun this figure of the earth will make some little difference in the place, where the sun shall appear wholly or in any given part covered. Let A B C D (in fig. 118.) represent the earth, A C the axis whereon it turns daily, E the center. Let F A G C represent a perfect globe inscribed within the earth. Let H I be a line drawn through the centers of the sun and moon, crossing the surface of the earth in K, and the surface of the globe inscribed in L. Draw E L, which will be perpendicular to the surface of the globe in L: and draw likewise K M, so that it shall be perpendicular to the surface of the earth in K. Now whereas the eclipse would appear central at L, if the earth were the globe A G C F, and does really appear so at K; I say, the latitude of the place K on the real earth is different from the latitude of the place L on the globe F A G C. What is called the latitude of any place is determined by the angle which the line perpendicular to the surface of the earth at that place makes with the axis; the difference between this angle, and that made by a perpendicular line or square being called the latitude of each place. But it might here be proved, that the angle which K M makes with M C is less, than the angle made between L E and E C: consequently[308] the latitude of the place K is greater, than the latitude, which the place L would have.
43. The next effect, which follows from this figure of the earth, is that gradual change in the distance of the fixed stars from the equinoctial points, which astronomers observe. But before this can be explained, it is necessary to say something more particular, than has yet been done, concerning the manner of the earth’s motion round the sun.
44. It has already been said, that the earth turns round each day on its own axis, while its whole body is carried round the sun once in a year. How these two motions are joined together may be conceived in some degree by the motion of a bowl on the ground, where the bowl in rouling on continually turns upon its axis, and at the same time the whole body thereof is carried straight on. But to be more express let A (in fig. 119) represent the sun B C D E four different situations of the earth in its orbit moving about the sun. In all these let F G represent the axis, about which the earth daily turns. The points F, G are called the poles of the earth; and this axis is supposed to keep always parallel to it self in every situation of the earth; at least that it would do so, were it not for a minute deviation, the cause whereof will be explained in what follows. When the earth is in B, the half H I K will be illuminated by the sun, and the other half H L K will be in darkness. Now if on the globe any point be taken[309] in the middle between the poles, this point shall describe by the motion of the globe the circle M N, half of which is in the enlightened part of the globe, and half in the dark part. But the earth is supposed to move round its axis with an equable motion; therefore on this point of the globe the sun will be seen just half the day, and be invisible the other half. And the same will happen to every point of this circle, in all situations of the earth during its whole revolution round the sun. This circle M N is called the equator, of which we have before made mention.
45. Now suppose any other point taken on the surface of the globe toward the pole F, which in the diurnal revolution of the globe shall describe the circle O P. Here it appears that more than half this circle is enlightned by the sun, and consequently that in any particular point of this circle the sun will be longer seen than lie hid, that is the day will be longer than the night. Again if we consider the same circle O P on the globe situated in D the opposite part of the orbit from B, we shall see, that here in any place of this circle the night will be as much longer than the day.
46. In these situations of the globe of earth a line drawn from the sun to the center of the earth will be obliquely inclined toward the axis F G. Now suppose, that such a line drawn from the sun to the center of the earth, when in C or E, would be perpendicular to the axis F G;[310] in which cases the sun will shine perpendicularly upon the equator, and consequently the line drawn from the center of the earth to the sun will cross the equator, as it passes through the surface of the earth; whereas in all other situations of the globe this line will pass through the surface of the globe at a distance from the equator either northward or southward. Now in both these cases half the circle O P will be in the light, and half in the dark; and therefore to every place in this circle the day will be equal to the night. Thus it appears, that in these two opposite situations of the earth the day is equal to the night in all parts of the globe; but in all other situations this equality will only be found in places situated in the very middle between the poles, that is, on the equator.
47. The times, wherein this universal equality between the day and night happens, are called the equinoxes. Now it has been long observed by astronomers, that after the earth hath set out from either equinox, suppose from E (which will be the spring equinox, if F be the north pole) the same equinox shall again return a little before the earth has made a compleat revolution round the sun. This return of the equinox preceding the intire revolution of the earth is called the precession of the equinox, and is caused by the protuberant figure of the earth.
49. Since the sun shines perpendicularly upon the equator, when the line drawn from the sun to the center of the earth is perpendicular to the earth’s axis, in this case[311] the plane, which should cut through the earth at the equator, may be extended to pass through the sun; but it will not do so in any other position of the earth. Now let us consider the prominent part of the earth about the equator, as a solid ring moving with the earth round the sun. At the time of the equinoxes, this ring will have the same kind of situation in respect of the sun, as the orbit of the moon has, when the line of the nodes is directed to the sun; and at all other times will resemble the moon’s orbit in other situations. Consequently this ring, which otherwise would keep throughout its motion parallel to it self, will receive some change in its position from the action of the sun upon it, except only at the time of the equinox. The manner of this change may be understood as follows. Let A B C D (in fig. 120) represent this ring, E the center of the earth, S the sun, A F C G a circle described in the plane of the earth’s motion to the center E. Here A and C are the two points, in which the earth’s equator crosses the plane of the earth’s motion; and the time of the equinox falls out, when the straight line A C continued would pass through the sun. Now let us recollect what was said above concerning the moon, when her orbit was in the same situation with this ring. From thence it will be understood, if a body were supposed to be moving in any part of this circle A B C D, what effect the action of the sun on the body would have toward changing the position of the line A C. In particular H I being drawn perpendicular to S E, if the body be in any part of this circle between A and H, or between C and I, the line A C[312] would be so turned, that the point A shall move toward B, and the point C toward D; but if it were in any other part of the circle, either between H and C, or between I and A, the line A C would be turned the contrary way. Hence it follows, that as this solid ring turns round the center of the earth, the parts of this ring between A and H, and between C and I, are so influenced by the sun, that they will endeavour, so to change the situation of the line A C as to cause the point A to move toward B, and the point C to move toward D; but all the parts of the ring between H and C, and between I and A, will have the opposite tendency, and dispose the line A C to move the contrary way. And since these last named parts are larger than the other, they will prevail over the other, so that by the action of the sun upon this ring, the line A C will be so turned, that A shall continually be more and more moving toward D, and C toward B. Thus no sooner shall the sun in its visible motion have departed from A, but the motion of the line A C shall hasten its meeting with C, and from thence the motion of this line shall again hasten the sun’s second conjunction with A; for as this line so turns, that A is continually moving toward D, so the sun’s visible motion is the same way as from S toward T.
49. The moon will have on this ring the like effect as the sun, and operate on it more strongly, in the same proportion as its force on the sea exceeded that of the sun on the same. But the effect of the action of both luminaries will be greatly diminished by reason of this ring’s being connected[313] to the rest of the earth; for by this means the sun and moon have not only this ring to move, but likewise the whole globe of the earth, upon whose spherical part they have no immediate influence. Beside the effect is also rendred less, by reason that the prominent part of the earth is not collected all under the equator, but spreads gradually from thence toward both poles. Upon the whole, though the sun alone carries the nodes of the moon through an intire revolution in about 19 years, the united force of both luminaries on the prominent parts of the earth will hardly carry round the equinox in a less space of time than 26000 years.
50. To this motion of the equinox we must add another consequence of this action of the sun and moon upon the elevated parts of the earth, that this annular part of the earth about the equator, and consequently the earth’s axis, will twice a year and twice a month change its inclination to the plane of the earth’s motion, and be again restored, just as the inclination of the moon’s orbit by the action of the sun is annually twice diminished, and as often recovers its original magnitude. But this change is very insensible.
51. I shall now finish the present chapter with our great author’s inquiry into the figure of the secondary planets, particularly of our moon, upon the figure of which its fluid parts will have an influence. The moon turns always the same side towards the earth, and consequently revolves but once round its axis in the space of an entire month;[314] for a spectator placed without the circle, in which the moon moves, would in that time observe all the parts of the moon successively to pass once before his view and no more, that is, that the whole globe of the moon has turned once round. Now the great slowness of this motion will render the centrifugal force of the parts of the waters very weak, so that the figure of the moon cannot, as in the earth, be much affected by this revolution upon its axis: but the figure of those waters are made different from spherical by another cause, viz. the action of the earth upon them; by which they will be reduced to an oblong oval form, whose axis prolonged would pass through the earth; for the same reason, as we have above observed, that the waters of the earth would take the like figure, if they had moved so slowly, as to keep pace with the moon. And the solid part of the moon must correspond with this figure of the fluid part: but this elevation of the parts of the moon is nothing near so great as is the protuberance of the earth at the equator, for it will not exceed 93 english feet.
52. The waters of the moon will have no tide, except what will arise from the motion of the moon round the earth. For the conversion of the moon about her axis is equable, whereby the inequality in the motion round the earth discovers to us at some times small parts of the moon’s surface towards the east or west, which at other times lie hid; and as the axis, whereon the moon turns, is oblique to her motion round the earth, sometimes small parts of her[315] surface toward the north, and sometimes the like toward the south are visible, which at other times are out of sight. These appearances make what is called the libration of the moon, discovered by Hevelius. But now as the axis of the oval figure of the waters will he pointed towards the earth, there must arise from hence some fluctuation in them; and beside, by the change of the moon’s distance from the earth, they will not always have the very same height.


BOOK III.
Chap I.
Concerning the cause of COLOURS inherent in the LIGHT.

AFTER this view which has been taken of Sir Isaac Newton’s mathematical principles of philosophy, and the use he has made of them, in explaining the system of the world, &c. the course of my design directs us to turn our eyes to that other philosophical work, his treatise of Optics, in which we shall find our great author’s inimitable genius discovering it self no less, than in[317] the former; nay perhaps even more, since this work gives as many instances of his singular force of reasoning, and of his unbounded invention, though unassisted in great measure by those rules and general precepts, which facilitate the invention of mathematical theorems. Nor yet is this work inferior to the other in usefulness; for as that has made known to us one great principle in nature, by which the celestial motions are continued, and by which the frame of each globe is preserved; so does this point out to us another principle no less universal, upon which depends all those operations in the smaller parts of matter, for whose sake the greater frame of the universe is erected; all those immense globes, with which the whole heavens are filled, being without doubt only design’d as so many convenient apartments for carrying on the more noble operations of nature in vegetation and animal life. Which single consideration gives abundant proof of the excellency of our author’s choice, in applying himself carefully to examine the action between light and bodies, so necessary in all the varieties of these productions, that none of them can be successfully promoted without the concurrence of heat in a greater or less degree.
2. ’Tis true, our author has not made so full a discovery of the principle, by which this mutual action between light and bodies is caused; as he has in relation to the power, by which the planets are kept in their courses: yet he has led us to the very entrance upon it, and pointed out the path so plainly which must be followed to reach it; that one may[318] be bold to say, whenever mankind shall be blessed with this improvement of their knowledge, it will be derived so directly from the principles laid down by our author in this book, that the greatest share of the praise due to the discovery will belong to him.
3. In speaking of the progress our author has made, I shall distinctly pursue three things, the two first relating to the colours of natural bodies: for in the first head shall be shewn, how those colours are derived from the properties of the light itself; and in the second upon what properties of the bodies they depend: but the third head of my discourse shall treat of the action of bodies upon light in refracting, reflecting, and inflecting it.
4. The first of these, which shall be the business of the present chapter, is contained in this one proposition: that the sun’s direct light is not uniform in respect of colour, not being disposed in every part of it to excite the idea of whiteness, which the whole raises; but on the contrary is a composition of different kinds of rays, one sort of which if alone would give the sense of red, another of orange, a third of yellow, a fourth of green, a fifth of light blue, a sixth of indigo, and a seventh of a violet purple; that all these rays together by the mixture of their sensations impress upon the organ of sight the sense of whiteness, though each ray always imprints there its own colour; and all the difference between the colours of bodies when viewed in open day light arises from this, that coloured bodies[319] do not reflect all the sorts of rays falling upon them in equal plenty, but some sorts much more copiously than others; the body appearing of that colour, of which the light coming from it is most composed.
5. That the light of the sun is compounded, as has been said, is proved by refracting it with a prism. By a prism I here mean a glass or other body of a triangular form, such as is represented in fig. 121. But before we proceed to the illustration of the proposition we have just now laid down, it will be necessary to spend a few words in explaining what is meant by the refraction of light; as the design of our present labour is to give some notion of the subject, we are engaged in, to such as are not versed in the mathematics.
6. It is well known, that when a ray of light passing through the air falls obliquely upon the surface of any transparent body, suppose water or glass, and enters it, the ray will not pass on in that body in the same line it described through the air, but be turned off from the surface, so as to be less inclined to it after passing it, than before. Let A B C D (in fig. 122.) represent a portion of water, or glass, A B the surface of it, upon which the ray of light E F falls obliquely; this ray shall not go right on in the course delineated by the line F G, but be turned off from the surface A B into the line F H, less inclined to the surface A B than the line E F is, in which the ray is incident upon that surface.
7. On the other hand, when the light passes out of any such body into the air, it is inflected the contrary way, being after its emergence rendred more oblique to the surface it passes through, than before. Thus the ray F H, when it goes out of the surface C D, will be turned up towards that surface, going out into the air in the line H I.
8. This turning of the light out of its way, as it passes from one transparent body into another is called its refraction. Both these cases may be tried by an easy experiment with a bason and water. For the first case set an empty bason in the sunshine or near a candle, making a mark upon the bottom at the extremity of the shadow cast by the brim of the bason, then by pouring water into the bason you will observe the shadow to shrink, and leave the bottom of the bason enlightned to a good distance from the mark. Let A B C (in fig. 123.) denote the empty bason, E A D the light shining over the brim of it, so that all the part A B D be shaded. Then a mark being made at D, if water be poured into the bason (as in fig. 124.) to F G, you shall observe the light, which before went on to D, now to come much short of the mark D, falling on the bottom in the point H, and leaving the mark D a good way within the enlightened part; which shews that the ray E A, when it enters the water at I, goes no longer straight forwards, but is at that place incurvated, and made to go nearer the perpendicular. The other case may be tryed by putting any small body into an empty bason, placed lower than your eye, and then receding from the bason, till you can but just[321] see the body over the brim. After which, if the bason be filled with water, you shall presently observe the body to be visible, though you go farther off from the bason. Let A B C (in fig. 125.) denote the bason as before, D the body in it, E the place of your eye, when the body is seen just over the edge A, while the bason is empty. If it be then filled with water, you will observe the body still to be visible, though you take your eye farther off. Suppose you see the body in this case just over the brim A, when your eye is at F, it is plain that the rays of light, which come from the body to your eye have not come straight on, but are bent at A, being turned downwards, and more inclined to the surface of the water, between A and your eye at F, than they are between A and the body D.
9. This we hope is sufficient to make all our readers apprehend, what the writers of optics mean, when they mention the refraction of the light, or speak of the rays of light being refracted. We shall therefore now go on to prove the assertion advanced in the forementioned proposition, in relation to the different kinds of colours, that the direct light of the sun exhibits to our sense: which may be done in the following manner.
10. If a room be darkened, and the sun permitted to shine into it through a small hole in the window shutter, and be made immediately to fall upon a glass prism, the beam of light shall in passing through such a prism be parted into rays, which exhibit all the forementioned colours. In this manner[322] if A B (in fig. 126) represent the window shutter; C the hole in it; D E F the prism; Z Y a beam of light coming from the sun, which passes through the hole, and falls upon the prism at Y, and if the prism were removed would go on to X, but in entring the surface B F of the glass it shall be turned off, as has been explained, into the course Y W falling upon the second surface of the prism D F in W, going out of which into the air it shall be again farther inflected. Let the light now, after it has passed the prism, be received upon a sheet of paper held at a proper distance, and it shall paint upon the paper the picture, image, or spectrum L M of an oblong figure, whose length shall much exceed its breadth; though the figure shall not be oval, the ends L and M being semicircular and the sides straight. But now this figure will be variegated with colours in this manner. From the extremity M to some length, suppose to the line n o, it shall be of an intense red; from n o to p q it shall be an orange; from p q to r s it shall be yellow; from thence to t u it shall be green; from thence to w x blue; from thence to y z indigo; and from thence to the end violet.
11. Thus it appears that the sun’s white light by its passage through the prism, is so changed as now to be divided into rays, which exhibit all these several colours. The question is, whether the rays while in the sun’s beam before this refraction possessed these properties distinctly; so that some part of that beam would without the rest have given a red colour, and another part alone have given an..orange, &c. That this is possible to be the case, appears from hence; that if a convex glass be placed between the paper and the prism, which may collect all the rays proceeding out of the prism into its focus, as a burning glass does the sun’s direct rays; and if that focus fall upon the paper, the spot formed by such a glass upon the paper shall appear white, just like the sun’s direct light.
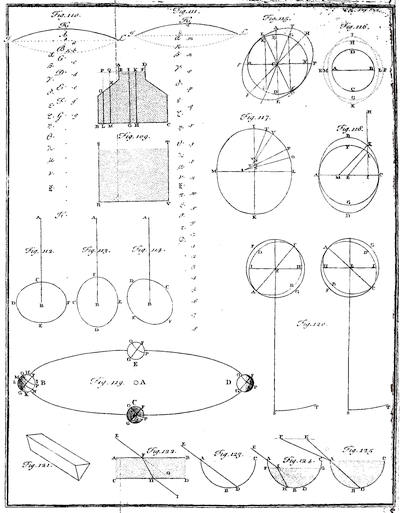
The rest remaining as before, let P Q. (in fig. 127.) be the convex glass, causing the rays to meet upon the paper H G I K in the point N, I say that point or rather spot of light shall appear white, without the least tincture of any colour. But it is evident that into this spot are now gathered all those rays, which before when separate gave all those different colours; which shews that whiteness may be made by mixing those colours: especially if we consider, it can be proved that the glass P Q does not alter the colour of the rays which pass through it. Which is done thus: if the paper be made to approach the glass P Q, the colours will manifest themselves as far as the magnitude of the spectrum, which the paper receives, will permit. Suppose it in the situation h g i k, and that it then receive the spectrum l m, this spectrum shall be much smaller, than if the glass P Q were removed, and therefore the colours cannot be so much separated; but yet the extremity m shall manifestly appear red, and the other extremity l shall be blue; and these colours as well as the intermediate ones shall discover themselves more perfectly, the farther the paper is removed from N, that is, the larger the spectrum is: the same thing happens, if the paper be removed farther off from P Q than N. Suppose[324] into the position θ γ η ϰ, the spectrum λ μ painted upon it shall again discover its colours, and that more distinctly, the farther the paper is removed, but only in an inverted order: for as before, when the paper was nearer the convex glass, than at N, the upper part of the image was blue, and the under red; now the upper part shall be red, and the under blue: because the rays cross at N.
12. Nay farther that the whiteness at the focus N, is made by the union of the colours may be proved without removing the paper out of the focus, by intercepting with any opake body part of the light near the glass; for if the under part, that is the red, or more properly the red-making rays, as they are styled by our author, are intercepted, the spot shall take a bluish hue; and if more of the inferior rays are cut off, so that neither the red-making nor orange-making rays, and if you please the yellow-making rays likewise, shall fall upon the spot; then shall the spot incline more and more to the remaining colours. In like manner if you cut off the upper part of the rays, that is the violet coloured or indigo-making rays, the spot shall turn reddish, and become, more so, the more of those opposite colours are intercepted.
13. This I think abundantly proves that whiteness may be produced by a mixture of all the colours of the spectrum. At least there is but one way of evading the present arguments, which is, by asserting that the rays of light after passing the prism have no different properties to exhibit this or the other colour, but are in that respect perfectly[325] homogeneal, so that the rays which pass to the under and red part of the image do not differ in any properties whatever from those, which go to the upper and violet part of it; but that the colours of the spectrum are produced only by some new modifications of the rays, made at their incidence upon the paper by the different terminations of light and shadow: if indeed this assertion can be allowed any place, after what has been said; for it seems to be sufficiently obviated by the latter part of the preceding experiment, that by intercepting the inferior part of the light, which comes from the prism, the white spot shall receive a bluish cast, and by stopping the upper part the spot shall turn red, and in both cases recover its colour, when the intercepted light is permitted to pass again; though in all these trials there is the like termination of light and shadow. However our author has contrived some experiments expresly to shew the absurdity of this supposition; all which he has explained and enlarged upon in so distinct and expressive a manner, that it would be wholly unnecessary to repeat them in this place[280]. I shall only mention that of them, which may be tried in the experiment before us. If you draw upon the paper H G I K, and through the spot N, the straight line w x parallel to the horizon, and then if the paper be much inclined into the situation r s v t the line w x still remaining parallel to the horizon, the spot N shall lose its whiteness and receive a blue tincture; but if it be inclined as much the contrary way, the same spot shall exchange its white colour for a reddish dye.[326] All which can never be accounted for by any difference in the termination of the light and shadow, which here is none at all; but are easily explained by supposing the upper part of the rays, whenever they enter the eye, disposed to give the sensation of the dark colours blue, indigo and violet; and that the under part is fitted to produce the bright colours yellow, orange and red: for when the paper is in the situation r s t u, it is plain that the upper part of the light falls more directly upon it, than the under part, and therefore those rays will be most plentifully reflected from it; and by their abounding in the reflected light will cause it to incline to their colour. Just so when the paper is inclined the contrary way, it will receive the inferior rays most directly, and therefore ting the light it reflects with their colour.
14. It is now to be proved that these dispositions of the rays of light to produce some one colour and some another, which manifest themselves after their being refracted, are not wrought by any action of the prism upon them, but are originally inherent in those rays; and that the prism only affords each species an occasion of shewing its distinct quality by separating them one from another, which before, while they were blended together in the direct beam of the sun’s light, lay conceal’d. But that this is so, will be proved, if it can be shewn that no prism has any power upon the rays, which after their passage through one prism are rendered uncompounded and contain in them but one colour, either to divide that colour into several, as the sun’s[327] light is divided, or so much as to change it into any other colour. This will be proved by the following experiment[281]. The same thing remaining, as in the first experiment, let another prism N O (in fig. 128.) be placed either immediately, or at some distance after the first, in a perpendicular posture, so that it shall refract the rays issuing from the first sideways. Now if this prism could divide the light falling upon it into coloured rays, as the first has done, it would divide the spectrum breadthwise into colours, as before it was divided lengthwise; but no such thing is observed. If L M were the spectrum, which the first prism D E F would paint upon the paper H G I K; P Q lying in an oblique posture shall be the spectrum projected by the second, and shall be divided lengthwise into colours corresponding to the colours of the spectrum L M, and occasioned like them by the refraction of the first prism, but its breadth shall receive no such division; on the contrary each colour shall be uniform from side to side, as much as in the spectrum L M, which proves the whole assertion.
15. The same is yet much farther confirmed by another experiment. Our author teaches that the colours of the spectrum L M in the first experiment are yet compounded, though not so much as in the sun’s direct light. He shews therefore how, by placing the prism at a distance from the hole, and by the use of a convex glass, to separate the colours of the spectrum, and make them uncompounded to any degree of exactness[282]. And he shews when this[328] is done sufficiently, if you make a small hole in the paper whereon the spectrum is received, through which any one sort of rays may pass, and then let that coloured ray fall so upon a prism, as to be refracted by it, it shall in no case whatever change its colour; but shall always retain it perfectly as at first, however it be refracted[283].
16. Nor yet will these colours after this full separation of them suffer any change by reflection from bodies of different colours; on the other hand they make all bodies placed in these colours appear of the colour which falls upon them[284]: for minium in red light will appear as in open day light; but in yellow light will appear yellow; and which is more extraordinary, in green light will appear green, in blue, blue; and in the violet-purple coloured light will appear of a purple colour; in like manner verdigrease, or blue bise, will put on the appearance of that colour, in which it is placed; so that neither bise placed in the red light shall be able to give that light the least blue tincture, or any other different from red; nor shall minium in the indigo or violet light exhibit the least appearance of red, or any other colour distinct from that it is placed in. The only difference is, that each of these bodies appears most luminous and bright in the colour, which corresponds with that it exhibits in the day light, and dimmed in the colours most remote from that; that is, though minium and bise placed in blue light shall both appear blue, yet the bise shall appear of a bright blue, and the minium of a dusky and obscure blue: but[329] if minium and bise be compared together in red light, the minium shall afford a brisk red, the bise a duller colour, though of the same species.
17. And this not only proves the immutability of all these simple and uncompounded colours; but likewise unfolds the whole mystery, why bodies appear in open day-light of such different colours, it consisting in nothing more than this, that whereas the white light of the day is composed of all sorts of colours, some bodies reflect the rays of one sort in greater abundance than the rays of any other[285]. Though it appears by the fore-cited experiment, that almost all these bodies reflect some portion of the rays of every colour, and give the sense of particular colours only by the predominancy of some sorts of rays above the rest. And what has before been explained of composing white by mingling all the colours of the spectrum together shews clearly, that nothing more is required to make bodies look white, than a power to reflect indifferently rays of every colour. But this will more fully appear by the following method: if near the coloured spectrum in our first experiment a piece of white paper be so held, as to be illuminated equally by all the parts of that spectrum, it shall appear white; whereas if it be held nearer to the red end of the image, than to the other, it shall turn reddish; if nearer the blue end, it shall seem bluish[286].
18. Our indefatigable and circumspect author farther examined his theory by mixing the powders which painters use of several colours, in order if possible to produce a white powder by such a composition[287]. But in this he found some difficulties for the following reasons. Each of these coloured powders reflects but part of the light, which is cast upon them; the red powders reflecting little green or blue, and the blue powders reflecting very little red or yellow, nor the green powders reflecting near so much of the red or indigo and purple, as of the other colours: and besides, when any of these are examined in homogeneal light, as our author calls the colours of the prism, when well separated, though each appears more bright and luminous in its own day-light colour, than in any other; yet white bodies, suppose white paper for instance, in those very colours exceed these coloured bodies themselves in brightness; so that white bodies reflect not only more of the whole light than coloured bodies do in the day-light, but even more of that very colour which they reflect most copiously. All which considerations make it manifest that a mixture of these will not reflect so great a quantity of light, as a white body of the same size; and therefore will compose such a colour as would result from a mixture of white and black, such as are all grey and dun colours, rather than a strong white. Now such a colour he compounded of certain ingredients, which he particularly sets down, in so much that when the composition was strongly illuminated by the sun’s direct beams, it would appear much whiter than even white paper,[331] if considerably shaded. Nay he found by trials how to proportion the degree of illumination of the mixture and paper, so that to a spectator at a proper distance it could not well be determined which was the more perfect colour; as he experienced not only by himself, but by the concurrent opinion of a friend, who chanced to visit him while he was trying this experiment. I must not here omit another method of trying the whiteness of such a mixture, proposed in one of our author’s letters on this subject[288]: which is to enlighten the composition by a beam of the sun let into a darkened room, and then to receive the light reflected from it upon a piece of white paper, observing whether the paper appears white by that reflection; for if it does, it gives proof of the composition’s being white; because when the paper receives the reflection from any coloured body, it looks of that colour. Agreeable to this is the trial he made upon water impregnated with soap, and agitated into a froth[289]: for when this froth after some short time exhibited upon the little bubbles, which composed it, a great variety of colours, though these colours to a spectator at a small distance discover’d themselves distinctly; yet when the eye was so far removed, that each little bubble could no longer be distinguished, the whole froth by the mixture of all these colours appeared intensly white.
19. Our author having fully satisfied himself by these and many other experiments, what the result is of mixing[332] together all the prismatic colours; he proceeds in the next place to examine, whether this appearance of whiteness be raised by the rays of these different kinds acting so, when they meet, upon one another, as to cause each of them to impress the sense of whiteness upon the optic nerve; or whether each ray does not make upon the organ of sight the same impression, as when separate and alone; so that the idea of whiteness is not excited by the impression from any one part of the rays, but results from the mixture of all those different sensations. And that the latter sentiment is the true one, he evinces by undeniable experiments.
20. In particular the foregoing experiment[290], wherein the convex glass was used, furnishes proofs of this: in that when the paper is brought into the situation θ γ η ϰ, beyond, beyond N the colours, that at N disappeared, begin to emerge again; which shews that by mingling at N they did not lose their colorific qualities, though for some reason they lay concealed. This farther appears by that part of the experiment, when the paper, while in the focus, was directed to be enclined different ways; for when the paper was in such a situation, that it must of necessity reflect the rays, which before their arrival at the point N would have given a blue colour, those rays in this very point itself by abounding in the reflected light tinged it with the same colour; so when the paper reflects most copiously the rays, which before they come to the point N exhibit redness, those same rays tincture[333] the light reflected by the paper from that very point with their own proper colour.
21. There is a certain condition relating to sight, which affords an opportunity of examining this still more fully: it is this, that the impressions of light remain some short space upon the eye; as when a burning coal is whirl’d about in a circle, if the motion be very quick, the eye shall not be able to distinguish the coal, but shall see an entire circle of fire. The reason of which appearance is, that the impression made by the coal upon the eye in any one situation is not worn out, before the coal returns again to the same place, and renews the sensation. This gives our author the hint to try, whether these colours might not be transmitted successively to the eye so quick, that no one of the colours should be distinctly perceived, but the mixture of the sensations should produce a uniform whiteness; when the rays could not act upon each other, because they never should meet, but come to the eye one after another. And this thought he executed by the following expedient[291]. He made an instrument in shape like a comb, which he applied near the convex glass, so that by moving it up and down slowly the teeth of it might intercept sometimes one and sometimes another colour; and accordingly the light reflected from the paper, placed at N, should change colour continually. But now when the comb-like instrument was moved very quick, the eye lost all preception of the distinct colours, which came to it from time to time, a perfect whiteness resulting from the[334] mixture of all those distinct impressions in the sensorium. Now in this case there can be no suspicion of the several coloured rays acting upon one another, and making any change in each other’s manner of affecting the eye, seeing they do not so much as meet together there.
22. Our author farther teaches us how to view the spectrum of colours produced in the first experiment with another prism, so that it shall appear to the eye under the shape of a round spot and perfectly white[292]. And in this case if the comb be used to intercept alternately some of the colours, which compose the spectrum, the round spot shall change its colour according to the colours intercepted; but if the comb be moved too swiftly for those changes to be distinctly perceived, the spot shall seem always white, as before[293].
23. Besides this whiteness, which results from an universal composition of all sorts of colours, our author particularly explains the effects of other less compounded mixtures; some of which compound other colours like some of the simple ones, but others produce colours different from any of them. For instance, a mixture of red and yellow compound a colour like in appearance to the orange, which in the spectrum lies between them; as a composition of yellow and blue is made use of in all dyes to make a green. But red and violet purple compounded make purples unlike to any of the prismatic colours, and these joined with[335] yellow or blue make yet new colours. Besides one rule is here to be observed, that when many different colours are mixed, the colour which arises from the mixture grows languid and degenerates into whiteness. So when yellow green and blue are mixed together, the compound will be green; but if to this you add red and purple, the colour shall first grow dull and less vivid, and at length by adding more of these colours it shall turn to whiteness, or some other colour[294].
24. Only here is one thing remarkable of those compounded colours, which are like in appearance to the simple ones; that the simple ones when viewed through a prism shall still retain their colour, but the compounded colours seen through such a glass shall be parted into the simple ones of which they are the aggregate. And for this reason any body illuminated by the simple light shall appear through a prism distinctly, and have its minutest parts observable, as may easily be tried with flies, or other such little bodies, which have very small parts; but the same viewed in this manner when enlighten’d with compounded colours shall appear confused, their smallest parts not being distinguishable. How the prism separates these compounded colours, as likewise how it divides the light of the sun into its colours, has not yet been explained; but is reserved for our third chapter.
25. In the mean time what has been said, I hope, will suffice to give a taste of our author’s way of arguing, and[336] in some measure to illustrate the proposition laid down in this chapter.
26. There are methods of separating the heterogeneous rays of the sun’s light by reflection, which perfectly conspire with and confirm this reasoning. One of which ways may be this. Let A B (in fig. 129) represent the window shutter of a darkened room; C a hole to let in the sun’s rays; D E F, G H I two prisms so applied together, that the sides E F and G I be contiguous, and the sides D F, G H parallel; by this means the light will pass through them without any separation into colours: but if it be afterwards received by a third prism I K L, it shall be divided so as to form upon any white body P Q the usual colours, violet at m, blue at n, green at o, yellow at r, and red at s. But because it never happens that the two adjacent surfaces E F and G I perfectly touch, part only of the light incident upon the surface E F shall be transmitted, and part shall be reflected. Let now the reflected part be received by a fourth prism Δ Θ Λ, and passing through it paint upon a white body Ζ Γ the colours of the prism, red at t, yellow at u, green at w, blue at x, violet at y. If the prisms D E F, G H I be slowly turned about while they remain contiguous, the colours upon the body P Q shall not sensibly change their situation, till such time as the rays become pretty oblique to the surface E F; but then the light incident upon the surface E F shall begin to be wholly reflected. And first of all the violet light shall be wholly reflected, and thereupon will disappear at m, appearing instead thereof[337] at y, and increasing the violet light falling there, the other colours remaining as before. If the prisms D E F, G H I be turned a little farther about, that the incident rays become yet more inclined to the surface E F, the blue shall be totally reflected, and shall disappear in n, but appear at x by making the colour there more intense. And the same may be continued, till all the colours are successively removed from the surface P Q to Ζ Γ. But in any case, suppose when the violet and the blue have forsaken the surface P Q, and appear upon the surface Ζ Γ, Ζ Γ, the green, yellow, and red only remaining upon the surface P Q; if the light be received upon a paper held any where in its whole passage between the light’s coming out of the prisms D E F, G I H and its incidence upon the prism I K L, it shall appear of the colour compounded of all the colours seen upon P Q; and the reflected ray, received upon a piece of white paper held any where between the prisms D E F and Δ Θ Σ shall exhibit the colour compounded of those the surface P Q is deprived of mixed with the sun’s light: whereas before any of the light was reflected from the surface E F, the rays between the prisms G H I and I K L would appear white; as will likewise the reflected ray both before and after the total reflection, provided the difference of refraction by the surfaces D F and D E be inconsiderable. I call here the sun’s light white, as I have all along done; but it is more exact to ascribe to it something of a yellowish tincture, occasioned by the brighter colours abounding in it; which caution is necessary in examining the colours of the reflected beam, when all the violet and blue are in it: for this[338] yellowish turn of the sun’s light causes the blue not to be quite so visible in it, as it should be, were the light perfectly white; but makes the beam of light incline rather towards a pale white.
Chap. II.
Of the properties of BODIES, upon which
their COLOURS depend.
AFTER having shewn in the last chapter, that the difference between the colours of bodies viewed in open day-light is only this, that some bodies are disposed to reflect rays of one colour in the greatest plenty, and other bodies rays of some other colour; order now requires us to examine more particularly into the property of bodies, which gives them this difference. But this our author shews to be nothing more, than the different magnitude of the particles, which compose each body: this I question not will appear no small paradox. And indeed this whole chapter will contain scarce any assertions, but what will be almost incredible, though the arguments for them are so strong and convincing, that they force our assent. In the former chapter have been explained properties of light, not in the least thought of before our author’s discovery of them; yet are they not difficult to admit, as soon as experiments are known to give proof of their reality; but some of the propositions to be stated here will, I fear, be accounted almost past belief; notwithstanding that the arguments, by which[339] they are established are unanswerable. For it is proved by our author, that bodies are rendered transparent by the minuteness of their pores, and become opake by having them large; and more, that the most transparent body by being reduced to a great thinness will become less pervious to the light.
2. But whereas it had been the received opinion, and yet remains so among all who have not studied this philosophy, that light is reflected from bodies by its impinging against their solid parts, rebounding from them, as a tennis ball or other elastic substance would do, when struck against any hard and resisting surface; it will be proper to begin with declaring our author’s sentiment concerning this, who shews by many arguments that reflection cannot be caused by any such means[295]: some few of his proofs I shall set down, referring the reader to our author himself for the rest.
3. It is well known, that when light falls upon any transparent body, glass for instance, part of it is reflected and part transmitted; for which it is ready to account, by saying that part of the light enters the pores of the glass, and part impinges upon its solid parts. But when the transmitted light arrives at the farther surface of the glass, in passing out of glass into air there is as strong a reflection caused, or rather something stronger. Now it is not to be conceived, how the light should find as many solid parts in the air to strike against as in the glass, or even a greater number[340] of them. And to augment the difficulty, if water be placed behind the glass, the reflection becomes much weaker. Can we therefore say, that water has fewer solid parts for the light to strike against, than the air? And if we should, what reason can be given for the reflection’s being stronger, when the air by the air-pump is removed from behind the glass, than when the air receives the rays of light. Besides the light may be so inclined to the hinder surface of the glass, that it shall wholly be reflected, which happens when the angle which the ray makes with the surface does not exceed about 49⅓ degrees; but if the inclination be a very little increased, great part of the light will be transmitted; and how the light in one case should meet with nothing but the solid parts of the air, and by so small a change of its inclination find pores in great plenty, is wholly inconceivable. It cannot be said, that the light is reflected by striking against the solid parts of the surface of the glass; because without making any change in that surface, only by placing water contiguous to it instead of air, great part of that light shall be transmitted, which could find no passage through the air. Moreover in the last experiment recited in the preceding chapter, when by turning the prisms D E F, G H I, the blue light became wholly reflected, while the rest was mostly transmitted, no possible reason can be assigned, why the blue-making rays should meet with nothing but the solid parts of the air between the prisms, and the rest of the light in the very same obliquity find pores in abundance. Nay farther, when two glasses touch each other, no reflection at all is made; though[341] it does not in the least appear, how the rays should avoid the solid parts of glass, when contiguous to other glass, any more than when contiguous to air. But in the last place upon this supposition it is not to be comprehended, how the most polished substances could reflect the light in that regular manner we find they do; for when a polished looking glass is covered over with quicksilver, we cannot suppose the particles of light so much larger than those of the quicksilver that they should not be scattered as much in reflection, as a parcel of marbles thrown down upon a rugged pavement. The only cause of so uniform and regular a reflection must be some more secret cause, uniformly spread over the whole surface of the glass.
4. But now, since the reflection of light from bodies does not depend upon its impinging against their solid parts, some other reason must be sought for. And first it is past doubt that the least parts of almost all bodies are transparent, even the microscope shewing as much[296]; besides that it may be experienced by this method. Take any thin plate of the opakest body, and apply it to a small hole designed for the admission of light into a darkened room; however opake that body may seem in open day-light, it shall under these circumstances sufficiently discover its transparency, provided only the body be very thin. White metals indeed do not easily shew themselves transparent in these trials, they reflecting almost all the light incident upon them at their first superficies; the cause of which will appear in what[342] follows[297]. But yet these substances, when reduced into parts of extraordinary minuteness by being dissolved in aqua fortis or the like corroding liquors do also become transparent.
5. Since therefore the light finds free passage through the least parts of bodies, let us consider the largeness of their pores, and we shall find, that whenever a ray of light has passed through any particle of a body, and is come to its farther surface, if it finds there another particle contiguous, it will without interruption pass into that particle; just as light will pass through one piece of glass into another piece in contact with it without any impediment, or any part being reflected: but as the light in passing out of glass, or any other transparent body, shall part of it be reflected back, if it enter into air or other transparent body of a different density from that it passes out of; the same thing will happen in the light’s passage through any particle of a body, whenever at its exit out of that particle it meets no other particle contiguous, but must enter into a pore, for in this case it shall not all pass through, but part of it be reflected back. Thus will the light, every time it enters a pore, be in part reflected; so that nothing more seems necessary to opacity, than that the particles, which compose any body, touch but in very few places, and that the pores of it are numerous and large, so that the light may in part be reflected from it, and the other part, which enters too deep to be returned out of the body, by numerous reflections may be stifled and lost[298]; which in all probability[343] happens, as often as it impinges against the solid part of the body, all the light which does so not being reflected back, but stopt, and deprived of any farther motion[299].
6. This notion of opacity is greatly confirmed by the observation, that opake bodies become transparent by filling up the pores with any substance of near the same density with their parts. As when paper is wet with water or oyl; when linnen cloth is either dipt in water, oyled, or varnished; or the oculus mundi stone steeped in water[300]. All which experiments confirm both the first assertion, that light is not reflected by striking upon the solid parts of bodies; and also the second, that its passage is obstructed by the reflections it undergoes in the pores; since we find it in these trials to pass in greater abundance through bodies, when the number of their solid parts is increased, only by taking away in great measure those reflections; which filling the pores with a substance of near the same density with the parts of the body will do. Besides as filling the pores of a dark body makes it transparent; so on the other hand evacuating the pores of a body transparent, or separating the parts of such a body, renders it opake. As salts or wet paper by being dried, glass by being reduced to powder or the surface made rough; and it is well known that glass vessels discover cracks in them by their opacity. Just so water itself becomes impervious to the light by being formed into many small bubbles, whether in froth, or by being mixed and agitated with any quantity of a liquor[344] with which it will not incorporate, such as oyl of turpentine, or oyl olive.
7. A certain electrical experiment made by Mr. Hauksbee may not perhaps be useless to clear up the present speculation, by shewing that something more is necessary besides mere porosity for transmitting freely other fine substances. The experiment is this; that a glass cane rubbed till it put forth its electric quality would agitate leaf brass inclosed under a glass vessel, though not at so great a distance, as if no body had intervened; yet the same cane would lose all its influence on the leaf brass by the interposition of a piece of the finest muslin, whose pores are immensely larger and more patent than those of glass.
8. Thus I have endeavoured to smooth my way, as much as I could, to the unfolding yet greater secrets in nature; for I shall now proceed to shew the reason why bodies appear of different colours. My reader no doubt will be sufficiently surprized, when I inform him that the knowledge of this is deduced from that ludicrous experiment, with which children divert themselves in blowing bubbles of water made tenacious by the solution of soap. And that these bubbles, as they gradually grow thinner and thinner till they break, change successively their colours from the same principle, as all natural bodies preserve theirs.
9. Our author after preparing water with soap, so as to render it very tenacious, blew it up into a bubble, and placing[345] it under a glass, that it might not be irregularly agitated by the air, observed as the water by subsiding changed the thickness of the bubble, making it gradually less and less till the bubble broke; there successively appeared colours at the top of the bubble, which spread themselves into rings surrounding the top and descending more and more, till they vanished at the bottom in the same order in which they appeared[301]. The colours emerged in this order: first red, then blue; to which succeeded red a second time, and blue immediately followed; after that red a third time, succeeded by blue; to which followed a fourth red, but succeeded by green; after this a more numerous order of colours, first red, then yellow, next green, and after that blue, and at last purple; then again red, yellow, green, blue, violet followed each other in order; and in the last place red, yellow, white, blue; to which succeeded a dark spot, which reflected scarce any light, though our author found it did make some very obscure reflection, for the image of the sun or a candle might be faintly discerned upon it; and this last spot spread itself more and more, till the bubble at last broke. These colours were not simple and uncompounded colours, like those which are exhibited by the prism, when due care is taken to separate them; but were made by a various mixture of those simple colours, as will be shewn in the next chapter: whence these colours, to which I have given the name of blue, green, or red, were not all alike, but differed as follows. The blue, which appeared next the dark spot, was a pure colour, but very faint, resembling the sky-colour; the[346] white next to it a very strong and intense white, brighter much than the white, which the bubble reflected, before any of the colours appeared. The yellow which preceded this was at first pretty good, but soon grew dilute; and the red which went before the yellow at first gave a tincture of scarlet inclining to violet, but soon changed into a brighter colour; the violet of the next series was deep with little or no redness in it; the blue a brisk colour, but came much short of the blue in the next order; the green was but dilute and pale; the yellow and red were very bright and full, the best of all the yellows which appeared among any of the colours: in the preceding orders the purple was reddish, but the blue, as was just now said, the brightest of all; the green pretty lively better than in the order which appeared before it, though that was a good willow green; the yellow but small in quantity, though bright; the red of this order not very pure: those which appeared before yet more obscure, being very dilute and dirty; as were likewise the three first blues.
10. Now it is evident, that these colours arose at the top of the bubble, as it grew by degrees thinner and thinner: but what the express thickness of the bubble was, where each of these colours appeared upon it, could not be determined by these experiments; but was found by another means, viz. by taking the object glass of a long telescope, which is in a small degree convex, and placing it upon a flat glass, so as to touch it in one point, and then water being put between them, the same colours appeared as in the[347] bubble, in the form of circles or rings surrounding the point where the glasses touched, which appeared black for want of any reflection from it, like the top of the bubble when thinnest[302]: next to this spot lay a blue circle, and next without that a white one; and so on in the same order as before, reckoning from the dark spot. And henceforward I shall speak of each colour, as being of the first, second, or any following order, as it is the first, second, or any following one, counting from the black spot in the center of these rings; which is contrary to the order in which I must have mentioned them, if I should have reputed them the first, second, or third, &c. in order, as they arise after one another upon the top of the bubble.
11. But now by measuring the diameters of each of these rings, and knowing the convexity of the telescope glass, the thickness of the water at each of those rings may be determined with great exactness: for instance the thickness of it, where the white light of the first order is reflected, is about 3⅞ such parts, of which an inch contains 1000000[303]. And this measure gives the thickness of the bubble, where it appeared of this white colour, as well as of the water between the glasses; though the transparent body which surrounds the water in these two cases be very different: for our author found, that the condition of the ambient body would not alter the species of the colour at all, though it might its strength and brightness; for pieces of Muscovy glass, which were so thin as to appear coloured by being[348] wet with water, would have their colours faded and made less bright thereby; but he could not observe their species at all to be changed. So that the thickness of any transparent body determines its colour, whatever body the light passes through in coming to it[304].
12. But it was found that different transparent bodies would not under the same thicknesses exhibit the same colours: for if the forementioned glasses were laid upon each other without any water between their surfaces, the air itself would afford the same colours as the water, but more expanded, insomuch that each ring had a larger diameter, and all in the same proportion. So that the thickness of the air proper to each colour was in the same proportion larger, than the thickness of the water appropriated to the same[305].
13. If we examine with care all the circumstances of these colours, which will be enumerated in the next chapter, we shall not be surprized, that our author takes them to bear a great analogy to the colours of natural bodies[306]. For the regularity of those various and strange appearances relating to them, which makes the most mysterious part of the action between light and bodies, as the next chapter will shew, is sufficient to convince us that the principle, from which they flow, is of the greatest importance in the frame of nature; and therefore without question is designed for no less a purpose than to give bodies their various colours, to which end it seems very fitly suited. For if any such transparent[349] substance of the thickness proper to produce any one colour should be cut into slender threads, or broken into fragments, it does not appear but these should retain the same colour; and a heap of such fragments should frame a body of that colour. So that this is without dispute the cause why bodies are of this or the other colour, that the particles of which they are composed are of different sizes. Which is farther confirmed by the analogy between the colours of thin plates, and the colours of many bodies. For example, these plates do not look of the same colour when viewed obliquely, as when seen direct; for if the rings and colours between a convex and plane glass are viewed first in a direct manner, and then at different degrees of obliquity, the rings will be observed to dilate themselves more and more as the obliquity is increased[307]; which shews that the transparent substance between the glasses does not exhibit the same colour at the same thickness in all situations of the eye: just so the colours in the very same part of a peacock’s tail change, as the tail changes posture in respect of the sight. Also the colours of silks, cloths, and other substances, which water or oyl can intimately penetrate, become faint and dull by the bodies being wet with such fluids, and recover their brightness again when dry; just as it was before said that plates of Muscovy glass grew faint and dim by wetting. To this may be added, that the colours which painters use will be a little changed by being ground very elaborately, without question by the diminution of their parts. All which particulars, and many more that[350] might be extracted from our author, give abundant proof of the present point. I shall only subjoin one more: these transparent plates transmit through them all the light they do not reflect; so that when looked through they exhibit those colours, which result from the depriving white light of the colour reflected. This may commodiously be tryed by the glasses so often mentioned; which if looked through exhibit coloured rings as by reflected light, but in a contrary order; for the middle spot, which in the other view appears black for want of reflected light, now looks perfectly white, opposite to the blue circle; next without this spot the light appears tinged with a yellowish red; where the white circle appeared before, it now seems dark; and so of the rest[308]. Now in the same manner, the light transmitted through foliated gold into a darkened room appears greenish by the loss of the yellow light, which gold reflects.
14. Hence it follows, that the colours of bodies give a very probable ground for making conjecture concerning the magnitude of their constituent particles[309]. My reason for calling it a conjecture is, its being difficult to fix certainly the order of any colour. The green of vegetables our author judges to be of the third order, partly because of the intenseness of their colour; and partly from the changes they suffer when they wither, turning at first into a greenish or more perfect yellow, and afterwards some of them to an orange or red; which changes seem to be effected from their ringing particles growing denser by the exhalation of their[351] moisture, and perhaps augmented likewise by the accretion of the earthy and oily parts of that moisture. How the mentioned colours should arise from increasing the bulk of those particles, is evident; seeing those colours lie without the ring of green between the glasses, and are therefore formed where the transparent substance which reflects them is thicker. And that the augmentation of the density of the colorific particles will conspire to the production of the same effect, will be evident; if we remember what was said of the different size of the rings, when air was included between the glasses, from their size when water was between them; which shewed that a substance of a greater density than another gives the same colour at a less thickness. Now the changes likely to be wrought in the density or magnitude of the parts of vegetables by withering seem not greater, than are sufficient to change their colour into those of the same order; but the yellow and red of the fourth order are not full enough to agree with those, into which these substances change, nor is the green of the second sufficiently good to be the colour of vegetables; so that their colour must of necessity be of the third order.
15. The blue colour of syrup of violets our author supposes to be of the third order; for acids, as vinegar, with this syrup change it red, and salt of tartar or other alcalies mixed therewith turn it green. But if the blue colour of the syrup were of the second order, the red colour, which acids by attenuating its parts give it, must be of the first order, and the green given it by alcalies by incrassating[352] its particles should be of the second; whereas neither of those colours is perfect enough, especially the green, to answer those produced by these changes; but the red may well enough be allowed to be of the second order, and the green of the third; in which case the blue must be likewise of the third order.
16. The azure colour of the skies our author takes to be of the first order, which requires the smallest particles of any colour, and therefore most like to be exhibited by vapours, before they have sufficiently coalesced to produce clouds of other colours.
17. The most intense and luminous white is of the first order, if less strong it is a mixture of the colours of all the orders. Of the latter sort he takes the colour of linnen, paper, and such like substances to be; but white metals to be of the former sort. The arguments for it are these. The opacity of all bodies has been shewn to arise from the number and strength of the reflections made within them; but all experiments shew, that the strongest reflection is made at those surfaces, which intercede transparent bodies differing most in density. Among other instances of this, the experiments before us afford one; for when air only is included between the glasses, the coloured rings are not only more dilated, as has before been said, than when water is between them; but are likewise much more luminous and bright. It follows therefore, that whatever medium pervades the pores of bodies, if so be there[353] is any, those substances must be most opake, the density of whose parts differs most from the density of the medium, which fills their pores. But it has been sufficiently proved in the former part of this tract, that there is no very dense medium lodging in, at least pervading at liberty the pores of bodies. And it is farther proved by the present experiments. For when air is inclosed by the denser substance of glass, the rings dilate themselves, as has been said, by being viewed obliquely; this they do so very much, that at different obliquities the same thickness of air will exhibit all sorts of colours. The bubble of water, though surrounded with the thinner substance of air, does likewise change its colour by being viewed obliquely; but not any thing near so much, as in the other case; for in that the same colour might be seen, when the rings were viewed most obliquely, at more than twelve times the thickness it appeared at under a direct view; whereas in this other case the thickness was never found considerably above half as much again. Now the colours of bodies not depending only on the light, that is incident upon them perpendicularly, but likewise upon that, which falls on them in all degrees of obliquity; if the medium surrounding their particles were denser than those particles, all sorts of colours must of necessity be reflected from them so copiously, as would make the colours of all bodies white, or grey, or at best very dilute and imperfect. But on the other hand, if the medium in the pores of bodies be much rarer than their particles, the colour reflected will be so little changed by the obliquity of the rays, that the colour produced by the rays, which fall near the perpendicular, may[354] so much abound in the reflected light, as to give the body their colour with little allay. To this may be added, that when the difference of the contiguous transparent substances is the same, a colour reflected from the denser substance reduced into a thin plate and surrounded by the rarer will be more brisk, than the same colour will be, when reflected from a thin plate formed of the rarer substance, and surrounded by the denser; as our author experienced by blowing glass very thin at a lamp furnace, which exhibited in the open air more vivid colours, than the air does between two glasses. From these considerations it is manifest, that if all other circumstances are alike, the densest bodies will be most opake. But it was observed before, that these white metals can hardly be made so thin, except by being dissolved in corroding liquors, as to be rendred transparent; though none of them are so dense as gold, which proves their great opacity to have some other cause besides their density; and none is more fit to produce this, than such a size of their particles, as qualifies them to reflect the white of the first order.
18. For producing black the particles ought to be smaller than for exhibiting any of the colours, viz. of a size answering to the thickness of the bubble, where by reflecting little or no light it appears colourless; but yet they must not be too small, for that will make them transparent through deficiency of reflections in the inward parts of the body, sufficient to stop the light from going through it; but they must be of a size bordering upon that[355] disposed to reflect the faint blue of the first order, which affords an evident reason why blacks usually partake a little of that colour. We see too, why bodies dissolved by fire or putrefaction turn black: and why in grinding glasses upon copper plates the dust of the glass, copper, and sand it is ground with, become very black: and in the last place why these black substances communicate so easily to others their hue; which is, that their particles by reason of the great minuteness of them easily overspread the grosser particles of others.
19. I shall now finish this chapter with one remark of the exceeding great porosity in bodies necessarily required in all that has here been said; which, when duly considered, must appear very surprizing; but perhaps it will be matter of greater surprize, when I affirm that the sagacity of our author has discovered a method, by which bodies may easily become so; nay how any the least portion of matter may be wrought into a body of any assigned dimensions how great so ever, and yet the pores of that body none of them greater, than any the smallest magnitude proposed at pleasure; notwithstanding which the parts of the body shall so touch, that the body itself shall be hard and solid[310]. The manner is this: suppose the body be compounded of particles of such figures, that when laid together the pores found between them may be equal in bigness to the particles; how this may be effected, and yet the body be hard and solid, is not difficult to understand; and the pores of such a body[356] may be made of any proposed degree of smallness. But the solid matter of a body so framed will take up only half the space occupied by the body; and if each constituent particle be composed of other less particles according to the same rule, the solid parts of such a body will be but a fourth part of its bulk; if every one of these lesser particles again be compounded in the same manner, the solid parts of the whole body shall be but one eighth of its bulk; and thus by continuing the composition the solid parts of the body may be made to bear as small a proportion to the whole magnitude of the body, as shall be desired, notwithstanding the body will be by the contiguity of its parts capable of being in any degree hard. Which shews that this whole globe of earth, nay all the known bodies in the universe together, as far as we know, may be compounded of no greater a portion of solid matter, than might be reduced into a globe of one inch only in diameter, or even less. We see therefore how by this means bodies may easily be made rare enough to transmit light, with all that freedom pellucid bodies are found to do. Though what is the real structure of bodies we yet know not.
Chap. III.
Of the Refraction, Reflection,
and Inflection of Light.
THUS much of the colours of natural bodies; our method now leads us to speculations yet greater, no[357] less than to lay open the causes of all that has hitherto been related. For it must in this chapter be explained, how the prism separates the colours of the sun’s light, as we found in the first chapter; and why the thin transparent plates discoursed of in the last chapter, and consequently the particles of coloured bodies, reflect that diversity of colours only by being of different thicknesses.
2. For the first it is proved by our author, that the colours of the sun’s light are manifested by the prism, from the rays undergoing different degrees of refraction; that the violet-making rays, which go to the upper part of the coloured image in the first experiment of the first chapter, are the most refracted; that the indigo-making rays are refracted, or turned out of their course by passing through the prism, something less than the violet-making rays, but more than the blue-making rays; and the blue-making rays more than the green; the green-making rays more than the yellow; the yellow more than the orange; and the orange-making rays more than the red-making, which are least of all refracted. The first proof of this, that rays of different colours are refracted unequally is this. If you take any body, and paint one half of it red and the other half blue, then upon viewing it through a prism those two parts shall appear separated from each other; which can be caused no otherwise than by the prism’s refracting the light of one half more than the light of the other half. But the blue half will be most refracted; for if the body be seen through the prism in such a situation, that the body shall appear[358] lifted upwards by the refraction, as a body within a bason of water, in the experiment mentioned in the first chapter, appeared to be lifted up by the refraction of the water, so as to be seen at a greater distance than when the bason is empty, then shall the blue part appear higher than the red; but if the refraction of the prism be the contrary way, the blue part shall be depressed more than the other. Again, after laying fine threads of black silk across each of the colours, and the body well inlightened, if the rays coming from it be received upon a convex glass, so that it may by refracting the rays cast the image of the body upon a piece of white paper held beyond the glass; then it will be seen that the black threads upon the red part of the image, and those upon the blue part, do not at the same time appear distinctly in the image of the body projected by the glass; but if the paper be held so, that the threads on the blue part may distinctly appear, the threads cannot be seen distinct upon the red part; but the paper must be drawn farther off from the convex glass to make the threads on this part visible; and when the distance is great enough for the threads to be seen in this red part, they become indistinct in the other. Whence it appears that the rays proceeding from each point of the blue part of the body are sooner united again by the convex glass than the rays which come from each point of the red parts[311]. But both these experiments prove that the blue-making rays, as well in the small refraction of the convex glass, as in the greater refraction of the prism, are more bent, than the red-making rays.
3. This seems already to explain the reason of the coloured spectrum made by refracting the sun’s light with a prism, though our author proceeds to examine that in particular, and proves that the different coloured rays in that spectrum are in different degrees refracted; by shewing how to place the prism in such a posture, that if all the rays were refracted in the same manner, the spectrum should of necessity be round: whereas in that case if the angle made by the two surfaces of the prism, through which the light passes, that is the angle D F E in fig. 126, be about 63 or 64 degrees, the image instead of being round shall be near five times as long as broad; a difference enough to shew a great inequality in the refractions of the rays, which go to the opposite extremities of the image. To leave no scruple unremoved, our author is very particular in shewing by a great number of experiments, that this inequality of refraction is not casual, and that it does not depend upon any irregularities of the glass; no nor that the rays are in their passage through the prism each split and divided; but on the contrary that every ray of the sun has its own peculiar degree of refraction proper to it, according to which it is more or less refracted in passing through pellucid substances always in the same manner[312]. That the rays are not split and multiplied by the refraction of the prism, the third of the experiments related in our first chapter shews very clearly; for if they were, and the length of the spectrum in the first refraction were thereby occasioned, the breadth should be no less dilated by the cross refraction of the second[360] prism; whereas the breadth is not at all increased, but the image is only thrown into an oblique posture by the upper part of the rays which were at first more refracted than the under part, being again turned farthest out of their course. But the experiment most expressly adapted to prove this regular diversity of refraction is this, which follows[313]. Two boards A B, C D (in fig. 130.) being erected in a darkened room at a proper distance, one of them A B being near the window-shutter E F, a space only being left for the prism G H I to be placed between them; so that the rays entring at the hole M of the window-shutter may after passing through the prism be trajected through a smaller hole K made in the board A B, and passing on from thence go out at another hole L made in the board C D of the same size as the hole K, and small enough to transmit the rays of one colour only at a time; let another prism N O P be placed after the board C D to receive the rays passing through the holes K and L, and after refraction by that prism let those rays fall upon the white surface Q R. Suppose first the violet light to pass through the holes, and to be refracted by the prism N O P to s, which if the prism N O P were removed should have passed right onto W. If the prism G H I be turned slowly about, while the boards and prism N O P remain fixed, in a little time another colour will fall upon the hole L, which, if the prism N O P were taken away, would proceed like the former rays to the same point W; but the refraction of the prism N O P shall not carry these rays to s, but to some place less distant from W as[361] to t. Suppose now the rays which go to t to be the indigo-making rays. It is manifest that the boards A B, C D, and prism N O P remaining immoveable, both the violet-making and indigo-making rays are incident alike upon the prism N O P, for they are equally inclined to its surface O P, and enter it in the same part of that surface; which shews that the indigo-making rays are less diverted out of their course by the refraction of the prism, than the violet-making rays under an exact parity of all circumstances. Farther, if the prism G H I be more turned about, ’till the blue-making rays pass through the hole L, these shall fall upon the surface Q R below I, as at v, and therefore are subjected to a less refraction than the indigo-making rays. And thus by proceeding it will be found that the green-making rays are less refracted than the blue-making rays, and so of the rest, according to the order in which they lie in the coloured spectrum.
4. This disposition of the different coloured rays to be refracted some more than others our author calls their respective degrees of refrangibility. And since this difference of refrangibility discovers it self to be so regular, the next step is to find the rule it observes.
5. It is a common principle in optics, that the sine of the angle of incidence bears to the sine of the refracted angle a given proportion. If A B (in fig. 131, 132) represent the surface of any refracting substance, suppose of water or glass, and C D a ray of light incident upon that face[362] in the point D, let D E be the ray, after it has passed the surface A B; if the ray pass out of the air into the substance whose surface is A B (as in fig. 131) it shall be turned from the surface, and if it pass out of that substance into air it shall be bent towards it (as in fig. 132) But if F G be drawn through the point D perpendicular to the surface A B, the angle under C D F made by the incident ray and this perpendicular is called the angle of incidence; and the angle under E D G, made by this perpendicular and the ray after refraction, is called the refracted angle. And if the circle H F I G be described with any interval cutting C D in H and D E in I, then the perpendiculars H K, I L being let fall upon F G, H K is called the sine of the angle under C D F the angle of incidence, and I L the sine of the angle under E D G the refracted angle. The first of these sines is called the sine of the angle of incidence, or more briefly the sine of incidence, the latter is the sine of the refracted angle, or the sine of refraction. And it has been found by numerous experiments that whatever proportion the sine of incidence H K bears to the sine of refraction I L in any one case, the same proportion shall hold in all cases; that is, the proportion between these sines will remain unalterably the same in the same refracting substance, whatever be the magnitude of the angle under C D F.
6. But now because optical writers did not observe that every beam of white light was divided by refraction, as has been here explained, this rule collected by them can only be understood in the gross of the whole beam after refraction,[363] and not so much of any particular part of it, or at most only of the middle part of the beam. It therefore was incumbent upon our author to find by what law the rays were parted from each other; whether each ray apart obtained this property, and that the separation was made by the proportion between the sines of incidence and refraction being in each species of rays different; or whether the light was divided by some other rule. But he proves by a certain experiment that each ray has its sine of incidence proportional to its sine of refraction; and farther shews by mathematical reasoning, that it must be so upon condition only that bodies refract the light by acting upon it, in a direction perpendicular to the surface of the refracting body, and upon the same sort of rays always in an equal degree at the same distances[314].
7. Our great author teaches in the next place how from the refraction of the most refrangible and least refrangible rays to find the refraction of all the intermediate ones[315]. The method is this: if the sine of incidence be to the sine of refraction in the least refrangible rays as A to B C, (in fig. 133) and to the sine of refraction in the most refrangible as A to B D; if C E be taken equal to C D, and then E D be so divided in F, G, H, I, K, L, that E D, E F, E G, E H, E I, E K, E L, E C, shall be proportional to the eight lengths of musical chords, which found the notes in an octave, E D being the length of the key, E F the length of the tone above[364] that key, E G the length of the lesser third, E H of the fourth, E I of the fifth, E K of the greater sixth, E L of the seventh, and E C of the octave above that key; that is if the lines E D, E F, E G, E H, E I, E K, E L, and E C bear the same proportion as the numbers, 1, 9/8, 5/6, ¾, ⅓, ¾, 9/61, ½, respectively then shall B D, B F, be the two limits of the sines of refraction of the violet-making rays, that is the violet-making rays shall not all of them have precisely the same sine of refraction, but none of them shall have a greater sine than B D, nor a less than B F, though there are violet-making rays which answer to any sine of refraction that can be taken between these two. In the same manner B F and B G are the limits of the sines of refraction of the indigo-making rays; B G, B H are the limits belonging to the blue-making rays; B H, B I the limits pertaining to the green-making rays, B I, B K the limits for the yellow-making rays; B K, B L the limits for the orange-making rays; and lastly, B L and B C the extreme limits of the sines of refraction belonging to the red-making rays. These are the proportions by which the heterogeneous rays of light are separated from each other in refraction.
8. When light passes out of glass into air, our author found A to B C as 50 to 77, and the same A to B D as 50 to 78. And when it goes out of any other refracting substance into air, the excess of the sine of refraction of any one species of rays above its sine of incidence bears a constant proportion, which holds the same in each species, to the excess of the sine of refraction of the same sort of rays[365] above the sine of incidence into the air out of glass; provided the sines of incidence both in glass and the other substance are equal. This our author verified by transmitting the light through prisms of glass included within a prismatic vessel of water; and draws from those experiments the following observations: that whenever the light in passing through so many surfaces parting diverse transparent substances is by contrary refractions made to emerge into the air in a direction parallel to that of its incidence, it will appear afterwards white at any distance from the prisms, where you shall please to examine it; but if the direction of its emergence be oblique to its incidence, in receding from the place of emergence its edges shall appear tinged with colours: which proves that in the first case there is no inequality in the refractions of each species of rays, but that when any one species is so refracted as to emerge parallel to the incident rays, every sort of rays after refraction shall likewise be parallel to the same incident rays, and to each other; whereas on the contrary, if the rays of any one sort are oblique to the incident light, the several species shall be oblique to each other, and be gradually separated by that obliquity. From hence he deduces both the forementioned theorem, and also this other; that in each sort of rays the proportion of the sine of incidence to the sine of refraction, in the passage of the ray out of any refracting substance into another, is compounded of the proportion to which the sine of incidence would have to the sine of refraction in the passage of that ray out of the first substance into any third, and of the proportion which[366] the sine of incidence would have to the sine of refraction in the passage of the ray out of that third substance into the second. From so simple and plain an experiment has our most judicious author deduced these important theorems, by which we may learn how very exact and circumspect he has been in this whole work of his optics; that notwithstanding his great particularity in explaining his doctrine, and the numerous collection of experiments he has made to clear up every doubt which could arise, yet at the same time he has used the greatest caution to make out every thing by the simplest and easiest means possible.
9. Our author adds but one remark more upon refraction, which is, that if refraction be performed in the manner he has supposed from the light’s being pressed by the refracting power perpendicularly toward the surface of the refracting body, and consequently be made to move swifter in the body than before its incidence; whether this power act equally at all distances or otherwise, provided only its power in the same body at the same distances remain without variation the same in one inclination of the incident rays as well as another; he observes that the refracting powers in different bodies will be in the duplicate proportion of the tangents of the lead angles, which the refracted light can make with the surfaces of the refracting bodies[316]. This observation may be explained thus. When the light passes into any refracting substance, it has been shewn above that the sine of incidence bears a constant proportion to the sine[367] of refraction. Suppose the light to pass to the refracting body A B C D (in fig. 134) in the line E F, and to fall upon it at the point F, and then to proceed within the body in the line F G. Let H I be drawn through F perpendicular to the surface A B, and any circle K L M N be described to the center F. Then from the points O and P where this circle cuts the incident and refracted ray, the perpendiculars O Q, P R being drawn, the proportion of O Q to P R will remain the same in all the different obliquities, in which the same ray of light can fall on the surface A B. Now O Q is less than F L the semidiameter of the circle K L M N, but the more the ray E F is inclined down toward the surface A B, the greater will O Q be, and will approach nearer to the magnitude of F L. But the proportion of O Q to P R remaining always the same, when O Q, is largest, P R will also be greatest; so that the more the incident ray E F is inclined toward the surface A B, the more the ray F G after refraction will be inclined toward the same. Now if the line F S T be so drawn, that S V being perpendicular to F I shall be to F L the semidiameter of the circle in the constant proportion of P R to O Q; then the angle under N F T is that which I meant by the least of all that can be made by the refracted ray with this surface, for the ray after refraction would proceed in this line, if it were to come to the point F lying on the very surface A B; for if the incident ray came to the point F in any line between A F and F H, the ray after refraction would proceed forward in some line between F T and F I. Here if N W be drawn perpendicular to F N, this line N W in the circle K L M N is called[368] the tangent of the angle under N F S. Thus much being premised, the sense of the forementioned proposition is this. Let there be two refracting substances (in fig. 135) A B C D, and E F G H. Take a point, as I, in the surface A B, and to the center I with any semidiameter describe the circle K L M. In like manner on the surface E F take some point N, as a center, and describe with the same semidiameter the circle O P Q. Let the angle under B I R be the least which the refracted light can make with the surface A B, and the angle under F N S the least which the refracted light can make with the surface E F. Then if L T be drawn perpendicular to A B, and P V perpendicular to E F; the whole power, wherewith the substance A B C D acts on the light, will bear to the whole power wherewith the substance E F G H acts on, the light, a proportion, which is duplicate of the proportion, which L T bears to P V.
10. Upon comparing according to this rule the refractive powers of a great many bodies it is found, that unctuous bodies which abound most with sulphureous parts refract the light two or three times more in proportion to their density than others: but that those bodies, which seem to receive in their composition like proportions of sulphureous parts, have their refractive powers proportional to their densities; as appears beyond contradiction by comparing the refractive power of so rare a substance as the air with that of common glass or rock crystal, though these substances are 2000 times denser than air; nay the same proportion[369] is found to hold without sensible difference in comparing air with pseudo-topar and glass of antimony, though the pseudo-topar be 3500 times denser than air, and glass of antimony no less than 4400 times denser. This power in other substances, as salts, common water, spirit of wine, &c. seems to bear a greater proportion to their densities than these last named, according as they abound with sulphurs more than these; which makes our author conclude it probable, that bodies act upon the light chiefly, if not altogether, by means of the sulphurs in them; which kind of substances it is likely enters in some degree the composition of all bodies. Of all the substances examined by our author, none has so great a refractive power, in respect of its density, as a diamond.
11. Our author finishes these remarks, and all he offers relating to refraction, with observing, that the action between light and bodies is mutual, since sulphureous bodies, which are most readily set on fire by the sun’s light, when collected upon them with a burning glass, act more upon light in refracting it, than other bodies of the same density do. And farther, that the densest bodies, which have been now shewn to act most upon light, contract the greatest heat by being exposed to the summer sun.
12. Having thus dispatched what relates to refraction, we must address ourselves to discourse of the other operation of bodies upon light in reflecting it. When light passes through a surface, which divides two transparent bodies[370] differing in density, part of it only is transmitted, another part being reflected. And if the light pass out of the denser body into the rarer, by being much inclined to the foresaid surface at length no part of it shall pass through, but be totally reflected. Now that part of the light, which suffers the greatest refraction, shall be wholly reflected with a less obliquity of the rays, than the parts of the light which undergo a less degree of refraction; as is evident from the last experiment recited in the first chapter; where, as the prisms D E F, G H I, (in fig. 129.) were turned about, the violet light was first totally reflected, and then the blue, next to that the green, and so of the rest. In consequence of which our author lays down this proportion; that the sun’s light differs in reflexibility, those rays being most reflexible, which are most refrangible. And collects from this, in conjunction with other arguments, that the refraction and reflection, of light are produced by the same cause, compassing those different effects only by the difference of circumstances with which it is attended. Another proof of this being taken by our author from what he has discovered of the passage of light through thin transparent plates, viz. that any particular species of light, suppose, for instance, the red-making rays, will enter and pass out of such a plate, if that plate be of some certain thicknesses; but if it be of other thicknesses, it will not break through it, but be reflected back: in which is seen, that the thickness of the plate determines whether the power, by which that plate acts upon the light, shall reflect it, or suffer it to pass through.
13. But this last mentioned surprising property of the action between light and bodies affords the reason of all that has been said in the preceding chapter concerning the colours of natural bodies; and must therefore more particularly be illustrated and explained, as being what will principally unfold the nature of the action of bodies upon light.
14. To begin: The object glass of a long telescope being laid upon a plane glass, as proposed in the foregoing chapter, in open day-light there will be exhibited rings of various colours, as was there related; but if in a darkened room the coloured spectrum be formed by the prism, as in the first experiment of the first chapter, and the glasses be illuminated by a reflection from the spectrum, the rings shall not in this case exhibit the diversity of colours before described, but appear all of the colour of the light which falls upon the glasses, having dark rings between. Which shews that the thin plate of air between the glasses at some thicknesses reflects the incident light, at other places does not reflect it, but is found in those places to give the light passage; for by holding the glasses in the light as it passes from the prism to the spectrum, suppose at such a distance from the prism that the several sorts of light must be sufficiently separated from each other, when any particular sort of light falls on the glasses, you will find by holding a piece of white paper at a small distance beyond the glasses, that at those intervals, where the dark lines appeared upon the glasses, the light is so transmitted,[372] as to paint upon the paper rings of light having that colour which falls upon the glasses. This experiment therefore opens to us this very strange property of reflection, that in these thin plates it should bear such a relation to the thickness of the plate, as is here shewn. Farther, by carefully measuring the diameters of each ring it is found, that whereas the glasses touch where the dark spot appears in the center of the rings made by reflexion, where the air is of twice the thickness at which the light of the first ring is reflected, there the light by being again transmitted makes the first dark ring; where the plate has three times that thickness which exhibits the first lucid ring, it again reflects the light forming the second lucid ring; when the thickness is four times the first, the light is again transmitted so as to make the second dark ring; where the air is five times the first thickness, the third lucid ring is made; where it has six times the thickness, the third dark ring appears, and so on: in so much that the thicknesses, at which the light is reflected, are in proportion to the numbers 1, 3, 5, 7, 9, &c. and the thicknesses, where the light is transmitted, are in the proportion of the numbers 0, 2, 4, 6, 8, &c. And these proportions between the thicknesses which reflect and transmit the light remain the same in all situations of the eye, as well when the rings are viewed obliquely, as when looked on perpendicularly. We must farther here observe, that the light, when it is reflected, as well as when it is transmitted, enters the thin plate, and is reflected from its farther surface; because, as was before remarked, the altering the transparent body behind the farther surface alters the degree[373] of reflection as when a thin piece of Muscovy glass has its farther surface wet with water, and the colour of the glass made dimmer by being so wet; which shews that the light reaches to the water, otherwise its reflection could not be influenced by it. But yet this reflection depends upon some power propagated from the first surface to the second; for though made at the second surface it depends also upon the first, because it depends upon the distance between the surfaces; and besides, the body through which the light passes to the first surface influences the reflection: for in a plate of Muscovy glass, wetting the surface, which first receives the light, diminishes the reflection, though not quite so much as wetting the farther surface will do. Since therefore the light in passing through these thin plates at some thicknesses is reflected, but at others transmitted without reflection, it is evident, that this reflection is caused by some power propagated from the first surface, which intermits and returns successively. Thus is every ray apart disposed to alternate reflections and transmissions at equal intervals; the successive returns of which disposition our author calls the fits of easy reflection, and of easy transmission. But these fits, which observe the same law of returning at equal intervals, whether the plates are viewed perpendicularly or obliquely, in different situations of the eye change their magnitude. For what was observed before in respect of those rings, which appear in open day-light, holds likewise in these rings exhibited by simple lights; namely, that these two alter in bigness according to the different angle under which they are seen: and our author[374] lays down a rule whereby to determine the thicknesses of the plate of air, which shall exhibit the same colour under different oblique views[317]. And the thickness of the aereal plate, which in different inclinations of the rays will exhibit to the eye in open day-light the same colour, is also varied by the same rule[318]. He contrived farther a method of comparing in the bubble of water the proportion between the thickness of its coat, which exhibited any colour when seen perpendicularly, to the thickness of it, where the same colour appeared by an oblique view; and he found the same rule to obtain here likewise[319]. But farther, if the glasses be enlightened successively by all the several species of light, the rings will appear of different magnitudes; in the red light they will be larger than in the orange colour, in that larger than in the yellow, in the yellow larger than in the green, less in the blue, less yet in the indigo, and least of all in the violet: which shew that the same thickness of the aereal plate is not fitted to reflect all colours, but that one colour is reflected where another would have been transmitted; and as the rays which are most strongly refracted form the least rings, a rule is laid down by our author for determining the relation, which the degree of refraction of each species of colour has to the thicknesses of the plate where it is reflected.
15. From these observations our author shews the reason of that great variety of colours, which appears in these thin plates in the open white light of the day. For when this white[375] light falls on the plate, each part of the light forms rings of its own colour; and the rings of the different colours not being of the same bigness are variously intermixed, and form a great variety of tints[320].
16. In certain experiments, which our author made with thick glasses, he found, that these fits of easy reflection and transmission returned for some thousands of times, and thereby farther confirmed his reasoning concerning them[321].
17. Upon the whole, our great author concludes from some of the experiments made by him, that the reason why all transparent bodies refract part of the light incident upon them, and reflect another part, is, because some of the light, when it comes to the surface of the body, is in a fit of easy transmission, and some part of it in a fit of easy reflection; and from the durableness of these fits he thinks it probable, that the light is put into these fits from their first emission out of the luminous body; and that these fits continue to return at equal intervals without end, unless those intervals be changed by the light’s entring into some refracting substance[322]. He likewise has taught how to determine the change which is made of the intervals of the fits of easy transmission and reflection, when the light passes out of one transparent space or substance into another. His rule is, that when the light passes perpendicularly to the surface, which parts any two transparent substances, these intervals in the substance, out of[376] which the light passes, bear to the intervals in the substance, whereinto the light enters, the same proportion, as the sine of incidence bears to the sine of refraction[323]. It is farther to be observed, that though the fits of easy reflection return at constant intervals, yet the reflecting power never operates, but at or near a surface where the light would suffer refraction; and if the thickness of any transparent body shall be less than the intervals of the fits, those intervals shall scarce be disturbed by such a body, but the light shall pass through without any reflection[324].
18. What the power in nature is, whereby this action between light and bodies is caused, our author has not discovered. But the effects, which he has discovered, of this power are very surprising, and altogether wide from any conjectures that had ever been framed concerning it; and from these discoveries of his no doubt this power is to be deduced, if we ever can come to the knowledge of it. Sir Isaac Newton has in general hinted at his opinion concerning it; that probably it is owing to some very subtle and elastic substance diffused through the universe, in which such vibrations may be excited by the rays of light, as they pass through it, that shall occasion it to operate so differently upon the light in different places as to give rise to these alternate fits of reflection and transmission, of which we have now been speaking[325]. He is of opinion, that such a substance may produce this and other effects also in nature, though it be so rare as not to give any sensible resistance to bodies in motion[326];[377] and therefore not inconsistent with what has been said above, that the planets move in spaces free from resistance[327].
19. In order for the more full discovery of this action between light and bodies, our author began another set of experiments, wherein he found the light to be acted on as it passes near the edges of solid bodies; in particular all small bodies, such as the hairs of a man’s head or the like, held in a very small beam of the sun’s light, cast extremely broad shadows. And in one of these experiments the shadow was 35 times the breadth of the body[328]. These shadows are also observed to be bordered with colours[329]. This our author calls the inflection of light; but as he informs us, that he was interrupted from prosecuting these experiments to any length, I need not detain my readers with a more particular account of them.
Chap. IV.
Of OPTIC GLASSES.
SIR Isaac Newton having deduced from his doctrine of light and colours a surprising improvement of telescopes, of which I intend here to give an account, I shall first premise something in general concerning those instruments.
2. It will be understood from what has been said above, that when light falls upon the surface of glass obliquely, after its entrance into the glass it is more inclined to the line drawn through the point of incidence perpendicular to that surface, than before. Suppose a ray of light issuing from the point A (in fig. 136) falls on a piece of glass B C D E, whose surface B C, whereon the ray falls, is of a spherical or globular figure, the center whereof is F. Let the ray proceed in the line A G falling on the surface B C in the point G, and draw F G H. Here the ray after its entrance into the glass will pass on in some line, as G I, more inclined toward the line F G H that the line A G is inclined thereto; for the line F G H is perpendicular to the surface B C in the point G. By this means, if a number of rays proceeding from any one point fall on a convex spherical surface of glass, they shall be inflected (as is represented in fig. 137,) so as to be gathered pretty close together about the line drawn through the center of the glass from the point, whence the rays proceed; which line henceforward we shall call the axis of the glass: or the point from whence the rays proceed may be so near the glass, that the rays shall after entring the glass still go on to spread themselves, but not so much as before; so that if the rays were to be continued backward (as in fig. 138,) they should gather together about the axis at a place more remote from the glass, than the point is, whence they actually proceed. In these and the following figures A denotes the point to which the rays are related before refraction, B the point to which they are directed afterwards, and C the center of the refracting surface. Here we may observe, that it is possible to form the glass of such a figure, that all the rays which proceed from one point[379] shall after refraction be reduced again exactly into one point on the axis of the glass. But in glasses of a spherical form though this does not happen; yet the rays, which fall within a moderate distance from the axis, will unite extremely near together. If the light fall on a concave spherical surface, after refraction it shall spread quicker than before (as in fig. 139,) unless the rays proceed from a point between the center and the surface of the glass. If we suppose the rays of light, which fall upon the glass, not to proceed from any point, but to move so as to tend all to some point in the axis of the glass beyond the surface; if the glass have a convex surface, the rays shall unite about the axis sooner, than otherwise they would do (as in fig. 140,) unless the point to which they tended was between the surface and the center of that surface. But if the surface be concave, they shall not meet so soon: nay perhaps converge. (See fig. 141 and 142.)
5. Farther, because the light in passing out of glass into the air is turned by the refraction farther off from the line drawn through the point of incidence perpendicular to the refracting surface, than it was before; the light which spreads from a point shall by parting through a convex surface of glass into the air be made either to spread less than before (as in fig. 143,) or to gather about the axis beyond the glass (as in fig. 144.) But if the rays of light were proceeding to a point in the axis of the glass, they should by the refraction be made to unite sooner about that axis (as in fig. 145.) If the surface of the glass be concave, rays which proceed from a point shall be made to spread faster (as in fig 146,) but rays which are tending to a point in the axis of[380] the glass, shall be made to gather about the axis farther from the glass (as in fig. 147) or even to diverge (as in fig. 148,) unless the point, to which the rays are directed, lies between the surface of the glass and its center.
4. The rays, which spread themselves from a point, are called diverging; and such as move toward a point, are called converging rays. And the point in the axis of the glass, about which the rays gather after refraction, is called the focus of those rays.
5. If a glass be formed of two convex spherical surfaces (as in fig. 149,) where the glass AB is formed of the surfaces A C B and A D B, the line drawn through the centers of the two surfaces, as the line E F, is called the axis of the glass; and rays, which diverge from any point of this axis, by the refraction of the glass will be caused to converge toward some part of the axis, or at least to diverge as from a point more remote from the glass, than that from whence they proceeded; for the two surfaces both conspire to produce this effect upon the rays. But converging rays will be caused by such a glass as this to converge sooner. If a glass be formed of two concave surfaces, as the glass A B (in fig. 150,) the line C D drawn through the centers, to which the two surfaces are formed, is called the axis of the glass. Such a glass shall cause diverging rays, which proceed from any point in the axis of the glass, to diverge much more, as if they came from some place in the axis of the glass nearer to it than the point, whence the rays actually proceed. But converging rays will be made either to converge less, or even to diverge.
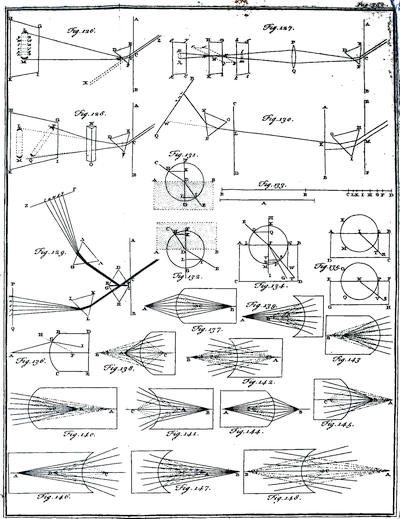
6. In these glasses rays, which proceed from any point near the axis, will be affected as it were in the same manner, as if they proceeded from the very axis it self, and such as converge toward a point at a small distance from the axis will suffer much the same effects from the glass, as if they converged to some point in the very axis. By this means any luminous body exposed to a convex glass may have an image formed upon any white body held beyond the glass. This may be easily tried with a common spectacle-glass. For if such a glass be held between a candle and a piece of white paper, if the distances of the candle, glass, and paper be properly adjusted, the image of the candle will appear very distinctly upon the paper, but be seen inverted; the reason whereof is this. Let A B (in fig. 151) be the glass, C D an object placed cross the axis of the glass. Let the rays of light, which issue from the point E, where the axis of the glass crosses the object, be so refracted by the glass, as to meet again about the point F. The rays, which diverge from the point C of the object, shall meet again almost at the same distance from the glass, but on the other side of the axis, as at G; for the rays at the glass cross the axis. In like manner the rays, which proceed from the point D, will meet about H on the other side of the axis. None of these rays, neither those which proceed from the point E in the axis, nor those which issue from C or D, will meet again exactly in one point; but yet in one place, as is here supposed at F, G, and H, they[382] will be crouded so close together, as to make a distinct image of the object upon any body proper to reflect it, which shall be held there.
7. If the object be too near the glass for the rays to converge after the refraction, the rays shall issue out of the glass, as if they diverged from a point more distant from the glass, than that from whence they really proceed (as in fig. 152,) where the rays coming from the point E of the object, which lies on the axis of the glass A B, issue out of the glass, as if they came from the point F more remote from the glass than E; and the rays proceeding from the point C issue out of the glass, as if they proceeded from the point G; likewise the rays which issue from the point D emerge out of the glass, as if they came from the point H. Here the point G is on the same side of the axis, as the point C; and the point H on the same side, as the point D. In this case to an eye placed beyond the glass the object should appear, as if it were in the situation G F H.
8. If the glass A B had been concave (as in, fig. 153,) to an eye beyond the glass the object C D would appear in the situation G H, nearer to the glass than really it is. Here also the object will not be inverted; but the point G is on the same side the axe with the point C, and H on the same side as D.
9. Hence may be understood, why spectacles made with convex glasses help the sight in old age: for the eye in that age becomes unfit to see objects distinctly, except such as are remov’d to a very great distance; whence all men, when they first stand in need of spectacles, are observed to read at arm’s length, and to hold the object at a greater distance, than they used to do before. But when an object is removed at too great a distance from the sight, it cannot be seen clearly, by reason that a less quantity of light from the object will enter the eye, and the whole object will also appear smaller. Now by help of a convex glass an object may be held near, and yet the rays of light issuing from it will enter the eye, as if the object were farther removed.
10. After the same manner concave glasses assist such, as are short sighted. For these require the object to be brought inconveniently near to the eye, in order to their seeing it distinctly; but by such a glass the object may be removed to a proper distance, and yet the rays of light enter the eye, as if they came from a place much nearer.
11. Whence these defects of the sight arise, that in old age objects cannot be seen distinct within a moderate distance, and in short-sightedness not without being brought too near, will be easily understood, when the manner of vision in general shall be explain’d; which I shall now endeavour to do, in order to be better understood in what[384] follows. The eye is form’d, as is represented in fig. 154. It is of a globular figure, the fore part whereof scarce more protuberant than the rest is transparent. Underneath this transparent part is a small collection of an humour in appearance like water, and it has also the same refractive power as common water; this is called the aqueous humour, and fills the space A B C D in the figure. Next beyond lies the body D E F G; this is solid but transparent, it is composed with two convex surfaces, the hinder surface E F G being more convex, than the anterior E D G. Between the outer membrane A B C, and this body E D G F is placed that membrane, which exhibits the colours, that are seen round the sight of the eye; and the black spot, which is called the sight or pupil, is a hole in this membrane, through which the light enters, whereby we see. This membrane is fixed only by its outward circuit, and has a muscular power, whereby it dilates the pupil in a weak light, and contracts it in a strong one. The body D E F G is called the crystalline humour, and has a greater refracting power than water. Behind this the bulk of the eye is filled up with what is called the vitreous humor, this has much the same refractive power with water. At the bottom of the eye toward the inner side next the nose the optic glass enters, as at H, and spreads it self all over the inside of the eye, till within a small diftance from A and C. Now any object, as I K, being placed before the eye, the rays of light issuing from each point of this object are so refracted by the convex surface of the aqueous humour, as to be caused to converge; after this being received by the convex surface E D G[385] of the crystalline humour, which has a greater refractive power than the aqueous, the rays, when they are entered into this surface, still more converge, and at going out of the surface E F G into a humour of a less refractive power than the crystalline they are made to converge yet farther. By all these successive refractions they are brought to converge at the bottom of the eye, so that a distinct image of the object as L M is impress’d on the nerve. And by this means the object is seen.
11. It has been made a difficulty, that the image of the object impressed on the nerve is inverted, so that the upper part of the image is impressed on the lower part of the eye. But this difficulty, I think, can no longer remain, if we only consider, that upper and lower are terms merely relative to the ordinary position of our bodies: and our bodies, when view’d by the eye, have their image as much inverted as other objects; so that the image of our own bodies, and of other objects, are impressed on the eye in the same relation to one another, as they really have.
12. The eye can see objects equally distinct at very different distances, but in one distance only at the same time. That the eye may accomodate itself to different distances, some change in its humours is requir’d. It is my opinion, that this change is made in the figure of the crystalline humour, as I have indeavoured to prove in another place.
13. If any of the humours of the eye are too flat, they will refract the light too little; which is the case in old age. If they are too convex, they refract too much; as in those who are short-sighted.
14. The manner of direct vision being thus explained, I proceed to give some account of telescopes, by which we view more distinctly remote objects; and also of microscopes, whereby we magnify the appearance of small objects. In the first place, the most simple sort of telescope is composed of two glasses, either both convex, or one convex, and the other concave. (The first sort of these is represented in fig. 155, the latter in fig. 156.)
15. In fig. 155 let A B represent the convex glass next the object, C D the other glass more convex near the eye. Suppose the object-glass A B to form the image of the object at E F; so that if a sheet of white paper were to be held in this place, the object would appear. Now suppose the rays, which pass the glass A B, and are united about F, to proceed to the eye glass C D, and be there refracted. Three only of these rays are drawn in the figure, those which pass by the extremities of the glass A B, and that which passes its middle. If the glass C D be placed at such a distance from the image E F, that the rays, which pass by the point F, after having proceeded through the glass diverge so much, as the rays do that come from an object, which is at such a distance from the eye as[387] to be seen distinctly, these being received by the eye will make on the bottom of the eye a distinct representation of the point F. In like manner the rays, which pass through the object glass A B to the point E after proceeding through the eye-glass C D will on the bottom of the eye make a distinct representation of the point E. But if the eye be placed where these rays, which proceed from E, cross those, which proceed from F, the eye will receive the distinct impression of both these points at the same time; and consequently will also receive a distinct impression from all the intermediate parts of the image E F, that is, the eye will see the object, to which the telescope is directed, distinctly. The place of the eye is about the point G, where the rays H E, H F cross, which pass through the middle of the object-glass A B to the points E and F; or at the place where the focus would be formed by rays coming from the point H, and refracted by the glass C D. To judge how much this instrument magnifies any object, we must first observe, that the angle under E H F, in which the eye at the point H would see the image E F, is nearly the same as the angle, under which the object appears by direct vision; but when the eye is in G, and views the object through the telescope, it sees the same under a greater angle; for the rays, which coming from E and F cross in G, make a greater angle than the rays, which proceed from the point H to these points E and F. The angle at G is greater than that at H in the proportion, as the distance between the glasses A B and C D is greater than the distance of the point G from the glass C D.
16. This telescope inverts the object; for the rays, which came from the right-hand side of the object, go to the point E the left side of the image; and the rays, which come from the left side of the object, go to F the right side of the image. These rays cross again in G, so that the rays, which come from the right side of the object, go to the right side of the eye; and the rays from the left side of the object go to the left side of the eye. Therefore in this telescope the image in the eye has the same situation as the object; and seeing that in direct vision the image in the eye has an inverted situation, here, where the situation is not inverted, the object must appear so. This is no inconvenience to astronomers in celestial observations; but for objects here on the earth it is usual to add two other convex glasses, which may turn the object again (as is represented in fig. 157,) or else to use the other kind of telescope with a concave eye-glass.
17. In this other kind of telescope the effect is founded on the same principles, as in the former. The distinctness of the appearance is procured in the same manner. But here the eye-glass C D (in fig. 156) is placed between the image E F, and the object glass A B. By this means the rays, which come from the right-hand side of the object, and proceed toward E the left side of the image, being intercepted by the eye-glass are carried to the left side of the eye; and the rays, which come from the left side of the object, go to the right side of the eye; so that the impression in the eye being inverted the object appears in the same situation,[389] as when view’d by the naked eye. The eye must here be placed close to the glass. The degree of magnifying in this instrument is thus to be found. Let the rays, which pass through the glass A B at H, after the refraction of the eye-glass C D diverge, as if they came from the point G; then the rays, which come from the extremities of the object, enter the eye under the angle at G; so that here also the object will be magnified in the proportion of the distance between the glasses, to the distance of G from the eye-glass.
18. The space, that can be taken in at one view in this telescope, depends on the breadth of the pupil of the eye; for as the rays, which go to the points E, F of the image, are something distant from each other, when they come out of the glass C D, if they are wider asunder than the pupil, it is evident, that they cannot both enter the eye at once. In the other telescope the eye is placed in the point G, where the rays that come from the points E or F cross each other, and therefore must enter the eye together. On this account the telescope with convex glasses takes in a larger view, than those with concave. But in these also the extent of the view is limited, because the eye-glass does not by the refraction towards its edges form so distinct a representation of the object, as near the middle.
18.Microscopes are of two sorts. One kind is only a very convex glass, by the means of which the object may be brought very near the eye, and yet be seen distinctly.[390] This microscope magnifies in proportion, as the object by being brought near the eye will form a broader impression on the optic nerve. The other kind made with convex glasses produces its effects in the same manner as the telescope. Let the object A B (in fig. 158) be placed under the glass C D, and by this glass let an image be formed of this object. Above this image let the glass G H be placed. By this glass let the rays, which proceed from the points A and B, be refracted, as is expressed in the figure. In particular, let the rays, which from each of these points pass through the middle of the glass C D, cross in I, and there let the eye be placed. Here the object will appear larger, when seen through the microscope, than if that instrument were removed, in proportion as the angle, in which these rays cross in I, is greater than the angle, which the lines would make, that should be drawn from I to A and B; that is, in the proportion made up of the proportion of the distance of the object A B from I, to the distance of I from the glass G H; and of the proportion of the distance between the glasses, to the distance of the object A B from the glass C D.
19. I shall now proceed to explain the imperfection in these instruments, occasioned by the different refrangibility of the light which comes from every object. This prevents the image of the object from being formed in the focus of the object glass with perfect distinctness; so that if the eye-glass magnify the image overmuch, the imperfections of it must be visible, and make the whole appear confused. Our author more fully to satisfy himself, that the different refrangibility of the[391] several sorts of rays is sufficient to produce this irregularity, underwent the labour of a very nice and difficult experiment, whose process he has at large set down, to prove, that the rays of light are refracted as differently in the small refraction of telescope glasses as in the larger of the prism; so exceeding careful has he been in searching out the true cause of this effect. And he used, I suppose, the greater caution, because another reason had before been generally assigned for it. It was the opinion of all mathematicians, that this defect in telescopes arose from the figure, in which the glasses were formed; a spherical refracting surface not collecting into an exact point all the rays which come from any one point of an object, as has before been said[330]. But after our author has proved, that in these small refractions, as well as in greater, the sine of incidence into air out of glass, to the sine of refraction in the red-making rays, is as 50 to 77, and in the blue-making rays 50 to 78; he proceeds to compare the inequalities of refraction arising from this different refrangibility of the rays, with the inequalities, which would follow from the figure of the glass, were light uniformly refracted. For this purpose he observes, that if rays issuing from a point so remote from the object glass of a telescope, as to be esteemed parallel, which is the case of the rays, which come from the heavenly bodies; then the distance from the glass of the point, in which the least refrangible rays are united, will be to the distance, at which the most refrangible rays unite, as 28 to 27; and therefore that the least space, into which[392] all the rays can be collected, will not be less than the 55th part of the breadth of the glass. For if A B (in fig. 159) be the glass, C D its axis, E A, F B two rays of the light parallel to that axis entring the glass near its edges; after refraction let the least refrangible part of these rays meet in G, the most refrangible in H; then, as has been said, G I will be to I H, as 28 to 27; that is, G H will be the 28th part of G I, and the 27th part of H I; whence if K L be drawn through G, and M N through H, perpendicular to C D, M N will be the a 28th part of A B, the breadth of the glass, and K L the 27th part of the same; so that O P the least space, into which the rays are gathered, will be about half the mean between these two, that is the 55th part of A B.
20. This is the error arising from the different refrangibility of the rays of light, which our author finds vastly to exceed the other, consequent upon the figure of the glass. In particular, if the telescope glass be flat on one side, and convex on the other; when the flat side is turned towards the object, by a theorem, which he has laid down, the error from the figure comes out above 5000 times less than the other. This other inequality is so great, that telescopes could not perform so well as they do, were it not that the light does not equally fill all the space O P, over which it is scattered, but is much more dense toward the middle of that space than at the extremities. And besides, all the kinds of rays affect not the sense equally strong, the yellow and orange being the strongest, the red and green next to them, the blue indigo and violet being much darker and fainter colours; and it is shewn that all the yellow and orange, and three fifths of the brighter half of the red next the orange, and as great a share of the brighter half of the green next the yellow, will be collected into a space whose breadth is not above the 250th part of the breadth of the glass.
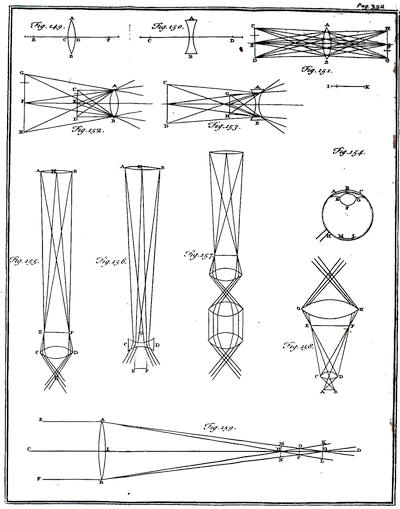
And the remaining colours, which fall without this space, as they are much more dull and obscure than these, so will they be likewise much more diffused; and therefore call hardly affect the sense in comparison of the other. And agreeable to this is the observation of astronomers, that telescopes between twenty and sixty feet in length represent the fixed stars, as being about 5 or 6, at most about 8 or 10 seconds in diameter. Whereas other arguments shew us, that they do not really appear to us of any sensible magnitude any otherwise than as their light is dilated by refraction. One proof that the fixed stars do not appear to us under any sensible angle is, that when the moon passes over any of them, their light does not, like the planets on the same occasion, disappear by degrees, but vanishes at once.
21. Our author being thus convinced, that telescopes were not capable of being brought to much greater perfection than at present by refractions, contrived one by reflection, in which there is no separation made of the different coloured light; for in every kind of light the rays after reflection have the same degree of inclination to the surface, from whence they are reflected, as they have at their incidence, so[394] that those rays which come to the surface in one line, will go off also in one line without any parting from one another. Accordingly in the attempt he succeeded so well, that a short one, not much exceeding six inches in length, equalled an ordinary telescope whose length was four feet. Instruments of this kind to greater lengths, have of late been made, which fully answer expectation[331].
Chap. V.
Of the RAINBOW.
I SHALL now explain the rainbow. The manner of its production was understood, in the general, before Sir Isaac Newton had discovered his theory of colours; but what caused the diversity of colours in it could not then be known, which obliges him to explain this appearance particularly; whom we shall imitate as follows. The first person, who expressly shewed the rainbow to be formed by the reflection of the sun-beams from drops of falling rain, was Antonio de Dominis. But this was afterwards more fully and distinctly explained by DesCartes.
2. There appears most frequently two rainbows; both of which are caused by the foresaid reflection of the sun-beams from the drops of falling rain, but are not produced by all the light which falls upon and are reflected from the drops. The inner bow is produced by those rays only which enter the drop, and at their entrance are so refracted as to unite into a point, as it were, upon the farther surface of the drop, as is represented in fig. 160; where the contiguous rays a b, c d, e f, coming from the[395] sun, and therefore to sense parallel, upon their entrance into the drop in the points b, d, f, are so refracted as to meet together in the point g, upon the farther surface of the drop. Now these rays being reflected nearly from the same point of the surface, the angle of incidence of each ray upon the point g being equal to the angle of reflection, the rays will return in the lines g h, g k, g l, in the same manner inclined to each other, as they were before their incidence upon the point g, and will make the same angles with the surface of the drop at the points b, k, l, as at the points b, d, f, after their entrance; and therefore after their emergence out of the drop each ray will be inclined to the surface in the same angle, as when it first entered it; whence the lines b m, k n, l o, in which the rays emerge, must be parallel to each other, as well as the lines a b, c d, e f, in which they were incident. But these emerging rays being parallel will not spread nor diverge from each other in their passage from the drop, and therefore will enter the eye conveniently situated in sufficient plenty to cause a sensation. Whereas all the other rays, whether those nearer the center of the drop, as p q, r s, or those farther off, as t u, w x, will be reflected from other points in the hinder surface of the drop; namely, the ray p q from the point y, r s from z, t v from α, and w x from β. And for this reason by their reflection and succeeding refraction they will be scattered after their emergence from the forementioned rays and from each other, and therefore cannot enter the eye placed to receive them copious enough to excite any distinct sensation.
3. The external rainbow is formed by two reflections made between the incidence and emergence of the rays; for it is to be noted, that the rays g h, g k, g l, at the points h, k, l, do not wholly pass out of the drop, but are in part reflected back; though the second reflection of these particular rays does not form the outer bow. For this bow is made by those rays, which after their entrance into the drop are by the refraction of it united, before they arrive at the farther surface, at such a distance from it, that when they fall upon that surface, they may be reflected in parallel lines, as is represented in fig. 161; where the rays a b, c d, e f, are collected by the refraction of the drop into the point g, and passing on from thence strike upon the surface of the drop in the points h, k, l, and are thence reflected to m, n, o, passing from h to m, from k to n, and from l to o in parallel lines. For these rays after reflection at m, n, o, will meet again in the point p, at the same distance from these points of reflection m, n, o, as the point g is from the former points of reflection h, k, l. Therefore these rays in passing from p to the surface of the drop will fall upon that surface in the points q, r, s in the same angles, as these rays made with the surface in b, d, f, after refraction. Consequently, when these rays emerge out of the drop into the air, each ray will make with the surface of the drop the same angle, as it made at its first incidence; so that the lines q t, r v, s w, in which they come from the drop, will be parallel to each other, as well as the lines a b, c d, e f, in which they came to the[397] drop. By this means these rays to a spectator commodiously situated will become visible. But all the other rays, as well those nearer the center of the drop x y, z α, as those more remote from it β γ, δ ε, will be reflected in lines not parallel to the lines h m, k n, l o; namely, the ray x y, in the line ζ η, the ray ϰ α in the line θ ϰ, the ray β γ in the line λ μ, and the ray δ ε in the line ν χ. Whence these rays after their next reflection and subsequent refraction will be scattered from the forementioned rays, and from one another, and by that means become invisible.
4. It is farther to be remarked, that if in the first case the incident rays a b, c d, e f, and their correspondent emergent rays h m, k n, l o, are produced till they meet, they will make with each other a greater angle, than any other incident ray will make with its corresponding emergent ray. And in the latter case, on the contrary, the emergent rays q t, r v, s w make with the incident rays an acuter angle, than is made by any other of the emergent rays.
5. Our author delivers a method of finding each of these extream angles from the degree of refraction being given; by which method it appears, that the first of these angles is the less, and the latter the greater, by how much the refractive power of the drop, or the refrangibility of the rays is greater. And this last consideration fully compleats the doctrine of the rainbow, and shews, why the colours of each bow are ranged in the order wherein they are seen.
6. Suppose A (in fig. 162.) to be the eye, B, C, D, E, F, drops of rain, M n, O p, Q r, S t, V w parcels of rays of the sun, which entring the drops B, C, D, E, F after one reflection pass out to the eye in A. Now let M n be produced to η till it meets with the emergent ray likewise produced, let O p produced meet its emergent ray produced in ϰ, let Q r meet its emergent ray in λ, let S t meet its emergent ray in μ, and let V w meet its emergent ray produced in ν. If the angle under M η A be that, which is derived from the refraction of the violet-making rays by the method we have here spoken of, it follows that the violet light will only enter the eye from the drop B, all the other coloured rays passing below it, that is, all those rays which are not scattered, but go out parallel so as to cause a sensation. For the angle, which these parallel emergent rays makes with the incident in the most refrangible or violet-making rays, being less than this angle in any other sort of rays, none of the rays which emerge parallel, except the violet-making, will enter the eye under the angle M η A, but the rest making with the incident ray M η a greater angle than this will pass below the eye. In like manner if the angle under O ϰ A agrees to the blue-making rays, the blue rays only shall enter the eye from the drop C, and all the other coloured rays will pass by the eye, the violet-coloured rays passing above, the other colours below. Farther, the angle Q λ A corresponding to the green-making rays, those only shall enter the eye from the drop D, the violet and blue-making rays passing above, and the other colours, that is the yellow and[399] red, below. And if the angle S μ A answers to the refraction of the yellow-making rays, they only shall come to the eye from the drop E. And in the last place, if the angle V ν A belongs to the red-making and least refrangible rays, they only shall enter the eye from the drop F, all the other coloured rays passing above.
7. But now it is evident, that all the drops of water found in any of the lines A ϰ, A λ, A μ, A ν, whether farther from the eye, or nearer than the drops B, C, D, E, F, will give the same colours as these do, all the drops upon each line giving the same colour; so that the light reflected from a number of these drops will become copious enough to be visible; whereas the reflection from one minute drop alone could not be perceived. But besides, it is farther manifest, that if the line A Ξ be drawn from the sun through the eye, that is, parallel to the lines M n, O p, Q r, S t, V w, and if drops of water are placed all round this line, the same colour will be exhibited by all the drops at the same distance from this line. Hence it follows, that when the sun is moderately elevated above the horizon, if it rains opposite to it, and the sun shines upon the drops as they fall, a spectator with his back turned to the sun must observe a coloured circular arch reaching to the horizon, being red without, next to that yellow, then green, blue, and on the inner edge violet; only this last colour appears faint by being diluted with the white light of the clouds, and from another cause to be mentioned hereafter[332].
8. Thus is caused the interior or primary bow. The drops of rain at some distance without this bow will cause the exterior or secondary bow by two reflections of the sun’s light. Let these drops be G, H, I, K, L; X y, Z α, Γ β, Δ ι, Θ ζ denoting parcels of rays which enter each drop. Now it has been remarked, that these rays make with the visible refracted rays the greatest angle in those rays, which are most refrangible. Suppose therefore the visible refracted rays, which pass out from each drop after two reflections, and enter the eye in A, to intersect the incident rays in π, ρ, σ, τ, φ respectively. It is manifest, that the angle under Θ φ A is the greatest of all, next to that the angle under Δ τ A, the next in bigness will be the angle under Γ σ A, the next to this the angle under Z ρ A, and the least of all the angle under X π A. From the drop L therefore will come to the eye the violet-making, or most refrangible rays, from K the blue, from I the green, from H the yellow, and from G the red-making rays; and the like will happen to all the drops in the lines A π, A ρ, A τ, A φ, and also to all the drops at the same distances from the line A Ξ all round that line. Whence appears the reason of the secondary bow, which is seen without the other, having its colours in a contrary order, violet without and red within; though the colours are fainter than in the other bow, as being made by two reflections, and two refractions; whereas the other bow is made by two refractions, and one reflection only.
9. There is a farther appearance in the rainbow particularly described about five years ago[333], which is, that under the upper part or the inner bow there appears often two or three orders of very faint colours, making alternate arches of green, and a reddish purple. At the time this appearance was taken notice of, I gave my thoughts concerning the cause of it[334], which I shall here repeat. Sir Isaac Newton has observed, that in glass, which is polished and quick-silvered, there is an irregular refraction made, whereby some small quantity of light is scattered from the principal reflected beam[335]. If we allow the same thing to happen in the reflection whereby the rainbow is caused, it seems sufficient to produce the appearance now mentioned.
10. Let A B (in fig. 162.) represent a globule of water, B the point from whence the rays of any determinate species being reflected to C, and afterwards emerging in the line C D, would proceed to the eye, and cause the appearance of that colour in the rainbow, which appertains to this species. Here suppose, that besides what is reflected regularly, some small part of the light is irregularly scattered every way; so that from the point B, besides the rays that are regularly reflected from B to C, some scattered rays will return in other lines, as in B E, B F, B G, B H, on each side the line B C. Now it has been observed above[336], that the rays of light in their passage from one superficies of a refracting body to the other undergo alternate fits of[402] easy transmission and reflection, succeeding each other at equal intervals; insomuch that if they reach the farther superficies in one sort of those fits, they shall be transmitted; if in the other kind of them, they shall rather be reflected back. Whence the rays that proceed from B to C, and emerge in the line C D, being in a fit of easy transmission, the scattered rays, that fall at a small distance without these on either side (suppose the rays that pass in the lines B E, B G) shall fall on the surface in a fit of easy reflection, and shall not emerge; but the scattered rays, that pass at some distance without these last, shall arrive at the surface of the globule in a fit of easy transmission, and break through that surface. Suppose these rays to pass in the lines B F, B H; the former of which rays shall have had one fit more of easy transmission, and the latter one fit less, than the rays that pass from B to C. Now both these rays, when they go out of the globule, will proceed by the refraction of the water In the lines F I, H K, that will be inclined almost equally to the rays incident on the globule, which come from the sun; but the angles of their inclination will be less than the angle, in which the rays emerging in the line C D are inclined to those incident rays. And after the same manner rays scattered from the point B at a certain distance without these will emerge out of the globule, while the intermediate rays are intercepted; and these emergent rays will be inclined to the rays incident on the globule in angles still less than the angles, in which the rays F I and H K are inclined to them; and without these rays will emerge other rays, that shall be inclined to the incident rays in angles yet less.
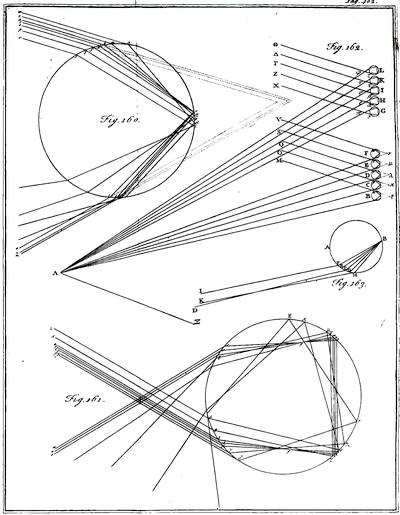
Now by this means may be formed of every kind of rays, besides the principal arch, which goes to the formation of the rainbow, other arches within every one of the principal of the same colour, though much more faint; and this for divers successions, as long as these weak lights, which in every arch grow more and more obscure, shall continue visible. Now as the arches produced by each colour will be variously mixed together, the diversity of colours observ’d in these secondary arches may very possibly arise from them.
11. In the darker colours these arches may reach below the bow, and be seen distinct. In the brighter colours these arches are lost in the inferior part of the principal light of the rainbow; but in all probability they contribute to the red tincture, which the purple of the rainbow usually has, and is most remarkable when these secondary colours appear strongest. However these secondary arches in the brightest colours may possibly extend with a very faint light below the bow, and tinge the purple of these secondary arches with a reddish hue.
12. The precise distances between the principal arch and these fainter arches depend on the magnitude of the drops, wherein they are formed. To make them any degree separate it is necessary the drop be exceeding small. It is most likely, that they are formed in the vapour of the cloud, which the air being put in motion by the fall of the rain may carry down along with the larger drops; and this may be the reason, why these colours appear under the upper[404] part of the bow only, this vapour not descending very low. As a farther confirmation of this, these colours are seen strongest, when the rain falls from very black clouds, which cause the fiercest rains, by the fall whereof the air will be most agitated.
13. To the like alternate return of the fits of easy transmission and reflection in the passage of light through the globules of water, which compose the clouds, Sir Isaac Newton ascribes some of those coloured circles, which at times appear about the sun and moon[337].


CONCLUSION.

SIR Isaac Newton having concluded each of his philosophical treatises with some general reflections, I shall now take leave of my readers with a short account of what he has there delivered. At the end of his mathematical principles of natural philosophy he has given us his thoughts concerning the Deity. Wherein he first observes, that the similitude found in all parts of the universe makes it undoubted, that the whole is governed by one supreme being, to whom the original is owing of the frame of nature, which evidently is the effect of choice and design. He then proceeds briefly to state the best metaphysical notions concerning God. In short, we cannot conceive either of space or time otherwise than as necessarily[406] existing; this Being therefore, on whom all others depend, must certainly exist by the same necessity of nature. Consequently wherever space and time is found, there God must also be. And as it appears impossible to us, that space should be limited, or that time should have had a beginning, the Deity must be both immense and eternal.
2. At the end of his treatise of optics he has proposed some thoughts concerning other parts of nature, which he had not distinctly searched into. He begins with some farther reflections concerning light, which he had not fully examined. In particular he declares his sentiments at large concerning the power, whereby bodies and light act on each other. In some parts of his book he had given short hints at his opinion concerning this[338], but here he expressly declares his conjecture, which we have already mentioned[339], that this power is lodged in a very subtle spirit of a great elastic force diffused thro’ the universe, producing not only this, but many other natural operations. He thinks it not impossible, that the power of gravity itself should be owing to it. On this occasion he enumerates many natural appearances, the chief of which are produced by chymical experiments. From numerous observations of this kind he makes no doubt, that the smallest parts of matter, when near contact, act strongly on each other, sometimes being mutually attracted, at other times repelled.
3. The attractive power is more manifest than the other, for the parts of all bodies adhere by this principle. And the[407] name of attraction, which our author has given to it, has been very freely made use of by many writers, and as much objected to by others. He has often complained to me of having been misunderstood in this matter. What he lays upon this head was not intended by him as a philosophical explanation of any appearances, but only to point out a power in nature not hitherto distinctly observed, the cause of which, and the manner of its acting, he thought was worthy of a diligent enquiry. To acquiesce in the explanation of any appearance by asserting it to be a general power of attraction, is not to improve our knowledge in philosophy, but rather to put a stop to our farther search.
FINIS.

FOOTNOTES:
[1] Philosoph. Nat. princ. math. L. iii. introduct.
[2] Nov. Org. Scient. L. i. Aphorism. 9.
[3] Nov. Org. L. i. Aph. 19.
[4] Ibid. Aph. 25.
[5] Aph. 30. Errores radicales & in prima digestione mentis ab excellentia functionum & remediorum sequentium non curantur.
[6] Aph. 38.
[7] Ibid.
[8] Aph. 39.
[9] Aph. 41.
[10] Aph. 10, 24.
[11] Aph. 45.
[12] De Cartes Princ. Phil. Part. 3. §. 52.
[13] Fermat, in Oper. pag. 156, &c.
[14] Nov. Org. Aph. 46.
[15] Aph. 50.
[16] Ibid.
[17] Aph 53.
[18] Aph. 54.
[19] Aph. 56.
[20] Aph. 55.
[21] Locke, On human understanding, B. iii.
[22] Nov. Org. Aph. 59.
[23] In the conclusion.
[24] Nov. Org. L. i. Aph. 59.
[25] Ibid. Aph. 60.
[26] Ibid. Aph. 62.
[27] Aph. 63.
[28] Aph. 64.
[29] Aph. 65.
[30] See above, § 4, 5.
[31] Nov. Org. L. i. Aph. 69.
[32] Ibid.
[33] Ibid. Aph. 109.
[34] Book III. Chap. iv.
[35] Book I. Chap. 2. § 14.
[36] Ibid. § 85, &c.
[37] See Book II. Ch. 3. § 3, 4. of this treatise.
[38] See Book II. Ch. 3. of this treatise.
[39] See Chap. 4.
[40] At the end of his Optics. in Qu. 21.
[41] See the same treatise, in Advertisement 2.
[42] Nov. Org. Lib. i. Ax. 105.
[43] Princip. philos. pag. 13, 14.
[44] Princ. Philos. L. II. prop. 24. corol. 7. See also B. II. Ch. 5. § 3. of this treatise.
[45] How this degree of elasticity is to be found by experiment, will be shewn below in § 74.
[46] In oper. posthum de Motu corpor. ex percussion. prop. 9.
[47] In the above-cited place.
[48] In the place above-cited.
[49] These experiments are described in § 73.
[50] Book II. Chap. 5.
[51] Chap. 1. § 25, 26, 27, compared with § 15, &c.
[52] Book II. Chap. 5. § 3.
[53] See Euclid’s Elements, Book XII. prop. 13.
[54] Archimed. de æquipond. prop. 11.
[55] Ibid. prop. 12.
[56] Lucas Valerius De centr. gravit. solid. L. I. prop. 2.
[57] Idem L. II. prop. 2.
[58] § 25.
[59] § 27.
[60] Pag. 65, 68.
[61] § 23.
[62] § 20
[63] § 17.
[64] § 27.
[65] Hugen. Horolog. oscillat. pag. 141, 142.
[66] See Hugen. Horolog. Oscillat. p. 142.
[67] Princip. Philos. pag. 22.
[68] Chap. 1. § 29.
[69] Princip. Philos. pag. 25.
[70] § 71.
[71] See Method. Increment. prop. 25.
[72] Lib. XI. Def.
[73] Chap. 2. § 17.
[74] See above Ch. 2. § 17.
[75] From B II. Ch. 3.
[76] Prin. Philos. pag. 7, &c.
[77] See Newton, princip. philos. pag. 9. lin. 30.
[78] Princip. Philos. pag. 10.
[79] Renat. Des Cart. Princ. Philos. Part. II. § 25.
[80] Ibid. § 30.
[81] § 85, &c.
[82] Princip. Philos. Lib. I. prop. 9.
[83] § 92.
[84] Ch. II. § 22.
[85] Viz. L. I. prop. 30, 29, & 26.
[86] Ch. II. § 21, 22.
[87] viz. His doctrine of prime and ultimate ratios.
[88] § 57
[89] § 3.
[90] Ch. 2. § 22.
[91] § 12.
[92] Ch. 1. sect. 21, 22.
[93] Elem. Book I. p. 37.
[94] § 12.
[95] Ch 1 § 24.
[96] Ch 2 select. 17.
[97] Newt. Princ. L. II. prop. 2; 5, 6, 7; 11, 12.
[98] Prop. 3; 8, 9; 13, 14.
[99] Prop. 4.
[100] Prælect. Geometr. pag. 123.
[101] Newton. Princ. Lib. II. prop. 10.
[102] Newton. Princ. Lib II. prop 10. in schol.
[103] Torricelli de motu gravium.
[104] Ch. 2 § 85, &c.
[105] Newt. Princ L. II. sect 6.
[106] L. II. sect. 4.
[107] See B. II. Ch 6. § 7. of this treatise.
[108] Lib. I. sect. 10.
[109] De la Pesanteur, pag. 169, and the following.
[110] Newton. Princ. L. II. prop 4. schol.
[111] See his Tract on the admirable rarifaction of the air.
[112] Book II. Ch. 6.
[113] Princ. philos. Lib. II. prop. 23.
[114] Book I. Ch. 2. § 30.
[115] Princ. philos. Lib. II. prop. 23, in schol.
[116] Princ. philos. Lib. II. prop. 33. coroll.
[117] Lib. II. Ch. 5.
[118] Ibid. Prop. 35. coroll. 2.
[119] Ibid. coroll. 3.
[120] Vid. ibid. coroll. 6.
[121] In § 2.
[122] Princ. philos. Lib. II. Prop. 35.
[123] Ibid.
[124] Id.
[125] h. 1. § 29.
[126] Princ. philos. Lib. II. Prop. 38, compared with coroll. 1 of prop. 35.
[127] L. II. Lem. 7. schol. pag. 341.
[128] Lib. II. Prop. 34.
[129] Lib. II. Lem. 7. p. 341.
[130] Schol. to Lem. 7.
[131] Prop. 34. schol.
[132] Ibid.
[133] Ibid.
[134] Book II. Ch. I. § 6.
[135] Vid. Newt. princ. in schol. to Lem. 7, of Lib. II. pag. 341.
[136] Sect. 17. of this chapter.
[137] See Princ. philos. Lib. II. prop. 34.
[138] Vid. Princ. philos. Lib. II. Lem. 5. p. 314.
[139] Lemm. 6.
[140] Ibid. 7.
[141] Newt. Princ. Lib. II. prop. 40, in schol.
[142] Lib. II. in schol. post prop. 31.
[143] Book I. ch. 2 § 82.
[144] Book I. Ch. 3 § 29.
[145] Ch. 3. of this present book.
[146] Ch. 4.
[147] In Princ. philos. part. 3.
[148] Philos. princ. mathem. Lib. II. prop. 2. & schol.
[149] Ibid. prop 53.
[150] Philos. princ. prop. 52. coroll. 4.
[151] Ibid.
[152] Coroll. 11.
[153] See ibid. schol. post prop. 53.
[154] Princ. philos. pag. 316, 317.
[155] Ch. I. § 7.
[156] Book I. Ch. 3.
[157] Book I. Ch. 3. § 29.
[158] Ibid. Ch. 2. § 30, 17.
[159] Book I. Ch. 3.
[160] Ch. 1. § 7.
[161] Chap. 5. § 8.
[162] Princ. pag. 60.
[163] Street, in Astron. Carolin.
[164] See Chap. 5. §9, &c.
[165] In the foregoing page.
[166] See Newton. Princ. Lib. III. prop. 13.
[167] Chap. 5. § 10.
[168] Princ. Lib. I. prop. 60.
[169] Book I, Chap. 2. § 80.
[170] Princ. philos. Lib. I. prop. 58. coroll. 3.
[171] Newt. Optics. pag. 378.
[172] Newton. Princ. Lib. III. prop. 1.
[173] Newton, Princ. Lib. III. pag. 390,391. compared with pag. 393.
[174] Book I. Ch. 3. § 29.
[175] Princ. philos. Lib. I. prop. 4.
[176] Ibid. coroll.
[177] Newt. Princ. philos. Lib. III. pag. 390.
[178] Newt. Princ. philos. Lib. III. pag. 391, 392.
[179] Book III. Ch. 4.
[180] Newt. Princ. philos. Lib. III. pag. 391.
[181] Ibid. pag. 392.
[182] See Book I. Ch. 2. § 60, 64.
[183] Book I. Ch. 2. § 17.
[184] See Ch. II. § 6.
[185] The second of the laws of motion laid down in Book I. Ch. 1.
[186] Newton. Princ. philos. Lib. III. prop. 6. pag. 401.
[187] Newton’s Princ. philos. Lib. III. prop. 22, 23.
[188] Newton. Princ. Lib. I. prop. 66. coroll. 7.
[189] Menelai Sphaeric. Lib. I. prop. 10.
[190] Vid. Newt. Princ. Lib. I. prop. 66. coroll. 10.
[191] Vid. Newt. Princ. Lib. III prop. 30. p. 440.
[192] Ibid. Lib. I. prop. 66. coroll. 10.
[193] What this proportion is, may be known from Coroll. 2 prop. 44. Lib. I. Princ. philos. Newton.
[194] Princ. Phil. Newt. Lib. I. prop. 45. Coroll. 1.
[195] Pr. Phil. Newt. Lib. I. prop. 66. Coroll. 7.
[196] See § 19 of this chapter.
[197] Phil. Nat. Pr. Math Lib. I. prop. 66. cor. 8.
[198] Ibid. Coroll. 8.
[199] Ibid.
[200] Ibid.
[201] Newt. Princ. Lib. III. prop. 29.
[202] Ibid. prop. 28.
[203] Ibid. prop. 31.
[204] Newt. Princ. pag. 459.
[205] In Princ. philos. part. 3. § 41.
[206] Chap. 1. § 11.
[207] Newton. Princ. philos. Lib. III. Lemm. 4. pag. 478.
[208] Princ. philos. Lib. III. prop. 40.
[209] Book I. chap. 2. § 82.
[210] Princ. philos. Lib. III. pag. 499, 500.
[211] Ibid. pag. 500, and 520, &c.
[212] Princ. Philos. Lib. III. prop. 40.
[213] Ibid. prop. 41.
[214] Ibid. pag. 522.
[215] Ibid. prop. 42.
[216] Newt. Princ. philos. edit. 2. p. 464, 465.
[217] Ibid. edit. 3. p 501, 502.
[218] Ibid. pag. 519.
[219] Ibid. pag. 524.
[220] Newt. Princ. philos. p. 525.
[221] Ibid.
[222] Ibid. pag. 508.
[223] Ibid.
[224] Ibid. pag. 484.
[225] Ibid. pag. 482, 483.
[226] Ibid. pag. 481.
[227] Ibid. pag. 509.
[228] See the fore-cited place.
[229] Ibid. and Cartes. Princ. Phil. part. 3. § 134, &c.
[230] Vid. Phil. Nat. princ. Math. p. 511.
[231] Book I. Ch. 4. § 11.
[232] Ch. 5.
[233] All these arguments are laid down in Philos. Nat. Princ. Lib. III. from p. 509, to 517.
[234] Philos. Nat. Princ. Lib. III. p. 515.
[235] Ch. 5.
[236] See Ch. 1. § 11.
[237] Newt. Princ. Philos. pag. 525, 526. An account of all the stars of both these kinds, which have appeared within the last 150 years may be seen in the Philosophical transactions, vol. 29. numb. 346.
[238] Newt. Princ. Philos. Nat. Lib. III. prop. 6.
[239] Ch. 3. § 6.
[240] Book I. Ch. 2. § 24.
[241] Newt. Princ. Lib. III. prop. 6.
[242] Ch. 3. § 6.
[243] Newt. Princ. philos. Lib. III. prop. 7. cor. 1.
[244] See Book I. Ch. 1. § 15.
[245] Ibid. § 5, 6.
[246] Chap. 2. § 8.
[247] Newt. Princ. Lib. I. prop. 63.
[248] § 8.
[249] See Introd. § 23.
[250] § 4, 5.
[251] Newt. Princ. philos. Lib. I. prop. 74.
[252] Ibid. coroll. 3.
[253] Lib. I. Prop. 75. and Lib. III. prop. 8.
[254] Lib. I. Prop. 76.
[255] Ibid. cor. 5.
[256] Vid. Lib. III. Prop. 7. coroll. 1
[257] Newt. Princ. Lib. III. prop. 8. coroll. 1.
[258] Ibid. coroll. 2.
[259] Book I. Ch. 4. § 2.
[260] Newt. Princ. Lib. III. prop. 8. coroll. 3.
[261] Ibid. coroll. 4.
[262] Book I. Ch. 4.
[263] Lib. II. prop. 20. cor. 2.
[264] Chap. 4. § 17.
[265] Ibid.
[266] Vid. Newt. Princ. Lib. II. prop. 46.
[267] Princ. philos. Lib. II. prop. 49.
[268] Chap. 3. § 18.
[269] Newt. Princ. philos. Lib. I. prop. 66. coroll. 18.
[270] § 8.
[271] Ch. 3. § 5.
[272] Ch. 3 § 17.
[273] Ibid.
[274] See below § 44.
[275] Newton Princ. Lib. III. prop. 19.
[276] Lib. III. prop. 19.
[277] Lib. I. prop. 73.
[278] Lib. III. prop. 20.
[279] Ibid.
[280] Opt. B. I. part. 2. prop. 1.
[281] Newt. Opt. B. 1. part 1. experim. 5.
[282] Ibid. prop. 4.
[283] Newt. Opt. B. 1. part 2. exper. 5.
[284] Ibid exper. 6.
[285] Newton Opt. B. I. prop. 10.
[286] Ibid exp. 9.
[287] Newt. Opt. B. I. part 1. exp 15.
[288] Philos. Transact. N. 88, p. 5099.
[289] Opt B. I. par. 2. exp. 14.
[290] Ibid. exp. 10.
[291] Opt. pag. 122.
[292] Opt. B. I. part 2. exp. 11.
[293] Ibid prop. 4, 6.
[294] Opt. pag. 51.
[295] Opt. Book II. prop. 8.
[296] Opt. Book II. par. 3. prop. 2.
[297] § 17.
[298] Opt. Book II. par. 3. prop. 4.
[299] Opt. Book II. pag. 241.
[300] Ibid. pag. 224.
[301] Ibid. Obs. 17. &c.
[302] Ibid. Obs. 10.
[303] Ibid. pag. 206.
[304] Obser. 21.
[305] Observ. 5. compared with Observ. 10
[306] Ibid. prop. 5.
[307] Observ. 7.
[308] Observ. 9.
[309] Ibid prop. 7.
[310] Opt. pag. 243.
[311] Newt. Opt. B. I. part. 1. prop. I.
[312] Opt. B. I. part. 1. prop. 2.
[313] Opt. B. I. part 1. Expec. 6.
[314] Opt. pag. 67, 68, &c.
[315] Ibid. B. 1. par. 2. prop. 3.
[316] Opt. B. II. par. 3. prop. 10.
[317] Opt. B. II. par. 3. prop. 15.
[318] Ibid. par. 1. observ. 7.
[319] Ibid. Observ. 19.
[320] Opt. B. II. par. 2. pag. 199. &c.
[321] Ibid. par. 4
[322] Ibid. part. 3. prop. 13.
[323] Ibid. prop. 17.
[324] Ibid. prop. 13.
[325] Opt. Qu. 18, &c.
[326] See Concl. S. 2.
[327] B. II. Ch. 1.
[328] Opt. B. III. Obs. 1.
[329] Ibid. Obs. 2.
[330] § 2.
[331] Philos. Trans. No. 378.
[332] § 11.
[333] Philos. Transact No. 375.
[334] Ibid.
[335] Opt. B. II. part 4.
[336] Ch. 3. § 14.
[337] Opt. B. II. part 4. obs. 13.
[338] Opt. pag. 255.
[339] Ch. 3. § 18.