Project Gutenberg's The Psychology of Arithmetic, by Edward L. Thorndike This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org/license Title: The Psychology of Arithmetic Author: Edward L. Thorndike Release Date: March 29, 2012 [EBook #39300] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK THE PSYCHOLOGY OF ARITHMETIC *** Produced by Jonathan Ingram and the Online Distributed Proofreading Team at http://www.pgdp.net

THE MACMILLAN COMPANY
NEW YORK · BOSTON · CHICAGO · DALLAS
ATLANTA · SAN FRANCISCO
MACMILLAN & CO., LIMITED
LONDON · BOMBAY · CALCUTTA
MELBOURNE
THE MACMILLAN COMPANY
OF CANADA, Limited
TORONTO
TEACHERS COLLEGE, COLUMBIA
UNIVERSITY
New York
THE MACMILLAN COMPANY
1929
All rights reserved
Copyright, 1922,
By THE MACMILLAN COMPANY.
Set up and electrotyped. Published January, 1922.
Reprinted October, 1924; May, 1926; August, 1927; October, 1929.
· PRINTED IN THE UNITED STATES OF AMERICA ·
[Pg v]
Within recent years there have been three lines of advance in psychology which are of notable significance for teaching. The first is the new point of view concerning the general process of learning. We now understand that learning is essentially the formation of connections or bonds between situations and responses, that the satisfyingness of the result is the chief force that forms them, and that habit rules in the realm of thought as truly and as fully as in the realm of action.
The second is the great increase in knowledge of the amount, rate, and conditions of improvement in those organized groups or hierarchies of habits which we call abilities, such as ability to add or ability to read. Practice and improvement are no longer vague generalities, but concern changes which are definable and measurable by standard tests and scales.
The third is the better understanding of the so-called "higher processes" of analysis, abstraction, the formation of general notions, and reasoning. The older view of a mental chemistry whereby sensations were compounded into percepts, percepts were duplicated by images, percepts and images were amalgamated into abstractions and concepts, and these were manipulated by reasoning, has given way to the understanding of the laws of response to elements or aspects of situations and to many situations or elements thereof in combination. James' view of reasoning as "selection of essentials" and "thinking things together" [Pg vi] in a revised and clarified form has important applications in the teaching of all the school subjects.
This book presents the applications of this newer dynamic psychology to the teaching of arithmetic. Its contents are substantially what have been included in a course of lectures on the psychology of the elementary school subjects given by the author for some years to students of elementary education at Teachers College. Many of these former students, now in supervisory charge of elementary schools, have urged that these lectures be made available to teachers in general. So they are now published in spite of the author's desire to clarify and reinforce certain matters by further researches.
A word of explanation is necessary concerning the exercises and problems cited to illustrate various matters, especially erroneous pedagogy. These are all genuine, having their source in actual textbooks, courses of study, state examinations, and the like. To avoid any possibility of invidious comparisons they are not quotations, but equivalent problems such as represent accurately the spirit and intent of the originals.
I take pleasure in acknowledging the courtesy of Mr. S. A. Courtis, Ginn and Company, D. C. Heath and Company, The Macmillan Company, The Oxford University Press, Rand, McNally and Company, Dr. C. W. Stone, The Teachers College Bureau of Publications, and The World Book Company, in permitting various quotations.
Edward L. Thorndike.
Teachers College
Columbia University
April 1, 1920
[Pg vii]
| CHAPTER | PAGE | |
| Introduction: The Psychology of the Elementary School Subjects | xi | |
| I. | The Nature of Arithmetical Abilities | 1 |
| Knowledge of the Meanings of Numbers | ||
| Arithmetical Language | ||
| Problem Solving | ||
| Arithmetical Reasoning | ||
| Summary | ||
| The Sociology of Arithmetic | ||
| II. | The Measurement of Arithmetical Abilities | 27 |
| A Sample Measurement of an Arithmetical Ability | ||
| Ability to Add Integers | ||
| Measurements of Ability in Computation | ||
| Measurements of Ability in Applied Arithmetic: the Solution of Problems | ||
| III. | The Constitution of Arithmetical Abilities | 51 |
| The Elementary Functions of Arithmetical Learning | ||
| Knowledge of the Meaning of a Fraction | ||
| Learning the Processes of Computation | ||
| IV. | The Constitution of Arithmetical Abilities (continued) | 70 |
| The Selection of the Bonds to Be Formed | ||
| The Importance of Habit Formation | ||
| Desirable Bonds Now Often Neglected | ||
| Wasteful and Harmful Bonds | ||
| Guiding Principles | ||
| V. | The Psychology of Drill in Arithmetic: The Strength of Bonds[Pg viii] | 102 |
| The Need of Stronger Elementary Bonds | ||
| Early Mastery | ||
| The Strength of Bonds for Temporary Service | ||
| The Strength of Bonds with Technical Facts and Terms | ||
| The Strength of Bonds Concerning the Reasons for Arithmetical Processes | ||
| Propædeutic Bonds | ||
| VI. | The Psychology of Drill in Arithmetic: The Amount of Practice and the Organization of Abilities | 122 |
| The Amount of Practice | ||
| Under-learning and Over-learning | ||
| The Organization of Abilities | ||
| VII. | The Sequence of Topics: The Order of Formation of Bonds | 141 |
| Conventional versus Effective Orders | ||
| Decreasing Interference and Increasing Facilitation | ||
| Interest | ||
| General Principles | ||
| VIII. | The Distribution of Practice | 156 |
| The Problem | ||
| Sample Distributions | ||
| Possible Improvements | ||
| IX. | The Psychology of Thinking: Abstract Ideas and General Notions in Arithmetic | 169 |
| Responses to Elements and Classes | ||
| Facilitating the Analysis of Elements | ||
| Systematic and Opportunistic Stimuli to Analysis | ||
| Adaptations to Elementary-school Pupils | ||
| X. | The Psychology of Thinking: Reasoning in Arithmetic | 185 |
| The Essentials of Arithmetical Reasoning | ||
| Reasoning as the Coöperation of Organized Habits | ||
| XI. | Original Tendencies and Acquisitions before School[Pg ix] | 195 |
| The Utilization of Instinctive Interests | ||
| The Order of Development of Original Tendencies | ||
| Inventories of Arithmetical Knowledge and Skill | ||
| The Perception of Number and Quantity | ||
| The Early Awareness of Number | ||
| XII. | Interest in Arithmetic | 209 |
| Censuses of Pupils' Interests | ||
| Relieving Eye Strain | ||
| Significance for Related Activities | ||
| Intrinsic Interest in Arithmetical Learning | ||
| XIII. | The Conditions of Learning | 227 |
| External Conditions | ||
| The Hygiene of the Eyes in Arithmetic | ||
| The Use of Concrete Objects in Arithmetic | ||
| Oral, Mental, and Written Arithmetic | ||
| XIV. | The Conditions of Learning: the Problem Attitude | 266 |
| Illustrative Cases | ||
| General Principles | ||
| Difficulty and Success as Stimuli | ||
| False Inferences | ||
| XV. | Individual Differences | 285 |
| Nature and Amount | ||
| Differences within One Class | ||
| The Causes of Individual Differences | ||
| The Interrelations of Individual Differences | ||
| Bibliography of References | 302 | |
| Index | 311 | |
The psychology of the elementary school subjects is concerned with the connections whereby a child is able to respond to the sight of printed words by thoughts of their meanings, to the thought of "six and eight" by thinking "fourteen," to certain sorts of stories, poems, songs, and pictures by appreciation thereof, to certain situations by acts of skill, to certain others by acts of courtesy and justice, and so on and on through the series of situations and responses which are provided by the systematic training of the school subjects and the less systematic training of school life during their study. The aims of elementary education, when fully defined, will be found to be the production of changes in human nature represented by an almost countless list of connections or bonds whereby the pupil thinks or feels or acts in certain ways in response to the situations the school has organized and is influenced to think and feel and act similarly to similar situations when life outside of school confronts him with them.
We are not at present able to define the work of the elementary school in detail as the formation of such and such bonds between certain detached situations and certain specified responses. As elsewhere in human learning, we are at present forced to think somewhat vaguely in terms of mental functions, like "ability to read the vernacular," "ability to spell common words," "ability to add, subtract, [Pg xii] multiply, and divide with integers," "knowledge of the history of the United States," "honesty in examinations," and "appreciation of good music," defined by some general results obtained rather than by the elementary bonds which constitute them.
The psychology of the school subjects begins where our common sense knowledge of these functions leaves off and tries to define the knowledge, interest, power, skill, or ideal in question more adequately, to measure improvement in it, to analyze it into its constituent bonds, to decide what bonds need to be formed and in what order as means to the most economical attainment of the desired improvement, to survey the original tendencies and the tendencies already acquired before entrance to school which help or hinder progress in the elementary school subjects, to examine the motives that are or may be used to make the desired connections satisfying, to examine any other special conditions of improvement, and to note any facts concerning individual differences that are of special importance to the conduct of elementary school work.
Put in terms of problems, the task of the psychology of the elementary school subjects is, in each case:—
(1) What is the function? For example, just what is "ability to read"? Just what does "the understanding of decimal notation" mean? Just what are "the moral effects to be sought from the teaching of literature"?
(2) How are degrees of ability or attainment, and degrees of progress or improvement in the function or a part of the function measured? For example, how can we determine how well a pupil should write, or how hard words we expect him to spell, or what good taste we expect him to show? How can we define to ourselves what knowledge of the meaning of a fraction we shall try to secure in grade 4?[Pg xiii]
(3) What can be done toward reducing the function to terms of particular situation-response connections, whose formation can be more surely and easily controlled? For example, how far does ability to spell involve the formation one by one of bonds between the thought of almost every word in the language and the thought of that word's letters in their correct order; and how far does, say, the bond leading from the situation of the sound of ceive in receive and deceive to their correct spelling insure the correct spelling of that part of perceive? Does "ability to add" involve special bonds leading from "27 and 4" to "31," from "27 and 5" to "32," and "27 and 6" to "33"; or will the bonds leading from "7 and 4" to "11," "7 and 5" to "12" and "7 and 6" to "13" (each plus a simple inference) serve as well? What are the situations and responses that represent in actual behavior the quality that we call school patriotism?
(4) In almost every case a certain desired change of knowledge or skill or power can be attained by any one of several sets of bonds. Which of them is the best? What are the advantages of each? For example, learning to add may include the bonds "0 and 0 are 0," "0 and 1 are 1," "0 and 2 are 2," "1 and 0 are 1," "2 and 0 are 2," etc.; or these may be all left unformed, the pupil being taught the habits of entering 0 as the sum of a column that is composed of zeros and otherwise neglecting 0 in addition. Are the rules of usage worth teaching as a means toward correct speech, or is the time better spent in detailed practice in correct speech itself?
(5) A bond to be formed may be formed in any one of many degrees of strength. Which of these is, at any given stage of learning the subject, the most desirable, all things considered? For example, shall the dates of all the early settlements of North America be learned so that the exact year will be [Pg xiv] remembered for ten years, or so that the exact date will be remembered for ten minutes and the date with an error plus or minus of ten years will be remembered for a year or two? Shall the tables of inches, feet, and yards, and pints, quarts, and gallons be learned at their first appearance so as to be remembered for a year, or shall they be learned only well enough to be usable in the work of that week, which in turn fixes them to last for a month or so? Should a pupil in the first year of study of French have such perfect connections between the sounds of French words and their meanings that he can understand simple sentences containing them spoken at an ordinary rate of speaking? Or is slow speech permissible, and even imperative, on the part of the teacher, with gradual increase of rate?
(6) In almost every case, any set of bonds may produce the desired change when presented in any one of several orders. Which is the best order? What are the advantages of each? Certain systems for teaching handwriting perfect the elementary movements one at a time and then teach their combination in words and sentences. Others begin and continue with the complex movement-series that actual words require. What do the latter lose and gain? The bonds constituting knowledge of the metric system are now formed late in the pupil's course. Would it be better if they were formed early as a means of facilitating knowledge of decimal fractions?
(7) What are the original tendencies and pre-school acquisitions upon which the connection-forming of the elementary school may be based or which it has to counteract? For example, if a pupil knows the meaning of a heard word, he may read it understandingly from getting its sound, as by phonic reconstruction. What words does the average beginner so know? What are the individual differences in [Pg xv] this respect? What do the instincts of gregariousness, attention-getting, approval, and helpfulness recommend concerning group-work versus individual-work, and concerning the size of a group that is most desirable? The original tendency of the eyes is certainly not to move along a line from left to right of a page, then back in one sweep and along the next line. What is their original tendency when confronted with the printed page, and what must we do with it in teaching reading?
(8) What armament of satisfiers and annoyers, of positive and negative interests and motives, stands ready for use in the formation of the intrinsically uninteresting connections between black marks and meanings, numerical exercises and their answers, words and their spelling, and the like? School practice has tried, more or less at random, incentives and deterrents from quasi-physical pain to the most sentimental fondling, from sheer cajolery to philosophical argument, from appeals to assumed savage and primitive traits to appeals to the interest in automobiles, flying-machines, and wireless telegraphy. Can not psychology give some rules for guidance, or at least limit experimentation to its more hopeful fields?
(9) The general conditions of efficient learning are described in manuals of educational psychology. How do these apply in the case of each task of the elementary school? For example, the arrangement of school drills in addition and in short division in the form of practice experiments has been found very effective in producing interest in the work and in improvement at it. In what other arithmetical functions may we expect the same?
(10) Beside the general principles concerning the nature and causation of individual differences, there must obviously be, in existence or obtainable as a possible result of proper investigation, [Pg xvi] a great fund of knowledge of special differences relevant to the learning of reading, spelling, geography, arithmetic, and the like. What are the facts as far as known? What are the means of learning more of them? Courtis finds that a child may be specially strong in addition and yet be specially weak in subtraction in comparison with others of his age and grade. It even seems that such subtle and intricate tendencies are inherited. How far is such specialization the rule? Is it, for example, the case that a child may have a special gift for spelling certain sorts of words, for drawing faces rather than flowers, for learning ancient history rather than modern?
Such are our problems: this volume discusses them in the case of arithmetic. The student who wishes to relate the discussion to the general pedagogy of arithmetic may profitably read, in connection with this volume: The Teaching of Elementary Mathematics, by D. E. Smith ['01], The Teaching of Primary Arithmetic, by H. Suzzallo ['11], How to Teach Arithmetic, by J. C. Brown and L. D. Coffman ['14], The Teaching of Arithmetic, by Paul Klapper ['16], and The New Methods in Arithmetic, by the author ['21].
According to common sense, the task of the elementary school is to teach:—(1) the meanings of numbers, (2) the nature of our system of decimal notation, (3) the meanings of addition, subtraction, multiplication, and division, and (4) the nature and relations of certain common measures; to secure (5) the ability to add, subtract, multiply, and divide with integers, common and decimal fractions, and denominate numbers, (6) the ability to apply the knowledge and power represented by (1) to (5) in solving problems, and (7) certain specific abilities to solve problems concerning percentage, interest, and other common occurrences in business life.
This statement of the functions to be developed and improved is sound and useful so far as it goes, but it does not go far enough to make the task entirely clear. If teachers had nothing but the statement above as a guide to what changes they were to make in their pupils, they would often leave out important features of arithmetical training, and[Pg 2] put in forms of training that a wise educational plan would not tolerate. It is also the case that different leaders in arithmetical teaching, though they might all subscribe to the general statement of the previous paragraph, certainly do not in practice have identical notions of what arithmetic should be for the elementary school pupil.
The ordinary view of the nature of arithmetical learning is obscure or inadequate in four respects. It does not define what 'knowledge of the meanings of numbers' is; it does not take account of the very large amount of teaching of language which is done and should be done as a part of the teaching of arithmetic; it does not distinguish between the ability to meet certain quantitative problems as life offers them and the ability to meet the problems provided by textbooks and courses of study; it leaves 'the ability to apply arithmetical knowledge and power' as a rather mystical general faculty to be improved by some educational magic. The four necessary amendments may be discussed briefly.
Knowledge of the meanings of the numbers from one to ten may mean knowledge that 'one' means a single thing of the sort named, that two means one more than one, that three means one more than two, and so on. This we may call the series meaning. To know the meaning of 'six' in this sense is to know that it is one more than five and one less than seven—that it is between five and seven in the number series. Or we may mean by knowledge of the meanings of numbers, knowledge that two fits a collection of two units, that three fits a collection of three units, and so on, each number being a name for a certain sized collection of discrete things, such as apples, pennies, boys, balls, fingers,[Pg 3] and the other customary objects of enumeration in the primary school. This we may call the collection meaning. To know the meaning of six in this sense is to be able to name correctly any collection of six separate, easily distinguishable individual objects. In the third place, knowledge of the numbers from one to ten may mean knowledge that two is twice whatever is called one, that three is three times whatever is one, and so on. This is, of course, the ratio meaning. To know the meaning of six in this sense is to know that if _________ is one, a line half a foot long is six, that if [ __ ] is one, [ ____________ ] is about six, while if [ _ ] is one, [ ______ ] is about six, and the like. In the fourth place, the meaning of a number may be a smaller or larger fraction of its implications—its numerical relations, facts about it. To know six in this sense is to know that it is more than five or four, less than seven or eight, twice three, three times two, the sum of five and one, or of four and two, or of three and three, two less than eight—that with four it makes ten, that it is half of twelve, and the like. This we may call the 'nucleus of facts' or relational meaning of a number.
Ordinary school practice has commonly accepted the second meaning as that which it is the task of the school to teach beginners, but each of the other meanings has been alleged to be the essential one—the series idea by Phillips ['97], the ratio idea by McLellan and Dewey ['95] and Speer ['97], and the relational idea by Grube and his followers.
This diversity of views concerning what the function is that is to be improved in the case of learning the meanings of the numbers one to ten is not a trifling matter of definition, but produces very great differences in school practice. Consider, for example, the predominant value assigned to counting by Phillips in the passage quoted below, and the [Pg 4] samples of the sort of work at which children were kept employed for months by too ardent followers of Speer and Grube.
"This is essentially the counting period, and any words that can be arranged into a series furnish all that is necessary. Counting is fundamental, and counting that is spontaneous, free from sensible observation, and from the strain of reason. A study of these original methods shows that multiplication was developed out of counting, and not from addition as nearly all textbooks treat it. Multiplication is counting. When children count by 4's, etc., they accent the same as counting gymnastics or music. When a child now counts on its fingers it simply reproduces a stage in the growth of the civilization of all nations.
I would emphasize again that during the counting period there is a somewhat spontaneous development of the number series-idea which Preyer has discussed in his Arithmogenesis; that an immense momentum is given by a systematic series of names; and that these names are generally first learned and applied to objects later. A lady teacher told me that the Superintendent did not wish the teachers to allow the children to count on their fingers, but she failed to see why counting with horse-chestnuts was any better. Her children could hardly avoid using their fingers in counting other objects yet they followed the series to 100 without hesitation or reference to their fingers. This spontaneous counting period, or naming and following the series, should precede its application to objects." [D.E. Phillips, '97, p. 238.]
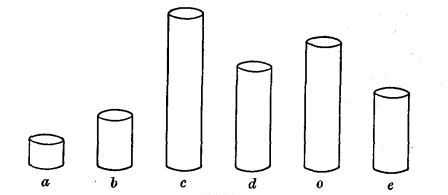 Fig. 1.
Fig. 1.
"Ratios.—1. Select solids having the relation, or ratio, of a, b, c, d, o, e.
2. Name the solids, a, b, c, d, o, e.
The means of expressing must be as freely supplied as the means of discovery. The pupil is not expected to invent terms.
3. Tell all you can about the relation of these units.
4. Unite units and tell what the sum equals.
5. Make statements like this: o less e equals b.
6. c can be separated into how many d's? into how many b's?
7. c can be separated into how many b's? What is the name of the largest unit that can be found in both c and d an exact number of times?
8. Each of the other units equals what part of c?
9. If b is 1, what is each of the other units?
10. If a is 1, what is each of the other units?
11. If b is 1, how many 1's are there in each of the other units?
12. If d is 1, how many 1's and parts of 1 in each of the other units?
13. 2 is the relation of what units?
14. 3 is the relation of what units?
15. 1⁄2 is the relation of what units?
16. 2⁄3 is the relation of what units?
17. Which units have the relation 3⁄2?
18. Which unit is 3 times as large as 1⁄2 of b?
19. c equals 6 times 1⁄3 of what unit?
20. 1⁄3 of what unit equals 1⁄6 of c?
21. What equals 1⁄2 of c? d equals how many sixths of c?
22. o equals 5 times 1⁄3 of what unit?
23. 1⁄3 of what unit equals 1⁄5 of o?
24. 2⁄3 of d equals what unit? b equals how many thirds of d?
25. 2 is the ratio of d to 1⁄3 of what unit? 3 is the ratio of d to 1⁄2 of what unit?
26. d equals 3⁄4 of what unit? 3⁄4 is the ratio of what units?" [Speer, '97, p. 9f.]
An inspection of books of the eighties which followed the "Grube method" (for example, the New Elementary Arithmetic by E.E. White ['83]) will show undue emphasis on the relational ideas. There will be over a hundred and fifty successive tasks all, or nearly all, on + 7 and − 7. There will be much written work of the sort shown below:
Add:
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 4 | 4 |
| 4 | 1 | 2 |
| —— | —— | —— |
which must have sorely tried the eyes of all concerned. Pupils are taught to "give the analysis and synthesis of each of the nine digits." Yet the author states that he does not carry the principle of the Grube method "to the extreme of useless repetition and mechanism."
It should be obvious that all four meanings have claims upon the attention of the elementary school. Four is the thing between three and five in the number series; it is the name for a certain sized collection of discrete objects; it is also the name for a continuous magnitude equal to four units—for four quarts of milk in a gallon pail as truly as for four separate quart-pails of milk; it is also, if we know it well, the thing got by adding one to three or subtracting six from ten or taking two two's or half of eight. To know the meaning of a number means to know somewhat about it in all of these respects. The difficulty has been the narrow vision of the extremists. A child must not be left interminably counting; in fact the one-more-ness of the number series can almost be had as a by-product. A child must not be restricted to exercises with collections objectified [Pg 7] as in Fig. 2 or stated in words as so many apples, oranges, hats, pens, etc., when work with measurement of continuous quantities with varying units—inches, feet, yards, glassfuls, [Pg 8] pints, quarts, seconds, minutes, hours, and the like—is so easy and so significant. On the other hand, the elaboration of artificial problems with fictitious units of measure just to have relative magnitudes as in the exercises on page 5 is a wasteful sacrifice. Similarly, special drills emphasizing the fact that eighteen is eleven and seven, twelve and six, three less than twenty-one, and the like, are simply idolatrous; these facts about eighteen, so far as they are needed, are better learned in the course of actual column-addition and -subtraction.
 Fig. 2.
Fig. 2.
The second improvement to be made in the ordinary notion of what the functions to be improved are in the case of arithmetic is to include among these functions the knowledge of certain words. The understanding of such words as both, all, in all, together, less, difference, sum, whole, part, equal, buy, sell, have left, measure, is contained in, and the like, is necessary in arithmetic as truly as is the understanding of numbers themselves. It must be provided for by the school; for pre-school and extra-school training does not furnish it, or furnishes it too late. It can be provided for much better in connection with the teaching of arithmetic than in connection with the teaching of English.
It has not been provided for. An examination of the first fifty pages of eight recent textbooks for beginners in arithmetic reveals very slight attention to this matter at the best and no attention at all in some cases. Three of the books do not even use the word sum, and one uses it only once in the fifty pages. In all the four hundred pages the word difference occurs only twenty times. When the words are used, no great ingenuity or care appears in [Pg 9] the means of making sure that their meanings are understood.
The chief reason why it has not been provided for is precisely that the common notion of what the functions are that arithmetic is to develop has left out of account this function of intelligent response to quantitative terms, other than the names of the numbers and processes.
Knowledge of language over a much wider range is a necessary element in arithmetical ability in so far as the latter includes ability to solve verbally stated problems. As arithmetic is now taught, it does include that ability, and a large part of the time of wise teaching is given to improving the function 'knowing what a problem states and what it asks for.' Since, however, this understanding of verbally stated problems may not be an absolutely necessary element of arithmetic, it is best to defer its consideration until we have seen what the general function of problem-solving is.
The third respect in which the function, 'ability in arithmetic,' needs clearer definition, is this 'problem-solving.' The aim of the elementary school is to provide for correct and economical response to genuine problems, such as knowing the total due for certain real quantities at certain real prices, knowing the correct change to give or get, keeping household accounts, calculating wages due, computing areas, percentages, and discounts, estimating quantities needed of certain materials to make certain household or shop products, and the like. Life brings these problems usually either with a real situation (as when one buys and counts the cost and his change), or with a situation that one imagines or describes to himself (as when one figures out how much money he must save per week to be able to buy [Pg 10] a forty-dollar bicycle before a certain date). Sometimes, however, the problem is described in words to the person who must solve it by another person (as when a life insurance agent says, 'You pay only 25 cents a week from now till—and you get $250 then'; or when an employer says, 'Your wages would be 9 dollars a week, with luncheon furnished and bonuses of such and such amounts'). Sometimes also the problem is described in printed or written words to the person who must solve it (as in an advertisement or in the letter of a customer asking for an estimate on this or that). The problem may be in part real, in part imagined or described to oneself, and in part described to one orally or in printed or written words (as when the proposed articles for purchase lie before one, the amount of money one has in the bank is imagined, the shopkeeper offers 10 percent discount, and the printed price list is there to be read).
To fit pupils to solve these real, personally imagined, or self-described problems, and 'described-by-another' problems, schools have relied almost exclusively on training with problems of the last sort only. The following page taken almost at random from one of the best recent textbooks could be paralleled by thousands of others; and the oral problems put by teachers have, as a rule, no real situation supporting them.
1. At 70 cents per 100 pounds, what will be the amount of duty on an invoice of 3622 steel rails, each rail being 27 feet long and weighing 60 pounds to the yard?
2. A man had property valued at $6500. What will be his taxes at the rate of $10.80 per $1000?
3. Multiply seventy thousand fourteen hundred-thousandths by one hundred nine millionths, and divide the product by five hundred forty-five.
4. What number multiplied by 43¾ will produce 2655⁄8?
[Pg 11]5. What decimal of a bushel is 3 quarts?
6. A man sells 5⁄8 of an acre of land for $93.75. What would be the value of his farm of 150¾ acres at the same rate?
7. A coal dealer buys 375 tons coal at $4.25 per ton of 2240 pounds. He sells it at $4.50 per ton of 2000 pounds. What is his profit?
8. Bought 60 yards of cloth at the rate of 2 yards for $5, and 80 yards more at the rate of 4 yards for $9. I immediately sold the whole of it at the rate of 5 yards for $12. How much did I gain?
9. A man purchased 40 bushels of apples at $1.50 per bushel. Twenty-five hundredths of them were damaged, and he sold them at 20 cents per peck. He sold the remainder at 50 cents per peck. How much did he gain or lose?
10. If oranges are 37½ cents per dozen, how many boxes, each containing 480, can be bought for $60?
11. A man can do a piece of work in 18¾ days. What part of it can he do in 62⁄3 days?
12. How old to-day is a boy that was born Oct. 29, 1896? [Walsh, '06, Part I, p. 165.]
As a result, teachers and textbook writers have come to think of the functions of solving arithmetical problems as identical with the function of solving the described problems which they give in school in books, examination papers, and the like. If they do not think explicitly that this is so, they still act in training and in testing pupils as if it were so.
It is not. Problems should be solved in school to the end that pupils may solve the problems which life offers. To know what change one should receive after a given real purchase, to keep one's accounts accurately, to adapt a recipe for six so as to make enough of the article for four persons, to estimate the amount of seed required for a plot of a given size from the statement of the amount required per acre, to make with surety the applications that the household, small stores, and ordinary trades require—such is the ability that the elementary school should develop. [Pg 12] Other things being equal, the school should set problems in arithmetic which life then and later will set, should favor the situations which life itself offers and the responses which life itself demands.
Other things are not always equal. The same amount of time and effort will often be more productive toward the final end if directed during school to 'made-up' problems. The keeping of personal financial accounts as a school exercise is usually impracticable, partly because some of the children have no earnings or allowance—no accounts to keep, and partly because the task of supervising work when each child has a different problem is too great for the teacher. The use of real household and shop problems will be easy only when the school program includes the household arts and industrial education, and when these subjects themselves are taught so as to improve the functions used by real life. Very often the most efficient course is to make sure that arithmetical procedures are applied to the real and personally initiated problems which they fit, by having a certain number of such problems arise and be solved; then to make sure that the similarity between these real problems and certain described problems of the textbook or teacher's giving is appreciated; and then to give the needed drill work with described problems. In many cases the school practice is fairly well justified in assuming that solving described problems will prepare the pupil to solve the corresponding real problems actually much better than the same amount of time spent on the real problems themselves.
All this is true, yet the general principle remains that, other things being equal, the school should favor real situations, should present issues as life will present them.
Where other things make the use of verbally described [Pg 13] problems of the ordinary type desirable, these should be chosen so as to give a maximum of preparation for the real applications of arithmetic in life. We should not, for example, carelessly use any problem that comes to mind in applying a certain principle, but should stop to consider just what the situations of life really require and show clearly the application of that principle. For example, contrast these two problems applying cancellation:—
A. A man sold 24 lambs at $18 apiece on each of six days, and bought 8 pounds of metal with the proceeds. How much did he pay per ounce for the metal?
B. How tall must a rectangular tank 16" long by 8" wide be to hold as much as a rectangular tank 24" by 18" by 6"?
The first problem not only presents a situation that would rarely or never occur, but also takes a way to find the answer that would not, in that situation, be taken since the price set by another would determine the amount.
Much thought and ingenuity should in the future be expended in eliminating problems whose solution does not improve the real function to be improved by applied arithmetic, or improves it at too great cost, and in devising problems which prepare directly for life's demands and still can fit into a curriculum that can be administered by one teacher in charge of thirty or forty pupils, under the limitations of school life.
The following illustrations will to some extent show concretely what the ability to apply the knowledge and power represented by abstract or pure arithmetic—the so-called fundamentals—in solving problems should mean and what it should not mean.
Keeping the scores and deciding which side beat and by how much in appropriate classroom games, spelling matches, and the like.
Computing costs, making and inspecting change, taking inventories, and the like with a real or play store.
Mapping the school garden, dividing it into allotments, planning for the purchase of seeds, and the like.
Measuring one's own achievement and progress in tests of word-knowledge, spelling, addition, subtraction, speed of writing, and the like. Measuring the rate of improvement per hour of practice or per week of school life, and the like.
Estimating costs of food cooked in the school kitchen, articles made in the school shops, and the like.
Computing the cost of telegrams, postage, expressage, for a real message or package, from the published tariffs.
Computing costs from mail order catalogues and the like.
The samples given here all concern the subtraction of fractions. Samples concerning any other arithmetical principle may be found in the appropriate pages of any text which contains problem-material selected with consideration of life's needs.
1. Dora is making jelly. The recipe calls for 24 cups of sugar and she has only 21½. She has no time to go to the store so she has to borrow the sugar from a neighbor. How much must she get?
Subtract
| 24 | Think "½ and ½ = 1." Write ½. |
| 21½ | Think "2 and 2 = 4." Write the 2. |
| ——— | |
| 2½ |
2. A box full of soap weighs 29½ lb. The empty box weighs 3½ lb. How much does the soap alone weigh?
3. On July 1, Mr. Lewis bought a 50-lb. bag of ice-cream salt. On July 15 there were just 11½ lb. left. How much had he used in the two weeks?
4. Grace promised to pick 30 qt. blueberries for her mother. So far she has picked 18½ qt. How many more quarts must she pick?
This table of numbers tells what Nell's baby sister Mary weighed every two months from the time she was born till she was a year old.
| Weight of Mary Adams | |
|---|---|
| When born | 73⁄8 lb. |
| 2 months old | 111⁄4 lb. |
| 4 months old | 141⁄8 lb. |
| 6 months old | 153⁄4 lb. |
| 8 months old | 175⁄8 lb. |
| 10 months old | 191⁄2 lb. |
| 12 months old | 213⁄8 lb. |
1. How much did the Adams baby gain in the first two months?
2. How much did the Adams baby gain in the second two months?
3. In the third two months?
4. In the fourth two months?
5. From the time it was 8 months old till it was 10 months old?
6. In the last two months?
7. From the time it was born till it was 6 months old?
1. Helen's exact average for December was 871⁄3. Kate's was 841⁄2. How much higher was Helen's than Kate's?
871⁄3
841⁄2
———
How do you think of 1⁄2 and 1⁄3?
How do you think of 12⁄6?
How do you change the 4?
2. Find the exact average for each girl in the following list. Write the answers clearly so that you can see them easily. You will use them in solving problems 3, 4, 5, 6, 7, and 8.
| Alice | Dora | Emma | Grace | Louise | Mary | Nell | Rebecca | |
|---|---|---|---|---|---|---|---|---|
| Reading | 91 | 87 | 83 | 81 | 79 | 77 | 76 | 73 |
| Language | 88 | 78 | 82 | 79 | 73 | 78 | 73 | 75 |
| Arithmetic | 89 | 85 | 79 | 75 | 84 | 87 | 89 | 80 |
| Spelling | 90 | 79 | 75 | 80 | 82 | 91 | 68 | 81 |
| Geography | 91 | 87 | 83 | 75 | 78 | 85 | 73 | 79 |
| Writing | 90 | 88 | 75 | 72 | 93 | 92 | 95 | 78 |
3. Which girl had the highest average?
4. How much higher was her average than the next highest?
5. How much difference was there between the highest and the lowest girl?
6. Was Emma's average higher or lower than Louise's? How much?
7. How much difference was there between Alice's average and Dora's?
8. How much difference was there between Mary's average and Nell's?
9. Write five other problems about these averages, and solve each of them.
Will has XXI marbles, XII jackstones, XXXVI pieces of string. How many things had he?
George's kite rose CDXXXV feet and Tom's went LXIII feet higher. How high did Tom's kite rise?
If from DCIV we take CCIV the result will be a number IV times as large as the number of dollars Mr. Dane paid for his horse. How much did he pay for his horse?
Hannah has 5⁄8 of a dollar, Susie 7⁄25, Nellie 3⁄4, Norah 13⁄16. How much money have they all together?
A man saves 317⁄80 dollars a week. How much does he save in a year?
A tree fell and was broken into 4 pieces, 131⁄6 feet, 103⁄7 feet, 81⁄2 feet, and 716⁄21 feet long. How tall was the tree?[Pg 17]
Annie's father gave her 20 apples to divide among her friends. She gave each one 22⁄9 apples apiece. How many playmates had she?
John had 172⁄5 apples. He divided his whole apples into fifths. How many pieces had he in all?
A landlady has 33⁄7 pies to be divided among her 8 boarders. How much will each boarder receive?
There are twenty columns of spelling words in Mary's lesson and 16 words in each column. How many words are in her lesson?
There are 9 nuts in a pint. How many pints in a pile of 5,888,673 nuts?
The Adams school contains eight rooms; each room contains 48 pupils; if each pupil has eight cents, how much have they together?
A pile of wood in the form of a cube contains 15½ cords. What are the dimensions to the nearest inch?
A man 6 ft. high weighs 175 lb. How tall is his wife who is of similar build, and weighs 125 lb.?
A stick of timber is in the shape of the frustum of a square pyramid, the lower base being 22 in. square and the upper 14 in. square. How many cubic feet in the log, if it is 22 ft. long?
Mr. Ames, being asked his age, replied: "If you cube one half of my age and add 41,472 to the result, the sum will be one half the cube of my age. How old am I?"
These samples, just given, of the kind of problem-solving that should not be emphasized in school training refer in some cases to books of forty years back, but the following represent the results of a collection made in 1910 from books then in excellent repute. It required only about an hour to collect them; and I am confident that a thousand such problems describing situations that the pupil will never encounter in real life, or putting questions that he will never be asked in real life, could easily be found in any ten textbooks of the decade from 1900 to 1910.
If there are 250 kernels of corn on one ear, how many are there on 24 ears of corn the same size?
Maud is four times as old as her sister, who is 4 years old. What is the sum of their ages?
If the first century began with the year 1, with what year does it end?
Every spider has 8 compound eyes. How many eyes have 21 spiders?
A nail 4 inches long is driven through a board so that it projects 1.695 inches on one side and 1.428 on the other. How thick is the board?
Find the perimeter of an envelope 5 in. by 3¼ in.
How many minutes in 5⁄9 of 9⁄4 of an hour?
Mrs. Knox is 3⁄4 as old as Mr. Knox, who is 48 years old. Their son Edward is 4⁄9 as old as his mother. How old is Edward?
Suppose a pie to be exactly round and 10½ miles in diameter. If it were cut into 6 equal pieces, how long would the curved edge of each piece be?
81⁄3% of a class of 36 boys were absent on a rainy day. 331⁄3% of those present went out of the room to the school yard. How many were left in the room?
Just after a ton of hay was weighed in market, a horse ate one pound of it. What was the ratio of what he ate to what was left?
If a fan having 15 rays opens out so that the outer rays form a straight line, how many degrees are there between any two adjacent rays?
One half of the distance between St. Louis and New Orleans is 280 miles more than 1⁄10 of the distance; what is the distance between these places?
If the pressure of the atmosphere is 14.7 lb. per square inch what is the pressure on the top of a table 1¼ yd. long and 2⁄3 yd. wide?
13⁄28 of the total acreage of barley in 1900 was 100,000 acres; what was the total acreage?
What is the least number of bananas that a mother can exactly divide between her 2 sons, or among her 4 daughters, or among all her children?
If Alice were two years older than four times her actual age she would be as old as her aunt, who is 38 years old. How old is Alice?
Three men walk around a circular island, the circumference of which is 360 miles. A walks 15 miles a day, B 18 miles a day, and C 24 miles a day. If they start together and walk in the same direction, how many days will elapse before they will be together again?
With only thirty or forty dollars a year to spend on a pupil's education, of which perhaps eight dollars are spent[Pg 19] on improving his arithmetical abilities, the immediate guidance of his responses to real situations and personally initiated problems has to be supplemented largely by guidance of his responses to problems described in words, diagrams, pictures, and the like. Of these latter, words will be used most often. As a consequence the understanding of the words used in these descriptions becomes a part of the ability required in arithmetic. Such word knowledge is also required in so far as the problems to be solved in real life are at times described, as in advertisements, business letters, and the like.
This is recognized by everybody in the case of words like remainder, profit, loss, gain, interest, cubic capacity, gross, net, and discount, but holds equally of let, suppose, balance, average, total, borrowed, retained, and many such semi-technical words, and may hold also of hundreds of other words unless the textbook and teacher are careful to use only words and sentence structures which daily life and the class work in English have made well known to the pupils. To apply arithmetic to a problem a pupil must understand what the problem is; problem-solving depends on problem-reading. In actual school practice training in problem-reading will be less and less necessary as we get rid of problems to be solved simply for the sake of solving them, unnecessarily unreal problems, and clumsy descriptions, but it will remain to some extent as an important joint task for the 'arithmetic' and 'reading' of the elementary school.
The last respect in which the nature of arithmetical abilities requires definition concerns arithmetical reasoning. An adequate treatment of the reasoning that may be expected of pupils in the elementary school and of the most [Pg 20] efficient ways to encourage and improve it cannot be given until we have studied the formation of habits. For reasoning is essentially the organization and control of habits of thought. Certain matters may, however, be decided here. The first concerns the use of computation and problems merely for discipline,—that is, the emphasis on training in reasoning regardless of whether the problem is otherwise worth reasoning about. It used to be thought that the mind was a set of faculties or abilities or powers which grew strong and competent by being exercised in a certain way, no matter on what they were exercised. Problems that could not occur in life, and were entirely devoid of any worthy interest, save the intellectual interest in solving them, were supposed to be nearly or quite as useful in training the mind to reason as the genuine problems of the home, shop, or trade. Anything that gave the mind a chance to reason would do; and pupils labored to find when the minute hand and hour hand would be together, or how many sheep a shepherd had if half of what he had plus ten was one third of twice what he had!
We now know that the training depends largely on the particular data used, so that efficient discipline in reasoning requires that the pupil reason about matters of real importance. There is no magic essence or faculty of reasoning that works in general and irrespective of the particular facts and relations reasoned about. So we should try to find problems which not only stimulate the pupil to reason, but also direct his reasoning in useful channels and reward it by results that are of real significance. We should replace the purely disciplinary problems by problems that are also valuable as special training for important particular situations of life. Reasoning sought for reasoning's sake alone is too wasteful an expenditure of time and is also likely to be inferior as reasoning.
The second matter concerns the relative merits of 'catch' problems, where the pupil has to go against some customary habit of thinking, and what we may call 'routine' problems, where the regular ways of thinking that have served him in the past will, except for some blunder, guide him rightly.
Consider, for example, these four problems:
1. "A man bought ten dozen eggs for $2.50 and sold them for 30 cents a dozen. How many cents did he lose?"
2. "I went into Smith's store at 9 A.M. and remained until 10 A.M. I bought six yards of gingham at 40 cents a yard and three yards of muslin at 20 cents a yard and gave a $5.00 bill. How long was I in the store?"
3. "What must you divide 48 by to get half of twice 6?"
4. "What must you add to 19 to get 30?"
The 'catch' problem is now in disrepute, the wise teacher feeling by a sort of intuition that to willfully require a pupil to reason to a result sharply contrary to that to which previous habits lead him is risky. The four illustrations just given show, however, that mere 'catchiness' or 'contra-previous-habit-ness' in a problem is not enough to condemn it. The fourth problem is a catch problem, but so useful a one that it has been adopted in many modern books as a routine drill! The first problem, on the contrary, all, save those who demand no higher criterion for a problem than that it make the pupil 'think,' would reject. It demands the reversal of fixed habits to no valid purpose; for in life the question in such case would never (or almost never) be 'How many cents did he lose?' but 'What was the result?' or simply 'What of it?' This problem weakens without excuse the child's confidence in the training he has had. Problems like (2) are given by teachers of excellent reputation, but probably do more harm than good. If a pupil should interrupt his teacher during the recitation in arithmetic by [Pg 22] saying, "I got up at 7 o'clock to multiply 9 by 2¾ and got 24¾ for my answer; was that the right time to get up?" the teacher would not thank fortune for the stimulus to thought but would think the child a fool. Such catch questions may be fairly useful as an object lesson on the value of search for the essential element in a situation if a great variety of them are given one after another with routine problems intermixed and with warning of the general nature of the exercise at the beginning. Even so, it should be remembered that reasoning should be chiefly a force organizing habits, not opposing them; and also that there are enough bad habits to be opposed to give all necessary training. Fabricated puzzle situations wherein a peculiar hidden element of the situation makes the good habits called up by the situation misleading are useful therefore rather as a relief and amusing variation in arithmetical work than as stimuli to thought.
Problems like the third quoted above we might call puzzling rather than 'catch' problems. They have value as drills in analysis of a situation into its elements that will amuse the gifted children, and as tests of certain abilities. They also require that of many confusing habits, the right one be chosen, rather than that ordinary habits be set aside by some hidden element in the situation. Not enough is known about their effect to enable us to decide whether or not the elementary school should include special facility with them as one of the arithmetical functions that it specially trains.
The fourth 'catch' quoted above, which all would admit is a good problem, is good because it opposes a good habit for the sake of another good habit, forces the analysis of an element whose analysis life very much requires, and does it with no obvious waste. It is not safe to leave a child with the one habit of responding to 'add, 19, 30' by 49, for in[Pg 23] life the 'have 19, must get .... to have 30' situation is very frequent and important.
On the whole, the ordinary problems which ordinary life proffers seem to be the sort that should be reasoned out, though the elementary school may include the less noxious forms of pure mental gymnastics for those pupils who like them.
These discussions of the meanings of numbers, the linguistic demands of arithmetic, the distinction between scholastic and real applications of arithmetic, and the possible restrictions of training in reasoning,—may serve as illustrations of the significance of the question, "What are the functions that the elementary school tries to improve in its teaching of arithmetic?" Other matters might well be considered in this connection, but the main outline of the work of the elementary school is now fairly clear. The arithmetical functions or abilities which it seeks to improve are, we may say:—
(1) Working knowledge of the meanings of numbers as names for certain sized collections, for certain relative magnitudes, the magnitude of unity being known, and for certain centers or nuclei of relations to other numbers.
(2) Working knowledge of the system of decimal notation.
(3) Working knowledge of the meanings of addition, subtraction, multiplication, and division.
(4) Working knowledge of the nature and relations of certain common measures.
(5) Working ability to add, subtract, multiply, and divide with integers, common and decimal fractions, and denominate numbers, all being real positive numbers.
(6) Working knowledge of words, symbols, diagrams, and[Pg 24] the like as required by life's simpler arithmetical demands or by economical preparation therefor.
(7) The ability to apply all the above as required by life's simpler arithmetical demands or by economical preparation therefor, including (7 a) certain specific abilities to solve problems concerning areas of rectangles, volumes of rectangular solids, percents, interest, and certain other common occurrences in household, factory, and business life.
The phrase 'life's simpler arithmetical demands' is necessarily left vague. Just what use is being made of arithmetic in this country in 1920 by each person therein, we know only very roughly. What may be called a 'sociology' of arithmetic is very much needed to investigate this matter. For rare or difficult demands the elementary school should not prepare; there are too many other desirable abilities that it should improve.
A most interesting beginning at such an inventory of the actual uses of arithmetic has been made by Wilson ['19] and Mitchell.[2] Although their studies need to be much extended and checked by other methods of inquiry, two main facts seem fairly certain.
First, the great majority of people in the great majority of their doings use only very elementary arithmetical processes. In 1737 cases of addition reported by Wilson, seven eighths were of five numbers or less. Over half of the multipliers reported were one-figure numbers. Over 95 per cent of the fractions operated with were included in this list: 1⁄2 1⁄4 3⁄4 1⁄3 2⁄3 1⁄8 3⁄8 1⁄5 2⁄5 4⁄5. Three fourths of all the cases reported were simple one-step computations with integers or United States money.
Second, they often use these very elementary processes, not because such are the quickest and most convenient, but because they have lost, or maybe never had, mastery of the more advanced processes which would do the work better. The 5 and 10 cent stores, the counter with "Anything on this counter for 25¢," and the arrangements for payments on the installment plan are familiar instances of human avoidance of arithmetic. Wilson found very slight use of decimals; and Mitchell found men computing with [Pg 25] 49ths as common fractions when the use of decimals would have been more efficient. If given 120 seconds to do a test like that shown below, leading lawyers, physicians, manufacturers, and business men and their wives will, according to my experience, get only about half the work right. Many women, finding on their meat bill "73⁄8 lb. roast beef $2.36," will spend time and money to telephone the butcher asking how much roast beef was per pound, because they have no sure power in dividing by a mixed number.
Test
Perform the operations indicated. Express all fractions in answers in lowest terms.
Add:
| 3⁄4 + 1⁄6 + .25 |
4 yr. 6 mo. 1 yr. 2 mo. 6 yr. 9 mo. 3 yr. 6 mo. 4 yr. 5 mo. |
Subtract:
| 8.6 − 6.05007 7⁄8 − 2⁄3 = 57⁄16 − 23⁄16 = |
Multiply:
| 7 × 8 × 4½ = | 29 ft. | 6 in. 8 |
Divide:
4½ ÷ 7 =
It seems probable that the school training in arithmetic of the past has not given enough attention to perfecting the more elementary abilities. And we shall later find further evidence of this. On the other hand, the fact that people in general do not at present use a process may not mean that they ought not to use it.
Life's simpler arithmetical demands certainly do not include matters like the rules for finding cube root or true discount, which no sensible person uses. They should not include matters like computing the lateral surface or volume of pyramids and cones, or knowing the customs of plasterers and paper hangers, which are used only by highly specialized trades. They should not include matters like interest on call loans, usury, exact interest, and[Pg 26] the rediscounting of notes, which concern only brokers, bank clerks, and rich men. They should not include the technique of customs which are vanishing from efficient practice, such as simple interest on amount for times longer than a year, days of grace, or extremes and means in proportions. They should not include any elaborate practice with very large numbers, or decimals beyond thousandths, or the addition and subtraction of fractions which not one person in a hundred has to add or subtract oftener than once a year.
When we have an adequate sociology of arithmetic, stating accurately just who should use each arithmetical ability and how often, we shall be able to define the task of the elementary school in this respect. For the present, we may proceed by common sense, guided by two limiting rules. The first is,—"It is no more desirable for the elementary school to teach all the facts of arithmetic than to teach all the words in the English language, or all the topography of the globe, or all the details of human physiology." The second is,—"It is not desirable to eliminate any element of arithmetical training until you have something better to put in its place."
One of the best ways to clear up notions of what the functions are which schools should develop and improve is to get measures of them. If any given knowledge or skill or power or ideal exists, it exists in some amount. A series of amounts of it, varying from less to more, defines the ability itself in a way that no general verbal description can do. Thus, a series of weights, 1 lb., 2 lb., 3 lb., 4 lb., etc., helps to tell us what we mean by weight. By finding a series of words like only, smoke, another, pretty, answer, tailor, circus, telephone, saucy, and beginning, which are spelled correctly by known and decreasing percentages of children of the same age, or of the same school grade, we know better what we mean by 'spelling-difficulty.' Indeed, until we can measure the efficiency and improvement of a function, we are likely to be vague and loose in our ideas of what the function is.
Consider first, as a sample, the measurement of ability to add integers.
The following were the examples used in the measurements made by Stone ['08]:[Pg 28]
| 596 | 4695 | |
| 428 | 872 | |
| 2375 | 94 | 7948 |
| 4052 | 75 | 6786 |
| 6354 | 304 | 567 |
| 260 | 645 | 858 |
| 5041 | 984 | 9447 |
| 1543 | 897 | 7499 |
| ——— | ——— | ——— |
The scoring was as follows: Credit of 1 for each column added correctly. Stone combined measures of other abilities with this in a total score for amount done correctly in 12 minutes. Stone also scored the correctness of the additions in certain work in multiplication.
Courtis uses a sheet of twenty-four tasks or 'examples,' each consisting of the addition of nine three-place numbers as shown below. Eight minutes is allowed. He scores the amount done by the number of examples, and also scores the number of examples done correctly, but does not suggest any combination of these two into a general-efficiency score.
927
379
756
837
924
110
854
965
344
———
The author long ago proposed that pupils be measured also with series like a to g shown below, in which the difficulty increases step by step.
| a. | 3 | 2 | 2 | 3 | 2 | 2 | 1 | 2 |
| 2 | 3 | 1 | 2 | 4 | 5 | 5 | 1 | |
| 4 | 2 | 3 | 3 | 3 | 2 | 2 | 2 | |
| — | — | — | — | — | — | — | — |
| b. | 21 | 32 | 12 | 24 | 34 | 34 | 22 | 12 |
| 23 | 12 | 52 | 31 | 33 | 12 | 23 | 13 | |
| 24 | 25 | 15 | 14 | 32 | 23 | 43 | 61 | |
| — | — | — | — | — | — | — | — |
| c. | 22 | 3 | 4 | 35 | 32 | 83 | 22 | 3 |
| 3 | 31 | 3 | 2 | 33 | 11 | 3 | 21 | |
| 38 | 45 | 52 | 52 | 2 | 4 | 33 | 64 | |
| — | — | — | — | — | — | — | — |
| d. | 30 | 20 | 10 | 22 | 10 | 20 | 52 | 12 |
| 20 | 50 | 40 | 43 | 30 | 4 | 6 | 22 | |
| 40 | 17 | 24 | 13 | 40 | 23 | 30 | 44 | |
| — | — | — | — | — | — | — | — |
| e. | 4 | 5 | 20 | 12 | 12 | 20 | 10 | |
| 20 | 30 | 3 | 40 | 4 | 11 | 20 | 20 | |
| 10 | 30 | 20 | 4 | 1 | 23 | 7 | 2 | |
| 20 | 2 | 40 | 23 | 40 | 11 | 10 | 30 | |
| 20 | 20 | 10 | 11 | 20 | 22 | 30 | 25 | |
| — | — | — | — | — | — | — | — |
| f. | 19 | 9 | 9 | |||||
| 14 | 2 | 19 | 24 | 9 | 4 | 13 | ||
| 9 | 14 | 13 | 12 | 13 | 13 | 9 | 14 | |
| 17 | 23 | 13 | 15 | 15 | 34 | 12 | 25 | |
| 26 | 29 | 18 | 19 | 25 | 28 | 18 | 39 | |
| — | — | — | — | — | — | — | — |
| g. | 13 | |||||||
| 13 | 9 | 14 | 12 | 9 | ||||
| 9 | 13 | 12 | 9 | 14 | 24 | |||
| 23 | 19 | 19 | 29 | 9 | 9 | 13 | 21 | |
| 28 | 26 | 26 | 14 | 8 | 8 | 29 | 23 | |
| 29 | 16 | 15 | 19 | 17 | 19 | 19 | 22 | |
| — | — | — | — | — | — | — | — |
Woody ['16] has constructed his well-known tests on this principle, though he uses only one example at each step of difficulty instead of eight or ten as suggested above. His test, so far as addition of integers goes, is:—
SERIES A. ADDITION SCALE (in part)
By Clifford Woody
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
|---|---|---|---|---|---|---|---|---|
| 2 3 — |
2 4 3 — |
17 2 — |
53 45 — |
72 26 — |
60 37 — |
3 + 1 = | 2 + 5 + 1 = | 20 10 2 30 25 — |
| (10) | (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) |
| 21 33 35 — |
32 59 17 — |
43 1 2 13 — |
23 25 16 — |
25 + 42 = | 100 33 45 201 46 — |
9 24 12 15 19 — |
199 194 295 156 —— |
2563 1387 4954 2065 —— |
| (19) | (20) | (21) | (22) | |||||
| $ .75 1.25 .49 —— |
$12.50 16.75 15.75 —— |
$8.00 5.75 2.33 4.16 .94 6.32 —— |
547 197 685 678 456 393 525 240 152 —— |
In his original report, Woody gives no scheme for scoring an individual, wisely assuming that, with so few samples at each degree of difficulty, a pupil's score would be too unreliable for individual diagnosis. The test is reliable for a class; and for a class Woody used the degree of difficulty such that a stated fraction of the class can do the work correctly, if twenty minutes is allowed for the thirty-eight examples of the entire test.
The measurement of even so simple a matter as the efficiency of a pupil's responses to these tests in adding integers is really rather complex. There is first of all the problem of combining speed and accuracy into some single estimate. Stone gives no credit for a column unless it is correctly added. Courtis evades the difficulty by reporting both number done and number correct. The author's scheme, which gives specified weights to speed and accuracy at each step of the series, involves a rather intricate computation.
This difficulty of equating speed and accuracy in adding means precisely that we have inadequate notions of what the ability is that the elementary school should improve. Until, for example, we have decided whether, for a given group of pupils, fifteen Courtis attempts with ten right, is or is not a better achievement than ten Courtis attempts with nine right, we have not decided just what the business of the teacher of addition is, in the case of that group of pupils.
There is also the difficulty of comparing results when short and long columns are used. Correctness with a short column, say of five figures, testifies to knowledge of the process and to the power to do four successive single additions without error. Correctness with a long column, say of ten digits, testifies to knowledge of the process and to the power to do nine successive single additions without error. Now if a pupil's precision was such that on the average he[Pg 32] made one mistake in eight single additions, he would get about half of his five-digit columns right and almost none of his ten-digit columns right. (He would do this, that is, if he added in the customary way. If he were taught to check results by repeated addition, by adding in half-columns and the like, his percentages of accurate answers might be greatly increased in both cases and be made approximately equal.) Length of column in a test of addition under ordinary conditions thus automatically overweights precision in the single additions as compared with knowledge of the process, and ability at carrying.
Further, in the case of a column of whatever size, the result as ordinarily scored does not distinguish between one, two, three, or more (up to the limit) errors in the single additions. Yet, obviously, a pupil who, adding with ten-digit columns, has half of his answer-figures wrong, probably often makes two or more errors within a column, whereas a pupil who has only one column-answer in ten wrong, probably almost never makes more than one error within a column. A short-column test is then advisable as a means of interpreting the results of a long-column test.
Finally, the choice of a short-column or of a long-column test is indicative of the measurer's notion of the kind of efficiency the world properly demands of the school. Twenty years ago the author would have been readier to accept a long-column test than he now is. In the world at large, long-column addition is being more and more done by machine, though it persists still in great frequency in the bookkeeping of weekly and monthly accounts in local groceries, butcher shops, and the like.
The search for a measure of ability to add thus puts the problem of speed versus precision, and of short-column versus long-column additions clearly before us. The latter[Pg 33] problem has hardly been realized at all by the ordinary definitions of ability to add.
It may be said further that the measurement of ability to add gives the scientific student a shock by the lack of precision found everywhere in schools. Of what value is it to a graduate of the elementary school to be able to add with examples like those of the Courtis test, getting only eight out of ten right? Nobody would pay a computer for that ability. The pupil could not keep his own accounts with it. The supposed disciplinary value of habits of precision runs the risk of turning negative in such a case. It appears, at least to the author, imperative that checking should be taught and required until a pupil can add single columns of ten digits with not over one wrong answer in twenty columns. Speed is useful, especially indirectly as an indication of control of the separate higher-decade additions, but the social demand for addition below a certain standard of precision is nil, and its disciplinary value is nil or negative. This will be made a matter of further study later.
Measurements of these abilities may be of two sorts—(1) of the speed and accuracy shown in doing one same sort of task, as illustrated by the Courtis test for addition shown on page 28; and (2) of how hard a task can be done perfectly (or with some specified precision) within a certain assigned time or less, as illustrated by the author's rough test for addition shown on pages 28 and 29, and by the Woody tests, when extended to include alternative forms.
The Courtis tests, originated as an improvement on the Stone tests and since elaborated by the persistent devotion of their author, are a standard instrument of the first sort for measuring the so-called 'fundamental' arithmetical[Pg 34] abilities with integers. They are shown on this and the following page.
Tests of the second sort are the Woody tests, which include operations with integers, common and decimal fractions, and denominate numbers, the Ballou test for common fractions ['16], and the "Ladder" exercises of the Thorndike arithmetics. Some of these are shown on pages 36 to 41.
Courtis Test
Arithmetic. Test No. 1. Addition
Series B
You will be given eight minutes to find the answers to as many of these addition examples as possible. Write the answers on this paper directly underneath the examples. You are not expected to be able to do them all. You will be marked for both speed and accuracy, but it is more important to have your answers right than to try a great many examples.
| 927 | 297 | 136 | 486 | 384 | 176 | 277 | 837 |
| 379 | 925 | 340 | 765 | 477 | 783 | 445 | 882 |
| 756 | 473 | 988 | 524 | 881 | 697 | 682 | 959 |
| 837 | 983 | 386 | 140 | 266 | 200 | 594 | 603 |
| 924 | 315 | 353 | 812 | 679 | 366 | 481 | 118 |
| 110 | 661 | 904 | 466 | 241 | 851 | 778 | 781 |
| 854 | 794 | 547 | 355 | 796 | 535 | 849 | 756 |
| 965 | 177 | 192 | 834 | 850 | 323 | 157 | 222 |
| 344 | 124 | 439 | 567 | 733 | 229 | 953 | 525 |
| —— | —— | —— | —— | —— | —— | —— | —— |
and sixteen more addition examples of nine three-place numbers.
Courtis Test
Arithmetic. Test No. 2. Subtraction
Series B
You will be given four minutes to find the answers to as many of these subtraction examples as possible. Write the answers on this paper directly underneath the examples. You are not[Pg 35] expected to be able to do them all. You will be marked for both speed and accuracy, but it is more important to have your answers right than to try a great many examples.
| 107795491 | 75088824 | 91500053 | 87939983 |
| 77197029 | 57406394 | 19901563 | 72207316 |
| ————— | ————— | ————— | ————— |
and twenty more tasks of the same sort.
Courtis Test
Arithmetic. Test No. 3. Multiplication
Series B
You will be given six minutes to work as many of these multiplication examples as possible. You are not expected to be able to do them all. Do your work directly on this paper; use no other. You will be marked for both speed and accuracy, but it is more important to get correct answers than to try a large number of examples.
| 8246 | 7843 | 4837 | 3478 | 6482 |
| 29 | 702 | 83 | 15 | 46 |
| —— | —— | —— | —— | —— |
and twenty more multiplication examples of the same sort.
Courtis Test
Arithmetic. Test No. 4. Division
Series B
You will be given eight minutes to work as many of these division examples as possible. You are not expected to be able to do them all. Do your work directly on this paper; use no other. You will be marked for both speed and accuracy, but it is more important to get correct answers than to try a large number of examples.
| 25 ) 6775 | 94 ) 85352 | 37 ) 9990 | 86 ) 80066 |
and twenty more division examples of the same sort.
SERIES B. MULTIPLICATION SCALE
By Clifford Woody
| (1) | (3) | (4) | (5) |
|---|---|---|---|
| 3 × 7 = | 2 × 3 = | 4 × 8 = | 23 3 — |
| (8) | (9) | (11) | (12) |
| 50 3 — |
254 6 — |
1036 8 — |
5096 6 — |
| (13) | (16) | (18) | (20) |
| 8754 8 —— |
7898 9 —— |
24 234 —— |
287 .05 —— |
| (24) | (26) | (27) | (29) |
| 16 25⁄8 —— |
9742 59 —— |
6.25 3.2 —— |
1⁄8 × 2 = |
| (33) | (35) | (37) | (38) |
| 2½ × 3½ = | 987¾ 25 ——— |
2¼ × 4½ × 1½ = | .09631⁄8 .084 —— |
SERIES B. DIVISION SCALE
By Clifford Woody
| (1) | (2) | (7) | (8) |
|---|---|---|---|
| 3 ) 6 | 9 ) 27 | 4 ÷ 2 = | 9 ) 0 |
| (11) | (14) | (15) | (17) |
| 2 ) 13 | 8 ) 5856 | ¼ of 128 = | 50 ÷ 7 = |
| (19) | (23) | (27) | (28) |
| 248 ÷ 7 = | 23 ) 469 | 7⁄8 of 624 = | .003 ) .0936 |
| (30) | (34) | (36) | |
| 3⁄4 ÷ 5 = | 62.50 ÷ 1¼ = | 9 ) 69 lbs. 9 oz. | |
Ballou Test
Addition of Fractions
| Test 1 | Test 2 | ||
|---|---|---|---|
| (1) ¼ ¼ — |
(2) 3⁄14 1⁄14 — |
(1) 1⁄3 1⁄6 — |
(2) 2⁄7 3⁄14 — |
| Test 3 | Test 4 | ||
| (1) 3⁄5 11⁄15 — |
(2) 5⁄6 1⁄2 — |
(1) 1⁄7 9⁄10 — |
(2) 7⁄9 1⁄4 — |
| Test 5 | Test 6 | ||
| (1) 1⁄10 1⁄6 — |
(2) 4⁄9 5⁄12 — |
(1) 1⁄6 9⁄10 — |
(2) 5⁄6 3⁄8 — |
An Addition Ladder [Thorndike, '17, III, 5]
Begin at the bottom of the ladder. See if you can climb to the top without making a mistake. Be sure to copy the numbers correctly.
| Step 6. | a. Add 11⁄3 yd., 7⁄8 yd., 1¼ yd., 3⁄4 yd., 7⁄8 yd., and 1½ yd. |
| b. Add 62½¢, 662⁄3¢, 56¼¢, 60¢, and 62½¢. | |
| c. Add 15⁄16, 19⁄32, 13⁄8, 111⁄32, and 17⁄16. | |
| d. Add 11⁄3 yd., 1¼ yd., 1½ yd., 2 yd., 3⁄4 yd., and 2⁄3 yd. | |
| Step 5. | a. Add 4 ft. 6½ in., 53¼ in., 5 ft. ½ in., 56¾ in., and 5 ft. |
| b. Add 7 lb., 6 lb. 11 oz., 7½ lb., 6 lb. 4½ oz., and 8½ lb. | |
| c. Add 1 hr. 6 min. 20 sec., 58 min. 15 sec., 1 hr. 4 min., and 55 min. | |
| d. Add 7 dollars, 13 half dollars, 21 quarters, 17 dimes, and 19 nickels. | |
| Step 4. | a. Add .05½, .06, .04¾, .02¾, and .05¼. |
| b. Add .331⁄3, .12½, .18, .162⁄3, .081⁄3 and .15. | |
| c. Add .081⁄3, .06¼, .21, .03¾, and .162⁄3. | |
| d. Add .62, .64½, .662⁄3, .10¼, and .68. | |
| [Pg 39] | |
| Step 3. | a. Add 7¼, 6½, 83⁄8, 5¾, 95⁄8 and 37⁄8. |
| b. Add 45⁄8, 12, 7½, 8¾, 6 and 5¼. | |
| c. Add 9¾, 57⁄8, 41⁄8, 6½, 7, 35⁄8. | |
| d. Add 12, 8½, 71⁄3, 5, 62⁄3, and 9½. | |
| Step 2. | a. Add 12.04, .96, 4.7, 9.625, 3.25, and 20. |
| b. Add .58, 6.03, .079, 4.206, 2.75, and 10.4. | |
| c. Add 52, 29.8, 41.07, 1.913, 2.6, and 110. | |
| d. Add 29.7, 315, 26.75, 19.004, 8.793, and 20.05. | |
| Step 1. | a. Add 103⁄5, 111⁄5, 104⁄5, 11, 112⁄5, 103⁄5, and 11. |
| b. Add 73⁄8, 65⁄8, 8, 91⁄8, 77⁄8, 53⁄8, and 81⁄8. | |
| c. Add 21½, 18¾, 31½, 19¼, 17¼, 22, and 16½. | |
| d. Add 145⁄12, 127⁄12, 911⁄12, 61⁄12, and 5. |
A Subtraction Ladder [Thorndike, '17, III, 11]
| Step 9. | |||||
|---|---|---|---|---|---|
| a. 2.16 mi. − 1¾ mi. c. 2 min. 10½ sec. − 93.4 sec. e. 10 gal. 2½ qt. − 4.623 gal. |
b. 5.72 ft. − 5 ft. 3 in. d. 30.28 A. − 101⁄5 A. |
||||
| Step 8. | a | b | c | d | e |
| 257⁄12 123⁄4 ——— |
101⁄4 71⁄3 ——— |
95⁄16 63⁄8 ——— |
57⁄16 23⁄4 ——— |
42⁄3 13⁄4 ——— |
|
| Step 7. | a | b | c | d | e |
| 283⁄4 161⁄8 ——— |
401⁄2 143⁄8 ——— |
101⁄4 61⁄2 ——— |
241⁄3 111⁄2 ——— |
371⁄2 143⁄4 ——— |
|
| Step 6. | a | b | c | d | e |
| 101⁄3 42⁄3 ——— |
71⁄4 23⁄4 ——— |
151⁄8 63⁄8 ——— |
121⁄5 114⁄5 ——— |
41⁄16 27⁄16 ——— |
|
| Step 5. | a | b | c | d | e |
| 584⁄5 521⁄5 ——— |
662⁄3 331⁄3 ——— |
287⁄8 75⁄8 ——— |
62½ 37½ —— |
97⁄12 45⁄12 —— |
|
| Step 4. | |||||
| a. 4 hr. − 2 hr. 17 min. c. 1 lb. 5 oz. − 13 oz. e. 1 bu. − 1 pk. |
b. 4 lb. 7 oz. − 2 lb. 11 oz. d. 7 ft. − 2 ft. 8 in. |
||||
| [Pg 40] | |||||
| Step 3. | a | b | c | d | e |
| 92 mi. 84.15 mi. ———— |
6735 mi. 6689 mi. ———— |
$3 − 89¢ ———— |
28.4 mi. 18.04 mi. ———— |
$508.40 208.62 ———— |
|
| Step 2. | a | b | c | d | e |
| $25.00 9.36 ——— |
$100.00 71.28 ——— |
$750.00 736.50 ——— |
6124 sq. mi. 2494 sq. mi. ————— |
7846 sq. mi. 2789 sq. mi. ————— |
|
| Step 1. | a | b | c | d | e |
| $18.64 7.40 ——— |
$25.39 13.37 ——— |
$56.70 45.60 ——— |
819.4 mi. 209.2 mi. ———— |
67.55 mi. 36.14 mi. ———— |
|
An Average Ladder [Thorndike, '17, III, 132]
Find the average of the quantities on each line. Begin with Step 1. Climb to the top without making a mistake. Be sure to copy the numbers correctly. Extend the division to two decimal places if necessary.
| Step 6. | a. 22⁄3, 17⁄8, 2¾, 4¼, 35⁄8, 3½ |
| b. 62½¢, 662⁄3¢, 40¢, 831⁄3¢, $1.75, $2.25 | |
| c. 311⁄16, 39⁄32, 33⁄8, 317⁄32, 37⁄16 | |
| d. .17, 19, .162⁄3, .15½, .23¼, .18 | |
| Step 5. | a. 5 ft. 3½ in., 61¼ in., 58¾ in., 4 ft. 11 in. |
| b. 6 lb. 9 oz., 6 lb. 11 oz., 7¼ lb., 73⁄8 lb. | |
| c. 1 hr. 4 min. 40 sec., 58 min. 35 sec., 1¼ hr. | |
| d. 2.8 miles, 3½ miles, 2.72 miles | |
| Step 4. | a. .03½, .06, .04¾, .05½, .05¼ |
| b. .043, .045, .049, .047, .046, .045 | |
| c. 2.20, .87½, 1.18, .93¾, 1.2925, .80 | |
| d. .14½, .12½, .331⁄3, .162⁄3, .15, .17 | |
| Step 3. | a. 5¼, 4½, 83⁄8, 7¾, 65⁄8, 93⁄8 |
| b. 95⁄8, 12, 8½, 8¾, 6, 5¼, 9 | |
| c. 93⁄8, 5¾, 41⁄8, 7½, 6 | |
| d. 11, 9½, 101⁄3, 13, 162⁄3, 9½ | |
| [Pg 41] | |
| Step 2. | a. 13.05, .97, 4.8, 10.625, 3.37 |
| b. 1.48, 7.02, .93, 5.307, 4.1, 7, 10.4 | |
| c. 68, 71.4, 59.8, 112, 96.1, 79.8 | |
| d. 2.079, 3.908, 4.165, 2.74 | |
| Step 1. | a. 4, 9½, 6, 5, 7½, 8, 10, 9 |
| b. 6, 5, 3.9, 7.1, 8 | |
| c. 1086, 1141, 1059, 1302, 1284 | |
| d. $100.82, $206.49, $317.25, $244.73 |
As such tests are widened to cover the whole task of the elementary school in respect to arithmetic, and accepted by competent authorities as adequate measures of achievement in computing, they will give, as has been said, a working definition of the task. The reader will observe, for example, that work such as the following, though still found in many textbooks and classrooms, does not, in general, appear in the modern tests and scales.
Reduce the following improper fractions to mixed numbers:—
19⁄13 43⁄21 176⁄25 198⁄14
Reduce to integral or mixed numbers:—
61381⁄37 2134⁄67 413⁄413 697⁄225
Simplify:—
3⁄4 of 8⁄9 of 3⁄5 of 15⁄22
Reduce to lowest terms:—
357⁄527 264⁄312 492⁄779 418⁄874 854⁄1769 30⁄735 44⁄242 77⁄847 18⁄243 96⁄224
Find differences:—
| 62⁄7 31⁄14 —— |
85⁄11 51⁄7 —— |
84⁄13 37⁄13 —— |
51⁄4 211⁄14 —— |
71⁄8 21⁄7 —— |
Square:—
2⁄3 4⁄5 5⁄7 6⁄9 10⁄11 12⁄13 2⁄7 15⁄16 19⁄20 17⁄18 25⁄30 41⁄53
Multiply:—
2⁄11 × 33
32 × 3⁄14
39 × 2⁄13
60 × 11⁄28
77 × 4⁄11
63 × 2⁄27
54 × 8⁄45
65 × 3⁄13
34416⁄21 4322⁄7
Stone ['08] measured achievement with the following problems, fifteen minutes being the time allowed.
"Solve as many of the following problems as you have time for; work them in order as numbered:
1. If you buy 2 tablets at 7 cents each and a book for 65 cents, how much change should you receive from a two-dollar bill?
2. John sold 4 Saturday Evening Posts at 5 cents each. He kept 1⁄2 the money and with the other 1⁄2 he bought Sunday papers at 2 cents each. How many did he buy?
3. If James had 4 times as much money as George, he would have $16. How much money has George?
4. How many pencils can you buy for 50 cents at the rate of 2 for 5 cents? '
5. The uniforms for a baseball nine cost $2.50 each. The shoes cost $2 a pair. What was the total cost of uniforms and shoes for the nine?
6. In the schools of a certain city there are 2200 pupils; 1⁄2 are in the primary grades, 1⁄4 in the grammar grades, 1⁄8 in the high school, and the rest in the night school. How many pupils are there in the night school?
7. If 3½ tons of coal cost $21, what will 5½ tons cost?
8. A news dealer bought some magazines for $1. He sold them for $1.20, gaining 5 cents on each magazine. How many magazines were there?
9. A girl spent 1⁄8 of her money for car fare, and three times as much for clothes. Half of what she had left was 80 cents. How much money did she have at first?
10. Two girls receive $2.10 for making buttonholes. One makes 42, the other 28. How shall they divide the money?
11. Mr. Brown paid one third of the cost of a building; Mr. Johnson paid 1⁄2 the cost. Mr. Johnson received $500 more annual rent than Mr. Brown. How much did each receive?
12. A freight train left Albany for New York at 6 o'clock. An express left on the same track at 8 o'clock. It went at the rate of 40 miles an hour. At what time of day will it overtake the freight train if the freight train stops after it has gone 56 miles?"
The criteria he had in mind in selecting the problems were as follows:—
"The main purpose of the reasoning test is the determination of the ability of VI A children to reason in arithmetic. To this end, the problems, as selected and arranged, are meant to embody the following conditions:—
1. Situations equally concrete to all VI A children.
2. Graduated difficulties.
a. As to arithmetical thinking.
b. As to familiarity with the situation presented.
3. The omission of
a. Large numbers.
b. Particular memory requirements.
c. Catch problems.
d. All subject matter except whole numbers, fractions, and United States money.
The test is purposely so long that only very rarely did any pupil fully complete it in the fifteen minute limit."
Credits were given of 1, for each of the first five problems, 1.4, 1.2, and 1.6 respectively for problems 6, 7, and 8, and of 2 for each of the others.
Courtis sought to improve the Stone test of problem-solving, replacing it by the two tests reproduced below.
ARITHMETIC—Test No. 6. Speed Test—Reasoning
Do not work the following examples. Read each example through, make up your mind what operation you would use if you were going to work it, then write the name of the operation selected in the blank space after the example. Use the following abbreviations:—"Add." for addition, "Sub." for subtraction, "Mul." for multiplication, and "Div." for division.
| Operation | ||
| 1. A girl brought a collection of 37 colored postal cards to school one day, and gave away 19 cards to her friends. How many cards did she have left to take home? | ||
| 2. Five boys played marbles. When the game was over, each boy had the same number of marbles. If there were 45 marbles altogether, how many did each boy have? | [Pg 44] | |
| 3. A girl, watching from a window, saw 27 automobiles pass the school the first hour, and 33 the second. How many autos passed by the school in the two hours? | ||
| 4. In a certain school there were eight rooms and each room had seats for 50 children. When all the places were taken, how many children were there in the school? | ||
| 5. A club of boys sent their treasurer to buy baseballs. They gave him $3.15 to spend. How many balls did they expect him to buy, if the balls cost 45¢. apiece? | ||
| 6. A teacher weighed all the girls in a certain grade. If one girl weighed 79 pounds and another 110 pounds, how many pounds heavier was one girl than the other? | ||
| 7. A girl wanted to buy a 5-pound box of candy to give as a present to a friend. She decided to get the kind worth 35¢. a pound. What did she pay for the present? | ||
| 8. One day in vacation a boy went on a fishing trip and caught 12 fish in the morning, and 7 in the afternoon. How many fish did he catch altogether? | ||
| 9. A boy lived 15 blocks east of a school; his chum lived on the same street, but 11 blocks west of the school. How many blocks apart were the two boys' houses? | ||
| 10. A girl was 5 times as strong as her small sister. If the little girl could lift a weight of 20 pounds, how large a weight could the older girl lift? | ||
| 11. The children of a school gave a sleigh-ride party. There were 270 children to go on the ride and each sleigh held 30 children. How many sleighs were needed? | ||
| 12. In September there were 43 children in the eighth grade of a certain school; by June there were 59. How many children entered the grade during the year? | ||
| 13. A girl who lived 17 blocks away walked to school and back twice a day. What was the total number of blocks the girl walked each day in going to and from school? | ||
| 14. A boy who made 67¢. a day carrying papers, was hired to run on a long errand for which he received 50¢. What was the total amount the boy earned that day? | ||
| Total Right |
(Two more similar problems follow.)
Test 6 and Test 8 are from the Courtis Standard Test. Used by permission of S. A. Courtis.
ARITHMETIC—Test No. 8. Reasoning
In the blank space below, work as many of the following examples as possible in the time allowed. Work them in order as numbered, entering each answer in the "answer" column before commencing a new example. Do not work on any other paper.
| Answer | ||
| 1. The children in a certain school gave a Christmas party. One of the presents was a box of candy. In filling the boxes, one grade used 16 pounds of candy, another 17 pounds, a third 12 pounds, and a fourth 13 pounds. What did the candy cost at 26¢. a pound? | ||
| 2. A school in a certain city used 2516 pieces of chalk in 37 school days. Three new rooms were opened, each room holding 50 children, and the school was then found to use 84 sticks of chalk per day. How many more sticks of chalk were used per day than at first? | ||
| 3. Several boys went on a bicycle trip of 1500 miles. The first week they rode 374 miles, the second week 264 miles, the third 423 miles, the fourth 401 miles. They finished the trip the next week. How many miles did they ride the last week? | ||
| 4. Forty-five boys were hired to pick apples from 15 trees in an apple orchard. In 50 minutes each boy had picked 48 choice apples. If all the apples picked were packed away carefully in 8 boxes of equal size, how many apples were put in each box? | ||
| 5. In a certain school 216 children gave a sleigh-ride party. They rented 7 sleighs at a cost of $30.00 and paid $24.00 for the refreshments. The party travelled 15 miles in 2½ hours and had a very pleasant time. What was each child's share of the expense? | ||
| 6. A girl found, by careful counting, that there were 2400 letters on one page of her history, and only 2295 letters on a page of her reader. How many more letters had she read in one book than in the other if she had read 47 pages in each of the books? | ||
| 7. Each of 59 rooms in the schools of a certain city contributed 25 presents to a Christmas entertainment for poor children. The stores of the city gave 1986 other articles for presents. What was the total number of presents given away at the entertainment? | ||
| 8. Forty-eight children from a certain school paid 10¢. apiece to ride 7 miles on the cars to a woods. There in a few hours they gathered 2765 nuts. 605 of these were bad, but the rest were shared equally among the children. How many good nuts did each one get? | ||
| Total |
These proposed measures of ability to apply arithmetic illustrate very nicely the differences of opinion concerning what applied arithmetic and arithmetical reasoning should be. The thinker who emphasizes the fact that in life out of school the situation demanding quantitative treatment is usually real rather than described, will condemn a test all of whose constituents are described problems. Unless we are excessively hopeful concerning the transfer of ideas of method and procedure from one mental function to another we shall protest against the artificiality of No. 3 of the Stone series, and of the entire Courtis Test 8 except No. 4. The Courtis speed-reasoning test (No. 6) is a striking example of the mixture of ability to understand quantitative relations with the ability to understand words. Consider these five, for example, in comparison with the revised versions attached.[3]
1. The children of a school gave a sleigh-ride party. There were 9 sleighs, and each sleigh held 30 children. How many children were there in the party?
Revision. If one sleigh holds 30 children, 9 sleighs hold .... children.
2. Two school-girls played a number-game. The score of the girl that lost was 57 points and she was beaten by 16 points. What was the score of the girl that won?
Revision. Mary and Nell played a game. Mary had a score of 57. Nell beat Mary by 16. Nell had a score of ....
3. A girl counted the automobiles that passed a school. The total was 60 in two hours. If the girl saw 27 pass the first hour how many did she see the second?
Revision. In two hours a girl saw 60 automobiles. She saw 27 the first hour. She saw .... the second hour.
4. On a playground there were five equal groups of children each playing a different game. If there were 75 children all together, how many were there in each group?
Revision. 75 pounds of salt just filled five boxes. The boxes were exactly alike. There were .... pounds in a box.
5. A teacher weighed all the children in a certain grade. One girl weighed 70 pounds. Her older sister was 49 pounds heavier. How many pounds did the sister weigh?
Revision. Mary weighs 70 lb. Jane weighs 49 pounds more than Mary. Jane weighs .... pounds.
The distinction between a problem described as clearly and simply as possible and the same problem put awkwardly or in ill-known words or willfully obscured should be regarded; and as a rule measurements of ability to apply arithmetic should eschew all needless obscurity or purely linguistic difficulty. For example,
A boy bought a two-cent stamp. He gave the man in the store 10 cents. The right change was .... cents.
is better as a test than
If a boy, purchasing a two-cent stamp, gave a ten-cent stamp in payment, what change should he be expected to receive in return?
The distinction between the description of a bona fide problem that a human being might be called on to solve out of school and the description of imaginary possibilities or puzzles should also be considered. Nos. 3 and 9 of Stone are bad because to frame the problems one must first know the answers, so that in reality there could never be any point in solving them. It is probably safe to say that nobody in the world ever did or ever will or ever should find the number of apples in a box by the task of No. 4 of the Courtis Test 8.
This attaches no blame to Dr. Stone or to Mr. Courtis. Until very recently we were all so used to the artificial problems of the traditional sort that we did not expect anything better; and so blind to the language demands of described problems that we did not see their very great influence. Courtis himself has been active in reform and has pointed out ('13, p. 4 f.) the defects in his Tests 6 and 8.[Pg 48]
"Tests Nos. 6 and 8, the so-called reasoning tests, have proved the least satisfactory of the series. The judgments of various teachers and superintendents as to the inequalities of the units in any one test, and of the differences between the different editions of the same test, have proved the need of investigating these questions. Tests of adults in many lines of commercial work have yielded in many cases lower scores than those of the average eighth grade children. At the same time the scores of certain individuals of marked ability have been high, and there appears to be a general relation between ability in these tests and accuracy in the abstract work. The most significant facts, however, have been the difficulties experienced by teachers in attempting to remedy the defects in reasoning. It is certain that the tests measure abilities of value but the abilities are probably not what they seem to be. In an attempt to measure the value of different units, for instance, as many problems as possible were constructed based upon a single situation. Twenty-one varieties were secured by varying the relative form of the question and the relative position of the different phrases. One of these proved nineteen times as hard as another as measured by the number of mistakes made by the children; yet the cause of the difference was merely the changes in the phrasing. This and other facts of the same kind seem to show that Tests 6 and 8 measure mainly the ability to read."
The scientific measurement of the abilities and achievements concerned with applied arithmetic or problem-solving is thus a matter for the future. In the case of described problems a beginning has been made in the series which form a part of the National Intelligence Tests ['20], one of which is shown on page 49 f. In the case of problems with real situations, nothing in systematic form is yet available.
Systematic tests and scales, besides defining the abil[Pg 49]ities we are to establish and improve, are of very great service in measuring the status and improvement of individuals and of classes, and the effects of various methods of instruction and of study. They are thus helpful to pupils, teachers, supervisors, and scientific investigators; and are being more and more widely used every year. Information concerning the merits of the different tests, the procedure to follow in giving and scoring them, the age and grade standards to be used in interpreting results, and the like, is available in the manuals of Educational Measurement, such as Courtis, Manual of Instructions for Giving and Scoring the Courtis Standard Tests in the Three R's ['14]; Starch, Educational Measurements ['16]; Chapman and Rush, Scientific Measurement of Classroom Products ['17]; Monroe, DeVoss, and Kelly, Educational Tests and Measurements ['17]; Wilson and Hoke, How to Measure ['20]; and McCall, How to Measure in Education ['21].
National Intelligence Tests.
Scale A. Form 1, Edition 1
Find the answers as quickly as you can.
Write the answers on the dotted lines.
Use the side of the page to figure on.
Begin here
| 1 | Five cents make 1 nickel. How many nickels make a dime? | Answer...... |
| 2 | John paid 5 dollars for a watch and 3 dollars for a chain. How many dollars did he pay for the watch and chain? | Answer...... |
| 3 | Nell is 13 years old. Mary is 9 years old. How much younger is Mary than Nell? | Answer...... |
| 4 | One quart of ice cream is enough for 5 persons. How many quarts of ice cream are needed for 25 persons? | Answer...... |
| 5 | John's grandmother is 86 years old. If she lives, in how many years will she be 100 years old? | Answer...... |
| 6 | If a man gets $2.50 a day, what will he be paid for six days' work? | Answer...... |
| 7 | How many inches are there in a foot and a half? | Answer...... |
| 8 | What is the cost of 12 cakes at 6 for 5 cents? | Answer...... |
| 9 | The uniforms for a baseball team of nine boys cost $2.50 each. The shoes cost $2 a pair. What was the total cost of uniforms and shoes for the nine? | Answer...... |
| 10 | A train that usually arrives at half-past ten was 17 minutes late. When did it arrive? | Answer...... |
| 11 | At 10¢ a yard, what is the cost of a piece 10½ ft. long? | Answer...... |
| 12 | A man earns $6 a day half the time, $4.50 a day one fourth of the time, and nothing on the remaining days for a total period of 40 days. What did he earn in all in the 40 days? | Answer...... |
| 13 | What per cent of $800 is 4% of $1000? | Answer...... |
| 14 | If 60 men need 1500 lb. flour per month, what is the requirement per man per day counting a month as 30 days? | Answer...... |
| 15 | A car goes at the rate of a mile a minute. A truck goes 20 miles an hour. How many times as far will the car go as the truck in 10 seconds? | Answer...... |
| 16 | The area of the base (inside measure) of a cylindrical tank is 90 square feet. How tall must it be to hold 100 cubic yards? | Answer...... |
From National Intelligence Tests by National Research Council.
Copyright, 1920, by The World Book Company, Yonkers-on-Hudson, New York.
Used by permission of the publishers.
It would be a useful work for some one to try to analyze arithmetical learning into the unitary abilities which compose it, showing just what, in detail, the mind has to do in order to be prepared to pass a thorough test on the whole of arithmetic. These unitary abilities would make a very long list. Examination of a well-planned textbook will show that such an ability as multiplication is treated as a composite of the following: knowledge of the multiplications up to 9 × 9; ability to multiply two (or more)-place numbers by 2, 3, and 4 when 'carrying' is not required and no zeros occur in the multiplicand; ability to multiply by 2, 3, ... 9, with carrying; the ability to handle zeros in the multiplicand; the ability to multiply with two-place numbers not ending in zero; the ability to handle zero in the multiplier as last number; the ability to multiply with three (or more)-place numbers not including a zero; the ability to multiply with three- and four-place numbers with zero in second or third, or second and third, as well as in last place; the ability to save time by annexing zeros; and so on and on through a long list of further abilities required to multiply with United States money, decimal fractions, common fractions, mixed numbers, and denominate numbers.[Pg 52]
The units or 'steps' thus recognized by careful teaching would make a long list, but it is probable that a still more careful study of arithmetical ability as a hierarchy of mental habits or connections would greatly increase the list. Consider, for example, ordinary column addition. The majority of teachers probably treat this as a simple application of the knowledge of the additions to 9 + 9, plus understanding of 'carrying.' On the contrary there are at least seven processes or minor functions involved in two-place column addition, each of which is psychologically distinct and requires distinct educational treatment.
These are:—
A. Learning to keep one's place in the column as one adds.
B. Learning to keep in mind the result of each addition until the next number is added to it.
C. Learning to add a seen to a thought-of number.
D. Learning to neglect an empty space in the columns.
E. Learning to neglect 0s in the columns.
F. Learning the application of the combinations to higher decades may for the less gifted pupils involve as much time and labor as learning all the original addition tables. And even for the most gifted child the formation of the connection '8 and 7 = 15' probably never quite insures the presence of the connections '38 and 7 = 45' and '18 + 7 = 25.'
G. Learning to write the figure signifying units rather than the total sum of a column. In particular, learning to write 0 in the cases where the sum of the column is 10, 20, etc. Learning to 'carry' also involves in itself at least two distinct processes, by whatever way it is taught.
We find evidence of such specialization of functions in the results with such tests as Woody's. For example, [Pg 53] 2 + 5 + 1 = .... surely involves abilities in part different from
2
4
3
—
because only 77 percent of children in grade 3 do the former correctly, whereas 95 percent of children in that grade do the latter correctly. In grade 2 the difference is even more marked. In the case of subtraction
4
4
—
involves abilities different from those involved in
9
3
—,
being much less often solved correctly in grades 2 and 4.
6
0
—
is much harder than either of the above.
| 43 1 2 13 | is much harder than | 21 33 35. |
| — | — |
It may be said that these differences in difficulty are due to different amounts of practice. This is probably not true, but if it were, it would not change the argument; if the two abilities were identical, the practice of one would improve the other equally.
I shall not undertake here this task of listing and describing the elementary functions which constitute arithmetical learning, partly because what they are is not fully known, partly because in many cases a final ability may be constituted in several different ways whose descriptions become necessarily tedious, and partly because an adequate statement of what is known would far outrun the space limits of this chapter. Instead, I shall illustrate the results by some samples.
As a first sample, consider knowledge of the meaning of a fraction. Is the ability in question simply to understand that a fraction is a statement of the number of parts, each of a certain size, the upper number or numerator telling how many parts are taken and the lower number or denominator telling what fraction of unity each part is? And is the educational treatment required simply to describe and illustrate such a statement and have the pupils apply it to the recognition of fractions and the interpretation of each of them? And is the learning process (1) the formation of the notions of part, size of part, number of part, (2) relating the last two to the numbers in a fraction, and, as a necessary consequence, (3) applying these notions adequately whenever one encounters a fraction in operation?
Precisely this was the notion a few generations ago. The nature of fractions was taught as one principle, in one step, and the habits of dealing with fractions were supposed to be deduced from the general law of a fraction's nature. As a result the subject of fractions had to be long delayed, was studied at great cost of time and effort, and, even so, remained a mystery to all save gifted pupils. These gifted pupils probably of their own accord built up the ability piecemeal out of constituent insights and habits.
At all events, scientific teaching now does build up the total ability as a fusion or organization of lesser abilities. What these are will be seen best by examining the means taken to get them. (1) First comes the association of ½ of a pie, ½ of a cake, ½ of an apple, and such like with their concrete meanings so that a pupil can properly name a clearly designated half of an obvious unit like an orange, pear, or piece of chalk. The same degree of understanding[Pg 55] of 1⁄4, 1⁄8, 1⁄3, 1⁄6, and 1⁄5 is secured. The pupil is taught that 1 pie = 2 1⁄2s, 3 1⁄3s, 4 1⁄4s, 5 1⁄5s, 6 1⁄6s, and 8 1⁄8s; similarly for 1 cake, 1 apple, and the like.
So far he understands 1⁄x of y in the sense of certain simple parts of obviously unitary ys.
(2) Next comes the association with ½ of an inch, ½ of a foot, ½ of a glassful and other cases where y is not so obviously a unitary object whose pieces still show their derivation from it. Similarly for 1⁄4, 1⁄3, etc.
(3) Next comes the association with 1⁄2 of a collection of eight pieces of candy, 1⁄3 of a dozen eggs, 1⁄5 of a squad of ten soldiers, etc., until 1⁄2, 1⁄3, 1⁄4, 1⁄5, 1⁄6, and 1⁄8 are understood as names of certain parts of a collection of objects.
(4) Next comes the similar association when the nature
of the collection is left undefined, the pupil responding to
1⁄2 of 6 is ..., 1⁄4 of 8 is ..., 2 is 1⁄5 of ...,
1⁄3 of 6 is ..., 1⁄3 of 9 is ..., 2 is 1⁄3 of ..., and the like.
Each of these abilities is justified in teaching by its intrinsic merits, irrespective of its later service in helping to constitute the general understanding of the meaning of a fraction. The habits thus formed in grades 3 or 4 are of constant service then and thereafter in and out of school.
(5) With these comes the use of 1⁄5 of 10, 15, 20, etc., 1⁄6 of 12, 18, 42, etc., as a useful variety of drill on the division tables, valuable in itself, and a means of making the notion of a unit fraction more general by adding 1⁄7 and 1⁄9 to the scheme.
(6) Next comes the connection of 3⁄4, 2⁄5, 3⁄5, 4⁄5, 2⁄3, 1⁄6, 5⁄6, 3⁄8, 5⁄8, 7⁄8, 3⁄10, 7⁄10, and 9⁄10, each with its meaning as a certain part of some conveniently divisible unit, and, (7) and (8), connections between these fractions and their meanings as parts of certain magnitudes (7) and collections (8) of convenient[Pg 56] size, and (9) connections between these fractions and their meanings when the nature of the magnitude or collection is unstated, as in 4⁄5 of 15 = ..., 5⁄8 of 32 = ....
(10) That the relation is general is shown by using it with numbers requiring written division and multiplication, such as 7⁄8 of 1736 = ..., and with United States money.
Elements (6) to (10) again are useful even if the pupil never goes farther in arithmetic. One of the commonest uses of fractions is in calculating the cost of fractions of yards of cloth, and fractions of pounds of meat, cheese, etc.
The next step (11) is to understand to some extent the principle that the value of any of these fractions is unaltered by multiplying or dividing the numerator and denominator by the same number. The drills in expressing fractions in lower and higher terms which accomplish this are paralleled by (12) and (13) simple exercises in adding and subtracting fractions to show that fractions are quantities that can be operated on like any quantities, and by (14) simple work with mixed numbers (addition and subtraction and reductions), and (15) improper fractions. All that is done with improper fractions is (a) to have the pupil use a few of them as he would any fractions and (b) to note their equivalent mixed numbers. In (12), (13), and (14) only fractions of the same denominators are added or subtracted, and in (12) (13), (14), and (15) only fractions with 2, 3, 4, 5, 6, 8, or 10 in the denominator are used. As hitherto, the work of (11) to (15) is useful in and of itself. (16) Definitions are given of the following type:—
Numbers like 2, 3, 4, 7, 11, 20, 36, 140, 921 are called whole numbers.
Numbers like 7⁄8, 1⁄5, 2⁄3, 3⁄4, 11⁄8, 7⁄6, 1⁄3, 4⁄3, 1⁄8, 1⁄6 are called fractions.
Numbers like 5¼, 73⁄8, 9½, 164⁄5, 3157⁄8, 11⁄3, 12⁄3 are called mixed numbers.[Pg 57]
(17) The terms numerator and denominator are connected with the upper and lower numbers composing a fraction.
Building this somewhat elaborate series of minor abilities seems to be a very roundabout way of getting knowledge of the meaning of a fraction, and is, if we take no account of what is got along with this knowledge. Taking account of the intrinsically useful habits that are built up, one might retort that the pupil gets his knowledge of the meaning of a fraction at zero cost.
Consider next the knowledge of the subtraction and division 'Tables.' The usual treatment presupposes that learning them consists of forming independently the bonds:—
| 3 − 1 = 2 | 4 ÷ 2 = 2 |
| 3 − 2 = 1 | 6 ÷ 2 = 3 |
| 4 − 1 = 3 | 6 ÷ 3 = 2 |
|
. . . |
. . . |
| 18 − 9 = 9 | 81 ÷ 9 = 9 |
In fact, however, these 126 bonds are not formed independently. Except perhaps in the case of the dullest twentieth of pupils, they are somewhat facilitated by the already learned additions and multiplications. And by proper arrangement of the learning they may be enormously facilitated thereby. Indeed, we may replace the independent memorizing of these facts by a set of instructive [Pg 58]exercises wherein the pupil derives the subtractions from the corresponding additions by simple acts of reasoning or selective thinking. As soon as the additions giving sums of 9 or less are learned, let the pupil attack an exercise like the following:—
Write the missing numbers:—
| A | B | C | D |
| 3 and ... are 5. | 5 and ... are 8. | 4 and ... are 5. | 4 and ... are 8. |
| 3 and ... are 9. | 3 and ... are 6. | 5 and ... are 6. | 1 and ... are 7. |
| 4 and ... are 7. | 4 and ... are 9. | 6 and ... are 9. | 6 and ... are 7. |
| 5 and ... are 7. | 2 and ... = 6. | 1 and ... are 8. | 8 and ... are 9. |
| 6 and ... are 8. | 5 and ... = 9. | 3 and ... are 7. | 3 + ... are 4. |
| 4 and ... are 6. | 2 and ... = 7. | 1 + ... are 3. | 7 + ... are 8. |
| 2 and ... are 5. | 3 and ... = 8. | 1 + ... are 5. | 4 + ... are 9. |
| 2 and ... = 8. | 1 and ... = 4. | 4 + ... are 8. | 2 + ... are 3. |
| 3 and ... = 6. | 2 and ... = 4. | 7 + ... are 9. | 1 + ... are 9. |
| 6 and ... = 9. | 3 and ... = 8. | 2 + ... = 4. | 3 + ... = 6. |
| 4 and ... = 6. | 6 and ... = 7. | 3 + ... = 8. | 5 + ... = 9. |
| 4 and ... = 7. | 2 and ... = 5. | 4 + ... = 5. | 1 + ... = 3. |
The task for reasoning is only to try, one after another, numbers that seem promising and to select the right one when found. With a little stimulus and direction children can thus derive the subtractions up to those with 9 as the larger number. Let them then be taught to do the same with the printed forms:—
Subtract
| 9 | 7 | 8 | 5 | 8 | 6 | |
| 3 | 5 | 6 | 2 | 2 | 4 | etc. |
| — | — | — | — | — | — |
and 9 − 7 = ..., 9 − 5 = ..., 7 − 5 = ..., etc.
In the case of the divisions, suppose that the pupil has learned his first table and gained surety in such exercises as:[Pg 59]—
| 4 5s = .... | 6 × 5 = .... | 9 nickels = .... cents. |
| 8 5s = .... | 4 × 5 = .... | 6 " = .... " |
| 3 5s = .... | 2 × 5 = .... | 5 " = .... " |
| 7 5s = .... | 9 × 5 = .... | 7 " = .... " |
If one ball costs 5 cents,
two balls cost .... cents,
three balls cost .... cents, etc.
He may then be set at once to work at the answers to exercises like the following:—
Write the answers and the missing numbers:—
| A | B | C | D |
| .... 5s = 15 | 40 = .... 5s | .... × 5 = 25 | 20 cents = .... nickels. |
| .... 5s = 20 | 20 = .... 5s | .... × 5 = 50 | 30 cents = .... nickels. |
| .... 5s = 40 | 15 = .... 5s | .... × 5 = 35 | 15 cents = .... nickels. |
| .... 5s = 25 | 45 = .... 5s | .... × 5 = 10 | 40 cents = .... nickels. |
| .... 5s = 30 | 50 = .... 5s | .... × 5 = 40 | |
| .... 5s = 35 | 25 = .... 5s | .... × 5 = 45 |
| E |
| For 5 cents you can buy 1 small loaf of bread. For 10 cents you can buy 2 small loaves of bread. For 25 cents you can buy .... small loaves of bread. For 45 cents you can buy .... small loaves of bread. For 35 cents you can buy .... small loaves of bread. |
| F |
| 5 cents pays 1 car fare. 15 cents pays .... car fares. 10 cents pays .... car fares. 20 cents pays .... car fares. |
| G |
| How many 5 cent balls can you buy with 30 cents? .... How many 5 cent balls can you buy with 35 cents? .... How many 5 cent balls can you buy with 25 cents? .... How many 5 cent balls can you buy with 15 cents? .... |
In the case of the meaning of a fraction, the ability, and so the learning, is much more elaborate than common [Pg 60] practice has assumed; in the case of the subtraction and division tables the learning is much less so. In neither case is the learning either mere memorizing of facts or the mere understanding of a principle in abstracto followed by its application to concrete cases. It is (and this we shall find true of almost all efficient learning in arithmetic) the formation of connections and their use in such an order that each helps the others to the maximum degree, and so that each will do the maximum amount for arithmetical abilities other than the one specially concerned, and for the general competence of the learner.
As another instructive topic in the constitution of arithmetical abilities, we may take the case of the reasoning involved in understanding the manipulations of figures in two (or more)-place addition and subtraction, multiplication and division involving a two (or more)-place number, and the manipulations of decimals in all four operations. The psychology of these is of special interest and importance. For there are two opposite explanations possible here, leading to two opposite theories of teaching.
The common explanation is that these methods of manipulation, if understood at all, are understood as deductions from the properties of our system of decimal notation. The other is that they are understood partly as inductions from the experience that they always give the right answer. The first explanation leads to the common preliminary deductive explanations of the textbooks. The other leads to explanations by verification; e.g., of addition by counting, of subtraction by addition, of multiplication by addition, of division by multiplication. Samples of these two sorts of explanation are given below.
SHORT MULTIPLICATION WITHOUT CARRYING: DEDUCTIVE EXPLANATION
Multiplication is the process of taking one number as many times as there are units in another number.
The Product is the result of the multiplication.
The Multiplicand is the number to be taken.
The Multiplier is the number denoting how many times the multiplicand is to be taken.
The multiplier and multiplicand are the Factors.
| Multiply 623 by 3 OPERATION | |
| Multiplicand | 623 |
| Multiplier | 3 |
| Product | 1869 |
Explanation.—For convenience we write the multiplier under the multiplicand, and begin with units to multiply. 3 times 3 units are 9 units. We write the nine units in units' place in the product. 3 times 2 tens are 6 tens. We write the 6 tens in tens' place in the product. 3 times 6 hundreds are 18 hundreds, or 1 thousand and 8 hundreds. The 1 thousand we write in thousands' place and the 8 hundreds in hundreds' place in the product. Therefore, the product is 1 thousand 8 hundreds, 6 tens and 9 units, or 1869.
SHORT MULTIPLICATION WITHOUT CARRYING: INDUCTIVE EXPLANATION
1. The children of the third grade are to have a picnic. 32 are going. How many sandwiches will they need if each of the 32 children has four sandwiches?
| 32 4 |
Here is a quick way to find out:— Think "4 × 2," write 8 under the 2 in the ones column. Think "4 × 3," write 12 under the 3 in the tens column. |
2. How many bananas will they need if each of the 32 children has two bananas? 32 × 2 or 2 × 32 will give the answer.
3. How many little cakes will they need if each child has three cakes? 32 × 3 or 3 × 32 will give the answer.
| 32 3 |
3 × 2 = .... Where do you write the 6? 3 × 3 = .... Where do you write the 9? |
4. Prove that 128, 64, and 96 are right by adding four 32s, two 32s, and three 32s.
| 32 32 32 32 |
32 32 32 |
32 32 |
Multiplication
You multiply when you find the answers to questions like
| How many are 9 × 3? How many are 3 × 32? How many are 8 × 5? How many are 4 × 42? |
1. Read these lines. Say the right numbers where the dots are:
If you add 3 to 32, you have .... 35 is the sum.
If you subtract 3 from 32, the result is .... 29 is the difference or remainder.
If you multiply 3 by 32 or 32 by 3, you have .... 96 is the product.
Find the products. Check your answers to the first line by adding.
| 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. |
| 41 | 33 | 42 | 44 | 53 | 43 | 34 | 24 |
| 3 | 2 | 4 | 2 | 3 | 2 | 2 | 2 |
| 10. | 11. | 12. | 13. | 14. | 15. | 16. | |
| 43 | 52 | 32 | 23 | 41 | 51 | 14 | |
| 3 | 3 | 3 | 3 | 2 | 4 | 2 | |
17. | |||
| 213 3 |
Write the 9 in the ones column. Write the 6 in the hundreds column. Write the 3 in the tens column. |
Check your answer by adding. | Add 213 213 213 |
| 18. | 19. | 20. | 21. | 22. | 23. | 24. |
| 214 | 312 | 432 | 231 | 132 | 314 | 243 |
| 2 | 3 | 2 | 3 | 3 | 2 | 2 |
SHORT DIVISION: DEDUCTIVE EXPLANATION
Divide 1825 by 4
Divisor 4 | 1825 Dividend
456¼
Quotient
Explanation.—For convenience we write the divisor at the left of the dividend, and the quotient below it, and begin at the left to divide. 4 is not contained in 1 thousand any thousand times, therefore the quotient contains no unit of any order higher than hundreds. Consequently we find how many times 4 is contained in the hundreds of the dividend. 1 thousand and 8 hundreds are 18 hundreds. 4 is contained in 18 hundreds 4 hundred times and 2 hundreds remaining. We write the 4 hundreds in the quotient. The 2 hundreds we consider as united with the 2 tens, making 22 tens. 4 is contained in 22 tens 5 tens times, and 2 tens remaining. We write the 5 tens in the quotient, and the remaining 2 tens we consider as united with the 5 units, making 25 units. 4 is contained in 25 units 6 units times and 1 unit remaining. We write the 6 units in the quotient and indicate the division of the remainder, 1 unit, by the divisor 4.
Therefore the quotient of 1825 divided by 4 is 456¼, or 456 and 1 remainder.
SHORT DIVISION: INDUCTIVE EXPLANATION
Dividing Large Numbers
1. Tom, Dick, Will, and Fred put in 2 cents each to buy an eight-cent bag of marbles. There are 128 marbles in it. How many should each boy have, if they divide the marbles equally among the four boys?
4 | 128
Think "12 = three 4s." Write the 3 over the 2 in the tens column.
Think "8 = two 4s." Write the 2 over the 8 in the ones column.
32 is right, because 4 × 32 = 128.
2. Mary, Nell, and Alice are going to buy a book as a present for their Sunday-school teacher. The present costs 69 cents. How much should each girl pay, if they divide the cost equally among the three girls?
3 | 69
Think "6 = .... 3s." Write the 2 over the 6 in the tens column.[Pg 64]
Think "9 = .... 3s." Write the 3 over the 9 in the ones column.
23 is right, for 3 × 23 = 69.
3. Divide the cost of a 96-cent present equally among three girls. How much should each girl pay? girls. How much should each girl pay? 3 | 96
4. Divide the cost of an 84-cent present equally among 4 girls. How much should each girl pay?
5. Learn this: (Read ÷ as "divided by.")
| 12 + 4 = 16. | 16 is the sum. |
| 12 − 4 = 8. | 8 is the difference or remainder. |
| 12 × 4 = 48. | 48 is the product. |
| 12 ÷ 4 = 3. | 3 is the quotient. |
6. Find the quotients. Check your answers by multiplying.
| 3 | 99 | 2 | 86 | 5 | 155 | 6 | 246 | 4 | 168 | 3 | 219 |
[Uneven division is taught by the same general plan, extended.]
LONG DIVISION: DEDUCTIVE EXPLANATION
To Divide by Long Division
1. Let it be required to divide 34531 by 15.
Operation
| Divisor |
Divided 15 ) 34531 ( 30 45 45 31 30 1 |
23021⁄15 Quotient |
| Remainder |
For convenience we write the divisor at the left and the quotient at the right of the dividend, and begin to divide as in Short Division.
15 is contained in 3 ten-thousands 0 ten-thousands times; therefore, there will be 0 ten-thousands in the quotient. Take 34 thousands; 15 is contained in 34 thousands 2 thousands times; we write the 2 thousands in the quotient. 15 × 2 thousands = 30 thousands, which, subtracted from 34 thousands, leaves 4 thousands = 40 hundreds. Adding the 5 hundreds, we have 45 hundreds.
15 in 45 hundreds 3 hundreds times; we write the 3 hundreds in the quotient. 15 × 3 hundreds = 45 hundreds, which subtracted from 45 hundreds, leaves nothing. Adding the 3 tens, we have 3 tens.[Pg 65]
15 in 3 tens 0 tens times; we write 0 tens in the quotient. Adding to the three tens, which equal 30 units, the 1 unit, we have 31 units.
15 in 31 units 2 units times; we write the 2 units in the quotient. 15 × 2 units = 30 units, which, subtracted from 31 units, leaves 1 unit as a remainder. Indicating the division of the 1 unit, we annex the fractional expression, 1⁄15 unit, to the integral part of the quotient.
Therefore, 34531 divided by 15 is equal to 23021⁄15.
[B. Greenleaf, Practical Arithmetic, '73, p. 49.]
LONG DIVISION: INDUCTIVE EXPLANATION
Dividing by Large Numbers
1. Just before Christmas Frank's father sent 360 oranges to be divided among the children in Frank's class. There are 29 children. How many oranges should each child receive? How many oranges will be left over?
Here is the best way to find out:
|
12 29|360 29 70 58 12 |
and 12 remainder |
Think how many 29s there are in 36. 1 is right. Write 1 over the 6 of 36. Multiply 29 by 1. Write the 29 under the 36. Subtract 29 from 36. Write the 0 of 360 after the 7. Think how many 29s there are in 70. 2 is right. Write 2 over the 0 of 360. Multiply 29 by 2. Write the 58 under 70. Subtract 58 from 70. There is 12 remainder. Each child gets 12 oranges, and there are 12 left over. This is right, for 12 multiplied by 29 = 348, and 348 + 12 = 360. |
| 8. 31 | 99,587 |
In No. 8, keep on dividing by 31 until you have used the 5, the 8, and the 7, and have four figures in the quotient. |
| 9. 22 | 253 |
10. 22 | 2895 |
11. 21 | 8891 |
12. 22 | 290 |
13. 32 | 16,368 |
Check your results for 9, 10, 11, 12, and 13.
1. The boys and girls of the Welfare Club plan to earn money to buy a victrola. There are 23 boys and girls. They can get a good second-hand victrola for $5.75. How much must each earn if they divide the cost equally?
Here is the best way to find out:
|
$.25 23|$5.75 46 115 115 |
Think how many 23s there are in 57. 2 is right. Write 2 over the 7 of 57. Multiply 23 by 2. Write 46 under 57 and subtract. Write the 5 of 575 after the 11. Think how many 23s there are in 115. 5 is right. Write 5 over the 5 of 575. Multiply 23 by 5. Write the 115 under the 115 that is there and subtract. There is no remainder. Put $ and the decimal point where they belong. Each child must earn 25 cents. This is right, for $.25 multiplied by 23 = $5.75. |
2. Divide $71.76 equally among 23 persons. How much is each person's share?
3. Check your result for No. 2 by multiplying the quotient by the divisor.
Find the quotients. Check each quotient by multiplying it by the divisor.
| 4. 23 | $99.13 |
5. 25 | $18.50 |
6. 21 | $129.15 |
7. 13 | $29.25 |
8. 32 | $73.92 |
1 bushel = 32 qt.
9. How many bushels are there in 288 qt.? 10. In 192 qt.? 11. In 416 qt.?
Crucial experiments are lacking, but there are several lines of well-attested evidence. First of all, there can be no doubt that the great majority of pupils learn these manipulations at the start from the placing of units under units, tens under tens, etc., in adding, to the placing of the decimal point in division with decimals, by imitation and blind[Pg 67] following of specific instructions, and that a very large proportion of the pupils do not to the end, that is to the fifth school-year, understand them as necessary deductions from decimal notation. It also seems probable that this proportion would not be much reduced no matter how ingeniously and carefully the deductions were explained by textbooks and teachers. Evidence of this fact will appear abundantly to any one who will observe schoolroom life. It also appears in the fact that after the properties of the decimal notation have been thus used again and again; e.g., for deducing 'carrying' in addition, 'borrowing' in subtraction, 'carrying' in multiplication, the value of the digits in the partial product, the value of each remainder in short division, the value of the quotient figures in division, the addition, subtraction, multiplication, and division of United States money, and the placing of the decimal point in multiplication, no competent teacher dares to rely upon the pupil, even though he now has four or more years' experience with decimal notation, to deduce the placing of the decimal point in division with decimals. It may be an illusion, but one seems to sense in the better textbooks a recognition of the futility of the attempt to secure deductive derivations of those manipulations. I refer to the brevity of the explanations and their insertion in such a form that they will influence the pupils' thinking as little as possible. At any rate the fact is sure that most pupils do not learn the manipulations by deductive reasoning, or understand them as necessary consequences of abstract principles.
It is a common opinion that the only alternative is knowing them by rote. This, of course, is one common alternative, but the other explanation suggests that understanding the manipulations by inductive reasoning from their results is another and an important alternative. The manipula[Pg 68]tions of 'long' multiplication, for instance, learned by imitation or mechanical drill, are found to give for 25 × A a result about twice as large as for 13 × A, for 38 or 39 × A a result about three times as large; for 115 × A a result about ten times as large as for 11 × A. With even the very dull pupils the procedure is verified at least to the extent that it gives a result which the scientific expert in the case—the teacher—calls right. With even the very bright pupils, who can appreciate the relation of the procedure to decimal notation, this relation may be used not as the sole deduction of the procedure beforehand, but as one partial means of verifying it afterward. Or there may be the condition of half-appreciation of the relation in which the pupil uses knowledge of the decimal notation to convince himself that the procedure does, but not that it must give the right answer, the answer being 'right' because the teacher, the answer-list, and collateral evidence assure him of it.
I have taken the manipulation of the partial products as an illustration because it is one of the least favored cases for the explanation I am presenting. If we take the first case where a manipulation may be deduced from decimal notation, known merely by rote, or verified inductively, namely, the addition of two-place numbers, it seems sure that the mental processes just described are almost the universal rule.
Surely in our schools at present children add the 3 of 23 to the 3 of 53 and the 2 of 23 to the 5 of 53 at the start, in nine cases out of ten because they see the teacher do so and are told to do so. They are protected from adding 3 + 3 + 2 + 5 not by any deduction of any sort but because they do not know how to add 8 and 5, because they have been taught the habit of adding figures that stand one above the other, or with a + between them; and because they are[Pg 69] shown or told what they are to do. They are protected from adding 3 + 5 and 2 + 3, again, by no deductive reasoning but for the second and third reasons just given. In nine cases out of ten they do not even think of the possibility of adding in any other way than the '3 + 3, 2 + 5' way, much less do they select that way on account of the facts that 53 = 50 + 3 and 23 = 20 + 3, that 50 + 20 = 70, that 3 + 3 = 6, and that (a + b) + (c + d) = (a + c) + (b + d)!
Just as surely all but the very dullest twentieth or so of children come in the end to something more than rote knowledge,—to understand, to know that the procedure in question is right.
Whether they know why 76 is right depends upon what is meant by why. If it means that 76 is the result which competent people agree upon, they do. If it means that 76 is the result which would come from accurate counting they perhaps know why as well as they would have, had they been given full explanations of the relation of the procedure in two-place addition to decimal notation. If why means because 53 = 50 + 3, 23 = 20 + 3, 50 + 20 = 70, and (a + b) + (c + d) = (a + c) + (b + d), they do not. Nor, I am tempted to add, would most of them by any sort of teaching whatever.
I conclude, therefore, that school children may and do reason about and understand the manipulations of numbers in this inductive, verifying way without being able to, or at least without, under present conditions, finding it profitable to derive them deductively. I believe, in fact, that pure arithmetic as it is learned and known is largely an inductive science. At one extreme is a minority to whom it is a series of deductions from principles; at the other extreme is a minority to whom it is a series of blind habits; between the two is the great majority, representing every gradation but centering about the type of the inductive thinker.
When the analysis of the mental functions involved in arithmetical learning is made thorough it turns into the question, 'What are the elementary bonds or connections that constitute these functions?' and when the problem of teaching arithmetic is regarded, as it should be in the light of present psychology, as a problem in the development of a hierarchy of intellectual habits, it becomes in large measure a problem of the choice of the bonds to be formed and of the discovery of the best order in which to form them and the best means of forming each in that order.
The importance of habit-formation or connection-making has been grossly underestimated by the majority of teachers and writers of textbooks. For, in the first place, mastery by deductive reasoning of such matters as 'carrying' in addition, 'borrowing' in subtraction, the value of the digits in the partial products in multiplication, the manipulation of the figures in division, the placing of the decimal point after multiplication or division with decimals, or the manipulation of the figures in the multiplication and division of [Pg 71] fractions, is impossible or extremely unlikely in the case of children of the ages and experience in question. They do not as a rule deduce the method of manipulation from their knowledge of decimal notation. Rather they learn about decimal notation by carrying, borrowing, writing the last figure of each partial product under the multiplier which gives that product, etc. They learn the method of manipulating numbers by seeing them employed, and by more or less blindly acquiring them as associative habits.
In the second place, we, who have already formed and long used the right habits and are thereby protected against the casual misleadings of unfortunate mental connections, can hardly realize the force of mere association. When a child writes sixteen as 61, or finds 428 as the sum of
15
19
16
18
or gives 642 as an answer to 27 × 36, or says that 4 divided by ¼ = 1, we are tempted to consider him mentally perverse, forgetting or perhaps never having understood that he goes wrong for exactly the same general reason that we go right; namely, the general law of habit-formation. If we study the cases of 61 for 16, we shall find them occurring in the work of pupils who after having been drilled in writing 26, 36, 46, 62, 63, and so on, in which the order of the six in writing is the same as it is in speech, return to writing the 'teen numbers. If our language said onety-one for eleven and onety-six for sixteen, we should probably never find such errors except as 'lapses' or as the results of misperception or lack of memory. They would then be more frequent before the 20s, 30s, etc., were learned.
If pupils are given much drill on written single column addition involving the higher decades (each time writing [Pg 72] the two-figure sum), they are forming a habit of writing 28 after the sum of 8, 6, 9, and 5 is reached; and it should not surprise us if the pupil still occasionally writes the two-figure sum for the first column though a second column is to be added also. On the contrary, unless some counter force influences him, he is absolutely sure to make this mistake.
The last mistake quoted (4 ÷ ¼ = 1) is interesting because here we have possibly one of the cases where deduction from psychology alone can give constructive aid to teaching. Multiplication and division by fractions have been notorious for their difficulty. The former is now alleviated by using of instead of × until the new habit is fixed. The latter is still approached with elaborate caution and with various means of showing why one must 'invert and multiply' or 'multiply by the reciprocal.'
But in the author's opinion it seems clear that the difficulty in multiplying and dividing by a fraction was not that children felt any logical objections to canceling or inverting. I fancy that the majority of them would cheerfully invert any fraction three times over or cancel numbers at random in a column if they were shown how to do so. But if you are a youngster inexperienced in numerical abstractions and if you have had divide connected with 'make smaller' three thousand times and never once connected with 'make bigger,' you are sure to be somewhat impelled to make the number smaller the three thousand and first time you are asked to divide it. Some of my readers will probably confess that even now they feel a slight irritation or doubt in saying or writing that 16⁄1 ÷ 1⁄8 = 128.
The habits that have been confirmed by every multiplication and division by integers are, in this particular of 'the ratio of result to number operated upon,' directly opposed to[Pg 73] the formation of the habits required with fractions. And that is, I believe, the main cause of the difficulty. Its treatment then becomes easy, as will be shown later.
These illustrations could be added to almost indefinitely, especially in the case of the responses made to the so-called 'catch' problems. The fact is that the learner rarely can, and almost never does, survey and analyze an arithmetical situation and justify what he is going to do by articulate deductions from principles. He usually feels the situation more or less vaguely and responds to it as he has responded to it or some situation like it in the past. Arithmetic is to him not a logical doctrine which he applies to various special instances, but a set of rather specialized habits of behavior toward certain sorts of quantities and relations. And in so far as he does come to know the doctrine it is chiefly by doing the will of the master. This is true even with the clearest expositions, the wisest use of objective aids, and full encouragement of originality on the pupil's part.
Lest the last few paragraphs be misunderstood, I hasten to add that the psychologists of to-day do not wish to make the learning of arithmetic a mere matter of acquiring thousands of disconnected habits, nor to decrease by one jot the pupil's genuine comprehension of its general truths. They wish him to reason not less than he has in the past, but more. They find, however, that you do not secure reasoning in a pupil by demanding it, and that his learning of a general truth without the proper development of organized habits back of it is likely to be, not a rational learning of that general truth, but only a mechanical memorizing of a verbal statement of it. They have come to know that reasoning is not a magic force working in independence of ordinary habits of thought, but an or[Pg 74]ganization and coöperation of those very habits on a higher level.
The older pedagogy of arithmetic stated a general law or truth or principle, ordered the pupil to learn it, and gave him tasks to do which he could not do profitably unless he understood the principle. It left him to build up himself the particular habits needed to give him understanding and mastery of the principle. The newer pedagogy is careful to help him build up these connections or bonds ahead of and along with the general truth or principle, so that he can understand it better. The older pedagogy commanded the pupil to reason and let him suffer the penalty of small profit from the work if he did not. The newer provides instructive experiences with numbers which will stimulate the pupil to reason so far as he has the capacity, but will still be profitable to him in concrete knowledge and skill, even if he lacks the ability to develop the experiences into a general understanding of the principles of numbers. The newer pedagogy secures more reasoning in reality by not pretending to secure so much.
The newer pedagogy of arithmetic, then, scrutinizes every element of knowledge, every connection made in the mind of the learner, so as to choose those which provide the most instructive experiences, those which will grow together into an orderly, rational system of thinking about numbers and quantitative facts. It is not enough for a problem to be a test of understanding of a principle; it must also be helpful in and of itself. It is not enough for an example to be a case of some rule; it must help review and consolidate habits already acquired or lead up to and facilitate habits to be acquired. Every detail of the pupil's work must do the maximum service in arithmetical learning.
As hitherto, I shall not try to list completely the elementary bonds that the course of study in arithmetic should provide for. The best means of preparing the student of this topic for sound criticism and helpful invention is to let him examine representative cases of bonds now often neglected which should be formed and representative cases of useless, or even harmful, bonds now often formed at considerable waste of time and effort.
(1) Numbers as measures of continuous quantities.—The numbers one, two, three, 1, 2, 3, etc., should be connected soon after the beginning of arithmetic each with the appropriate amount of some continuous quantity like length or volume or weight, as well as with the appropriate sized collection of apples, counters, blocks, and the like. Lines should be labeled 1 foot, 2 feet, 3 feet, etc.; one inch, two inches, three inches, etc.; weights should be lifted and called one pound, two pounds, etc.; things should be measured in glassfuls, handfuls, pints, and quarts. Otherwise the pupil is likely to limit the meaning of, say, four to four sensibly discrete things and to have difficulty in multiplication and division. Measuring, or counting by insensibly marked off repetitions of a unit, binds each number name to its meaning as —— times whatever 1 is, more surely than mere counting of the units in a collection can, and should reënforce the latter.
(2) Additions in the higher decades.—In the case of all save the very gifted children, the additions with higher decades—that is, the bonds, 16 + 7 = 23, 26 + 7 = 33, 36 + 7 = 43, 14 + 8 = 22, 24 + 8 = 32, and the like—need to be specifically practiced until the tendency becomes generalized. 'Counting' by 2s beginning with 1, and with 2,[Pg 76] counting by 3s beginning with 1, with 2, and with 3, counting by 4s beginning with 1, with 2, with 3, and with 4, and so on, make easy beginnings in the formation of the decade connections. Practice with isolated bonds should soon be added to get freer use of the bonds. The work of column addition should be checked for accuracy so that a pupil will continually get beneficial practice rather than 'practice in error.'
(3) The uneven divisions.—The quotients with remainders for the divisions of every number to 19 by 2, every number to 29 by 3, every number to 39 by 4, and so on should be taught as well as the even divisions. A table like the following will be found a convenient means of making these connections:—
|
10 = .... 2s 10 = .... 3s and .... rem. 10 = .... 4s and .... rem. 10 = .... 5s 11 = .... 2s and .... rem. 11 = .... 3s and .... rem. . . . 89 = .... 9s and .... rem. |
These bonds must be formed before short division can be efficient, are useful as a partial help toward selection of the proper quotient figures in long division, and are the chief instruments for one of the important problem series in applied arithmetic,—"How many xs can I buy for y cents at z cents per x and how much will I have left?" That these bonds are at present sadly neglected is shown by Kirby ['13], who found that pupils in the last half of grade 3 and the[Pg 77] first half of grade 4 could do only about four such examples per minute (in a ten-minute test), and even at that rate made far from perfect records, though they had been taught the regular division tables. Sixty minutes of practice resulted in a gain of nearly 75 percent in number done per minute, with an increase in accuracy as well.
(4) The equation form.—The equation form with an unknown quantity to be determined, or a missing number to be found, should be connected with its meaning and with the problem attitude long before a pupil begins algebra, and in the minds of pupils who never will study algebra.
Children who have just barely learned to add and subtract learn easily to do such work as the following:—
Write the missing numbers:—
|
4 + 8 = .... 5 + .... = 14 .... + 3 = 11 .... = 5 + 2 16 = 7 + .... 12 = .... + 5 |
The equation form is the simplest uniform way yet devised to state a quantitative issue. It is capable of indefinite extension if certain easily understood conventions about parentheses and fraction signs are learned. It should be employed widely in accounting and the treatment of commercial problems, and would be except for outworn conventions. It is a leading contribution of algebra to business and industrial life. Arithmetic can make it nearly as well. It saves more time in the case of drills on reducing fractions to higher and lower terms alone than is required to learn its meaning and use. To rewrite a quantitative problem[Pg 78] as an equation and then make the easy selection of the necessary technique to solve the equation is one of the most universally useful intellectual devices known to man. The words 'equals,' 'equal,' 'is,' 'are,' 'makes,' 'make,' 'gives,' 'give,' and their rarer equivalents should therefore early give way on many occasions to the '=' which so far surpasses them in ultimate convenience and simplicity.
(5) Addition and subtraction facts in the case of fractions.—In the case of adding and subtracting fractions, certain specific bonds—between the situation of halves and thirds to be added and the responses of thinking of the numbers as equal to so many sixths, between the situation thirds and fourths to be added and thinking of them as so many twelfths, between fourths and eighths to be added and thinking of them as eighths, and the like—should be formed separately. The general rule of thinking of fractions as their equivalents with some convenient denominator should come as an organization and extension of such special habits, not as an edict from the textbook or teacher.
(6) Fractional equivalents.—Efficiency requires that in the end the much used reductions should be firmly connected with the situations where they are needed. They may as well, therefore, be so connected from the beginning, with the gain of making the general process far easier for the dull pupils to master. We shall see later that, for all save the very gifted pupils, the economical way to get an understanding of arithmetical principles is not, usually, to learn a rule and then apply it, but to perform instructive operations and, in the course of performing them, to get insight into the principles.
(7) Protective habits in multiplying and dividing with fractions.—In multiplying and dividing with fractions special bonds should be formed to counteract the now harmful[Pg 79] influence of the 'multiply = get a larger number' and 'divide = get a smaller number' bonds which all work with integers has been reënforcing.
For example, at the beginning of the systematic work with multiplication by a fraction, let the following be printed clearly at the top of every relevant page of the textbook and displayed on the blackboard:—
When you multiply a number by anything more than 1 the result is larger than the number.
When you multiply a number by 1 the result is the same as the number.
When you multiply a number by anything less than 1 the result is smaller than the number.
Let the pupils establish the new habit by many such exercises as:—
|
18 × 4 = .... 4 × 4 = .... 2 × 4 = .... 1 × 4 = .... 1⁄2 × 4 = .... 1⁄4 × 4 = .... 1⁄8 × 4 = .... |
9 × 2 = .... 6 × 2 = .... 3 × 2 = .... 1 × 2 = .... 1⁄3 × 2 = .... 1⁄6 × 2 = .... 1⁄9 × 2 = .... |
In the case of division by a fraction the old harmful habit should be counteracted and refined by similar rules and exercises as follows:—
When you divide a number by anything more than 1 the result is smaller than the number.
When you divide a number by 1 the result is the same as the number.
When you divide a number by anything less than 1 the result is larger than the number.[Pg 80]
State the missing numbers:—
| 8 = .... 4s | 12 = .... 6s | 9 = .... 9s |
| 8 = .... 2s | 12 = .... 4s | 9 = .... 3s |
| 8 = .... 1s | 12 = .... 3s | 9 = .... 1s |
| 8 = .... 1⁄2s | 12 = .... 2s | 9 = .... 1⁄3s |
| 8 = .... 1⁄4s | 12 = .... 1s | 9 = .... 1⁄9s |
| 8 = .... 1⁄8s | 12 = .... 1⁄2s | |
| 12 = .... 1⁄3s | ||
| 12 = .... 1⁄4s |
| 16 ÷ 16 = | 9 ÷ 9 = | 10 ÷ 10 = | 12 ÷ 6 = |
| 16 ÷ 8 = | 9 ÷ 3 = | 10 ÷ 5 = | 12 ÷ 4 = |
| 16 ÷ 4 = | 9 ÷ 1 = | 10 ÷ 1 = | 12 ÷ 3 = |
| 16 ÷ 2 = | 9 ÷ 1⁄3 = | 10 ÷ 1⁄5 = | 12 ÷ 2 = |
| 16 ÷ 1 = | 9 ÷ 1⁄9 = | 10 ÷ 1⁄10 = | 12 ÷ 1 = |
| 16 ÷ 1⁄2 = | 12 ÷ 1⁄2 = | ||
| 16 ÷ 1⁄4 = | 12 ÷ 1⁄3 = | ||
| 16 ÷ 1⁄8 = | 12 ÷ 1⁄4 = | ||
| 12 ÷ 1⁄6 = |
(8) '% of' means 'hundredths times.'—In the case of percentage a series of bonds like the following should be formed:—
| 5 | percent | of | = .05 times | |
| 20 | " " | " | = .20 " | |
| 6 | " " | " | = .06 " | |
| 25 | % | " | = .25 × | |
| 12 | % | " | = .12 × | |
| 3 | % | " | = .03 × |
Four five-minute drills on such connections between 'x percent of' and 'its decimal equivalent times' are worth an hour's study of verbal definitions of the meaning of percent as per hundred or the like. The only use of the[Pg 81] study of such definitions is to facilitate the later formation of the bonds, and, with all save the brighter pupils, the bonds are more needed for an understanding of the definitions than the definitions are needed for the formation of the bonds.
(9) Habits of verifying results.—Bonds should early be formed between certain manipulations of numbers and certain means of checking, or verifying the correctness of, the manipulation in question. The additions to 9 + 9 and the subtractions to 18 − 9 should be verified by objective addition and subtraction and counting until the pupil has sure command; the multiplications to 9 × 9 should be verified by objective multiplication and counting of the result (in piles of tens and a pile of ones) eight or ten times,[4] and by addition eight or ten times;[4] the divisions to 81 ÷ 9 should be verified by multiplication and occasionally objectively until the pupil has sure command; column addition should be checked by adding the columns separately and adding the sums so obtained, and by making two shorter tasks of the given task and adding the two sums; 'short' multiplication should be verified eight or ten times by addition; 'long' multiplication should be checked by reversing multiplier and multiplicand and in other ways; 'short' and 'long' division should be verified by multiplication.
These habits of testing an obtained result are of threefold value. They enable the pupil to find his own errors, and to maintain a standard of accuracy by himself. They give him a sense of the relations of the processes and the reasons why the right ways of adding, subtracting, multiplying, and dividing are right, such as only the very bright [Pg 82] pupils can get from verbal explanations. They put his acquisition of a certain power, say multiplication, to a real and intelligible use, in checking the results of his practice of a new power, and so instill a respect for arithmetical power and skill in general. The time spent in such verification produces these results at little cost; for the practice in adding to verify multiplications, in multiplying to verify divisions, and the like is nearly as good for general drill and review of the addition and multiplication themselves as practice devised for that special purpose.
Early work in adding, subtracting, and reducing fractions should be verified by objective aids in the shape of lines and areas divided in suitable fractional parts. Early work with decimal fractions should be verified by the use of the equivalent common fractions for .25, .75, .125, .375, and the like. Multiplication and division with fractions, both common and decimal, should in the early stages be verified by objective aids. The placing of the decimal point in multiplication and division with decimal fractions should be verified by such exercises as:—
|
20 1.23 ) 24.60 246 |
It cannot be 200; for 200 × 1.23 is much more than 24.6. It cannot be 2; for 2 × 1.23 is much less than 24.6. |
The establishment of habits of verifying results and their use is very greatly needed. The percentage of wrong answers in arithmetical work in schools is now so high that the pupils are often being practiced in error. In many cases they can feel no genuine and effective confidence in the processes, since their own use of the processes brings wrong answers as often as right. In solving problems they often cannot decide whether they have done the right thing or the wrong, since even if they have done the right thing, they may[Pg 83] have done it inaccurately. A wrong answer to a problem is therefore too often ambiguous and uninstructive to them.[5]
These illustrations of the last few pages are samples of the procedures recommended by a consideration of all the bonds that one might form and of the contribution that each would make toward the abilities that the study of arithmetic should develop and improve. It is by doing more or less at haphazard what psychology teaches us to do deliberately and systematically in this respect that many of the past advances in the teaching of arithmetic have been made.
A scrutiny of the bonds now formed in the teaching of arithmetic with questions concerning the exact service of each, results in a list of bonds of small value or even no value, so far as a psychologist can determine. I present here samples of such psychologically unjustifiable bonds with some of the reasons for their deficiencies.
(1) Arbitrary units.—In drills intended to improve the ability to see and use the meanings of numbers as names for ratios or relative magnitudes, it is unwise to employ entirely arbitrary units. The procedure in II (on page 84) is better than that in I. Inches, half-inches, feet, and centimeters are better as units of length than arbitrary As. Square inches, square centimeters, and square feet are better for areas. Ounces and pounds should be lifted rather than arbitrary weights. Pints, quarts, glassfuls, cupfuls, handfuls, and cubic inches are better for volume.
All the real merit in the drills on relative magnitude advocated by Speer, McLellan and Dewey, and others can be secured without spending time in relating magnitudes [Pg 84] for the sake of relative magnitude alone. The use of units of measure in drills which will never be used in bona fide measuring is like the use of fractions like sevenths, elevenths, and thirteenths. A very little of it is perhaps desirable to test the appreciation of certain general principles, but for regular training it should give place to the use of units of practical significance.
 Fig. 3.
Fig. 3.
I. If A is 1 which line is 2? Which line is 4? Which line is 3? A and C together equal what line? A and B together equal what line? How much longer is B than A? How much longer is B than C? How much longer is D than A?
 Fig. 4.
Fig. 4.
II. A is 1 inch long. Which line is 2 inches long? Which line is 4 inches long? Which line is 3 inches long? A and C together make ... inches? A and B together make ... inches? B is ... ... longer than A? B is ... ... longer than C? D is ... ... longer than A?
(2) Multiples of 11.—The multiplications of 2 to 12 by 11 and 12 as single connections should be left for the pupil to acquire by himself as he needs them. These connections interfere with the process of learning two-place multiplication. The manipulations of numbers there required can be learned much more easily if 11 and 12 are used as multipliers in just the same way that 78 or 96 would be. Later the 12 × 2, 12 × 3, etc., may be taught. There is less reason for knowing the multiples of 11 than for knowing the multiples of 15, 16, or 25.
(3) Abstract and concrete numbers.—The elaborate emphasis of the supposed fact that we cannot multiply 726 by 8 dollars and the still more elaborate explanations of why nevertheless we find the cost of 726 articles at $8 each by multiplying 726 by 8 and calling the answer dollars are wasteful. The same holds of the corresponding pedantry about division. These imaginary difficulties should not be raised at all. The pupil should not think of multiplying or dividing men or dollars, but simply of the necessary equation and of the sort of thing that the missing number represents. "8 × 726 = .... Answer is dollars," or "8, 726, multiply. Answer is dollars," is all that he needs to think, and is in the best form for his thought. Concerning the distinction between abstract and concrete numbers, both logic and common sense as well as psychology support the contention of McDougle ['14, p. 206f.], who writes:—
"The most elementary counting, even that stage when the counts were not carried in the mind, but merely in notches on a stick or by DeMorgan's stones in a pot, requires some thought; and the most advanced counting implies memory of things. The terms, therefore, abstract and concrete number, have long since ceased to be used by thinking people.
"Recently the writer visited an arithmetic class in a[Pg 86] State Normal School and saw a group of practically adult students confused about this very question concerning abstract and concrete numbers, according to their previous training in the conventionalities of the textbook. Their teacher diverted the work of the hour and she and the class spent almost the whole period in reëstablishing the requirements 'that the product must always be the same kind of unit as the multiplicand,' and 'addends must all be alike to be added.' This is not an exceptional case. Throughout the whole range of teaching arithmetic in the public schools pupils are obfuscated by the philosophical encumbrances which have been imposed upon the simplest processes of numerical work. The time is surely ripe, now that we are readjusting our ideas of the subject of arithmetic, to revise some of these wasteful and disheartening practices. Algebra historically grew out of arithmetic, yet it has not been laden with this distinction. No pupil in algebra lets x equal the horses; he lets x equal the number of horses, and proceeds to drop the idea of horses out of his consideration. He multiplies, divides, and extracts the root of the number, sometimes handling fractions in the process, and finally interprets the result according to the conditions of his problem. Of course, in the early number work there have been the sense-objects from which number has been perceived, but the mind retreats naturally from objectivity to the pure conception of number, and then to the number symbol. The following is taken from the appendix to Horn's thesis, where a seventh grade girl gets the population of the United States in 1820:—
|
7,862,166 233,634 1,538,022 9,633,822 |
whites free negroes slaves |
In this problem three different kinds of addends are combined, if we accept the usual distinction. Some may say that this is a mistake,—that the pupil transformed the 'whites,' 'free negroes,' and 'slaves' into a common unit, such as 'people' of 'population' and then added these common units. But this 'explanation' is entirely gratuitous, as one will find if he questions the pupil about the process. It will be found that the child simply added the figures as numbers only and then interpreted the result, according to the statement of the problem, without so much mental gymnastics. The writer has questioned hundreds of students in Normal School work on this point, and he believes that the ordinary mind-movement is correctly set forth here, no matter how well one may maintain as an academic proposition that this is not logical. Many classes in the Eastern Kentucky State Normal have been given this problem to solve, and they invariably get the same result:—
'In a garden on the Summit are as many cabbage-heads as the total number of ladies and gentlemen in this class. How many cabbage-heads in the garden?'
And the blackboard solution looks like this each time:—
|
29 15 44 |
ladies gentlemen cabbage-heads |
So, also, one may say: I have 6 times as many sheep as you have cows. If you have 5 cows, how many sheep have I? Here we would multiply the number of cows, which is 5, by 6 and call the result 30, which must be linked with the idea of sheep because the conditions imposed by the problem demand it. The mind naturally in this work separates the pure number from its situation, as in algebra, handles it[Pg 88] according to the laws governing arithmetical combinations, and labels the result as the statement of the problem demands. This is expressed in the following, which is tacitly accepted in algebra, and should be accepted equally in arithmetic:
'In all computations and operations in arithmetic, all numbers are essentially abstract and should be so treated. They are concrete only in the thought process that attends the operation and interprets the result.'"
(4) Least common multiple.—The whole set of bonds involved in learning 'least common multiple' should be left out. In adding and subtracting fractions the pupil should not find the least common multiple of their denominators but should find any common multiple that he can find quickly and correctly. No intelligent person would ever waste time in searching for the least common multiple of sixths, thirds, and halves except for the unfortunate traditions of an oversystematized arithmetic, but would think of their equivalents in sixths or twelfths or twenty-fourths or any other convenient common multiple. The process of finding the least common multiple is of such exceedingly rare application in science or business or life generally that the textbooks have to resort to purely fantastic problems to give drill in its use.
(5) Greatest common divisor.—The whole set of bonds involved in learning 'greatest common divisor' should also be left out. In reducing fractions to lowest terms the pupil should divide by anything that he sees that he can divide by, favoring large divisors, and continue doing so until he gets the fraction in terms suitable for the purpose in hand. The reader probably never has had occasion to compute a greatest common divisor since he left school. If he has computed any, the chances are that he would have saved time by solving the problem in some other way![Pg 89]
The following problems are taken at random from those given by one of the best of the textbooks that make the attempt to apply the facts of Greatest Common Divisor and Least Common Multiple to problems.[6] Most of these problems are fantastic. The others are trivial, or are better solved by trial and adaptation.
1. A certain school consists of 132 pupils in the high school, 154 in the grammar, and 198 in the primary grades. If each group is divided into sections of the same number containing as many pupils as possible, how many pupils will there be in each section?
2. A farmer has 240 bu. of wheat and 920 bu. of oats, which he desires to put into the least number of boxes of the same capacity, without mixing the two kinds of grain. Find how many bushels each box must hold.
3. Four bells toll at intervals of 3, 7, 12, and 14 seconds respectively, and begin to toll at the same instant. When will they next toll together?
4. A, B, C, and D start together, and travel the same way around an island which is 600 mi. in circuit. A goes 20 mi. per day, B 30, C 25, and D 40. How long must their journeying continue, in order that they may all come together again?
5. The periods of three planets which move uniformly in circular orbits round the sun, are respectively 200, 250, and 300 da. Supposing their positions relatively to each other and the sun to be given at any moment, determine how many da. must elapse before they again have exactly the same relative positions.
(6) Rare and unimportant words.—The bonds between rare or unimportant words and their meanings should not be formed for the mere sake of verbal variety in the problems of the textbook. A pupil should not be expected to solve a problem that he cannot read. He should not be expected in grades 2 and 3, or even in grade 4, to read words that he has rarely or never seen before. He should not be given elaborate drill in reading during the time devoted to the treatment of quantitative facts and relations.
[Pg 90]All this is so obvious that it may seem needless to relate. It is not. With many textbooks it is now necessary to give definite drill in reading the words in the printed problems intended for grades 2, 3, and 4, or to replace them by oral statements, or to leave the pupils in confusion concerning what the problems are that they are to solve. Many good teachers make a regular reading-lesson out of every page of problems before having them solved. There should be no such necessity.
To define rare and unimportant concretely, I will say that for pupils up to the middle of grade 3, such words as the following are rare and unimportant (though each of them occurs in the very first fifty pages of some well-known beginner's book in arithmetic).
| absentees account Adele admitted Agnes agreed Albany Allen allowed alternate Andrew Arkansas arrived assembly automobile baking powder balance barley beggar Bertie Bessie bin Boston bouquet bronze buckwheat Byron camphor Carl Carrie Cecil Charlotte charity Chicago cinnamon Clara clothespins collect comma committee concert confectioner cranberries crane currants dairyman Daniel David dealer debt delivered Denver |
department deposited dictation discharged discover discovery dish-water drug due Edgar Eddie Edwin election electric Ella Emily enrolled entertainment envelope Esther Ethel exceeds explanation expression generally gentlemen Gilbert Grace grading Graham grammar Harold hatchet Heralds hesitation Horace Mann impossible income indicated inmost inserts installments instantly insurance Iowa Jack Jennie Johnny Joseph journey Julia Katherine |
lettuce-plant library Lottie Lula margin Martha Matthew Maud meadow mentally mercury mineral Missouri molasses Morton movements muslin Nellie nieces Oakland observing obtained offered office onions opposite original package packet palm Patrick Paul payments peep Peter perch phaeton photograph piano pigeons Pilgrims preserving proprietor purchased Rachel Ralph rapidity rather readily receipts register remanded |
respectively Robert Roger Ruth rye Samuel San Francisco seldom sheared shingles skyrockets sloop solve speckled sponges sprout stack Stephen strap successfully suggested sunny supply Susan Susie's syllable talcum term test thermometer Thomas torpedoes trader transaction treasury tricycle tube two-seated united usually vacant various vase velocipede votes walnuts Walter Washington watched whistle woodland worsted |
(7) Misleading facts and procedures.—Bonds should not be formed between articles of commerce and grossly inaccurate prices therefor, between events and grossly improbable consequences, or causes or accompaniments thereof, nor between things, qualities, and events which have no important connections one with another in the real world. In general, things should not be put together in the pupil's mind that do not belong together.
If the reader doubts the need of this warning let him examine problems 1 to 5, all from reputable books that are in common use, or have been within a few years, and con[Pg 92]sider how addition, subtraction, and the habits belonging with each are confused by exercise 6.
1. If a duck flying 3⁄5 as fast as a hawk flies 90 miles in an hour, how fast does the hawk fly?
2. At 5⁄8 of a cent apiece how many eggs can I buy for $60?
3. At $.68 a pair how many pairs of overshoes can you buy for $816?
4. At $.13 a dozen how many dozen bananas can you buy for $3.12?
5. How many pecks of beans can be put into a box that will hold just 21 bushels?
6. Write answers:
|
537 365 ? 36 1000 |
Beginning at the bottom say 11, 18, and 2 (writing it in its place) are 20. 5, 11, 14, and 6 (writing it) are 20, 5, 10. The number, omitted, is 62. |
| a. | 581 97 364 ? 1758 |
b. | 625 ? 90 417 2050 |
c. | 752 414 130 ? 2460 |
d. | 314 429 ? 76 1000 |
e. | ? 845 223 95 2367 |
(8) Trivialities and absurdities.—Bonds should not be formed between insignificant or foolish questions and the labor of answering them, nor between the general arithmetical work of the school and such insignificant or foolish questions. The following are samples from recent textbooks of excellent standing:—
On one side of George's slate there are 32 words, and on the other side 26 words. If he erases 6 words from one side, and 8 from the other, how many words remain on his slate?
A certain school has 14 rooms, and an average of 40 children in a room. If every one in the school should make 500 straight marks on each side of his slate, how many would be made in all?
8 times the number of stripes in our flag is the number of years from 1800 until Roosevelt was elected President. In what year was he elected President?
From the Declaration of Independence to the World's Fair in Chicago was 9 times as many years as there are stripes in the flag. How many years was it?
(9) Useless methods.—Bonds should not be formed between a described situation and a method of treating the situation which would not be a useful one to follow in the case of the real situation. For example, "If I set 96 trees in rows, sixteen trees in a row, how many rows will I have?" forms the habit of treating by division a problem that in reality would be solved by counting the rows. So also "I wish to give 25 cents to each of a group of boys and find that it will require $2.75. How many boys are in the group?" forms the habit of answering a question by division whose answer must already have been present to give the data of the problem.
(10) Problems whose answers would, in real life, be already known.—The custom of giving problems in textbooks which could not occur in reality because the answer has to be known to frame the problem is a natural result of the lazy author's tendency to work out a problem to fit a certain process and a certain answer. Such bogus problems are very, very common. In a random sampling of a dozen pages of "General Review" problems in one of the most widely used of recent textbooks, I find that about 6 percent of the problems are of this sort. Among the problems extemporized by teachers these bogus problems are probably still more frequent. Such are:—
A clerk in an office addressed letters according to a given list. After she had addressed 2500, 4⁄9 of the names on the list had not been used; how many names were in the entire list?
The Canadian power canal at Sault Ste. Marie furnished [Pg 94]20,000 horse power. The canal on the Michigan side furnished 2½ times as much. How many horse power does the latter furnish?
It may be asserted that the ideal of giving as described problems only problems that might occur and demand the same sort of process for solution with a real situation, is too exacting. If a problem is comprehensible and serves to illustrate a principle or give useful drill, that is enough, teachers may say. For really scientific teaching it is not enough. Moreover, if problems are given merely as tests of knowledge of a principle or as means to make some fact or principle clear or emphatic, and are not expected to be of direct service in the quantitative work of life, it is better to let the fact be known. For example, "I am thinking of a number. Half of this number is twice six. What is the number?" is better than "A man left his wife a certain sum of money. Half of what he left her was twice as much as he left to his son, who receives $6000. How much did he leave his wife?" The former is better because it makes no false pretenses.
(11) Needless linguistic difficulties.—It should be unnecessary to add that bonds should not be formed between the pupil's general attitude toward arithmetic and needless, useless difficulty in language or needless, useless, wrong reasoning. Our teaching is, however, still tainted by both of these unfortunate connections, which dispose the pupil to think of arithmetic as a mystery and folly.
Consider, for example, the profitless linguistic difficulty of problems 1-6, whose quantitative difficulties are simply those of:—
1. 5 + 8 + 3 + 7
2. 64 ÷ 8, and knowledge that 1 peck = 8 quarts
3. 12 ÷ 4
[Pg 95]4. 6 ÷ 2
5. 3 × 2
6. 4 × 4
1. What amount should you obtain by putting together 5 cents, 8 cents, 3 cents, and 7 cents? Did you find this result by adding or multiplying?
2. How many times must you empty a peck measure to fill a basket holding 64 quarts of beans?
3. If a girl commits to memory 4 pages of history in one day, in how many days will she commit to memory 12 pages?
4. If Fred had 6 chickens how many times could he give away 2 chickens to his companions?
5. If a croquet-player drove a ball through 2 arches at each stroke, through how many arches will he drive it by 3 strokes?
6. If mamma cut the pie into 4 pieces and gave each person a piece, how many persons did she have for dinner if she used 4 whole pies for dessert?
Arithmetically this work belongs in the first or second years of learning. But children of grades 2 and 3, save a few, would be utterly at a loss to understand the language.
We are not yet free from the follies illustrated in the lessons of pages 96 to 99, which mystified our parents.[Pg 96]
 Fig. 5.
Fig. 5.
LESSON I
1. In this picture, how many girls are in the swing?
2. How many girls are pulling the swing?
3. If you count both girls together, how many are they?
One girl and one other girl are how many?
4. How many kittens do you see on the stump?
5. How many on the ground?
6. How many kittens are in the picture? One kitten and one other kitten are how many?
7. If you should ask me how many girls are in the swing, or how many kittens are on the stump, I could answer aloud, One; or I could write One; or thus, 1.
8. If I write One, this is called the word One.
9. This, 1, is named a figure One, because it means the same as the word One, and stands for One.[Pg 97]
10. Write 1. What is this named? Why?
11. A figure 1 may stand for one girl, one kitten, or one anything.
12. When children first attend school, what do they begin to learn? Ans. Letters and words.
13. Could you read or write before you had learned either letters or words?
14. If we have all the letters together, they are named the Alphabet.
15. If we write or speak words, they are named Language.
16. You are commencing to study Arithmetic; and you can read and write in Arithmetic only as you learn the Alphabet and Language of Arithmetic. But little time will be required for this purpose.
 Fig. 6.
Fig. 6.
LESSON II
1. If we speak or write words, what do we name them, when taken together?
2. What are you commencing to study? Ans. Arithmetic.
3. What Language must you now learn?
4. What do we name this, 1? Why?
5. This figure, 1, is part of the Language of Arithmetic.
6. If I should write something to stand for Two—two girls, two kittens, or two things of any kind—what do you think we would name it?
7. A figure Two is written thus: 2. Make a figure two.
8. Why do we name this a figure two?
9. This figure two (2) is part of the Language of Arithmetic.[Pg 98]
10. In this picture one boy is sitting, playing a flageolet. What is the other boy doing? If the boy standing should sit down by the other, how many boys would be sitting together? One boy and one other boy are how many boys?
11. You see a flageolet and a violin. They are musical instruments. One musical instrument and one other musical instrument are how many?
12. I will write thus: 1 1 2. We say that 1 boy and 1 other boy, counted together, are 2 boys; or are equal to 2 boys. We will now write something to show that the first 1 and the other 1 are to be counted together.

13. We name a line drawn thus,—, a horizontal line. Draw such a line. Name it.
14. A line drawn thus, | , we name a vertical line. Draw such a line. Name it.[Pg 99]
15. Now I will put two such lines together; thus, +. What kind of a line do we name the first (—)? And what do we name the last? (|)? Are these lines long or short? Where do they cross each other?
16. Each of you write thus: —, | , +.
17. This, +, is named Plus. Plus means more; and + also means more.
18. I will write.
One and One More Equal Two.
19. Now I will write part of this in the Language of Arithmetic. I write the first One thus, 1; then the other One thus, 1. Afterward I write, for the word More, thus, +, placing the + between 1 and 1, so that the whole stands thus: 1 + 1. As I write, I say, One and One more.
20. Each of you write 1 + 1. Read what you have written.
21. This +, when written between the 1s, shows that they are to be put together, or counted together, so as to make 2.
22. Because + shows what is to be done, it is called a Sign. If we take its name, Plus, and the word Sign, and put both words together, we have Sign Plus, or Plus Sign. In speaking of this we may call it Sign Plus, or Plus Sign, or Plus.
23. 1, 2, +, are part of the Language of Arithmetic.
Write the following in the Language of Arithmetic:
24. One and one more.
25. One and two more.
26. Two and one more.
(12) Ambiguities and falsities.—Consider the ambiguities and false reasoning of these problems.
1. If you can earn 4 cents a day, how much can you earn in 6 weeks? (Are Sundays counted? Should a child who earns 4 cents some day expect to repeat the feat daily?)
2. How many lines must you make to draw ten triangles and five squares? (I can do this with 8 lines, though the answer the book requires is 50.)
3. A runner ran twice around an 1⁄8 mile track in two minutes. What distance did he run in 2⁄3 of a minute? (I do not know, but I do know that, save by chance, he did not run exactly 2⁄3 of 1⁄8 mile.)
4. John earned $4.35 in a week, and Henry earned $1.93. They put their money together and bought a gun. What did it cost? (Maybe $5, maybe $10. Did they pay for the whole of it? Did they use all their earnings, or less, or more?)
5. Richard has 12 nickels in his purse. How much more than 50 cents would you give him for them? (Would a wise child give 60 cents to a boy who wanted to swap 12 nickels therefor, or would he suspect a trick and hold on to his own coins?)
6. If a horse trots 10 miles in one hour how far will he travel in 9 hours?
7. If a girl can pick 3 quarts of berries in 1 hour how many quarts can she pick in 3 hours?
(These last two, with a teacher insisting on the 90 and 9, might well deprive a matter-of-fact boy of respect for arithmetic for weeks thereafter.)
The economics and physics of the next four problems speak for themselves.
8. I lost $15 by selling a horse for $85. What was the value of the horse?
9. If floating ice has 7 times as much of it under the surface of the water as above it, what part is above water? If an iceberg is 50 ft. above water, what is the entire height of the iceberg? How high above water would an iceberg 300 ft. high have to be?
10. A man's salary is $1000 a year and his expenses $625. [Pg 101] How many years will elapse before he is worth $10,000 if he is worth $2500 at the present time?
11. Sound travels 1120 ft. a second. How long after a cannon is fired in New York will the report be heard in Philadelphia, a distance of 90 miles?
The reader may be wearied of these special details concerning bonds now neglected that should be formed and useless or harmful bonds formed for no valid reason. Any one of them by itself is perhaps a minor matter, but when we have cured all our faults in this respect and found all the possibilities for wiser selection of bonds, we shall have enormously improved the teaching of arithmetic. The ideal is such choice of bonds (and, as will be shown later, such arrangement of them) as will most improve the functions in question at the least cost of time and effort. The guiding principles may be kept in mind in the form of seven simple but golden rules:—
1. Consider the situation the pupil faces.
2. Consider the response you wish to connect with it.
3. Form the bond; do not expect it to come by a miracle.
4. Other things being equal, form no bond that will have to be broken.
5. Other things being equal, do not form two or three bonds when one will serve.
6. Other things being equal, form bonds in the way that they are required later to act.
7. Favor, therefore, the situations which life itself will offer, and the responses which life itself will demand.
An inventory of the bonds to be formed in learning arithmetic should be accompanied by a statement of how strong each bond is to be made and kept year by year. Since, however, the inventory itself has been presented here only in samples, the detailed statement of desired strength for each bond cannot be made. Only certain general facts will be noted here.
The constituent bonds involved in the fundamental operations with numbers need to be much stronger than they now are. Inaccuracy in these operations means weakness of the constituent bonds. Inaccuracy exists, and to a degree that deprives the subject of much of its possible disciplinary value, makes the pupil's achievements of slight value for use in business or industry, and prevents the pupil from verifying his work with new processes by some previously acquired process.
The inaccuracy that exists may be seen in the measurements made by the many investigators who have used arithmetical tasks as tests of fatigue, practice, individual differences and the like, and in the special studies of arith[Pg 103]metical achievements for their own sake made by Courtis and others.
Burgerstein ['91], using such examples as
| 28704516938276546397 + 35869427359163827263 |
and similar long numbers to be multiplied by 2 or by 3 or by 4 or by 5 or by 6, found 851 errors in 28,267 answer-figures, or 3 per hundred answer-figures, or 3⁄5 of an error per example. The children were 9½ to 15 years old. Laser ['94], using the same sort of addition and multiplication, found somewhat over 3 errors per hundred answer-figures in the case of boys and girls averaging 11½ years, during the period of their most accurate work. Holmes ['95], using addition of the sort just described, found 346 errors in 23,713 answer-figures or about 1½ per hundred. The children were from all grades from the third to the eighth. In Laser's work, 21, 19, 13, and 10 answer-figures were obtained per minute. Friedrich ['97] with similar examples, giving the very long time of 20 minutes for obtaining about 200 answer-figures, found from 1 to 2 per hundred wrong. King ['07] had children in grade 5 do sums, each consisting of 5 two-place numbers. In the most accurate work-period, they made 1 error per 20 columns. In multiplying a four-place by a four-place number they had less than one total answer right out of three. In New York City Courtis found ['11-'12] with his Test 7 that in 12 minutes the average achievement of fourth-grade children is 8.8 units attempted with 4.2 right. In grade 5 the facts are 10.9 attempts with 5.8 right; in grade 6, 12.5 attempts with 7.0 right; in grade 7, 15 attempts with 8.5 right; in grade 8, 15.7 attempts with 10.1 right. These results are near enough to those obtained from the country at large to serve as a text here.[Pg 104]
The following were set as official standards, in an excellent school system, Courtis Series B being used:—
| Grade. | Speed Attempts. | Percent of Correct Answers. | |
|---|---|---|---|
| Addition | 8 | 12 | 80 |
| 7 | 11 | 80 | |
| 6 | 10 | 70 | |
| 5 | 9 | 70 | |
| 4 | 8 | 70 | |
| Subtraction | 8 | 12 | 90 |
| 7 | 11 | 90 | |
| 6 | 10 | 90 | |
| 5 | 9 | 80 | |
| 4 | 7 | 80 | |
| Multiplication | 8 | 11 | 80 |
| 7 | 10 | 80 | |
| 6 | 9 | 80 | |
| 5 | 7 | 70 | |
| 4 | 6 | 60 | |
| Division | 8 | 11 | 90 |
| 7 | 10 | 90 | |
| 6 | 8 | 80 | |
| 5 | 6 | 70 | |
| 4 | 4 | 60 | |
Kirby ['13, pp. 16 ff. and 55 ff.] found that, in adding columns like those printed below, children in grade 4 got on the average less than 80 percent of correct answers. Their average speed was about 2 columns per minute. In doing division of the sort printed below children of grades 3 B and 4 A got less than 95 percent of correct answers, the average speed being 4 divisions per minute. In both cases the slower computers were no more accurate than the faster ones. Practice improved the speed very rapidly, but the accuracy remained substantially unchanged. Brown ['11 and '12] found a similar low status of ability and notable improvement from a moderate amount of special practice.[Pg 105]
| 3 | 5 | 6 | 2 | 3 | 8 | 9 | 7 | 4 | 9 |
| 7 | 9 | 6 | 5 | 5 | 6 | 4 | 5 | 8 | 2 |
| 3 | 4 | 7 | 8 | 7 | 3 | 7 | 9 | 3 | 7 |
| 8 | 8 | 4 | 8 | 2 | 6 | 8 | 2 | 9 | 8 |
| 2 | 2 | 4 | 7 | 6 | 9 | 8 | 5 | 6 | 2 |
| 6 | 9 | 5 | 7 | 8 | 5 | 2 | 3 | 2 | 4 |
| 9 | 6 | 4 | 2 | 7 | 2 | 9 | 4 | 4 | 5 |
| 3 | 3 | 7 | 9 | 9 | 9 | 2 | 8 | 9 | 7 |
| 6 | 8 | 9 | 6 | 4 | 7 | 7 | 9 | 2 | 4 |
| 8 | 4 | 6 | 9 | 9 | 2 | 6 | 9 | 8 | 9 |
| — | — | — | — | — | — | — | — | — | — |
20 = .... 5s
56 = .... 9s and .... r.
30 = .... 7s and .... r.
89 = .... 9s and .... r.
20 = .... 8s and .... r.
56 = .... 6s and .... r.
31 = .... 4s and .... r.
86 = .... 9s and .... r.
It is clear that numerical work as inaccurate as this has little or no commercial or industrial value. If clerks got only six answers out of ten right as in the Courtis tests, one would need to have at least four clerks make each computation and would even then have to check many of their discrepancies by the work of still other clerks, if he wanted his accounts to show less than one error per hundred accounting units of the Courtis size.
It is also clear that the "habits of ... absolute accuracy, and satisfaction in truth as a result" which arithmetic is supposed to further must be largely mythical in pupils who get right answers only from three to nine times out of ten!
The bonds in question clearly must be made far stronger than they now are. They should in fact be strong enough to abolish errors in computation, except for those due to[Pg 106] temporary lapses. It is much better for a child to know half of the multiplication tables, and to know that he does not know the rest, than to half-know them all; and this holds good of all the elementary bonds required for computation. Any bond should be made to work perfectly, though slowly, very soon after its formation is begun. Speed can easily be added by proper practice.
The chief reasons why this is not done now seem to be the following: (1) Certain important bonds (like the additions with higher decades) are not given enough attention when they are first used. (2) The special training necessary when a bond is used in a different connection (as when the multiplications to 9 × 9 are used in examples like
| 729 8 |
where the pupil has also to choose the right number to multiply, keep in mind what is carried, use it properly, and write the right figure in the right place, and carry a figure, or remember that he carries none) is neglected. (3) The pupil is not taught to check his work. (4) He is not made responsible for substantially accurate results. Furthermore, the requirement of (4) without the training of (1), (2), and (3) will involve either a fruitless failure on the part of many pupils, or an utterly unjust requirement of time. The common error of supposing that the task of computation with integers consists merely in learning the additions to 9 + 9, the subtractions to 18 − 9, the multiplications to 8 × 9, and the divisions to 81 ÷ 9, and in applying this knowledge in connection with the principles of decimal notation, has had a large share in permitting the gross inaccuracy of arithmetical work. The bonds involved in 'knowing the tables' do not make up one fourth of the bonds involved in real adding, subtracting, multiplying, and dividing (with integers alone).[Pg 107]
It should be noted that if the training mentioned in (1) and (2) is well cared for, the checking of results as recommended in (3) becomes enormously more valuable than it is under present conditions, though even now it is one of our soundest practices. If a child knows the additions to higher decades so that he can add a seen one-place number to a thought-of two-place number in three seconds or less with a correct answer 199 times out of 200, there is only an infinitesimal chance that a ten-figure column twice added (once up, once down) a few minutes apart with identical answers will be wrong. Suppose that, in long multiplication, a pupil can multiply to 9 × 9 while keeping his place and keeping track of what he is 'carrying' and of where to write the figure he writes, and can add what he carries without losing track of what he is to add it to, where he is to write the unit figure, what he is to multiply next and by what, and what he will then have to carry, in each case to a surety of 99 percent of correct responses. Then two identical answers got by multiplying one three-place number by another a few minutes apart, and with reversal of the numbers, will not be wrong more than twice in his entire school career. Checks approach proofs when the constituent bonds are strong.
If, on the contrary, the fundamental bonds are so weak that they do not work accurately, checking becomes much less trustworthy and also very much more laborious. In fact, it is possible to show that below a certain point of strength of the fundamental bonds, the time required for checking is so great that part of it might better be spent in improving the fundamental bonds.
For example, suppose that a pupil has to find the sum of five numbers like $2.49, $5.25, $6.50, $7.89, and $3.75.[Pg 108] Counting each act of holding in mind the number to be carried and each writing of a column's result as equivalent in difficulty to one addition, such a sum equals nineteen single additions. On this basis and with certain additional estimates[7] we can compute the practical consequences for a pupil's use of addition in life according to the mastery of it that he has gained in school.
I have so computed the amount of checking a pupil will have to do to reach two agreeing numbers (out of two, or three, or four, or five, or whatever the number before he gets two that are alike), according to his mastery of the elementary processes. The facts appear in Table 1.
It is obvious that a pupil whose mastery of the elements is that denoted by getting them right 96 times out of 100 will require so much time for checking that, even if he were never to use this ability for anything save a few thousand sums in addition, he would do well to improve this ability before he tried to do the sums. An ability of 199 out of 200, or 995 out of 1000, seems likely to save much more time than would be taken to acquire it, and a reasonable defense could be made for requiring 996 or 997 out of 1000.
A precision of from 995 to 997 out of 1000 being required, and ordinary sagacity being used in the teaching, speed will substantially take care of itself. Counting on the fingers or in words will not give that precision. Slow recourse to memory of serial addition tables will not give that precision. Nothing save sure memory of the facts operating under the conditions of actual examples will give it. And such memories will operate with sufficient speed.
TABLE 1
The Effect of Mastery of the Elementary Facts of Addition upon the Labor Required to Secure Two Agreeing Answers When Adding Five Three-figure Numbers
| Mastery of the Elementary Additions Times Right in 1000 | Approximate Number of Wrong Answers in Sums of 5 Three-place Numbers per 1000 | Approximate Number of Agreeing Answers, after One Checking, per 1000 | Approximate Number of Agreeing Answers, after a Checking of the First Discrepancies | Approximate Number of Checkings Required (over and above the First General Checking of the 100 Sums) to Secure Two Agreeing Results |
|---|---|---|---|---|
| 960 | 700 | 90 | 216 | 4500 |
| 980 | 380 | 384 | 676 | 1200 |
| 990 | 190 | 656 | 906 | 470 |
| 995 | 95 | 819 | 975 | 210 |
| 996 | 76 | 854 | 984 | 165 |
| 997 | 54 | 895 | 992 | 115 |
| 998 | 38 | 925 | 996 | 80 |
| 999 | 19 | 962 | 999 | 40 |
There is one intelligent objection to the special practice necessary to establish arithmetical connections so fully as to give the accuracy which both utilitarian and disciplinary aims require. It may be said that the pupils in grades 3, 4, and 5 cannot appreciate the need and that consequently the work will be dull, barren, and alien, without close personal appropriation by the pupil's nature. It is true that no vehement life-purpose is directly involved by the problem of perfecting one's power to add 7 to 28 in grade 2, or by the problem of multiplying 253 by 8 accurately in grade 3[Pg 110] or by precise subtraction in long division in grade 4. It is also true, however, that the most humanly interesting of problems—one that the pupil attacks most whole-heartedly—will not be solved correctly unless the pupil has the necessary associative mechanisms in order; and the surer he is of them, the freer he is to think out the problem as such. Further, computation is not dull if the pupil can compute. He does not himself object to its barrenness of vital meaning, so long as the barrenness of failure is prevented. We must not forget that pupils like to learn. In teaching excessively dull individuals, who has not often observed the great interest which they display in anything that they are enabled to master? There is pathos in their joy in learning to recognize parts of speech, perform algebraic simplifications, or translate Latin sentences, and in other accomplishments equally meaningless to all their interests save the universal human interest in success and recognition. Still further, it is not very hard to show to pupils the imperative need of accuracy in scoring games, in the shop, in the store, and in the office. Finally, the argument that accurate work of this sort is alien to the pupil in these grades is still stronger against inaccurate work of the same sort. If we are to teach computation with two- and three- and four-place numbers at all, it should be taught as a reliable instrument, not as a combination of vague memories and faith. The author is ready to cut computation with numbers above 10 out of the curriculum of grades 1-6 as soon as more valuable educational instruments are offered in its place, but he is convinced that nothing in child-nature makes a large variety of inaccurate computing more interesting or educative or germane to felt needs, than a smaller variety of accurate computing!
The second general fact is that certain bonds are of service for only a limited time and so need to be formed only to a limited and slight degree of strength. The data of problems set to illustrate a principle or improve some habit of computation are, of course, the clearest cases. The pupil needs to remember that John bought 3 loaves of bread and that they were 5-cent loaves and that he gave 25 cents to the baker only long enough to use the data to decide what change John should receive. The connections between the total described situation and the answer obtained, supposing some considerable computation to intervene, is a bond that we let expire almost as soon as it is born.
It is sometimes assumed that the bond between a certain group of features which make a problem a 'Buy a things at b per thing, find total cost' problem or a 'Buy a things at b per thing, what change from c' problem or a 'What gain on buying for a and selling for b' problem or a 'How many things at a each can I buy for b cents' problem—it is assumed that the bond between these essential defining features and the operation or operations required for solution is as temporary as the bonds with the name of the buyer or the price of the thing. It is assumed that all problems are and should be solved by some pure act of reasoning without help or hindrance from bonds with the particular verbal structure and vocabulary of the problems. Whether or not they should be, they are not. Every time that a pupil solves a 'bought-sold' problem by subtraction he strengthens the tendency to respond to any problem whatsoever that contains the words 'bought for' and 'sold for' by subtraction; and he will by no means surely stop and survey every such problem in all its elements to make sure that no[Pg 112] other feature makes inapplicable the tendency to subtract which the 'bought sold' evokes.
To prevent pupils from responding to the form of statement rather than the essential facts, we should then not teach them to forget the form of statement, but rather give them all the common forms of statement to which the response in question is an appropriate response, and only such. If a certain form of statement does in life always signify a certain arithmetical procedure, the bond between it and that procedure may properly be made very strong.
Another case of the formation of bonds to only a slight degree of strength concerns the use of so-called 'crutches' such as writing +, −, and × in copying problems like those below:—
| Add | Subtract | Multiply |
| 23 61 — | 79 24 — | 32 3 — |
or altering the figures when 'borrowing' in subtraction, and the like. Since it is undesirable that the pupil should regard the 'crutch' response as essential to the total procedure, or become so used to having it that he will be disturbed by its absence later, it is supposed that the bond between the situation and the crutch should not be fully formed. There is a better way out of the difficulty, in case crutches are used at all. This is to associate the crutch with a special 'set,' and its non-use with the general set which is to be the permanent one. For example, children may be taught from the start never to write the crutch sign or crutch figure unless the work is accompanied by "Write ... to help you to...."[Pg 113]
| Write - to help you to remember that you must subtract in this row. |
Find the differences:— | ||||
| 39 23 | 67 44 | 78 36 | 56 26 | 45 24 | |
| Remember that you must subtract in this row. |
Find the differences:— | ||||
| 85 63 | 27 14 | 96 51 | 38 45 | 78 32 | |
The bond evoking the use of the crutch may then be formed thoroughly enough so that there is no hesitation, insecurity, or error, without interfering to any harmful extent with the more general bond from the situation to work without the crutch.
Another instructive case concerns the bonds between certain words and their meanings, and between certain situations of commerce, industry, or agriculture and useful facts about these situations. Illustrations of the former are the bonds between cube root, hectare, brokerage, commission, indorsement, vertex, adjacent, nonagon, sector, draft, bill of exchange, and their meanings. Illustrations of the latter are the bonds from "Money being lent 'with interest' at no specified rate, what rate is charged?" to "The legal rate of the state," from "$X per M as a rate for lumber" to "Means $X per thousand board feet, a board foot being 1 ft. by 1 ft. by 1 in."
It is argued by many that such bonds are valuable for a short time; namely, while arithmetical procedures in connection with which they serve are learned, but that their value is only to serve as a means for learning these procedures and that thereafter they may be forgotten. "They are formed only as accessory means to certain more purely arithmetical knowledge or discipline; after this is acquired[Pg 114] they may be forgotten. Everybody does in fact forget them, relearning them later if life requires." So runs the argument.
In some cases learning such words and facts only to use them in solving a certain sort of problems and then forget them may be profitable. The practice is, however, exceedingly risky. It is true that everybody does in fact forget many such meanings and facts, but this commonly means either that they should not have been learned at all at the time that they were learned, or that they should have been learned more permanently, or that details should have been learned with the expectation that they themselves would be forgotten but that a general fact or attitude would remain. For example, duodecagon should not be learned at all in the elementary school; indorsement should either not be learned at all there, or be learned for permanence of a year or more; the details of the metric system should be so taught as to leave for several years at least knowledge of the facts that there is a system so named that is important, whose tables go by tens, hundreds, or thousands, and a tendency (not necessarily strong) to connect meter, kilogram, and liter with measurement by the metric system and with approximate estimates of their several magnitudes.
If an arithmetical procedure seems to require accessory bonds which are to be forgotten, once the procedure is mastered, we should be suspicious of the value of the procedure itself. If pupils forget what compound interest is, we may be sure that they will usually also have forgotten how to compute it. Surely there is waste if they have learned what it is only to learn how to compute it only to forget how to compute it!
The next case of the formation of bonds to slight strength is the problematic one of forming the bonds involved in understanding the reasons for certain processes only to forget them after the process has become a habit. Should a pupil, that is, learn why he inverts and multiplies, only to forget it as soon as he can be trusted to divide by a fraction? Should he learn why he puts the units figure of each partial product in multiplication under the figure that he multiplies by, only to forget the reason as soon as he has command of the process? Should he learn why he gets the number of square inches in a rectangle by multiplying the length by the width, both being expressed in linear inches, and forget why as soon as he is competent to make computations of the areas of rectangles?
On general psychological grounds we should be suspicious of forming bonds only to let them die of starvation later, and tend to expect that elaborate explanations learned only to be forgotten either should not be learned at all, or should be learned at such a time and in such a way that they would not be forgotten. Especially we should expect that the general principles of arithmetic, the whys and wherefores of its fundamental ways of manipulating numbers, ought to be the last bonds of all to be forgotten. Details of how you arranged numbers to multiply might vanish, but the general reasons for the placing would be expected to persist and enable one to invent the detailed manipulations that had been forgotten.
This suspicion is, I think, justified by facts. The doctrine that the customary deductive explanations of why we invert and multiply, or place the partial products as we do[Pg 116] before adding, may be allowed to be forgotten once the actual habits are in working order, has a suspicious source. It arose to meet the criticism that so much time and effort were required to keep these deductive explanations in memory. The fact was that the pupil learned to compute correctly irrespective of the deductive explanations. They were only an added burden. His inductive learning that the procedure gave the right answer really taught him. So he wisely shuffled off the extra burden of facts about the consequences of the nature of a fraction or the place values of our decimal notation. The bonds weakened because they were not used. They were not used because they were not useful in the shape and at the time that they were formed, or because the pupil was unable to understand the explanations so as to form them at all.
The criticism was valid and should have been met in part by replacing the deductive explanations by inductive verifications, and in part by using the deductive reasoning as a check after the process itself is mastered. The very same discussions of place-value which are futile as proof that you must do a certain thing before you have done it, often become instructive as an explanation of why the thing that you have learned to do and are familiar with and have verified by other tests works as well as it does. The general deductive theory of arithmetic should not be learned only to be forgotten. Much of it should, by most pupils, not be learned at all. What is learned should be learned much later than now, as a synthesis and rationale of habits, not as their creator. What is learned of such deductive theory should rank among the most rather than least permanent of a pupil's stock of arithmetical knowledge and power. There are bonds which are formed only to be lost, and bonds formed only to be lost in their first form, being[Pg 117] used in a new organization as material for bonds of a higher order; but the bonds involved in deductive explanations of why certain processes are right are not such: they are not to be formed just to be forgotten, nor as mere propædeutics to routine manipulations.
The formation of bonds to a limited strength because they are to be lost in their first form, being worked over in different ways in other bonds to which they are propædeutic or contributing is the most important case of low strength, or rather low permanence, in bonds.
The bond between four 5s in a column to be added and the response of thinking '10, 15, 20' is worth forming, but it is displaced later by the multiplication bond or direct connection of 'four 5s to be added' with '20.' Counting by 2s from 2, 3s from 3, 4s from 4, 5s from 5, etc., forms serial bonds which as series might well be left to disappear. Their separate steps are kept as permanent bonds for use in column addition, but their serial nature is changed from 2 (and 2) 4, (and 2) 6, (and 2) 8, etc., to two 2s = 4, three 2s = 6, four 2s = 8, etc.; after playing their part in producing the bonds whereby any multiple of 2 by 2 to 9, can be got, the original serial bonds are, as series, needed no longer. The verbal response of saying 'and' in adding, after helping to establish the bonds whereby the general set of the mind toward adding coöperates with the numbers seen or thought of to produce their sum, should disappear; or remain so slurred in inner speech as to offer no bar to speed.
The rule for such bonds is, of course, to form them strongly enough so that they work quickly and accurately for the time being and facilitate the bonds that are to replace them,[Pg 118] but not to overlearn them. There is a difference between learning something to be held for a short time, and the same amount of energy spent in learning for long retention. The former sort of learning is, of course, appropriate with many of these propædeutic bonds.
The bonds mentioned as illustrations are not purely propædeutic, nor formed only to be transmuted into something else. Even the saying of 'and' in addition has some genuine, intrinsic value in distinguishing the process of addition, and may perhaps be usefully reviewed for a brief space during the first steps in adding common fractions. Some such propædeutic bonds may be worth while apart from their value in preparing for other bonds. Consider, for example, exercises like those shown below which are propædeutic to long division, giving the pupil some basis in experience for his selection of the quotient figures. These multiplications are intrinsically worth doing, especially the 12s and 25s. Whatever the pupil remembers of them will be to his advantage.
1. Count by 11s to 132, beginning 11, 22, 33.
2. Count by 12s to 144, beginning 12, 24, 36.
3. Count by 25s to 300, beginning 25, 50, 75.
4. State the missing numbers:—
| A. | B. | C. | D. |
|---|---|---|---|
| 3 11s = | 5 11s = | 8 ft. = .... in. | 2 dozen = |
| 4 12s = | 3 12s = | 10 ft. = .... in. | 4 dozen = |
| 5 12s = | 6 12s = | 7 ft. = .... in. | 10 dozen = |
| 6 11s = | 12 11s = | 4 ft. = .... in. | 5 dozen = |
| 9 11s = | 2 12s = | 6 ft. = .... in. | 7 dozen = |
| 7 12s = | 9 12s = | 9 ft. = .... in. | 12 dozen = |
| 8 12s = | 7 11s = | 11 ft. = .... in. | 9 dozen = |
| 11 11s = | 12 12s = | 5 ft. = .... in. | 6 dozen = |
5. Count by 25s to $2.50, saying, "25 cents, 50 cents, 75 cents, one dollar," and so on.
6. Count by 15s to $1.50.
7. Find the products. Do not use pencil. Think what they are.
| A. | B. | C. | D. | E. |
|---|---|---|---|---|
| 2 × 25 | 3 × 15 | 2 × 12 | 4 × 11 | 6 × 25 |
| 3 × 25 | 10 × 15 | 2 × 15 | 4 × 15 | 6 × 15 |
| 5 × 25 | 4 × 15 | 2 × 25 | 4 × 12 | 6 × 12 |
| 10 × 25 | 2 × 15 | 2 × 11 | 4 × 25 | 6 × 11 |
| 4 × 25 | 7 × 15 | 3 × 25 | 5 × 11 | 7 × 12 |
| 6 × 25 | 9 × 15 | 3 × 15 | 5 × 12 | 7 × 15 |
| 8 × 25 | 5 × 15 | 3 × 11 | 5 × 15 | 7 × 25 |
| 7 × 25 | 8 × 15 | 3 × 12 | 5 × 25 | 7 × 11 |
| 9 × 25 | 6 × 15 | 8 × 12 | 9 × 12 | 8 × 25 |
State the missing numbers:—
| A. 36 = .... 12s | B. 44 = .... 11s | C. 50 = .... 25s |
| 60 = .... 12s | 88 = .... 11s | 125 = .... 25s |
| 24 = .... 12s | 77 = .... 11s | 75 = .... 25s |
| 48 = .... 12s | 55 = .... 11s | 200 = .... 25s |
| 144 = .... 12s | 99 = .... 11s | 250 = .... 25s |
| 108 = .... 12s | 110 = .... 11s | 175 = .... 25s |
| 72 = .... 12s | 33 = .... 11s | 225 = .... 25s |
| 96 = .... 12s | 66 = .... 11s | 150 = .... 25s |
| 84 = .... 12s | 22 = .... 11s | 100 = .... 25s |
Find the quotients and remainders. If you need to use paper and pencil to find them, you may. But find as many as you can without pencil and paper. Do Row A first. Then do Row B. Then Row C, etc.
| Row A. | 11|45 | 12|45 | 25|45 | 15|45 | 21|45 | 22|45 |
| Row B. | 25|55 | 11|55 | 12|55 | 15|55 | 22|55 | 30|55 |
| Row C. | 12|60 | 25|60 | 15|60 | 11|60 | 30|60 | 21|60 |
| Row D. | 12|75 | 11|75 | 15|75 | 25|75 | 30|75 | 35|75 |
| Row E. | 11|100 | 12|100 | 25|100 | 15|100 | 30|100 | 22|100 |
| Row F. | 11|96 | 12|96 | 25|96 | 15|96 | 30|96 | 22|96 |
| Row G. | 25|105 | 11|105 | 15|105 | 12|105 | 22|105 | 35|105 |
| Row H. | 12|64 | 15|64 | 25|64 | 11|64 | 22|64 | 21|64 |
| Row I. | 11|80 | 12|80 | 15|80 | 25|80 | 35|80 | 21|80 |
| Row J. | 25|200 | 30|200 | 75|200 | 63|200 | 65|200 | 66|200 |
Do this section again. Do all the first column first. Then do the second column, then the third, and so on.
Consider, from the same point of view, exercises like (3 × 4) + 2, (7 × 6) + 5, (9 × 4) + 6, given as a preparation for written multiplication. The work of
| 48 3 |
68 7 |
47 9 |
and the like is facilitated if the pupil has easy control of the process of getting a product, and keeping it in mind while he adds a one-place number to it. The practice with (3 × 4) + 2 and the like is also good practice intrinsically. So some teachers provide systematic preparatory drills of this type just before or along with the beginning of short multiplication.
In some cases the bonds are purely propædeutic or are formed only for later reconstruction. They then differ little from 'crutches.' The typical crutch forms a habit which has actually to be broken, whereas the purely propædeutic bond forms a habit which is left to rust out from disuse.
For example, as an introduction to long division, a pupil may be given exercises using one-figure divisors in the long form, as:—
| 773 | and 5 remainder |
| 7 ) 5416 | |
| 49 | |
| 51 | |
| 49 | |
| 26 | |
| 21 | |
| 5 |
The important recommendation concerning these purely propædeutic bonds, and bonds formed only for later reconstruction, is to be very critical of them, and not indulge in them when, by the exercise of enough ingenuity, some bond worthy of a permanent place in the individual's equipment can be devised which will do the work as well. Arithmetical teaching has done very well in this respect, tending to err by leaving out really valuable preparatory drills rather than by inserting uneconomical ones. It is in the teaching of reading that we find the formation of propædeutic bonds of dubious value (with letters, phonograms, diacritical marks, and the like) often carried to demonstrably wasteful extremes.
It will be instructive if the reader will perform the following experiment as an introduction to the discussion of this chapter, before reading any of the discussion.
Suppose that a pupil does all the work, oral and written, computation and problem-solving, presented for grades 1 to 6 inclusive (that is, in the first two books of a three-book series) in the average textbook now used in the elementary school. How many times will he have exercised each of the various bonds involved in the four operations with integers shown below? That is, how many times will he have thought, "1 and 1 are 2," "1 and 2 are 3," etc.? Every case of the action of each bond is to be counted.
THE FUNDAMENTAL BONDS
| 1 + 1 | 2 − 1 | 1 × 1 | 2 ÷ 1 |
| 1 + 2 | 2 − 2 | 2 × 1 | 2 ÷ 2 |
| 1 + 3 | 3 × 1 | ||
| 1 + 4 | 4 × 1 | ||
| 1 + 5 | 3 − 1 | 5 × 1 | 3 ÷ 1 |
| 1 + 6 | 3 − 2 | 6 × 1 | 3 ÷ 2 |
| 1 + 7 | 3 − 3 | 7 × 1 | 3 ÷ 3 |
| 1 + 8 | 8 × 1 | ||
| 1 + 9 | 9 × 1 | ||
| [Pg 123] | 4 − 1 | 4 ÷ 1 | |
| 4 − 2 | 4 ÷ 2 | ||
| 11 (or 21 or 31, etc.) + 1 | 4 − 3 | 1 × 2 | 4 ÷ 3 |
| 11 " + 2 | 4 − 4 | 2 × 2 | 4 ÷ 4 |
| 11 " + 3 | 3 × 2 | ||
| 11 " + 4 | 4 × 2 | ||
| 11 " + 5 | 5 − 1 | 5 × 2 | 5 ÷ 1 |
| 11 " + 6 | 5 − 2 | 6 × 2 | 5 ÷ 2 |
| 11 " + 7 | 5 − 3 | 7 × 2 | 5 ÷ 3 |
| 11 " + 8 | 5 − 4 | 8 × 2 | 5 ÷ 4 |
| 11 " + 9 | 5 − 5 | 9 × 2 | 5 ÷ 5 |
| 6 − 1 | 1 × 3 | 6 ÷ 1 | |
| 2 + 1 | 6 − 2 | 2 × 3 | 6 ÷ 2 |
| 2 + 2 | 6 − 3 | 3 × 3 | 6 ÷ 3 |
| 2 + 3 | 6 − 4 | 4 × 3 | 6 ÷ 4 |
| 2 + 4 | 6 − 5 | 5 × 3 | 6 ÷ 5 |
| 2 + 5 | 6 − 6 | 6 × 3 | 6 ÷ 6 |
| 2 + 6 | 7 × 3 | ||
| 2 + 7 | 8 × 3 | ||
| 2 + 8 | 7 − 1 | 9 × 3 | 7 ÷ 1 |
| 2 + 9 | 7 − 2 | 7 ÷ 2 | |
| 7 − 3 | 7 ÷ 3 | ||
| 7 − 4 | 1 × 4 | 7 ÷ 4 | |
| 12 (or 22 or 32, etc.) + 1 | 7 − 5 | 2 × 4 | 7 ÷ 5 |
| 12 " + 2 | 7 − 6 | and so on | 7 ÷ 6 |
| 7 − 7 | to 9 × 9 | 7 ÷ 7 | |
| and so on to | and so on | and so on to | |
| 9 + 9 | to 18 − 9 | 82 ÷ 9 83 ÷ 9, etc. | |
| 19 (or 29 or 39, etc.) + 9 |
If estimating for the entire series is too long a task, it will be sufficient to use eight or ten from each, say:—
| 3 + 2 | 13, 23, etc. + 2 | 7 + 2 | 17, 27, etc. + 2 |
| " 3 | " 3 | " 3 | " 3 |
| " 4 | " 4 | " 4 | " 4 |
| " 5 | " 5 | " 5 | " 5 |
| " 6 | " 6 | " 6 | " 6 |
| " 7 | " 7 | " 7 | " 7 |
| " 8 | " 8 | " 8 | " 8 |
| " 9 | " 9 | " 9 | " 9 |
| 3 − 3 | 7 − 7 | 9 × 7 | 63 ÷ 9 |
| 4 " | 8 " | 7 × 9 | 64 " |
| 5 " | 9 " | 8 × 6 | 65 " |
| 6 " | 10 " | 6 × 8 | 66 " |
| 7 " | 11 " | 67 " | |
| 8 " | 12 " | 68 " | |
| 9 " | 13 " | 69 " | |
| 10 " | 14 " | 70 " | |
| 11 " | 15 " | 71 " | |
| 12 " | 16 " |
TABLE 2
Estimates of the Amount of Practice Provided in Books I and II of the Average Three-Book Text in Arithmetic; by 50 Experienced Teachers
| Arithmetical Fact | Lowest Estimate |
Median Estimate | Highest Estimate |
Range Required to Include Half of the Estimates |
|---|---|---|---|---|
| 3 or 13 or 23, etc. + 2 | 25 | 1500 | 1,000,000 | 800-5000 |
| " " 3 | 24 | 1450 | 80,000 | 475-5000 |
| " " 4 | 23 | 1150 | 50,000 | 750-5000 |
| " " 5 | 22 | 1400 | 44,000 | 700-5000 |
| " " 6 | 21 | 1350 | 41,000 | 700-4500 |
| " " 7 | 21 | 1500 | 37,000 | 600-4000 |
| " " 8 | 20 | 1400 | 33,000 | 550-4100 |
| " " 9 | 20 | 1150 | 28,000 | 650-4500 |
| 7 or 17 or 27, etc. + 2 | 20 | 1250 | 2,000,000 | 600-5000 |
| " " 3 | 19 | 1100 | 1,000,000 | 650-4900 |
| " " 4 | 18 | 1000 | 80,000 | 650-4900 |
| " " 5 | 17 | 1300 | 80,000 | 650-4400 |
| " " 6 | 16 | 1100 | 29,000 | 650-4500 |
| " " 7 | 15 | 1100 | 25,000 | 500-4500 |
| " " 8 | 13 | 1100 | 21,000 | 650-3800 |
| " " 9 | 10 | 1275 | 17,000 | 500-4000 |
| 3 − 3 | 25 | 1000 | 100,000 | 500-4000 |
| 4 − 3 | 20 | 1050 | 500,000 | 525-3000 |
| 5 − 3 | 20 | 1100 | 2,500,000 | 650-4200 |
| 6 − 3 | 10 | 1050 | 21,000 | 650-3250 |
| 7 − 3 | 22 | 1100 | 15,000 | 550-3050 |
| 8 − 3 | 21 | 1075 | 15,000 | 650-3000 |
| 9 − 3 | 21 | 1000 | 15,000 | 700-2600 |
| 10 − 3 | 20 | 1000 | 20,000 | 600-2500 |
| 11 − 3 | 20 | 1000 | 15,000 | 465-2550 |
| 12 − 3 | 18 | 1000 | 15,000 | 650-2100 |
| 7 − 7 | 10 | 1000 | 18,000 | 425-3000 |
| 8 − 7 | 15 | 1000 | 18,000 | 413-3100 |
| 9 − 7 | 15 | 950 | 18,000 | 550-3000 |
| 10 − 7 | 15 | 950 | 18,000 | 600-3950 |
| 11 − 7 | 10 | 900 | 18,000 | 550-3000 |
| 12 − 7 | 10 | 925 | 18,000 | 525-3100 |
| 13 − 7 | 10 | 900 | 18,000 | 500-2600 |
| 14 − 7 | 10 | 900 | 18,000 | 500-3100 |
| 15 − 7 | 10 | 925 | 18,000 | 500-3000 |
| 16 − 7 | 10 | 875 | 18,000 | 500-2500 |
| 9 × 7 | 10 | 700 | 20,000 | 500-2000 |
| 7 × 9 | 10 | 700 | 20,000 | 500-1750 |
| 8 × 6 | 10 | 750 | 20,000 | 500-2500 |
| 6 × 8 | 9 | 700 | 20,000 | 500-2500 |
| 63 ÷ 9 | 9 | 500 | 4,500 | 300-2500 |
| 64 ÷ 9 | 9 | 200 | 4,000 | 100- 700 |
| 65 ÷ 9 | 8 | 200 | 4,000 | 100- 600 |
| 66 ÷ 9 | 7 | 200 | 4,000 | 100- 550 |
| 67 ÷ 9 | 7 | 200 | 4,000 | 75- 450 |
| 68 ÷ 9 | 6 | 200 | 4,000 | 87- 575 |
| 69 ÷ 9 | 6 | 200 | 4,000 | 87- 450 |
| 70 ÷ 9 | 5 | 200 | 4,000 | 75- 575 |
| 71 ÷ 9 | 5 | 200 | 4,000 | 75- 700 |
| XX | 40 | 550 | 1,000,000 | 300-2000 |
| XO | 20 | 500 | 11,500 | 150-2000 |
| XXX | 15 | 450 | 12,000 | 100-1000 |
| XXO | 25 | 400 | 15,000 | 150-1000 |
| XOO | 15 | 400 | 5,000 | 100-1000 |
| XOX | 10 | 400 | 10,000 | 100- 975 |
Having made his estimates the reader should compare them first with similar estimates made by experienced teachers (shown on page 124 f.), and then with the results of actual counts for representative textbooks in arithmetic (shown on pages 126 to 132).
It will be observed in Table 2 that even experienced teachers vary enormously in their estimates of the amount [Pg 126] of practice given by an average textbook in arithmetic, and that most of them are in serious error by overestimating the amount of practice. In general it is the fact that we use textbooks in arithmetic with very vague and erroneous ideas of what is in them, and think they give much more practice than they do.
The authors of the textbooks as a rule also probably had only very vague and erroneous ideas of what was in them. If they had known, they would almost certainly have revised their books. Surely no author would intentionally provide nearly four times as much practice on 2 + 2 as on 8 + 8, or eight times as much practice on 2 × 2 as on 9 × 8, or eleven times as much practice on 2 − 2 as on 17 − 8, or over forty times as much practice on 2 ÷ 2 as on 75 ÷ 8 and 75 ÷ 9, both together. Surely no author would have provided intentionally only twenty to thirty occurrences each of 16 − 7, 16 − 8, 16 − 9, 17 − 8, 17 − 9, and 18 − 9 for the entire course through grade 6; or have left the practice on 60 ÷ 7, 60 ÷ 8, 60 ÷ 9, 61 ÷ 7, 61 ÷ 8, 61 ÷ 9, and the like to occur only about once a year!
TABLE 3
Amount of Practice: Addition Bonds in a Recent Textbook (A) of Excellent Repute. Books I and II, All Save Four Sections of Supplementary Material, to be Used at the Teacher's Discretion
The Table reads: 2 + 2 was used 226 times, 12 + 2 was used 74 times, 22 + 2, 32 + 2, 42 + 2, and so on were used 50 times.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total | |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 226 | 154 | 162 | 150 | 97 | 87 | 66 | 45 | |
| 12 | 74 | 53 | 76 | 46 | 51 | 37 | 36 | 33 | |
| 22, etc. | 50 | 60 | 68 | 63 | 42 | 50 | 38 | 26 | |
| [Pg 127] | |||||||||
| 3 | 216 | 141 | 127 | 89 | 82 | 54 | 58 | 40 | |
| 13 | 43 | 43 | 60 | 70 | 52 | 30 | 22 | 18 | |
| 23, etc. | 15 | 30 | 51 | 50 | 42 | 32 | 29 | 30 | |
| 7 | 85 | 90 | 103 | 103 | 84 | 81 | 61 | 47 | |
| 17 | 35 | 25 | 42 | 32 | 35 | 21 | 29 | 16 | |
| 27, etc. | 30 | 23 | 32 | 29 | 24 | 23 | 25 | 28 | |
| 8 | 185 | 112 | 146 | 99 | 75 | 71 | 73 | 61 | |
| 18 | 28 | 35 | 52 | 46 | 28 | 29 | 24 | 14 | |
| 28, etc. | 53 | 36 | 34 | 38 | 23 | 36 | 27 | 27 | |
| 9 | 104 | 81 | 112 | 96 | 63 | 74 | 58 | 57 | |
| 19 | 13 | 11 | 31 | 38 | 25 | 14 | 22 | 11 | |
| 29, etc. | 19 | 17 | 27 | 20 | 32 | 32 | 19 | 18 | |
| 2, 12, 22, etc. | 350 | 277 | 306 | 260 | 190 | 174 | 140 | 104 | 1801 |
| 3, 13, 23, etc. | 274 | 214 | 230 | 209 | 176 | 116 | 109 | 88 | 1406 |
| 7, 17, 27, etc. | 148 | 138 | 187 | 164 | 141 | 125 | 115 | 91 | 1109 |
| 8, 18, 28, etc. | 266 | 183 | 232 | 185 | 126 | 136 | 124 | 102 | 1354 |
| 9, 19, 29, etc. | 136 | 109 | 170 | 154 | 120 | 120 | 99 | 86 | 994 |
| Totals | 1164 | 921 | 1125 | 972 | 753 | 671 | 687 | 471 |
TABLE 4
Amount of Practice: Subtraction Bonds in a Recent Textbook (A) of Excellent Repute. Books I and II, All Save Four Sections of Supplementary Material, to be Used at the Teacher's Discretion
| Minuends | Subtrahends | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 372 | ||||||||
| 2 | 214 | 311 | |||||||
| 3 | 136 | 149 | 189 | ||||||
| 4 | 146 | 142 | 103 | 205 | |||||
| 5 | 171 | 91 | 92 | 164 | 136 | ||||
| [Pg 128]6 | 80 | 59 | 69 | 71 | 81 | 192 | |||
| 7 | 106 | 57 | 55 | 67 | 59 | 156 | 80 | ||
| 8 | 73 | 50 | 50 | 75 | 50 | 62 | 48 | 152 | |
| 9 | 71 | 75 | 54 | 74 | 48 | 55 | 55 | 124 | 133 |
| 10 | 261 | 84 | 63 | 100 | 193 | 83 | 57 | 124 | 91 |
| 11 | 48 | 31 | 50 | 36 | 41 | 32 | 46 | 35 | |
| 12 | 48 | 77 | 57 | 51 | 35 | 80 | 30 | ||
| 13 | 35 | 22 | 40 | 29 | 35 | 28 | |||
| 14 | 25 | 37 | 36 | 49 | 32 | ||||
| 15 | 33 | 19 | 48 | 20 | |||||
| 16 | 16 | 36 | 26 | ||||||
| 17 | 27 | 20 | |||||||
| 18 | 19 | ||||||||
| Total excluding 1 − 1, 2 − 2, etc. | 1258 | 755 | 565 | 713 | 571 | 558 | 327 | 569 | 301 |
TABLE 5
Frequencies of Subtractions not Included in Table 4
These are cases where the pupil would, by reason of his stage of advancement, probably operate 35 − 30, 46 − 46, etc., as one bond.
| Minuends | Subtrahends | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 11 21 etc. |
2 12 22 etc. |
3 13 23 etc. |
4 14 24 etc. |
5 15 25 etc. |
6 16 26 etc. |
7 17 27 etc. |
8 18 28 etc. |
9 19 29 etc. |
10 20 etc. | |
| 10, 20, 30, 40, etc. | 11 | 29 | 16 | 52 | 32 | 51 | 7 | 30 | 22 | 60 |
| 11, 21, 31, 41, etc. | 42 | 14 | 22 | 32 | 12 | 26 | 19 | 52 | 17 | 10 |
| 12, 22, 32, 42, etc. | 47 | 97 | 5 | 13 | 9 | 21 | 11 | 24 | 19 | 17 |
| 13, 23, 33, 43, etc. | 7 | 40 | 7 | 14 | 15 | 13 | 19 | 19 | 22 | 3 |
| 14, 24, 34, 44, etc. | 8 | 28 | 14 | 58 | 13 | 16 | 14 | 26 | 19 | 7[Pg 129] |
| 15, 25, 35, 45, etc. | 21 | 28 | 29 | 54 | 51 | 15 | 21 | 12 | 24 | 8 |
| 16, 26, 36, 46, etc. | 5 | 18 | 12 | 27 | 35 | 69 | 13 | 17 | 19 | 2 |
| 17, 27, 37, 47, etc. | 5 | 9 | 12 | 40 | 32 | 54 | 24 | 12 | 12 | 1 |
| 18, 28, 38, 48, etc. | 2 | 16 | 10 | 23 | 22 | 36 | 18 | 47 | 16 | 0 |
| 19, 29, 39, etc. | 5 | 7 | 7 | 10 | 13 | 28 | 14 | 23 | 16 | 0 |
| Totals | 153 | 286 | 134 | 323 | 234 | 329 | 160 | 262 | 186 | 108 |
TABLE 6
Amount of Practice: Multiplication Bonds in Another Recent Textbook (B) of Excellent Repute. Books I and II
| Multipliers | Multiplicands | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Totals | |
| 1 | 299 | 534 | 472 | 271 | 310 | 293 | 261 | 178 | 195 | 99 | 2912 |
| 2 | 350 | 644 | 668 | 480 | 458 | 377 | 332 | 238 | 239 | 155 | 3941 |
| 3 | 280 | 487 | 509 | 388 | 318 | 302 | 247 | 199 | 227 | 152 | 3109 |
| 4 | 186 | 375 | 398 | 242 | 203 | 265 | 197 | 163 | 159 | 93 | 2281 |
| 5 | 268 | 359 | 393 | 234 | 263 | 243 | 217 | 192 | 197 | 114 | 2480 |
| 6 | 180 | 284 | 265 | 199 | 196 | 191 | 168 | 169 | 165 | 106 | 1923 |
| 7 | 135 | 283 | 277 | 176 | 187 | 158 | 155 | 121 | 145 | 118 | 1755 |
| 8 | 137 | 272 | 292 | 175 | 192 | 164 | 158 | 157 | 126 | 126 | 1799 |
| 9 | 71 | 173 | 140 | 122 | 97 | 102 | 101 | 100 | 82 | 110 | 1098 |
| Totals | 1906 | 3411 | 3414 | 2287 | 2224 | 2095 | 1836 | 1517 | 1535 | 1073 | |
TABLE 7
Amount Of Practice: Divisions Without Remainder In Textbook B, Parts I And II
| Dividends | Divisors | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Totals | |||
| Integral multiples of 2 to 9 in sequence; i.e., 4 ÷ 2 occurred 397 times, 6 ÷ 2 occurred 256 times, 6 ÷ 3, 224 times, 9 ÷ 3, 124 times. |
397 | 224 | 250 | 130 | 93 | 44 | 98 | 23 | 1259 | ||
| 256 | 124 | 152 | 79 | 28 | 43 | 61 | 25 | 768 | |||
| 318 | 123 | 130 | 65 | 50 | 19 | 39 | 19 | 763 | |||
| 258 | 98 | 86 | 105 | 25 | 24 | 34 | 20 | 650 | |||
| 198 | 49 | 76 | 27 | 22 | 30 | 33 | 16 | 451 | |||
| 77 180 69 | 54 91 46 | 36 50 37 | 31 38 24 | 28 17 12 | 27 13 17 | 16 22 16 | 9 16 15 | 278 427 236 | |||
| Totals | 1753 | 809 | 817 | 499 | 275 | 217 | 319 | 142 | |||
TABLE 8
Division Bonds, With And Without Remainders. Book B
All work through grade 6, except estimates of quotient figures in long division.
| Dividend | 2 | 3 | 4 | 5 | ||||||||||||||
| Divisor | 1 | 2 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 5 | ||||
| Number of Occurrences | 41 | 386 | 27 | 189 | 240 | 26 | 397 | 66 | 185 | 23 | 136 | 43 | 53 | 135 | ||||
| Dividend | 6 | 7 | ||||||||||||||||
| Divisor | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||||
| Number of Occurrences | 21 | 256 | 224 | 68 | 43 | 83 | 23 | 72 | 55 | 38 | 46 | 32 | 54 | |||||
| Dividend | 8 | 9 | ||||||||||||||||
| Divisor | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Number of Occurrences | 17 | 318 | 30 | 250 | 22 | 28 | 39 | 91 | 19 | 50 | 124 | 49 | 25 | 15 | 18 | 30 | 38 | |
| Dividend | 10 | 11 | ||||||||||||||||
| Divisor | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Number of Occurrences | 258 | 38 | 46 | 120 | 19 | 9 | 24 | 24 | 32 | 21 | 16 | 3 | 7 | 11 | 14 | 3 | ||
| Dividend | 12 | 13 | ||||||||||||||||
| Divisor | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Number of Occurrences | 198 | 123 | 152 | 29 | 93 | 9 | 16 | 7 | 45 | 16 | 15 | 11 | 7 | 4 | 5 | 3 | ||
| Dividend | 14 | 15 | ||||||||||||||||
| Divisor | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Number of Occurrences | 77 | 20 | 13 | 5 | 8 | 44 | 8 | 6 | 69 | 98 | 16 | 79 | 8 | 8 | 4 | 6 | ||
| [Pg 131] | ||||||||||||||||||
| Dividend | 16 | 17 | ||||||||||||||||
| Divisor | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Number of Occurrences | 180 | 19 | 130 | 14 | 6 | 9 | 98 | 3 | 61 | 9 | 15 | 14 | 6 | 6 | 12 | 3 | ||
| Dividend | 18 | 19 | ||||||||||||||||
| Divisor | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Number of Occurrences | 69 | 49 | 13 | 6 | 28 | 7 | 7 | 23 | 21 | 6 | 10 | 5 | 3 | 4 | 10 | 4 | ||
| Dividend | 20 | 21 | ||||||||||||||||
| Divisor | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| Number of Occurrences | 24 | 86 | 65 | 11 | 3 | 23 | 5 | 54 | 12 | 8 | 5 | 43 | 10 | 5 | ||||
| Dividend | 22 | 23 | ||||||||||||||||
| Divisor | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| Number of Occurrences | 17 | 16 | 15 | 8 | 13 | 6 | 15 | 7 | 8 | 11 | 8 | 6 | 3 | 2 | ||||
| Dividend | 24 | 25 | ||||||||||||||||
| Divisor | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| Number of Occurrences | 91 | 76 | 18 | 50 | 5 | 61 | 1 | 11 | 13 | 105 | 5 | 6 | 5 | 3 | ||||
| Dividend | 26 | 27 | ||||||||||||||||
| Divisor | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| Number of Occurrences | 5 | 6 | 3 | 3 | 4 | 6 | 3 | 46 | 8 | 10 | 4 | 2 | 6 | 25 | ||||
| Dividend | 28 | 29 | ||||||||||||||||
| Divisor | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| Number of Occurrences | 4 | 36 | 8 | 3 | 19 | 3 | 7 | 6 | 8 | 0 | 5 | 11 | 2 | 3 | ||||
| Dividend | 30 | 31 | ||||||||||||||||
| Divisor | 4 | 5 | 6 | 7 | 8 | 9 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||
| Number of Occurrences | 21 | 27 | 25 | 6 | 7 | 13 | 4 | 3 | 1 | 1 | 4 | 2 | ||||||
| Dividend | 32 | 33 | ||||||||||||||||
| Divisor | 4 | 5 | 6 | 7 | 8 | 9 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||
| Number of Occurrences | 50 | 11 | 3 | 6 | 39 | 5 | 8 | 7 | 7 | 2 | 6 | 1 | ||||||
| Dividend | 34 | 35 | ||||||||||||||||
| Divisor | 4 | 5 | 6 | 7 | 8 | 9 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||
| Number of Occurrences | 8 | 3 | 5 | 2 | 1 | 1 | 10 | 31 | 5 | 24 | 5 | 3 | ||||||
| Dividend | 36 | 37 | ||||||||||||||||
| Divisor | 4 | 5 | 6 | 7 | 8 | 9 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||
| Number of Occurrences | 37 | 16 | 22 | 2 | 6 | 19 | 12 | 8 | 7 | 5 | 3 | 9 | ||||||
| Dividend | 38 | 39 | ||||||||||||||||
| Divisor | 4 | 5 | 6 | 7 | 8 | 9 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||
| Number of Occurrences | 7 | 8 | 7 | 1 | 1 | 5 | 4 | 3 | 7 | 4 | 3 | 1 | ||||||
| Dividend | 40 | 41 | 42 | |||||||||||||||
| Divisor | 5 | 6 | 7 | 8 | 9 | 5 | 6 | 7 | 8 | 9 | 5 | 6 | 7 | 8 | 9 | |||
| Number of Occurrences | 38 | 9 | 2 | 34 | 2 | 6 | 6 | 3 | 7 | 5 | 7 | 28 | 30 | 10 | 3 | |||
| Dividend | 43 | 44 | 45 | |||||||||||||||
| Divisor | 5 | 6 | 7 | 8 | 9 | 5 | 6 | 7 | 8 | 9 | 5 | 6 | 7 | 8 | 9 | |||
| Number of Occurrences | 7 | 5 | 10 | 3 | 2 | 7 | 6 | 4 | 5 | 0 | 24 | 6 | 7 | 10 | 20 | |||
| Dividend | 46 | 47 | 48 | |||||||||||||||
| Divisor | 5 | 6 | 7 | 8 | 9 | 5 | 6 | 7 | 8 | 9 | 5 | 6 | 7 | 8 | 9 | |||
| Number of Occurrences | 3 | 3 | 2 | 2 | 2 | 6 | 2 | 2 | 0 | 3 | 7 | 17 | 4 | 33 | 2 | |||
| Dividend | 49 | 50 | 51 | 52 | ||||||||||||||
| Divisor | 5 | 6 | 7 | 8 | 9 | 6 | 7 | 8 | 9 | 6 | 7 | 8 | 9 | 6 | 7 | 8 | 9 | |
| Number of Occurrences | 4 | 7 | 27 | 9 | 2 | 4 | 6 | 3 | 8 | 2 | 3 | 1 | 2 | 5 | 5 | 5 | 3 | |
| Dividend | 53 | 54 | 55 | 56 | ||||||||||||||
| Divisor | 6 | 7 | 8 | 9 | 6 | 7 | 8 | 9 | 6 | 7 | 8 | 9 | 6 | 7 | 8 | 9 | ||
| Number of Occurrences | 4 | 3 | 2 | 2 | 12 | 5 | 1 | 16 | 5 | 3 | 4 | 2 | 0 | 13 | 16 | 8 | ||
| [Pg 132] | ||||||||||||||||||
| Dividend | 57 | 58 | 59 | 60 | 61 | |||||||||||||
| Divisor | 6 | 7 | 8 | 9 | 6 | 7 | 8 | 9 | 6 | 7 | 8 | 9 | 7 | 8 | 9 | 7 | 8 | 9 |
| Number of Occurrences | 0 | 3 | 1 | 3 | 2 | 2 | 3 | 1 | 2 | 3 | 0 | 3 | 3 | 9 | 1 | 1 | 2 | 5 |
| Dividend | 62 | 63 | 64 | 65 | 66 | 67 | ||||||||||||
| Divisor | 7 | 8 | 9 | 7 | 8 | 9 | 7 | 8 | 9 | 7 | 8 | 9 | 7 | 8 | 9 | 7 | 8 | 9 |
| Number of Occurrences | 4 | 6 | 1 | 17 | 5 | 9 | 5 | 22 | 0 | 1 | 10 | 1 | 2 | 1 | 4 | 0 | 1 | 1 |
| Dividend | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | ||||||||||
| Divisor | 7 | 8 | 9 | 7 | 8 | 9 | 8 | 9 | 8 | 9 | 8 | 9 | 8 | 9 | 8 | 9 | 8 | 9 |
| Number of Occurrences | 1 | 3 | 2 | 0 | 6 | 1 | 6 | 2 | 1 | 0 | 16 | 10 | 7 | 5 | 3 | 3 | 5 | 3 |
| Dividend | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | ||||
| Divisor | 8 | 9 | 8 | 9 | 8 | 9 | 8 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| Number of Occurrences | 3 | 2 | 3 | 0 | 4 | 1 | 0 | 2 | 4 | 15 | 2 | 4 | 1 | 2 | 0 | 3 | 2 | 7 |
Tables 3 to 8 show that even gifted authors make instruments for instruction in arithmetic which contain much less practice on certain elementary facts than teachers suppose; and which contain relatively much more practice on the more easily learned facts than on those which are harder to learn.
How much practice should be given in arithmetic? How should it be divided among the different bonds to be formed? Below a certain amount there is waste because, as has been shown in Chapter VI, the pupil will need more time to detect and correct his errors than would have been required to give him mastery. Above a certain amount there is waste because of unproductive overlearning. If 668 is just enough for 2 × 2, 82 is not enough for 9 × 8. If 82 is just enough for 9 × 8, 668 is too much for 2 × 2.
It is possible to find the answers to these questions for the pupil of median ability (or any stated ability) by suitable experiments. The amount of practice will, of course, [Pg 133] vary according to the ability of the pupil. It will also vary according to the interest aroused in him and the satisfaction he feels in progress and mastery. It will also vary according to the amount of practice of other related bonds; 7 + 7 = 14 and 60 ÷ 7 = 8 and 4 remainder will help the formation of 7 + 8 = 15 and 61 ÷ 7 = 8 and 5 remainder. It will also, of course, vary with the general difficulty of the bond, 17 − 8 = 9 being under ordinary conditions of teaching harder to form than 7 − 2 = 5.
Until suitable experiments are at hand we may estimate for the fundamental bonds as follows, assuming that by the end of grade 6 a strength of 199 correct out of 200 is to be had, and that the teaching is by an intelligent person working in accord with psychological principles as to both ability and interest.
For one of the easier bonds, most facilitated by other bonds (such as 2 × 5 = 10, or 10 − 2 = 8, or the double bond 7 = two 3s and 1 remainder) in the case of the median or average pupil, twelve practices in the week of first learning, supported by twenty-five practices during the two months following, and maintained by thirty practices well spread over the later periods should be enough. For the more gifted pupils lesser amounts down to six, twelve, and fifteen may suffice. For the less gifted pupils more may be required up to thirty, fifty, and a hundred. It is to be doubted, however, whether pupils requiring nearly two hundred repetitions of each of these easy bonds should be taught arithmetic beyond a few matters of practical necessity.
For bonds of ordinary difficulty, with average facilitation from other bonds (such as 11 − 3, 4 × 7, or 48 ÷ 8 = 6) in the case of the median or average pupil, we may estimate twenty practices in the week of first learning, supported by thirty, and maintained by fifty practices well spread over the later[Pg 134] periods. Gifted pupils may gain and keep mastery with twelve, fifteen, and twenty practices respectively. Pupils dull at arithmetic may need up to twenty, sixty, and two hundred. Here, again, it is to be doubted whether a pupil for whom arithmetical facts, well taught and made interesting, are so hard to acquire as this, should learn many of them.
For bonds of greater difficulty, less facilitated by other bonds (such as 17 − 9, 8 × 7, or 12½% of = 1⁄8 of), the practice may be from ten to a hundred percent more than the above.
If we accept the above provisional estimates as reasonable, we may consider the harm done by giving less and by giving more than these reasonable amounts. Giving less is indefensible. The pupil's time is wasted in excessive checking to find his errors. He is in danger of being practiced in error. His attention is diverted from the learning of new facts and processes by the necessity of thinking out these supposedly mastered facts. All new bonds are harder to learn than they should be because the bonds which should facilitate them are not strong enough to do so. Giving more does harm to some extent by using up time that could be spent better for other purposes, and (though not necessarily) by detracting from the pupil's interest in arithmetic. In certain cases, however, such excess practice and overlearning are actually desirable. Three cases are of special importance.
The first is the case of a bond operating under a changed mental set or adjustment. A pupil may know 7 × 8 adequately as a thing by itself, but need more practice to operate it in
| 285 7 —— |
where he has to remember that 3 is to be added to the[Pg 135] 56 when he obtains it, and that only the 9 is to be written down, the 5 to be held in mind for later use. The practice required to operate the bond efficiently in this new set is desirable, even though it is excess from a narrower point of view, and causes the straightforward 'seven eights are fifty-six' to be overlearned. So also a pupil's work with 24, 34, 44, etc., + 9 may react to give what would be excess practice from the point of view of 4 + 9 alone; his work in estimating approximate quotient figures in long division may give excess practice on the division tables. There are many such cases. Even adding the 5 and 7 in 5⁄12 + 7⁄12 is not quite the same task as adding 5 and 7 undisturbed by the fact that they are twelfths. We know far too little about the amount of practice needed to adapt arithmetical bonds to efficient operation in these more complicated conditions to estimate even approximately the allowances to be made. But some allowance, and often a rather large allowance, must be made.
The second is the case where the computation in general should be made very easy and sure for the pupil except for some one new element that is being learned. For example, in teaching the meaning and uses of 'Averages' and of uneven division, we may deliberately use 2, 3, and 4 as divisors rather than 7 and 9, so as to let all the pupil's energy be spent in learning the new facts, and so that the fraction in the quotient may be something easily understood, real, and significant. In teaching the addition of mixed numbers, we may use, in the early steps,
| 11½ 13½ 24 —— |
rather than | 79½ 98½ 67 —— |
so as to save attention for the new process itself. In cancellation, we may give excess practice to divisions by 2, 3, 4, and 5 in order to make the transfer to the new habits of con[Pg 136]sidering two numbers together from the point of view of their divisibility by some number. In introducing trade discount, we may give excess practice on '5% of' and '10% of' deliberately, so that the meaning of discount may not be obscured by difficulties in the computation itself. Excess practice on, and overlearning of, certain bonds is thus very often justifiable.
The third case concerns bonds whose importance for practical uses in life or as notable facilitators of other bonds is so great that they may profitably be brought to a greater strength than 199 correct out of 200 at a speed of 2 sec. or less, or be brought to that degree of strength very early. Examples of bonds of such special practical use are the subtractions from 10, ½ + ½, ½ + ¼, ½ of 60, ¼ of 60, and the fractional parts of 12 and of $1.00. Examples of notable facilitating bonds are ten 10s = 100, ten 100s = 1000, additions like 2 + 2, 3 + 3, and 4 + 4, and all the multiplication tables to 9 × 9.
In consideration of these three modifying cases or principles, a volume could well be written concerning just how much practice to give to each bond, in each of the types of complex situations where it has to operate. There is evidently need for much experimentation to expose the facts, and for much sagacity and inventiveness in making sure of effective learning without wasteful overlearning.
The facts of primary importance are:—
(1) The textbook or other instrument of instruction which is a teacher's general guide may give far too little practice on certain bonds.
(2) It may divide the practice given in ways that are apparently unjustifiable.
(3) The teacher needs therefore to know how much practice it does give, where to supplement it, and what to omit.
(4) The omissions, on grounds of apparent excess practice, should be made only after careful consideration of the third principle described above.
(5) The amount of practice should always be considered in the light of its interest and appeal to the pupil's tendency to work with full power and zeal. Mere repetition of bonds when the learner does not care whether he is improving is rarely justifiable on any grounds.
(6) Practice that is actually in excess is not a very grave defect if it is enjoyed and improves the pupil's attitude toward arithmetic. Not much time is lost; a hundred practices for each of a thousand bonds after mastery to 199 in 200 at 2 seconds will use up less than 60 hours, or 15 hours per year in grades 3 to 6.
(7) By the proper division of practice among bonds, the arrangement of learning so that each bond helps the others, the adroit shifting of practice of a bond to each new type of situation requiring it to operate under changed conditions, and the elimination of excess practice where nothing substantial is gained, notable improvements over the past hit-and-miss customs may be expected.
(8) Unless the material for practice is adequate, well balanced and sufficiently motivated, the teacher must keep close account of the learning of pupils. Otherwise disastrous underlearning of many bonds is almost sure to occur and retard the pupil's development.
There is danger that the need of brevity and simplicity which has made us speak so often of a bond or an ability,[Pg 138] and of the amount of practice it requires, may mislead the reader into thinking that these bonds and abilities are to be formed each by itself alone and kept so. They should rarely be formed so and never kept so. This we have indicated from time to time by references to the importance of forming a bond in the way in which it is to be used, to the action of bonds in changed situations, to facilitation of one bond by others, to the coöperation of abilities, and to their integration into a total arithmetical ability.
As a matter of fact, only a small part of drill work in arithmetic should be the formation of isolated bonds. Even the very young pupil learning 5 and 3 are 8 should learn it with '5 and 5 = 10,' '5 and 2 = 7,' at the back of his mind, so to speak. Even so early, 5 + 3 = 8 should be part of an organized, coöperating system of bonds. Later 50 + 30 = 80 should become allied to it. Each bond should be considered, not simply as a separate tool to be put in a compartment until needed, but also as an improvement of one total tool or machine, arithmetical ability.
There are differences of course. Knowledge of square root can be regarded somewhat as a separate tool to be sharpened, polished, and used by itself, whereas knowledge of the multiplication tables cannot. Yet even square root is probably best made more closely a part of the total ability, being taught as a special case of dividing where divisor is to be the same as quotient, the process being one of estimating and correcting.
In general we do not wish the pupil to be a repository of separated abilities, each of which may operate only if you ask him the sort of questions which the teacher used to ask him, or otherwise indicate to him which particular arithmetical tool he is to use. Rather he is to be an effective organization of abilities, coöperating in useful ways to meet[Pg 139] the quantitative problems life offers. He should not as a rule have to think in such fashion as: "Is this interest or discount? Is it simple interest or compound interest? What did I do in compound interest? How do I multiply by 2 percent?" The situation that calls up interest should also call up the kind of interest that is appropriate, and the technique of operating with percents should be so welded together with interest in his mind that the right coöperation will occur almost without supervision by him.
As each new ability is acquired, then, we seek to have it take its place as an improvement of a thinking being, as a coöperative member of a total organization, as a soldier fighting together with others, as an element in an educated personality. Such an organization of bonds will not form itself any more than any one bond will create itself. If the elements of arithmetical ability are to act together as a total organized unified force they must be made to act together in the course of learning. What we wish to have work together we must put together and give practice in teamwork.
We can do much to secure such coöperative action when and where and as it is needed by a very simple expedient; namely, to give practice with computation and problems such as life provides, instead of making up drills and problems merely to apply each fact or principle by itself. Though a pupil has solved scores of problems reading, "A triangle has a base of a feet and an altitude of b feet, what is its area?" he may still be practically helpless in finding the area of a triangular plot of ground; still more helpless in using the formula for a triangle which is one of two into which a trapezoid is divided. Though a pupil has learned to solve problems in trade discount, simple interest, compound interest, and bank discount one at a time, stated in a few[Pg 140] set forms, he may be practically helpless before the actual series of problems confronting him in starting in business, and may take money out of the savings bank when he ought to borrow on a time loan, or delay payment on his bills when by paying cash he could save money as well as improve his standing with the wholesaler.
Instead of making up problems to fit the abilities given by school instruction, we should preferably modify school instruction so that arithmetical abilities will be organized into an effective total ability to meet the problems that life will offer. Still more generally, every bond formed should be formed with due consideration of every other bond that has been or will be formed; every ability should be practiced in the most effective possible relations with other abilities.
The bonds to be formed having been chosen, the next step is to arrange for their most economical order of formation—to arrange to have each help the others as much as possible—to arrange for the maximum of facilitation and the minimum of inhibition.
The principle is obvious enough and would probably be admitted in theory by any intelligent teacher, but in practice we are still wedded to conventional usages which arose long before the psychology of arithmetic was studied. For example, we inherit the convention of studying addition of integers thoroughly, and then subtraction, and then multiplication, and then division, and many of us follow it though nobody has ever given a proof that this is the best order for arithmetical learning. We inherit also the opposite convention of studying in a so-called "spiral" plan, a little addition, subtraction, multiplication, and division, and then some more of each, and then some more, and many of us follow this custom, with an unreasoned faith that changing about from one process to another is per se helpful.
Such conventions are very strong, illustrating our common tendency to cherish most those customs which we cannot justify! The reductions of denominate numbers ascending and descending were, until recently, in most courses of study,[Pg 142] kept until grade 4 or grade 5 was reached, although this material is of far greater value for drills on the multiplication and division tables than the customary problems about apples, eggs, oranges, tablets, and penholders. By some historical accident or for good reasons the general treatment of denominate numbers was put late; by our naïve notions of order and system we felt that any use of denominate numbers before this time was heretical; we thus became blind to the advantages of quarts and pints for the tables of 2s; yards and feet for the tables of 3s; gallons and quarts for the tables of 4s; nickels and cents for the 5s; weeks and days for the 7s; pecks and quarts for the 8s; and square yards and square feet for the 9s. Problems like 5 yards = __ feet or 15 feet = __ yards have not only the advantages of brevity, clearness, practical use, real reference, and ready variation, but also the very great advantage that part of the data have to be thought of in a useful way instead of read off from the page. In life, when a person has twenty cents with which to buy tablets of a certain sort, he thinks of the price in making his purchase, asking it of the clerk only in case he does not know it, and in planning his purchases beforehand he thinks of prices as a rule. In spite of these and other advantages, not one textbook in ten up to 1900 made early use of these exercises with denominate numbers. So strong is mere use and wont.
Besides these conventional customs, there has been, in those responsible for arithmetical instruction, an admiration for an arrangement of topics that is easy for a person, after he knows the subject, to use in thinking of its constituent parts and their relations. Such arrangements are often called 'logical' arrangements of subject matter, though they are often far from logical in any useful sense. Now the easiest order in which to think of a hierarchy of habits[Pg 143] after you have formed them all may be an extremely difficult order in which to form them. The criticism of other orders as 'scrappy,' or 'unsystematic,' valid enough if the course of study is thought of as an object of contemplation, may be foolish if the course of study is regarded as a working instrument for furthering arithmetical learning.
We must remember that all our systematizing and labeling is largely without meaning to the pupils. They cannot at any point appreciate the system as a progression from that point toward this and that, since they have no knowledge of the 'this or that.' They do not as a rule think of their work in grade 4 as an outcome of their work in grade 3 with extensions of a to a1, and additions of b2 and b3 to b and b1, and refinements of c and d by c4 and d5. They could give only the vaguest account of what they did in grade 3, much less of why it should have been done then. They are not much disturbed by a lack of so-called 'system' and 'logical' progression for the same reason that they are not much helped by their presence. What they need and can use is a dynamically effective system or order, one that they can learn easily and retain long by, regardless of how it would look in a museum of arithmetical systems. Unless their actual arithmetical habits are usefully related it does no good to see the so-called logical relations; and if their habits are usefully related, it does not very much matter whether or not they do see these; finally, they can be brought to see them best by first acquiring the right habits in a dynamically effective order.
Psychology offers no single, easy, royal road to discovering this dynamically best order. It can only survey the bonds, think what each demands as prerequisite and offers[Pg 144] as future help, recommend certain orders for trial, and measure the efficiency of each order as a means of attaining the ends desired. The ingenious thought and careful experimentation of many able workers will be required for many years to come.
Psychology can, however, even now, give solid constructive help in many instances, either by recommending orders that seem almost certainly better than those in vogue, or by proposing orders for trial which can be justified or rejected by crucial tests.
Consider, for example, the situation, 'a column of one-place numbers to be added, whose sum is over 9,' and the response 'writing down the sum.' This bond is commonly firmly fixed before addition with two-place numbers is undertaken. As a result the pupil has fixed a habit that he has to break when he learns two-place addition. If oral answers only are given with such single columns until two-place addition is well under way, the interference is avoided.
In many courses of study the order of systematic formation of the multiplication table bonds is : 1 × 1, 2 × 1, etc., 1 × 2, 2 × 2, etc., 1 × 3, 2 × 3, etc., 1 × 9, 2 × 9, etc. This is probably wrong in two respects. There is abundant reason to believe that the × 5s should be learned first, since they are easier to learn than the 1s or the 2s, and give the idea of multiplying more emphatically and clearly. There is also abundant reason to believe that the 1 × 5, 1 × 2, 1 × 3, etc., should be put very late—after at least three or four tables are learned, since the question "What is 1 times 2?" (or 3 or 5) is unnecessary until we come to multiplication of two- and three-place numbers, seems a foolish question until then, and obscures the notion of multiplication if put early. Also the facts are best learned once for all as the [Pg 145] habits "1 times k is the same as k," and "k times 1 is the same as k."[8]
In another connection it was recommended that the divisions to 81 ÷ 9 be learned by selective thinking or reasoning from the multiplications. This determines the order of bonds so far as to place the formation of the division bonds soon after the learning of the multiplications. For other reasons it is well to make the proximity close.
One of the arbitrary systematizations of the order of formation of bonds restricts operations at first to the numbers 1 to 10, then to numbers under 100, then to numbers under 1000, then to numbers under 10,000. Apart from the avoidance of unreal and pedantic problems in applied arithmetic to which work with large numbers in low grades does somewhat predispose a teacher, there is little merit in this restriction of the order of formation of bonds. Its demerits are many. For example, when the pupil is learning to 'carry' in addition he can be given better practice by soon including tasks with sums above 100, and can get a valuable sense of the general use of the process by being given a few examples with three- and four-place numbers to be added. The same holds for subtraction. Indeed, there is something to be said in favor of using six- or seven-place numbers in subtraction, enforcing the 'borrowing' process by having it done again and again in the same example, and putting it under control by having the decision between 'borrowing' and 'not borrowing' made again and again in the same example. When the multiplication [Pg 146] tables are learned the most important use for them is not in tedious reviews or trivial problems with answers under 100, but in regular 'short' multiplication of two- and three- and even four-place numbers. Just as the addition combinations function mainly in the higher-decade modifications of them, so the multiplication combinations function chiefly in the cases where the bond has to operate while the added tasks of keeping one's place, adding what has been carried, writing down the right figure in the right place, and holding the right number for later addition, are also taken care of. It seems best to introduce such short multiplication as soon as the × 5s, × 2s, × 3s, and × 4s are learned and to put the × 6s, × 7s, and the rest to work in such short multiplication as soon as each is learned.
Still surer is the need for four-, five-, and six-place numbers when two-place numbers are used in multiplying. When the process with a two-place multiplier is learned, multiplications by three-place numbers should soon follow. They are not more difficult then than later. On the contrary, if the pupil gets used to multiplying only as one does with two-place multipliers, he will suffer more by the resulting interference than he does from getting six- or seven-place answers whose meaning he cannot exactly realize. They teach the rationale and the manipulations of long multiplication with especial economy because the principles and the procedures are used two or three times over and the contrasts between the values which the partial products have in adding become three instead of one.
The entire matter of long multiplication with integers and United States money should be treated as a teaching unit and the bonds formed in close organization, even though numbers as large as 900,000 are occasionally involved. The reason is not that it is more logical, or less scrappy, but [Pg 147] that each of the bonds in question thus gets much help from, and gives much help to, the others.
In sharp contrast to a topic like 'long multiplication' stands a topic like denominate numbers. It most certainly should not be treated as a large teaching unit, and all the bonds involved in adding, subtracting, multiplying, and dividing with all the ordinary sorts of measures should certainly not be formed in close sequence. The reductions ascending and descending for many of the measures should be taught as drills on the appropriate multiplication and division tables. The reduction of feet and inches to inches, yards and feet to yards, gallons and quarts to quarts, and the like are admirable exercises in connection with the (a × b) + c = .... problems,—the 'Bought 3 lbs. of sugar at 7 cents and 5 cents worth of matches' problems. The reductions of inches to feet and inches and the like are admirable exercises in the d = (.... × b) + c or 'making change' problem, which in its small-number forms is an excellent preparatory step for short division. They are also of great service in early work with fractions. The feet-mile, square-foot-square-inch, and other simple relations give a genuine and intelligible demand for multiplication with large numbers.
Knowledge of the metric system for linear and square measure would perhaps, as an introduction to decimal fractions, more than save the time spent to learn it. It would even perhaps be worth while to invent a measure (call it the twoqua) midway between the quart and gallon and teach carrying in addition and borrowing in subtraction by teaching first the addition and subtraction of 'gallon, twoqua, quart, and pint' series! Many of the bonds which a system-made tradition huddled together uselessly in a chapter on denominate numbers should thus be formed[Pg 148] as helpful preparations for and applications of other bonds all the way from the first to the eighth half-year of instruction in arithmetic.
The bonds involved in the ability to respond correctly to the series:—
| 5 = .... 2s and .... remainder |
| 5 = .... 3s and .... remainder |
| 88 = .... 9s and .... remainder |
should be formed before, not during, the training in short division. They are admirable at that point as practice on the division tables; are of practical service in the making-change problems of the small purchase and the like; and simplify the otherwise intricate task of keeping one's place, choosing the quotient figure, multiplying by it, subtracting and holding in mind the new number to be divided, which is composed half of the remainder and half of a figure in the written dividend. This change of order is a good illustration of the nearly general rule that "When the practice or review required to perfect or hold certain bonds can, by an inexpensive modification, be turned into a useful preparation for new bonds, that modification should be made."
The bonds involved in the four operations with United States money should be formed in grades 3 and 4 along with or very soon after the corresponding bonds with three-place and four-place integers. This statement would have seemed preposterous to the pedagogues of fifty years ago. "United States money," they would have said, "is an application of decimals. How can it be learned until the essentials of decimal fractions are known? How will the child understand when multiplying $.75 by 3 that 3 times 5 cents is 1 dime and 5 cents, or that 3 times 70 cents is 2 dollars and 1 dime? Why perplex the young pupils with the difficulties of placing the decimal point? Why disturb [Pg 149] the learning of the four operations with integers by adding at each step a second 'procedure with United States money'?"
The case illustrates very well the error of the older oversystematic treatment of the order of topics and the still more important error of confusing the logic of proof with the psychology of learning. To prove that 3 × $.75 = $2.25 to the satisfaction of certain arithmeticians, you may need to know the theory of decimal fractions; but to do such multiplication all a child needs is to do just what he has been doing with integers and then "Put a $ before the answer to show that it means dollars and cents, and put a decimal point in the answer to show which figures mean dollars and which figures mean cents." And this is general. The ability to operate with integers plus the two habits of prefixing $ and separating dollars from cents in the result will enable him to operate with United States money.
Consequently good practice came to use United States money not as a consequence of decimal fractions, learned by their aid, but as an introduction to decimal fractions which aids the pupil to learn them. So it has gradually pushed work with United States money further and further back, though somewhat timidly.
We need not be timid. The pupil will have no difficulty in adding, subtracting, multiplying, and dividing with United States money—unless we create it by our explanations! If we simply form the two bonds described above and show by proper verification that the procedure always gives the right answer, the early teaching of the four operations with United States money will in fact actually show a learning profit! It will save more time in the work with integers than was spent in teaching it! For, in the first place, it will help to make work with four-place and five[Pg 150]-place numbers more intelligible and vital. A pupil can understand $16.75 or $28.79 more easily than 1675 or 2879. The former may be the prices of a suit or sewing machine or bicycle. In the second place, it permits the use of a large stock of genuine problems about spending, saving, sharing, and the like with advertisements and catalogues and school enterprises. In the third place, it permits the use of common-sense checks. A boy may find one fourth of 3000 as 7050 or 75 and not be disturbed, but he will much more easily realize that one fourth of $30.00 is not over $70 or less than $1. Even the decimal point of which we used to be so afraid may actually help the eye to keep its place in adding.
So far, the illustrations of improvements in the order of bonds so as to get less interference and more facilitation than the customary orders secure have sought chiefly to improve the mechanical organization of the bonds. Any gain in interest which the changes described effected would be largely due to the greater achievement itself. Dewey and others have emphasized a very different principle of improving the order of formation of bonds—the principle of determination of the bonds to be formed by some vital, engaging problem which arouses interest enough to lighten the labor and which goes beyond or even against cut-and-dried plans for sequences in order to get effective problems. For example, the work of the first month in grade 2B might sacrifice facilitations of the mechanical sort in order to put arithmetic to use in deciding what dimensions a rabbit's cage should have to give him 12 square feet of floor space, how much bread he should have per meal to get 6 ounces a day, how long a ten-cent loaf would last, how many loaves[Pg 151] should be bought per week, how much it costs to feed the rabbit, how much he has gained in weight since he was brought to the school, and so on.
Such sacrifices of the optimal order if interest were equal, in order to get greater interest or a healthier interest, are justifiable. Vital problems as nuclei around which to organize arithmetical learning are of prime importance. It is even safe probably to insist that some genuine problem-situation requiring a new process, such as addition with carrying, multiplication by two-place numbers, or division with decimals, be provided in every case as a part of the introduction to that process. The sacrifice should not be too great, however; the search for vital problems that fit an economical order of subject matter is as much needed as the amendment of that order to fit known interests; and the assurance that a problem helps the pupil to learn arithmetic is as important as the assurance that arithmetic is used to help the pupil solve his personal problems.
Much ingenuity and experimentation will be required to find the order that is satisfactory in both quality and quantity of interest or motive and helpfulness of the bonds one to another. The difficulty of organizing arithmetic around attractive problems is much increased by the fact of class instruction. For any one pupil vital, personal problems or projects could be found to provide for many arithmetical abilities; and any necessary knowledge and technique which these projects did not develop could be somehow fitted in along with them. But thirty children, half boys and half girls, varying by five years in age, coming from different homes, with different native capacities, will not, in September, 1920, unanimously feel a vital need to solve any one problem, and then conveniently feel another on, say, October 15! In the mechanical laws of learning[Pg 152] children are much alike, and the gain we may hope to make from reducing inhibitions and increasing facilitations is, for ordinary class-teaching, probably greater than that to be made from the discovery of attractive central problems. We should, however, get as much as possible of both.
The reader may by now feel rather helpless before the problem of the arrangement of arithmetical subject matter. "Sometimes you complete a topic, sometimes you take it piecemeal months or years apart, often you make queer twists and shifts to get a strategic advantage over the enemy," he may think, "but are there no guiding principles, no general rules?" There is only one that is absolutely general, to take the order that works best for arithmetical learning. There are particular rules, but there are so many and they are so limited by an 'other things being equal' clause, that probably a general eagerness to think out the pros and cons for any given proposal is better than a stiff attempt to adhere to these rules. I will state and illustrate some of them, and let the reader judge.
Other things being equal, one new sort of bonds should not be started until the previous set is fairly established, and two different sets should not be started at once. Thus, multiplication of two- and three-place numbers by 2, 3, 4, and 5 will first use numbers such that no carrying is required, and no zero difficulties are encountered, then introduce carrying, then introduce multiplicands like 206 and 320. If other things were equal, the carrying would be split into two steps—first drills with (4 × 6) + 2, (3 × 7) + 3, (5 × 4) + 1, and the like, and second the actual use of these habits in the multiplication. The objection to this separation of the double habit is that the first part of it in isolation is too [Pg 153] artificial—that it may be better to suffer the extra difficulty of forming the two together than to teach so rarely used habits as the (a × b) + c series. Experimental tests are needed to decide this point.
Other things being equal, bonds should be formed in such order that none will have to be broken later. For example, there is a strong argument for teaching long division first, or very early, with remainders, letting the case of zero remainder come in as one of many. If the pupils have been familiarized with the remainder notion by the drills recommended as preparation for short division,[9] the use of remainders in long division will offer little difficulty. The exclusive use of examples without remainders may form the habit of not being exact in computation, of trusting to 'coming out even' as a sole check, and even of writing down a number to fit the final number to be divided instead of obtaining it by honest multiplication.
For similar reasons additions with 2 and 3 as well as 1 to be 'carried' have much to recommend them in the very first stages of column addition with carrying. There is here the added advantage that a pupil will be more likely to remember to carry if he has to think what to carry. The present common practice of using small numbers for ease in the addition itself teaches many children to think of carrying as adding one.
Other things being equal, arrange to have variety. Thus it is probably, though not surely, wise to interrupt the monotony of learning the multiplication and division tables, by teaching the fundamentals of 'short' multiplication and perhaps of division after the 5s, 2s, 3s, and 4s are learned. This makes a break of several weeks. The facts for the 6s, 7s, 8s, and 9s can then be put to varied use as fast as learned. [Pg 154] It is almost certainly wise to interrupt the first half-year's work with addition and subtraction, by teaching 2 × 2, 2 × 3, 3 × 2, 2 × 4, 4 × 2, 2 × 5, later by 2 × 10, 3 × 10, 4 × 10, 5 × 10, later by ½ + ½, 1½ + ½, ½ of 2, ½ of 4, ½ of 6, and at some time by certain profitable exercises wherein a pupil tells all he knows about certain numbers which may be made nuclei of important facts (say, 5, 8, 10, 12, 15, and 20).
Other things being equal, use objective aids to verify an arithmetical process or inference after it is made, as well as to provoke it. It is well at times to let pupils do everything that they can with relations abstractly conceived, testing their results by objective counting, measuring, adding, and the like. For example, an early step in adding should be to show three things, put them under a book, show two more, put these under the book, and then ask how many there are under the book, letting the objective counting come later as the test of the correctness of the addition.
Other things being equal, reserve all explanations of why a process must be right until the pupils can use the process accurately, and have verified the fact that it is right. Except for the very gifted pupils, the ordinary preliminary deductive explanations of what must be done are probably useless as means of teaching the pupils what to do. They use up much time and are of so little permanent effect that, as we have seen, the very arithmeticians who advocate making them, admit that after a pupil has mastered the process he may be allowed to forget the reasons for it. I am not sure that the deductive proofs of why we place the decimal point as we do in division by a decimal, or invert and multiply in dividing by a fraction, and the like, are worth teaching at all. If they are to be taught at all, the time to teach them is (except for the very gifted) after the pupil has mastered the process and has confidence in it. He then at least[Pg 155] knows what process he is to prove is right, and that it is right, and has had some chance of seeing why it is right from his experience with it.
One more principle may be mentioned without illustration. Arrange the order of bonds with due regard for the aims of the other studies of the curriculum and the practical needs of the pupil outside of school. Arithmetic is not a book or a closed system of exercises. It is the quantitative work of the pupils in the elementary school. No narrower view of it is adequate.
The same amount of practice may be distributed in various ways. Figures 7 to 10, for example, show 200 practices with division by a fraction distributed over three and a half years of 10 months in four different ways. In Fig. 7, practice is somewhat equally distributed over the whole period. In Fig. 8 the practice is distributed at haphazard. In Fig. 9 there is a first main learning period, a review after about ten weeks, a review at the beginning of the seventh grade, another review at the beginning of the eighth grade, and some casual practice rather at random. In Fig. 10 there is a main learning period, with reviews diminishing in length and separated by wider and wider intervals, with occasional practice thereafter to keep the ability alive and healthy.
Plans I and II are obviously inferior to Plans III and IV; and Plan IV gives promise of being more effective than Plan III, since there seems danger that the pupil working by Plan III might in the ten weeks lose too much of what he had gained in the initial practice, and so again in the next ten weeks.

Fig. 7.—Plan I. 200 practices distributed somewhat evenly over 3½ years of 10 months. In Figs. 7, 8, 9, and 10, each tenth of an inch along the base line represents one month. Each hundredth of a square inch represents four practices, a little square 1⁄20 of an inch wide and 1⁄20 inch high representing one practice.
 Fig. 8.—Plan II. 200 practices distributed haphazard over 3½ years of 10 months.
Fig. 8.—Plan II. 200 practices distributed haphazard over 3½ years of 10 months.
 Fig. 9.—Plan III. A learning period, three reviews, and incidental practice.
Fig. 9.—Plan III. A learning period, three reviews, and incidental practice.
It is not wise, however, to try now to make close decisions in the case of practice with division by a fraction; or to determine what the best distribution of practice is for that or any other ability to be improved. The facts of psychology are as yet not adequate for very close decisions, nor are the[Pg 158] types of distribution of practice that are best adapted to different abilities even approximately worked out.
 Fig. 10.—Plan IV. A learning period with reviews of decreasing length at increasing intervals.
Fig. 10.—Plan IV. A learning period with reviews of decreasing length at increasing intervals.
Let us rather examine some actual cases of distribution of practice found in school work and consider, not the attainment of the best possible distribution, but simply the avoidance of gross blunders and the attainment of reasonable, defensible procedures in this regard.
Figures 11 to 18 show the distribution of examples in multiplication with multipliers of various sorts. X stands for any digit except zero. O stands for 0. XXO thus means a multiplier like 350 or 270 or 160; XOX means multipliers like 407, 905, or 206; XX means multipliers like 25, 17, 38. Each of these diagrams covers approximately 3½ years of school work, or from about the middle of grade 3 to the end of grade 6. They are made from counts of four textbooks (A, B, C, and D), the count being taken for each successive 8 pages.[10] [Pg 159] Each tenth of an inch along the base line equals 8 pages of the text in question. Each .01 sq. in. equals one example. The books, it will be observed, differ in the amount of practice given, as well as in the way in which it is distributed.
 Fig. 11.—Distribution of practise with multipliers of the XX type in the first two books of the three-book text A.
Fig. 11.—Distribution of practise with multipliers of the XX type in the first two books of the three-book text A.
Fig. 12.—Same as Fig. 11, but for text B. Following this period come certain pages of computation to be used by the teacher at her discretion, containing 24 XX multiplications.
These distributions are worthy of careful study; we shall note only a few salient facts about them here. Of the distributions of multiplications with multipliers of the XX type, that of book D (Fig. 14) is perhaps the best. A (Fig. 11) has too much of the practice too late; B (Fig. 12) gives too little practice in the first learning; C (Fig. 13) gives too much in the first learning and in grade 6. Among the distributions of multiplication with multipliers of the XOX type, that of book D (Fig. 18) is again probably the best. A, B, and C (Figs. 15, 16, and 17) have too much practice early and too long intervals between reviews. Book C (Fig. 17) by a careless oversight has one case of[Pg 161] this very difficult process, without any explanation, weeks before the process is taught!
 Fig. 13.—Same as Fig. 11, but for text C.
Fig. 13.—Same as Fig. 11, but for text C.
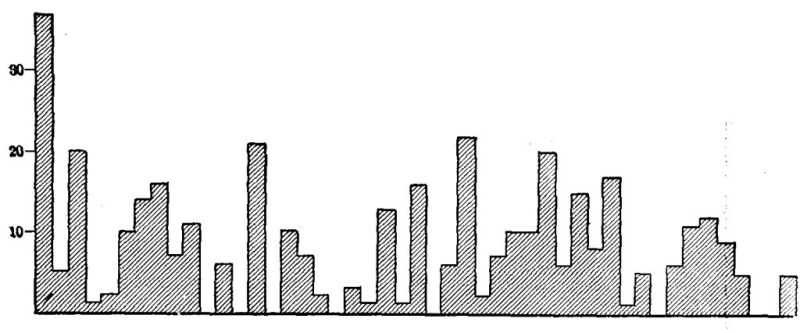 Fig. 14.—Same as Fig. 11, but for text D.
Fig. 14.—Same as Fig. 11, but for text D.
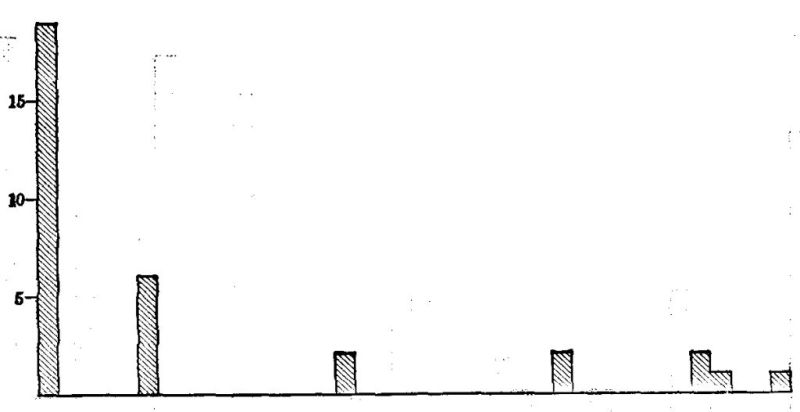 Fig. 15.—Distribution of practice with multipliers of the XOX type in the first
two books of the three-book text A.
Fig. 15.—Distribution of practice with multipliers of the XOX type in the first
two books of the three-book text A.
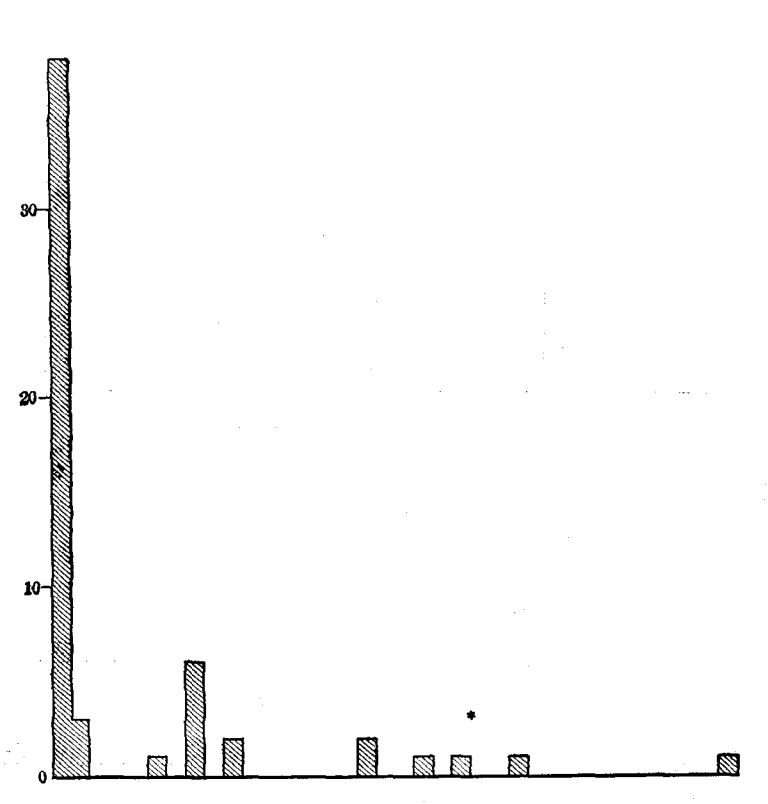
Fig. 16.—Same as Fig. 15, but for text B. Following this period come certain pages of computation to be used by the teacher at her discretion, containing 17 XOX multiplications.
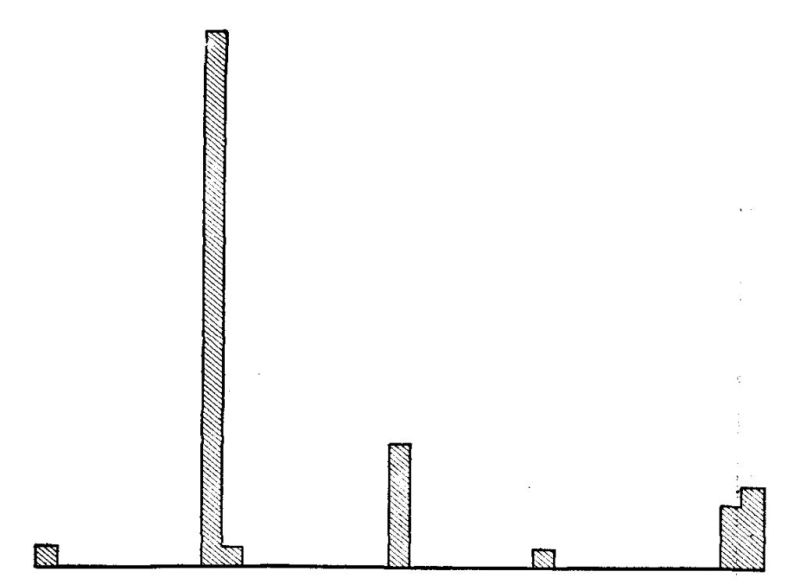 Fig. 17.—Same as Fig. 16, but for text C.
Fig. 17.—Same as Fig. 16, but for text C.
 Fig. 18.—Same as Fig. 16, but for text D.
Fig. 18.—Same as Fig. 16, but for text D.
Figures 19, 20, 21, 22, and 23 all concern the first two books of the three-book text E.
Figure 19 shows the distribution of practice on 5 × 5 in the first two books of text E. The plan is the same as in Figs. 11 to 18, except that each tenth of an inch along the base line represents ten pages. Figure 20 shows the dis[Pg 165]tribution of practice on 7 × 7; Fig. 21 shows it for 6 × 7 and 7 × 6 together. In Figs. 20 and 21 also, 0.1 inch along the base line equals ten pages.
Figures 22 and 23 show the distribution of practice on the divisions of 72, 73, 74, 75, 76, 77, 78, and 79 by either 8 or 9, and on the divisions of 81, 82 ... 89 by 9. Each tenth of an inch along the base line represents ten pages here also.
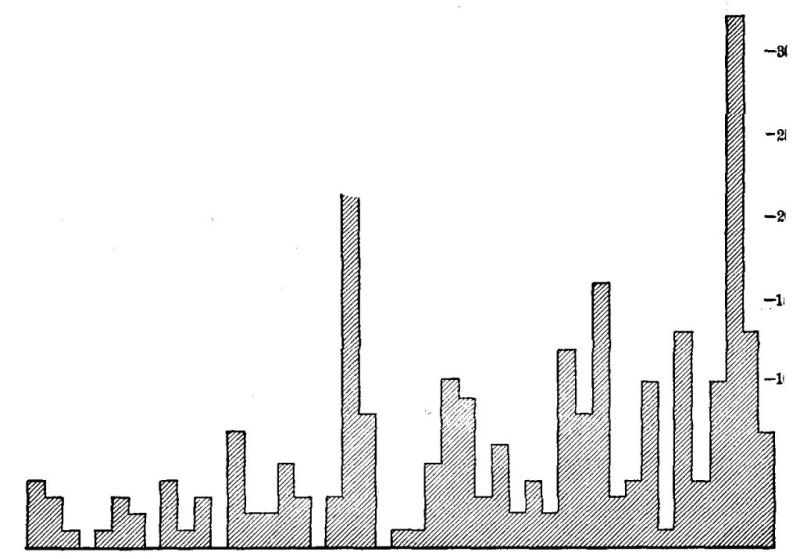 Fig. 19.—Distribution of practice with 5 × 5 in the first two books of the three-book
text E.
Fig. 19.—Distribution of practice with 5 × 5 in the first two books of the three-book
text E.
Figures 19 to 23 show no consistent plan for distributing practice. With 5 × 5 (Fig. 19) the amount of practice increases from the first treatment in grade 3 to the end of grade 6, so that the distribution would be better if the pupil began at the end and went backward! With 7 × 7 (Fig. 20)[Pg 166] the practice is distributed rather evenly and in small doses. With 6 × 7 and 7 × 6 (Fig. 21) much of it is in very large doses. With the divisions (Figs. 22 and 23) the practice is distributed more suitably, though in Fig. 23 there is too much of it given at one time in the middle of the period.
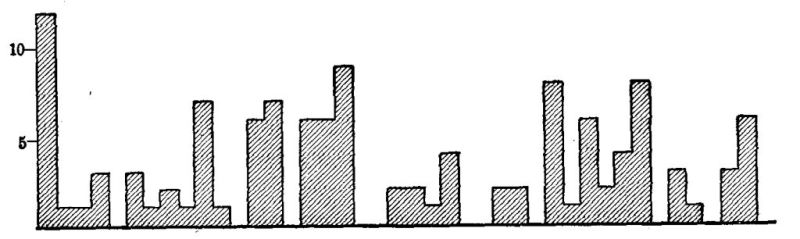 Fig. 20.—Distribution of practice with 7 × 7 in the first two books of text E.
Fig. 20.—Distribution of practice with 7 × 7 in the first two books of text E.
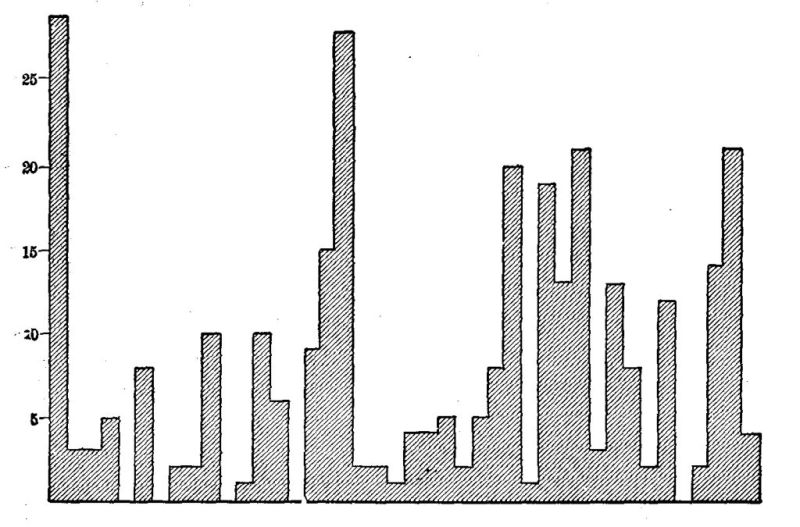 Fig. 21.—Distribution of practice with 6 × 7 or 7 × 6 in the first two books of text E.
Fig. 21.—Distribution of practice with 6 × 7 or 7 × 6 in the first two books of text E.
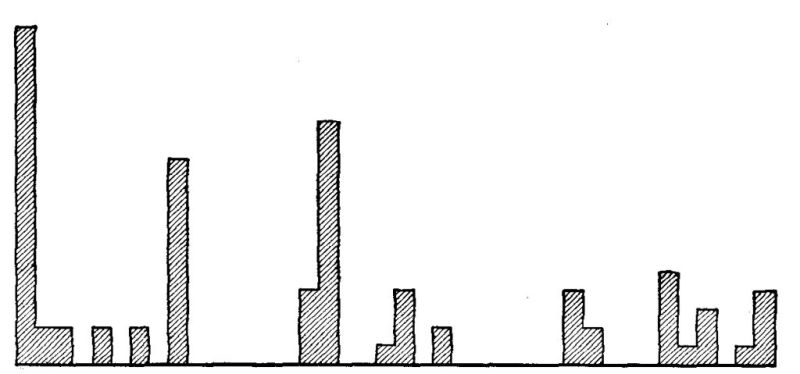 Fig. 22.—Distribution of practice with 72, 73 ... 79 ÷ 8 or 9 in the first two
books of text E.
Fig. 22.—Distribution of practice with 72, 73 ... 79 ÷ 8 or 9 in the first two
books of text E.
 Fig. 23.—Distribution of practice with 81, 82 ... 89 ÷ 9 in the first two books
of text E.
Fig. 23.—Distribution of practice with 81, 82 ... 89 ÷ 9 in the first two books
of text E.
Even if we knew what the best distribution of practice was for each ability of the many to be inculcated by arithmetical instruction, we could perhaps not provide it for all of them. For, in the first place, the allotments for some of[Pg 168] them might interfere with those for others. In the second place, there are many other considerations of importance in the ordering of topics besides giving the optimal distribution of practice to each ability. Such are considerations of interest, of welding separate abilities into an integrated total ability, and of the limitations due to the school schedule with its Saturdays, Sundays, holidays, and vacations.
Improvement can, however, be made over present practice in many respects. A scientific examination of the teaching of almost any class for a year, or of many of our standard instruments of instruction, will reveal opportunities for improving the distribution of practice with no sacrifice of interest, and with an actual gain in integrated functioning arithmetical power. In particular it will reveal cases where an ability is given practice and then, never being used again, left to die of inactivity. It will reveal cases where an ability is given practice and then left so long without practice that the first effect is nearly lost. There will be cases where practice is given and reviews are given, but all in such isolation from everything else in arithmetic that the ability, though existent, does not become a part of the pupil's general working equipment. There will be cases where more practice is given in the late than the earlier periods for no apparent extrinsic advantage; and cases where the practice is put where it is for no reason that is observable save that the teacher or author in question has decided to have some drill work at that time!
Each ability has its peculiar needs in this matter, and no set rules are at present of much value. It will be enough for the present if we are aroused to the problem of distribution, avoid obvious follies like those just noted, and exercise what ingenuity we have.
The plate which you see, the egg before you at the breakfast table, and this page are concrete things, but whiteness, whether of plate, egg, or paper, is, we say, an abstract quality. To be able to think of whiteness irrespective of any concrete white object is to be able to have an abstract idea or notion of white; to be able to respond to whiteness, irrespective of whether it is a part of china, eggshell, paper or whatever object, is to be able to respond to the abstract element of whiteness.
Learning arithmetic involves the formation of very many such ideas, the acquisition of very many such powers of response to elements regardless of the gross total situations in which they appear. To appreciate the fiveness of five boys, five pencils, five inches, five rings of a bell; to understand the division into eight equal parts of 40 cents, 32 feet, 64 minutes, or 16 ones; to respond correctly to the fraction relation in 2⁄3, 5⁄6, 3⁄4, 7⁄12, 1⁄8, or any other; to be sensitive to the common element of 9 = 3 × 3, 16 = 4 × 4, 625 = 25 × 25, .04 = .2 × .2, ¼ = ½ × ½,—these are obvious illustrations. All the numbers which the pupil learns to understand and manipulate are in fact abstractions; all the operations are abstractions; percent, discount, interest, height, length, area, volume, are abstractions; sum, difference, product, quotient, remainder, average, are facts that concern elements or aspects which may appear with countless different concrete surroundings or concomitants.
Towser is a particular dog; your house lot on Elm Street is a particular rectangle; Mr. and Mrs. I.S. Peterson and their daughter Louise are a particular family of three. In contrast to [Pg 170] these particulars, we mean by a dog, a rectangle, and a family of three, any specimens of these classes of facts. The idea of a dog, of rectangles in general, of any family of three is a general notion, a concept or idea of a class or species. The ability to respond to any dog, or rectangle, or family of three, regardless of which particular one it may be, is the general notion in action.
Learning arithmetic involves the formation of very many such general notions, such powers of response to any member of a certain class. Thus a hundred different sized lots may all be responded to as rectangles; 9⁄18, 12⁄27, 15⁄24, and 27⁄36 may all be responded to as members of the class, 'both members divisible by 3.' The same fact may be responded to in different ways according to the class to which it is assigned. Thus 4 in 3⁄4, 4⁄5, 45, 54, and 405 is classed respectively as 'a certain sized part of unity,' 'a certain number of parts of the size shown by the 5,' 'a certain number of tens,' 'a certain number of ones,' and 'a certain number of hundreds.' Each abstract quality may become the basis of a class of facts. So fourness as a quality corresponds to the class 'things four in number or size'; the fractional quality or relation corresponds to the class 'fractions.' The bonds formed with classes of facts and with elements or features by which one whole class of facts is distinguished from another, are in fact, a chief concern of arithmetical learning.[12]
Abstractions and generalizations then depend upon analysis and upon bonds formed with more or less subtle elements rather than with gross total concrete situations. The process involved is most easily understood by considering the means employed to facilitate it.
The first of these is having the learner respond to the total situations containing the element in question with the attitude of piecemeal examination, and with attentiveness to one element after another, especially to so near an approximation to the element in question as he can already select for attentive examination. This attentiveness to one element after another serves to [Pg 171] emphasize whatever appropriate minor bonds from the element in question the learner already possesses. Thus, in teaching children to respond to the 'fiveness' of various collections, we show five boys or five girls or five pencils, and say, "See how many boys are standing up. Is Jack the only boy that is standing here? Are there more than two boys standing? Name the boys while I point at them and count them. (Jack) is one, and (Fred) is one more, and (Henry) is one more. Jack and Fred make (two) boys. Jack and Fred and Henry make (three) boys." (And so on with the attentive counting.) The mental set or attitude is directed toward favoring the partial and predominant activity of 'how-many-ness' as far as may be; and the useful bonds that the 'fiveness,' the 'one and one and one and one and one-ness,' already have, are emphasized as far as may be.
The second of the means used to facilitate analysis is having the learner respond to many situations each containing the element in question (call it A), but with varying concomitants (call these V. C.) his response being so directed as, so far as may be, to separate each total response into an element bound to the A and an element bound to the V. C.
Thus the child is led to associate the responses—'Five boys,' 'Five girls,' 'Five pencils,' 'Five inches,' 'Five feet,' 'Five books,' 'He walked five steps,' 'I hit my desk five times,' and the like—each with its appropriate situation. The 'Five' element of the response is thus bound over and over again to the 'fiveness' element of the situation, the mental set being 'How many?,' but is bound only once to any one of the concomitants. These concomitants are also such as have preferred minor bonds of their own (the sight of a row of boys per se tends strongly to call up the 'Boys' element of the response). The other elements of the responses (boys, girls, pencils, etc.) have each only a slight connection with the 'fiveness' element of the situations. These slight connections also in large part[13] counteract each other, leaving the field clear for whatever uninhibited bond the 'fiveness' has.
The third means used to facilitate analysis is having the learner respond to situations which, pair by pair, present the element in a certain context and present that same context with the opposite of the element in question, or with something at least very unlike the element. Thus, a child who is being taught to respond to 'one fifth' is not only led to respond to 'one fifth of a cake,' 'one [Pg 172] fifth of a pie,' 'one fifth of an apple,' 'one fifth of ten inches,' 'one fifth of an army of twenty soldiers,' and the like; he is also led to respond to each of these in contrast with 'five cakes,' 'five pies,' 'five apples,' 'five times ten inches,' 'five armies of twenty soldiers.' Similarly the 'place values' of tenths, hundredths, and the rest are taught by contrast with the tens, hundreds, and thousands.
These means utilize the laws of connection-forming to disengage a response element from gross total responses and attach it to some situation element. The forces of use, disuse, satisfaction, and discomfort are so maneuvered that an element which never exists by itself in nature can influence man almost as if it did so exist, bonds being formed with it that act almost or quite irrespective of the gross total situation in which it inheres. What happens can be most conveniently put in a general statement by using symbols.
Denote by a + b, a + g, a + l, a + q, a + v, and a + B certain situations alike in the element a and different in all else. Suppose that, by original nature or training, a child responds to these situations respectively by r1 + r2, r1 + r7, r1 + r12, r1 + r17, r1 + r22, r1 + r27. Suppose that man's neurones are capable of such action that r1, r2, r7, r12, r22, and r27, can each be made singly.
Case I. Varying Concomitants
Suppose that a + b, a + g, a + l, etc., occur once each.
| We have | a + b | responded to by | r1 + r2, |
| a + g | " " | r1 + r7, | |
| a + l | " " | r1 + r12, | |
| a + q | " " | r1 + r17, | |
| a + v | " " | r1 + r22, and | |
| a + B | " " | r1 + r27, as shown in Scheme I. |
Scheme I
| a | b | g | l | q | v | B | |
| r1 | 6 | 1 | 1 | 1 | 1 | 1 | 1 |
| r2 | 1 | 1 | |||||
| r7 | 1 | 1 | |||||
| r12 | 1 | 1 | |||||
| r17 | 1 | 1 | |||||
| r22 | 1 | 1 | |||||
| r27 | 1 | 1 |
a is thus responded to by r1 (that is, connected with r1) each time, or six in all, but only once each with b, g, l, q, v, and B. b, g, l, q, v, and B are connected once each with r1 and once respectively with r2, r7, r12, etc. The bond from a to r1, has had six times as much exercise as the bond from a to r2, or from a to r7, etc. In any new gross situation, a 0, a will be more predominant in determining response than it would otherwise have been; and r1 will be more likely to be made than r2, r7, r12, etc., the other previous associates in the response to a situation containing a. That is, the bond from the element a to the response r1 has been notably strengthened.
Case II. Contrasting Concomitants
Now suppose that b and g are very dissimilar elements (e.g., white and black), that l and q are very dissimilar (e.g., long and short), and that v and B are also very dissimilar. To be very dissimilar means to be responded to very differently, so that r7, the response to g, will be very unlike r2, the response to b. So r7 may be thought of as rnot 2 or r-2. In the same way r12 may be thought of as rnot 12 or r-12, and r27 may be called rnot 22 or r-22.
Then, if the situations a b, a g, a l, a q, a v, and a B are responded to, each once, we have:—
| a + b | responded to by | r1 + r2, | |
| a + g | " " | r1 + rnot 2, | |
| a + l | " " | r1 + r12, | |
| a + q | " " | r1 + rnot 12, | |
| a + v | " " | r1 + r22, and | |
| a + B | " " | r1 + rnot 22, as shown in Scheme II. |
Scheme II
| a | b | g | l | q | v | B | |
| (opp. of b) | (opp. of l) | (opp. of v) | |||||
| r1 | 6 | 1 | 1 | 1 | 1 | 1 | 1 |
| rnot 1 | |||||||
| r2 | 1 | 1 | |||||
| rnot 2 | 1 | 1 | |||||
| r12 | 1 | 1 | |||||
| rnot 12 | 1 | 1 | |||||
| r22 | 1 | 1 | |||||
| rnot 22 | 1 | 1 |
r1 is connected to a by 6 repetitions. r2 and rnot 2 are each connected to a by 1 repetition, but since they interfere, canceling each[Pg 174] other so to speak, the net result is for a to have zero tendency to call up r2 or rnot 2. r12 and rnot 12 are each connected to a by 1 repetition, but they interfere with or cancel each other with the net result that a has zero tendency to call up r12 or rnot 12. So with r22 and rnot 22. Here then the net result of the six connections of a b, a g, a l, a q, a v, and a B is to connect a with r, and with nothing else.
Case III. Contrasting Concomitants and Contrasting Element
Suppose now that the facts are as in Case II, but with the addition of six experiences where a certain element which is the opposite of, or very dissimilar to, a is connected with the response rnot 1, or r-1 which is opposite to, or very dissimilar to r1. Call this opposite of a, − a.
That is, we have not only
| a + b | responded to by | r1 + r2, | |
| a + g | " " | r1 + rnot 2, | |
| a + l | " " | r1 + r12, | |
| a + q | " " | r1 + rnot 12, | |
| a + v | " " | r1 + r22, and | |
| a + B | " " | r1 + rnot 22, |
but also
| − a + b | responded to by | rnot 1 + r2, |
| − a + g | " " | rnot 1 + rnot 2, |
| − a + l | " " | rnot 1 + r12, |
| − a + q | " " | rnot 1 + rnot 12, |
| − a + v | " " | rnot 1 + r22, and |
| − a + B | " " | rnot 1 + rnot 22, as shown in Scheme III. |
Scheme III
| a | opp. | b | g | l | q | v | B | |
| of a | (opp. of b) | (opp. of l) | (opp. of v) | |||||
| r1 | 6 | 1 | 1 | 1 | 1 | 1 | 1 | |
| rnot 1 | 6 | 1 | 1 | 1 | 1 | 1 | 1 | |
| r2 | 1 | 1 | 2 | |||||
| rnot 2 | 1 | 1 | 2 | |||||
| r12 | 1 | 1 | 2[Pg 175] | |||||
| rnot 12 | 1 | 1 | 2 | |||||
| r22 | 1 | 1 | 2 | |||||
| rnot 22 | 1 | 1 | 2 | |||||
In this series of twelve experiences a connects with r1 six times and the opposite of a connects with rnot 1 six times. a connects equally often with three pairs of mutual destructives r2 and rnot 2, r12 and rnot 12, r22 and rnot 22, and so has zero tendency to call them up. − a has also zero tendency to call up any of these responses except its opposite, rnot 1. b, g, l, q, v, and B are made to connect equally often with r1 and rnot 1. So, of these elements, a is the only one left with a tendency to call up r1.
Thus, by the mere action of frequency of connection, r1 is connected with a; the bonds from a to anything except r1 are being counteracted, and the slight bonds from anything except a to r1 are being counteracted. The element a becomes predominant in situations containing it; and its bond toward r1 becomes relatively enormously strengthened and freed from competition.
These three processes occur in a similar, but more complicated, form if the situations a + b, a + g, etc., are replaced by a + b + c + d + e + f, a + g + h + i + j + k, etc., and the responses r1 + r2, r1 + r7, r1 + r12, etc., are replaced by r1 + r2 + r3 + r4 + r5 + r6, r1 + r7 + r8 + r9 + r10 + r11, etc.—provided the r1, r2, r3, r4, etc., can be made singly. In so far as any one of the responses is necessarily co-active with any one of the others (so that, for example, r13 always brings r26 with it and vice versa), the exact relations of the numbers recorded in schemes like schemes I, II, and III on pages 172 to 174 will change; but, unless r1 has such an inevitable co-actor, the general results of schemes I, II, and III will hold good. If r1 does have such an inseparable co-actor, say r2, then, of course, a can never acquire bonds with r1 alone, but everywhere that r1 or r2 appears in the preceding schemes the other element must appear also. r1 r2 would then have to be used as a unit in analysis.
The 'a + b,' 'a + g,' 'a + l,' ... 'a + B' situations may occur unequal numbers of times, altering the exact numerical relations of the connections formed and presented in schemes I, II, and III; but the process in general remains the same.
So much for the effect of use and disuse in attaching appropriate response elements to certain subtle elements of situations. There are three main series of effects of satisfaction and discomfort.[Pg 176] They serve, first, to emphasize, from the start, the desired bonds leading to the responses r1 + r2, r1 + r7, etc., to the total situations, and to weed out the undesirable ones. They also act to emphasize, in such comparisons and contrasts as have been described, every action of the bond from a to r1; and to eliminate every tendency of a to connect with aught save r1, and of aught save a to connect with r1. Their third service is to strengthen the bonds produced of appropriate responses to a wherever it occurs, whether or not any formal comparisons and contrasts take place.
The process of learning to respond to the difference of pitch in tones from whatever instrument, to the 'square-root-ness' of whatever number, to triangularity in whatever size or combination of lines, to equality of whatever pairs, or to honesty in whatever person or instance, is thus a consequence of associative learning, requiring no other forces than those of use, disuse, satisfaction, and discomfort. "What happens in such cases is that the response, by being connected with many situations alike in the presence of the element in question and different in other respects, is bound firmly to that element and loosely to each of its concomitants. Conversely any element is bound firmly to any one response that is made to all situations containing it and very, very loosely to each of those responses that are made to only a few of the situations containing it. The element of triangularity, for example, is bound firmly to the response of saying or thinking 'triangle' but only very loosely to the response of saying or thinking white, red, blue, large, small, iron, steel, wood, paper, and the like. A situation thus acquires bonds not only with some response to it as a gross total, but also with responses to any of its elements that have appeared in any other gross totals. Appropriate response to an element regardless of its concomitants is a necessary consequence of the laws of exercise and effect if an animal learns to make that response to the gross total situations that contain the element and not to make it to those that do not. Such prepotent determination of the response by one or another element of the situation is no transcendental mystery, but, given the circumstances, a general rule of all learning." Such are at bottom only extreme cases of the same learning as a cat exhibits that depresses a platform in a certain box whether it faces north or south, whether the temperature is 50 or 80 degrees, whether one or two persons are in sight, whether she is exceedingly or moderately hungry, whether fish or milk is outside the box. All learning is analytic, representing the activity of elements within a total situation. In man, by virtue of certain instincts and the course[Pg 177] of his training, very subtle elements of situations can so operate.
Learning by analysis does not often proceed in the carefully organized way represented by the most ingenious marshaling of comparing and contrasting activities. The associations with gross totals, whereby in the end an element is elevated to independent power to determine response, may come in a haphazard order over a long interval of time. Thus a gifted three-year-old boy will have the response element of 'saying or thinking two,' bound to the 'two-ness' element of very many situations in connection with the 'how-many' mental set; and he will have made this analysis without any formal, systematic training. An imperfect and inadequate analysis already made is indeed usually the starting point for whatever systematic abstraction the schools direct. Thus the kindergarten exercises in analyzing out number, color, size, and shape commonly assume that 'one-ness' versus 'more-than-one-ness,' black and white, big and little, round and not round are, at least vaguely, active as elements responded to in some independence of their contexts. Moreover, the tests of actual trial and success in further undirected exercises usually coöperate to confirm and extend and refine what the systematic drills have given. Thus the ordinary child in school is left, by the drills on decimal notation, with only imperfect power of response to the 'place-values.' He continues to learn to respond properly to them by finding that 4 × 40 = 160, 4 × 400 = 1600, 800 − 80 = 720, 800 − 8 = 792, 800 − 800 = 0, 42 × 48 = 2016, 24 × 48 = 1152, and the like, are satisfying; while 4 × 40 = 16, 23 × 48 = 832, 800 − 8 = 0, and the like, are not. The process of analysis is the same in such casual, unsystematized formation of connections with elements as in the deliberately man[Pg 178]aged, piecemeal inspection, comparison, and contrast described above.
The arrangement of a pupil's experiences so as to direct his attention to an element, vary its concomitants instructively, stimulate comparison, and throw the element into relief by contrast may be by fixed, formal, systematic exercises. Or it may be by much less formal exercises, spread over a longer time, and done more or less incidentally in other connections. We may call these two extremes the 'systematic' and 'opportunistic,' since the chief feature of the former is that it systematically provides experiences designed to build up the power of correct response to the element, whereas the chief feature of the latter is that it uses especially such opportunities as occur by reason of the pupil's activities and interests.
Each method has its advantages and disadvantages. The systematic method chooses experiences that are specially designed to stimulate the analysis; it provides these at a certain fixed time so that they may work together; it can then and there test the pupils to ascertain whether they really have the power to respond to the element or aspect or feature in question. Its disadvantages are, first, that many of the pupils will feel no need for and attach no interest or motive to these formal exercises; second, that some of the pupils may memorize the answers as a verbal task instead of acquiring insight into the facts; third, that the ability to respond to the element may remain restricted to the special cases devised for the systematic training, and not be available for the genuine uses of arithmetic.
The opportunistic method is strong just where the systematic is weak. Since it seizes upon opportunities created[Pg 179] by the pupil's abilities and interests, it has the attitude of interest more often. Since it builds up the experiences less formally and over a wider space of time, the pupils are less likely to learn verbal answers. Since its material comes more from the genuine uses of life, the power acquired is more likely to be applicable to life.
Its disadvantage is that it is harder to manage. More thought and experimentation are required to find the best experiences; greater care is required to keep track of the development of an abstraction which is taught not in two days, but over two months; and one may forget to test the pupils at the end. In so far as the textbook and teacher are able to overcome these disadvantages by ingenuity and care, the opportunistic method is better.
We may expect much improvement in the formation of abstract and general ideas in arithmetic from the application of three principles in addition to those already described. They are: (1) Provide enough actual experiences before asking the pupil to understand and use an abstract or general idea. (2) Develop such ideas gradually, not attempting to give complete and perfect ideas all at once. (3) Develop such ideas so far as possible from experiences which will be valuable to the pupil in and of themselves, quite apart from their merit as aids in developing the abstraction or general notion. Consider these three principles in order.
Children, especially the less gifted intellectually, need more experiences as a basis for and as applications of an arithmetical abstraction or concept than are usually given them. For example, in paving the way for the principle, "Any number times 0 equals 0," it is not safe to say, "John worked 8 days for 0 minutes per day. How many minutes[Pg 180] did he work?" and "How much is 0 times 4 cents?" It will be much better to spend ten or fifteen minutes as follows:[14] "What does zero mean? (Not any. No.) How many feet are there in eight yards? In 5 yards? In 3 yards? In 2 yards? In 1 yard? In 0 yard? How many inches are there in 4 ft.? In 2 ft.? In 0 ft.? 7 pk. = .... qt. 5 pk. = .... qt. 0 pk. = .... qt. A boy receives 60 cents an hour when he works. How much does he receive when he works 3 hr.? 8 hr.? 6 hr.? 0 hr.? A boy received 60 cents a day for 0 days. How much did he receive? How much is 0 times $600? How much is 0 times $5000? How much is 0 times a million dollars? 0 times any number equals....
| 232 | (At the blackboard.) 0 time 232 equals what? |
| 30 | I write 0 under the 0.[15] 3 times 232 equals what? |
| —— | |
| 6960 | Continue at the blackboard with |
| 734 | 321 | 312 | 41 | ||
| 20 | 40 | 30 | 60 | etc." | |
| —— | —— | —— | —— |
Pupils in the elementary school, except the most gifted, should not be expected to gain mastery over such concepts as common fraction, decimal fraction, factor, and root quickly. They can learn a definition quickly and learn to use it in very easy cases, where even a vague and imperfect understanding of it will guide response correctly. But complete [Pg 181] and exact understanding commonly requires them to take, not one intellectual step, but many; and mastery in use commonly comes only as a slow growth. For example, suppose that pupils are taught that .1, .2, .3, etc., mean 1⁄10, 2⁄10, 3⁄10, etc., that .01, .02, .03, etc., mean 1⁄100, 2⁄100, 3⁄100, etc., that .001, .002, .003, etc., mean 1⁄1000, 2⁄1000, 3⁄1000, etc., and that .1, .02, .001, etc., are decimal fractions. They may then respond correctly when asked to write a decimal fraction, or to state which of these,—1⁄4, .4, 3⁄8, .07, .002, 5⁄6,—are common fractions and which are decimal fractions. They may be able, though by no means all of them will be, to write decimal fractions which equal 1⁄2 and 1⁄5, and the common fractions which equal .1 and .09. Most of them will not, however, be able to respond correctly to "Write a decimal mixed number"; or to state which of these,—1⁄100 .4½, .007⁄350, $.25,—are common fractions, and which are decimals; or to write the decimal fractions which equal 3⁄4 and 1⁄3.
If now the teacher had given all at once the additional experiences needed to provide the ability to handle these more intricate and subtle features of decimal-fraction-ness, the result would have been confusion for most pupils. The general meaning of .32, .14, .99, and the like requires some understanding of .30, .10, .90, and .02, .04, .08; but it is not desirable to disturb the child with .30 while he is trying to master 2.3, 4.3, 6.3, and the like. Decimals in general require connection with place value and the contrasts of .41 with 41, 410, 4.1, and the like, but if the relation to place values in general is taught in the same lesson with the relation to ⁄10s, ⁄100s, ⁄1000s, the mind will suffer from violent indigestion.
A wise pedagogy in fact will break up the process of learn[Pg 182]ing the meaning and use of decimal fractions into many teaching units, for example, as follows:—
(1) Such familiarity with fractions with large denominators as is desirable for pupils to have, as by an exercise in reducing to lowest terms, 8⁄10, 36⁄64, 20⁄25, 18⁄24, 24⁄32, 21⁄30, 25⁄100, 40⁄100, and the like. This is good as a review of cancellation, and as an extension of the idea of a fraction.
(2) Objective work, showing 1⁄10 sq. ft., 1⁄50 sq. ft., 1⁄100 sq. ft., and 1⁄1000 sq. ft., and having these identified and the forms 1⁄10 sq. ft., 1⁄100 sq. ft., and 1⁄1000 sq. ft. learned. Finding how many feet = 1⁄10 mile and 1⁄100 mile.
(3) Familiarity with ⁄100s and ⁄1000s by reductions of 750⁄1000, 50⁄100, etc., to lowest terms and by writing the missing numerators in 500⁄1000 = ⁄100 = ⁄10 and the like, and by finding 1⁄10, 1⁄100, and 1⁄1000 of 3000, 6000, 9000, etc.
(4) Writing 1⁄10 as .1 and 1⁄100 as .01, 11⁄100, 12⁄100, 13⁄100, etc., as .11, .12, .13. United States money is used as the introduction. Application is made to miles.
(5) Mixed numbers with a first decimal place. The cyclometer or speedometer. Adding numbers like 9.1, 14.7, 11.4, etc.
(6) Place value in general from thousands to hundredths.
(7) Review of (1) to (6).
(8) Tenths and hundredths of a mile, subtraction when both numbers extend to hundredths, using a railroad table of distances.
(9) Thousandths. The names 'decimal fractions or decimals,' and 'decimal mixed numbers or decimals.' Drill in reading any number to thousandths. The work will continue with gradual extension and refinement of the understanding of decimals by learning how to operate with them in various ways.
Such may seem a slow progress, but in fact it is not, and[Pg 183] many of these exercises whereby the pupil acquires his mastery of decimals are useful as organizations and applications of other arithmetical facts.
That, it will be remembered, was the third principle:—"Develop abstract and general ideas by experiences which will be intrinsically valuable." The reason is that, even with the best of teaching, some pupils will not, within any reasonable limits of time expended, acquire ideas that are fully complete, rigorous when they should be, flexible when they should be, and absolutely exact. Many children (and adults, for that matter) could not within any reasonable limits of time be so taught the nature of a fraction that they could decide unerringly in original exercises like:—
Is 2.75⁄25 a common fraction?
Is $.25 a decimal fraction?
Is one xth of y a fraction?
Can the same words mean both a common fraction and a decimal fraction?
Express 1 as a common fraction.
Express 1 as a decimal fraction.
These same children can, however, be taught to operate correctly with fractions in the ordinary uses thereof. And that is the chief value of arithmetic to them. They should not be deprived of it because they cannot master its subtler principles. So we seek to provide experiences that will teach all pupils something of value, while stimulating in those who have the ability the growth of abstract ideas and general principles.
Finally, we should bear in mind that working with qualities and relations that are only partly understood or even misunderstood does under certain conditions give control over them. The general process of analytic learning in[Pg 184] life is to respond as well as one can; to get a clearer idea thereby; to respond better the next time; and so on. For instance, one gets some sort of notion of what 1⁄5 means; he then answers such questions as 1⁄5 of 10 = ? 1⁄5 of 5 = ? 1⁄5 of 20 = ?; by being told when he is right and when he is wrong, he gets from these experiences a better idea of 1⁄5; again he does his best with 1⁄5 = ⁄10, 1⁄5 = ⁄15, etc., and as before refines and enlarges his concept of 1⁄5. He adds 1⁄5 to 2⁄5, etc., 1⁄5 to 3⁄10, etc., 1⁄5 to 1⁄2, etc., and thereby gains still further, and so on.
What begins as a blind habit of manipulation started by imitation may thus grow into the power of correct response to the essential element. The pupil who has at the start no notion at all of 'multiplying' may learn what multiplying is by his experience that '4 6 multiplying gives 24'; '3 9 multiplying gives 27,' etc. If the pupil keeps on doing something with numbers and differentiates right results, he will often reach in the end the abstractions which he is supposed to need in the beginning. It may even be the case with some of the abstractions required in arithmetic that elaborate provision for comprehension beforehand is not so efficient as the same amount of energy devoted partly to provision for analysis itself beforehand and partly to practice in response to the element in question without full comprehension.
It certainly is not the best psychology and not the best educational theory to think that the pupil first masters a principle and then merely applies it—first does some thinking and then computes by mere routine. On the contrary, the applications should help to establish, extend, and refine the principle—the work a pupil does with numbers should be a main means of increasing his understanding of the principles of arithmetic as a science.
We distinguish aimless reverie, as when a child dreams of a vacation trip, from purposive thinking, as when he tries to work out the answer to "How many weeks of vacation can a family have for $120 if the cost is $22 a week for board, $2.25 a week for laundry, and $1.75 a week for incidental expenses, and if the railroad fares for the round trip are $12?" We distinguish the process of response to familiar situations, such as five integral numbers to be added, from the process of response to novel situations, such as (for a child who has not been trained with similar problems):—"A man has four pieces of wire. The lengths are 120 yd., 132 meters, 160 feet, and 1⁄8 mile. How much more does he need to have 1000 yd. in all?" We distinguish 'thinking things together,' as when a diagram or problem or proof is understood, from thinking of one thing after another as when a number of words are spelled or a poem in an unknown tongue is learned. In proportion as thinking is purposive, with selection from the ideas that come up, and in proportion as it deals with novel problems for which no ready-made habitual response is available, and in proportion as many bonds act together in an organized way to produce response, we call it reasoning.[Pg 186]
When the conclusion is reached as the effect of many particular experiences, the reasoning is called inductive. When some principle already established leads to another principle or to a conclusion about some particular fact, the reasoning is called deductive. In both cases the process involves the analysis of facts into their elements, the selection of the elements that are deemed significant for the question at hand, the attachment of a certain amount of importance or weight to each of them, and their use in the right relations. Thought may fail because it has not suitable facts, or does not select from them the right ones, or does not attach the right amount of weight to each, or does not put them together properly.
In the world at large, many of our failures in thinking are due to not having suitable facts. Some of my readers, for example, cannot solve the problem—"What are the chances that in drawing a card from an ordinary pack of playing-cards four times in succession, the same card will be drawn each time?" And it will be probably because they do not know certain facts about the theory of probabilities. The good thinkers among such would look the matter up in a suitable book. Similarly, if a person did not happen to know that there were fifty-two cards in all and that no two were alike, he could not reason out the answer, no matter what his mastery of the theory of probabilities. If a competent thinker, he would first ask about the size and nature of the pack. In the actual practice of reasoning, that is, we have to survey our facts to see if we lack any that are necessary. If we do, the first task of reasoning is to acquire those facts.
This is specially true of the reasoning about arithmetical facts in life. "Will 3½ yards of this be enough for a dress?" Reason directs you to learn how wide it is, what style of[Pg 187] dress you intend to make of it, how much material that style normally calls for, whether you are a careful or a wasteful cutter, and how big the person is for whom the dress is to be made. "How much cheaper as a diet is bread alone, than bread with butter added to the extent of 10% of the weight of the bread?" Reason directs you to learn the cost of bread, the cost of butter, the nutritive value of bread, and the nutritive value of butter.
In the arithmetic of the school this feature of reasoning appears in cases where some fact about common measures must be brought to bear, or some table of prices or discounts must be consulted, or some business custom must be remembered or looked up.
Thus "How many badges, each 9 inches long, can be made from 2½ yd. ribbon?" cannot be solved without getting into mind 1 yd. = 36 inches. "At Jones' prices, which costs more, 3¾ lb. butter or 6½ lb. lard? How much more?" is a problem which directs the thinker to ascertain Jones' prices.
It may be noted that such problems are, other things being equal, somewhat better training in thinking than problems where all the data are given in the problem itself (e.g., "Which costs more, 3¾ lb. butter at 48¢ per lb. or 6½ lb. lard at 27¢ per lb.? How much more?"). At least it is unwise to have so many problems of the latter sort that the pupil may come to think of a problem in applied arithmetic as a problem where everything is given and he has only to manipulate the data. Life does not present its problems so.
The process of selecting the right elements and attaching proper weight to them may be illustrated by the following problem:—"Which of these offers would you take, supposing that you wish a D.C.K. upright piano, have $50 saved,[Pg 188] can save a little over $20 per month, and can borrow from your father at 6% interest?"
A
A Reliable Piano. The Famous D.C.K. Upright. You pay $50 cash down and $21 a month for only a year and a half. No interest to pay. We ask you to pay only for the piano and allow you plenty of time.
B
We offer the well-known D.C.K. Piano for $390. $50 cash and $20 a month thereafter. Regular interest at 6%. The interest soon is reduced to less than $1 a month.
C
The D.C.K. Piano. Special Offer, $375, cash. Compare our prices with those of any reliable firm.
If you consider chiefly the "only," "No interest to pay," "only," and "plenty of time" in offer A, attaching much weight to them and little to the thought, "How much will $50 plus (18 × $21) be?", you will probably decide wrongly.
The situations of life are often complicated by many elements of little or even of no relevance to the correct solution. The offerer of A may belong to your church; your dearest friend may urge you to accept offer B; you may dislike to talk with the dealer who makes offer C; you may have a prejudice against owing money to a relative; that prejudice may be wise or foolish; you may have a suspicion that the B piano is shopworn; that suspicion may be well-founded or groundless; the salesman for C says, "You don't want your friends to say that you bought on the installment plan. Only low-class persons do that," etc. The statement of arithmetical problems in school usually assists the pupil to the extent of ruling out all save definitely quantitative elements,[Pg 189] and of ruling out all quantitative elements except those which should be considered. The first of the two simplifications is very beneficial, on the whole, since otherwise there might be different correct solutions to a problem according to the nature and circumstances of the persons involved. The second simplification is often desirable, since it will often produce greater improvement in the pupils, per hour of time spent, than would be produced by the problems requiring more selection. It should not, however, be a universal custom; for in that case the pupils are tempted to think that in every problem they must use all the quantities given, as one must use all the pieces in a puzzle picture.
It is obvious that the elements selected must not only be right but also be in the right relations to one another. For example, in the problems below, the 6 must be thought of in relation to a dozen and as being half of a dozen, and also as being 6 times 1. 1 must be mentally tied to "each." The 6 as half of a dozen must be related to the $1.00, $1.60, etc. The 6 as 6 times 1 must be related to the $.09, $.14, etc.
Buying in Quantity
These are a grocer's prices for certain things by the dozen and for a single one. He sells a half dozen at half the price of a dozen. Find out how much you save by buying 6 all at one time instead of buying them one at a time.
| Doz. | Each | |
|---|---|---|
| 1. Evaporated Milk | $1.00 | $.09 |
| 2. Puffed Rice | 1.60 | .14 |
| 3. Puffed Wheat | 1.10 | .10 |
| 4. Canned Soup | 1.90 | .17 |
| 5. Sardines | 1.80 | .16 |
| 6. Beans (No. 2 cans) | 1.50 | .13 |
| 7. Pork and Beans | 1.70 | .15 |
| 8. Peas (No. 2 cans) | 1.40 | .12 |
| 9. Tomatoes (extra cans) | 3.20 | .28 |
| 10. Ripe olives (qt. cans) | 7.20 | .65 |
It is obvious also that in such arithmetical work as we[Pg 190] have been describing, the pupil, to be successful, must 'think things together.' Many bonds must coöperate to determine his final response.
As a preface to reasoning about a problem we often have the discovery of the problem and the classification of just what it is, and as a postscript we have the critical inspection of the answer obtained to make sure that it is verified by experiment or is consistent with known facts. During the process of searching for, selecting, and weighting facts, there may be similar inspection and validation, item by item.
The pedagogy of the past made two notable errors in practice based on two errors about the psychology of reasoning. It considered reasoning as a somewhat magical power or essence which acted to counteract and overrule the ordinary laws of habit in man; and it separated too sharply the 'understanding of principles' by reasoning from the 'mechanical' work of computation, reading problems, remembering facts and the like, done by 'mere' habit and memory.
Reasoning or selective, inferential thinking is not at all opposed to, or independent of, the laws of habit, but really is their necessary result under the conditions imposed by man's nature and training. A closer examination of selective thinking will show that no principles beyond the laws of readiness, exercise, and effect are needed to explain it; that it is only an extreme case of what goes on in associative learning as described under the 'piecemeal' activity of situations; and that attributing certain features of learning to mysterious faculties of abstraction or reasoning gives no real help toward understanding or controlling them.[Pg 191]
It is true that man's behavior in meeting novel problems goes beyond, or even against, the habits represented by bonds leading from gross total situations and customarily abstracted elements thereof. One of the two reasons therefor, however, is simply that the finer, subtle, preferential bonds with subtler and less often abstracted elements go beyond, and at times against, the grosser and more usual bonds. One set is as much due to exercise and effect as the other. The other reason is that in meeting novel problems the mental set or attitude is likely to be one which rejects one after another response as their unfitness to satisfy a certain desideratum appears. What remains as the apparent course of thought includes only a few of the many bonds which did operate, but which, for the most part, were unsatisfying to the ruling attitude or adjustment.
Successful responses to novel data, associations by similarity and purposive behavior are in only apparent opposition to the fundamental laws of associative learning. Really they are beautiful examples of it. Man's successful responses to novel data—as when he argues that the diagonal on a right triangle of 796.278 mm. base and 137.294 mm. altitude will be 808.022 mm., or that Mary Jones, born this morning, will sometime die—are due to habits, notably the habits of response to certain elements or features, under the laws of piecemeal activity and assimilation.
Nothing is less like the mysterious operations of a faculty of reasoning transcending the laws of connection-forming, than the behavior of men in response to novel situations. Let children who have hitherto confronted only such arithmetical tasks, in addition and subtraction with one- and two-place numbers and multiplication with one-place numbers, as those exemplified in the first line below, be told to do the examples shown in the second line.[Pg 192]
| Add | Add | Add | Subt. | Subt. | Multiply | Multiply | Multiply |
| 8 5 — |
37 24 — |
35 68 23 19 — |
8 5 — |
37 24 — |
8 5 — |
9 7 — |
6 3 — |
| Multiply | Multiply | Multiply | |||||
| 32 23 — |
43 22 — |
34 26 — |
They will add the numbers, or subtract the lower from the upper number, or multiply 3 × 2 and 2 × 3, etc., getting 66, 86, and 624, or respond to the element of 'Multiply' attached to the two-place numbers by "I can't" or "I don't know what to do," or the like; or, if one is a child of great ability, he may consider the 'Multiply' element and the bigness of the numbers, be reminded by these two aspects of the situation of the fact that
'9
9 multiply'
—
gave only 81, and that
'10
10 multiply'
——
gave only 100, or the like; and so may report an intelligent and justified "I can't," or reject the plan of 3 × 2 and 2 × 3, with 66, 86, and 624 for answers, as unsatisfactory. What the children will do will, in every case, be a product of the elements in the situation that are potent with them, the responses which these evoke, and the further associates which these responses in turn evoke. If the child were one of sufficient genius, he might infer the procedure to be followed as a result of his knowledge of the principles of decimal notation and the meaning of 'Multiply,' responding correctly to the 'place-value' element of each digit and adding his 6 tens and 9 tens, 20 twos and 3 thirties; but if he did thus invent the shorthand addition of a collection of twenty-three collections, each of 32 units, he would still do it by the operation of bonds, subtle but real.[Pg 193]
Association by similarity is, as James showed long ago, simply the tendency of an element to provoke the responses which have been bound to it. abcde leads to vwxyz because a has been bound to vwxyz by original nature, exercise, or effect.
Purposive behavior is the most important case of the influence of the attitude or set or adjustment of an organism in determining (1) which bonds shall act, and (2) which results shall satisfy. James early described the former fact, showing that the mechanism of habit can give the directedness or purposefulness in thought's products, provided that mechanism includes something paralleling the problem, the aim, or need, in question.
The second fact, that the set or attitude of the man helps to determine which bonds shall satisfy, and which shall annoy, has commonly been somewhat obscured by vague assertions that the selection and retention is of what is "in point," or is "the right one," or is "appropriate," or the like. It is thus asserted, or at least hinted, that "the will," "the voluntary attention," "the consciousness of the problem," and other such entities are endowed with magic power to decide what is the "right" or "useful" bond and to kill off the others. The facts are that in purposive thinking and action, as everywhere else, bonds are selected and retained by the satisfyingness, and are killed off by the discomfort, which they produce; and that the potency of the man's set or attitude to make this satisfy and that annoy—to put certain conduction-units in readiness to act and others in unreadiness—is in every way as important as its potency to set certain conduction-units in actual operation.
Reasoning is not a radically different sort of force operating against habit but the organization and coöperation of many habits, thinking facts together. Reasoning is not[Pg 194] the negation of ordinary bonds, but the action of many of them, especially of bonds with subtle elements of the situation. Some outside power does not enter to select and criticize; the pupil's own total repertory of bonds relevant to the problem is what selects and rejects. An unsuitable idea is not killed off by some actus purus of intellect, but by the ideas which it itself calls up, in connection with the total set of mind of the pupil, and which show it to be inadequate.
Almost nothing in arithmetic need be taught as a matter of mere unreasoning habit or memory, nor need anything, first taught as a principle, ever become a matter of mere habit or memory. 5 × 4 = 20 should not be learned as an isolated fact, nor remembered as we remember that Jones' telephone number is 648 J 2. Almost everything in arithmetic should be taught as a habit that has connections with habits already acquired and will work in an organization with other habits to come. The use of this organized hierarchy of habits to solve novel problems is reasoning.
The activities essential to acquiring ability in arithmetic can rely on little in man's instinctive equipment beyond the purely intellectual tendencies of curiosity and the satisfyingness of thought for thought's sake, and the general enjoyment of success rather than failure in an enterprise to which one sets oneself. It is only by a certain amount of artifice that we can enlist other vehement inborn interests of childhood in the service of arithmetical knowledge and skill. When this can be done at no cost the gain is great. For example, marching in files of two, in files of three, in files of four, etc., raising the arms once, two times, three times, showing a foot, a yard, an inch with the hands, and the like are admirable because learning the meanings of numbers thus acquires some of the zest of the passion for physical action. Even in late grades chances to make pictures showing the relations of fractional parts, to cut strips, to fold paper, and the like will be useful.
Various social instincts can be utilized in matches after the pattern of the spelling match, contests between rows, certain number games, and the like. The scoring of both[Pg 196] the play and the work of the classroom is a useful field for control by the teacher of arithmetic.
Hunt ['12] has noted the more important games which have some considerable amount of arithmetical training as a by-product and which are more or less suitable for class use. Flynn ['12] has described games, most of them for home use, which give very definite arithmetical drill, though in many cases the drills are rather behind the needs of children old enough to understand and like the game itself.
It is possible to utilize the interests in mystery, tricks, and puzzles so as to arouse a certain form of respect for arithmetic and also to get computational work done. I quote one simple case from Miss Selkin's admirable collection ['12, p. 69 f.]:—
I. ADDITION
"We must admit that there is nothing particularly interesting in a long column of numbers to be added. Let the teacher, however, suggest that he can write the answer at sight, and the task will assume a totally different aspect.
"A very simple number trick of this kind can be performed by making use of the principle of complementary addition. The arithmetical complement of a number with respect to a larger number is the difference between these two numbers. Most interesting results can be obtained by using complements with respect to 9.
"The children may be called upon to suggest several numbers of two, three, or more digits. Below these write an equal number of addends and immediately announce the answer. The children, impressed by this apparently rapid addition, will set to work enthusiastically to test the results of this lightning calculation.
"Example:—
| 357 | } | 999 | |
| 682 | A | × 3 | |
| 793 | 2997 | ||
| 642 | } | ||
| 317 | B | ||
| 206 |
"Explanation:—The addends in group A are written down at random or suggested by the class. Those in group B are their complements. To write the first number in group B we look at the first number in group A and, starting at the left write 6, the complement of 3 with respect to 9; 4, the complement of 5; 2, the complement of 7. The second and third addends in group B are derived in the same way. Since we have three addends in each group, the problem reduces itself to multiplying 999 by 3, or to taking 3000 − 3. Any number of addends may be used and each addend may consist of any number of digits."
Respect for arithmetic as a source of tricks and magic is very much less important than respect for its everyday services; and computation to test such tricks is likely to be undertaken zealously only by the abler pupils. Consequently this source of interest should probably be used only sparingly, and perhaps the teacher should give such exhibitions only as a reward for efficiency in the regular work. For example, if the work for a week is well done in four days the fifth day might be given up to some semi-arithmetical entertainment, such as the demonstration of an adding machine, the story of primitive methods of counting, team races in computation, an exhibition of lightning calculation and intellectual sleight-of-hand by the teacher, or the voluntary study of arithmetical puzzles.
The interest in achievement, in success, mentioned above is stronger in children than is often realized and makes advisable the systematic use of the practice experiment as a method of teaching much of arithmetic. Children who thus compete with their own past records, keeping an exact score from week to week, make notable progress and enjoy hard work in making it.
Negatively the difficulty of the work that pupils should be expected to do is conditioned by the gradual maturing[Pg 198] of their capacities. Other things being equal, the common custom of reserving hard things for late in the elementary school course is, of course, sound. It seems probable that little is gained by using any of the child's time for arithmetic before grade 2, though there are many arithmetical facts that he can learn in grade 1. Postponement of systematic work in arithmetic to grade 3 or even grade 4 is allowable if better things are offered. With proper textbooks and oral and written exercises, however, a child in grades 2 and 3 can spend time profitably on arithmetical work. When all children can be held in school through the eighth grade it does not much matter whether arithmetic is begun early or late. If, however, many children are to leave in grades 5 and 6 as now, we may think it wise to provide somehow that certain minima of arithmetical ability be given them.
There are, so far as is known, no special times and seasons at which the human animal by inner growth is specially ripe for one or another section or aspect of arithmetic, except in so far as the general inner growth of intellectual powers makes the more abstruse and complex tasks suitable to later and later years.
Indeed, very few of even the most enthusiastic devotees of the recapitulation theory or culture-epoch theory have attempted to apply either to the learning of arithmetic, and Branford is the only mathematician, so far as I know, who has advocated such application, even tempered by elaborate shiftings and reversals of the racial order. He says:—
"Thus, for each age of the individual life—infancy, childhood, school, college—may be selected from the racial history the most appropriate form in which mathematical experience can be assimilated. Thus the capacity of the infant and early childhood is comparable with the capacity of animal consciousness and primitive man. The mathematics suitable to later childhood and boyhood (and, of course, girlhood) is comparable with Ar[Pg 199]chæan mathematics passing on through Greek and Hindu to mediæval European mathematics; while the student is become sufficiently mature to begin the assimilation of modern and highly abstract European thought. The filling in of details must necessarily be left to the individual teacher, and also, within some such broadly marked limits, the precise order of the marshalling of the material for each age. For, though, on the whole, mathematical development has gone forward, yet there have been lapses from advances already made. Witness the practical world-loss of much valuable Hindu thought, and, for long centuries, the neglect of Greek thought: witness the world-loss of the invention by the Babylonians of the Zero, until re-invented by the Hindus, passed on by them to the Arabs, and by these to Europe.
"Moreover, many blunders and false starts and false principles have marked the whole course of development. In a phrase, rivers have their backwaters. But it is precisely the teacher's function to avoid such racial mistakes, to take short cuts ultimately discovered, and to guide the young along the road ultimately found most accessible with such halts and retracings—returns up side-cuts—as the mental peculiarities of the pupils demand.
"All this, the practical realization of the spirit of the principle, is to be wisely left to the mathematical teacher, familiar with the history of mathematical science and with the particular limitations of his pupils and himself." ['08, p. 245.]
The latitude of modification suggested by Branford reduces the guidance to be derived from racial history to almost nil. Also it is apparent that the racial history in the case of arithmetical achievement is entirely a matter of acquisition and social transmission. Man's original nature is destitute of all arithmetical ideas. The human germs do not know even that one and one make two!
A scientific plan for teaching arithmetic would begin with an exact inventory of the knowledge and skill which the pupils already possessed. Our ordinary notions of what a child knows at entrance to grade 1, or grade 2, or grade 3,[Pg 200] and of what a first-grade child or second-grade child can do, are not adequate. If they were, we should not find reputable textbooks arranging to teach elaborately facts already sufficiently well known to over three quarters of the pupils when they enter school. Nor should we find other textbooks presupposing in their first fifty pages a knowledge of words which not half of the children can read even at the end of the 2 B grade.
We do find just such evidence that ordinary ideas about the abilities of children at the beginning of systematic school training in arithmetic may be in gross error. For example, a reputable and in many ways admirable recent book has fourteen pages of exercises to teach the meaning of two and the fact that one and one make two! As an example of the reverse error, consider putting all these words in the first twenty-five pages of a beginner's book:—absentees, attendance, blanks, continue, copy, during, examples, grouped, memorize, perfect, similar, splints, therefore, total!
Little, almost nothing, has been done toward providing an exact inventory compared with what needs to be done. We may note here (1) the facts relevant to arithmetic found by Stanley Hall, Hartmann, and others in their general investigations of the knowledge possessed by children at entrance to school, (2) the facts concerning the power of children to perceive differences in length, area, size of collection, and organization within a collection such as is shown in Fig. 24, and certain facts and theories about early awareness of number.
In the Berlin inquiry of 1869, knowledge of the meaning of two, three, and four appeared in 74, 74, and 73 percent of the children upon entrance to school. Some of those recorded as ignorant probably really knew, but failed to understand that they were expected to reply or were shy. Only[Pg 201] 85 percent were recorded as knowing their fathers' names. Seven eighths as many children knew the meanings of two, three, and four as knew their fathers' names. In a similar but more careful experiment with Boston children in September, 1880, Stanley Hall found that 92 percent knew three, 83 percent knew four, and 71½ percent knew five. Three was known about as well as the color red; four was known about as well as the color blue or yellow or green. Hartmann ['90] found that two thirds of the children entering school in Annaberg could count from one to ten. This is about as many as knew money, or the familiar objects of the town, or could repeat words spoken to them.
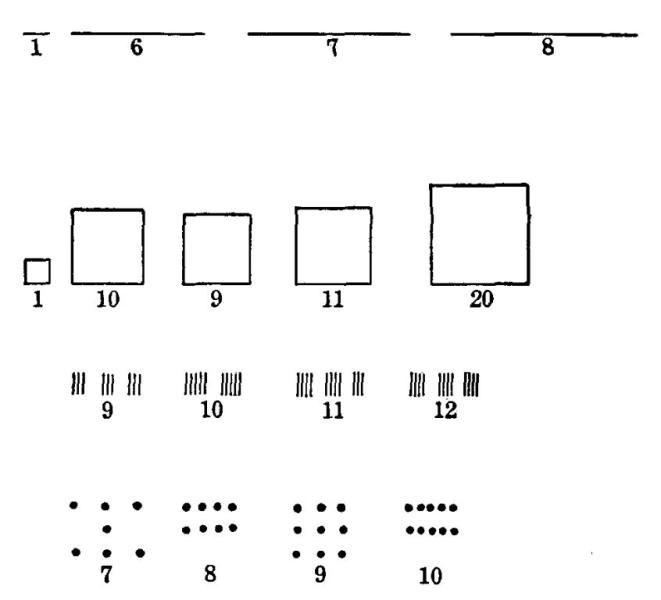 Fig. 24.—Objective presentation.
Fig. 24.—Objective presentation.
In the Stanford form of the Binet tests counting four pennies is given as an ability of the typical four-year-old. Counting 13 pennies correctly in at least one out of two[Pg 202] trials, and knowing three of the four coins,—penny, nickel, dime, and quarter,—are given as abilities of the typical six-year-old.
We know that educated adults can tell how many lines or dots, etc., they see in a single glance (with an exposure too short for the eye to move) up to four or more, according to the clearness of the objects and their grouping. For example, Nanu ['04] reports that when a number of bright circles on a dark background are shown to educated adults for only .033 second, ten can be counted when arranged to form a parallelogram, but only five when arranged in a row. With certain groupings, of course, their 'perception' involves much inference, even conscious addition and multiplication. Similarly they can tell, up to twenty and beyond, the number of taps, notes, or other sounds in a series too rapid for single counting if the sounds are grouped in a convenient rhythm.
These abilities are, however, the product of a long and elaborate learning, including the learning of arithmetic itself. Elementary psychology and common experience teach us that the mere observation of groups or quantities, no matter how clear their number quality appears to the person who already knows the meanings of numbers, does not of itself create the knowledge of the meanings of numbers in one who does not. The experiments of Messenger ['03] and Burnett ['06] showed that there is no direct intuitive apprehension even of two as distinct from one. We have to learn to feel the two touches or see the two dots or lines as two.

We do not know by exact measurements the growth in children of this ability to count or infer the number of elements in a collection seen or series heard. Still less do we[Pg 203] know what the growth would be without the influence of school training in counting, grouping, adding, and multiplying. Many textbooks and teachers seem to overestimate it greatly. Not all educated adults can, apart from measurement, decide with surety which of these lines is the longer, or which of these areas is the larger, or whether this is a ninth or a tenth or an eleventh of a circle.
Children upon entering school have not been tested carefully in respect to judgments of length and area, but we know from such studies as Gilbert's ['94] that the difference required in their case is probably over twice that required for children of 13 or 14. In judging weights, for example, a difference of 6 is perceived as easily by children 13 to 15 years of age as a difference of 15 by six-year-olds.
A teacher who has adult powers of estimating length or area or weight and who also knows already which of the two[Pg 204] is longer or larger or heavier, may use two lines to illustrate a difference which they really hide from the child. It is unlikely, for example, that the first of these lines ______________ ________________ would be recognized as shorter than the second by every child in a fourth-grade class, and it is extremely unlikely that it would be recognized as being 7⁄8 of the length of the latter, rather than 3⁄4 of it or 5⁄6 of it or 9⁄10 of it or 11⁄12 of it. If the two were shown to a second grade, with the question, "The first line is 7. How long is the other line?" there would be very many answers of 7 or 9; and these might be entirely correct arithmetically, the pupils' errors being all due to their inability to compare the lengths accurately.
The quantities used should be such that their mere discrimination offers no difficulty even to a child of blunted sense powers. If 7⁄8 and 1 are to be compared, A and B are not allowable. C, D, and E are much better.
Teachers probably often underestimate or neglect the sensory difficulties of the tasks they assign and of the material they use to illustrate absolute and relative magnitudes. The result may be more pernicious when the pupils answer correctly than when they fail. For their correct [Pg 205] answering may be due to their divination of what the teacher wants; and they may call a thing an inch larger to suit her which does not really seem larger to them at all. This, of course, is utterly destructive of their respect for arithmetic as an exact and matter-of-fact instrument. For example, if a teacher drew a series of lines 20, 21, 22, 23, 24, and 25 inches long on the blackboard in this form— _____ ________ and asked, "This is 20 inches long, how long is this?" she might, after some errors and correction thereof, finally secure successful response to all the lines by all the children. But their appreciation of the numbers 20, 21, 22, 23, 24, and 25 would be actually damaged by the exercise.
There has been some disagreement concerning the origin of awareness of number in the individual, in particular concerning the relative importance of the perception of how-many-ness and that of how-much-ness, of the perception of a defined aggregate and the perception of a defined ratio. (See McLellan and Dewey ['95], Phillips ['97 and '98], and Decroly and Degand ['12].)
The chief facts of significance for practice seem to be these: (1) Children with rare exceptions hear the names one, two, three, four, half, twice, two times, more, less, as many as, again, first, second, and third, long before they have analyzed out the qualities and relations to which these words refer so as to feel them at all clearly. (2) Their knowledge of the qualities and relations is developed in the main in close association with the use of these words to the child and by the child. (3) The ordinary experiences of the first five years so develop in the child awareness of the 'how many somethings' in various groups, of the relative magnitudes of two groups or quantities of any sort, and of groups and magnitudes as[Pg 206] related to others in a series. For instance, if fairly gifted, a child comes, by the age of five, to see that a row of four cakes is an aggregate of four, seeing each cake as a part of the four and the four as the sum of its parts, to know that two of them are as many as the other two, that half of them would be two, and to think, when it is useful for him to do so, of four as a step beyond three on the way to five, or to think of hot as a step from warm on the way to very hot. The degree of development of these abilities depends upon the activity of the law of analysis in the individual and the character of his experiences.
(4) He gets certain bad habits of response from the ambiguity of common usage of 2, 3, 4, etc., for second, third, fourth. Thus he sees or hears his parents or older children or others count pennies or rolls or eggs by saying one, two, three, four, and so on. He himself is perhaps misled into so counting. Thus the names properly belonging to a series of aggregations varying in amount come to be to him the names of the positions of the parts in a counted whole. This happens especially with numbers above 3 or 4, where the correct experience of the number as a name for the group has rarely been present. This attaching to the cardinal numbers above three or four the meanings of the ordinal numbers seems to affect many children on entrance to school. The numbering of pages in books, houses, streets, etc., and bad teaching of counting often prolong this error.
(5) He also gets the habit, not necessarily bad, but often indirectly so, of using many names such as eight, nine, ten, eleven, fifteen, a hundred, a million, without any meaning.
(6) The experiences of half, twice, three times as many, three times as long, etc., are rarer; even if they were not, they would still be less easily productive of the analysis of the proper abstract element than are the experiences of[Pg 207] two, three, four, etc., in connection with aggregates of things each of which is usually called one, such as boys, girls, balls, apples. Experiences of the names, two, three, and four, in connection with two twos, two threes, two fours, are very rare.
Hence, the names, two, three, etc., mean to these children in the main, "one something and one something," "one something usually called one, and one something usually called one, and another something usually called one," and more rarely and imperfectly "two times anything," "three times anything," etc.
With respect to Mr. Phillips' emphasis of the importance of the series-idea in children's minds, the matters of importance are: first, that the knowledge of a series of number names in order is of very little consequence to the teaching of arithmetic and of still less to the origin of awareness of number. Second, the habit of applying this series of words in counting in such a way that 8 is associated with the eighth thing, 9 with the ninth thing, etc., is of consequence because it does so much mischief. Third, the really valuable idea of the number series, the idea of a series of groups or of magnitudes varying by steps, is acquired later, as a result, not a cause, of awareness of numbers.
With respect to the McLellan-Dewey doctrine, the ratio aspect of numbers should be emphasized in schools, not because it is the main origin of the child's awareness of number, but because it is not, and because the ordinary practical issues of child life do not adequately stimulate its action. It also seems both more economical and more scientific to introduce it through multiplication, division, and fractions rather than to insist that 4 and 5 shall from the start mean 4 or 5 times anything that is called 1, for instance, that 8 inches shall be called 4 two-inches, or 10 cents, 5 two-cents. [Pg 208] If I interpret Professor Dewey's writings correctly, he would agree that the use of inch, foot, yard, pint, quart, ounce, pound, glassful, cupful, handful, spoonful, cent, nickel, dime, and dollar gives a sufficient range of units for the first two school years. Teaching the meanings of ½ of 4, ½ of 6, ½ of 8, ½ of 10, ½ of 20, 1⁄3 of 6, 1⁄3 of 9, 1⁄3 of 30, ¼ of 8, two 2s, five 2s, and the like, in early grades, each in connection with many different units of measure, provides a sufficient assurance that numbers will connect with relationships as well as with collections.
Arithmetic, although it makes little or no appeal to collecting, muscular manipulation, sensory curiosity, or the potent original interests in things and their mechanisms and people and their passions, is fairly well liked by children. The censuses of pupils' likes and dislikes that have been made are not models of scientific investigation, and the resulting percentages should not be used uncritically. They are, however, probably not on the average over-favorable to arithmetic in any unfair way. Some of their results are summarized below. In general they show arithmetic to be surpassed in interest clearly by only the manual arts (shopwork and manual training for boys, cooking and sewing for girls), drawing, certain forms of gymnastics, and history. It is about on a level with reading and science. It clearly surpasses grammar, language, spelling, geography, and religion.
Lobsien ['03], who asked one hundred children in each of the first five grades (Stufen) of the elementary schools of Kiel, "Which part of the school work (literally, 'which instruction period') do you like best?" found arithmetic led only by drawing and gymnastics in the case of the boys, and only by handwork in the case of the girls.[Pg 210]
This is an exaggerated picture of the facts, since no count is made of those who especially dislike arithmetic. Arithmetic is as unpopular with some as it is popular with others. When full allowance is made for this, arithmetic still has popularity above the average. Stern ['05] asked, "Which subject do you like most?" and "Which subject do you like least?" The balance was greatly in favor of gymnastics for boys (28-1), handwork for girls (32-1½), and drawing for both (16½-6). Writing (6½-4), arithmetic (14½-13), history (9-6½), reading (8½-8), and singing (6-7½) come next. Religion, nature study, physiology, geography, geometry, chemistry, language, and grammar are low.
McKnight ['07] found with boys and girls in grades 7 and 8 of certain American cities that arithmetic was liked better than any of the school subjects except gymnastics and manual training. The vote as compared with history was:—
| Arithmetic | 327 liked greatly, | 96 disliked greatly. |
| History | 164 liked greatly, | 113 disliked greatly. |
In a later study Lobsien ['09] had 6248 pupils from 9 to 15 years old representing all grades of the elementary school report, so far as they could, the subject most disliked, the subject most liked, the subject next most liked, and the subject next in order. No child was forced to report all of these four judgments, or even any of them. Lobsien counts the likes and the dislikes for each subject. Gymnastics, handwork, and cooking are by far the most popular. History and drawing are next, followed by arithmetic and reading. Below these are geography, writing, singing, nature study, biblical history, catechism, and three minor subjects.
Lewis ['13] secured records from English children in elementary schools of the order of preference of all the studies[Pg 211] listed below. He reports the results in the following table of percents:
| Top Third of Studies for Interest |
Middle Third of Studies for Interest |
Lowest Third of Studies for Interest |
|
|---|---|---|---|
| Drawing | 78 | 20 | 2 |
| Manual Subjects | 66 | 26 | 8 |
| History | 64 | 24 | 12 |
| Reading | 53 | 38 | 9 |
| Singing | 32 | 48 | 20 |
| Drill | 20 | 55 | 25 |
| Arithmetic | 16 | 53 | 31 |
| Science | 23 | 37 | 40 |
| Nature Study | 16 | 36 | 48 |
| Dictation | 4 | 57 | 39 |
| Composition | 18 | 28 | 54 |
| Scripture | 4 | 38 | 58 |
| Recitation | 9 | 23 | 68 |
| Geography | 4 | 24 | 72 |
| Grammar | — | 6 | 94 |
Brandell ['13] obtained data from 2137 Swedish children in Stockholm (327), Norrköping (870), and Gothenburg (940).
In general he found, as others have, that handwork, shopwork for boys and household work for girls, and drawing were reported as much better liked than arithmetic. So also was history, and (in this he differs from most students of this matter) so were reading and nature study. Gymnastics he finds less liked than arithmetic. Religion, geography, language, spelling, and writing are, as in other studies, much less popular than arithmetic.[Pg 212]
Other studies are by Lilius ['11] in Finland, Walsemann ['07], Wiederkehr ['07], Pommer ['14], Seekel ['14], and Stern ['13 and '14], in Germany. They confirm the general results stated.
The reasons for the good showing that arithmetic makes are probably the strength of its appeal to the interest in definite achievement, success, doing what one attempts to do; and of its appeal, in grades 5 to 8, to the practical interest of getting on in the world, acquiring abilities that the world pays for. Of these, the former is in my opinion much the more potent interest. Arithmetic satisfies it especially well, because, more than any other of the 'intellectual' studies of the elementary school, it permits the pupil to see his own progress and determine his own success or failure.
The most important applications of the psychology of satisfiers and annoyers to arithmetic will therefore be in the direction of utilizing still more effectively this interest in achievement. Next in importance come the plans to attach to arithmetical learning the satisfyingness of bodily action, play, sociability, cheerfulness, and the like, and of significance as a means of securing other desired ends than arithmetical abilities themselves. Next come plans to relieve arithmetical learning from certain discomforts such as the eyestrain of some computations and excessive copying of figures. These will be discussed here in the inverse order.
At present arithmetical work is, hour for hour, probably more of a tax upon the eyes than reading. The task of copying numbers from a book to a sheet of paper is one of the very hardest tasks that the eyes of a pupil in the ele[Pg 213]mentary schools have to perform. A certain amount of such work is desirable to teach a child to write numbers, to copy exactly, and to organize material in shape for computation. But beyond that, there is no more reason for a pupil to copy every number with which he is to compute than for him to copy every word he is to read. The meaningless drudgery of copying figures should be mitigated by arranging much work in the form of exercises like those shown on pages 216, 217, and 218, and by having many of the textbook examples in addition, subtraction, and multiplication done with a slip of paper laid below the numbers, the answers being written on it. There is not only a resulting gain in interest, but also a very great saving of time for the pupil (very often copying an example more than quadruples the time required to get its answer), and a much greater efficiency in supervision. Arithmetical errors are not confused with errors of copying,[16] and the teacher's task of following a pupil's work on the page is reduced to a minimum, each pupil having put the same part of the day's work in just the same place. The use of well-printed and well-spaced pages of exercises relieves the eyestrain of working with badly made gray figures, unevenly and too closely or too widely spaced. I reproduce in Fig. 25 specimens taken at random from one hundred random samples of arithmetical work by pupils in grade 8. Contrast the task of the eyes in working with these and their task in working with pages 216 to 218. The customary method of always copying the numbers to be used in computation from blackboard or book to a sheet of paper is an utterly unjustifiable cruelty and waste.[Pg 214]

Fig. 25a.—Specimens taken at random from the computation work of eighth-grade pupils. This computation occurred in a genuine test. In the original gray of the pencil marks the work is still harder to make out.
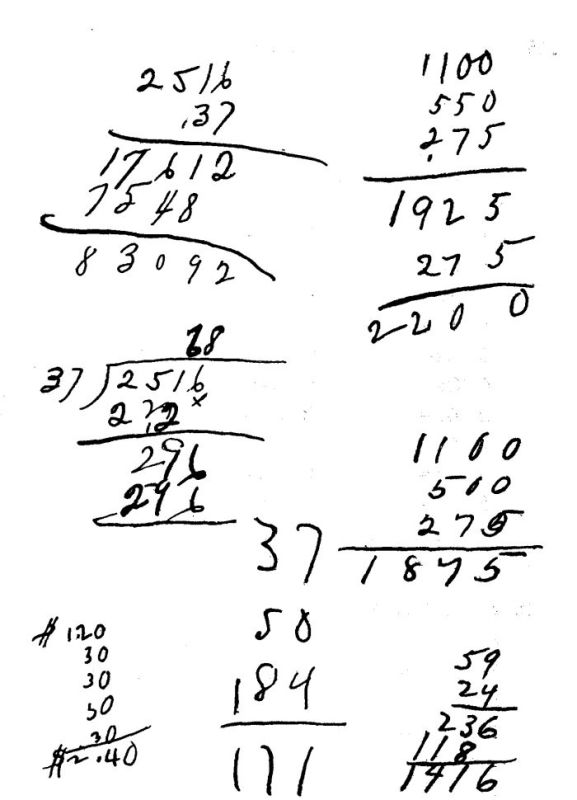
Fig. 25b.—Specimens taken at random from the computation work of eighth-grade pupils. This computation occurred in a genuine test. In the original gray of the pencil marks the work is still harder to make out.
Write the products:—
| A. 3 4s = | B. 5 7s = | C. 9 2s = |
| 5 2s = | 8 3s = | 4 4s = |
| 7 2s = | 4 2s = | 2 7s = |
| 1 6 = | 4 5s = | 6 4s = |
| 1 3 = | 4 7s = | 5 5s = |
| 3 7s = | 5 9s = | 3 6s = |
| 4 1s = | 7 5s = | 3 2s = |
| 6 8s = | 7 1s = | 3 9s = |
| 9 8s = | 6 3s = | 5 1s = |
| 4 3s = | 4 9s = | 8 6s = |
| 2 4s = | 3 5s = | 8 4s = |
| 2 2s = | 9 6s = | 8 5s = |
| 8 7s = | 2 5s = | 7 9s = |
| 5 8s = | 5 4s = | 6 2s = |
| 7 6s = | 8 2s = | 7 4s = |
| 7 3s = | 8 9s = | 9 3s = |
| D. 4 20s = | E. 9 60s = | F. 40 × 2 = 80 |
| 4 200s = | 9 600s = | 20 × 2 = |
| 6 30s = | 5 30s = | 30 × 2 = |
| 6 300s = | 5 300s = | 40 × 2 = |
| 7 × 50 = | 8 × 20 = | 20 × 3 = |
| 7 × 500 = | 8 × 200 = | 30 × 3 = |
| 3 × 40 = | 2 × 70 = | 300 × 3 = 900 |
| 3 × 400 = | 2 × 700 = | 300 × 2 = |
Write the missing numbers: (r stands for remainder.)
| 25 = .... 3s and .... r. | 30 = .... 4s and .... r. |
| 25 = .... 4s " .... r. | 30 = .... 5s " .... r. |
| 25 = .... 5s " .... r. | 30 = .... 6s " .... r. |
| 25 = .... 6s " .... r. | 30 = .... 7s " .... r. |
| 25 = .... 7s " .... r. | 30 = .... 8s " .... r. |
| 25 = .... 8s " .... r. | 30 = .... 9s " .... r. |
| 25 = .... 9s " .... r. | |
| 26 = .... 3s and .... r. | 31 = .... 4s and .... r. |
| 26 = .... 4s " .... r. | 31 = .... 5s " .... r. |
| 26 = .... 5s " .... r. | 31 = .... 6s " .... r. |
| 26 = .... 6s " .... r. | 31 = .... 7s " .... r. |
| 26 = .... 7s " .... r. | 31 = .... 8s " .... r. |
| 26 = .... 8s " .... r. | 31 = .... 9s " .... r. |
| 26 = .... 9s " .... r. |
Write the whole numbers or mixed numbers which these fractions equal:—
| 5 4 |
4 3 |
9 5 |
4 2 |
7 3 |
| 7 4 |
5 3 |
11 8 |
3 2 |
8 8 |
| 8 4 |
6 3 |
9 8 |
9 4 |
16 8 |
| 11 4 |
7 5 |
13 8 |
8 5 |
6 6 |
Write the missing figures:—
| 6 8 | = | 4 |
2 4 | = | 2 |
8 10 | = | 5 |
1 5 | = | 10 |
2 3 | = | 6 |
Write the missing numerators:—
| 1 2 | = | 12 |
8 |
10 |
4 |
16 |
6 |
14 |
||||||
| 1 3 | = | 12 |
9 |
18 |
6 |
15 |
24 |
21 |
||||||
| 1 4 | = | 12 |
16 |
8 |
24 |
20 |
28 |
32 |
||||||
| 1 5 | = | 10 |
20 |
15 |
25 |
40 |
35 |
30 |
||||||
| 2 3 | = | 12 |
18 |
21 |
6 |
15 |
24 |
9 |
||||||
| 3 4 | = | 8 |
16 |
12 |
20 |
24 |
32 |
28 |
Find the products. Cancel when you can:—
| 5 16 | × 4 = | 11 12 | × 3 = | 2 3 | × 5 = | ||
| 7 12 | × 8 = | 8 5 | × 15 = | 1 6 | × 8 = |
The use of bodily action, social games, and the like was discussed in the section on original tendencies. "Significance as a means of securing other desired ends than arithmetical learning itself" is therefore our next topic. Such significance can be given to arithmetical work by using that work as a means to present and future success in problems of sports, housekeeping, shopwork, dressmaking, self-management, other school studies than arithmetic, and general school life and affairs. Significance as a means to future ends alone can also be more clearly and extensively attached to it than it now is.
Whatever is done to supply greater strength of motive in studying arithmetic must be carefully devised so as not to get a strong but wrong motive, so as not to get abundant interest but in something other than arithmetic, and so as not to kill the goose that after all lays the golden eggs—the interest in intellectual activity and achievement itself. It is easy to secure an interest in laying out a baseball diamond, measuring ingredients for a cake, making a balloon of a certain capacity, or deciding the added cost of an extra trimming of ribbon for one's dress. The problem is to attach that interest to arithmetical learning. Nor should a teacher be satisfied with attaching the interest as a mere tail that steers the kite, so long as it stays on, or as a sugar-coating that deceives the pupil into swallowing the pill, or as an anodyne whose dose must be increased and increased if it is to retain its power. Until the interest permeates the arithmetical activity itself our task is only partly done, and perhaps is made harder for the next time.
One important means of really interfusing the arithmetical learning itself with these derived interests is to lead the pupil to seek the help of arithmetic himself—to lead him, in Dewey's phrase, to 'feel the need'—to take the[Pg 220] 'problem' attitude—and thus appreciate the technique which he actively hunts for to satisfy the need. In so far as arithmetical learning is organized to satisfy the practical demands of the pupil's life at the time, he should, so to speak, come part way to get its help.
Even if we do not make the most skillful use possible of these interests derived from the quantitative problems of sports, housekeeping, shopwork, dressmaking, self-management, other school studies, and school life and affairs, the gain will still be considerable. To have them in mind will certainly preserve us from giving to children of grades 3 and 4 problems so devoid of relation to their interests as those shown below, all found (in 1910) in thirty successive pages of a book of excellent repute:—
A chair has 4 legs. How many legs have 8 chairs? 5 chairs?
A fly has 6 legs. How many legs have 3 flies? 9 flies? 7 flies?
(Eight more of the same sort.)
In 1890 New York had 1,513,501 inhabitants, Milwaukee had 206,308, Boston had 447,720, San Francisco 297,990. How many had these cities together?
(Five more of the same sort.)
Milton was born in 1608 and died in 1674. How many years did he live?
(Several others of the same sort.)
The population of a certain city was 35,629 in 1880 and 106,670 in 1890. Find the increase.
(Several others of this sort.)
A number of others about the words in various inaugural addresses and the Psalms in the Bible.
It also seems probable that with enough care other systematic plans of textbooks can be much improved in this respect. From every point of view, for example, the early work in arithmetic should be adapted to some extent to the healthy childish interests in home affairs, the behavior of other children, and the activities of material things, animals, and plants.[Pg 221]
TABLE 9
Frequency of Appearance of Certain Words about Family Life, Play, and Action in Eight Elementary Textbooks in Arithmetic, pp. 1-50.
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| baby | 2 | 4 | ||||||
| brother | 2 | 6 | 1 | 1 | 1 | |||
| family | 2 | 2 | 4 | |||||
| father | 1 | 3 | 5 | 2 | 1 | |||
| help | ||||||||
| home | 2 | 4 | 4 | 2 | 2 | 7 | 1 | |
| mother | 4 | 2 | 9 | 5 | 5 | 1 | 7 | |
| sister | 1 | 2 | 2 | 9 | 1 | 1 | ||
| fork | ||||||||
| knife | ||||||||
| plate | 4 | 2 | 2 | 1 | ||||
| spoon | ||||||||
| doll | 10 | 1 | 10 | 6 | 10 | 9 | ||
| game | 1 | 3 | 5 | 5 | ||||
| jump | 4 | |||||||
| marbles | 10 | 4 | 10 | 10 | 1 | |||
| play | 1 | 3 | ||||||
| run | 1 | 3 | ||||||
| sing | ||||||||
| tag | ||||||||
| toy | 1 | |||||||
| car | 2 | 4 | 2 | 3 | 1 | |||
| cut | 10 | 6 | 2 | 8 | ||||
| dig | 2 | |||||||
| flower | 1 | 4 | 1 | 1 | 2 | |||
| grow | 1 | |||||||
| plant | 2 | |||||||
| seed | 3 | 1 | ||||||
| string | 1 | 10 | 1 | 1 | ||||
| wheel | 5 | 10 | ||||||
The words used by textbooks give some indication of how far this aim is being realized, or rather of how far short we are of realizing it. Consider, for example, the words home, mother, father, brother, sister, help, plate, knife, fork, spoon, play, game, toy, tag, marbles, doll, run, jump, sing, plant, seed, grow, flower, car, wheel, string, cut, dig. The frequency of appearance in the first fifty pages of eight beginners' arithmetics was as shown in Table 9. The eight columns refer to the eight books (the first fifty pages of each). The numbers refer to the number of times the word in question appeared, the number 10 meaning 10 or more times in the fifty pages. Plurals, past tenses, and the like were counted. Help, fork, knife, spoon, jump, sing, and tag did not appear at all! Toy and grow appeared each once in the 400 pages! Play, run, dig, plant, and seed appeared once in a hundred or more pages. Baby did not appear as often as buggy. Family appeared no oftener than fence or Friday. Father appears about a third as often as farmer.
Book A shows only 10 of these thirty words in the fifty pages; book B only 4; book C only 12; and books D, E, F, G, and H only 13, 8, 14, 13, 10, respectively. The total number of appearances (counting the 10s as only 10 in each case) is 40 for A, 9 for B, 60 for C, 42 for D, 25 for E, 62 for F, 30 for G, and 37 for H. The five words—apple, egg, Mary, milk, and orange—are used oftener than all these thirty together.
If it appeared that this apparent neglect of childish affairs and interests was deliberate to provide for a more systematic treatment of pure arithmetic, a better gradation of problems, and a better preparation for later genuine use than could be attained if the author of the textbook were tied to the child's apron strings, the neglect could be defended. It is not at all certain that children in grade 2 get much more enjoyment[Pg 223] or ability from adding the costs of purchases for Christmas or Fourth of July, or multiplying the number of cakes each child is to have at a party by the number of children who are to be there, than from adding gravestones or multiplying the number of hairs of bald-headed men. When, however, there is nothing gained by substituting remote facts for those of familiar concern to children, the safe policy is surely to favor the latter. In general, the neglect of childish data does not seem to be due to provision for some other end, but to the same inertia of tradition which has carried over the problems of laying walls and digging wells into city schools whose children never saw a stone wall or dug well.
I shall not go into details concerning the arrangement of courses of study, textbooks, and lesson-plans to make desirable connections between arithmetical learning and sports, housework, shopwork, and the rest. It may be worth while, however, to explain the term self-management, since this source of genuine problems of real concern to the pupils has been overlooked by most writers.
By self-management is meant the pupil's use of his time, his abilities, his knowledge, and the like. By the time he reaches grade 5, and to some extent before then, a boy should keep some account of himself, of how long it takes him to do specified tasks, of how much he gets done in a specified time at a certain sort of work and with how many errors, of how much improvement he makes month by month, of which things he can do best, and the like. Such objective, matter-of-fact, quantitative study of one's behavior is not a stimulus to morbid introspection or egotism; it is one of the best preventives of these. To treat oneself impersonally is one of the essential elements of mental balance and health. It need not, and should not, encourage[Pg 224] priggishness. On the contrary, this matter-of-fact study of what one is and does may well replace a certain amount of the exhortations and admonitions concerning what one ought to do and be. All this is still truer for a girl.
The demands which such an accounting of one's own activities make of arithmetic have the special value of connecting directly with the advanced work in computation. They involve the use of large numbers, decimals, averaging, percentages, approximations, and other facts and processes which the pupil has to learn for later life, but to which his childish activities as wage-earner, buyer and seller, or shopworker from 10 to 14 do not lead. Children have little money, but they have time in thousands of units! They do not get discounts or bonuses from commercial houses, but they can discount their quantity of examples done for the errors made, and credit themselves with bonuses of all sorts for extra achievements.
There remains the most important increase of interest in arithmetical learning—an increase in the interest directly bound to achievement and success in arithmetic itself. "Arithmetic," says David Eugene Smith, "is a game and all boys and girls are players." It should not be a mere game for them and they should not merely play, but their unpractical interest in doing it because they can do it and can see how well they do do it is one of the school's most precious assets. Any healthy means to give this interest more and better stimulus should therefore be eagerly sought and cherished.
Two such means have been suggested in other connections. The first is the extension of training in checking and verifying work so that the pupil may work to a standard of ap[Pg 225]proximately 100% success, and may know how nearly he is attaining it. The second is the use of standardized practice material and tests, whereby the pupil may measure himself against his own past, and have a clear, vivid, and trustworthy idea of just how much better or faster he can do the same tasks than he could do a month or a year ago, and of just how much harder things he can do now than then.
Another means of stimulating the essential interest in quantitative thinking itself is the arrangement of the work so that real arithmetical thinking is encouraged more than mere imitation and assiduity. This means the avoidance of long series of applied problems all of one type to be solved in the same way, the avoidance of miscellaneous series and review series which are almost verbatim repetitions of past problems, and in general the avoidance of excessive repetition of any one problem-situation. Stimulation to real arithmetical thinking is weak when a whole day's problem work requires no choice of methods, or when a review simply repeats without any step of organization or progress, or when a pupil meets a situation (say the 'buy x things at y per thing, how much pay' situation) for the five-hundredth time.
Another matter worthy of attention in this connection is the unwise tendency to omit or present in diluted form some of the topics that appeal most to real intellectual interests, just because they are hard. The best illustration, perhaps, is the problem of ratio or "How many times as large (long, heavy, expensive, etc.) as x is y?" Mastery of the 'times as' relation is hard to acquire, but it is well worth acquiring, not only because of its strong intellectual appeal, but also because of its prime importance in the applications of arithmetic to science. In the older arithmetics it was confused by pedantries and verbal difficulties and penalized[Pg 226] by unreal problems about fractions of men doing parts of a job in strange and devious times. Freed from these, it should be reinstated, beginning as early as grade 5 with such simple exercises as those shown below and progressing to the problems of food values, nutritive ratios, gears, speeds, and the like in grade 8.
John is 4 years old.
Fred is 6 years old.
Mary is 8 years old.
Nell is 10 years old.
Alice is 12 years old.
Bert is 15 years old.
Who is twice as old as John?
Who is half as old as Alice?
Who is three times as old as John?
Who is one and one half times as old as Nell?
Who is two thirds as old as Fred?
etc., etc., etc.
Alice is .... times as old as John.
John is .... as old as Mary.
Fred is .... times as old as John.
Alice is .... times as old as Fred.
Fred is .... as old as Mary.
etc., etc., etc.
Finally it should be remembered that all improvements in making arithmetic worth learning and helping the pupil to learn it will in the long run add to its interest. Pupils like to learn, to achieve, to gain mastery. Success is interesting. If the measures recommended in the previous chapters are carried out, there will be little need to entice pupils to take arithmetic or to sugar-coat it with illegitimate attractions.
We shall consider in this chapter the influence of time of day, size of class, and amount of time devoted to arithmetic in the school program, the hygiene of the eyes in arithmetical work, the use of concrete objects, and the use of sounds, sights, and thoughts as situations and of speech and writing and thought as responses.[17]
Computation of one or another sort has been used by several investigators as a test of efficiency at different times in the day. When freed from the effects of practice on the one hand and lack of interest due to repetition on the other, the results uniformly show an increase in speed late in the school session with a falling off in accuracy that about balances it.[18] There is no wisdom in putting arithmetic early in the session because of its difficulty. Lively and sociable exercises in mental arithmetic with oral answers in fact seem to be admirably fitted for use late in the session. Except for the general principles (1) of starting the day with work that will set a good standard of cheerful, efficient [Pg 228] production and (2) of getting the least interesting features of the day's work done fairly early in the day, psychology permits practical exigencies to rule the program, so far as present knowledge extends. Adequate measurements of the effect of time of day on improvement have not been made, but there is no reason to believe that any one time between 9 a.m. and 4 p.m. is appreciably more favorable to arithmetical learning than to learning geography, history, spelling, and the like.
The influence of size of class upon progress in school studies is very difficult to measure because (1) within the same city system the average of the six (or more) sizes of class that a pupil has experienced will tend to approximate closely to the corresponding average for any other child; because further (2) there may be a tendency of supervisory officers to assign more pupils to the better teachers; and because (3) separate systems which differ in respect to size of class probably differ in other respects also so that their differences in achievement may be referable to totally different differences.
Elliott ['14] has made a beginning by noting size of class during the year of test in connection with his own measures of the achievements of seventeen hundred pupils, supplemented by records from over four hundred other classes. As might be expected from the facts just stated, he finds no appreciable difference between classes of different sizes within the same school system, the effect of the few months in a small class being swamped by the antecedents or concomitants thereof.
The effect of the amount of time devoted to arithmetic in the school program has been studied extensively by Rice ['02 and '03] and Stone ['08].
Dr. Rice ['02] measured the arithmetical ability of some[Pg 229] 6000 children in 18 different schools in 7 different cities. The results of these measurements are summarized in Table 10. This table "gives two averages for each grade as well as for each school as a whole. Thus, the school at the top shows averages of 80.0 and 83.1, and the one at the bottom, 25.3 and 31.5. The first represents the percentage of answers which were absolutely correct; the second shows what per cent of the problems were correct in principle, i.e. the average that would have been received if no mechanical errors had been made."
The facts of Dr. Rice's table show that there is a positive relation between the general standing of a school system in the tests and the amount of time devoted to arithmetic by its program. The relation is not close, however, being that expressed by a correlation coefficient of .36½. Within any one school system there is no relation between the standing of a particular school and the amount of time devoted to arithmetic in that school's program. It must be kept in mind that the amount of time given in the school program may be counterbalanced by emphasizing work at home and during study periods, or, on the other hand, may be a symptom of correspondingly small or great emphasis on arithmetic in work set for the study periods at home.
A still more elaborate investigation of this same topic was made by Stone ['08]. I quote somewhat fully from it, since it is an instructive sample of the sort of studies that will doubtless soon be made in the case of every elementary school subject. He found that school systems differed notably in the achievements made by their sixth-grade pupils in his tests of computation (the so-called 'fundamentals') and of the solution of verbally described problems (the so-called 'reasoning'). The facts were as shown in Table 11.[Pg 230]
TABLE 10
Averages for Individual Schools in Arithmetic
| City | School | 6th Year | 7th Year | 8th Year | School Average | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Result | Principle | Result | Principle | Result | Principle | Result | Principle | Percent of Mechanical Errors | Minutes Daily | ||
| III | 1 | 79.3 | 80.3 | 81.1 | 82.3 | 91.7 | 93.9 | 80.0 | 83.1 | 3.7 | 53 |
| I | 1 | 80.4 | 81.5 | 64.2 | 67.2 | 80.9 | 82.8 | 76.6 | 80.3 | 4.6 | 60 |
| I | 2 | 80.9 | 83.4 | 43.5 | 50.9 | 72.7 | 79.1 | 69.3 | 75.1 | 7.7 | 25 |
| I | 3 | 72.2 | 74.0 | 63.5 | 66.2 | 74.5 | 76.6 | 67.8 | 72.2 | 6.1 | 45 |
| I | 4 | 69.9 | 72.2 | 54.6 | 57.8 | 66.5 | 69.1 | 64.3 | 70.3 | 8.5 | 45 |
| II | 1 | 71.2 | 75.3 | 33.6 | 35.7 | 36.8 | 40.0 | 60.2 | 64.8 | 7.1 | 60 |
| III | 2 | 43.7 | 45.0 | 53.9 | 56.7 | 51.1 | 53.1 | 54.5 | 58.9 | 7.4 | 60 |
| IV | 1 | 58.9 | 60.4 | 31.2 | 34.1 | 41.6 | 43.5 | 55.1 | 58.4 | 5.6 | 60 |
| IV | 2 | 59.8 | 63.1 | — | — | 22.5 | 22.5 | 53.9 | 58.8 | 8.3 | — |
| IV | 3 | 54.9 | 58.1 | 35.2 | 38.6 | 43.5 | 45.0 | 51.5 | 57.6 | 10.5 | 60 |
| IV | 4 | 42.3 | 45.1 | 16.1 | 19.2 | 48.7 | 48.7 | 42.8 | 48.2 | 11.2 | — |
| V | 1 | 44.1 | 48.7 | 29.2 | 32.5 | 51.1 | 58.3 | 45.9 | 51.3 | 10.5 | 40 |
| VI | 1 | 68.3 | 71.3 | 33.5 | 36.6 | 26.9 | 30.7 | 39.0 | 42.9 | 9.0 | 33 |
| VI | 2 | 46.1 | 49.5 | 19.5 | 24.2 | 30.2 | 40.6 | 36.5 | 43.6 | 16.2 | 30 |
| VI | 3 | 34.5 | 36.4 | 30.5 | 35.1 | 23.3 | 24.1 | 36.0 | 42.5 | 15.2 | 48 |
| VII | 1 | 35.2 | 37.7 | 29.1 | 32.5 | 25.1 | 27.2 | 40.5 | 45.9 | 11.7 | 42 |
| VII | 2 | 35.2 | 38.7 | 15.0 | 16.4 | 19.6 | 21.2 | 36.5 | 40.6 | 10.1 | 75 |
| VII | 3 | 27.6 | 33.7 | 8.9 | 10.1 | 11.3 | 11.3 | 25.3 | 31.5 | 19.6 | 45 |
High achievement by a system in computation went with high achievement in solving the problems, the correlation being about .50; and the system that scored high in addition or subtraction or multiplication or division usually showed closely similar excellence in the other three, the correlations being about .90.
TABLE 11
Scores Made by the Sixth-Grade Pupils of Each of Twenty-Six School Systems
| System | Score in Tests with Problems | Score in Tests in Computing |
|---|---|---|
| 23 | 356 | 1841 |
| 24 | 429 | 3513 |
| 17 | 444 | 3042 |
| 4 | 464 | 3563 |
| 25 | 464 | 2167 |
| 22 | 468 | 2311 |
| 16 | 469 | 3707 |
| 20 | 491 | 2168 |
| 18 | 509 | 3758 |
| 15 | 532 | 2779 |
| 3 | 533 | 2845 |
| 8 | 538 | 2747 |
| 6 | 550 | 3173 |
| 1 | 552 | 2935 |
| 10 | 601 | 2749 |
| 2 | 615 | 2958 |
| 21 | 627 | 2951 |
| 13 | 636 | 3049 |
| 14 | 661 | 3561 |
| 9 | 691 | 3404 |
| 7 | 734 | 3782 |
| 12 | 736 | 3410 |
| 11 | 759 | 3261 |
| 26 | 791 | 3682 |
| 19 | 848 | 4099 |
| 5 | 914 | 3569 |
Of the conditions under which arithmetical learning took place, the one most elaborately studied was the amount of time devoted to arithmetic. On the basis of replies by principals of schools to certain questions, he gave each of[Pg 231] the twenty-six school systems a measure for the probable time spent on arithmetic up through grade 6. Leaving home study out of account, there seems to be little or no correlation between the amount of time a system devotes to arithmetic and its score in problem-solving, and not much more between time expenditure and score in computation. With home study included there is little relation to[Pg 232] the achievement of the system in solving problems, but there is a clear effect on achievement in computation. The facts as given by Stone are:—
TABLE 12
Correlation of Time Expenditures with Abilities
| Without Home Study { | Reasoning and Time Expenditure | −.01 |
| Fundamentals and Time Expenditure | .09 | |
| Including Home Study { | Reasoning and Time Expenditure | .13 |
| Fundamentals and Time Expenditure | .49 | |
These correlations, it should be borne in mind, are for school systems, not for individual pupils. It might be that, though the system which devoted the most time to arithmetic did not show corresponding superiority in the product over the system devoting only half as much time, the pupils within the system did achieve in exact proportion to the time they gave to study. Neither correlation would permit inference concerning the effect of different amounts of time spent by the same pupil.
Stone considered also the printed announcements of the courses of study in arithmetic in these twenty-six systems. Nineteen judges rated these announced courses of study for excellence according to the instructions quoted below:—
Judges please read before scoring
I. Some Factors Determining Relative Excellence.
(N. B. The following enumeration is meant to be suggestive rather than complete or exclusive. And each scorer is urged to rely primarily on his own judgment.)
1. Helpfulness to the teacher in teaching the subject matter outlined.
2. Social value or concreteness of sources of problems.
3. The arrangement of subject matter.
4. The provision made for adequate drill.
5. A reasonable minimum requirement with suggestions for valuable additional work.
6. The relative values of any predominating so-called methods—such as Speer, Grube, etc.
7. The place of oral or so-called mental arithmetic.
8. The merit of textbook references.
II. Cautions and Directions.
(Judges please follow as implicitly as possible.)
1. Include references to textbooks as parts of the Course of Study.
This necessitates judging the parts of the texts referred to.
2. As far as possible become equally familiar with all courses before scoring any.
3. When you are ready to begin to score, (1) arrange in serial order according to excellence, (2) starting with the middle one score it 50, then score above and below 50 according as courses are better or poorer, indicating relative differences in excellence by relative differences in scores, i.e. in so far as you find that the courses differ by about equal steps, score those better than the middle one 51, 52, etc., and those poorer 49, 48, etc., but if you find that the courses differ by unequal steps show these inequalities by omitting numbers.
4. Write ratings on the slip of paper attached to each course.
The systems whose courses of study were thus rated highest did not manifest any greater achievement in Stone's tests than the rest. The thirteen with the most approved announcements of courses of study were in fact a little inferior in achievement to the other thirteen, and the correlation coefficients were slightly negative.
Stone also compared eighteen systems where there was supervision of the work by superintendents or supervisors as well as by principals with four systems where the principals and teachers had no such help. The scores in his tests were very much lower in the four latter cities.
 Fig. 26.—Type too large.
Fig. 26.—Type too large.
We have already noted that the task of reading and copying numbers is one of the hardest that the eyes have to perform in the elementary school, and that it should be alleviated by arranging much of the work so that only answers need be written by the pupil. The figures to be read and copied[Pg 235] should obviously be in type of suitable size and style, so arranged and spaced on the page or blackboard as to cause a minimum of effort and strain.
 Fig. 27.—12-point, 11-point, and 10-point type.
Fig. 27.—12-point, 11-point, and 10-point type.
Size.—Type may be too large as well as too small, though the latter is the commoner error. If it is too large, as in Fig. 26, which is a duplicate of type actually used in a form of practice pad, the eye has to make too many fixations to take in a given content. All things considered, 12-point type in grades 3 and 4, 11-point in grades 5 and 6, and 10-point in grades 7 and 8 seem the most desirable sizes. These are shown in Fig. 27. Too small type occurs oftenest in fractions and in the dimension-numbers or scale numbers of drawings. Figures 28, 29, and 30 are samples from actual school practice. Samples of the desirable size are shown in Figs. 31 and 32. The technique of modern typesetting makes it very difficult and expensive to make fractions of the horizontal type
| ( | 1 4 |
, | 3 8 |
, | 5 6 |
) |
large enough without making the whole-number figures with which they are mingled too large or giving an uncouth appearance to the total. Consequently fractions somewhat smaller than are desirable may have to be used occasionally in textbooks.[19] There is no valid excuse, however, for the excessively small fractions which often are made in blackboard work.
This is a picture of Mary's garden.
How many feet is it around the garden?
 Fig. 29.—Type too small.
Fig. 29.—Type too small.
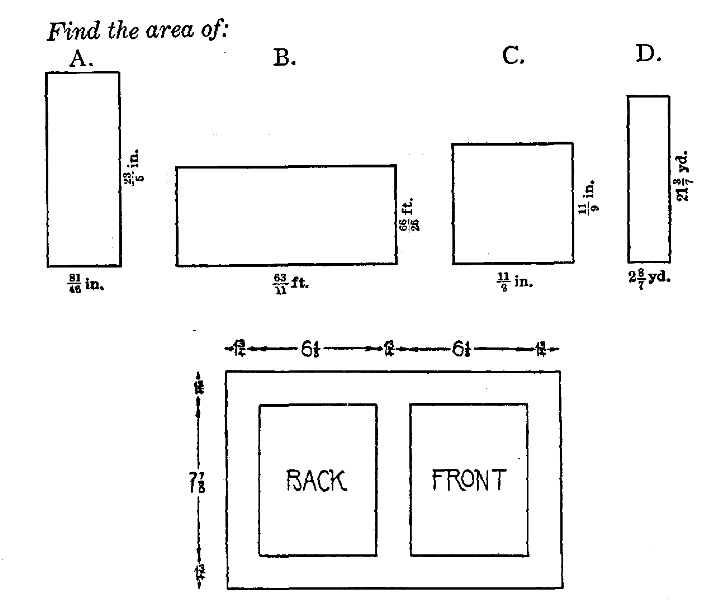 Fig. 30.—Numbers too small and badly designed.
Fig. 30.—Numbers too small and badly designed.
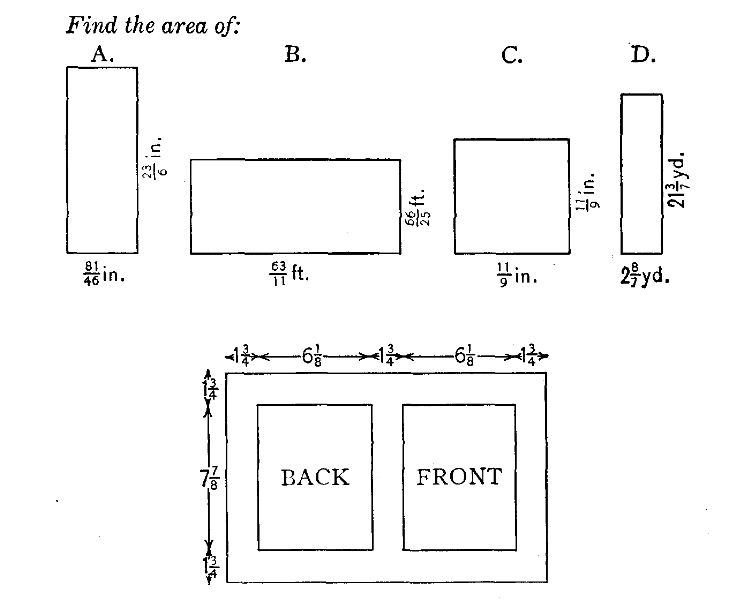 Fig. 32.—Figure 30 with suitable numbers.
Fig. 32.—Figure 30 with suitable numbers.
Style.—The ordinary type forms often have 3 and 8 so made as to require strain to distinguish them. 5 is sometimes easily confused with 3 and even with 8. 1, 4, and 7 may be less easily distinguishable than is desirable. Figure 33 shows a specially good type in which each figure is represented by its essential[20] features without any distracting shading or knobs or turns. Figure 34 shows some of the types in common use. There are no demonstrably great differences amongst these. In fractions there is a notable gain from using the slant form (2⁄3, 3⁄4) for exercises in addition [Pg 239] and subtraction, and for almost all mixed numbers. This appears clearly to the eye in the comparison of Fig. 35 below, where the same fractions all in 10-point type are displayed in horizontal and in slant form. The figures in the slant form are in general larger and the space between them and the fraction-line is wider. Also the slant form makes it easier for the eye to examine the denominators to see whether reductions are necessary. Except for a few cases to show that the operations can be done just as truly with the horizontal forms, the book and the blackboard should display mixed numbers and fractions to be added or subtracted in the slant form. The slant line should be at an angle of approximately 45 degrees. Pupils should be taught to use this form in their own work of this sort.


When script figures are presented they should be of simple design, showing clearly the essential features of the figure, the line being everywhere of equal or nearly equal width (that is, without shading, and without ornamentation or eccentricity of any sort). The opening of the 3 should be wide to prevent confusion with 8; the top of the 3 should be curved to aid its differentiation from 5; the down stroke of the 9 should be almost or quite straight; the 1, 4, 7, and 9 should be clearly distinguishable. There are many ways of distinguishing them clearly, the best probably being to use the straight line for 1, the open 4 with clear angularity, a wide top to the 7, and a clearly closed curve for the top of the 9.


| Fig. 36.—Good vertical spacing. | Fig. 37.—Bad vertical spacing. |
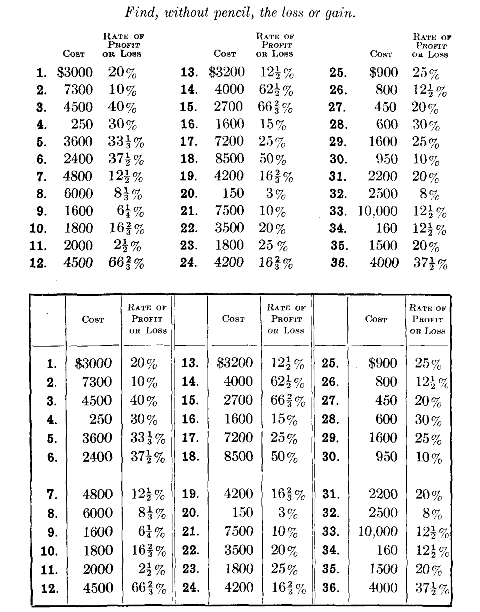 Figs. 38 (above) and 39 (below).—Good and bad left-right spacing.
Figs. 38 (above) and 39 (below).—Good and bad left-right spacing.
The pupil's writing of figures should be clear. He will thereby be saved eyestrain and errors in his school work as well as given a valuable ability for life. Handwriting of figures is used enormously in spite of the development of typewriters; illegible figures are commonly more harmful than illegible letters or words, since the context far less often tells what the figure is intended to be; the habit of making clear figures is not so hard to acquire, since they are written unjoined and require only the automatic action of ten minor acts of skill. The schools have missed a great opportunity in this respect. Whereas the hand writing of words is often better than it needs to be for life's purposes, the writing of figures is usually much worse. The figures presented in books on penmanship are also commonly bad, showing neglect or misunderstanding of the matter on the part of leaders in penmanship.
Spacing.—Spacing up and down the column is rarely too wide, but very often too narrow. The specimens shown in Figs. 36 and 37 show good practice contrasted with the common fault.
Spacing from right to left is generally fairly satisfactory in books, though there is a bad tendency to adopt some one routine throughout and so to miss chances to use reductions and increases of spacing so as to help the eye and the mind in special cases. Specimens of good and bad spacing are shown in Figs. 38 and 39. In the work of the pupils, the spacing from right to left is often too narrow. This crowding of letters, together with unevenness of spacing, adds notably to the task of eye and mind.
The composition or make-up of the page.—Other things being equal, that arrangement of the page is best which helps a child most to keep his place on a page and to find it after having looked away to work on the paper on which he computes, or for other good reasons. A good page and a bad page in this respect are shown in Figs. 40 and 41.[Pg 244]
 Fig. 40.—A page well made up to suit the action of the eye.
Fig. 40.—A page well made up to suit the action of the eye.
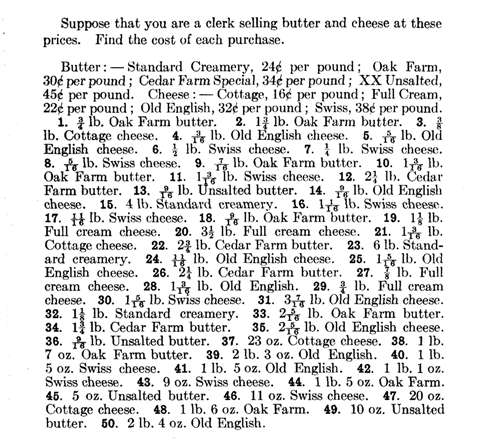
Objective presentations.—Pictures, diagrams, maps, and other presentations should not tax the eye unduly,
(a) by requiring too fine distinctions, or
(b) by inconvenient arrangement of the data, preventing easy counting, measuring, comparison, or whatever the task is, or
(c) by putting too many facts in one picture so that the eye and mind, when trying to make out any one, are confused by the others.
Illustrations of bad practices in these respects are shown in Figs. 42 to 52. A few specimens of work well arranged for the eye are shown in Figs. 53 to 56.
Good rules to remember are:—
Other things being equal, make distinctions by the clearest method, fit material to the tendency of the eye to see an 'eyeful' at a time (roughly 1½ inch by ½ inch in a book; 1½ ft. by ½ ft. on the blackboard), and let one picture teach only one fact or relation, or such facts and relations as do not interfere in perception.
The general conditions of seating, illumination, paper, and the like are even more important when the eyes are used with numbers than when they are used with words.
 Fig. 42.—Try to count the rungs on the ladder, or the shocks in the wagon.
Fig. 42.—Try to count the rungs on the ladder, or the shocks in the wagon.
 Fig. 43.—How many oars do you see? How many birds? How many fish?
Fig. 43.—How many oars do you see? How many birds? How many fish?
 Fig. 44.—Count the birds in each of the three flocks of birds.
Fig. 44.—Count the birds in each of the three flocks of birds.
 Fig. 45.—Note the lack of clear division of the hundreds. Consider the difficulty
of counting one of these columns of dots.
Fig. 45.—Note the lack of clear division of the hundreds. Consider the difficulty
of counting one of these columns of dots.
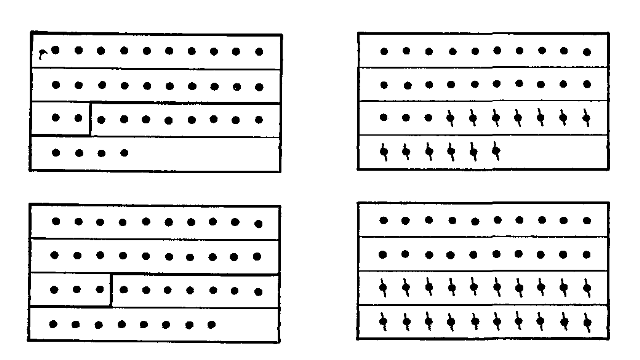 Fig. 46.—What do you suppose these pictures are intended to show?
Fig. 46.—What do you suppose these pictures are intended to show?
Fig. 47.—Would a beginner know that after THIRTEEN he was to switch around and begin at the other end? Could you read the SIX of TWENTY-SIX if you did not already know what it ought to be? What meaning would all the brackets have for a little child in grade 2? Does this picture illustrate or obfuscate?
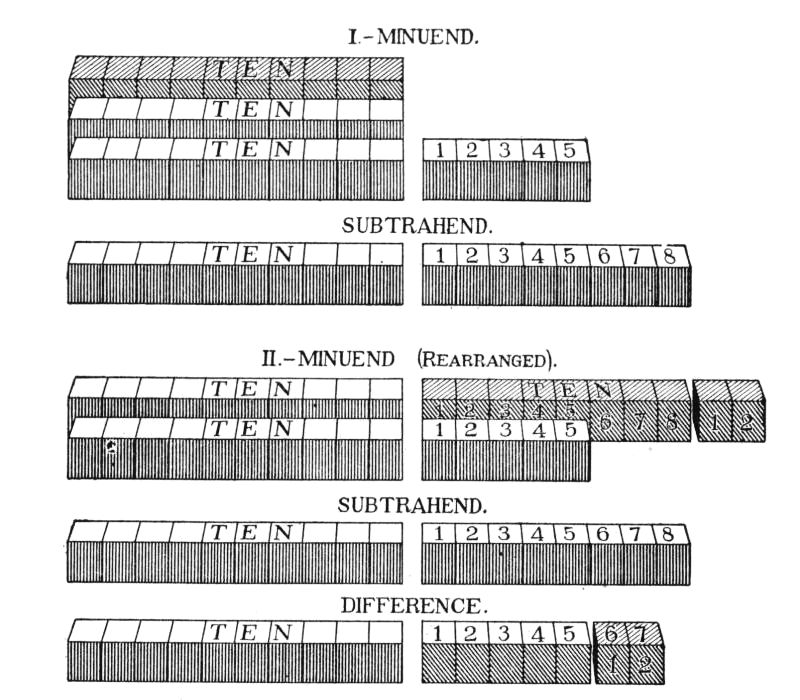 Fig. 48.—How long did it take you to find out what these pictures mean?
Fig. 48.—How long did it take you to find out what these pictures mean?

Fig. 49.—Count the figures in the first row, using your eyes alone; have some one make lines of 10, 11, 12, 13, and more repetitions of this figure spaced closely as here. Count 20 or 30 such lines, using the eye unaided by fingers, pencil, etc.
 Fig. 50.—Can you answer the question without measuring? Could a child of
seven or eight?
Fig. 50.—Can you answer the question without measuring? Could a child of
seven or eight?
 Fig. 52.—What are these drawings intended to show? What simple change would
make them show the facts much more clearly?
Fig. 52.—What are these drawings intended to show? What simple change would
make them show the facts much more clearly?
 Fig. 53.—Arranged in convenient "eye-fulls."
Fig. 53.—Arranged in convenient "eye-fulls."

Tell which bar has—
1. About 5 percent of its length black.
2. About 10 percent of its length black.
3. About 25 percent of its length black.
4. About 75 percent of its length black.
5. About 90 percent of its length black.
6. About 95 percent of its length black.
 Fig. 55.—Clear, simple, and well spaced.
Fig. 55.—Clear, simple, and well spaced.
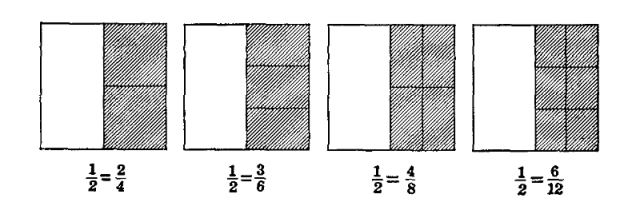 Fig. 56.—Well arranged, though a little wider spacing between the squares would
make it even better.
Fig. 56.—Well arranged, though a little wider spacing between the squares would
make it even better.
We mean by concrete objects actual things, events, and relations presented to sense, in contrast to words and numbers and symbols which mean or stand for these objects or for more abstract qualities and relations. Blocks, tooth-picks, coins, foot rules, squared paper, quart measures, bank books, and checks are such concrete things. A foot rule put successively along the three thirds of a yard rule, a bell rung five times, and a pound weight balancing sixteen ounce weights are such concrete events. A pint beside a quart, an inch beside a foot, an apple shown cut in halves display such concrete relations to a pupil who is attentive to the issue.
Concrete presentations are obviously useful in arithmetic to teach meanings under the general law that a word or number or sign or symbol acquires meaning by being connected with actual things, events, qualities, and relations.[Pg 254] We have also noted their usefulness as means to verifying the results of thinking and computing, as when a pupil, having solved, "How many badges each 5 inches long can be made from 31⁄3 yd. of ribbon?" by using 10 × 12⁄5, draws a line 31⁄3 yd. long and divides it into 5-inch lengths.
Concrete experiences are useful whenever the meaning of a number, like 9 or 7⁄8 or .004, or of an operation, like multiplying or dividing or cubing, or of some term, like rectangle or hypothenuse or discount, or some procedure, like voting or insuring property against fire or borrowing money from a bank, is absent or incomplete or faulty. Concrete work thus is by no means confined to the primary grades but may be appropriate at all stages when new facts, relations, and procedures are to be taught.
How much concrete material shall be presented will depend upon the fact or relation or procedure which is to be made intelligible, and the ability and knowledge of the pupil. Thus 'one half' will in general require less concrete illustration than 'five sixths'; and five sixths will require less in the case of a bright child who already knows 2⁄3, 3⁄4, 3⁄8, 5⁄8, 7⁄8, 2⁄5, 3⁄5, and 4⁄5 than in the case of a dull child or one who only knows 2⁄3 and 3⁄4. As a general rule the same topic will require less concrete material the later it appears in the school course. If the meanings of the numbers are taught in grade 2 instead of grade 1, there will be less need of blocks, counters, splints, beans, and the like. If 1½ + ½ = 2 is taught early in grade 3, there will be more gain from the use of 1½ inches and ½ inch on the foot rule than if the same relations were taught in connection with the general addition of like fractions late in grade 4. Sometimes the understanding can be had either by connecting the idea with the reality directly, or by connecting the two indirectly via some other idea. The amount of concrete material to be[Pg 255] used will depend on its relative advantage per unit of time spent. Thus it might be more economical to connect 5⁄12, 7⁄12, and 11⁄12 with real meanings indirectly by calling up the resemblance to the 2⁄3, 3⁄4, 3⁄8, 5⁄8, 7⁄8, 2⁄5, 3⁄5, 4⁄5, and 5⁄6 already studied, than by showing 5⁄12 of an apple, 7⁄12 of a yard, 11⁄12 of a foot, and the like.
In general the economical course is to test the understanding of the matter from time to time, using more concrete material if it is needed, but being careful to encourage pupils to proceed to the abstract ideas and general principles as fast as they can. It is wearisome and debauching to pupils' intellects for them to be put through elaborate concrete experiences to get a meaning which they could have got themselves by pure thought. We should also remember that the new idea, say of the meaning of decimal fractions, will be improved and clarified by using it (see page 183 f.), so that the attainment of a perfect conception of decimal fractions before doing anything with them is unnecessary and probably very wasteful.
A few illustrations may make these principles more instructive.
(a) Very large numbers, such as 1000, 10,000, 100,000, and 1,000,000, need more concrete aids than are commonly given. Guessing contests about the value in dollars of the school building and other buildings, the area of the schoolroom floor and other surfaces in square inches, the number of minutes in a week, and year, and the like, together with proper computations and measurements, are very useful to reënforce the concrete presentations and supply genuine problems in multiplication and subtraction with large numbers.
(b) Numbers very much smaller than one, such as 1⁄32, 1⁄64, .04, and .002, also need some concrete aids. A diagram like that of Fig. 57 is useful.[Pg 256]
(c) Majority and plurality should be understood by every citizen. They can be understood without concrete aid, but an actual vote is well worth while for the gain in vividness and surety.
(d) Insurance against loss by fire can be taught by explanation and analogy alone, but it will be economical to have some actual insuring and payment of premiums and a genuine loss which is reimbursed.[Pg 257]
(e) Four play banks in the corners of the room, receiving deposits, cashing checks, and later discounting notes will give good educational value for the time spent.
(f) Trade discount, on the contrary, hardly requires more concrete illustration than is found in the very problems to which it is applied.
(g) The process of finding the number of square units in a rectangle by multiplying with the appropriate numbers representing length and width is probably rather hindered than helped by the ordinary objective presentation as an introduction. The usual form of objective introduction is as follows:—

How long is this rectangle? How large is each square? How many square inches are there in the top row? How many rows are[Pg 258] there? How many square inches are there in the whole rectangle? Since there are three rows each containing 4 square inches, we have 3 × 4 square inches = 12 square inches.
Draw a rectangle 7 inches long and 2 inches wide. If you divide it into inch squares how many rows will there be? How many inch squares will there be in each row? How many square inches are there in the rectangle?
It is better actually to hide the individual square units as in Fig. 59. There are four reasons: (1) The concrete rows and columns rather distract attention from the essential thing to be learned. This is not that "x rows one square wide, y squares in a row will make xy squares in all," but that "by using proper units and the proper operation the area of any rectangle can be found from its length and width." (2) Children have little difficulty in learning to[Pg 259] multiply rather than add, subtract, or divide when computing area. (3) The habit so formed holds good for areas like 12⁄3 by 4½, with fractional dimensions, in which any effort to count up the areas of rows is very troublesome and confusing. (4) The notion that a square inch is an area 1' by 1' rather than ½' by 2' or 1⁄3 in. by 3 in. or 1½ in. by 2⁄3 in. is likely to be formed too emphatically if much time is spent upon the sort of concrete presentation shown above. It is then better to use concrete counting of rows of small areas as a means of verification after the procedure is learned, than as a means of deriving it.
There has been, especially in Germany, much argument concerning what sort of number-pictures (that is, arrangement of dots, lines, or the like, as shown in Fig. 60) is best for use in connection with the number names in the early years of the teaching of arithmetic.
Lay ['98 and '07], Walsemann ['07], Freeman ['10], Howell ['14], and others have measured the accuracy of children in estimating the number of dots in arrangements of one or more of these different types.[21] Many writers interpret a difference in favor of estimating, say, the square arrangements of Born or Lay as meaning that such is the best arrangement to use in teaching. The inference is, however, unjustified. That certain number-pictures are easier to estimate numerically does not necessarily mean that they are more instructive in learning. One set may be easier to estimate just because they are more familiar, having been oftener experienced. Even if the favored set was so after equal experience with all sets, accuracy of estimation would be a sign of superiority for use in instruction only if all other things were equal (or in favor of the arrangement [Pg 260] in question). Obviously the way to decide which of these is best to use in teaching is by using them in teaching and measuring all relevant results, not by merely recording which of them are most accurately estimated in certain time exposures.
 Fig. 60.—Various proposed arrangements of dots for use in teaching the meanings of the numbers 1 to 10.
Fig. 60.—Various proposed arrangements of dots for use in teaching the meanings of the numbers 1 to 10.
It may be noted that the Born, Lay, and Freeman pictures have claims for special consideration on grounds of probable instructiveness. Since they are also superior in the tests in respect to accuracy of estimate, choice should probably be made from these three by any teacher who wishes to connect one set of number-pictures systematically with the number names, as by drills with the blackboard or with cards.
Such drills are probably useful if undertaken with zeal, and if kept as supplementary to more realistic objective work with play money, children marching, material to be distributed, garden-plot lengths to be measured, and the like, and if so administered that the pupils soon get the generalized abstract meaning of the numbers freed from dependence on an inner picture of any sort. This freedom is so important that it may make the use of many types of number-pictures advisable rather than the use of the one which in and of itself is best.
As Meumann says: "Perceptual reckoning can be overdone. It had its chief significance for the surety and clearness of the first foundation of arithmetical instruction. If, however, it is continued after the first operations become familiar to the child, and extended to operations which develop from these elementary ones, it necessarily works as a retarding force and holds back the natural development of arithmetic. This moves on to work with abstract number and with mechanical association and reproduction." ['07, Vol. 2, p. 357.]
Such drills are commonly overdone by those who make[Pg 262] use of them, being given too often, and continued after their instructiveness has waned, and used instead of more significant, interesting, and varied work in counting and estimating and measuring real things. Consequently, there is now rather a prejudice against them in our better schools. They should probably be reinstated but to a moderate and judicious use.
There has been much dispute over the relative merits of oral and written work in arithmetic—a question which is much confused by the different meanings of 'oral' and 'written.' Oral has meant (1) work where the situations are presented orally and the pupil's final responses are given orally, or (2) work where the situations are presented orally and the pupils' final responses are written or partly written and partly oral, or (3) work where the situations are presented in writing or print and the final responses are oral. Written has meant (1) work where the situations are presented in writing or print and the final responses are made in writing, or (2) work where also many of the intermediate responses are written, or (3) work where the situations are presented orally but the final responses and a large percentage of the intermediate computational responses are written. There are other meanings than these.
It is better to drop these very ambiguous terms and ask clearly what are the merits and demerits, in the case of any specified arithmetical work, of auditory and of visual presentation of the situations, and of saying and of writing each specified step in the response.
The disputes over mental versus written arithmetic are also confused by ambiguities in the use of 'mental.' Mental has been used to mean "done without pencil and paper"[Pg 263] and also "done with few overt responses, either written or spoken, between the setting of the task and the announcement of the answer." In neither case is the word mental specially appropriate as a description of the total fact. As before, we should ask clearly, "What are the merits and demerits of making certain specified intermediate responses in inner speech or imaged sounds or visual images or imageless thought—that is, without actual writing or overt speech?"
It may be said at the outset that oral, written, and inner presentations of initial situations, oral, written, and inner announcements of final responses, and oral, written, and inner management of intermediate processes have varying degrees of merit according to the particular arithmetical exercise, pupil, and context. Devotion to oralness or mentalness as such is simply fanatical. Various combinations, such as the written presentation of the situation with inner management of the intermediate responses and oral announcement of the final response have their special merits for particular cases.
These merits the reader can evaluate for himself for any given sort of work for a given class by considering: (1) The amount of practice received by the class per hour spent; (2) the ease of correction of the work; (3) the ease of understanding the tasks; (4) the prevention of cheating; (5) the cheerfulness and sociability of the work; (6) the freedom from eyestrain, and other less important desiderata.
It should be noted that the stock schemes A, B, C, and D below are only a few of the many that are possible and that schemes E, F, G, and H have special merits.
The common practice of either having no use made of pencil and paper or having all computations and even much verbal analysis written out elaborately for examination is unfavorable for learning. The demands which life itself[Pg 264] will make of arithmetical knowledge and skill will range from tasks done with every percentage of written work from zero up to the case where every main result obtained by thought is recorded for later use by further thought. In school the best way is that which, for the pupils in question, has the best total effect upon quality of product, speed, and ease of production, reënforcement of training already given, and preparation for training to be given. There is nothing intellectually criminal about using a pencil as well as inner thought; on the other hand there is no magical value in writing out for the teacher's inspection figures that the pupil does not need in order to attain, preserve, verify, or correct his result.
| Presentation of Initial Situation | Management of Intermediate Processes | Announcement of Final Response |
|---|---|---|
| A. Printed or written | Written | Written |
| B. " " | Inner | Oral by one pupil, inner by the rest |
| C. Oral (by teacher) | Written | Written |
| D. " " | Inner | Oral by one pupil, inner by the rest |
| E. As in A or C | A mixture, the pupil writing what he needs | As in A or B or H |
| F. The real situation itself, in part at least | As in E | As in A or B or H |
| G. Both read by the pupil and put orally by the teacher | As in E | As in A or B or H |
| H. As in A or C or G | As in E | Written by all pupils, announced orally by one pupil |
The common practice of having the final responses of all easy tasks given orally has no sure justification. On the contrary, the great advantage of having all pupils really do the work should be secured in the easy work more than anywhere else. If the time cost of copying the figures is eliminated by the simple plan of having them printed, and if the supervision cost of examining the papers is eliminated by having the pupils correct each other's work in these easy tasks, written answers are often superior to oral except for the elements of sociability and 'go' and freedom from eyestrain of the oral exercise. Such written work provides the gifted pupils with from two to ten times as much practice as they would get in an oral drill on the same material, supposing them to give inner answers to every exercise done by the class as a whole; it makes sure that the dull pupils who would rarely get an inner answer at the rate demanded by the oral exercise, do as much as they are able to do.
Two arguments often made for the oral statement of problems by the teacher are that problems so put are better understood, especially in the grades up through the fifth, and that the problems are more likely to be genuine and related to the life the pupils know. When these statements are true, the first is a still better argument for having the pupils read the problems aided by the teacher's oral statement of them. For the difficulty is largely that the pupils cannot read well enough; and it is better to help them to surmount the difficulty rather than simply evade it. The second is not an argument for oralness versus writtenness, but for good problems versus bad; the teacher who makes up such good problems should, in fact, take special care to write them down for later use, which may be by voice or by the blackboard or by printed sheet, as is best.
Dewey, and others following him, have emphasized the desirability of having pupils do their work as active seekers, conscious of problems whose solution satisfies some real need of their own natures. Other things being equal, it is unwise, they argue, for pupils to be led along blindfold as it were by the teacher and textbook, not knowing where they are going or why they are going there. They ought rather to have some living purpose, and be zealous for its attainment.
This doctrine is in general sound, as we shall see, but it is often misused as a defense of practices which neglect the formation of fundamental habits, or as a recommendation to practices which are quite unworkable under ordinary classroom conditions. So it seems probable that its nature and limitations are not thoroughly known, even to its followers, and that a rather detailed treatment of it should be given here.
Consider first some cases where time spent in making pupils understand the end to be attained before attacking the task by which it is attained, or care about attaining the end (well or ill understood) is well spent.[Pg 267]
It is well for a pupil who has learned (1) the meanings of the numbers one to ten, (2) how to count a collection of ten or less, and (3) how to measure in inches a magnitude of ten, nine, eight inches, etc., to be confronted with the problem of true adding without counting or measuring, as in 'hidden' addition and measurement by inference. For example, the teacher has three pencils counted and put under a book; has two more counted and put under the book; and asks, "How many pencils are there under the book?" Answers, when obtained, are verified or refuted by actual counting and measuring.
The time here is well spent because the children can do the necessary thinking if the tasks are well chosen; because they are thereby prevented from beginning their study of addition by the bad habit of pseudo-adding by looking at the two groups of objects and counting their number instead of real adding, that is, thinking of the two numbers and inferring their sum; and further, because facing the problem of adding as a real problem is in the end more economical for learning arithmetic and for intellectual training in general than being enticed into adding by objective or other processes which conceal the difficulty while helping the pupil to master it.
The manipulation of short multiplication may be introduced by confronting the pupils with such problems as, "How to tell how many Uneeda biscuit there are in four boxes, by opening only one box." Correct solutions by addition should be accepted. Correct solutions by multiplication, if any gifted children think of this way, should be accepted, even if the children cannot justify their procedure. (Inferring the manipulation from the place-values of numbers is beyond all save the most gifted and probably beyond them.) Correct solution by multiplication by some child[Pg 268] who happens to have learned it elsewhere should be accepted. Let the main proof of the trustworthiness of the manipulation be by measurement and by addition. Proof by the stock arguments from the place-values of numbers may also be used. If no child hits on the manipulation in question, the problem of finding the length without adding may be set. If they still fail, the problem may be made easier by being put as "4 times 22 gives the answer. Write down what you think 4 times 22 will be." Other reductions of the difficulty of the problem may be made, or the teacher may give the answer without very great harm being done. The important requirement is that the pupils should be aware of the problem and treat the manipulation as a solution of it, not as a form of educational ceremonial which they learn to satisfy the whims of parents and teachers. In the case of any particular class a situation that is more appealing to the pupils' practical interests than the situation used here can probably be devised.
The time spent in this way is well spent (1) because all but the very dull pupils can solve the problem in some way, (2) because the significance of the manipulation as an economy over addition is worth bringing out, and (3) because there is no way of beginning training in short multiplication that is much better.
In the same fashion multiplication by two-place numbers may be introduced by confronting pupils with the problem of the number of sheets of paper in 72 pads, or pieces of chalk in 24 boxes, or square inches in 35 square feet, or the number of days in 32 years, or whatever similar problem can be brought up so as to be felt as a problem.
Suppose that it is the 35 square feet. Solutions by (5 × 144) + (30 × 144), however arranged, or by (10 × 144) + (10 × 144) + (10 × 144) + (5 × 144), or by 3500 + (35 × 40) + [Pg 269] (35 × 4), or by 7 × (5 × 144), however arranged, should all be listed for verification or rejection. The pupils need not be required to justify their procedures by a verbal statement. Answers like 432,720, or 720,432, or 1152, or 4220, or 3220 should be listed for verification or rejection. Verification may be by a mixture of short multiplication and objective work, or by a mixture of short multiplication and addition, or by addition abbreviated by taking ten 144s as 1440, or even (for very stupid pupils) by the authority of the teacher. Or the manipulation in cases like 53 × 9 or 84 × 7 may be verified by the reverse short multiplication. The deductive proof of the correctness of the manipulation may be given in whole or in part in connection with exercises like
| 10 × 2 = | 30 × 14 = |
| 10 × 3 = | 3 × 44 = |
| 10 × 4 = | 30 × 44 = |
| 10 × 14 = | 3 × 144 = |
| 10 × 44 = | 20 × 144 = |
| 10 × 144 = | 40 × 144 = |
| 20 × 2 = | 30 × 144 = |
| 20 × 3 = | 5 × 144 = |
| 30 × 3 = | 35 = 30 + .... |
| 30 × 4 = | 30 × 144 added to 5 × 144 = |
| 3 × 14 = |
Certain wrong answers may be shown to be wrong in many ways; e.g., 432,720 is too big, for 35 times a thousand square inches is only 35,000; 1152 is too small, for 35 times a hundred square inches would be 3500, or more than 1152.
The time spent in realizing the problem here is fairly well spent because (1) any successful original manipulation in [Pg 270] this case represents an excellent exercise of thought, because (2) failures show that it is useless to juggle the figures at random, and because (3) the previous experience with short multiplication makes it possible for the pupils to realize the problem in a very few minutes. It may, however, be still better to give the pupils the right method just as soon as the problem is realized, without having them spend more time in trying to solve it. Thus:—
1 square foot has 144 square inches. How many square inches are there in 35 square feet (marked out in chalk on the floor as a piece 10 ft. × 3 ft. plus a piece 5 ft. × 1 ft.)?
1 yard = 36 inches. How many inches long is this wall (found by measure to be 13 yards)?
Here is a quick way to find the answers:—
144
35
——
720
432
——
5040 sq. inches in 35 sq. ft.
36
13
——
108
36
——
468 inches in 13 yd.
Consider now the following introduction to dividing by a decimal:—
Dividing by a Decimal
1. How many minutes will it take a motorcycle, to go 12.675 miles at the rate of .75 mi. per minute?
| 16.9 |
| .75 | 12.675 |
| 7 5 |
| 5 17 |
| 4 50 |
| 675 |
| 675 |
2. Check by multiplying 16.9 by .75.
3. How do you know that the quotient cannot be as little as 1.69?
4. How do you know that the quotient cannot be as large as 169?
5. Find the quotient for 3.75 ÷ 1.5.
6. Check your result by multiplying the quotient by the divisor.
7. How do you know that the quotient cannot be .25 or 25 ?
8. Look at this problem. .25|7.5
How do you know that 3.0 is wrong for the quotient?
How do you know that 300 is wrong for the quotient?
State which quotient is right for each of these:—
9. .021 or .21 or 2.1 or 21 or 210
1.8|3.78
10. .021 or .21 or 21 or 210
1.8|37.8
11. .03 or .3 or 3 or 30 or 300
1.25|37.5
12. .03 or .3 or 3 or 30 or 300
12.5|37.5
13. .05 or .5 or 5 or 50 or 500
1.25|6.25
14. .05 or .5 or 5 or 50 or 500
12.5|6.25
15. Is this rule true? If it is true, learn it.
In a correct result, the number of decimal places in the divisor and quotient together equals the number of decimal places in the dividend.
These and similar exercises excite the problem attitude in children who have a general interest in getting right answers. Such a series carefully arranged is a desirable introduction to a statement of the rule for placing the decimal point in division with decimals. For it attracts attention to the general principle (divisor × quotient should equal dividend), which is more important than the rule for convenient location of the decimal point, and it gives training in placing the point by inspection of the divisor, quotient, and dividend, which suffices for nineteen out of twenty cases that the pupil will ever encounter outside of school. He is likely to remember this method by inspection long after he has forgotten the fixed rule.
It is well for the pupil to be introduced to many arith[Pg 272]metical facts by way of problems about their common uses. The clockface, the railroad distance table in hundredths of a mile, the cyclometer and speedometer, the recipe, and the like offer problems which enlist his interest and energy and also connect the resulting arithmetical learning with the activities where it is needed. There is no time cost, but a time-saving, for the learning as a means to the solution of the problems is quicker than the mere learning of the arithmetical facts by themselves alone. A few samples of such procedure are shown below:—
GRADE 3
To be Done at Home
Look at a watch. Has it any hands besides the hour hand and the minute hand? Find out all that you can about how a watch tells seconds, how long a second is, and how many seconds make a minute.
GRADE 5
Measuring Rainfall
| Rainfall per Week (cu. in. per sq. in. of area) | ||
| June | 1-7 | 1.056 |
| 8-14 | 1.103 | |
| 15-21 | 1.040 | |
| 22-28 | .960 | |
| 29-July 5 | .915 | |
| July | 6-12 | .782 |
| 13-19 | .790 | |
| 20-26 | .670 | |
| 27-Aug. 2 | .503 | |
| Aug. | 3-9 | .512 |
| 10-16 | .240 | |
| 17-23 | .215 | |
| 24-30 | .811 | |
1. In which weeks was the rainfall 1 or more?
2. Which week of August had the largest rainfall for that month?
3. Which was the driest week of the summer? (Driest means with the least rainfall.)
4. Which week was the next to the driest?
5. In which weeks was the rainfall between .800 and 1.000?
6. Look down the table and estimate whether the average rainfall for one week was about .5, or about .6, or about .7, or about .8, or about .9.
Dairy Records
| Record of Star Elsie | ||
| Pounds of Milk | Butter-Fat per Pound of Milk | |
|---|---|---|
| Jan. | 1742 | .0461 |
| Feb. | 1690 | .0485 |
| Mar. | 1574 | .0504 |
| Apr. | 1226 | .0490 |
| May | 1202 | .0466 |
| June | 1251 | .0481 |
Read this record of the milk given by the cow Star Elsie. The first column tells the number of pounds of milk given by Star Elsie each month. The second column tells what fraction of a pound of butter-fat each pound of milk contained.
1. Read the first line, saying, "In January this cow gave 1742 pounds of milk. There were 461 ten thousandths of a pound of butter-fat per pound of milk." Read the other lines in the same way.
2. How many pounds of butter-fat did the cow produce in Jan.? 3. In Feb.? 4. In Mar.? 5. In Apr.? 6. In May? 7. In June?
GRADE 5 OR LATER
Using Recipes to Make Larger or Smaller Quantities
I. State how much you would use of each material in the following recipes: (a) To make double the quantity. (b) To make half the quantity. (c) To make 1½ times the quantity. You may use pencil and paper when you cannot find the right amount mentally.
| 1. Peanut Penuche | 2. Molasses Candy |
| 1 tablespoon butter | ½ cup butter |
| 2 cups brown sugar | 2 cups sugar |
| 1⁄3 cup milk or cream | 1 cup molasses |
| ¾ cup chopped peanuts | 1½ cups boiling water |
| 1⁄3 teaspoon salt | |
| 3. Raisin Opera Caramels | 4. Walnut Molasses Squares |
| 2 cups light brown sugar | 2 tablespoons butter |
| 7⁄8 cup thin cream | 1 cup molasses |
| ½ cup raisins | 1⁄3 cup sugar |
| ½ cup walnut meats | |
| [Pg 274] | |
| 5. Reception Rolls | 6. Graham Raised Loaf |
| 1 cup scalded milk | 2 cups milk |
| 1½ tablespoons sugar | 6 tablespoons molasses |
| 1 teaspoon salt | 1½ teaspoons salt |
| ¼ cup lard | 1⁄3 yeast cake |
| 1 yeast cake | ¼ cup lukewarm water |
| ¼ cup lukewarm water | 2 cups sifted Graham flour |
| White of 1 egg | ½ cup Graham bran |
| 3½ cups flour | ¾ cup flour (to knead) |
II. How much would you use of each material in the following recipes: (a) To make 2⁄3 as large a quantity? (b) To make 11⁄3 times as much? (c) To make 2½ times as much?
| 1. English Dumplings | 2. White Mountain Angel Cake |
| ½ pound beef suet | 1½ cups egg whites |
| 1¼ cups flour | 1½ cups sugar |
| 3 teaspoons baking powder | 1 teaspoon cream of tartar |
| 1 teaspoon salt | 1 cup bread flour |
| ½ teaspoon pepper | ¼ teaspoon salt |
| 1 teaspoon minced parsley | 1 teaspoon vanilla |
| ¼ cup cold water |
In many cases arithmetical facts and principles can be well taught in connection with some problem or project which is not arithmetical, but which has special potency to arouse an intellectual activity in the pupil which by some ingenuity can be directed to arithmetical learning. Playing store is the most fundamental case. Planning for a party, seeing who wins a game of bean bag, understanding the calendar for a month, selecting Christmas presents, planning a picnic, arranging a garden, the clock, the watch with second hand, and drawing very simple maps are situations suggesting problems which may bring a living purpose into arithmetical learning in grade 2. These are all available under ordinary conditions of class instruction. A sample of such problems for a higher grade (6) is shown below.
Estimating Areas
The children in the geography class had a contest in estimating the areas of different surfaces. Each child wrote his estimates [Pg 275] for each of these maps, A, B, C, D, and E. (Only C and D are shown here.) In the arithmetic class they learned how to find the exact areas. Then they compared their estimates with the exact areas to find who came nearest.
Write your estimates for A, B, C, D, and E. Then study the next 6 pages and learn how to find the exact areas.
(The next 6 pages comprise training in the mensuration of parallelograms and triangles.)
In some cases the affairs of individual pupils include problems which may be used to guide the individual in question to a zealous study of arithmetic as a means of achieving his purpose—of making a canoe, surveying an island, keeping the accounts of a Girls' Canning Club, or the like. It requires much time and very great skill to direct the work of thirty or more pupils each busy with a special type of his own, so as to make the work instructive for each, but in some cases the expense of time and skill is justified.
In general what should be meant when one says that it is desirable to have pupils in the problem-attitude when they are studying arithmetic is substantially as follows:—
First.—Information that comes as an answer to questions[Pg 276] is better attended to, understood, and remembered than information that just comes.
Second.—Similarly, movements that come as a step toward achieving an end that the pupil has in view are better connected with their appropriate situations, and such connections are longer retained, than is the case with movements that just happen.
Third.—The more the pupil is set toward getting the question answered or getting the end achieved, the greater is the satisfyingness attached to the bonds of knowledge or skill which mean progress thereto.
Fourth.—It is bad policy to rely exclusively on the purely intellectualistic problems of "How can I do this?" "How can I get the right answer?" "What is the reason for this?" "Is there a better way to do that?" and the like. It is bad policy to supplement these intellectualistic problems by only the remote problems of "How can I be fitted to earn a higher wage?" "How can I make sure of graduating?" "How can I please my parents?" and the like. The purely intellectualistic problems have too weak an appeal for many pupils; the remote problems are weak so long as they are remote and, what is worse, may be deprived of the strength that they would have in due time if we attempt to use them too soon. It is the extreme of bad policy to neglect those personal and practical problems furnished by life outside the class in arithmetic the solution of which can really be furthered by arithmetic then and there. It is good policy to spend time in establishing certain mental sets—stimulating, or even creating, certain needs—setting up problems themselves—when the time so spent brings a sufficient improvement in the quality and quantity of the pupils' interest in arithmetical learning.
Fifth.—It would be still worse policy to rely exclusively[Pg 277] on problems arising outside arithmetic. To learn arithmetic is itself a series of problems of intrinsic interest and worth to healthy-minded children. The need for ability to multiply with United States money or to add fractions or to compute percents may be as truly vital and engaging as the need for skill to make a party dress or for money to buy it or for time to play baseball. The intellectualistic needs and problems should be considered along with all others, and given whatever weight their educational value deserves.
There are certain misconceptions of the doctrine of the problem-attitude. The most noteworthy is that difficulty—temporary failure—an inadequacy of already existing bonds—is the essential and necessary stimulus to thinking and learning. Dewey himself does not, as I understand him, mean this, but he has been interpreted as meaning it by some of his followers.[22]
Difficulty—temporary failure, inadequacy of existing bonds—on the contrary does nothing whatsoever in and of itself; and what is done by the annoying lack of success which sometimes accompanies difficulty sometimes hinders thinking and learning.
Mere difficulty, mere failure, mere inadequacy of existing bonds, does nothing. It is hard for me to add three eight-place numbers at a glance; I have failed to find as effective illustrations for pages 276 to 277 as I wished; my existing sensori-motor connections are inadequate to playing a golf course in 65. But these events and conditions have done nothing to stimulate me in respect to the behavior in question. In the first of the three there is no annoying lack and no dynamic influence at all; in the second there was to some [Pg 278] degree an annoying lack—a slight irritation at not getting just what I wanted,—and this might have impelled me to further thinking (though it did not, and getting one tiptop illustration would as a rule stimulate me to hunt for others more than failing to get such). In the third case the lack of the 65 does not annoy me or have any noteworthy dynamic effect. The lack of 90 instead of 95-100 is annoying and is at times a stimulus to further learning, though not nearly so strong a stimulus as the attainment of the 90 would be! At other times this annoying lack is distinctly inhibitory—a stimulus to ceasing to learn. In the intellectual life the inhibitory effect seems far the commoner of the two. Not getting answers seems as a rule to make us stop trying to get them. The annoying lack of success with a theoretical problem most often makes us desert it for problems to whose solution the existing bonds promise to be more adequate.
The real issue in all this concerns the relative strength, in the pupil's intellectual life, of the "negative reaction" of behavior in general. An animal whose life processes are interfered with so that an annoying state of affairs is set up, changes his behavior, making one after another responses as his instincts and learned tendencies prescribe, until the annoying state of affairs is terminated, or the animal dies, or suffers the annoyance as less than the alternatives which his responses have produced. When the annoying state of affairs is characterized by the failure of things as they are to minister to a craving—as in cases of hunger, loneliness, sex-pursuit, and the like,—we have stimulus to action by an annoying lack or need, with relief from action by the satisfaction of the need.
Such is in some measure true of man's intellectual life. In recalling a forgotten name, in solving certain puzzles, or in simplifying an algebraic complex, there is an annoying[Pg 279] lack of the name, solution, or factor, a trial of one after another response, until the annoyance is relieved by success or made less potent by fatigue or distraction. Even here the difficulty does not do anything—but only the annoying interference with our intellectual peace by the problem. Further, although for the particular problem, the annoying lack stimulates, and the successful attainment stops thinking, the later and more important general effect on thinking is the reverse. Successful attainment stops our thinking on that problem but makes us more predisposed later to thinking in general.
Overt negative reaction, however, plays a relatively small part in man's intellectual life. Filling intellectual voids or relieving intellectual strains in this way is much less frequent than being stimulated positively by things seen, words read, and past connections acting under modified circumstances. The notion of thinking as coming to a lack, filling it, meeting an obstacle, dodging it, being held up by a difficulty and overcoming it, is so one-sided as to verge on phantasy. The overt lacks, strains, and difficulties come perhaps once in five hours of smooth straightforward use and adaptation of existing connections, and they might as truly be called hindrances to thought—barriers which past successes help the thinker to surmount. Problems themselves come more often as cherished issues which new facts reveal, and whose contemplation the thinker enjoys, than as strains or lacks or 'problems which I need to solve.' It is just as true that the thinker gets many of his problems as results from, or bonuses along with, his information, as that he gets much of his information as results of his efforts to solve problems.
As between difficulty and success, success is in the long run more productive of thinking. Necessity is not the mother of invention. Knowledge of previous inventions is[Pg 280] the mother; original ability is the father. The solutions of previous problems are more potent in producing both new problems and their solutions than is the mere awareness of problems and desire to have them solved.
In the case of arithmetic, learning to cancel instead of getting the product of the dividends and the product of the divisors and dividing the former by the latter, is a clear case of very valuable learning, with ease emphasized rather than difficulty, with the adequacy of existing bonds (when slightly redirected) as the prime feature of the process rather than their inadequacy, and with no sense of failure or lack or conflict. It would be absurd to spend time in arousing in the pupil, before beginning cancellation, a sense of a difficulty—viz., that the full multiplying and dividing takes longer than one would like. A pupil in grade 4 or 5 might well contemplate that difficulty for years to no advantage. He should at once begin to cancel and prove by checking that errorless cancellation always gives the right answer. To emphasize before teaching cancellation the inadequacy of the old full multiplying and dividing would, moreover, not only be uneconomical as a means to teaching cancellation; it would amount to casting needless slurs on valuable past acquisitions, and it would, scientifically, be false. For, until a pupil has learned to cancel, the old full multiplying is not inadequate; it is admirable in every respect. The issue of its inadequacy does not truly appear until the new method is found. It is the best way until the better way is mastered.
In the same way it is unwise to spend time in making pupils aware of the annoying lacks to be supplied by the multiplication tables, the division tables, the casting out of nines, or the use of the product of the length and breadth of a rectangle as its area, the unit being changed to the[Pg 281] square erected on the linear unit as base. The annoying lack will be unproductive, while the learning takes place readily as a modification of existing habits, and is sufficiently appreciated as soon as it does take place. The multiplication tables come when instead of merely counting by 7s from 0 up saying "7, 14, 21," etc., the pupil counts by 7s from 0 up saying "Two sevens make 14, three sevens make 21, four sevens make 28," etc. The division tables come as easy selections from the known multiplications; the casting out of nines comes as an easy device. The computation of the area of a rectangle is best facilitated, not by awareness of the lack of a process for doing it, but by awareness of the success of the process as verified objectively.
In all these cases, too, the pupil would be misled if we aroused first a sense of the inadequacy of counting, adding, and objective division, an awareness of the difficulties which the multiplication and division tables and nines device and area theorem relieve. The displaced processes are admirable and no unnecessary fault should be found with them, and they are not inadequate until the shorter ways have been learned.
One false inference about the problem-attitude is that the pupil should always understand the aim or issue before beginning to form the bonds which give the method or process that provides the solution. On the contrary, he will often get the process more easily and value it more highly if he is taught what it is for gradually while he is learning it. The system of decimal notation, for example, may better be taken first as a mere fact, just as we teach a child to talk without trying first to have him understand the value of verbal intercourse, or to keep clean without trying first to have him understand the bacteriological consequences of filth.[Pg 282]
A second inference—that the pupil should always be taught to care about an issue and crave a process for managing it before beginning to learn the process—is equally false. On the contrary, the best way to become interested in certain issues and the ways of handling them is to learn the process—even to learn it by sheer habituation—and then note what it does for us. Such is the case with ".16662⁄3 × = divide by 6," ".3331⁄3 × = divide by 3," "multiply by .875 = divide the number by 8 and subtract the quotient from the number."
A third unwise tendency is to degrade the mere giving of information—to belittle the value of facts acquired in any other way than in the course of deliberate effort by the pupil to relieve a problem or conflict or difficulty. As a protest against merely verbal knowledge, and merely memoriter knowledge, and neglect of the active, questioning search for knowledge, this tendency to belittle mere facts has been healthy, but as a general doctrine it is itself equally one-sided. Mere facts not got by the pupil's thinking are often of enormous value. They may stimulate to active thinking just as truly as that may stimulate to the reception of facts. In arithmetic, for example, the names of the numbers, the use of the fractional form to signify that the upper number is divided by the lower number, the early use of the decimal point in U. S. money to distinguish dollars from cents, and the meanings of "each," "whole," "part," "together," "in all," "sum," "difference," "product," "quotient," and the like are self-justifying facts.
A fourth false inference is that whatever teaching makes the pupil face a question and think out its answer is thereby justified. This is not necessarily so unless the question is a worthy one and the answer that is thought out an intrinsically valuable one and the process of thinking used one that is[Pg 283] appropriate for that pupil for that question. Merely to think may be of little value. To rely much on formal discipline is just as pernicious here as elsewhere. The tendency to emphasize the methods of learning arithmetic at the expense of what is learned is likely to lead to abuses different in nature but as bad in effect as that to which the emphasis on disciplinary rather than content value has led in the study of languages and grammar, or in the old puzzle problems of arithmetic.
The last false inference that I shall discuss here is the inference that most of the problems by which arithmetical learning is stimulated had better be external to arithmetic itself—problems about Noah's Ark or Easter Flowers or the Merry Go Round or A Trip down the Rhine.
Outside interests should be kept in mind, as has been abundantly illustrated in this volume, but it is folly to neglect the power, even for very young or for very stupid children, of the problem "How can I get the right answer?" Children do have intellectual interests. They do like dominoes, checkers, anagrams, and riddles as truly as playing tag, picking flowers, and baking cake. With carefully graded work that is within their powers they like to learn to add, subtract, multiply, and divide with integers, fractions, and decimals, and to work out quantitative relations.
In some measure, learning arithmetic is like learning to typewrite. The learner of the latter has little desire to present attractive-looking excuses for being late, or to save expense for paper. He has no desire to hoard copies of such and such literary gems. He may gain zeal from the fact that a school party is to be given and invitations are to be sent out, but the problem "To typewrite better" is after all his main problem. Learning arithmetic is in some measure a game whose moves are motivated by the general[Pg 284] set of the mind toward victory—winning right answers. As a ball-player learns to throw the ball accurately to first-base, not primarily because of any particular problem concerning getting rid of the ball, or having the man at first-base possess it, or putting out an opponent against whom he has a grudge, but because that skill is required by the game as a whole, so the pupil, in some measure, learns the technique of arithmetic, not because of particular concrete problems whose solutions it furnishes, but because that technique is required by the game of arithmetic—a game that has intrinsic worth and many general recommendations.
The general facts concerning individual variations in abilities—that the variations are large, that they are continuous, and that for children of the same age they usually cluster around one typical or modal ability, becoming less and less frequent as we pass to very high or very low degrees of the ability—are all well illustrated by arithmetical abilities.
The surfaces of frequency shown in Figs. 61, 62, and 63 are samples. In these diagrams each space along the baseline represents a certain score or degree of ability, and the height of the surface above it represents the number of individuals obtaining that score. Thus in Fig. 61, 63 out of 1000 soldiers had no correct answer, 36 out of 1000 had one correct answer, 49 had two, 55 had three, 67 had four, and so on, in a test with problems (stated in words).
Figure 61 shows that these adults varied from no problems solved correctly to eighteen, around eight as a central tendency. Figure 62 shows that children of the same year-age (they were also from the same neighborhood and in the same school) varied from under 40 to over 200 figures correct. Figure 63 shows that even among children who have all reached the same school grade and so had rather [Pg 286] similar educational opportunities in arithmetic, the variation is still very great. It requires a range from 15 to over 30 examples right to include even nine tenths of them.
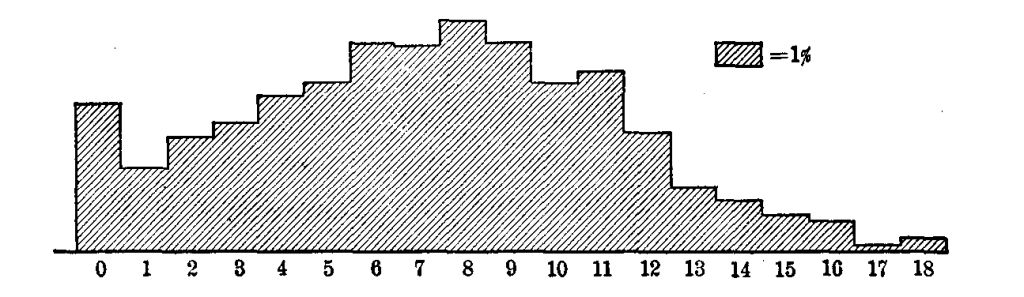
Fig. 61.—The scores of 1000 soldiers in the National Army born in English-speaking countries, in Test 2 of the Army Alpha. The score is the number of correct answers obtained in five minutes. Probably 10 to 15 percent of these men were unable to read or able to read only very easy sentences at a very slow rate. Data furnished by the Division of Psychology in the office of the Surgeon General.
It should, however, be noted that if each individual had been scored by the average of his work on eight or ten different days instead of by his work in just one test, the variability would have been somewhat less than appears in Figs. 61, 62, and 63.
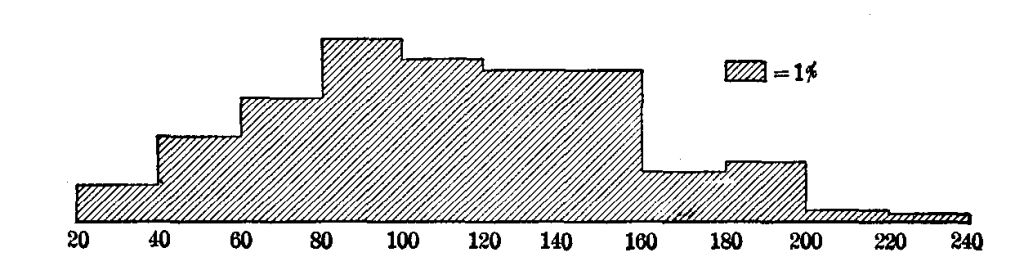
Fig. 62.—The scores of 100 11-year-old pupils in a test of computation. Estimated from the data given by Burt ['17, p. 68] for 10-, 11-, and 12-year-olds. The score equals the number of correct figures.
It is also the case that if each individual had been scored, not in problem-solving alone or division alone, but in an elaborate examination on the whole field of arithmetic, the variability would have been somewhat less than appears in Figs. 61, 62, and 63. On the other hand, if the officers and [Pg 287] the soldiers rejected for feeblemindedness had been included in Fig. 61, if the 11-year-olds in special classes for the very dull had been included in Fig. 62, and if all children who had been to school six years had been included in Fig. 63, no matter what grade they had reached, the effect would have been to increase the variability.
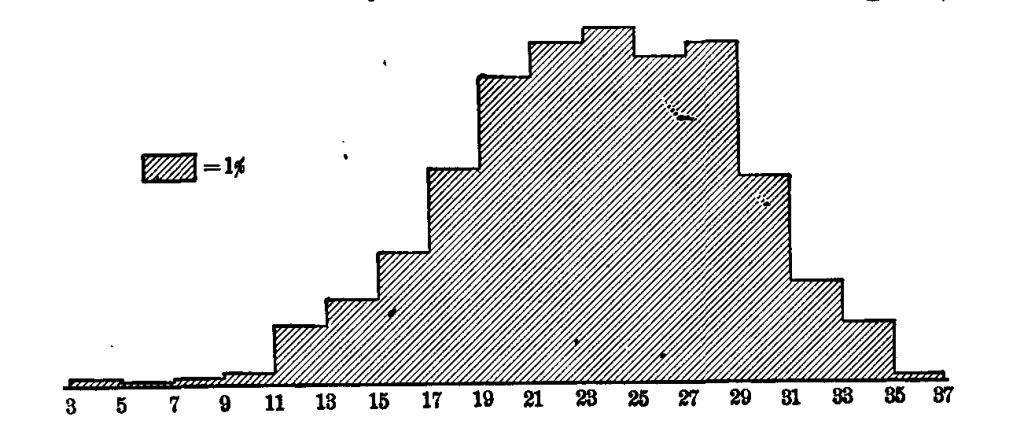
Fig. 63.—The scores of pupils in grade 6 in city schools in the Woody Division Test A. The score is the number of correct answers obtained in 20 minutes. From Woody ['16, p. 61].
In spite of the effort by school officers to collect in any one school grade those somewhat equal in ability or in achievement or in a mixture of the two, the population of the same grades in the same school system shows a very wide range in any arithmetical ability. This is partly because promotion is on a more general basis than arithmetical ability so that some very able arithmeticians are deliberately held back on account of other deficiencies, and some very incompetent arithmeticians are advanced on account of other excellencies. It is partly because of general inaccuracy in classifying and promoting pupils.
In a composite score made up of the sum of the scores in Woody tests,—Add. A, Subt. A, Mult. A, and Div. A, and two tests in problem-solving (ten and six graded problems, [Pg 288] with maximum attainable credits of 30 and 18), Kruse ['18] found facts from which I compute those of Table 13, and Figs. 64 to 66, for pupils all having the training of the same city system, one which sought to grade its pupils very carefully.
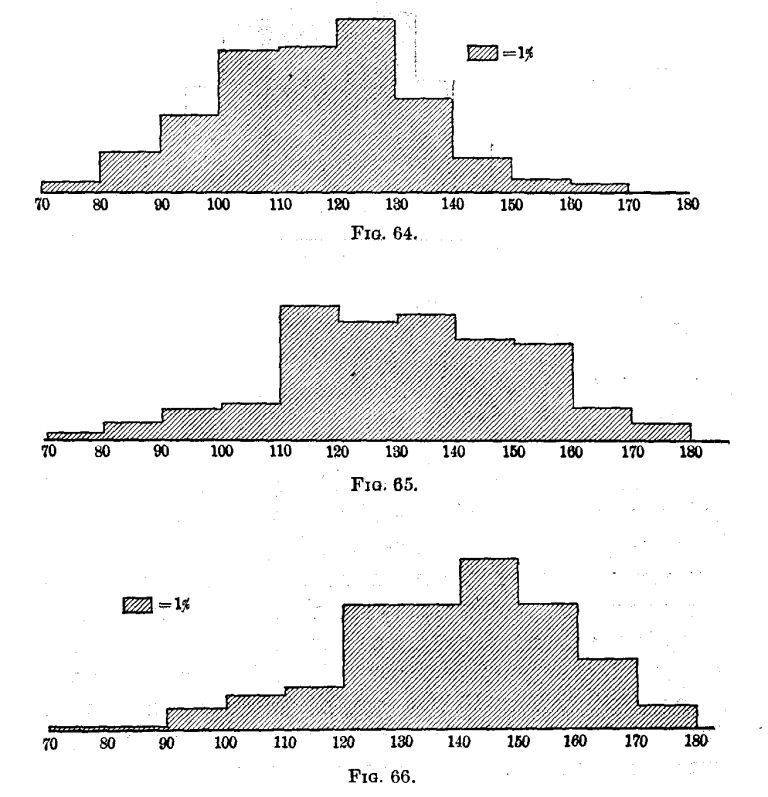
Figs. 64, 65, and 66.—The scores of pupils in grade 6 (Fig. 64), grade 7 (Fig. 65), and grade 8 (Fig. 66) in a composite of tests in computation and problem-solving. The time was about 120 minutes. The maximum score attainable was 196.
The overlapping of grade upon grade should be noted. Of the pupils in grade 6 about 18 percent do better than the average pupil in grade 7, and about 7 percent do better than the average pupil in grade 8. Of the pupils in grade 8 about 33 percent do worse than the average pupil in grade 7 and about 12 percent do worse than the average pupil in grade 6.
TABLE 13
Relative Frequencies of Scores in an Extensive Team of Arithmetical Tests.[23] In Percents
| Score | Grade 6 | Grade 7 | Grade 8 |
|---|---|---|---|
| 70 to 79 | 1.3 | .9 | .4 |
| 80 " 89 | 5.5 | 2.3 | .4 |
| 90 " 99 | 10.6 | 4.3 | 2.9 |
| 100 " 109 | 19.4 | 5.2 | 4.4 |
| 110 " 119 | 19.8 | 18.5 | 5.8 |
| 120 " 129 | 23.5 | 16.2 | 16.8 |
| 130 " 139 | 12.6 | 17.5 | 16.8 |
| 140 " 149 | 4.6 | 13.9 | 22.9 |
| 150 " 159 | 1.7 | 13.6 | 17.1 |
| 160 " 169 | 1.2 | 4.8 | 9.4 |
| 170 " 179 | 2.5 | 3.3 |
The variation within a single class for which a single teacher has to provide is great. Even when teaching is departmental and promotion is by subjects, and when also the school is a large one and classification within a grade is by ability—there may be a wide range for any given special component ability. Under ordinary circumstances the range is so great as to be one of the chief limiting conditions for the teaching of arithmetic. Many methods appropriate [Pg 290] to the top quarter of the class will be almost useless for the bottom quarter, and vice versa.
 Fig. 67.
Fig. 67.
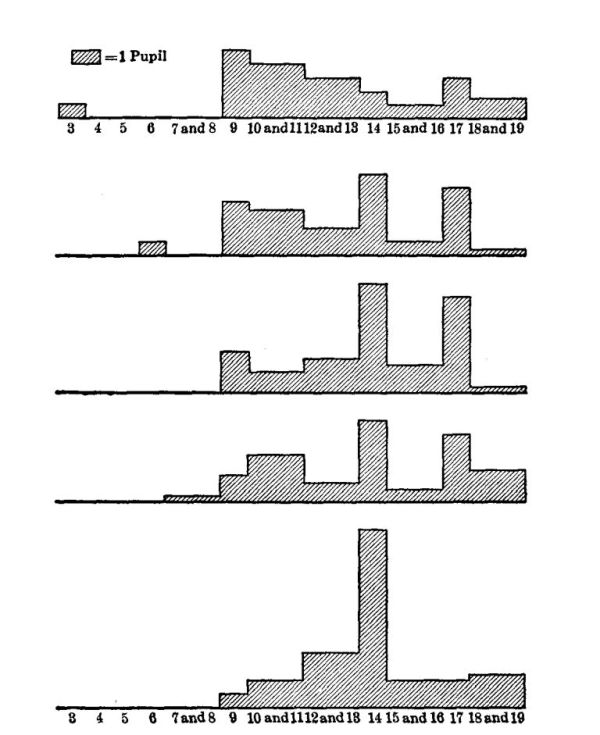 Fig. 68.
Fig. 68.Figs. 67 and 68.—The scores of ten 6 B classes in a 12-minute test in computation with integers (the Courtis Test 7). The score is the number of units done. Certain long tasks are counted as two units.
Figures 67 and 68 show the scores of ten classes taken at random from ninety 6 B classes in one city by Courtis ['13, p. 64] in amount of computation done in 12 minutes. Observe the very wide variation present in the case of every [Pg 292] class. The variation within a class would be somewhat reduced if each pupil were measured by his average in eight or ten such tests given on different days. If a rather generous allowance is made for this we still have a variation in speed as great as that shown in Fig. 69, as the fact to be expected for a class of thirty-two 6 B pupils.
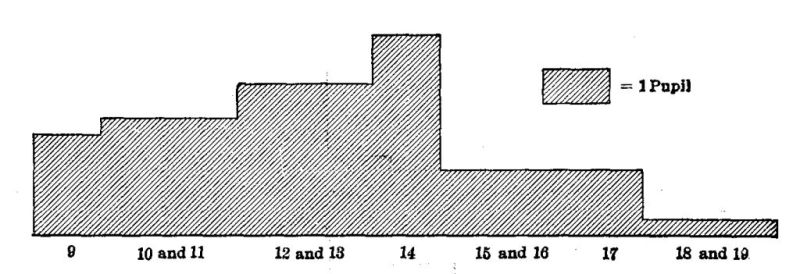
Fig. 69.—A conservative estimate of the amount of variation to be expected within a single class of 32 pupils in grade 6, in the number of units done in Courtis Test 7 when all chance variations are eliminated.
The variations within a class in respect to what processes are understood so as to be done with only occasional errors may be illustrated further as follows:—A teacher in grade 4 at or near the middle of the year in a city doing the customary work in arithmetic will probably find some pupil in her class who cannot do column addition even without carrying, or the easiest written subtraction
| ( | 8 | 9 | 78 | ), | |
| 5 | 3 | or | 37 |
who does not know his multiplication tables or how to derive them, or understand the meanings of + − × and ÷, or have any useful ideas whatever about division.
There will probably be some child in the class who can do such work as that shown below, and with very few errors.[Pg 293]
Add
| 3⁄8 + 5⁄8 + 7⁄8 + 1⁄8 | 2½ 63⁄8 3¾ |
1⁄6 + 3⁄8 |
Subtract
| 10.00 3.49 | 4 yd. 1 ft. 6 in. 2 yd. 2 ft. 3 in. |
Multiply
| 1¼ × 8 | 16 25⁄8 | 145 206 |
| —— | —— |
Divide
2 ) 13.50 25 ) 9750
The invention of means of teaching thirty so different children at once with the maximum help and minimum hindrance from their different capacities and acquisitions is one of the great opportunities for applied science.
Courtis, emphasizing the social demand for a certain moderate arithmetical attainment in the case of nearly all elementary school children of, say, grade 6, has urged that definite special means be taken to bring the deficient children up to certain standards, without causing undesirable 'overlearning' by the more gifted children. Certain experimental work to this end has been carried out by him and others, but probably much more must be done before an authoritative program for securing certain minimum standards for all or nearly all pupils can be arranged.
The differences found among children of the same grade in the same city are due in large measure to inborn differences in their original natures. If, by a miracle, the children studied by Courtis, or by Woody, or by Kruse had all re[Pg 294]ceived exactly the same nurture from birth to date, they would still have varied greatly in arithmetical ability, perhaps almost as much as they now do vary.
The evidence for this is the general evidence that variation in original nature is responsible for much of the eventual variation found in intellectual and moral traits, plus certain special evidence in the case of arithmetical abilities themselves.
Thorndike found ['05] that in tests with addition and multiplication twins were very much more alike than siblings[24] two or three years apart in age, though the resemblance in home and school training in arithmetic should be nearly as great for the latter as for the former. Also the young twins (9-11) showed as close a resemblance in addition and multiplication as the older twins (12-15), although the similarities of training in arithmetic have had twice as long to operate in the latter case.
If the differences found, say among children in grade 6 in addition, were due to differences in the quantity and quality of training in addition which they have had, then by giving each of them 200 minutes of additional identical training the differences should be reduced. For the 200 minutes of identical training is a step toward equalizing training. It has been found in many investigations of the matter that when we make training in arithmetic more nearly equal for any group the variation within the group is not reduced.
On the contrary, equalizing training seems rather to increase differences. The superior individual seems to have attained his superiority by his own superiority of nature rather than by superior past training, for, during a period of equal training for all, he increases his lead. For example, compare the gains of different individuals due to [Pg 295] about 300 minutes of practice in mental multiplication of a three-place number by a three-place number shown in Table 14 below, from data obtained by the author ['08].[25]
TABLE 14
The Effect of Equal Amounts of Practice upon Individual Difference in the Multiplication Of Three-Place Numbers
| Amount | Percentage of Correct Figures | |||
|---|---|---|---|---|
| Initial Score | Gain | Initial Score | Gain | |
| Initially highest five individuals | 85 | 61 | 70 | 18 |
| next five " | 56 | 51 | 68 | 10 |
| next six " | 46 | 22 | 74 | 8 |
| next six " | 38 | 8 | 58 | 12 |
| next six " | 29 | 24 | 56 | 14 |
Achievement in arithmetic depends upon a number of different abilities. For example, accuracy in copying numbers depends upon eyesight, ability to perceive visual details, and short-term memory for these. Long column addition depends chiefly upon great strength of the addition combinations especially in higher decades, 'carrying,' and keeping one's place in the column. The solution of problems framed in words requires understanding of language, the analysis of the situation described into its elements, the selection of the right elements for use at each step and their use in the right relations.
Since the abilities which together constitute arithmetic ability are thus specialized, the individual who is the best of a thousand of his age or grade in respect to, say, adding integers, may occupy different stations, perhaps from 1st to 600th, in multiplying with integers, placing the decimal point in division with decimals, solving novel problems, copying figures, etc., etc. Such specialization is in part due to his having had, relatively to the others in the thousand, more or better training in certain of these abilities than in others, and to various circumstances of life which have caused him to have, relatively to the others in the thousand, greater interest in certain of these achievements than in others. The specialization is not wholly due thereto, however. Certain inborn characteristics of an individual predispose him to different degrees of superiority or inferiority to other men in different features of arithmetic.
We measure the extent to which ability of one sort goes with or fails to go with ability of some other sort by the coefficient of correlation between the two. If every individual keeps the same rank in the second ability—if the individual who is the best of the thousand in one is the best of the group in the other, and so on down the list—the correlation is 1.00. In proportion as the ranks of individuals vary in the two abilities the coefficient drops from 1.00, a coefficient of 0 meaning that the best individual in ability A is no more likely to be in first place in ability B than to be in any other rank.
The meanings of coefficients of correlation of .90, .70, .50, and 0 are shown by Tables 15, 16, 17 and 18.[26]
TABLE 15
Distribution of Arrays in Successive Tenths of the Group When r = .90
| 10TH | 9TH | 8TH | 7TH | 6TH | 5TH | 4TH | 3D | 2D | 1ST | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1st tenth | .1 | .4 | 1.8 | 6.6 | 22.4 | 68.7 | ||||
| 2d tenth | .1 | .4 | 1.4 | 4.7 | 11.5 | 23.5 | 36.0 | 22.4 | ||
| 3d tenth | .1 | .5 | 2.1 | 5.8 | 12.8 | 21.1 | 27.4 | 23.5 | 6.6 | |
| 4th tenth | .4 | 2.1 | 6.4 | 12.8 | 20.1 | 23.8 | 21.2 | 11.5 | 1.8 | |
| 5th tenth | .1 | 1.4 | 5.8 | 12.8 | 19.3 | 22.6 | 20.1 | 12.8 | 4.7 | .4 |
| 6th tenth | .4 | 4.7 | 12.8 | 20.1 | 22.6 | 19.3 | 12.8 | 5.8 | 1.4 | .1 |
| 7th tenth | 1.8 | 11.5 | 21.2 | 23.8 | 20.1 | 12.8 | 6.4 | 2.1 | .4 | |
| 8th tenth | 6.6 | 23.5 | 27.4 | 21.1 | 12.8 | 5.8 | 2.1 | .5 | .1 | |
| 9th tenth | 22.4 | 36.0 | 23.5 | 11.5 | 4.7 | 1.4 | .4 | .1 | ||
| 10th tenth | 68.7 | 22.4 | 6.6 | 1.8 | .4 | .1 |
TABLE 16
Distribution of Arrays in Successive Tenths of the Group When r = .70
| 10TH | 9TH | 8TH | 7TH | 6TH | 5TH | 4TH | 3D | 2D | 1ST | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1st tenth | .2 | .7 | 1.5 | 2.8 | 4.8 | 8.0 | 13.0 | 22.3 | 46.7 | |
| 2d tenth | .2 | 1.2 | 2.6 | 4.5 | 7.0 | 9.8 | 13.4 | 17.3 | 21.7 | 22.3 |
| 3d tenth | .7 | 2.6 | 5.0 | 7.3 | 10.0 | 12.5 | 14.9 | 16.7 | 17.3 | 13.0 |
| 4th tenth | 1.5 | 4.5 | 7.3 | 9.8 | 12.0 | 13.7 | 14.8 | 14.9 | 13.4 | 8.0 |
| 5th tenth | 2.8 | 7.0 | 10.0 | 12.0 | 13.4 | 14.0 | 13.7 | 12.5 | 9.8 | 4.8 |
| 6th tenth | 4.8 | 9.8 | 12.5 | 13.7 | 14.0 | 13.4 | 12.0 | 10.0 | 7.0 | 2.8 |
| 7th tenth | 8.0 | 13.4 | 14.9 | 14.8 | 13.7 | 12.0 | 9.8 | 7.3 | 4.5 | 1.5 |
| 8th tenth | 13.0 | 17.3 | 16.7 | 14.9 | 12.5 | 10.0 | 7.3 | 5.0 | 2.6 | .7 |
| 9th tenth | 22.3 | 21.7 | 17.3 | 13.4 | 9.8 | 7.0 | 4.5 | 2.6 | 1.2 | .2 |
| 10th tenth | 46.7 | 22.3 | 13.0 | 8.0 | 4.8 | 2.8 | 1.5 | .7 | .2 |
TABLE 17
Distribution of Arrays of Successive Tenths of the Group When r = .50
| 10TH | 9TH | 8TH | 7TH | 6TH | 5TH | 4TH | 3D | 2D | 1ST | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1st tenth | .8 | 2.0 | 3.2 | 4.6 | 6.2 | 8.1 | 10.5 | 13.9 | 18.0 | 31.8 |
| 2d tenth | 2.0 | 4.1 | 5.7 | 7.3 | 8.8 | 10.5 | 12.2 | 14.1 | 16.4 | 18.9 |
| 3d tenth | 3.2 | 5.7 | 7.4 | 8.9 | 10.0 | 11.2 | 12.3 | 13.3 | 14.1 | 13.9 |
| 4th tenth | 4.6 | 7.3 | 8.8 | 9.9 | 10.8 | 11.6 | 12.0 | 12.3 | 12.2 | 10.5 |
| 5th tenth | 6.2 | 8.8 | 10.0 | 10.8 | 11.3 | 11.5 | 11.6 | 11.2 | 10.5 | 8.1 |
| 6th tenth | 8.1 | 10.5 | 11.2 | 11.6 | 11.5 | 11.3 | 10.8 | 10.0 | 8.8 | 6.2 |
| 7th tenth | 10.5 | 12.2 | 12.3 | 12.0 | 11.6 | 10.8 | 9.9 | 8.8 | 7.5 | 4.6 |
| 8th tenth | 13.9 | 14.1 | 13.3 | 12.3 | 11.2 | 10.0 | 8.8 | 7.4 | 5.7 | 3.2 |
| 9th tenth | 18.9 | 16.4 | 14.1 | 12.2 | 10.5 | 8.8 | 7.3 | 5.7 | 4.1 | 2.0 |
| 10th tenth | 31.8 | 18.9 | 13.9 | 10.5 | 8.1 | 6.2 | 4.6 | 3.2 | 2.0 | .8 |
TABLE 18
Distribution of Arrays, in Successive Tenths of the Group When r = .0
| 10TH | 9TH | 8TH | 7TH | 6TH | 5TH | 4TH | 3D | 2D | 1ST | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1st tenth | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 2d tenth | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 3d tenth | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 4th tenth | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 5th tenth | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 6th tenth | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 7th tenth | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 8th tenth | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 9th tenth | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 10th tenth | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
The significance of any coefficient of correlation depends upon the group of individuals for which it is determined. A correlation of .40 between computation and problem-solving [Pg 299] in eighth-grade pupils of 14 years would mean a much closer real relation than a correlation of .40 in all 14-year-olds, and a very, very much closer relation than a correlation of .40 for all children 8 to 15.
Unless the individuals concerned are very elaborately tested on several days, the correlations obtained are "attenuated" toward 0 by the "accidental" errors in the original measurements. This effect was not known until 1904; consequently the correlations in the earlier studies of arithmetic are all too low.
In general, the correlation between ability in any one important feature of computation and ability in any other important feature of computation is high. If we make enough tests to measure each individual exactly in:—
(A) Subtraction with integers and decimals,
(B) Multiplication with integers and decimals,
(C) Division with integers and decimals,
(D) Multiplication and division with common fractions, and
(E) Computing with percents,
we shall probably find the intercorrelations for a thousand 14-year-olds to be near .90. Addition of integers (F) will, however, correlate less closely with any of the above, being apparently dependent on simpler and more isolated abilities.
The correlation between problem-solving (G) and computation will be very much less, probably not over .60.
It should be noted that even when the correlation is as high as .90, there will be some individuals very high in one ability and very low in the other. Such disparities are to some extent, as Courtis ['13, pp. 67-75] and Cobb ['17] have argued, due to inborn characteristics of the individual in question which predispose him to very special sorts of [Pg 300] strength and weakness. They are often due, however, to defects in his learning whereby he has acquired more ability than he needs in one line of work or has failed to acquire some needed ability which was well within his capacity.
In general, all correlations between an individual's divergence from the common type or average of his age for one arithmetical function, and his divergences from the average for any other arithmetical function, are positive. The correlation due to original capacity more than counterbalances the effects that robbing Peter to pay Paul may have.
Speed and accuracy are thus positively correlated. The individuals who do the most work in ten minutes will be above the average in a test of accuracy. The common notion that speed is opposed to accuracy is correct when it means that the same person will tend to make more errors if he works at too rapid a rate; but it is entirely wrong when it means that the kind of person who works more rapidly than the average person is likely to be less accurate than the average person.
Interest in arithmetic and ability at arithmetic are probably correlated positively in the sense that the pupil who has more interest than other pupils of his age tends in the long run to have more ability than they. They are certainly correlated in the sense that the pupil who 'likes' arithmetic better than geography or history tends to have relatively more ability in arithmetic, or, in other words, that the pupil who is more gifted at arithmetic than at drawing or English tends also to like it better than he likes these. These correlations are high.
It is correct then to think of mathematical ability as, in a sense, a unitary ability of which any one individual may have much or little, most individuals possessing a moderate [Pg 301] amount of it. This is consistent, however, with the occasional appearance of individuals possessed of very great talents for this or that particular feature of mathematical ability and equally notable deficiencies in other features.
Finally it may be noted that ability in arithmetic, though occasionally found in men otherwise very stupid, is usually associated with superior intelligence in dealing with ideas and symbols of all sorts, and is one of the best early indications thereof.
[1] The following and later problems are taken from actual textbooks or courses of study or state examinations; to avoid invidious comparisons, they are not exact quotations, but are equivalents in principle and form, as stated in the preface.
[2] The work of Mitchell has not been published, but the author has had the privilege of examining it.
[3] The form of Test 6 quoted here is that given by Courtis ['11-'12, p. 20]. This differs a little from the other series of Test 6, shown on pages 43 and 44.
[4] Eight or ten times in all, not eight or ten times for each fact of the tables.
[5] The facts concerning the present inaccuracy of school work in arithmetic will be found on pages 102 to 105.
[6] McLellan and Ames, Public School Arithmetic [1900].
[7] These concern allowances for two errors occurring in the same example and for the same wrong answer being obtained in both original work and check work.
[8] The very early learning of 2 × 2, 2 × 3, 3 × 2, 2 × 4, 4 × 2, 3 × 3, and perhaps a few more multiplications is not considered here. It is advisable. The treatment of 0 × 0, 0 × 1, 1 × 0, etc., is not considered here. It is probably best to defer the '× 0' bonds until after all the others are formed and are being used in short multiplication, and to form them in close connection with their use in short multiplication. The '0 ×' bonds may well be deferred until they are needed in 'long' multiplication, 0 × 0 coming last of all.
[9] See page 76.
[10] At the end of a volume or part, the count may be from as few as 5 or as many as 12 pages.
[11] Certain paragraphs in this and the following chapter are taken from the author's Educational Psychology, with slight modifications.
[12] It should be noted that just as concretes give rise to abstractions, so these in turn give rise to still more abstract abstractions. Thus fourness, fiveness, twentyness, and the like give rise to 'integral-number-ness.' Similarly just as individuals are grouped into general classes, so classes are grouped into still more general classes. Half, quarter, sixth, and tenth are general notions, but 'one ...th' is more general; and 'fraction' is still more general.
[13] They may, of course, also result in a fusion or an alternation of responses, but only rarely.
[14] The more gifted children may be put to work using the principle after the first minute or two.
[15] If desired this form may be used, with the appropriate difference in the form of the questions and statements.
| 232 30 000 696 6960 |
[16] Courtis finds in the case of addition that "of all the individuals making mistakes at any given time in a class, at least one third, and usually two thirds, will be making mistakes in carrying or copying."
[17] Facts concerning the conditions of learning in general will be found in the author's Educational Psychology, Vol. 2, Chapter 8, or in the Educational Psychology, Briefer Course, Chapter 15.
[18] See Thorndike ['00], King ['07], and Heck ['13].
[19] A special type could be constructed that would use a large type body, say 14 point, with integers in 10 or 12 point and fractions much larger than now.
[20] It will be still better if the 4 is replaced by an open-top 4.
[21] For an account in English of their main findings see Howell ['14], pp. 149-251.
[22] In his How We Think.
[23] Compiled from data on p. 89 of Kruse ['18].
[24] Siblings is used for children of the same parents.
[25] Similar results have been obtained in the case of arithmetical and other abilities by Thorndike ['08, '10, '15, '16], Whitley ['11], Starch ['11], Wells ['12], Kirby ['13], Donovan and Thorndike ['13], Hahn and Thorndike ['14], and on a very large scale by Race in a study as yet unpublished.
[26] Unless he has a thorough understanding of the underlying theory, the student should be very cautious in making inferences from coefficients of correlation.
| Ames, A. F., and McLellan, J. F. | '00 | Public School Arithmetic. |
| Ballou, F. W. | '16 | Determining the Achievements of Pupils in the Addition of Fractions. School Document No. 3, 1916, Boston Public Schools. |
| Brandell, G. | '13 | Skolbarns intressen. Translated ['15] by W. Stern as, Das Interesse der Schulkinder an den Unterrichtsfächern. |
| Brandford, B. | '08 | A Study of Mathematical Education. |
| Brown, J. C. | '11, '12 | An Investigation on the Value of Drill Work in the Fundamental Operations in Arithmetic. Journal of Educational Psychology, vol. 2, pp. 81-88, vol. 3, pp. 485-492 and 561-570. |
| Brown, J. C. and Coffman, L. D. | '14 | How to Teach Arithmetic. |
| Burgerstein, L. | '91 | Die Arbeitscurve einer Schulstunde. Zeitschrift für Schulgesundheitspflege, vol. 4, pp. 543-562 and 607-627.[Pg 303] |
| Burnett, C. J. | '06 | The Estimation of Number. Harvard Psychological Studies, vol. 2, pp. 349-404. |
| Burt, C. | '17 | The Distribution and Relations of Educational Abilities. Report of The London County Council, No. 1868. |
| Chapman, J. C. | '14 | Individual Differences in Ability and Improvement and Their Correlations. Teachers College Contributions to Education, No. 63. |
| Chapman, J. C. | '17 | The Scientific Measurement of Classroom Products. (With G. P. Rush.) |
| Cobb, M. V. | '17 | A Preliminary Study of the Inheritance of Arithmetical Abilities. Jour. of Educational Psychology, vol. 8, pp. 1-20. Jan., 1917. |
| Coffman, L. D., and Brown, J. C. | '14 | How to Teach Arithmetic. |
| Coffman, L. D., and Jessup, W. A. | '16 | The Supervision of Arithmetic. |
| Courtis, S. A. | '09, '10, '11 | Measurement of Growth and Efficiency in Arithmetic. Elementary School Teacher, vol. 10, pp. 58-74 and 177-199, vol. 11, pp. 171-185, 360-370, and 528-539. |
| Courtis, S. A. | '11, '12 | Report on Educational Aspects of the Public School System of the City of New York. Part II, Subdivision 1, Section D. Report on the Courtis Tests in Arithmetic. |
| Courtis, S. A. | '13 | Courtis Standard Tests. Second Annual Accounting. |
| Courtis, S. A. | '14 | Manual of Instructions for Giving and Scoring the Courtis Standard [Pg 304]Tests in the Three R's. Department of Comparative Research, 82 Elliot St., Detroit, Mich., 1914. |
| Decroly, M., and Degand, J. | '12 | L'evolution des notions de quantités continues et discontinues chez l'enfant. Archives de psychologie, vol. 12, pp. 81-121. |
| Degand, J. See Decroly. | ||
| De Voss, J. C. See Monroe, De Voss, and Kelly. | ||
| Dewey, J. | '10 | How We Think. |
| Dewey, J., and McLellan, J. A. | '95 | Psychology of Number and Its Applications to Methods of Teaching Arithmetic. |
| Donovan, M. E., and Thorndike, E. L. | '13 | Improvement in a Practice Experiment under School Conditions. American Journal of Psychology, vol. 24, pp. 426-428. |
| Elliott, C. H. | '14 | Variation in the Achievements of Pupils. Teachers College, Columbia University, Contributions to Education, No. 72. |
| Flynn, F. J. | '12 | Mathematical Games—Adaptations from Games Old and New. Teachers College Record, vol. 13, pp. 399-412. |
| Freeman, F. N. | '10 | Untersuchungen über den Aufmerksamkeitsumfang und die Zahlauffassung. Pädagogische-Psychologische Arbeiten, I, 88-168. |
| Friedrich, J. | '97 | Untersuchungen über die Einflüsse der Arbeitsdauer und die Arbeitspausen auf die geistige Leistungsfähigkeit der Schulkinder. Zeitschrift für Psychologie, vol. 13, pp. 1-53. |
| Gilbert, J. A. | '94 | Researches on the Mental and[Pg 305] Physical Development of School Children. Studies from the Yale Psychological Laboratory, vol. 2, pp. 40-100. |
| Greenleaf, B. | '73 | Practical Arithmetic. |
| Hahn, H. H., and Thorndike, E. L. | '14 | Some Results of Practice in Addition under School Conditions. Journal of Educational Psychology, vol. 5, No. 2, pp. 65-84. |
| Hall, G. S. | '83 | The Contents of Children's Minds on Entering School. Princeton Review, vol. II, pp. 249-272, May, 1883. Reprinted in Aspects of Child Life and Education, 1907. |
| Hartmann, B. | '90 | Die Analyze des Kindlichen Gedanken-Kreises als die Naturgemässedes Ersten Schulunterrichts, 1890. |
| Heck, W. H. | '13 | A Study of Mental Fatigue. |
| Heck, W. H. | '13 | A Second Study in Mental Fatigue in the Daily School Program. Psychological Clinic, vol. 7, pp. 29-34. |
| Hoffmann, P. | '11 | Das Interesse der Schüler an den Unterrichtsfächern. Zeitschrift für pädagogische Psychologie, XII, 458-470. |
| Hoke, K. J., and Wilson, G. M. | '20 | How to Measure. |
| Holmes, M. E. | '95 | The Fatigue of a School Hour. Pedagogical Seminary, vol. 3, pp. 213-234. |
| Howell, H. B. | '14 | A Foundation Study in the Pedagogy of Arithmetic. |
| Hunt, C. W. | '12 | Play and Recreation in Arithmetic. Teachers College Record, vol. 13, pp. 388-398.[Pg 306] |
| Jessup, W. A., and Coffman, L. D. | '16 | The Supervision of Arithmetic. |
| Kelly, F. J. See Monroe, De Voss and Kelly. | ||
| King, A. C. | '07 | The Daily Program in Elementary Schools. MSS. |
| Kirby, T. J. | '13 | Practice in the Case of School Children. Teachers College Contributions to Education, No. 58. |
| Klapper, P. | '16 | The Teaching of Arithmetic. |
| Kruse, P. J. | '18 | The Overlapping of Attainments in Certain Sixth, Seventh, and Eighth Grades. Teachers College, Columbia University, Contributions to Education, No. 92. |
| Laser, H. | '94 | Ueber geistige Ermüdung beim Schulunterricht. Zeitschrift für Schulgesundheitspflege, vol. 7, pp. 2-22. |
| Lay, W. A. | '98 | Führer durch den ersten Rechenunterricht. |
| Lay, W. A. | '07 | Führer durch den Rechenunterricht der Unterstufe. |
| Lewis, E. O. | '13 | Popular and Unpopular School-Subjects. The Journal of Experimental Pedagogy, vol. 2, pp. 89-98. |
| Lobsien, M. | '03 | Kinderideale. Zeitschrift für pädagogische Psychologie, V, 323-344 and 457-494. |
| Lobsien, M. | '09 | Beliebtheit und Unbeliebtheit der Unterrichtsfächer. Pädagogisches Magazin, Heft 361. |
| McCall, W. A. | '21 | How to Measure in Education. |
| McDougle, E. C. | '14 | A Contribution to the Pedagogy of Arithmetic. Pedagogical Seminary, vol. 21, pp. 161-218.[Pg 307] |
| McKnight, J.A. | '07 | Differentiation of the Curriculum in the Upper Grammar Grades. MSS. in the library of Teachers College, Columbia University. |
| McLellan, J.A., and Dewey, J. | '95 | Psychology of Number and Its Applications to Methods of Teaching. |
| McLellan, J.A., and Ames, A.F. | '00 | Public School Arithmetic. |
| Messenger, J.F. | '03 | The Perception of Number. Psychological Review, Monograph Supplement No. 22. |
| Meumann, E. | '07 | Vorlesungen zur Einführung in die experimentelle Pädagogik. |
| Mitchell, H.E. | '20 | Unpublished studies of the uses of arithmetic in factories, shops, farms, and the like. |
| Monroe, W.S., De Voss, J.C., and Kelly, F.J. | '17 | Educational Tests and Measurements. |
| Nanu, H.A. | '04 | Zur Psychologie der Zahl Auffassung. |
| National Intelligence Tests | '20 | Scale A, Form 1, Edition 1. |
| Phillips, D.E. | '97 | Number and Its Application Psychologically Considered. Pedagogical Seminary, vol. 5, pp. 221-281. |
| Pommer, O. | '14 | Die Erforschung der Beliebtheit der Unterrichtsfächer. Ihre psychologischen Grundlagen und ihre pädagog. Bedeutung. VII. Jahresber. des k.k. Ssaatsgymn. im XVIII Bez. v. Wien. |
| Rice, J.M. | '02 | Test in Arithmetic. Forum, vol. 34, pp. 281-297. |
| Rice, J.M. | '03 | Causes of Success and Failure in Arithmetic. Forum, vol. 34, pp. 437-452. |
| Rush, G.P. | '17 | The Scientific Measurement of Classroom Products. (With J. C. Chapman.)[Pg 308] |
| Seekel, E. | '14 | Ueber die Beziehung zwischen der Beliebtheit und der Schwierigkeit der Schulfächer. Ergebnisse einer Erhebung. Zeitschrift für Angewandte Psychologie 9. S. 268-277. |
| Selkin, F. B. | '12 | Number Games Bordering on Arithmetic and Algebra. Teachers College Record, vol. 13, pp. 452-493. |
| Smith, D. E. | '01 | The Teaching of Elementary Mathematics. |
| Smith, D. E. | '11 | The Teaching of Arithmetic. |
| Speer, W. W. | '97 | Arithmetic: Elementary for Pupils. |
| Starch, D. | '11 | Transfer of Training in Arithmetical Operations. Journal of Educational Psychology, vol. 2, pp. 306-310. |
| Starch, D. | '16 | Educational Measurements. |
| Stern, W. | '05 | Ueber Beliebtheit und Unbeliebtheit der Schulfächer. Zeitschrift für pädagogische Psychologie, VII, 267-296. |
| Stern, C., and Stern, W. | '13 | Beliebtheit und Schwierigkeit der Schulfächer. (Freie Schulgemeinde Wickersdorf.) Auf Grund der von Herrn Luserke beschafften Materialien bearbeitet. In: "Die Ausstellung zur vergleichenden Jungendkunde der Geschlechter in Breslau." Arbeit 7 des Bundes für Schulreform. S. 24-26. |
| Stern, W. | '14 | Zur vergleichenden Jugendkunde der Geschlechter. Vortrag. III. Deutsch. Kongr. f. Jugendkunde [Pg 309]usw. Arbeiten 8 des Bundes für Schulreform. S. 17-38. |
| Stone, C.W. | '08 | Arithmetical Abilities and Some Factors Determining Them. Teachers College Contributions to Education, No. 19. |
| Suzzallo, H. | '11 | The Teaching of Primary Arithmetic. |
| Thorndike, E.L. | '00 | Mental Fatigue. Psychological Review, vol. 7, pp. 466-482 and 547-579. |
| Thorndike, E.L. | '08 | The Effect of Practice in the Case of a Purely Intellectual Function. American Journal of Psychology, vol. 10, pp. 374-384. |
| Thorndike, E.L. | '10 | Practice in the case of Addition. American Journal of Psychology, vol. 21, pp. 483-486. |
| Thorndike, E.L., and Donovan, M.E. | '13 | Improvement in a Practice Experiment under School Conditions. American Journal of Psychology, vol. 24, pp. 426-428. |
| Thorndike, E.L., and Donovan, M.E., and Hahn, H.H. | '14 | Some Results of Practice in Addition under School Conditions. Journal of Educational Psychology, vol. 5, No. 2, pp. 65-84. |
| Thorndike, E.L. | '15 | The Relation between Initial Ability and Improvement in a Substitution Test. School and Society, vol. 12, p. 429. |
| Thorndike, E.L. | '16 | Notes on Practice, Improvability and the Curve of Work. American Journal of Psychology, vol 27, pp. 550-565. |
| Walsh, J.H. | '06 | Grammar School Arithmetic. |
| Wells, F.L. | '12 | The Relation of Practice to Individual Differences. [Pg 310]American Journal of Psychology, vol. 23, pp. 75-88. |
| White, E. E. | '83 | A New Elementary Arithmetic. |
| Whitley, M. T. | '11 | An Empirical Study of Certain Tests for Individual Differences. Archives of Psychology, No. 19. |
| Wiederkehr, G. | '07 | Statistiche Untersuchungen über die Art und den Grad des Interesses bei Kindern der Volksschule. Neue Bahnen, vol. 19, pp. 241-251, 289-299. |
| Wilson, G. M. | '19 | A Survey of the Social and Business Usage of Arithmetic. Teachers College Contributions to Education, No. 100. |
| Wilson, G. M., and Hoke, K. J. | '20 | How to Measure. |
| Woody, C. | '10 | Measurements of Some Achievements in Arithmetic. Teachers College Contributions to Education, No. 80. |
Abilities, arithmetical, nature of, 1 ff.;
measurement of, 27 ff.;
constitution of, 51 ff.;
organization of, 137 ff.
Abstract numbers, 85 ff.
Abstraction, 169 ff.
Accuracy, in relation to speed, 31;
in fundamental operations, 102 ff.
Addition, measurement of, 27 ff., 34;
constitution of, 52 f.;
habit in relation to, 71 f.;
in the higher decades, 75 f.;
accuracy in, 108 f.;
amount of practice in, 122 ff.;
interest in 196 f.
Aims of the teaching of arithmetic, 23 f.
Ames, A. F., 89
Analysis, learning by, 169 ff.;
systematic and opportunistic stimuli to, 178 f.;
gradual progress in, 180 ff.
Area, 257 f., 275
Arithmetic, sociology of, 24 ff.
Arithmetical abilities. See Abilities.
Arithmetical language, 8 f., 19, 89 ff., 94 ff.
Arithmetical learning, before school, 199 ff.;
conditions of, 227 ff.;
in relation to time of day, 227 ff.;
in relation to time devoted to arithmetic, 228 ff.
Arithmetical reasoning. See Reasoning.
Arithmetical terms, 8, 19
Averages, 40 f.; 135 f.
Ballou, F. W., 34, 38
Banking, 256 f.
Binet, A., 201
Bonds, selection of, 70 ff.;
strength of, 102 ff.;
for temporary service, 111 ff.;
order of formation of, 141 ff.
See also Habits.
Brandell, G., 211
Brandford, B., 198 f.
Brown, J. C., xvi, 103
Burgerstein, L., 103
Burnett, C. J., 202
Burt, C., 286
Cardinal and ordinal numbers confused, 206
Catch problems, 21 ff.
Chapman, J. C., 49
Class, size of, in relation to arithmetical learning, 228;
variation within a, 289 ff.
Cobb, M. V., 299
Coffman, L. D., xvi
Collection meaning of numbers, 3 ff.
Computation, measurements of, 33 ff.;
explanations of the processes in, 60 ff.;
accuracy in, 102 ff.
See also Addition, Subtraction, Multiplication, Division, Fractions, Decimal numbers, Percents.
Concomitants, law of varying, 172 ff.;
law of contrasting, 173 ff.
Concrete numbers, 85 ff.
Concrete objects, use of, 253 ff.
Conditions of arithmetical learning, 227 ff.
Constitution of arithmetical abilities, 51 ff.
Copying of numbers, eyestrain due to, 212 f.
Correlations of arithmetical abilities, 295 ff.
Courses of study, 232 f.
Courtis, S. A., 28 ff., 43 ff., 49, 103, 291, 293, 299
Crutches, 112 f.
Culture-epoch theory, 198 f.
Dairy records, 273
Decimal numbers, uses of, 24 f.;
measurement of ability with, 36 ff.;
learning, 181 ff.;
division by, 270 f.
De Croly, M., 205
Deductive reasoning, 60 ff., 185 ff.
Degand, J., 205
Denominate numbers, 141 f., 147 f.
Described problems, 10 ff.
Development of knowledge of number, 205 ff.
[Pg 312]
De Voss, J. C., 49
Dewey, J., 3, 83, 150, 205, 207, 208, 219, 266, 277
Differences in arithmetical ability, 285 ff.;
within a class, 289 ff.
Difficulty as a stimulus, 277 ff.
Drill, 102 ff.
Discipline, mental, 20
Distribution of practice, 156 ff.
Division, measurement of, 35 f., 37;
constitution of, 57 ff.;
deductive explanations of, 63, 64 f.;
inductive explanations of, 63 f., 65 f.;
habit in relation to, 72;
with remainders, 76;
with fractions, 78 ff.;
amount of practice in, 122 ff.;
distribution of practice in, 167;
use of the problem attitude in teaching, 270 f.
Donovan, M. E., 295
Elements, responses to, 169 ff.
Eleven, multiples of, 85
Elliott, C. H., 228
Equation form, importance of, 77 f.
Explanations of the processes of computation, 60 ff.;
memory of, 115 f.;
time for giving, 154 ff.
Eyestrain in arithmetical work, 212 ff.
Facilitation, 143 ff.
Figures, printing of, 235 ff.;
writing of, 214 f., 241
Flynn, F. J., 196
Fractions, uses of, 24 f.;
measurement of ability with, 36 ff.;
knowledge of the meaning of, 54 ff.
Freeman, F. N., 259, 261
Friedrich, J., 103
Generalization, 169 ff.
Gilbert, J. A., 203
Graded tests, 28 ff., 36 ff.
Greatest common divisor, 88 f.
Habits, importance of, in arithmetical learning, 70 ff.;
now neglected, 75 ff.;
harmful or wasteful, 83 ff.; 91 ff.;
propædeutic, 117 ff.;
organization of, 137 ff.;
arrangement of, 141 ff.
Hahn, H. H., 295
Hall, G. S., 200 f.
Hartmann, B., 200 f.
Heck, W. H., 227
Heredity in arithmetical abilities, 293 ff.
Highest common factor, 88 f.
Hoke, K. J., 49
Holmes, M. E., 103
Howell, H. B., 259
Hunt, C. W., 196
Hygiene of arithmetic, 212 ff., 234 ff.
Individual differences, 285 ff.
Inductive reasoning, 60 ff., 169 ff.
Insurance, 256
Interest as a principle determining the order of topics, 150 ff.
Interests, instinctive 195 ff.;
censuses of, 209 ff.;
neglect of childish, 226 ff.;
in self-management, 223 f.;
intrinsic, 224 ff.
Interference, 143 ff.
Inventories of arithmetical knowledge and skill, 199 ff.
Jessup, W. A., xvi
Kelly, F. J., 49
King, A. C., 103, 227
Kirby, T. J., 76 f., 104, 295
Klapper, P., xvi
Kruse, P. J., 289, 293
Ladder tests, 28 ff., 36 ff.
Language in arithmetic, 8 f., 19, 89 ff., 94 ff.
Laser, H., 103
Lay, W. A., 259, 261
Learning, nature of arithmetical, 1 ff.
Least common multiple, 88 f.
Lewis, E. O., 210 f.
Lobsien, M., 209 f.
McCall, W. A., 49
McDougle, E. C., 85 ff.
McKnight, J. A., 210
McLellan, J. A., 3, 83, 89, 205, 207
Manipulation of numbers, 60 ff.
Meaning, of numbers, 2 ff., 171;
of a fraction, 54 ff.;
of decimals, 181 f.
Measurement of arithmetical abilities, 27 ff.
Mental arithmetic, 262 ff.
Messenger, J. F., 202
Metric system, 147
Meumann, E., 261
Mitchell, H. E., 24
[Pg 313]
Monroe, W. S., 49
Multiplication, measurement of, 35, 36;
constitution of, 51;
deductive explanations of, 61;
inductive explanations of, 61 f.;
with fractions, 78 ff.;
by eleven, 85;
amount of practice in, 122 ff.;
order of learning the elementary facts of, 144 f.;
distribution of practice in, 158 ff.;
use of the problem attitude in teaching, 267 ff.
Nanu, H. A., 202
National Intelligence Tests, 49 f.
Negative reaction in intellectual life, 278 f.
Number pictures, 259 ff.
Numbers, meaning of, 2;
as measures of continuous quantities, 75;
abstract and concrete, 85 ff.;
denominate, 141 f., 147 f.;
use of large, 145 f.;
perception of, 205 ff.;
early awareness of, 205 ff.;
confusion of cardinal and ordinal, 206.
See also Decimal numbers and Fractions.
Objective aids, used for verification, 154;
in general, 243 ff.
Oral arithmetic, 262 ff.
Order of topics, 141 ff.
Ordinal numbers, confused with cardinal, 206
Original tendencies and arithmetic, 195 ff.
Overlearning, 134 ff.
Percents, 80 f.
Perception of number, 202 ff.
Phillips, D. E., 3, 4, 205, 207
Pictures, hygiene of, 246 ff.;
number, 259 ff.
Pommer, O., 212
Practice, amount of, 122 ff.;
distribution of, 156 ff.
Precision in fundamental operations, 102 ff.
Problem attitude, 266 ff.
Problems, 9 ff.;
"catch," 21 ff.;
measurement of ability with, 42 ff.;
whose answer must be known in order to frame them, 93 f.;
verbal form of, 111 f.;
interest in, 220 ff.;
as introductions to arithmetical learning, 266 ff.
Propædeutic bonds, 117 ff.
Purposive thinking, 193 ff.
Quantity, number and, 85 ff.;
perception of, 202 ff.
Race, H., 295
Rainfall, 272
Ratio, 225 f.;
meaning of numbers, 3 ff.
Reaction, negative, 278 f.
Reality, in problems, 9 ff.
Reasoning, arithmetical, nature of, 19 ff.;
measurement of ability in, 42 ff.;
derivation of tables by, 58 f.;
about the rationale of computations, 60 ff.;
habit in relation to, 73 f., 190 ff.;
problems which provoke false, 100 f.;
the essentials of arithmetical, 185 ff.;
selection in, 187 ff.;
as the coöperation of organized habits, 190 ff.
Recapitulation theory, 198 f.
Recipes, 273 f.
Rectangle, area of, 257 f.
Rice, J. M., 228 ff.
Rush, G. P., 49
Seekel, E., 212
Selkin, F. B., 196 f.
Sequence of topics, 141 ff.
Series meaning of numbers, 2 ff.
Size of class in relation to arithmetical learning, 228
Smith, D. E., xvi, 224
Social instincts, use of, 195 f.
Sociology of arithmetic, 24 ff.
Speed in relation to accuracy, 31, 108
Speer, W. W., 3, 5, 83
Spiral order, 141, 145
Starch, D., 49, 295
Stern, W., 210, 212
Stone, C. W., 27 ff., 42 ff., 228 ff.
Subtraction, measurement of, 34 f.;
constitution of, 57 f.;
amount of practice in, 122 ff.
Supervision, 233 f.
Suzzallo, H., xvi
Temporary bonds, 111 ff.
Terms, 113 f.
Tests of arithmetical abilities, 27 ff.
Thorndike, E. L., 34, 38 ff., 227, 294
Time, devoted to arithmetic, 228 ff.;
of day, in relation to arithmetical learning, 227 f.
[Pg 314]
Type, hygiene of, 235 ff.
Underlearning, 134 ff.
United States money, 148 ff.
Units of measure, arbitrary, 5, 83 f.
Variation, among individuals, 285 ff.
Variety, in teaching, 153
Verification, 81 f.;
aided by greater strength of the fundamental bonds, 107 ff.
Walsh, J. H., 11
Wells, F. L., 295
White, E. E., 5
Whitley, M. T., 295
Wiederkehr, G., 212
Wilson, G. M., 24, 49
Woody, C., 29 ff., 52, 287, 293
Words. See Language and Terms.
Written arithmetic, 262 ff.
Zero in multiplication, 179 f.
TRANSCRIBER'S NOTE: Obvious errors in spelling and punctuation have been silently closed. Images have been moved from the middle of a paragraph to the closest paragraph break. Footnotes have been consolidated at the end of the HTML ebook.
End of the Project Gutenberg EBook of The Psychology of Arithmetic, by
Edward L. Thorndike
*** END OF THIS PROJECT GUTENBERG EBOOK THE PSYCHOLOGY OF ARITHMETIC ***
***** This file should be named 39300-h.htm or 39300-h.zip *****
This and all associated files of various formats will be found in:
http://www.gutenberg.org/3/9/3/0/39300/
Produced by Jonathan Ingram and the Online Distributed
Proofreading Team at http://www.pgdp.net
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
http://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org/license
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need, are critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at http://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
http://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at http://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit http://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including checks, online payments and credit card donations.
To donate, please visit: http://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart is the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
http://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.