image
(399 kB).VOL. I.
The Project Gutenberg EBook of Modern Machine-Shop Practice, Vol. I (of 2), by Joshua Rose This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Modern Machine-Shop Practice, Volumes I and II Author: Joshua Rose Release Date: March 21, 2012 [EBook #39225] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK MODERN MACHINE-SHOP PRACTICE, VOL 1 *** Produced by Ben Beasley, Harry Lamé and the Online Distributed Proofreading Team at http://www.pgdp.net
Please see Transcriber’s Notes at the end of this document.
| Large image (399 kB).VOL. I. |
MODERN MACHINE‑SHOP PRACTICE. | FRONTISPIECE |
 |
||
| Copyright, 1887 by Charles Scribner’s Sons. | ||
| MODERN AMERICAN FREIGHT LOCOMOTIVE. | ||
BY
JOSHUA ROSE, M.E.
ILLUSTRATED WITH MORE THAN 3000 ENGRAVINGS
VOLUME I.
NEW YORK
CHARLES SCRIBNER’S SONS
1887
Copyright, 1887, by
CHARLES SCRIBNER’S SONS
Press of J. J. Little & Co.
Astor Place, New York.
Modern Machine-Shop Practice is presented to American mechanics as a complete guide to the operations of the best equipped and best managed workshops, and to the care and management of engines and boilers.
The materials have been gathered in part from the author’s experience of thirty-one years as a practical mechanic; and in part from the many skilled workmen and eminent mechanics and engineers who have generously aided in its preparation. Grateful acknowledgment is here made to all who have contributed information about improved machines and details of new methods.
The object of the work is practical instruction, and it has been written throughout from the point of view, not of theory, but of approved practice. The language is that of the workshop. The mathematical problems and tables are in simple arithmetical terms, and involve no algebra or higher mathematics. The method of treatment is strictly progressive, following the successive steps necessary to becoming an intelligent and skilled mechanic.
The work is designed to form a complete manual of reference for all who handle tools or operate machinery of any kind, and treats exhaustively of the following general topics: I. The construction and use of machinery for making machines and tools; II. The construction and use of work-holding appliances and tools used in machines for working metal or wood; III. The construction and use of hand tools for working metal or wood; IV. The construction and management of steam engines and boilers. The reader is referred to the Table of Contents for a view of the multitude of special topics considered.
The work will also be found to give numerous details of practice never before in print, and known hitherto only to their originators, and aims to be useful as well to master-workmen as to apprentices, and to owners and managers of manufacturing establishments equally with their employees, whether machinists, draughtsmen, wood-workers, engineers, or operators of special machines.
The illustrations, over three thousand in number, are taken from modern practice; they represent the machines, tools, appliances and methods now used in the leading manufactories of the world, and the typical steam engines and boilers of American manufacture.
The new Pronouncing and Defining Dictionary at the end of the work, aims to include all the technical words and phrases of the machine shop, both those of recent origin and many old terms that have never before appeared in a vocabulary of this kind.
The wide range of subjects treated, their convenient arrangement and thorough illustration, with the exhaustive Table of Contents of each volume and the full Analytical Index to both, will, the author hopes, make the work serve as a fairly complete ready reference library and manual of self-instruction for all practical mechanics, and will lighten, while making more profitable, the labor of his fellow-workmen.
| CHAPTER I. | |||
| THE TEETH OF GEAR-WHEELS. | |||
| PAGE | |||
| Gear-Wheels. Spur-wheels, bevel-wheels, mitre-wheels, crown-wheels, annular or internal wheels | 1 | ||
| Trundle-wheels, rack and pinion-wheel and tangent screw, or worm and worm-wheel | 1 | ||
| The diameter of the pitch circle of | 1 | ||
| Gear-Wheel Teeth. The face, the flank, the depth or height | 1 | ||
| The space, the pitch line, the point, the arc pitch, the chord pitch, the line of centres | 2 | ||
| Rules for finding the chord pitch from the arc pitch; table of natural sines; diametral pitch; finding the arc from the diametral pitch; table of arc and diametral pitches | 3 | ||
| Gear-Wheels. The driver and follower, a train of gears | 3 | ||
| Intermediate gears | 3 | ||
| The velocity of compounded wheels | 4 | ||
| Finding the diameters of the pitch circles of | 4 | ||
| Considered as revolving levers | 5 | ||
| Calculating the revolutions of, and power transmitted by | 5 | ||
| The angular velocity of | 6 | ||
| Gear-Wheels. Hunting tooth in, stop motion of | 7 | ||
| Gear-Wheel Teeth. The requirements and nature of the teeth curves | 7 | ||
| Cycloidal curves for the faces of; epicycloidal and involute curves; the hypocycloidal curve; method of forming or generating the epicycloidal and hypocycloidal curves for the faces and flanks of gear teeth | 8 | ||
| Applications of the epicycloidal and hypocycloidal curves in the formation of gear teeth | 9 | ||
| The diameter of the circle for generating the epicycloidal and hypocycloidal curves; graphical demonstration that the flank curves are correctly formed to work with the face curves of the other wheel | 10 | ||
| Graphical demonstration that the curves are correct independent of either the respective sizes of the wheels, or of the curve generating circles | 11 | ||
| Gear-Wheels. Hand applications of the rolling or generating circle to mark the tooth curves for a pair of wheels | 12 | ||
| Gear-Wheel Teeth. The variation of curve due to different diameters of wheels or of rolling circles | 12 | ||
| Tracing the path of contact of tooth upon tooth in a pair of gear-wheels; definition of the “arc of approach;” definition of the “arc of recess;” demonstration that the flanks of the teeth on the driver or driving-wheel have contact with the faces of the driven wheel during the arc of approach, and with the flanks of the driven wheel during the arc of recess | 13 | ||
| Confining the action of the teeth to one side only of the line of centres, when motion rather than power is to be conveyed | 13 | ||
| Demonstration that the appearance or symmetry of a tooth has no significance with regard to its action | 14 | ||
| Finding how many teeth will be in constant action, the diameter of the wheels, the pitch of the teeth, and the diameter of the rolling circle being given | 15 | ||
| Example of the variation of tooth form due to variation of wheel diameter | 15 | ||
| Gear Teeth. Variation of shape from using different diameters of rolling circles | 16 | ||
| Thrust on the wheel shafts caused by different shapes of teeth | 16 | ||
| Gear-Wheels. Willis’ system of one size of rolling circle for trains of interchangeable gearing | 16 | ||
| Conditions necessary to obtain a uniform velocity of | 16 | ||
| Gear Teeth. The amount of rolling and of sliding motion of | 16 | ||
| The path of the point of contact of | 16 | ||
| The arcs of approaching and of receding contact | 16 | ||
| Lengths of the arcs of approach and of recess | 16 | ||
| The influence of the sizes of the wheels upon the arcs of contact | 17 | ||
| Influence of the size of the rolling circle upon the amount of flank contact | 18 | ||
| Demonstration that incorrectly formed teeth cannot correct themselves by wear | 18 | ||
| The smaller the diameter of the rolling circle, the less the sliding motion | 18 | ||
| Influence of the size of the rolling upon the number of teeth in contact in a given pair of wheels | 19 | ||
| Demonstration that the degrees of angle the teeth move through exceed those of the path of contact, unless the tooth faces meet in a point | 19 | ||
| Influence of the height of the teeth upon the number of teeth in contact | 20 | ||
| Increasing the arc of recess without increasing the arc of approach | 20 | ||
| Wheels for transmitting motion rather than power | 21 | ||
| Clock wheels | 21 | ||
| Forms of teeth having generating or rolling circles, as large or nearly as large as the diameters of the wheels | 21 | ||
| Gear-Wheels. Bevel | 21 | ||
| The principles governing the formation of the teeth of bevel- wheels | 22 | ||
| Demonstration that the faces of the wheels must be in line with the point of intersection of the axis of the two shafts | 22 | ||
| Gear Teeth. Method of finding the curves of, for bevel gear | 22 | ||
| Gear-Wheels. Internal or annular | 23 to 27 | ||
| Demonstration that the teeth of annular wheels correspond to the spaces of spur-wheels | 23 | ||
| Gear-Wheels Internal. Increase in the length of the path of contact on spur-wheels of the same diameter, and having the same diameter of generating or rolling circle | 23 | ||
| Demonstration that the teeth of internal wheels may interfere when spur-wheels would not do so | 23 | ||
| Methods of avoiding the above interference | 23 | ||
| Comparison of, with spur-wheels | 23 | ||
| The teeth of: demonstration that it is practicable to so form the teeth faces that they will have contact together as well as with the flanks of the other wheel | 24 | ||
| Intermediate rolling circle for accomplishing the above result | 24 | ||
| The application of two rolling circles for accomplishing the above result | 24 | ||
| Demonstration that the result reached by the employment of two rolling circles of proper diameter is theoretically and practically perfect | 24 | ||
| Limits of the diameters of the two rolling circles | 25 | ||
| Increase in the arc of contact obtained by using two rolling circles | 25 | ||
| Demonstration that the above increase is on the arc of recess or receding contact, and therefore gives a smooth action | 25 | ||
| Demonstration that by using two rolling circles each tooth has for a certain period two points of contact | 25 | ||
| The laws governing the diameters of the two rolling circles | 25 | ||
| Practical application of two rolling circles | 26 | ||
| Demonstration that by using two rolling circles the pinion may contain but one tooth less than the wheel | 26 | ||
| The sliding and rolling motion of the teeth of | 27 | ||
| CHAPTER II. | |||
| THE TEETH OF GEAR-WHEELS (Continued). | |||
| Worm and Worm-Wheel, or wheel and tangent screw | 28 to 31 | ||
| General description of | 28 | ||
| Qualifications of | 28 | ||
| The wear of | 28 | ||
| Worm-Wheel Teeth, the sliding motion of | 28 | ||
| When straight have contact on the centres only of the tooth sides | 28 | ||
| That envelop a part of the worm circumference | 28 | ||
| The location of the pitch line of the worm | 28 | ||
| [I-viii] | The proper number of teeth in the worm-wheel | 29 | |
| Locating the pitch line of the worm so as to insure durability | 29 | ||
| Rule for finding the best location for the pitch line of the worm | 29 | ||
| Increasing the face of the worm to obtain a smoother action | 29 | ||
| Worms, to work with a square thread | 29 | ||
| Worm-Wheels, applications of | 30 | ||
| Gear-Wheels with involute teeth | 31 to 34 | ||
| Gear Teeth. Generating the involute curve | 31 | ||
| Templates for marking the involute curve | 32 | ||
| Involute Teeth, the advantages of | 34 | ||
| Gear Teeth, Pratt and Whitney’s machine for cutting templates for | 35 | ||
| CHAPTER III. | |||
| THE TEETH OF GEAR-WHEELS (Continued). | |||
| Gear Teeth, revolving cutters for | 37 | ||
| Pantagraph engine for dressing the cutters for | 38 | ||
| Numbers of cutters used for a train of wheels | 39 | ||
| Gear-Wheel Teeth. Table of equidistant value of cutters | 41 | ||
| Depth of, in the Brown and Sharpe system | 42 | ||
| Cutting the teeth of worm-wheels | 42 | ||
| Finding the angle of the cutter for cutting worm-wheels | 43 | ||
| The construction of templates for rolling the tooth curves | 43 | ||
| Rolling the curves for gear teeth | 43 | ||
| Forms of templates for gear teeth | 44 | ||
| Pivoted arms for tooth templates | 44 | ||
| Marking the curves by hand | 45 | ||
| Former or Template of the Corliss bevel gear-wheel engine or cutting machine | 45 | ||
| The use of extra circles in marking the curves with compasses | 46 | ||
| Finding the face curves by geometrical constructions | 47 | ||
| The Willis odontograph for finding the radius for striking the curves by hand | 47 | ||
| The method of using the Willis odontograph | 48 | ||
| Professor Robinson’s odontograph | 49 | ||
| Method of using Professor Robinson’s odontograph | 49 | ||
| Application of Professor Robinson’s odontograph for trains of gearing | 51 | ||
| Tabular values and setting numbers for Professor Robinson’s odontograph | 51 | ||
| Walker’s patent wheel scale for marking the curves of cast teeth | 51 | ||
| The amount of side clearance in cast teeth | 53 | ||
| Filleting the roots of epicycloidal teeth with radial flanks | 53 | ||
| Scale of tooth proportions given by Professor Willis | 54 | ||
| The construction of a pattern for a spur-wheel that is to be cast with the teeth on | 54 | ||
| Template for planing the tooth to shape | 54 | ||
| Method of marking the curves on teeth that are to be glued on | 55 | ||
| Method of getting out the teeth of | 56 | ||
| Spacing the teeth on the wheel rim | 56 | ||
| Methods of accurately spacing the pattern when it has an even number of teeth | 58 | ||
| Method of spacing the wheel rim when it has an odd number of teeth | 58 | ||
| Gear-Wheels, Bevel Pinion, drawings for | 59 | ||
| Getting out the body for a bevel-wheel | 59 | ||
| Template for marking the division lines on the face of the wheel | 59 | ||
| Marking the lines of the division on the wheel | 60 | ||
| Gear-Wheels, Pinion, with dovetail teeth | 60 | ||
| Testing the angle of bevel-wheels while in the lathe | 60 | ||
| Gear-Wheels, Skew Bevel. Finding the line of contact | 61 | ||
| Marking the inclination of the teeth | 61 | ||
| Gear-Wheels, Bevel, drawing for built up | 61 | ||
| Gear-Wheels, Worm, or endless screw | 62 | ||
| Constructing a pattern from which the worm is to be cast | 62 | ||
| Tools for cutting the worm in a lathe | 62 | ||
| Cutting the teeth by hand | 62 | ||
| Gear-Wheels, Mortise or cogged | 63 | ||
| Methods of fastening cogs | 63 | ||
| Methods of getting out cogs for | 63 | ||
| Gear-Wheel Teeth, calculating the strength of epicycloidal | 64 | ||
| Factors of safety for | 64 | ||
| Tredgold’s rule for calculating the strength of | 65 | ||
| Cut, calculating the strength of | 65 | ||
| Gear-Wheel Teeth. The strength of cogs | 66 | ||
| The thickness of cogs | 66 | ||
| The durability of cogs | 66 | ||
| Table for calculating the strength of different kinds of | 67 | ||
| The contact of cast teeth | 67 | ||
| Table for determining the relation between pitch diameter, pitch, and number of teeth in gear-wheels | 68 | ||
| Examples of the use of the above table | 68 | ||
| With stepped teeth | 69 | ||
| Angular or helical teeth | 69 | ||
| End thrust of angular teeth | 69 | ||
| Herring-bone angular teeth | 69 | ||
| For transmitting motion at a right angle by means of angular or helical teeth | 69 | ||
| Cutting helical teeth in the lathe | 69 | ||
| For wheels whose shaft axes are neither parallel nor meeting | 70 | ||
| Elliptical | 70 | ||
| Elliptical, marking the pitch lines of | 70 | ||
| Elliptical, drawing the teeth curves of | 73 | ||
| For variable motion | 74 | ||
| Form of worm to give a period of rest | 74 | ||
| Various applications of | 74 | ||
| Gear-Wheels, arrangement of, for periodically reversing the direction of motion | 75 | ||
| Watt’s sun and planet motion | 75 | ||
| Arrangements for the rapid multiplication of motion | 75 | ||
| Arrangement of, for the steering gear of steam fire-engines | 75 | ||
| Various forms of mangle gearing | 79 | ||
| Gear-Wheel and Rack, for reciprocating motion | 77 | ||
| Friction Wheels. | 77 | ||
| The material for | 77 | ||
| Paper | 78 | ||
| For the feed motion of machines | 78 | ||
| The unequal wear upon grooved | 79 | ||
| Form of, for relieving the journals of strain | 79 | ||
| Cams, for irregular motion | 80 | ||
| Finding the pitch line of | 80 | ||
| Finding the working face of | 80 | ||
| The effect the diameter roller has upon the motion produced by a cam | 80 | ||
| Demonstration of the different motion produced by different diameters of rollers upon the same cam | 80 | ||
| Diagram of motion produced from the same cam with different diameters of rollers | 81 | ||
| Return or backing | 82 | ||
| Methods of finding the shape of return or backing | 82 | ||
| Cam Motion, for an engine slide valve without steam lap | 83 | ||
| For a slide valve with steam lap | 83 | ||
| Groove Cams, proper construction of | 84 | ||
| The wear of | 84 | ||
| Brady’s improved groove cam with rolling motion and adjustment for wear | 84 | ||
| CHAPTER IV. | |||
| SCREW-THREADS. | |||
| Screw Threads, the various forms of | 85 | ||
| The pitch of | 85 | ||
| Self-locking | 85 | ||
| The Whitworth | 86 | ||
| The United States standard | 86 | ||
| The Common V | 86 | ||
| The requirements of | 86 | ||
| Tools for cutting | 87 | ||
| Variation of pitch from hardening | 87 | ||
| The wear of thread-cutting tools | 88 | ||
| Methods of producing | 88 | ||
| Alteration of shape of, from the wear of the tools they are cut by | 89 | ||
| Screw Thread Cutting Tools. The wear of the tap and the die | 89 | ||
| Improved form of chaser to equalize the wear | 90 | ||
| Form of, to eliminate the effects of the wear in altering the fit | 90 | ||
| Originating standard angles for | 91 | ||
| Standard micrometer gauge for the United States standard screw thread | 91 | ||
| Standard plug and collar gauges for | 91 | ||
| Producing gauges for | 92 | ||
| Table of United States standard for bolts and nuts | 93 | ||
| Table of standard for the V-thread | 93 | ||
| United States standard for gas and steam pipes | 93 | ||
| Taper for standard pipe threads | 95 | ||
| Tables of the pitches and diameters at root of thread, of the Whitworth thread | 95 | ||
| Table of Whitworth’s screw threads for gas, water, and hydraulic piping | 96 | ||
| Whitworth’s standard gauges for watch and instrument makers | 96 | ||
| Screw-cutting hand tools | 96 | ||
| Thread-Cutting Tools. American and English forms of stocks and dies | 97 | ||
| Adjustable or jamb dies | 98 | ||
| The friction of jamb dies | 98 | ||
| The sizes of hobs that should be used on jamb dies | 99 | ||
| Cutting right or left-hand thread with either single, double, or treble threads with the same dies | 99 | ||
| Hobs for hobbing or threading dies | 100 | ||
| [I-ix] | Various forms of stocks with dies adjustable to take up the wear | 101 | |
| Dies for gas and steam pipes | 101 | ||
| Thread-Cutting Tool Taps. The general forms of taps | 102 | ||
| Reducing the friction of | 102 | ||
| Giving clearance to | 102 | ||
| The friction of taper | 103 | ||
| Improved forms of | 103 | ||
| Professor J. E. Sweet’s form of tap | 104 | ||
| Adjustable standard | 104 | ||
| The various shapes of flutes employed on taps | 105 | ||
| The number of flutes a tap should have | 105 | ||
| Demonstration that a tap should have four cutting edges rather than three | 106 | ||
| The position of the square or driving end, with relation to the cutting edges | 106 | ||
| Taper taps for blacksmiths | 106 | ||
| Collapsing taps for use in tapping machines | 107 | ||
| Collapsing tap for use in a screw machine | 107 | ||
| The alteration of pitch that occurs in hardening | 108 | ||
| Gauging the pitch after the hardening | 108 | ||
| Correcting the errors of pitch caused by the hardening | 109 | ||
| For lead | 109 | ||
| Elliptical in cross section | 109 | ||
| For very straight holes | 109 | ||
| Tap wrenches solid and adjustable | 110 | ||
| Thread-Cutting. Tapping | 110 | ||
| Appliances for tapping standard work | 111 | ||
| CHAPTER V. | |||
| FASTENING DEVICES. | |||
| Bolts, classification of, from the shapes of their heads | 112 | ||
| Classification of, from the shapes of their bodies | 112 | ||
| Countersunk | 112 | ||
| Holes for, classification of | 112 | ||
| For foundations, various forms of | 113 | ||
| Hook bolts | 113 | ||
| The United States standard for finished bolts and nuts | 113 | ||
| The United States standard for rough bolts and nuts, or black bolts | 114 | ||
| The Whitworth standard for bolts and nuts | 114 | ||
| Screws | 114 | ||
| Studs | 115 | ||
| Set Screws | 115 | ||
| Bolts for quick removal | 116 | ||
| That do not pass through the work | 117 | ||
| That self-lock in grooves and are readily removable | 117 | ||
| Heads and their bedding | 117 | ||
| Nuts, the forms of, when they are to be steam tight | 118 | ||
| Various forms of | 118 | ||
| Jamb nuts and lock nuts | 119 | ||
| Differential Threads for locking purposes | 119 | ||
| For fine adjustments | 119 | ||
| Nuts, taking up the wear of | 120 | ||
| Securing devices | 120 | ||
| Securing by taper pins | 121 | ||
| Securing by cotters | 121 | ||
| Securing by notched plates | 121 | ||
| Pins. Securing for exact adjustments | 121 | ||
| And double eyes fitting | 121 | ||
| Fixed | 122 | ||
| Working | 122 | ||
| Bolts, removing corroded | 122 | ||
| Nuts, removing corroded | 122 | ||
| Washers, standard sizes of | 122 | ||
| Wrench, the proper angles of | 123 | ||
| Box | 124 | ||
| Monkey | 125 | ||
| Adjustable, various forms of | 125 | ||
| Sockets | 125 | ||
| Novel for carriage bolts | 125 | ||
| Pin | 126 | ||
| Improved form of | 126 | ||
| Keys, the various kinds of | 126 | ||
| The bearing surfaces of | 126 | ||
| Set Screws, application of, to hubs or bosses | 127 | ||
| Keys, with set-screws | 127 | ||
| The draught of | 127 | ||
| Feathers, and their applications | 127 | ||
| Keys, for parallel rods | 128 | ||
| Taper Pins, proper position of, for locking purposes | 128 | ||
| Improved method of fitting | 128 | ||
| CHAPTER VI. | |||
| THE LATHE. | |||
| Lathe, the importance and advantages of | 129 | ||
| Classification of lathes | 129 | ||
| Foot | 130 | ||
| Methods of designating the sizes of | 130 | ||
| Bench | 130 | ||
| Power | 130 | ||
| Hand | 130 | ||
| Slide Rest for | 131 | ||
| American form of, their advantages and disadvantages | 132 | ||
| English forms of | 132 | ||
| For spherical work | 132 | ||
| Methods of taking up lost motion of | 133 | ||
| Engine Lathe, general construction of | 133 | ||
| The construction of the shears of | 134 | ||
| Construction of the headstock | 134 | ||
| Construction of the bearings | 134 | ||
| Construction of the back gear | 135 | ||
| Means of giving motion to the feed spindle | 135 | ||
| Construction of the tailstock | 135 | ||
| Method of rapidly securing and releasing the tailstock | 136 | ||
| Lathe Tailstock, setting over for turning tapers | 136 | ||
| Engine Lathe, construction of carriage | 137 | ||
| Feed motion for carriage or saddle | 137 | ||
| Lathe Apron, Construction of the feed traverse | 138 | ||
| Construction of the cross-feed motion | 138 | ||
| Engine Lathe, lead screw and change wheels of | 139 | ||
| Feed spindle and lead screw bearings | 139 | ||
| Swing frame for lead screw | 139 | ||
| Lead screw nuts | 140 | ||
| With compound slide rest | 140 | ||
| Construction of compound slide rest | 141 | ||
| Advantages of compound slide rest | 141 | ||
| For taper turning | 142 | ||
| Taper-turning attachments | 142 | ||
| With compound duplex slide rest | 143 | ||
| Detachable slide rest | 143 | ||
| Three-tool slide rest for turning shafting | 143 | ||
| With flat saddle for chucking work on | 143 | ||
| The Sellers Lathe | 143 | ||
| Construction of the headstock and treble gear | 144 | ||
| Construction of the tailstock and method of keeping it in line | 145 | ||
| Construction of the carriage and slide rest | 145 | ||
| Methods of engaging and disengaging the feed motions | 146 | ||
| Car Axle Lathe, with central driving motion and two slide rests | 147 | ||
| The feed motions of | 148 | ||
| Self-Acting Lathe, English form of | 148 | ||
| Pattern Maker’s Lathe | 148 | ||
| Brake for cone pulley | 149 | ||
| With wooden bed | 149 | ||
| Slide rest for | 149 | ||
| Chucking Lathe, English | 149 | ||
| Feed motions of | 150 | ||
| Pulley Lathe | 150 | ||
| Gap or Break Lathe | 151 | ||
| Extension Lathe | 151 | ||
| Wheel Lathe | 151 | ||
| Chucking Lathe for boring purposes | 152 | ||
| Lathe for turning crank axles | 152 | ||
| Construction of the headstock | 153 | ||
| Construction of the feed motions | 154 | ||
| For turning crank, Arrangements of the slide rests | 154 | ||
| Application of the slide rest to a crank | 155 | ||
| CHAPTER VII. | |||
| DETAILS IN LATHE CONSTRUCTION. | |||
| Live Spindle of a lathe, the fit of | 157 | ||
| With coned journals | 157 | ||
| Methods of taking up the end motion of | 158 | ||
| Arranging the swing frame for the change gears | 158 | ||
| Taking up the wear of the back bearing | 158 | ||
| The wear of the front bearing of | 158 | ||
| The Taper for the live centre | 159 | ||
| Methods of removing the lathe centres | 159 | ||
| Tapers for the live centres | 159 | ||
| Methods of removing the dead centre | 159 | ||
| Driving Cone, arranging the steps of | 159 | ||
| Requirements of proportioning the steps of | 159 | ||
| Rules for proportioning the diameters of the steps of, when the two pulleys are exactly alike and are connected by an open belt | 159 to 161 | ||
| When the two pulleys are unlike | 161 to 164 | ||
| Back Gear, methods of throwing in and out | 165 | ||
| Conveying motion to the lead screw | 165 | ||
| Attaching the swing frame | 166 | ||
| Feed Gear. Arrangement for cutting worm threads or tangent screws | 167 | ||
| Feed Motion for reversing the direction of tool traverse in screw cutting | 168 | ||
| For lathe aprons | 168 | ||
| Slide Rest, weighted elevated | 168 | ||
| Double tool holder for | 169 | ||
| [I-x] | Gibbed elevating | 169 | |
| Examples of feed motions | 170 | ||
| Feed Regulators for screw cutting | 171 | ||
| The star feed | 172 | ||
| Ratchet Feeds | 173 | ||
| Tool Holding devices, the various kinds of | 173 | ||
| Tool Rest swiveling | 174 | ||
| Tool Holder for compound slide rests | 174 | ||
| For octagon boring tools | 175 | ||
| Lathe Lead and Feed Screws | 175 | ||
| Lead screws, supporting, long | 176 | ||
| Position of the feed nut | 177 | ||
| Form of threads of lead screws | 177 | ||
| The effect the form of thread has in causing the nut to lock properly or improperly | 177 | ||
| Example of a lead screw with a pitch of three threads per inch | 177 | ||
| Example of a lead screw with five threads per inch | 178 | ||
| Example with a lead screw of five threads per inch | 179 | ||
| Device for correcting the errors of pitch of | 179 | ||
| Table for finding the change wheels for screw cutting when the teeth in the change wheels advance by four | 180 | ||
| For finding the change wheels when the teeth in the wheels advance by six | 180 | ||
| Constructing a table to cut fractional threads on any lathe | 181 | ||
| Finding the change wheels necessary to enable the lathe to cut threads of any given pitches | 181 | ||
| Finding the change wheels necessary to cut fractional pitches | 181 | ||
| Determining the pitches of the teeth for change wheels | 182 | ||
| Lathe Shears or beds | 182 | ||
| Advantages and disadvantages of, with raised V-guide-ways | 182 | ||
| Examples of various forms of | 183 | ||
| Lathe Shears with one V and one flat side | 183 | ||
| Methods of ribbing | 184 | ||
| The arrangement of the legs of | 184 | ||
| Lathe Tailblock | 185 | ||
| With rapid spindle motion | 185 | ||
| With rapid fastenings and releasing devices | 185 | ||
| The wear of the spindles of | 185 | ||
| Spindles, the various methods of locking | 186 | ||
| Testing, various methods of | 187 | ||
| CHAPTER VIII. | |||
| SPECIAL FORMS OF THE LATHE. | |||
| Watchmaker’s Lathes | 188 | ||
| Construction of the headstock | 188 | ||
| Construction of chucks for | 188 | ||
| Expanding chucks for | 188 | ||
| Contracting chucks for | 188 | ||
| Construction of the tailblock | 189 | ||
| Open spindle tailstocks for | 189 | ||
| Filing fixture for | 189 | ||
| Fixture for wheel and pinion cutting | 189 | ||
| Jewelers’ rest for | 189 | ||
| Watch Manufacturers’ Lathe | 190 | ||
| Special chucks for | 190 | ||
| Pump centre rest | 190 | ||
| Lathe, hand | 191 | ||
| Screw slotting | 192 | ||
| With variable speed for facing purposes | 192 | ||
| Cutting-off machine | 193 | ||
| Grinding Lathes | 193 | ||
| With elevating rest | 194 | ||
| Universal | 195 | ||
| Special chucks for | 196 | ||
| The Morton Poole calender roll grinding lathe | 196 | ||
| The construction of the bed and carriages | 197 | ||
| Principles of action of the carriages | 197, 198 | ||
| Construction of the emery-wheel arbors and the driving motion | 198, 199 | ||
| The advantages of | 199 | ||
| The method of driving the roll | 200 | ||
| Construction of the headstock | 200 | ||
| The transverse motion | 200 | ||
| The Brown and Sharpe Screw Machine, or screw-making lathe | 200 | ||
| Threading tools for | 203 | ||
| Examples of the use of | 203 | ||
| The Secor Screw Machine, construction of the headstock | 204 | ||
| The chuck | 205 | ||
| The feed gear | 205 | ||
| The turret | 205 | ||
| The cross slide | 205 | ||
| The stop motions | 206 | ||
| Pratt and Whitney’s Screw Machine | 206 | ||
| Parkhurst’s wire feed, construction of the headstock, chuck and feed motion | 207 | ||
| Box tools for | 208 | ||
| Applications of box tools | 208 | ||
| Threading tool for | 208 | ||
| Cutting-off tool for | 208 | ||
| Special Lathe for wood working | 208 | ||
| The construction of the carriage and reducing knife | 209 | ||
| Construction of the various feed motions | 209 | ||
| Construction of the tailstock | 209 | ||
| Lathes for irregular forms | 210 | ||
| Axe-handle | 210 | ||
| Back knife gauge | 210 | ||
| Special, for pulley turning | 211 | ||
| Boring and Turning mill or lathe | 211 | ||
| Construction of the feed motions | 213 | ||
| Construction of the framing and means of grinding the lathe | 214 | ||
| Construction of the vertical feed motions | 215 | ||
| The Morton Poole roll turning lathe | 215 | ||
| Construction of the slide rest | 216 | ||
| The tools for | 216 | ||
| Special Lathes for brass work | 216, 217 | ||
| Boring Lathe with traversing spindle | 218 | ||
| For engine cylinders | 219 | ||
| Cylinder, with facing slide rests | 219 | ||
| With double heads and facing rests | 220 | ||
| Lathe for turning Wheel hubs | 221 | ||
| CHAPTER IX. | |||
| DRIVING WORK IN THE LATHE. | |||
| Drivers, carriers, dogs, or clamps, and their defects | 222 | ||
| Lathe clamps | 222 | ||
| Equalizing drivers | 223 | ||
| The Clements driver | 223 | ||
| Driver and face plate for screw cutting | 223 | ||
| Forms of, for bolt heads | 224 | ||
| Adjustable, for bolt heads | 224 | ||
| For threaded work | 225 | ||
| For steady rest work | 225 | ||
| For cored work | 225 | ||
| For wood | 225 | ||
| Centres for hollow work | 226 | ||
| For taper work | 226 | ||
| Lathe Mandrels, or arbors | 227 | ||
| Drivers for | 227 | ||
| For tubular work | 227 | ||
| Expanding mandrels | 227 | ||
| With expanding cones | 228 | ||
| With expanding pieces | 228 | ||
| Expanding, for large work | 228 | ||
| For threaded work | 228 | ||
| For nuts, various forms of | 229 | ||
| For eccentric work | 229 | ||
| Centring devices for crank axles | 230 | ||
| The Steady Rest or back rest | 231 | ||
| Steady rest, improved form of | 232 | ||
| Cone chuck | 232 | ||
| Steady rest for square and taper work | 233 | ||
| The cat head | 233 | ||
| Clamps for | 233 | ||
| Follower rests | 234 | ||
| Chucks and Chucking | 234 | ||
| Simple forms of chucks | 234 | ||
| Adjustable chucks for true work | 235 | ||
| Two-jawed chucks | 236 | ||
| Box body chucks | 237 | ||
| Reversible jawed chucks | 237 | ||
| Three and four-jawed chucks | 237 | ||
| Combination chucks | 237 | ||
| The wear of scroll chuck threads | 237 | ||
| Universal chucks | 238 | ||
| The wear of chucks | 240 | ||
| Special forms of chucks | 241 | ||
| Expanding chucks for ring-work | 241 | ||
| Cement chuck | 241 | ||
| Chucks for wood-working lathes | 242 | ||
| Lathe Face Plates | 243 | ||
| Face plates, errors in, and their effects | 243 | ||
| Work-holding straps | 244 | ||
| Face plate, clamping work on | 245 | ||
| Forms of clamps for | 245 | ||
| Examples of chucking work on | 246, 247 | ||
| For wood work | 247 | ||
| Special Lathe Chuck for cranks | 248 | ||
| Face Plate Work, examples of | 249 | ||
| Errors in chucking | 250 | ||
| Movable dogs for | 250 | ||
| The angle plate | 251 | ||
| Applications of | 251 | ||
| Angle plate chucking, examples of | 251 | ||
| Cross-head chucking | 251-253 | ||
| CHAPTER X.[I-xi] | |||
| CUTTING TOOLS FOR LATHES. | |||
| Principles governing the shapes of lathe tools | 254 | ||
| Diamond-pointed, or front tool | 254 | ||
| Principles governing use of tools | 254 | ||
| Front rake and clearance of front tools | 254 | ||
| Influence of the height of a tool upon its clearance and keenness | 255 | ||
| Tools with side rake in various directions | 256 | ||
| The effect of side rake | 256 | ||
| The angle of clearance in lathe tools | 257 | ||
| Variation of clearance from different rates of feed and diameters of work | 257 | ||
| Round-nosed tools | 258 | ||
| Utmost Duty of cutting tools | 258 | ||
| Judging the quantity of the tool from the shape of its cutting | 259 | ||
| Square-nosed tools | 260 | ||
| The height of lathe tools | 260 | ||
| Side tools for lathe work | 261 | ||
| Cutting-off or grooving tools | 262 | ||
| Facing tools or knife tools | 262 | ||
| Spring tools | 263 | ||
| Brass Work, front tools for | 264 | ||
| Side tools for | 264 | ||
| Threading tools | 264 | ||
| Internal threading tools | 264 | ||
| The length of threading tools | 265 | ||
| The level of threading tools | 265 | ||
| Gauges for threading tools | 266 | ||
| Setting threading tools | 266 | ||
| Circular threading tools | 267 | ||
| Threading tool holders | 267 | ||
| Chasers | 268 | ||
| Chaser holders | 268 | ||
| Setting chasers | 268 | ||
| Square Threads, clearance of tools for | 269 | ||
| Diameter at the roots of threads | 269 | ||
| Cutting coarse pitch square threads | 269 | ||
| Dies for finishing square threads | 269 | ||
| Tool Holders for outside work | 270 | ||
| For circular cutters | 272 | ||
| Swiveled | 273 | ||
| Combined tool holders and cutting-off tools | 273 | ||
| Power Required to drive cutting tools | 273 | ||
| CHAPTER XI. | |||
| DRILLING AND BORING IN THE LATHE. | |||
| The Twist Drill | 274 | ||
| Twist drill holders | 274 | ||
| The diametral clearance of twist drills | 274 | ||
| The front rake of twist drills | 275 | ||
| The variable clearance on twist drills as usually ground | 275 | ||
| Demonstration of the common error in grinding twist drills | 276 | ||
| The effects of improper grinding upon twist drills | 276 | ||
| Table of speeds and feeds for twist drills | 277 | ||
| Grinding twist drills by hand | 279 | ||
| Twist drills for wood work | 279 | ||
| Tailstock Chucks for drilled work | 279 | ||
| Flat Drills for lathe work | 280 | ||
| Holders for lathe work | 281 | ||
| Half-round bit or pod auger | 281 | ||
| With front rake for wrought iron or steel | 281 | ||
| With adjustable cutter | 281 | ||
| For very true work | 281 | ||
| Chucking Reamer | 281 | ||
| The number of teeth for reamers | 282 | ||
| Spacing the teeth of reamers | 282 | ||
| Spiral teeth for reamers | 282 | ||
| Grinding the teeth of reamers | 282 | ||
| Various positions of emery-wheel in grinding reamers | 282 | ||
| Chucking reamers for true work | 283 | ||
| Shell reamers | 283 | ||
| Arbor for shell reamers | 283 | ||
| Rose-bit or rose reamers | 283 | ||
| Shell rose reamers | 284 | ||
| Adjustable reamers | 284 | ||
| Stepped reamers for taper work | 285 | ||
| Half-round reamers | 285 | ||
| Reamers for rifle barrels | 285 | ||
| Boring Tools for lathe work | 285 | ||
| Countersinks | 285 | ||
| Shapes of lathe boring tools | 285 | ||
| Boring tools for brass work | 286 | ||
| The spring of boring tools | 286 | ||
| Boring tools for small work | 287 | ||
| Boring tool holders | 287 | ||
| Boring Devices for Lathes | 288 | ||
| Boring Heads | 288 | ||
| Boring Bars | 289 | ||
| Boring bar cutters | 289 | ||
| Three versus four cutters for boring bars | 290 | ||
| Boring bars with fixed heads | 290 | ||
| With sliding heads | 290 | ||
| Bar cutters, the shapes of | 291 | ||
| Boring head with nut feed | 291 | ||
| Boring bars for taper work, various forms of | 292 | ||
| Boring double-coned work | 293 | ||
| Boring bar, centres for | 293 | ||
| Cutting Speeds and feeds for wrought iron | 294 | ||
| Examples of speeds taken from practice | 295 | ||
| CHAPTER XII. | |||
| EXAMPLES IN LATHE WORK. | |||
| Technical Terms used in the work | 296 | ||
| Lathe Centres | 296 | ||
| Devices for truing | 297 | ||
| Tools for testing the truth of, for fine work | 298 | ||
| Shapes of, for light and heavy work | 299 | ||
| Centre Drilling, attachment for lathes | 300 | ||
| The error induced by straightening work after | 300 | ||
| Machine | 300 | ||
| Combined centre-drill and countersink | 300 | ||
| Countersink with adjustable drill | 300 | ||
| Centring square | 300 | ||
| Centre-punch | 300 | ||
| Centre-punch guide | 301 | ||
| Centring work with the scribing block | 301 | ||
| Finding the centre of very rough work | 301 | ||
| Centre-drill chuck | 302 | ||
| The proper form of countersink for lathe work | 302 | ||
| Countersinks for lathe work | 302 | ||
| Various forms of square centres | 303 | ||
| The advantage of the square centre for countersinking | 303 | ||
| Novel form of countersink for hardened work | 303 | ||
| Chucks for centre-drilling and countersinking | 303 | ||
| Recentring turned work | 304 | ||
| Straightening Work. Straightening machine for bar iron | 304 | ||
| Hand device for straightening lathe work | 305 | ||
| Chuck for straightening wire | 305 | ||
| Cutting Rods into small pieces of exact length, tools for | 305 | ||
| Roughing cuts, the change of shape of work that occurs from removing the surface by | 306 | ||
| Feeds for | 306 | ||
| Rates of feed for | 307 | ||
| Finishing Work, the position of the tool for | 307 | ||
| Finishing cast-iron with water | 307 | ||
| Specks in finished cast-iron work | 307 | ||
| Scrapers for finishing cast-iron work | 307 | ||
| Method of polishing lathe work | 308 | ||
| Filing lathe work | 308 | ||
| The use of emery paper on lathe work | 308 | ||
| The direction of tool feed in finishing long work | 309 | ||
| Forms of laps for finishing gauges or other cylindrical lathe work | 310 | ||
| Forms of laps for finishing internal work | 311 | ||
| Grinding and polishing clamps for lathe work | 311 | ||
| Burnishing lathe work | 311 | ||
| Taper Work, turning | 312 | ||
| The wear of the centres of | 312 | ||
| Setting over the tailstock to turn | 312 | ||
| Gauge for setting over | 313 | ||
| Fitting | 313 | ||
| Grinding | 313 | ||
| The order of procedure in turning | 313 | ||
| The influence of the height of the tool in producing true | 314 | ||
| Special Forms. Curved work | 314, 315 | ||
| Standard gauges for taper work | 316 | ||
| Methods of turning an eccentric | 317 | ||
| Turning a cylinder cover | 318 | ||
| Turning pulleys | 318 | ||
| Chucking device for pulleys | 318 | ||
| Cutting Screws in the lathe | 319 | ||
| The arrangement of the change gears | 319 | ||
| The intermediate wheels | 319 | ||
| The compounded gears | 320 | ||
| Finding the change wheels to cut a given thread | 320 | ||
| Finding the change wheels for a lathe whose gears are compounded | 321 | ||
| Finding the change gears for cutting fractional pitches | 321 | ||
| To find what pitch of thread the wheels already on the lathe will cut | 322 | ||
| Cutting left-hand threads | 322 | ||
| Cutting double threads | 322 | ||
| Cutting screws whose pitches are given in the terms of the metric system | 322 | ||
| Cutting threads on taper work | 323 | ||
| Errors in cutting threads on taper work | 324 | ||
| CHAPTER XIII.[I-xii] | |||
| EXAMPLES IN LATHE WORK (Continued). | |||
| Ball Turning with tubular saw | 325 | ||
| With a single tooth on the end of a revolving tube | 325 | ||
| With a removable tool on an arbor | 325 | ||
| Tool holder with worm feed | 325 | ||
| By hand | 325 | ||
| Cams, cutting in the lathe | 326 | ||
| Improved method of originating cams in the lathe | 326 | ||
| Motions for turning cams in the lathe | 326, 327 | ||
| Application of cam motions to special work | 327 | ||
| Cam chuck for irregular work | 328 | ||
| Milling or knurling tool | 328 | ||
| Improved forms of | 328 | ||
| Winding Spiral Springs in the lathe | 329 | ||
| Hand Turning | 330 | ||
| The heel tool | 330 | ||
| The graver and its applications | 330, 331 | ||
| Hand side tools | 331 | ||
| Hand round-nosed tools for iron | 331 | ||
| Hand finishing tool | 331 | ||
| Hand Tools, for roughing out brass work | 332 | ||
| Various forms and applications of scrapers | 332, 333 | ||
| Clockmakers’ hand tool for special or standard work | 334 | ||
| Screw cutting with hand tools | 334 | ||
| Outside and inside chasers | 334 | ||
| Hobs and their uses | 335 | ||
| The application of chasers, and errors that may arise from the position in which they are presented to the work | 336 | ||
| Errors commonly made in cutting up inside chasers | 337 | ||
| V-tool for starting outside threads | 337 | ||
| Starting outside threads | 338 | ||
| Cutting taper threads | 338 | ||
| Wood turning hand tools | 338 | ||
| The gauge and how to use it | 338 | ||
| The chisel and its use | 339 | ||
| The skew chisel and how to use it | 339 | ||
| Wood turners’ boring tools for lathe work | 340 | ||
| CHAPTER XIV. | |||
| MEASURING MACHINES, TOOLS AND DEVICES. | |||
| Standards of Measurements, in various countries | 341 | ||
| Use of, by sight and by the sense of feeling | 341 | ||
| Variations in standard gauges | 341 | ||
| The necessity for accurate standards | 341 | ||
| The Rogers Bond standard measuring machine | 342 | ||
| Details of construction of | 343, 344 | ||
| The principle of construction of | 344 | ||
| The methods of using | 345 | ||
| The Whitworth measuring machine | 345 | ||
| The Betts Machine Company’s measuring machine | 346 | ||
| Professor Sweet’s measuring machine | 347 | ||
| Measuring machine for sheet metal | 348 | ||
| Circle, division of the | 348 | ||
| Troughton’s method of dividing the circle | 348, 349 | ||
| Ramsden’s dividing engine | 349 | ||
| The construction of | 350, 351 | ||
| Pratt and Whitney’s dividing device | 352 | ||
| Practical application of | 353 | ||
| Index wheel, method of originating, by R. Hoe & Co. | 353 | ||
| Application of the index wheel (Hoe & Co.’s system) | 353 | ||
| Classification of the measuring tools used by workmen | 354 | ||
| Micrometer Caliper and its principle of construction | 354, 355 | ||
| Gauges. Standard plug and collar gauges | 356 | ||
| Methods of comparing standard plug and collar gauges | 356 | ||
| The effects of variations of temperature upon standard gauges | 356 | ||
| Plug and collar gauges for taper work | 357 | ||
| The Baldwin standards for taper bolts | 359 | ||
| Workmen’s gauges for lathe work | 359 | ||
| Calipers, outside, the various forms of | 360 | ||
| Inside calipers | 360 | ||
| Calipers with locking devices | 360 | ||
| Spring calipers | 360 | ||
| The methods of holding and using | 361, 362 | ||
| Keyway calipers | 363 | ||
| The advantages of calipers | 363 | ||
| Fitting. The four kinds of fit in machine work | 363 | ||
| The influence of the diameter of the work in limiting the application of standard gauges | 363 | ||
| The wear of tools and its influence upon the application of the standard gauge system | 364 | ||
| The influence of the smoothness of the surface upon the allowance to be made for drilling or hydraulic fits | 365 | ||
| Examples of allowance for hydraulic fits | 365 | ||
| Parallel holes and taper plugs for hydraulic fits | 365 | ||
| Fitting. Practicable methods of testing the fit of axle brasses forced in by hydraulic pressure | 366 | ||
| Shrinkage or contraction fits | 366 | ||
| Allowances for | 366 | ||
| Gauge for | 367 | ||
| The shrinkage system at the Royal Gun Factory at Woolwich | 367 | ||
| Experiments by Thomas Wrightson upon the shrinkage of iron under repeated heatings and coolings | 368 to 374 | ||
| Shrinking work, to refit it | 374, 375 | ||
| CHAPTER XV. | |||
| MEASURING TOOLS. | |||
| End Measurements of large lathe work | 376 | ||
| Template gauges for | 376 | ||
| Trammels or Trains | 377 | ||
| Adjustable gauges for | 377 | ||
| Compasses—Dividers | 377 | ||
| Compass calipers | 378 | ||
| Key Seating rule | 378 | ||
| Surface Gauge | 378 | ||
| Pattern makers’ pipe gauge | 379 | ||
| Squares. The try square | 379 | ||
| The T square | 379 | ||
| Various methods of testing squares | 379, 380 | ||
| Bevel squares | 380 | ||
| Bevel Protractors | 380 | ||
| Hexagon Gauge | 381 | ||
| Straight Edge and its applications | 381, 382 | ||
| Winding strips and their application | 382 | ||
| Surface Plate or planimeter | 383 | ||
| Templates for curves | 384 | ||
| Wire Gauges, notch | 384 | ||
| Standard gauges for wire, &c. | 384, 386 | ||
| Gauge for music wire | 386 | ||
| Brown and Sharpe wire gauge | 387 | ||
| Birmingham wire gauge for rolled shell silver and gold | 387 | ||
| Sheet iron gauge, Russian | 387 | ||
| Galvanized iron | 387 | ||
| Belgian sheet zinc | 387 | ||
| American sheet zinc | 387 | ||
| Rifle Bore gauge | 387 | ||
| Strength of Wire, Kirkaldy’s experiments | 387, 388 | ||
| CHAPTER XVI. | |||
| SHAPING AND PLANING MACHINES. | |||
| General description of a shaping machine | 389 | ||
| Construction of swivel head | 389 | ||
| Slide | 390 | ||
| Vice chuck | 390 | ||
| Feed motion | 390 | ||
| Hand shaping machine | 392 | ||
| Quick Return Motion, Whitworth’s | 392 | ||
| Vice Chucks, the principles of construction of plain, for planing machine | 392 | ||
| The proper methods of chucking work in | 393 | ||
| Holding taper work in | 394 | ||
| Various forms of | 394 | ||
| Swiveling | 395 | ||
| Rapid motion | 396 | ||
| For vice work | 396 | ||
| Centres for shaping machines | 397 | ||
| Traveling Head in shaping machine | 397 | ||
| Planer Shapers or shaping machines, having a tappet motion for reversing the direction of motion | 398, 399 | ||
| Quick Return Motion shaping machines, link | 399 | ||
| The Whitworth | 400 | ||
| Comparisons of the link motion and Whitworth | 401 | ||
| Simple Crank, investigating the motion of | 401 | ||
| Planing Machines, or planer | 402 | ||
| The various motions of | 402, 403 | ||
| The table driving gear | 404 | ||
| Planing machine with double heads | 404 | ||
| Rotary planing machine | 405 | ||
| CHAPTER XVII. | |||
| PLANING MACHINERY. | |||
| The Sellers planing machine | 406 | ||
| The belt shifting mechanism | 406, 407 | ||
| The automatic feed motions | 408 | ||
| Sliding Head | 408 | ||
| Cross Bar | 409 | ||
| Slides of Planers, the various forms of construction of | 410 | ||
| [I-xiii]Wear of the Slides of planer heads, various methods of taking up the | 410 | ||
| Swivel Heads | 411 | ||
| Tool Aprons | 411 | ||
| Swivel Tool-holding devices for planers | 411 | ||
| Planer Heads, graduations of | 412 | ||
| Safety devices for | 413 | ||
| Feed motions for | 414 | ||
| V-guideways for | 414 | ||
| Flat guideways for | 415 | ||
| Oiling devices for | 415 | ||
| Planing Machine Tables | 415 | ||
| Slots and holes in planing machine tables | 416 | ||
| Forms of bolts for planer tables | 417 | ||
| Supplementary tables for planer tables | 417 | ||
| Angle plates for planer tables | 418 | ||
| Chucking devices for planer tables | 418 | ||
| Planer Centres | 418 | ||
| Planer Chucks | 419 | ||
| For spiral grooved work | 419 | ||
| For curved work | 420 | ||
| Chucking machine beds on planer tables | 420 | ||
| For large planing machines | 422 | ||
| Chucking the halves of large pulleys on a planer | 423 | ||
| Gauges for planing V-guideways in machine beds | 421 | ||
| Planing guideways in machine beds | 422 | ||
| Gauge for planer tools | 424 | ||
| Planer Tools, the shapes of | 424 | ||
| For coarse finishing feeds | 424 | ||
| The clearance of | 424 | ||
| For slotted work | 424 | ||
| Planer Tool Holder, with tool post | 425 | ||
| Various applications of | 425 | ||
| Simple and advantageous form of | 426 | ||
| Examples of application of | 426 | ||
| CHAPTER XVIII. | |||
| DRILLING MACHINES. | |||
| Drilling Machines. General description of a power drilling machine | 428 | ||
| Lever feed | 428 | ||
| With automatic and quick return feed motions | 428 | ||
| Improved, with simple belt and uniform motion, two series of rates of automatic feed, and guide for boring bar | 429, 430 | ||
| Radial | 430, 431 | ||
| For boiler shells | 436 | ||
| Cotter or keyway | 438 | ||
| Drilling Machine, three-spindle | 434 | ||
| Four-spindle | 434 | ||
| Drilling and Boring machine | 431 | ||
| Feed motion of | 432 | ||
| Combined Drilling Machine and lathe | 433 | ||
| Boring Machine, horizontal | 433 | ||
| For car wheels | 438 | ||
| For pulleys | 438 | ||
| Quartering Machine | 434 | ||
| Drilling and Turning Machine for boiler makers | 435 | ||
| Feed motions of | 436 | ||
| CHAPTER XIX. | |||
| DRILLS AND CUTTERS FOR DRILLING MACHINES. | |||
| Jigs or Fixtures for drilling machines | 439 | ||
| Limits of error in | 439 | ||
| Examples of, for simple work, as for links, &c. | 440 | ||
| Considerations in designing | 440 | ||
| For drilling engine cylinders | 440 to 441 | ||
| For cutting out steam ports | 441 | ||
| Drills and Cutters for drilling machines | 442 | ||
| Table of sizes of twist drills, and their shanks | 442 | ||
| Flat drills for drilling machines | 442 | ||
| Errors in grinding flat drills | 443 | ||
| The tit-drill | 443 | ||
| The lip drill | 443 | ||
| Cotter or keyway drills | 446 | ||
| Drilling holes true to location with flat drills | 444 | ||
| Drilling hard metal | 444 | ||
| Table of sizes of tapping holes | 445 | ||
| Drill Shanks and sockets | 445 | ||
| Improved form of drill shank | 446 | ||
| Square shanked drills and their disadvantages | 446 | ||
| Drill Chucks | 446 | ||
| Stocks and Cutters for drilling machines | 447 | ||
| Tube plate cutters | 448 | ||
| Stocks and Cutters. Adjustable stock and cutter | 448 | ||
| Facing tool with reamer pin | 449 | ||
| Counterbores for drilling machines | 449 | ||
| Drill and counterbore for wood work | 449 | ||
| Facing and countersink cutters | 449 | ||
| Device for drilling square holes | 450 | ||
| Device for drilling taper holes in a drilling machine | 451 | ||
| CHAPTER XX. | |||
| HAND-DRILLING AND BORING TOOLS, AND DEVICES. | |||
| The Brad-awl | 452 | ||
| Bits. The gimlet bit | 452 | ||
| The German bit | 452 | ||
| The nail bit | 452 | ||
| The spoon bit | 452 | ||
| The nose bit | 453 | ||
| The auger bit | 453 | ||
| Cook’s auger bit | 453 | ||
| Principles governing the shapes of the cutting edges of auger bits | 453 | ||
| Auger bit for boring end grain wood | 453 | ||
| The centre bit | 454 | ||
| The expanding bit | 454 | ||
| Drills. Drill for stone | 454 | ||
| The fiddle drill | 455 | ||
| The fiddle drill with feeding device | 455 | ||
| Drill with cord and spring motion | 455 | ||
| Drill stock with spiral grooves | 455 | ||
| Drill brace | 455 | ||
| Drill brace with ratchet motion | 456 | ||
| Universal joint for drill brace | 456 | ||
| Drill brace with multiplying gear and ratchet motion | 456 | ||
| Breast drill with double gear | 456 | ||
| Drilling levers for blacksmiths | 457 | ||
| Drill cranks | 457 | ||
| Ratchet brace | 457 | ||
| Flexible shaft for driving drills | 458 | ||
| Drilling device for lock work | 459 | ||
| Hand drilling machine | 459 | ||
| Slotting Machine | 459 | ||
| Sectional view of | 460 | ||
| Tool holders | 460, 461 | ||
| Tools | 461, 462 | ||
| CHAPTER XXI. | |||
| THREAD-CUTTING MACHINERY AND BROACHING PRESS. | |||
| Pipe Threading, die stock for, by hand | 463 | ||
| Die stock for, by power | 463 | ||
| Pipe threading machines, general construction of | 463 | ||
| Bolt Threading hand machine | 464 | ||
| With revolving head | 465 | ||
| Power threading machine | 465 | ||
| With automatic stop motion | 466 | ||
| Construction of the head | 466 | ||
| Construction of the chasers | 466 | ||
| Bolt threading machine with back gear | 467 | ||
| Single rapid bolt threading machine | 467 | ||
| Double rapid bolt threading machine | 467 | ||
| Construction of the heads of the rapid machines | 468 | ||
| Bolt threading machinery, the Acme | 468 | ||
| Construction of the head of | 468 to 470 | ||
| Capacity of | 470 | ||
| Cutting Edges for taps, the number of | 471 | ||
| Examples when three and when four cutting edges are used, and the results upon bolts that are not round | 471, 472 | ||
| Demonstration that four cutting edges are correct for bar iron | 472 | ||
| Positions of Dies, or chasers in the heads of bolt cutting machine | 473 | ||
| Dies, methods of hobbing, to avoid undue friction | 473 | ||
| The construction of, for bolt threading machines | 473 | ||
| Method of avoiding friction in thread cutting | 474 | ||
| Hob for threading | 474 | ||
| Cutting speeds for threading | 474 | ||
| Nut Tapping machine | 475 | ||
| Automatic socket for | 475 | ||
| Rotary | 475 | ||
| Three-spindle | 475 | ||
| Pipe Threading Machine | 475 to 477 | ||
| Tapping Machine for steam pipe fittings | 478 | ||
| Broaching Press | 478 | ||
| Principles of broaching | 478 | ||
| Examples in the construction of broaches | 479 | ||
| Facing | |||
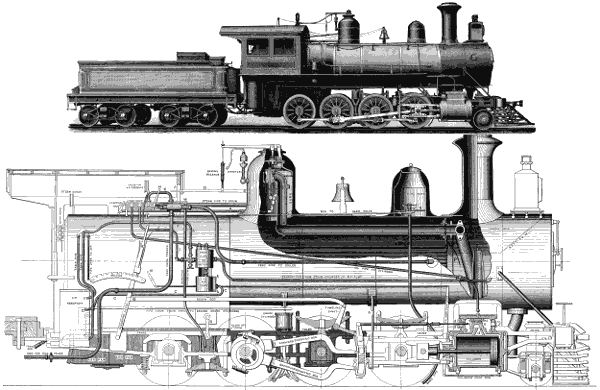
| Frontispiece. | MODERN LOCOMOTIVE ENGINE. | Title Page | |
| Plate | I. | TEMPLATE-CUTTING MACHINES FOR GEAR TEETH. | 34 |
| „ | II. | FORMS OF SCREW THREADS. | 85 |
| „ | III. | MEASURING AND GAUGING SCREW THREADS. | 93 |
| „ | IV. | END-ADJUSTMENT AND LOCKING DEVICES. | 120 |
| „ | V. | EXAMPLES IN LATHE CONSTRUCTION. | 148 |
| „ | VI. | CHUCKING LATHES. | 150 |
| „ | VII. | TOOL-HOLDING AND ADJUSTING APPLIANCES. | 174 |
| „ | VIII. | WATCHMAKER’S LATHE. | 188 |
| „ | IX. | DETAILS OF WATCHMAKER’S LATHE. | 188 |
| „ | X. | EXAMPLES OF SCREW MACHINES. | 200 |
| „ | XI. | ROLL-TURNING LATHE. | 215 |
| „ | XII. | EXAMPLES IN ANGLE-PLATE CHUCKING. | 252 |
| „ | XIII. | METHODS OF BALL-TURNING. | 325 |
| „ | XIV. | STANDARD MEASURING MACHINES. | 341 |
| „ | XV. | DIVIDING ENGINE AND MICROMETER. | 354 |
| „ | XVI. | SHAPING MACHINES AND TABLE-SWIVELING DEVICES. | 398 |
| „ | XVII. | EXAMPLES OF PLANING MACHINES. | 404 |
| „ | XVIII. | EXAMPLES IN PLANING WORK. | 422 |
| „ | XIX. | LIGHT DRILLING MACHINES. | 428 |
| „ | XX. | HEAVY DRILLING MACHINES. | 430 |
| „ | XXI. | EXAMPLES IN BORING MACHINERY. | 434 |
| „ | XXII. | BOILER-DRILLING MACHINERY. | 436 |
| „ | XXIII. | NUT-TAPPING MACHINERY. | 475 |
A wheel that is provided with teeth to mesh, engage, or gear with similar teeth upon another wheel, so that the motion of one may be imparted to the other, is called, in general terms, a gear-wheel.
When the teeth are arranged to be parallel to the wheel-axis, as in Fig. 1, the wheel is termed a spur-wheel. In the figure, a represents the axial line or axis of the wheel or of its shaft, to which the teeth are parallel while spaced equidistant around the rim, or face, as it is termed, of the wheel.
When the wheel has its teeth arranged at an angle to the shaft, as in Fig. 2, it is termed a bevel-wheel, or bevel gear; but when this angle is one of 45°, as in Fig. 3, as it must be if the pair of wheels are of the same diameter, so as to make the revolutions of their shafts equal, then the wheel is called a mitre-wheel. When the teeth are arranged upon the radial or side face of the wheel, as in Fig. 4, it is termed a crown-wheel. The smallest wheel of a pair, or of a train or set of gear-wheels, is termed the pinion; and when the teeth are composed of rungs, as in Fig. 5, it is termed a lantern, trundle, or wallower; and each cylindrical piece serving as a tooth is termed a stave, spindle, or round, and by some a leaf.
An annular or internal gear-wheel is one in which the faces of the teeth are within and the flanks without, or outside the pitch-circle, as in Fig. 6; hence the pinion p operates within the wheel.
When the teeth of a wheel are inserted in mortises or slots provided in the wheel-rim, it is termed a mortised-wheel, or a cogged-wheel, and the teeth are termed cogs.
When the teeth are arranged along a plane surface or straight line, as in Fig. 7, the toothed plane is termed a rack, and the wheel is termed a pinion.
A wheel that is driven by a revolving screw, or worm as it is termed, is called a worm-wheel, the arrangement of a worm and worm-wheel being shown in Fig. 8. The screw or worm is sometimes also called an endless screw, because its action upon the wheel does not come to an end as it does when it is revolved in one continuous direction and actuates a nut. So also, since the worm is tangent to the wheel, the arrangement is sometimes called a wheel and tangent screw.
The diameter of a gear-wheel is always taken at the pitch circle, unless otherwise specially stated as “diameter over all,” “diameter of addendum,” or “diameter at root of teeth,” &c., &c.
When the teeth of wheels engage to the proper distance, which is when the pitch circles meet, they are said to be in gear, or geared together. It is obvious that if two wheels are to be geared together their teeth must be the same distance apart, or the same pitch, as it is called.
The designations of the various parts or surfaces of a tooth of a gear-wheel are represented in Fig. 9, in which the surface a is the face of the tooth, while the dimension f is the width of face of the wheel, when its size is referred to. b is the flank or distance from the pitch line to the root of the tooth, and c the[I-2] point. h is the space, or the distance from the side of one tooth to the nearest side of the next tooth, the width of space being measured on the pitch circle p p. e is the depth of the tooth, and g its thickness, the latter also being measured on the pitch circle p p. When spoken of with reference to a tooth, p p is called the pitch line, but when the whole wheel is referred to it becomes the pitch circle.
The points c and the surface h are true to the wheel axis.
The teeth are designated for measurement by the pitch; the height or depth above and below pitch line; and the thickness.
The pitch, however, may be measured in two ways, to wit, around the pitch circle a, in Fig. 10, which is called the arc or circular pitch, and across b, which is termed the chord pitch.
In proportion as the diameter of a wheel (having a given pitch) is increased, or as the pitch of the teeth is made finer (on a wheel of a given diameter) the arc and chord pitches more nearly coincide in length. In the practical operations of marking out the teeth, however, the arc pitch is not necessarily referred to, for if the diameter of the pitch circle be made correct for the required number of teeth having the necessary arc pitch, and the wheel be accurately divided off into the requisite number of divisions with compasses set to the chord pitch, or by means of an index plate, then the arc pitch must necessarily be correct, although not referred to, save in determining the diameter of the wheel at the pitch circle.
The difference between the width of a space and the thickness of the tooth (both being measured on the pitch circle or pitch line) is termed the clearance or side clearance, which is necessary to prevent the teeth of one wheel from becoming locked in the spaces of the other. The amount of clearance is, when the teeth are cut to shape in a machine, made just sufficient to prevent contact on one side of the teeth when they are in proper gear (the pitch circles meeting in the line of centres). But when the teeth are cast upon the wheel the clearance is increased to allow for the slight inequalities of tooth shape that is incidental to casting them. The amount of clearance given is varied to suit the method employed to mould the wheels, as will be explained hereafter.
The line of centres is an imaginary line from the centre or axis of one wheel to the axis of the other when the two are in gear; hence each tooth is most deeply engaged, in the space of the other wheel, when it is on the line of centres.
There are three methods of designating the sizes of gear-wheels. First, by their diameters at the pitch circle or pitch diameter and the number of teeth they contain; second, by the number of teeth in the wheel and the pitch of the teeth; and third, by a system known as diametral pitch.
The first is objectionable because it involves a calculation to find the pitch of the teeth; furthermore, if this calculation be made by dividing the circumference of the pitch circle by the number of teeth in the wheel, the result gives the arc pitch, which cannot be measured correctly by a lineal measuring rule, especially if the wheel be a small one having but few teeth, or of coarse pitch, as, in that case, the arc pitch very sensibly differs from the chord pitch, and a second calculation may become necessary to find the chord pitch from the arc pitch.
The second method (the number and pitch of the teeth) possesses the disadvantage that it is necessary to state whether the pitch is the arc or the chord pitch.
If the arc pitch is given it is difficult to measure as before, while if the chord pitch is given it possesses the disadvantage that the diameters of the wheels will not be exactly proportional to the numbers of teeth in the respective wheels. For instance, a wheel with 20 teeth of 2 inch chord pitch is not exactly half the diameter of one of 40 teeth and 2 inch chord pitch.
To find the chord pitch of a wheel take 180 (= half the degrees in a circle) and divide it by the number of teeth in the wheel. In a table of natural sines find the sine for the number so found, which multiply by 2, and then by the radius of the wheel in inches.
Example.—What is the chord pitch of a wheel having 12 teeth and a diameter (at pitch circle) of 8 inches? Here 180 ÷ 12 = 15;[I-3] (sine of 15 is .25881). Then .25881 × 2 = .51762 × 4 (= radius of wheel) = 2.07048 inches = chord pitch.
| Degrees. | Sine. | Degrees. | Sine. | Degrees. | Sine. |
| 1 | .01745 | 16 | .27563 | 31 | .51503 |
| 2 | .03489 | 17 | .29237 | 32 | .52991 |
| 3 | .05233 | 18 | .30901 | 33 | .54463 |
| 4 | .06975 | 19 | .32556 | 34 | .55919 |
| 5 | .08715 | 20 | .34202 | 35 | .57357 |
| 6 | .10452 | 21 | .35836 | 36 | .58778 |
| 7 | .12186 | 22 | .37460 | 37 | .60181 |
| 8 | .13917 | 23 | .39073 | 38 | .61566 |
| 9 | .15643 | 24 | .40673 | 39 | .62932 |
| 10 | .17364 | 25 | .42261 | 40 | .64278 |
| 11 | .19080 | 26 | .43837 | 41 | .65605 |
| 12 | .20791 | 27 | .45399 | 42 | .66913 |
| 13 | .22495 | 28 | .46947 | 43 | .68199 |
| 14 | .24192 | 29 | .48480 | 44 | .69465 |
| 15 | .25881 | 30 | .50000 | 45 | .70710 |
The principle upon which diametral pitch is based is as follows:—
The diameter of the wheel at the pitch circle is supposed to be divided into as many equal parts or divisions as there are teeth in the wheel, and the length of one of these parts is the diametral pitch. The relationship which the diametral bears to the arc pitch is the same as the diameter to the circumference, hence a diametral pitch which measures 1 inch will accord with an arc pitch of 3.1416; and it becomes evident that, for all arc pitches of less than 3.1416 inches, the corresponding diametral pitch must be expressed in fractions of an inch, as 1⁄2, 1⁄3, 1⁄4, and so on, increasing the denominator until the fraction becomes so small that an arc with which it accords is too fine to be of practical service. The numerators of these fractions being 1, in each case, they are in practice discarded, the denominators only being used, so that, instead of saying diametral pitches of 1⁄2, 1⁄3, or 1⁄4, we say diametral pitches of 2, 3, or 4, meaning that there are 2, 3, or 4 teeth on the wheel for every inch in the diameter of the pitch circle.
Suppose now we are given a diametral pitch of 2. To obtain the corresponding arc pitch we divide 3.1416 (the relation of the circumference to the diameter) by 2 (the diametral pitch), and 3.1416 ÷ 2 = 1.57 = the arc pitch in inches and decimal parts of an inch. The reason of this is plain, because, an arc pitch of 3.1416 inches being represented by a diametral pitch of 1, a diametral pitch of 1⁄2 (or 2 as it is called) will be one half of 3.1416. The advantage of discarding the numerator is, then, that we avoid the use of fractions and are readily enabled to find any arc pitch from a given diametral pitch.
Examples.—Given a 5 diametral pitch; what is the arc pitch? First (using the full fraction 1⁄5) we have 1⁄5 × 3.1416 = .628 = the arc pitch. Second (discarding the numerator), we have 3.1416 ÷ 5 = .628 = arc pitch. If we are given an arc pitch to find a corresponding diametral pitch we again simply divide 3.1416 by the given arc pitch.
Example.—What is the diametral pitch of a wheel whose arc pitch is 11⁄2 inches? Here 3.1416 ÷ 1.5 = 2.09 = diametral pitch. The reason of this is also plain, for since the arc pitch is to the diametral pitch as the circumference is to the diameter we have: as 3.1416 is to 1, so is 1.5 to the required diametral pitch; then 3.1416 × 1 ÷ 1.5 = 2.09 = the required diametral pitch.
To find the number of teeth contained in a wheel when the diameter and diametral pitch is given, multiply the diameter in inches by the diametral pitch. The product is the answer. Thus, how many teeth in a wheel 36 inches diameter and of 3 diametral pitch? Here 36 × 3 = 108 = the number of teeth sought. Or, per contra, a wheel of 36 inches diameter has 108 teeth. What is the diametral pitch? 108 ÷ 36 = 3 = the diametral pitch. Thus it will be seen that, for determining the relative sizes of wheels, this system is excellent from its simplicity. It also possesses the advantage that, by adding two parts of the diametral pitch to the pitch diameter, the outside diameter of the wheel or the diameter of the addendum is obtained. For instance, a wheel containing 30 teeth of 10 pitch would be 3 inches diameter on the pitch circle and 32⁄10 outside or total diameter.
Again, a wheel having 40 teeth of 8 diametral pitch would have a pitch circle diameter of 5 inches, because 40 ÷ 8 = 5, and its full diameter would be 51⁄4 inches, because the diametral pitch is 1⁄8, and this multiplied by 2 gives 1⁄4, which added to the pitch circle diameter of 5 inches makes 51⁄4 inches, which is therefore the diameter of the addendum, or, in other words, the full diameter of the wheel.
Suppose now that a pair of wheels require to have pitch circles of 5 and 8 inches diameter respectively, and that the arc pitch requires to be, say, as near as may be 4⁄10 inch; to find a suitable pitch and the number of teeth by the diametral pitch system we proceed as follows:
In the following table are given various arc pitches, and the corresponding diametral pitch.
| Diametral Pitch. | Arc Pitch. | Arc Pitch. | Diametral Pitch. | ||||
| Inch. | |||||||
| 2 | 1 | .57 | 1 | .75 | 1 | .79 | |
| 2 | .25 | 1 | .39 | 1 | .5 | 2 | .09 |
| 2 | .5 | 1 | .25 | 1 | .4375 | 2 | .18 |
| 2 | .75 | 1 | .14 | 1 | .375 | 2 | .28 |
| 3 | 1 | .04 | 1 | .3125 | 2 | .39 | |
| 3 | .5 | .890 | 1 | .25 | 2 | .51 | |
| 4 | .785 | 1 | .1875 | 2 | .65 | ||
| 5 | .628 | 1 | .125 | 2 | .79 | ||
| 6 | .523 | 1 | .0625 | 2 | .96 | ||
| 7 | .448 | 1 | .0000 | 3 | .14 | ||
| 8 | .392 | 0 | .9375 | 3 | .35 | ||
| 9 | .350 | 0 | .875 | 3 | .59 | ||
| 10 | .314 | 0 | .8125 | 3 | .86 | ||
| 11 | .280 | 0 | .75 | 4 | .19 | ||
| 12 | .261 | 0 | .6875 | 4 | .57 | ||
| 14 | .224 | 0 | .625 | 5 | .03 | ||
| 16 | .196 | 0 | .5625 | 5 | .58 | ||
| 18 | .174 | 0 | .5 | 6 | .28 | ||
| 20 | .157 | 0 | .4375 | 7 | .18 | ||
| 22 | .143 | 0 | .375 | 8 | .38 | ||
| 24 | .130 | 0 | .3125 | 10 | .00 | ||
| 26 | .120 | 0 | .25 | 12 | .56 | ||
From this table we find that the nearest diametral pitch that will correspond to an arc pitch of 4⁄10 inch is a diametral pitch of 8, which equals an arc pitch of .392, hence we multiply the pitch circles (5 and 8,) by 8, and obtain 40 and 64 as the number of teeth, the arc pitch being .392 of an inch. To find the number of teeth and pitch by the arc pitch and circumference of the pitch circle, we should require to find the circumference of the pitch circle, and divide this by the nearest arc pitch that would divide the circumference without leaving a remainder, which would entail more calculating than by the diametral pitch system.
The designation of pitch by the diametral pitch system is, however, not applied in practice to coarse pitches, nor to gears in which the teeth are cast upon the wheels, pattern makers generally preferring to make the pitch to some measurement that accords with the divisions of the ordinary measuring rule.
Of two gear-wheels that which impels the other is termed the driver, and that which receives motion from the other is termed the driven wheel or follower; hence in a single pair of wheels in gear together, one is the driver and the other the driven wheel or follower. But if there are three wheels in gear together, the middle one will be the follower when spoken of with reference to the first or prime mover, and the driver, when mentioned with reference to the third wheel, which will be a follower. A series of more than two wheels in gear together is termed a train of wheels or of gearing. When the wheels in a train are in gear continuously, so that each wheel, save the first and last, both receives and imparts motion, it is a simple train, the first wheel being the driver, and the last the follower, the others being termed intermediate wheels. Each of these intermediates is a follower with reference to the wheel that drives it, and a driver to the one that it drives. But the velocity of all the wheels in the train is the same in fact per second (or in a given space of time), although the revolutions in[I-4] that space of time may vary; hence a simple train of wheels transmits motion without influencing its velocity. To alter the velocity (which is always taken at a point on the pitch circle) the gearing must be compounded, as in Fig. 11, in which a, b, c, e are four wheels in gear, b and c being compounded, that is, so held together on the shaft d that both make an equal number of revolutions in a given time. Hence the velocity of c will be less than that of b in proportion as the diameter, circumference, radius, or number of teeth in c, varies from the diameter, radius, circumference, or number of teeth (all the wheels being supposed to have teeth of the same pitch) in b, although the rotations of b and c are equal. It is most convenient, and therefore usual, to take the number of teeth, but if the teeth on c (and therefore those on e also) were of different pitch from those on b, the radius or diameters of the wheels must be taken instead of the pitch, when the velocities of the various wheels are to be computed. It is obvious that the compounded pair of wheels will diminish the velocity when the driver of the compounded pair (as c in the figure) is of less radius than the follower b, and conversely that the velocity will be increased when the driver is of greater radius than the follower of the compound pair.
The diameter of the addendum or outer circle of a wheel has no influence upon the velocity of the wheel. Suppose, for example, that we have a pair of wheels of 3 inch arc or circular pitch, and containing 20 teeth, the driver of the two making one revolution per minute. Suppose the driven wheel to have fast upon its shaft a pulley whose diameter is one foot, and that a weight is suspended from a line or cord wound around this pulley, then (not taking the thickness of the line into account) each rotation of the driven wheel would raise the weight 3.1416 feet (that being the circumference of the pulley). Now suppose that the addendum circle of either of the wheels were cut off down to the pitch circle, and that they were again set in motion, then each rotation of the driven wheel would still raise the weight 3.1416 feet as before.
It is obvious, however, that the addendum circle must be sufficiently larger than the pitch circle to enable at least one pair of teeth to be in continuous contact; that is to say, it is obvious that contact between any two teeth must not cease before contact between the next two has taken place, for otherwise the motion would not be conveyed continuously. The diameter of the pitch circle cannot be obtained from that of the addendum circle unless the pitch of the teeth and the proportion of the pitch allowed for the addendum be known. But if these be known the diameter of the pitch circle may be obtained by subtracting from that of the addendum circle twice the amount allowed for the addendum of the tooth.
Example.—A wheel has 19 teeth of 3 inch arc pitch; the addendum of the tooth or teeth equals 3⁄10 of the pitch, and its addendum circle measures 19.943 inches; what is the diameter of the pitch circle? Here the addendum on each side of the wheel equals (3⁄10 of 3 inches) = .9 inches, hence the .9 must be multiplied by 2 for the two sides of the wheel, thus, .9 × 2 = 1.8. Then, diameter of addendum circle 19.943 inches less 1.8 inches = 18.143 inches, which is the diameter of the pitch circle.
Proof.—Number of teeth = 19, arc pitch 3, hence 19 × 3 = 57 inches, which, divided by 3.1416 (the proportion of the circumference to the diameter) = 18.143 inches.
If the distance between the centres of a pair of wheels that are in gear be divided into two parts whose lengths are in the same proportion one to the other as are the numbers of teeth in the wheels, then these two parts will represent the radius of the pitch circles of the respective wheels. Thus, suppose one wheel to contain 100 and the other 50 teeth, and that the distance between their centres is 18 inches, then the pitch radius or pitch diameter of one will be twice that of the other, because one contains twice as many teeth as the other. In this case the radius of pitch circle for the large wheel will be 12 inches, and that for the small one 6 inches, because 12 added to 6 makes 18, which is the distance between the wheel centres, and 12 is in the same proportion to 6 that 100 is to 50.
A simple rule whereby to find the radius of the pitch circles of a pair of wheels is as follows:—
Rule.—Divide number of teeth in the large wheel by the number in the small one, and to the sum so obtained add 1. Take this amount and divide it into the distance between the centres of the wheels, and the result will be the radius of the smallest wheel. To obtain the radius of the largest wheel subtract the radius of the smallest wheel from the distance between the wheel centres.
Example.—Of a pair of wheels, one has 100 and the other 50 teeth, the distance between their centres is 18 inches; what is the pitch radius of each wheel?
Here 100 ÷ 50 = 2, and 2 + 1 = 3. Then 18 ÷ 3 = 6, hence the pitch radius of the small wheel is 6 inches. Then 18 - 6 = 12 = pitch radius of large wheel.
Example 2.—Of a pair of wheels one has 40 and the other 90 teeth. The distance between the wheel centres is 321⁄2 inches; what are the radii of the respective pitch circles? 90 ÷ 40 = 2.25 and 2.25 + 1 = 3.25. Then 32.5 ÷ 3.25 = 10 = pitch radius of small wheel, and 32.5 - 10 = 22.5, which is the pitch radius of the large wheel.
To prove this we may show that the pitch radii of the two wheels are in the same proportion as their numbers of teeth, thus:—
| Proof.— | Radius of small wheel | = | 10 | × | 4 | = | 40 |
| radius of large wheel | = | 22.5 | × | 4 | = | 90.0 |
Suppose now that a pair of wheels are constructed, having respectively 50 and 100 teeth, and that the radii of their true pitch circles are 12 and 6 respectively, but that from wear in their journals or journal bearings this 18 inches (12 + 6 = 18) between centres (or line of centres, as it is termed) has become 183⁄8 inches. Then the acting effective or operative radii of the pitch circles will bear the same proportion to the 183⁄8 as the numbers of teeth in the respective wheels, and will be 12.25 for the large, and 6.125 for the small wheel, instead of 12 and 6, as would be the case were the wheels 18 inches apart. Working this out under the rule given we have 100 ÷ 50 = 2, and 2 + 1 = 3. Then 18.375 ÷ 3 = 6.125 = pitch radius of small wheel, and 18.375 - 6.125 = 12.25 = pitch radius of the large wheel.
The true pitch line of a tooth is the line or point where the face curve joins the flank curve, and it is essential to the transmission of uniform motion that the pitch circles of epicycloidal wheels exactly coincide on the line of centres, but if they do not coincide (as by not meeting or by overlapping each other), then a false pitch circle becomes operative instead of the true one, and the motion of the driven wheel will be unequal at different instants of time, although the revolutions of the wheels will of course be in proportion to the respective numbers of their teeth.
If the pitch circle is not marked on a single wheel and its arc pitch is not known, it is practically a difficult matter to obtain either the arc pitch or diameter of the pitch circle. If the wheel[I-5] is a new one, and its teeth are of the proper curves, the pitch circle will be shown by the junction of the curves forming the faces with those forming the flanks of the teeth, because that is the location of the pitch circle; but in worn wheels, where from play or looseness between the journals and their bearings, this point of junction becomes rounded, it cannot be defined with certainty.
In wheels of large diameter the arc pitch so nearly coincides with the chord pitch, that if the pitch circle is not marked on the wheel and the arc pitch is not known, the chord pitch is in practice often assumed to represent the arc pitch, and the diameter of the wheel is obtained by multiplying the number of teeth by the chord pitch. This induces no error in wheels of coarse pitches, because those pitches advance by 1⁄4 or 1⁄2 inch at a step, and a pitch measuring about, say, 11⁄4 inch chord pitch, would be known to be 11⁄4 arc pitch, because the difference between the arc and chord pitch would be too minute to cause sensible error. Thus the next coarsest pitch to 1 inch would be 11⁄8, or more often 11⁄4 inch, and the difference between the arc and chord pitch of the smallest wheel would not amount to anything near 1⁄8 inch, hence there would be no liability to mistake a pitch of 11⁄8 for 1 inch or vice versâ. The diameter of wheel that will be large enough to transmit continuous motion is diminished in proportion as the pitch is decreased; in proportion, also, as the wheel diameter is reduced, the difference between the arc and chord pitch increases, and further the steps by which fine pitches advance are more minute (as 1⁄4, 9⁄32, 5⁄16, &c.). From these facts there is much more liability to err in estimating the arc from the measured chord pitch in fine pitches, hence the employment of diametral pitch for small wheels of fine pitches is on this account also very advantageous. In marking out a wheel the chord pitch will be correct if the pitch circle be of correct diameter and be divided off into as many points of equal division (with compasses) as there are to be teeth in the wheel. We may then mark from these points others giving the thickness of the teeth, which will make the spaces also correct. But when the wheel teeth are to be cut in a machine out of solid metal, the mechanism of the machine enables the marking out to be dispensed with, and all that is necessary is to turn the wheel to the required addendum diameter, and mark the pitch circle. The following are rules for the purposes they indicate.
The circumference of a circle is obtained by multiplying its diameter by 3.1416, and the diameter may be obtained by dividing the circumference by 3.1416.
The circumference of the pitch circle divided by the arc pitch gives the number of teeth in the wheel.
The arc pitch multiplied by the number of teeth in the wheel gives the circumference of the pitch circle.
Gear-wheels are simply rotating levers transmitting the power they receive, less the amount of friction necessary to rotate them under the given conditions. All that is accomplished by a simple train of gearing is, as has been said, to vary the number of revolutions, the speed or velocity measured in feet moved through per minute remaining the same for every wheel in the train. But in a compound train of gears the speed in feet per minute, as well as the revolutions, may be varied by means of the compounded pairs of wheels. In either a simple or a compound train of gearing the power remains the same in amount for every wheel in the train, because what is in a compound train lost in velocity is gained in force, or what is gained in velocity is lost in force, the word force being used to convey the idea of strain, pressure, or pull.
In Fig. 12, let a, b, and c represent the pitch circles of three gears of which a and b are in gear, while c is compounded with b; let e be the shaft of a, and g that for b and c. Let a be 60 inches, b = 30 inches, and c = 40 inches in diameter. Now suppose that shaft e suspends from its perimeter a weight of 50 lbs., the shaft being 4 inches in diameter. Then this weight will be at a leverage of 2 inches from the centre of e and the 50 must be multiplied by 2, making 100 lbs. at the centre of e. Then at the perimeter of a this 100 will become one-thirtieth of one hundred, because from the centre to the perimeter of a is 30. One-thirtieth of 100 is 333⁄100 lbs., which will be the force exerted by a on the perimeter of b. Now from the perimeter of b to its centre (or in other words its radius) is 15 inches, hence the 333⁄100 lbs. at its perimeter will become fifteen times as much at the centre g of b, and 333⁄100 × 15 = 4995⁄100 lbs. From the centre g to the perimeter of c being 20 inches, the 4995⁄100 lbs. at the centre will be only one-twentieth of that amount at the perimeter of c, hence 4995⁄100 ÷ 20 = 249⁄100 lbs., which is the amount of force at the perimeter of c.
Here we have treated the wheels as simple levers, dividing the weight by the length of the levers in all cases where it is transmitted from the shaft to the perimeter, and multiplying it by the length of the lever when it is transmitted from the perimeter of the wheel to the centre of the shaft. The precise same result will be reached if we take the diameter of the wheels or the number of the teeth, providing the pitch of the teeth on all the wheels is alike.
Suppose, for example, that a has 60 teeth, b has 30 teeth, and c has 40 teeth, all being of the same pitch. Suppose the 50 lb. weight be suspended as before, and that the circumference of the shaft be equal to that of a pinion having 4 teeth of the same pitch as the wheels. Then the 50 multiplied by the 4 becomes 200, which divided by 60 (the number of teeth on a) becomes 333⁄100, which multiplied by 30 (the number of teeth on b) becomes 9990⁄100, which divided by 40 (the number of teeth on c) becomes 249⁄100 lbs. as before.
It may now be explained why the shaft was taken as equal to a pinion having 4 teeth. Its diameter was taken as 4 inches and the wheel diameter was taken as being 60 inches, and it was supposed to contain 60 teeth, hence there was 1 tooth to each inch of diameter, and the 4 inches diameter of shaft was therefore equal to a pinion having 4 teeth. From this we may perceive the philosophy of the rule that to obtain the revolutions of wheels we multiply the given revolutions by the teeth in the driving wheels and divide by the teeth in the driven wheels.
Suppose that a (Fig. 13) makes 1 revolution per minute, how many will c make, a having 60 teeth, b 30 teeth, and c 40 teeth? In this case we have but one driving wheel a, and one driven wheel b, the driver having 60 teeth, the driven 30, hence 60 ÷ 30 = 2, equals revolutions of b and also of c, the two latter being on the same shaft.
It will be observed then that the revolutions are in the same proportion as the numbers of the teeth or the radii of the wheels, or what is the same thing, in the same proportion as their diameters. The number of teeth, however, is usually taken as being easier obtained than the diameter of the pitch circles, and easier to calculate, because the teeth will be represented by a whole number, whereas the diameter, radius, or circumference, will generally contain fractions.
[I-6]Suppose that the 4 wheels in Fig. 14 have the respective numbers of teeth marked beside them, and that the upper one having 40 teeth makes 60 revolutions per minute, then we may obtain the revolutions of the others as follows:—
| Revolu- tions. |
Teeth in first driver. |
Teeth in first driven. |
Teeth in second driver. |
Teeth in second driven. |
||||||
| 60 | × | 40 | ÷ | 60 | × | 20 | ÷ | 120 | = | 666⁄100 |
and a remainder of the reciprocating decimals. We may now prove this by reversing the question, thus. Suppose the 120 wheel to make 666⁄100 revolutions per minute, how many will the 40 wheel make?
| Revolu- tions. |
Teeth in first driver. |
Teeth in first driven. |
Teeth in second driver. |
Teeth in second driven. |
|||||||
| 6.66 | × | 120 | ÷ | 20 | × | 60 | ÷ | 40 | = | 5999⁄100 | = |
revolutions of the 40 wheel, the discrepancy of 1⁄100 being due to the 6.66 leaving a remainder and not therefore being absolutely correct.
That the amount of power transmitted by gearing, whether compounded or not, is equal throughout every wheel in the train, may be shown as follows:—
Referring again to Fig. 10, it has been shown that with a 50 lb. weight suspended from a 4 inch shaft e, there would be 3033⁄100 lbs. at the perimeter of a. Now suppose a rotation be made, then the 50 lb. weight would fall a distance equal to the circumference of the shaft, which is (3.1416 × 4 = 1256⁄100) 1256⁄100 inches. Now the circumference of the wheel is (60 dia. × 3.1416 = 18849⁄100 cir.) 18849⁄100 inches, which is the distance through which the 333⁄100 lbs. would move during one rotation of a. Now 3.33 lbs. moving through 188.49 inches represents the same amount of power as does 50 lbs. moving through a distance of 12.56 inches, as may be found by converting the two into inch lbs. (that is to say, into the number of inches moved by 1 lb.), bearing in mind that there will be a slight discrepancy due to the fact that the fractions .33 in the one case, and .56 in the other are not quite correct. Thus:
| 188.49 | inches | × | 3.33 | lbs. | = | 627 | .67 | inch | lbs., | and |
| 12.56 | „ | × | 50 | „ | = | 628 | „ | „ |
Taking the next wheels in Fig. 12, it has been shown that the 3.33 lbs. delivered from a to the perimeter of b, becomes 2.49 lbs. at the perimeter of c, and it has also been shown that c makes two revolutions to one of a, and its diameter being 40 inches, the distance this 2.49 lbs. will move through in one revolution of a will therefore be equal to twice its circumference, which is (40 dia. × 3.1416 = 125.666 cir., and 125.666 × 2 = 251.332) 251.332 inches. Now 2.49 lbs. moving through 251.332 gives when brought to inch lbs. 627.67 inch lbs., thus 251.332 × 2.49 = 627.67. Hence the amount of power remains constant, but is altered in form, merely being converted from a heavy weight moving a short distance, into a lighter one moving a distance exactly as much greater as the weight or force is lessened or lighter.
Gear-wheels therefore form a convenient method of either simply transmitting motion or power, as when the wheels are all of equal diameter, or of transmitting it and simultaneously varying its velocity of motion, as when the wheels are compounded either to reduce or increase the speed or velocity in feet per second of the prime mover or first driver of the train or pair, as the case may be.
In considering the action of gear-teeth, however, it sometimes is more convenient to denote their motion by the number of degrees of angle they move through during a certain portion of a revolution, and to refer to their relative velocities in terms of the ratio or proportion existing between their velocities. The first of these is termed the angular velocity, or the number of degrees of angle the wheel moves through during a given period, while the second is termed the velocity ratio of the pair of wheels. Let it be supposed that two wheels of equal diameter have contact at their perimeters so that one drives the other by friction without any slip, then the velocity of a point on the perimeter of one will equal that of a point on the other. Thus in Fig. 15 let a and b represent the pitch circles of two wheels, and c an imaginary line joining the axes of the two wheels and termed the line of centres. Now the point of contact of the two wheels will be on the line of[I-7] centres as at d, and if a point or dot be marked at d and motion be imparted from a to b, then when each wheel has made a quarter revolution the dot on a will have arrived at e while that on b will have arrived at f. As each wheel has moved through one quarter revolution, it has moved through 90° of angle, because in the whole circle there is 360°, one quarter of which is 90°, hence instead of saying that the wheels have each moved through one quarter of a revolution we may say they have moved through an angle of 90°, or, in other words, their angular velocity has, during this period, been 90°. And as both wheels have moved through an equal number of degrees of angle their velocity ratio or proportion of velocity has been equal.
Obviously then the angular velocity of a wheel represents a portion of a revolution irrespective of the diameter of the wheel, while the velocity ratio represents the diameter of one in proportion to that of the other irrespective of the actual diameter of either of them.
Now suppose that in Fig. 16 a is a wheel of twice the diameter of b; that the two are free to revolve about their fixed centres, but that there is frictional contact between their perimeters at the line of centres sufficient to cause the motion of one to be imparted to the other without slip or lost motion, and that a point be marked on both wheels at the point of contact d. Now let motion be communicated to a until the mark that was made at d has moved one-eighth of a revolution and it will have moved through an eighth of a circle, or 45°. But during this motion the mark on b will have moved a quarter of a revolution, or through an angle of 90° (which is one quarter of the 360° that there are in the whole circle). The angular velocities of the two are, therefore, in the same ratio as their diameters, or two to one, and the velocity ratio is also two to one. The angular velocity of each is therefore the number of degrees of angle that it moves through in a certain portion of a revolution, or during the period that the other wheel of the pair makes a certain portion of a revolution, while the velocity ratio is the proportion existing between the velocity of one wheel and that of the other; hence if the diameter of one only of the wheels be changed, its angular velocity will be changed and the velocity ratio of the pair will be changed. The velocity ratio may be obtained by dividing either the radius, pitch, diameter, or number of teeth of one wheel into that of the other.
Conversely, if a given velocity ratio is to be obtained, the radius, diameter, or number of teeth of the driver must bear the same relation to the radius, diameter, or number of teeth of the follower, as the velocity of the follower is desired to bear to that of the driver.
If a pair of wheels have an equal number of teeth, the same pairs of teeth will come into action at every revolution; but if of two wheels one is twice as large as the other, each tooth on the small wheel will come into action twice during each revolution of the large one, and will work during each successive revolution with the same two teeth on the large wheel; and an application of the principle of the hunting tooth is sometimes employed in clocks to prevent the overwinding of their springs, the device being shown in Fig. 17, which is from “Willis’ Principles of Mechanism.”
For this purpose the winding arbor c has a pinion a of 19 teeth fixed to it close to the front plate. A pinion b of 18 teeth is mounted on a stud so as to be in gear with the former. A radial plate c d is fixed to the face of the upper wheel a, and a similar plate f e to the lower wheel b. These plates terminate outward in semicircular noses d, e, so proportioned as to cause their extremities to abut against each other, as shown in the figure, when the motion given to the upper arbor by the winding has brought them into the position of contact. The clock being now wound up, the winding arbor and wheel a will begin to turn in the opposite direction. When its first complete rotation is effected the wheel b will have gained one tooth distance from the line of centres, so as to place the stop d in advance of e and thus avoid a contact with e, which would stop the motion. As each turn of the upper wheel increases the distance of the stops, it follows from the principle of the hunting cog, that after eighteen revolutions of a and nineteen of b the stops will come together again and the clock be prevented from running down too far. The winding key being applied, the upper wheel a will be rotated in the opposite direction, and the winding repeated as above.
Thus the teeth on one wheel will wear to imbed one upon the other. On the other hand the teeth of the two wheels may be of such numbers that those on one wheel will not fall into gear with the same teeth on the other except at intervals, and thus an inequality on any one tooth is subjected to correction by all the teeth in the other wheel. When a tooth is added to the number of teeth on a wheel to effect this purpose it is termed a hunting cog, or hunting tooth, because if one wheel have a tooth less, then any two teeth which meet in the first revolution are distant, one tooth in the second, two teeth in the third, three in the fourth, and so on. The odd tooth is on this account termed a hunting tooth.
It is obvious then that the shape or form to be given to the teeth must, to obtain correct results, be such that the motion of the driver will be communicated to the follower with the velocity due to the relative diameters of the wheels at the pitch circles, and since the teeth move in the arc of a circle it is also obvious that the sides of the teeth, which are the only parts that come into contact, must be of same curve. The nature of this curve must be such that the teeth shall possess the strength necessary to transmit the required amount of power, shall possess ample wearing surface, shall be as easily produced as possible for all the varying conditions, shall give as many teeth in constant contact as possible, and shall, as far as possible, exert a pressure in a direction to rotate the wheels without inducing undue wear upon the journals of the shafts upon which the wheels rotate. In cases, however, in which some of these requirements must be partly sacrificed to increase the value of the others, or of some of the others, to suit the special circumstances under which the wheels are to operate, the selection is left to the judgment of the designer, and the considerations which should influence his determinations will appear hereafter.
[I-8]Modern practice has accepted the curve known in general terms as the cycloid, as that best filling all the requirements of wheel teeth, and this curve is employed to produce two distinct forms of teeth, epicycloidal and involute. In epicycloidal teeth the curve forming the face of the tooth is designated an epicycloid, and that forming the flank an hypocycloid. An epicycloid may be traced or generated, as it is termed, by a point in the circumference of a circle that rolls without slip upon the circumference of another circle. Thus, in Fig. 18, a and b represent two wooden wheels, a having a pencil at p, to serve as a tracing or marking point. Now, if the wheels are laid upon a sheet of paper and while holding b in a fixed position, roll a in contact with b and let the tracing point touch the paper, the point p will trace the curve c c. Suppose now the diameter of the base circle b to be infinitely large, a portion of its circumference may be represented by a straight line, and the curve traced by a point on the circumference of the generating circle as it rolls along the base line b is termed a cycloid. Thus, in Fig. 19, b is the base line, a the rolling wheel or generating circle, and c c the cycloidal curve traced or marked by the point d when a is rolled along b. If now we suppose the base line b to represent the pitch line of a rack, it will be obvious that part of the cycloid at one end is suitable for the face on one side of the tooth, and a part at the other end is suitable for the face of the other side of the tooth.
A hypocycloid is a curve traced or generated by a point on the circumference of a circle rolling within and in contact (without slip) with another circle. Thus, in Fig. 20, a represents a wheel in contact with the internal circumference of b, and a point on its circumference will trace the two curves, c c, both curves starting from the same point, the upper having been traced by rolling the generating circle or wheel a in one direction and the lower curve by rolling it in the opposite direction.
To demonstrate that by the epicycloidal and hypocycloidal curves, forming the faces and flanks of what are known as epicycloidal teeth, motion may be communicated from one wheel to another with as much uniformity as by frictional contact of their circumferential surfaces, let a, b, in Fig. 21, represent two plain wheel disks at liberty to revolve about their fixed centres, and let c c represent a margin of stiff white paper attached to the face of b so as to revolve with it. Now suppose that a and b are in close contact at their perimeters at the point g, and that there is no slip, and that rotary motion commenced when the point e (where as tracing point a pencil is attached), in conjunction with the point f, formed the point of contact of the two wheels, and continued until the points e and f had arrived at their respective positions as shown in the figure; the pencil at e will have traced upon the margin of white paper the portion of an epicycloid denoted by the curve e f; and as the movement of the two wheels a, b, took place by reason of the contact of their circumferences, it is evident that the length of the arc e g must be equal to that of the arc g f, and that the motion of a (supposing it to be the driver) would be communicated uniformly to b.
Now suppose that the wheels had been rotated in the opposite direction and the same form of curve would be produced, but it would run in the opposite direction, and these two curves may be utilized to form teeth, as in Fig. 22, the points on the wheel a working against the curved sides of the teeth on b.
To render such a pair of wheels useful in practice, all that is necessary is to diminish the teeth on b without altering the[I-9] nature of the curves, and increase the diameter of the points on a, making them into rungs or pins, thus forming the wheels into what is termed a wheel and lantern, which are illustrated in Fig. 23.
a represents the pinion (or lantern), and b the wheel, and c, c, the primitive teeth reduced in thickness to receive the pins on a. This reduction we may make by setting a pair of compasses to the radius of the rung and describing half-circles at the bottom of the spaces in b. We may then set a pair of compasses to the curve of c, and mark off the faces of the teeth of b to meet the half-circles at the pitch line, and reduce the teeth heights so as to leave the points of the proper thickness; having in this operation maintained the same epicycloidal curves, but brought them closer together and made them shorter. It is obvious, however, that such a method of communicating rotary motion is unsuited to the transmission of much power; because of the weakness of, and small amount of wearing surface on, the points or rungs in a.
In place of points or rungs we may have radial lines, these lines, representing the surfaces of ribs, set equidistant on the radial face of the pinion, as in Fig. 24. To determine the epicycloidal curves for the faces of teeth to work with these radial lines, we may take a generating circle c, of half the diameter of a, and cause it to roll in contact with the internal circumference of a, and a tracing point fixed in the circumference of c will draw the radial lines shown upon a. The circumstances will not be altered if we suppose the three circles, a, b, c, to be movable about their fixed centres, and let their centres be in a straight line; and if, under these circumstances, we suppose rotation to be imparted to the three circles, through frictional contact of their perimeters, a tracing point on the circumference of c would trace the epicycloids shown upon b and the radial lines shown upon a, evidencing the capability of one to impart uniform rotary motion to the other.
To render the radial lines capable of use we must let them be the surfaces of lugs or projections on the face of the wheel, as shown in Fig. 25 at d, e, &c., or the faces of notches cut in the wheel as at f, g, h, &c., the metal between f and g forming a tooth j, having flanks only. The wheel b has the curves of each tooth brought closer together to give room for the reception of the teeth upon a. We have here a pair of gears that possess sufficient strength and are capable of working correctly in either direction.
But the form of tooth on one wheel is conformed simply to suit those on the other, hence, neither two of the wheels a, nor would two of b, work correctly together.
They may be qualified to do so, however, by simply adding to[I-10] the tops of the teeth on a, teeth of the form of those on b, and adding to those on b, and within the pitch circle, teeth corresponding to those on a, as in Fig. 26, where at k′ and j′ teeth are provided on b corresponding to j and k on a, while on a there are added teeth o′, n′, corresponding to o, n, on b, with the result that two wheels such as a or two such as b would work correctly together, either being the driver or either the follower, and rotation may occur in either direction. In this operation we have simply added faces to the teeth on a, and flanks to those on b, the curves being generated or obtained by rolling the generating, or curve marking, circle c upon the pitch circles p and p′. Thus, for the flanks of the teeth of a, c is rolled upon, and within the pitch circle p of a; while for the face curves of the same teeth c is rolled upon, but without or outside of p. Similarly for the teeth of wheel b the generating circle c is rolled within p′ for the flanks and without for the faces. With the curves rolled or produced with the same diameter of generating circle the wheels will work correctly together, no matter what their relative diameter may be, as will be shown hereafter.
In this demonstration, however, the curves for the faces of the teeth being produced by an operation distinct from that employed to produce the flank curves, it is not clearly seen that the curves for the flanks of one wheel are the proper curves to insure a uniform velocity to the other. This, however, may be made clear as follows:—
In Fig. 27 let a a and b b represent the pitch circles of two wheels of equal diameters, and therefore having the same number of teeth. On the left, the wheels are shown with the teeth in, while on the right-hand side of the line of centres a b, the wheels are shown blank; a a is the pitch line of one wheel, and b b that for the other. Now suppose that both wheels are capable of being rotated on their shafts, whose centres will of course be on the line a b, and suppose a third disk, q, be also capable of rotation upon its centre, c, which is also on the line a b. Let these three wheels have sufficient contact at their perimeters at the point n, that if one be rotated it will rotate both the others (by friction) without any slip or lost motion, and of course all three will rotate at an equal velocity. Suppose that there is fixed to wheel q a pencil whose point is at n. If then rotation be given to a a in the direction of the arrow s, all three wheels will rotate in that direction as denoted by their respective arrows s.
Assume, then, that rotation of the three has occurred until the pencil point at n has arrived at the point m, and during this period of rotation the point n will recede from the line of centres a b, and will also recede from the arcs or lines of the two pitch circles a a, b b. The pencil point being capable of marking its path, it will be found on reaching m to have marked inside the pitch circle b b the curve denoted by the full line m x, and simultaneously with this curve it has marked another curve outside of a a, as denoted by the dotted line y m. These two curves being marked by the pencil point at the same time and extending from y to m, and x also to m. They are prolonged respectively to p and to k for clearness of illustration only.
The rotation of the three wheels being continued, when the pencil point has arrived at o it will have continued the same curves as shown at o f, and o g, curve o f being the same as m x placed in a new position, and o g being the same as m y, but placed in a new position. Now since both these curves (o f and o g) were marked by the one pencil point, and at the same time, it follows that at every point in its course that point must have touched both curves at once. Now the pencil point having moved around the arc of the circle q from n to m, it is obvious that the two curves must always be in contact, or coincide with each other, at some point in the path of the pencil or describing point, or, in other words, the curves will always touch each other at some point on the curve of q, and between n and o. Thus when the pencil has arrived at m, curve m y touches curve k x at the point m, while when the pencil had arrived at point o, the curves o f and o g will touch at o. Now the pitch circles a a and b b, and the describing circle q, having had constant and uniform velocity while the traced curves had constant contact at some point in their lengths, it is evident that if instead of being mere lines, m y was the face of a tooth on a a, and m x was the flank of a tooth on b b, the same uniform motion may be transmitted from a a, to b b, by pressing the tooth face m y against[I-11] the tooth flank m x. Let it now be noted that the curve y m corresponds to the face of a tooth, as say the face e of a tooth on a a, and that curve x m corresponds to the flank of a tooth on b b, as say to the flank f, short portions only of the curves being used for those flanks. If the direction of rotation of the three wheels was reversed, the same shape of curves would be produced, but they would lie in an opposite direction, and would, therefore, be suitable for the other sides of the teeth. In this case, the contact of tooth upon tooth will be on the other side of the line of centres, as at some point between n and q.
In this illustration the diameter of the rolling or describing circle q, being less than the radius of the wheels a a or b b, the flanks of the teeth are curves, and the two wheels being of the same diameter, the teeth on the two are of the same shape. But the principles governing the proper formation of the curve remain the same whatever be the conditions. Thus in Fig. 28 are segments of a pair of wheels of equal diameter, but the describing, rolling, or curve-generating circle is equal in diameter to the radius of the wheels. Motion is supposed to have occurred in the direction of the arrows, and the tracing point to have moved from n to m. During this motion it will have marked a curve y m, a portion of the y end serving for the face of a tooth on one wheel, and also the line k x, a continuation of which serves for the flank of a tooth on the other wheel. In Fig. 29 the pitch circles only of the wheels are marked, a a being twice the diameter of b b, and the curve-generating circle being equal in diameter to the radius of wheel b b. Motion is assumed to have occurred until the pencil point, starting from n, had arrived at o, marking curves suitable for the face of the teeth on one wheel and for the flanks of the other as before, and the contact of tooth upon tooth still, at every point in the path of the teeth, occurring at some point of the arc n o. Thus when the point had proceeded as far as point m it will have marked the curve y and the radial line x, and when the point had arrived at o, it will have prolonged m y into o g and x into o f, while in either position the point is marking both lines. The velocities of the wheels remain the same notwithstanding their different diameters, for the arc n g must obviously (if the wheels rotate without slip by friction of their surfaces while the curves are traced) be equal in length to the arc n f or the arc n o.
In Fig. 30 a a and b b are the pitch circles of two wheels as before, and c c the pitch circle of an annular or internal gear, and d is the rolling or describing circle. When the describing point arrived at m, it will have marked the curve y for the face of a tooth on a a, the curve x for the flank of a tooth on b b, and the curve e for the face of a tooth on the internal wheel c c.[I-12] Motion being continued m y will be prolonged to o g, while simultaneously x will be extended into o f and e into h v, the velocity of all the wheels being uniform and equal. Thus the arcs n v, n f, and n g, are of equal length.
In Fig. 31 is shown the case of a rack and pinion; a a is the pitch line of the rack, b b that of the pinion, a b at a right angle to a a, the line of centres, and d the generating circle. The wheel and rack are shown with teeth n on one side simply for clearness of illustration. The pencil point n will, on arriving at m, have traced the flank curve x and the curve y for the face of the rack teeth.
It has been supposed that the three circles rotated together by the frictional contact of their perimeters on the line of centres, but the circumstances will remain the same if the wheels remain at rest while the generating or describing circle is rolled around them. Thus in Fig. 32 are two segments of wheels as before, c representing the centre of a tooth on a a, and d representing the centre of a tooth on b b. Now suppose that a generating or rolling circle be placed with its pencil point at e, and that it then be rolled around a a until it had reached the position marked 1, then it will have marked the curve from e to n, a part of this curve serving for the face of tooth c. Now let the rolling circle be placed within the pitch circle a a and its pencil point n be set to e, then, on being rolled to position 2, it will have marked the flank of tooth c. For the other wheel suppose the rolling wheel or circle to have started from f and rolled to the line of centres as in the cut, it will have traced the curve forming the face of the tooth d. For the flank of d the rolling circle or wheel is placed within b b, its tracing point set at f on the pitch circle, and on being rolled to position 3 it will have marked the flank curve. The curves thus produced will be precisely the same as those produced by rotating all three wheels about their axes, as in our previous demonstrations.
The curves both for the faces and for the flanks thus obtained will vary in their curvature with every variation in either the diameter of the generating circle or of the base or pitch circle of the wheel. Thus it will be observable to the eye that the face curve of tooth c is more curved than that of d, and also that the flank curve of d is more spread at the root than is that for c, which has in this case resulted from the difference between the diameter of the wheels a a and b b. But the curves obtained by a given diameter of rolling circle on a given diameter of pitch circle will be correct for any pitch of teeth that can be used upon wheels having that diameter of pitch circle. Thus, suppose we have a curve obtained by rolling a wheel of 20 inches circumference on a pitch circle of 40 inches circumference—now a wheel of 40 inches in circumference may contain 20 teeth of 2 inch arc pitch, or 10 teeth of 4 inch arc pitch, or 8 teeth of 5 inch arc pitch, and the curve may be used for either of those pitches.
If we trace the path of contact of each tooth, from the moment it takes until it leaves contact with a tooth upon the other wheel, we shall find that contact begins at the point where the flank of the tooth on the wheel that drives or imparts motion to the other wheel, meets the face of the tooth on the driven wheel, which will always be where the point of the driven tooth cuts or meets the generating or rolling circle of the driving tooth. Thus in Fig. 33 are represented segments of two spur-wheels marked respectively the driver and the driven, their generating circles being marked at g and g′, and x x representing the line of centres. Tooth a is shown in the position in which it commences its contact with tooth[I-13] b at b. Secondly, we shall find that as these two teeth approach the line of centres x, the point of contact between them moves or takes place along the thickened arc or curve c x, or along the path of the generating circle g.
Thus we may suppose tooth d to be another position of tooth a, the contact being at f, and as motion was continued the contact would pass along the thickened curve until it arrived at the line of centres x. Now since the teeth have during this path of contact approached the line of centres, this part of the whole arc of action or of the path of contact is termed the arc of approach. After the two teeth have passed the line of centres x, the path of contact of the teeth will be along the dotted arc from x to l, and as the teeth are during this period of motion receding from x this part of the contact path is termed the arc of recess.
That contact of the teeth would not occur earlier than at c nor later than at l, is shown by the dotted teeth sides; thus a and b would not touch when in the position denoted by the dotted teeth, nor would teeth i and k if in the position denoted by their dotted lines.
If we examine further into this path of contact we find that throughout its whole path the face of the tooth of one wheel has contact with the flank only of the tooth of the other wheel, and also that the flank only of the driving-wheel tooth has contact before the tooth reaches the line of centres, while the face of only the driving tooth has contact after the tooth has passed the line of centres.
Thus the flanks of tooth a and of tooth d are in driving contact with the faces of teeth b and e, while the face of tooth h is in contact with the flank of tooth i.
These conditions will always exist, whatever be the diameters of the wheels, their number of teeth or the diameter of the generating circle. That is to say, in fully developed epicycloidal teeth, no matter which of two wheels is the driver or which the driven wheel, contact on the teeth of the driver will always be on the tooth flank during the arc of approach and on the tooth face during the arc of recess; while on the driven wheel contact during the arc of approach will be on the tooth face only, and during the arc of recess on the tooth flank only, it being borne in mind that the arcs of approach and recess are reversed in location if the direction of revolution be reversed. Thus if the direction of wheel motion was opposite to that denoted by the arrows in Fig. 33 then the arc of approach would be from m to x, and the arc of recess from x to n.
It is laid down by Professor Willis that the motion of a pair of gear-wheels is smoother in cases where the path of contact begins at the line of centres, or, in other words, when there is no arc of approach; and this action may be secured by giving to the driven wheel flanks only, as in Fig. 34, in which the driver has fully developed teeth, while the teeth on the driven have no faces.
In this case, supposing the wheels to revolve in the direction of arrow p, the contact will begin at the line of centres x, move or pass along the thickened arc and end at b, and there will be contact during the arc of recess only. Similarly, if the direction of motion be reversed as denoted by arrow q, the driver will begin contact at x, and cease contact at h, having, as before, contact during the arc of recess only.
But if the wheel w were the driver and v the driven, then these conditions would be exactly reversed. Thus, suppose this to be the case and the direction of motion be as denoted by arrow p, the contact would occur during the arc of approach, from h to x, ceasing at x.
Or if w were the driver, and the direction of motion was as denoted by q, then, again, the path of contact would be during the arc of approach only, beginning at b and ceasing at x, as denoted by the thickened arc b x.
The action of the teeth will in either case serve to give a theoretically perfect motion so far as uniformity of velocity is concerned, or, in other words, the motion of the driver will be transmitted with perfect uniformity to the driven wheel. It will be observed, however, that by the removal of the faces of the teeth, there are a less number of teeth in contact at each instant of time; thus, in Fig. 33 there is driving contact at three points, c, f, and j, while in Fig. 34 there is driving contact at two points only. From the fact that the faces of the teeth work with the flanks only, and that one side only of the teeth comes into action, it becomes apparent that each tooth may have curves formed by four different diameters of rolling or generating circles and yet work correctly, no matter which wheel be the driver, or which the driven wheel or follower, or in which direction motion occurs. Thus in Fig. 35, suppose wheel v to be the driver, having motion in the direction of arrow p, then faces a on the teeth of v will work with flanks b of the teeth on w, and so long as the curves for these faces and flanks are obtained with the same diameter of rolling circle, the action of the teeth will be correct, no matter[I-14] what the shapes of the other parts of the teeth. Now suppose that v still being the driver, motion occurs in the other direction as denoted by q, then the faces c of the teeth on v will drive the flanks c of the teeth on w, and the motion will again be correct, providing that the same diameter (whatever it may be) of rolling circle be used for these faces and flanks, irrespective, of course, of what diameter of rolling circle is used for any other of the teeth curves. Now suppose that w is the driver, motion occurring in the direction of p, then faces e will drive flanks f, and the motion will be correct as before if the curves e and f are produced with the same diameter of rolling circle. Finally, let w be the driving wheel and motion occur in the direction of q, and faces g will drive flanks h, and yet another diameter of rolling circle may be used for these faces and flanks. Here then it is shown that four different diameters of rolling circles may be used upon a pair of wheels, giving teeth-forms that will fill all the requirements so far as correctly transmitting motion is concerned. In the case of a pair of wheels having an equal number of teeth, so that each tooth on one wheel will always fall into gear with the same tooth on the other wheel, every tooth may have its individual curves differing from all the others, providing that the corresponding teeth on the other wheel are formed to match them by using the same size of rolling circle for each flank and face that work together.
It is obvious, however, that such teeth would involve a great deal of labor in their formation and would possess no advantage, hence they are not employed. It is not unusual, however, in a pair of wheels that are to gear together and that are not intended to interchange with other wheels, to use such sizes as will give to[I-15] for the face of the teeth on the largest wheel of the pair and for the flanks of the teeth of the smallest wheel, a generating circle equal in diameter to the radius of the smallest wheel, and for the faces of the teeth of the small wheel and the flanks of the teeth of the large one, a generating circle whose diameter equals the radius of the large wheel.
It will now be evident that if we have planned a pair or a train of wheels we may find how many teeth will be in contact for any given pitch, as follows. In Fig. 36 let a, b, and c, represent three blanks for gear-wheels whose addendum circles are m, n and o; p representing the pitch circles, and q representing the circles for the roots of the teeth. Let x and y represent the lines of centres, and a, h, i and k the generating or rolling circle, whose centres are on the respective lines of centres—the diameter of the generating circle being equal to the radius of the pinion, as in the Willis system, then, the pinion m being the driver, and the wheels revolving in the direction denoted by the respective arrows, the arc or path of contact for the first pair will be from point d, where the generating circle g crosses circle n to e, where generating circle h crosses the circle m, this path being composed of two arcs of a circle. All that is necessary, therefore, is to set the compasses to the pitch the teeth are to have and step them along these arcs, and the number of steps will be the number of teeth that will be in contact. Similarly, for the second pair contact will begin at r and end at s, and the compasses applied as before (from r to s) along the arc of generating circle i to the line of centres, and thence along the arc of generating circle k to s, will give in the number of steps, the number of teeth that will be in contact. If for any given purpose the number of teeth thus found to be in contact is insufficient; the pitch may be made finer.
When a wheel is intended to be formed to work correctly with any other wheel having the same pitch, or when there are more than two wheels in the train, it is necessary that the same size of generating circle be used for all the faces and all the flanks in the set, and if this be done the wheels will work correctly together, no matter what the number of the teeth in each wheel may be, nor in what way they are interchanged. Thus in Fig. 37, let a represent the pitch line of a rack, and b and c the pitch circles of two wheels, then the generating circle would be rolled within b, as at 1, for the flank curves, and without it, as at 2, for the face curves of b. It would be rolled without the pitch line, as at 3, for the rack faces, and within it, as at 4, for the rack flanks, and without c, as at 5, for the faces, and within it, as at 6, for flanks of the teeth on c, and all the teeth will work correctly together however they be placed; thus c might receive motion from the rack, and b receive motion from c. Or if any number of different diameters of wheels are used they will all work correctly together and interchange perfectly, with the single condition that the same size of generating circle be used throughout. But the curves of the teeth so formed will not be alike. Thus in Fig. 38 are shown three teeth, all struck with the same size of generating circle, d being for a wheel of 12 teeth, e for a wheel of 50 teeth, and f a tooth of a rack; teeth e, f, being made wider so as to let the curves show clearly on each side, it being obvious that since the curves are due to the relative sizes of the pitch and generating circles they are equally applicable to any pitch or thickness of teeth on wheels having the same diameters of pitch circle.
In determining the diameter of a generating circle for a set or[I-16] train of wheels, we have the consideration that the smaller the diameter of the generating circle in proportion to that of the pitch circle the more the teeth are spread at the roots, and this creates a pressure tending to thrust the wheels apart, thus causing the axle journals to wear. In Fig. 39, for example, a a is the line of centres, and the contact of the curves at b c would cause a thrust in the direction of the arrows d, e. This thrust would exist throughout the whole path of contact save at the point f, on the line of centres. This thrust is reduced in proportion as the diameter of the generating circle is increased; thus in Fig. 40, is represented a pair of pinions of 12 teeth and 3 inch pitch, and c being the driver, there is contact at e, and at g, and e being a radial line, there is obviously a minimum of thrust.
What is known as the Willis system for interchangeable gearing, consists of using for every pitch of the teeth a generating circle whose diameter is equal to the radius of a pinion having 12 teeth, hence the pinion will in each pitch have radial flanks, and the roots of the teeth will be more spread as the number of teeth in the wheel is increased. Twelve teeth is the least number that it is considered practicable to use; hence it is obvious that under this system all wheels of the same pitch will work correctly together.
Unless the faces of the teeth and the flanks with which they work are curves produced from the same size of generating circle, the velocity of the teeth will not be uniform. Obviously the revolutions of the wheels will be proportionate to their numbers of teeth; hence in a pair of wheels having an equal number of teeth, the revolutions will per force be equal, but the driver will not impart uniform motion to the driven wheel, but each tooth will during the path of contact move irregularly.
The velocity of a pair of wheels will be uniform at each instant of time, if a line normal to the surfaces of the curves at their point of contact passes through the point of contact of the pitch circles on the line of centres of the wheels. Thus in Fig. 41, the line a a is tangent to the teeth curves where they touch, and d at a right angle to a a, and meets it at the point of the tooth curves, hence it is normal to the point of contact, and as it meets the pitch circles on the line of centres the velocity of the wheels will be uniform.
The amount of rolling motion of the teeth one upon the other while passing through the path of contact, will be a minimum when the tooth curves are correctly formed according to the rules given. But furthermore the sliding motion will be increased in proportion as the diameter of the generating circle is increased, and the number of teeth in contact will be increased because the[I-17] arc, or path, of contact is longer as the generating circle is made larger.
Thus in Fig. 42 is a pair of wheels whose tooth curves are from a generating circle equal to the radius of the wheels, hence the flanks are radial. The teeth are made of unusual depth to keep the lines in the engraving clear. Suppose v to be the driver, w the driven wheel or follower, and the direction of motion as at p, contact upon tooth a will begin at c, and while a is passing to the line of centres the path of contact will pass along the thickened line to x. During this time the whole length of face from c to r will have had contact with the length of flank from c to n, and it follows that the length of face on a that rolled on c n can only equal the length of c n, and that the amount of sliding motion must be represented by the length of r n on a, and the amount of rolling motion by the length n c. Again, during the arc of recess (marked by dots) the length of flank that will have had contact is the depth from s to ls, and over this depth the full length of tooth face on wheel v will have swept, and as l s equals c n, the amount of rolling and of sliding motion during the arc of recess is equal to that during the arc of approach, and the action is in both cases partly a rolling and partly a sliding one. The two wheels are here shown of the same diameter, and therefore contain an equal number of teeth, hence the arcs of approach and of recess are equal in length, which will not be the case when one wheel contains more teeth than the other. Thus in Fig. 43, let a represent a segment of a pinion, and b a segment of a spur-wheel, both segments being blank with their pitch circles, the tooth height and depth being marked by arcs of circles. Let c and d represent the generating circles shown in the two respective positions on the line of centres. Let pinion a be the driver moving in the direction of p, and the arc of approach will be from e to x along the thickened arc, while the arc of recess will be as denoted by the dotted arc from x to f. The distance e x being greater than distance x f, therefore the arc of approach is longer than that of recess.
But suppose b to be the driver and the reverse will be the case, the arc of approach will begin at g and end at x, while the arc of recess will begin at x and end at h, the latter being farther from the line of centres than g is. It will be found also that, one wheel being larger than the other, the amount of sliding and rolling contact is different for the two wheels, and that the flanks of the teeth on the larger wheel b, have contact along a greater portion of their depths than do the flanks of those on the smaller, as is shown by the dotted arc i being farther from the pitch circle than the dotted arc j is, these two dotted arcs representing the paths of the lowest points of flank contact, points f and g, marking the initial lowest contact for the two directions of revolution.
Thus it appears that there is more sliding action upon the teeth of the smaller than upon those of the larger wheel, and this is a condition that will always exist.
In Fig. 44 is represented portion of a pair of wheels corresponding to those shown in Fig. 42, except that in this case the diameter of the generating circle is reduced to one quarter that of the pitch diameter of the wheels. v is the driver in the direction[I-18] the teeth of v that will have contact is c n, which, the wheels, being of equal diameter, will remain the same whichever wheel be the driver, and in whatever direction motion occurs. The amount of rolling motion is, therefore, c n, and that of sliding is the difference between the distance c n and the length of the tooth face.
If now we examine the distance c n in Fig. 42, we find that reducing the diameter of generating circle in Fig. 44 has increased the depth of flank that has contact, and therefore increased the rolling motion of the tooth face along the flank, and correspondingly diminished the sliding action of the tooth contact. But at the same time we have diminished the number of teeth in contact. Thus in Fig. 42 there are three teeth in driving contact, while in Fig. 44 there are but two, viz., d and e.
In an article by Professor Robinson, attention is called to the fact that if the teeth of wheels are not formed to have correct curves when new, they cannot be improved by wear; and this will be clearly perceived from the preceding remarks upon the amount of rolling and sliding contact. It will also readily appear that the nearer the diameter of the generating to that of the base circle the more the teeth wear out of correct shape; hence, in a train of gearing in which the generating circle equals the radius of the pinion, the pinion will wear out of shape the quickest, and the largest wheel the least; because not only does each tooth on the pinion more frequently come into action on account of its increased revolutions, but furthermore the length of flank that has contact is less, while the amount of sliding action is greater. In Fig. 45, for example, are a wheel and pinion, the latter having radial flanks and the pinion being the driver, the arc of approach is the thickened arc from c to the line of centres, while the arc of recess is denoted by the dotted arc. As contact on the pinion flank begins at point c and ends at the line of centres, the total depth of flank that suffers wear from the contact is that from c to n; and as the whole length of the wheel tooth face sweeps over this depth c n, the pinion flanks must wear faster than the wheel faces, and the pinion flanks will wear underneath, as denoted by the dotted curve on the flanks of tooth w. In the case of the wheel, contact on its tooth flanks begins at the line of centres and ends at l, hence that flank can only wear between point l and the pitch line l; and as the whole length of pinion face sweeps on this short length l s, the pinion flank will wear most, the wear being in the direction of the dotted arc on the left-hand side v of the tooth. Now the pinion flank depth c n, being less than the wheel flank depth s l, and the same length of tooth face sweeping (during the path of contact) over both, obviously the pinion tooth will wear the most, while both will, as the wear proceeds, lose their proper flank curve. In Fig. 46 the generating arcs, g and g′, and the wheel are the same, but the pinion is larger. As a result the acting length c n, of pinion flank is increased, as is also the acting length s l, of wheel flank; hence, the flanks of both wheels would wear better, and also better preserve their correct and original shapes.
It has been shown, when referring to Figs. 42 and 44, when treating of the amount of sliding and of rolling motion, that the smaller the diameter of rolling circle in proportion to that of pitch circle, the longer the acting length of flank and the more the amount of rolling motion; and it follows that the teeth would also preserve their original and true shape better. But the wear of the teeth, and the alteration of tooth form by reason of that wear, will, in any event, be greater upon the pinion than upon the[I-19] wheel, and can only be equal when the two wheels are of equal diameter, in which case the tooth curves will be alike on both wheels, and the acting depths of flank will be equal, as shown in Fig. 47, the flanks being radial, and the acting depths of flank being shown at j k. In Fig. 48 is shown a pair of wheels with a generating circle, g and g′, of one quarter the diameter of the base circle or pitch diameter, and the acting length of flank is shown at l m. The wear of the teeth would, therefore, in this latter case, cause it in time to assume the form shown in Fig. 49. But it is to be noted that while the acting depth of flank has been increased the arcs of contact have been diminished, and that in Fig. 47 there are two teeth in contact, while in Fig. 48 there is but one, hence the pressure upon each tooth is less in proportion as the diameter of the generating circle is increased. If a train of wheels are to be constructed, or if the wheels are to be capable of interchanging with other combinations of wheels of the same pitch, the diameter of the generating circle must be equal to the smallest wheel or pinion, which is, under the Willis system, a pinion of 12 teeth; under the Pratt and Whitney, and Brown and Sharpe systems, a pinion of 15 teeth.
But if a pair or a particular train of gears are to be constructed, then a diameter of generating circle may be selected that is considered most suitable to the particular conditions; as, for example, it may be equal to the radius of the smallest wheel giving it radial flanks, or less than that radius giving parallel or spread flanks. But in any event, in order to transmit continuous motion, the diameter of generating circle must be such as to give arcs of action that are equal to the pitch, so that each pair of teeth will come into action before the preceding pair have gone out of action.
It may now be pointed out that the degrees of angle that the teeth move through always exceeds the number of degrees of angle contained in the paths of contact, or, in other words, exceeds the degrees contained in the arcs of approach and recess combined.
In Fig. 50, for example, are a wheel a and pinion b, the teeth on the wheel being extended to a point. Suppose that the wheel a is the driver, and contact will begin between the two teeth d and f on the dotted arc. Now suppose tooth d to have moved to position c, and f will have been moved to position h. The degrees of angle the pinion has been moved through are therefore denoted by i, whereas the degrees of angle the arcs of contact contain are therefore denoted by j.
The degrees of angle that the wheel a has moved through are obviously denoted by e, because the point of tooth d has during the arcs of contact moved from position d to position c. The degrees of angle contained in its path of contact are denoted by k, and are less than e, hence, in the case of teeth terminating in a point as tooth d, the excess of angle of action over path of contact is as many degrees as are contained in one-half the thickness[I-20] of the tooth, while when the points of the teeth are cut off, the excess is the number of degrees contained in the distance between the corner and the side of the tooth as marked on a tooth at p.
With a given diameter of pitch circle and pitch diameter of wheel, the length of the arc of contact will be influenced by the height of the addendum from the pitch circle, because, as has been shown, the arcs of approach and of recess, respectively, begin and end on the addendum circle.
If the height of the addendum on the follower be reduced, the arc of approach will be reduced, while the arc of recess will not be altered; and if the follower have no addendum, contact between the teeth will occur on the arc of recess only, which gives a smoother motion, because the action of the driver is that of dragging rather than that of pushing the follower. In this case, however, the arc of recess must, to produce continuous motion, be at least equal to the pitch.
It is obvious, however, that the follower having no addendum would, if acting as a driver to a third wheel, as in a train of wheels, act on its follower, or the fourth wheel of the train, on the arc of approach only; hence it follows that the addendum might be reduced to diminish, or dispensed with to eliminate action, on the arc of approach in the follower of a pair of wheels only, and not in the case of a train of wheels.
To make this clear to the reader it may be necessary to refer again to Fig. 33 or 34, from which it will be seen that the action of the teeth of the driver on the follower during the arc of approach is produced by the flanks of the driver on the faces of the follower. But if there are no such faces there can be no such contact.
On the arc of recess, however, the faces of the driver act on the flanks of the follower, hence the absence of faces on the follower is of no import.
From these considerations it also appears that by giving to the driver an increase of addendum the arc of recess may be increased without affecting the arc of approach. But the height of addendum in machinists’ practice is made a constant proportion of the pitch, so that the wheel may be used indiscriminately, as circumstances may require, as either a driver or a follower, the arcs of approach and of recess being equal. The height of addendum, however, is an element in determining the number of teeth in contact, and upon small pinions this is of importance.
In Fig. 51, for example, is shown a section of two pinions of equal diameters, and it will be observed that if the full line a determined the height of the addendum there would be contact either at c or b only (according to the direction in which the motion took place).
With the addendum extended to the dotted circle, contact would be just avoided, while with the addendum extended to d there would be contact either at e or at f, according to which direction the wheel had motion.
This, by dividing the strain over two teeth instead of placing it all upon one tooth, not only doubles the strength for driving capacity, but decreases the wear by giving more area of bearing surface at each instant of time, although not increasing that area in proportion to the number of teeth contained in the wheel.
In wheels of larger diameter, short teeth are more permissible, because there are more teeth in contact, the number increasing with the diameters of the wheels. It is to be observed, however, that from having radial flanks, the smallest wheel is always the weakest, and that from making the most revolutions in a given[I-21] time, it suffers the most from wear, and hence requires the greatest attainable number of teeth in constant contact at each period of time, as well as the largest possible area of bearing or wearing surface on the teeth.
It is true that increasing the “depth of tooth to pitch line” increases the whole length of tooth, and, therefore, weakens it; but this is far more than compensated for by distributing the strain over a greater number of teeth. This is in practice accomplished, when circumstances will permit, by making the pitch finer, giving to a wheel, of a given diameter, a greater number of teeth.
When the wheels are required to transmit motion rather than power (as in the case of clock wheels), to move as frictionless as possible, and to place a minimum of thrust on the journals of the shafts of the wheels, the generating circle may be made nearly as large as the diameter of the pitch circle, producing teeth of the form shown in Fig. 52. But the minimum of friction is attained when the two flanks for the tooth are drawn into one common hypocycloid, as in Fig. 53. The difference between the form of tooth shown in Fig. 52 and that shown in Fig. 53, is merely due to an increase in the diameter of the generating circle for the latter. It will be observed that in these forms the acting length of flank diminishes in proportion as the diameter of the generating circle is increased, the ultimate diameter of generating circle being as large as the pitch circles.
[1]This form is undesirable in that there is contact on one side only (on the arc of approach) of the line of centres, but the flanks of the teeth may be so modified as to give contact on the arc of recess also, by forming the flanks as shown in Fig. 54, the flanks, or rather the parts within the pitch circles, being nearly half circles, and the parts without with peculiarly formed faces, as shown in the figure. The pitch circles must still be regarded as the rolling circles rolling upon each other. Suppose b a tracing point on b, then as b rolls on a it will describe the epicycloid a b. A parallel line c d will work at a constant distance as at c d from a b, and this distance may be the radius of that part of d that is within the pitch line, the same process being applied to the teeth on both wheels. Each tooth is thus composed of a spur based upon a half cylinder.
[1] From an article by Professor Robinson.
Comparing Figs. 53 and 54, we see that the bases in 53 are flattest, and that the contact of faces upon them must range nearer the pitch line than in 54. Hence, 53 presents a more favorable obliquity of the line of direction of the pressures of tooth upon tooth. In seeking a still more favorable direction by going outside for the point of contact, we see by simply recalling the method of generating the tooth curves, that tooth contacts outside the pitch lines have no possible existence; and hence, Fig. 53 may be regarded as representing that form of toothed gear which will operate with less friction than any other known form.
This statement is intended to cover fixed teeth only, and not that complicated form of the trundle wheel in which the cylinder teeth are friction rollers. No doubt such would run still easier, even with their necessary one-sided contacts. Also, the statement is supposed to be confined to such forms of teeth as have good practical contacts at and near the line of centres.
Bevel-gear wheels are employed to transmit motion from one shaft to another when the axis of one is at an angle to that of the other. Thus in Fig. 55 is shown a pair of bevel-wheels to transmit motion from shafts at a right angle. In bevel-wheels all the lines of the teeth, both at the tops or points of the teeth, at the bottoms of the spaces, and on the sides of the teeth, radiate from the centre e, where the axes of the two shafts would meet if produced. Hence the depth, thickness, and height of the tooth decreases as[I-22] the point e is approached from the diameter of the wheel, which is always measured on the pitch circle at the largest end of the cone, or in other words, at the largest pitch diameter.
The principles governing the practical construction of the curves for the teeth of the bevel-wheels may be explained as follows:—
In Fig. 56 let f and g represent two shafts, rotating about their respective axes; and having cones whose greatest diameters are at a and b, and whose points are at e. The diameter a being equal to that of b their circumferences will be equal, and the angular and velocity ratios will therefore be equal.
Let c and d represent two circles about the respective cones, being equidistant from e, and therefore of equal diameters and circumferences, and it is obvious that at every point in the length of each cone the velocity will be equal to a point upon the other so long as both points are equidistant from the points of intersection of the axes of the two shafts; hence if one cone drive the other by frictional contact of surfaces, both shafts will be rotated at an equal speed of rotation, or if one cone be fixed and the other moved around it, the contact of the surfaces will be a rolling contact throughout. The line of contact between the two cones will be a straight line, radiating at all times from the point e. If such, however, is not the case, then the contact will no longer be a rolling one. Thus, in Fig. 57 the diameters or circumferences at a and b being equal, the surfaces would roll upon each other, but on account of the line of contact not radiating from e (which is the common centre of motion for the two shafts) the circumference c is less than that of d, rendering a rolling contact impossible.
We have supposed that the diameters of the cones be equal, but the conditions will remain the same when their diameters are unequal; thus, in Fig. 58 the circumference of a is twice that of b, hence the latter will make two rotations to one of the former, and the contact will still be a rolling one. Similarly the circumference of d is one half that of c, hence d will also make two rotations to one of c, and the contact will also be a rolling one; a condition which will always exist independent of the diameters of the wheels so long as the angles of the faces, or wheels, or (what is the same thing, the line of contact between the two,) radiates from the point e, which is located where the axes of the shafts would meet.
The principles governing the forms of the cones on which the teeth are to be located thus being explained, we may now consider the curves of the teeth. Suppose that in Fig. 59 the cone a is fixed, and that the cone whose axis is f be rotated upon it in the direction of the arrow. Then let a point be fixed in any part of the circumference of b (say at d), and it is evident that the path of this point will be as b rolls around the axis f, and at the same time around a from the centre of motion, e. The curve so generated or described by the point d will be a spherical epicycloid. In this case the exterior of one cone has rolled upon the coned surface of the other; but suppose it rolls upon the interior, as around the walls of a conical recess in a solid body; then a point in its circumference would describe a curve known as the spherical hypocycloid; both curves agreeing (except in their spherical property) to the epicycloid and hypocycloid of the spur-wheel. But this spherical property renders it very difficult indeed to practically delineate or mark the curves by rolling contact, and on account of this difficulty Tredgold devised a method of construction whereby the curves may be produced sufficiently accurate for all practical purposes, as follows:—
In Fig. 60 let a a represent the axis of one shaft, and b the axis of the other, the axes of the two meeting at w. Mark e,[I-23] representing the diameter of one wheel, and f that of the other (both lines representing the pitch circles of the respective wheels). Draw the line g g passing through the point w, and the point t, where the pitch circles e, f meet, and g g will be the line of contact between the cones. From w as a centre, draw on each side of g g dotted lines as p, representing the height of the teeth above and below the pitch line g g. At a right angle to g g mark the line j k, and from the junction of this line with axis b (as at q) as a centre, mark the arc a, which will represent the pitch circle for the large diameter of pinion d; mark also the arc b for the addendum and c for the roots of the teeth, so that from b to c will represent the height of the tooth at that end.
Similarly from p, as a centre, mark (for the large diameter of wheel c,) the pitch circle g, root circle h, and addendum i. On these arcs mark the curves in the same manner as for spur-wheels. To obtain these arcs for the small diameters of the wheels, draw m m parallel to j k. Set the compasses to the radius r l, and from p, as a centre, draw the pitch circle k. To obtain the depth for the tooth, draw the dotted line p, meeting the circle h, and the point w. A similar line from circle i to w will show the height of the addendum, or extreme diameter; and mark the tooth curves on k, l, m, in the same manner as for a spur-wheel.
Similarly for the pitch circle of the small end of the pinion teeth, set the compasses to the radius s l, and from q as a centre, mark the pitch circle d, outside of d mark e for the height of the addendum and inside of d mark f for the roots of the teeth at that end. The distance between the dotted lines (as p) represents the full height of the teeth, hence h meets line p, being the root of tooth for the large wheel, and to give clearance, the point of the pinion teeth is marked below, thus arc b does not meet h or p. Having obtained these arcs the curves are rolled as for a spur-wheel.
A tooth thus marked out is shown at x, and from its curves between b c, a template for the large diameter of the pinion tooth may be made, while from the tooth curves between the arcs e f, a template for the smallest tooth diameter of the pinion can be made.
Similarly for the wheel c the outer end curves are marked on the lines g, h, i, and those for the inner end on the lines k, l, m.
Internal or annular gear-wheels have their tooth curves formed by rolling the generating circle upon the pitch circle or base circle, upon the same general principle as external or spur-wheels. But the tooth of the annular wheel corresponds with the space in the spur-wheel, as is shown in Fig. 61, in which curve a forms the flank of a tooth on a spur-wheel p, and the face of a tooth on the annular wheel w. It is obvious then that the generating circle is rolled within the pitch circle for the face of the wheel and without for its flank, or the reverse of the process for spur-wheels. But in the case of internal or annular wheels the path of contact of tooth upon tooth with a pinion having a given number of teeth increases in proportion as the number of teeth in the wheel is diminished, which is also the reverse of what occurs in spur-wheels; as will readily be perceived when it is considered that if in an internal wheel the pinion have as many teeth as the wheel the contact would exist around the whole pitch circles of the wheel and pinion and the two would rotate together without any motion of tooth upon tooth. Obviously then we have, in the case of internal wheels, a consideration as to what is the greatest number (as well as what is the least number) of teeth a pinion may contain to work with a given wheel, whereas in spur-wheels the reverse is again the case, the consideration being how few teeth the wheel may contain to work with a given pinion. Now it is found that although the curves of the teeth in internal wheels and pinions may be rolled according to the principles already laid down for spur-wheels, yet cases may arise in which internal gears will not work under conditions in which spur-wheels would work, because the internal wheels will not engage together. Thus, in Fig. 62, is a pinion of 12 teeth and a wheel of 22 teeth, a generating circle having a diameter equal to the radius of the pinion having been used for all the tooth curves of both wheel and pinion. It will be observed that teeth a, b, and c clearly overlap teeth d, e, and f, and would therefore prevent the wheels from engaging to the requisite depth. This may of course be remedied by taking the faces off the pinion, as in Fig. 63, and thus confining the arc of contact to an arc of recess if the pinion drives, or an arc of approach if the wheel drives; or the number of teeth in the pinion may be reduced, or that in the wheel increased; either of which may be carried out to a degree sufficient to enable the teeth to engage and not interfere one with the other. In Fig. 64 the number of teeth in the pinion p is reduced from 12 to 6, the wheel w having 22 as before, and it will be observed that the teeth engage and properly clear each other.
By the introduction into the figure of a segment of a spur-wheel[I-24] also having 22 teeth and placed on the other side of the pinion, it is shown that the path of contact is greater, and therefore the angle of action is greater, in internal than in spur gearing. Thus suppose the pinion to drive in the direction of the arrows and the thickened arcs a b will be the arcs of approach, a measuring longer than b. The dotted arcs c d represent the arcs of receding contact and c is found longer than d, the angles of action being 66° for the spur-wheels and 72° for the annular wheel.
On referring again to Fig. 62 it will be observed that it is the faces of the teeth on the two wheels that interfere and will prevent them from engaging, hence it will readily occur to the mind that it is possible to form the curves of the pinion faces correct to work with the faces of the wheel teeth as well as with the flanks; or it is possible to form the wheel faces with curves that will work correctly with the faces, as well as with the flanks of the pinion teeth, which will therefore increase the angle of action, and Professor McCord has shown in an article in the London Engineering how to accomplish this in a simple and yet exceedingly ingenious manner which may be described as follows:—
It is required to find a describing circle that will roll the curves for the flanks of the pinion and the faces of the wheels, and also a describing circle for the flanks of the wheel and the faces of the pinion; the curve for the wheel faces to work correctly with the faces as well as with the flanks of the pinion, and the curve for the pinion faces to work correctly with both the flanks and faces of the internal wheel.
In Fig. 65 let p represent the pitch circle of an annular or internal wheel whose centre is at a, and q the pitch circle of a pinion whose centre is at b, and let r be a describing circle whose centre is at c, and which is to be used to roll all the curves for the teeth. For the flanks of the annular wheel we may roll r within p, while for the faces of the wheel we may roll r outside of p, but in the case of the pinion we cannot roll r within q, because r is larger than q, hence we must find some other rolling circle of less diameter than r, and that can be used in its stead (the radius of r always being greater than the radius of the axis of the wheel and pinion for reasons that will appear presently). Suppose then that in Fig. 66 we have a ring whose bore r corresponds in diameter to the intermediate describing circle r, Fig. 65 and that q represents the pinion. Then we may roll r around and in contact with the pinion q, and a tracing point in r will trace the curve m n o, giving a curve a portion of which may be used for the faces of the pinion. But suppose that instead of rolling the intermediate describing circle r around p, we roll the circle t around p, and it will trace precisely the same curve m n o; hence for the faces of the pinion we have found a rolling circle t which is a perfect substitute for the intermediate circle q, and which it will always be, no matter what the diameters of the pinion and of the intermediate describing circle may be, providing that the diameter of t is equal to the difference between the diameters of the pinion and that of the intermediate describing[I-25] circle as in the figure. If now we use this describing circle to roll the flanks of the annular wheel as well as the faces of the pinion, these faces and flanks will obviously work correctly together. Since this describing circle is rolled on the outside of the pinion and on the outside of the annular wheel we may distinguish it as the exterior describing circle.
Now instead of rolling the intermediate describing circle r within the annular wheel p for the face curves of the teeth upon p, we may find some other circle that will give the same curve and be small enough to be rolled within the pinion q for its teeth flanks. Thus in Fig. 67 p represents the pitch circle of the annular wheel and r the intermediate circle, and if r be rolled within p, a point on the circumference of r will trace the curve v w. But if we take the circle s, having a diameter equal to the difference between the diameter of r and that of p, and roll it within p, a point in its circumference will trace the same curve v w; hence s is a perfect substitute for r, and a portion of the curve v w may be used for the faces of the teeth on the annular wheel. The circle s being used for the pinion flanks, the wheel faces and pinion flanks will work correctly together, and as the circle s is rolled within the pinion for its flanks and within the wheel for its faces, it may be distinguished as the interior describing circle.
To prove the correctness of the construction it may be noted that with the particular diameter of intermediate describing circle used in Fig. 65, the interior and exterior describing circles are of equal diameters; hence, as the same diameter of describing circle is used for all the faces and flanks of the pair of wheels they will obviously work correctly together, in accordance with the rules laid down for spur gearing. The radius of s in Fig. 69 is equal to the radius of the annular wheel, less the radius of the intermediate circle, or the radius from a to c. The radius of the exterior describing circle t is the radius of the intermediate circle less the radius of the pinion, or radius c b in the figure.
Now the diameter of the intermediate circle may be determined at will, but cannot exceed that of the annular wheel or be less than the pinion. But having been selected between these two limits the interior and exterior describing circles derived from it give teeth that not only engage properly and avoid the interference shown in Fig. 62, but that will also have an additional arc of action during the recess, as is shown in Fig. 68, which represents the wheel and pinion shown in Fig. 62, but produced by means of the interior and exterior describing circles. Supposing the pinion to be the driver the arc of approach will be along the thickened arc of the interior describing circle, while during the arc of recess there will be an arc of contact along the dotted portion of the exterior describing circle as in ordinary gearing. But in addition there will be an arc of recess along the dotted portion of the intermediate circle r, which arc is due to the faces of the pinion acting upon the faces as well as upon the flanks of the wheel teeth. It is obvious from this that as soon as a tooth passes the line of centres it will, during a certain period, have two points of contact, one on the arc of the exterior describing circle, and another along the arc of r, this period continuing until the addendum circle of the pinion crosses the dotted arc of the exterior describing circle at z.
The diameters of the interior and exterior describing circles obviously depend upon the diameter of the intermediate circle, and as this may, as already stated, be selected, within certain limits, at will, it is evident that the relative diameters of the[I-26] interior and exterior describing circles will vary in proportion, the interior becoming smaller and the exterior larger, while from the very mode of construction the radius of the two will equal that of the axes of the wheel and pinion. Thus in Fig. 69 the radii of s, t, equal a b, or the line of centres, and their diameters, therefore, equal the radius of the annular wheel, as is shown by dotting them in at the upper half of the figure. But after their diameters have been determined by this construction either of them may be decreased in diameter and the teeth of the wheels will clear (and not interfere as in Fig. 62), but the action will be the same as in ordinary gear, or in other words there will be no arc of action on the circle r. But s cannot be increased without correspondingly decreasing t, nor can t be increased without correspondingly decreasing s.
Fig. 70 shows the same pair of gears as in Fig. 68 (the wheel having 22 and the pinion 12 teeth), the diameter of the intermediate circle having been enlarged to decrease the diameter of s and increase that of t, and as these are left of the diameter derived from the construction there is receding action along r from the line of centres to t.
In Fig. 71 are represented a wheel and pinion, the pinion having but four teeth less than the wheel, and a tooth, j, being shown in position in which it has contact at two places. Thus at k it is in contact with the flank of a tooth on the annular wheel, while at l it is in contact with the face of the same tooth.
As the faces of the teeth on the wheel do not have contact higher than point t, it is obvious that instead of having them 3⁄10 of the pitch as at the bottom of the figure, we may cut off the portion x without diminishing the arc of contact, leaving them formed as at the top of the figure. These faces being thus reduced in height we may correspondingly reduce the depth of flank on the pinion by filling in the portion g, leaving the teeth formed as at the top of the pinion. The teeth faces of the wheel being thus reduced we may, by using a sufficiently large intermediate circle, obtain interior and exterior describing circles that will form teeth that will permit of the pinion having but one tooth less than the wheel, or that will form a wheel having but one tooth more than the pinion.
The limits to the diameter of the intermediate describing circle are as follows: in Fig. 72 it is made equal in diameter to the pitch diameter of the pinion, hence b will represent the centre of the intermediate circle as well as of the pinion, and the pitch circle of the pinion will also represent the intermediate circle r. To obtain the radius for the interior describing circle we subtract the radius of the intermediate circle from the radius of the annular wheel, which gives a p, hence the pitch circle of the pinion also represents the interior circle r. But when we come to obtain the radius for the exterior describing circle (t), by subtracting[I-27] the radius of the pinion from that of the intermediate circle, we find that the two being equal give o for the radius of (t), hence there could be no flanks on the pinion.
Now suppose that the intermediate circle be made equal in diameter to the pitch circle of the annular wheel, and we may obtain the radius for the exterior describing circle t; by subtracting the radius of the pinion from that of the intermediate circle, we shall obtain the radius a b; hence the radius of (t) will equal that of the pinion. But when we come to obtain the radius for the interior describing circle by subtracting the radius of the intermediate circle from that of the annular wheel, we find these two to be equal, hence there would be no interior describing circle, and, therefore, no faces to the pinion.
The action of the teeth in internal wheels is less a sliding and more a rolling one than that in any other form of toothed gearing. This may be shown as follows: In Fig. 73 let a a represent the pitch circle of an external pinion, and b b that of an internal one, and p p the pitch circle of an external wheel for a a or an internal one for b b, the point of contact at the line of centres being at c, and the direction of rotation p p being as denoted by the arrow; the two pinions being driven, we suppose a point at c, on the pitch circle p p, to be coincident with a point on each of the two pinions at the line of centres. If p p be rotated so as to bring this point to the position denoted by d, the point on the external pinion having moved to e, while that on the internal pinion has moved to f, both having moved through an arc equal to c d, then the distance from e to d being greater than from d to f, more sliding motion must have accompanied the contact of the teeth at the point e than at the point f; and the difference in the length of the arc e d and that of f d, may be taken to represent the excess of sliding action for the teeth on e; for whatever, under any given condition, the amount of sliding contact may be, it will be in the proportion of the length of e d to that of f d. Presuming, then, that the amount of power transmitted be equal for the two pinions, and the friction of all other things being equal—being in proportion to the space passed (or in this case slid) over—it is obvious that the internal pinion has the least friction.
In Fig. 74 are shown a worm and worm gear partly in section on the line of centres. The worm or tangent screw w is simply one long tooth wound around a cylinder, and its form may be determined by the rules laid down for a rack and pinion, the tangent screw or worm being considered as a rack and the wheel as an ordinary spur-wheel.
Worm gearing is employed for transmitting motion at a right angle, while greatly reducing the motion. Thus one rotation of the screw will rotate the wheel to the amount of the pitch of its teeth only. Worm gearing possesses the qualification that, unless of very coarse pitch, the worm locks the wheel in any position in which the two may come to a state of rest, while at the same time the excess of movement of the worm over that of the wheel enables the movement of the latter, through a very minute portion of a revolution. And it is evident that, when the plane of rotation of the worm is at a right angle to that of the wheel, the contact of the teeth is wholly a sliding one. The wear of the worm is greater than that of the wheel, because its teeth are in continuous contact, whereas the wheel teeth are in contact only when passing through the angle of action. It may be noted, however, that each tooth upon the worm is longer than the teeth on the wheel in proportion as the circumference of the worm is to the length of wheel tooth.
If the teeth of the wheel are straight and are set at an angle equal to the angle of the worm thread to its axis, as in Fig. 75, p p representing the pitch line of the worm, c d the line of centres, and d the worm axis, the contact of tooth upon tooth will be at the centre only of the sides of the wheel teeth. It is generally preferred, however, to have the wheel teeth curved to envelop a part of the circumference of the worm, and thus increase the line of contact of tooth upon tooth, and thereby provide more ample wearing surface.
In this case the form of the teeth upon the worm wheel varies at every point in its length as the line of centres is departed from. Thus in Fig. 76 is shown an end view of a worm and a worm gear in section, c d being the line of centres, and it will be readily perceived that the shape of the teeth if taken on the line e f, will differ from that on the line of centres c d; hence the form of the wheel teeth must, if contact is to occur along the full length of the tooth, be conformed to fit to the worm, which may be done by taking a series of section of the worm thread at varying distances from, and parallel to, the line of centres and joining the wheel teeth to the shape so obtained. But if the teeth of the wheel are to be cut to shape, then obviously a worm may be provided with teeth (by serrating it along its length) and mounted in position upon the wheel so as to cut the teeth of the wheel to shape as the worm rotates. The pitch line of the wheel teeth, whether they be straight and are disposed at an angle as in Fig. 75, or curved as in Fig. 76, is at a right angle to the line of centres c d, or in other words in the plane of g h, in Fig. 76. This is evident because the pitch line must be parallel to the wheel axis, being at an equal radius from that axis, and therefore having an equal velocity of rotation at every point in the length of the pitch line of the wheel tooth.
If we multiply the number of teeth by their pitch to obtain the circumference of the pitch circle we shall obtain the circumference due to the radius of g h, from the wheel axis, and so long as g h is parallel to the wheel axis we shall by this means obtain the same diameter of pitch circle, so long as we measure it on a line parallel to the line of centres c d. The pitch of the worm is the same at whatever point in the tooth depth it may be measured, because the teeth curves are parallel one to the other, thus in Fig. 77 the pitch measures are equal at m, n, or o.
But the action of the worm and wheel will nevertheless not be correct unless the pitch line from which the curves were rolled coincides with the pitch line of the wheel on the line of centres, for although, if the pitch lines do not so coincide, the worm will at each revolution move the pitch line of the wheel through a distance equal to the pitch of the worm, yet the motion of the wheel will not[I-29] be uniform because, supposing the two pitch lines not to meet, the faces of the pinion teeth will act against those of the wheel, as shown in Fig. 78, instead of against their flanks, and as the faces are not formed to work correctly together the motion will be irregular.
The diameter of the worm is usually made equal to four times the pitch of the teeth, and if the teeth are curved as in figure 76 they are made to envelop not more than 30° of the worm.
The number of teeth in the wheel should not be less than thirty, a double worm being employed when a quicker ratio of wheel to worm motion is required.
When the teeth of the wheel are curved to partly envelop the worm circumference it has been found, from experiments made by Robert Briggs, that the worm and the wheel will be more durable, and will work with greatly diminished friction, if the pitch line of the worm be located to increase the length of face and diminish that of the flank, which will decrease the length of face and increase the length of flank on the wheel, as is shown in Fig. 79; the location for the pitch line of the worm being determined as follows:—
The full radius of the worm is made equal to twice the pitch of its teeth, and the total depth of its teeth is made equal to .65 of its pitch. The pitch line is then drawn at a radius of 1.606 of the pitch from the worm axis. The pitch line is thus determined in Fig. 76, with the result that the area of tooth face and of worm surface is equalized on the two sides of the pitch line in the figure. In addition to this, however, it may be observed that by thus locating the pitch line the arcs both of approach and of recess are altered. Thus in Fig. 80 is represented the same worm and wheel as in Fig. 79, but the pitch lines are here laid down as in ordinary gearing. In the two figures the arcs of approach are marked by the thickened part of the generating circle, while the arcs of recess are denoted by the dotted arc on the generating circle, and it is shown that increasing the worm face, as in Fig. 79, increases the arc of recess, while diminishing the worm flank diminishes the arc of approach, and the action of the worm is smoother because the worm exerts more pulling than pushing action, it being noted that the action of the worm on the wheel is a pushing one before reaching, and a pulling one after passing, the line of centres.
It may here be shown that a worm-wheel may be made to work correctly with a square thread. Suppose, for example, that the diameter of the generating circle be supposed to be infinite, and the sides of the thread may be accepted as rolled by the circle. On the wheel we roll a straight line, which gives a cycloidal curve suitable to work with the square thread. But the action will be confined to the points of the teeth, as is shown in Fig. 81, and also to the arc of approach. This is the same thing as taking the faces off the worm and filling in the flanks of the wheel. Obviously, then, we may reverse the process and give the worm faces only, and the wheel, flanks only, using such size of generating circle as will make the spaces of the wheel parallel in their depths and rolling the same generating circle upon the pitch line of the worm to obtain its face curve. This would enable the teeth on the wheel to be cut by a square-threaded tap, and would confine the contact of tooth upon tooth to the recess.
The diameter of generating circle used to roll the curves for a worm and worm-wheel should in all cases be larger than the radius of the worm-wheel, so that the flanks of the wheel teeth may be at least as thick at the root as they are at the pitch circle.
To find the diameter of a wheel, driven by a tangent-screw, which is required to make one revolution for a given number of turns of the screw, it is obvious, in the first place, that when the[I-30] screw is single-threaded, the number of teeth in the wheel must be equal to the number of turns of the screw. Consequently, the pitch being also given, the radius of the wheel will be found by multiplying the pitch by the number of turns of the screw during one turn of the wheel, and dividing the product by 6.28.
When a wheel pattern is to be made, the first consideration is the determination of the diameter to suit the required speed; the next is the pitch which the teeth ought to have, so that the wheel may be in accordance with the power which it is intended to transmit; the next, the number of the teeth in relation to the pitch and diameter; and, lastly, the proportions of the teeth, the clearance, length, and breadth.
When the amount of power to be transmitted is sufficient to cause excessive wear, or when the velocity is so great as to cause rapid wear, the worm instead of being made parallel in diameter from end to end, is sometimes given a curvature equal to that of the worm-wheel, as is shown in Fig. 82.
The object of this design is to increase the bearing area, and thus, by causing the power transmitted to be spread over a larger area of contact, to diminish the wear. A mechanical means of cutting a worm to the required form for this arrangement is shown in Fig. 83, which is extracted from “Willis’ Principles of Mechanism.” “a is a wheel driven by an endless screw or worm-wheel, b, c is a toothed wheel fixed to the axis of the endless screw b and in gear with another and equal toothed gear d, upon whose axis is mounted the smooth surfaced solid e, which it is desired to cut into Hindley’s[2] endless screw. For this purpose a cutting tooth f is clamped to the face of the wheel a. When the handle attached to the axis of b c is turned round, the wheel a and solid wheel e will revolve with the same relative velocity as a and b, and the tool f will trace upon the surface of the solid e a thread which will correspond to the conditions. For from the very mode of its formation the section of every thread through the axis will point to the centre of the wheel a. The axis of e lies considerably higher than that of b to enable the solid e to clear the wheel a.
[2] The inventor of this form of endless screw.
“The edges of the section of the solid e along its horizontal centre line exactly fit the segment of the toothed wheel, but if a section be made by a plane parallel to this the teeth will no longer be equally divided as they are in the common screw, and therefore this kind of screw can only be in contact with each tooth along a line corresponding to its middle section. So that the advantage of this form over the common one is not so great as appears at first sight.
“If the inclination of the thread of a screw be very great, one or more intermediate threads may be added, as in Fig. 84, in which case the screw is said to be double or triple according to the number of separate spiral threads that are so placed upon its surface. As every one of these will pass its own wheel-tooth across the line of centres in each revolution of the screw, it follows that as many teeth of the wheel will pass that line during one revolution of the screw as there are threads to the screw. If we suppose the number of these threads to be considerable, for example, equal to those of the wheel teeth, then the screw and wheel may be made exactly alike, as in Fig. 85; which may serve as an example of the disguised forms which some common arrangements may assume.”
In Fig. 86 is shown Hawkins’s worm gearing. The object of this ingenious mechanical device is to transmit motion by means of screw or worm gearing, either by a screw in which the threads are of equal diameter throughout its length, or by a spiral worm, in which the threads are not of equal diameter throughout, but increase in diameter each way from the centre of its length, or[I-31] about the centre of its length outwardly. Parallel screws are most applicable to this device when rectilinear motions are produced from circular motions of the driver, and spiral worms are applied when a circular motion is given by the driver, and imparted to the driven wheel. The threads of a spiral worm instead of gearing into teeth like those of an ordinary worm-wheel, actuate a series of rollers turning upon studs, which studs are attached to a wheel whose axis is not parallel to that of the worm, but placed at a suitable inclination thereto. When motion is given to the worm then rotation is produced in the roller wheel at a rate proportionable to the pitch of worm and diameter of wheel respectively.
In the arrangement for transmitting rectilinear motion from a screw, rollers may be employed whose axes are inclined to the axis of the driving screw, or else at right angles to or parallel to the same. When separate rollers are employed with inclined axes, or axes at right angles with that of the main driving screw, each thread in gear touches a roller at one part only; but when the rollers are employed with axes parallel to that of the driving screw a succession of grooves are turned in these rollers, into which the threads of the driving screw will be in gear throughout the entire length of the roller. These grooves may be separate and apart from each other, or else form a screw whose pitch is equal to that of the driving screw or some multiple thereof.
In Fig. 86 the spiral worm is made of such a length that the edge of one roller does not cease contact until the edge of the next comes into contact; a wheel carries four rollers which turn on studs, the latter being secured by cottars; the axis of the worm is at right angles with that of the wheel. The edges of the rollers come near together, leaving sufficient space for the thread of the worm to fit between any two contiguous rollers. The pitch line of the screw thread forms an arc of a circle, whose centre coincides with that of the wheel, therefore the thread will always bear fairly against the rollers and maintain rolling contact therewith during the whole of the time each roller is in gear, and by turning the screw in either direction the wheel will rotate.
To prevent end thrust on a worm shaft it may have a right-hand worm a, and a left-hand one c (Fig. 87), driving two wheels b and d which are in gear, and either of which may transmit the power. The thrust of the two worms a and c, being in opposite directions, one neutralizes the other, and it is obvious that as each revolution of the worm shaft moves both wheels to an amount equal to the pitch of the worms, the two wheels b d may, if desirable, be of different diameters.
Involute teeth.—These are teeth having their whole operative surfaces formed of one continuous involute curve. The diameter of the generating circle being supposed as infinite, then a portion of its circumference may be represented by a straight line, such as a in Fig. 88, and if this straight line be made to roll upon the circumference of a circle, as shown, then the curve traced will be involute p. In practice, a piece of flat spring steel, such as a piece of clock spring, is used for tracing involutes. It may be of any length, but at one end it should be filed so as to leave a scribing point that will come close to the base circle or line, and have a short handle, as shown in Fig. 89, in which s represents the piece of spring, having the point p′, and the handle h. The operation is, to make a template for the base circle, rest this template on drawing paper and mark a circle round its edge to represent on the paper the pitch circle, and to then bend the spring around the circle b, holding the point p′ in contact with the drawing paper, securing the other end of the piece of steel, so that it cannot slip upon b, and allowing the steel to unwind from the cylinder or circle b. The point p′ will mark the involute curve p. Another way to mark an involute is to use a piece of twine in place of the spring and a pencil instead of the tracing point; but this is not so accurate, unless, indeed, a piece of wood be laid on the drawing-board and the pencil held firmly against it, so as to steady the pencil point and prevent the variation in the curve that would arise from variation in the vertical position of the pencil.
The flanks being composed of the same curve as the faces of the teeth, it is obvious that the circle from which the tracing point starts, or around which the straight line rolls, must be of less diameter than the pitch circle, or the teeth would have no flanks.
A circle of less diameter than the pitch circle of the wheel is, therefore, introduced, wherefrom to produce the involute curves forming the full side of the tooth.
The depth below pitch line or the length of flank is, therefore, the distance between the pitch circle and the base circle. Now even supposing a straight line to be a portion of the circumference of a circle of infinite diameter or radius, the conditions would here appear to be imperfect, because the generating circle is not rolled upon the pitch circle but upon a circle of lesser diameter. But it can be shown that the requirements of a proper velocity ratio will be met, notwithstanding the employment of the base instead of the pitch circle. Thus, in Fig. 90, let a and b represent the respective centres of the two pitch circles, marked in dotted lines. Draw the base circle for b as e q, which may be[I-32] of any radius less than that of the pitch circle of b. Draw the straight line q d r touching this base circle at its perimeter and passing through the point of contact on the pitch circles as at d. Draw the circle whose radius is a r forming the base circle for wheel a. Thus the line r p q will meet the perimeters of the two circles while passing through the point of contact d at the line of centres (a condition which the relative diameters of the base circles must always be so proportioned as to attain).
If now we take any point on r q, as p in the figure, as a tracing point, and suppose the radius or distance p q to represent the steel spring shown in Fig. 89, and move the tracing point back to the base circle of b, it will trace the involute e p. Again we may take the tracing point p (supposing the line p r to represent the steel spring), and trace the involute p f, and these two involutes represent each one side of the teeth on the respective wheels.
The line r p q is at a right angle to the curves p e and p f, at their point of contact, and, therefore, fills the conditions referred to in Fig. 41. Now the line r p q denotes the path of contact of tooth upon tooth as the wheels revolve; or, in other words, the point of contact between the side of a tooth on one wheel, and the side of a tooth on the other wheel, will always move along the line q r, or upon a similar line passing through d, but meeting the base circles upon the opposite sides of the line of centres, and since line q r always cuts the line of centres at the point of contact of the pitch circles, the conditions necessary to obtain a correct angular velocity are completely fulfilled. The velocity ratio is, therefore, as the length of b q is to that of a r, or, what is the same thing, as the radius of the base circle of one wheel is to that of the other. It is to be observed that the line q r will vary in its angle to the line of centres a b, according to the diameter of the base circle from which it is struck, and it becomes a consideration as to what is its most desirable angle to produce the least possible amount of thrust tending to separate the wheels, because this thrust (described in Fig. 39) tends to wear the journals and bearings carrying the wheel shafts, and thus to permit the pitch circles to separate. To avoid, as far as possible, this thrust the proportions between the diameters of the base circles d and e, Fig. 91, must be such that the line d e passes through the point of contact on the line of centres, as at c, while the angles of the straight line d e should be as nearly 90° to a radial line, meeting it from the centres of the wheels (as shown in the figure, by the lines b e and d e), as is consistent with the length of d e, which in order to impart continuous motion must at least equal the pitch of the teeth. It is obvious, also, that, to give continuous motion, the length of d e must be more than the pitch in proportion, as the points of the teeth come short of passing through the base circles at d and e, as denoted by the dotted arcs, which should therefore represent the addendum circles. The least possible obliquity, or angle of d e, will be when the construction under any given conditions be made such by trial, that the base circles d and e coincide with the addendum circles on the line of centres, and thus, with a given depth of both beyond, the pitch circle, or addenda as it is termed, will cause the tooth contacts to extend over the greatest attainable length of line between the limits of the addendum circles, thus giving a maximum number of teeth in contact at any instant of time. These conditions are fulfilled in Fig. 92,[3] the addendum on the small wheel being longer than the depth below pitch line, while the faces of the teeth are the narrowest.
[3] From an article by Prof. Robinson.
In seeking the minimum obliquity or angle of d e in the figure, it is to be observed that the less it is, the nearer the base circle approaches the pitch circle; hence, the shorter the operative length of tooth flank and the greater its wear.
In comparing the merits of involute with those of epicycloidal teeth, the direction of the line of pressure at each point of contact must always be the common perpendicular to the surfaces at the point of contact, and these perpendiculars or normals must pass through the pitch circles on the line of centres, as was shown in Fig. 41, and it follows that a line drawn from c (Fig. 91) to any point of contact, is in the direction of the pressure on the surfaces at that point of contact. In involute teeth, the contact will always be on the line d e (Fig. 92), but in epicycloidal, on the line of the generating circle, when that circle is tangent at the line of centres; hence, the direction of pressure will be a chord of the circle drawn from the pitch circle at the line of centres to the position of contact considered. Comparing involute with radial flanked epicycloidal teeth, let c d a (Fig. 91) represent the rolling circle for the latter, and d c will be the direction of pressure for the contact at d; but for point of contact nearer c, the direction will be much nearer 90°, reaching that angle as the point of contact approaches c. Now, d is the most remote legitimate contact for involute teeth (and considering it so far as epicycloidal struck with a generating circle of infinite diameter), we find that the aggregate directions of the pressures of the teeth upon each other is much nearer perpendicular in epicycloidal, than in involute gearing; hence, the latter exert a greater pressure, tending to force the wheels apart. Hence, the former are, in this respect, preferable.
It is to be observed, however, that in some experiments made by Mr. Hawkins, he states that he found “no tendency to press the wheels apart, which tendency would exist if the angle of the line d e (Fig. 92) deviated more than 20° from the line of centres a b of the two wheels.”
A method commonly employed in practice to strike the curves of involute teeth, is as follows:—
In Fig. 93 let c represent the centre of a wheel, d d the full diameter, p p the pitch circle, and e the circle of the roots of the[I-33] teeth, while r is a radial line. Divide on r, the distance between the pitch circle and the wheel centre, into four equal parts, by 1, 2, 3, &c. From point or division 2, as a centre, describe the semicircle s, cutting the wheel centre and the pitch circle at its junction with r (as at a). From a, with compasses set to the length of one of the parts, as a 3, describe the arc b, cutting s at f, and f will be the centre from which one side of the tooth may be struck; hence from f as a centre, with the compasses set to the radius a b, mark the curve g. From the centre c strike, through f, a circle t t, and the centres wherefrom to strike all the teeth curves will fall on t t. Thus, to strike the other curve of the tooth, mark off from a the thickness of the tooth on the pitch circle p p, producing the point h. From h as a centre (with the same radius as before,) mark on t t the point i, and from i, as a centre, mark the curve j, forming the other side of the tooth.
In Fig. 94 the process is shown carried out for several teeth. On the pitch circle p p, divisions 1, 2, 3, 4, &c., for the thickness of teeth and the width of the spaces are marked. The compasses are set to the radius by the construction shown in Fig. 93, then from a, the point b on t is marked, and from b the curve c is struck.
In like manner, from d, g, j, the centres e, h, k, wherefrom to strike the respective curves, f, i, l, are obtained.
Then from m the point n, on t t, is marked, giving the centre wherefrom to strike the curve at h m, and from o is obtained the point p, on t t, serving as a centre for the curve e o.
A more simple method of finding point f is to make a sheet metal template, c, as in Fig. 95, its edges being at an angle one to the other of 75° and 30′. One of its edges is marked off in quarters of an inch, as 1, 2, 3, 4, &c. Place one of its edges coincident with the line r, its point touching the pitch circle at the side of a tooth, as at a, and the centre for marking the curve on that side of the tooth will be found on the graduated edge at a distance from a equal to one-fourth the length of r.
The result obtained in this process is precisely the same as that by the construction in Fig. 93, as will be plainly seen, because there are marked on Fig. 93 all the circles by which point f was arrived at in Fig. 95; and line 3, which in Fig. 95 gives the centre wherefrom to strike curve o, is coincident with point f, as is shown in Fig. 95. By marking the graduated edge of c in quarter-inch divisions, as 1, 2, 3, &c., then every division will represent the distance from a for the centre for every inch of wheel radius. Suppose, for example, that a wheel has 3 inches radius, then with the scale c set to the radial line r, the centre therefrom to strike the curve o will be at 3; were the radius of the wheel 4 inches, then the scale being set the same as before (one edge coincident with r), the centre for the curve o would be at 4, and arc t would require to meet the edge of c at 4. Having found the radius from the centre of the wheel of point f for one tooth, we may mark circle t, cutting point f, and mark off all the teeth by setting one point of the compasses (set to radius a f) on one side of the tooth and marking on circle t the centre wherefrom to mark the curve (as o), continuing the process all around the wheel and on both sides of the tooth.
This operation of finding the location for the centre wherefrom to strike the tooth curves, must be performed separately for each wheel, because the distance or radius of the tooth curves varies with the radius of each wheel.
In Fig. 96 this template is shown with all the lines necessary to set it, those shown in Fig. 95 to show the identity of its results with those given in Fig. 93 being omitted.
The principles involved in the construction of a rack to work correctly with a wheel or pinion, having involute teeth, are as in Fig. 97, in which the pitch circle is shown by a dotted circle and the base circle by a full line circle. Now the diameter of the base circle has been shown to be arbitrary, but being assumed the radius b q will be determined (since it extends from the centre b to the point of contact of d q, with the base circle); b d is a straight line from the centre b of the pinion to the pitch line of the rack, and (whatever the angle of q d to b d) the sides of the rack teeth must be straight lines inclined to the pitch line of the rack at an angle equal to that of b d q.
Involute teeth possess four great advantages—1st, they are[I-34] thickest at the roots, where they should be to have a maximum of strength, which is of great importance in pinions transmitting much power; 2nd, the action of the teeth will remain practically perfect, even though the wheels are spread apart so that the pitch circles do not meet on the line of centres; 3rd, they are much easier to mark, and truth in the marking is easier attained; and 4th, they are much easier to cut, because the full depth of the teeth can, on spur-wheels, in all cases be cut with one revolving cutter, and at one passage of the cutter, if there is sufficient power to drive it, which is not the case with epicycloidal teeth whenever the flank space is wider below than it is at the pitch circle. On account of the first-named advantage, they are largely employed upon small gears, having their teeth cut true in a gear-cutting machine; while on account of the second advantage, interchangeable wheels, which are merely required to transmit motion, may be put in gear without a fine adjustment of the pitch circle, in which case the wear of the teeth will not prove destructive to the curves of the teeth. Another advantage is, that a greater number of teeth of equal strength may be given to a wheel than in the epicycloidal form, for with the latter the space must at least equal the thickness of the tooth, while in involute the space may be considerably less in width than the tooth, both measured, of course, at the pitch circle. There are also more teeth in contact at the same time; hence, the strain is distributed over more teeth.
These advantages assume increased value from the following considerations.
In a train of epicycloidal gearing in which the pinion or smallest wheel has radial flanks, the flanks of the teeth will become spread as the diameters of the wheels in the train increase. Coincident with spread at the roots is the thrust shown with reference to Fig. 39, hence under the most favorable conditions the wear on the journals of the wheel axles and the bearings containing them will take place, and the pitch circles will separate. Now so soon as this separation takes place, the motion of the wheels will not be as uniformly equal as when the pitch circles were in contact on the line of centres, because the conditions under which the tooth curves, necessary to produce a uniform velocity of motion, were formed, will have become altered, and the value of those curves to produce constant regularity of motion will have become impaired in proportion as the pitch circles have separated.
In a single pair of epicycloidal wheels in which the flanks of the teeth are radial, the conditions are more favorable, but in this case the pinion teeth will be weaker than if of involute form, while the wear of the journals and bearings (which will take place to some extent) will have the injurious effect already stated, whereas in involute teeth, as has been noted, the separation of the pitch circles does not affect the uniformity of the motion or the correct working of the teeth.
If the teeth of wheels are to be cut to shape in a gear-cutting machine, either the cutters employed determine from their shapes the shapes or curves of the teeth, or else the cutting tool is so guided to the work that the curves are determined by the operations of the machine. In either case nothing is left to the machine operator but to select the proper tools and set them, and the work in proper position in the machine. But when the teeth are to be cast upon the wheel the pattern wherefrom the wheel is to be moulded must have the teeth proportioned and shaped to proper curve and form.
Wheels that require to run without noise or jar, and to have uniformity of motion, must be finished in gear-cutting machines, because it is impracticable to cast true wheels.
When the teeth are to be cast upon the wheels the pattern-maker makes templates of the tooth curves (by some one of the methods to be hereafter described), and carefully cuts the teeth to shape. But the production of these templates is a tedious and costly operation, and one which is very liable to error unless much experience has been had. The Pratt and Whitney Company have, however, produced a machine that will produce templates of far greater accuracy than can be made by hand work. These templates are in metal, and for epicycloidal teeth from 15 to a rack, and having a diametral pitch ranging from 11⁄2 to 32.
The principles of action of the machine are that a segment of a ring (representing a portion of the pitch circle of the wheel for whose teeth a template is to be produced) is fixed to the frame of the machine. Upon this ring rolls a disk representing the rolling, generating, or describing circle, this disk being carried by a frame mounted upon an arm representing the radius of the wheel, and therefore pivoted at a point central to the ring. The describing disk is rolled upon the ring describing the epicycloidal curve, and by suitable mechanical devices this curve is cut upon a piece of steel, thus producing a template by actually rolling the generating upon the base circle, and the rolling motion being produced by positive mechanical motion, there cannot possibly be any slip, hence the curves so produced are true epicycloids.
| VOL. I. | TEMPLATE‑CUTTING MACHINES FOR GEAR TEETH. | PLATE I. | |
 |
|||
| Fig. 98. | |||
 |
|||
| Fig. 99. | |||
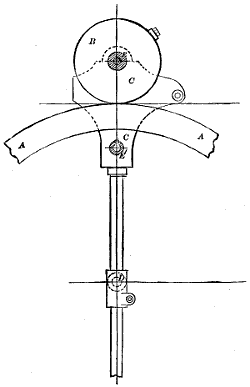 |
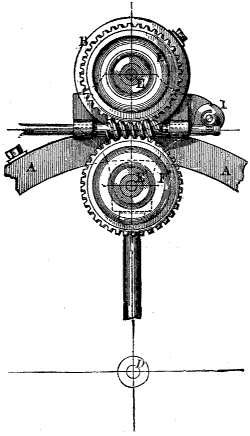 |
||
| Fig. 100. | Fig. 101. | ||
The general construction of the machine is shown in the side view, Fig. 98 (Plate I.), and top view, Fig. 99 (Plate I.), details of construction being shown in Figs. 100, 101 (Plate I.), 102, 103, 104, 105, and 106. a a is the segment of a ring whose outer edge represents a part of the pitch circle. b is a disk representing the rolling or generating circle carried by the frame c, which is attached to a rod pivoted at d. The axis of pivot d represents the axis of the base circle or pitch circle of the wheel, and d is adjustable along the rod to suit the radius of a a, or what is the same thing, to equal the radius of the wheel for whose teeth a template is to be produced.
When the frame c is moved its centre or axis of motion is therefore at d and its path of motion is around the circumference of a a, upon the edge of which it rolls. To prevent b from slipping instead of rolling upon a a, a flexible steel ribbon is fastened at one end upon a a, passes around the edge of a a and thence around the circumference of b, where its other end is fastened; due allowance for the thickness of this ribbon being made in adjusting the radii of a a and of b.
e′ is a tubular pivot or stud fixed on the centre line of pivots e and d, and distant from the edge of a a to the same amount that e is. These two studs e and e′ carry two worm-wheels f and f′ in Fig. 102, which stand above a and b, so that the axis of the worm g is vertically over the common tangent of the pitch and describing circles.
[I-35]The relative positions of these and other parts will be most clearly seen by a study of the vertical section, Fig. 102.[4] The worm g is supported in bearings secured to the carrier c and is driven by another small worm turned by the pulley i, as seen in Fig. 101 (Plate I.); the driving cord, passing through suitable guiding pulleys, is kept at uniform tension by a weight, however c moves; this is shown in Figs. 98 and 99 (Plate I.).
[4] From “The Teeth of Spur Wheels,” by Professor McCord.
Upon the same studs, in a plane still higher than the worm-wheels turn the two disks h, h′, Figs. 103, 104, 105. The diameters of these are equal, and precisely the same as those of the describing circles which they represent, with due allowance, again, for the thickness of a steel ribbon, by which these also are connected. It will be understood that each of these disks is secured to the worm-wheel below it, and the outer one of these, to the disk b, so that as the worm g turns, h and h′ are rotated in opposite directions, the motion of h being identical with that of b; this last is a rolling one upon the edge of a, the carrier c with all its attached mechanism moving around d at the same time. Ultimately, then, the motions of h, h′, are those of two equal describing circles rolling in external and internal contact with a fixed pitch circle.
In the edge of each disk a semicircular recess is formed, into which is accurately fitted a cylinder j, provided with flanges, between which the disks fit so as to prevent end play. This cylinder is perforated for the passage of the steel ribbon, the sides of the opening, as shown in Fig. 103, having the same curvature as the rims of the disks. Thus when these recesses are opposite each other, as in Fig. 104, the cylinder j fills them both, and the tendency of the steel ribbon is to carry it along with h when c moves to one side of this position, as in Fig. 105, and along with h′ when c moves to the other side, as in Fig. 103.
This action is made positively certain by means of the hooks k, k′, which catch into recesses formed in the upper flange of j, as seen in Fig. 104. The spindles, with which these hooks turn, extend through the hollow studs, and the coiled springs attached to their lower ends, as seen in Fig. 102, urge the hooks in the directions of their points; their motions being limited by stops o, o′, fixed, not in the disks h, h′, but in projecting collars on the upper ends of the tubular studs. The action will be readily traced by comparing Fig. 104 with Fig. 105; as c goes to the left, the hook k′ is left behind, but the other one, k, cannot escape from its engagement with the flange of j; which, accordingly, is carried along with h by the combined action of the hook and the steel ribbon.
On the top of the upper flange of j, is secured a bracket, carrying the bearing of a vertical spindle l, whose centre line is a prolongation of that of j itself. This spindle is driven by the spur-wheel n, keyed on its upper end, through a flexible train of gearing seen in Fig. 99; at its lower end it carries a small milling cutter m, which shapes the edge of the template t, Fig. 105, firmly clamped to the framing.
When the machine is in operation, a heavy weight, seen in Fig. 98 (Plate I.), acts to move c about the pivot d, being attached to the carrier by a cord guided by suitably arranged pulleys; this keeps the cutter m up to its work, while the spindle l is independently driven, and the duty left for the worm g to perform is merely that of controlling the motions of the cutter by the means above described, and regulating their speed.
The centre line of the cutter is thus automatically compelled to travel in the path r s, Fig. 105, composed of an epicycloid and a hypocycloid if a a be the segment of a circle as here shown; or of two cycloids, if a a be a straight bar. The radius of the cutter being constant, the edge of the template t is cut to an outline also composed of two curves; since the radius m is small, this outline closely resembles r s, but particular attention is called to the fact that it is not identical with it, nor yet composed of truly epicycloidal curves of any generation whatever: the result of which will be subsequently explained.
With a given pitch every additional tooth increases the diameter of the wheel, and changes the form of the epicycloid; so that it would appear necessary to have as many different cutters, as there are wheels to be made, of any one pitch.
[I-36]But the proportional increment, and the actual change of form, due to the addition of one tooth, becomes less as the wheel becomes larger; and the alteration in the outline soon becomes imperceptible. Going still farther, we can presently add more teeth without producing a sensible variation in the contour. That is to say, several wheels can be cut with the same cutter, without introducing a perceptible error. It is obvious that this variation in the form is least near the pitch circle, which is the only part of the epicycloid made use of; and Prof. Willis many years ago deduced theoretically, what has since been abundantly proved by practice, that instead of an infinite number of cutters, 24 are sufficient of one pitch, for making all wheels, from one with 12 teeth up to a rack.
Accordingly, in using the epicycloidal milling engine, for forming the template, segments of pitch circles are provided of the following diameters (in inches):
| 12, | 16, | 20, | 27, | 43, | 100, |
| 13, | 17, | 21, | 30, | 50, | 150, |
| 14, | 18, | 23, | 34, | 60, | 300. |
| 15, | 19, | 25, | 38, | 75, |
In Fig. 106, the edge t t is shaped by the cutter t t, whose centre travels in the path r s, therefore these two lines are at a constant normal distance from each other. Let a roller p, of any reasonable diameter, be run along t t, its centre will trace the line u v, which is at a constant normal distance from t t, and therefore from r s. Let the normal distance between u v and r s be the radius of another milling cutter n, having the same axis as the roller p, and carried by it, but in a different plane as shown in the side view; then whatever n cuts will have r s for its contour, if it lie upon the same side of the cutter as the template.
The diameter of the disks which act as describing circles is 71⁄2 inches, and that of the milling cutter which shapes the edge of the template is 1⁄8 of an inch.
Now if we make a set of 1-pitch wheels with the diameters above given, the smallest will have twelve teeth, and the one with fifteen teeth will have radial flanks. The curves will be the same whatever the pitch; but as shown in Fig. 106, the blank should be adjusted in the epicycloidal engine, so that its lower edge shall be 1⁄16th of an inch (the radius of the cutter m) above the bottom of the space; also its relation to the side of the proposed tooth should be as here shown. As previously explained, the depth of the space depends upon the pitch. In the system adopted by the Pratt & Whitney Company, the whole height of the tooth is 21⁄8 times the diametral pitch, the projection outside the pitch circle being just equal to the pitch, so that diameter of blank = diameter of pitch circle + 2 × diametral pitch.
We have now to show how, from a single set of what may be called 1-pitch templates, complete sets of cutters of the true epicycloidal contour may be made of the same or any less pitch.
Now if t t be a 1-pitch template as above mentioned, it is clear that n will correctly shape a cutting edge of a gear cutter for a 1-pitch wheel. The same figure, reduced to half size, would correctly represent the formation of a cutter for a 2-pitch wheel of the same number of teeth; if to quarter size, that of a cutter for a 4-pitch wheel, and so on.
But since the actual size and curvature of the contour thus determined depend upon the dimensions and motion of the cutter n, it will be seen that the same result will practically be accomplished, if these only be reduced; the size of the template, the diameter and the path of the roller remaining unchanged.
The nature of the mechanism by which this is effected in the Pratt & Whitney system of producing epicycloidal cutters will be hereafter explained in connection with cutters.
The revolving cutters employed in gear-cutting machines, gear-cutters, or cutting engines (as the machines for cutting the teeth of gear-wheels to shape are promiscuously termed), are of the form shown in Fig. 107, which represents what is known as a Brown and Sharpe patent cutter, whose peculiarities will be explained presently. This class of cutters is made as follows:—
A cast steel disk is turned in the lathe to the required form and outline. After turning, its circumference is serrated as shown, so as to provide protuberances, or teeth, on the face of which the cutting edges may be formed. To produce a cutting edge it is necessary that the metal behind that edge should slope or slant away leaving the cutting edge to project. Two methods of accomplishing this are employed: in the first, which is that embodied in the Brown and Sharpe system, each tooth has the curved outline, forming what may be termed its circumferential outline, of the same curvature and shape from end to end, and from front to back, as it may more properly be termed, the clearance being given by the back of the tooth approaching the centre of the cutter, so that if a line be traced along the circumference of a tooth, from the cutting edge to the back, it will approach the centre of the cutter as the back is approached, but the form of the tooth will be the same at every point in the line. It follows then that the radial faces of the teeth may be ground away to sharpen the teeth without affecting the shape of the tooth, which being made correct will remain correct.
This not only saves a great deal of labor in sharpening the teeth, but also saves the softening and rehardening process, otherwise necessary at each resharpening.
The ordinary method of producing the cutting edges after turning the cutter and serrating it, is to cut away the metal with a file or rotary cutter of some kind forming the cutting edge to correct shape, but paying no regard to the shape of the back of the tooth more than to give it the necessary amount of clearance. In this case the cutter must be softened and reset to sharpen it. To bring the cutting edge up to a sharp edge all around its profile, while still preserving the shape to which it was turned, the pantagraphic engine, shown in Fig. 108, has been made by the Pratt and Whitney Company. Figs. 109 and 110 show some details of its construction.[5] “The milling cutter n is driven by a flexible train acting upon the wheel o, whose spindle is carried by the bracket b, which can slide from right to left upon the piece b, and this again is free to slide in the frame f. These two motions are in horizontal planes, and perpendicular to each other.
[5] From “The Teeth of Spur Wheels,” by Professor McCord.
“The upper end of the long lever p c is formed into a ball, working in a socket which is fixed to p c. Over the cylindrical upper part of this lever slides an accurately fitted sleeve d, partly spherical externally, and working in a socket which can be clamped at any height on the frame f. The lower end p of this lever being accurately turned, corresponds to the roller p in Fig. 109, and is moved along the edge of the template t, which is fastened in the frame in an invariable position.
“By clamping d at various heights, the ratio of the lever arms p d, p d, may be varied at will, and the axis of n made to travel in a path similar to that of the axis of p, but as many times smaller as we choose; and the diameter of n must be made less than that of p in the same proportion.
“The template being on the left of the roller, the cutter to be shaped is placed on the right of n, as shown in the plan view at z, because the lever reverses the movement.
“This arrangement is not mathematically perfect, by reason of the angular vibration of the lever. This is, however, very small, owing to the length of the lever; it might have been compensated for by the introduction of another universal joint, which would practically have introduced an error greater than the one to be obviated, and it has, with good judgment, been omitted.
“The gear-cutter is turned nearly to the required form, the notches are cut in it, and the duty of the pantagraphic engine is merely to give the finishing touch to each cutting edge, and give[I-38] it the correct outline. It is obvious that this machine is in no way connected with, or dependent upon, the epicycloidal engine; but by the use of proper templates it will make cutters for any desired form of tooth; and by its aid exact duplicates may be made in any numbers with the greatest facility.
“It forms no part of our plan to represent as perfect that which is not so, and there are one or two facts, which at first thought might seem serious objections to the adoption of the epicycloidal system. These are:
“1. It is physically impossible to mill out a concave cycloid, by any means whatever, because at the pitch line its radius of curvature is zero, and a milling cutter must have a sensible diameter.
“2. It is impossible to mill out even a convex cycloid or epicycloid, by the means and in the manner above described.
“This is on account of a hitherto unnoticed peculiarity of the curve at a constant normal distance from the cycloid. In order to show this clearly, we have, in Fig. 110, enormously exaggerated the radius c d, of the milling cutter (m of Figs. 105 and 106). The outer curve h l, evidently, could be milled out by the cutter, whose centre travels in the cycloid c a; it resembles the cycloid somewhat in form, and presents no remarkable features. But the inner one is quite different; it starts at d, and at first goes down, inside the circle whose radius is c d, forms a cusp at e, then begins to rise, crossing this circle at g, and the base line at f. It will be seen, then, that if the centre of the cutter travel in the cycloid a c, its edge will cut away the part g e d, leaving the template of the form o g i. Now if a roller of the same radius c d, be rolled along this edge, its centre will travel in the cycloid from a, to the point p, where a normal from g, cuts it; then the roller will turn upon g as a fulcrum, and its centre will travel from p to c, in a circular arc whose radius g p = c d.
“That is to say even a roller of the same size as the original milling cutter, will not retrace completely the cycloidal path in which the cutter travelled.
“Now in making a rack template, the cutter, after reaching c, travels in the reversed cycloid c r, its left-hand edge, therefore, milling out a curve d k, similar to h l. This curve lies wholly outside the circle d i, and therefore cuts o g at a point between f and g, but very near to g. This point of intersection is marked s in Fig. 110, where the actual form of the template o s k is shown. The roller which is run along this template is larger, as has been explained, than the milling cutter. When the point of contact reaches s (which so nearly corresponds to g that they practically coincide), this roller cannot now swing about s through an angle so great as p g c of Fig. 110; because at the root d, the radius of curvature of d k is only equal to that of the cutter, and g and s are so near the root that the curvature of s k, near the latter point, is greater than that of the roller. Consequently there must be some point u in the path of the centre of the roller, such, that when the centre reaches it, the circumference will pass through s, and be also tangent to s k. Let t be the point of tangency; draw s u and t u, cutting the cycloidal path a r in x and y. Then, u y being the radius of the new milling cutter (corresponding to n of Fig. 109), it is clear that in the outline of the gear cutter shaped by it, the circular arc x y will be substituted for the true cycloid.
“The above defects undeniably exist; now, what do they amount to? The diagram is drawn purposely with these sources of error greatly exaggerated, in order to make their nature apparent and their existence sensible. The diameters used in practice, as previously stated, are: describing circle, 71⁄2 inches; cutter for shaping template, 1⁄8 of an inch; roller used against edge of template, 11⁄8 inches; cutter for shaping a 1-pitch gear cutter, 1 inch.
“With these data the writer has found that the total length of the arc x y of Fig. 110, which appears instead of the cycloid in the outline of a cutter for a 1-pitch rack, is less than 0.0175 inch; the real deviation from the true form, obviously, must be much less than that. It need hardly be stated that the effect upon the velocity ratio of an error so minute, and in that part of the contour, is so extremely small as to defy detection. And the best proof of the practical perfection of this system of making epicycloidal teeth[I-39] is found in the smoothness and precision with which the wheels run; a set of them is shown in gear in Fig. 111, the rack gearing as accurately with the largest as with the smallest. To which is to be added, finally, that objection taken, on whatever grounds, to the epicycloidal form of tooth, has no bearing upon the method above described of producing duplicate cutters for teeth of any form, which the pantagraphic engine will make with the same facility and exactness, if furnished with the proper templates.
“The front faces of the teeth of rotary cutters for gear-cutting are usually radial lines, and are ground square across so as to stand parallel with the axis of the cutter driving spindle, so that to whatever depth the cutter may have entered the wheel, the whole of the cutting edge within the wheel will meet the cut simultaneously. If this is not the case the pressure of the cut will spring the cutter, and also the arbor driving it, to one side. Suppose, for example, that the tooth faces not being square across, one side of the teeth meets the work first, then there will be as each tooth meets its cut an endeavour to crowd away from the cut until such time as the other side of the tooth also takes its cut.”
It is obvious that rotating cutters of this class cannot be used to cut teeth having the width of the space wider below than it is at the pitch line. Hence, if such cutters are required to be used upon epicycloidal teeth, the curves to be theoretically correct must be such as are due to a generating circle that will give at least parallel flanks. From this it becomes apparent that involute teeth being always thicker at the root than at the pitch line, and the spaces being, therefore, narrower at the root, may be cut with these cutters, no matter what the diameter of the base circle of the involute.
To produce with revolving cutters teeth of absolutely correct theoretical curvature of face and flank, it is essential that the cutter teeth be made of the exact curvature due to the diameter of pitch circle and generating circle of the wheel to be cut; while to produce a tooth thickness and space width, also theoretically correct, the thickness of the cutter must also be made to exactly answer the requirements of the particular wheel to be cut; hence, for every different number of teeth in wheels of an equal pitch a separate cutter is necessary if theoretical correctness is to be attained.
This requirement of curvature is necessary because it has been shown that the curvatures of the epicycloid and hypocycloid, as also of the involute, vary with every different diameter of base circle, even though, in the case of epicycloidal teeth, the diameter of the generating circle remain the same. The requirement of thickness is necessary because the difference between the arc and the chord pitch is greater in proportion as the diameter of the base or pitch circle is decreased.
But the difference in the curvature on the short portions of the curves used for the teeth of fine pitches (and therefore of but little height) due to a slight variation in the diameter of the base circle is so minute, that it is found in practice that no sensible error is produced if a cutter be used within certain limits upon wheels having a different number of teeth than that for which the cutter is theoretically correct.
The range of these limits, however, must (to avoid sensible error) be more confined as the diameter of the base circle (or what is the same thing, the number of the teeth in the wheel) is decreased, because the error of curvature referred to increases as the diameters of either the base or the generating circles decrease. Thus the difference in the curve struck on a base circle of 20 inches diameter, and one of 40 inches diameter, using the same diameter of generating circle, would be very much less than that between the curves produced by the same diameter of generating circle on base circles respectively 10 and 5 inches diameter.
For these reasons the cutters are limited to fewer wheels according as the number of teeth decreases, or, per contra, are allowed to be used over a greater range of wheels as the number of teeth in the wheels is increased.
Thus in the Brown and Sharpe system for involute teeth there are 8 cutters numbered numerically (for convenience in ordering) from 1 to 8, and in the following table the range of the respective cutters is shown, and the number of teeth for which the cutter is theoretically correct is also given.
| No. of cutter. | Involute teeth. | Teeth. | |||||||||
| 1 | Used | upon all | wheels | having | from | 135 | teeth | to a rack correct for | 200 | ||
| 2 | „ | „ | „ | „ | „ | 55 | „ | to | 134 | teeth, | 68 |
| 3 | „ | „ | „ | „ | „ | 35 | „ | to | 54 | „ | 40 |
| 4 | „ | „ | „ | „ | „ | 26 | „ | to | 34 | „ | 29 |
| 5 | „ | „ | „ | „ | „ | 21 | „ | to | 25 | „ | 22 |
| 6 | „ | „ | „ | „ | „ | 17 | „ | to | 20 | „ | 18 |
| 7 | „ | „ | „ | „ | „ | 14 | „ | to | 16 | „ | 16 |
| 8 | „ | „ | „ | „ | „ | 12 | „ | to | 14 | „ | 13 |
Suppose that it was required that of a pair of wheels one make twice the revolutions of the other; then, knowing the particular number of teeth for which the cutters are made correct, we may obtain the nearest theoretically true results as follows: If we select cutters Nos. 8 and 4 and cut wheels having respectively 13 and 26 teeth, the 13 wheel will be theoretically correct, and the 26 will contain the minute error due to the fact that the cutter is used upon a wheel having three less teeth than the number it is theoretically correct for. But we may select the cutters that are correct for 16 and 29 teeth respectively, the 16th tooth being theoretically correct, and the 29th cutter (or cutter No. 4 in the table) being used to cut 32 teeth, this wheel will contain the error due to cutting 3 more teeth than the cutter was made correct for. This will be nearer correct, because the error is in a larger wheel, and, therefore, less in actual amount. The pitch of teeth may be selected so that with the given number of teeth the diameters of the wheels will be that required.
We may now examine the effect of the variation of curvature in combination with that of the thickness, upon a wheel having less and upon one having more teeth than the number in the wheel for which the cutter is correct.
First, then, suppose a cutter to be used upon a wheel having less teeth and it will cut the spaces too wide, because of the variation of thickness, and the curves too straight or insufficiently curved because of the error of curvature. Upon a wheel having more teeth it will cut the spaces too narrow, and the curvature of the teeth too great; but, as before stated, the number of wheels assigned to each cutter may be so apportioned that the error will be confined to practically unappreciable limits.
If, however, the teeth are epicycloidal, it is apparent that the spaces of one wheel must be wide enough to admit the teeth of the other to a depth sufficient to permit the pitch lines to coincide on the line of centres; hence it is necessary in small diameters, in which there is a sensible difference between the arc and the chord pitches, to confine the use of a cutter to the special wheel for which it is designed, that is, having the same number of teeth as the cutter is designed for.
Thus the Pratt and Whitney arrangement of cutters for epicycloidal teeth is as follows:—
[All wheels having from 12 to 21 teeth have a special cutter for each number of teeth.][6]
| Cutter correct for | ||||||||
| No. of teeth. | ||||||||
| 23 | Used on | wheels | having | from | 22 | to | 24 | teeth. |
| 25 | „ | „ | „ | „ | 25 | to | 26 | „ |
| 27 | „ | „ | „ | „ | 26 | to | 29 | „ |
| 30 | „ | „ | „ | „ | 29 | to | 32 | „ |
| 34 | „ | „ | „ | „ | 32 | to | 36 | „ |
| 38 | „ | „ | „ | „ | 36 | to | 40 | „ |
| 43 | „ | „ | „ | „ | 40 | to | 46 | „ |
| 50 | „ | „ | „ | „ | 46 | to | 55 | „ |
| 60 | „ | „ | „ | „ | 55 | to | 67 | „ |
| 76 | „ | „ | „ | „ | 67 | to | 87 | „ |
| 100 | „ | „ | „ | „ | 87 | to | 123 | „ |
| 150 | „ | „ | „ | „ | 123 | to | 200 | „ |
| 300 | „ | „ | „ | „ | 200 | to | 600 | „ |
| Rack | „ | „ | „ | „ | 600 | to rack. | ||
[6] For wheels having less than 12 teeth the Pratt and Whitney Co. use involute cutters.
Here it will be observed that by a judicious selection of pitch and cutters, almost theoretically perfect results may be obtained[I-40] for almost any conditions, while at the same time the cutters are so numerous that there is no necessity for making any selection with a view to taking into consideration for what particular number of teeth the cutter is made correct.
For epicycloidal cutters made on the Brown and Sharpe system so as to enable the grinding of the face of the tooth to sharpen it, the Brown and Sharpe company make a separate cutter for wheels from 12 to 20 teeth, as is shown in the accompanying table, in which the cutters are for convenience of designation denoted by an alphabetical letter.
| Letter | A | cuts | 12 | teeth. | Letter | M | cuts | 27 | to | 29 | teeth. | ||
| B | „ | 13 | „ | N | „ | 30 | „ | 33 | „ | ||||
| C | „ | 14 | „ | O | „ | 34 | „ | 37 | „ | ||||
| D | „ | 15 | „ | P | „ | 38 | „ | 42 | „ | ||||
| E | „ | 16 | „ | Q | „ | 43 | „ | 49 | „ | ||||
| F | „ | 17 | „ | R | „ | 50 | „ | 59 | „ | ||||
| G | „ | 18 | „ | S | „ | 60 | „ | 74 | „ | ||||
| H | „ | 19 | „ | T | „ | 75 | „ | 99 | „ | ||||
| I | „ | 20 | „ | U | „ | 100 | „ | 149 | „ | ||||
| J | „ | 21 | to | 22 | „ | V | „ | 150 | „ | 249 | „ | ||
| K | „ | 23 | „ | 24 | „ | W | „ | 250 | „ | Rack. | |||
| L | „ | 25 | „ | 26 | „ | X | „ | Rack. | |||||
In these cutters a shoulder having no clearance is placed on each side of the cutter, so that when the cutter has entered the wheel until the shoulder meets the circumference of the wheel, the tooth is of the correct depth to make the pitch circles coincide.
In both the Brown and Sharpe and Pratt and Whitney systems, no side clearance is given other than that quite sufficient to prevent the teeth of one wheel from jambing into the spaces of the other. Pratt and Whitney allow 1⁄8 of the pitch for top and bottom clearance, while Brown and Sharpe allow 1⁄10 of the thickness of the tooth for top and bottom clearance.
It may be explained now, why the thickness of the cutter if employed upon a wheel having more teeth than the cutter is correct for, interferes with theoretical exactitude.
First, then, with regard to the thickness of tooth and width of space. Suppose, then, Fig. 112 to represent a section of a wheel having 12 teeth, then the pitch circle of the cutter will be represented by line a, and there will be the same difference between the arc and chord pitch on the cutter as there is on the wheel; but suppose that this same cutter be used on a wheel having 24 teeth, as in Fig. 113, then the pitch circle on the cutter will be more curved than that on the wheel as denoted at c, and there will be more difference between the arc and chord pitches on the cutter than there is on the wheel, and as a result the cutter will cut a groove too narrow.
The amount of error thus induced diminishes as the diameter of the pitch circle of the cutter is increased.
But to illustrate the amount. Suppose that a cutter is made to be theoretically correct in thickness at the pitch line for a wheel to contain 12 teeth, and having a pitch circle diameter of 8 inches, then we have
| 3.1416 | = | ratio of circumference to diameter. | ||||
| 8 | = | diameter. | ||||
| Number of teeth | = | 12 | ) | 25.1328 | = | circumference. |
| 2.0944 | = | arc pitch of wheel. | ||||
If now we subtract the chord pitch from the arc pitch, we shall obtain the difference between the arc and the chord pitches of the wheel; here
| 2 | .0944 | = | arc pitch. |
| 2 | .0706 | = | chord pitch. |
| .0238 | = | difference between the arc and the chord pitch. |
Now suppose this cutter to be used upon a wheel having the same pitch, but containing 18 teeth; then we have
| 2 | .0944 | = | arc pitch. |
| 2 | .0836 | = | chord pitch. |
| .0108 | = | difference between the arc and the chord pitch. |
Then
| .0238 | = | difference | on wheel | with | 12 | teeth. |
| .0108 | = | „ | „ | „ | 18 | „ |
| .0130 | = | variation between the differences. | ||||
And the thickness of the tooth equalling the width of the space, it becomes obvious that the thickness of the cutter at the pitch line being correct for the 12 teeth, is one half of .013 of an inch too thin for the 18 teeth, making the spaces too narrow and the teeth too thick by that amount.
Now let us suppose that a cutter is made correct for a wheel having 96 teeth of 2.0944 arc pitch, and that it be used upon a wheel having 144 teeth. The proportion of the wheels one to the other remains as before (for 96 bears the proportion to 144 as 12 does to 18).
Then we have for the 96 teeth
| 2 | .0944 | = | arc pitch. |
| 2 | .0934 | = | chord pitch. |
| .0010 | = | difference. |
For the 144 teeth we have
| 2 | .0944 | = | arc pitch. |
| 2 | .0937 | = | chord pitch. |
| .0007 | = | difference. |
We find, then, that the variation decreases as the size of the wheels increases, and is so small as to be of no practical consequence.
If our examples were to be put into practice, and it were actually required to make one cutter serve for wheels having, say, from 12 to 18 teeth, a greater degree of correctness would be obtained if the cutter were made to some other wheel than the smallest. But it should be made for a wheel having less than the mean diameter (within the range of 12 and 18), that is, having less than 15 teeth; because the difference between the arc and chord pitch increases as the diameter of the pitch circle increases, as already shown.
A rule for calculating the number of wheels to be cut by each cutter when the number of cutters in the set and the number of teeth in the smallest and largest wheel in the train are given is as follows:—
Rule.—Multiply the number of teeth in the smallest wheel of the train by the number of cutters it is proposed to have in the set, and divide the amount so obtained by a sum obtained as follows:—
From the number of cutters in the set subtract the number of the cutter, and to the remainder add the sum obtained by multiplying the number of the teeth in the smallest wheel of the set or train by the number of the cutter and dividing the product by the number of teeth in the largest wheel of the set or train.
Example.—I require to find how many wheels each cutter should cut, there being 8 cutters and the smallest wheel having 12 teeth, while the largest has 300.
| Number of teeth in smallest wheel. |
Number of cutters in the set. |
|||
| 12 | × | 8 | = | 96 |
Then
| Number of cutters in set. |
Number of cutter. |
|||
| 8 | - | 7 | = | 1 |
[I-41]Then
| Number of teeth in smallest wheel. |
The number of the cutter. |
The number of the teeth in largest wheel. |
||
| 12 | × | 8 | ÷ | 300 |
| 12 | |||||
| 8 | |||||
| 300 | ) | 96 | 0 | ( | 0.32 |
| 90 | 0 | ||||
| 6 | 00 | ||||
| 6 | 00 | ||||
Now add the 1 to the .32 and we have 1.32, which we must divide into the 96 first obtained.
Thus
| 1.32 | ) | 96 | .00 | ( | 72 | |
| 92 | 4 | |||||
| 3 | 60 | |||||
| 2 | 64 | |||||
| 96 | ||||||
Hence No. 8 cutter may be used for all wheels that have between 72 teeth and 300 teeth.
To find the range of wheels to be cut by the next cutter, which we will call No. 7, proceed again as before, but using 7 instead of 8 as the number of the cutter.
Thus
| Number of teeth in smallest wheel. |
Number of cutters in the set. |
|||
| 12 | × | 8 | = | 96 |
Then
| Number of cutters in the set. |
Number of cutters. |
|||
| 8 | - | 6 | = | 2 |
And
| Number of teeth in smallest wheel. |
The number of the cutter |
The number of teeth in the largest wheel. |
||
| 12 | × | 8 | ÷ | 300 |
Here
| 12 | |||||
| 8 | |||||
| 300 | ) | 96 | 0 | ( | 0.32 |
| 90 | 0 | ||||
| 6 | 00 | ||||
| 6 | 00 | ||||
Add the 2 to the .32 and we have 2.32 to divide into the 96.
Thus
| 2.32 | ) | 96 | .00 | ( | 41 |
| 92 | 8 | ||||
| 3 | 20 | ||||
| 2 | 32 | ||||
| 88 | |||||
Hence this cutter will cut all wheels having not less than the 41 teeth, and up to the 72 teeth where the other cutter begins. For the range of the next cutter proceed the same, using 6 as the number of the cutter, and so on.
By this rule we obtain the lowest number of teeth in a wheel for which the cutter should be used, and it follows that its range will continue upwards to the smallest wheel cut by the cutter above it.
Having by this means found the range of wheels for each cutter, it remains to find for what particular number of teeth within that range the cutter teeth should be made correct, in order to have whatever error there may be equal in amount on the largest and smallest wheel of its range. This is done by using precisely the same rule, but supposing there to be twice as many cutters as there actually are, and then taking the intermediate numbers as those to be used.
Applying this plan to the first of the two previous examples we have—
| Number of teeth in the smallest wheel. |
Number of cutters in the set. |
|||
| 12 | × | 16 | = | 192 |
Then
| Number of cutters in the set. |
Number of the cutter. |
|||
| 16 | - | 15 | = | 1 |
And
| Number of teeth in smallest wheel. |
The number of the cutter. |
The number of the teeth in the largest wheel. |
||
| 12 | × | 15 | ÷ | 300 |
| 1 | 2 | |||||
| 1 | 5 | |||||
| 6 | 0 | |||||
| 12 | ||||||
| 300 | ) | 18 | 0.0 | ( | 0.6 | |
| 18 | 00 | |||||
Then add the 1 to the .6 = 1.6, and this divided into 192 = 120.
By continuing this process for each of the 16 cutters we obtain the following table:—
| Number of Cutter. |
Number of Teeth. |
Number of Cutter. |
Number of Teeth. |
||||
| 1 | 12 | 9 | 26 | ||||
| *2 | 13 | *10 | 30 | ||||
| 3 | 14 | 11 | 35 | ||||
| *4 | 15 | *12 | 42 | ||||
| 5 | 17 | 13 | 54 | ||||
| *6 | 18 | *14 | 75 | ||||
| 7 | 20 | .61 | 15 | 120 | |||
| *8 | 23 | *16 | 300 | ||||
Suppose now we take for our 8 cutters those marked by an asterisk, and use cutter 2 for all wheels having either 12, 13, or 14 teeth, then the next cutter would be that numbered 4, cutting 14, 15, or 16 toothed wheels, and so on.
A similar table in which 8 cutters are required, but 16 are used in the calculation, the largest wheel having 200 teeth in the set, is given below.
| Number of Cutter. |
Number of Teeth. |
Number of Cutter. |
Number of Teeth. |
||||
| 1 | 12 | .7 | 9 | 26 | .5 | ||
| 2 | 13 | .5 | 10 | 29 | |||
| 3 | 14 | .5 | 11 | 35 | |||
| 4 | 15 | .6 | 12 | 40 | .6 | ||
| 5 | 16 | .9 | 13 | 52 | .9 | ||
| 6 | 18 | 14 | 67 | .6 | |||
| 7 | 21 | 15 | 101 | ||||
| 8 | 23 | .5 | 16 | 200 | |||
To assist in the selections as to what wheels in a given set the determined number of cutters should be made correct for, so as to obtain the least limit of error, Professor Willis has calculated the following table, by means of which cutters may be selected that will give the same difference of form between any two consecutive numbers, and this table he terms the table of equidistant value of cutters.
| Number of Teeth. |
| Rack—300, 150, 100, 76, 60, 50, 43, 38, 34, 30, 27, 25, 23, 21, 20, 19, 17, 16, 15, 14, 13, 12. |
The method of using the table is as follows:—Suppose it is required to make a set of wheels, the smallest of which is to contain 50 teeth and the largest 150, and it is determined to use but one cutter, then that cutter should be made correct for a wheel containing 76; because in the table 76 is midway between 50 and 150.
But suppose it were determined to employ two cutters, then one of them should be made correct for a wheel having 60 teeth, and used on all the wheels having between 50 and 76 teeth, while the other should be made correct for a wheel containing 100 teeth, and used on all wheels containing between 76 and 150 teeth.
In the following table, also arranged by Professor Willis, the most desirable selection of cutters for different circumstances is given, it being supposed that the set of wheels contains from 12 teeth to a rack.
| Number of cutters in the set. |
Number of Teeth in Wheel for which the Cutter is to be made correct. | |||||||||||||||||||||||
| 2 | 50 | 16 | ||||||||||||||||||||||
| 3 | 75 | 25 | 15 | |||||||||||||||||||||
| 4 | 100 | 34 | 20 | 14 | ||||||||||||||||||||
| 6 | 150 | 50 | 30 | 21 | 16 | 13 | ||||||||||||||||||
| 8 | 200 | 67 | 40 | 29 | 22 | 18 | 15 | 13 | ||||||||||||||||
| 10 | 200 | 77 | 50 | 35 | 27 | 22 | 19 | 16 | 14 | 13 | ||||||||||||||
| 12 | 300 | 100 | 60 | 43 | 34 | 27 | 23 | 20 | 17 | 15 | 14 | 13 | ||||||||||||
| 18 | 300 | 150 | 100 | 70 | 50 | 40 | 30 | 26 | 24 | 22 | 20 | 18 | 16 | 15 | 14 | 13 | 12 | |||||||
| 24 | Rack | 300 | 150 | 100 | 76 | 60 | 50 | 43 | 38 | 34 | 30 | 27 | 25 | 23 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 |
[I-42]Suppose now we take the cutters, of a given pitch, necessary to cut all the wheels from 12 teeth to a rack, then the thickness of the teeth at the pitch line will for the purposes of designation be the thickness of the teeth of all the wheels, which thickness may be a certain proportion of the pitch.
But in involute teeth while the depth of tooth on the cutter may be taken as the standard for all the wheels in the range, and the actual depth for the wheel for which the cutter is correct, yet the depth of the teeth in the other wheels in the range may be varied sufficiently on each wheel to make the thickness of the teeth equal the width of the spaces (notwithstanding the variation between the arc and chord pitches), so that by a variation in the tooth depth the error induced by that variation may be corrected. The following table gives the proportions in the Brown and Sharpe system.
| Arc Pitch. | Depth of Tooth. |
Depth in terms of the arc pitch. |
| inches. | inches. | inches. |
| 1.570 | 1.078 | .686 |
| 1.394 | .958 | .687 |
| 1.256 | .863 | .686 |
| 1.140 | .784 | .697 |
| 1.046 | .719 | .687 |
| .896 | .616 | .686 |
| .786 | .539 | .685 |
| .628 | .431 | .686 |
| .524 | .359 | .685 |
| .448 | .307 | .685 |
| .392 | .270 | .686 |
| .350 | .240 | .686 |
| .314 | .216 | .687 |
To avoid the trouble of measuring, and to assist in obtaining accuracy of depth, a gauge is employed to mark on the wheel face a line denoting the depth to which the cutter should be entered.
Suppose now that it be required to make a set of cutters for a certain range of wheels, and it be determined that the cutters be so constructed that the greatest permissible amount of error in any wheel of the set be 1⁄100 inch. Then the curves for the smallest wheel, and those for the largest in the set, and the amount of difference between them ascertained, and assuming this difference to amount to 1⁄16 inch, which is about 6⁄100, then it is evident that 6 cutters must be employed for the set.
It has been shown that on bevel-wheels the tooth curves vary at every point in the tooth breadth; hence it is obvious that the cutter being of a fixed curve will make the tooth to that curve. Again, the thickness of the teeth and breadth of the spaces vary at every point in the breadth, while with a cutter of fixed thickness the space cut will be parallel from end to end. To overcome these difficulties it is usual to give to the cutter a curve corresponding to the curve required at the middle of the wheel face and a thickness equal to the required width of space at its smallest end, which is at the smallest face diameter.
The cutter thus formed produces, when passed through the wheel once, and to the required depth, a tooth of one curve from end to end, having its thickness and width of space correct at the smaller face diameter only, the teeth being too thick and the spaces too narrow as the outer diameter of the wheel is approached. But the position and line of traverse of the cutter may be altered so as to take a second cut, widening the space and reducing the tooth thickness at the outer diameter.
By moving the cutter’s position two or three times the points of contact between the teeth may be made to occur at two or three points across the breadth of the teeth and their points of contact; the wear will soon spread out so that the teeth bear all the way across.
Another plan is to employ two or three cutters, one having the correct curve for the inner diameter, and of the correct thickness for that diameter, another having the correct curve for the pitch circle, and another having the correct curve at the largest diameter of the teeth.
The thickness of the first and second cutters must not exceed the required width of space at the small end, while that for the third may be the same as the others, or equal to the thickness of the smallest space breadth that it will encounter in its traverse along the teeth.
The second cutter must be so set that it will leave the inner end of the teeth intact, but cut the space to the required width in the middle of the wheel face. The third cutter must be so set as to leave the middle of the tooth breadth intact, and cut the teeth to the required thickness at the outer or largest diameter.
The most correct method of cutting the teeth of a worm-wheel is by means of a worm-cutter, which is a worm of the pitch and form of tooth that the working worm is intended to be, but of hardened steel, and having grooves cut lengthways of the worm so as to provide cutting edges similar to those on the cutter shown in Fig. 107.
The wheel is mounted on an arbor or mandril free to rotate on its axis and at a right angle to the cutter worm, which is rotated and brought to bear upon the perimeter of the worm-wheel in the same manner as the working worm-wheel when in action. The worm-cutter will thus cut out the spaces in the wheel, and must therefore be of a thickness equal to those spaces. The cutter worm acting as a screw causes the worm-wheel to rotate upon its axis, and therefore to feed to the cutter.
In wheels of fine pitch and small diameter this mode of procedure is a simple matter, especially if the form of tooth be such that it is thicker, as the root of the tooth is approached from the pitch line, because in that case the cutter worm may be entered a part of the depth in the worm-wheel and a cut be taken around the wheel. The cutter may then be moved farther into the wheel and a second cut taken around the wheel, so that by continuing the process until the pitch line of the cutter worm coincides with that of the worm-cutter, the worm-wheel may be cut with a number of light cuts, instead of at one heavy cut.
But in the case of large wheels the strain due to such a long line of cutting edge as is possessed by the cutter worm-teeth springs or bends the worm-wheel, and on account of the circular form of the breadth of the teeth this bending or spring causes that part of the tooth arc above the centre of the wheel thickness to lock against the cutter.
To prevent this, several means may be employed. Thus the grooves forming the cutting edges of the worm-cutter may wind spirally along instead of being parallel to the axis of the cutter.
The distance apart of these grooves may be greater than the breadth of tooth a width of worm-wheel face, in which case the cutting edge of one tooth only will meet the work at one time. In addition to this two stationary supports may be placed beneath the worm-wheel (one on each side of the cutter). But on coarse pitches with their corresponding depth of tooth, the difficulty presents itself, that the arbor driving the worm-cutter will spring, causing the cutter to lift and lock as before; hence it is necessary to operate on part of the space at a time, and shape it out to so nearly the correct form that the finishing cut may be a very light one indeed, in which case the worm-cutter will answer for the final cut.
The removal of the surplus metal preparatory to the introduction of the worm-cutter to finish, may be made with a cutter-worm that will cut out a narrow groove being of the thickness equal to the bottom of the tooth space and cutting on its circumference only. This cutter may be fed into the wheel to the permissible depth of cut, and after the cut is taken all around the wheel, it may be entered deeper and a second cut taken, and so on until it has entered the wheel to the necessary depth of tooth. A second cutter-worm may then be used, it being so shaped as to cut the face curve only of the teeth. A third may cut the flank curve only, and finally a worm-cutter of correct form may take a finishing cut over both the faces and the flanks. In this manner teeth of any pitch and depth may be cut. Another method is to use a revolving cutter such as shown in Fig. 107, and to set it at the required angle to the wheel, and then take a succession of cuts around the wheel, the first cut forming a certain part of the tooth depth, the second increasing this depth, and so on until the[I-43] final cut forms the tooth to the requisite depth. In this case the cutter operates on each space separately, or on one space only at a time, and the angle at which to set the cutter may be obtained as follows in Fig. 114. Let the length of the line a a equal the diameter of the worm at the pitch circle, and b b (a line at a right angle to a a) represent the axial line of the worm. Let the distance c equal the pitch of the teeth, and the angle of the line d with a a or b b according to circumstances, will be that to which the cutter must be set with reference to the tooth.
If then a piece of sheet metal be cut to the lines a, d, and the cutter so set that with the edge d of the piece held against the side face of the cutter (which must be flat or straight across), the edge a will stand truly vertical, and the cutter will be at the correct angle supposing the wheel to be horizontal.
In making patterns wherefrom gear-wheels may be cast in a mould, the true curves are frequently represented by arcs of circles struck from the requisite centres and of the most desirable radius with compasses, and this will be treated after explaining the pattern maker’s method of obtaining true curves by rolling segments by hand. If, then, the wheels are of small diameter, as say, less than 12 inches in diameter, and precision is required, it is best to turn in the lathe wooden disks representing in their diameters the base and generating circles. But otherwise, wooden segments to answer the same purpose may be made as from a piece of soft wood, such as pine or cedar, about three-eighths inch thick, make two pieces a and b, in Fig. 115, and trim the edges c and d to the circle of the pitch line of the required wheel. If the diameter of the pitch circle is marked on a drawing, the pieces may be laid on the drawing and sighted for curvature by the eye. In the absence of a drawing, strike a portion of the pitch circle with a pair of sharp-pointed compasses on a piece of zinc, which will show a very fine line quite clear. After the pieces are filed to the circle, try them together by laying them flat on a piece of board, bringing the curves in contact and sweeping a against b, and the places of contact will plainly show, and may be filed until continuous contact along the curves is obtained. Take another similar piece of wood and form it as shown in Fig. 116, the edge e representing a portion of the rolling circle. In preparing these segments it is an excellent plan to file the convex edges, as shown in Fig. 117, in which p is a piece of iron or wood having its surface s trued; f is a file held firmly to s, while its surface stands vertical, and t is the template laid flat on s, while swept against the file. This insures that the edge shall be square across or at least at the same angle all around, which is all that is absolutely necessary. It is better, however, that the edges be square. So likewise in fitting a and b (Fig. 115) together, they should be laid flat on a piece of board. This will insure that they will have contact clear across the edge, which will give more grip and make slip less likely when using the segments. Now take a piece of stiff drawing paper or of sheet zinc, lay segment a upon it, and mark a line coincident with the curved edge. Place the segment representing the generating circle flat on the paper or zinc, hold its edge against segment a, and roll it around a sufficient distance to give as much of the curve as may be required; the operation being illustrated in Fig. 118, in which a is the segment representing the pitch or base circle, e is the segment representing the generating circle, p is the paper, c the curve struck by the tracing point or pencil o.
This tracing point should be, if paper be used to trace on, a piece of the hardest pencil obtainable, and should be filed so that its edge, if flat, shall stand as near as may be in the line of motion when rolled, thus marking a fine line. If sheet zinc be used instead of paper a needle makes an excellent tracing point. Several of the curves, c, should be struck, moving the position of the generating segment a little each time.
On removing the segments from the paper, there will appear the lines shown in Fig. 119; a representing the pitch circle, and o o o the curves struck by the tracing point.
[I-44]Cut out a piece of sheet zinc so that its edge will coincide with the curve a and the epicycloid o, trying it with all four of the epicycloids to see that no slip has occurred when marking them; shape a template as shown in Fig. 120. Cutting the notches at a b, acts to let the file clear well when filing the template, and to allow the scriber to go clear into the corner. Now take the segment a in Fig. 118, and use it as a guide to carry the pitch circle across the template as at p, in Fig. 120. A zinc template for the flank curve is made after the same manner, using the rolling segment in conjunction with the segment b in Fig. 115.
But the form of template for the flank should be such as shown in Fig. 121, the curve p representing, and being of the same radius as the pitch circle, and the curve f being that of the hypocycloid. Both these templates are set to the pitch circles and to coincide with the marks made on the wheel teeth to denote the thickness, and with a hardened steel point a line is traced on the tooth showing the correct curve for the same.
An experienced hand will find no difficulty in producing true templates by this method, but to avoid all possibility of the segments slipping on coarse pitches, and with large segments, the segments may be connected, as shown in Fig. 122, in which o represents a strip of steel fastened at one end into one segment and at the other end to the other segment. Sometimes, indeed, where great accuracy is requisite, two pieces of steel are thus employed, the second one being shown at p p, in the figure. The surfaces of these pieces should exactly coincide with the edge of the segments.
The curve templates thus produced being shaped to apply to the pitch circle may be correctly applied to that circle independently of its concentricity to the wheel axis or of the points of the teeth, but if the points of the teeth are turned in the lathe so as to be true (that is, concentric to the wheel axis) the form of the template may be such as shown in Fig. 123, the radius of the arc a a equalling that of the addendum circle or circumference at the points of the teeth, and the width at b (the pitch circle) equaling the width of a space instead of the thickness of a tooth. The curves on each side of the template may in this case be filed for the full side of a tooth on each side of the template so that it will completely fill the finished space, or the sides of two contiguous teeth may be marked at one operation. This template may be set to the marks made on the teeth at the pitch circle to denote their requisite thickness, or for greater accuracy, a similar template made double so as to fill two finished tooth spaces may be employed, the advantage being that in this case the template also serves to mark or test the thickness of the teeth. Since, however, a double template is difficult to make, a more simple method is to provide for the thickness of a tooth, the template shown in Fig. 124, the width from a to b being either the thickness of tooth required or twice the thickness of a tooth plus the width of a space, so that it may be applied to the outsides of two contiguous teeth. The arc c may be made both in its radius and distance from the pitch circle d d to equal that of the addendum circle, so as to serve as a gauge for the tooth points, if the latter are not turned true in the lathe, or to rest on the addendum circle[I-45] (if the teeth points are turned true), and adjust the pitch circle d d to the pitch circle on the wheel.
The curves for the template must be very carefully filed to the lines produced by the rolling segments, because any error in the template is copied on every tooth marked from it. Furthermore, instead of drawing the pitch circle only, the addendum circle and circle for the roots of the teeth or spaces should also be drawn, so that the template may be first filed to them, and then adjusted to them while filing the edges to the curves.
Another form of template much used is shown in Fig. 125. The curves a and b are filed to the curve produced by rolling segments as before, and the holes c, d, e, are for fastening the template to an arm, such as shown in Fig. 126, which represents a section of a wheel w, with a plug p, fitting tightly into the hub h of the wheel. This plug carries at its centre a cylindrical pin on which pivots the arm a. The template t is fastened to the arm by screws, and set so that its pitch circle coincides with the pitch circle p on the wheel, when the curves for one side of all the teeth may be marked. The template must then be turned over to mark the other side of the teeth.
The objection to this form of template is that the length of arc representing the pitch circle is too short, for it is absolutely essential that the pitch line on the template (or line representing the arc of the addendum if that be used) be greater than the width of a single tooth, because an error of the thickness of a line (in the thickness of a tooth), in the coincidence of the pitch line of the template with that of the tooth, would throw the tooth curves out to an extent altogether inadmissible where true work is essential.
To overcome this objection the template may be made to equal half the thickness of a tooth and its edge filed to represent a radial line on the wheel. But there are other objections, as, for example, that the template can only be applied to the wheel when adjusted on the arm shown in Fig. 126, unless, indeed, a radial line be struck on every tooth of the wheel. Again, to produce the template a radial line representing the radius of the wheel must be produced, which is difficult where segments only are used to produce the curves. It is better, therefore, to form the template as shown in Fig. 127, the projections at a b having their edges filed to coincide with the pitch circle p, so that they may be applied to a length of one arc of pitch circle at least equal to the pitch of the teeth.
The templates for the tooth curves being obtained, the wheel must be divided off on the pitch circle for the thickness of the teeth and the width of the spaces, and the templates applied to the marks or points of division to serve as guides to mark the tooth curves. Since, however, as already stated, the tooth curves are as often struck by arcs of circles as by templates, the application of such arcs and their suitability may be discussed.
In the employment of arcs of circles several methods of finding the necessary radius are found in practice.
In the best practice the true curve is marked by the rolling segments already described, and the compass points are set by trial to that radius which gives an arc nearest approaching to the true face and flank curves respectively. The degree of curve error thus induced is sufficient that the form of tooth produced cannot with propriety be termed epicycloidal teeth, except in the case of fine pitches in which the arc of a circle may be employed to so nearly approach the true curve as to be permissible as a substitute. But in coarse pitches the error is of much importance. Thus in Fig. 128 is shown the curve of the former or template attachment used on the celebrated Corliss Bevel Gear Cutting Machine, to cut the teeth on the bevel-wheels employed upon the line shafting at the Centennial Exhibition. These gears, it may[I-46] be remarked, were marvels of smooth and noiseless running, and attracted wide attention both at home and abroad. The engraving is made from a drawing marked direct from the former itself, and kindly furnished me by Mr. George H. Corliss. a a is the face and b b the flank of the tooth, c c is the arc of a circle nearest approaching to the face curve, and d d the arc of a circle nearest approaching the flank curve. In the face curve, there are but two points where the circle coincides with the true curve, while in the flank there are three such points; a circle of smaller radius than c c would increase the error at b, but decrease it at a; one of a greater radius would decrease it at b, and increase it at a. Again, a circle larger in radius than d d would decrease the error at e and increase it at f; while one smaller would increase it at e and decrease it at f. Only the working part of the tooth is given in the illustration, and it will be noted that the error is greatest in the flank, although the circle has three points of coincidence.
In this case the depth of the former tooth is about three and three-quarter times greater than the depth of tooth cut on the bevel-wheels; hence, in the figure the actual error is magnified three and three-quarter times. It demonstrates, however, the impropriety of calling coarsely pitched teeth that are found by arcs of circles “epicycloidal” teeth.
When, however, the pitches of the teeth are fine as, say an inch or less, the coincidence of an arc of a circle with the true curve is sufficiently near for nearly all practical purposes, and in the case of cast gear the amount of variation in a pitch of 2 inches would be practically inappreciable.
To obtain the necessary set of the compasses to mark the curves, the following methods may be employed.
First by rolling the true curves with segments as already described, and the setting the compass points (by trial) to that radius which gives an arc nearest approaching the true curves. In this operation it is not found that the location for the centre from which the curve must be struck always falls on the pitch circle, and since that location will for every tooth curve lie at the same radius from the wheel centre it is obvious that after the proper location for one of the curves, as for the first tooth face or tooth flank as the case may be, is found, a circle may be struck denoting the radius of the location for all the teeth. In Fig. 129, for example, p p represents the pitch circle, a b the radius that will produce an arc nearest approaching the true curve produced by rolling segments, and a the location of the centre from which the face arc b should be struck. The point a being found by trial with the compasses applied to the curve b, the circle a c may be struck, and the location for the centres from which the face arcs of each tooth must be struck will also fall on this circle, and all that is necessary is to rest one point of the compasses on the side of the tooth as, say at e, and mark on the second circle a c the point c, which is the location wherefrom to mark the face arc d.
If the teeth flanks are not radial, the locations of the centre wherefrom to strike the flank curves are found in like manner by trial of the compasses with the true curves, and a third circle, as i in Fig. 130, is struck to intersect the first point found, as at g in the figure. Thus there will be upon the wheel face three circles, p p the pitch circle, j j wherefrom to mark the face curves, and i wherefrom to mark the flank curves.
When this method is pursued a little time may be saved, when dividing off the wheel, by dividing it into as many divisions as there are teeth in the wheel, and then find the locations for the curves as in Fig. 131, in which 1, 2, 3 are points of divisions on the pitch circle p p, while a, b, struck from point 2, are centres wherefrom to strike the arcs e, f; c, d, struck also from point 2 are centres wherefrom to strike the flank curves g, h.
It will be noted that all the points serving as centres for the face curves, in Fig. 130, fall within a space; hence if the teeth were rudely cast in the wheel, and were to be subsequently cut or trimmed to the lines, some provision would have to be made to receive the compass points.
To obviate the necessity of finding the necessary radius from rolling segments various forms of construction are sometimes employed.
Thus Rankine gives that shown in Fig. 132, which is obtained as follows. Draw the generating circle d, and a d the line of centres. From the point of contact at c, mark on circle d, a point distance from c one-half the amount of the pitch, as at p, and draw the line p c of indefinite length beyond c. Draw a line from p, passing through the line of centres at e, which is[I-47] equidistant between c and a. Then multiply the length from p to c by the distance from a to d, and divide by the distance between d and e. Take the length and radius so found, and mark it upon p c, as at f, and the latter will be the location of centre for compasses to strike the face curve.
Another method of finding the face curve, with compasses, is as follows: In Fig. 133, let p p represent the pitch circle of the wheel to be marked, and b c the path of the centre of the generating or describing circle as it rolls outside of p p. Let the point b represent the centre of the generating circle when that circle is in contact with the pitch circle at a. Then from b, mark off on b c any number of equidistant points, as d, e, f, g, h, and from a, mark on the pitch circle, points of division, as 1, 2, 3, 4, 5, at the intersection of radial lines from d, e, f, g, and h. With the radius of the generating circle, that is, a b, from b, as a centre, mark the arc i, from d the arc j, from e the arc k, &c., to m, marking as many arcs as there are points of division on b c. With the compasses set to the radius of divisions 1, 2, step off on arc m the five divisions, n, o, s, t, v, and v will be a point in the epicycloidal curves. From point of division 4, step off on l four points of division, as a, b, c, d, and d will be another point in the epicycloidal curve. From point 3 set off three divisions on k, from point 2 two dimensions on l, and so on, and through the points so obtained, draw by hand or with a scroll the curve represented in the cut by curve a v.
Hypocycloids for the flanks of the teeth may be traced in a similar manner. Thus in Fig. 134 p p is the pitch circle, and b c the line of motion of the centre of the generating circle to be rolled within p p, and r a radial line. From 1 to 6 are points of equal division on the pitch circle, and d to i are arc locations for the centre of the generating circle. Starting from a, which represents the supposed location for the centre of the generating circle, the point of contact between the generating and base circles will be at b. Then from 1 to 6 are points of equal division on the pitch circle, and from d to i are the corresponding locations for the centres of the generating circle. From these centres the arcs j, k, l, m, n, o, are struck. From 6 mark the six points of division from a to f, and f is a point in the curve. Five divisions on n, four on m, and so on, give respectively points in the curve which is marked in the figure from a to f.
There is this, however, to be noted concerning the constructions of the last two figures. Since the circle described by the centre of the generating circle is of different arc or curve to that of the pitch circle, the chord of an arc having an equal length on each will be different. The amount is so small as to be practically correct. The direction of the error is to give to the curves a less curvature, as though they had been produced by a generating circle of larger diameter. Suppose, for example, that the difference between the arc n 5 (Fig. 133) and its chord is .1, and that the difference between the arc 4 5, and its chord is .01, then the error in one step is .09, and, as the point v is formed in 5 steps, it will contain this error multiplied five times. Point d would contain it multiplied four times, because it has 4 steps, and so on.
The error will increase in proportion as the diameter of the generating is less than that of the pitch circle, and though in large wheels, working with large wheels (so that the difference between the radius of the generating circle and that of the smallest wheel is not excessive), it is so small as to be practically inappreciable, yet in small wheels, working with large ones, it may form a sensible error.
Fig. 135.
An instrument much employed in the best practice to find the radius which will strike an arc of a circle approximating the true epicycloidal curve, and for finding at the same time the location of the centre wherefrom that curve should be struck, is found in the Willis’ odontograph. This is, in reality, a scale of centres or radii for different and various diameters of wheels and generating circles. It consists of a scale, shown in Fig. 135, and is formed of a piece of sheet metal, one edge of which is marked or graduated in divisions of one-twentieth of an inch. The edge meeting the graduated edge at o is at angle of 75° to the graduated edge.
On one side of the odontograph is a table (as shown in the cut), for the flanks of the teeth, while on the other is the following table for the faces of the teeth:
CENTRES FOR THE FACES OF THE TEETH.
Pitch in Inches and Parts.
| No. of Teeth |
1⁄4 | 3⁄8 | 1⁄2 | 5⁄8 | 3⁄4 | 1 | 11⁄4 | 11⁄2 | 13⁄4 | 2 | 21⁄4 | 21⁄2 | 3 | 31⁄2 |
| 12 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 11 | 12 | 15 | 17 |
| 15 | .. | .. | 3 | .. | .. | .. | 7 | 8 | 10 | 11 | 12 | 14 | 17 | 19 |
| 20 | 2 | .. | .. | 4 | 5 | 6 | 8 | 9 | 11 | 12 | 14 | 15 | 18 | 21 |
| 30 | .. | 3 | 4 | .. | .. | 7 | 9 | 10 | 12 | 14 | 16 | 18 | 21 | 25 |
| 40 | .. | .. | .. | .. | 6 | 8 | .. | 11 | 13 | 15 | 17 | 19 | 23 | 26 |
| 60 | .. | .. | .. | 5 | .. | .. | 10 | 12 | 14 | 16 | 18 | 20 | 25 | 29 |
| 80 | .. | .. | .. | .. | .. | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 26 | 30 |
| 100 | .. | .. | .. | .. | 7 | .. | .. | .. | .. | 18 | 20 | 22 | .. | 31 |
| 150 | .. | .. | 5 | 6 | .. | .. | .. | 14 | 16 | 19 | 21 | 23 | 27 | 32 |
| Rack. | .. | 4 | .. | .. | .. | 10 | 12 | 15 | 17 | 20 | 22 | 25 | 30 | 34 |
[I-48]The method of using the instrument is as follows: In Fig. 136, let c represent the centre, and p the pitch circle of a wheel to contain 30 teeth of 3 inch arc pitch. Draw the radial line l, meeting the pitch circle at a. From a mark on the pitch circle, as at b, a radius equal to the pitch of the teeth, and the thickness of the tooth as a k. Draw from b to c the radial line e. Then for the flanks place the slant edge of the odontograph coincident and parallel with e, and let its corners coincide with the pitch circle as shown. In the table headed centres for the flanks of the teeth, look down the column of 3 inch pitch, and opposite to the 30 in the column of numbers of teeth, will be found the number 49, which indicates that the centre from which to draw an arc for the flank is at 49 on the graduated edge of the odontograph, as denoted in the cut by r. Thus from r to the side k of the tooth is the radius for the compasses, and at r, or 49, is the location for the centre to strike the flank curve f. For the face curve set the slant edge of the odontograph coincident with the radial line l, and in the table of centres for the faces of teeth, look down the column of 3-inch pitch, and opposite to 30 in the number of teeth column will be found the number 21, indicating that at 21 on the graduated edge of the odontograph, is the location of the centre wherefrom to strike the curve d for the face of the tooth, this location being denoted in the cut at r.
The requisite number on the graduated edge for pitches beyond 31⁄2 (the greatest given in the tables), may be obtained by direct proportion from those given in the tables. Thus for 4 inch pitch, by doubling the numbers given for a 2 inch pitch, containing the same number of teeth, for 41⁄2 inch pitch by doubling the numbers given for a 21⁄4 inch pitch. If the pitch be a fraction that cannot be so obtained, no serious error will be induced if the nearest number marked be taken.
An improved form of template odontograph, designed by Professor Robinson of the Illinois School of Industry, is shown in Fig. 137.
In this instrument the curved edge, having graduated lines, approaches more nearly to the curves produced by rolling circles than can be obtained from any system in which an arc of a circle is taken to represent the curve; hence, that edge is applied direct to the teeth and used as a template wherefrom to mark the curve. The curve is a logarithmic spiral, and the use of the instrument involves no other labor than that of setting it in position. The applicability of this curve, for the purpose, arises from two of its properties: first, that the involute of the logarithmic spiral is another like spiral with poles in common; and, second, that the obliquity or angle between a normal and radius sector is constant, the latter property being possessed by this curve only. By the first property it is known that a line, lying tangent to the curve c e h, will be normal or perpendicular to[I-49] the curve c d b; so that when the line d e f is tangent to the pitch line, the curve a d b will coincide very closely with the true epicycloidal curve, or, rather, with that portion of it which is applied to the tooth curve of the wheel. By the second quality, all sectors of the spiral, with given angle at the poles, are similar figures which admit of the same degree of coincidence for all similar epicycloids, whether great or small, and nearly the same for epicycloids in general; thus enabling the application of the instrument to epicycloids in general.
To set the instrument in position for drawing a tooth face a table which accompanies the instrument is used. From this table a numerical value is taken, which value depends upon the diameters of the wheels, and the number of teeth in the wheel for which the curve is sought. This tabular value, when multiplied by the pitch of the teeth, is to be found on the graduated edge on the instrument a d b in Fig. 137. This done, draw the line d e f tangent to the pitch line at the middle of the tooth, and mark off the half thickness of the tooth, as e, d, either on the tangent line or the pitch line. Then place the graduated edge of the odontograph at d, and in such a position that the number and division found as already stated shall come precisely on the tangent line at d, and at the same time so set the curved edge h f c so that it shall be tangent to the tangent line, that is to say, the curved edge c h must just meet the tangent line at some one point, as at f in the figure. A line drawn coincident with the graduated edge will then mark the face curve required, and the odontograph may be turned over, and the face on the other side of the tooth marked from a similar setting and process.
For the flanks of the teeth setting numbers are obtained from a separate table, and the instrument is turned upside down, and the tangent line d f, Fig. 137, is drawn from the side of the tooth (instead of from the centre), as shown in Fig. 138.
It is obvious that this odontograph may be set upon a radial arm and used as a template, as shown in Fig. 126, in which case the instrument would require but four settings for the whole wheel, while rolling segments and the making of templates are entirely dispensed with, and the degree of accuracy is greater than is obtainable by means of the employment of arcs of circles.
The tables wherefrom to find the number or mark on the graduated edge, which is to be placed coincident with the tangent line in each case, are as follows:—
| Ratios.[7] | Number of Teeth in Wheel Sought; or, Wheel for Which Teeth are Sought. | |||||||||||||||||||
| 8 | 12 | 16 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 120 | 150 | 200 | 300 | 500 | ||||
| For Faces: Flanks Radial or Curved. | ||||||||||||||||||||
| Draw Setting Tangent at Middle of Tooth.—Epicycloidal Spur or Bevel Gearing. | ||||||||||||||||||||
| 1⁄12 | = | .083 | .32 | .39 | .46 | .51 | ||||||||||||||
| 1⁄4 | = | .250 | .31 | .37 | .44 | .49 | .61 | .70 | .78 | .85 | .92 | .99 | 1.05 | 1.11 | 1.22 | 1.36 | 1.55 | 1.94 | 2.54 | |
| 1⁄2 | = | .500 | .28 | .34 | .41 | .46 | .57 | .66 | .73 | .80 | .87 | .93 | 1.00 | 1.06 | 1.15 | 1.29 | 1.50 | 1.86 | 2.41 | |
| 2⁄3 | = | .667 | .27 | .32 | .38 | .43 | .54 | .62 | .70 | .77 | .83 | .89 | .95 | 1.01 | 1.11 | 1.24 | 1.45 | 1.79 | 2.32 | |
| 1 | .23 | .28 | .34 | .39 | .49 | .58 | .65 | .72 | .78 | .83 | .89 | .94 | 1.03 | 1.15 | 1.36 | 1.65 | 2.10 | |||
| 3⁄2 | = | 1.50 | .19 | .25 | .29 | .34 | .44 | .51 | .58 | .64 | .69 | .74 | .79 | .84 | .93 | 1.05 | 1.25 | 1.53 | 1.94 | |
| 2 | .17 | .22 | .26 | .30 | .38 | .46 | .53 | .59 | .63 | .68 | .72 | .76 | .84 | .95 | 1.13 | 1.40 | 1.81 | |||
| 3 | .16 | .19 | .23 | .31 | .38 | .44 | .49 | .53 | .57 | .60 | .63 | .71 | .82 | .97 | 1.23 | 1.60 | ||||
| 4 | .14 | .17 | .20 | .26 | .33 | .38 | .42 | .46 | .49 | .53 | .56 | .63 | .73 | .87 | 1.08 | 1.42 | ||||
| 6 | .22 | .26 | .30 | .34 | .37 | .41 | .44 | .47 | .53 | .61 | .71 | .90 | 1.20 | |||||||
| 12 | .20 | .23 | .25 | .28 | .30 | .32 | .34 | .37 | .42 | .49 | .60 | .82 | ||||||||
| 24 | .19 | .21 | .23 | .26 | .31 | .40 | .57 | |||||||||||||
| For Flanks, when Curved. | ||||||||||||||||||||
| Draw Setting Tangent at Side of Tooth.—Epicycloidal Spur and Bevel Gearing. Faces of Internal, and Flanks of Pinion Teeth. | ||||||||||||||||||||
| De- | — | 1.5 | slight. | .77 | .98 | 1.18 | 1.36 | 1.75 | 2.05 | 2.31 | 2.56 | 2.75 | 2.92 | 3.08 | 3.24 | 3.52 | 3.87 | 4.51 | 5.50 | 7.20 |
| gree | 2 | good. | .44 | .54 | .63 | .72 | .92 | 1.09 | 1.24 | 1.38 | 1.49 | 1.59 | 1.79 | 1.79 | 1.98 | 2.23 | 2.67 | 3.22 | 4.50 | |
| of | 3 | more. | .20 | .28 | .35 | .40 | .54 | .65 | .76 | .86 | .95 | 1.02 | 1.10 | 1.18 | 1.31 | 1.46 | 1.67 | 2.08 | 2.76 | |
| flank | 4 | much. | .20 | .23 | .25 | .34 | .42 | .51 | .59 | .66 | .71 | .77 | .82 | .92 | 1.06 | 1.25 | 1.64 | 2.15 | ||
| cur- | 6 | .16 | .17 | .26 | .32 | .38 | .43 | .48 | .52 | .56 | .60 | .66 | .76 | .93 | 1.20 | 1.54 | ||||
| va- | 12 | .19 | .24 | .28 | .31 | .34 | .36 | .38 | .40 | .45 | .52 | .63 | .80 | .98 | ||||||
| ture | 24 | .22 | .25 | .28 | .33 | .47 | .60 | |||||||||||||
| For Faces of Racks; and of Pinions for Racks and Internal Gears; for Flanks of Internal and Sides of Involute Teeth. | ||||||||||||||||||||
| Draw Setting Tangent at Middle of Tooth, regarding Space as Tooth in Internal Teeth. For Rack use Number of Teeth in Pinion. | ||||||||||||||||||||
| Pinion. | .31 | .39 | .48 | .57 | .73 | .88 | 1.00 | 1.10 | 1.20 | 1.30 | 1.40 | 1.48 | 1.65 | 1.85 | 2.15 | 2.65 | 3.50 | |||
| Rack. | .32 | .38 | .44 | .50 | .62 | .72 | .80 | .87 | .93 | .99 | 1.03 | 1.08 | 1.16 | 1.27 | 1.49 | 1.86 | 2.44 | |||
[7] These ratios are obtained by dividing the radius of the wheel sought by the diameter of the generating circle.
From these tables may be found a tabular value which, multiplied by the pitch of the wheel to be marked (as stated at the head of the table), will give the setting number on the graduated edge of the instrument, the procedure being as follows:—
For the teeth of a pair of wheels intended to gear together only (and not with other wheels having a different number of teeth).
For the face of such teeth where the flanks are to be radial lines.
Rule.—Divide the pitch circle radius of the wheel to have its teeth marked by the pitch circle radius of the wheel with which it is to gear: or, what is the same thing, divide the number of teeth in the wheel to have its teeth marked by the number of teeth in the wheel with which it is to gear, and the quotient is the “ratio.” In the ratio column find this number, and look along that line, and in the column at the head of which is the number of teeth contained in the wheel to be marked, is a number termed the tabular value, which, multiplied by the arc pitch of the teeth, will give the number on the graduated edge by which to set the instrument to the tangent line.
Example.—What is the setting number for the face curves of a wheel to contain 12 teeth, of 3-inch arc pitch, and to gear with a wheel having 24 teeth?
Here number of teeth in wheel to be marked = 12, divided by the number of teeth (24) with which it gears; 12 ÷ 24 = .5. Now in column of ratios may be found 1⁄2 = .500 (which is the same thing as .5), and along the same horizontal line in the table, and in the column headed 12 (the number of teeth in the wheel) is found .34. This is the tabular value, which, multiplied by 3 (the arc[I-50] pitch of the teeth), gives 1.02, which is the setting number on the graduated edge. It will be noted, however, that the graduated edge is marked 1, 2, 3, &c., and that between each consecutive division are ten subdivisions; hence, for the decimal .02 an allowance may be made by setting the line 1 a proportionate amount below the tangent line marked on the wheel to set the instrument by.
Required now the setting number for the wheel to have the 24 teeth.
Here number of teeth on the wheel = 24, divided by the number of teeth (12) on the wheel with which it gears; 24 ÷ 12 = 2. Now, there is no column in the “number of teeth sought” for 24 teeth; but we may find the necessary tabular value from the columns given for 20 teeth and 30 teeth, thus:—opposite ratio 2, and under 20 teeth is given .30, and under 30 teeth is given .38—the difference between the two being .08. Now the difference between 20 teeth and 24 teeth is 4⁄10; hence, we take 4⁄10 of the .08 and add it to the tabular value given for 20 teeth, thus: .08 × 4 ÷ 10 = .032, and this added to .30 (the tabular value given for 20 teeth = .33, which is the tabular value for 24 teeth). The .33 multiplied by arc pitch (3) gives .99. This, therefore, is the setting number for the instrument, being sufficiently near to the 1 on the graduated edge to allow that 1 to be used instead of .99.
It is to be noted here that the pinion, having radial lines, the other wheel must have curved flanks; the rule for which is as follows:—
Note.—When the flanks are desired to be curved instead of radial, it is necessary to the use of the instrument to select and assume a value for the degree of curve, as is done in the table in the column marked “Degree for flank curving;” in which
1.5 slight—a slight curvature of flank.
2 good—an increased curvature of flank.
3 more—a degree of pronounced spread at root.
4 much—spread at root is a distinguishing feature of tooth form.
6—still increased spread in cases where the strength at root of
pinion is of much importance to give strength.
12—as above, under aggravated conditions.
24—undesirable (unless requirement of strength compels this
degree), because of excessive strain on pinion.
Rule.—For faces of teeth to have curved flanks.
Divide the number of teeth in the wheel to be marked by the number of teeth in the wheel with which it gears, and multiply by the degree of flank curve selected for the wheel with which that to be marked is to gear, and this will give the ratio. Find this number in ratio column, and the tabular number under the column of number of teeth of wheel to be marked; multiply tabular number so found by arc pitch of wheel to be marked, and the product will be the setting number for the instrument.
Example.—What is the setting number on the graduated edge of the odontograph for the faces of a wheel (of a pair) to contain 12 teeth of 2-inch arc pitch, and to gear with a wheel having 24 teeth and a flank curvature represented by 3 in “Degree of flank curving” column?
Here teeth in wheel to be marked (12) divided by number of teeth in the wheel it is to gear with (24), 12 ÷ 24 = .5, which multiplied by 3 (degree of curvature selected for flanks of 24-teeth wheel), .5 × 3 = 1.5. In column of ratio numbers find 1.5, and in 12-teeth column is .25, which multiplied by pitch (2) gives .5 as the setting number for the instrument; this being the fifth line on the instrument, and half way between the end and mark 1.
[I-51]Rule.—Assume the degree of curve desired for the flanks to be marked, select the corresponding value in the column of “Degrees of flank curving,” and find the tabular value under the number of teeth column.
Multiply tabular value so found by the arc pitch of the teeth, and the product is the setting number on the instrument.
Example.—What is the setting number on the odontograph for the flanks of a wheel to contain 12 teeth and gear with one having 24 teeth, the degree of curvature for the flanks being represented by 4 in the column of “Degree of flank curvature?”
Here in column of degrees of flank curvature on the 3 line and under 12 teeth is .20, which multiplied by pitch of teeth (2) is .20 × 2 = 40, or 4⁄10; hence, the fourth line of division on the curved corner is the setting line, it representing 4⁄10 of 1.
Rule—both for the faces and for the flanks. For each respective wheel divide the number of teeth in that wheel by some one number not greater than the number of teeth in the smallest wheel in the set, which gives the ratio number for the wheel to be marked. On that line of ratio numbers, and in the column of numbers of teeth, find the tabular value number; multiply this by the arc pitch of the wheel to be marked, and the product is the setting number of the instrument.
Example.—A set of wheels is to contain 10 wheels; the smallest is to contain 12 teeth; the arc pitch of the wheels is four inches. What is the setting number for the smallest wheel?
Here number of teeth in smallest wheel of set is 10; divide this by any number smaller than itself (as say 5), 10 ÷ 5 = 2 = the ratio number on ratio line for 2; and under column for 12 is .17, which is the tabular value, which multiplied by pitch (4) is .17 × 4 = 68, or 6⁄10 and 8⁄100; hence, the instrument must be set with its seventh line of division just above the tangent line marked on the wheel. It will be noted that, if the seventh line were used as the setting, the adjustment would be only the 2⁄100 of a division out, an amount scarcely practically appreciable.
Both for the faces and flanks, the second number is obtained in precisely the same manner for every wheel in the set, except that instead of 10 the number of teeth in each wheel must be substituted.
Rack and Pinion.—For radial flanks use for faces the two lower lines of table. For curved flanks find tabular value for pinion faces in lowest line. For flanks of pinion choose degree of curving, and find tabular value under “flanks,” as for other wheels. For faces of rack divide number of teeth in pinion by degree of curving, which take for number of teeth in looking opposite “rack.” Flanks of rack are still parallel, but may be arbitrarily curved beyond half way below pitch line.
Internal Gears.—For tooth curves within the pitch lines, divide radius of each wheel by any number not greater than radius of pinion, and look in the table under “flanks.” For curves outside pitch line use lower line of table; or, divide radii by any number and look under “faces.” In applying instrument draw tangents at middle and side of space, for internal teeth.
Involute Teeth.—For tabular values look opposite “Pinion,” under proper number of teeth, for each wheel. Draw setting tangent from “base circle” of involute, at middle of tooth. For this the instrument gives the whole side of tooth at once.
In all cases multiply the tabular value by the pitch in inches.
Bevel-Wheels.—Apply above rules, using the developed normal cone bases as pitch lines. For right-angled axes this is done by using in place of the actual ratio of radii, or of teeth numbers, the square of that ratio; and for number of teeth, the actual number multiplied by the square root of one plus square of ratio or radii; the numerator of ratio, and number of teeth, belonging to wheel sought.
When the first column ratio and teeth numbers fall between those given in the table, the tabular values are found by interpolating as seen in the following examples:
Take a pair of 16 and 56 teeth; radii 5.09 and 17.82 inches respectively; and 2 inches pitch.
| Kind of Gearing. | Number of Teeth. |
} | Kind of Flank. | Ratio Radii. |
First Column Ratio. | Tab. Val. | ||||||
| Flank. | Face. | Flank. | Face. | |||||||||
| Epicycloidal, | } | Small | Radial | . | 29 | Radial | . | 29 | .. | .44 | ||
| Radial Flanks | Large | Radial | 3. | 5 | Radial | 3. | 5 | .. | .44 | |||
| Epicycloidal, | } | Small | Curved 2 deg. | . | .29 | 2 | . | 87 | .63 | .36 | ||
| Curved Flanks. | Large | Curved 3 deg. | } | 3. | 5 | 3 | 7. | .82 | .30 | |||
| Epicycloidal, | } | Small | “Sets,” Divide | 2. | 2 | 2. | .63 | .26 | ||||
| Interchange’bl. | Large | Radii by 2.55 | 7. | 7 | 7. | .40 | .30 | |||||
| Epicycloidal, | } | Pinion | Curved 2 deg. | 2 | Pinion | .63 | .44 | |||||
| Internal. | Wheel | Int. face 7 deg. | 3. | 5 | Pinion | 7 | [8] | .84 | .39 | |||
| Epicycloidal, | } | Pinion | Curved 2 deg. | 2 | Pinion | .63 | .44 | |||||
| Rack & Pinion. | Rack | Parallel | Parallel | Rack | .. | .31 | ||||||
| Involute | } | Small | Face and Flank | Pinion. | .44 | |||||||
| Gearing. | Large | One Curve | Pinion. | .84 | ||||||||
[8] The face being here internal, the tabular value is to be found under “flanks.” If bevels, use ratio radii .082 and 12.25; and teeth numbers 16.6 and 203.8 respectively.
Walker’s Patent Wheel Scale.—This scale is used in many manufactories in the United States to mark off the teeth for patterns, wherefrom to mould cast gears, and consists of a diagram from which the compasses may be set to the required radius to strike the curves of the teeth.
The general form of this diagram is shown in Fig. 139. From[I-52] the portion a the length of the teeth, according to the pitch, is obtained. From the portion b half the thickness of the tooth at the pitch line is obtained. From the part c half the thickness at the root is obtained, and from the part d half the thickness at the point is obtained.
Each of these parts is marked with the number of teeth the wheel is to contain, and with the pitch of the teeth as shown in Fig. 140, which represents part c full size. Now suppose it is required to find the thickness at the root, for a tooth of a wheel having 60 teeth of one inch pitch, the circles from the point a, pitch line b and root c being drawn, and a radial line representing the middle of the tooth being marked, as is shown in Fig. 142, the compass points are set to the distance f b, Fig. 140—f being at the junction of line 1 with line 60; the compasses are then rested at g, and the points h i are marked. Then, from the portion b, Fig. 139 of the diagram, which is shown full-size in Fig. 141, the compasses may be set to half the thickness at the pitch circle, as in this case (for ordinary teeth) from e to e, and the points j k, Fig. 142, are marked. By a reference to the portion d of the diagram, half the thickness of the tooth at the point is obtained, and marked as at l m in Fig. 142. It now remains to set compasses to the radius for the face and that for the flank curves, both of which may be obtained from the part a of the diagram. The locations of the centres, wherefrom to strike these curves, are obtained as in Fig. 142. The compasses set for the face curve are rested at h, and the arc n is struck; they are then rested at j and the arc o struck; and from the intersection of n o, as a centre, the face curve h j is marked. By a similar process, reference to the portion d of the diagram, half the thickness of the tooth at the point is obtained, and marked as at l m in Fig. 142. It now remains to set the compasses to the radius to strike the respective face and flank curves, and for this purpose the operator turns to the portion a, Fig. 139, of the diagram or scale, and sets the compasses from the marks on that portion to the required radii.
It now remains to find the proper location from which to strike the curves.
The face curve on the other side of the tooth is struck. The compasses set to the flank radius is then rested at m, and the arc p is marked and rested at k to mark the arc q; and from the intersection of p q, as a centre, the flank curve k m is marked: that on the other side of the tooth being marked in a similar manner.
Additional scales or diagrams, not shown in Fig. 139, give similar distances to set the compasses for the teeth of internal wheels and racks.
It now remains to explain the method whereby the author of the scale has obtained the various radii, which is as follows: A wheel of 200 teeth was given the form of tooth curve that would be obtained by rolling it upon another wheel, containing 200 teeth of the same pitch. It was next given the form of tooth that would be obtained by rolling upon it a wheel having 10 teeth of the same pitch, and a line intermediate between the two curves was taken as representing the proper curve for the large wheel.[I-53] The wheel having 10 teeth was then given the form of tooth that would be obtained by rolling upon it another wheel of the same diameter of pitch circle and pitch of teeth. It was next given the form of tooth that would be given by rolling upon it a wheel having 200 teeth, and a curve intermediate between the two curves thus obtained was taken as representing the proper curve for the pinion of 10 teeth. By this means the inventor does not claim to produce wheels having an exactly equal velocity ratio, but he claims that he obtains a curve that is the nearest approximation to the proper epicycloidal curve. The radii for the curves for all other numbers of teeth (between 10 and 200) are obtained in precisely the same manner, the pinion for each pitch being supposed to contain 10 teeth. Thus the scale is intended for interchangeable cast gears.
The nature of the scale renders it necessary to assume a constant height of tooth for all wheels of the same pitch, and this Mr. Walker has assumed as .40 of the pitch, from the pitch line to the base, and .35 from the pitch line to the point.
The curves for the faces obtained by this method have rather more curvature than would be due to the true epicycloid, which causes the points to begin and leave contact more easily than would otherwise be the case.
For a pair of wheels Mr. Walker strikes the face curve by a point on the pitch rolling circle, and the flanks by a point on the addendum circle, fastening a piece of wood to the pitch circle to carry the tracing point. The flank of each wheel is struck with a tracing point, thus attached to the pitch circle of the other wheel.
The proportions of teeth and of the spaces between them are usually given in turns of the pitch, so that all teeth of a given pitch shall have an equal thickness, height, and breadth, with an equal addendum and flank, and the same amount of clearance.
The term “clearance” as applied to gear-wheel teeth means the amount of space left between the teeth of one wheel, and the spaces in the other, or, in other words, the difference between the width of the teeth and that of the spaces between the teeth.
This clearance exists at the sides of the teeth, as in Fig. 143, at a, and between the tops of the teeth and the bottoms or roots of the spaces as at b. When, however, the simple term clearance is employed it implies the side clearance as at a, the clearance at b being usually designated as top and bottom clearance. Clearance is necessary for two purposes; first, in teeth cut in a machine to accurate form and dimensions, to prevent the teeth of one wheel from binding in the spaces of the other, and second, in cast teeth, to allow for the imperfections in the teeth which are incidental to casting in a founder’s mould. In machine-cut teeth the amount of clearance is a minimum.
In wheels which are cast with their teeth complete and on the pattern, the amount of clearance must be a maximum, because, in the first place, the teeth on the pattern must be made taper to enable the extraction of the pattern from the mould without damage to the teeth in the mould, and the amount of this taper must be greater than in machine-moulded teeth, because the pattern cannot be lifted so truly vertical by hand as to avoid, in all cases, damage to the mould; in which case the moulder repairs the mould either with his moulding tools and by the aid of the eye, or else with a tooth and a space made on a piece of wood for the purpose. But even in this case the concentricity of the teeth is scarcely likely to be preserved.
It is obvious that by reason of this taper each wheel is larger in diameter on one side than on the other, hence to preserve the true curves to the teeth the pitch circle is made correspondingly smaller. But if in keying the wheels to their shafts the two large diameters of a pair of wheels be placed to work together, the teeth of the pair would have contact on that side of the wheel only, and to avoid this and give the teeth contact across their full breadth the wheels are so placed on their shafts that the large diameter of one shall work with the small one of the other, the amount of taper being the same in each wheel irrespective of their relative diameters. This also serves to keep the clearance equal in amount both top, and bottom, and sideways.
A second imperfection is that in order to loosen the pattern in the sand or mould, and enable its extraction by hand from the mould, the pattern requires to be rapped in the mould, the blows forcing back the sand of the mould and thus loosening the pattern. In ordinary practice the amount of this rapping is left entirely to the judgment of the moulder, who has nothing to guide him in securing an equal amount of pattern movement in each direction in the mould; hence, the finished mould may be of increased radius at the circumference in the direction in which the wheel moved most during the rapping. Again, the wood pattern is apt in time to shrink and become out of round, while even iron patterns are not entirely free from warping. Again, the cast metal is liable to contract in cooling more in one direction than in another. The amount of clearance usually allowed for pattern-moulded cast gearing is given by Professor Willis as follows:—Whole depth of tooth 7⁄10, of the pitch working depth 6⁄10; hence 1⁄10 of the pitch is allowed for top and bottom clearance, and this is the amount shown at b in Fig. 143. The amount of side clearance given by Willis as that ordinarily found in practice is as follows:—“Thickness of tooth 5⁄11 of the pitch; breadth of space 6⁄11; hence, the side clearance equals 1⁄11 of the pitch, which in a 3-inch pitch equals .27 of an inch in each wheel.” Calling this in round figures, which is near enough for our purpose, 1⁄4 inch, we have thickness of tooth 11⁄4, width of space 13⁄4, or 1⁄2 inch of clearance in a 3-inch pitch, an amount which on wheels of coarse pitch is evidently more than that necessary in view of the accuracy of modern moulding, however suitable it may have been for the less perfect practice of Professor Willis’s time. It is to be observed that the rapping of the pattern in the founder’s mould reduces the thickness of the teeth and increases the width of the spaces somewhat, and to that extent augments the amount of side clearance allowed on the pattern, and the amount of clearance thus obtained would be nearly sufficient for a small wheel, as say of 2 inches diameter. It is further to be observed that the amount of rapping is not proportionate to the diameter of the wheel; thus, in a wheel of 2 inches diameter, the rapping would increase the size of the mould about 1⁄32 inch. But in the proportion of 1⁄32 inch to every 2 inches of diameter, the rapping on a 6-foot wheel would amount to 11⁄16 inches, whereas, in actual practice, a 6-foot wheel would not enlarge the mould more than at most 1⁄8 inch from the rapping.
It is obvious, then, that it would be more in accordance with the requirements to proportion the amount of clearance to the diameter of the wheel, so as to keep the clearance as small as possible. This will possess the advantage that the teeth will be stronger, it being obvious that the teeth are weakened both from the loss of thickness and the increase of height due to the clearance.
It is usual in epicycloidal teeth to fill in the corner at the root of the tooth with a fillet, as at c, d, in Fig. 143, to strengthen it.[I-54] This is not requisite when the diameter of the generating circle is so small in proportion to the base circle as to produce teeth that are spread at the roots; but it is especially advantageous when the teeth have radial flanks, in which case the fillets may extend farther up the flanks than when they are spread; because, as shown in Fig. 47, the length of operative flank is a minimum in teeth having radial flanks, and as the smallest pinion in the set is that with radial flanks, and further as it has the least number of teeth in contact, it is the weakest, and requires all the strengthening that the fillets in the corners will give, and sometimes the addition of the flanges on the sides of the pinion, such gears being termed “shrouded.”
The proportion of the teeth to the pitch as found in ordinary practice is given by Professor Willis as follows:—
| Depth to pitch line | 3⁄10 | of the | pitch. |
| Working depth | 6⁄10 | „ | „ |
| Whole depth | 7⁄10 | „ | „ |
| Thickness of tooth | 5⁄11 | „ | „ |
| Breadth of space | 6⁄11 | „ | „ |
The depth to pitch line is, of course, the same thing as the height of the addendum, and is measured through the centre of the tooth from the point to the pitch line in the direction of a radial line and not following the curve of tooth face.
Referring to the working depth, it was shown in Figs. 42 and 44 that the height of the addendum remaining constant, it varies with the diameter of the generating circle.
From these proportions or such others as may be selected, in which the proportions bear a fixed relation to the pitch, a scale may be made and used as a gauge, to set the compasses by, and in marking off the teeth for any pitch within the capacity of the scale. A vertical line a b in Fig. 144, is drawn and marked off in inches and parts of an inch, to represent the pitches of the teeth; at a right angle to a b, the line b c is drawn, its length equalling the whole depth of tooth, which since the coarsest pitch in the scale is 4 inches will be 7⁄10 of 4 inches. From the end of line c we draw a diagonal line to a, and this gives us the whole depth of tooth for any pitch up to 4 inches: thus the whole depth for a 4-inch pitch is the full length of the horizontal line b c; the whole depth for a 3-inch pitch will be the length of the horizontal line running from the 3 on line a b, to line a c on the right hand of the figure; similarly for the full depth of tooth for a 2-inch pitch is the length of the horizontal line running from 2 to a c. The working depth of tooth being 6⁄10 of the pitch a diagonal is drawn from a meeting line c at a distance from b of 6⁄10 of 4 inches and we get the working depth for any other pitch by measuring (along the horizontal line corresponding to that pitch), from the line of pitches to the diagonal line for working depth of tooth. The thickness of tooth is 5⁄11 of the pitch and its diagonal is distant 5⁄11 of 4 (from b) on line b c, the thickness for other pitches being obtained on the horizontal line corresponding to those pitches as before.
The construction of a pattern wherefrom to make a foundry mould, in which to cast a spur gear-wheel, is as shown in section, and in plan of Fig. 145. The method of constructing these patterns depends somewhat on their size. Large patterns are constructed with the teeth separate, and the body of the wheel is built of separate pieces, forming the arms, the hub, the rim, and the teeth respectively. Pinion patterns, of six inches and less in diameter, are usually made out of a solid piece, in which case the grain of the wood must lie in the direction of the teeth height. The chuck or face plate of the lathe, for turning the piece, must be of smaller diameter than the pinion, so that it will permit access to a tool applied on both sides, so as to strike the pitch circle on both sides. A second circle is also struck for the roots or depths of the teeth, and also, if required, an extra circle for striking the curves of the teeth with compasses, as was described in Fig. 130. All these circles are to be struck on both sides of the pattern, and as the pattern is to be left slightly taper, to[I-55] permit of its leaving the mould easily, they must be made of smaller diameter on one side than on the other of the pattern; the reduction in diameter all being made on the same side of the pattern. The pinion body must then be divided off on the pitch line into as many equal divisions as there are to be teeth in it; the curves of the teeth are then marked by some one of the methods described in the remarks on curves of gear-teeth. The top of the face curves are then marked along the points of the teeth by means of a square and scribe, and from these lines the curves are marked in on the other side of the pinion, and the spaces cut out, leaving the teeth projecting. For a larger pinion, without arms, the hub or body is built up of courses of quadrants, the joints of the second course breaking joint with those of the first.
The quadrants are glued together, and when the whole is formed and the glue dry, it is turned in the lathe to the diameter of the wheel at the roots of the teeth. Blocks of wood, to form the teeth, are then planed up, one face being a hollow curve to fit the circle of the wheel. The circumference of the wheel is divided, or pitched off, as it is termed, into as many points of equal division as there are to be teeth, and at these points lines are drawn, using a square, having its back held firmly against the radial face of the pinion, while the blade is brought coincidal with the point of division, so as to act as a guide in converting that point into a line running exactly true with the pinion. All the points of division being thus carried into lines, the blocks for the teeth are glued to the body of the pinion, as denoted by a, in Fig. 145. Another method is to dovetail the teeth into the pinion, as in Fig. 145 at b. After the teeth blocks are set, the process is, as already described, for a solid pinion.
The construction of a wheel, such as shown in Fig. 145, is as follows: The rim r must be built up in segments, but when the courses of segments are high enough to reach the flat sides of the arms they should be turned in the lathe to the diameter on the inside, and the arms should be let in, as shown in the figure at o. The rest of the courses of segments should then be added. The arms are then put in, and the inside of the segments last added may then be turned up, and the outside of the rim turned. The hub should then be added, one-half on each side of the arms, as in the figure. The ribs c of the arms are then added, and the body is completed (ready to receive the teeth), by filleting in the corners. An excellent method of getting out the teeth is as follows: Shape a piece of hard wood, as in Fig. 146, making it some five or six inches longer than the teeth, and about three inches deeper, the thickness being not less than the thickness of the required teeth at the pitch line. Parallel to the edge b c, mark the line a d, distant from b c to an amount equal to the required depth of tooth. Mark off, about midway of the piece, the lines a b and c d, distant from each other to an amount equal to the breadth of the wheel rim, and make two saw cuts to those lines. Take a piece of board an inch or two longer than the radius of the gear-wheel and insert a piece of wood (which is termed a box) tightly into the board, as shown in Fig. 147, e representing the box. Let the point f on the board represent the centre of the wheel, and draw a radial line r from f through the centre of the box. From the centre f, with a trammel, mark the addendum line g g, pitch line h i, and line j k for the depth of the teeth (and also a line wherefrom to strike the teeth curves, as shown in Fig. 129 if necessary). From the radial line r, as a centre, mark off on the pitch circle, points of division for several teeth, so as to be able to test the accuracy of the spacing across the several points, as well as from one point to the next, and mark the curves for the teeth on the end of the box, as shown. Turn the box end for end in the board, and mark out a tooth by the same method on the other end of the box. The box being removed from the board must now have its sides planed to the lines, when it will be ready to shape the teeth in. The teeth are got out for length, breadth, and thickness at the pitch line as follows: The lumber from which they are cut should be very straight grained, and should be first cut into strips of a width and thickness slightly greater than that of the teeth at the pitch line. These strips (which should be about two feet long) should then be planed down on the sides to very nearly the thickness of the tooth at the pitch line, and hollow on one edge to fit the curvature of the wheel rim. From these strips, pieces a trifle longer than the breadth of the wheel rim are cut, these forming the teeth. The pieces are then planed on the ends to the exact width of the wheel rim. To facilitate this planing a number of the pieces or blank teeth may be set in a frame, as in Figs. 148 and 149, in which a is a piece having the blocks b b affixed to it. c is a clamp secured by the screws at s s, and 1, 2, 3, 4, 5, 6 are the ends of the blank teeth. The clamp need not be as wide as the[I-56] teeth, as in Fig. 148, but it is well to let the pieces a and b b equal the breadth of the wheel rim, so that they will act as a template to plane the blank teeth ends to. The ends of b b may be blackleaded, so as to show plainly if the plane blade happens to shave them, and hence to prevent planing b b with the teeth. The blank teeth may now be separately placed in the box (Fig. 146) and secured by a screw, as shown in that figure, in which s is the screw, and t the blank tooth. The sides of the tooth must be carefully planed down equal and level with the surface of the box. The rim of the wheel, having been divided off into as many divisions as there are to be teeth in the wheel, as shown in Fig. 150, at a, a, a, &c., the finished teeth are glued so that the same respective side of each tooth exactly meets one of the lines a. Only a few spots of glue should be applied, and these at the middle of the root thickness, so that the glue shall not exude and hide the line a, which would make it difficult to set the teeth true to the line. When the teeth are all dry they must be additionally secured to the rim by nails. Wheels sufficiently large to incur difficulty of transportation are composed of a number of sections, each usually consisting of an arm, with an equal length of the rim arc on each side of it, so that the joint where the rim segments are bolted together will be midway between the two arms.
This, however, is not absolutely necessary so long as the joints are so arranged as to occur in the middle of tooth spaces, and not in the thickness of the tooth. This sometimes necessitates that the rim sections have an unequal length of arc, in which event the pattern is made for the longest segment, and when these are cast the teeth superfluous for the shorter segments are stopped off by the foundry moulder. This saves cutting or altering the pattern, which, therefore, remains good for other wheels when required.
When the teeth of wheels are to be cut in a gear-cutting machine the accurate spacing of the teeth is determined by the index plate and gearing of the machine itself; but when the teeth are to be cast upon the wheel and a pattern is to be made, wherefrom to cast the wheel the points of division denoting the thickness of the teeth and the width of the spaces are usually marked by hand. This is often rendered necessary from the wheels being of too large a diameter to go into dividing machines of the sizes usually constructed.
To accurately divide off the pitch circle of a gear-wheel by hand, requires both patience and skilful manipulation, but it is time and trouble that well repays its cost, for in the accuracy of spaces lies the first requisite of a good gear-wheel.
It is a very difficult matter to set the compasses so that by commencing at any one point and stepping the compasses around the circle continuously in one direction, the compass point shall fall into the precise point from which it started, for if the compass point be set the 1⁄200th inch out, the last space will come an inch out in a circle having 200 points of divisions. It is, therefore, almost impossible and quite impracticable to accurately mark or divide off a circle having many points of division in this manner, not only on account of the fineness of the adjustment of the compass points, but because the frequent trials will leave so many marks upon the circle that the true ones will not be distinguishable from the false. Furthermore, the compass points are apt to spring and fall into the false marks when those marks come close to the true ones.
In Fig. 151 is shown a construction by means of which the compass points may be set more nearly than by dividing the circumference of the circle by the number of divisions it is required to be marked into and setting the compasses to the quotient, because such a calculation gives the length of the division measured around the arc of the circle, instead of the distance measured straight from point of division to point of division.
The construction of Fig. 151 is as follows: p p is a portion of the circle to be divided, and a b is a line at a tangent to the point c of the circle p p. The point d is set off distant from c, to an amount obtained by dividing the circumference of p p by the number of divisions it is to have. Take one-quarter of this distance c d, and mark it from c, giving the point e, set one point of the compass at e and the other at d, and draw the arc[I-57] d f, and the distance from f to c, as denoted by g, is the distance to which to set the compasses to divide the circle properly. The compasses being set to this distance g, we may rest one compass point at c, and mark the arc f h, and the distance between arc h and arc d, measured on the line a b, is the difference between the points c, f when measured around the circle p p, and straight across, as at g.
A pair of compasses set even by this construction will not, however, be entirely accurate, because there will be some degree of error, even though it be in placing the compass points on the lines and on the points marked, hence it is necessary to step the compasses around the circle, and the best method of doing this is as follows: Commencing at a, Fig. 152, we mark off continuously one from the other, and taking care to be very exact to place the compass point exactly coincident with the line of the circle, the points b, c, d, &c., continuing until we have marked half as many divisions as the circle is to contain, and arriving at e, starting again at a, we mark off similar divisions (one half of the total number), f, g, h, arriving at i, and the centre k, between the two lines e, i, will be the true position of the point diametrally opposite to point a, whence we started. These points are all marked inside the circle to keep them distinct from those subsequently marked.
It will be, perhaps, observed by the reader that it would be more expeditious, and perhaps cause less variation, were we to set the compasses to the radius of the circle and mark off the point k, as shown in Fig. 153, commencing at the point a, and marking off on the one side the lines b, c, and d, and on the other side e, f, and g, the junction or centre, between g and d, at the circle being the true position of the point k. For circles struck upon flat surfaces, this plan may be advantageous; and in cases where there are not at hand compasses large enough, a pair of trammels may be used for the purpose; but our instructions are intended to apply also to marking off equidistant points on such circumferences as the faces of pulleys or on the outsides of small rings or cylinders, in which cases the use of compasses is impracticable. The experienced hand may, it is true, adjust the compasses as instructed, and mark off three or four of the marks b, c, &c., in Fig. 152, and then open out the compasses to the distance between the two extreme marks, and proceed as before to find the centre k, but as a rule, the time saved will scarcely repay the trouble; and all that can be done to save time in such cases is, if the holes come reasonably close together, to mark off, after the compasses are adjusted, three or four spaces, as shown in Fig. 154. Commencing at the point a, and marking off the points b, c, and d, we then set another pair of compasses to the distance between a and d, and then mark, from d on one side and from a on the other, the marks from f to l and from m to t, thus obtaining the point k. This method, however expeditious and correct for certain work, is not applicable to circumferential work of small diameter and in which the distance between two of the adjacent points is, at the most, 1⁄20 of the circumference of the circle; because the angle of the surface of the metal to the compass point causes the latter to spring wider open in consequence of the pressure necessary to cause the compass point to mark the metal. This will be readily perceived on reference to Fig. 155 in which a represents the stationary, and b the scribing or marking point of the compasses.
The error in the set of the compasses as shown by the distance apart of the two marks e and i on the circle in Fig. 152 is too fine to render it practicable to remedy it by moving the compass legs, hence we effect the adjustment by oilstoning the points on the outside, throwing them closer together as the figure shows is necessary.
Having found the point k, we mark (on the outside of the circle, so as to keep the marks distinct from those first marked) the division b, c, d, Fig. 156, &c., up to g, the number of divisions between b and g being one quarter of those in the whole circle. Then, beginning at k, we mark off also one quarter of the number of divisions arriving at m in the figure and producing the point 3. By a similar operation on the other side of the circle, we get the true position of point No. 4. If, in obtaining points 3 and 4, the compasses are not found to be set dead true, the necessary adjustment must be made; and it will be seen that, so far, we have obtained four true positions, and the process of obtaining each of them has served as a justification of the distance of the compass points. From these four points we may proceed in like[I-58] manner to mark off the holes or points between them; and the whole will be as true as it is practicable to mark them off upon that size of circle. In cases, however, where mathematical precision is required upon flat and not circumferential surfaces, the marking off may be performed upon a circle of larger diameter, as shown in Fig. 157. If it is required to mark off the circle a, Fig. 157, into any even number of equidistant points, and if, in consequence of the closeness together of the points, it becomes difficult to mark them (as described) with the compasses, we mark a circle b b of larger diameter, and perform our marking upon it, carrying the marks across the smaller circle with a straightedge placed to intersect the centres of the circles and the points marked on each side of the diameter. Thus, in Fig. 157, the lines 1 and 2 on the smaller circle would be obtained from a line struck through 1 and 4 on the outer circle; and supposing the larger circle to be three times the size of the smaller, the deviation from truth in the latter will be only 1⁄3 of whatever it is in the former.
In this example we have supposed the number of divisions to be an even one, hence the point k, Fig. 152, falls diametrically opposite to a, whereas in an odd number of points of division this would not be the case, and we must proceed by either of the two following methods:—
In Fig. 158 is shown a circle requiring to be divided by 17 equidistant points. Starting from point 1 we mark on the outside of the circumference points 2, 3, 4, &c., up to point 9. Starting again from point 1 we mark points 10, 11, &c., up to 17. If, then, we try the compasses to 17 and 9 we shall find they come too close together, hence we take another pair of compasses (so as not to disturb the set of our first pair) and find the centre between 9 and 17 as shown by the point a. We then correct the set of our first pair of compasses, as near as the judgment dictates, and from point a, we mark with the second compasses (set to one half the new space of the first compasses) the points b, c. With the first pair of compasses, starting from b, we mark d, e, &c., to g; and from i, we mark divisions h, i, &c., to k, and if the compasses were set true, k and g would meet at the circle. We may, however, mark a point midway between k and g, as at 5. Starting again from points c and i, we mark the other side of the circle in a similar manner, producing the lines p and q, midway between which (the compasses not being set quite correct as yet) is the true point for another division. After again correcting the compasses, we start from b and 5 respectively, and mark point 7, again correcting the compasses. Then from c and the point between p and q, we may mark an intermediate point, and so on until all the points of division are made. This method is correct enough for most practical purposes, but the method shown in Fig. 159 is more correct for an odd number of points of division. Suppose that we have commenced at the point marked i, we mark off half the required number of holes on one side and arrive at the point 2; and then, commencing at the point i again, we mark off the other half of the required number of holes, arriving at the point 3. We then apply our compasses to the distance between the points 2 and 3; and if that distance is not exactly the same to which the compasses are set, we make the necessary adjustment, and try again and again until correct adjustment is secured.
It is highly necessary, in this case, to make the lines drawn at[I-59] each trial all on the same side of the circle and of equal length, but of a different length to those marked on previous trials. For example, left the lines a, b, c, d, in Fig. 159 represent those made on the first trial, and e, f, g, h, those made on the second trial; and when the adjustment is complete, let the last trial be made upon the outside or other side of the circle, as shown by the lines i, j, k, l. Having obtained the three true points, marked 1, 2, 3, we proceed to mark the intermediate divisions, as described for an even number of divisions, save that there will be a space, 2 and 3, opposite point 1, instead of a point, as in case of a circle having an even number of divisions.
The equal points of division thus obtained may be taken for the centres of the tooth at the pitch circle or for one side of the teeth, as the method to be pursued to mark the tooth curves may render most desirable. If, for example, a template be used to mark off the tooth curves, the marks may be used to best advantage as representing the side of a tooth, and from them the thickness of the tooth may be marked or not as the kind of template used may require. Thus, if the template shown in Fig. 21 be used, no other marks will be used, because the sides of a tooth on each side of a space may be marked at one setting of the template to the lines or marks of division. If, however, a template, such as shown in Fig. 81 be used, a second set of lines marked distant from the first to a radius equal to the thickness of a tooth becomes necessary so that the template may be set to each line marked. If the Willis odontograph or the Robinson template odontograph be used the second set of lines will also be necessary. In using the Walker scale a radial line, as g in Fig. 142, will require to be marked through the points of equal division, and the thickness of the tooth at the points on the pitch circle and at the root must be marked as was shown in Fig. 142.
But if the arcs for the tooth curves are to be marked by compasses, the location for the centres wherefrom to strike these arcs may be marked from the points of division as was shown in Fig. 130.
To construct a pattern wherefrom to cast a bevel gear-wheel.—When a pair of bevel-wheels are in gear and upon their respective shafts all the teeth on each wheel incline, as has been shown, to a single point, hence the pattern maker draws upon a piece of board a sketch representing the conditions under which the wheels are to operate. A sketch of this kind is shown in Fig. 160, in which a, b, c, d, represent in section the body of a bevel pinion. f g is the point of a tooth on one side, and e the point of a tooth on the other side of the pinion, while h i are pitch lines for the two teeth. Thus, the cone surface, the points, the pitch lines and the bottom of the spaces, projected as denoted by the dotted lines, would all meet at x, which represents the point where the axes of the shafts would meet.
In making wooden patterns wherefrom to cast the wheels, it is usual, therefore, to mark these lines on a drawing-board, so that they may be referred to by the workman in obtaining the degree of cone necessary for the body a b c d, to which the teeth are to be affixed. Suppose, then, that the diameter of the pinion is sufficiently small to permit the body a b c d to be formed of one piece instead of being put together in segments, the operation is as follows: The face d c is turned off on the lathe, and the piece is reversed on the lathe chuck, and the face a b is turned, leaving a slight recess at the centre to receive and hold the cone point true with the wheel. A bevel gauge is then set to the angle a b c, and the cone of the body is turned to coincide in angle with the gauge and to the required diameter, its surface being made true and straight so that the teeth may bed well. While turning the face d c in the lathe a fine line circle should be struck around the circumference of the cone and near d c, on which line the spacing for the teeth may be stepped off with the compasses. After this circle or line is divided off into as many equidistant points as there are to be teeth on the wheel, the points of division require to be drawn into lines, running across the cone surface of the wheel, and as the ordinary square is inapplicable for the purpose, a suitable square is improvised as follows: In Fig. 161 let the outline in full lines denote the body of a pinion ready to receive the teeth, and a b the circle referred to as necessary for the spacing or dividing with the compasses. On a b take any point, as c, as a centre, and with a pair of compasses mark equidistant on each side of it two lines, as d, d. From d, d as respective centres mark two lines, crossing each other as at f, and draw a line, joining the intersection of the lines at f with c, and the last line, so produced, will be in the place in which the teeth are to lie; hence the wheel will require as many of these lines as it is to contain teeth, and the sides of the teeth, being set to these lines all around the pinion, will be in their proper positions, with the pitch lines pointing to x, in Fig. 160.
To avoid, however, the labor involved in producing these lines for each tooth, two other plans may be adopted. The first is to make a square, such as shown in Fig. 162, the face f f being fitted to the surface c, in Fig. 161, while the edges of its blade[I-60] coincide with the line referred to; hence the edge of the blade may be placed coincident successively with each point of division, as d d, and the lines for the place of the length of each tooth be drawn. The second plan is to divide off the line a b before removing the body of the pinion from the lathe, and produce, as described, a line for one tooth. A piece of wood may then be placed so that when it lies on the surface of the hand-rest its upper surface will coincide with the line as shown in Fig. 163, in which w is the piece of wood, and a, b, c, &c., the lines referred to. If the teeth are to be glued and bradded to the body, they are first cut out in blocks, left a little larger every way than they are to be when finished, and the surfaces which are to bed on the cone are hollowed to fit it. Then blocks are glued to the body, one and the same relative side of each tooth being set fair to the lines. When the glue is dry, the pinion is again turned on the lathe, the gauge for the cone of the teeth being set in this case to the lines e, f, g in Fig. 160. The pitch circles must then be struck at the ends of the teeth. The turned wheel is then ready to have the curves of the teeth marked. The wheel must now again be divided off on the pitch circle at the large end of the cone into as many equidistant points as there are to be teeth on the wheel, and from these points, and on the same relative side of them, mark off a second series of points, distant from the points of division to an amount equal to the thickness the teeth are required to be. From these points draw in the outline of the teeth (upon the ends of the blocks to form the teeth) at the large end of the cone. Then, by use of the square, shown in Fig. 162, transfer the points of the teeth to the small end of the cone, and trace the outline of the teeth at the small end, taking centres and distances proportionate to the reduced diameter of the pitch circle at the small end, as shown in Fig. 160, where at j are three teeth so marked for the large end, and at k three for the small end, p p representing the pitch circle, and r r a circle for the compass points. The teeth for bevel pinions are sometimes put on by dovetails, as shown in Fig. 164, a plan which possesses points of advantage and disadvantage. Wood shrinks more across the grain than lengthwise with it, hence when the grain of the teeth crosses that of the body with every expansion or contraction of the wood (which always accompanies changes in the humidity of the atmosphere) there will be a movement between the two, because of the unequal expansion and contraction, causing the teeth to loosen or to move. In the employment of dovetails, however, a freedom of movement lengthways of the tooth is provided to accommodate the movement, while the teeth are detained in their proper positions. Again, if in making the founders’ mould, one of the mould teeth should break or fall down when the pattern is withdrawn, a tooth may be removed from the pattern and used by the moulder to build up the damaged part of the mould again. And if the teeth of a bevel pinion are too much undercut on the flank curves to permit the whole pattern from being extracted from the mould without damaging it, dovetailed teeth may be drawn, leaving the body of the pattern to be extracted from the mould last. On the other hand, the dovetail is a costly construction if applied to large wheels. If the teeth are to be affixed by dovetails, the construction varies as follows: Cut out a wooden template of the dovetail, leaving it a little narrower than the thickness of the tooth at the root, and set the template on the cone at a distance from one of the lines a, b, c, Fig. 163, equal to the margin allowed between the edge of the dovetail and the side of the root of the tooth, and set it true by the employment of the square, shown in Fig. 162, and draw along the cone surface of the body lines representing the location of the dovetail grooves. The lines so drawn will give a taper toward x (Fig. 160), providing that, the template sides being parallel, each side is set to the square. While the body is in the lathe, a circle on each end may be struck for the depth of the dovetails, which should be cut out to gauge and to template, so that the teeth will interchange to any dovetail. The bottom of the dovetails need not be circular, but flat, which is easier to make. Dovetail pieces or strips are fitted to the grooves, being left to project slightly above the face of the cone or body. They are drawn in tight enough to enable them to keep their position while being turned in the lathe when the projecting points are turned down level with the cone of the body. The teeth may then be got out as described for glued teeth, and the dovetails added, each being marked to its place, and finally the teeth are cut to shape.
In wheels too large to have their cones tested by a bevel gauge, a wooden gauge may be made by nailing two pieces of wood to stand at the required angle as shown in Fig. 165, which is extracted from The American Machinist, or the dead centre c and a straightedge may be used as follows. In the figure the other wheel of the pair is shown dotted in at b, and the dead centre is[I-61] set at the point where the axes of a and b would meet; hence if the largest diameter of the cone of a is turned to correct size, the cone will be correct when a straightedge applied as shown lies flat on the cone and meets the point of the dead centre e. The pinion b, however, is merely introduced to explain the principle, and obviously could not be so applied practically, the distance to set e, however, is the radius a.
Skew Bevel.[9]—When the axles of the shaft are inclined to each other instead of being in a straight line, and it is proposed to connect and communicate motion to the shafts by means of a single pair of bevel-gears, the teeth must be inclined to the base of the frustra to allow them to come into contact.
[9] From the “Engineer and Machinists’ Assistant.”
To find the line of contact upon a given frustrum of the tangent-cone; let the Fig. 166 be the plane of the frustrum; a the centre. Set off a e equal to the shortest distance between the axes (called the eccentricity), and divide it in c, so that a c is to e c as the mean radius of the frustrum to the mean radius of that with which it is to work; draw c p perpendicular to a e, and meeting the circumference of the conical surface at m; perform a similar operation on the base of the frustrum by drawing a line parallel to c m and at the same distance a c from the centre, meeting the circumference in p.
The line p c is then plainly the line of direction of the teeth. We are also at liberty to employ the equally inclined line c q in the opposite direction, observing only that, in laying out the two wheels, the pair of directions be taken, of which the inclinations correspond.
Fig. 167 renders this mode of laying off the outlines of the wheels at once obvious. In this figure the line a e corresponds to the line marked by the same letters in Fig. 166; and the division of it at c is determined in the manner directed. The line c m being thus found in direction, it is drawn indefinitely to d. Parallel to this line and from the point c draw e to e, and in this line take the centre of the second wheel. The line c m d gives the direction of the teeth; and if from the centre a with radius at c a circle be described, the direction of any tooth of the wheel will be a tangent to it, as at c, and similarly if a centre e be taken in the line e d, and with radius e d, c e a circle be drawn, the direction of the teeth of the second wheel will be tangents to this last, as at d.
Having thus found the direction of the teeth, these outlines may be formed as in the case of ordinary bevel-wheels and with equal exactness and facility, all that is necessary being to find the curves for the teeth as described for bevel-wheels, and follow precisely the same construction, except that the square, Fig. 162, marking the lines across the cones, requires to be set to the angle for the tooth instead of at a right angle, and this angle may be found by the construction shown in Fig. 167, it being there represented by line d c. It is obvious, however, that the bottoms of the blocks to form the teeth must be curved to bed on the cone along the line d c, Fig. 167, and this may best be done by bedding two teeth, testing them by trial of the actual surfaces.
Then two teeth may be set in as No. 1 and No. 6 in the box shown in Fig. 148, the intermediate ones being dressed down to them.
Where a bevel-wheel pattern is too large to be constructed in one piece and requires to be built up in pieces, the construction is as in Fig. 168, in which on the left is shown the courses of segments 1, 2, 3, 4, 5, &c., of which the rim is built up (as described for spur wheels), and on the right is shown the finished rim with a tooth, c, in position.
The tooth proper is of the length of face of the wheel as denoted by b b′; now all the lines bounding the teeth must converge to the point x. Suppose, then, that the teeth are to be shaped for curve of face and flank in a box as described for spur-wheel teeth in Fig. 146, then in Fig. 168 let a, a represent the[I-62] bottom and b b′ the top of the box, and c a tooth in the box, its ends filling the opening in the box at b b′ then the curve on the sides of the box at b′ must be of the form shown at f, and the curve on the sides of the box (at the point b of its length) must be as shown at g, the teeth shown in profile at g and u representing the forms of the teeth at their ends, on the outside of the wheel rim at b′, and on the inside at b; having thus made a box of the correct form on its sides, the teeth may be placed in it and planed down to it, thus giving all the teeth the same curve.
The spacing for the teeth and their fixing may be done as described for the bevel pinion.
To construct a pattern wherefrom to cast an endless screw, worm, or tangent screw, which is to have the worm or thread cut in a lathe.—Take two pieces, each to form one longitudinal half of the pattern; peg and screw them together at the ends, an excess of stuff being allowed at each end for the accommodation of two screws to hold the two halves together while turning them in the lathe, or dogs, if the latter are more convenient, as they might be in a large pattern. Turn the piece down to the size over the top of the thread, after which the core prints are turned. The body thus formed will be ready to have the worm or thread cut, and for this purpose the tools shown in Figs. 169 and 140 are necessary.
That shown in Fig. 169 should be flat on the face similar to a parting tool for cast iron, but should have a great deal more bottom rake, as strength is not so much an object, and the tool is more easily sharpened. It has also in addition two little projections a b like the point of a penknife, formed by filing away the steel in the centre; these points are to cut the fibres of the wood, the severed portion being scraped away by the flat part of the tool.
The degree of side rake given to the tool must be sufficient to let the tool sides well clear the thread or worm, and will therefore vary with the pitch of the worm.
The width of the tool must be a shade narrower than the narrowest part of the space in the worm. Having suitably adjusted the change wheels of the lathe to cut the pitch required the parting tool is fed in until the extreme points reach the bottom of the spaces, and a square nosed parting tool without any points or spurs will finish the worm to the required depth. This will have left a square thread, and this we have now to cut to the required curves on the thread or worm sides, and as the cutting will be performed on the end grain of the wood, the top face of the tool must be made keen by piercing through the tool a slot a, Fig. 170, and filing up the bevel faces b, c and d, and then carefully oilstoning them. This tool should be made slightly narrower than the width of the worm space, so that it may not cut on both sides at once, as it would have too great a length of cutting edge.
Furthermore, if the pattern is very large, it will be necessary to have two tools for finishing, one to cut from the pitch line inwards and the other to complete the form from the pitch line outwards. It is advisable to use hard wood for the pattern.
If it is decided to cut the thread by hand instead of with these lathe tools, then, the pattern being turned as before, separate the two halves by taking out the screws at the ends; select the half that has not the pegs, as being a little more convenient for tracing lines across. Set out the sections of the thread, a, b, c, and d, Fig. 171, similar to a rack; through the centres of a, b, c, and d, square lines across the piece; these lines, where they intersect the pitch line, will give the centres of teeth on that side: or if we draw lines, as e, f, through the centres of the spaces, they will pass through the centres of the teeth (so to speak) on the other side; in this position complete the outline on that side. It will be found, in drawing these outlines, that the centres of some of the arcs will lie outside the pattern. To obtain support for the compasses, we must fit over the pattern a piece of board such as shown by dotted lines at g h.
It now remains to draw in the top of the thread upon the curved surface of the half pattern; for this purpose take a piece of stiff card or other flexible material, wrap it around the pattern and fix it temporarily by tacks, we then trim off the edges true to the pattern, and mark upon the edges of the card the position of the tops of the thread upon each side; we remove the card and spread it out on a flat surface, join the points marked on the edges by lines as in Fig. 172, replace the card exactly as before upon the pattern, and with a fine scriber we prick through the lines. The cutting out is commenced by sawing, keeping, of course, well within the lines; and it is facilitated by attaching a stop to the saw so as to insure cutting at all parts nearly to the exact depth. This stop is a simple strip of wood and may be clamped to the saw, though it is much more convenient to have a couple of holes in the saw blade for the passage of screws. For finishing, a pair of templates, p and q, Fig. 173, right and left, will be found useful; and finally the work should be verified and slight imperfections corrected by the use of a form or template taking in three spaces, as shown at r in Fig. 173. In drawing the lines on the card, we must consider whether it is a right or left-handed worm that we desire. In the engraving the lines are those suitable for a right-handed thread. Having completed one half of the pattern, place the two halves together, and trace off the half that is uncut, using again the card template for drawing the lines on the curved surface. The cutting out will be the same as before.
[I-63]As the teeth of cast wheels are, from their deviation from accuracy in the tooth curves and the concentricity of the teeth to the wheel centre, apt to create noise in running, it is not unusual to cast one or both wheels with mortises in the rim to receive wooden teeth. In this case the wheel is termed a mortise wheel, and the teeth are termed cogs. If only one of a pair of wheels is to be cogged, the largest of the pair is usually selected, because there are in that case more teeth to withstand the wear, it being obvious that the wear is greatest upon the wheel having the fewest teeth, and that the iron wheel or pinion can better withstand the wear than the mortise wheel. The woods most used for cogs are hickory, maple, hornbeam and locust. The blocks wherefrom the teeth are to be formed are usually cut out to nearly the required dimensions, and kept in stock, so as to be thoroughly well-seasoned when required for use, and, therefore less liable to come loose from shrinkage after being fitted to the mortise in the wheel. The length of the shanks is made sufficient to project through the wheel rim and receive a pin, as shown in Fig. 174, in which b is a blank tooth, and c a finished tooth inserted in the wheel, the pin referred to being at p. But, if a mortise should fall in an arm of the wheel, this pin-hole must pass through the rim, as shown in the mortise a. The wheel, however, should be designed so that the mortises will not terminate in the arms of the wheel.
Another method of securing the teeth in the mortises is to dovetail them at the small end and drive wedges between them, as shown in Fig. 175, in which c c are two contiguous teeth, r the wheel rim and w w two of the wedges. On account of the dovetailing the wedges exert a pressure pressing the teeth into the mortises. This plan is preferable to that shown in the Fig. 174 inasmuch as from the small bearing area of the pins they become loose quicker, and furthermore there is more elasticity to take up the wear in the case of the wedges.
The mortises are first dressed out to a uniform size and taper, using two templates to test them with, one of which is for the breadth and the other for the width of the mortise. The height above the wheel requires to be considerably more than that due to the depth of the teeth, so that the surface bruised by driving the cogs or when fitting them into the mortises may be cut off. To avoid this damage as much as possible, a broad-face hammer should be employed—a copper, lead, lignum vitæ, or a raw hide hammer being preferable, and the last the best. The teeth are got out in a box and two guides, such as shown in Figs. 176, 177, and 178, similar letters of reference denoting the same parts in all three illustrations.
In Fig. 176, x is a frame or box containing and holding the operative part of the tooth, and resting on two guides c d. The height of d from the saw table is sufficiently greater than that of c to give the shank g the correct taper, e f representing the circular saw. t is a plain piece of the full size of the box or frame, and serving simply to close up on that side the mortise in the frame. The grain of t should run at a right angle to the other piece of the frame so as to strengthen it. s is a binding screw to hold the cog on the frame, and h is a guide for the edge of the frame to slide against. It is obvious, now, that if the piece d be adjusted at a proper distance from the circular saw e f, and the edge of the frame be moved in contact with the guide h, one side of the tooth shank will be sawn. Then, by reversing the frame end for end, the other side of the shank may be sawn. Turning the frame to a right angle the edges of the cog shank can be sawn from the same box or frame, and pieces c, d, as shown in Fig. 177.
The frame is now stood on edge, as in Fig. 178, and the underneath surfaces sawed off to the depth the saw entered when the shank taper was sawn. This operation requires to be performed on all four sides of the tooth.
After this operation is performed on one cog, it should be tried in the wheel mortises, to test its correctness before cutting out the shanks on all the teeth.
The shanks, being correctly sawn, may then be fitted to the mortises, and let in within 1⁄8 of butting down on the face of the wheel, this amount being left for the final driving. The cogs should be numbered to their places, and two of the mortises must be numbered to show the direction in which the numbers proceed. To mark the shoulders (which are now square) to the curvature of the rim, a fork scriber should be used, and the shanks of the cogs should have marked on them a line coincident with the inner edge of the wheel rim. This line serves as a guide in marking the pin-holes and for cutting the shanks to length; but it is to be remembered that the shanks will pass farther through to the amount of the distance marked by the fork scriber. The holes for the pins which pass through the shanks should be made slightly less in their distances (measured from the nearest edge of the pin-hole) from the shoulders of the cogs than is the thickness of the rim of the wheel, so that when the cogs are driven fully home the pin-holes will appear not quite full circles on the inside of the wheel rim; hence, the pins will bind tightly against the inside of the wheel rim, and act somewhat as keys, locking and drawing the shanks to their seats in the mortises.
[I-64]In cases where quietness of running is of more consequence than the durability of the teeth, or where the wear is not great, both wheels may be cogged, but as a rule the larger wheel is cogged, the smaller being of metal. This is done because the teeth of the smaller wheel are the most subject to wear. The teeth of the cogged wheel are usually made the thickest, so as to somewhat equalise the strength of the teeth on the two wheels.
Since the power transmitted by a wheel in a given time is composed of the pressure or weight upon the wheel, and the space a point on the pitch circle moves through in the given time, it is obvious that in a train of wheels single geared, the velocities of all the wheels in the train being equal at the pitch circle, the teeth require to be of equal pitch and thickness throughout the train. But when the gearing is compounded the variation of velocity at the pitch circle, which is due to the compounding, has an important bearing upon the necessary strength of the teeth.
Suppose, for example, that a wheel receives a tooth pressure of 100 lbs. at the pitch circle, which travels at the velocity of 100 feet per minute, and is keyed to the same shaft with another wheel whose velocity is 50 feet per minute. Now, in the power transmitted by the two wheels the element of time is 50 for one wheel and 100 for the other, hence the latter (supposing both wheels to have an equal number of teeth in contact with their driver or follower as the case may be) will be twice as strong in proportion to the duty, and it appears that in compounded gearing the strength in proportion to the duty may be varied in proportion as the velocity is modified by compounding of the wheels. Thus, when the velocity at the pitch circle is increased its strength is increased, and per contra when its velocity is decreased its strength is decreased, when considered in proportion to the duty. When, however, the wheels are upon long shafts, or when they overhang the bearing of the shaft, the corner contact will from tension of the shaft, continue much longer than when the shaft is maintained rigid.
It is obvious that if a wheel transmits a certain amount of power, the pressure of tooth upon tooth will depend upon the number of teeth in contact, but since, in the case of very small wheels, that is to say, pinions of the smallest diameter of the given pitch that will transmit continuous motion, it occurs that only one tooth is in continuous contact, it is obvious that each single tooth must have sufficient strength to withstand the whole of the pressure when worn to the limits to which the teeth are supposed to wear. But when the pinion is so small that it has but one tooth in continuous contact, that contact takes place nearer the line of centres and to the root of the tooth, and therefore at a less leverage to the line of fracture, hence the ultimate strength of the tooth is proportionately increased. On the other hand, however, the whole stress of the wheel being concentrated on the arc of contact of one tooth only (instead of upon two or more teeth as in larger wheels), the wear is proportionately greater; hence, in a short time the teeth of the pinion are found to be thinner than those on the other wheel or wheels. The multiplicity of conditions under which small wheels may work with relation to the number of teeth in contact, the average leverage of the point of contact from the root of the tooth, the shape of the tooth, &c., renders it desirable in a general rule to suppose that the whole strain falls upon one tooth, so that the calculation shall give results to meet the requirements when a single tooth only is in continuous contact.
It follows, then, that the thickness of tooth arrived at by calculation should be that which will give to a tooth, when worn to the extreme thinness allowed, sufficient strength (with a proper margin of safety) to transmit the whole of the power transmitted by the wheel.
The margin (or factor) of safety, or in other words, the number of times the strength of the tooth should exceed the amount of power transmitted, varies (according to the conditions under which the wheels work) between 5 and 10.
The lesser factor may be used for slow speeds when the power is continuously and uniformly transmitted. The greater factor is necessary when the wheels are subjected to violent shocks and the direction of revolution requires to be reversed.
In pattern-cast teeth, contact between the teeth of one wheel and those of the other frequently occurs at one corner only, as shown in Fig. 179, and the line of fracture is in the direction denoted by the diagonal dotted lines. The causes of this corner contact have been already explained, but it may be added that as the wheels wear, the contact extends across the full breadths of the teeth, and the strength in proportion to the duty, therefore, steadily increases from the time the new wheels have action until the wear has caused contact fully across the breadth. Tredgold’s rule for finding the proper thickness of tooth for a given stress upon cast-iron teeth loaded at the corner as in Fig. 179 and supposed to have a velocity of three feet per second of time, is as follows:—
Rule.—Divide the stress in pounds at the pitch circle by 1500, and the square root of the quotient is the required thickness of tooth in inches or parts of an inch.
In the results obtained by the employment of this rule, an allowance of one-third the thickness for wear, and the margin for safety is included, so that the thickness of tooth arrived at is that to be given to the actual tooth. Further, the rule supposes the breadth of the tooth to be not less than twice the height of the same, any extra breadth not affecting the result (as already explained), when the pressure falls on a corner of the tooth.
In practical application, however, the diameter of the wheel at the pitch circle is generally, or at least often a fixed quantity, as well as the amount of stress, and it will happen as a rule that taking the stress as a fixed element and arriving at the thickness of the tooth by calculation, the required diameter of wheel, or what is the same thing, its circumference, will not be such as to contain the exact number of teeth of the thickness found by the calculation, and still give the desired amount of side clearance. It is desirable, therefore, to deal with the stress upon the tooth at the pitch circle, and the diameter, radius, or circumference of the pitch circle, and its velocity, and deduce therefrom the required thickness for the teeth, and conform the pitch to the requirements as to clearance from the tooth thickness thus obtained.
To deduce the thickness of the teeth from these elements we have Robertson Buchanan’s rule, which is as follows:—
Find the amount of horse-power employed to move the wheel, and divide such horse-power by the velocity in feet per second of the pitch line of the wheel. Extract the square root of the quotient, and three-fourths of this root will be the least thickness of the tooth. To the result thus obtained, there must be added the allowance for wear of the teeth and the width of the space including the clearance which will determine the number of teeth in the wheel.
In conforming strictly to this rule the difficulty is met with that it would give fractional pitches not usually employed and difficult to measure on an existing wheel. Cast wheels kept on hand or in stock by machinists have usually the following standard:—
Beginning with an inch pitch, the pitches increase by 1⁄8 inch up to 3-inch pitch, from 3 to 4-inch pitches the increase is by 1⁄4 inch, and from 4-inch pitch and upwards the increase is by 1⁄2 inch. Now, under the rule the pitches would, with the clearance made to bear a certain proportion to the pitch, be in odd fractions of an inch.
It appears then, that, if in a calculation to obtain the necessary thickness of tooth, the diameter of the pitch circle is not an element, the rule cannot be strictly adhered to unless the diameter of the pitch circle be varied to suit the calculated thickness of[I-65] tooth; or unless either the clearance, factor of safety, or amount of tooth thickness allowed for wear be varied to admit of the thickness of tooth arrived at by the calculation. But if the diameter of the pitch circle is one of the elements considered in arriving at the thickness of tooth requisite under given conditions, the pitch must, as a rule, either be in odd fractions, or else the allowance for wear, factor of safety, or amount of side clearance cannot bear a definite proportion to the pitch. But the allowance for clearance is in practice always a constant proportion of the pitch, and under these circumstances, all that can be done when the circumstances require a definite circumference of pitch circle, is to select such a pitch as will nearest meet the requirements of tooth thickness as found by calculation, while following the rule of making the clearance a constant proportion of the pitch. When following this plan gives a thinner tooth than the calculation calls for, the factor of safety and the allowance for wear are reduced. But this is of little consequence whenever more than one tooth on each wheel is in contact, because the rules provide for all the stress falling on one tooth. When, however, the number of teeth in the pinion is so small that one tooth only is in contact, it is better to select a pitch that will give a thicker rather than a thinner tooth than called for by the calculation, providing, of course, that the pitch be less than the arc of contact, so that the motion shall be continuous.
But when the pinions are shrouded, that is, have flanges at each end, the teeth are strengthened; and since the wear will continue greater than in wheels having more teeth in contact, the shrouding may be regarded as a provision against breakage in consequence of the reduction of tooth thickness resulting from wear.
In the following table is given the thickness of the tooth for a given stress at the pitch circle, calculated from Tredgold’s rule for teeth supposed to have contact when new at one corner only.
| Stress in lbs. at pitch circle. |
Thickness of tooth in inches. |
Actual pitches to which wheels may be made. |
||||
| 400 | .52 | 1 | 1⁄8 | to | 1 | 1⁄4 |
| 800 | .75 | 1 | 1⁄2 | „ | 1 | 5⁄8 |
| 1,200 | .90 | 1 | 7⁄8 | „ | 2 | |
| 1,600 | 1.03 | 2 | „ | 2 | 1⁄8 | |
| 2,000 | 1.15 | 2 | 1⁄4 | „ | 2 | 3⁄8 |
| 2,400 | 1.26 | 2 | 1⁄2 | „ | 2 | 5⁄8 |
| 2,800 | 1.36 | 2 | 5⁄8 | „ | 2 | 3⁄4 |
| 3,200 | 1.43 | 2 | 7⁄8 | „ | 3 | |
| 3,600 | 1.56 | 3 | 1⁄8 | „ | 3 | 1⁄4 |
| 4,000 | 1.63 | 3 | 1⁄4 | „ | 3 | 3⁄8 |
| 4,400 | 1.70 | 3 | 3⁄8 | „ | 3 | 1⁄2 |
| 4,800 | 1.78 | 3 | 1⁄2 | „ | 3 | 5⁄8 |
| 5,200 | 1.86 | 3 | 5⁄8 | „ | 3 | 3⁄4 |
| 5,600 | 1.93 | 3 | 3⁄4 | „ | 4 | |
| 6,000 | 2.00 | 4 | „ | 4 | 1⁄4 | |
In wheels that have their teeth cut to form in a gear-cutting machine the thickness of tooth at any point in the depth is equal at any point across the breadth; hence, supposing the wheels to be properly keyed to their shafts so that the pitch line across the breadth of the wheel stands parallel to the axis of the shaft, the contact of tooth upon tooth occurs across the full breadth of the tooth.
As the practical result of these conditions we have three important advantages: first, that the stress being exerted along the full breadth of the tooth instead of on one corner only, the tooth is stronger (with a given breadth and thickness) in proportion to the duty; second, that with a given pitch, the thickness and therefore the margin for safety and allowance for wear are increased, because the tooth may be increased in thickness at the expense of the clearance, which need be merely sufficient to prevent contact on both sides of the spaces so as to prevent the teeth from locking in the spaces; and thirdly, because the teeth will not be subject to sudden impacts or shocks of tooth upon tooth by reason of back lash.
In determining the strength of cut gear-teeth we may suppose the weight to be disposed along the face at the extreme height of the tooth, in which case the theoretical shape of the tooth to possess equal strength at every point from the addendum circle to the root would be a parabola, as shown by the dotted lines in Fig. 180, which represents a tooth having radial flanks. In this case it is evident that the ultimate strength of the tooth is that due to the thickness at the root, because it is less than that at the pitch circle, and the strength, as a whole, is not greater than that at the weakest part. But since teeth with radial flanks are produced, as has been shown, with a generating circle equal in diameter to the radius of the pinion, and since with a generating circle bearing that ratio of diameter to diameter of pitch circle the acting part of the flank is limited, it is usual to fill in the corners with fillets or rounded corners, as shown in Fig. 129; hence, the weakest part of the tooth will be where the radial line of the flank joins the fillet and, therefore, nearer the pitch circle than is the root. But as only the smallest wheel of the set has radial flanks and the flanks thicken as the diameter of the wheels increase, it is usual to take the thickness of the tooth at the pitch circle as representing the weakest part of the tooth, and, therefore, that from which the strength of the tooth is to be computed. This, however, is not actually the case even in teeth which have considerable spread at the roots, as is shown in Fig. 181, in which the shape of the tooth to possess equal strength throughout its depth is denoted by the parabolic dotted lines.
Considering a tooth as simply a beam supporting the strain as a weight we may calculate its strength as follows:—
Multiply the breadth of the tooth by the square of its thickness, and the product by the strength of the material, per square inch of section, of which the teeth are composed, and divide this last product by the distance of the pitch line from the root, and the quotient will give a tooth thickness having a strength equal to the weight of the load, but having no margin for safety, and no allowance for wear; hence, the result thus obtained must be multiplied by the factor of safety (which for this class of tooth may be taken as 6), and must have an additional thickness added to allow for wear, so that the factor of safety will be constant notwithstanding the wear.
Another, and in some respects more convenient method, for obtaining the strength of a tooth, is to take the strength of a tooth having 1-inch pitch, and 1 inch of breadth, and multiply this quantity of strength by the pitch and the face of the tooth it is required to find the strength of, both teeth being of the same material.
Example.—The safe working pressure for a cast-iron tooth of[I-66] an inch pitch, and an inch broad will transmit, being taken as 400 lbs., what pressure will a tooth of 3⁄4-inch pitch and 3 inches broad transmit with safety?
Here 400 lbs. × 3⁄4 pitch × 3 breadth = 900 = safe working pressure of tooth 3⁄4-inch pitch and 3 inches broad.
Again, the safe working pressure of a cast-iron tooth, 1 inch in breadth and of 1-inch pitch, being considered as 400 lbs., what is the safe working pressure of a tooth of 1-inch pitch and 4-inch breadth?
Here 400 × 1 × 4 = 1600.
The philosophy of this is apparent when we consider that four wheels of 1-inch pitch and an inch face, placed together side by side, would constitute, if welded together, one wheel of an inch pitch and 4 inches face. (The term face is applied to the wheel, and the term breadth to the tooth, because such is the custom of the workshop, both terms, however, mean, in the case of spur-wheels, the dimension of the tooth in a direction parallel to the axis of the wheel shaft or wheel bore.)
The following table gives the safe working pressures for wheels having an inch pitch and an inch face when working at the given velocities, S.W.P. standing for “safe working pressure:”—
| Velocity of pitch circle in feet per second. |
S.W.P. for cast-iron spur gears. |
S.W.P. for spur mor- tise gears. |
S.W.P. for cast-iron bevel gears. |
S.W.P. for bevel mortise gears. |
| 2 | 368 | 178 | 258 | 178 |
| 3 | 322 | 178 | 225 | 157 |
| 6 | 255 | 178 | 178 | 125 |
| 12 | 203 | 142 | 142 | 99 |
| 18 | 177 | 124 | 124 | 87 |
| 24 | 161 | 113 | 113 | 79 |
| 30 | 150 | 105 | 105 | 74 |
| 36 | 140 | 98 | 98 | 69 |
| 42 | 133 | 93 | 93 | 65 |
| 48 | 127 | 88 | 88 | 62 |
For velocities less than 2 feet per second, use the same value as for 2 feet per second.
The proportions, in terms of the pitch, upon which this table is based, are as follows:—
| Thickness of | iron | teeth | . | 395 | of the pitch. |
| „ | wooden | „ | . | 595 | „ |
| Height of addendum | . | 28 | „ | ||
| Depth below pitch line | . | 32 | „ | ||
The table is based upon 400 lbs. per inch of face for an inch pitch, as the safe working pressure of mortise wheel teeth or cogs; it may be noted that there is considerable difference of opinion. They are claimed by some to be in many cases practically stronger than teeth of cast iron. This may be, and probably is, the case when the conditions are such that the teeth being rigid and rigidly held (as in the case of cast-iron teeth), there is but one tooth on each wheel in contact. But when there is so nearly contact between two teeth on each wheel that but little elasticity in the teeth would cause a second pair of teeth to have contact, then the elasticity of the wood would cause this second contact. Added to this, however, we have the fact that under conditions where violent shock occurs the cog would have sufficient elasticity to give, or spring, and thus break the shock which cast iron would resist to the point of rupture. It is under these conditions, which mainly occur in high velocities with one of the wheels having cast teeth, that mortise wheels, or cogging, is employed, possessing the advantage that a broken or worn-out tooth, or teeth, may be readily replaced. It is usual, however, to assign to wooden teeth a value of strength more nearly equal to that of its strength in proportion to that of cast iron; hence, Thomas Box allows a wood tooth a value of about 3⁄10ths the strength of cast iron; a value as high as 7⁄10ths is, however, assigned by other authorities. But the strength of the tooth cannot exceed that at the top of the shank, where it fits into the mortise of the wheel, and on account of the leverage of the pressure the width of the mortise should exceed the thickness of the tooth.
In some practice, the mortise teeth, or cogs, are made thicker in proportion to the pitch than the teeth on the iron wheel; thus Professor Unwin, in his “Elements of Machine Design,” gives the following as “good proportions”:—
| Thickness of | iron teeth | 0.395 | of the | pitch. |
| „ | wood cogs | 0.595 | „ | „ |
which makes the cogs 2⁄10ths inch thicker than the teeth.
The mortises in the wheel rim are made taper in both the breadth and the width, which enables the tooth shank to be more accurately fitted, and also of being driven more tightly home, than if parallel. The amount of this taper is a matter of judgment, but it may be observed that the greater the taper the more labor there is involved in fitting, and the more strain there is thrown upon the pins when locking the teeth with a given amount of strain. While the less the taper, the more care required to obtain an accurate fit. Taking these two elements into consideration, 1⁄8th inch of taper in a length of 4 inches may be given as a desirable proportion.
As an evidence of the durability of wooden teeth, there appeared in Engineering of January 7th, 1879, the illustration shown in Fig. 182, which represents a cog from a wheel of 14 ft. 1⁄2 in. diameter, and having a 10-inch face, its pinion being 4 ft. in diameter. This cog had been running for 261⁄2 years, day and night; not a cog in the wheel having been touched during that time. Its average revolutions were 38 per minute, the power developed by the engine being from 90 to 100 indicated horse-power. The teeth were composed of beech, and had been greased twice a week, with tallow and plumbago ore.
Since the width of the face of a wheel influences its wear (by providing a larger area of contact over which the pressure may be distributed, as well as increasing the strength), two methods of proportioning the breadth may be adopted. First, it may be made a certain proportion of the pitch; and secondly, it may be proportioned to the pressure transmitted and the number of revolutions. The desirability of the second is manifest when we consider that each tooth will pass through the arcs of contact (and thus be subjected to wear) once during each revolution; hence, by making the number of revolutions an element in the calculation to find the breadth, the latter is more in proportion to the wear than it would be if proportioned to the pitch.
It is obvious that the breadth should be sufficient to afford the required degree of strength with a suitable factor of safety, and allowance for wear of the smallest wheel in the pair or set, as the case may be.
According to Reuleaux, the face of a wheel should never be less than that obtained by multiplying the gross pressure, transmitted in lbs., by the revolutions per minute, and dividing the product by 28,000.
In the case of bevel-wheels the pitch increases, as the perimeter[I-67] of the wheel is approached, and the maximum pitch is usually taken as the designated pitch of the wheel. But the mean pitch is that which should be taken for the purposes of calculating the strength, it being in the middle of the tooth breadth. The mean pitch is also the diameter of the pitch circle, used for ascertaining the velocity of the wheel as an element in calculating the safe pressure, or the amount of power the wheel is capable of transmitting, and it is upon this basis that the values for bevel-wheels in the above table are computed.
In many cases it is required to find the amount of horse-power a wheel will transmit, or the proportions requisite for a wheel to transmit a given horse-power; and as an aid to the necessary calculations, the following table is given of the amount of horse-power that may be transmitted with safety, by the various wheels at the given velocities, with a wheel of an inch pitch and an inch face, from which that for other pitches and faces may be obtained by proportion.
| Velocity of Pitch Circle in Feet per Second. |
Spur-Wheels. H.P. |
Spur Mortise Wheels. H.P. |
Bevel-Wheels. H.P. |
Bevel Mortise Wheels. H.P. |
||||
| 2 | 1.3 | 38 | .6 | 47 | .9 | 38 | .6 | 47 |
| 3 | 1.7 | 56 | .9 | 71 | 1.2 | 27 | .8 | 56 |
| 6 | 2.7 | 82 | 1.7 | 6 | 1.7 | 6 | 1.3 | 63 |
| 12 | 4.4 | 3 | 3.1 | 3.1 | 2.1 | 6 | ||
| 18 | 5.7 | 93 | 4.0 | 58 | 4.0 | 58 | 2.8 | 47 |
| 24 | 7.0 | 25 | 4.9 | 31 | 4.9 | 31 | 3.4 | 47 |
| 30 | 8.1 | 82 | 5.7 | 27 | 5.7 | 27 | 4.0 | 36 |
| 36 | 9.1 | 63 | 6.4 | 14 | 6.4 | 14 | 4.5 | 16 |
| 42 | 10.1 | 56 | 7.1 | 02 | 7.1 | 02 | 4.9 | 63 |
| 48 | 11.0 | 83 | 7.6 | 80 | 7.6 | 80 | 5.4 | 11 |
In this table, as in the preceding one, the safe working pressure for 1-inch pitch and 1-inch breadth of face is supposed to be 400 lbs.
In cast gearing, the mould for which is made by a gear moulding machine, the element of draft to permit the extraction of the pattern is reduced: hence, the pressure of tooth upon tooth may be supposed to be along the full breadth of the tooth instead of at one corner only, as in the case of pattern-moulded teeth. But from the inaccuracies which may occur from unequal contraction in the cooling of the casting, and from possible warping of the casting while cooling, which is sure to occur to some extent, however small the amount may be, it is not to be presumed that the contact of the teeth of one wheel will be in all the teeth as perfect across the full breadth as in the case of machine-cut teeth. Furthermore, the clearance allowed for machine-moulded teeth, while considerably less than that allowed for pattern-moulded teeth, is greater than that allowed for machine-cut teeth; hence, the strength of machine-moulded teeth in proportion to the pitch lies somewhere between that of pattern-moulded and machine-cut teeth—but exactly where, it would be difficult to determine in the absence of experiments made for the purpose of ascertaining.
It is not improbable, however, that the contact of tooth upon tooth extends in cast gears across at least two-thirds of the breadth of the tooth, in which case the rules for ascertaining the strength of cut teeth of equal thickness may be employed, substituting 2⁄3rds of the actual tooth breadth as the breadth for the purposes of the calculation.
If instead of supposing all the strain to fall upon one tooth and calculating the necessary strength of the teeth upon that basis (as is necessary in interchangeable gearing, because these conditions may exist in the case of the smallest pinion that can be used in pitch), the actual working condition of each separate application of gears be considered, it will appear that with a given diameter of pitch circle, all other things being equal, the arc of contact will remain constant whatever the pitch of the teeth, or in other words is independent of the pitch, and it follows that when the thickness of iron necessary to withstand (with the allowances for wear and factor of safety) the given stress under the given velocity has been determined, it may be disposed in a coarse pitch that will give one tooth always in contact, or a finer pitch that will give two or more teeth always in contact, the strength in proportion to the duty remaining the same in both cases.
In this case the expense of producing the wheel patterns or in trimming the teeth is to be considered, because if there are a train of wheels the finer pitch would obviously involve the construction and dressing to shape of a much greater number of teeth on each wheel in the train, thus increasing the labor. When, however, it is required to reduce the pinion to a minimum diameter, it is obvious that this may be accomplished by selecting the finer pitch, because the finer the pitch, the less the diameter of the wheel may be. Thus with a given diameter of pitch circle it is possible to select a pitch so fine that motion from one wheel may be communicated to another, whatever the diameter of the pitch circle may be, the limit being bounded by the practicability of casting or producing teeth of the necessary fineness of pitch. The durability of a wheel having a fine pitch is greater for two reasons: first, because the metal nearest the cast surface of cast iron is stronger than the internal metal, and the finer pitch would have more of this surface to withstand the wear; and second, because in a wheel of a given width there would be two points, or twice the area of metal, to withstand the abrasion, it being remembered that the point of contact is a line which partly rolls and partly slides along the depth of the tooth as the wheel rotates, and that with two teeth in contact on each wheel there are two of such lines. There is also less sliding or rubbing action of the teeth, but this is offset by the fact that there are more teeth in contact, and that there are therefore a greater number of teeth simultaneously rubbing or sliding one upon the other.
But when we deal with the number of teeth the circumstances are altered; thus with teeth of epicycloidal form it is manifestly impossible to communicate constant motion with a driving wheel having but one tooth, or to receive motion on a follower having but one tooth. The number of teeth must always be such that there is at all times a tooth of each wheel within the arc of action, or in contact, so that one pair of teeth may come into contact before the contact of the preceding teeth has ceased.
In the construction of wheels designed to transmit power as well as simple motion, as is the case with the wheels employed in machine work, however, it is not considered desirable to employ wheels containing a less number of teeth than 12. The diameter of the wheel bearing such a relation to the pitch that both wheels containing the same number of teeth (12), the motion will be communicated from one to the other continuously.
It is obvious that as the number of teeth in one of the wheels (of a pair in gear) is increased the number of teeth in the other may be (within certain limits) diminished, and still be capable of transmitting continuous motion. Thus a pinion containing, say 8 teeth, may be capable of receiving continuous motion from a rack in continuous motion, while it would not be capable of receiving continuous motion from a pinion having 4 teeth; and as the requirements of machine construction often call for the transmission of motion from one pinion to another of equal diameters, and as small as possible, 12 teeth are the smallest number it is considered desirable for a pinion to contain, except it be in the case of an internal wheel, in which the arc of contact is greater in proportion to the diameters than in spur-wheels, and continuous motion can therefore be transmitted either with coarser pitches or smaller diameters of pinion.
For convenience in calculating the pitch diameter at pitch circle, or pitch diameter as it is termed, and the number of teeth of wheels, the following rules and table extracted from the Cincinnati Artisan and arranged from a table by D. A. Clarke, are given. The first column gives the pitch, the following nine columns give the pitch diameters of wheels for each pitch from 1 tooth to 9. By multiplying these numbers by 10 we have the pitch diameters from 10 to 90 teeth, increasing by tens; by multiplying by 100 we likewise have the pitch diameters from 100 to 900, increasing by hundreds.
| Pitch. | Number of Teeth. | |||||||||
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | ||
| 1 | .3183 | .6366 | .9549 | 1.2732 | 1.5915 | 1.9099 | 2.2282 | 2.5465 | 2.8648 | |
| 1 | 1⁄8 | .3581 | .7162 | 1.0743 | 1.4324 | 1.7905 | 2.1486 | 2.5067 | 2.8648 | 3.2229 |
| 1 | 1⁄4 | .3979 | .7958 | 1.1937 | 1.5915 | 1.9894 | 2.3873 | 2.7852 | 3.1831 | 3.5810 |
| 1 | 3⁄8 | .4377 | .8753 | 1.3130 | 1.7507 | 2.1884 | 2.6260 | 3.0637 | 3.5014 | 3.9391 |
| 1 | 1⁄2 | .4775 | .9549 | 1.4324 | 1.9099 | 2.3873 | 2.8648 | 3.3422 | 3.8197 | 4.2971 |
| 1 | 5⁄8 | .5173 | 1.0345 | 1.5517 | 2.0690 | 2.5862 | 3.1035 | 3.6207 | 4.1380 | 4.6552 |
| 1 | 3⁄4 | .5570 | 1.1141 | 1.6711 | 2.2282 | 2.7852 | 3.3422 | 3.8993 | 4.4563 | 5.0134 |
| 1 | 7⁄8 | .5968 | 1.1937 | 1.7905 | 2.3873 | 2.9841 | 3.5810 | 4.1778 | 4.7746 | 5.3714 |
| 2 | .6366 | 1.2732 | 1.9099 | 2.5465 | 3.1831 | 3.8197 | 4.4563 | 5.0929 | 5.7296 | |
| 2 | 1⁄8 | .6764 | 1.3528 | 2.0292 | 2.7056 | 3.3820 | 4.0584 | 4.7348 | 5.4112 | 6.0877 |
| 2 | 1⁄4 | .7162 | 1.4324 | 2.1486 | 2.8648 | 3.5810 | 4.2972 | 5.0134 | 5.7296 | 6.4457 |
| 2 | 3⁄8 | .7560 | 1.5120 | 2.2679 | 3.0239 | 3.7799 | 4.5359 | 5.2919 | 6.0479 | 6.8038 |
| 2 | 1⁄2 | .7958 | 1.5915 | 2.3873 | 3.1831 | 3.9789 | 4.7746 | 5.5704 | 6.3662 | 7.1619 |
| 2 | 5⁄8 | .8355 | 1.6711 | 2.5067 | 3.3422 | 4.1778 | 5.0133 | 5.8499 | 6.6845 | 7.5200 |
| 2 | 3⁄4 | .8753 | 1.7507 | 2.6260 | 3.5014 | 4.3767 | 5.2521 | 6.1274 | 7.0028 | 7.8781 |
| 2 | 7⁄8 | .9151 | 1.8303 | 2.7454 | 3.6605 | 4.5757 | 5.4908 | 6.4059 | 7.3211 | 8.2362 |
| 3 | .9549 | 1.9099 | 2.8648 | 3.8197 | 4.7746 | 5.7296 | 6.6845 | 7.6394 | 8.5943 | |
| 3 | 1⁄4 | 1.0345 | 2.0690 | 3.1035 | 4.1380 | 5.1725 | 6.2070 | 7.2415 | 8.2760 | 9.3105 |
| 3 | 1⁄2 | 1.1141 | 2.2282 | 3.3422 | 4.4563 | 5.5704 | 6.6845 | 7.7986 | 8.9126 | 10.0268 |
| 3 | 3⁄4 | 1.1937 | 2.3873 | 3.5810 | 4.7746 | 5.9683 | 7.1619 | 8.3556 | 9.5493 | 10.7429 |
| 4 | 1.2732 | 2.5465 | 3.8197 | 5.0929 | 6.3662 | 7.6394 | 8.9127 | 10.1839 | 11.4591 | |
| 4 | 1⁄2 | 1.4324 | 2.8648 | 4.2972 | 5.7296 | 7.1619 | 8.5943 | 10.0267 | 11.4591 | 12.8915 |
| 5 | 1.5915 | 3.1831 | 4.7746 | 6.3662 | 7.9577 | 9.5493 | 11.1408 | 12.7324 | 14.3240 | |
| 5 | 1⁄2 | 1.7507 | 3.5014 | 5.2521 | 7.0028 | 8.7535 | 10.5042 | 12.2549 | 14.0056 | 15.7563 |
| 6 | 1.9099 | 3.8196 | 5.7295 | 7.6394 | 9.5493 | 11.4591 | 13.3690 | 15.2788 | 17.1887 | |
The following rules and examples show how the table is used:
Rule 1.—Given —— number of teeth and pitch; to find —— pitch diameter.
Select from table in columns opposite the given pitch—
First, the value corresponding to the number of units in the number of teeth.
Second, the value corresponding to the number of tens, and multiply this by 10.
Third, the value corresponding to the number of hundreds, and multiply this by 100. Add these together, and their sum is the pitch diameter required.
Example.—What is the pitch diameter of a wheel with 128 teeth, 11⁄2 inches pitch?
We find in line corresponding to 11⁄2 inch pitch—
| Pitch | diameter for | 8 | teeth | 3.81 | 97 |
| „ | „ | 20 | „ | 9.54 | 9 |
| „ | „ | 100 | „ | 47.75 | |
| „ | „ | 128 | „ | 61.11 | 87 |
| Or about 611⁄8′′. Answer. | |||||
Rule 2.—Given —— pitch diameter and number of teeth; to find —— pitch.
First, ascertain by Rule 1 the pitch diameter for a wheel of 1-inch pitch, and the given number of teeth.
Second, divide given pitch diameter by the pitch diameter for 1-inch pitch.
The quotient is the pitch desired.
Example.—What is the pitch of a wheel with 148 teeth, the pitch diameter being 72′′?
First, pitch diameter for 148 teeth, 1-inch pitch, is—
| 8 | teeth | 2.54 | 65 | ||
| 40 | „ | 12.73 | 2 | ||
| 100 | „ | 31.83 | |||
| 148 | „ | 47.10 | 85 | ||
| Second, | 72 | = 1.53 inch equal to the pitch. | |||
| 47.1 | |||||
This is nearly 11⁄2-inch pitch, and if possible the diameter would be reduced or the number of teeth increased so as to make the wheel exactly 11⁄2-inch pitch.
Rule 3.—Given —— pitch and pitch diameter; to find —— number of teeth.
First, ascertain from table the pitch diameter for 1 tooth of the given pitch.
Second, divide the given pitch diameter by the value found in table.
The quotient is the number required.
Example.—What is the number of teeth in a wheel whose pitch diameter is 42 inches, and pitch is 21⁄2 inches?
First, the pitch diameter, 1 tooth, 21⁄2-inch pitch, is 0.7958 inches.
| Second. | 42 | = 52.8. Answer. |
| 0.7958 |
This gives a fractional number of teeth, which is impossible; so the pitch diameter will have to be increased to correspond to 53 teeth, or the pitch changed so as to have the number of teeth come an even number.
Whenever two parallel shafts are connected together by gearing, the distance between centres being a fixed quantity, and the speeds of the shafts being of a fixed ratio, then the pitch is generally the best proportion to be changed, and necessarily may not be of standard size. Suppose there are two shafts situated in this manner, so that the distance between their centres is 84 inches, and the speed of one is 21⁄2 times that of the other, what size wheels shall be used? In this case the pitch diameter and number of teeth of the wheel on the slow-running shaft have to be 21⁄2 times those of the wheel on the fast-running shaft; so that 84 inches must be divided into two parts, one of which is 21⁄2 times the other, and these quantities will be the pitch radii of the wheels; that is, 84 inches are to be divided into 31⁄2 equal parts, 1 of which is the radius of one wheel, and 21⁄2 of which the radius of the other, thus 84′′/31⁄2 = 24 inches. So that 24 inches is the pitch radius of pinion, pitch diameter = 48 inches; and 21⁄2 × 24 inches = 60 inches is the pitch radius of the wheel, pitch diameter = 120 inches. The pitch used depends upon the power to be transmitted; suppose that 25⁄8 inches had been decided as about the pitch to be used, it is found by Rule 3 that the number of teeth are respectively 143.6, and 57.4 for wheel and pinion. As this is impossible, some whole number of teeth, nearest these in value,[I-69] have to be taken, one of which is 21⁄2 times the other; thus 145 and 58 are the nearest, and the pitch for these values is found by Rule 2 to be 2.6 inches, being the best that can be done under the circumstances.
The forms of spur-gearing having their teeth at an angle to the axis, or formed in advancing steps shown in Figs. 183 and 184, were designed by Dr. Hooke, and “were intended,” says the inventor, “first to make a piece of wheel work so that both the wheel and pinion, though of never so small a size, shall have as great a number of teeth as shall be desired, and yet neither weaken the wheels nor make the teeth so small as not to be practicable by any ordinary workman. Next that the motion shall be so equally communicated from the wheel to the pinion that the work being well made there can be no inequality of force or motion communicated.
“Thirdly, that the point of touching and bearing shall be always in the line that joins the two centres together.
“Fourthly, that it shall have no manner of rubbing, nor be more difficult to make than common wheel work.”
The objections to this form of wheel lies in the difficulty of making the pattern and of moulding it in the foundry, and as a result it is rarely employed at the present day. For racks, however, two or more separate racks are cast and bolted together to form the full width of rack as shown in Fig. 185. This arrangement permits of the adjustment of the width of step so as to take up the lost motion due to the wear of the tooth curves.
Another objection to the sloping of the teeth, as in Fig. 183, is that it induces an end pressure tending to force the wheels apart laterally, and this causes end wear on the journals and bearings.
To obviate this difficulty the form of gear shown in Fig. 186 is employed, the angles of the teeth from each side of the wheel to its centre being made equal so as to equalize the lateral pressure. It is obvious that the stepped gear, Fig. 184, is simply equivalent to a number of thin wheels bolted together to form a thick one, but possessing the advantage that with a sufficient number of steps, as in the figure, there is always contact on the line of centres, and that the condition of constant contact at the line of centres will be approached in proportion to the number of steps in the wheel, providing that the steps progress in one continuous direction across the wheel as in Fig. 184. The action of the wheels will, in this event, be smoother, because there will be less pressure tending to force the wheels apart.
But in the form of gearing shown in Fig. 183, the contact of the teeth will bear every instant at a single point, which, as the wheels revolve, will pass from one end to the other of the tooth, a fresh contact always beginning on the first side immediately before the preceding contact has ceased on the opposite side. The contact, moreover, being always in the plane of the centres of the pair, the action is reduced to that of rolling, and as there is no sliding motion there is consequently no rubbing friction between the teeth.
A further modification of Dr. Hooke’s gearing has been somewhat extensively adopted, especially in cotton-spinning machines. This consists, when the direction of the motion is simply to be changed to an angle of 90°, in forming the teeth upon the periphery of the pair at an angle of 45° to the respective axes of the wheels, as in Figs. 187 and 188; it will then be perceived that if the sloped teeth be presented to each other in such a way as to have exactly the same horizontal angle, the wheels will gear together, and motion being communicated to one axis the same will be transmitted to the other at a right angle to it, as in a common bevel pair. Thus if the wheel a upon a horizontal shaft have the teeth formed upon its circumference at an angle of 45° to the plane of its axis it can gear with a similar wheel b upon a vertical axis. Let it be upon the driving shaft and the motion will be changed in direction as if a and b were a pair of bevel-wheels of the ordinary kind, and, as with bevels generally, the direction of motion will be changed through an equal angle to the sum of the angles which the teeth of the wheels of the pair form with their respective axes. The objection in respect of lateral or end pressure, however, applies to this form equally with that shown in Fig. 183, but in the case of a vertical shaft the end pressure may be (by sloping the teeth in the necessary direction) made to tend to lift the shaft and not force it down into the step bearing. This would act to keep the wheels in close contact by reason of the weight of the vertical shaft and at the same time reduce the friction between the end of that shaft and its step bearing. This renders this form of gearing preferable to skew bevels when employed upon vertical shafts.
It is obvious that gears, such as shown in Figs. 187 and 188 may be turned up in the lathe, because the teeth are simply portions of spirals wound about the circumference of the wheel. For a pair of wheels of equal diameter a cylindrical piece equal in length to the required breadth of the two wheels is turned up in the lathe, and the teeth may be cut in the same manner as cutting a thread in the lathe, that is to say, by traversing the tool the requisite distance per lathe revolution. In pitches above about 1⁄4 inch, it will be necessary to shape one side of the tooth at a time on account of the broadness of the cutting edges. After the spiral (for the teeth are really spirals) is finished the[I-70] piece may be cut in two in the lathe and each half will form a wheel.
To find the full diameter to which to turn a cylinder for a pair of these wheels we proceed as in the following example: Required to cut a spiral wheel 5 inches in diameter and to have 30 teeth. First find the diametral pitch, thus 30 (number of teeth) ÷ 5 (diameter of wheel at pitch circle) = 6; thus there are 6 teeth or 6 parts to every inch of the wheel’s diameter at the pitch circle; adding 2 of these parts to the diameter of the wheel, at the pitch circle we have 5 and 2⁄6 of another inch, or 52⁄6 inches, which is the full diameter of the wheel, or the diameter of the addendum, as it is termed.
It is now necessary to find what change wheels to put on the lathe to cut the teeth out the proper angle. Suppose then the axes of the shafts are at a right angle one to the other, and that the teeth therefore require to be at an angle of 45° to the axes of the respective wheels, then we have the following considerations. In Fig. 189 let the line a represent the circumference of the wheel, and b a line of equal length but at a right angle to it, then the line c, joining a, b, is at an angle of 45°. It is obvious then that if the traverse of the lathe tool be equal at each lathe revolution to the circumference of the wheel at the pitch circle, the angle of the teeth will be 45° to the axis of the wheel.
Hence, the change wheels on the lathe must be such as will traverse the tool a distance equal to the circumference at pitch circle of the wheel, and the wheels may be found as for ordinary screw cutting.
If, however, the axes of the shafts are at any other angle we may find the distance the lathe tool must travel per lathe revolution to give teeth of the required angle (or in other words the pitch of the spiral) by direct proportion, thus: Let it be required to find the angle or pitch for wheels to connect shafts at an angle of 25°, the wheels to have 20 teeth, and to be of 10 diametral pitch.
Here, 20 ÷ 10 = 2 = diameter of wheel at the pitch circle. The circumference of 2 inches being 6.28 inches we have, as the degrees of angle of the axes of the shafts are to 45°, so is 6.28 inches (the circumference of the wheels, to the pitch sought).
Here, 6.28 inches × 45° ÷ 25° = 11.3 inches, which is the required pitch for the spiral.
When the axes of the shafts are neither parallel nor meeting, motion from one shaft to another may be transmitted by means of a double gear. Thus (taking rolling cones of the diameters of the respective pitch circles as representing the wheels) in Fig. 190, let a be the shaft of gear h, and b b that of wheel e. Then a double gear-wheel having teeth on f, g may be placed as shown, and the face f will gear with e, while face g will gear with h, the cone surfaces meeting in a point as at c and d respectively, hence the velocity will be equal.
When the axial line of the shafts for two gear-wheels are nearly in line one with the other, motion may be transmitted by gearing the wheels as in Fig. 191. This is a very strong method of gearing, because there are a large number of teeth in contact, hence the strain is distributed by a larger number of teeth and the wear is diminished.
Fig. 192 (from Willis’s “Principles of Mechanism”) is another method of constructing the same combination, which admits of a steady support for the shafts at their point of intersection, a being a spherical bearing, and b, c being cupped to fit to a.
Rotary motion variable at different parts of a rotation may be obtained by means of gear-wheels varied in form from the true circle.
The commonest form of gearing for this purpose is elliptical gearing, the principles governing the construction of which are thus given by Professor McCord. “It is as well to begin at the foundation by defining the ellipse as a closed plane-curve, generated by the motion of a point subject to the condition that the sum of its distances from two fixed points within shall be constant: Thus, in Fig. 193, a and b are the two fixed points, called the foci; l, e, f, g, p are points in the curve; and a f + f b = a e + e b. Also, a l + l b = a p + p b = a g + g b. From this it follows that a g = l o, o being the centre of the curve, and g the extremity of the minor axis, whence the foci may be found if the axes be assumed, or, if the foci and one axis be given, the other axis may be determined. It is also apparent that if about either focus, as b, we describe an arc with a radius greater than b p and less than b l, for instance b e, and about a another arc with radius a e = l p-b e, the intersection, e, of these arcs will be on the ellipse; and in this manner any desired number of points may be found, and the curve drawn by the aid of sweeps.
“Having completed this ellipse, prolong its major axis, and draw[I-71] a similar and equal one, with its foci, c, d, upon that prolongation, and tangent to the first one at p; then b d = l p. About b describe an arc with any radius, cutting the first ellipse at y and the line l at z; about d describe an arc with radius d z, cutting the second ellipse in x; draw a y, b y, c x, and d x. Then a y = d x, and b y = c x, and because the ellipses are alike, the arcs p y and p x are equal. If then b and d are taken as fixed centres, and the ellipses turn about them as shown by the arrows, x and y will come together at z on the line of centres; and the same is true of any points equally distant from p on the two curves. But this is the condition of rolling contact. We see, then, that in order that two ellipses may roll together, and serve as the pitch-lines of wheels, they must be equal and similar, the fixed centres must be at corresponding foci, and the distance between these centres must be equal to the major axis. Were they to be toothless wheels, if would evidently be essential that the outlines should be truly elliptical; but the changes of curvature in the ellipse are gradual, and circular arcs may be drawn so nearly coinciding with it, that when teeth are employed, the errors resulting from the substitution are quite inappreciable. Nevertheless, the rapidity of these changes varies so much in ellipses of different proportions, that we believe it to be practically better to draw the curve accurately first, and to find the radii of the approximating arcs by trial and error, than to trust to any definite rule for determining them; and for this reason we give a second and more convenient method of finding points, in connection with the ellipse whose centre is r, Fig. 193. About the centre describe two circles, as shown, whose diameters are the major and minor axes; draw any radius, as r t, cutting the first circle in t, and the second in s; through t draw a parallel to one axis, through s a parallel to the other, and the intersection, v, will lie on the curve. In the left hand ellipse, the line bisecting the angle a f b is normal to the curve at f, and the perpendicular to it is tangent at the same point, and bisects the angles adjacent to a f b, formed by prolonging a f, b f.
“To mark the pitch line we proceed as follows:—
“In Fig. 194, a a and b b are centre lines passing through the major and minor axes of the ellipse, of which a is the axis or centre, b c is the major and a e half of the minor axis. Draw the rectangle b f g c, and then the diagonal line b e; at a right angle to b e draw line f h cutting b b at i. With radius a e and from a as a centre draw the dotted arc e j, giving the point j on the line b b. From centre k, which is on line b b, and central between b and j, draw the semicircle b m j, cutting a a at l. Draw the radius of the semicircle b m j cutting f g at n. With radius m n mark on a a, at and from a as a centre, the point o. With radius h o and from centre h draw the arc p o q. With radius a l and from b and c as centres draw arcs cutting p o q at the points p q. Draw the lines h p r and h q s, and also the lines p i t and q v w. From h as centre draw that part of the ellipse lying between r and s. With radius p r and from p as a centre draw that part of the ellipse lying between r and t. With radius q s and from q draw the ellipse from s to w. With radius i t and from i as a centre draw the ellipse from t to b. With radius v w and from v as a centre draw the ellipse from w to c, and one half the ellipse will be drawn. It will be seen that the whole construction has been performed to find the centres h p q i and v, and that while v and i may be used to carry the curve around the other side or half of the ellipse, new centres must be provided for h p and q; these new centres correspond in position to h p q.
“If it were possible to subdivide the ellipse into equal parts it would be unnecessary to resort to these processes of approximately representing the two curves by arcs of circles; but unless this be done, the spacing of the teeth can only be effected by the laborious process of stepping off the perimeter into such small subdivisions that the chords may be regarded as equal to the arcs, which after all is but an approximation; unless, indeed, we adopt the mechanical expedient of cutting out the ellipse in metal or other substance, measuring and subdividing it with a strip of paper or a steel tape, and wrapping back the divided measure in order to find the points of division on the curve.
“But these circular arcs may be rectified and subdivided with[I-72] great facility and accuracy by a very simple process, which we take from Prof. Rankine’s “Machinery and Mill Work,” and is illustrated in Fig. 195. Let o b be tangent at o to the arc o d, of which c is the centre. Draw the chord d o, bisect it in e, and produce it to a, making o a = o e; with centre a and radius a d describe an arc cutting the tangent in b; then o b will be very nearly equal in length to the arc o d, which, however, should not exceed about 60°; if it be 60°, the error is theoretically about 1⁄900 of the length of the arc, o b being so much too short; but this error varies with the fourth power of the angle subtended by the arc, so that for 30° it is reduced to 1⁄16 of that amount, that is, to 1⁄14400. Conversely, let o b be a tangent of given length; make o f = 1⁄4 o b; then with centre f and radius f b describe an arc cutting the circle o d g (tangent to o b at o) in the point d; then o d will be approximately equal to o b, the error being the same as in the other construction and following the same law.
“The extreme simplicity of these two constructions and the facility with which they may be made with ordinary drawing instruments make them exceedingly convenient, and they should be more widely known than they are. Their application to the present problem is shown in Fig. 196, which represents a quadrant of an ellipse, the approximate arcs c d, d e, e f, f a having been determined by trial and error. In order to space this off, for the positions of the teeth, a tangent is drawn at d, upon which is constructed the rectification of d c, which is d g, and also that of d e in the opposite direction, that is, d h, by the process just explained. Then, drawing the tangent at f, we set off in the same manner f i = f e, and f k = f a, and then measuring h l = i k, we have finally g l, equal to the whole quadrant of the ellipse.
“Let it now be required to lay out 24 teeth upon this ellipse; that is, 6 in each quadrant; and for symmetry’s sake we will suppose that the centre of one tooth is to be at a, and that of another at c, Fig. 196. We therefore divide l g into six equal parts at the points 1, 2, 3, &c., which will be the centres of the teeth upon the rectified ellipse. It is practically necessary to make the spaces a little greater than the teeth; but if the greatest attainable exactness in the operation of the wheel is aimed at, it is important to observe that backlash, in elliptical gearing, has an effect quite different from that resulting in the case of circular wheels. When the pitch-curves are circles, they are always in contact; and we may, if we choose, make the tooth only half the breadth of the space, so long as its outline is correct. When the motion of the driver is reversed, the follower will stand still until the backlash is taken up, when the motion will go on with a perfectly constant velocity ratio as before. But in the ease of two elliptical wheels, if the follower stand still while the driver moves, which must happen when the motion is reversed if backlash exists, the pitch-curves are thrown out of contact, and, although the continuity of the motion will not be interrupted, the velocity ratio will be affected. If the motion is never to be reversed, the perfect law of the velocity ratio due to the elliptical pitch-curve may be preserved by reducing the thickness of the tooth, not equally on each side, as is done in circular wheels, but wholly on the side not in action. But if the machine must be capable of acting indifferently in both directions, the reduction must be made on both sides of the tooth: evidently the action will be slightly impaired, for which reason the backlash should be reduced to a minimum. Precisely what is the minimum is not so easy to say, as it evidently depends much upon the excellence of the tools and the skill of the workmen. In many treatises on constructive mechanism it is variously stated that the backlash should be from one-fifteenth to one-eleventh of the pitch, which would seem to be an ample allowance in reasonably good castings not intended to be finished, and quite excessive if the teeth are to be cut; nor is it very obvious that its amount should depend upon the pitch any more than upon the precession of the equinoxes. On paper, at any rate, we may reduce it to zero, and make the teeth and spaces equal in breadth, as shown in the figure, the teeth being indicated by the double lines. Those upon the portion l h are then laid off upon k i, after which these divisions are transferred to curves. And since under that condition the motion of this third line, relatively to each of the others, is the same as though it rolled along each of them separately while they remained fixed, the process of constructing the generated curves becomes comparatively simple. For the describing line, we naturally select a circle, which, in order to fulfil the condition, must be small enough to roll within the pitch ellipse; its diameter is determined by the consideration, that if it be equal to a p, the radius of the arc a f, the flanks of the teeth in that region will be radial. We have, therefore, chosen a circle whose diameter, a b, is three-fourths of a p, as shown, so that the teeth, even at the ends of the wheels, will be broader at the base than on the pitch line. This circle ought strictly to roll upon the true elliptical curve, and assuming as usual the tracing-point upon the circumference, the generated curves would vary slightly from true epicycloids, and no two of those used in the same quadrant of the ellipse would be exactly alike. Were it possible to divide the ellipse accurately, there would be no difficulty in laying out these curves; but having substituted the circular arcs, we must now roll the generating circle upon these as bases, thus forming true epicycloidal teeth, of which those lying upon the same approximating arc will be exactly alike.[I-73] Should the junction of two of these arcs fall within the breadth of a tooth, as at d, evidently both the face and the flank on one side of that tooth will be different from those on the other side; should the junction coincide with the edge of a tooth, which is very nearly the case at f, then the face on that side will be the epicycloid belonging to one of the arcs, its flank a hypocycloid belonging to the other; and it is possible that either the face or the flank on one side should be generated by the rolling of the describing circle partly on one arc, partly on the one adjacent, which, upon a large scale and where the best results are aimed at, may make a sensible change in the form of the curve.
“The convenience of the constructions given in Fig. 194 is nowhere more apparent than in the drawing of the epicycloids, when, as in the case in hand, the base and generating circles may be of incommensurable diameters; for which reason we have, in Fig. 197, shown its application in connection with the most rapid and accurate mode yet known of describing those curves. Let c be the centre of the base circle; b that of the rolling one; a the point of contact. Divide the semi-circumference of b into six equal parts at 1, 2, 3, &c.; draw the common tangent at a, upon which rectify the arc a2 by process No. 1, then by process No. 2 set out an equal arc a2 on the base circle, and stepping it off three times to the right and left, bisect these spaces, thus making subdivisions on the base circle equal in length to those on the rolling one. Take in succession as radii the chords a1, a2, a3, &c., of the describing circle, and with centres 1, 2, 3, &c., on the base circle, strike arcs either externally or internally, as shown respectively on the right and left; the curve tangent to the external arcs is the epicycloid, that tangent to the internal ones the hypocycloid, forming the face and flank of a tooth for the base circle.
“In the diagram, Fig. 196, we have shown a part of an ellipse whose length is 10 inches and breadth 6, the figure being half size. In order to give an idea of the actual appearance of the combination when complete, we show in Fig. 198 the pair in gear, on a scale of 3 inches to the foot. The excessive eccentricity was selected merely for the purpose of illustration. Fig. 198 will serve also to call attention to another serious circumstance, which is that although the ellipses are alike, the wheels are not; nor can they be made so if there be an even number of teeth, for the obvious reason that a tooth upon one wheel must fit into a space on the other; and since in the first wheel, Fig. 196, we chose to place a tooth at the extremity of each axis, we must in the second one place there a space instead; because at one time the major axes must coincide, at another the minor axis, as in Fig. 191. If then we use even numbers, the distribution and even the forms of the teeth are not the same in the two wheels of the pair. But this complication may be avoided by using an odd number of teeth, since, placing a tooth at one extremity of the major axis, a space will come at the other.
“It is not, however, always necessary to cut teeth all round these wheels, as will be seen by an examination of Fig. 199, c and d being the fixed centres of the two ellipses in contact at p. Now p must be on the line c d, whence, considering the free foci, we see p b is equal to p c, and p a to p d; and the common tangent at p makes equal angles with c p and p a, as is also with p b and p d; therefore, c d being a straight line, a b is also a straight line and equal to c d. If then the wheels be overhung, that is, fixed on the ends of the shafts outside the bearings, leaving the outer faces free, the moving foci may be connected by a rigid link a b, as shown.
“This link will then communicate the same motion that would result from the use of the complete elliptical wheels, and we may therefore dispense with most of the teeth, retaining only those near the extremities of the major axes which are necessary in order to assist and control the motion of the link at and near the dead-points. The arc of the pitch-curves through which the teeth must extend will vary with their eccentricity: but in many cases it would not be greater than that which in the approximation may be struck about one centre, so that, in fact, it would not be necessary to go through the process of rectifying and subdividing the quarter of the ellipse at all, as in this case it can make no possible difference whether the spacing adopted for the teeth to be cut would “come out even” or not if carried around the curve. By this expedient, then, we may save not only the trouble of drawing, but a great deal of labor in making, the teeth round the whole ellipse. We might even omit the intermediate portions of the pitch ellipses themselves; but as they move in rolling contact their retention can do no harm, and in one part of the movement will be beneficial, as they will do part of the work; for if, when turning, as shown by the arrows, we consider the wheel whose axis is d as the driver, it will be noted that its radius of contact, c p, is on the increase; and so long as this is the case the other wheel will be compelled to move by contact of the pitch lines, although the link be omitted. And even if teeth be cut all round the wheels, this link is a comparatively inexpensive and a useful addition to the combination, especially if the eccentricity be considerable. Of course the wheels shown in Fig. 198 might also have been made alike, by placing a tooth at one end of the major axis and a space at the other, as above suggested. In regard to the variation in the velocity ratio, it will be seen, by reference to Fig. 199, that if d be the axis of the driver, the follower will in the position there shown move faster, the ratio of the angular velocities being pd/pb; if the driver turn uniformly the velocity of[I-74] the follower will diminish, until at the end of half a revolution, the velocity ratio will be pb/pd; in the other half of the revolution these changes will occur in a reverse order. But p d = l b; if then the centres b d are given in position, we know l p, the major axis; and in order to produce any assumed maximum or minimum velocity ratio, we have only to divide l p into segments whose ratio is equal to that assumed value, which will give the foci of the ellipse, whence the minor axis may be found and the curve described. For instance, in Fig. 198 the velocity ratio being nine to one at the maximum, the major axis is divided into two parts, of which one is nine times as long as the other; in Fig. 199 the ratio is as one to three, so that, the major axis being divided into four parts, the distance a c between the foci is equal to two of them, and the distance of either focus from the nearer extremity of the major axis equal to one, and from the more remote extremity equal to three of these parts.”
Another example of obtaining a variable motion is given in Fig. 200. The only condition necessary to the construction of wheels of this class is that the sum of the radii of the pitch circles on the line of centres shall equal the distance between the axes of the two wheels. The pitch curves are to be considered the same as pitch circles, “so that,” says Willis, “if any given circle or curve be assumed as a describing (or generating) curve, and if it be made to roll on the inside of one of these pitch curves and on the outside of the corresponding portion of the other pitch curve, then the motion communicated by the pressure and sliding contact of one of the curved teeth so traced upon the other will be exactly the same as that effected by the rolling contact (by friction) of the original pitch curves.”
It is obvious that on b the corner sections are formed of simple segments of a circle of which the centre is the axis of the shaft, and that the sections between them are simply racks. The corners of a are segments of a circle of which the axis of a is the centre, and the sections between the corners curves meeting the pitch circles of the rack at every point as it passes the line of centres.
Intermittent motion may also be obtained by means of a worm-wheel constructed as in Fig. 201, the worm having its teeth at a right angle to its axis for a distance around the circumference proportioned to the required duration of the period of rest; or the motion may be made variable by giving the worm teeth different degrees of inclination (to the axis), on different portions of the circumference.
In addition to the simple operation of two or more wheels transmitting motion by rotating about their fixed centres and in fixed positions, the following examples of wheel motion may be given.
In Fig. 202 are two gear-wheels, a, which is fast upon its stationary shaft, and b, which is free to rotate upon its shaft, the link c affording journal bearing to the two shafts. Suppose that a has 40 teeth, while b has 20 teeth, and that the link c is rotated once around the axis of a, how many revolutions will b make? By reason of there being twice as many teeth in a as in b the latter will make two rotations, and in addition to this it will, by reason of its connection to the arm c, also make a revolution, these being two distinct motions, one a rotation of b about the axis of a, and the other two rotations of b upon its own axis.
A simple arrangement of gearing for reversing the direction of rotation of a shaft is shown in Fig. 203. i and f are fast and loose pulleys for the shaft d, a and c are gears free to rotate upon d, n is a clutch driven by d; hence if n be moved so as to engage with c the latter will act as a driver to rotate the shaft b, the[I-75] wheel upon b rotating a in an opposite direction to the rotation of d. But if n be moved to engage with a the latter becomes the driving wheel, and b will be caused to rotate in the opposite direction. Since, however, the engagement of the clutch n with the clutch on the nut of the gear-wheels is accompanied with a violent shock and with noise, a preferable arrangement is shown in Fig. 204, in which the gears are all fast to their shafts, and the driving shaft for c passes through the core or bore of that for a, which is a sleeve, so that when the driving belt acts upon pulley f the shaft b rotates in one direction, while when the belt acts upon e, b rotates in the opposite direction, i being a loose pulley.
If the speed of rotation of b require to be greater in one direction than in the other, then the bevel-wheel on b is made a double one, that is to say, it has two annular toothed surfaces on its radial face, one of larger diameter than the other; a gearing with one of these toothed surfaces, and c with the other. It is obvious that the pinions a c, being of equal diameters, that gearing with the surface or gear of largest diameter will give to b the slowest speed of rotation.
Fig. 205 represents Watt’s sun-and-planet motion for converting reciprocating into rotary motion; b d is the working beam of the engine, whose centre of motion is at d. The gear a is so connected to the connecting rod that it cannot rotate, and is kept in gear with the wheel c on the fly-wheel shaft by means of the link shown. The wheel a being prevented from rotation on its axis causes rotary motion to the wheel c, which makes two revolutions for one orbit of a.
An arrangement for the rapid increase of motion by means of gears is shown in Fig. 206, in which a is a stationary gear, b is free to rotate upon its shaft, and being pivoted upon the shaft of a, at d, is capable of rotation around a while remaining in gear with c. Suppose now that the wheel a were absent, then if b were rotated around c with d as a centre of motion, c and its shaft e would make a revolution even though b would have no rotation upon its axis. But a will cause b to rotate upon its axis and thus communicate a second degree of motion to c, with the result that one revolution of b causes two rotations of c.
The relation of motion between b and c is in this case constant (2 to 1), but this relation may be made variable by a construction such as shown in Fig. 207, in which the wheel b is carried in a gear-wheel h, which rides upon the shaft d. Suppose now that h remains stationary while a revolves, then motion will be transmitted through b to c, and this motion will be constant and in proportion to the relative diameters of a and c. But suppose by means of an independent pinion the wheel h be rotated upon its axis, then increased motion will be imparted to c, and the amount of the increase will be determined by the speed of rotation of h, which may be made variable by means of cone pulleys or other suitable mechanical devices.
Fig. 208 represents an arrangement of gearing used upon steam fire-engines and traction engines to enable them to turn easily in a short radius, as in turning corners in narrow streets. The object is to enable the driving wheel on either side of the engine to increase or diminish its rotation to suit the conditions caused by the leading or front pair of steering wheels.
In the figures a is a plate wheel having the lugs l, by means of which it may be rotated by a chain. a is a working fit on the shaft s, and carries three pinions e pivoted upon their axes p. f is a bevel-gear, a working fit on s, while c is a similar gear fast to s. The pinions b, d are to drive gears on the wheels of the engine, the wheels being a working fit on the axle. Let it now be noted that if s be rotated, c and f will rotate in opposite directions and a will remain stationary. But if a be rotated, then all the gears will rotate with it, but e will not rotate upon p unless there be an unequal resistance to the motion of pinions d and b. So soon, however, as there exists an inequality of resistance between d and b then pinions e operate. For example, let b have more resistance than d, and b will rotate more slowly, causing pinion e to rotate and move c faster than is due to the motion of the chain wheel a, thus causing the wheel on one side of the engine to retard and the other to increase its motion, and thus enable the engine to turn easily. From its action this arrangement is termed the equalizing gear.
[I-76]In Figs. 209 to 214 are shown what are known as mangle-wheels from their having been first used in clothes mangling machines.
The mangle-wheel[10] in its simplest form is a revolving disc of metal with a centre of motion c (Fig. 209). Upon the face of the disc is fixed a projecting annulus a m, the outer and inner edges of which are cut into teeth. This annulus is interrupted at f, and the teeth are continued round the edges of the interrupted portion so as to form a continued series passing from the outer to the inner edge and back again.
[10] From Willis’s “Principles of Mechanism.”
A pinion b, whose teeth are of the same pitch as those of the wheel, is fixed to the end of an axis, and this axis is mounted so as to allow of a short travelling motion in the direction b c. This may be effected by supporting this end of it either in a swing-frame moving upon a centre as at d, or in a sliding piece, according to the nature of the train with which it is connected. A short pivot projects from the centre of the pinion, and this rests in and is guided by a groove b s f t b h k, which is cut in the surface of the disc, and made concentric to the pitch circles of the inner and outer rays of teeth, and at a normal distance from them equal to the pitch radius of the pinion.
Now when the pinion revolves it will, if it be on the outside, as in Fig. 209, act upon the spur teeth and turn the wheel in the opposite direction to its own, but when the interrupted portion f of the teeth is thus brought to the pinion the groove will guide the pinion while it passes from the outside to the inside, and thus bring its teeth into action with the annular or internal teeth. The wheel will then receive motion in the same direction as that of the pinion, and this will continue until the gap f is again brought to the pinion, when the latter will be carried outwards and the motion again be reversed. The velocity ratio in either direction will remain constant, but the ratio when the pinion is inside will differ slightly from the ratio when it is outside, because the pitch radius of the annular or internal teeth is necessarily somewhat less than that of the spur teeth. However, the change of direction is not instantaneous, for the form of the groove s f t, which connects the inner and outer grooves, is a semicircle, and when the axis of the pinion reaches s the velocity of the mangle-wheel begins to diminish gradually until it is brought to rest at f, and is again gradually set in motion from f to t, when the constant ratio begins; and this retardation will be increased by increasing the difference between the radius of the inner and outer pitch circles.
The teeth of a mangle-wheel are, however, most commonly formed by pins projecting from the face of the disc as in Fig. 210. In this manner the pitch circles for the inner and outer wheels coincide, and therefore the velocity ratio is the same within and without, also the space through which the pinion moves in shifting is reduced.
This space may be still further reduced by arranging the teeth as in Fig. 211, that is, by placing the spur-wheel within the annular or internal one; but at the same time the difference of the two velocity ratios is increased.
If it be required that the velocity ratio vary, then the pitch lines of the mangle-wheel must no longer be concentric.
Thus in Fig. 212 the groove k l is directed to the centre of the mangle-wheel, and therefore the pinion will proceed during this portion of its path without giving any motion to the wheel, and in the other lines of teeth the pitch radius varies, hence the angular velocity ratio will vary.
In Figs. 209, 210, and 211 the curves of the teeth are readily obtained by employing the same describing circle for the whole of[I-77] them. But when the form Fig. 212 is adopted, the shape of the teeth requires some consideration.
Every tooth of such a mangle-wheel may be considered as formed of two ordinary teeth set back to back, the pitch line passing through the middle. The outer half, therefore, appropriated to the action of the pinion on the outside of the wheel, resembles that portion of an ordinary spur-wheel tooth that lies beyond its pitch line, and the inner half which receives the inside action of the pinion resembles the half of an annular wheel that lies within the pitch circle. But the consequence of this arrangement is, that in both positions the action of the driving teeth must be confined to the approach of its teeth to the line of centres, and consequently these teeth must be wholly within their pitch line.
To obtain the forms of the teeth, therefore, take any convenient describing circle, and employ it to describe the teeth of the pinion by rolling within its pitch circle, and to describe the teeth of the wheel by rolling within and without its pitch circle, and the pinion will then work truly with the teeth of the wheel in both positions. The tooth at each extremity of the series must be a circular one, whose centre lies on the pitch line and whose diameter is equal to half the pitch.
If the reciprocating piece move in a straight line, as it very often does, then the mangle-wheel is transformed into a mangle-rack (Fig. 213) and its teeth may be simply made cylindrical pins, which those of the mangle-wheel do not admit of on correct principle. b b is the sliding piece, and a the driving pinion, whose axis must have the power of shifting from a to a through a space equal to its own diameter, to allow of the change from one side of the rack to the other at each extremity of the motion. The teeth of the mangle-rack may receive any of the forms which are given to common rack-teeth, if the arrangement be derived from either Fig. 210 or Fig. 211.
But the mangle-rack admits of an arrangement by which the shifting motion of the driving pinion, which is often inconvenient, may be dispensed with.
b b Fig. 214, is the piece which receives the reciprocating motion, and which may be either guided between rollers, as shown, or in any other usual way; a the driving pinion, whose axis of motion is fixed; the mangle rack c c is formed upon a separate plate, and in this example has the teeth upon the inside of the projecting ridge which borders it, and the guide-groove formed within the ring of teeth, similar to Fig. 211.
This rack is connected with the piece b b in such a manner as to allow of a short transverse motion with respect to that piece, by which the pinion, when it arrives at either end of the course, is enabled by shifting the rack to follow the course of the guide-groove, and thus to reverse the motion by acting upon the opposite row of teeth.
The best mode of connecting the rack and its sliding piece is that represented in the figure, and is the same which is adopted in the well-known cylinder printing-engines of Mr. Cowper. Two guide-rods k c, k c are jointed at one end k k to the reciprocating piece b b, and at the other end c c to the shifting-rack; these rods are moreover connected by a rod m m which is jointed to each midway between their extremities, so that the angular motion of these guide-rods round their centres k k will be the same; and as the angular motion is small and the rods nearly parallel to the path of the slide, their extremities c c may be supposed to move at a right angle to that path, and consequently the rack which is jointed to those extremities will also move upon b b in a direction at a right angle to its path, which is the thing required, and admits of no other motion with respect to b b.
To multiply plane motion the construction shown in Fig. 215 is frequently employed. a and b are two racks, and c is a wheel between them pivoted upon the rod r. A crank shaft or lever d is pivoted at e and also (at p) to r. If d be operated c traverses along a and also rotates upon its axis, thus giving to b a velocity equal to twice that of the lateral motion of c.
The diameter of the wheel is immaterial, for the motion of b will always be twice that of c.
Friction gearing-wheels which communicate motion one to the other by simple contact of their surfaces are termed friction-wheels, or friction-gearing. Thus in Fig. 216 let a and b be two wheels that touch each other at c, each being suspended upon a central shaft; then if either be made to revolve, it will cause the other to revolve also, by the friction of the surfaces meeting at c. The degree of force which will be thus conveyed from one to the other will depend upon the character of the surface and the length of the line of contact at c.
These surfaces should be made as concentric to the axis of the wheel and as flat and smooth as possible in order to obtain a maximum power of transmission. Mr. E. S. Wicklin states that under these conditions and proper forms of construction as much as 300 horse-power may be (and is in some of the Western States) transmitted.
In practice, small wheels of this class are often covered with some softer material, as leather; sometimes one wheel only is so covered, and it is preferred that the covered wheel drive the iron one, because, if a slip takes place and the iron wheel was the driver, it would be apt to wear a concave spot in the wood covered one, and the friction between the two would be so greatly diminished that there would be difficulty in starting them when the damaged spot was on the line of centre.
If, however, the iron wheel ceased motion, the wooden one continuing to revolve, the damage would be spread over that part of the circumference of the wooden one which continued while the iron one was at rest, and if this occurred throughout a whole revolution of the wooden wheel its roundness would not be apt to be impaired, except in so far as differences in the hardness of the wood and similar causes might effect.
“To select the best material for driving pulleys in friction-gearing has required considerable experience; nor is it certain[I-78] that this object has yet been attained. Few, if any, well-arranged and careful experiments have been made with a view of determining the comparative value of different materials as a frictional medium for driving iron pulleys. The various theories and notions of builders have, however, caused the application to this use of several varieties of wood, and also of leather, india-rubber, and paper; and thus an opportunity has been given to judge of their different degrees of efficiency. The materials most easily obtained, and most used, are the different varieties of wood, and of these several have given good results.
“For driving light machinery, running at high speed, as in sash, door, and blind factories, basswood, the linden of the Southern and Middle States (Tilia Americana) has been found to possess good qualities, having considerable durability and being unsurpassed in the smoothness and softness of its movement. Cotton wood (Populus monilifera) has been tried for small machinery with results somewhat similar to those of basswood, but is found to be more affected by atmospheric changes. And even white pine makes a driving surface which is, considering the softness of the wood, of astonishing efficiency and durability. But for all heavy work, where from twenty to sixty horse-power is transmitted by a single contact, soft maple (Acer rubrum) has, at present, no rival. Driving pulleys of this wood, if correctly proportioned and well built, will run for years with no perceptible wear.
“For very small pulleys, leather is an excellent driver and is very durable; and rubber also possesses great adhesion as a driver; but a surface of soft rubber undoubtedly requires more power than one of a less elastic substance.
“Recently paper has been introduced as a driver for small machinery, and has been applied in some situations where the test was most severe; and the remarkable manner in which it has thus far withstood the severity of these tests appears to point to it as the most efficient material yet tried.
“The proportioning, however, of friction-pulleys to the work required and their substantial and accurate construction are matters of perhaps more importance than the selection of material.
“Friction-wheels must be most accurately and substantially made and kept in perfect line so that the contact between the surfaces may not be diminished. The bodies are usually of iron lagged or covered with wooden segments.
“All large drivers, say from four to ten feet diameter and from twelve to thirty inch face, should have rims of soft maple six or seven inches deep. These should be made up of plank, one and a half or two inches thick, cut into ‘cants,’ one-sixth, eighth, or tenth of the circle, so as to place the grain of the wood as nearly as practicable in the direction of the circumference. The cants should be closely fitted, and put together with white lead or glue, strongly nailed and bolted. The wooden rim, thus made up to within about three inches of the width required for the finished pulley, is mounted upon one or two heavy iron ‘spiders,’ with six or eight radial arms. If the pulley is above six feet in diameter, there should be eight arms, and two spiders when the width of face is more than eighteen inches.
“Upon the ends of the arms are flat ‘pads,’ which should be of just sufficient width to extend across the inner face of the wooden rim, as described; that is, three inches less than the width of the finished pulley. These pads are gained into the inner side of the rim; the gains being cut large enough to admit keys under and beside the pads. When the keys are well driven, strong ‘lag’ screws are put through the ends of the arm into the rim. This done, an additional ‘round’ is put upon each side of the rim to cover bolt heads and secure the keys from ever working out. The pulley is now put to its place on the shaft and keyed, the edges trued up, and the face turned off with the utmost exactness.
“For small drivers, the best construction is to make an iron pulley of about eight inches less diameter and three inches less face than the pulley required. Have four lugs, about an inch square, cast across the face of this pulley. Make a wooden rim, four inches deep, with face equal to that of the iron pulley, and the inside diameter equal to the outer diameter of the iron. Drive this rim snugly on over the rim of the iron pulley having cut gains to receive the lugs, together with a hard wood key beside each. Now add a round of cants upon each side, with their inner diameter less than the first, so as to cover the iron rim. If the pulley is designed for heavy work, the wood should be maple, and should be well fastened by lag screws put through the iron rim; but for light work, it may be of basswood or pine, and the lag screws omitted. But in all cases, the wood should be thoroughly seasoned.
“In the early use of friction-gearing, when it was used only as backing gear in saw-mills, and for hoisting in grist-mills, the pulleys were made so as to present the head of the wood to the surface; and we occasionally yet meet with an instance where they are so made. But such pulleys never run so smoothly nor drive so well as those made with the fibre more nearly in a line with the work.”[11]
[11] By E. S. Wicklin.
The driving friction may be obtained from contact of the radial surfaces in two ways: thus, Fig. 217 represents three discs, a, b, and c; the edge of a being gripped by and between b and c, which must be held together by a spiral spring s or other equivalent device. These wheels may be made to give a variable speed of rotation by curving the surfaces of the pair b c as in the figure. By means of suitable lever-motion a may be made to advance towards or recede from the centre of b and c, giving to their shaft an increased or diminished speed of revolution.
A similar result may be obtained by the construction shown in Fig. 218, in which d and e are two discs fast upon their respective shafts, and c are discs of leather clamped in e. It is obvious that if d be the driver the speed of revolution of e will be diminished in proportion as it is moved nearer to the centre of d, and also that the direction of revolution of d remaining constant, that of e will be in one direction if on the side b of the centre of d, and in the other direction if it is on the side a of the centre of d, thus affording means of reversing the motion as well as of varying its speed. A similar arrangement is sometimes employed to enable the direction of rotation of the driver shaft to be reversed, or its motion to cease. Thus, in Fig. 219, r is a driving rope driving the discs a, b, and c, d, e, f, g are discs of yellow pine clamped between the flanges h i; when these five discs are forced (by lifting shaft h), against the face of a motion occurs in one direction, while if forced against b the direction of motion of h is reversed.
For many purposes, such as hoisting, for example, where considerable power requires to be transmitted, the form of friction wheels shown in Fig. 220 is employed, the object being to increase the line of contact between wheels of a given width of[I-79] face. In this case the strain due to the length of the line of contact partly counteracts itself, thus relieving to that extent the journals from friction. Thus in Fig. 221 is shown a single wedge and groove of a pair of wheels. The surface pressure on each side will be at a right angle to the face, or in the direction described by the arrows a and b. The surface contact acts to thrust the bearings of the two shafts apart. The effective length of surface acting to thrust the bearings apart being denoted by the dotted line c. The relative efficiency of this class of wheel, however, is not to be measured by the length of the line c, as compared to that of the two contacting sides of the groove, because it is increased from the wedge shape of the groove, and furthermore, no matter how solid the wheels may be, there will be some elasticity which will operate to increase the driving power due to the contact. It is to preserve the wedge principle that the wedges are made flat at the top, so that they shall not bottom in the grooves even after considerable wear has taken place. The object of employing this class of gear is to avoid noise and jar and to insure a uniform motion. The motion at the line of contact of such wheels is not a rolling, but, in part, a sliding one, which may readily be perceived from a consideration of the following. The circumference of the top of each wedge is greater than that of the bottom, and, in the case of the groove, the circumference of the top is greater than that of the bottom; and since the top or largest circumference of one contacts with the smallest circumference of the other, it follows that the difference between the two represents the amount of sliding motion that occurs in each revolution. Suppose, for example, we take two of such wheels 10 inches in diameter, having wedges and grooves 1⁄4 inch high and deep respectively; then the top of the groove will travel 31.416 inches in a revolution, and it will contact with the bottom of the wedge which travels (on account of its lesser diameter) 29.845 inches per revolution.
Fig. 222 shows the construction for a pair of bevel wheels on the same principle.
A form of friction-gearing in which the journals are relieved of the strain due to the pressure of contact, and in which slip is impossible, is shown in Fig. 223. It consists of projections on one wheel and corresponding depressions or cavities on the other. These projections and cavities are at opposite angles on each half of each wheel, so as to avoid the end pressure on the journals which would otherwise ensue. Their shapes may be formed at will, providing that the tops of the projections are narrower than their bases, which is necessary to enable the projections to enter and leave the cavities. In this class of positive gear great truth or exactness is possible, because both the projections and cavities may be turned in a lathe. Fig. 224 represents a similar kind of[I-80] gear with the projections running lengthways of the cylinder approaching more nearly in its action to toothed gearing, and in this case the curves for the teeth and groves should be formed by the rules already laid down for toothed gearing. The action of this latter class may be made very smooth, because a continuous contact on the line of centres may be maintained by reason of the longitudinal curve of the teeth.
Cams may be employed to impart either a uniform, an irregular, or an intermittent motion, the principles involved in their construction being as follows:—Let it be required to construct a cam that being revolved at a uniform velocity shall impart a uniform reciprocating motion. First draw an inner circle o, Fig. 225, whose radius must equal the radius of the shaft that is to drive it, plus the depth of the cam at its shallowest part, plus the radius of the roller the cam is to actuate. Then from the same centre draw an outer circle s, the radius between these two circles being equal to the amount the cam is to move the roller. Draw a line o p, and divide it into any convenient numbers of divisions (five being shown in the figure), and through these points draw circles. Divide the outer circle s into twice as many equal divisions as the line o p is divided into (as from 1 to 10 in the figure), and where these lines pass through the circles will be points through which the pitch line of the cam may be drawn.
Thus where circle 1 meets line 1, or at point a, is one point in the pitch line of the cam; where circle 2 meets line 2, or at b, is another point in the pitch line of the cam, and so on until we reach the point e, where circle 5 meets line 5. From this point we simply repeat the process, the point e where line 6 cuts circle 4, being a point on the pitch line, and so on throughout the whole 10 divisions, and through the points so obtained we draw the pitch line.
If we were to cut out a cam to the outline thus obtained, and revolve it at a uniform velocity, it would move a point held against its perimeter at a uniform velocity throughout the whole of the cam revolution. But such a point would rapidly become worn away and dulled, which would, as the point broadened, vary the motion imparted to it, as will be seen presently. To avoid this wear a roller is used in place of a point, and the diameter of the roller affects the action of the cam, causing it to accelerate the cam action at one and retard it at another part of the cam revolution, hence the pitch line obtained by the process in Fig. 225 represents the path of the centre of the roller, and from this pitch line we may mark out the actual cam by the construction shown in Fig. 226. A pair of compasses are set to the radius of the roller r, and from points (such as at a, b, e, f), as the pitch line, arcs of circles are struck, and a line drawn to just meet the crowns of these arcs will give the outline of the actual cam. The motion of the roller, however, in approaching and receding from the cam centre c, must be in a straight line g g that passes through the centre c of the cam. Suppose, for example, that instead of the roller lifting and falling in the line g g its arm is horizontal, as in Fig. 227, and that this arm being pivoted the roller moves in an arc of a circle as d d, and the motion imparted to the arm will no longer be uniform. Furthermore, different diameters of roller require different forms of cam to accomplish the same motion, or, in other words, with a given cam the action will vary with different diameters of roller. Suppose, for example, that in Fig. 228 we have a cam that is to operate a roller along the line a a, and that b represents a large[I-81] and c a small roller, and with the cam in the position shown in the figure, c will have contact with the cam edge at point d, while b will have contact at the point e, and it follows that on account of the enlarged diameter of roller b over roller c, its action is at this point quicker under a given amount of cam motion, which has occurred because the point of contact has advanced upon the roller surface—rolling along it, as it were. In Fig. 229 we find that as the cam moves forward this action continues on both the large and the small roller, its effect being greater upon the large than upon the small one, and as this rolling motion of the point of contact evidently occurs easily, a quick roller motion is obtained without shock or vibration. Continuing the cam motion, we find in Fig. 230 that the point of contact is receding toward the line of motion on the large roller and advancing upon the small one, while in Fig. 231 the two have contact at about the same point, the forward motion being about completed.
To compare the motions of the respective rollers along the line of motion a a we proceed as in Fig. 232, in which the two dots m and n are the same distance apart as are the centres of the two rollers b and c when in the positions they occupy in Fig. 228; hence a pair of compasses set to the radius from the axis of the cam to that of roller b will, if rested at n, strike the arc marked 1 above the line of motion a a, while a pair of compasses set to the radius from the axis of the cam to that of roller c in Fig. 228 will, if rested at m in Fig. 232, mark the arc 1 below the line of motion a a. Continuing this process, we set the compasses to the radius from the axis of the cam to that of roller b in Fig. 229, and mark this radius at arc 2 above the line a a in Fig. 232; hence the distance apart of these two arcs is the amount the roller travelled along the line a a while the cam moved from its position in Fig. 228 to its position in Fig. 229. Next we set the compasses from the axis of the cam to that of the large roller in Fig. 230, and then mark arc 3 above the line in Fig. 232, and repeat the process for Fig. 233, thus using the centre n for all the positions of the large roller and marking its motion above the line a a. To get the motion of the small roller c, we set the compasses to the radius from the axis of the cam to the small roller in Fig. 228, and then resting one point of these compasses on centre m in Fig. 232, we mark arc 1 below the line a a. Turning to Fig. 229 we set the compasses from the cam axis to the centre of roller c, and from centre n in Fig. 232 mark arc 2 below line a. From Figs. 230 and 231 proceed in the same way to get lines 3 and 4 below line a in Fig. 232, and we may at once compare the two motions. Thus we find that while the cam moved from the position in Fig. 228 to that in Fig. 229, the large roller moved twice as far as the small one, while at 230 the motions were rapidly equalizing again, the equalization being completed at 231.
We may now consider the return motion, and in Fig. 233 we find that the order of things is reversed, for the small roller has contact at o, while the large one has contact at p; hence the small one leads and gives the most rapid motion, which it continues to do, as is shown in Figs. 234, 235, and 236, and we may plot out the two motions as in Fig. 237—that for the large roller being above and that for the small one below the line a a. First we set a pair of compasses to the radius from the axis of the large and small roller when in the position shown in Fig. 231 (which corresponds to the same radius in Fig. 228), and mark two centres, m and n, as we did in Fig. 232. Of these n is the centre for plotting the motion of the large roller and m the centre for[I-82] plotting the motion of the small one. We set a pair of compasses to the radius from the axis of the cam and that of the large roller in Fig. 231, and then resting the compasses at n we mark arc 5 above the line a a, Fig. 237. The compasses are then set from the cam to the roller axis in Fig. 233, and arc 6 is marked above line a a. From Figs. 234, 235, and 236 we get the radii to mark arcs 7, 8, 9 above a a, and the motion of the large roller is plotted. We proceed in the same way for the small one, but use the centre m, Fig. 237, to mark the arcs 5, 6, 7, 8, and 9 below the line a a, and find that the small roller has moved quickest throughout. It appears, then, that the larger the roller the quicker the forward motion and the slower the return one, which is advantageous, because the object is to move the roller out quickly and close it slowly, so that under a quick speed the cam shall not run away from the roller as it is apt to do in the absence of a return or backing cam, which consists of a separate cam for moving the roller on its return stroke, thus dispensing with the use of springs or weights to keep the roller upon the cam and making the motion positive.
The return or backing cam obviously depends for its shape upon the forward cam, and the latter having been determined, the requisite form for the return cam may be found as follows. In Fig. 238 let a represent the forward cam fastened in any suitable or convenient way to a disc of paper, or, what is better, sheet zinc, b. The cam is pivoted by a pin passing through it and the zinc, and driven into the drawing-board. A frame f is made to carry two rollers r and r′, whose width apart exactly equals the extreme length of the forward cam. The faces d d of the frame f are in a line with a line passing through the centres of the rolls r r′, and the cam is also pivoted on this line, so that when the four pins p are driven into the drawing-board, the frame f will be guided by them to move in a line that crosses the centre of the cam a. Suppose then that, the pieces occupying the position shown in the engraving, we slide f so that roller r touches the edge of cam a, and we may then take a needle and mark an arc or line around the edge of r′. We then revolve cam a a trifle, and, being fast to b, the two will move together, and with r against a we mark a second arc, coincident with the edge of roller r′. By continuing this process we mark the numerous short arcs shown upon b, and the crowns of these arcs give us the outline of the return cam. It is obvious that, while the edge of the cam a will not let roller r (and therefore frame f) move to the right, roller r′ being against the edge of the backing or return cam as marked upon b, prevents the frame f from moving to the left; hence neither roll can leave its cam.
We have in this example supposed that the frame carrying the rollers is guided to move in a straight line, and it remains to give an example in which the rollers are carried on a pivoted shaft or rocking arm. In Fig. 239 we have the same cam a with a sheet of paper b fastened to it, the rollers r r′ being carried in a rock shaft pivoted at x. It is essential in this case that the rollers r and r′ and the centre upon which the cam revolves shall all three be in the arc of a circle whose centre is the axis of x, as is denoted by the arc d. The cam a is fastened to the piece of stiff paper or of sheet zinc b, and the two are pivoted by a pin passing[I-83] through the axis e of the cam and into the drawing-board, while the lever is pivoted at x by a pin passing into the drawing-board. The backing or return cam is obviously marked out the same way as was described with reference to Fig. 238.
In Fig. 240 we have as an example the construction of a cam to operate the slide valve of an engine which is to have the steam supply to the cylinder cut off at one-half the piston stroke, and that will admit the live steam as quickly as a valve having steam lap equal to, say, three-fourths the width of the port. In Fig. 240 let the line a represent a piston stroke of 24 inches, the outer circle b the path of the outer edge of the cam, and the inner circle c the inner edge of the cam, the radius between these circles representing the full width of the steam port. Now, in a valve having lap equal to three-fourths the width of the steam port, and travel enough to open both ports fully, the piston of a 24-inch-stroke engine will have moved about 2 inches before the steam port is fully opened, and to construct a cam that will effect the same movement we mark a dot d, distant from the end e of piston stroke 2⁄26 of the length of the line a, and by erecting the line f we get at point g, the point at which the cam must attain its greatest throw. It is obvious, therefore, that as the roller is at r the valve will be in mid-position, as shown at the bottom of the figure, and that when point g of the cam arrives at e the edge p of the valve will be moved fair with edge s of the steam port t, which will therefore be full open. To cut off at half stroke the valve must again be closed by the time point n of the cam meets the roller r; hence we may mark point n. We may then mark in the cam curve from n to m, making it as short as it will work properly without causing the roller to fail to follow the curve or strike a blow when reaching the circle c. To accomplish this end in a single cam, it is essential to make the curve as gradual as possible from point m to o, so as to start the roller motion easily. But once having fairly started, its motion may be rapidly accelerated, the descent from o to q being rapid. To prevent the roller from meeting circle c with a blow, the curve from q to n is again made gradual, so as to ease and retard the roller motion. The same remarks apply to the curve from r to g, the object being to cause the roller to begin and end its passage along the cam curve as slowly as the length of cam edge occupied by the curve will permit. There is one objection to starting the curve slowly at g, which is that the port s will be opened correspondingly slowly for the live steam. This, however, may be overcome by giving the valve an increased travel, as shown in Fig. 241, which will simply cause the valve edge to travel to a corresponding amount over the inside edge of the port. The increased travel is shown by the circles y and z, and it is seen that the cam curve from w to r is more gradual than in Fig. 240, while the roller r will be moved much more quickly in the position shown in Fig. 241 than it will in that shown in Fig. 240, both positions being that when the piston is at the end of the stroke and the port about to open. While that part of the cam curve from g to m in Fig. 241 is moving past the roller r, the valve will be moving over the bridge, the steam port remaining wide open, and therefore not affecting the steam distribution. After point m, Fig. 241, has passed the roller, we have from m to t to start the roller gradually, so that when it has arrived at t and the port begins to close for the cut-off it may move rapidly, and continue to do so until the point n reaches the roller and the cut-off has occurred, after which it does not matter how slowly the valve moves; hence we may make the curve from n to the circle y as gradual as we like.
Fig. 242 represents a cam for a valve having the amount of lap represented by the distance between circles c and y, the cam occupying the position it would do with the piston at one end of the stroke, as at e. Obviously, a full port is obtained when point g reaches the roller, and as point n is distant from e three-quarters of the diameter of the outer circle, the cut-off occurs at three-quarter stroke, and we have from n to y to make the curve as gradual as we like, and from w to r in moving the valve to open the port. We cannot, however, give more gradual curves at g and at m without retarding the roller motion, and therefore opening and closing the port slower, and it would simply be a matter of increase of speed to cause the roller to fail to follow[I-84] the cam surface at these two points unless a return cam be employed.
We have in these engine cams considered the steam supply and point of cut-off only, and it is obvious that a second and separate cam would be required to operate the exhaust valves.
Fig. 243 represents a groove-cam, and it is to be observed that the roller cannot be maintained in a close fit in the groove, because the friction on its two sides endeavours to drive it in opposite directions at the same time, causing an abrasion that soon widens the groove and reduces the roller diameter; furthermore, when the grooves are made of equal width all the way down (and these cams are often made in this way) the roller cannot have a rolling action only, but must have some sliding motion. Thus, referring to Fig. 243, the amount of sliding motion will be equal to the differences in the circumferences of the outer circle a and the inner one b. To obviate this the groove and roller must be made of such a taper that the axis of the cam and of the roller will meet on the line of the cam axes and in the middle of the width, as is shown in Fig. 244; but even in this case the cam will grind away the roller to some extent, on account of rubbing its sides in opposite directions. To obviate this, Mr. James Brady, of Brooklyn, N. Y., has patented the use of two rollers, as in Fig. 245, one acting against one side and the other against the other side of the groove, by which means lost motion and rapid wear are successfully avoided.
In making a cam of this form, the body of the cam is covered by a sleeve. The groove is cut through the sleeve and into the body, and is made wider than the diameter of the roller. When the rollers are in place on the spindle or journal, the sleeve is pushed forward, or rather endways, and fastened by a set-screw. This gives the desired bearing on both sides of the groove, while each roller touches one side only of the groove. The edges of the sleeve are then faced off even with the cam body, the whole appearing as in the figure.
| VOL. I. | FORMS OF SCREW THREADS. | PLATE II. | |
| THE V-THREAD. | THE UNITED STATES STANDARD THREAD. | ||
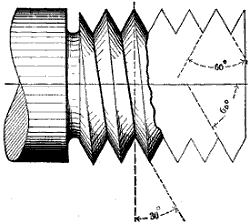 |
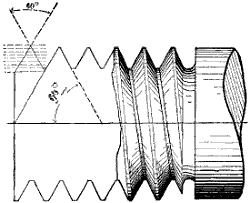 |
||
| Fig. 246. | Fig. 247. | ||
| THE WHITWORTH, OR ENGLISH STANDARD THREAD. | THE SQUARE THREAD. | ||
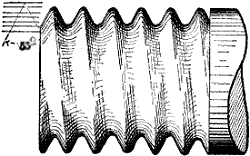 |
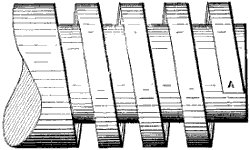 |
||
| Fig. 248. | Fig. 249. | ||
| THE PITCH OF A THREAD. | A DOUBLE THREAD. | ||
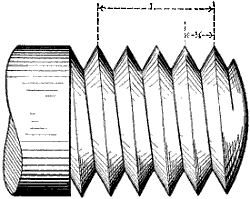 |
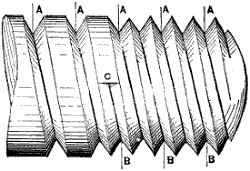 |
||
| Fig. 250. | Fig. 251. | ||
| THE RATCHET THREAD. | A “DRUNKEN” THREAD. | ||
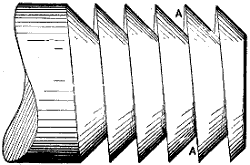 |
 |
||
| Fig. 252. | Fig. 253. | ||
| RIGHT AND LEFT HAND THREAD. | |||
 |
|||
| Fig. 254. | |||
Screw threads are employed for two principal purposes—for holding or securing, and for transmitting motion. There are in use, in ordinary machine shop practice, four forms of screw thread. There is, first, the sharp V-thread shown in Fig. 246; second, the United States standard thread, the Sellers thread, or the Franklin Institute thread, as it is sometimes called—all three designations signifying the same form of thread. This thread was originally proposed by William Sellers, and was afterward recommended by the Franklin Institute. It was finally adopted as a standard by the United States Navy Department. This form of thread is shown in Fig. 247. The third form is the Whitworth or English standard thread, shown in Fig. 248. It is sometimes termed the round top and bottom thread. The fourth form is the square thread shown in Fig. 249, which is used for coarse pitches, and usually for the transmission of motion.
The sharp V-thread, Fig. 246, has its sides at an angle of 60° one to the other, as shown; or, in other words, each side of the thread is at an angle of 60° to the axial line of the bolt. The United States Standard, Fig. 247, is formed by dividing the depth of the sharp V-thread into 8 equal divisions and taking off one of the divisions at the top and filling in another at the bottom, so as to leave a flat place at the top and bottom. The Whitworth thread, Fig. 248, has its sides at an angle of 55° to each other, or to the axial line of the bolt. In this the depth of the thread is divided into 6 equal parts, and the sides of the thread are joined by arcs of circles that cut off one of these parts at the top and another at the bottom of the thread. The centres from which these arcs are struck are located on the second lines of division, as denoted in the figure by the dots. Screw threads are designated by their pitch or the distance between the threads. In Fig. 250 the pitch is 1⁄4 inch, but it is usual to take the number of threads in an inch of length; hence the pitch in Fig. 250 would generally be termed a pitch of 4, or 4 to the inch. The number of threads per inch of length does not, however, govern the true pitch of the thread, unless it be a “single” thread.
A single thread is composed of one spiral projection, whose advance upon the bolt is equal in each revolution to the apparent pitch. In Fig. 251 is shown a double thread, which consists of two threads. In the figure, a denotes one spiral or thread, and b the other, the latter being carried as far as c only for the sake of illustration. The true pitch is in this case twice that of the apparent pitch, being, as is always the case, the number of revolutions the thread makes around the bolt (which gives the pitch per inch), or the distance along the bolt length that the nut or thread advances during one rotation. Threads may be made double, treble, quadruple and so on, the object being to increase the motion without the use of a coarser pitch single thread, whose increased depth would weaken the body of the bolt.
The “ratchet” thread shown in Fig. 252 is sometimes used upon bolts for ironwork, the object being to have the sides a a of the thread at a right angle to the axis of the bolt, and therefore in the direct line of the strain. Modifications of this form of thread are used in coarse pitches for screws that are to thread direct into woodwork.
A waved or drunken thread is one in which the path around the bolt is waved, as in Fig. 253, and not a continuous straight spiral, as it should be. All threads may be either left hand or right, according to their direction of inclination upon the bolt; thus, Fig. 254 is a cylinder having a right-hand thread at a and a left-hand one at b. When both ends of a piece have either right or left-hand threads, if the piece be rotated and the nuts be prevented from rotating, they will move in the same direction, and, if the pitches of the threads are alike, at the same rate of motion; but if one thread be a right and the other a left one, then, under the above conditions, the nuts will advance toward or recede from each other according to the direction of rotation of the male thread.
In Fig. 255 is represented a form of thread designed to enable the nut to fit the bolt, and the thread sides to have a bearing one upon the other, notwithstanding that the diameter of the nut and bolt may differ. The thread in the nut is what may be termed a reversed ratchet thread, and that in the bolt an undercut ratchet thread, the amount of undercut being about 2°. Where this form of thread is used, the diameter of the bolt may vary as much as 1⁄32d of an inch in a bolt 3⁄4 inch in diameter, and yet the nut will screw home and be a tight fit. The difference in the thread fit that ordinarily arises from differences in the standards of measurement from wear of the threading tools, does not in this form affect the fit of the nut to the bolt. In screwing the nut on, the threads conform one to the other, giving a bearing area extending over the full sides of the thread. The undercutting on the leading face of the bolt thread gives room for the metal to conform itself to the nut thread, which it does very completely. The result is that the nut may be passed up and down the bolt several times and still remain too tight a fit to be worked by hand. Experiment has demonstrated that it may be run up and down the bolt dozens of times without becoming as loose as an ordinary bolt and nut. On account of this capacity of the peculiar form of thread employed, to adapt itself, the threads may be made a tight fit when the threading tools are new. The extra tightness that arises from the wear of these tools is accommodated in the undercutting, which gives room for the thread to adjust itself to the opposite part or nut.
In a second form of self-locking thread, the thread on the bolt is made of the usual V-shape United States standard. The thread in the nut, however, is formed as illustrated in Fig. 256, which is a section of a 3⁄4-inch bolt, greatly enlarged for the sake of clearness of illustration. The leading threads are of the same angle as the thread on the bolt, but their diameters are 3⁄4 and 1⁄16th inch, which allows the nut to pass easily upon the bolt. The angle of the next thread following is 56°, the succeeding one 52°, and so on, each thread having 4° less angle than the one preceding, while the pitch remains the same throughout. As a result, the rear threads are deeper than the leading ones. As the nut is screwed home, the bolt thread is forced out or up, and fills the rear threads to a degree depending upon the diameter of the bolt thread. For example, if the bolt is 3⁄4 inch, its leading or end thread will simply change its angle from that of 60° to that of 44°, or if the bolt thread is 3⁄4 and 1⁄64th inch in diameter, its leading thread will change from an angle of 60° to one of 44°. It will almost completely fill the loose thread in the nut. The areas of spaces between the nut threads are very nearly equal, although[I-86] slightly greater at the back end of the nut, so that if the front end will enter at all, the nut will screw home, while the thread fit will be tight, even under a considerable variation in the bolt itself. From this description, it is evident that the employment of nuts threaded in this manner is only necessary in order to give to ordinary bolts all the advantages of tightness due to this form of thread.
The term “diameter” of a thread is understood to mean its diameter at the top of the thread and measured at a right angle to the axis of the bolt. When the diameter of the bottom or root of the thread is referred to it is usually specified as diameter at the bottom or at the root of the thread.
The depth of a thread is the vertical height of the thread upon the bolt, measured at a right angle to the bolt axis and not along the side of the thread.
A true thread is one that winds around the bolt in a continuous and even spiral and is not waved or drunken as is the thread in Fig. 253. An outside or male thread is one upon an external surface as upon a bolt; an internal or female thread is one produced in a bore or hole as in a nut.
The Whitworth or English standard thread, shown in Fig. 248, is that employed in Great Britain and her colonies, and to a small extent in the United States. The V-thread fig. 246 is that in most common use in the United States, but it is being displaced by the United States standard thread. The reasons for the adoption of the latter by the Franklin Institute are set forth in the report of a committee appointed by that Institute to consider the matter. From that report the following extracts are made.
“That in the course of their investigations they have become more deeply impressed with the necessity of some acknowledged standard, the varieties of threads in use being much greater than they had supposed possible; in fact, the difficulty of obtaining the exact pitch of a thread not a multiple or sub-multiple of the inch measure is sometimes a matter of extreme embarrassment.
“Such a state of things must evidently be prejudicial to the best interests of the whole country; a great and unnecessary waste is its certain consequence, for not only must the various parts of new machinery be adjusted to each other, in place of being interchangeable, but no adequate provision can be made for repairs, and a costly variety of screwing apparatus becomes a necessity. It may reasonably be hoped that should a uniformity of practice result from the efforts and investigations now undertaken, the advantages flowing from it will be so manifest, as to induce reform in other particulars of scarcely less importance.
“Your committee have held numerous meetings for the purpose of considering the various conditions required in any system which they could recommend for adoption. Strength, durability, with reference to wear from constant use, and ease of construction, would seem to be the principal requisites in any general system; for although in many cases, as, for instance, when a square thread is used, the strength of the thread and bolt are both sacrificed for the sake of securing some other advantage, yet all such have been considered as special cases, not affecting the general inquiry. With this in view, your committee decided that threads having their sides at an angle to each other must necessarily more nearly fulfil the first condition than any other form; but what this angle should be must be governed by a variety of considerations, for it is clear that if the two sides start from the same point at the top, the greater the angle contained between them, the greater will be the strength of the bolt; on the other hand, the greater this angle, supposing the apex of the thread to be over the centre of its base, the greater will be the tendency to burst the nut, and the greater the friction between the nut and the bolt, so that if carried to excess the bolt would be broken by torsional strain rather than by a strain in the direction of its length. If, however, we should make one side of the thread perpendicular to the axis of the bolt, and the other at an angle to the first, we should obtain the greatest amount of strength, together with the least frictional resistance; but we should have a thread only suitable for supporting strains in one direction, and constant care would be requisite to cut the thread in the nut in the proper direction to correspond with the bolt; we have consequently classed this form as exceptional, and decided that the two sides should be at an angle to each other and form equal angles with the base.
“The general form of the thread having been determined upon the above considerations, the angle which the sides should bear to each other has been fixed at 60°, not only because this seems to fulfil the conditions of least frictional resistance combined with the greatest strength, but because it is an angle more readily obtained than any other, and it is also in more general use. As this form is in common use almost to the exclusion of any other, your committee have carefully weighed its advantages and disadvantages before deciding to recommend any modification of it. It cannot be doubted that the sharp thread offers us the simplest form, and that its general adoption would require no special tools for its construction, but its liability to accident, always great, becomes a serious matter upon large bolts, whilst the small amount of strength at the sharp top is a strong inducement to sacrifice some of it for the sake of better protection to the remainder; when this conclusion is reached, it is at once evident a corresponding space may be filled up in the bottom of the thread, and thus give an increased strength to the bolt, which may compensate for the reduction in strength and wearing surface upon the thread. It is also clear that such a modification, by avoiding the fine points and angles in the tools of construction, will increase their durability; all of which being admitted, the question comes up, what form shall be given to the top and bottom of the thread? for it is evident one should be the converse of the other. It being admitted that the sharp thread can be made interchangeable more readily than any other, it is clear that this advantage would not be impaired if we should stop cutting out the space before we had made the thread full or sharp; but to give the same shape at the bottom of the threads would require that a similar quantity should be taken off the point of the cutting tool, thus necessitating the use of some instrument capable of measuring the required amount, but when this is done the thread having a flat top and bottom can be quite as readily formed as if it was sharp. A very slight examination sufficed to satisfy us that in point of construction the rounded top and bottom presents much greater difficulties—in fact, all taps and screws that are chased or cut in a lathe require to be finished or rounded by a second process. As the radius of the curve to form this must vary for every thread, it will be impossible to make one gauge to answer for all sizes, and very difficult, in fact impossible, without special tools, to shape it correctly for one.
“Your committee are of opinion that the introduction of a uniform system would be greatly facilitated by the adoption of such a form of thread as would enable any intelligent mechanic to construct it without any special tools, or if any are necessary, that they shall be as few and as simple as possible, so that although the round top and bottom presents some advantages when it is perfectly made, as increased strength to the thread and the best form to the cutting tools, yet we have considered that these are more than compensated by ease of construction,[I-87] the certainty of fit, and increased wearing surface offered by the flat top and bottom, and therefore recommend its adoption. The amount of flat to be taken off should be as small as possible, and only sufficient to protect the thread; for this purpose one-eighth of the pitch would seem to be ample, and this will leave three-fourths of the pitch for bearing surface. The considerations governing the pitch are so various that their discussion has consumed much time.
“As in every instance the threads now in use are stronger than their bolts, it became a question whether a finer scale would not be an advantage. It is possible that if the use of the screw thread was confined to wrought iron or brass, such a conclusion might have been reached, but as cast iron enters so largely into all engineering work, it was believed finer threads than those in general use might not be found an improvement; particularly when it was considered that so far as the vertical height of thread and strength of bolt are concerned, the adoption of a flat top and bottom thread was equivalent to decreasing the pitch of a sharp thread 25 per cent., or what is the same thing, increasing the number of threads per inch 33 per cent. If finer threads were adopted they would require also greater exactitude than at present exists in the machinery of construction, to avoid the liability of overriding, and the wearing surface would be diminished; moreover, we are of opinion that the average practice of the mechanical world would probably be found better adapted to the general want than any proportions founded upon theory alone.”
The principal requirements for a screw thread are as follows: 1. That it shall possess a strength that, in the length or depth of a nut, shall be equal to the strength of the weakest part of the bolt, which is at the bottom of the bolt thread. 2. That the tools required to produce it shall be easily made, and shall not alter their form by reason of wear. 3. That these tools shall (in the case of lathe work) be easily sharpened, and set to correct position in the lathe. 4. That a minimum of measuring and gauging shall be required to test the diameter and form of the thread. 5. That the angles of the sides shall be as acute as is consistent with the required strength. 6. That it shall not be unduly liable to become loose in cases where the nut may require to be fastened and loosened occasionally.
Referring to the first, by the term “the strength of a screw thread,” is not meant the strength of one thread, but of so many threads as are contained in the nut. This obviously depends upon the depth or thickness of the nut-piece. The standard thickness of nut, both in the United States and Whitworth systems, as well as in general practice, or where the common V-thread is used, is made equal to the diameter of the top of the thread. Therefore, by the term “strength of thread” is meant the combined strength of as many threads as are contained in a nut of the above named depth. It is obvious, then, when it is advantageous to increase the strength of a thread, that it may be done by increasing the depth of the nut, or in other words, by increasing the number of threads used in computing its strength. This is undesirable by reason of increasing the cost and labor of producing the nuts, especially as the threading tools used for nuts are the weakest, and are especially liable to breakage, even with the present depth of nuts.
It has been found from experiments that have been made that our present threads are stronger than their bolts, which is desirable, inasmuch as it gives a margin for wear on the sides of the threads. But for threads whose nuts are to remain permanently fastened and are not subject to wear, it is questionable whether it were not better for the bolts to be stronger than the threads. Suppose, for instance, that a thread strips, and the bolt will remain in place because the nut will not come off the bolt readily. Hence the pieces held by the bolt become loosened, but not disconnected. If, on the other hand, the bolt breaks, it is very liable to fall out, leaving the piece or pieces, as the case may be, to fall apart, or at least become disconnected, so far as the bolt is concerned. But since threads are used under conditions where the threads are liable to wear, and since it is undesirable to have more than one standard thread, it is better to have the threads, when new, stronger than the bolts.
Referring to the second requirement, screw threads or the tools that produce them are originated in the lathe, and the difficulty with making a round top and bottom thread lies in shaping the corner to cut the top of the thread. This is shown in Fig. 257, where a Whitworth thread and a single-toothed thread-cutting tool are represented. The rounded point a of the tool will not be difficult to produce, but the hollow at b would require special tools to cut it. This is, in fact, the plan pursued under the Whitworth system, in which a hob or chaser-cutting tool is used to produce all the thread-cutting tools. A chaser is simply a toothed tool such as is shown in Fig. 258. Now, it would manifestly be impracticable to produce a chaser having all the curves, a and b, at the top and at the bottom of the teeth alike, by the grinding operations usually employed in the workshop, and hence the employment of the hob. Fig. 259 represents a hob, which is a threaded piece of steel with a number of grooves such as shown at a, a, a, which divide the thread into teeth, the edges of which will cut a chaser, of a form corresponding to that of the thread upon the hob. The chaser is employed to produce taps and secondary hobs to be used for cutting the threads in dies, &c., so that the original hob is the source from which all the thread-cutting tools are derived.
For the United States standard or the common V-thread, however, no standard hob is necessary, because a single-pointed tool can be ground with the ordinary grinding appliances of the workshop. Thus, for the United States standard, a flat-pointed tool, Fig. 260, and for the common V-thread, a sharp-pointed tool, Fig. 260, may be used. So far as the correctness of angle of pitch and of thread depth are concerned, the United States standard and the common V-thread can both be produced, under skilful operation, more correctly than is possible with the Whitworth thread, for the following reasons:—
To enable a hob to cut, it must be hardened, and in the hardening process the pitch of the thread alters, becoming, as a[I-88] general rule (although not always) finer. This alteration of pitch is not only irregular in different threads, but also in different parts of the same thread. Now, whatever error the hob thread receives from hardening it transfers to the chaser it cuts. But the chaser also alters its form in hardening, the pitch, as a general rule, becoming coarser. It may happen that the error induced in the hob hardening is corrected by that induced by hardening the chaser, but such is not necessarily the case.
The single-pointed tool for the United States standard or for the common V-thread is accurately ground to form after the hardening, and hence need contain no error. On the other hand, however, the rounded top and bottom thread preserves its form and diameter upon the thread-cutting tools better than is the case with threads having sharp corners, for the reason that a rounded point will not wear away so quickly as a sharp point. To fully perceive the importance of this, it is necessary to consider the action of a tool in cutting a thread. In Fig. 261 there is shown a chaser, a, applied to a partly-formed thread, and it will be observed that the projecting ends or points of the teeth are in continuous action, cutting a groove deeper and deeper until a full thread is developed, at which time the bottoms of the chaser teeth will meet the perimeter of the work, but will perform no cutting duty upon it. As a result, the chaser points wear off, which they will do more quickly if they are pointed, and less quickly if they are rounded. This causes the thread cut to be of increased and improper diameter at the root.
The same defect occurs on the tools for cutting internal threads, or threads in holes or bores. In Fig. 262, for example, is shown a tool cutting an internal thread, which tool may be taken to represent one tooth of a tap. Here again the projecting point of the tool is in continuous cutting action, while this, being a single-toothed tool, has no bottom corners to suffer from wear. As a result of the wear upon the tools for cutting internal threads, the thread grooves, when cut to their full widths, will be too shallow in depth, or, more correctly speaking, the full diameter of the thread will be too small to an amount corresponding to twice the amount of wear that the tool point has suffered. In single-pointed tools, such as are used upon lathe work, this has but little significance, because it is the work of but a minute or two to grind up the tool to a full point again, but in taps and solid dies, or in chasers in heads (as in some bolt-cutting machines) it is highly important, because it impairs the fit of the threads, and it is difficult to bring the tools to shape after they are once worn.
The internal threads for the nuts of bolts are produced by a tap formed as at t in Fig. 263. It consists of a piece of steel having an external thread and longitudinal flutes or grooves which cut the thread into teeth. The end of the thread is tapered off as shown, to enable the end of the tap to enter the hole, and as it is rotated and the nut n held stationary, the teeth cut grooves as the tap winds through, thus forming the thread.
The threads upon bolts are usually produced either by a head containing chasers or by a solid die such as shown at a in Fig. 264, b representing a bolt being threaded. The bore of a is threaded and fluted to provide cutting teeth, and the threads are chamfered off at the mouth to assist the cutting by spreading it over several teeth, which enables the bolt to enter the die more easily.
We may now consider the effect of continued use and its consequent wear upon the threads or teeth of a tap and die or chaser.
The wear of the corners at the tops of the thread (as at a b in Fig. 265) of a tap is greater than the wear at the bottom corners at e f, because the tops perform more cutting duty.
First, the top has a larger circle of rotation than has the bottom, and, therefore, its cutting speed is greater, to an amount equal to the difference between the circumferences of the thread at the top and at the bottom. Secondly, the tops of the teeth of[I-89] tap perform nearly all the cutting duty, because the thread in the nut is formed by the tops and sides of the tap, which on entering cut a groove which they gradually deepen, until a full thread is formed, while the bottoms of the teeth (supposing the tapping hole to be of proper diameter and not too small) simply meet the bore of the tapping hole as the thread is finished. If, as in the case of hot punched nuts, the nut bore contains scale, this scale is about removed by the time the bottoms of the top teeth come into action, hence the teeth bottoms are less affected by the hardness of the scale.
In the case of the teeth on dies and chasers, the wear at the corners c d, in Fig. 266, is the greatest. Now, the tops of the teeth on the tap (a b, in Fig. 265) cut the bottom or full diameter of the thread in the nut, while the tops of the teeth (c d, in Fig. 266) in the die cut the bottom of the thread on the bolt; hence the rounded corners cut on the work by the tops of the teeth in the one case, meet the more square corners left by the tops of the teeth in the other, and providing that under these circumstances the thread in the nut were of equal diameter to that on the bolt the latter would not enter the former.
If the bolt were made of a diameter to enable the nut to wind a close fit upon the bolt, the corners only of the threads would fit, as shown in Fig. 267, which represents at n a thread in a portion of a nut and at s a portion of a thread upon a tap or bolt, the two threads being magnified and shown slightly apart for clearness of illustration. The corners a, b of the nut are then cut by the corners a b of the tap in Fig. 265, and the corners c, c, d correspond to those cut by the corners c, d of the die teeth in Fig. 266; corners e, f, Fig. 267, are cut by corners c, d, in Fig. 266, and corners g, h are cut by corners g, h in Fig. 266, and it is obvious that the roundness of the corners a, b, c, and d in Fig. 267 will not permit the tops of the thread on the bolt to meet the bottoms of the thread in the nut, but that the threads will bear at the corners only.
So far, however, we have only considered the wear tending to round off the sharp corners of the teeth, which wear is greater in proportion as the corners are sharp, and less as they are rounded or flattened, and we have to consider the wear as affecting the diameters of the male and female thread at their tops and bottoms respectively.
Now, since the tops of the tap teeth wear the most, the diameter of the thread decreases in depth, while, since the tops of the die teeth wear most, the depth of the thread in the die also decreases. The tops of the tap teeth cut the bottom of the thread in the nut and the tops of the die teeth cut the bottoms of the thread upon the bolt.
Let it be supposed then that the points of the teeth of a tap have worn off to a depth of the 1⁄2000th part of an inch, which they will by the time they become sufficiently dulled to require resharpening, and that the teeth of a die have become reduced by wear by the same amount, and the result will be the production of threads such as shown in Fig. 268, in which the diameter of the bolt is supposed to be an inch, and the proper thread depth 1⁄10th inch. Now, the diameter at the root of the thread on the bolt will be .802 inch in consequence of the wear, but the smallest diameter of the nut thread is .800 inch, and hence too small to admit the male or bolt thread. Again, the full diameter of the bolt thread is 1 inch, whereas the full diameter of the nut thread is but .998 inch, or, again, too small to admit the bolt thread. As a result, it is found in practice that any standard form of thread that makes no allowance for wear, cannot be rigidly adhered to, or if it is adhered to, the tap must be made when new above the standard diameter, causing the thread to be an easy fit, which fit will become closer as the thread-cutting tools wear, until finally it becomes too tight altogether. The fit, however, becomes too tight at the top and bottom, where it is not required, instead of at the sides, where it should occur. When this is the case, the nuts will soon wear loose because of their small amount of bearing area.
It may be pointed out, however, that from the form in which the chasers or solid dies for bolt machines, and also that in which taps are made, the finishing points of the teeth are greatly relieved of cutting duty, as is shown in Figs. 269 and 270. In the die the first two or three threads are chamfered off, while in the tap the thread is tapered off for a length usually equal to about two or three times the diameter for taps to be used by hand, and six or seven times the diameter for taps to be used in a machine. The wear of the die is, therefore, more than that of the tap, because the amount of cutting duty to produce a given[I-90] length of thread is obviously the same, whether the thread be an internal or an external one, and the die has less cutting edges to perform this duty than the tap has. The main part of the cutting is, it is true, in both cases borne by the beveled surfaces at the top of the chamfered teeth of the cutting tools, but the fact remains that the depth of the thread is finished by the extreme tops of the teeth, and these, therefore, must in time suffer from the consequent wear, while the bottoms of the teeth perform no cutting duty, providing that the hole in the one case and the bolt in the other are of just sufficient diameter to permit of a full thread being formed, as should be the case. In threads cut by chasers the same thing occurs; thus in Fig. 271 is shown at a a chaser having full teeth, as it must have when a full thread is to pass up to a shoulder, as up to the head of a bolt. Here the first tooth takes the whole depth of the cut, but if from wear this point becomes rounded, the next tooth may remedy the defect. When, however, a chaser is to be used upon a thread that terminates in a stem of smaller diameter, as c in Fig. 271, then the chaser may have its teeth bevelled off, as is shown on b.
The evils thus pointed out as attending the wear of screw-cutting tools for bolts and nuts, may be overcome by a slight variation in the form of the thread. Thus in Fig. 272, at a is shown a form of thread for the tools to cut internal threads, and at b a form of thread for dies to cut external threads. The sides of the thread are in both cases at the same angle, as say, 60°. The depth of the thread, supposing the angle of the sides to meet in a point, is divided off into 11, or any number of equal divisions. For a tap one of these divisions is taken off, forming a flat top, while at the bottom two of these divisions are taken off, or if desirable, 11⁄2 divisions may be taken off, since the exact amount is not of primary importance. On the external thread cutting tool b, as say a solid die, two divisions are taken off at the largest diameter, and one at the smallest diameter, or, if any other proportion be selected for the tap, the same proportion may be selected for the die, so long as the least is taken off the largest diameter of the tap thread, and of the smallest diameter of the die thread.
The diameter of the tap may still be standard to ring or collar gauge, as in the Franklin Institute thread, the angle at the sides being simply carried in a less distance. In the die the largest diameter of the thread has a flat equal to that on the bottom of the tap, while the smallest diameter has a flat equal to that on the tops of the tap teeth, the width or thickness of the threads remaining the same as in the Franklin Institute thread at each corresponding diameter in its depth.
The effect is to give to the threads on the work a certain amount of clearance at the top and bottom of the thread, leaving the angles just the same as before, and insuring that the contact shall be at the sides, as shown in Fig. 273.
This form of thread retains the valuable features of the Franklin Institute that it can be originated by any one, and that it can be formed with a single-toothed or single-pointed tool. Furthermore, the wear of the threading tools will not impair the diametral fit of the work, while the permissible limit of error in diameter will be increased.
By this means great accuracy in the diameters of the threads is rendered unnecessary, and the wear of the screw-cutting tools at their corners is rendered harmless, nor can any confusion occur, because the tools for external threads cannot be employed upon internal ones. The sides only of the thread will fit, and the whole contact and pressure of the fit will be on those sides only.
This is an important advantage, because if the tops of the thread are from the wear of the dies and taps of too large or small diameter, respectively, the threads cannot fit on the sides. Thus, suppose a bolt thread to be loose at the sides, but to be 1⁄1000 of an inch larger in diameter than the nut thread, then it cannot be screwed home until that amount has been worn or forced off the thread diameter, or has been bruised down by contact with the nut thread, and it would apparently be a tight fit at the[I-91] sides. Suppose a thread to have been cut in the lathe to the correct diameter at the bottom of the thread, the sides of the thread being at the correct angle, but let the diameter at the top of the thread (a Franklin Institute thread is here referred to), be 1⁄1000 too large, then the nut cannot be forced on until that 1⁄1000 is removed by some means or other, unless the nut thread be deepened to correspond.
Now take this last bolt and turn the 1⁄1000 inch off, and it will fit, turn off another 1⁄1000 or 1⁄64 inch, and it will still fit, and the fit will remain so nearly the same with the 1⁄64 inch off that the difference can scarcely be found. Furthermore, with a nut of a fit requiring a given amount of force to screw it upon the bolt, the area of contact will be much greater when that contact is on the sides than when it is upon the tops and bottoms of the thread, while the contact will be in a direction better to serve as an abutment to the thrust or strain.
In very fine pitches of thread such as are used in the manufacture of watches, this plan of easing or keeping free the extremities of the thread is found to be essential, and there appears every probability that its adoption would obviate the necessity of using check nuts.
It has been observed that the threads upon tools alter in pitch from the hardening operation, and this is an objection to the employment of chasers cut from hobs.
Suppose, for instance, that a nut is produced having a thread of true and uniform pitch, then after hardening, the pitch may be no longer correct. The chasers cut from the hob will contain the error of pitch existing in the hob, and upon being hardened may have added to it errors of its own. If this chaser be used to produce a new hob, the latter will contain the errors in the chaser added to whatever error it may itself obtain in the hardening. The errors may not, it is true, all exist in one direction, and those of one hardening may affect or correct those caused by another hardening, but this is not necessarily the case, and it is therefore preferable to employ a form of thread that can be cut by a tool ground to correct shape after having been hardened, as is the case with the V-thread and the United States standard.
It is obvious that in originating either the sharp V or the United States standard thread, the first requisite is to obtain a correct angle of 60°, which has been done in a very ingenious manner by Mr. J. H. Heyer for the Pratt and Whitney Company, the method being as follows. Fig. 274 is a face and an end view of an equilateral triangle employed as a guide in making standard triangles, and constructed as follows:—Three bars, a, a, a, of steel were made parallel and of exactly equal dimensions. Holes x were then pierced central in the width of each bar and the same distance apart in each bar; the method of insuring accuracy in this respect being shown in Figs. 275 and 276, in which s represents the live spindle of a lathe with its face-plate on and a plug, c, fitted into the live centre hole. The end of this plug is turned cylindrically true, and upon it is closely fitted a bush, the plug obviously holding the bush true by its hole. A rectangular piece e is provided with a slot closely fitting to the bush.
The rectangular piece e is then bolted to the lathe face-plate[I-92] and pierced with a hole, which from this method of chucking will be exactly central to its slot, and at a right angle to its base. The bush is now dispensed with and the piece e is chucked with its base against the face-plate and the hole pierced as above, closely fitting to the pin on the end of the plug c, which, therefore, holds e true.
The bars a are then chucked one at a time in the piece e (the outer end resting upon a parallel piece f), and a hole is pierced near one end, this hole being from this method of chucking exactly central to the width of the bar a, and at a right angle to its face.
The parallel piece f is then provided with a pin closely fitting the hole thus pierced in the bar. The bars were turned end for end with the hole enveloping the pin in f (the latter being firmly fixed to the face-plate), and the other end laid in the slot in e, while the second hole was pierced. The holes (x, Fig. 274) must be, from this method of chucking, exactly an equal distance apart on each bar. The bars were then let together at their ends, each being cut half-way through and closely fitting pins inserted in the holes x, thus producing an equilateral triangle entirely by machine work, and therefore as correct as it can possibly be made, and this triangle is kept as a standard gauge whereby others for shop use may be made by the following process:—
Into the interior walls of this triangle there is fitted a cylindrical bush b, it being obvious that this bush is held axially true or central to the triangle, and it is secured in place by screws y, y, y, passing through its flange and into bars a.
At one end of the bush b, is a cylindrical part d, whose diameter is 2 inches or equal to the length of one side of an equilateral triangle circumscribed about a circle whose diameter is 1.1547 inches, as shown in Fig. 278 and through this bush b passes a pin p, having a nut n. A small triangle is then roughed out, and its bore fitting to the stem of pin p, and by means of nut n, the small triangle is gripped between the under face of d and the head of p. The large triangle is then held to an angle-plate upon a machine while resting upon the machine-table, and the uppermost edge of the small triangle is dressed down level with the cylindrical stem d, which thus serves as a gauge to determine how much to take off each edge of the small triangle to bring it to correct dimensions.
The truth of the angles of the small triangle depends, of course, also upon the large one; thus with face h resting upon the machine-table, face g is cut down level with stem d; with face f upon the table, face e is cut down level with d; and with face l upon the table, face k is dressed down level with d. And we have a true equilateral triangle produced by a very ingenious system of chuckings, each of which may be known to be true.
The next operation is to cut upon the small triangle the flat representing the top and bottom of the United States standard thread, which is done by cutting off one-eighth part of its vertical height, and it then becomes a test piece or standard gauge of the form of thread. The next step is to provide a micrometer by means of which tools for various pitches may be tested both for angle and for width of flat, and this is accomplished as follows:—
In Fig. 278 f is a jaw fixed by a set screw to the bar of the micrometer, and e is a sliding jaw; these two jaws being fitted to the edges of the triangle or test piece t in the figure which[I-93] has been made as already described. To the sliding jaw e is attached the micrometer screw c, which has a pitch of 40 threads per inch; the drum a upon the screw has its circumference divided into 250 equidistant divisions, hence if the drum be moved through a space equal to one of these divisions the sliding jaw e will be moved the 1⁄250th part of 1⁄40th of an inch, or in other words the 1⁄10,000th of an inch. To properly adjust the position of the zero piece or pointer, the test piece t is placed in the position shown in Fig. 278, and when the jaws were so adjusted that light was excluded from the three edges of the test piece, the pointer r, Fig. 277, was set opposite to the zero mark on the drum and fastened.
To set the instrument for any required pitch of thread of the United States standard form the micrometer is used to move the sliding jaw e away from the fixed jaw f to an amount equal to the width of flat upon the top and bottom, of the required thread, while for the sharp V-thread the jaws are simply closed. The gauge being set the tool is ground to the gauge.
| VOL. I. | MEASURING AND GAUGING SCREW THREADS. | PLATE III. | |||
 |
 |
 |
|||
| Fig. 279. | Fig. 280. | Fig. 281. | |||
 |
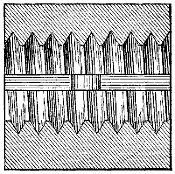 |
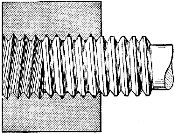 |
|||
| Fig. 282. | Fig. 285. | Fig. 286. | |||
 |
|||||
| Fig. 283. | |||||
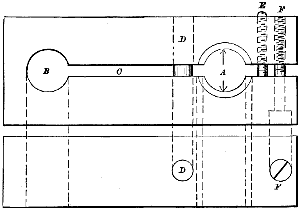 |
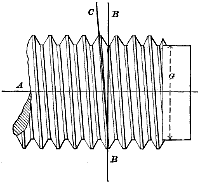 |
||||
| Fig. 284. | Fig. 287. | ||||
Referring to the third requirement, that the tools shall in the case of lathe work be easily sharpened and set to correct position in the lathe, it will be treated in connection with cutting screws in the lathe. Referring to the fourth requirement, that a minimum of measuring and gauging shall be required to test the diameter and form of thread, it is to be observed that in a Whitworth thread the angle and depth of the thread is determined by the chaser, which may be constantly ground to resharpen without altering the angles or depth of the thread, hence in cutting the tooth the full diameter of the thread is all that needs to be gauged or measured. In cutting a sharp V-thread, however, the thread top is apt to project (from the action of the single-pointed tool) slightly above the natural diameter of the work, producing a feather edge which it becomes necessary to file off to gauge the full diameter of the thread. In originating a sharp V-thread it is necessary first to grind the tool to correct angle; second, to set it at the correct height in the latter, and with the tool angles at the proper angle with the work (as is explained with reference to thread cutting in the lathe) and to gauge the thread to the proper diameter. In the absence of a standard cylindrical gauge or piece to measure from, a sheet metal gauge, such as in Fig. 279, may be applied to the thread; such gauges are, however, difficult to correctly produce.
So far as the diameter of a thread is concerned it may be measured by calipers applied between the threads as in Figs. 280 and 281, a plan that is commonly practised in the workshop when there is at hand a standard thread or gauge known to be of proper diameter; and this method of measuring may be used upon any form of thread, but if it is required to test the form of the thread, as may occur when its form depends upon the workman’s accuracy in producing the single-pointed threading tools, then, in the case of the United States standard thread, the top, the bottom, and the angle must be tested. The top of the thread may (for all threads) be readily measured, but the bottom is quite difficult to measure unless there is some standard to refer it to, to obtain its proper diameter, because the gauge or calipers applied to the bottom of the thread do not stand at a right angle to the axis of the bolt on which the thread is cut, but at an angle equal to the pitch of the thread, as shown in Fig. 282.
Now, the same pitch of thread is necessarily used in mechanical manipulation upon work of widely varying diameters, and as the angle of the calipers upon the same pitch of thread would vary (decreasing as the diameter of the thread increases), the diameter measured at the bottom of the thread would bear a constantly varying proportion to the diameter measured across the tops of the thread at a right angle to the axial line of the work. Thus in Fig. 282, a a is the axial line of two threaded pieces, b, c. d, d represents a gauge applied to b, its width covering the tops of two threads and measuring the diameter at a right angle to a a, as denoted by the dotted line e. The dotted line f represents the measurement at the bottom of the thread standing at an angle to e equal to half the pitch. The dotted line g is the measurement of c at the bottom of the thread.
Now suppose the diameter of b to be 11⁄2 inches at the top of the thread, and 11⁄8 inches at the bottom, while c is 11⁄8 inches on the top and 3⁄4 at the bottom of the thread, the pitches of the two threads being 1⁄4 inch; then the angle of f to e will be 1⁄8 inch (half the pitch) in its length of 11⁄8 inches. The angle of g to e will be 1⁄8 inch (half the pitch) in 3⁄4 (the diameter at the bottom or root of the thread).
It is obvious, then, that it is impracticable to gauge threads from their diameters at the bottom, or root.
On account of the minute exactitude necessary to produce with lathe tools threads of the sharp V and United States standard forms, the Pratt and Whitney Company manufacture thread-cutting tools which are made under a special system insuring accuracy, and provide standard gauges whereby the finished threads may be tested, and since these tools are more directly connected with the subject of lathe tools than with that of screw thread, they are illustrated in connection with such tools. It is upon the sides of threads that the contact should exist to make a fit, and the best method of testing the fit of a male and female thread is to try them together, winding them back and forth until the bright marks of contact show. Giving the male thread a faint tint of paint made of Venetian red mixed with lubricating oil, will cause the bearing of the threads to show very plainly.
Figs. 283 and 284 represent standard reference gauges for the United States standard thread. Fig. 283 is the plug or male gauge. The top of the thread has, it will be observed, the standard flat, while the bottom of the thread is sharp. In the collar, or female gauge, or the template, as it may be termed, a side and a top view of which are shown in Fig. 284, and a sectional end view in Fig. 285, the flat is made on the smallest diameter of the thread, while the largest diameter is left sharp; hence, if we put the two together they will appear as in Fig. 286, there being clearance at both the tops and bottoms of the threads. This enables the diameters of the threads to be in both cases tested by standard cylindrical gauges, while it facilitates the making of the screw gauges. The male or plug gauge is made with a plain part, a, whose diameter is the standard size for the[I-94] bottoms of the threads measured at a right angle to the axis of the gauge and taking the flats into account. The female gauge or template is constructed as follows:—A rectangular piece of steel is pierced with a plain hole at b, and a standard thread hole at a, and is split through at c. At d is a pin to prevent the two jaws from springing, this being an important element of the construction. e is a screw threaded through one jaw and abutting against the face of the other, while at f is another screw passing through one jaw and threaded into the other, and it is evident that while by operating these two screws the size of the gauge bore a may be adjusted, yet the screws will not move and destroy the adjustment, because the pressure of one acts as a lock to the other. It is obvious that in adjusting the female gauge to size, the thread of the male gauge may be used as a standard to set it by.
To produce sheet metal templates such as was shown in Fig. 279, the following method may be employed, it being assumed that we have a threading tool correctly formed.
Suppose it is required to make a gauge for a pitch of 6 per inch, then a piece of iron of any diameter may be put in the lathe and turned up to the required diameter for the top of the thread. The end of this piece should be turned up to the proper diameter for the bottom of the thread, as at g, in Fig. 287. Now, it will be seen that the angle of the thread to the axis a of the iron is that of line c to line a, and if we require to find the angle the thread passes through in once winding around the bolt, we proceed as in Fig. 288, in which d represents the circumference of the thread measured at a right angle to the bolt axis, as denoted by the line b in Fig. 287. f, Fig. 288 (at a right angle to d), is the pitch of the thread, and line c therefore represents the angle of the thread to the bolt axis, and corresponds to line c in Fig. 287. We now take a piece of iron whose length when turned true will equal its finished and threaded circumference, and after truing it up and leaving it a little above its required finished diameter, we put a pointed tool in the slide-rest and mark a line a a in Fig. 289, which will represent its axis. At one end of this line we mark off below a a the pitch of the thread, and then draw the line h j, its end h falling below a to an amount equal to the pitch of the thread to be cut. The piece is then put in a milling machine and a groove is cut along h j, this groove being to receive a tightly-fitting piece of sheet metal of which a thread gauge is to be made. This piece of sheet metal must be firmly secured in the groove by set-screws. The piece of iron is then again put in the lathe and its diameter finished to that of the required diameter of thread. Its two ends are then turned down to the required diameter for the bottom of the thread, leaving in the middle a section on which a full thread can be cut, as in Fig. 290, in which f f represents the sheet metal for the gauge. After the thread is cut, as in Fig. 290, we take out the gauge and it will appear as in Fig. 291, and all that is necessary is to file off the two outside teeth if only one tooth is wanted.
The philosophy of this process is that we have set the gauge at an angle of 90°, or a right angle to the thread, as is shown in Fig. 289, the line c representing the angle of the thread to the axis a a, and therefore corresponding to the line c in Fig. 287. A gauge made in this way will serve as a test of its own correctness for the following reasons: Taking the middle tooth in Fig. 291, it is clear that one of its sides was cut by one angle and the other by the other angle of the tool that cut it, and as a correctly formed thread is of exactly the same shape as the space between two threads, it follows that if the gauge be applied to any part of the thread that was cut in forming it, and if it fits properly when tried, and then turned end for end and tried again, it is proof that the gauge and the thread are both correct. Suppose, for example, that the tool was correct in its shape, but was not set with its two angles equal to the line of lathe centres, and in that case the two sides of the thread will not be alike and the gauge will not reverse end for end and in both cases fit to the thread. Or suppose the flat on the tool point was too narrow, and the flat at the bottom of the thread will not be like that at the top, and the gauge will show it.
Referring to the fifth requirement, that the angles of the sides of the threads shall be as acute as is consistent with the required strength, it is obvious that the more acute the angles of the sides of the thread one to the other the finer the pitch and the weaker the thread, but on the other hand, the more acute the angle the better the sides of the thread will conform one to the other. The importance of this arises from the fact that on account of the alteration of pitch, already explained, as accompanying the hardening of screw-cutting tools, the sides of threads cut even by unworn tools rarely have full contact, and a nut that is a tight fit on its first passage down its bolt may generally be caused to become quite easy by running it up and down the bolt a few times. Nuts that require a severe wrench force to wind them on the bolt, may, even though they be as large as a two-inch bolt, often be made to pass easily by hand, if while upon the bolt they are hammered on their sides with a hand hammer. The action is in both cases to cause the sides of the thread to conform one to the other, which they will the more readily do in proportion as their sides are more acute. Furthermore, the more acute the angles the less the importance of gauging the threads to precise diameter, especially if the tops and bottoms of the male and female thread are clear of one another, as in Fig. 273.
Referring to the sixth requirement, that the nut shall not be unduly liable to become loose of itself in cases where it may require to be fastened and loosened occasionally, it may be observed, that in such cases the threads are apt from the wear to become a loose fit, and the nuts, if under jar or vibration, are apt to turn back of themselves upon the bolt. This is best obviated by insuring a full bearing upon the whole area of the sides of the thread, and by the employment of as fine pitches as is consistent with sufficient strength, since the finer the pitch the nearer the thread stands at right angle to the bolt axis, and the less the tendency to unscrew from the pressure on the nut face.
The pitches, diameters, and widths of flat of the United States[I-95] standard thread are as per the following table:—
| Diameter of Screw. |
Threads per inch. |
Diameter at root of Thread. |
Width of Flat. | ||
| 1⁄4 | 20 | .1850 | .0063 | ||
| 5⁄16 | 18 | .2403 | .0069 | ||
| 3⁄8 | 16 | .2938 | .0078 | ||
| 7⁄16 | 14 | .3447 | .0089 | ||
| 1⁄2 | 13 | .4001 | .0096 | ||
| 9⁄16 | 12 | .4542 | .0104 | ||
| 5⁄8 | 11 | .5069 | .0114 | ||
| 3⁄4 | 10 | .6201 | .0125 | ||
| 7⁄8 | 9 | .7307 | .0139 | ||
| 1 | 8 | .8376 | .0156 | ||
| 1 | 1⁄8 | 7 | .9394 | .0179 | |
| 1 | 1⁄4 | 7 | 1.0644 | .0179 | |
| 1 | 3⁄8 | 6 | 1.1585 | .0208 | |
| 1 | 1⁄2 | 6 | 1.2835 | .0208 | |
| 1 | 5⁄8 | 5 | 1⁄2 | 1.3888 | .0227 |
| 1 | 3⁄4 | 5 | 1.4902 | .0250 | |
| 1 | 7⁄8 | 5 | 1.6152 | .0250 | |
| 2 | 4 | 1⁄2 | 1.7113 | .0278 | |
The standard pitches for the sharp V-thread are as follows:—
| 1⁄4 | 5⁄16 | 3⁄8 | 7⁄16 | 1⁄2 | 5⁄8 | 3⁄4 | 7⁄8 | 1 | 11⁄8 | 11⁄4 | 13⁄8 | 11⁄2 | 15⁄8 | 13⁄4 | 17⁄8 | 2 |
| Number of Threads to Inch. | ||||||||||||||||
| 20 | 18 | 16 | 14 | 12 | 11 | 10 | 9 | 8 | 7 | 7 | 6 | 6 | 5 | 5 | 41⁄2 | 41⁄2 |
The following table gives the threads per inch, pitches and diameters at root of thread of the Whitworth thread. The table being arranged from the diameter of the screw as a basis.
| Diameter of Screw. |
Threads per Inch. |
Pitch. | Diameter at Root or Bottom of Thread. |
||||
| Inch. | Inch. | ||||||
| 1⁄8 | 40 | .025 | .092 | 9 | |||
| 3⁄16 | 24 | .041 | .134 | 1 | |||
| 1⁄4 | 20 | .050 | .185 | 9 | |||
| 5⁄16 | 18 | .056 | .241 | 3 | |||
| 3⁄8 | 16 | .063 | .294 | 9 | |||
| 7⁄16 | 14 | .071 | .346 | ||||
| 1⁄2 | 12 | .083 | .393 | 2 | |||
| 9⁄16 | 12 | .083 | .455 | 7 | |||
| 5⁄8 | 11 | .091 | .508 | 5 | |||
| 11⁄16 | 11 | .095 | .571 | ||||
| 3⁄4 | 10 | .100 | .621 | 9 | |||
| 13⁄16 | 10 | .100 | .684 | 4 | |||
| 7⁄8 | 9 | .111 | .732 | 7 | |||
| 15⁄16 | 9 | .111 | .795 | 2 | |||
| 1 | 8 | .125 | .839 | 9 | |||
| 1 | 1⁄8 | 7 | .143 | .942 | |||
| 1 | 1⁄4 | 7 | .143 | 1.067 | |||
| 1 | 3⁄8 | 6 | .167 | 1.161 | 5 | ||
| 1 | 1⁄2 | 6 | .167 | 1.286 | 5 | ||
| 1 | 5⁄8 | 5 | .200 | 1.368 | 8 | ||
| 1 | 3⁄4 | 5 | .200 | 1.493 | 8 | ||
| 1 | 7⁄8 | 4 | 1⁄2 | .222 | 1.590 | 4 | |
| 2 | 4 | 1⁄2 | .222 | 1.715 | 4 | ||
| 2 | 1⁄8 | 4 | 1⁄2 | .222 | 1.840 | 4 | |
| 2 | 1⁄4 | 4 | .250 | 1.929 | 8 | ||
| 2 | 3⁄8 | 4 | .250 | 2.054 | 8 | ||
| 2 | 1⁄2 | 4 | .250 | 2.179 | 8 | ||
| 2 | 5⁄8 | 4 | .250 | 2.304 | 8 | ||
| 2 | 3⁄4 | 3 | 1⁄2 | .286 | 2.384 | ||
| 2 | 7⁄8 | 3 | 1⁄2 | .286 | 2.509 | ||
| 3 | 3 | 1⁄2 | .286 | 2.634 | |||
| 3 | 1⁄4 | 3 | 1⁄4 | .308 | 2.884 | ||
| 3 | 1⁄2 | 3 | 1⁄4 | .308 | 3.106 | ||
| 3 | 3⁄4 | 3 | .333 | 3.356 | |||
| 4 | 3 | .333 | 3.574 | ||||
| 4 | 1⁄4 | 2 | 7⁄8 | .348 | 3.824 | ||
| 4 | 1⁄2 | 2 | 7⁄8 | .348 | 4.055 | ||
| 4 | 3⁄4 | 2 | 3⁄4 | .364 | 4.305 | ||
| 5 | 2 | 3⁄4 | .364 | 4.534 | |||
| 5 | 1⁄4 | 2 | 5⁄8 | .381 | 4.764 | ||
| 5 | 1⁄2 | 2 | 5⁄8 | .381 | 5.014 | ||
| 5 | 3⁄4 | 2 | 1⁄2 | .400 | 5.238 | ||
| 6 | 2 | 1⁄2 | .400 | 5.488 | |||
The standard degree of taper, both for the taps and the dies, is 1⁄16 inch per inch, or 3⁄4 inch per foot, for all sizes up to 10-inch bore.
The sockets or couplings, however, are ordinarily tapped parallel and stretched to fit the pipe taper when forced on the pipe. For bores of pipe over 10 inches diameter the taper is reduced to 3⁄8 inch per foot. The pipes or casings for oil wells are given a taper of 3⁄8 inch per foot, and their couplings are tapped taper from both ends. There is, however, just enough difference made between the taper of the socket and that of the pipe to give the pipe threads a bearing at the pipe end first when tried with red marking, the threads increasing their bearing as the pieces are screwed together.
The United States standard thread for steam, gas and water pipe is given below, which is taken from the Report of the Committee on Standard Pipe and Pipe Threads of The American Society of Mechanical Engineers, submitted at the 8th Annual Meeting held in New York, November-December, 1886.
“A longitudinal section of the tapering tube end, with the screw-thread as actually formed, is shown full size in Fig. 291a for a nominal 21⁄2 inch tube, that is, a tube of about 21⁄2 inches internal diameter, and 27⁄8 inches actual external diameter.
“The thread employed has an angle of 60°; it is slightly rounded off both at the top and at the bottom, so that the height or depth of the thread, instead of being exactly equal to the pitch, is only four fifths of the pitch, or equal to 0.8 × 1/n if n be the number of threads per inch. For the length of tube end throughout which the screw thread continues perfect, the empirical formula used is (0.8D + 4.8) × 1/n, where D is the actual external diameter of the tube throughout its parallel length, and is expressed in inches. Further back, beyond the perfect threads, come two having the same taper at the bottom, but imperfect at the top. The remaining imperfect portion of the screw thread, furthest back from the extremity of the tube, is not essential in any way to this system of joint; and its imperfection is simply incidental to the process of cutting the thread at a single operation.”
The standard thicknesses of the pipes and pitches of thread are as follows:—
| DIAMETER OF TUBE. | THICKNESS OF METAL. |
SCREWED ENDS. | |||||
| Nominal Inside. |
Actual Inside. |
Actual Outside. |
Number of Threads per Inch. |
Length of Perfect Screw. |
|||
| Inches. | Inches. | Inches. | Inch. | No. | Inch. | ||
| 1⁄8 | 0.270 | 0.405 | 0.068 | 27 | 0.19 | ||
| 1⁄4 | 0.364 | 0.540 | 0.088 | 18 | 0.29 | ||
| 3⁄8 | 0.494 | 0.675 | 0.091 | 18 | 0.30 | ||
| 1⁄2 | 0.623 | 0.840 | 0.109 | 14 | 0.39 | ||
| 3⁄4 | 0.824 | 1.050 | 0.113 | 14 | 0.40 | ||
| 1 | 1.048 | 1.315 | 0.134 | 11 | 1⁄2 | 0.51 | |
| 1 | 1⁄4 | 1.380 | 1.660 | 0.140 | 11 | 1⁄2 | 0.54 |
| 1 | 1⁄2 | 1.610 | 1.900 | 0.145 | 11 | 1⁄2 | 0.55 |
| 2 | 2.067 | 2.375 | 0.154 | 11 | 1⁄2 | 0.58 | |
| 2 | 1⁄2 | 2.468 | 2.875 | 0.204 | 8 | 0.89 | |
| 3 | 3.067 | 3.500 | 0.217 | 8 | 0.95 | ||
| 3 | 1⁄2 | 3.548 | 4.000 | 0.226 | 8 | 1.00 | |
| 4 | 4.026 | 4.500 | 0.237 | 8 | 1.05 | ||
| 4 | 1⁄2 | 4.508 | 5.000 | 0.246 | 8 | 1.10 | |
| 5 | 5.045 | 5.563 | 0.259 | 8 | 1.16 | ||
| 6 | 6.065 | 6.625 | 0.280 | 8 | 1.26 | ||
| 7 | 7.023 | 7.625 | 0.301 | 8 | 1.36 | ||
| 8 | 8.982 | 8.625 | 0.322 | 8 | 1.46 | ||
| 9 | 9.000 | 9.688 | 0.344 | 8 | 1.57 | ||
| 10 | 10.019 | 10.750 | 0.366 | 8 | 1.68 | ||
The taper of the threads is 1⁄16 inch in diameter for each inch of length or 3⁄4 inch per foot.
Note.—The Internal and External diameters of Pipes, as given below, are those adopted by the firm of Messrs. James Russell & Sons, in Pipes of their manufacture.
| Gas and Water Piping. | Hydraulic Piping. | ||||||||||||||||||||||||
| Internal Diameter of Pipe. |
External Diameter of Pipe. |
No. of Threads per Inch. |
Internal Diamter of Pipe. |
External Diameter of Pipe. |
Pressure in lbs. per Square Inch. |
No. of Threads per Inch. |
Internal Diamter of Pipe. |
External Diameter of Pipe. |
Pressure in lbs. per Square Inch. |
No. of Threads per Inch. |
|||||||||||||||
| 1⁄8 | .385 | 28 | 1⁄4 | - | 5⁄8 | 4,000 | - | 14 | 1 | 1⁄4 | - | 1 | 3⁄4 | 4,000 | - | 11 | |||||||||
| 1⁄4 | .520 | 19 | 3⁄4 | 6,000 | 1 | 7⁄8 | 6,000 | ||||||||||||||||||
| 3⁄8 | .665 | 19 | 7⁄8 | 8,000 | 2 | 8,000 | |||||||||||||||||||
| 1⁄2 | .822 | 14 | 1 | 10,000 | 2 | 1⁄8 | 10,000 | ||||||||||||||||||
| 3⁄4 | 1.034 | 14 | 3⁄8 | - | 3⁄4 | 4,000 | - | 14 | 1 | 3⁄8 | - | 1 | 7⁄8 | 4,000 | - | 11 | |||||||||
| 1 | 1.302 | - | 11 | 7⁄8 | 6,000 | 2 | 6,000 | ||||||||||||||||||
| 1 | 1⁄8 | 1.492 | 1 | 8,000 | 2 | 1⁄8 | 8,000 | ||||||||||||||||||
| 1 | 1⁄4 | 1.650 | 1 | 1⁄8 | 10,000 | 2 | 1⁄4 | 10,000 | |||||||||||||||||
| 1 | 3⁄8 | 1.745 | 1⁄2 | - | 1 | 4,000 | - | 14 | 1 | 1⁄2 | - | 2 | 4,000 | - | 11 | ||||||||||
| 1 | 1⁄2 | 1.882 | 1 | 1⁄8 | 6,000 | 2 | 1⁄8 | 6,000 | |||||||||||||||||
| 1 | 5⁄8 | 2.021 | 1 | 1⁄4 | 8,000 | - | 11 | 2 | 1⁄4 | 8,000 | |||||||||||||||
| 1 | 3⁄4 | 2.047 | 1 | 3⁄8 | 10,000 | 2 | 3⁄8 | 10,000 | |||||||||||||||||
| 1 | 7⁄8 | 2.245 | 5⁄8 | - | 1 | 1⁄8 | 4,000 | 14 | 2 | 1⁄2 | 10,000 | ||||||||||||||
| 2 | 2.347 | 1 | 1⁄4 | 6,000 | - | 11 | 1 | 5⁄8 | - | 2 | 1⁄8 | 4,000 | - | 11 | |||||||||||
| 2 | 1⁄8 | 2.467 | 1 | 3⁄8 | 8,000 | 2 | 1⁄4 | 6,000 | |||||||||||||||||
| 2 | 1⁄4 | 2.587 | 1 | 1⁄2 | 10,000 | 2 | 3⁄8 | 8,000 | |||||||||||||||||
| 2 | 3⁄8 | 2.794 | 3⁄4 | - | 1 | 1⁄4 | 4,000 | - | 11 | 2 | 1⁄2 | 10,000 | |||||||||||||
| 2 | 1⁄2 | 3.001 | 1 | 3⁄8 | 6,000 | 1 | 3⁄4 | - | 2 | 1⁄4 | 3,000 | - | 11 | ||||||||||||
| 2 | 5⁄8 | 3.124 | 1 | 1⁄2 | 8,000 | 2 | 3⁄8 | 4,000 | |||||||||||||||||
| 2 | 3⁄4 | 3.247 | 1 | 5⁄8 | 10,000 | 2 | 1⁄2 | 6,000 | |||||||||||||||||
| 2 | 7⁄8 | 3.367 | 7⁄8 | - | 1 | 3⁄8 | 4,000 | - | 11 | 2 | 5⁄8 | 8,000 | |||||||||||||
| 3 | 3.485 | 1 | 1⁄2 | 6,000 | 2 | 3⁄4 | 10,000 | ||||||||||||||||||
| 3 | 1⁄4 | 3.698 | 1 | 5⁄8 | 8,000 | 1 | 7⁄8 | - | 2 | 3⁄8 | 3,000 | - | 11 | ||||||||||||
| 3 | 1⁄2 | 3.912 | 1 | 3⁄4 | 10,000 | 2 | 1⁄2 | 4,000 | |||||||||||||||||
| 3 | 3⁄4 | 4.125 | 1 | - | 1 | 1⁄2 | 4,000 | - | 11 | 2 | 5⁄8 | 6,000 | |||||||||||||
| 4 | 4.339 | 1 | 5⁄8 | 6,000 | 2 | 3⁄4 | 8,000 | ||||||||||||||||||
| 1 | 3⁄4 | 8,000 | 2 | 7⁄8 | 10,000 | ||||||||||||||||||||
| 1 | 7⁄8 | 10,000 | 2 | - | 2 | 1⁄2 | 3,000 | - | 11 | ||||||||||||||||
| 1 | 1⁄8 | - | 1 | 5⁄8 | 4,000 | - | 11 | 2 | 5⁄8 | 4,000 | |||||||||||||||
| 1 | 3⁄4 | 6,000 | 2 | 3⁄4 | 6,000 | ||||||||||||||||||||
| 1 | 7⁄8 | 8,000 | 2 | 7⁄8 | 8,000 | ||||||||||||||||||||
| 2 | 10,000 | 3 | 10,000 | ||||||||||||||||||||||
The English pipe thread is a sharp V-thread having its sides at an angle of 60°, and therefore corresponds to the American pipe thread except that the pitches are different.
The standard screw thread of The Royal Microscopical Society of London, England, is employed for microscope objectives, and the nose pieces of the microscope into which these objectives screw.
The thread is a Whitworth one, the original standard threading tools now in the cabinet of the society having been made especially for the society by Sir Joseph Whitworth. The pitch of the thread is 36 per inch. The cylinder, or male gauge, is .7626 inch in diameter.
The following table gives the Whitworth standard of thread pitches and diameters for watch and mathematical instrument makers.
| No. of each size in thou- sandths of an inch. |
Size in decimals of an inch. |
Number of Threads per inch. |
No. of each size in thou- sandths of an inch. |
Size in decimals of an inch. |
Number of Threads per inch. |
| 10 | .010 | 400 | 34 | .034 | 150 |
| 11 | .011 | „ | 36 | .036 | „ |
| 12 | .012 | 350 | 38 | .038 | 120 |
| 13 | .013 | „ | 40 | .040 | „ |
| 14 | .014 | 300 | 45 | .045 | „ |
| 15 | .015 | „ | 50 | .050 | 100 |
| 16 | .016 | „ | 55 | .055 | „ |
| 17 | .017 | 250 | 60 | .060 | „ |
| 18 | .018 | „ | 65 | .065 | 80 |
| 19 | .019 | „ | 70 | .070 | „ |
| 20 | .020 | 210 | 75 | .075 | „ |
| 22 | .022 | „ | 80 | .080 | 60 |
| 24 | .024 | „ | 85 | .085 | „ |
| 26 | .026 | 180 | 90 | .090 | „ |
| 28 | .028 | „ | 95 | .095 | „ |
| 30 | .030 | „ | 100 | .100 | 50 |
| 32 | .032 | 150 |
For the pitches of the threads of lag screws there is no standard, but the following pitches are largely used.
| Diameter of Screw. |
Threads per Inch. |
Diameter of Screw. |
Threads per Inch. |
| Inch. | Inch. | ||
| 1⁄4 | 10 | 5⁄8 | 5 |
| 5⁄16 | 9 | 11⁄16 | 5 |
| 3⁄8 | 8 | 3⁄4 | 5 |
| 7⁄16 | 7 | 7⁄8 | 4 |
| 1⁄2 | 6 | 1 | 4 |
| 9⁄16 | 6 |
Screw-Cutting Hand Tools.
For cutting external or male threads by hand three classes of tools are employed.
The first is the screw plate shown in Fig. 292. It consists of a hardened steel plate containing holes of varying diameters and threaded with screw threads of different pitches. These holes are provided with two diametrically opposite notches or slots so as to form cutting edges.
This tool is placed upon the end of the work and slowly rotated while under a hand pressure tending to force it upon the work, the teeth cutting grooves to form the thread and advancing along the bolt at a rate determined by the pitch of the thread.
The screw plate is suitable for the softer metals and upon[I-97] diameters of 1⁄8 inch and less, in which the cutting duty is light; hence the holes do not so rapidly wear larger.
The second class consists of a stock and dies such as shown in Fig. 293. For each stock there are provided a set of dies having different diameters and pitches of thread.
In this class of tool the dies are opened out and placed upon the bolt. The set screw is tightened up, forcing the dies to their cut, and the stock is slowly rotated and a traverse taken down the work.
In some cases the dies are then again forced to the work by the set screw, and a cut taken by winding the stocks up the bolt, the operation being continued until the thread is fully developed and cut to the required diameter. In other cases the cut is carried down the bolt, only the dies being wound back to the top of the bolt after each cut is carried down. The difference between these two operations will be shown presently.
The thread in dies which take successive cuts to form a thread may be left full clear through the die, and will thus cut a full thread close up to the head collar or shoulder of the work. It is usual, however, to chamfer off the half threads at the ends of the dies, because if left of their full height they are apt to break off when in use. It is sometimes the practice, however, to chamfer off the first two threads on one side of the dies, leaving the teeth on the other side full, and to use the chamfered as the leading side in all cases in which the thread on the work does not require to be cut up to a shoulder, but turning the dies over with the full threaded teeth as the leading ones when the thread does require to be carried up to a head or shoulder on the work.
To facilitate the insertion and extraction of the dies in and from their places in the stock, the Morse Twist Drill Co. employ the following construction. In Figs. 294 and 295 the pieces a, a′ which hold the dies are pivoted in the stock at b, so as to swing outward as in Fig. 295, and receive the dies which are slotted to fit them. These pieces are then swung into position in the stock. The lower die is provided with a hole to fit the pin c, hence when that die is placed home c acts as a detaining piece locking the pieces a, a′ through the medium of the bottom die.
In other dies of this class the two side pieces or levers which hold the dies are pivoted at the corner of the angle, as in Fig. 296. In the bottom of the stock is a sliding piece beveled at its top and meeting the bottom face of the levers; hence, by pressing this piece inwards the side pieces recede into a slot provided in the stock, and leave the opening free for the dies to pass into their places, when the pin is released and a spring brings the side pieces back. Now, since the bottom die rests upon the bottom angle of the side pieces the pressure of the set screw closes the side pieces to the dies holding them firmly.
In Fig. 297 is shown Whitworth’s stocks and dies, the cap that holds the guide die a and the two chasers b, c in their seats or recesses in the stock being removed to expose the interior parts. The ends of the chasers b, c are beveled and abut against correspondingly beveled recesses in the key d, so that by operating the nut e on the end of the key the dies are caused to move longitudinally. The principles of action are more clearly shown in Fig. 298. The two cutting chasers b and c move in lines that would meet at d, and therefore at a point behind the centre or axis of the bolt being threaded; this has the effect of[I-98] preserving their clearance. It is obvious, for example, that when these chasers cut a thread on the work it will move over toward guide a on account of the thread on the work sinking into the threads on a, and this motion would prevent the chasers b, c from cutting if they moved in a line pointing to the centre of the work. This is more clearly shown in Fig. 299, in which the guide die a and one of the cutting dies or chasers b is shown removed from the stock, while the bolt to be threaded is shown in two positions—one when the first cut is taken, and the other when the thread is finished. For the first cut the centre of the work is at e, for the last one it is at g, and this movement would, were the line of motion as denoted by the dotted lines, prevent the chaser from cutting, because, while the line of chaser motion would remain at j, pointing to the centre of work for the first cut, it would require a line at k to point to that centre for the last one; hence, when considered with relation to the work, the line of chaser motion has been moved forward, presenting the cutting edges at an angle that would prevent their cutting. By having their motion as shown in Fig. 299, however, the clearance of the chasers is preserved.
Referring now to the die a, it acts as a guide rather than as a cutting chaser, because it has virtually no clearance and cannot cut so freely as b and c; hence it offers a resistance to the moving of the bolt, or of the dies upon the bolt, in a lateral direction when the chaser teeth meet either a projection or a depression upon the work. The guide principle is, however, much more fully carried out in a design by Bodmer, which is shown in Fig. 300. Here there is but one cutting chaser c, the bush g being a guide let into a recess in the stock and secured thereon by a pin p. The chaser is set in a stock, d also let into a recess in the stock, and this recess, being circular, permits of stock d swinging. At s are two set-screws, which are employed to limit the amount of motion permitted to d. the handle e screws through d, and acts upon the edge of chaser c to put on the cut. The action of the tool is shown in Fig. 301, where it is shown upon a piece of work. Pulling the handle e causes d to swing in the stock, thus giving the chaser clearance, as shown. When the cut is carried down, a new cut may be put on by means of e, and on winding the stock in the opposite direction, d will swing in its seat, and cant or tilt the chaser in the opposite direction, giving it the necessary clearance to enable it to cut on the upward or back traverse. Another point of advantage is that the cutting edges are not rubbed by the work during the back stroke, and their sharpness is, therefore, greatly preserved. A die of this kind will produce work almost as true as the lathe, and, in the case of long, slender work, more true than the lathe; but it is obvious that, on account of the friction caused by the pressure of the work to the guide g, the tool will require more power to operate than the ordinary stock and die or the solid die.
In adjustable dies which require to take more than one cut along the bolt to produce a fully developed thread, there is always a certain amount of friction between the sides of the thread in the die and the grooves being cut, because the angle of the thread at the top of a thread is less than the angle at the bottom. Thus in Fig. 302 the pitch at the top of thread (at a, b) is the same as at the bottom (c, d). Now suppose that in Fig. 303 a b represents[I-99] the axial line of a bolt, and c d a line at a right angle to a b. The radius e f being equal to the circumference of the top of the thread, the pitch being represented by b; then k represents the angle of the top of the thread to the axial line a b. Now suppose that the radius e g represents the circumference at the bottom of the thread and to the pitch; then l is the angle of the bottom of the thread to the axial line of the work, and the difference in angle between k and l is the difference in angle between the top and bottom of the thread in the dies and the thread to be cut on the work.
Now the tops of the teeth on the die stand at the greatest angle l, in Fig. 303, when taking the first cut on the bolt, but the grooves they cut will be on the full diameter of the bolt, and will, therefore, stand at the angle k, hence the lengths of the teeth do not lie in the same planes as the grooves which they cut.
In cutting V-threads, however, the angle of the die threads gradually right themselves with the plane of the grooves attaining their nearest coincidence when closed to finish the thread.
Since, however, the full width of groove is in a square thread cut at the first cut taken by the dies, it is obvious that a square thread cannot be cut by this class of die, because the sides of the grooves would be cut away each time the dies were closed to take another cut.
Dies of this class require to have the threaded hole made of a larger diameter than is the diameter of the bolt they are intended to thread, the reason being as follows:—
Suppose the threaded hole in the dies to be cut by a hob or master tap of the same diameter as the thread to be cut by the dies; when the dies are opened out and placed upon the work as in Fig. 304, the edges a, b will meet the work, and there will be nothing to steady the dies, which will, therefore, wobble and start a drunken thread, that is to say, a thread such as was shown in Fig. 253.
Instances have been known in the use of dies made in this manner, wherein the workman using a right-hand single-threaded pair of dies has cut a right or left-hand double or treble thread; the teeth of the dies acting as chasers well canted over, as shown in Fig. 305. It is necessary to this operation, however, that the diameter of the work be larger than the size of hob the dies were threaded with.
In Fig. 306 is shown a single right-hand and a treble left-hand thread cut by the author with the same pair of dies.
All that is necessary to perform this operation is to rotate the dies from left to right to produce a right-hand thread, and from right to left for a left-hand thread, exerting a pressure to cause the dies to advance more rapidly along the bolt than is due to the pitch of the thread. A double thread is produced when the dies traverse along the work twice as fast as is due to the pitch of the thread in the dies, and so on.
It is obvious, also, that a piece of a cylindrical thread may be used to cut a left-hand external thread. Thus in Fig. 307 is shown a square piece of metal having a notch cut in on one side of it and a piece of an external thread (as a tap inserted) in the notch. By forcing a piece of cylindrical work through the hole while rotating it, the piece of tap would cut upon the work a thread of the pitch of the tap, but a left-handed thread, which occurs because, as shown by the dotted lines of the figure, the thread on one side of a bolt slopes in opposite directions to its direction on the other, and in the above operation the thread on one side is taken to cut the thread on the other.
These methods of cutting left-hand threads with right-handed ones are mentioned simply as curiosities of thread cutting, and not as being of any practical value.
To proceed, then: to avoid these difficulties it is usual to thread the dies with a hob or master tap of a diameter equal to twice the depth of the thread, larger than the size of bolt the dies are to thread. In this case the dies fit to the bolt at the first cut, as shown in Fig. 308, c, d being the cutting edges. The relation of the circle of the thread in the dies to that of the work during the final cut is shown in Fig. 309.
There is yet another objection to tapping the dies with a hob of the diameter of the bolt to be threaded, in that the teeth fit perfectly to the thread of the bolt when the latter is threaded to the proper diameter, producing a great deal of friction, and being[I-100] difficult to make cut, especially when the cutting edges have become slightly dulled from use.
Referring now to taking a cut up the bolt or work as well as down, it will be noted that supposing the dies to have a right-hand thread, and to be rotating from left to right, they will be passing down the bolt and the edges c, d (Fig. 308) will be the cutting ones. But when the dies are rotated from right to left to bring them to the end of the bolt again, c, d will be rubbed by the thread, which tends to abrade them and thus destroy their sharpness.
In some cases two or more pairs of dies are fitted to the same stock, as shown in Fig. 310, but this is objectionable, because it is always desirable to have the hole in the dies central to the length of the stock, so that when placed to the work the stock shall be balanced, which will render it easier to start the thread true with the axial line of the bolt.
From what has been said with reference to Fig. 303, it is obvious that a square thread cannot be cut by a die that opens and closes to take successive cuts along the work, but such threads may be cut upon work that is of sufficient strength to withstand the twisting pressure of the dies, by making a solid die, and tapering off the threads for some distance at the mouth of the die, so as to enable the die to take its bite or grip upon the work, and start itself. It is necessary, however, to give to the die as many flutes (and therefore cutting edges), as possible, or else to make flutes wide and the teeth as short as will leave them sufficiently strong, both these means serving to avoid friction.
The teeth for adjustable dies, such as shown in Fig. 293, are cut as follows:—There is inserted between the two dies a piece of metal, separating them when set together to a distance equal to twice the depth of the thread, added to the distance the faces of the dies are to be apart when the dies are set to cut to this designated or proper diameter. The tapping hole is then drilled (with the pieces in place) to the diameter of the bolt the die is for. The form of hob used by the Morse Twist Drill & Machine Company, to cut the thread, is shown in Fig. 311. The unthreaded part at the entering end is made to a diameter equal to that of the work the dies are to be used in; the thread at the entering end is made sunk in one half the height of the full thread, and is flattened off one half the height of a full thread, so that the top of the thread is even with the diameter of the unthreaded part at the entering end. The thread then runs a straight taper up the hob until a distance equal to the diameter of the nut is reached, and the length of hob equal to its diameter is made a full and parallel thread for finishing the die teeth with. The thread on the taper part has more taper at the root of the thread than it has at the top of the same, and the diameter of the full and parallel part at the shank end of the thread is made of a diameter equal to twice the height or depth of a full thread, larger than the diameter at the entering end of the hob. The hob thus becomes a taper and relieved tap cutting a full thread at one passage through the dies. If the hob is made parallel and a full thread from end to end, as in Fig. 312, the dies must traverse up and down the hob, or the hob through the dies to form a full thread.
The third class of stock and die is intended to cut a full thread at one passage along the work, while at the same time provision is made, whereby, to take up the wear due to the abrasion of the cutting edges, which wear would cause the diameter of thread cut to be above the standard.
In Fig. 313 is shown the Grant adjustable die made by the Pratt & Whitney Company. It consists of four chasers or toothed cutting tools, inserted in radial recesses or slots in an iron disc or collet encircled by an iron ring. Each chaser is beveled at its end to fit a corresponding bevel in the ring, and is grooved on one of its side faces to receive the hardened point of a screw that is inserted in the collet to hold the chaser in its adjusted position. Four screws extend up through the central flange or body of the collet, two of which serve to draw down the ring, and by reason of the taper on the ring move the chasers equally towards the centre and reduce the cutting diameter of the die, while the other two hold the ring in the desired position, or force it upward to enlarge the cutting diameter of the die. The range of adjustment permitted by this arrangement is 1⁄32 inch. The dies may be taken out and ground up to sharpen.
The object of cutting grooves in the sides of the chasers is that the fine burrs formed by the ends of the set screws do not prevent the chasers from moving easily in the collet during the process of adjustment; the groove also acts as a shoulder for the screw end to press the chaser down to its seat. These chasers are marked to their respective places in the collet, and are so made that if one chaser should break, a new one can be supplied to fit to its place, the teeth of the new one falling exactly in line with the teeth on the other three, whereas under ordinary conditions if one chaser breaks, a full set of four new ones must be obtained.
In this die, as in all others which cut a full thread at one passage along the work, the front teeth of the chasers are beveled off as shown in the cut; this is necessary to enable the dies to take hold of or “bite” the work, the chamfer giving a relief to the cutting edge, while at the same time forming to a certain extent a wedge facilitating the entrance of the work into the die.
Fig. 314 represents J. J. Grant’s patent die, termed by its makers (Wiley and Russel) the “lightening die.” In this, as in other similar stocks, several collets with dies of various pitches and diameters of thread, fit to one stock. The nut of the stock is split on one side, and is provided with lugs on that side to receive a screw, which operates to open and enlarge the bore to[I-101] release a collet, or close thereon and grip it, as may be required when inserting or extracting the same. The dies are formed as shown in Fig. 315, in which a, a are the dies, and b the collet. To open the dies within the collet, the screws e are loosened and the screws d are tightened, while to close the dies d, d are loosened and e are tightened; thus the adjustment to size is effected by these four screws, while the screws d also serve to hold the dies to the collet b. The collets are provided with a collar having a bore f, through which the work passes, so that the dies may be guided true when starting upon the work; but if it is required to cut a thread close up to a head or shoulder, the stock is turned upside down, not only to have the collet out of the way of the head or shoulder, but also because the thread of the dies on the collet side are chamfered off (as is necessary in all solid dies, or dies which cut a full thread at one traverse down the work) so as to enable them to grip or bite the work, and start the thread upon it as before stated.
In Fig. 316 is shown Stetson’s die, which cuts a full thread at one passage, is adjustable to take up its wear, and has a guide to steady it upon the work and assist it in cutting a true thread. The guide piece consists of a hub (through which the work passes) having a flange fitting into the dies and being secured thereto by the two screws shown. The holes in the flanges are slotted to permit of the dies being closed (to take up wear) by means of the small screws shown at the end of the die, which screws pass through one die in a plain hole and screw into the other.
In Fig. 317 is shown Everett’s stocks and dies. In this tool the dies are set up by a cam lever, the dies being set to standard size when the lever arm stands parallel with the arm of the stock. By turning the straight side of the cam lever opposite to the dies, the latter may be instantly removed and another size of die inserted. The dies may be used to cut on their passage up and down the bolt or by operating the cam. When the dies are at the end of a cut the dies may be opened, lifted to the top of the work and another cut taken, thus saving the time necessary to wind the stock back. When the final cut is taken the dies may be opened and lifted off the work.
The hardening process usually increases the thickness of these dies, making the pitch of the thread coarser. The amount of expansion due to hardening is variable, but increases with the thickness of the die. The hob as a rule shortens during the tempering, but the amount being variable, no rule for its quantity can be given.[12]
Stocks and dies for pipe work are made in the form shown in Fig. 318, in which b is the stock having the detachable handles (for ease of conveyance) a, h, the latter being shown detached. The solid screw-cutting dies c are placed in the square recess at b, and are secured in b by the cap d, which swings over (upon its pivoted end as a centre) and is locked by the thumbscrew e. To guide the stocks and cause them to cut a true thread, the bushes f are provided. These fit into the lower end of b and are locked in position by four set screws g. The bores of the bushes f are made an easy fit to the outside of the pipe to be threaded, there being a separate bush for each size of pipe.
The dies employed in stocks for threading steam and gas pipes by hand are sometimes solid, as in Fig. 318 at c, and at others adjustable. In Fig. 319 is shown Stetson’s adjustable pipe die containing four chasers or toothed thread-cutting tools. These are set to cut the required diameter by means of a small screw in each corner of the die, while they are locked in their adjusted position by four screws on the face.
The tap is a tool employed to cut screw threads in internal surfaces, as holes or bores. A set of taps for hand use usually consist of three: the taper tap, Fig. 320; plug tap, Fig. 321; and bottoming tap, Fig. 322. (In England these taps are termed respectively the taper, second, and plug tap.) The taper tap is[I-102] the first to be inserted, and (when the hole to be threaded passes entirely through the work) rotated until it passes through the work, thus cutting a thread parallel in diameter through the full length of the hole. If, however, the hole does not pass through the work, the taper tap leaves a taper-threaded hole containing more or less of a fully developed thread according to the distance the tap has entered.
To further complete the thread the plug tap is inserted, it being parallel from four or five threads from the entering end of the tap to the other end. If the work will admit it, this tap is also passed through, which not only saves time in many cases, by avoiding the necessity to wind the tap back, but preserves the cutting edge which suffers abrasion from being wound back. To cut a full thread as near as possible to the bottom of a hole the bottoming tap is used, but when the circumstances will admit, it is best to drill the hole rather deeper than is actually necessary, to avoid the trouble incident to tapping a hole clear to the bottom.
On wrought iron and steel, which are fibrous and tough, the tap, when used by hand, will not (if the hole be deeper than the diameter of the tap) readily operate by a continuous rotary motion, but requires to be rotated about half a revolution back occasionally, which gives opportunity for the oil to penetrate to the cutting edges of the tap, frees the tap and considerably facilitates the tapping operation, especially if the hole be a deep one.
When the tap is intended to pass entirely through the work with a continuous rotary motion, as is the case, for example, in tapping nuts in a tapping machine, it is made of similar form to the taper hand tap, but longer, as shown in Fig. 323, the thread being full and parallel at the shank end for a distance at least equal to the full diameter of the tap measured across the tops of the thread.
If the thread of a tap be in diametral section a full circle, the sides of the thread rub against the grooves cut by the teeth, producing a friction which augments as the sharp edge of the teeth become dulled from use, but the tap cuts a thread of great diametral accuracy.
To reduce this friction to a minimum as much as is consistent with maintaining the standard size of the tapped hole, taps are sometimes given clearance in the thread, that is to say, the back of each tooth recedes from a true circle, as shown in Fig. 324, in which a a represents a washer, and b a tap in the same, the back of the teeth receding at c, d, e, from the true circle of the bore of a a, the tap cutting when revolved in the direction of the arrow. The objection to this is that when the tap is revolved backwards, as it must be to extract it unless the hole passes clear through the work, the cuttings lodge between the teeth and the thread in the work, rendering the extraction of the tap difficult, unless, indeed, the clearance be small enough in amount to clear the sides of the thread in the work sufficiently to avoid friction without leaving room for the cuttings to enter. If an excess of clearance be allowed upon taps that require to be used by hand, the tap will thread the hole taper, the diameter being largest at the top of the hole. This occurs because the tap is not so well steadied by its thread, which fails to act as a guide, and it is impossible to revolve the tap steadily by hand. Taps that are revolved by machine tools may be given clearance because both the taps and the work are detained in line, hence the tap cannot wobble.
In some cases clearance is given by filing or cutting off the tops of the threads along the middle of the teeth, as shown in Fig. 325 at a, b, c, which considerably reduces the friction. If clearance were given to a tap after this manner but extended to the sides and to the bottom of the thread, it would produce the best of results (for all taps that do not pass entirely through the hole), reducing the friction and leaving no room for the cuttings to jam in the threads when the tap is being backed out. The threads of Sir Joseph Whitworth’s taper hand taps are made parallel, measured at the bottom of the thread, and parallel at the tops of the thread for a distance equal to the diameter of the tap at the shank end; thence, to the entering end of the tap, the tops of the thread are turned off a straight taper, the amount of taper being slightly more than twice the depth of the thread: hence, the thread is just turned out at the entering end of the tap, and that end is the exact proper size for the tapping hole.
This enables the tap to enter the tapping hole for a distance enveloping one or perhaps two of the tap threads, leaving the extreme end of the tap with the thread just turned out. In the practice of some tap makers the diameter of the thread at the[I-103] top is made the same as in the Whitworth system, but there is more depth at the root of the thread and near the entering end of the tap, hence the bottoms of the thread at that end perform no cutting duty. This is done to enable the tap to take hold of, and start a thread in, the work more readily, which it does for the following reasons. In Fig. 326 is a piece of work with a tap a, having a tapered thread, and a tap b, in which the taper is given by turning off the thread. In the case of a the teeth points cut a groove that is gradually widened and deepened as the tap enters, until a full thread is finally produced. In the case of b the teeth cut at first a wide groove, leaving a small projection, that is a part of the actual finished thread, and the groove gets narrower as the tap enters; so that in the one case no part of the thread is finished until the tap has entered to its full diameter, while in the other the thread is finished as it is produced. On entering, therefore, more cutting duty is performed by b than by a, because a greater length of cutting edge is in operation and more metal is being removed, and as a result b requires more power to start it, so that in practice it is necessary to exert a pressure upon it, tending to force it into the hole while rotating it. The cutting duty on b decreases as the tap enters, because it gets less width and area of groove to cut, while the cutting duty on a increases as the tap enters, because it gets a greater width and area of groove to cut. In the latter case the maximum of pressure falls on the tap when it has entered the hole deepest, and hence can be operated steadiest, which, independent of its entering easiest, is an advantage. When, however, the bottom of a thread is taper (as must be the case to enable it to cut as at a), the cutting edge of each tooth does not cut a groove sufficiently large in diameter to permit the tooth itself to pass through. In Fig. 327, for example, is shown a tap which is taper and has a full thread from end to end (as is necessary for pipe tapping). Its diameter increases as the thread proceeds from the end towards the line a b. Now take the tooth o p, which stands lengthwise, in the plane c d. Its cutting edge is at p, but the diameter of the tap at p is less than it is at o, while o has to pass through the groove that p cuts. To obviate this difficulty the tap is given clearance, as shown in Fig. 324, the amount being slightly more than the difference in the diameter of the tap at o and at p in that figure. It follows, therefore, that a tap having taper from end to end and a full thread also, as shown in the lower tap in Fig. 328, is wrong in principle, and from the unsteady manner in which it operates is undesirable, even though its thread be given clearance.
In some cases the thread is made parallel at the tops and turned taper for a distance of 1⁄3 or 1⁄2 the length of the tap, the root of the thread at the taper part being deepened and the tops being given a slight clearance. This answers very well for shallow holes, because the taper tap cuts more thread on entering a given depth so that the second tap can follow more easily, but the tap will not operate so steadily as when the taper part is longer.
It is on account of the tops of the teeth performing the main part of the cutting that a tap taper may be sharpened by simply grinding the teeth tops. In the Pratt and Whitney taps, the hand taper tap is made parallel at the shank end for a distance equal in length to the diameter of the tap.
The entering end of the taper tap is made straight or parallel for a distance equal in length to one half the diameter of the tap, the diameter at this end being the exact proper size of tapping hole. The parallel part serves as a guide, causing the tap to enter and keep axially true with the hole to be tapped. The plug and bottoming taps are made parallel in the thread, the former being tapered slightly at and for two or three threads from the entering, as shown in Fig. 328. The threads are made parallel at the roots.
The Pratt and Whitney taper taps for use in machines are of the following form:—
The entering end of the tap is equal in diameter to the diameter of the tapping hole into which the tap will enter for a distance of two or three threads. The thread at the shank end is parallel both at the top and at the root for a distance equal, in length, to twice the diameter of the tap. The top of the thread has a straight taper running from the parallel part at the shank to the point or entering end, while the roots of the thread are made along this taper twice the taper that there is at the top of the thread, which is done to make the tap enter and take hold of the nut more easily.
A form of tap that cuts very freely on account of the absence of friction on the sides of the thread is shown in Fig. 329. The thread is cut in parallel steps, increasing in size towards the shank, the last step (from d to e in the figure) being the full size. The end of the tap at a being the proper size for the tapping hole, and the flutes not being carried through a, insures that the tap shall not be used in holes too small for the size of the tap, and thus is prevented a great deal of tap breakage. The bottom of the thread of the first parallel step (from a to b) is below the diameter of a, so as to relieve the sides of the thread of[I-104] friction and cause the tap to enter easily. The first tooth of each step does all the cutting, thus acting as a turning tool, while the step within the work holds the tooth to its cut, as shown in Fig. 330, in which n represents a nut and t the tap, both in section. The step c holds the tap to its work, and it is obvious that, as the tooth b enters, it will cut the thread to its own diameter, the rest of the teeth on that step merely following frictionless until the front tooth on the next step takes hold. Thus, to sharpen the tap equal to new, all that is required is to grind away the front tooth on each step, and it becomes practicable to sharpen the tap a dozen times without softening it at all. As a sample of duty, it may be mentioned that, at the Harris-Corliss Works, a tap of this class, 27⁄8 inches diameter, with a 4 pitch, and 10 inches long, will tap a hole 5 inches deep, passing the tap continuously through without any backing motion, two men performing the duty with a wrench 4 feet long over all, the work being of cast iron.
Another form of free cutting tap especially applicable to taps of large diameter has been designed by Professor Sweet. Its principles may be explained as follows:—
In the ordinary tap, with the taper four or five diameters in length, there are far more cutting-edges than are necessary to do the work; and if the taper is made shorter, the difficulty of too little room for chips presents itself. The evil results arising from the extra cutting edges are that, if all cut, then it is cutting the metal uselessly fine—consuming power for nothing; or if some of the cutting edges fail to cut, they burnish down the metal, not only wasting power, but making it all the harder for the following cutters. One plan to avoid this is to file away a portion of the cutting edges; but the method adopted in the Cornell University tap is still better. Assume that it is desired to make three following cutters, to remove the stock down to the dotted line in Fig. 331. Instead of each cutter taking off a layer one-third the thickness and the full width, the first cutter is cut away on each side to about one-third its full width, so that it cuts out the centre to its full depth, as shown in Fig. 331, the next cutter cutting out the metal at a, and so on. This is accomplished by filing, or in any other way cutting away the sides of one row of the teeth all the way up; next cutting away the upper sides of the next row and the lower sides of the third, leaving the fourth row (if it be a four-fluted tap) as it is left by the lathe, to insure a uniform pitch and a smooth thread.
Figs. 333, 334 and 335 represent an adjustable tap designed by C. R. French, of Providence, R. I., to thread holes accurate in diameter.
The plug tap, Fig. 333, has at its end a taper screw, and the tap is split up as far as the flutes extend, a second screw binds the two sides of the tap together, hence by means of the two screws the size of the tap may be regulated at will. In the third or bottoming tap, Fig. 334, the split extends farther up the shank, and four adjusting screws are used as shown, hence the parallelism of the tap is maintained.
In the machine tap, Fig. 335, there are six adjusting screws, two of those acting to close the tap being at the extreme ends so as to strengthen it as much as possible.
In determining the number, the width, the depth, and the form of flutes for a tap, we have the following considerations. In a tap to be used in a machine and to pass entirely through the work, as in the case of tapping nuts, the flute need not be deep, because the taper part of the tap being long the cutting teeth extend farther along the tap; hence, each tooth takes a less amount of cut, producing less cuttings, and therefore less flute is required to hold them. In taps of this class, the thread being given clearance, the length of the teeth may be a maximum, because they are relieved of friction; on the other hand, however, the shallower and narrower the flute the stronger the tap, so long as there is room for the cuttings so that they shall not become wedged in the flutes. Taps for general use by hand are frequently used to tap holes that do not pass entirely through the work; hence, the taper tap must have a short length of taper so that the second tap may be enabled to carry a full thread as near as possible to the bottom of the hole without carrying so heavy a cut as to render it liable to breakage, and the second or plug tap must in turn have so short a length of its end tapered that it will not throw too much duty upon the bottoming tap. Now, according as the length of the taper on the taper tap is reduced, the duty of the teeth is increased, and more room is necessary in the flute to[I-105] receive the cuttings, and supposing the tap to be rotated continuously to its duty the flute must possess space enough to contain all the cuttings produced by the teeth, but on account of the cuttings filling the flutes and preventing the oil fed to the tap from flowing down the flute to the teeth it is found necessary in hand taps (when they cannot pass through the work, or when the depth of the hole is equal to more than about the tap diameter), to withdraw the tap and remove the cuttings. On account of the tap not being accurately guided in hand-tapping it produces a hole that is largest at its mouth, and it is found undesirable on this account to give any clearance to hand taps, because such clearance gives more liberty to the tap to wobble in the hole and to enlarge its diameter at the mouth. It is obvious also, that the less of the tap circumference removed to form the flutes the longer the tap-teeth and the more steadily the tap may be operated. On the other hand, however, the longer the teeth the greater the amount of friction between them and the thread in the hole and the more work there is involved in the tapping, because the tap must occasionally be rotated back a little to ease its cut, which it is found to do.
Fig. 336 represents a form of flute recommended by Brown and Sharp. The teeth are short, thus avoiding friction, and the flutes are shallow, which leaves the tap strong. The inclination of the cutting edges, as a b (the cutting direction of rotation being denoted by the arrow), is shown by the dotted lines, being in a direction to curve the chip or cutting somewhat upward and not throw them down upon the bottom of the flute. A more common form, and one that perhaps represents average American practice, is shown in Fig. 337, the cutting edges forming a radial line as denoted by the dotted line. The flute is deeper, giving more room for the chips, which is an advantage when the tap is required to cut a thread continuously without being moved back at all, but the tap is weaker on account of the increased flute depth, the teeth are longer and produce more friction, and the flutes are deeper than necessary for a tap having a long taper or that requires to be removed to clear out the cuttings. Fig. 338 shows the form of flute in the Pratt and Whitney Company’s hand taps, the cutting edges forming radial lines and the bottoms of the flutes being more rounded than is usual. It may here be remarked that if the flutes have comparatively sharp corners, as at c in Fig. 339, the tap will be liable to crack in the hardening process. The form of flute employed in the Whitworth tap is shown in Fig. 340; here there being but three flutes the teeth are comparatively long, and on this account there is increased friction. But, on the other hand, such a tap produces, when used by hand, more accurate work, the threaded hole being more parallel and of a diameter more nearly equal to that of the tap, it being observed that even though a hand tap have no clearance it will usually tap a hole somewhat larger than itself so that it will unwind easily. If a hand tap is given clearance not only will it cut a hole widest at the mouth, but it will cut a thread larger than itself in an increased degree, and, furthermore, when the tap requires to be wound back to extract it the fine cuttings will become locked in the threads and the points of the tap teeth are liable to become broken off. To ease the friction of long teeth, therefore, it is preferable to do so either as in Fig. 325 at a, b, c, or as in Fig. 341. In Fig. 325 the tops of the teeth are shown filed away, leaving each end full, so that the cuttings cannot get in, no matter in which direction the tap is rotated; but the clearance is not so complete as in Fig. 341, in which the teeth are supposed to be eased away within the area enclosed by dotted lines, which gives clearance to the bottom as well as to the tops and sides of the thread and leaves the ends of each tooth a full thread.
Concerning the number of flutes in taps, it is to be observed that the duty the tap is to be put to, has much influence in this respect. In hand tapping the object is to tap as parallel and straight as possible with the least expenditure of power. Now, the greater the number of flutes the less the tap is guided, because more of the circumferential guiding surface is cut away. But on the other hand, the less the number of flutes, and therefore the less the number of cutting edges, the more power it takes to operate the tap on account of the greater amount of friction between the tap and the walls of the hole. In hand tapping on what may be termed frame work (as distinguished from such loose work as nuts, &c.), the object is to tap the holes as parallel as possible with the least expenditure of power while avoiding having to remove the tap from the hole to clear it of the cuttings. Obviously the more flutes and cutting edges there are the more room there is for the cuttings and the less frequent the tap requires to be cleaned. If the tapping hole is round and straight the tapping may be made true and parallel if due care is taken, whatever the number of flutes, but less care will be required in proportion as there are less flutes, while, as before noted, more power and more frequent tap removals will be necessary. But if the hole is not round, other considerations intervene.
Thus in Fig. 342 we have a three-flute tap in a hole out of round at a, and it is obvious that when a cutting edge meets the recess at a, all three teeth will cease to cut; hence there will be no inducement for the tap to move over toward a. But in the case of the four-flute tap in Fig. 343, when the teeth come to a there will be a strain tending to force the teeth over toward the depression a. How much a given tap would actually move over would, of course, depend upon the amount of clearance; but whether the tap has clearance or not, the three-flute tap will not move over, while with four flutes the tap would certainly do so. Again, with an equal width of flute there is more of the circumference[I-106] tending to guide and steady the three-flute than the four-flute tap. If the hole has a projection instead of a depression, as at b, Figs. 344 and 345, then the advantage still remains with the three-flute tap, because in the case of the three flutes, any lateral movement of the tap will be resisted at the two points c and d, neither of which are directly opposite to the location of the projection b; hence, if the projection caused the tap to move laterally, say, 1⁄100th inch, the effect at c and d would be very small, whereas in the four-flute, Fig. 345, the effect at e would be equal to the full amount of lateral motion of the tap.
In hand taps the position of the square at the head of the tap with relation to the cutting-edges is of consequence; thus, in Fig. 346, there being a cutting-edge a opposite to the handle, any undue pressure on that end of the handle would cause a to cut too freely and the tap to enlarge the hole; whereas in Fig. 347 this tendency would be greatly removed, because the cutting-edges are not in line with the handle. In a three-flute tap it makes but little difference what are the relative positions of the square to the flutes, as will be seen in Fig. 348, where one handle of the wrench comes in the most favorable and the other in the most unfavorable position. Taps for use by hand and not intended to pass through the work are sometimes made with the shank and the square end which receive the wrench of enlarged diameter. This is done to avoid the twisting of the shank which sometimes occurs when the tap is employed in deep holes, giving it much strain, and also to avoid as much as possible the wearing and twisting of the square which occurs, because in the course of time the square holes in solid wrenches enlarge from wear, and the larger the square the less the wear under a given amount of strain.
Brass finishers frequently form the heads of their taps as in Fig. 349, using a wrench with a slot in it that is longer than the flat of the tap head.
The thickness of the flat head at a is made equal for all the taps intended to be used with the same wrench. By this means one wrench may be used for many different diameters of taps.
For gas, steam pipe, and other connections made by means of screw threads, and which require to be without leak when under pressure, the tap shown in Fig. 350 is employed. It is made taper and full threaded from end to end, so that the fittings may be entered easily into their places and screwed home sufficiently to form a tight joint.
The standard degree of taper for steam-pipe taps is 3⁄4 inch per foot of length, the taper being the same in the dies as on the taps. The threading tools for the pipes or casings for petroleum oil wells are given a taper of 3⁄8 inch per foot, because it was not found practicable to tap such large fittings with a quick taper, because of the excessive strain upon the threading tools. Ordinary pipe couplings are, however, tapped straight and stretch to[I-107] fit when screwed home on the pipe. Oil-well pipe couplings are tapped taper from both ends, and there is just enough difference in the taper on the pipe and that in the socket to show a bearing mark at the end only when the pipe and socket are tested with red marking.
| Diameter. | Length. | No. of Threads to Inch. |
Diameter. | Length. | No. of Threads to Inch. |
||||||||||
| 1⁄4 | 2 | 3⁄4 | 16, | 18 | & | 20 | 3⁄4 | 5 | 13⁄16 | 10, | 11 | & | 12 | ||
| 5⁄16 | 2 | 7⁄8 | 16 | & | 18 | 13⁄16 | 6 | 10 | |||||||
| 3⁄8 | 3 | 1⁄2 | 14 | & | 16 | 7⁄8 | 6 | 1⁄8 | 9 | & | 10 | ||||
| 7⁄16 | 3 | 13⁄16 | 14 | & | 16 | 15⁄16 | 6 | 3⁄8 | 9 | ||||||
| 1⁄2 | 4 | 5⁄16 | 12, | 13 | & | 14 | 1 | 6 | 13⁄16 | 8 | |||||
| 9⁄16 | 4 | 3⁄4 | 12 | & | 14 | 1 | 1⁄8 | 7 | 1⁄4 | 7 | & | 8 | |||
| 5⁄8 | 5 | 1⁄8 | 10, | 11 | & | 12 | 1 | 1⁄4 | 8 | 7 | & | 8 | |||
| 11⁄16 | 5 | 3⁄8 | 11 | & | 12 | ||||||||||
Fig. 351 represents the form of tap employed by blacksmiths for rough work, and for the axles of wagon wheels. These taps are given a taper of 1⁄2 inch per foot of length, and are made with right and left-hand threads, so that the direction of rotation on both sides of a wagon wheel shall be in a direction to screw up the nuts and not to unscrew the nut, as would be the case if both ends of the axle were provided with right-hand threads.
Taps that are used in a machine are sometimes so constructed that upon having tapped the holes to the required depth, the pieces containing the tap teeth recede from the walls of the hole, so that the tap may be instantly withdrawn from the hole instead of requiring to be rotated backwards. This is an advantage, not only on account of the time saved, but also because the cutting edges of the teeth are saved from the abrasion and its consequent wear which occur in rotating a tap backwards.
Figs. 352 and 353 represent a collapsing tap that is much used in manufactories of pipe fittings.
a is driven by the spindle of the machine, and drives b through the medium of the pin h. In b are three chasers c, fitting into the dovetail and taper grooves d. These chasers are provided with lugs fitting into an annular groove e sunk in a, so that if the piece h rises, the chasers will not rise with it, but will simply close together by reason of the lifting or rising of the core b, with its taper dovetail grooves; or, on the other hand, if the core b descends, the taper grooves in b force the chasers outward, increasing their cutting diameter.
When the tap is cutting, it is driven as denoted by the arrow, and the pin h is driven by the ends of the grooves, of which there are two, one diametrically opposite the other, inclined in the same direction. But when the tap has cut a thread to the required depth on the work, the handles h may be pulled or pushed the working way, passing along the grooves i, and causing b to lift within a, and allowing the chasers to close away from the thread just cut, and the tap may be instantly withdrawn, and handles h pushed back to expand the chasers, ready for the next piece of work.
Fig. 354 represents a collapsing tap used in Boston, Massachusetts, at the Hancock Inspirator Works, in a monitor or turret lathe. It consists of an outer shell a carrying three chasers b, pivoted to a at c, having a small lug e at one end, and being coned at the inner end d. The inner shell f is reduced along part of its length to receive the lug e of the chaser, and permit the chasers to open out full at their cutting end. f has a cone at[I-108] the end g, fitting to the internal cone on the chasers at d. At the other end of f is a washer h, against which abuts the spiral spring shown, the other end of this spring abutting against a shoulder provided in a. The washer h is bevelled on its outer or end face to correspond with the bevel on a notch provided in lever i, as is shown. Within the inner tube f is the stem j, into the end of which is fitted the piece k, and on which is fixed the cone l. Piece k, and therefore l, is prevented from rotating by a spline in k, into which spline the pin m projects.
The operation is as follows. In the position in which the parts are shown in the engraving, f is pushed forward so that its coned end g has opened out the chaser to its fullest extent, which opening is governed by contact of the lug e with the reduced diameter of f. Suppose that the tap is operating in the work, then, when the foot n of k meets with a resistance (as the end of the hole being tapped), j, and therefore l, will be gradually pushed to the right, until, finally, the cone on l will raise the end of lever i until the notch on i is clear of h, when the spiral spring, acting against h, will force f to the right, and the shoulder on f, at x, will lift the end e of the chaser, causing the cutting end to collapse within a, the pivot c being its centre of motion. The whole device may then be withdrawn from the work. To open the chasers out again the rod j is forced, by hand, to the left, the cone-piece l meeting the face of h and pushing it to the left until cone g meets cone d, when the chasers open until the end e meets the body of f, as in the cut. The rod j is then pulled to the right until l again meets the curved end of lever i and all the parts assume the positions shown in the cut. To regulate the depth of thread the tap shall cut, the body a is provided with a thread to receive the nut o, by means of which the collar p may be moved along a. This collar carries the pivots q for levers i, so that, by shifting o, the position of i is varied, hence the point at which l will act upon the end of i and lift it to release h is adjustable.
When used upon steel, wrought iron, cast iron, copper, or brass, a tap should be freely supplied with oil, which preserves its cutting edge as well as causes it to cut more freely, but for cutting the soft metals such as tin, lead, &c., oil is unnecessary.
The diameters of tapping holes should be equal to the diameter of the thread at the root, but in the case of cast iron there is much difference of opinion and practice. On the one hand, it is claimed that the size of the tapping hole should be such as to permit of a full thread when it is tapped; on the other hand, it is claimed that two-thirds or even one-half of a full thread is all that is necessary in holes in cast iron, because such a thread is, it is claimed, equally as strong as a full one, and much easier to tap. In cases where it is not necessary for the thread to be steamtight, and where the depth of the thread is greater by at least 1⁄8 inch than the diameter of the bolt or stud, three-quarters of a full thread is all that is necessary, and can be tapped with much less labor than would be the case if the hole were small enough to admit of a full thread, partly because of the diminished duty performed by the tap, and partly because the oil (which should always be freely supplied to a tap) obtains so much more free access to the cutting edges of the tap. If a long tap is employed to cut a three-quarter full thread, it may be wound continuously down the hole, without requiring to be turned backwards at every revolution or so of the tap, to free it from the tap cuttings or shavings, as would be necessary in case a full thread were being cut. The saving of time in consequence of this advantage is equal to at least 50 per cent. in favor of the three-quarter full thread.
As round bar iron is usually rolled about 1⁄32 inch larger than its designated diameter, a practice has arisen to cut the threads upon the rough iron just sufficiently to produce a full thread, leaving the latter 1⁄32 inch above the proper diameter, hence taps 1⁄32 inch above size are required to thread nuts to fit the bolts. This practice should be discountenanced as destroying in a great measure the interchangeability of bolts and nuts, because 1⁄32 inch is too small a measurement to be detected by the eye, and a measurement or trial of the bolt and nut becomes necessary.
A defect in taps which it has been found so far impracticable to eliminate is the alteration of pitch which takes place during the hardening process. The direction as well as the amount of this variation is variable even with the most uniform grades of steel, and under the most careful manipulation. Mr. John J. Grant, in reply to a communication upon this subject, informs me that, using Jones and Colver’s (Sheffield) steel, which is very uniform in grade, he finds that of one hundred taps, about 5 per cent. will increase in length, the pitch of the thread becoming coarser; 15 per cent. will suffer no appreciable alteration of pitch, and 80 per cent. will shrink in length, the pitch becoming finer, and these last not alike. But it must be borne in mind that with different steel the results will be different, and the greater the variation in the grade of the steel the greater the difference in the alteration of pitch due to hardening.
It is further to be observed that the expansion or contraction of the steel is not constant throughout the same tap; thus the pitches of three or four consecutive teeth may measure correct to pitch, while the next three or four may be of too coarse or too fine a pitch.
There is no general rule, even using the same grade of steel, for the direction in which the size of a tap may alter in hardening, as is attested by the following answers made by Mr. J. J. Grant to the respective questions:—
“Do the taps that shorten most in length increase the most in diameter?”
Answer.—“Not always; sometimes a tap that shortens by hardening becomes also smaller in diameter, while sometimes a tap will increase in length, and also in diameter from hardening.”
“Do taps that remain of true pitch after hardening remain true, or increase or diminish in diameter?”
Answer.—“They will generally be of larger diameter.”
“Do small taps alter more in diameter from hardening than large ones?”
Answer.—“No; the proportion is about the same, and is about .002 per inch of diameter.”
“What increase in diameter do you allow for shrinkage in hardening of hob taps for tapping solid dies?”
Answer.—“As follows:—
| Diameter of Hob Tap |
Shrinkage about |
||
| 1⁄4 | inch | .003 | |
| 1⁄2 | „ | .003 | |
| 3⁄4 | „ | .005 | |
| 1 | „ | .008 | ” |
“Suppose a tap that had been hardened and tempered to a straw color contained an error 1⁄1000 inch both in diameter and in pitch, was softened again, would it when soft retain the errors, or in what way would softening affect the tap?”
Answer.—“We have repeatedly tried annealing or softening taps that were of long or short pitch caused by tempering, and invariably found them about the same as before the annealing. The second tempering will generally shorten them more than the first. Sometimes, however, a second tempering will bring a long pitch nearer correct.”
“Do you soften your taps after roughing them out in the lathe?”
Answer.—“Never, if we can possibly avoid it. Sometimes it is necessary because of improper annealing at first. The more times steel is annealed the worse the results obtained in making the tool, and the less durable the tool.”
The following are answers to similar questions addressed to the Morse Twist Drill and Machine Co.:—
“The expansion of taps during hardening varies with the diameter. A 1-inch tap would expand in diameter from 1⁄1000 to 3⁄1000 inch.”
“Taps above 1⁄2 inch diameter expand in diameter to stop the gauge every time.”
“The great majority of taps contract in pitch during the hardening, they seldom expand in length.”
“The shortening of the pitch and the expansion in diameter have not much connection necessarily, though steel that did not alter in one direction would be more likely to remain correct in the other.”
“There does not seem to be any change in the diameter or pitch[I-109] of taps if measured after hardening (and before tempering) and again after tempering them.”
“Taps once out in length seem to get worse at every heating, whether to anneal or to harden.”
It will now be obvious to the reader that the diameter of a tap, to give a standard sized bolt a required tightness of fit, will, as a general rule, require to vary according to the depth of hole to be tapped, because the greater that depth the greater the error in the pitch. Suppose a tap, for example, to get of finer pitch to the amount of .002 per inch of length, then a hole an inch deep and tapped with that tap would err .002 in its depth, while a hole two inches deep would err twice as much in its depth.
Therefore a bolt that would be a hand fit (that is, screw in under hand pressure) in the hole an inch deep would require more force, and probably the use of a wrench, to wind it through the hole 2 inches deep; hence in cases where a definite degree of fit is essential, the reduction in diameter of the male screw or thread necessary to compensate for the error in the tap pitch must vary according to the depth of the hole, and the degree of error in the tap.
It is obvious that the longer a tap is the greater the error induced by hardening, and it often becomes a consideration how to tap a long hole, and obtain a thread true to pitch. This may be accomplished as follows. Several taps are made of slightly different diameters, the largest being of the required finished size. Each tap is made taper for a distance of two or three threads only, and is hardened at this tapered end, but left soft for the remainder of its length. The smallest tap is used first, and when it has tapped a certain distance, a larger one is inserted, and by continuing this interchange of taps and slightly varying the length of the taper, the work may be satisfactorily done.
To test the accuracy, or rather the uniformity, of a thread that has been hardened, a sheet metal gauge, such as at g or at g′ (Fig. 355), may be used, there being at a and b teeth to fit the threads. If the edge of the gauge meets the tops of the threads, then their depth is correct. If it is desired to test only the pitch, then the gauge may be made as at g′, where, as is shown in the figure, the edge of the gauge clears the tops of the threads, and in this way may be tried at various points along the thread length.
A method of truing hardened threads proposed by the author of this work in 1877, and since employed by the Pratt and Whitney Company to true their hardened steel plug-thread gauges, is as follows:—A soft steel wheel about 31⁄2 inches in diameter, whose circumference is turned off to the shape of the thread, is mounted upon the slide rest of a lathe, and driven by a separate belt after the manner of driving emery wheels; this wheel is charged with diamond dust, which is pressed into its surface by a roller, hence it grinds the thread true.
The amount allowed for grinding is 3⁄1000 inch measured in the angles of the thread, as was shown in Figs. 280 and 281.
In charging the wheel with diamond dust it is necessary to use a roller shaped as in Fig. 356, so that the axis of the roller r and wheel w shall be at a right angle, as denoted by the dotted lines. If the roller is not made to the correct cone its action will be partly a rolling and partly a sliding one, and it will strip the diamond dust from the wheel rather than force it in, the reasons for this being shown in Figs. 57 and 58 upon the subject of bevel-wheels.
Taps for lead and similar soft metal are sometimes made with three flat sides instead of grooves. The tapping holes may in this case be made of larger diameter than the diameter of the end of the tap thread, because the metal in the hole will compress into the tap thread, and so form a full thread. Taps for other metal have also been made of half-round section. Fig. 357 represents a tap of oval cross section, having two flutes, as shown, but it may be observed that neither half-round nor oval taps possess any points of advantage over the ordinary forms of three or four fluted taps, while the former are more troublesome and costly to manufacture.
When it is required to tap a hole very straight and true, it is sometimes the practice to provide a parallel stem to the tap, as[I-110] shown in figure at c. This stem is made a neat working fit to the tapping hole, so that the latter serves as a guide to the tap, causing it to enter and to operate truly.
Tap Wrench.—Wrenches for rotating a tap are divided into two principal classes, single and double wrenches. The former has the hole which receives the squared end of the tap in the middle of its length, as shown in Fig. 358 at e, there being a handle on each side to turn it by.
The single wrench has its hole at one end, as shown in Fig. 359 at d, and is employed for tapping holes in locations where the double wrench could not be got in.
In some cases double tap wrenches are made with two or three sizes of square holes to serve as many different sizes of taps, but this is objectionable, because unless the handles of the wrench extend equally on each side of the tap, the overhanging weight on one side of the tap exerts an influence to pull the tap over to one side and tap the hole out of straight. For taps that have square heads the wrench should be a close but an easy fit to the tap head, otherwise the square corners of the tap become rounded. For the smaller sizes of taps, adjustable wrenches, such as shown in Fig. 360, are sometimes employed. These contain two dies; the upper one, which meets the threaded end of c, being a sliding fit, and the joint faces being formed as shown at a, b. By rotating the handle c its end leaves the upper die, which may be opened out, leaving the square hole between the dies large enough to admit the squared tap end. After the wrench is placed on the tap, c is rotated so as to close the dies upon the tap.
When the location of the tapping hole leaves room for the wrench to rotate a full circle, c is screwed up so that the dies firmly grip the tap head, which preserves the tap head; but when the wrench can only be rotated a part of a revolution, c is adjusted to leave the dies an easy fit to the tap head, so as to enable the wrench to be removed from the tap head with facility and again placed upon the tap head. c is operated by a round lever or pin introduced in a hole in the collar, or the collar may be squared to receive a wrench.
To insure that a tap shall tap a hole straight, the machinist, in the case of hand tapping, applies a square to the work and the tap, as shown in Fig. 361, in which w represents a piece of work, t a tap, and s s two squares. If the tap is a taper one the square is sighted with the shank of the tap, as shown in position 1, but if the thread of the tap is parallel, the square may be applied to the thread of the tap, as in position 2. If the tap leans over to one side, as in Fig. 362, it is brought upright by exerting a pressure on the tap wrench handle b (on the high side) in the direction of the arrow a, while the wrench is rotated; but if the tap leans much to one side it is necessary to rotate the tap back and forth, exerting the pressure on the forward stroke only.
It is necessary to correct the errors before the tap has entered the hole deeply, because the deeper the tap has entered the greater the difficulty in making the correction. If the pressure on the tap wrench be made excessive, it is very liable to cause the tap to break, especially in the case of small taps, that is to say, those of 5⁄8 inch or less in diameter. The square should be applied as soon as the tap has entered the hole sufficiently to operate steadily, and should be applied several times during the tapping operation.
When the tap does not pass through the hole it may be employed with a guide which will keep it true, as shown in Fig. 363, in which w is a piece of work, t the tap, and s a guide, the latter being bolted or clamped to the work at b. In this case the shank of the tap is made fully as large in diameter as the thread. In cases where a number of equidistant holes require tapping, as in the case of cylinder ends, this device saves a great deal of time and insures that the tapping be performed true, the hole to receive the bolt b and that to receive the tap being distant apart to the same amount as are the holes in the work.
In shops where small work is made to standard gauge, and on the interchangeable system, devices are employed, by means of[I-111] which a piece that has been threaded will screw firmly home to its place, and come to some definite position, as in the following examples. In Fig. 364 let it be required that the stud a shall screw in the slide s; the arm a to stand vertical when collar b is firmly home, and a device such as in Fig. 365 may be employed. p is a plate on which is fixed a chuck c to receive the slide s. In plate p is a groove g to hold the head h at a right angle to the slideway in c, there being a projection beneath h and beneath c to fit into g. The tap t is threaded through h, but not fluted at the part that winds through h when the tapping is being done, so as not to cause the thread in h to wear. h acts as a guide to the tap and causes it to start the thread at the same point in the bore of each piece s, and the stem will be so threaded that the screw starts at the same point in the circumference of each piece.
A second example of uniform tapping is shown in Figs. 366, 367, and 368. The piece, Fig. 366, is to have its bore a tapped in line with the slot c, and the thread is to start at a certain point in its bore. In Fig. 367 this piece is shown chucked on a plate d. f is a chuck having a lug e fitting into the slot (c, Fig. 366) of the work. This adjusts the work in one direction. The face d of the plate adjusts the vertical height of the work, and the alignment of the hole to the axis of the tap is secured in the construction of the chuck, as is shown in Fig. 369. A lug k is at a right angle to the face b of the chuck and stands in a line with lug e, as denoted by the dotted line g g, and as lug k fits into the slot g, Fig. 367, the work will adjust itself true when bolted to the plate.
Fig. 368 shows a method of tapping or hobbing four chasers (as for a bolt cutter), so that if the chasers are marked 1, 2, 3 and 4, as shown, any chaser of No. 1 will work with the others, although not tapped at the same operation. c is a chuck with four dies (a, b, c, d) placed between the chasers. By tightening the set-screws s, the dies and chasers are locked ready for the tapping. n is a hub to receive a guide-pin p, which is passed through to hold the chasers true while being set in the chuck, and it is withdrawn before the tapping commences; d e f are simply to take hold of when inserting and removing the dies. It is obvious that a chuck such as this used upon a plate, as in Fig. 365, with the hob guided in the head h there shown, would tap each successive set of chasers alike as a set, and individually alike, provided, of course, that the hob guide or head h is at each setting placed the same distance from the face of the chuck, a condition that applies to all this class of work. In the case of work like chasers, where the tap or hob does not have much bearing to guide it in the work, a three-flute hob should be used for four chasers, or a four-flute hob for three chasers, which is necessary so that the hob may work steadily and tap all to the same diameter.
Bolts are usually designated for size by their diameters measured at the cylindrical stem or body, and by their lengths measured from the inner side of the head to the end of the thread, so that if a nut be used, the length of the bolt, less the thickness of the nut and washer (if the latter be used), is the thickness of work the bolt will hold. If the work is tapped, and no nut is used, the full length of the bolt stem is taken as the length of the bolt.
A black bolt is one left as forged. A finished bolt has its body, and usually its head also, machine finished, but a finished bolt sometimes has a black head, the body only being turned.
A square-headed bolt usually has a square nut, but if the nut is in a situation difficult of access for the wrench, or where the head of the bolt is entirely out of sight (as secluded beneath a flange) the nut is often made hexagon. A machine-finished bolt usually has a machine-finished and hexagon nut. Square nuts are usually left black.
The heads of bolts are designated by their shapes, irrespective of whether they are left black or finished. Fig. 370 represents the various forms: a, square head; b, hexagon head; c, capstan head; d, cheese head; e, snap head; f, oval head, or button head; g, conical head; h, pan head; i, countersink head.
The square heads a are usually left black, though in exceptional cases they are finished. Hexagon heads are left black or finished as circumstances may require; when a bolt head is to receive a wrench and is to be finished, it is usually made hexagon. Heads c and d are almost invariably finished when used on operative parts of machines, as are also e and f. Heads g are usually left black, while h and i are finished if used on machine work, and left black when used as rivets or on rough unfinished work.
The heads from e to i assume various degrees of curve or angle to suit the requirements, but when the other end of the bolt is threaded to receive a nut, some means is necessary to prevent them from rotating in their holes when the nut is screwed up, thus preventing the nut from screwing up sufficiently tight. This is accomplished in woodwork by forging either a square under the head, as in Fig. 371, or by forging under the head a tit or stop, such as shown in Figs. 372 and 373 at p. Since, however, forging such stops on the bolt would prevent the heads from being turned up in the lathe, they are for lathe-turned bolts put in after the bolts have been finished in the lathe, a hole being subsequently drilled beneath the head to receive the pin or stop, p, Fig. 372, which may be tightly driven in. A small slot is cut in the edge of the hole to receive the stop.
Bolts are designated for kinds, as in Fig. 374, in which k is a machine bolt; l a collar bolt, from having a collar on it; m a cotter bolt, from having a cotter or key passing through it to serve in place of a nut; n a carriage bolt, from having a square part under the head to sink in the wood and prevent the bolt from turning with the nut; and o a countersink bolt for cases where the head of the bolt comes flush.
The simple designation “machine bolt” is understood to mean a black or unfinished bolt having a square head and nut, and threaded, when the length of the bolt will admit it, and still leave an unthreaded part under the bolt head, for a length equal to about four times the diameter of the bolt head. If the bolt is to have other than a square head it is still called a machine bolt, but the shape of the head or nut is specially designated as “hexagon head machine bolt,” this naturally implying that a hexagon nut also is required.
In addition to these general names for bolts, there are others applied to special cases. Thus Fig. 375 represents a patch bolt or a bolt for fastening patches (as plate c to plate d), its peculiarity being that it has a square stem a for the wrench to screw it in by. When the piece the patch bolt screws into is thin, as in the case of patches on steam boilers, the pitch of the thread may, to avoid leakage, be finer than the usual standard.
In countersink head bolts, such as the patch bolt in Fig. 375, the head is very liable to come off unless the countersink in the work (as in c) is quite fair with the tapped hole (as in d) because the thread of the bolt is made a tight fit to the hole, and all the bending that may take place is in the neck beneath the head, where fracture usually occurs. These bolts are provided with a square head a to screw them in by, and are turned in as at b to a diameter less than that at the bottom of the thread, so that if screwed up until they twist off, they will break in the neck at b.
Instead of the hole being countersunk, however, it may be cupped or counterbored, as in Fig. 376, in which the names of the various forms of the enlargement of holes are given. The difference between a faced and a counterbored hole is that in a counterbored hole the head or collar of the pin passes within the counterbore, the use of the counterbore being in this case to cause the pin to stand firmly and straight. The difference between a dished and a cupped is merely that cupped is deeper than dished, and that between grooved and recessed is that a recess is a wide groove.
Eye bolts are those having an eye in place of a head, as in Fig. 377, being secured by a pin passing through the eye, or by a second bolt, as in the figure. When the bolt requires to pivot, that[I-113] part that is within the eye may be made of larger diameter than the thread, so as to form a shoulder against which the bolt may be screwed firmly home to secure it without gripping the eye bolt.
Fig. 378 represents a foundation bolt for holding frames to the stone block of a foundation. The bolt head is coned and jagged with chisel cuts. It is let into a conical hole (widest at the bottom) in the stone block, and melted lead is poured around it to fill the hole and secure the bolt head.
Another method of securing a foundation bolt head within a stone block is shown in Fig. 379; a similar coned hole is cut in the block, and besides the bolt head b a block w is inserted, the faces of the block and bolt being taper to fit to a taper key k, so that driving k locks both the bolt and the block in the stone. When the bolt can pass entirely through the foundation (as when the latter is brickwork) it is formed as in Fig. 380, in which b is a bolt threaded to receive a nut at the top. At the bottom it has a keyway for a key k, which abuts against the plate p. To prevent the key from slackening and coming out, it has a recess as shown in the figure at the sectional view of the bolt on the right of the illustration, the recess fitting down into the end of the keyway as shown.
Another method is to give the bolt head the form at b in Fig. 381, and to cast a plate with a rectangular slot through, and with two lugs a c. The plate is bricked in and a hole large enough to pass the bolt head through is left in the brickwork. The bolt head is passed down through the brickwork in the position shown at the top, and when it has passed through the slot in the plate it is given a quarter turn, and then occupies the position shown in the lower view, the lugs a c preventing it from turning when the nut is screwed home. The objection to this is that the hole through the brickwork must be large enough to admit the bolt head. Obviously the bolt may have a solid square head, and a square shoulder fitting into a square hole in the plate, the whole being bricked in.
Figs. 382 and 383 represent two forms of hook bolt for use in cases where it is not desired to have bolt holes through both pieces of the work. In Fig. 382 the head projects under the work and for some distance beneath and beyond the washer, as is denoted by the dotted line, hence it would suspend piece a from b or piece b from a. But in Fig. 383 the nut pressure is not beneath the part where the hook d grips the work, hence the nut would exert a pressure to pull piece b in the direction of the arrow; hence if b were a fixed piece the bolt would suspend a from it, but it could not suspend b from a.
In woodwork the pressure of the nut is apt to compress the wood, causing the bolt head and nut to sink into the wood, and to obviate this, anchor plates are used to increase the area receiving the pressure; thus in Fig. 384 a plate is tapped to serve instead of a nut, and a similar plate may of course be placed under the bolt head.
The Franklin Institute or United States Standard for the dimensions of bolt heads and nuts is as follows. In Fig. 385, d represents the diameter of the bolt, j represents the short diameter or width across flats of the bolt head or of the nut, being equal to one and a half times the diameter of the bolt, plus 1⁄16 inch for finished heads or nuts, and plus 1⁄8 inch for rough or unfinished heads or nuts. k represents the depth or thickness of the head or nut, which in finished heads or nuts equals the diameter of the bolt minus 1⁄16 inch, and in rough heads equals one half the distance between the parallel sides of the head, or in other words one half the width across the flats of the head.
h represents the thickness or depth of the nut, which for finished nuts is made equal to the diameter of the bolt less 1⁄16 inch, and therefore[I-114] the same thickness as the finished bolt head, while for rough or unfinished nuts it is made equal to the diameter of the bolt or the same as the rough bolt head. i represents the long diameter or diameter across corners, which, however, is a dimension not used to work to, and is inserted in the following tables merely for reference:—
| Diameter at top of Thread. |
Diameter at bottom of Thread. |
Number of Threads per inch. |
Diameter across Flats, or short diameter. |
Thickness or Depth. |
||||
| 1⁄4 | .185 | 20 | 7⁄16 | 3⁄16 | ||||
| 5⁄16 | .240 | 18 | 17⁄32 | 1⁄4 | ||||
| 3⁄8 | .294 | 16 | 5⁄8 | 5⁄16 | ||||
| 7⁄16 | .345 | 14 | 23⁄32 | 3⁄8 | ||||
| 1⁄2 | .400 | 13 | 13⁄16 | 7⁄16 | ||||
| 9⁄16 | .454 | 12 | 29⁄32 | 1⁄2 | ||||
| 5⁄8 | .507 | 11 | 1 | 9⁄16 | ||||
| 3⁄4 | .620 | 10 | 1 | 3⁄16 | 11⁄16 | |||
| 7⁄8 | .731 | 9 | 1 | 3⁄8 | 13⁄16 | |||
| 1 | .837 | 8 | 1 | 9⁄16 | 15⁄16 | |||
| 1 | 1⁄8 | .940 | 7 | 1 | 3⁄4 | 1 | 1⁄16 | |
| 1 | 1⁄4 | 1.065 | 7 | 1 | 15⁄16 | 1 | 3⁄16 | |
| 1 | 3⁄8 | 1.160 | 6 | 2 | 1⁄8 | 1 | 5⁄16 | |
| 1 | 1⁄2 | 1.284 | 6 | 2 | 5⁄16 | 1 | 7⁄16 | |
| 1 | 5⁄8 | 1.389 | 5 | 1⁄2 | 2 | 1⁄2 | 1 | 9⁄16 |
| 1 | 3⁄4 | 1.491 | 5 | 2 | 11⁄16 | 1 | 11⁄16 | |
| 1 | 7⁄8 | 1.616 | 5 | 2 | 7⁄8 | 1 | 13⁄16 | |
| 2 | 1.712 | 4 | 1⁄2 | 3 | 1⁄16 | 1 | 15⁄16 | |
| 2 | 1⁄4 | 1.962 | 4 | 1⁄2 | 3 | 7⁄16 | 2 | 3⁄16 |
| 2 | 1⁄2 | 2.176 | 4 | 3 | 13⁄16 | 2 | 7⁄16 | |
| 2 | 3⁄4 | 2.426 | 4 | 4 | 3⁄16 | 2 | 11⁄16 | |
| 3 | 2.629 | 3 | 1⁄2 | 4 | 9⁄16 | 2 | 15⁄16 | |
| 3 | 1⁄4 | 2.879 | 3 | 1⁄2 | 4 | 15⁄16 | 3 | 3⁄16 |
| 3 | 1⁄2 | 3.100 | 3 | 1⁄4 | 5 | 5⁄16 | 3 | 7⁄16 |
| 3 | 3⁄4 | 3.377 | 3 | 5 | 11⁄16 | 3 | 13⁄16 | |
| 4 | 3.567 | 3 | 6 | 1⁄16 | 3 | 15⁄16 | ||
| 4 | 1⁄4 | 3.798 | 2 | 7⁄8 | 6 | 7⁄16 | 4 | 3⁄16 |
| 4 | 1⁄2 | 4.028 | 2 | 7⁄8 | 6 | 13⁄16 | 4 | 7⁄16 |
| 4 | 3⁄4 | 4.256 | 2 | 5⁄8 | 7 | 3⁄16 | 4 | 11⁄16 |
| 5 | 4.480 | 2 | 1⁄2 | 7 | 9⁄16 | 4 | 15⁄16 | |
| 5 | 1⁄4 | 4.730 | 2 | 1⁄2 | 7 | 15⁄16 | 5 | 3⁄16 |
| 5 | 1⁄2 | 4.953 | 2 | 3⁄8 | 8 | 5⁄16 | 5 | 7⁄16 |
| 5 | 3⁄4 | 5.203 | 2 | 3⁄8 | 8 | 11⁄16 | 5 | 11⁄16 |
| 6 | 5.423 | 2 | 1⁄4 | 9 | 1⁄16 | 5 | 15⁄16 | |
Note that square heads are supposed to be always unfinished, hence there is no standard for their sizes if finished.
The Franklin Institute standard dimensions for hexagon and square bolt heads and nuts when the same are left unfinished or rough, as forged, are as follows:—
| Bolt Diameter in Inches. |
Diameter across corners, or long diameter of hexagon heads. |
Diameter across corners or long diameter of square heads. |
Short diameter, or diameter across flats for square or hexagon heads and nuts. |
Thickness or depth for square or hexagon heads. |
|||||
| Inch. | Inch. | Inch. | Inch. | ||||||
| 1⁄4 | 37⁄64 | 7⁄10 | 1⁄2 | 1⁄4 | |||||
| 5⁄16 | 11⁄16 | 10⁄12 | 19⁄32 | 19⁄64 | |||||
| 3⁄8 | 51⁄64 | 63⁄64 | 11⁄16 | 11⁄32 | |||||
| 7⁄16 | 9⁄10 | 1 | 7⁄64 | 25⁄32 | 25⁄64 | ||||
| 1⁄2 | 1 | 1 | 15⁄64 | 7⁄8 | 7⁄16 | ||||
| 9⁄16 | 1 | 1⁄8 | 1 | 23⁄64 | 31⁄32 | 31⁄64 | |||
| 5⁄8 | 1 | 7⁄32 | 1 | 1⁄2 | 1 | 1⁄16 | 17⁄32 | ||
| 3⁄4 | 1 | 7⁄16 | 1 | 49⁄64 | 1 | 1⁄4 | 5⁄8 | ||
| 7⁄8 | 1 | 21⁄32 | 2 | 1⁄32 | 1 | 7⁄16 | 23⁄32 | ||
| 1 | 1 | 7⁄8 | 2 | 19⁄64 | 1 | 5⁄8 | 13⁄16 | ||
| 1 | 1⁄8 | 2 | 2⁄32 | 2 | 9⁄16 | 1 | 13⁄16 | 29⁄32 | |
| 1 | 1⁄4 | 2 | 5⁄16 | 2 | 53⁄64 | 2 | 1 | ||
| 1 | 3⁄8 | 2 | 17⁄32 | 3 | 3⁄32 | 2 | 3⁄16 | 1 | 3⁄32 |
| 1 | 1⁄2 | 2 | 3⁄4 | 3 | 23⁄64 | 2 | 3⁄8 | 1 | 3⁄16 |
| 1 | 5⁄8 | 2 | 31⁄32 | 3 | 5⁄8 | 2 | 9⁄16 | 1 | 9⁄32 |
| 1 | 3⁄4 | 3 | 3⁄16 | 3 | 57⁄64 | 2 | 3⁄4 | 1 | 3⁄8 |
| 1 | 7⁄8 | 3 | 13⁄32 | 4 | 5⁄32 | 2 | 15⁄16 | 1 | 15⁄32 |
| 2 | 3 | 5⁄8 | 4 | 27⁄64 | 3 | 1⁄8 | 1 | 9⁄16 | |
| 2 | 1⁄4 | 4 | 1⁄16 | 4 | 61⁄64 | 3 | 1⁄2 | 1 | 3⁄4 |
| 2 | 1⁄2 | 4 | 1⁄2 | 5 | 31⁄64 | 3 | 7⁄8 | 1 | 15⁄16 |
| 2 | 3⁄4 | 4 | 29⁄32 | 6 | 4 | 1⁄4 | 2 | 1⁄8 | |
| 3 | 5 | 3⁄8 | 6 | 17⁄32 | 4 | 5⁄8 | 2 | 5⁄16 | |
| 3 | 1⁄4 | 5 | 13⁄16 | 7 | 1⁄16 | 5 | 2 | 1⁄2 | |
| 3 | 1⁄2 | 6 | 7⁄64 | 7 | 39⁄64 | 5 | 3⁄8 | 2 | 11⁄16 |
| 3 | 3⁄4 | 6 | 21⁄32 | 8 | 1⁄8 | 5 | 3⁄4 | 2 | 7⁄8 |
| 4 | 7 | 3⁄32 | 8 | 41⁄64 | 6 | 1⁄8 | 3 | 1⁄16 | |
| 4 | 1⁄4 | 7 | 9⁄16 | 9 | 3⁄16 | 6 | 1⁄2 | 3 | 1⁄4 |
| 4 | 1⁄2 | 7 | 31⁄32 | 9 | 3⁄4 | 6 | 7⁄8 | 3 | 7⁄16 |
| 4 | 3⁄4 | 8 | 13⁄32 | 10 | 1⁄4 | 7 | 1⁄4 | 3 | 5⁄8 |
| 5 | 8 | 27⁄32 | 10 | 49⁄64 | 7 | 5⁄8 | 3 | 13⁄16 | |
| 5 | 1⁄4 | 9 | 9⁄32 | 11 | 23⁄64 | 8 | 4 | ||
| 5 | 1⁄2 | 9 | 23⁄32 | 11 | 7⁄8 | 8 | 3⁄8 | 4 | 3⁄16 |
| 5 | 3⁄4 | 10 | 5⁄32 | 12 | 3⁄8 | 8 | 3⁄4 | 4 | 3⁄8 |
| 6 | 10 | 19⁄32 | 12 | 15⁄16 | 9 | 1⁄8 | 4 | 9⁄16 | |
The depth or thickness of both the hexagon and square nuts when left rough or unfinished is, according to the above standard, equal to the diameter of the bolt.
The following are the sizes of finished bolts and nuts according to the present Whitworth Standard. The exact sizes are given in decimals, and the nearest approximate sizes in sixty-fourths of an inch:—
| Diameter of bolts. |
Width of nuts across flats. | Height of bolt heads. | |||||||||
| 1⁄8 | .33 | 8 | 21⁄64 | f | .10 | 93 | 7⁄64 | ||||
| 3⁄16 | .44 | 8 | 29⁄64 | b | .16 | 40 | 5⁄32 | ||||
| 1⁄4 | .52 | 5 | 33⁄64 | f | .21 | 87 | 7⁄32 | ||||
| 5⁄16 | .60 | 14 | 19⁄32 | f | .27 | 34 | 17⁄64 | ||||
| 3⁄8 | .70 | 94 | 45⁄64 | f | .32 | 81 | 21⁄64 | ||||
| 7⁄16 | .82 | 04 | 53⁄64 | b | .38 | 28 | 3⁄8 | f | |||
| 1⁄2 | .91 | 91 | 29⁄32 | b | .43 | 75 | 7⁄16 | ||||
| 9⁄16 | 1.01 | 1 | 1 | 1⁄64 | b | .49 | 21 | 31⁄64 | f | ||
| 5⁄8 | 1.10 | 1 | 1 | 3⁄32 | f | .54 | 68 | 35⁄64 | |||
| 11⁄16 | 1.20 | 11 | 1 | 13⁄64 | b | .60 | 15 | 19⁄32 | f | ||
| 3⁄4 | 1.30 | 12 | 1 | 19⁄64 | f | .65 | 62 | 21⁄32 | |||
| 13⁄16 | 1.39 | 1 | 25⁄64 | b | .71 | 09 | 45⁄64 | f | |||
| 7⁄8 | 1.47 | 88 | 1 | 31⁄64 | b | .76 | 56 | 49⁄64 | |||
| 15⁄16 | 1.57 | 45 | 1 | 37⁄64 | b | .82 | 03 | 13⁄16 | f | ||
| 1 | 1.67 | 01 | 1 | 43⁄64 | b | .87 | 5 | 7⁄8 | |||
| 1 | 1⁄8 | 1.86 | 05 | 1 | 55⁄64 | f | .98 | 43 | 63⁄64 | ||
| 1 | 1⁄4 | 2.04 | 83 | 2 | 3⁄64 | f | 1.09 | 37 | 1 | 3⁄32 | |
| 1 | 3⁄8 | 2.21 | 46 | 2 | 7⁄32 | b | 1.20 | 31 | 1 | 13⁄64 | |
| 1 | 1⁄2 | 2.41 | 34 | 2 | 13⁄32 | f | 1.31 | 25 | 1 | 5⁄16 | |
| 1 | 5⁄8 | 2.57 | 63 | 2 | 37⁄64 | b | 1.41 | 28 | 1 | 27⁄64 | |
| 1 | 3⁄4 | 2.75 | 78 | 2 | 3⁄4 | f | 1.53 | 12 | 1 | 17⁄32 | |
| 1 | 7⁄8 | 3.01 | 83 | 3 | 1⁄16 | f | 1.64 | 06 | 1 | 41⁄64 | |
| 2 | 3.14 | 91 | 3 | 5⁄32 | b | 1.75 | 1 | 3⁄4 | |||
| 2 | 1⁄8 | 3.33 | 7 | 3 | 11⁄32 | b | 1.85 | 23 | 1 | 55⁄64 | |
| 2 | 1⁄4 | 3.54 | 6 | 3 | 35⁄64 | b | 1.96 | 87 | 1 | 31⁄32 | |
| 2 | 3⁄8 | 3.75 | 3 | 3⁄4 | 2.07 | 81 | 2 | 5⁄64 | |||
| 2 | 1⁄2 | 3.89 | 4 | 3 | 57⁄64 | f | 2.18 | 75 | 2 | 3⁄16 | |
| 2 | 5⁄8 | 4.04 | 9 | 4 | 3⁄64 | f | 2.29 | 68 | 2 | 19⁄64 | |
| 2 | 3⁄4 | 4.18 | 1 | 4 | 3⁄16 | b | 2.40 | 62 | 2 | 13⁄32 | |
| 2 | 7⁄8 | 4.34 | 56 | 4 | 11⁄32 | f | 2.51 | 56 | 2 | 33⁄64 | |
| 3 | 4.53 | 1 | 4 | 17⁄32 | b | 2.62 | 5 | 2 | 5⁄8 | ||
The thickness of the nuts is in every case the same as the diameter of the bolts: f = full, b = bare.
[I-115]When bolts screw directly into the work instead of passing through it and receiving a nut, they come under the head of either tap bolts, set screws, cap screws, or machine screws. A tap bolt is one in which the full length of the stem or body is threaded, and differs from a set screw, which is similarly threaded, in the respect that in a set screw the head is square and its diameter is the same as the square bar of steel or iron (as the case may be) from which the screw was made, while in the tap bolt the head is larger in diameter than the bar it was made from. Furthermore a tap bolt may have a hexagon head, which is usually left unfinished unless ordered to be finished, as is also the case with set screws.
Cap screws are made with heads either hexagon, square, or round, and also with a square head and round collar, as in Fig. 386, the square heads being of larger diameter than the iron from which they were made. When the heads of cap screws are finished they are designated as “milled heads.”
A machine screw is a small screw, such as in Fig. 387, the diameter of the body being made to the Birmingham wire gauge, the heads being formed by upsetting the wire of which they are made. They have saw slots s for a screw driver, the threads having special pitches, which are given hereafter. The forms of the heads are as in Fig. 387, a being termed a Fillister, b a countersink, and c a round head. The difference between a Fillister head of a machine screw and the same form of head in a cap screw is that the former is upset cold, and the latter is either forged or cut out of the solid metal.
When the end of a screw abuts against the work to secure it, it is termed a set screw. The ordinary form of set screw is shown in Fig. 389, the head being square and either black or polished as may be required. The ends of the set screws of commerce, that is to say, that are kept on sale, are usually either pointed as at a, Fig. 388, slightly bevelled as at b, or cupped as at d. If left flat or only slightly bevelled as at b, they are liable, if of steel and not hardened, or if of iron and case-hardened only, to bulge out as at c. This prevents them from slacking back easily or prevents removal if necessary, and even though of hardened steel they do not grip very firmly. On this account their points are sometimes made conical, as at a. This form, however, possesses a disadvantage when applied to a piece of work that requires accurate adjustment for position, inasmuch as it makes a conical indentation in the work, and unless the point be moved sufficiently to clear this indentation the point will fall back into it; hence the conical point is not desirable when the piece may require temporary fixture to find the adjustment before being finally screwed home. For these reasons the best form of set screw end is shown at d, the outside of the end being chamfered off and the inside being cupped, as denoted by the dotted lines. This form cuts a ring in the work, but will hold sufficiently for purposes of adjustment without being screwed home firmly.
In some cases the end of the set screw is tapped through the enveloping piece (as a hub) and its end projects into a plain hole in the internal piece of the work, and in this case the end of the thread is turned off for a distance of two or three threads, as at a in Fig. 390. Similarly, when the head of the screw is to act or bear upon the work, the thread may be turned off as at b in the figure.
When a bolt has no head, but is intended to screw into the work at one end, and receive a nut at the other, it is termed a stud or standing bolt. The simplest form of standing bolt is that in which it is parallel from end to end with a thread at each end, and an unthreaded part in the middle, but since standing bolts or studs require to remain fixed in the work, it is necessary to screw them tightly into their places, and therefore firmly home. This induces the difficulty that some studs may screw a trifle farther into the work than others, so that some of the stud ends may project farther through the nuts than others, giving an appearance that the studs have been made of different lengths. The causes of this may be slight variations in the tapping of the holes and the threading of the studs. If those that appear longest are taken out and reduced to the lengths of the others, it will be found sometimes that the stud on the second insertion will pass farther into the work than at the first, and the stud will project less through the nut than the others. To avoid this those protruding most may be worked backward and forward with the wrench and thus induced to screw home to the required distance, but it is better to provide to the stud a shoulder against which it may screw firmly home; thus in Fig. 391 is a stud, whose end a is to screw into the work, part b is to enter the hole in the work (the thread in the hole being cut away at the mouth to receive b). In this case the shoulder between b and c screwing firmly against the face of the work, all the studs being made of equal length from this shoulder to end e, then the thickness of the flange or work secured by the nut being equal, the nuts will pass an equal distance on end d, and e will project equally through all the nuts. The length of the plain part c is always made slightly less than the thickness of the flange or foot of the work to be bolted up, so that the nut shall not meet c before gripping the flange surface.
There are, however, other considerations in determining the shape and size of the parts a and c of studs.
Thus, suppose a stud to have been in place some time, the nut on end e being screwed firmly home on the work, and perhaps somewhat corroded on e. Then the wrench pressure applied to the nut will be in a direction to unscrew the stud out of the work, and if there be less friction between a and the thread in the work than there is between d and the thread in the nut, the stud and not the nut will unscrew. It is for this purpose that the end a requires firmly screwing into the work. But in the case of much corrosion this is not always sufficient, and the thread a is therefore sometimes made of a larger diameter than the thread at d. In this case the question at once arises, What shall be the diameter of the plain part c?
If it be left slightly larger than d, but the depth of the thread less than a, then it may be held sufficiently firmly by the fit of the threads (without the aid of screwing against a shoulder) to prevent unscrewing when releasing the nut, and may be screwed within the work until its end projects the required distance; thus all the studs may project an equal distance, but there will be the disadvantage that when the studs require removing and are corroded the plain part is apt to twist off, leaving the end a plugging the hole. The plain part c may be left of same diameter as a, both being larger than d; but in this case the difficulty of having all the studs project equally when screwed home, as previously mentioned, is induced; hence c may be larger than a, and a shoulder left at b, as in the figure; this would afford excellent[I-116] facility for unscrewing the stud to remove it, as well as insuring equal projection of e. The best method of all is, so far as quality goes, to make the plain part c square, as in Fig. 392, which is an English practice, the square affording a shoulder to screw up against and secure an equal projection while serving to receive a wrench to put in or remove the stud. In this case the holes in the flange or piece bolted up being squared, the stud cannot in any case unscrew with the nut. The objection to this squared stud is that the studs cannot be made from round bar iron, and are therefore not so easily made, and that the squaring of the holes in the flange or part of the work supported by the stud is again extra work, and for these reasons studs with square instead of cylindrical mid-sections have not found favor in the United States.
An excellent method of preventing the stud from unscrewing with the nut is to make the end a longer than the nut end, as in Fig. 393, so that its threads will have more friction; and this has the further advantage that in cast iron it serves also to make the strength of the thread equal to that of the stud. As the faces of the nuts are apt when screwed home to score or mark the face of the work, it adds to the neatness of the appearance to use a washer w beneath the nut, which distributes the pressure over a greater area of work surface.
In some practice the ends a of studs are threaded taper, which insures that they shall fit tight and enables their more easy extraction.
An excellent tool for inserting studs of this kind to the proper distance is shown in Fig. 394. It consists of a square body a threaded to receive the stud whose end is shown at c. The upper end is threaded to receive an adjusting screw b, which is screwed in so that its end d meets the end c of the stud. It is obvious that b may be so adjusted that when a is operated by a wrench applied to its body until its end face meets the work and the stud is inserted to the proper depth, all subsequent studs may be put into the same depth.
When the work pivots upon a stem, as in Fig. 395, the bolt is termed a standing pin, and as in such cases the stem requires to stand firm and true it is usual to provide the pin with a collar, as shown in the figure, and to secure the pivoted piece in place with a washer and a taper pin because nuts are liable to loosen back of themselves. Furthermore, a pin and washer admit of more speedy disconnection than a nut does, and also give a more delicate adjustment for end fit.
In drilling the tapping holes for standing bolts, it is the practice with some to drill the holes in cast iron of such a size that the tap will cut three-quarters only of a full thread, the claim being that it is as strong as a full thread. The difference in strength between a three-quarter and a full thread in cast iron is no doubt practically very small indeed, while the process of tapping is very much easier for the three-quarter full thread, because the tap may, in that case, be wound continuously forward without backing it at every quarter or half revolution, as would otherwise be necessary, in order to give the oil access to the cutting edges of the tap—and oil should always be used in the process of tapping (even though on cast iron it causes the cuttings to clog in the flutes of the tap, necessitating in many cases that the tap be once or twice during the operation taken out, and the cuttings removed) because the oil preserves the cutting edges of the tap teeth from undue abrasion, and, therefore, from unnecessarily rapid dulling. With a tap having ordinarily wide and deep flutes, and used upon a hole but little deeper than the diameter of the tap, the cuttings due to making a three-quarter full thread will not more than fill the flutes of the tap by the time its duty is performed. We have also to consider that with a three-quarter full thread it is much easier to extract the standing bolt when it is necessary to do so, so that all things considered it is permissible to have such a thread, providing the tapping hole does not pass through into a cylinder or chamber requiring to be kept steam-tight, for in that case the bolt would be almost sure to leak. As a preventive against such leakage, the threads are sometimes cut upon the standing bolts without having a terminal groove, and are then screwed in as far as they will go; the termination of the thread upon the standing bolt at the standing or short end being relied upon to jam into and close up the thread in the hole. A great objection to this, however, is the fact that the bolts are liable to screw into the holes to unequal depths, so that the outer ends will not project an equal distance through the nuts, and this has a bad appearance upon fine work. It is better, then, in such a case, to tap the holes a full thread, the extra trouble involved in the tapping being to some extent compensated for in the fact that a smaller hole, which can be more quickly drilled, is required for the full than for the three-quarter thread.
The depth of the tapping hole should be made if possible equal to one and a half times the diameter of the tap, so that in case the hole bottoms and the tap cannot pass through, the taper, and what is called in England the second, and in the United States the plug tap, will finish the thread deep enough without employing a third tap, for the labor employed in drilling the hole deeper is less than that necessary to the employment of a third tap. If the hole passes through the work, its depth need not, except for cast-iron holes, be greater than 1⁄8 inch more than the diameter of the bolt thread, which amount of excess is desirable so that in case the nut corrodes, the nut being as thick as the diameter of the tap, and therefore an inch less than the depth of the hole at the standing end, will be more likely to leave the stud standing than to carry it with it when being unscrewed.
When it is desirable to provide that bolts may be quickly removed, the flanges may be furnished with slots, as in Fig. 396, so that the bolts may be passed in from the outside, and in this case it is simply necessary to slacken back the nut only. It is preferable, however, in this case to have the bolt square under the head, as in Fig. 397, so as to prevent the bolt from turning when screwing up or unscrewing the nut. The bolt is squared at a, which fits easily into the flange. The flanges, however, should in this case be of ample depth or thickness to prevent[I-117] their breakage, twice the depth of the nut being a common proportion.
In cases where it is inconvenient for the bolt head to pass through the work a T groove is employed, as in Fig. 398. In this case the bolt head may fit easily at a b to the sides a b of the groove, so that while the bolt head will slide freely along the groove, the head, being square, cannot turn in the slot when the nut is screwed home. This, however, is more efficiently attained when there is a square part beneath the bolt head, as in Fig. 399, the square a of the bolt fitting easily to the slot b of the groove.
When it is undesirable that the slots run out to the edge of the work they may terminate in a recess, as at a in Fig. 400, which affords ingress of the bolt head to the slot; or the bolt head may be formed as in Fig. 401, the width a b of the bolt head passing easily through the top a b of the slot, and the bolt head after its insertion being turned in the direction of the arrow, which it is enabled to do by reason of the rounded corners c d. In this case, also, there may be a square under the head to prevent the bolt head from locking in the slot, but the corners of the square must also be rounded as in Fig. 402.
The underneath or gripping surface of a bolt head should be hollow, as at a in Fig. 403, rather than rounding as at b, because, if rounding, the bolt will rotate with the nut when the latter grips the work surface. It should also be true with the axial line of the bolt so as to bear fairly upon the work without bending. The same remarks apply to the bedding surface of the nut, because to whatever amount the face is out of true it will bend the threaded end of the bolt, and this may be sufficient to cause the bolt to break.
In Fig. 404, for example, is shown a bolt and nut, neither of which bed fair, being open at a and b respectively, and it is obvious that the strain will tend to bend or break the bolt across the respective dotted lines c, d. In the case of the nut there is sufficient elasticity in the thread to allow of the nut forcing itself to a bed on the work, the bolt bending; but in the case of the bolt head the bending is very apt to break off the bolt short in the neck under the head. In a tap bolt where the wrench is applied to the bolt head, the rotation, under severe strain, of the head will usually cause it to break off in all cases where the bolt is rigidly held, so that it cannot cant over and allow the head to bed fair.
A plain tap bolt should be turned up along its body, because if out of true the hole it passes through must be made large enough to suit the eccentricity of the bolt, or else a portion of the wrench pressure will be expended in rotating the bolt in the hole instead of being expended solely in screwing the bolt farther into the work.
It is obvious therefore, that if a tap bolt be left black the hole it passes through must be sufficiently large to make full allowance for the want of truth in the bolt. For the same reasons the holes for tapped bolts require to be tapped very true.
Black studs possess an advantage (over tap bolts) in this respect, inasmuch as that if the holes are not tapped quite straight the error may be to some extent remedied by screwing them fully home and then bending them by hammer blows.
[I-118]Nuts are varied in form to suit the nature of the work. For ordinary work, as upon bolts, their shape is usually made to conform to the shape of the bolt head, but when the nut is exposed to view and the bolt head hidden, the bolt end and the nut are (for finished work) finished while the bolt heads are left black.
The most common form of hexagon nut is shown in Fig. 405, the upper edge being chamfered off at an angle of about 40°. In some cases the lower edge is cut away at the corners, as in Fig. 405 at a, the object being to prevent the corners of the nut from leaving a circle of bearing marks upon the work, but this gives an appearance at the corners that the nut does not bed fair. Another shape used by some for the end faces of deep nuts, that is to say, those whose depth exceeds the diameter of the bolt, is shown in Fig. 406. Nuts of extra depth are used when, from the nut being often tightened and released, the thread wear is increased, and the extra thread length is to diminish the wear.
To avoid the difficulty of having some of the bolt ends project farther through some nuts than others on a given piece of work, as is liable to occur where the flanges to be bolted together are not turned on all four radial faces, the form of nut shown in Fig. 407 is sometimes employed, the thread in the nut extending beyond the bolt end.
As an example of the application of this nut, suppose a cylinder cover to be held by bolts, then the cylinder flange not being turned on its back face is usually of unequal thickness; hence to have the bolt ends project equally through the nuts, each bolt would require to be made of a length to suit a particular hole, and this would demand that each hole and bolt be marked so that they may be replaced when taken out, without trying them in their places. Another application of this nut is to make a joint where the threads may be apt to leak. In this case the mouth of the hole is recessed and coned at the edge; the nut is chamfered off with a similar cone, and a washer w, Fig. 408, is placed beneath the nut to compress and conform to the coned recess; thus with the aid of a cement of some kind, as red or white lead (usually red lead), a tight joint may be made independent of the fit of the threads.
When the hole through which the bolt passes is considerably larger in diameter than the bolt, the flange nut shown in Fig. 409 is employed, the flange covering the hole. A detached washer may be used for the same purpose, providing that its hole fit the bolt and it be of a sufficient thickness to withstand the pressure and not bend or sink into the hole.
Circular nuts are employed where, on account of their rotating at high speed, it is necessary that they be balanced as nearly as possible so as not to generate unbalanced centrifugal force. Fig. 410 represents a nut of this kind: two diametrically opposite flat sides, as a, affording a hold for the wrench. Other forms of circular nuts are shown in Figs. 411 and 412. These are employed where the nuts are not subject to great strain, and where lightness is an object.
That in Fig. 411 is pierced around its circumference with cylindrical holes, as a, b, c, to receive a round lever or rod or a wrench, such as shown in Fig. 459.
That shown in Fig. 412 has slots instead of holes in its circumference, and the form of its wrench is shown in Fig. 461.
When nuts are employed upon bolts in which the strain of the duty is longitudinal to the bolt, and especially if the direction of motion is periodically reversed, and also when a bolt is subject to shocks or vibrations, a single nut is liable to become loose upon the bolt, and a second nut, termed a check nut, jamb nut, or safety nut, becomes necessary, because it is found that if two nuts be employed, as in Fig. 413, and the second nut be screwed firmly home against the first, they are much less liable to come loose on the bolt.
Considerable difference of practice exists in relation to the thickness of the two nuts when a check nut is employed. The first or ordinary nut is screwed home, and the second or check nut is then screwed home. If the second nut is screwed home as firmly as the first, it is obvious that the strain will fall mainly on the second. If it be screwed home more firmly than the first, the latter may be theoretically considered to be relieved entirely of the strain, while if it be screwed less firmly home, the first will be relieved to a proportionate degree of the strain. It is usual to screw the second home with the same force as applied to the first, and it would, therefore, appear that the first nut, being relieved of strain, need not be so thick as the first, but it is to be considered that, practically, the first nut will always have some contact with the bolt threads, because from the imperfections in the threads of ordinary bolts the area and the force of contact is not usually the same nor in the same direction in both nuts, unless both nuts were tapped with the same tap and at about the same time.
When, for example, a tap is put into the tapping machine, it is at its normal temperature, and of a diameter due to that temperature, but as its work proceeds its temperature increases, notwithstanding that it may be freely supplied with oil, because the oil cannot, over the limited area of the tap, carry off all the heat generated by the cutting of a tap rotated at the speeds usually employed in practice. As a result of this increase of temperature, we have a corresponding increase in the diameter of the tap, and a variation in the diameter of the threads in the nuts. The variation in the nuts, however, is less than that in the tap diameter, because as the heated tap passes through the nut it imparts some of its heat to the nut, causing it also to expand, and hence to contract in cooling after it has been tapped, and, therefore, when cold, to be of a diameter nearer to that of the tap.
Furthermore, as the tap becomes heated it expands in length, and its pitch increases, hence here is another influence tending[I-119] to cause the pitches of the nut threads to vary, because although the temperature of the tap when in constant use reaches a limit beyond which, so long as its speed of rotation is constant, it never proceeds; yet, when the tap is taken from the machine to remove the tapped nuts which have collected on its shank, and it is cooled in the oil to prevent it from becoming heated any more than necessary, the pitch as well as the diameter of the tap is reduced nearer to its normal standard.
So far, then, as theoretical correctness, either of pitch or diameter in nut threads, is concerned, it could only be attained (supposing that the errors induced by hardening the tap could be eliminated) by employing the taps at a speed of rotation sufficiently slow to give the oil time to carry off all the heat generated by the cutting process. But this would require a speed so comparatively slow as not to be commercially practicable, unless followed by all manufacturers. Practically, however, it may be considered that if two nuts be tapped by a tap that has become warmed by use, they will be of the same diameter and pitch, and should, therefore, have an equal area and nature of contact with the bolt thread, supposing that the bolt thread itself is of equal and uniform pitch. But the dies which cut the thread upon the bolt also become heated and expanded in pitch. But if the temperature of the dies be the same as that of the tap, the pitches on both the bolt and in the nut will correspond, though neither may be theoretically true to the designated standard.
In some machines for nut tapping the tap is submerged in oil, and thus the error due to variations of temperature is practically eliminated, though even in this case the temperature of the oil will gradually increase, but not sufficiently to be of practical moment.
Let it now be noted that from the hardening process the taps shrink in length and become of finer pitch, while the dies expand and become of coarser pitch, and that this alone precludes the possibility of having the nut threads fit perfectly to those on the bolt. It becomes apparent, then, that only by cutting the threads in the lathe, and with a single-toothed lathe tool that can be ground to correct angle after hardening, can a bolt and nut be theoretically or accurately threaded. Under skilful operation, however, both in the manufacture of the screw-cutting tools and in their operation, a degree of accuracy can be obtained in tapped nuts and die-threaded bolts that is sufficient with a single nut for ordinary uses, but in situations in which the direction of pressure on the nut is periodically reversed, or in which it is subject to shocks or vibrations, the check nut becomes necessary, as before stated.
An excellent method of preventing a nut from slackening back of itself is shown in the safety nut in Fig. 414; it consists of a second nut having a finer thread than the first one, so that the motion of the first would in unscrewing exceed that of the second, hence the locking is effectually secured.
Work may be very securely fastened together by the employment of what are called differential screws, the principle of whose action may be explained with reference to Fig. 415, which is extracted from “Mechanics.” It represents a piston head and piston rod secured together by means of a differential screw nut. The nut contains an internal thread to screw on the rod, and an external one to screw into the piston head, but the internal thread and that on the rod differ from the external one, and that in the head by a certain amount, as say one tenth of the pitch. The nut itself is furnished with a hexagonal head, and when screwed into place draws the two parts together with the same power as a screw having a pitch equal to the difference between the two pitches.
When putting the parts together the nut is first screwed upon the rod b. The outside threads are then entered into the thread in the piston c, and by means of a suitable wrench the nut is screwed into the proper depth. As shown in the engraving, the nut goes on to the rod a couple of threads before it is entered in the piston. The tightening then takes place precisely as though the nut had a solid bearing on the piston and a fine thread on the rod, the pitch of which is equal to the difference between the pitches of the two threads. Fig. 416 shows its application to the securing of a pump plunger upon the end of a piston-rod. In this case, as the rod does not pass through the nut, the latter is provided with a cap, which covers the end of the rod entirely.
The principle of the differential screw may be employed to effect very fine adjustments in place of using a very fine thread, which would soon wear out or wear loose. Thus in Fig. 417 is shown the differential foot screws employed to level astronomical instruments. c d is a foot of the instrument to be levelled. It is threaded to receive screw a, which is in turn threaded to receive the screw b, whose foot rests in the recess or cup in e f. Suppose the pitch of screw a is 30 per inch, and that of b is 40, and we have as follows. If a and b are turned together the foot c d is moved the amount due to the pitch of a. If b is turned within a the foot is moved the amount due to the pitch of b. If a is turned the friction of the foot of b will hold b stationary, and the motion of c d will equal the difference between the pitches of the threads of a and b. Thus one revolution of a forward causes it to descend through c d 1⁄30 inch (its pitch), tending to raise c d [I-120]1⁄30 inch. But while doing this it has screwed down upon the thread of b 1⁄40 inch (the pitch of b) and this tends to lower c d, hence c d is moved 1⁄120 inch, because 1⁄30 - 1⁄40 = 1⁄120.
| VOL. I. | END‑ADJUSTMENT AND LOCKING DEVICES. | PLATE IV. | |||
 |
 |
 |
|||
| Fig. 418. | Fig. 419. | Fig. 420. | |||
 |
 |
 |
|||
| Fig. 421. | Fig. 422. | Fig. 423. | |||
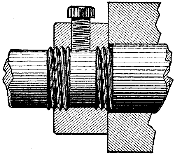 |
 |
 |
|||
| Fig. 424. | Fig. 425. | Fig. 426. | |||
 |
 |
||||
| Fig. 427. | Fig. 428. | ||||
To cause a single nut to lock itself and dispense with the second or jamb nut, various expedients have been employed. Thus in Fig. 418 is shown a nut split on one side; after being threaded the split is closed by hammer blows, appearing as shown in the detached nut. Upon screwing the nut upon the bolt the latter forces the split nut open again by thread pressure, and this pressure locks the nut. Now there will be considerable elasticity in the nut, so that if the thread compresses on its bearing area, this elasticity will take up the wear or compression and still cause the threads to bind. Sometimes a set screw is added to the split, as in Fig. 419, in which case the split need not be closed with the hammer.
Another method is to split the nut across the end as shown in Fig. 420, tapping the nut with the split open, then closing the split by hammer blows. Here as before the nut would pass easily upon the bolt until the bolt reached the split, when the subsequent threads would bind. In yet another design, shown in Fig. 421, four splits are made across the end, while the face of the nut is hollowed, so that a flat place near each corner meets the work surface. The pressure induced on these corners by screwing the nut home is relied on in this case to spring the nut, causing the thread at the split end to close upon and grip the bolt thread.
Check nuts are sometimes employed to lock in position a screw that is screwed into the work, thus screws that require to be operated to effect an adjustment of length (as in the case of eccentric rods and eccentric straps) are supplied with a check nut, the object being to firmly lock the screw in its adjusted position.
The following are forms of nuts employed to effect end adjustments of length, or to prevent end motion in spindles or shafts that rotate in bearings.
Fig. 422 shows two cylindrical check nuts, the inner one forming a flange for the bearing. The objection to this is that in screwing up the check nut the adjustment of the first nut is liable to become altered in screwing up the second one, notwithstanding that the first be held by a lever or wrench while the second is screwed home.
Another method is to insert a threaded feather in the adjustment nut and having at its back a set screw to hold the nut in its adjusted position, as in Fig. 423. In this case the protruding head of the set screw is objectionable. In place of the feather the thread of the spindle may be turned off and a simple set screw employed, as in Fig. 424; here again, however, the projecting set screw head is objectionable. The grip of an adjustment nut may be increased by splitting it and using a pinching or binding screw, as in Fig. 425, in which case the bore of the thread is closed by the screw, and the nut may be countersunk to obviate the objection of a projecting head. For adjusting the length of rods or spindles a split nut with binding screws, such as shown in Fig. 426, is an excellent and substantial device. The bore is threaded with a right-hand thread at one end and a left-hand one at the other, so that by rotating the nut the rod is lengthened or shortened according to the direction of rod rotation. Obviously a clamp nut of this class, but intended to take up lost motion or effect end adjustment, may be formed as in Fig. 427, but the projecting ears or screw are objectionable.
Where there is sufficient length to admit it an adjustment nut, such as in Fig. 428, is a substantial arrangement. The nut a is threaded on the spindle and has a taper threaded split nut to receive the nut b. Nut a effects the end adjustment by screwing upon the spindle, and is additionally locked thereon by screwing b up the taper split nut, causing it to close upon and grip the spindle.
Lost motion in square threads and nuts may be taken up by forming the nut in two halves, a and b, in Fig. 429 (a being shown in section) and securing them together by the screws c c. The lost motion is taken up by letting the two halves together by filing away the joint face d of either half, causing the thread in the nut to bear against one side only of the thread of the screw. The same end may be accomplished in nuts for V-shaped threads by forming the nut either in two halves, as shown in Fig. 430, in which a is a cap secured by screws b, the joint face c being filed away to take up the lost motion. Or the nut may be in one piece with the joint c left open, the screws b crossing the nut upon the screw by pressure. In this case the nut closes upon the circumference of the thread, taking up the wear by closing upon both sides of the thread instead of on one side only as in the case of the square thread.
In cases where nuts are placed under rapid vibration or motion they are sometimes detained in their places by pins or cotters. The simplest form of pin used for this purpose is the split pin, shown in Fig. 431. It is made from half round wire and is parallel, and does not, therefore, possess the capability of being tightened when the nut has become loosened from wear. As the wire from which these pins are made is not usually a full half circle the pins should, if the best results are to be obtained, be filed to fit the hole, and in doing this, care should be taken to have the pin bear fully in the direction of the split which is longitudinal to the bolt, as shown in Fig. 432, where the pin is shown with its ends opened out as is required to prevent the pin from coming out. If the pin bears in a direction across the bolt as at a d, in Fig. 433, it will soon become loose.
Pins of this class are sometimes passed through the nut itself[I-121] as well as through the bolt; but when this is the case, there is the objection that the nut cannot be screwed up to take up any wear, because in that case the hole in the nut would not come fair with that in the bolt, and the pin could not be inserted. When, therefore, such a pin passes through the nut, lost motion must be taken up by placing an additional or a thicker washer behind the nut. The efficiency of this pin as a locking device is much increased by passing it through the nut, because its bearing, and, therefore, wearing area, is increased, and the pin is prevented from bending after the manner shown in Fig. 434, as it is apt to do under excessive wear, with the result that the end pressure of the nut almost shears or severs the pin close to the perimeter of the bolt.
To enable the pin to take up the wear, it is a good plan to file on it a flat place, which must be parallel to the sides of the pin-head and placed against the nut-face. The hole in the bolt is in this case made to fall slightly under the nut, as in Fig. 435, so that the flat place is necessary to enable the pin to enter. By filing the flat place taper, the lost motion that may ensue from wear may be taken up by simply driving the pin in farther.
In place of this class of split pin, solid taper pins are sometimes used, but these, if employed in situations where they are subject to jar and vibration, are apt sometimes to come loose, especially if they be given much taper, because in that case they do not wedge so tightly in the hole. But if a taper pin be made too nearly parallel, it will drive through too easily, and has less capability to take up the play due to wear. An ordinary degree of taper is about 5⁄8 inch per foot of length, but in long pins having ample bearing area, 1⁄2 inch per foot of length is ample. To prevent taper pins from coming loose from vibration, they are sometimes forged split at the small end, as in Fig. 436, and opened out at that end after the manner shown in Fig. 432. This forms a very secure locking device, and one easily applied. The split ends are closed by hammer blows to remove the pin, and it is found that such pins may be opened and closed many times without breaking, even though made of cast steel. The heads and ends are rounded so as to prevent them from swelling from the hammer blows necessary to drive them in and out. When a taper pin is passed through a nut and bolt, it simply serves as a locking device to secure the nut in position, and the lost motion due to wear must be taken up by the application of a washer beneath the nut, as already described. If, however, the taper pin be applied outside the nut, it may be made to take up the wear, by filing on it a flat place, and locating the hole in the bolt so that it will fall partly beneath the nut, as shown in Fig. 435. In this case, the nut may be screwed up to take up the wear, and the pin by being driven farther in will still bear against the nut and prevent its slacking back.
Another and excellent locking device for bolts or nuts, is the cotter shown in Fig. 437, which is sometimes forged solid and sometimes split, as in the figure. By being made taper from a to b, it will take up the wear if driven farther in. Its width gives it strength in the direction in which it acts to lock, the overhanging head is to drive it out by, and the bevelled corner c is to enable its easy insertion, because if left sharp it would be liable to catch against the edge of the cotter-way and burr up. If made split, its ends are opened out after it is inserted, as shown at d. When closing the ends of either split cotters or split pins to extract them it is better to close one side first and bend it over a trifle too much, so that, when closing the other side, by the time the pin is straightened the two ends will be closed together, and extraction becomes easy.
A very safe method in the case of a single nut or bolt head is to provide a separate plate, as in Fig. 438. The plate p is provided with three sides, corresponding to the sides of the hexagon, as shown, and in the middle of these sides are cut the notches a b c, so that by giving the nut n one-twelfth of a turn its corners d e would be held by the notches b c, s being a small screw to hold p. It is obvious that a simple set screw passed through the walls of the nut would grip the bolt thread and serve to hold the nut, but this would damage the bolt thread, and, furthermore, that thread would under jar or vibration compress and let the set screw come loose.
A better plan than this is to provide a thick washer beneath the nut and let a set screw pass through the washer and grip the bolt, fastening or setting up the set screw after the nut is screwed home. This, however, makes the washer a gripping piece and in no wise serves to lock the nut. In addition to the washer a pin may project through the radial face of the washer and into the work surface, which will prevent, in connection with the set screw, both the bolt and the washer from turning.
When a bolt has no thread but is secured by a taper pin, set screw, cotter, or device other than a nut, it is termed a pin. So, likewise, a cylindrical piece serving as a pivot, or to hold two pieces together and having no head, is termed a pin.
The usual method of securing a pin is by a set screw or by a taper pin and a washer; and since the term pin applying to both may lead to misunderstanding, the term bolt will here be applied to the large and the term pin to the small or securing pin only.
The object of pins and washers is to secure an exact degree of fit and permit of rapid connection or disconnection. An application of a taper pin and washer to a double eye is shown in Fig. 439. It is obvious, in this case, the pin e will drive home until it fills the hole through the bolt, and hence always to the same spot, so that the parts may be taken apart and put together again rapidly, while the fit is self-adjusting, providing that the pin fills the hole, bears upon the groove in the washer, and is driven home, so that by first letting the pin bind the washer w slightly too tight, and then filing the radial faces of the joint to a proper fit (which will ease the bearing of the pin on the washer), an exact degree of fit and great accuracy may be obtained, whereas when a nut is used it is difficult to bring the nut to the exact same position when screwing it home. When the joints are to be thus fitted, it is a good plan to drill the pin-hole (through[I-122] the bolt) so that its centre falls coincident with the face of the washer; to then file out the grooves in the washer not quite deep enough. The pin may then be filed to fit the hole through the bolt, but left slightly too large, so that it shall not pass quite far enough through the bolt. The joint faces may then be filed true, and when finished, the parts may be put together, and the groove through the washer and hole through the bolt may be simultaneously finished by reaming with a taper reamer. This will leave the job a good fit, with a full bearing, without much trouble, the final reaming letting the taper pin pass to its proper distance through the bolt.
Taper pins are sometimes employed to secure in position a bolt that rotates, or one that requires locking in position, in situations in which there is no room for the bolt end to project and receive a nut or washer. Examples of these kinds are shown in section in Figs. 440 and 441. In 441, b is a stud pin, to rotate in the bore of a. c is a semi circular groove in b, and p a taper pin entering one-half in the groove c and one-half in b, thus preventing b from moving endwise in a, while at the same time permitting its free rotation. In this case it is best to fit b to its place, a fit tight enough to hold it firmly while the pin-hole is drilled and reamed through a and b simultaneously, then b can be put in the lathe, and the groove cut in to coincide with the half-hole or groove caused in the pin by the drilling, and after the groove is turned the stud pin may be eased to the required degree of working fit. The process for Fig. 440 is precisely the same, except that no groove turning or easing of the pin will be necessary, because the pin being locked in position may be left a tight fit. If, however, it is considered desirable to give the taper pin in Fig. 440 a little draft, so that any looseness (that may occur to the pin or stud) from wear may be taken up, then after the taper pin-hole has been drilled and reamed, the pin or stud (d in the figure) may be taken out, and its taper pin-hole in the arm e may be filed out all the way through on one side, as denoted by the dotted half-circle. This will give draft to the pin and allow it to drive farther through and grip the pin as it wears smaller.
If a bolt and nut fit too tightly in their threads the nut may be wound back and forth upon the bolt under free lubrication, which will ease the fit by wearing away or compressing that part of the thread surface that is in contact. If this should not suffice we may generally ease a nut that fits so tight that it cannot be screwed upon the bolt with an ordinary wrench, by screwing the nut on a thread or two, then rest it on an iron block, and lightly hammer its sides; it will loosen its fit, and if continued, the nut may be made to pass down the bolt comparatively easily. Now, in this operation, it is not that the nut has been stretched, but that the points of contact on the threads have become compressed and imbedded; we have, in other words, caused the shape of each thread to conform nearer to that of the other than it is practicable to make them, because of reasons explained in the remarks on screw threads, and on taps.
To remove nuts or bolts that have become corroded in their places, we may adopt the following methods:—
If the nuts are so corroded that they will not unscrew with an ordinary wrench, we may, if the standing bolts and the wrench are strong enough to stand it, place a piece of gas or other pipe on the end of the wrench, so as to get a longer leverage; and, while applying the power to the wrench, we may strike the end face of the nut a few sharp blows with the hammer, interposing a set chisel, if the nut is a small one, so as to be sure to strike the nut in the proper place, and not rivet the screw end. If the joint is made with tap bolts we may strike the bolt heads with the hammer direct, using as before a light hammer and sharp blows, which will, in a majority of cases, start the thread, after which the wrench alone will usually suffice to unscrew it. If, however, this is not effective, we should take a thick washer, large enough in its bore to pass over the nut, and heat it to a yellow heat and place it over the nut, and the nut heating more rapidly than the stud or standing bolt, will be proportionately expanded and loosened; and, furthermore, the iron becomes stronger by being heated, providing the temperature does not exceed about 400°. If standing bolts or studs are employed on the joint, the heating is still advantageous, for the increase of strength more than compensates for the expansion. In this case the heating, however, may be performed more slowly, so that the hole may also become heated, and the bolt, therefore, not made a tighter fit by its excessive expansion. So also, in taking out the standing bolts or studs, heating them will often enable one to extract them without breaking them off in the hole, which would necessitate drilling out the broken piece or part. If, however, this should become necessary, we may drill a hole a little smaller than the diameter of the bottom of the bolt thread, and then drive into the hole a taper square reamer, as shown in Fig. 442, in which w represents the work, r the square reamer, and s the drilled screw end, and then, with a wrench applied to the reamer, unscrew the bolt thread. If this plan fails there is no alternative, after drilling the hole, but to take a round-nosed cape or cross-cut chisel and cut out the screw as nearly as possible, then pick out the thread at the entrance of the hole, and insert a plug tap to cut out the remaining bolt thread.
To take out a standing bolt, take two nuts and screw them on the bolt end; then hold the outer one still with a wrench and[I-123] unscrew the inner one tightly against it. We may then remove the wrench from the outer or top nut, and unscrew the bolt by a wrench applied to the bottom or inner one. If the thread of a standing bolt has become damaged or burred, we can easily correct the evil by screwing a solid die or die nut down it, applying a little oil to preserve the cutting edge of the nut. If it is found impossible to take off a corroded nut without twisting off the standing bolt, it is the better plan to sacrifice the nut in order to save the bolt; and we may first hold a hammer beneath the nut, and take a cold chisel, and holding it so that the cutting edge stands parallel with the chamfered edge of the nut, and slanting it at an angle obtuse to the direction in which the nut in unscrewing would travel, strike it a few sharp blows, using a light hand-hammer; and this will often start it, especially if the nut is heated as before directed. The hammer held beneath the nut should be a heavy one, and should be pressed firmly against the square or hexagon side of the nut, the object being to support it, and thus prevent the standing bolt from bending or breaking, as it would otherwise be very apt to do. If this plan succeeds, the nut may, for rough work, be used over again, the burr raised by the chisel head being hammered down to close it as much as possible before filing it off. By holding the chisel precisely as directed, the seating of the nut acts to support it, and thus aids the heavy hammer in its duty. If this procedure fails we may cut the nut off, and thus preserve the bolt.
To do this, we must use a cross-cut or cape chisel, and cut a groove from the end face to the seating of the nut—a narrow groove will do, and two may be cut if necessary; light cuts should be taken, and the chisel should be ground at a keen angle, so that it will keep to its cut when held at an angle, as nearly parallel to the centre line of the length of the bolt as possible, in which case the force of the blows delivered upon the chisel head will be in a direction not so liable to bend the bolt. The groove or grooves should be cut down nearly to the tops of the bolt threads, and then a wrench will unscrew the nut or else cause it to open if one, and break in halves, if two grooves were cut.
After the nuts are all taken off, we may take a hammer and two or three wedges, or chisels (according to the size of the joint), and drive them an equal distance into the joint, striking one chisel first, and the diametrically opposite one next, and going over all the wedges to keep an equal strain upon each. If the joint resists this method, we may take a hammer and strike blows between the standing bolts on the outside face, interposing a block of hard wood to prevent damage to the face, and holding the wood so that the hammer strikes it endwise of the grain; and this will, in most cases, loosen the material of which the joint is made, and break the joint. If, however, the joint, after repeated trials, still resists, we may employ the hammer without the interposition of the wood, using a copper or lead hammer, if one is at hand, so as not to cause damage to the face of the work. To facilitate the entrance of the wedges, grooves should be cut in the joint of one face, their widths being about an inch, and their depth 1⁄16 inch.
Washers.—Washers are placed upon bolts for the following purposes. First, to provide a smooth seating for the nut in the case of rough castings. Second, to prevent the nut corners from marking and marring the surface of finished work. Thirdly, to give a neat finish, and in some cases to increase the bearing area of the nut and provide an elastic cushion to prevent the nut from loosening. Washers are usually of wrought iron, except in the case of brass nuts, when the washers also are of brass. The standard sizes adopted by the manufacturers in the United States for wrought iron washers is given in the following table:—
Adopted by “The Association of Bolt and Nut Manufacturers of the
United States,” at their meeting in New York, December 11th, 1872.
| Diameter. | Size of Hole. |
Thickness Wire Gauge. |
Size of Bolt. |
||||
| 1⁄2 | 1⁄4 | No. | 18 | 3⁄16 | |||
| 5⁄8 | 5⁄16 | „ | 16 | 1⁄4 | |||
| 3⁄4 | 5⁄16 | „ | 16 | 1⁄4 | |||
| 7⁄8 | 3⁄8 | „ | 16 | 5⁄16 | |||
| 1 | 7⁄16 | „ | 14 | 3⁄8 | |||
| 1 | 1⁄4 | 1⁄2 | „ | 14 | 7⁄16 | ||
| 1 | 3⁄8 | 9⁄16 | „ | 12 | 1⁄2 | ||
| 1 | 1⁄2 | 5⁄8 | „ | 12 | 9⁄16 | ||
| 1 | 3⁄4 | 11⁄16 | „ | 10 | 5⁄8 | ||
| 2 | 13⁄16 | „ | 10 | 3⁄4 | |||
| 2 | 1⁄4 | 15⁄16 | „ | 9 | 7⁄8 | ||
| 2 | 1⁄2 | 1 | 1⁄16 | „ | 9 | 1 | |
| 2 | 3⁄4 | 1 | 1⁄4 | „ | 9 | 1 | 1⁄8 |
| 3 | 1 | 3⁄8 | „ | 9 | 1 | 1⁄4 | |
| 3 | 1⁄2 | 1 | 1⁄2 | „ | 9 | 1 | 3⁄8 |
The various forms of wrenches employed to screw nuts home or to remove them are represented in the following figures. Fig. 443 represents what is known as a solid wrench, the width between the jaws a being an easy fit to the nuts across the flats. The opening between the jaws being at an angle to the body enables the wrench to be employed in a corner which would be too confined to receive a wrench in which the handle stood in a line with the[I-124] jaws, because in that common form of wrench the position of the jaws relative to the handle would be the same whether the wrench be turned over or not, whereas with the jaws at an angle as in the figure, the wrench may be applied to the nut, rotating it a certain distance until its handle meet an abutting piece, flange, or other obstruction, and then turned over and the jaw embracing the same two sides of the nut the handle will be out of the way and may again operate the nut.
In some cases each end of the wrench is provided with jaws, those at one end standing at the same angle but being on the opposite side of the wrench.
The proper angle of the jaws to the centre line of the jaws may be determined as follows:—The most desirable angle is that which will enable the wrench to operate the nut with the least amount of wrench-motion, an object that is of great importance in cases where an opening has to be provided to admit the wrench to the nut, it being desirable to leave this opening as small as possible so as to impair the solidity of the work as little as practicable. For a hexagon nut this angle may be shown to be one of 15°, as in Fig. 444.
In Fig. 445, for example, the wrench is shown in the position in which it will just engage the nut, and at the first movement it will move the nut to the position shown in Fig. 446. The wrench is then turned upside down and placed upon the nut as in Fig. 447, and moved to the position shown in Fig. 448, thus moving the nut the sixth part of a revolution, and bringing it to a position corresponding to that in Fig. 445, except that it has moved the nut around to a distance equal to one of its sides. Since the wrench has been moved twice to move the nut this distance, and since there are six sides, it will take twelve movements to give the nut a full revolution, and, there being 360° in the circle, each movement will move the nut 30°, or one-twelfth of 360°, and one-half of this must be the angle of the gripping faces of the jaws to the body of the wrench. The width of the opening in the work to admit the wrench in such a case as in Fig. 445 must be not less than 30°, plus the width of the wrench handle, at the radius of the outer corner of the opening.
In the case of wrenches for square nuts it is similarly obvious that when the nut makes one-eighth of a revolution its sides will stand in the same position to receive the wrench that the nut started from, and in one-eighth of a revolution there are 45°. As the wrench is applied twice to the same side of the nut, its jaws must stand at one half this angle (or 221⁄2°) to the handle.
When a nut is in such a position that it can only be operated upon from the direction of and in a line with the axis of the bolt, a box wrench such as shown in Fig. 449, is employed, the cavity[I-125] at b fitting over the bolt head; but if there is no room to admit the cross handle, a hub or boss is employed instead, and this hub is pierced with four radial holes into which the point of a round lever may be inserted to turn the wrench. Adjustable wrenches that may be opened and closed to suit the varying sizes of nuts are represented in Figs. 450, 451, and 452. In Fig. 450, a is the fixed jaw solid upon the square or rectangular bar e, and passing through the wooden handle d. b is a sliding jaw embracing e, and operated thereon by the screw c, whose head is serrated to afford a good finger grip. Various modifications of this form of wrench are made; thus, for example, in Fig. 451 a is the jaw, b a slotted shank, c the handle, all made in one piece. d is the movable jaw having a sleeve extension d′, and recesses which permit the jaw to slide on the shank longitudinally, but which prevent it from turning. The movable jaw is run to and from the nut or bolt head to be turned, by means of the screw g.
In another class of adjustable wrench the jaws slide one within the other; thus in Fig. 452, the fixed jaw of the wrench forms a part of the handle, and is hollowed out and slotted to receive the stem of the loose jaw, which plays therein, being guided by ribs in the slot, which take into grooves in the stem of the loose jaw. A screw with a milled head and a grooved neck serves to propel the loose jaw, being stopped from moving longitudinally by a partly open fixed collar on the fixed jaw, which admits the screw and engages the grooved neck of the same. The threaded extremity of the screw engages a female screw in the loose jaw, and while the same are engaged the screw cannot be released from the embrace of the fixed collar, as it requires considerable lateral movement to accomplish this.
Adjustable wrenches are not suited for heavy work because the jaws are liable to spring open under heavy pressure and thus cause damage to the edges of finished nuts, and indeed these wrenches are not suitable for ordinary use on finely finished work unless the duty be light. Furthermore, the jaws being of larger size than the jaws of solid wrenches, will not pass so readily into corners, as may be seen from the S wrench shown in Fig. 453. In the adjustable S wrench in Fig. 454, each half is provided with a groove at one end and a tongue in the other, so that when put together the tongues are detained in the grooves. To open or close the wrench a right and left-hand screw is tapped into the wrench as shown, the head being knurled or milled to afford increased finger-grip.
In all wrenches the location of contact and of pressure on the nut is mainly at the corners of the nut, and unless the wrench be a very close fit, the nut corners become damaged. A common method of avoiding this is to interpose between the wrench jaw and the nut a piece of soft metal, as copper, sheet zinc, or even a piece of leather. The jaws of the wrench are also formed to receive babbitt metal linings which may be renewed as often as required. To save the trouble of adjusting an accurately fitting wrench to the nut, Professor Sweet forms the jaws as in Fig. 455, so that when moved in one direction the jaws will pass around the nut without gripping it, but when moved in the opposite direction the jaws will grip the nut but not damage the corners, while to change the direction of a nut rotation it is simply necessary to turn the wrench over.
Fig. 456 represents a key wrench which is suitable for nuts of very large size. The sliding jaw j is held by the key or wedge s, which is operated by hammer blows. The projection at r is necessary to give sufficient bearing to the sliding jaw.
For use in confined places where but little handle-motion is obtainable, the ratchet wrench is employed, consisting of a lever affording journal bearing to a socket that fits the head of the bolt. The socket is provided with a ratchet or toothed wheel in which a catch or pawl engages. Fig. 457 represents the Lowell Wrench Company’s ratchet wrench in which a lag screw socket is shown affixed. The socket is removable so that various sizes and shapes may be used with the same wrench. Each socket takes two sizes of square and one of hexagon heads or nuts. So long as the screw runs easily, it can be turned by the wooden handle more conveniently and faster than by the fingers, and independently of the ratchet motion. When this can no longer be done with ease, the twelve-inch handle is brought into use to turn the screw home.
For carriage bolts used in woodwork that turn with the nut notwithstanding the square under the head (as they are apt to do from decay of the wood or from the bolt gradually working loose) the form of wrench shown in Fig. 458 is exceedingly useful, it is[I-126] driven into the wood by hammer blows at a. The bevelled edges cause the jaws to close upon the head in addition to the handle-pressure.
For circular nuts such as was shown in Fig. 411, the pin wrench or spanner wrench shown in Fig. 459 is employed, the pin p fitting into the holes in the nut circumference. The pin p should be parallel and slope very slightly in the direction of a, so that it may not meet and bruise the mouths of the pin-holes, a, b, c. The pin must, of course, pass easily into the pin-holes, and would, if vertical, therefore meet the edge of the hole at the top, bruising it and causing the wrench to spring or slip out, as would be the case if the pin stood in the direction of b.
It is obvious that to reverse the motion of the nut it is necessary to reverse the position of the wrench, because the handle end must, to enable the wrench to grip the work, travel in advance of the pin end. To avoid this necessity Professor Sweet forms the wrench as in Fig. 460, in which case it can operate on the nut in either direction without being reversed.
When a circular nut has its circumference provided with notches as was shown in Fig. 412 the wrench is provided with a rectangular piece as shown in Fig. 461. This piece should slope in the direction of a for the reasons already explained with reference to the cylindrical pin in Fig. 459. It is obvious, however, that this wrench also may be made upon Professor Sweet’s plan, in which case the pin should be straight.
Keys and Keyways.—Keys and keyways are employed for two purposes—for locking permanently in a fixed position, and for locking and adjusting at the same time. Keys that simply permanently lock are usually simply embedded in the work, while those that adjust the parts and secure them in their adjusted position usually pass entirely through the work. The first are termed sunk keys and keyways, the latter adjusting keys and through keyways.
The usual forms of sunk keyways are as follows:—Fig. 462 represents the common sunk key, the head h forming a gib for use in extracting the key, which is done by driving a wedge between the head and the hub of the work.
The flat key, sunk key, and feather shown in Fig. 463, are alike of rectangular form, their differences being in their respective thicknesses, which is varied to meet the form of key way which receives them. The flat key beds upon a flat place upon the shaft, the sunk key beds in a recess provided in the shaft, and the feather is fastened permanently in position in the shaft. The hollow key is employed in places where the wheel or pulley may require moving occasionally on the shaft, and it is undesirable that the latter have any flat place upon it or recess cut in it. The flat key is used where it is necessary to secure the wheel more firmly without weakening the shaft by cutting a keyway in it. The sunk key is that most commonly used; it is employed in all cases where the strain upon the parts is great. The feather is used in cases where the keyway extends along the shaft beyond the pulley or wheel, the feather being fast in the wheel, and its protruding part a working fit in the shaft keyway. This permits the wheel to be moved along the shaft while being driven through the medium of the feather along the keyway or spline. The heads of the taper keys are sometimes provided with a set screw as in Fig. 464, which may be screwed in to assist in extracting the key.
Fig. 465 represents an application of keys to a square shaft that has not been planed true. The wheel is hung upon the shaft and four temporary gib-headed keys are inserted in the spaces a, a, a, a, in Fig. 465. (It may be mentioned here that similar heads are generally forged upon keys to facilitate their withdrawal while fitting them to their seats, the heads being cut off after the key is finally driven home.) These sustain the wheel while the permanent keys, eight in number, as shown in the figure at b, b, b, b, b, b, b, b, are fitted, the wheel being rotated and tested for truth from a fixed point, the fitting of the keys being made subservient to making the wheel run true.
The proportions of sunk keys are thus given by the Manchester[I-127] (England) rule. The key is square in cross section and its width or depth is obtained by subtracting 1⁄2 from the diameter of the shaft and dividing the sum thus obtained by 8, and then adding to the subtrahend 1⁄4.
Example.—A shaft is 6 inches in diameter, what should be the cross section dimensions of its key diameter of shaft?
6 - 1⁄2 = 51⁄2, 51⁄2 ÷ 8 = .687, and .687 + .25 = 937⁄1000 inch.
In general practice, however, the width of a key is made slightly greater than its depth, and one-half its depth should be sunk in the shaft.
Taper keys are tapered on their surfaces a and b in Fig. 466, and are usually given 1⁄8-inch taper per foot of length. There is a tendency either in a key or a set screw to force the hub out of true in the direction of the arrow. It therefore causes the hub bore to grip the shaft, and this gives a driving duty more efficient than the friction of the key itself. But the sides also of the key being a sliding fit they perform driving duty in the same manner as a feather which fits on the sides a, d in Fig. 467, but are clear either top or bottom. In the figure the feather is supposed to be fast in the hub and therefore free at c, but were it fast in the shaft it would be free on the top face.
Fig. 468 represents a shaft held by a single set screw, the strain being in the direction of the arrow, hence the driving duty is performed by the end of the set screw and the opposite half circumference of the bore and shaft. On account, however, of the small area of surface of the set screw point the metal of the shaft is apt, under heavy duty and when the direction of shaft rotation is periodically reversed, to compress (as will also the set screw point unless it is of steel and hardened), permitting the grip to become partly released no matter how tightly the set screw be screwed home. On this account a taper key will under a given amount of strain upon the hub perform more driving duty, because the increased area of contact prevents compression. Furthermore, the taper key will not become loose even though it suffer an equal amount of compression. Suppose, for example, that a key be driven lightly to a fair seating, then all the rest of the distance to which the key is driven home causes the hub to stretch as it were, and even though the metal of the key were to compress, the elasticity thus induced would take up the compression, preventing the key from coming loose. It is obvious, then, that set screws are suitable for light duty only, and keys for either heavy or light duty. It is advanced by some authorities that keys are more apt to cause a wheel or pulley to run out of true than a set screw, but such is not the case, because, as shown in Figs. 466 and 468, both of them tend to throw the wheel out of true in one direction; but a key may be made with proper fitting to cause a wheel to run true that would not run true if held by a set screw, as is explained in the directions for fitting keys given in examples in vice work.
If two set screws be used they should both be in the same line (parallel to the shaft axis) or else at a right angle one to the other as in Fig. 469, so that the shaft and bore may drive by frictional contact on the side opposite to the screws. Theoretically the contact of their surface will be at a point only, but on account of the elasticity of the metal the contact will spread around the bore in the arc of a circle, the length of the arc depending upon the closeness of fit between the pulley bore and the shaft. If the bore is a close fit to the shaft it is by reason of the elasticity of the metal relieved of contact pressure on the side on which the set screw or key is to an amount depending upon the closeness of the bore fit, but this will not in a bore or driving fit to the shaft be sufficient to set the wheel out of true.
If two set screws are placed diametrally opposite they will drive by the contact of their ends only, and not by reason of their inducing frictional contact between the bore and the shaft.
A very true method of securing a hub to a shaft is to bore it larger than the shaft and to a taper of one inch to the foot. A bushing is then bored to fit the shaft and turned to the same taper as the hub is turned, but left, say, 1⁄100 inch larger in diameter and 1⁄4 or 3⁄8 longer. The bush is then cut into three pieces and these pieces are driven in the same as keys, but care must be taken to drive them equally to keep the hub true.
Feathers are used under the following conditions:—When the wheel driven by a shaft requires to slide along the shaft during its rotation, in which case the feather is fast in the wheel and the shaft is provided with a keyway or spline (as it is termed when the sliding action takes place), of the necessary length, the sides of the feather being a close but sliding fit in the spline while fixed fast in the wheel.
It is obvious that the feather might extend along the shaft to the requisite distance and the spline or keyway be made in the wheel: but in this case the work is greater, because the shaft would still require grooving to receive the feather, and the feather instead of being the simple width of the wheel would require to be the width of the wheel longer than the traverse of the wheel on the shaft. Nor would this method be any more durable, because the keyway’s bearing length would be equal to the width of the wheel only.
When a feather is used to enable the easy movement of a wheel from one position to another a set screw may be used to fix the wheel in position through the medium of the feather as is shown in Fig. 470.
Through keys and keyways are employed to lock two pieces, and sometimes to enable the taking up of the wear of the parts. Fig. 471 represents an example in which the key is used to lock a taper shaft end into a socket by means of a key passing through both of them. When the keyway is completely filled by the key as in the figure it is termed a solid key and keyway, indicating that there is no draft to the keyway. Fig. 472 represents a key and keyway having draft. One edge, a c, of the key binds against the socket edges only, and the other edge e binds against the edge b of the enveloped piece or plug, so that by driving in the key with a hammer the two parts are forced together. The space or distance between the edge d and the key, and between edges e and f, is termed the draft. The amount of this draft is made equal to the taper of the key, hence, when the key is driven[I-128] in so that its head comes level with the socket or work surface, the draft will be all taken up and the key will fill the keyway.
Draft is given to ensure all the strain of the key forcing the parts together, to enable the key to be driven in to take up any wear and to adjust movable parts, as straps, journal boxes or brasses, &c. When the bore of the socket and the end of the rod are parallel, the end of the rod f, Fig. 473, should key firmly against the end e of the socket, while the end d of the socket should be clear of the shoulder on the rod; otherwise instead of the key merely compressing the metal at f it will exert a force tending to burst the end f from g of the rod, furthermore, the area of contact at the shoulder d being small the metal would be apt to compress and the key would soon come loose.
In some cases two keys are employed passing through a sleeve, the arrangement being termed a coupling, or a butt coupling.
The usual proportions for this class of key, when the rod ends and socket boxes are parallel, is width of key equals diameter of socket bore, thickness of key equals one-fourth its width, with a taper edgeways of about 1⁄4 inch in 10 inches of length.
As the keys in through keyways often require to be driven in very tight, and as the parts keyed together often remain a long time without being taken apart and in some situations become rusted together, it is often a difficult matter to get them apart. First, it is difficult to drive it out because the blows swell the end of the key so that it cannot pass through the keyway, and secondly, driving the socket off the plug of the two parts keyed together often damages the socket and may bend the rod to which it is keyed. Furthermore, as the diameter of the socket is usually not more than half as much again as the diameter of the plug, misdirected blows are apt to fall upon the rod instead of upon the socket end and damage it. Hence, a piece of copper, of lead, or a block of wood should always be placed against the socket end to receive the hammer blows. To force a plug out of a socket, we may use reverse keys. These are pieces formed as shown in Fig. 474. a, a and b, b are edge and face views respectively of two pieces of metal, formed as shown, which are inserted in the keyway as shown in Fig. 475, in which a is the plug or taper end of a rod and b the socket, c is one and d the other of the reverse keys, while e is a taper key inserted between them, b driving e through the keyway, a and b are forced apart. The action of the reverse keys is simply to reverse the direction of the draft in the keyway so that the pressure due to driving e through the keyway is brought to bear upon the rod end in the part that was previously the draft side of the keyway, and in like manner upon the keyway in the socket on the side that previously served as draft.
Reverse keys are especially serviceable to take off cross heads, piston heads, keyed crank-pins, and parts that are keyed very firmly together.
Hubs are sometimes fastened to their shafts by pins passing through both the hub and the shaft. These pieces may be made parallel or taper, but the latter obviously secures the most firmly. If the pin is located as in Fig. 476, its resisting strength is that due to its cross sectional area at a and b. But if the pin be located as in Fig. 477 it secures the hub more firmly, because it draws the bore (on the side opposite to the pin) against the shaft, causing a certain amount of friction, and, furthermore, the area resisting the pressure of the hub is increased, and that pressure is to a certain degree in a crushing as well as a shearing direction.
If unturned pins are used and the holes are rough or drilled but not reamed, it is better that two sides of the pin should be eased off with a file or on the emery wheel, so that all the locking pressure of the pin shall fall where it is the most important that it should—that is, where it performs locking duty. This is shown in Fig. 478, the hole being round and the pin being very slightly oval (not, of course, so much as shown in the drawing), so that it will bind at a b, and just escape touching at c, d, so that all the pressure of contact is in the direction to bind the hub to the shaft.
The lathe may be justly termed the most important of all metal-cutting machine tools. Not only on account of the rapidity of its execution which is due to its cutting continuously while many others cut intermittently, but also because of the great variety of the duty it will perform to advantage. In the general operations of the lathe, drilling, boring, reaming, and other processes corresponding to those performed by the drilling machine, are executed, while many operations usually performed by the planing machine, or planer as it is sometimes termed, may be so efficiently performed by the lathe that it sometimes becomes a matter of consideration whether the lathe or the planer is the best machine to use for the purpose.
The forms of cutting tools employed in the planer, drilling machine, shaping machine, and boring machine, are all to be found among lathe tools, while the work-holding devices employed on lathe work include, substantially, very nearly all those employed on all other machines and, in addition, a great many that are peculiar to itself. In former times, and in England even at the present day, an efficient turner (as a lathe operator is termed), or lathe hand, is deemed capable of skilfully operating a planer, boring machine, screw-cutting machine, drilling machine, or any of the ordinary machine tools, whereas those who have learned to operate any or all of those machine tools would prove altogether inefficient if put to operate a lathe.
In almost all the mechanic arts the lathe in some form or other is to be found, varying in weight from the jewellers’ lathe of a few pounds to the pulley or fly-wheel lathe of the engine builder, weighing many tons.
The lathe is the oldest of machine tools and exists in a greater variety of forms than any other machine tool. Fig. 479 represents a lathe of primitive construction actually in use at the present day, and concerning which the “Engineering” of London (England), says, “At the Vienna Exhibition there were exhibited wood, glasses, bottles, vases, &c., made by the Hucules, the remnant of an old Asiatic nation which had settled at the time of the general migration of nations in the remotest parts of Galicia, in the dense forests of the Carpathian Mountains. The lathe they are using has been employed by them from time immemorial. They make the cones b, b (of maple) serve as centres, one being fixed and the other movable (longitudinally). They rough out the work with a hatchet, making one end a cylindrical, to receive the rope for giving rotary motion. The cross-bar d is fastened to the trees so as to form a rest for the cutting tool, which consists of a chisel.” c, of course, is the treadle, the lathe or pole being a sapling.
In other forms of ancient lathes a wooden frame was made to receive the work-centres, and one of these centres was carried in a block capable of adjustment along the frame to suit different lengths of work. In place of a sapling a pole or lath was employed, and from this lath is probably derived the term lathe.
It is obvious, however, that with such a lathe no cutting operation can be performed while the work is rotating backwards, and further, that during the period of rest of the cutting tool it is liable to move and not meet the cut properly when the direction of work rotation is reversed and cutting recommences, hence the operation is crude in the extreme, being merely mentioned as a curiosity.
The various forms in which the lathe appears in ordinary machine shop manipulation may be classified as follows:—
The foot lathe, signifying that the lathe is driven by foot.
The hand lathe, denoting that the cutting tools must be held in the hands, there being no tool-carrying or feeding device on the lathe.
The single-geared lathe, signifying that it has no gear-wheels to reduce the speed of rotation of the live spindle from that of the cone.
The back-geared lathe, in which gear-wheels at the back of the headstock are employed to reduce the speed of the lathe.
The self-acting lathe, or engine lathe, implying that there is a slide rest actuated automatically to traverse the tool to its cut or feed.
The screw-cutting lathe, which is provided with a lead screw, by means of which other screws may be cut.
The screw-cutting lathe with independent feed, which denotes that the lathe has two feed motions, one for cutting threads and another for ordinary tool feeding; and
The chucking lathe, which implies that the lathe has a face plate of larger diameter than usual, and that the bed is somewhat short, so as to adapt it mainly to work held by being chucked, that is to say, held by other means than between the lathe centres.
There are other special applications of the lathe, as the boring lathe, the grinding lathe, the lathe for irregular forms, &c., &c.
This classification, however, merely indicates the nature of the lathe with reference to the individual feature indicated in the title; thus, although a foot lathe is one run by foot, yet it may be a single or double gear (back-geared) lathe, or a hand or self-acting lathe, with lead screw and independent feed motion.
Again, a hand lathe may have a hand slide rest, and in that case it may also be a back-geared lathe, and a back-geared lathe may have a hand slide rest or a self-acting feed motion or motions.
Fig. 480 represents a simple form of foot lathe. The office of the shears or bed is to support the headstock and tailstock or tailblock, and to hold them so that the axes of their respective spindles shall be in line in whatever position the tailstock may be placed along the bed. The duty of the headstock is to carry the live spindle, which is driven by the cone, the latter being connected by the belt to the wheel upon the crank shaft driven by the crank hook and the treadle, which are pivoted by eyes w to the rod x, the operation of the treadle motion being obvious. The work is shown to be carried between the live centre, which is fitted to the live spindle, and the dead centre fitting into the tail spindle, and as it has an arm at the end, it is shown to be driven by a pin fixed in the face plate, this being the simplest method of holding and driving work. The lathe is shown provided with a hand tool rest, and in this case the cutting tools are supported upon the top of the tool rest n, whose height may be adjusted to bring the tool edge to the required height on the[I-130] work by operating the set screw s, which secures the stem of n in the bore of the rest.
To maintain the axes of the live and dead spindles in line, they are fitted to a slide or guideway on the shears, the headstock being fixed in position, while the tailstock is adjustable along the shears to suit the length of the work.
To lock the tailstock in its adjusted position along the shears, it has a bolt projecting down through the plate c, which bolt receives the hand nut d. To secure the hand rest in position at any point along the shears, it sets upon a plate a and receives a bolt whose head fits into a T-shaped groove, and which, after passing through the plate p receives the nut n, by which the rest is secured to the shears.
To adjust the end fit of the live spindle a bracket k receives an adjusting screw l, whose coned end has a seat in the end j of the live spindle, m being a check nut to secure l in its adjusted position.
The sizes of lathes are designated in three ways, as follows:— First by the swing of the lathe and the total length of the bed, the term swing meaning the largest diameter of work that the lathe is capable of revolving or swinging. The second is by the height of the centres (from the nearest corner of the bed) and the length of the shears. The height of the centres is obviously equal to half the swing of the lathe, hence, for example, a lathe of 28-inch swing is the same size as one of 14-inch centres. The third method is by the swing or height of centres and by the greatest length of work that can be held between the lathe centres, which is equal to the length of the bed less the lengths of the head and tailstock together.
The effective size of a lathe, however, may be measured in yet another way, because since the hand rest or slide rest, as the case may be, rests upon the shears or bed, therefore the full diameter of work that the lathe will swing on the face plate cannot be held between the centres on account of the height of the body of the hand rest or slide rest above the shears.
Fig. 481 shows a hand lathe by F. E. Reed, of Worcester, Massachusetts, the mechanism of the head and tail stock being shown by dotted lines. The live spindle is hollow, so that if the work is to be made from a piece of rod and held in any of the forms of chucks to be hereafter described, it may be passed through the spindle, which saves cutting the rod into short lengths. The front bearing of the headstock has two brasses or boxes, a and b, set together by a cap c.
The rear bearing has also a bearing box, the lower half d being threaded to receive an adjustment screw f and check nut g to adjust the end fit of the spindle in its bearings. In place of grooved steps for the belt the cone has flat ones to receive a flat belt.
The tail spindle is shown, in Fig. 482, to be operated by a screw h, having journal bearing at i, and threaded into a nut fast in the tail spindle at j. To hold the tail spindle firmly the end of the tail stock is split, and the hand screw k may be screwed up to close the split and cause the bore at l to clasp the tail spindle at that end.
To lock the tail stock to the shears the bolt m receives the lever n at one end and at the other passes through the plate or clamp o, and receives the nut p, so that the tail stock is gripped to or released from the shears by operating n in the necessary direction. The hand rest, Fig. 483, has a wheel w in place of a nut, which dispenses with the use of a wrench.
What are termed bench lathes are those having very short legs, so that they may for convenience be mounted on a bench or fastened to a second frame, as shown in Fig. 484.
It is obvious that when work is turned by hand tools, the parallelism of the work depends upon the amount of metal cut off at every part of its length, which to obtain work of straight outline, whether parallel or taper, involves a great deal of testing and considerable skill, and to obviate these disadvantages various methods of carrying and accurately guiding tools are employed. The simplest of these methods is by means of a slide rest, such as shown in Fig. 485.
The tool t is carried in the tool post p, being secured therein by the set screw shown, which at the same time locks the tool post to the upper slider. This upper slider fits closely to the[I-131] cross slide, and has a nut projecting down into the slot shown in the same, and enveloping the cross feed screw, whose handle is shown at c, so that operating c traverses the upper slider on the cross slide and regulates the depth to which the tool enters the work, or in other words, the depth of cut.
The cross slide is formed on the top of the lower slider, which has beneath a nut for the feed screw, whose handle is shown at a, hence rotating a will cause the lower slider to traverse along the lower slide and carry the tool along the work to its cut. To maintain the fit of the sliders to the slides a slip of metal is inserted, as at e and at c, and these are set up by screws as at f, f and b, b.
The lower or feed traverse slide is pivoted to its base b, so that it may be swung horizontally upon the same, and is provided with means to secure it in its adjusted position, which is necessary to enable it to turn taper as well as parallel work. To set this lower slide to a given degree of angle it may be marked with a line and the edge of base b may be divided into degrees as shown at d.
When a piece of work is rotated between the lathe centres its axis of rotation may be represented by an imaginary straight line and the lower slides must, to obtain parallel work, be set parallel to this straight line, while for taper work the slide rest must be set at an angle to it. Now, in the form of slide rest shown in figure the cross slide is carried by the lower or feed[I-132] traverse slide, hence setting the lower slide out of parallel with the work axis sets the cross slide out of a right angle to the work axis, with the result that when a taper piece of work is turned that has a collar or flange on it, the face of that collar or flange will be turned not at a right angle to the work axis as it should be, but at a right angle to the surface of the cone. Thus in Fig. 486 a represents the axis of a piece of work, and the slide nut having been set parallel to the work axis, the face c will be at a right angle to the surface b or axis a, but with the slide nut set at an angle to turn the cone d, the cross slide will be at an angle to a, hence the face e will be undercut as shown, and at a right angle to the surface d instead of to a a. This may be obviated by letting the cross slide be the lower one as in the English form of slide rest shown in Fig. 487, in which the upper slide is pivoted at its centre to the cross slide and may be swung at an angle thereto and secured in its adjusted position by the bolt at f. The projection at the bottom of the lower slider fits between the shears of the lathe and holds the lower slider parallel with the line of lathe centres, which causes the slide rest to cut all faces at a sight angle to the work axis whether the feed traverse slide be set to turn parallel or taper. In either case, however, there is nothing to serve as a guide to set the feed traverse slide parallel to the work axis, and this must, therefore, be done as near as may be by the eye and by taking a cut and testing its parallelism.
The rest may be set approximately true by bringing the operator’s eye into such a position that the edge a a, Fig. 488, of the slide rest come into line with the edge b b of the lathe shears, because that edge is parallel to the line of lathe centres, and therefore to the work axis.
Slide rests which have a slide for traversing the tool along the work to its cut are but little used in the United States, being confined to very small lathes, and then (except in the case of watchmakers’ lathes whose forms of slide rest will be shown hereafter), mainly as an expedient to save expense in the cost of the lathe, it being preferred to feed the tool for the feed traverse (as the motion of the cutting tool along the work is termed) by mechanism operated from the live spindle and to be hereafter described. In England, however, slide rests are much used, a specimen construction being shown in Fig. 489. The end face a of the rest comes flush so that the tool shall be carried firmly when taking facing cuts in which solidity in the rest is of most importance. The tool is held by two clamps instead of by single tool posts, because the slide rest is employed to take heavy cuts, and when this is the case with boring tools whose cutting edges stand far out from the slide rest, a single tool post will not hold the tool sufficiently firm.
The gib e, Fig. 485, is sometimes placed on the front side of the slider, as in the figure, and at others on the back; when it is placed in the front the strain of the cut causes it to be compressed against the slide, and there is a strain placed upon the screws f which lifts them up, whereas if placed on the other side the screws are relieved of strain, save such as is caused by the setting of the gib up.
On the other hand, the screws are easier to get at for adjustment if placed in front. When the screws b of the upper gib c, Fig. 485, are on the right-hand side, as in that figure, there is considerable strain on the screws when a boring tool is used to stand far out, as for boring deep holes. On the other hand, however, the screws can be readily got at in this position, and may therefore be screwed up tightly to lock the upper slider firmly to the cross slide, which will be a great advantage in boring and also in facing operations. But the screws must not in this case have simple saw slot heads, such as shown on a[I-133] larger scale in Fig. 490, but should have square heads to receive a wrench, and if these four screws are used, the two end ones may be set to adjust the slicing fit of the slider, while the two middle ones may be used to set the slider form on its slide when either facing or boring. The corners of the gibs as well as those of the slider and slide may with advantage be rounded so that they may not become bruised or burred, and, furthermore, the slider is strengthened, and hence less liable to spring under the pressure of a heavy cut.
A slide rest for turning spherical work is shown in Fig. 491. a is the lower slide way on which is traversed the slide b, upon which is fitted the piece c, pivoted by the bolt d; there is provided upon c a half-circle rack, shown at e, and into this rack gears a worm-wheel having journal bearing on b, and operated by the handle f. As f is rotated c would rotate on d as a centre of motion, hence the tool point would move in an arc of a circle whose radius would depend upon the distance of the tool point from d as denoted by j, which should be coincident with the line of centres of the lathe.
The slide g is constructed in the ordinary manner, but the way on which it slides should be short, so as not to come into contact with the work. If the base slide way a be capable of being traversed along the lathe shears s s by a separate motion, then the upper slide way and slide may be omitted, g and c being in one piece. It is to be noted in a rest of this kind, however, that the tool must be for the roughing cut set too far from d to an amount equal to about the depth of cut allowed to finish with, and for the finishing cut to the radius of the finished sphere in order to obtain a true sphere, because if b be operated so that d does not stand directly coincident with the line of lathe centres, the centre of motion, or of the circle described by the tool point, will not be coincident with the centre on which the work rotates, hence the work though running true would not be a true sphere but an oval. This oval would be longest in the direction parallel with the line of centres whenever the pivot d was past the line of centres, and an oval of largest diameter at the middle or largest diameter turned by the tool whenever the pivot d was on the handle h side of the line of centres. To steady c it may be provided with a circular dovetail, as shown at the end i, provision being made (by set screw or otherwise) for locking c in a fixed position when using the rest for other than spherical work.
To construct such a rest for turning curves or hollows whose outline required to be an arc of a circle, the pivot d would require to be directly beneath the tool post, which must in this case occupy a fixed position. The radius of the arc would here again be determined by the distance of the tool point from the centre of rotation of the pivot, or, what would be the same thing, from that of the tool post.
Next to the hand slide rest lathe comes the self-acting or engine lathe. These are usually provided with a feed motion for traversing the slide rest in the direction of the length of the bed, and sometimes with a self-acting cross feed, that is to say, a feed motion that will traverse the tool to or from the line of centres and at a right angle to the same.
In an engine lathe the parallelism or truth of the work depends upon the parallelism of the line of centres with the shears of the lathe, and therefore upon the truth of the shears or bed, and its alignment with the cone spindle and tail spindle, while the truth of the radial faces on the turned work depends upon the tool rest moving on the cross slide at a true right angle to the line of centres.
Fig. 492 represents an 18-inch engine (or self-acting) lathe designed by and containing the patented improvements of S. W. Putnam, of the Putnam Tool Company, of Fitchburg, Massachusetts. The lathe has an elevating slide rest self-acting feed traverse and self-acting cross feed, both feeds being operative in either direction. It has also a feed rod for the ordinary tool feeding and a lead screw for screw-cutting purposes.
Fig. 493 represents a cross-sectional view of the shears beneath the headstock; a a are the shears or bed having the raised Vs marked v′ and v on which the headstock and tailstock rest, and v′′ and v′′′ on which the carriage slides. a and a′ are the shears[I-134] connected at intervals by cross girts or webs b to stiffen them. c c are the bolts to secure the headstock to the shears. d is a bracket bolted to a′ and affording at e journal bearing for the spindle that operates the independent feed spindle. e is split at f and a piece of soft wood or similar compressible material is inserted in the split. The bolt f is operated to close the split, and, therefore, to adjust the bore e to properly fit the journal of the feed spindle, and as similar means are provided in various parts of the lathe to adjust the fits of journals and bearings the advantages of the system may here be pointed out. First, then, the fit of the bearing may be adjusted by simply operating the screw, and, therefore, without either disconnecting the parts or performing any fitting operation, as by filing. Secondly, the presence of the wood prevents the ingress of dust, &c., which would cause the bearings and journals to abrade; and, thirdly, the compression of the wood causes a resistance and pressure on the adjusting screw thread, which pressure serves to lock it and prevent it from loosening back of itself, as such screws are otherwise apt to do.
As the pressure of the tool cut falls mainly on the front side of the carriage, and as the weight of the carriage itself is greatest on that side, the wear is greatest; this is counteracted by forming the front V, marked v′′′ in figure, at a less acute angle, which gives it more wearing area and causes the rest to lower less under a given amount of wear.
The rib a′′ which is introduced to strengthen the shears against torsional strains, extends the full length of the shears.
Fig. 494 is a sectional side elevation of the headstock; a a′ represents the headstock carrying the bearing boxes b and b′, which are capable of bore closure so as to be made to accurately fit the spindle s by the construction of the front bearing b, being more clearly shown in Fig. 495; b is of composition brass, its external diameter being coned to fit the taper hole in the head; it is split through longitudinally, and is threaded at each end to receive the ring nuts c and c′. If c be loosened from contact with the radial face of a, then c′ may be screwed up, drawing b through the coned hole in a, and, therefore, causing its bore to close upon s.
At the other end of s, Fig. 496, c′′ is a ring nut for drawing the journal box b′ through a′ to adjust the bore of b′ to fit the journal of s, space to admit the passage of b′ being provided at e. d is a box nut serving to withdraw b′ or to secure it firmly in its adjusted position, and also to carry the end adjusting step e. f is a check nut to lock e in its adjusted position.
The method of preventing end motion to s is more clearly shown in Fig. 496, in which h is a steel washer enveloping s, having contact with the radial face of b′ and secured in its adjusted position by the check nuts g, hence it prevents s from moving forward to the right. f is a disk of raw hide let into e; the latter is threaded in d and is squared at the end within f to admit of the application of a wrench, hence e may be screwed in until it causes contact between the face of f and the end of s, thus preventing its motion to the left. By this construction the whole adjustment laterally of s is made with the short length from h to f, hence any difference of expansion (under varying temperature) between the spindle and the head a a′, or between the boxes and the spindle s, has no effect towards impairing the end fit of s in its bearings.
The method of adjusting the bearings to the spindle is as follows:—c′′ and c′ are slackened back by means of a “spanner wrench” inserted in the holes provided for that purpose. c and d are then screwed up, withdrawing b and b′ respectively, and leaving the journal fit too easy. c′ is then screwed up until b is closed upon the spindle sufficiently that the belt being loose on the cone pulley, the latter moved by the hand placed upon the smallest step of the cone can just detect that there is contact between the bore of b and the spindle, then, while still moving the[I-135] cone, turn c′ back very slowly and a very little, the object being to relieve the bore of b from pressure against s. c may then be screwed up, firmly locking b in its adjusted position. c′′ may then be operated to adjust b′ in a similar manner, and d screwed up to lock it in its adjusted position. Before, however, screwing up d it is better to remove f and release e from pressure against f, adjusting the end pressure of e after d has been screwed home against a′.
To prevent b and b′ from rotating in the head when the ring nuts are operated, each is provided with a pin, q, grooves c and c′ permitting of the lateral movement of b and b′ for adjustment. The boxes b, b′ admit of being rotated in their sockets in a and a′ so as to assume different positions, the pins q and q′ being removable from one to another of a series of holes in the boxes b, b′ when it is desired to partly rotate those boxes. The tops of the boxes are provided with oil holes, and the oil ways shown at r, s being the oil groove through the head and a simply a stopper to prevent the ingress of dust, &c.
The thread on s at z, Fig. 494, is to receive and drive the face plates, chucks, &c., which are bored and threaded to fit over z. To cause the radial faces of such face plates or chucks to run true, there is provided the plain cylindrical part l, to which the bore in the hub of the face plate or chuck is an accurate fit when the radial face of that hub meets the radial face m.
Referring again to Fig. 494, g′ is the pinion to drive the back gear while g receives motion from the back-gear pinion. The object of the back gear is to reduce the speed of rotation of s and to enable it to drive a heavier cut, which is accomplished as follows:—g′′ is secured within the end k of the cone and is free to rotate with the cone upon s; at the other end the cone is secured to m, which is free to rotate upon s so far as its bore is concerned. g is fixed upon s and hence rotates at all times with it; but g may be locked to or released from m as follows:—
In g is a radial slot through which passes a bolt i provided with a cap nut h, in m is an annular groove j. When i is lifted its head passes into a recess in m, then h is screwed up and g is locked to m. This is the position of i when the back gear is not in use, the motion of the cone being communicated to s through i. But if h be loosened and i be moved inwards towards s, the head of i passes into the annular groove j, and the cone is free to rotate upon s while the latter and g remain stationary unless the back gear is put into operation. In this latter case the pinion g′ rotating with the cone drives the large gear of the back gear and the small pinion of the latter drives g, whose speed of rotation is reduced by reason of the relative proportions of the gear wheels.
In this case it is obvious that since the pulley rotates upon the spindle it requires lubrication, which is accomplished through the oil hole tubes l.
The means of giving motion to the feed spindle and lead screw are as follows:—n, Fig. 494, is a pinion fast upon s and operating the gear o, which is fast upon the spindle p, having journal bearing in a stem in a′ and also at g′′. p drives the three-stepped cone r, which is connected by belt to a similar cone fast upon the independent feed spindle. The seat for the driving gear of the change wheels for the lead screw is on p at v. To provide ample bearing surface for p in a′ the bush or sleeve shown is employed, but this sleeve also serves to pivot the swing frame w which carries the studs for the change wheels that go between the wheel on v and that on the lead screw; x y are simply oil holes to lubricate p in its bearings.
To provide a wider range of tool feed than that obtainable by the steps on the feed cones, as r, they are provided at their ends with seats for change wheels, the swing frame w carrying the intermediate wheels for transmitting motion from v to a similar seat on the cone on the feed spindle.
Fig. 497 represents the tailstock (or tailblock as it is sometimes termed), shown in section. a represents the base which slides upon the raised Vs on the bed and carries the upper part b, in which slides the tail spindle c, which is operated longitudinally by the tail screw d, having journal bearing in e, and threaded through the nut f which is fast in c. The hand wheel g is for rotating d, whose thread operating in the nut f, causes c to slide within b in a direction determined by the direction of rotation of g. To lock c in its adjusted position the handled nut h is employed in connection with the bolt i, which is shown in dotted lines; c is split as shown by the dotted lines at f; j is the dead centre fitting accurately into a conical hole in c. When it is required to remove j from c the wheel g is operated to withdraw c entirely within b, and the end d of d meets the end e of j and forces j from the coned hole in c.
[I-136]The method of securing the tailstock to the shears or releasing it from the same is as follows. A vertical prolongation of b affords at b′′ a bearing surface for the nut-handle l and washer m. k is a bolt threaded into l passing through m, b′′ and n, the latter of which it carries. n spans the shears beneath the two Vs on which the tailstock slides. Moving or rather partly rotating the handle l in the necessary direction lifts k and causes n to rise, and grip the shears beneath, while the pressure of m on b′′ causes b to grip a and the latter to grip the raised Vs on the shears. If l be rotated in the opposite direction it will cause n to fall, leaving a free to slide along the shears. To prevent n from partly rotating when free, its ends are shaped to fit loosely between the shears as shown at n.
To give to n sufficient rise and fall to enable it to grip or fall entirely free from the shears with the small amount of rotary motion which the handle-lever l is enabled from its position to have, the following device is provided. m is a washer interposed between l and b′′. This washer has upon it steps of different thickness as shown at m and m, the two thicknesses being formed by an incline as shown. The face of l has, as shown, similar steps; now as shown in the cut the step l on lever l meets the steps m of the washer, the handle having receded to the limit of its motion. The bolt k then has fallen to the amount due to unscrewing the threaded or nut end of l, and also to the amount of the difference of thickness at m and at m of the washer, the plate n being clear of the lathe-shears. But suppose the handle l be pulled towards the operator, then the surface l passing from a thin section on to a thick one as m of the washer, will lift the bolt k, causing n to meet the under surface of the shears, and then the motion of l continuing the pressure of the thread will bind or lock n to the bed.
The surface a′ in Fig. 497 affords a shelf or table whereon tools, &c., may be placed instead of lying on the lathe bed, where they may cause or receive damage.
Fig. 498 represents an end view of the tailstock viewed from the dead centre end, the same letters of reference applying to like parts that are shown in Fig. 497. The split at f is here shown to be filled with a piece of soft wood which prevents the ingress of dust, &c. At d is a cup or receptacle for oil, e being a stopper, having attached to it a wire pin flattened and of barb shape at the end, the object being to cause the wire to withdraw from the cup a drop of oil to lubricate the dead centre and centre in the work. The proximity of e to the dead centre makes this a great convenience, while the device uses much less oil than would be used by an oil can.
The method of setting over the upper part b to enable the turning of the diameter of work conical or taper instead of parallel is shown in Fig. 498: p and p′ are square-headed screws threaded into the walls of a and meeting at their ends the surface of b′. In a there is at a a wide groove or way, and on b there is at b a projection fitting into the way a so as to guide b when it slides across a, as it will when p is unscrewed in a and p′ is screwed into a. This operation is termed setting over the tailstock, and its effect is as follows:—Suppose it be required to turn a piece of work of smaller diameter at the end which runs on the dead centre, then, by operating the screw p towards the front of the lathe (or to the left as shown in the cut) and screwing p′ farther into a, the end of p′ will meet the surface of b′, causing b′ to move over, and the centre of the dead centre j (which is the axis of rotation of the work at that end) will be nearer to the point of the cutting tool. Or suppose the work requires to be turned a taper having its largest diameter at the end running on the dead centre, then p′ would be unscrewed and p screwed farther into a, carrying b farther towards the back of the lathe.
[I-137]The V grooves q and q′ fit upon the inner raised Vs shown at v, v′ in Fig. 499.
Fig. 499 is a side view of the slide rest for holding and traversing the cutting tool. a represents the carriage resting upon the raised Vs marked v′′ and v′′′ and prevented from lifting by its own weight, and in front also by the gib a secured to a by the bolt b and having contact at c with the shears. a carries at d a pivot for the cross slide b and at e a ball pivot for the cross slide elevating screw c. This screw is threaded through the end of b so that by operating it that end of b may be raised or lowered to adjust the height of the cutting tool point to suit the work. To steady b there is provided (in addition to the pivots at d) on a two lugs f, between the vertical surfaces of which b is a close working fit. The upper surface of b is provided with a V-slide-way g, to which is fitted the tool rest d (the construction being more clearly shown in Fig. 500).
The means for traversing d along the slide g on b is as follows:—
A nut i is secured to d by the screw bolt j, and threaded through the nut i is the cross-feed screw e, which has journal bearing in the piece k, which is screwed into the end face of b; there is a collar on e which meets the inner end of k, and the handle f being secured by nut to that end of e its radial face forms a shoulder at m which with the collar prevents any end motion of e, so that when f is rotated e rotates and winds through the nut i which moves d along b.
An end view of a, b, and d is shown in Fig. 500, in which the letters of reference correspond to those in Fig. 499. b′ and b′′ are the projections that pass into a and receive the pivoting screws d and d. To adjust the fit and take up any wear that may ensue on the slide g, on b and on the corresponding surface on d, the piece n is provided, being set up by the adjusting screws o.
To adjust the fit and take up the wear at the pivots d they are made slightly taper, fitting into correspondingly taper holes in b.
The dotted circle t′, represents a pinion fast upon the cross-feed screw (e, Fig. 499); the similar circles t and s′′ also represent pinions, the three composing a part of the method of providing an automatic or self-acting cross feed or cross traverse to d by rotating it through a gear-wheel motion derived from the rotation of the independent feed spindle, as is described with reference to Fig. 501.
m in Fig. 500 represents a cavity or pocket to receive wool, cotton or other elastic or fibrous material to be saturated with oil and thus lubricate the raised Vs while keeping dirt from passing between the rest and the Vs. The shape of these pockets is such as to enable them to hold the cotton with a slight degree of pressure against the slides, thus insuring contact between them.
The mechanical devices for giving to the carriage a self-acting traverse in either direction along the bed, so as to feed the tool automatically to its cut, and for giving to the tool rest (d, Fig. 499) traverse motion so as to feed the tool to or from the line of centres along the cross slide, are shown in Fig. 501, which presents two views of the feed table or apron. The lower view supposes the feed table to be detached from the carriage and turned around so as to present a side elevation of the mechanism. The upper view is a plan of the same with two pinions (n and n′), omitted. a represents the part of the lathe carriage shown at a in Fig. 500. It has two bolts p and p′, which secure the apron g, Fig. 501, to a. At h is the independent feed spindle or feed rod operated by belt from the cone pulley r, Fig. 494, or by a gear on stud p at v. h is carried in bearings fixed to each end of the lathe shears or bed, both of these bearings being seen in Fig. 492. h is also provided with a bearing fixed on the feed apron as seen in Fig. 501, and is splined as shown at h. At i is a bracket fast upon the apron g and affording journal bearing to j, which is a bevel pinion having a hub which has journal bearing in the bracket i. The fit of the bearing to the journal is here again adjusted by a split in the bearing with a screw passing through the split and threaded in the lower half (similar to the construction of d in Fig. 493); j is bored to receive h, and is driven by means of a feather projecting into the spline h. When therefore, the carriage a is moved it carries with it the apron g, and this carries the bracket i holding the bevel pinion j, which is in[I-138] gear with the bevel-wheel k, and therefore operates it when h has rotary motion. At the back of k, and in one piece with it, is a pinion k′, both being carried upon the stud l; pivoted upon this same stud is a plate lever m, carrying two pinions n and n′ in gear together, but n only is in gear with k′, hence k′ drives n and n drives n′. Now in the position shown neither n or n′ is in gear with the gear-wheel o, but either of them may be placed in gear with it by means of the following construction:—
At the upper end of m there is provided a handle stud m′ passing through the slot m′′ in g. Screwing up this stud locks m fast by binding it against the surface of g. Suppose, then, m′ to be unscrewed, then if it be moved to the right in the slot m′′, n will be brought into gear with o and the motion will be transmitted in the direction of the arrows, and screwing up n would retain the gear in that position. But suppose that instead of moving m′ to the right it be moved to the left, then n′ will be brought into gear with o and the direction of rotation of o will be reversed.
Thus, then, o may be made to remain stationary or to rotate in either direction according to the position of m′ in the slot m′′, and this position may be regulated at will.
The gear o contains in its radial face a conical recess, and upon the same stud or pin (p) upon which o is pivoted, there is fixed the disk p′, which is in one piece with the pinion p′′; the edge of p′ is coned to fit the recess in the wheel o, so that if the stud p is operated to force the disk p′ into the coned recess in o the motion of wheel o will be communicated to disk p′, by reason of the friction between their two coned surfaces. Or if p be operated to force the coned edge of the disk out of contact with the coned bore or recess in gear o, then o will rotate while p′ and p′′ will remain stationary. Suppose the coned surfaces to be brought (by operating x) into contact and p′ to rotate with o, then p′′ being in gear with wheel q will cause it to rotate. Now q is fast to the pinion q′, hence it will also rotate, and being in contact with the rack which is fixed along the shears of the lathe and a section of which is shown in the cut, the whole feed table or apron will be made to traverse along the lathe shears.
The direction in which this traverse will take place depends upon the adjusted position of m′ in m′′, or in other words upon whether n or n′ be the pinion placed in gear with o. As shown in the cut neither of them is in gear, and motion from h would be communicated to n and n′ and would there cease; but if m′ be raised in the slot m′′, n would drive o, and supposing p′ to be held to o, the motion of all the gears would be as denoted by the arrows, and the lathe carriage a would traverse along the lathe bed in the direction of arrow q′′. But if n′ be made to drive o all the motions would be in the opposite directions. The self-acting feed motion thus described is obviously employed to feed the cutting tool, being too slow in its operation for use to simply move the carriage from one part of the lathe bed to another; means for this purpose or for feeding the carriage and cutting tool by hand are provided as follows:—r is a pinion in gear with q and fast upon the stud r′, which is operated by the handle r′′. The motion of r′′ passes from r to q and q′ which is in gear with the rack. But q′ being in gear with p′′ the latter also rotates, motion ceasing at this point because the cone on p′ is not in contact with the coned recess in o. When, however, p′ and o are in contact and in motion, that motion is transmitted to r′′, which cannot then be operated by hand.
It is often necessary when operating the cross feed to lock the carriage upon the lathe bed so that it shall not move and alter the depth of the tool-cut on the radial face of the work. One method of doing this is to throw off the belt that operates the feed spindle h, place n in gear with o and p′ in contact with o, so that the transverse feed motion will be in action, and then pull by hand the cone pulley driving h, thus feeding the tool to its necessary depth of cut. The objection to this method, however, is that when the operator is at the end of the lathe, operating the feed[I-139] cone by hand he cannot see the tool and can but guess how deep a cut he has put on. To overcome this difficulty a brake is provided to the pinion r as follows:—
The brake whose handle is shown at v has a hub v′ enveloping the hub r′′′ which affords journal bearing to the stud r′. In the bore of this hub v′ is an eccentric groove, and in r′′′ is a pin projecting into the eccentric groove and meeting at its other end the surface of the stud r′. When, therefore, v is swung in the required direction (to the left as presented in the cut), the cam groove in v′ forces r inwards, gripping it and preventing it from moving, and hence the movement of r which also locks q and q′.
It remains now to describe the method of giving rotary motion to the cross-feed screw e (Fig. 499) so as to enable it to self-act in either direction. s is a lever pivoted upon the hub of o and carrying at one end the pinion s′′, while at the other end is a stud s′ passing through a slot in g. The pinion s′′ is in gear with o and would therefore receive rotary motion from it and communicate such motion to pinion t, which in turn imparts rotary motion to t′. Now t′ is fast upon the cross-feed screw as shown in Fig. 499 and the cross-feed screw e in that figure would by reason of the nut i in figure cause the tool rest d to traverse along the cross-slide in a direction depending upon the direction of motion of t′, which may be governed as follows:—
If s′ be moved to the left s′′ will be out of gear with t and the cross-feed screw may be operated by the handle (f, Fig. 499). If s′ be in the position shown in cut and m′′ also in the position there shown (Fig. 501), operating the feed screw by its handle would cause its pinion t′ to operate t, s′′, and o; hence s′ should always be placed to disconnect s′′ from t when the cross-feed screw is to be operated by hand, and s′ operated to connect them only when the self-acting cross feed is to operate. In this way when the cross feed is operated by hand t′ and t will be the only gears having motion. It has been shown that the direction of motion of o is governed by the position of m′, or in other words, is governed by which of the two pinions n or n′ operates, and as o drives s′′ its motion, and therefore that of t′, is reversible by operating m′.
The construction of s′ is as follows:—Within the apron as shown in the side elevation it consists of what may be described as a crank, its pin being at t; in the feed table is a slot through which the shaft of the crank passes; s is a handle for operating the crank. By rotating s the end s′ of s is caused to swing, the crank journal moving in the slot to accommodate the motion and permit s to swing on its centre.
The device for forcing the cone disk p′ into contact with or releasing it from o is as follows:—The stud p is fast at the other end in p′ and has a collar at b; the face of this collar forms one radial face, and the nut w affords the other radial face, preventing end motion to x without moving p endwise. If x be rotated its thread at x′ causes it to move laterally, carrying p with it, and p being fast to p′ also moves it laterally. p′ is maintained from end motion by a groove at o′ in which the end of a screw a projects, a screwing through w and into the groove o′.
The lead screw of a lathe is a screw for operating the lathe carriage when it is desired to cut threads upon the work. It is carried parallel to the lathe shears after the same manner as the independent feed spindle, and is operated by the change wheels shown in Fig. 492 at the end of the lathe. These wheels are termed change wheels on account of their requiring to be changed for every varying pitch of thread to be cut, so that their relative diameters, or, what is the same thing, their relative number of teeth, shall be such as to give to the lead screw the speed of rotation per lathe revolution necessary to cut upon the work a thread or screw of the required pitch.
The construction of the bearings which carry the lead screw in the S. W. Putnam’s improved lathe is shown in Fig. 502, in which a represents the bearing box for the headstock end of the lathe, having the foot a′ as a base to bolt it to the lathe shears. l represents the lead screw, having on one side of a the collar l′ and on the other the nut and washer n and n′. The seat for the change wheel that operates the lead screw is at l′′, the stop pin l fitting into a recess in the change wheel so as to form a driving pin to the lead screw. The washer n′ is provided with a feather fitting into a recess into l so that it shall rotate with l and shall prevent the nut n from loosening back as it would be otherwise apt to do. End motion to l is therefore prevented by the radial faces of l′ and n′.
At the other end of the lathe there are no collars on the lead screw, hence when it expands or contracts, which it will do throughout its whole length under variations of atmospheric temperature, it is free to pass through the bearing and will not be deflected, bent, or under any tension, as would be the case if there were collars at the ends of both bearings. The amount of this variation under given temperatures depends upon the difference in the coefficients of expansion for the metal of which the lead screw and the lathe shears are composed, the shears being of cast iron while lead screws are sometimes of wrought iron and sometimes of steel.
The bearings at both ends are split, with soft wood placed in the split and a screw to close the split and adjust the bearing bore to fit the journal, in the manner already described with reference to other parts of this lathe.
The construction of the swing frame for carrying the change wheels that go between the driving stud v, Fig. 494, and that on the seat l′′, Fig. 502, are as follows:—
Fig. 503 represents the change wheel swing frame, an edge view of which is partly shown at w in Fig. 494. s is a slot narrower at a than at b. Into this slot fit the studs for carrying the change wheels.
By enabling a feed traverse in either direction the lathe carriage may be traversed back (for screw-cutting operations) without the aid of an extra overhead pulley to reverse the direction of rotation of the lathe, but in long screws it is an advantage to have such extra overhead pulley and to so proportion it as to make the lathe rotate quicker backwards than forward, so as to save time in running the carriage back.
The mechanical devices for transmitting motion from the lead screw to the carriage are shown in Fig. 504, representing a view from the end and one from the back of the lathe. b is a frame or casting bolted by the bolt b to the carriage a of the lathe. c is a disk having a handle c′ and having rotary motion from its centre. Instead of being pivoted at its centre, however, it is guided in its rotary motion by fitting at d d into a cylindrical recess provided[I-140] in b to receive it. c contains two slots d and d′ running entirely through it. These slots are not concentric but eccentric to the centre of motion of c. Through these slots there pass two stud bolts e and e′ shown by dotted lines in Fig. 504, and these bolts perform two services: first by reason of the nuts f and f′ they hold c to its place in b, and next they screw into and operate the two halves g and g′ of a nut.
Suppose, now, that the handle c′ be operated or moved towards arrow e, then the dot at f being the centre of its motion and the slots d and d′ gradually receding from f as their ends g are approached they will cause e to move vertically upward and e′ to move vertically downward, a slot in b (which slot is denoted by the dotted lines h) guiding them and permitting this vertical movement.
Since e and e′ carry the two halves of the nut which envelops the lead screw l it is obvious that operating c′ will either close or release the half nuts from l according to which direction it (c′) is moved in.
The screws h and h′ screw tightly into b, and the radial faces of their heads are made to have a fair and full bearing against the underside of the shears, so that they serve as back gibs to hold the carriage to the shears and may be operated to adjust the fit or to lock the carriage to the bed if occasion may require. This lathe is made with a simple tool rest as shown in the engravings or with a compound slide rest. In some sizes the rest is held to the carriage by a weight upon a principle to be hereafter described. The bed is made (as is usual) of any length to suit the purposes for which the lathe is to be used.
The next addition to the lathe as it appears in the United States is that of a compound slide rest.
Fig. 505 represents a 28-inch swing lathe by the Ames Manufacturing Company, of Chicopee, Massachusetts. It is provided with the usual self-acting feed motion and also with a compound slide rest. The swing frame for the studs carrying the change wheels for screw cutting here swings upon the end of the lead screw, the same spindle that carries the driving cone for the independent feed rod which is in front of the lathe, also carries the driving gear for the change wheels used for screw cutting.
The construction of the compound rest is shown in Figs. 506 and 507. n is the nut for the cross-feed screw (not shown in the cut) and is carried in the slide a. a and the piece l above it are virtually in one, since the latter is made separate for convenience of construction and then secured to it firmly by screws. b is made separate from c also for convenience of construction and fixed to it by screws; l is provided with a conical circular recess into which the foot b of c fits. e is a segment of a circle operated by the set screw f to either grip or release b. The bolt d simply serves as a pivot for piece b c; at its foot c is circular and is divided[I-141] off into the degrees of a circle to facilitate setting it to any designated angle.
If, then, f be unscrewed, c may be rotated and set to the required angle, in which position screwing up f will lock it through the medium of e. g is the feed nut for the upper slider h, which operates along a slide way provided on c, the upper feed screw having journal bearing at c′. i is the tool post, having a stepped washer j, by means of which the height of the tool k may be regulated to suit the work.
Suppose, now, that it be required to turn a shaft having a parallel and a taper part; then the carriage may be traversed to turn the parallel part, and the compound slide c may be set to turn the taper part, while the lower feed screw operating in n may be used to turn radial faces.
The object of making a and l in two pieces is to enable the boring and insertion of b, which is done as follows:—The front end of l as l′ is planed out, leaving in it a groove equal in diameter and depth to the diameter and depth of b, so that b may be inserted laterally along this groove to its place in l. The segment e is then inserted and a piece is then fitted in at l′ and held fast to a by screws. It is into this piece that the set screw f is threaded.
Various forms of construction are designed for compound rests, but the object in all is to provide an upper sliding piece carrying the tool holder, such sliding piece being capable of being so set and firmly fixed that it will feed the tool at an angle to the line of the lathe centres.
Another and valuable feature of the compound rest is that it affords an excellent method of putting on a very fine cut or of accurately setting the depth of cut to turn to an exact diameter; this is accomplished by setting the upper slide at a slight angle to the line of centres and feeding the tool to the depth of cut by means of the screw operating the upper slide. In this way the amount of feed screw handle motion is increased in proportion to the amount to which the tool point moves towards the line of lathe centres, hence a delicate adjustment of depth of cut may be more easily made.
Suppose, for example, that a cut be started and that it is not quite sufficiently deep, then, while the carriage traverse is still proceeding, the compound rest may be operated to increase the cut depth, or if it be started to have too deep a cut the compound rest may be operated to withdraw the tool and lessen its depth of cut. Or it may be used to feed the tool in sharp corners when the feed traverse is thrown out, or to turn the tops of[I-142] collars or flanges when the tailstock is set over to turn a taper.
It is obvious, however, that comparatively short tapers only can be conveniently turned by a compound slide rest; but most tapers, however, are short.
To turn long tapers the tailstock of the lathe is set over as described with reference to the Putnam lathe, but for boring deep holes the slide rest must either be a compound one or a taper turning former or attachment must be employed.
When, however, the tailstock is set over, the centres in the work are apt to wear out of true and move their location (the causes of which will be hereafter explained).
In addition to this, however, the employment of a taper turning attachment enables the boring of taper holes without the use of a compound slide rest, thus increasing the capacity of the lathe not having a simple or single rest.
In Fig. 508 is shown a back view of a Pratt and Whitney weighted lathe having a Slate’s taper turning attachment, the construction of which is as follows:—Upon the back of the lathe shears are three brackets having their upper surfaces parallel with and in the same plane as the surface of the lathe shears. Pivoted to the middle bracket is a bar which has at each end a projection or lug fitting into grooves provided in the end brackets, these grooves being arcs of a circle whose centre is the axis of the pivot in the middle bracket.
The end brackets are provided with handled nuts upon bolts, by which means the bar may be fixed at any adjusted angle to the lathe shears. Upon the upper surface of the bar is a groove or way in which slides a sliding block or die, so that this die in traversing the groove will move in a straight line but at an angle to the lathe bed corresponding to the angle at which the bar may be adjusted. The slide rest upon being connected by a bar or rod to the die or sliding block is therefore made to travel at the same angle to the lathe bed or line of centres as that to which the bar is set. The method of accomplishing this in the lathe, shown in Fig. 508, is as follows:—
In Fig. 509 a is the bar pivoted at c upon the centre bracket b; e is the sliding block pivoted to the nut bar f. This nut bar carries the cross-feed nut, which in turn carries the feed screw and hence the tool rest. When the nut bar is attached to the sliding block to turn a taper it is free to move endways upon the lower part of the carriage in which it slides, but when the taper attachment is not in use the bar is fastened to the lower part of the carriage by a set screw.
The screw at d is provided to enable an accurate adjustment for the angle of the bar a. g and h are screws simply serving to adjust the diameter to which the tool will turn after the manner shown in Fig. 588, g being for external and h for internal work.
When the lathe has a bed of sufficient length to require it, a slide is provided to receive the brackets, which may be adjusted to any required position along the slide, as shown in Fig. 510. This is a gibbed instead of a weighted lathe, and the method of attaching the sliding block to the lathe rest is as follows:—
A separate rod is pivoted to the sliding block. This rod carries at its other end a small cross head which affords general bearing to the end of the cross-feed screw, which has a collar on one side of the cross head and a fixed washer on the other, to prevent any end motion of the said screw.
The cross-feed nut is attached to the traversing cross slide. The other or handle end of the cross-feed screw has simple journal bearing in the slide rest, but no radial faces to prevent end motion, so that one may from the rod attached to the sliding-block traverse the cross-feed slide, which will carry with it the feed screw. As a result, the line of motion of the tool rest is governed by the sliding die, but the diameter to which the tool will turn is determined by the feed screw in the usual manner. When it is not required to use the taper attachment, the rod or spindle is detached from the sliding die and is locked by a clamp, when the rest may be operated in the usual manner.
Fig. 511 represents a compound duplex lathe of a design constructed by Sir Joseph Whitworth, of Manchester, England.[I-143] The two rests are here operated on the same cross slide by means of a right and left-hand cross-feed screw.
The tool for the back rest is here obviously turned upside down.
The lead screw is engaged at two places by the feed nut, which is in two pieces attached to levers; while at a third point in its circumference it is supported by a bracket, bolted to the lathe bed.
Fig. 512 represents the New Haven Manufacturing Company’s three tool slide rest, for turning shafting. It is provided with a follower rest, in front of which are two cutting tools for the roughing cuts, and behind which is a third tool for the finishing cut. The follower rest receives bushes, bored to the requisite diameter, to leave a finishing cut. The first tool takes the preliminary roughing cut; the second tool turns the shaft down to fit the bush or collar in the follower rest; and, as stated, the last tool finishes the work.
Fig. 513 represents a 44-inch swing lathe, showing an extra and detachable slide rest, bolted on one side of the carriage and intended for turning work of too large a diameter to swing over the slide rest. By means of this extra rest the cutting tool can be held close in the rest, instead of requiring to stand out from the tool-post to a distance equal to the width of the work. The ordinary tool post is placed in this extra rest.
When it is desired to bolt work on the lathe carriage and rotate the cutting tools, as in the case of using boring bars, the cross slide is sunk into instead of standing above the top surface of the carriage so as to leave a flat surface to bolt the work to, and T-shaped slots are provided in the carriage, to receive bolts for fastening the work to the carriage, an example of this kind being shown in Fig. 514.
Fig. 515 represents a self-acting slide or engine lathe by William Sellers and Co., of Philadelphia. These lathes are made in various sizes from 12 inches up to 48 inches swing on the same general design, possessing the following features:—The beds or shears are made with flat tops, the carriage being gibbed to the edges of the shears, these edges being at a right angle to the top face of the bed. The dead centre spindle is locked at each end of its bearing in the tailstock, thus securing it firmly in line with the live spindle. The ordinary tool feed is operated by a feed rod in front of the lathe, and this rod is operated by a disc feed, which may be altered without stopping the lathe so as to vary the rate of tool feed; and an index is provided whereby the operator may at once set the discs to give the required rate of feed. The lead screw for screw cutting is placed in a trough running inside the lathe bed, so that it is nearer to the cutting tool than if placed outside that bed, while it is entirely protected from the lathe cuttings and from dirt or dust; and the feed-driving mechanism is so arranged that both may be in gear with the live spindle, and either the rod feed or screw-cutting feed may be put into action instantly, while putting one into action throws the other out, and thus avoid the breakage that occurs when both may be put into action at the same time. The direction of the turning feed is determined by the motion of a lever conveniently placed on the lathe carriage, and the feed may be stopped or started in either direction instantly. The mechanism for putting the cross feed in action is so constructed (in those lathes having a self-acting cross feed) that the cross feed cannot be in action at the same time as the turning feed or carriage traverse by rod feed.
Lathes of 12 and 16 inches swing are back-geared, affording six changes of speed, and the lathe tool has a vertical adjustment on a single slide rest. Lathes of 20 inches swing are back-geared with eight changes of speed. Lathes of 25 inches and up to 48 inches swing inclusive are triple-geared, affording fifteen changes of speed, having a uniformly progressive variation at each change.
The construction of the live head or headstock for a 36-inch[I-144] lathe is shown in the sectional side view in Fig. 516, and in the top view in Fig. 517, and it will be seen that there are five changes of speed on the cone, five with the ordinary back-gear, and five additional ones obtained by means of an extra pinion on the end of the back-gear spindle, and gearing with the teeth on the circumference of the face plate, the ordinary pinion of the back-gear moving on the back-gear spindle so as to be out of the way and clear the large gear on the cone spindle when the wheel of the extra back-gear pinion is in use, as shown in Fig. 517.
The front bearing of the live spindle is made of large diameter to give rigidity, and the usual collar for the face plate to screw against is thus dispensed with. End motion to the live spindle is prevented by a collar of hardened steel, this collar being fast on the live spindle and abutting on one side against the end face of the back bearing and on the other against a hardened steel thrust collar.
All these parts are enclosed in a tight cast-iron tail-block, which serves as an oil well to insure constant and perfect lubrication. The surfaces which confine the revolving collar back and front are so adjusted as to allow perfect freedom of rotary motion to the spindle and collar, but no perceptible end motion. The securing of the live spindle endwise is thus confined to the thickness of the steel collar only, and this is so enclosed in a large mass of cast iron as to insure uniformity of temperature in all its parts, hence there is no liability for the live spindle to stick or jam in its bearings, while the expansion of the live spindle endways from this collar (if it expands more than the lathe head) is allowed for in freedom of end motion through the front journal, which is a little longer than the bearing it runs in. In turning work held between the lathe centres the end thrust is taken against the hardened steel collar on the live spindle, and the hardened steel collar at the back of it, while in turning work chucked to the face plate the spindle is held in place endways by the confinement of the steel collar on the spindle between the steel collar behind it and the back end of the back bearing. With this arrangement of the spindle the change from turning between the lathe centres and turning chucked work requires no thought or attention to be given to any adjustment of the live spindle to accommodate it for the changed condition of end pressure between turning between the centres and turning chucked work, as is the case in ordinary lathes.
The double-geared lathes, as those of 12, 16 and 20 inches swing, are provided with face plates that unscrew from the live spindle to afford convenience for changing from one size of face plate to another, and all such lathes have their front live spindle journal made of sufficiently enlarged diameter above that of the screw, to afford a shoulder for the face plate to abut against. The nose of the live spindle is not threaded along its entire length, but a portion next to the shoulder is made truly cylindrical but without any thread upon it, and to this unthreaded part the face plate accurately fits so that it is held true thereby, and the screw may fit somewhat loosely so that all the friction acts to hold the[I-145] face plate true and hard up against the trued face of the spindle journal. Face plates fitted in this way may be taken off and replaced as often as need be, with the assurance that they will be true when in place unless the surfaces have been abused in their fitting parts.
The construction of the tailstock or poppet-head, as it is sometimes termed, is shown in Figs. 518, 519, and 520. To hold it in line with the live spindle it is fitted between the inner edges of the bed, and it will be seen that one of the bed flanges (that on the left of the figure) is provided on its under side with a V, and the clamp is provided with a corresponding V, so that in tightening up the bolt that secures the tailstock to the bed the tailstock is drawn up to the edge of the shears, and therefore truly in line with the live spindle, while when this bolt is released the tailstock is quite free to be moved to its required position in the length of the bed. As a result of this form of design there is no wear between the clamp and the underneath V, and the tailstock need not fit tightly between the edges of the bed, hence wear between these surfaces is also avoided, while the tailstock is firmly clamped against one edge of the bed as soon as the clamp is tightened up by the bolt on that side.
Fig. 520 shows the method of locking the tailstock spindle and of preventing its lateral motion in the bearing in the tailstock. At the front or dead centre end of this bearing there is between the spindle a sleeve enveloping the spindle, and coned at its outer end, fitting into a corresponding cone in the bore of the tailstock. Its bore is a fit to the dead spindle, and it is split through on the lower side. Its inner end is threaded to a sleeve that is within the headstock, and whose end is coned to fit a corresponding cone at the inner end of the bore of the tailstock.
To this second sleeve the line shown standing vertically on the left of the hand wheel is attached, so that operating this handle revolves the second sleeve and the two sleeves screw together, their coned ends abutting in their correspondingly coned seats in the tailstock bore, and thus causing the first-mentioned and split sleeve to close upon the dead centre spindle and yet be locked to the tailstock.
As the bore of the tailstock is exactly in line with the live spindle, it follows that the dead spindle will be locked also in line with it.
Figs. 521 and 522 represent sectional views of the carriage and slide rest of these lathes of a size over 16 inches swing. On the feed rod there are two bevel pinions p, one on each side of the bevel-wheel a, and by a clutch movement either of these wheels may be placed in gear with bevel-wheel a.
The clutch motion is operated by a lever which, when swung over to the right, causes the bevel pinion on the right to engage[I-146] with the bevel-wheel a, and the carriage feeds to the right, while with the lever swung over to the left the carriage feeds to the left.
On the inclined shaft is a worm, or, as the makers term it, a spiral pinion of several teeth which gears into a straight toothed spur gear-wheel, giving a smooth and rolling tooth contact, and therefore producing an even and uniform feed motion.
This spur gear is fast on a shaft c, which is capable of end motion and is provided on each of its side faces with an annular toothed clutch. On each side of this spur-wheel is a clutch, one of which connects with the train of gears for the turning feed, and the other with the cross-feed gear b.
When the shaft (whose end is shown at c, and to which the spur gear referred to is fast) is pulled endways outwards from the lathe bed, its front annular clutch engages with the clutch that sets the cross-feed gear b in motion, and b engages with a pinion which forms the nut of the cross-feed screw.
When shaft c is moved endways inwards its other annular clutch engages the clutch on that side of it, and the turning feed is put into operation. The method of operating shaft c endways is as follows:—
In a horizontal bearing d is a shaft at whose end is a weighted lever l, and on the end of this shaft is a crank pin shown engaging a sleeve e which affords journal bearing to the outer end of shaft c, so that operating the weighted lever l operates e, and therefore shaft c with the spur gear receiving motion from the worm. A simple catch confines lever l to either of its required limits of motion, and allows the free motion of the operating lever to start or stop either the longitudinal or the cross feed, either of which is started or stopped by this lever, but no mistake can occur as to which feed is operated, because the catch above mentioned requires to be shifted to permit the feed to be operated.
The lower end of the bell crank f engages with the sleeve e, so that when the shaft c is operated outwards the horizontal arm of bell crank f is depressed and the spur pinion of the cross-feed nut is free to revolve, being driven by the cross-feed motion. When the lever f is moved towards the lathe bed (which occurs when the stop or catch is set to allow the longitudinal feed to be used) the nut of the cross feed is locked fast by the horizontal arm of the bell crank f. This device makes the whole action from one direction of feed to another automatic, and the attention of the workman is not needed for any complicated adjustment of parts preparatory to a change from one feed to the other.
At h is a hand wheel for hand feeding, the pinion r meshing into the rack that extends along the front of the lathe bed; back of the hand wheel and at h′ a clamp is provided whereby the saddle or carriage may be locked to the lathe bed when the cross feed is being used, thus obviating the use of a separate clamp on the bed.
The top slide of the compound rest is long and its guideway is short, the nut being in the stationary piece g, and it will be observed that by this arrangement at no time does the bearing surfaces of the slides become exposed to the action of chips or dirt.
Fig. 523 is a sectional view of the carriage and slide rest as arranged for 12 and 16-inch lathes when not provided with a self-acting cross feed. In this case end motion to shaft c is given by lever h, which is held in its adjusted position by the tongue t. In this lathe the screw-cutting and the turning feed cannot be put into gear at the same time.
The tool nut is arranged to enable the tool to be adjusted for height after it is fastened in the tool post by pivoting it to the cross slide, a spring s forcing it upwards at its outer end, thus holding the tool point down and in the direction in which the pressure of the cut forces it, thus preventing the wear of the pivot from letting the tool move when it first meets the cut. The nut n is operated to adjust the tool height, and at the same time enables the depth of cut to be adjusted very minutely. A trough catches the water, cuttings, &c., and thus protects the slides and slideways from undue wear.
In all these lathes the feeding mechanism is so arranged that there are no overhanging or suspended shaft pins or spindles, each of such parts having a bearing at each end and not depending on the face surface of a collar or pin, as is common in many[I-147] lathes. Furthermore, in these lathes the handle for the hand carriage feed moves to the right when the carriage moves to the right; the cross-feed screw (and the upper screw also in compound slide rests) has a left-hand thread, so that the nut being fixed the slides move in the same direction as though the nut moved as in ordinary lathes. The tailstock or poppet-head screw is a right hand because the nut moves in this case. The object of employing right-hand screws in some cases, and left-hand ones in others, is that it comes most natural in operating a screw to move it from right to left to unscrew, and from left to right to screw up a piece, this being the action of a right-hand screw, left-hand screws being comparatively rarely used in mechanism, save when to attain the object above referred to.
Fig. 524 represents the Niles Tool Works car axle lathe, forming an example in which the work is driven from the middle of its length, leaving both ends free to be operated upon simultaneously by separate slide rests.
The work being driven from its centre enables it to rotate upon two dead centres, possessing the advantage that both being locked fast there is no liberty for the work to move, as is the case when an ordinary lathe having one live or running spindle is used, because in that case the live spindle must be held less firmly and rigidly than a dead centre, so as to avoid undue wear in the live spindle bearings; furthermore, the liability of the workman to neglect to properly adjust the bearings to take up the wear is avoided in the case of two dead centres, and no error can occur because of either of the centres running out of true, as may be the case with a rotating centre.
The cone pulley and back gear are here placed at the head of the lathe driving a shaft which runs between the lathe shears and drives a pinion which gears with the gear on the work driving head shown to stand on the middle of the shears. This head is hollow so that the axle passes through it. On the face of this gear is a Clement’s equalizing driver constructed upon the principle of that shown hereafter in Fig. 756.
The means for giving motion to the feed screw and for enabling a quick change from the coarse roughing feed to a finer finishing feed to the cutting tool without requiring to change the gears or alter their positions, is shown in Fig. 525. a and b are two separate pinions bored a working fit to the end of the driving shaft s, but pierced in the bore with a recess and having four notches or featherways h. The end of the driving shaft s is pierced or bored to receive the handled pin i, and contains four slots to receive the four feathers j which are fast in i. In the position shown in the figure these feathers engage with neither a nor b, hence the driving shaft would remain motionless, but it is obvious that if pin i be pushed in the feathers would engage b and therefore drive it; or if i were pulled outwards the feathers would engage a and drive it, because a and b are separate pinions with a space or annular recess between them sufficient in dimensions to receive the feathers. The difference in the rate of feed is obviously obtained through the difference in diameters of the pair of wheels a, c and the pair d, b, the lathe giving to the lead screw the slowest motion and, therefore, the finest feed.
The means for throwing the carriage in and out of feed gear with the feed screw and of providing a hand feed for operating the tool in corners or for quickly traversing the carriage, is shown in Fig. 526, in which s represents the feed screw and b a bracket[I-148] or casting bolted to the carriage and carrying the hand wheel and feed mechanism shown in the general cut figure.
b provides a slide way denoted by the dotted lines at b, for the two halves n and n′ of the feed nut. It also carries a pivot pin shown at p in the front elevation, which screws into b as denoted by p′ in the end view; upon this pivot operates the piece d, having the handle d. In d are two cam grooves a a; two pins n, which are fast in the two half-nuts n n′, pass through slots c c in b, and into the cam grooves a a respectively.
As shown in the cut the handle d of d is at its lowest point, and the half-nuts n′ and n are in gear upon the feed screw; but suppose d be raised, then the grooves a a would force their respective pins n up the slots c, and these pins n being each fast to a half of the nut, the two half-nuts would be opened clear of the feed screw, and the carriage would cease to be fed.
The hand-feed or guide-carriage traverse motion is accomplished as follows:—b provides at e journal bearing to a stud on which is the hand wheel shown in the general cut; attached to this hand wheel is a pinion operating a large gear (also seen in general cut) whose pitch line is seen at g, in figure. The stud carrying g has journal bearing at f, and carries a pinion whose pitch circle is at h and which gears with the rack.
| VOL. I. | EXAMPLES IN LATHE CONSTRUCTION. | PLATE V. |
|
Large image (60 kB). 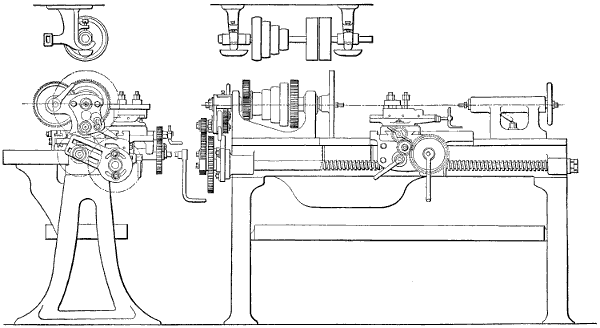 |
||
| Fig. 527. | ||
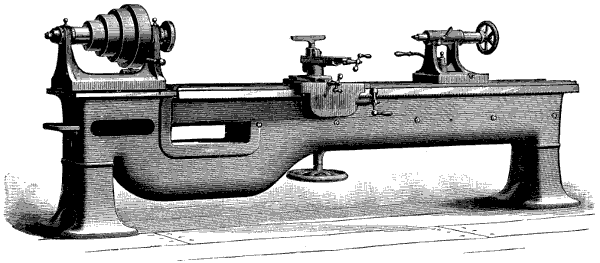 |
||
| Fig. 528. | ||
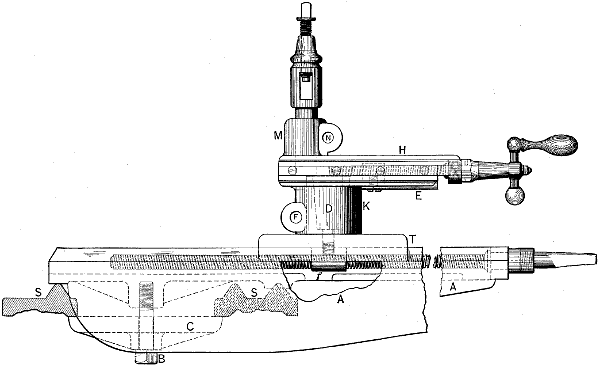 |
||
| Fig. 529. | ||
Fig. 527, which is taken from The American Machinist, represents an English self-acting lathe capable of swinging work of 12 inches diameter over the top of the lathe shears, which are provided with a removable piece beneath the live centre, which when removed leaves a gap, increasing the capacity of the lathe swing. The gears for reversing the direction of feed screw motion are here placed at the end of the live head or headstock, the screw being used for feeding as well as for screw cutting.
Fig. 528 represents a pattern-maker’s lathe, by the Putnam Tool Co., of Fitchburg, Massachusetts. This lathe is provided with convenient means of feeding the tool to its cut by mechanism instead of by hand, as is usually done by pattern-makers, and this improvement saves considerable time, because the necessity of frequently testing the straightness of the work is avoided.
It is provided with an iron extension shears, the upper shears sliding in V-ways provided in the lower one. The hand-wheel is connected with a shaft and pinion, which works in a rack, and is used for the purpose of changing the position of the upper bed, which is secured in its adjusted position by means of the tie bolts and nuts, as shown on the front of the lower shears. This enables the gap in the lower shears to be left open to receive work of large diameter, and has the advantage that the gap need be opened no more than is necessary to receive the required length of work. The slide-rest is operated by a worm set at an angle, so as to operate with a rolling rather than a sliding motion of the teeth, and the handle for operating the worm-shaft is balanced. The carriage is gibbed to the bed. The largest and smallest steps of the cone pulley are of iron, the intermediate steps being of wood, and a brake is provided to enable the lathe to be stopped quickly. This is an excellent improvement, because much time is often lost in stopping the lathe while running at a high velocity, or when work of large diameter is being turned. The lathe will swing work of 50 inches within the gap, and the upper shears will move sufficiently to take in 4 additional feet between the centres.
In the general view of the lathe, Fig. 528, the slide-rest is shown provided with a T-rest for hand tools, but as this sets in a clip or split bore, it may readily be removed and replaced by a screw tool, poppet for holding a gauge, or other necessary tool. To enable the facing of work when the gap is used, the extra attachment shown in Figs. 529 and 530 is employed. It consists of an arm or bar a, bolted to the upper shears s by a bolt b, and clamp c, in the usual manner, and is provided with the usual slideway and feed-screw f for operating the lower slide t, which carries a hollow stem d; over d fits a hub k, upon the upper slide e, which hub is split and has a bolt at f, by means of which the upper slide may be clamped to its adjusted angle or position. The upper slider h receives the tool-post, which is parallel and fits in a split hub, so that when relieved it may be rapidly raised or lowered to adjust the height of the tool.
[I-149]The construction of the brake for the cone pulley is shown in Figs. 531 and 532, in which p represents the pulley rim, l the brake lever, s a wooden shoe, and w a counter-weight. The lever is pivoted at g to a lug r, provided on the live headstock, and the brake obviously operates on the lowest part of the cone flange; hence the lever handle is depressed to put the brake in action.
The construction of the front and back bearings for the live spindle is the same as that shown in Figs. 495 and 496.
Wood turners sometimes have their lathes so made that the headstock can be turned end for end on the lathe shears, so that the face plate may project beyond the bed, enabling it to turn work of large diameter. A better method than this is to provide the projecting end of the lathe with a screw to receive the face plate as shown in Fig. 533, which represents a lathe constructed by Walker Brothers of Philadelphia. At the end of the lathe is shown a hand rest upon a frame that can be moved about the floor to accommodate the location, requiring to be turned upon the work.
For very large work, wood-workers sometimes improvise a facing lathe, as shown in Fig. 534, in which a is a headstock bolted to the upright b; c is the cone pulley, and e a face plate built up of wood, and fastened to an iron face plate by bolts. The legs a, of the tripod hand rest, Fig. 535, are weighted by means of the weights b.
| VOL. I. | CHUCKING LATHES. | PLATE VI. |
 |
||
| Fig. 536. | ||
 |
||
| Fig. 537. | ||
In Fig. 536 is shown a chucking lathe, especially adapted for boring and facing discs, wheels, &c. The live spindle is driven by a worm-wheel, provided around the circumference of the face plate. The driving worm (which runs in a cup of oil) is on a driving shaft, running across the lathe and standing parallel with the face of the face plate. This shaft is driven by a pulley as shown, changes of speed being effected by having a cone pulley on the counter-shaft and one on the line of shafting.
This lathe is provided with two compound slide rests. One of which may be used for boring, while the other is employed for facing purposes. These rests are adjustable for location across the bed of the lathe by means of bolts in slots, running entirely across the lathe bed.
These slide rests are given a self-acting motion by the following arrangement of parts: at the back of the live spindle is an eccentric rod, operating a connecting rod, which is attached at its lower end to the arm of a shaft running beneath the bed, and parallel to the lathe spindle. This shaft passes beyond the bed where it carries a bevel gear-wheel, which meshes with a bevel gear-wheel upon a cross shaft. This cross shaft carries three arms, one at each end and inside its journal bearings in the bed, and one beneath and at a right angle to the other two. These receive oscillating motion by reason of the eccentric connecting rod, &c.
[I-150]For each compound rest there are provided two handles as usual, and in addition an L lever, one arm of the latter being provided with a series of holes, while the other carries a weight.
The L lever carries a pawl which operates a ratchet wheel, placed on the handle end of the slide rest cross feed screw. If then a chain be attached to one of the holes of the L lever, and to the oscillating arm, the motion in one direction of the latter will be imparted to the L lever (when the chain is pulled). On the return motion of the oscillating arm, the chain hangs loose, and the weight on the L lever causes that lever arm to fall, taking up the slack of the chain, the feed taking place (when the pawl is made to engage with the ratchet wheel) during the motion of the oscillating arm from right to left, or while pulling the chain.
The rate of feed is varied by attaching the chain to different holes in the L lever.
To operate the rests in a line parallel to the lathe spindle, a similar L lever is attached by chain to the third oscillating arm, which is placed on the cross shaft, mid-way of the bed, or between the two slide rests. It is obvious then that with an L lever attachment on each feed screw, both slides of each rest may be simultaneously operated, while either one may be stopped either by detaching the chain or removing the L lever.
For operating the rests by hand, the usual feed-screw handles are used.
Fig. 537 represents a 90-inch swing lathe by the Ames Manufacturing Company of Chicopee, Massachusetts.
The distinguishing feature of this lathe is that the tailstock spindle is made square, to better enable it to bear the strain due to carrying cutting tools in place of the dead centre; and by means of a pulley instead of a simple hand wheel for operating the tail spindle, that spindle may be operated from an overhead countershaft, and a tool may be put in to cut key-ways in pulleys, wheels, &c., chucked on the face plate (which of course remains stationary during the operation), thus dispensing with the necessity of cutting out such key-ways by hammer, chisel, and file, in wheel bores too large and heavy to be operated upon in a slotting machine.
On account of the weight of the tailstock it is fitted with rollers, which may be operated to lift it from the bed when it is to be moved along the lathe bed.
Fig. 538 represents a 50-inch swing lathe by the New Haven[I-151] Manufacturing Company of New Haven, Connecticut. The compound rest is here provided with automatic feed so that it may be set at an angle to bore tapers with a uniform feed. The tailstock is provided with a bracket, carrying a pinion in gear with the hand-feed rack, so as to move the tailstock along the bed by means of the pinion. The feed screw is splined to give an independent feed, and the swing frame is operated by a worm as shown.
The gap lathe is one in which the bed is provided with a gap beneath the face plate, so as to enable that plate or the chucks to swing work of larger diameter, an example being given in Fig. 539.
It is obvious, however, that the existence of the gap deprives the slide rest of support on one side, when it is used close to the face plate. This is obviated in some forms of gap lathes by fitting into the gap a short piece of bed that may be taken out when the use of the gap is required.
The gap lathe has not found favor in the United States, the same result being more frequently obtained by means of the extension lathe, which possesses the advantages of the gap lathe, while at the same time enabling the width of the gap to be varied to suit the length of the work. Fig. 540 represents an extension lathe by Edwin Harrington and Son, of Philadelphia. There are two beds a and b, the former sliding upon the latter when operated by the hand-wheel e, which is upon the end of a screw that passes between the two beds, has journal bearing in the upper bed, and engages a nut in the lower one, so that as the screw is operated the wheel moves longitudinally with the upper bed. c is the feed rod which communicates motion to the feeding screw d, which has journal bearing on the upper bed and therefore travels with it when it is moved or adjusted longitudinally. The cross slide has sufficient length to enable the slide rest to face work of the full diameter that will swing in the gap, and to support the slide rest when moved outwards to the full limit, it is provided with a piece f, which slides at its base upon the guideway or slide g.
Fig. 541 represents a double face plate lathe such as is used for turning the wheels for locomotives. The circumference of both[I-152] the face plates are provided with spur teeth, so that both are driven by pinions, which by being capable of moving endways into or out of gear, enable either face plate to be used singly, if required, as for boring purposes.
The slide rests are operated by ratchet arms for the self feed, these arms being operated by an overhead shaft, with arms and chains.
Fig. 542 represents a chucking lathe adapted more especially for boring purposes. Thus the cone pulley is of small diameter and the parts are light, so that the lathe is more handy than would be the case with a heavier built lathe, while at the same time it is sufficiently rigid for large work that is comparatively light.
The compound rest is upon a pedestal that can be bolted in any required position on the lower cross slide, and is made self-acting for the feed traverse by the change wheels and feed screw, while the self-acting cross feed is operated by a ratchet handle, actuated by a chain from an overhead reciprocating lever; the latter being actuated from the crank pin at a, which is adjustable in a slot in the crank disk b. A lathe of this kind is very suitable for brass work of unusually large diameter, because in such work the cuts and feeds are light, and the cutting speed is quick, hence a heavy construction is not essential.
Figs. 543 and 544 represent a large lathe built by Thomas Shanks and Co., of Johnstone, near Glasgow, Scotland; all the figures of this lathe being from The American Machinist.
Fig. 543 shows the headstock and two of the slide rests, while Fig. 544 represents the remainder of the bed, the tailstock, and two of the slide rests.
It will be seen from the figures that there are a compound rest and a column or pillar rest both at the front and at the back of the lathe, and that there is an additional rest on the front end of the tailstock which may be used for facing the ends of the work.
Fig. 545 represents a section through, and a partial plan of the headstock, and it will be seen that the live spindle is free from the cone pulley and from the gearing, the chuck plate being driven from a pinion engaging an internal gear at the back of the chuck plate. By this construction the balancing of such work as crank shafts is facilitated, because the chuck plate is not affected by the friction of the driving gears, and may therefore be easily revolved to test the balance of the work.
Fig. 546 represents a cross section through the bed, and through one of the compound rests, and one of the pillar rests, the latter rests being made thin so that they may pass between the cheeks of crank shafts, to turn their faces and the crank journals.
Fig. 547 represents a view from the back end of the headstock, and Fig. 548 a view of the lathe from the tailstock end.
Figs. 549 and 550 represent a plan and a side view of the headstock and the two slide rests nearest to it. The lathe being shown at work on the crank shaft of the steamship service, which is shown in dotted lines, and it will be seen that for turning the stem of the shaft all the rests can be used at once, those at the[I-153] back of the lathe having their cutting tools turned upside down (as will be more clearly seen in the cross-sectional view of the rests in Fig. 546).
Figs. 551 and 552 represent a plan and a side view of the other half of the lathe in operation upon the same crank shaft, which is again shown in dotted lines.
Referring now to the general construction of the lathe, the headstock or live spindle has a front journal bearing 18 inches diameter and 24 inches long, and a back bearing 12 inches diameter and 15 inches long, the bearings being parallel. The driving cone has five changes of speed for a 6-inch belt, and is carried on an independent spindle. The cone is turned inside as well as outside, so as to be in balance at high speeds.
The face plate is 12 feet diameter, cast with internal gear at the back. It is provided with T-slots and square holes for fixing work. It is bolted to a large flange in one piece with the spindle, and fitted with four steel expanding gripping jaws worked with screws and toothed blocks. These are for doing chuck work, or for gripping work to be driven, as the collars of propeller or crank shafts, or work of a similar character. By the system of gearing adopted, when desired, the face plate can be revolved almost free, which facilitates balancing for turning crank shafts, as well as other operations. The thrust against the live spindle is taken by an adjustable steel tail piece.
The
beds are double, 10 feet in width over all, the sections being
joined together by massive ground plates and bolts. They are
made with square lips to resist the upward strain of cutting.
The[I-154/
155]
front bed is fitted with two saddles, each carrying a compound
slide rest having the following movements: First, screw-cutting,
by means of a leading screw, situated inside the bed, with a
sliding disengaging nut and reversing motion for right or left-hand
threads, or for instantaneously stopping the longitudinal
movement of the saddle. This is accomplished by a set of clutch
mitres placed inside the bed at headstock end, and actuated by
a lever in front: Second, a self-acting surfacing motion to slide
rest by means of a longitudinal shaft at the front of the bed, and
clutch mitres for reversing the saddle screw.
Third, power motion for moving the saddles quickly to position along the bed. This is done through the fast and loose pulleys at the headstock end of lathe.
Fourth, hand rack motion to saddle. The back bed is fitted with two saddles, each carrying a pillar rest, fitted for all movements in plain turning like the front rests, and also with swiveling motion for corner turning.
The tailstock has a spindle 9 inches diameter. It is fitted in Vs on the bed, and held down by three T-head bolts on each side. The top section is adjustable for turning tapers. It is moved along the ways by engaging a nut with the main screw. An end-cutting rest is fitted to the tailstock, which is adapted for operating on flanged couplings and similar work.
There is a separate set of change wheels for each saddle, so arranged as to cut standard pitches up to 3-inch pitch, and for self-acting feeds down to 50 per inch. By this means, when both[I-156] tools are in operation on a piece of work, one tool may be used with coarse feed for roughing out, while the other may be taking a fine or finishing cut either on the same or a different part of the piece; or one tool may be cutting towards and the other from the face plate, always maintaining the balance of a front and back cut.
Complete counter driving motion, consisting of wall brackets, shaft, cone, and sets of fast and loose pulleys for quick reversing motion in screw cutting, also belt bar shipping motion, and full set of case-hardened wrenches are provided.
Although in each class of lathe the requirements may be practically the same, yet there is a variety of different details of construction by means of which these requirements may be met or filled, and it may be profitable to enter somewhat into these requirements and the different constructions generally employed to meet them.
The cone spindle or live spindle of a lathe should be a close working fit to its boxes or bearings, so that it will not lift under a heavy cut, or lift and fall under a cut of varying pressure. This lifting and falling may occur even though the work be true, and the cut therefore of even depth all around the work, because of hard seams or spots in the metal.
It is obvious that the bearings should form a guide, compelling the live spindle to revolve in a true circle and in a fixed plane, the axis of revolution being in line with the centre line of the tail spindle and that means should be provided to maintain this alignment while preserving the fit, or in other words taking up the wear. The spindle journals must, to produce truly cylindrical work, be cylindrically true, or otherwise the axis of its revolution will change as it revolves, and this change will be communicated through the live centre to the work, or through the chuck plate to the work, as the case may be.
The construction of the bearings should be such, that end motion to the spindle is prevented in as short a length of the spindle as possible, the thrust in either direction being resisted by the mechanism contained in one bearing.
In Fig. 553 is a form of construction for the front bearing (as that nearest to the live centre is called), in which end motion to the spindle is prevented at the same time as the diametral fit is adjusted. The spindle is provided with a cone at c and is threaded at t to receive two nuts n which draw the spindle cone within the bearing. In this case the journal at the back end may be made parallel, so that if the spindle either expands or contracts more under variations of temperature than the frame or head carrying the bearings or bearing boxes, it will not bind endwise, nor will the fit be impaired save inasmuch as there may be an inequality of expansion in the length of the front journal and its box. In this case, however, the end pressure caused by holding the work between the lathe centres acts to force the spindle into its bearing and increase the tightness of its fit, hence it is not unusual to provide at the back bearing additional means to resist the thrust of the dead centre.
Fig. 554, which is taken from “Mechanics,” represents Wohlemberg’s patent lathe spindle, in which both journals are coned, fitting into bushes which can be replaced by new ones when worn; the end thrust is here taken by a steel screw, while the end fit is adjusted by means of a ring nut which binds the face of the large cone gear against the inside face of the front bearing and by the face of the gear that drives the change gears. It may be pointed out, however, that in this construction the spindle must be drawn within to adjust the fit of the front bearing, which can only be done by adjusting the pinion that drives the change gears, or by screwing up the nut that is inside the cone, and therefore cannot[I-158] be got at. The back bearing can be adjusted by means of the ring nuts provided at each of its ends.
Fig. 555 represents another design of cone bearing, in which the spindle is threaded to receive the nuts a which draw it within the front bearing and thus adjust the fit, and at the same time prevent end motion. The back bearing is provided with a bush parallel outside, and furnished with a nut at b to adjust the fit of the end bearing. To prevent the end pressure of the dead centre from forcing the spindle cones too tightly within their bearings a cross piece p is employed (being supported by two studs provided in the head), and through p passes an adjusting screw d, having nuts n and c, one on each side of p. Between the end of d and of the lathe spindle a washer of leather or of raw hide is placed to prevent the end faces from abrading. A similar device for taking up the end thrust is often provided to lathes in which the journals are both parallel, fitting in ordinary boxes, a top view of the device being illustrated in Fig. 556, in which b is the back bearing box, s s two studs supporting cross-piece p, and n and c are adjusting nuts. g is the gear for driving the change wheels for screw cutting or for ordinary feeding as the case may be. In this design the gear wheel g remains fixed and the combinations of gears necessary to cut various pitches of thread must be made on the lead screw and on the swing frame, which must be long enough to permit the change gear stud to pass up to permit the smallest change wheel to gear with wheel g, and which is provided with two grooves e and f, Fig. 557, for two studs to carry two compounded pairs of change wheels. This compounding in two places on the swing frame enables gear g to be comparatively large, and thus saves the teeth from rapid wear, while it facilitates the cutting of left-hand threads, because it affords more convenience for putting in a gear to change the direction of feed screw revolution.
In many lathes of American design the journals are made parallel, and the end play is taken up at the back bearing, an example being given in Fig. 558, in which the back bearing boxes are made in two halves a and b, the latter having a set screw (with check nut) threaded through it and bearing against a washer that meets the end of the spindle.
A simple method of preventing end motion is shown in Fig. 559, a bracket b affording a support for a threaded adjusting screw, which is sometimes made pointed and at others flat. When pointed it acts to support the spindle, but on the other hand it also acts to prevent the journal from bedding fairly in the boxes. In some cases of small lathes the back bearing is dispensed with, and a similar pointed adjusting screw takes its place, which answers very well for very small work.
Since the strain of the cut carried by the cutting tool falls mainly upon the live centre end of the cone spindle, it is obvious that the bearing at that end has a greater tendency to wear.
In addition to this the weight of the cone itself is greatest at that end, and furthermore the weight of the face plate or chuck, and of the work, is carried mainly at that end. If, however, one journal and bearing wears more than the other, the spindle is thrown out of line with the lathe shears, and with the tail block spindle. The usual method of obviating this as far as possible is to give that end a larger journal-bearing area.
The direction in which this wear will take place depends in a great measure upon the kind of work done in the lathe; thus in a lathe running slowly and doing heavy work carried by chucks, or on the face plate, the wear would be downwards and towards the operator, the weight of the chuck, &c., causing the downward, and the resistance or work-lifting tendency of the cut causing the lateral wear. As a general rule the wear will be least in a lateral direction towards the back of the lathe, but the direction of wear is so variable that provision for its special prevention or adjustment is not usually made. In the S. W. Putnam lathe, provision is made that the bearing boxes may be rotated in the head, so that when the lathe is used on a class of work that caused the live spindle to wear the bearing boxes on one side more than on another, the boxes may be periodically partly rotated in the head so that further wear will correct the evil.
[I-159]The coned hole to receive the live centre should run quite true, so that the live centre will run true without requiring, when inserted, to be placed in exactly the same position it occupied when being turned up at its conical point. But when this hole does not run true a centre punch dot is made on the end of the spindle, and another on the centre, so that by placing the two dots to coincide at all times, the centre will run true.
The taper given to lathe centres varies from 9⁄16 per foot to 1 inch per foot. In the practice of Pratt and Whitney a taper of 9⁄16 per foot is given to all lathes, the lengths of the tapers for different sizes of lathes being as follows:
| Swing of Lathe. | Length of Taper Socket for Live Centre. |
|||||
| 13 | inches | 5 | inches. | |||
| 16 | „ | 3 | 3⁄4 | „ | ||
| 18 | and 19 | inches | 7 | 11⁄16 | „ | |
| „ | „ | with hollow spindle 5 inches long | ||||
| and 11⁄16 diameter at the small end. | ||||||
The less the amount of taper the more firmly the centre is held, but the more difficult it becomes to remove the centre when necessary.
The principal methods of removing live centres are shown in Fig. 560, in which is shown at b a square part to receive a wrench, it being found that if not less than about 1⁄2-inch taper per foot of length be given to the live spindle socket, then revolving the centre with a wrench will cause it to release itself, enabling it to be removed by hand. Another method employed on small lathes is to drill a hole through the live spindle to receive a taper pin p, the live centre end being shown at c.
Another and excellent plan for large lathes, is to thread the centre and provide it with a nut m, which on being screwed against the end face of the live spindle will release the centre. The objection to the use of the pin p is that it is apt to become mislaid, and it is not advisable to use a hammer about the parts of the lathe, especially in such an awkward place as between the journal bearing and the cone, which is where the pin hole requires to be located. The square section is, therefore, the best method for small lathes, and the nut for large ones.
In cases where the live spindle is made hollow a bar may be passed through from the rear end to remove the centre; this also enables rods of iron to be passed through the spindle, leaving the end projecting through the chuck for any length necessary for the work to be turned out of its exposed end.
The dead centre may be extracted from the tail spindle by a pin and hole as in Fig. 560, or, what is better, by contact with the end of the tail screw as described when referring to the tail stock of the S. W. Putnam lathe.
The cone pulley should be perfectly balanced, otherwise at high speeds the lathe will shake or tremble from the unbalanced centrifugal motion, and the tremors will be produced to some extent on the work. The steps of the cone should be amply wide, so that it may have sufficient power, without overstraining the belt, to drive the heaviest cut the lathe is supposed to take without the aid of the back gear.
In some cases, as in spinning lathes, the order of the steps is reversed, the smallest step of the cone being nearest to the live centre, the object being to have the largest step on the left, and therefore more out of the way.
The steps of the cone should be so proportioned that the belt will shift from one to the other, and have the same degree of tension, while at the same time they should give a uniform graduation or variation of speed throughout, whether the lathe runs in single gear or with the back gear in. This is not usually quite the case although the graduation is sufficiently accurate for practical purposes. The variation in the diameter of the steps of a lathe cone varies from an inch for lathes of about 12-inch swing, up to 2 inches for lathes of about 30-inch swing, and 3 inches for lathes of 5 or more feet of swing.
To enable the graduation of speed of the cone to be uniform throughout, while the tension of the belt is maintained the same on whatever step the cone may be, the graduation of the steps may be varied, and this graduation may be so proportioned as to answer all practical purposes if the overhead or countershaft cone and that on the lathe are alike.
The following on this subject is from the pen of Professor D. E. Klein, of Yale College.
“The numbers given in the following tables are the differences between the diameters of the adjacent steps on either cone pulley, and are accurate within half a hundredth of an inch, which is a degree of accuracy sufficient for practical purposes.
By simply omitting a step at each end of the cone, the two tables given will be found equally well adapted for determining the diameters of cones having four and three steps respectively.
The following are examples in the use of the tables. Suppose the centres of a pair of pulley shafts to be 60 inches apart, and that the difference of diameter between the adjacent steps is to be as near to 21⁄2 inches as can be, to obtain a uniformity of speed graduation and belt tension, also that each cone is to have six steps, the smallest of which is to be of five inches diameter.
| The numbers given in table are the differences between the diameters of the adjacent steps on either cone pulley, and can be employed when there are either six or four steps on a cone. When there are six steps, the largest is the first, and the smallest the sixth step of the table. When there are four steps, the largest is the second, and the smallest the fifth step of the table. | |||||||||||||||
| Average difference between the adjacent steps. |
Adjacent steps, whose difference is given in table. |
Distance between the Centres of Cone Pulleys. | |||||||||||||
| 10 inches. |
20 inches. |
30 inches. |
40 inches. |
50 inches. |
60 inches. |
70 inches. |
80 inches. |
90 inches. |
100 inches. |
120 inches. |
240 inches. |
||||
| 1 inch | 1st | and | 2nd | 0.87 | 0.94 | 0.96 | 0.97 | 0.98 | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 1.00 |
| 2nd | „ | 3rd | 0.94 | 0.97 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 | |
| 3rd | „ | 4th | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4th | „ | 5th | 1.06 | 1.03 | 1.02 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | |
| 5th | „ | 6th | 1.13 | 1.06 | 1.04 | 1.03 | 1.02 | 1.02 | 1.02 | 1.02 | 1.01 | 1.01 | 1.01 | 1.00 | |
| 11⁄2 inch | 1st | and | 2nd | 1.21 | 1.36 | 1.40 | 1.43 | 1.44 | 1.45 | 1.46 | 1.46 | 1.47 | 1.47 | 1.48 | 1.49 |
| 2nd | „ | 3rd | 1.36 | 1.43 | 1.45 | 1.46 | 1.47 | 1.48 | 1.48 | 1.48 | 1.49 | 1.49 | 1.49 | 1.49 | |
| 3rd | „ | 4th | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | |
| 4th | „ | 5th | 1.64 | 1.57 | 1.55 | 1.54 | 1.53 | 1.52 | 1.52 | 1.52 | 1.51 | 1.51 | 1.51 | 1.51 | |
| 5th | „ | 6th | 1.79 | 1.64 | 1.60 | 1.57 | 1.56 | 1.55 | 1.54 | 1.54 | 1.53 | 1.53 | 1.52 | 1.51 | |
| 2 inches | 1st | and | 2nd | 1.47 | 1.74 | 1.83 | 1.87 | 1.90 | 1.92 | 1.93 | 1.93 | 1.94 | 1.95 | 1.96 | 1.98 |
| 2nd | „ | 3rd | 1.74 | 1.87 | 1.92 | 1.93 | 1.95 | 1.96 | 1.96 | 1.97 | 1.97 | 1.97 | 1.98 | 1.99 | |
| 3rd | „ | 4th | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | |
| 4th | „ | 5th | 2.26 | 2.13 | 2.08 | 2.07 | 2.05 | 2.04 | 2.04 | 2.03 | 2.03 | 2.03 | 2.02 | 2.01 | |
| 5th | „ | 6th | 2.53 | 2.26 | 2.17 | 2.13 | 2.10 | 2.08 | 2.07 | 2.07 | 2.06 | 2.05 | 2.04 | 2.02 | |
| 21⁄2 inches | 1st | and | 2nd | 1.66 | 2.10 | 2.23 | 2.30 | 2.34 | 2.37 | 2.39 | 2.40 | 2.41 | 2.42 | 2.43 | 2.47 |
| 2nd | „ | 3rd | 2.10 | 2.30 | 2.37 | 2.40 | 2.42 | 2.43 | 2.44 | 2.45 | 2.46 | 2.46 | 2.47 | 2.49 | |
| 3rd | „ | 4th | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | |
| 4th | „ | 5th | 2.90 | 2.70 | 2.63 | 2.60 | 2.58 | 2.57 | 2.56 | 2.55 | 2.54 | 2.54 | 2.53 | 2.51 | |
| 5th | „ | 6th | 3.34 | 2.90 | 2.77 | 2.70 | 2.66 | 2.63 | 2.61 | 2.60 | 2.59 | 2.58 | 2.57 | 2.53 | |
| 3 inches | 1st | and | 2nd | 1.76 | 2.42 | 2.62 | 2.71 | 2.77 | 2.81 | 2.84 | 2.86 | 2.87 | 2.88 | 2.90 | 2.95 |
| 2nd | „ | 3rd | 2.42 | 2.71 | 2.81 | 2.86 | 2.88 | 2.90 | 2.92 | 2.93 | 2.94 | 2.94 | 2.95 | 2.98 | |
| 3rd | „ | 4th | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | |
| 4th | „ | 5th | 3.58 | 3.29 | 3.19 | 3.14 | 3.12 | 3.10 | 3.08 | 3.07 | 3.06 | 2.06 | 3.05 | 3.02 | |
| 5th | „ | 6th | 4.24 | 3.58 | 3.38 | 3.29 | 3.23 | 3.19 | 3.16 | 3.14 | 3.13 | 3.12 | 3.10 | 3.05 | |
| 4 inches | 1st | and | 2nd | 3.95 | 3.31 | 3.49 | 3.59 | 3.66 | 3.71 | 3.75 | 3.78 | 3.80 | 3.83 | 3.91 | |
| 2nd | „ | 3rd | 2.94 | 3.49 | 3.66 | 3.75 | 3.80 | 3.83 | 3.85 | 3.87 | 3.88 | 3.89 | 3.91 | 3.96 | |
| 3rd | „ | 4th | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | |
| 4th | „ | 5th | 5.06 | 4.51 | 4.34 | 4.25 | 4.20 | 4.17 | 4.15 | 4.13 | 4.12 | 4.11 | 4.09 | 4.04 | |
| 5th | „ | 6th | 5.05 | 4.69 | 4.51 | 4.41 | 4.34 | 4.29 | 4.25 | 4.22 | 4.20 | 4.17 | 4.09 | ||
| 5 inches | 1st | and | 2nd | 3.33 | 3.92 | 4.20 | 4.36 | 4.47 | 4.55 | 4.60 | 4.64 | 4.68 | 4.74 | 4.87 | |
| 2nd | „ | 3rd | 3.31 | 4.19 | 4.47 | 4.60 | 4.68 | 4.74 | 4.77 | 4.80 | 4.82 | 4.84 | 4.86 | 4.93 | |
| 3rd | „ | 4th | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | |
| 4th | „ | 5th | 6.69 | 5.81 | 5.53 | 5.40 | 5.32 | 5.26 | 5.23 | 5.20 | 5.18 | 5.16 | 5.14 | 5.07 | |
| 5th | „ | 6th | 6.67 | 6.09 | 5.80 | 5.64 | 5.53 | 5.45 | 5.40 | 5.36 | 5.32 | 5.26 | 5.13 | ||
| 6 inches | 1st | and | 2nd | 3.52 | 4.42 | 4.83 | 5.08 | 5.23 | 5.34 | 5.42 | 5.49 | 5.55 | 5.62 | 5.80 | |
| 2nd | „ | 3rd | 4.83 | 5.23 | 5.42 | 5.54 | 5.62 | 5.67 | 5.71 | 5.75 | 5.77 | 5.81 | 5.90 | ||
| 3rd | „ | 4th | 6.00 | 6.00 | 6.00 | 6.00 | 6.00 | 6.00 | 6.00 | 6.00 | 6.00 | 6.00 | 6.00 | ||
| 4th | „ | 5th | 7.17 | 6.77 | 6.58 | 6.46 | 6.38 | 6.33 | 6.29 | 6.25 | 6.23 | 6.19 | 6.10 | ||
| 5th | „ | 6th | 8.48 | 7.58 | 7.17 | 6.92 | 6.77 | 6.66 | 6.58 | 6.51 | 6.45 | 6.38 | 6.20 | ||
To find the diameters for the remaining steps, we look in Table I. (corresponding to cone pulleys with six steps), under 60 in. and opposite 21⁄2 in. and obtain the differences,
| 2.37 | 2.43 | 2.50 | 2.57 | 2.63 |
Each of these differences is subtracted from the larger diameter of the two adjacent steps to which it corresponds, thus:
| 17.50 | = | 1st | step. | |||||
| Difference of | 1st | and | 2nd | = | 2.37 | |||
| 15.13 | = | 2nd | „ | |||||
| „ | 2nd | „ | 3rd | = | 2.43 | |||
| 12.70 | = | 3rd | „ | |||||
| „ | 3rd | „ | 4th | = | 2.50 | |||
| 10.20 | = | 4th | „ | |||||
| „ | 4th | „ | 5th | = | 2.57 | |||
| 7.63 | = | 5th | „ | |||||
| „ | 5th | „ | 6th | = | 2.63 | |||
| 5.00 | = | 6th | „ | |||||
Example 2. If we suppose the same conditions as in Example 1, with the exception that each cone is to have four steps instead of six, the largest diameter will, in this case, equal 121⁄2 in. and we may obtain the remaining diameters by omitting the end differences of the above example, and then subtracting the remaining differences as follows:
| 12.50 | = | 2nd | step. | |||||
| Difference of | 2nd | and | 3rd | = | 2.43 | |||
| 10.07 | = | 3rd | „ | |||||
| „ | 3rd | „ | 4th | = | 2.50 | |||
| 7.57 | = | 4th | „ | |||||
| „ | 4th | „ | 5th | = | 2.57 | |||
| 5.00 | = | 5th | „ | |||||
The 2nd, 3rd, 4th, and 5th steps of the table correspond respectively to the 1st, 2nd, 3rd, and 4th steps of the cone, having but four steps. If the smallest diameter had not been assumed equal to 5 in. we might have dropped a step at each end of the six-step cone of the preceding example, and employed the remaining four diameters, 15.13 in. 12.70 in. 10.20 in. and 7.63 in. for one four-step cone.
The present and the previous examples show that we can assume the size of the smallest step anything that we please,[I-160] and, other things being equal, can make the required cones large or small.
| The numbers given in table are the differences between the diameters of the adjacent steps on either cone pulley, and can be employed when there are either five or three steps on a cone. | |||||||||||||||
| Average difference between the adjacent steps. |
Adjacent steps, whose difference is given in table. |
Distance between the Centres of Cone Pulleys. | |||||||||||||
| 10 inches. |
20 inches. |
30 inches. |
40 inches. |
50 inches. |
60 inches. |
70 inches. |
80 inches. |
90 inches. |
100 inches. |
120 inches. |
240 inches. |
||||
| 1 inch | 1st | and | 2nd | 0.90 | 0.95 | 0.97 | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 |
| 2nd | „ | 3rd | 0.97 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 3rd | „ | 4th | 1.03 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4th | „ | 5th | 1.10 | 1.05 | 1.03 | 1.02 | 1.02 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | |
| 11⁄2 inch | 1st | and | 2nd | 1.28 | 1.39 | 1.43 | 1.45 | 1.46 | 1.46 | 1.47 | 1.47 | 1.48 | 1.48 | 1.48 | 1.49 |
| 2nd | „ | 3rd | 1.43 | 1.46 | 1.48 | 1.48 | 1.48 | 1.49 | 1.49 | 1.49 | 1.49 | 1.49 | 1.49 | 1.49 | |
| 3rd | „ | 4th | 1.57 | 1.54 | 1.52 | 1.52 | 1.52 | 1.51 | 1.51 | 1.51 | 1.51 | 1.51 | 1.51 | 1.51 | |
| 4th | „ | 5th | 1.72 | 1.61 | 1.57 | 1.55 | 1.54 | 1.54 | 1.53 | 1.53 | 1.52 | 1.52 | 1.52 | 1.51 | |
| 2 inches | 1st | and | 2nd | 1.61 | 1.81 | 1.87 | 1.90 | 1.92 | 1.93 | 1.94 | 1.95 | 1.96 | 1.96 | 1.97 | 1.98 |
| 2nd | „ | 3rd | 1.87 | 1.94 | 1.96 | 1.97 | 1.97 | 1.98 | 1.98 | 1.98 | 1.99 | 1.99 | 1.99 | 1.99 | |
| 3rd | „ | 4th | 2.13 | 2.06 | 2.04 | 2.03 | 2.03 | 2.02 | 2.02 | 2.02 | 2.01 | 2.01 | 2.01 | 2.01 | |
| 4th | „ | 5th | 2.39 | 2.19 | 2.13 | 2.10 | 2.08 | 2.07 | 2.06 | 2.05 | 2.04 | 2.04 | 2.03 | 2.02 | |
| 21⁄2 inch | 1st | and | 2nd | 1.89 | 2.20 | 2.30 | 2.35 | 1.38 | 2.40 | 2.41 | 2.42 | 2.43 | 2.44 | 2.45 | 2.47 |
| 2nd | „ | 3rd | 2.30 | 2.40 | 2.43 | 2.45 | 2.46 | 2.47 | 2.47 | 2.47 | 2.48 | 2.48 | 2.48 | 2.49 | |
| 3rd | „ | 4th | 2.70 | 2.60 | 2.57 | 2.55 | 2.54 | 2.53 | 2.53 | 2.53 | 2.52 | 2.52 | 2.52 | 2.51 | |
| 4th | „ | 5th | 3.11 | 2.80 | 2.70 | 2.65 | 2.62 | 2.60 | 2.59 | 2.58 | 2.57 | 2.56 | 2.55 | 2.53 | |
| 3 inches | 1st | and | 2nd | 2.10 | 2.57 | 2.71 | 2.78 | 2.83 | 2.86 | 2.87 | 2.89 | 2.90 | 2.91 | 2.93 | 2.96 |
| 2nd | „ | 3rd | 2.71 | 2.86 | 2.90 | 2.93 | 2.94 | 2.95 | 2.96 | 2.96 | 2.97 | 2.97 | 2.98 | 2.99 | |
| 3rd | „ | 4th | 3.29 | 3.14 | 3.10 | 3.07 | 3.06 | 3.05 | 3.04 | 3.04 | 3.03 | 3.03 | 3.02 | 3.01 | |
| 4th | „ | 5th | 3.90 | 3.43 | 3.29 | 3.22 | 3.17 | 3.14 | 3.13 | 3.11 | 3.10 | 3.09 | 3.07 | 3.04 | |
| 4 inches | 1st | and | 2nd | 3.22 | 3.49 | 3.62 | 3.69 | 3.75 | 3.78 | 3.81 | 3.83 | 3.84 | 3.87 | 3.94 | |
| 2nd | „ | 3rd | 3.48 | 3.74 | 3.83 | 3.87 | 3.90 | 3.91 | 3.92 | 3.94 | 3.94 | 3.95 | 3.96 | 3.98 | |
| 3rd | „ | 4th | 4.52 | 4.26 | 4.17 | 4.13 | 4.10 | 4.09 | 4.08 | 4.06 | 4.06 | 4.05 | 4.04 | 4.02 | |
| 4th | „ | 5th | 4.78 | 4.51 | 4.38 | 4.31 | 4.25 | 4.22 | 4.19 | 4.17 | 4.16 | 4.13 | 4.06 | ||
| 5 inches | 1st | and | 2nd | 3.77 | 4.20 | 4.40 | 4.52 | 4.60 | 4.66 | 4.71 | 4.73 | 4.76 | 4.80 | 4.90 | |
| 2nd | „ | 3rd | 4.19 | 4.60 | 4.73 | 4.80 | 4.84 | 4.87 | 4.89 | 4.90 | 4.91 | 4.92 | 4.93 | 4.96 | |
| 3rd | „ | 4th | 5.81 | 5.40 | 5.27 | 5.20 | 5.16 | 5.13 | 5.11 | 5.10 | 5.09 | 5.08 | 5.07 | 5.04 | |
| 4th | „ | 5th | 6.23 | 5.80 | 5.60 | 5.48 | 5.40 | 5.34 | 5.29 | 5.27 | 5.24 | 5.20 | 5.10 | ||
| 6 inches | 1st | and | 2nd | 4.21 | 4.83 | 5.13 | 5.31 | 5.42 | 5.51 | 5.57 | 5.62 | 5.66 | 5.71 | 5.86 | |
| 2nd | „ | 3rd | 4.82 | 5.42 | 5.62 | 5.71 | 5.77 | 5.81 | 5.83 | 5.86 | 5.87 | 5.88 | 5.90 | 5.95 | |
| 3rd | „ | 4th | 7.18 | 6.58 | 6.38 | 6.29 | 6.23 | 6.19 | 6.17 | 6.14 | 6.13 | 6.12 | 6.10 | 6.05 | |
| 4th | „ | 5th | 7.79 | 7.17 | 6.87 | 6.69 | 6.58 | 6.49 | 6.43 | 6.38 | 6.34 | 6.29 | 6.14 | ||
Example 3. Let distance apart of the centres = 30 in. the average difference between adjacent steps = 2 in. the diameter of the smallest step = 4 in., and the number of steps on each of the cones = 5. The largest step will then equal 12 in., and from Table II., under 30 in. and opposite 2 in., we obtain the differences
| 1.87 | 1.96 | 2.04 | 2.13 |
and then subtracting as before we get the required diameters
| 12 in. | 10.30 in. | 8.17 in. | 6.13 in. | 4 in. |
Example 4. Let the conditions be as in the preceding example, the cone pulley having, however, three steps instead of five, the largest diameter will then equal 8 in.; and by dropping the end differences and subtracting
| 8.00 | = | 2nd | step. | |||||
| Difference of | 2nd | and | 3rd | = | 1.96 | |||
| 6.04 | = | 3rd | „ | |||||
| „ | 3rd | „ | 4th | = | 2.04 | |||
| 4.00 | = | 4th | „ | |||||
we get the diameters 8 in., 6.04, and 4 in., which correspond respectively to 2nd, 3rd, and 4th steps of the table, and to the 1st, 2nd, and 3rd steps of the three-step cone.
Example 5. Let the distance apart of the centres be 60 in., the average difference between the adjacent steps be 21⁄8 in., the smallest step 7 in. and the number of steps = 5. The largest step will then be 7 in. + (4 × 21⁄8) = 151⁄2 inches.
Now an inspection of Table II. will show that it contains no horizontal lines corresponding to the average difference 21⁄8 inches, we cannot, therefore, as heretofore, obtain the required differences directly, but must interpolate as follows: since 21⁄8 inches is quarter way between 2 inches and 21⁄2 inches, the numbers corresponding to 21⁄8 inches (for any given distance apart of the centres), will be quarter way between the numbers of the table corresponding to 2 inches and 21⁄2 inches. Thus, in Table II., we have under 60 inches,
| and opposite | 2 | 1⁄2 | in.: | 2.40 | 2.47 | 2.53 | 2.60 | ||||
| „ | 2 | 1.93 | 1.98 | 2.02 | 2.07 | ||||||
| .47 | .49 | .51 | .53 | ||||||||
Dividing these differences by 4, we get:
| .12 | .12 | .13 | .13 |
to which we add,
| 1.93 | 1.98 | 2.02 | 2.07 |
[I-161]and get for the differences corresponding to 21⁄8 inches
| 2.05 | 2.10 | 2.15 | 2.20 |
and subtracting as before,
| 15.5 | 1st | step. | |||||||
| difference of | 1st | and | 2nd | = | 2.0 | 5 | |||
| 13.4 | 5 | = | 2nd | „ | |||||
| „ | 2nd | „ | 3rd | = | 2.1 | 0 | |||
| 11.3 | 5 | = | 3rd | „ | |||||
| „ | 3rd | „ | 4th | = | 2.1 | 5 | |||
| 9.2 | 0 | = | 4th | „ | |||||
| „ | 4th | „ | 5th | = | 2.2 | 0 | |||
| 7.0 | 0 | = | 5th | „ | |||||
| Each vertical cone of the table corresponds to a given length of belt, and the numbers in these columns are the required effective diameters of the steps when the centres of the pulleys are a Unit’s distance apart. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Length of Belt When the Centres of the Cone Pulleys Are A Unit’s Distance Apart. | Assumed diameter of steps, divided by distance between the centres of Cone Pulleys |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.09 | 42 | 2.18 | 85 | 2.28 | 27 | 2.37 | 70 | 2.47 | 12 | 2.56 | 55 | 2.65 | 97 | 2.75 | 40 | 2.84 | 82 | 2.94 | 25 | 3.03 | 67 | 3.13 | 10 | 3.22 | 52 | 3.31 | 95 | 3.41 | 37 | 3.50 | 80 | 3.60 | 22 | 3.69 | 65 | 3.79 | 07 | 3.88 | 50 | 3.97 | 92 | 4.07 | 35 | 4.16 | 77 | 4.26 | 20 | 4.35 | 62 | 4.45 | 04 | 4.54 | 47 | 4.63 | 89 | 4.73 | 32 | 4.82 | 74 | 4.92 | 17 | 5.01 | 59 | 5.11 | 02 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | ||||||||||||||||||||||||||||||||||
| .05 | 94 | .11 | 77 | .17 | 50 | .23 | 13 | .28 | 67 | .34 | 13 | .39 | 50 | .44 | 79 | .50 | 00 | .55 | 14 | .60 | 20 | .65 | 18 | .70 | 10 | .74 | 95 | .79 | 74 | .84 | 47 | .89 | 13 | .93 | 73 | .98 | 28 | 1.02 | 77 | 1.07 | 21 | 1.11 | 59 | 1.15 | 93 | 1.20 | 21 | 1.24 | 44 | 1.28 | 61 | 1.32 | 74 | 1.36 | 82 | 1.40 | 85 | 1.44 | 84 | 1.48 | 77 | 1.52 | 66 | 1.56 | 50 | 0.00 |
| .03 | .08 | 94 | .14 | 77 | .20 | 50 | .26 | 13 | .31 | 67 | .37 | 13 | .42 | 50 | .47 | 79 | .53 | 00 | .58 | 14 | .63 | 20 | .68 | 18 | .73 | 10 | .77 | 95 | .82 | 74 | .87 | 47 | .92 | 13 | .96 | 73 | 1.01 | 28 | 1.05 | 77 | 1.10 | 21 | 1.14 | 59 | 1.18 | 93 | 1.23 | 21 | 1.27 | 44 | 1.31 | 61 | 1.35 | 74 | 1.39 | 82 | 1.43 | 85 | 1.47 | 84 | 1.51 | 77 | 1.55 | 66 | 0.03 | |
| .06 | .11 | 94 | .17 | 77 | .23 | 50 | .29 | 13 | .34 | 67 | .40 | 13 | .45 | 50 | .50 | 79 | .56 | 00 | .61 | 14 | .66 | 20 | .71 | 18 | .76 | 10 | .80 | 95 | .85 | 74 | .90 | 47 | .95 | 13 | .99 | 73 | 1.04 | 28 | 1.08 | 77 | 1.13 | 21 | 1.17 | 59 | 1.21 | 93 | 1.26 | 21 | 1.30 | 44 | 1.34 | 61 | 1.38 | 74 | 1.42 | 82 | 1.46 | 85 | 1.50 | 84 | 1.54 | 77 | 0.06 | |||
| .02 | 94 | .09 | .14 | 94 | .20 | 77 | .26 | 50 | .32 | 13 | .37 | 67 | .43 | 13 | .48 | 50 | .53 | 79 | .59 | 00 | .64 | 14 | .69 | 20 | .74 | 18 | .79 | 10 | .83 | 95 | .88 | 74 | .93 | 47 | .98 | 13 | 1.02 | 73 | 1.07 | 28 | 1.11 | 77 | 1.16 | 21 | 1.20 | 59 | 1.24 | 93 | 1.29 | 21 | 1.33 | 44 | 1.37 | 61 | 1.41 | 74 | 1.45 | 82 | 1.49 | 85 | 1.53 | 84 | 0.09 | |||
| .05 | 94 | .12 | .17 | 94 | .23 | 77 | .29 | 50 | .35 | 13 | .40 | 67 | .46 | 13 | .51 | 50 | .56 | 79 | .62 | 00 | .67 | 14 | .72 | 20 | .77 | 18 | .82 | 10 | .86 | 95 | .91 | 74 | .96 | 47 | 1.01 | 13 | 1.05 | 73 | 1.10 | 28 | 1.14 | 77 | 1.19 | 21 | 1.23 | 59 | 1.27 | 93 | 1.32 | 21 | 1.36 | 44 | 1.40 | 61 | 1.44 | 74 | 1.48 | 82 | 1.52 | 85 | 0.12 | |||||
| .02 | 75 | .08 | 94 | .15 | .20 | 94 | .26 | 77 | .32 | 50 | .38 | 13 | .43 | 67 | .49 | 13 | .54 | 50 | .59 | 79 | .65 | 00 | .70 | 14 | .75 | 20 | .80 | 18 | .85 | 10 | .89 | 95 | .94 | 74 | .99 | 47 | 1.04 | 13 | 1.08 | 73 | 1.13 | 28 | 1.17 | 77 | 1.22 | 21 | 1.26 | 59 | 1.30 | 93 | 1.35 | 21 | 1.39 | 44 | 1.43 | 61 | 1.47 | 74 | 1.51 | 82 | 0.15 | |||||
| .05 | 75 | .11 | 94 | .18 | .23 | 94 | .29 | 77 | .35 | 50 | .41 | 13 | .46 | 67 | .52 | 13 | .57 | 50 | .62 | 79 | .68 | 00 | .73 | 14 | .78 | 20 | .83 | 18 | .88 | 10 | .92 | 95 | .97 | 74 | 1.02 | 47 | 1.07 | 13 | 1.11 | 73 | 1.16 | 28 | 1.20 | 77 | 1.25 | 21 | 1.29 | 59 | 1.33 | 93 | 1.38 | 21 | 1.42 | 44 | 1.46 | 61 | 1.50 | 74 | 0.18 | |||||||
| .02 | 44 | .08 | 75 | .14 | 94 | .21 | .26 | 94 | .32 | 77 | .38 | 50 | .44 | 13 | .49 | 67 | .55 | 13 | .60 | 50 | .65 | 79 | .71 | 00 | .76 | 14 | .81 | 20 | .86 | 18 | .91 | 10 | .95 | 95 | 1.00 | 74 | 1.05 | 47 | 1.10 | 13 | 1.14 | 73 | 1.19 | 28 | 1.23 | 77 | 1.28 | 21 | 1.32 | 59 | 1.36 | 93 | 1.41 | 21 | 1.45 | 44 | 1.49 | 61 | 0.21 | |||||||
| .05 | 44 | .11 | 75 | .17 | 94 | .24 | .29 | 94 | .35 | 77 | .41 | 50 | .47 | 13 | .52 | 67 | .58 | 13 | .63 | 50 | .68 | 79 | .74 | 00 | .79 | 14 | .84 | 20 | .89 | 18 | .94 | 10 | .98 | 95 | 1.03 | 74 | 1.08 | 47 | 1.13 | 13 | 1.17 | 73 | 1.22 | 28 | 1.26 | 77 | 1.31 | 21 | 1.35 | 59 | 1.39 | 93 | 1.44 | 21 | 1.48 | 44 | 0.24 | |||||||||
| .02 | 00 | .08 | 44 | .14 | 75 | .20 | 94 | .27 | .32 | 94 | .38 | 77 | .44 | 50 | .50 | 13 | .55 | 67 | .61 | 13 | .66 | 50 | .71 | 79 | .77 | 00 | .82 | 14 | .87 | 20 | .92 | 18 | .97 | 10 | 1.01 | 95 | 1.06 | 74 | 1.11 | 47 | 1.16 | 13 | 1.20 | 73 | 1.25 | 28 | 1.29 | 77 | 1.34 | 21 | 1.38 | 59 | 1.42 | 93 | 1.47 | 21 | 0.27 | |||||||||
| .05 | 00 | .11 | 44 | .17 | 75 | .23 | 94 | .30 | .35 | 94 | .41 | 77 | .47 | 50 | .53 | 13 | .58 | 67 | .64 | 13 | .69 | 50 | .74 | 79 | .80 | 00 | .85 | 14 | .90 | 20 | .95 | 18 | 1.00 | 10 | 1.04 | 95 | 1.09 | 74 | 1.14 | 47 | 1.19 | 13 | 1.23 | 73 | 1.28 | 28 | 1.32 | 77 | 1.37 | 21 | 1.41 | 59 | 1.45 | 93 | 0.30 | |||||||||||
| .01 | 40 | .08 | 00 | .14 | 44 | .20 | 75 | .26 | 94 | .33 | .38 | 94 | .44 | 77 | .50 | 50 | .56 | 13 | .61 | 67 | .67 | 13 | .72 | 50 | .77 | 79 | .83 | 00 | .88 | 14 | .93 | 20 | .98 | 18 | 1.03 | 10 | 1.07 | 95 | 1.12 | 74 | 1.17 | 47 | 1.22 | 13 | 1.26 | 73 | 1.31 | 28 | 1.35 | 77 | 1.40 | 21 | 1.44 | 59 | 0.33 | |||||||||||
| .04 | 40 | .11 | 00 | .17 | 44 | .23 | 75 | .29 | 94 | .36 | .41 | 94 | .47 | 77 | .53 | 50 | .59 | 13 | .64 | 67 | .70 | 13 | .75 | 50 | .80 | 79 | .86 | 00 | .91 | 14 | .96 | 20 | 1.01 | 18 | 1.06 | 10 | 1.10 | 95 | 1.15 | 74 | 1.20 | 47 | 1.25 | 13 | 1.29 | 73 | 1.34 | 28 | 1.38 | 77 | 1.43 | 21 | 0.36 | |||||||||||||
| .00 | 64 | .07 | 40 | .14 | 00 | .20 | 44 | .26 | 75 | .32 | 94 | .39 | .44 | 94 | .50 | 77 | .56 | 50 | .62 | 13 | .67 | 67 | .73 | 13 | .78 | 50 | .83 | 79 | .89 | 00 | .94 | 14 | .99 | 20 | 1.04 | 18 | 1.09 | 10 | 1.13 | 95 | 1.18 | 74 | 1.23 | 47 | 1.28 | 13 | 1.32 | 73 | 1.37 | 28 | 1.41 | 77 | 0.39 | |||||||||||||
| .03 | 64 | .10 | 40 | .17 | 00 | .23 | 44 | .29 | 75 | .35 | 94 | .42 | .47 | 94 | .53 | 77 | .59 | 50 | .65 | 13 | .70 | 67 | .76 | 13 | .81 | 50 | .86 | 79 | .92 | 00 | .97 | 14 | 1.02 | 20 | 1.07 | 18 | 1.12 | 10 | 1.16 | 95 | 1.21 | 74 | 1.26 | 47 | 1.31 | 13 | 1.35 | 73 | 1.40 | 28 | 0.42 | |||||||||||||||
| .06 | 64 | .13 | 40 | .20 | 00 | .26 | 44 | .32 | 75 | .38 | 94 | .45 | .50 | 94 | .56 | 77 | .62 | 50 | .68 | 13 | .73 | 67 | .79 | 13 | .84 | 50 | .89 | 79 | .95 | 00 | 1.00 | 14 | 1.05 | 20 | 1.10 | 18 | 1.15 | 10 | 1.19 | 95 | 1.24 | 74 | 1.29 | 47 | 1.34 | 13 | 1.38 | 73 | 0.45 | |||||||||||||||||
| .02 | 71 | .09 | 64 | .16 | 40 | .23 | 00 | .29 | 44 | .35 | 75 | .41 | 94 | .48 | .53 | 94 | .59 | 77 | .65 | 50 | .71 | 13 | .76 | 67 | .82 | 13 | .87 | 50 | .92 | 79 | .98 | 00 | 1.03 | 14 | 1.08 | 20 | 1.13 | 18 | 1.18 | 10 | 1.22 | 95 | 1.27 | 74 | 1.32 | 47 | 1.37 | 13 | 0.48 | |||||||||||||||||
| .05 | 71 | .12 | 64 | .19 | 40 | .26 | 00 | .32 | 44 | .38 | 75 | .44 | 94 | .51 | .56 | 94 | .62 | 77 | .68 | 50 | .74 | 13 | .79 | 67 | .85 | 13 | .90 | 50 | .95 | 79 | 1.01 | 00 | 1.06 | 14 | 1.11 | 20 | 1.16 | 18 | 1.21 | 10 | 1.25 | 95 | 1.30 | 74 | 1.35 | 47 | 0.51 | |||||||||||||||||||
| .01 | 60 | .08 | 71 | .15 | 64 | .22 | 40 | .29 | 00 | .35 | 44 | .41 | 75 | .47 | 94 | .54 | .59 | 94 | .65 | 77 | .71 | 50 | .77 | 13 | .82 | 67 | .88 | 13 | .93 | 50 | .98 | 79 | 1.04 | 00 | 1.09 | 14 | 1.14 | 20 | 1.19 | 18 | 1.24 | 10 | 1.28 | 95 | 1.33 | 74 | 0.54 | |||||||||||||||||||
| .04 | 60 | .11 | 71 | .18 | 64 | .25 | 40 | .32 | 00 | .38 | 44 | .44 | 75 | .50 | 94 | .57 | .62 | 94 | .68 | 77 | .74 | 50 | .80 | 13 | .85 | 67 | .91 | 13 | .96 | 50 | 1.01 | 79 | 1.07 | 00 | 1.12 | 14 | 1.17 | 20 | 1.22 | 18 | 1.27 | 10 | 1.31 | 95 | 0.57 | |||||||||||||||||||||
| .00 | 29 | .07 | 60 | .14 | 71 | .21 | 64 | .28 | 40 | .35 | 00 | .41 | 44 | .47 | 75 | .53 | 94 | .60 | .65 | 94 | .71 | 77 | .77 | 50 | .83 | 13 | .88 | 67 | .94 | 13 | .99 | 50 | 1.04 | 79 | 1.10 | 00 | 1.15 | 14 | 1.20 | 20 | 1.25 | 18 | 1.30 | 10 | 0.60 | |||||||||||||||||||||
| .03 | 29 | .10 | 60 | .17 | 71 | .24 | 64 | .31 | 40 | .38 | 00 | .44 | 44 | .50 | 75 | .56 | 94 | .63 | .68 | 94 | .74 | 77 | .80 | 50 | .86 | 13 | .91 | 67 | .97 | 13 | 1.02 | 50 | 1.07 | 79 | 1.13 | 00 | 1.18 | 14 | 1.23 | 20 | 1.28 | 18 | 0.63 | |||||||||||||||||||||||
| .06 | 29 | .13 | 60 | .20 | 71 | .27 | 64 | .34 | 40 | .41 | 00 | .47 | 44 | .53 | 75 | .59 | 94 | .66 | .71 | 94 | .77 | 77 | .83 | 50 | .89 | 13 | .94 | 67 | 1.00 | 13 | 1.05 | 50 | 1.10 | 79 | 1.16 | 00 | 1.21 | 14 | 1.26 | 20 | 0.66 | |||||||||||||||||||||||||
| .01 | 74 | .09 | 29 | .16 | 60 | .23 | 71 | .30 | 64 | .37 | 40 | .44 | 00 | .50 | 44 | .56 | 75 | .62 | 94 | .69 | .74 | 94 | .80 | 77 | .86 | 50 | .92 | 13 | .97 | 67 | 1.03 | 13 | 1.08 | 50 | 1.13 | 79 | 1.19 | 00 | 1.24 | 14 | 0.69 | |||||||||||||||||||||||||
| .04 | 74 | .12 | 29 | .19 | 60 | .26 | 71 | .33 | 64 | .40 | 40 | .47 | 00 | .53 | 44 | .59 | 75 | .65 | 94 | .72 | .77 | 94 | .83 | 77 | .89 | 50 | .95 | 13 | 1.00 | 67 | 1.06 | 13 | 1.11 | 50 | 1.16 | 79 | 1.22 | 00 | 0.72 | |||||||||||||||||||||||||||
| .07 | 74 | .15 | 29 | .22 | 60 | .29 | 71 | .36 | 64 | .43 | 40 | .50 | 00 | .56 | 44 | .62 | 75 | .68 | 94 | .75 | .80 | 94 | .86 | 77 | .92 | 50 | .98 | 13 | 1.03 | 67 | 1.09 | 13 | 1.14 | 50 | 1.19 | 79 | 0.75 | |||||||||||||||||||||||||||||
| .02 | 92 | .10 | 74 | .18 | 29 | .25 | 60 | .32 | 71 | .39 | 64 | .46 | 40 | .53 | 00 | .59 | 44 | .65 | 75 | .71 | 94 | .78 | .83 | 94 | .89 | 77 | .95 | 50 | 1.01 | 13 | 1.06 | 67 | 1.12 | 13 | 1.17 | 50 | 0.78 | |||||||||||||||||||||||||||||
| .05 | 92 | .13 | 74 | .21 | 29 | .28 | 60 | .35 | 71 | .42 | 64 | .49 | 40 | .56 | 00 | .62 | 44 | .68 | 75 | .74 | 94 | .81 | .86 | 94 | .92 | 77 | .98 | 50 | 1.04 | 13 | 1.09 | 67 | 1.15 | 13 | 0.81 | |||||||||||||||||||||||||||||||
| .00 | 81 | .08 | 92 | .16 | 74 | .24 | 29 | .31 | 60 | .38 | 71 | .45 | 64 | .52 | 40 | .59 | 00 | .65 | 44 | .71 | 75 | .77 | 94 | .84 | .89 | 94 | .95 | 77 | 1.01 | 50 | 1.07 | 13 | 1.12 | 67 | 0.84 | |||||||||||||||||||||||||||||||
| .03 | 81 | .11 | 92 | .19 | 74 | .27 | 29 | .34 | 60 | .41 | 71 | .48 | 64 | .55 | 40 | .62 | 00 | .68 | 44 | .74 | 75 | .80 | 94 | .87 | .92 | 94 | .98 | 77 | 1.04 | 50 | 1.10 | 13 | 0.87 | |||||||||||||||||||||||||||||||||
| .06 | 81 | .14 | 92 | .22 | 74 | .30 | 29 | .37 | 60 | .44 | 71 | .51 | 64 | .58 | 40 | .65 | 00 | .71 | 44 | .77 | 75 | .83 | 94 | .90 | .95 | 94 | 1.01 | 77 | 1.07 | 50 | 0.90 | |||||||||||||||||||||||||||||||||||
| .01 | 38 | .09 | 81 | .17 | 92 | .25 | 74 | .33 | 29 | .40 | 60 | .47 | 71 | .54 | 64 | .61 | 40 | .68 | 00 | .74 | 44 | .80 | 75 | .86 | 94 | .93 | .98 | 94 | 1.04 | 77 | 0.93 | |||||||||||||||||||||||||||||||||||
| .04 | 38 | .12 | 81 | .20 | 92 | .28 | 74 | .36 | 29 | .43 | 60 | .50 | 71 | .57 | 64 | .64 | 40 | .71 | 00 | .77 | 44 | .83 | 75 | .89 | 94 | .96 | 1.01 | 94 | 0.96 | |||||||||||||||||||||||||||||||||||||
| .07 | 38 | .15 | 81 | .23 | 92 | .31 | 74 | .39 | 29 | .46 | 60 | .53 | 71 | .60 | 64 | .67 | 40 | .74 | 00 | .80 | 44 | .86 | 75 | .92 | 94 | .99 | 0.99 | |||||||||||||||||||||||||||||||||||||||
| .01 | 57 | .10 | 38 | .18 | 81 | .26 | 92 | .34 | 74 | .42 | 29 | .49 | 60 | .56 | 71 | .63 | 64 | .70 | 40 | .77 | 00 | .83 | 44 | .89 | 75 | .95 | 94 | 1.02 | ||||||||||||||||||||||||||||||||||||||
| .04 | 57 | .13 | 38 | .21 | 81 | .29 | 92 | .37 | 74 | .45 | 29 | .52 | 60 | .59 | 71 | .66 | 64 | .73 | 40 | .80 | 00 | .86 | 44 | .92 | 75 | 1.05 | ||||||||||||||||||||||||||||||||||||||||
| .07 | 57 | .16 | 38 | .24 | 81 | .32 | 92 | .40 | 74 | .48 | 29 | .55 | 60 | .62 | 71 | .69 | 64 | .76 | 40 | .83 | 00 | .89 | 44 | 1.08 | ||||||||||||||||||||||||||||||||||||||||||
| .01 | 31 | .10 | 57 | .19 | 38 | .27 | 81 | .35 | 92 | .43 | 74 | .51 | 29 | .58 | 60 | .65 | 71 | .72 | 64 | .79 | 40 | .86 | 00 | 1.11 | ||||||||||||||||||||||||||||||||||||||||||
| .04 | 31 | .13 | 57 | .22 | 38 | .30 | 81 | .38 | 92 | .46 | 74 | .54 | 29 | .61 | 60 | .68 | 71 | .75 | 64 | .82 | 40 | 1.14 | ||||||||||||||||||||||||||||||||||||||||||||
| .07 | 31 | .16 | 57 | .25 | 38 | .33 | 81 | .41 | 92 | .49 | 74 | .57 | 29 | .64 | 60 | .71 | 71 | .78 | 64 | 1.17 | ||||||||||||||||||||||||||||||||||||||||||||||
| .00 | 50 | .10 | 31 | .19 | 57 | .28 | 38 | .36 | 81 | .44 | 92 | .52 | 74 | .60 | 29 | .67 | 60 | .74 | 71 | 1.20 | ||||||||||||||||||||||||||||||||||||||||||||||
| .03 | 50 | .13 | 31 | .22 | 57 | .31 | 38 | .39 | 81 | .47 | 92 | .55 | 74 | .63 | 29 | .70 | 60 | 1.23 | ||||||||||||||||||||||||||||||||||||||||||||||||
| .06 | 50 | .16 | 31 | .25 | 57 | .34 | 38 | .42 | 81 | .50 | 92 | .58 | 74 | .66 | 29 | 1.26 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| .09 | 50 | .19 | 31 | .28 | 57 | .37 | 38 | .45 | 81 | .53 | 92 | .61 | 74 | 1.29 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| .02 | 00 | .12 | 50 | .22 | 31 | .31 | 57 | .40 | 38 | .48 | 81 | .56 | 92 | 1.32 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| .05 | 00 | .15 | 50 | .25 | 31 | .34 | 57 | .43 | 38 | .51 | 81 | 1.35 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .08 | 00 | .18 | 50 | .28 | 31 | .37 | 57 | .46 | 38 | 1.38 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .11 | 00 | .21 | 50 | .31 | 31 | .40 | 57 | 1.41 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .02 | 55 | .14 | 00 | .24 | 50 | .34 | 31 | 1.44 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .05 | 55 | .17 | 00 | .27 | 50 | 1.47 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .08 | 55 | .20 | 00 | 1.50 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Thus far, however, we have considered only the case where the two cone pulleys were exactly alike. Now although this case occurs much more frequently than the case in which the cone pulleys are unlike, it is nevertheless true that unlike cone pulleys occur with sufficient frequency to make it desirable that convenient means be established for obtaining the diameters of their steps rapidly and accurately, and Table III. was calculated by the writer for this purpose; its accuracy is more than sufficient for the requirements of practice, the numbers in the table being correct to within a unit of the fourth decimal place (i.e. within .0001). It should be noticed that the tabular quantities are not the diameters of the steps, but these diameters divided by the distance between the centres of the cone pulleys; in other words, the tabular quantities are the effective diameters of the steps only when the centres of the pulleys are a unit’s distance apart. By thus expressing the tabular quantities in terms of the distance apart of the axis, the table becomes applicable to all cone pulleys whatever their distance from each other, the effective diameters of the steps being obtained by multiplying the proper tabular quantities by the distance between the centres of the pulleys.
Before describing and applying the table, we will call attention to the term “effective” diameter. The effective radius—as is well known—extends from the centre of the pulley to the centre of the belt; the effective diameter, being twice this effective radius, must also equal the actual diameter plus thickness of belt.
The table is so arranged that the diameter (divided by distance between centres) of one step of a belted pair will always be found in the extreme right-hand column; while its companion step will be found on the same horizontal line, and in that vertical column of the table corresponding to the length of belt employed. For example, if column 14 of the table corresponded to the length of belt employed, some of the possible pairs of diameters would be as follows:
| .71 | 18 | .58 | 13 | .42 | .21 | 64 | .04 | 74 | |
| .06 | .24 | .42 | .60 | .72 |
The upper row of this series of pairs being taken from column 14, and the lower row from the extreme right-hand column, the numbers in each pair being on the same horizontal line. If the distance between the centers of the pulleys were 60 ins. the effective diameters of the steps corresponding to the above pairs would be:
| 42.7 | 1 | 34.8 | 8 | 25.2 | 12.9 | 8 | 2.8 | 4 | ins. | |
| 3.6 | 14.4 | 25.2 | 36.0 | 43.2 | 0 |
being obtained by multiplying the first series of pairs by 60; the length of belt which would be equally tight on each of these pairs would be 3.3195 × 60 ins. = 199.17 ins.
[I-162-
163]To
get the actual diameters of these steps when thickness of belt
= 7⁄32 = 0.22 in., we have simply to subtract 0.22 in. from the effective
diameters just given, thus:
| 42.49 | 34.66 | 24.98 | 12.76 | 2.62 | in. |
| 3.38 | 14.18 | 24.98 | 35.78 | 42.98 |
would be the series of pairs of actual diameters.
In solving problems relating to the diameters of cone pulleys by means of the accompanying table, we must have, besides the distance between centres, sufficient data to determine the column representing the length of belt. The length of belt is seldom known because it is of small practical importance to know its exact length; but it may be estimated approximately, and then the determination of suitable diameters of the steps becomes an extremely simple matter, as may be seen from what has already preceded. When the length of the belt is not known, and has not been assumed, we indirectly prescribe the length of belt by assuming the effective diameters of the two steps of a belted pair; thus, in the following Figure (561), the length of belt is prescribed when the distance a b, and any one of the pairs of steps d1d1, d2d2, d3d3 and d4d4 are given. We will show in the following examples how the length of belt and its corresponding column of diameter may be found when a pair of steps (like d1d1), are given.
Example 1. Given the effective diameters
| 4.5 | in. | 9 | in. | 15 | in. | 21 | in. | on cone | A, |
| — | — | 15 | in. | — | „ | B, | |||
and the distance between centres equal to 50 inches.
Required the remaining diameters on cone b.
Since in this example the steps of the given pair are equal, we look for 15⁄50 = 0.30, in the extreme right-hand column of table; we will find it in the 11th line from the top; now looking along this line for the diameter of the other step, = 15⁄50 = 0.30, we will find it in column 10; consequently the numbers of this column may be taken as the diameters of the steps which are the companions or partners of those in the extreme right-hand column.
We can now easily determine the remaining members of the pairs to which 4.5 in., 9 in., and 21 in. steps respectively belong. To find the partner of the 4.5 step, we find 4.5⁄50 = 0.09 in the right-hand column, and look along the horizontal line on which 0.09 is placed till we come to column 10, in which we will find the number 0.4850; 0.4850 × 50 in. = 24.25 in. will be the effective diameter of the companion to the 4.5 in. step.
To find the partner to the 9 in. step, we proceed as before, looking for 9⁄50 = 0.18 in the right-hand column, and then along the horizontal line of 0.18 to column 10, then will 0.4113 × 50 in. = 20.57 in. be the required companion to the 9 in. step of cone a.
In like manner for the partner of the 21 in. step we get 0.1700 × 50 in. = 8.5 in. The effective diameter therefore will be,
| 4 | .5 | in. | 9 | in. | 15 | in. | 21 | in. | on cone | A, | |||
| 24 | .25 | 20 | .57 | 15 | in. | 8 | .5 | „ | B. |
If the thickness of belt employed were 0.25 in. the actual diameters of steps would be,
| 4.25 | 8.75 | 14.75 | 20.75 | on cone | A, |
| 24.00 | 20.32 | 14.75 | 8.25 | „ | B, |
and the length of belt would be 2.9425 × 50 = 147.125 in.
Example 2. Given the effective diameters
| 6 | in. | 12 | in. | 18 | in. | 24 | in. | on cone | A, |
| 30 | in. | — | — | — | „ | B, | |||
and the distance between centres = 40 in.
Required the unknown diameters on cone B.
We must, as before, first find the vertical column corresponding to the length of belt which joins the pair of steps 6 in/30 in. We find the number 6⁄40 = .15 in the right-hand column, and then look along its horizontal line for its partner 30⁄40 = 0.75. Since we do not find any number exactly equal to .7500, we must interpolate. For the benefit of those not familiar with the method of interpolation we will give in detail the method of finding intermediate columns of the table. On the aforesaid horizontal line we find in column 16 a number 0.7520, larger than the required 0.7500, and in column 15 a number 0.7014, smaller than 0.7500; evidently the intermediate column, containing the required 0.7500, must lie between columns 16 and 15. To find how far the required column is from column 16, we subtract as follows:
| 0.7520 | 0.7520 | |
| 0.7500 | 0.7014 | |
| .0020 | 0.0506 |
then the fraction .0020⁄.00506 = 0.04 nearly will represent the position of the required intermediate column; namely, that its distance from column 16 is about 4⁄100 of the distance between the adjacent columns, 15 and 16.
To find other numbers in this intermediate column we have only to multiply the difference between the adjacent numbers of columns 16 and 15 by 0.04, and subtract the product from the number in column 16. But it is not necessary to find as many numbers of the intermediate columns as are contained in either of the adjacent columns; it is only necessary to find as many numbers as there are steps in each of the cone pulleys. We will now illustrate what has preceded, by finding the partner to the 12 in. step of cone a. Find, as before, the horizontal line corresponding to 12⁄40 = 0.30, then take the difference between the numbers 0.6413 and 0.5867 of columns 16 and 15, and multiply this difference, 0.0546, by 0.04; this product = 0.0022 subtracted from 0.6413, will give 0.6391, a number of the intermediate columns corresponding to the length of belt of the present problem. Multiplying by the distance between the axes = 40 in. we get 0.6391 × 40 = 25.56, for the diameter of the step of cone b which is partner to the 12 in. step of cone a.
To find the companion to the 18 in. step, we proceed in the same manner, looking for the horizontal line 18⁄40 = 0.45, and interpolating as follows:
0.5094 - (0.5094 - 0.4500) × 0.04 = 0.5070.
Consequently, 0.5070 × 40 in. = 20.28 in. will be the required partner of the 18 in. step.
In like manner, for the 24 in. step, we have
0.3500 - (0.3500 - 0.2840) × 0.04 = 0.3474, and 0.3474 × 40 = 13.90.
The effective diameters are therefore
| 6 | in. | 12 | in. | 18 | in. | 24 | in. | on cone | A. | |||
| 30 | 25 | .56 | 20 | .28 | 13 | .9 | „ | B. |
[I-164]The actual diameters, when thickness of belt = 0.20 in., are:
| 5 | .8 | 11 | .8 | 17 | .8 | 23 | .8 | on cone | A. |
| 29 | .8 | 25 | .36 | 20 | .08 | 13 | .7 | „ | B. |
And the length of belt will be:
[3.5080 - (3.5080 - 3.4137) × 0.04] × 40 in. = 140.17 in.
Example 3. Given the effective diameters:
| 12 | in. | 18 | in. | 24 | in. | 30 | in. | on cone | A, |
| 33 | in. | — | — | — | „ | B, | |||
and the distance between the centres = 60 in.
Required the remaining diameters on cone b.
The horizontal corresponding to 12⁄60 = 0.20 lies 2⁄3rd way between the horizontal line, corresponding to 0.18 and 0.21; the number 33⁄60 = 0.5500, corresponding to the companion of the 12 in. step, will therefore lie 2⁄3rd way between the horizontal lines 0.18 and 0.21. We have now to find two numbers on this 2⁄3rd line, of which one will be less and the other greater than 0.5500. An inspection of the table will show that these greater and less numbers must lie in columns 13 and 12. The numbers on the 2⁄3rd line itself may now be found as follows:
In column 13, 0.5750 - 2⁄3(0.5750 - 0.5513) = 0.5592.
In column 12, 0.5213 - 2⁄3(0.5213 - 0.4967) = 0.5049.
0.5592 will be the number on the 2⁄3rd line, which is greater than 0.5500, and 0.5049 will be the one which is less than 0.5500. The position of the intermediate column, corresponding to the length of belt of the present example, may now be found, as before, briefly. It is:
| 0.5592 | - | 0.5500 | = | 0.0092 | = | 0.17. |
| 0.5592 | - | 0.5049 | = | 0.0543 |
Consequently the required column lies nearest column 13, 17⁄100th way between columns 13 and 12. To find any other number in the required column, we have only to multiply the difference between two adjacent numbers of columns 13 and 12 by 17⁄100, and subtract the product from the number in column 13. For example, to find the diameter of the partner to the 18 in. step of cone a, we find the numbers 0.4750 and 0.4177 of columns 13 and 12, which lie on the horizontal line corresponding to 18⁄60 = 0.30; the difference, 0.0573, between the two numbers is multiplied by 0.17, and the product, 0.0573 × 0.17 = 0.0097, subtracted from 0.4750. This last difference will equal 0.4653, and will be the number sought. If we now multiply by 60, we will get 27.92 in. as the effective diameter of that step on cone b which is the partner to the 18 in. step of cone a.
To find the companion of the 24 in. step, we proceed after the same fashion; the horizontal line 24⁄60 = 0.40 lies 1⁄3rd way between 0.39 and 0.42; hence,
In column 13, 0.3900 - 1⁄3(0.3900 - 0.3594) = 0.3798;
In column 12, 0.3294 - 1⁄3(0.3294 - 0.2975) = 0.3188;
And 0.3798 - (0.3798 - 0.3188) × 0.17 = 0.3694.
The required effective diameter of the step, which is partner to the 24 in. step, will therefore be 0.3694 × 60 = 22.16 in.
In like manner we obtain partner for the 30 in. step, thus:
In column 13, 0.2944 - 2⁄3(0.2944 - 0.2600) = 0.2715.
In column 12, 0.2300 - 2⁄3(0.2300 - 0.1940) = 0.2060.
Also 0.2715 - (0.2715 - 0.2060) × 0.17 = 0.2604, and 0.2604 × 60 in. = 15.62 in. = diam. of step belonging to the same belted pair as the 30 in. step of cone a.
The effective diameters will be:
| 12 | in. | 18 | in. | 24 | in. | 30 | in. | on cone | A, | |||
| 33 | 27 | .92 | 22 | .16 | 15 | .62 | „ | B, |
and the actual diameters when belt is 0.22′′ thick:
| 11.78 | 17.78 | 23.78 | 29.78 | in. |
| 32.78 | 27.70 | 21.94 | 15.40 |
and the length of belt is found to be:
[3.2252 - (3.2252 - 3.1310) × 0.17] × 60 in. = 192.55 in.
In all the preceding problems it should be noticed that we arbitrarily assumed all the steps on one cone, and one of the steps on the other cone. It will be found that all of the practical problems relating to cone-pulley diameters can finally be reduced to this form, and can consequently be solved according to the methods just given.
For those who find difficulty in interpolating, the following procedure will be found convenient: Estimate approximately the necessary length of belt, then divide this length by the distance between the centres of the cone pulleys; now find which one of the 33 lengths of belt (per unit’s distance apart of the centres) given in the table is most nearly equal to the quotient just obtained, and then take the vertical column, at the head of which it stands, for the companion to the right-hand column. Those numbers of these companion columns which are on the same horizontal line will be the companion steps of a belted pair. The table is so large, that in the great majority of cases not only exact, but otherwise satisfactory values can be obtained by this method, without any interpolation whatever.”
The teeth of the back gear should be accurately cut so that there is no lost motion between the teeth of one wheel, and the spaces of the other, because on account of the work being of large diameter or of hard metal (so as to require the slow speed), the strain of the cut is nearly always heavy when the back gear is in use, and the strain on the teeth is correspondingly great, causing a certain amount of spring or deflection in the live spindle and back gear spindle. Suppose then, that at certain parts of the work there is no cut, then when the tool again meets the cut the work will meet the tool and stand still until the lost motion in the gear teeth and the spring of the spindles is taken up, when the cut will proceed with a jump that will leave a mark on the work and very often break the tool. When the cut again leaves the tool a second jump also leaving a mark on the work will be made. If the teeth of the gears are cut at an angle to the axial line of the spindle, as is sometimes the case, this jumping from the play between the teeth will be magnified on account of a given amount of play, affording more back lash in such gears.
The teeth of the wheels should always be of involute and not of epicycloidal form, for the following reasons. The transmission of motion by epicycloidal teeth is exactly uniform only when their pitch circles exactly coincide, and this may not be the case in time because of wear in the parts as in the live spindle journals and the bearings, and the back gear spindle and its bearings, and every variation of speed in the cut, however slight it may be, produces a corresponding mark upon the work. In involute teeth the motion transmitted will be smooth and equal whether the pitch lines of the wheels coincide or not, hence the wear of the journals and bearings does not impair their action.
The object of cutting the teeth at an angle is to have the point of contact move or roll as it were from one end to the other of the teeth, and thus preserve a more conterminous contact on the line of centres of the two wheels, the supposition being that this would remove the marks on the work produced by the tremor of the back gear. But such tremor is due to errors in the form of the teeth, and also in the case of epicycloidal teeth from the pitch lines of the teeth not exactly coinciding when in gear.
The pitch of the teeth should be as fine as the requisite strength, with the usual allowance of margin for wear and safety will allow, so as to have as many teeth in continuous contact as possible.
Various methods of moving the back gear into and out of gear with the cone spindle gears are employed. The object is to place the back gears into gear to the exact proper depth to hold them securely in position, and to enable the operator to operate the gears without passing to the back of the lathe. Sometimes a sliding bearing box, such as shown in Fig. 562, is employed; a is the back gear spindle, b its bearing box, and d a pin which when on[I-165] the side shown holds b in position, when the back gear is in action. To throw it out of action d is removed, b pushed back, and d inserted in a hole on the right hand of b; the objection is that there is no means of taking up the wear of b, and it is necessary to pass to the back of the lathe to operate the device.
Another plan is to let the back gear move endwise and bush its bearing holes with hardened steel bushes. This possesses the advantage that the gear is sure, if made right, to keep so, but it has some decided disadvantages: first, the pinion a, Fig. 563, must be enough larger than the smallest cone-step b to give room between b and c for the belt, and this necessitates that d also be larger than otherwise; secondly, the gear-spindle f projects through the bearing at f, and this often comes in the way of the bolt-heads used for chucking work to the face plate. The method of securing the spindle from end motion is as follows: On the back of the head is pivoted at i, a catch g, and on the gear shaft f are two grooves. As shown in the sketch, g is in one of these grooves while h is the other, but when the back gear is in, g would be in h.
Sometimes a simple eccentric bush and pin is used as in Fig. 564, in which a is the spindle journal, b a bush having bearing in the lathe head, and d a taper pin to secure b in its adjusted position.
In large heavy lathes having many changes of speed, there are various other constructions, as will be seen upon the lathes themselves in the various illustrations concerning the methods of throwing the back gear in and out. The eccentric motion shown in Fig. 573 of the Putnam lathe, is far preferable to any means in which the back-gear spindle moves endways, because, as before stated, the end of the back-gear spindle often comes in the way of the bolts used to fasten work to the large face plate. This occurs mainly in chucked work of the largest diameter within the capacity of the lathe.
In many American lathes the construction of the gearing that conveys motion from the live spindle is such that facility is afforded to throw the change gears out of action when the lathe is running fast, as for polishing purposes, so as to save the teeth from wear. Means are also provided to reverse the direction of lead screw or feed screw revolution. An example of a common construction of this kind is shown in Fig. 565, in which the driving wheel a is on the inner side of the back bearing as shown. It drives (when in gear) a pair of gears, one only of which is seen in the figure at b, which drives c, and through r, d, i, and s, the lead screw. A side view of the wheel a and the mechanism in connection therewith is shown in Fig. 566, in which s represents the live spindle and r is a spindle or shaft corresponding to r in Fig. 565. l is a lever pivoted upon r and carrying two pinions b and e; pinion b is of larger diameter than e, so that b gears with both c and e (c corresponding to wheel c in Fig. 565), while e gears with b only.
With the lever l in the position shown, neither b nor e engages with a, hence they are at rest; but if lever l be raised as in Fig. 567, b will gear with wheels a and c, and motion will be conveyed from a to c, wheel e running as an idle wheel, thus c will revolve in the same direction as the lathe spindle.
But if lever l be lowered as in fig. 568, then wheel e will gear with and receive motion from a, which it will convey to b, and c will revolve in the opposite direction to that in which the lathe spindle runs. To secure lever l in position, a pin f passes through it and into holes as i, j, provided in the lathe head. Lever l is sometimes placed inside the head, and sometimes outside as in[I-166] Fig. 569, and it will be obvious that it may be used to cut left-hand threads without the use of an extra intermediate change gear, which is necessary in the construction shown in Fig. 570, in order to reverse the direction of lead screw revolution.
Sometimes the pin f is operated by a small spring lever attached to l, so that the hand grasps the end of l and the spring lever simultaneously, removing f from the hole in h, and therefore freeing l, so as to permit its operation. By relaxing the pressure on the small spring lever pin f finds its own way into the necessary hole in h, when opposite to it, without requiring any hand manipulation.
In larger lathes the lever l is generally attached to its stud outside the end bearing of the head h.
It is preferable, however, that the device for changing the direction of feed traverse be operative from the lathe carriage as in the Sellers lathe, so that the operator need not leave it when it is necessary to reverse the direction of traverse.
The swing frame, when the driving gear d is outside of the back bearing (as it is in Fig. 570), is swung from the axis of the lead screw as a centre of motion, and has two slots for receiving studs for change wheels. But when the driving gear is inside the back bearing as in Fig. 571, the swing frame may be suspended from the spindle (r, Fig. 565) that passes through the lathe head, which may also carry the cone for the independent feed as shown in Fig. 571, no matter on which side of the lathe the lead screw and feed rod are. This affords the convenience that when both lead screw and feed rod are in front of the lathe, the feed may be changed from the screw cutting to the rod feed, or vice versâ, by suitable mechanism in the apron, without requiring any change to be made in the driving gears.
In the lathe shown in Fig. 572, which is from the design of S. W. Putnam, of the Putnam Tool Company of Fitchburg, Massachusetts, the cone pinion for the back gear, and that for driving the feed motion, are of the same diameter and pitch, so that the gear-wheel l in Fig. 573 may (by means of a lever shown dotted in) be caused to engage with either of them. When the latter is used in single gear it would obviously make no difference which wheel drives l, but when the back gear is put in and l is engaged with the cone pinion, its speed corresponds to that of the cone, which being nine times faster than the live spindle, enables the cutting of threads nine times as coarse as if the back gear was not in use. This affords very great advantages for cutting worms and threads of coarse pitches.
An excellent method of changing the direction of feed motion, and of starting or stopping the same, is shown in Fig. 574, which represents the design of the Ames Manufacturing Company’s lathe.
In the figure, a is the small step of the lathe cone, b the pinion to drive the back gear, c a pinion to drive the feed gear, giving motion to d, which drives e, the latter being fast to g and rotating freely upon the shaft f, g drives h, which in turn drives i. The clutch j has a featherway into which fits the feather c, on the shaft f, so that when the clutch rotates it rotates j through the medium of c; k is a circular fork in a groove in j, and operated by a lever operated by a rod running along the front of the lathe bed. This rod is splined so that a lever carried by the apron or feed-table, having a hub and enveloping the rod, may by means of a feather filling into the spline operate the rod by partly rotating it, and hence operate k. Suppose now that this lever stands horizontal, then the clutch j would stand in the position shown in the cut, and d, e, g, h, and i, would rotate, while f would remain stationary. By lifting the lever, however, j would be moved laterally on f (by means of k) and the lug a on j would engage with lug b on g, and g would drive j, which through c would drive f, on which is placed a change gear at l, thus traversing the carriage forward. To traverse it backward the lever would be lowered or depressed below the horizontal level moving k, and therefore j, to the right, so that lug a would engage with lug b on i, hence f [I-167] would be driven by i, whose motion is in an opposite direction to g, as is denoted by the respective arrows.
To throw all the feed motion out of gear, to run the lathe at its quickest for polishing, &c., the operation is as follows.
m is tubular and fast in n and affords journal bearing to wheel d. Through m passes stud o, having a knob handle at p. At the end of the hub of d is a cap fast in d, the latter being held endways between the shoulder shown on o and the washer and nut t. If then p be pulled outwards o will slide through m, and through the medium of t will cause d to slide over m, in the direction of the arrow, and pass out of gear from c, motion therefore ceasing at c.
q is the swing frame for the studs to carry the change wheels, and r a bolt for securing q in its adjusted position. s is a journal and bearing for h.
If it be considered sufficient the feed motion on small lathes (instead of feeding in both directions on the lateral and cross feeds[I-168] as in the Putnam Lathe), may feed in the direction from the dead to the live centre, and in one direction only on the cross slide.
An example of a feed motion of this kind is shown in Figs. 575 and 576; f f is the feed spindle splined and through the medium of a feather driving the bevel pinion a having journal bearing in b. Pinion a drives the bevel gear c, which is in one piece with pinion d. The latter drives gear f, which drives pinion k, which is carried on a lever l, pivoted on the stud which carries f, so that by operating l, pinion k is brought into gear with pinion p, which is fast upon the cross-feed screw, and therefore rotates it to effect the automatic cross feed.
As shown in the cut, the lever l is in such a position as to throw k out of gear with p, and the cross feed screw is free to be operated by the handle by hand. At m is a slot in l in which operates a cam or eccentric, one end of which projects into l, while at the other end is the round handle r, Fig. 575, which is rotated to raise or lower that end of l so as to operate k. To operate the saddle or carriage the motion is continued as follows:—at the centre of f is a pinion gear g which operates a gear h, which is in one piece with the pinion i, and the latter is in gear with the rack running along the lathe bed.
If the motion from a to i was continuous, the carriage feed or traverse would be continuous, but means are provided whereby motion from f to i may be discontinued, as follows:—A hand traverse or feed is provided. j, Figs. 575 and 576, is carried by a stud having journal bearing in a hub on x and receiving the handle q; hence by operating q, j is rotated, operating the gear h, upon which is the pinion i, which is in gear with the rack running along the lathe bed.
To lock the carriage in a fixed position, as is necessary when operating the cross feed on large radial surfaces, the following device is provided:—n is a stud fixed in a hub on x, and having a head which overlaps the rim of h, as shown in figure. On the other side of that rim is a washer z on the same stud having a radial face also overlapping the rim of h, but its back face is bevelled to a corresponding bevel on the radial face on the hub of lever o (the hub of o being pivoted on the same stud). When therefore o is depressed the two-bevel face of the hub of o forces the washer z against the face of the wheel h, whose radial faces at the rim are therefore gripped between the face of the collar n and that of the washer z, hence h is locked fast. By raising the end of lever o, z is released and h is free to rotate.
Both the carriage feed and cross feed can only be traversed in one direction so far as these gears and levers are concerned, but means are provided on the lathe headstock for reversing the direction of motion of the feed spindle f so as to reverse the direction of the feeds. It will be observed that so long as f rotates, a, c, d, and f rotate, the remaining motions only operating when s is screwed up.
In order to obtain a delicate tool motion from the handle q it is necessary to reduce the motion between j and i as much as possible, a point in which a great many lathes as at present constructed are deficient, because q, although used to simply traverse the carriage along the bed, in which case rapid motion of the latter is desirable, is also used to feed the tool into corners when the lathe has no compound rest to put on light cuts on radial faces, hence it should be capable of giving a delicate tool motion.
On account of the deficiency referred to it is often necessary to put on a fine radial cut by putting the feed traverse in gear, and, throwing the feed screw gear out of contact with the other change wheels, pull it around by hand to put on the cut. In compound slide rests these remarks do not apply, because the upper part of the rest may be used instead of the handle q.
Many small lathes are provided with a tool rest known as the elevating rest, or weighted lathe.
[I-169]An excellent example of an elevating rest for a weighted lathe is shown in Figs. 577 and 578, which represent the construction in the Pratt and Whitney lathe. a is the lathe shears upon which slides the carriage provided with V slideways r for the sliding piece b, and provided at the other end with the guides h. The cross slide s is pivoted upon b at d, and fits at the other end between the guides h. At e is the elevating screw which when operated raises or lowers that end of the elevating rest to adjust the tool height. This also affords an excellent means of making a minute adjustment for depth of tool cut. The tool rest f is bolted to s.
The weight w is suspended from s and, therefore, holds one end of s to b, the lathe to c, and c to a; at the other end the weight holds s to c (through the medium of the elevating screw e) and c to a. The cross feed nut n is fast to s, the cross feed screw being operated by hand wheel g. b is provided with the V slideways r, which slide upon corresponding V slides r′ upon c; p is a lug cast upon c, and k is a screw threaded in b. When the end of screw k abuts against p the motion of s, and, therefore, of the cutting tool t, towards the work is arrested, hence when the tool is adjusted to the proper depth of cut, k is operated to abut firmly against p, and successive pieces may be turned to the same diameter without requiring each piece to be measured for diameter. n is the handle for opening and closing the nut for the feed screw q, and z is the wheel for the hand feed traverse. The length of cross feed motion is determined by the length of the cross V slides r′.
This class of rest possesses the advantage that no lost motion in the slides occurs by reason of the wear, because the weight keeps the parts in constant contact notwithstanding such wear; on the other hand, however, the slide Vs sustain the extra wear due to the weight w in addition to the weight of the carriage. Lathes of this class are intended for light work, and are less suited for boring than for plain turning; they are, however, very convenient, and are preferred by many to any other kind of lathe for short and light work.
The tool rest being removable may be supplanted by other special forms of rest. Thus Figs. 579 and 580 represent a special rest for carrying two tools to cut pieces of work to the exact same length. Bolts d and e are to secure the rest a to the elevating rest, and c c are the clamps for the two tools b.
Fig. 581 represents a cross sectional view of the Putnam Tool Company’s gibbed elevating rest, there being a gib on the underneath side of the front shear. The elevating screw is pivoted by a ball joint. By employing a gib instead of a weight, the bed may be provided with cross girts or ribs joining the two sides of the shear, thus giving much greater stiffness to it.
Figs. 582, 583, and 584 represent a lathe feed motion by William Munzer, of New York. The object in this motion is to insure that no two feeds can be put into operation simultaneously, because putting the feed in motion in one direction throws it out of gear for either of the others. Another object is to have the transmitting motion as direct as possible so as to avoid the rotation of any wheels not actually necessary for the transmission of the motion; and a third object is to enable the throwing out of gear of all wheels (when no feed motion at all is required) without leaving the apron.
The means employed to effect these objects are as follows:—
In Fig. 582 f represents the independent feed spindle and s the lead-screw: f is splined to drive a, a′ and a′′, which is a sleeve in one piece, and consists of a circular rack at a, a bevel pinion at a′, and a second bevel pinion at a′′. This sleeve may be operated in either direction along f by rotating the pinion b. As shown in the cut a′ and a′′ are both out of gear with the bevel-wheel c, but if b be rotated to the right then a′ will be in gear with c, or if it be operated to the left then a′′ will be in gear with c. Now the direction of rotation of c will be governed by which pinion, a′ or a′′, drives it, and these are the means by which the direction of the feed traverse and also of the cross feed is determined.
If none of the feeds are required to operate, the sleeve occupies the position shown in the cut, and the circular rack at a simply rotates while b and all other parts remain at rest. On the same central pin as c is the pinion d driving a spur gear e′′. On the same centre pin as e is the gear f driving g, which is on the same central pin as c and d. The gear h is fixed to and rotates with g and drives i; all these gears serving to reduce the speed of motion when operating to feed the carriage traverse in either direction.
A gear j is carried on the end of a lever k, being pivoted at l. In the position shown j is out of gear with all gears, but it may be swung to the right so as to engage with wheel i and wheel m, and convey the motion of i to m. Upon the same spindle as m is the pinion n, engaging with the rack o, which is fast on the lathe bed. This completes the automatic feed traverse.
[I-170]For a hand feed traverse, pinion p is employed to drive m, which is fast to n. The cross feed is self-acted by moving lever k to the left, causing it to engage with pinion q as well as with t, q being fast on the cross feed screw. To lock j in either of its three positions there is provided on lever k a spring locking pin r, shown clearly in Fig. 584, which represents an irregular section of the gearing viewed from the headstock of the lathe. The pin r is pressed inward by the spiral spring shown, and has a conical end fitting into holes provided in the apron to receive it. There are three of these holes, shown in dotted lines at a b c in Fig. 582. When the pin is in a the lever k, and therefore wheel j, Fig. 582, is locked out of gear; when it is in hole b wheel j is locked in gear with i and m, and when it is in c the wheel j is in gear with t and q, and the cross feed is actuated.
A similar locking device is provided for the pinion b for actuating a; thus in Fig. 582 b is the lever, the spring pin being at r′′; or referring to Fig. 584, x is the lever fast at x on the pin driving b, and r′ is the spring pin.
The nut for the lead screw is secured either in or out of gear with the screw in the same manner, x′, Fig. 583, being the lever and r′′ the spring pin.
In screw cutting the cutting tool requires to be withdrawn from the thread while the carriage traverses back, and it is somewhat difficult to know just how far to move the tool in again in order to put on a proper depth of cut. To facilitate this the device shown in Fig. 585 (which is taken from the “American Machinist,”) is sometimes employed.
It consists of a ring c inserted between the cross slide d and the handle hub b having journal bearing on and rotating with the latter. When the first cut is put on, the mark on c is coincident with that on d, and the ring is then, while the first cut is traversing, moved (supposing the cross feed screw to have a right-hand thread) to the left, as shown in the figure, to the amount the handle will be required to move to the right to put on the next[I-171] cut, and when the next cut is put on the handle will be moved the distance it was moved to withdraw the tool for the back traverse, and in addition enough to make the marks coincide, then while the second cut is being taken the ring is again moved to the left, as in the cut, to give the depth of cut for the next traverse, and so on.
If the cross feed screw has a left-hand thread, the mark on the ring would require to be moved to the right instead of to the left of the mark on d. It is obvious that this answers the same purpose, but is more exact than the chalk mark before referred to, and, indeed, that chalk mark could be used in the same way, leaving the chalk mark d and rubbing out that on c while the cut is proceeding and making a new one for the next cut.
Another device for use on lathes specially designed for screw-cutting is shown in Fig. 586, in which a represents the cross feed screw. It is fast to the notched wheel b, and is operated by it in the usual way. c is a short screw which provides journal bearing for the screw a by a plain hole. It is screwed on the outside, and the plate in which it fits acts as its nut. It is fast to the handle d, and is in fact operated by it. The handle or lever is provided with a catch e, pivoted in the enclosed box f, which also contains a means of detaining the catch in the notches of the wheel, or of holding it free from the same when it is placed clear. If, then, the lever d be moved back and forth the feed screw a, and hence the slide rest, will be operated; while, if the catch be placed in one of the notches on the wheel b, both the screws, a and c, will act to operate the rests. When, therefore, the tool is set to touch the diameter of the work, the catch e is lifted and the feed wheel b rotated, putting on the cut until the catch e will fall into the next notch in b, the lever d resting in the meantime on the stud g. When the cut is carried along the work to the required distance the tool is withdrawn by moving d over until it rests upon stud or stop h. While the slide rest is traversing back e is lifted and b rotated so that e will fall into the next notch, and when the tool starts forward again d is moved over from h to g, as shown in the figure, and the tool cut is put on.
When the device is not required to be used e is thrown out, d rests on e, and the feed is operated in the ordinary manner.
A simple attachment for regulating on a slide rest the depth of tool cut in screw cutting or for adjusting the cut to a requisite diameter when a number of pieces are to be turned to diameter[I-172] by a finishing cut, is shown in Fig. 587, in which b represents the slide rest carriage, and e the cross slide on which the slide rest a is traversed by means of the cross feed screw f. A screw is screwed into the rest, as shown, carrying the two circular milled edge nuts r p; the screw passes an easy fit through the piece c, which is capable of being fixed in any position along the slide e by means of the set screw s; the nut r is set in such a position on the screw that it will abut against c when the tool is clear of the work surface (for the back traverse) while p may be used in two ways:—First it may be set so that when it comes against c the thread is cut to the required depth, and thus act as stop to give the thread depth without trying the gauge: or it may be used to answer the same purpose and in the same way as the ring c in Fig. 585.
The use of this device as a stop to gauge the thread depth is confined to such lengths of work as enable the tool to cut several pieces without requiring regrinding, because when the tool is removed to grind it, it is impracticable to set it exactly the same distance out from the tool post, hence the adjustment of p becomes destroyed. It is better, therefore, in most cases where a number of threads of equal pitch and diameter are to be cut, to rough them all out, cutting the threads a little above the gauge diameter so as to leave a finishing cut to be taken. In roughing out, however, the nut p may still be used to regulate the depth.
For the finishing cut the tool may be ground and p adjusted to give the requisite depth of cut, taking a single traverse over each thread to finish it. This, of course, preserves the tool and enables it to finish a larger number of threads without regrinding, and the consequent readjustment of p.
It is obvious that the nut p may be employed in the same manner to turn a number of plain pieces to an equal diameter.
It is preferable in a device of this kind, however, to employ the two adjusting nuts p and q in Fig. 588, q being a clamp nut that can be closed by a screw so as to firmly grip the threaded stud. q is adjusted so that when p abuts against it the tool will cut to the correct diameter when it is moved in as far as nuts p q will permit. The use of the second nut p is as follows:—Suppose a first cut has been taken and p may be screwed up to just meet the face of clamp c. Then while the carriage is traversing, p may be screwed back towards q sufficiently to put on the next cut, and so on, so that p is used to adjust the depths of the roughing, and q that of the finishing cut.
Sometimes a feed motion to a slide rest is improvised by what is known as the star feed, the principle of action of which is as follows: Upon the outer end of the feed screw of the boring bar or slide rest, as the case may be, is fastened a piece of iron plate, which, from having the form in which stars are usually represented, is called the star. If the feed is for a slide rest a pin is fastened to the lathe face plate or other revolving part, in such a position that during the portion of the revolution in which it passes the star it will strike one of the star wings, and move it around sufficiently to bring the next wing into position to be struck by the pin during its succeeding revolution. When the feed is applied to a revolving boring bar the construction is the same, but in this case the pin is stationary and the star revolves with the feed screw of the bar.
In Fig. 589 is shown a star feed applied to a slide rest. a is the slide rest, upon the end of the feed screw of which the star, b, is fitted. c is a pin attached to the face plate of the lathe, which, as it revolves, strikes one of the star wings, causing it to partly rotate, and thus move the feed screw. The amount of rotation of the feed screw will depend upon the size of the star and how far the circle described by the pin c intersects the circle described by the extreme points of the star wings. Thus the circles denoted by d e show the path of the pin c; the circle f h the path of the star points, and the distance from f to g the amount which one intersects the other. It follows that at each revolution of c an arm or wing of the star will be carried from the point g to point f, which, in this case, is a sixth of a revolution. If more feed is required, we may move the pin c, so that it may describe a smaller circle than d e, and cause it to intersect f h to a greater extent, in which case it will move the star through a greater portion of its revolution, striking every other wing and doubling the amount of feed.
It will be observed that the points f and g are both below the horizontal level of the slide rest’s feed screw, and therefore that the sliding motion of the pin c upon the face of the star wings will be from the centre towards the points. This is better, because the motion is easier and involves less friction than would be the case if the pin contact first approached and then receded from the centre, a remark which applies equally to all forms of gearing, for a star feed is only a form of gearing in which the star represents a tooth wheel, and the pin a tooth in a wheel or a rack, according to whether its line of motion is a circle or a straight line.
It is obvious that in designing a star feed, the pitch of the feed screw is of primary importance. Suppose, for example, that the pitch of a slide rest feed screw is 4 to an inch, and we require to feed the tool an inch to every 24 lathe revolutions; then the star must have 6 wings, because each revolution of the screw will move the rest 1⁄6 in., while each revolution of the pin c will move the star 1⁄6 of a revolution, and 4 × 6 = 24. To obtain a very coarse feed the star attachment would require to have two multiplying cogs placed between it and the feed screw, the smaller of the cogs being placed upon the feed screw.
In many lathes of European design, the feeds or some of them,[I-173] are actuated by ratchet handles, operated by an overhead shaft, having arms which rock back and forth. Thus in Fig. 590 is a lathe on which there is provided at a crank disc, carrying in a dovetail slot a pin p, for rocking the overhead shaft from whose arms a chain is attached which may be connected to the ratchet handle shown on the cross-feed screw, the weight being for the purpose of carrying that handle down while the chain pulls it up. To regulate the amount of feed the pin p is adjusted in the slot in a, or the chain may be attached in different positions along the length of the ratchet arm, the weight being provided with a set screw so that it may be set in any required position along the ratchet arm.
Tool-holding Devices.—Perhaps no part of a lathe is found in American practice with so many different forms of construction as the device for holding the cutting tool. The requirements for a lathe to be used on light work and where frequent changes in the position of the tool are necessary, are quite different from those for a lathe intended to take as heavy a cut as the lathe will properly drive, and wherein tools having the cutting edge at times standing a long way out from the tool post (as sometimes occurs in the use of boring tools). In the former case a single holding screw will suffice, possessing the advantage that the tool may be quickly inserted, adjusted for height and set to one side or the other, with a range of motion which often permits of a tool that has taken a parallel cut being moved in position to capacitate it to take a facing one, which would not be the case were its capacity for side adjustment limited.
| VOL. I. | TOOL‑HOLDING AND ADJUSTING APPLIANCES. | PLATE VII. | |||
 |
 |
 |
|||
| Fig. 591. | Fig. 592. | Fig. 593. | |||
 |
 |
 |
|||
| Fig. 594. | Fig. 595. | Fig. 596. | |||
 |
 |
 |
|||
| Fig. 597. | Fig. 598. | Fig. 599. | |||
 |
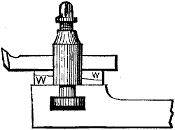 |
 |
|||
| Fig. 600. | Fig. 601. | Fig. 602. | |||
 |
 |
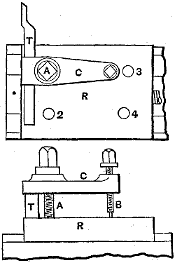 |
|||
| Fig. 603. | Fig. 604. | ||||
 |
|||||
| Fig. 606. | Fig. 605. | ||||
In the case of the common American lathe having a self-acting feed and no compound rest, the tool post is usually employed, the rest being provided with a T slot such as shown in Fig. 577. This enables the tool post to be moved from side to side of the tool rest, and swing around in any required position. In connection with such tool posts various contrivances are employed to enable the height of the cutting edge of the tool to be readily adjusted. Thus in the Fig. 591, the tool post is surrounded by a cupped washer w, and through the slot in the tool post passes a gib g, which may be moved endways in the slot and thus elevates or depresses the tool point.
The objection to this is that the tool is not lifted parallel, or in other words is caused to stand out of its proper horizontal position which alters the clearance of the tool, and by presenting the angles forming the tool edge in an improper position, with relation to the work, impair its cutting qualification, as will be shown hereafter when treating of lathe cutting tools.
An improvement on this form has been pointed out by Professor John E. Sweet, whose device is shown in Fig. 592. Here the washer or ring is rounded and the bottom surface of the gib is hollowed, so that chips or dirt will to a great extent fall off, and every time the tool post is swung the gib acts to push off whatever dirt may lodge on the washer.
In the design shown in Fig. 593, the tool rests upon two washers w that are tapered, and its height is adjusted by revolving one of these washers, it being obvious that the limit of action to depress the tool point is obtained when the two thin sides of the washers are placed together, and on the same side of the tool post as the cutting edge of the tool, while the limit of action to raise the tool point is obtained when the washers have their thick sides together and nearest to the tool point.
Here again the tool is thrown out of level, and to obviate this difficulty the stepped washer shown in Fig. 594 may be used, the steps on opposite sides of the washer being of an equal height. This enables the tool to be raised or lowered without being set out of the horizontal position; but it has the defect that the adjustment cannot be made any finer than the height of the steps, and if the height is made to vary but slightly, in order to refine, as it were, the adjustment, the range of tool elevation or depression is correspondingly limited. Another form of stepped washer is shown in Fig. 595, in which no two steps are of the same height. This affords a wider range of adjustment, because the same two steps will alter the height of the tool by simply turning the washer one-half revolution. It has two defects, however; first, the least amount of adjustment is that due to the difference in height of the steps; and, second, when the tool is elevated it grips the washer at a, so that the tool is not supported across the full width of face of the washer, as it should be.
A defect common to all devices in which the tool is thrown out of level, is that the binding screw does not bed fair upon the tool, and as a result it is apt, if screwed home very firmly, as is necessary to hold boring tools that stand far out from the tool post, to spread the screw end as in Fig. 596, or to bend it.
A very convenient tool-adjusting device is shown in Fig. 597. It consists of a threaded ring n receiving the threaded bush m, the tool height being adjusted by screwing or unscrewing one within the other.
The objection to this is, that it occupies so much vertical height that there is not always room to admit it, which occurs, for example, in compound slide rests on small lathes.
On these rests, therefore, a single washer is more frequently used, which answers very well when the tool post is in a slot, so that it can be moved from side to side of the rest as occasion may require. When, however, the position of the tool post is fixed it has the disadvantage that the point p, Fig. 598, where the tool takes its leverage, is too far removed, and the tool is therefore liable to bend or spring from the pressure of the cut.
[I-174]In Fig. 599 is an elevating device sometimes used on the compound rests of large lathes. The top of the rest is provided with a hub h, threaded externally to receive a ring nut r, around whose edge there are numerous holes to receive a pin for operating the nut. The tool-post is situated central in the hub. When the tool is loose the ring nut can be operated by hand or the tool may be gripped lightly and the ring nut operated by a pin. The level of the tool is here maintained; it is supported to about the edge of the rest on account of the large diameter of the ring nut, and a very delicate adjustment for height can be made, but such a device is only suitable for large lathes on account of the depth of the ring nut and hub.
On small slide-rests the device shown in Fig. 600 is often found. It consists of a holder h, in which is cut a seat for the tool, this seat being inclined to give the piece of steel used as a tool a certain constant degree of angle, and at the same time to permit of the tool being moved endwise in the holder to set it for height; but, as the tool requires to be pushed farther and farther through the holder to raise it, it is not so well supported as is desirable when slight tools are used, unless the holder is made long, so as to pass through the tool post with the tool. Again, it does not support the tool sideways unless the tool steel is dressed up and closely fits the groove in the holder.
In Fig. 601 w w are two inverted wedges which afford an accurate adjustment, but the range is limited, because if the wedges have much taper they are apt to move endways when the tool is fastened.
A convenient device for the compound rests of small lathes is shown in Fig. 602. It consists of a holder pivoted upon a central post and carrying two tool-binding screws, hence it can be revolved to set the tool in any required position. A similar device is shown in Fig. 603, in which the central post is slotted at a to receive the tool, and also carries a plate c, held by the nut n, and provided with tool-holding screws b and b′, which abut against the top of the rest, a top view of the device being shown in Fig. 604. Plate c may thus be swung around to set the tool in any required position on either side of the rest.
In Maudslay’s slide rest, the tool clamp shown in Fig. 605 is employed. Screws a are employed to grip the tool moderately firm, and a turn of screws b (whose ends abut against the top of the slide rest) very firmly secures the tool, since it moves the clamp c as a lever, whose fulcrum is the screw a.
Figs. 606 and 607 represent the Whitworth tool clamp, the clamping plates of which change about upon the four studs, and are supported at their inner ends by a block equal in height to the height of the tool steel.
Figs. 608, 609, 610, and 611 represent the “Lipe” tool post, so called from the name of its inventor. The top of the cross slide is cylindrical, and is bored to receive the tool post which has a cylindrical stem. The cylindrical part of the tool post is split vertically, and has two lips, the bolt d passing through one lip and threading into the other, so that by operating bolt d the tool post may be gripped very firmly or released, so that it may be revolved to bring the tool into any required position after it is fastened in the tool post, which is a great advantage because the tool is brought to a solid seating in the post before its height is adjusted, and will not therefore be altered in height by setting up the set screws as often occurs in ordinary tool posts. From the shape of the tool post, the tool may be gripped by one set screw only, when required for light duty, or by two set screws for heavy duty or for boring, while in either case it is supported clear to the edge of the rest.
Fig. 608 shows the tool in position, held by a single screw, for work requiring the tool to be close up to the work driver. In Fig. 609 a tool is shown held as is required by work between centres, but both set-screws are used. Fig. 610 shows a tool in position for boring, two set-screws being used. Fig. 611 shows a tool being held for the same purpose, but by a single screw, and it will be observed that the advantage of the second set-screw is obtained without in any way sacrificing the handiness of the post, when used with a single screw. Whether one or two set-screws are used, the boring tool may be forged from a single bar of octagon steel, which can be seated in a piece like that shown at e in Fig. 610, which is grooved so as to receive and hold the tool. As is well known, boring tools are the most troublesome both to forge and to adjust in the lathe, and, as the result, a light tool is often used because no other is at hand and it is costly to make a new one. When, however, the tool can be forged from a plain piece of steel, these objections are overcome, and a sufficient number of tools may be had so that one can always be found suitable for any ordinary sized hole, the object being to use as rigid a tool as can be got into the hole bored.[I-175] The feature of maintaining the tool level is of great importance in boring work, because when the tool requires to be set out of level to adjust its height, it will generally strike against the mouth of the hole if the latter is of much depth. This annoyance is also frequently met with in boring tools which are forged out of rectangular steel, because the rounded stem is generally left taper. The largest end of the taper is generally nearest the tool post. Hence the capacity to use octagon steel and keep it level while adjusting its height, added to the fact that the tool is supported clear to the edge of the tool rest, and the tool post is so blocked as to virtually become a part of the rest, constitute a very important advantage.
A common device on large lathes is shown in Fig. 612, the two clamps being shown in position for outside turning, and being changed (so as to stand at a right angle to the position they occupy in the figure) for holding boring tools. The bolts are enveloped by spiral springs which support the clamps.
Figs. 613 and 614 represent the tool holders employed in the Brown and Sharpe small screw machines. In the front rest, Fig. 613, the piece r receives two adjusting and tool-gripping screws s, upon which sits the gib g, and upon this the tool is placed. The surface e at the top of the tool post slot is curved so that it will bear upon the top of the tool at a point only. The tool is here supported along the full length of the gib, and there is no set-screw at the top of the tool post, which enables a much more unobstructed view of the tool.
Fig. 614 is the tool post used at the back of the rest, the piece b passing through the tool post slot. The tool rests upon the top of screw e and upon the top of b at f, and is secured by set-screw s; its height is therefore adjusted by means of screw e, which is threaded in b. The set-screw s is not in this case objectionable, because it is at the back of the rest, and therefore does not obstruct the view of the work, while it is at the same time convenient to get at.
When the screw for traversing a lathe carriage is used for plain feeding, it is termed the feed screw, but when it is used to cut threads it is termed the lead screw.
A lead screw should be used for screw cutting only, so that it may be preserved as much as possible from wear. As the greater portion of threads cut in a lathe of a given size are short in comparison[I-176] with the length of the lathe, it follows that the part of the lead screw that is in operation when the carriage or saddle is traversing over short work is most worn, while the other end is least worn, hence it is not unusual to so construct the screw and its bearings that it may be changed end for end in the lathe, to equalize the wear. By turning a lead screw end for end, therefore, to equalize the wear, the middle of the length of the screw will become the least worn, and, therefore, the most true. Hence it is better to use one end of the lead screw for general work, and to reverse it and use the other end only for screws requiring to be of very correct pitch.
To obviate the wear as much as possible the feed nut should embrace as great a length of the screw as convenient, and should be of a material that will suffer more from wear than the lead screw, or in other words shall relieve the feed screw from wear as much as possible. The wear on the nut being equal from end to end, the wearing away of one side of its thread does not vary its pitch; hence the only consideration as to its wearing qualification are the expense of its renewal and the length of time that may occur between its being engaged with the lead screw and giving motion to the lathe carriage, this time increasing in proportion as the nut thread is worn. Under quick speeds or when the lathe is in single gear, the rotation of the feed screw is so quick that not much time is lost before the carriage feeds, but when the back gear is in operation at the slowest speeds, the loss of time due to a nut much worn is an item of importance.
In some lathes the feed screw is employed for screw cutting and for operating an independent feed also. This is accomplished by cutting a feather way or spline along it, so that a worm having journal bearing in the apron of the rest carriage may envelop the lead screw and be driven by it, through the medium of a feather fast into the worm gear. The motion obtained from the worm gear is transferred through suitable gearing to the rack pinion.
The spline is cut deeper than the thread, so as to prevent the latter as far as possible from wear, by reason of the friction of the spline.
The lead screw if long should be supported, to prevent its sagging of its own weight. In some cases the lead screw is supported[I-177] in a trough along its whole length, as is done in the Sellers lathe. In other cases, bearings hanging from the V-slides, and movable along the bed, are employed.
It is desirable that the feed screw and nut be as near the middle of the carriage as possible, so that it shall pull the carriage at as short a leverage as possible, thus avoiding the liability to tilt or twist the carriage; but it is not practicable to place it midway between the lathe shears, because in that case the cuttings, &c., from the work would fall upon it, and cause excessive and rapid wear of the screw and nut.
In general the lead screw is located either in front, or at the back of the lathe, and in considering the more desirable of the two locations, we have as follows:
The feed nut should obviously remain axially true with the lead screw, as by reason of the extra weight of the front of the carriage, both it and the lathe shears wear most at the front, and the carriage, therefore, falls to the amount of its own wear and the wear of the shears. If the lead screw is used to feed with (as it should not be), the nut wears coincidently with the carriage and the shears, and the screw alignment is not impaired; but with an independent feed, only a small portion of the carriage traversing is done with the lead screw, hence the carriage lowers from the wear due to the independent feeding, and when the lead screw comes to be used its nut is not in true alignment with it. It is obviously preferable, then, to place the lead screw at the back, where the carriage and shears wear the least. Furthermore, this relieves the carriage front from the weight of the nut, &c., tending to equalize the back and front wear, while removing the nut-operating device from the front to the back of the shears, and thus reducing the number of handles in front, and thus avoid complication in small lathes.
Lathe Lead Screws.—Lead screws have their pitches in terms of the inch throughout all parts of the world; or, in other words, the lead screws of all lathes contain so many full threads per inch of length.
Lead screws are usually provided with square threads of the usual form, or with threads whose sides have about fifteen degrees of angle, so that the two halves of the feed nut may be let together to take up the wear. It is obvious that in a V-thread or in a thread whose sides are at an angle, the feeding strain tends to force the two halves of the feed nut apart, and therefore places a strain on the feed-nut operating mechanism that does not exist in the case of a square thread. Furthermore it can be shown that with a V-thread the opportunities to lock the carriage on a wrong place, after traversing it back by hand in screw cutting, are increased, thus augmenting the liability to cut intermediate and improper threads.
In Fig. 615, for example, we have a pitch of lead screw of three threads per inch, and the gears arranged to cut six threads per inch on the work. As the bottom wheel has twice as many teeth as the top one, it is clear that, while the top one makes one, the bottom one will make half revolution, and the lead screw will make half a turn for every turn the work makes. Now, suppose the tool point to stand opposite to space a, and the nut (supposing it to have but one thread only, which is all that is required for our purpose), stand opposite to space d. Suppose, further, that the lathe makes one revolution, and space b on the work will have moved to occupy the position occupied by space a, or, rather, there will still be a place at a fully in front of the tool, as should be the case, but the lead screw will have made half revolution, the top e of the thread coming opposite to the feed nut, as in the position of tool and nut shown in the figure at t and n; hence the nut would not engage, without moving the lathe carriage sideways, and thus throwing the tool to one side of the thread in the work. When, however, the work had made another revolution, both the feed screw and the work would again come into position for the tool and nut to engage properly, and it follows that in this case the tool will always fall into proper position for the nut to be locked.
It is obvious, however, that had the lead screw thread been a square one, and the nut thread to accurately fit to the lead screw thread, so as to completely fill it, then the nut could not engage[I-178] with the lead screw until the lathe had made a complete revolution, at which time the work will have made two full or complete revolutions, and the tool would, therefore, fall into proper position to follow in the groove or part of a thread cut at the first tool traverse.
In Fig. 616, we have the same lead screw geared to cut five or an odd number of threads per inch. The tool and the nut are shown in position to properly engage, but suppose, the nut being disengaged, that the work makes one revolution, and during this period the lead screw will have made 3⁄5ths of a revolution, hence the nut will not be in position to engage properly, because, although space b will have travelled forward so as to occupy the position of space a in the figure (that is, there will be a space fairly in front of the tool point), yet the nut will not engage properly, because the nut point will not be opposite to the bottom of the lead screw thread. When the work has made its second revolution, and space c moves to the position occupied by a, the lead screw will have made 6⁄5 or 11⁄5 revolutions, and the nut cannot engage properly; when the lathe has made its third revolution, the lead screw will have made 14⁄5 revolutions and the nut will still fall to one side of the thread space, and will not lock properly. The work having made its fourth turn, the lead screw will have made 22⁄5 turns, and the nut will not be in position to lock fairly. The work having made its fifth turn, however, the lead screw will have made three turns, and the threads will fall into the same position that they occupy in the figure, and both tool and feed nut will fall into their proper positions in their respective threads. It does not follow, however, that, the lead screw having a V-shaped thread, the nut cannot be forced to engage but once in every five turns of the lead screw, because, were this the case, it would be impossible to lock the nut in an improper position.
Suppose, for example, that we have in Fig. 617, the same piece of work and lead screw as in Fig. 616, and that a first groove, a, has been cut with the tool in the position shown, and the nut engaged in the position marked 1. Now, suppose the nut be disengaged and the work allowed to make one revolution, then the lead screw will, during this revolution, revolve 3⁄5 of a revolution, and the position of the nut point with relation to the lead screw will be as at position 2. If, then, the nut was forced into the lead screw thread, it would, acting on the wedge principle, move the carriage to the right sufficiently to permit the nut to engage fully in thread g, and the tool would then cut a second groove on thread b. If the nut then be withdrawn from thread g, and the work allowed to make another revolution, the nut will stand in a precisely similar position with relation to the lead screw thread as it did in position 2, and by forcing it down into thread h the carriage would be again forced to the right, causing a third thread, c, to be cut. By repeating the operation of withdrawing the nut, letting the work make another revolution and then engaging the nut again, it will seat in thread k, and a fourth thread d will be cut. On again repeating the operation, however, the nut will come into position 5, and, on being drawn home into thread, or, rather, into space l, the tool will fall into groove a again. Thus there will be four threads, each having a pitch equal to that of the lead screw. The second (b) of these four will fall to the left of thread a to an amount or distance equal to 2⁄5 of the pitch of the lead screw, because, in forcing the nut from position 2 down into the lead screw, the slide rest, and therefore the tool, will be moved to the right 2⁄5 of the pitch of the lead screw. The third thread c will fall to the left of thread b also to an amount equal to 2⁄5 of the pitch of the lead screw, because, in forcing the thread to seat itself into thread h from position 3, the slide rest was again moved (to that amount) to the right. The fourth thread d will fall to the left of thread c to the same amount and for the same reason.
But in this case, as before, if the lead screw had a square thread and the nut threads completely filled the spaces between the lead screw threads, then the nut could not engage at the 2nd, 3rd, or 4th work revolution, hence the false threads b, c, and d, could not have been cut, even though the feed nut was disengaged and the lathe carriage was traversed back by hand.
Now, suppose that two threads on the work measure less than the amount the lead screw advances during the time that the work makes a revolution, and if the lead screw has a V-shaped thread, the case is altered. We have, for example, in Fig. 618, a pitch of lead screw of 3 to cut 12 and 13 threads respectively. In the case of the 13 threads it will be seen that, supposing there to have been a first cut taken on the work, and the feed nut to be disengaged while the work makes a revolution, then the lead screw will revolve 3⁄13 revolution and the point a on the lead screw will have moved up to point b, and the nut point remaining at n, seating it in the thread, would cause it to engage with the same thread that it did before, and no second thread would be cut. If the nut be then released, the work allowed to make another revolution and the nut again closed, the operation would be the same as[I-179] before, and no error would be induced, and so on. Suppose, further, that after the nut was disengaged the lathe was permitted to make two revolutions, and the lead screw would make 6⁄13, or less than half a turn, and closing it would still cause it to pass back into the same thread on the lead screw and produce correct work. But if after the nut was released the work made three turns, the lead screw would make 9⁄13 of a turn, and the nut would fall on the right-hand side of the lead screw thread, and in closing would move the lathe carriage to the right, causing the tool to cut a second thread. Now, the same operation that occurred with the first thread would during the next three trials occur with the second thread, and at the next or seventh trial a third thread would be cut, which would be again operated upon during the next succeeding three trials. At the eleventh trial a fourth thread would be cut, but on the next three trials the tool would again fall into the groove first cut and the work proceed correctly. In the case of the 12 threads, the thread cut at the first and second trials would be correct. At the third trial the nut would seat itself in the groove c of the lead screw, causing the carriage to move to the right to a distance equal to twice the pitch of thread being cut, but the tool would still fall into the same groove in the work, as it also would on the fourth. At the fifth trial the process would be repeated, and so on, so that no second thread would be cut.
It may now be noted that if we draw the lead screw and the thread to be cut as in the figure, and draw the dotted lines shown, then those that meet the bottom of the thread on the lead screw, and also meet the groove cut on the work, at the first trial, represent the cases in which the nut will fall naturally into its proper position for the tool to fall into the correct groove, while whenever the nut is being forced home it seats in a groove in the lead screw, the bottom of which groove meets a line drawn from the first thread cut; the results obtained will be made correct by reason of the movement given to the slide nut when artificially seating the nut. This is shown to be the case in Fig. 619, which represents a lead screw having an even number of threads per inch, and from which it appears that in cutting 12 threads (an even number also) the nut cannot be engaged wrong, whereas in the case of 13 threads it can be engaged right three times in 13 trials, and 10 times wrong, the latter causing the tool to cut three wrong threads.
To prevent end motion of a lead screw it should have collars on both sides of one bearing, and not one at each bearing. By this means the screw will be permitted to expand and contract under variations of atmospheric temperature, without binding against the bearing faces.
When a lead screw is long it requires to be supported, otherwise, either its weight will be supported or lifted by the feed nut in gear, or if that nut does not lift the screw, the thread cut will be finer than that due to the pitch of the lead screw, by reason of its deflection or sag.
A lead screw should preferably be as near as possible to the middle of the lathe shears, and as close to the surface as possible, so as to bring it as nearly in line with the strain on the tool as possible, but on account of the cuttings, which falling upon the screw would cause it to wear rapidly, it is usual to locate it on one side, so as to protect it from the cuttings. It is better to locate it on the front side of the lathe rather than on the back, because the strain of the cut falls mainly on the front side (especially in work of large diameter when this strain is usually greatest) and it is desirable to pull the carriage as near in a line with the resistance of the cut as possible, because the farther off the feed nut from the cutting tool point, the greater the tendency to twist the carriage on the shears.
To preserve the nut from wear, it should be made as long as convenient, as, say, five or six times the diameter of the lead screw; it is usually made, however, three or four diameters.
It is obvious that the pitch of the thread should be as accurate as possible, but it has not as yet been found practicable to produce a screw so accurate that it would not show an error, if sufficient of its length be tested, as, say, several feet.
If the error in a screw be equal, and in the same direction at all parts of its length, various devices may be employed to correct it. Thus Fig. 620 represents a device employed by the Pratt and Whitney Co.
It was first ascertained by testing the lathe that its lead screw was too short by 7⁄100ths of a revolution in a length of 2 feet, the pitch of its thread being 6 to an inch. Now in 2 feet of the screw there would be 144 threads, and since 7⁄100ths (the part of a revolution the thread was too short) × 1⁄6 (the pitch of the thread) = 7⁄600ths (which was called 1⁄85th), the error amounted to 1⁄85th inch in 144 turns of the screw. The construction of the device employed to correct this error is as follows: In Fig. 620, a represents the bearing of the feed screw of the lathe, and b b a sleeve, a sliding fit upon a, prevented from revolving by the pin h, while still having liberty to move endways. c represents a casing affording journal bearing to b b, having a fixed gear-wheel at its end c′, and an external thread upon a hub at that end. d is the flange of c to fasten the device to the shears of the latter, being held by screws. e represents an arm fast upon the collar of the feed screw, and carrying the pinion f, the latter being in gear with the pinion c′, and also with g, which is a pinion containing two[I-180] internal threads, one fitting to b at b, and the other fitting to c at c, the former having a pitch of 27 threads to an inch, the latter a pitch of 25 to an inch.
The operation is as follows:—The ordinary change wheels are connected to the feed screw, or lead screw, as it is sometimes termed, at j in the usual manner. The arm e being fast to the feed screw will revolve with it, and cause the pinion f to revolve around the stationary gear-wheel c′. f also gears with g. Now, f is of 12 diametrical pitch and contains 26 teeth, c′ is of 12 diametrical pitch and contains 37 teeth, and g is of 12 diametrical pitch and contains 36 teeth. It follows that the pinion f, while moving around the fixed gear c′, will revolve the pinion g (which acts as a nut), to an amount depending upon the difference in the number of its teeth and those of fixed gear c′ (in this case as 36 is to 37), and upon the difference in the pitches of the two threads, so that at each revolution g will move the feed screw ahead of the speed imparted by the change gears, the end of the sleeve b abutting against the collar of the feed screw to move it forward.
In this case there are 36 turns of the feed screw a for one turn of the nut pinion g, the thread on sleeve b being 27, and that on the hub of c being 25 to the inch; hence, 36 turns of the feed screw gives an end motion to the sleeve b of 1⁄25 minus 1⁄27 = 2⁄675, and 1⁄36 of that = 1⁄12150 of an inch = the amount of sliding motion of the sleeve b, for each revolution of the lathe feed screw. By varying the proportions between the number of teeth in c′ and g and the pitches of the two threads in a proper and suitable ratio, the device enables the cutting of a true thread from any untrue one in which the variation is regular.
It is usual to fasten to the side of the lathe head stock a brass plate, giving a table of threads, and the wheels that will cut them, and obviously such tables vary according to the pitch of the lead screw, but a universal table may be constructed, such as the following table (prepared by the author) that will serve for any lathe.
At the top of the table is the number of teeth in wheels, advancing by four from 12 to 80 teeth, but it may be carried as much beyond 80 as desired. On the left hand of the table is a column of the same wheels. At the bottom of the scale are pitches of lead screw from 3 up to 20 threads per inch. Over each lead screw pitch are thread pitches, thus on lead screw pitch 4 we have 20, 19, 18, and so on.
| Lead Screw. |
12 | *16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 12 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 16 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 20 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 24 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| 28 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| 32 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| 36 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| 40 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 44 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| 48 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| *52 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| 56 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 |
| 60 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| 64 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| 68 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 |
| 72 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 |
| 76 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 |
| 80 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| Lead Screw Pitch 3. |
Lead Screw Pitch 4. |
Lead Screw Pitch 5. |
Lead Screw Pitch 6. |
Lead Screw Pitch 7. |
Lead Screw Pitch 8. |
Lead Screw Pitch 9. |
Lead Screw Pitch 10. |
Lead Screw Pitch 11. |
Lead Screw Pitch 12. |
Lead Screw Pitch 13. |
Lead Screw Pitch 14. |
Lead Screw Pitch 15. |
Lead Screw Pitch 16. |
Lead Screw Pitch 17. |
Lead Screw Pitch 18. |
Lead Screw Pitch 19. |
Lead Screw Pitch 20. |
The use of the table is as follows:—
Find the pitch of the lead screw, and at the head of that column is the number of teeth for the lathe stud or mandril. Then find in that column the number of threads to be cut, and on the same line, but at the left hand, will be found the number of teeth for the lead screw.
Example.—The lead screw has a pitch of 4, and I require to cut 13 threads per inch. At the head of the column is 16, and on a line with the 13 of the column, but on the left is 52, each number being marked by a * hence the 16 and 52 are the wheels; if we have not those wheels, multiply both by 2 and 32, and 104 will answer.
If the pitch of the lead screw is 2 threads per inch, the wheels must advance by 6 teeth, as indicated below:—
| Number of Teeth for Wheel to go on Lead Screw. |
Lead Screw. |
12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 |
| 12 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| 18 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |
| 24 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 30 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| 36 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | |
| 42 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | |
| 48 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | |
| 54 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |
| 60 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |
| Pitch of Lead Screw. |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
This table may be used for compound lathes by simply dividing the pitch of the lead screw by the ratio of the compounded pair of wheels. For example, for the wheels to cut 8 threads per inch, the pitch of lead screw being 4 and the compounded gears 2 to 1, as the ratio of the compounded pair is 2 to 1, we divide the pitch of lead screw by 2, which gives us 2, and we thus find the wheels in the column of pitch of lead screw 2, getting 12 and 48 as the required wheels, the 12 going on top of the lathe because it is at the top of the table, and the 48 on the lead screw because it is at the left-hand end of the table, and the lead screw gear is at the left-hand end of the lathe.
The table may be made for half threads as well as whole ones by[I-181] simply advancing the left-hand column by two teeth, instead of by four, thus:—
| Teeth for Wheel on Lead Screw. |
Teeth for Wheel on Stud. | |||||||||||||||||
| 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | ||||||||||
| 12 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |||||||||
| 14 | 3 | 1⁄2 | 3 | 1⁄2 | 3 | 1⁄2 | 3 | 1⁄2 | 3 | 1⁄2 | 3 | 1⁄2 | 3 | 1⁄2 | 3 | 1⁄2 | 3 | 1⁄2 |
| 16 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |||||||||
| 18 | 4 | 1⁄2 | 4 | 1⁄2 | 4 | 1⁄2 | 4 | 1⁄2 | 4 | 1⁄2 | 4 | 1⁄2 | 4 | 1⁄2 | 4 | 1⁄2 | 4 | 1⁄2 |
| 20 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |||||||||
| 22 | 5 | 1⁄2 | 5 | 1⁄2 | 5 | 1⁄2 | 5 | 1⁄2 | 5 | 1⁄2 | 5 | 1⁄2 | 5 | 1⁄2 | 5 | 1⁄2 | 5 | 1⁄2 |
| 24 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | |||||||||
| 26 | 6 | 1⁄2 | 6 | 1⁄2 | 6 | 1⁄2 | 6 | 1⁄2 | 6 | 1⁄2 | 6 | 1⁄2 | 6 | 1⁄2 | 6 | 1⁄2 | 6 | 1⁄2 |
| 28 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | |||||||||
| 30 | 7 | 1⁄2 | 7 | 1⁄2 | 7 | 1⁄2 | 7 | 1⁄2 | 7 | 1⁄2 | 7 | 1⁄2 | 7 | 1⁄2 | 7 | 1⁄2 | 7 | 1⁄2 |
| 32 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | |||||||||
| 34 | 8 | 1⁄2 | 8 | 1⁄2 | 8 | 1⁄2 | 8 | 1⁄2 | 8 | 1⁄2 | 8 | 1⁄2 | 8 | 1⁄2 | 8 | 1⁄2 | 8 | 1⁄2 |
| 36 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |||||||||
| 38 | 9 | 1⁄2 | 9 | 1⁄2 | 9 | 1⁄2 | 9 | 1⁄2 | 9 | 1⁄2 | 9 | 1⁄2 | 9 | 1⁄2 | 9 | 1⁄2 | 9 | 1⁄2 |
| 40 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |||||||||
| 42 | 10 | 1⁄2 | 10 | 1⁄2 | 10 | 1⁄2 | 10 | 1⁄2 | 10 | 1⁄2 | 10 | 1⁄2 | 10 | 1⁄2 | 10 | 1⁄2 | 10 | 1⁄2 |
| Pitch of Lead Screw. |
3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |||||||||
For quarter threads we advance the left-hand column by one tooth, or for thirds of threads by three teeth, and so on.
If we require to find what wheels to provide for a lathe, we take the pitch of the lead screw for the numerator, and the pitch required for the denominator, and multiply them first by 2, then by 3, then by 4, and so on, continuing until the numerator or denominator is as large as it can be to give the required proportion of teeth, and not exceed the greatest number that the largest wheel can contain.
For example: A lathe has single gear, and its lead screw pitch is 8 per inch, what wheels will cut 18, 17, 16, 15, 14, or 13 threads per inch?
| Wheels. | |||||||||
| Pitch of lead screw | 8 | × 2 = | 16 | 24 | 32 | ||||
| Pitch required | 18 | 36 | 54 | 72 | |||||
| Pitch of lead screw | 8 | „ | 16 | 24 | 32 | ||||
| Pitch required | 17 | 34 | 51 | 68 | |||||
| Pitch of lead screw | 8 | „ | 16 | 24 | 32 | ||||
| Pitch required | 16 | 32 | 48 | 64 | |||||
| Pitch of lead screw | 8 | „ | 16 | 24 | 32 | ||||
| Pitch required | 15 | 30 | 45 | 60 | |||||
| Pitch of lead screw | 8 | „ | 16 | 24 | 32 | ||||
| Pitch required | 14 | 28 | 42 | 56 | |||||
| Pitch of lead screw | 8 | „ | 16 | 24 | 32 | 40 | |||
| Pitch required | 13 | 26 | 39 | 52 | 65 | ||||
If we suppose that the greatest number of teeth permissible in one wheel is not to exceed 100, then in this table we have all the combinations of wheels that can be used to cut the given pitches; and having made out such a table, comprising all the pitches to be cut, we may select therefrom the least number of wheels that will cut those pitches. The whole table being made out it will be found, of course, that the numerators of the fractions are the same in each case; that is, in this case, 16, 18, 24, 32, and so on as far as we choose to carry the multiplication of the numerator. We shall also find that the denominators diminish in a regular order: thus taking the fractions whose numerators are in each case 16, we find their denominators are, as we pass down the column, 36, 34, 32, 30, 28, and 26, respectively, thus decreasing by 2, which is the number we multiplied the left-hand column by to obtain them. Similarly in the fractions whose numerators are 24, the denominators diminish by 3, being respectively 54, 51, 48, 45, 42, and 39; hence the construction of such a table is a very simple matter so far as whole numbered threads are concerned, as no multiplication is necessary save for the first line representing the finest pitch to be cut.
For fractional threads, however, instead of using the pitch of the lead screw for the numerator, we must reduce it to terms of the fraction it is required to cut. For example, for 51⁄2 threads we proceed as follows. The pitch of the lead screw is 8, and in 8 there are 16 halves, hence we use 16 instead of 8, and as in the 51⁄2 there are 11 halves we use the fraction 16⁄11 and multiply it first by 2, then by 3, and then by 4, and so on, obtaining as follows: 16⁄11, 32⁄22, 48⁄33, 64⁄44, obtaining as before three sets of wheels either of which will cut the required pitch. In selecting from such a table the wheels to cut any required number of pitches, the set must, in order to cut a thread of the same pitch as the lead screw, contain two wheels having the same number of teeth.
Now, suppose that the pitch of the lead screw was 6 instead of 8 threads per inch, and the table will be as follows:—
| 6 | 12 | 18 | 24 | |||
| 18 | 36 | 54 | 72 | |||
| 6 | 12 | 18 | 24 | |||
| 17 | 34 | 51 | 68 | |||
| 6 | 12 | 18 | 24 | |||
| 16 | 32 | 48 | 64 | |||
| 6 | 12 | 18 | 24 | |||
| 15 | 30 | 45 | 60 | |||
| 6 | 12 | 18 | 24 | |||
| 14 | 28 | 42 | 56 | |||
| 6 | 12 | 18 | 24 | |||
| 13 | 26 | 39 | 52 | |||
Here, again, we find that in the first vertical column the denominators decrease by two for each thread less per inch, in the second column they decrease by three, and in the third by four; this decrease equalling the number the first fraction was multiplied by.
But suppose the lead screw pitch is an odd one, as, say, 3 threads per inch, and we construct the table as before, thus—
| Pitch of lead screw | 3 | 6 | 9 | 12 | 15 | ||||
| Pitch to be cut | 18 | 32 | 54 | 72 | 90 |
Now it is useless to multiply by 2 or by 3, because they give a less number of teeth than the smallest wheel should have, hence the first multiplier should be 4, giving the following table:—
| 3 | 12 | 15 | 18 | |||
| 18 | 72 | 90 | 108 | |||
| 3 | 12 | 15 | 18 | |||
| 17 | 68 | 85 | 102 | |||
| 3 | 12 | 15 | 18 | |||
| 16 | 64 | 80 | 96 | |||
| 3 | 12 | 15 | 18 | |||
| 15 | 60 | 75 | 90 | |||
By continuing the table for other pitches we shall find that in the first vertical column the denominators diminish by 4, the second column by 5, and the third by 6; and it is seen that by diminishing the pitch of the lead screw, we have rendered necessary one of two things, which is, that either larger wheels containing more teeth must be used, or the change gears must be compounded.
Assuming that the pitch of the lead screw was 5 per inch, the table would be as follows:—
| 5 | × 3 = | 15 | 20 | 25 | ||
| 18 | 54 | 72 | 90 | |||
| 5 | „ | 15 | 20 | 25 | ||
| 17 | 51 | 68 | 85 | |||
| 5 | „ | 15 | 20 | 25 | ||
| 16 | 48 | 64 | 80 |
[I-182]The wheels in the first column here decrease by 3, the second by 4, and the third by 5.
In nearly all lathes the advance or decrease is by 4 or by 6. In determining this rate of advance or decrease, there are several elements, among which are the following. Suppose the lathe to be geared without compounding, then the distance between the lathe spindle and the lead screw will determine what shall be the diameters of the largest and of the smallest wheel in the set, it being understood that the smallest wheel must not contain less than 12 teeth. Assume that in a given case the distance is 10 inches, and it is obvious that the pitch of the teeth at once commands consideration, because the finer the pitch the smaller the wheel that will contain 12 teeth, and the larger the wheel on the lead screw may be made. Of course the pitch must be coarse enough to give the required tooth strength.
Let it be supposed that the arc pitch is 3⁄4-inch, then the pitch circumference of a 12-toothed wheel would be 9 inches and its radius 1.432 in.; this subtracted from the 10 leaves 8.568 in. as the radius, or 17.136 in. as the largest diameter of wheel that can be used on the lead screw, supposing there to be no intermediate gears. Now a wheel of this diameter would be capable of containing more than 75 teeth, but less than 76. But from the foregoing tables it will be seen that it should contain a number of teeth divisible either by 4 or by 6 without leaving a remainder, and what that number should be is easily determined by means of a table constructed as before explained. Thus from the tables it would be found that 72 teeth would be best for a lead screw having a pitch of either 8, 6, 5, or 3 threads per inch, and the screw-cutting capacity of the lathe would (unless compounded) be confined to such pitches as may be cut with wheels containing between 12 and 72 teeth both inclusive.
But assume that an arc pitch of 3⁄8-inch be used for the wheel teeth, and we have as follows: A wheel of this pitch and containing 12 teeth will have a radius of 716⁄1000 inches, leaving 9.284 in. as the radius of the largest wheel, assuming it to gear direct with the 12-tooth pinion. With this radius it would contain 155 teeth and a fraction of a tooth; we must, therefore, take some less number, and from what has been said, it will be obvious that this lesser number should be one divisible by either 4 or 6. If made divisible by 6, the number will be 150, because that is the highest number less than 155 that is divisible by 6 without leaving a remainder. But if made divisible by 4, it may contain 152 teeth, because that number is divisible by 4 without leaving a remainder. With 150 teeth the latter could cut a thread 121⁄2 times as fine as the lead screw, because the largest wheel contains 121⁄2 times as many teeth as the smallest one; or it would cut a thread 121⁄2 times as coarse as the lead screw, if the largest wheel be placed on the mandril and the smallest on the lead screw. With 152 teeth the lathe would be able to cut a thread 1284⁄100 times as fine or as coarse as the lead screw. Unless, however, the lathe be required to cut fractional pitches, it is unnecessary that the largest wheel have more teeth than divisible, without leaving a remainder, by the number of teeth in the smallest wheel, which being 12 we have 144 as the number of teeth for the largest wheel. In the United States standard pitches of thread, however, there are several pitches in fractions of an inch, hence it is desirable to have wheels that will cut these pitches.
Lathe Shears or Beds.—The forms of the shears and beds may be classified as follows.
The term shear is generally applied when the lathe is provided with legs, while the term bed is used when there are no legs; it may be noted, however, that by some workmen the two terms of shear and bed are used indiscriminately.
The forms of shears in use on common lathes are, in the United States, the raised V, the flat shear and the shear, with the edge at an angle of 90° or with parallel edges. In England and on the continent of Europe, the flat shear is almost exclusively employed.
Referring to the raised V it possesses an important advantage in that, first, the slide rest does not get loosely guided from the wear; and second, the wear is in the direction that least affects the diameter of the work.
In Fig. 621, for example, is a section of a lathe shear, with a slide rest shown in place, and it will be observed that the wear of the V upon the lathe bed, and of the V-groove in the slide rest, will cause the rest to fall in the direction of arrow a, and that a given amount of motion in that direction will have less effect in altering the diameter than it would in any other direction. This is shown on the right hand of the figure as follows: Suppose the cutting point of the tool is at a, and the work will be of the diameter shown by the full circle in the figure. If we suppose the tool point to drop down to f, the work would be turned to the diameter denoted by dotted arc g, while if the tool were moved outwards from a to c the work would be turned to the diameter e. Now since f and c are equidistant from the point a, therefore the difference in the diameters of e and g represents the difference of effect between the wear letting the rest merely fall, or moving it outwards, and it follows that, as already stated, the diameter of the work is less affected by a given amount of wear, when this wear is in the direction of a, than when it is in the direction of b. When the carriage is held down by a weight as is shown in Figs. 577 and 578, there is therefore no lost motion or play in the carriage, which therefore moves steadily upon the shears, unless the pressure of the cut is sufficient in amount, and also in a direction to lift the carriage (as it is in the case of boring with boring tools); but to enable the carriage to remain firm upon the shears under all conditions, it is necessary to provide means to hold it down upon the Vs, which is done by means of gibs g, g, which are secured to the carriage, and fit against the bottom of the bed flange as shown.
Now since lathes are generally used much more frequently on short than on long work, therefore the carriage traverses one part of the shears more than another, and the Vs wear more at the part most traversed, and it follows that if gibs g are set to slide properly at some parts they will not be properly set at another or other parts of the length of the shears; hence the carriage will in some parts have liberty to move from the bed, there being nothing but the weight of the carriage, &c., to hold it down to the Vs. Now, the wear in the direction of a acts directly to cause this inequality of gib fit, whereas that in the direction of b does so to a less extent, as will appear hereafter.
Meantime it may be noted that when the carriage is held down by a suspended weight the shears cannot be provided with cross girts, and are therefore less rigid and more subject to torsion under the strain of the cut; furthermore the amount of the weight must be sufficient to hold the carriage down under the maximum of cut, and this weight acts continuously to wear the Vs, whether the carriage is under cutting duty or not, but the advantage of keeping the carriage firmly down upon the Vs is sufficiently great[I-183] to cause many to prefer the weighted carriage for light work driven between the lathe centres.
Fig. 622 represents the flat shear, the edges being at an angle and the fit of the carriage to the shears being adjusted by the gibs at a a, which are set up by bolts c c and d d. In this case there is a large amount of wearing surface at b b, to prevent the fall of the carriage c, but the amount of end motion (in the direction of b, Fig. 621), permitted to the carriage by reason of the wear of the gibs and shear edges, is greater than the amount of the wear because of the edges being at an angle. It is true that the amount of fall of the carriage on the raised V is also (on account of the angle of the V) greater than the actual amount of the wear, but the effect upon the work diameter is in this case much greater, as will be readily understood from what has already been said. The wearing surface of the raised V may obviously be increased by providing broader Vs, or two Vs instead of having four. This would tend to keep the lathe in line, because the wear due to moving the tailblock would act upon those parts of the shear length that are less acted upon by the carriage, and since the front journal and bearing of the live spindle wear the most, the alignment of the lathe centres would be more nearly preserved.
Fig. 623 represents another form of parallel edged shears in which the fit of the carriage to the shears is effected at the front end only, the other or back edge being clear of contact with the carriage, but provided with a gib to prevent the carriage from lifting. This allows for any difference in expansion and contraction between the carriage and the shears, while maintaining the fit of the carriage to the bed.
A modification of this form (both these forms being taken from “Mechanics”) is shown in Fig. 624, in which the underneath side of the front edge is beveled so that but one row of screws is required to effect the adjustment.
Fig. 625 represents a form of bed in which the fit adjustment is also made at the front end only of the bed, and there is a flange or slip at a, which receives the thrust outwards of the carriage; and a similar design, but with a bevelled edge, is shown in Fig. 626.
In Fig. 627 is shown a lathe shear with parallel edges, the fit being adjusted by a single gib d, set up by set-screws s. In this case the carriage will fall or move endwise, to an amount equal to whatever the amount of the wear may be, and no more, but it may be observed that in all the forms that admit of wear endways (that is to say in the direction of b in Fig. 621), the straightness of the shears is impaired in proportion as its edges are more worn at one part than at another.
A compromise between the flat and the raised V-shear is shown in Fig. 628, there being a V-guide on one side only, as at j. When the carriage is moved by mechanism on the front side of the lathe, and close to the V, this plan may be used, but if the feed screw or other mechanism for traversing the carriage is within the two shears, the carriage should be guided at each end, or if the operating mechanism is at the back of the lathe, the carriage should be guided at the back end, if not at both ends.
In flat shear lathes the tailstock is fitted between the inside edges of the two shears, and the alignment of the tailstock depends upon maintaining a proper fit notwithstanding the wear that will naturally take place in time. The inside edges of the shears are sometimes tapered; this taper makes it much easier to obtain a correct fit of the tailstock to the shears, but at the same time more hard to move the tailstock along the bed. To remedy this difficulty, rollers are sometimes mounted upon eccentrics having journal bearing in the tailstock, so that by operating these eccentrics one half a turn, the rollers will be brought down upon the upper face of the shears, lifting the tailstock and enabling it to be easily moved along the bed to its required position.
In many of the watchmakers’ lathes the outer edges are beveled off as in Fig. 629, the bearing surfaces being on the faces b as well as on the edges a. As a result, edges a are relieved of weight, and therefore to some extent of wear also, and whatever wear faces b have helps the fit at a a.
In the Barnes lathe, as in several other forms in which the lathe is made (as, for example, in screw-making lathes) the form of bed in Fig. 630 is employed. The tailblock may rest on the surfaces a, a′, b, c, d, and e, or as in the Barnes lathe the tailstock may[I-184] fit to angles a b, but not to e d, while the carriage fits to b e, and c d, but not to a, the intention being to equalize the wear as much as possible.
The shears of lathes require to be as rigid as possible, because the pressure of the cut, as well as the weight of the carriage, slide rest, and tailstock, and of the work, tends to bend and twist them.
The pressure of the dead centre against the end of the work considered individually, is in a direction to bend the lathe shears upward, but the weight of the work itself acts in an opposite direction.
The strain due to the cut falls in a direction variable with the shape of the cutting tool, but mainly in a direction towards the operator, and, therefore, tending to twist the shears. To resist these strains, lathe shears are usually given the I form shown in the cuts.
Figs. 631 and 632 represent the ribbing in the Putnam Tool Company’s lathe; a middle rib running the entire length, which greatly stiffens it.
The legs supporting lathe shears are, in lathes of ordinary length, placed at each end of the bed, so that the weight of the two heads, that of the work, and that of the carriage and slide rest, as well as the downward pressure of the cut, act combined to cause it to deflect or bend. It is necessary, therefore, in long beds to provide intermediate resting or supporting points to prevent this deflection.
Professor Sweet has pointed out that a lathe shears will be more truly supported on three than on four resting points, if the foundation on which the legs rest do not remain permanently level, and in lathes designed by him has given the right-hand end of the shears a single supporting point, as shown at a in Fig. 633.
J. Richards in an article in “Engineering,” has pointed out also that, when the lathe legs rest upon a floor that is liable from moving loads upon it to move its level, it is preferable that the legs be shaped as in Fig. 634, being narrowest at the foot, whereas when upon a permanent foundation, in which the foundation is intended to impart rigidity to the legs, they should be broader at the base, as in Fig. 635.
The rack on a lathe bed should be a cut one, and not simply a cast one, because when a cutting tool is running up to a corner as against a radial face, the self-acting motion must be stopped and the tool fed into the corner by hand. As a very delicate tool movement is required to cut the corner out just square, it should be capable of easy and steady movement, but in the case of cast racks, the rest will, from defects in the rack teeth, move in little jumps, especially if the pitch of the teeth be coarse. On the other hand it is difficult to cast fine pitches of teeth perfectly, hence the racks as well as the gear teeth should be cut gear and of fine pitch.
The tailblock of a lathe should be capable of easy motion for adjustment along the shears, or bed of the lathe, and readily fixable in its adjusted position. The design should be such as to hold the axial line of its spindle true with the axial line of the live spindle. If the lathe bed has raised Vs there are usually provided two special Vs for the tailblock to slide on, the slide rest carriage sliding on two separate ones. In this case the truth of the axial line of the tail spindle depends upon the truth of the Vs.
If the lathe bed is provided with ways having a flat surface, as was shown in Fig. 622, the surfaces of the edges and of the projection are apt in time to wear, permitting an amount of play which gives room for the tailblock to move out of line. To obviate this, various methods are resorted to, an example being given in the Sellers lathe, Fig. 518.
In wood turners’ lathes, where tools are often used in place of the dead centre, and in which a good deal of boring is done by such use of the tail spindle, it is not unusual to provide a device for the rapid motion of that spindle. Such a device is shown in Fig. 636; it consists of an arm a to receive the end c of the lever b, c being pivoted to a. The spindle is provided with an eye at e, the wheel w is removed and a pin passed through d and e, so that by operating the handle the spindle can be traversed in and out without any rotary motion of the screw.
When the tailblock of a lathe fits between the edges of the shears, instead of upon raised Vs, it is sometimes the practice to[I-185] give them a slight taper fitting accurately a corresponding taper on the edges of the shears. This enables the obtenance of a very good fit between the surfaces, giving an increased area of contact, because the surfaces can be filed on their bearing marks to fit them together; but this taper is apt to cause the tailstock to fit so tightly between the shears as to render it difficult to move it along them, and in any event the friction is apt to cause the fit to be destroyed from the wear. An excellent method of obviating these difficulties is by the employment of rollers, such as shown at r in Figs. 637 and 638, which represent the tailstock of the Putnam Tool Company’s lathe. In some cases such rollers are carried on eccentric shafts so that they may be operated to lift the tailstock from the bed when moving it.
A very ready method of securing or releasing a small tailstock to a lathe shears is shown applied to a wood turner’s hand rest in Fig. 639, in which a a represents the lathe shears, b the hand rest, c the fastening bolt, d a piece hinged at each end and having through its centre a hole to receive the fastening bolt, and a counter-sink or recess to receive the nut and prevent it unscrewing. e represents a hinged plate, and f a lever, having a cam at its pivoted end. A slot for the fastening bolt to pass through is provided in the plate e. In this arrangement a very moderate amount of force applied to bring up the cam lever will cause the plate d to be pressed down, carrying with it the nut, and binding the tailstock or the tool rest, as the case may be, with sufficient force for a small lathe.
When a piece of work is driven between the lathe centres, the weight of the work tends to deflect or bend down the tail spindle. The pressure of the cut has also to be resisted by the tail spindle, but this pressure is variable in direction, according to the shape of the tool and the direction of the feed; usually it is laterally towards the operator and upwards. In any event, however, the spindle requires locking in its adjusted position, so as to keep it steady. The pressure on the conical point of the dead centre is in a direction to cause the tail screw to unwind, unless it be a left-hand thread, as is sometimes the case.
If the spindle and the bore in which it operates have worn, the resulting looseness affords facility for the spindle to move in the bore as the pressure of the cut varies, especially when the spindle is far out from the tailstock.
Now, in locking the tail spindle to obviate these difficulties, it is desirable that the locking device shall hold that spindle axially true with the live spindle of the lathe, notwithstanding any wear that may have taken place. The spindle is released from the pressure of the locking device whenever it is adjusted to the work, whether the cut be proceeding or not. Hence, the wear takes place on the bottom of the spindle and of the hole, wear only ensuing on the top of the spindle and bore when the spindle is operated under a slight locking pressure, while the cut is proceeding in order to take up the looseness that may have arisen from wear in the work centres.
In all cases the feed of the cut should be stopped while the centre is adjusted, so as to relieve the spindle and bore from[I-186] undue wear; but most workmen pay little heed to this; hence the wear ensues, being, as already stated, mainly at the bottom. It is obvious, then, that, if the spindle is to be locked to the side of the bore on which it slides, it will be held most truly in line if it be locked to that side which has suffered least from wear, and this has been shown to be at the top.
The methods usually employed to effect this locking are as follows:—In Fig. 640, s is the tail spindle, b part of the tailblock in section, r a ring-bolt, and h a handled nut. Screwing up the nut h causes r to clamp s to the upper part of the bore of b; while releasing h leaves s free to slide. There are three objections to this plan. The ring r tends to spring or bend s. The weight of r tends to produce wear upon the top of the spindle, and the spindle is not gripped so near to its dead centre end as it might be. If s is a close fit in b the pressure of r could not spring or bend s; but, so soon as wear has taken place, s becomes simply suspended at r, having the pressure of r, and the weight of the work tending to bend it. Another locking device is shown in Fig. 641. It consists of a shoe placed beneath s, and a wedge-bolt beneath it, operated by the handled nut c. Here the pressure is again in a direction to lift s, as denoted by the arrow; but when the wedge w is released the shoe falls away from s, hence the locking device produces no wear upon s. This device may be placed nearer to the end of b, since the wedge may pass through the front leg of the tailstock instead of to the right of it, as in Fig. 640. But s is still suspended from the point of contact of the shoe, and the weight of the work still bends it as much as its play in b will permit.
Another clamping device is shown in Fig. 642. In this the cylindrical part b of the tailblock is split on one side, and is provided with two lugs. A handled screw passes through the upper lug, and is threaded into the lower one, so that by operating the handle c, the bore may be closed, so as to grip s, or opened to relieve it. This possesses the advantages: First, that it will cause s to be gripped most firmly at the end of b, and give a longer length of bearing of b upon s; and, secondly, that it will grip s top and bottom, and, therefore, prevent its springing from the weight of the work. But, on the other hand, b will close mainly on the side of the split, as denoted by the dotted half-circle, and therefore tend to throw s somewhat in the direction of the arrow, which it will do to an amount answerable to the amount of looseness of s in b. In the Pratt and Whitney lathes this device is somewhat modified, as is shown in Fig. 643. A stud e screws into the lower lug d, having a collar at e let into the upper lug, with a square extending above the upper lug so that the stud may be screwed into d, exerting sufficient pressure to close the bore of b to a neat working fit to the spindle. The handled nut, when screwed up, causes b to grip the spindle firmly; but when released, leaves the spindle a neat working fit and not loose to the amount of the play; hence, the locking device may be released, and the centre adjusted to take up the wear in the work centres while the cut is proceeding, without any movement of the spindle in b, because there is no play between the spindle and b.
In the design shown in Fig. 644, the end b of the tailblock is threaded and is provided with a handled cap nut a a. In the end of the tailblock where the spindle emerges, is provided a cone, and into this cone fits a wedge-shaped ring, as shown. This ring is split quite through on one side, while there are two other slots nearly but not quite splitting the wedge-ring. When the handle c is pulled towards the operator it screws a up on the end b, and forces the wedge-ring up in the conical bore in b. From the split the ring closes upon the spindle s, and grips it. Now, as the ring is weakened by slots in two places besides the split, it closes more nearly cylindrically true than if it had only a split, there being three points where the ring can spring when closing upon s; and from the cone being axially true with the live spindle of the lathe, s is held axially true, notwithstanding any wear of the spindle, because the locking device, being at the extreme end of b, is as near to the dead centre as it is possible to get it; and, furthermore, when c is operated for the release, the wedge-ring opens clear of s, so that s does not touch it when moved laterally. The wear of the bore of b has, therefore, no effect to throw s out of line, nor has the gripping device any tendency to bend or spring s, while the latter is held as close to the work as possible; hence the weight of the work has less influence in bending it. The pitch of the thread and the degree of cone are so proportioned that less than one-quarter rotation of a will suffice to grip or release s, the handle c being so placed on a as to be about vertical when the split ring binds s; hence c is always in a convenient position for the hand to grasp.
In this case, however, the spindle being locked at the extreme end of the hole, there is more liability of the other end moving from the pressure of the cut, or from the weight of the work; hence it would seem desirable that a tail spindle should be locked in two places; one at the dead centre end of the hole, and the other as near the actuating wheel, or handle, as possible, and also that each device should either hold it central to the original bore, notwithstanding the wear, an end that is attained in the Sellers lathes already described.
Slide rests for self-acting or engine lathes are divided into seven kinds, termed respectively as follows: simple, or single, elevating, weighted, gibbed, compound, duplex, and duplex compound. A simple, or single, slide rest contains a carriage and one cross slide, as in Fig. 621. An elevating slide rest is one capable of elevation at one end to adjust the cutting tool height, as in Fig. 499. A weighted slide rest is one held to the shears by a weight, as in Fig. 577. A gibbed slide rest is held to the shears by gibs, as in Fig. 621. A compound slide rest has above the cross slide, a second slide carrying the tool holder, this second slide pivoting to stand at any required angle, as in Fig. 505. A duplex slide rest has two rests on the same cross slide, and in a compound duplex both these two rests are compound, as in Fig. 511. The rest shown on the Putnam lathe in Figs. 492 and 499, is thus an elevating gibbed single rest.
Testing a Lathe.—To test a lathe to find if its live and dead spindles are axially in line one with the other and with the guides on the lathe bed, the following methods may be employed in addition to those referred to under the heading of Erecting.
To test if the live spindle is true with the bed or shear guides, a piece such as in Fig. 645 may be turned up between the lathe centres, the end a fitting into the live spindle in place of the live centre, and the collars b c being turned to an equal diameter, and the end face d squared off true. The end a must then be placed in the lathe in place of the live centre, the dead centre being removed from contact with the work; with the lathe at rest a tool point may be set to just touch collar c, and if when the carriage[I-187] is moved to feed the tool past collar b, the tool draws a line along it of equal depth to that it drew along c, the live head is true; the dead centre may then be moved up to engage the work end d, and the lathe must be revolved so that (the tool not having been moved at all by the cross-feed screw) the tool may be traversed back to draw another line along c, and if all three lines are of equal depth the lathe is true. The tool should be fine pointed and set so as to mark as fine a line as possible.
| Any View. | Side View. | Side View. | Top View. |
 |
 |
 |
 |
| Fig. 646. | Fig. 647. | Fig. 648. | Fig. 649. |
Another method is to turn up two discs, such as in Fig. 646, their stems a and b fitting in place of the live and dead centres. One of these discs is put in the place of the live, and the other in that of the dead centre, and if then the lathe tailstock be set up so that the face of b meets that of a, their coincidence will denote the truth of the live and dead spindles. The faces of the discs may be recessed to save work and to meet at their edges only, but their diameters must be equal. If the discs come one higher than the other, as in Fig. 647, the centres are of unequal height. If the faces meet at the top and are open at the bottom, as in Fig. 648, it shows that the back bearing of the live spindle is too high, or that the tail spindle is too low at the dead centre end. If the discs, when viewed from above, come as in Fig. 649, it is proof that either the live spindle or the tail spindle does not stand true with the lathe shears. If the disc faces come so nearly fair that it is difficult to see if they are in contact all around, four pieces of thin paper may be placed equidistant between them, and the grip upon them tested by pulling.
If the tailstock has been set over to turn taper and it is required to set it back to turn parallel again, place a long rod (that has been accurately centred and centre-drilled) between the lathe centres, and turn up one end for a distance of an inch or two.
Then turn it end for end in the lathe and let it run a few moments so that the work centre, running on the dead centre of the lathe, may wear to a proper bed or fit to the lathe centre, and then turn up a similar length at the dead centre end, taking two cuts, the last a fine finishing cut taken with a sharp tool, and feeding the finishing cut from left to right, so that it will be clear of the work end when the cut is finished. Without moving the cross-feed screw of the lathe after the finishing cut is set, take the bar out of the lathe and wind the slide rest carriage, so that the turning tool will stand close to the live centre. Place the bar of iron again in the lathe, with the turned end next to the live centre, and move the lathe carriage, so that the tool is on the turned end of the bar.
Rotate the bar by hand, and if the tool just touches the work without taking a cut the line of centres is parallel with the ways. If there is space between the tool point and the turned end of the bar, the tailstock requires setting over towards the back of the lathe, while if the tool takes a cut the tailstock requires to be set over towards the operator. If a bar is at hand that is known to be true, a pointed tool may be adjusted to just make a mark on the end of the bar when the slide rest is traversed. On the bar being reversed, the tool should leave, when traversed along the bar, a similar mark on the bar.
To test the workmanship of the back head or tailstock, place the forefinger on the spindle close to the hub whence it emerges, and observe how much the hand wheel can be moved without moving the spindle; this will show how much, if any, lost motion there is between the screw and the nut in the spindle. Next wind the back spindle about three quarters of its length out of the tailstock, take hold of the dead centre and pull it back and forth laterally, when an imperfect fit between the spindle and the hole in which it slides will be shown by the lateral motion of the dead centre. Wind the dead centre in again, and tighten and loosen the spindle clamp, and see if doing so moves the spindle in the socket.
To examine the slide rest, move the screw handles back and forth to find how much they may be moved without giving motion to the slides; this will determine the amount of lost motion between the collars of the screws and between the screws themselves and the nuts in which they operate. To try the fit of the slide rest slides, in the stationary sliding ways or Vs, remove the feed screws and move the slide so that only about one-half inch is in contact with the Vs, then move the slide back and forth laterally to see if there is any play. Move the slide to the other end of the Vs, and make a similar test, adjusting the slide to take up any play at either end. Then clean the bearing surfaces and move the slide back and forth on the Vs, and the marks will show the fit, while the power required to move the slide will show the parallelism of the Vs.
If the lathe carriage have a rack feed, operate it slowly by hand, to ascertain if it can be fed slowly and regularly by hand, which is of great importance. Then put the automatic feed in gear, and operate the feed gear back and forth, to determine how much it can be moved without moving the slide rest. To test the fit of the feed screw to the feed nut, put the latter in gear and operate the rack motion back and forth.
To determine whether the cross slide is at a right angle with the ways or shears, take a fine cut over a radial face, such, for example, as the largest face plate, and test the finished plate with a straight edge. If the face plate runs true and shows true with a straight edge, so that it is unnecessary to take a cut over it, grind a piece of steel a little rounding on its end, and fasten it in the tool post or clamp, with the rounded end next to the face plate. Let the rounded end be about 1⁄4 in. away from the face plate, and then put the feed motion into gear, and, with the steel near the periphery of the face plate, let the carriage feed up until the rounded steel end will just grip a piece of thin paper against the face plate tight enough to cause a slight strain in pulling the paper out, then wind the tool in towards the lathe centre and try the friction of the paper there; if equal, the cross slide is true.
To find the amount of lost motion in the screw feed gear, adjust it ready to feed the saddle, and pull the lathe belt so as to revolve the cone spindle backward, until the slide rest saddle begins to move, then mark a fine line on the lathe bed making the line coincident with the end of the lathe saddle or carriage. Then revolve the cone spindle forward, and note how much the cone spindle rotates before the saddle begins to traverse.
If the lathe has an independent feed motion it may be tested in the same manner as above.
In large lathes this is of great consideration, because the work revolves very slowly, and if there is much lost motion in the feed gear, it may take considerable time after the feed is put in gear before the carriage begins to travel. Suppose, for example, a 14-foot pulley is being turned, and that the tool cuts at 15 feet per minute, it will take nearly three minutes for the work to make a revolution.
The lathe is made in many special or limited forms, to suit particular purposes, the object being to increase its efficiency for those purposes, which necessarily diminishes its capacity for general work.
In addition to this, however, there are machine tools whose construction varies considerably from the ordinary form of lathe, which nevertheless belong to the same family, and must, therefore, be classified with it, because they operate upon what is essentially lathe work. Thus boring and turning mills are essentially what may be termed horizontal lathes.
| VOL. I. | WATCHMAKER’S LATHE. | PLATE VIII. | |||
 |
|||||
| Fig. 650. | |||||
 |
|||||
| Fig. 651. | |||||
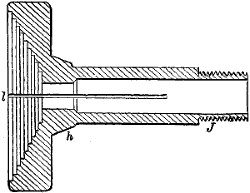 |
 |
||||
| Fig. 653. | |||||
 |
|||||
| Fig. 652. | Fig. 654. | ||||
Figs. 650 to 655 inclusive, represent the American Watch Tool Company’s special lathes for watch-makers, which occupy a prominent position in Europe, as well as in the United States.
In lathes of this class, refinement of fit, alignment, truth, and durability of parts are of the first importance, because of the smallness of the work they perform, and the accuracy to which that work must be made. Furthermore, such lathes must be constructed to hold and release the work as rapidly as possible, because in such small work the time occupied by the tools in cutting is less, while that occupied in the insertion and removal of it is greater in comparison than in larger jobs; it often takes longer to insert and remove the work than to perform it.
These facts apply with equal force to all such parts as require the removal to or from the lathe-bed, or frequent adjustment upon the same. Thus the devices for holding and releasing the tool post or hand rest and tailblock are each so constructed that they may be set without the use of detached wrenches.
Fig. 650 represents a general view of the lathe, while Fig. 651 represents a sectional view of the headstock. The live spindle consists of two parts, an outer sleeve a a, having journal bearing in the head, and an inner hollow spindle b b, threaded at its front end e, to receive the chucks. The main spindle at the front end works in a journal box c, that is cylindrical to fit the headstock, but double coned within to afford journal bearing to the spindle a. The inner step of this double cone is relied upon mainly to adjust the diametral fit of the bearing, while the outer step is relied upon mainly to adjust the end fit of the spindle; but it is obvious in both cases there is an action securing simultaneously the diametral and the end fit. In the back bearing there are two cones. The outer one r is cylindrical outside where it fits into the head, and coned in its bore to receive the second cone s, which rotates with spindle a. The nut f is threaded upon a, so that by operating f, a is drawn within c, and s is simultaneously moved within r, so that both bearings are simultaneously adjusted. d d are dust rings, being ring-caps which cover the ends of the bearings and the oil holes so as to prevent the ingress of dust.
The inner spindle b has a bearing in a at the back end to steady it, and a bearing at end e, and is provided with the hand wheel h, by which it may be rotated to attach the chucks which screw into its mouth at e. To rotate or drive the chucks there is in a a feather at g, the chucks having a groove to receive this feather and screwing into b at e, when b is rotated.
The mouth of a is coned, as shown at h, and the chucks are provided with a corresponding male cone, as shown at h in Figs. 652 and 653, so that the chucks are supported and guided by the cone, and are therefore as close to the work as possible while having a bearing at g. But the cone on the chucks being split, (as is shown in Fig. 652), rotating b while holding a stationary (which may be done by means of the band pulley p), causes the chucks to move endwise in a, and if the motion is in the direction to draw the chuck within a, the cone h causes the chuck to close upon and grip the work. Thus in Fig. 652 is shown a step chuck. The thread at j enters the end e of b, in Fig. 651, which screws upon it. Cone h fits mouth h in Fig. 651, and l represents the splits in the chuck, which enable it to close when the cone h is drawn within the mouth h of spindle a.
The chuck is employed to hold cylindrical plates or discs, such as wheels and barrels, and the various steps are to suit the varying diameters of these parts in different sizes of watches.
Fig. 653 represents a wire chuck, having the cone at h, and the three splits at l, as before, the cone-mouth h closing the chuck as the latter is drawn within the spindle a.
In both the chucks thus far described, the construction has been arranged to close the splits and thus grip the circumferences of cylindrical bodies, but in Fig. 654 is shown the arrangement for enabling the chuck to expand and grip the bores of hollow work, such as rings, &c.
The outer spindle a corresponds to the outer spindle a in Fig. 651, and the inner one to spindle b in that figure. The chuck is here made in two separate parts, a sleeve v fitting in and driven by a, and a plug x fitting into a cone in the mouth of v, and screwing into the end of drawing spindle b. But while v is driven by and prevented from rotating within a by means of the feather at g, so likewise x is prevented from rotating within v by means of a feather h fast in x and fitting into a groove or featherway in v. It follows then that when b is rotated x may be traversed endways in v, to open or close the steps y according to the direction of rotation of b.
It will now be apparent that in the case of chucks requiring to grip external diameters, the gripping jaws of the chucks will, when out of the lathe, be at their largest diameter, the splits l being open to their fullest, and that when by the action of the cones, they are closed to grip the work, such closure must be effected against a slight spring or resistance of the jaws, and this it is that enables and causes the chuck to open out of itself, when the enveloping cone permits it to do so.
But in the case of the opening or expanding chuck, the reverse is the case, and the chuck is at its smallest diameter (the splits l being at their closest) when the chuck is removed from the lathe, as is obviously necessary. In reality the action is the same in both cases, for the chuck moves to grip the work under a slight resistance, and this it is that enables it to readily release the work when moved in the necessary endwise direction.
The band pulley p is fast upon a, and is provided with an index of 60 holes on its face g, and which are adjusted for any especial work by a pin q, so that a piece of work may have marked on it either 60, 30, 20, 15, 12, 10, 6, 5, 4, 3, or 2 equidistant lines of division, each of those numbers being divisors of 60. In marking such lines of division upon the work a sharp point may be used, supported by the face of the hand rest as a guide; or a sharp-pointed tool may be placed in the slide rest to cut a deeper line upon the work. The index plates used for cutting wheels and pinions may be placed on the rear end of a, the pawl being secured to the work-bench. The wheel h is for rotating spindle b to screw the chucks on or off the same.
| VOL. I. | DETAILS OF WATCHMAKER’S LATHE. | PLATE IX. | ||
 |
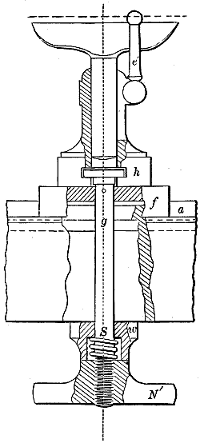 |
 |
||
| Fig. 657. | ||||
 |
||||
| Fig. 655. | Fig. 656. | Fig. 658. | ||
 |
 |
|||
| Fig. 659. | Fig. 660. | |||
 |
 |
|||
| Fig. 661. | Fig. 662. | |||
Fig. 655 represents an end view from the tailstock end of the lathe; a′ is the bed having the angles a a to align the heads and rests. The means of holding or releasing the tailstock, on the lathe-bed, is the same as that for holding the headstock, the construction being as follows: b is the shoulder of a bolt through which passes the shaft c, with a lever d to operate it. This shaft is eccentric where it passes through the bolt, so that by using the lever aforesaid the bolt secures or releases the head according to the direction in which it is moved. A very small amount of motion is needed for this. The standard for the hand rest is split,[I-189] and a screw is used to tighten it in an obvious manner, the screw being operated by the handle e′. An end view of the rest, showing the device for securing the foot h to the bed, is shown in Fig. 656, f is a shoe spanning the bed and fitting to the bed angles a. Through f passes the bolt g, its head passing into the T-shaped groove h; n′ is a hand wheel for operating bolt g. At s is a spiral spring, which by exerting an end pressure on washer w and nut n′, pulls g and the head h down upon f, and therefore f down upon the bed, whether the rest be locked to the bed or not; hence when n′ is released to remove or adjust the rest, neither dust nor fine cuttings can pass either between the rest and shoe or the shoe and the lathe-bed, and the abrasion that would otherwise occur is thus avoided.
Two qualities of these lathes are made: in the better quality all the working parts are hardened and afterwards ground true. In the other the parts are also ground true, but the parts (which in either case are of steel) are left soft for the sake of reducing the cost. In all, the parts are made to gauge and template, so that a new head, tailstock, or any other part in whole or in detail may be obtained from the factory, either to make additions to the lathe or to replace worn parts.
Two styles of slide rest are made with these lathes: in the first, shown in Fig. 657, the swivel for setting the top slide at an angle for taper turning is at the base of the top slide, hence the lower slide turns all radial faces at a right angle to the line of lathe centres. In the second, Fig. 658, there is a third slide added at the top, so that the bottom slide turns radial faces to a right angle with the line of lathe centres, the next slide turns the taper and the top slide may be used to turn a radial face at a right angle to the surface of the taper, and not at a right angle to the axis of the work. Both these rests are provided with tool post clamps, to hold tools made of round wire, such clamps being shown in position in figure 657.
Fig. 659 represents an additional tailstock for this lathe, the tail spindle lying in open bearings so that it can be laid in, which enables the rapid employment of several spindles holding tools for performing different duties, as drilling, counter-boring, chamfering, &c.
Fig. 660 represents a filing fixture to be attached to the bed in the same manner as the slide rest. It consists of a base supporting a link, carrying two hardened steel rolls, upon which the file may rest, the rolls rotating by friction during the file strokes, and serving to keep the file flat and fair upon the work.
Fig. 661 represents a fixture for wheel and pinion cutting; it is attached to the slide rest. When the cutter spindle is vertical the belt runs directly to it from the overhead counter shaft, but when it is horizontal the belt passes over idler pulleys, held above the lathe. The cutter spindle is carried on a frame, pivoted to the sliding piece on the vertical slide, so that it may be swivelled to set in either the vertical or horizontal position.
Fig. 662 represents a jewelers’ rest for this lathe. It fits on the bed in the place of the tailstock, and is used for cutting out the seats for jewels, in plates, or settings. It is especially constructed so as to receive the jewel at the top and bore the seating to the proper diameter, without requiring any measurements or fitting by trial, and the manner in which this is accomplished is as follows:—
Fig. 663 is a side elevation, Fig. 664 an end elevation, and Fig. 665 a plan view of this rest, and similar letters of reference indicate like parts in each of the three figures. a is the base, held to the lathe bed by the bolt b, whose operation is the same as that already described for the head and tailstocks.
In one piece with a is the arm c, carrying at its head three gauge tongues or pieces d e f, which are adjustable by means of the screws d e f, which move the gauge tongues horizontally. Through a suitable guide i is a standard or head; pivoted to a at j j, and carrying at its top three gauge tongues k l m.
Midway between pivots j j and the ends of the gauge tongues, is the centre or tool carrying spindle o. If a piece of work, as a jewel, be placed between the tongues f and m, Fig. 664 [swinging m, and with it i (which is pivoted at j), laterally], then the point of the centre n will be thrown out of line with the lathe live spindle half the diameter of the jewel, because from j to the centre n, of o, is exactly one half of the vertical distance from j to the jewel. If then a tool be placed in the dead centre and its cutting edge is in line with the axis of spindle o, it will bore a hole that will just fit the jewel. Hence placing the jewel between the two tongues sets the diameter to which the tool will bore and determines that it shall equal the diameter of the jewel.
The object of having three pair of gauge tongues is to enable the obtaining of three degrees of fit; thus with a piece placed between d k the hole may be bored to fit the piece easily, with it placed between e l the fit may be made barely movable, while with it placed between f m the fit may be too tight to be a movable one save by pressure or driving, each degree of fit being adjusted by means of the screws e f g.
The tool is fed by moving spindle o by hand, the screw p being adjusted so that its end abuts against stop q, when the hole is bored to the requisite depth; r is simply a guide for the piece s, which being attached to o, prevents it from rotating.
[I-190]In watch manufactories special chucks and appliances are necessary to meet their particular requirements. There is found to exist, for example, in different rods of wire of the same nominal diameter, a slight variation in the actual diameter, and it is obvious that with the smaller diameters of wire the split chucks will pass farther within the mouth h of a, Fig. 651, because the splits of the chucks will close to a greater extent, and the cones on the chucks therefore become reduced in diameter.
If then it be required to turn a number of pieces of work to an exact end measurement, or a number of flanges or wheels to equal thicknesses, without adjusting the depth of cut for each it becomes necessary to insure that the successive pieces of work shall enter the chucks to an equal distance, notwithstanding any slight variation in the work diameter at the place or part where it is gripped by the chuck.
To accomplish this end what is termed a sliding-spindle head is employed. In this the outer spindle has the end motion necessary to open and close the chuck, the chuck having no end motion.
The construction of this sliding-spindle head is shown in Fig. 666, in which a wire chuck is shown in position in the spindles; l is the live spindle passing through parallel bearings, so that it may have end motion when the nut m is operated. The inner spindle n to which the chucks are screwed is prevented from having end motion by means of the collar p and nut q at the rear bearing. When nut m is rotated and n is held stationary by means of the pulley p, l slides endways, and the chuck opens or closes according to the direction in which the nut moves the spindle l.
To regulate the exact distance to which the work shall be placed within the chuck, a piece of wire rod may be placed within the hollow spindle n being detained in its adjusted position by the set screw s.
The construction whereby the nut is permitted to revolve with spindle l, and be operated by hand to move spindle l when the lathe is at rest, is as follows.
The cylindrical rim t of the nut is provided with a series of notches arranged around its circumference. r is a lever whose hub envelops nut m, but has journal bearing on v. r receives the pin s, which rests upon a spiral spring t. When, therefore, s is pushed down it depresses the spring t and its end w enters some one of the notches in the rim t, and operates the nut after the manner of a ratchet. But so soon as the end pressure on r is released, the spiral spring lifts it and m is free to revolve with l as before. The inner spindle is driven by means of the feather g.
Pulley p has two steps y for the belt, and a friction step z, around which passes a friction band operated by the operator’s foot to stop the lathe quickly. This performs two functions, as follows. The thread of m is a left-hand one so that the inertia of the nut will not, when the lathe is started, operate to screw the nut back, and release the chuck jaws from the work, by moving spindle l endwise. Per contra, however, in stopping the lathe suddenly by means of the brake, there is a tendency of nut m to stop less quickly than spindle l, and this operates to unscrew nut n and release the work. To assist this r is sometimes in lathes for watch manufactories provided with a hand wheel whose weight is made sufficient for the purpose.
Figs. 667 and 668 represent a pump centre head for watch manufactories, being a device for so chucking a piece of work that a hole may be chucked true and enlarged or otherwise operated upon, with the assurance that the work will be chucked true with the hole. Suppose two discs be secured together at their edges, their centres being a certain distance apart, as, for example, a top and bottom plate of a watch movement, and that the holes of one plate require to be transferred to the other, then by means of this head they may be transferred with the assurance that they shall be axially in line one with the other, and at a right[I-191] angle to the faces of the plates, as is necessary in setting jewels in a watch movement.
In holes of such small diameters as are used in watch work, it is manifestly very difficult to set them true by the ordinary methods of chucking and it is tedious to test if they are true, and it is to obviate these difficulties that the pump centre head is designed. Its operation is as follows.
There are in this case three spindles a, b, and c, in Fig. 667; a corresponds to spindle a in Fig. 651, driving the chuck d which screws on a as shown; b simply holds the work against the face d of d, and c holds the work true by means of the centre e, which enters the hole or centre in the work and is withdrawn when the work is secured by spindle b.
The chuck d is open on two sides as shown at e e in Fig. 668, which is an end face view of the chuck, and through these openings the work is admitted to the chuck. The rod or spindle c is then pushed, by hand, endwise, its centre e entering the hole or centre in the work (so as to hold the same axially true) and forcing the work against the inside faces d, spindle b is then operated, the face p forcing the work against face d, and between these two faces d p the work is held and driven by friction. The spindle c and its centre e is then withdrawn by hand, leaving the hole in the work free to be operated upon.
The journal bearings for spindle a are constructed as described for a in Fig. 666; spindle b is operated endways within a as follows. a is threaded at g to receive the hub h of wheel i, at the end of b is a collar which is held to and prevented from end motion within the hub h: hence when wheel i is rotated and a is held stationary (by means of the band pulley), h traverses on g and carries b with it. Operating i in one direction, therefore moves p against the work, while operating it in the other direction releases face p from contact with the work.
It is obviously of the first importance that the spindle c be held and maintained axially true, notwithstanding any wear, and that it be a close fit within b so as to remain in any position when the lathe is running, and thus obviate requiring to remove it. To maintain this closeness of fit the following construction is designed. Between spindle a and spindle b, at the chuck end of the two, is a steel bush which can be replaced by a new one when any appreciable wear has taken place. Between b and c are two inverted conical steel bushes, which can also be replaced by new ones, to take up any wear that may have taken place.
Fig. 669 represents an improved hand lathe by the Brown and Sharpe Manufacturing Company, of Providence, R. I. It is specially designed for the rapid production of such cylindrical work as may be held in a chuck, or cut from a rod of metal passing through the live spindle, which is hollow, so that the rod may pass through it. Short pieces may be driven by the chuck or between the centres of a face plate (shown on the floor at e) screwing on in the ordinary manner. When, however, this face plate is removed a nut d screws on in its stead, to protect the thread on the live spindle.
The chuck for driving work in the absence of face plate e (as when the rod from which the work is to be made is passed through the live spindle) may be actuated to grip or release the work without stopping the lathe. The pieces j j are to support the hand tool shown in Figs. 1313 and 1314, in connection with hand turning, the tool stock or handle being shown at k on the floor. The lever for securing the tailstock to or releasing it from the shears is shown at t. The tail spindle is operated by a lever pivoted at g so that it may be operated quickly and easily, while the force with which the tail spindle is fed may be more sensitively felt than would be the case with the ordinary wheel and screw, this being a great advantage in small work. The tail spindle is also provided with a collar r, that may be set at any desired location on the spindle to act as a stop, determining how far the tail spindle can be fed forward, thus enabling it to drill holes, &c., of a uniform depth, in successive pieces of work.
The live spindle is of steel and will receive rods up to 1⁄2 inch in diameter. Its journals are hardened and ground cylindrically true after the hardening. It runs in bearings which are split and are coned externally, fitting into correspondingly coned holes in the headstock. These bearings are provided with a nut by means of which they may be drawn through the headstock to take up such wear in the journal and bearing fit, as may from time to time occur.
[I-192]It is obvious that the lathe may be removed from the lower legs and frame and bolted to a bench, forming in that case a bench lathe.
Fig. 670 represents a special lathe or screw slotting machine, as it is termed, for cutting the slots in the heads of machine or other screws. The live spindle drives a cutter or saw e, beneath which is the device for holding the screws to be slotted, this device also being shown detached and upon the floor.
The screw-holding end of the lever a acts similarly to a pair of pliers, one jaw of which is provided on handle a, while the other is upon the piece to which a is pivoted. The screw to be slotted is placed between the jaws of a beneath e; handle a is then moved to the left, gripping the screw stem; by depressing a, the screw head is brought up to the cutter e and the slot is cut to a depth depending upon the amount to which a is depressed, which is regulated by a screw at b; hence after b is properly adjusted, all screw heads will be slotted to the same depth.
The frame carrying the piece to which a is pivoted may be raised or lowered to suit screws having different thicknesses of head by means of a screw, whose hand nut is shown at d.
The frame for the head of the machine is hollow, and is divided into compartments as shown, in which are placed the bushings used in connection with the screw-gripping device, to capacitate it for different diameters of screws, and also for the wrenches, cutters, &c.
Figs. 671, 672, and 673, represent a lathe having a special feed motion designed and patented by Mr. Horace Lord, of Hartford, Connecticut. Its object is to give to a cutting tool a uniform rate of cutting speed (when used upon either flat or spherical surfaces), by causing the rotations of the work to be retarded as the cutting tool traverses from the centre to the perimeter of the work, or to increase as the tool traverses from a larger to a smaller diameter. If work of small diameter be turned at too slow a rate of cutting speed, it is difficult to obtain a true and smooth surface; hence, as the tool approaches the centre, it is necessary to increase the speed of rotation. As lathes are at present constructed, it is necessary to pass the belt from one step to another of the driving cone, to increase the speed. In this two disadvantages are met with. First, that the increase of speed occurs suddenly and does not meet the requirements with uniformity. Second, that the strain upon the cutting tool varies with the alteration of cutting speed. As a result, the spring of the parts of the lathe, as well as of the cutting tool, varies, so that the cut shows plainly where the sudden increase or decrease (as the case may be) of cutting speed has occurred. The greatest attainable degree of trueness is secured when the cutting speed and the strain due to the cut are maintained constant, notwithstanding variations of the diameter.
This, Mr. Lord accomplishes by the following mechanism: Instead of driving the lathe from an ordinary countershaft, he introduces a pair of cones which will vary the speed of the lathe as shown in Fig. 672 as applied to ball turning. l is a belt cone upon the counter-shaft driven from the line shaft. l drives h, which may be termed the lathe countershaft, and from the stepped cone k the belt is connected to the lathe in the usual manner. p is a shipper bar to move the belt n upon and along the belt cones, and thus vary the speed. r is a vertical shaft extending up at the end of the lathe and carrying a segment. This segment is connected to the belt shipper bar p by two cords, one passing from r1 around half the segment to r2, and the other passing from r3 to r4, so that if the segment be rotated, say to the right, it and the bar will move as denoted by the dotted lines, or if moved in an opposite direction, the bar motion will correspond and move the belt n along the cones respectively left or right.
At the back of the lathe is a horizontal shaft s, similar to an ordinary feed spindle, and connected to the segment shaft by a pair of bevel gears s2. Between the two ears e e, at the rear of the lathe carriage, is a pinion t, which drives the splined shaft s, which works in a rack t′. The tool rest is pivoted directly beneath the ball, to be turned after the usual manner of spherical slide rests, and carries a gear a2, which, as the rest turns, rotates a gear a3. Upon the face of the latter is a pin a4 working in a slot a5 at the end of the rack t′; hence as the tool rest feeds, motion [I-193]is transmitted from a2 through a3, a4, a, t′, t, and s s2 to r, which operates the belt shipper p. As it is the rate of tool feed that governs the speed of these motions, the effect is not influenced by irregularity in feeding; hence the speed of the work will be equalized with the tool feed under all conditions. The direction of motion of all the parts will correspond to that of the tool feed from which their motion is directed, and therefore the work speed will augment or diminish automatically to meet the requirements.
Fig. 673 illustrates the action of the mechanism when used for surfaces, like a lathe face plate. In this case the two gears and the rack t′ simply traverse with the cross-feed slider, and the mechanism is actuated as before. In Fig. 674 a different method of actuating the belt shipper is illustrated. A pulley is attached to the intermediate stud of the change gears, being connected by belt to the shipper, which is threaded as shown at d, the belt guiding forks, as p2, being carried on a nut actuated by the screw d.
Cutting-off Machine.—The cutting-off machine is employed to cut up into the requisite lengths pieces of iron from the bar. As the cutting is done by a tool, the end of the work is left true and square and a great saving of time is effected over the process of heating and cutting off the pieces in the blacksmith’s forge, in which case the pieces must be cut off too long and the ends left rough.
Fig. 675 represents Hyde’s cutting-off machine, which consists of a hollow live spindle through which the bar of iron is passed and gripped by the chucks c c. At g is a gauge rod whose distance from the tool rest r determines the length of the work. f is a feed cone driven by a corresponding cone on the live spindle and driving the worm w, which actuates the self-acting tool feed, which is provided with an automatic motion, which throws the feed out of action when the work is cut off from the bar. The stand s is movable and is employed to support the ends of long or heavy bars.
To finish work smooth and more true than can be done with steel cutting tools in a lathe, what are known as grinding lathes are employed. These lathes are not intended to remove a mass of metal, but simply to reduce the surfaces to cylindrical truth, to true outline and to standard diameter, hence the work is usually first turned up in the common lathe to the required form and very nearly to the required diameter, and then passed to the grinding lathe to be finished. The grinding lathe affords the best means we have of producing true and smooth cylindrical parallel work, and in the case of hardened work the only means. In place of steel cutting tools an emery wheel, revolved at high speed from an independent[I-194] drum or wide pulley, is employed, the direction of rotation of the emery wheel being opposite to that of the work.
Fig. 676 represents Pratt and Whitney’s weighted grinding lathe. The headstock and tailstock are attached to the bed in the usual manner, the frame carrying the emery wheel is bolted to the slide rest as shown, the rest traversing by a feed spindle motion. The carriage traverse is self-acting and has three changes of feed, by means of the feed cones shown.
To enable the lathe to grind taper work (whether internal or external) the lathe is fitted with the Slate taper attachment shown in Figs. 508 and 509.
It is obvious that in a lathe of this kind, there must be an extra overhead shaft, driving a drum of a length equal to the full traverse of the lathe carriage, or of the plate carrying the head and tailstocks, and the arrangement of this drum with its belt connection to the pulley on the emery wheel arbor, is sufficiently shown in figure. To protect the ways of the bed from the abrasion that would be caused by the emery and water falling upon them, guards are attached to the carriage extending for some distance over the raised Vs.
It is essential that the work revolve in a direction opposite to that of the emery wheel, for the following reasons. In Fig. 677 let a represent a reamer and b a segment of an emery wheel. Now suppose a and b to revolve in the direction that would exist if one drove the other from frictional contact of the circumferential surfaces, then the pressure of the cut would cause the reamer a to spring vertically and a wedging action between the reamer and wheel would take place, the reamer vibrating back and forth under varying degrees of this wedging; as a result the surface of a would show waves and would be neither round nor smooth.
In the absence of a proper grinding lathe, an ordinary lathe is sometimes improvised for grinding purposes, by attaching to the slide rest a simple frame and emery wheel arbor with pulley attached as in Fig. 678, in which a is the emery wheel, c the pulley for driving the arbor, and b the frame, d being a lug for a bolt hole to hold the frame to the lathe rest.
[I-195]In some cases the work may remain stationary and the emery wheel only rotate. Thus, suppose it was required to grind the necessary clearance to relieve the cutting edge c of the reamer, then a could be rotated until c stood in the required position with relation to b, and the revolving emery wheel may either be traversed along, or the work may traverse past the wheel, according to the design of the grinding lathe, but in either case a remains stationary during each cut traverse; after each successive traverse a may be rotated sufficiently to give a cut for the next traverse.
Fig. 679 represents Brown and Sharpe’s universal grinding lathe.
This lathe is constructed to accomplish the following ends. First, to have the lathe centres axially true with the work when grinding tapers, so that the lathe centres shall not wear and gradually throw the work out of true from the causes explained in the remarks on turning tapers in a lathe of ordinary construction.
Second, to have the headstock b capable of lateral swing, so as to enable the grinding of taper holes.
The manner in which these results are accomplished is as follows:
The headstock b and the tailstock are attached to the bed or table a, which is pivoted at its centre to a table beneath it, this latter table being denoted by c. This permits table a to swing laterally upon c and stand at any required angle. To enable a delicate adjustment of this angle, a screw a having journal bearing in a lug on c is threaded through a piece carried in projection on the end of a.
The table c traverses back and forth past the emery wheel, after the manner of an ordinary iron planing machine, the mechanical parts effecting this motion being placed within the bed upon which c slides. The carriage supporting the emery frame and table d remains stationary in its adjusted position, while c (carrying a with it) traverses back and forth.
Now, if a be adjusted so that the line of centres is parallel with the line of motion of c, then the work will be ground parallel, but if a be operated to move a upon its pivoted centre and draw the tailstock end of a towards the operator, then the work will be ground of larger diameter at the tailblock end. Conversely, by operating screw a in the opposite direction, it will be of smaller diameter at that end.
But whatever the degree of angle of a to c, the line of centres of the head and tailstocks will be axially true with the axial line of the work, hence the work centres are not liable to wear off true, as is the case when the tailstock only sets over (as will be fully explained in the remarks on taper turning).
To grind conical holes the headstock b is pivoted at its centre upon a piece held by bolts to the table a, so that it is capable of being swung laterally to the degree requisite for the required amount of taper in the work bore, and of being locked in that adjusted position, the work being held in a chuck screwed upon the spindle in the usual manner. The pulley d being removed to enable the grinding of cones, chamfers, or tapers of too great an angle to permit of a setting over to the required degree. The line of cross-feed motion of the emery wheel may be set to the required angle as follows.
The frame carrying the emery wheel arbor is fixed to a table d, which is capable of being operated (in a direction across the table a) upon a carriage beneath a. This carriage, or saddle (as it may perhaps be more properly termed), is pivoted so as to allow of its movement and adjustment in a horizontal plane, and since d operates in the slide of the carriage, its line of motion in approaching or receding from the line of centres will be that to which the saddle is set. This enables the grinding of such short cones as the circumferences of bevelled cutters, chamfers, &c., at whatever angle the saddle may be set, however, d may be operated from the feed screw disc and handle f.
The lever handle at the left hand is for operating or rather traversing c by hand; b is a pan to catch the grit and water, the water being led to the back of machine into a pail; c is a back rest to steady the work when it is slight and liable to deflection.
The slot and stops shown upon the edge of c are to regulate the points of termination of the traverse (in the respective directions) of c. A guard is placed over the emery wheel to arrest and collect the water cuttings, &c., which would otherwise fly about.
A large amount of work which has usually been filed in a lathe, can be much more expeditiously and accurately finished by grinding in this machine.
Work to be ground may obviously be held in the same chucks or work-holding appliances as would be required to hold it to turn it with cutting tools, or where a quantity of similar work is to be done special chucks may be made.
[I-196]Fig. 680 (from The American Machinist) shows a special chuck for grinding the faces of thin discs, such as very thin milling cutters, which could not be held true by their bores alone. The object of the device is to hold the cutter by its bore and then draw it back against the face of the chuck, which, therefore, sets it true on the faces. The construction of the chuck is as follows. The hub screws upon the lathe like an ordinary face plate, and has a slot running diametrically through it. Upon its circumference is a knurled or milled nut c, which is threaded internally to receive the threaded wings of the bush b. A collar behind c holds it in place upon the hub. To admit piece b the front of the chuck is bored out, and after b is inserted and its threaded wings are engaged in the ring nut c a collar is fitted over it and into the counter-bore to prevent b from having end motion unless c is revolved. d is a split bushing that fits into b, its stem fitting the bore of the disc, or cutter to be ground: the enlarged end of d is countersunk to receive the head of the screw e, whose stem passes through d and threads at its end into b, so that when e is screwed up its head expands d and causes it to grip the bore of the disc or cutter to be ground. After e is screwed up the ring nut c is revolved, drawing b within the chuck and therefore bringing the inside face of the disc or cutter against the face of the chuck or face plate, and truing it upon the bushing d. All that is necessary therefore in using the chuck is to employ a bushing of the necessary diameter for the bore of the cutter, insert it in b, then screw up the screw e and then revolve the ring nut c until the work is brought to bear evenly and fair against the face of the chuck, and to insure this it is best not to screw e very tightly up until after the ring nut c has been operated and brought the work up fair against the chuck face.
Fig. 681 represents the J. Morton Poole calender roll grinding lathe, which has attained pre-eminence both in Europe and the United States from the great accuracy and fine finish of the work it produces.
In all other machine tools, surfaces are made true either by guiding the tool to the work or the work to the tool, and, in either case, guide-ways and slides are employed to determine the line of motion of the tool or the work, as the case may be. These guideways and slides are usually carried by a framing really independent of the work, so that the cutting depends entirely upon the truth or straightness of the guideways, and is not determined by the truth, straightness, or parallelism of the work itself. As a result, the surface produced depends for its truth upon the truth of the tool-guiding ways. In the Poole lathe, however, while guideways are necessarily employed to guide the emery wheels in as straight a line as is possible, by means of such guides, the roll[I-197] itself is employed as a corrective agent to eliminate whatever errors may exist in the guide. The rolls come to this machine turned (in the lathe Fig. 730), and with their journals ground true (on dead centres).
Fig. 681 represents a perspective view of the machine, as a whole. It consists of a driving head, answering to the headstock of an ordinary lathe. b b are bearings in which the rolls are revolved to be ground. c is a carriage answering to the carriage of an ordinary lathe, but seated in sunken V-guideways, corresponding to those on an ordinary iron planing machine. Referring to Fig. 682, f is a swing-frame suspended by four links at g, h, i, j, which are upon shafts having at their ends knife edges resting in small V-grooves on the surface of standards s, which are fixed to carriage c. The frame f being thus suspended and being in no way fixed to c, it may be swung back and forth crosswise of the latter, the links at g, h, i, j, swinging as pendulums. At the top of f are two slide rests a a, one on each end, carrying emery or corundum wheels w, and the roll r, which rests in the bearings b, rotates between these emery wheels. The carriage c is fed along the bed as an ordinary lathe carriage, and the emery wheels are revolved from an overhead countershaft. Now, it will be found that from this form of construction the surface of the roll, when ground true, serves as a guide to determine the line of motion of the emery wheels, and that the emery wheels may be compared to a pair of grinding calipers that will operate on such part of the roll length as may be of larger diameter than the distance apart of the perimeters of the emery wheels, and escape such parts in the roll length as may be of less diameter than the width apart of those perimeters; hence parallelism in the roll is inevitable, because it is governed solely by the width apart of the wheel perimeters, which remain the same, while the wheels traverse the roll, except in so far as it may be affected by wear of emery-wheel diameters in one traverse along the roll.
Supposing now that we have a roll r (Fig. 683), placed in position and slowly revolved, and that the carriage c is fed along by feed screw e, then the line of motion of the emery wheels will be parallel to the axis of the roll, provided, of course, that the bearings b (Figs. 681 and 687) are set parallel to the V-guideways in the bed, and that these guideways are straight and parallel. But the line of travel of the emery wheels is not guided by the Vs except in so far as concerns their height from those Vs, because the swing-frame is quite free to swing either to the right or to the left, as the case may be. Its natural tendency is, from its weight, to swing into its lowest position, and this it will obviously do unless some pressure is put on it in a direction tending to swing it. Suppose, then, that instead of the roll running true, it runs eccentrically, or out of true, as it is termed, as shown in Fig. 683, when the high side meets the left-hand wheel it will push against it, causing the carriage c to swing to the left and to slightly raise. The pressure thus induced between the emery wheel and the roll[I-198] causes the roll surface to be ground, and the grinding will continue until the roll has permitted the swing-frame to swing back to its lowest and normal position. When the high side of the roll meets the right-hand emery wheel it will bear against it, causing the swing-frame to move to the right, and the pressure between the wheel and the roll will again cause the high side of the latter to be reduced by grinding. This action will continue so long as the roll runs out of true, but when it runs true both emery wheels will operate, grinding it to a diameter equal to the distance between the emery-wheel perimeters, which are, of course, adjusted by the slide rests a a. If the roll is out of true in the same direction and to the same amount throughout its length, the emery wheel will act on an equal area (for equal lengths of roll) throughout the roll length; but the roll may be out in one direction at one part and in another at some other part of the length; still the emery wheel will only act on the high side, no matter where that high side may be or how often it may change in location as the carriage and wheels traverse along the roll. Now, the roll does not run true until its circumference is equidistant at every point of its surface from the axis on which the roll revolves, and obviously when it does run true its circumference is parallel to the axis of revolution of the roll, because this axis is the line which determines whether the roll runs true or not, and therefore the swing-frame is actually guided by the axis of revolution of the roll, and will therefore move parallel to it.
It is obvious that if by any means the swinging of frame f is slightly resisted, as by a plate between it and c, with a spring to set up the plate against f, then the emery wheels will be capacitated to take a deeper cut than if the frame swing freely, this plan being adopted until such time as the roll is ground true, when both wheels will act continuously and simultaneously, and f may swing freely.
A screw may be used to set up the spring and plate when they are required to act.
Suppose now that the roll was not set exactly level with the V-guideways of the bed, there being a slight error in the adjustment of the roll journals in the bearings on b, and the emery-wheels would vary in height with relation to the height of the roll axis, and theoretically they would grind the roll of larger diameter at one end than at the other.
This, however, is a theoretical, rather than a practical point, as may be perceived from Fig. 684, in which r is a part of a section of a roll, and w a part of a section of a wheel. Now, assuming that the V-ways were as much as even a sixteenth out of true, so far as height is concerned, all the influence of the variation in height is shown by the second line of emery-wheel perimeter, shown in the figure, the two arcs being drawn from centres, one of which is 1⁄16th inch higher than the other. It is plain, then, that with the ordinary errors found in such V-guideways, which will not be found to exceed 1⁄30th of an inch, no practical effect will be produced upon the roll. Again, if one V is not in line with the other, no practical effect is produced, because if the carriage c were inclined at an angle, though the plane of rotation of the emery-wheel would be varied, its face would yet be parallel to the roll axis. If the Vs were to vary in their widths apart (the angles of the Vs being 45° apart), all the effect it would have would be to raise or lower the carriage c to one-half the amount the Vs were in error. It will be thus perceived that correctness of the roll both for parallelism and cylindricity is obtained independent of absolute truth in the V-guides.
Referring now to some of the details of construction of the lathe, the slide rest a, Fig. 683, is bored to receive sockets d d, Fig. 685, and is provided with caps, so that the sockets may be firmly[I-199] gripped and held axially true one with the other. The socket-bores are taper, to receive the taper ends of the arbor x, and are provided with oil pockets at each end. There is a driving pulley on each side of the emery-wheel, and equal belt-speed is obtained as follows: Two belt driving drums m n are employed, and each belt passes over both, as in Figs. 683 and 685, and down around the pulleys p. The diameter of the drum n is less than the diameter of the drum m by twice the thickness of the belt, thus equalizing inside and outside belt diameters, since they both pass over the pulley of the emery-arbor. The piece t is a guard to catch the water from the emery-wheels, and is hinged at the back so that the top is a lid that may be swung back out of the way when necessary.
The method of securing the emery-wheels is shown in Fig. 686. Two flanges z (made in halves) are let into the wheel, and clamp the wheel by means of the screws shown. The bore of these flanges z is larger than the diameter of pulleys p, so that the emery-wheels may be changed on the arbor without removing the pulley. Fig. 687 represents an end view of the bearings b for the roll to revolve in, being provided with three pieces, the two side ones of which are adjustable by the set-screws, so as to facilitate setting the roll parallel with the bed of the lathe. The height is adjusted by means of screws k, k, which may also be used in grinding a roll of large diameter at the middle of its length, by occasionally raising the roll as the carriage c proceeds along the roll (the principle of this action is hereafter explained with reference to turning tapers on ordinary lathe work). When the wheels have traversed half the length of the roll, the screws k are operated to lower it again, it being found that the effect of a slight operating of the screws k is so small that the workman’s judgment may be relied upon to use them to give to a roll with practical accuracy any required degree of enlarged diameter at the middle of its length with sufficient accuracy for all practical purposes.
There are, however, other advantages of this system, which may be noted as follows. When a single emery-wheel is used there is evidently twice the amount of wear to take a given amount of metal off (per traverse) that there is when two wheels are used, and furthermore the reduction of every wheel diameter per traverse is evidently twice as great with one wheel as it is with two. From some experiments made by Messrs. Morton Poole, it was found that using a pair of 10-inch emery-wheels it would take 40,000 wheel traverses along an average sized calender roll, to reduce its diameter an inch, hence the amount of error due to the reduction of the emery-wheel diameters, per traverse, may be stated as 1⁄40000 of an inch per traverse, for the two wheels.
Now referring to Fig. 688, let r represent a roll and w w the two emery-wheels.
Suppose the wheels being at the end of a traverse, the roll is 1⁄40000 inch larger at that end on account of the wear of the emery-wheels, then each wheel will have worn 1⁄40000 inch diameter or 1⁄80000 inch radius, hence the increase of roll diameter is equal to the wear of wheel diameter.
Now, suppose that one wheel be used as in Fig. 689, and its reduction of diameter will be equal to that of the two wheels[I-200] added together, or 1⁄20000 inch, this would be 1⁄40000 in the radius of the wheel, producing a difference of 1⁄20000 difference in the diameter of the wheel.
There is another advantage, however, in that a finer cut can be easier put on in the Poole system, because if a feed be put on of 1⁄100th inch, the roll is only reduced 1⁄100th inch in diameter, but if the same amount of feed be put on with a single wheel, it will reduce the roll 1⁄50th inch, hence for a given amount of feed or movement of emery-wheel towards the roll axis, the amount of cut taken is only half as much as it would be if a single wheel is used. This enables a minimum of feed to be put on the wheel, wear being obviously reduced in proportion as the feed is lighter and the duty therefore diminished.
The method of driving the roll is as follows: Shaft t, Fig. 681, runs in bearings in the head, and spindle r r′ passes through, and is driven by shaft t. A driving pulley is fitted on the spindle at end r′, at the other end is a driving chuck p for driving the roll through the medium of a wabbler, whose construction will be shown presently. Spindle r may be adjusted endwise in t, so that it may be adjusted to suit different lengths of rolls without moving the bearing blocks b.
The wabbler is driven by p and receives the end of the roll to be ground, as shown in Fig. 690, the end of the roll being a taper square and fitting very loosely in a square taper hole in the end of the wabbler; similarly p may have a taper square hole loosely fitting the squared end of the wabbler. The looseness of fit enables the wabbler to drive the roll without putting any strain on it tending to lift or twist it in its bearings in block b, and obviates the necessity for the axis of the rolls to be dead in line with the axis of r r′. Various lengths of wabblers may be used to suit the lengths of roll and avoid moving blocks b, and it is obvious also that if the ends of the roll are round instead of square, two set-screws may be used to hold the roll end being set diametrically opposite, and if set screws are used in p to drive the wabbler they should be two in number, set diametrically opposite, and at a right angle to the two in the wabbler, so that it may act as a universal joint.
The method of automatically traversing the carriage c is as follows: Referring to Fig. 681, two gears a, b are fast upon shaft t, gear a drives c which is on the same shaft as e, gear b drives d which drives a gear not seen in the cut, but which we will term x, it being on the same shaft as c and e. Now if e is driven through the medium of a c, it runs in one direction, while if it is driven through the medium of b d x, it revolves e in the opposite direction, and since e drives g and g is on the end of the feed screw (e, Fig. 682) the direction of motion of carriage c is determined by which of the wheels a or b drives e. At h is a stand affording journal bearing to a shaft n, whose end engages a clutch upon the shaft of wheels c, x and e. On the outer end of shaft n is ball lever l′′, whose lower end is attached to a rod k, upon which are stops l l′ adjustable along rod k by means of set-screws. At m is a bracket embracing rod k.
Now suppose carriage c to traverse to the left, and m will meet l moving rod k to the left, the ball i will move up to a vertical position and then fall over to the right, causing the clutch to disengage from gear c and engage with the unseen gear x, reversing the motion of e and of g, and therefore of carriage c, which moves to the right until m meets l′ and pushes it to the right, causing i to move back to the position it occupies in the engraving, the clutch engaging c, which is then the driving wheel for e.
Screw Machine.—The screw machine is a special form of lathe in which the work is cut direct from the bar, without the intervention of forging operations, and it follows therefore that the bar must be large enough in diameter to suit the largest diameter of the work, the steps or sections of smaller diameter being turned down from the full size of the bar. The advantages of the screw machine are, that the work requires no centring since it is held in a chuck, that forging operations are dispensed with, that any number of pieces may be made of uniform dimensions without any measuring operations save those necessary when adjusting the tool for the first piece, and that it does not require skilled labor to operate the machine after the tools are once set.
The capacity of the screw machine is, therefore, many times greater than that of a lathe, while the diameters and lengths of the various parts of the work will be more uniform than can be done by caliper measurements, being in this case varied by the wear of the cutting edges of the tools only, which eliminates the errors liable to independent caliper measurement. Hollow work, as nuts and washers, may be equally operated on being driven by a mandril held in the chuck.
| VOL. I. | EXAMPLES OF SCREW MACHINES. | PLATE X. | |
 |
|||
| Fig. 691. | |||
 |
|||
| Fig. 692. | |||
Fig. 691 represents Brown and Sharpe’s Number 1 screw machine, which is designed for the rapid production of small work.
Three separate tool-holding devices may be employed: first, cutting tools may be placed in the holes shown to pierce (horizontally) the circular head f; second, tools may be fixed in the tool posts shown in the double slide rest, which has two slides (one in the front and one at the back of the line of centres); and third, tools may be placed in what may be termed the screw-cutting slide-rest j.
f is a head pierced horizontally with seven holes, and is capable of rotation upon l; when certain mechanism is operated l slides on d and the mechanism of these three parts is arranged to operate as follows. The lever arms k traverse l in d. When k is operated from right to left, l advances towards the live spindle until arrested at some particular point by a suitable stop motion, this stop motion being capable of adjustment so as to allow f to approach the live spindle a distance suitable for the work in hand.
When, however, k is operated from left to right l moves back, and when it has traversed a certain distance, the head f rotates 1⁄7 of a rotation, and becomes again locked so far as rotation is concerned. Now the relation between the seven holes in f is such that when f has rotated its 1⁄7 rotation, one of the seven holes is in line with the live spindle. Suppose then seven cutting tools to be secured in the holes in f, then k may be operated from right to left, traversing l and f forward, and one of the cutting tools will operate upon the work until l meets the stop; k may then be moved from left to right, l and f will traverse back, then f will rotate 1⁄7 rotation and l and f may be traversed by k, and a second tool will operate upon the work, and so on.
The diameter of the work is determined by the distance of the cutting edge of the tool from the line of centres, when such tool is in line with the work, or, in other words, is in position to operate upon the work. The end measurements of the work are secured by placing the cutting edges of the tools the requisite distance out from f, when l is moved forward as far as the stop motion will permit. But it is evident that the length of cut taken along the work, would under these simple conditions vary with the distance of the end of the work from the face of the chuck driving it, but this is obviated as follows:—
The live spindle is made hollow so that the rod of metal, of which the work is to be made, may pass through that spindle. A chuck on the spindle holds the work or releases it in the usual manner. Suppose then the chuck to be open and the bar free to be moved, then there is placed in the hole in f, that is in line with the work, a stop instead of a cutting tool. The end of the work may then, for the first piece turned, be squared up by a tool placed in the slide rest and then released from the chuck and pushed through the live spindle until it abuts against the stop so adjusted and affixed in the hole in f; k may then be operated to act on the work. The first tool may reduce the work to its largest required diameter, the second turn down a plain shoulder, the third may be a die cutting a thread a certain distance up the work, the fourth may be a tool turning a plain part at the beginning of the thread, the fifth may round off the end of the work, and the sixth may be a drill to pierce a hole a certain distance up the end of the work.
Now suppose the work to require its edge at the other end to be chamfered, then there may be placed in the slide rest tool posts a tool to sever the work from the bar out of which it has been[I-201] made, while the other may be used to chamfer the required edge, or to round it if needs be to any required form.
Work held in the chuck but not formed from a rod may be, of course, operated upon in a similar manner.
In the case, however, of work of large diameter requiring to be threaded, the threading tool may be held and operated differently and more rigidly as follows. i is a lever carrying under its bend and over the projecting end of the live spindle, a segment of a nut whose thread must equal in pitch the pitch of thread to be given to the work. A collar or ring, oftentimes called the leader, having a thread of the same pitch, is then secured upon the live spindle, so as to rotate with it, and have no end motion; when therefore i is depressed, the nut will come into work with the collar or ring, and i will be traversed at a speed proportioned to the pitch of the threads on the collar and nut.
Now i is attached to a shaft having journal bearing (and capable of end motion) at the back of the lathe head, and on this bar is attached the slide rest j, in which the turning or threading tool may be placed. The shaft above referred to having end motion, may be operated (when the nut in the lever i is lifted clear of the collar) laterally by means of the lever i; hence to traverse j to the right, or for the back traverse, i is raised and pulled to the right, i is then lowered, the nut engages with the collar, and the tool is traversed to the cut. The cut is adjusted for diameter by the slide rest, which is provided with an adjustable stop to determine the depth to which the tool shall enter the work.
It is obvious that this part of the machine, may be employed for ordinary turning operations, if the collar be of suitable pitch for the feed.
Figs. 692 and 693 represent a screw machine for general work.
a is a chuck with hardened steel V-shaped jaws. It is fast on the hollow arbor of the machine. b is a steadying chuck on the rear end of the arbor. The arbor has a two and one-sixteenth hole through it and its journals are very large and stiff. It is of steel, and runs in gun-metal boxes. The cone pulley and back gear is of the full proportion and power of an eighteen-inch lathe. c is an ordinary lathe carriage fitted to slide on the bed, and be operated by hand-wheel d and a rack pinion as usual. Across this carriage slides a tool rest e operated by screw as usual, and having two tool posts, one to the front and one to the rear of the work. This tool rest, instead of sliding directly in the carriage as is the case with lathes, slides on an intermediate slide which fits and slides in the carriage. This intermediate slide is moved in and out, a short distance only, by means of cam lever g. An apron on the front end of this slide carries the lead screw nut h. When the cam lever is raised it brings the slide outward about half an inch, and the tool rest e comes out with it and at the same time the nut leaves the lead screw. The inward movement of the slide is always to the same point, thus engaging the lead screw and resetting the tool. In cutting threads with a tool in the front tool post the tool is set by moving the tool rest as usual, and at the end of the cut the cam lever serves to quickly withdraw the tool and lead screw nut so that the carriage can be run back. The tool rest is then advanced slightly and the new cut taken. By this means threads are cut without any false motions, and the threads may be cut close up to a shoulder.
i is the lead screw. This screw does not extend, as is usual, to the head of the machine. It is short and is socketed into a shaft which runs to the head of the machine and is driven by gearing as usual. The lead screw is thus a plain shaft with a short, removable, threaded end. The gearing is never changed. Different lead screws are used for different threads, thus permitting threads to be cut without running back. The lead screws are changed in an instant by removing knob j. The lead screw nut h is a sectional nut, double ended, so that each nut will do for two pitches, by turning end for end in the apron. l is an adjustable stop which determines the position of the carriage in cutting off, facing, &c. k is an arm pivoted to the rear of the carriage and carrying three open dies like a bolt cutter head. At m is a block sliding or capable of being fed along the bed. n is a gauge screw attached to this block and provided with two nuts. The stop lever shown in the cut turns up to straddle[I-202] this screw, and the position of the nuts determines how far each way the block may slide. o is the turret fitted to turn on the block. It has six holes in its rim to receive sundry tools. It can be turned to bring any of these tools into action, and is secured by the lock lever p.
The turret slide is moved quickly by hand, by means of the capstan levers u, which, by an in-and-out motion, also serve to lock the turret at any point. The turret slide is fed, in heavy work, by the crank-wheel r on its tail screw. This tail screw carries, inside the crank-wheel, two gears s, which are driven at different speeds by a back shaft behind the machine. These two gears are loose on the tail screw, and a clutch operated by lever t locks either one to the screw. Both the carriage and turret are provided with oil pots not shown in the cuts.
A top view of the turret is shown in Fig. 694, a set of tools being shown in place.
The end gauge which is shown removed from the chuck in Fig. 695, is composed of a hollow shank a fitting the hole in the turret, and a gauge rod b fitting the bore of the shank. The shank a may be set farther in or out of the turret, and the rod b may be set farther in or out of the shank, the two combined being so set that when the turret is clear back against its stop the end of the rod b will gauge the proper distance that the bar iron requires to project outwards from the chuck of the machine. The centre shown in Fig. 696 corresponds to an ordinary lathe centre, and is only used when chasing long work in steel.
The turner shown removed from the chuck in Fig. 697, consists of a hollow shank a, fitting the turret and having at its front end a hardened bushing b secured to a by a set screw. It has also a heavy mortised bolt c in the front lug of the shank; an end-cutting tool d shaped like a carpenter’s mortising chisel, and clamped by the mortised bolt; a collar screw e to hold the tool endwise; and a pair of set-screws f to swivel the tool and its bolt. Bushing b is to suit the work in hand. The tool d is a piece of square steel hardened throughout. It is held by its bolt with just the proper clearance on its face. It cuts with its end without any springing, and will on this account stand a very keen angle of cutting edge. There is hardly any limit to its cutting power. It will cut an inch bar away at one trip with a coarse feed. It does not do smooth work, and is, therefore, used only to remove the bulk of the metal, leaving the sizer to follow.
The sizer Fig. 698, consists of a hollow shank a fitting the turret and carrying in its front end a hardened bushing b and a flat cutting tool c. The sizer follows the turner and takes a light finishing cut with oil or water, giving size and finish with a coarse feed, and having only a light and clean duty it maintains its size.
The die holder shown in Figs. 699 and 700, is arranged to automatically stop cutting when the thread is cut far enough along the work. It will cut a full thread cleanly up against a solid shoulder. It consists of a hollow shank a fitting the turret; a sleeve b fitted to revolve and slide on the front end of the shank c; a groove e bored inside the sleeve; a pin d on the shank fitting freely in the groove e; a keyway f at one point in the groove and leading out each way from it; and a thread die g held in the front end of the[I-203] sleeve. When the turret is run forward, the thread die takes hold of the bolt to be cut, but it revolves idly instead of standing still to cut, until the pin d comes opposite the keyway f when, the turret still being moved forward, the pin enters the back of the keyway. The sleeve now stands still, the die cuts the thread and pulls the turret along by the friction of the pin in the keyway. Finally the turret comes against its front stop and can move forward no farther. Consequently the sleeve is drawn forward on its shank c, and the instant the pin d reaches the groove e the die and sleeve commence to revolve with the work and cease cutting. The machine is then run backward, and the turret moved back a trifle. This causes the pin to catch in the front end of the keyway and the sleeve is again locked. The die then unscrews, and, in doing so, pushes the turret back. A tap holder may be inserted in place of the die, and plug taps may be run to an exact depth without danger.
Drills and other boring tools are held in suitable sockets, which fit into the turret.
The following are the operations necessary to produce in this machine an hexagon-headed bolt.
First operation: The bar is inserted through the open chuck.
Second operation: Turret being clear back against its stop and revolved to bring present the end gauge, the bar is set against the end gauge, and the chuck is tightened. This chucks the bar and leaves the proper length projecting from the chuck.
Third operation: Front tool in the carriage, a bevelled side tool cones the end of the bar so turret tools will start nicely.
Fourth operation: Turret being revolved to present the turner, the bar is reduced, at one heavy cut, to near the proper size, the turret stop determining the length of the reduced portion.
Fifth operation: Turret being revolved to present the sizer, the body of the bolt is brought to exact size by a light, quick, sliding cut.
Sixth operation: Open die arm being brought down, the bolt is threaded; the left carriage stop indicating the length of the threaded part.
Seventh operation: Turret being revolved to present the die holder, the solid die is run over the bolt, bringing it to exact size with a light cut, and cutting full thread to the exact point desired.
Eighth operation: Front tool in the carriage chamfers off the end thread.
Ninth operation: Back tool of carriage, a parting tool, cuts off the bolt; the left carriage stop determining the proper length of head.
Tenth operation: Bolt being reversed in chuck, the top of the head is water cut finished by a front tool in the carriage. This operation is deferred till all the bolts of the lot are ready for it.
Fig. 703 represents a general view of a screw machine designed by Jerome B. Secor, of Bridgeport, Connecticut. The details of the machine are shown in Figs. 704, 705, 706, 707, 708, 709, 710, and 711.[13] The live spindle is of steel and is hollow, and its journals are ground. The boxes are lined with babbitt, so that no other metal touches the spindle, and may, by a special device, be re-babbitted and bored exactly parallel with the planing of the bed.
[13] From Mechanics.
A steel collar j, Fig. 704, between the front end of the forward box and the spindles, receives the thrust due to the cut, and a nut on the spindle acts against the cone to adjust it forward on a feather k in the spindle to take up end wear. The wire or rod[I-204] from which the work is to be made is passed through the spindle and collar on the stand, and is held by a thumb-screw in the collar, which is influenced by the weight and cords, so that when the wire is released in the chuck the weight pulls the collar and wire forward, forcing the wire out through the front end of the chuck until it comes against the stop in the turret, which gauges the length needed to make the piece required. From time to time, as the rod is used up, the thumb-screw in the sliding collar is loosened, and the collar is shoved back on the rod as far as it will go, and the set-screw is again tightened.
Fig. 704 shows in section the front bearing and the automatic chuck. m is a hollow spindle within which is the hollow spindle h, through which the rod or wire to make the work passes. It is prevented from end motion by the cone hub on one side and the collar j on the other side of the bearing, while h may be operated endwise within m by means of the hand-lever shown on the left-hand of the headstock in the general view. The core a of the chuck screws upon m, and is threaded to receive the adjustment nut b, which receives and holds the adjustment wedges c at their ends by the talon shown. The shell d is secured to h by the screws i, which pass through slots in a, and therefore move endwise when h is operated by its hand-lever. Now the mouth of d, against which the adjustment wedges c rest, is coned 21⁄2°, as marked; hence the end motion of d to the left causes c, and therefore f, to approach the axis of the chuck and grip the rod or wire, while its motion to the right causes c, and therefore f, to recede from the chuck axis and to release the wire. Since b is screwed upon a, and c is guided at the end by b, and since also f is detained endwise in a, the motions of c and of f are at a right angle to the chuck axis. Hence in gripping the rod or wire there is no tendency to move it endways, as there is where the gripping jaws have, as in many machines, a certain amount of end motion while closing. When this end motion exists, tightening the jaws upon the work draws it away from the stop in the turret and impairs the adjustment for length of work. The gripping jaws are closely guided in slots in d and in a, and three sets of these jaws are necessary to cover a range of work from the full diameter of the bore of h down to zero. The capacity of each of these sets of jaws, however, may be varied as follows: The adjustment ring b is threaded upon a, and may be operated along a to move c endwise by means of the tangent screw e, whose threads engage with teeth parallel to the axis of b, and running across its width all around its circumference, hence rotating e, rotates b, causing it to move along a, and carry c beneath f. By this method of adjustment f need be given only enough motion to and from the chuck axis to grip and release the work, and the reduction of motion between the hand-lever operating h and the motion of f is so great, that with a very moderate force at the lever the wire may be held so that its projecting end may be twisted off without slipping the wire within the jaws or impairing the jaw grip.
[I-205]Fig. 705 is a sectional and end view of the core a of the chuck, and Fig. 706 a sectional and end view of the shell d.
Fig. 707 represents a sectional side view and an end view of the cross slide, or cutting-off slide, which carries two tool posts, and therefore two cutting tools, one of which is at the back of the rest. In place of a feed screw and nut, or of a hand lever and link, it is provided with a segment of a gear-wheel p operating in a rack r, which avoids the tendency to twist the cross slides in its guides which exists when a hand lever and link is used.
The cross slide is adjusted to fit in its guideway by a jaw s1, Fig. 707, which is firmly screwed to and recessed into r. To take up the wear, the face of s1 is simply reduced. This possesses a valuable advantage, because it is rigid and solid, does not admit of improper adjustment, nor can the adjustment become impaired at the hands of the operator.
To adjust the position of the cross slide upon the shears a screw passes between the shears and is threaded into the stud q. This screw is operated by a hand wheel shown in the general view, Fig. 703, beneath the rear bearing of the headstock.
A special and excellent feature of the machine is the stop device for the motion of the cross slide which is shown in Fig. 707.
The screw s has one collar c, solid on it, and the screwed end is tapped into the sliding sleeve t, which is held from turning by the stud a. Between the solid collar c and the loose collar b there is a short, stiff spiral spring, as shown; by means of the fast and loose collars, the spring and the screwed thimble d, a strong friction is had on the collar b, which is ample to keep the screw from turning while in use as a stop, although it permits the screw to turn easily enough when a wrench is applied to the square end. Precisely the same device is used at the other end of the slide to stop it in the opposite direction.
Details of the mechanism of the turret and turret slide are shown in Figs. 708, 709, and 710. Fig. 708 is an end sectional view of the turret slide, which is traversed on its base by a segment d of a gear operating in a rack r (in the same manner as the cutting-off slide), the segment being connected by stud n to handle m. o represents the body of the slide, which is grooved at the sides to receive the gibs x, which secure it to the base p on which it slides. p is clamped to its adjusted position on the shears or bed by means of the gib, shown in dotted lines, which is pulled laterally forward by the screw s, which is tapped into the stem of the gib. The method of rotating the slide and of locking it in position is shown in Fig. 709, which is a top view of the turret head, and Fig. 710, which shows o removed from p and turned[I-206] upside down. Pivoted to segment d is a rod e having at k a pin that as motion proceeds falls into s and rotates t, which is fast to the bottom of the turret. Upon the handle m being moved backward the segment begins its motion forward, as indicated by the arrow in Fig. 710, thereby moving the slide backward upon the gibs by the working of its cogs into the rack r, Fig. 708, which is attached to the base p. When the segment d has accomplished about one-half its motion the pin h, which is on the upper side of the segment d, comes in contact with the projection or lug on the side of the cam f, as shown by the arrow head in Fig. 710, bringing the opposite side of the cam against the pin g, Fig. 709, thereby moving it backward, compressing the spring u, and drawing the bolt l from its seat in the disc v. This operation is completed before the motion of the segment brings the pin k in contact with the ratchet-wheel t. The segment d in continuing its motion after the pin k is brought into the notch s, begins the revolution of the turret on its axis. As will be seen by the inspection of Fig. 710, the pin h works upon a much longer radius than the projection upon the cam with which it comes in contact, and therefore, after a given part of its motion is complete, gets beyond the reach of the cam, thereby releasing its hold and allowing the bolt l, Fig. 709, to be forced against the disc v by the expansion of the spring u, which occurs soon after the turret has commenced its revolution by the contact of pin k with the wheel t. The completion of the movement of the handle m (and the segment d) completes the revolution of the turret one-sixth of its circumference, thereby allowing the bolt l, by the further expansion of the spring u, to be forced into its next opening or seat in the disc v. The forward motion of the handle m brings the turret forward to its position at the work and restores the parts to their former positions, as shown in the illustrations.
The stop motion for the forward motion of m, and that therefore determines the length of turret traverse forward, and hence the distance each tool shall carry its cut along the work, is shown in Fig. 711. The end of the screw a abuts against the stop b in the usual manner; it is, however, threaded through the eye of a bolt c, as well as through the end of the turret slide, so that it may be locked by simply operating the nut d. Thus the use of a wrench is obviated, and the adjustment is more readily effected.
Figs. 712 and 713 represent a screw machine by the Pratt and Whitney Company, of Hartford, Connecticut, and having Parkhurst’s patent wire or rod feed for moving the work through the hollow spindle and into position to be operated upon by the tools. The reference letters correspond in both figures.
At a is the front and at b the back bearing, affording journal bearing to a hollow spindle c, which carries the shell d of the work-gripping chuck, the clutch ring h and a collar i, in which is pivoted, at j, the clutch levers g. This collar is threaded upon c and is locked in position by a ring lock nut j′. The clutch arm k slides upon a rod x, and has a feather projecting into a spline in x. The core e of the work-gripping chuck is fast upon the inner spindle f, which revolves with the outer one c. The left-hand end of f abuts[I-207] against the short arms of the clutch levers g, and it is obvious that when k is operated back and forth upon x, it moves the clutch h endways upon c, and the cone upon h operates the levers g, causing them to move the inner spindle f endways and the inner cone e of the chuck to open or close. Suppose, for example, that k (and hence h) is moved to the right, and the long ends of g will be released and may close moving their short ends away from the end of f, and therefore releasing e from its grip upon the work. In moving k to the right the sleeve l is also moved to the right, and its serrations at l′ being engaged with the tongue p, the sleeve m is pulled forward. Now the bar or rod of which the work is made is held at one end by the chuck, it is supported by the bushing z in the end of spindle c, and in the bushing s in the arm of sleeve m, while it has fast upon it a collar t. When therefore m is pulled forward or to the right, its arm meets t and pulls the rod or bar for the work through the chuck e.
On the other hand when k and therefore h, l, and m, are moved to the left, levers g are opened at their long ends by the cone of h. The short ends of g push the inner spindle f to the right, e passes through d, and being split, closes upon the work and grips it, the parts occupying the positions shown in the figure. The same motion of k passes l through the sleeve m (the teeth at n raise the catch p, allowing l′ to pass through m) so that at the next movement of k to the right, m will be pulled a second step forward, again passing the work through the chuck. q is merely a pin wherewith to lift p and enable m to be moved back, when putting in a new rod for the work; k is operated by a link from u to v, the handle for moving this link being shown at w in the general view.
To prevent the sleeve m from moving back with l it is provided with a shoe o, pressed by the spring r against x, thus producing a friction between m and x that holds m while l slides through it. r′ is to regulate the tension of the spring at r. y is merely a sleeve to protect the clutch mechanism from dust, &c.
Box tools for screw machines are used for a great variety of special work. They are simply boxes or heads carrying tools and a work-steadying rest.
Fig. 714 represents a box tool for a screw machine. The cylindrical stem fits into the turret holes and contains a steadying piece or rest g to support the work and keep it to its cut. In the box tool shown in the figure, there are four cutting tools set in to the depth of cut by the screws a, b, c, and d respectively, and a fifth for rounding off the end of the work is shown at e.
[I-208]Fig. 715 represents a top view, Fig. 715a a front view, and Fig. 715b an end view, of a box tool for shaping the handles for the wheels of the feeding mechanism of machines. The work is first turned true and to its required diameter, and the rest is set to just bear against the work to steady it and hold it against the pressure of the cut. The cutter is cylindrical with a gap cut in it at g, so as to give a cutting edge. By grinding the face of this gap the tool is sharpened without altering its shape, as is explained with reference to circular or disc tools for lathe work. The cutter is provided with a stem by which it is held in the slide, through the medium of the clamp. The slide is operated by an eccentric on the spindle or rod r, which is operated by the handle h. The stop obviously arrests the motion of the slide when it meets the box b, and this determines the diameter of the work, which is represented by w in the end view figure.
Fig. 716 represents the die holder and die for the Pratt and Whitney Co.’s screw machine. The die is cut through on four sides, and is enveloped by a split ring having a screw through its two lugs, so that by operating the screw the die may be closed to take up the wear and adjust it for diameter. It is secured in a collar by the set-screw shown, and this collar is clutch shaped on its back face, engaging a similar clutch face on the shoulder of the arbor, the object of this arrangement being as follows. Suppose it is required to cut a thread a certain distance, as say, 3⁄4 inch, along a stud, and that the depth of the clutch is 1⁄4 inch. Suppose that when the turret is fed forward sufficiently the thread is cut half an inch along the work at the moment that the turret meets its stop and comes to rest, then the die will continue to feed forward one-quarter of an inch, moving along the body or stem of the holder until its clutch face disengages, when the die will revolve with the work.
Fig. 717 represents a cutting-off tool and holder for a screw machine. The tool fits into a dovetail groove in the split end of the holder, and is ground taper in thickness to give the necessary clearance on the sides. It is held by the screw shown, which closes the split and grips the dovetail; obviously the top face only is ground to resharpen it.
Fig. 718 represents a special lathe for wood work designed and constructed by Charles W. Wilder, of Fitchburg, Massachusetts. It is intended to produce small articles in large quantities, cutting them to duplicate form and size without any further measurements than those necessary to set the tools in their proper respective positions. It is employed mainly for such work as druggists’ boxes, tool handles, straight spokes for toy vehicles, piano pins, balls, rings, and similar work.
Its movements are such that the tools are guided by stops determining the length and the diameter of the work so as to make it exactly uniform, while the form of the cutting tools determines the form of the work, which must therefore be uniform.
The lathe may be described as one having a carriage rest spanning the bed of the lathe, which rest holds the work axially true with the lathe centres without the aid of the dead centre, while it at the same time trues the end of the work and leaves it free to be operated upon by other tools, which, after once being[I-209] set and adjusted, shape any number of pieces of work to exact and uniform diameter and shape.
The manner in which this is accomplished is as follows: Fig. 718 is a general external view of the lathe; Fig. 719 is an end elevation view of the rest from the cone spindle end, and Fig. 720 is an end view of the rest viewed from the tailstock end of the lathe. a is a ring fastened in the rest r by the set-screw b. The mouth c of the ring which first meets the work is coned, or beveled, as shown, and an opening on one side of the ring admits a cutting tool t. Now the work is placed one end in the cone driving chuck on the lathe spindle, and the other end in the cone or mouth c, Fig. 719, being kept up to the driving chuck by the end pressure of c. As the work rotates, the tool t cuts it to the diameter d of the ring bore, the carriage or rest r traversing along the lathe bed as fast as tool cuts; hence the bore d serves as a guide to hold the work and make it run true, this bore being axially true with the lathe centres. The cone surface of c thus operates the same as the sole of an ordinary carpenter’s plane, the tool t cutting more or less rapidly according as its cutting edge is set to project more or less in advance of the surface of the cone or recess c. This admits of the tool cutting at a rate of feed that may best suit the diameter of the work and the nature of the wood. The tool t, is operated laterally to increase or diminish the rate of feed by the screw e, which also serves as a pivot, so that by operating the thumb-screw f, the tool point may be adjusted for distance from the centre of the bore d, or in other words the diameter to which the tool t will turn the work is adjusted by the thumb-screw f. g is the head of the pivot screw that the swing tool holder h works upon, and this swing motion carries the forming tool or cutter x, which shapes the work to the required form. i is a shaft upon which a lever, carrying the tool holder j, works, the latter carrying the severing tool k, which severs the finished work from the stick of wood from which the work is made.
The tool holders h and j are connected by means of the arms l and m to the stud o, fast in wheel p, operated by a knee lever q, which is pivoted at s to u, which is fast to one of the gibs that hold the carriage to the lathe Vs. The knee lever q is connected to the wheel p by a raw-hide strap, or belt v, so that the operator, by pressing his knee upon the end of the lever q, causes the wheel p, to partly rotate, carrying o with it (o being fast in p), and gives a forward radial motion to tool holder h and cutter x, causing the latter to enter the work until such time as the stud o and the screw stud w are in line, horizontally with the centre of the wheel p, after which tool holder h will move back, while the severing tool k (which has a continuous upward or vertical movement) is cutting off the finished work, which has been formed to shape, and reduced to the required diameter by the forward movement of the tool or cutter x. The object of the backward or retiring motion of h is to relieve the shaping tool x from contact with the work, while k cuts it off, or otherwise the work might meet x when cut off, and receive damage from contact with it. The stud w, connecting tool holder h with the wheel p, is threaded with a right and left-hand screw, by operating which the tool x may be operated to reduce the work to any required diameter.
The rest or carriage r traverses along the lathe shears or bed z, carrying with it all the levers and tools, so far described.
The tailstock, or back head, carries a tool holder in the rear of the spindle, in which fits also a drill bit or other cutting tool. The method of traversing and operating the carriage r and the back head is as follows:
At the back of the bed or shears is a table, shown at t, in Fig. 718. Upon this table is a stand to which is pivoted the end of a lever, as is shown at 1 in figure. This lever has a joint at 2, and is connected to the tailstock spindle at a joint marked 3. It is obvious that by operating the lever laterally, joint 2 will double, and the tail spindle will be moved along the bed. If the tail spindle is not locked it will simply feed through the tailstock and[I-210] the tool in the spindle will operate, but if it is locked (by the ordinary screw shown), then the handle will slide the whole tailstock and the tool in the holder at the back of the tail spindle may operate.
At 4 is an adjusting screw, which, by coming into contact with the carriage r causes it also to traverse, which it will do until it meets against a screw on the other side, marked 5, in Fig. 718, which, standing farther out than the chuck prevents the cutting tool from meeting the chuck.
The movement of the carriage continues until the stop-gauge 6 meets the end of the work, hence the length of the work is from the cutting-off tool to the face of stop 6. The adjustment for the length of the work is made by means of screw 4, which will slide the carriage r, as soon as it meets it, independent of what distance the stop 6 may be from the work end. The tailstock carries two tool holders, similar to those on an ordinary lathe. When the cutting tools are used to cut completely over the end of the work, as in ball turning or a round ended handle, the stop 6 is not used, the tool which rounds the end acting as a stop of itself.
When bits are used they are held in the tail spindle and are made of a proper length to give the required depth of hole, or sometimes the face of the bit-holder may be used as a stop.
When the tools, cutters, and belts are all properly adjusted in position to cut to the required respective diameters or lengths the operator has simply to place a stick of wood in the lathe and operate the respective handles or levers in their proper consecutive order, and the work will be finished and cut off, the operation being repeated until the stick is used up, when a new one may be inserted, and so on.
Lathes for Irregular Forms.—In lathes for irregular forms (which are chiefly applied to wood and very rarely to metal turning), the work is performed by rotary cutting tools carried in a rapidly rotating head. The work itself is rotated slowly, and the carriage or frame carrying the cutting tools is caused to follow the outline of the pattern or former at every point in its circumference as well as in its length. The principle of action by means of which these ends are attained is represented in Fig. 721, in which s represents a slide which carries the sliding head, affording journal bearing to the rotating head h, driven by the belt e, and carrying the cutters, and also the wheel w. f represents the pattern or former, and b a piece of wood requiring to be turned to the same form as that of f. Suppose then that f be slowly rotated by a and c, receiving rotary motion from a (through the medium of d), then the rotations of c will equal those of f, because the diameter of a is equal to that of c. The diameter of the circle described by the cutters at h is also equal to the diameter of w, hence the motion of the extremities of the cutters is precisely the same as that of the circumference of w, and as w receives its motion from f it is obvious that the cutters will reduce g to the same form and size as f, and if the head be traversed in the same direction as the axis of f, then the diameter and form of b will be made to correspond to that of f at every corresponding point throughout its length. Contact between w and f is maintained by means of a weight or spring, the rotation of f being sufficiently slow to insure its being continuous, while the necessary rapidity of cutting speed for the tools is attained by rotating h at the required speed of rotation.
This class of lathe is termed the “Blanchard” lathe from the name of the inventor, or “Lathe for irregular forms,” from the chief characteristic of the work, but is sometimes designated from the special article it is intended to turn, as “The Shoe-last lathe,” “Axe-handle lathe,” “Spoke lathe,” &c., &c.
Let Fig. 722 represent a lathe of this kind provided with a frame a affording journal bearing to the shaft of the drum b, which is driven by the pulleys c. Let e represent a pulley receiving motion from b by the belt d. The cutting tools are carried by the head f which is rotated by pulley e. Let the carriage or frame carrying the shaft of e carry a dull pointed tracer, with continuous contact with the former h by means of a weight or spring, the carriage being so connected to the way n on which it traverses that it is capable of rocking motion, and if h be rotated the carriage will, by reason of the tracing point, have a motion (at a right angle to the axis of h) that will be governed by the shape of h; hence since g rotates equally with h, the form of the blank work g will be similar to that of h, but modified by reason of the tracing point being at a greater distance than f from the centre of rocking motion.
All that is necessary to render this motion positive throughout the lengths of g and h is to connect them together by gears of[I-211] equal diameter, and traverse the carriage along n for the full length of the pieces. But the effect will be precisely the same if the frame carrying g and h be pivoted below, capable of a rocking motion, and h be kept against the tracing point by means of a spring or weight, in which case the carriage may travel in a straight line upon n and without any rocking motion. This would permit of the carriage operating in a slide way on n enabling it to traverse more steadily.
To maintain continuous contact between the tracing point and the former h, the rotations of h are slow, the necessary rapidity of tool cutting action being obtained by means of the rapid rotation of the head and cutters f.
Since motion from the line shaft to the machine is communicated at c it is obvious that the gears or devices for giving motion to h and g may be conveniently derived from the shaft carrying c and b, for which purpose it extends beyond the frame at one end as shown. Lathes of this kind are made in various forms, but the principles of action in all are based upon the principles above described.
Back Knife Gauge Lathe.—This lathe, Fig. 723, has a carriage similar to that described with reference to Fig. 718, and carries similar tools upon the tailstock. It is further provided, however, with a self-acting feed traverse to the carriage, and by means of a rope and a weight, with a rapid carriage feed back or from left to right on the bed, and also with a knife at the back. This knife stands, as seen in the engraving, at an angle, and is carried (by means of an arm at each end) on a pivoted shaft that can be revolved by the vertical handle shown. The purpose of this knife is first to shape the work and then to steady and polish the wood or work. Obviously when the knife is brought over upon the work its cutting edge meets it at an angle and cuts it to size and to shape; the surface behind the cutting edge having no clearance rubs against the work, thus steadying it while polishing it at the same time. These lathes are used for turning the parts of chairs, balusters, and other parts of household furniture, the beads or other curves or members being produced on the work by suitably shaped knives, which obviously cut the work to equal shape and length as well as diameter, and it is from this qualification that the term “gauge” is applied to it.
Fig. 724 represents the Niles Tool Works special pulley turning lathe, in which motion from the cone spindle to the live spindle is conveyed by means of a worm on the cone spindle and a worm-wheel on the live spindle. Two compound slide rests are provided, the tool on the rear one being turned upside down as shown. These rests may be operated singly or simultaneously, and by hand or by a self-acting motion provided as follows:—A screw running parallel to the cone spindle is driven by suitable gearing from the cone spindle. At each end of this screw it gears into a worm-wheel having journal bearing on the end of the slide rest feed screw as shown. By a small hand wheel on the end of the slide rest feed screw the worm-wheel may be caused to impart motion to the feed screw by friction causing the slide rest to feed. But releasing this hand wheel or circular nut releases its grip upon the feed screw, and permits of its being operated by the handle provided at the other end. The rail carrying the slide rest is adjustable in and out to suit varying diameters of pulleys, being secured in its adjusted position by the bolts shown.
The cut is put on by means of the upper part of the compound rest. To turn a crowning pulley the rails carrying the slide rests are set at an angle, the graduations shown on the edge of the ways to which they are bolted being to determine the degree of angle. When the pulley surface of the pulley is to be “straight” both tools may commence to operate on one edge of the pulley surface, the advance tool taking a roughing and the follower tool a finishing cut; but for crowning pulleys the tools may start from opposite edges of the pulley, the cuts meeting at the middle of the face; hence the angles at which the respective rails are set will be in opposite directions.
The pulleys to be turned are placed upon mandrels and driven by two arms engaging opposite arms of the pulley. To drive both arms with an equal pressure, as is necessary to produce work cylindrically true, an equalizing driver on Clements’ principle (which is explained in Fig. 756, and its accompanying remarks) is employed.
For driving the pulleys to polish them after they are turned the cone spindle is hollow at the rear end and receives a mandrel. The high speed at which the cone spindle runs renders this possible, which would not be the case if wheels and pinions, instead of worm-gear, were employed to communicate motion from the cone to the live spindle. A wheel shown in position for polishing is exhibited in the cut, the pivoted arm in front affording a rest for the polishing stick or lever.
Boring and Turning Mills.—The boring and turning mill patented in England by Bodmer in 1839, has developed into its present improved form in the United States, being but little known in other countries. It possesses great advantages over the lathe for some kinds of turning and boring, as wheels, pulleys, &c.
The principal advantages of its form of construction are:—
1st. That its work table is supported by the bed at its perimeter as well as at its centre, whereas in a lathe the weight of the[I-213] chuck plate as well as that of the work overhangs a journal of comparatively small diameter, and is therefore more subject to spring or deflection and vibration.
2nd. It will carry two slide rests more readily adjustable to an angle, and more readily operated simultaneously, than a lathe slide rest.
3rd. It is much more easy to chuck work on a boring mill table than on a lathe, because on the former the work is more readily placed upon the table, and rests upon the table, so that in wedging up or setting any part of the circumference of the work to the work table, there is no liability to move the work beneath the other holding plates; whereas in a lathe the work standing vertical is apt when moving or setting one part to become unset at other points, and furthermore requires to be held and steadied while first being gripped by the chucking dogs, plates, or other holding devices.
Figs. 725, 726, 727, 728, and 729 represent the design of the Niles Tool Works (of Hamilton, Ohio), boring and turning mill. In this design provision is made to raise the table so that it takes its bearing at the centre spindle only when used upon small work where a quick speed of rotation is necessary, or it may be lowered so as to take its circumferential bearing for large heavy work where slower speeds and greater pressure are to be sustained.
The bearing surfaces are, in either case, protected from dust, &c., and provided with ample means of lubrication. Each tool bar is so balanced that the strain due to the balancing weights is in a line parallel to the bar axis in whatever position and at whatever angle to the work table the bar may be set. This prevents the friction that is induced between the bar and its bearings when the balancing strain is at an angle to the bar axis, and consequently pulls the bar to one side of or in a line to twist the bar. The bar is therefore more easily operated, and the feed gear is therefore correspondingly relieved of strain and wear.
The general construction of the machine is shown in Fig. 725. It consists of a base or bed, affording journal bearing and support to a horizontal work table, rotated by devices carried upon the bed. To each side of the bed are attached uprights or standards, forming a rigid support to a cross slide or rail for the two sliding heads carrying the tool bars.
The various motions of the machine are as follows: There are 16 speeds of work table, 8 with the single, and the same with the back gear. The cross slide is capable of being raised or lowered, to suit the height of the work, by an automatic motion. Both tool rests are capable of hand or automatic feed motion at various rates of speed, in a line parallel to the surface of the work table. Both are also capable of automatic or hand feed motion, either vertically or at any required angle to the work table, and have a quick return motion for raising them, while each may be firmly locked while taking radial or surfacing cuts, thus preventing spring or vibration to the tool bar. In addition to this, however, there is provided, when required, a tailstock, carrying a dead centre after the manner of a lathe, so that the work may be steadied from above as well as by the work table. In Figs. 726 and 727 are shown the devices for raising the work table and those for actuating the feed screws and the feed rod; thus operating the sliding heads horizontally and the tool bars vertically. a is the base or bed supporting the work carrying table b′, and affording its spindle journal bearing at d′. A step within and at the foot of d′ rests upon the wedge f′ so that when the wedge is caused to pass within d′ it lifts the step, which in turn lifts the table spindle, and hence the table, sufficiently to relieve its contact with the outer diameter of the bed. f′ is operated as follows: The lever g′ is pivoted at e′ and carries at its upper end a nut h′, operated by a screw on the end of the bolt i′; hence rotating i′, operates wedge f′.
For operating the automatic feed motions, f is a disc upon a shaft that is rotated by suitable gears beneath the work table; g is a disc composed of two plates, having a leather disc between them, the perimeter of the disc having sufficient frictional contact with f to cause g to rotate when f does so: g drives the vertical spindle i, which has a worm at j′ driving a worm-wheel which rotates the gears upon the feed spindles v, f, w, in the figures; f rotates in a continuous direction, but the spindle i is caused to rotate in either direction, according to whether it has contact with the top or bottom of the face of f, it being obvious that the motion of f above its centre is in the opposite direction to that below its centre of rotation. The means of raising and lowering g to effect this reversal of rotative direction is as follows: It is carried on a sleeve g′ which is provided with a rack operated by a pinion that is rotated by means of hand wheel h; hence, operating h raises or lowers g′, and therefore g; h′ is a hand wheel for locking the pinion, and hence detaining the rack (and therefore g) in its adjusted position. This design is an excellent example of advanced American practice for obtaining a variable rate of feed motion in either direction, it being obvious that g, being driven by the radial face of f, its speed of rotation will be greater according as it is nearer to the perimeter of f and less as it approaches the centre of f, at which point the rotary motion of g would cease. Here, then, we have a simple device, by means of which the direction and rate of feed may be governed at will with the mechanism under continuous motion, and conveniently situated for the operator, without his requiring to move from the position he naturally occupies when working the machine.
The means of raising or lowering the height of the rail r on the side standards z are as follows: k is a pulley driven by belt from the countershaft and operating pinion l, which operates pinion n, driving m. o is a gear on the shaft driving the pinions p, p, which operate the gears q, q, on the vertical screws which engage with nuts attached to r; m and n are carried on a bell-crank r pivoted on the shaft of pulley k. Pinion n is always in gear with pinion[I-214] l, and pinion m is always in gear with pinion n (and not with pinion l). With the bell-crank in one position, motion passes from l to n and to o; but with it in the other position, motion passes from l to n, thence to m, and from it to o. The motion of m, therefore, is always in a direction opposite to that of n; hence o, and gears p and q, may be operated in either direction by regulating which of the two gears n, m shall drive o, and this is accomplished as follows: The bell-crank r is connected by an arm to rod s, and the latter is connected by a strap to an eccentric t, operated by the handle shown. When this handle stands horizontally, both m and n are disengaged from pinion o; but if the handle be raised, rod s is raised, and m is brought into gear with o. If, however, it be lowered from the horizontal position, n is brought into gear with o, and m becomes an idle wheel.
There are two feed screws—one for operating each boring bar-head, and a spindle for operating the vertical feeds of the bars in the sliding heads. Fig. 728 shows the arrangement for engaging and disengaging the feed nuts of these heads. a is the slide that traverses the rail. It carries a nut made in two halves, n and n′, which are carried in a guide or slide-way, and which open from or close upon the screw f when the handle o is operated in the necessary direction. Each half of the nut is provided with a pin projecting into eccentric slots x in the face of a pivoted plate (shown dotted in), to which the handle o is attached. w, w represent bearings for the vertical feed [I-215] spindle w in Fig. 726. a is the annular groove for the bolts b in Fig. 729.
For a quick hand traverse for the head the ratchet, p is provided, operating a pinion s, which engages with a rack t, running along the underneath side of the cross-rail r. To adjust the fit of a to the rail the gibs y and y′ and the wedge x are employed.
Fig. 729 represents the automatic feed motion within the head for operating the tool bars vertically. r is the cross rail on which slides a carrying b, and permitting it to swivel at any angle by means of bolts b, whose heads pass within an annular groove, a in a. In b is carried the boring bar g, having the rack shown. p is a pinion to operate the rack. w is the feed-rod driving the worm h, which drives the worm-wheel i. This worm-wheel is provided with a coned recess, into which the friction plate c fits, so that when the two are forced together rotary motion from i is communicated to c, and thence to c′ (which is a sleeve upon c), where it drives pinion p by means of pin p′. i rotates upon and is supported by the stud j, which is threaded into c2 (the latter being also a continuation of c); hence when hand-wheel k is operated in one direction, c2 acting as a nut causes j to clamp i to c, and the tool bar to therefore feed. Conversely, when k is operated in the opposite direction, i is released from c, and may, therefore, rotate while c remains at rest. For feeding the tool bar g by hand, or for moving it rapidly, the hand-wheel m is provided, being fast to the sleeve at its section c2, and, therefore, capable of rotating pinion p. d affords journal bearing to c at its section c′. The chain from the weights which counterbalance the bars g pass over sheaves which are fixed to the piece b in which the bar slides, so that they occupy the same position with relation to the axis of the bar at whatever angle the latter may be set, and thus the counterbalancing weight is delivered upon the bar in a line parallel to its axis. As an example of the efficiency of the machine, it may be mentioned that at the Buckeye Engine Co.’s Works, at Salem, Ohio, a pulley 12 feet in diameter, weighing 8860 pounds, and having a 27-inch face, was bored and turned on one of these machines in 17 hours, taking three cuts across the face, turning the edge of the rim facing off the hub and recessing the bore in the middle of its length for a distance of several inches, the bore being in all 18 inches deep. The machine is made in different sizes, and with some slight variations in each, but the main features of the design, as clearly shown in our engravings, are common to all sizes.
| VOL. I. | ROLL‑TURNING LATHE. | PLATE XI. |
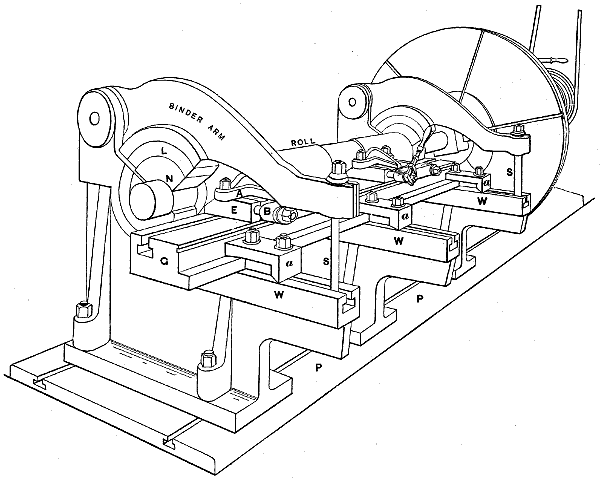 |
||
| Fig. 730. | ||
 |
||
| Fig. 731. | ||
Fig. 730 represents a lathe for turning chilled rolls such as are used for paper calendering machines, and is constructed by the J. Morton Poole Company of Wilmington, Delaware.
In the figure a roll is shown in position in the lathe. The journals of the rolls are first turned in a separate lathe, and form the guide by which the body of the roll is turned in the lathe shown in the figure. The lathe consists of a bed plate p, at one end of which is mounted the driving head. Upon this bed plate are also mounted three standards or vertical frames, to the two end ones of which are pivoted the binder arms shown. These frames hold the bushes at l and n, in which the journals of the roll revolve. They also carry the bar g, secured to the arm w of the frame by clamps a, a, a. Upon the bar g are two slide rests, consisting of a tool rest e, a tool clamp a, and a feed yoke b, which is screwed up by a wrench applied to the nuts as shown on the right-hand tool rest in the figure. The binder arm is adjusted to hold the bushings l n (which are varied to suit the size of the roll journal) a fair working fit upon the roll journals, the bolts s holding the binder arms firmly against the enormous pressure due to the cut. It is obvious that the frames w may be adjusted anywhere along the bed plate p to suit the length of roll to be turned, and that the slide rests may be moved to any required position along the bar g. Further details of the construction are as follows. Fig. 731 is an end, and Fig. 732 is a top view of the tool rest; a is the tool clamp securing the tool to the rest e, r representing a section of the roll, b is the feed yoke, which to put on a cut is screwed inwards by operating the nuts d. The pins c are fast in b, and their ends abut against the tool, which is fed in under the full pressure of the clamp a. The tool is shown at f in figure, and also at f in Fig. 733, which is a view of the rest with the clamp a removed. The form of tool employed is shown in Fig. 734, its length varying from five to six inches. As the tool feeds in and does not traverse along the roll it is obvious that it cuts along its entire length, the cuttings coming off like a bundle of fine ragged needles.
When the tool has been fed in cutting the roll to the required diameter the rest is moved along the bar g, a distance equal to the length of the tool, and the operation is repeated until the full length of the roll has been turned. It is obvious that to feed the tool in parallel, both nuts d of the tool rest are operated. The tool is held as close in to the rest as the depth of cut to be taken will permit, and is used at a cutting speed varying from about 21⁄3 feet to 5 feet per minute according to the hardness of the roll. The tool has four cutting edges, and each cutting edge will carry in at least one cut, and may sometimes be used for a second one. The tools are used dry and the amount of clearance is just sufficient to clear the roll and no more.
The rolls are driven by a socket bolted to the lathe face plate, and containing a square hole, in which fits loosely the square end of the roll. The object of this arrangement is to permit the roll[I-216] to be guided entirely by the bearings in which it rotates, uninfluenced by the guiding effect that accompanies the use of centres in the ordinary method of turning.
Fig. 735 represents a lathe designed and constructed by the American Tool and Machine Company, of Boston, Mass. This class of lathe is strictly of American origin, and has become the most important tool in the brass finishing shop.
In its design the following advantages are obtained:—
1st. The front of the lathe is entirely unobstructed by the ordinary lathe carriage and slide rest, hence the work may be more easily chucked and examined, while in the case of work requiring to be ground together, while one part is in the chuck, the trouble of moving the slide rest out of the way is entirely obviated.
2nd. In place of the single cutting tool carried in a slide rest and of the tailstock of the ordinary lathe, there is provided, what is known as a turret, or turret rest, carrying 6 tools, each of which can be successively brought into action upon the work by the simple motion of a lever or handle.
3rd. The rest for traversing single pointed screw cutting tools or chasers (for internal threads) is at the back of the lathe where it is out of the way.
4th. In place of the usual change wheels required to operate the lead screw, the chasing bar is operated by a single threaded collar or hob, which is more easy of application and removal.
5th. The slide rest carrying the screw cutting tool is capable of such adjustment, that the tool will thread successive pieces of duplicate work to an exactly equal diameter, so as to obviate the[I-217] necessity of either measuring or trying the work after the tool has been accurately set for the first piece.
6th. When the threading tool has traversed to the end of its cut it may be lifted from the same and pulled back by hand, ready to take a second cut, thus avoiding the loss of time involved in traversing it back by a lead screw or its equivalent.
7th. Each of the tools in the turret may be set so as to operate to an equal depth and diameter upon successive pieces of work.
In the particular lathe shown in our example, there is another and special advantage as follows:—
In lathes operating upon small work and upon the softer metals, as composition, brass, &c., the time occupied in traversing the cutting tool is comparatively short, and from the comparative softness of the metal the speed of lathe rotation is quick, and the tool motions must be correspondingly quick. In addition to this the work being so much more quickly performed, changes and readjustments of the parts are necessarily more frequent, hence the rests traverse the bed more rapidly as well as more frequently and the wear of the Vs on the lathe, and the corresponding V-grooves in the tool rest, slide rest, or turret, is increased; as a result, tools carried in the tailstock or the turret, as the case may be, which tools should for a great many purposes stand axially true with the live spindle, stand below it, and hence instead of boring a hole equal to their own diameter, bore one of larger diameter. In the case of tools, however, which, as in the case of drills, endeavour to find their own centre in the work, this action takes place to some extent as the tool enters the work, and as a result the hole is made a taper, whose largest diameter is at the mouth. This induces another evil in that it dulls the advance edge of the drill flute, and wears away the clearance which is of such vital importance to the free action of the drill.
The manner in which these advantages are obtained is as follows:—
In place of the ordinary tailstock a back head is provided which has a cross slide operating after the manner of the ordinary slide rest; this carries an upper slide, thus forming a compound slide rest. On the top of this rest is carried a rotating head or turret head, serving the same purpose as the head shown in Fig. 694, and carrying a series of tool holders. These tool holders may be operated by the feed screw of the compound rest, or may be operated by the hand lever shown standing horizontally. In addition to the ordinary back gear for reducing the live spindle speed there is provided on the live spindle a second small pinion, driving at the back of the lathe head a shaft, on the left-hand end of which is a seat for collars or hobs, operating a bar running along the back of the lathe, and forming what is termed the screw apparatus, whose operation is as follows:—
This bar carries the slide rest shown, a handle or lever for partly rotating the slide rest, spanning the bed of the lathe. When this handle is lifted, the bar at the back of the lathe rotates in its journals. On this bar is an arm which carries a segment of a circle, containing a thread corresponding in pitch to the thread on the collar or hob. When the lever is raised the segment moves away from the hob, and the bar may be moved laterally by hand, but when the lever is lowered the arm falls, and the segment comes into contact with the hob thread, which therefore feeds the bar; all that is necessary for thread cutting is, therefore, to place on the lathe a hob having the required pitch for the thread to be cut, and place in the slide rest a chaser or single-pointed threading tool, and set the tool to the work by means of the slide rest, depressing the lever to cause the tool to feed forward, and elevating it to move the bar back by a lateral hand pressure. To put on successive cuts the slide rest is operated, the lever always being lowered till it meets the surface of the lathe bed. To cause the slide rest to cut successive threads to the same diameter, a suitable stop motion is provided to the slide rest, and when the rest has been operated as far as the stop will permit it, the thread is cut to the required depth and diameter.
A stop motion is also provided to the lateral motion of the turret, so that the tools being set to enter the work to their respectively required distances, all pieces will be turned to equal depths or lengths.
To enable the centres of the tool holders to maintain true alignment with the live spindle, notwithstanding the wear of the lathe bed and back head, the bed is made in two parts. One of them carries the headstock, and on the vertical face of this part is a slide in which the end of the second part fits, so that by means of adjusting screws the second part may be elevated to effect the true alignment when necessary.
Fig. 736 represents a square arbor brass-finisher’s lathe. The object of the square arbor or tail spindle is to enable it to carry cutting tools in place of the dead centre. A cross slide is provided to the tailstock, and upon this slide the head of the tailstock is pivoted so as to bore taper holes; the tailstock thus virtually becomes a compound slide rest. This lathe is provided at the back of the bed with a bar carrying a slide rest, operated in the same way and for the same purpose as that described with[I-218] reference to Fig. 735. Both these lathes are furnished with separate compound slide rests, and with a hand rest.
When work of considerable weight requires to be bored with holes of moderate diameter, it is more convenient that it remain fixed upon a table, and that the boring tools rotate, and a machine constructed by the Ames Manufacturing Company for this purpose is shown in Fig. 737; a standard occupies the position of the ordinary tailstock. It carries an horizontal table, or angle plate, on which the work may be chucked. This table is capable of a vertical and a cross shear movement, so that when the work is chucked upon it, holes whose axes are parallel, but situated in different locations upon the same surface, may be drilled or bored by so moving the table as to bring each successive hole into line with the live spindle. The feed motions are as follows:—
At the back of the smallest step on the cone and fast on the cone spindle is a gear-wheel gearing into a pinion, which drives the lower shaft shown behind the back bearing, and on this shaft are two pinions. One drives the upper feed cone, shown at the back of the back bearing, which cone connects by belt to the feed cone below, which operates a traverse feed for the work table; the other drives the tool holding spindle which passes through the cone spindle. This tool holding or driving spindle is threaded at its back end, passing through a nut which causes it to self-feed from left to right, or in other words, towards the work table. To throw this feed out of operation the pinion on the end of the lower or feed driving spindle is moved laterally out of gear with the pinion driving it.
To provide a quick hand-feed traverse the shaft or spindle, shown with a hand-wheel, is provided, being connected to the tool driving spindle by gearing.
When employed to operate a boring bar, a bearing to support[I-219] the bar at the tail or footstock end may be bolted to the table, such bearing carrying a bushing which may be changed to suit the diameter of the boring bar.
Fig. 738 represents a cylinder boring lathe. d is the driving cone, on whose shaft is the worm w, driving the worm-wheel g, which is fast upon the boring bar g, having journal bearing in the standards h and h′, the latter of which must be moved out of the way to get the work over the bar. h is a head provided with slots to carry the cutting tools; h is a close sliding fit to the bar g, and is traversed along g as follows:—g is hollow and there passes through it a feed screw, which operates a nut on h, which nut passes through a longitudinal opening in the bar g. At the end of this feed screw is the gear-wheel d. Now fast upon the end of g, and therefore rotating with it, is the gear a, driving gear b, which is fast on the same sleeve as c, which it therefore drives; c drives d. The diameter of a is less than that of b, while that of c is less than that of d; hence the rotation of d is slower than that of a, and the difference in the relative velocities of d and a causes the feed screw to rotate upon its axis and feed the head h along the bar. If c be placed out of gear with d, the feed screw (and hence the head h) may be operated by the handle e.
There are several objections to this form of machine, as will be seen when comparison is made with Fig. 739, which represents a special cylinder boring lathe, designed and constructed by William Sellers and Co., of Philadelphia, Pennsylvania. The boring bar is here supported in two heads, and is hollow, the feed screw for traversing the head carrying the boring cutters being within the bar. The feed is effected through the medium of the train of gearing shown at the end. The two face plates shown which drive the boring bar, also carry two slide rests which are used to face off the ends of cylinders while the boring bar is in operation, these slide rests being operated by a star feed, acting on the principle described with reference to Fig. 589. The boring bar in this case being driven from each side of the work the torsion due to the strain of the cut is divided between the two halves of the bar; or in other words, when a boring bar is driven from one end the strain due to the cut falls upon that part of the bar that lies between the boring-head and the point at which the bar is driven; but when the bar is driven from each end then the strain is divided between the two ends, causing a bar of a given strength to operate more steadily and take a heavier cut for roughing, and a smoother one for finishing. A greater advantage, however, is that it gives to the bar a rigidity, enabling it to carry a cutter having a long cutting edge without chattering, thus allowing a very coarse finishing feed, which will finish a bore with less wear to the tool edge (and therefore more parallel) because for a given amount of work the cutting-edge is under duty for a less period of time, the cutting speed remaining the same, or even slower than would be desirable for a fine feed. The driving-cone, which is shown to be below the boring-bar, is so situated to accomplish two objects, which are to operate the two face plates by a shaft having two pinions (within the bed) gearing with the circumferential teeth on the face plates, and to operate at the same time the table (shown on the bed between the face-plates) to which the cylinder is bolted.
In a boring machine it is of the utmost consequence that the bar shall be as free from vibration as possible, while lost motion, or looseness from wear, is especially to be avoided. By carrying the bar in two bearings, as it were, the wear is greatly reduced.
The duty of facing the cylinder ends is sometimes done by facing cutters carried in the head. Such cutters, however, must have a cutting edge equal to the breadth of the surface faced by them, because the cutter cannot be fed radially to its cut. Furthermore, the cut is carried by the bar at a considerable leverage, and as a result it is very difficult indeed to make the radial faces true or even nearly true, the cutter dipping into the softer parts of the iron or into spongy places if there are any. In any event springing away from its cut, resisting it until forced to cut, and then cutting deeper than should be, so that on a finished surface it is often apparent to the eye where the cutter began and left off. When, however, the radial faces are operated upon by a slide rest, as in the Sellers machine, the tool is more firmly held, and may be fed radially to the cut, producing true faces, and saving a great deal of time in making the cylinder cover joints, as well as in the boring and facing operations.
Fig. 740 represents a double boring and facing lathe by G. A. Gray, Junior, of Cincinnati, Ohio. Two driving heads are provided, each having a main spindle, but holding the boring bar after the manner of an ordinary lathe, and within each spindle is another capable of longitudinal traverse. The main spindle is provided with a head corresponding to a slide rest and carrying a cutting tool for facing purposes, the feed being obtained by means of a star-feed. The work is bolted to the carriage and fed to the cut for boring purposes. It is provided with an automatic feed and also with hand feed. When facing is to be done the carriage may be firmly locked to the lathe shears.
In boring and facing a steam pump centre, or other similar piece, the casting is fastened to the carriage in a special fixture. The carriage is then moved so that the work will come nearly in[I-220] contact with tool in the fast head, the loose head is moved up to the work, and both the carriage and loose head are clamped.
Both ends of the casting may be operated upon at the same time or separately, as occasion requires, the object being, however, to work upon as many places at one time as the nature of the work will permit; this being the main point in the economical performance of work. It is evident also that if the machine is true, and the piece is finished at one setting, the work will be true.
In the detail engravings, Fig. 741 represents boring, tapping, and facing steam pump centres, in which operations the carriage is locked.
Fig. 742 illustrates the manner of boring and facing cylinders and similar pieces, the loose head stock being used as a tailstock[I-221] and the fast headstock as the driver. The facing is done either before or after the boring, all the work obviously being done at one chucking.
Fig. 743 shows a longitudinal cross section of the headstocks showing the main and the internal spindles.
Fig. 744 represents a lathe constructed by the Defiance Machine Works for turning the hubs for carriage and wagon wheels.
The blank from which the hub is turned is driven by a mandrel having a square stem fitting in the live or driving-spindle, this mandrel being supported at the other end by the ordinary dead centre operated by the upper hand-wheel. The bed is provided (between the driving-spindle and tailstock) with the usual raised Vs on which rests a carriage carrying a cross slide. This cross slide carries, at the back of the lathe, a head or stock containing the roughing-knives, and at the front a table carrying the finishing-knives, hence, by operating the large hand-wheel (which gives transverse motion to the cross slide) in one direction the roughing-knives are brought into operation, while by operating it in the opposite direction the finishing-knives are brought into operation (the roughing-knives receding). By suitable stops, the motion of the roughing and finishing-knives respectively are arrested when those knives have cut the blanks to the desired diameter, the finishing-knives shaping the work correctly by reason of their form of outline. Upon the same cross slide are the equalizing-knives, one on each side of the front table. These knives operate simultaneously with the finishing-knives, cutting the hubs to uniform length. Thus the hubs are cut to exact uniformity of diameter, shape and length, by simply operating the large hand-wheel first in one direction and then in the other.
If it be required to cup the hubs, as in the case of standard wagon hubs, suitable cutters carried in a bar (having sliding motion in a guide way on the tailstock) are caused to do such cupping, the cupper-bar being operated by the left-hand lever.
The live, or driving, spindle is started and stopped by a tight and loose pulley, the belt being passed from one to the other by means of the lever on the right, which simultaneously operates a brake attached to the belt stopper, operating upon the tight pulley. By this means the lathe can be started and stopped more quickly than would be the case with a cone pulley, whose extra weight and inertia would take time to overcome.
The devices employed to drive work that is suspended between the lathe centres are shown in the following illustrations.
They are termed lathe dogs, drivers, or carriers. It is to be observed, however, that since the term dog is also applied to a device for holding work to the lathe face plate, as well as to the jaws of chucks, either the term driver or the English term carrier is preferable to the term dog.
Fig. 745 represents a lathe dog, driver, or carrier d, in position to drive a piece of work in the lathe. It is obvious that the work is secured within the carrier or driver by means of the set-screw shown. The tail of the driver here shown is bent around to pass within the slot provided in the face plate, a plan which is convenient, but is objectionable, because in this manner of driving the work two improper strains are induced, both of which act to spring or bend the work. The first of these strains is caused by the carrier being driven at a leverage to the work, as shown at a in the figure, which causes the live centre to act as a fulcrum, from which the work may be bent by the strain caused by the cut.
The second strain is caused by driving the carrier from one side or end only, and is shown in Fig. 746, where the dog receives the face-plate pressure at the point a, and the cut or resistance being on the opposite side of the work, the leverage of the driving point causes a tendency to lift the work in the direction of the arrow c. The direction of this latter strain, however, varies as the work revolves. For example, in Fig. 747 the dog is shown in position at another point in its revolution, and the point a, where the power is applied to the carrier, is here on the same side as the tool cut; hence there is less tendency to spring the work. It becomes obvious then, that work driven in this manner will be liable to be oval, or out of round, as it is commonly termed.
The methods of overcoming these two sources of error are as follows: Instead of the end of the dog being bent around to pass within the slot in the face plate, as in Fig. 745, the leverage a in that figure may be avoided by the means shown in Fig. 748, in which a driver having straight ends is used, and a pin p is fastened to the face plate to drive the carrier. But this does not remove the tendency (shown in Fig. 746) acting to spring the work from the pressure of the cut; hence, to obviate this latter tendency, two driving-pins p p, in Fig. 749, are sometimes used with the idea of driving the work from both sides, and thus equalizing the strain. But this is effective only when each pin is in working contact with the dog. This condition is difficult to secure for several reasons. First, suppose the two ends of the carrier to be of equal thickness, and the driving-pins to be of equal diameter, while the work receiving hole of the carrier is quite central to these two ends, then the work also must be true, in order to cause the pins to act equally on the ends of the carrier. Hence, this method is only applicable, even if all the above conditions be fulfilled, to the finishing cuts, and these would have to be taken on work that had been sprung in the roughing cuts, so that it would be difficult to obtain accurate results. A nearer approach to correctness is therefore sought by various means. Thus, Fig. 750 represents a face plate provided with an annular T-groove, having a cut at h to admit two nuts into which the pins p are screwed. These pins may be tightened lightly, so that they will slip under the pressure of the roughing cut, and thus come to an equal bearing upon the carrier or work, as in case of the arms of a pulley where a carrier is not used. When the pins have adjusted themselves to have as near as may be an equal driving bearing, they may be tightened up. By this means the pins are compelled to act at an equal leverage upon the carrier or work, but there is no assurance of an equal degree of pressure of the pins p.
Another method is shown in Fig. 751, in which a clamp in two parts is employed, the driving-pins p fitting into two holes equidistant from the lathe centre, while loosening one bolt, j or k, and tightening the other is resorted to, to equalize the driving contact on the two arms, but in this case again there is no certainty that the two pins will drive equally, and there is danger of drawing the work somewhat out of true. Another form is shown in Fig. 752, the idea being to equalize the pressure of the driving pins, by means of the four screws, but here again, there is no means of knowing whether the driving pressure is equalized.
[I-223]The best form of driver is shown in Fig. 753, which represents a Clement’s driver. The driving-plate f has four slots; two of them, a and b, pass entirely through this plate to admit bolts c d, which have a shoulder, so that they may be secured firmly to the lathe face plate, but which are an easy fit in the plate f, so as to permit it to move upon the lathe face plate. The other two are T-shaped slots to receive nuts, into which the pins p p are to be screwed. The bolts c d drive f, and the pins p drive the work, the freedom of the plate e to move upon the lathe face plate permitting this strain-equalizing action of the driving-plate and driving-pins.
Sometimes, as in cutting screws, the work requires to be revolved backwards, without having any lost motion between the arm and carrier, or in other words, the carrier must revolve backwards as soon as the face plate does. To accomplish this, a common plan is to tie the driver or carrier to the driving-pin, but a better plan is to employ a bent tailed dog and secure its end in the face-plate slot. A convenient form of face plate for this purpose is shown in Fig. 754, a, b, c, and d, being slots, and e a set-screw for binding the dog as shown in Fig. 755.
For special lathes in which the work is of uniform diameter, the driving pins p, Fig. 753, may be replaced by solid jaws, thus in Fig. 756 is a Clement driver, such as is used on axle lathes, c c being driving lugs in place of the pins p in figure.
To prevent the ends of the set-screw or screws of the driver from damaging the surface of finished work, the form of driver shown in Fig. 757 has been patented in England. It consists of a disc arched to receive a lever c, which is pivoted in the disc at d. A set-screw provided in the disc binds one end of the lever to the work, and as the pressure to drive the work is applied at the other end of the same lever, it serves to assist (to some extent) the set-screw in binding the lever to the work. The work is held between a V in the disc and one on the lever, the object being to provide a large area of contact, and thus prevent the damage to finished work which screw ends are apt to cause.
The same end may be obtained for ordinary drivers by using a copper or brass ring, such as shown in Fig. 758, which may be opened or closed, within certain limits, to suit the diameter of the work, being placed on the end of the work, and within the dog, to receive the pressure of the set-screws.
One such ring will serve for several diameters of work, springing open when forced, under hand pressure, upon the work, or closing upon the work as the pressure of the dog set-screw is received. It is obvious that the split of the ring should be placed diametrally opposite to the dog set-screw.
[I-224]In very small lathes the driver is sometimes driven by the device shown in Fig. 759, which consists of a small chuck, screwed on the live spindle, and containing the live centre and a driving arm b, which passes through the chuck, and is set to any required distance out, by the set-screw c. The objection to this is, first, that either the live centre must be very short, or the arm b must be very long; and, second, if the chuck wears out of true, it carries the live centre also out of true; hence this class of driver is but little used, even in foot lathes.
In small drivers of this kind it is sometimes the practice to cut away rather more than one quarter of the thread on each side of the live spindle as shown in Fig. 760 at a, and to then cut away one quarter of the thread on each side of the bore of the driver as at b in the figure. This enables the driver to be passed upon the spindle and screwed home with one quarter of a turn, thus saving time in putting on and taking off the driver.
Fig. 761 illustrates a work driver very convenient for turning bolts. It consists of a piece of iron or plate p bolted to the lathe face plate f, and having jaws so as to fit to the sides of the bolt b and drive it. This not only saves the time that would otherwise be required to put on a driver or carrier but leaves the underneath face of the bolt clear to be faced up by the turning tool, an example of its use being shown in connection with the knife tool or facing tool.
Fig. 762 represents a driver of this kind having a sliding jaw so that it may be set for different sizes of bolt heads. When the driving end of the work is threaded an ordinary dog or driver cannot be used because its screw would damage the thread on the work. A common method of overcoming this difficulty is to place over the ring a split ring of copper, or to place on it two nuts, putting a common dog on the end nut. It is better, however, to use a driver, threaded part of the way through, as in figure 762 (from The American Machinist) and to screw it upon the work.
Fig. 763 represents a very useful form of work driver designed by Mr. William A. Lorenz. It consists of two jaws a, a held together by two screws, and threaded to receive two driving screws d, e in the figure, which enable it to be used to hold work to the live centre as is necessary when using the steady rest, as is shown in the figure, in which b represents the work and c the jaws of the steady rest. It is obvious that the dog may be thus employed to chuck work independently of the steady rest, because the live centre may be removed, and the face of the work held against the face of the chuck, the short screws h being used instead of the long ones d, e.
If the carrier is used to simply drive the work without clamping it to the live centre or face plate, one or both of the screw pins j, k may be used in place of bolts d, e, the carrier being balanced when both are used.[I-225]
Fig. 764 represents a driver, carrier, or dog threaded in its bore to drive threaded work, which the screw of the ordinary dog would obviously damage.
Fig. 765 represents an excellent driver for cored work such as the piece w. Its hub a is screwed on the live spindle in place of the face plate, and carries the rods b, b′, both of which are adjustable in the distance they stand out from a, so that b may be set to suit the work, and b′ set out sufficiently to balance b and d. The driving arm d is adjustable along b, and by being bent to the form shown is more out of the way, and obviates the necessity of using a dog on many kinds of work. The other end of the work is shown supported by a cone centre c, whose construction is shown in Figs. 766 and 767. Its object is to avoid the wear that occurs at the mouth of the hole in cored work, when it is run on the dead centre, and to avoid the necessity of plugging the hole to provide a temporary centre. In the figures, a represents a stem (fitting into the tailstock spindle s, in place of the ordinary dead centre), having a collar b and carrying the cone c. The work is supported upon c, which revolves upon the stem of a. At e is a raw-hide washer, intended to prevent the abrasion which would occur on the faces of b and c. The pin f prevents c from coming off d, one half of its cross section being in c, and the other half in a semicircular groove running around d. An oil groove is provided through the collar b, and passes along the stem d. This is an exceedingly handy device for cored work, and may also be used to sustain work against the lathe face plate, while chucking the work true by its bore.
The work drivers employed by wood turners, for work held between the lathe centres, are as follows:—
Fig. 768 represents two views of a fork centre to be placed in the cone spindle of the lathe, and serve as a live centre, while also driving the work; c is a sharp conical point, which should run true, because it serves to centre the work; d, e are two wings which enter the wood to drive it. This device answers well for work that can be finished without taking it in and out of the lathe, it being difficult to place the work in the lathe so as to run true after removal therefrom; in case, however, that this should become necessary, the work should be replaced so that each wing falls into its original impression. For heavy work this device is unsuitable, hence the two plates shown in Fig. 769 are employed, being termed centre plates. They are composed of iron and are held to the work by screws passing through the respective holes shown at the corners of the plates. The plate having the round centre hole is for the dead centre end of the work, while that[I-226] having the rectangular slot is for the live centre end of the work. The rectangular slot is made a close fit to the wings of the fork centre shown in figure. Figs. 770 and 771 represent a spur centre designed to hold pieces of soft wood, that may be liable to split from the pressure of the centres. The spurs are made parallel on their outer surfaces, while the inner ones are at an angle, so as to close the wood around the central point, and not spread the wood outwards. The plate for the dead centre is formed on the same principle as is shown in figure 769.
Another form of chuck centre or driving centre for wood work is shown in Fig. 772, being especially useful when the work cannot be supported by the lathe dead centre. The body a screws on to the thread on the live spindle of the lathe, while the work screws on the pointed screw b, which will hold disc-shaped pieces of moderate diameter, as about 4 or 5 inches, leaving its face to be operated on as may be desired. To prevent b from splitting the work, or when hard wood is to be turned, a small hole may be bored up the work to permit b to enter sufficiently easily.
When a piece of work to be turned between the lathe centres is of such a form that there is no place to receive centres, provision must be made to supply the deficiency.
In Fig. 773, for example, a temporary centre b is fitted into the socket to receive the centre.
In small work that has been drilled or bored, a short mandrel is used instead of the piece b.
If a half-round piece is to be turned it should be forged with a small projecting piece to receive the lathe centre, as in Fig. 774.
When the end of the work is flat and not in line with the axial line of the main body of the work, a piece of metal to contain the centre may be held to the work by a driving clamp, as in Fig. 775, in which a represents the end of the work and b a temporary piece containing the centre c. In this case it is best to make the centre c after the piece b is clamped to the work.
To provide a temporary centre for a piece having a taper hole, a taper plug is used, as shown in Fig. 776, w representing the work and p the plug, which must be an accurate fit to the taper of the hole, and must not reach to the bottom of the hole.
Mandrels or Arbors.—Work (of about 6 inches and less in diameter) that is bored is driven by the aid of the mandrel or arbor, which is held between the lathe centres, as in Fig. 777, in which w represents a washer and m the mandrel, driven into the washer bore so as to drive it by friction. At a is a flat place to receive the set-screw of the driver or lathe dog, and at b a flat place upon which the diameter of the mandrel is marked. The[I-227] mandrel diameter is made slightly larger at d than at c, so as to accommodate any slight variation in the diameter of holes bored by standard reamers, which gradually reduce in diameter by wear; thus if a reamer be made 11⁄1000 inch diameter, with a limit of wear of 1⁄1000 inch, then the mandrel may be made 1 inch at c and 11⁄1000 inch at d. It is well to taper the end of the mandrel from c to e about 1⁄2000 inch, so that it may enter the work easily before being driven in. Instead, however, of driving mandrels into work, it is better to force them in under a press. If driving be resorted to a lead hammer, or for very light mandrels a raw-hide mallet, may be used.
In the absence of a lead hammer, a driver, such as in Fig. 778, is a good substitute, consisting of a socket containing babbitt or some other soft metal at b (the mandrel being represented by m). If copper be used instead of babbitt a hole may be drilled through it, as denoted by the dotted lines.
The centres of mandrels should either have an extra countersink, as at a in Fig. 779, or else the cut should be recessed as at b, Fig. 780. Mandrels are best made of steel hardened and ground up after hardening.
If the bore of the work is coned, and of too great a cone to permit the mandrel to be driven, and drive the work by friction, the cone mandrel shown in Fig. 781 may be used. m is the mandrel in one piece with the collar c. The work w is held between two cones a, a, which slide a close fit upon the mandrel, and grip the work by screwing up the nut n, there being a thread upon the mandrel, as at s, to receive the nut. It is obvious, however, that work having a parallel bore may also be held by the cone mandrel, as shown in Fig. 782.
To obviate the necessity of having the large number of mandrels that would be necessary so as to have on hand a mandrel of any size that might happen to be required, mandrels with provision for expanding or contracting the diameter of the parts used to hold the work are made.
Thus in Fig. 783 is shown Le Count’s expanding mandrel, in which g h is the body of the mandrel, turned parallel along a certain distance, to fit the bore of the sleeve a, which is a close-sliding fit on this parallel part of e.
From the end h of the mandrel there extends towards the end g four dovetail grooves, which receive four keys b. The heads of these four keys are enclosed and fit into an annular groove provided in the head c of the sleeve a, so that moving the sleeve a along the mandrel causes the four keys to slide simultaneously in their respective grooves.
Now these grooves, while concentric at any one point in their transverse section to the axis of the mandrel, are taper to that axis, so that sliding the sleeve a along the parallel part of the mandrel increases or decreases (according to the direction in which a is moved) the diameter of the keys.
If the sleeve be moved towards the end g, the keys while sliding in their taper grooves recede from the axis of the mandrel, while if moved towards h they approach the axis of the mandrel, or what is the same thing, if the sleeve be held stationary and the body of the mandrel be moved, the keys open or close in diameter in the same manner; hence all that is necessary is to insert the mandrel in the bore of the work, and drive the end g, when the keys will expand radially and grip the work bore.
The keys, it will be observed, are stepped on their diametral or work-gripping surfaces, which is done to increase the capacity of the tool, since each step will expand to the amount equal to the whole movement of the keys in their grooves or slots.
Mandrels or arbors are sometimes made adjustable for diameter by forcing a split cone upon a coned plug, examples being given in the following figures, which are extracted from Mechanics. In Fig. 784, a is a cone having the driving head extending on both sides of the centre so as to balance it. Over its coned body fits the shell b, which is split, as shown in Fig. 785, the splits c, d being at a right angle to splits e, f.
It is obvious that the range of adjustment for such a shell is small, but several diameters of shell may be fitted to one cone, the thickness being increased to augment the diameter. The diameter of the shell should be made to enter the work without driving, the tightening being effected by screwing the nut up to force the shell up the cone.
Figs. 786, 787, 788, and 789 represent an expanding mandrel designed by Mr. Hugh Thomas, of New York City. The body b[I-229] of the mandrel is provided with a taper section g, and either three or four gripping pieces a, a, a, a, let through mortises or slots in a sleeve c, which fits the body of the mandrel at each end.
This sleeve when forced up the mandrel by the nut d, carries the gripping pieces along the cone at g, and causes them to expand outwards and grip the bore of the work, which is shown in the end view in Fig. 788 to be a ring or washer w.
The advantage of this form is that the cone at g can be easily turned or ground to keep it true, and the gripping pieces a may be fastened in their mortises by means of the screws shown at h in the end view, and thus kept true. It is obvious that for long work there may be gripping pieces at each end of the mandrel, as in Fig. 789, and the work will be held true whether its bore be parallel, stepped, or taper, a valuable feature not usually found in expanding mandrels.
When a mandrel is used upon work having its bore threaded the mandrel also must be threaded, and must abut against a radial face, as at a, in Fig. 790, because otherwise the pressure of the cut would hold the work still while the mandrel revolved, thus causing the work to traverse along the mandrel. If the thread of the mandrel be made so tight a fit that it will drive the work by friction it will require considerable force to remove the work from the mandrel, so much so, in fact, that finished pieces would be much damaged in the operation. It is better therefore to have the work such a fit that it can be just screwed home against the radial face of the mandrel under heavy hand pressure (if the work be not too heavy for this, in which case a clamp may be employed). Small work, as nuts, &c., are turned on a mandrel of this kind, which has a stem, and fits into the cone or live spindle in the same manner as the live centre, which will drive work up to about 1 inch in diameter without fear of slipping. Threaded mandrels that are in frequent use soon become a loose fit to the work by reason of the thread wear, with the result that if the face of the work is not true with the thread, it meets the mandrel shoulder, as in Fig. 791, and as the nut cants over, one side as t in the figure, is turned too thick. When the nut is reversed on the mandrel, the turned face will screw up fair against the mandrel shoulder, and the faces of the nut, though true one with the other, are not square with the axis of the thread, and will not therefore bed fair when placed in position upon the work.
To obviate this difficulty we have Boardman’s device, which is shown in Fig. 792. It consists of a threaded mandrel provided with a ring, with two rounded projections a, a and b, b, on each radial face, those on one side being at a right angle to those on the other. This ring adapts itself to the irregular surface of the nut and by equally distributing the pressure on each side of the nut destroys the tendency to cant over, hence the nut may be turned true, notwithstanding any irregularity of its radial faces, and independently of its fitting the arbor or mandrel thread tightly.
Another form of mandrel for the same purpose is shown in Fig. 793, the mandrel being turned spherical, instead of having a square shoulder, and the washer w being cupped to fit, so that the washer will cant over and conform to the nut surface.
The mandrel thread may be caused to fill the nut thread better if it be provided with three or more splits a, b, c, Fig. 794, a hole d being drilled up the centre of the mandrel, the thread may then be turned somewhat large, the splits permitting the thread to close from the nut thread pressure.
When a mandrel is fitted to the sockets for the lathe centre, it should have a thread and nut, as shown in Fig. 795, so as to enable its extraction from the socket without striking it, as has been described with reference to lathe centres.
Mandrels may be employed to turn work, requiring its outside diameter to be eccentric to the bore, by the following means:—In Fig. 796, let the centre c represent the centre of the mandrel, and d a centre provided in each end of the mandrel, distant from c to one half the amount the work is required to be eccentric. The mandrel must be placed with the centres d receiving the lathe centres. In this operation great care must be taken that a radial line drawn on each end of the mandrel, and passing through the centre of the centres d, shall exactly meet and coincide with the line l drawn parallel to the axis of the mandrel. If this be not the case the work will be less eccentric at one end than at the other. As it is a somewhat difficult matter to test this and ascertain if the mandrel has become out of true from use, it is an excellent plan to turn such a mandrel down at each end, as shown in Fig. 797, and draw on it the lines l, l, which correspond to the line l l in Fig. 796. If then a steel point be put in the lathe rest and fed in to the work, so that revolving the latter just causes[I-230] the tool point to touch the lines l at each end, or if the tool point makes long lines as at a, a, the two lines l, l, should intersect the lines a, a at the centre of their respective lengths. The lines l l should be marked as fine as possible, but deep enough to remain permanently, so that the truth of the eccentricity of the mandrel may be tested at any time. An equivalent device is employed in turning the journals of crank shafts, as is shown in Figs. 798 and 799, in which d, d are two pieces fitted on the ends of the crank shaft, being equal in thickness to the crank throw, as shown at a, b in the figure, so that when d, d lie in the same plane as the crank cheeks (as when all will lie level on a plate, as in the figure) the centres c will be in line with the journal in the crank throw. Pieces d are broadened at one end to counterbalance the weight of the crank, which will produce more true work than counterbalancing by means of weights bolted to the face plate of the lathe, as is sometimes done, causing the crank throw to be turned oval instead of round. In the case of a double crank, however, the centre pieces cannot be widened to counterbalance, because what would counterbalance when the centres a in Fig. 799 were used, would throw the crank more out of balance when centres b were used for the throw b. In this case, therefore, the centre pieces are provided with seats for the bars e, e, which may be bolted on to carry the counterbalancing weights, the bars being changed on the centre pieces when the centres are changed. The bars, for example, are shown in their position when the centres a are being used to turn up the journal a, the necessary amount of weight for counterbalancing being bolted on them with a set-screw through the weight.
The centres are steel plugs screwed tightly into the pieces d, and are hardened after being properly centre-drilled and countersunk.
To enable the pieces d to be easily put on and taken off, it is a good plan to make the bore a tight fit to the shaft and then cut it away as at e, as shown in Fig. 801, using set-screws to hold it.
Great care is necessary in putting in the work centres, since they must, if the crank throws are to be at a right angle one to the other, as for steam engines, be true to the dotted lines in figure, these dotted lines passing through the centre of the axle and being at a right angle one to the other. If the thickness of the centre pieces are greater than the crank throws they may be adjusted as in Fig. 800, in which b, b′ represent the centre pieces, and c the crank, while s is a straight-edge; the edge surfaces of b, b being made true planes parallel to each other on each arm, and parallel to the axial line of the bore fitting the end of the crank axle.
The straight-edge is pressed at one end, as at f, firmly to an edge face of b, the other end being aslant so as not to cover the edge of the piece b′ at the opposite end of the crank (as shown at g, Fig. 801). While being so pressed the other end must be swung over the end arm of b′ at the opposite end of the crank, when the edge of the straight-edge should just meet and have slight contact[I-231] with the surface of the edge of b′. This test should be applied to all four edges of b, and in two positions on each, as at g, h—i, j, and for great exactitude may be applied from each end of the crank. It is to be observed, however, that the tests made on the edges standing vertical, as at i, j, will be the most correct, because the straightness of the straight-edge is when applied in those positions not affected by deflection of the straight-edge from its own weight.
In shops where such a job as this is a constantly recurring one attachments are added to a press of some kind, so that the axle and the pieces b may be guided automatically and forced to their proper places, without requiring to be tested afterwards.
When the work is sufficiently long or slender to cause it to sag and bend from its own weight, or bend from the pressure of the cut, it is supported by means of special guides or rests. Fig. 802 represents a steady rest of the ordinary pattern; its construction being as follows:—f is a base fitting to the Vs of the lathe shears at f, and capable of being fastened thereto by the bolt c, nut n, and clamp a. f′ is the top half of the frame, being pivoted at p to f, the bolt p′ forming the pivot for both halves (f and f′), of the frame, which may be secured together by the nut of p′. On the other side of the frame the bolt is pivoted at b to f. This bolt passes through an open slot in f′, so that its nut being loose, it may swing out of the way as denoted by the arrow e, and the top half frame f′ may be swung over in the direction of arrow g, the centre of motion or pivot being on the bolt p′. With f′ out of the way the work may be placed within the frame, the nut of b and also that of p′ may be tightened up so as to lock the two halves of the frame firmly together.
On this frame and forming a part of it are the three ways, g g′ g′′, which contain cavities or slide ways to which are fitted and in which may slide the respective jaws j, and to operate these jaws are the respective square-headed screws s, which are threaded through the tops of the respective ways g, g′, and g′. The screws are operated until the ends of the jaws j have contact with the work w, and hold it axially true with the line of centres of the lathe, or otherwise, as the nature of the work may require. When adjusted the jaws are locked to the frame by means of the bolts d, which are squared to fit in the rectangular openings, shown at h in the respective jaws, so as to prevent the bolts from rotating when their locking nuts d are screwed home.
As an example of the use of this device as a steadying rest, suppose a long shaft to require turning from end to end and to be so slight as to require steadying, then a short piece of the shaft situated somewhat nearer the live centre than the middle of the length of the work is turned upon the work, so that this place shall be round and true to receive the jaws, or plates p, and revolve smoothly in them. The jaws are then adjusted to fit the turned part a close sliding fit, but not a tight fit, as that would cause the jaws to score the work. To prevent this even under a light pressure of contact, oil should be occasionally supplied. This steadies the work at its middle, preventing it from springing or trembling when under the pressure of the cut.
By placing the steady rest to one side of the middle of the work length, at least one half of that length may be turned before reversing the work in the lathe centres. After reversing the work end for end in the lathe centres, the jaws, or plates p, are adjusted to the turned part, and the turning may be completed.
In adjusting the plates p to the work, great care is necessary or they will spring the work out of its normal line of straightness, and cause it to be out of parallel, or to run out of true in the middle of its length, as explained in the remarks referring to the cat head shown in Fig. 809.
The plates p should be gripped to the frame by the nuts with sufficient force to permit them to be moved by the set-screw s under a slight pressure, which will help their proper adjustment. They should also be adjusted to just touch the work, without springing it, the two lower ones being set up to the work first, so that their contact shall serve to relieve the work of its spring or deflection, due to its own weight. This is especially necessary in long slender spindles, in which the deflection may occur to a sensible degree.
If the work does not require turning on its full length, the steady rest may be applied but a short distance from the length of the part to be turned, so as to hold the work more steadily against the pressure of the cuts.
Steady rests are often used to support the end of work without the aid of the dead centre, but it is not altogether suitable for this class of work, because it has no provision to prevent the work from moving endways and becoming loose on the dead centre. A provision of this kind is sometimes made by tying the work driver to the face plate or to the pins driving the work driver or dog, or bolts and plates holding the work driver towards the lathe face plate; but these are all objectionable in that unless the pressure thus exerted be equal, it tends to spring or bend the work.
Another method of preventing this is to drive the work by means of a universal chuck; but this again is objectionable, because the jaws of these chucks do not keep dead true under the wear, and indeed if made to run concentrically true (in cases where the chuck has provision for that purpose) the gripping surfaces of the chuck jaws have more wear at the outer than at the inner ends, hence those surfaces become in time tapering. Again the jaws wear in time so easy a fit in their radial slots that they spring under pressure, and the wear not being equal, the amount of spring is not equal, so that it is impracticable to do dead true work chucked in this way.
The reasons that the chuck jaws do not wear equal in the radial slots may be various, as the more frequent presence of grit in one than in the other, less perfect lubrication, inequalities in the fit, less perfect cleaning, and so on, so that it is not often that the wear is precisely equal. In addition to these considerations there are others rendering the use of the steady rest in some cases objectionable; suppose, for example, a piece of cylindrical work, say 6 feet long, to have in one end a hole of 2 inches diameter, which requires to be very true (as, for example, the cone spindle for a lathe). Now let the face plate end be driven as it may, it will be a difficult matter to set the steady rest so as to hold the other end of the work in perfect line, so that its axial line shall be dead true with the line of lathe centres, because the work will run true though its axial line does not stand true in the lathe.
Here it may be added that it will not materially aid the holding of the work true at the live centre end, by placing it on the live centre and then tightening the universal chuck jaws on it, because the pressure of those jaws will spring it away to some extent from the live centres. This will occur even though the work be placed between the two lathe centres, and held firmly by screwing up the dead centre tight upon the work, before tightening the chuck jaws upon the work, because so soon as the pressure of the dead centre is removed, the work will to some extent relieve its contact with the live one.
If the jaws of the chuck are not hardened, they may be trued[I-232] up to suit a job of this kind as follows:—A ring (of such a size that when gripped in the outer steps of the chuck jaws, the inner steps will be open to an amount about equal to the diameter of the work at the live centre end) may be fastened in the chuck, and the inner ends of the jaws may be turned up with a turning tool, in which case the jaws will be made true while under pressure, and while in the locations upon the chuck in which they will stand when gripping the work, under which conditions they ought to hold the work fairly upon the live centre. But even in this case the weight of the work will aid to spring it, and relieve it from contact with the live centre.
Now let us suppose that the piece of work is taper on its external diameter at each end, even truing of the chuck jaws will be of no avail, nor will the steady rest be of avail, if the taper be largest at the dead centre end. Another form of steady rest designed to overcome these objectionable features is shown in Fig. 803. In this case the stand that is bolted to the lathe bed is bored to receive a ring. This ring is made with its middle section of enlarged diameter, as denoted by the dotted circle c. Into the wide part of the stand fits a ring f, its external diameter fitting into c. The ring carries the jaws, hence the ring is passed over the work, and is then inserted into the stand, while the work is placed between the lathe centres.
The ring revolves with the work and has journal bearing in the stand, the enlarged diameter c preventing end motion. There is nothing here to take up the lost motion that would in time ensue from the wear of the radial faces of the ring, hence it is better to use the cone-plate shown in Fig. 805.
When, however, the work will admit of being sufficiently reduced in diameter, it may be turned down, leaving a face f in Fig. 804, that may bear against the radial faces of the jaws of the steady rest; or a collar may be set upon the work as in Fig. 804 at c. But these are merely makeshifts involving extra labor and not producing the best of results, because the radial face is difficult to keep properly lubricated, and the work is apt to become loose on the live centre.
For these reasons the cone plate shown in Fig. 805 is employed; a is a standard fitting the shears or bed of the lathe and carrying the circular plate c by means of the stud b, which is fitted so as to just clamp the plate c firmly to the frame a when the nut of b is screwed firmly home with a wrench.
The plate c contains a number of conical holes, 1, 2, 3, &c., (as shown in section at d) of various diameters to suit varying diameters of work.
The frame is fitted to the lathe bed so that the centre stud b stands sufficiently out of the line of lathe centres to bring the centres of the conical holes true with the line of lathe centres. The centres of the conical holes are all concentric to b. Around the outer diameter of the cone plate are arranged taper holes g, so situated with reference to the coned holes that when the pin, shown at g in the sectional view, will pass through the plate and into the frame a as shown, one of the coned holes will stand axially true with the line of lathe centres. Hence it is simply necessary to place one end of the work in the live centre, with a work driver attached in the usual manner; to select a coned hole of suitable size; to move the frame a along the lathe bed until it supports the overhanging end of the work in a suitably sized coned hole without allowing the work any end motion, and to then fasten the frame a to the lathe bed, and the work will be ready to operate on. The advantages of this device are that the pin shown at g in the sectional view holds the conical hole true, and thus saves all need of adjustment and liability to error, nor will the work be sprung out of true, furthermore the tool feed may traverse back and forth, without pulling the work off the live centre. With this device a coarse pitch left-hand internal thread may be cut as easily as if it were an external thread and the work was held between the lathe centres, heavy cuts being taken which would scarcely be practicable in the ordinary form of steady rest.
The pins b and g and the coned holes should be of cast steel hardened, so as to avoid wear as much as possible. The plate may be made of cast iron with hardened steel bushes to fit the coned holes.
It is obvious that the radial face of the work at the cone plate end, as well as the circumference, must be trued up, so that the work end may have equal contact around the bore of the coned rings.
Figs. 806 and 807 represent a class of work that it would be very difficult to chuck and operate on without the aid of a cone plate. The former requires to have a left-hand thread cut in its bore a, and the latter a similar thread in end a. A universal chuck cannot be used to drive the work, because in the former case it would damage its thin edge, and in the latter the jaws would force the work out of the chuck; a steady rest cannot be used on the former on account of its being taper, while if used on the latter there would be nothing to prevent the work from moving endwise, unless a collar be improvised on the stem, which on[I-233] account of the reduced diameter of the stem would require to be made in two halves. It can, however, be driven on the live centre by a driver or dog, and supported at the other end by the cone plate without any trouble, and with an assurance of true work.
Fig. 808 represents a form of steady rest designed by Wm. MacFaul, of the Freeland Tool Works, for taper work. The frame affords journal bearing to a ring a, having four projections b, to which are a close but easy sliding fit, the steadying jaws c. These are held to the work or cue blank w by the spiral springs shown in the projections or sockets b, which act against the ends of c. It will be observed that the work being square could not move in any direction without moving sideways the two of the steadying jaws c which stand at a right angle to that direction. But the jaws c fit the bore of the sockets, and cannot, therefore, move sideways; hence it is evident that the work is firmly supported, although the steadying jaws are capable of expanding or contracting to follow the taper of the blank cue or other piece of work. This enables the steady rest to lead the cutting tool instead of following it, so that the work is steadied on both sides of the tool. Obviously, the stand may be fastened to the leading side of the lathe carriage or fitted upon the cross-slide, as may be most convenient.
To steady work that is unturned and of so great a length that it springs too much to permit of its being turned true, the sleeve or cat head shown in Fig. 809 is employed; it may contain three or four screws c, to true it upon the work. The body b is turned true.
The set-screws are so adjusted upon the work, that the outside runs quite true from end to end. The jaws of the steady rest are then set to just touch the circumference of the sleeve, care being taken that their pressure does not spring the axial line of the work out of its normal straight line. If the shaft is to be turned from end to end, the cat head should be placed sufficiently to one side of the centre of the length of the work and nearer the live centre, that the lathe tool may turn up the work for a distance of at least half its length, or slightly more than half. One half of the work being turned, the shaft is reversed end for end in the lathe, when the cat head may be moved to envelop the turned part, and again set true, or the jaws of the steady rest may be set direct upon the work; in this latter case, however, the friction between the jaws and the work will be apt to leave rings or marks upon the latter.
If the cat head is not set to run quite true upon the work, the latter will not run true when the steady rest is removed, and if the jaws of the steady rest spring the axial line of the work out of its normal straightness, the work will be turned either larger or smaller in diameter in the middle of its length, according to the direction in which the work is sprung.
Suppose, for example, that the work is sprung laterally towards the tool point, then the work will be turned smaller in the middle, or if the work were sprung laterally in the opposite direction, it would be turned larger in the middle than at the ends. If the work is sprung vertically so as to approach or recede from the lathe bed, the amount of the error will be less than if it were sprung laterally, and the nature of the error will depend upon the height of the cutting tool with relation to the work. If, for example, the point is above the centre of the work, and the latter is sprung towards the lathe bed, the work will turn of largest diameter in the middle of its length; or with the tool point placed at the centre of the work, the same result will follow, whether the work be sprung up or down; but if the work be sprung up or away from the lathe bed, and the tool point be placed above the centre, the diameter of the work will be turned smaller than that at the ends.
When the work is to be turned from end to end or for a considerable distance, a follower rest such as shown in Fig. 810 should be employed, being similar to the steady rest shown in Fig. 802, except that it is open in front, and being fastened to the slide rest carriage, of course travels with the tool; hence the plates p may be either directly in front of the tool or following it, but if the work w has been turned true and parallel, the plates p may be in front of the tool, or rather may lead it.
The follower rest should always be set to the work when as near as practicable to the dead centre, in which case it will be easier to set it without springing the work.
For work of small diameter for which the plates p would be too large, and therefore in the way, the plate p, Fig. 811, may be used, being bolted to the follower rest. For work of larger diameter the device shown in Fig. 812 is sometimes used. It consists of a[I-234] plate p with a cap c, and bolts for holding the bearings b, b. These bearings are bored slightly larger in diameter than the finished diameter of the work.
The advantage of the use of this device is that bearings of the requisite bore having been selected they may be inserted and adjusted a proper fit to the work before p is fastened to the follower rest, thus avoiding the liability of being either too tight or too loose as may happen when the plates cannot be moved or rotated to test the fit. Another and great advantage is that if after the adjustment of the bearings b, b to the work, the plate p is carefully bolted to the follower rest, the liability of springing the work is eliminated, hence truer work will be produced.
A representative of another class of follower rest is shown in Fig. 813, the hub h is accurately bored to receive collars or rings of various diameters of bore to suit the work. The bore of h may be made to stand axially true with the lathe centres, and thus avoid the trouble of setting, by employing the steady pin s, which, being a close fit in the follower rest and in the lathe carriage will bring the rest to its proper distance from the lathe centres, where it may be secured by the bolt b, which may screw into the metal of the carriage or operate to lift a wedge or guide slip so as to grip the V-slide of the carriage and take up any lost motion between the slide in the rest and that in the lathe carriage.
Fig. 814 shows a follower rest in position on the cross slide of a lathe.
There is a large class of small work that could be held between the lathe centres, but that can be more conveniently held in chucks. Chucks are devices for holding work to the live spindle, and may be divided into classes as follows:
1st. Those in which the work is secured by a simple set-screw.
2nd. Drill chucks, which are applied mainly to drive drills, but which may also be used to drive very small work to be operated upon by cutting tools, the mechanism causing the jaws to move simultaneously to grip or release the work.
3rd. Independent chucks, in which the jaws are operated separately.
4th. Universal chucks, which are larger than drill chucks, and in which the jaws operate simultaneously.
5th. Combination chucks, in which the jaws may be operated either separately or simultaneously as may be required.
Referring to the first, Fig. 815 represents a simple form of set-screw chuck, the stem s fitting into the live centre hole, and the outer end being pierced to receive a drill shank, and the iron from which a piece of work may require to be turned, which is secured in the chuck by the set-screw b. In the case of drill or other cutting tools, however, it is better that they be provided with a flat place a, to receive the set-screw pressure, and enable it to hold them more securely. The objections to this class of chuck are threefold: First, each chuck is suitable for one diameter of work only; secondly the screw head b is in the way; and thirdly, the set-screw pressure is in a direction to set the work out of true, which it will do unless the work is a tight fit to the bore of the chuck. In this case, however, it is troublesome to insert and remove the drill, unless the bore of the socket is relieved on the half circumference nearest to the set-screw, as shown at c in the end view, in which case the efficiency of the chuck is greatly enhanced.
Referring to the second class they are made to contain either two or three jaws.
When two jaws are employed they are made to slide in one slideway, and are operated therein by a right and left-handed screw, causing them to simultaneously advance or recede from the chuck axis. Fig. 816 represents a chuck of this class, the jaws fitting one into the other to maintain each other in line, and prevent their tilting over from the pressure.
In scroll chucks the mechanism for operating the jaws is constructed upon two general principles. The first may be understood from Fig. 817, in which the body of the chuck is provided upon its end face with a scroll c, with which the ends of the jaws a engage. These jaws fit into radial slots in the shell e, which is[I-235] capable of rotation upon b and is held thereto by the cap d; hence rotating e carries around the jaws a, and the thread c causes them to approach or recede from the chuck axis, according to their direction of rotation.
The second general principle upon which small drill chucks are constructed may be understood from Fig. 818, in which c may be taken to represent the end of a lathe spindle or a stem fitting into the live centre hole in the same. At the other end it is to receive the shell d which screws upon it. d is coned at the outer end of its bore, and the jaws e are made to fit the cone, and it is obvious that if d be rotated to screw farther upon c, the coned bore of d will act to force the jaws e nearer to the chuck axis and cause them to close upon and grip the work. To operate d it is knurled or milled at g, or it may have pin spanner holes as at h. In this class of chuck it is essential that the direction of rotation of d to close the jaws must be opposite to that in which the drill rotates, otherwise the resistance of the work against the jaws would cause d to rotate upon c, and the work to become released from the jaw grip. Furthermore, as the larger the work the more severe the duty in driving it, it is usually provided by the construction of such chucks that the jaws shall be opened to their maximum when at their nearest approach to the body (as c) of the chuck, and shall close as they move outward or away from the same. This principle of moving the jaws radially by means of a cone sliding upon a cone is applied in numerous ways, thus sometimes the jaws are provided with wings that slide upon a cone or in slide ways that are at an angle to the chuck axis.
Figs. 819, 820, and 821 represent Gage’s patent chuck, in which the gripping surfaces of the jaws are serrated to increase the grip, and to further secure the same object the jaws move at an angle instead of in a radial line, so that the body of the jaws is more directly in the line of strain, and therefore resists it better. The serrations are left-handed, so that the tendency is to force the drill forward and toward the cut, supposing them to act as a nut and screw upon the drill shank. The jaws are supported by the central cylindrical piece that contains them out to the extreme end, and have in addition a lug which slides in radial grooves. Fig. 819 is a side elevation, with a piece of the shell removed to show the jaw and its slide way, and an end view showing the arrangement of the jaws. Fig. 820 is a sectional side elevation, and Fig. 821, two views of the jaws removed from the chuck; a represents the jaws with the lug e to slide in the radial slots provided in b. The wings a′ of the jaws slide in the ways in b, the ways passing through the opening f in Fig. 821; c is the cone for causing the jaws to open and close radially. The driving piece h has a left-hand thread operating in b. It also has a collar abutting over one side against the end of b, and secured on the other by the cap i, which threads into the shell g. A pin in c secures it to the cap i, so that if rotated both move together. On the other hand, if h be rotated and g is held stationary, the thread on h operates on b as a nut, causing it to slide, carrying the jaws with it, and the jaws are simultaneously opened or closed according to the direction of rotation of h. Fig. 819 shows the jaws screwed partly out, and therefore partially closed, while in Fig. 820 the jaws are shown within the chuck, and therefore opened to their fullest extent.
Figs. 822 and 823 represent a chuck employed by the Hancock Inspirator Co., of Boston, for very true work. This chuck will not get out of true by wear, and holds brass work against a good lathe-cut without indenting it.
Fig. 822 shows the chuck complete. Fig. 823 is a mid-section of chuck complete. Fig. 824 is a side and an end of the work-gripping piece. The chuck is composed of three pieces, a, b and c. Piece a screws upon the lathe spindle and is bored to receive c; piece b screws upon a and receives the outer end of c, which is provided with a double cone d e, and is split nearly its full length at three places, one of which is shown at f, so that when b is screwed upon a the two cones upon a, b compress c, and cause the diameter of its bore to decrease and grip the work. The splits f are made long, so that c shall not close at its outer end only, but on both sides of the cones, and thus grip the work parallel.
There are several advantages in this form of construction; thus[I-236] the parallel bore of a, in which c fits, is not subject to strain or wear, and therefore remains true and holds c true. Furthermore, b has no tendency to wear out of true, because it fits upon a at the part g, as well as at its threaded end, while the cone e of c also acts to keep it true. As b is screwed up with a wrench fitting its hexagon exterior, the work can be held against any amount of cut that the lathe will drive.
It is obvious that the capacity of the chuck, so far as taking in range of different diameters, is quite limited, but the excellence of its execution far more than compensates for this when work is to be turned out true and correct to standard gauge.
To increase the range of capacity of the chuck, the split piece only needs to be changed. Before hardening the split piece the jaws should be sprung well apart, so that they will spring open when released by unscrewing the outside shell to release the work and insert another piece.
In proportion as the diameter of the work is increased it requires to be more firmly held, and the chucks are made with jaws moved by screws operated by wrench power. These chucks are made with two, three, or four jaws, and the bite of the jaw is shaped to suit the nature of the work, the gripping area being reduced for very small work, and serrated parallel to the chuck axis so as to form gripping teeth for firmly gripping rough work, as shown in some of the following examples:—
Figs. 825 and 826 represent the Horton two-jawed chucks with false or slip jaws, which are removable so that jaws of various shapes in the bore may be fitted to the same chuck, thus enabling the jaws to be varied to suit the shape of the work to be held. The jaws are secured in place by the pins shown.
Fig. 827 shows a two-jawed solid jaw chuck, the bite of the jaws being made hollow, so as not to mark the surface of the work, while they will hold it very firmly.
In Fig. 828 is shown what is termed a box-body two-jawed chuck, which is mainly used by brass turners. The object of this form of body is to permit the flanges, &c., of castings escaping the face of the chuck.
Fig. 829 also represents a two-jawed chuck, the body being cylindrical, and having a V-groove at a to receive the work. The screws c, d may act independently of each other, or a continuous screw may be used, having, as in the figure, a left-hand thread at c, and a right-hand one at d, so that the jaws move simultaneously when the screw is operated. The difference between these two methods being as follows:—
When one screw is used the jaws will hold the work so that the centre of rotation will be midway between the points of contact of the jaws of the chuck and the work, hence work cannot be set eccentrically, unless pieces of iron are inserted between it and one of the jaws. When two screws are used the jaws may be operated separately, and one jaw may be set to such distance from the centre of rotation as the necessities of the work may require; but in this case more adjustment is required to set either square or cylindrical work to rotate on its axis than when the jaws operate simultaneously as with a right and left-hand screw. It is obvious that the axial line of the screw or screws must stand parallel with the plane of the face f. It will be observed that the back of each jaw is cut away at b: this serves two purposes, first it permits of a piece of work having a small flange, head or projection being held in the Vs of the jaws; and secondly, it equalizes the wear on the jaws of the chuck, because in jaw chucks generally there is more wear at the outer than at the inner end of the jaws, because work shorter than the length of the jaws, or requiring to be held as far out from the jaws as possible, does not have contact at the back end of the work holding jaw faces, hence the jaws are apt to wear, in course of time, taper. By cutting away the jaws at the back, the tendency to unequal wear is greatly reduced, hence this plan is adopted to a more or less[I-237] degree in the dogs or jaws of all chucks, being in many cases merely a small recess from 1⁄16 to 1⁄8 inch deep only.
When the jaws have a V-groove as in the cut, the face f of the chuck does not form a guide in setting the work, the truth of the V-grooves being solely relied upon for that purpose.
The form of two-jawed chuck shown in Fig. 830 is intended for square or rectangular work, and is mainly used by wood workers. It may be operated by a right and left-hand screw, but is generally preferred with independent screws. The face f of the chuck may be employed to serve as a guide in setting the work as shown in the cut, in which w represents a piece of work held between the jaws a, a, and resting against the face f, which therefore serves as a guide against which to set the work to insure that its axial line shall stand parallel with the face f, or in other words at a right angle to the line of centres of the lathe.
In Fig. 831 is an example of a machinist’s two-jawed chuck. The jaws are operated simultaneously by a right and left-hand screw. The jaws are provided with slides to receive the two separate pieces shown in figure, which may be made to suit the form of special work. The two screws shown on each side of the chuck face are to support a piece of work that is too large to be otherwise held firmly by the chuck. These screws may be operated by screw-driver wrench, to enable the face of the work to rest on them, and therefore be supported parallel or true with the chuck face. The jaws may be turned end for end in their slide ways as shown in Fig. 833, to enable them to grip work of small diameter, the separate pieces shown in Fig. 832, being placed on the jaws for such small pieces as drills, &c.
In the larger sizes, lathe chucks are provided with either three or four jaws, which are caused to operate either independently or simultaneously, and in some cases the construction is such that the same chuck may be used as an independent or as a universal one at will, in which case they are termed combination chucks. Concerning the number of jaws it may be observed that a three-jawed chuck will hold the work with an equal pressure on all three jaws, whether it be cylindrical or not, but in a four-jawed chuck the jaws will not have an equal grip upon the work, unless the[I-238] same be either cylindrically true or square, hence it is obvious that a three-jawed chuck is less liable to wear out of true, and is also preferable for holding unturned cylindrical work, while it is equal to a four-jawed one for true, but unsuitable for square work.
Fig. 834 represents the construction of the Horton chuck. Upon the screws that operate the jaws are placed pinions that gear into a circular rack, so that by operating one jaw with a wrench the rack is revolved and the remaining jaws are operated simultaneously. The chuck being constructed in two halves, the rack may be removed and the jaws operated separately, or independently as it is termed.
Fig. 835 represents one of the jaws with its operating screw and pinion removed from the chuck. The gripping surfaces of the steps in the jaws are serrated to increase their grip upon the work, and the nuts a, a, against which the works rests, are ground true with the face of the chuck. The corner between the faces a and the bite or gripping surfaces of the jaws are recessed so that the work cannot bind in them, but will bed fairly against the faces a, a, which serve to set the work against and hold it true instead of the face of the chuck.
Fig. 836 represents a Horton chuck for work up to four inches diameter.
Fig. 837 represents a similar chuck for all sizes between 4 and 15 inches, the designated sizes of the chuck being 6, 9, and 12 inches, these diameters being the largest the chucks will take in.
Fig. 838 represents a Horton chuck with outside bites for opening out to grip the bores of rings or other hollow work.
The term scroll chuck is applied to universal chucks in which the jaws are operated throughout their full range by means of a scroll thread such as was shown in Fig. 817. The objection to this form is that the threads on the jaws cannot be made to have a full bearing in the scroll thread.
In Fig. 839, for example, let a a and b b represent grooves between the scroll threads, and if the thread on the jaws be made to the curve and width of a a, it would not pass in that of b b, and vice-versâ, and it would take but five revolutions of the thread to pass a nut thread from a to b. To overcome this difficulty the jaw threads are not made correct to either curvature but so formed as to fit at points c, d, e, when in the groove a and at points f, g, h, when in groove b. This obviously reduces their bearing area and therefore their durability. To avoid this defect the jaws of many universal chucks are operated by screws in the same way as independent jaw chucks, but provision is made whereby the operation of any one of the jaw screws will simultaneously operate all[I-239] the others, so that all the jaws are moved by the operation of one screw.
Thus in the following figures is shown the Sweetland chuck.
Fig. 840 represents the chuck partly cut away to show the mechanism, which consists of a pinion on each jaw screw, and a circular rack beneath. The rack is shown in gear with a pinion at o, and out of gear with a pinion at c, which is effected as follows:—
The rack is stepped, being thicker at its outer diameter, and the thin part forms a recess and the shoulder between the thick and thin part forms a bevel or cone. Between this circular rack and the face of the plate at the back of the chuck is placed, beneath each jaw, a cam block bevelled to correspond with the bevelled edge of the recess in the ring. The cam block stem passes through radial slots in the face of the chuck, so that it can be moved to and from the centre of the chuck. When it is moved in, its cam head passes into the recess in the ring rack, which then falls out of gear with the jaw screw pinion; but when it is moved outward the cam head slides (on account of the bevelled edges) under the ring rack and puts it in gear with the jaw screw pinion. Thus, to change the chuck from an independent one to a universal one all that is necessary is to push out the bolt heads on the cam block stems, the said heads being outside the chuck. The washers beneath these heads are dished to give them elasticity and enable them to steady the cams without undue friction.
To enable the setting of the jaws true for using the chuck as a universal one, after it has been used as an independent one, a ring is marked on the face, and to this ring the edges of all the jaws must be set before operating the cams radially to put the rack ring in gear. In Fig. 841 a three-jawed chuck on this principle is shown acting as an independent one to hold an eccentric. On account of the spring of the parts, which occurs when the strain is transmitted from one part to another, it is desirable when using the chuck as a universal one to first operate one screw to grip the work and then pass to the others and operate them so that they may receive the pressure direct from the screw head and not entirely through the medium of the rack, and there will be found enough movement of the screws when thus operated to effect the object of relieving the rack to some extent from strain.
Figs. 842, 843, 844, and 845 represent Cushman’s patent combination chuck, in which each jaw may be operated independently by means of its screw thread, or a circular rack may be made to engage with the respective pinions, as shown in Fig. 844, in which[I-240] case operating any one of the screws operates simultaneously all the jaws. The method of engaging and disengaging is shown in Fig. 845. c represents the circular rack and d a circular ring beneath it. This ring is threaded on its circumference, screwing into the body of the chuck, so that revolving it in one direction moves the circular rack forward and into mesh with the pinions, while revolving it backward causes the rack to recede from the pinions. To operate this ring the lug shown near the top of the chuck in figure is simply pushed in the required direction, while to lock the ring when out of gear with the pinions the spring catch shown on the left of that figure is moved radially. When the rack is in gear, the chuck is a universal one, all the jaws moving simultaneously and equally, whether they be set in such position in their slots as may be necessary to grip an oval or round piece of work; when the rack is out of gear the jaws may be moved by their respective screws so as to run true as for round work, or to hold the work to any degree of eccentricity required.
The jaws may be reversed in their slots and operated simultaneously as a universal chuck, or independently as a simple jaw chuck.
It is obvious that the truth of the jaws for concentricity may be adjusted within the degree of accuracy due to the number of teeth in one pinion divided into the pitch of the jaw operating screw, because each screw may be revolved separately to bring each successive tooth into mesh until the greatest obtainable jaw truth is secured.
Fig. 846 represents a front, and Fig. 847 a sectional view, of the Westcott combination chuck. f is the main body of the chuck screwing on to the lathe spindle. f carries the annular ring d, which has a thread on its face, as shown. d is kept in place by the ring e, which screws in an annular recess provided in the back of the chuck. c is a box fitting in the radial slots of the chuck. The back of the box c meshes into the radial thread on d, hence, when d is revolved, the boxes c move radially in the slots. Now the boxes c afford journal bearing to, and carry the worm or screws b as well as the chuck jaws a, hence revolving d operates the jaws simultaneously and concentrically as in a scroll or universal chuck. By means of the screws b, the jaws may be operated individually (the boxes c and ring d remaining stationary) as in an independent jaw chuck.
Suppose, now, the jaws to have been used independently, and that they require to be set to work simultaneously and concentric to the centre of the chuck, then the screws b may be operated until the jaws at their outer edge are even with the circumference of the chuck (or, if the jaws are nearer the centre of the chuck, they may be set true with a pointer), and the ring d may be operated. In like manner, if a number of pieces of work are eccentric, the screws b may be used to chuck the work to the required eccentricity, and when the next piece is to be chucked the ring d may be operated, and the chuck will be used as a universal one, although the shape of the work be irregular, all that is necessary being to place the same part of the work to the same jaw on each occasion.
The faces of the jaws of jaw chucks when they are true with the face of the chuck (or what is the same thing, run true, and are at a right angle to the axial line of the lathe centres), form guides wherefrom to set the work true, but this will only be the case when they remain true, notwithstanding the pressure of the jaws upon the work. Their truth, however, is often impaired by their wear in the chuck slots which gives them play and permits them to cant over. Thus in Fig. 848 is shown a chuck gripping a piece of work w, and it is obvious that to whatever extent the jaws may spring, or have lost motion in the ways or slots in the chucks, the jaws will move in the direction of the dotted lines a a, the face of the jaw then standing in the direction of dotted lines b b, instead of being parallel to the chuck face. If the spring or wear of the mechanism were equal for each jaw, the work would be held true, notwithstanding that the jaws be out of line, but such is not found to be the case, and as a result the work cannot be set quite true.
When the jaws are applied within the work, as in Fig. 849 (representing the jaws of the chuck within the bore of a ring or piece of work w), the jaws spring in the opposite direction as[I-241] denoted by dotted lines c, c, and when the jaws are locked to the work the latter moves in the direction of d and away from the chuck face. It will be observed that there is no true surface to put the face of the work against in either case.
This is remedied in independent dog chucks by the construction shown in Fig. 850, in which each jaw has a square a, fitting in the grooves of the chuck, and a nut and washer at b secure the jaw to the face of the chuck so that the lost motion due to wear of the parts may be taken up.
The Judson patent chuck is designed to overcome this difficulty, and is constructed as shown in Figs. 851 and 852, the former being a face view and the latter a sectional edge view of the chuck.
The jaws a of the chuck are hollow, and the nut instead of being solid in the jaw is a separate piece, having two wings, the outer of which bears upon a pin in the jaw, while the inner bears upon an inclined surface as plainly shown in the cut, so that the pressure of the screw is distributed equally upon the pin and the inclined surface. The nut b being below the centre of the pin and inclined surface causes the pressure to throw the jaw fair against the face of the chuck, hence the faces of the jaws will serve (equally as well as the surface of the chuck) as a guide to set the work against.
From the short length of gripping surface on the jaws of jaw chucks, they are incapable of holding work of any greater length than, say, about 6 inches, without the aid of the dead centre at the other end of the work; but if the dead centre be used in this way the work will be out of true, unless the jaws of the chuck be quite true, which is not always the case, especially after the chuck has been much in use. Furthermore, it is at times a difficult if not even an impracticable job to set work quite true in this way.
For special work made in quantities the form of the chuck may be varied to conform to the special requirements of the work. The variety of chucks that may thus be formed is obviously as infinite as the variations in form of the work. Thus threaded work may be screwed into threaded chucks, or cylindrical work may be driven into bored blocks forming chucks, or a ring may be chucked and then used as a mandrel to drive the work by friction.
An excellent example of special chuck is shown in Fig. 853, representing a chuck for holding piston rings. It resembles a face plate screwing on the live spindle at b, and having 8 radial dogs or jaws a, let into the face d, and secured thereto, when adjusted by the bolts and nuts e. A mandrel is fast in the centre of the chuck carrying the cone c, upon which rest the cone surfaces on the ends of the dogs a, so that screwing up c, by means of the nut shown, throws the dogs a outwards, causing them to grip the inside of the piston ring as shown in the face view of the chuck.
In Fig. 854 is shown Swazey’s expanding chuck. b is the body of the chuck driven on an arbor a. The hub of b is turned taper to receive a disc c, which is split partly through in three places, and wholly through at z. By means of the nut and washer d e, the disc is forced up the taper hub and caused to expand in diameter and grip the bore of the work, or ring r, the face of b serving to set the face of the ring against to hold it true sideways.
The chucks employed by wood workers for driving work without, the aid of the back or dead centre of the lathe are as follows:— On account of the fast speed at which the wood-workers’ lathe revolves, it would be undesirable to have their chucks of iron, because of the time it would take the lathe to start them to full speed, and also to stop them after shifting the belt from the driving to the loose pulley of the countershaft, and further because[I-242] of the damage the tool edges would receive if they accidentally came into contact with the face of the chuck. For these reasons wood workers’ chucks are usually built up upon small iron face plates.
Fig. 855 represents a cement chuck, consisting of a disc of hard wood a, screwed firmly to the face plate b; at c is a round steel point located at the axis of the chuck.
This chuck is employed to drive very thin work by the adhesion between the surface of the work and that of the chuck. The surface of the chuck is coated with a mixture of 8 parts of resin to one part of beeswax run into sticks. The chuck is waxed or cemented by rotating it at high velocity while holding the sticks against it. The whole surface of the chuck being thus coated, the centre of the work is forced on the steel point c, and the lathe is kept running until the surface of the work nearly touches that of the chuck, when the belt is passed to the loose pulley overhead and the work forced against the chuck surface until it stops or else revolves the work against the hand pressure, the friction between the surfaces having melted the wax or cement, and cemented the work to the chuck. This leaves the face and the circumference of the work free to be operated upon. The work is removed from the chuck by the gradual insertion between the two of a long thin-bladed knife.
For work of large diameter, however, a mere disc of wood will not answer, it being too weak across the grain: and here it may be remarked that the work often supports the chuck, and therefore we should always, in fixing, make the grain of the work cross that of the chuck, because the centrifugal force due to the high velocity is so great that both the chuck and the work have before now been rent asunder by reason of the non-observance of this apparently small matter. When it is considered that the chuck has not sufficient strength across the grain, battens should be screwed on at the back; but a chuck so strengthened will require truing frequently on account of the strains to which its fibres will be subjected from the unequal expansion or contraction of its component parts. Fig. 856 shows the back of a chuck strengthened by the battens a, a, a.
Another and superior method of making a chuck suitable for work of about the same diameter is shown in Fig. 857. Its construction enables it to better resist outward strains in every direction, while the strains to which it must necessarily be subject, from variations of temperature and humidity, are less than in the former. It will also be found that it can be trued with greater facility, especially on the diameter, as the turning tool will not be exposed to the end grain of the wood.
The crossed bars at the back of the chuck are half checked, as shown at a, so that both pieces may extend clear across the chuck and not terminate at the centre. They are fastened together at the centre by glue, and also with screws. Upon these bars as a frame, the four pieces composing the body or face of the chuck are fastened by both glue and screws. These pieces need not extend clear to the centre, but may leave an open square as shown, because the centre of a large chuck rarely requires to be used.
For very large chucks a cross of this kind would not afford sufficient strength, hence, the form shown in Fig. 858 is employed. The arms are bolted to an iron face plate, as shown, their number increasing with the diameter of the chuck. To keep the chuck true, the arms should have a level and fair bed upon the face plate, the segments composing the rim being fairly bedded to the arms and well jointed at the ends. They should be both glued and screwed, care being taken that the points of the screws do not meet the face of the chuck, in which case they would damage the turning tools used to true the chuck.
As wooden chucks are liable to warp and become out of true it is requisite to test them on each occasion before use, and true them if necessary. The work is fastened to these chucks by means of screws whose heads are sunk beneath the work surface a sufficient depth so that there is no danger of their coming into contact with the turning tools. In other cases the work is glued to the chuck, a piece of paper being interposed between the work and the chuck, which, by being damped, will enable the more ready removal of the work from the chuck.
Another form of chuck used by wood workers is shown in Fig. 859. It consists of a disc of wood a; screwed to the face plate[I-243] and carrying the two pieces b, b. The pieces c, c are wedges which slide endways to grip the work. This chuck is especially handy for small work of rectangular form.
From the shape of some work, it cannot be chucked in jaw chucks of any description, and this is especially the case with work of large diameter, hence, large lathes, as, say those that will swing more than three feet, are not usually provided with universal chucks, although sometimes provided with independent jaw-chucks. So likewise in small lathes there are many forms of work that cannot be chucked in jaw chucks, and yet other forms that can be more conveniently held or chucked on face or chuck plates, &c.
If, for example, the surface of the chuck requires to be used in setting the work, the jaws will often be in the way of the tools or instruments employed to set the work. Again, there may be projections on the work which will require the body of the work to be held too far from the face of the chuck to enable its jaws to grip the work.
To meet the requirements of these classes of work chucking devices, which may be classified as follows, are employed:—
1st. Chucking by bolting work to the face plate or chuck plate with bolts and plates.
2nd. Chucking between dogs movable about the face chuck plate, and holding the work from that plate.
3rd. Chucking with the aid of the angle plate, or with the angle plate employed in conjunction with the chuck plate.
The chuck plate is simply a face as large in diameter as the lathe will swing, and is sometimes termed the large face plate. Chuck plates for smaller lathes, as 30 inches swing, or less, are sometimes provided with numerous round or square holes to receive the bolts which hold the work, but usually with slots and holes as in Fig. 860. The larger sizes of chuck plates are similarly formed, but are sometimes provided with short slots that meet the circumference of the plate as in Fig. 861, which represents a chuck plate of the Whitworth pattern. The face of the chuck plate must be maintained true in order that true work may be produced, and it is necessary when putting it upon the lathe to carefully clean its threads and those of the live spindle, as, on account of its large diameter, a very little dirt between it and the live spindle will throw it considerably out of truth at the circumference.
It is better if there be any error in a chuck plate or face plate that it be hollow rather than rounding when tested with a straightedge, because in that case a given amount of error in the plate will produce less error in the work.
In Fig. 862, for example, a represents a chuck plate hollow across the face, and b a link requiring to be bored through its double eye c, the centre line of the lathe being line e e, and the centre line of the hole in the hub d of the link being denoted by f, and as e and f are not parallel one to the other it is obvious that the holes will not be parallel. Suppose, now, that the chuck face was rounding, and the centre line of d would stand at g g, and the holes in c and d would be out of true in the opposite direction. In this case the error would be equal, but suppose we have a ring or disc such as b in Fig. 863 to chuck by bolts and plates c, d and it will be chucked true, notwithstanding that the face of the plate is hollow. But were the face of the plate rounding the disc may be chucked as in Fig. 864, the face f of the work not being held at a right angle to the line of centres e as it is in Fig. 863. The truth of the chucking in Fig. 864 depends upon whether the clamps c were screwed up with equal force upon the work. A hollow chuck plate will lose this advantage in proportion as the work covers more of one side of the chuck plate than it does of the other, but in any event it will chuck more true than a rounding[I-244] one. Suppose we have, for example, a ring chucked eccentrically as in Figs. 865 and 866, the chuck being as much hollow in the one case as it is rounding in the other, and that shown in Fig. 866 will stand out of true to an amount greater than the chuck is in an equal amount of its radius. While that shown in Fig. 865 would be nearer true than the chuck is in an equal length of its radius, both amounts being in proportion to the length of the line a to that of line b.
If the chuck plate is known to be either rounding or hollow, pieces of paper of sufficient thickness to remedy the error may be placed at c and d respectively. It is better, however, to true up the faces of plates so that the surface of the work bolted against it will be true and stand at a right angle to the line of lathe centres.
In truing up a face plate, the bearings of the live spindle should be adjusted so that there is no play on them, and the screw or other device used to prevent end motion to the live spindle should be properly adjusted.
A bar or rod of iron should also be placed between the lathe centres to further steady the live spindle, and the square holes or radial slots should have the edges rounded or bevelled off, as shown in Fig. 867, so that when the tool point strikes the sides a of the holes or slots it will leave its cut gradually and not with a sudden jerk or jump, while, when it again takes its cut on the side b, it will also meet it gradually and will not meet the sand or hard skin on the face of the casting, which would rapidly dull the tool.
In facing or truing up a chuck plate, the feed nut should be put in gear with the feed screw or feed spindle, and the cut should be put on by revolving the feed spindle or feed screw. This will take up any lost motion in the feeding mechanism, after which the carriage may, if there are devices for the purpose, be locked to the lathe bed so as to prevent its moving.
It is better that the thread of the chuck be not too tight a fit upon that on the lathe spindle, the radial face of the chuck hub and of the cone spindle collar being relied upon to set the chuck true, because it is somewhat difficult to produce threads so true as to hold the faces true.
To preserve the threads both upon the chuck bore and the lathe spindle from undue wear, the chuck when taken off the lathe should be stood on edge so that falling dust may not accumulate in the thread. Before putting the chuck upon the lathe spindle the threads of both and the radial faces of the chuck hub and cone spindle collar should be carefully cleaned, because the presence of any dirt or dust on those faces will throw the face of the chuck plate out of true to an amount that may be of importance at and near the chuck’s circumference.
As an example of simple chucking on a face plate, or chuck plate, let it be required to bore, cut a thread in the bore, and recess the piece of work shown in Fig. 868, the radial faces being already true planes not requiring to be turned.
This could be held as shown in Fig. 869, in which c is the chuck plate, w the work, s a strap plate, and b, b are bolts and nuts, a face view of the work already chucked being shown in Fig. 870. The surface of the work being bolted direct against the face of the chuck plate will be held true to that face, and all that is necessary is to set it true concentrically. While performing this setting, the work should not be bolted too firmly, but just firm enough to permit of its being moved on the chuck plate by light blows, the final tightening of the clamps being effected after the work is set true. The bolts should be tightened upon the work equally, otherwise one end of the plate will grip the work firmly, while the other being comparatively slack, the work will be apt to move under the pressure of a heavy cut.
A form of strap not unusually employed for work chucked in this manner is shown in Fig. 871, its advantage being that it is capable of more adjustment about the chuck plate, because the slots afford a greater range for the bolts to come even with the holes in the chuck plate.
If the work be light, it may be held to the face plate while the holding or clamping plates are applied as shown in Fig. 872, in[I-245] which f is the face plate or chuck plate, w the work, p a plate of iron, d a rod, and c the back lathe centre. The latter is forced out by the hand wheel of the tailstock with sufficient force to hold the work by friction while the bolts and plates are applied. It is obvious, however, that if the work has no hole in its centre, the plate p may be dispensed with, and that if a strap plate, such as shown in Fig. 871, be employed, it must first be hung on the tail spindle so that it may be passed over the rod d to the work. Strap plates are suitable for work not exceeding about 6 inches in diameter. For larger work, bolts and plates are used, as shown, for example, in Fig. 873, which represents a piece of work w held to the chuck plate by plates p and bolts b, there being at e e packing pieces or pieces of iron to support those ends of the clamps or clamping plates p. It is necessary that these packing pieces e be of such a height as to cause the plates p to stand parallel to the face of the chuck for the following reasons:—
Suppose that in Fig. 874, w is a piece of work clamped to the chuck plate, and that packing piece e is too high, and packing piece e′ is too low, as shown, both pieces throwing the plates p out of level, then in setting the hole in the work to run true it will be found difficult to move it in the direction of the arrow, because moving it in that direction acts to force it farther under plate p′, and therefore, to tighten its nut. In the case of plate p, the packing piece e will be gripped by the plate more firmly than the work is, which will be held too loosely, receiving so little of the plate pressure as to be liable to move under the pressure of the tool cut. It is better, however, that the packing piece be slightly above, rather than below the level of the work surface. The position of the plates with relation to the work should be such as to drive rather than to pull it, which is accomplished in narrow work by placing them as in Fig. 873.
The position of the bolts should be as close as possible or convenient to the work, because in that case a larger proportion of its pressure falls upon the work than upon the packing piece. For the same reason, the packing piece should be placed at the end of the plates. This explains one reason why it is preferable that the packing piece be slightly above rather than below the level of the work surface, because, the bolt being nearer to the work than to the packing piece, will offset in its increased pressure on the work the tendency of the packing piece to take the most bolt pressure on account of standing the highest.
If a packing piece of the necessary height be not at hand, two or more pieces may be used, one being placed upon the other. Another plan is to bend the end of the clamping plate around, as in Fig. 875, in which case a less number of packing pieces will be required, or, in case the part bent around is of the right length or height, packing pieces may be dispensed with altogether. This is desirable because it is somewhat difficult to hold simultaneously the plate in its proper position and the packing pieces in place while the nut is screwed up, there being too many operations for the operator’s two hands. To facilitate this handling, the nuts upon the bolts should not be a tight fit, because, in that case, the bolt will turn around in the bolt holes or slot of the chuck, requiring a wrench to hold the head of the bolt while the nut is screwed up, which, with holding the plate, would be more than one operator could perform. If the holes in the chuck plate are square, as they should be, the bolt may be made square under the head, as in Fig. 876 at a, which will prevent it from turning in the hole. This, however, necessitates that the head of the bolt be placed at the back of the chuck, the nut end of the bolt being on the work side, which is permissible providing that the bolt is not too long, for in that case the end of the bolt projecting beyond the nut would prevent the slide rest from traversing close up to the work, which would necessitate that the cutting tools stand farther out from the slide rest, which is always undesirable. Bolts that are not square under the head should, therefore, be placed with the head in the work side of the chuck plate, because it is of little consequence if the bolt ends project beyond the nuts at the back of the chuck plate.
The heads of the bolts should be of larger diameter than the[I-246] nuts, because the increased area under the head will tend to prevent the bolt from turning when the nut is screwed up.
It sometimes happens that a projection on the work prevents the surface that should go against the surface of the chuck plate from meeting the latter. In this case, what are known as parallel pieces are employed. These are pieces of metal, such as shown in Fig. 877, the thickness a varying from the width b so as to be suitable for work requiring to stand at different distances from the chuck plate surface, it being always desirable to have the work held as near as possible to the chuck plate so that it may not overhang the live spindle bearings any more than necessary.
An example of chucking with bolts and plates and with parallel pieces is given in Fig. 878, in which the work has projections a, a and b, b, which prevent it going against the face of the chuck; e, e are the parallel pieces which, being of equal thickness, hold the inside face of the work parallel to the chuck face.
Another example of the employment of parallel pieces is shown in Fig. 879, which represents a connecting rod strap with its brasses in place, and chucked to be bored. b is a small block of iron inserted so that the key may bind the brasses in the strap and p p is one parallel piece, the other being hidden beneath the key and gib. The object in this case is to chuck the brasses true with the face a of the strap, the plates s being placed directly above or over the parallel pieces. This is a point requiring the strictest attention, for otherwise the pressure of the clamping plates will bend both the work and the chuck plate.
In Fig. 880, for example, the parallel pieces being placed at p, p, and the clamping plates at p, p, the pressure of the latter will bend the work as denoted by the dotted lines, and the chuck plate in the opposite direction, and in this case the work being weaker than the chuck plate will bend the most.
As a result the face of the work will not be true when released from the pressure of the bolts and nuts holding it. Parallel pieces should therefore always be placed directly beneath the clamping plates, especially in the case of light work, because if they be but an inch away the work will be bent, or spring as it is termed, from the holding plate pressure. In very large work the want of truth thus induced would be practically discernible, even though the work be quite thick, as, say, three inches, if the parallel pieces were as much as, say, 6 inches from the holding plates.
Fig. 881 shows an example of chucking by means of parallel strips in conjunction with parallel pieces. b, b are a pair of brasses clamped by the strips s, s, which are bolted together by the bolts a, a; p, p are the parallel pieces.
The strips being thus held parallel to the surface of the chuck plate, all that is necessary is to set the flanges of the work fair against the surface of the strips and true with the dotted circle, and the brass bore will be bored at a true right angle to the inside face of the flange. If the inside face of the brasses was true, the parallel pieces might be omitted, but this is rarely the case.
An excellent example of bolt and plate chucking is given in a heavy ring of, say, three feet diameter, and 5 or 6 inches cross section, requiring to be turned quite true, and of equal thickness all over. This job may be chucked in three different ways; for example, in Fig. 882, a, b, c, d are four-chucking dogs, so holding the work that its two radial faces and outside diameter may be turned. This being done, four more dogs may be placed to grip the diameter of the work, and the inside ones may then be removed and the bore turned out. In this way the work would not be unchucked until finished. There is danger, however, that the dogs applied outside may spring the work out of true, in which case it would require setting by a pointer in the slide rest.
Another plan would be to hold the work by dogs applied on the outside, and turn the bore and both of the faces. To these fasten four plates on the chuck plate, and turn their ends to the size of the bore and place the work on them, as in Fig. 883, in which a, b, c, d are the four plates, and are clamping plates. This plan is often employed, but it is not a desirable one in heavy work, because the weight of the work is quite apt to move the plates during its setting. A better plan than either of these is to[I-247] first turn off one face and then turn the work around in the lathe and hold it as in Fig. 884. The bore may then be turned, and all that part of the face not covered by the plates. Four holding plates must then be applied with the bolts within the bore, and when screwed firmly down the outside plates may be removed, leaving the work free to have the remainder of its face and its circumference turned up. In this way the work may be turned more true than by either of the two previously described methods, because it has no opportunity to move or become out of true.
Cylindrical work to be chucked with its axis parallel to the face plate is chucked by wood workers as shown in Fig. 885, in which b, b are two blocks screwed to the chuck c, and having Vs in to receive the work as shown; the work is held to the blocks b, by means of the straps s, s, which are held to b, b by screws. An example of a different class of chucking by bolts and clamps may be given in the engine crank. A common method of chucking such a crank is to level the surface of the crank in a planing machine, and to hold that surface to the chuck-plate by bolts and plates, while boring both the holes, merely reversing the crank end for end for the second chucking.
This method has several inherent defects, especially in the case of large cranks. First, it is a difficult matter to maintain large chuck plates quite true, and as a result by this method of chucking any want of truth in the surface of the chuck will be doubled in the want of parallelism in the bores of the crank.
Suppose, for example, that the chuck surface is either slightly hollow or rounding as tested with a straight-edge placed across its face, then the axial line of the hole bored in the crank will not be at a true right angle with the planed surface of the crank. When the crank is turned end for end on the chuck-plate and again bolted with its plain surface against the surface of the chuck, the second hole bored will again not stand at a true right angle to the planed surface, and furthermore the error in one hole will be in a directly opposite direction to that of the other hole, so that the error in the crank will be double the amount that it is on the chuck surface. To this it may be answered that if such an error is known to exist it may be corrected by placing a piece of paper of the requisite thickness at the necessary end of the crank for both chuckings. But this necessitates testing the chuck on each occasion of using it, and the selection of a sheet of paper of the exact proper thickness, which is labor thrown away so long as an equally easy and more true way of chucking can be found. Furthermore there is a second and more important element than want of truth in the chuck to be found, which is that of the alteration of form which occurs in the crank (as each part of its surface is cut away) as explained in the remarks with which the subject of chucking is prefaced.
First, the planed surface of the crank will alter in truth so soon as the crank is released from the pressure of the holding devices on the planer or planing machine; second, that surface will again alter in form and truth from the removal of the metal around the surface of the hole first bored; and third, the planed surface will be to some extent sprung from the pressure of the plates holding the crank to the chuck plate, hence the following method is far preferable.
If it is intended to plane the back surface of the crank let that be done first as before, and let it be held to the face-plate by bolts and plates as before, while the hole and its radial face at the large end of the crank are turned and finished. In doing this, however, first rough out the radial face, and then rough out the hole, so that if the work alters in form a fine finishing cut on both the radial face and the bore will correct the evil. Then release the crank from the pressure of the holding plates; and it[I-248] is obvious that however the planed surface may have altered in truth from removing the surface metal, the radial face just turned will be true with the bore turned at the same chucking. Now to chuck the crank to bore the second hole, turn it end for end as in Fig. 886, and bolt the face already turned to the chuck plate (as at a in the figure) with one or more bolts and strap plates. To steady the other end of the crank, and prevent it from moving under the pressure of the cut, take two bolts and plates b, and place a washer between them and the chuck surface as shown at c, then bolt the plates to the chuck plate, so adjusting them that their ends just have contact with the crank when it is set true. In setting it true it may be moved by striking the outer ends of the plates.
In this method of chucking, we have the following advantages:—
1st. If the chuck plate is not true we may place a piece of paper beneath the crank surface a, to correct the error as in the former method, or if this is neglected, the second hole bored will be out of true to an amount answerable to the want of truth in the chuck, and not to twice as much as in the former method.
2nd. Any alteration of form that may take place during the first chucking does not affect the truth of the second chucking as in the other case.
3rd. The crank being suspended during the second chucking, any alteration of form that may accompany the boring of the second hole will be corrected by the finishing cut, hence the crank will be bored with its two holes as axially true as they can be produced in the lathe.
It now remains to explain the uses of the pieces w in Fig. 886, simply weights termed counterbalances bolted to the chuck plate to balance it against the overhanging weight of the crank on one side of the chuck plate. If these weights are omitted the holes in the work will be bored oval, because the centrifugal force generated by the revolution of the work will take up any lost motion there may be between the cone spindle journal and its bearings, or if there be no such lost motion the centrifugal force will in many cases be sufficient to spring the cone spindle.
In selecting these weights it is well to have them as nearly as possible heavy enough to counterbalance the work when placed at the same distance from the lathe centre as the outer end of the work. The proper adjustment of the weight is ascertained by revolving the lathe and letting it slowly come to rest, when, if the outer end, or overhanging end as it termed, of the work comes to rest at the bottom of the circle of revolution on two or three successive trials the weight of the counterbalance must be increased by the addition of another weight, or the weight may be moved farther from the lathe centre.
To enable a piece of work, such as a crank for example, to have two or more holes bored at one chucking, a class of chuck such as shown in Fig. 887 is sometimes employed. s is a slide in one piece with the hub that screws on the live spindle and standing at a true right angle with the axial line of the cone spindle and made as long as will swing over the lathe bed. It contains a dovetail groove (as shown in the edge view) into which a bar t, running across the back of the face plate p, passes. To cause the bar t to accurately fit the dovetail, notwithstanding any wear of the surfaces, a slip g is introduced, being set up to t by set-screws passing through that side of the dovetailed piece. The work, as the crank c, is bolted to the face plate, and the set-screws on g are eased so that the plate can be moved to set the work true; when true, the set-screws are tightened, and the first hole may be bored. To bore the second hole all that is necessary is to slacken the set-screws on g, move the plate, which will slide in the dovetail groove, and set the work; when the set-screws are again set up tight, the boring may again be proceeded with. In this way both holes may be bored without unclamping the work. The whole truth of the job, before being unclamped from the chuck plate, depends in this case upon the dovetail groove being at a true right angle to the axial line of the lathe cone spindle, it being of no consequence whether the face plate stands true or not. But suppose the removal of the metal to have released strains in the casting or forging, then the clamping plates will have prevented the crank from quite assuming its normal shape after the release of those strains, and the crank, when finished, though true while clamped, will change its form the instant the clamping plates are removed, and the holes bored will in all probability not have their axial lines true one with the other. Another objection is that throwing the chuck plate out of balance on the lathe spindle as well as the crank induces the evils due to the centrifugal motion. This may be offset by increased counterbalancing, of course, but the counterbalancing becomes cumbersome, and is not so easy a matter. For these reasons, chucks of this class are not desirable unless it may be for comparatively small and light work. It is obvious that the dovetail groove may be provided with a screw, and the back of the plate with a nut, so as to move the plate along the groove by revolving the screw. This will assist in adjusting or setting the work, but it will increase the amount of weight requiring to be counterbalanced.
When a number of pieces are to be bored with their holes of equal diameters and of the same distance apart, the chucking should be performed as in Figs. 888 and 889; one and the same end of each link should be bored and faced, the links being held by the stem, placed on parallel pieces with plates. A pin such as shown in Fig. 889 should then be provided, its diameter across a being a close sliding fit into the bores of the links; while the length of a should be slightly less than the length of the hole in the link, the part d should be made to accurately fit the hole bored by any suitably sized reamer; a washer b should be provided, and each end should be threaded to receive nuts. There should then be provided in the chuck plate a hole whose distance from the centre of the chuck must exactly equal the distance apart the holes in the links are required to be, and into whose bore the end d of the pin shown in Fig. 889 must drive easily. The pin should be locked in this hole by a nut as shown in Fig. 889. The bored ends of the links may then be placed on the pin and[I-249] fastened by a nut as in Fig. 888, which will regulate the distance apart of the holes.
It is obvious that the pin may be passed through one of the radial slots in the chuck, and set the required distance from the centre, but in this case the pin would be liable to become moved in its position in the slot.
Side plates to prevent the link from moving should of course be applied as at d, d in the figure.
The whole process of the second chucking will thus consist of fastening the links on the pin, and setting the free end to the circle made to mark its location. This is done as shown in Fig. 890, which represents the free end of a link, d is the circle marked to set the link by, and p a pointed tool held firmly in the slide rest tool post. The link is obviously set true when the dotted circle on its end face runs true, the pointer merely serving to test the dotted circle.
When, however, one or two links only require to be turned it will not pay to make the pins shown in Fig. 888, especially if the holes of the different links vary in diameter, hence the work must be set by lines.
In the promiscuous practice of the general workshop, where it may and often does happen that two pieces of work are rarely of the same shape and size, lines whereby to set the work are an absolute necessity, not only to set the work by in chucking it, but also to denote the quantity of metal requiring to be taken off one face in order to bring its distance correct with relation to other faces. An example of this kind is given in Fig. 891, which represents a lever to be bored and faced at the two ends, the radial faces standing at different distances from the centre of the lever stem as denoted by the lines (defined by centre punch dots) e, f, g, h, i, j, k, l. It will be noted that at h, i, f, and e there is but little metal to be taken off, while there is ample at l. Suppose then that the face l were the first one turned, and it was only just trued up, then when f or h were turned there would be no metal to turn, for they may be too near the plane of l already.
The necessity for these lines now being shown, we may proceed to show how they should be located and their services in setting the work. The line a is called the centre line, it passing through the centre of the thickness of the link body on both edges of the link. From it all the other lines, as j, f, l, g, e, k, and h, i, are marked.
The first question that arises in the chucking is, which of the holes b, c, or d, shall be bored first. Now the faces k and l are those that project farthest from the centre line a, hence if the hole at that end be bored and the faces k, l, be turned first, we may bolt those faces against the chuck plate, and thus insure that all three holes shall stand axially true one with the other. If the holes b or c were bored first, l projecting beyond j and f (which are the faces of holes b, c) would prevent the radial face first turned from serving as a guide in the subsequent chuckings, unless a parallel piece were placed between the face and the chuck. In this case, however, there is not only the extra trouble of using the parallel piece, but there would obviously be more liability of error, as from the parallel piece not being dead true and the amount of the error multiplying in the length of the lever, and so on.
The hole d is the one, therefore, to be bored first, the chucking proceeding as follows:—Two parallel pieces of sufficient thickness to keep l clear of the chuck plate should be placed one on each side of the hub e, and bolts and plates placed directly over them. The work must be set so that the line a on each side of the link stands exactly parallel with the face of the chuck, the parallelism being tried at each end of the line, because any error that may be made in setting the work by the full length of the line will have a less effect upon the work than the same amount of error in a shorter length of line. For this reason the centre line should always be marked as long as possible and used to set by, unless there is a longer line running parallel to it and marked on both sides of the link, as would be the case if the dotted line at j and[I-250] that at l were equidistant from a, in which event they may preferably be used.
The work is set true to the lines by a scribing block, or surface gauge, but as that instrument is more used in setting work with chuck dogs its application will be shown in connection with chucking by dogs; hence to proceed: To set the work true to the line a it may be necessary to place a thickness of paper, a piece of sheet tin, or the equivalent, beneath one of the parallel pieces to bring a parallel with the chuck plate surface. This being done, however, and the circle d being set to run true, the hole may be bored and the radial face l turned off so as to just split the dotted line at l, and this radial face may be used instead of the line a for all subsequent chuckings, so as to avoid the errors that might occur in referring to the line, and from the alterations that might occur in the form of the work from removing the surface metal.
Fig. 892 represents a view of the end l as held for the second chucking. c is a section of the chuck plate, and o o represents the line of centres of the lathe, and it is obvious that the radial face of the lever end (which is here represented by l) being used for all but the first chucking, the holes will all stand axially true one with the other, no matter how many chuckings and holes there may be, hence it becomes obvious that the face that will meet the chuck plate is the one that should be turned at the first chucking. It is of no consequence in the case of a single lever whether the pin fits the hole in the end of l, Fig. 892, or not, because the dotted circles at b, c, d in Fig. 891 form the guides whereby to set the holes for distance apart, and any bolt may be used to clamp the work.
It is usual in an example of this kind to turn the stem of the lever to its proper thickness for a short distance from the hubs, so as to have the stem true with the bores, and form a guide whereby to set the lever in the planer or shaper when cutting down the lever stem to size. The rules of chucking and the balance weighting described with reference to chucking a crank, of course also apply to this example.
It will now be observed that in all cases in which work is chucked by bolts and plates, the whole of the faces cannot be turned at one chucking unless the shape of the work is such that it will permit the plates and the bolts to pass or be below the level of the work surface. It will further be noticed that if one face of the work is held against the chuck surface it cannot be turned at the same chucking that the other face is turned at. Now it may be very desirable that a part or the whole of the back face as well as the front one be turned at the same chucking as that at which the hole is bored, so as to have the hole and those two faces true without incurring the errors that might arise from a second chucking. Again, the diameter of the work may be equal to that of the chuck so as to preclude the possibility of using bolts and plates outside of the circumference, and though there be cavities or slots running through the work through which the bolts might be passed, yet the presence of the plates would prevent the face from being turned.
To meet these and many other requirements that might be named, chucking by the aid of chucking dogs is resorted to, one of these dogs being shown in Fig. 893. b represents a section of the chuck plate with a piece broken out to show the stem a of the dog, which is squared to prevent its revolving when the nut d, which holds the dog to the chuck plate, is tightened, the holes of the chuck, of course, being square also; e is the set-screw which holds the work, its end at e being turned down below the thread, and the head squared to receive a wrench.
Fig. 894 represents an example of chucking by dogs, it being required to face the work off to the dotted line f f. Three of the four dogs used are shown at d, d, d. To set the work the scribing block shown in the figure is employed, the point of the needle being set to the line at any one spot, and the scribing block or surface gauge carried around the work rested with its base against the chuck plate and the needle point tried for coincidence with the line at various points in the work’s circumference. The work is not at first held too firmly by the dogs, so that light blows will suffice to so move the work that the surface gauge needle point applied as shown and at any point around the work will coincide with the line. It will here be observed that using the dogs obviates the necessity for parallel pieces, when the work has projections at the back face as shown in the cut.
Fig. 895 represents another example in chucking by dogs. It is required to surface the whole of the surfaces shown, to bore the hole c and to face a face similar to a, but on the other side or chuck side of the work. Then the work is placed so that its outer face will project beyond the extreme surface of the dogs, and the whole of the operations can be performed at one chucking. It[I-251] will be observed that in this case the surface of the chuck plate does not automatically serve to guide the work in the chucking, because there is no contact between the two, but the chuck surface can be used as a guide whereby to chuck the work as has just been shown. Or suppose the work to require to be set as true as can be to its exposed face, then the work end of the surface gauge is applied as shown in Fig. 896 at e.
The surface gauge may indeed be dispensed with if the work is sufficiently light that the lathe can be swung around by pulling the chuck plate with the hand, and the work merely requires to be set to run true on its exposed radial face. A pointer held in the slide rest, and applied as in Fig. 890, will denote the setting of the work, which must be tapped until the pointer touches it equally on four equidistant points of the surface; but if it is essential to take as little as possible off the face while truing it up, the tool point should be held stationary, while the work should be so set that the four most distant points (in that circle on the work which is equivalent in radius to the radius to which the tool point stands from the chuck centre) are equidistant as measured by a rule from the tool point. The philosophy of this will be understood from a reference to Fig. 894 and the remarks thereon, this being a parallel case, but applied to a radial face instead of to a circumference.
Now suppose we have the piece of work shown in Fig. 897, which requires to have its surfaces a and b parallel and at a right angle to c and d, the end faces e and f parallel to each other, and at a right angle to both a, b, c, and d, the hole at g is to be axially true with the surfaces a, b, c, and d, as well as with the pin at i, and the hole at h at a dead right angle to that at g.
We may put a plug in g and turn up the surfaces e and f, and turn the pin i; this, however, would leave the hole g unbored, whereas it should be bored when the surface e is turned; again, after these surfaces are turned they are of no advantage as guides in the subsequent chuckings.
We may grip the surfaces e and f in a jaw chuck to turn the surfaces a, b, c and d, but depending upon the face jaws of the dogs to set the work surface true by; but this would not be apt to produce true work on account of the spring of the jaws, as explained in the remarks upon jaw chucks; furthermore, the work, supposing it to be a foot long, could not be held in a dog chuck sufficiently firmly to enable the turning of the end face e or the pin i, and this brings us to that most excellent adjunct to a general chucking lathe, the angle plate shown in Fig. 898.
It is simply a plate of the form shown in the figure, having two flat and true surfaces, one at a right angle to the other; one of these surfaces bolts to the chuck plate, while the other is to fasten the work on. The slots shown are to pass the bolts through to fasten the angle plate to the chuck plate, and the work surface of the plate contains similar slots and holes to receive the bolts used to fasten the work.
Suppose, then, we fasten the piece of work to the angle plate as shown in Fig. 899, and face off the surface c, and bore the hole h, the work being set true with its surface, or to a line, by the aid of a surface gauge, as may be required. We then turn surface c down to meet the surface of the angle plate, fasten it to the same with bolts and plates and setting it as before, and on turning its surface a we shall have the two surfaces a and c at a right angle to one another. We then turn the surface a down upon the angle plate and bolt it again as before. But we have now to set it so that the surface c shall be quite parallel with the surface of the chuck plate. This we may do by placing one or more parallel strips behind it, as at s s, in the plan view, Fig. 900, setting the work so that it binds the parallel strips tight against the chuck plate along their full lengths; or we may measure the distance of c from the chuck plate surface with a pair of inside calipers; or we may turn the bent end of a surface-gauge needle outwards and gauge the work as shown in the plan view, trying the work all along. On turning the surface d, Fig. 897, we shall have three of the surfaces done at right angles and with c and d parallel.
It is obvious that the surface d may be turned down on the angle plate and bolted as before, the surface a being set parallel to the chuck plate surface as before, and all four of these surfaces will be finished true as required. Next come the two end surfaces and the pin i. For f and the pin i we chuck the work on the angle plate, as shown in the plan view, Fig. 901, p, p representing the clamping-plates. The angle plate will here again serve to hold the work true one way, and all we have to do to set it true the other way is to fasten a pointer in the tool post and bring it up to just touch the corners of the work at the outer end, as at k. Now run the carriage up so as to bring the pointer to position l, and when the work is so set that all four corners just touch the[I-252] pointer, tried in their two positions, without touching the cross-feed screw, the work is true, and the end surface e and hole g may be turned; e will then be at a true right angle to the four faces, a, b, c, d, while g will be axially true with them.
We may, instead of using the pointer at k and l, or in addition to so using it, apply a square against the chuck plate and bring the blade against the work, as shown at r.
We have now to turn the pin i and end face, and to do this we simply reverse the work, end for end, and bolt it as before. But we may now employ the trued surface e as an aid in setting by causing it to abut against the chuck plate surface, and, as an aid to finding that it abuts fair, we may put two strips of the same piece of paper behind it, one on each side of the square, and, after the work is bolted, see that both are held firm; but it is necessary to test with the pointer as before, as well as with the square.
It is obvious that the angle plate requires counterbalancing, which is done by means of the weight w. (Fig. 900).
An excellent example of angle plate chucking is furnished in a pipe bend requiring both flanges to be turned up. The method of chucking is shown in Figs. 902 and 903, the flanges being simply bolted to the angle plate. The work may be set true to the body of the bend close to the neck of the flange or by the circumference of the flange. The face of the flange will be held true one way by the face on the angle plate, but must be set true the other way. The truest flange should be the one first bolted to the angle plate.
A common but good example of angle plate chucking is shown in Fig. 904, which represents a cross head requiring to have its two holes bored one at a right angle to the other, the jaws faced inside and outside, and the hub or boss turned.
It would be proper to mark the cross-head out by lines, giving dotted circles to set the work by, and dotted lines to give the thickness of the jaws. In thus marking out two centre lines a a and b b in Fig. 905 would be used to locate the centres of the holes; and the thickness of the jaws would be marked from the line b b. In marking these lines the cross head should be rested upon a table or plate as in Fig. 905, and the line a a should be made with the jaws of the cross head lying flat on the table, that is without the interposition of any packing or paper between them and the plate, so that the edges of the jaws on that side will be true with the line a a, and will therefore serve to apply a square against when chucking to bore the hole through the jaws. If the jaw edges are not sufficiently true to permit of their lying on the table, they should be made so by filing a flat place on them, so that when a square is applied to them as in Fig. 906, the edges c, c will be parallel with the axis a a of the holes in the chucks or jaws. The first chucking should be as in Fig. 907, the cross head being bolted to an angle plate set true by the circle on the end face of its hub d, and a square being applied to the centre line a, as in Fig. 908, and to the dotted lines on the jaws as shown in Fig. 909. A balance weight w, Fig. 907, is necessary to counterbalance the weight of the angle plate.
| VOL. I. | EXAMPLES IN ANGLE‑PLATE CHUCKING. | PLATE XII. | |
 |
|||
| Fig. 907. | |||
 |
 |
||
| Fig. 908. | Fig. 909. | ||
 |
 |
||
| Fig. 910. | Fig. 911. | ||
The second chucking to bore the cheeks and face them inside and out to the required thickness would be as in Fig. 910, a single plate and two bolts being used to hold the cross head to the angle plate. To set the cross head true in one direction, the outer circle shown marked upon the face of the cheek is used.
It remains to so set the face of the cheeks that the hole through them shall be central with that already bored through the hub d and all that is necessary to accomplish this is to set the edge true as shown in the top view in Fig. 911, in which s is a square rested against the face of the chuck and applied to the edges of the cheeks, these edges being those that were rested on the plate when marking the line a a in Fig. 905, or that were filed square if it was found necessary as already mentioned.
The inside faces of the cheeks are turned to the dotted lines shown in Fig. 909, and the outside faces being turned each to the proper thickness measured from the outside ones, the job will be complete and true in every direction.
An excellent example of angle plate chucking is shown in Fig. 912—the actual dimension of the piece, measuring, say, 24 inches[I-253] in length. It is required to have the cylindrical stems a, b turned parallel to each other, of equal diameters, equidistant from the central hole c, and true with the hub d. A large piece of work of this kind would be marked off with lines defined by centre-punch dots, as shown. The ends of a, b, d would require dotted circles to set them by. Now, in all work of this kind it is advisable to turn that surface first that will afford the greatest length of finished surface, to serve as a guide for the subsequent chucking, which in this case is the hub d, and the face on that side as denoted by the dotted line which has to be cut to that line. The method of chucking would, for this purpose, be as in Fig. 913.
The second chucking would be as in Fig. 914 to bore the hole at c, while, at the same time, the surface from f to g may be turned. Either inside calipers or a surface gauge may be employed to set e e parallel to the chuck plate surface. It is supposed that the location c is defined by a dotted circle, by which the work may be set for concentricity, as should be the case. At the next chucking it will simply be necessary to move the work on the angle plate to the position shown in Fig. 915, setting the circle on the end of a to run true, and the surface e parallel to the chuck surface as before. The third chucking is made by simply moving the work on the angle plate again, and setting as in the last instance.
The cutting tools for lathes are composed of a fine grain of cast steel termed “tool-steel,” and are made hard, to enable them to cut, by heating them to a red heat and dipping them in water, and subsequently reheating them to temper them or lower their degree of hardness, which is necessary for weak tools.
These cutting tools may be divided into two principal classes, viz., slide rest tools, or those held in the slide rest, and hand tools, which are held by hand.
The latter, however, have lost most of their former importance in the practice of the machine shop, by reason of the employment of self-acting lathes.
The proper shape for lathe slide rest tools depends upon—
1st. The kind of metal to be cut.
2nd. Upon the amount of metal to be cut off.
3rd. Upon the purpose of the cut, as whether to rough out or to finish the surface.
4th. Upon the degree of hardness of the metal to be cut.
5th. Upon the distance the tool edge is required to stand out from the tool clamp, or part that supports it.
Lathe tools are designated either from the nature of their duty, or from some characteristic peculiar to the tool itself.
The term “diamond point” is given because the face of the tool is diamond shaped; but in England and in some practice in the United States the same tool is termed a front tool, because it is employed on the front of external work.
A side tool is one intended for use on the side faces of the work, as the side of a collar or the face of a face plate. An outside tool is one for use on external surfaces, and an inside one for internal, as the walls or bores of holes, &c.
A spring tool is formed to spring or yield to excessive pressure rather than dig or jump into the work.
A boring tool is one used for boring purposes.
The principal forms of cutting tools for lathes are the diamond points or front tools, the side tools (right and left), and the cutting off or parting tool. The cutting edges of lathe tools are formed by grinding the upper surface, as a in Fig. 916, and the bottom or side faces as b, so that the cutting edges c and d shall be brought to a clean and sharp edge, the figure representing a common form of front tool. The manner in which this tool is used to cut is shown in Fig. 917, in which the work is supposed to be revolved between the lathe centres in the manner already described with reference to driving work in the lathe. The tool is firmly held in the tool post or tool clamp, as the case may be, and is fed into the work by the cross-feed screw taking a cut to reduce the work diameter and make it cylindrically true; the depth to which the tool enters the work is the depth of the cut. The tool is traversed, or fed, or moved parallel to the work axis, and the motion in that is termed the feed, or feed traverse.
The cutting action of the tool depends upon the angles one to the other of faces b, d (Fig. 918), and the position in which they are presented to the work, and in discussing these elements the face d will be termed the top face, and its inclination or angle above an horizontal line, or in the direction of the arrow in Fig. 918, will be termed the rake, this angle being considered with relation to the top a a, or what is the same thing, the bottom e e of the tool steel. The angle of the bottom face b to the line c is the bottom rake, or more properly, the clearance.
In the form of diamond point or front tool, shown in Fig. 916, there is an unnecessary amount of surface to grind at b, hence the form shown in Fig. 919 is also employed on light work, while it is in its main features also employed on large work, hence it will be here employed in preference to that shown in Fig. 916, the cutting action of the two being precisely alike so long as the angles of the faces are equal in the two tools.
The strength of the cutting edge is determined by the angles of the rake and clearance, but in this combination the clearance has the greater strength value. On the other hand the keenness of the tool though dependent in some degree upon the amount of[I-255] clearance, is much more dependent upon the angle of the top face.
It follows therefore that for copper, tin, lead, and other metals that may be comparatively easily severed, a tool may be given a maximum of top rake, and it is found in practice that top rake can be employed to advantage upon steel, wrought iron, and cast iron, but the amount must be decreased in proportion as the nature of either of those metals is hard.
For the combinations of copper and tin which are generally termed brass or composition, either no top rake or negative top rake is employed according to the conditions.
It may be pointed out, however, that in a given tool the cutting qualification is governed to a great extent by the position in which the tool is presented to the work, thus in Fig. 920, let c represent a piece of work and b, b, b, b, four tools having their top and bottom faces ground at the same angle to each other. In position 1, the top face of the tool is at an acute angle below the radial line a, hence the tool possesses top rake, the amount being about suitable for hard steel or hard cast iron.
In position 2 the top face is at an acute angle above the radial line a, hence the tool has negative top rake, the amount being about suitable for brass work under some conditions.
In position 3 the top face has no rake of any kind, and the tool is suitable (in this respect) for ordinary brass work.
In position 4 the tool possesses an amount of top rake about suitable for ordinary wrought-iron work.
If the tool was presented to brass work in positions 1 or 4 it would rip or tear the metal instead of cutting it, while if the tool was presented to iron or steel (of an ordinary degree of hardness) in positions 2 or 3, it would force rather than cut the metal.
Furthermore it will be readily perceived that though each tool may have its faces, whose junction forms the cutting edge, at the same angles, yet the strength of the cutting edge is varied by the position in which the tool is presented to the work, thus the edge in position 2, will be weaker than that in position 4.
We have now to consider another point bearing upon the proper presentment of top rake and the presentment of the tool to the work. It is obvious that the strain of the cut falls upon the top face of the tool, and therefore the direction in which this strain is exerted is the direction in which the tool will endeavour to move if the strain is sufficient to bend the tool and cause motion.
In Fig. 921 let w represent the work having a cut c being taken off by the tool t; let e represent the slide rest, and f the extreme point at which the tool is supported; then the pressure placed by c on the top face of the tool will be at a right angle to the plane of that top face, or in the direction of the arrow b; to whatever amount therefore the tool sprung under the cut pressure (its motion being in an arc of a circle, of which f is the centre) it would enter the work deeper, and as a result, the rough work not being cylindrically true, the tool will dip farthest beyond its proper line of work where the cut is deepest, and therefore will not cut the work cylindrically true; as this, however, naturally leads to a variation in the direction of the top rake, and as the cutting action of the point of such a tool differs from that of the side edge, which also leads to a variation in the direction of the top rake, it becomes necessary to consider just what the cutting action is both at the point and on the side of the tool.
Suppose, then, that the tool carries so fine a cut that it cuts at the point only, and the pressure will be as denoted by the arrow b in Fig. 921.
If the tool be given no traverse, but be merely moved in towards the centre of the work, the cut will move outward and in a line with the body of the tool, the cutting coming off as shown in Fig. 922.
So soon, however, as the tool is fed to its feed traverse the form of the cutting alters to the special form shown in Fig. 917, and moves to one side of the tool, as well as outwards from the work.
Fig. 923 is a top view of a tool and piece of work, and the arrow a denotes the direction of the resistance of the work to the cut, being at a right angle to plane of the cutting edge.
Now the duty of the side edge is simply to remove metal, while that of the point is to finish the surface, and it is obvious that for finishing purposes the most important part of the tool edge is the point, and this it is that requires to be kept sharp, hence the angle or rake should be in the direction of the point. But when the object is to remove metal and prepare the work for the finishing cut the duty falls heavily on the side edge of the tool, and the angle of the top face and the direction of its rake may be varied with a view to increase the efficiency of the side edge, and at the same time to diminish the amount of power necessary to pull the tool along to its feed traverse. This may be accomplished by altering the top rake from front to side rake, which is done in varying degrees according to the nature of the work.
In Fig. 924 the angle of the top face in the direction of a is the front, and that in the direction of b is the side rake.
[I-256]In small work where the cuts are not great, and where but one roughing cut is taken, it is an object to have the roughing cut leave the work with as smooth a surface as possible, and the amount of side rake may be small as in Fig. 924. For heavy deep cuts, however, a maximum of side rake may be used.
Thus in Fig. 925 is an engraving of a tool used for roughing in the Morgan Iron Works, its top rake being all side rake.
When a tool has side rake, its cutting capacity is obviously increased on one side only, hence it should be fed to cut on that side only. It is for this reason that no side rake is given to tools for very small and short work, because it is then more convenient to traverse the tool to cut in either direction at will.
In long and large work, however, where the motion of the slide rest is slow, tools having right and left-hand side rake are used. The tools in Figs. 924 and 925 are right-hand tools, their direction of feed travel being to the left.
In Fig. 926 is a left-hand tool, its direction of feed traverse being from left to right; hence edge g is the cutting one, edge f being dulled by the side angle b.
It is obvious that various combinations of side rake and front rake may be given to produce the same degree of keenness to the tool. For example, a tool may have its keenness from side rake alone, or it may have the same degree of keenness by using less side rake and some front rake. The principles governing the selections of these combinations are as follows:—
Suppose that in addition to say 20 degrees of side rake a tool is given a certain amount of front rake as denoted in Fig. 927 by e e, and suppose that the tool is moved in to its cut by the cross feed screw. During this motion and until the tool point meets the work surface the contact between the cross feed screw and feed nut will be on the sides of the threads facing the line of lathe centres, and all the play between those threads will be on their other sides, but so soon as the tool meets the cut it will jump forward and into the work to the amount that the play between the threads will allow it, and this is very apt to cause the tool to break. Furthermore the point of the tool is apt from its extreme keenness to become dulled quickly.
The amount of side rake may, however, be considerably increased if the heel d, Fig. 928, be made higher than the point a in that figure, the plane of the middle being denoted by the arrow at a; a view of the other side of this tool is shown in Fig. 929, the plane of the cutting edge being denoted by the dotted line.
A tool thus formed will require a slight cross feed screw pressure to force it to its cut, thus causing the cross feed nut to have contact with the sides of the thread in contact when winding the tool into its cut, hence the tendency to jump into the depth of cut is eliminated, and regulating the depth of the cut is much more easily accomplished.
In proportion as a tool is given side rake, it is more easily traversed to its cut, as will be perceived from the following:—
Fig. 930 represents a section of a tool t, whose feed traverse is in the direction of a. Now all the force that is expended in bending the cutting c out of the straight line, or in other words the pressure on the top face of the tool, acts to a great extent to force the tool to the left, and therefore traverse it to its feed. The more side rake a tool has the nearer the thickness of its cutting will accord to the thickness of the feed traverse. For example, if a tool having a side rake of say 35 degrees of angle feeds forward 1⁄32 inch per work revolution, the thickness of the cutting will but slightly exceed 1⁄32 inch, but if no top rake at all be given, as shown in Fig. 931, then the cutting will come off nearly straight, will be considerably thicker than 1⁄32 inch, and will be ragged and broken up, and it follows that the thickening and the bending of the cutting has required an expenditure of the driving power of the lathe, diminishing the depth of cut the lathe[I-257] will be capable of driving. With such a tool the pressure of the cut will fall downwards as denoted by the arrow b.
In the practice of many tool makers in the Eastern States the tool is ground to a point a, Fig. 932, that is, ground sharp and merely rounded off with an oil-stone. This may serve when the lathe has an exceedingly fine feed, and the strain being in that case very slight the tool point may be made to stand well above the level of the body of the steel, as in the figure, and thus save forging; but this is a slow method of procedure, and produces no better work than a tool which is rounded at the point, and therefore capable of producing smoother work with a much coarser feed.
The diameter of the curls of the cutting, shaving, or chip produced by a turning and also the direction in which it moves after leaving the tool, depends upon the amount of the top rake and the direction in which it is provided. The greater the amount of rake, whether it be front or side rake, the larger the coils of the cutting, and, therefore, the less the amount of power expended in bending it. Furthermore, it may be remarked that the thickness of the cutting is always greater than is due to the amount of feed traverse, and it requires power to produce this thickening of the cutting. The larger the coils of the cutting the nearer the thickness accords with the rate of feed.
In these considerations we have referred to the angle of the top face only, but if we consider the angle of the two faces one to the other we shall see that they form a wedge, and that all cutting tools are simply wedges which enter the material the more easily in proportion as the angles are more acute, providing always that they are presented to the work in the most desirable position, as was explained with reference to Fig. 920.
We may now consider the degree of a bottom rake or clearance desirable for a tool, and this it can be shown depends entirely upon the conditions of work, diameter, and rate of tool traverse, and cannot, therefore, be made a constant degree of angle. This is shown in Fig. 934, in which a tool t is represented in three positions, marked respectively 1, 2, and 3. Line a a is at a right angle to the axis of the work w, and the side of the tool is given in each case 5° of angle from this line a a. In position 1 the tool has 3° of clearance from the side of the cut; in position 2 it has 2° clearance, but in position 3 it would require to have 2° more clearance given to it to enable the cutting-edge to meet the side of the cut, without even then having the clearance necessary to enable it to cut. This occurs because the side of the cut is not at a right angle to the work axis, but at an angle the degree of which depends upon the rate of feed.
Thus in Fig. 935 the three tools have the same amount of clearance, and if they are supposed to be facing off the work they will maintain that clearance under all conditions of work, diameter, and rate of feed, but if they were traversed along instead of across the work the angle of the tool (both on the top and bottom face) to the cut will become changed, and will continue to change with every change of work diameter, so that the same tool stands at a different angle at each successive cut taken off the work, even though the lathe were used at or possessed but one rate of feed. But lathe tools are used at widely varying rates of feed, and we may therefore take an example in which a tool is at work taking a cut of the same diameter and depth at different rates of feed.
This is shown in Fig. 936, tool 1 taking the coarsest, and 2 the[I-258] finest feed, and it is seen that the finer the rate of feed the more clearance the tool has with a given degree of side clearance (for all the three tools have 7° of side angle). The only way to obtain an equal degree of clearance from the cut, therefore, clearly lies in giving to a tool a different angle for every variation, either in work diameter or in rate of feed traverse, and to show how much this will affect the shape of the tool, we have Fig. 937, in which the same rate of feed is used for all three cuts, and the tool is given in each position 5° of clearance from the cut. In position 1 the tool side stands at 81⁄2° of angle from line a, which is at a right angle to the work axis. In position 2 it stands at 101⁄2°, and in position 3 at 15° of angle from line a, a variation of 61⁄2°. Referring now to the top face of the tool, the variations occur to the same extent and from the same causes. It is in a fine degree of perception of these points that constitutes the skill of expert workmen in grinding their lathe tools, varying the angle of the tool at every grinding to suit the varying requirements.
It has been shown that for freedom of cutting and ease of driving a given cut, the direction of top rake as well as its degree needs to be a maximum that the nature of the material and its degree of hardness will admit; but this is not the only consideration, because in a finishing cut the surface requires to be left as smooth and clean cut as possible, and it remains to consider how this may best be accomplished. Now let it again be considered that it is that part of the cutting edge that lies at a right angle to the axial line of the work that removes the metal, while it is that part that lies parallel to the work axis (or in other words parallel to the finished work surface) that performs the finishing cutting duty.
Now, in proportion as the length of the cutting edge is disposed parallel to the work axis, the tool has a tendency to spring (under an increase of cut) into the work, and also to dip into soft places or seams in the work, and the amount of its front rake must be decreased, because such rake causes a pressure pulling the tool deeper into its cut, as was explained with reference to Fig. 921. Round-nosed front tools, therefore, such as in Fig. 938, cannot be given so much front rake as ordinary ones, such as in the preceding figures.
Round-nosed tools are used to cut out round corners, and the roughing tools are given a less curvature than that to be formed on the work, thus in Fig. 939 is an ordinary form of small round nose shown operating in what is termed a hollow corner, the directions of tool feed being marked by arrows. The tool may be fed by the feed traverse, and the tool gradually withdrawn, thus forming the work to the required curve.
The amount of cut a lathe will drive, the degree of hardness which the tool may be given, the length of time the tool will last without grinding, the speed at which the work may run, and the cleanness and truth of the cut, depend almost entirely upon the perfect adaptability of the tool to the conditions under which it is to be used. Upon the same kind of work, and using the same kind of tools, some workmen will give a tool from 20° to 30° more angle than others.
It is a difficult matter to determine at just what point the utmost duty is being obtained from cutting tools, because the conditions of use are so variable; but one good general guide is the speed at which the tool cuts, and another is the appearance of the cuttings or chips.
Both these guides, however, can only be applied to metal not unusually hard, and to tools rigidly held, and having their cutting edges sufficiently close to the tool point or clamp that the tool itself will not bend and spring from the pressure of the cut. The cutting speed for chilled cast-iron rolls, such, for example, as calender rolls, is but about 7 feet per minute, and the angles one to the other of the tool faces is about 75 degrees, the top face being horizontally level, and standing level with the axis of the roll.
When a tool has front rake only, the form of its cutting will depend upon the depth of its cut. With a very fine cut the cutting will come off after the manner shown in Fig. 940, while as the depth of the cut is increased, the cutting becomes a coil such as shown in Fig. 941. These coils lie closer together in proportion[I-259] as the top face of the tool is given less rake, as is necessary for steel and other hard metal. Thus Fig. 940 represents a cutting from steel, the tool having front rake only, while Fig. 941 represents a cutting from a steel crank pin, the tool having side rake. The following observations apply generally to the cuttings.
The cleaner the surface of a cutting, and the less ragged its edges are, the keener the tool has cut; thus, in Fig. 941, the raggedness shows that the tool was slightly dulled, although not sufficiently so to warrant the regrinding of the tool. Such a cutting, however, taken off wrought iron would show a tool too much dulled, or else possessing too little top rake to cut to the best advantage. In wrought iron, the tool having a keener top face, the cuttings will coil larger, and the direction in which they coil and move as they leave the tool will depend upon the shape of the tool and its height to the work.
In Fig. 942, for example, is a tool having front and side angle in about an equal degree, and its cutting is shown in Fig. 943, the side angle causing it to move to the right, and the front angle causing it to move towards the tool post.
The tool in Fig. 944 has side rake mainly, and the point is slightly depressed, hence its cutting would leave the work moving horizontally and towards the right hand.
In Fig. 945 the point of the tool is made considerably lower than the point b, and as a result the cutting would rise somewhat vertically as in Fig. 946. Indeed the heel b may be raised so as to cause the cutting to move but little to the right, but rise up almost vertically, being thrown over towards the work, and in extreme cases the cutting will rub against the surface of the work and the friction will prevent the cutting from moving to the right, hence it will roll up forming a ball, the direction of the rotation occasionally changing.
Whatever irregularities may appear in the coil of the cuttings will, if the tool is not dulled from use, arise from irregularities in the work and not from any cause attributable to the tool.
The strength of a cutting forms to a great extent a guide as to the quality of the tool, since the stronger the cutting the less it has become disintegrated, and therefore less power has been expended in removing it from the work.
The cutting speed for wrought iron should be sufficiently great that water being allowed to fall upon the work in a quick succession of drops as, say, three per second, the cuttings will leave the work so hot as to be almost unbearable in the hands, if the cut is a heavy one, as, say, reducing the work diameter 1⁄2 inch at a cut.
If wrought-iron cuttings break off in short pieces it may occur from black seams in the work, but if they break off short and show no tendency to coil, the tool has too little rake. If the tool gets dull too quickly and the cutting speed is not excessive, then the tool has too much clearance. If the tool edge breaks there is too much rake (providing of course that the tool has not been burnt in the forging or hardening), a fine feed will generally produce longer and closer coiled cuttings (that is of smaller diameter)[I-260] than a coarse feed, especially if the work be turned dry or without the application of water.
Aside from these general considerations which apply to all tools, there are peculiar characteristics of particular metals; thus, for example, cast iron will admit of the tool having a greater width of cutting edge in a line with the finished surface of the metal than either steel, wrought iron, copper or brass, which renders it possible to use a finishing tool of the form shown in Fig. 947, whose breadth of cutting edge a, lying parallel with the line of feed traverse, may always exceed that for other metals, and may in the case of cast iron be increased according to the rigidity of the work, especially when held close in to the tool post.
The corners b c may for roughing the work be rounded so as to be more durable, but for finishing cuts they should be bevelled as shown, because by this means face a can more easily be left straight than would be the case with a rounded corner. In the absence of the bevels there would be a sharp corner that would soon become dull. For finishing purposes the corners need not be so much bevelled as in figure, but may be very slightly relieved at the corners a and b, in Fig. 948, the width of the flat nose being slightly greater than the amount of feed per lathe revolution. Such tools produce the quickest and best work without chattering when the conditions are such that the work and the tool are held sufficiently rigid, and in that case may be used for the harder and tougher metals, as wrought iron and steel.
We have now to consider the height of the tool with relation to the work, which is a very important point.
In Fig. 949, for example, let e be the washer or ring under the tool, and f therefore the fulcrum from which the tool will bend. Let the horizontal dotted line a represent the centre of the work, and it is plain that to whatever amount the tool may spring under the pressure of the cut, its motion from this spring will be in the direction of the dotted arc h, causing the tool to dip deeper into the work in proportion as the tool point is set above the work centre line a. Now the amount of tool spring will even under the most rigid conditions vary in a heavy cut with every variation in the depth of cut or in the hardness of the metal. Furthermore, as the cutting edge of the tool becomes dulled from use, its spring will increase, because the pressure required to force it to its cut becomes greater, and as a result when the conditions are such that a perceptible amount of tool spring or deflection occurs, the work will not be turned cylindrically true. Obviously the work under these conditions will be most true when the tool point is set level with the line a, passing through the work axis.
There are two advantages, however, in setting the tool above the work centre: first it severs the metal easier; and second, it enables the employment of more bottom rake without increasing the bottom clearance.
Thus in Figs. 950 and 951 the diameters of the work w and the top rake of the respective tools are equal, but the tool that is set above the centre, Fig. 950, has more bottom rake but no more clearance, which occurs from the manner in which the cutting edge is presented to the work; the dotted lines represent the line of severance for each, and it is obvious that in Fig. 950, being of the shortest length for the depth of the cut will require least power to drive, because it is, as presented to the work, the sharpest wedge, as will be perceived by referring to Fig. 952, in which the tool shown in Fig. 950 is simply placed below the work centre, all other conditions as angle, &c., being equal.
From these considerations it appears that while for roughing cuts it is advantageous to set the tool above the centre, it is better where great cylindrical truth is required to set it at the centre for finishing cut.
It may also be observed that if the lathe bed be worn it will usually be most worn at the live centre end, where it is most used, and a tool set above the centre will gradually fall as the cut proceeds towards the live centre, entering the work farther, and therefore reducing its diameter. This can be offset by setting the tailstock over, but in this case the wear of the work centres is increased, and the work will be more liable to gradually run out of true, as explained with reference to turning taper work. Sir Joseph Whitworth recommends that the tool edge be placed at the “centre” of the work, while at the same time on a line with the middle of the body of the steel. To accomplish this result it is necessary that the form of the tool be such as shown in Fig. 953, in which w represents a piece of work, r the slide rest, a the[I-261] fulcrum of the tool support, the dotted line the centre of the work, and the arrow the direction in which the tool point would move from its deflection or spring. Now take the conditions shown in Fig. 954, and it will be perceived at once that the least tool deflection will have an appreciable effect in causing the tool point to advance into the work in the direction denoted by the arrow. This would impair the cylindrical truth of the work, because metals are not homogeneous but contain in forged metals seams and harder and softer places, and in cast metals different degrees of density, that part laying at the bottom of the mould being densest (and therefore hardest) by reason of having supported the weight of the metal above it when cooling in the mould.
This brings us to another consideration, inasmuch as supposing the tool edge to be set level with the work centre (as in Figs. 951 and 953), the arc of deflection of the tool point will vary in its direction with relation to the work according to the vertical distance of the top of the tool rest (r in Figs. 953 and 954) from the horizontal centre of the work.
Thus the vertical distance between the point a in Fig. 953 and the work centre is less than that between a and the horizontal work centre in Fig. 954, as may be measured by prolonging the dotted lines in both figures until they pass over a, and then measuring the respective vertical distances between a and those dotted lines. It is to be noted that this distance is governed by the vertical distance of the top of the tool rest r from the work centre, but where this distance is required or desired to be reduced a strip of metal may be placed beneath the tool and between it and the slide rest.
It will now be obvious that to produce work as nearly cylindrical as possible, the tool edge should stand as near to the slide rest as the circumstances will permit, which will hold the tool more firmly and prevent, as far as possible, its deflection or spring from the cut pressure. Both in roughing out and in finishing, this is of great importance, influencing in many cases the depth of cut the tool will carry as well as the cylindrical truth of the work.
We may now present some others of the ordinary forms of tools used in the slide rests on external or outside work, bearing in mind, however, that these are merely the principal forms, and that the conditions of practice require frequent changes in their forms, to suit the conditions of access to the work, &c.
Fig. 955 represents a diamond point tool much used by eastern tool makers. The sides are ground flat and the point is merely oil-stoned to take off the sharp corner. This tool is used with very fine feeds as, say, 180 work revolutions to an inch of tool traverse, taking very fine cuts, and in sharpening it the top face only is ground; hence as the height of the tool varies greatly before it is worn out, the tool elevating device must have a great range of action.
In Fig. 956 is shown a side tool for use on wrought iron; it is bent around so that its cutting edge a may be in advance of the side of the steel, and thus permit the cutting edge to pass up into a corner. When it is bent to the left as in the figure, it is termed a right-hand side tool, and per contra when bent to the right it is a left-hand tool. The edge a must form an acute angle to edge b, so that when in a corner the point only will cut, or when the edge a meets a radial face, as in Fig. 957, the cutting edge b will be clear of the work as shown.
If the angle of a to b is such that both those edges cut at once, the pressure due to such a broad cutting surface would cause the tool to spring or dip into the work, breaking off the tool point and perhaps forcing the work from between the lathe centres.
This tool may be fed from right to left on parallel work, or inwards and outwards on radial faces, but it produces the truest work when fed inwards on radial faces, and to the left on parallel work, while it cuts the smoothest in both cases when fed in the opposite direction.
It is a very desirable tool on small work, since it may be used on both the stem of the work, and on the radial face, which saves the trouble of having to put in a front tool to turn the stem, and a separate tool for the radial face.
In cutting down a radial face with this tool, it is best (especially if much metal is to be cut off), if the face of the metal is hard, to carry the cut from the circumference to the centre, as shown in the plan view in Fig. 958, in which a is the cutting edge of the[I-262] tool, b a collar on a piece of work, c the depth of the cut, and d a hard skin surface. Thus the point of the tool cuts beneath the hard surface, which breaks away without requiring to be actually cut.
Fig. 959 represents a cutting off or parting tool for wrought iron, its feed being directly into the metal, as denoted by the arrow. This tool should be set exactly level with the work centre when it is desired to completely sever the work. When, however, it is used to merely cut a groove, it may be set slightly above the centre.
When the tool is very narrow at c, Fig. 960, or long as in Fig. 961, it may be strengthened by being deepened, the bottom b projecting below the level of the tool steel, which will prevent undue spring and the chattering to which this tool is liable.
To enable the sides of the tool to clear the groove it cuts, the width at c should slightly exceed that at d, and the thickness along the top a should slightly exceed that at the bottom b.
When the tool is used to cut a wide groove as, say, 3⁄8-inch wide, in a small lathe, it is necessary to carry down two cuts, making the tool about 1⁄4 inch wide at c, which is a convenient size, affording sufficient strength for ordinary uses.
When used on wrought iron the top face may, with advantage, be given top rake as in Fig. 962, which on account of causing the tool to cut easier, will reduce the spring of the work w in the direction of arrow a. For brass work, however, the top should be ground in an opposite direction, as in Figs. 963 and 964, which will enable it to cut smoother and with less liability to rip into the metal, especially if the tool requires to be held far out from the tool post. To capacitate the tool to cut a groove close up to a shoulder, it should be forged to the shape shown in Fig. 965. As it is very subject to spring, it should not, unless the conditions are such as to give rigidity to both the work and the tool, be set above the work centres.
When a grooving or parting tool is to be used close up to the lathe dog, its cutting end may be bent at an angle, as in Fig. 966, so that it may be adjusted on the lathe rest, so that the work driver will not strike against the slide rest.
In Figs. 967, 968, and 969, are represented the facing tool, side[I-263] tool, or knife tool, as it is promiscuously termed, which is sometimes made thicker at the bottom as in Fig. 969. It is mainly used for squaring up side faces, as upon the ends of work or the sides of heads or collars. a is the cutting edge which may be ground so as to cut at and near the end, for large work in which it is necessary to feed the tool in with the cross slide, or to cut along its full length for small work in which the longitudinal feed is used. To facilitate the grinding, the bottom may be cut away, as at b in Fig. 968.
In some practice the bottom b, Fig. 969, of the tool, is made thicker than the top a, which is, however, unnecessary, unless for heavy cuts, for which the tool would be otherwise unsuitable on account of weakness. For all ordinary facing purposes, it should be made of equal thickness, which will reduce the area to be ground in sharpening the tool.
On small work the edge a a should be ground straight, and set at a right angle to the work, so that it may face off the whole surface at once, but for work of large diameter it should be ground and set as in Figs. 970 and 971, so that it will cut deepest at the end e, enabling it to carry a finishing cut from the circumference to the centre, by feeding it with the cross-feed screw.
The cutting edge should be level with the centre of the work, the angle of the top face d being about 35 degrees in the direction of the arrow c for wrought iron, and level if used for brass. When this tool is to be used for a face close to the work driver it should be bent at an angle as in Fig. 972, so as to enable the driver to clear the slide rest, and when used for countersunk head bolts, it may be bent at an angle as in Fig. 973, so that when it is once set to give the head the correct degree of taper, it will turn successive heads to the correct taper without requiring each head to be fitted to its place.
In Fig. 974 is shown the spring tool which is employed to finish smoothly round corners or sweeps, which it will do to better advantage than any other slide rest tool, because it is capable of carrying a larger amount of cutting edge in simultaneous operation. This property is due to the shape of the tool, the bend or curve serving as a spring to enable the tool to bend rather than dig into the work.
This form of tool is sometimes objected to on the ground that it does not turn true, but this is not the case if the tool is properly formed and placed at the correct height with relation to the work. In the first place the top face should, even on wrought iron, have but very little top rake, and indeed none at all if held far out from the tool post, while for brass, negative top rake may be employed to advantage. The height of the cutting edge b should be level with the top of the tool steel as denoted by the dotted line in the figure, and in no case should it stand above that level. The[I-264] cutting edge should be placed about level with the horizontal centre of the work, but in no case above it. It is from this error that the tool is frequently condemned, because if placed above, the broad cutting edge causes the tool to spring slightly and dig into the metal, whereas when placed at the middle of the height of the work the spring will not have that effect, as already explained when referring to front tools. Furthermore, the spring of the tool (from inequalities in the texture or from seams in the metal) will be in a line so nearly coincident with the work surface that the latter will be practically true, and from the smoothness and the evenness of the curve this tool will produce a much better work than any other tool, unless indeed the curve be of a very small radius, as, say, about 1⁄4 inch only, in which case a hand tool such as shown in Fig. 1292 may be employed; spring tools are intended to finish only, and not to rough out the work.
The curves, as b in Fig. 974 for a round corner and c for a bead, should be carefully and smoothly finished to the required curve and the top face only ground to sharpen the tool, so as to maintain the curve as nearly as possible; but if the curve is a very large one, the tool will require to be a part of the curve only, and must be operated by the slide rest around the curve.
For finishing the curves or round corners in cast-iron work the spring tool is especially advantageous, as it will produce a polished clean surface of exquisite finish if used with water, and the cutting speed is exceedingly slow, as about 7 feet per minute.
Nearly all the tools used in the slide rest upon iron work may be employed upon brass work, but the top faces should not have rake, that is to say, they should have their top faces lying in the same plane as the bottom plane of the tool steel which rests on the slide rest. For if the top face is too keen it rips rather than cuts the brass, giving it a patchy, mottled appearance.
Fig. 975 represents a front tool for brass, which is used for carrying cuts along outside work or for facing purposes, corresponding, so far as its use is concerned, to the diamond point or front tool for iron. The top face of this tool must in no case be given rake of any kind, as that would cause it to tear rather than to cut the metal, and also to chatter. The point a should be slightly rounded and the width at b and depth at c must be regulated to suit the depth of cut taken, the rule being that slightness in either of these directions causes the tool to chatter. When held far out from the tool post or under other conditions in which the tool cannot be rigidly held, the top face should be ground away towards the end, thus depressing the point a, after the manner shown with reference to the cutting-off tool for brass in Fig. 963. The manner in which the cuttings come off brass work when a front tool is used, depends upon the hardness of the brass and the speed at which the tool cuts.
In the harder kinds of brass, such as that termed gun metal, composition, or bell metal, the cuttings will fly off the tool in short angular grains, such as indicated in Fig. 976, travelling a yard or two after leaving the tool if a fairly quick cutting speed is used. But if the cutting speed is too slow the cuttings will come off slowly and fly but a few inches. In the softer kinds of brass, such as yellow brass, the cuttings are longer and inclined to form short curls, which will, if cut at a high speed, fly a few inches only after leaving the tool.
In Fig. 977 is shown a right-hand side tool for brass work. It is used to carry cuts along short work, and to carry facing cuts at the same time, thus avoiding the necessity to move the position of the tool to enable it to carry a facing cut, as would be necessary if a front tool for brass were used. It is peculiarly adapted, therefore, for brass bolts, or other short work having a head or collar to be faced especially; hence, it may be traversed to its cut in either direction without requiring to be moved in the tool post. It may also be used to advantage for boring purposes. It will be found that this tool will cut smoother and will be less liable to chatter if its top face is ground slightly down towards the point and if it be not forged too slight either in depth or across b. Its clearance on the side is given by forging it to the diamond shape shown in the sectional view. To make the tool a left-handed one it must be bent to the right, the clearance being in any case on the inside of the curve.
The forms of single-pointed slide rest tools employed to cut V-threads in the lathe are shown in Fig. 978, which represents a tool for external, and Fig. 979, which represents one for an internal V-thread, the latter being a tool ground to accurate shape and secured in a holder by the set screw s.
It is obvious that a Whitworth thread might be cut with a single-pointed tool such as shown in Fig. 980, the corner at b being rounded to cut the rounded tops of the thread. It is more usual, however, to employ a chaser set in the tool point in the same manner as a single-pointed tool, or in a holder fixed in the tool post. When a single-pointed tool is employed to cut a thread, the angles of its sides are not the same as the angle of the thread it produces, which occurs because the tool must have clearance to enable it to cut. In Fig. 981, for example, is a single-pointed[I-265] tool without any clearance, and, as a result, it cannot enter the work to cut it. In Fig. 982 the tool is shown with clearance, and, as a result, the angle of the cutting edge is not the same angle as the sides of the tool are, because the top face is not at a right angle to the sides of the tool. It is obvious that the angle of the sides of the tool must be taken along the dotted line in Fig. 982.
It follows then that a tool whose sides are at a given angle will cut a different angle of thread for every variation in the amount of clearance. But whatever the amount of clearance may be, the tool will produce correct results providing that the gauge to which the tool is ground is held level, as in Fig. 983 at a, and not at an angle as at b.
The tool, however, must be set at the correct height with relation to the work, and its top surface must point to the work axis to produce correct results.
Suppose, for example, that in Fig. 984 a is a piece of work, its horizontal centre being represented by the dotted line c, and its centre of revolution being at c. Now suppose d is a screw-cutting tool cutting a depth of thread denoted by e. g is another lathe tool having teeth of the same form and angle as d, but lifted above the horizontal centre of the work. The depth of thread cut by g is denoted by f, which is shallower, though it will be seen that the point of g has entered the work to the same depth or distance (of the tool point) as d has. It is obvious, however, that for any fixed height, a tool suitable to cut any required depth or angle can be made, but it would be difficult to gauge when the tool stood at its proper height.
To facilitate setting the height of the tool, a gauge such as shown in Fig. 985 may be used, the height of the line a from the base equalling the height or distance between the top surface of the cross slides and the axial line of the lathe centres. If the lathe, however, have an elevating slide rest, the rest must be set level before applying the gauge. Or in place of using the gauge, the tool stool or tool holder, as the case may be, may be made of such height that when level in the tool post its top face points to the axis of the lathe centre, the tool being sharpened on the angles and not ground on the top face.
But in the case of a tool holder, or of a chaser holder, the tool may be ground on the top face, and adjusted for height by any suitable means, the top of the holder serving as a guide to set the tool by.
The line of the cutting edge of the tool must, to obtain correct results, be presented to the work in the same manner as it was presented to the gauge to which its angles were ground, so that if the tool were in position in the tool post, and the gauge were applied, it would point to the axis of the lathe centre, for if this is not the case the thread cut will not be of correct angle or depth. Thus, in Figs. 986 and 987 the tool t would cut threads too shallow, although placed at the correct height, because the cutting edges are at an angle to the radial lines c c.
It becomes obvious, then, that it is improper to set the height of a screw-cutting tool by means of any tool elevating or setting-device that throws it out of the horizontal position. To enable the correct setting of threading tools, and to avoid having to grind the angles correct to gauge every time the tool requires[I-266] sharpening, various kinds of tool holders have been designed by means of which the tool may be ground on the top face, and set at correct height and in the proper plane.
To facilitate grinding the tools to a correct angle, the gauge shown in Fig. 988 is employed, the various notches being for the pitches of thread for which they are respectively marked, but, the edge of the gauge being circular, does not afford much guide to the eye in grinding the angles equal from the sides of the body of the tool; hence the form of gauge shown in Fig. 989 is preferable, because the tool can be so ground that the edge of the gauge stands parallel with the side of the tool steel, so that the tool will, when in correct position, point straight to the work axis. To insure correctness in setting the tool, it may then be set with a square s in Fig. 990, held firmly with its back against the side of the tool, which may be adjusted in the tool post until the blade b comes fair with the work.
Another method of setting the tool is with a gauge as in Fig. 991, which sets it true with the angle independent of whether the angle is true with the side of the tool or not. In Fig. 992 is a form of gauge that will serve to grind the tool by to correct angle, and also to set it in the lathe by the angles, independent of the side of the tool.
The same gauge may be used for setting internal threading tools by first facing the work quite true and then applying the gauge as in Fig. 993.
By reason of the comparatively sharp points of thread-cutting tools, they are more readily dulled than the rounder pointed ordinary lathe tool, and by reason of their cutting edges extending along a greater length of the work, and therefore causing it to spring or bend more from the strain of the cut, they cannot be employed to take such heavy cuts as ordinary tools. Hence, in all thread cutting, it is necessary to turn the work down to the finished diameter before using the threading tool, so that the thread will be finished when it is cut to the proper depth. To test that depth on a piece of work having a United States standard, or a sharp V-thread, a gauge such as shown in Fig. 994 may be used, consisting of a piece of sheet steel about 1⁄50 inch thick, having a single tooth formed correct for the space of the thread, so that the edge of the gauge will meet the tops of the thread when the space is cut to admit the tooth on the gauge; the most accurate method of producing such a gauge having been described in the remarks upon screw threads.
If the tool is known to be ground to the correct angle and is set properly, the gauge for depth may be dispensed with by turning the body of the work to correct diameter, and also turning a small[I-267] part, as a in Fig. 995, down to the correct diameter for the bottom of the thread, so that when the tool point meets a the thread will be cut to correct depth.
Figs. 996 and 997 represent a method of cutting a round top and bottom, or any other form of thread, by means of a single-pointed circular cutting tool, which is mounted on a holder. On the circumference of the cutter is cut a single thread, and a piece is cut out at e to form a cutting edge. To cut a right-hand thread on the work, a left-hand one must be cut on the cutter, so as to make its thread slant in the proper direction. The tool is sharpened by grinding the top face, and moved on the holding pin to set it to the proper height or in position to enable it to cut. A top view of the tool and holder is shown in figure 997.
It is obvious that two gaps may be cut in the wheel or cutter so as to provide two cutting edges, one of which may be used for roughing, and the other for finishing cuts.
In roughing out coarse threads, a single-pointed tool, formed as in Fig. 998, and set considerably above the centre as shown, may be used to great advantage. It will carry a heavy cut and throw off a cutting but very little curved; hence but little power is absorbed in bending the cutting. To preserve the cutting edge, the point of the tool should be slightly rounded. Such a tool, however, requires to be rigidly held, and requires experience to use it to the best advantage.
An English tool holder for a single-pointed tool for cutting coarse pitch threads, such as square threads, is shown in Fig. 999. The stem of the holder is cylindrical, and is held between two clamping pieces, while the short piece of steel used as a tool (which is thinnest at the bottom, so as to provide for the clearance without grinding it) is clamped in a swiveled post, so that it may be set at the angle sideways required for the particular pitch of thread to be cut, as is shown in the end view.
The difficulty of adjusting the height of threading tools that are ground on their top faces to sharpen them is obviated in a very satisfactory manner by the tool holder patented by the Pratt and Whitney Company, and represented in Figs. 1000 and 1001. a is the body of the holder, c is the tool clamp, and b the set screw for c; d is a pin fast in a and projecting into c to adjust it square upon a. The threading tool g has a groove h, into which the projection e fits, so that the tool is held accurately in position. f is the screw which adjusts the height of the tool, being threaded into a and partly into g, as is shown at i. The holder once being set in correct position, the threading tool may be removed for grinding, and reset with accuracy. The face k of the holder is made at 30° to the front or leading face of the holder, so that the stem or body of the holder will be at an angle and out of the way of the work driver.
[I-268]If a chaser instead of a single-pointed tool be used to cut a thread, the thread requires to be gauged for its full diameter only, because both the angles of the thread sides and the thread depth are determined by the chaser itself. Chasers are also preferable to a single-pointed tool when the work does not require to be cut to an exact diameter, nor to have a fully developed thread clear up to a shoulder; but when such is the case a single-pointed tool is preferable, because if the leading tooth should happen to run against the shoulder the whole of the teeth dig into the work, and more damage is done to it than with a single-pointed tool. When the thread does not run up to a shoulder, or in cases where the thread may be permitted to run gradually out, and, again, where the thread is upon a part of enlarged diameter, a chaser may have its efficiency increased in two ways, the first of which is shown in Fig. 1002. When the chaser is set and formed as at a in the figure, the leading tooth takes all the cut, and the following tooth will only cut as it is permitted to do so from the wear of the leading bolt. This causes the tooth to wear, but the teeth may be caused to each take a proportion of the cut by chamfering them as at b in the figure, which will relieve the front tooth of a great part of its duty and let the following teeth perform duty, and thus preserve the sharpness of the cutting edges. We are limited in the degree of chamfer that may be given to the teeth, first, because as the cutting edge is broader and the strain of the cut is greater it causes the tool to spring or bend more under the cut pressure; and secondly, because if the tool be given many teeth in order to lengthen the chamfer, then the pitch is altered to a greater extent by reason of the expansion which accompanies the hardening of the chaser.
A chaser thus chamfered may be set square in the tool post by placing a scale against the work as at s in Fig. 1003, and setting the bottoms of the chaser teeth fair with the outer edge of the scale as in the figure.
The second method of increasing the efficiency of a chaser is to grind the top face at an angle as from a to b in Fig. 1004, and set it so that the last tooth b is at or a little above the work axis d. This causes the last tooth b to stand sufficiently nearer the work axis than the other teeth to enable it to take a light scraping cut, producing a smooth cut, because the duty on the last tooth being light it preserves its cutting edge, and therefore its form.
Chasers are often in shops, doing general work, formed in one piece in the same way as an ordinary tool, but it is preferable to use short chasers and secure them in holders.
Figs. 1005 and 1006 show a convenient form of holder, the chaser a being accurately fitted into a recess in the holder d, so that it may be set square in the holder without requiring to be adjusted to come fair with the thread grooves after having been ground to resharpen it. The short chasers are held by the clamp b, which has at c a projection fitting into a recess in the holder to cause the clamp to adjust itself fairly.
In setting a chaser to correct position in a tool post the points of the teeth may be set to the surface of the work as in Fig. 1007, or if the thread is partly produced and the lathe has a compound slide rest, the tool may be set to the tops of the thread as in Fig. 1008, and then brought into position to meet the thread grooves by operating the slide rest.
It is obvious that the height and position of a chaser require to be as accurately set as a single-pointed tool, but it is more difficult to set it because it can only be sharpened by grinding the top face, and this alters the height at each grinding.
Thus, suppose that when new its teeth are of correct height, when the bottom face i, Fig. 1009, lies upon the rest r, the face h being in line with the centre b b of the work, then as face h is ground the tool must be lifted to adjust its height. On account, however, of the curve of the teeth it is very difficult to find when the chaser is in the exact proper position, which in an ordinary chaser will be when it has just sufficient clearance to enable it to cut, as is explained with reference to cutting up chasers and using them by hand.
[I-269]To obviate these difficulties, an excellent form of chaser holder is shown in Figs. 1010 and 1011. Its top face c being made of such a height that when the holder rests on the surface of the slide rest and is in the tool box, c will stand horizontally level with the horizontal centre of the work, as denoted by the horizontal line d e; then the tool proper may have long teeth as denoted by a, and the surface of the teeth may always be brought up level with the top surface of the tool holder as tested with a straight-edge. This is a ready and accurate mode of adjustment. A top view of the tool holder is shown in Fig. 1011, in which a is the tool holder, b the threading tool, with a clamp to hold b, and a screw to tighten the clamp.
It may now be pointed out that a common sharp V-chaser may be used to cut a United States standard thread by simply grinding off the necessary flats at the points of the teeth, because when the chaser has entered the work to the proper depth it will leave the necessary flat places at the top of the thread, as is shown in Fig. 1012.
In cutting internal, inside, or female threads (these terms being synonymous) the diameter of the bore or hole requires to be made of the diameter of the male thread at the root.
Since, however, it is impracticable to measure male threads at the root, it becomes a problem as to the proper size of hole to bore for any given diameter and pitch of thread. This, however, may be done by the following rules:—
To find the diameter at the roots or bottom of the thread of United States standard threads:
Rule.—Diameter - (1.299 ÷ pitch) = diameter at root.
Example.—What is the diameter at the root of a United States standard thread measuring an inch in diameter at the top of the thread and having an 8 pitch?
| Here 1.299 ÷ 8 = .162375. | |||||
| 1.000000 | |||||
| Then 1 - .162375 | .162375 | = | .8376. | ||
| .837635 | |||||
For the sharp V-thread the following rule is employed:
Rule.—Diameter-(1.73205 ÷ pitch) = diameter at root.
Example.—What is the diameter at the root of a sharp V-thread of 8 pitch, and measuring 1 inch diameter at the top of the thread?
| Here 1.73205 ÷ 8 = .21650. | |||||
| 1.0000 | |||||
| Then 1 - .2165 | .2165 | = | .7835. | ||
| .7835 | |||||
For cutting square threads the class of tool shown in Fig. 1013 is employed, being made wider at the cutting point c than at b or at d, so that the cutting may be done by the edge c, and the sides a may clear, which is necessary to reduce the length of cutting edge and prevent an undue pressure of cut from springing the work.
The sides of the tool from a to b must be inclined to the body of the tool steel, as shown in Fig. 1014, the degree of the inclination depending upon the pitch of thread to be cut. It may be determined, however, by the means shown in Fig. 1015.
Draw the line a, and at a right angle to it line b, whose length must equal the circumference of the thread to be cut and measured at its root. On the line a set off from b the pitch of thread to be cut as at c, then draw the diagonal d, which will represent the angle of the bottom of the thread to the work axis, and the angle of the tool sides must be sufficiently greater to give the necessary clearance. The width of the point c of the tool should be made sufficiently less than the width of the thread groove to permit of the sides of the thread being pinched (after the thread is cut to depth) with a tool such as was shown in Fig. 968.
For coarser pitches the thread is cut as shown in Fig. 1016.[I-270] The tool is made one-half the width of the thread groove, and a groove, a, a, a, is cut on the work. The tool is then moved laterally and a second cut as at b b is taken, this second cut being shown in the engraving to have progressed as far as c only for clearness of illustration. When the thread has in this manner been cut to its proper depth, the side tools are introduced to finish the sides of the thread. If the thread is a shallow one each side may be finished at one cut by a side tool ground and set very true; but in the case of a deep one the tool may be made to cut at and wear its end only, and after taking a cut, the tool fed in and another cut taken, and so on until, having begun at the top of the thread, the tool operated or fed, after each traverse, by the cross feed, finally reaches the bottom of the thread. If a very fine or small amount of cut is taken, both sides of the thread may in this way be finished together, the tool being made to the exact proper width.
When used on wrought iron the tool is sometimes given top rake, which greatly facilitates the operation, as the tool will then take a heavier as well as a cleaner cut.
After the first thread cut is taken along the work, it is usual to remove it from the lathe and drill, at the point where it is desired that the thread shall terminate, a hole equal in diameter to the width of the thread groove, and in depth to the depth of the thread. This affords relief to the cutting tool at the end of the cut, enables the thread to end abruptly, and leaves a neat finish.
On account of the broad cutting edge on a screw-cutting tool, the lathe is always run at a slower speed than it would be on the same diameter of work using an ordinary turning tool. After the tool is set to just clear the diameter of the work it is moved (for a right-hand thread) past the end of the work at the dead centre, and a cut is put on by operating the cross-feed screw. The feed nut is then engaged with the feed screw and the tool takes its cut as far along the work as the thread is to be, when the tool is rapidly withdrawn from the work and the lathe carriage traversed back again, ready to take another cut. If, however, the thread to be cut runs close up to a shoulder, head, or collar, the lathe may be run slower as the tool approaches that shoulder by operating the belt shipper and moving the overhead belt partly off the tight pulley and on to the loose one, or the lathe may be stopped when the tool is near the shoulder and the belt pulled by hand.
An excellent method of finishing square threads after having cut them in the lathe to very nearly the finished dimensions is with an adjustable die in a suitable stock, such as in Figs. 1017 and 1018, in which s is a stock having handle h, and containing a die d, secured by a cap c, pivoted at p. To adjust the size of the die, two screws, a and b, are used, a passing through the top half of the die and threading into the half below the split, while b threads into the lower half and abuts against the face of the split in the die, so that, by adjusting these two screws, the wear may be taken up and the size maintained standard. This device is used to take a very light finishing cut only, and is found to answer very well, because it obviates the necessity of fine measurement in finishing the thread. The die d is seated in a recess at the top and at the bottom so as to prevent it moving sideways and coming out.
Lathe Tool Holders for Outside Tools.—When a lathe cutting tool is made from a rectangular bar of steel it requires to be forged to bring it to the required shape at the cutting end, and to avoid this labor, and at the same time attain some other advantages which will be referred to presently, various forms of tool holders are employed.
These holders fasten in the tool post, or tool clamp, and carry short tools, which, from their shapes and the manner in which they are presented to the work, require no forging, and maintain their shapes while requiring a minimum of grinding.
Fig. 1019 represents a side view of Woodbridge’s tool holder at work in the lathe, and Fig. 1020 is a view of the same set at an angle to the tool rest. Fig. 1021 is an end view of the tool and holder removed from the lathe.
The tool seat a is at an angle of about 4 degrees to the base of holder (a greater degree being shown in the cut for clearness of illustration), so that the side j of the tool will stand at an angle and have clearance without requiring such clearance to be produced by grinding. The seat b of the cap c upon the tool is curved, so that the cap will bind the middle of the tool and escape[I-271] the edges, besides binding the tool fair upon its seat a. The top face is formed at the angle necessary for free and clean cutting, and the tools are, when the cutting edge is provided at one end only, hardened for half their length.
The holder, and therefore the tool, may obviously be swung at any chosen angle of the work or to suit the requirements.
Fig. 1022 shows a right and left-hand diamond-point tool in position in the holder with the cap removed, the cutting edge being at g, the angle of the top face being from f to e. The tool, it will be observed from the dotted line, is supported close up to its cutting corner.
Fig. 1023 shows a right and left-hand side tool in position, the dotted line showing that it is supported as close to the cutting edge d as the nature of facing work will permit. When left-hand tools are used the holder is turned end for end, so as to support the tools in the same manner as for right-hand ones, and for this purpose it is that the holder is beveled off at each end.
By grinding both ends of one tool, however, to the necessary shape and angle, one tool may be made to serve for both right and left, the tool holder being simply reversed end for end in the tool post. There are, however, furnished with each holder a right and left-hand diamond point and a right and left-hand side tool, each being hardened for half its full length.
It is obvious, however, that there is no front rake to the tool, and that it therefore derives its keenness from the amount of side rake, which may be regulated to suit the conditions.
When tool holders of this class are employed, the end face only of the tool requires grinding to resharpen the cutting edges; hence the area of metal requiring to be ground is much less than that on forged tools, and therefore the grinding occupies less time; and if the workman grinds the tools, he is enabled to run more lathes and not keep them idle so long while grinding the tool. Or if the tools are kept ground in stock (about 200 of the tools or cutters serving to run 24 lathes a week) the workman has but to slip in a new tool as the old one becomes dull, no adjustment for height being necessary as in the forged tool.
When the tool requires to be set to an exact position, as in the case of screw cutting, it is desirable that the tool holder be so constructed that the tool may be removed therefrom and replaced without disturbing the position of the tool holder in the tool post or tool clamp; and means must therefore be provided for securing the tool to the holder independently of the tool post or clamp screw. Fig. 1024 represents a tool holder possessing these features: h is the holder provided with a clamp c, secured by a screw b, t representing the tool, which is in this case a chaser, having teeth down the full length of its front face; k is a key or feather fast in the holder h, and fitting into a groove provided in the side of the tool. The vertical angle of this feather obviously determines the angle of clearance at which the tool shall stand to the work.
The Pratt and Whitney Company, who are the manufacturers of this holder, make this angle of clearance 15 degrees. The height of the tool in the holder is adjusted by the screw s, which has journal bearing in the holder, and threads to the end edge of the tool.
Now it is obvious that the holder h, once being set to its proper position in the tool post, the tool t may be removed from and replaced in the exact same position, both in the holder and with reference to the work.
In Fig. 1025, for example, is a top view of the holder with a single-pointed threading tool t in place. w represents a piece of work supposed to be in the lathe, and g a tool-setting gauge; and it is obvious that, if the holder is not moved, the tool t may be removed, ground up, and replaced with the assurance that it will stand in the exact same position as before, producing the exact same effect upon the work, providing that the height is maintained equal, and the tool is not altered in shape by the grinding. To maintain the height equal, all that is necessary is to have the upper face (h, Fig. 1024) of the holder horizontally level and in line with the line of centres of the lathe, and to set the top face of the tool level with that of the holder. In sharpening the tool the top face only is ground; hence the angles are not altered.
[I-272]Fig. 1026 represents the holder with a tool in position to true up a lathe centre, the angle of the tool holder to the line of centres being the same as in Fig. 1025; and Fig. 1027 represents various forms of tools for curves. All these serve to illustrate the advantages of such a tool holder.
If, for example, a piece of work requires the use of two or more such tools, and the holder is once set, the tools may be removed and interchanged with a certainty that each one put into place will stand at the exact angle and position required, not only with relation to the work, but also in relation to the other tools that have preceded it. Each hollow or round will not only be correct in its sweep, but will also stand correct in relation to the other sweeps and curves, no matter how often the tools may be changed. Inasmuch as the tool is ground at the top only for the purpose of resharpening, it maintains a correct shape until worn out.
The pin shown at f in Fig. 1024 is fast in the holder, and fits loosely in clamp c to prevent it from swinging around on b when b is loosened.
When the tool requires to preserve its exact shape it may also be made circular with the required form for the cutting edge formed round the perimeter. Thus Figs. 1028 and 1029, which are extracted from The American Machinist, represent tool holders with circular cutting tools.
The holder a fits the lathe tool post, carrying the cutting tool b, which is bolted to the holder and has at f a piece cut out to form the cutting edge.
To facilitate the grinding, holes are drilled at intervals through b. A plan view of this tool and holder is shown at c, the shape of the cutting edge being shown at d. The cutting edge is shown in the side view to be level with the centre of the tool holder height, but it may be raised to the level of the top of the tool steel by raising the hole to receive the bolt that fastens the cutter, as is shown at e; or the cutter may be mounted on top of the holder as shown at h, having a stem passing down through the holder, and capable of being secured by the taper pin i. A plan view of this arrangement is shown at j.
Another form of circular cutter is shown in Fig. 1030. It consists of a disk or cutter secured to a holder fitted to the tool post, the cutter edge being formed by a gap in the disk, as shown in the figure, which represents a cutter for a simple bead or round corner. The front end of the holder has a face a, whose height is level with the line of lathe centre when the holder is set level in the tool post. Hence the top face of the cutting edge may be known to be set level with the line of centres when it is fair with the face a of the holder. The bottom clearance is given by the circular shape of the cutter, while side clearance may be given by inclining the face b of the holder (against which the face of the cutter is bolted) to the necessary angle from a vertical line. The[I-273] face c is ground up to resharpen the cutting edge, and may be reground until the circumference of the wheel is used up.
Figs. 1031, 1032, 1033, and 1034 represent lathe tool holders by Messrs. Bental Brothers, of Fullbridge Works, Maldon, England. The holder consists of a bar a, having at the front end a hub h, containing a bush in two halves, through which the tool t passes; this tool consisting of a piece of V-shaped steel. A set screw on top of the hub clamps the two half-bushes together, and these, as their faces do not meet, grip the tool.
The advantage possessed by this form of holder is that the top face of the tool may be given any desired degree of side rake or angle required by the nature of the work by simply revolving the bushes in the hub of the holder. Thus, in Fig. 1034 the top face of the tool stands level, as would be required for brass work; in Fig. 1032 the tool is canted over, giving its top face angle a rake in the direction necessary when cutting wrought iron and feeding toward the dead centre; and in Fig. 1033 the tool is in position for carrying a cut on wrought iron, the feed being toward the live centre of the lathe. This capacity to govern the angle of the top face of the tool is a great advantage, and one not possessed by ordinary tool holders, especially since it does not sensibly alter the height of the tool point with relation to the work. Again, the V-shape of the tool steel causes the bushes to grip and support the tool sideways, and, by reducing the area of tool surface requiring to be ground, facilitates the tool grinding to that extent. Altogether, this is an exceedingly handy device. It is obvious, however, that it cannot be moved from side to side of the tool rest unless a right and left-hand tool holder be used; that is to say, there must be two holders having the hub on the opposite side of the body a.
Figs. 1035, 1036, 1037, and 1038 represent tool holders in which the tools consist of short pieces of steel held end-wise and at a given angle, so that the amount of clearance is constant. The holders Figs. 1035 and 1036 are split, and the tool is secured by the screw shown. Fig. 1037 represents a tool holder in which the tool is held by a clamp, whose stem passes through the body of the holder so as to bring the fastening nut out at the end, where it is more convenient to get at than are the screw heads in Figs. 1035 and 1036. It is obvious, however, that such a holder is weak and unsuitable for any tools save those used for very light duty indeed, while all this class of holders is open to the objection that the side of the holder prevents the tool from passing up into a corner, hence the cut cannot be carried up to a shoulder on the work. This may, however, be accomplished by bending the end of the holder round; but in this case two holders, a right and a left, will be necessary.
Fig. 1038 represents a form of tool holder of this kind in which the tool may be set for height by a set screw beneath it.
Fig. 1039 represents a tool holder and work-steadying device combined. The holder is held in the lathe tool rest in the usual manner, and affords slideway to a slide operated by the handle shown at the right-hand end.
The tool is carried at the other end of this slide, there being shown in the figure a cutting-off tool in position. At the end of the holder is a hub and three adjusting screws whose ends steady the work, and which are locked in their adjusted position by the chuck nuts shown.
The Power Required to Drive Cutting Tools.—From experiments made by Dr. Hartig, he concluded that by multiplying the weight of the metal cuttings removed per hour by certain decimal figures (or constants) the horse-power required to cut off that quantity of metal might be obtained. These decimal constants are as follows:
| Lbs. of metal | cut off per hour, | cast iron | × | .0314 | = | horse‑power required to drive the lathe. |
| „ | „ | wrought iron | × | .0327 | = | „ |
| „ | „ | steel | × | .4470 | = | „ |
For Planing Tools.
| Lbs. of | steel | cut off per hour | × | .1120 | = | horse-power required | to drive planer. |
| „ | wrought iron | „ | × | .0520 | = | „ | „ |
| „ | gun metal | „ | × | .0127 | = | „ | „ |
For drilling in the lathe, the twist drill is employed not only on account of its capacity to drill true, straight, and smooth holes, but also because its flutes afford free egress to the cuttings and obviate the necessity of frequently withdrawing the drill to clear the hole of the cuttings.
In the smaller sizes of twist drill, the stem or shank is made parallel, as in Fig. 1040, while in the larger sizes it is made taper, as in Fig. 1041, for reasons which will appear hereafter.
The taper shanks of twist drills are given a standard degree of taper of 5⁄8 inch per foot of length, which is termed the Morse taper. A former standard, termed the American standard, is still used to a limited extent, its degree of taper being 9⁄16 inch per foot.
Parallel shanked twist drills are driven by chucks, while taper, shanked ones, are driven by sockets, such as in Fig. 1042, from c to d, fitting into the lathe centre hole, while the bore at the other end is the Morse standard taper, to receive the drills e e, which have a projection such as shown at a, which by fitting into a slot that meets the end of the taper holes in the socket, lock the drill and prevent its revolving in the socket, while affording a means of forcing the drill out by inserting a key k, as shown in the figure.[14]
Each socket takes a certain number of different sized drills, the shanks of the smaller drills being in some cases longer than the drill body.
| Number | 1 | socket receives | drills from | 1⁄8 | to | 19⁄32 | inch | inclusive. | ||
| „ | 2 | „ | „ | 5⁄8 | „ | 29⁄32 | „ | „ | ||
| „ | 3 | „ | „ | 15⁄16 | „ | 1 | 1⁄4 | „ | „ | |
| „ | 4 | „ | „ | 1 | 9⁄32 | „ | 2 | „ | „ | |
| „ | 5 | „ | „ | 2 | 1⁄32 | „ | 2 | 1⁄2 | „ | „ |
These sockets are manufactured ready to receive the drills, but are left unturned at the shank end so that they may be fitted to the particular lathe or machine in which they are to be used, no standard size or degree of taper having as yet been adopted.
A twist drill possesses three cutting edges marked a, b, c respectively in Fig. 1043, and of these c is the least effective, because it cannot be made as keen as is desirable for rapid and clean cutting, and therefore necessitates that the drill be given an unusually fine rate of feed as compared with other cutting tools.
The land of the drill—or, in other words, the circumference between the flutes—is backed off to give clearance, as is shown in Fig. 1044, a true circle being marked with a dotted line, and the drill being of full diameter from a to b only. The object of this clearance is to prevent the drill from seizing or grinding against the walls of the hole, as it would otherwise be apt to do when the outer corner wore off, as is likely to be the case.
Twist drills having three and more flutes have been devised and made, but the increased cost and the weakness induced by the extra flutes have been found to more than counterbalance the gain due to an increase in the number of cutting edges, Further, the increase in the number of flutes renders the grinding of the drill a more delicate and complicated operation.
[I-275]The keenness and durability of the cutting edge of a twist drill are governed by the amount of clearance given by the grinding to the cutting edge, by the angle of one cutting edge to the other, and by the degree of twist of the flute. Beginning with the angle of the front face, we shall find that it varies at every point in the diameter of the drill, being greatest at the outer corner and least at the centre of the drill, whatever degree of spirality the groove or flute may possess. In Fig. 1045, for example, we may consider the angle at the corner c and at the point f in the length of the cutting edge. The angle or front rake of the corner c is obviously that of the outer edge of the spiral c d, while that of the point f is denoted by the line f f, more nearly parallel to the drill axis, and it is seen that the front rake increases in proportion as the corner c is approached, and diminishes as the drill centre or point is approached.
It follows, then, that if the angle of the bottom face of the drill be the same from the centre to the corner of the drill, and we consider the cutting edge simply as a wedge and independent of its angle presentation to the work, we find that it has a varying degree of acuteness at every point in its length. This may be seen from Fig. 1046, in which the end face is ground at a constant angle from end to end to the centre line of the drill, and it is seen that the angle a represents the wedge at point c and the angle b the wedge at the point f in the length of the cutting edge, and it follows that the wedge becomes less acute as the centre of the drill is approached from the point c. If, then, we give to the end face a degree of clearance best suited for the corner c, it will be an improper one for the cutting edge near the drill point; or if we adopt an angle suitable for the point, it will be an improper one for the corner c.
This corner performs the most cutting duty, because its path of revolution is the longest, or rather of the greatest circumference, and it operates at the highest rate of cutting speed for the same reason, hence it naturally wears and gets dull the quickest.
As this wear proceeds the circumferential surface near this corner grinds against the walls of the hole, causing the drill to heat and finally to cease cutting altogether.
For these reasons it is desirable that the angle of the end face, or the angle of clearance, be made that most suitable to obtain endurance at this corner. It may be pointed out, however, that the angle of one cutting edge to the other, or, what is the same thing, its angle to the centre line of the drill, influences the keenness of this corner. In Fig. 1045, for example, each edge is at an angle of 60° to the drill axis, this being the angle given to drills by the manufacturers as most suitable for general use. In Fig. 1047, the angle is 45°, and it will be clearly seen that the corner c is much less acute; an angle of 45° is suitable for brass work or for any work in which the holes have been cored out and the drill is to be used to enlarge them.
Referring again to the angle of clearance of the end faces, it can be shown that in the usual manner of grinding twist drills the conditions compel the amount of clearance to be made suitable for the point of the drill, and therefore unsuitable for the corner c, giving to it too much clearance in order to obtain sufficient clearance for the remainder of the cutting edge. Suppose, for example, that we have in Fig. 1048 a spiral representing the path of corner c during one revolution, the rate of feed being shown magnified by the distance p, and the spiral will represent the inclination of that part of the bottom of the hole that is cut by corner c, and the angle of the end face of the drill to the drill axis will be angle r. The actual clearance will be represented by the angle between the end face s of the drill and the spiral beneath it, as denoted by t. But if we take the path of the point f, Fig. 1045, during the same revolution, which is represented by the spiral in Fig. 1049, we find that, in order to clear the end of the hole, it must have more angle to the centre line of the drill, as is clearly shown, in order to have the clearance necessary to enable the point f to cut, because of the increased spiral. It follows that, if the same degree of clearance is given throughout the full length of the cutting edge, it must be made suitable for the point of the drill, and will therefore be excessive for the corner c.
This fault is inseparable from the method of grinding drills in ordinary drill-grinding machines, which is shown in Fig. 1050, [I-276] the line a a representing the axis of the motion given to the drill in these machines. It is obvious that the line a a being parallel to the face of the emery-wheel, the angle of clearance is made equal throughout the whole length of the cutting edge. This is, perhaps, made more clear in Fig. 1051, in which we have supposed the drill to take a full revolution upon the axis a a, and as a result it would be ground to the cylinder represented by the dotted lines. We may, however, place the axis on which the drill is moved to grind it at an angle to the emery-wheel face, as at b, Fig. 1052, and by this means we shall obtain two important results: (1) The angle of b may be made such that the clearance will be the same to the actual surface it cuts at every point in the length of the cutting edge, making every point in that length equally keen and equally strong, the clearance being such as it is determined is the most desirable. (2) The clearance may be made to increase as the heels of each end face are approached from the cutting edge. This is an advantage, inasmuch as it affords freer access to the oil or other lubricating or cooling material. If we were to prolong the point of the drill sufficiently, and give it a complete revolution on the axis b, we should grind it to a cone, as shown by the dotted lines in Fig. 1052.
In Fig. 1053 we have a top, and in Fig. 1054 a sectional, view of a conical recess cut by a drill, with a cylinder r lying in the same. p represents in both views the outer arc or circle which would be described by the outer corner, Fig. 1045, of the drill, and q the path or arc described or moved through by the point at f, Fig. 1045, of the drill. At v and w are sectional views of the cylinder r, showing that the clearance is greater at v than at w. The cylinder obviously represents the end of a drill as usually ground. In Figs. 1055 and 1056 we have two views of a cone lying in a recess cut by a drill, the arcs and circles p and q corresponding to those shown in Fig. 1055, and it is seen that in this case the amount of clearance between v and p and between w and q are equal, v representing a cross-section of the cone at its largest end,[I-277] and w a cross-section at the point where the cone meets the circle q. It follows, therefore, that drills ground upon this principle may be given an equal degree of clearance throughout the full length of each cutting edge, or may have the clearance increase or diminished towards the point at will, according to the angle of the line b in Fig. 1052.
In order that the greatest possible amount of duty may be obtained from a twist drill, it is essential that it be ground perfectly true, so that the point of the drill shall be central to the drill and in line with the axis on which it revolves. The cutting edges must be of exactly equal length and at an equal degree of angle from the drill axis. To obtain truth in these respects it is necessary to grind the drill in a grinding machine, as the eye will not form a sufficiently accurate guide if a maximum of duty is to be obtained. The cutting speeds and rates of feed recommended by the Morse Twist Drill and Machine Company are given in the following table.
The following table shows the revolutions per minute for drills from 1⁄16 in. to 2 in. diameter, as usually applied:—
| Diameter of Drills. |
Speed for Steel. |
Speed for Iron. |
Speed for Brass. |
Diameter of Drills. |
Speed for Steel. |
Speed for Iron. |
Speed for Brass. |
||
| inch. | inch. | ||||||||
| 1⁄16 | 940 | 1280 | 1560 | 1 | 1⁄16 | 54 | 75 | 95 | |
| 1⁄8 | 460 | 660 | 785 | 1 | 1⁄8 | 52 | 70 | 90 | |
| 3⁄16 | 310 | 420 | 540 | 1 | 3⁄16 | 49 | 66 | 85 | |
| 1⁄4 | 230 | 320 | 400 | 1 | 1⁄4 | 46 | 62 | 80 | |
| 5⁄16 | 190 | 260 | 320 | 1 | 5⁄16 | 44 | 60 | 75 | |
| 3⁄8 | 150 | 220 | 260 | 1 | 3⁄8 | 42 | 58 | 72 | |
| 7⁄16 | 130 | 185 | 230 | 1 | 7⁄16 | 40 | 56 | 69 | |
| 1⁄2 | 115 | 160 | 200 | 1 | 1⁄2 | 39 | 54 | 66 | |
| 9⁄16 | 100 | 140 | 180 | 1 | 9⁄16 | 37 | 51 | 63 | |
| 5⁄8 | 95 | 130 | 160 | 1 | 5⁄8 | 36 | 49 | 60 | |
| 11⁄16 | 85 | 115 | 145 | 1 | 11⁄16 | 34 | 47 | 58 | |
| 3⁄4 | 75 | 105 | 130 | 1 | 3⁄4 | 33 | 45 | 56 | |
| 13⁄16 | 70 | 100 | 120 | 1 | 13⁄16 | 32 | 43 | 54 | |
| 7⁄8 | 65 | 90 | 115 | 1 | 7⁄8 | 31 | 41 | 52 | |
| 15⁄16 | 62 | 85 | 110 | 1 | 15⁄16 | 30 | 40 | 51 | |
| 1 | 58 | 80 | 100 | 2 | 29 | 39 | 49 | ||
To drill one inch in soft cast iron will usually require: For 1⁄4 in. drill, 125 revolutions; for 1⁄2 in. drill, 120 revolutions; for 3⁄4 in. drill, 100 revolutions; for 1 in. drill, 95 revolutions.
The rates of feed for twist drills are thus given by the same Company:—
| Diameter of drill. |
Revolutions per inch depth of hole. |
|||||||
| 1⁄16 | inch | 125 | ||||||
| 1⁄4 | „ | „ | ||||||
| 3⁄8 | „ | 120 to | 140 | |||||
| 1⁄2 | „ | „ | „ | |||||
| 3⁄4 | „ | 1 inch | feed per | minute | ||||
| 1 | „ | „ | „ | „ | ||||
| 1 | 1⁄2 | „ | „ | „ | „ | |||
Taking an inch drill as an example, we find from this table that the rate of feed is for iron 1⁄100th inch per drill revolution, and as the drill has two cutting edges it is obvious that the rate of feed for each edge is 1⁄200th inch per revolution. But it can be shown that this will only be the case when the drill is ground perfectly true; or, in other words, when the drill is so ground that each edge will take a separate cut, or so that one edge only will cut, and that in either case the rate of feed will be diminished one-half.
In Fig. 1057, for example, is shown a twist drill in which one cutting edge (e) is ground longer than the other, and the effect this would produce is as follows. First, suppose the drill to be fed automatically, the rate of feed being 1⁄100th inch, and the whole of this feed would fall on cutting edge e, and, being double what it should be, would in the first place cause the corner c to dull very rapidly, and in the second place be liable to cause the drill to break when c became dull.
In the second place the drill would make a hole of larger diameter than itself, because the point of the drill will naturally be forced by the feed to be the axis or centre of cutting edge revolution, which would therefore be on the line b b. This would cause the diameter of hole drilled to be determined by the radius of the cutting edge e rather than by the diameter of the drill. Again, the side of the drill in line with corner c would bind against the side of the hole, tending to grind away the clearance at the corner c, which, it has been shown, it is of the utmost importance to keep sharp. But assuming 1⁄200th inch to be the proper feed for each cutting edge, and the most it can carry without involving excessive grinding, then the duty of the drill can only be one-half what it would be were both cutting edges in action.
In Fig. 1058 is shown a twist drill in which one cutting edge is ground longer than the other, and the two cutting edges are not at the same angle to the axis a a of the drill.
[I-278]Here we find that the axis of drill rotation will be on the line b from the point of the drill as before, but both cutting edges will perform some duty. Thus edge e will drill a hole which the outer end of f will enlarge as shown. Thus the diameter of hole drilled will be determined by the radius of corner c, from the axis of drill revolution, and will still be larger than the drill. A drill thus ground would drill a more true and round hole than one ground as in Fig. 1057, because as both cutting edges perform duty the drill would be steadied.
The rate of feed, however, would require to be governed by that length of cutting edge on f that acts to enlarge the hole made by e, and therefore would be but one-half what would be practicable if the drill were ground true. Furthermore, the corner c would rapidly dull because of its performing an undue amount of duty, or in other words, because it performs double duty, since it is not assisted by the other corner as it should be. In both these examples the drill if rigidly held would be sprung or bent to the amount denoted by the distance between the line a a, representing the true axis of the drill, and line b b, representing the line on which the drill point being ground and one-sided compels the drill to revolve; hence one side of the drill would continuously rub against the walls of the hole the drill produced, acting, as before observed, to grind away the clearance that was shown in figure and also to dull corner c.
Fig. 1059 shows a case in which the point of the drill is central to the drill axis d d, but the two cutting edges are not at the same angle. As a result all the duty falls on one cutting edge, and the hole drilled will still be larger in diameter than the drill is, because there is a tendency for the cutting edge e to push or crowd the drill over to the opposite side of the hole.
It will be obvious from these considerations that the more correctly the drill is ground, the longer it will last without regrinding, the greater its amount of feed may be to take an equal depth of cut, and the nearer the diameter of the hole drilled to that of the drill—the most correct results being obtained when the drill will closely fit into the hole it has drilled and will not fall through of its own gravity, a result it is somewhat difficult to attain.
Professor John E. Sweet advocates grinding twist drills as in Fig. 1060 (which is from The American Machinist), the object being to have a keener cutting edge at the extreme point of the drill.
In a paper on cutting tools read before the British Institution of Mechanical Engineers the following examples of the efficiency of the twist drill are given—
Referring to a 1⁄2 inch twist drill, it is said:
“The time occupied from the starting of each hole in a hammered scrap-iron bar till the drill pierced through it varied from 1 minute 20 seconds to 11⁄2 minutes. The holes drilled were perfectly straight. The speed at which the drill was cutting was nearly 20 feet per minute in its periphery, and the feed was 100 revolutions per inch of depth drilled. The drill was lubricated with soap and water, and went clean through the 23⁄4 inches without being withdrawn, and after it had drilled each hole it felt quite cool to the hand, its temperature being about 75°. It is found that 120 to 130 such holes can be drilled before it is advisable to resharpen the twist drill. This ought to be done immediately the drill exhibits the slightest sign of distress. If carefully examined after this number of holes has been drilled, the prominent cutting parts of the lips which have removed the metal will be found very slightly blunted or rounded to the extent of about 1⁄100th inch, and on this length being carefully ground by the machine off the end of the twist drill, the lips are brought up to perfectly sharp cutting edges again.
“The same sized holes, 1⁄2 inch diameter and 23⁄4 inches deep, have been drilled through the same hammered scrap-iron at the extraordinary speed of 23⁄4 inches deep in 1 minute and 5 seconds, the number of revolutions per inch being 75. An average number of 70 holes can be drilled in this case before the drill requires resharpening. The writer considers this test to be rather too severe, and prefers the former speed.
“In London, upward of 3000 holes were drilled 5⁄8 inch diameter and 3⁄8 inch deep through steel bars by one drill without regrinding it. The cutting speed was in this instance too great for cutting steel, being from 18 to 20 feet per minute, and the result is extraordinary. Many thousands of holes were drilled 1⁄8 inch diameter, through cast iron 7⁄16ths inch deep with straight-shank twist drills gripped by an eccentric chuck in the end of the spindle of a quick-speed drilling machine. The time occupied for each hole was from 9 to 10 seconds only. Again, 1⁄4-inch holes have been drilled through wrought copper 13⁄8 inches thick at the speed of one hole in 10 seconds. With special twist drills, made for piercing hard Bessemer steel, rail holes, 13⁄16ths inch deep and 29⁄32nds inch diameter, have been drilled at the rate of one hole in 1 minute and 20 seconds in an ordinary drilling machine. Had the machine been stiffer and more powerful, better results could have been obtained. A similar twist drill, 29⁄32nds inch in diameter, drilled a hard steel rail 13⁄16ths inch deep in 1 minute, and another in 1 minute 10 seconds. Another drill, 5⁄8 inch diameter, drilled 3⁄4 inch deep in 38 seconds, the cutting speed being 22 feet per minute. This speed of cutting rather distressed the drill; a speed of 16 feet per minute would have been better. The steel rail was specially selected as being one of the hardest of the lot.”
Drills ground by hand may be tested for angle by a protractor, as in Fig. 1061, and for equal length of cutting edge by resting them upon a flat surface, as b in Fig. 1062, and applying a scale as at s in the figure. In the case of very small drills, it is difficult to apply either the protractor or the scale, as well as to determine the amount of clearance on the end face. This latter, however, may be known from the appearance of the cutting edge at the point a in Fig. 1063, for if the line a is at a right angle to e, there is no clearance, and as clearance is given this line inclines as shown at b in the figure, the inclination increasing with increased clearance, as is shown at c. When this part of the edge inclines in the opposite direction, as at d in the figure, the curved edges e f stand the highest, and the drill cannot cut. The circumferential[I-279] surface of a drill should never be ground, nor should the front face or straight side of the flute be ground unless under unusual conditions, such as when it is essential, as in drilling very thin sheet metal, to somewhat flatten the corner (c in Fig. 1062), in order to reduce its tendency to run forward, in which case care must be taken not to grind the front face sufficiently to reduce the full diameter. In Fig. 1064, for example, that part of the circumference lying between a and b being left of full circle, the faces of the flutes might be ground away as denoted by the dotted lines c d without affecting the drill diameter.
Fig. 1065 represents the Farmer lathe drill, in which the flutes are straight and not spiral, by which means the tendency to run forward when emerging through the work is obviated.
When a twist drill is to be used for wood and is driven by a machine it is termed a bit, and is provided with a conical point to steady it, and two wings or spurs, as in Fig. 1066, which sever the fibres of the wood in advance of their meeting the main cutting edges and thus produce a smooth hole. The sharp conical point is used in place of the conical screw of the ordinary wood auger to avoid the necessity of revolving the drill or bit backwards to release the screw in cases in which the hole is not bored entirely through the work.
When the drill revolves and the work is to be held in the hands a rest or table whereon to rest the work and hold it fair is shown in Fig. 1067, the taper shank fitting in the dead centre hole and the tailstock spindle being fed up by hand to feed the drill to its cut. The face a a of the chuck is at a right angle to the shank, and a coned recess is provided at the centre, as denoted by the dotted lines, to permit the drill point to pass through the work without cutting the chuck.
For larger work a table, such as shown in Fig. 1068, is used, the cavity c permitting the drilling tool to pass through the work, there being a hole h provided for that purpose. The stem s fits in place of the dead centre. For cylindrical work the rest or chuck shown in Figs. 1069 and 1070 may be employed. It consists of a piece fitted to the tail spindle in place of the dead centre, its end being provided with V-grooves. These grooves are made true with the line of centres of the lathe, so that when the work is laid in them it will be held true. It is obvious that one groove would be sufficient, but two are more convenient—one[I-280] for large work and one for small work—so that the side of the shaft to be drilled shall not pass within the fork, but will protrude, so that the progress of the work can be clearly seen. In Fig. 1070 an end view of this chuck is shown. It may be observed, however, that when starting the drill care must be taken to have it start true, or the drill may bend, and thus throw the work out of the true. For this reason the drills should be as short as possible when their diameters are small.
For square work this class of work table or chuck may be formed so as to envelop the work and prevent its revolving, thus relieving the fingers of that duty, and it may be so formed as to carry the work back or off the drill when the latter is retired after the drilling is performed.
Another and quite convenient method of holding work to be drilled by a revolving drill in the lathe is shown in Fig. 1071. It consists of simply a bracket, a b, fitted to the tool-box of the slide rest, carrying a spindle with one end screwed to receive any face plates or chucks that fit the lathe live spindle. The bracket is kept in position by two pins in the under side of it, fitting into holes in the bottom piece of tool-box. If it be required to drill a straight row of holes, the spindle is fixed by the set-screws in its bracket, and the work is bolted to the face plate at the proper level, and traversed across opposite the drill in the lathe mandrel, by the cross screw of the slide rest, while it is fed up to the drill by the upper screw or the rack and pinion.
For circular rows of holes the centre line of the spindle is adjusted parallel with and at a proper distance from that of the mandrel. For holes in the edge of the work, the whole top of slide rest is turned round till the spindle is at right angles with the mandrel.
Work merely requiring to be held fast for drilling is bolted on one side of the face plate, and can then be adjusted exactly to the drill by the combined motions of the cross screw and the face plate on its centre. Small round work, while drilled in the end, can be held in a scroll chuck screwed on the spindle the same as a face plate.
The convenience of this device consists in this, that the work turned on the chuck may be drilled without moving it from the chuck, which may be so set as to cause the drilled holes to be at any required angle to the work surface, which is quite difficult of accomplishment by other ordinary means.
On account of the readiness with which a flat drill may be made to suit an odd size or employed to recess work with a flat or other required shape of recess, flat drills are not uncommonly used upon lathe work, and in this case they may be driven in the drill chucks already shown. A very convenient form of drill chuck for small drills is shown in Fig. 1072. It consists of a cylindrical chuck fitting from a to b into the coned hole in the live spindle so as to be driven thereby. At the protruding end c there is drilled a hole of the diameter of the wire forming the drill. At the end of this hole there is filed a slot d extending to the centre of the chuck. The end of the drill is filed half round and slightly taper, as shown in Fig. 1073 at d, so that the half-round end of the drill will pass into the slot of the chuck, therefore forming a driving piece which effectually prevents the drill from slipping, as is apt to occur with cylindrical stem or shank drills. If one size of wire be used for all drills, and the drill size be determined by the forging, the drill will run true, being held quite firmly, and may be very readily inserted in or removed from the chuck.
But the flat drill possesses several disadvantages: thus, referring to figure, it must be enough smaller at a than at b to permit the cuttings to find egress, and this taper causes the diameter of the drill to be reduced at each drill grinding. The end b may, it is true, be made parallel for a short distance, but in this case the cuttings will be apt to clog in the hole unless the drill be frequently removed from deep holes to clear the cuttings. For these reasons the fluted drill or the twist drill is preferable, especially as their diameters are maintained without forging. For deep holes, as, say, those having a depth equal to more than twice the diameter, the flat drill, if of small diameter, as, say, an inch or less, is unsuitable because of the frequency with which it must be removed from the hole to clear it of cuttings.
For fluted or twist drills the lathe may run quicker than for a flat drill, which is again an advantage. It sometimes becomes convenient in the exigencies which occur in the work of a general machine shop to hold a drill in a dog or clamp and feed it into the work with the lathe dead centre. In this case the drill should be held very firmly against the dead centre, or otherwise the drill may, when emerging through the back of the hole, feed itself forward, slipping off the dead centre, and causing the drill to catch and break, or moving the work in the chuck, to avoid which the drill should have a deep and well countersunk centre.
A very effective drill for holes that are above two inches in diameter and require enlarging is shown in Fig. 1074. It consists of a piece of flat steel a, with the pieces of wood b fastened on the flat faces, the wood serving to steady the drill and prevent it from running to one side in the work. This drill is sometimes used to finish holes to standard size, in which case the hole to be bored or drilled should be trued out a close fit to the drill for a distance equal to about the diameter of the drill, and the face at the entrance of the hole should be true up. This is necessary to enable the drill to start true, which is indispensable to the proper operation of the drill.
This drill is made by being turned up in the lathe, and should have at the stock end a deep and somewhat large centre, so that[I-281] when in use it may not be liable to slip off the dead centre of the lathe. The drill is held at the stock end by being placed in the lathe dead centre and is steadied, close to the entrance of the hole in the work, by means of a hook which at one end embraces the drill, as shown in Fig. 1075, in which a represents the hook and b the drill.
This drill will bore a parallel hole, but if the same be a long or a deep one it is apt to bore gradually out of true unless the bore of the hole is first trued from end to end with a boring tool before using the drill. It is often employed to enlarge a hole so as to admit a stout boring tool, and to remove the hard surface skin from which the boring tool is apt to spring away.
Half-round Bit or Pod Auger.—For drilling or enlarging holes of great depth (in which case it is difficult to drill straight holes with ordinary drills), the half-round bit—Figs. 1076 and 1077—is an excellent tool. Its diameter d is made that of the required hole, the cutting being done at the end only from a to b, from b to c being ground at a slight angle to permit the edge from a to b to enter the cut. When a half-round bit is to be used on iron or steel, and not upon brass, it may be made to cut more freely by giving the front face rake as at e f, Fig. 1078.
To enable a bit of this kind to be adjusted to take up the wear, it may be formed as in Fig. 1079, in which a quarter of the circumference is cut away at a, and a cutter c is bolted in position projecting into a recess at b to secure the cutter in addition to the bolts. Pieces of paper may be inserted at b to set out the cutter.
An excellent form of boring bar and cutter is shown in Figs. 1080 and 1081.
Fig. 1082 shows a side view of the cutter removed from the bar; Fig. 1081 an end, and Fig. 1080 a side view of the bar and cutter. The cutter is turned at a and b to fit the bore of the bar. The cutting edge c extends to the centre of the bar, while that at d does not quite reach the centre. These edges are in a line as shown in the end view. On account of the thickness of the cutter not equaling the diameter of the bore through the bar there is room for a stream of water to be forced through the bar, thus keeping it cool and forcing out the cuttings which pass through the passages g and h in the bar. The cutter drives lightly into the bar. By reason of one cutting edge not extending clear to the centre of the cutter there is formed a slight projection at the centre of the hole bored which serves as a guide to keep the cutter true, causing it to bore the hole very true.
For finishing the walls of holes more true, smooth, and straight, and of more uniform diameter than it is found possible to produce them with a drill, the reamer, or rymer, is employed. It consists of a hardened piece of steel having flutes, at the top of which are the cutting edges, the general form of solid reamer for lathe work being shown in Fig. 1083. The reamer is fed end-ways into the work at a cutting speed of about 15 to 18 feet per minute.
The main considerations in determining the form of a reamer are as follows:—
1. The number of its cutting edges.
2. The spacing of the teeth.
3. The angles of the faces forming the cutting edges.
4. Its maintenance to standard diameter.
As to the first, it is obvious that the greater the number of cutting edges the more lines of contact there are to steady it on the walls of the hole; but in any case there should be more than three teeth, for if three teeth are used, and one of them is either relieved of its cut or takes an excess of cut by reason of imperfections in the roundness of the hole, the other two are similarly affected and the hole is thus made out of round.
[I-282]An even number of teeth will not work so steadily as an odd one, for the following reasons.
In Fig. 1084 is represented a reamer having 6 teeth and each of these teeth has a tooth opposite to it; hence, if the hole is out of round two teeth only will operate to enlarge its smallest diameter. In Fig. 1085 is a reamer having 7 teeth, and it will be seen that if any one tooth cuts there will be two teeth on the opposite side of the reamer that must also cut; hence, there are three lines of contact to steady the reamer instead of two only as in the case of the 6 teeth. An even number of teeth, however, may be made to operate more steadily by spacing the teeth irregularly, and thus causing three teeth to operate if the hole is out of round. Thus, in Fig. 1086 the teeth are spaced irregularly, and it will be seen that as no two teeth are exactly opposite, if a tooth on one side takes a cut there must be two on the opposite side that will also cut. The objection to irregular spacing is that the diameter of the reamer cannot be measured by calipers. Another method of obtaining steadiness, however, is to make the flutes and the cutting edges spiral instead of parallel to the axis, but in this case the spiral must be left-handed, as in Fig. 1087, or else the cutting edges acting on the principle of a screw thread will force the reamer forward, causing it to feed too rapidly to its cut. If, however, a reamer have considerable degree of taper, it may be given right-hand flutes, which will assist in feeding it.
Referring to the second, the spacing of the teeth must be determined to a great extent by the size of the reamer, and the facility afforded by that size to grind the cutting edges to sharpen them.
The method employed to grind a reamer is shown in Fig. 1088, in which is shown a rapidly-revolving emery-wheel, above the reamer, and also a gauge against which the front face of each tooth is held while its top or circumferential face is being sharpened. The reamer is held true to its axis and is pushed end-ways beneath the revolving emery-wheel. In order that the wheel may leave the right-hand or cutting edge the highest (as it must be to enable it to cut), the axis of the emery-wheel must be on the left hand of that of the reamer, and the spacing of the teeth must be such that the periphery of the emery-wheel will escape tooth b, for otherwise it would grind away its cutting edge. It is obvious, however, that the less the diameter of the emery-wheel the closer the teeth may be spaced; but there is an objection to this, inasmuch as that the top of the tooth is naturally ground to the curvature of the wheel, as is shown in Fig. 1089, in which two different-sized emery-wheels are represented operating on the same diameter of reamer. The cutting edge of a has the most clearance, and is therefore the weakest and least durable; hence it is desirable to employ as large a wheel as the spacing of the teeth will allow, there being at least four teeth, and preferably six, on small reamers, and their number increasing with the diameter of the reamer.
It would appear that this defect might be remedied by placing the emery-wheel parallel to the teeth as in Fig. 1090; but if this were done, the wear of the emery-wheel would cause the formation of a shoulder at s in the figure, which would round off the cutting edge of the tooth. This, however, might be overcome by giving the emery-wheel enough end motion to cause it to cross and recross the width of the top facet; or the reamer r may be presented to the wheel w at an angle to the plane of wheel rotation, as in Fig. 1091, which would leave a straight instead of a curved facet, and, therefore, a stronger and more durable cutting edge.
Another method of accomplishing the same object would be to mount the emery-wheel as in Fig. 1092, using its side face, which might be recessed on the side, leaving an annular ring of sufficient diameter to pass clear across the tooth, and thus prevent a shoulder from forming on the side face of the wheel.
Yet another method is to use an emery-wheel bevelled on its edge, and mount it as in Fig. 1093, in which case it would be preferable to make the bevel face narrow enough that all parts would cross the facet of the tooth.
Referring to the third, viz., the angles of the faces forming the cutting edges, it is found that the front faces, as a and b in Fig. 1094, should be a radial line, for if given rake as at c, the tooth will spring off the fulcrum at point e in the direction of d, and cause the reamer to cut a hole of larger diameter than itself, an action that is found to occur to some extent even where the front face is a radial line. As this spring augments with any increase[I-283] of cut-pressure, it is obvious that if a number of holes are to be reamed to the same diameter it is essential that the reamer take the same depth of cut in each, so that the tooth spring may be equal in each case. This may be accomplished to a great extent by using two reamers, one for equalizing the diameters of the holes, and the other for the final finishing. The clearance at the top of the teeth is obviously governed by the position of the reamer with relation to the wheel, and the diameter of the wheel, being less in proportion as the reamer is placed farther beneath the wheel, and the wheel diameter is increased. In some forms of reamer the teeth are formed by circular flutes, such as at h in Fig. 1094, and but three flutes are used. This leaves the teeth so strong and broad at the base that the teeth are not so liable to spring; but, on the other hand, the clearance is much more difficult to produce and to grind in the resharpening.
As to the maintenance of the reamer to standard diameter, it is a matter of great importance, for the following reasons: The great advantage of the standard reamer is to enable holes to be made and pieces to be turned to fit in them without requiring any particular piece to be fitted to some particular hole, and in order to accomplish this it is necessary that all the holes and all the pieces be exactly alike in diameter. But the cutting edges of the reamer begin to wear—and the reamer diameter, therefore, to reduce—from the very first hole that it reams, and it is only a question of time when the holes will become too small for the turned pieces to enter or fit properly. In all pieces that are made a sliding or a working fit, as it is termed when one piece moves upon the other, there must be allowed a certain latitude of wear before the one piece must be renewed.
One course is to make the reamer when new enough larger than the proper size to bore the holes as much larger as this limit of wear, and to restore it to size when it has worn down so that the holes fit too tightly to the pieces that fit them. But this plan has the great disadvantage that the pieces generally require to have other cutting operations performed on them after the reaming, and to hold them for these operations it is necessary to insert in them tightly-fitting plugs, or arbors, as they are termed. If, therefore, the holes are not of equal diameter the arbor must be fitted to the holes, whereas the arbor should be to standard diameter to save the necessity of fitting, which would be almost as costly as fitting each turned piece to its own hole. It follows, therefore, that the holes and arbors should both be made to a certain standard, and the only way to do this is to so construct the reamer that it may be readily adjusted to size by moving its teeth.
It is obvious that a reamer must, to produce parallel holes, be held axially true with the holes, or else be given liberty to adjust itself true. Fig. 1095 shows a method of accomplishing this object. The reamer is made to have a slight freedom or play in the sleeve, being 1⁄32 inch smaller, and the hole for the pin is also made large so that the reamer may adjust itself for alignment.
For short holes the shell reamer shown in Fig. 1096 may be employed. Its bore is coned so that it will have sufficient friction upon its driving arbor to prevent its coming off; when it is to be withdrawn from the work it is provided with two slots into which fit corresponding lugs on the driving arbor. Fig. 1097 shows the Morse Twist Drill and Machine Company’s arbor.
The rose reamer, or rose bit, has its cutting edges on the end only, as shown in Fig. 1098, the grooves being to supply lubricating material (as oil or water) only, and, as a result, will bore a more parallel hole than the ordinary reamer in cases in which the reamer has liberty to move sideways, from looseness in the mechanism driving it. Furthermore, when the work is composed of two parts, the outer one, through which the reamer must pass before it meets the inner one, guides the reamer without becoming enlarged by reason of the reamer having cutting edges, which is especially advantageous when the inner hole requires to be made true with the outer one, or in cases where a piece has two holes with a[I-284] space between them, and one hole requires to be made true with the other, and both require to be made to the same diameter as the reamer.
Fig. 1099 represents the Morse Twist Drill Company’s shell rose reamer for short holes, corresponding in principle to the solid rose reamer, but fitting to an arbor for the same purposes as the shell reamer.
Instead of having upon a reamer a flat tooth top to provide clearance, very accurate and smooth work may be produced by letting the back of the tooth, as a in Fig. 1100, proceed in a straight line to b, leaving the reamer, when soft, too large, so that after hardening it may be ground by an emery-wheel to size; and the clearance may be given by simply oilstoning the top of each tooth lengthwise, the oilstone marks barely effacing the emery marks at the cutting edge and removing slightly more as the back of the tooth is approached from the cutting edge. This produces cutting edges that are very easily fed to the cut, which must obviously, however, be a light one, as should always be the case for finishing, so that the wear of the teeth may be a minimum, and the reamer may therefore maintain its standard diameter as long as possible.
When a solid reamer has worn below its required diameter, the same may be restored by upsetting the teeth with a set chisel, by driving it against the front face; and in determining the proper diameter for a reamer for work to be made to gauge under the interchangeable system the following considerations occur.
Obviously the diameter of a reamer reduces as it wears; hence there must be determined a limit to which the reamer may wear before being restored to its original diameter. Suppose that this limit be determined as 1⁄1000 inch, then as the reamer wears less in diameter the bolts to fit the holes it reams must also be made less as the reamer wear proceeds, or otherwise they will not enter the reamed holes. But it is to be observed that while the reamer wears smaller, the standard gauges to which the pins or bolts are turned wear larger, and the wear is here again in a direction to prevent the work from fitting together. It is better then to make the reamer when new too large to the amount that has been determined upon as the limit of wear, so that when the work begins to go together too tight, the reamer requires resharpening and restoring.
A still better plan, however, is to use reamers adjustable for diameter, so that the wear may be taken up, and also the reamer sharpened, without being softened, which always deteriorates the quality of the steel.
Reamers that are too small to be made adjustable for size by a combination of parts may be constructed as in Fig. 1101, in which the reamer is drilled and threaded, and countersunk at the end to receive a taper-headed screw s, which may be screwed in to expand the reamer, which contains three longitudinal splits to allow it to open. To cause s to become locked in its adjusted position a plug screw p is inserted for the end of s to abut against. It is obvious that in this form the reamer is expanded most at the end.
Fig. 1102 represents a single-tooth adjustable reamer, in which the body a is ground to the standard diameter, and the wear of the cutter c is taken up by placing paper beneath the cutter. In this case the reamer cannot, by reason of the wear of the cutting edge, ream too small, because the body a forms a gauge of the smallest diameter to which the reamer will cut. The cutter may, however, be set up to the limit allowed for wear of cutting edge, which for work to fit should not be more than 1⁄5000 inch.
An adjustable reamer designed and used by the author for holes not less than 11⁄2 inches in diameter, is shown in Fig. 1103, in which a represents the body of the reamer containing dovetail grooves tapered in depth with the least depth at the entering end. The grooves receive cutters b, having gib heads. c is a ring or washer interposed between the gib heads of the cutter and the face or shoulder of a, the cutters being locked against that face by a nut and a washer e. By varying the thickness of c, the cutters are locked in a different position in the length of the grooves, whose taper depth therefore causes the cutters to vary in diameter. Suppose, for example, that with a given thickness of washer c, the cutters are adjusted in diameter so as to produce a hole a tight working fit to a plug turned to a 2-inch standard gauge: a slightly thinner washer may be used, setting the cutters so as to bore a hole an easy working fit to the plug; or a slightly thicker washer may be employed so as to produce a hole a driving fit to the same plug. Three or more washers may thus be used for every standard size, their thickness varying to suit the nature of the fit required.
It will be noted that it is mentioned that three or more washers may be used, and this occurs because a diameter of fit that would be a driving fit for a hole of one length would be too tight for a driving fit of a much longer hole, the friction of course increasing with the length of hole, because of the increase of bearing area.
For large sizes, a reamer of this description is an excellent tool, because if it be required to guide the reamer by means of a plain cylindrical shank, a washer, or sleeve, having a bore to fit the shank at the termination of the thread, may be used, but such a[I-285] reamer is not suitable for small diameters, because of the reduction of shank necessary to provide for the nut and thread.
Reamers for roughing out taper holes may be made with steps, as in Fig. 1104, which is taken from The American Machinist, there being a cutting edge where each step meets a flute. Such a reamer may be used to enlarge parallel holes, or to rough out taper ones, and the flutes (if not to be used for brass work) may be spiral, as in the figure. The end step being guided by the hole serves as a guide to the first cutting edge; the second step serves as a guide for the cutting edge that follows it, and so on.
The steps are best turned a trifle larger, say 1⁄1000 inch larger, at the cutting end. Half-round taper reamers, such as shown in Fig. 1105, are used for finishing holes. The flat face is cut down, leaving rather more than a half circle; the clearance being filed or ground on the cutting side so as to enable the reamer to cut, and extending from the cutting edge to nearly half-way to the bottom of the reamer.
For holes, however, that are large enough to admit a tool of sufficient strength, the single-pointed boring tool produces the most true work.
Brass finishers use square taper reamers, which produce upon brass more true work than the half-round reamer.
For reaming the bores of rifles, a square reamer, such as shown in Fig. 1106, is employed; the edges a b are the cutting ones, the edges c d being rounded off; e is a piece of wood, beneath which slips of paper are placed to restore the size as the wear proceeds. The entering end of the reamer is slightly tapered. On account of the extreme length of this reamer in proportion to its diameter, it is fed to its cut by being pulled instead of pushed as is usually the case, the pull placing the rod of the reamer under tension and thus stiffening it; the line of pull is of course true with the axis of the rifle bore. The reamer is revolved at high speed and freely supplied with oil.
By means of the slips of paper successive cuts and minute increases of diameter may be taken with the same reamer.
Fig. 1107 represents a class of rose bit employed to reduce pins to a uniform diameter, and face off the shoulder under the head, or it may be used to cut a recess round a pin, or to cut a recess and leave a pin.
For making a recess round a hole, or, in other words, for cutting a flat-bottom countersink, a facing countersink, Fig. 1108, may be used, its cutting edges being at a, b, c, &c. The clearance is given at the ends of the teeth only, being shown from b to d. The pin p steadies the tool, and is made a working fit to the hole in the work. Or if too small, a ferrule may be placed upon it, thus increasing the capacity of the tool. When a tool of this kind is to be used on iron, steel, or copper, and not upon brass, the front face of the teeth may be given rake by cutting the grooves at an angle, as in Fig. 1109.
Boring Tools for Lathe Work.—The principal object in forming a boring tool to be held in a slide rest is to have the body of the tool as large as can be conveniently got into the size of the hole to be bored; hence the cutting edge should not stand above the level of the top of the steel. By this means the tool will be as stiff as possible, and less liable to spring away from its cut, as boring tools are apt to do, especially when the cut or hole is a long one.
It is so difficult a matter to bore a long hole parallel with a long boring tool that cutters of various forms are usually preferred, and these will be described hereafter.
The boring tool is, upon cast iron and brass, exceedingly liable to chatter, but this may always be avoided by making the angles forming the cutting edge less acute: thus, in Fig. 1110 are three boring tools, a, b, c, operating in a piece of work d. Now the lateral pressure of a cut is exerted upon the tool at a right angle to the length of the cutting edge; hence (in addition to the vertical pressure) the lateral pressure of the tool a will be in the direction of the dotted line and arrow a, that on b in the direction of dotted line and arrow b, and that on c in the direction of dotted line and arrow c; hence the pressure of the cut would tend to force a towards the centre of the hole and off or away from its cut, b back from its cut, and c deeper into its cut. Now as the cut proceeds, the tool edge dulls, hence it would appear that a compromise between c and b would be the most desirable, as giving to the tool enough of the tendency to deepen its cut to compensate for the tendency to spring away from its cut, as the cutting edge dulls (which it does from the moment the cut begins).[I-286] This is quite practicable in tools to be used on wrought iron, as shown in Fig. 1111, which represents the most desirable form.
In this form the part of the cutting edge performing duty under a deep cut will be mainly in front of the tool, but in light cuts the cutting edge would be farther back, where it is more nearly parallel to the line of the work bore, and will hence cut smoother.
Where a boring tool is intended for light cuts only on wrought iron it may have all, or nearly all, its rake at the top, as shown in Fig. 1112, from a to b representing the cut, and c the tool.
Under ordinary conditions that in the form of tool shown in Fig. 1113[15] is best for brass work, the face a being horizontal or slightly depressed towards the point. Boring tools require very little bottom rake, and the cutting points should be as rounded as they can be made without chattering. On wrought iron the top rake may be as much as is consistent with strength, and water should be freely applied to the cut. For cast iron the best form of tool is that shown in Fig. 1114, the edge a being parallel with the bore of the hole, and the feed being a coarse one, taking a very light cut when finishing.
[15] From “The Complete Practical Machinist.”
In cases, however, where the tool point requires to cut up to a sharp corner, the form of tool shown in Fig. 1115 (which represents a top and end view) may be used. Its end face c is at an obtuse angle to the length of the tool, so that on passing up a bore and meeting a radial face the point only will meet that face. This angle, however, gives to the tool a keenness that will cause chattering on brass work unless the top face be bevelled to the tool body, as is a to b in the figure.
It frequently happens in boring cast iron that the skin or the surface of the metal is very hard, rapidly dulling the tool and forcing it away from its cut, unless the cut is deep enough to allow the point of the tool to cut beneath it, as shown in Fig. 1116, in which the hardness is supposed to extend from the bore to the dotted line.
In this case a tool formed as at c is employed, the point cutting in advance of the rest of the tool, and entering the soft metal beneath the hard metal; the hard metal will then break away in lumps or pieces, without requiring to be absolutely cut into chips or turnings, because of being undercut, as shown at b.
The cross slider or tool rest of a lathe should be adjusted to closely fit the cross slide of the lathe if true and parallel work is to be bored, because any lost motion that may exist in the slide is multiplied by the length the tool stands out from the tool post. Thus the centre of motion of the rest if it has play, as at b, Fig. 1117, and the direction of motion at the tool point, will be an arc of a circle of which b is the centre, the bend of the tool from the pressure of the cut will have its point of least motion or fulcrum at a; hence, both tend to cause the tool point to dip and spring unequally under the varying cut pressure that may arise from hard or soft places in the metal, and from inequalities in the cut depth.
The pressure of the cut increases as the tool point loses its sharpness, and this makes sufficient difference for the amount of tool spring in light boring tools or in long holes to cause the tool to bore a larger hole at the beginning than it does at the end of its feed traverse; or, in other words, to bore a taper hole, whose largest end is that at which the cut was started. If, therefore, the cut is traversed from the front to the back of the hole the latter will be of the smallest diameter at the back, and conversely if the cut proceeds from the back to the front of the hole the front will be of smallest diameter. The amount of the taper so caused (or in other words the error from parallelism) will obviously increase with the length of the hole.
To obviate this taper, the slide of the rest should for the finishing cut be set up firmly, and the tool after being sharpened should take a finishing cut through the hole, and then let traverse back, which can be done providing that care be taken not to bore the hole too large.
A boring tool will take a smoother cut and chatter less if the final cut be from the back to the front of the hole, and for the following reasons: When the tool is fed in, the strain or pressure of the cut is in a direction to partly compress and partly bend the steel which is being pushed to its cut, but when it is fed in the opposite direction it is pulled to its cut and the strain is in a direction to stretch the steel, and this the tool is more capable of resisting, hence it does not so readily vibrate to cause chattering.
In consequence, however, of the liability of a boring tool to spring away from its cut, it is far preferable to finish holes with standard cutters, reamers, or bits, in which case the boring tool may be[I-287] employed to rough out and true up the hole, leaving a fine cut for the finishing cutter or bit, so as to wear its cutting edge as little as possible. To further attain this latter object, the cutter or bit should be used at a slow cutting speed and with a coarse feed.
If cutters or bits are not at hand, tool holders are desirable, and the forms of these depend upon the nature, or rather the diameter, of the hole to be bored. In all cases, however, the best results will be obtained when the diameter of the tool holder is as near that of the hole to be bored as will give it clearance. This occurs on account of the rigidity of the holder being greater than that of the tool.
For large work tool holders are desirable, in that the tools, being short, are easier to forge, to handle, and to grind.
For example, a tool holder of a cross section of two inches square may contain a tool whose cross section is 1 by 3⁄4 inch, in which case it is necessary to forge, grind, &c., the small tool only, whereas in the absence of the holder the tool would require to be of a cross section equal to that of the holder to obtain an equal degree of rigidity.
A boring tool holder suitable for holes of from 2 to 4 or 5 inches is shown in Fig. 1118, in which a represents a round bar shaped at the end b to fit into the tool post of the slide rest, and having a groove across the diameter of the end c d to receive a short tool. The slot and tool may be either square or V-shaped, the tool being locked by a wedge. It is obvious that instead of shaping the end b as shown, the bar may be held (if the slide-rest head is provided with a clamp instead of a tool post) by two diametrically opposite flat faces.
For holes of a greater diameter a holder such as shown in Fig. 1119 should be used, the body being a square bar, and the tool being held in the box a a by two set screws b. For holes of small diameter, as, say, less than 11⁄2 inches, a tool holder is especially desirable, because when a boring tool is forged out of a piece of tool steel, its length is determined, and in order to have tools suitable for various depths of hole a number of tools of varying lengths are requisite. Suppose, for example, that a piece of steel be forged into a boring tool suitable for a hole of an inch diameter, and 4 inches deep, then the steel must be forged round for a distance of at least 4 inches from the cutting end, and if such a tool were applied to a hole, say, two inches deep, the cutting edge would stand out from the tool post at least two inches more than is necessary, which would cause the employment of a tool weaker than necessary for the work. To enable the use of one tool for various depths of work, and yet hold it in each case as close to the tool post as the work depth admits, tool-clamping devices, such as in Fig. 1120 (which are extracted from The American Machinist), are employed. 1 and 2 are pieces of steel fitting in the tool post and clamping the tool, which for very small holes is made of octagon or round forged steel. The tool may be passed to any required distance through the clamp, so as to project only to the amount necessary for the particular depth of hole requiring to be bored. These clamping pieces 1 and 2 should bed upon the tool fairly along their full length; or, what is better, they may bed the firmest at their extremities, which will insure that the tool is gripped firmly as near to the cutting edge as possible.
In place of a steel tool, a tool holder turned cylindrically true and parallel may be used to carry a short boring tool, as shown in Fig. 1121, in which a is the tool secured by the set-screw b into the holder c. The latter may be provided with a line running true longitudinally, and may have a fine groove similar to a thread, and having a pitch measuring some part of an inch, as 1⁄8, 1⁄4, 1⁄2 inch, &c., so that the distance the tool projects from the holder may be known without measuring the same. But when a tool and holder of this description are used, the tool cannot be employed unless the hole passes entirely through the work, which occurs because of the presence of the set-screw b.
It is obvious that for a tool-holding bar such as this, a clamping device such as shown in Fig. 1120 is requisite, and that the position of the clamping device may be adjusted to suit the work by setting it more or less through the tool post.
The manner in which the deflection of a boring tool will affect the bore of the work depends upon the height of the boring tool in the work. If the tool is above the horizontal centre of the work, as in Fig. 1122, the spring vertically will cause it to leave the cut, and bore the hole to a corresponding amount smaller; and since the tool gets duller as the wear proceeds, it will spring more at the[I-288] latter end of each tool traverse, leaving the end of the hole last cut of smallest diameter.
If, on the other hand, the tool be below the horizontal centre, as in Fig. 1123, the vertical spring will be in a direction to increase the amount of the cut, and thus offset the tapering effect of the increased tool spring due to the wear of the tool. Furthermore, the shaving will be easier bent if the tool be below than if above the horizontal centre, because the metal will be less supported by the metal behind it. It is always desirable therefore to have the cutting edge of a boring tool used on small work below rather than above the horizontal centre of the work. On large work, however, as say, having a bore of 6 inches and over, the curve of the bore in the length of the circumference affected by the cut or bending of the cut is so small, that the height of the tool is of less consequence.
To enable the use of a stout-bodied boring tool, while keeping its cutting edge below the centre, the top face of the tool may be depressed, as shown in Fig. 1123.
An excellent attachment for boring parallel holes is shown in Figs. 1124 and 1125, in which there is fixed to the cross slide a the bracket b, which is bored to receive a number of bushes c, whose bores are made to suit varying diameters of boring-bars or reamers d. The hub of the bracket is split on one side to enable it to be closed (by the bolt e) upon the bush c and grip it firmly, the bush also being split at f. The bracket b is provided with a taper pin g, which brings it in position upon the slide so that the bushes c are true with the line of lathe centres. It is also provided with the screws h, which lock it firmly to the cross slide and prevent any spring or movement from play or looseness.
When the bracket is adjusted and the bar fastened up (by screw e), the lathe-carriage feeds the boring tool to the cut in the usual manner. Now suppose that, as shown in our illustrations, a pulley p requires to be bored, and the boring tool or reamer may be set to have its cutting end stand out just as far as the length of the hub requires, and no farther, so that the bar will be held and supported as close to the pulley hub as is possible from the nature of the job. There need not be a separate bush for every size of reamer, because the bodies of several size bars may fit to one size of bush, especially if the set of reamers for every size of bush be made with its smallest size equal to the bore of the bush; because in that case the whole of the set may be adjusted to bore any required depth of hole by sliding the reamer through the bush to the required distance. If there are a number of lathes in a shop, each lathe may have its own bracket b, all these brackets being bored to receive the same bushes, and therefore the same boring-bars or reamers.
A bracket or stand of this kind may obviously be used to carry a bar, having a head such as is shown in Fig. 1126, each dovetail groove carrying a cutting tool, and for wrought iron or steel work these grooves may be at an angle to the bar axis, as in the figure, to give each cutter front rake, and increase its keenness.
Boring Bars for Lathe Work.—Boring bars for lathe work are of two kinds, those in which the cutters are held in a fixed position in the length of the bar, and those in which the cutters are held in a head which traverses along the work. The former[I-289] are the least desirable, because they require to be more than twice the length of the work, which must be on one side of the cutter at the commencement of the cut, and on the other at the termination of the same. But to traverse the head carrying the tools along the bar necessitates a feed screw either within the bar or outside of it. If within, the metal removed to give it place weakens the bar, while in small holes there is no room for it; hence solid bars with fixed cutting tools are used for small holes, and tools held in a traversing head for those sufficiently large to give room for a head without weakening the bar too much. A boring bar is best driven from both ends.
“The boring bar is one of the most important tools to be found in a machine shop, because the work it has to perform requires to be very accurately done; and since it is a somewhat expensive tool to make, and occupies a large amount of shop room, it is necessary to make one size of boring bar answer for as many sizes of hole as possible, which end can only be attained by making it thoroughly stiff and rigid. To this end a large amount of bearing and close fitting, using cast iron as the material, are necessary, because cast iron does not spring or deflect so easily as wrought iron; but the centres into which the lathe centres fit are, if of cast iron, very liable to cut and shift their position, thus throwing the bar out of true. It is, therefore, always preferable to bore and tap the ends of such bars, and to screw in a wrought-iron or steel plug, taking care to screw it in very tightly, so that it shall not at any time become loose. The centres should be well drilled and of a comparatively large size, so as to have surface enough to suffer little from wear, and to well sustain the weight of the bar. The end surface surrounding the centres should be turned off quite true to keep the latter from wearing away from the high side, as they would do were one side higher than the other.”[16]
[16] From “The Complete Practical Machinist.”
The common form of the smaller sizes of boring bar is that shown in Fig. 1127. a a being the bar, d d the lathe centres, b the cutter passing through a slot or keyway in the bar, and c a key tapered (as is also the back edge of the cutter) to wedge or fasten the cutter to the bar. It is obvious that, if the cutter is turned up in the bar, and is of the exact size of the hole to be bored, it will require to stand true in the bar, and will therefore be able to cut on both ends, in which case the work may be fed up to it twice as fast as though only one edge were performing duty. To facilitate setting the cutter quite true, a flat and slightly taper surface should be filed on the bar at each end of the keyway, and the cutter should have a recess filed in it, as shown in Fig. 1128, the recess being shown at a, and the edges b b forming the diameter of the cutters. The backing off is shown at c, from which it will be observed that the cutting duty is performed by the edge c, and not along the edge b, further than is shown by the backing off. The recess must be made taper, and to fit closely to the flat places filed on the bar. Such a cutter, if required to be adjustable, must not be provided with the recess a, but must be left plain, so that it may be made to extend out on one side of the bar to cut any requisite size of bore; it is far preferable, however, to employ the recess and have a sufficient number of cutters to suit any size of hole, since, as already stated (there being in that case two cutting edges performing duty), the work may be fed up twice as fast as in the former case, in which only one cutting edge operates.
Messrs. Wm. Sellers and Co. form the cutters for their celebrated car wheel boring bar machine as in Fig. 1129, the bottom or plain edge performing the cutting. By this means the recess to fit the bar is not reduced in depth from sharpening the tool. The tool is sharpened by grinding the ends of the lower face as shown by the unshaded parts, and the cutter is said to work better after the cutting part has begun to be oblique from grinding.
The cutter is hardened at the ends and left soft in the middle, so that the standard size of the cutter may be restored when necessary, by pening and stretching the soft metal in the middle. These cutters will bore from 50 to 250 car wheels, without appreciable reduction of size.
The description of bar shown in Fig. 1127 may be provided with several slots or keyways in its length, to facilitate facing off the ends of work which requires it. Since the work is fed to the cutter, it is obvious that the bar must be at least twice the length of the work, because the work is all on one side of the cutter at the commencement, and all on the other side at the conclusion of the boring operation. The excessive length of bar, thus rendered necessary, is the principal objection to this form of boring bar, because of its liability to spring. There should always be a keyway, slot, or cutter way, near to the centre of the length of the bar, so as to enable it to bore a hole as long as possible in proportion to the length of the boring bar, and a keyway or cutter way at each end of the bar, for use in facing off the end faces of the work.
If a boring bar is to be used only for work that does not require facing at the ends, the cutter, slot, or keyway should be placed in such position in the length of the bar as will best suit the work (keeping in mind the desirability of having the bar as short as possible), and the bar should be tapering from the middle towards each end, as shown in Fig. 1130. This will make the bar stronger in proportion to its weight, and better able to resist the pressure of the cut and the tendency to deflect. The parallel part at a is to receive the driving clamp, but sometimes a lug cast on at that end is used instead of a clamp.
For bores too large to be bored by the bar alone, a tool-carrying head is provided, being sometimes fixed upon the bar by means of a locking key, and at others fed along the bar by a feed screw provided on the bar.
When the head is fixed on the bar the latter must be twice as long as the bore of the work, as the work is on one side of the head at the beginning, and on the other at the end of a cut; hence it follows that the sliding or feeding head is preferable, being the shortest, and therefore the most rigid, unless the bar slides through bearings at each end of the head.
Fig. 1131 represents a bar with a fixed head in operation in a cylinder, and having three cutting tools, and it will be observed that if tool a meets a low spot and loses its cut, the pressure on tools b and c, both being on the opposite side of the head, would cause the bar to spring over towards a, producing a hole or bore out of round, and it follows that four tools are preferable.
[I-290]Fig. 1132 is a side view of a bar with four cutters, and Fig. 1133 an end view of the same shown within a cylinder, and it will be seen that should one of the cutters lose its cut, the two at right angles to it will steady the bar.
When the cutters require to stand far out from the head, the bar will work more steadily if the cutters, instead of standing radially in the head, are placed as in Fig. 1134, so that they will be pulled rather than pushed to their cut.
An excellent form of boring bar fixed head, employed by Messrs. Wm. Sellers and Co. on their horizontal cylinder boring machine, is shown in Fig. 1135. The boring head is split at a, so that by means of the bolt b it may be gripped firmly to the bar d, or readily loosened and slid along it. The head is provided with cutters c (of which there are four in the latest design of bar), fitting into the radial slots e. These cutters are secured to the head by the clamps and nuts at g.
Fig. 1136 represents a boring bar, with a sliding head fed by a feed screw running along the bar, and having at its end a pinion that meshes upon a gear or pinion upon the dead centre of the lathe.
The tools employed for the roughing cuts of boring bars should, for wrought iron, cast iron, steel, or copper, have a little front rake, the cutting corner being at a in Fig. 1137.
If the cutters are to be used for one diameter of bore only, they will work more steadily if but little or no clearance is given them on the end b, Fig. 1138, but it is obvious that if they are to be used on different diameters of bores they must have clearance on these ends. The same tool may be used both for roughing and finishing cuts.
The lip or top rake must, in case the bar should tremble during the finishing cut, be ground off, leaving the face level; and if, [I-291] from the bar being too slight for its duty, it should still either chatter or jar, it will pay best to reduce the revolutions per minute of the bar, keeping the feed as coarse as possible, which will give the best results in a given time. In cases where, from the excessive length and smallness of the bar, it is difficult to prevent it from springing, the cutters must be made as in Fig. 1139, having no lip, and but a small amount of cutting surface; and the corner a should be bevelled off as shown. Under these conditions, the tool is the least likely to chatter or spring into the cut.
The shape of the cutting corner of a cutter depends entirely upon the position of its clearance or rake. If the edge forming the diameter has no clearance upon it, the cutting being performed by the end edges, the cutter may be left with a square, slightly rounded, or bevelled corner; but if the cutter have clearance on its outside or diametrical edge, as shown on the cutters in Fig. 1137, the cutting corner should be bevelled or rounded off, otherwise it will jar in taking a roughing cut, and chatter in taking a moderate cut. The principle is that bevelling off the front edge of the cutter, as shown in Fig. 1139, tends greatly to counteract a disposition to either jarring or chattering, especially as applied to brass work.
The only other precaution which can be taken to prevent, in exceptional cases, the spring of a boring bar is to provide a bearing at each end of the work, as, for instance, by bolting to the end of the work four iron plates, the ends being hollowed to fit the bar, and being so adjusted as to barely touch it; so that, while the bar will not be sprung by the plates, yet, if it tends to spring out of true, it will be prevented from doing so by contact with the hollow ends of the plates, which latter should have a wide bearing, and be kept well lubricated.
It sometimes happens that, from play in the journals of the machine, or from other causes, a boring bar will jar or chatter at the commencement of a bore, and will gradually cease to do so as the cut proceeds and the cutter gets a broader bearing upon the work. Especially is this liable to occur in using cutters having no clearance on the diametrical edge; because, so soon as such a cutter has entered the bore for a short distance, the diametrical edge (fitting closely to the bore) acts as a guide to steady the cutter. If, however, the cutter has such clearance, the only perceptible reason is that the chattering ceases as soon as the cutting edge of the tool or cutter has lost its fibrous edges. The natural remedy for this would appear to be to apply the oil-stone; this, however, will either have no effect or make matters worse. It is, indeed, a far better plan to take the tool (after grinding) and rub the cutting edge into a piece of soft wood, and to apply oil to the tool during its first two or three cutting revolutions. The application of oil will often remedy a slight existing chattering of a boring bar, but it is an expedient to be avoided, if possible, since the diameter or bore cut with oil will vary from that cut dry, the latter being a trifle the larger.
The considerations, therefore, which determine the shape of a cutter to be employed are as follows: Cutters for use on a certain and unvarying size of bore should have no clearance on the diametrical edges, the cutting being performed by the end edge only. Cutters intended to be adjusted to suit bores of varying diameter should have clearance on the end and on the diametrical edges. For use on brass work the cutting corner should be rounded off, and there should be no lip given to the cutting edge. For wrought iron the cutter should be lipped, and oil or soapy water should be supplied to it during the operation. A slight lip should be given to cutters for use on cast iron, unless, from slightness in the bar or other cause, there is a tendency to jarring, in which case no lip or front rake should be given.
“In boring work chucked and revolved in the lathe, such, for instance, as axle boxes for locomotives, the bar shown in Fig. 1140 is an excellent tool. a represents a cutter head, which slides along, at a close working fit, upon the bar d d, and is provided with the cutters b, b, b, which are fastened into slots provided in the head a by the keys shown. The bar d d has a thread cut upon part of its length, the remainder being plain, to fit the sliding head. One end is squared to receive a wrench, which resting against the bed of the lathe, prevents the bar from revolving upon the lathe centres f, f, by which the bar is held in the lathe. g, g, g are plain washers, provided to make up the distance between the thread and plain part of the bar in cases where the sliding head a requires considerable lateral movement, there being more or less washers employed according to the distance along which the sliding head is required to move. The edges of these washers are chamfered off to prevent them from burring easily. To feed the cutters, the nut h is screwed up with a wrench.
“The cutter head a is provided in its bore with two feathers, which slide in grooves provided in the bar d d, thus preventing the head from revolving upon the bar. It is obvious that this bar will, in consequence of its rigidity, take out a much heavier cut than would be possible with any boring tool, and furthermore that, there being four cutters, they can be fed up four times as fast as would be possible with a single tool or cutter. Care must, however, be exercised to so set the cutters that they will all project true radially, so that the depth of cut taken by each will be equal, or practically so; otherwise the feeding cannot progress any faster than if one cutter only were employed.”[17]
[17] From Rose’s “Complete Practical Machinist.”
For use on bores of a standard size, the cutters may be made with a projecting feather, fitting into a groove provided in the head to receive it, as shown in Fig. 1141, which shows the boring bar and head, the nuts and washers being removed. a, a represent cutters, b the bar, c the sliding head, and d, d keys which fasten the cutters in the head. The cutters should be fitted to their places, and each marked to its place; so that, if the keyways should vary a little in their radius from their centre of the bar, they will nevertheless be true when in use, if always placed in the slot in which they were turned up when made. By fitting in several sets of cutters and turning them up to standard sizes, correctness in the size of bore may be at all times insured, and the feeding may be performed very fast indeed.
[I-292]For boring cannon the form of bar shown in Fig. 1142 is employed. The cannon is attached to the carriage or saddle of the lathe and fed to the boring bar. The working end only of the bar is shown in the figure, the shank stem or body of the bar being reduced in diameter to afford easy access to the cuttings. The cutters occupy the positions indicated by the letters a, a, a, being carefully adjusted as to distance from the axis of the bar by packing them at the back with very thin paper. As may be observed they are arranged in two sets of three each, of which the first set performs almost the whole of the work, the second being chiefly added as a safeguard against error in the size of the bore on account of wear of the cutting edges, which takes place to a small but an appreciable extent in the course of even a single boring. Following the cutters is a series of six guide-bars (b b b), arranged spirally, which are made exactly to fit the bore. Provided that the length of these is sufficient, and their fit perfect, it is evident that the cutters cannot advance except in a straight line. The spiral arrangement of the cutters is employed to steady the bar and to give it front rake.
Boring Tapers with a Boring Bar or Attachment.—In cases where the degree of taper is very great a live centre may be bolted to a chuck plate, as in Fig. 1143, by which means any degree of taper may be bored. Instead of a star feed, a gear feed may be provided by fastening one gear, as a, on the dead centre, and another, as b, on the feed-screw. The cutting tool must stand on the side of the sliding-head—that is, farthest from the line of lathe centres.
Small holes may readily be bored taper with a bar set over as in Fig. 1144, the work being carried by a chuck. The head h carries the cutting tool, having a feather which projects into the spline s to prevent the head from rotating on the bar. To prevent the bar from rotating, it is squared on the end f to receive a wrench. The head is fed by the nut n, which is screwed upon the bar. w, w, w, w are merely washers used to bring the nut n at the end of the thread when the head is near the mouth of the work, their number, therefore, depending upon the depth of the work. A bar of this kind is more rigid than a tool held in the tool post.
Instead of setting the dead centre of the lathe over, the bar may be set over, as in Fig. 1145, in which the boring tool is carried in the sliding head at t, and is fed by a screw having a star feed on its end. At b is a block sliding in the end of the bar and capable of movement along the same, to adjust the degree of taper by means of the screw shown in the end view, Fig. 1146. n is a nut to secure b in its adjusted position.
In this case the work must be bolted to the lathe carriage, and the tool feeds to the cut, and the largest end of the hole bored will be at the live spindle end of the lathe.
But we may turn the bar around, as in Fig. 1147, driving the work in a chuck, and holding the dead centre end of the bar stationary, feeding the sliding head to the cut by the feed screw f.
To increase the steadiness of the sliding head it may with[I-293] advantage, be made long, as in Fig. 1148, in which s is a long sleeve fitting to the bar b at the head end h, and recessed as denoted by the dotted lines. The short cutting tool c may be fastened to h by a set-screw in the end of h, or by a wedge, as may be most desirable. The bar may obviously set over to bore tapers as in the cut, and the sliding head may be prevented from turning by a driver resting on the top of the tool rest, and pushed by a tool secured to the tool post, the self-acting carriage feed being put in operation.
It is obvious that when a boring bar is set over to bore a taper, the lathe centres do not bed fair in the work centres, hence the latter are subject to excessive wear and liable to wear to one side more than to another, thus throwing the bar out of true and altering the taper it will bore. This, however, may be prevented by fitting to the bar at each end a ball-and-socket centre, such as shown in section in Fig. 1149. A spherical recess is cut in the bar, a spherical piece is fitted to this recess and secured therein by a cap as shown, the device having been designed by Mr. George B. Foote.
Boring Double Tapers.—To prevent end play in journal bearings where it is essential to do so, the form of journal shown in Fig. 1150 is sometimes employed, hence the journal bearing requires to be bored to fit.
Fig. 1151 represents a bearing box for such a journal, the brasses a, b having flanges fitting outside the box as shown. The ordinary method of doing such a job would be to chuck the box on the face plate of the lathe, setting it true by the circle (marked for the purpose of setting) upon the face of the brasses, and by placing a scribing point tool in the lathe tool post and revolving the box, making the circle run true to the point, which would set the box one way, and then setting the flanges of the box parallel with the face plate of the lathe to set the box true the other way; to then bore the box half way through from one side and then turn it round upon the face plate, reset it and bore the other half; thus the taper of the slide rest would not require altering. This plan, however, is a tedious and troublesome one, because, as the flanges protrude, parallel pieces have to be placed between them and the lathe face plate to keep them from touching; and as the face of the casting may not be parallel with the slide ways, and will not be unless it has been planed parallel, pieces of packing, of paper or tin, as the case may be, must be placed to true the ways with the face plate, and the setting becomes tedious and difficult. But the two tapers may be bored at one chucking, as shown in Fig. 1152, in which a represents the lathe chuck, and b is a sectional view of the bearing chucked thereon, c, c being the parallel pieces. Now it will be observed that the plane of the cone on the front end and on one side stands parallel with the plane of the cone on the back end at an exactly opposite diameter, as shown by the dotted lines d and e. If then the top slide of the lathe rest be set parallel with those lines, we may bore the front end by feeding the tool from the front of the bore to the middle as marked from f to g, and then, by turning the turning tool upside down, we may traverse or feed it along the line from h to j, and bore out the back half of the double cone without either shifting the set of the lathe rest or chucking the box after it is once set.
In considering the most desirable speed and feed for the cutting tools of lathes, it may be remarked that the speeds for boring tools[I-294] are always less than those for tools used on external diameters, and that when the tool rotates and the work is stationary, the cutting speed is a minimum, rarely exceeding 18 feet per minute, while the feed, especially upon cast iron, is a maximum.
The number of machines or lathes attended by one man may render it desirable to use a less cutting speed and feed then is attainable, so as to give the attendant time to attend to more than one, or a greater number of lathes. In the following remarks outside work and a man to one lathe is referred to.
The most desirable cutting speeds for lathe tools varies with the rigidity with which the tool is held, the rigidity of the work, the purpose of the cut, as whether to remove metal or to produce finish and parallelism, the hardness of the metal and stoutness of the tool, the kind of metal to be cut, and the length the tool may be required to carry the cut without being reground. The more rigid the tool and the work the coarser the feed may be, and the more true and smooth the work requires to be the finer the feed. In a roughing cut the object is to remove the surplus metal as quickly as possible, and prepare the work for the finishing cut, hence there is no objection to removing the tool to regrind it, providing time is saved. Suppose, for example, that at a given speed and feed the tool will carry a cut 12 inches along the work in 20 minutes, and that the tool would then require regrinding, which would occupy four minutes, then the duty obtained will be 12 inches turned in 24 minutes; suppose, however, that by reducing the speed of rotation, say, one-half, the tool would carry a cut 24 inches before requiring to be reground, then the rate of tool traverse remaining the same per lathe revolution, it would take twice as long (in actual cutting time) to turn a foot in length of the work. If we take the comparison upon two feet of work length, we shall have for the fast speed 24 inches turned in 40 minutes of actual cutting time, and 10 minutes for twice grinding the tool, or 24 inches in 50 minutes; for the slow speed of rotation we shall have 24 inches turned in 80 minutes.
In this case therefore, it would pay to run the lathe so fast that the tool would require to be ground after every foot of traverse. But in the case of the finishing cut, it is essential that the tool carry the cut its full length without regrinding, because of the difficulty of resetting the tool to cut to the exact diameter. It does not follow from this that finishing cuts in all cases require to be taken at a slower rate of cutting speed, because, as a rule, the opposite is the case, because of the lightness of the cut; but in cases where the work is long, the rate of cutting speed for the finishing cut should be sufficiently slow to enable the tool to take a cut the whole work length without grinding, if this can be done without an undue loss of time, which is a matter in which the workman must exercise his judgment, according to the circumstances. In tools designed for special purposes, and especially upon cast iron the work being rigid the tool may be carried so rigidly that very coarse feeds may be used to great advantage, because the time that the cutting edge is under cutting duty is diminished, and the cutting speed may be reduced and still obtain a maximum of duty; but the surfaces produced are not, strictly speaking, smooth ones, although they may be made to correct diameter measured at the tops of the tool marks, or as far as that goes at the bottom of the tool marks also, if it be practicable.
In the following table of cutting feeds and speeds, it is assumed that the metals are of the ordinary degree of hardness, that the conditions are such that neither the tool nor the work is unduly subject to spring or deflection, and that the tool is required to carry a cut of at least 12 inches without being reground; but it may be observed that the 12 inches is considered continuous, because on account of the tool having time to cool, it would carry more than the equivalent in shorter cuts, thus if the work was 2 inches long and the tool had time to cool while one piece of work was taken out and another put in the lathe, it would probably turn up a dozen such pieces without suffering more in sharpness than it would in carrying a continuous cut of 12 inches long. The rates of feed here given are for work held between the lathe centres in the usual manner.
| For Wrought Iron. | ||||||
| Work diameter. Inches. |
Roughing cuts. Feet per minute. |
Roughing cuts. Lathe revolutions per minute. |
Feed as lathe revolutions per inch of tool travel. |
Finishing cuts. Lathe revolutions per minute. |
Finishing cuts. Lathe revolutions per inch; tool travel. |
|
| 1⁄2 | 40 | 305 | 30 | 305 | 60 | |
| 1 | 35 | 133 | 30 | 133 | 60 | |
| 1 | 1⁄2 | 30 | 76 | 30 | 76 | 60 |
| 2 | 28 | 53 | 25 | 53 | 60 | |
| 2 | 1⁄2 | 28 | 42 | 25 | 42 | 50 |
| 3 | 28 | 35 | 25 | 35 | 50 | |
| 3 | 1⁄2 | 26 | 28 | 25 | 30 | 50 |
| 4 | 26 | 24 | 20 | 26 | 50 | |
| 5 | 25 | 18 | 20 | 21 | 50 | |
| 6 | 25 | 15 | 20 | 16 | 50 | |
| Cast Iron. | ||||||
| 1 | 45 | 163 | 30 | 163 | 40 | |
| 1 | 1⁄2 | 45 | 135 | 25 | 135 | 30 |
| 2 | 40 | 76 | 25 | 76 | 25 | |
| 2 | 1⁄2 | 40 | 61 | 20 | 61 | 20 |
| 3 | 35 | 44 | 20 | 50 | 16 | |
| 3 | 1⁄2 | 35 | 38 | 18 | 43 | 16 |
| 4 | 35 | 33 | 18 | 38 | 16 | |
| 4 | 1⁄2 | 30 | 25 | 16 | 28 | 14 |
| 5 | 30 | 22 | 16 | 26 | 14 | |
| 5 | 1⁄2 | 30 | 20 | 14 | 24 | 12 |
| 6 | 30 | 19 | 14 | 22 | 12 | |
| Brass. | ||||||
| 1⁄2 | 120 | 910 | 25 | 910 | 40 | |
| 3⁄4 | 110 | 556 | 25 | 556 | 40 | |
| 1 | 100 | 382 | 25 | 382 | 40 | |
| 1 | 1⁄4 | 90 | 275 | 25 | 275 | 40 |
| 1 | 1⁄2 | 80 | 203 | 25 | 203 | 40 |
| 1 | 3⁄4 | 80 | 174 | 25 | 174 | 40 |
| 2 | 75 | 143 | 25 | 143 | 40 | |
| 2 | 1⁄2 | 75 | 114 | 25 | 114 | 40 |
| 3 | 70 | 89 | 25 | 89 | 40 | |
| 3 | 1⁄2 | 70 | 76 | 25 | 76 | 40 |
| 4 | 70 | 66 | 25 | 66 | 40 | |
| 4 | 1⁄2 | 65 | 55 | 25 | 55 | 40 |
| 5 | 65 | 50 | 25 | 50 | 40 | |
| 5 | 1⁄2 | 65 | 45 | 25 | 45 | 40 |
| 6 | 65 | 41 | 25 | 41 | 40 | |
| Tool Steel. | ||||||
| 3⁄8 | 24 | 245 | 60 | 245 | 60 | |
| 1⁄2 | 24 | 184 | 60 | 184 | 60 | |
| 5⁄8 | 24 | 147 | 50 | 147 | 60 | |
| 3⁄4 | 24 | 122 | 40 | 122 | 60 | |
| 7⁄8 | 20 | 87 | 30 | 87 | 60 | |
| 1 | 20 | 76 | 30 | 76 | 60 | |
| 1 | 1⁄4 | 20 | 61 | 25 | 61 | 50 |
| 1 | 1⁄2 | 18 | 45 | 25 | 45 | 50 |
| 2 | 18 | 34 | 25 | 34 | 50 | |
| 2 | 1⁄2 | 18 | 27 | 25 | 27 | 50 |
| 3 | 18 | 22 | 25 | 22 | 40 | |
| 3 | 1⁄2 | 18 | 19 | 25 | 19 | 40 |
| 4 | 18 | 17 | 25 | 17 | 40 | |
| 4 | 1⁄2 | 18 | 15 | 25 | 15 | 40 |
These cutting speeds and feeds are not given as the very highest that can be attained under average conditions, but those that can be readily obtained, and that are to be found used by skilful workmen. It will be observed that the speeds are higher as the work is smaller, which is practicable not only on account of the less amount of work surface in a given length as the diameter decreases, but also because with an equal depth of cut the tool endures less strain in small work, because there is less power required to bend the cutting, as has been already explained.
When it is required to remove metal it is better to take it off at a single cut, even though this may render it necessary to reduce the cutting speed to enable the tool to stand an increase of feed better than excessive speed. Suppose, for example, that a pulley requires 1⁄4 inch taken off its face, whose circumference is 5 feet and width 8 inches. Now the tool will carry across a cut reducing the diameter 1⁄8 inch, at a cutting speed of 40 feet per minute, or 10 lathe revolutions per minute; but if the speed be reduced to about 35 feet per minute, the tool would be able to stand the full depth of cut required, that is, 1⁄8 inch deep, reducing the diameter[I-295] of the pulley 1⁄4 inch. Now with the fast speed two cuts would be required, while with the slow one a single cut would serve; the difference is therefore two to one in favor of the deep cut, so far as depth of cut is concerned.
The loss of time due to the reduced rotative speed of work would of course be in proportion to that reduction, or in the ratio of 35 to 50. It is apparent then that the tool should, for roughing cuts, be set to take off all the surplus metal at one cut, whenever the lathe has power enough to drive the cut, and that the cutting speed should be as fast as the depth of cut will allow.
Concerning the rate of feed, it is advisable in all cases, both for roughing and finishing cuts, to let it be as coarse as the conditions will permit, the rates given in the table being in close approximation of those employed in the practice of expert lathe hands.
It is to be observed, however, that under equal conditions, so far as the lathe and the work is concerned, it is not unusual to find as much difference as 30 per cent. in the rate of cutting speed or lathe rotation, and on small work 50 per cent. in the rate of tool traverse employed by different workmen, and here it is that the difference is between an indifferent and a very expert workman.
An English authority (Mr. Wilson Hartnell), who made some observations (in different workshops and with different workmen) on this subject, stated that taking the square feet of work surface tooled over in a given time, he had often found as much as from 100 to 200 per cent. difference, and that he had found the rate of tooling small fly-wheels vary from 2 to 8 square feet per hour without any sufficient reason. The author has himself observed a difference of as much as 20 feet of work rotation per minute on work of 18 and less inches in diameter, and as much as 50 per cent. in the rate of tool traverse per lathe revolution.
It is only by keeping the speed rotation at the greatest consistent with the depth of cut, and by exercising a fine discretion in regulating the rotations of feed and cutting speed, that a maximum of duty can under any given conditions be obtained.
It has hitherto been assumed that the workman’s attention is confined to running one lathe, but cases are found in practice where the lathes, having automatic feed and stop motions, one man can attend to several lathes, and in this case the feeds and speeds may be considerably reduced, so as to give the operator time to attend to a greater number of lathes. As an example, in the use of automatic lathes, several of which are run by one man, the following details of the practice in the Pratt and Whitney Company’s tap and die department are given.
Lathe Number 1.—Lathe turning tool steel 3⁄8 inch in diameter and 11⁄4 long, reducing the diameter of the work 1⁄8 inch. Revolutions of work per minute 125. Feed one inch of tool travel to 200 lathe revolutions.
Lathe Number 2.—Turning tool steel 2 inches long and 1⁄2 inch diameter, reducing diameter 1⁄8 inch. Revolutions of work 100 per minute. Feed 200 lathe revolutions per inch of tool travel.
Lathe Number 3.—Turning tool steel 4 inches long and 7⁄8 inch in diameter, reducing the diameter 1⁄8 inch. Revolutions of work 40 per minute. Feed 200 lathe revolutions per inch of tool travel.
Lathe Number 4.—Turning tool steel 6 to 8 inches long and 13⁄16 diameter, reducing work 1⁄8 inch in diameter. Revolutions of work 35 per minute. Feed 200 lathe revolutions per inch of tool travel.
Lathe Number 5.—Turning tool steel 8 to 10 inches long, and 2 inches in diameter, reducing diameter 1⁄8 inch. Lathe revolutions 30 per minute. Feed 200 lathe revolutions per inch of tool travel.
Lathe Number 6.—Turning tool steel 5 inches long and 31⁄2 inches diameter, reducing diameter 3⁄16. Lathe revolutions 19 per minute. Feed 200 lathe revolutions per inch of tool travel.
The power required to drive the work under a given depth of cut varies greatly with the following elements:—
1st. The diameter of the work, all other conditions being equal.
2nd. The degree of hardness of the metal, all other conditions being equal.
3rd. Upon the shape of the cutting tool; and—
4th. Upon the quality of the steel composing the cutting tool, and the degree of its hardness.
That the diameter of the work is an important element in small work may be shown as follows:—
In Fig. 1153 let w represent a piece of work having a cut taken off it, and the line of detachment of the metal from the body of the work will be represented by the part of the dotted line passing through the depth of the cut (denoted by c). Let Fig. 1154 represent a similar tool with the same depth of cut on a piece of work of larger diameter, and it will be observed that the dotted line of severance is much longer, involving the expenditure of more power.
In boring these effects are magnified: thus in Fig. 1155 let w represent a washer to be bored with the tool t, and let the same depth of cut be taken by the tool, the diameter of the work being simply increased. It is manifest that the cutting would require to be bent considerably more in the case of the small diameter of work than in that of the large, and would thus require more power for an equal depth of cut.
Again, from a reference to Figs. 950 and 952, it will be observed that the height of the tool will make a difference in the power required to drive a given depth of cut, the shaving being bent more when the tool is above the centre in the case of boring tools, and below the centre in the case of outside tools. But when the diameter of the work exceeds about 6 inches, it has little effect in the respects here enumerated.
The following, however, are the general rules applicable when considering the power required for the cutting of metal with lathe or planer tools. The harder the metal, the more power required to cut off a given weight of metal. The deeper the cut the less power required to cut off a given weight of metal. The quicker the feed the less power required to cut off a given weight of metal. The smaller the diameter of outside work, and the larger the diameter of inside or bored work, the less power required.
Copper requires less power than brass; yellow, and other brass containing zinc, less than brass containing a greater proportion of tin. Brass containing lead requires less power than that not containing it. Cast iron requires more power than brass, but less than wrought iron; steel requires more power than wrought iron.
Technical Terms used with Reference to Lathe Work.—Work held between the lathe centres is said to run true, when a fixed point set to touch its perimeter will have an equal degree of contact all around the circumference, and at any part of the length of the same when the work is cylindrical and is rotated. When such a fixed point has contact at one part more than at another of the work circumference, it is said to run “out of true,” “out of truth,” or not to run true.
Radial or side faces (as they are sometimes called) also run true when a fixed point has equal contact (at all parts of the revolution) with the work surface.
Work that is held in chucks is said to be set true when it is adjusted in the intended position.
To true up is to take off the work a cut of sufficient depth to cause a fixed point to touch the work surface equally at each point in the revolution.
To clean work up is to take off it a cut sufficiently deep to cause it to run true, and at the same time removes the rough surface or scale from the metal.
Roughing out work is taking off a cut which reduces it to nearly the finishing size, leaving sufficient metal to take a finishing cut, and reduce it to the proper size.
Facing a piece of work is taking a cut off its radial face.
When a radial face or surface is convex, it is said to be rounding or round, and when it is concave it is said to be hollow.
When a radial face is at a right angle to a cylindrical parallel surface, it is said to be square; but in taper work, it is said to be square when it is at a right angle to the axis of the taper.
Outside work includes all operations performed on a piece of work except those executed within the bores of holes or recesses, which is termed inside or internal work.
Jarring or chattering is the term applied to a condition in which the tool does not cut the work smooth, but leaves a succession of elevations and depressions on it, these forming sometimes a regular pattern on the work. In this case the projections only will have contact with the measuring tools, or with the enveloped or enveloping work surface, when the two pieces are put together.
Jarring or chattering more commonly occurs in the bores of holes or upon radial surfaces, than upon plain cylindrical surfaces, unless the latter be very long and slender. It occurs more also upon brass than upon iron work, and more upon cast than upon wrought iron or steel. It is caused mainly by vibrations of either the work or the tool.
It is induced by weakness (or want of support) in the work, by weakness in the tool, or by its being improperly formed for the duty. Thus, if a tool have too broad a cutting surface it will jar; if it be held out far from the tool post it may jar; if it have too keen a top face for the conditions it will jar.
Jarring may almost always be remedied on brass work by reducing the keenness of the top face, giving it if necessary negative rake, as shown in Fig. 964. On iron or steel work it may be avoided by using as stiff a cutting tool as possible, holding its cutting edge as close to the tool post as convenient, and reducing the length of cutting edge to a minimum.
It may be prevented sometimes by simply placing the finger or a weight upon the tool, or by applying oil to the work, but if this be done it should be supplied continuously throughout the cut, as a tool will cut to a different depth when dry from what it will when lubricated.
In using hand tools such as scrapers, too thin a tool may cause jarring, which may be obviated by keeping the tool rest as close to the work as possible, and placing a piece of leather between the work and the rest.
Examples in Lathe Work.—The simplest class of lathe work is that cut from rods or short lengths of rod metal, which may be turned by being held in a small chuck, or between the lathe centres.
Such work is usually of small diameter and short length, and is therefore difficult to get at if turned between the lathe centres, because the dog that drives it, the lathe face plate, and the dead centre are in the way; such work may be more conveniently driven by a small chuck.
It is usually made of round wire or rod, cut into lengths to suit the conditions; thus if the lathe have a hollow spindle, the rod lengths may be so long as to pass entirely through the spindle, otherwise the lengths may be passed through the chuck, and as far as possible into the live spindle centre hole.
In any event it is desirable to let the rod project so far out from the chuck as to enable its being finished and cut off, without removal from or moving it in the chuck, because such chucks are apt in course of time to wear, so that the jaws do not grip the work quite concentric to the line of centres; hence, if the work be moved in the chuck after having been turned, it is apt to run out of true.
Sometimes, however, the existence of a collar on the work prevents it from being trued for fit at both ends without being cut off from the rod, in which case, if it requires correction after being cut off, it must be rechucked, and it may be necessary at this rechucking to grip it in several successive positions (partly rotating it in the chuck at each trial) before it will run true.
Sometimes the length of work that may advantageously be driven by such a chuck is so great as to render the use of the dead centre to support one end necessary, in which case the rod should be removed from the chuck before each piece is turned, so as to centre drill the dead centre end.
There is one special advantage in driving small work in a chuck of this kind, inasmuch as the work can be tried for fit without removing it from the lathe, while in some cases operations can be performed on it which would otherwise require its removal to the vice; suppose, for example, a thread of very small diameter and pitch requires to be cut on the work end, then a pair of dies or a screw plate may be placed on it, and the lathe pulled round by the belt; after the dies have commenced to start the thread, they may be released and allowed to rotate with the lathe, which will show if they are starting the thread true upon the work.
In cases also where the end of the work requires fitting to a seat, or where it requires turning to a conical point, there is the advantage that the work can be tried to the seat, or turned to the point without taking from the lathe, or without any subsequent operations, whereas in the case of a conical point, the existence of a work centre would necessitate turning the cone some distance from the end, and cutting off the work centre.
As the size of the work increases, the form of the chuck is varied to make it more powerful and strong to resist the strains, but when the size of the chuck becomes so large that it is as much in the way as the face place would be, it is better to turn the work between the lathe centres.
For work to be turned between the lathe centres, it is essential that those centres run true, and be axially in line, and that both centres be turned to the same degree of angle or cone, which is usually for small lathes an angle of 60°, and for lathes of about 30 inches swing and over an angle of about 70°. Both centres should be of an equal angle, for the following reasons.
It is obvious that the work centres wear to fit the dead centre, because of the friction between the two. Now in order to turn a piece of work from end to end, it is necessary to reverse it in the[I-297] lathe, because at the first turning one end is covered by the carrier or driver driving it. At the first turning one work centre only will have worn to fit the lathe centre; hence when at the second, the other work centre wears to fit the dead centre and in the process of such wearing moves (as it always does to some degree) its location, the part first turned will no longer run true. To obviate this difficulty it is proper at the first turning to cut the work down to nearly the finished size, and then reverse it in the lathe and turn up the other end. At this second turning the work will have had both work centres worn to fit the dead centre, hence if it be of the same angle as the live centre, the work will properly bed to both centres, otherwise it will plainly not bed well to the live centre, and in consequence will be apt to run in some degree out of true at the live centre end.
The lathe centres should, for parallel work, stand axially true one with the other, and this can only be the case when the live centre runs true. If the live centre does not run true the following difficulties are met with.
If one end only of the work requires to be turned and it can be completely finished without moving the work driver, the work will be true (assuming the live spindle to run true in its bearings and to fit the same). It will also run true if the work be taken from the lathe and replaced without moving the driver or carrier, providing that the driver be so placed as to receive the driving pressure at the same end as it did when the work was driven; and it is therefore desirable, on this account alone, to always so place the work in the lathe that the driver is driven by its tail end, and not from the screw or screw head. But if the work be turned end for end it will not run true, because the work centre at the unturned end of the work will not be true or central to the turned part of the work.
It is obvious then that lathe centres should run true. But this will not be the case unless the holes into which they fit in the lathe are axially true one with the other and with the lathe spindles. If these holes are true, and the centres are turned true and properly cleaned before insertion, the centres may be put into their places without any adjustment of position. Otherwise, however, a centre punch mark is made on the radial or end face of the live spindle, and another is made on the live centre, so that both for turning up and for subsequent use the centre will run true when these centre punch marks are exactly opposite to each other.
The best way to true lathe centres is with an emery-wheel. In some lathes there are special fixtures for emery grinding, while in others an attachment to go in the tool post is used. Fig. 1156 shows such an attachment.
In the figure a is a frame to be fastened in the slide rest tool post at the stem a′. It affords journal bearing to the hand wheel b, to the shaft of which is attached the gear-wheel c, which drives a pinion d, on a shaft carrying the emery-wheel e, the operation being obviously to rotate wheel b, and drive the emery-wheel e, through the medium of the multiplying gear-wheels c, d.
The emery-wheel is fed to its depth of cut on the lathe centre p, by the cross feed screw of the lathe, and is traversed by pulling or pushing the knob f, the construction of this part of the device being as follows: g and h are two bushes, a sliding fit in the arms of frame a, but having on top flat places i and j, against which touch the ends of the two set-screws k, l, to prevent them from rotating. The emery-wheel and gear pinion d are fast together, and a pin passes through and holds g and h together. Hence the knob f pushes or pulls, as the case may be, the bushes through the bearings g, h, in the frame a, the pinion and emery-wheel traversing with them. Hence pinion d is traversed to and fro by hand, and it is to admit of this traverse that it requires its great length. The stem a is at such an angle that, if it be placed true with the line of cross feed, the lathe centre will be ground to the proper angle.
Fig. 1157 represents a centre grinding attachment by Trump Brothers, of Wilmington, Delaware. In this device the emery-wheel is driven by belt power as follows. A driving wheel a is bolted to the lathe face plate, and a stand carries at its top the over-head belt pulleys, and at its base the emery-wheel and spindle. This stand at c sets over the tool post, and is secured by a bar passing through c and through the tool post, whose set-screw therefore holds the stand in position. On the end of the emery-wheel spindle is a feed lever, by means of which the emery-wheel may be fed along the lathe centre. Cup piece b is for enabling wheel a to be readily set true on the lathe face plate, one end of b fitting the hub of a, while the other receives the dead centre which is screwed up so that b will hold a in place, while[I-298] it is bolted to the lathe face plate, and at the same time will hold it true.
In the absence of a centre grinding attachment, lathe centres may be turned true with a cutting tool, and finished with water applied to the tool so as to leave a bright and true surface. They should not, for the finest of work, be finished by filing, even though the file be a dead smooth one, because the file marks cause undue wear both to the lathe centres and the work centres.
The dead centres should be hardened to a straw color, and the live centre to a blue; the former so as to have sufficient strength to resist the strain, and enough hardness to resist abrasion, and the latter to enable it to be trued up without softening it.
When, after turning them up, the centres are put into their places, the tailstock may be moved up the bed so that the dead centre projects but very little from the tailstock, and is yet close to the live centre, and the lathe should be run at its fastest speed to enable the eye to perceive if the live centre runs true, and whether the dead centre is in line with the live one, and the process repeated so that both centres may be tested.
A more correct test, however, may be made with the centre indicator.
Centre Indicators.—On account of the difficulty of ascertaining when a centre runs quite true, or when a very small hole or fine cone as a centre punch mark runs true when chucked in a lathe, the centre indicator is used to make such tests, its object being to magnify any error, and locate its direction. Fig. 1158, from The American Machinist, represents a simple form of this tool, designed by Mr. G. B. Foote, for testing lathe centres. a is a piece of iron about 8 inches long to fit the lathe tool post, b is a leather disk secured to a by a plate c, and serving to act as a holding fulcrum to the indicator needle, which has freedom of movement on account of the elasticity of the leather washer, and on account of the hole shown to pass through a. It is obvious that if the countersunk end of the needle does not run true, the pointed end will magnify the error by as many times as the distance from the needle point to the leather washer is greater than that from the leather washer to the countersunk end of the needle. It is necessary to make several tests with the indicator, rotating the lathe centre a quarter turn in its socket for each test, so as to prove that the centre runs true in any position in the lathe spindle. If it does not run true the error should be corrected, or the centre and the lathe spindle end may be marked by a centre punch done to show in what position the centre must stand to run true.
The tension of the leather washer serves to keep the countersunk against the lathe centre without a very minute end adjustment. Or the same end may be attained by the means shown in Fig. 1159, which is a design communicated by Mr. C. E. Simonds to The American Machinist. The holder is cupped on one side to receive a ball as shown, and has a countersink on the other to permit a free vibration of the needle. The ball is fitted to slide easily upon the needle, and between the ball and a fixed collar is a spiral spring that keeps the ball in contact with its seat in the holder.
One end of the needle is pointed for very small holes or conical recesses, while the other is countersunk for pointed work, as lathe centres. The countersink of the needle may be made less acute than the lathe centre, so that the contact will be at the very point of the lathe centre, the needle not being centre-drilled. The end of the needle that is placed against the work should be as near to the ball or fulcrum as convenient, so as to multiply the errors of work truth as much as possible.
In some forms of centre indicators the ball is pivoted, so that the needle only needs to be removed to reverse it end for end, or[I-299] for adjusting its distance, it being made a close sliding fit through the ball. Thus, in Fig. 1160 the ball e is held in a bearing cut half in the holder a, and half in cap b, which is screwed to a by screws c d.
Or the ball may be held in a universal joint, and thus work more frictionless. Thus, in Fig. 1161 it is held by the conical points of two screws diametrically opposite in a ring which is held by the conical points of two screws threading through an outer ring, these latter screws being at a right angle to those in the inner ring. The outer ring is held to the holder by the conical points of two screws, all the conical points seating in conical recesses.
It is obvious that the contact of the point of the needle and the work may be more delicately made when there is some elasticity provided, as is the case with the spiral spring in Fig. 1159.
Indicators of this class may be used to test the truth of cylindrical work: thus, in Fig. 1162 is an application to a piece of work between the lathe centres, there being fitted to one end of the needle a fork a that may be removed at pleasure.
One of the difficulties in turning up a lathe centre to run true arises from the difference in cutting speed at the point and at the full diameter of the cone, the speed necessary to produce true smooth work at the point being too fast for the full diameter. This may be remedied on centres for small work, as, say, three inches and less in diameter, by cutting away the back part of the cone, leaving but a short part to be turned up to true the centre.
To permit the cutting off or squaring tool to pass close up to the centre, and thus prevent leaving a burr or projection on the work end, the centre may be thus relieved at the back and have a small parallel relief, as in Fig. 1164 at a, the coned point being left as large as possible, but still small enough to pass within the countersink.
In centres for large and heavy work it is not unusual to provide some kind of an oil way to afford means of lubrication, and an excellent method of accomplishing this object is to drill a hole a, Fig. 1163, to the axis of the centre and let it pass thence to the point as denoted by the dotted line; there may also be a small groove at b in the figure to distribute the oil along the centre, but grooves of this kind make the returning of the centre more difficult and are apt to cause the work centres to enlarge more from wear, especially in turning tapers with the tailstock set over the lathe centre, these being out of line with the work centre.
To enable a broad tool such as a chaser to meet work of smaller diameter than the lathe centre, the latter is cut away on one side as in Fig. 1164. It is obvious also that the flat place being turned uppermost, will facilitate the use of the file on work of smaller diameter than the lathe centre, and that placed in the position shown in the cut, it will permit a squaring tool to pass clear down to the centre and avoid leaving the projecting burr which is left when the tool cannot pass clear down the face to the edge of the countersink of the work centre.
The method to be employed for centring work depends upon its diameter, and upon whether its ends are square or not. When the pieces are cut from a rod or bar in a cutting-off machine, the ends are square, and they may be utilized to set the work by in centring it. Thus, in Fig. 1165 is a top, and in Fig. 1166 is an end view of a simple device, or lathe attachment for centre drilling. s is a stand bolted to the lathe shears and carrying two pins p, which act as guides to the cup chuck or work guide g; between the heads of pins p and the hubs of g are spiral springs, forcing it forward, but permitting it to advance over the drill chuck; the work w is fed forward to the drill. At the dead centre end the work is supported by a female cone centre d in the tail spindle t. The work rests in mouths of g and d, and as the pieces are cut from the rod they are sufficiently straight, and being cut off in a cutting-off machine the ends are presumably square; hence the coned chucks will hold them sufficiently true with the ends, and the alignment of the centre drilled holes will not be impaired by any subsequent straightening processes; for it is to be observed,[I-300] that if work is centre-drilled and straightened afterwards, the straightening throws the centre holes out of line one with the other, and the work will be more liable to gradually run out of true as its centres wear.
Thus, in Fig. 1167, let w represent a bent piece of work centre-drilled, and the axis of the holes will be in line as denoted by the dotted line, but after the piece is straightened the holes will lie in the planes denoted by the dotted line in Fig. 1168, and there will be a tendency for the work centres to move over towards the sides c d as the wear proceeds.
In Fig. 1169 is shown a centre-drilling machine, which consists of a live spindle carrying the centre-drilling tool, and capable of end motion for the drill feed. The work is held in a universal chuck, and if long is supported by a stay as shown in the figure. The axis of the work being in line with that of the chuck, the work requires no setting.
In this case the centre hole will be drilled true with that part of the work that is held in the chuck, and the alignment of the centre hole will depend upon the length of the rod being supported with its axis in line with the live spindle. If the work is not straightened after drilling, the results produced are sufficiently correct for the requirements; but it follows from what has been said, that work which requires to be straightened and tried for straightness in the lathe should be centred temporarily and not centre-drilled until after the straightening has been done.
In Fig. 1170 is shown a combined centre-drill and countersink not unfrequently used in centring machines. The objection to it is, that the cutting edges of the drill get dull quicker than those of the countersink, and in regrinding them the drill gets shorter. Of course the drill may be made longer than necessary so as to admit of successive grindings, but this entails drilling the centre holes deeper than necessary, until such time as the drill has worn to its proper length. To overcome this difficulty the countersink may be pierced to receive a drill as in Fig. 1171, the drill being secured by a set-screw s.
Among the devices for centring work by hand, or of pricking the centre preparatory for centre-drilling, are the following:—
In Fig. 1172 is a centre-marking square. a b c d represents the back and e the blade of the square. Suppose then that the dotted circle f represents the end of a piece of work, and we apply the square as shown in the cut and mark a line on the end of the work, and then moving the square a quarter turn around the work, draw another line, the point of contact of these two lines (as at g in the cut) will be the centre of the work, or if the work is of large diameter as denoted by the circle h h, by a similar process we obtain the centre e. In this case, however, the ends a b of the square back must be of equal lengths, so that the end faces at a b will form a right angle to the edge of the blade, and this enables the use of the square for ordinary purposes as well as for marking centres.
The point a of the centre punch shown in Fig. 1173 is then placed at the intersection of the two lines thus marked, and a hammer blow produces the required indentation. The centre punch must be held upright or it will move laterally while entering the metal. The part b of the centre punch is tapered so as to obstruct the vision as little as possible, while it is made hexagon or octagon at the upper end to afford a better grip. By increasing the diameter at c, the tool is stiffened and is much less liable to fly out of the fingers when the hammer blow does not fall quite fair.
In Fig. 1174 is shown a device for guiding the centre punch true with the axis of the work, so as to avoid the necessity of finding the same by lines for the centres. It consists of a guide piece b and a parallel cylindrical centre punch a, c representing a piece of work. b is pierced above with a parallel hole fitting and[I-301] guiding the centre punch, and has a conical hole at the lower end to rest on the work, so that if the device be held upright and pressed down upon the end of the work, and the top of the centre punch is struck with the hammer, the indentation made will be central to the points of contact of the end of the work with the coned hole of b. If then the end of the work has no projecting burrs the centring will be centred true.
In the absence of these devices, lines denoting the location for the conical recess or centre may be made, when either of the following methods may be pursued.
In Fig. 1175 is shown what is known as a pair of hermaphrodite calipers, which consists of two legs pivoted at the upper end; the bent leg is placed against the perimeter of the work, as shown, and held steadily, while with the point a line is marked on the work. This operation is performed from four equidistant (or thereabouts) points on the work, which will appear as shown in Fig. 1176, providing the radius to which the point was set be equal to the radius of the work. The point at which the lines meet is in this case the location for the centre. If, however, the radius to which the points are set is less than the radius of the work, the lines will appear as in Fig. 1177, in which case the location is in the centre of the inscribed square, as denoted by the dot; or if the radius be set too great the lines will appear as in Fig. 1178, and the location for the centre will again be as denoted by the dot.
Another and very old method of marking these lines is to place the work on a pair of parallel pieces and draw the lines across it, as shown in Fig. 1179, in which w represents the work, p, p the parallel pieces of equal thickness, s a stand (termed a scribing block) carrying a needle n, which is held by a thumb screw and bolt at b. The point of the needle is adjusted for the centre of the work, a line is drawn, the work is then rotated, another line drawn, and so on, until the four lines are drawn as in Fig. 1180, when the work may be turned end for end if light, or if heavy the scribing block may be moved to the other end of the work.
The centre locations are here made true with the part of the work that rests on the parallel pieces, and this is in some cases an essential element in the centring.
Thus, in Fig. 1181, it is required to centre a piece true with the journals a b, and it is obvious that those journals may be rested on parallel pieces p, p, and the centres marked by the scribing block on the faces e, f in the manner before described.
If there is a spot in the length of a long piece of work where the metal is scant and out of round, so that it is necessary to centre the work true by that part, the surface gauge and parallel pieces may be used with advantage, but for ordinary centring it is a slow process. When a piece of work is not cylindrical, and it is doubtful if it will clean up, the centring requires care, for it must not always be assumed, that if two diametrically opposite points meet the turning tool at an equal depth of cut, the piece is centred so as to true up to the largest possible diameter.
This is pointed out in Fig. 1182, which is extracted from an article by Professor Sweet. “In a piece of the irregular form a, the points a and b might be even and still be no indication of the best location for the centre, and in the piece b it is evident that if c and d were even, nothing like the largest cylinder could be got from it. In the case of shape a, the two points e and f should be equidistant from the centre, and in the case of shape b, the three points g, h, i should be equidistant from the centre.”
The depth of the centre drill holes should be such as to leave[I-302] them in the work after it is cut off to its proper length, and will, therefore, be deeper as the amount to be cut off is greater.
The diameter of the centre drill is larger as the size of the work increases, and may be stated as about 3⁄64 for work of about 1⁄2 inch, increasing up to 1⁄8 inch for work of about an inch, and up to three inches in diameter; for work of a foot or over the centre drill may be 3⁄16 inch in diameter.
The centre drilling and countersinking may, when the work is cut to length, be performed at one operation, but when it requires to be cut to length in the lathe, that should be done before the countersinking. A very simple chuck for centre drilling is shown in Fig. 1183, with a twist drill (which is an excellent tool for centre-drilling). If the work is held in the hand and fed to the drill by the lathe dead centre, the weight of the work will cause the hole to be out of straight with the work axis, unless the grip is occasionally relaxed, and the work made to rotate a half or a quarter turn as the drilling proceeds.
After the work is centre-drilled and cut off to length, it must be finally countersunk, so as to provide ample bearing area for the lathe centres.
The countersinking should be true to the centre hole; and it is sometimes made to exactly fit the lathe centres, and in other cases it is made more acute than the lathe centre, so that the oil may pass up the countersink, while it is bedding itself to the lathe centres.
If the countersinking is done before the end of the work is squared, it will not be true with the centre-drilled hole.
In order that the countersinking may wear true with the centre-drilled hole, it may be made of a more obtuse angle (as, say, one degree) than the lathe centre, as in Fig. 1184, so that the hole may form a guide to cause the lathe centre to wear the countersinking true to the hole, and thus correct any error that may exist.
If the countersink is made more acute than the lathe centre, as shown in Fig. 1185, the wear of its mouth will act as a guide, causing the centre to be true with the countersinking; and when the bearing area extends to the centre-drilled hole, there will be introduced, if that hole does not run true, an element tending to cause the work to run out of true again, because the countersinking will have more bearing area on one side than on the other.
It is to be observed, however, that if the difference between the countersink angle and that of the lathe centre be not more than about one degree, the work centre will bed itself fully to the lathe centre very rapidly, and usually before the first cut is carried over the work, unless the work centres have been made to have unduly large countersinks.
Fig. 1186 represents a half-round countersink, in which the cutting edge is produced by cutting away the coned point slightly below the dotted axial line. This secures two advantages: first, it gives the cutting edge clearance without requiring the grinding or filing such clearance; and, secondly, the cone being the same angle as the lathe centres, filing away more than half of it causes it to give the lathe centre at first a bearing at the small end of the countersink, as in Fig. 1184, and this secures the advantage mentioned with reference to that figure. It is obvious that such a reamer, however, does not produce strictly a cone countersink, as is shown in Fig. 1187, where the cutting away of the cone is carried to excess simply to explain the principle, and the cone becomes an hyperbolic curve.
The small amount, however, that it is necessary to carry the face below the line of centres, practically serves to make the cone somewhat less acute, and is not therefore undesirable.
Another method of forming the half-round countersink is shown in Fig. 1188, in which the cone is of the same angle as the lathe centres; the back a is ground away to avoid its contact with the work and give clearance, while clearance to the cutting edge is obtained by filing or grinding a flat surface b at the necessary angle to the upper face of the cone. In this case it is assumed that the centre-drilling and countersinking are true one with the other. Yet another form of countersink is shown in Fig. 1189, consisting of a cone having three or four teeth. It may be provided with a tit, which will serve as a guide to keep the countersink true with the hole, and this tit may be made a trifle larger in diameter than the hole, and given teeth like a reamer, so as to ream the hole out while the countersinking is proceeding.
Unless one side of a half-round reamer is filed away so as to give the cutting edge alone contact with the bore of the hole, an improper strain is produced both upon the work and the countersink.
[I-303]In Fig. 1190, for example, is shown, enlarged for clearness of illustration, a hole, and a half-round countersink in section, and it is evident that if the countersink is set central to the hole, it will have contact at a and at b, and a cannot enter the metal to cut without springing towards c.
But when the lathe has made rather more than one-half a revolution, the forcible contact at b will be relieved, and either the work or the countersink will move back towards d. This may be remedied by setting the countersink to one side, as in Fig. 1191, or by cutting it away on one side, as in Fig. 1192, when the half-round reamer will, if the work be rigidly held while being countersunk, act as a cutting tool. But it is more troublesome to hold the work rigidly while countersinking it than it is to simply hold it in the hands, and for these reasons the square centre is an excellent tool to produce true countersinking.
Fig. 1193 represents a square centre, the conical end being provided with four flat sides, two of which appear at a b, or it may have three flat sides which will give it keener cutting edges, and will serve equally well to keep it true with the drilled hole. But it is questionable whether it is not an advantage not to have the cutting edges so keen as is given by the three flat faces, because the less keen the cutting edges are, the more true the countersinking will be with the hole, the extra pressure required to feed the square centre tending to cause it to remain true with the hole notwithstanding any unequal density of the metal on different sides of the hole. An objection to the square centre is that it involves more labor in the grinding to resharpen it, and is not so easy to grind true, but for fine work this is more than compensated for in the better quality of its work.
This labor, however, may be lessened in two ways: first, the faces may be fluted, as in Fig. 1194, at a and at b, or its diameter may be turned down, as in Fig. 1195. In using the square centre it is placed in the position of the live centre and revolved at high speed, all the cutting edges operating simultaneously; the work is fed up by the dead centre and held in the hand.
To prevent the weight of the work from causing the countersinking being out of true with the hole, the work should be occasionally allowed (by relaxing the grip upon it) to make part of a revolution, as explained with reference to centre-drilling without a work guide. Another and simple form of square centre for countersinking is shown in Fig. 1196. It consists of a piece of square steel set into a stock or holder.
Work that is to be hardened and whose centres are, therefore, liable to warp in the hardening, may be countersunk as in Fig. 1197, there being three indentations in the countersink as shown. This insures that there shall be three points of contact, and the work will run steadily and true. Furthermore, the indentations form passages for the oil, facilitating the lubrication and preventing wear both to the work and to the lathe centres.
These indentations are produced after the countersinking by the punch, shown in Fig. 1198. Except when tapers are turned by setting the lathe centres out of line with the lathe shears (as in setting the tailstock over), all the wear falls on the dead centre end of the work, as there is no motion of the work centre on the live centre, hence the work centres will not have worn to a full bearing until the work has been reversed end for end in the lathe.
If it be attempted to countersink a piece of work whose end face is not square, the countersinking will not be true with the centre hole, and furthermore the causes producing this want of truth will continue to operate to throw the work out of true while it is being turned. Thus, in Fig. 1199, a represents a piece of work and b the dead centre; if the side c is higher than side d of the work end, the increased bearing area at c will cause the most wear to occur at d, and the countersink in the work will move over towards d, and it follows that the face of a rough piece of work should be faced before being countersunk. Professor Sweet designed the centre-drilling device shown in Fig. 1200, which consists of a stock fitting the holes for the lathe centres, and carrying what may be called a turret head, in which are the centre drills, facing tools, and countersinks. The turret has 6 holes corresponding to the number of tools it carries, and each tool is held in[I-304] position by a pin, upon a spring, which projects into the necessary hole, the construction being obvious. The facing tool is placed next to the drill and is followed by a countersink, in whatever direction the turret is rotated to bring the next tool into operation. The work should, on account of the power necessary for the facing, be driven in a chuck.
A similar tool, which may, however, be used for other work besides centring and countersinking, is shown in Fig. 1201. It consists of a stem fitting into the hole of the tail spindle, and carrying a base having a pin d, on which fits a cap having holes b, and set-screws c for fastening drills, countersinks, or cutting tools. The cap is pierced with six taper holes, and a pin projects through the base into these holes to lock the cap in position, this pin being operated by the spring lever shown.
Work that has already been turned, but has had its centres cut off, may be recentred as follows. One end may be held and driven by a chuck, while the other end is held in a steady rest such as was shown in Fig. 802, and the centre may then be formed in the free end by a half-round reamer, such as shown in Fig. 1190, placed in the position of the dead centre, or the square centre may be used in place of the dead centre, being so placed that one of its faces stands vertically, and therefore that two of its edges will operate to cut. The location for the work centre should be centre punched as accurately as possible, and the work is then placed in the lathe with a driver on it, as for turning it up; a crotch, such as shown in Fig. 1202, is then fastened in the lathe tool post, and fed up by the cross-feed screw until it causes the work to run true, and the square centre should then be fed slowly up and into the work, with a liberal supply of oil. If the work runs out of true, the crotch should be fed in again, but care must be taken not to feed it too far. So long as the square centre is altering the position of the centre in the work, it will be found that the feed-wheel of the tailstock will feed by jumps and starts; and after the feeding feels to proceed evenly, the crotch may be withdrawn and the work tried for being true. The crotch, as well as the square centre, should be oiled to prevent its damaging the work surface. It is obvious that in order to prevent the lathe dead centre point from seating at the point or bottom of the work centre, the square centre should be two or three degrees more acute in angle than the lathe dead centre. If the work is tried for truth while running on the square centre, the latter is apt to enlarge the work centre, while the work will not run steadily, hence it is better (and necessary where truth is a requisite) to try the work with the dead centre in place of the square one.
In thus using a square centre to true work, great care should be taken not to cut the work centres too large, and this may be avoided by making the temporary centre-punch centres small, and feeding the crotch rapidly up to the work, until the latter runs true, while the square centre is fed up only sufficiently to just hold the work steady.
To test the truth of a piece of rough work, it may, if sufficiently light, be placed between the lathe centres with a light contact, and rotated by drawing the hand across it, a piece of chalk being held in the right hand sufficiently near to just touch the work, and if the chalk mark extends all round the work, the latter is as true as can be tested by so crude a test, and a more correct test may be made by a tool held in the tool rest. If the test made at various positions in the length of the work shows the work to be bent enough to require straightening, such straightening may be done by a straightening lever.
In shops where large quantities of shafting are produced, there are special straightening tools or devices: thus, Figs. 1203 and 1204 represent two views of a straightening machine. The shaft to be straightened is rotated by the friction caused by its own weight as it lies between rollers, which saves the trouble of placing the shaft upon centres. Furthermore, the belt that is the prime mover of the gears driving these rollers is driven from the line shaft itself without the aid of any belt pulley. The tension of this driving belt is so adjusted that it will just drive the heaviest shaft the machine will straighten; but if the operator grasps the shaft in his hand, the driving mechanism will stop and the belt will slip, the shaft remaining stationary until the operator sets it in motion again with his hand, when the belt ceases to slip and the mechanism again acts to drive the shaft.
Fig. 1203 represents the mechanism for driving the shaft s, to[I-305] be straightened, which lies upon and between two rollers, r, r′. Upon the shafts of these rollers are the gear-wheels a and b, which are in gear with wheel c, the latter being driven by gear-wheel d. Motion to d is derived from a pair of gears, the pinion of which is driven by the belt from the line shaft. h is a head carrying all these gears (and the rollers) except d. There are two of these heads, one at each end of the machine, the two wheels d being connected by a rod running between the shears, but the motion is communicated at one end only of this rod, the shaft is driven between four rollers, of which two, r r′, are shown in the engraving.
In Fig. 1204 the straightening device is shown. A frame consisting of two parts, f, f′, is gibbed to the edge of the shears at g and h. The upper part of this frame carries a square-threaded screw i, and is capable of sliding across the shears upon the part f′. It rests upon the shears through the medium of four small rollers (which are encased), two of which are at j, k, and two are similarly situated at the back of the frame f′. The motion of f across the machine is provided so that the upper part f may be pushed back out of the way, to permit the shaft being easily put on and taken off the friction rollers r r′. The motion along the shears is provided to enable the straightening device to be moved to the required spot along the shaft s′. The shaft s is laid on two pieces n, p, and a similar piece r is placed above to receive the pressure of the screw i, which is operated by a hand lever to perform the straightening. The pieces n, p rest upon two square taper blocks v, which are provided with circular knobs at their outer ends to enable them to be held and pushed in or pulled out so as to cause n, p to meet the shaft before i is operated. This is necessary to accommodate the different diameters of shaft s. The operator simply marks the rotating shaft with chalk in the usual manner to show where it is out of true, and then straightens wherever it is found necessary.
Fig. 1205 represents a similar device for straightening rods or shafts while they are in the lathe. a is a frame or box which is fitted to rest on the Vs of the lathe shears, the straightening frame resting on the box. Instead, however, of simply adjusting the height of the pieces p to suit different diameters of the shaft, the whole frame is adjusted by means of the wedge w, which is inserted between the frame f and the upper surface of the box a. At h is a hole to admit the operator’s hand to move a along the lathe shears.
A method of straightening wire or small rods that are too rigid to be straightened by hand, and on which it is inadvisable to use hammer blows, is shown in Fig. 1206. It consists of a head revolved in a suitable machine, and having a hole passing endways through it. In the middle is a slot and through the body pass the pins a, being so located that their perimeters just press the rod or wire when it is straight, and in line with the axis of the bore through the head, each successive pin a touching an opposite side of the wire or rod. It is obvious that these pins in revolving force out any crooks or bent places in the wire or rod, and that as the work may be pulled somewhat rapidly through the head or frame, the operation is a rapid one.
When pieces of lathe work are to be made from rod or bar iron, they should be cut off to the proper length in a cutting-off machine, such as described in special forms of the lathe, and for the reasons set forth in describing that machine.
An excellent tool, however, for cutting up rods of not more than 1⁄2 inch in diameter, is Elliott’s cutting-off tool shown in Fig. 1207. It consists of a jaw carrying steadying pieces for the rod to be cut up, these pieces being adjusted to fit the rod by the screw and nut shown. On the same jaw is pivoted a tool-holder, carrying a[I-306] cutting-off tool, which is fed to its cut by the upper handle being pressed towards the lower one.
An adjustable stop or gauge is attached, by means of a small rod, to the swinging arm which carries the cutting tool, and can be removed when its use is not desirable.
The operation of this tool is as follows:—The rod to be cut up is held in the lathe chuck, projecting beyond any desired distance, and arranged to revolve at the same speed as for turning. The tool is placed upon the rod, and the movable jaw of the rest adjusted to a bearing. If several pieces are to be cut to a length, the gauge is adjusted, the tool moved along the rod till the gauge-stop comes in contact with the end, the handles pressed together, which moves the cutting tool up to the work in such a way that it will come exactly to the centre, thus cutting the piece entirely off, no adjustment of the tool ever being necessary to provide for its cutting to the centre, except keeping the cutting edge (which is not in this respect changed by grinding) at a distance specified in the directions from the part in which it is clamped. As the tool is moved up to cut, by the same operation the gauge is moved back out of contact with the end. When the pressure on the handles is removed, a spring returns the cutting tool to its original position, and also brings the gauge in position for determining the length of the next piece to be cut. The operation is repeated by simply moving the tool along the rod, the cutting up being done with great rapidity and accuracy. It will be noticed that all the appliances for cutting, gauging, &c., being a part of the tool itself, if the rod runs out of truth—in other words, wabbles—it will have no effect on the cutting, the rod to be cut forming the gauge for all the operations required; also that comparatively no time is lost in adjustment between the several pieces to be cut from a rod.
The cutting tool is a piece of steel of the proper thickness, cleared on the sides by concave grinding. It is held in place by a clamp and two small screws, and requires grinding on the end only.
When the work is centred, it should, for reasons already explained, have its end faces trued up.
In doing this, however, it is desirable in some cases to cut off the work to its exact finished length. This possesses the advantage, that when the work is finished, the work centres will be left intact, and the work may be put into the lathe at any time, and it will run true to the original centres. But this is not always the best plan; suppose, for example, that there are a number of collars or flanges on the work, then it is better to leave a little extra length to the work when truing up the ends, so that if any of the collars are scant of metal, or if it be desirable to turn off more on one side of a collar than on another, as may be necessary to turn out a faulty place in the material, the end measurements on the work may be conformed to accommodate this requirement, and not confined to an exact measurement from the end of the work.
Again, in the case of work having a taper part to be fitted, it is very difficult to obtain the exact proper fit and entrance of taper to an exact distance, hence it is best to leave the work a little too long, with its collars too thick, and to then fit the taper properly and adjust all other end measurements to suit the taper after it is fitted.
Before any one part of a piece of work turned between the lathe centres is finished to diameter, all the parts to be turned should be roughed out, and for the following reasons, which apply with additional force to work chucked instead of being turned between the lathe centres.
It is found, that all iron work changes its form if the surface metal be removed from it. Thus, though the lathe centres be true, and a piece of work be turned for half its length in the lathe, after it has been turned end for end in the lathe to turn the other half of its length, the part already turned will run out of true after the second half is turned up. This occurs from the tension and unequal internal strains which exist in the metal from its being forged or rolled at a constantly diminishing temperature, and from the fact that the surface of the metal receives the greatest amount of compression during the forging.
In castings it is caused by the unequal and internal strains set up by the unequal cooling of the casting in the mould, because of one part being thicker than another.
When the whole of the work surfaces have been cut down to nearly the finished size, this alteration will have taken place, and the finishing may be proceeded with, leaving the work as true as possible. In chucked work, or the most of it rather, it is impracticable (from being too troublesome) to rough out all over before finishing; hence at each chucking all the work to be done at that chucking is finished.
The roughing cuts on a piece of work should always be taken with as coarse a feed as possible, because the object is to remove the mass of the metal to be cut away rather than to produce a finish, and this may be most quickly done by a deep cut and coarse feed. Theoretically also the finishing should be done with a coarse feed, since the coarser the feed, the less the length of time the cutting edge is in action. But the length of cutting edge in action, with a given tool and under a given depth of cut, increases as that edge is made longer to carry the coarse feed, and the long cutting edge produces a strain that tends to spring or bend the work, and that causes the tool to dip into seams or soft spots, or into spongy or other places, where the cutting strain is reduced, and also to spring away from hard spots or seams, where the cutting strain is increased. The most desirable rate of feed, therefore, is that which is as coarse as can be used without springing either the work or the tool, and this will depend upon the rigidity of the work of the lathe, and of the cutting tool. Short or slight work may be turned very true by a light cut fine feed and quick cutting speed, but the speed must obviously be slower in proportion as the length of the work increases, because the finishing cut should be taken without taking the tool out to resharpen it, since it is very difficult to set the tool to the exact proper depth a second time.
Since the cutting edge will, at any given rate of cutting speed, retain its keenness better for a given surface of work in proportion as the time it is under duty is diminished, it follows, therefore, that the coarser the feed the better (so long as both the work and the tool are sufficiently rigid to withstand the rate of feed without springing).
Under conditions of rigidity that are sufficiently favorable a tool, such as in Fig. 948, may be used on wrought or cast iron, at[I-307] a feed of 1⁄2 or even 3⁄4 inch of traverse per lathe revolution, producing true and smooth work, providing that the tool be given a very slight degree of clearance, that its cutting edge is ground quite straight, that it is set parallel to the line of feed, or what is the same thing, to the work axis, and that the length of cutting edge is greater than the amount of tool traverse per lathe revolution, as is shown in the figure, the amount of tool traverse per lathe revolution obviously being from a to b. It may also be observed that the leading corner of the tool may with advantage be very slightly rounded as shown, so that there shall be no pointed corner to dull rapidly.
In proportion as the work is light and the pressure of the cut may spring it, the feed must be lessened, so that on very slender work a feed of 100 lathe revolutions per inch of tool travel may be used. On cast-iron work the feeds may be coarser than for wrought-iron, the other conditions being equal, because cast iron cuts easier and therefore springs the work less for a given depth of cut. But since cast iron is apt to break out, exposing the pores of the metal, and thus leaving small holes plainly visible on the work surface, the finishing cut should be of very small depth, indeed a mere scrape; and if the surface is to be polished, a fine feed and a quick speed will leave a cleaner cut surface, and one that will require the least polishing operations to produce a clean and spotless surface. Brass work also is best finished with a fine feed and a quick speed.
It is obvious that the top face of the tool should be given more rake for wrought iron than for cast iron or steel, and that in the case of the very fine feeds, the form of tool shown in figure is the best for finishing these metals.
In turning a number of pieces requiring to be of the same diameter, it is to be borne in mind that a great part of the time is consumed in accurately setting the tool for the finishing cut, and that if one piece is finished at a time, this operation will require to be done separately for each piece.
It is more expeditious, therefore, to rough all the pieces out, leaving enough metal for a fine finishing cut to be taken, and then finish these pieces without moving the tool; which may be done, after the tool is once set, by letting the tool stand still at the end of the first finishing cut, and taking the work out of the lathe. The carriage is then traversed back to the dead centre, and another piece of work is put in, and it is obvious that as the cross-feed screw is not operated after the tool is once set, the work will all be turned to the same diameter without any further measuring than that necessary for the first piece.
If the tool is traversed back to the dead centre before the lathe is stopped or before the work is removed from the lathe, one of two results is liable to follow. If the lathe is left running, the tool will probably cut a spiral groove on the work, during its back traverse; or if the lathe be stopped, the tool point will mark a line along the work, and the contact of the tool point with the work will dull the cutting edge of the tool. The reason of this is as follows: When the slide rest and carriage are traversing in one direction, the resistance between the tool and the cut causes all the play in the carriage and rest, and all the spring or deflection of those parts, to be in an opposite direction. Now if the play and spring were precisely equal for both directions, the tool should cut to an equal diameter with the carriage traversed in either direction, but the carriage in feeding is fed by the feed nut or friction feed device, while when being traversed back the traversing handle is used; thus the power is applied to the carriage in the two cases at two different points, hence the spring of the parts, whether from lost motion, or play from wear, or from deflection, is variable. Again, even with the tool fed both to its cut and on the back traverse with the hand feed handle, the play is, from the altered direction of resistance of the cut, reversed in direction, and the depth of cut is therefore altered.
Thus, in Fig. 1208, let s s represent the cross slide on the carriage and r r the cross slide of the tool rest shown in section, and suppose the tool to be traversing towards the live centre, then to whatever amount there may be play or spring between the slide and the slide way, the slide will from the pressure of the cut twist over, bearing against the slide way at a and b, and being clear of it at g and h. On reversing the direction of traverse of the rest, so as to feed the tool towards the dead centre, the exactly opposite condition will set in, that is, the pressure of the cut will force the slides in the opposite direction, or in other words, the contact will be as in Fig. 1209, at c, d, and the play at e, f. During the change of location of bearing between the slides and the way, there will have been a certain amount of tool motion altering the distance of the tool point from the line of centres, and therefore the diameter to which it will cut. The angle at which the body of the tool stands will influence the effect: thus, if when traversing towards the live centre the tool stands at an angle pointing towards the live centre, it would recede and cause the tool to clear the cut, if removed on the back traverse without being moved to or from the line of centres. Conversely, if the body of the tool was at an angle, so that it pointed towards the dead centre, and a cut was taken towards the live centre, and the tool was traversed back without being moved in or out, it would take another cut while being moved back.
The conditions, however, are so uncertain, that it is always advisable to be on the safe side, and either wind the tool out from its cut before winding the rest and carriage back (thus destroying its set for diameter), or else to stop the lathe and remove the work before traversing the carriage back as already directed. If the latter plan is followed the trouble of setting the tool is avoided and much time is saved, while greater accuracy of work diameter is obtained. It is obvious that this plan may be adopted for roughing cuts in cases where two cuts only are to be taken, so as to leave finishing cuts of equal depths; or if three cuts are to be taken, it may advantageously be followed for the second and last cuts, the depth of the first cut being of less importance in this case.
The following rules apply to all tools and metals:
When the pressure between the tool and the work is sufficient, from the proportions of the work, to cause the work to spring or bend, the length of acting cutting edge on the tool should be reduced.
As the diameter and rigidity of the work increases, the length of tool cutting edge may increase. The cutting edge of the tool should be kept as close as the work will conveniently admit to the slide rest tool post, 1⁄4 inch even of this distance being important.
The slide rest tool should always be resharpened to take the finishing cut, with which, for wrought iron or steel, soapy water with soda in it should be used, the soda serving to prevent the dripping water from rusting the parts of the lathe.
Cast iron will cut with an exquisite polish if finished at a very slow rate of cutting speed, and turned with a spring tool, such as was shown in Fig. 974, and water is used. But being a slow process it is not usual to finish it in this manner, though for round corners, curves, &c., this method is highly advantageous.
For cast iron the tool should be as keen as the hardness of the metal of the work will permit. If an insufficiently keen tool, or too deep a cut, or too coarse a feed be taken, the metal will break out instead of cutting clean, and numerous fine holes will be perceived over the whole surface, impairing that dead flatness which is necessary to an even and fine polish.
To remove these specks or holes in cylindrical work, the file may be used, but for radial faces hand-scrapers, such as shown in Fig. 1295, are used, the work rotating in either case at high speed. Such scrapers are oilstoned and held with the handle end above the horizontal level.
The rest should be so conformed to suit the shape of the work, that the scraper will be supported close to the work, which will[I-308] prevent chattering, and a piece of leather should (as a further preventive of chattering) be placed beneath the scraper. A very good method of using a scraper is to adjust it to the work, and holding it still on the rest, traverse the slide rest to move the scraper to its cut.
After the scraping, three methods of polishing radial faces are commonly employed; the first is to use emery paper only, and the second is by the use first of grain, emery, and oil, and the subsequent use of emery paper or cloth, and the third is by the use of emery wheels and crocus cloth.
If the work is finished by emery paper only, and it requires much application of the same to efface the scraper marks, the evil will be induced that the emery cuts out the metal most where it is most porous, so that the finished surface is composed of minute hills and hollows, and the polish, though bright and free from marks, will not have that dead flat smooth appearance necessary to a really fine polish and finish; indeed, the finish is in this case to some extent sacrificed to obtain the polish.
It is for this reason that stoning the work (as hereafter described) is resorted to, and that grain emery and lead is employed, which is done as follows:—
For a flat radial face, a flat piece of lead, say 3⁄8 inch thick, and of a size to suit the work, may be pivoted to the end of a piece of wood of convenient length and used with grain emery and oil, the work rotating quickly. To afford a fulcrum for the piece of wood, a lever or rest of some kind, as either a hand rest or a piece fastened in the tool post, is used.
The rest should be placed a short distance from the work surface and the lever held partly vertical until the lead meets the work surface, when depressing the lever end will force the lead against the work. The lever end must be quickly moved laterally, so that the lead will approach and then recede from the work centre; this is necessary for two reasons. First, to prevent the emery from cutting rings in the work surface, and secondly, to prevent the formation of grooves behind any hollow spots or specks the work may contain. The reason of the formation of these grooves is that the emery lodges in them and works out from the contact of the lead, so that if on working out they move always in the same line they cut grooves.
When a lathe is provided with belt motion to run both ways, it is an excellent plan to apply the lead with the lathe running forward and then with it running backward.
When by this means the scraper marks are removed, the next object is to let the marks left by the lead be as fine and smooth as possible, for which purpose flour emery should be used; but towards the last no emery, but oil only, should be applied, the lead being kept in constant lateral motion, first quickly and then slowly, so that the marks on the work cross and recross it at different angles.
For round or hollow corners the lead need not be pivoted to the stick, but should be spherical at the end, the marks being made to cross by partly rotating the lever first in one direction and then in the other.
Sometimes the end of the lever is used without the addition of lead, but this does not produce so flat a surface, as it cuts out hollows in the pores of the metal.
For polishing to be done entirely in the lathe, emery paper and crocus may follow the lead, being used dry and kept also in constant lateral motion. Each successive grade of emery paper must entirely remove all marks existing on the work at the time of its (the paper’s) first application, and, furthermore, each successive grade should be continued until it is well worn, because of two pieces of emery paper of the same grade that most worn will cut the smoothest and polish the best. For the final polishing a piece of the finest emery paper should be prepared in the manner hereafter described for polishing plain cylindrical surfaces.
The radial faces of wrought iron must be finished as smoothly and true as possible, because being harder than cast iron the emery acts less rapidly upon it. For radial faces on brass the surfaces should be finished as smooth as possible with the slide rest tool, which should be round nosed, with the round flattened somewhat where the tool cuts, and the tool should not, under any condition, have any rake on its top face, while the feed should be fine as, say, 32 revolutions per inch of tool travel. Under skillful manipulation scraping may then be dispensed with, although it may be used to a slight extent without impairing the truth.
Very small radial surfaces of brass may best be finished by the scraper and polished with emery paper, while large ones may be finished with dry emery paper.
Round corners on brass work should be finished with a spring tool, such as shown in Fig. 974, but having negative top rake; but if the corners are of small radius a well oilstoned hand-scraper is best.
To enable the smooth and true turning of all radial faces of large diameter, the lathe head should, when it is possible, be steadied for end motion by placing a rod between the lathe centres, but if the radial face is solid at the centre so that such a rod cannot be put in, the end motion adjusting device of the lathe should be adjusted. The slides of the lathe should also be set up to have good firm contact, and the tool should be brought up to the work by putting the feed motion in gear and operating it by hand at the cone pulley, or gear-wheel on the feed spindle. If the lathe has no compound rest, the cut should be put on by this means, but otherwise the tool may be brought near the work by the feed motion and the cut put on by the compound rest, the object in both cases being to take up all lost motion and hold the rest firmly or steadily on the lathe shears, so that it shall not move back as the cut proceeds.
Work of cast iron or brass and of small dimensions and irregular or curved outline should be finished with scraping tools, such as shown in Figs. 1303 and 1310, polished with emery cloth or paper. But whenever scrapers are made with curves to suit the form of the work, such tool curves should be so formed (for all metals) as not to cut along the whole length of cutting edge at once, unless the curve be of very small length as, say, 1⁄4 inch. This is necessary, because if the cutting edge operates on too great a length it will jar or chatter.
For convex surfaces the curve on the scraper should be of greater radius than that of the work, while in the case of concave curves the tool should have a less radius. In both cases the tool will require a lateral movement to cause it to operate over the full width of work curve.
If the work curves are sufficiently large, and the same is sufficiently rigid that a slide rest tool may be used, the length of cutting edge may be increased, so that under very favorable conditions of rigidity the tool edge may cut along its whole length without inducing either jarring or chattering, but the best results will always be obtained when with a broad cutting edge the tool is of the spring tool form shown in Fig. 974.
Work of wrought iron or steel of small dimensions and of irregular form, must also be finished by hand tools, such as the graver shown in Figs. 1285 and 1286, and the finishing tool shown in Figs. 1289 and 1292, the shape of the tool varying to suit the shape of the work.
Round corners or sweeps cannot on any kind of work be finished by a file, because the latter is apt to pin and cut scratches in the work.
For the final tool finishing of lathe work of plain cylindrical outline, no tool equals the flat file if it be used under proper conditions, which are, that the work be turned true and smooth with slide rest tools, the marks left by these tools being exceedingly shallow and smooth.
A dead smooth file that has been used enough to wear down the projecting teeth (which would cut scratches) should then be used, the work rotating at as fast a speed as the file teeth will stand without undue wear. The file strokes should be made under a light pressure, which will prevent the cuttings from clogging its teeth, and the cuttings should be cleaned from the file after every few strokes. Under these conditions work of moderate diameter may be turned to the greatest degree of smoothness and truth attainable with steel cutting tools, providing that the work makes several revolutions during each file stroke, and it therefore follows that the file strokes may be more rapid as the diameter of the work decreases, and should be more slow as that diameter increases. Allowing[I-309] the greatest speed of the filed surface permissible, without too rapid destruction of the file teeth, to be 200 feet per minute, and the slowest speed of file stroke that will prevent the file teeth from being ground away or from becoming pinned (when used on wrought iron) to be one stroke in two seconds, the greatest diameter of work that can be finished by filing under the condition that the work must make more than one rotation per file stroke, is about 25 inches in diameter, running about 30 revolutions per minute. The same diameter and speed may be also taken for cast iron, but brass may be filed under increased speed, rendering it practicable to file it up to a diameter of about 36 inches under the above conditions of work rotation and file stroke speed.
Supposing, however, that from hardness of the metal or from its increased diameter the work cannot make a rotation per file stroke unless that stroke be more slowly performed, then the cuttings gather in the teeth of the file, become locked and form projections, termed pins, above the file teeth, and these projections cut scratches in the work, and this it is that renders it impracticable to hold the file still while the work rotates. But suppose the file be applied to work of such a diameter that, with a stroke in two seconds and the work surface rotating at 200 feet per minute, each stroke acts on a fraction of the circumference only, then there can be no assurance that the filed surface will be cylindrical, because there is no means of applying the file equally over the whole surface. But it is to be noted, nevertheless, that the file acts with greater effect in proportion as the area filed is decreased, and that as the tool marks are filed out the area of surface operated upon is increased. Suppose, then, that starting from any point on the work circumference a file stroke be taken, and that it extends around one-third of the circumference, that the second file stroke extends around one-third also, but that there is an unfiled space of, say, two inches between the area of surface filed by these two strokes, and that at the third file stroke the file starts on the surface filed at the first stroke, passes over the two inches previously unfiled and terminates on the surface filed by the second stroke; then the conditions will be as follows:—
Part of the surface filed at the first stroke will have been filed twice, part of the surface filed at the second stroke will also have been filed twice, while the two inches will have been filed once only. But this latter part will have had much more taken off it during the third stroke than did the rest of the surface filed at that stroke, because it operated on the ridges or tool marks where, being unfiled, their area in contact with the file teeth was at a minimum. This condition will prevail until the tool marks are effaced, and tends to preserve the truth of the work up to that point, hence the necessity of leaving very fine tool marks becomes obvious.
Apart from these considerations, however, there is the fact that filing work in the lathe is a very slow operation, and therefore inapplicable to large work; and furthermore, on large work the surface is not needed to be so smooth as in small work; for example, tool feed marks 1⁄1000 inch deep would upon work of 1⁄2 inch diameter leave a surface appearing very uneven, and the wearing away of those ridges or marks would destroy the fit of the piece; but in a piece, say, six feet in diameter, tool marks of that depth would not appear to much disadvantage, and their wearing away would have but little effect upon the fit of the piece.
Finishing with the file, therefore, is usually applied to work of about 24 inches in diameter, and less, larger work being finished with the cutting tool or by emery grinding, where a greater degree of finish is required.
Small work—as, say, of six inches, or less, in diameter—may be finished with the file so cylindrically true, that no error can be discovered by measurement with measuring tools of the calipering class, though the marks of contact if made apparent by gently forcing the work through a closely fitting ring-gauge may not appear to entirely cover the surface.
To produce filed work thus true, all that is necessary is to set the cutting edge of the finishing tool at the horizontal centre of the work, properly adjust the live spindle of the lathe for fit to its bearings, adjust the slides of the slide rest so that there is no lost motion, and follow the rules already given with reference to the shape of the tool cutting edge, employing a cutting speed not so fast as to dull the tool before it has finished its cut, using a fine feed except in the case of cast iron, as already explained.
The requirement that the tool shall not become dull before it has finished its cut, brings us to the fact that the length of work that can be thus accurately turned is limited, as the diameter of the work increases.
Indeed, the length of the work in proportion to its diameter is a very important element. Thus, it would be very difficult indeed to turn up a spindle of an inch in diameter and, say, 14 feet long, and finish it cylindrically true, parallel, and smooth, because
1st. The slightness of the work would cause it to spring or deflect from the pressure or strain due to the cut. This may to some extent be remedied by steadying the work in a follower rest, but the bore of such follower itself wears as the cut proceeds, though the amount may be so small as to be almost inappreciable.
2nd. The work being better supported (by the lathe centres) at the two ends than in the middle of its length, the duty placed on the follower rest will increase as the middle of the work length is approached, hence the spring or deflection of the follower rest will be a disturbing element.
3rd. The tool gets duller as the cut proceeds, causing more strain from the cut, and, therefore, placing more strain on the follower rest; and,
4th. It would be necessary, on account of the length of the cut, to resharpen the tool before the cut was carried from end to end of the spindle, and it would be almost impracticable to set the reground tool to cut to the exact diameter.
The second, third, and fourth of the above reasons operate together in causing increased work spring as the tool approaches the middle of the work length; thus the deflection of the follower rest, the increased weakness of the work, and the comparative dullness of the tool would all operate to cause the work to gradually increase in diameter as the cut proceeded towards the work centre (of length).
Suppose, for example, a cut to have been carried from the dead centre, say, five feet along the work; at the end of this five feet the tool will be at its dullest, the shaft at its weakest, and supported the least from the dead centre and follower rest.
Suppose, then, that the reground tool be placed in the rest again and set to just meet the turned surface without cutting it, then when it meets the cut to carry it farther along the work the cut will produce (on account of the tool being sharper) less strain on the work, which will therefore spring or deflect less. Precisely what effect this may have upon the diameter to which the tool will turn the work will depend upon various conditions: thus, if the top face of the tool be sufficiently keen to cause the strain due to bending the shaving cut or chip to pull the work forward, the tool would turn to a smaller diameter. If the depth of the cut be sufficient to cause the work to endeavor to lift, and the tool edge be above the centre of the work, it would be cut to smaller diameter. If the tool cutting edge were below the centre, or if its top face be at an angle tending to force the work away from the tool point, the diameter of the work would be increased.
From these considerations it is obvious that the finishing cut should be started at the centre of the work length, and carried towards the lathe centres, because in this case the tool will be sharpest, and therefore will produce less tensional strain on the work at the point where the latter is the weakest, while the resisting strength of the work would increase as the cut proceeded, and the tool became dull from use. Furthermore, if it were necessary to regrind the tool, it would be reset nearer to the lathe centres, where the work would be more rigidly held; hence the tool could be more accurately set to the diameter of the finishing cut.
By following this plan, however, it becomes necessary to have the shaft as near true and parallel as possible before taking the finishing cut, for the following reasons:—
Let the diameter of the spindle before the finishing cut be 11⁄32 inches, leaving 1⁄32 inch to be taken off at the finishing cut, then the ring in the follower rest must be at starting that cut 11⁄32 inch bore, and if the rest is to follow the cut the bush must be changed[I-310] (so soon as it meets the finishing cut) to one of an inch bore. But if the spindle be turned as true and parallel as possible before the finishing cut the rest may lead the tool, in which case the bush need not be changed. There are differences of opinion as to the desirability of either changing the bush or letting the tool follow the rest, but there can be no dispute that (from the considerations already given) a spindle turned as true and parallel as may be with the tool started from the dead centre and carried forward can be improved by carrying yet another cut from the middle towards the dead centre. In any event, however, work liable to spring or too long to be finished at one cut without removing the tool to grind it, can be more accurately finished by grinding in a lathe, such as was shown in Figs. 676 or 679, than by steel-cutting tools, and for the following reasons:—
If it be attempted with steel tools to take a very fine cut, as, say, one of sufficient depth to reduce a diameter, say 1⁄500 inch, the tool is apt to turn an uneven surface. There appears, indeed, to be a necessity to have the cut produce sufficient strain to bring the bearing surfaces of the rest into close contact and to place a slight strain on the tool, because under very light cuts, such as named above, the tool will generally momentarily leave the cut or take a reduced cut, and subsequently an increased one.
It may be accepted that from these causes a finishing cut taken with a steel tool should not be less than that sufficient to reduce the diameter of the work 1⁄64 inch. Now an emery-wheel will take a cut whose fineness is simply limited by the wear of the wheel in the length of the cut. Some experiments made by Messrs. J. Morton Poole and Sons, of Wilmington, Delaware, upon this subject led to the conclusion that with corundum wheels of the best quality the cut could be made so fine that a 12-inch wheel used upon a piece of work (a calender roll) 16 inches in diameter and 6 feet long, would require about forty thousand traverses to reduce the diameter of the work an inch, leading to the conclusion that the wear of the wheel diameter was less than one eighty-thousandth part of an inch per traverse.
Now the strain placed upon the work of an emery-wheel taking a cut of, say, 1⁄1000 inch, is infinitely less than that caused by a cutting tool taking a cut of 1⁄120 inch in diameter; hence the accuracy of grinding consists as much in the small amount of strain and, therefore, of deflection it places upon the work, as upon the endurance of the wheel itself.
Since both in finishing and in polishing a piece of work the object is to obtain as true and smooth a surface as possible, the processes are to a certain extent similar, but there is this difference between the two: where polishing alone is to be done, the truth of the work or refined truth in its cylindrical form or parallelism may be made subservient to the convenience of polish. Thus, in the case of the stem of the connecting rod that has been turned and filed and finished as true as possible, the polishing processes may be continued with emery-cloth, &c., producing the finest of polish without impairing the quality of the work, whereas the degree of error in straightness or parallelism induced by the polishing may impair the degree of truth desirable for a piston rod.
The degree of finish or polish for any piece of work is, therefore, governed to some extent by the nature of its use. Thus a piston rod may be finished and polished to the maximum degree consistent with maintaining its parallelism and truth, while a connecting rod stem may be polished to any required attainable degree.
In finishing for truth, as in the case of journal bearings, the work, being turned as true and smooth as possible, may be filed with the finest of cut files, and polished with a fine grade of emery-cloth or paper; the amount of metal removed by filing and polishing being so small as not to impair to any practically important degree the truth of the work: a journal so finished will be as true as it is possible to make it without the use of a grinding lathe.
Instead of using emery-paper, grain emery and oil may be used, but the work will not be so true, because in this case much more metal will be removed from the work in the finishing or polishing process.
When it is required to polish and to keep the work as true and parallel as possible, these ends may be simultaneously obtained by means of clamps, such as shown in Fig. 1210, which represents a form of grinding and polishing clamp used by the Pratt and Whitney Company for grinding their standard cylindrical gauges. A cast-iron cylindrical body a is split partly through at b and entirely through at c, being closed by the screw d to take up the wear. The split b not only weakens the body a and enables its easy closure, but it affords ingress to the grinding material. It may be noted that cast iron is the best metal that can be used for this purpose, not only on account of the dead smooth surface it will take, but also because its porosity enables it to carry the oil better than a closer grained metal. For work of larger diameter, as, say, 2 or 3 inches, the form of lap shown in Fig. 1211 is used for external grinding, there being a hinge b c instead of a split, and handles are added to permit the holding and moving of the lap. The bore of this clamp is sometimes recessed and filled with lead. It is then reamed out to fit the work and used with emery and oil, the lathe running at about 300 feet per minute.
For grinding and polishing the bores of pieces, many different forms of expanding grinding mandrels have been devised, in most of which the mandrel has been given a slight degree of curvature in its length; or in other words, the diameter is slightly increased as the middle of the mandrel length is approached from either end. But with this curvature of outline, as small as it may be, it rather increases the difficulty of grinding a bore parallel instead of diminishing it. When expanding mandrels are caused to expand by a wedge acting upon split sections of the mandrel, they rarely expand evenly and do not maintain a true cylindrical form.
Fig. 1212 represents a superior form of expanding mandrel for this purpose. The length a is taper and contains a flute c. The lead is cast on and turned upon the mandrel, the metal in the flute c driving the lead. The diameter of the lap is increased by driving the taper mandrel through it, and the lead is therefore maintained cylindrically true.
While these appliances are supplied with the flour emery and oil, their action is to grind rather than to polish, but as they are used without the addition of emery, the action becomes more a polishing one.
[I-311]Fig. 1213 represents at a a a wooden clamp for rough polishing with emery and oil. It consists of two arms hinged by leather at b and having circular recesses, as c, d, to receive the work. At j j is represented a similar grinding and polishing clamp for more accurate work. g and h are screws passing through the top arm and threaded into the lower, while e, f are threaded into the lower arm, and abut at their ends against the face of the upper arm. It is obvious that by means of these screws the clamp may be set to size, adjusted to give the required degree of pressure, and held firmly together. Lead bushes may be inserted in the bores as grinding laps. As this clamp is used by hand, it must be moved along the work at an exactly even speed of traverse, or else it will operate on the work for a longer period of time at some parts than at others; hence the greatest care is necessary in its use.
The best method of polishing cylindrical work to be operated on entirely in the lathe, the primary object being the polish, is by means of emery paper, and as follows:—
In all polishing the lathe should run at a fast speed; hence special high speeded lathes, termed speed lathes, are provided for polishing purposes only.
The emery paper or cloth should be of a fine grade, which is all that is necessary if the work has been properly filed, if cylindrical, and scraped if radial or of curved outline.
In determining whether emery paper or cloth should be used, the following is pertinent:—
The same grade of emery cuts more freely on cloth than on paper, because the surface of the cloth is more uneven; hence the emery grains project in places, causing them to cut more freely until worn down. If, then, the surface is narrow, so that there is no opportunity to move the emery cloth endways on the work, emery paper should be used. It should be wrapped closely (with not more than one, or at least two folds) around a smooth file, and not a coarse one, whose teeth would press the emery to the work at the points of its coarse teeth only. The file should be given short, rapid, light strokes.
For work of curved outline emery cloth should be used, because it will bend without cracking, and the cloth should be moved quickly backwards and forwards across, and not round, the curve; and when the work is long enough to permit it, the emery paper or cloth should be moved rapidly backwards and forwards along the work so that its marks cross and recross at an obtuse angle.
Now, suppose the grade of emery paper first used to be flour emery, and the final polish is to be of the highest order, then 0000 French emery paper will be required to finish, and it is to be observed that nothing will polish a metal so exquisitely as an impalpable powder of the metal itself: hence, while performing the earlier stages of polishing, it is well to prepare the final finishing piece, so as to give it a glaze of metal from the work surface.
When, therefore, all the file marks are removed by the use of the flour emery cloth, the surface of the work should be slightly oiled and then wiped, so as not to appear oily and yet not quite dry, with a piece of rag or waste, then the piece of 0000 emery paper, or, what is equally as good, a piece of crocus cloth, to be used for the final finishing should be applied to the work, and the slightly oily surface will cause the cuttings to clog and fill the crocus cloth. The cloth should be frequently changed in position so as to bring all parts of its surface in contact with the work and wear down all projections on the cloth as well as filling it with fine cuttings from the work. Then a finer grade, as, say, No. 0 French emery paper, must be used, moving it rapidly endwise of the work, as before, and using it until all the marks left by the flour emery have been removed.
One, or at most two drops of lard oil should then be put on the work, and spread over as far as it will extend with the palm of the hand, when the finishing crocus may again be applied and reversed as before in every direction; 00 emery paper may then be used until all the marks of the 0 are removed, and with the work left quite dry the crocus for final finishing may again be applied; 000 emery paper may then be used to efface all the marks left by the 00. This 000 emery paper should be used until it is very much worn, the final finish being laid with the glazed crocus.
If this crocus has been properly prepared, its whole surface will be covered with a film of fine particles of metal, so that if the metal be brass the crocus surface will appear like gold leaf. If cast iron, the crocus surface will appear as though polished with plumbago or blacklead, while in any case the crocus surface will be polished and quite dry. The crocus should be pressed lightly to the work, so that its polishing marks will not be visible to the naked eye.
If emery paper be applied to work finished to exact diameter it should be borne in mind that the process reduces to some extent the size of the work, and that the amount under proper conditions though small is yet of importance, where preciseness of diameter is a requisite.
In the practice, however, of some of the best machine shops of the United States, the lathe alone is not relied upon to produce the best of polish. Thus, in the engine works of Charles H. Brown, of Fitchburg, Massachusetts, whose engines are unsurpassed for finish and polish, and which the majority of mechanics would suppose were finely silver plated, the following is the process adopted for polishing connecting rods.
The rod is carefully tool-finished with a fine feed. The tool marks are then erased with a fine smooth file, and these file marks by a dead-smooth file, the work rotating at a quick speed, little metal being left, so as to file as little as possible. Next comes fine emery cloth to smooth down and remove the file marks. The lathe is then stopped and the rod stoned lengthwise with Hindostan stone and benzine, removing all streaks. The Scotch stone used with water follows, until the surface is without scratches or marks, as near perfect as possible. The next process is, for the finest work, the burnisher used by hand. But if not quite so exquisite a polish is required, the rod is finished by the use of three grades of emery cloth, the last being very fine.
Sometimes, however, the streaks made by polishing with emery paper used before the application of the stones are too difficult to remove by them. In this case, for a very fine finish, the lathe is stopped and draw-filing with the finest of files is performed, removing all streaks; and the stones then follow the draw-filing. All stoning is done by hand with the work at rest, as is also all burnishing.
After the burnisher comes fine imported crocus cloth, well worn, which makes the surface more even and dead than that left by the burnisher. The crocus is used with the lathe at its quickest speed, and is moved as slowly and as evenly as possible, the[I-312] slower and more even the crocus movement along the rod, the more even the finish. If the rod has filleted corners, such corners are in all cases draw-filed before the stoning.
The method of polishing a cylinder cover at the Brown Engine Works is as follows.
The finishing cut is taken with a feed of 32 lathe-revolutions per inch of tool traverse, and at as quick a cutting speed as the hardness of the iron will permit. This is necessary in order to have the tool-edge cut the metal without breaking it out as a coarse one would do. With the fine feed and quick speed the pores of the iron do not show; with a coarse feed the pores show very plainly and are exposed for quite a depth.
After the lathe-tool comes a well oil-stoned hand-scraper, with a piece of leather between it and the tool rest to prevent the scraper from chattering. The scraper not only smooths the surface, but it cuts without opening the pores. It is used at a quick speed, as quick indeed as it will stand, which varies with the hardness of the metal, but is always greater than is possible with a slide-rest tool.
After the scraper the cover is removed from the lathe, and all flat surfaces are filed as level as possible with a second-cut file, and then stoned with soft Hindostan stone, used with benzine or turpentine, so as to wash away the cuttings and prevent them from clogging the stone or forming scratches. In using all stones the direction of motion is frequently reversed so as to level the surface. Next comes stoning with Scotch stone (Water of Ayr), used with water; in this part of the operation great care must be taken, otherwise the cuttings will induce scratches. When the Scotch stone marks have removed all those left by the Hindostan stone, and left the surface as smooth as possible, the cover is again put in the lathe and the grain is laid and finished with very fine emery cloth and oil. The emery cloth is pressed lightly to the work and allowed to become well worn so as to obtain a fine lustre without leaving any streaks.
It will be noticed here that the use of the emery stick and oil is entirely dispensed with; but for a less fine polish it may be used, providing it be kept in quick motion radially on the work. The objection to its use is that if there be any speck on the work it is apt to cut a streak or groove following the spot like a comet’s tail.
Turning Tapers.—There are five methods of turning outside tapers; 1st, by setting over the tailstock of the lathe; 2nd, by the use of a former or taper turning attachment such as was shown in Fig. 508; 3rd, by the use of a compound slide rest; 4th, by means of a lathe in which the head and tailstock are upon a bed that can be set at an angle to the lathe shears on which the lathe carriage slides; and 5th, by causing the cross-feed screw to operate simultaneously with the feed traverse.
Referring to the first method, it is objectionable, inasmuch as that the work axis is thrown at an angle to the axis of the lathe centres, which causes the work centres to wear rapidly, and this often induces them to move their positions and throw the work out of true. Furthermore, the tailstock has to be moved back in line with the live spindle axis for turning parallel again, and this is a troublesome matter, especially when the work is long.
Fig. 1214 shows the manner in which the lathe centres and the work centres have contact, l being the live and b the dead centre; hence c c is the axis of the live spindle which is parallel to the lathe shear slides, which are represented by g; obviously a is the work axis. The wear is greatest at the dead centre end of the work, but there is some wear at the live centre end, because there is at that end also a certain amount of motion of the work centre upon the live centre. Thus, in Fig. 1215, let c represent the live centre axis, a the work axis, d the lathe face plate, and e f the plane of the driver or dog upon the work, and it is obvious that the tail of the driver will when at one part of the lathe revolution stand at e, while when diametrically opposite it will stand at f; hence, during each work revolution the driver moves, first towards and then away from the face plate d, and care must be taken in adjusting the position of the driver to see that it has liberty to move in this direction, for if obstructed in its motion it will spring or bend the work.
To determine how much the tailstock of a lathe must be set over to turn a given taper, the construction shown in Fig. 1216 may be employed. Draw the outline of the work and mark its axis d, draw line c parallel to one side of the taper end, and the distance a between this line and the work axis is the amount the tailstock requires to be set over. This construction is proved in Fig. 1217, in which the piece of work is shown set over, c representing the line of the lathe ways, with which the side f of the taper must be parallel. d is the line of the live spindle, and e that of the work, and the distance b will be found the same as distance a in Fig. 1216.
It may be remarked, however, that in setting the tailstock over it is the point of the dead centre when set adjusted to the work length that must be measured, and not the tailblock itself.
Other methods of setting tailstocks for taper turning are as follows: If a new piece is to be made from an old one, or a duplicate of a piece of work is to be turned, the one already turned, or the old piece as the case may be, may be put in the lathe and we may put a tool in the tool post and set the tailstock over until the tool traversed along the work (the latter remaining stationary) will touch the taper surface from end to end.
If, however, the taper is given as so much per foot, the distance to set the tailstock over can be readily calculated.
Thus, suppose a piece of work has a taper part, having a taper of an inch per foot, the work being three feet long, then there would be three inches of taper in the whole length of the piece and the tailstock requires to be set over one-half of the three inches, or 11⁄2 inches. It will not matter how long the taper part of the work is, nor in what part of the work it is, the rule will be found correct so long as the tailstock is set over one-half the amount obtained by multiplying the full length of the work per foot by the amount of taper per foot.
If we have no pattern we may turn at each end of the part that is to be taper a short parallel place, truing it up and leaving it larger to the same amount at each end than the finished size, and taking care that the parallel part at the small end will all turn out in the finishing. We then fasten a tool in the lathe tool post,[I-313] place it so that it will clear the metal of the part requiring to be turned taper, and placing it at one extreme end of said part, we take a wedge, or a piece of metal sufficiently thick, and place it to just contact with the turned part of the work and the tool point (adjusting the tool with the cross-feed screw), we then wind the rest to the other end of the required taper part, and inserting same wedge or piece of iron, gauge the distance from the tool point to the work, it being obvious that when the tool point wound along is found to stand at an equal distance from each end of the turned part, the lathe is set to the requisite taper.
Figs. 1218 and 1219 illustrate this method of setting. a represents a piece of work requiring to be turned taper from b to c, and turned down to within 1⁄32 inch of the required size at e and f. If then we place the tool point h first at one end and then at the other, and insert the piece i and adjust the lathe so that the piece of metal i will just fit between the tool point and the work at each extreme end of the required taper part, the lathe will be set to the requisite taper as near as practicable without trying the work to the taper hole. The parallel part at the small end of the work should be turned as true as possible, or the marks may not be obliterated in finishing the work.
Fig. 1220 (from The American Machinist) represents a gauge for setting the tailstock over for a taper. A groove is cut as at e and d, these diameters corresponding to the required taper; a holder a is then put in the tool point, and to this holder is pivoted the gauge b. The tailstock is set over until the point of b will just touch the bottom of the groove at each end of the work.
To try a taper into its place, we either make a chalked stripe along it from end to end, smoothing the chalked surface with the finger, or else apply red marking to it, and then while pressing it firmly into its place, revolve it backwards and forwards, holding it the while firmly to its seat in the hole; we move the longest outwardly projecting end up and down and sideways, carefully noting at which end of the taper there is the most movement. The amount of such movement will denote how far the taper is from fitting the hole, while the end having the least movement will require to have the most taken off it, because the fulcrum off which the movement takes place is the highest part, and hence requires the greatest amount of metal to be taken off.
Having fitted a taper as nearly as possible with the lathe tool, that is to say, so nearly that we cannot find any movement or unequal movement at the ends of the taper (for there is sure to be movement if the tapers do not agree, or if the surfaces do not touch at more than one part of their lengths), we must finish it with a fine smooth file as follows: After marking the inside of the hole with a very light coat of red marking, taking care that there is no dirt or grit in it, we press the taper into the hole firmly, forcing it to its seat while revolving it backwards and forwards.
By advancing it gradually on the forward stroke, the movement will be a reciprocating and yet a revolving one. The work must then be run in the lathe at a high speed, and a smooth file used to ease off the mark visible on the taper, applying the file the most to parts or marks having the darkest appearance, since the darker the marks the harder the bearing has been. Too much care in trying the taper to its hole cannot be taken, because it is apt to mark itself in the hole as though it were a correct fit when at the same time it is not; it is necessary therefore at each insertion to minutely examine the fit by the lateral and vertical movement of projecting part of the taper, as before directed.
A taper or cone should be fitted to great exactitude before it is attempted to grind it, the latter process being merely intended to make the surfaces even.
For wrought-iron, cast-iron, or steel work, oil and emery may be used as the grinding materials (for brass, burnt sand and water are the best). The oil and emery should be spread evenly with the finger over the surfaces of the hole and the taper; the latter should then be placed carefully in its place and pressed firmly to its seat while it is being revolved backwards and forwards, and slowly rotated forward by moving it farther during the forward than during the backward movement of the reciprocating motion.
After about every dozen strokes the taper should be carefully removed from the hole and the emery again spread evenly over the surfaces with the finger, and at and during about every fourth one of the back strokes of the reciprocating movement the taper should be slightly lifted from its bed in the hole, being pressed lightly home again on the return stroke, which procedure acts to spread the grinding material and to make the grinding smooth and even. The emery used should be about number 60 to 70 for large work, about 80 to 100 for small, and flour emery for very fine work.
Any attempt to grind work by revolving it steady in one direction will cause it to cut rings and destroy the surface.
Referring to the second method, all that is necessary in setting a former or taper attachment bar is to set it out of line with the lathe shears to half the amount of taper that is to be turned, the bar being measured along a length equal to that of the work. Turning tapers with a bar or taper-turning attachment possesses the advantage that the tailstock not being set over, the work centres are not thrown out of line with the live centres, and the latter are not subject to the wear explained with reference to Fig. 1214. Furthermore, the tailstock being kept set to turn parallel, the operator may readily change from turning taper to turning parallel, and may, therefore, rough out all parts before finishing any of them, and thus keep the work more true, whereas in turning tapers by setting the tailstock over we are confronted by the following considerations:—
If we turn up and finish the plain part first, the removing of the skin and the wear of the centres during the operation of turning the taper part will cause the work to run out of true, and hence it will not, when finished, be true; or if, on the other hand, we turn up the taper part first, the same effects will be experienced in afterwards turning the plain part. We may, it is true, first rough out the plain part, then rough out the taper part, and finish first the one and then the other; to do this, however, we shall require to set the lathe twice for the taper and once for the parallel part.
It is found in practice that the work will be more true by turning the taper part the last, because the work will alter less upon the lathe centres when changed from parallel to taper turning than when changed from the latter to the former. In cases, however, in which the parts fitting the taper part require turning, it is better to finish the parallel part last, and to then turn up the work[I-314] fastened upon the taper part while it is fast upon its place: thus, in the case of a piston rod and piston, were we to turn up the parallel part of the rod first and the taper last, and the centres altered during the last operation, when the piston head was placed upon the rod, and the latter was placed in the lathe, the plain part or stem would not run true, and we should require to true the centres to make the rod run true before turning up the piston head. If, however, we first rough out the plain part or stem of the rod, and then rough out and finish the taper part, we may then fasten the head to its place on the rod, and turn the two together; that is to say, rough out the piston head and finish its taper hole; then rough out the parallel part of the rod, but finish its taper end. The rod may then be put together and finished at one operation; thus the head will be true with the rod whether the taper is true with the parallel part of the rod or not. With a taper-turning attachment the rod may be finished separately, which is a great advantage.
If, however, one part of the length of a taper turning attachment is much more used than another, it is apt to wear more, which impairs the use of the bar for longer work, as it affects its straightness and causes the slide to be loose in the part most used, and on account of the wear of the sliding block it is proper to wind the tool out from its cut on the back traverse, or otherwise the tool may cut deeper on the back than on the forward traverse, and thus leave a mark on the work surface.
Referring to the third method, a compound slide rest provides an excellent method of turning tapers whose lengths are within the capacity of the upper slide of the compound rest, because that slide may be used to turn the taper, while the ordinary carriage feed may be used for the parallel parts of the work, and as the tailstock does not require to set over, the work centres are not subject to undue wear.
If the seat for the upper slide of the rest is circular, and the taper is given in degrees of angle, a mark may be made on the seat, and the base of the upper slide may be marked in degrees of a circle, as shown in Fig. 1221, which will facilitate the setting; or the following construction, which is extracted from Mechanics, may be employed. Measure the diameter of the slide rest seat, and scribe on a flat surface a circle of corresponding diameter. Mark its centre, as a in Fig. 1222, and mark the line a b. From the centre a mark the point b, whose radius is that of the small end of the hole to be bored. Mark the length of the taper to be turned on the line a g and draw the line g d distant from a b equal to the diameter of the large end of the hole to be bored. Draw the line b d. Then the distance e f is the amount the rest must be swiveled to turn the required taper.
It is obvious that the same method may also be used for setting the rest.
Referring to the fourth method, by having an upper bed or base plate for the head and tailstock, so that the line of lathe centres may be set at the required angle to the Vs or slides on which the carriage traverses, it affords an excellent means of turning tapers, since it avoids the disadvantages mentioned with regard to other systems, while at the same time it enables the turning of tapers of the full length of the carriage traverse, but it is obvious that the head and tailstock are less rigidly supported than when they are bolted direct to the lathe shears.
In turning tapers it is essential that the tool point be set to the exact height of the work axis, or, in other words, level with the line of centres. If this is not the case the taper will have a curved outline along its length. Furthermore, it may be shown that if a straight taper be turned and the tool be afterwards either raised or lowered, the amount of taper will be diminished as well as the length being turned to a curve.
Figs. 1223 and 1224 demonstrate that the amount of taper will be changed by any alteration in the height of the tool. In Fig. 1223, a b represents the line of centres of the spindle of a lathe, or, in other words, the axis of the work w, when the lathe is set to turn parallel; a c represents the axis of the work or cone when the lathe tailstock is set over to turn the taper or cone; hence the length of the line c b represents the amount the tailstock is set over. Referring now to Fig. 1224, the cone is supposed to stand level, as it will do in the end view, because the lathe centres remain at an equal height from the lathe bed or Vs, notwithstanding that the tailstock is set over. The tool therefore travels at the same height throughout its whole length of feed; hence, if it is set, as at t, level with the line of centres, its line of feed while travelling from[I-315] end to end of the cone is shone by the line a b. The length of the line a b is equal to the length of the line b c Fig. 1223. Hence, the line a b, Fig. 1224, represents two things: first, the line of motion of the point of tool t as it feeds along the cone, and second its length represents the amount the work axis is out of parallel with the line of lathe centres. Now, suppose that the tool be lowered to the position shown at i; its line of motion as it feeds will be the line c d, which is equal in length to the line a b. It is obvious, therefore, that though the tool is set to the diameter of the small end, it will turn at the large end a diameter represented by the dotted circle h. The result is precisely the same if the taper is turned by a taper-turning attachment instead of setting the tailstock out of line.
The demonstration is more readily understood when made with reference to such an attachment as the one just mentioned, because the line a b represents the line of tool feed along the work, and its length represents the amount the attachment causes the tool to recede from the work axis. Now as this amount depends upon the set-over of the attachment it will be governed by the degree of that set over, and is, therefore, with any given degree, the same whatever the length of the tool travel may be. All that is required, then, to find the result of placing the tool in any particular position, as at i in the end view, is to draw from the tool point a line parallel to a b and equal in length to it, as c d. The two ends of that line will represent in their distances from the work axis the radius the work will be turned to at each end with the tool in that position. Thus, at one end of the line c d is the circle k, representing the diameter the tool i would turn the cone at the small end, while at the other end the dotted circle h gives the diameter at the large end that the tool would turn to when at the end of its traverse. But if the tool be placed as at t, it will turn the same diameter k at the small end, and the diameter of the circle p at the large end.
We have here taken account of the diameters at the ends only of the work, without reference to the result given at any intermediate point along the cone surface, but this we may now proceed to do, in order to prove that a curved instead of a straight taper is produced if the tool be placed either above or below the line of lathe centres.
In Fig. 1225, d e f c represents the complete outline of a straight taper, whose diameter at the ends is represented in the end view by the outer and inner circles. Now, a line from a to b will represent the axis of the work, and also the line of tool point motion or traverse, if that point is set level with the axis. The line i k in the end view corresponds to the line a b in the side view, in so far that it represents the line of tool traverse when the tool point is set level with the line of centres. Now, suppose the tool point to be raised to stand level with the line g h, instead of at i k, and its line of feed traverse be along the line g h, whose length is equal to that of i k. If we divide the length of g h into six equal divisions, as marked from 1 to 6, and also divide the length of the work in the side view into six equal divisions (a to f), we shall have the length of line g h in the first division in the end view (that is, the length from h to g), representing the same amount or length of tool traverse as from the end b of the cone to the line a in the side view. Now, suppose the tool point has arrived at 1; the diameter of work it will turn when in that position is evidently given by the arc or half-circle h, which meets the point 1 on g h. To mark that diameter on the side view, we first draw a horizontal line, as h p, just touching the top of h; a perpendicular dropped from it cutting the line a b, gives the radius of work transferred from the end view to the side view. When the tool point has arrived at 2 on g h in the end view, its position will be shown in the side view at the line b, and the diameter of work it will turn is shown in the end view by the half-circle k. To transfer this diameter to the side view we draw the line k g, and where it cuts the line b in the side view is the radius of the work diameter when the tool has arrived at the point b in the side view. Continuing this process, we mark half-circles, as l, m, n, o, and the lines l r, m s, n t, o u, by means of which we find in the side view the work radius when the tool has arrived at c, d, e, and f respectively. All that remains to be done is to draw on the side view a line, as u e, that shall pass through the points. This line will represent the outline of the work turned by the tool when its height is that denoted by g h. Now, the line u e is shown to be a curve, hence it is proved that with the tool at the height g h a curved, and not a straight, taper will be turned.
It may now be proved that if the tool point is placed level with the line of centres, a straight taper will be turned. Thus its line of traverse will be denoted by a b in the side view and the line i k in the end view; hence we may divide i k into six equal divisions, and a b into six equal divisions (as a, b, c, &c.). From the points of division i k, we may draw half-circles as before, and from these half-circles horizontal lines, and where the lines meet the lines of division in the side view will be points in the outline of the work, as before. Through these points we draw a line, as before, and this line c f, being straight, it is proven that with the tool point level with the work axis, it will turn a straight taper.
It may now be shown that it is possible to turn a piece of work to a curve of equal curvature on each side of the middle of the work length. Suppose, for example, that the cutting tool stands on top of the work, as in the end view in Fig. 1226, and that while the tool is feeding along the work it also has a certain amount of motion in a direction at right angles to the work axis, so that its line of motion is denoted by the line b b in the top view. The outline of the work turned will be a curve, as is shown in Fig. 1227, in which the line of tool traverse is the line c d. Now the[I-316] amount of tool motion that occurs during this traverse in a direction at right angles to the work axis is represented by the line f e, because the upper end is opposite to the upper end of c d, while the lower end is opposite the lower end of c d. We may then divide one-half of the length of f e into the divisions marked from 1 to 6. Now, as we have taken half the length of f e, we must also take half the length of the work and divide it into six equal divisions marked from a to f. Now, suppose the tool point to stand in the line f s in the end view, its position in the top view will be at c. When it is at 1 on the end view it will have arrived at p in the top view. The radius of work it will then turn is shown in the end view by the length of line running from 1 to the work centre. Take this length, and from a in the work axis set it off on the line a h, and make the length equal the height of 1 s. In like manner, when the tool point has arrived at 2, the radius it will cut the work is shown by the length of line i; hence from 2 on the work axis we may set off the length of 2 s, making 2 s and b i of equal length. Continuing this process, we make the length of c k equal that of 3 s, the length of d l equal 4 s, and so on. All that remains then is to draw a line, o g, that shall meet the tops of these lines. This line will show the curve to which that half of the work length will be turned to. The other half of the work length will obviously be turned to the same curvature.
It is obvious that the curvature of the work outline will be determined by the proportion existing between the length of the work and the amount of tool motion in a direction at right angles to the work axis, or, in other words, between the length of the work and that of the line f e. It is evident, also, that with a given amount of tool motion across the work, the curvature of outline turned will be less in proportion as the work length is greater. Now, suppose that the smaller and the larger diameter of the work, together with its length, are given, and it is required to find how much curvature the tool must have, we may find this and work out the curve it will cut by the construction shown in Fig. 1228, in which the circle k is the smallest and the circle p the largest diameter. The line m c is drawn to just touch the perimeter of k, and this at once gives the amount of cross-motion for the tool. Hence, we may draw the line m b and c b, and from their extremities draw the line b b representing the path of traverse of the tool point. We may then obtain the full curve on one side of the work by dividing one-half the length of m c into six equal divisions and proceeding as before, except that we have here added the lines of division in the second half as from f to l. It will be observed that the centre of the curve is at the point where the tool point crosses the axis of the work; hence, by giving to the tool more traverse on one side than on the other of the work axis, the location of the smallest point of work diameter may be made to fall on one side of the middle of the work length.
In either turning or boring tapers that are to drive or force in or together, the amount to be allowed for the fit may be ascertained, so that the work may be made correct without driving each piece to its place to try its fit.
Suppose, for example, that the pieces are turned, and the holes are to be reamed, then the first hole reamed may be made to correct diameter by fit and trial, and a collar may be put on the reamer to permit it to enter the holes so far and no farther.
A taper gauge may then be made as in Fig. 1229, the line a representing the bore of the hole, and line b the diameter of the internal piece, the distance between the two being the amount found by trial to be necessary for the forcing or driving. The same gauge obviously serves for testing the taper of the holes reamed.
Chucked or Face Plate Work.—This class of work requires the most skillful manipulation, because the order in which the work may most advantageously proceed and the method of chucking are often matters for mature consideration.
In a piece of work driven between the lathe centres, the truth of any one part may be perceived at any time while operating upon the others, but in chucked work, such is not always the case, and truth in the work is then only to be obtained by holding it truly. Again, the work is apt to be sprung or deflected by the pressure of the devices holding it, and furthermore the removal of the skin or surface will in light work sometimes throw it out of true as the work proceeds, the reason being already given, when referring to turning plain cylindrical work.
To Turn a Gland.—There are three methods of turning a gland: first, the hole and the face on the outside of the flange may be turned first, the subsequent turning being done on a mandrel; second, the hole only may be bored at the first chucking, all the remaining work being done on a mandrel; and, third, the hole, hub, and one radial face may be turned at one chucking, and the remaining face turned at a separate chucking.
If the first plan be adopted, any error in the truth of the mandrel will throw the hole out of true with the hub, which would be a serious defect, causing the gland to jamb against one side of the piston rod, and also of the gland bore. The same evil is liable to result from the second method; it is best, therefore, to chuck the gland by the hub in a universal chuck, and simply face the outer face of the flange, and also its edge. The gland may then be turned end for end, and the hole, the hub, the inside radial flange face, and the hub radial face, may then all be turned at one chucking; there is but one disadvantage in this method, which is that the gland must be unchucked to try its fit in the gland hole, but if standard gauges are used such trial will not be necessary, while if such is not the case and an error of measurement should occur, the gland may still be put on a mandrel and reduced if necessary.
In either method of chucking, the fit of the hole to the rod it is intended for cannot be tested without removing the gland from the chuck.
To Turn a Plain Cylindrical Ring all over in a Universal Chuck.—Three methods may be pursued in doing this simple job: first, the hole may be bored at one chucking, and the two radial faces and the circumference turned at a second chucking; second, the diameter may be turned, first on the hole and two radial faces turned at a second chucking; and third the hole and[I-317] one radial face may be turned at one chucking, and the diameter and second radial face at a second chucking. The last method is best for the following reasons. The tool can pass clear over the surfaces at each chucking without danger of coming into contact with the chuck jaws, which would cause damage to both; second, at the last chucking, the chuck jaws being inside the ring, the latter may be tested for truth with a pointer fixed in the tool rest, and therefore set quite true.
It is obvious that at neither chucking should the ring be set so far within the chuck jaws that there will be danger of the tool touching them when turning the radial face.
In the case of a ring too thin to permit this, and of too large a bore to warrant making a mandrel for it, the ring may be held on the outside and bored, and both radial faces turned to within a short distance of the chuck jaws; at the second chucking, the chuck jaws being within the ring bore, the work may be set true with a pointer, as before, and finished.
If, however, a number of such rings were to be turned, it would pay to turn up another and thicker ring, and use it as a mandrel after the bore and one radial face of the ring had been turned.
To Turn an Eccentric Strap and Eccentric.—The eccentric strap should be turned first, because it can then be taken apart and its fit to the eccentric tried while the latter is in the lathe, which is not the case with the eccentric. The strap should first be held in a universal chuck bolted to the face plate, or held in dogs such as shown in Fig. 893 at c, and one face should be turned. It should then be turned round on the chuck to bore it, and face the other side.
If the shape of the strap will admit it, it is best chucked by plates and bolts holding the face first turned to the face plate, because in this case there will be no pressure tending to spring the straps out of their natural shape; otherwise, however, it may be held in a universal or independent jaw chuck, or if too large for insertion in chucks of this kind (which are rarely made for large lathes) it may be held in dogs such as shown in Fig. 893 at c.
If after an eccentric strap is bored, and the bolts that hold its two halves together have been slackened, its diameter at a and at c, Fig. 1230, be measured, it will be found that a is less than c. The cause of this is partly explained under the head of tension of castings; but it is necessary to add that the diameters at a and at c in the figure are equal while the strap is in the lathe, or until the bolts holding the two halves of the strap together are released, yet so soon as this is done the diameter at a will reduce, the bore becoming an oval.[18]
[18] This occurs in all castings of similar form, as brasses, &c.
Now, it is obvious that the eccentric must be turned to the diameter at c, or otherwise it will have lost motion in the strap. If, however, the eccentric be turned to the diameter of c, the strap cannot be tried on, as it will bind at the corners, as shown in Fig. 1231. To remedy this evil it is usual to put a piece of sheet tin or metal between the joint faces of the two halves of the eccentric straps before they are chucked to turn them, and to bore them too large to the amount of the thickness of sheet metal so employed. After the straps are bored these pieces of metal are removed, and the strap halves bolted together as in Fig. 1230, the diameter at c being that to which the eccentric must be turned.
If the sheet metal so inserted were thick enough, the strap bore will measure the same at a as at c, Fig. 1230. If it were too thick the diameter at a will be greatest, while if too thin the diameter at a will be the least. There is no rule whereby the necessary thickness for a given size of strap may be known, and the workman is usually governed by his experience on castings of similar metal, or from the same moulding shop.
He prefers, however, to be on the safe side by not putting in too great a thickness, because it is easier to scrape away the bore at the joint than it is to file away the joint faces. The following thicknesses for the respective diameters may be considered safe for castings that have not been reheated after casting.
| Diameter of bore. |
Thickness of metal to place between the strap valves. |
|
| Inches. | Inch. | |
| 6 | 1⁄64 | |
| 12 | 1⁄32 | |
| 18 | 3⁄64 | |
| 24 | 1⁄8 |
In turning a new strap for an old eccentric, it will be necessary, when taking the diameter of the eccentric, to take a piece of tin of the same thickness as that placed between the eccentric lugs or jaws, and place it between the caliper leg and the eccentric, so that the diameter of the strap across c, Fig. 1230, may be made equal when the tin is removed to the diameter of the eccentric.
In turning up the eccentric, the plain face should be faced first, setting it true, or nearly so, with the circumference of the eccentric, as will be the case if the circumference is held in a universal chuck, but if the hub is so long that this cannot be done because the chuck jaws cannot reach the circumference, the hub itself may be held in an independent jaw chuck.
The face turned may then be turned round, so as to meet the face of the chuck against which it should bed fairly, so as to run true. At this chucking the hole bore, the hub, and the radial faces should be turned, all these surfaces being roughed out before any one surface is finished.
The eccentric must then be again reversed, so that the face of the hub meets, the face plate being held by bolts as shown for a crank in figure, when the work being set to the lines marked (so as to give it the correct amount of throw) may be turned to fit the bore of the strap, the strap being taken apart so as to try it on, which this method of chucking will readily permit.
Now, in an eccentric, the surfaces requiring to be most true one with the other are those of the bore and of the circumference where the strap fits, and since the latter was turned with the hub face to the chuck, and that hub face was turned at the same chucking as the hole was bored (and must, therefore, be true to the bore), the bore and circumference will be as true as it is practicable to get them, because upon the truth of the last chucking alone will the truth of the work depend.
Small eccentrics may be held for all their chuckings in jaw chucks, but not so truly as if chucked on a face plate, because of the difficulty of keeping the radial faces of such jaws true, which occurs by reason of the causes explained with reference to Figs. 848 and 849.
Eccentrics having so much throw upon them as to render it difficult to hold them for the last chucking by the method above given (by bolts through the bore), usually have openings through them on the throw side, and in this case parallel pieces may be placed behind the radial face (on the hub side of the eccentric), such parallel pieces being thick enough to keep the hub face clear of the chuck face, and bolts may be passed through the said opening to hold the eccentric. Another method would be as follows:—
The outside diameter of the eccentric may be gripped in a dog chuck, if the dogs of the chuck project out far enough to reach it (otherwise the dogs may grip the hub of the eccentric), while the hole is bored and the plain face of the eccentric turned. The eccentric must then be reversed in the lathe, and the hub and the radial face on that side must be turned. Then the plain face of the eccentric must be bolted to the face plate by plates placed across the spaces which are made to lighten the eccentric, and by a plate across the face of the hub. The eccentric, being set true to the lines, may then be turned on its outside diameter to fit the[I-318] strap; to facilitate which fitting, thin parallel strips may be placed between the face plate and the plain face of the eccentric at this last chucking. It will be observed that, in either method of chucking, the outside diameter of the eccentric (that is to say, the part on which the strap fits) is turned with the face which was turned at the same chucking at which the hole was bored, clamped to the face plate. In cases where a number of eccentrics having the same size of bore and the same amount of throw are turned, there may be fitted to the face plate of the lathe a disk (such as shown in Fig. 888), of sufficient diameter to fit the hole of the eccentric, the said disk being fastened to the face plate at the required distance from the centre of the lathe to give the necessary amount of throw to the eccentric. The best method of fastening such a disk to the face plate is to provide it with a plain pin turned true with the disk, and let it fit a hole (bored in the face plate to receive it) sufficiently tightly to be just able to be taken in and out by the hand, the pin being provided with a screw at the end, so that it can be screwed tight by a nut to the face plate. The last chucking of the eccentric is then performed by placing the hole of the eccentric on the disk, which will insure the correctness of the throw without the aid of any lines on the eccentric which may be set as true as the diameter of the casting will permit, and then turned to fit the strap.
To Turn a Cylinder Cover.—A cylinder cover affords an example of chucking in which the work done at one chucking requires to be very true with that done at a subsequent chucking, thus the gland hole which is on one side requires to be quite true with the diameter that fits into the cylinder bore, this diameter being on the opposite side.
If the polished or gland side of the cover be turned first, the hole for the packing ring and that for the gland may be bored with the assurance that one will be true with the other, while the polished outside face may be turned at the same chucking.
But when the cover is turned round in the lathe to turn the straight face, though the hole may be set true as far as can be ascertained in its short length, yet that length is too short to be an accurate guide, and the hole for the packing ring may appear true, while that for the gland, being longer, will have any error in the setting, multiplied by reason of its greater length. It is better, therefore, to turn the plain face first, gripping the cover by the gland flange so that the plain radial face, the step that fits the cylinder bore, and the outer edge of the cover flange may be turned at one chucking; then when the cover is turned round in the chuck, the flat face may be set true by resting against the radial surface of the chuck jaws, and the concentric truth may be set by the outer edge of the flange, which, being of the extreme diameter of the cover, will most readily show any want of truth in the setting. If in this case a universal chuck be used, and the work does not run quite true, it may be corrected by slacking the necessary dog or jaw on one side, and tightening up again from the screw of the necessary jaw on the other.
This occurs because from the wear, &c., there is always some small amount of play or lost motion in the jaw screws, and in the mechanism operating them, and by the above means this is taken advantage of to true the work.
If from any cause the work cannot be held for the first chucking by means of the gland hole flange, it must be held by the circumferential edge of the cover, letting the jaws envelop as small a distance over that edge as possible, the protruding part of it may then be turned up as close to the chuck jaws as possible, and this turned part may still be used to set the cover concentrically true at the second chucking.
In a very small cover the gland hole may have a mandrel fitted to it and be turned therefrom on both radial faces, or on one face only, the other being turned at the chucking at which the holes were bored.
In a cover too large to be held in a jaw chuck, the cover may be held in chucking dogs such as shown at c in Fig. 893, the edge protruding as much as possible from the dog screws, and being turned half way across at one chucking, and finished at the second chucking. To set the radial face at the second chucking, the surface gauge, applied as shown in Fig. 894, may be employed. If the bore of the packing ring or piston rod hole is large enough to permit it, that hole and the gland hole may be bored at the same chucking as that at which the plain face and step that fits in the cylinder bore is turned, thus ensuring truth in all the essential parts of the cover.
But in this case these operations should be performed at the last of the two chuckings, so as to eliminate any error that might arise from the casting altering its shape by reason of the removal of the metal on the radial face of the gland hole side of the cover.
To Turn a Pulley.—A pulley affords an excellent example of lathe work, because it may be operated upon by several different methods: thus, for boring it may be held, if small, in a dog chuck, with the jaws inside the rim; in a dog chuck with the jaws outside the rim; in a dog chuck by the hub itself (if the hub is long enough). A larger pulley may be chucked for boring by the rim held in a jaw chuck; by the rim held by bolts and plates, or by the rim held by dogs, such as shown in Fig. 893, or by the arms rested on pieces placed between them and the chuck, and then bolts and plates applied to those arms.
The rim may be turned by placing the pulley on a mandrel and driving that mandrel by a dog or carrier; by placing it on a mandrel and driving it by a Clements driver such as shown in Fig. 753, and having two diametrically opposite driving pins, placed to bear against diametrically opposite arms; by holding the arms to the chuck as before described, and performing the boring and facing at one chucking; or by holding the rim on its inside by the chuck jaws, so as to turn and bore the pulley at one chucking, which can be done when the inside of the rim is parallel, or not sufficiently coned to cause it to slip off the jaws, or when the jaws will reach to the centre of the rim width.
The advantages and disadvantages of these various methods are as follows:—
From the weakness of the pulley rim it is apt to distort when held with sufficient chuck-jaw pressure to enable the turning of the rim face and edge. But this would not affect the truth of the hole; hence the rim may be gripped in a chuck to bore the hole and face the hub. If so held it should be held true to the inside face of the rim, so that the bore will be true to the same, and then in turning the outside diameter it will be made as true as possible with the rim, which will preserve the balance of the pulley as much as possible. For these reasons the inside of the rim should be the part set to run true, whatever method of chucking be employed; hence, if the circumstances will permit of holding the hub to bore it, an independent jaw chuck should be employed (that is, of course, a chuck capable of independent jaw movement).
If the pulley be chucked by the arms, it is well-nigh impossible to avoid springing those arms from the pressure of the bolts, &c., holding them, and as a result the pulley face, though turned true, will not be true of itself, nor true with the hole, when the arms are released from such pressure.
If the pulley is of such a large size that its rim must be held by bolts and plates while the boring is progressing, such bolts, &c., must be placed on the outside of the rim, so as not to be in the way when setting the pulley true to the inside of the rim.
A small pulley may be turned on a mandrel driven by a dog, which is the truest method of turning, because the rim is in this case strained by the pressure of the cut only. But a dog will not drive a cut at such a leverage as exists at the rim of a pulley above about 18 inches in diameter; furthermore, in a large wheel there would not be sufficient friction between a mandrel and the pulley bore to drive the roughing cut on the pulley face.
It is necessary, therefore, to drive the pulley from the arms, while holding it on a mandrel, but if it be driven by one arm the whole strain due to driving will fall on that one arm, and on one side of the pulley only, and this will have a tendency to cause the rim at and near its junction with that arm to spring or deflect from its natural position, and, therefore, to be not quite true; all that can be done, therefore, is to drive by two arms with a Clements driver, so as to equalize the pressure on them.
An excellent method of chucking a pulley, and one that with care avoids the disadvantages mentioned in the foregoing methods,[I-319] is shown in Figs. 1232 and 1233. It consists of a clamping dog, Fig. 1234, that fastens to the lathe face plate, and secures the pulley by its arms, while supporting the rim and preventing it from chattering, if it is weak or slight.
This dog is bolted to the face plate by the two studs a and b. At c is a set screw for clamping the pulley arms against the screw d, and at f is a screw that steadies the pulley rim between the arms.
Cutting Screws in the Lathe with Slide Rest Tools.—In order to cut a thread in the lathe with a slide rest tool, it is necessary that the gear-wheels which transmit motion from the cone spindle to the feed screw shall be of the proportions necessary to give to the lathe carriage and slide rest sufficient lateral movement or traverse for lathe revolution to cut a thread of the desired pitch.
Suppose now that the feed screw makes a revolution in the same time that the cone spindle does, and it is evident that the thread cut by the slide rest tool will be of the same pitch as is the pitch of the lathe feed screw. If the feed screw gear-wheels of the lathe are what is called single geared (which means that no one stud in the change gearing carries more than one gear-wheel), it does not matter what are the sizes or how many teeth there are in the wheels used to convey or transmit motion from the cone spindle to the feed screw, for so long as the number of teeth on the cone spindle gear and that on the feed screw are equal, the feed screw will make one revolution in the same time as the cone spindle makes a revolution, and the cutting tool will travel a lateral distance equal to the pitch of the lead screw.
Suppose, for example, that Fig. 1235 represents the screw cutting gear or change wheels of a lathe, wheel d being the driver, i an intermediate wheel for transmitting motion from the driver d to the lead-screw wheel s. Suppose, also, that d has 32, i 80, and s 32 teeth, and we have a simple or single-geared lathe. In this case it may first be proved that we need not concern ourselves with the number of teeth in the intermediate i, because its number of teeth is of no consequence. For example, the 32 teeth in d will in a revolution move 32 of the teeth in i past the line of centres, and it is obvious that i will move the 32 teeth in s past the line of centres, causing it to make one revolution the same as d. If any other size of wheel be used for an intermediate, the effect will be precisely the same, the revolutions of d and of s remaining equal. Under these conditions the lathe would cut a thread whose pitch would be the same as that of the thread on the lead screw.
Now let us turn to Fig. 1236, representing an arrangement of gearing common in American practice, and we have within the lathe-head three gears, a, b, and c, which cannot be changed. Of these, b and c are simply intermediate wheels, the respective diameters of which have no effect upon the revolutions of the lead screw, except that they convey the motion to d. To demonstrate this, suppose the wheels to have the number of teeth marked respectively against them in the end view of the figure, c and d having each 20 teeth, and the one revolution of the live spindle wheel a will cause the lead-screw wheel to make one revolution, because a and s contain the same number of teeth. This may be made plain as follows: The 20 teeth in a will in one revolution cause b to make two revolutions, because b has but half as many teeth as a. The two revolutions of b will cause c to make but one[I-320] revolution, because c has twice as many teeth as b has. Now, c and d are fast on the same shaft r; hence they revolve together, the one revolution of c simply being conveyed by the shaft r to d, and it is clear that the one revolution of a has been conveyed without change to d, and that, therefore, d may be considered to have simply taken the place of a, unaffected by the wheels b, c. Wheel i is again an intermediate, so that, whatever its diameter or number of teeth, one revolution of d will cause one revolution of s. Thus in this arrangement the lead screw will again revolve at the same speed as the live spindle, and the thread cut will be of the same pitch as the pitch of the lead screw. Practically, then, all the wheels between a and s, as thus arranged, act as simple intermediates, the same as though it were a single-geared lathe, which occurs because c and d have the same number of teeth, and we have, therefore, made no use of the shaft r to compound the gearing.
The term “compounded” as applied to the change gears of a lathe, means that there exists in it a shaft or some equivalent means by which the velocity of the wheels may be changed. Such a shaft is shown at r in Fig. 1236, and it affords a means of compounding by placing on its outer end, as at d, a wheel that has a different number of teeth to that in wheel c. In Fig. 1237 this change is made, wheel d having 40 teeth instead of the 20 it had before. As in the former case, however, it will make one revolution to one of c or one of a, but having 40 teeth it will move 40 of the teeth in i past the line of centres, and this will cause the lead screw wheel s to make two revolutions, because it has 20 teeth only. Thus, the compounding of c and d on shaft r has caused s to make two revolutions to one of a, or, what is the same thing, one revolution of a will in this case cause s to make two revolutions, and the thread cut would be twice as coarse as the lead-screw thread. In the case of a lathe geared as in either Fig. 1235 or 1236, all the wheels that we require to consider in calculating the change wheels are d and s. Now, the shaft r is called the “mandrel,” the “stud,” or the “spindle,” all three terms being used, and the wheel d is the wheel on the stud, mandrel, or spindle, while in every case s is that on the lead screw, and the revolutions of this wheel d and those of the lead screw will be in the same proportion as exists between their numbers of teeth. In considering their revolutions it is to be borne in mind that when d has more teeth than s the speed of the lead screw is increased, and the lathe will cut a thread coarser than that of its lead screw, or when d has less teeth than s the speed of the lead screw is diminished, and the pitch of thread cut will be finer than that of the lead screw.
Another method of compounding is shown in Fig. 1238, the compounded pair c d being on a stud carried in the swing frame f. Now, suppose a has 32, c 64, d 32, and s 64 teeth, the revolution being in the same proportion as the numbers of teeth, c will make one-half a revolution to one revolution of a, and d, being fast to the same stud as c, will also make one-half revolution to one revolution of a. This one-half revolution of d will cause s to make one-quarter of a revolution; hence the thread cut will be four times as fine as the pitch of the thread on the lead screw, because while the lathe makes one turn the lead screw makes one-quarter of a turn. In this arrangement we are enabled to change wheel c as well as wheel d (which could not be done in the arrangement shown in Fig. 1236), and for this reason more changes can be made with the same number of wheels. When the wheel c makes either more or less revolutions than the driver a, it must be taken into account in calculating the change wheels. As arranged in Fig. 1236, it makes the same number as a, which is a very common, arrangement, but in Fig. 1238 it is shown to have twice as many teeth as a; hence it makes half as many revolutions. In the latter case we have two pairs of wheels, in each of which the driven wheel is twice the size of the driver; hence the revolutions are reduced four times.
Suppose it is required to cut a thread of eight to an inch on a lathe such as shown in Fig. 1235, the lead screw pitch being four per inch, and for such simple trains of gearing we have a very simple rule, as follows:—
Rule.—Put down the pitch of the lead screw as the numerator, and the pitch of thread you want to cut as the denominator of a vulgar fraction, and multiply both by the pitch of the lead screw, thus:
| Pitch of lead screw. |
||||||||
| Pitch of lead screw | 4 | × | 4 | = | 16 | = | { | the number of teeth for the wheel on the spindle. |
| Pitch to be cut | 8 | 4 | 32 | = | { | the number of teeth for the wheel on the lead screw. | ||
There are three things to be noted in this rule; and the first is, that when the pitch of the lead screw and the pitch of thread you want to cut is put down as a fraction, the numerator at once represents the wheel to go on the stud, and the denominator represents the wheel to go on the lead screw, and no figuring would require to be done providing there were gear-wheels having as few teeth as there are threads per inch in the lead screw, and that there was a gear-wheel having as many teeth as the threads per inch required to be cut. For example, suppose the lathe in Fig. 1236 to have a lead screw of 20 per inch, and that the change wheels are required to cut a pitch 40, then we have 20⁄40, the 20 to go on at d in Fig. 1236 and the 40 to go on the lead screw. But since lead screws are not made of such fine pitch, but vary from two threads to about six per inch, we simply multiply the fraction by any number we choose that will give us numbers corresponding to the teeth in the change wheels. Suppose, for example, the pitch of lead screw is 2, and we wish to cut 6, then we have 2⁄6, and as the smallest change wheel has, say, 12 teeth we multiply the fraction by 6, thus: 2⁄6 × 6⁄6 = 12⁄36. If we have not a 12 and a 36 wheel, we may multiply the fraction by any other number, as, say, 8; thus: 2⁄6 × 8⁄8 = 16⁄48 giving us a 16 wheel for d, Fig. 1236, and a 48 wheel for the lead screw.
The second notable feature in this rule is that it applies just the same whether the pitch to be cut is coarser or finer than the lead screw; thus: Suppose the pitch of the lead screw is 4, and we want to cut 2. We put these figures down as before 4⁄2, and proceed to multiply, say, by 8; thus: 4⁄2 × 8⁄8 = 32⁄16, giving a 32 and a 16 as the necessary wheels.
[I-321]The third feature is, that no matter whether the pitch to be cut is coarser or finer than the lead screw, the wheels go on the lathe just as they stand in the fraction; the top figure goes on top in the lathe, as, for example, on the driving stud, and the bottom figures of the fraction are for the teeth in the wheel that goes on the bottom of the lathe or on the lead screw. No rule can possibly be simpler than this. Suppose now that the pitch of the lead screw is 4 per inch and we want to cut 11⁄2 per inch. As the required pitch is expressed in half inches, we express the pitch of the lead in half inches, and employ the rule precisely as before. Thus, in four there are eight halves; hence, we put down 8 as the numerator, and in 11⁄2 there are three halves, so we put down 3 and get the fraction 8⁄3. This will multiply by any number, as, say, 6; thus: (8⁄3) × (6⁄6) = (48⁄18), giving us 48 teeth for the wheel d in Fig. 1236, and 18 for the lead screw wheel s.
In a lathe geared as in Fig. 1235 the top wheel d could not be readily changed, and it would be more convenient to change the lead screw wheel s only. Suppose, then, that the lead screw pitch is 2 per inch, and we want to cut 8. Putting down the fraction as before, we have 2⁄8, and to get the wheel s for the lead screw we may multiply the number of teeth in d by 8 and divide it by 2; thus: 32 × 8 = 256, and 256 ÷ 2 = 128; hence all we have to do is to put on the lead screw a wheel having 128 teeth. But suppose the pitch to be cut is 41⁄4, the pitch of the lead screw being 2. Then we put both numbers into quarters, thus: In 2 there are 8 quarters, and in 41⁄4 there are 17 quarters; hence the fraction is 8⁄17. If now we multiply both terms of this 8⁄17 by 4 we get 32⁄68, and all we have to do is to put on the lead screw a wheel having 68 teeth.
When we have to deal with a lathe compounded as in Fig. 1238, in which the combination can be altered in two places—that is, between a and c and between d and s—the wheel a remaining fixed, and the pitch of the lead screw is 2 per inch, and it is required to cut 8 per inch—this gives us the fraction 2⁄8, which is at once the proportion that must exist between the revolutions of the wheel a and the wheel s. But in this case the fraction gives us the number of revolutions that wheel s must make while the wheel a is making two revolutions, and it is more convenient to obtain the number that s requires to make while a is making one revolution, which we may do by simply dividing the pitch required to be cut by the pitch of the lead screw, as follows: Pitch of thread required, 8; pitch of lead screw, 2; 8 ÷ 2 = 4 = the revolutions s must make while a makes one. We have then to reduce the revolutions four times, which we may do by putting on at c a wheel with twice as many teeth in it as there are in a, and as a has 32, therefore c must have 64 teeth. When we come to the second pair of wheels, d and s, we may put any wheel we like in place of d, providing we put on s a wheel having twice as many.
But suppose we require to cut a fractional pitch, as, say, 41⁄8 per inch, the pitch of lead screw being 2, all we have to do is to put the pitch of the lead screw into eighths, and also put the number of teeth in a into eighths; thus: In two there are 16 eighths, and in the pitch required there are 33 eighths; hence for the pitch of the lead screw we use the 16, and for the thread required we use the 33, and proceed as before; thus:
| Pitch of thread required. |
Pitch of lead screw. |
|||||
| 33 | ÷ | 16 | = | 21⁄16 | = | the revolution which a must make while wheel b makes one revolution. |
The simplest method of doing this would be to put on at c a wheel having 21⁄16 times as many teeth as there are in a. Suppose then that a has 32 teeth, and one sixteenth of 32 = 2, because 32 ÷ 16 = 2. Then twice 32 is 64, and if we add the 2 to this we get 66; hence, if we give wheel c 66 teeth, we have reduced the motion the 21⁄16 times, and we may put on d and s wheels having an equal number of teeth. Or we may put on a wheel at c having the same number as a has, and then put on any two wheels at d and c, so long as that at s has 21⁄16 times as many teeth as that at d.
Again, suppose that the pitch of a lead screw is 4 threads per inch, and that it be required to find what wheels to use to cut a thread of 11⁄16 inch pitch, that is to say, a thread that measures 11⁄16 inch from one thread to the other, and not a pitch of 11⁄16 threads per inch: First we must bring the pitch of the lead screw and the pitch to be cut to the same terms, and as the pitch to be cut is expressed in sixteenths we must bring the lead screw pitch to sixteenths also. Thus, in an inch of the length of the lead screw there are 16 sixteenths, and in this inch there are 4 threads; hence each thread is 4⁄16 pitch, because 16 ÷ 4 = 4. Our pitch of lead screw expressed in sixteenths is, therefore, 4, and as the pitch to be cut is 11⁄16 it is expressed in sixteenths by 11; hence we have the fraction 4⁄11, which is the proportion that must exist between the wheels, or in other words, while the lathe spindle (or what is the same thing, the work) makes 4 revolutions the lead screw must make 11.
Suppose the lathe to be single geared, and not compounded, and we multiply this fraction and get—
| 4 | × | 4 | = | 16 | = | wheel | to go on | lead screw. | |
| 11 | × | 4 | 44 | = | „ | „ | stud or mandrel. | ||
| Or, | 4 | × | 5 | = | 20 | = | wheel | to go on | lead screw. |
| 11 | × | 5 | 55 | = | „ | „ | stud or mandrel. | ||
| Or, | 4 | × | 6 | = | 24 | = | wheel | to go on | lead screw. |
| 11 | × | 6 | 66 | = | „ | „ | stud or mandrel. | ||
But suppose the lathe to be compounded as in Fig. 1235, and we may arrange the wheels in several ways, and in order to make the problem more practical, we may suppose the lathe to have wheels with the following numbers of teeth, 18, 24, 36, 36, 48, 60, 66, 72, 84, 90, 96, 102, 108, and 132.
Here we have two wheels having each 36 teeth; hence we may place one of them on the lathe spindle and one on the lead screw, as in Fig. 1239; and putting down the pitch of the lead screw, expressed in sixteenths as before, and beneath it the thread to cut also in sixteenths, we have:
| 4 | × | 6 | = | 24 | = | wheel | to be driven by lathe spindle, |
| 11 | × | 6 | 66 | = | „ | to drive lead screw wheel; |
the arrangement of the wheels being shown in Fig. 1239.
We may prove the correctness of this arrangement as follows: The 36 teeth on the lathe spindle will in a revolution cause the 24 wheel to make 11⁄2 revolutions, because there are one and a half times as many teeth in the one wheel as there are in the other; thus: 36 ÷ 24 = 11⁄2. Now, while the 24 wheel makes 11⁄2, the 66 will also make 11⁄2, because they are both on the same sleeve and revolve together. In revolving 11⁄2 times the 66 will cause the 36 on the lead screw to make 23⁄4 turns, because 99 ÷ 36 = 23⁄4 (or expressed in decimals 2.75), and it thus appears that while the lathe spindle makes one turn, the lead screw will make 23⁄4 turns.
Now, the proportion between 1 and 23⁄4 is the same as that existing between the pitch of the lead screw and the pitch of the thread we want to cut, both being expressed in sixteenths; thus:
| Pitch | of lead screw in sixteenths | 4 | , and 11 ÷ 4 = 23⁄4; |
| „ | to be cut in sixteenths | 11 |
that is to say, 11 is 23⁄4 times 4.
[I-322]Suppose it is required, however, to find what thread a set of gears already on the lathe will cut, and we have the following rule:
Rule.—Take either of the driven wheels and divide its number of teeth by the number of teeth in the wheel that drives it, then multiply by the number of teeth in the other driving wheel, and divide by the teeth in the last driven wheel. Then multiply by the pitch of the lead screw.
Example.—In Fig. 1240 are a set of change wheels, the first pair of which has a driving wheel having 36 teeth, and a driven wheel having 18 teeth. The second pair has a driving wheel of 66 teeth, and a driven wheel of 48.
Let us begin with the first pair and we have 36 ÷ 18 = 2, and this multiplied by 66 is 132. Then 132 ÷ 48 = 2.75, and 2.75 multiplied by 4 is 11, which is the pitch of thread that will be cut. Now, whether this 11 will be eleven threads per inch, or as in our previous examples a pitch of 11⁄16 inch from one thread to another or to the next one, depends upon what the pitch of the lead screw was measured in.
If it is a pitch of 4 threads per inch, the wheels will cut a thread of 11 per inch, while if it were a thread of 4⁄16 pitch, the thread cut will be 11⁄16 pitch.
Let us now work out the same gears beginning from the lead screw pair, and we have as follows:
Number of teeth in driver is 66, which divided by the number in the driven, 48, gives 1.375. This multiplied by the number of teeth in the driver of the other pair = 36 gives 49.5, which divided by the number of teeth in the driven wheel of the first pair gives 2.75, which multiplied by the pitch of the lead screw 4 gives 11 as before.
Taking now the second example as in Fig. 1240, and beginning from the first pair of gears, we have, according to the rule, 36 ÷ 48 × 66 ÷ 18 × 4 = 11 = pitch the gears will cut; or proceeding from the second pair of gears, we have by the rule, 66 ÷ 18 × 36 ÷ 48 × 4 = 11 = the pitch the gears will cut. It is not often, however, that it is required to determine what threads the wheels already on a lathe will cut, the problem usually being to find the wheels to cut some required pitch. But it may be pointed out that when the problem is to find the result produced by a given set of wheels, it is simpler to begin the calculation from the wheel already on the lathe spindle, rather than beginning with that on the lead screw, because in that case we begin at the first wheel and calculate the successive ones in the same order in which we find them on the lathe, instead of having to take the last pair in their reverse order, as has been done in the examples, when we began at the wheel on the lead screw, which we have termed the second pair.
The wheels necessary to cut a left-hand thread are obviously the same as those for a right-hand one having an equal pitch; all the alteration that is necessary is to employ an additional intermediate wheel, as at i in Fig. 1241, which will reverse the direction of motion of the lead screw. For a lathe such as shown in Fig. 1235, this intermediate wheel may be interposed between wheels d and i or between i and s. In Fig. 1236, it may be placed between d and i or between i and s, and in Fig. 1238 it may be placed between a and c or between d and s.
Here it may be well to add instructions as to how to arrange the change wheels to cut threads in terms of the French centimètre. Thus, an inch equals 254⁄100 of a centimètre, or, in other words, 1 inch bears the same proportion to a centimètre as 254 does to 100, and we may take the fraction 254⁄100 and reduce it by any number that will divide both terms of the fraction without leaving a remainder; thus, 254⁄100 ÷ 2 = 127⁄50. If, then, we take a pair of wheels having respectively 127 and 50 teeth, they will form a compound pair that if placed as in Fig. 1242 will enable the cutting of threads in terms of the centimètre instead of in terms of the inch.
Thus, for example, to cut 6 threads to the centimètre, we use the same change wheels on the stud and on the lead screw that would be used to cut 6 threads to the inch, and so on throughout all other pitches.
Cutting Double or other Multiple Threads in the Lathe.—In cutting a double thread the change wheels are obviously arranged for the pitch of the thread, and one thread, as a in Fig. 251 is cut first, and the other, b, afterwards. In order to insure that b shall be exactly midway between a, the following method is pursued. Suppose the pitch of the lead screw is 4 threads per inch, and that we require to cut a double thread, whose actual pitch is 8 per inch, and apparent pitch 16 per inch, then the lead screw requires to make half a turn to one turn of the lathe spindle; or what is the same thing, the lathe spindle must make two turns to one of the lead screw, hence the gears will be two to one, and in a single-geared lathe we may put on a 36 and a 72, as in Fig. 1243, in which the intermediate wheels are omitted, as they do not affect the case. With these wheels we cut a thread of 8 per inch[I-323] and then, leaving the lead screw nut still engaged with the lead screw and the tool still in position to cut the thread already formed, we make on the change wheels a mark as at s t, and after taking off the driving gear we make a mark at space u, which is 18 teeth distant from s, or half-way around the wheel. We then pull the lathe around half a turn and put the driving gear on again with the space u engaged with the tooth t, and the lathe will cut the second thread exactly intermediate to the first one. If it were three threads that we require to cut, we should after the driving gear was taken off give the lathe one-third a revolution, and put it back again, engaging the twelfth space from s with tooth t, because one-third of 36 is 12.
It is obviously necessary, in cutting multiple threads in this way, to so select the change wheels that the driving gear contains a number of teeth that is divisible without leaving a remainder by the thread to be cut: thus, for a double thread the teeth must be divisible by two, hence a 24, 30, 34, 36, or any even number of teeth will do. For a triple thread the number of teeth in the driving gear must be divisible by 3, and so on.
But suppose the driving gear is fast upon the lathe spindle and cannot be taken off, and we may then change the position of the lead screw gear to accomplish the same object as moving the lathe spindle. Thus for a double thread we would require to remove the driving gear as before, and then pull round the lead screw so that the eighteenth tooth from t would engage with space s, which is obviously the same thing as moving the driving gear round 18 teeth.
In short work of small diameter the tool will retain its sharpness so long, that one tool will rough out and finish a number of pieces without requiring regrinding, and in this case the finishing cuts can be set by noting the position of the feed screw handle when the first piece is finished to size and the tool is touching the work, so that it may be brought to the same position in taking finishing cuts on the succeeding pieces; but the calipers should nevertheless be used, being applied to the threads as in Figs. 1244 and 1245, which is the best method when there is a standard to set the calipers by.
After a threading tool has carried its cut along the required length of the work, the carriage must be traversed back, so that the second cut may be started. In short work the overhead cross belt that runs the lathe backwards is sufficiently convenient and rapid for this purpose, but in long screws much time would be lost in waiting while the carriage runs back. In the Ames lathe there is a device that enables the carriage to be traversed back by hand, and the feed nut to be engaged without danger of cutting a double thread, or of the tool coursing to one side of the proper thread groove, which is a great convenience.
The construction of this device is shown in Fig. 574. In lathes not having a device for this purpose, the workman makes a chalk mark on the tail of the work driver, and another on the top of the lead screw gear, and by always moving the carriage back to the same point on the lathe bed, and engaging the lead screw nut when these two chalk marks are at the top of their paths of revolution, the tool will fall into its correct position and there will be no danger of cutting a double thread.
In cutting V threads of very coarse pitch it will save time, if the thread is a round top and bottom one, to use a single-pointed slide rest tool, and cut up the thread to nearly the finished depth, leaving just sufficient metal for the chaser to finish the thread.
In using the single-pointed tool on the roughing cuts of very coarse pitches, it is an advantage to move the tool laterally a trifle, so that it will cut on one side or edge only. This prevents excessive tool spring, and avoids tool breakage.
This lateral movement should be sufficient to let the follower side or edge of the tool just escape the side of the thread, and all the cut be taken by the leading side or edge of the tool.
This is necessary because the tool will not cut so steadily on the follower as on the leading cutting edge, for the reason that[I-324] the pressure of the cut assists to keep the feed screw nut against the sides of the feed screw thread, taking up the lost motion between them, whereas the pressure of a cut taken on the follower side of the thread tends to force the thread of the feed nut away from the sides of the feed screw thread and into the space between the nut thread afforded by the lost motion, and as a result the slide rest will move forward when the tool edges meet exceptionally hard places or spots in the metal of the work, while in any event the tool will not operate so steadily and smoothly.
If the screw is a long one, the cutting should be done with a liberal supply of oil or water to keep it cool, otherwise the contraction of the metal in cooling will leave the thread finer than it was when cut. This is of special importance where accuracy of pitch is requisite.
In cutting a taper thread in a lathe, it is preferable that the taper be given by setting over the lathe tailstock, rather than by operating the cross slider from a taper-turning attachment, because the latter causes the thread to be cut of improper pitch. Thus, in Fig. 1246 is a piece of work between the lathe centres, and it will be readily seen that supposing the lathe to be geared to cut, say, 10 threads per inch, and the length a of the work to be 2 inches long, when the tool has traversed the distance a it will have cut 20 threads, and it will have passed along the whole length of the side b of the work and have cut 20 threads upon it, but since the length of line b is greater than that of a, the pitch of the thread cut will be coarser than that due to the change wheels. The amount of the error is shown by the arc c, which is struck from d as a centre; hence from c to e is the total amount of error of thread pitch.
But if the lathe tailstock sets over as in Fig. 1247, then the pitch of the thread will be cut correct, because the length of b will equal the length of tool traverse; hence at each work revolution the tool would advance one-twentieth of the length of the surface on which the thread is cut, which is correct for the conditions.
| VOL. I. | METHODS OF BALL TURNING. | PLATE XIII. | |||
 |
 |
 |
|||
| Fig. 1248. | Fig. 1249. | Fig. 1250. | |||
 |
 |
||||
| Fig. 1251. | Fig. 1252. | ||||
 |
|||||
| Fig. 1253. | |||||
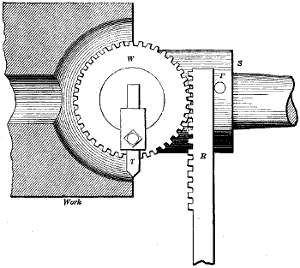 |
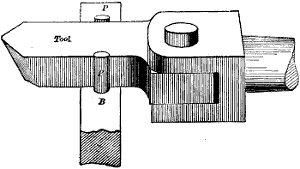 |
||||
| Fig. 1254. | Fig. 1255. | ||||
BALL TURNING.—One of the best methods of turning balls of the softer materials, such as wood, bone, or ivory, is shown in Figs. 1248 and 1249, in which are shown a blank piece of material and a tubular saw, each revolving in the direction denoted by the respective arrows. The saw is fed into the work and performs the job, cutting the ball completely off. In this case the saw requires to be revolved quicker than the work—indeed, as quickly as the nature of the material will permit, the revolving of the work serving to help the feed. Of course, the teeth of such a saw require very accurate sharpening if smooth work is to be produced, but the process is so quickly performed that it will pay to do whatever smoothing and polishing may be required at a separate operation. This method of ball cutting undoubtedly gave rise to the idea of using a single tooth, as in Fig. 1250. But when a single tooth is employed the work must revolve at the proper cutting speed, while the tooth simply advances to the feed. If the work was cut from a cylindrical blank the cutter would require to be advanced toward the work axis to put on a cut and then revolved to carry that cut over the work, when another cut may be put on, and so on until the work is completed. The diameter of ball that can be cut by one cutter is here obviously confined to that of the bore of the cutter, since it is the inside edge of the cutter that does the finishing.
This naturally suggests the employment of a single-pointed and removable tool, such as in Fig. 1251, which can be set to turn the required diameter of ball, and readily resharpened. To preserve the tool for the finishing cut several of such tools and holders may be carried in a revolving head provided to the lathe or machine, as the case may be. In any event, however, a single-pointed tool will not give the smoothness and polish of the ball cutter shown in Fig. 1252, which produces a surface like a mirror. It consists of a hardened steel tube c, whose bore is ground cylindrically true after it has been hardened. The ball b is driven in a chuck composed of equal parts of tin and lead, and the cutter is forced to the ball by hand. The ball requires to revolve at a quick speed (say 100 feet per minute for composition brass), while the cutter is slowly revolved.
A simple attachment for ball turning in an ordinary lathe is shown in Fig. 1253. It consists of a base a, carrying a plate b, which is pivoted in a; has worm-wheel teeth provided upon its circumference and a slideway at s, upon which slides a tool rest r, operated by the feed-screw handle h. The cut is put on by operating h, and the feed carried around by means of the screw at w. The base plate a may be made suitable to bolt on the tool rest, or clamped on in place of the tool, as the circumstances may permit; or in some cases it might be provided with a stem to fit in place of the dead centre. For boring the seats for balls or other curved internal surfaces the device shown in Fig. 1254 may be used. It consists of a stem or socket s, fitting to the dead spindle in place of the dead centre, and upon which is pivoted a wheel w, carrying a tool t. r is a rack-bar that may be held in the lathe tool post and fed in to revolve wheel w and feed the tool to its cut. At p is a pin to maintain the rack in gear with the wheel. Obviously, a set-screw may be placed to bear against the end of the tool to move it endwise and put on the cut. An equivalent device is shown in Fig. 1255, in which the tool is pivoted direct into the stem and moved by a bar b, held in the tool post. The cut is here put on by operating the tail spindle, a plan that may also be used in the device shown in Fig. 1254. The pins p upon the bar are for moving or feeding the tool to its cut. It is obvious that in all these cases the point of the tool must be out of true vertically with the axis of the work.
In turning metal balls by hand it is best to cast them with a stem at each end, as in Fig. 1257.
To rough them out to shape, a gauge or template, such as in Fig. 1256, is used, being about 1⁄32 inch thick, which envelops about one-sixth of the ball’s circumference. After the ball is roughed out as near as may be to the gauge, the stems may be nicked in, as in Fig. 1257, and broken off, the remaining bits, a, b, being carefully filed down to the template. The balls are then finished by chucking them in a chuck such as shown in Fig. 1258,[19] and a narrow band, shown in black in the figure, is scraped, bringing the ball to the proper diameter. The ball is then reversed in the chuck, as in Fig. 1259, and scraped by hand until the turning marks cross those denoted by the black band. The ball is then reversed, so that the remaining part of the black band that is within the chuck in Fig. 1259 may be scraped down, and when by successive chuckings of this kind the lightest of scrape marks cross and recross each other when the ball is reversed, it may be finished by the ball cutter, applied as shown in Fig. 1252,[I-326] and finally ground to its seat with the red-burnt sand from the foundry, which is better than flour emery or other coarser cutting grinding material.
[19] From The American Machinist.
Cutting Cams in the Lathe.—Fig. 1260 represents an end view of cam to be produced, having four depressions alike in form and depth, and arranged equidistant round the circumference, which is concentric to the central bore. The body of a cam is first turned up true, and one of the depressions is filed in it to the required form and curvature. On its end face there is then drilled the four holes, a, b, c, d, Fig. 1261, these being equidistant from the bore e. A similar piece is then turned up in the lathe, and in its end is fitted a pin of a diameter to fit the holes a, b, &c., it being an equal distance from bore e. These two pieces are then placed together, or rather side by side, on an arbor or mandrel, with the pin of the one fitting into one of the holes, as a. Two tool posts are then placed in position, one carrying a dull-pointed tool or tracer, and the other a cutting tool. The dull-pointed tracer is set to bear against the cam shown in Fig. 1262, while the cutting tool is set to take a cut off the blank cam piece. The cross feed screw of the lathe is disengaged, and a weight w, Fig. 1262, attached to the slider to pull the tracer into contact with the cam f. As a result, the slide rest is caused to advance to and recede from the line of lathe centres when the cam depression passes the tracer point, the weight w maintaining contact between the two. Successive cuts are taken until the tool cuts a depression of the required depth. To produce a second cam groove, the piece is moved on the mandrel so that the pin will fall into a second hole (as, say, b, Fig. 1261), when, by a repetition of the lathe operation, another groove is turned. The whole four grooves being produced by the same means, they must necessarily be alike in form, the depths being equal, provided a finishing cut were taken over each without moving the cutting tool.
It will be observed that this can be done in any lathe having a slide rest, and that the grooves cut in one piece will be an exact duplicate of that in the other, or guide groove, save such variation as may occur from the thickness of the tracer point, which may be allowed for in forming the guide or originating groove. From the wear, however, of the tracer point, and from having to move the cutting tool to take successive depths of cut, this method would be undesirable for continuous use, though it would serve excellently for producing a single cam. An arrangement for continuous use is shown in Fig. 1263, applied to a lathe having a feed spindle at its back, with a cam g upon it. This cam g may be supposed to have been produced by the method already described. A tracer point h, or a small roller, may be attached to the end of the slide-rest and held against g by the weight w, which may be within the lathe shears if they have no cross girts, as in the case of weighted lathes. The slide-rest may be arranged to have an end motion slightly exceeding the motion, caused by the cam, of the tracer h. Change gears may then be used to cause the cam g to make one rotation per lathe rotation, cutting four recesses in the work; or by varying the rotations of g per lathe rotation, the number of recesses cut by the tool t may be varied. Successive depths of cut may then be put on by operating the feed screw in the ordinary manner. In this arrangement the depth and form of groove cut upon the work will correspond to the form of groove upon the cam-roller g; or each groove upon g being of a different character, those cut on the work will correspond. The wear on the cross slide will, in this case, be considerable, however, in consequence of the continuous motion of the tool-carrying slider, and to prevent this another arrangement may be used, it being shown in Fig. 1264 as applied to a weighted and elevating slide rest. The elevating part of the slide rest is here pivoted to the lathe carriage at i, the weight w preventing play (from the wear) at i. A bracket j is shown fast to the elevating slide of the rest, carrying a roller meeting the actuating cam g. In this arrangement the cut may be put on by the feed screw traversing the slider in the usual manner, or the elevating screw k may be operated, causing the roller at the end of j to gradually descend as each cut is put on into more continuous contact with g as the latter rotates. The form of groove cut by the tool does not, in this case, correspond to the form on g, because the tool lifts and falls in the arc of a circle of which pivot i is the centre of motion, and its radius from i being less than the radius of g, its motion is less. But in[I-327] addition to this the direction of its motion is not that of advancing and receding directly toward and away from the line of lathe centres, and the cam action is reduced by both these causes.
The location of pivot i is of considerable importance, since the nearer it is to the line of centres the less the action of the cam g is reduced upon the work. As this is not at first sight apparent, a few words may be said in explanation of it. It is obvious that the farther the pivot i is from the tool point the greater will be the amount of motion of the tool point, but this motion is not in a direction to produce the greatest amount of effect upon the work, as is demonstrated in Fig. 1265; referring to which, suppose line a b c to represent a lever pivoted at b, and that end a be lifted so that the lever assumes the position denoted by the dotted lines d and e, then the end of c will have moved from circle f to circle g, as denoted by arc h; arm c of the lever being one-half the length of arm a b, and from circle f to circle g, measured along the line h, being one-half the distance between a and the end of the line d, the difference in the diameters of circles f and g will represent the effect of the cam motion on the tool under these conditions. Now, suppose a j is a lever pivoted at k, and that end a is raised to the dotted line d, then arm j, being one-half the length of a k, will move half as much as end a, and will assume the position denoted by dotted line l, and the difference in the diameter of circles f and m will represent the cam motion upon the tool motion under these conditions. From this it appears that the more nearly vertical beneath the tool point the pivoted point is, the greater the effect produced by a given amount of cam motion. On this account, as well as on account of the direction of motion, the shape of the actuating cam may be more nearly that of the form required to be produced in proportion as the pivoted centre falls directly beneath the tool point. But, on the other hand, the wear of the pivot, if directly beneath the tool point, would cause more unsteadiness to the tool; hence it is desirable that it be somewhere between points k and b, the location being so made that (b representing the pivoted point of the rest) the line b c forms an angle of 50° with the line b a. It is obvious that when the work is to be cam-grooved on a radial face the pivoted design is unsuitable, and either that in Fig. 1262 or 1263 is suitable.
Similar cam motions may be given to the cross feed of a lathe: thus, the Lane and Bodley Company of Cincinnati, Ohio, employ the following method for turning the spherical surfaces of their swiveling bearings for line shafting.
The half bearing b, Fig. 1266, is chucked upon a half-round mandrel, c being the spherical surface to be turned, a sectional view of c being shown in Fig. 1267.
In Fig. 1268 is a plan view of the chuck, work, and lathe rest; d is a former attachment bolted to the slider of the rest, and e a rod passing through the lathe block. The weight w, Fig. 1269, is suspended by a cord attached to the slide rest so as to keep the former d firmly against the end of e.
As the slider is operated, the rest is caused by e to slide upon the lathe bed, and the cutting tool forms a spherical curve corresponding to the curve on the former d. The weight w of course lifts or falls according to the direction of motion of the slider.
The cut is put on by operating handle g, thus causing e to advance.
The weight w causes any play between the slider and the cross slide to be taken up in the same direction as the tool pressure would take it up, hence the cut taken is a very smooth one. The half-round mandrel being fixed to the lathe face plate will remain true, obviating the liability of the centre of the spherical surface being out of line with the axis of the bearing-bore.
A method of producing cams without a lathe especially adopted[I-328] for the purpose is shown in Figs. 1270 and 1272, which are extracted from Mechanics. The apparatus consists of a frame e, which fits on the cross ways of an ordinary lathe. The cross-feed screw is removed, so that e may slide backwards and forthwards freely. The frame e carries the worm-wheel a and the worm-gear b, which is operated by the crank f. The cam c to be cut is bolted on to the face of the worm-wheel, which faces the headstock of the lathe. The form for the cam, which may be made of sheet steel, or thicker material, according to the wear it is to have, is fastened to the face of the cam.
A cutter, like a fluted reamer, such as is shown in Fig. 1271, is then put in the live centre of the lathe. Care must be taken that the shank is the same size as the fluted part, and that the flutes are not cut up farther than the thickness that the cam grooves are to be cut in the blank. Having attached a cord to the back of e, pass it over a pulley h, fastened on the rear of the lathe, and hang on a weight g. Fig. 1272 is an edge view of the device, looking from the back of the lathe. It shows the worm a, blank c, and former d all bolted together, while the cutter i is ready in its place on a line with the centre of the worm, and just at back of the former. The machine is operated by turning the crank f, which causes the worm a, also c and d, to revolve slowly, while the cutter i has a rather rapid rotation. The weight causes the cutter to be held firmly against the form f, and to follow its curves in and out.
Knurling or Milling Tools.—In Fig. 1273 is shown the method of using the knurling tool in the slide rest of a lathe. It represents the tool at work producing the indentations which are employed to increase the hand grip of screw heads, or of cylindrical bodies, as shown in the figure by the crossed lines. Fig. 1274 is an end view of the tool, which consists of a holder to go in the slide rest tool post, and carrying two small hardened steel wheels, each of which is serrated all round its circumference, the serrations of one being in an opposite direction to those of the other. The method of using the tool is shown in Fig. 1275, where it is represented operating upon a cylindrical piece of work. If the knurling is to be carried along the work to a greater length than the thickness of the knurl wheels, the lathe slide rest is slowly traversed the same as for a cutting tool.
As the knurling tool requires to be forced against the work with considerable pressure, there is induced a strain tending to force the tool directly away from the work, as denoted by the arrow in Fig. 1276, and this, in a weighted lathe, acts to raise the lathe carriage and weight. This is avoided by setting the tool at an angle, as in Fig. 1277, so that the direction of strain is below and not above the pivot on which the cross slide rests. This is accomplished by pivoting the piece carrying the wheels to the main body of the stem, as shown in Fig. 1277.
For use by hand the knurling or milling tool is fitted to a holder and handle, as in Fig. 1278, and the hand tool rest is placed some[I-329] little distance from the work so that the knurl can pass over it, and below the centre of the work.
Knurls for screw heads are made convex, concave, or parallel, to fit the heads of the screws, and may be indented with various patterns.
Winding Spiral Springs in the Lathe.—Spiral springs whose coils are close, and which therefore act on distension only, may be wound by simply starting the first coil true, and keeping the wire as it winds on the mandrel close to that already wound thereon.
Spiral springs with open coils may be best wound as shown in Fig. 1279, in which is shown a mandrel held between the lathe centres and driven by a dog that also grips one end of the wire w, of which the spring is to be made. The wire is passed through two blocks b, which, by means of the set-screw in the lathe tool post, place a friction on it sufficient to place it under a slight tension which keeps it straight. The change gears of the lathe are arranged as they would be to cut a screw of a pitch equal to the thickness of the wire added to the space there is to be between the coils of the spring. The first turn of the lathe should wind a coil straight round the mandrel when the self-acting feed motion is put in operation and the winding proceeds, and when the spring is sufficiently long, the feed motion is disconnected, and the last coil is allowed to wind straight round the mandrel, thus giving each end of the spring a flat or level end.
If the wire is of brass it will be necessary to close it upon the mandrel with blows from a lead mallet to prevent it from uncoiling on the mandrel when the end is released, which it will do to some extent in any event.
If it is of steel it may be necessary to heat the coil red-hot to prevent its uncoiling, and in the coiling it will, if of stout wire, require to be bent against the mandrel during winding with a piece of steel placed in the tool post, as in Fig. 1280, in which a represents the mandrel, b the spring wire, and d the lathe tool post.
In the absence of a lathe with a self-acting feed motion, the mandrel may have a spiral groove in it and the piece of steel or other hard metal shown in figure must be used, the feed screw of the slide rest being removed so that the wire can feed itself along as the mandrel rotates. Near one end of the mandrel a small hole is drilled through, there being sufficient space between the hole and the end of the mandrel to admit of a loose washer being placed thereon; the bore of this washer requires to be rather larger in diameter than the outside diameter of the spring, when wound upon the mandrel, and also requires to be provided with a keyway and key. The washer d (Fig. 1281), is slipped over the mandrel, the end of the wire c is inserted in the hole b and the spring being wound, the washer is passed up to the end, and the key driven home as in Fig. 1282; when the wire is cut off and the mandrel may be taken from the lathe with the spring closely wound round it to be hammered if of brass, and heated if of steel. The hammering should be done over the whole circumference, not promiscuously, but beginning at one end and following along the wire with the blows delivered not more than 1⁄4 of an inch apart; for unless we do this we cannot maintain any definite[I-330] relation between the size of the mandrel and the size of the spring.
When a grooved mandrel is used, its diameter should be slightly less than the required diameter of spring, as when released the coils expand in diameter.
If it is not essential that the coils be exactly true, take a plain mandrel, such as shown in Fig. 1283, and a hook, such as shown at a, fasten the end of the wire either round the lathe dog, or in a hole in the mandrel as before, and wind one full coil of the spring upon the mandrel, then force this coil open until the hook end of a can be inserted between it and over the mandrel, the other end hanging down between the lathe shears, which will prevent it from rotating, starting the lathe while holding the unwound end of the wire against the hook with a slight pressure, and the winding will proceed as shown in the figure, the thickness of a regulating the width apart of the coils. It is obvious that if the coil is to be a right-handed one and is started at the carrier end, the lathe must revolve backwards.
Spiral springs for railroad cars are wound while red-hot in special spring-winding lathes and with special appliances.
Tools for Hand Turning.—Many of the tools formerly used in hand turning have become entirely obsolete, because they were suitable for larger work than any to which hand turning is now applied; hence, reference to such tools will be omitted, and only such hand tools will be treated of as are applicable to foot lathes and wood turning, their purposes being those for which hand tools are now used.
To the learner, practice with hand tools is especially advantageous, inasmuch as the strain due to the cut is felt by the operator; hence, the effects of alterations in the shape of the tools, its height or position with relation to the work, and also the resistance of the metal to severance, are more readily understood and appreciated than is the case where the tool is held in a slide rest or other mechanical device. If under certain conditions the hand tool does not operate to advantage, these conditions may be varied by a simple movement of the hands, altering the height of the tool to the work, the angle of the cutting edges to the work, or the rate of feed, as the case may be, and instantly perceiving the effects; whereas with tools held by mechanical means, such alterations would involve the expenditure of considerable time in loosening, packing, and fastening the tool, and adjusting it to position.
Small work that is turned by hand may, under exceptionally expert manipulation, be made as interchangeable and more accurate in dimensions than it could be turned by tools operated in special machines. That is to say, it is possible to turn by hand a number of similar small pieces that will be when finished as true, more nearly corresponding in dimensions, and have a finer finish, than it is practicable to obtain with tools operated or guided by parts of a machine. This occurs because of the wear of the cutting tools, which upon small work may be compensated for in the hand manipulation in cases where it could not be in machine manipulation. But with ordinary skill, and under ordinary conditions, the liability to error in hand work induces greater variation in the work than is due to the wear of the tool cutting edges in special machine work; hence, the practical result is that work made by special machinery is more uniform and true to size and shape than that made by hand, while also the quantity turned out by special machines is very much greater.
The most desirable form of tool for taking a heavy hand cut is the heel tool shown in Fig. 1284, which, it may be remarked, is at present but little used on account of the greater expedition of tools held in slide rests. It consists of a steel bar, about 3⁄8 or 1⁄2 inch square, forged with a heel at f, so that it may firmly grip the hand rest, and having a cutting edge at e. This bar is about 8 inches long, and is held in a groove in a wooden stock by a strap passing over it, and having a stem which passes down through the handle d, in which is fixed a nut, so that by screwing up or unscrewing d the bar is gripped or released, as the case may be, in a groove in the stock. In use, the end h of the stock is held firmly against the operator’s shoulder, the left hand grasps the stock and presses the tool firmly down upon the face of the hand rest, while with the right the handle d is moved laterally, causing the tool to move to its cut. The depth of the cut is put on and regulated by elevating the end h of the stock. The heel f is placed close enough to the work to keep e f nearly vertical, for if it inclines too much in any direction the tool gets beyond the operator’s control. The position of the heel f is moved from time to time along the hand rest to carry the cut along.
A cut of 1⁄8 inch deep, that is, reducing the work diameter 1⁄4 inch, may readily be taken with this tool, which, however, requires skilful handling to prevent it from digging into the work.
The shorter the distance from the face e to the heel f the more easily the tool can be controlled; hence, as f serves simply as a sharp and gripping fulcrum it need not project much from the body of the steel; indeed, in many cases it is omitted altogether, the bottom of the steel bar being slightly hollowed out instead. No oil or water is required with the heel tool.
The hand rest should be so adjusted for height that the cutting edge of the tool stands slightly above the horizontal level of the work, a rule which obtains with all hand tools used upon wrought iron and steel.
The graver is the most useful of all hand turning tools, since it is applicable to all metals, and for finishing as well as roughing out the work. It is formed by a square piece of steel whose end is ground at an angle, as shown in the top and the bottom view, Fig. 1285, a a being the cutting edges, c c the points, and d d the heels.
It is held in a wooden handle, which should be long enough to grasp in both hands, so that the tool may be held firmly. For cutting off a maximum of metal in roughing out the work the graver is held as in Fig. 1286, the heel being pressed down firmly[I-331] upon the tool rest. The cut is carried along the work by revolving the handle upon its axis, and from the right towards the left, at the same time that the handle is moved bodily from the left towards the right. By this combination of the two movements, if properly performed, the point of the graver will move in a line parallel to the centres of the lathe, because, while the twisting of the graver handle causes the graver point to move away from the centre of the diameter of the work, the moving of the handle bodily from left to right causes the point of the graver to approach the centre of that diameter; hence the one movement counteracts the other, producing a parallel movement, and at the same time enables the graver point to follow up the cut, using the heel as a pivotal fulcrum, and hence obviating the necessity of an inconveniently frequent moving of the heel of the tool along the rest. The most desirable range of these two movements will be very readily observed by the operator, because an excess in either of them destroys the efficacy of the heel of the graver as a fulcrum, and gives it less power to cut, and the operator has less control over the tool.
For finishing or smoothing the work the graver is held as in Fig. 1287, the edge being brought parallel to the work surface. For brass work the top faces of the graver should be slightly bevelled in the direction shown in Fig. 1288.
The graver cuts most efficiently with the work revolving at a fast speed, or, say, at about 60 feet per minute, and for finishing wrought iron or steel requires an application of water.
To finish work that has been operated upon by a heel tool or by a graver, the finishing tool shown in Fig. 1289 may be employed. It is usually made about 5⁄8 or 3⁄4 inch wide, as the graver is employed for shorter work. It is ground so as not to let the extreme corners cut, and is used at a slow speed with water. The edge of this tool is sometimes oilstoned, causing it to cut with a clean polish. The tool is held level, brought up to the work, and a cut put on by elevating the handle end. To carry the cut forward, the tool is moved along the hand rest to nearly the amount of its width, and is brought to its cut by elevating the handle as before. When the work has been finished as near as may be with this tool, it may be finished by fine filing, the lathe running at its quickest speed; or the file may be used to show the high spots while using the finishing tool.
For facing the ends of work the tool shown in Fig. 1290, or that shown in Fig. 1291, may be used, either of them being made from an old three-cornered file. The cutting edge at a, Fig. 1290, should be slightly curved, as shown. The point of the tool is usually brought to cut at the smallest diameter of the work, with the handle end of the tool somewhat elevated. As the cut is carried outwards the handle end of the tool is depressed, and the point correspondingly elevated. It may be used dry or with water, but the latter is necessary for finishing purposes.
Another form of this tool is shown in Fig. 1291. It has two cutting edges a a, one of which rests on the hand rest while the other is cutting, the tool being shown in position for cutting a right-and a left-hand face, the face nearest to the work being shown in the lower view. This face should be placed against the radial face of the work, and the cut put on by turning the upper edge over towards the work while pressing the tool firmly to the lathe rest.
For cutting out a round corner the tool shown in Fig. 1292, employed either for roughing or smoothing purposes (water being used with it for the latter), the heel causes it to grip the hand rest firmly, and acts as a pivotal fulcrum from which the tool may be swept right and left round the curve, or a portion of it.
This tool, as in the case of all tools used upon wrought iron or steel, should not cut all round its edge simultaneously, as in that case, unless indeed it is a very narrow tool, the force placed upon it by the cut will be too great to enable the operator to hold and control it; hence the cut should be carried first on one side and then on the other, and then at the point, or else the handle end should be moved laterally, so that the point sweeps round the work. It should be brought to its cut by placing its heel close to the work, and elevating the handle end until the cutting edge meets the work.
[I-332]The point or nose of the tool may obviously be made straight or square, as it is termed, to suit the work, the top rake being omitted for brass work.
In using this tool for cutting a groove it is better (if it be a deep groove, and imperative if it be a broad one, especially if the work be slight and apt to spring) to use a grooving tool narrower in width than the groove it is to cut, the process being shown in Fig. 1293, in which w represents a piece of work requiring the two grooves at a and b cut in it. For a narrow groove as a the tool is made about half as wide as the groove, and a cut is taken first on one side as at c, and then on the other as at d. For a wider groove three or more cuts may be made, as at e, f, g. In all cases the tool while sinking the groove is allowed to cut on the end face only; but when the groove is cut to depth, the side edges of the tool may be used to finish the sides of the groove, but the side and end edge must not cut simultaneously, or the tool will be liable to rip into the work.
Hand Tools for Brass Work.—In addition to the graver as a roughing-out tool for brass work, we have the tool shown in Fig. 1294, the cutting edge being at the rounded end a. It is held firmly to the rest, which is not placed close to the work (as in the case of other tools), so as to give the tool a wide range of movement, and hence permit of the cut being carried farther along without moving its position on the rest. It may be used upon either internal or external work.
For finishing brass work, tools termed scrapers are employed.
Fig. 1295 represents a flat scraper, the two end edges a and the side edges along the bevel forming the cutting edges.
In this tool the thickness of the end a is of importance, since if it be too thin it will jar or chatter. This is especially liable to occur when a broad scraper is used, having a great length of cutting edge in operation. This may be obviated to some extent by inclining the scraper as in Fig. 1296, which has the same effect as giving the top face negative rake, causing the tool to scrape rather than cut. The dividing line between the cutting and scraping action of a tool is found in the depth of the cut, and the presentation of the tool to the work, as well as in the shape of the tool. Suppose, for example, that we have in Fig. 1297, a piece of work w and a tool s, and the cut being light will be a scraping one. Now suppose that the relative positions of the size of the work and of the tool remain the same, but that the cut be deepened as in Fig. 1298, and the scraping action is converted into that class of severing known as shearing, or we may reduce the depth of cut as in Fig. 1299, and the action will become a cutting one.
But let the depth of cut be what it may, the tool will cut and not scrape whenever the angle of its front face is more than 90° to the line of tool motion if the tool moves, or of work motion if the work moves to the cut. In Fig. 1300, for example, the tool is in position to cut the angle of the front face, being 110° to the direction of tool motion.
We may consider this question from another stand-point, however, inasmuch as that the tool action is a cutting one whenever the pressure of the cut is in a direction to force the tool deeper into the work, and a scraping one whenever this pressure tends to force the tool away from the work, assuming of course that the tool has no front rake, and that the cut is light or a “mere scrape,” as workmen say. This is illustrated in Fig. 1301, the tool at a acting to cut, and at b to scrape, and the pressure of the cut upon a acting to force the tool into the work as denoted by the arrow d, while that upon b acts to force it in the direction of arrow c, or away from the work.
In addition to these distinctions between a cutting and a scraping action we have another, inasmuch as that if a tool is pulled or dragged to its cut its action partakes of a scraping one, no matter at what angle its front face may stand with relation to the work.
The end face of a flat scraper should be at a right angle to the body of the tool, so that both edges may be equally keen, for if otherwise, as in Fig. 1302, one edge as a will be keener than the other and will be liable to jar or chatter.
[I-333]The flat scraper can be applied to all surfaces having a straight outline, whether the work is parallel or taper, providing that there is no obstruction to prevent its application to the work.
Thus, in Fig. 1303 we have a piece of work taper at a and c, parallel at e, and with a collar at d, the scraper s being shown applied to each of these sections, and it is obvious that it cannot be applied to section a because the collar d is in the way. This is remedied by grinding the scraper as in Fig. 1304, enabling it to be applied to the work as in Fig. 1305. Another example of the use of a bevelled scraper is shown in Fig. 1306, the scraper s having its cutting edge parallel to the work and well clear of the arm h.
The round-nosed scraper is used for rounding out hollow corners, or may be made to conform to any required curve or shape. It is limited in capacity, however, by an element that affects all scraping tools, that if too great a length of cutting edge is brought into action at one time, chattering will ensue, and to prevent this the scraper is only made of the exact curvature of the work when it is very narrow, as at s in Fig. 1307.
For broad curves it is made of more curvature, so as to limit the length of cutting edge, as is shown in the same figure at s′, and is swept round the work so as to carry the cut around the curve.
There are, however, other means employed to prevent chattering, and as these affect the flat scraper as well as the round-nosed one, they may as well be explained with reference to the flat one.
First, then, a thin scraper is liable to chatter, especially if used upon slight work. But the narrower the face on the end of the scraper, the easier it is to resharpen it on the oilstone, because there is less area to oilstone. A fair thickness is about 1⁄20 inch; but if the scraper was no thicker than this throughout its whole length, it would chatter violently, and it is for this reason that it is thinned at its cutting end only. Chattering is prevented in small and slight work by holding the scraper as in Fig. 1308, applying it to the top of the work; and to reduce the acting length of cutting edge, so as to still further avoid chattering, it is sometimes held at an angle as in the top view in Fig. 1309, s being the scraper and r the tool rest.
When the scraper is applied to side faces, or in other cases in which a great length of cutting edge is brought into action, a piece of leather laid beneath the scraper deadens the vibration and avoids chattering.
[I-334]It is obvious that the scraper may be given any required shape to meet the work, Fig. 1310 representing a scraper of this kind; but it must in this case be fed endways only to its cut, if the work is to be cut to fit the scraper.
In Fig. 1311 is shown a half-round scraper, which is shown in Fig. 1312 in position to scrape out a bore or hole. This tool is made by grinding the flat face and the two edges of a worn-out half-round smooth file, and is used to ease out bores that fit too tightly. The cutting edges are carefully oilstoned, and the work revolved at a very quick feed.
When a number of small pieces of duplicate form are to be turned by hand, a great deal of measuring may be saved and the work very much expedited by means of the device shown in Fig. 1313. It consists of a tool stock or holder, the middle of which, denoted by a, is square, and contains three or four square slots, with a set-screw to each slot to hold different turning tools. Each end of the stock is turned parallel, as denoted by b, c. In Figs. 1313 and 1314, d, e, and f are the tools, and g, h, are the set-screws.
Fig. 1315 represents top and side view of a plate, of which there must be two, one to fasten on the headstock and one on the tailstock of the lathe, as shown in Fig. 1316. In Fig. 1317 the manner of using the tool is shown, similar letters of reference denoting similar parts in all the figures.
The plates p p are bolted by screws to the headblock h and the tailstock t of the lathe. The tool holder is placed so that the cylindrical ends b, c, rest on the ends of these plates, and in the angles p′ p′. The cutting tool d is sustained, as shown, upon the lathe rest r. In use the operator holds the stock a in his hands in the most convenient manner, using the tool e as a handle when there is a tool in the position of e. The cutting point of the tool is pressed up to the work w, and the feed is carried along by hand. It is obvious, however, that when the perimeters of a b meet the shoulders o o, Fig. 1315, of the plates p p, the tool cannot approach any nearer to the diametrical centre of the work; hence the diameter to which the tool will turn is determined by the distance of the shoulder o of the plate p from the centre of the lathe centres, as shown in Fig. 1316 by the line l. In carrying the cut along it is also obvious that the lateral travel of the stock or holder must end when the end of the square part a comes against the side face of either of the plates. In the engraving we have shown the tool d cutting a groove in the work w, while the shoulder of the holder is against the plate fastened to the lathe tailstock t; and so long as the operator, in each case, keeps the shoulder against that plate, the grooves upon each piece of work will be cut in the same position, for it will be observed that the position in the length of the work performed by each tool is determined by the distance of the cutting part of each tool from the end of the square part a of the tool holder. All that is necessary, then, is to adjust each tool so that it projects the proper distance to turn the requisite diameter and stands the required distance from the shoulders of the square to cut to the desired length, and when once set error cannot occur.
[I-335]This plain description of the device, however, does not convey an adequate idea of its importance. Suppose, for example, that it is required to turn a number of duplicate pieces, each with a certain taper: all that is necessary is to adjust the plates p in their distances from the lathe centres. If the large end of the taper on the work is required to stand nearest the lathe headstock a, the plate p on the headstock must be moved until its shoulder o is farther from the lathe centre. If, however, the work requires to be made parallel, the plates p must be set the same distance for the axial line of the centres. If it be desired to have a parallel and a taper in proximity upon the same piece of work, the tool must have one of its cylindrical ends taper and use it upon the taper part of the work.
In Fig. 1317 the tool d is shown cutting a square groove. The tool at f serves to turn the parallel part x, and the tool e would cut the V-shaped groove i.
All kinds of irregular work may be turned by varying the parallelism and form of the cylindrical ends b c; but in this event the shoulders o o, Fig. 1315, should be made V-shaped and hardened to prevent them from rapid wear.
Screw Cutting with Hand Tools.—Screw threads are cut by hand in the lathe with chasers, of which there are two kinds, the outside and the inside chaser. In Fig. 1319 is shown an outside, or male, and in Fig. 1318 an inside, or female chaser. The width of a chaser should be sufficient to give at least four teeth, and for the finer thread pitches it is better to have six or eight teeth, the number increasing as the pitch is finer, and the length of the work will permit. The leading tooth should be a full one, or otherwise it will break off, and if in cutting up the chaser a half or less than a full tooth is formed it should be ground off. The tooth points should not be in a plane at a right angle to the chaser length, but slightly diagonal thereto, as in Fig. 1319, so that the front edge of the chaser will clear a bolt head or shoulder, and permit the leading tooth to pass clear up to the head without fear of the front edge of the steel meeting the shoulder.
The method of producing a chaser from a hob is shown in Fig. 1320, in which h is a hob, which is a piece of steel threaded and serrated, as shown, to give cutting edges to act, as the hob rotates, upon the chaser c. If the chaser is cut while held in a constant horizontal plane, its teeth will have the same curvature as the hob, or, in other words, they will fit its circumference. Suppose that the chaser, being cut up by the hob and then hardened, is applied to a piece of work of the same diameter as the hob and held in the same vertical plane, as in Fig. 1320, it is obvious that, there being no clearance, the teeth cannot cut. Or, suppose it be applied to a piece of work of smaller diameter, as in Fig. 1324, it cannot cut unless its position be lowered, as in Fig. 1322, or else it must be elevated, as in Fig. 1323. In either case the angle[I-336] of the thread cut will be different from the angle of the sides of the chaser teeth, and the thread will be of improper depth. Thus, on referring to Fig. 1321, it will be seen that the chaser c has a tooth depth corresponding to that on the work w along the horizontal dotted line e only, because the true depth of thread on the work is its depth measured along a radial line, as line f or g, and the chaser teeth are, at the cutting edge, of a different angle. This becomes more apparent if we suppose the chaser thickness to be extended up to the dotted line h, and compare that part of its length that lies within the two circles i j, representing the top and bottom of the thread, with the length of radial line g, that lies within these circles. If, then, the chaser be lowered, to enable it to act, it will cut a thread whose sides will be of more acute angle than are the sides of the chaser teeth or of the hob from which it was cut. The same effect is caused by using a chaser upon a larger diameter of work than that of the hob from which the chaser was cut, because the increased curvature of the chaser teeth acts to give the teeth less contact with the work, as is shown in Fig. 1325, for the teeth cannot cut without either the lower corners a of the teeth being forced into the metal, or else the chaser being tilted to relieve them of contact. To obviate these difficulties and enable a chaser to be used upon various diameters of work, it is, while being cut up by the hob, moved continuously up and down, as denoted in Fig. 1326, by a and b, which represent two positions of the chaser. The amount of this movement is sufficient to make the chaser teeth more straight in their lengths, and to give them a certain amount of clearance, an example of the form of chaser thus produced being shown in Fig. 1327, applied to two different diameters of work, as denoted by the circle a and segment of a circle b, c representing the chaser.
To obtain the most correct results with such a chaser, it must be applied to the work in such a way that it has as little clearance as will barely enable it to cut, because it follows from what has been said with reference to single-pointed threading tools that to whatever amount the chaser has clearance, a corresponding error of thread angle and depth is induced. In hand use, therefore, it does not matter at what height the chaser is applied so long as it is elevated sufficiently to barely enable it to cut.
After the chaser is cut on the hob, its edges, as at c, and the corner, as at d, in Fig. 1328, should be rounded off, so that they may not catch in any burr which the heel of the hand tools may leave on the surface of the hand rest.
For roughing out the threads on wrought iron or steel the top face should be hollowed out, as shown in Fig. 1328, which will enable the chaser to cut very freely. For use on cast iron the top face should be straight, as shown in Fig. 1328 at a, while for use on soft metal, as brass, the top face must be ground off, as shown in Fig. 1329.
The Pratt and Whitney Co. cut up chasers by the following method: In place of a hob, a milling cutter is made, having concentric rings instead of a thread. The cutters are revolved on a milling machine in the ordinary manner. The chaser is fastened in a chuck fixed on the milling machine table, and stands at an angle of 15°. It is traversed beneath the milling cutter, and thus cut up with teeth whose lengths are at a right angle to the top and bottom faces of the chaser; hence the planes of the length of the teeth are not in the same plane as that of the grooves of the thread to be cut. Thus, let a, b, c, and d, Fig. 1330, represent the planes of the thread on the work, and e, f, g, h, will be the planes of the lengths of the chaser teeth.
The chaser, however, is given 15° of bottom rake or clearance, and this causes the sides of the chaser teeth to clear the sides of the thread.
Now, suppose the top face a, Fig. 1331, of the chaser to be[I-337] parallel with the face of the tool steel, and to lie truly horizontal and in the same plane as the centre of the work. This clearance will cause the thread cut by the chaser to be deeper than the natural depth of the chaser teeth. Thus, in Fig. 1331 is shown a chaser (with increased clearance to illustrate the point desired), the natural depth of whose thread is represented by the line f, but it is shown on the section of work that the thread cut by the tool will be of the depth of the line d, which is greater than the length or depth of f, as may be more clearly observed by making a line e, which, being parallel to a, is equal in length to d, but longer than f. Hence, the clearance causes the chaser under these conditions to cut a thread of the same pitch, but deeper than the grooves of the hub, and this would alter the angles of the thread. This, however, is taken into account in forming the angles of the thread upon the milling cutter, and, therefore, of the chaser, which are such that with the tool set level with the work centre, the thread cut will be of correct angle, notwithstanding the clearance given to the teeth.
In order to enable the cutting of an inside chaser from a hub, it requires to be bent as in Fig. 1332, in which h is the hub, r the lathe rest, and c the chaser. After the chaser is cut, it has to be straightened out, as shown in Fig. 1318, in which is represented a washer being threaded and shown in section; c is the chaser and r the lathe rest, while p is a pin sometimes let into the lathe rest to act as a fulcrum for the back of the chaser to force it to its cut, the handle end of the chaser being pressed inwards.
When an inside chaser is cut from a hub (which is the usual method) or male thread, its teeth slant the same as does the male thread on the side of the hub on which it is cut, and in an opposite direction to that of the thread on the other side of the hub. Thus, in Fig. 1333, h is the hub, c the chaser, and r the lathe rest. The slope of the chaser-teeth is shown by the dotted line b. Now, the slant of the thread on the half circumference of the hub not shown or seen in the cut will be in an opposite direction, and in turning the chaser over from the position in which it is cut (Fig. 1333) to the position in which it is used (Fig. 1334), and applying it from a male to a female thread, we reverse the direction with relation to the work in which the chaser-teeth slant; or, in other words, whereas the teeth of the chaser should lie as shown in Fig. 1334 at a a, they actually lie as denoted in that figure by the dotted line b b. As a consequence, the chaser has to be tilted over enough to cause the sides of the chaser-teeth to clear the sides of the thread being cut, which, as they lie at opposite angles, is sufficient to cause the female thread cut by the chaser to be perceptibly shallower than the chaser-teeth, for reasons which have been explained with reference to Fig. 1321. It may be noted however, that an inside chaser cannot well be used with rake, hence the tilting in this case makes the thread shallower instead of deeper.
To obviate these difficulties the hub for cutting a right-hand inside chaser should have a left-hand thread upon it, and per contra, an inside chaser for cutting a left-hand thread should be cut from a hub having a right-hand thread.
The method of starting an outside thread upon wrought iron or steel to cut it up with a chaser is as follows:—
The work is turned up to the required diameter, and the V-tool shown in Fig. 1335 is applied; the lathe is run at a quick speed, and the heel of the tool is pressed firmly to the face of the lathe rest, the handle of the tool must be revolved from right to left at the same time as it is moved laterally from the left to the right, the movement being similar to that already described for the graver, save that it must be performed more rapidly. It is in fact the relative quickness with which these combined movements are performed which will determine the pitch of the thread. The appearance of the work after striking the thread will be as shown in Fig. 1336, a being the work, and b a fine groove cut upon it by the V-tool.
The reason for running the lathe at a comparatively fast speed[I-338] is that the tool is then less likely to be checked in its movement by a seam or hard place in the metal of the bolt, and that, even if the metal is soft and uniform in its texture, it is easier to move the tool at a regular speed than it would be if the lathe ran comparatively slowly.
If the tool is moved irregularly or becomes checked in its forward movement, the thread will become waved or “drunken”—that is, it will not move forward at a uniform speed;[20] and if the thread is drunken when it is started, the chaser will not only fail to rectify it, but, if the drunken part occurs in a part of the iron either harder or softer than the rest of the metal, the thread will become more drunken as the chaser proceeds. It is preferable, therefore, if the thread is not started truly, to try again, and, if there is not sufficient metal to permit of the starting groove first struck being turned out, to make another farther along the bolt. It takes much time and patience to learn to strike the requisite pitch at the first trial; and it is therefore requisite for a beginner to leave the end of the work larger in diameter than the required finished size, as shown in Fig. 1336, so as to have sufficient metal to turn out the groove cut by the V-tool at the first trial cut, and try again.
If the thread is to be cut on brass the V-tool must not have any top rake. Some turners start threads upon brass by placing the chaser itself against the end of the work and sweeping it rapidly from left to right (for a right-hand thread), thus obviating the use of the V-tool.
In all cases the work should be rounded off at the end to prevent the chaser-teeth from catching.
In applying the chaser to the groove cut by the V-tool the leading tooth should be held just clear of the work at first, and only be brought to touch the work after the rear teeth have found and are traversing in the groove. By this means the chaser will carry the thread forward more readily and true. The thread must be carried forward but a short distance at each passage of the chaser, gradually deepening the thread while carrying it forward.
To start an inside thread the corner of the hole at its entrance should be rounded off and the back teeth of the chaser placed to touch the bore while the front teeth are clear. The lathe is to be run at a quick speed, and the chaser moved forward at as near the proper speed as can be judged. When the chaser is moved at the proper speed, the rear teeth will fall into the fine grooves cut by the advance ones, and start a thread, while otherwise promiscuous grooves only will be cut. It is an easy matter, however, to start a double thread with an inside chaser; hence, when the thread is started the lathe should be stopped and the thread examined.
The chaser should be placed with its top face straight above the horizontal level of the work and held quite horizontal, and the handle end then elevated just sufficient to give the teeth clearance enough to enable them to cut; otherwise, with a chaser having top rake, the thread cut will be too deep, and its sides will be of improper angle one to the other.
Thus, in Fig. 1337, w represents a piece of work, r the lathe rest, and t the chaser. The depth of the thread cut in this case will be from the circle a to the circle b; whereas the depth of the chaser teeth, and therefore the proper depth for the thread, is from c to d. Thus tilting the handle end of the chaser too much has caused the chaser teeth to cut a thread too deep. If on brass work the chaser has its top face ground off as in figure, tilting the handle too much will cause the thread cut to be too shallow, and in both cases the error in thread depth induces a corresponding error in the angles of the sides of the thread one to the other and relative to the axial line of the bolt or work.
If the chaser teeth are held at an angle to the work surface, the thread cut will be of finer pitch than the chaser, and the angles of the sides of the thread on the work will not be the same as those of the teeth. It is permissible, however, during the early cuts taken with a hand chaser to give the chaser a slight degree of such angle, because it diminishes the length of cutting edge, and causes the chaser to cut more freely, especially when the pitch of the thread is coarse and the chaser is becoming dull.
In the case of a taper thread the same rule, that the thread may be roughed out with the chaser teeth at an angle to the surface lengthways of the work, but must be finished with the teeth parallel to the surface, holds good.
Thus, in Fig. 1338 is a taper plug fitting in a ring having a threaded taper bore, the threads matching, and having the thread sides in both cases at an equal angle to the surface, lengthways of the work, though the tops and bottoms of the thread are not parallel with the axial line of the work.
Wood Turning Tools.—Wood turning in the ordinary lathe is generally performed by hand tools, and of these the principal is the gouge, which in skillful hands may be used to finish as well as to rough out the work (although there are other more useful finishing tools to be hereafter described).
It is used mainly, however, to rough out the work and to round out corners and sweeps. The proper form for this tool is shown in Fig. 1339, the bevel on the end of the back or convex side being carried well round at the corners, so as to bring those corners up to a full sharp cutting edge on the convex or front side.
The proper way to hold a gouge is shown in Fig. 1340, in which the cut taken by the tool is being carried from right to left, the face plate of the lathe being on the left side, so that by holding it in the manner shown the body and arms are as much as possible out of the way of the face plate, which is a great consideration in short work. But if the cut is to be carried from left to right, the relative position of the hands may be changed.
When the work runs very much out of true, or has corners upon it, as in the case of square wood, the forefinger may be placed under the hand rest, and the thumb laid in the trough of the gouge, pressing the latter firmly against the lathe rest to prevent the tool edge from entering the work too far, or, in other words, to regulate the depth of the cut, and prevent its becoming so great as to force the tool from the hands or break it, as is sometimes[I-339] the case under such circumstances. When the gouge is thus held, its point of rest upon the lathe rest may be used as a fulcrum, the tool handle being moved laterally to feed it to the cut, which is a very easy and safe plan for learners to adopt, until practice gives them confidence. The main point in the use of the gouge is the plane in which the trough shall lie. Suppose, for example, that in Fig. 1341 is shown a piece of work with three separate gouge cuts being taken along it, that on the right being carried in the direction of the arrow. Now the gouge merely acts as a wedge, and the whole of the pressure placed by the cut on the trough side or face of the gouge is tending to force the gouge in the direction of the arrow, and therefore forward into its cut, and this it does, ripping along the work and often throwing it out of the lathe. To avoid this the gouge is canted, so that when cutting from right to left it lies as shown at b, in which case the pressure of the cut tends rather to force the gouge back from the cut, rendering a slight pressure necessary to feed it forward. The gouge trough should lie nearly horizontal lengthwise, the cutting edge being slightly elevated. The gouge should never (for turning work) be ground in the trough (as the concave side is termed), and should always be oilstoned, the trough being stoned with a slip of stone lying flat along the trough, the back being rotated upon a piece of flat stone, and held with the ground surface flat on the surface of the stone, and so pressed to it as to give most pressure at and near the cutting edge.
For finishing flat surfaces, the chisel shown in Fig. 1342 is employed. It should be short, as shown. It should be held to the work in a horizontal position, or it is apt to dig or rip into the work, especially when it is used upon soft wood. Some expert workmen hold it at an angle for finishing purposes, which makes it cut very freely and clean, but increases the liability to dig into the work; hence learners should hold it as shown.
Another excellent finishing tool is the skew-chisel, Fig. 1343, so called because its cutting edge is at an angle, or askew with the body of the tool. This tool will cut very clean, leaving a polish on the work. It also has the advantage that the body of the tool may be kept out of the way of flanges or radial faces when turning cylindrical work, or may, by turning it on edge, be used to finish radial faces. It is shown in Fig. 1343 by itself, and in Fig. 1344 turning up a stem. It is held so that the middle of the edge does[I-340] the cutting, and this tends to keep it from digging into the work. The bevels forming the cutting edge require to be very smoothly oilstoned.
The whole secret of the skillful and successful use of this valuable tool lies in giving it the proper inclination to the work. It is shown in Fig. 1344, at e, in the proper position for taking a cut from right to left, and at f in position for taking a cut from left to right. The face of the tool lying on the work must be tilted over, for e as denoted by line a, and for f as denoted by the line b, the tilt being only sufficient to permit the edge to cut. If tilted too much it will dig into the work; if not tilted, the edge will not meet the work, and therefore cannot cut. For cutting down the ends of the work, or down a side face, it must be tilted very slightly, as denoted in figure by c d, the amount of the tilt regulating the depth of the cut, so that when the cutting edge of the tool has entered the wood to the requisite depth, the flat face of the tool will prevent the edge from entering any deeper. In cutting down a radial face the acute corner of the tool leads the cut, whereas in in plain cylindrical work the obtuse is better to lead.
For cutting down the ends, for getting into small square corners, and especially for small work, the skew chisel is more handy than the ordinary chisel, and leaves less work for the sand-paper to do. Beginners will do well to practise upon black walnut, or any wood that is not too soft, roughly preparing it with an axe to something near a round shape.
For finishing hollow curves the tool shown in Fig. 1345 is employed, the cutting edge being at b; the degree of the curve determines the width of the tool, and, for internal work the tool is usually made long and without a handle.
The tool shown in Fig. 1346 is employed in place of the gouge in cases where the broad cutting edge of the latter would cause tremulousness. It may be used upon internal or external work, being usually about two feet long. For boring purposes, the tools shown in Fig. 1347 are employed, the cutting edges being from the respective points along the edges c, d, respectively. But when the bore is too small to admit of the application of tools having their cutting edges on the side, the tool shown in Fig. 1347 at e is employed, which has its cutting edge on the end.
Measurements are primarily derived in Great Britain and her colonies, and in the United States, from the English Imperial or standard yard. This yard is marked upon a bar of “Bailey’s metal” (composed of 16 parts copper, 21⁄2 parts tin, and 1 part zinc), an inch square and 38 inches long. One inch from each end is drilled a hole about three-quarters through the whole depth of the bar, into which are fitted gold plugs, whose upper end faces are level with the axis of the bar. Across each plug is marked a fine line, and the distance between these lines was finally made the standard English yard by an Act of Parliament passed in 1855. A copy of this bar is in the possession of the United States Government at Washington, and all the standard measuring tools for feet, inches, &c., are derived from subdivisions of this bar.
The standard of measurement in France and her colonies, Italy, Germany, Portugal, British India, Mexico, Roumania, Greece, Brazil, Peru, New Granada, Uruguay, Chili, Venezuela, and the Argentine Confederation, is the French mètre, which is also partially the standard in Austria, Bavaria, Wurtemberg, Baden, Hesse, Denmark, Turkey, and Switzerland. It consists of a platinum bar, called the “mètre des archives,” whose end faces are parallel, and the length of this bar is the standard mètre. But as measuring from the ends of this bar would (from the wear) impair its accuracy, a second bar, composed of platinum and iridium, has been made from the “mètre des archives.” This second bar has ruled upon it two lines whose distance apart corresponds to the length of the “mètre des archives,” and from the distance between these lines the subdivisions of the mètre have been obtained.
As all metals expand or contract under variations of temperature, it is obvious that these standards of length can only be accurate when at some given temperature: thus the English bar gives a standard yard when it is at a temperature of 62° Fahr., while the French standard bar is standard at a temperature of 32° Fahr., which corresponds to 0 in the centigrade thermometer. But if a bar is copied from a standard, and is found to be too short, it is obvious that if its amount of expansion under an increase of temperature be accurately known, it will be an accurate standard at some higher temperature, or in other words, at a temperature sufficiently higher to cause it to expand enough to compensate for its error, and no more.
As all bars of metal deflect from their own weight, it is obvious that the bar must be supported at the same points at which it rested when the lines were marked, and it has been determined by Sir George Airy, that the best position for the points of support for any bar may be obtained as follows: Multiply the number of the points of support by itself (or, as it is commonly called, “square it”), and from the sum so obtained subtract 1. Then subtract the square root of the remainder, which gives a sum that divided into the length of the bar will represent the distance apart for the points of support. It will be obvious that the points of support must be at an equal distance from each end of the bar.
Measurement may be compared in two ways, by sight and by the sense of feeling. Measurement by sight is made by comparing the coincidence of lines, and is called “line measurement.” Measurement by feeling or touch is called “end measurement,” because the measurement is taken at the ends. If, for example, we measure the diameter of a cylindrical bar, it is an end measurement, because the measurement is in a line at a right angle to the axis of the bar, and the points of touch on each side of the bar are the ends of the measurement, which is supposed to have no width.
In measuring by sight we may, for rude measurements, trust to the unaided eye, as in using the common foot rule, but for such minute comparisons as are necessary in subdividing or transferring a standard, we may call in the aid of the microscope.
The standard gauges, &c., in use in the United States have been obtained from Sir Joseph Whitworth, or duplicated from those made by him with the aid of measuring and comparing machines. It has been found, however, that different sets of these gauges did not measure alike, the variations being thus given by Mr. Stetson, superintendent of the Morse Twist Drill and Machine Co.
At the time the Government established the use of the standard system of screw threads in the navy yards, ten sets of gauges were ordered from a manufacturer. His firm procured a duplicate set of these and took them to the navy yard in Boston and found that they were practically interchangeable. He also took them to the Brooklyn Yard Navy. The following tabular statement shows the difference between them:—
| Size. | Navy Yard Male Gauge. |
Morse Twist Drill and Machine Co. Male Gauge. |
Morse Twist Drill and Machine Co. Female Gauge. |
|||||||||||
| 1⁄4 | 0 | .25 | 0 | .25 | Interchanged | |||||||||
| 5⁄16 | .313 | .313 | „ | |||||||||||
| 3⁄8 | .375 | .3759 | ||||||||||||
| 7⁄16 | .437 | .437 | Interchanged | |||||||||||
| 1⁄2 | .505 | .505 | „ | |||||||||||
| 9⁄16 | .562 | .564 (-) | „ | |||||||||||
| 5⁄8 | Damaged | .626 | „ | |||||||||||
| 3⁄4 | .7505 | .751 | „ | |||||||||||
| 7⁄8 | .876 | .8758 | „ | |||||||||||
| 1 | 1 | .00075 | 1 | .00075 | „ | |||||||||
| 1 | 1⁄8 | 1 | .125 (+) | 1 | .125 (-) |
|
||||||||
| 1 | 1⁄4 | 1 | .25 | 1 | .25 | Interchanged | ||||||||
| 1 | 3⁄8 | 1 | .375 | 1 | .375 | „ | ||||||||
| 1 | 1⁄2 | 1 | .5 | 1 | .5 (-) | (-) | ||||||||
| 1 | 5⁄8 | 1 | .6245 | 1 | .624 | (-) | ||||||||
| 1 | 3⁄4 | 1 | .749 | 1 | .749 | Interchanged | ||||||||
| 1 | 7⁄8 | 1 | .8745 | 1 | .874 | (-) | ||||||||
| 2 | 1 | .999 | 1 | .999 | ||||||||||
| The sign (-) means that the piece is small, but not enough to measure. | ||||||||||||||
| The sign (+) means that the piece is large, but not enough to measure. | ||||||||||||||
The advantages to be derived from having universally accepted standard subdivisions of the yard into inches and parts of an inch are as follows:—
When a number of pieces of work of the same shape and size are to be made to fit together, then, if their exact size is not known and there is no gauge or test piece to fit them to, each piece must be fitted by trial and correction to its place, with the probability that no two pieces will be of exactly the same size. As a result, each piece in a machine would have to be fitted to its place on that particular machine, hence each machine is made individually.
Furthermore, if another lot of machines are afterwards to be made, the work involved in fitting the parts together in the first lot of machines affords no guide or aid in fitting up the second lot. But suppose the measurements of all the parts of the first lot are known to within the one ten-thousandth part of an inch, which is sufficiently accurate for practical purposes, then the parts may be made to measurement, each part being made in quantities and kept together throughout the whole process of manufacture, so that when all the parts are finished they may go to the assembling or erecting room, and one piece of each part may be taken indiscriminately from each lot, and put together to make a complete machine. By this means the manufacture of the machine may be greatly simplified and cheapened, and the fit of any part may be known from its size, while at the same time a new part may be made at[I-342] any time without reference to the machine or the part to which it is to fit.
Again, work made to standard size in one shop will fit to that made to standard size in another, providing the standard gauges agree.
The Pratt and Whitney Company, of Hartford, Connecticut, in union with Professor Rogers, of Cambridge University, in Massachusetts, determined to inspect the Imperial British yard, to obtain a copy of it, and to make a machine that would subdivide this copy into feet and inches, as well as transfer the line measurements employed in the subdivisions into end measures for use in the workshops, the degree of accuracy being greater than is necessary in making the most refined mechanism, made under the interchangeable or standard gauge system. The machine made under these auspices is the Rogers-Bond Universal Comparator; Mr. Bond having been engaged in conjunction with Professor Rogers in its construction.
The machine consists of two cylindrical guides, upon which are mounted two heads, carrying microscopes which may be reversed in the heads, so as to be used at the front of the machine for line measurements and on the back for end measurements.
| VOL. I. | THE ROGERS‑BOND UNIVERSAL COMPARATOR. | PLATE XIV. |
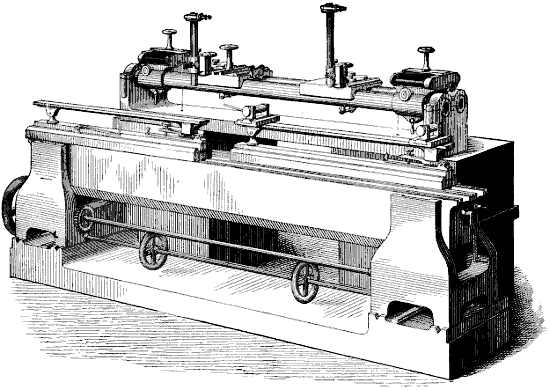 |
||
| Fig. 1348. | ||
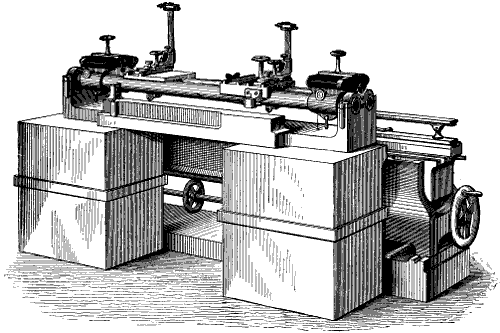 |
||
| Fig. 1349. | ||
Fig. 1348 is a front, and Fig. 1349 a rear view of the machine, whose details of construction are more clearly shown in the enlarged views, Fig. 1350 and 1352.
Fig. 1350 is a top view, and Fig. 1352 a front view, the upper part of the machine being lifted up for clearness of illustration. x, x, are the cylindrical guides, upon which are the carriages i, k, for the microscopes. The construction of these carriages is more fully seen in Fig. 1351, which represents carriage k. It is provided with a hand-wheel r, operating a pinion in a rack (shown at t in the plan view figure of the machine) and affording means to traverse the carriage along the cylindrical guides. The microscope may be adjusted virtually by the screw m4. The base upon which the microscope stands is adjustable upon a plate n, by means of the two slots and binding screws shown, and the plate n fits in a slideway running across the carriage. u is one of the stops used in making end measurements, the other being fixed upon the frame of the machine at v in the plan view, Fig. 1350. The micrometric arrangement for the microscope is shown more clearly in Fig. 1353. The screw b holds the box in position, the edge of the circular base on which it sits being graduated, so that the position of m may be easily read. In the frame m is a piece of glass having ruled upon it the crossed lines, or in place of this a frame may be used, having in it crossed spider web lines. These lines are so arranged as to be exactly in focus of the upper glass of the microscope, this adjustment being made by means of the screw s. The lines upon the bar are in the focus of the lower glass; hence, both sets of lines can be seen[I-344] simultaneously, and by suitable adjustment of the microscope can be brought to coincide.
Beneath the cylindrical guides, and supported by the rack t that runs between and beneath them, are the levers p, in Fig. 1352, upon which weights may be placed to take up the flexure or sag of the cylindrical guides.
In Fig. 1352, h, h, are heads that may be fixed to the cylindrical guides at any required point, and contain metallic stops, against which corresponding stops on the microscope carriages may abut, to limit and determine the amount to which these carriages may be moved along the cylindrical guides.
The pressure of contact between the carriage and the fixed stops is found to be sufficiently uniform or constant if the carriage is brought up to the stops (by means of the hand-wheel r, Fig. 1351) several times, and a microscope reading taken for each time of contact. But this pressure of contact may be made uniform or constant for all readings by means of an electric current applied to the carriage through the metallic stops on heads h, h, and those on the carriage.
We have now to describe the devices for supporting the work and adjusting it beneath the microscopes.
Referring, then, to Fig. 1352, e is a bed or frame that may be raised or lowered by means of the hand-wheel c, so as to bring the plate s (on which rests the bar whose line measure is to be compared) within range of the microscopes. The upper face of e is provided with raised V slideways, which are more clearly seen in the end view of this part of the machine shown in Fig. 1354. Upon these raised Vs are the devices for adjusting the height of the eccentric rollers s3, upon which the bars to be tested are laid, s2 representing one of these bars. To adjust the bars in focus under the microscope, these eccentric rollers are revolved by means of levers s4. At s5 is a device for giving to the table a slight degree of longitudinal movement in the base plate that rests upon the raised Vs; on the upper face of e and at s6 is a mechanism for adjusting the height of that end of the plate s. The base plate may be moved along the raised Vs of e by the hand-wheel d.
To test whether the cylindrical guides are deflected by their own weight or are level, a trough of mercury may be set upon the eccentric rollers s3, Fig. 1352, and the fine particles of dust on its surface may be brought into focus in the microscope, whose carriage may then be traversed to various positions along the cylindrical guides, and if these dust particles remain in focus it is proof that the guides are level with the mercury surface.
The methods of using the machine are as follows: The standard bar has marked upon its upper face (which is made as true as possible and highly polished) a line b (Fig. 1355), which is called the horizontal line, and is necessary in order to set the bar parallel to the cylindrical guides of the machine. The lines a, a, are those defining the measurement as a yard, a foot, or whatever the case may be, and these are called the vertical lines or lines of measurement. Now, suppose we require to test a bar with the standard and the lines on its face are marked to correspond to those on the standard.
The first operation will be to set the standard bar on the eccentric rollers s3 in Fig. 1352, and it and the microscopes are so adjusted that the spider web lines in the microscope exactly intersect the lines a and b on the standard, when the microscope carriage abuts against the heads h, Fig. 1352. The standard bar is then replaced by the bar to be tested, which is adjusted without altering the microscope adjustment or the heads h, and if the spider web lines in the microscope exactly coincide with and intersect the lines a and b, the copy corresponds to the standard. But if they do not coincide, then the amount of error may be found by the micrometer wheel g, Fig. 1353.
In this test the carriage is moved up against the stops h several times, and several readings or tests are made, so as to see that the force of the contact of the carriage against the stops h is uniform at each test, and if any variation is found, the average of a number of readings is taken. It is found, however, that with practice the carriage may be moved against the head h by means of the hand-wheel with such an equal degree of force that an error of not more than one fifty-thousandth of an inch is induced. It is found, however, that if too much time is occupied in this test, the heat of the operator’s body will affect the temperature of the bars, and therefore expand them and vitiate the comparison. But in this connection it may be noted that if a bar is at a temperature of 40°, and is placed in an ice bath, it does not show any contraction in less than one minute, and that when it does so, the contraction is irregular, taking place in sudden movements or impulses.
Professor Rogers’ methods of testing end measures are as follows: To compare a line with an end measure, a standard bar is[I-345] set upon the machine, its horizontal and vertical lines being adjusted true to the cylindrical guides by the means already described, and the microscope carriage is so adjusted that the spider web lines of the microscope coincide with the horizontal and vertical lines marked on the standard, while at the same time the stop (u, Fig. 1350) on the carriage k has contact with the fixed stop (v, Fig. 1350.) Carriage k is then moved along the cylindrical guides so as to admit the bar (whose end measure is to be compared with the lines on the standard) between the two stops, and if, with the bar touched by both stops u and v, the microscope spider lines intersect the vertical and horizontal line on the standard bar, then the end measure corresponds to the line measure; whereas, if such is not the case, the amount of error may be found by noting how much movement of the micrometer wheel of the microscope is required to cause the lines to intersect.
It is obvious that in this test, if the cylindrical guides had a horizontal curvature, the test would not be perfect.
The Horizontal Curvature.—The copy or bar to be tested may be set between the stops, and the standard bar may be placed on one side of it, as in Fig. 1356, and the test be made as already described. It is then set the same distance from the bar to be tested, but on the other side of it, as in figure, and again adjusted for position and tested, and if the readings on the standard bar are the same in both tests, it is proof that the measurements are correct.
Suppose, for example, that the cylindrical guides were curved as in Fig. 1356, it is evident that the vertical lines would appear closer together on the standard bar when in the first position than when in the second position.
In the Rogers machine the amount of error due to curvature in the cylindrical guides in this direction is found to be about 1⁄5000 part of an inch in 39 inches, corresponding to a radius of curvature of five miles.
Another method of testing an end with a line measure is as follows: The bar to be measured is shaped as in Fig. 1357, the end measurement being taken at a, and the projection b at each end serving to preserve the end surfaces a from damage. The standard bar is then set upon the machine and its horizontal and vertical lines adjusted in position as before described. In connection with this adjustment, however, the bar to be tested is set as in Fig. 1358; c being a block of metal (having marked centrally upon it horizontal and vertical lines), placed between the bar and the fixed stop u, its vertical line being in line with the vertical line on the standard. This adjustment being made, the block c is removed and placed at the other end of the bar, as shown in Fig. 1359, when, if the end measure on the bar corresponds with the line measure on the standard, the vertical line at the other end of the standard will correspond with the vertical line on block c.
To prove that the vertical line is exactly equidistant from each end of the block c, all that is necessary is to place it between the bar and the fixed stop u, Fig. 1350, adjust the microscope to it and then turn it end for end, and if its vertical line is still in line with the spider web of the microscope it is proof that it is central on the block, while if it is not central the necessary correction may be made. It is obvious that it is no matter what the length of c may be so long as its vertical line is central in its length.
In this process the coincidence of the vertical lines on the standard and on the piece c are employed to test the end measure on the bar with the line measure on the standard.
Figs. 1360 and 1361 represent the Whitworth Millionth Measuring Machine, in which the measurement is taken by the readings of an index wheel, and the contact is determined from the sense of touch and the force of gravity.
It is obvious that in measuring very minute fractions of an inch one of the main difficulties that arise is that the pressure of contact between the measuring machine and the surfaces measured must be maintained constant in degree, because any difference in this pressure vitiates the accuracy of the measurement. This pressure should also be as small as is consistent with the assurance that contact actually exists, otherwise the parts will spring, and this would again impair the accuracy of the measurement.
If the degree of contact is regulated by devices connected with the moving mechanism of the machine it is indirect, and may vary from causes acting upon that mechanism. But if it is regulated between the work and the moving piece that measures it, nothing remains but to devise some means of making its degree or amount constant for all measurements; so that if a duplicate requires to be compared with a standard, the latter may first be measured and the duplicate be afterwards measured for comparison.
All that is essential is that the two be touched with an equal[I-346] degree of contact, and the most ingenious and delicate method yet devised to accomplish this result is that in the Whitworth machine, whose construction is as follows:—
In a box frame a, is provided a slide-way for two square bars, b, c, which are operated by micrometer screws, one of which is shown at j (the cap over b being removed to expose b and j to view). The bars b, c, are made truly square, and each side a true plane. The groove or slide-way in which they traverse is made with its two sides true planes at a right angle to each other; so that the bars in approaching or receding from each other move with their axes in a straight line. At the two ends of the frame the micrometer screws are afforded journal bearings. The ends of the bars b, c, are true planes at a right angle to the axes of b, c. Bar b is operated as follows: Its operating screw j has a thread of 1⁄20 inch pitch; or in other words, there are twenty threads in an inch of its length. It is rotated by the hand-wheel f, whose rim-face is graduated by 250 equidistant lines of division. Moving f through a distance equal to that between, or from centre to centre of its lines of division, moves b through a distance equal to one five-thousandth part of an inch.
The screw in head i for operating bar c also has a pitch of 1⁄20 inch (or twenty threads in an inch of its length), and is driven by a worm-wheel w, having 200 teeth. This worm-wheel w is driven by a worm or tangent-screw h, having upon its stem a graduated wheel g, having 250 equidistant lines marked upon the face of its rim.
Suppose, then, that wheel g be moved through a distance equal to that between its lines of division, that is 1⁄250th of a rotation, then the worm h will move through 1⁄250th of a rotation, and the worm-wheel on the micrometer screw will be rotated 1⁄250th part of its pitch expressed in inches; because a full rotation of g would move the worm one rotation, and thus would move the worm-wheel on the screw one tooth only, whereas it has 200 teeth in its circumference; hence it is obvious that moving graduated wheel g, through a distance equal to one of its rim divisions will move the bar c the one-millionth of an inch; because:
| Pitch of thread |
Rotation of worm‑wheel |
Rotation of graduated wheel |
||||
| 1⁄20 inch | × | 1⁄200 | × | 1⁄250 | = | 1⁄1000000 |
Fixed pointers, as k, Fig. 1362, enable the amount of movement or rotation of the respective wheels f, g, to be read.
A peculiarly valuable feature of this machine is the means by which it enables an equal pressure of contact to be had upon the standards, and the duplicates to be tested therewith. This feature is of great importance where fine and accurate measurements are to be taken. The means of accomplishing this end are as follows:—
In the figures, d is a piece in position to be measured, and between it and the bar c is a feeler consisting of a small flat strip of steel, e e, having parallel sides, which are true planes.
When the pressure of contact upon this piece e e is such that if one end be supported independently the other will just be supported by friction, and yet may be easily moved between d and c by a touch of the finger, the adjustment is complete. At the sides of the frame a are two small brackets, shown at k, in the end view, Fig. 1362, e e being shown in full lines resting upon them, and in dotted lines with one end suspended. The contact-adjustment may thus be made with much greater delicacy and accuracy than in those machines in which the friction is applied to the graduated wheel-rim, because in the latter case, whatever friction there may be is multiplied by the difference in the amount of movement of the graduated rim and that of the bar touching the work.
All that is necessary in the Whitworth machine is to let e e be easy of movement under a slight touch, though capable of suspending one end by friction, and to note the position of the lines of graduation on c with reference to its pointer. By reason of having two operative bars, b, c, that which can be most readily moved may be operated to admit the piece or to adjust the bars to suit the length of the work, while that having the finer adjustive motion, as c, may be used for the final measuring only, thus preserving it from use, and therefore from wear as much as possible; or coarser measurements may be made with one bar, and more minute ones with the other.
So delicate and accurate are the measurements taken with this machine, that it is stated by C. P. B. Shelley, C.E., in his “Workshop Appliances,” that if well protected from changes of temperature and from dust, a momentary contact of the finger-nail will suffice to produce a measurable expansion by reason of the heat imparted to the metal. In an iron bar 36 inches long, a space equal to half a division on the wheel g having been rendered distinctly measurable by it, this space indicating an amount of expansion in the 36-inch bar equals the one two-millionth part of an inch!
The following figures, which are taken from Mechanics, represent a measuring machine made by the Betts Machine Company, of Wilmington, Delaware.
Fig. 1363 shows a vertical section through the length of the machine, which consists of a bed carrying a fixed and an adjustable head, the fixed head carrying the measuring screw and vernier while the adjustable one carries a screw for approximate adjustment in setting the points of the standard bars.
These screws have a pitch of ten threads per inch, and the range of the measuring screw has a range of 4 inches, and the machine is[I-347] furnished with firm standard steel bars (4-inch, 6-inch, 18-inch, and 24-inch). The measuring points of the screws are of hardened steel, secured axially in line with the screws, and of two forms, with spherical and flat points, one set of each being used at a time. The larger wheel c is indexed to 1000 divisions, each division representing the ten-thousandth of an inch at the points; the smaller wheel has 100 divisions, each representing the one-thousandth part of an inch at the points. Beside, and almost in contact with, the larger wheel is a movable or adjustable pointer e, upon which the error of the screw is indexed for each inch of its length; the screw error is of the utmost importance when positive results are desired. The screw is immersed in oil to maintain a uniform temperature throughout its length, and to avoid particles of dust accumulating on its surface.
As stated above, the readings are indexed to the ten-thousandth part of an inch, but variations to the hundred-thousandth part of an inch can be indicated. The machine will take in pieces to 24 inches in length, and to 4 inches in diameter. In measuring, the points are brought into easy contact and then expanded by turning the larger wheel, counting the revolutions or parts of revolutions to determine the distance between the points or the size of what is to be measured. The smaller machine is constructed so as to indicate by means of vernier attachment to the ten-thousandth part of an inch, and is of value in tool-rooms where standard and special tools are continually being prepared. By its use, gauges and other exact tools can be made, and at the same time keep gauges of all kinds to standard size by detecting wear or derangement. The machine consists of a frame with one fixed head; the other head is moved by a screw; on both heads are hardened steel points. As with the larger machine, the screw error is indicated in such a manner as to permit the operator to guard against reproducing its error in its work. These machines are used for making gauges, reamers, drills, mandrels, taps, and so on.
The errors that may exist in the pitch of the measuring screw are taken into account as follows: The points of the measuring machine should be brought into light contact, the position of index-wheel, vernier, and the adjustable pointer which has the screw error indexed upon it should be as in Fig. 1364; that is, the zeros on index-wheel and vernier should be in exact line, the vernier covering half of the zero line on pointer. To measure 1⁄2 inch, for illustration, five complete revolutions of index-wheel should produce 1⁄2 inch, and would if we had a perfect screw, but the screw is not perfect, and we must add to the measurement already obtained one-half of the space, stamped upon corrective devise, 0-1. This space 0-1 represents the whole error in the screw from zero to 1 inch. The backlash of the screw should always be taken up.
The details of this machine are as follows:—
In Fig. 1363 the points g are those between which the measuring is done, and the slide held by the nut k in position is adjusted by means of inch bars to the distance to be measured; h, the hand-wheel for moving one point, and f the wheel which moves the other. Fig. 1366 is a cross section of the movable head through the nut k and stud m, by which the movable head is adjusted, and Fig. 1365 is a cross section through the fixed head. The bars used in setting the machine are shown in Fig. 1367, and in Fig. 1368 the points of the measuring screws are shown on a large scale. The other figures show various details of the machine and their method of construction. The vernier, it will be observed, is a double one. This is shown in Fig. 1364, and is so arranged that the zero is made movable in order to correct the errors of the screw itself. These errors are carefully investigated and a record made of each. Thus, in Fig. 1363 the arm e is graduated so as to show the true zero for different parts of the screw; d can then be adjusted to a correct reading, and the divisions on the large wheel will then be correct to an exceedingly small fraction. This method of construction enables the machine to be used for indicating very minute variations of length.
In Fig. 1369 is shown a measuring machine designed by Professor John E. Sweet, late of Cornell University. The bed of the machine rests on three feet, so that the amount of support at each leg may remain the same, whether the surface upon which it rests be a true plane or otherwise. This bed carries a headstock and a tailstock similar to a lathe. The tailstock carries a stationary feeler, and the headstock a movable one, operated horizontally by a screw passing through a nut provided in the headstock, the axial lines of the two feelers being parallel and in the same plane. The diameters of the two feelers are equal at the ends, so that each feeler shall present the same amount of end area to the work. The nut for the screw operating the headstock feeler is of the same length as the screw itself, so that the wear of the screw shall be equalized as near as possible from end to end, and not be the most at and near the[I-348] middle of its length, as occurs when the thread on the screw is longer than that in the nut.
The pitch of the thread on the screw is 16 threads in an inch of length, hence one revolution of the screw advances the feeler 1⁄16 inch. The screw carries a wheel whose circumference is marked or graduated by 625 equidistant lines of division. If, therefore, this wheel be moved through a part of a rotation equal to one of these divisions, the feeler will move a distance equal to 1⁄625 of the 1⁄16th of an inch, which is the ten thousandth part of an inch, and as the bed of the machine is long enough to permit the feelers to be placed 12 inches apart, the machine will measure from zero to 12 inches by the ten-thousandth of an inch.
To assist the eye in reading the lines of division, each tenth line is marked longer than the rest, and every hundredth, still longer. The pitch of the screw being 16 threads to an inch enables the feeler to be advanced or retired (according to the direction of the rotation of the wheel) a sixteenth inch by a simple rotation of the wheel, an eighth inch by two wheel rotations, a thirty-second inch by a quarter rotation, and so on; and this renders the use of that machine very simple for testing the accuracy of caliper gauges, that are graduated to 1⁄8, 1⁄16, 1⁄32, 1⁄64th inch, and so on, such a gauge being shown (in the cut) between the feelers.
The bar or arm shown fixed to the headstock and passing over the circumference of the wheel at the top affords a fixed line or point wherefrom to note the motion of the wheel, or in other words, the number of graduations it moves through at each wheel movement. It is evident that in a machine of this kind it is essential that the work to be measured have contact with the feelers, but that it shall not be sufficient to cause a strain or force that will spring or deflect either the work itself (if it be slight) or the parts of the machine. It is also essential that at excessive measurements the feelers shall touch the work with the same amount of force. The manner of attaining this end in Professor Sweet’s machine is as follows: Upon the same shaft as the wheel is an arm having contact at both ends with the edge of the wheel rim whose face is graduated. This arm is free to rotate upon the shaft carrying the graduated wheel, which it therefore drives by multiple friction on its edges at diametrically opposite points; by means of a nut the degree of this friction may be adjusted so as to be just sufficient to drive the wheel without slip when the wheel is moved slowly. So long, then, as the feelers have no contact with the piece to be measured, the arm will drive the graduated wheel, but when contact does take place the wheel will be arrested and the arm will slip. The greatest accuracy will therefore be obtained if the arm be moved at an equal speed for all measurements.
Fig. 1370 represents a Brown and Sharpe measuring machine for sheet metal. It consists of a stand a with a slotted upright having an adjusting screw c above, and a screw d, with a milled head and carrying a dial, passing through its lower part. One turn of the screw, whose threads are 1⁄10th inch apart, causes one rotation of the dial, the edge of which is divided into one hundred parts, enabling measurements to be made to thousandths of an inch. The sheet-metal to be gauged is inserted in the slot of the upright. The adjusting-screw is set so that when the points of the two screws meet, the zero of the dial shall be opposite an index or pointer which shows the number of divisions passed over, and is firmly secured by a set-screw.
Next in importance to line and end measurements is the accurate division of the circle, to accomplish which the following means have been taken.
What is known as “Troughton’s” method (which was invented by Edward Troughton about 1809) is as follows: A disk or circle of 4 feet radius was accurately turned, both on its face and its inner and outer edges. A roller was next provided of such diameter that it revolved sixteen times on its own axis, while rolling once round the outer edge of the circle. This roller was pivoted in a framework which could be slid freely, yet tightly, along the circle, the roller meanwhile revolving by frictional contact on the outer edge. The roller was also, after having been properly adjusted as to size, divided as accurately as possible into sixteen equal parts by lines parallel to its axis. While the frame carrying the roller was moved once round along the circle, the points of contact of the roller divisions with the circle were accurately observed by two microscopes attached to the frames, one of which commanded the ring on the circle near its edge, which was to receive the divisions, and the other viewed the roller divisions. The exact points of contact thus ascertained were marked with faint dots, and the meridian circle thereby divided into 256 very nearly equal parts.
The next part of the operation was to find out and tabulate the errors of these dots, which are called apparent errors, because the error of each dot was ascertained on the supposition that all its neighbors were correct. For this purpose two microscopes, which we shall call a and c, were taken with cross-wires and micrometer adjustments, consisting of a screw and head divided into 100 divisions, 50 of which read in the one and 50 in the opposite direction. These microscopes, a and b, were fixed so that their cross-wires respectively bisected the dots 0 and 128, which were supposed to be diametrically opposite. The circle was now turned half way round on its axis, so that dot 128 coincided with the wire of a, and should dot 0 be found to coincide with b, then the dots were sure to be 180° apart. If not, the cross-wire of b was moved till it coincided with the dot 0 and the number of divisions of micrometer head noted. Half this number gave clearly the error of dot 128 and was tabulated plus or minus according as the arcual distance between 0 and 128 was found to exceed or fall short of the removing part of the circumference. The microscope b was now shifted, a remaining opposite dot 0 as before, till its wire bisected dot 64, and by giving the circle one-quarter of a turn on its axis, the difference of the arcs between dots 0 and 64, and between 64 and 128 was obtained. The half of this distance gave the apparent error of dot 64, which was tabulated with its proper sign. With the microscope a still in the same position, the error of dot 192 was obtained, and in the same way, by shifting b to dot 32, the errors of dots 32, 96, 160 and 224 were successively ascertained. By proceeding in this way the apparent errors of all the 256 dots were tabulated.
In order to make this method fully understood, we have prepared the accompanying diagrams, which clearly show the plan pursued.
Fig. 1371 illustrates the plan of dividing the large circle by means of the roller b.
[I-349]Fig. 1372 shows the general adjustment of the microscope for the purpose of proving the correctness of the divisions.
Fig. 1373 shows the location of the microscope over the points 0 and 128.
Fig. 1374 shows the circle turned half-way round, the points 0 and 128 coinciding with the cross threads of the microscope.
Fig. 1375 shows a similar reading, in which the points do not coincide with the cross threads of the microscope.
Fig. 1376 shows the microscope adjusted for testing by turning the circle a quarter revolution.
Fig. 1377 represents one of the later forms of Ramsden’s dividing engine.[21] It consists first of a three-legged table, braced so as to be exceedingly stiff. Upon this is placed a horizontal wheel with deep webs, and a flat rim. The webs stiffen the wheel as much as possible, and one of these webs, which runs round the wheel about half-way between the centre and the circumference, rests upon a series of rollers which support it, and prevent, as far as possible, the arms from being deflected by their own weight. An outer circle, which receives the graduation, is laid upon the rim of the wheel and secured in place. The edge of this circle is made concave. A very fine screw, mounted in boxes and supported independently, is then brought against this hollow edge, and, being pressed against it, the screw, when revolved, of course cuts a series of teeth in the circumference, and this tooth-cutting, facilitated by having the screw threads made with teeth, was continued until perfect V-shaped teeth were cut all around the edge of the wheel. This Mr. Ramsden calls ratching the wheel. The number of teeth, the circumference of the wheel, and the pitch of the screw were all carefully adjusted, so that by using 2160 teeth, six revolutions of the screw would move the wheel the space of 1°. When this work was finished, and the adjustment had been made as perfect as possible, a screw without teeth—that is, one in which the thread was perfect—was put in the place of that which had cut the teeth from the wheel, and the machine was perfected. The wheel a b c in the drawings is made of bell metal, and turns in a socket under the stand, which prevents the wheel from sliding from the supporting or friction rolls z, z. The centre r, working against the spindle m, is made so as to fit instruments of various sizes. The large wheel has a radius of 45 inches, and has 10 arms. The ring b is 24 inches in diameter by 3 inches deep. The ring c is of very fine brass, fitting exactly on the circumference of the wheel, and fastened by screws, which, after being screwed home, were well riveted. Great care was taken in making the centre on which the wheel worked exceedingly true and perfect, and in making the socket for the wheel fit as exactly as possible. The revolving mechanism is all carried on the pillar p, resting on the socket c′. We may state here that the machine, as shown in the engravings, now in the possession of the Stevens Institute, is in some respects slightly improved on that shown in the original drawings published in “Rees’ Cyclopædia” in 1819. After the wheel was put on its stand, and the pulleys in place, the instrument was ready for the turning mechanism. The upper part of this pillar p carries the framework in which the traversing screw revolves.
[21] From Mechanics.
In Fig. 1378 d is the head of this pillar, p the screw which turns the wheel. e1 e1 are the boxes, which are made conical so as to prevent any shake and to hold the screw firmly. Circles of brass, f and v, are placed on the arbor of the screw, and as their circumference is[I-350] divided into 60 parts, each division consequently amounts to a motion of the wheel of 10 seconds, and 60 of them will equal 1 minute. Revolution is given to the screw by means of the treadle b′ and the cord y, which runs over the guiding screw w, Fig. 1379, and is finally attached to the box u. A spring enclosed in the box u causes it to revolve, and winds up the slack of the cord whenever the treadle is relieved. In the original drawing the head of the pillar p was carried in a parallel slip in the piece surrounding its head. The construction as shown in Fig. 1379 is somewhat different. The result attained, however, is identical, and the spindles and attachments are held so as to have no lateral motion. The wheels v and x have stops upon them, so arranged that the screw may be turned definitely to a given point and stopped. These wheels are at the opposite ends of the screw w. A detail of one of them is shown at v in Fig. 1380, where x is the ratchet-wheel. This figure also illustrates the construction of the bearings for the screw arbor. We have not space to explain the method by which the perfection of the screw was obtained, nor to discuss the means by which was obtained the success of so eliminating the errors as to make the division of the instrument more perfect than anything which had been attempted previously. Success, however, was obtained, and by means of the first or tooth-cutting screw the teeth were brought to such a considerable uniformity that, together with the fact that the screw took hold of a number of teeth at one time, most of the errors which would have been expected from this method of operation were eliminated. The method of ruling lines upon the instrument was most ingenious. The frame l l, is connected to the head d, of the pillar p in front, by the clamps i and k, and to the centre m by the block r. A frame n n stiffens the back. The blocks o, o on the frame q′ are secured to the frame l l, by set-screws c, c.
Fig. 1381 shows a side view of the frame q′, which it is seen carries a V-shaped piece q, which in turn carries another V-shaped piece s, Fig. 1378. The piece q is supported on pointed screws d, d, and the piece s is supported on two similar screws f, f. The point of this piece s carries the cutting tool e, Fig. 1378. Of course s can move only in a radial line from the centre m towards the circumference. If the sextant, octant, or other instrument be fastened to the large wheel a, with its centre at m, and the large wheel be rotated by the screw, all lines drawn upon it by e will be radial, and the distances apart will be governed by the number of turns made by the screw. This improvement, we think, was originated by Mr. Ramsden, and was a very great advance over the old method of the straight-edge, and has been used in some of the Government comparators and dividing engines. The following is Mr. Ramsden’s own description of the graduation of the machine, and of his method of operating it. It shows the extreme care which he took in correcting the mechanical errors in the construction:—
“From a very exact centre a circle was described on the ring c, about 4⁄10 inch within where the bottom of the teeth would come. This circle was divided with the greatest exactness I was capable of, first into five parts, and each of these into three. These parts were then bisected four times; that is to say, supposing the whole circumference of the wheel to contain 2160 teeth, this being divided into five parts, and these again divided into three parts, each third part would contain 144, and this space, bisected four times, would give 72, 36, 18, 9; therefore, each of the last divisions would contain 9 teeth. But, as I was apprehensive some error might arise from quinquesection and trisection, in order to examine the accuracy of the divisions, I described another circle on the ring c, Fig. 1378, 1⁄10 inch within the first, and divided it by continual bisection, as 2160, 1080, 540, 270, 135, 671⁄2, 333⁄4, and, as the fixed wire (to be described presently) crossed both the circles, I could examine their agreement at every 135 revolutions (after ratching could examine it at every 333⁄4); but not finding any sensible difference between the two sets of divisions, I, for ratching, made choice of the former, and, as the coincidence of the fixed wire with an intersection could be more exactly determined with a dot or division, I therefore made use of intersections on both sides, before described.
“The arms of the frame l, Fig. 1381, were connected by a thin[I-351] piece of brass, 3⁄4 inch broad, having a hole in the middle 4⁄10 inch in diameter; across this hole a silver wire was fixed, exactly in a line to the centre of the wheel; the coincidence of this wire with the intersections was examined by a lens of 1⁄10 inch focus, fixed in a tube which was attached to one of the arms l. Now (a handle or winch being fixed on the end of the screw) the division marked 10 on the circle f was set to its index, and, by means of a clamp and adjusting-screw for that purpose, the intersection marked i on the circle c′ was set exactly to coincide with the fixed wire. The screw was then carefully pressed against the circumference of the wheel by turning the finger-screw h; then, removing the clamp, I turned the screw by its handle nine revolutions, till the intersection marked 240 came nearly to the wire. Then, turning the finger-screw h, I released the screw from the wheel, and turned the wheel back till the intersection marked 2 exactly coincided with the wire, and by means of the clamp before mentioned, the division 10 on the circle being set to its index, the screw was pressed against the edges of the wheel by the finger-screw h, the clamps were removed, and the screw turned nine revolutions, till the intersection marked i nearly coincided with the fixed wire; the screw was released from the wheel by turning finger-screw h as before, the wheel was turned back till intersection marked 3 coincided with the fixed wire; the division 10 in the circle being set to its index, the screw was pressed against the wheel as before, and the screw turned nine revolutions, till intersection 2 was nearly coincident with the fixed wire, and the screw released, and I proceeded in this manner till the teeth were marked round the whole circumference of the wheel. This was repeated three times round to make the impressions deeper. I then ratched the wheel round continuously in the same direction, without ever disengaging the screw, and, in ratching the wheel about 300 times round, the teeth were finished.
“Now, it is evident that if the circumference of the wheel was even one tooth, or ten minutes, greater than the screw would require, this error would, in the first instance, be reduced by 1⁄240 part of a revolution, or two seconds and a half, and these errors or inequalities of the teeth were equally distributed round the wheel at the distance of nine teeth from each other. Now, as the screw in ratching had continual hold of several teeth at the same time and thus constantly changing, the above-mentioned irregularities soon corrected themselves, and the teeth were reduced to a perfect equality. The piece of brass which carried the wire was now taken away, and the cutting-screw was also removed, and a plain one put in its place. At one end of the screw arbor, or mandrel was a small brass circle f, having its edge divided into 60 parts, numbered at every sixth division, as before mentioned. On the other end of the screw is a ratchet-wheel v (x, Fig. 1380) having 60 teeth, covered by the hollow circle (v, Fig. 1380), which carries two clicks that catch upon opposite sides of the ratchet-wheel. When the screw is to be moved forward, the cylinder w turns on a strong steel arbor e′′, which passes through the piece x′; this piece, for greater firmness, is attached to the screw-frame by the braces w. A spiral groove or thread is cut upon the outside of the cylinder w, which serves both for holding the string and also giving motion to the lever i on its centre, by means of a[I-352] steel tooth v, that works between the threads of the spiral. To the lever is attached a strong steel pin m, on which a brass socket turns; this socket passes through a slit in the piece u, and may be tightened in any part of the slit by the finger-nut y. This piece serves to regulate the number of revolutions of the screw for each tread of the treadle b′.”
Figs. 1382, 1383, and 1384 represent a method adopted to divide a circle by the Pratt and Whitney Company. The principle of the device is to enable the wheel to be marked, to be moved through a part of a revolution equal to the length of a division, and to test the accuracy of the divisions by the coincidence of the line first marked with that marked last when the wheel has been moved as many times as it is to contain divisions. By this means any error in the division multiplies, so that the last division marked will exhibit it multiplied by as many times as there are divisions in the whole wheel. The accuracy of this method, so long as variations of temperature are avoided, both in the marking and the drilling of the wheel, appears to be beyond question. In the figures, w represents a segment of the wheel to be divided, and c what may be termed a dividing chuck. The wheel is mounted on an arbor in a gear-cutting machine. On the hub of the wheel (which has been turned up for the purpose) there is fitted, to a close working fit, a bore at the end of an arm, the other end of the arm being denoted by a in the figures. The dividing chuck is fitted to the slide s of the gear-cutting machine, and is of the following construction.
Between two lugs, b and b′, it receives the end of arm a. These lugs are provided with set-screws, the distance between the ends of which regulate the amount of movement of the end of arm a. Upon a is the slide d, carrying the piece e, in which is the marking tool f, the latter being lifted by a spring g, and, therefore, having no contact with the wheel surface until the spring is depressed. h is an opening through the arm a to permit the marking tool f to meet the wheel face, as shown in Fig. 1384, which is an end view of the slide showing the arm a in section. The face of the wheel rests upon the chuck on each side of the arm at the points i, j, and may be clamped thereto by the clamps k. The arm may be clamped to the wheel by the clamp shown dotted in at l, the bolt passing up and through the screw handle m. n is simply a lever with which to move the arm a, or arm a and the wheel. Suppose all the parts to be in the position shown in the cuts, the clamps being all tightened up, the slide d may be moved forward towards k, while[I-353] the spring is depressed, and f will mark a line upon the wheel. The handle m may then be released and arm a moved until it touches the set-screw in b′, when m may be tightened and another line marked. Clamps k are then tightened, and the wheel, with the arm a fast to it, moved back to the position shown in the cut, when the clamps may be tightened again and another line marked, the process being continued all round the wheel. To detect and enable the correction of any discoverable error in a division, there is provided the plate p, having upon it three lines of division (which have been marked simultaneously with three of the lines marked on the wheel). This plate is supported by an arm or bracket q, on the rear edge of which are three notches r to hold a microscope, by means of which the lines on p may be compared with those on the wheel face, so that if any discrepancy should appear it may be determined which line is in error. The labor involved in the operation of marking a large wheel is very great. Suppose, for example, that a wheel has 200 lines of division, and that after going round the wheel as described it is found that the last division is 100th inch out; then in each division the error is the two-hundredth part of this 100th inch, and that is all the alteration that must be made in the distance between set-screws b and b′.
| VOL. I. | DIVIDING ENGINE AND MICROMETER. | PLATE XV. | |
 |
|||
| Fig. 1385. | |||
 |
 |
||
| Fig. 1386. | Fig. 1387. | ||
 |
 |
||
| Fig. 1388. | Fig. 1389. | ||
 |
|
||
| Fig. 1390. | Fig. 1391. | ||
Figs. 1385 and 1386 represent a method of originating an index wheel, adopted by R. Hoe and Co., of New York City.
In this method the plan was adopted of fitting round a wheel 180 tapering blocks, which should form a complete and perfect circle. These blocks were to serve the same purpose as is ordinarily accomplished by holes perforated on the face of an index wheel. In their construction, means of correcting any errors that might be found, without the necessity of throwing away any portion of the work done, would also be provided. Further, this means would provide for taking up wear, should any occur in the course of time, and thus restore the original truth of the wheel.
Fig. 1385 of the engravings shows the originating wheel mounted upon a machine or cutting engine. Upon the opposite end of the shaft is the worm-wheel in the process of cutting. After the master worm-wheel has been thus prepared by means of the originating wheel, it is used upon the front end of the shaft, in the position now occupied by the originating wheel, and operated by a worm in the usual manner. Subdivisions are made by change wheels. The construction of the originating wheel will be understood by the smaller engravings.
Fig. 1386 is an enlarged section of a segment of the wheel, while Fig. 1387 is an edge view of this segment. Fig. 1388 is a view of one of the blocks employed in the construction of the wheel, drawn to full size.
In the rim of the originating wheel there was turned a shoulder, c, Fig. 1387, 5 feet in diameter. Upon this shoulder there were clamped 180 blocks, of the character shown in Fig. 1386, as indicated by the section, Fig. 1387. These blocks were secured to the face of the wheel d by screws e, and were held down to the shoulder by the screw and clamp g f, shown in Fig. 1387. (They are omitted in Fig. 1385 for clearness of illustration.) In the preparation of these blocks each was fitted to a template t, in Fig. 1388, and was provided with a recess b, to save trouble in fitting and to insure each block seating firmly on the shoulder c. The shoulder, after successive trials, was finally reduced to such a diameter that the last block exactly filled the space left for it when it was fully seated on the shoulder c. The wheel thus prepared was mounted on a Whitworth cutting engine, as shown in Fig. 1385. The general process of using this wheel is as follows: The blocks forming the periphery of the originating wheel are used in place of the holes ordinarily seen in the index plates. One of them is removed to receive a tongue, shown in the centre of Fig. 1385, which, exactly filling the opening or notch thus made, holds the wheel firmly in place. After a tooth has been cut in the master worm-wheel, shown at the back of Fig. 1385, the block in the edge of the originating wheel corresponding to the next tooth to be cut is removed. The tongue is withdrawn from the first notch, the wheel is revolved, and the tongue is inserted in the second position. The block first removed is then replaced, and the cutting proceeds as before. This operation is repeated until all the teeth in the master wheel have been cut. The space being a taper, the tongue holds the originating wheel more firmly than is possible by means of cylindrical pins fitting into holes. The number of blocks in the originating wheel being 180, the teeth cut in the master wheel may be 180 or some exact divisor of this number.
The advantages of this method of origination are quite evident. Since 180 blocks were made to fill the circle, the edges of each had 2° taper. This taper enabled the blocks to be fitted perfectly to the template, because any error in fit would be remedied by letting the block farther down into the template. Hence, it was possible to correct any error that was discovered without throwing the block away. Further, as the blocks themselves are removed to form a recess for locking the originating wheel in position while cutting the worm-wheel, the truth of the work is not subject to the errors that creep in when holes or notches require to be pierced in the originating wheel. Such errors arise from the heating due to the drilling or cutting, from the wear of the tools or from their guides, from soft or hard spots in the metal and other similar causes. To avoid any error from the heating due to the cut on the worm-wheel, in producing master wheels, Messrs. Hoe and Co. allowed the wheel to cool after each cut. The teeth were cut in the following order: The first three were cut at equidistant points in the circumference of the wheel. The next three[I-354] also were at equidistant points, and midway between those first cut. This plan was continued until all the teeth were cut, thus making the expansion of the wheel from the heat as nearly equal as possible in all directions.
There is one feature in this plan that is of value. It is that a certain number of blocks, for example six, may be taken out at two or three different parts of the originating wheel and interchanged, thus affording a means of testing that does not exist in any other method of dividing.
The tools applied by the workmen to measure or to test work may be divided into classes.
1st. Those used to determine the actual size or dimension of the work, which may be properly termed measuring tools.
2nd. Those used as standards of a certain size, which may be termed gauges.
3rd. Those used to compare one dimension with another, as in the common calipers.
4th. Those used to transfer measurements or distances defined by lines.
5th. Those used to test the accuracy of plane or flat surfaces, or to test the alignment of one surface to another.
Referring to the first, their distinctive feature is that they give the actual dimensions of the piece, whether it be of the required dimension or not.
The second determine whether the piece tested is of correct size or not, but do not show what the amount of error is, if there be any.
The third show whatever error there may be, but do not define its amount; and the same is true of the fifth and sixth.
Fig. 1389 represents a micrometer caliper for taking minute end measurements. This instrument is capable of being set to a standard measurement or of giving the actual size of a piece, and is therefore strictly speaking a combined measuring tool and a gauge. The U-shaped body of the instrument is provided with a hub a, which is threaded to receive a screw c, the latter being in one piece with the stem d, which envelops for a certain distance the hub a. The thread of c has a pitch of 40 per inch; hence one revolution of d causes the screw to move endways 1⁄40 of an inch.
The vertical lines of division shown on the hub a are also 1⁄40 of an inch apart, hence the bevelled edge of the sleeve advances one of the divisions on a at each rotation.
This bevelled edge is divided into 25 equal divisions round its circumference, as denoted by the lines marked 5, 10, &c. If, then, d be rotated to an amount equal to one of its points of division, the screw will advance 1⁄25 of 1⁄40 of an inch. In the cut, for example, the line 5 on the sleeve coincides with the zero line which runs parallel to the axial line of the hub. Now suppose sleeve d to be rotated so that the next line of division on the bevelled edge of d comes opposite to the zero line, then 1⁄25 part of a revolution of d will have been made, and as a full revolution of d would advance the screw 1⁄40 of an inch, then 1⁄25 of a revolution will advance it 1⁄25 of 1⁄40 inch, which is 1⁄1000 inch.
The zero line being divided by lines of equal division into 40ths of an inch, then, as shown in the cut, the instrument is set to measure 3⁄40ths and 5⁄25ths of a fortieth.
It is to be observed that to obtain correct measurements the work must be held true with the face of the foot b, and the contact between the end of screw c and the work must be just barely perceptible, otherwise the pressure of the screw will cause the U-piece to bend and vitiate the accuracy of the measurement. Furthermore, if the screw be rotated under pressure upon the work, its end will wear and in time impair the accuracy of the instrument. To take up any wear that may occur, the foot-piece b is screwed through the hub, holding it so that it may be screwed through the hub to the amount of the wear.
To avoid wear as much as possible, the screws of instruments of this kind are sometimes hardened, and to correct the error of pitch induced in the hardening, each screw is carefully tested to find in what direction the pitch of the hardened thread has varied, and provision is made for the correction as follows:—
The zero line on the hub a stands, if the thread is true to pitch, parallel to the axis of the screw c, but if the pitch of the thread has become coarser from hardening, this zero line is marked at an angle, as shown in Fig. 1390, in which a a represents the axial line of the screw and b the zero line.
If the screw pitch becomes finer from hardening, the zero line is made at an angle in the opposite direction, as shown in Fig. 1391, the amount of the angle being that necessary to correct the error in the screw pitch. The philosophy of this is, that if the pitch has become coarser a less amount of movement of the screw is necessary, while if it has become finer an increased movement is necessary. It is obvious, also, that if the pitch of the thread should become coarser at one end and finer at the other the zero line may be curved to suit.
Fig. 1392 represents a vernier caliper, in which the measurement is read by the coincidence of ruled lines upon the following principle. The vernier is a device for subdividing the readings of any equidistant lines of division. Its principle of action may be explained as follows: Suppose in Fig. 1393 a to be a rule or scale divided into inches and tenths of an inch, and b a vernier so divided that its ten equidistant divisions are equal to nine of the divisions on a; then the distance apart of the lines of division on a will be 1⁄10 inch; but, as the whole ten divisions on b measure less than an inch, by 1⁄10 inch, then each line of division is a tenth part of the lacking tenth less than 1⁄10 inch apart. Thus, were we to take a space equal to the 1⁄10 inch between 9 and 10 on a, and divide it into 10 equal parts (which would give ten parts each measuring 1⁄100th of an inch) and add one of said parts to each of the distances between the lines of division on b, then the whole of the lines on a would coincide with those on b. It becomes evident, then, that line 1 on b is 1⁄100 inch below line 1 on a, that line 2 on b is 2⁄100 inch below line 2 on a, line 3 on the vernier b is 3⁄100 inch below line 3 on the rule a, and so on, until we arrive at line 10 on the vernier, which is 10⁄100 or 1⁄10 inch below line 10 on a. Suppose, then, the rule or scale to rest vertically on a truly surfaced plate, and a piece of metal be placed beneath b, the thickness of the piece will be shown by which of the lines on b coincides with a line on a. For more minute divisions it is simply necessary to have more lines of division in a given length on a and b. Thus, if the rule be divided into inches and fiftieths, and the vernier is so divided that it has 20 equidistant lines of division to 19 lines on[I-355] the rule, it will then lack one division, or 1⁄50 inch in 20⁄50 inch, each division on the vernier will then be the one-twentieth of a fiftieth too short, and as 1⁄20 of 1⁄50 is 1⁄1000, the instrument will read to one-thousandth of an inch.
Let it now be noted that, instead of making the lines of division closer together to obtain minute measurements, the same end may be obtained by making the vernier longer. For example, suppose it be required to measure to 1⁄2000 part of an inch, then, if the rule or scale be graduated to inches and fiftieths, and the vernier be graduated to have 40 equidistant lines of division, and 39 of the lines on the scale, the reading will be to the 1⁄2000 part of an inch. But, in any event, the whole of the readings on the vernier may be read, or will be passed through, while it is traversing a division equal to one of the divisions on the scale or rule.
In Fig. 1392 is shown a vernier caliper, in which the vernier is attached to and carried by a slide operating against the inside edge of the instrument. The bar is marked or graduated on one side by lines showing inches and fiftieths of an inch, with a vernier graduated to have 20 equidistant lines of division in 19 of the lines of division on the bar, and therefore measuring to the 1⁄1000th of an inch, while the other side is marked in millimètres with a vernier reading to 1⁄40th millimètre, there being also 20 lines of division on the vernier to 19 on the bar.
The inside surfaces of the feet or jaws are relieved from the bar to about the middle of their lengths, so as to confine the measuring surfaces to dimensions sufficiently small to insure accurate measurement, while large enough to provide a bearing area not subject to rapid wear. If the jaw surface had contact from the point to the bar, it would be impossible to employ the instrument upon a rectangular having a burr, or slight projection, on the edge. Again, by confining the bearing area to as small limits as consistent with the requirements of durability a smaller area of the measured work is covered, and the undulations of the same may be more minutely followed.
To maintain the surface of the movable jaw parallel with that of the bar-jaw, it is necessary that the edge of the slide carrying the vernier be maintained in proper contact with the edge of the instrument, which, while adjusting the vernier, should be accomplished as follows:—
The thumb-screw most distant from the vernier should be set up tight, so that that jaw is fixed in position. The other thumb-screw should be set so as to exert, on the small spring between its end and the edge of the bar, a pressure sufficient to bend that spring to almost its full limit, but not so as to let it grip the bar. The elasticity of the spring will then hold the edge of the vernier slide sufficiently firmly to the under edge of the bar to keep the jaw-surfaces parallel; to enable the correct adjustment of the vernier, and to permit the nut-wheel to move the slide without undue wear upon its thread, or undue wear between the edge of the slide and that of the bar, both of which evils will ensue if the thumb-screw nearest the vernier is screwed firmly home before the final measuring adjustment of the vernier is accomplished.
When the measurement is completed the second thumb-screw must be set home and the reading examined again, for correctness, to ascertain if tightening the screw has altered it, as it would be apt to do if the thumb-screw was adjusted too loose.
The jaws are tempered to resist wear, and are ground to a true plane surface, standing at a right angle to the body of the bar. The method of setting the instrument to a standard size is as follows:—
The zero line marked 0 on the vernier coincides with the line 0 on the bar when the jaws are close together; hence, when the 0 line on the vernier coincides with the inch line on the bar, the instrument is set to an inch between the jaws. When the line next to the 0 line on the vernier coincides with the line to the left of the inch line on the bar, the instrument is set to 11⁄1000 inches. If the vernier slide then be moved so that the second line on the vernier coincides with the second line, on the left of the inch on the bar, the instrument is set to 12⁄1000 inches, and so on, the measurement of inches and fiftieths of an inch being obtained by the coincidence of the zero line on the vernier with the necessary line on the bar, and the measurements of one-thousands being taken as described.
But if it is required to measure, or find the diameter of an existing piece of work, the method of measuring is as follows:—
The thumb-screws must be so adjusted as to allow the slide to move easily or freely upon the work without there being any play or looseness between the slide and the bar. The slide should be moved up so as to very nearly touch the work when the latter is placed between the jaws. The thumb-screw farthest from the vernier should then be screwed home, and the other thumb-screw operated to further depress the spring without causing it to lock upon the bar. The nut-wheel is then operated so that the jaws, placed squarely across the work, shall just have perceptible contact with it. (If the jaws were set to grip the work tight they would spring from the pressure, and impair the accuracy of the measurements.) The thumb-screw over the vernier may then be screwed home, and the adjustment of the instrument to the work again tried. If a correction should be found necessary, it is better to ease the pressure of the thumb-screw over the vernier before making such correction, tightening it again afterwards. The reading of the measurement is taken as follows:—
If the 0 line on the vernier coincides with a line on the bar, the measurement will, of course, be shown by the distance of that line from the 0 line on the bar, the measurement being in fiftieths of inches, or inches and fiftieths (as the case may be), but if the 0 line on the vernier does not coincide with any line of division on the bar, then the measurement in inches and fiftieths will be from the next line (on the bar) to the right of the vernier, while the thousandths of an inch may be read by the line on the vernier which coincides with a line on the bar.
Suppose, for example, that the zero line of the vernier stands somewhere between the 1 inch and the 11⁄50 inch line of division on the bar, then the measurement must be more than an inch, but less than 11⁄50 inches. If the tenth or middle line on the vernier is the one that coincides with a line on the bar, the reading is 110⁄1000 inches. If the line marked 5 on the vernier is the one that coincides with a line on the bar, the measurement is an inch and 5⁄1000, and so on.
For measuring the diameters of bores or holes, the external edges of the jaws are employed; the width of the jaw at the ends being reduced in diameter to enable the jaw ends to enter a small hole. These edges are formed to a circle, having a radius smaller than the smallest diameter of hole they will enter when the jaws are closed, which insures that the point of contact shall be in the middle of the thickness of each jaw. In this case the outside diameter of the jaws must be deducted from the measurement taken by the vernier, or if it be required to set the instrument to a standard diameter, the zero line on the vernier must be set to a distance on the bar less than that of the measurement required to an amount equal to the diameter of the jaw edges when the jaws are closed. This diameter is, as far as possible, made to correspond to the lines of division on the bar. Thus in the instrument shown in Fig. 1392, these lines of division are 1⁄50 inch; hence the diameter across the closed bars should, to suit the reading (for internal measurements) on the bar, be measurable also in fiftieths of an inch; but the other side of the bar is divided into millimètres, hence to suit internal measurements (in millimètres or fractions thereof) the width of the jaws, when closed, should be measurable in millimètres; hence, it becomes apparent that the diameter of the jaws used for internal measurements can be made to suit the readings on one side only of the bar, unless the divisions on one side are divisible into those on the other side of the bar. When the diameter of the jaws is measurable in terms of the lines of division on the bar, the instrument may be set to a given diameter by placing the zero of the vernier as much towards the zero on the bar as the width of the jaws when closed. Thus, suppose that width (or diameter, as it may be termed) be 10⁄50 of an inch, and it be required to set the instrument for an inch interval or bore measurement, then the zero on the vernier must be placed to coincide with the line on the bar which denotes 40⁄50 of an inch, the lacking 10⁄50 inch being accounted for in the diameter or width of the two jaws.
But when the width of the jaws when closed is not measurable[I-356] in terms of the lines of division on the bar, the measurement shown by the vernier will, of course, be too small by the amount of the widths of the two jaws, and the measurement shown by the vernier must be reduced to the terms of measurement of the width of the jaws, or what is the same thing, the measurement of the diameter of the jaws must be reduced to the terms of measurement on the bar, in order to subtract one from the other, or add the two together, as the case may require.
For example: Suppose the diameter of the jaws to measure, when they are close together, 250⁄1000 of an inch, and that the bar be divided into inches and fiftieths. Now set the zero of the vernier opposite to the line denoting 49⁄50 inch on the bar. What, then, is the measurement between the outside edges of the jaws? In this case we require to add the 250⁄1000 to the 49⁄50 in order to read the measurement in terms of fiftieths and thousandths of an inch, or we may read the measurement to one hundredths of an inch, thus: 49⁄50 equal 98⁄100, and 250⁄1000 equal 25⁄100, and 98⁄1000 added to 25⁄100 are 123⁄100, or an inch and 23⁄100. To read in 1⁄1000ths of an inch, we have that 49⁄50 of an inch are equal to 980⁄1000, because each 1⁄50 inch contains 20⁄1000 inch, and this added to 250⁄1000 makes 1230⁄1000, that is 1230⁄1000 inches.
The accuracy of the instrument may be maintained, notwithstanding any wear which may in the course of time take place on the inside faces of the jaws, by adjusting the zero line on the vernier to exactly coincide with the zero line on the bar, but the fineness of the lines renders this a difficult matter with the naked eye, hence it is desirable to read the instrument with the aid of a magnifying glass. If the outer edges of the jaws should wear, it is simply necessary to alter the allowance made for their widths.
Fig. 1394 represents standard plug and collar gauges. These tools are made to represent exact standard measurements, and obviously do no more than to disclose whether the piece measured is exactly to size or not. If the work is not to size they will not determine how much the error or difference is, hence they are gauges rather than measuring tools. It is obvious, however, that if the work is sufficiently near to size, the plug or male gauge may be forced in, or the collar or female gauge may be forced on, and in this case the tightness of the fit would indicate that the work was very near to standard size. But the use of such gauges in this way would rapidly wear them out, causing the plug gauge and also the collar to get smaller than its designated size, hence such gauges are intended to fit the work without friction, and at the same time without any play or looseness whatever. Probably the most accurate degree of fit would be indicated when the plug gauge would fit into the collar sufficiently to just hold its own weight when brought to rest while within the collar, and then slowly fall through if put in motion within the collar. It is obvious that both the plug and the collar cannot theoretically be of the same size or one would not pass within the other, but the difference that is sufficient to enable this to be done is so minute that it is practically too small to measure and of no importance.
When these gauges are used by the workmen, to fit the work to their wear is sufficient to render it necessary to have some other standard gauge to which they can be from time to time referred to test their accuracy, and for this purpose a standard such as in Fig. 1395 may be employed. It consists of a number of steel disks mounted on an arbor and carefully ground after hardening each to its standard size.
But a set of plug and collar gauges provide within themselves to a certain extent the means of testing them. Thus we may take a collar or female gauge of a certain size and place therein two or three plug gauges whose added diameters equal that of the female or collar gauge.
In Fig. 1396, for example, the size of the female gauge a being 11⁄2 inches, that of the male b may be one inch, and that of c 1⁄2 an inch, and the two together should just fit the female. On the other hand, were we to use instead of b and c two males, 7⁄8 and 5⁄8 inches respectively, they should fit the female; or a 1⁄2 inch, a 5⁄8 inch and a 3⁄8 inch male gauge together should fit the female. By a series of tests of this description, the accuracy of the whole set may be tested; and by judicious combinations, a defect in the size of any gauge in the set may be detected.
The wear of these gauges is the most at their ends, and the fit may be tested by placing the plug within the collar, as in Fig. 1397, and testing the same with the plug inserted various distances within the collar, exerting a slight pressure first in the direction of a and then of b, the amount of motion thus induced in the plug denoting the closeness of the fit.
In trying the fit of the plug by passing it well into or through the collar, the axis of the plug should be held true with that of the collar, and the plug while being pressed forward should be slightly rotated, which will cause the plug to enter more true and therefore more easily. The plug should be kept in motion and not allowed[I-357] to come to rest while in the collar, because in that case the globules of the oil with which the surfaces are lubricated maintain a circular form and induce rolling friction so long as the plug is kept in motion, but flatten out, leaving sliding friction, so soon as the plug is at rest, the result being that the plug will become too tight in the collar to permit of its being removed by hand.
The surfaces of both the plug and the collar should be very carefully cleaned and oiled before being tried together, it being found that a film of oil will be interposed between the surfaces, notwithstanding the utmost accuracy of fit of the two, and this film of oil prevents undue abrasion or wear of the surfaces.
When great refinement of gauge diameter is necessary, it is obvious that all the gauges in a set should be adjusted to diameter while under an equal temperature, because a plug measuring an inch in diameter when at a temperature of, say, 60° will be of more than an inch diameter when under a temperature of, say, 90°.
It follows also that to carry this refinement still farther, the work to be measured if of the same material as the standard gauge should be of the same temperature as the gauge, when it will fit the gauge if applied under varying temperatures; but if a piece of work composed, say, of copper, be made to true gauge diameter when both it and the gauge are at a temperature of, say, 60°, it will not be to gauge diameter, and will not fit the gauge, if both be raised to 90° of temperature, because copper expands more than steel.
To carry the refinement to its extreme limit then, the gauge should be of the same metal as the work it is applied to whenever the two fitting parts of the work are of the same material. But suppose a steel pin is to be fitted as accurately as possible to a brass bush, how is it to be done to secure as accurate a fit as possible under varying temperatures? The two must be fitted at some equal temperature; if this be the lowest they will be subject to, the fit will vary by getting looser, if the highest, by getting tighter; in either case all the variation will be in one direction. If the medium temperature be selected, the fit will get tighter or looser as the temperature falls or rises. Now in workshop practice, where fit is the object sought and not a theoretical standard of size, the range of variation due to temperature and, generally, that due to a difference between the metals, is too minute to be of practical importance. To the latter, however, attention must, in the case of work of large diameter, be paid: thus, a brass piston a free fit at a temperature of 100° to a 12-inch cast-iron cylinder, will seize fast when both are at a temperature of, say, 250°. In such cases an allowance is made in conformity with the co-efficients of expansion.
In the case of the gauges, all that is practicable for ordinary work-shop variation of temperature is to make them of one kind and quality of material—as hard as possible and of standard diameter, when at about the mean temperature at which they will be when in use. In this case the limit of error, so far as variation from temperature is concerned, will be simply that due to the varying co-efficients of expansion of the metals of which the work is composed.
To provide a standard of lineal measurement which shall not vary under changes of temperature it has been proposed to construct a gauge such as shown in Fig. 1398, in which a and b are bars of different metals whose lengths are in the inverse ratio of their co-efficients of expansion. It is evident that the difference of their lengths will be a constant quantity, and that if the two bars be fastened together at one end, the distance from the free end of b to the free end of a will not vary with ordinary differences in temperature.
Plug and collar gauges may be used for taper as well as for parallel fits, the taper fit possessing the advantage that the bolt or pin may be let farther into its hole to take up the wear. In a report to the Master Mechanics Association upon the subject of the propriety of recommending a standard taper for bolts for locomotive work, Mr. Coleman Sellers says:—
“As the commission given to me calls for a decision as to the taper of bolts used in locomotive work, it presupposes that taper bolts are a necessity. In our own practice we divide bolts into several classes, and our rule is that in every case where a through bolt can be used it must be used. If we cannot use a through bolt we use a stud, and where a stud cannot be used we put in a tap bolt, and the reason why a tap bolt comes last is because it is part and parcel of the machine itself. There are also black bolts and body bound bolts, the former being put into holes 1⁄16 inch larger than the bolt. It is possible in fastening a machine or locomotive together to use black bolts and body bound bolts. With body bound bolts it is customary for machine builders to use a straight reamer to true the hole, then turn the bolt and fit it into its place. It is held by many locomotive builders that the use of straight bolts is objectionable, on the score that if they are driven in tight there is much difficulty in getting them out, and where they are got out two or three times they become loose, and there is no means of making them tighter.
“There is no difficulty in making two bolts of commercially the same size. But there is a vast difference between absolute accuracy and commercial accuracy. Absolute accuracy is a thing that is not obtainable. What we have to strive for, then, is commercial accuracy. What system can we adopt that will enable workmen of limited capacity to do work that will be practically accurate? The taper bolt for certain purposes presents a very decided advantage. Bolts may be made practically of the same diameter, but holes cannot be made practically of the same diameter. Each one is only an approximation to correctness. We have here an ordinary fluted reamer (showing an excellent specimen of Betts Machine Company’s make). That reamer is intended to produce a straight hole, but having once passed through a hole the reamer will be slightly worn. The next time you pass it through it is a little duller, and every time you pass it through the hole must become smaller. There have been many attempts made to produce a reamer that should be adjustable. That, thanks to the gentlemen who are making such tools a speciality, has added a very useful tool to the machine shop—a reamer where the cutters are put in tapered and can be set up and the reamer enlarged and made to suit the gauge. This will enable us to make and maintain a commercially uniform hole in our work. But the successful use of a reamer of this kind depends upon the drill that precedes this reamer being made as nearly right as possible, so that the reamer will have little work to do. The less you give a reamer to do the longer it will maintain its size.
“The question of tapered bolts involves at once this difficulty: that we have to drill a straight hole, then the tapered reamer must take out all the metal that must be removed in order to convert a straight into a tapered hole. The straight hole is maintained in its size by taking out the least amount of metal. It follows that the tapered reamer would be nearest right which would also take out the least amount of metal.
“Then you come to the question of the shape of the taper. When I was engaged building locomotives in Cincinnati, a great many years ago, we used bolts the taper of which was greater than I shall recommend to you. In regard to the compression that would take place in bolts, no piece of iron can go into another piece of iron without being smaller than the hole into which it is intended to go. If it is in any degree larger, it must[I-358] compress the piece itself or stretch the material that is round it. So, if you adopt a tapered bolt, you cannot adopt a certain distance that it shall stand out before you begin to drive it, for there will be more material to compress in a large piece than in a small one. Metal is elastic. Within the elastic limit of the metal you may assume the compression to be a spring. In a large bolt you have a long spring, and in a short one you have a short spring. If you drive a half-inch bolt into a large piece of iron, it is the small bolt which you compress; therefore the larger the bolt the more pressure you can give to produce the same result. Hence, if you adopt the taper bolt, you will have to use your own discretion, unless you go into elaborate experiments to show how far the bolt head should be away from the metal when you begin to drive it.
“Certain builders of locomotives put their stub ends together with tapered bolts, but do not use tapered bolts in any other part of the structure. The Baldwin Works use tapered bolts wherever they are body bound bolts. They make a universal taper of 1⁄16 inch to the foot. An inch bolt 12 inches long would be 11⁄16 inches diameter under the head. They make all their bolts under 9 inches long 1⁄16 larger under the head than the name of the bolt implies. Thus a 3⁄4 inch bolt would be 13⁄16 inch under the head, provided it was 9 inches long or under. Anything over 9 inches long is made 1⁄8 inch larger under the head, and still made a taper of 1⁄16 inch to the foot. A locomotive builder informs me that a taper of 1⁄8 inch to the foot is sometimes called for, and the Pennsylvania road calls for 3⁄32 inch to the foot. But the majority of specifications call for 1⁄16 inch to the foot. The advantage of 1⁄16 inch taper lies in the fact that a bolt headed in the ordinary manner can be made to fill the requirements, provided it is made of iron. You may decide that bolts should be tapered, for the reason that when a tapered bolt is driven into its place it can be readily knocked loose, or if that bolt, when in its place, proves to be too loose, you have merely to drive it in a little farther: these are arguments in favor of tapered bolts, showing their advantage. It is easier to repair work that has tapered bolts than work that has straight bolts. If you adopt a tapered bolt, say, with a taper of 1⁄16 inch to the foot, you are going to effect the making of those bolts and the boring of those holes in a commercially accurate manner, so that they can be brought into the interchangeable system. To carry this out, you require some standard to start with, and the simplest system that one can conceive is this: Let us imagine that we have a steel plug and grind it perfectly true. We have the means of determining whether that is a taper of 1⁄16 inch, thanks to the gentlemen who are now making these admirable gauges. We have a lathe that can turn that taper. I think if you go into the manufacture of these bolts, you will be obliged to use a lathe which will always turn a uniform taper. Having made a female gauge, Fig. 1399, 8 inches long and 11⁄16 inches diameter with a taper of 1⁄16 inch to the foot, this is the standard of what? The area of the bolt, not of the hole it goes into. We now make a plug, Fig. 1399. Taking that tapered plug we should be able to drop it into the hole. Your taper reamer is made to fit this, but you require to know how deep the hole should be. Remember, I said this is the gauge that the bolts are made by. Now let us suppose that we have this as a standard, and to that standard these reamers are made. We decide by practice how much compression we can put upon the metal. For inch bolts, and, say, all above 1⁄2 inch, we might, say, allow the head to stand up 1⁄8 of an inch. Let us make another female gauge like Fig. 1399, but turned down 1⁄8 of an inch shorter. We then shall have the hole smaller than it was before. It is this degree smaller, .0065 of an inch; that is a decimal representing how much smaller that hole is when you have gone down 1⁄8 of an inch on a taper of 1⁄16 inch to the foot.
“Having got this tapered plug, you then must have the means of making the bolts commercially accurate in the shop. For that purpose you must have some cast-iron plugs. Those are reamed with a reamer that has no guard on it, but is pushed into it until the plug—this standard plug—is flush with the end of it. If you go in a little too far it is no matter. Having produced that gauge, we gauge first the one that is used on the lathe for the workman to work by, and he will fit his bolt in until the head will be pushed up against it. If you have a bolt to make from a straight piece of iron, I should advise its being done in two lathes. Here are those beautiful gauges of the Pratt and Whitney Company, which will answer the present purpose; one of these gauges measuring what the outside of the bolt will be, the other gauge 1⁄16 of an inch larger will mark the part under the head. Messrs. Baldwin have a very good system of gauges. All the cast-iron plugs which they use for this purpose are square. Holes are cut in the blocks the exact size of the bolts to be turned up, as shown in Fig. 1400. The object of this is that there shall be no mistake as to what the gauge is. These gauges can be readily maintained, because they have to go back into the room to the inspector. He puts this plug in. If it goes in and fits flush, it is all right. If the plug goes in too far, it is worn. He then turns a little off the end and adjusts it.
“Now practically through machine shops we find that we have to use cast-iron gauges. We take, for instance, 2-inch shafting. Shafting can only be commercially accurate. Therefore we make cast-iron rings and if those rings will go on the shafting it is near enough accurate for merchantable purposes. But this ring will wear in a certain time. Therefore it must not be used more than a certain number of days or hours. Here you have a system that is simple in the extreme. You have all this in two gauges, one gauge being made as a mere check on that tapered plug which is the origin of all things, the origin being 1⁄8 or 7⁄16, or 1⁄4 of an inch shorter if the bolt is very large. There is where you have to use your own judgment. But having adopted something practical you then can use your reamer which is necessary to produce a hole of a given size. If this reamer wears, you then turn off this wrought-iron collar far enough back to let it go in that much farther. I know of no other way by which you can accomplish this result so well as by that in use at the Baldwin Locomotive Works. I think that the system originated with Mr. Baldwin himself.
[I-359]“I do not feel disposed to recommend to you any particular taper to be adopted, because it is not a question like that of screw-threads. In screw-threads we throw away the dies that are used upon bolts, which are perishable articles. The taper that has once been adopted in locomotive establishments is a perpetual thing. If the Pennsylvania railroad and all its branches have adopted 3⁄32, it is folly to ask them to change it to 1⁄16 of an inch, because their own connections are large enough to make them independent of almost any other corporation, and the need of absolute uniformity in their work would cause them to stick to that particular thing. Any of you having five, six, seven, or two or three hundred engines, must make up your minds what you will do. When we adopt a standard for screw-threads, a screw-thread is adopted which has a manifest advantage. A bolt that has one screw thread can be used on any machine. But once having adopted a taper on a road, it is very difficult to make a change; and whether it is wisdom for this Association to say that thus-and-so shall be the standard taper, is a question I am unable to answer. Therefore I am unwilling to present any taper to you, and only present the facts, but will say that 1⁄16 inch is enough. The less taper you have the less material you have to cut away. But to say that 1⁄16 inch is preferable to 1⁄32 inch is folly, because no human being could tell the difference. If a bolt has 5° taper on the side, it may set in place; if it has 7°, it may jump out. That is the angle of friction for iron or other metals. Five degrees would be an absurd angle for a taper bolt. Anything, then, that will hold; that is, if you drive the bolt it will set there.
“This presentation may enable you to arrive at some conclusion. Nothing is more desirable than an interchangeable system. In making turning lathes we try to make all parts interchangeable, and we so fit the sliding spindle. Every sliding spindle in the dead head of the lathe has to be fitted into its own place. We know of no method of making all holes of exactly the same size that shall be commercially profitable. The only way we could surmount that difficulty was to put two conical sleeves in that should compress. We have so solved the problem. We now make spindles that are interchangeable, and we do not fit one part to the other. But that is not the case with bolts. You cannot put the compressing thimbles on them, therefore, you have to consider the question, How can you make holes near enough, and how can you turn the bolts near enough alike?”
Fig. 1401 represents, and the following table gives the taper adopted by the Baldwin Locomotive Works.
Bolt threads, American standard, except stay bolts and boiler studs, V-threads, 12 per inch; valves, cocks and plugs, V-threads, 14 per inch, and 1⁄8 inch taper per 1 inch.
Standard bolt taper 1⁄16 inch per foot.
Length of bolts from head to end of thread equals a.
Diameter of bolt under the head as follows:—
| 3⁄64 | inch | larger at b | for 9 inch and under | |||||
| 1⁄16 | „ | „ | over | 9 | inch | to | 12 | inch |
| 3⁄32 | „ | „ | „ | 12 | „ | to | 18 | „ |
| 1⁄8 | „ | „ | „ | 18 | „ | to | 24 | „ |
| 5⁄32 | „ | „ | „ | 24 | „ | to | 30 | „ |
| 3⁄16 | „ | „ | „ | 30 | „ | to | 36 | „ |
It is obvious that a plug or collar gauge simply determines what is the largest dimension of the work, and that although it will demonstrate that a piece of work is not true or round yet it will not measure the amount of the error. The work may be oval or elliptical, or of any other form, and yet fit the gauge so far as the fit can be determined by the sense of feeling. Or suppose there is a flat place upon the work, then except in so far as the bearing marks made upon the work by moving it within the gauge may indicate, there is no means of knowing whether the work is true or not. Furthermore, in the case of lathe work held between the lathe centres it is necessary to remove the work from the lathe before the collar gauge can be applied, and to obviate these difficulties we have the caliper gauge shown in Fig. 1402. The caliper end is here shown to be for 3⁄4 inch, and the plug end for 13⁄16 inch. If the two ends were for the same diameter one gauge only would be used for measuring external and internal work of the same diameter, but in this case the male cannot be tested with the female gauge; whereas if the two ends are for different diameters the end of one gauge may be tested with that of another, and their correctness tested, but the workman will require two gauges to measure an external and internal piece of the same diameter.
For small lathe work of odd size as when it is required to turn work to fit holes reamed by a worn reamer that is below the standard size, a gauge such as in Fig. 1403, is sometimes used, the mouth a serving as a caliper and the hole b as a collar gauge for the same diameter of work. It is obvious that such a gauge may be applied to the work while it is running in the lathe, and that when the size at a wears too large the jaw may be closed to correct it; a plan that is also pursued to rectify the caliper gauge shown in Fig. 1402.
On large work, as, say, of six inches in diameter, a gauge, such as in Fig. 1404, is used, being short so that it may be light enough[I-360] to be conveniently handled; or sometimes a piece such as in Fig. 1405 is used as a gauge, the ends being fitted to the curvature of the bore to be tested. Gauges of these two kinds, however, are generally used more in the sense of being templates rather than measuring tools, since they determine whether a bore is of the required size rather than determine what that size is.
For gauging work of very large diameter, as, say, several feet, to minute fractions of an inch, as is necessary, for example, for a shrinkage fit on a locomotive tire, the following method is employed. In Fig. 1406 let a represent a ring, say, 5 feet bore, and requiring its bore to be gauged to within, say, 1⁄100 inch. Then r represents a rod made, say, 1⁄2 inch shorter than the required diameter of bore, and w, Fig. 1407, represents a wedge whose upper surface c d is curved, its lower surface being a true plane. The thickness at the end c is made, say, 51⁄100 inch, while that at d is 48⁄100 inch; or in other words, there is 3⁄100 of an inch taper in the length of the wedge. Suppose then that the rod r is placed in the bore of a as in figure, and that the wedge just has contact with the work bore and with the end of the rod when it has entered as far as e in Fig. 1407, and that point e is one-third of the length of the wedge, then the bore of a will measure the length of the rod r plus 49⁄100 of an inch. But if the wedge passed in to line f, the latter being two-thirds the length of the wedge from d, then the bore would be 50⁄100 larger than the length of the rod r. It is obvious that with this method the work may be measured very minutely, and the amount of error, if there be any, may be measured.
The rod must be applied to the work in the same position in which its measurement was made, otherwise its deflection may vitiate the measurement. Thus, if the rod measures 4 feet 111⁄2 inches when standing vertical, it must be applied to the work standing vertical; but if it was measured lying horizontal, it must be applied to the work lying horizontal, as there will be a difference in its length when measured in the two positions, which occurs on account of variations in its deflection from its own weight.
For simply measuring a piece of work to fit it to another irrespective of its exact size as expressed in inches and parts of an inch the common calipers are used. Fig. 1408 represents a pair of spring calipers, the bow acting as a spring to keep the two legs apart, and the screw and nut being used to close them against the spring pressure. The slightness of the legs enables these calipers to be forced or to spring over the work, and thus indicate by the amount of pressure it requires to pass them over the work how much it is above size, and therefore how much it requires to be reduced. But, on the other hand, this slightness renders it somewhat difficult to measure with great correctness. A better form of outside calipers is shown in Fig. 1409, in which in addition to the stiffness of the pivoted joint a bow spring acts to close the caliper legs, which are operated, to open or close them, by operating the hand screw shown, the nuts in which the screw operates being pivoted to the caliper legs. The advantage of this form is that the calipers may be set very readily, while there is no danger of the set or adjustment of the calipers altering from any slight blow or jar received in laying them down upon the bench.
Fig. 1410 gives views of a common pair of outside calipers such as the workman usually makes for himself. When this form is made with a sufficiently large joint, and with the legs broad and stiff as in the figure, they will serve for very fine and accurate adjustments.
Fig. 1411 represents a pair of inside calipers for measuring the diameters of holes or bores. The points of these calipers should be at an angle as shown in the Fig. 1412, which will enable the points to enter a long distance in a small hole, as is denoted by the dotted lines in the figure. This will also enable[I-361] the extreme points to reach the end of a recess, as in Fig. 1413, which the rounded end calipers, such as in this figure, will not do.
Fig. 1414 represents a pair of inside calipers with an adjustment screw having a right-hand screw at a and a left-hand one at b, threaded into two nuts pivoted into the arms, so that by operating the screw the legs are opened or closed, and are locked in position, so that they cannot move from an accidental blow. But as the threads are apt to wear loose, it is preferable to provide a set screw to one of the nuts so as to take up the wear and produce sufficient friction to prevent looseness of the legs.
Calipers are sometimes made double, that is to say, the inside and the outside calipers are provided in the one tool, as in Fig. 1415, which represents a pair of combined inside and outside calipers having a set screw at c to secure the legs together after the adjustment is made. The object of this form is to have the measuring points equidistant from the centre of the pivot a in Fig. 1416, so that when the outside legs are set to the diameter of the work as at b, the inside ones will be set to measure a hole or bore of the same diameter as at c.
This, however, is not a desirable form for several reasons, among which are the following:—
In the first place outside calipers are much more used than inside ones, hence the wear on the points are greatest. Again, the pivot is apt to wear, destroying the equality of length of the points from the centre of the pivot; and in the third place the shape of the points of calipers as usually made vitiates the correctness of the measurements.
Fig. 1417, for example, represents the ordinary form, the points being rounded; hence, when the legs are closed the point of contact between the inside and outside calipers will be at a, while when they are opened out to their fullest the points of contact will be at b. This may, however, be remedied to a great extent by bevelling off the ends from the outside as shown in Fig. 1416.
The end faces of outside calipers should be curved in their widths, as in Fig. 1418, so that contact shall occur at the middle, and it will then be known just where to apply the points of the inside calipers when testing them with the outside ones.
Inside and outside calipers are capable of adjustment for very fine measurements; indeed, from some tests made by the Pratt and Whitney Company among their workmen it was found that the average good workman could take a measurement with them to within the twenty-five thousandth part of an inch. But the workman of the general machine shop who has no experience in measuring by thousandths has no idea of the accuracy with which he sets two calipers in his ordinary practice. The great difference that the one-thousandth of an inch makes in the fit of two pieces may be shown as in Fig. 1419, which represents a collar gauge of 5⁄8 inch in diameter, and a plug 1⁄1000 inch less in diameter, and it was found that with the plug inserted 1⁄8 inch in the collar it could be moved from a to b, a distance of about 5⁄16 inch, which an ordinary workman would at once recognise as a very loose fit.
If the joints of outside calipers are well made the calipers may upon small work be closed upon the work as in Fig. 1420, and the adjustment may be made without requiring to tap or lightly knock the caliper legs against the work as is usually done to set them. But to test the adjustment very finely the work should be held up to the light, as in Fig. 1421, the lower leg of the calipers rested against the little finger so as to steady it and prevent it from moving while the top leg is moved over the work, and at the same time moving it sideways to find when it is held[I-362] directly across the work. For testing the inside and outside calipers together they should for small diameters be held as in Fig. 1422, the middle finger serving to steady one inside and one outside leg, while one leg only of either calipers is grasped in the fingers.
For larger dimensions, as six or eight inches, it is better, however, to hold the calipers as in Fig. 1423, the forefinger of the left hand serving to rest one leg of each pair on the contact being thus tested between the legs that are nearest to the operator.
The adjustment of caliper legs should be such that contact between the caliper points and the work is scarcely, if at all, perceptible. If with the closest of observation contact is plainly perceptible, the outside calipers will be set smaller than the work, while in the case of inside calipers, they would be set larger; and for this reason it follows that if a bore is to be measured to have a plug fitted to it, the inside calipers should have barely perceptible contact with the work bore, and the outside calipers should have the same degree of contact, or, if anything, a very minute degree of increased contact. On the other hand, if a bore is to be fitted to a cylindrical rod the outside calipers should be set to have the slightest possible contact with the rod, and the inside ones set to have as nearly as possible the same degree of contact with the outside ones, or, if anything, slightly less contact. For if in any case the calipers have forcible contact with the work the caliper legs will spring open and will therefore be improperly set.
Calipers should be set both to the gauge and to the work in the same relative position. Let it be required, for example, to set a pair of inside calipers to a bore, and a pair of outside calipers to the inside ones, and to then apply the latter to the[I-363] work. If the legs of the inside calipers stand vertical to the bore for setting they should stand vertical while the outside calipers are set to them, and if the outside calipers are held horizontally while set to the inside ones they should be applied horizontally to the work, so as to eliminate any error due to the caliper legs deflecting from their own weight.
To adjust calipers so finely that a piece of work may be turned by caliper measurement to just fit a hole; a working or a driving fit without trying the pieces together, is a refinement of measurement requiring considerable experience and skill, because, as will be readily understood from the remarks made when referring to gauge measurements, there are certain minute allowances to be made in the set of the calipers to obtain the desired degree of fit.
In using inside calipers upon flat surfaces it will be found that they can be adjusted finer by trusting to the ear than the eye. Suppose, for example, we are measuring between the jaws of a pillow-block. We hold one point of the calipers stationary, as before, and adjust the other point, so that, by moving it very rapidly, we can just detect a scraping sound, giving evidence of contact between the calipers and the work. If, then, we move the calipers slowly, we shall be unable, with the closest scrutiny, to detect any contact between the two.
Calipers possess one great advantage over more rigid and solid gauges, in that the calipers may be forced over the work when the degree of force necessary to pass them on indicates how much the work is too large, and therefore how much it requires reducing. Thus, suppose a cylindrical piece of work requires to be turned to fit a hole, and the inside calipers are set to the bore of the latter, then the outside calipers may be set to the inside ones and applied to the work, and when the work is reduced to within, say, 1⁄100 inch the calipers will spring open if pressed firmly to the work, and disclose to the workman that the work is reduced to nearly the required size. So accustomed do workmen become in estimating from this pressure of contact how nearly the work is reduced to the required diameter, that they are enabled to estimate, by forcing the calipers over the work, the depth of the cut required to be taken off the work, with great exactitude, whereas with solid gauges, or even caliper gauges of solid proportions, this cannot be done, because they will not spring open.
The amount to which a pair of calipers will spring open without altering their set depends upon the shape: thus, with a given joint they will do so to a greater extent in proportion as the legs are slight, whereas with a given strength of leg they will do so more as the diameter of the joint is large and the fit of the joint is a tight one. But if the joint is so weak as to move too easily, or the legs are so weak as to spring too easily, the calipers will be apt in one case to shift when applied to the work, and in the other to spring so easily that it will be difficult to tell by contact when the points just touch the work and yet are not sprung by the degree of contact. For these reasons the points of calipers should be made larger in diameter than they are usually made: thus, for a pair of calipers of the shape shown in Fig. 1410, the joint should be about 11⁄4 inches diameter to every 6 inches of length of leg. The joint should be sufficiently tight that the legs can just be moved when the two legs are taken in one hand and compressed under heavy hand pressure.
For measuring the distance of a slot or keyway from a surface, the form of calipers shown in Fig. 1424 is employed; the straight leg has its surface a true plane, and is held flat against the surface b of the slot or keyway, and the outside or curved leg is set to meet the distance of the work surface measuring the distance c. These are termed keyway calipers.
There are in general machine work four kinds of fit, as follow: The working or sliding fit; the driving fit; the hydraulic press fit; and the shrinkage fit. In the first of these a proper fit is obtained when the surfaces are in full contact, and the enveloped piece will move without undue friction or lost motion when the surfaces are oiled. In the second, third, and fourth, the enveloped piece is made larger than the enveloping piece, so that when the two pieces are put together they will be firmly locked.
It is obvious that in a working or sliding fit the enveloped piece must be smaller than that enveloping it, or one piece could not pass within the other. But the amount of difference, although too small to be of practical importance in pieces of an inch or two in diameter and but few inches in length, is appreciable in large work, as, say, of two or more feet in diameter. A journal, for example, of 1⁄10 inch diameter, running in a bearing having a bore of 1⁄1000 inch larger diameter, and being two diameters in length, would be instantly recognised as a bad fit; but a journal 6 inches in diameter and two diameters or 12 inches long would be a fair fit in a bearing having a bore of 61⁄1000 inches. In the one case the play would be equal to one one-hundredth of the shaft’s diameter, while in the other case the play would equal but one six-thousandth part of the shaft’s diameter. In small work the limit of wear is so small, and the length of the pieces so short, that the 1⁄1000 of an inch assumes an importance that does not exist in larger work. Thus, in watch work, an error of 1⁄1000 inch in diameter may render the piece useless; in sewing machine work it may be the limit to which the tools are allowed to wear; while in a steamship or locomotive engine it may be of no practical importance whatever.
A journal 1⁄10 inch in diameter would require to run, under ordinary conditions, several years to become 1⁄1000 inch loose in its bearing. Some of this looseness, and probably nearly one half of it, will occur from wear of the bearing bore; hence, if a new shaft of the original standard diameter be supplied the looseness will be reduced by one-half. But a 6-inch journal and bearing would probably wear nearly 1⁄1000 inch loose in wearing down to a bearing which may take but a week or two, and for[I-364] these reasons among others, standard gauges and measuring tools are less applicable to large than to small work.
The great majority of fits made under the standard gauge system consist of cylindrical pieces fitting into holes or bores. Suppose then that we have a plug and a collar gauge each of an inch diameter, and a reamer to fit the collar gauge, and we commence to ream holes and to turn plugs to fit the collar gauge, then as our work proceeds we shall find that as the reamer wears, the holes it makes will get smaller, and that as the collar gauge wears, its bore gets larger, and it is obvious that the work will not go together. The wear of the gauge obviously proceeds slowly, but the wear of the reamer begins from the very first hole that it reams, although it may perform considerable duty before its wear sensibly affects the size of the hole. Theoretically, however, its size decreases from the moment it commences to perform cutting duty until it has worn out, and the point at which the wearing-out process may have proceeded to its greatest permissible limit is determined by its reduction of size rather than by the loss of its sharpness or cutting capacity. Obviously then either the reamer must be so made that its size may be constantly adjusted to take up the wear, as in the adjustable reamer, or else if solid reamers are used there must be a certain limit fixed upon as the utmost permissible amount of wear, and the reamer must be made above the standard size to an amount equal to the amount of this limit, so that when the reamer has worn down it will still bore a hole large enough to admit the plug gauge. To maintain the standard there should be in this case two sets of gauges, one representing the correct standard and the other the size to which the reamer is to be made when new or restored to its proper size.
The limit allowed for reamer wear varies in practice from 1⁄1000 to 1⁄10000 of an inch, according to the requirements of the work. As regards the wear of the standard gauges used by the workmen they are obviously subject to appreciable wear, and must be returned at intervals to the tool room to be corrected from gauges used for no other purpose.
To test if a hole is within the determined limit of size a limit gauge may be used. Suppose, for example, that the limit is 1⁄1000 of an inch, then a plug gauge may be made that is 1⁄1000 of an inch taper, and if the large end of this plug will enter the hole, the latter is too large, while if the small end will not enter, the hole is too small.
When only a single set of plug and collar gauges are at hand the plug or the collar gauge may be kept to maintain the standard, the other being used to work to, both for inside and outside work. Suppose, for example, that a plug and collar gauge are used for a certain piece of work and that both are new, then the reamer may be made from either of them, because their sizes agree, but after they have become worn either one or the other must be accepted as the standard of size to make the reamer to. If it be the collar gauge, then the plug gauge is virtually discarded as a standard, except in that if the plug gauge be not used at all it may be kept as a standard of the size to which the collar gauge must be restored when it has worn sufficiently to render restoration to size necessary. If this system be adopted the size of the reamer will be constantly varying to suit the wear of the collar gauge, and the difficulty is encountered that the standard lathe arbors or mandrels will not fit the holes produced, and it follows that if standard mandrels are to be used the reamers must when worn be restored to a standard size irrespective of the wear of the gauges, and that the standard mandrels must be made to have as much taper in their lengths as the limit of wear that is allowed to the reamers. Suppose, for example, that it is determined to permit the reamer to wear the 1⁄2000 of an inch before restoring it to size, then in an inch mandrel the smallest end may be made an inch in diameter and the largest 11⁄2000 inch in diameter, so that however much the reamer may be worn within the limit allowed for wear the hole it produces will fit at some part in the length of the standard mandrel. But as the reamer wears smaller its size must be made as much above its designated standard size as the limit allowed for wear; hence, when new or when restored to size, the reamer would measure 11⁄2000 inches, and the hole it produced would fit the large end of the mandrel. But as the reamer wore, the hole would be reamed smaller and would not pass so far along the mandrel, until finally the limit of reamer wear being reached the work would fit the small end of the mandrel. The small end of the mandrel is thus the standard of its size, and the wear of the collar gauge is in the same direction as that of the reamer. Thus, so long as the collar gauge has not worn more than the 1⁄2000 of an inch it will, if placed upon the mandrel, fit it at some part of its length.
Now suppose that the plug gauge be accepted as the standard to which the reamer is to be made, and that to allow for reamer wear the reamer is made, say, 1⁄2000 inch larger than the plug gauge, the work being made to the collar gauge. Then with a new reamer and new or unworn gauges the hole will be reamed above the standard size to the 1⁄2000 inch allowed for reamer wear. As the reamer wears, the hole it produces will become smaller, and as the collar gauge wears, the work turned to it will be larger, and the effect will be that, to whatever extent the collar gauge wears, it will reduce the permissible amount of reamer wear, so that when the collar gauge had worn the 1⁄2000 inch the work would not go together unless the reamer was entirely new or unworn.
In a driving fit one piece is driven within the other by means of hammer blows, and it follows that one piece must be of larger diameter than the other, the amount of the difference depending largely upon the diameter and length of the work.
It is obvious, however, that the difference may be so great that with sufficiently forcible blows the enveloping piece may be burst open. When a number of pieces are to be made a driving fit, the two pieces may be made to fit correctly by trial and correction, and from these pieces gauges may be made so that subsequent pieces may be made correct by these gauges, thus avoiding the necessity to try them together.
In fitting the first two pieces by fit and trial, or rather by trial and correction, the workman is guided as to the correctness of the fit by the sound of the hammer blows, the rebound of the hammer, and the distance the piece moves at each blow. Thus the less the movement the more solid the blow sounds, and the greater the rebound of the hammer the tighter the fit, and from these elements the experienced workman is enabled to know how tightly the pieces may be driven together without danger of bursting the outer one.
What the actual difference in diameter between two pieces may require to be to make a driving fit is governed, as already said, to a great extent by the dimensions of the pieces, and also by the nature of the material and the amount of area in contact. Suppose, for example, that the plug is 6 inches long, and the amount of pressure required to force it within the collar will increase with the distance to which it is enveloped by the collar. Or suppose one plug to be 3 inches and another to be 6 inches in circumference, and each to have entered its collar to the depth of an inch, while the two inside or enveloped pieces are larger than the outside pieces by the same amount, the outside pieces being of equal strength in proportion to their plugs, so that all other elements are equal, and then it is self-evident that the largest plug will require twice as much power as the small one will to force it in another inch into the collar, because the area of contact is twice as great. It is usual, therefore, under definite conditions to find by experiment what allowance to make to obtain a driving or a forcing fit. Thus, Mr. Coleman Sellers, at a meeting of the Car Builders Association, referring to the proper amount of difference to be allowed between the diameters of car axles and wheel bores in order to obtain a proper forcing or hydraulic fit, said, “Several years ago some experiments were made to determine the difference which should be made between the size of the hole and that of the axle. The conclusion reached was that if the axle of standard size was turned 0.007 inch larger than the wheel was bored it would require a pressure of about 30 tons to press the axle into the wheel.” The wheel seat on the axle here referred to was 47⁄8 inches in diameter and 7 inches long. It is to be remarked, however, that the wheel bore being of cast iron and the axle of wrought iron the friction between the surfaces was not the same as it would be were the[I-365] two composed of the same metal. This brings us to a consideration of what difference in the forcing fit there will be in the case of different metals, the allowance for forcing being the same and the work being of the same dimensions.
Suppose, for example, that a wrought-iron plug of an inch in diameter is so fitted to a bore that when inserted therein to a distance of, say, 2 inches, it requires a pressure of 3 lbs. to cause it to enter farther, then how much pressure would it take if the bore was of cast iron, of yellow brass, or of steel, instead of wrought iron. This brings us to another consideration, inasmuch as the elasticity and the strength of the enveloping piece has great influence in determining how much to allow for a driving, forcing, or a shrinkage fit.
Obviously the allowance can be more if the enveloping piece be of wrought iron, copper, or brass, than for cast iron or steel, because of the greater elasticity of the former. Leaving the elasticity out of the question, it would appear a natural assumption that the pieces, being of the same dimensions, the amount of force necessary to force one piece within the other would increase in proportion as the equivalents of friction of the different metals increased.
This has an important bearing in practice, because the fit of pieces not made to standard gauge diameter is governed to a great extent by the pressure or power required to move the pieces. Thus, let a steel crosshead pin be required to be as tight a fit into the crosshead as is compatible with its extraction by hand, and its diameter in proportion to that of the bore into which it fits will not be the same if that bore be of wrought iron, as it would be were the bore of steel, because the coefficient of friction for cast steel on cast iron is not the same as that for steel on wrought iron. In other words, the lower the coefficient of friction on the two surfaces the less the power required to force one into the other, the gauge diameters being equal. In this connection it may be remarked that the amount of area in contact is of primary importance, because in ordinary practice the surfaces of work left as finished by the steel cutting tools are not sufficiently true and smooth to give a bearing over the full area of the surfaces.
This occurs for the following reasons. First, work to be bored must be held (by bolts, plates, chuck-jaws, or similar appliances) with sufficient force to withstand the pressure of the cut taken by the cutting tool, and this pressure exerts more or less influence to spring or deflect the work from its normal shape, so that a hole bored true while clamped will not be so true when released from the pressure of the holding clamps.
To obviate this as far as possible, expert workmen screw up the holding devices as tight as may be necessary for the heavy roughing cuts, and then slack them off before taking the finishing cuts.
Secondly, under ordinary conditions of workshop practice, the steel cutting tools do not leave a surface that is a true plane in the direction of the length of the work, but leave a spiral projection of more or less prominence and of greater or less height, according to the width of that part of the cutting edge which lies parallel to the line of motion of the tool feed, taken in proportion to the rate of feed per revolution of the work.
Let the distance, Fig. 1424a, a to b lie in the plane of motion of the tool feed, and measure, say, 1⁄4 inch, the tool moving, say, 5⁄16 inch along the cut per lathe revolution. Suppose the edge from b to d to lie at a minute angle to the line of tool traverse, and the depth of the cut to be such that the part from b to c performs a slight cutting or scraping duty, then the part from b to c will leave a slight ridge on the work plainly discernible to the naked eye in what are termed the tool marks.
The obvious means of correcting this is to have the part a b of greater width than the tool will feed along the cut, during one revolution of the work (or the cutter, as the case may be); but there are practicable obstacles to this, especially when applied to wrought iron, steel, or brass, because the broader the cutting edge of a tool the more liable it is to spring, as well as to jar or chatter, leaving a surface showing minute depressions lying parallel to the line of tool feed.
If the cutting tool be made parallel and cylindrical on its edges, and clearance be given on the front end of its diameter only, so as to cut along a certain distance only of its cylindrical edge, the rest being a close fit to the bore of the work, the part having no cutting edge, that is, the part without clearance, will be apt to cause friction by rubbing the bore of the work as the tool edge wears, and the friction will cause heat, which will increase as the cut proceeds, causing the hole to expand as the cut proceeds, and to be taper when cooled to an equal degree all over. This may be partly obviated by giving the tool a slow rate of cutting speed, and a quick rate of feed, which will greatly reduce the friction and consequently the heating of the tool and the work. On cast iron it is possible to have a much broader cutting edge to the tool, without inducing the chattering referred to, than is the case with wrought iron, steel, or brass, especially when the finishing cut is a very light one. If the finishing cut be too deep, the surface of the work, if of cast iron, will be pitted with numerous minute holes, which occur because the metal breaks out from the strain placed on it (and due to the cut) just before it meets the cutting edge of the tool. Especially is this the case if the tool be dull or be ground at an insufficiently acute angle.
When the work shows the tool marks very plainly, or if of cast iron shows the pitting referred to (instead of having a smooth and somewhat glossy appearance), there will be less of its surface in contact with the surface to which it fits, and the fit will soon become destroyed, because the wearing surface or the gripping surface, as the case may be, will the sooner become impaired, causing looseness of the fit. In the one case the abrasion which should be distributed over the whole area of the fitting parts is at first confined to the projections having contact, which, therefore, soon wear away. In the other case the projecting area in contact compresses, causing looseness of the fit.
Hydraulic press or forcing fits.—For securing pieces together by forcing one within the other by means of an hydraulic press, the plug piece is made a certain amount larger than the bore it is to enter, this amount being termed the allowance for forcing. What this allowance should be under any given conditions for a given metal, will depend upon the truth and smoothness of the surfaces, and on this account no universal rule obtains in general practice. From some experiments made by William Sellers & Co., it was determined that if a wheel seat (on an axle) measuring 47⁄8 inches in diameter and 7 inches long was turned 7⁄1000 of an inch larger than the wheel bore, it would require a pressure of about thirty tons to force the wheel home on the axle.
At the Susquehanna shops of the Erie railroad the measurements are determined by judgment, the operatives using ordinary calipers. If an axle 31⁄2 diameter and 6 inches long requires less than 25 tons it is rejected, and if more than 35 tons it is corrected by reducing the axle.
In order to insure a proper fit of pieces to be a driven or forced fit it is sometimes the practice to make them taper, and there is a difference of opinion among practical mechanics as to whether taper or parallel fits are the best. Upon this point it may be remarked that it is much easier to measure the parts when they are parallel than when they are taper, and it is easier to make them parallel than taper.
On the elevated railroads in New York city, the wheel bores being 41⁄8 inches in diameter and 5 inches long, the measurements are taken by ordinary calipers, the workmen judging how much to allow, and the rule is to reject wheels requiring less than about 26 tons, or more than about 35 tons, to force them on. These wheels form excellent examples, because of the excessive duty to which they are subjected by reason of the frequency of their stoppage under the pressure of the vacuum brake. The practice with these wheels is to bore them parallel, finishing with a feed of 1⁄4 inch per lathe revolution, and to turn the axle seats taper just discernible by calipers.
This may, at first sight, seem strange, but examination makes it reasonable and plain. Let a wheel having a parallel bore be forced upon a parallel axle, and then forced off again, and the bore of the wheel will be found taper to an appreciable amount, but increasing in proportion as the surface of the hole varied from a dead smoothness; in other words, varying with the depth of the tool marks in the bore and the smoothness of the cut.
Let the length of the wheel bore be 7 inches long, and the[I-366] amount allowed for forcing be .004 inch, and one end of the wheel bore will have been forced (by the time it is home on the axle) over the length of 7 inches of the axle-seat, whose diameter was .004 larger than the bore: a condensation, abrasion, or smoothing of the metal must have ensued.
Now the other end of the same bore, when it takes its bearing on the shaft, is just iron, and iron without having suffered any condensation. If the tool marks be deep, those on one end will be smoothed down while those at the other remain practically intact. Clearly then, for a parallel hole, a shaft having as much taper as the wheel bore will get in being forced over the shaft best meets the requirements; or, for a parallel shaft or seat, and a taper hole (the taper being proportioned as before), the small end of the taper hole should be first entered on the shaft, and then when home both the axle and the wheel-bore will be parallel.
It may be remarked that the wheel seat on the axle will also be affected, which is quite true, but the axle is usually of the hardest metal and has the smoothest surface, hence it suffers but little; not an amount of any practical importance.
In an experiment upon this point made in the presence of the author by Mr. Howard Fry and the master mechanic of the Renovo shops of the Philadelphia and Erie railroad, an axle seat finished by a Whitney “doctor,” and parallel in diameter, was forced into a wheel having a parallel bore, and removed immediately. On again measuring the axle, the wheel-seat was found to be 1⁄1000 taper in its length.
The wheel-bore was found to be but slightly affected in its diameter, which is explained because it being very smooth, while the turning marks in the axle were plainly visible, the abrasion fell mainly upon the latter.
When the enveloping piece or bore is not solid or continuous, but is open on one side, the degree of the fit may be judged from the amount that it opens under the pressure of the plug piece.
Thus the axle brasses of American locomotives are often made circular at the back, as shown in Fig. 1425, and are forced in endways by hydraulic pressure. The degree of tightness of the brass within the box may, of course, be determined by the amount of pressure it requires to force it in, but another method is to mark a centre punch dot as at j, and before the brass is put in mark from this dot as a centre an arc of a circle as l l. When the brass is home in the box a second arc k is marked, the distance between l and k showing how much the brass has sprung the box open widening at h. In an axle box whose bore is about 4 inches to 5 inches in diameter, and 6 inches long, 1⁄32 inch is the allowance usually made.
Shrinkage fits are employed when a hole or bore requires to be very firmly and permanently fastened to a cylindrical piece as a shaft. The bore is turned of smaller diameter than its shaft, and the amount of difference is termed the allowance for shrinkage. The enveloping piece is heated so as to expand its bore; the shaft is then inserted and the cooling of the bore causes it to close or contract upon the shaft with an amount of force varying of course with the amount allowed for contraction. If this allowance is excessive, sufficient strain will be generated to burst the enveloping piece asunder, while if the allowance for shrinking is insufficient the enveloping piece may become loose.
The amount of allowance for shrinkage varies with the diameter thickness, and kind of the material; but more may be allowed for wrought iron, brass, and copper, than for cast iron or steel.
Again, the smoothness and truth of the surfaces is an important element, because the measurement of a bore will naturally be taken at the tops of the tool marks, and these will compress under the shrinkage strain, hence less allowance for contraction is required in proportion as the bore is smoother.
In ordinary workshop practice, therefore, no special rule for the amount of allowance for shrinkage obtains, the amount for a desultory piece of work generally being left to the judgment of the workman, while in cases where such work is often performed on particular pieces, the amount of allowance is governed by experience, increasing it if the pieces are found in time to become loose, and decreasing it if it is found impossible to get the parts together without making the enveloping piece too hot, or if it is found to be liable to split from the strain.
The strength of the enveloping piece is again an element to be considered in determining the amount to be allowed for shrinkage. It is obvious, for example, that a ring of 8 inches thick, and having a bore of, say, 6 inches diameter, would be less liable to crack from the strain due to an allowance of 1⁄50 inch for contraction, than would a ring of equal bore and one inch thick having the same allowance. The strength or resistance to compression of the piece enveloped in proportion to that enveloping it, is yet another consideration.
The tires for railway wheels are usually contracted on, and Herr Krupp states the allowance for contraction to be for steel tires 1⁄100 inch for every foot of diameter; in American practice, however, a greater amount is often employed. Thus upon the Erie railroad a 5 foot tire is given 1⁄16 inch contraction. The allowance for wrought iron or brass should be slightly more than it is for steel or cast iron, on account of the greater elasticity of those metals.
Examples of the practice at the Renovo shops of the Pennsylvania road are as follows:
Class E, diameter of wheel centre, 44 inches; bore of steel tire, 4315⁄16 inches.
Class D, diameter of wheel, 50 inches; bore of tire, 499⁄16 inches.
It is found that the shrinkage of the tire springs or distorts the wheel centre, hence the tires are always shrunk on before the crank-pin holes are bored.
Much of the work formerly shrunk on is now forced on by an hydraulic press. But in many cases the work cannot be taken to an hydraulic press, and shrinkage becomes the best means. Thus, a new crank pin may be required to be shrunk in while the crank is on the engine shaft, the method of procedure being as follows: In heating the crank, it is necessary to heat it as equally as possible all round the bore, and not to heat it above a very dark red. In heating it some dirt will necessarily get into the hole, and this is best cleaned out with a piece of emery paper, wrapped round a half-round file, carefully blowing out the hole after using the emery paper. Waste or rag, whether oiled or not, is not proper to clean the hole with, as the fibres may burn and lodge in the hole; indeed, nothing is so good as emery paper.
It is desirable to heat the crank as little as will serve the purpose, and it is usual to heat it enough to allow the pin to push home by hand. It is better, however, to overheat the crank than to underheat it, providing that the heat in no case exceeds a barely perceptible red heat. If, however, the crank once grips the pin before it is home, in a few seconds the pin will be held so fast that no sledge hammer will move it. It is well, therefore, to have a man stationed on each side of the crank, each with a sledge hammer, and to push the crank pin in with a slam, giving the man in front orders to strike it as quickly as possible at a given signal; but if the pin does not move home so rapidly at each blow as to make it appear certain that it will go home, the man at the rear, who should have a ten-pound sledge, should be signalled to drive out the crank pin as quickly as he possibly can for every second is of consequence. All this should be done so[I-367] quickly that the pin has not had time to get heated to say 100° at the part within the crank.
So soon as the pin is home, a large piece of wetted cotton waste should be wrapped round its journal, and a stream of water kept running on it, to keep the crank pin cold. At the other end water should be poured on the pin end in a fine stream, but in neither case should the water run on the crank more than can be avoided. Of course, if the crank is off the shaft, the pin may be turned downward, and let project into water.
The reasons for cooling the pin and not the crank are as follows: If the crank be of cast iron, sudden cooling it would be liable to cause it to split or crack. If the crank pin is allowed to cool of itself, the pin will get as hot as the crank itself, and in so doing will expand, placing a strain on the crank that will to some extent stretch it. Indeed, when the pin has become equally hot with the crank it is as tight a fit as it will ever be, because after that point both pieces will cool together, and shrink or contract together, and hence the fit will be a looser or less tight one to the amount that the pin expanded in heating up to an equal temperature with the crank.
The correct process of shrinking is to keep the plug piece as cold as possible, while the outside is cooled as rapidly as can be without danger of cracking or splitting.
The ends of crank pins are often riveted after being shrunk in, in which case it is best to recess the end, which makes the riveting easier, and causes the water poured upon its face to be thrown outward, thus keeping it from running down the crank face and causing the crank to crack or split.
It sometimes becomes necessary and difficult to take out a piece that has been shrunk in, and in this event, as also in the case of a piece that has become locked before getting fully home in the shrinking process, there is no alternative but to reheat the enveloping piece while keeping the enveloped piece as cold as can be by an application of water.
The whole aim in this case is to heat the enveloping piece as quickly as possible, so that there shall be but little time for its heat to be transmitted to the piece enveloped. To accomplish this end melted metal, as cast iron, is probably the most efficient agent; indeed it has been found to answer when all other means failed.
The fine measurements necessary for shrinkage purposes render it necessary, where pieces of the same form and kind are shrunk on, to provide the workmen with standard gauges with which the work may be correctly gauged. These often consist of simple rods or pieces of iron wire of the required length. Figs. 1426 and 1427, however, represent an adjustable shrinkage gauge designed by H. S. Brown, of Hartford, Connecticut. Fig. 1427 is a sectional, and Fig. 1426 a plan side view of the gauge. a is a frame, containing at its lower end a fixed measuring piece b, and provided at its upper end with a threaded and taper split hub to receive externally the taper-threaded screw cap c, and threaded internally to receive a tube e, which is plugged at the bottom by the fixed plug f. The adjustable measuring leg g is threaded with the tube e, so as to be adjustable for various diameters of boxes, but it is locked when adjusted by the jamb-nut h. The operation is as follows: The cap-nut c and jamb-nut h are loosened and screwed back, allowing stem g and tube e to be adjusted to the exact size of the shaft for which a shrinkage fit is to be bored, as, say, in an engine crank. In setting the gauge to the diameter of the shaft, the cap end c and jamb-nut h are screwed home, so as to obtain a correct measurement while all parts are locked secure. The cap-nut c draws the split hub upon the tube e, and the jamb-nut h locks up g to e, so that the shaft measurement is taken with all lost motion, play and spring of the mechanism taken into account, so that they shall not vitiate the measurement. This being done, c is loosened so that e can be rotated, and raised up (by rotating) to admit the shrinkage gauge-piece j, whose thickness equals the amount to be allowed for the size of borer to be shrunk on the shaft. j being inserted, e is rotated back so as to bind j between the end of e and the foot piece b, when c is screwed down, clamping e again. Thus the measuring diameter of the gauge is increased to an amount due to the thickness of the gauge-piece j. At the right of Fig. 1426 an edge and side elevation of j is shown, the 12⁄1000 indicating its thickness, which is the amount allowed for shrinkage, and the 6-inch indicating that this gauge-piece is to be used for bores of 6 inches in diameter. The dotted circle k k l l represents a bore to which the gauge is shown applied.
The system of shrinking employed at the Royal Gun Factory at Woolwich, England, is thus described by Colonel Maitland, superintendent of that factory:—
“The inside diameter of the outer tube, when cold, must be rather smaller than the outside diameter of the inner tube: this difference in the diameter is called the ‘shrinkage.’ While the outer coil is cooling and contracting it compresses the inner one: the amount by which the diameter of the inner coil is decreased is termed the ‘compression.’ Again, the outer coil itself is stretched on account of the resistance of the inner one, and its diameter is increased; this increase in the diameter of an outer coil is called ‘extension.’ The shrinkage is equal to compression plus the extension, and the amount must be regulated by the known extension and compression under certain stresses and given circumstances. The compression varies inversely as the density and rigidity of the interior mass; the first layer of coils will therefore undergo more compression than the secondhand the second more than the third, and so on.
“Shrinking is employed not only as an easy and efficient mode of binding the successive coils of a built-up gun firmly together, but also for regulating as far as possible the tension of the several layers, so that each and all may contribute fairly to the strength of the gun.
“The operation of shrinking is very simple; the outer coil is expanded by heat until it is sufficiently large to fit easily over the inner coil or tube (if a large mass, such as the jacket of a Fraser gun, by means of a wood fire, for which the tube itself forms a flue; if a small mass, such as a coil, in a reverberatory furnace at a low temperature, or by means of gas). It is then raised up by a travelling crane overhead and dropped over the part on to which it is to be shrunk, which is placed vertically in a pit ready to receive it.
“The heat required in shrinking is not very great. Wrought iron, on being heated from 62° Fahr. (the ordinary temperature) to 212°, expands linearly about 1⁄1000th part of its length; that is to say, if a ring of iron 1000 inches in circumference were put into a vat of boiling water, it would increase to 1001 inches, and according to Dulong and Petit the coefficient of expansion, which[I-368] is constant up to 212°, increases more and more from that point upward, so that if the iron ring were raised 150° higher still (i.e. to 362°) its circumference would be more than 1002 inches. No coil is ever shrunk on with so great a shrinkage as the 2⁄1000th part of its circumference or diameter, for it would be strained beyond its elastic limit. Allowing, therefore, a good working margin, it is only necessary to raise a coil to about 500° Fahr.,[22] though in point of fact coils are often raised to a higher degree of temperature than this in some parts, on account of the mode of heating employed. Were a coil plunged in molten lead or boiling oil (600° Fahr.) it would be uniformly and sufficiently expanded for all the practical purposes of shrinking, but as shrinkings do not take place in large numbers or at regular times, the improvised fire or ordinary furnace is the more economical mode, and answers the purpose very well.
[22] The temperature may be judged by color; at 500° F. iron has a blackish appearance; at 575° it is blue; at 775° red in the dark; at 1,500° cherry red, and so on, getting lighter in color, until it becomes white, or fit for welding, at about 3,000°.
“Heating a coil beyond the required amount is of no consequence, provided it is not raised to such a degree of temperature that scales would form; and in all cases the interior must be swept clean of ashes, &c., when it is withdrawn from the fire. With respect to the modes of cooling during the process of shrinking, care must be taken to prevent a long coil or tube cooling simultaneously at both ends, for this would cause the middle portion to be drawn out to an undue state of longitudinal tension. In some cases, therefore, water is projected on one side of a coil so as to cool it first. In the case of a long tube of different thickness, like the tube of a R. M. L. gun, water is not only used at the thick end, but a ring of gas or a heated iron cylinder is applied at the thin or muzzle end, and when the thick end cools the gas or cylinder is withdrawn from the muzzle, and the ring of water raised upward slowly to cool the remainder of the tube gradually.
“As a rule, the water is supplied whenever there is a shoulder, so that that portion may be cooled first and a close joint secured there; and water is invariably allowed to circulate through the interior of the mass to prevent its expanding and obstructing or delaying the operation; for example, when a tube is to be shrunk on a steel barrel, the latter is placed upright on its breech end, and when the tube is dropped down on it, a continual flow of cold water is kept up in the barrel by means of a pipe and syphon at the muzzle. The same effect is produced by a water jet underneath, when it is necessary to place the steel tube muzzle downward for the reception of a breech coil. As to the absolute amount of shrinkage given when building up our guns, let us take the 121⁄2-inch muzzle-loading gun of 38 tons as an example.
| Coils. | Shrinkages. | Remarks. | |||||||
| In Inches. | In terms of diameter. |
||||||||
| Rear. | Front. | Rear. | Front. | ||||||
| Breech‑piece | .02 | 2 | .02 | 6 | D | D | Shrunk on | A tube. | |
| 857 | 807 | ||||||||
| B coil | .05 | 5 | .01 | D | D | „ | „ | ||
| 561 | 190 | ||||||||
| B tube | .03 | 5 | nil. | D | nil. | „ | „ | ||
| 668 | |||||||||
| C coil | .03 | .06 | D | D | Shrunk on to breech piece and rear end |
||||
| 1134 | 729 | ||||||||
| of 1 B coil.” | |||||||||
The objections to fitting work by contraction where accuracy is required in the work are, that if the enveloping piece is of cast iron its form is apt to change from being heated. Furthermore, if the enveloping piece, which is always the piece to be heated, is of unequal thickness all round the bore, the thin parts are apt to become heated the most, and to therefore give way to the strain induced by contraction when cooling, which, while not, perhaps, impairing the fit, may vitiate the alignment of parts attached to it. Thus, a crank pin may be thrown out of true by the alteration of form induced first by unequal heating of the metal round the crank eye, enveloping the shaft; and secondly, because of the weakest side of the eye giving way, to some extent, to the pressure of the contracting strain. To counteract this, the strongest part of the enveloping piece should be heated the most, or if the enveloping piece be of equal strength all round its bore, it should be heated equally all round. To effect this object heated liquids, as boiling water, or heated fluids, as melted lead, may advantageously be employed.
In some practice, locomotive wheel tires are heated for shrinking in boiling water. The allowance for shrinkage is from .075 millimètre to every mètre in diameter, which is .02952 inch to every 39.37079 inches of diameter.
The employment of hot water, however, necessitates that the tires be bored very smoothly and truly, and that the wheel rim be similarly true and smooth, otherwise the amount of expansion thus obtained will be insufficient to maintain a permanent fit under the duty to which a wheel tire is submitted.
Shrinking is often employed to strengthen a weak place or part, or one that has cracked. The required size is, in this case, a cylindrical surface that is not a true cylinder, obtained by a rolling wheel rotated by friction over the surface to be enveloped by the band. Or if the surface is of a nature not to admit of this, a strip of lead or piece of lead wire may be lapped round it to get the necessary measurements.
The bands for this purpose are usually of wrought iron, and require in the case of irregular surfaces to be driven on by hammer blows, so that the fit may be correct. As the band is forced on a heavy hammer is held against it, to prevent its moving back and off the work as the other parts are forced on.
Very slight bands may be forced on by levers: thus, wagon makers use a lever or jack, such as in Fig. 1428, for forcing the tires on their wheels. The wheel is laid horizontally on a table as shown, and the tire a forced out by the vertical lever, the arm b affording a fulcrum for the lever, and itself resting against the hub c of the wheel.
The following extracts are from a paper read by Thomas Wrightson, before the Iron and Steel Institute of Great Britain.
“The large amount of attention bestowed upon the chemical properties of metals, and the scientific methods adopted for their investigation, have led to the most brilliant results in the history of iron and steel industries. It must not, however, be overlooked that iron and steel have highly important properties other than those which can be examined by chemical methods. The cause for so little having been done in accurate observation of the physical properties of iron is twofold: 1. The molecular changes of the metals are so slow, when at ordinary temperatures and when under ordinary conditions of strain, that reliable observations, necessarily extending over long periods, are difficult to obtain: 2. When the temperatures are high—at which times the greatest and most rapid molecular changes are occurring—the difficulties of observation are multiplied to such an extent that the results have not the scientific accuracy which characterizes the knowledge we have of the chemical properties of metals.
“The object of the present paper is to draw attention to some[I-369] phenomena connected with the physical properties of iron and steel, and to record some experiments showing the behavior of these metals under certain conditions.
“In experimenting the author has endeavored to adopt methods which would, as far as possible, eliminate the two great difficulties mentioned.
“It is obvious that the possible conditions under which experiments may be made are so numerous that all which any one experimenter can do is to record faithfully and accurately his observations, carefully specifying the exact conditions of each observation, and this must eventually lead to a more complete knowledge of the physical properties of the metals.
“The author’s observations have been led in the following directions:—
“1. The changes in wrought and cast iron when subjected to repeated heatings and coolings.
“2. The effect upon bars and rings when different parts are cooled at different rates.
“3. These changes occurring in molten iron when passing from the solid to the liquid state, and vice versâ.
PART I.
“To illustrate the practical importance of knowing the effects of reiterated heating and cooling on iron plates, one of the most obvious examples is the action of heat upon the plates of boilers which are alternately heated and cooled, as in use or otherwise. When in use, the plates above the fire are subjected to the fierce flame of the furnace on one side, and on the other side to a temperature approximating to that of the steam and water in the boiler. Where the conducting surfaces of the metal are thickened at the riveted seams, a source of danger is frequently revealed in the appearance of what are known as ‘seam-rips.’
“The long egg-ended boilers, much used in the North of England, are very subject to this breaking away of the seams. From some tests made by the writer on iron cut from the plates of two different boilers which had ripped at the seams, and one of which seam-rips had led to an explosion resulting in the destruction of much property, though happily of no lives, it was found that the heat acting on the bottom of the boiler had, through time, so affected the iron at the seam as to make it brittle, apparently crystalline in fracture, and of small tensile strength. Farther from the seam the iron appeared in both cases less injuriously affected. But although the alternate heating and cooling of the plates over a long period had produced this change in the molecular condition of the iron, a method of restoration presents itself in the process of annealing. In subjecting the pieces cut from the seam-rips to a dull red heat, and then allowing them to cool slowly in sawdust, the writer found that the fibrous character of the iron appeared again, and renewed testing showed that the ductility and tensile strength were restored.
“The same process of annealing is equally effectual in restoring the tenacity of iron in chains rendered brittle, and apparently crystalline, by long use, and is periodically applied where safety depends upon material in this form. Thus the heating and cooling of iron may be looked upon as the bane or the antidote according to the conditions under which the process is carried out. This affords an example of the importance of the physical effects produced by repeated changes of temperature. The change effected by one heating and cooling is so small that a cumulative method of experiment is the only one by which an observable result can be obtained, and this is the method adopted by the writer in the investigation now to be described.
“It is well known that if a wrought-iron bar be heated to redness, a certain expansion takes place, which is most distinctly observed in the direction of its length. It is also known, although not generally so, that if a bar be thus heated and then suddenly cooled in water, a contraction in length takes place, the amount of this contraction exceeding that of the previous expansion, insomuch that the bar when cooled is permanently shorter than it originally was. If this process of heating and cooling be repeated, a further amount of contraction is found to follow for many successive operations.
“Experiments Nos. 1 and 2 were made to verify this, and to show the increment of contraction after each operation.
| Experiment No. 1. | Experiment No. 2. | |||||
| Common Iron. | Best Iron. | |||||
| Contraction. | Percentage on original length. |
Contraction. | Percentage on original length. |
|||
| Inches. | Inches. | |||||
| After | 1st | cooling | .04 | .13 | .04 | .13 |
| „ | 2nd | „ | .10 | .33 | .10 | .33 |
| „ | 3rd | „ | .16 | .53 | .14 | .46 |
| „ | 4th | „ | .17 | .56 | .16 | .53 |
| „ | 5th | „ | .23 | .76 | .20 | .66 |
| „ | 6th | „ | .28 | .93 | .24 | .80 |
| „ | 7th | „ | .31 | 1.03 | .27 | .89 |
| „ | 8th | „ | .33 | 1.10 | .30 | 1.00 |
| „ | 9th | „ | .40 | 1.33 | .33 | 1.10 |
| „ | 10th | „ | .47 | 1.56 | .39 | 1.30 |
| „ | 11th | „ | .52 | 1.73 | .42 | 1.40 |
| „ | 12th | „ | .54 | 1.80 | .47 | 1.56 |
| „ | 13th | „ | .58 | 1.93 | .51 | 1.70 |
| „ | 14th | „ | .62 | 2.06 | .54 | 1.80 |
| „ | 15th | „ | .68 | 2.26 | .56 | 1.86 |
“The Table of Experiment No. 5 shows that at the twenty-fifth cooling a contraction of 3.05 per cent. had taken place, or an average of .122 per cent. after each cooling. This is almost identically the same average result as shown in Experiment No. 1 with straight bars.
“The above experiments only having reference to the permanent contraction of the iron in the direction of its length, the author made the following experiments to ascertain the effect in the other dimensions, and to see whether the specific gravity of the iron was affected in the reduction of dimensions.
“Experiment No. 6.—Wrought-iron plate, .74 inch thick, planed on both surfaces and all edges to a form nearly rectangular, and of the dimensions given in Fig. 1429.
“Specific Gravity.—Two small samples were cut out of different parts of the same piece of plate from which the experimental piece was planed, and the specific gravity determined as follows:—
| No. 1 piece | 7.629 | } | Mean, 7.64. |
| No. 2 piece | 7.651 |
“Quality.—Subjecting a piece to tensile strain in the direction of the grain, it broke at 21.2 tons per square inch of section, the ductility being such that an elongation of 8.3 per cent. occurred before fracture, with a reduction of 9.6 per cent. of the area of fracture. This may be looked upon as representing a fairly good quality of iron.
“A bar of wrought iron, 11⁄8 inches square and 30.00 inches long, was heated to redness, and then allowed to cool gradually in air. Measurements after each of five coolings showed no perceptible change of length.
“Experiment No. 4.—Wrought-iron bar, 11⁄8 inches square by 30 inches long, heated to a white heat and cooling gradually in air.
| Contraction. | Percentage on original length. |
Remarks. | |||
| Inches. | |||||
| After | 1st | cooling | No change. | —— | |
| „ | 2nd | „ | „ | —— | |
| „ | 3rd | „ | .02 | .07 | —— |
| „ | 4th | „ | .05 | .17 | —— |
| „ | 5th | „ | .05 | .17 | —— |
[I-370]“It may be remarked, that if the bars be heated to white heat a slight contraction does occur, as shown by Experiment No. 4, where a bar of the same dimensions as No. 3 contracted .17 per cent. after the fifth cooling. As, however, the further remarks on this subject have only reference to bars heated to redness and then cooled, the writer would summarize the results of Experiments Nos. 1, 2, and 3, by stating that wrought-iron bars heated to redness permanently contract in their length along the fibre when cooled in water of ordinary temperature; but when cooled in air, they remain unchanged in length.
“To show that this is true as applied to circular hoops, Experiment No. 5 was made upon a wrought-iron bar of 11⁄8 inches square in section, welded into a circular hoop, 57.7 inches outside circumference.
“Experiment No. 5.—Wrought-iron hoop, 11⁄8 inches square by 57.7 inches outside circumference, heated to a dull red, then cooled suddenly in water.
| Contraction. | Percentage of original circumference. |
Remarks. | |||
| Inches. | |||||
| After | 1st | cooling | .06 | .10 | Red heat. |
| „ | 2nd | „ | .06 | .10 | This was nearly white, but before cooling red hot. |
| „ | 3rd | „ | .16 | .28 | |
| „ | 4th | „ | .26 | .45 | |
| „ | 5th | „ | .35 | .61 | |
| „ | 6th | „ | .46 | .80 | |
| „ | 7th | „ | .54 | .93 | |
| „ | 8th | „ | .60 | 1.04 | |
| „ | 9th | „ | .68 | 1.18 | |
| „ | 10th | „ | .76 | 1.32 | |
| „ | 11th | „ | .80 | 1.38 | |
| „ | 12th | „ | .87 | 1.51 | |
| „ | 13th | „ | .94 | 1.63 | |
| „ | 14th | „ | 1.00 | 1.73 | |
| „ | 15th | „ | 1.08 | 1.90 | |
| „ | 20th | „ | 1.30 | 2.25 | On opposite edge 1.66; hoop splitting. |
| „ | 25th | „ | 1.76 | 3.05 | |
“This hoop was heated to redness and cooled in water twenty-five times, the circumference of the hoop being accurately measured after each cooling.[23]
[23] The lengths of circumference were taken, in this and other hoops, after each cooling, by encircling the periphery with a very fine piece of “crinoline” steel, the ends of which were made just to meet round the original hoop. By again encircling the hoop with the same piece of steel the expansion was shown by a gap between the ends, and a contraction by an overlap, either of which was measured with great accuracy by means of a finely divided scale.
“Two wrought-iron bars, 11⁄8 inches square and 30.05 inches long, were selected.[24] No. 1 was of common “Crown” quality; No. 2 of a superior quality known as “Tudhoe Crown.” These bars were heated to redness in a furnace and then plunged into water of ordinary temperature, the length being accurately measured after each cooling. After fifteen heatings and coolings the permanent contraction on No. 1 bar was 2.26 per cent. of the original length, and that on No. 2 bar 1.86 per cent., or an average on the two bars of about .13 per cent. after each cooling, the increment of contraction being nearly equal after each successive operation. It is noticeable that after the first two coolings the better quality of iron did not contract quite so much as the common quality, and that in the latter the contraction was going on as vigorously at the fifteenth as at the first cooling.
[24] In some of these experiments the original sizes of the iron were only measured with an ordinary foot-rule, in which case the dimensions are given in the ordinary fraction used in expressing the mercantile sizes of iron. When accurate measurement was taken decimals are invariably used both in this paper and the Tables of Experiment.
“Similar bars of wrought iron, heated to redness and then allowed to cool in air at ordinary temperature, do not appear to suffer any permanent change in their length.
“Experiment No. 3 was made to verify this.
“Experiment No. 3.—Wrought-iron bar, 11⁄8 inches square by 30 inches long heated to a dull red and cooled gradually in air.
| Contraction. | Percentage on original length. |
Remarks. | |||
| After | 1st | cooling | No change. | —— | —— |
| „ | 2nd | „ | „ | —— | —— |
| „ | 3rd | „ | „ | —— | —— |
| „ | 4th | „ | „ | —— | —— |
| „ | 5th | „ | „ | —— | —— |
Wrought iron rectangular plate. 14” thick × 11” 995 × 598 planed on both surface and edges. Heated to redness, and cooled in water 50 times. The dotted lines show original form, the black lines the form after the eperiment.
(Two-ninths of full size.)
Fig. 1430.
The plate was subjected to fifty heatings to redness and subsequent coolings in water of ordinary temperature. At every tenth cooling accurate measurements were taken of the contraction in superficial dimensions, and Fig. 1430 shows the final form after fifty coolings. The intermediate measurements at every tenth cooling showed a uniform and gradual decrease in the superficial dimensions, but the thicknesses were only measured after the fifty coolings had been completed. The thickness appears to have varied considerably; in some places, notably towards the centre and outside edges, being much reduced. Between the centre and outside edges the thickness appears to have increased, and in some few places the plate has been split open. The average dimensions in inches before and after the experiment were as follows (dimensions of cracks being allowed for):—
| Average length. |
Average breadth. |
Average thickness. |
Cubic inches capacity. |
||||||
| Inches. | Inches. | Inches. | |||||||
| Original | 11.99 | 5 | 5.98 | .74 | 53.08 | ||||
| After 50 coolings | 11.25 | 5.59 | .77 | 4 | 48.72 | ||||
| Per cent. variation from original |
- | Decrease | Decrease | Increase | Decrease | ||||
| of | of | of | of | ||||||
| 6.2 p. c. | 6.52 p. c. | 4.6 p. c. | 8.2 p. c. | ||||||
[I-371]“Three triangular pieces of iron were then cut out of the plate from positions indicated on the diagram; No. 1a from the part most reduced in thickness, No. 3a from the part most increased in thickness, and No. 2a from a part where the thickness was a mean between the thickest and thinnest part. The specific gravities were accurately determined as follows:—
| No. 1a | 7.552 thinnest part. |
| No. 2a | 7.574 average thickness. |
| No. 3a | 7.560 thickest part. |
“The average of these specific gravities is 7.562.
“The average before experiment was 7.64. Hence the average loss in specific gravity has been 1.02 per cent.
“The small triangular piece No. 1a, specific gravity 7.552 (already subjected to fifty heatings when forming part of the solid plate), was next heated and cooled fifty times more. The specific gravity at the end of the one hundred total coolings was 7.52, being .43 per cent. lower than after fifty heatings in plate, and 1.57 per cent. lower than 7.64, the original mean specific gravity of the plate.
“The same piece, 1a, was then heated twenty-five times more, making 125 in all. On taking the specific gravity it was found to be 7.526, or practically the same as after 100 total heatings and coolings.
“It thus appears that there is an undoubted decrease in specific gravity on repeated heating and cooling as described up to one hundred coolings, the specific gravity decreasing as much as 1.57 per cent.; that this percentage appears to be less when the pieces of iron operated upon are very small; that while there is a decrease of specific gravity there is also a decrease of total volume.
“From the above it was evident that the volume was affected by several causes:—
“1. By the permanent contraction of the outer skin, either the volume would be lessened, or relief by bulging out the sides must occur.
“2. By the decrease of specific gravity an increase of volume must occur, which could also find relief in bulging.
“3. A diminution of the whole mass must occur through scaling of the surface.
“Having determined the change in specific gravity by Experiment 6, we only now want to determine the loss of volume due to surface scaling, and we can then infer the actual contraction of the outer skin.
“Experiment No. 7.—To ascertain the amount of scaling which took place in heating and cooling under same conditions as Experiment No. 6, a wrought-iron plate was cut from the same piece as No. 6, thickness .74 in., planed on both surfaces and all edges to a form nearly rectangular, and to the dimensions given in Fig. 1431.
“The only difference (except the very small difference in the dimensions) between this and 1430, was that the principal grain of the iron was in 1431 in the direction of the arrow, whereas in the other it was lengthwise of the plate.
“This piece was subjected to fifty heatings to redness and sudden coolings in water of ordinary temperature, as in the case of No. 6. The change in form was exactly the same in general character, but the contraction was not quite so great either in length or breadth; the increase in thickness, however, was proportionately greater, the volume (measured by displacement of water) after fifty heatings being 48.6 cubic inches, which is nearly the same as in No. 6 after the same number of heatings. The weight of the piece:—
| Avoirdupois. | |||
| lbs. | oz. | dr. | |
| Before heating | 14 | 10 | 15 |
| After fifty heatings | 13 | 5 | 10 |
| Difference | 1 | 1 | 5 |
“This represents a loss of 9.07 per cent. of the original weight by scaling, and upon the whole original surface (sides and edges) represents a thickness of .0284 of an inch for the fifty immersions, or .00057 of an inch for the thickness of the film lost at each immersion over the whole surface.
“Calculating the weight of No. 6 before and after experiment from the volumes and specific gravities, we find the following:—
| Volume. | Mean specific gravity. |
Weight of cubic inch water. |
Pounds. | ||||||||
| Weight | before | heating | should be | 53.08 | × | 7.64 | × | .036 | = | 14.599 | |
| „ | after | „ | „ | 48.72 | × | 7.56 | 2 | × | .036 | = | 13.262 |
| Difference in weight | 1.337 | ||||||||||
the ascertained difference in the case of No. 7 being 1.332, thus sufficiently accounting for the discrepancy between specific gravity and change of volume by the scaling.
“By Experiment 7 it has been shown that the loss of thickness due to scaling after fifty immersions was .0284 inch over the whole surface (sides and edges.) Therefore, assuming this scaling as uniform over the surface, the girth, whether measured lengthwise or breadthwise, should be eight times .0284, or .23 inch less after immersion than before. Now the gross loss of girth is:—
| Lengthwise. | Breadthwise. | ||
| Inches. | Inches. | ||
| In No. 6 | 1.3 | 8 | .86 |
| In No. 7 | 1.2 | .52 | |
| Or for both experiments a mean of | 1.2 | 9 | .69 |
| Deducting from them the loss of girth due to scaling | .2 | 3 | .23 |
| Net contraction after fifty immersions | 1.0 | 6 | .46 |
| Or in percentage of original girths, which were | 25.4 | 6 | 13.43 |
| per cent. | per cent. | ||
| We have a percentage of | 4.1 | 6 | 3.42 |
| Or for each immersion an average of | .0 | 83 | .07 |
“Comparing these results with those of Experiments Nos. 1, 2, and 5, we find that the contraction of the skin of the plate is less for each immersion than that of a bar or hoop, in the proportion of .125 to .083. This is what might be expected, as the contraction of the plate is resisted by the volume of heated matter inside, which is eventually displaced by bulging, while the bar finds relief endwise without having to displace the interior.
“We have now before us the following facts, substantiated by the experiments described:—
“1. That in heating to redness, and then cooling suddenly in water at ordinary temperatures, bars and plates of wrought iron, a reduction of specific gravity takes place, the amount being about 1 per cent. after fifty immersions, and 1.57 per cent. after one hundred immersions, further heatings and coolings not appearing to produce further change.
“2. That a reduction of the surface takes place after each heating and cooling, this being due to two causes:—
“a. The scaling of the surface, which is shown to amount to a film over the (sides and edges) entire area of .00057 inch in thickness for each immersion, or 0.284 inch for fifty immersions (Experiment 7).
“b. A persistent contraction, which takes place after each immersion. This varies according to the form of the iron, being in plates from .07 per cent. to 0.83 per cent. (Experiment 6), while in long bars it varies from .122 to .15 per cent. (Experiments 1, 2, and 5). This contraction continues vigorously up to fifty immersions, and probably much farther.
“3. That in the case of plates a bulging takes place on the largest surfaces, increasing the thickness towards the centres, although the edges diminish in thickness.
[I-372]“4. That wrought-iron bars heated to redness, and allowed to cool slowly in air, do not show any change in dimensions (Experiment 3).
“The reduction of specific gravity, and the bulging out of the sides, have been explained as follows by the learned Secretary of the Royal Society, Professor Stokes, who has taken considerable interest in these experiments, and who has kindly allowed the author to publish the explanation:
“‘When the heated iron is plunged into water, the skin tends everywhere to contract. It cannot, however, do so to any significant extent by a contraction which would leave it similar to itself, because that would imply a squeezing in of the interior metal, which is still expanded by heat, and is almost incompressible. The endeavor, then, of the skin to contract is best satisfied, consistently with the retention of volume of the interior, by a contraction of the skin in the two longish lateral directions, combined with a bulging out in the short direction. The still plastic state of the interior permits of this change.
“‘Conceive an india-rubber skin of the form of the plate in its first state, the skin being free from tension, and having its interior filled with water, treacle, or pitch. I make abstraction of gravity. It would retain its shape. But suppose, now, the india-rubber to be endowed with a tension the same everywhere similar to that of india-rubber that has been pulled out, what would take place? Why, the flat faces of considerable area, being comparatively weak to resist the interior pressure, would be bulged out, and the vessel would contract considerably in the long directions, increasing in thickness. This is just what takes place with the iron in the first instance. But when the cooling has made further progress, and the solidified skin has become comparatively thick and strong, the further cooling of the interior tends to make it contract. But this it cannot well do, being encased in a strong hide, and accordingly the interior tends to be left in a porous condition.’
“The reduction by scaling does not require any explanation. The only fact which appears unaccounted for is this persistent contraction of the cooled iron skin, which does not appear to be explicable on any mechanical grounds; and we are, therefore, obliged to look upon it as the result of a change in the distance of the molecules of the iron, caused by the sudden change of temperature in the successive coolings.
“Our next subject is the curious effect of cooling bars or rings by partial immersion in water. Bearing in mind the results at which we have arrived, viz., that wrought iron contracts when immersed in water after heating, and that when allowed to cool in air it remains of the same dimensions, let us ask what would be the behavior of a bar or circular hoop of iron cooled half in water and half in air, the surface of the water being parallel to the fibre and at right angles to the axis of the hoop?
“Arguing from the results of Experiments 1, 2, and 5, it might be expected that the lower portion cooled in water would suffer permanent contraction; and, arguing from Experiment 3, that the upper or air-cooled edge would not alter. This apparently legitimate conclusion is completely disproved by experiments. This will be seen by a reference to Experiments 8, 9, and 10.

Fig. 1432.—Experiments with a circular hoop of wrought iron. Appearance of the hoop at the beginning.
“In No. 8 a circular hoop of wrought iron was forged out of a 31⁄2-inch by 1⁄2-inch bar, the external diameter being about 18 inches, the breadth, 1⁄2 inch, being parallel to the axis of the hoop. This hoop, Fig. 1432, was heated to redness, then plunged into cold water half its depth, the upper half cooling in air. The changes in the external circumference of the hoop were accurately measured after each of twenty successive coolings, at the end of which the external circumference of the water-cooled edge had increased 1.24 inches, or 2.14 per cent. of its original length, and the air-cooled edge had contracted 7.9 inches, or 13.65 per cent.
“Experiment No. 8.—Wrought-iron hoop, 31⁄2 inches by 1⁄2 inch by about 18 inches in diameter, or exactly 57.85 inches in circumference at top, and 57.95 inches at bottom edge.
| Top Edge. | Bottom Edge. | Remarks. | |||||
| Contraction. | Percentage of original circum- ference. |
Expansion. | Percentage of original circum- ference. |
||||
| Ins. | Ins. | ||||||
| After | 1st | dip | .50 | .86 | .08 | .14 | |
| „ | 2nd | „ | .99 | 1.71 | .08 | .14 | |
| „ | 3rd | „ | 1.47 | 2.54 | .26 | .45 | |
| „ | 4th | „ | 1.92 | 3.32 | .30 | .52 | |
| „ | 5th | „ | 2.30 | 3.97 | .34 | .59 | |
| „ | 6th | „ | 2.60 | 4.49 | .40 | .70 | Slight crack in expanded edge. |
| „ | 7th | „ | 2.94 | 5.25 | .44 | .76 | |
| „ | 8th | „ | 3.40 | 5.98 | .50 | .86 | |
| „ | 9th | „ | 3.70 | 6.39 | .56 | .96 | |
| „ | 10th | „ | 4.40 | 7.60 | .62 | 1.07 | |
| „ | 11th | „ | 4.42 | 7.64 | .66 | 1.14 | |
| „ | 12th | „ | 4.85 | 8.40 | .70 | 1.22 | |
| „ | 13th | „ | 5.24 | 9.02 | .78 | 1.34 | |
| „ | 14th | „ | 5.74 | 9.92 | .80 | 1.39 | |
| „ | 15th | „ | 6.00 | 10.37 | .86 | 1.49 | |
| „ | 20th | „ | 7.90 | 13.65 | 1.24 | 2.14 | After deducting for a crack .06 inch wide which appeared at sixth dip. |
“It will be observed that we have here two remarkable phenomena: 1. The reversal of the expansion and contraction as described. 2. The very large amount of contraction on the upper edge compared with what was exhibited in Experiment 5 of entire submersion.
“The table showing Experiment 5 gives a contraction of 2.25 per cent. after the twentieth cooling, whereas the contraction on the air-cooled edge of Experiment 8 is 13.65 per cent., or six times the contraction of an entirely submerged hoop.
“To ascertain whether these unexpected phenomena had any connection with the circular form of the hoop, Experiment 9 was made with a straight bar of iron 31⁄2 inches deep by 1⁄2 inch thick by 28.4 inches long.
“Experiment No. 9.—Wrought-iron bar, 31⁄2 inches by 1⁄2 inch by 28.4 inches long, heated to a dull red, then quenched half its depth in water.
| Bottom Edge. | Top Edge. | |||||
| Expan- sion. |
Percentage on original length. |
Contrac- tion. |
Percentage on original length. |
|||
| Inches. | Inches. | |||||
| After | 1st | cooling | .05 | .18 | .26 | .91 |
| „ | 2nd | „ | .10 | .35 | .43 | 1.51 |
| „ | 3rd | „ | .10 | .35 | .54 | 1.90 |
| „ | 4th | „ | .14 | .49 | .75 | 2.64 |
| „ | 5th | „ | .20 | .70 | .92 | 3.24 |
| „ | 6th | „ | .30 | 1.05 | 1.25 | 4.40 |
| „ | 7th | „ | .34 | 1.20 | 1.50 | 5.28 |
| „ | 8th | „ | .38 | 1.34 | 1.56 | 5.53 |
| „ | 9th | „ | .39 | 1.37 | 1.66 | 5.84 |
| „ | 10th | „ | .40 | 1.40 | 1.76 | 6.19 |
| „ | 11th | „ | .41 | 1.43 | 1.84 | 6.48 |
| „ | 12th | „ | .44 | 1.55 | 1.96 | 6.90 |
“This was cooled half in air and half in water, and the length of the two edges measured accurately after each of twelve coolings. At the end of this experiment the air-cooled edge had contracted 6.9 per cent., while the water-cooled edge had expanded 1.55 per cent. of the original length. The effect on the[I-373] bar was to make it gradually curve, the water-cooled or extended edge becoming convex, the air-cooled or contracted edge concave.

Fig. 1436.—After the preceding experiment the same bar was reheated and reversed in the water, the eleventh cooling resulting in the above form, the bar bending in the opposite direction from that previously shown.
“Experiment No. 10 was made in order to show the effect of reversing this cooling process. After five coolings, a bar of iron, 28 inches long, 31⁄2 inches deep, and 1⁄2 inch thick, was curved so that the versed sine of its air-cooled edge was 11⁄2 inches. The coolings were then reversed, what was the air-cooled edge being then immersed in water. After five more coolings the bar was restored to within 1⁄8 inch of being straight, and the eleventh cooling threw the concavity on the other side of the bar.
“Experiment No. 10.—Wrought-iron flat bar, 28 inches long by 31⁄2 inches by 1⁄2 inch, heated to dull red, then quenched half its depth in water, up to five heats, then the opposite edge dipped.
| Versed sine of concave, i.e. air- cooled edge. |
Reversed Cooling. | |||||||
| Versed sine of concave, i.e. now water- cooled edge. |
||||||||
| Inches. | Inches. | |||||||
| 1st | cooling | 5⁄16 | 6th | cooling | 1 | 3⁄16 | ||
| 2nd | „ | 9⁄16 | 7th | „ | 7⁄8 | |||
| 3rd | „ | 13⁄16 | 8th | „ | 3⁄4 | scant. | ||
| 4th | „ | 1 | 3⁄8 | 9th | „ | 3⁄8 | full. | |
| 5th | „ | 1 | 1⁄2 | 10th | „ | 1⁄8 | ||
| 11th | „ | Brought concavity 1⁄8 in. on other side. |
||||||
“When the author had proceeded thus far, these curious results were shown to several leading scientific men, who expressed interest in the subject, which encouraged the author to extend his experiments under varied conditions with a view of ascertaining the cause for these anomalous effects. These experiments (Nos. 11 to 17) are fully recorded, and the results shown on the diagrams; the actual rings are also on the table before you.
“Experiment No. 11.—Wrought-iron hoop, turned and bored, 37.1 inches, outside circumference, by 2.95 inches deep by .44 inch thick, the grain of the iron running the short way of the bar from which the hoop was made, heated to redness, then cooled half its depth in water (see Fig. 1437 at a for final form of hoop after ten heatings and coolings).
| Top Edge. | Bottom Edge. | ||||||
| Contrac- tion. |
Percentage on original length. |
Expan- sion. |
Percentage on original length. |
||||
| Inches. | Inches. | ||||||
| After | 1st | cooling | .3 | .83 | .05 | .13 | |
| „ | 2nd | „ | .6 | 4 | 1.72 | .12 | .32 |
| „ | 3rd | „ | 1.0 | 2 | 2.75 | .22 | .60 |
| „ | 4th | „ | 1.3 | 8 | 3.72 | .30 | .80 |
| „ | 5th | „ | 1.6 | 2 | 4.37 | .37 | 1.00 |
| „ | 10th | „ | 3.1 | 4 | 8.46 | .76 | 2.05 |
“Experiment No. 12.—Wrought-iron hoop, turned and bored, 6 inches diameter (18.85 inches circumference) outside, by 2 inches deep by .375 inch thick, heated to redness, then cooled, with lower edge barely touching the water (see Fig. 1437 at b for final form of hoop after twenty heatings and coolings).
| Top Edge. | Bottom Edge. | |||||
| Contrac- tion. Outside circum- ference. |
Percentage of original circum- ference. |
Contrac- tion. Outside circum- ference. |
Percentage of original circum- ference. |
|||
| Inches. | Inches. | |||||
| After | 5th | cooling | .10 | .53 | .16 | .85 |
| „ | 10th | „ | .22 | 1.17 | .34 | 1.80 |
| „ | 15th | „ | .32 | 1.70 | .48 | 2.54 |
| „ | 20th | „ | .48 | 2.54 | .62 | 3.30 |
“Experiment No. 13.—Wrought-iron hoop, turned and bored, 6 inches diameter (18.85 inches circumference) outside by 2 inches deep by .375 inch thick, heated to redness, then cooled one-fourth its depth in water (see Fig. 1437 at c for final form of hoop after twenty heatings and coolings).
| Top Edge. | Bottom Edge. | ||||||
| Contrac- tion. |
Percentage of original circum- ference. |
Extension. | Percentage of original circum- ference. |
||||
| Inches. | Inches. | ||||||
| After | 1st | cooling | .06 | .32 | .02 | .10 | |
| „ | 5th | „ | .28 | 1.50 | { | A hair’s breadth contraction. |
|
| „ | 10th | „ | .56 | 3.00 | { | Returned to original circumference. |
|
| „ | 15th | „ | .78 | 4.14 | .02 contraction. | .10 | |
| „ | 20th | „ | 1.12 | 6.00 | .02 contraction. | .10 | |
“Experiment No. 14.—Wrought-iron hoop, turned and bored. 6 inches diameter (18.85 inches circumference) outside by 2 inches deep by .375 inch thick, heated to redness, then cooled one-half its depth in water (see Fig. 1437 at d for final form of hoop after twenty heatings and coolings).
| Top Edge. | Bottom Edge. | |||||
| Contrac- tion. |
Percentage of original circum- ference. |
Expan- sion. |
Percentage of original circum- ference. |
|||
| Inches. | Inches. | |||||
| After | 5th | cooling | .46 | 2.44 | .06 | .32 |
| „ | 10th | „ | .96 | 5.00 | .09 | .48 |
| „ | 15th | „ | 1.34 | 7.10 | .18 | .96 |
| „ | 20th | „ | 1.80 | 9.10 | .26 | 1.38 |
“Experiment No. 15.—Wrought-iron hoop turned and bored, 6 inches in diameter (18.85 inches circumference) outside by 2 inches deep by .375 inch thick, heated to redness, then cooled three-fourths its depth in water (see Fig. 1437 at e for final form of hoop after twenty heatings and coolings).
| Top Edge. | Bottom Edge. | |||||||
| Contrac- tion. |
Percentage of original circum- ference. |
Expansion. | Percentage of original circum- ference. |
|||||
| Inches. | Inches. | |||||||
| After | 1st | cooling | .05 | .26 | .015 | .08 | ||
| „ | 5th | „ | .30 | 1.60 | .02 | .10 | ||
| „ | 10th | „ | .56 | 3.00 | { | A hair’s breadth contraction. |
||
| „ | 15th | „ | .74 | 3.92 | { | .02 contraction. |
} | .10 |
| „ | 20th | „ | 1.02 | 5.40 | { | .03 contraction. |
} | .10 |
“Experiment No. 16.—Cast-copper ring, turned and bored to same dimensions as Nos. 12, 13, 14, and 15, heated to redness, then cooled half its depth in water (see Fig. 1437 at f for final form of hoop after twenty heatings and coolings).
| Top Edge. | Bottom Edge. | ||||||||
| Contrac- tion. |
Percentage of original circum- ference. |
Expan- sion. |
Percentage of original circum- ference. |
||||||
| Inches. | Inches. | ||||||||
| After | 1st | cooling | .01 | .05 | .05 | .26 | |||
| „ | 2nd | „ | .01 | .05 | .08 | .42 | |||
| „ | 3rd | „ | .02 | .10 | .14 | .75 | |||
| „ | 4th | „ | .02 | .10 | .17 | .90 | |||
| „ | 5th | „ | - | No change from original size from 5th to 20th cooling. |
.22 | 1.17 | |||
| „ | 10th | „ | .40 | 2.13 | |||||
| „ | 15th | „ | .56 | 3.00 | |||||
| „ | 20th | „ | .70 | 3.70 | |||||
“It will be unnecessary to occupy much time in analyzing the experiments, as any one who takes a practical interest in the subject will have full information in the diagrams and tables. Professor Stokes drew attention to the fact that, in 1863, similar phenomena had been noticed by Colonel Clark, of the Royal Engineers. His experiments, made at the Royal Arsenal, Woolwich, were published in the ‘Proceedings of the Royal Society,’ and Professor Stokes had himself attached an explanatory note, the outline of which was as follows:—
“Imagine a cylinder divided into two parts by a horizontal plane at the water-line, and in this state immersed after heating. The under part, being in contact with water, would rapidly cool and contract, while the upper part would cool but slowly. Consequently by the time the under part had pretty well cooled, the upper part would be left jutting out; but when both parts had cooled their diameters would again agree. Now in the actual experiments the independent motion of the two parts is impossible on account of the continuity of the metal; the under part tends to pull in the upper, and the upper to pull out the under. In this contest the cooler metal, being the stronger, prevails, and so the upper part gets pulled in a little above the water-line while still hot. But it has still to contract in cooling, and this it will do to the full extent due to its temperature, except in so far as it may be prevented by its connection with the rest. Hence, on the whole, the effect of this cause is to leave a permanent contraction a little above the water-line, and it is easy to see that the contraction must be so much nearer to the water-line as the thickness of the metal is less, the other dimensions of the hollow cylinder and the nature of the metal being given. When the hollow cylinder is very short, so as to be reduced to a mere hoop, the same cause operates, but there is not room for more than a general inclination of the surface, leaving the hoop bevelled.
“The expansion of the bottom edge was not noticed in Colonel Clark’s paper, perhaps owing to the much smaller hoops which he used in experimenting. Accepting Professor Stokes’ explanation of the top contraction, it appears that expansion of the bottom may be accounted for by the reacting strain put on the cooled edge when forcing in the top edge, acting in such a way as to prevent the cooled edge coming quite to its natural contraction, and this, when sufficiently great, expresses itself in the form of a slight expansion.
“Experiment No. 14.—Forged steel hoop, turned and bored, 18.53 inches in circumference outside by 2.375 inches deep by .27 inch thick, heated to redness, then cooled one-half its depth in water (see Fig. 1437 at g for final form of hoop after three heatings and coolings).
| Top Edge. | Bottom Edge. | |||||||
| Contrac- tion. |
Percentage of original length. |
Expan- sion. |
Percentage of original length. |
|||||
| Inches. | Inches. | |||||||
| Afer | 1st | cooling | .06 | .32 | — | — | { | Cracked at water‑cooled edge one‑third depth of ring. |
| „ | 2nd | „ | .12 | .64 | — | — | ||
| „ | 3rd | „ | .20 | 1.08 | .05 | .27 | { | After allowing for three small cracks in bottom edge.” |
The shrinkage of iron and steel by cooling rapidly is sometimes taken advantage of by workmen to refit work, the principles involved in the process being as follows:—
Suppose in Fig. 1438 a a represents a piece of wrought-iron tube that has been heated to a bright red and immersed in cold water c c from the end b to d, until that end is cold. The part submerged and cold will be contracted to its normal diameter and have regained its normal strength, while the part above the[I-375] water, remaining red-hot, will be expanded and weak. There will be, then, a narrow section of the tube, joining the heated and expanded part to the cooled and contracted part, and its form will be conical, as shown at d d. Now, suppose the tube to be slowly lowered in the water, the cold metal below will compress the heated metal immediately above the water-line, the cone section d being carried up into the metal before it has had time to cool; and the tube removed from the water when cold will be as shown in Fig. 1438, from c to d, representing the part first immersed and cooled. To complete the operation the tube must be heated again from the end c to a short distance past d, and then immersed from e nearly to d, and held still until the submerged part is cold, when the tube must be slowly lowered to compress the end c d, making the tube parallel, but smaller in diameter and in bore, while leaving it of its original length, but thickening its wall.
This process may, in many cases, be artificially assisted. Suppose, for example, a washer is too large in its bore; it should have its hole and part of its radial faces filled with fire-clay, as shown in Fig. 1439, in which a is the washer and b b the clay, c c being pieces of wire to hold the fire-clay and prevent its falling off. The washer should be heated to a clear red and plunged in the water d d, which will cool and shrink the exterior and exposed metal in advance of the interior, which will compress to accommodate the contraction of the outer metal, hence the hole will be reduced. This operation may be repeated until the hole be entirely closed.
Another method of closing such a piece as an eye of large diameter compared to its section, is shown in Fig. 1440; first dipping the heated eye at a and holding it there till cold and then slowly lowering it into the water, which would close the diameter across c, and, after reheating, dipping at d till cold, and then slowly immersing, which would close the eye across e. To shrink a square ring, the whole ring would require to be heated and a side of the square dipped, as shown in Fig. 1441, until quite cold, and then immersed slowly for about an inch, the operation being performed with a separate heating for each side. Connecting rod straps, wheel-tires, and a large variety of work may be refitted by this process, but in each case the outside diameter will be reduced.
For what may be termed the length measurements of lathe work it is obvious that caliper gauges, such as shown in Fig. 1402, may be employed. Since, however, these length measurements rarely require to be so accurate as the diametrical measurements, the ordinary lineal rule is very commonly employed in work not done under the standard gauge system. It is obvious, however, that when a number of pieces are to be turned to corresponding lengths, a strip of sheet iron, or of iron rod made to the required length, may be employed; a piece of sheet iron filed to have the necessary steps being used where there are several steps in the work; but if the lineal measuring rule is used, and more than one measurement of length is to be taken, some one point, as one end of the work, should be taken wherefrom to measure all the other distances. Suppose, for example, that Fig. 1442 represents a crank pin requiring to have its end collar 1⁄4 inch thick, the part a 2 inches long, part b 3 inches long, collar c 1⁄2 inch thick, and the part d 7 inches long. If the length of each piece were taken separately and independently of the others, any errors of measurement would multiply; whereas, if some one point be taken as a point wherefrom to measure all the other distances, error is less liable to occur, while at the same time an error in one measurement would not affect the correctness of the others. In the case of the crank pin shown, the collar c would be the best point wherefrom to take all the other measurements. First, it would require to be made to its proper thickness, and the lengths of b, a, and the end collar should be measured from its nearest radial face. The length of d should then be measured from the same radial face, the thickness of the collar being added to the required length of d, or d may be measured from the nearest radial face of c, providing c be of its exact proper thickness. In measuring the length of the taper part d, a correct measurement will not be obtained by laying the rule along its surface, because that surface does not lie parallel to its axis, hence it is necessary to apply the measuring rule, as shown in Fig. 1443, in which s is a straight-edge held firmly against the radial face of the crank pin (the radial face being of course turned true), and r is the measuring rule placed true with the axial line of the crank pin. Whenever the diameters of the lengths to be measured vary, this mode of measuring must be employed. On small work, or on short distances requiring to be very exact, a gauge such as shown in Fig. 1444 at a may be employed, which will not only give more correct results, but because it is more convenient, as it can be conveniently held or tried to the work with one hand while the other hand is applied to the feed screw handle to withdraw the cutting tool at the proper moment, and to the feed nut to unlock it and stop the feed.
On long work a wooden strip is the best, especially if the work has varying diameters and a number of pieces of work require to be made exactly alike. In Fig. 1445 s represents the wooden strip, and w the work. The strip is marked across by lines representing the distances apart the shoulders of the work require to be; thus the lines a, b, c, d, e, f, g, represent the distances apart of the radial faces a, b, c, d, e, f, g, on the work, and these lines will be in the same plane as the shoulders if the latter are turned to correct lengths. To compare the radial faces with the lines, a straight-edge must be held to each successive shoulder (as already described) that is of smaller diameter than the largest radial face on the work.
If the wooden strip be made the full length of the work the dog or clamp driving the work will require to be removed every time the wooden gauge is applied, and since the work must be turned end for end in the lathe to be finished, it would be as well to let the length of the wood gauge terminate before reaching the work driver, as, say, midway between e and f.
When a lineal distance is marked by lines, and this distance is to be transferred to another piece of work and marked thereon by lines, the operation may be performed, for short distances or radii, by the common compasses employed to mark circles, but for greater distances where compasses would be cumbersome, the trammels are employed.
Fig. 1446 represents a pair of trammels made entirely of metal, and therefore suitable for machinists’ use, in which the points require to be pressed to the work to mark the lines. a a represents a bar of square steel; or for very long trammels wood may be used. b represents a head fastened tightly to one end, and through b passes the leg or pointer c, which is thus adjustable as to its projecting distance, as c can be fastened in any position by the thumb-screw d. The head e is made to a good sliding fit upon the bottom and two side faces of a a; but at the top there is sufficient space to admit a spring, which passes through e. f is the leg screwed into e, which is locked in position by the thumb-screw g. The head e is thus adjustable along the whole length of the bar or rod a a. The object of the spring is as follows:—If the head e were made to fit the bar a a closely on all four sides, the burrs raised upon the top side of the rod a a by the end of the thumb-screw g would be likely to impede its easy motion. Then again, when the sliding head e has worn a trifle loose upon the bar a a, and is loosened for adjustment, it would be liable to hang on one side, and only to right itself when the screw g brought it to a proper bearing upon the under side of the bar a a, and thus tightening the head e would alter the adjustment[I-377] of the point. The spring, however, always keeps the lower face of the square hole through e bearing evenly against the corresponding face of the bar, so that tightening the screw g does not affect the adjustment, and, furthermore, the end of the set-screw, bearing against the spring instead of against the top of the rod, prevents the latter from getting burred.
The flat place at i i is to prevent the burrs raised by the thumb-screw end from preventing the easy sliding of leg c through b.
In some cases a gib is employed, as shown at a in Fig. 1447, instead of a spring, the advantage being that it is less liable to come out of place when moving the head along the bar.
The trammels should always be tried to the work in the same relative position as that in which they were set, otherwise the deflection of the bar may vitiate the correctness of the measurement; thus, if the rod or bar stood vertical when the points were adjusted for distance to set them to the required distance, it should also stand vertical upon the work when applied to transfer that distance, otherwise the deflection of the bar from its own weight will affect the correctness of the operation. Again, when applied to the work the latter should be suspended as nearly as convenient in the same position as the work will occupy when erected to its place.
Thus, suppose the trammels be set to the crank pin centres of a locomotive, then the bar will stand horizontally. Now the side rod, or coupling rod, as it may be more properly termed, should be stood on edge and should rest on its ends, because its bearings wherever it will rest when on the engine are at the ends; thus the deflection of the trammel rod will be in the same direction when applied to the work as it was when applied to the engine, and the deflection of the coupling rod will be in the same direction when tried by the trammel as when on the engine. The importance of this may be understood when it is mentioned that if the coupling rod be a long one, resting it on its side and supporting it in the middle instead of at its ends will cause a difference of 1⁄50th inch in its length.
Another lineal measuring gauge employed in the machine shop is shown in Fig. 1448. It is employed to measure the distance between two faces, and therefore in place of inside calipers, in cases where from the extreme distance to be measured it would require the use of inside calipers too large to be conveniently handled. Its application is more general upon planing machine work than any other, although it is frequently used by the lathe hand or turner, and by the vice hand and erector. It consists of two legs a and b, held together by the screws c d, which screw into nuts. These nuts should have a shoulder fitting into the slots in both legs, so as to form a guide to the legs. The screws are set up so as to just bind both legs together but leaving them free enough to move under a slight friction. The gauge is then set to length by lightly striking the ends e, and when adjusted the screws c d are screwed firmly home. The ends e are rounded somewhat, as is shown, to prevent them from swelling or burring by reason of the blows given to adjust them.
For striking circles we have the compasses or dividers, which are made in various forms.
Thus, Fig. 1449 represents a pair of spring dividers, the bow spring at the head acting to keep the points apart, and the screw and nut being employed to close and to adjust them.
Another form is shown in Fig. 1450, the legs being operated by a right and left-hand screw, which may be locked in position by the set-screw shown.
For very small circles the fork scriber shown in Fig. 1451 is an excellent tool, since it may be used with great pressure so as to cut a deep line in the surface of the work. This tool is much used by boiler makers, but is a very useful one for the machinist for a variety of marking purposes, which will be described with reference to vice work.
For larger work we have the compasses, a common form of which is shown in Fig. 1452, in which the leg a is slotted to receive the arc piece c, which has a threaded stem passing through e, and is provided with a nut at b; at d is a spring which holds the face of the nut b firmly against the leg e; at a is a thumb-screw for securing the leg to the arm c. The thumb-screw a being loosened, the compass legs may be rudely adjusted for distance apart, and a is then tightened. The adjustment is finally made by operating the nut b, which, on account of its fine thread, enables a very fine adjustment to be easily made.
[I-378]It is often very convenient to be able to set one leg of a pair of dividers to be longer than the other, for which purpose a socket b, Fig. 1453, is provided, being pierced to receive a movable piece a, and split so that by means of a set-screw c the movable piece a may be gripped or released at pleasure.
For finding the centres of bodies or for testing the truth of a centre already marked, the compass calipers shown in Fig. 1454, are employed. It is composed of one leg similar to the leg of a pair of compasses, while the other is formed the same as the leg of an inside caliper. The uses of the compass calipers are manifold, the principal being illustrated as follows:—
Let it be required to find the centre of a rectangular block, and they are applied as in Fig. 1455, the curved leg being rested against the edge and a mark being made with the compass leg. This being done from all four sides of the work gives the centre of the piece.
In the case of a hole its bore must be plugged and the compass calipers applied as in Fig. 1456.
For marking a line true with the axial line of a cylindrical body, we have the instrument w in Fig. 1457, which is shown applied to a shaft s. The two angles of the instrument are at a right angle one to another, so that when placed on a cylindrical body the contact will cause the edge of w to be parallel with the axis of the shaft. The edge is bevelled, as shown, so that the lines of division of inches and parts may come close to the work surface, and a scriber may be used to mark a line of the required length. A scriber is a piece of steel wire having a hardened sharp point wherewith to draw lines.
On account of the instrument w finding its principal application in marking key seats upon shafts, it is termed the “key-seat rule.”
For marking upon one surface a line parallel to another surface, the scribing block or surface gauge shown in Fig. 1458 is employed. It consists of a foot piece or stand d, carrying a stem. In the form shown this stem contains a slot running centrally up it. Through this slot passes a bolt whose diameter close to the head is larger than the width of the slot, so that it is necessary to file flat places on the side of the slot to permit the bolt to pass through it.
On the stem of the bolt close to the head, and between the bolt head and the stem of the stand, passes the piece shown at f. This consists of a piece of brass having a full hole through which the bolt passes clear up to the bolt head. On the edge view there is shown a slot, and on each side of the slot a section of a hole to receive a needle. A view of the bolt is given at e, the flat place to fit the slot in the stem being shown in dotted lines, and the space between the flat place and the bolt head is where the piece of brass, shown in figure, passes. This piece of brass being placed on the bolt, and the bolt being passed through the slot in the stem, the needle is passed through the split in the brass, and the thumb-nut is screwed on so that tightening up the thumb-nut causes the needle to be gripped in the brass split in any position in the length of the stem slot in which the bolt may be placed. The advantage of this form over all others is that the needle may be made of a simple piece of wire, and therefore very readily. Again, the piece of brass carrying the needle may be rotated upon the pin any number of consecutive rotations backwards and forwards, and there is no danger of slacking the thumb-nut, because the needle is on the opposite side of the stem to what the thumb-nut is, and the flat place prevents the bolt from rotating. Furthermore, the needle can be rotated on the bolt for adjustment for height without becoming loosened, whereas when the thumb-nut is screwed up firmly the needle is held very fast indeed, and finally all adjustments are made with a single thumb-nut.
[I-379]The figure represents a view of this gauge from the bolt head and needle side of the stem, the thumb-nut being on the opposite side.
This tool finds its field of application upon lathe work, planer work, and, indeed, for one purpose or another upon all machine tools, and in vice work and erecting, examples of its employment being given in connection with all these operations.
Fig. 1459 represents a scribing block for marking the curves to which to cut the ends of a cylindrical body that joins another, as in the case of a T-pipe. It is much used by pattern-makers. In the figure a is a stem on a stand e. A loose sleeve b slides on a carrying an arm c, holding a pencil at d. A piece of truly surfaced wood or iron w, has marked on it the line j. Two Vs, g, g, receive the work p. Now, if the centres of g, g and of the stand e all coincide with the line j then e will stand central to p, and d may be moved by the hand round p, being allowed to lift and fall so as to conform to the cylindrical surface of p, and a line will be marked showing where to cut away the wood on that side, and all that remains to do is to turn the work over and mark a similar line diametrically opposite, the second line being dotted in at k.
The try square, Fig. 1460, is composed of a rectangular back f, holding a blade, the edges of the two being at a right angle one to the other and as straight as it is possible to make them. The form shown in the figure is an L-square.
Fig. 1461 represents the T-square, whose blade is some distance from the end of the back and is sometimes placed in the middle. When the square edges are at a true right angle the square is said to be true or square, the latter being a technical term meaning at practically a true right angle.
The machinists’ square is in fact a gauge whereby to test if one face stands at a right angle to another. It is applied by holding one edge firmly and fairly bedded against the work, while the other edge is brought to touch at some part against the face to be tested.
If in applying a square it be pressed firmly into the corner of the work, any error in the latter is apt to escape observation, because the square will tilt and the error be divided between the two surfaces tested. To avoid this the back should be pressed firmly against one surface of the work and the square edge then brought down or up to just touch the work, which it will do at one end only if the work surface is out of square or not at a right angle to the face to which the square back is applied.
An application of the T-square is shown in Fig. 1462, in which w is a piece of work requiring to have the face a of the jaw c at a right angle to the face b c. Sometimes the L-square is employed in conjunction with a straight-edge in place of the T-square. This is usually done in cases where the faces against which the square rests are so far apart as to require a larger T-square than is at hand. It is obvious that if the face a of the work is the one to be tested, the edge b is the part pressed to the work; or per contra, if b c is the face to be tested, the edge of the blade is pressed to the work.
The plane of the edges of a square should, both on the blade and on the back, stand at a right angle to the side faces of the body or stock, and the side of the blade should be parallel to the sides of the back and not at an angle to either side, nor should it be curved or bent, because if under these conditions the plane of the square edge is not applied parallel with the surface of the work the square will not test the work properly. This is shown in Fig. 1463, in which w is a piece of work, and s a square having its blade bent or curved and applied slightly out of the vertical, so that presuming the plane of the blade edge to be a right angle to the stock or back of the square the plane of the blade edge will not be parallel with the plane of the work, hence it touches the work at the ends a b only,[I-380] whereas if placed vertically the blade edge would coincide with the work surface all the way along. It is obvious then that by making the edge of the blade at a right angle, crossways as well as in its length, to the stock, the latter will serve as a guide to the eye in adjusting the surface of the blade edge parallel to that of the work by placing the stock at a right angle to the same.
There are three methods of testing the angle of a square blade to the square back. The first is shown in Fig. 1464, in which a is a surface plate having its edge a true plane. The square s is placed in the position shown by full lines pressed firmly to the edge of the surface plate and a fine line is drawn with a needle point on the face of the surface plate, using the edge of the square blade as denoted by the arrow c as a guide. The square is then turned over as denoted by the dotted lines and the edge is again brought up to the line and the parallelism of the edge with the line denotes the truth, for whatever amount the blade may be out of true will be doubled in the want of coincidence of the blade edge with the line.
A better plan is shown in Fig. 1465, in which a is the surface plate, b a cylindrical piece of iron turned true and parallel in the lathe and having its end face true and cupped as denoted by the dotted lines so as to insure that it shall stand steadily and true. The surface of a and the vertical outline of b forming a true right angle we have nothing to do but make the square s true to them when placed in the position shown.
If we have two squares that are trued and have their edges parallel, we may test them for being at a right angle by trying them together as in Figs. 1466 and 1467, in which a, b, are the two squares which, having their back edges pressed firmly together (when quite clean), must coincide along the blade edges; this being so we may place them on a truly surfaced plate as shown in Fig. 1468, in which s is one square and s′ the other, p being the surface plate. Any want of truth in the right angle will be shown doubled in amount by a want of coincidence of the blade edges.
For some purposes, as for marking out work on a surface plate, it is better that the square be formed of a single piece having the back and blade of equal thickness, as shown in Fig. 1469, which represents a side and edge view of an L-and T-square respectively.
For angles other than a right angle we have the bevel or bevel square (as it is sometimes called), shown in Fig. 1470, a representing the stock or back, and b the blade, the latter being provided with a slot so that it may be extended to any required distance (within its scope) on either side of the stock. c is the rivet, which is made sufficiently tight to permit of the movement by hand of the blade, and yet it must hold firmly enough to be used without moving in the stock. Instead of the rivet c, however, a thumb-screw and nut may be employed, in which case, after the blade is set to the required angle, it may be locked in the stock by the thumb-screw.
Fig. 1471 represents a Brown and Sharpe bevel protractor, with a pivot and thumb-nut in the middle of the back with a half-circle struck from the centre of the pivot and marked to angular degrees. The pointer for denoting the degrees of angle has also a thumb-screw and nut so that the blade may, by loosening the[I-381] pivot and pointer, be moved to project to the required distance on either side of the back.
Swasey’s improved protractor, however, is capable of direct and easy application to the work, forming a draughtsman’s protractor, and at the same time a machinist’s bevel or bevel square, while possessing the advantage that there is no protruding back or set-screw to prevent the close application of the blade to the work. This instrument is shown in Fig. 1472. The blade a is attached to the circular piece d, the latter being recessed into the square b b, and marked with the necessary degrees of angle, as shown, while the mark f upon the square b serves as an index point. The faces of a, b b, and d are all quite level, so that the edges will meet the lines upon the work and obviate any liability to error. The piece d is of the shape shown in section at g, which secures it in b b, the fit being sufficient to permit of its ready adjustment and retain it by friction in any required position. The dotted lines indicate the blade as it would appear when set to an angle, the point e being the centre of d, and hence that from which the blade a operates.
On account, however, of the numerous applications in machine work of the hexagon (as, for instance, on the sides of both heads and nuts), a special gauge for that angle is requisite, the usual form being shown in Fig. 1473. The edges a, b, form a hexagon gauge, and edges c, d, form a square, while the edge e serves as a straight-edge.
All these tools should be made of cast steel, the blades being made of straight saw blade, so that they will not be apt to permanently set from an ordinary accidental blow; while, on the other hand, if it becomes, as it does at times, necessary to bend the blade over to the work, it will resume its straightness and not remain bent.
For testing the straightness, in one direction only, of a surface the straight-edge is employed. It consists in the small sizes of a piece of steel whose edges are made straight and parallel one to the other. When used to test the straightness of a surface without reference to its alignment with another one, it is simply laid upon the work and sighted by the eye, or it may have its edge coated with red marking, and be moved upon the work so that its marking will be transferred to the high spots upon the work. The marking will look of the darkest colour in the places where the straight-edge bears the hardest. The most refined use of the straight-edge is that of testing the alignment of one surface to the other, and as this class of work often requires straight-edges of great length, as six or ten feet, which if made of metal would bend of its own weight, therefore they are made of wood.
Fig. 1474 represents an example of the use of straight-edge for alignment purposes. It represents a fork and connecting rod, and it is required to find if the side faces of the end b are in line with the fork jaws. A straight-edge is held firmly against the side faces of b in the two positions s and s′, and it is obvious that if they are in line the other end will be equidistant from the jaw faces, at the two measurements.
Figs. 1474, 1475, 1476, 1477, and 1478 represent the process of testing the alignment of a link with a straight-edge. First to test if the single eye e is in line with the double eye f at the other end, the straight-edge is pressed against the face of e, as in Fig. 1475, and the distance i is measured. The straight-edge is then applied on the other side of e, as in Fig. 1476, and the distance h is measured, and it is clear that if distances h and i are equal, then e is in line with the double eye. To test if the double eye f is in line with the single eye e, the straight-edge is pressed against the face of the double eye in the positions shown in Figs. 1477 [I-382]and 1478, and when distances j and k measure equal the jaws of the double eye f are in line with those of the single eye e.
It is obvious, however, that we have here tested the alignment in one direction only. But to test in the other direction we may use a pair of straight-edges termed winding strips, applying them as in Fig. 1479, to test the stem, and as in Fig. 1480 to test the eye e, and finally placing the winding strip c on the eye of f while strip d remains upon e, as in Fig. 1480. The two strips are sighted together by the eye, as is shown in Fig. 1481, in which s and s′′ are the strips laid upon a connecting rod, their upper edges being level with the eye, hence if they are not in line the eye will readily detect the error. Fig. 1482 represents an application to a fork ended connecting rod. Pattern-makers let into their winding strips pieces of light-coloured wood as at c, c, c, c, in Fig. 1483, so that the eye may be assisted in sighting them.
It is obvious that in using winding strips they should be parallel one to the other; thus, for example, the ends a, b, in Fig. 1481, should be the same distance apart as ends c, d.
If less than three straight-edges or parallel strips are to be trued they must be trued to a surface plate or its equivalent, but if a pair are to be made they should have the side faces made true, and be riveted together so that their edges may be trued together, and equal width may be more easily obtained. For this purpose copper rivets should be used, because they are more readily removable, as well as less likely to strain the work in the riveting.
By riveting the straight-edges together the surface becomes broader and the file operates steadier, while the edges of the straight-edge are left more square. Furthermore parallelism is more easily obtained as one measurement at each end of the batch will test the parallelism instead of having to measure each one separately at each end. If three straight-edges are to be made they may be riveted together and filed as true as may be with the testing conveniences at hand, but they should be finally trued as described for the surface plate.
In using straight-edges to set work, the latter is often heated to facilitate the setting, and in this case the straight-edge or parallel strips should be occasionally turned upside down upon the work, for if the heated work heats one side of the straightedge more than the other the increased expansion of the side most heated will bend the straight-edge or strips, and throw them out of true.
In applying a straight-edge to test work it must never be pressed to the work surface, because in that case it will show contact with the work immediately beneath the parts where such pressure is applied. Suppose, for example, a true straight-edge be given a faint marking, and be applied to a true surface, the straight-edge itself being true; then if the hands are placed at each end of the straight-edge, and press it to the work while the straight-edge is given motion, it will leave the heaviest marks at and near the ends as though the work surface was slightly hollow in its length; while were the hand pressure applied to the middle of the length of the straight-edge the marks on the work would show the heaviest in the middle as though the work surface were rounding. This arises from the deflection due to the weakness of the straight-edge.
For testing the truth of flat or plane surfaces the machinist employs the surface plate or planometer. The surface plate is a plate or casting having a true flat surface to be used as a test plate for other surfaces. It is usually made of cast iron, and sometimes of chilled cast iron or hardened cast steel, the surface in either of these two latter cases being ground true because their hardness precludes the possibility of cutting them with steel tools. A chilled or hardened surface plate cannot, however, be so truly surfaced as one that is finished with either the scraper or the file.
The shape of the surface plate is an element of the first importance, because as even the strongest bars of metal deflect from their own weight, it is necessary to shape the plate with a view to make this deflection as small as possible in any given size and weight of plate. In connection, also, with the shape we must[I-383] consider the effect of varying temperatures upon the metal, for if one part of the plate is thinner than another it will, under an increasing temperature, heat more rapidly, and the expansion due to the heating will cause that part to warp the plate out of its normal form, and hence out of true. The amount that a plate will deflect of its own weight can only be appreciated by those who have had experience in getting up true surfaces, but an idea may be had when it is stated that it can be shown that it is easily detected, in a piece of steel three inches square and a foot long.
Now this deflection will vary in direction according to the points upon which the plate rests. For instance, take two plates, clean them properly, and rest one upon two pieces of wood, one piece under each end, and then place another plate upon the lower one and its face will show hollow, and, if the upper plate is moved backwards and forwards laterally it will be found to move from the ends as centres of motion. Then rest the lower plate upon a piece of wood placed under the middle of its length, and we shall find that (if the plates are reasonably true) the top one will move laterally with the middle of its length as a centre of motion. Now although this method of testing will prove deflection to exist, it will not show its amount, because the top plate deflects to a certain extent, conforming itself to the deflection of the lower one, and if the test is accurately made it will be found that the two plates will contact at whatever points the lower one is supported.
If plates, tested in this manner, show each other to have contact all along however the lower one is supported, it is because they are so light that the upper one will readily bend to suit the deflection of the lower one, and true work is, with such a plate, out of the question.
To obviate these difficulties the body of the plate is heavily ribbed, and these ribs are so arranged as to be of equal lengths, and are made equal in thickness to the plate, so that under variations of temperature the ribs will not expand or contract more quickly or slowly than the body of the plate, and the twisting that would accompany unequal expansion is avoided.
In Fig. 1484 is shown the form of surface plate designed by Sir Joseph Whitworth for plates to be rested upon their feet. The resting points of the plate are small projections shown at a, b, and c. The object of this arrangement of feet is to enable the plate to rest with as nearly as possible an equal degree of weight upon each foot, the three feet accommodating themselves to an uneven surface. It is obvious, however, that more of the weight will fall upon c than upon a or b, because c supports the whole weight at one end, while at the other end a and b divide the weight.
Fig. 1485 shows the form of plate designed by Professor Sweet.
In Fig. 1486 is shown a pair of angle surface plates resting upon a flat one. The angle plates may be used for a variety of purposes where it is necessary to true a surface standing at a true right angle to another.
The best methods of making surface plates are as follows:—
The edges of the plates should be planed first, care being taken to make them square and flat. The surfaces should then be planed, the plates being secured to the planer by the edges, which will prevent as far as possible the pressure necessary to hold them against the planing tool cut from springing, warping, or bending the plates. Before the finishing cut is taken, the plates or screws holding the surface plate should be slackened back a little so as to hold them as lightly as may be, the finishing cut being a very light one, and under these circumstances the plates may be planed sufficiently true that one will lift the other from the partial vacuum between them.
After the plates are planed, and before any hand work is done on them, they should be heated to a temperature of at least 200° Fahr., so that any local tension in the casting may be as far as possible removed.
Surface plates for long and narrow surfaces are themselves formed long and narrow, as shown in Fig. 1487, which represents the straight-edge surface plate made at Cornell University.
The Whitworth surfacing straight-edge, or long narrow surface plate, is ribbed as in Fig. 1488, so as to give it increased strength in proportion to its weight, and diminish its deflection from its own weight. The lugs d are simply feet to rest it on.
Straight-edges are sometimes made of cast steel and trued on both edges. These will answer well enough for small work, but if made of a length to exceed about four feet their deflection from their own weight seriously affects their reliability. The author made an experiment upon this point with a very rigid surface plate six feet long, and three cast steel straight-edges 6 feet long, 41⁄2 inches wide, and 1⁄2 inch thick. Both edges of the straight-edges were trued to the surface plate until the light was excluded from between them, while the bearing surface appeared perfect;[I-384] thin tissue paper was placed between the straight-edges and the plate, and on being pulled showed an equal degree of tension. The straight-edges were tried one with the other in the same way and interchanged without any apparent error, but on measuring them it was found that each was about 1⁄50 inch wider in the middle of its length than at the ends, the cause being the deflection. They were finished by filing them parallel to calipers, using the bearing marks produced by rubbing them together and also upon the plate; but, save by the caliper test, the improvement was not discernible.
In rubbing them together no pressure was used, but they were caused to slide under their own weight only.
A separate and distinct class of gauge is used in practice to copy the form of one piece and transfer it to another, so that the one may conform to or fit the other. To accomplish this end, what are termed male and female templates or gauges are employed. These are usually termed templates, but their application to the work is termed gauging it.
Suppose, for example, that a piece is to be fitted to the rounded corner of a piece f, Fig. 1489, and the maker takes a piece of sheet metal a, and cuts it out to the line b c d, leaving a female gauge e, which will fit to the work f. We then make a male gauge g, and apply this to the work, thus gauging the round corner.
Fig. 1490 represents small templates applied to a journal bearing, and it is seen that we may make the template as at t, gauging one corner only, or we may make it as at t′, thus gauging the length of the journal as well as the corners.
Fig. 1491 represents a female gauge applied to the corner of a bearing or brass for the above journal, it being obvious that the male and female templates when put together will fit as in Fig. 1492.
For measuring the diameters of metal wire and the thickness of rolled sheet metal, measuring instruments termed wire gauges and sheet metal measuring machines are employed. A simple wire gauge is usually formed of a piece of steel containing numerous notches, whose widths are equal to the intended thickness to be measured in each respective notch. These notches are marked with figures denoting the gauge-number which is represented by the notch.
For wire, however, a gauge having holes instead of notches is sometimes employed, the wire being measured by insertion in the hole, an operation manifestly impracticable in the case of sheet metal.
In Fig. 1493 is shown one of Brown and Sharpe’s notch wire-gauges, the notches being arranged round the edge as shown:
The thickness of a given number of wire-gauge varies according to the system governing the numbering of the gauge, which also varies with the class of metal or wire for which the gauge has been adopted by manufacturers. Thus, in the following table are given the gauge-numbers and their respective sizes in decimal parts of an inch, as determined by Holtzapffel in 1843, and to which sizes the Birmingham wire-gauge is made. The following table gives the numbers and sizes of the Birmingham wire-gauge.
| Mark. | Size. | Mark. | Size. | Mark. | Size. | Mark. | Size. |
| 36 | .004 | 26 | .018 | 16 | .065 | 6 | .203 |
| 35 | .005 | 25 | .020 | 15 | .072 | 5 | .220 |
| 34 | .007 | 24 | .022 | 14 | .083 | 4 | .238 |
| 33 | .008 | 23 | .025 | 13 | .095 | 3 | .259 |
| 32 | .009 | 22 | .028 | 12 | .109 | 2 | .284 |
| 31 | .010 | 21 | .032 | 11 | .120 | 1 | .300 |
| 30 | .012 | 20 | .035 | 10 | .134 | 0 | .340 |
| 29 | .013 | 19 | .042 | 9 | .148 | 00 | .380 |
| 28 | .014 | 18 | .049 | 8 | .165 | 000 | .425 |
| 27 | .016 | 17 | .058 | 7 | .180 | 0000 | .454 |
In this gauge it will be observed that the progressive wire gauge numbers do not progress by a regular increment.
This gauge is sometimes termed the Stubs wire-gauge, Mr. Stubs being a manufacturer of instruments whose notches are spaced according to the Birmingham wire-gauge. Since, however, Mr. Stubs has also a wire-gauge of his own, whose numbers and gauge-sizes do not correspond to those of the Birmingham gauge, the two Stubs gauges are sometimes confounded. The second Stubs gauge is employed for a special drawn steel wire, made by that gentleman to very accurate gauge measurement for purposes in which accuracy is of primary importance.
From the wear of the drawing dies in which wire is drawn, it is impracticable, however, to attain absolute correctness of gauge measurement. The dies are made to correct gauge when new, and when they have become worn larger, to a certain extent, they are renewed. As a result the average wire is slightly larger than the designated gauge-number. To determine the amount of this error the Morse Twist-Drill and Machine Company measured the wire used by them during an extended period of time, the result being given in table No. 2, in which the first column gives the gauge-number, the second column gives the thickness of the gauge-number in decimal parts of an inch, and the third column the actual size of the wire in decimal parts of an inch as measured by the above Company.
| No. by Stubs’s wire- gauge. |
Stubs’s Dimen- sions. |
Measure- ment by Morse Twist- Drill & Machine Co. |
No. by Stubs’s wire- gauge. |
Stubs’s Dimen- sions. |
Measure- ment by Morse Twist- Drill & Machine Co. |
No. by Stubs’s wire- gauge. |
Stubs’s Dimen- sions. |
Measure- ment by Morse Twist- Drill & Machine Co. |
| 1 | .227 | .228 | 23 | .153 | .154 | 45 | .081 | .082 |
| 2 | .219 | .221 | 24 | .151 | .152 | 46 | .079 | .080 |
| 3 | .212 | .213 | 25 | .148 | .150 | 47 | .077 | .079 |
| 4 | .207 | .209 | 26 | .146 | .148 | 48 | .075 | .076 |
| 5 | .204 | .206 | 27 | .143 | .145 | 49 | .072 | .073 |
| 6 | .201 | .204 | 28 | .139 | .141 | 50 | .069 | .070 |
| 7 | .199 | .201 | 29 | .134 | .136 | 51 | .066 | .067 |
| 8 | .197 | .199 | 30 | .127 | .129 | 52 | .063 | .064 |
| 9 | .194 | .196 | 31 | .120 | .120 | 53 | .058 | .060 |
| 10 | .191 | .194 | 32 | .115 | .116 | 54 | .055 | .054 |
| 11 | .188 | .191 | 33 | .112 | .113 | 55 | .050 | .052 |
| 12 | .185 | .188 | 34 | .110 | .111 | 56 | .045 | .047 |
| 13 | .182 | .185 | 35 | .108 | .110 | 57 | .042 | .044 |
| 14 | .180 | .182 | 36 | .106 | .106 | 58 | .041 | .042 |
| 15 | .178 | .180 | 37 | .103 | .104 | 59 | .040 | .041 |
| 16 | .175 | .177 | 38 | .101 | .101 | 60 | .039 | .040 |
| 17 | .172 | .173 | 39 | .099 | .100 | 61 | .038 | .039 |
| 18 | .168 | .170 | 40 | .097 | .098 | 62 | .037 | .038 |
| 19 | .164 | .166 | 41 | .095 | .096 | 63 | .036 | .037 |
| 20 | .161 | .161 | 42 | .092 | .094 | 64 | .035 | .036 |
| 21 | .157 | .159 | 43 | .088 | .089 | 65 | .033 | .035 |
| 22 | .155 | .156 | 44 | .085 | .086 |
The following table represents the letter sizes of the same wire:—
| A. | 0.234 | J. | 0.277 | S. | 0.348 |
| B. | 0.238 | K. | 0.281 | T. | 0.358 |
| C. | 0.242 | L. | 0.290 | U. | 0.368 |
| D. | 0.246 | M. | 0.295 | V. | 0.377 |
| E. | 0.250 | N. | 0.302 | W. | 0.386 |
| F. | 0.257 | O. | 0.316 | X. | 0.397 |
| G. | 0.261 | P. | 0.323 | Y. | 0.404 |
| H. | 0.266 | Q. | 0.332 | Z. | 0.413 |
| I. | 0.272 | R. | 0.339 |
By an Order in Council dated August 23rd, 1883, and which took effect on March 1st, 1884, the standard department of the British Board of Trade substituted for the old Birmingham wire-gauge the following:—
| Descriptive number B. W. G. No. |
Equivalents in parts of an inch. |
Descriptive number B. W. G. No. |
Equivalents in parts of an inch. |
||
| No. | Inch. | No. | Inch. | ||
| 7 | /0 | 0.500 | 23 | 0.024 | |
| 6 | /0 | .464 | 24 | .022 | |
| 5 | /0 | .432 | 25 | .020 | |
| 4 | /0 | .400 | 26 | .018 | |
| 3 | /0 | .372 | 27 | .016 | 4 |
| 2 | /0 | .348 | 28 | .014 | 8 |
| 0 | .324 | 29 | .013 | 6 | |
| 1 | .300 | 30 | .012 | 4 | |
| 2 | .276 | 31 | .011 | 6 | |
| 3 | .252 | 32 | .010 | 8 | |
| 4 | .232 | 33 | .010 | 0 | |
| 5 | .212 | 34 | .009 | 2 | |
| 6 | .192 | 35 | .008 | 4 | |
| 7 | .176 | 36 | .007 | 6 | |
| 8 | .160 | 37 | .006 | 8 | |
| 9 | .144 | 38 | .006 | 0 | |
| 10 | .128 | 39 | .005 | 2 | |
| 11 | .116 | 40 | .004 | 8 | |
| 12 | .104 | 41 | .004 | 4 | |
| 13 | .092 | 42 | .004 | 0 | |
| 14 | .080 | 43 | .003 | 6 | |
| 15 | .072 | 44 | .003 | 2 | |
| 16 | .064 | 45 | .002 | 8 | |
| 17 | .056 | 46 | .002 | 4 | |
| 18 | .048 | 47 | .002 | 0 | |
| 19 | .040 | 48 | .001 | 6 | |
| 20 | .036 | 49 | .001 | 2 | |
| 21 | .032 | 50 | .001 | 0 | |
| 22 | .028 | ||||
The gauge known as the American Standard Wire-Gauge was designed by Messrs. Brown and Sharpe to correct the discrepancies of the old Birmingham wire-gauge by establishing a regular proportion of the thirty-nine successive steps between the 0000 and 36 gauge-number of that gauge. In the American Standard (which is also called the Brown and Sharpe gauge) the value of 0.46 or 46⁄100 has been taken as that for 0000 or the largest dimension of the gauge. Then by successive and uniform decrements, each number following being obtained from multiplying its predecessor by 0.890522 (which is the same thing as deducting 10.9478 per cent.), the final value for number 36 is reached at 0.005, which corresponds with number 35 of the Birmingham wire-gauge. The principle of the gauge is shown in Fig. 1495, which represents a gauge for jewelers, having an angular aperture with the gauge-numbers marked on the edge, the lines and numbers being equidistant.
The advantage of this system is that the instrument is easy to produce, the difference between any two gauge-numbers being easily found by calculation; and the gauge is easy to originate, since the opening, being of the proper width at the open end, the sides terminating at the proper distance and being made straight, the intermediate gauge-sizes may be accurately marked by the necessary number of equidistant lines.
Wire, to be measured by such a gauge, is simply inserted into and passed up the aperture until it meets the sides of the same, which gives the advantage that the size of the wire may be obtained, even though its diameter vary from a gauge-number. This could not be done with a gauge in which each gauge-number and size is given in a separate aperture or notch. A comparison between the Brown and Sharpe and the Birmingham wire-gauge is shown in Fig. 1494, in which a piece of wire is[I-386] inserted, showing that No. 15 by the Birmingham gauge is No. 13 by the Brown and Sharpe gauge.
The gauge-numbers and sizes of the same in decimal parts of an inch, of the American standard or Brown and Sharpe gauge, are given in the table following:—
| No. of Wire- Gauge. |
American or New Standard. | No. of Wire- Gauge. |
American or New Standard. | ||
| Size of each number in decimal parts of an inch. |
Difference between consecutive numbers in decimal parts of an inch. |
Size of each number in decimal parts of an inch. |
Difference between consecutive numbers in decimal parts of an inch. |
||
| 0000 | .460 | —— | 19 | .03589 | .00441 |
| 000 | .40964 | .05036 | 20 | .03196 | .00393 |
| 00 | .36480 | .04484 | 21 | .02846 | .00350 |
| 0 | .32495 | .03994 | 22 | .02535 | .00311 |
| 1 | .28930 | .03556 | 23 | .02257 | .00278 |
| 2 | .25763 | .03167 | 24 | .0201 | .00247 |
| 3 | .22942 | .02821 | 25 | .0179 | .00220 |
| 4 | .20431 | .02511 | 26 | .01594 | .00196 |
| 5 | .18194 | .02237 | 27 | .01419 | .00174 |
| 6 | .16202 | .01992 | 28 | .01264 | .00155 |
| 7 | .14428 | .01774 | 29 | .01126 | .00138 |
| 8 | .12849 | .01579 | 30 | .01002 | .00123 |
| 9 | .11443 | .01406 | 31 | .00893 | .00110 |
| 10 | .10189 | .01254 | 32 | .00795 | .00098 |
| 11 | .09074 | .01105 | 33 | .00708 | .00087 |
| 12 | .08081 | .00993 | 34 | .0063 | .00078 |
| 13 | .07196 | .00885 | 35 | .00561 | .00069 |
| 14 | .06408 | .00788 | 36 | .005 | .00061 |
| 15 | .05707 | .00702 | 37 | .00445 | .00055 |
| 16 | .05082 | .00625 | 38 | .00396 | .00049 |
| 17 | .04525 | .00556 | 39 | .00353 | .00043 |
| 18 | .0403 | .00495 | 40 | .00314 | .00039 |
This gauge is now the standard by which rolled sheet brass and seamless brass tubing is made in the United States. It is also sometimes used as a gauge for the copper wire used for electrical purposes, being termed the American Standard; but unless the words “American Standard” are employed, the above wire is supplied by the Birmingham wire-gauge numbers. The brass wire manufacturers have not yet adopted the Brown and Sharpe gauge; hence, for brass wire the Birmingham gauge is the standard.
Gauges having simple notches are not suitable for measuring accurately the thickness of metal, because the edges of the sheets or plates frequently vary from the thickness of the body of the plate. This may occur from the wear of the rolls employed to roll out the sheet, or because the sheets have been sheared to cut them to the required width, or to remove cracks at the edges, which shearing is apt to form a burr or projection on one side of the edge, and a slight depression on the other.
Again, a gauge formed by a notch requires to slide over the metal of the plate, and friction and a wear causing an enlargement of the notch ensues, which destroys the accuracy of the gauge. To avoid this source of error the form of gauge that was shown in Fig. 1370 may be used, it having the further advantage that it will measure thicknesses intermediate between the sizes of two contiguous notches, thus measuring the actual thickness of the sheet when it is not to any accurate sheet metal gauge thickness.
It is to be observed that in the process of rolling, the sheet is reduced from a greater to a lesser thickness, hence the gauge will not pass upon the plate until the latter is reduced to its proper thickness.
In applying the gauge, therefore, there is great inducement for the workman to force the gauge on to the sheet, in order to ascertain how nearly the sheet is to the required size, and this forcing process causes rapid wear to the gauge.
It follows, therefore, that a gauge should in no case be forced on, but should be applied lightly and easily to the sheet to prevent wear. Here may be mentioned another advantage of the Brown and Sharpe gauge, in that its gauge-number measurements being uniform, it may be more readily known to what extent a given plate varies from its required gauge thickness.
Suppose, for example, a sheet requiring to be of Number 1 Birmingham gauge is above the required thickness, but will pass easily through the 0 notch of the gauge, the excessive variation of those two gauge numbers (over the variations between other consecutive numbers of the gauge) leaves a wider margin in estimating how much the thickness is excessive than would be the case in using the Brown and Sharpe gauge. Indeed, if the edge of the plate be of uniform thickness with the body of the plate, the variation from the required thickness may be readily ascertained by a Brown and Sharpe gauge, by the distance the plate will pass up the aperture beyond the line denoting the 0 gauge number, or by the distance it stands from the 1 on the gauge when passed up the aperture until it meets both sides of the same.
In addition to these standard gauges, some firms in the United States employ a standard of their own; the principal of these are given in comparison with others in the table following.
| Number of Wire Gauge. |
American or Brown & Sharpe. |
Birming- ham, or Stubs’s. |
Washburn & Moen Mfg. Co., Worcester, Ms. |
Trenton Iron Co., Trenton, N. J. |
G. W. Prentiss, Holyoke, Mass. |
Old English, from Brass Manu- facturers’ List. |
| 000000 | —— | —— | .46 | —— | —— | —— |
| 00000 | —— | —— | .43 | .45 | —— | —— |
| 0000 | .46 | .454 | .393 | .4 | —— | —— |
| 000 | .40964 | .425 | .362 | .36 | .3586 | —— |
| 00 | .3648 | .38 | .331 | .33 | .3282 | —— |
| 0 | .32495 | .34 | .307 | .305 | .2994 | —— |
| 1 | .2893 | .3 | .283 | .285 | .2777 | —— |
| 2 | .25763 | .284 | .263 | .265 | .2591 | —— |
| 3 | .22942 | .259 | .244 | .245 | .2401 | —— |
| 4 | .20431 | .238 | .225 | .225 | .223 | —— |
| 5 | .18194 | .22 | .207 | .205 | .2047 | —— |
| 6 | .16202 | .203 | .192 | .19 | .1885 | —— |
| 7 | .14428 | .18 | .177 | .175 | .1758 | —— |
| 8 | .12849 | .165 | .162 | .16 | .1605 | —— |
| 9 | .11443 | .148 | .148 | .145 | .1471 | —— |
| 10 | .10189 | .134 | .135 | .13 | .1351 | —— |
| 11 | .090742 | .12 | .12 | .1175 | .1205 | —— |
| 12 | .080808 | .109 | .105 | .105 | .1065 | —— |
| 13 | .071961 | .095 | .092 | .0925 | .0928 | —— |
| 14 | .064084 | .083 | .08 | .08 | .0816 | .083 |
| 15 | .057068 | .072 | .072 | .07 | .0726 | .072 |
| 16 | .05082 | .065 | .063 | .061 | .0627 | .065 |
| 17 | .045257 | .058 | .054 | .0525 | .0546 | .058 |
| 18 | .040303 | .049 | .047 | .045 | .0478 | .049 |
| 19 | .03539 | .042 | .041 | .039 | .0411 | .04 |
| 20 | .031961 | .035 | .035 | .034 | .0351 | .035 |
| 21 | .028462 | .032 | .032 | .03 | .0321 | .0315 |
| 22 | .025347 | .028 | .028 | .027 | .029 | .0295 |
| 23 | .022571 | .025 | .025 | .024 | .0261 | .027 |
| 24 | .0201 | .022 | .023 | .0215 | .0231 | .025 |
| 2S | .0179 | .02 | .02 | .019 | .0212 | .023 |
| 26 | .01594 | .018 | .018 | .018 | .0194 | .0205 |
| 27 | .014195 | .016 | .017 | .017 | .0182 | .01875 |
| 28 | .012641 | .014 | .016 | .016 | .017 | .0165 |
| 29 | .011257 | .013 | .015 | .015 | .0163 | .0155 |
| 30 | .010025 | .012 | .014 | .014 | .0156 | .01375 |
| 31 | .008928 | .01 | .0135 | .013 | .0146 | .01225 |
| 32 | .00795 | .009 | .013 | .012 | .0136 | .01125 |
| 33 | .00708 | .008 | .011 | .011 | .013 | .01025 |
| 34 | .006304 | .007 | .01 | .01 | .0118 | .0095 |
| 35 | .005614 | .005 | .0095 | .009 | .0109 | .009 |
| 36 | .005 | .004 | .009 | .008 | .01 | .0075 |
| 37 | .004453 | —— | .0085 | .00725 | .0095 | .0065 |
| 38 | .003965 | —— | .008 | .0065 | .009 | .00575 |
In the Whitworth wire-gauge, the mark or number on the gauge simply denotes the number of 1⁄1000ths of an inch the wire is in diameter; thus Number 1 on the gauge is 1⁄1000 inch, Number 2 is 2⁄1000ths inch in diameter, and so on.
Below is given the Washburn and Moen Manufacturing Company’s music wire-gauge.
| No. of Gauge. |
Size of each No. in decimal parts of an inch. |
No. of Gauge. |
Size of each No. in decimal parts of an inch. |
| 12 | .0295 | 21 | .0461 |
| 13 | .0311 | 22 | .0481 |
| 14 | .0325 | 23 | .0506 |
| 15 | .0343 | 24 | .0547 |
| 16 | .0359 | 25 | .0585 |
| 17 | .0378 | 26 | .0626 |
| 18 | .0395 | 27 | .0663 |
| 19 | .0414 | 28 | .0719 |
| 20 | .043 | —— | —— |
These sizes are those used by the Washburn and Moen Manufacturing Company, of Worcester, Mass., manufacturers of steel music wire.
[I-387]In the following table is the French Limoges wire-gauge.
| Number on gauge. |
Diameter, millimètre. |
Inch. | Number on gauge. |
Diameter, millimètre. |
Inch. |
| 0 | .39 | .0154 | 13 | 1.91 | .0725 |
| 1 | .45 | .0177 | 14 | 2.02 | .0795 |
| 2 | .56 | .0221 | 15 | 2.14 | .0843 |
| 3 | .67 | .0264 | 16 | 2.25 | .0886 |
| 4 | .79 | .0311 | 17 | 2.84 | .112 |
| 5 | .90 | .0354 | 18 | 3.40 | .134 |
| 6 | 1.01 | .0398 | 19 | 3.95 | .156 |
| 7 | 1.12 | .0441 | 20 | 4.50 | .177 |
| 8 | 1.24 | .0488 | 21 | 5.10 | .201 |
| 9 | 1.35 | .0532 | 22 | 5.65 | .222 |
| 10 | 1.46 | .0575 | 23 | 6.20 | .244 |
| 11 | 1.68 | .0661 | 24 | 6.80 | .268 |
| 12 | 1.80 | .0706 |
The following table gives the Birmingham wire-gauge for rolled sheet silver and gold.
| Gauge number. |
Thickness. | Gauge number. |
Thickness. |
| Inch. | Inch. | ||
| 1 | .004 | 19 | .064 |
| 2 | .005 | 20 | .067 |
| 3 | .008 | 21 | .072 |
| 4 | .010 | 22 | .074 |
| 5 | .013 | 23 | .077 |
| 6 | .013 | 24 | .082 |
| 7 | .015 | 25 | .095 |
| 8 | .016 | 26 | .103 |
| 9 | .019 | 27 | .113 |
| 10 | .024 | 28 | .120 |
| 11 | .029 | 29 | .124 |
| 12 | .034 | 30 | .126 |
| 13 | .036 | 31 | .133 |
| 14 | .041 | 32 | .143 |
| 15 | .047 | 33 | .145 |
| 16 | .051 | 34 | .148 |
| 17 | .057 | 35 | .158 |
| 18 | .061 | 36 | .167 |
The following table gives the gauge thickness of Russia sheet iron,[25] the corresponding numbers by Birmingham wire gauge, and the thicknesses in decimal parts of an inch.
[25] This iron comes in sheets 28 × 56 inches = 10.88 square feet of area.
| Russia gauge number. |
Birmingham wire-gauge number. |
Thickness in decimal parts of an inch. |
|
| 7 | 29 | .013 | |
| 8 | 28 | .014 | |
| 9 | 27 | .016 | |
| 10 | 26 | .018 | |
| 11 | 25 | .020 | |
| 12 | 24 | 1⁄2 | .021 |
| 13 | 24 | .022 | |
| 14 | 23 | 1⁄4 | —— |
| 15 | 22 | 3⁄8 | —— |
| 16 | 21 | 1⁄2 | —— |
The following table gives the gauge numbers to which galvanized iron is made.[26]
[26] Galvanized iron is made to the Birmingham wire-gauge, the thickness includes the galvanizing, the sheets being rolled thinner to allow for it.
| Gauge number. |
Thickness. | Gauge number. |
Thickness. |
| Inch. | Inch. | ||
| 14 | .083 | 23 | .025 |
| 16 | .065 | 24 | .022 |
| 17 | .058 | 25 | .02 |
| 18 | .049 | 26 | .018 |
| 19 | .042 | 27 | .016 |
| 20 | .035 | 28 | .014 |
| 21 | .032 | 29 | .013 |
| 22 | .028 |
In the following table is given the American gauge sizes and their respective thicknesses for sheet zinc.
| Gauge and Thickness. | Gauge and Thickness. | ||||
| Number. | Approximate Birmingham wire-gauge. |
Thickness in fractions of an inch. |
Number. | Approximate Birmingham wire-gauge. |
Thickness in fractions of an inch. |
| 1 | —— | 0.0039 | 16 | —— | 0.0447 |
| 5 | —— | 0.0113 | 17 | —— | 0.0521 |
| 6 | —— | 0.0132 | 18 | —— | 0.0596 |
| 7 | —— | 0.0150 | 19 | —— | 0.0670 |
| 8 | 28 | 0.0169 | 20 | —— | 0.0744 |
| 9 | 27 | 0.0187 | 21 | —— | 0.0818 |
| 10 | 26 | 0.0224 | 22 | —— | 0.0892 |
| 11 | 25 | 0.0261 | 23 | —— | 0.0966 |
| 12 | 24 | 0.0298 | 24 | —— | 0.1040 |
| 13 | —— | 0.0336 | 25 | —— | 0.1114 |
| 14 | —— | 0.0373 | 26 | —— | 0.1189 |
| 15 | —— | 0.0410 | |||
The Belgian sheet zinc gauge is as follows:
| Gauge number. |
Thickness in decimal parts of an inch. |
Gauge number. |
Thickness in decimal parts of an inch. |
| 1 | .004 | 14 | .037 |
| 2 | .006 | 15 | .041 |
| 3 | .008 | 16 | .045 |
| 4 | .009 | 17 | .052 |
| 5 | .011 | 18 | .059 |
| 6 | .013 | 19 | .067 |
| 7 | .015 | 20 | .074 |
| 8 | .017 | 21 | .082 |
| 9 | .019 | 22 | .089 |
| 10 | .022 | 23 | .097 |
| 11 | .026 | 24 | .104 |
| 12 | .030 | 25 | .111 |
| 13 | .034 | 26 | .120 |
The gauge sizes of the bores of rifles are given in the following table,[27] in which the first column gives the proper gauge diameter of bore, and the second the actual diameter containing the errors found to exist from errors of workmanship. The standard diameters are supposed to be based upon the number of spherical bullets to the pound weight, if of the same diameter as the respective gauge sizes.
[27] From The English Mechanic.
| No. of Gauge. |
Diameter of Bore. | No. of Gauge. |
Diameter of Bore. | ||||||
| 4 | varies from | 1.052 | to | 1.000 | 14 | varies from | .693 | to | .680 |
| 6 | „ | .919 | „ | .900 | 16 | „ | .662 | „ | .650 |
| 8 | „ | .835 | „ | .820 | 20 | „ | .615 | „ | .610 |
| 10 | „ | .775 | „ | .760 | 24 | „ | .579 | „ | .577 |
| 12 | „ | .729 | „ | .750 | 28 | „ | .550 | „ | .548 |
The following table gives the result of some recent experiments made by Mr. David Kirkaldy, of London, to ascertain the tensile strength and resistance to torsion of wire made of various materials:
| Kind of wire tested. | Pulling stress per sq. in. | ||
| Unannealed. | Annealed. | ||
| Pounds. | Pounds. | ||
| Copper | 63,122 | 37,002 | |
| Brass | 81,156 | 51,550 | |
| Charcoal iron | 65,834 | 46,160 | |
| Coke iron | 64,321 | 61,294 | |
| Steel | 120,976 | 74,637 | |
| Phosphor bronze, | No. 1 | 159,515 | 58,853 |
| „ | No. 2 | 151,119 | 64,569 |
| „ | No. 3 | 139,141 | 54,111 |
| „ | No. 4 | 120,900 | 53,381 |
| Kind of wire tested. | Ultimate extension in per cent. Annealed. |
No. of twists in 5 inches. |
||||
| Unannealed. | Annealed. | |||||
| Copper | 34 | .1 | 86 | .8 | 96 | |
| Brass | 36 | .5 | 14 | .7 | 57 | |
| Charcoal iron | 28 | 48 | 87 | |||
| Coke iron | 17 | 26 | 44 | |||
| Steel | 10 | .9 | [28] | 79 | ||
| Phosphor bronze, | No. 1 | 46 | .6 | 13 | .3 | 66 |
| „ | No. 2 | 42 | .8 | 15 | .8 | 60 |
| „ | No. 3 | 44 | .9 | 17 | .3 | 53 |
| „ | No. 4 | 42 | .4 | 13 | 124 | |
[28] Of the eight pieces of steel tested, three stood from forty to forty-five twists, and five stood one and a half to four twists.
[I-388]The following, on some experiments upon the elasticity of wires, is from the report of a committee read before the British Association at Sheffield, England.
“The most important of these experiments form a series that have been made on the elastic properties of very soft iron wire. The wire used was drawn for the purpose, and is extremely soft and very uniform. It is about No. 20 B.W.G., and its breaking weight, tested in the ordinary way, is about 45 lbs. This wire has been hung up in lengths of about 20 ft., and broken by weights applied, the breaking being performed more or less slowly.
“In the first place some experiments have been tried as to the smallest weight which, applied very cautiously and with precautions against letting the weight run down with sensible velocity, will break the wire. These experiments have not yet been very satisfactorily carried out, but it is intended to complete them.
“The other experiments have been carried out in the following way: It was found that a weight of 28 lbs. does not give permanent elongation to the wire taken as it was supplied by the wire drawer. Each length of the wire, therefore, as soon as it was hung up for experiment, was weighted with 28 lbs., and this weight was left hanging on the wire for 24 hours. Weights were then added till the wire broke, measurements as to elongation being taken at the same time. A large number of wires were broken with equal additions of weight, a pound at a time, at intervals of from three to five minutes—care being taken in all cases, however, not to add fresh weight if the wire could be seen to be running down under the effect of the weight last added. Some were broken with weights added at the rate of 1 lb. per day, some with 3⁄4 lb. per day, and some with 1⁄2 lb. per day. One experiment was commenced in which it was intended to break the wire at a very much slower rate than any of these. It was carried on for some months, but the wire unfortunately rusted, and broke at a place which was seen to be very much eaten away by rust, and with a very low breaking weight. A fresh wire has been suspended, and is now being tested. It has been painted with oil, and has now been under experiment for several months.
“The following tables will show the general results of these experiments. It will be seen, in the first place, that the prolonged application of stress has a very remarkable effect in increasing the strength of soft iron wire. Comparing the breaking weights for the wire quickly broken with those for the same wire slowly broken, it will be seen that in the latter case the strength of the wire is from two to ten per cent. higher than in the former, and is on the average about five or six per cent. higher. The result as to elongation is even more remarkable, and was certainly more unexpected. It will be seen from the tables that, in the case of the wire quickly drawn out, the elongation is on the average more than three times as great as in the case of the wire drawn out slowly. There are two wires for which the breaking weights and elongations are given in the tables, both of them ‘bright’ wires, which showed this difference very remarkably. They broke without showing any special peculiarity as to breaking weight, and without known difference as to treatment, except in the time during which the application of the breaking weight was made. One of them broke with 441⁄4 lbs., the experiment lasting one hour and a half; the other with 47 lbs., the time occupied in applying the weight being 39 days. The former was drawn out by 28.5 per cent. on its original length, the latter by only 4.79 per cent.
“It is found during the breaking of these wires that the wire becomes alternately more yielding and less yielding to stress applied. Thus from weights applied gradually between 28 lbs. and 31 lbs. or 32 lbs., there is very little yielding, and very little elongation of the wire. For equal additions of weight between 33 lbs. and about 37 lbs. the elongation is very great. After 37 lbs. have been put on, the wire seems to get stiff again, till a weight of about 40 lbs. has been applied. Then there is a rapid running down till 45 lbs. has been reached. The wire then becomes stiff again, and often remains so till it breaks. It is evident that this subject requires careful investigation.”
| Rate of adding weight. | Breaking weight in pounds. |
Per cent. of elongation on original length. |
|||||
| Dark Wire.[29] | |||||||
| 01⁄4 | lb. per | minute | 45 | 25 | .4 | ||
| 1 | „ | 5 | minutes | 45 | 1⁄4 | 25 | .9 |
| „ | 5 | „ | 45 | 1⁄4 | 24 | .9 | |
| „ | 4 | „ | 44 | 1⁄4 | 24 | .58 | |
| „ | 3 | „ | 44 | 1⁄4 | 24 | .88 | |
| „ | 3 | „ | 45 | 1⁄4 | 29 | .58 | |
| „ | 5 | „ | 44 | 1⁄4 | 27 | .78 | |
| Bright Wire.[29] | |||||||
| 1 | lb. per | 5 | minutes | 44 | 1⁄4 | 28 | .5 |
| „ | 5 | „ | 44 | 1⁄4 | 27 | .0 | |
| „ | 4 | „ | 44 | 1⁄4 | 27 | .1 | |
[29] The wire used was all of the same quality and gauge, but the “dark” and “bright” wire had gone through slightly different processes for the purpose of annealing.
| Weight added and number of experiment. |
Breaking weight in pounds. |
Per cent. of elongation on original length. |
||||||
| 1. | 1 | lb. per | day | 48 | 7.58 | |||
| 2. | „ | „ | 46 | 8.13 | ||||
| 3. | „ | „ | 47 | 7.05 | ||||
| 4. | „ | „ | 47 | 6.51 | ||||
| 5. | „ | „ | 47 | 8.62 | ||||
| 6. | „ | „ | 47 | 5.17 | ||||
| 7. | „ | „ | 46 | 5.50 | ||||
| 8. | „ | „ | 47 | 6.92 | bright wire | |||
| 1. | 3⁄4 | lb. per | day | 49 | 8.50 | |||
| 2. | „ | „ | 48 | 1⁄4 | 8.81 | |||
| 3. | „ | „ | Broken by accident. | |||||
| 4. | „ | „ | 46 | 7.55 | ||||
| 5. | „ | „ | 46 | 6.41 | ||||
| 6. | „ | „ | 45 | 1⁄2 | 6.62 | |||
| 1. | 1⁄2 | lb. per | day | 48 | 8.26 | |||
| 2. | „ | „ | 50 | 8.42 | ||||
| 3. | „ | „ | 49 | 7.18 | ||||
| 4. | „ | „ | 47 | 4.79 | } | bright wires | ||
| 5. | „ | „ | 46 | 1⁄2 | 6.00 | |||
The American Standard diameters of solid drawn or seamless brass and copper tube are as in the following table.
| Outside diameter. |
Thickness Stubs’s wire-gauge. |
Weight per running foot. Brass tubes. |
Weight per running foot. Copper tubes. |
|||||
| 5⁄8 | 18 | 3⁄8 | 3⁄8 | |||||
| 3⁄4 | 17 | 1⁄2 | 1⁄2 | |||||
| 13⁄16 | 17 | 9⁄16 | 9⁄16 | |||||
| 7⁄8 | 17 | 5⁄8 | 5⁄8 | |||||
| 15⁄16 | 16 | 11⁄16 | 11⁄16 | |||||
| 1 | 16 | 3⁄4 | 3⁄4 | |||||
| 1 | 1⁄8 | 16 | 7⁄8 | 7⁄8 | ||||
| 1 | 1⁄4 | 12 | and | 14 | 1 | 1⁄4 | 1 | 1⁄4 |
| 1 | 3⁄8 | 12 | „ | 14 | 1 | 3⁄8 | 1 | 3⁄8 |
| 1 | 1⁄2 | 12 | „ | 14 | 1 | 1⁄2 | 1 | 6⁄10 |
| 1 | 5⁄8 | 12 | „ | 14 | 1 | 5⁄8 | 1 | 7⁄10 |
| 1 | 3⁄4 | 12 | „ | 14 | 1 | 3⁄4 | 1 | 8⁄10 |
| 1 | 13⁄16 | 12 | „ | 14 | 1 | 13⁄16 | 1 | 9⁄10 |
| 1 | 7⁄8 | 12 | „ | 14 | 1 | 7⁄8 | 1 | 15⁄16 |
| 1 | 15⁄16 | 12 | „ | 14 | 2 | 2 | 1⁄10 | |
| 2 | 12 | „ | 14 | 2 | 1⁄8 | 2 | 1⁄4 | |
| 2 | 1⁄8 | 12 | „ | 14 | 2 | 1⁄4 | 2 | 3⁄8 |
| 2 | 1⁄4 | 12 | „ | 14 | 2 | 3⁄8 | 2 | 1⁄3 |
| 2 | 3⁄8 | 12 | „ | 14 | 2 | 1⁄2 | 2 | 2⁄3 |
| 2 | 1⁄2 | 11 | „ | 13 | 2 | 3⁄4 | 3 | |
| 2 | 5⁄8 | 11 | „ | 13 | 3 | 3 | 1⁄8 | |
| 2 | 3⁄4 | 11 | „ | 13 | 3 | 1⁄8 | 3 | 1⁄4 |
| 2 | 7⁄8 | 11 | „ | 13 | 3 | 1⁄4 | 3 | 3⁄8 |
| 3 | 11 | „ | 13 | 3 | 3⁄8 | 3 | 1⁄2 | |
| 3 | 1⁄8 | 11 | „ | 13 | 3 | 1⁄2 | 3 | 3⁄4 |
| 3 | 1⁄4 | 11 | „ | 13 | 3 | 7⁄8 | 4 | 1⁄8 |
| 3 | 3⁄8 | 11 | „ | 13 | 4 | 1⁄8 | 4 | 1⁄4 |
| 3 | 1⁄2 | 11 | „ | 13 | 4 | 1⁄4 | 4 | 3⁄8 |
| 4 | 11 | „ | 13 | 5 | 5 | 1⁄4 | ||
| 4 | 1⁄4 | 11 | „ | 13 | 6 | 6 | 1⁄2 | |
| 5 | 10 | „ | 12 | 7 | 8 | |||
| 6 | 10 | „ | 12 | 9 | 10 | |||
The office of the shaping machine is to dress or cut to shape such surfaces as can be most conveniently cut by a tool moving across the work in a straight line.
The positions occupied among machine tools at the present time by shaping and planing machines are not as important as was the case a few years ago, because of the advent of the milling machine, which requires less skill to operate, and produces superior work.
All the cutting tools used upon shaping and planing machines have already been described with reference to outside tools for lathe work, and it may be remarked that a great deal of the chucking done on the shaping and planing machine corresponds to face plate chucking in the lathe. Both shaping machines and small planing machines, however, are provided with special chucks and work-holding appliances that are not used in lathe work, and these will be treated of presently. On large planing machines chucks are rarely used, on account of the work being too large to be held in a chuck. Shaping machines are also known as shapers and planing machines as planers.
The simplest form of shaping machine, or shaper as it is usually termed in the United States, is that in which a tool-carrying slide is reciprocated across the work, the latter moving at the end of each back stroke so that on the next stroke the tool may be fed to its cut on the work. Fig. 1496 represents a shaper of this kind constructed by Messrs. Hewes and Phillips, of Newark, New Jersey, in which p is a cone pulley receiving motion from a countershaft, and driving a pinion which revolves the gear-wheel q, whose shaft has journal bearing in the frame of the machine. This shaft drives a bevel pinion gearing with a bevel-wheel in one piece with the eccentric spur-wheel s, which is upon a shaft having at its lower end the bevel-wheel b to operate the work-feeding mechanism. s drives an eccentric gear wheel r, fast upon the upper face of which is a projection e, in which is a T-shaped groove to receive and secure a wrist or crank pin which drives a connecting rod secured to the slide a by means of a bolt passing through a, and secured to the same by a nut d.
When the gear-wheel r revolves, the connecting rod causes slide a to traverse to and fro endways in a guideway, provided on the top of the frame at x. On the end of this slide is a head carrying a cutting tool t, which, therefore, moves across the work, the latter being held in the vise v, which is fast upon a table w upon a carriage saddle or slider p, which is upon a horizontal slide that in turn fits to a slide vertical upon the front of the machine, and may be raised or lowered thereon by means of an elevating screw driven by a pair of mitre-wheels at f. The slider and table w (and therefore the vise and the work) are moved along the horizontal slide to feed the work to the tool cut as follows. A short horizontal shaft (driven by the bevel pinions at b), drives at its outer end a piece c, having a slot to receive a crank pin driving the feed rod n, which operates a pawl k engaging a ratchet wheel which is fast upon the horizontal screw that operates slider p.
The diameters of the eccentric gear-wheels e and s are equal; hence, c makes a revolution and the cross feed is actuated once for every cutting stroke. The swivel head h is bolted to the end of the slide or ram, as it is sometimes called, a, and is provided with a slide i upon which is a slider j, carrying an apron containing the tool post holding the cutting tool, the construction of this part of the mechanism being more fully shown in Fig. 1497. The eccentric gear-wheels r s are so geared that the motion of the slide a during the cutting stroke (which is in the direction of the arrow) is slower than the return stroke, which on account of being accelerated is termed a quick return. Various mechanisms for obtaining a quick return motion are employed, the object being to increase the number of cutting strokes in a given time, without accelerating the cutting speed of the tool, and some of these mechanisms will be given hereafter.
Referring again to the mechanism for carrying the cutting tool and actuating it to regulate the depth of cut in Fig. 1497, g is the end of the slide a to which the swivel head h is bolted by the bolts a b. The heads of these bolts pass into T-shaped annular grooves in g, so that h may be set to have its slides at any required angle. i is a slider actuated on the slide by means of the vertical feed screw which has journal bearing in the top of h, and passes through a nut provided in i. To i is fastened the apron swivel j, being held by a central bolt not seen in the cut,[I-390] and also by the bolt at c. In j is a slot, which when c is loosened permits j to be swung at an angle. The apron k is pivoted by a taper pin l, which fits into both j and k. During the cutting stroke the apron k beds down upon j, but during the back stroke the tool may lift the apron k swinging upon the pivot l. This prevents the cutting edge of the tool from rubbing against the work during the return stroke.
Thus in Fig. 1498 is a piece of work, and it is supposed that a cut is being carried down the vertical face or shoulder at a; by setting the apron swivel at an angle and lifting the tool during the return stroke, its end will move away from the face of the shoulder. The slider i obviously moves in a vertical line upon slides m.
To take up the wear of the sliding bar a, various forms of guideways and guides are employed, a common form being shown in Fig. 1499. There are two gibs, one on each side of the bar, and these gibs are set up by screws to adjust the fit. In some cases only one gib is used, and in that event the wear causes the slide to move to one side, but as the wear proceeds exceedingly slowly in consequence of the long bearing surface of the bar in its guides, this is of but little practical moment. On the other hand, when two gibs are used great care must be taken to so adjust the screws that the slide bar is maintained in a line at a right angle to the jaws of the work-holding vice, so that the tool will cut the vertical surfaces or side faces of the work at a right angle to the work surface that is gripped by the vice.
To enable the length of stroke of slide a, Fig. 1496, to be varied to suit the length of the work, and thus not lose time by uselessly traversing that slide, e is provided with a T-slot as before stated, and the distance of the wrist pin (in this slot) from the centre of wheel e determines the amount of motion imparted to the connecting rod, and therefore to slide a. The wrist pin is set so as to give to a a rather longer stroke than the work requires, so that this tool may pass clear of the work on the forward stroke, and an inch or so past the work on the return stroke, the latter giving time to feed the tool down before it meets the work.
The length of the stroke being set, the crank piece e (for its slot and wrist pin correspond to a crank) is, by pulling round the pulley p, brought to the end of a stroke, the connecting rod being in line with slide a. The nut d is then loosened and slide a may then be moved by hand in its slideway until the tool clears the work at the end corresponding to the connecting rod position when nut d is tightened and the stroke is set.
Now suppose it is required to shape or surface the faces f and f′, the round curve s and the hollow curve c of the piece of work shown held in a vice chuck in Fig. 1500, and during the cutting stroke the slide a will travel in the direction of n in the figure, while during its return stroke it will traverse back in the direction of i. The sliding table w in Fig. 1496 would continuously but gradually be fed or moved (so much per tool traverse, and by the feeding mechanism described with reference to Fig. 1501) carrying with it the vice chuck, and therefore the work. When this feeding brought the surface of curve s, Fig. 1500, into contact with the tool, the feed screw handle in figure would be operated by hand so much per feed traverse, thus raising the slider, and therefore the tool, in the direction of l, and motion of the work to the right and the left of the tool (by means of the feed handle) would (if the amount of tool lift per tool stroke is properly proportioned to the amount of work feed to the right) cause the tool to cut the work to the required curvature. When the work had traversed until the tool had arrived at the top of curve s, the direction of motion of the feed-screw handle z in Fig. 1496 must be reversed, the tool being fed down so much per tool traverse (in the direction of m) so as to cut out the curves from the top of s to the bottom of c, the face f′ being shaped by the automatic feed motion only.
The feed obviously occurs once for each cutting stroke of the tool and for the vertical motion of the tool, or when the tool is operated by the hand feed-screw handle in Fig. 1496, the handle motion, and therefore the feed should occur at the end of the back stroke and before the tool again meets the work, so as to prevent the cutting edge of the tool from scraping against the work during its back traverse.
In this connection it may be remarked that by setting the apron swivel over, as in Fig. 1498, the tool is relieved from rubbing on the back stroke for two reasons, the first having been already explained, and the second being that to whatever amount the tool may spring, bend, or deflect during the cutting stroke (from the pressure of the cut), it will dip into the work surface and cut deeper; hence on the back stroke it will naturally clear the surface, providing that the next cut is not put on until the tool has passed back and is clear of the work.
Referring now to the automatic feed of the sliding table w, in Fig. 1496, the principle of its construction may be explained with reference to Fig. 1501, which may be taken to represent a class of such feeding mechanisms. a is a wheel corresponding to the wheel marked m in Fig. 1496, or, it may be an independent wheel in gear with the feed wheel. On the same shaft as a is pivoted an arm b having a slot s at one end to receive a pin to which the feed rod e may connect. f is a disk rotated from the driving mechanism of the shaping machine, and having a T-shaped slot g g, in which is secured a pin to actuate the rod e. As f rotates e is vibrated to and fro and the catch c on one stroke falls into the notches or teeth in a and causes it to partly rotate, while on the return stroke of e it lifts over the teeth, leaving a stationary.
The amount of motion of b, and therefore the quantity of the feed, may be regulated at either end of e; as, for example, the farther the pin from the centre of g the longer the stroke of e, or[I-391] the nearer the pin in s is to the centre of b the longer the stroke, but usually this provision is made at one end only of e.
To stop the feed motion from actuating, the catch c may be lifted to stand vertically, as shown in dotted lines in position 2, and to actuate the feed traverse in an opposite direction, c may be swung over so as to occupy the position marked 3, and to prevent it moving out of either position in which it may be set a small spring is usually employed.
Now suppose that the tool-carrying slide a, Fig. 1496, is traversing forward and the tool will be moving across the work on the cutting stroke, as denoted by the arrow k in Fig. 1502, the line of tool motion for that stroke being as denoted by the line c a. At a is the point where the tool will begin its return stroke, and if the work is moved by the feeding mechanism in the direction of arrow e, then the line of motion during the return stroke will be in the direction of the dotted line a b, and as a result the tool will rub against the side of the cut.
It is to obviate the friction this would cause to the tool edge, and the dulling thereto that would ensue, that the pivot pin l for the apron is employed as shown in Fig. 1497, this pin permitting the apron to lift and causing the tool to bear against the cut with only such force as the weight of the apron and of the tool may cause. Now suppose that in Fig. 1503 we have a piece of work whose edge a a stands parallel to the line of forward tool motion, there being no feed either to the tool or the work, and if the tool be set to the corner f its line of motion during a stroke will be represented by the line f g. Suppose that on the next stroke the feed motion is put into action and that feeding takes place during the forward stroke, and the amount of the feed per stroke being the distance from g to h, then the dotted line from f to h represents the line of cut. On the return stroke the line of tool motion will be from h along the dotted line h k, and the tool will rest against the cut as before. Suppose again that the feed is put on during the return stroke, and that c c′ represents the line of tool motion during a cutting stroke, and the return stroke will then be along the line from c′ to b, from c to b representing the amount of feed per stroke; hence, it is made apparent that the tool will rub against the cut whether the feed is put on during the cutting or during the return stroke. Obviously then it would be preferable to feed the work between the period that occurs after the tool has left the work surface on the return stroke and before it meets it again on the next cutting stroke. It is to be observed, however, that by placing the pin actuating the rod e, Fig. 1501, on the other side of the centre of the slot g in f, the motion of e will be reversed with relation to the motion j of the slide; hence, with the work feeding in either direction, the feed may be made to occur during either the cutting or return stroke at will by locating the driving pin on the requisite side of the centre of g.
An arrangement by Professor Sweet, whereby the feed may be actuated during the cutting or return stroke (as may be determined in designing the machine), no matter in which direction the work table is being fed, is shown in Fig. 1504. Here there are two gears a and d, and the pawl or catch c may be moved on its pivoted end so as to engage either with a or d to feed in the required direction.
Suppose the slide to be on its return stroke in the direction of l, and f be rotated as denoted by the arrow, then the pawl c will be actuating wheel a as denoted by its arrow, but if c be moved over so as to engage d as denoted by the dotted outline, then with the slide moving in the same direction, c will pull d in the direction of arrow k′, and wheel a will be actuated in the opposite direction, thus reversing the direction of the feed while still causing it to actuate on the return stroke.
Since the feed wheel a must be in a fixed position with relation to the work table feed screw, and since the height of this table varies to meet the work, it is obvious that as the work table is raised the distance between the centres of a and f in the figure is lessened, or conversely as that table is lowered the distance between those centres is increased; hence, where the work table has much capacity of adjustment for height, means must be provided to adjust the length of rod e to suit the conditions. This may be accomplished by so arranging the construction that the rod may pass through its connection with wheel f, in the figure, or to pass through its connection with b.
Fig. 1505 represents a shaper that may be driven either by hand or by belt power. The cone pulley shaft has a pinion that drives the gear-wheel shown, and at the other end of this gear-wheel shaft is a slotted crank carrying a pin that drives a connecting rod that actuates the sliding bar, or ram, as it is sometimes termed. The fly-wheel also affords ready means of moving the ram to any required position when setting the tool or the work.
Fig. 1506 represents a shaping machine by the Hewes and Phillips Iron Works, of Newark, N.J. The slide or ram is operated by the Whitworth quick return motion, whose construction will be shown hereafter. The vice sets upon a knee or angle plate fitting to vertical slideways on the cross slide, and may be raised or lowered thereon to suit the height of the work by means of the crank handle shown in front. The vice may be removed and replaced by the supplemental table shown at the foot of the machine. Both the vice and the supplemental table are capable of being swivelled when in position on the machine. The machine is provided with a device for planing circular work, such as[I-392] sectors, cranks, &c., the cone mandrel shown at the foot of the machine bolting up in place of the angle plate.
Holding Work in the Shaper or Planer Vice.—The simplest method of holding work in a shaper is by means of a shaper vice, which may be employed to hold almost any shape of work whose size is within the capacity of the chuck. Before describing, however, the various forms of shaper vices, it may be well to discuss points to be considered in its use.
The bottom surface a a, Fig. 1507, of a planer vice is parallel with the surfaces d, d′ and as surface a is secured to the upper face of the slider table shown in figure, and this face is parallel to the line of motion of the slide a, and also parallel with the cross slide in that figure, it follows that the face d is also parallel both with the line of motion of slide a and with the surface of the slider table. Parallel work to be held in the vice may therefore be set down upon the surface d (between the jaws), which surface will then form a guide to set the work by. The work-gripping surfaces b and e, Fig. 1507, of the jaws are at a right angle to surface a, and therefore also to d, therefore the upper surface of work that beds fair upon d, or beds fair against b, will be held parallel to the line of motion x of the tool and the line z of the feed traverse. Similarly the upper surfaces a, b of the gripping jaws are parallel to a a, hence they may be used to set the work true with the line of feed traverse. The sliding jaw, however, must be a sufficiently easy fit to the slideways that guide it to enable it to be moved by the screw that operates it, and as a result it has a tendency to lift upon its guideways so that its face e will not stand parallel to b or at a right angle to d. In Fig. 1508, for example, is a side view of a vice holding a piece of work w, the face f of the work being at an angle. As a consequence there is a tendency to lift in the direction of c. If the jaw does lift or spring in this direction it will move the work, so that instead of its lower face bedding down upon face d, Fig. 1507, it will lie in the direction of h, Fig. 1508, while its face parallel to f, instead of bedding fair against the face of jaw j, will lie as denoted by the line g, and as a result the work will not be held fair with either of those faces and the value of faces b, d and e in Fig. 1507 is impaired.
This lifting of the movable or sliding jaw is prevented in some forms of chuck, to be hereafter described, by bolts passing through which hold it down, but the tendency is nevertheless present,[I-393] and it is necessary to recognise it in treating of chucking or holding work in such vices.
The work gripping face b, Fig. 1507, of the fixed jaw, however, is not subject to spring, hence it and the surface d are those by which the work may be set. The work, however, is held by the force of the screw operating the sliding jaw, hence the strain is in the direction of the arrow p in Fig. 1508, which forces it against the face of the fixed jaw. All the pressure that can be exerted to hold work down upon the surface d, Fig. 1507, is that due to the weight of the work added to whatever effort in that direction there may be induced by driving the work down by blows upon surface d after the jaws are tightened upon the work. This, however, is not to be relied upon whenever there is any tendency for the work not to bed down fair. It follows, then, that surface b of the work-gripping jaw is that to be most depended upon in setting the work, and that the surface that is to act as a guide at each chucking should be placed against this surface unless there are other considerations that require to be taken into account.
For example, suppose we have a thin piece of work, as in Fig. 1509, and the amount of surface bearing against the fixed jaw is so small in comparison to its width between the jaws that e would form no practical guide in setting the work. If then the edges of such a piece of work were shaped first the face or faces may or may not be made at a right angle to them, or square as it is termed. But if the faces were shaped first, then when the work was held by them to have the edges shaped there would be so broad an area of work surface bedding against the jaw surface, that the edges would naturally be shaped square with the faces.
In cases, therefore, where the area of bedding surface of the work against the faces of the jaws is too small to form an accurate guide and the work is not thick enough to rest upon the surface d, Fig. 1507, it is set true to that surface by a parallel piece.
If the work is wide or long enough to require it, two parallel pieces must be used, both being of the same thickness, so that they will keep the work true with the surface d.
Pieces such as p, Fig. 1510, are also used to set work not requiring to be parallel. Thus in figure are a number of keys placed side by side and set to have their edges shaped, and piece p is inserted not only to lift the narrow ends of the keys up, but also to maintain their lower edges fair one with the other, and thus insure that the keys shall all be made of equal width.
They are also serviceable to interpose between the work and the vice jaws when the work has a projection that would receive damage from the jaw pressure.
Thus in Fig. 1511 the work w has such a projection and a parallel piece p is inserted to take the jaw pressure. By placing the broadest work surface g against the fixed jaw the work will be held true whether the movable jaw springs or not, because there will be surface g and surface h guiding it.
But if the work were reversed, as in Fig. 1512, with the broadest surface against k, then if k sprung in the direction of c, the work would not be shaped true.
When the work is very narrow, however, the use of a parallel piece to regulate its height is dispensed with, and the top surface b of the jaw, in Fig. 1513, is used to set the work by. A line is marked on the work surface to set it by and a surface gauge is set upon the face b, its needle point being set to the line in a manner similar to that already explained with reference to chucking work in the lathe.
All work should be so set that the tool will traverse across the longest length of the work, as denoted by the tool in Fig. 1502, and the arrow marking its direction of traverse.
The general principles governing the use of the shaper vice having been explained, we may now select some examples in its use.
Fig. 1514 represents a simple rectangular piece, and in order to have the tool marks run lengthwise of each surface (which is, as[I-394] already stated the most expeditious) they must be in the direction of the respective arrows. In a piece of such relative proportions there would be little choice as to the order in which the surfaces should be shaped, but whatever surface be operated on first, that at a right angle to it should be shaped second; thus, if a be first, either b or d should be second, for the following reasons.
All the surfaces have sufficient area to enable them to serve as guides in setting the work, hence the object is to utilize them as much as possible for that purpose. Now, suppose that surface a has been trued first, and if c be the next one, then the bedding of surface a upon the vice surface or the parallel pieces must be depended upon to set a true while truing c. Now the surfaces b and d may both, or at least one of them, may be untrue enough to cause the work to tilt or cant over, so that a will not bed fair, and c will then not be made parallel to a. It will be preferable then to shape a first and at the second chucking to set a against the stationary jaw of the vice, so that it may be held true.
The sliding jaw will in this case be against face c, and if that face is out of true enough to cant the work so that a will not bed fair, then a narrow parallel piece may be inserted between the sliding jaw and the work, which will cause a to bed fair. The third face should be face c, in which case face a will rest on one surface and face b will be against the fixed jaw, and there will be two surfaces to guide the work true while c is being trued. In this case also, however, it is better to use a parallel piece p, Fig. 1515, between the work and the sliding jaw, so as to insure that the work shall bed fair against the fixed jaw; and if necessary to bring up the top surface above the jaws, a second parallel piece p′ should be used.
Suppose now that we have a connecting rod key to shape, and it is to be considered whether the faces or the edges shall be shaped first. Now if the side faces are out of parallel it will take more filing to correct them than it will to correct the same degree of error in the edges; hence it is obviously desirable to proceed with a view to make all surfaces true, but more especially the side faces. As the set of the key while shaping these faces is most influenced by the manner in which the fixed jaw surface meets the work, and as an edge will be the surface to meet the fixed jaw faces when the side faces are shaped, it will be best to dress one edge first, setting the key or keys, as the case may be, as was shown in Fig. 1510, so as to cut them with the tool operating lengthways of the key; one edge being finished, then one face of each key must be shaped, the key being set for this purpose with the surfaced edge against the fixed jaw. As the width of the key is taper, either a chuck with a taper attachment that will permit the sliding jaw to conform itself to the taper of the key must be used (vices having this construction being specially made for taper work as will be shown hereafter), or else the key must be held as in Fig. 1516, in which k represents the key with its trued edge against the fixed jaw, at p is a piece put in to compensate for the taper of the key, and to cause the other edge to bed firmly and fairly against the fixed jaw.
The first side face being trued, it should be placed against the fixed jaw while the other edge is shaped. For the remaining side face we shall then be able to set the key with a trued edge against the fixed jaw, and a true face resting upon a parallel piece, while the other edge will be true for the piece p, Fig. 1516, to press against, and all the elements will be in favor of setting the key so that the sides will be parallel one to the other, and the edges square with the faces.
In putting in the piece p, Fig. 1516, the key should be gripped so lightly that it will about bear its own weight; piece p may then be pushed firmly in with the fingers, and the vice tightened up.
If there are two keys the edges and one face may be trued up as just described, and both keys k, Fig. 1517, chucked at once by inverting their tapers as shown in figure. But in this case unless the edges are quite true they may cause the keys not to bed fair on the underneath face, and the faces therefore to be out of parallel on either or both of the keys. If there are a number of keys to be cut to the same thickness it may be done as follows:—
Plane or shape first one edge of all the keys; then plane up one face, chucking them with one planed edge against each vice jaw, and put little blocks (a, b, c, d, Fig. 1518) between the rough edges; then turn them over, chuck them the same way and plane the other face, resting them on parallel pieces; then plane the other edges last.
In place of the small blocks a, b, c, d, a strip of lead, pasteboard, or wood, or for very thin work a piece of lead wire, may be used.
Cylindrical work may be held in a vice chuck, providing that the top of the vice jaws is equal in height to the centre of the work, as in Fig. 1519, a parallel piece being used to set the work true. When, however, the work is to be shaped at one end only, it is preferable to hold it as in Fig. 1520, letting its end project out from the side of the chuck. In some vices the jaws are wider than the body of the chuck, so that cylindrical work may be held vertical, as in Fig. 1521, when the end is to be operated upon.
[I-395]Fig. 1522 represents a simple form of shaper or planer chuck, such chucks being used upon small planing machines as well as upon shaping machines.
The base a is bolted to the work table, and is in one piece with the fixed jaw b. The movable jaw c is set up to meet the work by hand, and being free to move upon a may be used for either taper or parallel work. To fasten c upon the work, three screws threaded through f abut against the end of c; f being secured to the upper surface of a by a key or slip, which fits into a groove in f, and projects down into such of the grooves in the upper surface of a as may best suit the width of work to be held in the vice; c is held down by the bolts and nuts at g.
The operation of securing work in such a chuck is as follows:—The screws both at f and at g being loosened, and jaw c moved up to meet the work and hold it against the fixed jaw b, then nuts g should be set up lightly so that the sliding jaw will be set up under a slight pressure, screws f may then be set up and finally nuts g tightened.
This is necessary for the following reasons:—The work must, in most cases, project above the level of the jaws so that the tool may travel clear across it; hence, the strain due to holding the work is above the level of the three screws, and the tendency, therefore, is to turn the jaw c upwards, and this tendency the screws g resist. A similar chuck mounted upon a circular base so that it may be swivelled without moving the base on the work table is shown in Fig. 1523. The capacity to swivel the upper part of the chuck without requiring the base of the chuck to be moved upon the table is a great convenience in many cases.
Fig. 1524 represents an English chuck in which the fixed jaw is composed of two parts, a which is solid with the base g, and d which is pivoted to a at f. The movable jaw also consists of two parts, b which carries the nut for the screw that operates b, and c which is pivoted to b at e. The two pivots e, f being above the surface of the gripping jaws c, d, causes them to force down upon the surface of g as the screw is tightened, the work, if thin, being rested, as in the case of the chuck shown in Fig. 1523, upon parallel pieces.
Fig. 1525 represents a chuck made by W. A. Harris, of Providence. The jaws in this case carry two pivoted wings a, b, between the ends of which the work c is held, and the pivots being above the level of the work the tendency is here again to force the work down into the chuck, the strain being in the direction denoted by the arrows.
Here the work rests on four pins which are threaded in the collars h, so that by rotating the pins they will stand at different heights to suit different thicknesses of work, or they may be set to plane tapers by adjusting their height to suit the amount of taper required. The spiral springs simply support the pins, but as the jaws close the pins lower until the washer nuts h meet the surface of recess i.
Figs. 1526 and 1527 represent Thomas’s patent vice, which possesses some excellent conveniences and features.
In Fig. 1526 it is shown without, and in Fig. 1527 with a swivel motion. The arrangement of the jaws upon the base in Fig. 1526 is similar to that of the chuck shown in Fig. 1522, but instead of there being a key to secure the piece f to the base, there is provided on each side of the base a row of ratchet teeth, and there is within f a circular piece g (in Fig. 1528) which is serrated to engage the[I-396] ratchet teeth. This piece may be lifted clear of the ratchet teeth by means of the pin at h, and then the piece f may be moved freely by hand backwards or forwards upon the base and swung at any required angle, as in Fig. 1528, or set parallel as in Fig. 1527; f becoming locked, so far as its backward motion is concerned, so soon as h is released and g engages with the ratchet teeth on the base. But f may be pushed forward toward the fixed jaw without lifting h, hence the adjustment of the sliding jaw to the work may be made instantaneously without requiring any moving or setting of locking keys or other devices.
It is obvious that it is the capability of g to rotate in their sockets that enables f to be set at an angle and still have the teeth of g engage properly with those on the base plate.
The mechanism for swivelling the upper part or body upon the base and for locking it in its adjusted position is shown in Figs. 1529 and 1530. The body d is provided with an annular ring fitting into the bore of the base, which is coned at q. The half-circular disks r fit this cone and are held to the body of the chuck by four bolts n, which are adjusted to admit disks r to move without undue friction. k is a key having on it the nut v, which receives a screw whose squared end is shown at s. By operating s in one direction key k expands disks r, causing them to firmly grip the base at the bevel q, hence the base and the body are locked together. By operating s to unscrew in the nut v, k is moved in the opposite direction and r, r release their grip at q and the body d may be swung round in any position, carrying with it all the mechanism except base p.
To enable the body to be readily moved a quarter revolution, or in other words, moved to a right angle, there is provided a taper pin, the base having holes so situated that the body will have been moved a quarter revolution when the pin having been removed from one hole in the base is seated firmly home in the other.
Referring again to Fig. 1526, there are shown one pair of parallel pieces marked respectively a, having bevelled edges, and another pair marked respectively b. Both pairs are provided with a small rib fitting into a groove in the jaws of the chuck, as shown in the figure.
These ribs and grooves are so arranged that the upper pair (a, a) may be used in the place of the lower ones, and the uses of these pieces are as follows:—
Suppose a very thin piece of work is to be planed, and in order to plane it parallel, which is ordinarily a difficult matter, it must bed fair down upon the face of the vice, which it is caused to do when chucked as in Fig. 1531, in which the work is shown laid flat upon the face of the vice, and gripped at its edges by the pieces a, a.
These pieces, it may be noted, do not bed fair against the gripping faces of the jaws, but are a trifle open at the bottom as at e, e, hence when they are pressed against the work they cant over slightly and press the work down upon the chuck face causing it to bed fair. Furthermore, the work is supported beneath its whole surface, and has, therefore, less tendency to spring or bend from the holding pressure; and as a result of these two elements much thinner work can be planed true and parallel than is possible when the work is lifted up and supported upon separate parallel pieces, because in the latter case the work, being unsupported between the parallel pieces, has more liberty to bend from the pressure due to the tool cut, as well as from the holding pressure.
[I-397]Fig. 1532 shows the chuck holding a bracket, having a projection or eye. The work rests on pieces b, b, and is gripped by pieces a, a. It will be observed that a, a being beveled enables the cut to be carried clear across the work.
Fig. 1533 represents the chuck in use for holding a piece of shafting s to cut a keyway or spline in it. In this case a bevelled piece j is employed, its bevelled face holding the work down upon the chuck face.
Fig. 1534 represents a chuck termed shaper centres, because the work is held between centres as in the case of lathe work. The live spindle is carried in and is capable of motion in a sleeve, the latter having upon it a worm-wheel, operated by a worm, so that it can be moved through any given part of a circle, and has index holes upon its face to determine when the wheel has been moved to the required amount.
For work that is too large to be operated upon in the class of shaping machine shown in Fig. 1506, and yet can be more conveniently shaped than planed, a class of machine is employed in which the tool-carrying slide is fed to the work, which is chucked to a fixed table or to two tables.
Fig. 1535 represents a machine of this class. The tool-carrying slide a, in this case, operates in guideways provided in b, the latter being fitted to a slideway running the full length of the top of the frame m. The base slider b is fed along the bed by means of a screw operating in a nut on the under side of b, this screw being operated once during each stroke of the tool-carrying slide a, by means of a pawl feeding arrangement at f, which corresponds to the feeding device shown in Fig. 1501.
Two vertical frame pieces d, d are bolted against the front face of the machine, being adjustable along any part of the bed or frame length, because their holding bolts have heads capable of being moved (with the frame pieces d) along the two T-shaped grooves shown, their T-shape being visible at the end of the frame or bed. To frames d are bolted the work-holding tables e, e, the bolts securing them passing into vertical T-grooves in d, so that e may be adjusted at such height upon d as may be found necessary to bring the work within proper range of the cutting tool. The work tables e, e are raised or lowered upon d by means of a vertical screw, which is operated by the handle h, this part of the mechanism accomplishing the same end as the elevating mechanism shown in Fig. 1496. The swivel head j is here provided at its top with a segment of a worm-wheel which may be actuated to swivel that head by the worm g.
The swivel head may thus be operated upon its pivot, causing the tool point to describe an arc of a circle of which the pivot is the centre. To steady the swivel head when thus actuated, there is behind the worm segment a V-slide that is an arc, whose centre is also the centre of the pivot.
The tool-carrying slide a is operated as follows: The driving pulley p rotates a shaft lying horizontal at the back of the machine. Along this shaft there is cut a featherway or spline driving a pinion which operates a link mechanism such as described with reference to Fig. 1550.
The means of adjusting the distance the head of a shall stand out from b, are similar to that described for Fig. 1496, a bolt passing through a, and in both cases attaching to a connecting rod or bar.
At k is a cone mandrel such as has been described with reference to lathe work upon which is chucked a cross-head c. By means of suitable mechanism, this mandrel is rotated to feed the circular circumference of the cross-head jaws to the cut, the slider b remaining in a fixed position upon the bed m.
To support the outer end of the cone mandrel a beam l is bolted to the two tables e, e. On l is a slideway for the piece p. At s is a lug upon e through which threads a screw r, which adjusts the height of the piece p, while q is a bolt for securing p in its adjusted position. This cone mandrel and support is merely an attachment to be put on the machine as occasion may require.
| VOL. I. | SHAPING MACHINES AND TABLE‑SWIVELING DEVICES. | PLATE XVI. | |
 |
 |
||
| Fig. 1536. | Fig. 1537. | ||
 |
 |
||
| Fig. 1538. | Fig. 1539. | ||
Fig. 1536 represents a shaping machine by the Pratt and Whitney Company. In this machine a single sliding head is used and the work remains stationary as in the case of the machine shown in Fig. 1535. The vice is here mounted on a slide which enables the work to be finely adjusted beneath the sliding bar independently of that bar, which is provided with a Whitworth quick-return motion.
As the tool-carrying slide of a shaping machine leaves its guideways during each stroke, the tool is less rigidly guided as the length of slide stroke is increased, and on this account its use is limited to work that does not require a greater tool stroke than about 18 inches, and in small machines not to exceed 12 inches. The capacity of the machine, however, is obviously greatest when[I-398] the length of the work is parallel to the line of motion of the feed traverse. Work whose dimension is within the limit of capacity of the shaper can, however, be more expeditiously shaped than planed because the speed of the cutting tool can be varied to suit the nature of the work, by reason of the machine having a cone pulley, whereas in a planing machine the cutting speed of the tool is the same for all sizes of work, and all kinds of metal. In shaping machines such as shown in Fig. 1537, or in similar machines in which the work table is capable of being traversed instead of the head, the efficiency of the work-holding table and of the chucking devices may be greatly increased by constructing the table so that it will swivel, as in Fig. 1538, which may be done by means of the employment of Thomas’s swivelling device in Fig. 1530. By this means the ends of the work may be operated upon without removing it from the chuck. Or the work may be shaped taper at one part and parallel at another without unchucking it.
Fig. 1539 shows a circular table swivelled by the same device, sitting upon a work table also swivelled.
Fig. 1540 represents a general view of a shaping machine having the motion corresponding in effect to a planing machine, the object being to give a uniform rate of speed to the tool throughout, both on its cutting and return stroke. The feed always takes place at the end of the return stroke, so as to preserve the edge of the tool, and the length of the stroke may be varied, without stopping the machine, by simply adjusting the tappets or dogs, the range of stroke being variable from 1⁄4 inch to 20 inches, while the return stroke is 40 per cent. quicker than the cutting one. There are two different rates of cutting speed, one for steel and the other for the softer metals.
The ram or bar is provided with a rack (z, Fig. 1545) which engages with a pinion s, Fig. 1541, h being the driving shaft driven by the belt cones a and b. These two cones are driven by separate belts, but from the same counter-shaft, one being an open and the other a crossed belt. The open belt drives either the largest step of pulley b, giving a cutting speed suitable for steel, or the smaller step, giving a cutting speed for softer metals, as cast iron, &c. The crossed belt drives, in either case, the pulley a for the quick-return stroke, and this pulley revolve upon a sleeve or hub c, which revolves upon the shaft h. The sleeve or hub c is in one piece with a pulley c, whose diameter is such as to leave an annular opening between its face and the bore of the largest step of cone pulley b, and pulley a is fast to the hub or sleeve c. It will be seen that as the driving belts from the counter-shaft are one open and one crossed, therefore pulley a runs constantly in one direction, while pulley b runs constantly in the other, so that the direction of motion of the driving shaft h depends upon whether it is locked to pulley a or to pulley b.
In the annular space left between the face of pulley c and the cone b is a steel band g, Fig. 1542, forming within a fraction a complete circle, and lined inside and out with leather, and this band is brought, by alternately expanding and contracting it, into contact with either the bore of the largest cone step of b or with the outside face of pulley c. The ends of this band are pivoted upon two pins f, which are fast in two arms e and d, in Fig. 1542. Arm e is fastened to the driving shaft h, and its hub has two roller studs k, Fig. 1541, these being diametrically opposite on the said hub. The hub of arm d is a working fit upon the hub[I-399] of e, and has two slots to admit the above rollers. Hub d is also provided with two studs and rollers placed midway between the studs k. These latter rollers project into the spiral slots k′ of the ring in Fig. 1543, this ring enveloping the hub of d and being enveloped by the sleeve m, which contains two spiral grooves diametrically opposite, and lying in an opposite direction to grooves k′, Fig. 1543. Sleeve m is prevented from revolving by rollers on the studs o, which are screwed into the bearing bush r, and carry rollers projecting into the slots in m.
It is evident that if the ring l, Fig. 1543, is moved endways with m, then the arms e, d, together with the band g, will be expanded or contracted according to the direction of motion of the ring, because the motion of m, by means of its spiral grooves, gives a certain amount of rotary motion to the ring l, and the spiral grooves in the ring give a certain amount of rotary motion to the arms d and e, Fig. 1542. When this rotary motion is in one direction the band is expanded; while when it is reversed it is contracted, and the direction of motion of shaft h is reversed.
The outer sleeve m carries the rod t, Figs. 1544 and 1545, which is connected to the lever u, the upper arm of which is operated by the tappets or dogs x on the ram or sliding bar, and it is obvious that when u is vibrated sleeve m is operated in a corresponding direction, and the ring l also is moved endwise in a corresponding direction, actuating the band as before described, the direction of motion being governed, therefore, by the direction in which u is moved by the tappets or dogs. A certain degree of friction is opposed to the motion of lever u in order to keep it steady, the construction being shown in Fig. 1546, where it is seen that there is on each side of its nut a leather washer, giving a certain amount of elasticity to the pressure of the nut holding it in place on the shaft u.
The mechanism for actuating the feed at the end of the return stroke only, is shown in Fig. 1547. The shaft v (which is also seen in a dotted circle in Fig. 1545) carries a flange c, on each side of which is a leather disk, so that the pressure of the bolts which secure b to the sleeve a causes c to revolve under friction, unless sleeve a, slotted bar b, and flange c all revolve together, or, in other words, c revolves under friction when it revolves within a b.
Fig. 1548 is an end view of Fig. 1547.
Fig. 1549 gives a cross-sectional view of the shaft sleeve, &c. The sleeve a is provided with two pins i, i, and a pin k is fast in the frame of the machine, and it is seen that a and v may revolve together in either direction until such time as one of the pins i meets the stationary pin k, whereupon the further revolving of a will be arrested and v will revolve within a, and as flange c, Fig. 1547, revolves with v, it will do so under the friction of the leather washers. The pins i and the pin k are so located that a can have motion only when the ram or sliding-bar is at the end of the return stroke, and the feed-rod f, being connected to b, is therefore actuated at the same time.
Among the various mechanisms employed to give a quick return to the tool-carrying slide of shaping machines, those most frequently employed are a simple crank, a vibrating link, and the Whitworth quick-return motion, the latter being the most general one.
The principle of action when a vibrating link is employed may be understood from Fig. 1550, in which p is a pinion driven by the cone pulley and imparting motion to d. At l is a link pivoted at c. At a is a link block or die capable of sliding in the slot or opening in the link and a working fit upon a pin which is fast in[I-400] the wheel d. As d rotates the link block slides in the slot and the link is caused to travel as denoted by the dotted lines. r is a rod connecting the tool-carrying slide s to the upper end of link l, and therefore causing it to reciprocate with l. But s being guided by its slide in the guideway traverses in a straight line.
Since the rotation of p and d is uniform, the vibrations of the link l will vary in velocity, because while the link block is working in the lower half of the link slot it will be nearer to the centre of motion c of the link, and the upper end of c will move proportionately faster. The arrangement is such that during this time the tool-carrying slide is moved on its return stroke, the cutting stroke being made while the link block is traversing the upper half of the slot, or in other words, during the period in which the crank pin in a is above the horizontal centre of wheel d.
Now suppose the arrangement of the parts is such that the front of the machine or the cutting tool end of the slide is at the end k of s, then s will be pushed to its cut by the rod r at an angle which will tend to lift s in the slideways. But suppose the direction of rotation of wheel d instead of being as denoted by the arrow at d be as denoted by the arrow at e, then s will be on its back stroke, the front of the machine being at j. In this case rod r will pull s to the cut, and s will, from the angularity of r, be pulled down upon the bed of the slideway guiding it, and will therefore be more rigidly held and less subject to spring, because the tendency to lift is resisted on one side by the adjustable gib only, and on the other by the projecting v, whereas the tendency to be pulled downwards is resisted by the strength of the frame of the machine.
Furthermore, as the pressure on the cutting tool is below the level of the tool-carrying slide it tends to force that slide down upon the slideway, and it will therefore be more rigidly and steadily guided when the force moving the slide and the tool pressure both act in the same direction.
To vary the length of stroke of s pin a is so attached to wheel d that it may be adjusted in its distance from the centre of d.
The Whitworth quick-return motion is represented in Fig. 1551. At p is the pinion receiving motion from the cone pulley or driving pulley of the machine and imparting motion to the gear-wheel g, whose bearing is denoted by the dotted circle b. Through b passes a shaft c, which is eccentric to b and carries at its end a piece a in which is a slot to receive the pin x, which drives rod r whose end z is attached to the ram of the machine. At d is a pin fast in gear-wheel g and passing into a slot in a.
Taking the position the parts occupy in the figures, and it is seen that the axis of b is the centre of motion of g and is the fulcrum from which the pin d is driven, the power being delivered at x. The path of motion of the driving pin d is denoted by the dotted circle h′, and it is apparent that as it moves from the position shown in the figure it recedes from the axis of c, and as the motion of g is uniform in velocity therefore d will move a faster while moving below the line m than it will while moving above it, thus giving a quick return, because the cutting stroke of the ram occurs while d is above the line m and the return stroke occurs while d is below m.
In some constructions the pin x and pin d work in opposite ends of the piece a, as shown in Fig. 1552. This, however, is an undesirable construction because the shaft c becomes the fulcrum, and as the power and resistance are on opposite ends of the lever a, the wheel g is therefore forced against its bearing, and this induces unnecessary friction and wear.
We may now consider the tool motion given by other kinds of slide operating mechanism.
In Fig. 1553 is a diagram of the tool motion given when the slide is operated by a simple crank c, the thickened line r[I-401] representing the rod actuating the slide and line on the line of motion of the cutting tool. The circle h denotes the path of revolution of the crank pin, and the black dots 1, 2, 3, 4, &c., equidistant positions of the crank pin.
Line m represents the path of motion of the cutting tool.
If a pair of compasses be set to the full length of the thick line r, that is from the centre of the crank pin to end b of line r, and these compasses be then applied to the centre of crank pin position 1, and to the line m, they will meet m at a point denoted by line a, which will, therefore, represent the position of the tool point when the crank pin was in position 1. To find how far the tool point is moved while the crank pin moves from position 1 to position 2, we place the compass point on the centre of crank pin position 2 and mark line b. For crank position 3 we have by the same process line c, and so on, the twelve lines from a to l representing crank positions from 1 to 12.
Now let it be noted that since the path of the crank pin is a circle, the tool point will on the backward stroke occupy the same position when the crank pin is at corresponding positions on the forward and backward strokes. For example, when the crank pin is in position 7 the tool point will be at point g on the forward stroke, and when the crank pin is in position 17 the tool will be at point g on the backward stroke, as will be found by trial with the compasses; and it follows that the lines a, b, c, &c., for the forward stroke will also serve for the backward one, which enables us to keep the engraving clear, by marking the first seven positions on one side of line m, and the remaining five on the other side of m, as has been done in the figure.
Obviously the distances apart of the lines a, b, c, d, &c., represent the amount of tool motion during equal periods of time, because the motion of the crank pin being uniform it will move from position 1 to position 2 in the same time as it moves from position 2 to position 3, and it follows that the cutting speed of the tool varies at every instant in its path across the work, and also that since the crank pin operates during a full one-half of its revolution to push the tool forward, and during a full one-half to pull it backward, therefore the speed of the two strokes are equal.
We may now plot out the motion of the link quick return that was shown in Fig. 1550, the dotted circle h′, in Fig. 1554, representing the path of the pin a, and the arc h representing the line of motion of the upper end of link l, and lines n, o, its centre line at the extreme ends of its vibrating motion. In Fig. 1554 the letters of reference refer to the same parts as those in Fig. 1550. We divide the circle h′ of pin motion into twenty-four equidistant parts marked by dots, and through these we draw lines radiating from centre c and cutting arc h, obtaining on the arc h the various positions for end z of rod r, these positions being marked respectively 1, 2, 3, 4, &c., up to 24. With a pair of compasses set to the length of rod r from 1 on h, as a centre, we mark on the line of motion of the slide line a, which shows where the other end of the rod r will be (or, in other words, it shows the position of bolt b in Fig. 1550), when the centre of a, Fig. 1550, is in position 1, Fig. 1554.
From 2 on arc h, we mark with the compasses line b on line m, showing that while the pin moved from 1 to 2, the rod r would move slide s, Fig. 1550, from a to b, in Fig. 1554. From 3 we mark c, and so on, all these marks being above the horizontal line m, representing the line of motion, and being for the forward stroke. For the backward stroke we draw the dotted line from position 17 up to arc h, and with the compasses at 17 mark a line beneath the line m of motion, pursuing the same course for all the other pin positions, as 18, 19, &c., until the pin arrives again at position 24, and the link at o, and has made a full revolution, and we shall have the motion of the forward stroke above and that of the backward one below the line of motion of the slide.
On comparing this with the crank and with the Whitworth motion hereafter described, we find that the cutting speed is much more uniform than either of them, the irregularity of motion occurring mainly at the two ends of the stroke.
In Fig. 1555 we have the motion of the Whitworth quick return described in Fig. 1551, h′ representing the path of motion of the driving-pin d about the centre of b, and h′ the path of motion of x about the centre c, these two centres corresponding to the centres of b and c respectively in Fig. 1551. Let the line m correspond to the line of motion m in Fig. 1551. Now, since pin d, Fig. 1551, drives, and since its speed of revolution is uniform, we divide its circle of motion h′ into twenty-four equal divisions, and by drawing lines radiating from centre b, and passing through the lines of division on h′, we get on circle h twenty-four positions for the pin x in Fig. 1551. Then setting the compasses to the[I-402] length of the rod (r, Fig. 1551), we mark from position 1 on circle h as a centre, line a; from position 2 on h we mark line b, and so on for the whole twenty-four positions on circle h, obtaining from a to n for the forward, and from n to y for the motion during the backward stroke. Suppose, now, that the mechanism remaining precisely the same as before, the line m of motion be in a line with the centres c, b, instead of at a right angle to it, as it is in Fig. 1551, and the motion under this new condition will be as in Fig. 1556, the process for finding the amount of motion along m from the motion around h being precisely as before.
The iron planing machine, or iron planer as it is termed in the United States, is employed to plane such surfaces as may be operated upon by traversing a work table back and forth in a straight line beneath the cutting tool. It consists essentially of a frame or bed a, Fig. 1557, provided on its upper surface with guideways, on which a work carrying table t may be moved by suitable mechanism back and forth in a straight line.
This frame or bed carries two upright frames or stanchions b, which support a cross-bar or slide c, to which is fitted a head which carries the cutting tool.
To enable the setting of the tool at such a height from the table as the height of the work may require, the cross slide c may be raised higher upon the uprights b by means of the bevel gears f, g, h, and t, the latter being on a shaft at the top of the machine, and operating the former, which are on vertical screws n, which pass down through nuts that are fast upon the cross slide c.
To secure c at its adjusted height, the uprights are provided with T-shaped slots h h, and bolts pass through c, their heads being in the T-grooves, and their nuts exposed so that a wrench may be applied to them.
The faces of the cross slide c are parallel one to the other, and stand at a right angle to the V-guideways on which the work table (or platen as it is sometimes termed) slides; hence the cross slide will, if the table is planed true or parallel with this cross slide, be parallel with the table at whatever height above the table it is set, providing that the elevating screws, when operated, lift each end of c equally.
The construction of the head d corresponds to that of the head shown in Figs. 1497 and 1498 for a shaper, except that in this case the swivel head is secured to a saddle that slides along c, being provided with a nut operated by a feed screw j, which moves d along c.
The mechanism for operating the work table or platen t is as follows:—p p′ are two loose pulleys and p′′ is a driving pulley fast on the same shaft. This shaft drives, within the casing at q, a worm operating a worm-wheel, which actuates inside the frame a and beneath the work table a train of gears, the last of which gears with a rack, provided on the underneath side of the table.
The revolutions of this last wheel obviously cause the work table to slide back and forth while resting on the V-guideways provided on top of the frame a, the direction of table motion being governed by the direction in which the wheel revolves.
This direction is periodically reversed as follows:—The pulley p is driven by a crossed belt, while pulley p′ is driven by an open or uncrossed one, hence the direction of revolution of the driving pulley p′′ will be in one direction if the belt is moved from p to p′′, and in the other if the belt is moved from p′ to p′′. Mechanism is provided whereby first one and then the other of these belts is moved so as to pass over upon p′′ and drive it, the construction being as follows:—
To the edge of the work table there is fixed a stop r, which as the table traverses to the right meets and moves a lever arm s, which through the medium of a second lever operates the rod x, which operates a lever u, which has a slot through which one of the driving belts passes. The lever u operates a second lever w on the other side of the pulleys, and this lever also has a slot through which the other driving belt passes.
When the stop r moves the lever arm s levers u and w therefore move their respective belts, one moving from the tight pulley p′′ to a loose one as p, and the other moving its belt from the loose pulley as p′ to the tight one p′′, and as the directions of belt motions are opposite the direction of revolution of p′′ is reversed by the change of belt operating it. There are two of the stops r, one on each side of the lever s, hence one of these stops moves the lever s from left to right and the other from right to left.
Suppose, then, that the table is moving from right to left, which is its cutting stroke, and the driving belt will be on the pulley p′′ while the other belt will be on pulley p. Then as the stop r moves s and operates x the arm u will move its belt from p′′ to p′, and arm w will move its belt from p to p′′, reversing the direction of motion of p′′, and therefore causing the table t to move from left to right, which it will continue to do until the other stop corresponding to r meets s and moves it from right to left, when the belts will be shifted back again. The stroke of the table, therefore, is determined by the distance apart of the stops r, and these may be adjusted as follows:—
They are carried by bolts whose heads fit in a dovetail groove z provided along the edge of the table, and by loosening a set screw may therefore be moved to any required location along the bed.
To give the table a quick return so that less time may be occupied for the non-cutting stroke, all that is necessary is to make the countershaft pulley that operates during the back traverse of larger diameter than that which drives during the cutting traverse of the table.
In order that one belt may have passed completely off the driving pulley p′′ before the other moves on it the lever motions of u and w are so arranged that when the belt is moving from p′′ to p lever u moves in advance of lever w, while when the other belt is being moved from p′′ to p′ lever w moves in advance of lever u.
To enable the work table to remain at rest, one driving belt must be upon p and the other upon p′, which is the case when the lever arm s is in mid position, and to enable it to be moved to this position it is provided with a handle k forming part of lever s.
[I-403]To cause the tool to be fed to its cut before it meets the cut and thus prevent it from rubbing against the side of the cut, as was described with reference to Fig. 1503, the feed takes place when the table motion is reversed from the back or return stroke to the cutting or forward stroke by the following mechanism:—
At a is a rack that is operated simultaneously with s and by the same stop r. This rack operates a pinion b, which rotates the slotted piece c, in which is a block that operates the vertical rod d, which is attached to a segmental rack e, which in turn operates a pinion which may be placed either upon the cross-feed screw j, or upon the rod above it; the latter operates the vertical feed of the tool through mechanism within the head d and not therefore shown in the engraving. Thus the self-acting tool feed may take place vertically or across the work table at will by simply placing the pinion upon the cross-feed screw or upon the feed rod, as the case may be.
Fig. 1558 represents a planer by David W. Pond, of Worcester, Massachusetts, in which the rod x is connected direct from s to a pivoted piece y in which is a cam-shaped slot through which pass pins from the belt-moving arms u and w. The shape of the slot in y is such as to move the belt-moving arms one in advance of the other, as described with reference to Fig. 1566.
The feed motions are here operated by a disk c, which is actuated one-half a revolution when the work table is reversed. This disk is provided on its face with a slide-way in which is a sliding block that may be moved to or from the centre of c by the screw shown, thus varying at will the amount of stroke imparted to the rod which moves the rack by means of which the feed is actuated through the medium of the gear-wheels at f. The handle g is for operating the feed screw when the self-acting feed is thrown out of operation, which is done by means of a catch corresponding in its action to the catch shown in Fig. 1501. s and s′ are in one piece, s′ being to move the two driving belts on to the loose pulleys so as to stop the work table from traversing.
The size of a planer is designated from the size of work it will plane, and this is determined by the greatest height the tool can be raised above the planer table, the width between the stanchions, and the length of table motion that can be utilized while the tool is cutting; which length is less than the full length of table stroke, because in the first place it is undesirable that the rack should pass so far over the driving wheel or pinion that any of the teeth disengage, and, furthermore, a certain amount of table motion is necessary to reverse after the work has passed the tool at the end of each stroke.
Fig. 1559 represents a method employed in some English planing machines to drive the work table and to give it a quick return motion. In this design but one belt is used, being shifted from pulley a, which operates the table for the cutting stroke, to pulley j, which actuates the table for the return stroke. The middle pulley k is loose upon shaft b, as is also pulley j, which is in one piece with pinion j′. Motion from a is conveyed through shaft b and through gear c, d, e to f, and is reduced by reason of the[I-404] difference in diameter between d and e and between f and g. Motion for the quick return passes from j direct to f without being reduced by gears d, e, hence the difference between the cutting speed and the speed of the return stroke is proportionate to the relative diameters or numbers of teeth in d and e, and as e contains 12 and d 20 teeth, it follows that the return is 8⁄12 quicker than the cutting stroke.
In this design the belt is for each reversal of table motion moved across the loose pulley k from one driving pulley to the other, and therefore across two pulleys instead of across the width of one pulley only as in American machines.
In American practice the rack r, Fig. 1559, is driven by a large gear instead of by a pinion, so that the strain on the last driving shaft s, in Fig. 1560, shall be less, and also the wheel less liable to vibration than a pinion would be, because in the one case, as in Fig. 1559, the power is transmitted through the shaft, while in the other, as in Fig. 1560, it is transmitted through the wheel from the pinion p to the rack r.
| VOL. I. | EXAMPLES OF PLANING MACHINES. | PLATE XVII. | |
 |
|||
| Fig. 1561. | |||
 |
|||
| Fig. 1563. | |||
Fig. 1561 represents a planer, designed for use in situations where a solid foundation cannot be obtained, hence the bed is made of unusual depth to give sufficient strength and make it firm and solid on unstable foundations, such as the floors in the upper stories of buildings. In all other respects the machine answers to the general features of improved planing machines.
As the sizes of planing machines increase, they are given increased tool-carrying heads; thus, Fig. 1562 represents a class in which two sliding heads are used, so that two cutting tools may operate simultaneously. Each head, however, is capable of independent operation; hence, one tool may be actuated automatically along the cross slide to plane the surfaces of the work, while the other may be used to carry a cut down the sides of the work, or one tool may take the roughing and the other follow with the finishing cut, thus doubling the capacity of the machine.
In other large planers the uprights are provided with separate heads as shown in the planer in Fig. 1563, in which each upright is provided with a head shown below the cross slide. Either or both these heads may be employed to operate upon the vertical side faces of work, while the upper surface of the work is being planed.
The automatic feed motion for these side heads is obtained in the Sellers machine from a rod actuated from the disk or plate in figure, this rod passing through the bed and operating each feed by a pawl and feed wheel, the latter being clearly seen in the figure.
To enable the amount of feed to be varied the feed rod is driven by a stud capable of adjustment in a slot in the disk.
Fig. 1563 represents a planing machine designed by Francis Berry & Sons, of Lowerby Bridge, England. The bed of the machine is, it will be seen, L-shaped, the extension being to[I-405] provide a slide to carry the right-hand standard, and permit of its adjustment at distances varying from the left-hand standard to suit the width of the work. This obviously increases the capacity of the machine, and is a desirable feature in the large planers used upon the large parts of marine engines.
Rotary Planing Machine.—Fig. 1564 is a rotary planing machine. The tools are here carried on a revolving disk or cutter head, whose spindle bearing is in an upper slide with 2 inches of motion to move the bearing endways, and thereby adjust the depth of cut by means of a screw. The carriage on which the spindle bearing is mounted is traversed back and forth (by a worm and worm-wheel at the back of the machine) along a horizontal slide, which, having a circular base, may be set either parallel to the fixed work table or at any required angle thereto.
By traversing the cutter head instead of the work, less floor space is occupied, because the head requires to travel the length of the work only, whereas when the work moves to the cut it is all on one side of the cutter at the beginning of the cut, and all on the other at the end, hence the amount of floor space required is equal to twice the length of the work.
The disk or cutter head is in one piece with the spindle, and carries twenty-four cutters arranged in a circle of 36 inches in diameter. These cutters are made from the square bar, and each cutting point should have the same form and position as referred to one face, side, or square of the bar, so that each cutter may take its proper share of the cutting duty; and it is obvious that all the cutting edges must project an equal distance from the face of the disk, in which case smooth work will be produced with a feed suitable for the whole twenty-four cutters, whereas if a tool cuts deeper than the others it will leave a groove at each passage across the work, unless the feed were sufficiently fine for that one tool, in which case the advantage of the number of tools is lost.
The cutters may be ground while in their places in the head by a suitable emery-wheel attachment, or if ground separately they must be very carefully set by a gauge applied to the face of the disk.
Fig. 1565 represents a planer by William Sellers and Co., of Philadelphia, Pennsylvania. This planer is provided with an automatic feed to the sliding head, both horizontally and vertically, and with mechanism which lifts the apron, and therefore the cutting tool, during the backward stroke of the work table, and thus prevents the abrasion of the tool edge that occurs when the tool is allowed to drag during the return stroke. The machine is also provided with a quick return motion, and in the larger sizes with other conveniences to be described hereafter.
The platen or table is driven by a worm set at such an angle to the table rack as to enable the teeth of the rack to stand at a right angle to the table length, and as a result the line of thrust between the worm and the rack is parallel to the V-guideways, which prevents wear between the Vs of the table and of the bed.
The driving pulleys are set at a right angle to the length of the machine, their planes of revolution being, therefore, parallel to the plane of revolution of the line or driving shaft overhead, and parallel with the lathes and other machines driven from the same line of shafting, thus taking up less floor space, while the passage ways between the different lines of machines is less obstructed.
By setting the worm driving shaft at an angle the teeth of the worm rotate in a plane at a right angle to the length of the work-table rack, and as a result the teeth of the worm have contact across the full width of the rack teeth instead of in the middle only, as is the case when the axis of a worm is at a right angle to the axis of the wheel or rack that it drives.
Furthermore, by inclining the worm shaft at an angle the teeth of the rack may be straight (and not curved to suit the curvature of the worm after the manner of worm-wheels), because the contact between the worm and rack teeth begins at one side of the rack and passes by a rolling motion to the other, after the manner and possessing the advantages of Hook’s gearing as described in the remarks made with reference to gear-wheel teeth.
By inclining the worm shaft, however, the side thrust incidental to Hook’s gearing is avoided, the pressure of contact of tooth upon tooth being in the same direction and in line with the rack motion. As the contact between the worm teeth and the rack is uniform in amount and is also continuous, a very smooth and uniform motion is imparted to the work table, and the vibration usually accompanying the action of spur-gearing is avoided.
The worm has four separate spirals or teeth, hence the table rack is moved four teeth at each worm revolution, and a quick belt motion is obtained by the employment of pulleys of large diameter.
It is desirable that the belt motion of a planing machine be as quick as the conditions will permit, because the amount of power necessary to drive the machine can thus be obtained by a narrower belt, it being obvious that since the driving power of the belt is the product of its tension and velocity the greater the velocity the less the amount of tension may be to transmit a given amount of power.
The mechanism for shifting the belt to reverse the direction of table motion is shown in Fig. 1566 removed from all the other mechanism.
To the bracket or arm b are pivoted the arms or belt guides c and d and the piece g. In the position occupied by the parts in the figure the belt for the forward or cutting stroke would be upon the loose pulley p′, and that for the quick return stroke would be upon the loose pulley p, hence the machine table would remain at rest. But suppose the rod f be moved by hand in the direction of arrow f, then g would be moved upon its pivot x, and its lug h would meet the jaw i of c, moving c in the direction of arrow a, and therefore carrying the belt from loose pulley p′ on to the driving pulley p′′, which would start the machine work table, causing it to move in the direction of arrow w until such time as the stop a meets the lug r, operating lever e and moving rod f in the direction of arrow d. This would move g, causing its lug h to meet the jaw j, which would move c from p′′ back to the position it occupies in the figure, and as the motion of g continued its shoulder at g′ would meet the shoulder or lug t of k (the latter being connected to d) and move arm d in the direction of b, and therefore carrying the crossed belt upon p, and causing the machine table to run backward, which it would do at a greater speed than during the cutting traverse, because of the overhead pulley on the countershaft being of greater diameter than that for the cutting stroke.
It is obvious that since each belt passes from its loose pulley to the fast one, the width of the overhead or countershaft pulleys must be twice as wide as the belt, and also that to reverse the direction of pulley revolution one driving belt must be crossed; and as on the countershaft the smallest pulley is that for driving the cutting stroke, its belt is made the crossed one, so as to cause it to envelop as much of the pulley circumference as possible, and thereby increase its driving power. The arrangement of the countershaft pulleys and belts is shown in Fig. 1567, in which s is the countershaft and n, o the fast and loose pulleys for the belt from the line shaft pulley; q′ is the pulley for operating the table on the cutting stroke (with the crossed belt), while q is the pulley for operating the table on its return stroke. The difference in the speed of the table during the two strokes is obviously in the same proportions as the diameters of pulleys q′ and q.
The feed rod, and feed screw, and rope for lifting the tool on the back stroke are operated as follows:—
Fig. 1568 is an end view of the mechanism viewed from the front of the machine, and Fig. 1569 is a side view of the same.
The shaft of the driving pulleys (p p′ and p′′, Fig. 1567) drives a pinion operating the gear wheel w, upon the face of which is a serrated internal wheel answering to a ratchet wheel, and with which a pawl engages each time the direction of pulley revolution (or, which is the same thing, the direction of motion w) reverses, and causes the pawl and the shaft, to which the plate p, Fig. 1569, is fast, to make one-half a revolution, when the pawl disengages and all parts save the wheel w come to rest.
From this plate p the feed motions are actuated, and the tool is lifted during the back traverse of the work table by the following mechanisms.
Referring to Fig. 1570, upon the plate p is pivoted a lever q, carrying a universal joint at z, and a nut pivoted at v, and it is obvious that at each half-revolution of p, the rod r is moved vertically.[I-408] This rod connects to a universal joint j (shown in Fig. 1571) that is pivoted in a toothed segment (k, in the same figure) which engages with a pinion on the feed screw, this pinion being provided with a ratchet and feed pawl (of the usual construction) for reversing the direction of the feed or throwing it out of action.
The amount of feed is regulated as follows:—
Referring to Figs. 1569 and 1570, the amount of vertical motion of rod r is obviously determined by the distance of the universal joint z from the centre of the plate p, and this is set by operating the hand wheel t, which revolves the screw y in the nut v.
For lifting the tool during the return motion of the work and work table, there is provided in the plate p, Fig. 1570, a pin which actuates the rod b, which in turn actuates the grooved segment c.
From this segment a cord is stretched passing over the grooved pulley d, Fig. 1571, thence over pulley e, and after taking a turn around the pulley f, Fig. 1571, it passes to the other end of the cross slide, where it is secured.
This pulley f is therefore revolved at each motion of the plate p, Figs. 1569 or 1570, or in other words each time the work table reverses its motion.
In reference to Figs. 1571 and 1572, f, Fig. 1571, is fast upon a pin g, at whose other end is a pinion operating a gear-wheel h. Upon the face of this gear-wheel is secured a steel plate shown at m in Fig. 1572, which is a vertical section of the sliding head. In a cam groove in m, projects a pin that is secured to the sleeve n, which envelops the vertical feed screw o. This sleeve n has frictional contact at p with the bar q, whose lower end receives the bell crank r, which on each return stroke is depressed, and thus moves the tool apron s, and with it the tool, which is therefore relieved from contact with the cut upon the work.
The self-acting vertical feed is actuated as follows:—
Referring to Figs. 1571 and 1572 the gear segment k operates a pinion upon the squared end of the feed rod l, this pinion l having the usual pawl and ratchet for reversing the direction of rod revolution.
The splined feed rod l actuates the bevel pinion m, which is in gear with bevel pinion n, the latter driving pinion p, which is threaded to receive the vertical feed screw o; hence when p is revolved it moves the feed screw o endways, and this moves the vertical slide r upon which is the apron box t and the apron s. To prevent the possibility of the friction of the threads causing the feed screw o to revolve with the pinion p, the journal e of the feed screw o is made shorter than its bearing in r, so that the nut f may be used to secure the feed screw o to the slide r.
Planer Sliding Heads.—In order that the best work may be produced, it is essential that the sliding head of a planer or planing machine be constructed as rigid as possible, and it follows that the slides and slideways should be of that form that will suffer the least from wear, resist the tool strain as directly as possible, and at the same time enable the taking up of any wear that may occur from the constant use of the parts.
Between the tool point that receives the cutting strain and the cross bar or cross slide that resists it there are the pivoted joint of the apron, the sliding joint of the vertical feed, and the sliding joint of the saddle upon the cross slide, and it is difficult to maintain a sliding fit without some movements or spring to the parts, especially when, as in the case of a planer head, the pressure on the tool point is at considerable leverage to the sliding surfaces, thus augmenting the strain due to the cut.
The wear on the cross slide is greater at and towards the middle than at the ends, but it is also greater at the end nearest to the operator than at the other end, because work that is narrower than the width of the planing machine table is usually chucked on the side nearest to the operator or near the middle of the table width, because it is easier to chuck it there and more convenient to set the tool and watch the cut, for the reason that the means for stopping and starting the machine, and for pulling the feed motions in and out of operation, are on that side.
The form of cross bar usually employed in the United States is represented in Fig. 1573, and it is clear that the pressure of the cut is in the direction of the arrow c, and that the fulcrum off which the strain will act on the cross bar is at its lowest point d, tending to pull the top of the saddle or slider in the direction of arrow e, which is directly resisted by the vertical face of the gib, while the horizontal face f of the gib directly resists the tendency of the saddle to fall vertically, and, therefore, the amount of looseness that may occur by reason of the wear cannot exceed the amount of metal lost by the wear, which may be taken up as far as possible by means of the screws a and b, which thread through the saddle and abut against the gib. The gib is adjusted by these screws to fit to the least worn and therefore, the tightest[I-409] part of the cross bar slideway, and the saddle is more loosely held at other parts of the cross bar in proportion as its slideway is worn.
In this construction the faces of the saddle are brought to bear over the whole area of the slideways surface of the cross bar, because the bevel at g brings the two faces at m into contact, and the set-screw b brings the faces in together. Instead of the screws a and b having slotted heads for a screw driver, however, it is preferable to provide square-headed screws, having check nuts, as in Fig. 1574, so that after the adjustment is made the parts may be firmly locked by the check nuts, and there will be no danger of the adjustment altering.
The wear between the slider and the raised slideways s is taken up by gibs and screws corresponding to those at a and c in the Fig. 1575, and concerning these gibs and screws J. Richards has pointed out that two methods may be employed in their construction, these two methods being illustrated in Figs. 1575 and 1576, which are taken from “Engineering.”
In Fig. 1575 the end s of the adjustment screw a is plain, and is let into the gib c abutting against a flat seat, and as a result while the screw pressure forces the gib c against the bevelled edge of the slideway it does not act to draw the surfaces together at m m as it should do. This may be remedied by making the point of the screw of such a cone that it will bed fair against gib c, without passing into a recess, the construction being as in Fig. 1576, in which case the screw point forces the gib flat against the bevelled face and there is no tendency for the gib to pass down into the corner e, Fig. 1575, while the pressure on the screw point acts to force the slide a down upon the slideway, thus giving contact at m m.
The bearing area of such screw points is, however, so small that the pressure due to the tool cut is liable to cause the screw to indent the gib and thus destroy the adjustment, and on this account a wedge such as shown in Fig. 1577 is preferable, being operated endwise to take up the wear by means of a screw passing through a lug at the outer or exposed end of the wedge.
The corners at i, Figs. 1575 and 1576, are sometimes planed out to the dotted lines, but this does not increase the bearing area between the gib c and the slide, while it obviously weakens the slider and renders it more liable to spring under heavy tool cuts.
Fig. 1578 represents a form of cross bar and gib found in many English and in some American planing machines. In this case the strain due to the cut is resisted directly by the vertical face of the top slide of the cross bar, the gib being a triangular piece set up by the screws at a, and the wear is diminished because of[I-410] the increased wearing surface of the gib due to its lower face being diagonal.
On the other hand, however, this diagonal surface does not directly resist the falling of the saddle from wear, and furthermore in taking up the wear the vertical face of the saddle is relieved from contact with the vertical face of the cross bar, because the screws a when set up move the top of the saddle away from the cross bar, whereas in Fig. 1573, setting up screw b brings the saddle back upon the vertical face of the cross bar slideway.
Fig. 1579 is a front view, and Fig. 1580 a sectional top view, of a sunk vertical slide, corresponding to that shown in Figs. 1573 and 1578, but in this case the gib has a tongue t, closely fitted into a recess or channel in the vertical slider s, and to allow room for adjustment, the channel is made somewhat deeper than the tongue requires when newly fitted. The adjustment is effected by means of two sets of screws, a and b, of which the former, being tapped into the gib, serve to tighten, and the latter, being tapped into the slide, serve to loosen the gib. By thus acting in opposite directions the screws serve to check each other, holding the gib rigidly in place. To insure a close contact of the gib against the vertical surface of the slide, the screws b are placed in a line slightly outside of the line of the screws a.
Fig. 1581 represents a similar construction when the slideways on the swing frame project outwards, instead of being sunk within that frame.
Fig. 1582 represents the construction of the Pratt & Whitney Company’s planer head, in which the swivel head instead of pivoting upon a central pin and being locked in position by bolts, whose nuts project outside and on the front face of the swing frame, is constructed as follows:—
A circular dovetail recess in the saddle receives a corresponding dovetail projection on the swivel head or swing frame, and the two are secured together at that point by a set-screw a. In addition to this the upper edge b of the saddle is an arc of a circle of which the centre is the centre of the dovetail groove, and a clamp is employed to fasten the swivel head to the saddle, being held to that head by a bolt, and therefore swinging with it. Thus the swivel head is secured to its saddle at its upper edge, as well as at its centre, which affords a better support.
The tool box is pivoted upon the vertical slider, and is secured in its adjusted position by the bolts n in Fig. 1573, the object of swinging it being to enable the tool to be lifted on the back stroke and clear the cut, when cutting vertical faces, as was explained with reference to shaping machines.
The tool apron is in American practice pivoted between two jaws, which prevent its motion sideways, and to prevent any play[I-411] or lost motion that might arise from the wear of the taper pivoting pin b, in Fig. 1583, the apron beds upon a bevel as at a, so that in falling to its seat it will be pulled down, taking up any lost motion upon b.
The bevel at a would also prevent any side motion to the apron should wear occur between it and the jaws. In addition to this bevel, however, there may be employed two vertical bevels c in the top view in Fig. 1584. In English practice, and especially upon large planing machines, the apron is sometimes made to embrace or fit the outsides of the tool box, as in Fig. 1585, the object being to spread the bearings as wide apart as possible, and thus diminish the effect of any lost motion or wear of the pivoting pin, and to enable the tool post or holder to be set to the extreme edge of the tool box as shown in the figure.
It is desirable that the tool apron bed as firmly as possible back against its seat in the tool box, and this end is much more effectively secured when it is pivoted as far back as possible, as in Fig. 1585, because in that case nearly all the weight of the apron, as well as that of the tool and its clamp, acts to seat the apron, whereas when the pivot is more in front, as m, in Fig. 1573, it is the weight of the tool post and tool only that acts to keep the apron seated.
In small planing machines it is a great advantage to provide an extra apron carrying two tool posts, as in Fig. 1586, so that in planing a number of pieces, that are to be of the same dimension, one tool may be used for roughing and one for finishing the work. The tools should be wider apart than the width of the work, so that the finishing tool will not come into operation until after the roughing tool has carried its cut across.
When the roughing tool has become dulled it should, after being ground up, be set to the last roughing cut taken, so that it will leave the same amount of finishing cut as before.
The advantage of this system is that the finishing tool will last to finish a great many pieces without being disturbed, and as a result the trouble of setting its cut for each piece is avoided; on which account all the pieces are sure to be cut to the same dimension without any further measuring than is necessary for the first piece, whereas if one tool only is used it rapidly dulls from the roughing cut, and will not cut sufficiently smooth for the finishing one, and must therefore be more frequently ground up to resharpen it, while it must be accurately set for each finishing cut. A double tool apron of this kind is especially serviceable upon such work as planing large nuts, for it will save half the time and give more accurate work.
In some planing machines, and notably those made by Sir Joseph Whitworth, a swiveling tool holder is made so that at each end of the stroke the cutting tool makes half a revolution, and may therefore be used to cut during both strokes of the planer table. A device answering this purpose is shown in Fig. 1587. The tool-holding box is pivoted upon a pin a, and has attached to[I-412] it a segment of a circular rack or worm-wheel, operated by a worm upon a shaft having at its upper end the pulley shown, so that by operating this pulley, part of a revolution at the end of each work-table stroke, one or the other of the two tools shown in the tool box, is brought into position to carry the cut along. Thus two tools are placed back to back, and it is obvious that when the tool box is moved to the right, the front tool is brought into position, while when it is moved to the left, the back or right-hand tool is brought into position to cut, the other tool being raised clear of the work.
The objections to either revolving one tool or using two tools so as to cut on both strokes are twofold: first, the tools are difficult to set correctly; and, secondly, the device cannot be used upon vertical faces or those at an angle, or in other words, can only be used upon surfaces that are nearly parallel to the surface of the work table.
Figs. 1588 and 1589 represent the sliding head of the large planer at the Washington Navy Yard, the sectional view, Fig. 1589, being taken on the line x x in Fig. 1588. c is the cross bar and s the saddle, f being the swing frame or fiddle, as some term it, and s′ the vertical slider; b is the tool box, and a the apron.
The wear of the cross slider is taken up by the set screws a, and that of the vertical slide by the screws b.
The graduations of the degrees of a circle for setting over the swing frame f, as is necessary when planing surfaces that are at an angle to the bed and to the cross slide, are marked on the face of the saddle, and the pointer (f, Fig. 1578) is fastened to the edge of the swing frame. When the swing frame is vertical the pointer is at 90° on the graduated arc, which accords with English practice generally. In American practice, however, it is customary to mark the graduations on the edge of the swing frame as in Fig. 1590, so that the pointer stands at the zero point o when the swing frame is vertical, and the graduations are marked on the edge of the swing frame as shown, the zero line o being marked on the edge of the saddle.
In the English practice the swing frame is supposed to stand in its neutral or zero position when it is vertical, and all angles are assumed to be measured from this vertical zero line, so that if the index point be set to such figure upon the graduated arc as the angle of the work is to be to a vertical line, correct results will be obtained.
Thus in Fig. 1591 (which is from The American Machinist) the pointer is set to 40° and the bevelled face is cut to an angle of 40° with the vertical face as marked. But if the head be graduated as in Fig. 1592, the face of the planer table being taken as the zero line o, then the swing frame would require to be set over to 30°[I-413] out of its normal or neutral vertical position as is shown in figure, the bevelled face being at an angle of 50° from a vertical, and 40° from a horizontal line, hence the operator requires to consider whether the number of degrees of angle are marked on the drawing from a zero line that is vertical on one that is horizontal.
Referring again to Fig. 1588 the slots for the tool post extend fully across the apron, so that the tool posts may be set at any required point in the tool-box width, and the tool or tool holder may be set nearer to the edge of the tool box than is the case when fixed bolts, as in Fig. 1590, are used, because these bolts come in the way.
This is mainly important when the tool is required to carry a deep vertical cut, in which case it is important to keep the tool point as close in to the holder as possible so that it may not bend and spring from the pressure of the cut.
The tool or holder may be held still closer to the edge of the head, and therefore brought still closer to the work, when the apron embraces the outside of the tool box, as was shown in Fig. 1585, and referred to in connection therewith.
A sectional side view and a top view of Fig. 1588 through the centre of the head is given in Figs. 1595 and 1596, exposing the mechanism for the self-acting feed traverse, and for the vertical feed. For the feed traverse the feed screw (m, Fig. 1588) passes through the feed nut n. For the vertical feed the feed rod (n, Fig. 1588) drives a pair of bevel-gears at p, which drives a second pair at q, one of which is fast on a spindle which passes through the vertical feed screw, and is secured thereto by the set screw e. The object of this arrangement is that if the self-acting vertical feed should be in action and the tool or swing frame s′ should meet any undue obstruction, the set screw e will slip and the feed would stop, thus preventing any breakage to the gears at p or q. The feed screw is threaded into the top of s′. At e is the pin on which the tool box pivots to swing it at an angle.
The mechanism for actuating the cross-feed screw and the feed rod is shown in the top view, Fig. 1597, and the side view, Fig. 1598, in which a is a rod operated vertically and actuated from the stop (corresponding to stop r in Fig. 1558) that actuates the belt shifting gear. Upon a is the sleeve b, which actuates rod c, which operates the frame d. This frame is pivoted upon a stud which is secured to the cross bar c, and is secured by the nut at e. Frame d carries pawls f and g, the former of which engages gear-wheel h, which drives the pinion n, Fig. 1598, that is fast on the feed rod, while the latter drives the gear k, which in turn drives pinion p, which is fast upon the feed screw in Fig. 1588.
[I-414]The feeds are put into or thrown out of action as follows:—On the same shaft or pin as the pawls g and f, is secured a tongue t, Fig. 1599, whose end is wedge shaped and has a correspondingly shaped seat in a plate v, whose cylindrical stem passes into a recess provided in d, and is surrounded by a spiral spring which acts to force v outwards from the recess.
In the position shown in the figure the end of t is seated in the groove in v, and the pressure of the spring acts to hold t still and keep the pawl g from engaging with the teeth of gear-wheel h. But suppose the handle w (which is fast on the pawl g) is pulled upwards, and t will move downwards, disengaging from the groove in v, and the upper end of pawl g will engage with the teeth of h, actuating in the direction of the arrow during the upward motion of rod a, and thus actuating pinion n and putting the vertical feed in motion in one direction. When the rod a makes its downward stroke the pawl g will slip over the teeth of h, because there is nothing but the spiral spring to prevent the end of the pawl from slipping over these teeth. To place the vertical feed in action in the other direction, handle w is pressed downwards, causing the bottom end x of the pawl to engage with the teeth of h.
Planer Beds and Tables.—The general forms of the beds of small planers are such as in Figs. 1557 and 1558, and those of the larger sizes such as shown in Fig. 1563.
It is of the first importance that the V-guideways in these beds should be straight and true, and that the corresponding guides on the planer table should fit accurately to those in the bed; for which purpose it is necessary, if the greatest attainable accuracy is to be had, that the guideways in the bed first be made correct, and those on the table then fitted, using the bed to test them by.
The angle of these guides and guideways ranges from about 60° in the smallest sizes to about 110° in the largest sizes of planers. Whatever the angle may be, however, it is essential that all the angles be exactly equal, in order that the fit of the table may not be destroyed by the wear.
In addition to this, however, it is important that each side of the guides stand at an equal height, or otherwise the table will not fit, notwithstanding that all the angles may be equal.
Suppose, for example, that in Fig. 1600 all the sides are at an equal angle, but that side e was planed down to the dotted line e, then all the weight of the table would fall on side a, and, moreover, the table would be liable to rock in the guideways, for whenever the combined weight of the table and the pressure of the cut was greatest on the right-hand of the middle x of the table width and the feed was carried from right to left, then the table would move over, as shown exaggerated in Fig. 1601, because the weight would press guide g down into its guideways, and guide h would then rise up slightly and not fit on one side at all, while on the other side it would bear heaviest at point p. Great care is therefore necessary in planing and fitting these guides and ways, the processes for which are explained under the respective headings of “Examples in Planer Work,” and “Erecting Planers.”
In some designs the bed and table are provided with but one V-guideway, the other side of the table being supported on a flat side, and in yet another form the table is supported on two flat guideways.
Referring to the former the bearing surface of the V and of the[I-415] flat guide must be so proportioned to that of the V that the wear will let the table down equally, or otherwise it would become out of parallel with the cross slide, and would plane the work of unequal thickness across its width.
Referring to the second, which is illustrated in Fig. 1602, it possesses several disadvantages.
Thus, if there be four gibs as at a, b, and e, f, set up by their respective set-screws, the very means provided to take up the wear affords a means of setting the bed out of line, so that the slots in the table (and, therefore, the chucks fitting to these slots) will not be in the line of motion of the table, and the work depending upon these chucks will not be true. This may be avoided by taking up the wear on two edges only, as in Fig. 1603 at a, b, but in this case the bearing at e and f would eventually cease by reason of the wear.
Suppose, for example, that the pressure of the tool cut tends to throw the table in the direction of arrow j, and the surfaces at a and f resist the thrust and both will wear. But when the strain on the table is in the direction of arrow k, the surfaces b, e, will both wear; hence while the width apart of the table slides becomes greater, the width apart of the bed slideways wears less, and the fit cannot be maintained on the inner edges of the guideways. It is furthermore to be noted that with flat guideways the table will move sideways very easily, since there is nothing but the friction of the slides to prevent it, but in the case of V-guides the table must lift before it can move sideways; hence, it lies very firmly in its seat, its weight resisting any side motion.
It is found in practice that the wear of the guides and guideways in planer tables and beds is greatest at the ends, and the reason of this is as follows:—
In Fig. 1604 is a top view of a planer table, the cutting tool being assumed to be at t, and as the driving gear is at g forcing the table in the direction of the arrow a, and the resistance is at t, the tendency is to throw the table around in the direction of arrows b and c. When the tool is on the other side of the middle of the table width as at f, the tendency is to throw the table in the opposite direction as denoted by the arrows d and e, which obviously causes the most wear to be at the ends of the slides.
As the feed motions are placed on the right-hand side of the machines the operator stands on that side of the machine at x, and starts the cut from that side of the table; hence unless the work is placed in the middle of the table width, the wear will be most in the direction of arrows b and c.
The methods of fitting the guideways and guides of planer beds and tables is given in the examples of erecting.
A very good method of testing them, however, is as follows:—Suppose that we have in Fig. 1605 a plate that has been planed on both edges g, h, and that in consequence of a want of truth in the planer guideways edge g is rounding and edge h hollow, the plate being supposed to lie upon the planer table in the position in which it was planed.
Now, suppose that it be turned over on the planer, as in Fig. 1606, the rounding edge, instead of standing on the right-hand side of the planer table, will stand on the left-hand side, so that if that edge were planed again in its new position it would be made hollow instead of rounding in its length. It is obvious, therefore, that if a planed edge shows true when turned over on the planer table, the Vs of the planer are true, inasmuch as the table moves in a straight line in one direction, which is that affecting the truth of all surfaces of the work that are not parallel to the cross feed of the tool, or, what is the same thing, parallel to the surface of the planer table.
Planing Machine Tables.—In order that the guides on the table of a planer may not unduly wear, it is essential that they be kept well lubricated, which is a difficult matter when the table takes short strokes and has work upon it that takes a long time to perform, in which case it is necessary to stop the planing operations and run the work back so as to expose the guideways in the bed, so that they may be cleaned and oiled.
It will often occur that the work will not pass beneath the cross slide, and in that case it should be raised out of the ways to enable[I-416] proper oiling, because insufficient lubrication frequently causes the guides and guideways to tear one another, or cut as it is commonly termed.
The means commonly employed for oiling planer Vs or guideways are as follows:—At the top of the guideways small grooves, g g, Fig. 1609, are provided, and at the bottom a groove x. In the guides on the table there are provided pockets or slots in which are pivoted pendulums of the form shown in Fig. 1607 at a. Each pendulum passes down to the bottom of groove x in which the oil lies, and is provided on each side with recesses e, which are also seen in the edge view on the right of the figure.
The pendulums are provided with a long slot to enable them when the table motion reverses to swing over and drag in the opposite direction (as shown in Fig. 1607); as they drag on the bottom of groove x of the bed they lift the oil it contains, which passes up the sides of the pendulum as denoted by the arrow, and into grooves provided on the surface of the table guide, as at h in Fig. 1608, in which v′ is the table guide, v the guideway in the bed, g oil grooves, (see sectional view, Fig. 1613), x the oil groove at the bottom of the bed v, and h h the oil grooves which receive the oil the pendulum lifts.
The oil grooves h on the table guide run into the grooves g in the V-guideway in the bed, hence grooves g g become filled with oil. But after the end of the table has passed and left the bed v exposed, the oil flows out of grooves g down the sides of the guideway, and constant lubrication is thus afforded at all times when the stroke of the table is sufficient to enable the pendulums to force the oil sufficiently far along oil way h. When the table reverses the pendulum will swing over and lift the oil up into grooves or oil ways h′.
Another and excellent method of oiling, also invented by Mr. Hugh Thomas, of New York, is shown in Figs. 1609 and 1610, in which p represents an oiling roll or wheel, V-shaped, to correspond to the shape of the Vs. This roll is laced with cotton wick or braid, as shown by the dark zigzag lines, and is carried in a frame f, capable of sliding vertically in a box c, which is set in a pocket in the bed v, and contains oil. By means of a screw s, the roll p is set to touch the face of the table V, and the friction between the roll and the V, as the table traverses, rotates the roll, which carries up the oil and lubricates the table V over its whole surface. The dust, &c., that may get into the oil settles in the bottom of the box c, which can occasionally be cleaned out. In this case the oil is not only presented to the oil grooves (h, Fig. 1608), but spread out upon the Vs; but it is nevertheless advisable to have the grooves h so as to permit of an accumulation of oil that will aid in the distribution along the Vs of the bed.
This method of oiling has been adopted in some large and heavy planers built by R. Hoe & Co., and has been found to operate admirably, keeping the guides and guideways clean, bright, and well lubricated.
Mr. Thomas has also patented a system of forced oil circulation for large planers. In this system a pump p, Fig. 1611, draws the oil from the cellars c (which are usually provided on the ends of planer beds) and delivers it through pipes passing up to the sides of the Vs, thus affording a constant flow of oil. A reservoir at the foot of the pump enables the dirt, &c., in the oil to settle before it enters the pump, which can be operated from any desirable part of the planer mechanism. The pendulums are also used in connection with the forced circulation.
As the work is fastened to the upper face of a planing machine table either directly or through the intervention of chucking devices, the table must be pierced with holes and grooves to receive bolts or other appliances by means of which the work or chuck, as the case may be, may be secured.
For receiving the heads of bolts, T-shaped grooves running the full length of the table are provided, and in addition there are sometimes provided short T-grooves, to be shown presently.
For receiving stops and other similar chucking devices, the tables are provided with either round or square holes.
In Fig. 1612 is shown a section of a table provided with T-grooves and rows of round holes, a, b, c, d, e, which pass entirely through the table, and hence must not be placed so that they will let dirt fall through to the V-guides or the rack. Tables with this arrangement[I-417] of holes and grooves are usually used upon small planers in the United States, and sometimes to large ones also.
It is obvious that the dirt, fine cuttings, &c., will pass through the holes and may find its way to the V-guideways. Especially will this be the case when water is used upon the tool to take smooth cuts upon wrought iron and steel. To obviate this the construction shown in Fig. 1613 is employed.
Fig. 1613 represents a section of one guideway of a table and bed. On each side of the table V there is cut a groove leaving projecting ribs b, c, and whatever water, oil, or dirt may pass through the holes (Fig. 1612), will fall off these points b, c, Fig. 1613, and thus escape the guideways, while falling dust will be excluded by the wings b, c, from the Vs.
The capacity of a planer table may be increased by fitting thereto two supplementary short tables, as shown in Fig. 1614, several applications of its use being given with reference to examples in planer work. These supplementary tables are secured to the main table by set-screws at a, and have been found of great value for a large variety of work, especially upon planing machines in which the table width is considerably less than the width between the uprights or stanchions.
Fig. 1615 represents the arrangement of square holes and T-grooves employed upon large planers. The square holes are cast in the table, and are slightly tapered to receive taper plugs or stops against which the work may abut, or which may be used to wedge against, as will be hereafter described, one of these stops being shown at s in the figure.
The T-shaped slots f, g, h, are to receive the heads of bolts as shown in Fig. 1616. The bolt head is rounded at corners a, b, and the square under the head has the corresponding diagonal corners as c also rounded, so that the width of the head being slightly less than that of the slot it may be passed down in the slot and then given a quarter revolution in the direction of the arrow, causing the wings of the head to pass under the recess of the T-groove, as shown in Fig. 1617, which is a sectional end view of the groove with the bolt in place. The square corners at e and at f prevent the bolt from turning round more than the quarter revolution when screwing up the bolt nut, and when the nut is loosened a turn the bolt can be rotated a quarter revolution and lifted out of the groove.
Now it is obvious that these slots serve the same purpose as the longitudinal T-grooves, since they receive the bolt heads, and it might therefore appear that they could be dispensed with, but it is a great convenience to be able to adjust the position of the bolt across the table width, which cannot be done if longitudinal grooves only are employed. Indeed, it might easily occur that the longitudinal[I-418] grooves be covered by the work when the short transverse ones would serve to advantage, and in the wide range of work that large planers generally perform, it is desirable to give every means for disposing the bolts about the table to suit the size and shape of the work.
It is obvious that the form of bolt head shown in Fig. 1616 is equally applicable to the longitudinal grooves as to the cross slots, enabling the bolt to be inserted, notwithstanding that the work may cover the ends of the longitudinal slots.
The round holes a, b, c, &c., in Fig. 1612, are preferable to the square ones, inasmuch as they weaken the table less and are equally effective. Being drilled and reamed parallel the plugs that fit them may be passed through them to any desirable distance, whereas the square plugs being taper must be set down home in their holes, necessitating the use of plugs of varying length, so that when in their places they may stand at varying heights from the table, and thus suit different heights of work. Whatever kind of holes are used it is obvious that they must be arranged in line both lengthways of the table and across it, so that they will not come in the way of the ribs r, which are placed beneath it to strengthen it.
The longitudinal grooves are planed out to make them straight and true with the V-guides and guideways, so that chucking appliances fitting into the grooves may be known to be set true upon the table.
In Fig. 1618, for example, is shown an angle piece a having a projection fitting into a longitudinal groove, the screws whose heads are visible passing through a into nuts that are in the widened part of the groove, so that operating the screws secures a to the table. The vertical face of a being planed true, a piece of work, as a shaft s, may be known to be set in line with the table when it is clamped against a by clamps as at p, or by other holding devices. Angle pieces such as a are made of varying lengths and heights to suit different forms and sizes of work.
In some planing machine tables a V-groove is cut along the centre for the purpose of holding spindles to have featherways or splines cut in them, the method of chucking being shown in Fig. 1619. This, however, is not a good plan, as the bolts and plates are apt to bend the shaft out of straight, so that the groove cut in the work will not be straight when the spindle is removed from the clamp pressure. The proper method of chucking such work will, however, be given in connection with examples on planer work.
For the round holes in planer tables several kinds of plugs or stops are employed, the simplest of them being a plain cylindrical plug or stop.
Fig. 1620 represents a stop provided with a screw b. The stem a fits into the round holes, and the screw is operated to press against the work. By placing the screw at an angle, as shown, its pressure tends to force the work down upon the planer table.
A similar stop, termed a bunter screw, s, Fig. 1621, may be used in the longitudinal slots, the shape of its hook enabling it to be readily inserted and removed from the slot. These screws may be applied direct to the work when the circumstances will permit, or a wedge w may be interposed between the screw and the work, as shown.
Fig. 1622 represents a form of planer chuck used on the smaller sizes of planers, and commonly called planer centres. a is the base or frame bolted to the planer table at the lugs l; at b is a fixed head carrying what may be termed the live centre d, and c is a head similar to the tailstock of a lathe carrying a dead centre; f is an index plate having worm-teeth on its edge and being operated by the worm g. At s is a spring carrying at its end the pin for the index holes. To bring this pin opposite to the requisite circle of holes, the bolt holding s to a is eased back and s moved as required. On the live centre d is a clamp for securing the work or mandrel holding dog. Head c is split as shown, and is held to the surface of a by the bolt h, which is tapped into the metal on one side of the split.
It is obvious that polygons may be planed by placing the work between the centres and rotating it by means of g after each successive side of the polygon has been planed or shaped, the number[I-419] of sides being determined by the amount of rotation of the index plate.
Fig. 1623 shows a useful chuck for holding cylindrical work, such as rolls. The base is split at e, so that by means of the bolt and nut d the V-block a may be gripped firmly; b and c are screws for adjusting the height of the V-block a. At f is the bolt for clamping the chuck to the planer table, and g is a cap to clamp the work w in the block a. It will be seen that this chuck can be set for taper as well as parallel work.
Fig. 1624 represents a chucking device useful for supporting or packing up work, or for adjusting it in position ready to fasten it to the work table, it being obvious that its hollow seat at a enables it to set steadily upon the table, and that its screw affords a simple means of adjusting its height. It may also be used between the jaws of a connecting rod strap or other similar piece of work to support it, as in Fig. 1625, and prevent the jaws from springing together under the pressure of the tool cut.
Another and very useful device for this purpose is shown in Fig. 1626, consisting of a pair of inverted wedges, of which one is dovetailed into the other and having a screw to operate them endwise, the purpose being to hold the two jaws the proper distance apart and prevent their closure under pressure of the planer vice jaws. It is obvious that the device in Fig. 1625 is most useful for work that has not been faced between the jaws, because the device in Fig. 1626 would, upon rough work that is not true, be apt to spring the work true with the inside faces, which may not be true with the outside ones, and when the wedges were removed the jaws would spring back again, and the work performed while the inverted wedges were in place would no longer be true when they were removed.
Fig. 1627 represents a centre chuck to enable the cutting of spirals. The principle of the design is to rotate the work as it traverses, and this is accomplished as follows:—
Upon the bed of the machine alongside of the table is bolted the rack a a, into which gears the pinion b, which is fixed to the same shaft as the bevel-gear c, which meshes with the bevel-wheel d. Upon the same shaft as d is the face plate e, and in the spindle upon which d and e are fixed is a centre, so that the plate e answers to the face plate of a lathe. f is a bearing for the shaft carrying b and c, and g is a bearing carrying the spindle to which e and d are fixed. h is a standard carrying the screw and centre, shown at i, and hence answers to the tailstock of a lathe. k represents a frame or plate carrying the bearings f and g, and the standard h. l represents the table of the planing machine to which k is bolted. The reciprocating motion of the table l causes the pinion b to revolve upon the rack a a. The pinion b revolves c, which imparts its motion to d, and the work w being placed between the centres as shown, is revolved in unison with e, revolving in one direction when the table k is going one way, and in the other when the motion of the table is reversed; hence a tool in the tool post will cut a spiral groove in the work.
To enable the device to cut grooves of different spirals or twist, all that is necessary is to provide different sizes of wheels to take the places of c and d, so that the revolutions of e, and hence of the work w, may be increased or diminished with relation to the revolutions of b; or, what is the same thing, to a given amount of table movement, or a stud may be put in so as to enable the employment of change gears.
Figs. 1628 and 1629 represent a universal planer chuck, designed and patented by John H. Greenwood, of Columbus, Ohio, for planing concave or convex surfaces, as well as ordinary plane ones, with the cross feed of the common planer.
The base l of the chuck is bolted to the planer work table in the ordinary manner.[I-420]
The work-holding frame or vice is supported, for circular surfaces, by being pivoted to the base at o, o, and by the gibbed head d, which has journal bearing at e. The work is held between the stationary jaw b or b′ (at option) and the movable jaw c which may face either b or b′ (by turning c round). Suppose then, that while the chuck is passing the cutting tool, end i of the work-holding frame is raised, lifting that end of the work above the horizontal level (the work-holding frame swinging at the other end on the pivots o, o), then the tool will obviously cut a convex surface. Or if end i of the work-holding frame be lowered while the cut is proceeding, the tool will cut a concave surface.
Now end i is caused to rise or lower as follows:—The head d is adjusted by means of its gibs to be a sliding fit on the bar g in Fig. 1629, which bar is rigidly fixed at p to the planer bed; hence as the planer table and the chuck traverse, d slides along bar g. If this bar is fixed at an angle to the length of the planer head, d must travel at that same angle, causing end i of the work-holding frame to rise or lower (from o, o, as a centre of motion) as it traverses according to the direction of motion of the planer table.
Suppose that in Fig. 1629, the planer table is moving on the back or non-cutting stroke, then head d will be moving towards the point of suspension p of the bar g, and will therefore gradually lower as it proceeds, thus lowering end i of the work-holding frame and causing the curved link to pass beneath the tool with a curved motion or suppose the table to be on its cutting traverse, then head d will be raised as the table moves and the cut proceeds, and the surface cut by the tool will be concave.
Now, suppose that the bar g were fixed at an angle, with its end, that is towards the back end of the planer, inclined towards the table instead of away from it as in Fig. 1629, and then on the cutting traverse head d would cause end i (Fig. 1628) of the work-holding vice or frame to lower as the cut proceeded, and the tool would therefore plane a convex surface.
Thus the direction of the angle in which g is fixed governs whether the surface planed shall be a concave or a convex one, and it is plain that the amount of concavity or convexity will be governed and determined by the amount of angle to which g is set to the planer table.
When the chuck is not required to plane curved surfaces the bar g is altogether dispensed with, and the chuck becomes an ordinary one possessing extra facilities for planing taper work.
Thus for taper work the work-holding frame may be set out of parallel with the base of the chuck to an amount answering to the required amount of taper, being raised or lowered (as may be most convenient) at one end by means of the gears m, of which there is one on each side meshing into the segmental rack shown, the work-holding frame being secured in its adjusted position by means of a set bolt.
To set the work-holding frame parallel for parallel planing, a steady pin is employed, the frame being parallel to the base when that pin is home in its place.
The construction of the chuck is solid, and the various adjustments may be quickly and readily made, giving to it a range of capacity and usefulness that are not possessed by the ordinary forms of planer chucks.
Planing Machine Beds.—In long castings such as lathe or planer beds, the greatest care is required in setting the work upon the planer table, because the work will twist and bend of its own weight, and may have considerable deflection and twist upon it notwithstanding that it appears to bed fair upon the table. To avoid this it is necessary to know that the casting is supported with equal pressure at each point of support. In all such work the surface that is to rest upon the foundation or legs should be planed first.
Thus supposing the casting in Fig. 1630 to represent a lathe shears, the surfaces f whereon the lathe legs are to be bolted should be planed first, the method of chucking being as follows:—
The bed is balanced by two wedges a, in Fig. 1630, one being placed at each end of the bed, and the position of the wedges being adjusted so that it lies level. A line coincident with the face of the bed (as face d) is then drawn across the upper face of each wedge. Wedges (as b, c,) are then put in on each side of the bed until they each just meet the bed, and a line coincident with the bed surface is drawn across their upper surfaces. Wedge b is then driven in until it relieves a of the weight of the bed, and a second line is drawn across its upper face. It is then withdrawn to the first line, and the wedge on the opposite side of the bed is driven in until a is relieved of the weight, when a second line is drawn on this wedge’s face. The wedges at the other end (as c) are then similarly driven in and withdrawn, being also marked with two lines, and then the four wedges (b, c, and the two corresponding ones on the opposite side of the bed) are withdrawn, having upon their surfaces two lines each (as a, b, in Fig. 1631). Midway between these two lines a third (as c) is drawn, and all four wedges are then driven in until line c is coincident with the bed surface, when it may be assumed that the bed is supported equally at all the four[I-421] points. When the bed is turned over, surfaces f may lie on the table surface without any packing whatever, as they will be true.
Another excellent method is to balance the bed on three points, two at one end and one at the other, and to then pack it up equally at all four corners.
To test if the surface of a piece of such work has been planed straight, the following plan may be pursued:—
Suppose that surface e, Fig. 1632, is to be tested, it having been planed in the position it occupies in the figure, and the casting may be turned over so that face e stands vertical, as in Fig. 1632, and a tool may be put in the tool post of the planer, the bed being adjusted on the planer table so that the tool point will just touch the surface at each end of the bed. The planer table is then run so that the tool point may be tried with the middle of the bed length, when, if the face e is true, it will just meet the tool point at the middle of its length as well as at the ends.
In the planing of the V-guides and guideways of a bed for a machine tool, such as, for example, a planer bed and table, the greatest of care is necessary, the process being as follows:—
Beginning with the bed it has been shown in Fig. 1601 that the sides of the guideways must all be of the same height as well as at the same angle, and an excellent method of testing this point is as follows:—
In Fig. 1633 is shown at a a male gauge for testing the V-guideways in the bed, and at b a female gauge for testing those on the table. These two gauges are accurately made to the correct angle and width, and fitted together as true as they can be made, being corrected as long as any error can be found, either by testing one with the other or by the application of a surface plate to each separate face of the guides and guideways. The surfaces c and d of the respective gauges are made parallel with the V-surfaces, a point that is of importance, as will be seen hereafter. It is obvious that the female gauge b is turned upside down when tried upon the table.
Suppose it is required to test the sides e, f, of the bed guideways in Fig. 1634, and the gauge must be pulled over in the direction of the arrow so that it touches those two sides only; a spirit-level laid upon the top of the gauge will then show whether the two faces e, f, are of equal height. It is obvious that to test the other two faces the gauge must be pulled over in the opposite direction.
This test must be applied while fitting the Vs to the gauge. Suppose, for example, that when the gauge is applied and allowed to seat itself in the ways, the two outside angles e, g, are found to bear while the two inside ones do not touch the gauge at all, then by this test it can be found whether the correction should be made by taking a cut off e or off g, for if the spirit-level stood level when the gauge was pulled in either direction, then both faces would require to be operated upon equally, but suppose that the gauge and spirit-level applied as shown proved end e to be high, then it would be the one to be operated on, or if when the gauge was pulled over in the opposite direction end g was shown (by the spirit-level) to be high, then it would be the one to be operated upon.
By careful operation the table and bed may thus be made to fit more perfectly than is possible by any other method. To test the fit of the gauge to the Vs it is a good plan to make a light chalk mark down each V and to then apply the gauge, letting it seat itself and moving it back and forth endways, when if it is a proper fit it will rub the chalk mark entirely out. It may be noted, however, that a light touch of red marking is probably better than chalk for this purpose.
It is of importance that the Vs be planed as smooth as possible, and to enable this a stiff tool holder holding a short tool, as in Fig. 1635 should be used, the holder being held close up to the tool box as shown. It will be obvious that when the head is set over to an angle it should be moved along the cross slide to plane the corresponding angle on the other side of the bed.
| VOL. I. | EXAMPLES IN PLANING WORK. | PLATE XVIII. |
 |
 |
|
| Fig. 1636. | Fig. 1637. | |
 |
||
| Fig. 1638. | ||
 |
||
| Fig. 1639. | ||
Fig. 1636 represents a planer chuck by Mr. Hugh Thomas. The angle piece a is made to stand at an angle, as shown, for cylindrical work, such as shafts, so that the work will be held firmly down upon the table. The base plate b has ratchet teeth at each end c, into which mesh the pawls d, and has slotted holes for the bolts which hold it down to the table, so that it has a certain range of movement to or from the angle piece a, and may therefore be adjusted to suit the diameter or width of the work.
The movable jaw e is set up by the set-screw f and is held down by the bolts shown. The pawls d are constructed as shown in Fig. 1637, the pin or stem s fitting the holes in the planer table and the tongue p being pivoted to the body r of the pawl. As the pawls can be moved into any of the holes in the table, the base plate b may be set at an angle, enabling the chuck to be used for taper as well as for parallel work, while the chuck has a wide range of capacity.
In Fig. 1614 is shown a supplementary table for increasing the capacity of planer tables, and which has already been referred to, and Fig. 1638 represents an application of the table as a chucking device. a, a, &c., are frames whose upper surfaces are to be planed. An angle plate is bolted to the planer table and the supplementary[I-422] table is bolted to the angle plate. The first frame is set against the vertical face of the supplementary table, and the remaining ones set as near as possible, b, b, &c., being small blocks placed between the frames which are bolted to the planer table as at c.
In many cases this method of chucking possesses great advantages. Thus in the figure there are six frames to be planed, and as they would be too long to be set down upon the planer table, only three or four could be done at a time, and a good deal of measuring and trying would be necessary in order to get the second lot like the first. This can all be avoided by chucking the whole six at once, as in figure.
Another application of the same tables as useful chucking devices is shown in Fig. 1639, where two frames e, f, are shown bolted to the machine table and supported by the supplementary tables t, which are bolted to the main table and supported by angle-pieces b, b. Work that stands high up from the planer table may be very effectively steadied in this way, enabling heavier cuts and coarser feeds while producing smoother work.
As horizontal surfaces can be planed very much quicker than vertical ones, it frequently occurs that it will pay to take extra trouble in order to chuck the work so as to plane it horizontally, an excellent example being the planing of the faces of the two halves of a large pulley, the chucking of which is illustrated in Fig. 1640.
Four pieces, as at a, are made to engage the rims of the two halves of the pulley and hold them true, one with the other. The two plates t′ and t′ are set under the pulley halves to level the upper faces, and wooden clamps c, c, are bolted up to hold the pulleys together at the top, w representing wedges between the hubs. s represents supports to block up the pulley near its upper face, and at p are clamps to hold the two halves to the table. It is found that by this method of chucking more than half the time is saved, and the work is made truer than it is possible to get it by planing each half separately and laying them down on the table.
Supplemental tables may also be made in two parts, the upper one being capable of swiveling as in Fig. 1641, the swiveling device corresponding to that shown for the Thomas shaper chuck in Fig. 1530. This enables the work to be operated upon on several different faces without being released from the chuck. Thus in figure the segment could be planed on one edge and the upper table swiveled to bring the other edge in true with the table, which would be a great advantage, especially if the face it is chucked by has not been trued.
Figs. 1642 and 1643 show other applications of the same swiveling device.
It is obvious that the chuck shown in Fig. 1636 can be mounted on a supplemental and swiveling table as shown in Fig. 1644, thus greatly facilitating the chucking of the work and facilitating the means of presenting different surfaces or parts of the work to the tool without requiring to unchuck it. The pawls, also, may in heavy work have two pins to enter the work-table holes and be connected by a strap as in Fig. 1645.
In the exigencies of the general machine shop it sometimes happens that it is required to plane a piece that is too wide to pass between the uprights of the planing machine, in which case one standard or upright may be taken down and the cross slide bolted to the other, as in Fig. 1646, the blocks a, a, being necessary on account of the arched form of the back of the cross slide. In the example given the plates to be planed were nearly twice as wide as the planer table and were chucked as shown, the beam d resting on blocks e, f, and forming a pathway for the piece c, which was provided with rollers at each end so as to move easily upon d. The outer end of the plate was clamped between b and c, and the work was found to be easily and rapidly done. In this chucking, however, it is of importance that beam d be carefully levelled to stand parallel with the planer table face, while its height must be so adjusted that it does not act to cant or tilt the table sideways as that would cause one V of the planer ways to carry all or most of the weight, and be liable to cause it to cut and abrade the slide surfaces.
Cutting Tools for Shaping and Planing Machines.—All
the cutting tools forged to finished shape from rectangular bar
steel, and described in connection with lathe work, are used in the
planer and in the shaper, and the principles governing the rake of
the top face remain the same. But in the matter of the clearance
[I-423/
424]
there is the difference that in a planing tool it may be made
constant, because the tool feeds to its cut after having left
the work surface at the end of the back stroke, hence the
clearance remains the same whatever the amount or rate of feed
may be.
On this account it is desirable to use a gauge as a guide to grind the tool by, the application of such a gauge being shown in Fig. 1647. It consists of a disk turned to the requisite taper and laid upon a plate, whereon the tool also may be laid to test it. The tool should not be given more than 10° of clearance, unless in the case of broad flat-nosed tools for finishing, for which 5° are sufficient.
The principle of pulling rather than pushing the tool to its cut, can, however, be more readily and advantageously carried out in planer than in lathe tools, because the spring of the tool and of the head carrying it only need be considered, the position of the tool with relation to the work being otherwise immaterial. As a consequence it is not unusual to forge the tools to the end of pulling, rather than of pushing the cutting edge.
In Figs. 1648 and 1649, for example, are two tools, w representing the work, and a the points off which the respective tools will spring in consequence of the pressure; hence the respective arrows denote the direction of the tool spring. As a result of this spring it is obvious the tool in Fig. 1648 will dip deeper into the work when the pressure of the cut increases, as it will from any increase of the depth of the cut in roughing out the work, or from any seams or hard places in the metal during the finishing cut. On the other hand, however, this deflection or spring will have the effect of releasing the cutting edge of the tool from contact with the work surface during the back stroke, thus rendering it unnecessary to lift the tool to prevent the abrasion, on its back stroke, from dulling its cutting edge.
It will be noted that the radius from the point of support a is less for the tool in Fig. 1649 than for that in Fig. 1648, although both tools are at an equal height from the work, which enables that in Fig. 1649 to operate more firmly. In these two figures the extremes of the two systems are shown, but a compromise between the two is shown in Fig. 1650, the cutting edge coming even with the centre of the body of the steel, which makes the tool easier to forge and grind, and keeps the cutting edge in plainer view when at work, while avoiding the evils attending the shape shown in Fig. 1648.
It is sometimes necessary, however, that a tool of the form in Fig. 1652 be used, as, for example, to shape out the surface of a slot, and when this is the case the tool should be shaped as in Fig. 1651, the bottom face having ample clearance (as, say, 15°) from the heel a to about the point b, and about 3° from b to the front end. The front face should have little or no clearance, because it causes the tool to dig into the work. A tool so shaped will clear itself well on the back stroke, whereas if but little clearance and front rake be given as in Fig. 1652, the tool will not only dig in, but its cutting edge will rub on the back or return stroke.
For broad feed finishing cuts the shape of tool shown in Fig. 1653 is employed, the cutting edge near the two corners being eased off very slightly with the oilstone. The amount of clearance should be very slight indeed, only just enough to enable the tool to cut as is shown in the figure, by the line a a. The amount of front rake may be varied to suit the nature and hardness of the metal, and the tool should be held as close in as possible to the tool clamp.
Smoother work may be obtained in shaping and in planing machine tools when the tool is carried in a holder, such as in Fig. 1654, which is taken from The American Machinist because in this case any spring or deflection either in the tool or in the shaper head acts to cause the tool to relieve itself of the cut instead of digging in, as would be the case were the tool put in front of the[I-425] tool post as in Fig. 1654. In finishing large curves this is of great importance, because to obtain true and smooth curves it is necessary to shape the tool to cut upon the whole of the curve at once, and this gives so great a length of cutting edge, that the tool is sure to chatter if held in front of the tool post.
It is essential, therefore, to carry the tool at the back of the tool post as shown, and for curves that are arcs of circles tools such as in Fig. 1655 may be employed, or a circular disk will answer, possessing the advantage that its shape may be maintained by grinding its flat face to resharpen it.
Cutters of the kind shown in Fig. 1655 may be made to possess several important advantages aside from their smooth action: thus they may be made after the principle explained with reference to the Brown & Sharpe rotary cutters for gear-teeth, in which case the front face only need be ground to resharpen them, and their shapes will remain unaltered, and they may be given different degrees of front rake by placing packing between one side and the holder, and any number of different shaped cutters may be fitted to the same stock.
Tool Holders for Planing Machines.—The advantages of tool holders for planing machines are equally as great as those already described for lathes, but as applied to planing machines there is the additional advantage that the clearance necessary on the tool is less variable for planer work than for lathe work, because in lathe work the diameter of the work as well as the rate of tool feed affects the tool clearance, whereas in planer work the tool feed is put on before the tool begins its cutting action; hence the degree of clearance is neither affected by the size of the work nor by the rate of feed, and as a result the tools may be given a definite and constant amount of clearance.
Fig. 1656 represents a planer tool holder (by Messrs. Smith & Coventry), in which what is, in effect, a swivel tool post is attached to the end of the holder, thus enabling the tool to be used on either the right or left-hand of the holder at will. The shape of the tool steel is shown in section on the right-hand of the engraving, being narrow at the bottom, which enables the tool to be very firmly held and reduces the area to be ground in sharpening the tool. A side and end view of the holder is shown in Fig. 1657, in which it is seen that the tool may be given top rake or angle to render it suitable for wrought iron or steel or may be set level for brass work.
In Fig. 1658 the tool and holder are shown in position on the planer head, the front rake on the tool being that suitable for wrought iron.
It is to be noted, however, that the amount of front rake should, to obtain the best results, be less for steel than for wrought iron, and less for cast iron than for wrought, while for brass there should be none; hence the tool post should be made to accomplish these different degrees of rake in order to capacitate such holders for the four above-named metals. It is an advantage, however, that by inclining the tool to give the top rake, this rake may be kept constant by grinding the end only of the tool to sharpen it, and as the end may be ground to a gauge it is very easy to maintain a constant shape of tool. Furthermore as the tool is held by one binding screw only, it may be more readily adjusted in position for the work than is the case when the two apron clamp nuts require to be operated.
Figs. 1659 to 1661, show this tool-holder applied to various kinds of work, thus in Fig. 1659 the tool is planing under the underneath side of a lathe bed flange, while in Fig. 1660 it is acting upon a V-slideway and escaping an overhanging arm, and[I-426] in Fig. 1661 it is shown operating on a V-slideway and in a T-groove.
Fig. 1662 represents a tool holder by Messrs. Bental Brothers, the tool being held in a swivelled tool post, so that it may be used as a right or left-hand tool. In this case the front rake must be forged or ground on the tool, and there is the further objection common to many tool holders, that the tool if held close in to the tool post is partly hidden from view, thus increasing the difficulty of setting it to the depth of cut.
Another form of planer or shaper tool-holder is shown in Fig. 1663, in which a tool post is mounted on a tool bar, and may be used as a right or left-hand tool at will.
Fig. 1664 represents a tool holder in which two tools may be held as shown, or a single tool right-hand or left-hand as may be required, or the tool may be held at the end of the holder as in Fig. 1665. The advantage of such a holder is well illustrated in the case of cutting out a T-shaped groove, because with such a holder a straight tool can be used for the first cuts, its position being shown in Fig. 1665, whereas in the absence of such a holder a tool bent as in Fig. 1666 would require to be used, this bend giving extra trouble in the forging, rendering the tool unfit for ordinary plain work, and being unable to carry so heavy a cut or to cut so smooth as the straight tool in Fig. 1665. In cutting out the widest part of such a groove the advantage of the holder is still greater, because by its use a tool with one bend, as in Fig. 1667, will serve, whereas without a holder the tool must have two bends, as shown in the figure, and would be able to carry a very light cut, while liable to dig into the work and break off.
The tool itself should be so forged that one side is flush with the side of the tool steel as shown at a in Fig. 1668, for if there is a shoulder, as at c, it sometimes prevents the tool from entering the work as shown in the figure.
Other examples in the use of this tool holder are given in Figs. 1669 and 1670.
In Fig. 1669, we have the case of cutting out the V-slideways of a planer bed, and it is seen that the tool point may be held close to the holder, the side of the tool box still clearing the side of[I-427] the V-slideway, whereas in the absence of the holder the tool would require to have a considerable bend in it, or else would have to stand out from the bottom of the tool apron to a distance equal to the length of one side of the slideway.
In Fig. 1670 it is also seen that by the use of the holder the tool point may also be held as close as necessary to the holder, and still permit the side of the vertical slide s′ and the tool box b to clear the vertical face of the work.
In all planer work it is an essential in the production of true and smooth surfaces that the tool be held as close in to the tool clamp or tool box as possible, and this forms one of the main advantages of tool holders.
Power Drilling Machines.—The drilling machine consists essentially of a rotating spindle to drive the drill, a work-holding table, and means of feeding the drill to its cut. The spindle speed and the force with which it is driven are varied to suit the work. The feeding is sometimes given to the spindle, and at others to the work table. In either case, however, the feeding mechanism should be capable of varying the rate of feed and of permitting a quick withdrawal of the drill. The spindle should be supported as near to its drill-holding end as possible. When the table feeds to the work the spindles may be held rigidly, because of their not requiring to pass so far out or down from the bearing supporting them; but when the spindle feeds, it must either pass through its bearings, or the bearing, or one of them, must either be capable of travel with the spindle or adjustable with relation to the machine framing.
In using small drills in a machine it is of the first importance that the amount of pressure necessary to feed the drill be plainly perceptible at the hand lever or other device for feeding the drill or the work, as the case may be, as any undue pressure causes the drills to break. To attain sensitiveness in this respect the parts must be light and easy both to move and to operate.
| VOL. I. | LIGHT DRILLING MACHINES. | PLATE XIX. | |
 |
 |
||
| Fig. 1671. | |||
 |
|||
| Fig. 1672. | |||
 |
|||
| Fig. 1673. | |||
 |
|||
| Fig. 1674. | Fig. 1675. | ||
Fig. 1671 represents the American Tool Company’s delicate drilling machine for holes of 1⁄4 inch and less in diameter. It consists of a head fixed upon a cylindrical column and affording journal bearing to the drill-driving spindle, which is driven by belt. The table on which the work is placed is carried by a knee that may be fixed at any required height upon the same round column. The knee and table may be swung out of the way, the column serving as a pivot. The table has journal bearing in the knee, and is fed upwards by the small lever shown.
Fig. 1672 represents Elliott’s drilling machine for drills from 1⁄32 inch to 3⁄4 inch in diameter. The work table may be revolved in the arm that carries it, and this arm may be swung round the column or post. It is operated upwards for the feed by the hand lever shown. The conical chuck shown lying on the work table fits into the hole that is central in the table, and is used to receive the end of cylindrical work and hold it true while the upper end is operated upon.
The construction of the live spindle and its cone are shown in Fig. 1673. The drill chuck q is attached to and driven by a one-inch steel spindle 19 inches long, which is accurately fitted through the sleeve bearings, within which it is free to move up and down, but is made to revolve with the cone by means of the connection o, one end of which slides upon the rods l. The drill is held up by means of the spiral spring m acting from the bottom of cone to the collar o. The weight of cone and spindle is carried upon a raw-hide washer, beneath which is the cupped brass p which retains the oil. The thrust of the feed lever g is also taken by a raw-hide washer r.
The machine is provided with a hand and a foot feed by means of the compound lever w z, Fig. 1674, actuating the feed rod j, which passes up within the column and connects to the lever k, the latter being suspended by a link h.
Fig. 1675 represents Slate’s sensitive drilling machine, in which the lower bearing for the live spindle is carried in a head h that fits to a slide on the vertical face of the frame, so that it may be adjusted for height from the work table w to suit the height of the work. l is a lever operating a pinion engaging a rack on the sleeve s to feed the spindle. The table w swings out of the way and a conically recessed cup chuck c is carried in a bracket fitting into a guideway in the vertical bed g. The cone of the cup chuck is central to or axially in line with the live spindle, hence cylindrical work may have its end rested in the cone of the cup chuck, and thus be held axially true with the live spindle.
Fig. 1676 represents a drilling machine in which the spindle has four changes of feed, and is fed by a lever handle operating a pinion that engages a rack placed at the back of a sleeve forming the lower journal bearing for the spindle. This lever is provided with a ratchet so that it may be maintained in a handy position for operating. The work table is raised or lowered by a pinion operating in a rack fast upon the face of the column, a pawl and ratchet wheel holding it in position when its height has been set. A lever is used to operate the pinion, being inserted in a hub fast upon the same spindle that carries the pinion and the ratchet wheel.
Fig. 1677 represents a drilling machine by Prentice Brothers, of Worcester, Massachusetts. Motion for the cone pulley a is received by pulleys b and is conveyed by belt to cone pulley c, which is provided with back gear, as shown; the driving spindle d drives the bevel pinion e, which gears with the bevel-wheel f, which drives the drill spindle g by means of a feather fitting in a keyway or spline that runs along that spindle. Journal bearing is provided to the upper end of the spindle at h and to the lower end by bearings in the head j, which may be adjusted to stand at, and be secured upon any part of the length of the slideway k. By this arrangement the spindle is guided as near as possible to the end l to which the drill is fixed and upon which the strain of the drilling primarily falls. This tends to steady the spindle and prevent the undue wear that occurs when the drill spindle feeds below or through the lower bearing.
The feed motions are obtained as follows:—
On the drill spindle is a feed cone m which is connected by belt to cone n, which drives a pinion o, that engages a gear p upon the feed spindle q, which has at its lower end a bevel pinion, which drives a bevel gear upon the worm shaft r. The worm shown on r drives the worm-wheel s, whose spindle has a pinion in gear with the rack t, which is on a sleeve u on the drill spindle[I-429] g. It is obvious that when the rack t is operated by its pinion the sleeve u is moved endways, carrying the feed spindle with it and therefore feeding the drill to its cut, and that as the feed cone m has three steps there are three different rates of automatic feed.
To throw the self-feed into or out of action the following construction is employed:—
The worm-wheel s has on its hub face teeth after the manner of a clutch, and when these teeth are disengaged from the clutch sleeve w the worm-wheel s rides or revolves idly upon its shaft or spindle, which therefore remains at rest. Now the clutch sleeve s has a feather fitting to its spindle or shaft, so that the two must, if motion takes place, revolve together, hence when w is pushed in so as to engage with s, then s drives w and the latter drives the spindle, whose pinion operates the rack t.
A powerful hand feed to the drill spindle is provided as follows:—
The worm shaft r is hollow, and through it passes a rod having at one end the hand nut v and at the other a friction disk fitting to the bevel gear shown at the right-hand end of the worm-shaft. This friction disk is fast upon the worm-shaft and serves to lock the bevel gear to the worm-shaft when the nut v is screwed up, or to release it from that shaft when v is unscrewed.
Suppose, then, that v is unscrewed and shaft r will be unlocked from the bevel-wheel and may be operated by the hand wheel x, which is fast upon the worm-shaft, and therefore operates it and worm-wheel s, so that w being in gear with s the hand feed occurs when x is operated and v is released. But as the motion of s is, when operated by its worm, a very slow one, a second and quick hand feed or motion is given to the spindle g as follows, this being termed the quick return, as it is mainly useful in quickly removing the drill from a deep hole or bore.
The spindle carrying s and w projects through on the other side of the head j and has at its end the lever y, hence w being released from s, lever y may be operated, thus operating the pinion that moves rack t, one revolution of y giving one revolution to the pinion, both being on the same shaft or spindle.
The work is carried and adjusted in position beneath the drill as follows:—
The base of the column or frame is turned cylindrically true at a, and to it is fitted a knee b which carries a rack c. The knee b affords journal bearing to a spindle which has a pinion gearing with the rack c, and at the end of this spindle is a ratchet-wheel d operated by the lever shown. A catch may be engaged with or disengaged from ratchet d. When it is disengaged the lever may be operated, causing the pinion to operate on rack c and the knee b to raise or lower on a according to the direction in which the lever is operated. As the knee b carries the rack the knee may be swung entirely from beneath the drill spindle and the work be set upon the base plate e if necessary, or it may be set upon the work table f which has journal bearing in the knee b, so that it may be revolved to bring the work in position beneath the drill.
In the Sellers drilling machine, Fig. 1678, the drill spindle when in single gear is driven by belt direct, producing a uniform and smooth motion that is found of great advantage in drilling the smaller sizes of holes. The back gear is arranged to drive the spindle direct without the power requiring to be transmitted through a shaft, which induces vibration. The drill spindle is provided with variable rates of self-acting feed, but may also be moved rapidly by hand, and is counterbalanced. The work table is capable of revolving upon its axis, and the arm on which it is carried is pivoted in a slide upon a vertical slideway on the front of the main frame, so that[I-430] the table and the arm may be swung out of the way for work that can be more advantageously rested on the base plate of the machine. A central hole is bored in the table, being true to the drill spindle when the arm is in its mid position, and clamps are provided to secure the circular table against rotation when it is set to place, and also to secure the swinging bracket to any required position. This form of table, like the compound table, has the advantage of permitting all parts of the table being brought in turn under the drill, but the motion is not in right lines. Holes are provided in the circular table to admit holding-down bolts.
The rates of feed are proportioned to the kind of drilling to be done. When the back gear is not in use and small drills are to be driven, the range of feeds is through a finer series than when the back gear is being used, and large drills or boring bars are [I-431] to be driven.
| VOL. I. | HEAVY DRILLING MACHINE. | PLATE XX. | |
 |
|||
| Fig. 1679 | |||
Fig. 1679 represents a drilling machine of English design. The cone pulley a is provided with back gear b placed beneath it, the live spindle driving the drill spindle through the bevel gears c, one of which is fast upon a sleeve d through which the drill spindle e passes. The feed motions are obtained as follows:— i is the feed cone driving cone j, which drives a worm and worm-wheel at k. In one piece with the worm-wheel is a ratchet wheel l, and at m is a handle with a pawl that may be engaged with or disengaged from ratchet-wheel l. When it is engaged the handle, which is fast upon the vertical feed spindle n, is revolved by the worm-wheel and the automatic feed is put in operation; but when the pawl is disengaged the worm and worm-wheel revolve in the bearing while the spindle n remains at rest, unless it be operated by the handle m, which obviously revolves the spindle n more quickly than the worm and gives to a corresponding extent a quick motion to the drill spindle. Spindle n is provided with the gear-wheel o, which drives gear p, which is threaded upon the feed screw f and has journal bearing at q. The sleeve d has journal bearing at g and at h. At r is a hand wheel upon a horizontal shaft at whose other end is a bevel gear engaging with a bevel gear on the vertical screw for the knee t which fits to the vertical slides v. The work table w is fitted to a horizontal slide upon the arm x, which is pivoted to the knee t at y, the handle for operating the screw of the table being at z.
Radial Drilling Machine.—Fig. 1680 represents a radial drilling machine, the column of which envelops a sleeve round which it may be swung or revolved, the sleeve extending some distance up from the base plate. The arm fits to the column and may be raised or lowered to any desired height to suit the work, the construction being as follows:—
Motion by belt is given to the spindle shown extending above the top of the column, and the pair of gears beneath it convey motion to the pair of bevels which drive the upper cone pulley which connects by belt to the lower one, which is provided with back gears to give the necessary changes of speed and power for the wide range of work the machine is intended for; the live spindle of the lower cone pulley extends past the collar and runs beneath the horizontal arm, giving motion to the drill spindle, which is carried in a sliding head. The spindle may be set at any required angle to the arm.
The vertical screw on the right hand of the column passes through a nut in the column, so that by throwing the gearing at the upper end of the screw into action, the arm may be raised or lowered by power.
The vertical rod appearing in the front of the column and having an arm at its top, is for putting this gearing in or out of action, the arm being raised or lowered according to the direction in which the rod is operated by the lever handle shown upon it, and in front of the column. The gearing at the top of the raising and lowering screw is constructed on the principle that was shown in Fig. 566, for reversing the direction of a lathe feed.
The capacity to swing the drill spindle at an angle enables the drilling of long work such as the flanges of pipes, by setting the pipe at an angle and swinging the spindle so as to stand parallel to it, while the facility with which the arm may be moved to any required position makes it easier to move the arm to the work, so that the latter will require but one chucking or setting.
Radial drilling machines are of various constructions. In some the drilling head is carried by an arm standing at a right angle to the main column or frame, and is capable of being moved to any required position upon the length of this arm. The arm itself is sometimes made capable of swinging upon its own axis, as shown in Fig. 1682.
It is also capable of being adjusted at any height from the bed or base plate upon which the upright or main frame sits, or above the work table when one is used as in the figure.
The advantage given by these facilities is that a heavy piece of work may be set upon the base plate or work table, and be drilled in various places without requiring to be moved.
Figs. 1681 and 1682 represent a radial drilling machine, in which the radial arm is carried on a head, which fits a vertical slideway provided on the face of the upright column, and may be moved to any required height on this slideway by means of a rack and worm gear, the latter being shown in the front view.
The seat of the arm on this head is cylindrical, the head being pivoted upon it in order that it may permit of its being rotated to hold the drill at an angle. The drill spindle is carried in a head sliding on the radial arm as already stated, and is driven as follows:—
Motion from the shop driving shaft is communicated by belt to the cone pulley shown at the base of the upright column.
The spindle of this cone pulley drives a belt which passes up the column over an idle pulley on the sliding head that carries the radial arm; hence it passes along the front of the radial arm and partly round a pulley on the drill spindle, two idle pulleys holding it in contact with the drill spindle pulley. Hence it passes over a small pulley at the outer end of the radial arm, and returns along that arm through the sliding head, over an idle pulley to the pulley seen at the head of the vertical column, and from this pulley it passes to the pulley that is on the cone spindle shaft at the base of the column. The drill is provided with an automatic feed actuated by the worm shown on the drill spindle.
In Figs. 1683, 1684, and 1685 is represented a combined drilling and boring machine.
It is provided with an horizontal as well as with a vertical spindle, either of which may be used for boring as well as for drilling. In the case of the vertical spindle the boring bar may extend down and have journal bearing in a block, or bearing secured to the base plate i.
Each spindle has eight changes of speed, four in single, and four in double gear, that is when the back gears at a are in operation.
Motion from the pulley k on the cone spindle is conveyed by belt b to pulley l, whose hub extends through the frame at r and affords journal bearing to that end of spindle s which has a feed motion at h. Motion is conveyed from the cone spindle to vertical spindle m as follows:—
Referring to Fig. 1685, bevel-wheel f is on the end of the cone spindle and drives bevel-wheel g, which drives spindle m. This spindle is provided with an automatic as well as a hand-feed motion, the construction being as follows:—
Referring first to the automatic feed, the cone pulley e′, Fig. 1685, which is upon the main cone spindle of the machine, drives cone e, Fig. 1683, and the latter operates a worm w, Fig.1684, engaging a worm-wheel w, which drives the bevel gear a, shown by dotted circles in Fig. 1685; a drives the bevel gear c upon the sleeve o, which has journal bearing (in the frame a of the machine) both at its upper end and immediately above c. The upper end of the sleeve o is threaded to receive an inner sleeve n, within which is a spindle v, having journal bearing at each end of n and being fast to m, so as to revolve with it. End motion to n is prevented by a collar at its upper end r and by three steel washers at i, the latter taking the thread when the drill spindle m is in operation. The inner sleeve n is prevented from revolving by means of a lug or projection which passes into a slot or groove running vertically in the bore of the outer casing a; hence when o is revolved by a it acts as a nut to n, causing the latter to move endways and feed the drill spindle m.
To enable the engagement or disengagement of the automatic feed, there is at f, Fig. 1684, a friction disk, the female half of which is fast upon the spindle that drives bevel gear a in Fig. 1685, while the male half is in one piece with the hand wheel z, Fig. 1684, which has journal bearing upon the spindle of a. g is a hand nut for engaging or disengaging the friction disks. In addition to the ordinary work table t, the knee u carries on a projection x a work-holding vice v, which is a great convenience, especially for cylindrical work. The base of the machine is provided with a plate upon which work may be secured independent of the work table t, or the lower end of a boring bar may be steadied by a step bolted to the base plate.
[I-433]The construction of the machine, as will be seen, is very substantial throughout, since all the strains are central, the spindles are well supported, and there is a commendable absence of springs, pull-pins, and other light parts that are liable to get out of order from the wear and tear of the ordinary machine-shop tool. It may also be remarked that the combination of the two spindles is effected without impairing either the usefulness or handiness of the vertical spindle.
In Fig. 1686, which is taken from Mechanics, is illustrated a combined drilling and turning machine. In this machine the motion for both drilling and turning is received by belt on the cone pulley shown on the right, which is provided with back gear similar to that of a lathe. The live spindle thus driven has a face plate at the left-hand end, whereon work may be chucked to be operated upon by a tool in the compound slide rest shown on the cylindrical column. Motion to the drill spindle is conveyed by belt from a pulley on this same live spindle, hence the same cone pulley and back gear are utilized for either drilling or turning. The self-acting feed for the drill spindle is actuated by an eccentric on that spindle operating an arm, having a pawl engaging with the ratchet wheel on the lower end of the vertical feed spindle. Obviously when the pawl is thrown out of engagement with the ratchet wheel, the horizontal hand wheel may be used to feed the drill spindle by hand or to withdraw it, as the case may be.
The work table for drilling operations has motion laterally in two directions (one at a right angle to the other) by means of being carried on slides, and is fitted to a vertical slide on the face of the column so that it may be raised and lowered to suit the height of the work by means of the worm and worm-wheel shown, the latter being on the same shaft as a pinion engaging with a vertical rack on the face of the upright frame or column.
| VOL. I. | EXAMPLES IN BORING MACHINERY. | PLATE XXI. | |
 |
|||
| Fig. 1687. | |||
 |
|||
| Fig. 1688. | |||
 |
|||
| Fig. 1689. | |||
In Fig. 1687 is represented a horizontal drilling and boring machine. In this machine the work-holding table is provided with a hand feed, and the drilling or boring spindle with hand and self-acting feed, the latter being variable to suit different kinds of work. The table has a compound motion upon suitable[I-434] slideways and rests upon a frame or knee that is elevated by two vertical screws that are operated by hand wheel. This knee fits to a vertical slideway on the main frame, so that its upper face, and therefore the face also of the work table, is maintained parallel with the drill spindle at whatever height it may be set from it.
The arbor that carries the drill spindle is arranged with a face plate so that the machine can be used as a facing lathe. The feeds are arranged in two separate series, a fine and a coarse, and both of these series are applicable to any speed or any size of drill. The value of the coarse feed will be felt in all kinds of boring with bars and cutters, inasmuch as it is possible to rough out with a fine feed and finish with a light cut and a very coarse feed.
For work that is too large to be conveniently lifted to the table of a machine the floor boring machine is employed.
Fig. 1688 represents a machine of this class, which consists of two heads that may be moved about upon, and secured to, any part of its base or bed plate to which the work is secured. The boring bar it will be seen stands horizontal, and may be set at any height from the base plate between the limits of 14 inches and 6 feet 4 inches, the driving head being raised on its slideway on the face of its standard or column by automatic mechanism. The feed is automatic and variable in amount to suit the nature of the duty.
The bar has eight speeds, four in single and four in double gear.
In order to insure that the crank pins of locomotive driving wheels shall stand with their axes parallel to that of the wheel shaft, and that they shall also stand 90° apart when measured on the wheel circle, it is necessary that the holes for these pins be bored after the wheels are upon their shaft, it being found that if the crank pin holes are bored before the wheels are upon the shaft they are liable to be out of parallel and out of quarter.
To avoid these errors a quartering machine is employed, such as shown in Fig. 1689. This machine consists of two heads carrying stationary or dead centres to hold the wheel axle, as in a lathe. Each of these heads is provided with a boring bar having an automatic and adjustable feed, the axes of these bars being 90°, or one quarter of a circle, apart.
As both crank pin holes are bored simultaneously and with the wheel rigidly fixed and held upon centres the work will obviously be true. This machine may also be used as an ordinary horizontal boring machine.
Multiple drilling machines are employed for two general purposes: first, those in which a number of holes may be advantageously drilled simultaneously; and second, where a number of operations require to be performed upon one and the same hole. When the object is to drill a number of holes spaced a certain distance apart in one piece of work, the spindles may be so constructed that their distances one from the other may be adjustable, so that they may be set to drill the holes equally or unequally spaced as may be required.
In such machines it will be more convenient to feed the work to the drill, so as to have but one feed motion, instead of having a separate feed motion to each drill spindle. When, however, a number of separate operations are to be performed upon the same hole, it is preferable to rotate the table so that the work may be carried from one spindle to the other, the spindles feeding automatically and simultaneously.
Fig. 1690 represents a three-spindle drilling machine. The main driving spindle is vertical and within the top of the column, having three pulleys to connect by belt to the vertical drill driving spindles, whose driving pulleys are of different diameters to vary the speed to suit different diameters of drilling tools. A foot feed is provided by means of the treadle, and a hand feed by means of the lever, the weight of the work table being balanced by means of the ball weight shown. The work table is adjustable for height in a main table, that is adjustable for height on the face of the column. Similar machines are made with four or more spindles.
Fig. 1691 represents a four-spindle machine, in which each spindle has a separate and independent feed, which may be operated in unison or separately as may be required.
The four spindles are driven by means of a gear-wheel engaging[I-435] with a gear on the central or main driving spindle. The work-holding table rotates about the column of the machine, and is arranged with a stop motion that locks the table in position when the work-holding chucks are exactly in line with the drill spindles. Suppose, then, one spindle to drive a drill, the second driving an enlarging drill, a third driving a countersink, and a fourth a reamer. A piece of work may then be fastened beneath the first spindle and be drilled. The table may then be rotated one-fourth of a revolution, bringing it beneath the enlarging drill, while a second piece of work is placed beneath the first or piercing drill. The table may then be given another quarter rotation, bringing the piece of work first put in beneath the countersink, the second beneath the enlarging drill, while a third piece may be placed beneath the first or piercing drill. The table being again given one-quarter rotation the first piece will be brought beneath the reamer, the second beneath the countersink, the third beneath the enlarging drill, and a fourth may be placed beneath the piercing drill; all that will then be necessary is to remove the first piece when it arrives at the piercing drill and insert a new piece; the four spindles operating simultaneously, and the process continuing, the four operations proceed together.
Thus the piece of work is finished without being released from the holding devices, which insures truth while requiring a minimum of attendance. The amount of feed being equal for all four spindles the depth to which each tool will operate is gauged by the distance it stands down from the feeding head, each spindle being capable of independent adjustment in this respect, so that the tool requiring to move the farthest through the work will meet it the first, and so on.
Figs. 1692 and 1693 represent a combined drilling and turning machine for boiler-maker’s use. The machine consists of two uprights or drill standards which can be traversed along horizontal slides on beds which are fixed at right angles one to the other. The work to be drilled is carried on a turntable or work-holding table, the pivot and carrying frame of which can be traversed along a third set of guides lying between the other two and forming an angle of 45° with either of them.
Thus, by adjusting the relative positions of the turntable and the drill standards (each of which carries two drills), either a large or a small boiler can be conveniently operated on. Worm-gear is provided for revolving the turntable, either to divide the pitch of the holes, or when the machine is used for turning the edges of flanged plates, or for boring the large holes for flue tubes. Longitudinal seams may be drilled by laying the boiler horizontally on chucks alongside one of the beds, and traversing the drill standard from hole to hole.
Referring especially to Fig. 1693, a1 and a2 are the two wings of the bed plate, each being provided with V-slides to carry the uprights or standards b1, b2, on each of which is a drilling head c1, c2, these being each adjustable vertically on its respective standard by means of rack and pinion and hand wheels d1 and d2. The heads are balanced so that the least possible exertion is sufficient to adjust them. The vertical standards b1 and b2 are provided at their bases with a gear wheel operated by means of pinions at g1, g2, so that they may be rotated upon the sliders e1 and e2, by means of which they may be traversed along their respective bed slides. The drilling heads are composed of a slider on a vertical slide on the face of the vertical standard or upright, rotary motion and the feed being operated as follows: Power is applied to the machine through the cones k1 and k2, working the horizontal and vertical shafts l1 and l2, &c. On the vertical shafts are fitted coarse pitch worms sliding on feather keys, and carried with the heads c1 and c2, &c. The worms gearing with the worm-wheels m1 and m2 are fitted on the sleeves of the steel spindles n1 and n2. The spindles are fitted with self-acting motions o1 and o2, which are easily thrown in and out of gear.
The shell to be drilled is placed upon the circular table h, which is carried by suitable framework adjustable by means of screw on the V-slide i, placed at an angle of 45° with the horizontal bed plates. By this arrangement, when the table is moved along i it will approach to or recede from all the drills equally. j1 and j2 are girders forming additional bearings for the framework of the table. The bed plates and slides for the table are bolted and braced together, making the whole machine very firm and rigid.
The machine is also used for turning the edge of the flanges which some makers prefer to have on the end plates of marine boilers. The plates are very readily fixed to the circular table h, and the edge of the flange trued up much quicker than by the ordinary means of chipping. When the machine is used for this purpose, the cross beam p, which is removable, is fastened to the[I-436] two upright brackets r1 and r2. The cross beam is cast with V-slides at one side for a little more than half its length from one end, and on the opposite side for the same length, but from the opposite end. The V-slides are each fitted with a tool box s1 and s2, having a screw adjustment for setting the tool to the depth of cut, and adjustable on the V-slides of the cross beam to the diameter of the plate to be turned. This arrangement of the machine is also used for cutting out the furnace mouths in the boiler ends. The plate is fastened to the circular table, the centre of the hole to be cut out being placed over the centre of table; one or both of the tool boxes may be used. There is sufficient space between the upright brackets r1 and r2 to allow that section of a boiler end which contains the furnace mouths to revolve while the holes are being cut out; the plate belonging to the end of a boiler of the largest diameter that the machine will take in for drilling. The holes cut out will be from 2 ft. 3 in. diameter and upwards. Power for using the turntable is applied through the cone t. The bevel-wheels, worms, worm-wheels and pinions for driving the tables are of cast steel, which is necessary for the rough work of turning the flanges.
As to the practical results of using the machine, the drills are driven at a speed of 34 feet per minute at the cutting edges. A jet of soapsuds plays on each drill from an orifice 1⁄32 in. in diameter, and at a pressure of 60 lbs. per square inch. A joint composed of two 1-inch plates, and having holes 11⁄8 in. in diameter, can be drilled in about 21⁄2 minutes, and allowing about half a minute for adjusting the drill, each drill will do about 20 holes per hour. The machine is designed to stand any amount of work that the drills will bear. The time required for putting on the end of a boiler and turning the flange thereon (say, 14 ft. diameter), is about 21⁄2 hours; much, however, depends on the state of the flanges, as sometimes they are very rough, while at others very little is necessary to true them up. The time required for putting on the plate containing the furnace mouths and cutting out three holes 2 ft. 6 in. in diameter, the plate being 11⁄8 inches thick, is three hours. Of course, if several boilers of one size are being made at the same time, the holes in two or more of these plates can be cut out at once. The machine is of such design that it can be placed with one of the horizontal bed plates (say a1) parallel and close up to a wall of the boiler shop; and when the turning apparatus is being used, the vertical arm b2 can be swivelled half way round on its square box e2, and used for drilling and tapping the stay holes in marine boiler ends after they are put together; of course sufficient room must be left between bed plate a2 and the wall of boiler shop parallel with it, to allow for reception of the boiler to be operated upon.
| VOL. I. | BOILER‑DRILLING MACHINERY. | PLATE XXII. | |
 |
|||
| Fig. 1694. | |||
 |
|||
| Fig. 1695. | |||
In Figs. 1694 and 1695 is represented a machine which is constructed for the drilling of shells of steam boilers, to effect which the boiler is set upon a table, round which are placed four standards, each carrying a drilling head, so that four[I-438] holes may be drilled simultaneously, and is provided with a dividing motion that enables the table to be revolved a certain distance, corresponding to and determining the pitch of the rivet holes.
It is capable of drilling locker shells of any diameter between four and eight feet. The feed motion to each drill is driven from one source of power, but each drill is adjustable on its own account. The depth of feed is regulated by a patent detent lever which engages with the teeth of a ratchet wheel, till released therefrom by contact with the adjustable stop. The drill spindle is then instantly forced back by the spiral spring and the forward feed motion continues.
It is the duty of the attendant to turn his dividing apparatus handle the required distance for the next hole, directly the drills are withdrawn, the amount of clearance between the drill point and the boiler shell being such as to give him proper time for this purpose, but no more. Self-acting water jets to the drills, and reflectors to enable the operator to see each drill, will be provided, but were not in action at the time views of the machine were made.
With an ordinary boiler shell formed in three plates, the three drills work simultaneously, and the one movement of the dividing apparatus, of course, applies to all. If the object to be drilled be not divisible into multiples of three, any other divisions can be produced by the dividing gear, either one, two, or three drills being used, as the circumstances may permit. Two heads can be shifted round from the angle of 120°, at which they are shown, to positions diametrically opposite, as may be desired, and the third can be used or disused as wished.
Vertical gauge rods are provided, duly marked out to the various pitches that may be needed for the vertical rows of holes, and the movement of the drill spindle saddles is so simple and steady that accurate adjustment can be made without the least difficulty. In the same way when the drill would, in its natural course, come in contact with one of the bolts by which the plates are held together, the attendant can run all the drills downwards a couple of inches or so, then turn the dividing apparatus two pitches instead of one, and on raising the three drills again he can continue the circular row as before. The entire control of the machine is governed by the attention of one man to two levers and the one dividing handle, which are all conveniently placed for the purpose.
In Fig. 1696 is represented a machine for boring car wheels. The chuck is driven by a crown gear operated beneath by a pinion on the cone spindle. The feed motion for the boring bar is operated from the small cone shown on the cone spindle, there being three rates of automatic feed, which are communicated to the bar by a worm and worm-wheel operating a spindle carrying a pinion in gear with a rack on the back of a boring bar.
The worm-wheel is provided with a friction disk operated by the small hand-wheel shown, to start and stop the automatic feed, the large hand-wheel operating the rack spindle direct, and therefore giving a rapid hand-feed or quick return motion for the boring bar. The boring bar is counterbalanced by a weight within the frame. On the side of the frame is a small crane for handing the car wheels.
Fig. 1697 represents a special machine for boring pulleys, &c. The advantage possessed by this class of machine is fully set forth in the remarks upon Boring and Turning Mills, and with reference to Fig. 725. The tool bar is fed vertically to the rotating pulley, and has three changes of feed; viz. .0648, .0441, and .0279 of an inch per rotation of the work. Its weight is counterbalanced.
The speed of rotation of the work table or chuck plate may, by means of the four steps on the cone pulley, be varied as follows:—63, 43, 19, or 10 revolutions per minute, which speeds are suitable for work bores ranging from 1 to 71⁄2 inches in diameter, the power exerted at the tool-point being for the latter diameter 1800 lbs.
The tool bar feed is operated by the upper cone pulley, and the worm and worm-wheel shown, the small wheel giving the automatic feed by a suitable friction plate, and the large hand wheel operating the bar quickly to elevate it after it has carried its cut through. When the drill is given a traverse back and forth, it obviously cuts out a slot or keyway whose width is equal to the diameter of the drill, and whose length equals the amount of traverse given to the drill. Special forms of drill are used for this purpose, and their forms will be shown hereafter. The machines for using these drills are termed traverse or cotter drilling machines. In Fig. 1698 is represented a combined drilling and cotter drilling machine. This machine consists essentially of a drilling machine provided with automatic feed motions for cotter drilling; these motions consisting of a self-acting traverse to the sliding head carrying the drill spindle, and a vertical feed, which occurs at the end of each traverse, and during a short period of rest given to the sliding head carriage, or saddle as it is promiscuously termed. The slideway for this head stands vertical and extends across the top of the frame.
The belt motion is conveyed up one end and then on the top of the slideway, driving the spindle direct by means of a pulley. The traverse of the head or saddle in cotter drilling is accomplished by means of a peculiar arrangement of screws and adjustable nuts, which can be instantly set to the required length of slot, and insures a uniform motion, back and forth, at each stroke, the length of the stroke being uniform, as is also the rate of its advance. The vertical position of the drill spindle is of great advantage in cotter drilling wrought iron or steel, as the slot in process of cutting can be kept full of oil.
The feed motions for cotter drilling may be instantly thrown out of gear when not required, remaining at rest and leaving the machine a simple traverse drill with automatic feeds.
Drilling Jigs, Guides, or Fixtures.—When a large number of pieces are to be drilled alike, as in the case when work is done to special gauges, special chucking devices called jigs, or fixtures, are employed to guide the drill, and insure that the holes shall be pierced accurately in the required location, and test pieces or gauges are provided to test the work from time to time to insure that errors have not arisen by reason of the wear of these drill-guiding devices.
Suppose, for example, that we have a link, such as in Fig. 1699, and that we require to have the holes throughout a large number of them of equal diameter at each end and the same distance apart, and if we could prevent the wear of the tools, and so continue to produce any number of links all exactly alike, we could provide a simple test gauge, such as shown in the figure, making it pass the proper distance apart, and of a diameter to fit the holes; but as we cannot prevent wear to the tools we must fix a limit to which such wear may be permitted to occur, and having reached that point they must be restored and corrected. We must at the same time possess means of testing in what direction the wear has induced error. Let it be assumed that the bore at a should be 1⁄2 inch and that at b 3⁄8 inch in diameter, that their distance from centre is to be, say, six inches, and that either bore may vary in diameter to the amount of 1⁄1000 inch, while the distance from centre to centre of the bores may also vary 1⁄1000 inch. Now let it be noted that if one piece be made 1⁄2000 inch too short, and another 1⁄2000 inch too long we have reached the extent of the limit, there being 1⁄1000 inch difference between them, although neither piece varies more than 1⁄2000 inch from the standard. Similarly in the bore diameters, if the bore, say at a, is 1⁄2000 inch too large in one piece and 1⁄2000 too small in another, there is a difference of 1⁄1000 between them, although each varies only the 1⁄2000 inch from the standard. In making test gauges for the holes, therefore, we must consider in what direction the tool will wear; thus, suppose that the finishing reamer for the holes is made when new to the standard diameter, and it can only wear smaller, hence a plug gauge of the standard diameter and 1⁄1000 inch smaller would serve thus, as so long as the smaller one will go in the limit of wear is not reached; when it will not go in sufficiently easily the reamer must be restored to fit the standard gauge. On the other hand, the reamer when new may be made 1⁄1000 inch above the standard size and restored when it has worn down to the standard size. In this case the bore diameter is still within the limit as long as the small gauge will enter; but when it fits too tight the reamer must be restored to the large plug gauge, the forms of these gauges being shown in Fig. 1700.
In Figs. 1701 and 1702 we have a jig or fixture for holding the link during the drilling process. It consists of two parts, c and d, between which the link is held by the screws e and f. The two hubs, g and h, are provided with hardened steel bushes, i and j, which are pierced with holes to receive and guide the drilling tool or reamer, and it is evident that in time the bore of these bushes will wear, and if they wear on one side more than on another they may wear longer or shorter between the centres or axis; hence we require gauges such as shown in Fig. 1703, one being longer between centres and the other shorter, in each case to the amount of the prescribed limit. In this case, so long as the holes are kept within the prescribed limit of diameter, the distance apart of the two holes will be within the limit so long as neither of the limit gauges will enter; and when they will enter the bushes i j must be restored.
It is to be remarked, however, that the variation in the diameter of the holes affects these standards, since if the holes are made sufficiently large either gauge would enter, although the axis of the holes and of the pins on the gauge might be the proper distance apart; hence the gauging for length depends to some degree upon the degree of accuracy in gauging for diameter.
Referring now to the construction of the jig, or fixture for drilling the link shown in Figs. 1701 and 1702: the base piece is provided with two short hubs, r and s, upon which the link is to sit, and it is obvious that these hubs must be faced off true with the bottom face of the base, while the link must also be faced so that it will be level, and not be bent or sprung when clamped by the screws e f. It is obvious that the hubs r and s may be omitted, and the link be flat on the base plate; but this would not be apt to hold the link so steadily, and greater care would be required to keep the surface clean. It is also obvious that in the form of jig shown there is a tendency of the screws e and f to[I-440] bend the piece d; but in the case of small pieces, as, say, not exceeding 8 inches long, piece d may be made strong enough to resist the screw pressure without bending. If, however, the link were, say, 18 inches long, it would be preferable to have projections in place of the hubs r, s, and to let these projections extend some distance along each end of the link, using four holding screws, and clamping the piece d on the inside of the hubs h g. To facilitate the rapid insertion and removal of the link into and from the jig cap-piece, d is pivoted on screw f, while a slot v is cut at the other end, so that when the two screws e, f are loosened, the cap-piece d may be swung out of the way without entirely removing it.
In Fig. 1704 we have a link in which a hole is to be bored at one end at a certain distance from a pin at the other, and the fixture, or jig for drilling, is shown in the sectional view, Fig. 1705, the side view, Fig. 1706, and the top view, Fig. 1707. It is obvious that the pin p and the face w of the link must be made true, and that a hardened steel bush may be placed in the hub to receive the pin p. The screw e binds one end of the cap d, and eye-bolts with thumb-nuts f bind the other, these bolts being pivoted at their lower ends, and passing through slots in d, so that as soon as nuts f are loosened, their bolts may be swung out clear of the cap, which may be swung on one side from the pin n as a pivot.
In Fig. 1708 we have a piece containing three holes, which are to be drilled in a certain position with regard to each other, and with regard to the face a. This brings us to the consideration that in all cases the work must be chucked or held true by the faces to which it is necessary that the holes must be true, and as in this case it is the face a, the jig must be made to hold the piece true by a, the construction being as in Fig. 1709, which represents a top view, and a sectional side view. The upper plate d carries three hardened steel bushes, a, b, and c, to receive the drilling tools, and thus determine that the holes shall be drilled at their proper positions with relation to each other, and is provided with a face n, against which the face (a, Fig. 1708) may be secured by the screw h, and thus determine the positions of the holes with, regard to that face. At e, f, and g are eye-bolts for clamping the work between the cap and the base plate, which is made large so that it may lie steadily on the table of the drilling machine. When the nuts e, f, and g and the screw h are loosened the cap d may be lifted off and the work removed.
If the holes are required to be made very exact in their positions with relation to one edge, as well as to the face a of the work, two screws k would be required, one binding the cap against the lug m of the base, and the other binding the edge of the work against the same lug.
The usefulness of jigs, or fixtures, is mainly confined to small work in which a great many duplicate pieces are to be made, and their designing calls for a great deal of close study and ingenuity. They can obviously be applied to all kinds of small work, and as a general principle the holes and pins of the work are taken as the prime points from which the work is to be held.
Drilling fixtures may, however, be applied with great advantage to work of considerable size in cases where a number of duplicate parts are to be made, an example of this kind being given in the fixtures for drilling the bolt holes, &c., in locomotive cylinders.
For drilling the cylinder covers and the tapping holes in the cylinder, the following device or fixture is employed: The flanges of the cylinder covers are turned all of one diameter, and a ring is made, the inside diameter of which is, say, an inch smaller than the bore of the cylinder; and its outside diameter is, say, an inch larger than the diameter of the cover. On the outside of the ring is a projecting flange which fits on the cover, as in Fig. 1710, a being the cylinder cover, and b b a section of the ring, which is provided with holes, the positions in the ring of which correspond with the required positions of the holes in the cover and cylinder; the diameter of these holes (in the ring, or template, as it is termed) is at least one quarter inch larger than the clearing holes in the cylinder are required to be. Into the holes of the template are fitted two bushes, one having in its centre a hole of the size necessary for the tapping drill, the other a hole the size of the clearing drill; both these bushes are provided with a handle by which to lift them in and out of the template, as shown in Fig. 1711, and both are hardened to prevent the drill cutting them, or the borings of the drill from gradually wearing their holes larger. The operation is to place the cover on the cylinder and[I-441] the template upon the cover, and to clamp them together, taking care that both cover and template are in their proper positions, the latter having a flat place or deep line across a segment of its circumference, which is placed in line with the part cut away on the inside of the cover to give free ingress to the steam, and the cover being placed in the cylinder so that the part so cut away will be opposite to the port in the cylinder, by which means the holes in the covers will all stand in the same relative position to any definite part of the cylinder, as, say, to the top or bottom, or to the steam port, which is sometimes of great importance (so as to enable the wrench to be applied to some particular nut, and prevent the latter from coming into contact with a projecting part of the frame or other obstacle): the positions of the cylinder, cover, template, and bush, when placed as described, being such as shown in Fig. 1712, a a being the cylinder, b the steam port, c the cylinder cover, d the template, and e the bush placed in position. The bush e having a hole in it of the size of the clearance hole, is the one first used, the drill (the clearance size) is passed through the bush, which guides it while it drills through the cover, and the point cuts a countersink in the cylinder face. The clearing holes are drilled all round the cover, and the bush, having the tapping size hole in it, is then brought into requisition, the tapping drill being placed in the drilling machine, and the tapping holes drilled in the cylinder flange, the bush serving as a guide to the drill, as shown in Fig. 1712, thus causing the holes in the cover and those in the cylinder to be quite true with each other. A similar template and bush is provided for drilling the holes in the steam chest face on the cylinder, and in the steam chest itself. While, however, the cylinder is in position to have the holes for the steam chest studs drilled, the cylinder ports may be cut as follows:—
The holes in the steam chest face of the cylinder being drilled and tapped, a false face or plate is bolted thereon, which plate is provided with false ports or slots, about three-eighths of an inch wider and three-fourths of an inch longer than the finished width and length of the steam ports in the cylinder (which excess in width and length is to allow for the thickness of the die). Into these false ports or slots is fitted a die to slide (a good fit) from end to end of the slots. Through this die is a hole, the diameter of which is that of the required finished width of the steam ports of the cylinder; the whole appliance, when in position to commence the operation of cutting out the cylinder ports, being as illustrated in Fig. 1713, a a being the cylinder, b b the false plate, c the sliding die, and d d the slots or false ports into which the die c fits. Into the hole of the die c is fitted a reamer, with cutting edges on its end face and running about an inch up its sides, terminating in the plain round parallel body of the reamer, whose length is rather more than the depth of the die c. The operation is to place the reamer into the drilling machine, taking care that it runs true. Place the die in one end of the port, as shown in Fig. 1713, and then wind the reamer down through the die so that it will cut its way through the port of the cylinder at one end; the spindle driving the drill is then wound along. The reamer thus carries the die with it, the slot in the false face acting as a guide to the die.
In the case of the exhaust port, only one side is cut out at a time. It is obvious that, in order to perform the above operation, the drilling machine must either have a sliding head or a sliding table, the sliding head being preferable.
The end of the slot at which the die must be placed when the reamer is wound down through the die and cylinder port, that is to say, the end of the port at which the operation of cutting it must be commenced, depends solely on which side of the port in the cylinder requires most metal to be cut off, since the reamer, or cutter, as it may be more properly termed, must cut underneath the heaviest cut, so that the heaviest cut will be forcing the reamer back, as shown in Fig. 1714, a being a sectional view of the cutter, b the hole cast in the cylinder for the port, c the side of the port having the most cut taken off, d the direction in which the cutter a revolves, and the arrow e the direction in which the cutter a is travelling up to its cut. If the side f of the port were the one requiring the most to be cut off, the cutter a would require to commence at the end f, and to then travel in the direction of the arrow g. The reason for the necessity of observing these conditions, as to the depth of cut and direction of cutter travel, is that the pressure of the cut upon the reamer is in a direction to force the reamer forward and into its cut on one side, and backward and away from its cut on the other side, the side having the most cut exerting the most pressure. If, therefore, the cutter is fed in such a direction that this pressure is the one tending to force the cutter forward, the cutter will spring forward a trifle, the teeth of the cutter taking, in consequence, a deep cut, and, springing more as the cut deepens, terminate in a pressure which breaks the teeth out of the cutter.
If, however, the side exerting the most pressure upon the reamer is always made the one forcing the cutter back, as shown in Fig. 1714, by reason of the direction in which the cutter is travelled to its cut, the reamer, in springing away from the undue pressure, will also spring away from its cut, and will not, therefore, rip in or break, as in the former case.
In cutting out the exhaust port, only one side, in consequence of its extreme width, may be cut at one operation; hence there[I-442] are two of the slots d, Fig. 1713, provided in the false plate or template for the exhaust port. The cutter a must, in this case, perform its cut so that the pressure of the cut is in a direction to force the cutter backwards from its cut. The time required to cut out the ports of an ordinary locomotive cylinder, by the above appliance, is thirty minutes, the operation making them as true, parallel, and square as can possibly be desired.
Drills and Cutters for Drilling Machines.—In the drilling machine, as in the lathe, the twist drill is the best tool that can be used for all ordinary work, since it produces the best work with the least skill, and is the cheapest in the end. As, however, the twist drill has been fully discussed with reference to its use upon lathe work, it is unnecessary to refer to it again more than to say that it possesses even greater advantages when used in the drilling machine than it does when used in the lathe; because as the drill stands vertical the flat drill will not relieve itself of the cuttings, and in deep holes must be occasionally withdrawn from the hole in order to permit the cuttings to be extracted, an operation that often consumes more time than is required for the cutting duty. Furthermore, as flat drills rarely run true they place excessive wear upon the drilling machine spindle, causing it to wear loose in its bearings, which is a great detriment to the machine.
Fig. 1715 represents a piece of work that can be readily drilled with a twist drill but not with a flat one, such work being very advantageous in cutting out keyways. All that is necessary is to drill the three holes b first, and if the drill runs true and the work is properly held and the drill fed slowly while run at a quick speed the operation may be readily performed.
The speeds and feeds for twist drills are given in connection with the use of the drill in the lathe, but it may be remarked here that more duty may be obtained by hand than by automatically feeding a drill, because in hand feeding the resistance of the feed motion indicates the amount of pressure on the drill, and the feed may be increased when the conditions (such as soft metal) permits, and reduced for hard spots or places, thus preserving the drill. Furthermore, the dulling of the drill edges becomes more plainly perceptible under hand feeding.
The commercial sizes of both taper and straight shank twist drills are as follows:—
| Diameter. | Length. | Diameter. | Length. | Diameter. | Length. | Diameter. | Length. | ||||||||
| 1⁄4 | 6 | 1⁄8 | 25⁄32 | 9 | 7⁄8 | 1 | 5⁄16 | 14 | 1⁄4 | 1 | 27⁄32 | 16 | 3⁄8 | ||
| 9⁄32 | 6 | 1⁄4 | 13⁄16 | 10 | 1 | 11⁄32 | 14 | 3⁄8 | 1 | 7⁄8 | 16 | 1⁄2 | |||
| 5⁄16 | 6 | 3⁄8 | 27⁄32 | 10 | 1⁄4 | 1 | 3⁄8 | 14 | 1⁄2 | 1 | 29⁄32 | 16 | 1⁄2 | ||
| 11⁄32 | 6 | 1⁄2 | 7⁄8 | 10 | 1⁄2 | 1 | 13⁄32 | 14 | 5⁄8 | 1 | 15⁄32 | 16 | 1⁄2 | ||
| 3⁄8 | 6 | 3⁄4 | 29⁄32 | 10 | 5⁄8 | 1 | 7⁄16 | 14 | 3⁄4 | 1 | 31⁄32 | 16 | 1⁄2 | ||
| 13⁄32 | 7 | 15⁄16 | 10 | 3⁄4 | 1 | 15⁄32 | 14 | 7⁄8 | 2 | 16 | 1⁄2 | ||||
| 7⁄16 | 7 | 1⁄4 | 31⁄32 | 10 | 7⁄8 | 1 | 1⁄2 | 15 | 2 | 1⁄32 | 16 | 1⁄2 | |||
| 15⁄32 | 7 | 1⁄2 | 1 | 11 | 1 | 17⁄32 | 15 | 1⁄8 | 2 | 1⁄16 | 17 | ||||
| 1⁄2 | 7 | 3⁄4 | 1 | 1⁄32 | 11 | 1⁄8 | 1 | 9⁄16 | 15 | 1⁄4 | 2 | 1⁄8 | 17 | ||
| 17⁄32 | 8 | 1 | 1⁄16 | 11 | 1⁄4 | 1 | 19⁄32 | 15 | 3⁄8 | 2 | 3⁄16 | 17 | |||
| 9⁄16 | 8 | 1⁄4 | 1 | 3⁄32 | 11 | 1⁄2 | 1 | 5⁄8 | 15 | 1⁄2 | 2 | 1⁄4 | 17 | 1⁄2 | |
| 19⁄32 | 8 | 1⁄2 | 1 | 1⁄8 | 11 | 3⁄4 | 1 | 21⁄32 | 15 | 5⁄8 | 2 | 5⁄16 | 17 | 1⁄2 | |
| 5⁄8 | 8 | 3⁄4 | 1 | 5⁄32 | 11 | 7⁄8 | 1 | 11⁄16 | 15 | 3⁄4 | 2 | 3⁄8 | 18 | ||
| 21⁄32 | 9 | 1 | 3⁄16 | 12 | 1 | 23⁄32 | 15 | 7⁄8 | 2 | 7⁄16 | 18 | 1⁄2 | |||
| 11⁄16 | 9 | 1⁄4 | 1 | 7⁄32 | 12 | 1⁄8 | 1 | 3⁄4 | 16 | 2 | 1⁄2 | 19 | |||
| 23⁄32 | 9 | 1⁄2 | 1 | 1⁄4 | 12 | 1⁄2 | 1 | 25⁄32 | 16 | 1⁄8 | |||||
| 3⁄4 | 9 | 3⁄4 | 1 | 9⁄32 | 14 | 1⁄8 | 1 | 13⁄16 | 16 | 1⁄4 | |||||
Twist drills are also made to the Stubs wire gauge as follows:—
| Numbers by gauge. | Length. | Numbers by gauge. | Length. | ||||||
| 1 | to | 5 | 4 | 31 | to | 35 | 2 | 5⁄8 | |
| 6 | „ | 10 | 3 | 11⁄16 | 36 | „ | 40 | 2 | 7⁄16 |
| 11 | „ | 15 | 3 | 1⁄2 | 41 | „ | 45 | 2 | 1⁄4 |
| 16 | „ | 20 | 3 | 1⁄4 | 46 | „ | 50 | 2 | 1⁄16 |
| 21 | „ | 25 | 3 | 1⁄16 | 51 | „ | 60 | 1 | 3⁄4 |
| 26 | „ | 30 | 2 | 13⁄16 | 61 | „ | 70 | 1 | 1⁄2 |
Fig. 1716 represents the flat drill, which has three cutting edges, a, b, and c. The only advantages possessed by the flat drill are that it will stand rougher usage than the twist drill, and may be fed faster, while it can be more easily made. Furthermore, when the work is unusually hard the flat drill can be conveniently shaped and tempered to suit the conditions.
The drill is flattened out and tapered thinnest at the point c. The side edges that form the diameter of the drill are for rough work given clearance, but for finer work are made nearly cylindrical, as in the figure.
The flattening serves two purposes: first, it reduces the point of the drill down to its proper thinness, enabling it to enter the metal of the work easily, and secondly, it enables the cuttings to pass upward and find egress at the top of the hole being drilled.
The cutting edges are formed by grinding the end facets at an angle as shown, and this angle varies from 5° for drilling hard metal, such as steel, to 20° for soft metal, such as brass or copper.
The angle of one cutting edge to the other varies from 45° for steel to about 35° or 40° for soft metals. The object of these two variations of angles is that in hard metal the strain and abrasion is greatest and the cutting edge is stronger with the lesser degree of angle, while in drilling the softer metals the strain being less the cutting edge need not be so strong and the angles may be made more acute, which enables the drill to enter the metal more easily. The most imperfect cutting edge in a drill is that running diagonally across the point, as denoted by a in Fig. 1717, because it is less acute than the other cutting edges, but this becomes more acute and, therefore, more effective, as the angles of the facets forming it are increased as denoted by the dotted lines in the figure. It is obvious, however, that the more acute these angles the weaker the cutting edge, hence an angle of about 5° is that usually employed.
It is an advantage to make the cutting edge at a, Fig. 1717, as short as possible, which may be done by keeping the drill point thin; but if too thin it will be apt either to break or to operate in jumps (especially upon brass), drilling a hole that is a polygon instead of a true circle.
The cutting edges should not only stand at an equal degree of angle to the axial line of the drill, but should be of equal lengths, so that the point of the drill will be in line with the axial line of the drill. If the drill runs true the point will then be in the axial line of rotation, and the diameter of hole drilled will be equal to the diameter of the drill.
[I-443]If, however, one cutting edge is longer than the other the hole drilled will be larger than is due to the diameter of the drill.
Suppose, for example, the drill to be ground as in Fig. 1718, the cutting edge f being the longest and at the least angle, then the point g of the drill, when clear of the work, will naturally revolve in a circle around the axial line h of the drill’s rotation. But when the drilling begins, the point of the drill meets the metal first and naturally endeavours to become the centre of rotation, drilling a straight conical recess, the work moving around with the point of the drill. If the work is prevented from moving, either the drill will spring or bend, the point of the drill remaining (at first) the centre of rotation at that end of the drill, or else the recess cut by the drill will be as in the figure, and the hole will be larger in diameter than the drill.
If, however, the drill is ground as shown in Fig. 1719, the edge e being nearest to a right angle to the axial line h of the drill, the drilling will be performed as shown in the figure, the edge e cutting the cone l, the edge f serving simply to enlarge the hole drilled by e. Here, again, if the work is held so that it cannot move, the point of the drill will revolve in a circle, and in either case, so soon as the point of the drill emerges the diameter of the hole drilled will decrease, the finished hole being conical as shown in Fig. 1720 at a.
It may be remarked that the eye of the workman is (for rough work, such as tapping or clearing holes) sufficient guide to enable the grinding of the drill true enough to partly avoid the conditions shown in these two figures (in which the errors are magnified for clearness of illustration), because when the want of truth is less in amount than the thickness of the drill point, the centre of motion of the drill point when the drill has entered the work to its full diameter becomes neither at the point of the drill nor in the centre of its diameter, but intermediate between the two.
Thus, in Fig. 1721, a is the centre of the diameter of the drill, but the cutting edge c being shorter than d throws the point of the drill towards e, hence the extra pressure of d on the incline of the recess it cuts, over the like pressure exerted by c tends to throw the centre of rotation towards e, the natural endeavor of the drill point to press into the centre of the recess acting in the same direction. This is in part resisted by the strength of the drill, hence the centre of rotation is intermediate as at b in figure. The dotted circle is drawn from the axial line of the drill as a centre, while the full circle is drawn from b as a centre. The result of this would be that the point of the drill would perform more duty than is due to its thickness, and the recess cut would have a flat place at the bottom, as shown in Fig. 1722 at o. This, from the want of keenness of the cutting edge running diagonally across the drill point, would cause the drill to cut badly and require more power to drive and feed.
The edges at the flat end of the drill, as at a, a in Fig. 1723, should have a little clearance back from the cutting edge though they may be left the full circle as, at a, a, but in any event they should not have clearance sufficient to form them as at b, b, Fig. 1723, because in that case the side edges c, c would cut the sides of the hole. In large drills, especially, it is necessary that the edges have but little clearance, and that the form of the clearance be as shown in Fig. 1044, with reference to twist drills. When no edge clearance whatever is given the edges act to a certain extent as guides to the drill, but if the drill is not ground quite true this induces a great deal of friction between the edges of the drill and the side of the hole.
In any case of improper grinding the power required to drive the drill will be increased, because of the improper friction induced between the sides of the drill and the walls of the hole.
For use on steel, wrought iron, and cast iron the lip drill shown in Fig. 1724 is a very efficient tool. It is similar to the flat drill but has its cutting edge bent forward. It possesses the keenness of the twist drill and the strength of the flat drill, but as in the case of all drills whose diameters are restored by forging and hand grinding, it is suitable for the rougher classes of work only, and requires great care in order to have it run true and keep both cutting edges in action. It is sometimes attempted to give a greater cutting angle to a flat drill by grinding a recess in the front face, as at a in Fig. 1725, but this is a poor expedient.
Fig. 1726 represents what is known as the tit drill. It is employed to flatten the bottoms of holes, and has a tit t which serves to steady it. The edges a, b of this drill may be turned true and left without clearance, which will also serve to steady the drill. The tit t should be tapered towards the point, as shown, which will enable it to feed more easily and cut more freely. The speed of the drill must be as slow again as for the ordinary flat drill, and not more than one-third as fast as the twist drill.
To enable a drill to start a hole in the intended location the[I-444] centre-punch recess in the centre of that location should be large enough in diameter at the top to admit the point of the drill, that is to say, the recess should not be less in diameter at the top than the thickness of the drill point.
If the drill does not enter true the alteration is effected as shown in Fig. 1727, in which a represents the work, b a circle of the size of the hole to be drilled, and c the recess cut by the drill, while d is a recess cut with a round-nosed chisel, which recess will cause the drill to run over in that direction.
It is a good plan when the hole requires to be very correctly located to strike two circles, as shown in Fig. 1728, and to define them with centre-punch marks so that the cuttings and oil shall not erase them, as is apt to be the case with lines only. The outer circle is of the size of hole to be drilled, the inner one serves merely as a guide to true the drilling by.
If the work is to be clamped to the work table an alteration in the location of the recess cut by the drill point may be made by moving the work. In this case the point of the drill may be fed up so as to enter into and press against the centre-punch mark made in the centre of the location of the hole to be drilled, which, if the drill runs true will set the work true enough to clamp it by. The alteration to the recess cut by the drill when first starting to bring the hole in its true position should be made as soon as a want of truth is discernible, because the shallower the recess the more easily the alteration may be made.
Sometimes a small hole is drilled as true to location as may be, and tested, any error discovered being corrected by a file; a larger drill is then used and the location again tested, and so on; in this way great precision of location may be obtained.
The more acute angle the cutting edges form one to the other, or in other words, the longer the cutting edges are in a drill of a given diameter, the more readily the drill will move over if one side of the recess be cut out as in Fig. 1727, and from some experiments made by Messrs. William Sellers and Co., it was determined that if the angle of one cutting edge to the other was more than 104° the drill would cease to move over.
In drilling wrought iron or the commoner qualities of steel the drill should be liberally supplied with either water or oil, but soapy water is better than pure. This keeps the drill cool and keeps the cutting edge clean, whereas otherwise the cuttings under a coarse feed are apt to stick fast to the drill point if the speed of the drill is great. Furthermore, under excessive duty the drill is apt to become heated and softened.
For cast steel oil is preferable, or if the steel be very hard it will cut best dry under a slow speed and heavy pressure.
For brass and cast iron the drill should run dry, otherwise the cuttings clog and jam in the hole. When the drill squeaks either the cutting edge is dulled and the drill requires regrinding, or else the cuttings have jammed in the hole, and either defect should be remedied at once.
As soon as the point of the drill emerges through the work the feed should be lessened, otherwise the drill is apt to force through the weakened metal and become locked, which will very often either break or twist the drill. This may be accomplished when there is any end play to the drilling machine spindle by operating the feed motion in a direction to relieve the feed as soon as the point of the drill has emerged through the bottom of the hole, thus permitting the weight of the spindle to feed the drill. In a drilling machine, however, in which the weight of the spindle is counterbalanced, the feed may be simply reduced while the drill is passing through the bottom of the hole.
Drills for work of ordinary hardness are tempered to an orange purple, but if the metal to be cut is very hard a straw color is preferable, or the drill may be left as hard as it leaves the water; that is to say hardened, but not tempered. In these cases the speed of the drill must be reduced.
To assist a drill in taking hold of hard metal it is an excellent plan to jag the surface of the metal with a chisel which will often start the drill to its cut when all other means have failed. It is obvious from previous remarks that the harder the drill the less the angle of the end facets.
In cases of extreme hardness two drills may with advantage be used intermittently upon the same hole; one of these should have its cutting edges ground at a more acute angle one to the other than is the case with the other drill, thus the cutting edge will be lessened in length while the drill will retain the strength due to[I-445] its diameter, so that a maximum of pressure may be placed upon it. When one drill has cut deep enough to bring its full length of cutting edge into action, it may be removed and the other drill employed, and so on.
The drill (for hard steel) should be kept dry until it has begun to cut, when a very little oil may be employed, but for chilled cast iron it should be kept dry.
Small work to be drilled while resting upon a horizontal table may generally be held by hand, and need not therefore be secured in a chuck or to the table, because the pressure of the drill forces the work surface to the table, creating sufficient friction to hold the work from rotating with the drill. For large holes, however, the work may be secured in chucks or by bolts and plates as described for lathe and planer work, or held in a vice.
The following table for the sizes of tapping holes is that issued by the Morse Twist Drill and Machine Co. In reply to a communication upon the subject that company states. “If in our estimate the necessary diameter of a tap drill to give a full thread comes nearest to a 1⁄64 inch measurement, we give the size of the drill in 64ths of an inch. If nearest to a 32nd size of drill we give the drill size in 32nds of an inch.”
In the following table are given the sizes of tapping drills, to give full threads, the diameters being practically but not decimally correct:—
| Diameter of tap. |
Number threads to inch. |
Drill for V‑thread. |
Drill for U.S.S. thread. |
Drill for Whitworth thread. |
|||||||||||||||||||||
| 1⁄4 | 16 | 18 | 20 | 5⁄32 | 5⁄32 | 11⁄64 | — | — | 3⁄16 | — | — | 3⁄16 | |||||||||||||
| 9⁄32 | 16 | 18 | 20 | 3⁄16 | 13⁄64 | 13⁄64 | — | — | — | — | — | — | |||||||||||||
| 5⁄16 | 16 | 18 | — | 7⁄32 | 15⁄64 | — | — | 1⁄4 | — | — | 15⁄64 | — | |||||||||||||
| 11⁄32 | 16 | 18 | — | 1⁄4 | 17⁄64 | — | — | — | — | — | — | — | |||||||||||||
| 3⁄8 | 14 | 16 | 18 | 1⁄4 | 9⁄32 | 9⁄32 | — | 9⁄32 | — | — | 9⁄32 | — | |||||||||||||
| 13⁄32 | 14 | 16 | 18 | 19⁄64 | 21⁄64 | 21⁄64 | — | — | — | — | — | — | |||||||||||||
| 7⁄16 | 14 | 16 | — | 21⁄64 | 11⁄32 | — | 11⁄32 | — | — | 11⁄32 | — | — | |||||||||||||
| 15⁄32 | 14 | 16 | — | 23⁄64 | 3⁄8 | — | — | — | — | — | — | — | |||||||||||||
| 1⁄2 | 12 | 13 | 14 | 3⁄8 | 25⁄64 | 25⁄64 | — | 13⁄32 | — | 3⁄8 | — | — | |||||||||||||
| 17⁄32 | 12 | 13 | 14 | 13⁄32 | 27⁄64 | 27⁄64 | — | — | — | — | — | — | |||||||||||||
| 9⁄16 | 12 | 14 | — | 7⁄16 | 29⁄64 | — | 7⁄16 | — | — | — | — | — | |||||||||||||
| 19⁄32 | 12 | 14 | — | 15⁄32 | 31⁄64 | — | — | — | — | — | — | — | |||||||||||||
| 5⁄8 | 10 | 11 | 12 | 15⁄32 | 1⁄2 | 1⁄2 | — | 1⁄2 | — | — | 1⁄2 | — | |||||||||||||
| 21⁄32 | 10 | 11 | 12 | 1⁄2 | 17⁄32 | 17⁄32 | — | — | — | — | — | — | |||||||||||||
| 11⁄16 | 11 | 12 | — | 9⁄16 | 9⁄16 | — | — | — | — | — | — | — | |||||||||||||
| 23⁄32 | 11 | 12 | — | 19⁄32 | 19⁄32 | — | — | — | — | — | — | — | |||||||||||||
| 3⁄4 | 10 | 11 | 12 | 19⁄32 | 5⁄8 | 5⁄8 | 5⁄8 | — | — | 5⁄8 | — | — | |||||||||||||
| 25⁄32 | 10 | 11 | 12 | 5⁄8 | 21⁄32 | 21⁄32 | — | — | — | — | — | — | |||||||||||||
| 13⁄16 | 10 | — | — | 21⁄32 | — | — | — | — | — | — | — | — | |||||||||||||
| 27⁄32 | 10 | — | — | 11⁄16 | — | — | — | — | — | — | — | — | |||||||||||||
| 7⁄8 | 9 | 10 | — | 45⁄64 | 23⁄32 | — | 23⁄32 | — | — | 23⁄32 | — | — | |||||||||||||
| 29⁄32 | 9 | 10 | — | 47⁄64 | 3⁄4 | — | — | — | — | — | — | — | |||||||||||||
| 15⁄16 | 9 | — | — | 49⁄64 | — | — | — | — | — | — | — | — | |||||||||||||
| 21⁄32 | 9 | — | — | 51⁄64 | — | — | — | — | — | — | — | — | |||||||||||||
| 1 | 8 | — | — | 13⁄16 | — | — | 27⁄32 | — | — | 27⁄32 | — | — | |||||||||||||
| 1 | 1⁄32 | 8 | — | — | 53⁄64 | — | — | — | — | — | — | — | — | ||||||||||||
| 1 | 1⁄16 | 8 | — | — | 55⁄64 | — | — | — | — | — | — | — | — | ||||||||||||
| 1 | 3⁄32 | 8 | — | — | 57⁄64 | — | — | — | — | — | — | — | — | ||||||||||||
| 1 | 1⁄8 | 7 | 8 | — | 29⁄32 | 15⁄16 | — | 15⁄16 | — | — | 15⁄16 | — | — | ||||||||||||
| 1 | 5⁄32 | 7 | 8 | — | 15⁄16 | 31⁄32 | — | — | — | — | — | — | — | ||||||||||||
| 1 | 3⁄16 | 7 | 8 | — | 31⁄32 | 1 | — | — | — | — | — | — | — | ||||||||||||
| 1 | 7⁄32 | 7 | 8 | — | 1 | 1 | 1⁄32 | — | — | — | — | — | — | — | |||||||||||
| 1 | 1⁄4 | 7 | — | — | 1 | 1⁄32 | — | — | 1 | 1⁄16 | — | — | 1 | 1⁄16 | — | — | |||||||||
| 1 | 9⁄32 | 7 | — | — | 1 | 1⁄16 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 5⁄16 | 7 | — | — | 1 | 3⁄32 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 11⁄32 | 7 | — | — | 1 | 1⁄8 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 3⁄8 | 6 | — | — | 1 | 1⁄8 | — | — | 1 | 5⁄32 | — | — | 1 | 5⁄32 | — | — | |||||||||
| 1 | 13⁄32 | 6 | — | — | 1 | 5⁄32 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 7⁄16 | 6 | — | — | 1 | 5⁄32 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 15⁄32 | 6 | — | — | 1 | 3⁄16 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 1⁄2 | 6 | — | — | 1 | 15⁄64 | — | — | 1 | 9⁄32 | — | — | 1 | 9⁄32 | — | — | |||||||||
| 1 | 17⁄32 | 6 | — | — | 1 | 9⁄32 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 9⁄16 | 6 | — | — | 1 | 9⁄32 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 19⁄32 | 6 | — | — | 1 | 5⁄16 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 5⁄8 | 5 | 5 | 1⁄2 | — | 1 | 9⁄32 | 1 | 5⁄16 | — | — | 1 | 3⁄8 | — | 1 | 23⁄64 | — | — | |||||||
| 1 | 21⁄32 | 5 | 5 | 1⁄2 | — | 1 | 5⁄16 | 1 | 11⁄32 | — | — | — | — | — | — | — | |||||||||
| 1 | 11⁄16 | 5 | 5 | 1⁄2 | — | 1 | 11⁄32 | 1 | 3⁄8 | — | — | — | — | — | — | — | |||||||||
| 1 | 23⁄32 | 5 | 5 | 1⁄2 | — | 1 | 3⁄8 | 1 | 13⁄32 | — | — | — | — | — | — | — | |||||||||
| 1 | 3⁄4 | 5 | — | — | 1 | 13⁄32 | — | — | 1 | 1⁄2 | — | — | 1 | 1⁄2 | — | — | |||||||||
| 1 | 25⁄32 | 5 | — | — | 1 | 7⁄16 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 13⁄16 | 5 | — | — | 1 | 15⁄32 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 27⁄32 | 5 | — | — | 1 | 1⁄2 | — | — | — | — | — | — | — | — | |||||||||||
| 1 | 7⁄8 | 4 | 1⁄2 | 5 | — | 1 | 17⁄32 | 1 | 17⁄32 | — | — | 1 | 5⁄8 | — | 1 | 37⁄64 | — | — | |||||||
| 1 | 29⁄32 | 4 | 1⁄2 | 5 | — | 1 | 9⁄16 | 1 | 9⁄16 | — | — | — | — | — | — | — | |||||||||
| 1 | 15⁄16 | 4 | 1⁄2 | 5 | — | 1 | 19⁄32 | 1 | 19⁄32 | — | — | — | — | — | — | — | |||||||||
| 1 | 31⁄32 | 4 | 1⁄2 | 5 | — | 1 | 5⁄8 | 1 | 5⁄8 | — | — | — | — | — | — | — | |||||||||
| 2 | 4 | 1⁄2 | — | — | 1 | 21⁄32 | — | — | 1 | 23⁄32 | — | — | 1 | 45⁄64 | — | — | |||||||||
To drive all drills by placing them directly in the socket of the drilling machine spindle would necessitate that all the drills should have their shanks to fit the drilling machine socket. This would involve a great deal of extra labor in making the drills, because the socket in the machine spindle must be large enough to fit the size of shank that will be strong enough to drive the largest drill used in the machine, hence the small drills would require to be forged down from steel equal to the full diameter of the shank of the largest drill. To obviate this difficulty the sockets already described with reference to drilling in the lathe are used.
The employment of these sockets preserves the truth of the bore of the drilling machine spindle by greatly diminishing the necessity to insert and remove the shank from the drill spindle, because each socket carrying several sizes of drills (as given with reference to lathe work) the sockets require less frequent changing.
Drill shanks are sometimes made parallel, with a flat place as at a in Fig. 1729, to receive the pressure of the set-screw by which it is driven. To enable the shank to run true it must be a close fit to the socket and should be about five diameters long. The objection to this form is that the pressure of the set-screw tends to force the drill out of true, as does also the wear of the socket bore.
These objections will obviously be diminished in proportion as the drill shank is made a tight fit to the socket, and to effect this and still enable the drill to be easily inserted and removed from the socket, the drill shank may be first made a tight fit to the socket bore, and then eased away on the half circumference on the side of the flat place, leaving it to fit on the other half circumference which is shown below the dotted line b in the end view in the figure. The set-screw is also objectionable, since it requires the use of a wrench, and is in the way and liable to catch the operator’s clothing.
There is, however, one advantage in employing a set-screw for twist drills, inasmuch as that, on account of the front rake on a twist drill, there is a strong tendency for the drill, as soon as the point emerges through the work, to run forward into the work and by ripping in become locked. This is very apt to be the case if there is any end play in the driving spindle, because the pressure of the cut forces the spindle back from the cut; but so soon as the drill point emerges and the pressure is reduced, the weight of the spindle acting in concert with the front rake on the drill causes the spindle to drop, taking up the lost motion in the opposite direction. In addition to this the work will from the same cause lift and run up the drill, often causing an increase in the duty sufficient to break the drill.
If the spindle has no lost motion and the work is bolted or fastened to the table or in a chuck, the drill if it has a taper shank only will sometimes run forward and slip loose in the driving socket. This, however, may be obviated by feeding the drill very slowly after its point emerges through the work.
[I-446]Yet another form in which the cylindrical shanks of drills have been driven is shown in Fig. 1730. The shank is provided with a longitudinal groove turning at a right angle; at its termination the socket is provided with a screw whose point projects and fits into the shank groove. The drill is inserted and turned to the right, the end of the screw driving the drill and preventing it from coming out or running forward.
Flat drills are usually provided with a square taper shank such as shown in Fig. 1730, an average amount of taper being 11⁄4 inches per foot.
There are several disadvantages in the use of a square shank.
1st. It is difficult to forge the drill true and straight with the shank.
2nd. It is difficult to make the square socket true with the axial line of the machine spindle, and concentric with the same from end to end.
3rd. It is difficult to fit the shank of the drill to the socket and have its square sides true with the axial line of the drill.
4th. It is an expensive form of shank to fit. It is a necessity, however, when the cutting duty is very heavy, as in the case of stocks carrying cutters for holes of large diameter.
In order to properly fit a square shank to a socket it should be pressed into the socket by hand only, and pressed laterally in the direction of each side of the square. If there is no lateral movement the shank is a fit, and the spindle may be revolved to see if the drill runs true, as it should do if the body of the drill is true with the shank (and this must always be the case to obtain correct results). The drill must be tried for running true at each end of the cylindrical body of the drill, which, being true with the square shank, may be taken as the standard of truth in grinding the drill, so that supposing the hole in the driving spindle to be true and the drill shank to be properly fitted, the drill will run true whichever way inserted. If the body of the drill runs out of true it will cause a great deal of friction by rubbing and forcing the cuttings against the sides of holes, especially if the clearance be small or the hole a deep one.
In fitting the shank, the fitting or bearing marks will show most correctly when the shank is driven very lightly home, for if driven in too firmly the bearing marks will extend too far in consequence of the elasticity of the metal. If the hole in the spindle is not true with the axial line of the spindle, or if the sides of the hole are not a true square or are not equidistant from the axial line of the spindle, the drill must be fitted with one side of its square shank always placed to the same side of the square in the socket, and these two sides must therefore be marked so as to denote how to insert the drill without having to try it in the socket. Usually a centre-punch mark, as at e, Fig. 1731, is made on the drill and another on the collar as at f.
To enable the extraction of the drill from the socket the latter is provided with a slot, shown in figure at c, the slot passing through the spindle and the end of the drill protruding into the slot, so that a key driven into the slot will force the drill from the socket. The key employed for this purpose should be of some soft metal, as brass or hard composition brass, so that the key shall not condense or press the metal of the keyway, and after the key is inserted it should be lightly tapped with a hammer, travelling in the direction of the line of the spindle and not driven through the keyway.
The drill should not be given a blow or tap to loose it in the spindle, as this is sure in time to make its socket hole out of true.
The thread shown on the end of the drill spindle in figure is to receive chucks for holding and driving drills.
The various forms of small drill chucks illustrated in connection with the subject of lathe chucks are equally suitable for driving drills in the drilling machine.
Fig. 1732, however, represents an excellent three-jawed chuck for driving drills, the bite being very narrow and holding the drill with great firmness.
Fig. 1733 represents a two-jawed drill chuck in which the[I-447] screws operate a pair of dies for gripping parallel shank drills, the screws being operated independently.
In other forms of similar chucks the bite is a V recess parallel to the chuck axis, the only difference between a drill chuck for a drilling machine and one for a lathe being that for the former the jaws do not require outside bites nor to be reversible.
Holes that are to be made parallel, straight, cylindrically true in the drilling machine, are finished by the reamer as already described with reference to lathe work, and it is found as in lathe work that in order that a reamer may finish holes to the same diameter, it is necessary that it take the same depth of finishing cut in each case, an end that is best obtained by the use of three reamers, the first taking out the irregularities of the drilled hole, and the second preparing it for the light finishing cut to be taken by the third.
All the remarks made upon the reamer when considered with reference to lathe work apply equally to its use in the drilling machine.
Another tool for taking a very light cut to smooth out a hole and cut it to exact size is the shell reamer shown in Fig. 1734, which fits on a taper mandrel through which passes a square key fitting into the square slot shown in the shell reamer.
Reamers may be driven by drill chucks, but when very true and parallel work is required, and the holes are made true before using the reamer, it is preferable to drive them by a socket that permits of their moving laterally. Especially is this the case with rose-bits. Fig. 1735, which is taken from The American Machinist, represents a socket of this kind, being pivoted at its driving or shank end, and supported at the other by two small spiral springs. The effect is that if the socket does not run quite true the reamer is permitted to adjust itself straight and true in the hole being reamed, instead of rubbing and binding against its walls, which would tend to enlarge its mouth and therefore impair its parallelism.
Cotter drills, slotting drills, or keyway drills, three names designating the same tool, are employed to cut out keyways, mortises, or slots.
Fig. 1736 represents a common form of cotter or keyway drill, the cutting edges being at a, a, and clearance being given by grinding the curve as denoted by the line c. In some cases a stock s and two detachable bits or cutters c, c, are used as in Fig. 1737, the bits being simple tools secured in slots in the stock by set-screws, and thus being adjustable for width so that they may be used to cut keyways of different widths.
The feed of keyway drills should be light, and especial care must be taken where two spindles are used, to keep them in line, or otherwise the keyway will not come fair, as is shown in Fig. 1738, where the half drilled from side a and that drilled from side b are shown not to come fair at their point of junction c. This is more apt to occur when a deep keyway is drilled one half from each side. Hence in such a case great care must be exercised in setting the work true, because the labor in filing out such a keyway is both tedious and expensive.
In producing holes of above or about two inches in diameter, cutters such as shown in Fig. 1739 may be employed. a is a stock carrying a cutter b secured in place by a key c. Holes are first drilled to receive the pin d, which serves as a guide to steady the stock. The amount of cutting duty is obviously confined to the production of the holes to receive the pin and the metal removed from the groove cut by the cutters, so that at completion of the cutter duty there comes from the work a ferrule or annular ring that has been cut out of the work.
For use on wrought iron or steel the front faces of the cutters may be given rake as denoted by the dotted line at e, and smooth and more rapid duty may be obtained if the cutter be set back, as in Fig. 1740, the cutting edge being about in a line with line a, in which case the front face may be hollowed out as at b, and take a good cut without the digging in and jumping that is apt to occur in large holes if the cutter is not thus set back. The larger the diameter of the work the greater the necessity of setting the cutting edge back, thus in Fig. 1741 the cutter is to be used to cut a large circle out of a plate p, as, say, a man-hole in a boiler sheet. The cutter c is carried in a bar b secured in the stock a by a screw, and unless the cutter is set well back it is liable to dip into the work and break.[I-448]
It is obvious that the pin e in the figure must be long enough to pass into the hole in the plate before the cutter meets the plate surface and begins to cut, so that the pin shall act as a guide to steady the cutter, and also that in all cutters or cutter driving stocks the shank must be either of large diameter or else made square, in order to be able to drive the cut at the increased leverage over that in drilling.
In these forms of tube plate cutters it is necessary to drill a hole to receive the pin d. But this necessity may be removed by means of a cutter, such as shown in Fig. 1742, which is given simply as a representative of a class of such cutters. a is a cutter stock having the two cutters b b fitted in slots and bolted to it. c is a spiral spring inserted in a hole in a and pressing upon the pin d, which has a conical point. The work is provided with a deep centre-punch mark denoting the centre of the hole to be cut. The point of d projects slightly beyond the cutting edges of the cutters, and as it enters the centre-punch mark in the work it forms a guide point to steady the cutters as they rotate. As the cutters are fed to their cut, the pin d simply compresses the spiral spring c and passes further up the cutter stock. Thus the point of d serves instead of a hole and pin guide.
A simple form of adjustable cutter is shown in Figs. 1743 and 1744. It consists of a stock a a with the shank b, made tapering to fit the socket of a boring or drilling machine. Through the body of the stock is a keyway or slot, in which is placed the cutter c, provided in the centre of the upper edge with a notch or recess. Into this slot fits the end of the piece d, which is pivoted upon the pin e. The radial edge of d has female worm teeth upon it. f is a worm screw in gear with the radial edge of d. Upon the outer end of f is a square projection to receive a handle, and it is obvious that by revolving the screw f, the cutter c will be moved through the slot in the stock, and hence the size of the circle which the cutter will describe in a revolution of the stock a may be determined by operating the screw f. Thus the tool is adjustable for different sizes of work, while it is rigidly held to any size without any tendency whatever either to slip or alter its form. The pin g is[I-449] not an absolutely necessary part of the tool, but it is a valuable addition, as it steadies the tool. This is necessary when the spindle of the machine in which it is used has play in the bearings, which is very often the case with boring and drilling machines. The use of g is to act as a guide fixed in the table upon which the work is held, to prevent the tool from springing away from the cut, and hence enabling it to do much smoother work. It is usual to make the width of the cutter c to suit some piece of work of which there is a large quantity to do, because when the cutter is in the centre of the stock both edges may perform cutting duty; in which case the tool can be fed to the cut twice as fast as when the cutter is used for an increased diameter, and one cutting edge only is operative. The tool may be put between the lathe centres and revolved, the work being fastened to the lathe saddle. In this way it is exceedingly useful in cutting out plain cores in half-core boxes.
In addition to its value as an adjustable boring tool this device may be used to cut out sweeps and curves, and is especially adapted to cutting those of double eyes. This operation is shown in Fig. 1744, in which d is the double eye, a is the tool stock, f is the adjusting screw, and c is the cutter. The circular ends of connecting rod strips and other similar work also fall within the province of this tool, and in the case of such work upon rods too long to be revolved this is an important item, as such work has now to be relegated to that slowest and most unhandy of all machine tools, the slotting machine.
It is obvious that any of the ordinary forms of cutter may be used in this stock.
For enlarging a hole for a certain distance the counterbore is employed. Fig. 1745 represents a counterbore or pin drill, in which the pin is cut like a reamer, so as to ream the hole and insure that the pin shall fit accurately. The sides are left with but little clearance and with a dull edge, so that they will not cut, the cutting edges being at e, c and the clearance on the end faces.
For counterboring small holes or for facing the metal around their ends, the form of counterbore shown in Fig. 1746 is employed. The pin must be an accurate fit to the hole, and to capacitate one tool for various sizes of holes the bit is made interchangeable. The stock has a flat place on it to receive the pressure of the screw that secures the counterbore, and the end of the stock is reduced in diameter, so that the counterbore comes against a shoulder and cannot push up the stock from the pressure of the feed; the end of the counterbore is bored to receive the tit pin, thus making it permissible to exchange the pin, and use various sizes in the same counterbore.
Twist drills for use in wood work are given a conical point, as was shown with reference to lathe drills, and when the holes are to be countersunk, an attachment, such as shown in Fig. 1747, may be used. It is a split and threaded taper, so that by operating the nut in one direction it may be locked to the drill, while by operating it in the other it will be loosened, and may be adjusted to any required distance from the point of the drill, as shown in Fig. 1748.
For larger sizes of holes a stock and cutter, such as shown in Fig. 1749, may be employed, receiving a facing of counterboring cutter such as a, or a countersink bit such as b, and the bit may be made to suit various sizes of holes by making its diameter suitable for the smallest size of hole the tool is intended for, and putting ferrules to bring it up to size for larger diameters.
The cutters are fastened into the stock by a small key or wedge, as shown. By having the cutter a separate piece from the stock, the cutting edges may be ground with greater facility, while one stock may serve for various sizes of cutters. The slot in the stock should be made to have an amount of taper equal to that given to the key, so that all the cutters may be made parallel in their widths or depths, and thus be more easily made, while at the same time the upper edge will serve as a guide to grind the cutting edges parallel to, and thus insure that they shall stand at a right angle to the axis of the stock, and that both will therefore take an equal share of the cutting duty.
When cutters of this kind are used to enlarge holes of large diameter it is necessary that the pin be long enough to pass down into a bushing provided in the table of the machine, and thus steady the bar or stock at that end.
For coning the mouths of holes the countersink is employed,[I-450] being provided with a pin, as shown in Fig. 1750; and it is obvious that the pin may be provided with bushings or ferrules. The smaller sizes of countersinks are sometimes made as in Fig. 1751, the coned end being filed away slightly below the axis so as to give clearance to the cutting edge.
Fig. 1752 refers to a device for drilling square holes. The chuck for driving the drill is so constructed as to permit to the drill a certain amount of lateral motion, which is rendered necessary by the peculiar movement of the cutting edges of the drill which does not rotate on a fixed central point, but diverges laterally to a degree proportional to the size of the hole. For the chuck the upper part of the cavity of a metal cylinder is bored out so as to fit on the driving spindle. Below this bore a square recess is made, and below this latter and coming well within the diameter of the square recess, is a circular hole passing through the end of the chuck. The drill holder or socket is in a separate piece, the bottom portion of which is provided with a square or round recess for holding the drill shanks, and is held firmly in its socket by means of a set-screw. The upper part of the socket consists first of a screw (Fig. 1752) at s; secondly, of a squared shoulder b; thirdly, of a cylindrical shoulder d, and the circular part e, the drill shank being inserted at h. n is a nut holding the drill socket in the chuck. The socket being inserted in the chuck, the loose square collar c, which has an oblong rectangular slot in it, is put in, passing over the squared part of the socket. The nut n is then screwed up, bringing the face of e up to the face of the chuck, but not binding c, because c is thinner than the recess in which it lies. When this is done the socket will readily move in a horizontal plane to such a distance as the play between the two sides of the loose collar c and two of the sides of the recess will permit, while in the other direction it will move in a horizontal plane such distance as the play between the two sides of the square shoulder of the socket and the ends of the rectangular slot in the loose collar c will permit. The amount of this horizontal motion is varied to suit the size of the square hole to be drilled. Near to the lower end or cutting edges of the drill, there is fixed above the work a metal guide plate f having a square hole of the size requiring to be drilled. The drill is made three-sided, as shown, the dimensions of the three sides being such that the distance from the base to the apex of the triangle is the same as the length of the sides of the hole to be drilled. The drill may then be rotated through f as a guide, when it will drill a square hole.
The method of operation is as follows: The three-sided drill being fixed in the self-adjusting chuck, the guide bar with the square guide hole therein rigidly fixed above the point in the work where it is required to drill, the drilling spindle carrying the chuck drill is made to revolve, and is screwed or pressed downwards, upon which the drill works downwards through the square guide hole, and drills holes similar in size and form to that in the guide. The triangular drill for drilling dead square holes may also be used without the self-adjusting drill chuck in any ordinary chuck, when the substance operated upon is not very heavy nor stationary; then, instead of the lateral movement of the drill, such lateral movement will be communicated by the drill to the substance operated upon.
In making oblong dead square-cornered holes, either the substance to be operated upon must be allowed to move in one direction more than another, or the hole in the guide plate must be made to the shape required, and the drill chuck made to give the drill greater play in one direction.
[I-451]The boring bars and cutters employed in drilling and boring machines are usually solid bars having fixed cutters, the bars feeding to the cut.
Figs. 1753, 1754, 1755, and 1756, however, represent a bar having a device for boring tapers in a drilling or boring machine. It consists of a sleeve a fixed to the bar s, and having a slideway at an angle to the bar axis. In this slideway is a slide carrying the cutting tool and having at its upper end a feed screw with a star feed. Fig. 1753 shows the device without, and Fig. 1754 with, the boring bar. a is a sleeve having ribs b to provide the slideway c for the slide d carrying the cutting-tool t. The feed screw f is furnished with the star g between two lugs h k. A stationary pin bolted upon the work catches one arm of the star at each revolution of the bar, and thus puts on the feed. To take up the wear of the tool-carrying slide, a gib m and set-screws p are provided, and to clamp the device to the boring-bar it is split at q and furnished with screws r. The boring-bar s, furthermore, has a collar at the top and a nut n at the bottom. The tool, it will be observed, can be closely held and guided, the degree of taper of the hole bored being governed by the angle of the slideway c to the axis of the sleeve.
Hand Drilling and Boring Tools.—The tools used for piercing holes in wood are generally termed boring tools, while those for metal are termed drilling tools when they cut the hole from the solid metal, and boring tools when they are used to enlarge an existing hole. Wood-boring tools must have their cutting edges so shaped that they sever the fibre of the wood before dislodging it, or otherwise the cutting edges wedge themselves in the fibre. This is accomplished, in cutting across the grain of the wood, in two ways: first, by severing the fibre around the walls of the hole and in a line parallel to the axial line of the boring tool, and removing it afterwards with a second cutting edge at a right angle to the axis of the boring tool; or else by employing a cutting edge that is curved in its length so as to begin to cut at the centre and operate on the walls of the hole, gradually enlarging it, as in the case of Good’s auger bit (to be hereafter described), the action being to cut off successive layers from the end of the grain or fibre of the wood. Tools for very small holes or holes not above one-quarter inch in diameter usually operate on this second principle, as do also some of the larger tools, such as the nail bit or spoon bit and the German bit.
The simplest form of wood-piercing tool is the awl or bradawl, shown in Figs. 1757 and 1758, its cutting end being tapered to a wedge shape whose width is sometimes made parallel with the stem and at others spread, as at c d in figure. It is obvious that when the end is spread the stem affords less assistance as a guide to pierce the hole straight.
It is obvious that the action of an awl is that of wedging and tearing rather than of cutting, especially when it is operating endways of the grain.
Thus in Fig. 1758 is shown an awl operating, on the right, across the grain, and, on the left, endwise of the same. In the former position it breaks the grain endwise, while in the latter it wedges it apart. Awls are used for holes up to about three-sixteenths of an inch in diameter.
Fig. 1759 represents the gimlet bit having a spiral flute at f and a spiral projection at s s, which, acting on the principle of a screw, pulls the bit forward and into its cut. These bits are used in sizes from 1⁄16 inch to 1⁄2 inch. The edge of the spiral flute or groove here does the cutting, producing a conical hole and cutting off successive layers of the fibre until the full diameter of hole is produced. The upper part of the fluted end is reduced in diameter so as to avoid its rubbing against the walls of the hole and producing friction, which would make the tool hard to drive.
Figs. 1760 and 1761 represent the German bit, which is used for holes from 1⁄16 inch to 3⁄8 inch in diameter. This, as well as all other bits or augers, have a tapered square by which they are driven with a brace, the notch shown at n being to receive the spring catch of the brace that holds them in place. The cutting edges at a and b are produced by cutting away the metal behind them.
Fig. 1762 represents the nail bit, which is used for boring across the grain of the wood. Its cutting edge severs the fibre around the walls of the hole, leaving a centre core uncut, which therefore remains in the hole unless the hole is pierced entirely through the[I-453] material. If used to bore endways or parallel with the direction of the fibre or grain of the wood it wedges itself therein.
The groove of the nail bit extends to the point, as shown by the dotted line in the figure. Nail bits are used in sizes from 1⁄16 to 3⁄8 inch.
Fig. 1763 represents the spoon bit whose groove extends close to the point, as shown by the dotted line c.
Fig. 1764 represents the pod or nose bit, whose cutting edge extends half way across its end and therefore cuts off successive layers of the fibres, which peculiarly adapts it for boring endways of the grain, making a straight and smooth hole. It is made in sizes up to as large as four inches, and is largely used for the bores of wooden pipes and pumps, producing holes of great length, sometimes passing entirely through the length of the log.
Fig. 1765 represents the auger bit, which is provided with a conical screw s which pulls it forward into the wood. Its two wings w have cutting edges at d, d, which, being in advance of the cutting edges a, b, sever the fibre of the wood, which is afterwards cut off in layers whose thickness is equal to the pitch of the thread upon its cone s. The sides of the wings w obviously steady the auger in the hole, as do also the tops t of the twist. This tool is more suitable for boring across the grain than lengthways of it, because when boring lengthways the wings w obviously wedge themselves between the fibres of the wood.
This is obviated in Cook’s auger bit, shown in Fig. 1766, in which the cutting edge is curved, so that whether used either across or with the grain the cutting edge produces a dished seat and cuts the fibre endways while removing the material in a spiral layer. The curve of the cutting edge is such that near the corners it lies more nearly parallel to the stem of the auger than at any other part, which tends to smooth the walls of the hole. This tool while very serviceable for cross grain is especially advantageous for the end grain of the wood.
In the smaller sizes of auger bits the twist of the spiral is made coarser, as in Fig. 1767, which is necessary to provide sufficient strength to the tool. For the larger sizes the width of the top of the flute (t, Fig. 1765), or the land, as it is termed, is made narrow, as in Fig. 1768, for holes not requiring to be very exact in their straightness, while for holes requiring to be straight and smooth they are made wider, as at d, in Fig. 1769, and the wings a, b in the figure extend farther up the flutes so as to steady the tool in the walls of the hole and make them smoother. It is obvious that the conical screw requires to force or wedge itself into the wood, which in thin work is apt to split the wood, especially when it is provided with a double thread as it usually is (the top of one thread meeting the cutting edge a in Fig. 1765, while the top of the other thread meets cutting edge b).
In boring end-grain wood, or in other words lengthways of the grain of the wood, the thread is very apt to strip or pull out of the wood and clog the screw of the auger; especially is this the case in hard woods. This may be to a great extent avoided by cutting a spiral flute or groove along the thread, as in Fig. 1770, which enables the screw to cut its way into the wood on first[I-454] starting, acts to obviate the stripping and affords an easy means of cleaning. The groove also enables the screw to cut its way through knots and enables the auger to bore straight.
In boring holes that are parallel with the grain or fibre of the wood, much more pressure is required to keep the auger up to its cut and to prevent the thread cut by the auger point from pulling or stripping out of the wood, in which case it clogs the thread of the auger point and is very difficult to clean it out, especially in the case of hard woods.
Furthermore, after the thread has once stripped it is quite difficult to force the auger to start its cut again. To obviate these difficulties, the screw is fluted as shown. It is obvious also that this flute by imparting a certain amount of cutting action, and thereby lessening the wedging action of the screw, enables it to bore, without splitting it, thinner work than the ordinary auger. But it will split very thin work nevertheless; hence for such work as well as for holes in any kind of wood, when the hole does not require to be more than about twice as deep as that diameter, the centre bit shown in Figs. 1771 and 1772 is employed, being an excellent tool either for boring with the grain or across it. The centre b is triangular and therefore cuts its way into the work, and the spur or wing a extends lower than the cutting edge c, which on account of its angle cuts very keenly.
Fig. 1773 represents the twist drill which is used by the wood-worker for drilling iron, its end being squared to fit the carpenter’s brace.
Fig. 1774 represents an extension bit, being adjustable for diameter by reason of having its cutting edge upon a piece that can be moved endways in the holder or stem. This piece is ruled with lines on its face so that it may be set to the required size. Its upper edge is serrated with notches into which a dish screw or worm meshes, so that by revolving the worm the bit piece is moved farther out on the spur or wing side or end, it being obvious that the spur must meet the walls of the hole. A better form of extension bit for the end grain of wood is shown in Fig. 1775, the cutting edge being a curve to adapt it to severing the fibre in end-grained wood, as was explained with reference to Good’s auger bit.
Fig. 1776 represents a drill for stone work, whose edge is made curved to steady it. This tool is caused to cut by hammer blows, being slightly revolved upon its axis after each blow, hence the curved shape of its cutting edge causes it to sink a dish-shaped recess in the work which holds that end steady. The end of the tool is spread because the corners are subject to rapid wear, especially when used upon hard stone, and the sides of the drill would bend or jam in the walls of the hole in the absence of the clearance caused by the spread. To prevent undue abrasion water is used.
In soft stones the hammer blows must be delivered lightly or the cutting edge will produce corrugations in the seat or bottom of the hole, and falling into the same recesses when revolved after each blow the chipping action is impaired and finally ceases. To[I-455] prevent this the cutting edge is sometimes curved in its length so that the indentations cross each other as the drill is revolved, which greatly increases the capacity of the drill, but is harder to forge and to grind.
The simplest hand-drilling device employed for metal is the fiddle bow drill shown in Fig. 1777. It consists of an elastic bow b, having a cord c, which passes around the reel r, at one end of which is the drill d, and at the other a stem having a conical or centre point fitting into a conical recess in a curved breast-plate. The operator presses against this plate to force the drill to cut, and by moving the bow back and forth the cord revolves the drill.
As the direction of drill revolution is reversed at each passage of the bow, its cutting edges must be formed so as to cut when revolved in either direction, the shape necessary to accomplish this being shown in the enlarged side and edge views at the foot of the engraving. It is obvious that a device of this kind is suitable for small holes only, as, say, those having a diameter of one-eighth inch or less. But for these sizes it is an excellent tool, since it is light and very sensitive to the drill pressure, and the operator can regulate the amount of pressure to suit the resistance offered to the drill, and therefore prevent the drill from breakage by reason of excessive feed. In place of the breast-plate the bow drill may be used with a frame, such as in Fig. 1778. the frame being gripped in a vice and having a pin or screw a. If a pin be used, its weight may give the feed, or it may be pressed down by the fingers, while if a screw is used it must be revolved occasionally to put on the feed.
Fig. 1779 represents a hand-drilling device in which the cord passes around a drum containing a coiled spring which winds up the cord, the latter passing around the drill spindle, so that pulling the cord revolves the spindle and the drill, the drum and spiral spring revolving the drill backwards.
Fig. 1780 represents a drilling device in which the drill is carried in a chuck on the end of the spindle which has right and left spiral grooves in it, and is provided with a barrel-shaped nut, which when operated up and down the spindle causes it to revolve back and forth.
The nut or slide carries at one hand a right-hand, and at the other a left-hand nut fitting into the spindle grooves, and cut like a ratchet on their faces. Between these is a sleeve, also ratchet cut, but sufficiently short that when one nut engages, the other is released, with the result that the drill is revolved in one continuous direction instead of back and forth, and can therefore be shaped as an ordinary flat drill instead of as was shown in Fig. 1777. The drill is fed to its cut by hand pressure on the handle or knob at the top.
Fig. 1781 represents Backus’ brace for driving bits, augers, &c., the construction of the chuck being shown in Fig. 1782. The two tongues are held at their inner ends by springs and are coned at their outer ends, there being a corresponding cone in the threaded sleeve, so that screwing up this sleeve firmly grips the tool shank and thus holds it true, independent of the squared end which fits into the inner tongue that drives it.
In another form this brace is supplied with a ratchet between[I-456] the chuck and the cranked handle, as shown in Fig. 1783, the construction of the ratchet being shown in Fig. 1784. The ring is provided on its inner edge with three notches, so that by pulling it back and setting it in the required notch the ratchet will operate the chuck in either direction or lock it for use as an ordinary brace. The ratchet enables the tool to be used in a corner in which there would be no room to turn the crank a full revolution. This end may, however, be better accomplished by means of the Backus’ patent angular wrench shown in Fig. 1785, which consists of a frame carrying a ball-and-socket joint between it and the chuck, as shown.
Figs. 1786 and 1787 represent the brace arranged to have a gear-wheel connected or disconnected at will, the object of this addition being to enable a quick speed to the chuck when the same is advantageous.
For drilling small holes in metal, the breast drill shown in Fig. 1788 is employed. It consists of a spindle having journal bearing in a breast-plate at the head, and in a frame carrying a bevel gear-wheel engaging with two gear-pinions that are fast upon the spindle, this frame and the bevel gear-wheel being steadied by the handle shown on the right. At the lower end of the spindle is a chuck for holding and driving the drill, which is obviously operated by revolving the handled crank which is fast upon the large bevel gear. The feed is put on by pressing the body against the breast-plate.
It is obvious that but one bevel pinion would serve, but it is found that if one only is used the spindle is apt to wear so as to run out of true, and the bore of the gear-wheel rapidly enlarges from the strain falling on one side only. To avoid this the spindle is driven by two pinions, one on each side of the driving gear as in figure.
Breast-drills do not possess enough driving power to capacitate them for drills of above about quarter inch in diameter, for which various forms of drill cranks are employed.
[I-457]Fig. 1789 represents a drill crank which receives the drill at a, and is threaded at b to receive a feed screw c, which is pointed at d; at e is a loose tube or sleeve that prevents the crank from rubbing in the operator’s hands when it is revolved.
To use such a drill crank a frame a, Fig. 1790, is employed, being held in a vice and having at t a table whereon the work w may be rested. The feed is put on by unscrewing the screw s in this figure against the upper jaws of a; holes of about half inch and less in diameter may be drilled with this device.
A very old but a very excellent device for hand drilling when no drilling machine is at hand is the drilling frame shown in Fig. 1791, which consists of two upright posts a, and two b, placed side by side with space enough between them to receive and guide the fulcrum lever and the lifting lever. The fulcrum lever is pivoted at c, and has an iron plate at e, and suspends a weight at its end which serves to put on the feed. The lifting lever is pivoted at d, and at f hooks on to the fulcrum lever. At its other end is a rope and eye g, and it is obvious that the effect of the weight upon the fulcrum lever is offset by any pressure applied to g, so that by applying the operator’s foot at g the weight of drill feed may be regulated to suit the size of hole and strength of drill being used. The work is rested on a bench, and a drill crank or other device such as a ratchet brace may be used to drive the drill. This drill frame is capable of drilling holes up to about two inches in diameter, but it possesses the fault that the upper end of the brace or drilling device moves as the drill passes into the work in an arc h of a circle, of which the pin c is the centre. The posts a are provided with numerous holes for the pin c, so that the fulcrum lever may be raised or lowered at that end to suit the height of the work above the work bench. Another objection to this device is, it takes up a good deal of shop room.
Ratchet braces are employed to drill holes that are of too large a bore to be drilled by tread drills, and that cannot be conveniently taken to a drilling machine.
In Fig. 1792 is represented a self-feeding ratchet brace. a is the body of the brace, having a taper square hole in its end to receive the square shank of the drill. l is a lever pivoted upon a, and having a pawl or catch b, which acts upon ratchet teeth provided upon a. When the lever l is moved backward the pawl b being pivoted rides over the ratchet teeth, but when l is pulled forward b engages the ratchet teeth and rotates a and therefore the drill. At f is a screw threaded into a, its pointed end abutting against some firm piece, so that unscrewing f forces the drill forward and into its cut. These features are essential to all forms of ratchet braces, but the peculiar feature of this brace consists in its exceedingly simple self-feeding devices, the feed screw f requiring in ordinary braces to be operated by hand when the drill requires to be fed.
The construction and operation of the self-feeding device is as follows: The feed screw f is provided with a feather way or spline and with a feed collar c, operated by the pawl e. The feed-collar c has at d a groove, into which a flange on pawl e fits, and on its side face there is a groove receiving an annular ring on the face of lever l, these two keeping it in place. The pawl e is a double one, and may be tripped to operate c in opposite directions to feed or release the drill, as the case may be, or it may be placed in hind position to throw the feed off—all these operations being easily performed while the lever l is in motion. Collar c is in effect a double ratchet, since its circumference is provided with two sets of notches, one at g and the other at h. Each set is equally spaced around the circumference, but one set or circle is coarser spaced than the other, while both are finer spaced than is the ratchet operated by pawl b. Suppose, now, that the lever l is at the end of a back stroke, and pawl e will fall into one of the notches on side g of the feed-ratchet, and when lever l is moved on its forward stroke it will operate the feed ratchet and move it forward, a standing still until such time as pawl b meets a tooth of the ratchet on a. The feed screw f is provided with a left-hand thread, and the feed ratchet has a feather projecting into the spline in the feed screw; hence moving the feed ratchet at the beginning of the forward motion of l and before a is operated, puts a feed on, and the amount of this feed depends upon how much finer the notches into which pawl e falls are than those into which b falls. The feed takes place, be it noted, at the beginning of the lever stroke, and ceases so soon as pawl b operates a and the drill begins to cut.
As shown in the figure, the feed collar is set for large drills (which will stand a coarser feed than small ones), because the notches are finer spaced at g than at h. For small drills and finer feeds the collar is slipped off the screw and reversed so that[I-458] side h will fall under e, it being obvious that the finer the notches are spaced the more feed is put on per stroke. The spacings are made to suit very moderate feeds, both for large and small drills, because the operator can increase the feed at any stroke quite independently of the spacings on the feed ratchet. All he has to do is to give the lever handle a short stroke and more feed is put on; if still more feed is wanted, another short stroke may be made, and so on, the least possible amount of feed being put on when the longest strokes are made. In any event, however, there will be a certain amount of average feed per stroke if equal length of strokes is taken, the spacing being made to suit such ordinary variations of stroke as are met within every-day practice. When it is desired to stop feeding altogether, or to release the drill entirely from the cut, all that is necessary is to trip the feed-pawl e (without stopping the lever motion), and it will operate the feed screw in the opposite direction sufficiently to release the drill in a single backward stroke of the lever. The range of feed that is obtainable with a single feed ratchet is sufficient for all practical purposes, although it is obvious that if any special purpose should require it, a special feed ratchet may be made to suit either an unusually fine or coarse rate of feed. The feed screw is not provided with either a squared head or with the usual pin holes, because the feed ratchet is so readily operated that these, with their accompanying wrench or pin, are unnecessary.
Figs. 1793 and 1794 represent a self-feeding ratchet brace for hand drilling in which the feed is obtained as follows: The inside or feed sleeve b, which screws upon the drill spindle, is fitted with a friction or outer sleeve a, in the head of which is secured a steel chisel-shaped pin c, the lower end of which is pointed and rests upon a hardened steel bearing d, fixed in the head of the inner sleeve b. This sleeve, with its bearing d, revolves upon the point of the pin c, and within the friction sleeve a. Having thus described its construction, we will now describe the operation of the self-feeding device. The head of the pin c being chisel-shaped, prevents the pin and the outer sleeve a from revolving. If the thumb or friction screw f is unscrewed, it will permit the inner sleeve b to rotate freely upon the bearing of pin c, and within the friction sleeve a. As the screw f is tightened, the friction upon the inner sleeve b is increased, causing it to remain stationary, and consequently causing the screw on the drill spindle to feed the drill until the friction on the drill becomes greater than the friction on the sleeve b. This then commences to rotate again within the outer sleeve a, and continues until the chip which the drill has commenced to cut is finished, when the same operation is repeated, thus giving a continuous feed, capable of being instantly adjusted to feed fast or slow as desired, by tightening or loosening the friction screw f, thereby causing a greater or less friction upon the inside or feed sleeve b.
To afford a fulcrum or point of resistance for the chisel-piece c, or the pointed centre used in the common forms of ratchet brace feed screws, various supporting arms, or stands are employed. Thus Fig. 1795[30] represents a boiler shell a, to which is attached an angle frame or knee b, carrying the angle piece c (which may be adjusted for vertical height on b by means of the bolt shown) affording a fulcrum for the feed sleeve d. This sleeve is sometimes made hexagonal on its outside to receive a wrench or to be held by the hand when feeding, or it may have holes near its centre end to receive a small pin or piece of wire; e is a chain to pass around the boiler to secure b to it, which is done by means of the device at f.
[30] From The American Machinist.
For many purposes a simple stand having an upright cylindrical bar carrying an arm that may be set at any height and set to its required position on the bar by a set-screw is sufficient, the base of the stand being secured to the work by a clamp or other convenient device.
Fig. 1796 represents a flexible shaft for drilling holes inaccessible to a drilling machine, and in situations or under conditions under which a ratchet brace would otherwise require to be used. It consists of a shaft so constructed as to be capable of transmitting rotary motion though the shaft be bent to any curve or angle. A round belt driven from a line shaft rotates the grooved pulley, and the shaft transmits the rotary motion to bevel-wheels contained in a portable drilling frame, the fulcrum for the feed being afforded by a drilling post after the manner employed in ratchet drilling. The shaft is built up of several layers of wire (as shown in the view to the left), the number of layers depending upon the size and strength of shaft required, wound one upon the other helically. The layers are put on in groups of three to eight wires, parallel to each other, each successive layer containing groups of varying numbers of wires, thus giving a different pitch to the helices for each layer, the direction of each twist or helix being the reverse of the one upon which it is wound. When the shaft is laid up in this manner, the wires at each end for a short distance are brazed solidly together, and to these solidified ends the piercers are secured for the attachment of the pulley and tool which it is to drive.
This construction, it will be readily seen, produces a shaft which will have considerable transverse elasticity, while it must necessarily offer great resistance to torsional strain, the reversed[I-459] helices forming a kind of helical trussing, which effectually braces it against torsion. The case within which it turns is simply an elastic tube of leather or other suitable material, within which is wound a single helix of wire fitting its inside tightly, the inside diameter of the helix being a little greater than the outside diameter of the shaft, and wound in a contrary direction to the outer helices of the shaft. This forms a continuous bearing for the shaft; or at least serves as a bearing at the points of contact between the shaft and case which are brought about in the various bending of the whole when in use.
In order to give to the instrument all the transverse elasticity possible, that end of the shaft carrying the pulley is made with a feather so that it may slide endways in the pulley, while the latter is secured to the case, the case, however, not rotating with it. It will be readily seen that this is a necessary precaution, inasmuch as in the varying curves given to the instrument in use a difference will occur in the relative lengths of the shaft and tube.
It might be supposed that the friction of the shaft within the tube would be so considerable as to militate against the success of the apparatus; but in practice, and under test for the determination of this, it has been found that the friction generated by running it when bent at a right angle does not exceed that when used in a straight line more than 15 per cent. of the latter.
In the running of it in a bent position, not only will there be friction between the shaft and tube, but there must also be some little motion of the layers of wire one upon another in the shaft itself; and to provide against the wear and friction which would otherwise occur in this way, provision is made for not only oiling the bearings at the ends, but also for confining a small quantity of oil within the tube, by which all motion of the wires upon one another, or the shaft upon the interior of the tube, is made easy by its being well lubricated.
In the figure the shaft is shown complete with a wood-boring auger in place at the shaft end. Shafts of similar but very light construction are employed by dentists for driving their dental drills and plugging tools, many of them having ingenious mechanical movements derived from the rotary motion of the shaft.
In Fig. 1797 is represented a drilling device in position for drilling a hole from the inside of a steam boiler. a represents a base piece made with a journal stud b. This base piece is provided with radial arms a, with threaded ends and nuts made with conical projecting ends, as shown at a2. One of these pieces is used at each end of the machine when convenient, their use for centring and holding the frame being apparent. When not convenient to use two of them, one end of the frame is sustained as shown in the engraving, or in some other manner that may suggest itself. The casting b is made in two pieces, and is provided with a bearing for the pin b, and holds the ends of the rods c c. The actuating shaft g carries the bevel-wheel g, more clearly seen in the figure at side, which drives the drill spindle, whose ends are of different lengths, for convenience in reaching to different distances. The cross-head e may be slid along as required on the rods, and the revolving frame and drill turned around to different positions.
Fig. 1798 represents a small hand drilling machine to be fastened to a work bench. A suitable frame affords journal bearing to the upright spindle, upon which is a bevel-gear g, which is driven by a gear upon the same shaft as the wheel w. The spindle is threaded at s and is fed by the hand wheel f, which is threaded upon the screw s and has journal bearing in the cap c.
Fig. 1799 represents a hand drilling machine for fixture against a post, the larger wheel serving as a fly-wheel and the smaller one being to feed with.
Slotting Machine.—In the slotting machine the cutting tools are carried in a ram or slide that operates vertically, and the work table lies horizontal and beneath the ram.
Fig. 1800 represents a slotting machine, and Fig. 1801 is a sectional view of the same machine.
The cone spindle shaft has a pinion which drives a spur-wheel[I-460] upon an horizontal shaft above. Upon the inside face of this spur gear is a cam groove for operating the feed motions, at the other end of the shaft is a Whitworth quick-return motion, such as has already been described with reference to shaping machines. The connecting rod from the quick-return motion attaches to the ram, which operates on a guide passing through a way provided at the upper end of the main frame, and bolting to the front face of the main body of the frame. The object of this arrangement is that by adjusting the height of this guide to suit the height of the work, the ram will be guided as close to the top of the work as the height of the latter will permit; whereas when the guide for the ram is fixed in position on the frame the ram passes as far through the guide when doing this as it does when doing thick work, and is therefore less closely guided than is necessary so far as the work is concerned.
The ram, or slotting bar as it is sometimes termed, is counterbalanced by the weighted lever shown, so that the ram is always held up, and there is no jump when the tool post meets the work, because the tool motion is always taken up by the lever.
The work is held upon a circular table capable of being revolved upon its axis to feed the work to the cut. This table is carried upon a compound slide having two horizontal motions, one at a right angle to the other. The lower of these is operated by a rod running through the centre of the machine, as seen in the sectional view in Fig. 1801. The upper is operated through the larger of the two gear-wheels, seen at the side of the machine in the general view of the machine in Fig. 1800. The upper and smaller of these wheels operates a worm, which engages with worm-teeth cut on the periphery of the circular table to rotate the latter. Either or all of these feed motions may be put in simultaneous action, or all may be thrown out and the feeds operated by hand.
As the tool is in many cases rigid on the ram or bar of a slotting machine, it is preferable that the feed should occur while the tool is at the top of its stroke and before it meets the work, so that it may not rub on the return stroke, and thus become rapidly dulled.
Fig. 1802 represents a slotting machine in which the guideway for the slotting bar or ram is fixed in position, and the feed motions are entirely on the outside of the machine. In this case the worm-gear pinion is on the side of the machine not seen in the engraving.
The cutting tools for slotting machines are carried in one of these ways: first, bolted direct to the slotting bar or ram, in which case they stand vertically; secondly, in a box that is bolted to the end of the ram and standing horizontally; and thirdly, held in a tool bar, in which case the tool may stand either horizontally or vertically.
Fig. 1803 shows a tool b secured in a hole provided in a stout bar a by the set-screw c. The tool in this case being rigidly held the cutting edge is apt to rub against the work during the upward stroke and become rapidly dulled. To avoid this, various devices have been employed, but before describing them it will be well to point out that the shape of the tool has an important bearing upon this point.
In Fig. 1804, for example, is a tool t bolted to the box b at the end of the slide s. w is a piece of work having the cut c taken off it. Now suppose that a is the centre of motion or fulcrum from which the spring of the tool takes place (and there is sure to be a little spring under a heavy cut), then the point of the tool will spring in the direction of the arrow e, and will cut deeper to the amount of its spring; but during the up stroke the tool being released from pressure will not spring, and therefore will partly[I-461] or quite clear the cut according to the amount of the spring. This desirable action may be increased by giving the face of the tool which meets the cutting a slight degree of side rake, as shown in Fig. 1805, in which s is the slide, t the tool, b the box, and f the direction of the tool spring, which takes place in this case from the pressure of the cutting in its resistance to being bent out of the straight line.
In Fig. 1806 is a device for obviating to some extent this defect. a a is the tool box or bar containing a tool-holding piece pivoted at c, the tool being secured therein by the set-screw e b. A spiral spring sustains the weight of the pivoted piece and of the tool. During the down stroke the spiral spring holds the pivoted piece against the box or bar a, while during the up stroke the pivoted piece allows the tool to swing from the pivot c as denoted[I-462] by the arrow d. In this case the friction on the tool edge is that due to overcoming the resistance of the spring only.
In round-nose tools that are slight, and which from having a maximum length of cutting edge are very subject to spring, additional strength may be given the tool by swelling it out at the back, as denoted by the dotted line b in Fig. 1807.
Excessively heavy cuts may be taken by the form of tool shown in Fig. 1808, in which a is the tool, b the tool box, and c the work, the depth of cut being from d to e, which may be made 21⁄3 inches if necessary. The face f of the tool is ground at an angle in the direction of i, so that the tool shall take its cut gradually, and that the whole length of the tool cutting edge shall not strike the cut at the same instant, which would cause a sudden strain liable to break either the tool or some part of the machine itself. So likewise the tool will leave its cut gradually and not with a jump. As shown in the cut, but a small part of the cutting edge would first meet the work, exerting for an instant of time only enough pressure and resistance to bring all the working parts of the machine up to a bearing, and as the tool descends (as denoted by the arrow g), the strain would increase until the whole length of tool cutting edge was in operation. For such heavy duty as this the tool is tempered down to a purple to give it strength.
In Fig. 1809 is represented a front view of a patent die stock for threading pipe up to six inches in diameter. In the figure the three bits or chasers are shown locked in position by the face plate, which is shown removed in Fig. 1810. Fig. 1811 shows the machine with the face plate removed, the bit or chasers having pins in them which fit into the slots in the face plate, so that by rotating the plate the chasers may be set to size.
The head carrying the chasers is revolved by means of the gear-wheel and pinion, and Fig. 1812 represents a ratchet lever for revolving the pinion, and is useful when the pipe is in the ground and the die stock is used to cut it off and thread it without lifting it from its position.
The method of gripping the pipe is shown in Fig. 1813, in which the machine is represented as arranged for operating by belt power, the pinion being operated by a worm and worm-gear.
Referring to the pipe-gripping vice it is seen in the figure that the back of the machine is provided with ways in which the gripping jaws slide. The lower jaw is adjusted for height to suit the size of pipe to be operated upon, and is firmly locked in its adjusted position. It is provided with an index pointer, and the face of the slideway is marked by lines to suit the different diameters of pipe, so that this jaw may at once be set to the proper height to bring the pipe central to the bits. The lower jaw being set, all that is necessary is, by means of the hand wheel, to operate the upper one to firmly grip the pipe. Fig. 1814 shows the front of the machine when arranged for belt power.
The No. 1 die stock threads pipe from one to two inches in diameter, but has no cut-off. The large gear has cut teeth, and the pinion is of steel, working in gun-metal bearings. The gripping jaws are fitted with cast-steel faces, hardened.
By a simple change the stock may be used to cut left-hand as well as right-hand threads, this change consisting in putting in left-hand bits and in replacing the right-hand screw ring with a left-hand one. After a piece of pipe has been threaded, all that is necessary is to turn the head in the opposite direction, and the bits retire from the pipe thread, so that the pipe may at once be withdrawn, which preserves the cutting edges of the bits as well as saves the time usually lost in winding the dies back.
In threading machines the bolt (or pipe, as the case may be) may be revolved and the die held stationary, or the die may be revolved and the pipe held from revolving, the differences between the two systems being as follows, which is from The American Machinist:—
Fig. 1815 may be taken to represent a machine in which the pipe is held and the die revolved, and Fig. 1816 one in which the pipe is revolved and the dies are held in a head, which allows them to move laterally to suit the pipe that may not run true, while it prevents them from revolving.
In the former figure the bolt or pipe is shown to be out of line with the die driving spindle, and the result will be that the thread will not be parallel with the axis of the pipe. Whereas in Fig. 1816 the thread will be true with the axis of the work, because the latter revolves, and as the die is permitted more lateral motion it can move to accommodate itself to the eccentric motion of the work, if the latter should not run true.
If the end of a piece of pipe is not cut off square or at a right angle to the pipe axis, and the die has liberty to move, it will thread or take hold of one part, the longest one, of the pipe circumference first, and the die will cant over out of square with[I-464] the pipe axis, and the thread cut will not be in line with the pipe axis.
The two important points in operating threading machines is to keep the dies sharp and to well lubricate them with oil. When dies are run at a maximum speed and continuously at work they should be sharpened once or, if the duty is heavy, twice a day, a very little grinding sufficing.
In nut tapping the oil lubrication is of the utmost importance, and is more difficult because the cuttings are apt to clog the tap flutes and prevent the oil from flowing into the cutting teeth.
When the tap stands vertical and the nuts are put on at the upper end (the point of the tap being uppermost), the cuttings are apt to pass upwards and prevent perfect lubrication by the descending oil. When the taps stand horizontally, gravity does not assist the oil to pass into the nut, and it falls rapidly from the tap, hence it is preferable that the tap should stand vertical with its point downwards, and running in oil and water.
In machines which cut the bolt threads with a solid die, it is obvious that after the thread is cut upon the bolt to the required distance, the direction of rotation of the bolt or die, as the case may be, requires to be reversed in order to remove the bolt from the die, and during this reversal of rotation the thread upon the bolt is apt to rub against and impair the cutting edges of the chasers or die teeth.
To obviate this difficulty in power machines the dies are sometimes caused to open when the bolt is threaded to the required distance, which enables the instant removal of the finished work, and this saves time as well as preserving the cutting edges of the die or chaser teeth.
In machines in which the bolt rotates, the machine must be stopped to take out each finished bolt and insert the blank one, which is unnecessary when the bolt is stationary, because so soon as the bolt is threaded to the required distance the dies may open automatically, the carriage holding the bolt at once withdrawn and a new one inserted.
When the dies open automatically the further advantage is secured that the bolts will all be threaded to an equal distance or length without care on the part of the operator.
A hand machine for threading bolts from 1⁄4 inch to 3⁄4 inch in diameter is shown in Fig. 1817. It consists of a head carrying a live spindle revolved by hand, by the lever shown at the right-hand end of the machine, being secured to the live spindle by a set-screw, so that the handle may be used at a greater or less leverage to suit the size of the thread to be cut; on the front end of this spindle are the dies, consisting of four chasers held in a collet that is readily removable from the spindle, being held by a spring bolt which, when pressed downwards, frees the collet from the spindle.
The work is held in a pair of vice jaws operated by the hand wheel shown, and this vice is moved endwise in its slideways on the bed by means of the vertical lever shown. The bolt being stationary, the small diameter of the die enables it to thread bent or crooked pieces, such as staples, &c.
For bolts of larger diameter requiring more force than can be exerted by a hand lever, a geared hand bolt cutter is employed.
[I-465]In Fig. 1818 is represented a hand bolt cutter. In this cutter the bolt is rotated, being held in a suitable chuck. The revolving spindle is hollow in order to receive rods of any length, and is operated by bevel-wheels as shown, so as to increase the driving power of the spindle by decreasing its speed of rotation. To provide for a greater speed of rotation than that due to the diameters of the bevel-pinion and wheel, the lever is made to slide through the pinion, effecting the same object and convenience as described for the machine shown in Fig. 1817.
The threading dies are held in collets carried by a head or cylinder mounted horizontally on a carriage capable of being moved along the bed by means of a rack and pinion, the latter being operated by a handle passing through the side of the bed as shown. The cylinder also carries a collet adapted for recessed plates so as to receive square or hexagon nuts of different sizes for tapping purposes, the taps being held in the rotating chuck. The collets are capable of ready and separate extraction, and by removing the collet that is opposite to the one that is at work, the end of a bolt may pass if necessary entirely through the head or cylinder threading the work to any required length or distance.
To insure that the die shall stand axially true with the revolving spindle, bolt holes are drilled in the lower part of the cylinder, and a pin passes through the carriage carrying the head, and projects into these holes, which are so situated that when the pin end projects into a hole and locks the head a collet is in line with the spindle.
The dies consist of four chasers inserted in radial slots in collets held in place and bound together by a flat steel ring, which is let into the face of the collet and the external radial face of the chasers, and secured to the collet by screws. One chaser only is capable of radial motion for adjusting the diameter of thread the die will cut, and this chaser is adjusted and set by a screw in the periphery of the collet.
The other two chasers being held rigidly in a fixed position in the ring act as back rests and cut to the diameter or size to which they are made, or according to the adjustment of the first chaser. The shanks of the collets are secured in the cylindrical head by means of either a bolt and key or by a set-screw.
The chasers are sharpened by grinding the face on an ordinary grindstone or emery wheel.
The chasers are numbered to their places and are so constructed that if a single chaser of a set of three should require renewal, a chaser can be obtained from the manufacturers that will match with the remaining two of the set, the threads on the one falling exactly in line with those on the other two, whereas in other dies the renewal of one chaser involves the renewal of the whole[I-466] number contained in the die. This is accomplished by so threading the dies that the thread starts from the same chaser (as No. 1) in each set.
In Fig. 1819 is represented one of these machines, which is intended for threads from 3⁄8 to 1 inch in diameter. It is arranged to be driven by belt power, being provided with a pulley having three steps; on this pulley spindle is a pinion operating a gear-wheel on the die driving spindle, as shown.
The oil and cuttings fall into a trough provided in the bed of the machine, but the oil drains through a strainer into the cylindrical receiver shown beneath the bed, whence it may be drawn off and used over again.
In Fig. 1820 is represented a bolt threading machine which is designed for bolts from 3⁄16 to 1 inch in diameter.
The bolt to be threaded is gripped in the vice l, operated by hand by the hand wheel m, and is moved by hand up to the head d, by the hand wheel q operating the pinion in the rack shown at the back of the machine. When the dies or chasers have cut or threaded the bolt to the required distance, the threading dies are opened automatically as follows:—-
At h is a clutch ring for opening and closing the threading chasers, and at n is the lever operating the shoes in the groove of the clutch ring. This lever is upon a shaft running across the machine and having at its end the catch piece p; at z is a catch for holding p upright against the pressure of a spring that is beneath the bed of the machine, and presses on an arm on the same shaft as the catch piece p. On the back jaw of the vice l is a bracket carrying a rod r, and the bolt or work is threaded until the end of rod r lifts catch z, when the before-mentioned spring pulls lever n and clutch ring h forward, opening the dies and therefore stopping the threading operation. The length of thread cut upon the work is obviously determined by adjusting the distance rod r projects through v. The handle w is upon the same shaft as catch piece p and clutch lever n, and therefore affords means of opening the dies by hand.
The operation of the machine obviously consists of gripping the work in vice l, moving it up to the head d by the hand wheel q, setting the rod r to open the dies when the bolt is threaded to the required length, and moving the vice back to receive a subsequent piece of work.
The construction of the head d and clutch and ring h is shown in Figs. 1821 and 1822.
The body f is bolted by the flange i to a face plate in the live spindle or shaft of the machine, and through slots in this body pass the holders or cases c containing the chasers or dies. Upon f is the piece d provided with a slot to receive the die cases and a tongue to move them. This slot and tongue, which are shown at e′, are at an angle to the axis of f; hence if d be moved endways upon f the cases and dies are operated radially in or through the body f. To operate d laterally or endwise upon f the clutch ring h and the toggles g are provided, the latter being pivoted in the body f, and h being operated endwise upon f by the lever shown at n in the general view, Fig. 1820. The amount to which the dies will be closed is adjustable by means of the adjusting screws e, which are secured in their adjusted position by the set-screws r, Fig. 1821; it being obvious that when h meets the shoulder s of g and depresses that end of the toggle, head d is moved to the right and the dies are closed when the end of g meets e, and ceases to close when g has seated itself in f and can no longer move e. The backward motion of the clutch ring h, and therefore the amount to which the dies are opened, is regulated by the screw b and stop a in Fig. 1822, it being obvious that when b meets a the motion of h and d to the left upon f ceases and the dies are fully opened. The amount of their opening is therefore adjustable by means of screw b. j is simply a cap to hold the dies and cases in their places.
[I-467]In the end view, Fig. 1823, e, e are the adjustment screws for the amount of die closure, and b, b those for the amount they will open to, t representing the screws for the cap j, which is removed for the insertion and extraction of the dies and die cases.
The construction of the dies p and cases c is shown in Fig. 1824. Two screws at n secure the dies in their cases and a screw m adjusts them endways so as to set them forward when recutting them. By inserting the dies in cases they may be made of simple pieces of rectangular steel, saving cost in their renewal when worn too short.
Fig. 1825 shows the machine arranged with back gear for bolts from 2 to 21⁄2 inches in diameter, the essential principles of construction being the same as in Fig. 1820.
In Fig. 1826 is represented a single and in Fig. 1827 a double “rapid” machine, constructed for sizes up to 5⁄8 inch in diameter, the double machine having a pump to supply oil to the dies. This pump is operated by an eccentric upon the end of the shaft of the cone pulley.
The construction of the head of this machine is shown in Fig. 1827a. z is the live or driving spindle, upon which is fast the head a. In a are pivoted at m the levers l which carry the dies d, which are secured in place in the levers by the set-screws b and adjusted to cut to the required diameter by the screws e. The levers l are closed upon the clutch c by means of the springs r and s, each of these springs acting upon two diametrically opposite levers, hence the action of the springs is to open the dies d. The clutch c has a cone at t and slides endways upon the live spindle z. The clutch lever and shoes are upon a shaft[I-468] running across the machine and actuated by a rod corresponding to the rod r in Fig. 1820. When the clutch and levers l are in the position shown in the figures the dies are closed for threading the bolt, and when this threading has proceeded to the required distance along the work, clutch c is moved by the aforesaid rod and lever in the direction of arrow w, and the springs r, s close the ends p of lever l down upon the body x of the clutch opening the dies and causing the threading to cease.
Fig. 1828 represents a “double” rapid machine for threading work up to four inches in diameter, and therefore having back gear so as to provide sufficient power. The gauge rod from the carriage here disengages a bell crank from the end of the long lever shown, and thus prevents the spring to operate the cross shaft and open the dies.
In Fig. 1829 is represented a bolt threading machine or bolt cutter, which consists of a head carrying a live spindle upon which is a head carrying four bits or chasers that may be set to cut the work to the required diameter, and opened out after the work is threaded to the required length and the bolt withdrawn without losing the time that occurs when the dies require to run backward to release the work, and also preventing the abrasion and wear that occurs to the cutting edges of the die bits or chasers when revolved backward upon the work. This head is operated by the upright lever shown in the figure, this lever being connected to the clutch shown upon the live spindle. The details of construction of the clutch and of the head are shown in Figs. 1830, 1831, 1832, and 1833. The work to be threaded is gripped between jaws operated by the large hand wheel shown, while the vice moves the work up to or away from the head by means of the small hand wheel which operates pinions geared with racks on each side of the bed of the machine as clearly shown in the figure.
Fig. 1830 is a longitudinal section of the head, and Fig. 1831 an end view of the same. p are the threading dies or chasers held in slots in the body a by the annular ring face plate k. The ends of the dies are provided with T-shaped caps t fitting into corresponding grooves or slideways in the die ring b, and it is obvious that as the heads of their caps are at an angle therefore sliding the ring b along a and to the right of the position it occupies in the figure will cause the dies p to close concentrically towards the centre or axis of the head a. At c is a ring capable of sliding upon a and operated by the upright lever shown in the general view in Fig. 1829.
The connection between the die ring b and the clutch ring c is shown in Figs. 1832 and 1833, the former being also a longitudinal sectional view of the head, but taken in a different plane from that in Fig. 1830. The barrel or body a a of the head is provided with two diametrically opposite curved rocking levers which are pivoted in recesses in a a. The clutch ring c envelops body a and passes between the curved ends of these rocking levers. The upper of the two rocker levers shown in the engraving connects with a lever e, which connects to a stud or plunger p, threaded to receive the adjusting screw i, which is threaded into the die ring b. Obviously when c is moved to the right along a it operates the rocking lever and causes b to move to the right and to close the dies upon the work. The amount of die closure, and therefore the diameter to which the dies will thread the work, is adjustable by means of the adjusting screw i, which has a coarse thread in b and a finer one in p, hence screwing up i draws b to the left and farther over the plunger p, thus shortening the distance between the centre of the curved lever and limiting the motion of b to the right. On the other hand, unscrewing i moves b to the right, and it is obvious that in doing this the cap t in Fig. 1830 is forced down by the groove in b and the dies are moved endwise towards the axis a a, or in other words, closed.
It will be clear that a greater amount of power will be necessary[I-469] to hold the dies to their cut than to release them from it, and on that account the lower curved rocking arm d connects through e to a solid plunger g, the screw h abutting against the end of g and not threading into it, because g is only operative in pushing b forward in conjunction with p, while p pulls b backward, the duty being light. It is obvious, however, that after the adjustment screw i is operated to set the dies to cut to the proper diameter, adjustment screw h must be operated to bring the ring b fair and true upon a a and prevent any lateral strain that might otherwise ensue.
These two adjustments being made the clutch ring c is operated to the left to its full limit of motion to open the dies and to its full limit to the right to close them.
It will be seen, by the lines that are marked to pass through the pivoting pins of the rocking lever d, that the joints marked 2 in Fig. 1832 are below these lines, and as a result the links e form in effect a toggle joint locking firmer in proportion as the strain upon them is greater.
Fig. 1834 represents a bolt threading machine having two heads each of which is capable of threading bolts from 1⁄2 up to 11⁄2 inches in diameter.
The levers for operating the clutch rings are here placed[I-471] horizontal, so that they may extend to the end of the machine and be convenient to operate, and a pump is employed to supply oil to the dies.
The capacity of a double machine of this kind is about one ton of railroad track bolts per day of 10 hours’ working time.
In American practice it is usual to employ four cutting dies, bits, or chasers, in the heads of bolt threading machines, while in European practice it is common to employ but three. Considering this matter independently of the amount of clearance given to the teeth, we have as follows:—
If a die or internal reamer, the cutting points of which were all equidistant from a common centre, were placed over a piece of work, as a bar of iron shown in Fig. 1835, and set to take a certain cut, as shown by the circle outside the section, it is evident that if revolved, but left free to move laterally, or “wabble,” the cutter would tend to adjust itself at all times in a manner to equalize the cutting duty—that is, if the die had two opposite cutting edges or points, and the piece operated upon were not of circular form, then, when one cutter reached the part that was not round, it would have either more or less cutting to do than before, and hence, the opposite cutter having the same amount, the tendency would be for the two cutting edges to travel over and equalize the cuts, and hence the pressure. With three cutting points, no two being opposite, the tendency would all the while be to equalize the cuts taken by all three; with four, spaced equally, the tendency would always be to equalize the cuts of those diametrically opposite; with five, the tendency would be to equalize the duty on each, and so on. Thus it will be noticed that there is a difference between the acting principle of a die having an even or an odd number of cutters, independent of the difference in the actual number of cutting edges, or points, as we are now considering them.
To take an example, in Fig. 1835 is represented a die having four cutting points, placed upon a piece of iron of a round section, with the exception of a flat place, as shown. Now, in this position each one of the cutting points a, b, c, and d, is in contact with the true cylindrical part of the work only; hence, if the die were set to take the amount of cut shown, each point would enter the iron an equal distance, and the inner circle through the points would be the smallest diameter of the die. Upon revolving the die in the direction denoted by the arrow, an equal cut would continue to be taken off, and hence the circular form maintained, until cutter d had reached the edge x of the flat, the opposite one b, being at y (a at r and c at v), proceeding as d moved from x towards a, its cutting duty would continually become less and its pressure decrease, but as it is the cutting pressure of d that holds the opposite point b to its cut, as the pressure in d, after reaching x, continually becomes less, the die would gradually travel over so as to carry d toward the centre and cause it to take more cut, while b, on the opposite side, would travel out a corresponding distance and take less, thus keeping the duty equalized until the cutter d had reached h, the lowest part of the flat, when the die would have moved the greatest distance off the centre, assuming the position shown by dotted lines. Thus the cutting point at h has passed inside the true circle that all the cutters commenced to follow, while f has passed outside. Meanwhile, as h and f have shifted over, e and g have, of course, moved an equal amount and in the same direction, but the diameter of e and g being at right angles to that of h and f, the distances of e and g from the centre would be changed but an infinitesimal amount; hence, they would virtually continue to follow the true circle, notwithstanding the deviation of the other pair. As the die continues to revolve and h passes toward a, the lateral motion is reversed, the die tending to resume its original central position, which it does upon the completion of another quarter of a revolution, when the cutter that started at d has passed to h and finally to a. A cutting has now been removed from the entire circumference of the iron, leaving it of a form shown approximately in Fig. 1836, where a z, b y, c v, and d x, are the four true circular portions cut respectively by the points a, b, c, and d, before the flat place was reached. After the flat place was reached x a is the depression cut by d, y c the elevation formed by b, and z b and v d are the arcs, differing almost imperceptibly from the true circular ones cut by a and c.
Fig. 1837 represents a die having three instead of four cutting points—that is, the point c of Fig. 1835 is left out, and the remaining ones a, b, and d, are equally spaced. This, placed upon a similar bar and taking an equal cut, would produce a truly circular form until d had reached x—with a and b at z and y—after which the die would move laterally, tending to carry d toward the centre of the work and a and b away from it, so as to equalize the cuts on all three. Hence, when d had reached h and the three-cutter die attained the position shown by dotted lines in Fig. 1837, h would have made an indentation inside the true circle, while e and f have travelled away from it, thus forming protuberances. From h to a the lateral movement is reversed, and finally upon the completion of a third of a revolution, the die is again central and a cut has been carried completely around the bar, leaving it as shown in Fig. 1838. Comparing this with Fig. 1836, it will be seen that there are three truly cylindrical portions—viz., a z, b y, and d x instead of four in Fig. 1836, but each one is longer; that there is a depressed place, x a, of equal length to that in Fig. 1836, and two elevations, z b and y d, each of equal length to the one (y c) in Fig. 1836.
Now, suppose the bar to have an equal flat place on its opposite side, becoming of a section shown in Fig. 1839, upon applying the dies and pursuing a similar course of reasoning, the die with four points would reduce the bar to the size and shape shown in Fig. 1840, or a true cylinder, while the triple-pointed cutter would produce the form shown in Fig. 1841, which is a sort of hexagon, coinciding with the true circle in six places—a, z, b, y, d, and x—while between a and z, and opposite, between y and d, there is an elevation; also from z to b and from d to x. A flattened[I-472] portion, a x, with a similar one b y, opposite, completes the profile. Suppose, now, that a bar of the form shown in Fig. 1842, having two flat places not opposite, be taken, and the four-cutter and three-cutter dies are applied. The product of the four is shown in Fig. 1843, and that produced by the three-cutter die in Fig. 1844. The section cut with four coincides with the true circle at four points, a, b, c, d, and differs from it almost imperceptibly at z, y, v, and x. There are two elevations between a and b and between b and c; also two depressions between c and d and between d and a. The section from the three-cutter die is the perfect circular form between a z, b y, and d x, with a projection from z to b and two depressions from y to d and from x to a. The four-die, applied to a section having three flats like Fig. 1845, would produce Fig. 1846, which does not absolutely coincide with the true circle at any point, although the difference is inconsiderable at a, z, y, c, v and x; three equidistant sections a z, y c, and v x, are elevated and the three alternate ones depressed.
The three-cutter die would in this case cut the perfectly circular form of Fig. 1847.
Now, suppose both of the dies to have been made or set to some certain diameter—in fact, presume them to be made by taking a ring of steel having a round hole of the required diameter, say 1 inch, and removing the metal shown by the dotted lines, Fig. 1848, and leaving only the four cutting points in one case (and the three in the other). Then it is evident that our dies are both of the same diameter, and likewise both of the assumed diameter, or 1 inch; then it is fair to presume that the plugs or sections just cut by either one of the dies should enter a round hole of the same diameter as the dies; but it is obvious that only two, Figs. 1840 and 1847, will do so, all the rest being considerably too large, from their irregularity of form, notwithstanding the fact that the diameter of any of those cut by four cutters is never more than that of the die, while any one of the equal radii, taken at equal distances on any of the forms cut by the three-cutter die, will not exceed the radius of the die. Now, six of the pieces being too large when referred to the standard of a round hole of the size of the die, while two are of the correct size, it is obvious that if the four-die, for example, which cut Fig. 1846, were reduced enough to make Fig. 1843 just enter the standard, that, Fig. 1840, which is now just correct in size and form, would, when cut, be altogether too small. The same would be the case also with the three-cutter die.
Now let us consider the two productions (Figs. 1840 and 1847) that answer the requirements, the two different sections (Figs. 1839 and 1845) from which they were cut, and also the other two pieces (Figs. 1841 and 1846) that were cut from the same bars at the same time. The general shape of Fig. 1839, is oval or four-sided, and while the four cutters operated upon it to produce perfectly circular work, the three cutters reproduced the general shape started with, only somewhat modified, as Fig. 1841 plainly shows. Upon the blank, Fig. 1845, the general shape of which is triangular, the very opposite is the case, for the three cutters now produce a perfect circle, while the four modify only the figure that they commenced to operate upon.
Considering that every irregular form may be approximated by a square, an equilateral triangle, or in general by either a parallelogram or a regular polygon, it will be found that from a flat, oval, or square piece of metal the four cutters will produce a true circle; from a triangular piece the three; from a heptagon neither will do so, while from a hexagon both the three and four cutters are calculated to do so. Following in the same manner, and increasing the sides, it will be found that the four cutters will produce a true circle from every parallelogram, whether all the sides are equal or not, while the three cutters will produce a true circle also from every regular polygon the number of sides of which is a multiple of three—that is, four cutters would operate correctly upon a figure having 4, 6, 8, 10, 12, &c., parallel sides, while the three would do so upon a figure having 3, 6, 9, 12, 15, &c., equal sides. Thus, for regular forms varying between these two series neither one would be adapted. Hence, if the general form of the work is represented by the first series, the four cutters are the best; if the general and average form of the material to be operated upon corresponds to the second series, then the three dies are the best adapted, so far as their two principles of action, mentioned at the outset, are concerned; hence, if it is considered that the material or bars of metal to be wrought vary from a circular form indifferently, then there is no choice between an even and an odd number merely on that account.
Placing the same dies that cut these six irregular figures upon their respective productions would not serve to correct their form; as, for instance, if the die that cut Fig. 1846 were revolved around it—even if set up or reduced in diameter to take a cut—it would remove an equal amount all round and leave the same figure still. Similarly with, say, Fig. 1841, cut by the three; but if the three were run over Fig. 1846, cut by the four, it would tend to correct the errors, and likewise if the four were run over Fig. 1841, the tendency would be to modify the discrepancies left by the three that cut it.
As regards the number of cutting points, suppose that there were a certain number, as three, shown in Fig. 1849, all taking an equal cut; then, when the position indicated by the dotted lines[I-473] was reached, where cutter h runs out, the entire duty would be only two-thirds as much as it was, and the die would shift laterally in the direction of the arrow enough to equalize this smaller amount of duty on all three, or make h, e, and d each cut two-thirds as much as at first. With four as shown in Fig. 1850 when h reached the depression where its cut would run out, the entire duty would be three-fourths of what it was at first, and the die would travel laterally in the direction of the arrow sufficiently to equalise the pressure upon h and f, and upon e and g. With five, as shown in Fig. 1851, in similar position the entire duty would be four-fifths as much; with six, five-sixths, and so on. Thus it can be seen that the variation between the least amount to be cut and the full amount is relatively less, the greater the number of cutting points that it is divided between, and hence the lateral movement would be less; therefore the general tendency of an increase in the number of cutting points would be to promote true work.
Hence, from these considerations it appears that it is not material whether the number is odd or even merely on that account; so four would be preferable to three only on account of being one more, and, in turn, five would be better than four, and six better than five, and so on. It is found, however, that bar iron usually inclines to the elliptical form, and that an even number is, therefore, preferable.
Thus far the cutting edges of the die have been assumed to be points equidistant about a circle—that is, it has been supposed to have absolute clearance, so that its movements would be regulated entirely by the depth of cut taken, in order to ascertain the inherent tendency to untruth caused by an odd or an even, a greater or a less, number of cutters. This tendency is, of course, modified in each case by the amount of clearance.
The position of the dies in the head and with relation to the work is, in bolt cutting machines, a matter of great importance, and in all cases the dies should be held in the same position when being hobbed (that is, having their teeth cut by the hob or master tap) as they will stand in when put to work, and the diameter of the hob must be governed by the position of the dies in the head. If they are placed as in Fig. 1852 the diameter of the hob must be 1⁄32 inch larger than the diameter of bolt the dies are intended to thread, so that the point or cutting edge may meet the work first and the heel may have clearance, it being borne in mind that the clearance is less at the tops than it is at the bottoms of the teeth, because of their difference in curvature. In this position the teeth are keen and yet retain their strength, acting somewhat as a chaser. If placed in the position shown in Fig. 1853 the hob or master tap must be 1⁄32 inch smaller than the diameter of bolt they are to thread, so as to give the teeth clearance. In this case the dies are somewhat harder to feed into their cut and do not cut quite so freely, but on the other hand they work more steadily as the bolt is better guided, while left-hand dies may be used in the same head. If placed as in Fig. 1854 they must be cut with a hob 1⁄32 inch larger in diameter than the bolt they are to thread, so that the teeth will have less curvature than the work, and will, therefore, have clearance. In this position the dies do not cut so freely as in Fig. 1852.
The dies should be broad enough to contain at least as many teeth as there are in a length of bolt equal to its diameter, and should be thick enough to withstand the pressure of the cut without perceptible spring or deflection.
The cutting edges of dies may be brought in their best cutting position and the dies placed in radial slots in the head by forming the dies as in Fig. 1855. Face x is at an angle of 18° to the leading or front face of the die steel, and the heel is filed off at an angle of 45° and extends to the centre line of the die. This gives a strong and a keen die, and by using a hob 1⁄32 inch smaller than the diameter of bolt to be cut, the clearance is sufficiently maintained.
The heel of the die should not when the cutting edge is in front extend past the axis of the work, but should be cut off so as to terminate at the work axis as denoted by the dotted line g in Fig. 1856.
In hobbing the dies it is necessary that they be all of equal length so that the hob may cut an equal depth in each, and may, therefore, work steadily and hob them true. After the dies are hobbed their front ends should be reamed with a taper reamer as in Fig. 1857, chamfering off not more than three threads, and the chamfered teeth must then be filed, just bringing the front[I-474] edges up to a cutting edge, but filing nothing off them, the reamed chamfer acting as a guide to file them by.
This will cause each tooth to take its proper share of the cut, thus preserving the teeth and causing the dies to cut steadily. Back from the cutting edge towards the heels of the teeth the clearance may gradually increase so that the heel will not meet the work and cause friction.
The chasers or dies are obviously changed for each diameter of bolt, and it follows that as the chasers all fit in the same slots in the head they must all be made of the same size of steel whatever diameter of bolt they are intended to cut, and this leads to the following considerations.
Suppose the capacity of the machine is for bolts between 1⁄4 inch and 11⁄4 inches in diameter, and the size of the chaser or die will be 11⁄4 inches wide and 1⁄2 inch thick.
The width of a die or chaser should never be less than the diameter of bolt it is to thread, so that it may contain as many threads as are contained in a length of bolt equal to the bolt diameter. Now the 11⁄4-inch chaser equals in width the diameter of bolt it is to cut, viz. 11⁄4 inches; but if the chaser for 1⁄4-inch bolts was threaded parallel and left its full width it would be five times as wide as the diameter of the bolt and the thread cut would be imperfect, because the chasers alter their pitches in the hardening process, as was explained with reference to taps, and it is found that the error induced in the hardening varies in amount and sometimes in direction: thus of the four chasers three may expand and become of coarser pitch, each varying in degree from the other two, and the other may remain true, or contract and become of finer pitch.
As a rule the dies expand, but do not so equally. The more teeth there are in the die the more the pitch error from the hardening; or in other words, there is obviously more error in an inch than there is in half an inch of length. Suppose then that we have a die for 20 threads per inch, and as the chaser is 11⁄4 inches wide, it will contain 25 teeth, and the amount of pitch error due to 11⁄4 inches of length; and this amount not being equal in all the chasers, the result is that the dies cut the sides of the thread away, leaving it sharp at the top but widened at the bottom, as shown in Fig. 1858, weakening it and impairing its durability while placing excessive duty on the dies and on the machine.
A common method of avoiding this is to cut away all the teeth save for a width of die equal to the diameter of the bolt, as shown in Fig. 1859. An equally effective and much simpler plan is to form the dies as in Fig. 1860, the diameter at the back b being slightly larger than that at the mouth a, so that the back teeth are relieved of cutting duty. This enables the dies to undergo more grindings and still retain sufficient teeth. For example, the chamfer at a may be ground farther towards b, and still leave in action sufficient teeth to equal in width of chaser the diameter of the bolt. To enable the threading of dies in this manner the hobs or master taps employed to thread them are formed as in Fig. 1861, the proportions of the master taps for the different sizes of bolts being as given in the following table:—
| Diameter of bolt. |
—— | —— | Length at A. |
Length at B. |
Length at C. |
Length at D. |
Length at E. |
||||||||||
| 1⁄4 | Dia. from | G to H | 15⁄64 | At J | 7⁄32 | 1⁄2 | 1 | 1 | 1 | 1⁄2 | 1⁄2 | ||||||
| 5⁄16 | „ | „ | 19⁄64 | „ | 9⁄32 | 1⁄2 | 1 | 1 | 1 | 1⁄2 | 1⁄2 | ||||||
| 3⁄8 | „ | „ | 23⁄64 | „ | 11⁄32 | 1⁄2 | 1 | 1 | 1 | 1⁄2 | 1⁄2 | ||||||
| 7⁄16 | „ | „ | 27⁄64 | „ | 13⁄32 | 1⁄2 | 1 | 1 | 1 | 1⁄2 | 1⁄2 | ||||||
| 1⁄2 | „ | „ | 31⁄64 | „ | 15⁄32 | 1⁄2 | 1 | 1⁄2 | 1 | 1⁄2 | 1 | 1⁄2 | 3⁄4 | ||||
| 5⁄8 | „ | „ | 39⁄64 | „ | 19⁄32 | 1⁄2 | 1 | 1⁄2 | 1 | 1⁄2 | 1 | 1⁄2 | 3⁄4 | ||||
| 3⁄4 | „ | „ | 47⁄64 | „ | 23⁄32 | 1⁄2 | 1 | 1⁄2 | 2 | 1 | 1⁄2 | 3⁄4 | |||||
| 7⁄8 | „ | „ | 55⁄64 | „ | 27⁄32 | 1⁄2 | 1 | 1⁄2 | 2 | 1 | 1⁄2 | 3⁄4 | |||||
| 1 | Dia. at G | 31⁄32 | At J 1⁄100 less | 1⁄2 | 4 | 4 | 1 | 1⁄2 | 1 | ||||||||
| 1 | 1⁄8 | „ | 1 | 3⁄32 | —— | 1 | 4 | 4 | 1 | 1⁄2 | 1 | ||||||
| 1 | 1⁄4 | „ | 1 | 7⁄32 | —— | 1 | 4 | 4 | 1 | 1⁄2 | 1 | ||||||
| 1 | 3⁄8 | „ | 1 | 11⁄32 | —— | 1 | 4 | 4 | 1 | 1⁄2 | 1 | ||||||
| 1 | 1⁄2 | „ | 1 | 15⁄32 | —— | 1 | 4 | 4 | 1 | 1⁄2 | 1 | 1⁄4 | |||||
| 1 | 5⁄8 | „ | 1 | 19⁄32 | —— | 1 | 5 | 5 | 2 | 1 | 1⁄2 | ||||||
| 1 | 3⁄4 | „ | 1 | 23⁄32 | —— | 1 | 5 | 5 | 2 | 1 | 1⁄2 | ||||||
| 1 | 7⁄8 | „ | 1 | 27⁄32 | —— | 1 | 6 | 6 | 2 | 1 | 3⁄4 | ||||||
| 2 | „ | 1 | 31⁄32 | —— | 1 | 6 | 6 | 2 | 1 | 3⁄4 | |||||||
| All over 2 in. same length as the 2 in. Shanks J turned to bottom of last thread. | |||||||||||||||||
The cutting speeds for the dies and taps are as given in the following table, in which it will be seen that the speeds for bolt factories are greater than for machine shops. This occurs on account of the greater experience of the operators and the greater care taken in lubricating the dies and keeping them sharp:—
| Diameter of bolt. |
Revolutions of dies for machine shops. |
Revolutions of dies for bolt factories. |
Diameter of bolt. |
Revolutions of dies for machine shops. |
Revolutions of dies for bolt factories. |
||
| inch. | inch. | ||||||
| 1⁄8 | 450 | 600 | 1 | 5⁄8 | 33 | 48 | |
| 1⁄4 | 230 | 300 | 1 | 3⁄4 | 30 | 45 | |
| 3⁄8 | 150 | 200 | 1 | 7⁄8 | 28 | 40 | |
| 1⁄2 | 100 | 150 | 2 | 25 | 38 | ||
| 5⁄8 | 75 | 125 | 2 | 1⁄8 | 23 | 36 | |
| 3⁄4 | 65 | 100 | 2 | 1⁄4 | 22 | 34 | |
| 7⁄8 | 55 | 85 | 2 | 3⁄8 | 21 | 32 | |
| 1 | 45 | 75 | 2 | 1⁄2 | 20 | 30 | |
| 1 | 1⁄8 | 42 | 65 | 2 | 5⁄8 | 18 | 25 |
| 1 | 1⁄4 | 40 | 60 | 2 | 3⁄4 | 15 | 20 |
| 1 | 3⁄8 | 38 | 55 | 2 | 7⁄8 | 12 | 18 |
| 1 | 1⁄2 | 35 | 50 | 3 | 10 | 15 | |
| Taps same speed as dies. | |||||||
[I-475]In Fig. 1862 is represented a nut threading or tapping machine. The vertical spindles have spring sockets in which the taps are held, so that they can be inserted or removed without stopping the machine. The nuts are fed down the slots of the inclined plates shown on the upper face of the circular base, and the spindles are raised and lowered by the pivoted levers shown. The nuts lie in a dish that contains water up to the level of the bottom of the nuts, the object being to prevent the taps from getting hot and therefore expanding in diameter. Upon the top of the water floats a body of oil about 1⁄2 inch deep, which lubricates the cutting edges of the tap. These machines are also made with six instead of four spindles, which in both machines run at different speeds to suit different sizes of nuts, and which are balanced by weights hanging inside the central hollow column or frame.
Fig. 1863 represents the socket for driving the tap, so devised that when the tap is strung for its intended length with nuts, the top nut releases the tap of itself, the construction being as follows: s is the socket that fits into the driving spindle of the machine; its bore, which fits the stem of the tap easily, receives two headless screws b, a pin p, which is a sliding fit, and the screw a. r is a ring or sleeve fitting easily to the socket, and is prevented from falling off by screw a. The tap is provided with an annular groove g. The flattened end of the tap passes up between and is driven by the ends of screws b, the weight of the collar ring or sleeve r forcing pin p into the groove g, thus holding the tap up. When the tap is full of nuts the top nut meets face v of ring r, lifting this ring upon the socket and relieving pin p of the weight of r, the weight of the tap and the nuts then causes the tap to be released. By this construction the tap can be inserted or removed while the machine is in motion.
| VOL. I. | NUT‑TAPPING MACHINERY. | PLATE XXIII. | |
 |
 |
||
| Fig. 1864. | Fig. 1865. | ||
 |
 |
||
| Fig. 1866. | Fig. 1867. | ||
In Fig. 1864 is represented a rotary nut tapper, and in Fig. 1865, is also represented a sectional view of the same machine.
The tap driving spindles are driven from a central vertical shaft s, driven by bevel-gear b. The horizontal driving shaft operates a worm c, to drive a worm-wheel in a vertical shaft, which drives a pinion a, driving a spur wheel w in the base of the spindle head, by which means this head is revolved so as to bring the successive spindles in front of the operator. A trough is provided at t to cool the tap with oil and water after it has passed through the nut.
Fig. 1866 represents a nut tapping machine designed for light work, the spindles are raised after each nut is tapped by the foot levers and rods shown, the latter connecting to a shoe fitting into a groove in a collar directly beneath the driving pulleys of the spindles.
Fig. 1867 represents a three-spindle nut tapping machine, in which the spindles are horizontal and the nuts are held in three separate heads or horizontal slideways and are traversed by the ball levers shown, and a self-acting pump supplies them with oil. The three spindles are driven by a cone pulley having four changes of speed to suit different diameters of taps.
Pipe Threading Machinery.—In Fig. 1868 is represented a machine for threading and cutting off pipe of large diameter. This machine consists of a driving head corresponding to the headstock of a lathe, but having a hollow spindle through which the pipe may pass. The pipe is driven by a three-jawed chuck, and the threading and cutting off tools are carried on a carriage which has a threading head for ordinary lengths of pipe, and one for short pieces such as nipples, the latter swinging out of the way when not in use. Between these two is a pair of steadying jaws for the pipe. A side view of the front of the carriage is shown in Fig. 1869, h h, &c., representing the threading dies used for nipples. It is movable along a slideway e and pivoted upon its slider. The dies are carried in a chuck g, and are opened or closed by the lever n; at l is the handle for the screw that operates the guide jaws a a.
[I-476]The threading head at h (right-hand end of Fig. 1868), is represented in Fig. 1870, being pivoted so that it also can be swung out of the way to permit of the removal of the pipe. The dies c are opened or closed by the hand wheel b, operating a worm meshing into a segment of a worm-wheel upon the body of the head, the amount of motion being regulated by the stop screw at f, which therefore regulates the size to which the dies can be closed, and therefore the diameter of thread the dies will cut. The construction of the cutting-off head is shown in Fig. 1871, t representing the cutting tool which is operated by the hand wheel k. The carriage is fed or traversed by means of two pinions operated by the six-handled wheel shown at w, Fig. 1868; these two pinions engaging racks beneath the carriage, and near the[I-477] inside edges of the bed, one of them being seen at the extreme right-hand end of Fig. 1868.
In Fig. 1872 is represented a machine for threading or tapping the fittings for steam and gas pipe. The tap is carried in the end of the vertical spindle, and the work may be held in the vice upon the work table, or if too large the table may be swung out of the way.
The general design of the machine corresponds somewhat to that of a drilling machine.
Broaching Press.—Broaching consists in forcing cutters through keyways or apertures, to dress their sides to shape.
In Fig. 1873 is represented a broaching press. Its driving gear which is within the box frame is so constructed that it may be started and stopped instantly, notwithstanding its heavy fly wheel.
[I-478]Figs. 1874 to 1877 represent the method of cutting out a keyway by broaching.
In Fig. 1874 a represents the end of a connecting rod having three holes, b, c, and d, pierced through it, their diameters nearly equalling the total finished width of keyway required. The punch d′ is first forced through, thus making the three holes into one.
The V-shape of the end of the cutting punch d′ tends to steady it while in operation, forces the cut outwards into the next hole, preventing them from jambing, and causes the strain upon the punch to begin and end gradually; thus it prevents violent action during the ingress and egress of the cutting punch. This roughing out process dispenses with the use of the hammer and chisel, and saves much time, since it is done at one stroke of the press. The next part of the process is the introduction of a series of broaches such as shown in Fig. 1875, the principles involved being as follow: It is obvious that from the large amount of cutting edge possessed by a single tooth extending all around such a broach, it would be impracticable to take much of a cut at once; hence a succession of broaches is used, some of them performing duty on the sides only, others at the ends only, but the last and[I-479] final broach is usually made to take a very fine cut all over. All these broaches are made slightly taper; that is to say, the breadth of the lower tooth at a in Fig. 1875 is made less than that at b, the amount allowed varying according to the dimensions and depth of the keyway.
The smallest of the set of broaches is entered first and forced through until its end stands level with the upper face of the work. Each broach is provided with a conical teat at one end and a corresponding conical recess at the other, so that when the second broach is placed on top of the first, the teat fitting into the recess below it, will hold the two broaches central one to the other.
The head of each broach is made somewhat conical or tapered, and sets in a corresponding recess in the driving head in the machine, which, therefore, holds the broaches parallel one to the other. A succession of these broaches is used, each requiring one stroke of the press to force it within the keyway, and another to force it out.
The following is an example of broaching, relating to which, the dotted lines shown on the broaches, Fig. 1876, indicate the depths and shapes of the teeth. The small end of each broach corresponds to the large end of the one that preceded it, which is necessary in order to permit it to enter easily. Of the ten broaches used the first two operate to straighten the side walls of the hole, No. 3 being the first to operate upon the circular corners, which are not cut to the rectangle until No. 8 has passed through. But as the duty in cutting out the corners diminishes, the walls and ends of the hole are operated upon to finish them to size; thus broach No. 3 leaves the hole 11⁄8 or 1.125 inches wide, and 2.7501 inches long, which No. 4 increases to 1.1354 inches wide and 2.7605 inches long. This increase of width and depth, or breadth, as it may more properly be termed, continues up to the last or tenth cutter, which is parallel and of the same dimensions as the large end of cutter No. 9. Fig. 1877 gives two views of the No. 10 broach.
Broaches require a very free lubrication in order to prevent them from tearing the walls of the hole, and to enable them to cut easily and smoothly; hence it is found highly advantageous after the teeth are cut to cut out grooves or passages lengthways of the broach, and extending nearly to the bottom of the teeth, which eases the cut as well as affords the required lubrication; but it is obvious that the finishing cutter must not have such oil ways.
MODERN
MACHINE-SHOP
PRACTICE
VOL. II.MODERN MACHINE‑SHOP PRACTICE.FRONTISPIECE

COMPOUND MARINE ENGINE.
Modern
Machine-Shop Practice
BY
JOSHUA ROSE, M.E.
ILLUSTRATED WITH MORE THAN 3000 ENGRAVINGS
VOLUME II.
NEW YORK
CHARLES SCRIBNER’S SONS
1888
Copyright, 1887, 1888 by
CHARLES SCRIBNER’S SONS
Press of J. J. Little & Co.
Astor Place, New York.
| PAGE | ||||
| CHAPTER XXII. | ||||
| MILLING MACHINERY AND MILLING TOOLS. | ||||
| The Milling Machine; Advantages possessed by | 1 | |||
| The hand milling machine | 1 | |||
| Power milling machine | 2 | |||
| Universal milling machines | 2, 3 | |||
| The Brown and Sharpe Universal Milling Machine, general view of | 4 | |||
| The construction of the bearings and of the head | 5 | |||
| Sectional view of head | 6 | |||
| The dividing mechanism | 6 | |||
| The index plate | 7 | |||
| Table of index holes for gear cutting | 7 | |||
| The automatic feed motion | 8, 9 | |||
| Special index plate for gear cutting | 9 | |||
| The Brainard Milling Machine | 9 | |||
| The various attachments of | 10 | |||
| The rotary vise | 10 | |||
| Universal head and back centre | 10 | |||
| Universal head for gear cutting | 11 | |||
| The head for cutting spirals | 12 | |||
| The cam cutting attachment | 12 | |||
| The Lipe Universal Milling Machine | 12 | |||
| Sectional view of the Lipe machine | 13 | |||
| The feed motions of the Lipe machine | 13 | |||
| The index head of the Lipe machine | 14 | |||
| The adjustable centre rest | 14 | |||
| The Universal Milling Machine for heavy work | 15 | |||
| Construction of the driving gear and feed motion | 15 | |||
| Pratt and Whitney’s double spindle milling machine | 16 | |||
| Milling Cutters or Mills | 16 to 24 | |||
| Cutters with spiral teeth | 17 | |||
| Table of sizes of Brown and Sharpe standard cutters | 17 | |||
| Table of standard sizes of Brainard cutters | 17 | |||
| Face cutters | 17 | |||
| Twin cutters and right and left hand cutters | 18 | |||
| Advantages and disadvantages of face cutters | 18 | |||
| Angular cutters | 19 | |||
| Right and left angular cutters | 19 | |||
| The Brown and Sharpe patent cutters | 19 | |||
| Shank cutters | 19 | |||
| The direction of the feed for shank cutters | 20 | |||
| Applications of shank cutters | 21 | |||
| Sizes of shank cutters | 21 | |||
| Fly cutters | 21 | |||
| Different methods of making fly cutters, and the advantages and defects of each method | 21 | |||
| Circular cutters, and holders for fly cutters | 22 | |||
| Matched cutters; methods of matching cutters | 23 | |||
| Gang or composite cutters; cutters with inserted teeth | 24 | |||
| Cutter Arbors | 25 | |||
| Milling | 25 to 30 | |||
| Comparison of the advantages of end milling, face milling, and twin milling | 25 | |||
| The length of feed in face milling | 26 | |||
| Cutting grooves in cylindrical work | 27 | |||
| Angular cutters for groove cutting | 27 | |||
| The crowding of grooving cutters and how to avoid it | 27 | |||
| The direction of the feed in cutting spiral grooves | 27 | |||
| Setting angular grooving cutters | 28 | |||
| Cutting right and left hand grooves and determining the direction of the feed for the same | 29 | |||
| Fluting twist drills | 29 | |||
| Finding the angle of the cutter in cutting spiral grooves | 29 | |||
| Producing different shaped grooves with the same cutter | 29, 30 | |||
| Holding work on the milling machine; milling taper work | 30 | |||
| Chucks for Milling Machines | 31 | |||
| Vertical Milling Machine | 31 | |||
| Profiling Machine | 31, 32 | |||
| Grinding Machine, for milling cutters | 32 to 37 | |||
| Fixture for grinding parallel cutters | 32 | |||
| Errors in grinding milling cutters | 32 | |||
| Grinding thin cutters | 33 | |||
| Grinding taper cutters | 33 | |||
| Fixture for grinding taper work | 33 | |||
| Fixture for taper cutters and for face cutters | 34 | |||
| The position of the emery wheel and clearance on the cutter | 35 | |||
| Grinding the teeth of spiral cutters | 36 | |||
| Positions of emery wheels in cutter grinding as affecting the strength of the cutting edges | 36, 37 | |||
| CHAPTER XXIII. | ||||
| EMERY WHEELS AND GRINDING MACHINERY. | ||||
| Grinding Operations; Classification of | 38 | |||
| The qualifications of emery wheels | 38 | |||
| Cements used in the manufacture of emery wheels | 38 | |||
| Grades of coarseness and fineness of emery wheels | 38 | |||
| Grades of wheels and the work they are suitable for | 39 | |||
| Speeds of emery wheels | 39 | |||
| Balancing emery wheels | 39 | |||
| Emery Grinding Machines | 40 | |||
| The Sellers drill grinding machine | 41 | |||
| The construction of the drill holding chuck | 41 | |||
| Varying the drill position to suit the diameter of the drill, and thus maintain equal conditions for all diameters of drills | 41 | |||
| Errors of construction in ordinary drill grinding machines | 41 | |||
| The construction whereby the Sellers machine maintains an equal degree of clearance from end to end of the cutting edge upon all sizes of drills | 41, 42, 43, 44 |
|||
| The Sellers attachment for thinning the points of large twist drills | 44 | |||
| The front rake of twist drills | 44 | |||
| Emery grinder for true surfaces | 45 | |||
| For engine guide bars | 45 | |||
| For car axle boxes | 45 | |||
| Emery grinder with traversing emery wheel | 46 | |||
| For rough work | 46 | |||
| For planing machine knives or cutters | 46 | |||
| Emery wheel swing frame for dressing large castings, &c. | 46 | |||
| Emery belt grinding machine | 47 | |||
| Presenting emery wheels to the work, or the work to the wheels | 47 | |||
| Annular emery wheels | 48 | |||
| Recessed emery wheel | 48 | |||
| The wear of emery wheels | 48 | |||
| Polishing Wheels | 49 to 51 | |||
| The construction of | 49 | |||
| Lapping the leather on | 49 | |||
| Method of keeping them true | 50 | |||
| Charging with emery | 50 | |||
| The speed of | 50 | |||
| Polishing materials for | 50 | |||
| Brush wheels for polishing | 50 | |||
| Speed of brush wheels | 50 | |||
| Polishing materials for brush wheels for brass work | 50 | |||
| Solid leather wheels | 51 | |||
| Rag polishing wheels | 51 | |||
| Polishing materials for rag wheels | 51 | |||
| Polishing device for engravers’ steel plates | 51 | |||
| Grindstones and Tool Grinding | 51 | |||
| The various kinds of | 51 | |||
| Suitable for wood working tools | 52 | |||
| Suitable for saws or iron plates | 52 | |||
| The speeds of | 52 | |||
| The changes of pulley diameter necessary as the diameter of the stone decreases in order to maintain a nearly uniform circumferential speed of grindstone | 52 | |||
| Arrangement of, for saw plates | 52 | |||
| Hacking | 53 | |||
| [II-vi] | Device for truing | 53 | ||
| Automatic traversing device for | 53 | |||
| Considerations that determine the position in which the work should be applied to | 53 | |||
| Oil-stones, the various kinds of | 54 | |||
| Truing oil-stones | 54 | |||
| Removing the feather edge left by | 54 | |||
| Oil-stoning edge tools | 54 | |||
| CHAPTER XXIV. | ||||
| GEAR CUTTING MACHINES. | ||||
| Gear Cutters—The Brainard Automatic | 55 | |||
| Plan view of the mechanism | 55 | |||
| Method of operating the cutter slide | 55 | |||
| The arrangement of the positive feed shipping motion | 55 | |||
| Arrangement and construction of the dividing mechanism | 55 | |||
| The Brainard half automatic gear cutting machine | 56 | |||
| Gear cutting engine with vertical cutter spindle | 56 | |||
| Gear planing machine | 56 | |||
| Piat’s French gear cutting machine | 56 to 61 | |||
| CHAPTER XXV. | ||||
| VISE WORK. | ||||
| Definition of Vise Work | 62 | |||
| The Vise | 62 | |||
| The height of vise jaws | 62 | |||
| The wood-worker’s vise | 62 | |||
| The Stephens vise | 62 | |||
| Swivelling vises | 62 | |||
| The Prentiss vise | 62 | |||
| Leg vise with parallel motion | 63 | |||
| Various forms of vise clamps | 64 | |||
| Hammers | 64 | |||
| The effects of the speed of a hammer blow | 65 | |||
| Experiments by Robert Sabine on the duration of a blow | 65 | |||
| Machinists’ hand hammers | 66 | |||
| Shapes of hammer eyes | 66 | |||
| The proper method of putting handles in | 67 | |||
| Paning of pening hammers | 68 | |||
| The plate straightener’s and saw maker’s hammers | 69 | |||
| The principles involved in straightening plates | 69 | |||
| The dog-head hammer | 69 | |||
| The effects of hammer blows upon plates | 69 | |||
| Saw straightening and saw hammering | 70, 71 | |||
| Machinist’s sledge hammer | 71 | |||
| The file cutter’s hammers | 71 | |||
| Riveter’s hammer | 71 | |||
| The cooper’s hammer | 71 | |||
| The mallet | 72 | |||
| Pening or paning | 72 | |||
| Applications of pening to straighten work or refit it | 72 | |||
| Riveting crank pins | 73 | |||
| Chisels | 73 | |||
| Forms of bar steel for chisels | 73 | |||
| The widths and thicknesses of the cutting ends of | 74 | |||
| Angles of the cutting edges of | 74 | |||
| Shapes of the cutting edges of | 74 | |||
| Chisel holders | 74 | |||
| Cape or cross-cut | 74 | |||
| Round nosed | 75 | |||
| The cow-mouthed | 75 | |||
| Curved or oil groove | 76 | |||
| The diamond point chisel | 76 | |||
| Applications of machinists’ chisels | 76 | |||
| The carpenter’s chisel | 77 | |||
| The angle of presentation of chisels | 77 | |||
| Plane Blades | 77 | |||
| The form of, necessary to produce a given shape of moulding | 77 | |||
| Finding the shape of knives, plane blades, or cutters necessary to produce given shapes upon the work | 78 to 83 | |||
| Scale for marking out the necessary shapes of moulding knives | 83 | |||
| Instruments for | 84 | |||
| Files | 85 | |||
| Shapes of file teeth | 85 | |||
| The cut of files | 85 | |||
| Sizes and kinds of flat files | 86 | |||
| Groubet files | 87 | |||
| Rasps, the kinds and cut of | 88 | |||
| The names of files | 88, 89 | |||
| Round, half-round, and three-square files | 90 | |||
| Knife files, cross files, reaper files, tumbler files | 91 | |||
| The selection of files | 91 | |||
| Putting handles on files | 92 | |||
| Instruction on holding files | 92 | |||
| Slim files | 92 | |||
| The warping of files | 93 | |||
| Using bent files | 93 | |||
| Cross filing | 93 | |||
| Draw filing | 94 | |||
| Cleaning files | 94 | |||
| Filing out round corners | 95 | |||
| Using round files | 95 | |||
| Files for soft metals | 95 | |||
| Resharpening files | 95 | |||
| The Sand Blast process | 96 | |||
| Red Marking for vise work | 96 | |||
| Hack Saw | 97 | |||
| Screw Drivers and their proper shape | 97 | |||
| Scrapers for true surfaces | 97 | |||
| Angles for the facets of scrapers | 97 | |||
| Various forms of scrapers | 97 | |||
| Reamers | 98 | |||
| The spacing of reamer teeth | 98 | |||
| Odd and even numbers of reamer teeth | 98 | |||
| Adjustable reamers | 98 | |||
| Taper reamers | 99 | |||
| Reamers for framing | 99 | |||
| Half-round reamers | 99 | |||
| Square reamers | 99 | |||
| CHAPTER XXVI. | ||||
| VISE WORK (Continued). | ||||
| Examples in Vise Work | 100 to 113 | |||
| The use of chisels | 100 | |||
| File cutting | 100 | |||
| Cutting key seats | 101 | |||
| Sinking feathers in shafts | 101 | |||
| Methods of securing feathers | 102 | |||
| Filing up a double eye or knuckle joint | 103 | |||
| Filing pins | 103 | |||
| Blocks for filing pins | 104 | |||
| Hand vise | 104 | |||
| Filing bolt heads and nuts | 104, 105 | |||
| Making outside calipers | 105, 106 | |||
| Fitting keys | 107 | |||
| Cutting keyways by hand | 108 | |||
| Cutting out keyways by drifts | 109 | |||
| Forms of drifts | 109 | |||
| Methods of using drifts | 109 | |||
| Templates | 110 | |||
| Making male and female templates | 110 to 112 | |||
| CHAPTER XXVII. | ||||
| VISE WORK (Continued). | ||||
| Examples in Vise Work | 113 to 127 | |||
| The various form of connecting rods | 113 | |||
| Solid ended connecting rods | 113 | |||
| Clip ended connecting rod | 114 | |||
| Strap ended connecting rod | 115 | |||
| Double gibbed connecting rod | 115 | |||
| Locomotive connecting rod | 115 | |||
| Bolted connecting rod straps | 115 | |||
| Marine engine connecting rod | 116 | |||
| Tapered connecting rod ends and their advantages | 117 | |||
| Stepped connecting rod straps and their advantages | 117 | |||
| Fitting up connecting rods | 117, 119 | |||
| Welding up stub ends of connecting rods | 118 | |||
| Aligning welded connecting rods | 118 | |||
| Fitting on connecting rod straps | 119 | |||
| Filing out connecting rod keyways | 119 | |||
| Fitting the keys and gibs | 119 | |||
| Fitting connecting rod brasses to their straps | 120, 122 | |||
| The joint faces of connecting rod straps | 121 | |||
| Disadvantages of joints left open to take up the wear | 121 | |||
| Obviating this disadvantage | 121 | |||
| Marking the lengths of connecting rods | 122 | |||
| Fitting up a fork end connecting rod | 122 | |||
| Aligning fork end connecting rods | 123 | |||
| Repairing connecting rods | 124 | |||
| Setting connecting rod brasses together | 125 | |||
| Lining up connecting rod brasses | 126 | |||
| Adjusting the lengths of connecting rods | 126 | |||
| Setting up the keys of connecting rods | 126 | |||
| Shapes of the crowns of brasses | 127 | |||
| Fitting up a link motion | 127 | |||
| Templates for filing the link slot | 127 | |||
| Case-hardening | 128 to 133 | |||
| Sheehan’s case-hardening process | 128 | |||
| Preparing work for | 129 | |||
| Setting work after | 129 | |||
| Fitting brasses to pillow blocks or axle-boxes | 130 | |||
| [II-vii] | Bedding brasses | 132 | ||
| The proper shape for the patterns of brasses | 132 | |||
| Originating a True Plane | 133 | |||
| Finding which of three surfaces is the nearest to a true plane | 133 | |||
| Methods of testing the surfaces | 134 | |||
| A new process of originating surface plates | 134 | |||
| The deflection of surface plates | 134 | |||
| The Friction of Plane Surfaces | 135 | |||
| Oiling True Surfaces | 135 | |||
| CHAPTER XXVIII. | ||||
| ERECTING. | ||||
| Spirit-level | 136 | |||
| Plumb-level | 136 | |||
| Joints | 136 to 141 | |||
| Filing or making joints | 137 | |||
| Ground joints | 137 | |||
| Scraped joints | 137 | |||
| Cylinder covered joints | 137 | |||
| Making a scraped joint with the studs in their places | 138 | |||
| Joints for rough surfaces | 138 | |||
| Gauze wire joints | 138 | |||
| Water joints | 138 | |||
| Joints to withstand great heat | 138 | |||
| Rubber joints | 139 | |||
| Boiler fitting joints | 139 | |||
| Easily removable joints | 140 | |||
| Rust or caulked joints; caulking tools | 141 | |||
| Thimble joints | 141 | |||
| Expansion joint | 141 | |||
| Pipes, Cocks and Plugs | 141 to 145 | |||
| Pipe cutters | 141 | |||
| Pipe vises | 141 | |||
| Pipe tongs | 143 | |||
| Erecting pipe work | 144 | |||
| Refitting leaky cocks and plugs | 144 | |||
| Grinding cocks and-plugs | 145 | |||
| Boxes and Brasses | 145 to 149 | |||
| Fitting brasses to their journals | 145 | |||
| Various forms of bearings and brasses or boxes | 147 | |||
| Locomotive axle boxes | 148 | |||
| Lead lined brasses | 148 | |||
| Open brasses | 149 | |||
| Lubrication | 149 to 154 | |||
| Examples of oil cavities and oil grooves for brasses | 150 | |||
| Qualities of lubricants | 151 | |||
| Testing lubricants | 151 | |||
| Best method of using thin oils | 152 | |||
| The influence of the atmosphere on oils | 153 | |||
| Longevity of lubricants | 153 | |||
| Testing oils for salts and acids | 153 | |||
| Swiss watchmakers’ oil tests | 153 | |||
| The blotting paper oil test | 154 | |||
| Friction and Wear | 154 | |||
| Morin’s experiments on | 154 | |||
| Order of the value of metals to resist wear | 154 | |||
| White metal or babbitt metal lined boxes | 155 | |||
| Methods of babbitting boxes | 156 | |||
| The pressure on journals | 156 | |||
| Cranks | 156 | |||
| Placing at right angles | 156, 157 | |||
| Engine Cylinders | 158 to 161 | |||
| Fitting | 158 | |||
| Setting | 159 | |||
| Reboring cylinders in their places | 160 | |||
| Scraping out cylinder ends | 161 | |||
| CHAPTER XXIX. | ||||
| ERECTING ENGINES AND MACHINERY. | ||||
| Engine Guide Bars | 162 | |||
| Setting | 162 | |||
| The spring of | 162 | |||
| Testing | 163 | |||
| Setting by stretched lines | 163 | |||
| Heating and Knocking of Engines | 164 | |||
| The ordinary causes of | 164, 166 | |||
| Aligning New Engines | 166 to 171 | |||
| Classification of the errors in engine alignment | 166 | |||
| Testing the alignment of the crank | 167 | |||
| Showing separately the causes of beating and pounding | 168 | |||
| Methods of discovery and determining the errors of alignment | 169 | |||
| Errors of alignment in crank pins | 170 | |||
| Methods of discovering errors of crank pin alignment | 170 | |||
| Remedying errors of crank pin alignment | 171, 172 | |||
| Slide Valves | 173 to 175 | |||
| Finding the dead centre of the crank | 173 | |||
| Taking up the lost motion when setting the valve | 174 | |||
| Measuring the valve lead | 174 | |||
| Finding the dead centre with a spirit level | 174 | |||
| Setting Eccentrics on crank shafts | 175 | |||
| Setting double eccentrics by lines | 175 | |||
| Erecting the Framework of machinery | 176, 177 | |||
| Repairing and Patching broken frames | 178 | |||
| Erecting an Iron Planer | 179 | |||
| Foundations for an iron planer | 180 | |||
| Fitting up and erecting a lathe | 181 | |||
| Testing Lathes | 181 | |||
| Instruments for testing lathes | 182 | |||
| Testing lathe carriages | 183 | |||
| Erecting Line Shafting | 184 to 186 | |||
| CHAPTER XXX. | ||||
| LINE SHAFTING. | ||||
| Line Shafting | 187 to 190 | |||
| Sizes of | 187 | |||
| Cold rolled shafting | 187 | |||
| Distance between bearings of line shafting | 187 | |||
| Tests of hot rolled and cold rolled shafting | 188 | |||
| Collars for shafting | 189 | |||
| Diameters of line shafting | 189 | |||
| The strength of line shafting | 190 | |||
| Speeds for shafting | 190 | |||
| Counter Shafts | 191 | |||
| Friction Clutches | 192 | |||
| Shafting Hangers | 193 | |||
| Various forms of | 193 | |||
| Open-sided | 193 | |||
| Wall hangers | 194 | |||
| Pillow Blocks for shafting | 194 | |||
| Couplings | 194 to 199 | |||
| For line shafts | 194 | |||
| With split sleeves | 195 | |||
| Errors in | 196 | |||
| Self-adjusting | 196 | |||
| Plate | 196 | |||
| Clamp | 197, 198 | |||
| For light shafting | 199 | |||
| Universal | 199 | |||
| CHAPTER XXXI. | ||||
| PULLEYS. | ||||
| Classification | 200, 201 | |||
| Wood pulleys | 200 | |||
| Solid and split pulleys | 200 | |||
| Expansion pulleys | 200 | |||
| Self-oiling pulleys | 200 | |||
| Crowned pulleys | 201 | |||
| Fastening pulleys to their shafts | 201 | |||
| Balancing pulleys | 202 | |||
| The Transmitting Power of pulleys | 204 | |||
| Size of pulleys for countershafts | 205 | |||
| Calculating the Speeds of pulleys | 206 | |||
| CHAPTER XXXII. | ||||
| LEATHER BELTING. | ||||
| Hides | 207, 208 | |||
| The parts of a hide used for belting | 207 | |||
| The thickness and stretch of the parts of a hide | 207 | |||
| Experiments on the strength of the parts of a hide | 208 | |||
| Single and double belts | 208 | |||
| Grain Side of Leather | 208 | |||
| Weakness of the | 208 | |||
| Why the grain side should go next to a pulley | 208 | |||
| Belts | 209 to 217 | |||
| The length of | 209 | |||
| Belt clamp | 210 | |||
| The sag of belts | 210 | |||
| Belt connection at an angle | 211 | |||
| Guide pulleys for belts | 211 | |||
| The tension and creep of belts | 212 | |||
| Methods of joining the ends of belts | 213 | |||
| Forms of belt lacings | 214 | |||
| Covers for belt lacings | 215 | |||
| Lap joints for belts | 215 | |||
| Joining thin belts | 215 | |||
| Bevelled joints for belts | 215 | |||
| Pegged belts | 215 | |||
| Belt hooks and belt screws | 216 | |||
| Angular or V-belts | 217 | |||
| The line of motion of belts | 217 | |||
| [II-viii] | Changing or shipping belts | 217 | ||
| Automatic belt replacer | 218 | |||
| Pull of a belt | 218 | |||
| The Sellers experiments on transmission of power | 218 to 225 | |||
| Belt 51⁄2′′ wide by 7⁄32′′ thick | 219 | |||
| Belt 21⁄4′′ wide by 5⁄16′′ thick | 219 | |||
| Rawhide belt 4′′ by 9⁄32′′ | 220 | |||
| Double oak tanned belt 4′′ by 5⁄16′′ | 220, 221 | |||
| Oak tanned belt 2′′ by 3⁄16′′ | 222 | |||
| Coefficient of friction and velocity of slip | 222 | |||
| Torsional moment | 223 | |||
| Increase of tensions | 224 | |||
| CHAPTER XXXIII. | ||||
| FORGING. | ||||
| Testing Iron by bending it | 226 | |||
| Testing machines | 227, 228 | |||
| Tools for Blacksmiths | 228 to 232 | |||
| Forges | 228, 229 | |||
| Chisels, &c. | 230 | |||
| Anvils | 230 | |||
| Swages | 230, 231 | |||
| Spring swages | 231 | |||
| Swage blocks | 232 | |||
| Swaging | 232, 233 | |||
| Examples in Welding | 233, 235 | |||
| Iron | 233, 234 | |||
| Steel to iron | 234 | |||
| Best method of | 234, 237 | |||
| Examples in Forging | 238 to 252 | |||
| Device for bolt forging | 238 | |||
| Forging turn buckles | 239 | |||
| Methods of bending iron | 240 | |||
| Device for bending iron | 240, 241 | |||
| Forging steel forks | 241 | |||
| Forging under the hammer | 242, 243 | |||
| Forging rope sockets | 243, 244 | |||
| Forging wrought iron wheels for locomotives | 244, 245 | |||
| Forging rudder frames | 245, 246 | |||
| Welding scrap iron for large shafts | 247 | |||
| Construction of furnace for heating scrap | 247 | |||
| Forging crank shafts | 248, 249 | |||
| Forging large crank shafts | 249, 252 | |||
| Forging machines | 252 to 263 | |||
| Foot-power hammer or Oliver | 252, 253 | |||
| Standish’s foot-power hammer | 252, 253 | |||
| Power hammers and steam hammers | 252, 253 | |||
| Bradley’s cushioned hammer | 252, 253 | |||
| Corr’s power hammer | 254, 255 | |||
| Kingsley’s trip hammer | 255 | |||
| The drop hammer | 255, 256 | |||
| Steam hammers | 257, 258 | |||
| Double frame steam hammer | 258 | |||
| Double frame steam drop hammer | 258 | |||
| Double frame steam drop hammer for locomotive and car axles and truck bars | 259 | |||
| The Edgemore Iron Works’ hydraulic forging press | 260 | |||
| Dies for forging eye bars | 260 | |||
| Nail forging machine | 260 | |||
| Rolls for forming knife blades | 261 | |||
| Machine for forging threads on rods | 261, 262 | |||
| Finishing machine for horseshoes | 262, 263 | |||
| Circular saw for cutting hot iron | 263 | |||
| CHAPTER XXXIV. | ||||
| WOOD WORKING. | ||||
| Pattern Making | 264, 267 | |||
| Choice and preservation of wood for | 264 | |||
| Bending Timber | 265, 266 | |||
| The bending block | 265, 266 | |||
| Steaming wood for bending | 266, 267 | |||
| Wood Working Tools | 267 to 274 | |||
| Planes for pattern making | 267 | |||
| Compass planes | 268 | |||
| Stanley’s iron frame block plane | 269 | |||
| Stanley’s bull-nose rabbet plane | 269 | |||
| Bailey’s patent adjustable planes | 269 | |||
| The combination plane | 269, 270 | |||
| The beading bit | 270, 271 | |||
| Tool for cutting material into parallel slips | 271 | |||
| The chisel and chisel handles | 271 | |||
| Firmer and paring chisels and gouges | 272 | |||
| Rip saws | 272, 273 | |||
| Cross cut saw | 273 | |||
| Common gauges for marking off work | 274 | |||
| Mortise gauge | 274 | |||
| Cutting gauge | 274 | |||
| Wood Joints | 274, 275 | |||
| Mortise joint | 274 | |||
| Tenon joint | 274 | |||
| Dovetail joint | 275 | |||
| Mitre joint | 275 | |||
| Half check joint | 275 | |||
| Examples of Pattern Making | 275 to 285 | |||
| Patterns for piston gland | 275 | |||
| Construction of piston gland pattern | 276, 277 | |||
| Rapping small cast gears | 277 | |||
| Casting pillow block | 277 | |||
| Pattern for pillow block | 277 | |||
| Pulley pattern | 278, 279 | |||
| Building up segments for patterns | 278, 279 | |||
| Getting out arms for pulleys | 280 | |||
| Making pipe patterns | 280, 281 | |||
| Globe valve pattern | 281, 282 | |||
| Angle valve pattern | 283, 284 | |||
| Branch pipes | 284 to 286 | |||
| CHAPTER XXXV. | ||||
| WOOD WORKING MACHINERY. | ||||
| Classification | 287 | |||
| Circular Saws | 287 to 305 | |||
| Gauges for circular saws | 287 | |||
| Table of diameters | 287 | |||
| Thickness | 287 | |||
| Size of mandrel hole | 287 | |||
| Shingle saw | 287, 288 | |||
| Concave saw | 287, 288 | |||
| Stretching of circular saws by heat | 288 | |||
| The tension of circular saws | 288 | |||
| Causes of alteration of tension and method of discovering the same | 288 | |||
| Truth of circular saws | 288 | |||
| Various effects of circular saws heating | 288 | |||
| Truing circular saws | 288 | |||
| Sharpening the teeth of circular saws | 289, 290 | |||
| The gumming, gulleting or chamfering machine | 290 | |||
| Inserted teeth of saws | 290 | |||
| Chisel teeth saws | 290, 291 | |||
| Inserting teeth in circular saws | 290, 291 | |||
| Swing frame saws | 290, 292 | |||
| Fence for swing frame saws | 293 | |||
| Examples of work done on swing frame machine | 293 | |||
| Swing machine with fixed table | 294 | |||
| Double saw machine | 294, 295 | |||
| Gauges for sawing machine | 294 | |||
| Method of employing the mitre gauge | 294 | |||
| Cropping and gauging gauge | 296 | |||
| Bevel or mitre sawing machines | 296, 298 | |||
| Roll feed circular saw machine | 298, 300 | |||
| Segmental circular saws | 300 | |||
| Fastening saw segments to their disks | 301 | |||
| Gang edging machines | 301 | |||
| Rack feed saw bench | 301 | |||
| Construction of the feed motion | 301 to 304 | |||
| Fibrous packing for circular saw | 305 | |||
| Tubular Saw Machine | 305 | |||
| Cross Cutting or Gaining Machine | 305, 306 | |||
| Scroll Sawing Machine | 306 | |||
| Construction of various scroll sawing machines | 306, 307 | |||
| Band Sawing Machine | 308 to 312 | |||
| Various kinds of teeth for band saws | 308, 309 | |||
| Pitch of teeth for band saws | 309 | |||
| The adjustment of the saws of band saw machines | 309, 310 | |||
| Filing the teeth of band saw machines | 309 | |||
| Re-sawing band saw machine | 309, 310 | |||
| To regulate the tension of band saws | 310, 311 | |||
| Construction of band saw guides | 311 | |||
| Various band saw machines | 311, 312 | |||
| Reciprocating Cross Cutting Saw | 312 | |||
| Construction of | 312 | |||
| Horizontal Saw Frame Machine | 312 to 315 | |||
| Construction of the saw driving mechanism | 314 | |||
| Construction of the feed motion | 315 | |||
| Construction of the saw | 315 | |||
| Planing Machines | 315 to 341 | |||
| Buzz planer | 315 | |||
| Construction of the work table | 316 | |||
| Construction of the cutter head | 316 | |||
| Skew knives | 316 | |||
| Roll feed wood planing machine | 317 | |||
| The construction of the feed rolls | 317 | |||
| Adjustment of the feed rolls | 317 | |||
| Construction of the pressure bars | 317 | |||
| Adjustment of the roll pressure | 318 | |||
| Adjustment of the work table | 318 | |||
| [II-ix] | The roll driving mechanism | 319 | ||
| The cutter head | 320 | |||
| Three feed roll wood planing machine | 322, 323 | |||
| Pony planer | 323 | |||
| Construction of the feed mechanism | 324 | |||
| Balancing cutter heads and knives | 324, 326 | |||
| Farrar planing machine | 326, 327 | |||
| Planing and matching machine | 328 | |||
| Construction of the feed rolls | 329 | |||
| Construction of the upper cylinder | 329 | |||
| Construction of the lower cylinder | 329 | |||
| Construction of a matcher hanger | 329 | |||
| The timber planer | 330, 331 | |||
| Construction of parts of the timber planer | 331 | |||
| How the timber planer operates | 331, 332 | |||
| Panel planing and trying up machine | 332, 334 | |||
| Moulding machine | 334 | |||
| Double head panel raiser and double sticker | 335, 336 | |||
| Moulding cutters | 336, 337 | |||
| Cutter heads and circular cutters | 337 | |||
| The Shimer head | 337 | |||
| Head for producing match board grooves | 337, 338 | |||
| Jointing machine | 338 | |||
| Knives of jointing machine | 338 | |||
| Speed of cutter head or disc | 338 | |||
| Stroke jointers | 338, 339 | |||
| Machine for cutting mitre joints | 339 | |||
| Moulding or friezing machines | 339 | |||
| Important points of friezing machines | 339 | |||
| Construction of moulding and friezing machines | 340, 341 | |||
| Shape of cutters for moulding and friezing machine | 341 | |||
| Rotary cutters for all kinds of work, and for edge moulding and friezing machine | 341 to 343 | |||
| Boring Machines | 342 | |||
| Fences for | 342 | |||
| Augers or bits for | 342 | |||
| Boring machines for heavy work | 343 | |||
| Mortising Machines | 344 | |||
| Tools used in mortising machines | 344 | |||
| Motion of chisel bar and auger | 344 | |||
| Construction of bed | 344 | |||
| Adjustment of carriage | 344 | |||
| Tenoning Machines | 344, 345 | |||
| Construction of revolving heads | 344, 345 | |||
| Tenoning machine for heavy work | 346 | |||
| Sand-papering Machines | 346, 349 | |||
| Construction of sand-papering machines | 347, 348 | |||
| Movements of sand-papering machine | 347 | |||
| Cylinder sand-papering machines | 348 | |||
| Self-feeding sand-papering machine | 348 | |||
| Sizes of machines | 348 | |||
| Construction of feed rolls | 348 | |||
| Finishing and roughing cylinders | 348 | |||
| Brush attachment | 348 | |||
| Double wheel sanding machines | 348, 349 | |||
| CHAPTER XXXVI. | ||||
| STEAM BOILERS. | ||||
| Strength of Boiler Shells | 350 | |||
| Strength of Boiler Plate | 351 | |||
| Explanation of pressure in steam boilers | 351 | |||
| Boiler Joints or Seams | 351 to 357 | |||
| Forms of rivet joints | 351 | |||
| Single riveted lap joint | 351 | |||
| Double riveted lap joint | 352 | |||
| Single riveted butt joint with straps | 352 | |||
| Double riveted butt joint with straps zigzag riveted | 352 | |||
| Triple riveted lap joint zigzag riveted | 352 | |||
| Lap joint with covering plate | 352 | |||
| Double riveted lap joint chain riveted | 353 | |||
| Double riveted butt joints with double straps | 353 | |||
| Treble riveted butt joint with double straps | 353, 354 | |||
| Rules for spacing the rivets in boiler seams | 353 | |||
| Rule for finding diagonal pitch of riveted joints | 353 | |||
| High percentage joint | 353 | |||
| Rivets unevenly pitched | 354 | |||
| Rule for calculating the percentage strength of joint with unevenly pitched rivets | 354 | |||
| Strength of circumferential seams of stationary engine boilers | 354, 355 | |||
| Table of additions to be made to the factor of safety for various constructions of riveted joints | 355 | |||
| Table of diameter of rivets for single riveted lap joints | 356 | |||
| Rule for making rivet and plate area equal | 336 | |||
| Table of rivet diameter and pitch for single riveted lap joints | 356 | |||
| Rule for finding the pitch for double, diagonal riveted lap joints | 356 | |||
| Example in the use of rule for diagonal pitch of rivets | 356 | |||
| Rule for finding distance V where the diagonal pitch has been found | 357 | |||
| Comparing chain with zigzag riveted joints | 357 | |||
| Interior of Boilers | 358 to 364 | |||
| The internally fired flue boiler | 358, 359 | |||
| Boiler with Field tubes | 350 | |||
| Vertical water tube boiler | 360 | |||
| Construction of field tubes | 360 | |||
| Arrangement of field tubes | 360 | |||
| Vertical boilers with external uptakes | 361 | |||
| Horizontal return tubular boiler | 361, 362 | |||
| Construction of horizontal return tubular boiler | 362, 363 | |||
| Various arrangements of tubes in boilers | 364 | |||
| Setting Boilers | 364, 366 | |||
| Ground plan of brickwork | 365 | |||
| Setting full arch front boilers | 365 | |||
| Table of measurements for setting tubular stationary boilers with full arch front | 366 | |||
| Table of measurements for setting stationary boilers with half arch front | 366 | |||
| The Evaporative Efficiencies of Boilers | 366 to 368 | |||
| Table of the pressure, temperature and volume of steam | 367 | |||
| Calculating the evaporation of a boiler | 368 | |||
| Care and Management of Boilers | 368 to 371 | |||
| Examining safety valves | 368 | |||
| Water gauge glass | 368 | |||
| Gauge cocks | 368 | |||
| Lighting boiler fires | 368 | |||
| The thickness of the fire for boilers | 368 | |||
| Managing the fire | 368 | |||
| Shaking grate bars | 369 | |||
| The slice bar | 369 | |||
| The hoe | 369 | |||
| The poker | 369 | |||
| The clinker hook | 369 | |||
| The rake | 369 | |||
| The quantity of water in a boiler | 369 | |||
| Leaving the fire for the night | 369 | |||
| Leaving the safety valve for the night | 369 | |||
| Regulating the boiler feed | 369 | |||
| Dirty feed water | 370 | |||
| Defective feed pumps | 370 | |||
| Scale in boilers | 370 | |||
| Preventing the formation of scale | 370 | |||
| Feed water heaters | 370 | |||
| Low water in boilers | 370 | |||
| Priming or foaming | 370 | |||
| The known causes of priming | 370 | |||
| Wastefulness of priming | 370 | |||
| The detection of priming | 370 | |||
| To prevent or stop priming | 370 | |||
| Surface blow off cock or mechanical boiler cleaner | 370 | |||
| Blowing off a boiler | 370 | |||
| Blowing down a boiler | 370 | |||
| Washing out a boiler | 371 | |||
| Cleaning a boiler | 371 | |||
| Scaling a boiler | 371 | |||
| Examining a boiler | 371 | |||
| CHAPTER XXXVII. | ||||
| STEAM ENGINES. | ||||
| Engine Cylinders | 372 to 374 | |||
| The bores of | 372 | |||
| Sizes of | 372 | |||
| Wear of | 372 | |||
| Counterbore of | 372 | |||
| Clearance in | 372 | |||
| Lubrication of | 373 | |||
| The cocks of | 373 | |||
| Relief valves of | 373 | |||
| The steam ports of | 373 | |||
| Lagging | 374 | |||
| Jacketed cylinders | 374 | |||
| Engine Pistons | 374 | |||
| The speeds of | 374 | |||
| With releasing gears | 374 | |||
| With positive valve gears | 374 | |||
| The rings of | 374 | |||
| The follower | 374 | |||
| Testing the rings of | 374 | |||
| Engine Piston Rods | 375 | |||
| Methods of securing | 375 | |||
| Packing | 375 | |||
| Glands for | 375 | |||
| Engine Cross Heads | 375 | |||
| Engine Guide Bars | 375 | |||
| Engine Connecting Rods | 375 | |||
| Connecting rod keys | 375 | |||
| Angularity of | 375 | |||
| The lengths of | 375 | |||
| Valves | 376 to 378 | |||
| [II-x] | The D-valve | 376 | ||
| The point of cut off | 376 | |||
| Period of expansion of the steam | 376 | |||
| Point of release of the steam | 376 | |||
| Point of compression of the steam | 376 | |||
| Lead of | 376 | |||
| Point of admission of the steam | 376 | |||
| The lip | 376 | |||
| Exhaust lap | 376 | |||
| Steam lap | 376 | |||
| Tracing the action of | 376 | |||
| Double ported valves | 377 | |||
| The Allen valve | 377 | |||
| Webb’s patent valve | 377 | |||
| Balanced valves | 377 | |||
| Circular valves | 377 | |||
| Piston valves | 378 | |||
| Separate cut off valves | 378 | |||
| Meyer’s cut off valves | 378 | |||
| Gonzenback’s cut off valve | 378 | |||
| Eccentrics | 378 | |||
| Shifting eccentrics | 378 | |||
| The action of | 378 | |||
| The angular advance of | 378 | |||
| Designing Slide Valves | 380 | |||
| Valve Motions | 381 | |||
| Diagram for designing | 381 | |||
| Link Motion | 383 | |||
| In full gear forward | 383 | |||
| In full gear backward | 383 | |||
| The action of | 383 | |||
| Setting the valves | 383 | |||
| Governors | 384 | |||
| Fly ball or throttling | 384 | |||
| Isochronal | 384 | |||
| Dancing | 384 | |||
| Speed of | 384 | |||
| Spring adjustment of | 384 | |||
| Sawyer’s valve for | 384 | |||
| Speeder for | 384 | |||
| Starting a Slide Valve Engine | 384 | |||
| Crank position in | 384 | |||
| Examination of an Engine | 385, 387 | |||
| Adjusting connecting rod brasses | 385 | |||
| Adjusting main bearing | 386 | |||
| Taking a lead | 386 | |||
| Squaring a valve | 386 | |||
| Heating, to avoid | 386 | |||
| Setting a valve | 386 | |||
| Leaky throttle valves | 386 | |||
| Freezing an engine, prevention of | 386, 387 | |||
| Pumps | 387, 388 | |||
| Lift and force | 387 | |||
| Plunger | 387 | |||
| Rotary | 387 | |||
| Single-acting | 387 | |||
| Double-acting | 387 | |||
| Displacement of | 387 | |||
| Principles of action of | 387, 388 | |||
| Speed of | 388 | |||
| Capacity of | 388 | |||
| Air chamber of | 388 | |||
| Belt | 388 | |||
| CHAPTER XXXVIII. | ||||
| THE LOCOMOTIVE. | ||||
| Modern Freight Locomotive | 389, 390 | |||
| General construction | 389 | |||
| Course of steam from boiler to smoke stack | 389 | |||
| Boiler feed | 389 | |||
| Position of parts for starting | 389 | |||
| Steam supply to injectors | 389 | |||
| Oil supply to slide valve and cylinder | 389 | |||
| Control of safety valve | 389 | |||
| Pop valve | 389 | |||
| Automatic air brake | 390 | |||
| Draught of fire | 390 | |||
| Sand valves | 390 | |||
| American Passenger Locomotive | 390 to 393 | |||
| General construction | 390 | |||
| Steam reversing gear | 390, 391 | |||
| Link motion in full gear forward | 391 | |||
| In mid gear | 392 | |||
| In full gear backward | 392 | |||
| Reversing gear | 392 | |||
| Changing gear of link motion | 393 | |||
| Running forward | 393 | |||
| Running backward | 393 | |||
| Special Operations | 394 | |||
| Setting the slide valves | 394 | |||
| Getting the length of eccentric rods | 394 | |||
| Setting the lead | 394 | |||
| Backward eccentric | 394 | |||
| Marking sector notches | 394 | |||
| Setting Allen valves | 395 | |||
| Special Parts | 395 to 400 | |||
| The injector | 395 to 397 | |||
| Westinghouse automatic air brake | 398 to 400 | |||
| Locomotive Running | 400 to 404 | |||
| General discussion | 400 | |||
| Getting the engine ready | 400 | |||
| Laying the fire | 400 | |||
| Banking the fire | 401 | |||
| Starting up a banked fire | 401 | |||
| Examining the engine | 401 | |||
| Oiling the engine | 401 | |||
| Starting the engine | 401 | |||
| Saving fuel | 402 | |||
| Methods of firing | 402 | |||
| Examples of trips | 402 | |||
| Accidents on the Road | 402 | |||
| Knocking out cylinder heads | 402 | |||
| Heating of piston rods | 403 | |||
| Throwing off a wheel tire | 403 | |||
| Throwing off a driving wheel | 403 | |||
| Breaking a spring | 403 | |||
| Bursted tubes | 403 | |||
| Slipping eccentrics | 403 | |||
| Hot axle boxes | 403 | |||
| Breaking a lifting link | 403 | |||
| Breaking the saddle pin | 403 | |||
| Adjusting the wedges of the axle boxes | 404 | |||
| CHAPTER XXXIX. | ||||
| THE MECHANICAL POWERS. | ||||
| Power | 405 | |||
| Lever | 405 | |||
| The principles of | 405 | |||
| Wheels and pulleys considered as levers | 405, 406 | |||
| Power transmitted by gear wheels and pulleys combined | 407 | |||
| Horse Power | 407 | |||
| Calculating the horse power of an engine | 407 | |||
| Testing the horse power of an engine | 408 | |||
| Safety Valve Calculations | 409 | |||
| Heat | 410 | |||
| Latent heat | 410 | |||
| Water | 410 | |||
| Steam | 410 | |||
| Saturated | 410 | |||
| Superheated | 410 | |||
| Expansion of | 411 | |||
| Absolute pressure of | 411 | |||
| Weight of | 411 | |||
| Volume and pressure of | 411 | |||
| Heat | 411 | |||
| Conversion of heat into work | 411 | |||
| Joule’s equivalent | 411 | |||
| Mechanical equivalent of heat | 411 | |||
| Mariotte’s law | 411 | |||
| Radiation of heat | 412 | |||
| Conduction of heat | 412 | |||
| Convection of heat | 412 | |||
| CHAPTER XL. | ||||
| THE INDICATOR. | ||||
| Computations from Indicator Diagrams | 413 | |||
| Indicators | 413 | |||
| Description of | 413 | |||
| Thompson indicator | 413 | |||
| Tabor indicator | 413 | |||
| Diagrams | 414 | |||
| Admission of steam to indicator | 414 | |||
| Expansion line or curve | 414 | |||
| Exhaust line | 414 | |||
| Back pressure line | 414 | |||
| Atmospheric line | 414 | |||
| Theoretical diagram | 414 | |||
| Compression line or curve | 415 | |||
| Condensing engine diagram | 415 | |||
| Vacuum line of indicator diagram | 415 | |||
| (Barometer, construction of) | 415 | |||
| (Barometer, graduation of) | 416 | |||
| Indicator springs | 416 | |||
| Tables of springs for indicators | 416 | |||
| [II-xi] | Attachment of indicators to an engine | 416, 417 | ||
| Pantagraph motions | 417 | |||
| Expansion curve, testing of | 417, 418 | |||
| Theoretical expansion curve | 417, 418 | |||
| Calculations from diagrams | 418 to 421 | |||
| Horse power | 418, 419 | |||
| Area | 419 | |||
| Rule for calculating horse power | 419 | |||
| Mean effective pressure | 420 | |||
| Steam used in engines | 420 | |||
| Water consumption | 420, 421 | |||
| Defective diagrams of engines | 421 | |||
| Excessive lead of engines | 421 | |||
| Theoretical compression curve of engines | 422 | |||
| CHAPTER XLI. | ||||
| AUTOMATIC CUT-OFF ENGINES. | ||||
| Definition | 423 | |||
| Corliss Automatic Cut-off Engine | 423, 424 | |||
| Valve gear of | 424, 425 | |||
| Governor of | 425, 426 | |||
| Admission of steam into | 426 | |||
| Lap of valve of | 426, 427 | |||
| High Speed Automatic Engines | 427, 428 | |||
| Speed of | 427 | |||
| Wheel governors for | 427, 428 | |||
| Straight Line Automatic Engine | 428, 429 | |||
| Important details of | 429, 430 | |||
| Steam Fire Engine | 430, 431 | |||
| Boilers of | 430, 433 | |||
| Pumps | 431, 432 | |||
| Heaters for | 432, 433 | |||
| CHAPTER XLII. | ||||
| MARINE ENGINES. | ||||
| Various Kinds of Marine Engines | 434 to 451 | |||
| High pressure engines | 434 | |||
| Compound condensing engines | 434, 435 | |||
| Triple expansion engines | 436 | |||
| Donkey engines | 442 | |||
| Trunk engines | 446 | |||
| Oscillating engines | 446 | |||
| Geared engine | 446 | |||
| Compound engine of the steamship Poplar | 447, 450, 451 | |||
| Arrangement of Marine Engine Pumps | 436 | |||
| Boilers of Marine Engines, Arrangement of | 436, 437 | |||
| Various Parts of Marine Engines, etc. | 438 to 449 | |||
| Valve for intermediate cylinder of triple expansion engines | 438 | |||
| Link motions for triple expansion engines | 438 | |||
| Auxiliary or by-pass valve | 438, 439 | |||
| Oiling apparatus | 439, 440 | |||
| Surface condensers | 440 | |||
| Circulating pumps | 440 | |||
| The snifting valve | 440 | |||
| The blow-through valve | 440 | |||
| Air pumps | 441 | |||
| The air chamber | 441 | |||
| Feed escape or feed relief valve | 441 | |||
| Bilge injections for marine engines | 441, 442 | |||
| Surface condensing, advantages of | 442 | |||
| Valves of the surface condensing engine | 442 | |||
| Case hardening | 442 | |||
| Link motion for marine engines | 443 | |||
| The separate expansion valve | 443 | |||
| Friction of slide valves | 443 | |||
| Double beat valves | 443 | |||
| The siphon | 443 | |||
| Steam lubricators | 444 | |||
| Marine engine valves that are worked by hand | 444 | |||
| Vacuum gauge | 444 | |||
| Condenser, to find the total pressure in the | 444 | |||
| Paddle wheels | 444, 445 | |||
| Screw propeller | 445 | |||
| The thrust bearing | 445 | |||
| Marine engine, the principal parts of | 445 | |||
| Lagging marine engines | 446 | |||
| Propeller cylinders | 446 | |||
| Fuel required | 446 | |||
| Freezing of pipes | 446 | |||
| Failure of engine to start, causes of | 446, 447 | |||
| Defective vacuum, causes of | 447 | |||
| Heating, causes of | 447 | |||
| Construction of a triple expansion engine | 447 to 449 | |||
| CHAPTER XLIII. | ||||
| MARINE BOILERS. | ||||
| Plates for Marine Boilers | 452 | |||
| Iron | 452 | |||
| Steel | 452 | |||
| Strength of | 452 | |||
| Boiler Stays | 452 | |||
| Methods of securing | 452 | |||
| Boiler Tubes | 452 | |||
| Methods of securing | 452 | |||
| Causes of leaks | 452 | |||
| Repairing leaks | 452 | |||
| The Up-take | 453 | |||
| The Receiver | 453 | |||
| The Fittings and their Uses | 453, 454 | |||
| Valves | 453, 454 | |||
| Gauges | 453, 454 | |||
| Cocks | 454 | |||
| Important Features and Facts | 454, 455 | |||
| Boiler scale | 454 | |||
| The salinometer | 454 | |||
| Priming, the prevention of | 454 | |||
| Supplemental parts | 454, 455 | |||
| The superheater | 454 | |||
| The draught | 455 | |||
| Wasting of plates | 455 | |||
| Fuel, the quantity of | 455 | |||
| To Relieve the Boiler in Case of Accident | 455 | |||
| Steel Marine Boiler | 456 | |||
| The “Martin” Boiler | 456 | |||
| Testing and Examining Boilers | 456 to 459 | |||
| Hydraulic tests | 456 | |||
| Related to stays | 456, 457 | |||
| On new and old boilers | 456, 457 | |||
| Internal examinations | 458 | |||
| Preparation for | 458 | |||
| Safety valves | 458 | |||
| Bottom of the boiler | 458 | |||
| Bottom and sides of the furnace | 458 | |||
| Boxes and stays | 458 | |||
| Use of chipping hammer | 458 | |||
| Pit holes in the bottom of a furnace | 458 | |||
| Drilling through the plates | 458 | |||
| Flanges of furnaces | 458 | |||
| Deposits on the necks of stays | 458 | |||
| Man-hole door | 458 | |||
| Superheater | 459 | |||
| Proportions for grate surface | 459 | |||
| Outside examination | 458 | |||
| Cement beds for boilers | 458 | |||
| Proportions for circular tubular boilers | 459 | |||
| CHAPTER XLIV. | ||||
| HARDENING AND TEMPERING. | ||||
| Purposes | 460 | |||
| To resist wear | 460 | |||
| To increase elasticity | 460 | |||
| To provide a cutting edge | 460 | |||
| Manufacturer’s Temper | 460 | |||
| Blacksmith’s Temper | 460 | |||
| Color Tempering | 460 | |||
| Practical Processes | 461 to 464 | |||
| The muffle | 461 | |||
| Warping | 461 | |||
| Rapidity of reduction of temper | 461 | |||
| Brown and Sharpe’s practice | 461 | |||
| Waltham Watch Co.’s practice | 461 | |||
| Pratt and Whitney Co.’s practice | 461 | |||
| Morse Twist Drill Co.’s practice | 461 | |||
| Outside hardening | 462 | |||
| Heating in fluxes | 462 | |||
| Monitor Sewing Machine Co.’s practice | 462 | |||
| Hardening saws | 462 | |||
| Drawing the temper | 462 | |||
| 1. Lying in an open furnace | 462 | |||
| 2. Stretched in a frame | 462 | |||
| 3. Between dies | 462 | |||
| Stiffening saws | 463 | |||
| Tomlinson Carriage Spring Co.’s practice | 463 | |||
| Columbia Car Spring Co.’s practice | 463 | |||
| New Haven Clock Co.’s practice | 464 | |||
| APPENDIX. | ||||
| Part I.—Test Questions for Engineers | 467 | |||
| Part II.—Dictionary of Workshop Terms | 473 | |||
| Facing | |||
| Frontispiece. | COMPOUND MARINE ENGINE. | Title Page |
|
| Plate | I. | EXAMPLE OF MILLING MACHINE. | 10 |
| „ | II. | EXAMPLES OF MILLING MACHINES. | 12 |
| „ | III. | EXAMPLES OF MILLING MACHINES. | 16 |
| „ | IV. | EMERY GRINDING MACHINERY. | 45 |
| „ | V. | GRINDSTONE GRINDING. | 54 |
| „ | VI. | FULL AUTOMATIC GEAR CUTTER. | 55 |
| „ | VII. | GEAR CUTTING MACHINES. | 56 |
| „ | VIII. | THE HAMMER AND ITS USES. | 71 |
| „ | IX. | SCRAPERS AND SCRAPING. | 97 |
| „ | X. | OIL-TESTING MACHINES. | 153 |
| „ | XI. | TESTING PLANER BEDS AND TABLES. | 180 |
| „ | XII. | EXAMPLES OF PULLEYS. | 200 |
| „ | XIII. | THE ACTION OF SAW TEETH. | 273 |
| „ | XIV. | EXAMPLE IN PATTERN WORK. | 276 |
| „ | XV. | EXAMPLES IN STEAM HAMMER WORK. | 232 |
| „ | XVI. | EXAMPLES IN HAND FORGING. | 239 |
| „ | XVII. | FORGING UNDER THE HAMMER. | 249 |
| „ | XIX. | DIMENSION SAWING MACHINE. | 292 |
| „ | XIX. | RACK-FEED SAW BENCH. | 302 |
| „ | XX. | PLANTATION SAW MILL. | 305 |
| „ | XXI. | GAINING OR GROOVING MACHINE. | 306 |
| „ | XXII. | BAND SAW WITH ADJUSTABLE FRAME. | 311 |
| „ | XXIII. | BAND SAW MILL. | 311 |
| „ | XXIV. | LOG CROSS-CUTTING MACHINE. | 312 |
| „ | XXV. | HORIZONTAL SAW FRAME. | 314[II-xiv] |
| „ | XXVI. | TRYING-UP MACHINE. | 333 |
| „ | XXVII. | SANDING MACHINES. | 348 |
| „ | XXVIII. | BOILER FOR STATIONARY ENGINES. | 360 |
| „ | XXIX. | AMERICAN FREIGHT LOCOMOTIVE. | 388 |
| „ | XXX. | AMERICAN PASSENGER LOCOMOTIVE. | 390 |
| „ | XXXI. | LOCOMOTIVE LINK MOTION. | 392 |
| „ | XXXII. | INJECTOR AS APPLIED TO A LOCOMOTIVE. | 395 |
| „ | XXXIII. | LOCOMOTIVE AIR BRAKES. | 396 |
| „ | XXXIV. | THE CORLISS VALVE GEAR. | 425 |
| „ | XXXV. | STEAM FIRE ENGINE. | 430 |
| „ | XXXVI. | COMPOUND MARINE ENGINE. | 436 |
| „ | XXXVII. | TRIPLE EXPANSION MARINE ENGINE. | 440 |
The Milling Machine.—The advantages of the milling machine lie first in its capacity to produce work as true and uniform as the wear of cutting edges will permit (which is of especial value in work having other than one continuous plane surface); second, in the number of cutting edges its tools will utilize in one tool or cutter; and third, in its adaptability to a very wide range of work, and in the fact that when the work and the cutters are once set the operator may turn out the best quality of work without requiring to be a skilled machinist.
The extended use of the milling machine, which is an especial feature of modern machine shop practice, is due, in a very large degree, to the solid emery wheel, which provides a simple method of sharpening the cutters without requiring them to be annealed and rehardened, it being found that annealing and rehardening reduces the cutting qualifications of the steel, and also impairs the truth of the cutting edges by reason of the warping or distortion that accompanies the hardening process. Rotary cutters are somewhat costly to make, but this is more than compensated for in the uniformity of their action, since in the case of the cutter the expense is merely that involved in forming the cutting edges with exactitude to shape; once shaped the cutter will produce a great quantity of work uniform in shape, whereas in the absence of such cutters each piece of work would require, to bring it to precise form, as much precision and skill as is required in shaping the cutter.
If a piece of work is shaped in a planing machine, the different steps, curves, or members must be cut or acted upon by the tool separately, and the dimensions must be measured individually, giving increased liability to error of measurement, and requiring a fine adjustment of the cutting tool for each step or member. Furthermore, neither a planing machine or any other machine tool can have in simultaneous cutting operation so great a length of cutting edge as is possible with a rotary cutter.
Again, in the planing machine each cut requires to be set individually, and cannot be so accurately gauged for its depth, whereas with a rotary cutter an error in this respect is impossible, because the diameters of the various steps on the cutter determine the depth of the respective cuts or steps in the work.
In a milling machine the cut is carried continuously from its commencement to its end, whereas in a shaping or planing machine the tool does not usually cut during the back or return stroke. In either of these machines, therefore, the operator’s skill is required as much in measuring the work, setting the tools feeds, &c., as in shaping the tools, whereas in the milling machine all the skill required lies in the chucking and adjustment of the work to the cutter, rather than in operating the machine, which may therefore be operated by comparatively unskilled labor.
The multiplicity of cutting edges on a rotary cutter so increases its durability, and the intervals at which it must be sharpened are so prolonged, that, with the aid of the present improved cutter grinding machines, one tool maker can make and keep in order the cutters for many machines.
The speed at which milling cutters are run varies very widely in the practice in different workshops. Thus upon cast iron, cutting speeds of 15 circumferential feet per minute will be employed upon the same class of work that in another shop would be done at a cutting speed of as high as fifty feet per minute. With the quick speeds, however, lighter feeds are employed. As the teeth of milling cutters are in cutting action throughout but a small portion of a revolution, they have ample time to cool, and may be freely supplied with oil, which enables them to be used at a higher rate of cutting speed than would otherwise be the case. Yet another element of importance in this connection is that when the cut is once started on a plain cutter, the cutting edges do not meet the surface skin of the metal, this skin always being hard and destructive to the cutting edges.
The simplest form in which the milling machine appears is termed the hand milling machine, and an example of this is shown in Fig. 1878. This machine consists of a head carrying a live spindle which drives the cutting tools, which latter are called cutters or mills. The front of the head is provided with a vertical slideway for the knee or bracket that carries an upper compound slide upon which the work-holding devices or chucks are held. The work is fed to the revolving cutter by the two levers shown, the end one of which is for the vertical and the other for the horizontal motion, which is in a direction at a right angle to the live spindle axis.
[II-2]In other forms of the hand milling machine the live spindle is capable of end motion by a lever.
In Fig. 1878a is shown Messrs. Brown and Sharpe’s plain milling machine, or in other words a milling machine having but one feed motion, and therefore suitable for such work only as may be performed by feeding the work in a straight line under the cutter, the line of feed motion being at a right angle to the axis of the cutter spindle.
Machines of this class are capable of taking heavy cuts because the construction admits of great rigidity of the parts, there being but one slideway, and therefore but one place in the machine in which the rigidity is impaired by the necessity for a sliding surface.
The construction of this machine is as follows: The head a which carries the cutter spindle is pivoted at c to a stiff and solid projection on the frame f, and means are provided to solidly clamp the two together.
A bracket b supports the outer end of the head; at its upper end b is split so that by means of a bolt it may firmly clamp the cylindrical end of a, which carries the dead centre piece d. The two lower ends of b are bolted to the frame f.
The work table t is gibbed to slideways in f, and is provided with suitable automatic feed and stop motion, and of course with a hand feed also.
To adjust the height of the cutter, the lower ends of b are released from f and the head a is swung on its centre c.
It is obvious that a machine of this class is suitable for cases where a large quantity of work of one kind is to be done and frequent changes of the adjustments are not required, and that for such work the solidity of the construction and the convenience of having all the handles employed in operating the machine accessible from one position are desirable elements obtained by a very simple construction.
Fig. 1879 represents Pratt & Whitney’s power milling machine. The cone and live spindle are here carried in boxes carried in vertical slideways in the headstock, so as to be adjustable in height from the work table, and is provided with a footstock for supporting the outer end of the live spindle, which is necessary in all heavy milling. The carriage is adjustable along the bed, being operated by a screw whose operating hand wheel is shown at the left-hand end of the bed.
The automatic feed is obtained as follows: The large gear on the right of the main driving cone operates a pinion driving a small four-step cone connected by belt to the cone below, which, through the medium of a pair of spur-gears, drives the feed rod, on which is seen a long worm engaging a worm-wheel which drives the feed screw. A suitable stop motion is provided.
What is termed a universal milling machine is one possessing the capacity to cut spiral grooves on either taper or parallel work, and is capable of cutting the teeth of spur and bevel-gears or similar work other than that which can be held in an ordinary vice. These features may be given to a machine by devices forming virtually an integral part of the machine, or by providing the machine with separate devices which are attachable to the work table.
In Fig. 1880 is represented a small size universal milling machine, in which a is the frame that affords journal bearing to the live spindle, in the coned mouth a of which the mandrel carrying the rotary cutter is fitted, means being afforded for taking up the wear of the live spindle journal and bearings. b is the cone pulley for driving a. Upon the front face of a is a vertical slide upon which may be traversed the knee or table c, which by being[II-3] raised, regulates the depth to which the cutters enter the work. To operate c the vertical screw b is provided, it being operated (by bevel-gears) from a horizontal shaft whose handle end is shown at c.
The nut for elevating screw b is formed by a projecting lug from or on the main frame a. To enable c to be raised to a definite height so that the cutters shall enter successive pieces of work to an equal depth, a stop motion is provided in the rod d, which passes through a plain hole in the lug on a that forms a nut for b. Rod d is threaded and is provided with a nut and chuck nut whose location on the length of the rod determines the height to which c can be raised, which ceases when the faces of the nuts meet the face of the projecting lug.
The upper surface of c is provided with a slide on which is a slider d, which, by means of a feed screw whose handle end is shown at e, may be traversed in a line parallel to the axial line of[II-4] the live spindle or arbor, as it is more often termed, this motion being employed to set the width of the work in the necessary position with relation to the rotary cutters. To d is attached e, which is pivoted at its centre so as to be capable of swinging horizontally, means being provided to fasten it to d in its adjusted position. This is necessary to enable the line of traverse of the work to be at other than a right angle to the axial line of the cutter spindle when such is desired, as in the case of cutting spirals; e serves as a guide to the carriage f, the latter being operated endwise by means of a screw whose handle is shown at e′′, the nut being attached to e, handle e′′ being to traverse e by hand. To feed f automatically gear-wheel f is attached to the other end of the same screw, this automatic feed being actuated as follows:—
At the rear end of the live spindle is a three-stepped cone pulley attached by belt to cone pulley g, which connects by rod to and drives gear f. The construction of the rod is so designed as to transmit the rotary motion from g to f without requiring any adjustment of parts when c is raised or lowered or f traversed back or forth, which is accomplished as follows:—
At g g are two universal joints attached respectively to g and f, and to two shafts which are telescoped one within the other. The inner rod is splined to receive a feather in the outer. The rotary motion is communicated from g to the universal joint, through that joint to the outer or enveloping shaft which drives the inner shaft, the latter driving a universal joint which drives f, the inner shaft passing freely within the outer or sliding out from it (while the rotary motion is continuing) to suit the varying distance from and position of f with relation to g. This automatic feed motion may be adjusted to cease at any point in the traverse of e by a stop and lever provided for the purpose, so that if an attendant operates more than one machine, or if the feed require to be carried a definite distance, it will stop automatically when that point has been reached.
The carriage f may carry various chucks or attachments to suit the nature of the work. As shown in the cut it carries a tailblock i and head j, both fitting into a way provided in f so that they will be in line one with the other at whatever part in the length of f they may be set or fixed. Both i and j carry centres between which the work may be held, as in the case of lathe work. Part j is pivoted to j so that it may be set at an angle if required, thus setting the centre, which fits in the hole at h, above the level of that in i, as may be necessary in milling taper work, the raising of j answering to the setting over of the tailstock of a lathe for taper turning.
To enable the accurate milling of a polygon, the spindle h may be rotated through any given portion of a circle by means of the index wheel at i, it being obvious that if a piece of work be[II-5] traversed beneath the cutter, and h be rotated a certain portion of a circle after each traverse, the work will be cut to a polygon having a number of sides answering to the portion of a circle through which h is rotated after each traverse. Means are also provided to rotate h while f is traversing beneath the cutter; hence when these two feed motions act simultaneously the path of the work beneath the cutter is a spiral, and the action of the cutter in the work is therefore spiral; hence spiral grooves may be cut or spiral projections left on the work, as may be determined by the shape of the cutters. k is a chuck that may be connected to h to drive the work, and h a work-holding vice, that may be used instead upon f in place of heads i j.
The countershaft shown at the foot of the machine has two loose pulleys and a tight one between them, this being necessary because, in cutting spiral work, the work must rotate while on the back traverse as well as on the forward one, hence a crossed as well as an open belt is necessary.
Fig. 1881 represents a large Brown & Sharp universal milling machine, in which the cone spindle is provided with back gear, and a supporting arm is also provided for the outer end of the cutter arbor. The feed motions for this machine correspond to those already described for the smaller one, Fig. 1880, the construction of the important parts being shown in the following figures.
The construction of the bearings for the cutter driving spindle of the machine is as in Figs. 1882 and 1883. a is the spindle having a double cone to fit corresponding cones in the sleeve b, the fit of one to the other being adjusted by means of the nut c, which is threaded upon a. The mouth of a is coned to receive the arbors or mandrels for driving the mills or cutters. At the back bearing, Fig. 1883, the journal a′, and bore of the sleeve b′, is parallel, this sleeve being split at the top so that when it is (by means of nut d) drawn within the head e its coned exterior will cause it to close to a proper fit upon a′, by which means the wear of the parts may be taken up as they become perceptible.
The head j, Fig. 1880, is used (in connection with the foot block i) to suspend or hold work by or between centres, its centre fitting into the spindle at h, which is capable of being revolved continuously (to enable the cutting of spirals), by means of change gears, and intermittently through a given part of a circle by means of the index wheel i. The block j carrying the spindle is also capable of elevation for conical or taper work, two examples of such uses being shown in Figs. 1884 and 1885, in which c is the cutter and w the work.
[II-6]Fig. 1886 is a sectional view in a vertical plane through the centre of the head, and showing the construction of the spindle and the means of elevating the block j; h is the spindle having journal bearing in j, and secured from end motion by the cone at a and the nut b; its bore is coned at the front end to receive the arbor c carrying the centre d, upon which is the piece e for[II-7] driving the work dog, which is secured within e by the set-screw f. Fast upon spindle h is a worm-wheel f made in two halves, which are secured together by the screws g. At g is the worm-wheel (for driving f) fast upon the shaft h′.
It is obvious that the block j may be raised at its centre end upon h as a centre of motion, the worm f simply moving around upon g. At v is a bolt to lock j to j, and thus secure it in its adjusted position. w w are lugs or blocks fitting into the slot in the work table, and serving to secure the head, being in line with the foot block (shown at 1 in Fig. 1880). A sleeve z is used to cover the thread and protect it when a chuck is not used.
Fig. 1887 is an end view partly in section to show the construction of the worm shaft and the index plate. h is a sleeve upon which j pivots, and h′ the worm shaft, which may be revolved by hand by the lever l, or automatically by means of the bevel-gear k, which connects with the train of change gears; these change gears being thrown out of operation when gear k (and therefore h) is not required to revolve automatically nor continuously. l is an arm for carrying the index pin l for the index plate i. The pin l is adjustable for radius from the centre of h (so as to come opposite to the necessary circle of holes on the plate i), the arm l being slotted to permit of this adjustment, and being secured in its adjusted position by the nut on the end of h′. Pin l is pushed into the index holes by means of the spiral spring coiled around l at m, which permits l to be withdrawn from i under an end pressure, but pushes it into i when that pressure is released. To indicate the amount of rotation of i, without counting the number of holes, a sector n n′ is employed, it having two arms adjustable for their widths apart so as to embrace any given number of holes on the required circle. At r′ is a pin which is pulled forward and into holes provided in the plate i to prevent its turning when using the lever l. n and n′ are held to the face of i by the friction of the spring q. A face view of index plate i is shown in Fig. 1888, the lever l, Fig. 1887, being removed to expose n and n′.
The surface of the plate is provided with rings of holes marked respectively 20, 19, 18, &c., the holes in each ring or circle being equidistantly spaced.
The sector arms n and n′ may be opened apart or closed together so as to embrace any required number of holes in either of the circles. As shown in the cut they embrace one quarter of the circle of 20, there being five divisions between the holes s and t. The screw w secures them in their adjustment apart. Suppose that pin l (Fig. 1887), is in s, and arm n′ is moved up against it, the arm n leaves t open, and indicates that t is the next hole for pin l, which is withdrawn from s, and lever l (Fig. 1887) is moved around until the pin will enter t, and the sector is then moved into the position shown in Fig. 1888a, indicating that hole u is the next one for the pin. This obviates the necessity of counting the holes, and prevents liability to error in the counting. Three of these index plates are provided, each having different numbers of holes in the circles, and in the following tables are given those specially prepared for use in cutting the teeth of gear-wheels:
| No. of teeth. |
Index circle. |
No. of turns of index. |
No. of teeth. |
Index circle. |
No. of turns of index. |
||
| 2 | ANY | 20 | 80 | 20 | 10⁄20 | ||
| 3 | 39 | 13 | 13⁄39 | 82 | 41 | 20⁄41 | |
| 4 | ANY | 10 | 84 | 21 | 10⁄21 | ||
| 5 | „ | 8 | 85 | 17 | 8⁄17 | ||
| 6 | 39 | 6 | 26⁄39 | 86 | 43 | 20⁄43 | |
| 7 | 49 | 5 | 35⁄49 | 88 | 33 | 15⁄33 | |
| 8 | ANY | 5 | 90 | 27 | 12⁄27 | ||
| 9 | 27 | 4 | 12⁄27 | 92 | 23 | 10⁄23 | |
| 10 | ANY | 4 | 94 | 47 | 20⁄47 | ||
| 11 | 33 | 3 | 21⁄33 | 95 | 19 | 8⁄19 | |
| 12 | 39 | 3 | 13⁄39 | 98 | 49 | 20⁄49 | |
| 13 | 39 | 3 | 3⁄39 | 100 | 20 | 8⁄20 | |
| 14 | 49 | 2 | 42⁄49 | 104 | 39 | 15⁄39 | |
| 15 | 39 | 2 | 26⁄39 | 108 | 27 | 10⁄27 | |
| 16 | 20 | 2 | 10⁄20 | 110 | 33 | 12⁄33 | |
| 17 | 17 | 2 | 6⁄17 | 115 | 23 | 8⁄23 | |
| 18 | 27 | 2 | 6⁄27 | 116 | 29 | 10⁄29 | |
| 19 | 19 | 2 | 2⁄19 | 120 | 39 | 13⁄39 | |
| 20 | ANY | 2 | 124 | 31 | 10⁄31 | ||
| 21 | 21 | 1 | 19⁄21 | 128 | 16 | 6⁄16 | |
| 22 | 33 | 1 | 27⁄37 | 130 | 39 | 12⁄39 | |
| 23 | 23 | 1 | 17⁄23 | 132 | 33 | 10⁄33 | |
| 24 | 39 | 1 | 26⁄39 | 135 | 27 | 8⁄27 | |
| 25 | 20 | 1 | 12⁄20 | 136 | 17 | 5⁄17 | |
| 26 | 39 | 1 | 21⁄39 | 140 | 49 | 14⁄49 | |
| 27 | 27 | 1 | 13⁄27 | 144 | 18 | 5⁄18 | |
| 28 | 49 | 1 | 21⁄49 | 145 | 29 | 8⁄29 | |
| 29 | 29 | 1 | 11⁄29 | 148 | 37 | 10⁄37 | |
| 30 | 39 | 1 | 13⁄39 | 150 | 15 | 4⁄15 | |
| 31 | 31 | 1 | 9⁄31 | 152 | 19 | 5⁄19 | |
| 32 | 20 | 1 | 5⁄20 | 155 | 31 | 8⁄31 | |
| 33 | 33 | 1 | 7⁄33 | 156 | 39 | 10⁄39 | |
| 34 | 17 | 1 | 3⁄17 | 160 | 20 | 5⁄20 | |
| 35 | 49 | 1 | 7⁄49 | 164 | 41 | 10⁄41 | |
| 36 | 27 | 1 | 3⁄27 | 165 | 33 | 8⁄33 | |
| 37 | 37 | 1 | 3⁄37 | 168 | 21 | 5⁄21 | |
| 38 | 19 | 1 | 1⁄19 | 170 | 17 | 4⁄17 | |
| 39 | 39 | 1 | 1⁄39 | 172 | 43 | 10⁄43 | |
| 40 | ANY | 1 | 180 | 27 | 6⁄27 | ||
| 41 | 41 | 40⁄41 | 184 | 23 | 5⁄23 | ||
| 42 | 21 | 20⁄21 | 185 | 37 | 8⁄37 | ||
| 43 | 43 | 40⁄43 | 188 | 47 | 10⁄47 | ||
| 44 | 33 | 30⁄33 | 190 | 19 | 4⁄19 | ||
| 45 | 27 | 24⁄27 | 195 | 39 | 8⁄39 | ||
| 46 | 23 | 20⁄23 | 196 | 49 | 10⁄49 | ||
| 47 | 47 | 04⁄47 | 200 | 20 | 4⁄20 | ||
| 48 | 18 | 15⁄18 | 205 | 41 | 8⁄41 | ||
| 49 | 49 | 20⁄49 | 210 | 21 | 4⁄21 | ||
| 50 | 20 | 16⁄20 | 215 | 43 | 8⁄43 | ||
| 52 | 39 | 30⁄39 | 216 | 27 | 6⁄27 | ||
| 54 | 27 | 20⁄27 | 220 | 33 | 6⁄33 | ||
| 55 | 33 | 24⁄33 | 230 | 23 | 4⁄23 | ||
| 56 | 49 | 35⁄49 | 232 | 29 | 5⁄29 | ||
| 58 | 29 | 20⁄29 | 235 | 47 | 8⁄47 | ||
| 60 | 39 | 26⁄39 | 240 | 18 | 3⁄18 | ||
| 62 | 31 | 20⁄31 | 245 | 49 | 8⁄49 | ||
| 64 | 16 | 10⁄16 | 248 | 31 | 5⁄31 | ||
| 65 | 39 | 24⁄39 | 260 | 39 | 6⁄39 | ||
| 66 | 33 | 20⁄33 | 264 | 33 | 5⁄33 | ||
| 68 | 17 | 10⁄17 | 270 | 27 | 4⁄27 | ||
| 70 | 49 | 28⁄49 | 280 | 49 | 7⁄49 | ||
| 72 | 27 | 15⁄27 | 290 | 29 | 4⁄29 | ||
| 74 | 37 | 20⁄37 | 296 | 37 | 5⁄37 | ||
| 75 | 15 | 8⁄15 | 300 | 15 | 2⁄15 | ||
| 76 | 19 | 10⁄19 | 310 | 31 | 4⁄31 | ||
| 78 | 39 | 20⁄39 | 312 | 39 | 5⁄39 | ||
[II-8]A plan view of one-half of the head is shown in Fig. 1889, the edge of j being graduated for a guide in elevating the head at an angle, at v is the bevel-gear for driving k, and at s is a pinion receiving motion from the change gears.
The feed motions for the traversing table (f, Fig. 1880) is shown in Figs. 1889, 1890, and 1891, g represents the universal joint rotating continuously the spindle a, which provides journal bearing to bevel pinion b and the clutch c, these two being fixed together; d is a clutch which rotates with a, but is capable of a certain amount of end motion on or along a to enable it to engage or disengage with its mate c. When d engages with c the rotary motion of a is transmitted through d, c, b, to f, which actuates the feed screw a, while when d is disengaged from c, it rotates, leaving c b f idle. d is operated to engage with or disengage from c, its hub is enveloped by the fork e, which is attached to rod h, which is provided with a recess to receive one end of the bell crank l, the other end of which lies in a recess in the rod m, to the end of which is connected the lever handle n, which is pivoted at o; hence operating n laterally as denoted by the arrows, throws d in or out of gear with c, according to the direction of motion, direction p being that to throw it out of, and q to throw it into gear or engagement. At r is a stop that can be fixed at any adjusted position or desired location along the bed upon which the feed table or carriage (f, Fig. 1880) slides, so that when that carriage is being self-actuated it will traverse until the inner end of n meets the stop, whereupon the stop will move n and thereby disengage d from c, causing the automatic feed to cease. All that is necessary, therefore, is to set r in such a position along the bed that it will operate n when the milling cutter has operated to the required distance along or over the work; s is the stud arm that carries wheel t to engage with and drive the pinions shown in Fig. 1889, and u is the stud for carrying the wheels for giving the required changes of rotation to k, Fig. 1889, the wheels on u receiving motion from a gear placed at the seat v on the feed screw a. The stud arm s being slotted, can be moved forward, transmitting motion from the change wheels on u to wheel s, Fig. 1890, causing the automatic spiral feed to actuate; or by moving s outwards, this feed is thrown out of action, and either the hand feed of handle w or the self-acting feed traverse may be employed.
Thus the hand, and all the automatic feed motions are driven from the feed screw a, and each of the automatic feed motions may be started or stopped by operating the lever n, while the stop r causes each of them to cease when the work has traversed to the required distance beneath the milling cutter.
Fig. 1892 represents an attachment to this machine to facilitate cutting the teeth of gears, which it does because its index plate operates the work-holding mandrel direct, and may, therefore, be[II-9] set quicker. The base bolts to the machine table and the index head and tailblock are traversed in the base by means of the four-levered handle shown.
Figs. from 1893 to 1899 represent a universal milling machine. This machine is so constructed that all the features essential to a universal milling machine are obtained by means of attachments (each complete in itself) which may be removed, leaving the work table clear, and, therefore, serviceable for large work, or work which may be more conveniently held without the use of attachments.
The T-slots in the table are furnished to standard size, and are at right angles, so that the attachments will be held exactly parallel with, or at a right angle, as the case may be, to the live spindle of the machine; hence the machine will accomplish all the varied results required in the tool room or for machine work generally.
Thus for the cutting of spirals, a fixture capable of originating any spiral right or left hand, from 2 inches to 6 feet pitch, is provided. Two bolts secure it to the machine table, and when the job is finished it is removed. Similarly for the cutting of cams, an attachment fastened to the work table by three bolts is used, which cuts either cylinder or face cams of considerable size, and as conveniently as a machine built solely for cam cutting. A gear-cutting device is also applied in the same manner, as well as plain or universal work-holding centres.
| VOL. II. | EXAMPLE OF MILLING MACHINE. | PLATE I. |
 |
||
| Fig. 1893. | ||
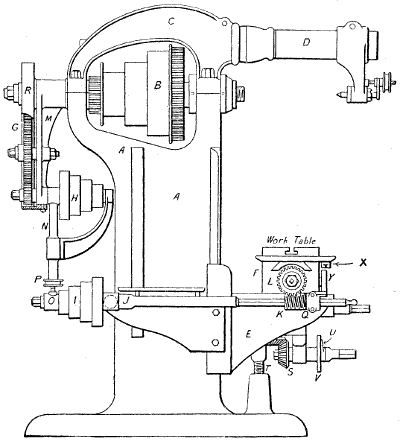 |
||
| Fig. 1894. | ||
The essential features of the machine are a standard a, Fig. 1894, with spreading base, carrying upon its top a driving cone b, which is fully back-geared like an engine lathe. The driving cone operates also the feed mechanism. Above the driving cone is an arch c, in which is inserted an arm d for supporting the outer end of the mill arbor when used for heavy work. Upon the face or front of the standard slides a knee e, which in its turn supports a carriage f, which traverses crosswise upon it and carries above it the work table, which is provided with an automatic feed at right[II-10] angles with the movement of the carriage. These three movements, vertical, cross, and longitudinal, cover all that is usually required in a universal milling machine.
Coming to details we start with the spindle or arbor, the front end of which runs in bearings of bronze. These are made in two parts, tapering upon the outside and straight upon the inside, a corresponding taper hole to receive the spindle bearings being bored in the solid iron of the standard. A check nut upon each end of the bushing or bearing abuts against the end faces of the standard bearing, and by drawing the bushing or bearing through the taper hole in the standard, produces the exact required closeness of fit between the spindle journal and its bearing bore, and thus compensates for the wear of either the spindle journal or its bearing or bushing bore, the front check nut also providing a dust cap.
The back journal of the spindle runs in a bushing of considerable length. Upon the back end of the spindle is secured a train of feed gears g, the lower of which is upon a shaft that on its other end carries the first feed cone h. The corresponding feed cone i is fixed to the longer shaft j, carrying a worm (or tangent screw) k, which engages with the worm-gear l connected directly with the feed screw, for the longitudinal motion of the work table.
This whole feed work is shown fully in outline in Fig. 1894. The arm m that supports the two lower feed gears pivots upon the outboard end of the back bushing, hence its centre coincides with that of the spindle. At its lower end a projection inwards forms a hub upon which a second lug or arm n is pivoted. The lower end of this arm is bored out to receive the threaded end of a lug o with the bearing of the second feed cone i. This threaded end carries a milled or hand nut p, so that to tighten or loosen the feed belt a turn of the nut is sufficient, the effect being to increase or diminish the distance between the feed cones h and i. The front end of the feed rod is supported in a drop box q, and is splined to allow the worm k to travel upon it. It will be seen, therefore, that the feed mechanism is undisturbed either by the vertical movement of the knee, or the cross motion of the carriage, or the longitudinal feed of the table. The feed gears are covered with a shield r, a part of which is shown broken away. The knee with its appendages is actuated vertically by means of a crank connected with bevel gearing at s, which moves a perpendicular screw t under the centre of the knee. Rotating with this crank-shaft is a finger u held by friction. This finger is in close proximity to a dial v graduated to thousandths of an inch, and as one revolution of the finger indicates 1⁄8 of an inch of elevation to the knee e, the ordinary subdivisions of an inch are obtained either with or without an inner circle of graduations on the dial. A similar dial upon the cross feed motion (not shown in the engraving) is also put on, which likewise reads to thousandths of an inch.
The feed of the work table is accomplished by means of a screw whose thread is in shape a half V and does not bear upon the bottom of the thread in the feed nut, which is in halves, with provision for closing up to compensate for wear, while check nuts on one end of the feed screw take up all end play.
The automatic feed is self-stopping (so as to enable one attendant to operate several machines) by means of the following construction:—
In the general view, Fig. 1893, there is seen a stop that is secured in the required position in the T-groove shown at x in the outline view, Fig. 1894, and when this stop meets the bell crank y it unlatches it from a lug which is on the drop box q, Fig. 1893, hence this box falls and with it that end of the worm shaft j, throwing it out of gear with the worm-wheel l, and therefore stopping the feed.
The attachments giving to this machine its universal qualifications are as follows:—
The rotary vice is shown on the work table in the general view, Fig. 1893; and requires but little description. Upon the underside of the base is a circular projection having beneath it a projection fitting into the T-slots in the work table. Two segmental slots in the base admit of a rotary movement of the vice within a range of 90°, and it is held to the table by two bolts. The crank or handle of the vice is made more convenient by means of two square holes that fit the end of the screw that actuates the movable jaw. Using the central hole allows the handle to clear the work table, but when the vice jaws need to be closed with considerable force the handle is shifted to the end or outer hole, thus doubling the leverage.
The Universal Head and Back Centre.—This tool is used for making milling cutters either straight or angular, cutting small gears either spur or bevel, fluting taps or reamers, finishing nuts or bolt-heads, and a multitude of other jobs too numerous to particularise. The head consists, as seen in Fig. 1895, of a swinging block mounted centrally between the two upright sides or jaws of a base, and is clamped in any position by a set-screw on either side. The face of one side or jaw is laid out in degrees, and a finger or pointer on the block indicates its angle of elevation. On the front end of the spindle is secured a worm-wheel[II-11] divided longitudinally, each half being used as a corrector (in the making) for the other half till all errors are eliminated. A dial is fixed upon the bushing through which passes the shaft that actuates the worm, and consequently revolves the worm-gear and the spindle. A pointer arm carrying a handle with a pointer and appendages is secured to the end of this shaft. Under it are the usual spaces for laying off or indicating the proper number of index holes for the required fraction of a circle the spindle is to be moved through. The spindle is hollow and has a screw on the outer end for taking a chuck or face plate. It has a taper hole for receiving the proper centre, which carries a lug for holding the dog used when the work to be finished is held between centres. Three index dials, which are made interchangeable, provide for most divisions except a few prime numbers to 360.
To prevent or take up lost motion between the worm and the worm-gear the entire bracket carrying the worm and indexing mechanism is made adjustable as follows:—
Through the base of the bracket thread two sleeves whose ends abut against the top of the block, and therefore determine the engagement of the worm with the worm-wheel. Through these sleeves pass the bolts which thread into the block and lock the bracket in its adjusted position. A simple screw bolts the back end of the bracket. The degree of fit between the worm and the wheel may be very sensitively made by revolving the worm spindle by hand.
The block carrying the back centre has some peculiar features, which enable it to be set in line with the axis of the work, whether the latter be parallel or taper, so as to suit the elevation or depression of the head, and enable the centre to fill the countersink of work held on centres, keeping it central and avoiding wear to one side. It consists of a block held between two uprights or jaws, and clamped thereto by two screw bolts. The block is slotted entirely through from side to side, the front slot being only wide enough to receive the bolt and making a changeable centre for the block to partially rotate upon. The rear slot is wider and is a segment of a circle. The screw bolts being slackened the back centre is raised, lowered, or tilted to any required position to bring the centre in line with the work axis, and is then clamped in place. One bolt holds this part of the machine to the work table. The centre is adjusted to place in the end of the work in the ordinary way, with a hand nut, &c.
For gear cutting, the universal head is enlarged and somewhat modified in design, as is shown in Fig. 1896, the worm and worm-wheel being much larger in diameter and exceedingly accurate by the following method having been adopted to test them: Two cast-iron disks were placed side by side on an arbor or mandrel held between the centres, and lines of division were marked across the edges of both of them (the index plate, of course, being used for the division). The disks were then separated and one of them moved and the lines of division again compared with a microscope, and no sensible errors were apparent.
The provisions for taking up the wear of the worm and its bearings, and of the worm and its wheel, are as follows: The worm-shaft runs in compensating bearings of phosphor bronze,[II-12] and the bracket carrying the worm-shaft is adjustable towards the worm-wheel by the means already described for the ordinary universal head, and this head is said to be capable of making divisions as fine as one minute of an arc, or dividing the circle into 21,600 parts.
The employment of a worm and a worm-wheel necessitates that the index pointer arm be given a certain number of revolutions, in order to move the spindle the requisite amount for all divisions except those equal in number to the number of teeth contained in the worm-wheel, and to avoid any mistake in counting the number of revolutions of this index pointer arm the following device is employed: On the worm shaft is a pin, and to the right of the index plate is a dial plate which is clearly shown in the engraving. The circumference of the latter is cut with ratchet teeth, and the length of the pin on the worm-shaft is such that at each revolution it moves one tooth of the dial plate. In front of the dial plate is a fixed pointer, and as the face of the ratchet wheel is graduated and marked 1, 2, 3, &c., it is obvious that the pointer shows how many revolutions the dial plate, and therefore the worm shaft, has made. After the requisite number has been made and the index pin has been set in the index wheel, the small lever, shown on the right of the dial plate, is moved and a spring brings the dial plate back so that its zero number comes back to the pointer ready to count the number of revolutions when the worm-shaft is revolved for the next division or movement of the worm and wheel. For this head there are three index plates drilled with 23 circles of holes, making, in combination with the worm and wheel, all divisions up to 90, all even divisions up to 180, with most of the other divisions between 90 and 180, or 135 divisions and multiples of these divisions up to 16,200. The index plates are interchangeable, and additional ones for other divisions may obviously be added.
The device for cutting spirals as arranged for hand feeding is shown in Fig. 1897, while in Fig. 1898 it is shown arranged for automatic feeding, and is shown in position on the machine.
Referring to Fig. 1897 the hand wheel operates a worm engaging with a worm-wheel on the shaft of the largest gear shown in the engraving. From this gear motion is conveyed through intermediate wheels to the pinion on the same shaft as the first bevel-gear, which obviously drives the bevel-gear shown on the end of the head. The back face of this latter gear is provided with index holes, and the usual index arm and pin are provided.
The change gears provided for this device are sufficient to cut twelve different pitches, ranging from one turn in 2 inches to one turn in 6 feet. Obviously right or left-hand spirals are produced according to the direction of revolution of the hand wheel.
| VOL. II. | EXAMPLES OF MILLING MACHINES. | PLATE II. |
 |
||
| Fig. 1898. | ||
 |
||
| Fig. 1900. | ||
In the general view, Fig. 1898, the device is placed upon a box bolted to the work table, and obtains its automatic feed through the medium of the worm for the table feed.
The cam-cutting attachment, Fig. 1899, consists of a base bolted to the machine table and adjustable to any required position thereon. This base has a slide way in which a gibbed slide carrying a head is free to travel longitudinally. The pattern or former cam and the work are carried on the live spindle of the head, and the former cam is supported by circumferential contact with a roll carried on the vertical bracket shown on the right of the engraving. As shown, the device is arranged for cutting face cams, the cam-holding spindle being placed in line with the machine spindle. All that is necessary for cutting cylinder cams is to set the device with its spindle at a right angle to the machine spindle and move the supporting bracket so that its roller will meet the perimeter of the former cam. In either case the slide carrying the head is pulled forward by weights suspended over the wheel shown on the end of the base, and the feed is put on by revolving the spindle by means of the worm and worm-wheel shown in the engraving, the ordinary crank handle of the machine fitting the worm shaft.
A hand feed for cam cutters is preferable to the automatic feed, because in turning corners or curves the rate of the feed requires to be reduced in order to obtain smooth work.
Fig. 1900 represents a universal milling machine. The live spindle head is fitted to a horizontal slide on the top of the main frame, and may therefore be moved on that slideway to adjust the cutters to the work, the motion being effected by a pinion operating a rack on the underside of the head, as shown in Fig. 1901, which is a sectional view of the machine.
At the handle end of the pinion shaft there is provided a dial (which is seen in the general view of the machine) having an outer[II-13] circle graduated to sixty-fourths of an inch, and an inner one graduated to fortieths of an inch. The driving shaft is at a right angle to the live spindle, and drives it by means of a hardened steel worm operating a bronze worm-wheel fast on the live spindle, and which runs in a trough of oil to provide ample lubrication.
The spindle is hollow and has tapered journals. The arm for supporting the outer end of the cutter arbor is cylindrical, and fits to a bore provided in the top of the frame of the head, which is split and has two binding screws. When these screws are loosened the arm may be readily adjusted for position, while when they are screwed up they lock the arm in its adjusted position. By this means the arm only projects out as far as the particular work in hand requires.
The knee for carrying the work table and chucking devices terminates at its top in a circular box cast open on top. This box is covered with a circular cap, in the upper face of which are the slideways or guides for the work table. The cap is recessed into the box so as to be kept central, and is fastened therein by an expanding ring operated by a single stud which projects through the walls of the box. This ring has a V-shaped groove on its periphery, which in expanding closes over corresponding bevelled ledges on the inside of both the cap and the box. The edge of the cap is graduated for cutting spirals.
By this arrangement the table can be set to move at any required angle with the live spindle and quickly clamped in position, while the ring being of larger diameter and bearing evenly around the entire circle, the cap is rigidly held. In this box, securely protected from the cuttings or dirt, is a large worm-gear secured to a short vertical shaft, on the upper end of which is a pinion projecting through the cap and engaging with a rack upon the underneath side or face of the work table. This shaft also carries a bevel-pinion which meshes with a pinion on the end of the short shaft seen projecting through the front of the box and provided with a hand crank, the hand lever shown behind this crank being for securing or releasing the cap to or from the box. The gearing is so arranged that one revolution of the hand crank traverses the work table a distance of 2 inches, thus providing for the rapid motion of the table to expedite putting in and taking out the work.
The knee is operated vertically by a pair of bevel-gears, the shaft for operating which is shown on the left-hand side of the knee. On this shaft is a pointer for an indexed dial, which has two graduated circles, the outer of which is divided so that each division corresponds to a knee motion of 1⁄32 of an inch, while the inner one denotes a knee motion of 1⁄1000 inch.
Automatic feed motion for the work table is provided as follows: The cone shaft projects through the live head and carries a leather-covered friction disk which drives a vertical shaft carried by a bracket hinged to the head. A small pulley splined on this shaft, and held at any point by a spring-pressed catch, bears against the leather-covered face of the disk, and it is obvious that the nearer to the centre of the disk the pulley is set the slower the latter will be revolved, and therefore the finer the feed will be, while the direction of revolution of the small pulley will be reversed if it be set on the upper half or above the centre of the disk, thus providing for reversing the direction of feed. By this arrangement both the rate and direction of the feed can be set without stopping the machine.
This vertical feed shaft carries a splined worm driving a worm-gear splined on a horizontal shaft which is carried by the knee, which has a projecting arm or bracket for carrying the back end of the shaft, so that the latter rises or falls with the knee. A worm on this horizontal shaft engages a large worm-wheel within the box and fast upon the short upright shaft, whose pinion engages the table rack and thus completes the feed motion.
It will be seen in the sectional view that the worm-wheel for the automatic feed is in one piece, with a smaller bevel-wheel engaging with a bevel-pinion for the hand feed.
A clutch joint near the centre of the horizontal shaft affords the means for putting the automatic feed either into or out of action.
The table can be fed its full length in either direction, and when placed so that one end will pass the main frame or column[II-14] may be swung around parallel to the spindle, thus enabling the machine to be used as a boring mill for short holes, or by turning the table a half revolution work may be done on both sides of a piece at one chucking, thus insuring perfect parallelism.
The construction of the index head of this machine is as follows: Fig. 1902 represents it on a plate with a back centre and a centre rest, and Fig. 1903 represents the head elevated. The head is a hollow box, the outline of which is about two-thirds of a circle. The opening, in front or chord side, is surrounded by a flange, and bored out as large as permissible. This forms the front bearing of the spindle and face plate, which is cast in one piece. A rear and smaller bearing is provided on the circular part of the case. The end of the spindle projects through the case, and is held from coming out by a recessed nut and washer. The spindle also carries an accurately-divided steel gear of sixty teeth. This gear is made as large as will go through the opening in front, or about 6 inches in diameter. Directly under this gear the box is pierced from the side. In this opening is inserted a long bush, through which a steel worm engages with the gear. An index plate secured to the outer end of the bush, and an adjustable arm and index pin attached to the projecting end of the worm, complete the dividing mechanism. Substantial but delicate adjustments are provided for eliminating lost motion.
On the periphery of the case is turned a dovetail shoulder, which slides around in a corresponding groove in the quadrant-shaped base. The case is graduated on its edge, and may be clamped at any angle of elevation from 15 degrees below a horizontal line to a vertical position, being equally stable in all positions. The face plate is no farther from the bed in one position than another, and being seated to the case, and adapted to hold work directly on its face, forms a stiff and substantial device for cutting bevel-gears and other work requiring angular motion. The tail centre is also of a strong and substantial design.
An adjustable centre rest of novel design also accompanies the outfit, and an extra bed or table, with straps for securing it to the table of the machine. With the centres arranged on this bed the line of centres may be set at any angle with the sliding table, A sufficient number of index plates are provided to divide all numbers up to 100 and all even numbers to 200.
Fig. 1904 represents a machine in which the base column and the head are constructed upon the same design as that in Fig. 1900, but the circular top and cap are replaced with a larger and heavier knee of rectangular form, and the table is longer. A cross sectional view of the head is shown in Fig. 1905. The bearings for the live spindle are solid bushes slightly tapered, and are driven into the head from each end up to and against the flanges.
The spindle is of tool steel 31⁄2 inches in diameter at the front bearing, tapering uniformly 3⁄4 inch per foot to the back end. This simple construction allows the spindle to be perfectly ground, and accurately fitted to the boxes by scraping. After this is done the spindle is withdrawn about the 1⁄100 part of an inch, and a flat babbitt metal washer fitted to exactly the space between the shoulder on the spindle and the front box. A check nut and sliding collar on the back end holds the spindle in place. A perfectly uniform space for oil is thus formed between the spindle and bearings. The worm-gear is forced tightly on the taper spindle with a nut, and keyed to prevent turning.
The spindle has a hole 19⁄16 inches through its centre, tapering in front to receive the arbor to 17⁄8 inches. The taper is made 1⁄2 inch per foot, and for ordinary work is sufficient to prevent the arbor turning, but for driving gangs or large mills an arbor is used having a hexagon enlargement just outside the spindle. A cap to screw over the end of the spindle, having a hexagon opening in it to fit the arbor, completes a positive driver that has none of the objections to cutting a mortise or keyway in the spindle or otherwise disfiguring it. This cap protects the thread on the spindle, and may be readily removed for a face plate or large facing mills.
The cone shaft and its bearings are made independent of the head. A long sleeve, which is provided with a large flange, projects through cored openings in the side of the head. The bosses around these openings are faced off square and parallel, and a[II-15] large flat ring threaded on the end of the sleeve draws the flange against the opposite face. The large end of the sleeve is counterbored to receive the worm, and is cut away on the under side to allow the worm to drop into mesh with the gear. The worm is feathered on the shaft, the thrust of the worm being taken in one direction against the shoulder in the sleeve, and in the opposite[II-16] direction (the machine can be driven either right or left-handed) against the end of a bush, which is screwed in the sleeve and forms one bearing for the cone shaft. Friction washers are placed to form the step, and all wear or lost motion can be removed by screwing in the bearing, which, when adjusted, is prevented from turning by a small set-screw. The cone-shaft bearings are babbitt lined, but the spindle bearings are made of cast iron, in which steel scrap has been melted. The worm-gear has 40 teeth, and the worm is triple threaded, thus making a back gear equivalent to 40⁄3, or 131⁄3 to 1. As the sleeve does not fit the openings in the head, the worm and gear may be readily adjusted to each other at all times, and held firmly and squarely in place by drawing the flange tight against the side of the head. Set-screws through the head prevent accidental displacement of the sleeve after being adjusted.
Fig. 1906 represents a double spindle milling machine. The second spindle is for driving the finishing cutters, so that as the two spindles are capable of independent adjustment, the work may be finished at one feed traverse, thus avoiding the necessity of removing the work or making special adjustments.
| VOL. II. | EXAMPLES OF MILLING MACHINES. | PLATE III. |
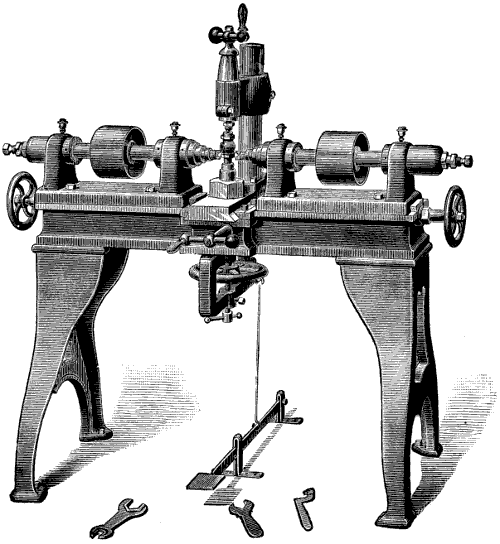 |
||
| Fig. 1907. | ||
 |
||
| Fig. 1908. | ||
Fig. 1907 represents a milling machine for globe valves and other similar work. Here there are two cutter-driving spindles, one on each end of the bed, and the work is held vertically. It is provided with an index wheel for milling squares, hexagons, or octagons, and the pen for the index wheel is operated by treadle. The work is fed across the bed, the chucking devices being carried on a slide rest. In the figure a globe valve is shown chucked between two plugs or arbors fitting its bore, but it is obvious that centres or other work-holding appliances may be used to suit the kind of work.
Fig. 1908 represents an eighty-inch milling machine, the table of which has longitudinal motion; and provision for vertical and crosswise movements are made in the head which carries the driving mechanism.
The machine table sets low on a bed supported by four box legs, and is actuated by a steel screw driven by a worm and worm-gear connected with a pair of spur-gears. The gearing is outside the bed, and therefore accessible, and is protected by a shield, as shown in cut. The arrangement for belting to feed works is also shown too plainly to need description. The head upon which the spindle carrier is mounted travels in ways upon the bed, and is adjusted crosswise on it by means of a screw connected with a hand wheel, partially shown at the left of engraving. For convenience and ease in fine adjustment this wheel, and also the wheel at top of machine, connected with the elevating screw, are worked by a hand lever, the wheels having sockets in their periphery for this purpose.
The carrier, upon which is mounted the driving spindle, is gibbed to the head, and has a vertical range sufficient to allow work 18 inches high to pass under centres. From this carrier projects a large arm for outside centre support of mill spindle, intended for use on work where a back stand is not admissible. There is, however, as may be seen, a back stand or tailstock of a very solid character. The arm is readily removable, when desired, or the tailstock can be slid off its seat if required. In most cases, however, the arm need not be removed, the yoke on it being swung up out of the way, leaving the centre of mill arbor free to engage with that on the back stand. This combination provides for operating on a wide range of work.
As shown in the engraving, the space between head and tailstock is about 24 inches, but if required the tailstock can be made to travel in line with the head, and its support be extended to any distance desired.
The method of driving the spindle is simple and strong, and allows of free adjustment of the spindle without disarrangement of the driving and feed belts.
The cone, which is made for 31⁄2 inch belt, is mounted in a stirrup which is pivoted to the bed, and the pinion which engages with the driving gear on the spindle is held at correct distance by a connecting yoke, and is driven by a feather.
The machine has longitudinal feed only, but where it is desired an automatic feed motion can be applied to the elevating screw in the head, giving feed in a vertical direction.
The table is arranged to be run back rapidly by power, by a device which is not seen in the engraving. As the table weighs one ton, the relief to the operator by this improvement is obvious.
All the operations of the machine are intended to be conducted from the front side, without any change in the position of the operator. The feed can be thrown out by hand at any moment by means of a rod which connects with the latch shown in the front of the cut, and the power quick-return applied; or the table can be run back by hand, and the feed thrown in by a foot lever, which lifts the drop box shown in front of cut. Adjustable dogs automatically drop the feed motion at any point.
The machine is massive in all its parts, and is intended for heavy milling of any description, but more particularly for shafting, railroad, or engineering shops, being specially adapted for key-seating long and heavy shafting, finishing guide bars, connecting rods, &c.
Its weight is 7,500 pounds. The work table is 7 feet long by 20 inches wide; length of longitudinal feed, 84 inches; distance between uprights, 24 inches. The cast-steel spindle is 4 inches in diameter, and the mill arbor 21⁄2 inches diameter. Arm for outer centre support 5 inches diameter at its smallest part.
Milling Cutters or Mills.—The simplest form of milling cutter is that shown in Fig. 1909, the teeth being equidistantly arranged upon the circumference only. Its size is usually designated by its length, which is termed the face. Thus a cutter[II-17] having its teeth parallel to its axis and an inch long would be said to have 1 inch face. Cutters of more than about half an inch face usually, however, have their teeth cut spirally, as in Fig. 1910; the degree of spiral is one turn in a length of 3 feet for cutters between 21⁄4 and 4 inches in diameter. For cutters of less than 21⁄4 the degree in the spiral is increased; thus for an inch cutter, the degree is one turn in 15 inches, while for 6 inches one turn in about 60 inches is used.
In the following table is given the sizes of cutters as made by one company, the bores being 1 inch.
| Width of face. |
Diameter of cutter. | Width of face. |
Diameter of cutter. | ||||||||
| inch. | inch. | inch. | inch. | inch. | inch. | inch. | inch. | ||||
| 1⁄8 | 2 | 1⁄2 | 3 | 4 | 15⁄16 | 2 | 1⁄2 | 3 | 4 | ||
| 3⁄16 | 2 | 1⁄2 | 3 | 4 | 1 | 2 | 1⁄2 | 3 | 4 | ||
| 1⁄4 | 2 | 1⁄2 | 3 | 4 | 1 | 1⁄8 | 2 | 1⁄2 | 3 | 4 | |
| 5⁄16 | 2 | 1⁄2 | 3 | 4 | 1 | 1⁄4 | 2 | 1⁄2 | 3 | 4 | |
| 3⁄8 | 2 | 1⁄2 | 3 | 4 | 1 | 1⁄2 | 2 | 1⁄2 | 3 | 4 | |
| 7⁄16 | 2 | 1⁄2 | 3 | 4 | 1 | 3⁄4 | 2 | 1⁄2 | 3 | 4 | |
| 1⁄2 | 2 | 1⁄2 | 3 | 4 | 2 | 2 | 1⁄2 | 3 | 4 | ||
| 9⁄16 | 2 | 1⁄2 | 3 | 4 | 2 | 1⁄4 | 2 | 1⁄2 | 3 | 4 | |
| 5⁄8 | 2 | 1⁄2 | 3 | 4 | 2 | 1⁄2 | 2 | 1⁄2 | 3 | 4 | |
| 11⁄16 | 2 | 1⁄2 | 3 | 4 | 3 | 2 | 1⁄2 | 3 | 4 | ||
| 3⁄4 | 2 | 1⁄2 | 3 | 4 | 3 | 1⁄2 | 2 | 1⁄2 | 3 | 4 | |
| 13⁄16 | 2 | 1⁄2 | 3 | 4 | 4 | 2 | 1⁄2 | 3 | 4 | ||
| 7⁄8 | 2 | 1⁄2 | 3 | 4 | |||||||
The keyways are semicircular, the key being composed of a piece of No. 25 Stubbs steel wire.
The following is a table of the sizes of milling cutters made by another company.
| Width of face. |
Diameter of cutter. |
Size of hole. |
Width of face. |
Diameter of cutter. |
Size of hole. |
||||
| inch. | inch. | inch. | inch. | inch. | inch. | ||||
| 1⁄8 | 2 | 1⁄4 | 1 | 3⁄4 | 2 | 7⁄8 | 1 | ||
| 3⁄16 | 2 | 1⁄4 | 1 | 7⁄8 | 2 | 7⁄8 | 1 | ||
| 1⁄4 | 2 | 1⁄2 | 1 | 1 | 2 | 1⁄2 | 1 | ||
| 5⁄16 | 2 | 1⁄2 | 1 | 1 | 1⁄4 | 2 | 1⁄2 | 1 | |
| 3⁄8 | 2 | 5⁄8 | 1 | 1 | 1⁄2 | 2 | 1⁄2 | 1 | |
| 7⁄16 | 2 | 5⁄8 | 1 | 1 | 3⁄4 | 2 | 1⁄2 | 1 | |
| 1⁄2 | 2 | 3⁄4 | 1 | 2 | 2 | 1⁄2 | 1 | ||
| 9⁄16 | 2 | 3⁄4 | 1 | 2 | 1⁄2 | 2 | 1⁄2 | 1 | |
| 5⁄8 | 2 | 3⁄4 | 1 | 3 | 2 | 1⁄2 | 1 | ||
| 11⁄16 | 2 | 7⁄8 | 1 | ||||||
Cutters of 1 inch face and over have teeth of a spiral form.
The object of providing spiral teeth is to maintain a uniformity of cutting duty at each instant of time.
Suppose, for example, that the teeth are parallel to the cutter axis, when the cutter first meets the work the tooth will take its cut along its full length at the same instant, causing in wide cuts a jump to the work because of the spring of the various parts of the work-holding devices, and of the cutter driving spindle; furthermore as the cutter revolves the number of teeth in action upon the work varies. Thus in Fig. 1912 it is seen that one tooth only is in action, but when the cutter has revolved a little more there will be two teeth in action, as shown in Fig. 1913. This variation causes a corresponding variation of spring or give to the machine, producing a surface very slightly marked by undulations. But if the teeth are cut spiral the cut begins at one end of the tooth and proceeds gradually along it, thus avoiding violent shock, and after the cut is fairly started across the work the length of cutting edge in action is maintained uniform, producing smoother work, especially in the case of wide surfaces and deep cuts.
When the cutter is required to cut on the sides of the work as well as on its upper face it is termed a face cutter, and its side faces are provided with teeth, as shown in Fig. 1914; and when these cutters are arranged in pairs as in Fig. 1915, so as to cut in the side faces only of the work d, they are termed twin or straddle mills, both being of the same diameter.
In mills or cutters used in this way the cutting duty is excessive[II-18] on the outer corners of the teeth, which, therefore, rapidly dull; hence it is usual to provide teeth on both sides of the cutter, as in Fig. 1916, so that after having been used in the position shown in the engraving until the teeth are dull the positions of cutters may be changed, bringing the unused cutting edges into use.
Twin or heading cutters are right and left hand, a right-hand one being that in which the teeth at the top of the wheel revolves towards the right, while a left-hand one revolves (at the top) towards the left.
If the machine is belted so that it can be revolved in either direction, both sides of the cutter may be utilised by taking the cutters off the arbor, turning them around and then replacing them in their original positions on the same. Thus in Fig. 1917 we have at a a left-hand cutter that if reversed upon its arbor would be a right-hand one as at b, and it is obvious that the direction of revolution must be in each case as denoted by the arrows f g, which are in opposite directions. In this case the direction of work feed must be reversed, the work for a feeding in the direction of c, and that for b in the direction of d. It is to be observed, however, that the cutter could not be reversed if it was driven by an arbor that screwed upon the driving spindle of the milling machine. For if the machine has a right-hand thread then the cutter must revolve in the direction of g, and the work feed must be in that of c; whereas if the machine spindle drives its chucks, arbors, &c., by a left-hand thread, then the direction of cutter revolution must be as at f, and that of work feed as at d. But if the cutters are upon an arbor that is driven by a conical seat in the machine spindle, or by any other means enabling the arbor to revolve in either direction without becoming released from that spindle, then the cutter may be simply turned around and the feed direction reversed, as already explained. The reason for reversing the direction of feed when the direction of cutter revolution is reversed is as follows:—
In Fig. 1918 a and b represent two pieces of work of which b is to be fed in the direction of arrow c, so that the pressure of the cut tends to force the work back from under the cutter, whereas in the case of the work a, feeding in the direction of d, the teeth act to pull the work beneath the cutter, which causes tooth breakage.
Suppose, for example, that in Fig. 1919 p is a piece of work fastened to the table t, feeding in the direction of a, the cutter w revolving in the direction of arrow b, n representing the feed nut operated by the feed screw s. Now while the table is being pulled in the direction of a, the sides c of the feed screw thread will bear against the sides of the thread in the nut, and whatever amount of looseness there may be between the threads of the screw and nut will in this case be on the sides d of the threads. So soon, therefore, as the wheel meets the work p, it will suddenly pull the work forward to the amount of the play or looseness on the sides d of the threads, and this in addition to the feed given by the rotating screw s, would cause the wheel to lock upon the work surface.
[II-19]In all milling operations, therefore, the work is fed against the cutter as at b, in Fig. 1918, unless, in the case of twin mills, it is fed (as at e and f in the same figure) in the middle of the cutters, in which case it is preferable to present it as at f, so that the pressure of the cut will tend to hold the work down to the table, and the table down upon its guideways. This position of the work presents some advantages for small work which will be explained hereafter.
Fig. 1920 represents angular cutters, the teeth being at an angle to the cutter axis. These cutters are made right and left as at a and b in Fig. 1921, the teeth of a being cut in the opposite direction to those at b, so as to be able to cut equal angles on the work when these angles lie in opposite directions, as c and d in the figure. Furthermore these cutters are sometimes screwed to their arbors, and can therefore be revolved in one direction only, which prevents their being turned around end for end, even though the machine be so belted as to be capable of revolving its spindle in either direction.
The angular cutters shown in Fig. 1921 have their teeth arranged for a Brainard milling machine, in which the live spindle has a right-hand thread for driving the chucks, arbors, &c.; hence the direction of cutter revolution, and the arrangement of the teeth are as in the figure.
In Fig. 1922 are segments of two wheels, a and b (corresponding to a and b in Fig. 1921), but with their teeth arranged for a Brown and Sharpe milling machine, in which the machine spindle has a left-hand thread; hence the direction of cutter revolution is reversed, as denoted by the arrows in the two figures.
Fig. 1923 represents a round edge cutter; and it is obvious that the curvature or roundness of the cutting edges may be made to suit the nature of the work, whether the same be of regular or irregular form. In cutters of this description it would be a difficult matter to resharpen the teeth by grinding their backs, hence they are ground on the front faces; and to maintain the form or profile of the cutting edges, notwithstanding the grinding, we have a patent form of cutter, an example of which is shown in the gear tooth cutter in Fig. 1924. The backs of the teeth are of the same form throughout their entire length, so that grinding away the front face to sharpen the cutting edge does not alter the contour or shape of the cutting edge. This is of especial advantage in cutters for gear teeth, and those for irregular forms, Figs. 1925, 1926, and 1927 forming prominent examples.
End mills or shank cutters are formed as in Fig. 1928, the shank sometimes being made parallel with a flat place at a, to receive the set-screw pressure, and at others taper, the degree of taper being 1⁄2 inch per foot. The hole at the end facilitates both[II-20] the cutting of the tooth in the making and also the grinding. Shank cutters may be used to cut their way into the work, with the teeth on the end face, and then carry it along, bringing the circumferential teeth into operation; or the end teeth may be used to carry the cut after the manner of a face cutter.
Shank cutters are rarely made above an inch in diameter, and are largely used for cutting grooves or recesses, and sometimes to dress out slots or grooves that have been cast in the work, as in the case of the steam and exhaust ports of steam engine cylinders. In work of this kind the direction of the feed is of great importance and must be varied according to the depth of cut taken on the respective sides of the cutter. Suppose, for example, that the conditions are such as illustrated in Fig. 1929, the cut being deepest on the side a of the slot, and the cutter must be entered at the end of the slot and fed in the direction of d, so that the pressure of the cut may tend to push the cutter back, it being obvious that on the side b the cutter has a tendency to walk or move forward too rapidly to its cut, and if the cut was heaviest on that side it would do, this increasing the cut rapidly and causing tooth breakage.
This tendency, however, is resisted by the pressure on the side a of the slot, which acts, as already stated, to push the cutter back. In starting the cutter therefore, it is necessary to do so at that end of the slot that will cause the deepest cut to act in the direction to retard the feed. Suppose, for example, that the heaviest or deepest cut, instead of being on the side a of the slot, as in Fig. 1929, was on the side b, and in that case it would be necessary to start the cut from the other end of the slot as in Fig. 1930, the arrow c denoting the direction of feed.
[31] Figs. 1928, 1931, 1932, 1933, are from an article by John J. Grant, in The American Machinist.
Similarly when a groove has been roughed out from the solid, and it is determined to take a finishing cut, the direction of the feed for the latter is of importance. Suppose, for example, a T-groove is to be cut, and that a slot is first cut with a shank cutter as in Fig. 1931, leaving a light finishing cut of, say, 3⁄64 inch to finish the neck to the dotted lines a b, and entering to within 1⁄16 inch of the full depth as denoted by line c. The enlarged part of the groove may then be cut out, leaving about 3⁄64 inch at the top and bottom, d and e, the cutter having a plain shank (as in Fig. 1933), whose diameter should just clear the narrow part of the groove already roughed out. The work will then be ready for the finishing cutter, formed as in Fig. 1932, whose teeth (on both the shank and the enlarged end) should have a diameter of 3⁄32 less than that of the finished slot. In taking the finishing cut this cutter must be set first to cut the sides b e to finished size, the direction of the feed being such that the pressure of the cut acts to push the cutter back as already explained, and when the cut is finished on this side the finishing cut may be put on the side a d, without traversing the cutter back, or in other words the feed must be carried in the opposite direction, so that the cutter will run under the cut and be pushed back by it, so as to prevent it from running forward as explained with reference to figure.
For ordinary work not requiring great truth, however, the first cutter, Fig. 1931, may be made of the finished diameter, and be followed by a cutter such as in Fig. 1933, also of the finished diameter.
[32] Figs. 1934, 1935, 1936, are from articles by John J. Grant, in The American Machinist.
When a shank-cutter is required to enter solid metal endways, as in the case of cutting grooves around the circumferential surface of a cylinder, it is necessary to drill a hole to admit the cutter, leaving a light finishing cut for the diameter of the cutter, and sufficient in the depth to let the end face of the cutter remove or square up the cone seat left by the drill. Shank cutters may[II-21] obviously be made taper, or to any other required angle or curvature, Figs. 1934 and 1935 being examples which can be used in situations where other cutters could not, as for example on the arms or spokes of wheels.
Fig. 1936, from The American Machinist, represents an example of the employment of shank cutters, the work being a handle for a lathe cross-feed screw, and it is obvious that the double cornering cutter may be used upon both edges, and the cut being carried around the hub by the parallel part of the cutter; the whole of the work on the handle including the boring, if the hole is cast in, may be done by the shank cutter, the handle end being finished and the boring done first, the hub being finished on an arbor.
Shank mills may obviously be made of various shapes; thus in Fig. 1937 is shown two applications of an end or shank mill, one for cutting a dovetailed groove and the other an angular one. In the case of the dovetail groove the cutter will work equally well, whether it be used on straight or spiral grooves; but this is not the case with angular grooves for reasons which are explained with reference to angular cutters and spiral groove cutting.
Shank cutters are provided with finer teeth than ordinary cutters, the following being the numbers of teeth commonly employed for the respective diameters:—
| Diameter | of cutter | 1⁄8 or 3⁄16 | inch, | number | of teeth | 6 |
| „ | „ | 1⁄4 | „ | „ | „ | 7 |
| „ | „ | 3⁄8 | „ | „ | „ | 8 |
| „ | „ | 1⁄2 | „ | „ | „ | 8 |
| „ | „ | 5⁄8 | „ | „ | „ | 10 |
| „ | „ | 3⁄4 | „ | „ | „ | 10 |
| „ | „ | 7⁄8 | „ | „ | „ | 12 |
| „ | „ | 1 | „ | „ | „ | 14 |
The front faces of the teeth are radial as in other cutters, the angle of the back of the tooth being 40° for the smaller, 50° for the medium, and 60° for an inch cutter.
Fly cutters are single-toothed cutters, or rather tools, that are largely used by watchmakers for cutting their fine pitches of gear wheels.
Fig. 1938 represents a fly cutter in place in its holder or arbor, its front face d being in line with the axis c of the arbor.
Let it be required to make a fly cutter for a very fine pitch of gear tooth, such as used for watches, and a template, shown greatly magnified at t in Fig. 1939, is made to fill a space and one half of each of the neighboring teeth. From this template a cutting tool is made, being carefully brought to shape with an oil-stone slip and a magnifying glass. This tool is used for the production of fly cutters, and may be employed by either of the following methods:—
The piece of steel to form the cutter is fastened in an arbor back from the centre, as at d in Fig. 1940, and is then cut to shape by the tool before referred to. It is then set for use in the milling machine, or in such other machine as it may be used in, in the position shown in Fig. 1938, its front face d being in line with the axis c of the arbor. The change of position has the effect of giving the tool clearance, thus enabling it to cut while being of the same shape throughout its whole thickness; face d may be ground to resharpen the cutter without altering the shape it will produce. It is this capacity to preserve its shape that makes the fly cutter so useful as a milling machine tool, since it obviates the necessity of making the more expensive[II-22] milling cutters, which, unless made on the principle of the Brown and Sharpe cutters, do not preserve their shapes.
It is to be observed, however, that a fly cutter made as above does not produce work to exactly correspond to the template it was made from, because moving it from the position it was made in (Fig. 1938) to the position it is used in (Fig. 1940) causes it to cut slightly shallower, but does not affect its width.
Another method of cutting up a fly cutter by the tool made to the template is shown in Fig. 1941. The blank cutter is placed at an angle to an arbor axis, and is cut to shape by the tool. For use it is placed in line with the arbor axis as in Fig. 1942, the change of position here again giving clearance as shown by the dotted arcs, the inside ones showing the arc the cutter revolved on when it was in the arbor in Fig. 1938. Here again, however, the change of position causes the fly cutter to produce a shape slightly different from the template to which the first tool was made, hence the best method is as follows:—
The blank is let into an arbor of small diameter, as in Fig. 1943, its face d being in line with the arbor axis. It is then cut up with the tool made from the template. For use it is set in a larger arbor, as in Fig. 1944, the difference in its path of revolution giving it the necessary clearance. Thus, in the figure the inner dotted arcs show the path of revolution of the cutter when it was in the small arbor, and the outer arc of the path in the large arbor. The front face can be ground without altering the shapes; the cutter will produce this front face, being kept in line with the arbor axis by grinding the body of the steel as much as the front face is ground when it is resharpened. Curves or irregular shapes may be readily produced and preserved by fly cutters.
It is obvious, however, that when the tool made to the original template is worn out, another must be made, and to avoid this trouble and preserve the original shape beyond possible error, we have recourse to the following additional method:—
With the tool made from the template we may cut up a wheel, such as in Fig. 1945, and this wheel we may use as a turning tool to cut up fly cutters, the principle of the wheel cutter having been shown in connection with lathe tools. It may here be pointed out, however, that if a wheel or circular cutter, as it is termed, is to be used, we may make the template, and the master tool we make from it, for one side of a tooth only, and use the master tool to cut up one side only of the corner of the circular cutter, as shown in Fig. 1945.
The method of using the circular cutter is illustrated in Fig. 1946, in which h is a holder, whose end face p is level with the axis of the cutter, which is held to the holder by a screw. The side face of the holder is out of the vertical so as to give the cutter side clearance. A second holder has its side face inclined in the opposite direction, thus enabling the one edge of the circular cutter to be used as a right or as a left-hand tool and insuring uniformity, because the same edge of the circular cutter[II-23] is used in both cases, so that if used for say a tool for a gear tooth, both sides of the tool will be cut from the same side of the circular cutter.
It is obvious that instead of having one continuous cutter, the necessary breadth of cutter face may be obtained by means of two or more cutters placed side by side. Thus to mill a piece of work two inches wide we may use two cutters of an inch face each (both of course being of equal diameter), or we may use one cutter, of 11⁄4 inch and another of 3⁄4 inch face. It is preferable, however, to use two cutters of an inch face each, and to set one beam left-hand and the other right-hand spiral teeth, because spiral teeth have considerable tendency to draw the machine spindle endways in its bearings, because the teeth correspond to a certain extent to a screw, and the work to a nut. A cutter with a left-hand spiral exerts end pressure tending to draw the driving spindle out from its bearings, while a right-hand one tends to push it within them; hence by making the two cutters of equal length and of the same degree of spiral, the effect of one cutter offsets that of the other. Furthermore, it is found that the tendency to chatter which increases with an increase in the width of the work, is diminished by using right and left spiral cutters side by side.
In order that the cutting edges of cutters placed side by side in this way may be practically continuous so as not to leave a line on the finished work, the teeth may be made to overlap in two ways as in Fig. 1948, both representing magnified portions of cutters. In the method shown on the left of the figure the usefulness of either cutter to be used singly is not impaired, all that is necessary to insure the overlapping being to cut the keyways in different positions with relation to the teeth; whereas on the left of the figure neither cutter would be efficient if used singly, except upon work as narrow as the narrowest part of the cutter. On the other hand, however, it affords excellent facilities for grinding, since the two cutters may be ground together, thus ensuring that they be of equal diameters except in so far as may be influenced by the wear of the emery wheel, which is, however, almost inappreciable even in cutters of considerable width of face. In the method shown on the left there is the further advantage that as the teeth are not in line the cutting action is more continuous and less intermittent, the arrangement having in a modified degree the same advantage as the spiral cutter.
In both methods some latitude is given to adjust the total width of face by placing paper washers between the cutters. If the plan on the right is employed the projections may occupy one-fourth of the circumference, there being two projections and two depressions on one end of the cutter. When cutters of different diameters and shapes are put together side by side on the same arbor the operation is termed gang milling.
Thus, in Fig. 1949 is shown a sectional view of a gang of three mills or cutters, a, b, and c, of which a and c are recessed to admit of the ends of b passing within them. The heavy black line representing a paper washer inserted to adjust the distance apart of a and c, it being obvious that this gives a means of letting them together after their side teeth at d and e have been ground. As shown in the figure, a has teeth on one only of its sides, while c has them on both sides as well as in its circumference, while all three are of different widths of face. This would capacitate a only for the inside cutter, as in the figure, while b would be serviceable only when there was a cutter on each side of it; or if used singly, only when its face overlapped the width of the work on each side. But c, being cut on each side, could be used singly for grooving or recessing, or for plain milling, or in the position of b or a in the figure; hence it is preferable in gang milling for general purposes to provide teeth on both sides as well as on the circumference of the mill or cutter. But if a gang of mills are to be made for some special purpose, and used for no other, the teeth may be provided on the sides or not, as the circumstances may require.
Suppose, for example, that steps, such as shown in Fig. 1950, were required to be cut in a piece of brass work, and that, the work requiring to be very true, a set of roughing and one of finishing cutters be used, then the latter may be put together as in Fig. 1951, there being eight separate cutters, and their ends being slightly recessed but without teeth. Such cutters would wear a long time and may be readily sharpened, and there being no side teeth, the widths of the cutters, individually and collectively, would not be altered by the grinding; hence no readjustment with washers would be necessary. The tooth corners must, however, be kept sharp, for in proportion as they get dull or blunt, the sides of the cutter wedge in the work, causing friction and extra power to drive them as well as producing inferior work.[II-24]
Fig. 1952, which is from an article by John J. Grant, represents a gang of cutters arranged to mill out the jaws and the top faces of a head for a lathe; and it is obvious that a number of such heads may be set in line and all milled exactly alike.
The Number of Teeth in Mills or Cutters.—The teeth of cutters must obviously be spaced wide enough apart to admit of the emery wheel grinding one tooth without touching the next one, and the front faces of the teeth are always made in the plane of a line radiating from the axis of the cutter.
In cutters up to 3 inches in diameter, it is good practice to provide 8 teeth per inch of diameter, while in cutters above that diameter the spacing may be coarser, as follows:—
| Diameter | of cutter | 6 | inches, | number of | teeth in cutter | 40 |
| „ | „ | 7 | „ | „ | „ | 45 |
| „ | „ | 8 | „ | „ | „ | 50 |
Milling Cutters with Inserted Teeth.—When it is required to use milling cutters of a greater diameter than about 8 inches, it is preferable to insert the teeth in a disk or head, so as to avoid the expense of making solid cutters and the difficulty of hardening them, not merely because of the risk of breakage in hardening them, but also on account of the difficulty in obtaining the uniform degree of hardness or temper. The requirements for the heads for inserted teeth are, that the teeth shall be locked firmly in position without lost motion, and be easily set to gauge, ease of insertion and of removal being of secondary consideration, as such teeth should be ground in their places in the head, and are therefore rarely removed. The manner in which these requirements are attained in the Brainard heads are, as shown in Fig. 1953. A disk of wrought iron of suitable thickness and diameter is turned and squared, then a circle of index holes corresponding to the number of teeth required is drilled in its face; this circle of holes is used to insure the accurate spacing of the dovetail seats for the teeth, and to attain accuracy in grinding the teeth. All the teeth are a driving fit, and being milled are, of course, interchangeable. In order to obtain a larger number of teeth in a given size of head than could be got into the face, only one-half of the teeth are dovetailed into the periphery of the head and the other half into its face, but yet all the teeth are effective for face cutting, the construction being as follows:—
Between each pair of face teeth is a slit sleeve, which meets them and has a taper base, through which passes a taper bolt having a nut on the back face of the head. Tightening this nut expands the sleeve, thus locking the pair of teeth in their dovetail grooves. The circumferential teeth are each counter-based to receive a screw tapped in the head, and are firmly locked thereby. This affords a simple and reliable means of inserting and adjusting other teeth with the certainty that they will be true with those already in use.
The large size of some of these heads makes it convenient and desirable to grind them in their places on the machine, and for this purpose a special grinder is made by the same company. This grinder sets upon the machine table and has a point or pin for the index holes or the cutter head; by this means the grinding may be made as accurate as in small milling cutters.
The head shown in figure represents one that has been in use ten years, its cutters having been renewed but once; it is 28 inches in diameter, contains 84 teeth, and weighs 400 lbs.
Arbors for milling cutters may be driven in two ways. In the first the shank is made taper to fit the taper bore of the live spindle. The standard taper is 1⁄2 inch per foot of length. The keyway is semicircular, as shown at g in Fig. 1954, the key consisting of a piece of No. 25 Stubbs steel wire, which being of uniform diameter enables a number of keys of different lengths to be easily obtained or made, and the nut is usually cylindrical, having two flat sides, a.
Fig. 1955 (from The American Machinist) represents an arbor, having a cone at a, so that the cutter bore being coned to correspond, the cutter will run true, notwithstanding that it may not fit the stem b. It is obvious, however, that the nut and washer must be made quite true or the cutter will be thrown out of line with the[II-25] arbor axis and therefore out of true, and also that such an arbor is not suitable for cutters of a less width of face than the length of the cone a.
Shank cutters that have parallel shanks as in Fig. 1928 should have their sockets eased away on the upper half of the bore as denoted by the dotted arc d in Fig. 1956, which will enable the cutter shanks to be made the full size of the socket bore proper, and thus run true while enabling their easy insertion and extraction from the socket. Or the same thing may be accomplished by leaving the socket bore a true circle fitting the cutter shanks in tight, and then easing away that half of the circumference that is above the centre line c in the figure. It is preferable, however, to ease away the bore of the socket, which entails less work than easing away the shanks of all the cutters that fit to the one socket. When the cutter is held in a socket of this kind it allows it to be set further in or out, to suit the convenience of the work in hand, which cannot be done when the cutter has a taper shank fitting into the coned bore of the machine spindles.
It is obvious that when the cutter requires to pass within the work, or cut its way, as in the case of milling out grooves, a nut cannot be used; hence, inch cutters are driven by a key as usual, but secured by a screw, as in Fig. 1957, which is from the pen of John J. Grant, in The American Machinist.
In many cases it becomes a question whether it is better to do a piece of work with plain mills, with an end mill, or with face mills, a common hexagon nut forming an example. Thus, in Fig. 1958, we have a nut being operated upon by a plain mill; in Fig. 1959 by an end mill, and in Fig. 1960 by a pair of twin face mills.
In the case of the plain mill, it is obvious that only one side of the nut is operated upon at a time, and as the whole of the pressure of the cut falls on one side of the work it acts to spring or bend the mandrel or arbor used to hold the nut, and this spring is sufficient, if several nuts are milled at once on the same arbor, to make the arbor bend and cause the nuts in the middle to be thicker than those at the ends of the arbor. In the case of hand-forged nuts in which there may be more metal to take off some nuts or some sides of nuts than off others, the extra spring due to an increased depth of cut will make a sensible difference to the size the work is milled to. In the case of the end mill the pressure of the cut falls in line with the arbor axis and downwards; hence the arbor spring is less and does not affect the depth of the cut.
In the case of the face mills the pressure of the cut falls on both sides of the work, and the spring is mainly endways of the nut arbor; hence, it does not affect the depth of the cut nor the truth of the work. Furthermore, in both the end and the face mills, the work will be true notwithstanding that the cutter may not be quite true, because each point of the work surface is passed over by every tooth in the cutter, so that the work will be true whether the cutter runs true or not; whereas in the plain mill or cutter[II-26] each tooth does its individual and independent proportion of finishing. This is shown in Figs. 1961 and 1962. In Fig. 1961 we have the plain mill, and it is obvious that the tooth does the finishing on the vertical line b, that being the lowest point in its revolution. After a tooth has passed that point the work in feeding moves forward a certain distance before the next tooth comes into action; hence to whatever amount a tooth is too high it leaves its mark on the work in the form of a depression, or vice versâ, a low tooth will leave a projection.
In Fig. 1962 we have a piece of work being operated on by a face mill, and it is obvious that while the teeth perform cutting duty throughout the distance a, yet after the work has fed past the line a it is met by the cutter teeth during the whole time that the work is feeding a distance equal to a on the other side; hence the prolonged action of the teeth insures truth in the work. On the other hand, however, it is clear that the work requires to feed this extra distance before it is finished.
Suppose, however, that the cutter being dead true the cutting action ceases on the centre line, and therefore exists through the distance a only, and if we take a plain cutter of the same diameter as in Fig. 1963 we see that its period of feed only extends through the length b, and it becomes apparent that to perform an equal amount of work the face cutter is longer under feed, and therefore does less work in a given time than the plain cutter, the difference equalling twice that between a and b in the two figures, because it occurs at the beginning and at the end of the cut.
There is, however, another question to be considered, inasmuch as that the face cutter must necessarily be of larger diameter than the plain one, because the work must necessarily pass beneath the washer (c, Fig. 1915), that is between the two cutters; hence the cutter is more expensive to make.
We may in very short work overcome this objection by feeding the work, as at k in Fig. 1964, the face l to be milled requiring to feed the length of the teeth instead of the distance h in the figure. In the end mill the amount of feed also is greater for a given length of finished surface than it is in the plain cutter, as will be readily understood from what has already been said with reference to face mills.
Face milling possesses the following points of advantage and disadvantage, in addition to those already enumerated: If the work is sprung by the pressure of the holding devices it is in a line with the plane of motion of the teeth, hence the truth of the work is not impaired. On the other hand, the teeth meet the scale or skin of the work at each cut, whereas in a cylindrical cutter this only occurs when the cutter first meets the work surface.
The strain of the cut has more tendency to lift the work table than in the case of a cylindrical cutter. The work must be held by end pressure; hence the chuck or holding jaws must be narrower than the work, rendering necessary more work-holding devices. Since, however, both sides of the work are simultaneously operated on, there is no liability of error in parallelism from errors in the second chucking, as is the case with plain cutters.
[II-27]To cut V-shaped grooves in cylindrical work, when it is required that one face or side of the groove shall be a radial line from the centre of the work, two methods may be employed. First we may form the cutter, as in Fig. 1965, the side b of the cutter being straight and the point of the cutter being set over the centre of the work. The objection to this is that the finished groove will have a projection or burr on the radial side of the groove, as shown at d in the figure, entailing the extra labor of filing or grinding, to remove it; furthermore, that face will have fine scored marks upon it, as denoted by the arcs at c, these scores showing very plainly if the cutter has any high teeth upon it, and more especially in the case of cutting spirals, as will appear presently. The reason of this is that the side b of the cutter being straight or flat the whole of the teeth that are within the groove have contact with the side c of the groove, that is to say, all the teeth included in the angle e in the figure, because the teeth on the side a tend, from the pressure of the cut to force the cutter over towards the side c of the groove. The second method referred to, which is that commonly adopted for cutting the flutes of tapes, reamers, milling cutters, &c., is to form the cutter on the general principle illustrated in Fig. 1966, and set it to one side of the centre of the work so that one of its faces forms a radial line, as shown in the figure, the distance to which it is set to one side depending upon the angle of its cutting edge to the face of the cutter.
Fig. 1967 represents a common form of cutter of this class that is used for cutting spiral grooves on milling cutters up to 3 inches in diameter, which contain eight teeth per inch of diameter. The angle of the teeth on b is 12° to the side face a of the cutter, and the angle of the teeth at c is 40° to the face d.
The effect produced by making face b at an angle instead of leaving it straight, or in other words, instead of cutting the teeth on the face a, may be shown as follows:—
Suppose that in Fig. 1968 we have a sectional view taken through the middle of the thickness of a cutter for a rectangular groove, the circumferential surface being at a right angle to the side faces, and it is evident that the teeth, at every point in their length across the cutter, except at the extreme corner that meets the side faces as c, will have contact with the seat of the groove while passing through the angle f only (which is only one half of the angle e in Fig. 1965); or in other words, each tooth will have contact with the seat of the groove as soon as it passes the line g, which passes through the axis of the cutter; whereas, when the teeth are parallel with the side of the cutter, as was shown in Fig. 1965, the teeth continue to have contact with the side walls of the groove after passing the line g.
By forming the cutter as in Fig. 1967, therefore, we confine the action to the angle f, Fig. 1968, the teeth having contact with the walls of the groove as soon as they pass the line g.
In cutting spiral grooves this is of increased importance, for the following reasons: In Fig. 1969 we have a cutter shown in section, and lying in a spiral groove. Now suppose a tooth to be in action at the bottom of the groove, and therefore on the line g g, and during the time that it moves from that line until it has moved above the level of the top of the groove, the work will have performed some part of a revolution in the direction of the arrow, and has therefore moved over towards that side of the cutter; hence, if that side of the cutter had teeth lying parallel, as shown at b in Fig. 1965, the walls of the groove would be scored as at c in that figure, whereas by placing the teeth at an angle to the side face, they recede from the walls after passing line g, and therefore produce smoother work.
A cutter of this kind must, for cutting the teeth of cutters, be accurately set to the work, and the depth of cut must be[II-28] accurate in order to cut the grooves so that one face shall stand on a radial line, and the top of the teeth shall not be cut to a feather edge. If the teeth were brought up to a sharp edge the width of the groove at the top would be obtained with sufficient accuracy by dividing the circumference of the work by the number of flutes or teeth the work is to contain, but it is usual to enter the cutter sufficiently deep into the work to bring the teeth tops up to not quite a sharp edge. The method of setting the cutter is to mark on the end of the work a central line r, Fig. 1970, and make the distance e in same figure equal to about one tenth the diameter of the work.
Obviously the cutter is set on opposite sides of the work centre, according to which side of the groove is to have the radial face. Thus for example, in Fig. 1970, the cutter is set to the left of line r, the radial face of the groove being on the left, while in Fig. 1971 the cutter is set on the right of line r, because the radial face is on the right hand side of it, the work consisting (in these examples) in cutting up a right and a left-hand mill or cutter.
The acting cutter j may in both cases be used to cut either a right or a left-hand flute, according to the direction in which the work w is revolved, as it is fed beneath the cutter j.
In Fig. 1972 we have an example of cutting straight grooves or teeth, with an angular cutter having one side straight, and it is seen that we may use the operating or producing cutter in two ways: first, so that the feed is horizontal, as at a, or vertical, as at b; the first produces a right-hand, and the second a left-hand cutter, as is clearly seen in the plan, or top view. The feeds must, however, be as denoted by the respective arrows being carried upwards for b, so that the cutter may run under the cut and avoid cutter breakage.
The number of grooves or flutes producible by an angular cutter depends upon the depth of the groove and the width of land or tooth between the grooves. Thus Fig. 1973 represents a cutter producing in one case four and in the other eight flutes with the same form of cutter, the left being for taps, and the right for reamers.
For cutting the teeth of cutters or mills above 3 inches in diameter, the angles of the acting or producing cutter are changed from the 12° and 40° shown in Fig. 1967, to 12° as before on one side, and a greater number on the other; thus in the practice of one company it is changed to 12° and 48°, the 12° giving the radial face as before, and the 48° giving a stronger and less deep tooth, the deep tooth in the small cutters being necessary to facilitate the grinding of the teeth to sharpen them.
In cutting angular grooves in which the angle is greater on one side than on the other of the groove, the direction of cutter revolution and the end of the work at which the groove is started; or in other words, the direction of the feed, is of importance, and it can be shown that the feed should preferably be so arranged that the side of the groove having the least angle to the side of the cutter should be the one to move away from the cutter after passing the lowest point of cutter revolution.
In Fig. 1974, for example, we have at r a cylinder with a right-hand groove in it, whose side c, representing the face of a tooth, is supposed to be a radial line from the cylinder axis, the side b representing the back of a cutter tooth, being at an angle of 40°.
[II-29]Now if the work revolves in the direction of arrow a, and the cut be started at end g (as it must to cut a right-hand groove with the work revolving as at a), then the side c of the groove will move over towards and upon the side of the cutter for the reasons explained with reference to Fig. 1969, and the teeth on this side being at the least angle to the side of the cutter, do not clear the cut so well, the teeth doing some cutting after passing their lowest point of revolution—or in other words, after passing the line g in Fig. 1968. The effect of this is to cause the cutter to drag, as it is termed, producing a less smooth surface on that side (c) of the groove or tooth.
We may, however, for a right-hand groove revolve cylinder r, as denoted by arrow e, and start the cut at end d. The result of this is that the side c of the groove, as the roller revolves, moves away from the side of the cutter, whose teeth therefore do no cutting after passing their lowest point of revolution (g, Fig. 1968), and the dragging action is therefore avoided, and the cut smoother on this which is the most important side of the tooth, since it is the one possessing the cutting edge. When “dragging” takes place the burr that was shown in Fig. 1965 at d, is formed, and must, as stated with reference to that figure, be removed either by filing or grinding.
Obviously if the direction of cutter revolution and of feed is arranged to cause side c to move away from the side of the cutter, then side b will move over towards the other side of the cutter; but on account of the cutter teeth on this side being at a greater angle to the side of the cutter, they clear better, as was explained with reference to Fig. 1968, and the dragging effect caused by the revolving of the work is therefore reduced.
We have now to examine the case of a left-hand groove, and in Fig. 1975 we have such a groove in a cylinder l. Let it be supposed that the direction of its revolution is as denoted by arrow f, and if the cutter is started at h (as it must be to cut a left-hand groove if the work revolves as at f), then the side c moves over towards the cutter, and the dragging or crowding action occurs on that side; whereas if the direction of revolution is as at k, and the cutter starts at n and feeds to h, then side b of the groove moves towards the cutter; hence face c of the groove is cut the smoothest. Obviously then the direction of cutter and work revolution and of feed, in cutting angular grooves in which one angle of the cutter is at a greater degree of angle than the other to the side of the cutter, should be so arranged that the work revolves towards that side of the cutter on which its teeth have the greater angle, whether the spiral be a right-hand or a left-hand one. In cutting grooves not truly circular the same principle should be observed.
In Fig. 1976, for example, it is better if the side b is the one that moves towards the cutter, the direction of revolution being as denoted by the arrow, whether the groove be a right-hand or left-hand (supposing, of course, that the cutter starts from end e of the work).
Obviously, also, the greater the degree of spiral the more important this is, because the work revolves faster in proportion to the rate of feed, and therefore moves over towards the outer faster.
In cutting spirals it is necessary first to put on such change gears as are required to revolve the work at the required speed for the given spiral, and to then set the work at such an angle that the cutter will be parallel to the groove it cuts, for if this latter is not the case the groove will not be of the same shape as the cutter that produces it.
In Fig. 1977 we have a spiral so set, the centre of the cutter and of the groove being in the line o o, and the work axis (which is also the line in which the work feeds beneath the cutter) being on the line c c. The degrees of angle between the centre of the cutter, or line o o, and the axis of the work, or line c c, are the number of degrees it is necessary to set the work over to bring the cutter and the groove parallel, this number being shown to be 20 in the example.
To find this angle for any given case we have two elements: first, the pitch of the spiral, or in other words, the length or distance in which it makes one complete turn or revolution; and second, the circumference of the work; for in a spiral of a given pitch the angle is greater in proportion as the diameter is increased as may be seen in Fig. 1978, in which the pitch of the spirals is that in Fig. 1977, while the angle is obviously different.
To find the required angle for any given case we may adopt either of two plans, of which the first is to divide the circumference of the work in inches by the number of inches which the spiral takes to make one turn. This gives us the tangent of angle of the spiral.
The second method of setting the work to cut a given spiral is to chuck the work and put on the necessary change gears. The cutter is then set to just touch the work and the machine is started, letting the work traverse beneath the cutter just as though the work was set at the required angle to the cutter:
When the cutter has arrived at the end of the work it will have marked on it a line, as in Fig. 1979, this line representing the spiral it will cut with those change gears, and all that remains to do is to swing the work over so that this line is parallel with the face of the cutter, as shown in Fig. 1980. If the diameter of the cutter is small we may obviously secure greater accuracy by placing a straight-edge upon the side of the cutter so as to have a greater length to sight by the eye in bringing the line fair with the cutter. This being done it remains to merely set the cutter in its required position with reference to the work diameter.
If an error be made in setting the angle of the work to the cutter the form of groove cut will not correspond to that of the[II-30] cutter. This is shown in Fig. 1981, in which the cutter being at an angle to the groove the latter is wider than the cutter thickness, and it is obvious that by this means different shapes of grooves may be produced by the same cutter. In proportion, however, as the cutter is placed out of true the cutting duty falls on the cutting edges on one side only of the cutter, which is the leading side c in the figure, while the duty on the other side, b, is correspondingly diminished.
The simplest method of holding work to be operated upon in the milling machine is either between the centres or in the vice that is provided with the machine. The principles involved in holding work in the vise so as to keep it true and avoid springing it for milling machine work, are the same as those already described with reference to shaping machine vises.
In milling tapers the work, if held in centres, should be so held that its axial line is in line with the axes of both centres, for the following reasons:—
In Figs. 1982 and 1983 we have a piece of work in which the axes of the centres and of the work are not in line, and it is clear that the horn d of the dog d will, in passing from the highest to the lowest point in its revolution, move nearer to the axis of the work. Suppose, then, that the driver e is moved a certain portion of a revolution with tail d at its highest point, and is then moved through the same portion of a revolution with d at its lowest point in its path of revolution, and being at a greater distance or leverage when at the top than when at the bottom it will revolve the work less. Or if the tail d of the dog is taper in thickness, then in moving endways in the driver e (as it does when the work is revolved) it will revolve the work upon the centres. Suppose, then, that the piece of work in the figures required to be milled square in cross-section, and the sides would not be milled to a right angle one to another. This is avoided by the construction of the Brainard back centre, shown in Fig. 1984, in which t represents the surface of the work table and h the back centre. The block b is fitted within head h, and has two slots a a, through which the bolts s s pass, these bolts securing b in its adjusted position in h. The centre slide c operates in b; hence b, and therefore c, may be set in line with the work axis.
For heads in which the back centre cannot thus be set in line, the form of dog shown in Fig. 1985 (which is from The American[II-31] Machinist) may be employed to accommodate the movement of the tail or horns through the driver. Its horn or tail b is made parallel so as to lie flat against the face of the slot in the driver. The other end of tail b is pivoted into a stud whose other end is cylindrical, and passes into a hub provided in one jaw of the dog, the set-screw a being loosened to permit this sliding motion. This locks the horn in the clamp and permits the dog to adjust itself to accommodate the motion endwise that occurs when it is revolved. The amount of this motion obviously depends upon the degree of taper, it being obvious (referring to Fig. 1982) that horn d would pass through the chuck, as denoted by the dotted lines, when at the bottom of its path of revolution.
It is obvious that when the head or universal head of the machine is elevated so that it stands vertical, it may have a chuck screwed on and thus possess the capacity of the swiveled vise. It is preferable, however, to have a separate swiveled chuck, such as in Fig. 1986 (from The American Machinist), which will not stand so high up from the machine bed, and will therefore be more solid and suitable for heavy work.
Another very handy form of chuck for general work is the angle chuck shown in Fig. 1987, which is from an article by John J. Grant, in The American Machinist. The work-holding plate has T-grooves to chuck the work on and is pivoted at one end, while at the other is a segment and bolt to secure it in its adjusted angle. Two applications of the chuck are shown in the figure.
Fig. 1988 represents a top, and Fig. 1989 an end view of a chuck to hold rectangular bars that are to be cut into pieces by a gang of mills. a, a, a, are grooves through the chuck jaws through which the cutters pass, severing the bar through the dotted lines. Each piece of the bar is held by a single screw on one side and by two screws on the other, which is necessary in order to obtain equal pressure on all the screws and prevent the pieces from moving when cut through, and by moving, gripping the cutters and causing them to break.
In chucking the bar the two end screws d d must be the first to be set up to just meet the bar: next the screws b c on the other side must be set up, holding the bar firmly. The two screws between d d are then set up to just bind the bar, and then the middle four on the other side are screwed up firmly. By this method all the screws will hold firmly and the pieces cannot move.
Vertical Milling, Die Sinking, or Routing Machine.—Fig. 1990 represents Warner & Swazey’s die sinking machine. The cutter driving spindle is here driven by belt direct, imparting a smooth motion. The knee is adjustable for height on the vertical slideway on the face of the column, which is provided with a stop adjustable to determine how high the knee and work-holding devices can be raised, and, therefore, the depth to which the cutter can enter the work, and a former pin is placed 6 inches behind the cutter to act as a stop against which a pattern may be moved when work is to be copied from a former or pattern piece. The work-holding device consists of a compound rest and a vise capable of being swiveled to any angle or of being revolved to feed the work to the cutter, hence the work may be moved in any required direction, in either a straight line, in a circle, or in any irregular manner to suit the shape of the work.
Profiling Machine.—The profiling machine is employed mainly to cut the edges of work, and to sink recesses or grooves in the upper surface of the same to correspond to a pattern. A provisional template of the form of the work is fastened on the bed of the machine, and from this is cut in the machine a thicker one termed the “former,” which is then used to copy the work from.
Fig. 1991 represents Pratt & Whitney’s profiling machine. On the cross slide are two separate sliding heads, each of which carries a live spindle for the cutting tool, and beside it a spindle to receive a pin, which by being kept against the pattern or former causes the work to be cut to the same shape as the former.
[II-32]The work is fastened to the table, which is operated upon the raised Vs shown by the handle on the left, which operates a pinion geared to a rack on the underneath side of the table. The handle on the right operates the heads along the cross slide also by a rack and pinion motion. The gearing and racks in both cases are double, so that by two independent adjusting screws the wear of the teeth may be taken up and lost motion prevented. By means of these two handles the work may be moved about the cutter with a motion governed by the form or shape of the former, of which the work is thus made a perfect pattern both in size and shape. The tool used is a shank or end mill, such as was shown in Fig. 1928. In some profiling machines the spindle carrying the guide or former pin is stationary, in which case the provisional template is put beneath it and the former is cut by the live spindle, and for use must be moved from the position in which it was cut and reset beneath the former spindle. This machine, however, is provided with Parkhurst’s improvement, in which the former spindle is provided with a gear-wheel, by which it may be revolved from the live spindle, hence the provisional template may be set beneath the live spindle in which the guide pin is then placed. The cutter is then placed in the former spindle, and the former cut to shape from the provisional template while in the actual position it will occupy when used.
Fig. 1992 represents Brainard’s machine for grinding milling cutters. It consists of a threaded column a to which is fitted the knee b, which as it fits the top of the threads on the column may be swung or revolved about the column without being altered in its height upon the same except by means of the threaded ring c. At d is a lever for clamping the knee b to the column after adjustment; w represents the emery wheel mounted on the end of the horizontal spindle having journal bearing at the top of the column. The face of the knee b has a slideway d for the fixtures, &c., which hold the cutters to be ground, and at e is a lug pierced to receive an arbor whereon to place cutters to be ground, the lug being split and having a binding screw to lock the arbor firmly in place. f is a slide for receiving the grinding attachments, one of which is shown at k carrying a milling cutter in position to be ground on the face.
Fig. 1993 shows the fixture employed to grind parallel cutters, s representing a stand upon slide f (which corresponds to slide f in the general view of the machine in Fig. 1992) in which is fixed the arbor h. The cutter c is slid by hand along arbor h and beneath the emery wheel, the method of guiding the cutter to the wheel being shown in Fig. 1994, which represents a front view of the machine. At e is the lug (shown also at e in the general view) which has a hole to receive a rod p, and is split through at s, so that operating binding screw l locks rod p in e. At r is a rod secured to the rod p, and g is a gauge capable of swivelling in the end of r and of being secured in its adjusted position. The end of this gauge is adjusted to touch the front face of the tooth to be ground on the cutter c, which must be held close against the end of the gauge in order to grind the cutting edge to a straight line parallel to its axis.
A not uncommon error is to place the gauge g against the tooth in front of that which is being ground, as in Fig. 1995, the gauge being against tooth c while tooth b is the one being ground. In this case the truth of the grinding depends upon the accuracy of the tooth spacing. Suppose, for example, that teeth b and c are too widely spaced,[II-33] tooth c being too far ahead, and this error of spacing would cause tooth b to be too near the centre of the emery wheel and its cutting edge to be ground too low.
The object of feeding the cutter by hand along the arbor h is twofold: first, the amount of cut must be very light and the feed very delicate, for if the grinding proceeds too fast the cutting edge will be what is termed burned, that is to say, enough heat will be generated to soften the extreme cutting edge, which may be discovered by holding the front face of the tooth to the light, when a fine blue tint will be found along the cutting edge, showing that it has been softened in the grinding, and this will cause it to dull very rapidly.
The second object is to insure parallelism in the cutter. Suppose, for example, that the cutter c was fast upon arbor h and was fed to the wheel by moving slide f, and if the arbor h stood at an angle, as in Fig. 1996, to the slide upon which f moved, the cutter would be ground taper, whereas if the cutter is fed along the arbor it will be ground parallel whether the arbor is true or not with the slideway of f, the only essential being that the arbor h be parallel and straight, which is much easier to test and to maintain than it is in the slideway (d, Fig. 1992). Here it may be noted that oil should not be applied either to arbor h or to the cutter bore or slideway d, as lubrication only increases the wear of the parts, causing the fine emery particles that inevitably fall upon them to cut more freely.
As thin cutters would not have sufficient length of bore to steady them upon the arbor and insure parallelism, the cutter sleeve shown in Fig. 1997, which is from The American Machinist, is employed to hold them. It is provided with a collar, is threaded at t for the nut n to hold the cutter against collar c, and is bored to fit the cutter arbor h, which corresponds to h in Fig. 1993.
This device also affords an excellent means of holding two or more thin cutters requiring to be ground of exactly equal diameters.
It follows from what has been said that taper tools, such as taper reamers, must be held with their upper face parallel to the line of their motion in being fed to the wheel, as in Fig. 1998, in which line m represents this line of motion, line n the axis of the reamer, and line o the line on which the fixture that holds the reamer must move, o being parallel to m.
Fig. 1999 represents Slate’s fixture for this class of work. a is a stand that bolts upon the slideway d in Fig. 1992. Upon a is fixed a rectangular bar b, upon which (a sliding fit) is the shoe c. Upon c fits the piece d, which is pivoted to shoe c by the pin at e. At the other end of d is a lug, against which abuts the end of screw g, which is threaded through the end of c, so that by operating the screw g, d may be set to any required angle upon c, and at f is a set-screw threaded through d and abutting against c, so as to[II-34] lock d in its adjusted position. At p is a pointer for the graduations on c, which are marked to correspond with the graduations upon the taper turning attachment of a lathe.
The work is held between centres, the head h fitting to a slideway on the top of d, and being secured in its adjusted position by the screw i. The work should obviously be set so that its upper face lies horizontal, and is fed to the wheel by moving shoe c by hand along bar b, the long bearing keeping c steady, and the lightness of the moving parts making the feeding more sensitive than it would be were it required to move bar b.
The tooth being ground is held by hand against the gauge g in Fig. 1994, as was described with reference to that figure, and the reamer, therefore, in the case of having spiral grooves, revolves upon its centre while being fed to the emery wheel.
For tapers that are beyond the capacity of this device, and also for holding cutters to have their face teeth ground, the device shown in Fig. 2000 is employed. Upon the slide f is fixed knee k (the corresponding parts to which are seen in the general view, Fig. 1992), whose disk face at r is graduated as shown. Piece s is pivoted by a pin passing through the hub of k and having a nut t to secure it in its adjusted position. s is bored to receive the cutter arbor h, and is split through so that by means of the screw at v the arbor may be gripped and locked in s. The stud w for holding the gauge g passes into a bore in the bracket x, and is secured therein by the screw at y, the lugs through which y passes being split through into the bore for w. As shown in the figure, the arbor h is set for grinding the side teeth of the cutter, but it is obvious that s being pivoted to k may be swung out of the vertical and to any required angle, so as to bring the face of the tooth that is to be ground horizontally beneath the emery wheel, as shown in Fig. 2001, which represents an angular cutter in position. We have now to consider the adjustment of the cutter to the emery wheel, necessary in order that the cutting edges may be given the necessary clearance.
First, then, suppose in Fig. 2002 that the line a a represents the line of centres of the emery-wheel spindle and the cutter arbor, and if the front face b of the tooth be set coincident with this line, as in the figure, then the top of the tooth partaking of the curvature of the wheel that grinds it would have its heel c the highest; hence the edge at b could not cut.
If, however, the line a a in Fig. 2003, still representing the line of centres, we so set the gauge (g, Fig. 1994) that the heel c of[II-35] the tooth comes up to line a a, then the curvature of the emery wheel would give clearance to the heel c, and therefore a cutting edge to face b of the tooth.
The amount of clearance that may be given in this way is limited by the spacing of the teeth and the diameter of the emery wheel, as is seen from Fig. 2004, it being obvious that when tooth a is being ground the emery wheel must clear the rear tooth b or it will grind its edge off, and it is obvious that the smaller the emery-wheel diameter the more the tooth to be ground may be set in advance of the line of centres of the wheel and spindle. It may be pointed out, however, that there are two methods of adjusting the cutter to the wheel.
In Fig. 2005, for example, let a a represent the line of centres of the cutter and the wheel, and line b the plane of the front face of the tooth being ground; and in Fig. 2006 let line a represent a vertical line from the axis of the wheel, and b a vertical line passing through the axis of the cutter, the tooth edge c occupying the same position in both figures. Now suppose we employ cutting edge c as a centre and swing the cutter until its axis or centre moves along the arc d to the dot e, and it is evident that during this motion the heel of the tooth will have approached the axis of the emery wheel and that more clearance will therefore have been given to the cutting edge c.
The actual curve of the top face, as c, Fig. 2007, of the tooth t will remain the same in either case, but its position with relation to the front face will be altered. As this curve is greater in proportion as the diameter of the emery wheel is diminished, and as the curvature weakens the cutting edge of the tooth, it is obviously desirable to employ a wheel of as large a diameter as possible.
To eliminate this curvature it would appear that the position of the emery wheel might be reversed, as in Fig. 2008, but as the emery wheel would wear only where in contact with the tooth, it would gradually assume the shape in Fig. 2009, there being a shoulder at s that would destroy the cutting edge of the tooth.
This may to a great extent be remedied by presenting the[II-36] cutter diagonally to the wheel, as in Fig. 2010, employing a wheel so thin that the whole of its face will cross the tooth top during a revolution. Or if the side faces of the wheel be recessed, leaving only a narrow annular grinding ring at the circumference, the wheel might be mounted as in Fig. 2011, thus making the top of the tooth quite flat. It may be observed, however, that the usual plan is to revolve the wheel at a right angle to the work axis, as was shown in Fig. 1994.
In grinding cutters having their teeth a right-hand spiral, care must be taken that in grinding one tooth the emery wheel does not touch the cutting edge of the next tooth.
Thus in Fig. 2013 it is seen that the corner c of the emery wheel is closer than corner d, and being at the back of the wheel and out of sight it is apt to touch at c unless a thin emery wheel be used.
In a left-hand spiral, Fig. 2012, it is the corner d that is apt to touch the next tooth, the liability obviously being greatest in cutters of large diameter.
The emery wheel should be of a grade of not less than 60 or more than 70. If it is too coarse it leaves a rough edge, which may, however, be smoothed with an oilstone slip. If the wheel is too fine it is apt to burn the cutter, or in other words, to soften the cutting edge, which may be known by a fine blue burr that may be seen on the front face of the tooth, the metal along this line being softened.
The diameter of the wheel may be larger for small cutters than for large ones, since the teeth of small cutters clear the wheel[II-37] better. The larger the wheel the less the curvature on the top of the tooth.
For general work a diameter of 21⁄2 inches will serve well, the thickness being about 5⁄16 inch or 3⁄8 inch. The speed of a wheel of this diameter varies in practice from 3,000 to 4,500 revolutions per minute, but either too fast or too slow a speed will cause the wheel to burn the cutter, and the same thing will occur if the cutter is fed too fast to the wheel, or if too deep a cut is taken. The finishing cut should obviously be very small in amount, especially in cutters of large diameter, for otherwise the wear in the diameter of the wheel will sensibly affect the teeth height, those last ground being the highest.
Emery Wheels and Grinding.—Emery grinding operations may be divided into four classes as follow:—
1st. Tool or cutter grinding, in which the emery wheel is used to sharpen tools which, from their shape, were formerly softened and sharpened by the file, already largely treated in the preceding chapter.
2nd. Cylindrical grinding, in which both the work and the emery wheel are revolved, as has been explained with reference to grinding-lathes.
3rd. Flat surface grinding, in which the emery wheel takes the place of the ordinary steel cutting tool; and
4th. Surface grinding, in which the object is to remove metal or to smoothen surfaces.
The distinctive feature of the various makes of solid emery wheels lies in the material used to cement the emery together, and much thought and experiment are now directed to the end of discovering some cementing substance which will completely meet all the requisite qualifications. Such a material must bind the emery together with sufficient strength to withstand the centrifugal force due to the high speeds at which these wheels must be run to work economically; and it must neither soften by heat nor become brittle by cold. It must not be so hard as to project above the surface of the wheel; or in other words, it should wear away about as fast as does the emery. It must be capable of being mixed uniformly throughout the emery, so that the wheel may be uniform in strength, texture, and density. It must be of a nature that will not spread over the surface of the emery, or combine with the cuttings and form a glaze on the wheel, which will prevent it from cutting. This glazing is, in fact, one of the most serious difficulties to be encountered in the use of emery wheels for grinding purposes, while it is a requisite for polishing uses, as will be explained farther on. Many of the experiments to prevent glazing have been in the direction of discovering a cement which would wear away under about the same amount of duty as is necessary to wear away the cutting angles of the grains of emery, thus allowing the emery to become detached from the wheel, rather than to remain upon it in a glazed condition.
With the same grade of emery the wheel will cut more freely and glaze less in proportion as the cementing material leaves the wheel softer, but the softer the wheel the more rapidly it will wear away; indeed it is the dislodgement of the emery points as soon as they have become dulled that produces freedom from glazing. It may be remarked, however, that the nature of the material operated upon has a good deal to do with the glazing; thus wrought iron will glaze a wheel more quickly than hardened steel, and brass more quickly than wrought iron, while on the other hand soft cast iron has less tendency than either of them to glaze. Glazing occurs more readily in all cases upon fine than upon coarse wheels. Glazing is more apt to occur as the work is pressed more firmly to the wheel, and with broad and flat surfaces rather than with cylindrical ones. An excellent material for removing the glaze from an emery wheel is a piece of ordinary pumice stone.
The principal cements used in the manufacture of emery wheels are as follows, each representing the cement for one make of wheel:—
1. Hard rubber. 2. Chemical charcoal (leather cut down by acid and used to prevent shrinkage), and glue. 3. Oxychloride of zinc. 4. Shellac. 5. Linseed oil and litharge. 6. Silicate of soda and chloride of calcium. 7. Celluloid. 8. Oxychloride of magnesium. 9. Infusoria. 10. Ordinary glue.
The vitrified emery wheel is made with a cement which contracts slightly while cooling, leaving small pores or cells through which water, introduced at the centre, is thrown (by centrifugal force) to the surface. This causes, when the wheel is rotating, a constant flow of water from the centre to the surface, carrying off the cuttings and the detached emery.
In order that an emery wheel shall run true with its bore it must fit the driving spindle, and in order that it may do this closely the wheel bore is sometimes filled with lead, the latter being bored out to fit the spindle. If the bore of the emery wheel itself were made a tight fit to the spindle it would abrade the spindle in being put on, and the pressure of the fit if any would tend to split the wheel. A common method of securing emery wheels to their spindles is to fill the bore of the wheel with lead, and bore it out to fit the spindle of the emery grinding machine. The flanges between which the wheel is held are recessed so as to grip the wheel at and near their perimeters only. Between the flange and the wheel a thin disk of sheet-rubber is sometimes used to afford a good bedding for the flange.
The forms of the perimeters of emery wheels are conformed to suit the form of the work to be ground, and it is found that from the great strength of the emery wheel it can be used to a degree of thinness that cannot be approached in any kind of grinding stone. For instance, vulcanite emery wheels 18 inches in diameter and having 3⁄16 inch thickness, or face as it is commonly termed, are not unfrequently used at a speed of some 5,000 feet of circumferential feet per minute, whereas it would be altogether impracticable to use a grindstone of such size and shape, because the side pressure would break it, no matter at what speed it were run. Indeed, in the superior strength of the emery wheels of the smaller sizes lies their main advantage, because they can be made to suit narrow curvatures, sweeps, recesses, &c., and run at any requisite speed under 5,000 feet per minute, and with considerable pressure upon either their circumferential or radial faces.
Grades of Coarseness or Fineness of Emery Wheels.—Emery is found in the form of rock, and is crushed into the various grades of fineness. The crushing is done either between rollers or by means of stamps, the latter, however, leaves the corners of the grains the sharpest, and hence the best for cutting, though not for polishing purposes. The grades of emery are determined by passing the crushed rock through sieves or wire cloths having from eight to ninety wires to the inch; thus, emery that will pass through a sieve of sixty wires to the inch is called No. 60 grade.
The finest grade obtained from the manufactory is that which floats in the atmosphere of the stamping room, and is deposited on the beams and shelves, from where it is occasionally collected. Washed emery is used by plate-glass workers, opticians, and others that require a greater degree of fineness than can be obtained by the sieve.
The numbers representing the grades of emery run from 8 to 120, and the degree of smoothness of surface they leave may be compared to that left by files as follows:
| 8 | and | 10 | represent the | cut of a | wood rasp | |
| 16 | „ | 20 | „ | „ | coarse rough file | |
| 24 | „ | 30 | „ | „ | ordinary rough | file |
| 36 | „ | 40 | „ | „ | bastard | „ |
| 46 | „ | 60 | „ | „ | second cut | „ |
| 70 | „ | 80 | „ | „ | smooth | „ |
| 90 | „ | 100 | „ | „ | superfine | „ |
| 120, F & FF | „ | „ | dead smooth | „ | ||
The f and ff emery is flour emery which has been washed to purify it.
The following are the kinds of wheel suitable for the respective purposes named:—
| Kind of work. | Kind of wheel. | |
| For rough grinding, such as on the edges of iron or steel plates, for removing the protuberances on castings or on narrow surfaces where rough grinding is sufficient. | } | Coarse grain and hard texture. |
| For narrow surfaces, such as moulding knives, lathe tools, saw gumming, &c. | } | Medium grain and hard texture. |
| For free cutting without gumming on broad surfaces on iron, steel, or brass. | } | Medium grain and soft texture. |
| For grinding fine tools, such as milling machine cutters, or for work in which the duty is not great while the wheel requires to keep its shape and keep true. | } | Fine grain and soft texture. |
| For smooth grinding on soft metals, as cast iron and brass. | } | Fine grain and hard texture. |
When the work is presented to the wheel unguided, the wheel wears out of true, because the work can follow the wheel, hence it becomes necessary to true the wheel occasionally. This can be done by a tool such as in Fig. 2014, which is applied by hand on the hand rest, and corresponds to the tool shown in Fig. 2061 for grindstones, or by the use of a diamond set in a tool to be held by hand or in a slide rest. The diamond produces the most true and smooth work, but the cut of the wheel is at first impaired by the action of the diamond, which is not the case with the tool in Fig. 2014.
Corundum is a mineral similar to emery, and corundum wheels are made and used in the same manner as emery wheels. Their cutting qualifications are, however, superior to those of the emery wheel, both cutting more freely and being more durable with less liability to glaze.
Speeds for Emery Wheels.—The speed at which an emery wheel may be run without danger of bursting varies according to the thickness or breadth of face of the wheel, as well as according to the quality of the cementing material and excellence of manufacture. Hence, although a majority of manufacturers recommend a speed of about 5,000 circumferential feet per minute, that speed may be largely exceeded in some cases, while it would be positively dangerous in others. It is, in fact, impracticable in the operations of the workshop to maintain a stated circumferential speed, because that would entail a constant increase of revolutions to compensate for the wear in the diameter of the wheel. Suppose, for example, that a wheel when new is a foot in diameter: a speed of about 1,600 revolutions per minute would equal about 5,000 circumferential feet; whereas, when worn down to 2 inches in diameter, the revolutions would require, to maintain the same circumferential speed, to be about 9,500 per minute, entailing so many changes of pulleys and counter-shafting as to be impracticable. In practice, therefore, a uniform circumferential speed does not exist, the usual plan adopted being to run the large-sized wheels, when new, at about the speed recommended by the manufacturer of the kind of wheel used, and to make such changes in the speed of the wheel during wear as can be accomplished by changing the belt upon a three-stepped cone pulley, and perhaps one, or at most two, changes of pulley upon the counter-shaft. It is sometimes practicable to use wheels of a certain diameter upon machines speeded to suit that diameter, and to transfer them to faster speeded machines as they diminish in diameter. Even by this plan, however, only an approximation to a uniform speed can in most cases be obtained, because as a rule certain machines are adapted to certain work, and the breadth of face and form of the edge of the emery wheel are very often made to suit that particular work. Furthermore, a new wheel is generally purchased of such a size, form, and grade of emery as are demanded by the work it is intended at first to perform. Neither is it, as a rule, practicable to transfer the work with the diametrically reduced wheel to the lighter and faster-speeded grinding machine. So that, while it is desirable to run all emery wheels as fast as their composition will with safety admit, yet there are practical objections to running small wheels at a rate of speed sufficient to make their circumferential velocities equal to those of large wheels. The speeds recommended for the various kinds of wheels now in use vary from about 2,700 to 5,600 circumferential feet per minute; but the speeds obtaining in workshops average between 2,000 and 4,000 feet for wheels 3 inches and less in diameter, and from about 3,000 to 5,600 feet for wheels above 12 inches in diameter. Wheels above 15 inches in diameter, and of ample breadth of face, are not unfrequently run at much greater velocities.
On account of the high velocity at which emery wheels operate, it is necessary that they be very accurately balanced, otherwise the unequal centrifugal motion causes them to vibrate very rapidly, every vibration leaving its mark upon the work.
The method of balancing adopted by one firm is as follows: The arbors are of cast iron, and are cast standing vertical so as to induce equal density in the metal, it having been found that if the arbors were cast horizontally the lower part of the metal would from the weight of the molten metal be more dense than that at the top of the casting. In casting the arbors upright, the difference in the density of metal simply causes one end of the arbor to be more dense than the other, and the difference being at a right angle to the plane of revolution has no tendency to cause vibration. The driving pulleys are cast horizontal to obtain equal density, and after being turned are carefully balanced. The driving pulleys are held to the arbors by being bored a driving fit, and are driven on so as to avoid the use of keys, which would throw the wheels out of balance.
The centrepiece and flange to hold the wheel to the arbor are turned and balanced. The nut to hold the wheel is a round one, which is easier to balance than a hexagon nut. After the centrepiece is put on the arbor, the whole is tried for balance, and corrected if necessary. The pulley is then put on and the whole is again balanced, and so on, the arbor being balanced after each piece is added, so that while each piece is balanced of itself the whole is balanced after the addition of each separate piece.
The emery or corundum wheel is then put on the arbor and tried for being in balance. The method of correcting the balance of the wheel is as follows: The arbor with the wheel on is placed in the lathe, the wheel turned true with a diamond tool (the wheel revolving at a comparatively slow speed). The arbor is then revolved at its proper speed (5,000 circumferential feet per minute), and a point applied to just meet the circumference will touch the wheel where it is heaviest, leaving a line as shown in Fig. 2015 at a. The centre of the arbor is then moved over towards this line as shown in Fig. 2016, in which w is the wheel, the location of the line a (marked as above) being as denoted by the arc a,[II-40] and c represents the arbor whose centre is moved over towards the arc a. When therefore the arbor is again put in the lathe, it will run out of true by reason of the centre at one end having been altered. A cut is taken down that radial face of the wheel which faces the end of the arbor that has had its centre moved so that the wheel is turned thinner where the mark (a, Fig. 2016) is. The amount of cut to be taken off is a matter of judgment and trial, since it must be just sufficient to compensate for the greater density of the wheel on that side. This greater density, be it noted, occurs from the difficulty in mixing the corundum or other abrasive grains with the cementing material with entire uniformity throughout the mass.
By this method of balancing, the wheel will remain in true balance notwithstanding its wear, because the balancing proceeds equally from the perimeter towards the centre of the wheel.
Emery Grinding Machines. (For grinding-lathes and roll grinding, see article on Lathes.)—Fig. 2017 represents Brown & Sharpe’s grinding machine. The bed, the table, and the cross-feed motion of this machine closely resemble those of the planing machine, but its work is far more smoothly and accurately done than can be performed in a planing machine. The table traverses to and fro, accurately guided in ways, and the revolving emery wheel takes the place of the ordinary cutting tool, being carried in a sliding head upon a cross slide or cross bar. The drum for driving the emery wheel is at the back of the machine, as shown in the cut.
The vertical feed motion for adjusting the depth of cut of the emery wheel is capable of very minute adjustment, thus avoiding a difficulty commonly experienced in iron planing machines on account of the coarseness of feed-screw pitch, which coarseness is necessary to insure their durability. The means by which this capability of minute adjustment is effected is shown in Fig. 2018, in which d is the cross head of the machine and c the sliding head having the arm c′, which provides at b a pivot for the wheel-carrying arm a. f is a stud fast in c and carrying e, which forms the nut for the feed screw. Outside this nut is the spiral spring s, whose force steadies the upper end of a.
Now suppose the feed wheel g be operated a full rotation, and[II-41] the motion of that end of a will be that due to the pitch of the feed screw, but the motion at the centre h of the emery wheel will be the pitch of the screw divided by the difference between the length from the centre of h to the centre of the feed screw, and that from the centre of h to the centre of b. But even this diminished motion at h is still further reduced, so far as the depth of cut put on is concerned, because the motion of h is not directly vertical but an arc p, of which b is the centre.
The standards carrying the cross slide are segments of a circle struck from the centre of the driving drum, which is necessary to enable the raising and lowering of the cross slide, and maintain a uniform tension on the belt driving the emery wheel without employing an idler wheel or belt tightener.
Fig. 2019 represents Wm. Sellers & Co.’s drill-grinding machine, in which the drill is held in a chuck operated by the hand wheel a. The jaws of the chuck grip the drill at the outer corners of the cutting edge as shown in Fig. 2020, and so as to grind the point of the drill central to those corners. In order to give to the cutting edges a suitable degree of clearance in their lengths, and to allow for the difference in thickness at their points between large and small drills, the following construction is employed.
Fig. 2020 represents the jaws j j holding on the left a small, and on the right a large drill. The line of motion of the right-hand jaw in opening and closing to grip the drill is along the line r, while that of the left-hand is along the line p p, the centre upon which the chuck is revolved to grind the drill being denoted by the small circle at s. x′ represents the centre line of the large drill when held in the chuck, and it is seen that the action of the jaws in closing upon small drills is to lift the drill point closer to the centre s upon which the chuck revolves (the cutting edge being ground to be on the line y′ y′). The reason for this peculiar and simple but exceedingly ingenious construction is, as before remarked, to maintain the cutting edge in its proper relation to the thickness of the drill point (which thickness varies in different diameters of drills), and to maintain a proper degree of clearance at every point along the length of the cutting edge. In other drill grinding machines the drill when rotated to grind the clearance is moved on the axis a a in Fig. 2022 as a centre of motion, and as this line is parallel to the face of the emery wheel it follows that if the drill were given a full revolution its circumference would be ground to a cylinder as shown in Fig. 2021 by the dotted lines.
In this machine the drill is rocked on the line b, Fig. 2023, as a centre of motion, this line corresponding to the axis of the shaft of lever f in Fig. 2019 upon which the chuck swings, and to the line b in Fig. 2024. As a result the surface is ground to the form of a cone as denoted by the dotted lines in Fig. 2024. The results of the two systems are shown in Figs. 2025 and 2026, which represent the conical holes made by a drill.
Section.
Fig. 2025.
Section.
Fig. 2026.
[II-42]In Fig. 2025 a cylinder r is shown lying in a conical recess, and end views of the cylinder are shown at v and w. Now suppose the line of contact of the roll or cylinder upon the recess represents the cutting edge of the drill, and that we consider the clearance at the outer end, and at that part that in revolving would describe the circle q, and on referring to circle v and the outer circle of the recess, and also to circles w and q, it is seen that there is more clearance for v than there is for w, and that the clearance of the latter would be still less if q were of smaller diameter, and it follows that the clearance is less in proportion as the point of the drill is approached. In determining the amount of clearance, therefore, we are compelled to make it sufficient for the point of the drill, and this under this system of grinding is excessive for the outer diameter of the drill, causing it to dull quickly, it being borne in mind that as the outer corner of the cutting edge of a drill describes the largest circle of any point of the cutting edge it obviously performs the most cutting duty in removing metal, and furthermore revolves at the highest rate of cutting speed, both of which cause it to dull the most rapidly. In Fig. 2026 we have a cone r lying in the coned recess, an end view of the cone being shown at v and w, and if we again consider the line of contact of the cone on the recess to represent the cutting edge and the circumferential surface of the cone as the end surface of the drill, we observe in the end views v and w that the clearance is equal for the two positions, or by varying the degree of taper of the cone we may regulate the amount of clearance at will. It is found preferable, however, to give more clearance as the point of the drill is approached so as to increase the cutting capacity; hence, in this case, the outer corner of the drill has the least clearance, which greatly increases its endurance for the reasons already mentioned, and which were further pointed out in the remarks upon drilling in the lathe. There remains, however, an additional advantage in this method of grinding which may be pointed out, inasmuch as that the clearance produced by the method shown in Fig. 2019, while capable of being governed from end to end of the cutting edge, yet increases as the heel of the land is approached, making the central cutting edge (c, Fig. 2028) more curved in its length so that it approaches[II-43] the form of cutting edge of the fiddle drill and this enhances its cutting capability.
Referring again to the general view of the machine in Fig. 2019, the chuck is supported or carried by the shaft having the ball lever f, which is clearly seen in the rear view, Fig. 2027, and the rod carrying the sleeve b (which holds the centre for supporting the shank end of the drill) is secured to the back of the chuck, as seen in the same figure. When, therefore, lever f is moved over, the drill is moved through an arc of a circle of which the axis of the shaft of f is the centre, and this it is that gives clearance to the cutting edge of the drill.
The drill being chucked, the emery wheel is brought up to it by means of the hand wheel e, which moves the frame c laterally, the grinding being done by the side face of the emery wheel. On the same shaft as e is a lever which may be used in connection with the stop or pin (against which it is shown lying) to enable an adjustment of the depth of cut taken by the wheel separately when grinding each lip, and yet to permit both cutting edges of the drill to be gauged to the same length.
Suppose, for example, that the point of a drill has been broken so that it requires several cuts or traverses of the emery wheel to bring it up to a point again; then when this has been done on one cutting edge the lever may be set to the stop, so that when the grinding of the second cutting edge has proceeded until the lever meets the stop both edges will be known to be ground of the same length, and will, therefore, perform equal cutting duty when at work.
The depth of cut being adjusted, the lever d is operated to pass the side face of the emery wheel back and forth along the cutting edge of the drill, this lever rocking the frame c on which the emery wheel is mounted back and forth in a line parallel to the cutting edge of the drill. Different angles of one cutting edge of the drill to the other are obtained by swivelling the frame carrying the shaft of lever f. The emery wheel is cased in except at a small opening where it operates upon the drill, and may, therefore, be liberally supplied with water without the latter splashing over. Water is continuously supplied to the emery wheel by an endless belt pump, which also delivers water on the end of the drill, enabling heavy grinding cuts to be taken without danger of softening the drill at the cutting edge, which is otherwise apt to occur. The following is the method of operating the machine: Open the jaws of the chuck by means of the hand wheel a, insert the drill from the back of the chuck towards the face of the stone, letting the end of the drill rest on the lower jaw, with the cutting edge just touching the end stop; close the jaws temporarily, while the back centre b is run up and clamped; then release the jaws, hold the drill back against the back centre b with the left hand, at the same time rotating hard against the two side stops on the jaws; then tightly closing the jaws, clamp the drill by means of the hand wheel a, using the right hand for this purpose. Throw ball-handle f part way back, and by means of hand wheel e feed up the stone until it just touches the drill. Bring ball-handle f forward and give additional feed; pass the stone over the face of the drill, back and forth, by lever d, moving ball-handle f back a little between each two cuts. This slices off the stock to be removed; then when entirely over the face of the lip being ground, hold lever d stationary, and rotate the drill against the stone by means of ball-handle f. By this means a heavy slicing cut can be taken and a final smooth finish obtained without any risk of drawing the temper of the drill.
When one lip has been thus formed, slack up the jaws of the chuck, turn the drill half around, pressing its lips as before against the side stops on jaws, and at the same time be sure to hold the drill firmly back against the back centre b (pay no attention to the end stop, which is only used in locating the drill endways in the first setting), tighten chuck, and grind the second lip without any readjustment of the stone. The lips will then be of equal length. During all these manipulations the stop that is arranged in connection with hand wheel e can be slack, and may rest against the pin in the bed made to receive it.
Fig. 2027 represents a rear view of the machine, at which there is an attachment for thinning the point of the drill, which is advantageous for the following reasons. In Fig. 2028 we have a side and an end view of a twist drill, and it can be shown that the angular piece of cutting edge c that connects the two edges a and b cannot be given sufficient angle to make it efficient as a cutting edge without giving clearance and angle excessive to the edges a and b.
In Fig. 2029 we may consider the angle of the cutting edge at the corner h and at the points f and g. First, then, it is obvious that the front face for the point h is represented by the line h h, that for f by line f f, and that for g by g g, and it appears that[II-44] on account of the spiral of the flute the front face has less angle to the drill axis as the point of the drill is approached.
Considering the end of the drill, therefore, as a cutting wedge, and considering the cutting edge at the two points c and e, in Fig. 2030, the end face being at the same angle, we see that the point c has the angle a and point e the angle b; at the drill point there will be still less cutting angle, and it has, therefore, the least cutting capacity. To remedy this the attachment shown in the figure is employed, consisting of a frame or head carrying a thin emery wheel, and capable of adjustment to any angle to suit the degree of spiral of the drill flute.
By means of this emery wheel a groove is cut in the flute at the point of the drill, as shown in Fig. 2031, at a and b, thus reducing the length of c, and therefore increasing the cutting capacity and correspondingly facilitating the feed of the drill. It is found, indeed, that by this means the drill will perform 15 per cent. more duty.
It is obvious, however, that as the thickness of drills at the point increases in proportion to the diameter of the drill, this improvement is of greater advantage with large than with small drills. The reason for augmenting the thickness at the centre with the drill diameter is that the pressure of the cut acts to unwind the spiral of the drill, and if the drill were sufficiently weak at its axis this unwinding would occur, sensibly enlarging the diameter of hole drilled, more especially when the drill became partly dulled and the resistance of the cut increased. By means of the small grooves a and b, however, the point is thinned while the strength of the drill is left unimpaired.
| VOL. II. | EMERY GRINDING MACHINERY. | PLATE IV. |
 |
||
| Fig. 2032. | ||
 |
||
| Fig. 2033. | ||
[II-45]Fig. 2032 represents Brown & Sharpe’s surfacing grinder, designed to produce true and smooth surfaces by grinding instead of by filing. In truing surfaces with a file a great part of the operator’s time is occupied in testing the work for parallelism, and applying it to the surface plate to test its flatness or truth, whereas in a machine of this kind both the parallelism and the truth of the work are effected by the accurate guiding of the machine table in its guideways. Furthermore, a high order of skill is essential to the production of work by filing that shall equal for parallelism and truth work that is much more easily operated upon in the machine. The machine is provided with two feed motions, the first of which is in a line parallel with the axis of the emery wheel driving spindle, and is communicated (by means of the small hand wheel on the right) to the lower table, which moves in V-guides provided upon the base plate of the machine. Upon this lower, and what may be termed cross-feed table slides, in suitable guideways, the work-holding or upper table, which is operated (by the large hand wheel) to traverse the work back and forth beneath the grinding wheel. Both these feed motions are operated by hand, automatic feed motions being unnecessary for work of the size intended to be operated upon in this machine. The grinding wheel spindle is carried in a bearing carried in a vertical slide, and is fed to its depth of cut by means of the vertical feed screw and hand wheel shown. The spindle passes through the bearing and carries a pulley at the back of the machine, which pulley is driven by a belt passing over idler pulleys at the back of the machine, by means of which the tension of the driving belt may be regulated.
Fig. 2033 represents The Tanite Co.’s machine for surface grinding such work as locomotive guide bars. The emery wheel n is mounted beneath a table t, whose upper surface is planed true, and which has two cylindrical stems c d fitting into the bored guides e. The stems are threaded at their lower ends to receive a screw, on the lower end of which is a bevel-gear f meshing into a similar gear g on the shaft actuated by the hand wheel w, hence by operating w the height of the table face may be adjusted to suit the diameter of the wheel.
The surface to be ground is laid upon the face of the table, and the operator moves it by hand, slowly passing it over the emery wheel, which projects slightly through the opening shown through the centre of the table. The operator stands at the end of the machine so as to be within reach of the wheel, and the direction of rotation is towards him, so that the work requires to be pushed to the cut and is not liable to be pulled too quickly across the table by the emery wheel.
Fig. 2034 represents an emery grinding machine for grinding the bores of railroad car axle-boxes. The circumference of the emery wheel is dressed to the curvature of the box bore by a diamond tool a which swings on a centre in its frame, and can be adjusted to any arc. Once set, it can only turn the prescribed arc with accuracy. In order to avoid the necessity of the foreman having to set the tool, a gauge is also furnished. This consists of a spindle adjustable with a nut in such a way that its two points rest in the centres on which the diamond tool revolves. It is only necessary for a disk b turned accurately to the diameter of the bearing, to be prepared, and this the apprentice can place on the spindle, adjust the latter, and screw down the diamond tool until it touches the periphery of the disk. A nut is then fastened on the diamond tool, and the frame is lifted on the ways beneath the wheel, when the moving of the handle turns the face of the wheel to the exact circle desired.
To adjust the brass in the chuck c, it is first set on the axle d. The chuck is then placed on frame e, in such a way that the Vs fit. Handle f then moves a cam that clamps the brass between the jaws g, one set of which swings on a pivot at h. The brass is thus adjusted in such a manner that, despite the imperfections in moulding, it is ground accurately with the least removal of metal. The chuck c fits into planed guides on the table i, and is thus brought in exact line with the motion of the wheel. The crank j serves to move the table to and fro on the rods k, and the table also rises and falls on planed ways, being pressed up by springs. The hand wheel gives vertical adjustment to the whole bed by means of a chain beneath it. There is a pulley by which a suction fan, to remove dust, &c., may be driven. The machine is capable of fitting from 150 to 500 car brasses per day.
Fig. 2035 represents an emery planing machine. The emery wheel, which takes the place of the cutting tool of an ordinary shaping machine, is upon a spindle driven by the pulley a upon the spindle b, which is traversed endways by means of the connecting rod which is actuated by a crank e driven by the cone pulley c. The work-holding table g is traversed by the handle k or automatically through wheel h, which through suitable gearing drives the spindle i. The blower or fan is to draw off the cuttings and emery. It is obvious that any of the usual forms of work-holding devices may be employed.
Fig. 2036 represents an ordinary form of emery grinding machine for general purposes. a represents the frame affording journal bearing for the driving spindle driven by the cone pulley p, having the fast flanges f and collars c, which are screwed up to hold the emery wheel by the nut n, the direction of spindle rotation being denoted by the arrows. The thread at the end k of the spindle must be a right-hand one, and that at the other end l must be a left-hand, so that the resistance against the nut shall in both cases be in a direction to screw the nuts up and cause them to bind or grip the wheels more firmly, and not unscrew and release the wheels. Upon the frame a are the lugs d to carry the hand rests r and s, which are adjustable, and are secured in their adjusted position by the handle nuts e. The rest s is of the same form and construction as a lathe hand rest, while that at r is angular, to support the tool while applying it to the side as well as to the circumference of the wheel.
Fig. 2037 represents a machine for grinding the knives for wood-planing machines, and having a hand feed only. It consists of an emery wheel mounted upon a spindle and with a slide rest in front of it. Mounted on the slide rest is a frame for holding the knife, and a set-screw for adjusting the angle of the knife to the wheel. The slide rest is traversed by means of the hand wheel operating a pinion in the rack shown.
Fig. 2038 represents a swing frame for carrying and driving an emery wheel to be used on the surfaces of castings, its construction permitting it to be moved about the casting to dress its surface. The overhead countershaft carries the grooved driving wheel a. At b is a vertical shaft pivoted at i by the forked bearing which swings upon the countershaft. The fork l at the lower end of shaft b carries a shaft on which is the fork c′, c having journal bearing on it, and the driving pulley j. Fork d has journal bearing on the same shaft as pulley j, and is fast upon the rod or arm e, which affords journal bearing to the emery wheel k on a shaft having handles h h. Motion to the emery wheel is conveyed through the belts f and g. To counterbalance the frame the weight w is employed, permitting the frame to be readily swung. The upper fork carrying b, being pivoted to the shaft of a, permits b to swing to any required position. The pivot at i permits b to rotate in a vertical plane; the pivot of c′ c at d affords vertical movement to e; the pivot at d allows e to rotate about its own[II-47] axis, hence the wheel k can be moved about laterally, raised, lowered, or have its plane of revolution varied at will by simply swinging the handles h h to the required plane. The emery-wheel shaft is pivoted upon the fork carrying it, so that the emery wheel can be turned to stand in a horizontal plane if desired.
Fig. 2039 represents an emery belt machine, in which the belt runs vertically and its tension is adjusted by the idler pulley shown at the top of the frame.
It is obvious that if a piece of work, as a in Fig. 2040, be held steadily upon the rest r, its end will be ground to the curvature of the emery wheel w, and that if it be required to grind the surface flat the piece must be raised and lowered as denoted by the dotted lines, the amount of this motion being determined by the thickness of the piece.
Furthermore, if the piece of work be of a less width than the thickness of the wheel, as in the top view in Fig. 2041, the work a will wear a groove on the wheel, and its side edges will therefore become rounded off unless it be given sufficient motion in the direction of d and e to cause it to traverse across the full width of the wheel face, and as this motion would require to be simultaneous with the vertical motion explained with reference to Fig. 2040, it is not practicable to grind true level surfaces upon the perimeter of the wheel. As the sides of the wheel are flat, however, it is self-suggestive to apply the work to the side faces. But in this case, also, that part of the wheel surface that performs grinding duty will gradually wear away, leaving a shoulder or projecting surface upon the wheel.
Suppose, for example, that in Fig. 2042 the duty has been confined to that part of the wheel face from a to the perimeter and the wheel would wear as shown, the result being the same whether the width or distance from the shoulder a to the perimeter of the wheel represents the width of the work held steadily against the wheel or the traverse of a narrower piece of work.
This difficulty may be overcome by recessing the wheel face, as in Fig. 2043, in which the wheel is shown in section.
In some cases, as for grinding the knives for wood-working machines, hollow cylindrical wheels, such as in Fig. 2044. are used, the duty being performed on the end face b b of the wheel, and the work being traversed in the direction of the arrows. The wheel is here gripped between the flange f and the collar c, which fits accurately to the end of the driving spindle s, so as to be held true, and secured by screws passing through c and into f, or the end of s may be threaded to receive a nut to screw against c.
The circumferential surface of a wheel may be employed to grind a flat surface, providing that the work be traversed to the wheel, as in the side view in Fig. 2045. In this case, however, the cut must be taken while the work p is travelling in the direction denoted by the arrow j, and no cutting must be done while the work is travelling back in the direction of k. After the work has traversed back in the direction of k, and is clear of the wheel, the cut is carried farther across the work by moving or feeding the work in the direction of the arrow in the front view, Fig. 2046. In this case the whole surface of the work passes beneath the wheel thickness, and the wheel face wears parallel to the wheel axis, producing a true plane (supposing the work to be moved in straight lines), save in so far as it may have been affected by the reduction of the diameter of the emery wheel from[II-48] wear, which is not found sufficient to be of practical importance. If the whole surface of the work does not pass across or beneath the wheel thickness the wheel face may wear taper. Suppose, for example, that in Fig. 2047, p is a piece of work requiring to have produced in it a groove whose bottom is to be parallel to the lower surface f. Then the upper work surface being taper the thick side a would wear away the side b of the wheel, and the groove ground would not be parallel to f.
Another method of grinding flat surfaces is to mount the emery wheel beneath a table t in Fig. 2048, letting the top of the wheel emerge through an opening in the table, and sliding the work upon the trued upper surface of the table. The surface of the table thus becomes a guide for the work. To obtain true work in this way, however, it is necessary that the cut taken by the emery wheel be a very light one, as will be perceived from the following considerations.
In Fig. 2049 t represents a table and b a guide bar thereon. The depth of cut taken will be equal to the height the emery wheel projects above the surface a of the table, hence when the bar has been moved nearly half-way across the table its surface will be as in Fig. 2050, the bar occupying the position shown in Fig. 2051. Now the part of the bar that has passed over the table will not rest upon it as is shown in Fig. 2051. When the bar has passed over the emery wheel more than half of the bar length, its end f, Fig. 2052, will fall to meet the half d of the table, and end e will lift from the half c of the table, causing the bar surface to be ground rounding in its length. If, however, the cut taken be a very light one the surface may be ground[II-49] practically true, because the bar will bend of its own weight and lap down to fit the table at both ends. Furthermore it will be noted that in the case of a large surface in which the wheel might sensibly wear in diameter before it had operated over the whole of the work surface, the table may be lowered or the wheel may be raised (according to the construction of the machine), to offset the wear of the wheel, or rather to take it up as it were.
Polishing Wheels.—For polishing purposes as distinguished from that of grinding, various forms of polishing wheels are employed. For the rougher class of polishing, wooden wheels covered with leather coated with fine emery that is allowed to glaze are employed. For a finer degree of polish the wheels are covered with lead to which various polishing materials are occasionally applied, while for the finest polishing rag or buff wheels are the best. Wooden polishing wheels are built up of sections of soft wood fastened together by gluing, and with wooden pegs in place of nails or screws.
The joints of the sections or segments are broken—that is to say, suppose in Fig. 2053 that 1, 2, 3, &c., up to 6, represent the joints of the six sections of wood forming one layer of the wheel, the next six sections would have their joints come at the dotted lines a, b, c, &c., up to f. To prevent them from warping after being made into a wheel it is advisable to cut out the sections somewhere near the size in the rough and allow them to lie a day or two before planing them up and fitting them together; the object being to allow any warping that may take place to do so before the pieces are worked up into the wheel, because if the warping takes place afterwards it will be apt to throw the wheel out of true, whereas it is necessary that these wheels be very true, not only so that they may not prove destructive to their shaft bearings, but that they may run steady, and not shake or terrible, and because the work can be made much more true and smooth with a true than with an untrue wheel. Only one layer of segments should be put on in one day, and they should be put on as quickly as possible after the glue is applied, so that the latter shall not get cold. So soon as each segment is put into its place it should be clamped firmly to its seat and driven firmly up to the joint of the next one, and when the layer is completed it should be left clamped all night to dry. In the morning one clamp should be removed, and that section fastened by boring small holes and driving therein round and slightly tapered soft-wood pegs of about 1⁄4 inch diameter. The whole of the sections being pegged the next layer of segments may be added, and so on until the required width of wheel is attained. The whole wheel should then be kept two days before it is turned, and as little as possible should be taken off in the turning process. The circumferential surface should be turned slightly rounding across its width, and as smoothly as possible. It is practicable to proceed with the construction of the wheel without waiting between the various operations so long as here advised, but the wheel will in that case be more apt to get, in time, out of true. To cover the circumference of the wheel sole leather is used, its thickness being about 1⁄4 inch; it should be put on soft and not hardened by hammering at all, and with the flesh side to the wood. The joint of the leather should not be made straight but diagonal with the wheel face, the leather at the edge of the joint being chamfered off, as shown in Fig. 2054 at a, and the joint made diagonal, as shown in Fig. 2055 at a.
If the leather were put on with a square butt joint there would likely be a crease in the joint, and the emery or other polishing material would then strike the work with a blow, as well as presenting a keener cutting edge, which would make marks in[II-50] the work no matter what pains might be taken to prevent it. This, indeed, is found to occur to a slight extent upon very fine polishing, even when the joint of the leather is made as above; and the means taken to obviate it is to not put any polishing material on the immediate joint and to wipe off any that may get there, leaving 1⁄10 inch clear of polishing material. It is obvious that in fastening the wheel to its shaft it should be put on so that it will run in the direction of the arrow, providing the operator works with the wheel running from him, as is usually the case with large wheels, that is to say, wheels over 18 inches in diameter. In any event, however, the wheel should be put on so that the action of the work is to smooth the edge of the leather joint down upon the wheel, and not catch against the edge of the joint, which would tend to rough it up and tear it apart. The leather should be glued to the wheel, which may be slightly soaked first in hot water. The glue should be applied very hot, and the leather applied quickly and bound tightly to the wheel with a band. One end of the leather may be first glued to the wheel and fastened with a few tacks to hold it while it is stretched tightly round the wheel; the leather itself should be softened by an application of hot water, but not too much should be applied. After the leather is glued to the wheel it is fastened with soft wooden pegs, about 3⁄16 inch in diameter, driven through the leather into the wood and cut off slightly below the surface of the leather.
Wheels of this kind are sometimes made as large as 5 or 6 feet in diameter, in which case the truth of the wheel may be preserved by letting in a wrought-iron ring, as shown in Fig. 2056, fastening the rings with wood screws. The wheels thus constructed are covered with emery of grades varying from No. 60 to 120, and flour emery. The coarser grades perform considerable cutting duty as well as polishing. The manner of putting the emery, and fastening it, upon the wheel is as follows:—The face of the wheel is well supplied with hot glue of the best quality, and some roll the wheel in the emery, in which case the emery does not adhere so well to the leather as it does when the operation is performed as follows:—Let the wheel either remain in its place upon the shaft, or else rest it upon a round mandrel, so that the wheel can revolve upon the same. Then apply the hot glue to about a foot of the circumference of the wheel, and cover it as quickly as possible with the emery. Then take a piece of board about 3⁄4 inch thick and 28 inches long, the width being somewhat greater than that of the polishing wheel, and placing the flat face of the board upon the circumferential surface of the wheel, work it by hand, and under as much pressure as possible, back and forth, so that each end will alternately approach the circumference of the wheel, as illustrated in Fig. 2057, the movement being indicated by the dotted lines. By adopting this method the whole pressure placed upon the board is brought to bear upon a small area of the emery and leather, and the two hold much more firmly together than would be the case if the circumference of the wheel were glued and then rolled in a trough of emery, because the time occupied in spreading the glue evenly and properly over the whole wheel surface would permit it to cool before receiving the emery, whereas it is essential that the glue be hot so that it may conform itself to the shape of the grains of emery and hold them firmly.
The speed at which such wheels are used is about 7,000 feet per minute. The finest of emery applied upon such wheels is used for cast iron, wrought iron, and steel, to give to the work a good ordinary machine finish; but if a high polish or glaze is required, the wheels are coated with flour emery, and the wheel is made into a glaze-wheel by wearing the emery down until it gets glazed, applying occasionally a little grease to the surface of the wheel. Another kind of glaze-wheel is made by covering the wooden wheel with a band of lead instead of a band of leather, and then applying to the lead surface a mixture of rouge, crocus and wax, worn smooth by applying to it a piece of sheet steel or a piece of flint-stone before applying the work. Others add to this composition a little Vienna lime. For flat surfaces, or those requiring to have the corners or edges kept sharp, it is imperative that such wheels as above described—that is to say, those having an unyielding surface—be used; but where such a consideration does not exist, brush and rag wheels may be used. In Europe comparatively large flat surfaces requiring a high polish are finished upon wooden wheels made of soft wood and not emeried, the polishing material employed being Vienna lime. The lime for ordinary use is mixed with water, and is applied by an assistant on the opposite side of the wheel to the operator. For superfine surfaces the Vienna lime is mixed with alcohol, which increases its efficiency; and here it may be as well to note that Vienna lime rapidly deteriorates from exposure to the air, so that it should be kept as little exposed as possible.
Brush-Wheels.—These are polishing wheels of wood with a hair brush provided around the circumference. These wheels are excellent appliances, whether employed upon iron, steel, or brass. Their sizes run from 11⁄2 inch to about 8 inches in diameter, and the hair of the brush should not exceed from 1 to 11⁄4 inches in length. The speed at which they should be run is about 2,500 for the largest, and up to 4,500 revolutions per minute for the smaller sizes. In ordinary grinding and polishing practice in the United States, brush wheels are used with Vienna lime in all cases in which the lime is used by itself—that is to say, unmixed with wax, crocus, or rouge, or a mixture of the same. In watchmaking, however, and for other purposes in which the truth of the work is an important element, Vienna lime is applied to wooden or even metal, such as steel, polishing wheels, which are in this latter case always of small diameter. An excellent polishing composition is formed of water 1 gill, sperm oil 3 drops, and sufficient Vienna lime to well whiten the mixture. The brush may be let run dry during the final finishing. For polishing articles of intricate shape, brush wheels are superior to all others. If the articles to be polished are of iron, or steel, the first stage of the process is performed with a mixture of oil and emery, Vienna lime being used for final finishing only. The wheels to which Vienna lime is applied should not be used with any other polishing material, and should be kept covered when not in use, so as to keep them free from dust.
For brass work, brush wheels are used with crocus, with rouge, or with a mixture of the two, with sufficient water, and sometimes with oil, to cause the material to hold to the brush and not fly off from the centrifugal force. For very fine brass polishing, the first stages are performed with powdered pumice-stone mixed with sufficient oil to hold it together. This material has considerable[II-51] cutting qualifications. The next process is with rouge and crocus mixed, and for very fine finishing rotten-stone.
Solid leather wheels are much used by brass-finishers. The wheels are made of walrus hide glued together in disks, so as to obtain the necessary thickness of wheel. The disks are clamped between pieces of board so soon as the glue is applied, so as to make a good joint, and also keep the wheel flat and prevent it from warping during the drying process. Such wheels may be run at a velocity of 8,000 feet per minute, and with any of the polishing materials already referred to. After the wheel is made and placed upon its spindle or mandrel it may be turned true with ordinary wood-turning tools—and it may here be remarked that rag wheels may be trued in the same way. The spongy nature of these wheels renders them very efficient for polishing purposes, for the following reasons: The polishing materials become imbedded in the leather and are retained, and become mixed and glazed with a fine film of the material being polished, which film possesses the very highest polishing qualifications. These walrus wheels may be used with pumice, crocus, rouge, or Vienna lime, according to the requirements of the case, or even with a mixture of flour emery and oil; and they possess the advantage of being less harsh than leather or lead-covered wheels, while they are more effectual than the latter, and will answer very well for flat surfaces.
Rag polishing wheels are formed of disks of rags, either woollen or strong cotton, placed loosely side by side, and clamped together upon the mandrel at the centre only. Their sizes range usually from 4 to 8 inches in diameter, and they are run at a speed of about 7,000 feet per minute. They assume a disk form when in motion from the centrifugal force generated from the great speed of rotation. They are used for the fine polishing only, and not upon work requiring the surfaces to be kept very flat or the corners very sharp. For use upon steel or iron, they are supplied with a polishing material composed of Vienna lime 3 parts, crocus 3 parts, beeswax 3 parts, boiled up together, allowed to cool off, and then cut into cakes. These cakes are dipped in oil at the end, which is then applied to the rag wheel occasionally during the polishing process. For brass-work, an excellent polishing composition is composed of crocus 2 parts, wax 1 part, rouge 1⁄8 part, the wax being melted, and the ingredients thoroughly mixed. This mixture gives to the metal a rich color. It is dipped in oil and then applied to the rag wheel. It may be used to polish fine nickel-plating, for which purpose it is an excellent material. Nickel-plated articles having sharp corners should be polished with fine rouge mixed with clear water and a drop of oil, the mixture being applied to the rag wheel with the finger of the operator. Any of the compositions of rouge, crocus, and rotten-stone may be used for brass, copper, or nickel-plated work upon rag wheels, while for iron or steel work the same materials, separate or in combination, may be used, though they are greatly improved by the addition of Vienna lime. When, however, either of these materials is used singly, it should be applied to the rag wheels with a brush; and if it is used dry, it must be at a greatly reduced speed for the wheel, which is sometimes resorted to for very fine polishing.
Fig. 2058 represents a polishing device used to polish the surface of engravers’ plates. It consists of a spindle d, carried in bearings b, and, having no collars, it is capable of end motion through those bearings. The spindle is pressed downward by a spring a, carrying at its end a piece c, which is capped to receive the end of the spindle d and the piece e which threads into the spindle, thus making a sort of universal joint. The spindle d is run by the pulley p, and carries a piece of stone s, the work w resting upon the plate or table t. The stone being set to one side of the centre of the spindle, each part of its surface describes a circle, the centre of which is outside of the stone, thus making the effectiveness of the centre of the stone greater by increase of motion. To raise the stone from the work the spindle is raised by means of the chord f, or the table t may have a simple lever motion. The work is moved about and around and beneath the revolving stone. Water, oil, benzine or alcohol is used to keep the stone clear and wash away the cuttings. The device saves a good deal of hand work in the preparatory stages of grinding, although it can be used only with soft stones.
Grindstones and Tool Grinding.—The general characteristics of grindstones are as follow:—
For rapid grinding a coarse and an open grit is the most effective. The harder the grit the more durable the stone, but the liability of the stone to become coated or glazed with particles of the metal ground from the work is increased. With a given degree of coarseness a soft grit stone will grind a smoother surface than a hard grit one.
The finer the grit the smoother the surface it will grind. In all stones, however, it is of prime importance that the texture be even throughout the stone, because the soft or open-grained part will wear more rapidly than the close or hard grained. All grindstones are softer when water-soaked than when dry, and will cut more freely, because the water washes away the particles of metal ground from the work, and prevents them from glazing the stone. It follows from this, however, that a stone should not be allowed to rest overnight with its lower part resting in water, as the wear of the stone will be unequal until such time as it has become equally saturated. Furthermore the balance of the stone is destroyed, and if run at a maximum speed, as in the case of stones used to grind up large edge tools, the unbalanced centrifugal force generated on the water-soaked side may cause the stone to burst. The following stones are suitable for the class of work named:—
| FOR GRINDING MACHINISTS’ TOOLS. | |||
| Name of stone. | Kind of grit. | Texture of stone. | Color of stone. |
| Nova Scotia. | All kinds, from finest to coarsest. | All kinds, from hardest to softest. | Blue or yellowish grey. |
| Bay Chaleur (New Brunswick). | Medium to finest. | Soft and sharp. | Uniformly light blue. |
| Liverpool or Melling. | Medium to fine. | Soft, with sharp grit. | Reddish. |
| FOR WOOD-WORKING TOOLS.[II-52] | |||
| Name of stone. | Kind of grit. | Texture of stone. | Color of stone. |
| Wickersly. | Medium to fine. | Very soft. | Greyish yellow. |
| Liverpool or Melling. | Medium to fine. | Soft, with sharp grit. | Reddish. |
| Bay Chaleur (New Brunswick). | Medium to finest. | Soft and sharp. | Uniform light blue. |
| Huron, Michigan. | Fine. | Soft and sharp. | Uniform light blue. |
| FOR GRINDING BROAD SURFACES, AS SAWS OR IRON PLATES. | |||
| Name of stone. | Kind of grit. | Texture of stone. | Color of stone. |
| Newcastle. | Coarse to medium. | The hard ones. | Yellow. |
| Independence. | Coarse. | Hard to medium. | Greyish white. |
| Massillon. | Coarse. | Hard to medium. | Yellowish white. |
The flanges for grindstones should be trued on both faces, and should pass easily over the grindstone shaft, and there should be between these collars and the stone an elastic disk, as of wood or felt, which will bed fully against the surface of the stone. It is preferable also if the under faces of these collars be recessed to within an inch of their perimeters so as to confine the grip to the outer edges of the faces.
The process of grinding large surfaces is entirely distinct from that of small ones, because of the difficulty in the former of getting rid of the cuttings. As an illustration of this point it may be remarked that a stone that has become dulled and glazed from operating upon a broad area of surface, as say a large plate, may be both cleaned of the cuttings and sharpened by grinding upon it a roller of, say, 1 or 11⁄4 inches in diameter. This roller is laid across the “horn” or rut of the stone, and pressed firmly against it, the bar being allowed to slowly rotate. What is commonly termed grinding is the class of grinding that is followed as a trade, such as file grinding, saw grinding, plate grinding, edge tool and cutlery grinding. In all this class of grinding the speeds of the stones is very much greater than for machine-shop tool grinding. For all the above, save cutlery grinding, the stones when new are of a diameter from 5 to 8 feet, and of a width of from 8 to 15 inches. The stones used by cutlers are about 15 inches in diameter, and from 1⁄2 inch to 3 inches thick. The average speed of grindstones in workshops may be given as follows:—
| Circumferential speed of stone. |
||||
| For grinding | machinists’ | tools, about | 900 | feet per minute. |
| „ | carpenters’ | „ | 600 | „ |
The speeds of stones for file grinding and other similar rapid grinding is thus given in the “Grinders’ List.”
| Diameter of stone. |
Revolutions per minute. |
|
| ft. | in. | |
| 8 | 0 | 135 |
| 7 | 6 | 144 |
| 7 | 0 | 151 |
| 6 | 6 | 166 |
| 6 | 0 | 180 |
| 5 | 6 | 196 |
| 5 | 0 | 216 |
| 4 | 6 | 240 |
| 4 | 0 | 270 |
| 3 | 6 | 308 |
| 3 | 0 | 360 |
These speeds are obviously obtained by reducing the diameter of the pulley on the grindstone shaft each time the stone has worn down 6 inches less in diameter, and give a uniform velocity of stone if the 8 feet stone be driven with a pulley 32 inches in diameter. Each shift (or change of pulley) giving a pulley 2 inches less in diameter.
The following table (from the Mechanical World) is for the diameter of stones and the number of revolutions they should run per minute (not to be exceeded), with the diameter of change or shift pulleys required, varying each shift or change 21⁄2 inches, 21⁄4 inches, or 2 inches in diameter for each reduction of 6 inches in the diameter of the stone:—
| Diameter of stone. |
Revolutions per minute. |
Shift of pulleys in inches. | |||||
| 2 | 1⁄2 | 2 | 1⁄4 | 2 | |||
| ft. | in. | ||||||
| 8 | 0 | 135 | 40 | 36 | 32 | ||
| 7 | 6 | 144 | 37 | 1⁄2 | 33 | 3⁄4 | 30 |
| 7 | 0 | 154 | 35 | 31 | 1⁄2 | 28 | |
| 6 | 6 | 166 | 32 | 1⁄2 | 29 | 1⁄4 | 26 |
| 6 | 0 | 180 | 30 | 27 | 24 | ||
| 5 | 6 | 196 | 27 | 1⁄2 | 24 | 3⁄4 | 22 |
| 5 | 0 | 216 | 25 | 22 | 1⁄2 | 20 | |
| 4 | 6 | 240 | 22 | 1⁄2 | 20 | 1⁄4 | 18 |
| 4 | 0 | 270 | 20 | 18 | 16 | ||
| 3 | 6 | 308 | 17 | 1⁄2 | 15 | 3⁄4 | 14 |
| 3 | 0 | 360 | 15 | 13 | 1⁄2 | 12 | |
| 1 | 2 | 3 | 4 | 5 | |||
“Columns 3, 4, and 5 are given to show that if you start an 8 feet stone with, say, a countershaft pulley driving a 40 inch pulley on the grindstone spindle, and the stone makes the right number (135) of revolutions per minute, the reduction in the diameter of the pulley on the grinding-stone spindle, when the stone has been reduced 6 inches in diameter, will require to be also reduced 21⁄2 inches in diameter, or to shift from 40 inches to 371⁄2 inches, and so on similarly for columns 4 and 5. Any other suitable dimensions of pulley may be used for the stone when 8 feet in diameter, but the number of inches in each shift named, in order to be correct, will have to be proportional to the number of revolutions the stone should run, as given in column 2 of the table.”
In all grinding operations it is necessary that the stone should run true. This is sometimes accomplished by so mounting the stones in their frames that their perimeters touch at the back of each stone, one stone running slightly faster than the other. Or sometimes the work is placed between the two stones, as in Fig. 2059, which represents a plan frequently used to grind circular saws; c in the figure represents the grinding-stone and a the saw. Long saws are mounted vertically as in Fig. 2060, a representing a frame to which the upper end of the saw is attached and driven by a disk crank and connecting rod as shown, the two stones c e may, in this case, be of equal diameter.
[II-53]Fig. 2061 represents a grindstone truing device (for tool-grinding stones) in which a series of serrated disks are employed in place on a threaded roll. The disks are fed to the stone by the hand wheel and screw, and are traversed back and forth across the stone face by means of the lever handle shown.
The fast running grindstones used for heavy and coarse grinding are trued by a process known as hacking. The high spots of the stone are marked by holding a piece of coal to the stone while it revolves slowly, and a tool similar to an adze is used to cut or chop indentations in the stone. The highest spots will be most plainly marked by the coal, and the hacking is spaced closer together in these places, the hacking marks crossing each other and varying in depth to suit, obviously being deepest where the marks are blackest. The hacking also sharpens the stone. To prevent the stone from wearing uneven across its face the file grinder mounts the stone in a very ingenious manner, causing it to traverse automatically, back and forth, while rotating.
This device is shown in Fig. 2062, in which a represents the grindstone spindle having journal bearing at b b, but as there are no collars on the journals, a can move endwise through b b. Fast to a are the collars c and c′ (sometimes the face of the pulley hub is made to serve instead of c′); s is a sleeve fitting easily to a, and containing a return groove, as shown; d is a fixed arm carrying a pin which projects down into the groove of s, as shown; p is the pulley driving a, and w w are suspended weights. The operation is self-acting, as follows: The shaft revolving causes the sleeve to revolve by friction, and the pin causes the sleeve to move endwise; its end face abutting against the face of the collar on one side, or the face of the pulley on the other side, as the case may be, causing the shaft to travel in that lateral direction. When the pin has arrived at the end of the groove, the stone ceases lateral motion (there being left a little play between the faces of the sleeve and of the collar and pulley face for this special purpose), while the cam travels in the opposite lateral direction, getting fairly in motion until it strikes the face, when it slowly crowds the face over. In travelling to the right it crowds against the face of the collar c′, and in traveling to the left, as shown in the figure, against the face of the collar c. The swing thus given to the stone is a slow and very regular one, the motion exciting surprise from its simplicity and effectiveness, especially when it is considered that the friction of the rotation of a shaft about 21⁄2 inches diameter in a smooth hole about 6 inches long is all that is relied upon to swing a ponderous stone.
The following are the considerations that determine in grinding tools or pieces held by the hands to the grindstone. Upon the edge of a tool that last receives the action of the stone there is formed what is termed a feather-edge, which consists of a fine web of metal that bends as the tool is ground, and does not become detached from the tool in the grinding. The amount or length of this feather-edge increases as the work is thinner, and is greater in soft than in hardened steel. It also increases as the tool or piece is pressed more firmly to the stone.
| VOL. II. | GRINDSTONE GRINDING. | PLATE V. | |||
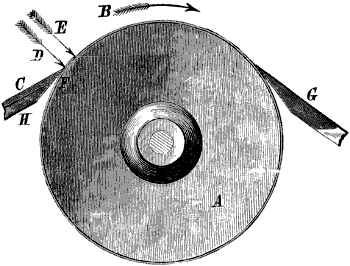 |
|||||
| Fig. 2063. | |||||
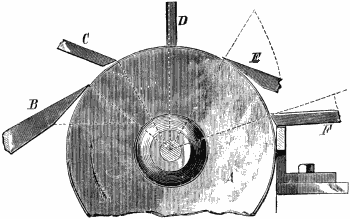 |
 |
||||
| Fig. 2064. | |||||
 |
Fig. 2065. | ||||
| Fig. 2066. | |||||
 |
|||||
| Fig. 2067. | |||||
To prevent its formation on such tools as plane blades or others having thin edges, the tool is held as at g in Fig. 2063, the top[II-54] of the stone running towards the workman, and the tool is held lightly to the stone during the latter part of the grinding operation. With the tool held on the other side of the stone as at c, and pressed heavily to the stone, a feather-edge extending as long as from d to e may be formed if the tool has a moderate degree only of temper, as, say, tempered to a dark purple. The feather-edge breaks off when the tool is put to work, or when it is applied to an oil-stone, leaving a flat place instead of a sharp cutting edge. In well-hardened and massive tools, such as the majority of lathe tools, the amount of feather-edge is very small and of little moment, but in thin tapered edges, even in well-hardened tools, it is a matter of importance.
After a tool is ground it is often necessary to remove the feather-edge without having recourse to an oil stone. This may be accomplished by pressing the edge into a piece of wood lengthways with the grain of the wood, and while holding the cutting edge parallel with the line of motion, draw it towards you and along the grain of the wood, which removes the feather-edge without breaking it off low down, as would be the case if the length of the cutting edge stood at a right angle to the line of motion.
The positions in which to hold cutting tools while grinding them are as follows: The bottom faces of lathe tools and the end faces of tools such as scrapers should be ground with the tool laid upon the grindstone rest as in Fig. 2064, the stone running in the direction of the arrow. The best position for thin work as blades is at f providing the stone runs true, for otherwise the tool edge will be liable to catch in the stone. With an untrue stone the position shown in Fig. 2065 is the best, the blade being slowly reciprocated across the face of the stone.
If the facet requires to be ground rounding and not flat the position at c, Fig. 2064, is the best, the work being moved to produce the roundness of surface. If the tool is to be ground hollow or somewhat to the curvature of the stone, as in Fig. 2066, the curve being from b to c, the position at b is the best. At position d the tool cannot be held steadily; hence, that position is altogether unsuitable for tool grinding purposes.
For grinding the top faces of lathe or planer tools or other similar shaped pieces that must be held with their length at a right angle (or thereabouts) to the plane of the rotation of the stone, the tool is held in the hands, and the hands are supported by the grindstone rest as in Fig. 2067, the fingers being so placed that should the tool catch in the stone it will slip from between the fingers and not carry them down with it upon the tool rest.
Tools to be ground to a sharp point should be ground at the back of the stone, that is to say, with the top of the stone running away from the operator, and the point should be slowly moved across the width of the stone to prevent wearing grooves in its surface.
To produce a finer edge than is possible with the grindstone, the oil-stone is brought into requisition, the shape of the oil-stone being varied to suit the shape of the tool. Three kinds of oilstone are in general use, Turkey stone, Arkansas stone, and Washita stone, the latter being softer and of inferior quality to the two former. The best quality of Arkansas stone is of a milky white color, of very fine and even grain, and very hard, being impervious to a file; but there are softer grades. An oil-stone should be of even grain throughout, so that it may wear even throughout, and produce a smooth and unscored edge. Arkansas stone is rarely obtainable in lengths above 6 inches, on account of the presence of fine seams of hard quartz, which wears less than the stone, and forms a projection that scores the cutting edge of the tool, and the same applies to the Turkey stones.
For tools fully hardened and not tempered the hardest oilstones are best; but for tools that are tempered, as tools for woodwork, a softer grade of stone is preferable, since it will cut the most free.
When an oil-stone has worn out of shape it may be dressed on a grindstone; but if a flat surface is required it is best to true it by a piece of coarse sand-paper laid upon a flat true surface.
The action of an oil-stone is to smooth the surfaces; but while doing this the oil-stone itself forms what is termed a wire-edge, which resembles a feather-edge, except that it is smoother and more continuous. It is caused by the weak edge of the blade giving way under the pressure with which it is held to the stone. To reduce the wire-edge as much as possible the tool is pressed very lightly to the oil-stone during the latter part of the stoning, and is frequently turned over. If the motion of the tool upon the oil-stone is parallel with the line of cutting edge, the wire-edge will be greater than if the line of motion were at a right angle to it.
Again, the strokes performed while the cutting edge is advancing upon the oil-stone produce less wire-edge than the return strokes, hence the finishing process consists of a few light strokes upon one and then upon the other facet repeated several times. Now let it be observed that, the wire-edge will never be turned toward the facet last oil-stoned, and cannot be obviated by the most delicate use of the stone; but after the stoning proper is finished, the operator will lay one facet quite level with the face of the stone, and then give to the blade, under a very light pressure, forward diagonal motion, and then perform the same operation with the other facet upon the stone, the last facet operated upon being usually the straight and not the bevelled one. To still further reduce the wire-edge for very fine work, the operator sometimes uses a piece of leather belt, either glued to a piece of wood, as upon the lid of the oil-stone box, or some attach it at each end to projecting pieces of wood, while yet others lap the tool upon the palm of the hand. In giving an edge to a razor, the process may be carried forward in the usual way by means of straps, the first strokes being long ones made under a slight pressure, the strokes getting shorter and the pressure lighter as the process proceeds, until at last the motion and contact are scarcely perceptible.
When, as in the case of plane blades and carpenters’ chisels, the area of face is large, it is advantageous to grind the face somewhat concave, as in Fig. 2068, so that the heel and the point only of the tool has contact with the oil-stone, thus reducing the area to be stoned and steadying the tool, because, the area being small, the heel as well as the edge may be allowed to rest upon the oil-stone without unduly prolonging the stoning operation.
| VOL. II. | FULL AUTOMATIC GEAR CUTTER. | PLATE VI. |
 |
||
| Fig. 2069. | ||
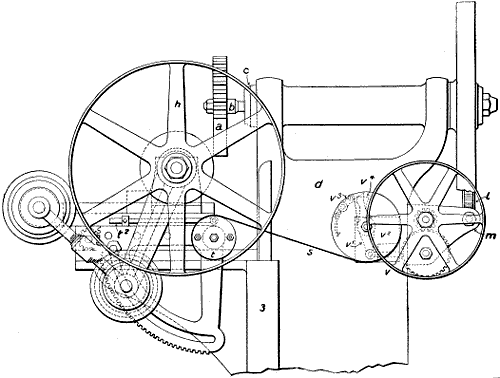 |
||
| Fig. 2070. | ||
The Brainard automatic gear cutter, Figs. 2069, 2070, 2071 and 2072 is arranged to cut spur, bevel, and worm-wheels, and is of that class where the manipulations required in gear cutting are all performed by the machine itself, thus dispensing with the care of an attendant except to place the wheels in position and set the machine for the proper depth and length of cut. The manner in which these results are accomplished will be seen from the following description, reference being had to the engravings. The wheel to be cut (a, Fig. 2070) is held upon a mandrel b fitted to the spindle c, which is mounted in firm bearings upon a column or standard d. To the face of the standard is gibbed a sliding knee e. Upon this knee is placed the cutter slide f, which is arranged to be inclined for bevel-gear cutting, and to be swung aside in cutting worm-wheels. Rotary cutters are carried on arbors fitted to the cutting spindle (g, Fig. 2071). Power for driving the cutter is applied to the pulley h, mounted upon the cutter spindle.
The cutter slide f is operated through the medium of a screw and bevel-gears from a shaft h1, which is arranged to revolve alternately in opposite directions from a continuous motion of the driving cone pulley t, receiving, motion from the feed pulley i, through the means of a swinging arm, carrying a receiving pulley and cone as is shown in Fig. 2069.
The method of obtaining these opposite motions of the shaft h1 will be seen in Fig. 2071. To the block h2 which supports the shaft h1 is secured a gear h3, which engages with a pinion h4 mounted loosely on the cone pulley i1. Side by side with this gear is placed a second gear h5 also engaging with the pinion h4 and having one tooth less than the gear h3. This gear is mounted loosely on the shaft h1 and is sleeved through the block h2, and to it is secured a ratchet clutch j.
This arrangement produces a motion analogous to that of worm gearing; the revolution of the cone i1 carrying the pinion h4, causes the gear h5 to be moved in the opposite direction to that of the cone i1, and at a speed of one tooth for each revolution of the cone. The cone i1 carries on its outer end a second clutch j1. The shaft h1 is made hollow, and two clutches are secured to a rod playing loosely on the hollow shaft, and arranged to be engaged alternately with the clutches j and j1. This engagement is effected by means of a bell crank k, operated by a shipper rod k1 on which adjustable dogs are placed, arranged to be operated by the cutter slide f.
This arrangement of feed shipping motion is very positive in its action, and allows of a very quick return of the cutter slide. The parts are so proportioned that the slide returns thirty-three times as fast as the forward motion, and yet on the very fastest speeds there is no perceptible jar of the parts. The entire mechanism can be disconnected from the feed screw, when desired, by disengaging the clutch j3 on the feed screw. The means employed for spacing the wheel blank are shown in Figs. 2070 and 2072. At the rear end of the spindle c is secured a worm-wheel l. This worm-wheel is made in two parts screwed firmly together. By this construction the wheel is made very accurately. The screw holes in the ring l1 are slightly elliptic. After the wheel has been hobbed out the position of the ring is changed and the wheel re-hobbed, and so on until the teeth will match perfectly in any position of the ring, when the ring is pinned and screwed on permanently. This wheel is driven by a worm m in connection with change gearing m1, m2, in such a way that one turn of the shaft m3 serves for all divisions. To the shaft m3 is secured a graduated plate o, to which is secured a latch plate o1 by means of a T-slot and bolts. The latch plate o1 is secured in this manner in order that the plate o may be turned any desired amount of “set over” in bevel-gear cutting, without disturbing the change gearing or latch. This dividing mechanism is driven by an independent belt from the countershaft to the pulley p, which is secured to a pinion p1, running loose on a stud. The pinion p1 engages with a gear p2 mounted loosely on the shaft m3. This gear is made to drive the latch plate o1 at the proper time by means of friction plates, which are set to the required tension by check nuts. The latch plate o1 is held by a spring latch v, which is secured to an arm v1 mounted loosely on a stud. The arm v1 is moved by a disk v2 carrying a secondary latch v3. This secondary latch v3 has on one side a roll which engages with a fixed cam v4 which trips the latch v3 from its connection with the arm v1, thus allowing the spring on the latch v to return it to its seat in the latch plate o1.
The disk v2 is moved by a steel ribbon (s, Fig. 2070) which is connected to a pair of plates, t t1, held together by a T-slot and bolts, and mounted loosely upon the carriage which carries the cutter slide f. The object of the double plates is to take up the slack ribbon, in any required position of the carriage, on the knee e. To the inside plate t1 is connected a shipper rod t2, which carries a dog and is operated by the return motion of the cutter slide f. A spiral spring coiled on the stud supporting the disk v2 returns the disk to its original position on the forward motion of the cutter slide f and reseats the secondary latch v3 in its seat in the arm v1. This arrangement of dividing mechanism requiring but one turn of the shaft m3 possesses some very decided advantages over the ordinary way of simple gearing and multiplied turns. The latch v is tripped immediately after leaving its seat in the plate o1, and is returned by its spring against the periphery of the plate, and is surely seated by means of a lip on the upper side of the plate. Should it, however, fail by reason of[II-56] any accident no harm will be done as the gear will be correctly spaced whenever the latch is seated, only one or more spaces will have been missed. Another advantage is that the feed gear can be disconnected and the latch withdrawn, thus allowing the gear to be revolved for the purpose of examination without any necessity for remembering the exact number of turns. When the latch is again seated the gear will be always properly spaced.
Fig. 2073 represents the same machine made half automatic, or in other words the feed is automatic, but when the cut is through, the worm that actuates the feed is thrown out of gear by a catch which lets the box or bearing at the left hand of the worm shaft drop vertically, this catch being operated by a stop on the side of the cutter slide. The method of arranging the feed mechanism so that it shall remain undisturbed, and require no alteration or adjustment at whatever height the knee carrying the cutter slide may be, is substantially the same as that already described with reference to the universal milling machine in Fig. 1893, while the dividing mechanism and other general features are the same as in the full automatic, with the exception of the mechanism for operating the cutter during the return stroke, and operating the dividing mechanism, both of which operations are done by hand in the half-automatic machine.
| VOL. II. | GEAR-CUTTING MACHINES. | PLATE VII. |
 |
||
| Fig. 2074. | ||
 |
||
| Fig. 2075. | ||
Fig. 2074 represents a Whitworth machine in which the cutter is carried in a vertical spindle carried in a sliding head. a is the driving pulley, b a pair of bevel-gears, and c a pinion driving the cutter spindle d, the cutter being at e. The cutter spindle has journal bearing at each end in arms upon the sliding head f, which is operated along the slideway of h by the gear-wheel g, receiving motion from the worm at c; at k is the index wheel, the wheel to be cut being carried on its shaft at m. The head n, carrying the index-wheel shaft, may be moved along the bed on which it slides by the handle p, which operates a screw within the bed, and engaging a nut on the under side of n. The worm for the worm-wheel k is carried beneath the wheel by a bracket from n, and being on a splined shaft moves with n. p is the handle for the divisions, the latter being obtained by means of change wheels at j, which connect with the worm shaft. By employing change gears the handle p makes a complete turn for any division, and is locked in a recess, which determines when an exact turn has been made. The range of a machine of this design is very great, because of the length of the bed on which the head n slides, which may be longer than would be practical if it stood upright.
Fig. 2075 represents a gear planing machine, shown with a bevel-gear in place. The main spindle is horizontal upon a fixed head, and has its dividing mechanism at the back of the machine. A single pointed tool is used in a slide rest, operated (by crank motion) upon the horizontal slideway shown, which may be set at any required angle for bevel-wheels. The cut is carried from the point to the flank of the tooth, and is put on by a rod and ratchet motion, the rod striking against the stop seen beneath the cross slide for the slide rest, and on the side of the horizontal slideway.
Figs. 2076, 2077, 2078, 2079, 2080, 2081, and 2082 represent different views of a gear-cutting machine, which consists of a bed plate a a, Figs. 2077, 2078, and 2079, having an extension at end a2, to support the hollow cylindrical column a3, which carries an overhead shaft a, at one end of which is a four-step cone a3, for driving the cutter feed motions. At the other end are the tight and loose pulleys for driving this shaft, upon which is also a series of grooved pulleys a5, arranged in the form of a cone. The object of this is to drive the cutter. At the base of the column a3 is a corresponding series of grooved pulleys, also arranged in the form of a cone a6. A round belt is employed. The shaft on which a6 is placed extends through the column, and on its opposite end a grooved pulley is also placed. This serves to drive a belt which, passing over a series of idle pulleys, as will be seen by reference to Figs. 2076 and 2077, drives the rotary cutter.
The wheel to be cut is carried as follows: Upon the bed-plate of the machine is placed a head b, Fig. 2078, corresponding to the headstock of a lathe, opposite which is a head b′, answering to the tailstock of a lathe. These two carry a mandrel d, to which is fastened a face-plate d′ against which the work is chucked. At the end of d′′ is fixed, in the usual manner, the worm-wheel for the dividing mechanism. The cutting arbor is held in a head that is carried in a cross slide c2, Fig. 2077, this cross slide being a carriage that may be fed along the side extension of the bed, which is broken off in the plan view of the machine, Fig. 2078. The two slides thus provided in this machine form in effect a longitudinal and cross feed, answering to the feeds of a lathe carriage and tool rest.
The cutter head m, Fig. 2077, is composed of two parts, c and m. Provision is made to swing the head in two directions, one of[II-57] which is noted by the plain arrow and the other by the feathered arrow in the engravings. Between the two the cutter arbor, it will be perceived, may be set at an angle in whatever direction the nature of the work may require. Referring to Figs. 2076 and 2077, it will be seen that the cutter-driver mechanism operates as follows: The tight pulley a1, driven in the direction noted by the arrow, turns the cone a6 which drives the pulley b. The belt from b passes over grooved idlers, b1, b2, b3, &c., to the grooved pulley b8, which is fast on its shaft and drives a train of gearing that operates the cutter arbor, the train being best shown in Fig. 2077. The train of gearing thus driven is composed of gears c1, c2 and c5, the latter being on the cutter arbor. The object of this arrangement is to obtain a high belt velocity. It will be seen that all these gears have their teeth at an angle to their axes, a feature that has been introduced to obtain smoothness of action. To maintain equal tension of belt at whatever angle the cutter may be set, the idle pulley b2 acts as a belt tightener, being carried by the rods t and t1.
Referring now to the feed motions, the machine is provided with a quick return for the cutter, the mechanism of which is as follows: The cone pulley a4, Fig. 2077, is mounted upon a driver shaft d, Fig. 2079. Upon this shaft are two loose bevelled pinions d2 d4, between which, and splined to the shaft, is a clutch f. For the feed traverse the clutch f is moved to engage with the pinion d4, while for the quick return it engages with d2. This device corresponds to the old-style quick-return motion used in some of the heavy English planing machines. The clutch f is operated by a rod l′, and drives the bevelled pinions d2 d4 by friction. The hub of the clutch is coned to fit a coned recess in the hubs of the two pinions. A pair of gears, d6 d7, transmit the motion of d5 to the shaft d1, on the end of which is the pinion e1, Motion is conveyed from this pinion to the feed-screw e, Fig. 2081, by the intermediate gears e2, e3, e4 and e5, and also by the helical pinions e6 and e7, the latter two being also shown in Fig. 2081.
Referring to the dividing mechanism, e, Fig. 2077, is an index-wheel operated by a worm. e1 is an arm with a locking tongue. Motion from e is conveyed to the shaft g through a swing-frame, shown in dotted lines in Fig. 2077, and a train of gears g2, g3, g4, g5, g6. On shaft g, Fig. 2078, is a pair of angular-toothed beveled pinions, h1 h2, and on shaft h, Fig. 2080, is a pinion h3, driving a pinion h4, which in turn drives pinions i i1. The latter drive the worm h′ which operates the wheel h. The two shafts carrying i i1 are supported by a piece f, the arm of which appears in section. This is fixed on the large toothed wheel g, indicated by the dotted lines in the same figure. The piece f above referred to is not fully shown in the engraving, portions of it having been omitted in order to show the mechanism previously mentioned. The wheel h is mounted on shaft d′′, and is used to revolve the face plate d′, all as shown in Fig. 2078. The wheels g2 g3 are change wheels, whose relative diameters determine the number of turns the wheel e must make for a given [II-58]pitch. The arm e1, Fig. 2077, is provided with a spring to hold the index pin into the notch of the index wheel. From this description it is obvious that when the number of the teeth of the wheel to be cut is a multiple of that of the wheel h, the number of turns to be given to the tangent screw h′, Fig. 2080, is exactly determined by the ratio existing between these two numbers. On the other hand, where the number of teeth required is not a multiple of the teeth in the wheel h, the number of turns to be given to the screw will be equal to n plus a fraction. In the first case, if all the intermediate gears between the dividing apparatus and the tangent screw are arranged to transmit to the former a number of definite turns, it will suffice to make the crank describe the number of turns indicated by the ratio the wheel e bears to the worm-wheel. In the second case, in order to give the tangent screw n turns plus a fraction by giving the crank n + turns, it is necessary to employ several wheels, for which the ratio must be calculated. If the division so obtained is not an exact divisor of the number of teeth of the wheel h, it is necessary that one of the wheels forming the combination shall have a number of teeth which is a multiple of the division mentioned.
Another consideration with reference to the number of turns to be given to the crank of the dividing apparatus is mentioned in the inventor’s description of this machine. The smaller the number the greater will be the chance of error in the result; for example, if it be supposed that a division corresponding to one turn of the tangent screw is to be made, if only one turn of the crank is made, the play unavoidable where easy movement is secured will be repeated and multiplied in the same way that an error is produced after a certain number of divisions. If, on the contrary, the mechanism be arranged so that the number of turns of the crank is multiplied in obtaining one turn of the tangent screw, the error will be appreciably reduced. It is therefore recommended by the designer of this machine to arrange the train of gears so as to give a certain number of full turns to the crank in all cases. If, after having cut the teeth in the blank, it is desirable to go over them again, it is simply necessary to turn the screw j which engages with the gear-wheel j1.
The next feature to be described is the adjustment of the cutter. In some cases it is necessary to incline the cutter in such a way that the axis of the shaft carrying it forms a certain angle with the vertical. This is the case in cutting angle teeth, as shown in Fig. 2076. In order to produce the necessary angle for such teeth, it is only necessary to turn the worm k that engages with the worm-wheel k1, Fig. 2077. This wheel is fast on to the piece m, and the latter, when set to the desired inclination, is kept in place by means of bolts o, Figs. 2077 and 2081. In some cases it is necessary to incline the cutter in such a way that the[II-59] axis of the shaft that carries it does not cease to be in a vertical plane perpendicular to the shaft d, this being the case as illustrated in Fig. 2082. In order to obtain this obliquity the small shaft m is turned, and the movement so obtained is transmitted by means of two small pinions m2 m3 to the shaft carrying at its extremity the screw n′. This screw gears with the segment n′′. The latter is fixed to a piece j, furnished with bearings for the reception of the shaft that drives the cutter spindle, which is adjusted endways by means of the nuts shown.
If it is desired to produce a wheel with angle teeth it is necessary, after having arranged the cutter as shown in Fig. 2076, and while the forward motion of the carriage takes place, that the wheel r shall turn with a slow, regular movement until the tooth operated upon is finished. After this the tool retraces its path at a somewhat higher speed. This automatic motion is obtained from a shaft (Fig. 2076), on which are placed the pinions e2 e3. This shaft carries a third pinion p2, which, by means of one or more pairs of wheels mounted two by two on a swinging frame p, as shown by p3 p4 p5, turns the shaft p′ (Fig. 2080), which carries at one of its extremities the wheel p5 and at the other the screw h3. This screw, by proper intermediates, operates the toothed wheel g, Fig. 2080, which in its rotation carries along the piece f, with all the parts supported by it. In this movement the pinion h3 does not turn, nor does the second pinion h4, which slides on the former. The screw h′ slightly turns the large wheel h, which, as previously mentioned, is mounted on the shaft d, Fig. 2078. When the special tooth operated upon is finished the movement is reversed by operating the lever l. The table and the wheel r, Fig. 2077, then move in the opposite direction. When the original position is reached by the cutter, the reversing lever is thrown out of gear; the handle e′ is then used so as to effect the proper division, and the machine is again started.
As has been shown, only a small portion of the circumference of the wheel g is subjected to wear. In this way it would be possible to limit the operation of cutting the teeth to a certain length of arc only. In that case, however, considerable wear would be produced; for this reason the constructor has preferred to provide the whole circumference with teeth, in order to change the working point from time to time, so as to distribute the wear. In order to permit this displacement it is necessary to disengage the worm k (Fig. 2076), which is accomplished by turning the hand wheel v, mounted on the shaft v′, Fig. 2078. This shaft carries at each extremity small pinions, v2, v3, gearing with other pinions fixed at the extremity of each of the supports of the shaft p′.
[II-60]In order to make the operation of this machine better understood, we will conclude our description by some practical examples of the calculations required in making helical teeth. It will be observed that the two small movements necessary in cutting an angle tooth in a given inclination are obtained first by the screw e, Fig. 2077, feeding the cutter head, and second by the tangent screw k, Fig. 2076, that governs the rotary motion of the wheel g, and consequently of the shaft d, carrying the face plate and the blank to be cut. The second wheel h, mounted on this shaft, is driven by the endless screw h′, Fig. 2080, the supports of which are fixed on the wheel g. It will be observed at the same time that the speed of the screw e acting upon the tool holder is the same as that of the shaft carrying the wheels e2 e3 and p2, since the wheels e4 e5 e6 e7 have the same number of teeth. It is obvious, therefore, that that ratio of speed which will exist between the tangent screw k and the shaft of wheels e2 e3 and p2 will have to be the same as that between the driving screw e of the cutter head and the tangent screw k. Consequently, the combinations of wheels that connect this tangent screw k to the shaft e2 e3 and p2 will produce the same effect as if they were connected directly with the feed screw e. This being established, the general formulæ determining the gearing to be employed in order to produce helical teeth inclined at a certain angle are obtained in the following manner: It should here be observed that the teeth produced will be what in the United States are called angle teeth, corresponding, however, so nearly to the helix as to be considered helical. Suppose that the number of teeth in the wheel g is 300, and that the pitch of the driving screw of the cutter head is 5 mm., using for convenience the French system of measurements. Let x/y be the ratio of the four wheels that it is necessary to mount. Let m designate the degrees of inclination of the teeth. Let p equal the pitch of the desired helix, and d the diameter of the wheel to be operated upon. We then have cotan. m = p/(d × 3.14), from which we find p = cotan. m × d × 3.14, and in order to make the cutter head run over a distance corresponding to this pitch, the driving screw e must make a number of turns equal to
| cotan. m × d × 3.141 |
| 5 |
But while the cutter head passes over a distance equal to the[II-61] pitch, the wheel g makes one turn and the tangent screw 300 turns; consequently, the ratio to be established between the speed of the tangent screw and between that of the screw driving the carriage will be represented by
| x | = | 1500 |
| y | cotan. m × d × 3.141 |
Thus, for a wheel with a diameter of 1.75 inches, the machine ought to have an inclination of 15° to the primitive circumference, and we would have, for the ratio to be established between the tangent screw and the driving screw,
| x | = | 1500 | = | 1500 |
| y | cotan. 15° × 1.75 × 3.141 | 20.51778 |
It should be remarked that, according as the angle should be either to right or to left, one or two intermediate pieces are placed on the swing-frame, the slide of which is nearly horizontal. The speed of the driving shaft, supported by the column mentioned in introductory remarks, is 120 revolutions; that of cutter equals from 20 to 30 revolutions; that of screw of cutter head, advance from 1 to 42 revolutions, return from 7 to 66 revolutions.
Vice work may be said to include all those operations performed by the machinist that are not included in the work done by machine tools. In England vice work is divided into two distinct classes, viz., fitting and erecting. The fitter fits the work together after it has been operated upon by the lathe planer and other machine tools, and the erector receives the work from the fitter and erects it in place upon the engine or machine. Fitting requires more skill than turning, and erecting still more than fitting, but it is at the same time to be observed that the operations of the erector includes a great many of those of the fitter. In treating of the subjects of vice work and erecting, it appears to the author desirable to treat at the same time of some operations that are not usually included in those trades, because they are performed with tools similar to those used by the fitter, and may be treated equally as well in this way as in any other, while a knowledge of them cannot fail to be of great service to both the fitter and erector. Among the operations here referred to are some of the uses of the hammer; such, for example, as in straightening metal plates.
The vice used by the machinist varies both in construction and size according to the class of work it is to hold. For ordinary work the vice may possess the conveniences of swiveling and a quick return motion, but when heavy chipping constitutes a large proportion of the work to be done the legged vice is preferable.
The height of vice jaws from the floor is usually greater for very small work than for the ordinary work of the machine shop, because the work needs to be more clearly observed without compelling the operator to stoop to examine it. The gripping surfaces of vice jaws are usually made to meet a little the closest at the top, so as to grip the work close to the top and enable work cut off with a chisel to be cut clean and level with the jaws.
The jaws of the wood-worker’s vice are made then as in Fig. 2083, and reach higher above the screw than the vices used for iron work, because the work is often of considerable depth, and being light will not lie still of its own weight, as is the case with iron.
An example of the ordinary vice of the machine shop is shown in Fig. 2084, which represents partly in section a patent swivel vice. a is the jaw in one piece with the body of the vice, and b is the movable jaw, being the one nearest to the[II-63] operator. The movable jaw is allowed to slide freely through the fixed one (being pushed or pulled by hand), or is drawn upon and grips the work by operating the handle or lever h. The means of accomplishing this result are as follows: As shown in the cut, b is free to be moved in or out, but if h be pulled away from the vice, the shoulder c, meeting the shoulder n, will move the toggle g, and this, through the medium of g′, moves the tooth bar t, so as to engage with the teeth on the side of the movable jaw bar shown at t. As soon as the teeth t meet the teeth t the two travel together, and the jaw b closes on and grips the work. But as the motion is small in amount, the jaw b should be placed so to nearly or quite touch the work before h is operated. To unloose the work, the handle h is operated in an opposite direction, and the hook m meets m and pulls t to the position shown. The spring s operates upon a hook at u, to engage the teeth t, with the rack t, as soon as the handle h is moved in the tightening direction. The vice grips with great force, because during the tightening the toggle, g is nearly straight, and its movement less than would be the case with a screw-vice having the ordinary pitch of thread and under an equal amount of handle movement.
In this vice the fixed jaw is made to fasten permanently to the work bench, but in others having a similar tightening mechanism the fixed jaw is so attached to the bench as to allow of being swivelled. The method of accomplishing this is shown in Fig. 2085, in which s is the foot of the vice bored conical to receive a cone on the casting r, which is fastened to the bench b. w is a washer and h the double arm nut. Loosening this nut permits of the vice being rotated upon r.
When handle h is operated to release the movable jaw it can be moved rapidly to open and receive the work, and to close upon the work, when by a second handle movement the work can be gripped, the operation being much quicker than when the movable jaw is traversed by a screw and nut.
In this vice the gripping surface of the jaws are always parallel one to the other, and attachments are employed to grip taper work as wedges.
In Fig. 2086 is represented a patent adjustable jaw vice, which is also shown in Fig. 2087 with the adjustable jaw removed and upside down. From the construction it is apparent that the groove g, being an arc of a circle of which c is the centre, the jaw is, as it were, pivoted horizontally, and can swing so as to let the plane of the jaw surfaces conform to the plane of the work; hence a wedge can be gripped all along the length enveloped by the jaws, and not at one corner or end only. When the pin a is inserted the jaw stands fixed parallel to the sliding jaw. The pin a engages in a ratchet in the base below it to secure the back vice jaw in position when it is set to any required angle.
A second convenience in this vice is that the whole vice can be swivelled upon the base that bolts to the bench, which is provided with a central hole and annular groove into which the base of the field jaw pivots; at b is a spring pin passing into holes in the bench plate, so that by lifting the pin b, the whole vice can be swung or rotated upon the base or bench plate, until the pin b falls into another hole in the base plate, which is provided with eight of these holes. The movable jaw is here operated by a screw and nut.
Fig. 2088 represents a form of leg vice for heavy work. In the ordinary forms of this class of vice the two gripping surfaces of the jaws, only stand parallel and vertical when at one position, because the movable leg is pivoted at p; but in that shown in the figure the movable jaw is supported by the arm a, passing through the fixed leg l, which carries a nut n. A screw s, having journal bearing in the movable leg, screws through the nut n, and is connected to the upper screw by the chain c, which passes around a chain wheel provided on each screw, so that the movable leg moves in an upright position and the jaw faces stand parallel, no matter what the width of the work. This is a very substantial method of obtaining a desirable and important object, and greatly enhances the gripping capability of the vice. Fig. 2089 represents a sectional view of another patent vice. a is the sliding and b the fixed jaw. p is the bed plate carrying the steel rack plate h. Attached to each side of the base of the handle is a disk. These disks are carried on the outer end of the movable jaw a, and are held in place by the friction straps t, adjusted by the screws s. On the radial face of the disk is the pin k, which, when the handle or lever is lifted or raised, depresses the end of lever j, which at its other end raises the clutch g, disengaging the same from the rack h, as shown in the engraving. The jaw a is thus free to be moved by[II-64] hand, so as to have contact with the work. To tighten the vice the handle is depressed, whereon k releases j and the latter permits the toothed clutch g to engage with the teeth of h. At the same time the bar d, which is pivoted to the disks, is drawn outward. The end of the bar d, meeting the surface of the lug shown on a, acts (in conjunction with the toothed clutch h) as a toggle fulcrum from which the disks may force the movable jaw to grip the work.
This action may be more minutely described as follows: The end d of d is pivoted upon the disks, as shown; hence when the handle is depressed the effort of the end d is to move to the right, but d being fixed at the other end the pressure is exerted to force the movable jaw to the left, and therefore upon the work. The amount of jaw movement due to the depression of the handle is such that if that jaw is pushed near or close to the work the handle will stand about vertical downward when the vice firmly grips the work.
For vices whose jaws cannot be swiveled horizontally to enable them to conform to taper work, attachments for the jaws are sometimes provided, these attachments having the necessary swiveling feature. So likewise for gripping pipes, and similar purposes, attachments are made having circular recesses to receive the pipes.
To prevent the vice jaws from damaging the work surface, and also to hold some kinds of work more firmly, various forms of clamps, or coverings for the vice jaws are used. Thus Figs. 2090 and 2091 represent clamps for holding round or square pins. In the former the grooves pass entirely through the clamp jaws, so as to receive long pieces of wire, while in the latter the recesses are short, so as to form an abutment for the end of the pins, and act as a gauge in filing or cutting them off to length.
An excellent form of pin clamp is shown in Fig. 2092, the spring bow at the bottom acting to hold the jaws open and force the faces against the vice jaws when the latter are opened. The flanges at b b rest upon the tops of the vice jaws; hence it will be seen that the clamp is not liable to fall off when the vice is opened to receive the work, which is placed either in the hole at a or that at b, as may be most desirable.
Fig. 2093 shows such a clamp holding a screw, the clamp jaws being forced against the screw by the vice jaw pressure, when the vice jaws are opened the spring of the bow will cause the clamp jaws to open and release the screw.
Clamps such as shown in Figs. 2090 and 2091, but without the pin holes, are also provided, being made one pair of copper and another of lead, the latter being preferable for highly finished work. As the filings are apt to imbed in the copper, and, furthermore, as the copper gradually hardens upon its surface, the copper clamps require to be annealed occasionally, which may be done by heating them to a low red heat and dipping them in water. Lead clamps will hold small work very firmly, and are absolutely essential for triangular or other finished work having sharp corners, and also for highly finished cylindrical work, which may be held in them sufficiently firmly to be clipped without suffering damage from the vice jaws. A piece of thick leather, such as sole leather, also forms a very good clamp for finished work, but to prevent its falling off the vice jaws it is necessary to cut it nearly through on the outside and at the bent corner.
The hammer in some form or other is used in almost all kinds of mechanical manipulation, and in each of these applications it assumes a form varied to suit the nature of its duty, and of the material to be operated upon. In the machine shop it is used to drive, to stretch, and to straighten.
The most skilful of these operations are those involving stretching operations, as saw and plate straightening, examples of which will be given.
In using a hammer to drive, the weight and velocity of the hammer head are the main considerations. For example, the force of a blow delivered by a hammer weighing 1 lb., and travelling 40 feet in a second, will be equal to that weighing 2 lbs, and[II-65] travelling 20 feet in a second; but the mechanical effects will be different. If received on the same area of impact the effects will sink deeper into the metal with the greater velocity, and they will extend to a less radius surrounding the area of impact. Thus in driving out a key that is fast in its seat, a quick blow is more effective than a slow one, both being assumed to have at the moment of impact an equal amount of mechanical force stored up in them. On the other hand, for riveting the reverse will be the case. In the stretching processes the hammer requires to fall with as dead a blow as possible. Thus the hammer handle is, for saw stretching, placed at such an angle to the length of the hammer that the latter stands about vertical when the blow is delivered. In straightening, the blow is varied to accommodate the nature of the work; thus a short crook or bend would be best straightened by a quick blow with a light hammer, and a long one by a slower blow with a heavier hammer, which would cause the effects of the blow to affect a greater radius around the part receiving the impact.
As an example of the difference in mechanical effect between a number of blows aggregating a given amount of energy and a single blow having an equal amount of energy, suppose the case of a key requiring a given amount of power to start it from its seat, and every blow delivered upon it with insufficient force to loosen its hold simply tends to swell and rivet it more firmly in the keyway.
Probably the most expert use of the hammer is required in the straightening of engravers’ plates, as bank-note plates; and next to this comes the ornamental repoussé work of the manufacturing jeweller.
The most expert hammer process of the machine shop is that of straightening rifle barrels and straightening saws and sheet metal plates.
In straightening rifle barrels, the operator is guided as to the straightness as follows: A black line is drawn across a piece of glass elevated to the light, and the straightener looks through the bore at this line, which throws a dark line of shadow along the rifle bore. If this line appears straight while the barrel is rotated the bore is straight; but if the line waves the barrel requires straightening, the judgment of the operator being relied upon to determine the amount of the error, its location, and the force and nature of the blow necessary to rectify it.
The following information on the duration of a blow is taken from Engineering, the results having been obtained from some experiments by Mr. Robert Sabine. These experiments, which were intended as preliminary to a more extended inquiry, were made with a view to find approximately how the duration of a blow varied with the weight of the hammer, its velocity of descent, and with the materials. An iron ball weighing 1⁄4 lb. was suspended by a fine wire from an insulated support upon the ceiling; so that when it hung vertically it just grazed the vertical face of an ordinary blacksmith’s anvil placed upon its side on a table. By raising the ball and letting it swing against the face of the anvil a blow of varying force could be struck. On rebounding, the ball was arrested whilst the excursion of the galvanometer needle was observed. By measuring the angle through which the ball was separated, its vertical fall and final velocity could be easily deduced. In this way the greatest vertical height from which the iron ball was let fall on to the face of the iron anvil was 4 ft., the least about 1⁄80 inch. Six readings were taken for each height, and they were invariably found to agree amongst each other. The averages only are given in the following records:
| Vertical fall in inches. |
Duration of contact in seconds. |
|
| 48 | 0.00008 | |
| 36 | 0.00008 | |
| 28 | 0.00008 | |
| 17 | 0.00009 | |
| 9 | 1⁄4 | 0.00010 |
| 4 | 0.00011 | |
| 1 | 0.00013 | |
| 0 | 1⁄4 | 0.00016 |
| 0 | 1⁄16 | 0.00018 |
| 0 | 1⁄32 | 0.00021 |
| 0 | 1⁄80 | 0.00030 |
From this it would appear that when the velocity of a blow is increased, the duration is decreased within a certain limit; but that it reaches a minimum. The velocity of impact in the first experiment was about sixty times as great as in the last one; but the duration of the blow appears to be reduced only to about one-fourth of the time. The blows given by two hammers of different weights were compared. No. 1 weighed 4 ozs., No. 2 weighed only 21⁄4 ozs. The durations of the blows were as follows:
| Vertical fall. | Duration of contact. | |
| Ball No. 1. | Ball No. 2. | |
| inch. | seconds. | seconds. |
| 1 | 0.000135 | 0.000098 |
| 4 | 0.000096 | 0.000083 |
It appears from this that a heavier hammer of the same material gives a longer duration of blow.
In the course of these experiments it was observed that the ball after striking the anvil rebounded irregularly, sometimes to a greater, at others to a less height, and that some relation appeared to exist between the heights to which the ball rebounded and the excursions of the galvanometer needle due to the residue of the charge.
In the next series, therefore, the rebounds of the iron ball from the iron anvil were measured and recorded, from which it appeared that when the rebound was greater the duration of contact was shorter, and vice versâ.
| Vertical fall. | Vertical rebound. | Duration of blow. | ||
| inch. | inch. | seconds. | ||
| 6 | 2 | 0.000120 | ||
| 6 | 2 | 1⁄2 | 0.000111 | |
| 6 | 3 | 1⁄4 | 0.000101 | |
| 6 | 3 | 1⁄2 | 0.000091 | |
| 14 | 1⁄2 | 3 | 1⁄4 | 0.000106 |
| 14 | 1⁄2 | 4 | 1⁄2 | 0.000103 |
| 14 | 1⁄2 | 5 | 1⁄4 | 0.000095 |
| 14 | 1⁄2 | 6 | 1⁄2 | 0.000086 |
| 25 | 7 | 3⁄4 | 0.000096 | |
| 25 | 8 | 1⁄4 | 0.000091 | |
| 25 | 9 | 1⁄2 | 0.000086 | |
| 25 | 12 | 0.000078 | ||
The explanation of this is probably that when the energy of the blow is expended in bruising or permanently altering the form of the hammer or anvil by which the contact of the two is prolonged, it has less energy left to enable it to rebound, and vice versâ. Substituting a brass anvil and brass ball, it was found that the blow was duller, the rebound much less, and the duration contact nearly three times as great as when the iron ball and anvil were used.
| Vertical fall. | Vertical rebound. | Duration of contact. | ||
| inch. | inch. | seconds. | ||
| 1 | 3⁄4 | 0 | 1⁄3 | 0.00036 |
| 6 | 1 | 0.00033 | ||
| 14 | 1⁄2 | 1 | 1⁄2 | 0.00026 |
| 25 | 2 | 0.00027 | ||
This series also shows the longer duration of the blow when its velocity is small. Using a brass anvil and iron ball the duration of the blow was greater than when both were of iron, but less than when both were of brass.
| Vertical fall. | Vertical rebound. | Duration of contact. | ||
| inch. | inch. | seconds. | ||
| 1 | 3⁄4 | 0 | 1⁄8 | 0.00021 |
| 6 | 0 | 1⁄2 | 0.00018 | |
| 14 | 1⁄2 | 1 | 1⁄3 | 0.00015 |
| 25 | 2 | 0.00014 | ||
[II-66]Striking the brass anvil with a common hammer, the duration of the blow appeared shorter when struck sharply.
| Duration of contact. | |
| seconds. | |
| Moderate blow | 0.00027 |
| Harder blow | 0.00019 |
Striking the blacksmith’s anvil with a common carpenter’s hammer, the duration appeared to be nearly constant.
| Duration of contact. | |
| seconds. | |
| Moderate blow | 0.00011 |
| Harder blow | 0.00010 |
It was, of course, necessary to allow in each case the hammer to rebound freely, and not to prevent it doing so by continuing to exert any pressure at the instant of the blow. When this condition was observed, it was invariably found that the harder and sharper the blow the shorter was its duration. It was also noticed that whenever the anvil gave out a sharp ringing sound, the duration of the blow was much shorter than when the sound was dull.
A very slight error would be introduced by reason of thermo-currents set up between the metals at the moment of the blow. By reversing the direction of charge of the accumulator, however, the effect from this cause was found to be quite inappreciable.
The machinists’ hand hammer is usually made in one of the three forms shown in Figs. 2094, 2095 and 2096, and varies in weight from about 13⁄4 lbs. for heavy chipping to about 1⁄2 lb. for light work, the handle being about 15 inches long for the heavy, and about 10 or 12 for the light business. The round face is usually somewhat convex on its surface with its edge slightly rounded or beveled. The pane or pene a, Fig. 2097, is usually made in European practice to stand at a right angle to the axis of the handle as shown, while in the United States it is usually made to stand parallel with the handle as in Fig. 2096. The face end is sometimes given taper as in Figs. 2094 and 2095, and at others parallel as in Figs. 2097 and 2098, or nearly so. The pene is mostly used for riveting purposes, and it is obvious that with the pene at a right angle to the handle axis as in Fig. 2097, it will not matter whether the pene meets the work quite fair or not, especially as the pene is made slightly curved in its length, and it is easier to hold the hammer level sideways than it is to hold it so true lengthways that the pene, when forward, as in Fig. 2096, will meet the work fair.
The proper shape for the eye of a hammer is that shown in Figs. 2099 and 2100, a representing the top of the hammer. The two sides of the eye are rounded out from the centre towards each end, while the ends of the eye are made parallel. The form of the eye as viewed from the top a is as shown in Fig. 2102, while Fig. 2101 represents a view from the bottom b. The handle is fitted a driving fit and is driven in from side b, and is shaped as in Figs. 2103 and 2104 which are side and edge views.
From c to d the handle fills the eye, but from d to e it fills the[II-67] eye lengthways only of the oval. A saw-slot, to receive a wedge, is cut in the handle, as shown in Fig. 2104. The wedge is best made of soft wood, which will compress and conform itself to the shape of the slot. To drive the handle into the eye, preparatory to wedging it permanently, it should be placed in the eye held vertically, with the tool head hanging downward, and the upper end struck with a mallet or hammer, which is better than resting the tool head on a block. The wedge should be made longer than will fill the slot, so that its upper end may project well, and the protruding part, which may split or bulge in the driving, may be cut off after the wedge is driven home.
The wedge should be driven first with a mallet and finally with a hammer. After every few blows on the wedge, the tool should be suspended by the handle and the end of the latter struck to keep the handle firmly home in the eye. This is necessary, because driving the wedge in is apt to drive the handle partly out of the eye.
The width of the wedge should equal the full length of the oval at the top of the eye, so that one wedge will spread the handle out to completely fill the eye, as shown in Fig. 2105. Metal wedges are not so good as wooden ones, because they have less elasticity and do not so readily conform to the shape of the saw-slot, for which reasons they are more apt to get loose. The taper on the wedge should be regulated to suit the amount of taper in the eye, while the thickness of the wedge should be sufficiently in excess of the width of the saw-cut, added to the taper in the eye, that there will be no danger of the end of the wedge meeting the bottom of the saw-slot.
By this method, the tool handle is locked to the tool eye by being spread at each end of the same. If the top end of the tool eye were rounded out both ways of the oval, two wedges would be required to spread the handle end to fit the eye, one wedge standing at a right angle to the other. In this case, one wedge may be of wood and one of metal, the one standing across the width of the oval usually being the metal one. The thin edge of the metal wedge is by some twisted, as shown by Fig. 2106, which causes the wedge to become somewhat locked when driven in.
In fitting the handle, care must be taken that its oval is made to stand true with the oval of the tool eye. Especially is this necessary in the case of a hammer. Suppose, for example, that in Fig. 2107 the length of the oval of the handle lies in the plane a b, while that of the eye lies in the plane c d, then the face of the hammer will meet the work on one side, and the hammer will wear on one side, as shown in figure at e. If, however, the eye is not true in the hammer, the handle must be fitted true to the body of the hammer; that is to say, to the line c d. The reason for this is that the hand naturally grasps the handle in such a manner that the length of the oval of the handle lies in the plane of the line of motion when striking a blow, and it is obvious that to strike a fair blow the length of the hammer should also stand in the plane of motion.
The handle should also stand at a right angle to the plane of the length of the hammer head, viewed from the side elevation, as shown in Fig. 2108, in which the dotted line is the plane of the hammer’s length, while b represents a line at a right angle to a, and should, therefore, represent the axial line of the hammer handle. But suppose the handle stood as denoted by the dotted line c, then the face of the hammer would wear to one side, as shown in the figure at d.
In the operation of straightening iron or steel plates by hammer blows, the process when correctly carried out is one of liberating the strains (whose existence throws the plate out of a true plane) by stretching those parts that are unduly contracted. Every hammer blow should, therefore, be directed towards this end, for[II-68] one misdirected blow entails the delivery of many others to correct its evil influence; hence, if several of such misdirected blows are given, the plate will have upon it a great many more hammer marks, or “hammer sinks” or chops, as they are sometimes termed, than are necessary. As a result, not only will the painter (in fine work) be given extra trouble in stopping the hollows to make a smooth surface, but the following evil will result: Every blow struck by the hammer compresses and proportionately stiffens the small surface upon which it is delivered, and creates a local tension upon the surrounding metal. The misdirected blows then cause a tension acting in opposition to the effect of the properly delivered ones; and though the whole plate may be stiffened by the gross amount of blows, yet there will be created local tensions in various parts of the plate, rendering it very likely to spring or buckle out of truth again. If, for example, we take a plate of iron and hammer it indiscriminately all over its surface, we shall find it very difficult to straighten it afterwards, not only on account of the foregoing reasons, but for the additional and most important one that the effect of the straightening blows will be less, on account of the hammered surface of the plate offering increased resistance to the effects of each blow; and after the plate is straightened, there will exist in it conflicting strains, an equilibrium of which holds the plate straight, but the weakening of any of which will cause the preponderance of the others to throw the plate out of straight; for the effects of the blows cannot be permanent unless the whole body of the iron is acted upon to an equal extent by the hammer. Suppose, for example, that we take a flat plate, and deliver upon it a series of blows round about its centre. The effect will be to make it hollow on one side and rounding on the other, the effect of the blows being, not only to indent the plate in the spots where they fell, but to carry the whole body of the middle out of true; because, the area of the iron being increased by the stretching effect of the blows, the centre leaves the straight line to accommodate the increased area. Thus, if we mark off a circle of, say, a foot in diameter, in the middle of a plate, and hammer it so as to stretch it and increase its area 1⁄8 inch each way, the form of the plate must alter to suit this added area, and the form of a dish or curve is the only one it can assume.
The skilful workman, so soon as he has ascertained where the plate is out of true, sets to work to stretch it, so as to draw the crooked place straight, taking care that the shape and weight of the hammer and the weight of the blows delivered shall bear a proper relation to the thickness of the plate and the material of which it is composed. If it is of consequence that the finished work shall bear no marks of the hammering (as in the case of engravers’ plates), an almost flat-faced hammer is employed; but for other work the shapes, as well as the weights, of the hammers vary.
Fig. 2109 represents what is called the long cross-face hammer, used in saw straightening for the first part of the process which is called the smithing. The face that is parallel to the handle is called the long one, and the other is the cross-face. These faces are at a right angle one to the other, so that without changing his position the operator may strike blows that will be lengthways in one direction, as at a, in Fig. 2110, and by turning the other face towards the work he may strike a second series standing as at b. Now, suppose we had a straight plate and delivered these two series of blows upon it, and it will bend to the shape shown in Fig. 2111, there being a straight wave at a, and another across the plate at b, but rounded in its length, so that the plate will be highest in the middle, or at c; if we turn the plate over and repeat the blows against the same places, it will become flat again. Both faces of this hammer are made alike, being rounded across the width and slightly rounded in the length, the amount of this rounding in either direction being important, because if the hammer leaves indentations, or what are technically called “chops,” they will appear after the saw has been ground up, even though the marks themselves are ground out, because in the grinding the hard skin of the plate is removed, and it goes back to a certain, but minute, extent towards its original shape. This it will do more in the spaces between the hammer blows than it will where the blows actually fell, giving the surface a slightly waved appearance.
The amount of roundness across the face regulates the widths, and the amount of roundness in the face length regulates the length of the hammer marks under any given force of blow. As the thicker the plate the more forcible the blow, therefore the larger the dimensions of the hammer mark.
The twist hammer, shown in Fig. 2112, is used for precisely the same purposes as the long cross-face, but on long and heavy saws or plates, and for the following reasons, namely: When the operator is engaged in straightening a short saw he can stand close to the spot he is hammering, and the arm using the hammer may be well bent at the elbow, which enables him to see the work plainly, and does not interfere with the use of the hammer, while the shape of the smithing hammer enables him to bend his elbow[II-69] and still deliver the blows lengthways, in the required direction. But when a long and heavy plate is to be straightened, the end not on the anvil must be supported with the left hand, and it stands so far away from the anvil that he could not bend his elbow and still reach the anvil. With the twist hammer, however, he can reach his arm out straight forward to the anvil, to reach the work there, while still holding up the other end, which he could not do if his elbow were bent. By turning the twist hammer over he can vary the direction of the blow the same as with the long cross-face.
It is obvious that by slightly bending the elbow and turning either of these hammers over the blows may be caused to be in any required direction, as shown in Fig. 2113. These two hammers are used for the straightening or smithing processes, and not to regulate the tension, because the effects of their blows do not extend equally around the part struck, but follow the form of the hammer marks, whose shapes are shown in Fig. 2114, at a and b, the radiating lines denoting the directions in which the effects extend; obviously the size of these marks depends upon the shape of the hammer face and the force of the blow.
An inspection of hammered saw plates, however, will show that the marks (which are scarcely visible, having a merely dulled surface), are usually about one-half wider than the thickness of the plate, and about four or five times as long as they are wide. Obviously, also, the direction of the effects of a blow follow the direction in which the hammer travels. If, for example, the long cross-face falls vertically its effects will extend equally all around the hammer mark, as at a in Fig. 2115, but if the hammer moved laterally to the left while falling its blows would have more effect on the left-hand side of the mark as at b, or if it moved away from the operator its effects would extend most in front as at c, the amount increasing with the force of the blow, and it may be remarked that quick blows are not used, because they would produce indentations or chops; hence, the force of the blow is regulated by the weight of the hammer rather than by the velocity it travels at. On account of the oval shape of the blow delivered by the long cross-face and by the twist hammers, the dog-head hammer, shown in Fig. 2116, is used to regulate the tension of the plate or saw, the effects of its blow when delivered vertically being circular, as at a, in Fig. 2117; obviously, however, if in falling it moved vertically in the direction of arrow c the effects would extend as at b. But while the dog-head is used entirely for regulating the tension, it may also be used for the same purposes as either the long cross-face or the twist hammer, because the smith operates to equalize the tension at the same time that he is taking down the lumps; hence he changes from one hammer to the other in an instant, and if after regulating the tension with the dog-head he should happen to require to do some smithing, before regulating the tension in another, he would go right on with the dog-head and do the intermediate smithing without changing to the smithing hammer. Or, in some cases, he may use the long cross-face to produce a similar effect to that of the dog-head, by letting the blows cross each other, thus distributing the hammer’s effects more equally than if the blows all lay in one direction.
In circular saws, which usually run at high velocity, there is generated a centrifugal force that is sufficient to actually stretch the saw and make it of larger diameter. As the outer edge of the saw runs at a greater velocity than the eye it stretches most, and therefore the equality of tension throughout the saw is destroyed, the outer surface becoming loose and causing the saw to wabble as it revolves, or to run to one side if one side of the timber happens to be harder than the other, as in the case of meeting the edge of a knot.
The amount of looseness obviously depends upon the amount the saw expands from the centrifugal force, and this clearly depends upon the speed the saw is to run at; so the saw straightener requires to know at what speed the saw is to run, and, knowing this, he gives it more tension at the outside than at the eye; or, in other words, while the eye is the loosest, the tension gradually increases towards the circumference, the amount of increase being such that when the saw is running the centrifugal force, and consequent stretching of the saw, will equalize the tension and cause the saw to run steadily.
If the eye of a circular saw is loose, or, in other words, if it is rim bound when running, it will dish, as in Fig. 2118, and the rounded side rubbing against the side of the saw slot or kerf, will cause the saw to become heated and the eye to expand more than the outer edges, thus increasing the dish. But if the saw strikes a knot on the hollow side it may throw the dish over to the other side of the saw in an instant. The remedy is to hammer the saw with the dog-head as shown in the figure, not touching the eye,[II-70] and letting the blows fall closer together towards the circumference.
On the other hand, if the eye is tight and the circumference loose the saw will flop from side to side as it runs, and the remedy is to stretch it round about the eye, letting the blows fall wider apart as the outer edge of the saw is approached. The combinations of tight and loose places may be so numerous in circular saws that as the smith proceeds in testing with the straight-edge he marks them, drawing a circular mark, as at g, in Fig. 2119, to denote loose, and the zig-zag marks to indicate tight places. To cite some practical examples of the principles here laid down, suppose we have in Fig. 2120 a plate with a kink or bend in the edge, and as this would stiffen the plate there, it would be called a tight place. To take this out, the hammer marks would be delivered on one side, radiating from the top of the convexity, as on the left, and on the other as shown radiating from the other end of the concavity, as on the right, the smithing hammer being used. This would induce a tight place at a which would be removed by dog-head blows delivered on both sides of the plate. Suppose we had a plate with a loose place, as at g in Fig. 2121. We may take it out by long cross-face blows, as at a and b, delivered on both sides of the plate, or we might run the dog-head on both sides of the plate, both at a and at b, the effect being in either case to stretch out the metal on both sides of the loose place g, and pull it out. In doing this, however, we shall have caused tight places at e and f, which we remove with dog-head blows, as shown. If a plate had a simple bend in it, as in Fig. 2122, hammer blows would first be delivered on one side, as at a, and on the other side, as at b. A much more complicated case would be a loose place at g, in Fig. 2123, with tight places at h, j, k, and l, for which the hammer blows would be delivered as marked, and on both sides of the plate. Another complicated case is given in Fig. 2124, g g being two loose places, with tight places between them and on each side. In this case, the hammering with the long cross-face would induce tight places at d and e, requiring hammer blows as denoted by the marks.
The saw or plate straightener’s anvil or block is about 12 by 18 inches on its face, which must be very smooth and is slightly convex, because it is necessary that the plate should be solid on the block, directly beneath the part of its surface which is being hammered, otherwise the effect of the blows will be entirely altered. If, for instance, a, in Fig. 2125, represents the straightening block, and b a plate resting thereon, then the blows struck upon the plate anywhere save over the very edges of the anvil will have but little effect, because of the spring and rebound of the plate; and the effect of the blow will be distributed over a large area of the metal, tending to spring it rather than give it a permanent set. If the blow is a quick one, it may indeed indent the plate without having any straightening effect. On the other hand, by stretching the skin on the upper side of the plate, it will actually, under a succession of blows, become more bent. In fact, to use a straightening block, so large in proportion to the size of the plate that the latter cannot be adjusted so that the part of the plate struck lies solid on the block, renders all the principles above explained almost valueless, and is a process of[II-71] pounding, in a promiscuous way, productive of hammer marks, and altogether fatal to the production of true work.
To straighten the plate shown in Fig. 2125, we place it upon the anvil, as shown in Fig. 2126, striking blows as denoted at a, and placing but a very small portion of the plate over the anvil at first; and as it is straightened, we pass it gradually farther over the anvil, taking care that it is not, at any part of the process, placed so far over the anvil as to drum, which will always take place if the part of the plate struck does not bed, under the force of the blow, well upon the anvil.
| VOL. II. | THE HAMMER AND ITS USES. | PLATE VIII. | |||
 |
 |
||||
| Fig. 2127. | Fig. 2128. | ||||
 |
 |
||||
| Fig. 2129. | |||||
|
|
|||||
| Fig. 2130. | Fig. 2131. | ||||
 |
 |
||||
| Fig. 2132. | Fig. 2133. | ||||
 |
|||||
| Fig. 2134. | |||||
The methods employed to discover in what parts a plate requires stretching, in order to straighten it and to equalize its tension, are as follow: Suppose we have a plate, say 18 inches by 24, and having a thickness of 19 gauge, and we rest one end of it upon the block and support the other end in the left hand, as shown in Fig. 2127; then with the right hand we exert a sudden pressure in the middle of the plate; and quickly releasing this pressure, we watch where its bending movement takes place. If it occurs most at the outer edges, it proves that the plate is contracted in the middle; while, if the centre of the plate moves the most, it demonstrates that it is expanded in the middle. And the same rule applies to any part of the plate. This way of testing may be implicitly relied upon for all plates or sheets thin enough to be sprung by hand pressure.
Another plan, applicable for either thick or thin plates, and used conjointly with the first named, is to stand the plate on edge with the light in front, as in Fig. 2128; we then cast one eye along the face of the plate upon which the light falls, and any unevenness will be made plainly visible by the shadows upon the surface of the plate. The eye should also be cast along the edges to note any twist or locate any kinks.
We may take a thin piece of plate in the hands, and if it is loose in the middle and we lay a straight-edge upon its upper surface, and try to bend the middle of the plate downward with the fingers, it will go down under the finger pressure, the straight-edge showing a hollow place in the middle; and the same thing will occur if the straight-edge be tried with either side of the plate uppermost. But if the piece be tight in the middle and we test with the fingers and straight-edge in the same way, the middle instead of bending downwards, appears to rise up, the straight-edge showing it to be rounded. In the first case the middle moves because it is loose, and in the second the edges move because they are loose.
Fig. 2129 represents a plate for a circular saw that is loose in the middle, and if we bend the middle down it will become concave on the top, as shown in the figure. But if it were tight in the middle and loose at the outer edge, it would become, under the same pressure, convex on the top, as in Fig. 2130, and here again the part that is loose moves the most.
In thin saws, such as hand saws, the workman takes the saw in his hands, as in Fig. 2131, and bends it up and down so that by close observation he may see where it moves the most, and then discover the loose places, or he may watch for the tight places, since these are the places he must attack.
The sledge hammer used by the machinist is usually made in one of the two forms shown in Figs. 2132 and 2133, the latter being the most serviceable because it has two faces which may be used for driving purposes, which is the only use the machinist has for the sledge hammer. The coppersmith varies the shape of his hammer faces to suit the nature of the work, thus Fig. 2134 represents a coppersmith’s hammer, its two faces being of different sizes and of different curvature, and both being used to form convex surfaces having different degrees of curvature, it being noted that the curvature of the hammer face is always less than that of the work. In other forms of coppersmith’s hammers there are two penes and no face, one being at a right angle to the other, as in Fig. 2135, the penes being rounded as in the figure, or sometimes square.
Fig. 2136 represents a coppersmith’s hammer with a square nosed pene, which is sometimes made to stand at a right angle to the handle as in the figure, and at others parallel to it.
Fig. 2137 represents the file cutter’s hammer, whose handle is at the angle shown because the chisel is held at an angle, the point or cutting edge being nearest to the workman; hence if the handle were at a right angle to the hammer length his arm would require to be considerably elevated in order to let the hammer face fall fair on the chisel head, whereas by setting the handle at the angle shown the arm need not be elevated, and the blow may be given by a movement of the wrist.
Figs. 2138 and 2139 represent hammers used by boiler-makers for riveting boiler seams. The faces are made small so that if the blows are properly directed the edge of the face will not meet the boiler plate and indent it. These hammers are made long and narrow so that the weight may lie in the same direction as the hammer travels in when delivering the blow, and thus cause the effects of the hammer blows to penetrate deeper than if the hammer was wider.
In the cooper’s hammer, shown in Fig. 2140, the face extends flush up to the head, thus enabling it to strike a hoop upon a[II-72] barrel without danger of the extreme end or top of the hammer meeting the barrel, and preventing the hammer face from meeting the edge of the barrel hoop when driving it on the barrel. The face is square and its front edge therefore a straight line, which is necessary on account of the circular shape of the hoop of the barrel.
The mallet is made in various forms to suit the nature of the work and the tools it is to be used upon. Thus the carpenter’s mallet is a rectangular block, such as shown in Fig. 2141. It is composed of wood, because the carpenter’s tools are held in wooden handles, and a metal hammer would split them in course of time. It is rectangular in shape so that it may be applied to tools held in a corner of the work, where a round mallet could not, if of sufficient diameter, give the necessary weight. For such carpenters’ or wood-workers’ tools as are for heavy duty, and the tools for which have ferrules at the head of their handles to prevent them from splitting, the mallet is made cylindrical or round, as it is termed, and has an iron band at each end to prevent the face from spreading or splitting.
The stonemason’s mallet is also of wood, and is disk-shaped, with the handle in the centre, the circumferential surface forming the face. The reason for this is that his tools are of steel and have no handles; hence if the blow continually fell on the same part or spot of the mallet face it would sink or indent holes in it, which is prevented by utilising the whole circumference of the mallet for the face.
An excellent mallet for the machinist’s use, for driving finished work without damaging it, is formed of raw hide secured in a metal eye that receives the handle. Or for the same purpose a lead hammer is used, being especially serviceable for setting work in machines.
What is known as pening, or paning, consists of hammering the skin of metal to stretch it on the side that is hammered. It may be employed either to bend or to straighten. Suppose, for example, we have a piece of metal that is bent to a half circle, and if we take a light hammer and hammer it on the concave side and all over its surface the piece will straighten out to an amount depending on the amount of pening. Or if he hammers the convex side the piece will bend to a smaller circle. The principle involved is, that if one side of a piece is elongated and the other remains of its original length, the only shape it can assume to accommodate or permit the elongation is that of a curve of which the convex side is the longest. It follows, therefore, that the hammer blows must in pening be sufficiently light to condense or stretch the metal on one side only of the metal, and not forcible enough to effect it all through.
In order to accomplish this stretching as rapidly as possible it is necessary to use a light hammer, with sufficient force to be expended in condensing the metal at its surface, and to so form the hammer that it shall expend its force upon the work with a dead blow, that is, with as little rebound as possible. These results are best accomplished with a ball pened hammer, such as shown in Fig. 2108 and weighing about 1⁄2 lb. The blows should fall dead; that is, the hammer should fall, to a great extent, by its own weight, the number rather than the force of the blows being depended upon; hence, the hammer marks will not be deep. This is of especial importance when pening has to be performed upon finished work, because, if the marks sink deeply, proportionately more grinding or filing is required to efface them; and for this reason the force of the blows should be as near equal as possible. Another and a more important reason, however, is that the effect of the pening does not penetrate deeply; and if much of the pened surface is removed, the effects of the pening will be also removed. The work should not be rested upon metal, but upon wood.
The following are examples of pening. Fig. 2142 represents a shaft bent as shown, the arms being too wide at a, which may be corrected by pening at b. If the error was in the arms themselves and not in the stem, the side faces of the arms would require to be pened. Thus in Fig. 2143 the distance a is too short, and the pening must be at b c.
Fig. 2144 represents a strap requiring to be closed across a, the pening being at c or d. But as pening at d would bend the crown and unpair the bed of the brasses, it is preferable to pene at c. In either case the jaws will close as denoted by the dotted lines.
Fig. 2145 represents another common form of connecting rod strap, and in this case the pening may be most quickly and effectively done at the crown as denoted by the dots; and as this would alter the inside curve, the brass or box fitting into it must be refitted. In case the pening should be overdone it is better to modify it by filing away some of the pened surface.
Cast iron is more rapidly affected by pening than either wrought iron or steel. One of the most useful applications of pening is in the case of moulding patterns, which in time may become warped[II-73] from the rapping of the pattern in the mould, and this warping may be corrected by judicious pening, or suppose that a number of plates, such as represented in Fig. 2146, having been cast, it is found that the ends of the tongues a b curl up when cooling in the mould, then the tongues may be pened as at c d, throwing them down to the requisite amount, and thus moulding the pattern to accommodate the curling in cooling.
The riveting usually performed by the machinist is generally upon cold metal. The blows in this case should fall dead and the riveting be performed with a view to stretching the metal uniformly and evenly over the surface to be riveted.
An excellent example of cold riveting is given in the crank pin p in Figs. 2147 and 2148. c is the crank (both being shown in section). The end of the pin should be recessed as shown at a, so that it may be the more readily riveted outward to fill the countersink shown in the crank at b, b. The crank-pin is rested upon a piece of copper d interposed between it and the iron block e to prevent damage to the finished face of the crank-pin.
The riveting blows should be given with a ball-faced hammer, and delivered with a view to stretch the whole end face of the crank-pin evenly. Otherwise the riveted surface will be apt to split as shown. This usually occurs from not riveting the area at and near the circumference sufficiently, although it may occur from riveting that part of the area too much. The line of travel of the hammer should not be directly vertical, but somewhat lateral in a direction from the centre towards the circumference. If the countersink is a deep one, it is desirable to leave the crank-pin sufficiently too long, so that after the riveting has proceeded some time the surface of the metal which has become condensed and crystallized from the direct impact of the hammer blows, may be chipped away, leaving a surface that is swollen by the riveting without being so much condensed. This enables a much greater spreading of the metal without splitting it.
If in this class of work the riveted piece (as the crank-pin) is not driven in very tight before riveting, the riveting blows will be apt to jar the pin back. Hence, it is necessary to occasionally drive the pin home. The riveting should proceed equally all over, as if one side be riveted in advance of the other it tends to throw the pin out of true. When, however, the riveting begins to bed the pin, four equidistant places may be riveted home in advance so as to bring the pin home and hold it firmly.
The Chisel.—The machinist’s cold chisel is made from the two forms of steel shown in Figs. 2149, 2150, and 2151, and of these the former is preferable because it has two broad flats diametrally opposite and these form a guide to the eye in holding the chisel on the grindstone, and aid in grinding the facets that form the cutting edge true. Furthermore, as the cutting edge is in the same plane as these flats they serve as a guide to denote when the chisel edge lies parallel to the work surface, which is necessary to produce true and smooth chipping.
The width of the chisel may be made greater, as in Figs. 2152 and 2153, for brass or cast-iron work than for wrought iron or steel for the following reasons. On account of the toughness and hardness of wrought iron and steel the full force of a 13⁄4 lb. hammer, having a handle 13 inches long, may be used on a chisel about 7⁄8 inch wide without danger of causing the metal to break out below the chipping line, but if such a chisel be used with full force blows upon cast iron or brass the metal is apt to break out[II-74] in front of the chisel, the line of fracture often passing below the level it is intended to chip down to. Hence if a narrow chisel is used lighter blows must be delivered. But by using a broader chisel the force of the blow is distributed over a longer length of cutting edge, and full force blows may be used without danger of breaking out the metal.
The cutting end of the chisel should be kept thin, as in that case it cuts both easier and smoother. The total length of a chisel should not when new exceed 8 inches, for if made longer it is not suitable for heavy or smooth chipping, as it will bend and spring under heavy blows, and cannot be held steadily. The forged part should not exceed about 21⁄2 or 3 inches in length, as a long taper greatly conduces to springiness, whereas solidity is of great importance both to rapid and smooth work. The facets forming the cutting edge should be straight in their widths, as at b in Fig. 2154, and not rounded as at a, so that the face next to the work may form a guide in holding the chisel at the proper angle to maintain the depth of the cut. This angle depends upon the nature of the material to be cut; the facets forming an angle one to the other of about 65° for cast steel and about 50° for gun metal or brass. The more acute these angles the nearer the body of the chisel lies parallel with the work and the more effective the hammer blows. Thus in Fig. 2155 chisel c is the position of the chisel for wrought iron, and position d is for steel. The angles should always be made, therefore, as acute as the hardness of the material will permit. If they are too acute the cutting edge will be apt to bend in its length, while if not sufficiently acute they will not cut keen enough; hence the object is to make them as acute as possible without causing the cutting edge to bend in its length. For copper and other soft metals the angle may be about 30° or 35°, the chisel end being kept thin so that it may not become wedged between the work and the chipping, which will bend but little, and is, therefore, apt to grip the wedge end of the chisel. The cutting edge should be slightly rounded in its length, which will strengthen it and also enable a fine finishing clip to be taken off, as in Fig. 2156, the width of the chip not extending fully across the chisel width so that the corners are not under duty and are not, therefore, liable to break, or dig in and prevent smooth chipping. In some practice the edge is made straight in its length, as shown in Fig. 2149, which is permissible in heavy chipping when a cape chisel has been used, but in any event an edge rounded in its length is preferable. If the edge is hollow in its length, as shown in Fig. 2157, and magnified in Fig. 2158, the chip acts as a wedge to force the corners outwards as denoted by the arrows, causing them to break under a heavy cut, and, furthermore, a smooth cut cannot be taken when the corners of the chisel meet the work surface.
If the facets are ground under on one side, those on the other, as in Fig. 2159, the edge will not be parallel with the flats of the chisel, so that in holding it the flats will not form a guide to determine when the edge lies parallel to the work surface as it should do. The edge should also be at a right angle to the length of[II-75] chisel, as denoted by the lines, as in Fig. 2160, for if not at a right angle the chisel will be apt to move sideways after each blow, and cannot be held steadily.
The chisel should be held as close to its head as possible, so that the hand will steady the head as much as possible, and should be pushed forward firmly and steadily to its cut, which will greatly facilitate rapid and smooth chipping, and for wrought iron and copper it is found better to occasionally moisten the chisel with oil or water, the former being preferable.
Messrs Tangye, of Birmingham, have introduced the employment of chisel holders, such as shown in Fig. 2161, the object being to fit to each holder a number of short pieces of steel for chisels so that a number can be ground or forged at one time; obviously chisels of different shapes require different forms of handle.
When a heavy cut is to be taken the cape (Fig. 2162) chisel is used, first to carry through grooves or channels, such as shown in Fig. 2176 at a, b, and c, the distance apart of these grooves being slightly less than the width of the flat chisel, whose cut is shown partly carried across at d in the figure. The width of a cape chisel should gradually decrease from a to b in Fig. 2163, so that its side will be free in the groove it cuts, and the chisel head will be free to be moved sideways, and the direction of the groove may be governed thereby. If the chisel end be made parallel, as at c in Fig. 2164, it will have no play in the groove and the head cannot be moved; hence if the groove is started out of line, as it is apt to be, it will continue so.
The round-nosed chisel, Figs. 2165 and 2166, may be straight from h nearly to the point g, but should be bevelled at and near g, so that the chisel head may be raised or lowered to govern the depth of the cut. Its round nose should also be wider than the metal higher up, so that the chisel head may be moved sideways to govern the direction of the cut as in the cape chisel. The cow mouth chisel, Figs. 2167 and 2168, should be bevelled from g to[II-76] the point to enable the governing of the depth of the cut, and should be of greater curvature than the corner it is to cut out, so that its corners cannot wedge in the work.
The oil groove chisel, Figs. 2169 and 2170, should be wider at the cutting edge than at a for reasons already stated, and of less curvature than the bore of the brass or bearing it is to cut the oil groove in.
The diamond point chisel, Figs. 2171 and 2172, may be made in two ways. First, as in Figs. 2173 and 2174, for shallow holes, and as in Figs. 2171 and 2172 for deep ones. In shallow holes the chisel can be leaned over, as in Fig. 2176 at y, whereas in deep ones it must be held straight so that the chisel body may not meet the other side of the hole, slot, or keyway. The form shown in Fig. 2172 is the strongest, because its point is brought into line with the body of the steel, as shown by the line q. The side chisel, Fig. 2175, for cutting out the sides of keyways or slots, should be bevelled from w to the cutting edge for the reasons already given, and straight from w to v, the line v w projecting slightly above or beyond the body u. An application of the cow mouth chisel is shown at l, and one of the side chisel is shown at z in Fig. 2176. All these chisels are tempered to a blue color.
The chisel that is driven by hammer blows may be said to be to some extent a connecting link between the hammer and the cutting tool, the main difference being that the chisel moves to the work, while the work generally moves to the cutting tool. In many stone-dressing tools the chisel and hammer are combined, inasmuch as that the end of the hammer is chisel shaped; an example of this kind of tool being given in the pick that flour millers use to dress their grinding stones. On the other hand we may show the connection between the chisel and the cutting tool by the fact that the wood-worker uses the chisel by driving it with a mallet, and also by using it for a cutting tool for work driven in the lathe. Indeed, we may take one of these carpenter’s chisels and fasten it to the revolving shaft of a wood-planing[II-77] machine, and it becomes a planing knife; or we may put it into a carpenter’s hand plane, and by pushing it to the work it becomes a plane blade. In each case it is simply a wedge whose end is made more or less acute so as to make it as sharp as possible, while still retaining strength enough to sever the material it is to operate upon.
In whatever form we may apply this wedge, there are certain well-defined mechanical principles that govern its use. Thus when we employ it as a hand tool its direction of motion, under hammer blows, is governed by the inclination of the face which meets the strongest side of the work, while it is the weakest side of the material that moves the most to admit the wedge and therefore becomes the chip, cutting, or shaving. In Fig. 2177, for example, we have the carpenter’s chisel operating at a and b to cut out a recess or mortise, and it is seen that so long as the face of the chisel that is next to the work is placed level with the straight surface of the work the depth of cut will be equal; or in other words, the line of motion of the chisel is that of the chisel face that lies against the work. At c and d is a chisel with, in the one instance, the straight, and in the other the bevelled face toward the work surface. In both cases the cut would gradually deepen because the lower surface of the chisel is not parallel to the face of the work.
If now we consider the extreme cutting edge of chisel or wedge-shaped tools it will readily occur that but for the metal behind this fine edge the shaving or cutting would come off in a straight ribbon, and that the bend or curl that the cutting assumes increases with the angle of the face of the wedge that meets the cutting, shaving, or chip.
I may, for example, take a piece of lead, and with a penknife held as at a, Fig. 2178, cut off a curl bent to a large curve, but if I hold the same knife as at b it will cause the shaving to curl up more. Now it has taken some power to effect this extra bending or curling, and it is therefore desirable to avoid it as far as possible. For the purpose of distinction we may call that face of the chisel which meets the shaving the top face, and that which lies next to the main body of the work the bottom face. Now at whatever angle either face of the chisel may be to the other, and in whatever way we present the chisel to the work, the strength of the cutting edge depends upon the angle of the bottom face to the line of motion of the chisel, and this is a principle that applies to all tools embodying the wedge principle, whether they are moved by a machine or by hand.
Thus, in Fig. 2179 we have placed the bottom face at an angle of 80° to the line of tool motion, which is denoted by the arrow, and we at once perceive its weakness. If the angle of the top face to the line of tool motion is determined upon, we may therefore obtain the strongest cutting edge in a hand-moved tool by causing the bottom angle to lie flat upon the work surface.
But in tools driven by power, and therefore accurately guided in their line of motion, it is preferable to let the bottom face clear the work surface, save at the extreme cutting edge. The front face of the wedge or tool is that which mainly determines its keenness, as may be seen from Fig. 2180, in which we have the wedge or tool differently placed with relation to the work, that in position a obviously being the keenest and less liable to break from the strain of the cutting process.
If we now turn our attention to that class of chisel or wedge-shaped tools in which the cutting edge is not a straight line, but may be stepped or curved—as, for example, the carpenter’s plane blade—we shall find that so long as the blade stands at a right angle to the surface it is operating upon, as in Fig. 2183 at b, the shape of surface it cuts will exactly correspond to the shape of its cutting edge; but so soon as the tool is inclined to its line of motion its cutting edge will, if curved, produce a different degree of curvature on the work.
Suppose, for instance, that we have in the figure a piece of moulding m and a plane blade b, and the length of the cutting edge is denoted by a, Fig. 2182; now suppose that the blade is inclined to its line of motion (as in the case of carpenters’ planes) and stands at c, Fig. 2183: we then find that the cutting edge must extend to the length or depth d, and it is plain that the depth of the curve on the moulding is less than the depth of the cutting edge that produces it; the radius e being less than of d, so that if we place the cutter c upright on the moulding it will appear as shown in Fig. 2181. If, therefore, we are required to make a blade that will produce a given depth of moulding when moved in a straight line and presented at a given angle to the work, we must find out what shape the blade must be to produce the given shape of moulding, which we may do as follows:[II-78]
In Fig. 2184 let a be a section of the moulding, and if the blade or knife is to stand perpendicular, as shown at b, Fig. 2183, and if it is moved in a straight line in the direction of the length of the work, then its shape would necessarily be that shown at b, Fig. 2184, or merely the reverse of a. In the position mentioned it could be used only as a sweep applicable to some few uses, but not adapted to cutting. To become a cutting tool it must be inclined and stand at some angle of less than 90° to its line of motion.
Thus in Fig. 2185 d b e represents the bottom of the moulding and line of motion of the cutter, and a b the cutter perpendicular to it, the highest point of the cutting edge, as c of Fig. 2184, being at c, Fig. 2185. The height or thickness of the moulding cut would be the space between the lines e b d and e c f, but the cutter assuming the position b c at an angle of 30° from a b, the point c is brought to d; consequently the highest line of the moulding would now be g d h, and its thickness less. This is further exhibited in Fig. 2186, where a represents the original depth section of Fig. 2184 that would be formed by knife b of Fig. 2184 when standing perpendicular; and g shows the depth with the same knife when placed as b c, Fig. 2185, or at 30° inclination, and h shows the depth that would be cut with the same knife or cutter at 45°. It is now evident that every change in the inclination of the same cutter would effect a change in the shape of moulding which it cuts, and to produce a given style of moulding the shape of the cutter must be decided by its inclination, or the angle at which it is used.
The method of projecting a given section of moulding in order to exhibit the form that the curve of the opening should assume on the face of the knife, is shown in Fig. 2187. Upon a horizontal line a b c d draw a section of the required style of moulding, as shown at a e b. To the right of this draw a line, as f c, to meet the base line a b c d, and as f c represents the cutter, it must stand at the same angle that the proposed cutter is to have—in this particular example 30° from the perpendicular. From the highest point of the section a e b draw a horizontal line e g, meeting f c in g. From points g and c draw lines, as c j and g h, of any convenient length, at right angles to f c. At any distance from g h draw k l parallel to g h, and upon k l trace the section of moulding a e b, as k m l. Draw lines from the extreme edges k and l of k m l, as k n, l j, perpendicular to k l, cutting g h and meeting c j at n and j. e g being parallel to a b c d, g will be the point on the cutter where the top e of the moulding will come on the highest point of the cutting edge, and c g will be the entire length of cutting edge or height of opening measured on the face of the cutter f c. c j being drawn from the lowest point c of the cutter and g h being drawn from g, the highest cutting point, both lines at right angles to g c, then their distance from each other, as p o, must obviously represent the extreme height of opening in the cutter in its new position or front view, and k l, representing the width of moulding transferred to n j by the parallel lines k n and l j, will show the width of opening in the cutter. Having now the height and width, it only remains to project an indefinite number of points and trace the curve through them. Divide a b into a number of parts, and[II-79] to avoid confusion mark the points of division thus obtained upon a b—1, 2, 3, 4, &c. Divide k l in an exactly similar manner and into the same number of parts, and mark the divisions i., ii., iii., iv., &c. Erect perpendiculars from points 1, 2, 3, 4, &c., meeting the curve a e b, and from the points thus found on a e b draw horizontal lines to f c; from the termini of these horizontals on f c draw the remaining lines parallel to and between g h and c j. From the divisions i., ii., iii., iv., &c., on k l, let drop the perpendiculars, cutting the other series of lines at right angles. A point of the curve will then be at the intersection of the line from 1 on a b, with line i on k l; another at the intersection of the line originating at 2 with that from ii, and so on, and the proper curve is found by tracing from n through the intersections to p, and from p to j. Then k n being one side of the cutter and l j the other, n p j is the curve that the opening or cutting edges must have to cut the profile a e b, with the cutter set at f c, or 30°.
The same method is shown in Fig. 2188, except that in this case, instead of dividing a b and k l, the divisions are made directly on the peripheries a 6 b and k vi. l by stepping round with the dividers. The cutter f c is shown in this case at an angle of 45°, in order that the change in form which the curve assumes with the cutter at different angles may be clearly seen by comparing the curve n p j of Fig. 2187 with the same in Fig. 2188. The two figures are similar in other respects, and as the lettering is the same on each, the description of Fig. 2187 will apply equally to Fig. 2188.
There remains one more case of cutters moving in right lines, and that is where, besides having an inclination backward, as at f c, Fig. 2187, making a vertical angle to the line of motion, they are placed at an angle across the guiding piece also, or “skewing,” thus making an angle to the line of motion on a horizontal plane as well as on a vertical one. Thus, suppose an ordinary carpenter’s plane to have the cutter or “iron” turned partly round and placed so that the cutting edge, instead of lying at a right angle across the body, crosses it at some other angle. Fig. 2189 represents an ordinary carpenter’s plane with the blade so placed. Here the edge, or rather side, d b, of the blade inclines back at an angle, as a b d, which is 45° in this case, to the perpendicular line a b on the side of the plane. For convenience call a b d the vertical angle. The lower or cutting edge e b of the blade also crosses the bottom of the plane at an angle e b c—30° in this instance—to a line b c, crossing the bottom at right angles. Now, it is evident that this latter angle e b c will influence the form of the cutter, if, instead of being a flat plane, as represented for clearness in Fig. 2189, it had a cutting edge of curved outline for cutting mouldings or similar work. But in either case the angle that d b or one side of the blade makes to e b, or the cutting edge—that is, the angle d b e—must be found in order to cut off the blank for the cutter or knife at the right “slant.”
The method given in Figs. 2187 and 2188 of determining the form of cutter to produce a moulding of given profile now undergoes a modification where there are two angles to be taken into consideration instead of one. As an example, suppose a cutter is required that is to be fixed in such a position in its carrier or block that the handle a b d, or “vertical angle,” of Fig. 2189 is, say, 45°, and the angle e b c, or “horizontal angle,” of Fig. 2189 shall be 30°. Required the angle at which the bottom of the blank for the cutter must be cut off; or the angle that the side d b and lower edge b e of Fig. 2189 would make to each other, measured on the face of the cutter, and required the outline of cutting edge to be traced on the face of cutter to cut the section of moulding a e b, Fig. 2190: draw a horizontal line, as a b c d, and erect a perpendicular, as c r. From c draw c f, making an angle to c r equal to the “vertical angle,” or angle a b d, Fig. 2189, which is 45° in this case. Draw a profile of the required moulding, as a e b, with its back a b coincident to the horizontal line a b c d. Draw a horizontal line from the highest point of the profile, as e, to meet f c in g. Draw parallel lines c j and g h, from c and g respectively, of any convenient length and making right angles to f c. At right angles to g h and c j, and parallel to f c, draw k h j to represent one side or edge of the cutter, but the angle of the lower end or angle d b e of Fig. 2189 must now be determined; to do this, draw an indefinite horizontal line, a b c, Fig. 2191, and from any point, as b, drop a perpendicular b d; now, from b set off on a b c the distance c b of Fig. 2190, obtaining point e, and from e extend a perpendicular above and below a b c, as f e h. From e on e f set off distance g b of Fig. 2190, obtaining j on e f. From b draw a line, making the same angle to b d that the angle e b c is in Fig. 2189, or 30° in this case, and cutting e h in k. Set off distance e k from e on a c, obtaining l; draw l j. Now, on Fig. 2190, with centre at h, and radius l j of Fig. 2191, describe arc w x, and from j as centre, on Fig. 2190, and b k of Fig. 2191 as radius, describe arc y z. Through the intersection v of arcs y z and w x, j l m must be drawn, making the proper angle to the side j h k of the cutter; this angle is 69° in this case, as found by construction. From h draw h n parallel to j l, and from h draw h o at the same angle to h n that b k is to b d,[II-80] Fig. 2191, or angle e b c, Fig. 2189. Place a duplicate of a e b, with its base coincident to h o and corner a at h, as h p r. From r draw r n at right angles to h r and cutting h n at n; through n draw s n l parallel to k h j. Then while k h j represents one edge of the cutter, s n l will be the other, and j l the cutting edge before the opening is cut out. Divide the curves e b and p r similarly, obtaining points 1, 2, 3, &c., and i., ii., iii., &c., respectively. From points 1, 2, 3, &c., lines are to be drawn parallel to e g, meeting g c, continued from g c parallel to g h, and meeting h j, and from h j parallel to h n, meeting n l. From points i., ii., iii., &c., lines are to be drawn perpendicular to h r, meeting h n and continued from h n, parallel to h j, to j l, thus intersecting the first series. Lines from points 1, 2, 3, &c., then determine the height of different points of the curve, and those from i., ii., iii., &c., their location laterally; hence, by tracing through the intersections of 1 with i., 2 with ii., &c., the curve h t l is obtained. The two outside lines k h j and s n l may now represent the edges of a piece of steel of which the cutter is to be made, and h t l will be the contour of cutting edge that must be given it in order that when, fixed for use at the angles named, it will form the required moulding a e b.
If the chisel, knife, or cutter revolves in a circle, instead of in a right or straight line, the problem is again different, and the shape of cutting edge necessary to produce a given shape of moulding is again altered. Let Fig. 2192, for example, represent the bar or head of a wood moulding machine, the bar or head revolving in the direction of the arrow, and the moulding being moved beneath it in a straight line endways as denoted by the arrow at n.
In order that the nut that holds the cutter to the head may clear the top of the moulding the highest cutting point of the cutter must not come nearer to the corner of the head than 1⁄4 inch. This is shown in the end view of a 21⁄2 inch cutter head in Fig. 2193, the circle b representing the path of revolution of the nut. In larger heads the nut will clear better.
Now we may consider that the cutter simply revolves about a circle whose diameter is the largest that can be described on the end of the square bar that drives it.
If, for instance, we look at the end of the bar as it is presented in Fig. 2195, we see that the circle just fills the square, and that if we cut off all four corners, leaving the bar round, as denoted by the circle, the chisel will revolve in the same path as before. Now suppose we place beneath the revolving chisel a piece of square timber, and raise this timber while holding it horizontally, as would be done by raising the work table. It will cut the work to the shape shown in the two views in the figure, enabling us to observe the important point that the only part of the work that the chisel has cut to its finished shape is that which lies on the line a a. This line passes through the axis on which the bar and cutter revolve, and represents the line of motion of the work in feeding upward to the chisel.
If now we were to move the work endways upon the table, we should simply cause the moulding to be finished to shape as it passes the line a; because all the cutting is done before and up to the time that the chisel edge reaches this line; or in other words, each part of the chisel edge begins to cut as soon as it meets the moulding, and ceases to cut as soon as it reaches this line. We may now draw this circle and put on it a chisel in two positions, one at the time its lowest cutting point is crossing the line a and the other at the time the highest point on its cutting[II-81] edge is passing the line, these positions being marked 1 and 2 in Fig. 2196; the depth of moulding to be cut being shown at s. Now, since the chisel revolves on the centre of the circle, the path of motion on its highest cutting point c will be as shown by the circle b, and that of the lowest point or end e of its cutting edge will be that of the circle d, while the depth of moulding it will cut is the distance between c and e, measured along the line a a, this depth corresponding to depth shown at s.
Clearly when the chisel has arrived at position 2, the moulding will be finished to shape, and it is therefore plain that it takes a length of cutter-edge from c to f to cut a moulding whose depth is s, or what is the same thing, c e.
But to solve the question in this way, we require for every different depth of moulding to make such a sketch, and the square bar that drives the chisel is made in various sizes, each different size again altering the length or depth of chisel edge necessary for a given depth of moulding.
But we may carry the solution forward to the greatest simplicity for each size of square bar, and for any depth of moulding that can be dressed on that size of bar, by the following means:—In Fig. 2197 we have the circle and the line a as before; the depth from c to e being the greatest depth of moulding to which the square bar is intended to drive the chisels; while point c is the nearest point to the square bar at which the top of the moulding must be placed. Line a represents a chisel cutting at its highest point; line b a chisel cutting the moulding to final shape at 1⁄4 inch below c, on the line a; line c a chisel cutting the moulding to final shape at a distance of 1⁄2 inch below point c and measured on the line a; lines d, e, f, g, h, and i represent similar chisel positions, the last meeting the point e, which is the lowest point at which the chisel will cut. Suppose, now, we set a pair of compasses one point at the centre a of the circle, and strike the arc j; this arc will represent the path of motion of that part of the chisel edge that would finish the moulding to shape at c; similarly arc k represents the path of motion of that part of the chisel edge[II-83] that cuts the moulding to final shape on the line a, and at a distance of 1⁄4 inch below c, and so on until we come to arc r, which represents the path of motion of the end of the chisel. All these arcs are carried to meet the first chisel position c a, and from these points of intersection with this line c a we mark lines representing those on a common measuring rule. The first of these from c we mark 1⁄4, the next 1⁄2, the next 3⁄4, and so on to 2, these denoting the measurement or depth of chisel necessary to cut the corresponding depth of moulding. If, for example, we are asked to set a pair of compasses to the depth of cutting edge necessary to cut a moulding that is an inch deep, all we do is to set one leg of the compasses at c, and the other at line 1 on the line c a; or if the moulding is to be 2 inches deep, we set the compasses from c to 2 on line c a. We have here, in fact, constructed a graduated scale that is destined to be found among the tools of every workman who forms moulding cutters, and if we examine it we shall find that the line that is marked 1⁄4 inch from c is not 1⁄4 inch but about 5⁄16 inch; its distance from c being the depth of chisel edge necessary to cut a moulding that is 1⁄4 inch deep.
Again, the line marked 1 measures 13⁄16 inch from c, because it requires a chisel edge 13⁄16 deep to cut a moulding that is one inch deep. But if we measure from c to the line marked 2 we find that it is 21⁄4 inches from c, and since it represents a chisel that will cut a moulding two inches deep, we observe that the deeper the moulding is the nearer the depth of cutting edge is to the depth of moulding it will produce. This occurs because the longer the chisel the more nearly it stands parallel to the line a, at the time when its point is crossing the line a. Thus, line i is more nearly parallel to a than line a is, and our scale has taken this into account, for it has no two lines equally spaced; thus, while that marked 1⁄4 is 5⁄16 inch distant from c, that marked 1⁄2 is less than 5⁄16 inch distant from that marked 1⁄4, and this continues so that the line marked 2 is but very little more than 1⁄4 inch from that marked 13⁄4. Having constructed such a scale we may rub out the circle, the arcs, the line a, and all the lines except the line from c to a and its graduations, and we have a permanent scale for any kind of moulding that can be brought to us.
If, for example, the moulding has the four steps or members s, t, u, v, in the figure, each 1⁄2 inch deep, then we get the depth of cutter edge for the first member s on our scale, by measuring from c to the line 1⁄2 on line c a. Now the next member t extends from 1⁄2 to 1 on the moulding, and we get length of cutter edge necessary to produce it from 1⁄2 to 1 on the scale. Member u on the moulding extends from 1 to 13⁄4; that is to say, its highest point is 1 inch and its lowest 13⁄4 inch from the top of the moulding, and we get the length for this member on a scale from the 1 to the 13⁄4; and so on for any number of members.
After the depth of cutting edge for each member has thus been found, it remains to find the exact curve of cutting edge for each step, and, in doing this, the same scale may be used, saving much labor in this part also of the process, especially where a new piece of moulding must be inserted to repair part of an old piece that needs renewal in places only, as is often the case in railroad cars.
In Fig. 2197a we have a scale or rule constructed upon the foregoing[II-84] principles, but marked to sixteenths, and it may now be shown that the same scale may be used in finding the actual curve as well as the depth of cutter edge necessary to produce the moulding of any member of it. Let the lower curves s, t, for example, represent the moulding to be produced, and the upper outline represent the blank piece of steel of which the cutter is to be made, the edges c, d being placed in line one with the other. We may then draw across both the moulding and the steel, lines such as e e, f f, g g, h h, i i, j j, all these lines being parallel to the edges c, d. To get the total depth of cutter edge for the moulding we measure with a common measuring rule the total height of the moulding, and supposing it to measure an inch, we set a pair of compasses to an inch on our cutter scale, and with them mark from the base m of the steel, the line p giving total depth of cutter edge. We next measure with a common rule the depth of member s of the moulding, and as it measures 1⁄2 inch we set the compasses to the 1⁄2 on the cutter scale, and with these compasses mark from line m line b, showing the depth of member s. In order to find the exact curve for each member, we have first to find a number of points in the curve and then mark in the curve by hand, and it is for the purpose of finding these points that the lines e e, f f, g g, h h, i i, j j, have been drawn. These lines, it may be remembered, need not be equally spaced, but they must be parallel, and as many of them may be used as convenient, because the greater their number the more correctly the curve can be drawn.
The upper edge or base line, m m, both of the steel and of the drawing, is that from which all measurements are to be taken in finding the points in the curve, which is done as follows: With an ordinary measuring rule we measure on the moulding and from line m m of the moulding as a base the length of the line f f below m m, to the curve, which in this case measures say 5⁄16 inch; we then set a pair of compasses or compass calipers to the 5⁄16 on the cutter scale, and from base m m on the cutter[II-85] steel, mark, on line f f, an arc, and where the arc cuts f f is one point in the curve.
Similarly we measure on the moulding, or drawing of the moulding, the length of line g g from line m m to the moulding curve, and find that it measures, say 7⁄16 inch, hence we mark from base line m m of the steel, on line g g, arc v, distant 7⁄16 according to the cutter scale. Similar measurements are taken at each vertical line of the drawing which represents the moulding, and by means of the corresponding divisions of the cutter scale, arcs are marked on the vertical lines on the cutter steel, and where the arcs cut the vertical lines are points in the curve, and through these points the curve may be drawn by hand. We may make a cutter scale from an ordinary parallel rule, marking one end to correct inches and the other end for a cutter scale. Measurements from the moulding may then be made on one end of the rule; measurements for the cutter may be taken from the other end of the rule, and the rule may be used at the same time to draw the parallel lines e e, &c. Or, as each size of cutter head requires a different cutter scale, we may make a rule out of a piece of box or other close-grained wood, say 3⁄4 inch square, using one side for each size of cutter head. One end of each face of this rule may be marked in correct inches and parts of an inch (the divisions being thirty-seconds of an inch), and the other end may be marked as a cutter scale, the divisions being found as described with reference to Fig. 2197.
An instrument, patented by R. Drummond, for finding the depth of cutting edge and also for finding the curves, is shown in Figs. 2198 and 2199. It consists essentially of a bar g bent at a right angle, thus making two arms. Upon one arm is a slide w (best seen in Fig. 2199) secured by a set-screw b, and having at a a pivot to carry a second bar h, which is slotted throughout its length to permit bar g to slide freely through it. Upon the other arm of g is a slide p secured by a set-screw c, and carrying a compass point e. The bar h carries an adjustable slide z secured by a set-screw d and carrying the compass point f.
In using the instrument but three very simple operations are necessary. First, the two slides w and p are set to the numerals on the bar, which correspond to the size of the head on the moulding machine the cutter is to be used upon; thus in Fig. 2199 they are shown set to numeral 2, as they would be for a 2-inch cutter head. The instrument is next opened, its two bars occupying the position shown in Fig. 2199, and the two compass points are set to the height of the moulding or to any desired member of it, as the case may be. The bars are then opened out into the position shown in Fig. 2200, and the compass points at once give the depth of cutter edge necessary to produce the required depth of moulding.
It will be noted that the pivot a represents the centre upon which the cutter revolves, and that while the face of the bar h corresponds to the line of moulding formation answering to line a a in Fig. 2196, the face of bar g corresponds to the face c f of the cutter in Fig. 2196; hence the instrument simply represents a skeleton head and cutter, having motions corresponding to those of an actual cutter head and cutter.
The File.—The file is a piece of hardened steel having teeth produced upon its surface by means of rows of chisel cuts which run more or less diagonally across its width at an angle that is varied to suit the nature of the material the file is to be used upon. The vertical inclination of the tooth depends upon the inclination of the face of the chisel with which it is cut, the two being equal, as is shown in Fig. 2201, which is an enlarged view of a chisel and some file teeth. In order that the tops of the teeth shall be sharp, and not rounded or curved, as in Fig. 2202, it is necessary that the edge of the chisel be kept sharp, an end that is greatly aided by the improved form of chisel shown in Fig. 2203. When a file possesses curved points, or caps, as they are technically termed, a few strokes upon a narrow surface will cause them to break off, reducing the depth of the teeth and causing the cuttings to clog in them. If, however, the file is used upon a broad surface these caps will remain, obviously impairing the cutting qualifications of the file, even when new, and as they[II-86] soon get dulled the file loses its grip upon the work and becomes comparatively valueless.
Files were, until the past few years, cut entirely by hand—file cutting by machinery having previously been a wide field of mechanical experiment and failure. Among the most prominent causes of failure was that the teeth produced by the earlier machines were cut too regular, both as to their spacing and their height; hence the points of the rear teeth fell into the same channels as those in advance of them, thus giving the tooth points too little opportunity to grip the work. This also gives too broad a length of cutting edge and causes the file to vibrate on the forward or cutting stroke, an action that is technically known as chattering, and that obviously impairs its cutting capacity. The greatest amount of duty is obtained from a file when the rear tooth cuts off the projection left by the preceding one, because in that case the duty of the tooth is confined to cutting off a projection that is already weakened and partly separated from the main body by having the metal cut away around its base. Workmen always practically recognise this fact, and cause the file marks to cross each other after every few strokes. In the machine-cut files made by The Nicholson File Co., the teeth are arranged to attain this object by the following means:—1. The rows of teeth are spaced progressively wider apart from the point towards the middle of the file length by regular increments of spacing, and progressively narrower from the middle toward the heel. 2. This general law of the spacing is modified by introducing as the teeth are cut an element of controllable irregularity in the spacing, which irregularity is confined within certain limits, so that neither the increment nor decrement of spacing is entirely regular. 3. In arranging the teeth so that the successive rows shall not be exactly parallel one to the other, the angle of inclination being reversed as necessity requires. The irregularity of spacing, while sufficient to accomplish the intended object, is not enough to practically vary the cut of the file, or, in other words, it is insufficient to vary its degree of coarseness or fineness to any observable extent. But it enables the file to grip the work with as little pressure as possible, and enables the teeth to cut easily without producing deep file marks or furrows.
Files and rasps have three distinguishing features: 1. Their length, which is always measured exclusively of their tangs. 2. Their cut, which relates not only to the character, but also to the relative degree of coarseness of the teeth. 3. Their kind or name, which has reference to the shape or style. In general, the length of files bears no fixed proportion to either their width or thickness, even though of the same kind. The tang is the spiked-shaped portion of the file prepared for the reception of a handle, and in size and shape should always be proportioned to the size of the file and to the work to be performed. The heel is that part of the file to which the tang is affixed.
Of the cut of files we may say that it consists of three distinct forms; viz.: “single cut,” “double cut” and “rasp,” which have different degrees of coarseness, designated by terms as follows viz.:—
| Single-cut. | Double-cut. | Rasp. |
| Rough | Coarse | Coarse |
| Coarse | Bastard | Bastard |
| Bastard | Second-cut | Second-cut |
| Second-cut | Smooth | Smooth |
| Smooth | Dead-smooth |
The terms “rough,” “coarse,” “bastard,” “second-cut,” “smooth” and “dead-smooth,” have reference only to the coarseness of the teeth, while the terms “single-cut,” “double-cut” and “rasp” have special reference to the character of the teeth. The single-cut files (the coarser grades of which are sometimes called “floats”) are those in which the teeth are unbroken, the blanks having had a single course of chisel-cuts across their surface, arranged parallel to each other, but with a horizontal obliquity to the central line, varying from 5° to 20° in different files, according to requirements. Its several gradations of coarseness are designated by the terms “rough,” “coarse,” “bastard,” “second-cut” and “smooth.” The rough and coarse are adapted to files used upon soft metals, as lead, pewter, &c., and, to some extent, upon wood. The bastard and second-cut are applied principally upon files used to sharpen the thin edges of saw teeth, which from their nature are very destructive to the delicate points of double-cut files. The smooth is seldom applied upon other than the round files and the backs of the half-rounds. Fig. 2204 represents the cut of single-cut rough files, their lengths ranging from 16 inches down to 4 inches. Fig. 2205 shows the cut of the coarse, bastard, and second-cut, whose lengths also range from 16 to 4 inches, and whose cut is also finer as the length decreases. The float is used to some extent upon bone, horn, and ivory, but principally by plumbers and workers in lead, pewter, and similar soft metals. It will be seen that the teeth are nearly straight across the file and are very open, both of these features being essential requirements for files to be used on the above-named metals.
Double-cut files are those having two courses of chisel cuts crossing each other. The first course is called the over cut, and has a horizontal obliquity with the central line of the file, ranging from 35° to 55°. The second course, which crosses the first, and in most double cuts is finer, is called the up-cut, and has a horizontal obliquity varying from 5° to 15°. These two courses fill the surface of the file with teeth inclined toward its point, the points of which resemble somewhat, when magnified, those of the diamond-shaped cutting tools in general use. This form of cut[II-87] is made in several gradations of coarseness, which are designated by the terms “coarse,” “bastard,” “second-cut,” “smooth” and “dead-smooth.” Fig. 2206 represents the cut of double-cut bastard files, from the 16 inch down to the 4 inch, and Fig. 2207 the cut of the coarse, second-cut, and smooth. For very fine finishing a still finer cut, called the dead-smooth, is made, being like the smooth, but considerably finer. It is a superior file for finishing work in the lathe, or for draw-filing machine work that is to be highly finished. The double-cut is applied to most of the files used by the machinist, and, in fact, to most of the larger number in general use. For unusually fine work, tool-makers and watch-makers use the Swiss or Groubet files—so called from their being made by M. Groubet, of Switzerland. These files are double-cut, and their degree of coarseness is denoted by number; thus, the coarsest is a bastard and the finest number 8. The prominent characteristics of these files are their exceedingly even curvature and straightness, and, in the finer grades, the unusual fineness of the cut, which feels soft and velvety to the touch. They are made in sizes ranging from 2 to 10 inches, and are always double-cut.
Rasps differ from the single or double-cut files in that the teeth are disconnected from each other, each tooth being made by a single-pointed tool, denominated by file-makers a punch, the essential requirement being that the teeth thus formed shall be so[II-88] irregularly intermingled as to produce, when put in use, the smoothest possible work consistent with the number of teeth contained in the surface of the rasp. Rasps, like files, have different degrees of coarseness, designated as “coarse,” “bastard,” “second-cut” and “smooth.” The character and general coarseness of these cuts, as found in the different sizes, are shown in Figs. 2208 and 2209. Generally speaking, the coarse teeth are applied to rasps used by horseshoers, the bastard to those used by carriage makers and wheelwrights, the second-cut to shoe-rasps, and the smooth to the rasps used by cabinet-makers.
Figs. 2210, 2211 and 2212 are respectively coarse, bastard, and finishing second-cut files, the first two being for brass.
Fig. 2210 represents a file open in both its over and up-cut, which is not, therefore, expected to file fine, but fast, and is adapted for very rough work on the softer metals, as in filing off sprues from brass and bronze castings, filing the ends of rods, and work of a similar nature. It is also, to some extent, used upon wood. The essential difference between the bastard file shown in Fig. 2211 and that just described is the degree of fineness of the up-cut, which is nearly straight across the tool. This form of teeth, which may be applied to any of the finer cuts, and upon any of the shapes usually made double-cut, is especially adapted to finishing brass, bronze, copper and similar soft metals, and is not so well adapted to the rougher work upon these metals as the coarse brass file previously described. Fig. 2212 is a finishing file. The first or over-cut in this case is very fine, and, contrary to the general rule, has the least obliquity, while the up-cut has an unusual obliquity, and is the coarser of the two cuts. The advantages in this arrangement of the teeth are that the file will finish finer, and by freeing itself from the filings is less liable to clog or pin than files cut for general use. This form of cut is especially useful when a considerable quantity of finishing of a light nature is required upon steel or iron. It is not recommended for brass or the softer metals, nor should it be made of a coarser grade than the second-cut.
The names of files are sometimes derived from the purpose for which they are to be used. Thus, we have saw files, slitting files, warding files, and cotter files. The term “warding” implies that the file is suitable for use on the wards of keys, while “cotter” implies that it is suitable for filing the slots for that class of key which the machinist terms a cotter. In other cases files are named from their sections, as in the case of “square,” “round,” “half-round,” and “triangular,” or “three-square” files, as they are often termed.
The term “flat” may be considered strictly as meaning any[II-89] file of rectangular section whose width exceeds the thickness. Hence, “mill files,” “hand files,” and “pillar files” all come under the head of flat files, although each has its own distinguishing features. The general form of the flat file is shown in Fig. 2213, while the cross-sections of various quadrangular files are shown in Figs. from 2214 to 2218. From these views it will be seen that the thicknesses gradually increase from the mill to the square file. Mill files are slightly tapered from the middle to the point both in their width and thickness. They are single-cut, and are usually either bastard or second-cut, although they are sometimes double-cut. Mill files of both cuts are principally used for sharpening mill saws, mowing-machine knives and ploughs, and in some machine shops for rough lathe work, and, to some extent, in finishing composition brasswork. Mill sections are occasionally made blunt—that is to say, their sectional shape is alike from end to end—in which case they are mostly double-cut, and seldom less than 8 inches in length. They are suitable for filing out keyways, mortises, &c., and for these purposes should have at least one safe edge. A safe edge is one having no teeth upon it, which allows the file to be used in a corner without cutting more than one of the work surfaces. When the corner requires to be very sharp it is preferable to take a file that has teeth upon its edge and grind the teeth off, so as to bring the corner of the file up sharp, which it will not be from the cutting, because the teeth do not come fully up to a sharp corner.
Hand-files are tapered in thickness from their middle towards both the point and the tang, and are, therefore, well curved or bellied on each side. This fits them for the most accurate of work, on which account they are generally preferred by expert workmen. They are nearly parallel in width and have one safe edge and one edge cut single, while the face is cut double. Hand-files are also made equaling, the term equaling meaning that, although apparently blunt or of even thickness throughout the length, yet, in fact, there is a slight curvature, due to the file being thickest in the middle of its length. An equaling hand-file is especially suitable for such purposes as filing out long keyways, in which a great part of the file length is in action, and it can, therefore, be easily pushed in a straight line.
The flat file, Fig. 2213, when 10 inches and under in length, is made taper on both its sides and edges, from the middle to the front of the file, and when longer than 10 inches they should be made full taper—that is to say, the taper should extend from the middle toward the heel, as well as toward the point. Flat files are usually double-cut, the coarse-cut being used upon leather, wood, and the soft metals. The flat bastard is that most commonly used, the flat second-cut, smooth, and dead-smooth being used by machinists for finishing purposes, the latter preceding the polishing processes.
Pillar files are tapered in thickness from the middle to each end; the width is nearly parallel, and one of the edges is left safe. They are double-cut, and, although not in general use, are especially adapted to narrow work, such as in making rifles,[II-90] locks, &c. The square file ranges from 3 to 16 inches in length, and is made for general purposes with considerable taper. It is usually double-cut, the bastard being the principal cut, the second-cut and smooth being mainly used by the machinist.
Square blunt files range from 10 to 20 inches in length, of the same sectional sizes as the square taper, and are cut double, usually bastard. For machinists’ use, however, they are used in the second-cut also, and are provided with sometimes one and sometimes two safe sides. Square equalling files are in every respect like the square blunt, except in the care taken to prepare a slight curve or belly in the length of the file, which greatly enhances their value in filing out the edges of keyways, splines, or mortises. The fault of the square blunt, when used for fine, or true work, is that the heel, having no belly, is apt to come into too prominent action.
Warding files, Fig. 2218, are made parallel in thickness, but are considerably tapered on their edges. They range in size from 3 to 8 inches in length, progressing by half-inches in the sizes below 6 inches. They are cut double, and usually on both edges, and are mainly used by locksmiths and jewellers, and to but a limited extent by machinists. Some of the warding files are provided with teeth upon their edges only, which are made quite rounding, the cut usually being second-cut, single.
Files deriving their sections from the circle are shown from Figs. 2219 to 2222. “Round files” are circular in section, as shown in Fig. 2219, their lengths ranging from 2 to 16 inches, and are usually of considerable taper. The small bastards are mostly single-cut and the larger sizes double-cut. The second-cuts and smooths are rarely double-cut, except in some of the very large sizes. In imitation of double-cut, however, they are sometimes made with the first, or overcut, very open, called “hopped,” which adds, however, but very little to the cutting capacity of the file. The very small sizes—as, say, those of one-quarter inch and less in diameter—are often called “rat-tailed” files. For some classes of work—as for instance, the circular edges of deep keyways—round, blunt files are used, their sizes running up to 18 and 20 inches, their principal cut being bastard and double.
The gulleting file is a round, blunt saw file, and, like most other files for this purpose, is single-cut (except for a small space at the point, which is left uncut). Its principal use is for extending the gullet of what are known as gullet-tooth and briar-toothed saws.
Half-round files are of the cross-section shown in Fig. 2220, and although their name implies a semicircle, yet, as generally made, their curvature does not exceed the third part of a circle. They are made taper; the bastard is usually double cut on both its sides; the second-cut and smooth is double-cut on their flat sides, and single-cut on the curve side, except occasionally in the larger sizes, when it is double-cut or hopped. Half-round files for wood usually range in size from 10 to 14 inches, and are of the same shape and taper as the regular half-rounds. They are cut coarse and double, and are used by wood-workers generally. Half-round rasps are also like the regular half-round in shape, the sizes usually called for being 10, 12, and 14-inch. They are used principally by wheelwrights and carriage builders, but are to some extent used by plumbers and marble workers.
Cabinet files are of the section shown in Fig. 2222, being both wider and thinner than the half-rounds, the sectional curvature being somewhat less than the fifth part of a circle. They are made taper from near the middle to the point, while both the files and the rasps are made from 6 to 14 inches in length; 8, 10, and 12 inches are the sizes in most common use. As usually known, the cabinet file is a bastard double-cut. The cabinet rasp is punched smooth, and both the cabinet rasp and file are rarely made of any other degree of coarseness. They are used by cabinet, saddle-tree, pattern, and shoe-last makers, and also by gunstockers and wood-workers generally.
Three-square files are made with equilateral triangular sections, as in Fig. 2223. They are tapered to a small point with considerable[II-91] curve, and are double-cut. The larger sizes—say, from 10 to 14 inches—are usually bastard, and are used to a considerable extent in rolling mills. The smaller sizes are not unfrequently smooth or dead-smooth, and are used in machine shops quite generally for filing interval angles more acute than the rectangle, clearing out square corners, sharpening cutters, &c. Three-square blued files of sizes from 3 to 6 inches are sometimes made. They are mostly second-cut, or smooth and double-cut, and are principally used in machine shops for filing up cutters for working metals.
Cant files, whose cross-sections are shown in Fig. 2224, are usually made blunt and double-cut, mostly bastard, on all three sides. These sizes are usually 6, 8, and 10 inches. Lightning files are of the cross-section shown in Fig. 2225, the term lightning being known principally by those using the saws of this name, and to some extent by those using other cross-cut, M-shaped saw teeth. The obtuse angle of this file is five-canted, while the regular cant is hexagon or six-canted, and it is found to be too obtuse for the purposes required of the saw file. They are made blunt, and range in length from 4 to 12 inches, and are cut (except for a short space near the point) single on their three sides.
Knife files are of the section shown in Fig. 2226, and rarely exceed 10 inches in length, the principal sizes being 4, 5, and 6-inch. They are tapered, resembling somewhat the blade of a knife, and are cut double. The very acute angle of the sides of this file makes it especially useful in filing the inner angles of the rear and main springs of a rifle lock and work of similar shape. These files are also made blunt. Cross files (sometimes called double half-round or crossing files) are of the section shown in Fig. 2227. They are mostly made to order, either blunt or tapered, and usually double-cut. “Feather-edge” files (Fig. 2227) are but little used by the mechanics of this day. They were formerly used in filing feather springs (as the rear spring of a gun lock is sometimes called), and also the niches in currycombs, which led them to be called by some currycomb files. The few files of this kind which are now made are usually blunt and double-cut. Half-round “shoe rasps” as generally made are of the cross-section shown in Fig. 2228, their sizes ranging from 6 to 12 inches, while 8, 9, and 10 inch are the most common. They are made parallel in width, but with their sides slightly tapered from the middle; the ends are rounded and cut single; the edges are safe or uncut, or if cut are usually made half-file and half-rasp reversed (1⁄4 rasp and 3⁄4 file, while sometimes made, are the exception). The file quarters are bastard double-cut, and the rasp quarters second-cut. This form of shoe rasp is the one in general use at this time, having almost entirely superseded the flat and swaged rasps formerly in use.
Reaper files (b, Fig. 2229), so called from their use in sharpening the knives of reaping and mowing machines, are of the cross-section shown. They range in length from 7 to 10 inches, are slightly tapered, and are cut single and on their sides only.
Tumbler files, whose cross-section is shown at a, Fig. 2229, were formerly much used to file the tumblers of gun locks, but are now rarely called for. They are taper and cut double. It will be seen, however, that unless for some special purpose, the pitsaw round or half-round file will be found to answer the same purpose as the tumbler file.
It is obvious that in the use of files the coarser cuts are for use when it is required to remove a maximum quantity of material, and the finer to produce a more smooth and true surface, and also that the form of file selected is that which will best conform to the shape of the work, or can be best admitted upon or into the work.
In selecting the length of the file, the size of the work and the delicacy of the same are the determining considerations; thus, a 14-inch file would be a clumsy tool upon a small piece of work, as, say, one having an area of 1⁄2 inch square. In selecting the shape of the file there are, however, other considerations than the shape of the work. Among these considerations may be enumerated that, in proportion as the number of teeth on any given file, performing cutting duty simultaneously, is increased, the less metal will be taken off, because the pressure on each tooth is reduced, and the file does not bite or take hold of the work so well; hence it cuts smoother.
To fit the handles to small files, as 6-inch or less, it is simply necessary to bore suitable-sized holes in the handles, and force in[II-92] the tang of the file. In doing this care should be taken to bore the hole axially true with the handle, so that the latter may stand true with the file, which greatly assists the production of true and rapid filing.
For larger files the handle should have a small hole bored up it as before, the file tang should be made red hot (a piece of wet rag or cotton waste being wrapped around the heel of the file, so that it shall not get hot and be softened), and forced into the handle by hand, the file and handle being rotated during the operation, and sighted to insure that the handle is kept true with the centre line of the file. So soon as the tang of the file has entered three-quarters or thereabouts of its length it should be removed and gradually cooled by dipping in water.
When the surface of the work is so large that the file handle would meet the work before the point had reached fully across it, the raised handle shown in Fig. 2230 is employed. The square end of the handle has a dovetail groove into which the tang of the file is fitted. In the figure the file is shown applied to a connecting rod end, and in such broad surfaces it is especially necessary to vary the line of motion of the file after every few strokes, so as to cause the file marks to cross and recross, as shown in Fig. 2231.
The height at which work should be held to file it to the best advantage depends entirely upon its size, the amount of metal to be filed off, and the precision to which the filing requires to be executed.
Under ordinary conditions the work should stand about level with the operator’s elbow when he stands in position to file the work. This is desirable so that the joint of the arm from the elbow to the wrist may be in the same plane as the line of motion of the file, which will give the workman the least fatigue. But when the work surface is very broad it should be lower down, so that the operator may reach over all parts of its surface. On the other hand, on very small round work, or work so small as to require but one hand to hold the file, the work may be so high as to require the operator to stoop but very little, in which case the fatigue will be less, while the work will be more in sight, and can be better scrutinized.
When the file is pushed endways it is termed cross-filing, and the teeth cut on the forward or pushing stroke only, and in this case the file should be held as in Fig. 2232, the end of the file handle abutting against the palm of the right hand. But when the file is held in one hand only, the forefinger may be placed uppermost, and either on the file handle or on the file itself, as may be found most convenient. In cross-filing the file should be relieved of cutting duty on the return or back stroke, but should not be removed from the work surface.
For heavy cross-filing on iron or brass, a 15-inch file is sufficiently large for any of the ordinary duty required by the machinist, and will require all the pressure one man can put on it to enable it to cut freely, and move at a suitable speed.
The workman should for heavy cross-filing stand well off or away from the work so as to require to bend the body well forward. His feet should in this case be spread apart so that when the pressure of the hands is placed upon the file it will relieve the forward foot of a great part of the weight of the workman’s body, which will be thrown upon the file. The rear foot operates during the forward stroke as a fulcrum, wherefrom to push the file.
At each forward stroke the workman’s body should move somewhat in unison with the file; his arms being less extended than would otherwise be the case, and the file being under more pressure and better control.
During the backward stroke the forward foot should again take the workman’s weight, while he recovers the upright position.
For less heavy filing and for smooth filing, the workman should stand more nearly upright and nearer to the work.
The heavier the pressure (either in cross-filing or draw-filing), the coarser the file cuts, and the more liable it is to pin and scratch.
In the case, however, of slim files, the pressure is apt to bend the file, causing it to cut at the edges or ends only of the work, as shown at a, in Fig. 2233. This may be avoided by holding the file as in the figure, the pressure of the fingers in the direction of the arrows causing the file to bend, and produce more straight work.
From the nature of the processes employed to cut the teeth of files, they are unequal in height, and as the file in addition to this varies in its straightness or warps in the process of hardening, it becomes necessary in many cases to choose for certain work files whose shape is best suited for it. Suppose, however, that files were produced whose teeth or tops or points were equal in height from end to end of the file, and it would be necessary for the workman to move the file in a true straight line in order to file a straight surface. This the most expert filers cannot accomplish. It is for this reason that hand files are made as in Fig. 2234, being thickest in the middle m, and of a curved taper both towards the point p and the heel h, so that when applied to the work the file will bear on the work at a, Fig. 2235, and be clear of it at b and c, which allows the file motion to deviate from a straight line without cutting away the work too much at b and c. The file curvature also enables any part of the file length to be brought into contact with the work or with any required part of the surface of the same, so as to locate or limit its action to any desired part.
If a bellied file (as this shape of file is sometimes termed) be[II-93] moved in a straight line it will file flat so long as it is moved to have contact clear across the work, but if the file is concave in its length it can only cut at that part which is in contact with the edge of the work, and the latter must be filed convex.
It becomes obvious then that for flat work a bellied file must be used, and that the belly should preferably be of even sweep from end to end.
But files, whatever their shape, and however evenly formed when soft, warp (as already remarked) in the hardening process, sometimes having crooks or bends in them, such as at e and d, in Fig. 2236. In such a file the teeth at e would perform no duty unless upon work narrower than the length of the concavity at e, while on the other side d, the extra convexity would give the file great value for work, in which particular spots only required to be filed, because the teeth at d could be brought to bear on the required spot without fear of cutting elsewhere.
If, however, we have a taper flat file, such as in Fig. 2234, the thickness being equal from h to m, and a curved taper from m to p only, then it would be impossible to file flat unless only that part from m to p be used, because the heel h would meet the work at the same time as m, and it could not be known where the file would cut, more than that the most prominent teeth would cut the most.
An excellent method of testing the truth of a file, and of finding its high spots is to chalk a piece of board, press the file firmly to it and take several strokes and the chalk will be transferred to the highest parts of the file, showing very distinctly every hill and hollow in the teeth, even on the finest of Groubet files, and it will be found from this test that but very few of the best-made files are true, and that very great care is necessary in selecting a file for flat and true work.
The curvature or belly on a file not only enables but few teeth to be brought into action at any one turn, and thus cause it to cut more freely; but it also enables all parts of the file length to be used and worn equally. Thus in Fig. 2238 are shown two positions of a file, one cutting at a and the other at b, these different locations being due to different levels of the file which may be given by elevating or depressing it at the handle end.
If a file is hollow in one side of its width, and rounding on the other, as in Fig. 2239, the hollow side is unfit for any but the roughest of work, since it will not file any kind of work true; but the rounded side is very effective for flat surfaces, since the number of teeth in action is more limited and their grip is therefore greater, while by canting the file any part of its width may be brought into action. The rounded side is especially advantageous for draw-filing (a process to be hereafter explained).
In all cross-filing, whether performed to clean up a surface, remove a maximum of metal, or prepare the work for draw-filing, [II-94] or for reducing the work to shape, the file should be given a slight lateral as well as a forward motion, and it will be found that this lateral motion is more effective if made from right to left, leaving the file marks in the direction of marks b, in Fig. 2240, because the workman has more control over the file (especially if a large one) than when the lateral motion is from left to right; but this latter motion must be given occasionally to prevent the file from cutting deep scratches, and to keep the file surface true.
A new file should be used at first on broad surfaces so that the teeth may not grip or bite the work so firmly that the strain will cause their fine sharp edges to break off, which is apt to occur unless their edges are slightly worn off. As a file becomes worn it may be used on narrower work, because the narrower the surface the more readily the file will bite. When a file is much worn, or when it is desired to remove a quantity of metal as quickly as possible, the file may be used at different angles upon the work, as shown in Fig. 2241, which by reducing the number of teeth in action facilitates the cutting, but if this be done with a new file it will break off the points of the teeth.
Cast iron, brass, and copper require a sharper file than do either steel or wrought iron, hence for the first named metals (especially brass and copper) new files are used, and these should not be used upon wrought iron or steel until worn out for the above metals.
In the case of unusually hard cast iron or tempered steel a second-cut file will cut more freely than a coarser grade.
Work to be draw-filed should first be cross-filed with smooth or at the coarsest with second-cut files, so as to remove the scratches of the bastard or rough file before the draw-filing, which should not be done with a rough or bastard file.
Draw-filing consists in moving the file in a line at a right angle to its length, the file being grasped at each end independently of its handle, which may be removed from the file if it be in the way, as in the case of files used on broad surfaces.
Draw-filing is employed for two purposes: first and most important, to fit work more accurately than can be done by cross-filing, and secondly to finish surfaces more smoothly, and lay the grain of the finish lengthwise of the work. The greater accuracy of draw-filing occurs because the high parts of the file can be selected and the file so balanced that this high part covers the place on the work requiring to be filed, while the strokes may be made to suit the length of the spot to be filed.
In draw-filing the file can be moved more steadily than in cross-filing, and will, therefore, rock so much less that even the novice can with care produce very true work.
Suppose, for example, that a piece of work requires filing in the middle of its length and half way along its width and half along its length, and a well bellied file may be balanced upon c, Fig. 2242, and grasped at its two ends a and b, and used with strokes of a sufficient length to file half the work length as required.
In draw-filing the file should be pressed to the cut on the pushing stroke only, and not on the return or pulling stroke.
Draw-filing produces with a given cut of file a smoother surface than cross-filing, but it will not remove so much metal in a given time.
In draw-filing short strokes will produce better work than long ones, because with the latter the file cuttings are apt to become locked in the teeth of the file, and cut scratches in the work. This is called pinning, and the pins cutting deeper than the file teeth produce the scratches.
To avoid this pinning the file surface may be well chalked, which will at the same time cause the file to cut smoother although not quite so freely. It is necessary, however, to clean the file after every ten or twelve draw-filing strokes so as to remove the filings. This removes the chalk also, hence it requires occasional renewal. For this purpose lumps of chalk are employed, but great care is necessary in its selection, because it sometimes contains small pieces of flint or other stones, and these score and greatly damage the file teeth.
To dislodge the chalk and filings the file surface may be rubbed two or three strokes with the hand, and the file lightly tapped on the vice back. But it will also be found necessary to occasionally clean the file with a file-brush or file-card. The file-card is brushed across the width of the file so that the wire may reach the bottoms of the rows of teeth and clean them out.
If the pins have lodged too firmly in the teeth to be removed, the scorer shown in Fig. 2243 is employed. This scorer is a piece of copper or brass wire flattened out thin at the end e, which end is pressed firmly to the file teeth and pushed across the width of the file. By this means the thin edge becomes serrated, and the points of the teeth forming the serrations pass down the bottoms of the rows of file teeth and force out the pins. Here it may be remarked that pinning takes place in cross-filing as well as in draw-filing, and is at all times destructive to either good or quick work.
Oil is sometimes used to prevent pinning and produce a dead finish, which will hide scratches, but it is much more dirty than chalk and no more effective. Neither of these substances, however, is employed upon cast iron, brass, copper, or other than the fibrous metals.
In removing the cross-file marks it will be found that the file will cut more freely if it be slightly canted so that it cuts most at and near the edge, as shown in Fig. 2244, the edge a b meeting the work, the file stroke having progressed from c as shown. This is especially advantageous if the metal be somewhat hard or have a hard skin upon it, or in case of a hard spot, because it will enable the file to bite when, if pressed flat upon the work, it would slip over it.[II-95]
When draw-filing is resorted to, to obtain a very fine surface, to be finished with emery paper and crocus cloth, it is best to reverse the direction of the file strokes so as to cause the file marks to cross and recross as shown in Fig. 2244, where the marks c cross those previously made, which will not only produce smoother work, but it will partly prevent the file from pinning. It will also be found that the draw-filing will be smoother and pinning less liable to occur when the file strokes cross the fibres or grain of the metal than when they are parallel to that grain; hence when the finishing marks are to be left in a line with the grain and a very smooth surface is required, the draw-filing marks should, just before the final finishing, be across the grain, the final finishing being with the grain simply to reverse the direction of the marks.
Half-round files should be well curved in their lengths on the half-round side, so that when applied to the work any part of the file’s length may be brought to bear upon the required spot on the work, as was explained for the flat file, and shown in Fig. 2238. If the flat side is straight or hollow in its length it is of little consequence, because it can be used upon convex or upon narrow surfaces. The sweep or curve of the file should in its cross-section always be less than the curve of the work it is to operate upon, and the teeth should be brought up sharp on the edges, and over the whole area of the half-round side, which is in inferior files not always the case, because the rows of chisel cuts are too far apart in the width of the file; hence, there is along the length of the file between the rows of full teeth, rows that are not brought fully up, which impair the cutting qualifications of the file.
In using a half-round file to cross file it should at each stroke be swept first from right to left, and after a few strokes from left to right, so that the file marks appear first as in Fig. 2245, running somewhat diagonal from right to left, and then, when the side sweep of the file is reversed in direction, the file marks will cross after the manner shown exaggerated in Fig. 2247. Unless this is done, the curve will be apt to have a wave in it as in Fig. 2246, or in large curves there may be several waves, and the same thing may occur if the direction of side sweep is not reversed sufficiently often. The file should also be partly swept around the curve, so that if at the beginning of a stroke it meets the work at the upper position in Fig. 2247, then at the end of the stroke it should be as at the lower one, which will also prevent the formation of waves. The larger the curve the less the amount of this sweep can be, the operator giving as much as convenient for the size of curve being filed.
In draw-filing the file should be slightly rotated, so that if at the beginning of a stroke it stands as at a, Fig. 2247, at the end of that stroke it should stand as at position b, and it should at the same time be given sufficient end motion, so as to cause the file marks to cross as shown.
A round file should always be a little smaller at its greatest diameter than the hole in the work. Before inserting it in the hole it should be rotated in the fingers, and the eye cast along it, to select the part having the most belly, which may then be brought to bear on the required spot in the work, without filing any other place, and without filing away the edges at the ends of the hole. For very accurate work it is sometimes desirable to grind on a round file, a flat place forming a safe edge. So likewise a safe edge flat file requires grinding on its safe edge, because in cutting the teeth a burr is thrown over on the safe edge, rendering it capable of scoring the work when filing close up to a shoulder.
The work should be held as near down to the surface of the jaws of the vice as will allow the required amount of metal to be filed off without danger of the file teeth coming into contact with those jaws, and should be placed so that the filing operation when finished shall be as near as possible parallel with the top of the vice jaws. These jaws then serve somewhat as a guide to the filing operation, showing where the metal requires filing away.
For cutting steel that contains hard spots or places, a second-cut file is more effective than a rough or bastard file.
Rough files are more suitable for soft metals, the bastard cut being usually employed upon wrought iron, cast iron, and steel by the machinist. But in any case the edge of the file is employed to remove small spots that are excessively hard. The file should be clean and dry to cut hard places or spots, and used with short strokes under a heavy pressure, with a slow movement.
When a file has been used until its cutting edges have become too dull for use, it may be to some extent resharpened by immersion in acid solutions; but the degree of resharpening thus obtained has not proved sufficient to bring this process into general or ordinary application; hence, the files are either considered useless, or the teeth are ground off and new ones formed by recutting them.
A recut file is of course thinned by the process, but if properly done is nearly, if not quite, as serviceable as a new one, providing that in grinding out the old teeth the file be ground properly true to curve; but, unfortunately, this is rarely found to be the case.
An excellent method of resharpening files, and also of increasing the bite of new files (which is an especial advantage for brass work), is by the means of the sand blast. The process consists of injecting fine sand against the backs of the teeth by means of a steam jet, and is applicable to all files, from the rasp to the finest of Groubet files. The action of the sand is to cut away the backs of the file teeth, thus forming a straight bevel on the teeth back, and giving a new cutting edge, and the process occupies from three to five minutes.
[II-96]Fig. 2248 represents a machine constructed for this purpose. Steam is conveyed by the piping to the nozzles a, a, which connect by rubber hose h, h to sand pipe k, so that the steam jets passing through a, a carry with them the mixture of quartz, sand, and water in the sand box. By means of the overhead guide frame at d, e the file clamp c is caused to travel when moved by hand in a straight line between the nozzles a, a in the steam box, from which the expended sand and water flow down back to the sand box. Thus both sides of the file are sharpened simultaneously, and from the fixed angles of the nozzles and true horizontal motion of the file the angles of all the teeth are equal and uniform.
To distribute the sharpening effects of the sand equally across the width of the file, the carriage has lateral or side motion, as well as endwise, and on the apparatus represented adjustable rollers regulate this side movement. Having the two motions, any part of the file can be presented to the blast.
The following is from Engineering:—“A comparative trial of the cutting power of the sharpened files was lately made with the following results: A piece of soft wrought iron was filed clean and weighed; 1200 strokes were made by a skilled workman with one side of a new 10-inch bastard file, the iron was again weighed, and the loss noted. The other side of this file was then subjected to the sand blast for five seconds, and 1200 strokes were made with this sand-blasted side on the same piece of iron, great care being taken to give strokes of equal length and pressure in both cases. The iron was then weighed, and the loss found to be double as much as in the first case.
“These operations were repeated many times, counting the strokes and weighing the metal each time, and the quantity cut was found to gradually become less for both sides as these became worn. When the weight of metal cut away by 1200 strokes of the sand-blasted side was found to be no greater than had been cut by the first 1200 strokes of the ordinary side when quite new, a second sand blasting was applied to it for 10 seconds, and in the next 1200 strokes its rate of cutting rose to nearly its first figure. When the cut made by the ordinary side of the file fell to about four-tenths of its cut when new, it was considered by the workman as worn out, and a new file of the same size and maker was used to continue the comparison with the one sand-blasted side; 83 sets of 1200 strokes each and 13 sand-blastings were made on the same side of this file, and in that time it cut as much metal as six ordinary sides. In 99,600 strokes it cut away 14 ozs. avoirdupois of wrought iron, and 16.4 ozs. of steel.
“With an equal number of strokes its average rate of cutting was, on wrought iron, 50 per cent. greater than the average of the ordinary sides, and on steel 20 per cent. greater. As the teeth became more worn, the time of the application of the sand blast was lengthened up to one minute. After the thirteenth re-sharpening its rate of cutting was nine-tenths that of the ordinary side when quite new.
“When the teeth become so much worn that the sand blast ceases to sharpen them effectively, the file can be recut in the usual way, and each set of teeth can be made to do six times as much work as an ordinary file, and to do it with less time and labor, because it is done with edges constantly kept sharp. The time required to sharpen a worn-out 14-inch bastard file is about four minutes, or proportionately less if sharpened before being entirely worn out. Smooth files require much less time. About 4 horse power of 60 lb. steam used during four minutes, and one pint per minute of sand (passed through a No. 120 sieve), and the time of a boy are the elements of cost of the operation.”
Red Marking or Marking.—This is a paint used by machinists to try the fit of one piece to another, or to try the work by a test piece or surface plate. It should be composed of dry Venetian red, mixed with lubricating oil of any kind.
Instead of Venetian red, red lead is sometimes used for marking, but it is too heavy and separates from the oil, and furthermore will not spread either evenly or sufficiently thin, and is therefore much inferior to Venetian red.
It is applied to the surface of the test piece or piece of work, and the latter is brought to bear on the surface to be tested, so that it leaves paint marks disclosing where the surfaces had contact, and therefore what parts of the surface require removing in order to make the surfaces have the desired degree of contact.
When either the test piece or the work can be put in motion while testing, one piece is rubbed upon the other or passed along the same in order that the bearing marks may receive the marking more readily and show the bearing spots more plainly, the operation coming under the head of fitting. When neither piece can be given motion, one is made to mark the other by being struck with a mallet or hammer, or to avoid damage to the work from the hammer blows, a piece of wood or copper is interposed. This operation is termed “bedding.”
The thickness of the coating of marking varies with the kind of work, the finer fit the work requires to be, the thinner the coat of marking. Thus in chipping a thick coat is applied, for rough filing a thinner, for smooth filing a still thinner coat, and so on, until for the finest of work the coat is so thin as to be barely perceptible to the naked eye. When either the work or the testing piece can be given motion and the surfaces rubbed together, a thinner coat of marking may be used. Marking is usually applied with a piece of rag doubled over and over, and bound round with a piece of twine so as to form a kind of paint-brush. This will give the surface a lighter and more evenly spread coat than would be[II-97] possible with a brush of any kind. For very fine work red marking may be spread the lightest and the most even with the palm of the hand, which will readily detect any grit, dirt, or other foreign substance which the marking may contain from being left exposed.
The Hack-Saw.—The hack-saw is employed by the machinist for severing purposes, and also for sawing slots in the heads of screws. The blade should be tightly strained in the frame, which will prevent saw breakage. The ordinary method of doing this is to provide the end of the saw frame with a sliding stud threaded at its end to receive a thumb nut. The studs at each end of the blade should be squared where they pass through the frame, as at a, b in Fig. 2249, so that the blade shall not be permitted to twist. An improved form is shown in Fig. 2250, in which the end e has a saw slot to receive the blade f. At the handle end of the blade it is held by a stud sliding through the frame, being squared at b; at c is a nut let into and screwed in the handle, and into or through the nut is threaded the end of the stud, so that by rotating the handle the blade is strained. The curve in the back at a gives a little elasticity to it, and therefore a better strain to the blade. A hack-saw should always be used with oil, which preserves the cutting edge of the teeth.
In sharpening a hack-saw it is best to rest the smooth edge of the blade on a piece of hard wood or a piece of lead, and spread the tops of the teeth by light hammer blows, which serves a two-fold purpose, first it thickens them and enables them to cut a groove wide enough to let the blade pass freely through, and secondly it enables the teeth to be filed up to a sharp cutting edge with less filing.
The screw-driver to be used in saw slots should have its end shaped as at a in Fig. 2251, which will tend to prevent it from slipping out of the saw slot, as it will be apt to do if wedge-shaped as at b, because in that case the action of the torsional pressure or twist is to lift the screw-driver out of the slot.
Scrapers and Scraping.—The process of scraping is used by the machinist to true work, and to increase the bearing area of surfaces, while the brass finisher employs it to prepare surfaces for polishing, applying it mainly to hollow corners and sweeps.
For scraping work to fit it together the flat scraper is used, ordinary forms being shown in Figs. 2252 and 2256.
| VOL. II. | SCRAPERS AND SCRAPING. | PLATE IX. | |
 |
 |
||
| Fig. 2252. | Fig. 2253. | ||
 |
 |
||
| Fig. 2254. | Fig. 2255. | ||
 |
 |
||
| Fig. 2256. | Fig. 2257. | ||
 |
 |
||
| Fig. 2258. | Fig. 2259. | ||
 |
|||
| Fig. 2260. | |||
That shown in Fig. 2252 may be made of a flat smooth file, of about an inch wide, and 3⁄16-inch thick, which is large enough for any kind of work. Two opposite faces, one of which is shown at a, are ground beveled so as to leave the end face b about 1⁄16-inch thick. This end face is then ground square as denoted by the dotted lines, producing two cutting edges of equal angles, and therefore equally keen. If it were attempted to grind face b at an angle as denoted by the dotted lines g, in Fig. 2253, the lower edge h would cut too keenly, causing the scraper to chatter and cut roughly, while the upper one i would not cut sufficiently easily.
For very smooth work the scraper may be formed as in Fig. 2256, the front face e being ground slightly out of square as shown, and the bottom face f being given considerable angle to the body of the scraper. For very rapid cutting, however, the front face e may be at an angle of less than 90° to the top of the scraper.
The only objection to this form is that the eye lends no assistance in bringing the edge fair with the work surface. The scraper should not exceed about 6 inches in length, exclusive of the handle, for if longer it will not cut well or smoothly, and its end face should be slightly rounded as in Fig. 2254. Its facets should be ground square or straight and carefully oil-stoned after the grinding, the oil-stoning process being repeated for two or three resharpenings, after which it must be reground upon the grindstone.
The scraper should be grasped very firmly in the hands, and held as in Fig. 2255. It requires to be pressed hard to the work during the cutting and lightly during the backward stroke.
The strokes should not exceed for the roughing courses, say, half an inch in length, the first course leaving the work as represented in Fig. 2257.
The second course should be at a right angle to the first, leaving the work as in Fig. 2258, and after these two courses the work should be tested by surface plate, or with the part to which it is to fit, as the case may be. Previous to the testing, however, the work must be carefully wiped clean with old rag, as new rag or waste is apt to leave ravelings behind. The surface plate should be given a light coat of red marking, and then moved backward, forward, and sideways over the work, or, if the work is small, it may be taken from the vice and rubbed upon the surface plate, and the high spots upon the work will be shown very plainly by the marks left by the plate. The harder the plate bears upon the work the darker the marks will appear, so that the darkest parts should be scraped the heaviest.
After applying the plate, the scraper may again be applied, the marks being at an angle to the previous operation, the testing and marking by the plate and scraping process being continued until the job is complete, appearing as shown in Fig. 2259.
It will be noted that the scraper marks are much smaller and finer at and during the last few scrapings; and it may be here remarked that the scrapings are very light during the last few finishing processes.
The strokes of the scraper being made of a length about equal to the acting width of its edge cuts, makes the scraper mark approximately square, on which account it is sometimes termed “block” scraping. It gives an excellent finish, while not sacrificing the truth of the work to obtain the finish.
The scraper will not remove a quantity of metal so quickly as a file, and on this account it is always preferable to surface the work[II-98] with a file before using the scraper, even though the work be well and smoothly planed. Not until the file has almost entirely removed the planer marks, and the surface plate shows the surface to be level and true, should the scraper be brought into requisition, the first courses being applied vigorously to break down the surface.
It would appear that scraping might be more quickly done by taking long scraper strokes promiscuously over the work, but in this case the bearing marks are not well defined and do not show plainly, which leads to confusion and causes indecision as to where the most or heaviest scraping requires to be done, whereas in the block scraping the marks are clearly defined and the high patches or spots on the work show very plainly, and the workman is able to proceed intelligently and with precision.
Fig. 2260 represents a three-cornered or “three-square” scraper, which is used principally upon hollow or very small flat surfaces. The half-round scraper is employed upon holes, bores, or large concave surfaces, such as brasses. Both these tools are for vice work, used in the same manner as described for flat scrapers, while all scrapers cut smoother when the edge is kept wetted with water, as is essential when used upon wrought iron, copper, and steel.
Hand Reamers or Rymers.—The hand reamer is employed for two purposes, first, to make holes of standard diameter and smooth their walls, and second, to bring holes in line one with the other.
Fig. 2261 represents an ordinary solid hand reamer for parallel holes. The teeth are ground so that their tops form a true circle, this grinding being done after the reamer has been hardened and tempered, because in these processes the reamer is apt to get both out of round and out of straight.
In some practice the reamers are formed as shown in Fig. 2262, and are made in sets of three for each size; the first is slightly taper from end to end, the second is slightly tapered at the entering end for a length about or nearly equal to the diameter, and the third is parallel and rounded on the end like the second, and in many cases only three teeth are employed.
Fig. 2263 represents a reamer in which the distance between the cutting edges a b, Fig. 2264, is greater than between b c, and so on, the spacing decreasing from tooth a to tooth a. The spacing of a, b, &c. to f on the other side is also irregular, so that if the reamer be given half a revolution no two teeth will have arrived at similar positions except a and a, the former arriving at the position occupied by the latter.
Now suppose that a hole to be reamed has a hollow or spongy seam along it, and if the reamer be regularly spaced, there will at this point occur a lateral movement of the reamer that will impair the roundness of the hole, and this lateral movement the irregular spacing tends to prevent.
If a solid reamer is made to standard gauge diameter when new, and the bolts or pins turned to standard diameter, then by reason of the wear of the reamer the work will become gradually a tighter fit and finally will not go together, hence the reamer must be restored to standard diameter, which may be done by upsetting the teeth with a set chisel. Furthermore the workman’s measuring gauges are themselves subject to wear, those for measuring the pins wearing larger and those for the holes wearing smaller, and this again is in a direction to prevent the work from fitting together. It is preferable, therefore, to employ adjustable reamers.
Thus Fig. 2265 represents an adjustable reamer in which the teeth fit tightly into dovetail grooves, that are deeper at the entering than at the shank end of the reamer, so that by forcing the teeth up the grooves towards the shank the diameter is increased.
Both castings and forgings are found to alter somewhat in shape in proportion as their surfaces are removed by the machine tools, so that the shape of the work undergoes continuous alteration.
Suppose, for example, that a piece of metal two inches square and four inches long, has a hole cast in it of an inch in diameter, and when finished it is to be 13⁄4 inches square, 33⁄4 inches long, and have a hole 11⁄8 diameter. Let it be chucked in a lathe or shaping machine and have its surfaces cut down to the required dimensions. Removing the metal to true the first surface will reduce the strain on that side of the casting and alter the shape of the whole body, but this alteration of form will not occur to its full extent until the piece is removed from the pressure of the chuck jaws, or other clamping device holding it in the machine, because this pressure holds it; as a result the surface will not be so true after leaving the machine as it was before. On surfacing the second side of the piece, the internal strain is still further reduced, and a second alteration of form ensues, and so on at the surfacing of every side of the piece. Now let the piece be chucked true to have the hole[II-99] bored out, and the removal of the metal in the hole will again reduce the internal strain and the form of the body will again alter.
Suppose, however, that the piece after having its surfaces thus removed, and its hole bored as true as may be, were again trued over each surface, and in its bore there will still be at each surfacing and at the boring an alteration of form, although it may be to a very minute degree, and from these causes the use of the reamer for work requiring to be very true becomes indispensable.
Fig. 2266 represents a taper hand reamer with straight flutes. It is preferable, however, to give the flutes a left-hand spiral, as was explained with reference to reamers for lathe work.
The frames of large machines are frequently composed of parts that are bolted together after having the holes for shafts, &c. bored, and to insure the alignment of these holes after the frames are put together a hand reaming bar, such as in Fig. 2267, is employed, a and b being two shell reamers fastened to the bar by a pin.
Reamers are sometimes employed to enlarge holes or bring them fair one with another, without reference to their being precise to a designated diameter; thus Fig. 2268 represents a half-round reamer of the form used by boiler makers to bring rivet holes fair, and sometimes by machinists to ream the holes for taper securing pins. The flat face is cut down to below the centre line, so that the back requires no clearance ground upon it.
The square reamer shown in Fig. 2269 is used for rough work generally, although with careful grinding and use it will produce excellent results upon work of small diameter. Brass finishers generally prefer a square reamer to all others for reaming the bores of brass cocks, &c., and some of them prefer that one edge only be sharpened to cut, the other three being oilstoned off so as not to cut, but simply serve as guides. The square reamer is very easily sharpened whether by grinding or oil-stoning; the flat sides are operated on, taking care to keep them straight and the thickness even on the two diameters, so that, the sides being straight and the reamer square, it will cut taper holes whose sides will be straight. If the reamer is not ground square, two only of the edges will be liable to have contact with the work bore, causing the reamer to wabble, and rendering it liable to break.
Another and very good form of reamer for the rapid removal of metal is shown in Fig. 2270, having three teeth and a good deal of clearance, which enables it to work steadily and cut freely.
In most of the operations of the machine-shop, the work of the chisel is followed by that of the file; hence, as an example in the use of the chisel independent of that of the file, the cutting of the teeth upon files may be given as follows:—
The largest and smallest chisels commonly used in cutting files are represented in two views and half size in Figs. 2271 and 2272. The first is a chisel for large rough files; the length is about 3 inches, the width 21⁄2 inches, and the angle of the edge about 50°; the edge is perfectly straight, but the one bevel is a little more inclined than the other; this chisel requires a hammer of about 7 or 8 pounds weight. Fig. 2272 is the chisel used for small superfine files; its length is 2 inches, the width 1⁄2 inch; it is very thin, and sharpened at about the angle of 35°; it is used with a hammer weighing only 1 or 2 ounces; as it will be seen, the weight of the blow mainly determines the distance between the teeth. Other chisels are made of intermediate proportions, but the width of the edge always exceeds that of the file to be cut. The first cut is made at the point of the file; the chisel is held in the left hand, at a horizontal angle of about 55° with the central line of the file, as at a a, 2273, and with a vertical inclination of about 12° to 4° from the perpendicular, as represented in Fig. 2274, supposing the tang of the file to be on the left-hand side. The following are nearly the usual angles for the vertical inclination of the chisels, namely: For rough rasps, 15° beyond the perpendicular; rough files, 12°; bastard files, 10°; second-cut files 5°, and dead-smooth-cut files 4°. The blow of the hammer upon the chisel causes the latter to indent and slightly to drive forward the steel, thereby throwing up a trifling ridge or burr; the chisel is immediately replaced on the blank, and slid from the operator until it encounters the ridge previously thrown up, which arrests the chisel or prevents it from slipping farther back, and thereby determines the succeeding position of the chisel. The chisel having been placed in its second position, is again struck with the hammer, which is made to give the blows as nearly as possible of uniform strength, and the process is repeated with considerable rapidity and regularity, 60 to 80 cuts being made in one minute, until the entire length of the file has been cut with inclined parallel and equidistant ridges, which are collectively denominated the “first course.” So far as this one face is concerned, the file, if intended to be single-cut, would be then ready for hardening, and when greatly enlarged its section would be somewhat as in Fig. 2274.
The teeth of some single-cut files are much less inclined than 58°; those of floats are in general square across the instrument. Most files, however, are double-cut, and for these the surface of the file is now smoothed by passing a smooth file once or twice along the face of the teeth, to remove only so much of the roughness as would obstruct the chisel from sliding along the face in receiving its successive positions, and the file is again greased. The second course of teeth is now cut, the chisel being inclined vertically as before, or at about 12°, but horizontally about 5° to 10° from the rectangle, as at b b, Fig. 2273. The blows are now given a little less strongly, so as barely to penetrate to the bottom of the first cuts, and consequently the second course of cuts is somewhat finer than the first. The two series of courses fill the surface of the file with teeth which are inclined toward the point of the file. If the file is flat and to be cut on two faces, it is now turned over; but to protect the teeth from the hard face of the anvil a thin plate of pewter is interposed. Triangular and other files require blocks of lead having grooves of the appropriate sections to support the blanks, so that the surface to be cut may be placed horizontally. Taper files require the teeth to be somewhat finer toward the point, to avoid the risk of the blank being weakened or broken in the act of its being cut, which might occur if as much force were used in cutting the teeth at the point of the file as in those at its central and stronger part. Eight courses of cuts are required to complete a double-cut rectangular file that is cut on all faces, but eight, ten, or even more courses are required in cutting only the one rounded face of a half-round file. There are various objections to employing chisels with concave edges, and therefore, in cutting round and half-round files, the ordinary straight chisel is used and applied as a tangent to the[II-101] curve. It will be found that in a smooth, half-round file 1 inch in width, about twenty courses are required for the convex side, and two courses alone serve for the flat side. In some of the double-cut, gullet-tooth saw-files, as many as twenty-three courses are sometimes used for the convex face, and but two for the flat. The same difficulty occurs in a round file, and the surfaces of curvilinear files do not therefore present, under ordinary circumstances, the same uniformity as those of flat files.
The teeth of rasps are cut with a punch, which is represented in two views, Fig. 2275. The punch for a fine cabinet rasp is about 31⁄2 inches long and 5⁄8 inch square at its widest part. Viewed in front, the two sides of the point meet at an angle of about 60°; viewed edgewise, or on profile, the edge forms an angle of about 50°, the one face being only a little inclined to the body of the tool. In cutting rasps, the punch is sloped rather more from the operator than the chisel in cutting files, but the distance between the teeth of the rasp cannot be determined, as in the file, by placing the punch in contact with the burr of the tooth previously made. By dint of habit the workman moves—or, technically, hops—the punch the required distance; to facilitate this movement, he places a piece of woollen cloth under his left hand, which prevents his hand from coming immediately in contact with and adhering to the anvil.
As an example in the use of the chisel for chipping purposes, let it be required to fasten a feather on a shaft.
There are four methods of inserting feathers: First, a shaft may have a parallel recess sunk into it and a parallel feather may be driven in; second, the feather may be made slightly taper and driven in; third, the feather may be dovetailed on the sides and ends both, or on the ends only, and as one or the other of these is the proper method, and the process is the same for both, one only need be described.
In Fig. 2276 let s represent a shaft and f a feather, required by the drawing to be permanently fixed therein. The drawing will not, in ordinary shop practice, give any instructions as to how the feather is to be fastened; hence the mechanic usually exercises his own judgment about the matter, or is governed by the practice of the shop. If left to his own judgment he may determine to so fix it that it may be locked on all four sides, as in Fig. 2277, or he may simply set it in as in the similar views shown in Fig. 2278.
The method shown in Fig. 2277 is the most secure and best job; but, on the other hand, it is the most difficult and costly. The difficulty consists in filing the parallel part above the surface of the shaft to a line that shall be quite even with the surface of the shaft. This difficulty may be overcome by leaving the sides parallel, and making the length a equal to the length of the acting part of the key, and the bottom b as much longer as may be required to get the required amount of dovetail on the feather ends.
The first thing to do is to mark off the keyway by scribing lines on the surface of the shaft, indicating the location for the feather seat; and for this purpose nothing is better than the key seat rule shown in Fig. 2279, in which w is the key seat rule, and s the shaft. After the lines are drawn they should be defined by centre-punch dots, as in Fig. 2280, and then the metal should be cut out on the sides first, using a cape chisel, and cutting close to the side lines, as in Fig. 2281, in which a is a cape chisel cut taken along one side, d a second cape chisel cut, being carried along the other side, c the cape chisel, c′ the cut taken by the chisel, and b a piece of metal to be cut out after the cape chisel has done its work. Suppose, now, the mass of the metal is removed, then the dovetailing is performed as follows: Next the setting or upsetting is proceeded with as shown in Fig. 2282, which is a side sectional view. s is a set chisel driven[II-102] by hammer blows against the walls of the feather seat (as against the end e), causing it to bulge up, as shown at f. This setting will enlarge the feather seat or recess, so that the wide part of the dovetail on the feather will just pass in (the dotted lines shown in Fig. 2281 having, of course, been marked to the size of the feather, where it will, when fixed, meet the surface of the shaft). The feather is then placed in its seat and bedded properly by red marking applied to its bottom surface to show the high spots on the seat of the recess, and when properly bedded it is fastened, as in Fig. 2283, in which s is a set chisel, which, by being struck with hammer blows, closes the bulged metal back again on the dovetail of the feather, and firmly locks it in the shaft. And all that remains is to file the shaft surface around the feather level with the surrounding surface, there being usually a little surplus metal from the upsetting.
As an example of chipping and filing let it be required to chip and file to shape and to fit a knuckle joint (or a double and single eye, as it may more properly be termed), such as in Fig. 2284. The eye being marked out by lines, the first operation will be to remove the surplus metal around the edges by chipping, which should be done (with the pin in place, so that it may support the eye) before the joint faces are filed at all, and should be carried in a direction around the eye, as shown in Fig. 2285, in which v is the vice jaw, e a lead clamp, c the cut, and d the chisel. By chipping in this direction two ends are served: first, the force of the chipping blows is less likely to bend the eye if it is a light one, and, secondly, the chipping will not break out the metal at the edge of the eye, which it would be apt to do if the chipping was carried across. This is shown in Fig. 2286, where a chisel cut is supposed to have been carried across from a to b and a piece has broken out at b. If the width of the eye is too broad for one chisel cut, a cape chisel should be run around it, as in Fig. 2287, a d showing the cutting, the flat chisel cuts b, c being taken separately afterwards.
In order to illustrate the filing clearly, it will be necessary to show more metal to be filed off than would be the case in practice, unless the eye were very small, in which case it would not pay to chip.
Put the eyes together with the pin in and let the two lowest places on the edges coincide. Then file a flat place clear across them, as shown in Fig. 2288 at f, making it parallel to the pin, and, say, down to within 1⁄100 of the finished depth. To test the parallelism of the flat place, take out the pin and apply to the flat place a square, rested against the radial face of the double eye, or measure its distance from the hole of the eye on each side of the double eye, that is at each end of the hole.
When it is true and down to the required size, put the eyes together and let their relative positions be such that the flat places do not coincide, and that on the double eye will serve as a guide to carry the filing around the single eye, while that on the single eye will serve as a guide to carry the filing around the double eye, as will be seen on reference to Fig. 2289, in which the flat places a, b on the double eye serve as a guide to file c down to, while the flat place on the single eye at d is a guide to file the metal at e, f down to, and it is obvious that by moving the eyes to different positions the eye may on that side be filed true and to circle.
When the filing has thus been carried around as far as the movement of the eyes permits on that side, turn the single eye over in the double eye, and they will appear as shown in the end view, [II-103] Fig. 2290, a being the filed side of the single and e d that of the double eye; hence the metal at c, b must be filed down level with a, and that at f down level with e, d.
We have assumed that the edges only required finishing irrespective of the joint faces; but let it be assumed that the whole of the eye has been dressed up by machine tools, and that it requires fitting and finishing by the file both on its joint faces and on its edges.
If the eye has been bored and faced in the lathe the faces will be about true with the hole, but if it has had its faces trued in a machine, as a planer or slotter, and the hole bored subsequently in a slotting machine, the hole may not be true to the faces. This may occur from want of truth in the chucking devices, from these devices having been held to a table or carriage moving on slides, and having lost motion or play, in which case from the leverage of the pressure of the boring tool-reamer or bit, this table may have lifted to the extent of such play, in which case the hole will not be at a right angle to the face or faces.
First, then, these faces must be tested for truth and smoothed by filing. The best testing device is a pin and washer, the pin neatly fitting the hole in the eye and the washer neatly fitting the pin. The radial face of the pin head and of the washer should then be given a light coat of marking, and be inserted in the eye, as shown in Fig. 2291, in which a is the pin head and b the washer. If each be then rotated under pressure against the eye, they will mark the high spots, which may be filed and draw-filed until an even contact all around is shown.
The single eye should be similarly faced and fitted, a somewhat tight fit, into the double eye. In a job of this kind, where accuracy of fit is essential, it is usual to bore the hole about 1⁄100 inch smaller than its finished diameter, and after fitting the two eyes, to ream out the eyes while bolted together.
For the reaming the two eyes should be clamped together. The single eye is left somewhat too tight a fit to the double eye to permit of the finishing being done after the holes are reamed, because the reaming may slightly alter the axial line of the hole. The two bolts holding the clamping plates should be brought just home on the plates, and then tightened up gradually and alternately, so that the eyes may be gripped fair, and not liable to move during the reaming. The bores of the eyes should be set as true as possible one with the other before the plates are tightened upon the eyes, for if it is attempted to set the eyes true by hammer blows afterwards, the pressure of the plates would cause the arm or hub of the double eye which received the hammer blow to move more than the other, or, in other words, to spring out of its normal position, and the eye will be distorted. But when released from the pressure of the clamping plate the double eye will resume its normal shape, and the holes will not be axially true in the two eyes.
After the holes are reamed the temporary pin and washer used for the facing will be too loose, and the proper pin should be used for all future operations. The eyes should be put together with a light coat of marking on both faces of the single eye, and, with the pin in place, one eye should be moved back and forth, when they may be taken apart again and filed on the high spots. When by repetition of this process they fit properly the outside edges may be filed up, as already described.
It is obvious, however, that the pin and washer shown in the figure may be hardened and used to file the edges up before the reaming, in which case, their diameters being equal, and equal to that of the required finished diameter of the eye, it is easy to file the eye edges true and to size; but even in this case the eyes should be finished by reversing and moving as before described. There is, however, the objection to filing the edges—first, that the joint will show plainer, because in filing the side faces to fit the single into the double eye, that part of each face near the edge is apt to be filed away slightly too much, causing the joint to show; but if the circumferential edges of the eye be filed last, the part so filed away is removed and the joint may be made almost invisible.
The best plan of all is to first fit the eyes, then ream them out and then provide a hardened pin and washer to fit the reamed hole, then file down the circumferential edges nearly level with the pin and washer and finish by reversing and moving the eyes as before described.
In the absence of any pin and washer, such as shown in Fig. 2291, the inside faces of the jaws of the double eye must be filed parallel to the outside radial faces of the single eye, the outside surfaces being trued when the hole is bored. If none of the surfaces have been trued with the hole, the outer ones should first be trued, using a T-square (if there is no pin) to test the truth of the face with the hole, and the inside jaw faces must be trued with the outside, measuring each jaw with outside calipers, and the width between the jaws with inside calipers.
Let us now suppose that it were attempted to first fit the single to the double eye a tight fit, then to ream the hole and then to make the joint an easy working fit. In this case the finished hole in one eye may become out of true with that in the other, that is, it may not be parallel with that in the other, and for the following reasons:—The holes of the two eyes will rarely come quite true with each other, even though the radial faces of the eyes be turned in the lathe or faced in a machine when the holes are bored, and it is the duty of the reamer to true as well as smooth them in whatever direction they may be out of true or face one with the other until they are put together. Now, if they be put together a tight fit, the outside jaws are sprung open to some extent. Again, they may be sprung slightly atwist, and if the hole be reamed true and this twist taken out afterwards the hole will come atwist or out of fair in proportion as the jaws lose their twist from being fitted.
Again, reaming the hole slightly alters its axial line, and the radial faces, if at a right angle to the hole before reaming, will not be so after reaming, and it is not practicable to discover in just what direction and to what degree reaming the hole will alter its axial direction; hence, the single eye must be fitted as near as may be before the holes are reamed, and finished afterwards as described.
Let it be required to reduce by filing, the diameter of a round pin[II-104] or to file it to fit a taper hole, and the diameter of the pin being small it may be held by one end in the vice jaws or by means of the clamps, shown in Fig. 2091 or those in Fig. 2092. But the filing can be more truly and easily finished as in Fig. 2292, in which there is shown fastened in the vice a filing block having V-grooves (of varying width to suit varying diameters of work), in which the pin to be filed may be rested.
The pin is held by the hand vice shown, and is rotated towards the operator during the forward file stroke (one hand holding the hand vice and the other the file), and in the opposite direction during the back stroke. After every few file strokes the hand vice is partly rotated in the hand so that the whole of the pin surface may be subjected to the file. The hand vice enables the pin to be forced into its hole and rotated, to show by the contact or bearing marks where it requires filing to adjust the fit.
Fig. 2293 represents an excellent form of hand vice for holding pins, &c., the jaws being pivoted to a cross piece and opened by a cone, the handle threading to the stem of the cross piece, and being hollow so that the work may pass through it. The work is thus very firmly gripped and not liable to move in the jaws as it is when the hand vice is fastened upon the work by a thumb nut.
Very thin pieces of metal cannot be well held in the vice jaws, and as an example of this kind of work holding, let it be required to file up a caliper leg, which being curved cannot well be held in any of the vice fixtures heretofore shown.
In Fig. 2294 there is a block of wood having an extension at a that may be gripped in the vice jaws. Upon the surface of the block the caliper leg is held by brads or nails driven around its edge, as shown, or it is obvious screws may be used.
An excellent example of filing is to file up a hexagon nut or a bolt head. This is apparently a simple piece of work, but it is in fact a job that requires a good deal of care and precision to properly accomplish. The requirements are that the nut shall measure alike across the flats, that each flat shall be parallel to the axial line of the bolt, and at a proper and equal angle to both of its neighbors, and that the nut shall be of equal thickness all round. The method of accomplishing this result is as follows: Let Fig. 2295 represent a bolt head, after it has been turned in the lathe. It will be observed that the end face of the bolt head is rounded. Now a bolt head of this form gives a very neat appearance, but it presents difficulties in the filing up, as we shall see presently.
Suppose that one flat (which we will call flat a) of a nut, is nearest to the bore, then to make the nut of equal thickness all around, the other flats must be so filed down as to approach the bore as nearly as a does, and it is assumed that there is metal enough to permit this. The flat a will then be the first one to be filed up, taking off just sufficient to make it true when tested by the nut gauge, applied as in Fig. 2296, in which n is the nut, and g the gauge. The flat must also be filed true when tested by the gauge, as in Figs. 2297 and 2298, the gauge g being tried rested on a and applied to b, and then rested on a and applied to c. a should be filed so that, if possible, it will be at the proper angle to both b and c, but if, from errors in the angles of b and c, this is impossible, the error should be divided between the two, as shown, for example, in Figs. 2299 and 2300, where the gauge is shown in the two positions necessary to test each respective flat, b and c; the amount of error being equal at h and i.
[II-105]The next flat to file will be e, Fig. 2299. Now, in a small nut, the chamfer of the nut edge will be sufficient guide to the eye in filing e to an equal thickness (that is, equal for distance from the bore to a).
In order that the finished nut shall be so true that the nut gauge shall show that the flats or angles are true one with the other all around the nut, it is necessary that the flat e shall stand parallel to a; hence it should be made so by measurement with calipers, irrespective of its angle to either d or f. After e is filed it will serve as a base from which d and f may be filed to angle, while a will serve as a base from which the flats d and c may be filed to angle; but, while testing the angle with the gauge, c and d should be tried for parallelism, and f and b for parallelism, while the diameters across these flats should be equal on all sides.
If it were attempted to go all around the nut, filing to the gauge, as, for example, filing c, Fig. 2300, from a, f from c, e from f, d from e, and b from d, all the error in the angle of the gauge, or errors of workmanship, will (supposing the latter to be always in the same direction) be multiplied upon, or rather added to b when tested with a, and these two will not be of correct angle. Again, any error made upon one flat will be copied upon the one filed to gauge angle from it; whereas, filing e parallel to a insures the correctness of these two, and testing the parallelism of the others, as b, f, serves to discover and correct any error of angle that may exist. It is obvious that in filing each flat the gauge must be applied as in Fig. 2296, as well as in Fig. 2298.
In filing the opposite flats to diameter to fit the wrench or gauge, if one be used, it is best to leave them a tight fit until all are nearly finished, so that any error that may be discovered may be corrected while finishing them.
In small nuts, if two are to be filed, a better plan may be followed. The two nuts may be put upon a short piece of screw, as shown in Fig. 2301, and screwed firmly together. In doing this, however, it may be found that the nuts will not tighten against each other, with the flats fair one with the other. This, however, may be accomplished by winding around the piece of screw, and between the nuts, a piece of waste, twine, or rag, and then screwing them together until they bind sufficiently and the sides come fair; the nuts may then be put in the vice, the jaws of the latter meeting the end a of the screw and the face b of the nut in the figure. Select the thinnest flat on either of the two nuts, and file it and the one coincident to it, but on the other nut, at the same time taking care that both are filed equidistant from the screw. To test this, apply the gauge as shown in Fig. 2296. File these faces down a little above size, and then loose the nuts and put in an addition of waste or twine, so that the same faces shall not coincide, and the two filed faces will serve as guides, down to which their new contiguous faces may be filed, the hexagon gauge being applied as before. By adding waste or twine, this process may be repeated, the original, or first-filed faces serving as guides down to which to file all the others, which will insure equal thickness of all the flats. After roughing out all the flats in this manner, reverse the nuts on the screw, so that the two chamfered faces come together, as in Fig. 2302, and any want of truth in the parallelism of the flats one with the other, or with the axial line of the screw, will become at once apparent, and will be corrected in the finishing, providing that an equal amount be filed off the respective sides that are in the same plane as are a and b in the figure. Of course nuts filed in this way require the application of the calipers and gauges, the same as described for a single nut; but uniformity will be assured and the filing truer, because the filing in small nuts, as an inch or less, will be more true on account of there being a larger area for the file to rest and steady upon. It is obvious that a plain cylindrical piece, instead of a piece of screw, may be used, in which case the waste or twine will be unnecessary; but in this case the plug, or cylindrical piece, should be shorter than the length of the two nuts, and should not be so tight a fit to the bores as to damage the threads.
In small nuts it will not pay to chip off the surplus metal, because they cannot be held sufficiently firmly in the vice without suffering damage from the vice-jaws, or even from copper clamps, while lead ones are too soft to hold them.
The finishing marks, if any, should be in a line with the bore of the nut, which gives the neatest appearance. The process is the same for a bolt head, such as shown in Fig. 2295, as for a single nut, with the exception that the gauge must be applied as in Fig. 2303, when testing the truth of the flats with the axial line of the bolt, this being necessary because of the roundness of the end face a, in Fig. 2303. The distances d and c will be equal when the flat is true in that direction.
A pair of outside calipers form an excellent example in vice work. The material should be good cast steel of an even thickness, and therefore (unless for very large ones) saw blade will answer the purpose. It should be well softened by being made to a low red heat and buried in fine cinder ashes or lime, and allowed to cool there; the proper width of this piece of steel being sufficiently greater than the size of the caliper washer, to allow room for a chisel cut and leave a little to file off in truing up the joint. The length should be somewhat more than that required to make the legs, because a piece will be required to be cut off the narrow end to give substance enough for the points. The size of the washer should be drawn at each end of the steel, the centre of the washer should be centrepunch-marked, and a line should then be drawn to set off the two legs. The steel is then severed along this line, thus getting out the two rough legs. When shears are not at hand, or when it is not designed to use them for this purpose, three methods of dividing may be pursued: First, we may drill small holes along the line, and cut between the holes with a chisel. The objection to this is that the blade is sometimes very[II-106] hard to drill. Secondly, we may make centrepunch marks along the line, and then cut along the line with a chisel; and thirdly, we may drill a few holes at each end, and cut the middle with the centrepunch and chisel. The entire drilling is the safest, and the centrepunching the most hazardous, but it can be accomplished if the centrepunching is done lightly and gone over several times, with the chisel applied between the centrepunch marks, which will be much the quickest plan of the three.
The hole is next drilled for the rivet, care being taken to make it about 1⁄32 inch smaller than the proper size, because the drill will not make a sufficiently true and parallel hole, and the latter must be reamed or trued out; and again because the legs have to go into the fire to be bent, and hence the holes may become damaged. There is another consideration, however, in determining the size to drill this hole, which is that the two legs require to be riveted together to bend them, and it is as well to drill the hole to suit the piece of metal intended to be used for this temporary rivet, which should be of brass or copper, so as to drive out easily after the bending is done. During the bending process the points should be thickened, care being taken not to twist them in the process. If the vice hand does the bending, the following instructions are pertinent: Heat the steel slowly and turn it over and over in the fire so that the points may not get burned before the wider parts are sufficiently heated. Let the fire be a clean one, that is, with no gaseous or blazing coal about it, or the coal will stick to the sides of the calipers, and they will get cool while being cleaned of adhering coal after being taken from the fire. Begin the bending from the thick end, carrying it forward by degrees. Strike light but rapidly succeeding blows, placing the steel upon the round point of the anvil.
The bending completed, and the points being thickened, the edges of the legs are trimmed upon an emery wheel or with a file, using the latter lengthwise of the edges if a new one, or crosswise if an old one. A full 1⁄32 inch may be left to trim off after the calipers are put together. The temporary rivet may next be driven out, first, however, gripping the legs firmly and near to the rivet end with a hand vice, putting a piece of sheet brass between each jaw of the hand vice and the steel; otherwise the teeth of the latter will mark the steel, entailing a great deal of extra labor to file the marks out. The rivet hole is then reamed out to the required size, the two legs being held together by the hand vice to render the reaming more steady and true by making the hole longer when the two are together.
The next operation is to turn the rivet and washers. It is a very common practice to turn two separate washers and a rivet. On account, however, of the small amount of bearing in the washer holes, such washers are apt to rivet up out of fair one with the other, making an unsightly joint and causing them to be out of round when the edges of the joint are filed up. A better plan is to turn a pin and washer, taking care to make the diameters of the two exactly equal and the flat faces of each quite level. The pin should be turned about 1⁄64 inch taper, the small end being made a neat fit to the holes in the caliper legs, and should be made of cast steel properly annealed. When finished, the head of the pin should be gripped by a pair of lead clamps in the vice, the end being left protruding so that the legs can be put upon it and revolved back and forth with a good supply of oil and under hard pressure, so that the pin will be forced a good and rather tight fit into the holes. This process will also smooth out the holes and condense the metal around both the holes and the pin. It is well to leave the pin to fit about one half as tight as the finished joint requires to be. The washer should be countersunk about three-quarters of the way through the hole, the latter being left a close working fit to the pin.
The legs should be rough filed, second-cut filed, and smooth filed before being draw-filed, care being used to keep the files clean, so as to avoid scratches. During this filing, however, the pin should be tried in the hole to see if the head comes fair down upon the face; thus the pin forms a guide and test in facing up the joint of the leg, and this is one of its advantages over the two-washer plan. After carefully draw-filing and polishing the sides of the legs the fitting of the joint is finished as follows: Place the two legs upon the pin in their proper position, and then put the washer into its place. Then behind the washer place another temporary one that will protrude beyond the end of the pin; then grip the whole tightly between a pair of lead clamps or pieces of thick leather in the vice; this will bring all parts of the joint home. Take hold of one leg in each hand and move them backward and forward as far as the vice will let them go, repeating the operation about a dozen times or more. This will mark the high spots upon the legs, which may then be taken apart again and have the bright parts removed by a scraper. It is also well to place the flat face of the washer upon a smooth file and rub it backward and forward under finger pressure, which will tend to correct any defect in its flatness. When the faces of the joint bear all over, it may be put together with oil and placed in the vice as before. Work it well back and forth, take it apart again and cut off the rivet to the required length, taking care very slightly to recess the end to assist the riveting. The whole joint should then be wiped quite clean, freely oiled, and put together ready to rivet. The head of the pin should be rested upon a block of lead, so that it will not get damaged. The riveting should be done with a small light ball-pened hammer, the blows being delivered very lightly and evenly all round the edge. As the riveting continues it is necessary to move the legs occasionally to see how the tightening proceeds, and when the legs are sufficiently tight, one of them may be gripped between pieces of leather in the vice, while the other is well worked and lubricated with oil. Then the riveted end should be filed off to very nearly its proper height and shape, and the joint well worked back and forth and round and round in the hand until it gets quite warm, when it may be cooled in water and tried for tightness. If too tight, it may be either worked until easy, or the riveted end of the pin may be tapped with a hammer to loosen it slightly. The riveting being completed, and the end filed smooth, the rounded part of the washer and the pin head should be draw-filed with a very fine file moved in varying directions, and then the polishing may be done with emery paper.
Fitting Keys.—Keys that have been planed or milled will still require fitting with the file to insure that they bed properly. If the key to be fitted is taper and intended to fit top and bottom, the sides should first be filed true to a surface plate, and fitted into the keyway in the shaft, so that it can be slid up and down a good working fit. While fitting it, however, it is well to try it once or twice in the keyway in the wheel, as well as in the shaft, so as to see by the marks whether the keyways in the shaft and wheel require any fitting at all, either to make them quite square with the outside face, supposing it to be turned off, or to give them a good even bearing surface. The key being fitted sideways we must give the two keyseats a coating of red marking just sufficient to show that the surface is of a red tint, and then put the wheel in its place on the shaft. Then we bevel off the edges of the key at each end, leaving a chamfer of 1⁄16 inch, and after facing off the top of the key with a bastard file, we place it in the keyway and tap it very lightly to a gentle bearing. After driving the key lightly home and taking it out again, we may file it on the top and bed it on the bottom, according to the indication of the marking, and re-insert it, tapping it up until it is home, top and bottom, without being a driven fit at all; on taking it out we file it according to the marks again, and if we continue this process until the key is a good fit, it will not spring the wheel the least out of true, no matter how tight, reasonably, it is finally driven. The key must never be driven in or out dry, for it will, in that case, inevitably cut during the first part of the operation; the marking put on the keyway is sufficient lubrication, but after two or three insertions the key also should be itself given a light coat, which will serve as lubrication, as well as denote the fit.
The bearing or contact marks upon a key driven home very lightly may show at one end or on one side only, while if the key was driven farther in those marks may show all over, making the key appear to fit much better than it actually does. This occurs from the elasticity and compression of the metal of the keyway and key, the metal giving most where the contact is hardest; from this it is apparent that a wheel truly bored and a good fit may be set out of true by the key.
In Fig. 2304, for example, is a wheel hub w, assumed to be a good fit to the shaft s, while the key k fits at the end a only. If[II-107] the key be driven tightly home, the wheel will spring over, so that instead of the plane of its diameter standing at a right angle to the axial line of the shaft as at d in Fig. 2305, it will stand at an angle as at e, throwing the wheel out of true in that direction. This would occur not only on account of the elasticity and compression of the metal of the keyway, but also because the surface of the bore of the wheel and of the shaft is not, even under the best of turning, smooth enough to come into close contact all over, but are covered with slight projections or protuberances, which may occur in spirals because of the turning tool marks, or in localities because of differences in the texture of the metal. In driving the key home these protuberances give way, and they do so most where the contact pressure is greatest, which would be at g in Fig. 2305, causing the wheel to cant over. If the wheel is not a good fit to the shaft it will not in this case touch the shaft at c, Fig. 2305.
Now suppose the key to bear at a and b, Fig. 2306, only, then the wheel would be thrown out of true in a direction at a right angle to the length of the key as denoted by the line e, which should stand as at d.
A properly bedded key binds the opposite half of the circumference of the wheel bore to the corresponding half circumference of the shaft; but if the key binds at one end only, as in Fig. 2304, the contact will be at the end h only; hence the surfaces will soon compress, on account of all the strain of the key falling on a small area, and the key will get loose.
It is obvious then that if a wheel has not been bored to run true the error may be to some extent corrected in fitting the key, but in this case the key must be driven well home, and the wheel rim tried for running true during the fitting process, the key being so bedded as to true the wheel as far as the elasticity and compression will permit; but a key thus bedded will not hold so firmly.
The distance a key of a certain length, breadth, and thickness, and of a given taper, will drive after being pushed home by hand or lightly tapped in with a hand hammer depends upon how closely it fits to its seat, and upon the elasticity of the metal, as well as upon the force with which it is driven. The workman usually, while fitting the key, drives it well home occasionally, to see how much of its length to allow for the final driving, and while doing so, if the key is a small one, a hand set chisel or a piece of copper should be interposed between the key head and the hammer (a blacksmith’s set chisel is used for large keys) to prevent the hammer from damaging the key.
In fitting keys to old keyways the key is made too long, and cut off after being driven home. A long key is apt to bend in the driving, hence it is not unusual to support it by holding a second hammer beneath and against it to support it while being driven. In driving a key out, especially if it is fast home, a quick heavy blow is best, as it is less likely to burr, swell, or bulge the end of the key. But after the key has started lighter blows will answer.
To make a key for an old sunk keyway, it is as well to fit a piece of wood thereto as a guide in forging and fitting the key. If a fast running grindstone or emery wheel is at hand, many will forge the key a trifle large and then grind it as near as possible, and finish by filing. This, however, does not produce good work; it is better to plane the key all over, leaving a little in size for fitting. In preparing the piece of wood referred to, it should not in the fitting be driven or even forced in and out to try the fit, for the wood will compress and the marks mislead as to the actual fit. The proper way is to chalk the piece of wood and push it up the keyway just tightly home, then withdraw and fit it again.
In cases where the key is forged to very nearly the finished size, and is finished by the file, as sometimes occurs when away from the shop, it is best to forge the key with a gib head, as in Fig. 462, to assist in extracting it, especially when it is difficult to drive the key out from the back end, or when the keyway does not pass entirely through. The key should be finished with a smooth file and with the file marks lengthways; it is, in fact, better to use a small smooth file and draw-file it, taking care to ease the high spots the most; and before driving it home both it and the keyway should be oiled.
If a keyway is to be cut by hand through a bore, as in a pulley or gear-wheel bore, its width should be marked with a T-square. If its width does not exceed 1⁄2 inch a cape chisel a little less (say 1⁄32 inch less) than the finished width of keyway should be used, which will leave a little metal for the sides to be filed true. If the keyway be an inch wide it is better to take a cape chisel about 1⁄4 inch wide and cut a groove along each side of the keyway (keeping close to the marked line), and then cut out the middle with a flat chisel. The sides and bottom of the keyway should be surfaced true with the file.
If a keyway is to be cut in a shaft the cape chisel should be used in the same manner as above. But in both cases it is best, when filing, to occasionally ease out the corners with the edge of a half-round file, for reasons which will be explained presently.
In chipping a keyway in a bore the cut must not be carried[II-108] entirely through from one side, or the metal at the end of the cut will break out, and even in wrought iron this is apt to occur, so that it is necessary to cut the keyway from each end, or, at least, nick it in at one and cut it from the other end. In long key ways it is handiest to cut them half-way from each side, using, in the absence of anything better, a piece of planed wood and red marking or chalk to try the keyway with.
In cutting out through keyways by hand the location of the keyway is marked off by lines on both sides of the stub end of the rod, and then the mass of the metal is removed by drilling through as many holes as can be got in the size of keyway required, as shown in Fig. 2307, in which w is the work, b c d e the location of the keyway, and 1, 2, 3, 4 are the holes, taking care to have the drill rather smaller than the width of requisite keyway. The holes are drilled half-way through from each side, which is done to keep the keyway true; for if the drills were to run a little to one side, as they are apt to do from a variety of causes, a great deal of work would be required to correct the error.
If the keyway is of sufficient dimensions to admit of the use of a chisel, the pieces left between the drilled holes are chipped out, and for this purpose a side chisel is found very useful, not only to nick the sides of the pieces left by the drilling, but also to take the finishing chipping cuts on the sides of the keyway. To cut out the square corners of the keyway, the diamond-point chisel shown in Fig. 2171 is employed.
If, however, the keyway is a very deep one, requiring long and slight chisels, the chipping process may be greatly reduced, or in fact entirely dispensed with, by plugging up the holes first drilled in the stub end by driving pieces of round iron tightly into them, and then drilling new holes, having their centres midway between the pieces so driven in, as at a in Fig. 2308. After the latter drilling, the remaining pieces of plugs are driven out, leaving the centre of the keyway cut clear through and the sides with a series of flutes in them, as shown at b, Fig. 2308 (in which 1 2 are the plugs and a is a centre for the new hole at that end), which should be filed away with a file as thick or strong as the clear space will allow. These plugs must be of the same metal as that in which the keyway is cut, otherwise the drill will be apt to run to one side.
To insure truth in the surfaces, a surface plate to test with is an absolute necessity, while to test the parallelism, a small sheet iron gauge is used, which gauge may afterwards be employed as a guide whereby to plane the thickness of the gib and key.
In cases where a slotting machine is at hand, it is sometimes the practice to cut out one end of the keyway to a sufficient length to admit a slotting tool, and then to slot out the remainder. This plan is often resorted to in getting out keyways of unusually large dimensions.
A much more usual method, however, is to employ slotting or keyway drills.
It is obvious that the ends of the keyways cut by drills are half round; hence, if square corners are required, they must be cut out square with the chisel shown in Fig. 2176, and afterwards filed out true. As a general rule, keyways cut with these drills require filing on the sides to get proper smoothness and bearing for the keys; and here it may be remarked that, in filing the corners of the keyway, a safe-edge file must be used, so that the two faces forming the corner will not be operated upon simultaneously, because that would require that the file be used in a straight line laterally as well as horizontally, and this is impracticable even in the hands of the most skilful.
Even the square file should have a safe edge upon it, and such an edge is usually produced by grinding the teeth off one face of the file. In selecting the face to have the teeth ground off, choose a face that is hollow in its length, or, if none of the faces is hollow, then select a face that is at a right angle to a good face of the file. It will be noted that with one safe edge only the square file will require turning over in order to operate upon both corners and maintain in each case a safe edge of the file against the flat sides of the keyway. For this reason many workmen select the two best parallel faces of the file and grind off the two other faces, giving to the file two safe edges, one opposite to the other. In this case either of the cutting faces of the file may be used upon the whole end face of the keyway operating close up to the corner, or if the file is much narrower than the keyway it may be used with a side sweep that will prevent the file from pinning, and produce much truer filing.
It is useless to attempt to cut out a square corner with a square file unless one edge of the latter is ground safe, because the teeth of the file itself do not form a square corner, and it is therefore only by grinding the teeth off one side that the points of the file teeth can be brought full up to a sharp angle. Here, however, it may be noted that even if the filing is performed with the best of safe-edge files, and as carefully as possible, it will still be necessary to square out the fine corners with the edge of a fine smooth half-round file.
If the edges of the keyways are rounding, as they are sometimes made where strength is required in the strap, it is better to take a file nearly or about 1⁄8 inch larger in diameter than the width of the keyway, and grind two safe edges on it, otherwise the round file is very apt to go astray and cut the sides as well as the edge of the keyway.
An equaling file is much better for keyways than one actually parallel.
Another way employed to finish small keyways is by the aid of the tools shown in Figs. 2309 and 2310, which are termed drifts, because they are driven through with a hand hammer. That shown in Fig. 2309 is intended for holes having but little depth and not requiring to be very true, such, for instance, as those cut in the ends of keyways or bolts to receive cotters; the thickness at a a is made greater than at b c to give the cutting edge clearance.
The form shown in Fig. 2309 is for use by hand, the teeth being cut diagonally instead of across, as at a a, to preserve the strength.[II-109] This end may also be attained by making the serrations round at the bottom, as shown in the figure.
The slant of the teeth on one side of the drift should cross the slant of the teeth on the diametrally opposite side, because if the teeth on opposite sides were parallel one to the other the drift would have a tendency to move over to one side, and crowd there during the process of drifting.
In using these drifts the keyway should first be filed out to very nearly the finished size, leaving very little duty for the drift to perform, although the drift may be driven a short distance into the keyway occasionally during the filing, so as to show where filing is requisite. The work must lie flat and level upon a metal block, lead being preferable, and oil freely supplied to the drift. “If the hole is a deep one, and the cuttings clog in the teeth, or if the cut becomes too great (which may be detected by the drift making but little progress, or by the blows sounding solid) the drift must be driven out again, the cuttings removed, and the surplus metal, if any, removed by filing. The drift must again be freely oiled, and driven in as before, and the operation continued until the drift is driven through the keyway. After the drift has passed once through it should be reversed (or, if a square one, turned a quarter revolution) and again driven through, so that each side of the drift will have cut on each side of the hole, which is done to correct any variation in the size of the drift” (“Complete Practical Machinist”).
The great desideratum in using these drifts is to drive them true, and to strike fair blows, otherwise they will break. While the drift is first used, it should be examined for straightness at almost every blow; and if it requires drawing to one side, it should be done by altering the direction in which the hammer travels, and not by tilting the hammer face.
In Fig. 2311, suppose a to be a piece of wood and b and c drifts which have entered the keyways out of plumb, as shown by the dotted lines d and e. If, to right the drift c, it was struck by the hammer f in the position shown, and travelling in the direction denoted by g, the drift c would be almost sure to break; but if the drift b was struck by the hammer h, as shown, and travelling in the direction denoted by i, it would draw the drift b upright without breaking; or, in other words, the hammer face should always strike the head of the drift level and true with it, the drawing of the drift, if any is required, being done by the direction in which the hammer travels. When it is desired to cut a very smooth hole, two or more drifts should be used, each successive one being a trifle larger in diameter than its predecessor. Drifts slight in cross-section or slight in proportion to their lengths would be tempered evenly all over to a blue, while those of stout proportions would be tempered to a deep brown, bordering upon a bright purple.
For cutting out long narrow keyways, that are too narrow to admit of a machine cutting tool, and for very true holes, not to be cut out in quantities all of the same dimensions, it has no equal.
Hand drifts are sometimes used to cut keyways in small bores, as in small hubs, the method being shown in Fig. 2312, in which a represents a pulley with a keyway to be cut in the hub b; c is a plug, and d slips of iron placed between c and the drift e to press the latter to its cut. It is obvious that in this case the keyway in the pulley will be cut parallel, and the taper must be provided for in the key seat in the shaft. Keyways cut in this way are more true than those filed out. It is also obvious that the sides of the keyway, as well as its depth, may be finished by a drift, and this is very desirable (on account of insuring parallelism) when the key is to act as a feather that is to have contact on the sides and not bind top and bottom.
The most improved form and method of using this class of tool, however, is as follows:—If a keyway is to be cut out of solid metal, holes are drilled as closely together as the length of the keyway will admit, their diameter nearly equaling the required width of keyway, after these holes are drilled through the metal remaining between them.
Templates.—Templates for vice work are used for two purposes: first to serve as guides in filing work to shape and size, and secondly to test the finished work. When used as guides to file the work they are mainly used to work of irregular, curved, or angular form, to which the square and other ordinary vice tools cannot be applied.
Fig. 2313 represents a template for filing out a square hole. The edges a, b are at a right angle to each other, the wire simply serving as a handle.
There are two methods of applying this template; the first is to file out two opposite surfaces of the hole to the required diameter, making them true and parallel one to the other, and to then employ the template while filing out the remaining two sides; the[II-110] other is to file out one side and apply the template from that as a base for the other sides. The first is preferable because the liability to error is a minimum.
When work is to be from a template, the latter obviously becomes the original standard, and in many cases the best method of forming it so as to insure correctness and enable its proper application to the work is a matter of great consideration. The shape of the template must, of course, be marked by lines which should be as fine and as deep as possible. But it does not matter how closely the template may be filed to these lines, it will still have some error, and this can in many cases be discovered and corrected during its application to the work. In the following examples there are principles which will be found of general application:—
Let it be required to make or test a piece of work such as in Fig. 2314, the teeth to be equally spaced, of the same angle, and of equal height. A template must be made of one of the two forms shown in Fig. 2315. To begin with, take a piece of sheet metal equal in width to at least two teeth, and, assuming that the template is to have two teeth, file its sides p q, in Fig. 2316, parallel, and make the width equal to twice the pitch of the teeth. We next divide its width into four equal parts by lines, and mark the height, as shown in Fig. 2316. If we desire to make the template such as at a, we cut out the shaded portion; or for the template at b, the shaded portion. It will be observed, however, that in template a there are two corners c and d to be filed out, while at b there is but one e, the latter being the easier to make, since the corners are the most difficult to file and keep true. The best method of producing such a corner is to grind the teeth off the convex side and at the edge of a half-round file, producing a sharper corner than the teeth possess, while giving at the same time a safe edge on the rounded side that will not cut one angle while the other is being filed. But when we come to apply these templates to the work, we shall find that a is the better of the two, because we can apply the square s, Fig. 2317, to the outside of the template, and also to the edge f of the work, which cannot be done to the edges g of the work and h of the template, because the template edge overhangs. We can, however, apply a square s′ to the other edge of b, but this is not so convenient unless the tops of the teeth are level.
Assuming, therefore, that the template a is the one to be made, we proceed to test its accuracy, bearing in mind that for this purpose the same method is to be employed whatever shape the template may be. Consequently, we make from the male template a, Fig. 2318, a female template k, beginning at one end of k and filing it to fit a until the edges of a and k are in line when tested by a straight-edge s. We then move the template a one tooth to the right, and file another tooth in k, and proceed in this way until a number of teeth have been made, applying a square as at s, Fig. 2319, to see that the template a is kept upright upon k. When k has been thus provided with several teeth that would fit a in any position in which the latter may be placed, we must turn template a around upon k to test the equality of the angles. Thus, suppose at the first filing the edges a, b, c, d, upon a accurately fit the template k, and the straight-edge shows the edges fair; then if we simply turn the template a around, its angles, which were before on the right, will now be on the left, as is shown at the right of Fig. 2318.[II-111] Thus in one position a fits to e, in the other it fits to h, or b fits to f, and when turned around it fits to g, and so on. Supposing that when thus turned around the angles do not coincide, then half the error will be in the teeth of a and one-half in those of k, and the best plan will be to correct them on a to the necessary amount as near as judgment will dictate, and then to apply k as before, continuing this process until a will fit anywhere in k, and may be turned around without showing any error. But at each correction the straight-edge must be applied, and finally should be tried to prove if the teeth tops are level. We thus have two interchangeable templates, of which a may be used on the work and k kept to correct a when the latter becomes worn. It may be as well to add, however, that in first applying a to k it is best to press the straight-edge s against the edge of k, and hold it there, and then to place a against s, and slide it down into k.
Fig. 2320 represents an example in which, the form being a curve, it would be best to have the template touch more than two teeth, as shown in the cut. By letting the side a, Fig. 2321, of the template t terminate at the centre line of the two curves, and the end b terminate at the top of a curve, turning the template around would cause end a to envelop side c of the middle curve, thus increasing the scope of the template. Suppose, however, that the base curve d required to be true with the teeth, then a second template t′ must be used, its ends at e and f measuring an equal length or height, so that when they are placed even with the ends of the work, the distances g h being equal, the corrugations will be true to the curve d d. Now let it be supposed that, instead of making a template to test a piece of work such as in Fig. 2321, it is required to make a template for use in making another piece of work that is to fit to piece w, then template t in Fig. 2321 will not answer, because it is a female template, whereas a male one is required, so that the edge of the template may coincide with that of the work. But we may convert t, Fig. 2321, into a male template by simply cutting off the edge a as far as the line j, and causing its right-hand edge to coincide with the edge of the work so that the latter, after being fitted to the template, may be turned upside down and fit upon the piece of work.
In Fig. 2323 is an example in which the forms of both sides of a piece require to be exactly alike, and the easiest method of accomplishing this is as follows:—The face a should first be made true, and face b made parallel to a. A centre line c may then be drawn, and from it the lines e, e may be marked. The lines d are then drawn parallel to a a, lines e being made square to d and to a. The sides e may be calipered to width and parallelism, and all that will then remain is to file the angles f, f and the ends g, g to their required lengths. For f, f all that is necessary is a template formed as in Fig. 2324. The object of dressing the ends g, g last is that if they were finished before, their faces e would have to be made at exactly correct distances from them, which would render the job considerably more difficult.
Fig. 2325 represents a sketch for a piece of work whose two sides are to be shaped exactly alike, requiring a template of the form of the work, as shown. From this a second template, Fig. 2326, is made, and to this latter the work may be filed. To make the template in Fig. 2325, which represents the work, the edge x x must be made straight, and the edge d parallel to it at the proper height. A centre line s is then marked, and the edges at e may be filed equidistant from s and square to d; hence they will be parallel to each other. The side sections f should then be filed equidistant from s and parallel to each other. They should be the proper width apart and square to d, being tested in each of these[II-112] respects. The line joining e and f should be left full, as denoted by the dotted line at a on the right. The edges at c, c should then be filed, calipering them from the edge x x. Edges g, g are obviously equidistant from s and parallel to s, or, what is the same thing, at a right angle to x x, from which they may therefore be tested with a square, and, finally, the edges b are made parallel to x x, and the ends h made square to x and equidistant from s. We have now to file the angular groove at a, and to get this true after marking its depth from the lines at a, we file it first to the lines as near as may be by the eye and very nearly to the full depth. We then make a small supplemental male template t, Fig. 2327, equal in width to the distance e f, or, in other words, to the width of the step at a, and having its edges quite parallel. Its end is then filed to fit the groove at a, when its edge meets and coincides with edge e, as in Fig. 2327, t representing the supplemental template. It is clear that when the V-groove a is so filed that t will fit it with either of its edges against e, the angles of the groove will be alike, and we may then make a male gauge, as in Fig. 2326, that may be used to mark or line out the work and to use as a template to file it to, its edge h being kept parallel to face d, Fig. 2325, of the work.
There are two principal kinds of connecting rods, first those in which the brasses fit in spaces provided in the solid rod, and which are known as solid-ended connecting rods, and second those in which the brasses fit in a strap secured by bolts or keys to the end of the rod. In Fig. 2328 is shown the simplest form of solid-end connecting rod. It consists of a rod enlarged at its end to receive a brass held up to the journal by a set-screw as shown, one-half the bore being provided in the rod and one-half in the brass. The objection to this kind of rod is that as the bore wears the rod gets shorter and no means is provided to restore its length, and that during the pulling stroke of the rod the whole of the strain is concentrated on the end area of the set-screw, and this causes it to imbed in the brass, giving play to the brass unless frequent adjustment is made. It is, therefore, difficult to readily maintain a very accurate adjustment of fit with a simple set-screw of this kind. This may be to some extent remedied by the construction shown in Fig. 2329 in which the half brass a threads upon the stem of the rod, so that when it wears shorter to the amount of half the pitch of the thread upon the rod end, the brass may be unscrewed half a turn, and the original length will be restored. The cap is held on by two screws, which may have slotted heads as shown, or screws with check-nuts to prevent the screws from slackening back, as all screws are apt to do that receive alternating strains in reverse directions.
Yet another simple form of solid-end connecting rod is shown in Fig. 2330, there being two brasses with a key on one side and a set-screw on the other. In this case, as soon as either brass is moved by the key it can fit the rod at the top and at the bottom only; hence there is but little to hold the brasses sideways in the rod, and furthermore the brasses are damaged from the key and the set-screw acting directly upon them, as will be explained with reference to strap-ended rods. In Fig. 2333 is shown a very substantial form of solid-ended rod, a sectional view being shown in Fig. 2331. The bottom or back brass a has a flange, as shown in Figs. 2331 and 2332 at a, which secures it to the rod end at the back. The top or key brass b has the keyway partly sunk in it, and the key binds against one side as well as on the bottom of the keyway, and this draws that brass close down to the face of the rod, as shown in Fig. 2331.
In this as in all other connecting rods in which one edge of the key beds against the back of the brass, the taper for the key should be cut in the rod so that the edge which meets the brass will stand square across the opening for the brass; in this way the back of the brass will also stand square across, which is easier to mark off and cut, plane, and fit. If the taper for the key is cut on the brass, marking the latter and fitting it become more difficult, as it must be put in and out of its place to fit and bed the taper for the key edge, whereas, in the other case, it can be squared with a square while planing and fitting. As the bore of connecting-rod brasses wears, and the lost motion incident thereto is taken up (by driving in the key) the location of the brasses in the rod end is altered, making the rod longer or shorter according to the location of the key. But when this wear has been sufficient to let the key pass through the rod, slips of iron termed liners are inserted between the backs or bedding faces of the brasses and the end of the rod or crown of the strap, as the case may be. In putting in these liners the location of the brasses in the rod end may be adjusted so as to bring the brass back to its original position and restore the rod to its proper length, and in doing so the back brass, as distinguished from the key brass, is the one to be lined first.
In the rod ends shown in Figs. 2333 and 2334 the joint faces (that is the faces where the brasses meet) must be filed away to take up the wear, hence the rods get shorter. In Fig. 2333 the liner may be placed behind either brass, a or b, or behind both, the thickness of that behind a adjusting the length of the rod (which is always measured from centre to centre of the respective brass bores), while the thickness of that placed behind b would simply act to prevent the key from passing so far through the keyway. To prevent as far as possible the wear from altering the length of the rod, the key at one end of the rod is placed outside the crank pin or at the outer end of the rod, as in Fig. 2333, while at the other end it is placed between the brasses and the stem of the rod, as in Fig. 2334. In this latter case the thickness of liner placed behind the key brass b (as the brass against which the key bears, or the brass next to the key, is always termed) would adjust the length of the rod, while the thickness of liner placed behind the back brass (as the other brass is termed) would be the one to adjust the distance the key would pass through the keyway.
In this form of rod end, as in many other solid-ended rods, the flange or collar of the crank pin, if solid with the pin, requires to pass through the opening in the rod end which receives the brasses. This may be accomplished by making that opening large or wide enough to pass over the crank-pin collar (which will increase the width of the brasses, and hence that of the rod end); or else the crank-pin collar may have two flat places filed on it, as in the end view shown in Fig. 2335. The objection to[II-114] this plan is that the rod can only be taken on and off in one position of the engine; that is, when the two flat places a and b, Fig. 2335, stand parallel with the length of the rod.
It will be noticed in Fig. 2331 that the brass b does not fill the space in the rod. This is because that brass has to pass in over crank-pin collar and push up into the journal after it is in the rod. To make this space as small as possible, and to enable giving the crank pin as large a collar as possible, the key brass is sometimes beveled off, as shown in Fig. 2336 at a b. Another form of this rod end is shown in Fig. 2336, in which there are two keys to the brasses, the object being to adjust the keys to maintain the rod of its proper length. In order to facilitate making this adjustment, there should always be upon the face of the rod end centrepunch marks, as shown in Fig. 2338 at f and g, or else two deep marks, as shown at c d in Fig. 2337. Then, in lining up the brasses to set the key back, the rod may be restored to its original length by putting behind the back brass a piece of metal of such thickness as will bring the centre of the bore of the back brass b even with the centrepunch or other marks. This being the case, it does not matter about the exact thickness of the piece of metal put behind the other brass, since a variation in that will only act to let the key come more or less through the rod end without affecting the length of the rod. In Fig. 2337 is shown a form of rod end sometimes used. The end being open, the brasses pass through it. In this case the whole strain of the pull of the rod falls upon the edge of the gib at top and bottom of the strap, causing the gib to wear out very fast; furthermore, the back brass condenses the metal at the back of the brass opening, acting to pene it and throw the points of the rod end open, which it always does, the jaws of the gib imbedding in the jaws of the rod. This opening of the rod jaws makes the brasses loose in their places; hence this is a weak and undesirable form of rod end, though very convenient to take on and off. In Figs. 2338, 2339, 2340, and 2341 is shown a form of solid-ended rod of more modern construction. In this case a wedge a is used instead of a key, being adjusted by screws passing through the rod at the top and bottom, it being obvious that the set-screws may have check-nuts added. b is the back brass, and c the key brass. In this case the flange of the brass goes next to the crank pin, and a plate d is provided to serve as a flange on the front face of the brass. In Fig. 2338 this plate is removed to show the wedge a; but it is shown in the plan view, 2339, and the end view, 2340, and by itself in Fig. 2341. A groove is cut on each side of the two brasses and the plate spans the brasses, passing up the groove being held in position by a screw at e. The opening for the brass (in the rod end) is here shown wide enough for the rod end to pass over the collar of the crank pin, but in many cases, with this as well as with other forms of solid-ended rods, the crank pin may be made plain—that is, without a flange—and have a washer secured by a screw, so that by removing the washer the rod may be put on with the brasses already in place, and made no thicker (at the joint face) than is necessary for strength. In Fig. 2342 is shown what may be termed a clip-end connecting rod, the screw closing the rod end (to take up the wear) against the spring of the metal. It is obvious that in this case the hole may receive a brass bush split as is the rod end and secured from turning by a pin. Fig. 2343 presents another form of solid-end rod, which admits of the use of a brass having a flange on both sides of the strap, and will take on and off by removing the cap b. If the crank-pin collar is solid, the brasses must be placed on the crank pin, and the rod, with the wedge in place, lifted or lowered to the brasses; but if the crank pin has a washer and bolt, the rod may be put together and slipped on its place.
A compromise between the solid and the strap-rod end is shown in Fig. 2344, which represents a design used upon the fast engines of the Pennsylvania Railway. The piece a takes out to enable[II-115] putting on the rod or taking it off, a being secured in position by the bolt and nuts shown. This forms a solid and durable rod that is much less costly to make than strap-ended rods.
The simplest form of strap-ended connecting rod is that shown in Fig. 2345; s is the strap, secured to the rod end by the key d and gib c. a is the top, and b the bottom, or crown brass, and e the set-screw for securing the key in its place. [When the rod ends are forged in separate pieces, to be afterwards welded to the stem of the rod after the strap brasses are fitted up (which is done for convenience in handling them while fitting them up), they are termed stub ends.] This form of rod affords great facility for connection with the journals as the strap is easily removed. As the strap, however, is only secured to the rod by the gib and key, and as these have a small amount of area on the sides, it is not unusual to employ two gibs and one key, as in Fig. 2346, which holds the strap more securely, and more effectually prevents its movement sideways upon the rod end. In rods in which gibs and keys alone are used to hold the strap to the rod, the strap moves along the rod as the key passes farther through the strap, and the fit of the strap to the rod must be easy enough to permit of this motion; hence it cannot be locked to the rod. This, however, may be done by the employment of a bolt as well as a gib and key, as is shown in Fig. 2347. The edge of the gib here abuts against the back of the top brass, or key brass, as it is sometimes termed, which is objectionable, inasmuch as that it is apt to indent the brass, as shown in Fig. 2348 at b. This causes the bore to close at a, and causes the journal to heat, while it makes the brass fit loosely between the jaws of the strap, because it stretches the metal at the back of the brass, which has the same effect as pening it with the hammer.
In Fig. 2349 is shown an end of a connecting rod, such as is employed on American locomotives, the use of a gib being dispensed with, and the strap being held by two bolts. To prevent the edge of the key from imbedding in the brass, a piece of hardened steel is sometimes placed between the key and the brass, as shown in the figure.
In some designs this method is reversed, the gib being prolonged in a screw-thread, as shown in Fig. 2350, and the key head is carried over as shown. Two wing nuts are provided for adjusting the key, which enables its adjustment without the employment of a wrench or hammer.
To prevent the end of the set-screw from raising a burr on the key, which would prevent its easy motion through the keyway, a shallow groove is sometimes cut along the key, as in Fig. 2351 at a, the end of the set-screw binding on the bottom of that groove.
In other forms of rod a gib and key are used as well as two bolts. This not only holds the strap very firmly, but it prevents to a certain extent the pening of the back of the brass, explained with reference to Fig. 2348. It is obvious that in the absence of a gib the key[II-116] moving under friction against the brass stretches the metal more than a gib that presses against the brass, but has no motion endways.
In Fig. 2352 the strap is held by bolts having nuts at each end, instead of a solid head at one end and nuts at the other. The single nuts at the top serve to draw the bolts out when the rod is to be taken apart, thus saving the use of the hammer for that purpose.
In Fig. 2353 is shown a form of rod in which the strap is held by two dies a b, and a bolt which passes through the strap, the dies, and the rod end.
In Fig. 2354 is a form of rod end in which the strap ends are keyed against abutments on the rod by means of the key a. The abutments and strap ends being bevelled, keying up the strap with a closes it down upon the rod.
In Fig. 2355 is a form of rod end largely used upon marine engine work; a is the end of the rod, b, b the brasses, and d, d bolts passing through the brasses. Here we have no means of correcting the alteration of length due to the wear, unless a line is marked on the rod end, as at c, and the distance that line should stand from the centre of the brass bore is marked beside it, as is denoted by the figure in the cut, indicating that the line should stand 9 inches from the cuts of the brass bore.
In general practice the inside jaw faces of connecting rod straps and the faces of the rod are made parallel, which serves very well when the duty and wear is not great; but when the wear and tear is great, as in locomotive work, it is much better to make them taper; indeed, they are in any event better taper, because in that case the brasses can be made a tighter fit. The reason for making them parallel is because they can be more readily planed so than taper; but a parallel strap is more difficult to fit, and cannot be made so good a fit as a taper one, even when new, while it is very much more difficult and expensive to repair.
When the faces of the stub end (or, more properly speaking, of the block) are parallel one to the other, and the inside faces of the strap are also parallel, the strap must be made a very easy fit to the block, in order to be an equal fit from end to end; for if the strap fits as tightly as it should to be a good job, it will, when put on the rod, spring open, fitting across a, Fig. 2356, only; this because the strap springs open from contact at a. The fit, then, can only be such as will not have force enough to spring the strap open, and this is very small indeed even in a very strong strap. It is within the mark to state that in a strap measuring 4 inches between jaws, at a in Fig. 2356, it can be forced by hand on the rod sufficiently tight to spring them open 1⁄16th of an inch at b, b. When the brasses are fitted into the strap a second difficulty arises, inasmuch as they must be made a very easy fit, or else they will spring the strap open so that it will neither fit at a nor at b, whereas it is desirable that the bottom brass drive home, and the top brass, or one nearest the rod, just push home by hand.
When the rod requires repairing a more serious difficulty arises. Suppose, for example, that the strap requires refitting to the rod, then it must evidently be closed between the jaws, especially if the rod end requires filing up, as it usually does. Now the jaws being parallel cannot be closed without being taken to the blacksmith shop and closed across the crown, as at a in Fig. 2357; for if the jaws are closed (as they might be) by pening the corners b, c the[II-117] jaws would close as denoted by the dotted lines. The brasses will have to be made larger than the diameter at d, in order to fill the space at a, and will be an easier fit as they pass from d to a, whereas the opposite should be the case. The strap must therefore be closed across a in the blacksmith’s fire; this will scale the crown end and render it necessary to file down the whole of the surface on each of the side faces of the strap and rod in order to make them parallel, as they must be to have the flanges of the brasses fit when home in the strap.
The blacksmithing will in most cases render it necessary to file out the keyways, and this again entails the making of a new gib and key. All this extra work may be avoided by making the block and strap a little taper. But before proving this it may be noted that when the rod is made parallel the strap may be made to fit tightly by making the jaws taper, as shown by dotted lines in Fig. 2357; so that when the strap is on the rod, and the jaws spring open by reason of the close fit, the fitting surfaces will be parallel. Such a construction would be faulty however, for the brasses would fit too tight when entering the strap, and get easier as they passed to their places, whereas, as already stated, the exact opposite should be the case.
Let us now observe the advantages of a strap, whose inside faces are made as in Fig. 2358; smaller at a than at b, and also at c than at d, while the thickness from a to b is greater than that from c to d, while the widths c d are less than the corresponding width of the rod.
First, as to fitting the strap to the rod. It may be made so tight to the rod that it will only just pass on when pushed by the hand.
Second, this will render possible a tighter fit than would be possible with a parallel strap and rod.
Third, the width b a being taper, the brasses may be easier made a good fit, because there will be some metal to fit on after they enter at b.
Fourth, the brasses may be made a tighter fit, the bottom brass being tight enough to spring the strap a trifle, easing but not destroying its fit on the rod.
Fifth, the top brass may be made a handsliding fit to the strap without springing the strap open, which being already under a tension because of the spring due to the bottom brass, will be more rigid and permit of a tighter degree of top brass fit, without springing open and away from the rod.
Sixth, this will leave the bottom brass a tight driving fit, and the top a hand sliding fit, which is desirable, because the top brass has to be taken out to get the rod off while the bottom brass remains in its place.
Seventh, what is of more consequence than all, the strap can be more easily and cheaply refitted to repair it. Thus, in Fig. 2359, suppose the strap to have been closed by pening at d; then whether the end d will be narrowed will depend on the amount the strap was closed, and the amount of taper it had before closing. Let us take, however, the most unfavorable conditions, and suppose that the amount of taper was so small, and the amount of closing by pening so great, that the jaws were made taper and smallest at d. Then the amount to be filed off to bring the width of jaw correct, and a fit to the strap, will be less than if the strap jaws were formed as in Fig. 2357, as will be seen by comparing Fig. 2357 with Fig. 2359, the amount to be filed away being that between the dotted and the full lines in both figures; the amount of closure being the same in the two figures.
But there is another great advantage, inasmuch as in pening, the strap may be pened and tried on the rod, the strap being pened and tried alternately until the required fit is obtained, which is not practicable with upsetting in the blacksmith’s shop.
Again, the keyways in the strap will not be set out of true with those in the rod, as they are apt to be when upsetting is resorted to, nor will the strap be scaled; hence the side faces will require but little filing.
Furthermore the step may be located so as to come against the rod end when the wear has let the key down, and this will prevent the strap from passing too far upon the rod, and, therefore, tend to prevent the rod length from being improperly altered from errors in the thickness of the liners placed behind the brasses to take up the wear.
Fitting up Connecting Rods.—The method of fitting up a connecting rod depends entirely upon its size. Very small rods to be made in numbers are usually got out by means of special devices which leave the fitter but little to do; indeed, sometimes the machine work is so accurately and finely fitted and finished as to finish the rod without the aid of the vice hand, save to put it into its place upon the engine or machine. As, however, the dimensions of the rod increase, this method of manipulation is in practice departed from, and the filing, fitting, and adjusting operations increase. In any event, however, the principles to be observed in the manipulation are the same, because the points to be observed in the fitting by hand work must be accomplished by the machine if the rods are to be finished by machine work.
Let Fig. 2360 represent a connecting rod; a representing the centre line in the side, and f the centre line in the edge view, and it is obvious that the axial lines, b and c, of the brass bores must stand at a right angle to line f, and be parallel to each other, because the journals on which they fit will do so. Furthermore, the faces of the brasses, as e, must stand their proper distance from the centre line f, this distance being at each end respectively half the whole width d, and the faces e must be in the same plane whatever their widths may be. The centre lines a and f are imaginary lines not worked to (except it be in marking or lining the rod out for the planing operations); but the method employed to fit up the rod must be such as will make all parts true to those lines if they were tested by them.
The process of fitting up a connecting rod may be tersely stated as follows: 1st, the rod is planed; 2nd, the straps are planed; 3rd, the straps are fitted to the rods; 4th, the straps are drilled and bolted to the rod; 5th, the keyways are cut, and the keys and gibs fitted; 6th, the side faces of the rod ends are again planed with the straps on; 7th, the brasses are fitted and the rods marked[II-118] off for length and the brasses bored; and, 8th, the file finishing and polishing done.
In the case of very large rods the two ends are made and fitted up as separate pieces, and are afterwards welded to the body or stem of the rod, and the setting of the ends true one to the other after the welding affords such an excellent insight into the alignment of rods that it may be well to describe it. First, then, the rod being laid on its side, two straight-edges, or rather winding strips, s and s′, Fig. 2361, are placed on the side faces, and the rod will be set in this direction when their ends a, b, c, d, appear parallel when sighted by the eye. If the winding strips are adjusted to stand straight across the rod, and, therefore, parallel one to the other, any twist or wind in the two rod faces will be very plainly discernible by the sighting process. The rod is then stood on edge, as in Fig. 2362, to test the alignment of the side faces. A straight-edge s is pressed firmly against one of the faces, as h in the figure, with the other end elevated as shown. The elevated end is then lowered, the motion serving to keep the end fairly bedded against face h. The distance, i j, Fig. 2363, is then measured. The straight-edge is then used in the same manner on the other side of the rod as at s in the figure, and the distance k l is measured, the setting in this direction being correct when distances i j and j k are equal. The straight-edge is then applied to the edge faces of end h of the rod, as in Fig. 2364, at m and at n, the distances o, p, are made equal. During these operations a straight-edge is applied along the body of the rod to see where to set it to effect any required adjustment, and if that body is straight the adjustment is made near the end at which the straight-edge is pressed to the rod.
The setting of the small end i is effected in the same manner, but the straight-edge will in this case fall over the face at the larger end, as is shown in Fig. 2365; hence, instead of measuring, lines as g and t are marked coincident with the edge of the[II-119] straight-edge and the distances t u, i g, are made equal. Winding strips are applied to the edge faces as well as to the side faces, and as making one adjustment or alignment may alter another, the whole process must be repeated until the whole of the tests prove the setting to be true.
Now suppose the rod to have been forged solid and all these faces to have been made true in the planing, and the first operation is to fit the straps to the rod ends. The strap should be put in place on the rod and moved laterally, when the centre of its motion where it moves the least will be the place where it binds and therefore requires filing. If its side faces come atwist with the side faces of the rod end, as shown in section in Fig. 2366, either the faces of the rod end or the inside faces of the jaw are out of square as denoted by the dotted lines. In any event the face e, Fig. 2367, of the rod end should be surfaced true and made at a right angle to the side face, and if to be made parallel to m, also at a right angle to k, a square and a surface plate are used to test them. If the diameter j is to be smaller than that at h, then the angle of both face e, and its opposite, should be equal with reference to k. These faces should be finished by draw-filing, with the file marks lengthwise of the rod. To fit the strap, proceed as follows: To find where it requires filing, place it on the rod (having previously put red marking on the rod end), and move it endwise and sideways, observing where the least motion takes place when the strap is moved sideways by pressing its crown end, for this point of least motion is always where it fits the tightest. To test the jaw faces for being square apply a straight-edge s, and a square p, Fig. 2368, pressing s against the strap, and p firmly against s.
When the strap shows to bed well on the rod and its motion is an ambling one (and not a pivoted one), it fits properly, and if both rod and strap have been filed square, their side faces will come fair or even. The keyways being drilled, may then if necessary be filed out, for which purpose it is necessary to bolt the strap to the rod, a process that requires very skilful treatment, because if the tightening of the bolts moves the strap on the rod, or if the strap be moved on the rod after the clamp is tightened, the keyways will not come fair when the clamp is taken off. In Fig. 2369 the strap is shown held to the rod by plates c and bolts b, the rod being shown in position ready to file out the keyway. It is better, however, to let the side face of the rod stand vertical as the strap will stand steadier that way. The strap should be set fair with the outside faces, which will bring the keyway fair if it is properly located. The bolt nuts should be tightened gradually, first one a little and then another, going over all four once or twice before they are fully tightened, and if the strap is not fair when they are all tight, all must be loosened before the strap is adjusted, or the clamp pressure will cause the strap jaws to spring out of true, and the keyways will not come fair when the clamp is removed.
Should the keyways not come fair when the strap sets fair on the rod the strap may be set to accommodate the keyways, and thus save filing, but this must be done before clamping it to the rod end. Care must, however, be taken to see if cutting the strap out to suit the keyway may not leave too little metal on one side of the keyway when the strap is subsequently planed.
The sides of the keyway should be filed true to a surface plate, using a well-bellied file and as stout a one as possible, so that it may not bend under the pressure, and file away the edges of the keyway.
The keyway should be made parallel to the side face of the strap, so that it may be fair with the centre line f in Fig. 2360. It should be made of equal width throughout, a piece of iron being used as a gauge in place of the key, and this same piece of sheet iron will serve as a gauge to plane the keys to thickness.
The corners of the keyway, if to be made square, should be filed out with the corner of a smooth half-round file, because the corners even of safe-edge files do not come up sharp enough.
For filing out the end faces of rectangular keyways, a square file with both edges safe must be used, the safe edges being on opposite sides of the file. For roughing out, a taper square, but for finishing, a parallel, or equalizing file is preferable.
The next operation is to fit the keys and gibs. The key should first be fitted and should be filed true to a surface plate, for in no other way can a really good reliable gib be obtained, no matter how well the keys may have been planed or milled. It should be filed a tight fit to the keyway so that it may be used (with a light coat of red marking) to show tight places in the keyway, driving the key in for that purpose from first one and then the other end of the keyway. If, however, it is driven too forcibly, it may seize or cut, and it will be difficult to get it out, besides damaging both it and the keyway. When the keys are reduced so that they will drive lightly into the keyway, they should be tried in the rod and in the strap separately, moving the key laterally or edgeways, so that it may mark any high places in the keyway of either of them.
The finished key and gib should be left tight enough, that they will hold themselves in any position in the keyway of the strap or of the rod when standing vertical.
[II-120]The head of the gib should be chamfered as in Fig. 2370, so that it may be driven in and out to fit without raising burrs which would prevent it from passing into the keyway, and the key should be similarly chamfered and rounded in its width.
The width of the key and gib should be such as to just fill the key ways, leaving no draw when the key is down in the keyway so that its head is level with the head of the gib, as in Fig. 2371, a equaling the keyway width; and their edges should bed fairly one against the other, and against the edges of the keyway. The strap must then be keyed upon the rod, and the side faces of the rod and strap planed to thickness, placing a bolt and nut in the rod end in place of the brasses, so that the key may lock the strap and bind it in position. The rod end should be planed to thickness for the brasses and of equal thickness on each side of the keyway. The brasses should be planed after the rod end is planed to thickness. The width for the brasses should be measured while the strap is on the rod end, because the width between the jaws of the strap is greater when the strap is in place on the rod end than when it is off, because in order to make the strap jaws a tight fit to the rod end it is made narrower between the jaws than the width of the rod end, so that the jaws spring open when the strap is pushed on the rod end. The sizes for the brasses to be planed to will then be the width of the strap across its edge face, and the width of the strap between the jaws when it is on the rod; and for these sizes a wire gauge should be made; or an adjustable gauge may of course be set.
The method to be pursued in planing the brasses is an important consideration. It is most convenient to plane both the brasses together, by which means much time is saved. To obtain this end the brasses are sometimes cast together, as in Fig. 2372, and after planing and before boring are cut in two at the narrow section a. In this case the brasses are cast sufficiently wide from crown to crown as denoted by b to allow for the length cut away in separating them. In other practice the joint faces of the brasses are faced first and then soldered together for the planing; but very large brasses are planed separately. In either case the joint face of the brass should be made at a right angle to the faces of the brass that fit the strap.
The brasses should be fitted separately to the strap, and hence should, if joined, be separated, being cut in two in a shaper, if of the form shown in Fig. 2372, and split by driving a keen chisel between the corners of the joint faces, if the latter have been soldered. The back or crown brass, and not the key brass, should be fitted first. The corners of the ways, in the brass, for the strap should be eased just clear with the edge of a smooth half-round file, because otherwise they will rub down the sharp edges of the strap, and make the strap jaws appear to be a bad fit when on the rod. The brass should be driven in and out of the strap to fit, using a block of wood to strike on, otherwise the skin of the bore may become pened, and when the brasses are bored they will close in at the sides and become loose in the strap.
As a guide when fitting the bottom brass in the strap, place the strap on the rod as in Fig. 2373, and take the measure of the strap at a a, the strap overlapping the rod to admit the calipers or gauge. Each time the brass is driven in the strap to try the fit, the calipers so set should be tried in the strap (the brass being in the strap), as in the figure, and when the calipers very nearly touch the strap jaws, the strap with the back brass still in should be tried on the rod end, or in the case of a very heavy strap the caliper measurement minutely taken may be relied on to show that the brass does not spring the strap jaws too wide open. It is better, however, to leave the brasses a little too tight in the strap as they close slightly in the boring, becoming easier in the strap.
After the brass has been tried in the strap, and before it is filed again, it should be tried with a square, using a straight-edge also if the square back is too short to cross both faces of the brass. The method of testing is shown in Fig. 2374, in which b represents the brass, s the square, and t the straight-edge. The inside face of the flange should also be tried as in Fig. 2375, in which p represents the surface plate, s the square, and b the brass. This will insure that the brass face joint is square as it should be, and is further necessary because the bearing marks on the brass are not to be altogether relied upon.
In Fig. 2376, for example, the brass is shown in section in the strap, and the side a of the brass has a bearing against the jaw b of the strap, and hence would show marks of contact. The succeeding blows in driving the brass, however, may cause the brass to have contact on the side c with the jaw d; hence the bearing marks would show the brass to fit well when such was not the case. This may be detected by striking the brass on its joint face, and then measuring from e and from f to the end of the strap, and then striking the joint face at f and again measuring both distances, when any canting of the brass will readily be detected. It is better, however, to also apply the square, as shown in Figs. 2374 and 2375, because by this means the joint faces e f being parallel to the crown face g of the brass, the brass will be fitted so that when g meets the crown face h of the strap, the two will be parallel to each other and require but little filing to fit or bed together.
The crown of the brass should be bedded very finely to the strap, or it will spring the strap jaws away from the rod when the key is driven home.
Suppose, for example, that the crown of the brass did not bed well at a in Fig. 2377, then keying up the strap would spring its[II-121] jaws away from the rod end, as shown at b c, the least error in the bedding having this effect notwithstanding the fit of the gib jaws.
The second brass must be made to just fit the strap when the back brass is in its place, and is small enough when the calipers, set as shown in Fig. 2373, and tried as shown in Fig. 2376, just fit the strap. This will insure that both brasses fit the strap when it is in its place on the rod.
When both pairs of brasses have been fitted to their straps, the latter should (if held by bolts) be bolted to their places on the rod, and the centre of the respective spaces for the brasses will be the location for the marks g, g, Fig. 2360. A pair of trammels should, however, be set to the proper length of the rod and these marks tested. If the strap is held by gibs and keys, as in the small end in Fig. 2360, the strap should be put on its place with the gibs in, and drawn up the rod by slowly forcing the key in until the mark g at that end stands in its proper distance from g at the other end, at which time the key should come through its proper distance.
The thickness of the brasses must be measured from these marks g, g to the crowns of the straps and the ends of the rod respectively. If the rod is of its proper length and the straps are in their proper positions, these marks will come in the centre of the space for the brasses. If, however, there is any error, as there is apt sometimes to be in very large rods, the course to be pursued depends upon the kind of rod end. If both straps are bolted to the rod end, the error may be divided equally at each end. If one end has a key and gib or gibs, but no bolt, as at the small end in Fig. 2360, the key brass may be made of such thickness as to butt against the end of the rod and meet the mark g.
For the large end, the thickness of the key brass, or, in other words, the distance d in Fig. 2378, must be taken after the face of the crown brass has been squared up, as described with reference to Figs. 2374 and 2375, the connecting rod strap being placed in such position that the key will be up in its proper place.
When the joint faces of brasses do not meet, but are left open to take up the wear, it is a difficult matter to properly adjust the brass bore to the journal. If the flanges of the brasses do not quite fit the length of the journal, as is very commonly the case, it is customary to tighten the key until the rod end can just be moved by hand so as to force the brass flanges against first one and then the other end of the journal. This is an approximate adjustment; and if the journal heats at all, the key is slacked back a trifle; whereas if it pounds, the key is set up a little. As a matter of fact, then, nothing is actually known of the precise fit of the brass to the journal; and while looseness may be detected by the pounding, the brass may be tight enough to cause undue wear without very sensibly heating the journal, especially if the latter is freely lubricated. If, however, the brasses fit the length of the journal, and do not butt, it is usual to drive the key in till the brasses bind the journal, and to then slack the key back to the necessary amount. What that amount should be cannot be stated, because it varies with the taper of the key and the force with which it is driven home. As a result, then, the operation is left to the judgment, or, in other words, to guess-work, of men, many of whom are not well experienced in the operation; while under any circumstances the actual fit is not positively known. A plan not infrequently adopted is to insert a piece of lead wire of small diameter between the brasses, the key is first driven tightly home, and then slacked back until the lead wire is just freed. It is estimated that the adjustment will then be correct; there is no actual certainty of the fit, however, even in this case.
Another objection is that the oil is apt to flow out of the opening, and the brass having communication with the oil cup is better lubricated than the other brass.
In cases where the brasses are difficult to get out of the strap, because of the location or of the size and weight of the parts, a piece of sheet brass is sometimes placed between the joint faces, and this piece is filed thinner to let the brasses together, the necessary thickness for the piece being ascertained by the lead wire process described. If the strap is held to the rod end by a gib and key only, and the joint faces are left open, there is nothing to lock the strap to the rod end save the jaws of the gib, whereas when the brasses butt, the key binds the brasses to the end face of the rod and the strap to the brasses, which if there is any wear sideways (as in locomotives), prevents the keys from wearing the sides of the key ways and the brass flanges from wearing the straps.
A method of overcoming this defect is shown in Fig. 2379, where the joint faces are left open, and four set-screws s, s, two on each side of the rod, pass through the flange of one brass and abut against the face of the other, serving to adjust the fit of the brasses to the journal, and lock them in their adjusted position, locking at the same time the brasses to the strap and the strap to the rod end.
When the rods are finished so far as the fitting of its various[II-122] parts are concerned, the brasses should be marked so that the bore, when bored out, will leave an equal thickness of metal between the brass and the strap on each side of the bore, while the rod will be of proper length. To accomplish this, mark on the outside face of the top brass two lines level with the faces which fit against the inside jaws of the strap, as shown in Fig. 2380, a, b being the lines referred to. We then key up the brasses in their places in the rod and fasten a centre piece in the brasses at each end of the rod. Upon these centre pieces we first mark a line parallel with and central between the lines a, b, and then a line across the joint of the brasses if the joint faces meet, and in the centre of the space between them if they do not meet.
Before applying the trammels to test the rod length, the latter should be stood or placed in the position in which it works when on the engine; for all rods deflect by their weight, the amount of such deflection depending upon the position in which the rod is suspended. The trammels also deflect, it is true, but their deflection is allowed for in setting them, whereas the deflection of the rod will not be accounted for unless it is trammelled when standing or lying in the position in which it works.
Fitting up Solid-ended Connecting Rods.—In fitting up solid-ended rods the side faces require to be filed up first and the jaws to receive the brasses next, taking care to file them out either square with the faces, or if slightly taper, as they should be, then each inside face should be an equal degree of taper to the side faces. This is necessary so that if the brasses are bored true to their own faces, the bore of the brasses at one end of the rod shall stand parallel to the bore of those at the other end.
The fitting of the keys and brasses is performed as described for strap-ended rods.
The reason that the jaws or box that receives the brasses is but a trifle taper is that in that case they are easier made a good fit, as they can be tried in their places while being fitted and before being reduced to the finished size, and furthermore because they can be put in and taken out easier.
Fitting up a Fork-end Connecting Rod.—A fork-end connecting rod affords as good an example of vice work as can be found, because any faulty workmanship, either in the individual truth of the parts, or their relative truth one part to another, will make itself very plainly apparent.
Fig. 2381 represents a side and plan view of an ordinary form of fork-end rod, and the requirements are that the centre line a of the brass bores at the fork end shall be parallel with the centre line b of the bore at the butt end; that the side faces of all the brasses shall be parallel one to the other; that the side faces at the fork end shall be equidistant, or at the required distance, from the side faces at the butt end as denoted by c, d; that the bores of the brasses shall be at the proper distance apart to make the length of the rod come right; that the brasses at the fork end shall be the right distance apart, and that they shall stand parallel to each other, as well as to the bore at the butt end, as denoted by the line e in Fig. 2382.
If the rod were of a size that it could be conveniently handled and planed, if forged solid, the fitting up would be much simplified, because the setting of the rod for the machine operation would, to a great extent, insure truth in the relative alignment of the parts. Thus all the side faces of the rod ends could be planed at one chucking, in which case they would necessarily be parallel, and their proper relative distances apart, if the rod was properly marked out by lines and planed to the lines. The jaws or ways to receive[II-123] the brasses would be slotted out together, and necessarily true, if the rod was chucked true on the machine table. But even in this case the rod has to be marked out by lines denoting where the metal is to be cut off to, and the principles involved in the lining are just the same as those involved in the fitting up.
If the rod be large, the ends may be, and usually are, forged and fitted up separately, and subsequently welded to the body of the rod, which has been forged separately. In this case, the alignment of the parts is a part of the process in welding the rod, and setting it after welding. All the principles involved in making the rod ends separate, and afterwards welding them, or in marking out a small and complete forged rod, are, however, involved in the process of refitting an old rod in the jaws, and putting in new brasses; hence a description of that process will cover the whole ground. The first thing to do is to file up the side faces, as f, g, Fig. 2381, and, in doing this, all that is necessary is to file f up true, when tested by a straight-edge applied as in Fig. 2383, in which r is the fork and s a straight-edge, whose edge should measure the same distance at h as it does at i from the side face f, while the face c measures the same distance from face a of the other fork end, or from the imaginary centre line x, Fig. 2381. Then turning the rod on its side, a straight-edge should be placed across the face f, and one across the face g, as in Fig. 2384, at s and s′; and the edges of the two straight-edges should stand parallel, when sighted in such a position that the edges are very nearly in line with the eye, as shown in the figure.
The inside faces of the fork jaws may be filed to measurement from the outside ones.
The ways for the brasses should be filed square with the outside faces, as shown in Fig. 2385, in which s is a T-square; but if one jaw is wider than the other, as sometimes occurs, it will not matter, providing that, with the square applied, resting against the side and the face of the ways on the narrow jaw, the ways of the other jaw are equidistant from the square blade, as would be the case; for example, if the width of the ways of the jaw j extended to the dotted lines at k, l, because the line p would still form the centre line of both jaws, standing at a right angle to the side faces of the fork end, and parallel to the bore of the brasses at the butt end. Before filing up the side faces at the butt end, the strap should be fitted on and keyed up, so that its side faces may be filed up with those on the rod. To test the truth of the side faces at the butt end, a straight-edge should be applied, as at s and s′′, Fig. 2386, being pressed firmly to the side faces at the butt b, the fork faces being measured from the edge of the straight-edge at that end, and also with straight-edges, as in Fig. 2384. The brasses, after being fitted into the ways of the jaws, should have their joint faces squared, as in Fig. 2387, the top of each jaw being shown broken away, so as to fully expose the brasses. s is a square held firmly against the side face of a jaw, the brasses having their joint faces true with the square blade, and true also when tested with a[II-124] square, applied as in Fig. 2388, in which b is the brass and s the square. The brasses at the other end should be filed true to the side faces of the strap in a similar manner, and, the fitting being completed, it simply remains to mark off the brasses for boring. The joint faces of the brasses should form the centre of their respective bores; hence, all that is necessary, is to insure that the brasses be of equal thickness, top and bottom, and this may be accomplished as follows: Mark across each face a line even with the ways of the brass, as shown in Fig. 2389, at a, c, and carry these lines around the side face, as shown in the figure at b, d. Place the brasses in the strap, put in a piece of wood whereon the compasses may be rested, as shown in Fig. 2390, which represents one jaw, and mark on this piece of wood a line even with the joint faces of the brasses, and on this line a centre-punch dot equidistant between the lines b, d. From this dot, as a centre, strike the circle shown, and define it by centre-punch dots, and if the lathe-hand chucks the brasses true to the ways that fit the rod jaws, and to the dotted circle, the bores will stand true in every respect.
Repairing Connecting Rods.—In repairing connecting rods the following is the work usually required to be done, and in the order named: Refitting straps, refitting gibs, and perhaps new gibs and keys, filing up the side faces of rod ends and straps, lining up brasses to make them fit the strap, lining up the rod to length and fitting the brasses together so as to fit their journals.
If the strap is taper and can be closed by pening, the outside of the back should be pened; but if the strap requires closing in the blacksmith’s shop, then it should be tested by winding strips as shown in Fig. 2391, to insure that the faces are true, and thus save filing at the key ways and on the side faces to make them come fair with the rod ends. The rod ends should then be filed up and the straps fitted on.
Next comes putting in the new key and gib, or refitting the old gib. If the jaw of the gib has cut into the strap, as it will do in some cases (especially in marine and locomotive rods), this may be repaired as follows: Cut out the recess shown in Fig. 2392 at a, making it dovetail-shaped as shown, and with a set chisel set up its sides as shown in Fig. 2393, which is a sectional side elevation through the line of b. Cut out a piece of wrought iron and bevel its edges as shown in Fig. 2394, filing it to fit into the recess cut at a, Fig. 2392, and letting the bevelled edge be uppermost. Then take a set chisel and close down again upon the bevelled edge of the piece the metal that was set up, as shown in Fig. 2393, and the piece will be riveted, and it and the gib jaw may be refitted to touch the piece thus let in.
The jaws of the gib are sometimes made slightly taper at a, Fig. 2395.
To refit the brasses to the jaws of the strap, the flanges which do not as a rule wear much are usually tinned with a soldering iron, and given a lining of babbitt metal. This must be done all around the flanges (of both pairs of brasses) that come on the same side of the rod, so as to keep the faces of the brasses leading fair.
The fit between the jaws is restored by riveting pieces of sheet brass to that side of the brasses that has worn the most (usually the top which carries the weight of the rod). Fig. 2396 shows this operation carried out, a being the pieces of sheet brass which are sometimes soldered as well as held by rivets. These rivets are screwed into the brass, being composed of softened brass wire riveted after being screwed in.
If these pieces, which are called liners, are placed on the top of the brasses at one end, they should also be placed at the top of the brasses at the other end of the rod. They should not be less than about the 1⁄24 inch thick, the body of the brass being cut off to admit them if necessary.
In filing the joint faces of the brasses to let them together so as to take up the lost motion due to the wear of the brass bore and of the crank pin, the following considerations are met.
If the brass faces are to come “brass and brass,” that is, butt together, when their bore is of the diameter of the journal, file those faces away until the bore appears just perceptibly too large for the journal, when measured with calipers, as in Fig. 2397, the[II-125] bore measuring parallel all the way through. But, in doing this, it is necessary to be careful to file each brass so that it shall embrace one-half the journal diameter, which will be the case when the two brasses measure correctly as above, and alike, when tested, as in Fig. 2398, in which p is a planed surface, c a pair of inside calipers, and b a brass resting on p. When filing the joint faces, test them with a square as in Fig. 2399, in which s is a square and b a brass, and also in Fig. 2400, in which s is a square and b the brass shown in section, thus making the faces quite square.
The necessity of having their faces quite square when the brasses come brass and brass may be shown as follows:—
Suppose the joint to be at an angle as at a, a, Fig. 2401, instead of square across, as denoted by the dotted lines b, b, then the respective brasses will be forced by the key-pressure in the direction of the respective arrows, and there will be a tendency to twist the brasses in the strap. Or suppose the joint faces to be out of square as at c, c, instead of square as at d, then there will be a tendency to twist the respective brasses in the direction of e, f, and therefore to cause these to move in the direction of g, h, and as a result the brasses will spring the strap away from the rod, as shown at i, j.
To line up the brasses for length we proceed as follows: One of the liners adjusts the length of the rod and the other simply serves to set the key back to its proper height, so that it shall not pass too far through the keyway, as the wear of the brasses lets it down. Which of the liners will be the one by which to alter or adjust the length of the rod depends upon the design of the rod itself; but, in the case of all solid-ended rods, or those in which the position of the strap is fixed by means of bolts, it is the liner behind the end brass, as d, in Fig. 2402, as stated in the opening of this discussion, and it is the first one, therefore, to be fitted. The space at e is where the second liner requires to be placed, its thickness being that necessary to lift up the key from its bottom or lowest position, as shown in the cut, to the highest position.
In strap-ended rods in which the strap is not bolted to the rod, but moves farther upon the rod as the key passes farther through the keyway, it is the brass next to the rod end, as b, in Fig. 2403, by which to adjust the length of the rod, and its liner l is, therefore, the one to be fitted first; the space e is, in this case, the one to be fitted with a liner of sufficient thickness to lift the key up. It will now be noted that the thickness of l in both figures requires to be exact, so that the rod may be of correct length, which is necessary, so that there may be the same amount of clearance or space between the piston head and the cylinder cover when the piston is at the respective ends of the stroke. But the liners to fill the respective spaces e need not necessarily be of the exact thickness (although it is better that they should be), because if too thin the only effect will be that the key will pass farther through the keyway than otherwise. In considering in any form of rod which is the liner to be put in first to bring the rod to length, we have the general rule that the brass that moves in the strap or rod end when the key is moved farther through the keyway is the one to be lined last. The method of obtaining the proper thickness of the liners l, Figs. 2402 and 2403, are as follows: If the rods have been correctly made at first, the centre of the brass bores will be midway in the spaces for the brasses (denoted by f in the two figures). If the oil-holes in the strap or rod end (as the case may be) have been drilled in the centre of this space f as they should be, then the line g will represent the centre of f and the centre of the oil-holes, and all that will be necessary will be to place behind d and b respectively a liner of sufficient thickness to bring the joint face of these brasses (d and b) even with the line g. To ascertain the thickness of liner necessary for this purpose, suppose the case of a rod end of the design shown in Fig. 2402, then, with the strap off the rod, drive the brass d down until its crown face beds fairly against the strap c, and with a scriber mark on the inside face of the jaw of the strap a line coincident with the joint face of the brass, then set the brass up the strap until its joint face comes fair with the centre of the oil-hole or the central line g, and then mark a second line so that on taking the brass out of the strap there will appear two lines, and the distance between these two lines is the necessary thickness of liner. In the case of the form of rod end shown[II-126] in Fig. 2403, the process would be as follows: Let the strap have placed in it the brass b only, place it upon the rod, and set it so that it binds the gib and key, when the key is lifted up to its required position, then, with the brass b bedding fairly against the rod end, mark on the strap a line coincident with the joint face of the brass as before. Then move the brass in the strap until its face comes fair with the centre of the oil-hole or line g, and mark another line, and the thickness between these lines is the thickness of liner required at l.
If the brass is to be lined sufficiently to merely bring the key up without respect to the length of the rod we may drive the key home as in Fig. 2404, and mark on it a line coincident with the edge a of the strap. We then lift the key up to its proper height and mark a second line, so that when removed from the keyway the key will have on it the two lines shown in Fig. 2405, a being the first and b the second line; and the difference between the width of the key at a and its width at b will be the thickness of the liner necessary to be placed behind the brass nearest to the key. To ascertain the precise amount of this difference (because a very small error as to this amount causes a great deal of extra labor), we set a pair of outside calipers to the width at a; and then passing the caliper points down to b, we keep one of the points even with the line b, and insert a wedge until it just fills the space between the other point and the side of the key, as shown in Fig. 2406, c being the wedge, which should be chalked along its surface so that, when inserted until it touches against the caliper point, the latter will leave a mark on the wedge, denoting exactly how far the wedge entered, and hence the exact required thickness of liner.
It has thus far been supposed that the joint faces of the brasses are made to come brass and brass, that is to say, butt close together from the key pressure, when the brass bores properly fit the journal. Suppose, however, that the joint of the brass is left open as in Fig. 2407, and in that case a strip of metal f, whose diameter equals that of the journal, may be inserted between the brasses as shown, and at its centre should be provided a small centre-punch mark, denoting the centre of the bore. A piece of this kind should be inserted in the brasses at each end of the rod and placed in the middle of the length of the bore, the centre-punch marks being to apply the trammels to. Or if the rod was made of correct length when new, and the bore of the brasses, therefore, requires to stand central in space f, Fig. 2403, then the pieces f, Fig. 2407, may be dispensed with by marking a line b, Fig. 2408, central to space f, Fig. 2403. Then put the strap on the rod (with the brasses, gib, and key in place), and pull the strap back to hold the key up to its proper height.
The two brasses should then be placed as far apart as possible in the strap, each bedding fairly against its back or crown. Then, using the joint face of the back brass as a straight-edge or guide, a line should be marked on the side face of the strap, this line representing the position of that face when the brass is bedded fairly home, and being shown in Fig. 2408 at a. This brass should then be moved forward until the bore of the pair of brasses at d, Fig. 2408, measures equal to the diameter of the journal (of the crank pin or of the cross-head pin as the case may be) and a second line b, also coincident with the joint face of the brass, should be marked upon the strap, and the strap will then have marked on it the two lines shown in Fig. 2409, in which it is shown removed from the rod; the distance apart of these two lines will be the thickness of the two liners combined, hence half this thickness will be the thickness necessary for each liner. Suppose, however, that it is not known whether the rod has been correctly made, and therefore it be unknown whether, in order to have the rod of the correct length, the brass bore should stand in the centre of the space or not.
This is often the case in repairs, and sometimes on new rods, in which slight inaccuracies of workmanship are apt to occur. In this case it is best to mark a line, as g, in Fig. 2410, representing at each end of the rod the centre of the space f in that figure. Then set a[II-127] pair of trammels to the correct length of the rod, and with one point of the trammel resting on the point at the intersection of line c with line d (the latter being the line g transferred to the centre of the bore) at the small end of the rod, we mark a line at the other end. If the lines d are too far apart, making the rod too long, the trammels will mark a line r, and the distance between lines r and d at the large end will be the amount the rod is too long, while half this distance will be the thickness of liner to go behind each bottom brass if the error of length is to be equally divided between the two ends of the rod, in which case a line t, midway between d and r, must be marked, the trammel then being rested on t, and the line s marked. These two lines, s and t, are then the centre lines for the bores of the brasses.
If it is determined that one pair of brasses shall be central in its space f, all the error being thrown on the other pair, this may be done by lining one pair up so that its bore is true to line d, and putting behind the back brass at the other end a liner whose thickness is equal to the distance between d and r at the large end of the rod. It is obvious that the measurement for rod length must be taken on the line c.
Having thus determined what thickness of liner is necessary to bring the rod to its proper length, it remains to find the thickness of liner necessary for the other half brass, to bring the key up to its proper position, the process for which has already been explained. After, however, the various liner thicknesses have been found, and the sheet metal selected to cut them from, it is well to try if the thickness is correct by cutting off a small piece of the metal, putting it in place behind the brass, and then, after keying up the brasses, the rod length may be trammelled.
As the liners placed behind connecting-rod brasses require to be very finely bedded, the facility with which their forms permit them to be fitted is an important consideration.
In Fig. 2411 is shown the forms commonly given, the requisite form of liner being shown beneath each. Form 1 will bed very firmly to its seat, but it will be observed that its liner is a difficult one to make, the bottom section a being thicker than the sides or wings b. This is a troublesome form of liner to fit as well as to make. If it be made of wrought iron, the wings b must be either forged or filed to their reduced thickness.
In the form at 2 in the figure we have the same defect, while in addition the liner will not adjust itself so readily in position to its bed.
This latter is an easier form to make in the moulding pattern, and easier to mould, and somewhat easier to fit, but it is not so firm as the first. To cause this form of brass to bed easily to its proper position it is sometimes given a lug on the bottom, as at 3 in the figure, the lug extending part of the width across only, because if it extended fully across, the liner would require to be in two pieces, causing trouble both in fitting them and in getting them into their places. When the lug extends partly across, the liner must have a slot to pass over and admit the lug, and this causes trouble in bending the liner to the required curve.
In the form shown at 4 in the figure all these difficulties are avoided, while, if the lower corners are made square instead of rounding, a simple piece of sheet metal will serve as a liner requiring but little fitting and bedding if it be of the proper thickness.
To fit up a link motion, assuming the machine work to be done, the first thing to do is to face up the side faces of the links, making them parallel, and true to a surface plate. The slot is then filed out square to the side faces, its curve being filed to a template t, Fig. 2412, which is provided with a piece of wire for a handle. It is supplied with red marking, and is rubbed upon the slot to mark the high spots. The same template may be used to prepare the link block or die; but as soon as the block can be moved in the slot with slight hammer blows (using a mallet or a block of wood) it should be used instead of the template, the bearing marks serving to correct and finish the block as well as the slot. In filing up the block care should be taken to make it of even thickness on each side of its hole and with its sides parallel to the hole, the latter being of great importance. When the block is a sufficiently easy fit in the slot to permit it, a round stick of wood may be put through it and used to move it up and down the link slot for the marking process.
The next operation is to fit the eccentric rod eyes to the link, and to then ream out the holes in both the link and the eyes while they are put together. The block may then be placed in the link, and the rocker pin passed through the block and into the rocker arm, so that the working fit of these parts when put together may be tested and adjusted if necessary. The link hanger may then be fitted to the saddle pin, when the whole will be ready for the file finishing and polishing, after which it may be case-hardened.
[II-128]Case-hardening.—Case-hardening consists in the conversion of the surface of wrought iron into steel, or in converting the grade of a low steel into a sufficiently high grade to render it capable of hardening. The depth to which this conversion occurs depends upon the material used to produce it, and the length of time the process is continued, varying from 1⁄64 inch under the prussiate of potash process to 1⁄16 or 1⁄8 inch in the case of long-continued box case-hardening.
Work that is thoroughly case-hardened has a dull white, frosted-looking surface. If the surface of the work is mottled, or has patches of fancy water-mark colors, it may be hard, but it is not so to the highest attainable degree.
To thoroughly test this, take a new dead-smooth file and apply its corner edge under heavy pressure to the work on an edge where the fancy colours are, and then on an edge where the surface is white, and the latter will be found to be the hardest as well as hardened the deepest.
The simplest method of case-hardening is by the prussiate of potash process, for which it is essential that the prussiate of potash be finely powdered, and contain no small lumps. The piece being heated may then, if small, be dipped in the prussiate of potash, or if large have the same spread upon it. In either case, however, the work must be hot enough to cause the potash to fuse and run over the work surface, and this action may be assisted by using a piece of iron wire, spoon-shaped at the end, wherewith to apply potash to the work and rub it upon the work surface.
After the potash has thoroughly fused and run over the entire surface of the work it will usually have become somewhat cooled, and will require reheating before quenching in the water.
If this reheating be done in the blacksmith’s fire, it is not well to put the blast on; it is better to let the blast on gently while applying the potash to the work, so as to have a live clear fire to put the work in, and reheat it with the blast turned off.
While the work is in the fire it should be constantly rotated, not only to heat it evenly, but to let the adhering potash run over the entire surface, and as soon as the required heat is attained the work should be removed from the fire quickly and quenched in water.
It may be added, however, that if after the potash has been applied and fused more potash be added, so that it will adhere to the work and not fuse until the work is put into the fire a second time, then, after the work is quenched and taken from the water, there will be found on it a thick white and closely adhering fur of melted potash, and the work will be a dead white, with no fancy colors on it, and as hard as it is possible to make it.
The prussiate of potash process is, of course, from its expensiveness, both in material and labor, too costly for work to be done in quantities, and box-hardening is therefore resorted to.
In box case-hardening the work is case-hardened all over. It consists in packing the work in an iron box containing the hardening material, and subjecting the whole to a cherry-red heat for some hours.
A very common process is to fill a sheet-iron box with the work closely packed about with bone-dust, the pieces of the work having at least a thickness of 3⁄8ths of an inch of bone-dust around them. The seams of the box are well luted with clay to prevent the gases from the consumed bone-dust from escaping, and to exclude air.
Various ingredients are used to effect case-hardening. One process is as follows: 20 lbs. of scrap leather and 15 lbs. of hoofs (cut into pieces of about an inch square), 4 lbs. of salt, and one gallon of urine are prepared, and a wrought iron box with a lid capable of being fastened on is obtained. The fastenings must be capable of ready unfastening when hot. A layer of leather and pieces of hoofs about 11⁄2 inches thick is first laid in the box, then a layer of salt, and then a layer of work. Leather and hoof are then packed closely around the work and above it for a thickness of about an inch, and a second layer of work added, and so on, the last layer being of leather, &c., completely filling the box; the urine is then added, and the box well sealed with clay.
The box is placed in a furnace and kept at a red heat for about fourteen hours, and is then taken to a deep tank, and the work quickly immersed, so as not to be exposed to the air after the box is opened.
If the pieces are of solid proportions, so as not to be liable to bend or warp in the cooling, the contents of the box are simply dumped into the tank, the water being allowed to flow freely in the tank to keep up a circulation and cool the work quickly; some work, however, requires careful dipping to prevent it from warping. Thus a link or a double-eye would be dipped endwise, a plate edgewise; but all pieces should be immersed as quickly as possible after the box is opened.
Sheehan’s patent process for box case-hardening, which is considered a very good one, is thus described by the inventor:
No. 1 is common salt.
No. 2 is sal soda.
No. 3 is charcoal pulverized.
No. 4 is black oxide of manganese.
No. 5 is common black rosin.
No. 6 is raw limestone (not burned).
Take of No. 1, 45 lbs., and of No. 2, 12 lbs. Pulverize finely and dissolve in as much water as will dissolve it and no more—say 14 gallons of water in a tight barrel; and let it be well dissolved before using it.
Then take three bushels of No. 3, hardwood charcoal broken small and sifted through a No. 4 sieve. Put the charcoal in a wooden or iron box of suitable size made water-tight.
Next take of No. 4, 5 lbs., and of No. 5, 5 lbs., the rosin pulverized very fine. Mix thoroughly No. 4 and No. 5 with the charcoal in your box.
Then take of the liquid made by dissolving No. 1 and No. 2 in a barrel as stated, and thoroughly wet the charcoal with the whole of said liquid, and mix well.
The charcoal compound is now ready for use.
A suitable box of wrought or cast iron (wrought iron is preferable) should next be provided, large enough for the work intended to be steelified.
Now take No. 6, raw limestone broken small (about the size of peas), and put a layer of the broken limestone, about 11⁄2 inches thick, in the bottom of the box. A plate of sheet iron, one-tenth of an inch in thickness, is perforated with 1⁄4-inch holes one inch apart. Let this plate drop loose on the limestone inside the box. Place a layer of the charcoal compound, two inches thick, on the top of said perforated plate. Then put a layer of the work intended to be steelified on the layer of charcoal compound, and alternate layers of iron and of the compound until the box is full, taking care to finish with a thick layer of compound on the top of the box. Care should also be taken not to let the work in the box come in contact with the sides or ends of the box. Place a suitable cover on the box and lute it with fire-clay or yellow mud. The cover should have a quarter-inch hole in it to permit the steam to escape while heating.
The box should now be put in an open fire or furnace (furnace preferred), and subjected to a strong heat for five to ten hours, according to the size of the box, and the bulk of iron to be steelified. Remove the pieces from the box one by one and clean with a broom, taking care not to waste the residue, after which, chill in a sufficient body of clear, cold water, and there will be a uniform coat of actual steel on the entire surface of the work to the depth of 1⁄16 or 1⁄8 of an inch, according to the time it is left in the fire. The longer it is left in the fire the deeper will be the coat of steel.
Then remove the residue that remains in the box, and cool with the liquid of No. 1 and No. 2, made for the purpose with 20 gallons of water, instead of 14 gallons, as first used with the charcoal compound.
The residue must be cooled off while it is hot, on a piece of sheet iron or an iron box made for the purpose. Turn the residue into the supply box, and it will be ready for use again. The more it is used, the better and stronger it will be for future work.
There is nothing to be renewed for each batch of work but the limestone, and that, after each job, will be good burned lime.
A process used at the Elevated R.R. shops in New York city is as follows: The materials used are: leather, 1 part; bone dust, [II-129] 5 parts; salt, 1 part. Heat for 48 hours to a red heat in a box sealed with fire clay, and quench in a solution of 3 pounds of potash to 30 gallons of water.
The wrought iron thus treated is impervious to a new smooth file at a depth of 1⁄16 of an inch.
The potash water is said to prevent both warping and the formation of blister marks on the work.
The durability of work case-hardened is greatly enhanced, but it is an expensive process; not so much by reason of the cost of it, but because it involves resetting and a refitting of the parts. The resetting is necessary because the work warps under or during the process. This warping can be prevented to some extent by placing the heaviest pieces in the bottom of the box, and so packing the same that the weight of the top pieces shall not tend to bend those beneath them when the hardening material has burned away, and so placing the upper pieces that they shall not be bent by their own weight. Thus both in packing and locating the work in the box the utmost care is necessary.
Setting Work after hardening it.—Work that has been hardened or case-hardened usually swells during the hardening process, and therefore requires refitting afterwards. This swelling usually occurs in all directions, thus holes and bores become of smaller dimensions, while the outside dimensions also increase, bolts become of larger diameter and sometimes increase in length.
In very exceptional cases, however, the dimensions of a piece of work will not alter.
This renders it usually necessary to refit the work after it has been hardened, thus holes which are ground out by laps or bolts may be ground to diameter in a grinding lathe.
In some practice, however, the work to be hardened is made a somewhat too easy fit, the holes tapped out and the bolts ground in by direct application of the bolts to their holes in connection with flour emery and oil. This latter plan is also adopted for forms not easily ground out in a machine, as, for example, a die in a link of a link motion.
To prevent surfaces or forms of this class from altering their shape or dimensions during the hardening process, slips of iron are sometimes fitted to them before they are placed in the hardening box. Thus Fig. 2414 represents a double eye, and Fig. 2413 a link having thin pieces fitted in as shown at a in both figures.
The heating for the hardening process is also apt to impair the alignment of the work, causing it to require resetting by the aid of parallel strips and straight-edges.
The faces of the link having been set, the width of the link slot must be set, for it may open or close in places. If it opens it may be closed by the jaws of a powerful vice, while if it closes it may be opened by a pair of inverted keys, inserted as shown in Fig. 2415, and driven in by the hammer. At each trial, however, a mark should be made on the driven key, so that it may be known how far to drive it at the next trial.
Fig. 2416 represents a link that is supposed to have been case-hardened, and to therefore require resetting. The stem from a to b should first be straightened to a straight-edge on both its side and edge faces. It should then be tested for winding with the winding strips, c, d, placed as in Fig. 2416, and then as in Fig. 2417.
To test the alignment of end e, press a straight-edge s fair against its side face, as in Fig. 2418, and measure the distance h. Then place the straight-edge on the other side face of e and measure the distance i, Fig. 2419, and these distances both measuring alike, e will be true providing that the jaws at end f have not altered from their proper width apart.
To test the alignment of the jaws at end f, press a straightedge against the outside face of the hub and measure the[II-130] distance j, Fig. 2420, then apply it on the other side and measure distance k, Fig. 2421, and when distances j and k are equal and the width l between the jaws is correct, end f is in line in one direction. To test it in the other direction, apply a pair of parallel strips, placing one on end e as in Fig. 2417, and the other across the face of the hub of end f to see if there is any twist.
Suppose, however, that distances j k are unequal, then if distance l is too narrow (when tested by the piece that fits between the jaws) then the jaw at f that gives the widest distance at e is the one that requires correction, or if distance l is too wide, the jaw that shows the least distance at end e is the one requiring correction.
The link should be warmed to about 300°, or nearly black hot, and pieces of sheet copper placed between the work and the anvil, and between the blacksmith’s tools and the work, so that the latter may not be bruised by the blows delivered to effect the straightening.
After the process has been performed at each end individually the testing should be repeated, because setting the end f may have impaired the setting of end e, in the alignment to f.
It is obvious that the same setting or aligning process would be required in the case of a large link, where the ends were forged separately and welded to the body after the machine work and fitting had been done to them.
Fitting Brasses to Boxes or to Pillar Blocks.—In the operation of fitting brasses to their boxes or to pillar blocks there are two things to be especially guarded against: First, having the brass let down one-sided, as shown in Fig. 2422; and next, aslant, as shown in Fig. 2423. The first depends on taking the proper amount off the two side faces, and the second in cutting the inside of the flanges fair. To cut the side faces fair, grip the brass in the vice, as shown in Fig. 2424 (the brass being shown in section), in which a is a block of wood. Take the measure of the box, down where the brass will come when home, and, if there be any taper to the box, set the inside calipers to the top of the location for the brass, and after the brass is in the vice place a square under one side-face, as at b in Fig. 2426, and see how much there is to come off. This saves the use of outside calipers, and is better because, not only is the trouble of setting the latter avoided, but the inside calipers can be tried to the box and the work in an instant, and a correction can at once be made if the calipers have got shifted. The cape chisel, or cross-cut, as it is sometimes termed, should first be used, taking a cut close to the flange, and making it half as deep as the calipers (applied as shown in Fig. 2426) show there is metal to come off. Then a similar cut should be taken close to the other flange, especial[II-131] care being taken to take both cuts equally deep, and leaving as much to come off the other side face of the brass; otherwise, the brass will come atwist. Then take a straight-edge, and, placing its edge fair with the two chisel-grooves, while holding it firmly against the joint face of the brass, mark a line running from one chisel groove to the other; this line serving as a guide for the depth of all the other cape-chisel grooves. Now cut off the intermediate spaces with the flat chisel, using a straight-edge as a guide. If the box is taper, chip the side face to a corresponding taper, using a bevel-square, or estimating the amount by the eye if it is not too much. Now file the chipped surface flat and true, and then turn the brass upside down, gripping it with the wood as before, and dress the other side face (applying the inside calipers as in Fig. 2426), and bring that face down to within about 1⁄64 inch of the size to which the calipers are set. If the block of wood is made a little shorter than the length of the brass, the calipers can be applied without moving the brass from or in the vice. The method of applying the square to these side faces is shown in Fig. 2425, in which a is the brass in section, b a straight-edge, and c a square.
We now turn our attention to the flanges, and apply a square to the crown of the box, bringing the edge of the blade fair with the edge of the box, as shown in Fig. 2428, a representing the box in section, and b the square. Supposing the crown of the box to stand square, as shown in the engraving, and as it should do, we set the brass upon a truly-surfaced iron plate and square up the joint face, as shown in Fig. 2427, in which a is the surfaced iron, b the brass, and c the square. Since, however, the joint face of the brass may not be parallel with the crown face, we may place the square so that its blade edge comes fair with the crown face—that is, as shown at d in Fig. 2427—and set the brass crown (by means of inserting a wooden wedge under its face) truly perpendicular or parallel with the square blade edge. Now try the square with the side face of the brass, setting the latter true with the square blade, as in Fig. 2430; a being the iron plate and b the square; and, supposing the box to be true, as it usually is, we may set a scribing-block, as shown in Fig. 2427, and mark off how much is to come off the flanges by scribing a line around the flange, sufficiently depressing the scriber-point to allow an equal amount to come off each of the flanges. Sometimes, however, the inside faces of the box are not true with the outside face. To test this, we place a straight-edge across the outside face, place a square on it, and apply it to the inside face of the box, as in Fig. 2429, which is a plan view of the box, a being the straight-edge and b the square. If the square thus applied shows a want of truth in the box, we may set the brass over when adjusting it (as in Fig. 2427) to a corresponding amount, and thus mark off the flanges to suit the box.
To hold the brass while operating on the flanges, we resort to the device shown in Fig. 2431, in which a is a bolt, b the brass, c a piece of hard wood, and p a clamp fastened down by a nut d. To sustain the plate p, so that it shall not fall down on the piece of wood every time the brass is taken out to try it in the box, we may insert the spiral spring s, shown in the separate view of the bolt, nut, and plate. One such holding device will do for different sizes of brasses, by either gripping the bolt lower down in the vice jaws or putting washers between the nut and the plate. This will hold the brass very firmly, and at the same time leave the whole of the flange easily got at. When the flanges are dressed, we may try the brass in the box, putting red-lead marking on the box to mark where the brass binds. While letting the brass down, however, we must be careful to let it down fair, to avoid the state of things shown in Figs. 2422 and 2423. A ready method of doing this is (supposing the box to be true, as it should be, and making the necessary allowance if it is not), to set a pair of inside calipers to the joint face of the brass and the top of the box, as shown in Fig. 2432, trying the calipers (in the two positions there shown) on both sides of the box. This should be done every time the brass is tried in the box, until such time as the brass begins to bed against the bottom of the box.
[II-132]We now come to the bedding of the brass to its seat in the box. This requires skillful treatment; for one mistake will involve a great deal of extra work to rectify it.
In fitting the brass to the box care must be taken to leave it a rather tighter fit to the box than it requires to be when finished, that is after the bore has been made, because in the boring operation the sides of the brass are apt to close and loosen the fit of the brass to the box.
When the side faces and flanges are so far fitted as to render probable the brass driving home at the next trial, the bed of the box should be given a coat of red-lead marking, and small pellets of stiff red lead or putty should be stuck on the bottom of the box, two at each end of each bevel, and two at each end of the bottom, with one in the middle of the bottom and each bevel, as shown at a, b, c, d, e, f, in Fig. 2433, by the black spots. Then when the brass comes home, it will flatten these pellets, and their thickness (when the brass is taken out) will show how much the bevels are out, and how much to take off the brass to make it bed. These pellets must be restored to their original shape every time the brass is tried; otherwise, they may mislead. To insure their sticking to the box, and not coming out with the brass, the bottom of the box must have red-lead marking kept upon it. The chipping should continue until the pellets flatten out equally on the two bevels, but are left a little thicker on the bottom. If this is not done, the bottom will bed first, causing a great deal of extra filing, because filing the side bevels will let the bottom down too far.
In driving the brass in and out of the box while fitting it, a piece of wood must be used to strike on, otherwise the brass will stretch during the fitting and come loose in the box during the boring.[33]
The patterns from which the castings for brasses are moulded should not be made of the same angle or sweep on the bedding part or bottom as the bottom of the box, pedestal, or pillar block, because the brass casting, in cooling in the mould, contracts across the bore; thus if in Figs. 2434 and 2435 the full lines denote the shape of the pattern the dotted lines denote the shape the casting will be.
The result of this is that when the brass is let down in the box it will bed on the crown and not at the sides. Thus in Fig. 2436, a is a pedestal, and b a brass which beds at c, but not at d or e. In Fig. 2437 is shown an example of a brass, with a circular bottom, which would bed at the crown c, but not at the sides d e, until the metal was cut down to the dotted circle f.
The amount to which this contraction in the mould occurs varies with the size of the brass, the difference in the thickness at the crown and at the face joint, the composition of the metal of which the casting is made, and the temperature of the metal when poured into the mould. It should always be allowed for, however, for the following reasons. Referring again to Fig. 2436, it will be noted that it requires a heavy cut off c to bring e, d to a bearing, while it is apparent that if the brass met the box at e, d before it did at c, but little filing at e, d would let the brass down a long way. It saves work, therefore, to so make the pattern as to insure that the brass casting shall have bedding contact at d and e before it does at c. As an example of the allowance to be made for this purpose, it may be stated that in brasses of 6 inches bore and 9 inches long, the hexagon of the brass pattern at d, e, Fig. 2436, would require about 1⁄16 inch put on them to compensate for the contraction, supposing that the hexagon on the brass pattern were made at first to fit the hexagon of the pedestal or axle box.
To originate a true flat surface we proceed as follows: In the absence of a standard plate to go by, we must have three plates, and one of them must be accepted as a provisional or temporary standard. This we will call No. 1, and we fit Nos. 2 and 3 to it and then try them together, and if they also fit it is proof that No. 1 was true, and that all three are therefore true. It will very rarely happen, however, that this is the case; but Nos. 2 and 3 merely serve to show how much No. 1 was out of true.
Suppose, for example, that No. 1 is concave in its length, and we fit No. 2 to it, as in Fig. 2438, and then fit No. 3 to it as in[II-133] Fig. 2439, and when we come to put Nos. 2 and 3 together, as in Fig. 2440, we find that they are out of true to twice the amount that No. 1 is, and that all the work that has been done to them to fit them to No. 1 has been thrown away, and possibly to make them worse instead of better. It becomes important therefore to select the most true plate for No. 1, and this we may do as follows:—
If we have a straight-edge that is known to be true, we may lay it on the face of a plate and move it laterally from each end alternately, and if it swings from the centre the plate face is rounding, while if it shuffles across moving first at one end and then at the other the face is hollow; but if it glides as it were across, the surface is nearer true. The straight-edge must not be pressed to the plate, but merely touched laterally to make it move laterally, for if we take a true straight-edge and press it vertically to a true surface while moving it, it will show the marks of contact the most plainly immediately beneath the parts where it is pressed. Selecting by this means the two plates that appear to be the most true we proceed to test them further as follows: We give to one of them which we will call No. 1 a light coat of red marking, and placing it upon the other or No. 2, we move it about in all directions and then take the two apart to examine the bearing marks. Suppose then that No. 1 shows the bearing marks to be at the shaded places, a and b, in Fig. 2441, while the bearing marks on No. 2 are as at the shaded parts a and b in Fig. 2442, the two ends a having been placed together; then we know that b is a high spot on No. 1, and a a high spot on No. 1 for the following reasons. The marks at a, No. 2, have been made by the marking at a on No. 1, and will extend across No. 2, a distance depending upon how much No. 1 has moved across No. 2, for if corner a of No. 1 had only moved half-way across No. 2, it could only have marked half-way across it. Similarly spot b on No. 1 has marked spot b in No. 2, because it has been moved all the way across, it being evident that the marking on b, No. 1, can only mark plate 2 as far across its width as it is moved across it. From this it follows that the higher or more prominent a spot is the less will be the area of the bearing mark at that spot.
Now suppose that the two plates were curved to an equal degree as in Fig. 2443, and the bearing marks would extend all over both surfaces; but we may discover this error by turning one plate at a right angle, as in Fig. 2444, in which case the bearing marks would show along the edges of No. 1 and along the middle of No. 2, and we may correct each with the file until both plates mark all across and from end to end when tried together lengthways as in Fig. 2443, and one across the other as in Fig. 2444.[II-134] But the plates may be curved to a different degree, as in Fig. 2445, and it then becomes necessary to know which to file the most in correcting them and fitting them together, which we may discover as follows:—
We give one plate a light coat of red marking and rub it upon the other both sideways and lengthways. Suppose that on being separated and examined the bearing marks, shown as at a a and b b, Fig. 2446, on one plate, and at c c and d d, Fig. 2447, on the other, and as those at a a and b b are the narrowest, or in other words extend the least distance across the plate, it is proof that this plate is more concave than the other plate is convex, and therefore needs the most correction. This is plain because whatever part of a plate touches another, will, if the two are merely pressed together, only leave a bearing mark equal in area to itself, while this area will obviously be increased in proportion as one plate is moved about upon the other.
When the object is to merely produce a flat surface, independent of the thickness or parallelism of the plate, it is not always necessary to file or scrape the whole of the area showing bearing marks. Suppose, for example, that the marks appear as in Fig. 2448, and as the bearing marks at a a show that edge of the plate to be straight already, all that is necessary is to ease the surface at b in order to let that side of the plate come up.
When we have fitted two of the three plates together we must accept one of them as a true one and (calling it No. 1) fit Nos. 3 and also 2 to it, and then try Nos. 2 and 3 together. If these require correcting the amount of correction must be made equal on each, and when this is done we must accept one of these two (say No. 3) as the standard, fit No. 1 to it, so that Nos. 1 and 2 both having been fitted to No. 3 may be tried together and both corrected equally; nor will the surfaces of any of them be true until all three will interchange in this manner and show a perfect contact.
It is to be noted, however, that in this process we have not altogether eliminated the error due to the deflection of each plate. Suppose, for example, a plate to be resting on its feet and its middle will sag or deflect to some extent (very minute though it may be in a small plate), and when we place another plate upon it the latter will also sag or deflect if its points of contact are far apart, and in any event the truing is performed by the bearing-marks, which the operator knows show the darkest and the brightest where the contact is greatest; hence by the time the contact marks show equally strong all over, the top plate will have been fitted to suit the deflection of the lower one. Since, however, the nearer the points of contact (between the plates) are together the less the degree of deflection, it is better in trying them to place the test plate on the top of the one being operated on. If the plates are long ones it will not answer to have more than three points of rest for the lower plate, unless the foundation on which the plate rests is made so true that each resting point of the plate will bear with equal pressure on the foundation plate or stone.
To eliminate as far as possible the deflection, the three plates may be got up by the process described, and then finished by trying them when resting on their edges (the trued surfaces standing vertical), interchanging the three plates as before.
In this case the surface will be true when standing vertical as finished, but there will still be some untruth from deflection when the plates are rested on their feet, though it will be less in amount than if the plates were finished on their feet as first described.
In finishing surface plates with a hand scraper, we have a surface that bears in fine spots only, these spots being the tops only of the scraper marks. Now the depth of the scraper marks are unequal, because immediately after the scraper is sharpened it cuts the easiest and the deepest, the scraper cutting less deep as its edge dulls. The operator regulates this to some extent by applying a greater pressure to the scraper as it gets dull, but from differences in the texture of the metal and from other causes it is impracticable to make the scraper cut equally deep at each stroke, as a result the tops of the scraper marks, which are the points of contact of the plates, wear away quickest, and the plate soon loses, to some extent, its truth.
Again, work that is so small as to cover part of the plate surface only, wears the part of the plate to which it is applied, and although the careful workman usually applies small work at and near the outside edges of the plate only, still these are all elements tending to produce increased local wear and to throw the plate out of true.
To obviate this difficulty the surface should be got up to bear all over, thus greatly increasing its bearing area and proportionately decreasing its wear. To produce such a surface the following plan was adopted by the author in 1876.
The filing process was continued with fine Groubet files, and testing the plates, rubbing them together sufficiently to mark them without the use of oil. Very short file strokes must be employed, and great care taken to apply the file to the exact necessary spots and places.
Then instead of using the scraper, No. 0 French emery paper was used, wrapped over the end of a flat file. The plates being interchanged and trued with No. 0, No. 00 was used, and the testing and interchanging repeated. These grades of emery paper were then wrapped or folded over the curved end of a piece of wood, the plates interchanged and rubbed together as before, and the emery paper used as described for the scraper. Subsequently[II-135] Nos. 000 and 0000 French emery paper were similarly applied until the plates were finished. Much assistance to this method may be rendered by taking a piece of Water of Ayr stone, and truing its surfaces by rubbing them on the plates after the fine filing and before the emery papering. Then while applying the finer grades of emery paper the stone may be rubbed (with oil or water) in various directions over the surface. This has the effect of wearing off the very fine protuberances due to the emery paper cutting the metal most around its pores, and furthermore it causes the marks made in testing to show more plainly.
In skillful hands this process very far surpasses, both in the superiority of its results and in rapidity of execution, the scraping process, leaving a brilliant polished surface, so smooth that it feels as soft as satin, and the contact becomes so complete that no bearing marks can be distinguished.
In this process great care must be taken in cleaning the surfaces before applying them together, as the finest particle of dust will cut scratches, which though imperceptible on scraped surfaces, appear very coarse and deep on these smooth ones.
The amount of metal taken off by the finer grades of emery paper is so small as to be scarcely appreciable, save that it slightly discolors the emery paper.
The finest test for plates finished in this way is to rest the lower one quite level, clean it with alcohol, wipe it clean with old linen rag and finally with the palm of the hand, which if quite dry is more effective than anything else. The eye should carefully sight the plate surface with the light reflecting on that surface, when particles too fine to be felt may be observed and wiped off with the hand. In dry weather it is a difficult matter to clean the plates perfectly, as while one is being cleaned the fine particles of matter floating in the air rest upon the other; but in rainy weather the cleaning is much easier.
The plates being cleaned one must be lowered vertically on the other where it will float, there being a film of air between the two which it is almost impossible to exclude by pressure even though the plates be moved while pressed together.
If under these conditions the surfaces are not true and the top plate be set in motion in various directions, by a light finger touch it will swing round, the parts of the surface most in contact being the centre of motion. Suppose then the top plate to swing from one end it should be turned end for end on the bottom plate, and if the location of the centre of motion is still at the same end of the top plate, that plate is high there, while if the centre of motion in both cases is at the same end of the bottom plate it is the one that contains the error.
If the top plate swings upon its own centre of motion it must be moved farther off the bottom one, first on one side and then on the other, to discover if it or the bottom plate is in error; while if the top plate swings first from one end and then from the other, one or both of the plates are hollow and the top one must again be moved farther off the lower one, and the test by motion continued. The error discoverable in this way is very much finer than can be discovered by the marks of contact, since a plate showing quite even contact when quite dry and clean, and tested as lightly and carefully as may be will show error by this motion test. The error being so small in amount that it may be corrected by rubbing the plate with rag and oil, applied under hand pressure to the plate.
To cause the plates to bind together so that rubbing one on the other will leave contact marks, the top plate must be placed about an inch over the corner of the bottom one, pressed closely to it and forced laterally over it. A pair of plates of the Whitworth pattern (such as shown in Fig. 2449) placed by the author in the Centennial Exhibition, required, when put together dry as above, 3411⁄2 lbs to slide the top one over the other, which was due to the friction caused between the surfaces by the atmospheric pressure acting on the back surface of the plate, the latter having a superficial area of 12 by 8 inches.
Here it may be added that a plate of the same dimensions, and having its surface finished simply by filing with a dead smooth file, which plate was made for exhibition at a lecture on hand work, delivered before the Spring Garden Institute of Philadelphia, required a force of 22 lbs. to slide on the one on which it rested.
If two plates finished by the above method be placed together by sliding one upon the other it will be found that with the hands applied as in Fig. 2449, they can be separated or pulled apart with less force than it requires to slide one upon the other, because the plates bend and unlap, as would be the case if two sheets of paper were wetted and placed together and then taken apart by pulling two edges in opposite directions. But if the power to pull the plates apart be applied at the middle of the plate it will require a much greater force to separate them, although how much is problematical, no experiments having been made upon the subject. Furthermore the friction between two such plates will be greater if the surfaces be lubricated than if quite dry.
Thus, with the surfaces cleaned by alcohol, the top plate will move comparatively easily, but if the surfaces be slightly oiled and then wiped apparently quite clean with old dry rags, the friction will be a maximum. If then a piece of rag, say of an area of an inch, have one drop of oil upon it and be then applied to the surfaces of two plates after they have been cleaned with alcohol, the friction will still be about 3 lbs. per inch of area of one plate. With the surfaces well lubricated it will still require more power to slide one plate upon the other than would be the case were both plates quite dry.
The reason of this is that when quite dry it is impracticable to exclude the air from between the surfaces, whereas with the lubrication the air is more perfectly excluded and the atmospheric pressure forces the plates together.
ERECTING.—The term erecting is applied in large work to the operations involved in fitting the parts to their places on the engine or machine, as well as to placing them upon their foundations and putting them together ready to run.
In vice work or fitting, the various parts are put together ready to be erected, each part being complete in itself, but not adjusted with relation to the others. Thus, while a link motion may be complete in itself, the length of its eccentric rods will usually require correcting when placed upon the engine. Furthermore the position of the eccentric is to be adjusted.
The boiler fittings may be complete in themselves, but will still require to be fitted or erected upon or to their places.
Erecting requires the greatest of skill, care, and judgment, in order that the work may be put together properly aligned and any defects of construction corrected in the finished machine.
In erecting a machine, as in building a house—or, indeed, as in everything that man constructs—the work must be begun at the foundation.
In a machine in which the working parts are carried and contained upon framework, such framework becomes the foundation so far as the erector is concerned.
In a stationary steam engine the cylinder and bed plate form the erector’s foundation while the engine is in the shop, the mason’s foundation being an after consideration.
In a locomotive the boiler is the foundation to which all the other parts are either directly or indirectly affixed.
The erector uses all the measuring tools used by the fitter or vice hand, and in addition many others, as stretched lines, the spirit-level and plumb-level. Either of these tools forms the readiest means of testing whether surfaces that are widely removed and in different positions about a machine are parallel one to the other, it being evident that all surfaces standing vertical will be parallel, or all those standing horizontal will also be parallel, one to the other.
Spirit-levels are often made of wood, which is very objectionable for the erector’s use, because the lower or testing surface is apt to catch and hold particles of metal, and furthermore it is very susceptible to abrasion, and wears rapidly. It is preferable, therefore, that it be of iron or steel. The test of a spirit-level is its sensitiveness, and it is found in a properly constructed one that the bubble will move to a perceptible extent if a piece of gold leaf be inserted under one end. In a spirit-level which came into the hands of the author of this work he found the warmth of the finger when placed on its top sufficient to cause the bubble to move nearly the full length of its tube, the body of the level being a block of iron 11⁄4 inches square and 9 inches long. The movement of the bulb was caused by the heat of the finger expanding the top of the spirit-level and causing it to bend. To test the truth of a spirit-level, it should be placed upon a true surface, as a surface plate, and if the bubble comes to rest at the same spot in the length of the spirit tube when the level is tried turned end for end, the level is true. The test should be made several times.
The plumb-rule, though less used by machinists than formerly, is better for machinists’ use than the ordinary wooden-bodied spirit-level, since it is more delicate if properly constructed. It should be formed as in Fig. 2450, the sides a a and b b being straight and parallel one to the other; c and d are two plugs of soft yellow brass let in so as to keep the line l l clear of the face of the level, so that there shall be no friction between them. At n are notches to secure the line, which should be as fine and as closely spun as possible.
The plumb-level, Fig. 2451, is also preferable to the ordinary spirit-level; its edges a, b must be straight and at a right angle one to the other, c and d representing brass plugs as before. The edge a of the rule or of the level should be laid upon a surface plate, and a fine line drawn on the face of these plugs with a scribing block, the coincidence of the line l with these marked lines testing the truth of the work.
Fitting or Making Joints.—The best form of joint to withstand pressure is the ground joint, and next to this, but more expensive, is the scraped joint. The difference between the two is as follows:—
For a ground joint the fitting with files or scrapers is only carried far enough to bring the fit sufficiently near that it may be finished by grinding the surfaces by rotating one upon the other with oil and emery interposed between them.
To grind a joint it is obvious that all the bolts or studs must be removed.
In a scraped joint the scraping is carried to such a point of correctness that the fit will be tight without grinding.
Joints in new work are easily ground, because the bolts or studs being new have not become rusted in their places and may therefore be readily removed; furthermore the joint may be ground before the studs are inserted. But in the case of old joints the studs may have become so rusted to their places as to render them liable to break off in the effort to extract them, and in such case it is better in most cases to make a scraped joint, which may be done with the studs left standing in their places.
To make a ground joint, as say a cylinder cover joint, proceed as follows:—
Put a thin coat of red marking upon the joint face of the cover, and after it is coated lightly and smoothly all over, the hand should be passed over the whole surface marked, because any grit left on the surface will cut the faces of the joint when they are rubbed together to fit them, and there is no wiping material that will so effectually clean dust from the surface as the hand will; and furthermore, the sense of touch will instantly detect any grit present. The cover may now be put into its place on the cylinder and rotated back and forth a turn or so to insure that it is properly seated; then we may strike it a light blow in different [II-137] places with a piece of wood or the end of the handle of the chipping hammer; and if the cover does not fit pretty closely to its seat, a sharp metallic sound will be distinctly heard when the blow is struck over the parts of the face that are much out of true. Hence, by striking the blows all around the flange, we can easily find not only the high and low spots, but can determine, after a little practice, by the degree of the sound, how much the faces are out of true. We next rub the cover back and forth on its seat, so that the marking on the cover will mark the high spots on the cylinder face. If, however, we make the forward reciprocating movement of the cover a longer one than the backward, we shall give to it a gradually rotary as well as a reciprocating movement, and this will tell us if the face of the cover is true or not, for if the marking is removed from the face of the cover in two diametrically opposite places only, it shows that the cover itself is not true; and if the cylinder face also marks on two diametrically opposite places only, it is proof that both the faces are a good deal out of true: but there is no knowing which one is the most out, and so we must file off each an equal amount. If either face marks in more than two places it is evidence that it is pretty nearly true, and it follows that that face does not need much filing. Here it becomes necessary to state why the movement of the cover must, when being tried to its place, be back and forth, as well as rotated by the movement already explained. If we revolve a radial surface of metal upon a similar surface they are extremely liable to cut or abrade each other, and the presence of the least grit will inevitably cause them to cut; and if cutting once begins, the metal gathers upon the cutting part, increasing its size so that the groove cut will get deeper until a complete revolution has been made, and this rule applies to all revolving surfaces, but more particularly to radial or conical ones.
By making the movement a partly reciprocating one we destroy this tendency, and either imbed the grit into the iron or else work it out. To proceed, however. If during our testing the blows induced a secondary and metallic sound as above described, we take a rough file and ease the high spots on both the cover and the cylinder face, filing a good deal off the face that shows diametrically opposite bearing spots only, and but very little off the face that shows three or more bearing spots. In this latter case, indeed, it is better to use a second-cut than a rough file. We next wipe both faces quite clean, apply the marking to the cover as before, and try it to its seat again; rubbing it in the same manner to its seat and testing it for the metallic sound as in the first case. So soon as this sound ceases we may take a second-cut file and fit the faces until they bear in at least four different places, when a smooth file should be used and the fitting and trying continued, until a very light coat of the red marking will show both the cover and the cylinder face to mark in spots not more than an inch apart; and we may then take a flat scraper, ease away the high spots, pressing the scraper firmly to its work and making it cut fine scrapings, using the scraper in strokes of about 1⁄2 inch for a large face and 1⁄4 inch for a small one. When the two faces show about an even contact all over, the grinding may be performed as follows:—
The two faces must be wiped quite clean, and then with an oil-can we can run a line of oil around both the cylinder and cover faces, and then with the fingers sprinkle on them some dry grain emery, of a grade of about 50 for a cylinder whose diameter is, say, 14 inches or over, and of a grade of about 60 to 65 for smaller diameters; if, however, only coarser grades of emery are at hand it may be ground finer by abrasion on an iron block, using a hammer face to grind it with. The emery and oil being applied, we place the cover in its place upon the cylinder, and give to it the reciprocative rotatory movement already described, continuing the movement until the cover moves so smoothly and noiselessly that it is evident that the emery has done its duty. We then take the cover off and examine the faces.
If there are prominently bright spots upon either face, denoting that the emery has not operated upon them, it will pay to take the scraper again and ease away the dullest and most frosted-looking spots, which denote that they have suffered most during the grinding operation. The difference between the spots that have been the most and those the least affected by the grinding will be very plainly visible if the faces are wiped clean. We must continue the grinding operation with this grade of emery until the marks show the grinding to have been performed pretty evenly all over the faces, and we then apply a coating of oil and emery, as in the previous operations, the latter being in this case of a grade of about 70, moving the cover as before until it revolves so smoothly and noiselessly as to indicate that the emery is no longer doing any duty. Having continued this process, applying fresh emery and oil until the face appears true, we may perform the finishing and testing process, which is of the utmost importance, since it will detect the faintest possible defect in the job. Wiping the faces quite clean, we put the cover in place upon the cylinder again, and move it as before back and forth, and yet slowly advancing; but it must be borne in mind that if the cover makes the least jarring noise during the operation we must at once remove it and wipe it clean again, or the faces will abrade and become destroyed. There is no danger of this, however, if the cover be at once removed when the jarring sound is heard. If it be not heard, we continue the operation until the cover has made four or five revolutions, and then remove it, and we shall find that the emery and oil, which had impregnated the surfaces, have worked out. We again wipe the faces clean and put them together and rub one upon the other as before, bearing in mind that if the faces cling much one to the other, we must wipe them clean again. Usually the finishing process requires performing about three times, and then the faces will have become as bright and clear as a mirror, magnifying the slightest defect in the joint. Joints made in this way will stand any pressure without leaking (unless the pressure be so great as to spring the metal of the cover). It is well, however, when making the joint, to put a little oil or pure tallow on it, and it is from this that it is called in England a grease joint, while in the United States it is termed the ground joint. It is common, however, in England to finish the whole joint by scraping; but this is a much more tedious job, and not so good a one, after all. Here it becomes necessary to remark, that in order to be able to handle the cover readily, it is best to bolt to it a wooden lever overhanging both sides of the cover, and to serve as a handle in moving it. And during the grinding we may place a weight on the cover, which will greatly expedite the process. It would appear that this is a long job, but such is not the case; indeed, a 16-inch cylinder face and cover 1⁄32 inch out of true one with the other can be got up in half an hour.
It is to be observed, however, that the cylinder cover that contains the stuffing box for the piston rod often carries one end of the guide bars, and in any event carries the gland whose bore requires to stand in line with the cylinder bore. It must be remembered that if more is filed off the top than off the bottom of the face, or vice versâ, the gland bore may be thrown out of parallel with the cylinder bore, and the guide bar seatings will be thrown out of parallel in the same direction.
To facilitate the making of ground and scraped joints it is preferable that the surface of the joint, both on the cylinder and the cover, project from the rest of the flange, from the bolt holes to the bore in the one case, and from the bolt holes to the body in the cover in the other, so that the bearing surface of the joint shall extend from the inside edge of the bolt holes to the cylinder bore only. This provides ample surface to make a joint, while reducing the surface to be operated upon.
To make a Scraped Joint.—Let us now suppose that the studs are in their places, and it is decided, for fear of breaking them in taking them out, to make a scraped joint, and the process is as follows:—
The testing and marking of the high spots or places must be made by giving to one of the surfaces a light coat of red marking and then bolting up the cover moderately tight, screwing up the nuts at first until they just grip the work all around, and not letting one part of the cover face bear at any time with greater pressure against the cylinder face than there is on the diametrically opposite side of the cover, for the side under most pressure will receive the marking most readily. Especially is this the case when the two faces first meet, because even a low part of the face will show most contact under such circumstances, and then easing such marks away will make the[II-138] cover a worse fit than it was before. When the cover is bolted home, the marking on the cylinder face may be made to transfer itself on to the high spots of the cylinder cover face more plainly if a piece of wood be placed on the cover and struck lightly with a hammer, moving the wood around and between the studs. If the wood be struck heavily it will cause an almost endless and assuredly a faulty job, because the force of the blow will spring that part of the cover to its seat on the cylinder face, whether it fits in that particular spot to its seat or not, and hence the filing or scraping may be done in places where it is not required, because the marking misleads. If the bolt holes are very close together, as in English practice, lightly striking the cover will prove an assistance; but where they are several inches apart, as in American practice, it is better to omit it, for the bedding marks will show plainly and properly if the marking be evenly distributed by the hand over the cylinder face, and the cover is bolted at each trial tightly to its seat, providing of course that the red marking is free from grit.
In a job of this kind it is difficult to know, when a leak occurs, whether the defect is in the cylinder face or the cover, and it is very desirable to perform the operation with a view to correct the defect rather than bed one face to the incorrectness of the other.
If then the stud holes are equidistant apart and concentric (so as to permit it), the cover may be tried on in one or two positions, and, if the bearing marks occur on the cover at each trial in the same places it is the cover that is out; or if this occurs on the cylinder face, it is that face which is out. Since the studs are in their places the cylinder face may be best operated on by a scraper, while for the first part of the operation on the cylinder cover a file may be used. The corner at the junction of the cylindrical part of the cover (where it fits into the cylinder bore) should be scraped well clear, or it will be apt to bind on the edge of the cylinder bore and prevent the cover from screwing fairly home to the cylinder face. The joint should be made to bed well inside of the bolt holes, and coated with oil or grease when finally put together.
Joints for Rough or Untrue Surfaces.—The most permanent form of joint for a rough or untrue surface is, for steam pressure, a gauze, and for water pressure, a pasteboard, or a duck or canvas joint.
A gauze joint is composed of copper wire gauze, having square meshes of about 1⁄32 inch square; this gauze is cut out to fit over the joint surfaces, a single, double, or treble thickness being used according to the unevenness of the surfaces. A coating of red-lead putty is first spread over the joint with a piece of smooth surfaced metal; the wire gauze is then put on, and over it another coating of red lead; the cover is then put on, and the nuts screwed lightly home so as to bring the cover to bear against the red lead. Then any nut may be given a quarter or a half-turn, and the diametrically opposite one also given a half-turn, this process being continued until all the nuts have been screwed home a half-turn, when the process may be continued until the nuts are screwed firmly home. This is necessary, because if the nuts on one side are screwed home in advance of those on the other, the red lead on that side may be squeezed out too much and the joint will leak. In joints of this class the surfaces being rough it is not unusual to cut out the gauze wire as follows: Lay the sheet of gauze over the joint and cut it to the size by lightly hammering it over the sharp edges of the joint, which will cause the sharp edges to cut the copper wire. To cut out the holes place the ball piece of a hand hammer on the wire and over a hole and strike the hammer face several light blows, and the corners of the hole will cut the wire through.
The gauze joint will answer equally well for hot water as for steam joints, provided that it be given time to dry and become hard. If the joint can have a week in which to dry the red-lead putty may have about one-sixth of its bulk of white lead mixed with it, being made to a consistency of soft dough so that it will spread easily; and the amount being sufficient to fairly cover the gauze and no more, the soundness of the joint may be known by the lead squeezing out all around the joint edge as the bolts are screwed home. If the joint is to be used in a day or so after being made, the white lead should be omitted. In either case the lead should be mixed stiffly at first; the best lead should be used and it should be well hammered on an iron block, after which it may be thinned with boiled oil, or with a little varnish, which will cause it to harden more quickly.
For water joints requiring to stand high pressure, and to be used as soon as made, a paper, pasteboard, or a duck or canvas joint are best. The joint is made by using, in place of the gauze wire, one or two thicknesses of the pasteboard, duck, or canvas, cut out to the size of the flange, and with the necessary holes to receive the standing bolts and leave the bore of the pipe clear. If the flange of the joint is of copper, brass, or wrought iron, or, if of cast iron, is of sufficient strength to permit it, one disk may be made the full size of the flange, and a second may be made to have an external diameter sufficiently large to fit snugly inside of the bolt holes, which will form sufficient thicknesses if the flange is a fair fit to its seat; if it is not, however, three, or even four, thicknesses may be used, in which case at least one of them should fit inside the diameter of the flange across the bolt holes, as described. The disks being prepared, we spread on the first one a thin coating of red-lead putty, and then lay another canvas disk on, again adding the putty until the whole is completed. We then spread a thin layer of the putty around the hole of the seat and that of the flange, place the disk in position and screw the joint up, tightening down the nuts until they bring the flange to an equal seating all around and not sooner on one side than on another, for in that case the red-lead putty will be squeezed unevenly, and too much on the side screwed up to excess. The nuts should be screwed up very tight; the joint wiped, the protruding canvas cut off, and the joint is complete.
For very rude and rough joints, whether used under pressure or not, we may make, for either water or steam, a joint as follows: Taking four or five strands of hemp, we saturate them with a coating of white lead ground in oil, applying just sufficient to make the fibres of the hemp cling well together. We then plait the strands and coat the whole rope thus formed with red-lead putty, and place the strand around the hole of the joint, taking care that the ends lap evenly, so that the joint shall be of even thickness. It is better, however, to bend a piece of lead or iron wire to suit the size and shape of the hole in the joint, and then wind the hemp and red lead around the wire. And in cases where the flanges of the joint are sufficiently strong to have no danger of their breaking from the pressure due to screwing up the nuts, the piece of lead wire, if given a neat butt joint or neatly lapped, may be employed without any red-lead putty or hemp; this does not, however, make a good permanent joint. In cases where a joint requires to be made thick to accommodate the length of the pipe, pasteboard may be used in the place of canvas, giving to it a thinly-spread coating of red-lead putty on each side, and, if possible, leaving the pasteboard a trifle too thick and springing open the flanges of the joint to get the pasteboard into position without scraping off the red-lead putty.
Where it is required that a joint stand great heat or fire, asbestos board, about 1⁄16 inch thick, makes a good and permanent joint. It is coated with red lead mixed thinly with boiled oil, containing as much as it will soak up, leaving a thin layer of the lead upon the surface of the asbestos. The holes for the bolts to pass through in the duck, canvas, pasteboard, or asbestos joint should be cut large enough to well clear the bolts.
For cold water, where it is not subject to great variations of temperature, common sheet lead makes a very good joint; but under excessive changes of temperature the expansion of the pipes will soon cause the sheet lead to squeeze out and the joint to leak.
Joints are frequently made with copper wire rings, made of a diameter to pass around the hole of the joint and lie within the diameter of the bolt holes, and brazed together at the ends; but if the joint be rectangular instead of circular the wire must either lie in a recess, or else a shoulder must be left for the wire to abut against, which will prevent its blowing or becoming forced out by the pressure.
In some practice softened sheet copper about 1⁄32 inch thick is[II-139] used to make joints on surfaces that have been planed. Joints of this kind are used for locomotive steam chests.
Rubber joints are used to make steam, water, and air-tight joints, and are usually made from what is known as combination rubber—that is, sheet rubber having a linen or other web running through it; with one such web it is called single, and with two webs two-ply, and so on. There is in many cases, however, an objection to this form of joint, in that it compresses; and hence in the case of the steam chest, for example, it affects the distance of the slide-spindle hole in the chest from the seat, and throws it somewhat out of line with the eccentric. In long eccentric rods the variation is of course minute; but still it exists, and must exist, since it is impossible to tell exactly how much the rubber will compress in making the joint. Furthermore, if it is required to break such a joint, the rubber will very often cling so tenaciously to the seat in one place and to the chest in the other, that it will tear asunder in breaking the joint. To obviate this as much as possible, however, we may chalk the rubber on one face and slightly oil it on the other, so that the oil will aid the rubber in clinging to one face, while the chalk will assist it in separating from the other face of the joint.
Rubber joints slowly compress after being under pressure a day or so, and also if subjected to heat; hence they should have their bolts screwed up after becoming heated, or after having stood some time. It is advisable also that the rubber be as thin as the truth of the surfaces will admit. If it is necessary to use more than one thickness of rubber, the thickness may be made up of rings, whose diameter will just pass within the bolt holes.
The holes in a rubber gasket should be made larger than the bolt holes, so that there shall be no danger of the bolt, when being inserted, catching the gasket.
If the flanges should not come fair, and it is determined not to set them fair, the rubber should be as thick as the widest part of the opening between them, and shaved off to suit the thin side of the joint, and in this case the bolts must be tightened very uniformly and gradually around the joint to secure a tight one. If there is room to shave the gasket to the amount of taper, and use in addition a ring around the bolt holes, it will make a safer job.
When the gasket requires to be split to pass it around or over a rod, it should be cut through to the canvas on one side, and a short distance off cut through to the canvas on the other side; the rubber may then be stripped carefully back from the canvas and the latter cut through and passed over the rod, when the rubber may be put back and sewed to the canvas again.
Sheet rubber with a gauze wire insertion instead of canvas makes an excellent joint.
In Fig. 2452 is shown a method of making a steam-tight joint largely employed in England, upon the steam chest joint where the cylinders of crank shaft (inside cylinder) engines are bolted together. a is the flange of one cylinder, which is bolted to the other by the bolt b. c is a strip of copper let into a dovetail groove cut one half in one cylinder, and the other half in the other. After the bolts b are all firmly screwed home, hammer blows are delivered upon the top of the copper strip as denoted by the arrow e, expanding the copper so that it completely and closely fills the dovetail groove, and makes a steam-tight groove.
In riveting the copper it is necessary to hammer it evenly all along lightly, and only sufficiently to make it closely fill the groove, otherwise it will spring the joint open, and cause it to leak, notwithstanding the bolts b, which will give under the extreme strain.
Temporary joints are sometimes made by bending a piece of lead wire into a ring or frame, of such a size as to well clear the inside of the bolt holes. The ends are neatly joined, and the lead wire compressing and accommodating itself to the inequalities of the surfaces forms a joint.
Joints for Boiler Fittings.—Let it be assumed that the casting shown in Figs. 2453 and 2454 requires to be fitted to a boiler, both being new. In this case, the holes for the studs or bolts should first be drilled in the flange of the casting, which will reduce its weight and render it easier to handle. The casting should then be held against the boiler in its proper position and location; and, with a fork scriber whose width of points is equal to the widest space between the face of the casting flange and the boiler, pass the fork scriber around the fitting or casting with one point against the boiler shell and the other pressed against the edge of the casting, the result being to mark around the flange of the latter a line exactly following the surface or contour of the boiler, and at a distance from the boiler the nearest that will suffice to properly bed the casting to the boiler surface, or, in other words, the line that will exactly mark the amount of metal requiring to be cut off the flange face to make it bed all over; and that face may, therefore, be cut down to the line. In chipping and filing it, however, the straight-edge may be used to advantage as follows:—
Suppose the casting flange to be gripped in the vice facing the operator, as in Fig. 2455, and that l l represents the scribed line: then the cape chisel cuts may be carried clear across the flange, coming exactly down to the line on each side of the flange, while a straight-edge s may be used as shown to show when the cut is carried across level. Then, when the intermediate spaces are cut out with the flat chisel the surface will be of correct shape, and the surface may be rough filed. The casting should be cut clear down to the lines, and if the job has been properly set, marked and faced, no further trying will be necessary previous to marking the bolt or stud holes in the boiler. It is well, however, if the[II-140] operator is inexperienced in this kind of work, to again set the casting in its proper position to correct the fit. But, with proper care, all the holes in the boiler may be marked without any second fitting of the flange, since the operation properly performed is bound to give correct results. In doing a job of this kind it must be borne in mind that it is very easy to consume more time in trying and altering the job than is required under proper conditions to do the entire job; hence, in setting the casting, preparatory to marking it with the fork scriber, nothing is near enough that does not carry with it a conviction of perfect reliability; and if any doubt exists it is better to go through the process again. If the casting flange varies much in shape from its seat, and rocks or is unsteady, wooden wedges may be placed beneath it, or a few pellets of stiffly mixed red lead may be placed on the boiler where there is most room between it and the casting, the boiler surface being coated or painted with red marking, so that the pellets shall adhere to it and not to the flange face. If the casting is too heavy to be steadied by hand, one hole may be drilled in the boiler and a temporary bolt inserted to hold the casting while setting it in position, and marking with the fork scriber.
When the flange is approaching a fit, it must be placed in position on the boiler and the stud holes marked on the boiler with an ordinary scriber, its point being pressed against the boiler while it is pressed against the side of the hole in the casting flange and traversed around it, so as to scribe on the boiler surface circles corresponding to the holes in the flange. From the centres of these circles others of the proper size of the tapping holes may be struck and the tapping holes may then be drilled, and the studs put in. The remainder of the fitting operation consists in applying red marking on the boiler surface, bolting the casting to its place and filing the high spots. The marking is made to show plainly upon the flange by light hammer blows with a piece of wood interposed between the hammer and the flange face to prevent piercing the latter. These blows, however, should be lightly delivered, or they will cause the marking to be deceptive.
The fit of the flange to the boiler, however, should vary according to the kind of bolt used to hold the fitting to the boiler. If stud bolts are used they are supposed to screw into the boiler steam-tight, hence the flange may be fitted so that it has the closest contact with an annular ring extending from the outside of the bolt holes to the central hole of the flange, as shown in Fig. 2456, in which the area within the dotted circle c encloses the area to be most closely bedded. This is a highly important consideration in flange joints of every description, for, if a joint is made there, that is all that is necessary, and the fit outside of the bolt holes—that is to say from the bolt holes to the perimeter of the flange—has nothing to do with making the joint, unless the studs or bolts leak, and in that case the leak will find egress beneath the nut, unless grummets are used. A grummet is a washer made of twisted hemp, cotton, or other material, and coated with red-lead putty, and is placed beneath the heads of bolts, or under washers placed beneath nuts to stop leaks. It is not necessary to ease the flange from the bolt holes outward much, but to merely make the flange, or fitting, bed clearly and distinctly the most around the main hole, and outwards to the inside of the bolt holes; for, if there was given too much clearance, the flange would bend from the pressure of the nuts, and would in consequence spring if made of brass, or perhaps break if made of cast iron.
To make the joint, gauze wire, pasteboard, or asbestos board may be used, or if the joint is to have ample time to set, a red-lead joint without the gauze may be used; but in this case it is an advantage to cut up into pieces about 3⁄8 inch long, and thoroughly shred some hemp, and well mix it in the lead, well beating the same with a hammer.
To preserve red-lead putty from becoming hard and dry, as it will do if exposed to the air, it should be kept covered with water.
In some cases joints of flanges to boilers are made by riveting the flanges to the boiler and caulking or closing the edge of the flanges to the boiler shell; but this possesses the disadvantage that the rivets must be cut off to remove the fitting from the boiler when necessary, and access to the interior of the boiler is necessary in order to attach the fitting again by rivets.
Fig. 2457 (which is taken from The American Machinist), represents a joint for boiler fittings, designed to facilitate the breaking and re-making of the joint. c represents, say, a boiler plate, b a piece having a ball joint seat in c ground steam tight, and a a flange, say, for a feed pipe; the studs d thread permanently into c, and the joint is bolted up by the stud nuts e. It is obvious that the ball joint between b and c permits the flange a to set at an angle if necessary.
Rust Joints.—These are joints made by means of filling the space between the flanges, or annular spaces, as the case may be, with cast-iron turnings, and compacting them with a caulking tool. Any interstices through which steam or water, &c., might leak become filled by the subsequent rusting of the iron cuttings, the rust occupying considerably more space than the iron from which it was formed.
Rust joints are employed upon very uneven surfaces, and for pipes for mains to go under ground. In former times this class of joints was much used in engine and boiler work, but of late years it has been to a great extent abandoned. In Fig. 2458 is[II-141] shown the method of construction for a rust joint for what are known as spigot and socket joints for pipe work. s is the spigot and p the socket. r r is a metal ring, bound over with either dry hemp fibre or tarred twine or rope. The remainder of the space between the pipes at a a being filled with a cement composed of
| Sifted cast-iron borings | 100 | lbs. |
| Sal-ammoniac | 1⁄2 | lb. |
| Sulphur | 1⁄2 | lb. |
but when required to set quickly, 1 lb. sal-ammoniac may be used. These ingredients are thoroughly mixed with water immediately before being used, and just covered with water when used intermittently. The cement is put into the space a a, in quantities sufficient to fill up about 3⁄4 inch in length of the annular space a a, and then caulked by being driven in with the tool shown in Fig. 2459. Cement is then again put in and the caulking repeated, the process being continued until the whole space is filled.
In some cases (as in gas mains) the space a a is filled with melted lead, and when cold caulked with the tool described.
In Fig. 2460 is shown the method of making a rust flange joint; a a being a ring covered with hemp twisted around it, the cast-iron cement being caulked in as before.
The wire rings should be firmly gripped by the bolts to prevent them from moving from the caulking blows, which should be at first delivered lightly.
In some cases pipes are joined with rust joints, as in Fig. 2461 in which a a is a sleeve, there being two rings of wire and hemp inserted as shown.
When flanged joints are made with a scraper, or ground joint, or with rubber, duck, or other similar material to make the joint, the length of the pipe, from face to face of the joint, must be made accurate.
Fig. 2462 is a face, and Fig. 2463 (which are from Mechanics), a sectional edge view of an expansion joint, being that used by the New York Steam Supply Company for the steam pipes laid under the streets to convey steam to buildings. The object is to provide a joint which shall permit and accommodate the expansion and contraction of the pipe under varying temperatures. p p are corrugated copper disks secured to the faces of the pipe ends by flanges, as shown, and gripped at their edges by the flanges of the cast-iron casing, and it is obvious that the ends of the pipe may move longitudinally carrying the corrugated disks with it. The cavity a is filled with steam, and to support the disks p against the pressure segmental blocks b of cast iron are placed behind them, the number of these blocks being as indicated by the dotted radial lines in the figure. It may be added that this joint has been found to answer its purpose to great perfection.
Pipe cutters, for cutting steam or gas pipe by hand, are usually provided with either a rotary wheel which severs by rolling an indentation, or else are provided with cutting tools. The rolling wheel has the advantage that it makes no cuttings, cuts very readily and is not apt to break; on the other hand it is apt to raise around the severed end of the pipe a slight ridge, which with a worn cutter may be sufficiently great as to require to be filed off[II-142] before the threading dies will grip the pipe. Cutting tools are apt to break and require frequent grinding; hence, as a rule, the rolling wheel cutter is generally preferred.
Fig. 2464 represents a cutter of this kind, the piece a carrying the cutter b, which is operated in the stock c by means of the threaded handle h.
Fig. 2465 represents a pipe cutter in which are a pair of anti-friction rollers and a severing tool bevelled on one edge only so as to leave the end of the pipe face cut square, and the piece cut off bevelled on its face; or by turning the cutter round the reverse will be the case, the piece cut off being flat on its end.
The action of this cutter is, as in the case of the wheel cutter, simply that of a wedge, hence no cuttings are formed.
Fig. 2466 represents a pipe cutter in which a cutting tool is employed, being fed to its cut by the handle which is threaded similar to the handle shown in Fig. 2464. The end jaw is operated to suit different diameters of pipe by means of the milled nut shown, which receives a threaded stem on the adjustable jaw.
Pipe Vice.—The ordinary bench vice is sometimes provided with an attachment to enable it to grip pipe at three points, and, therefore, hold it sufficiently firmly without squeezing it oval, but it is preferable to use a proper pipe vice, such as shown in Fig. 2467, which consists of a base frame bolted to the work bench and receiving a serrated die to grip the pipe. The upper die is carried to a frame pivoted on both sides to the base, and is operated to grip or release the pipes by means of the handled screw shown.
To change the dies one pivot is removed and the upper frame swung open, as in Fig. 2468.
The proper shape for pipe tongs depends upon the number of sizes of pipe the tongs are intended for, but in all cases the point at which the gripping point should be is about as shown in Fig. 2469. This enables the edge at a to enter the work and grip it. If this point of contact were nearer to c it would be apt to slip upon the pipe, whereas, were it farther towards b, it would present a less acute angle to the pipe, which would be apt to jam in the tongs.
It is obvious that, if the tongs be moved in the direction of h, the whole power applied to f acts to cause the edge at a to grip the pipe, and that the length from a to g has an important bearing on the grip of a to the pipe; because the nearer a is to g not only the greater the leverage of the leg f, but also the less a, with a given amount of movement of f on its pivot, endeavors to enter the pipe; hence the movement of a in a direction to grip the pipe is less in proportion to the movement of f, and has a corresponding increase of force. It follows then that the nearer the grip of a is to c, the less, and the nearer the grip to b the greater, its grip[II-143] upon the pipe. But, by making the length of a such as to grip the pipe in about the position shown in the cut, there is latitude enough in the location at which it will grip the pipe to permit of the tongs being used upon pipe of a somewhat greater or less external diameter, increasing the availability of the tongs. Furthermore, if a gripped the pipe at or too near to b, it would be apt to indent it. The crown of the jaw d may be made to fit to the pipe or to be clear of it; for thin pipe, as solid drawn brass pipe, it should fit so that the pressure will not indent the pipe, but for strong iron pipe it is better to let it clear, which will not only afford a firmer grip, but will also better fit the tongs to take in different diameters of pipe. In some cases, as in adjustable pipe tongs, the jaw surface d is, for this purpose, considerably V-shaped, as will be seen presently.
It is obvious that as a grips the pipe automatically, the tongs may be moved through any portion of a rotation that the location may render most desirable. Pipe tongs are designated for size by the diameter of the pipe they are intended for; thus, a pair of inch tongs are suitable for pipe an inch in diameter of bore, the handles or legs of the tongs coming so close together that both can be readily grasped in one hand applied at their extreme ends. If, however, the tongs be applied to pipe of a larger diameter the legs will be wider apart, and one hand will be required to be applied to each leg to force them together. A complete set of pipe tongs, therefore, includes as many pairs as there are diameters of pipe, unless adjustable tongs be used.
Adjustable tongs are made of various forms; thus a simple plan is shown in Fig. 2470. The gripping surface of the jaw is shaped as at v, so as to admit varying diameters of pipe, the smaller diameters passing farther up the v, the distance of the end a of jaw, or leg f, being regulated to grip the pipe in the proper place by operating the screw s, which is tapped into the jaw f and pivoted in b, the slot c enabling f to move along b. The capacity of tongs of this design is about three diameters of pipe, as 1, 11⁄4, and 11⁄2 inches. There are various other forms of adjustable pipe tongs, but most of them possess the disadvantage that the adjustable jaw hangs loosely, involving some extra trouble in placing them upon the pipe, because one hand must be employed to guide the loose jaw and adjust its position on the pipe. Fig. 2471 represents tongs of this class, the gripping size being varied by moving the jaw a upon b at the various notches. The end of b is serrated to afford a firmer grip upon the pipe. Fig. 2472 represents another adjustable pipe tongs, which is made in two parts, a straight lever a and hooked lever b, the former passing through a slot in the latter. The back of the straight lever is notched and a serrated fulcrum piece c is pivoted in the slotted lever by a pin upon which the lever b receives its support when the tongs are in operation. The fulcrum piece is provided with a spring which retains the serrated edge in proper position to engage the notches in the lever a. By means of the thumb piece d, the piece c can be moved in either direction to increase or diminish the gripping size of the tongs. When the tongs are open the lever a can be moved within the slot and adjusted so that the tongs will fit the pipe. The fulcrum piece c, being pivoted, allows the full length of its serrated edge to come into contact with the corresponding portion of the lever a, so that the parts always have a firm bearing and are subjected to an equal wear.
A common form of pipe tongs of this class is shown in Fig. 2473, b being pivoted to a by a pin, and changing to various holes in a to suit different diameters of pipe.
Erecting Pipe Work.—In erecting pipe work care must be taken to have it align as true as possible, as well as to have the joints tight enough to stand the required pressure without leakage. If the elbows, tees, or other fittings are not threaded true, a pipe[II-144] whose thread is not true with its axis may be selected or cut purposely to suit the error in the fitting, so as not to leave an unsightly finish to the job.
Suppose, for example, that in Fig. 2474, e is a pipe erected parallel to the wall, but that the holes in its elbows are tapped at an acute instead of at a right angle, then by cutting the thread on the end of pipe d untrue with its axis, its far end will rotate out of true as denoted by the shaded and by the plain lines, and all that will be necessary is to screw up the pipe sufficiently firm to make the joint, but to leave it in the position shown in the plain lines.
If the pipe tightens sufficiently before it has reached that position it may generally be eased by rotating it back and forth in the elbow with the pipe tongs. If this does not suffice, the pipe must of course be threaded sufficiently further along. To cut a pipe out of true to suit an untrue elbow, a very good plan is to cut the end of the pipe at an angle to its axis, which will cause the dies to cant over when starting the thread, but little practice being required to educate the judgment as to how much to do this to suit any given degree of error.
In erecting pipe it is best to begin at one end and screw each successive piece firmly home to its place before attaching another, so that the lengths of the pieces may be accurate and not vitiated by screwing them up and causing them to enter farther into the fittings. If it is probable that the piping may have to be taken down after erection, it should be put up at first screwed together rather tighter than will be necessary, as the thread fits become eased by being moved one within the other. This is especially the case with brass fittings, upon which it is best in cutting the lengths of pipe to have it of full length, as the threads will conform to each other sufficiently to cause the pipe to enter a thread or so farther if the pipe be rotated back and forth a few times in the fitting.
The fit should in all cases be made by tightness of thread fit, and not by the union or elbow face jambing against the end of the thread or the pipe, as joints in which this is the case will usually leak if used under pressure.
The thread of both the pipe and the fitting should be smeared with a thick lead paint. If the pipe is to be used as soon as erected, plain red lead and boiled oil should be used for the paint; but if it may stand a few days it is better to mix white and red lead in about equal quantities, as this, if given time to dry, makes a tighter job. The quantity of this paint should not be more than will thinly cover the threads, otherwise it will squeeze out when the pipes are screwed home, and falling from the end of the pipe within the fitting be apt to be carried by the steam or water to the valves, and getting between them and their seats cause them to leak. The iron cuttings should be carefully cleaned both from the pipe and the fitting for the same reason.
In cases where the piping may require to be used under heavy pressure as soon as erected, it is a good plan to use dry red lead in varnish, thoroughly hammering it to mix it well, and thinning it after it has been so hammered.
In case of emergency a loose pipe may be somewhat improved by wrapping around its thread a piece of lamp wick saturated with this varnish lead, beginning at the end of the pipe and wrapping the thread from end to end.
It is preferable that the stem of the valve stand nearly horizontal, so that any water of condensation may pass freely away with the steam and not collect and lie in the pipe as it does when vertical. If it be quite horizontal the water of condensation will drip through the stuffing box; hence it is better that it stand 10 or 12 degrees from the horizontal.
It is better in all cases to purchase nipples than to make them by hand, because when made in a machine the threads are more true to the axis than those made by hand; especially is this the case in short nipples in which there is not sufficient length to use the guide socket when engaged in threading the nipple with the hand dies.
It is a very good plan in making such short nipples to cut them off the end of a length of pipe that has been threaded by machine, and to screw on the threaded end a coupling. Into this coupling a piece of pipe may be threaded to afford a hold in the vice. If then the nipple is long enough, a guide to suit the size of the nipple may be used in the threading dies, or a guide socket to fit the diameter of the coupling may be used.
A globe valve should be so placed on the pipe that the pressure will, when the valve is closed, fall on the bottom face of the valve, so that the steam may be shut off while the valve stem is being packed.
Cotton lamp wick plaited to fit the packing space, and well oiled, is as good as anything to pack the stem with.
In taking old pipe down a refractory joint may be sometimes loosened by striking it with a hammer while it is under full pipe tongs pressure; or these means failing, the elbow or tee may be heated, which should be done as quickly as possible, so that the fitting may be hotter than the pipe. A very good method of doing this, where it is desired to save the fitting, is to pour red-hot lead over the fitting.
If it is not important to save the fitting, it may be split by a flat chisel, or by cutting a groove along it with a narrow cape chisel; or if the pipe is free the elbow may be rested on an anvil and hammered around its circumference, which will either free it or break it, if of cast iron.
When pipes are to be taken down and re-erected elsewhere they should all be marked to their fittings and places before being taken down, as this will preserve their lengths as near as possible for re-erection. Black japan is an excellent marking for this purpose because it dries quickly.
Re-fitting the Leaky Plugs and Barrels of Cocks.—When a cock leaks, be it large or small, it should be refitted as follows, which will take less time than it would to ream or bore out the cock or to turn the plug, unless the latter be very much worn indeed, while in either case the plug will last much longer if refitted, as hereinafter directed, because less metal will be taken off it in the re-fitting.
After removing the plug from the cock, remove the scale or dirt which will sometimes be found on the larger end, and lightly draw-file, with a smooth file, the plug all over from end to end. If there is a shoulder worn by the cock at the large end of the plug, file the shoulder off even and level. Then carefully clean out the inside of the cock, and apply a very light coat of red marking to the plug, and putting it into the cock press it firmly to its seat, moving it back and forth part of a revolution; then, while it is firmly home to its seat, take hold of the handle end of the plug, and pressing it back and forth at a right angle to its length note if the front or back end moves in the cock; if it moves at the front or large end, it shows that the plug is binding at the small end, while if it moves at the back or small end, it demonstrates that it binds at the front or large end. In either case the amount of movement is a guide as to the quantity of metal to be taken off the plug at the requisite end to make it fit the cock along the whole length of its taper bore.
[II-145]If the plug shows a good deal of movement when tested as above, it will be economical to take it to a lathe, and, being careful to set the taper as required, take a light cut over it. Supposing, however, there is no lathe at hand, or that it is required to do the job by hand, which is, in a majority of cases, the best method, the end of the cock bearing against the plug must be smooth-filed, first moving the file round the circumference, and then draw-filing; taking care to take most off at that end of the plug, and less and less as the other end of the plug is approached. The plug should then be tried in the cock again, according to the instructions already given, and the filing and testing process continued until the plug fits perfectly in the cock. In trying the plug to the cock, it will not do to revolve the plug continuously in one direction, for that would cut rings in both the cock and the plug, and spoil the job; the proper plan is to move the plug back and forth at the same time that it is being slowly revolved. As soon as the plug fits the cock from end to end, we may test the cock to see if it is oval or out of round. The manner of testing the cock is as follows:—
First give it a very light coat of red marking, just sufficient, in fact, to well dull the surface, and then insert the plug, press it firmly home, and revolve it as above directed, then remove the plug, and where the plug has been bearing against the surface of the cock the latter will appear bright. If, then, the bore of the cock appears to be much oval, which will be the case if the amount of surface appearing bright is small, and on opposite sides of the diameter of the bore, those bright spots may be removed with a half-round scraper.
Having eased off the high spots as much as deemed sufficient, the cock should be carefully cleaned out (for if any metal scrapings remain they will cut grooves in the plug), and the red marking re-applied, after which the plug may be again applied. If the plug has required much scraping, it will pay to take a half-round smooth file that is well rounding lengthwise of its half-round side, so that it will only bear upon the particular teeth required to cut, and selecting the highest spot on the file, by looking down its length, apply that spot to the part of the bore of the cock that has been scraped, draw-filing it sufficient to nearly efface the scraper marks. The process of scraping and draw-filing should be continued until the cock shows that it bears about evenly all over its bore, when both the plug and the cock will be ready for grinding.
Here, however, it may be as well to remark that in the case of large cocks we may save a little time and insure a good fit by pursuing the following course, and for the given reasons. If a barrel bears all around its water-way only for a distance equal to about 1⁄16th of the circumference of the bore, and the plug is true, the cock will be tight, the objection being that it has an insufficiency of wearing surface. It will, however, in such case wear better as the wearing proceeds. Plug and barrel being fitted as directed, we may take a smooth file and ease away very lightly all parts of the barrel save and except to within, say, 3⁄8 inch around the water or steam-way. The amount taken off must be very small indeed, just sufficient, in fact to ease it from bearing hard against the plug, and the result will be that the grinding will bed the barrel all over to the plug, and insure that the metal around the water or steam-way on the barrel shall be a good fit, and hence that the cock be tight.
The best material to use for the grinding apparatus is the red burnt sand from the core of a brass casting, which should be sifted through fine gauze and riddled on the work from a box made of, say, a piece of 11⁄2 pipe 4 inches long, closed at one end and having fine gauze instead of a lid.
A very good material, however, is Bath brick rubbed to a powder on a piece of clean board. Neither emery nor ground glass is a good material, because they cut too freely and coarsely, which is unnecessary if the plug has been well fitted.
Both the barrel and the plug should be wiped clean and free from filings, &c., before the sand is applied; the inside of the barrel should be wetted in and the plug dipped in water, the sand being sifted a light coat evenly over the barrel and the plug. The plug must then be inserted in the barrel without being revolved at all till it is home to its seat, when it should be pressed firmly home, and operated back and forth while being slowly revolved. It should also be occasionally taken a little way out from the barrel and immediately pressed back to its seat and revolved as before, which will spread the sand evenly over the surfaces and prevent it from cutting rings in either the barrel or the plug. This process of grinding may be repeated, with fresh applications of sand, several times, when the sand may be washed clean from the barrel and the plug, both of them wiped comparatively dry and clean, and the plug be re-inserted in the barrel, and revolved, as before, a few revolutions; then take it out, wipe it dry, re-insert and revolve it again, after which an examination of the barrel and plug will disclose how closely they fit together, the parts that bind the hardest being of the deepest colour. If, after the test made subsequent to the first grinding operation, the plug does not show to be a good even fit, it will pay to ease away the high parts with a smooth file, and repeat afterwards the grinding and testing operation.
To finish the grinding, we proceed as follows: Give the plug a light coat of sand and water, press it firmly to its seat and move it back and forth while revolving it, lift it out a little to its seat at about every fourth movement, and when the sand has ground down and worked out, remove the plug, and smear over it evenly with the fingers, the ground sand that has accumulated on the ends of the plug and barrel, then replace it in the barrel and revolve as before until the plug moves smoothly in the barrel, bearing in mind that if at any time the plug, while being revolved in the barrel, makes a jarring or grating sound, it is cutting or abrading from being too dry. Finally, wipe both the barrel and the plug clean and dry, and revolve as before until the surfaces assume a rich brown, smooth and glossy, showing very plainly the exact nature of the fit. Then apply a little tallow, and the job is complete and perfect.
In place of the tallow a soft paste of good beeswax and castor oil is an excellent application, the two being heated in order to thoroughly mix them.
The grinding material must be frequently changed to produce smooth work, because if the grinding cuttings accumulate in it, they will scratch and score the work. Indeed, it is a good plan when convenient, to hold the cock and plug under water while grinding them, and to occasionally lift the plug out, so as to wash out the cuttings.
The surface of a well-ground plug will be in all cases polished, and not have that frosted appearance which exists so long as active grinding is proceeding, and all that is necessary to produce this polish is to well work the plug in its barrel while keeping it quite clean.
Fitting Brasses to their Journals.—Brass bores always require fitting to their journals after having been bored, because the finished hole is not a true circle, but too narrow across the joint face, as at f in Fig. 2475, in which the full lines represent the form of the brass before, and the dotted line its form after being bored and released from the pressure of the devices or chuck that held it while it was being bored. This almost always occurs to a greater or less degree, and it arises from local strains induced from the unequal cooling of the casting in the mould, which strains are released as the metal is removed (in the process of boring) from the surface of the bore. It would appear, however, that if the finishing cut taken by the boring cutter be a very fine one it should leave the hole true and round, but the pressure which is placed upon the bearing to hold it against the force of the cut prevents[II-146] the bearing from assuming its natural form until released from that pressure.
If a bearing be bored to very nearly its finished size and first released altogether from the pressure of the holding chuck, or other device, and then re-chucked, it is probable that the finished bore would be practically quite round and true, but such re-chucking is not the usual practice.
Suppose, however, that the bearing shown in Fig. 2475, be properly fitted to a journal, still improper conditions arise from wear, because the area of the surface d becomes from the weight and from vibration condensed, and finally it stretches, causing the bore at f to close upon the journal and bind it with undue friction.
If the shape of the bedding part of the brass, or bearing, be such as shown in Fig. 2476, the surfaces a b and c will condense and stretch, closing the diameter of the bore at e and making the sides g g fit loosely in their places. It is to be observed that a similar condensation of the metal occurs to some extent around the bore of the bearing; but this surface is being continuously worn away by the journal, and it is, therefore, at all times less stretched and condensed than that on the bedding surface.
There is, therefore, a constant action causing the brass to bind unduly hard at and near its joint face e, Fig. 2476, and thus to cause heating and undue abrasion and wear. To prevent this it is necessary to ease away that part of the brass bore, as is shown in Fig. 2477 from j to k, clear of the journal.
But in the case of bearings receiving thrust, as in engine main bearings, the line of pressure is in a horizontal direction; and hence the most effective bore area to resist that pressure has been removed. Furthermore, the bearing area of the brass bore has been reduced, thus increasing the pressure per square inch on the remaining area.
The methods employed to avoid this evil are as follows:—In the form shown in Fig. 2478 the joint faces are at an angle instead of being horizontal and parallel to the line of the thrust, or the joint faces may be made to stand at a right angle to the line of journal thrust, so that the crown of the brass will receive the thrust. But the brasses will still close across the joint faces (as already described) as the wear proceeds, and the areas from j to k in Fig. 2477, must still be eased away, requiring frequent attention and giving a reduced bearing area. Furthermore, in proportion as the line of the joint faces of the brasses is at an angle to the line of thrust, the strain on the top or cap brass will fall on the bolts, so that if those joint faces be at a right angle to the line of thrust, the whole strain of that thrust will fall on the bolts that hold the cap and cap brass.
Another plan is to make the bearing in parts, as in Fig. 2479, in which the top and bottom parts of the bearing extend to the joint face on one side, but admit a chock or gib, a in the figure, which may be adjusted by a set-screw as shown. By this means the bearing area may extend all around the bore. In some cases two of such chocks and set-screws, one on each side of the journal, are employed.
In place of the set-screws, whose ends, from receiving the pressure of the thrust, are apt to imbed themselves into the chock and to thus loosen the adjustment, wedges lifted by bolts passing up through the cap, as shown in Fig. 2480, are employed, being preferable to the screws.
In the Porter Allen engine the wedges pass clear through the bearing, as in Fig. 2481, so that they may be pushed up after the manner of a key and their pressure against the side chocks judged independently of the nuts at the top.
In some designs the top and bottom parts of the bearing are free to move in the line of the thrust, and the side chocks or blocks alone are relied on to resist the thrust.
When the brasses are in two halves, they may be fitted so as to have a known degree of bearing pressure upon the journal, and the fit may thus be accurately adjusted, in which case they will wear[II-147] a long time before requiring re-adjustment. On the other hand when the side chocks are used the wear in the line of the thrust may be taken up as it proceeds. In one case the attending engineer cannot alter the fit of the bearing nor the alignment of the shaft, while in the other he can do both. Thus the facilities that enable him to make these adjustments properly also enable him to make them improperly. But this would be of no consequence, providing it could be determined whether the adjustment were improving the conditions without first making it. With an engine at rest it is easy to determine, by means of the connecting rod, whether the chock adjustment is correct, so far as the adjustment of the shaft is concerned, but it is not easy so to determine the pressure of the chock on the journal; nor when each chock has two adjusting screws is it easy to determine when they both bear alike.
When the bearing is in four pieces, and three of them have two screws each, it is still more difficult to operate all so as to have the bearing equal on the journal. The fit to the journal can only be determined by the results: if too easy, the bearing pounds; if too tight, the bearing heats and wears.
But undue wear may take place without heating, and this is one of the greatest objections to this method of adjustment.
A design of bearing used in American locomotive practice is shown in Fig. 2482. Here the joint faces c, b of the brass is bevelled, fitting into a corresponding bevel in the box, which prevents the brass from closing across the joint face; hence, the bearing on the journal may extend all around the brass bore from the oil cavity a to the edges b c. The brass is, in this case, forced to its place in the axle box under hydraulic pressure, and this pressure springs the box open at h, making it wider; but when the box is put to work the brass compresses somewhat, and its surfaces conform more closely to the bedding surface of the box than when first put in, and this causes the box to close slightly at h.
To prevent this closure from carrying the brass with it and close it across the joint face (as in the case of the brass shown in Fig. 2476) the following plan is adopted. The brasses, after having been turned in the lathe, are filed along the entire surface (on each side) for a distance of about 11⁄2 or 2 inches, so as to clear the bore of the box near the bevels b, c. When the box is put into the hydraulic press, to have the brass forced in, a centre-punch mark j is made, and part of a circle l l is struck; when the brass is home in the box the arc of circle k is made, the distance between k and l showing how much the box has been sprung open by the brass; the amount allowed is about 1⁄32 of an inch. If, as the brass is pressed in, it is found that this will be exceeded, it is taken out and eased. When the engine is running and the boxes spring to some extent they do not carry the brass with them, because the sides being eased away gives liberty to the box to come and go slightly; the bevels also tend to keep the brass bore open.
Here, then, the brasses may be fitted to align the axle perfectly, and it is not permitted to the engineer to alter that alignment, while at the same time the fit of the brass to the journal being made correct, the engineer cannot alter it. Under these conditions the whole area of the brass is effective in holding the journal, which increases the durability of the brass by keeping the pressure per square inch on the brass bore at a minimum.
If side chocks are used, however, it is better to set them up by wedges than by screw bolts, because from the tightness of the fit of such screws in the tapped holes, it is difficult to determine, with precision, with what degree of pressure the chocks are forced against the journal. Furthermore, the screws may not fit with an equal degree of tightness; hence, when screwed up with an equal degree of pressure, one end of the same chock may be set tighter to the journal than the other end, and any undue pressure of fit at either end tends to throw the shaft out of line as well as inducing undue wear. But when wedges are used to set up the side chocks the nuts operating those wedges may be an easy fit without fear of their becoming loosened (as set-screws in the line of thrust are apt to do).
On the fast engines of the Pennsylvania Railroad solid bronze boxes, without brasses, are used, and when the boxes require truing from having cut or from having worn oval they close them under a steam hammer, closing the bore across and enabling it to be trued out in the lathe without taking much metal out of the crown of the bore. The wedges and adjusting shoes are thickened when this becomes necessary by reason of the box closure or width.
If a brass bore does not bed fully and equally over the entire intended bearing area the part not fitting will at first perform no duty as bearing area, and the whole strain will be thrown upon a less area than is intended by the construction, causing undue abrasion until the brass bore has what is termed worn down to a bearing. The amount of this wearing down to a bearing may be so small as to be scarcely perceptible to ordinary observation, but if the oil that has passed through the journal be smeared upon stiff white paper, as writing paper, it will be found to contain the particles of abraded metal, which will be plainly distinguishable. Under these conditions the journal will have a dull, though perhaps a smooth appearance, and will not have that mirror-like surface which is characteristic of a properly fitted and smooth working bearing, while under a magnifying glass the journal will show a series of fine rings or wearing marks. It is necessary, therefore, that each brass be properly fitted to its journal so that it shall bed fairly and evenly over all the area of its bore that is intended to bear upon the journal.
The most expeditious method of fitting a new bearing box or brass to its journal is to first file the bore until it fits the journal when simply placed thereon by hand, and without going to the trouble to put the brass or the journal in position in the frame which holds them. So soon, however, as the crown of the brass beds to the journal along its whole length, the brass should be placed in its box, or in the frame, and the journal adjusted in its place and rotated so as to leave its bearing marks upon the brass bore, to assist which it may have a faint coat of red marking on its surface. The fitting should be continued both with file and scraper until the whole area of the part intended to bed fits well and is[II-148] smooth and polished. To produce this result the finishing should be done with a very smooth half-round file, draw-filing so as to leave the marks in a line with the circumference of the bore, and finally with a half round scraper, which will remove the file marks. The degree of contact should be such that, when the bearing is bolted up, brass and brass, as it is termed (which means that the joint faces of the brasses are held firmly together), the journal will rotate as freely as when the top brass is removed, while the contact marks on the top brass have been removed by scraping. By this means the fit will be just sufficient to permit the lubricating oil to pass between the journal and the bearing, and the journal will work freely and easily without any play, knock, or pound. If, when the top brass or bearing is bolted home and the shaft is rotated by hand, that brass on removal shows contact marks on its bore, although it may rotate comparatively easily it will be so tight a fit that the oil cannot pass, and as a result the wear, instead of producing a glossy surface, will produce a dull one, and undue abrasion will ensue even though no rings appear.
When brasses are held in rods that connect two journals together the fitting of the brass bore must be conducted with a view to have the brasses fit their journals all over the intended bearing area of their bores, which can only be accomplished by trying the brass bores to their journals while in the rod, in the manner to be hereafter described with reference to connecting rods and to lining engines.
When a journal is worn in rings, or so rough as to cause destructive abrasion and undue friction, it may be refitted as follows:—First, with a smooth file draw-file the journal in the direction of its length, taking off all the projecting rings. Then sweep a very smooth file that is somewhat worn (which will cut smoother than a sharp file) around the circumference of the journal so that the file marks will be in the plane of revolution. Then wrap a piece of fine and somewhat worn emery paper around the journal, and wrap around it (say twice around) a piece of coarse string, leaving the two ends about two feet long. Take one end of the string in each hand and pull first one end and then the other, causing the emery paper to revolve around the journal and smooth it.
To refit the bearings, first with a smooth half-round file remove the rings or rough surface, and then fit the surface with the file, so that when in its place the journal is rotated the contact marks show a proper bearing. Then draw-file the bore with a smooth half-round file and finish with a half-round scraper, easing away the high spots until the bore shows proper contact and is smooth. A piece of fine emery paper may then be wrapped around a half-round file and the surface smoothed with the emery paper moved across the bore and not in the direction of the circumference of the same. The emery paper should be well worn for the finishing and of a fine grade number, so as to leave a bright polish and not dull marks.
In some practice the bores of brasses are left rough-filed, the file marks being lengthways of the bearing of bore. If the journal requires smoothing it is draw-filed lengthways of the journal. The philosophy of this is, that the file marks will hold the oil and afford unusually free lubrication while the bearing and journal are wearing down to a bearing.
But where the framework holding the bearings and journals are rigid, these bearings and journals may, with care, be fitted to a polished and equal bearing, leaving a smoother surface than that produced by wearing down to a bearing. But if, as in the case of a locomotive, the framework is subject to torsion, rough surfaces left to adjust themselves are possibly better than those accurately fitted, because the whole framework holding the bearings changes its form when the full load is upon it and after put to work, and the fitting done when there was no load upon the parts is no longer quite correct. The lubrication of the bearing, however, should be very free, and the effort appears at present to be to afford more ample oil ways than hitherto even at some sacrifice of bearing area.
Lead-lined Journal Bearings.—If a journal is worn in grooves or undulations it becomes impracticable to properly fit the brass to it without reducing its diameter to remove the rings, and to obviate the cutting and heating which necessarily follow, as well as to obviate the necessity of fitting the brasses at all, Mr. D. A. Hopkins introduced lead-lined bearings; the lead lining being merely auxiliary to the bearing proper, which is made preferably of hard bronze, and to which the thin layer or facing of lead is firmly attached by a soldering process, so that the two metals are virtually one piece. Into this lead facing the journal, under the pressure of the car, moulds or imbeds itself from the start, and afterwards gradually wears its way through it into the hard metal. The perfect fit thus secured under all conditions of the journal, aided with proper lubrication, not only prevents heating, but secures the full wear of the brasses, and makes them at all times perfect counterparts of the journal surfaces.
Fig. 2483 shows at the top an unfitted bearing without the lead lining, resting upon a worn and badly-cut journal, the only points of contact being near the ends. For obvious reasons such a journal is sure to run hot.
The engraving below shows the application of the lead lining to the same journal, the dark shading between the journal and bearing representing the lead which has been pressed into the worn and hollow surface of the journal, forming a complete bearing and distributing the weight equally upon its surface.
Fig. 2484 represents an end view of an unfitted journal and the same lead lined.
The lead compresses until the brass meets the journal and thus permits between the two contact over the area that does fit or touch; while the lead fills the remaining area of the brass bore, giving it a bearing on the journal, thus relieving the touching points from receiving the whole weight of the load, and preventing the cutting or abrasion that would otherwise occur. As, however, the wear takes place the lead compresses, permitting the journal and brass to come into bearing over its full area, being obviously effective providing the bearing be kept free from grit, which would imbed in the bearing and cause it to unduly wear the journal.
If a brass is too tight a fit upon its journal, heating and abrasion, or “cutting” as it is termed, ensues. But if a brass or box does not fit close to its journal, lost motion and sometimes knocking[II-149] or pounding ensues. When the joint faces of brasses abut, or come brass and brass as it is termed, they should be a proper fit to the journal when they are keyed, or otherwise set up close together; hence there is no danger of either having a pound in the brass, or of heating and cutting. The objection to this plan is that the brasses must be removed from their boxes and the joint faces filed away to let the brasses together, to take up the wear; hence, in positions in which it is difficult to get the brasses out, the joints should be left open, while in all cases where they can be readily removed they should be made brass and brass.
It is to be observed that brasses that come brass and brass require less adjusting and last longer than those left open, because the latter often suffer from the abrasion due to an improper adjustment.
In brasses that are left open, it is not an uncommon practice to adjust the fit as follows: Between the brass joint faces at each of the four corners a piece of lead wire is inserted; the brasses are keyed as close home as can be upon the journals, which compresses the lead wire; the top brass is then released until the piece of lead wire can be moved freely between the brass joints.
A compromise between the brass and brass and the open joint is sometimes effected by the insertion of slips, as shown in Fig. 2485 at a, b. These slips may be taken out by simply removing the top brass, while their reduction of thickness lets the brasses together to take up the wear. The thickness for these strips may be readily obtained by means of the pieces of lead wire used as already described.
In the case of large brasses which come brass and brass, much of the filing on the joint faces to let them together may be saved by reducing their thickness and area by cutting away part of the metal, as at a a in Fig. 2486.
To enable the removal of bearings for renewal, or to refit them without taking the shaft out, various forms of construction are employed, of which Fig. 2487, which shows a main bearing, is an example.
Thus, when the cap is removed the side chocks, or gibs as they are sometimes called, can be lifted out by eye-bolts screwed into the holes at c; the weight of the shaft can then be sustained while the bottom piece d is removed.
A great deal of trouble in fitting journals and bearings may be avoided if the best conditions are observed in their manufacture. If, for example, the conditions of casting are uniform, and the diameter of the bearing bore and journal bores are constant, that is to say, when a great number of pieces are to be bored, the amount the bearings will close across the joint being definitely determined, the conditions of boring may be made such as to allow for the closure, and the fitting in this respect may be facilitated; but this applies to small bores only, as, say, three inches and less in diameter, because in larger diameters there will be sufficient variation in the amounts of contraction across the joint face to render it necessary to fit to some extent at least the bores to their journals.
In some cases slips of paper are placed between the joint faces of the bearings, or if the joint faces do not meet, slips of brass may be placed between them; or again the conditions of chucking or holding the bearings to bore them may be such as to hold them a certain amount farther apart than they will require to be when on the journal. The bore is then made sufficiently larger than the diameter of the journal that it will be as nearly as possible round after being removed from the boring machine, and will bed down fairly upon the journal without being fitted with a file, which saves considerable labor. But unless the bearings are so held as to be to some extent self-adjusting for alignment, there is liability of the axis of the bore not being quite true with the axis of the journal, the amount being so small as to escape detection save by trial for fit with the shaft, and the bearings in their respective positions. It is a difficult matter, in the absence of special holding devices, to chuck a bearing, especially if a long one, so true in a boring machine or lathe as to insure that its bore shall stand in absolutely correct alignment with the journal when placed in its position in the framing where it is to operate, and it is for this reason that many bearings are bored while in their frames. In some cases, however, this difficulty is overcome by so constructing the bores and the pieces holding them that the boxes may swivel and adjust themselves, as in the case of the bearings of line shafting.
Examples of the oil cavities for bearings are given as follows:—
For journals of small diameter oil cups screwing into the bearing cups, with feed-regulating devices, are generally used, and the same are used in the case of two half-brasses. But if the journals are of large diameter, as, say, 5 inches or more, oil receptacles are often cast in the caps.
In the absence of side chocks in the bearing all the oiling usually proceeds from the top, save perhaps that an oil groove may be provided in the crown of the bottom brass.
Fig. 2488 represents a bearing lubricated from the top and bottom; thus in the cap is an oil cup or cavity from which passes nearly down to the bearing a brass tube containing cotton wick, which slowly feeds the oil to the bearing.
Fig. 2489 represents this tube and wick removed from the bearing. This plan of feeding is largely used on marine engines and on locomotives. When used upon stationary bearings the[II-150] cotton wick need not fill the tube, but if used on reciprocating parts it should fill so that the oil may not spill over and pass too freely down the tube. In either case, however, it is desirable to twist in the cotton a piece of fine copper wire, and bend the ends over the top of the tube to keep the wick in place in the tube.
The bottom of the bearing, Fig. 2488, is provided with an oil cavity and a similar tube and wick. Usually, however, the oil is fed in at the top only, except in the case of locomotives, because in them all the weight falls on the top brass; hence, the bottom may be utilised as an oil receptacle. In English locomotive practice this receptacle as a rule merely catches the oil that has passed through the bearing box, but sometimes a roller is inserted and forced against the journal by springs so as to rotate, by friction, with the rotating journal.
The bottom of the roller runs in oil so that the roller feeds the journal with oil, but ceases to feed when the journal ceases to rotate, an advantage not possessed by self-feeding oil cups, or by the cotton wick syphons shown in Fig. 2489.
The oil ways or oil grooves are usually provided in small journal brasses as follows:—
It is obvious that if the joint faces of the brasses are left open and oil be supplied to one brass only, a great part of the oil supplied will pass out between the joint faces before reaching the other brass, and one brass will therefore be better lubricated than the other, unless each brass be lubricated independently. Even in this event, however, a great part of the lubricating material will be lost from finding rapid egress through the opening of the brasses. This may be to some extent prevented in brasses whose joint faces lie horizontally by chamfering the edges of the bore so as to form a trough extending nearly to the ends of the brass, as shown in Fig. 2492. Now it is obvious that the oil hole must always be above the journal or bearing bore; hence when the joint faces stand horizontal, the oil hole should come through the crown of the brass, and oil grooves are necessary to convey and distribute the oil along the bore. A single groove, as in Fig. 2490, is sufficient for light duty, but for heavy duty a double groove, such as shown in Fig. 2491, is necessary.
When, however, the joint faces stand vertically and come brass and brass, the oil hole may be filed half in the joint face of each brass, and the edges chamfered off as in Figs. 2492 and 2493, a b representing the chamfers and c the oil hole, the two brasses put together appearing as shown in section in Fig. 2493.
This plan has the advantage that the oil is confined within the journal, except in so far as it may in time work through the ends of the journal bore, while there are two oil grooves provided without reducing the bearing or bedding area of the brass. When the oil grooves run diagonally, as in Fig. 2491, there is the advantage that the length is greater, and lying nearer to the plane of rotation the oil flows along the grooves easier, being assisted by its frictional contact with the journal, but on the other hand the bearing area of the brass on the journal is so much the more reduced.
Oil holes that are not provided with oil cups should be provided with small wooden plugs, which will serve to keep the dirt and dust out; they should be made of as small diameter as the quantity and nature of the lubricant to pass through them will admit of, and should be left plain at the top and not countersunk, because the countersinking simply forms a dish that will collect dust, &c., which the oil applied will carry down into the bearing.
In some cases there is provided an oil dish around the oil hole, and this dish is filled with tallow that will not melt under the normal temperature at which the brass is supposed to operate. But if from defective oil lubrication or other cause the bearing begins to heat, the tallow will melt, and flowing through the oil hole afford the needed lubrication.
It is to be observed that the lubrication of a bearing in which the pressure is moved alternately from one half of the bearing to the other is far easier to attain, and more perfect, than in one in which the direction of the journal pressure is constant, because in the latter case the journal pressure acts to squeeze out and exclude the oil continuously, whereas when the pressure is relieved alternately on each brass, the oil has an opportunity to pass back[II-151] between the relieved surfaces. Again the lubrication is more perfect when the direction of the journal motion is periodically reversed, as the passage of the oil through the bearing is retarded by the motion, and yet again the abrasion is reduced because, as stated when referring to rotating radial surfaces, the particles of metal abraded add themselves together and form cutting pieces when the motion is continuous in one direction, whereas in a reversing motion the particles are kept separated and flow out more freely with the oil that passes through the journal.
If a shaft having a continuous direction of rotation be given end play so that while rotating it may move endwise, the particles abraded are again kept separated, and the conditions of lubrication are such as to give a minimum of wear, because the formation of fine rings or serration is avoided, the end motion serving to cause the wear to smooth the surfaces.
When a shaft has a collar, that is subject to end pressure, the oil way may be carried up the face of the collar as in Fig. 2494 at b. So also where very free lubrication is required, an oil groove may also be cut in the journal itself, as at c in the figure. This plan is adopted by some American engineers upon the crank pins of steam engines, the grooves being cut on diametrally opposite sides of the pin in a line with the throw of the crank.
Referring now to the oil itself, it is generally conceded that a pure sperm or lard oil is equal to any that can be used for general journal lubrication, but the ordinary purchaser has no means of knowing if the oil is pure. The requirements of an oil for lubricating purposes are given in the following paper on testing the value of lubricants, which was read by Mr. W. H. Bailey before the Manchester (England) Institution of Employers, Foremen and Draughtsmen:—
“A fact in connection with oil and lubrication is probably about as difficult a thing to describe as anything which agitates the minds of engineers and mechanical men. We appear to have very little published information on the subject, except that which describes the labors of Morin, of France, about forty years ago, and that which has been given to us by Professor Rankine more recently in this country. Those investigators who preceded Morin do not appear to have published information of very much value, or which can be used with profit for the discussion of lubricants, for their researches have been more concerning the proportions of bearings, and the value of different materials of construction, rather than the value of different lubricants.
“At the present moment so little is known generally concerning the performance of different oils, that the public are much at the mercy of the vendors of these oils, who can make almost any assertion they like without fear of contradiction.
“The valuable discoveries of our distinguished townsman, Dr. Joule, have enabled us to look upon the cost of friction and the cash value of heat as mere questions of arithmetic. Dr. Joule’s investigations have been put into such forcible and elegant English by Professor Tyndall, and other students of the science of force, as to cause us to understand that when friction is produced heat is lost, and that all energy thus wasted passes away in this heat, which may be measured and valued with nearly as much facility as any article of commerce. We may gather from this knowledge, when we apply it to workshop economy, that if a pedestal or bearing becomes so hot through friction as to cause 1 lb. of water to be raised only one degree Fahrenheit in temperature in one minute, that heat has been lost equal to that which would be created by a weight of one pound falling through a space of 772 feet. We are told that if we apply this conversely, that heat has been lost which would lift 1 lb. weight 772 feet; and if we apply these illustrations still further, and imagine forty-two pedestals or bearings losing heat by friction in a similar manner, we may inform ourselves that we are losing nearly 1 horse-power, because they represent 32,424 foot-pounds of force; and if we know from our books what our coal costs, it will take very little trouble to give us the exact cash value of this friction and destructive action.
“What is friction? It may be described as the effect produced by two bodies sliding one upon the other, which have upon their opposing surfaces minute asperities, which interlock with each other. The sliding movement which forcibly removes these minute irregularities creates what we call friction. Friction is reduced when these asperities are small, and lubrication is resorted to to prevent that loss of power caused by motion under these conditions. The chief lubricants used are oil and tallow, which have a less coefficient of friction than the parts in contact. It may be well now to state that the term ‘coefficient of friction’ is an expression which indicates the proportion which resistance to sliding bears to the force which presses the surfaces together. There is little friction when this amounts to only one-twentieth, it is moderate when it is one-tenth, and it is very high when it is a quarter or twenty-five per cent. of the force which presses the surfaces, together, as I before said.
“Qualities of Lubricants.—Good lubricants should have the following qualities: (1) Sufficient body to keep the surfaces free from contact under maximum pressure. (2) The greatest possible fluidity consistent with the foregoing condition. (3) The lowest possible coefficient of friction. (4) The greatest capacity for storing and carrying away heat. (5) A high temperature of decomposition. (6) Power to resist oxidation; or in other words, the influence of the atmosphere upon them. (7) Freedom from corrosive action on the metals upon which they are used. It will thus be seen that many conditions have to be carefully taken into consideration; and further, it may be stated that an oil which may be good for heavy bearings may not be desirable for use on light spindles, and for delicate machinery like clocks and watches, where very little power is required to be transmitted beyond that of overcoming their own inertia; and also that oil which is good for small machinery running at quick speeds is very often useless for heavy pressures and large shafting. For very heavy bearings tallow and other solid lubricants are used, such as mixtures of sulphur and tallow, asbestos, soapstone with asbestos, graphite, caustic soda, beeswax, and other similar mixtures, which find favor among locomotive engineers and those in charge of heavy machinery. The pressure that can be borne by a good lubricant for a useful length of time depends upon the nature of the bearings as well as upon the lubricant itself. The velocity of the rubbing action also must be taken into consideration. The maximum of pressure that solid lubricants will bear without destruction is unknown. For steel surfaces, lubricated with best sperm oil moving slowly, 1,200 lbs. pressure per square inch of bearing surface has been found permissible. Under the pivots of swinging bridges several thousand pounds per square inch have been found to work, and for iron journals 800 lbs. per square inch should not be exceeded.
“Lubricants in the market vary much in cost as well as in quality, and very often it is found that the varying prices bear little or no relation to the value of the article purchased. Probably the best test of value is one with which I was familiar some years ago. It consisted of a small engine very much overworked, which stopped and refused to move or go at the proper speed if the shafting had not been lubricated with good oil.
“Testing by Destruction.—The instrument here illustrated, in Figs. from 2495 to 2501, to which I call attention, consists of a bed-plate, having upon it a piece of shafting upon which friction is created by means of two brass steps, the speed at which it is driven being about 300 revolutions per minute. The friction is brought to bear by levers and weights somewhat after the manner of a friction brake as shown in Figs. 2495 and 2500. In the top step is a thermometer for indicating any increase of temperature [II-152] caused by the friction. A small index indicates the number of revolutions that the shaft makes for any given temperature which the friction causes the thermometer to indicate. The machines used for testing oil have the friction shaft where the oil is destroyed three inches in diameter. Those for tallow are of larger dimensions. It will be seen that on ascertaining the number of revolutions which may be obtained without generating heat, or with the lowest possible increase of heat, that the value of the oil can be obtained. That oil which allows the greatest heat to accumulate with the fewest revolutions must be a bad lubricant. This tabular method of keeping an account of experiments has been found useful. The machine is stopped when the thermometer indicates 200 degrees, as it is considered that an oil has not much lubricating power left if it permits that heat.
| Name of oil. | Price. | Revolutions to 200 degrees F. |
Temperature of atmosphere. |
No. of revolutions to each degree. |
“When testing with this machine a definite quantity of oil should be placed on the friction roller, the top step being removed for that purpose; the quantity should be about five drops. A glass tube or small tin measure should be used, as drops vary in size according to the temperature of the oil, and also differ with the specific gravity. The inventor of this machine is Mr. Heinrich Stapfer. I believe he may be considered the inventor of the first instrument for testing oils by destroying them by friction under the actual conditions in which oils are used as lubricants. In using this machine I found that, although it was supposed to test lubricants in the way in which they are used in manufactories, a slight difference existed, which prevented accurate results.
“Behavior of Thin Oils.—The first machines were made with the brass steps lipped or recessed, to prevent the oil running away, (see Fig. 2496), which, when thus tested, gave results very much different to those which are accepted by those who are familiar with the use of lubricants. For instance, some thin mineral oils were found to be quite as valuable as, and in some cases superior to, sperm; and this was caused by the lips on the sides, which prevented the oil from running off the bearing when an increased fluidity was caused by friction, and by any slight elevation of temperature. This is a very important quality in lubricating oils, probably next to the capacity to resist oxidation, the most important to be criticised by those who wish to value a lubricant. Although this experiment points out to us that it may be advisable to make the journals of heavy bearings similar to these, if we wish to obtain the best results from cheap thin oils, yet, as oil should be criticised and prepared to be used on bearings with parallel necks, such as are used in works, it was considered proper to alter the tester to that shape to make the conditions similar. This illustration (see Fig. 2497) permits the oil when tested to run away from the bearing if its increased fluidity gives it a tendency to do so. It is this severe test which has enabled sperm oil to rise superior to all rivals, because it has these two apparently opposite attributes—body or thickness, which keep it on its bearing, combined with sufficient fluidity for lubricating purposes. Permit me further to illustrate what I mean in another manner. Suppose we take an oil, good as a lubricant in all other respects, and place it on a bearing, and that 40 per cent. works quickly away because of its extra fluidity when subjected to an increase of frictional temperature, and then compare it with another oil under similar conditions which only wastes, say, 5 per cent. This latter will be 35 per cent. superior as an oil having body, and even if slightly inferior as a lubricant, it may be the most valuable, because strong in this one great quality of remaining at its duty when placed in position. Still another illustration will inform us that in the one case we obtain, say, 60 gallons of lubricating material out of every 100 purchased, and in the other we obtain 95 gallons.
“The Best Methods of Using Thin Oils.—This will show us that oils which are deficient in body, but which are good in other respects, may be used with good results if doled out in small quantities, as required, by automatic oil-cups like the Lieuvain needle lubricator, Fig. 2498, or any other means. Journals which cannot be fed by means of automatic oil-cups in positions difficult of access should be fed with oil which has a good body. If time permitted, much might be said of the proper shape for bearings of machinery—a subject which would lead to valuable results if discussed by the members of this Society, many of whom must have great experience of those designs which have produced the best results, as well as of those mixtures of metals which are the most durable for light high speed and heavy slow shafting. If any member will take up this subject, or if several members will read short notes, giving their actual experience of different sorts of footsteps, pedestals, and spindles, as well as of the use of different sorts of oil-cups and lubricators, it will be highly advantageous knowledge, which must be of great value to all who use machinery.
“Fluidity of Oils.—Continuing my remarks on the thinness or fluidity of oils, I wish to call attention to an ingenious arrangement for testing the fluidity when subject to a slight increase of temperature, and also for detecting any tendency which they may have for combining with the oxygen of the atmosphere; this latter quality being advantageous in oils which are used to mix with paint, but which is a great evil when used for lubricating purposes. A piece of plate-glass placed at an angle is made warm to 200° Fahr. A drop of oil when placed on the upper end of this glass will flow down a few inches and thus indicate its fluidity when subjected to increase of temperature. Fig. 2499 shows a ready method I have designed for testing oil in this way. It consists of a tin box in which is fixed the glass, through which can be seen a thermometer. A graduated scale at the side of the box enables the track of the oil to be measured. The box has a door at the back which enables a copper vessel full of boiling water to be introduced; the box is lined with felt to prevent rapid radiation, and when the door is closed it will be seen that several experiments may be conducted before the apparatus becomes too cool for use. I think this a cleaner way than using a lamp for the purpose. The copper may also be used by itself for indicating [II-153] the behavior of oil on copper when slightly warm in making it discolored or otherwise. As I have before stated, there are many oils which are good lubricants, but which become too thin when exposed to slight heat, and I do not hesitate to reiterate the statement, as I wish to have some influence on the future designs of bearing in this district. A correspondent writing to Engineer from Queensland says that for six months in the year oil runs off the machinery like water and seems to have no lubricating power; he says that the thermometer registers in the summer 140° in the sun, and 110° in the shade. Great difficulty seems to have been experienced by him in keeping oil on the bearings; his experiments on locomotives show that it costs for lubricating a locomotive there about a halfpenny to three farthings a mile, according to the mixture used.
“Influence of the Atmosphere on Oils.—There are some oils which are excellent lubricants for the first few hours of use, but which have a low capacity for resisting the influence of the oxygen of the atmosphere upon them. The warm glass test may be used for indicating this weakness. If after the test for fluidity the oil be permitted to remain on the glass any exhibition of a resinous or varnish quality may be observed. Another test for this resinous or gummy quality is one which has been suggested to me by Mr. F. R. Wheeldon, of Bilston. He has made many experiments. He found that by permitting oil to remain on a Stapfer friction tester after one test which had been recorded, he tested again on the following day, without adding any fresh oil. This is a severe test, as the thermometer was made to indicate 200° Fahr. each time.
“Longevity of Lubricants.—Supposing an oil to possess all the qualities which we think a good lubricant should have—that it has fluidity in season, and that it does not combine with the atmosphere and become varnish, that it does not become like water in summer and like mutton suet in winter, and is in most respects satisfactory. We then want to know its powers of endurance, its capacity to resist wear and tear—in other words, its longevity. A good test for longevity or durability of oil when subject to either heavy or light frictional pressure is one suggested by Mr. W. H. Hatcher, a very careful investigator, and chief of the Laboratory of Price’s Patent Candle Company, who are extensive oil manufacturers. It consists in taking away the bottom step of the Stapfer tester and placing a small dish containing oil underneath the friction roller (as in Fig. 2500). This oil is carefully weighed before and after several hours’ frictional wear and tear. The drawing (Fig. 2501) shows the application of this mode, which I have designed, for testing solid lubricants, such as lard and sulphur and other railway and steamship mixtures. It will be seen that the material is kept to its duty by the weighted lever, and its progress of diminution can be tested in its place by the scale-beam arrangement. When it is used with the pressure on the top step it is advisable to drive it at about 2,000 revolutions per minute; otherwise much time will be occupied in destroying a weighable quantity of oil. The large Stapfer tester (Fig. 2502) was designed a few months ago for this purpose for the Government railways of New South Wales, and it is also used by the Manchester, Sheffield, and Lincolnshire, the Lancashire and Yorkshire, and other railways. I have not been able to get any results of these tests in time for our subject on this occasion, but hope to do so at some future time. The frictional roller is 6 inches in diameter, the pressure amounts to 1 cwt. on each step. As it takes a considerable time to wear away half a pound of solid lubricant, it may be advisable to measure by minutes instead of using the speed index. The speed should be at least 1,500 revolutions per minute. The Stapfer tester should be used in a room of equal temperature, and should not be subject to draughts of cold air, as it will be obvious these will interfere with the indications of the thermometer. A recent alteration in the Stapfer tester permits the quantity of oil used for testing to be measured with greater accuracy than before. A small oil-hole is made in the top step (see Fig. 2502 at a and at c) in which is placed a glass tube. This only holds a few drops, and can be filled by simply dropping the oil in, holding the finger at the bottom to prevent it running away, and then place it in the hole. If a small needle lubricator be weighed and then filled with oil of a definite weight, and placed in this hole (see Fig. 2502 at b), oil may be tested for longevity and for its anti-frictional properties for a longer period than with the small tube. If oil be placed in this at the same time that oil is placed in the lubricators in the works and the oil tester be driven from the same shafting, permitting it to stop and start when the engine stops and starts, the effect of a week’s work upon the weight of the oil may be seen; notice should be taken of the difference of the temperature between the thermometer on the instrument and the temperature of the atmosphere of the workshop.
| VOL. II. | OIL-TESTING MACHINE. | PLATE X. |
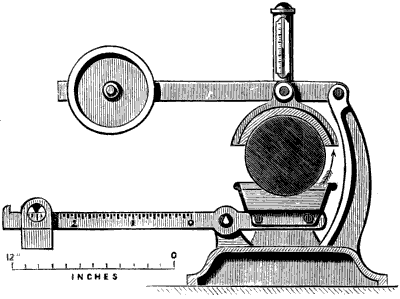 |
||
| Fig. 2501. | ||
|
Large image (213 kB). 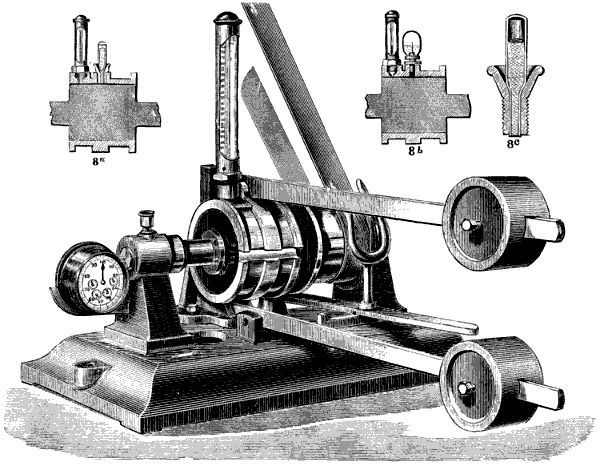 |
||
| Fig. 2502. | ||
“Testing for Salts and Acids, etc.—It will be obvious that however good as a lubricant an oil is, and however valuable its properties may be when examined, if it possesses any corrosive quality which will be injurious to the metals upon which it is placed, it will soon become detrimental to the machinery, and may also cease to be valuable as a lubricant. Mr. William Thomson, analytical chemist, of Manchester, read a paper on this subject at the British Association at Glasgow, and he stated the results of elaborate experiments conducted by him to discover the influence of various oils of commerce upon bright strips of copper. He permitted the copper strips to remain entirely covered by oil. He also conducted similar tests with half of the strip below the surface of the oil, and the other half exposed to the atmosphere, in order to see what influence the oil had, when the surface line touching the metal would, of course, be acted on by the atmosphere. After noticing the effect upon the brightness or dulness of the copper, he carefully tested the oils in order to detect the quantity of metal which had been dissolved. Mr. Thomson found the following oils dissolved the largest proportions of copper, leaving the surfaces of the copper slips bright—rape, linseed, sperm, raw cod-liver, Newfoundland cod, and common seal oils; and that the following dissolved much smaller proportions of copper, also leaving the slips bright—seal, whale, cod, shark, and East Indian fish oils; and that mineral oils seem to have no dissolving power on the copper, the only effect being a slight discoloration on the copper slip of a greyish color.
“Swiss Watchmakers’ Test for Fluidity and Capacity to Resist Cold.—It seems, according to the Watchmaker and Jeweller (a monthly trade journal), that the plan I have described, and what may be called the warm glass test, seems to be looked upon with favor for testing oil in Switzerland. The degree of[II-154] heat used for testing the fluidity of oil is 200° Fahr., and if this causes the oil to become a varnish two or three days after the test the oil is considered unfit for use. Another test is one to which I have not alluded, and that is, capacity to resist low temperatures. Oils are tried for their capability to withstand low temperature in the following manner: Fifteen parts of Glauber salts are put into a small glass vessel, a small bottle of oil to be tested is immersed into this; this done, a mixture of five parts of muriatic acid and five parts of cold water is placed over the salt. By means of a thermometer the temperature is indicated, and when it shows a very low temperature, the behavior of the oil, subject to this freezing mixture, may be observed and noted. Mr. Thomson, however, considers that this mixture is not so good or so cheap as ice alone, or a mixture of ice and common salt.
“Blotting-paper Test.—It seems it is considered that the blotting-paper test for fluidity is more reliable, according to the writer of the article, than the inclined plane experiment. In order to use this test we must saturate the strip of blotting-paper with oil, and watch whether the drops fall off in pearls or have an inclination to spread out. The latter is a certain sign, the writer says, of a viscid oil. Although this may be considered viscid oil, and may not be valuable for watches, it may, however, be a good oil for heavier machinery.”
The amount of friction between a journal and its bearing varies with the kind of metal of which the journal and bearing are composed; on the area of surface in contact in proportion to the load or pressure sustained by the bearing surfaces; on the nature or degree of the lubrication afforded; on the diameter of the journal in proportion to its length; on the manner in which the journal fits or beds to its bearing, and on the kind of motion, as whether the same be continuous, intermittent, rotatory, or reciprocating.
Referring to the friction as influenced by the nature of the metals in contact: the friction varies with the hardness of the metal; thus, with hard cast iron, there will, under equal conditions, be less friction than with soft cast iron. The friction is greater when the surfaces in contact are both of the same metal than when they are of different metals. Mr. Rankine summarizes General Morin’s experiments on the friction of various bodies not lubricated as follows:—
| Surfaces. | Angle of repose. |
Friction in terms of the weight. |
|||||||||
| degrees. | |||||||||||
| Wood | on | wood, | dry | 14 | to | 26 | 1⁄2 | .25 | to | .5 | |
| „ | „ | soaped | 11 | 1⁄2 | „ | 2 | .2 | „ | .04 | ||
| Metals | on | oak, | dry | 26 | 1⁄2 | „ | 31 | .5 | „ | .6 | |
| „ | „ | wet | 13 | 1⁄2 | „ | 14 | 1⁄2 | .24 | „ | .26 | |
| „ | „ | soapy | 11 | 1⁄2 | .2 | ||||||
| „ | elm, | dry | 11 | 1⁄2 | „ | 14 | .2 | „ | .25 | ||
| Hemp | on | oak, | dry | 28 | .53 | ||||||
| „ | „ | wet | 18 | 1⁄2 | .33 | ||||||
| Leather | on | oak | 15 | „ | 19 | 1⁄2 | .27 | „ | .38 | ||
| „ | metals, | dry | 29 | 1⁄2 | .56 | ||||||
| „ | „ | wet | 20 | .36 | |||||||
| „ | „ | greasy | 13 | .23 | |||||||
| „ | „ | oily | 8 | 1⁄2 | .15 | ||||||
| Metals | on | metals, | dry | 8 | 1⁄2 | „ | 11 | 1⁄2 | .15 | „ | .2 |
| „ | „ | wet | 16 | 1⁄2 | .3 | ||||||
| Smooth | metal | surfaces | occasionally greased | 4 | „ | 4 | 1⁄2 | .07 | „ | .08 | |
| „ | „ | „ | continuously greased | 3 | .05 | ||||||
| „ | „ | „ | best results | 1 | 3⁄4 | „ | 2 | .03 | „ | .036 | |
| Bronze on lignum-vitæ, constantly wet | 3 | (?) | .05 | (?) | |||||||
“The ‘angle of repose’ given in the first column is the angle which a flat surface will make with the horizon when a weight placed upon it just ceases to move by gravity. The column of ‘friction in terms of the weight’ means the proportion of the weight which must be employed to draw the body by a string in order to overcome its friction, and the proportionate weight is sometimes called the coefficient of friction.”[34]
[34] From Bourne’s “Handbook of the Steam Engine.”
In the following table are given some of the results obtained from Morin’s experiments with unguents interposed.
| Nature of surfaces in contact. | Coefficient of friction during motion. |
Kind of unguent. |
|||
| Brass upon brass | .058 | Olive oil. | |||
| Cast | iron | upon | brass | .078 | „ |
| „ | „ | „ | cast iron | .314 | Water. |
| Steel | upon | cast iron | .079 | Olive oil. | |
| „ | „ | brass | .056 | Tallow or olive oil. | |
| Wrought | iron | upon | brass | .103 | Tallow. |
| „ | „ | „ | cast iron | .066 | Olive oil. |
| „ | „ | „ | wrought iron | .136 | „ |
Morin’s experiments demonstrated that friction is always proportional to the pressure and independent of the area pressed in contact, providing that the pressure is not so great as to cause the surfaces to abrade in the manner or to the degree commonly known as cutting, which occurs when the area of bearing surface in proportion to the pressure is so small as to press out the lubricating material.
Now, between the degree of abrasion that is sufficient to cause a bearing to heat and the minimum, possibly lies a wide range that is very difficult of classification, and that influences the friction of the bearing and journal. Under any given dimensions of journal area and any given pressure of the same to its bearing, the abrasion, and, therefore, the friction, will be less in proportion as the fit of the journal to its bearing extends over its whole area and with an equal pressure of contact. Under these conditions, and with a bearing area ample for the given pressure, the surfaces of a journal and bearing have a smooth, glossy appearance, with a surface as glossy as plate-glass.
This degree of perfection, however, is only occasionally reached in practice, because of imperfections in the fitting and lubrication.
Now, between this condition of glossy smoothness and the degree of abrasion known to practical men as cutting lies, as already stated, a wide range of degrees of abrasion, and each of these has its own coefficient of friction. This may be readily proved by freely lubricating the bearings of a number of journals working under the usual conditions of practice and smearing the oil just as it passes through the bearings upon a sheet of white note paper, when it will be found to contain fine particles of metal, the number and size of particles in a given quantity of the oil decreasing as the surfaces of the bearings are glossy, and increasing as those surfaces appear dull.
The order of value to resist wear is generally considered in practice to be as follows:—
1st in value, hardened steel running on hardened steel.
2nd (and by some considered equal to the first when the pressure per square inch of area is light), cast iron either upon cast iron, hardened wrought iron, or hardened steel.
3rd, under light duty cast iron upon wrought iron or steel not hardened.
4th, wrought iron upon hard composition or brass.
5th, wrought iron upon some anti-friction metal, as Babbitt metal.
Cast iron appears to be an exception to the general rule, that the harder the metal the greater the resistance to wear, because cast iron is softer in its texture and easier to cut with steel tools than steel or wrought iron, but in some situations it is far more durable than hardened steel; thus when surrounded by steam it will wear better than will any other metal. Thus, for instance, experience has demonstrated that piston-rings of cast iron will wear smoother, better, and equally as long as those of steel, and longer than those of either wrought iron or brass, whether the cylinder in which it works be composed of brass, steel, wrought iron, or cast iron—the latter being the more noteworthy, since two surfaces of the same metal do not, as a rule, wear or work well together. So also slide-valves of brass are not found to wear so long or so smoothly as those of cast iron, let the metal of which the seating is composed be whatever it may; while, on the other hand, a cast-iron slide-valve will wear longer of itself, and cause less wear to its seat, if the latter is of cast iron, than if of steel, wrought iron, or brass. The duty in each of these cases is light; the pressure on the cast iron, in the first instance cited, probably[II-155] never exceeding a pressure of ten pounds per inch, while in the latter case two hundred pounds per square inch of area is probably the extreme limit under which slide-valves work; and what the result under much heavier pressures would be is entirely problematical.
Cast iron in bearings or boxes is found to work exceedingly smoothly and well under light duty, provided the lubrication is perfect and the surfaces can be kept practically free from grit and dust. The reason of this is that cast iron forms a hard surface skin when rubbed under a light pressure, and so long as the pressure is not sufficient to abrade this hard skin, it will wear bright and very smooth, becoming so hard that a sharp file or a scraper made as hard as fire and water will make it will scarcely cut the skin referred to. Thus in making cast-iron and wrought-iron surface plates or planometers, we may rub two such plates of cast iron together under moderate pressure for an indefinite length of time, and the tops of the scraper marks will become bright and smooth, but will not wear off; while if we rub one of cast iron and one of wrought iron, or two of wrought iron, well together, the wrought-iron surfaces will abrade so that the protruding scraper marks will entirely disappear, while the slight amount of lubrication placed between such surfaces to prevent them from cutting will become, in consequence of the presence of the wrought iron, thick and of a dark blue color, and will cling to the surfaces, so that after a time it becomes difficult to move the one surface upon the other. If, however, the surfaces are pressed together sufficiently to abrade the hard skin from the cast iron, a rapid cutting immediately takes place, which is very difficult to remove.
To obtain the best results from cast-iron bearings the bedding of the journal to the bearing must be full and perfect, and the surfaces bright and smooth, in which case it will wear better than hardened steel, unless it be very heavily loaded.
Again, a cast-iron surface will hold the lubricating oil better than either steel, wrought iron, or brass of any kind. Indeed, if a cast-iron surface be made very true and smooth so that it is polished and no marks are visible upon its surface, it will take much patient rubbing and cleaning with a dry clean rag to remove the oil entirely, whereas other metals will clean comparatively easy. In testing this matter upon surface plates the author has found that the only safe method, and by far the quickest, of removing the oil from cast iron is an application of alcohol or spirits of turpentine, because the oil will enter and to some extent soak into the pores of cast iron and gradually work out again as it is continuously wiped, so that if apparently quite clean (after having been oiled and wiped) a short period of rest will cause oil to again be present to some extent upon the surface.
As a general rule motion in a continuous direction causes more wear under equal conditions than does a reciprocating one, because when a revolving surface commences to abrade, the particles of metal being cut are forced into and add themselves, in a great measure, to the particles performing the cutting, increasing its size and the strain of contact of the surfaces, causing them to cut deeper and deeper until at least an entire revolution has been made, when the severed particles of metal release themselves, and are for the most part forced into the grooves made by the cutting.
In reciprocating surfaces, when any part commences to cut, the edge of the protruding cutting part is abraded by the return stroke; which fact is clearly demonstrated in either fitting or grinding in the plugs of cocks, in which operation it is found absolutely necessary to revolve the plugs back and forth, to prevent the cutting which inevitably and invariably takes place if the plug is revolved in a continuous direction. Furthermore, when a surface revolves in a continuous direction, any grit that may lodge in a speck, hollow spot, or soft place in the metal, will cut a groove and not easily work its way out, as is demonstrated in polishing work in a lathe; for be the polishing material as fine as it may, it will not polish so smoothly unless kept in rapid motion back and forth. Grain emery used upon a side face, such as the radial face of a cylinder cover, will lodge in any small hollow spots in the metal and cut grooves, unless the polishing stick be moved rapidly back and forth between the centre and the outer diameter. If a revolving surface abrades so much as to seize and come to a standstill, it will be found very difficult to force it forward, while it will be comparatively easy to move it backward, which will not only release the particles of metal already severed from the main body, and permit them to lodge in the grooves due to the cutting, but will also dislodge the projecting particles which are performing the cutting, so that a few reciprocating movements and ample lubrication will, in most cases, stop the cutting and wash out the particles already cut from the surfaces of the metal.
In determining the metals to be used for a journal and bearing it is preferable to use the softer metal, or that which will wear the most, in the position in which it can be the most easily and cheaply replaced, which is usually in the bearing rather than in the journal; and since two metals of a different kind run better together than two of the same kind, the bearing is usually of a different kind of metal from that composing the journal. It may be stated, however, that under light duty cast iron will wear upon cast iron better than wrought iron or brass upon cast iron (for reasons which have already been stated), especially if the bearing area be broad and the lubrication ample and perfect.
To facilitate the removal of the bearings, brasses or boxes are provided, but in the case of small journals, as, say, of about 3 inches and less in diameter, the duty being light, the lubrication ample and equally distributed, and the journals an easy working fit when new, it is found that solid cast-iron boxes will last for a great length of time without sensible wear.
In some cases cast-iron boxes are cast with a receptacle for some soft metal, such as the various compound metals known under the general name of Babbitt metal.
Babbitt metal is composed of tin, antimony, and copper, mixed in varying proportions. A good mixture for general use where the duty is light is composed of 50 parts tin, 5 parts antimony, and 1 part copper. A harder composition, sometimes termed white metal, is composed of tin 96 parts, copper 4 parts, and antimony 8 parts. This mixture is especially suitable for journal boxes or bearings. It is mixed as follows: Twelve parts of copper are first melted, and then 36 parts of tin are added; 24 parts of antimony are put in, and then 36 parts of tin, the temperature being lowered as soon as the copper is melted in order not to oxidize the tin and antimony; the surface of the bath being protected from contact with the air. The alloy thus made is subsequently remelted in the proportion of 50 parts of alloy to 100 tin.
For brass bearings or boxes a mixture of 64 parts copper, 8 parts tin, and 1 part zinc is found to answer well; but for bearings not requiring so hard a metal, the quantity of zinc is increased, and that of the tin diminished.
Bearings or boxes that are to be babbitted are usually cast as in Fig. 2503, there being a rib at a, b, and c, forming a cavity at d, into which the melted metal is poured. The ribs (in new boxes) are sometimes bored out, or for rougher work may be chipped and filed out to fit the shaft, and hold it in line; and to prevent the ribs a, b, &c., from bearing and cutting the shaft, a piece of pasteboard is laid on ribs a and b, thus confining the journal bearing to the babbitt. The best method is to pour the bearing and then rivet the babbitt well into the cavity d, which is made wider at the bottom, to prevent the babbitt from coming loose, and then bore out the bearing in the usual manner.
[II-156]The principal advantage of a babbitted bearing is the ease with which it can be renewed, and the fact that the metal will soon bed itself to the journal. This is of great advantage in the case of solid bearings in the framing of fast-running machines, and in situations where it would be awkward or difficult to take brasses or bushes out to fit them, or align them to the shaft, which in many cases would also require to be taken out to remove the brasses. On the other hand, any particles of grit that may find ingress to babbitted boxes are apt to become bedded into the babbitt metal and cut or grind away the journal.
Since the babbitt metal in a bearing is apt to close across the bore when cooling after being poured, a mandrel of slightly larger diameter than the diameter of the journal should be used in place of the working journal to run the bearing on. Some effect the same purpose by wrapping writing paper around the journal; but it is wrong to use the journal, for the following reasons: To get a good, sound, well-fitting babbitt metal box, the metal should be poured as cool as possible, for if made red hot it contracts so much in cooling that it does not fit well in the box or frame of the machine. On the other hand unless the metal be well hot it is apt to cool and set too soon and be unsound. To remedy this the journal, or whatever represents it, must be heated. The heating is very apt to bend it. It is obvious then that instead of the journal a temporary bar of iron of slightly larger diameter than the working journal should be used, heating it to a good black hot heat, so that the babbitt metal may be poured less hot than would otherwise be permissible, and the contraction of the babbitt in the box reduced to a minimum. A little powdered resin sprinkled in the box will help the babbitt to flow easily and make a sound casting.
The temporary spindle, or journal, should also be oiled, and as soon as the metal has well set, the temporary journal should be revolved to free it. Babbitt bearings cast in two halves should be fitted to the journal as already described for brasses, which will well repay the cost and trouble.
To prevent the metal from running out of the bearing, its ends are closed by means of either clay or putty closely packed against the bearing ends and the shaft, and in pouring in the melted metal it is best to pour it on the top of the shaft, and let it run down its sides into the cavity of the bearing. This heats the shaft equally, and prevents it bending from unequal expansion, as it would do if it met the heated metal on its lower half only, it being obvious that if the shaft bends the bore of the bearing will not be cast in line; hence, the shaft will bear at the end only, and will require to wear the babbitt down to a bearing.
Babbitting is sometimes employed to refit parts that have worn loose, or to bush the bores of work. Suppose, for example, that in a case of emergency a pulley of a certain diameter is required, and that the only one at hand has too large a bore, then we may take a mandrel or arbor of the diameter of the shaft the pulley is required for, and drive on it two thin washers and turn them to fit the bore of the pulley, and cut a recess in each to enable the metal to be poured through. We may then put the arbor and washers in the pulley (the washers serving to hold the arbor true), and fill in the bore with babbitt metal, leaving the pulley set-screw in place and set to just touch the arbor, so as to cast the thread in the babbitt bushing, and thus save drilling and tapping.
Proportions of Journals.—It follows from what has been already said that under a given amount of duty the friction will be less and the durability greater in proportion as the bearing area of a journal is increased. But it is an important consideration whether such area shall be obtained in the diameter or in the length of the journal, or, in other words, what shall be the proportions between the diameter and length of a journal. It is found in practice that a journal wears better in proportion as its length exceeds its diameter, providing that the stress is not sufficient to cause sensible flexure, because in that case the pressure is reduced at that part of the journal where the most flexure occurs, and increased where the journal is most rigid. As a result, the abrasion increasing with the pressure becomes locally excessive, the glossy smoothness is lost and increased friction ensues.
If, however, the length of a journal is limited by the exigencies of its location or the design of the machine, the diameter of journal must be increased if necessary in order to obtain sufficient bearing area to withstand the stress without causing undue abrasion.
Referring to the bearing area in proportion to the load, Prof. R. H. Thurston writes, in an article in the Railroad Gazette of January 18th, 1878, as follows:—
“A pressure of 800 pounds to the square inch can rarely be attained on wrought iron at even low speeds, while 1,200 pounds is not infrequently adopted on the steel crank-pins of steamboat engines. I have known of several thousand pounds pressure per inch being reached on the slow-working and rarely moved pivots of swing bridges. In my own practice, I never, if I can avoid it, use higher pressures than 600 and 1,000 on iron and on steel, and, for general practice, make the pressure less as the speed is greater.”
W. Sellers and Co. state that under a pressure of 50 lbs. per square inch, and with oil well distributed over the surface of the box, the metal of the journal will not touch that of the bearing box bore.
In practice bearings are made with a length varying from that equal to the diameter of the journal to about four times that diameter, and but few cases occur in which these limits are exceeded in either direction. It is to be observed, however, that diminishing the length is apt to increase the abrasion unless the duty is very light indeed, while increasing it increases the durability while not affecting the friction, unless the shaft bends.
There are special cases in which within certain limits the proportions of journals are nearly uniform in practice; thus the length of engine crank-pin bearings rarely exceeds once and a half times the diameter, while the main shaft bearings are often similarly limited in width from the exigencies of designing the engine so that the eccentric shall come in line with the slide-valve spindle. In the case of crank-pins the pin cannot be held sufficiently rigidly to prevent spring or flexure; hence it is desirable to limit its length so that its pressure shall be as short a leverage as possible to the crank. The solid bearings in the framing of machines usually admit of room enough to make their lengths three or four times the diameter. Again, in the case of line shafting, boxes having a length equal to three or four times the diameter may be employed, providing that the alignment be made correct, or that the boxes are self-adjusting. But in all cases the longer the bearings the greater the necessity for correct alignment, so that the axis of the bearing bore may be in line with the axis of the shaft, the error manifestly increasing with the length of the bearing.
Placing two Cranks on a Shaft so that their Centre Lines shall stand at a Right Angle.—It is obvious that the keyways in both the crank and the shaft must be cut accurately in their proper positions, because it is a tedious operation to file out the sides of the keyways when the cranks are placed upon the shaft. To mark the keyways in the absence of any tools or appliances specially designed for the purpose we proceed as follows: Placing the shaft upon a marking-off table, we plug up the centres upon which the shaft has been turned by driving a piece of lead in them, leaving the surface level with those of the shaft; and then from the perimeter of the shaft we carefully mark, upon the lead plugs, the centres of the shaft. From this centre we describe a circle whose diameter will be equal to the required widths of the keyway, and then taking a square we place its stock upon the face of the marking-table, and bringing the edge of the blade even with the edge of the circle, we mark a perpendicular line upwards from the circle to the perimeter of the shaft, and then draw a similar line on the other side of the circle, as shown in Fig. 2504, in which a represents the shaft and b the circle, c the perpendicular line struck on one side of the circle, and d the square placed upon the marking-table e, in position to mark the line on the other side of the circle, f and g being wedges to keep the shaft a from moving its position upon the table. We next mark with a scribing-block or surface gauge the depth of the keyway as denoted by the line h, and the marking at that end of the shaft is completed. Passing to the other end of the shaft we find the centre of the shaft, and describe around it a circle equal in diameter to the required width[II-157] of keyway, and from the edges of the circle to the perimeter of the shaft draw two lines with a scribing-block, as shown in Fig. 2505, a representing the shaft, b the circle, c d the breadth of the keyway, e the marking-off table, f and g the wedges, and h the depth of the keyway, which must, in this case, be marked with a square resting on the table.
If, however, the shaft is too heavy or large to be placed on a marking-off table, we may proceed as follows: Strike as before the circle b, Fig. 2504, equal in diameter to the required width of keyway, and adjust a straight-edge held firmly against the end face of the shaft, so that its upper edge is coincident with the perimeter of this circle, while the straight is horizontally level-tested by a spirit-level. Draw a line along the shaft face, using the straight-edge as a guide. This will give us the line c in Fig. 2505. By a similar process the line d, Fig. 2505, may be drawn. At the other end of the shaft similar lines, but standing vertical, may be marked, which will give the positions of the keyways.
We have now marked off on the end faces of the shaft a keyway at each end, one standing at a right angle to the other; but it must be borne in mind that we have paid no attention as to which crank shall lead; that is to say, suppose in Fig. 2506 a and b represent cranks placed upon the shaft c, and running in the direction indicated by arrow d, it is evident that the crank b leads in the direction in which the engine is to run, and hence the keyway e stands in advance of the keyway f; and therefore, as shown in the figure, the right-hand crank leads. To have made the left-hand crank lead, when the engine runs in the direction of the arrow d, we should, supposing the keyway f to be already cut, have to cut the keyway e on the directly opposite side of the shaft; or, what is the same thing, supposing the keyway e to be already cut, the keyway f would require to be cut on the diametrally opposite side of the shaft. It is obvious that if the engine ran in the direction of the arrow g, the left-hand crank would lead, supposing in each case the cylinders to stand at h. Here it may be necessary to explain the manner of determining which is the right-hand and which the left-hand crank. Suppose then that the figure represents a locomotive crank, the cylinders being at h, then as the engineer stands in the cab, facing his engine, a will be the left-hand and b the right-hand crank. It is usual in locomotives to make the left-hand crank lead when the engine is running forward, the practical difference being, that if the workman were by mistake to make the right-hand crank lead, the engine would run forward when the reversing lever was placed to run backward, and vice versâ. It makes no difference whether the shaft can be turned end for end or not: if the right or left crank is required to lead when the crank is required to revolve in a given direction the keyways in the shaft must be marked off in the relative positions on the shaft necessary to obtain that result.
The keyways may be carried along the circumference of the shaft by a square applied to its end face, or if that face is not flat by the ordinary keyway marking tool.
To mark off the keyways in the cranks, we place a centre-piece in the bore of the crank, as shown in Fig. 2507, in which a represents a crank having a centre-piece of sheet iron b placed in the bore. On the face of this centre-piece we mark the centre of the hole into which it fits, and from that centre we describe the circle c, which must be of exactly same diameter as the crank-pin if it is in its place, or otherwise of the crank-pin hole. We then draw the lines d and e, using as a guide a straight-edge placed one end upon the crank-pin journal, or even with the edge of the crank-pin hole, as the case may be, and the other end (of the same edge of the straight-edge) exactly even with the circumference of the circle c. From d and e we find the centre of the circle f, which must be central between d and e, and whose diameter must be exactly equal to the required width of keyway; and we then mark the circle g, describing it from the centre of the hole, and therefore of the circle c. By drawing the lines h and i, which must be even with the circumference of the circles f and g, using a straight-edge as a guide, we shall obtain the correct position for the keyway k, and the whole of the keyways may be cut, care being taken to cut them quite true with the lines, and of an exact equal width.
To put the cranks on the shaft, first provide a temporary key, a close fit on the sides, but clear top and bottom, so that it will bind just easily on the sides of the keyways in both the shaft and the crank. The shaft must be placed and wedged with its keyway downwards, so that in putting the crank on, the pin end may hang downwards, which will render it more easy both to put on, handle, and adjust. As soon as the shaft has entered the crank, say a quarter of an inch, we must insert the temporary key (which may have its end edges well tapered off to assist the operation of entering it) sufficiently far into the keyway of the shaft that it will[II-158] not fall out, and we may then proceed to put the crank on the shaft to the necessary distance, keeping the temporary key sufficiently far in the keyway to enable it to act as a guide—that is to say, up to at least half the length of the keyway.
To put on the second crank, we first place the shaft so that the crank already on stands exactly horizontal, setting it by placing a spirit-level, as shown in Fig. 2508, in which a represents either the crank-pin journal or the crank-pin hole in the crank, and b a circle struck on the end face of the shaft and from its centre, the diameter of the circle b being exactly the same as that of a. If then we so adjust the position of the crank that a spirit-level applied to the exact circumferences of the circles a and b stands level, the crank will stand level, and we have only to put the second crank on with its centre-line standing perpendicular, and the two cranks will be at a right angle one to the other. We now proceed to put on the second crank, pursuing the same method employed in putting on the first one, save that the temporary key need not be inserted so far into the keyway, because, if the keyways have been cut the least out of true, it will make a great difference at the crank-pin, because of the increased distance of the latter from the centre of the crank-shaft. As soon as the second crank is placed to its position on the shaft we must ascertain if it stands vertical, which we may do by applying the spirit-level as shown in Fig. 2509, bringing its edges exactly fair with the edges of the circles a and b, and moving the crank until the bubble of the level stands true, and taking out the temporary key if it is necessary to adjust the crank at all.
If, however, the crank is to be forced on by hydraulic pressure, this latter adjustment should be made when the crank is just sufficiently far on the crank shaft to enable it to bind enough to well support its own weight, to facilitate which the end of the shaft is sometimes slightly tapered for a very short distance—a practice which is sometimes rendered unnecessary by reason of there being attachments fitted to the hydraulic presses which of themselves adjust the position of the cranks, and insure their being at a right angle one to the other.
After the cranks are on their places the keys may be fitted, care being taken that, if the crank last put on had to be moved to adjust it, the sides of the keyways be filed even, otherwise driving the key will tend to move the crank.
Fitting Engine Cylinders.[35]—When engine cylinders are made in quantities, as in locomotive building shops, a great deal of the fitting work is saved by the machine work; but when a single cylinder or a pair of cylinders only are to be fitted up it will not pay to make jigs and appliances; hence, they are usually fitted up entirely by hand. The first thing to do is to mark off all the holes requiring to be drilled, and have the drilling done.
[35] From the “Complete Practical Machinist.”
In marking the holes in the cylinder covers it is to be noted whether that part of the cylinder cover which fits into the cylinder has a portion cut away to give room for the steam to enter (as is usually the case), and if so, first mark a line across the inside flange of the cover, parallel to the part cut away, and then scribe each end of the line across the edge of the flange. Then mark a similar line across the cylinder end, parallel to the steam port where it enters the cylinder, and scribe each end of this line across the cylinder flange, so that, when the cylinder cover is placed into the cylinder and the lines on the flanges of the cylinder and the cover are placed parallel to each other, the piece cut away on the cover will stand exactly opposite to the steam port, as it is intended to do. The cover may then be clamped to the cylinder, and holes of the requisite size for the tap (the tapping holes, as they are commonly called) may be drilled through the cover and the requisite depth into the cylinder at the same time.
The cylinder covers must, after being drilled, as above, be taken from the cylinder, and the clearing drill put through the holes already drilled so that they will admit the bolts or studs, the clearing holes being made 1⁄16 inch larger than the diameter of the bolts or studs. The steam chest may be either clamped to the cylinder, and tapping holes drilled through it and the cylinder (the same as done in the case of the covers), or it may have its clearing holes drilled in it while so clamped, care being taken to let the point of the drill enter deep enough to pass completely through the steam chest, and into the cylinder deep enough to cut or drill a countersink nearly or quite equal to the diameter of the drill. If, however, the steam chest is already drilled, it may be set upon the cylinder, and the holes marked on the cylinder face by a scriber or by the end of a piece of wood or of a bolt, which end may be made either conical or flat for the purpose, marking being placed upon it; so that, by putting it through the hole of the chest, permitting it to rest upon the cylinder face (which may be chalked so as to show the marks plainly), and then revolving it with the hand, it will mark the cylinder face. This plan is generally resorted to when the holes in the chest are too deep to permit of being scribed. To true the back face, round a hole against which face the bolt head or the face of the nut may bed, in cases where such facing cannot be done by a pin countersink or a cutter used in a machine, the tool shown in Fig. 2510 may be employed, a being a pin provided with a slot at one end to admit the cutter b, which is held fast by the key c, and is also provided with a square end f, by which it may be turned or revolved by means of a wrench, and with a thread to receive the nut e, d being a washer; so that, by screwing up the nut e, the cutting-edges of the cutter are forced against the cylinder g, and will, when revolved, cut the face, against which they are forced, true with the hole in the cylinder through which the pin a is passed.
After the drilling the cylinder should be placed on end and all[II-159] the holes that can be got at should be tapped. Then the cover joint, supposing it to be a ground joint, should be made according to the directions given for making ground joints, when the cylinder may be turned upside down and the other cover fitted. Then the holes for the cylinder cocks and for the steam and exhaust pipe should be tapped, and the faces for these pipe joints fitted as required.
The steam-chest holes should then be tapped and the ports marked out and chipped and filed to the lines, such lines being marked as described in the remarks on lining out work.
The face for the steam-chest seat and the steam-chest cover may then be prepared by filing, scraping, or grinding, as may be required, and simultaneously the valve seat and valve face may be fitted. If the cylinders are to be bolted together as in a locomotive, the holes for holding them together should be drilled about 1⁄64 inch smaller than the bolts, so that they may be reamed out together after the cylinder bores are aligned.
One cylinder face should be marked and drilled first, and the two cylinder bores being set to align true the other cylinder should be marked from the other, or if there is a saddle between the two cylinders both cylinders may be marked and drilled, and also the holes on one side of the saddle. Temporary bolts may then be put through the holes that are drilled in the cylinder and saddle and clamps used to hold the undrilled cylinder to the saddle, when the cylinder bores may be set true one to the other, and the holes on the remaining side of the saddle marked through those already drilled in the cylinder. These latter holes being drilled, temporary bolts of smaller diameter than the holes (so as to give room to move the cylinders to align their bores) may be used to bolt the cylinders together while their bores are accurately aligned, which alignment may be effected as follows:—
The bores should be set as near true as possible, tested by a spirit-level rested on the bore and placed as near true as can be judged with the length of the bore, and a plumb rule may be applied to the end faces where the cover joint comes. Then a straight-edge should be applied, as in Fig. 2511, in which s is the straight-edge, and c and d the two cylinder ends.
The method of testing is shown in Fig. 2511, where the straight-edge s is shown in three positions, marked respectively 1, 2, and 3 at one end, and f, g, and h at the other.
The first test should be made by simply placing the straight-edge across the two cylinder faces, as at g 3; and when the cylinders are set apparently true and the spirit-level applied to the respective bores shows them true, greater accuracy may be secured by placing the straight-edge in position 1 h, being pressed firmly to its cylinder face with end 1 above the other cylinder face. Then, while end h is held firmly to its cylinder, let end 1 lower until it passes entirely over the face of cylinder c, whose face it should just touch; if on meeting c the straight-edge strikes it or does not meet it, further adjustment of the cylinder positions is necessary. Next place the straight-edge in position 2, pressing end f firmly against cylinder d, and passing the other end entirely over the end of cylinder c, which it should just touch, and no more. It will then be necessary to repeat this process, pressing the straight-edge against cylinder c and testing the other end with cylinder d, and the cylinders thus set will be (if the end faces are true, as they should be, and usually are) more truly aligned than is possible by the use of the spirit-level. This method also brings the end faces of the cylinders in the same plane, so that each piston head will travel central in the length of the cylinder bore, approaching the cylinder covers equally, and therefore keeps the clearance equal. Incidentally, also, this secures accuracy in the cross-head traverse on the guide bars (supposing these bars to be bolted to[II-160] the cylinder cover). The holes for bolting the cylinders together may then be reamed and the bolts driven in and screwed up.
To guide the tap when tapping the cylinder cover and steam-chest holes the guide stand s, shown in Fig. 2512, should be employed. It is bolted to the cylinder face by the bolt b, which passes through a slot in the stand.
The tap t is inserted through the two arms of the stand and its end inserted in the hole to be tapped when bolt b is tightened up.
The stem of the tap should be of slightly larger diameter than the tap thread, so as to fit in the holes of the guide or stand.
When, however, one end of the guide bars is carried on the cylinder cover, it is necessary when setting that cover to be marked for the drilling, to so set it that the seats for the guide bar ends shall be horizontally level when the cylinder is on the engine; and when setting the bores of the cylinder in line to mark the holes for bolting the cylinders together or to the saddle, this point should also be looked to, as if these seats are not in line the faces of the guide bars will not be in line, and will not, therefore, bed fair to the cross-head guide unless the error is in some way corrected.
It is desirable that these seatings be quite true and in line one with the other on both cylinders, so that if liners require to be made, or if the ends of the bars require to be filed to let the bars together at any time, the surfaces may be filed true to the face of the bar, and thus be set true and to fit the cross-head guides without requiring to put the bars on and off to fit them true by trial.
Reboring Cylinders in their Places on the Engine.—When a cylinder bore becomes so worn out of cylindrical truth, or becomes grooved or cut, as it is termed, as to require to be rebored, it may be done with the class of boring bar shown in Fig. 2513. It consists of a bar having journal bearing in castings which bolt on to the two ends of the cylinder in place of the cylinder covers. On the bar is fitted a sliding head carrying the cutting tool and fed by a screw passing within the bar. To operate the bar and simultaneously the feed screw, the hand-wheel and worm-wheel is employed, giving rotary motion to the worm-wheel which is fast upon the bar. Fast also upon the bar is the inside one of the two small gears shown, which operates the inner of the two small gears shown above it. The outer of the upper gears engages with the outer of the lower ones, the latter being fast upon the feed screw. In the inner pair the lower is of largest diameter, but in the outer pair the upper is the largest, and as a result the outer of the lower rotates the fastest, and hence rotates the feed screw, causing the tool to feed to its cut.
The proportions of these wheels are, first or inside pair, lower wheel 36, upper 37; outside pair, upper 37, lower 36, so that the feed per bar rotation is in amount that produced by moving the outer lower gear a part of a rotation equal to twice the pitch of the teeth, the cutting tool motion depending upon the pitch of the feed screw.
To enable the rapid traverse of the head from end to end of the bar, the upper pair of gears are mounted on an eccentric stud, so that by operating the small handle shown they may be disengaged from the lower feed gears and the feed screw operated direct by means of the handle shown.
In setting such a bar to a cylinder bore it is to be remembered that two methods may be employed. First, the bar may be set to accommodate the cylinder bore, truing it out with as light a cut as possible. In this case the bore of the cylinder may be made out of line with the guide bars and with the centre of the length of the crank-pin journal.
In the second the bar may be set with a view to bore it out in line with the guide bars and crank pin, and then taking as much cut as will be necessary to true the bore.
The latter plan is the preferable of the two, unless the repairs are so extensive as to require the guide bars to be redressed and the main bearing renewed, in which case those parts requiring to be re-aligned, the cylinder may be rebored with a view to take out as little metal as possible, and the other parts set to suit the new bore.
To set the bar true to the guide bars and crank pin, and thus retain the axis of the new bore true with that of the original bore, the bar should be set true with the recessed counterbore at each end of the cylinder, which being unworn remains true.
If, however, only one cylinder cover can be conveniently taken off, the piece of wood will require to fit in the counterbore at the open end, and in the cylinder bore at the closed end of the cylinder; hence we make it large enough for the counterbore, and after having removed the ridge at that end we cut the length of the wood down to fit the cylinder bore, whereas if we made our rest to fit the bore at first we should require to use wedges to make[II-161] it fit the counterbore. In some cases holes might be bored near the ends of the rest or fulcrum to serve the same purpose as the notches.
The method of using the scraper, Fig. 2516, is shown in Fig. 2514, which latter represents an engine cylinder. At b is shown the wooden rest or fulcrum; and at c the lever scraper operating on the ridge at the closed end of the cylinder. The lever c is worked on the pulling stroke only, and is so held that the edge presents a keen scraping tool which will cut very freely. The fulcrum b should be adjusted as closely as convenient to the work, so as to obtain good leverage for the scraper. It should be moved in its position, so that during the roughing out only the lower notches in the fulcrum are used.
A plan was lately resorted to on the White Star Line of steamships for re-boring a cylinder. The cylinder heads and piston follower were taken off; a groove was cut from the outer end of the cylinder along the bore as far and as deep as the counterboring was required to be done. The counterboring was then accomplished in the manner shown in Fig. 2515. The junk ring was provided with a small tool holder, such as is used upon boring bars. The tool was fastened in the holder while its cutting edge was in the groove referred to, cut as deep and as far up the cylinder as the counterboring was to be. To the junk ring was fastened, by two long bolts, a wooden lever extending above and across the cylinder. Two men walked around pushing the lever, and when the tool at each revolution arrived at the groove, a fresh cut was taken by moving the engine so as to raise the piston the necessary amount. It is obvious that the piston head may be steadied and held true in the bore of the cylinder by means of a few wooden wedges. Thus we see that in this operation the junk ring was made to serve as a boring bar head, the men furnishing the necessary rotative motion, the feed motion to the tool being obtained by advancing the piston toward the end of the cylinder where the work was being done.
The ridges which in time form at the two ends of a cylinder bore are usually removed by the hand-boring bar shown in Fig. 2513, but they may, in cylinders of from 12 to 24 or 30 inches in diameter, be readily cut out by hand as follows:—
Take a bar of steel 9⁄16 inch square and 3 feet 6 inches long; forge it at one end to the shape shown in Fig. 2516, in which from a to b is the forged end. This end must then be heated along its entire length to a cherry red, and dipped vertically into cold water to harden it; after which it must be ground from a to b on all four faces square across, and as nearly of an even curve as can be ascertained by the eye. Next take a piece of hard wood—oak, for instance—about an inch thick and 3 inches wide; cut it to such a length that when placed upright its ends will wedge tightly into the counterbore of the cylinder. Into the edges of this piece of wood saw out a series of notches, making its finished appearance to be such as shown in Fig. 2517. The object of fitting its length tightly into the counterbore of the cylinder is as follows: If both cylinder covers are off or can be conveniently taken off, the ridge can be operated upon at each end of the cylinder; hence our piece of wood, which is merely an improvised rest to act as a fulcrum for the bar scraper shown at the top of the figure, would require to fit into the counterbore.
In engines having suspended guide bars, it is not uncommon to set those bars by the working parts of the engine, instead of by lines. This is an advantage when the parts of the engines are not taken down, and, if care is taken, will make a true and smooth working job; but otherwise, it is likely to introduce errors in the lining of the engine, which throw it out of proper line, and cause a great deal of friction.
The proper method of setting the bars depends upon the condition of the engine as to wear. Suppose, for example, that a new piston head has been put in, then, if the gland is new also, or is a good fit to both the piston rod and the bar of the stuffing box, the bars may be set as follows:—
Place the piston at the back end of the cylinder, and put the cross head and guide blocks in proper place on the rod. Put up the bottom guide bars so that they just touch the cross-head guides. Now, in adjusting these bottom bars there are two essential points: first, that the plane of their upper surfaces shall stand parallel with the axial line of the main shaft, and secondly, to place the upper surface parallel with the axial line of the cylinder (it being of course assumed that the cylinder and crank shaft are in proper line). The first of these essential points will be attained when a spirit-level, placed truly along the bore of the cylinder, shows the bubble to stand in the same position in the tube, as it does when placed upon and along the bar. The second will be attained when a spirit-level, placed across the bars, as in Fig. 2518, at a, shows the bubble to stand the same as it does when the level is placed on a parallel part of the shaft, as in the figure at b. When the bars are thus temporarily set, the liners, or pieces of iron, may be fitted to the proper thickness, so that the gland will pass in and out of the stuffing box easily by hand, no matter in what position the piston may be in the cylinder.
To get the thickness of these liners, take wedges made of iron, wood, or lead, and insert the thin end between the faces of the bars and those of the supports, forcing the wedges in sufficiently to leave a mark upon them. By chalking the faces of the wedges they will exhibit the marks more plainly. The wedges should be inserted at each end and on both sides of the bar, for one bar at a time, the liners being got out a trifle too thick so as to allow some for fitting.
If the liners require to be very thin and are difficult to hold in the vice without springing, take a piece of soft wood faced true, and grip it in the vice, and fasten the liner on it by means of brads driven in around the edge of the liner.
When the four liners are ready place them in position between the bars and their seatings. Bolt the bars firmly in position, wipe them clean and test them lengthwise with the spirit-level to ascertain if they are parallel with the cylinder bore, and place the level across the bars at each end to test parallelism with the engine shaft, as in Fig. 2518, and, having noted where further adjustment is necessary, put marking upon the bars and move the cross head back and forth to ascertain how much the respective liners require reducing. If the gland is a fit upon the piston rod and in the stuffing box, moving the gland in and out of the stuffing box will be an admirable test of the guide-bar adjustment.
The straight-edge should also be applied to test if the surfaces of the bars lead true one to the other; thus, in Fig. 2519, a and b are the bars and e the straight-edge, which by being pressed firmly to the surface of a discloses that the surface of a is not in line with b, because if it were so the straight-edge would meet the face of b as in Fig. 2519, where the straight-edge f pressed to the surface of c leads true to the surface of the bar d. All four of the bars require testing in this manner. If the seatings for the bars or the liners are not made flat and of equal thickness, or if from any other cause the bars do not bed properly upon the liners, then bolting up the bars will spring them as shown in Fig. 2520, in which, at a, is shown a bar sprung in the bolting up, because the liners fit at the ends b c only; while at e is shown a bar sprung or bent because the liners fit at the ends d d only. In either case the cross head would be forced to travel in a curve, bending the piston rod, and inducing much friction. The way to test the bars in this respect is, after the above operations, and before loosening the bolts, place a long straight-edge lengthwise along each bar and move it laterally at one end. If it swings from the centre the bar is rounding, while if it shuffles across first at one end and then at the other the bar is hollow in its length and we must find at which end of the bar this spring exists.[II-163] To do this, slightly slacken the bolt or bolts at one end and again apply the straight-edge, if the spring is removed the error lies in the bedding of the liner at that end. If not removed, retighten the bolts at that end and slacken those or that at the other end, and again apply the straight-edge, and thus may it be determined how much of the spring is due to each of the liners, and this must be remembered and allowed for in filing the liner to its final adjustment. Before putting the liners in a second time it is better to give them a light coat of marking to show where they bear. At each trial of the bars the spirit-level and straight-edge should be applied and the cross head should be moved back and forth to show by the bearing marks how the cross-head guides fit to the bars. These marks are a great deal finer test than any spirit-level adjustment, hence the last part of the fitting should be performed with strict reference to the bearing marks upon both the bars and the cross-head guides as well as upon the liner, the cross-head flanges being adjusted and fitted at the same time as the face fitting.
To set the top bars place the cross head in the middle of its stroke, and place them upon the cross-head guides. Then, with the wedges applied as before, ascertain the required thickness of the respective liners one at a time, leaving them, as previously, a trifle too thick, and testing them while fitting by marking placed upon their faces. The top bars may be entirely adjusted from the contact marks left by the cross-head guides when moved along the bars, thus dispensing with the use of the straight-edge and spirit-level.
As the bolts supporting the bottom bars often require to be loosened to get the top bars off, pieces of wood may be placed beneath the bottom bars to retain them in position when the bolts are loosened. These pieces must be removed during the testing, for if left so as to wedge the bars they may spring them, and thus mislead in the adjustment. After the top bars are adjusted the whole bearing surfaces should be oiled, and the cross head pulled back and forth by hand without the use of a lever, providing the size of the piston does not exceed about eighteen inches diameter. The bars when set true should be clamped to their seatings and the holes reamed out to receive the proper bolts, and, finally, mark each bolt, bar, and liner to its place.
When the bars, tested with the straight-edge and spirit-level as described, show true, if the gland will pass freely in and out of the stuffing box with the cross head at any part of its stroke, the guide bars are set.
In this operation let it be noted that the close fit of the piston to the cylinder bore and of the gland to the stuffing box is alone depended upon as a guide whereby to so set the guide bars that the axial line of the piston rod and its plane of motion shall be in line with the centre of the crank shaft.
Suppose, however, that the piston head is a new one, and the gland is worn a loose fit to the stuffing box, then setting the bar to the gland would produce the result shown in Fig. 2521, in which the dotted line a a is a line or cord stretched axially true with the cylinder bore, and coincident with the centre of the pillow block at b. The gland being a loose fit permits the piston rod to fall below its proper level, and the surface of the bars, if set by the gland only, without using the spirit-level, would be set true to the full line c c, and therefore out of true line. If the bars are set by spirit-level true to the length of the cylinder bore, the gland becomes useless as a guide to set the bars by. It is a not uncommon practice, when the gland has play, to insert in the stuffing-box bore, at the bottom, a piece of tin or sheet brass, equal in thickness to one-half the amount to which the gland is too small, or to insert a similar piece beneath the piston head if it is too small. As a rule, however, there will be at least as much play between the piston rod and the gland bore as between the gland and the stuffing-box bore; hence, if there is any play, it is better to discard the use of the gland altogether.
The proper method of setting guide bars by a stretched line is as follows:—
The cord or line is set true to the cylinder bore, and coincident with the centre of the pillow block, as at a a in Fig. 2521, and the two bottom bars are put up in line horizontally with the axial line of the crank shaft, and at a distance below the stretched line equal to one-half the height of the guides for the cross head, as in Fig. 2522, in which a represents the stretched line, b, b the bottom bars, c c a straight-edge, and d a piece of wire whose length from point to point is equal to one-half the height or thickness of the guide blocks. The width apart of the bars is set to suit the width apart of the flanges of the guide blocks on the cross head, by means of a square. The square is applied in the following manner: On a straight-edge mark two lines a and d, Fig. 2523, a distance apart equal to the distance between the flange edges of the cross-head guides. Midway between a and d mark the line c; place the straight-edge across the bars as shown, and when the edge of a square, placed on the straight-edge, coincides with c and the stretched line, and the marks a and d coincide with the edges of the bars, the latter are set true, and will come right for distance apart, and distance from the centre line, supposing the flange edges of the cross-head guides to be equidistant from the centre of the length of the cross-head journal. If, however, such is not the case, the width from a to c and from c to d must be made to suit, c representing the centre of the length of the cross head journal, d the flange on one guide and a the flange on the other guide. Here it may also be remarked that, if the thicknesses of the cross-head guides vary, or if they are not central to the axial line of the[II-164] cross-head journal, the bars must be set for distance from a in Fig. 2523, to suit the error, because in that figure the straight-edge is supposed to stand parallel to the axial line of the shaft, as it is also in Fig. 2522, the aim in both cases being to so set the bars that the cross-head journal shall stand parallel with the crank shaft.
It is the liability of variation in the thickness of the guide blocks, and of their not being central to the cross-head journal, that constitutes the disadvantage of setting the bars by lines, it being obvious that the bars must be either set to suit any errors in the guides, or those errors must be eliminated before setting the bars. The top bars must be set parallel to the bottom ones, at a distance from the bottom ones equal to the thickness of the guide blocks, and parallel to one another. It is preferable to set the top ones with the cross head and guides in place, observing all the precautions as to springing them given in the case of the bottom bars.
The bars thus set will be in line with the crank axle, but unless the piston accurately fits the cylinder bore, they will not long remain in line with the line of motion of the piston rod. For example, Fig. 2524 shows a piston head too small for the cylinder bore, the guides fitting the bars properly, and the gland and stuffing box fitting the piston rod; the piston will be suspended in the cylinder, its overhanging weight being supported by the guides b, the gland, and packing ring. This would cause friction and rapid wear of the gland bore and guide surfaces in a direction parallel to the line c, which would gradually let the piston fall to the bottom of the cylinder bore, touching at the end of d first. In some engines provision is made to adjust the piston to take up its wear, which is, it will be seen, a great advantage.
The Heating and Pounding, or Knocking, of Engines.—The heating of any part of an engine occurs from one of two causes, viz., either the fit of the parts is too close, inducing undue friction, or the parts are not in line.
When the former is the cause the remedy is to ease the fit. If the parts are not in line, the heating may also be remedied by loosening the fit of the parts; but this will often induce a pound or knock, hence the true remedy is to properly align the parts.
The location of a pound may be discovered by placing a piece of metal wire between the teeth, and resting the other end of the wire upon each end of the cylinder, guide bars, and bearings of the main shaft, repeating the operation in each place, and the sense of feeling will distinctly indicate the location of the knock, by imparting a more severe shock to the teeth when the vicinity of the knock is approached.
The most prominent location of the causes of a pound are, first, in the crank pin, from causes to be hereafter explained, and from its wearing oval at the cross-head journal; and second, at the ends of the cylinders, or the ends of the guide bars, because of a ridge forming there as the wear proceeds.
A crank pin cannot wear oval if the brasses are kept adjusted to fit it, because in that case the brass bore must wear it round; but if there is any play it wears oval, because the pressure of contact between the journal and the brass bores is least when the pin is at and near the points of dead centre, and the most when it is at and near half stroke.
The cross-head pin wears oval because the pressure between the pin and its bearing is in a line with the connecting rod, and there is but little wear on the pin in a direction at right angles to the rod.
Ridges form at the ends of the cylinder bore and at the ends of the guides for the following reasons:—
Referring to the cylinder, the location of the piston stroke in the cylinder bore alters as the connecting-rod keys pass through the rod, because that alters the length of the connecting rod, and therefore the path of the cross-head guides on the guide bars, and also that of the piston in the cylinder.
As the piston rod is shortened there is less wear at the extreme end of the cylinder bore farthest from the crank, and the same remark applies to the guide bars.
If the piston head travels past the end of the cylinder bore and into the counterbore at each end, a distance equal to the amount of taper on the connecting-rod keys, or equal to the amount the connecting-rod length will alter while those keys are passed through the rod (to take up the journal and brass wear), the piston head will (if the rod is kept to its original length within that amount) always travel to the end of the cylinder bore, and no ridge should form on account of the length of the rod altering; but even then a slight ridge may form because the wear is naturally less at the ends. Thus in the middle of the cylinder length the whole thickness of the piston head, piston rings, and of the follower passes over the bore, while at the ends only the flange of the piston head at one end and the follower at the other passes over the metal of the bore; hence the friction and wear are less.
The ordinary cause of pounding and heating is a want of truth in the alignment of the crank pin, or in that of the cylinder, main shaft, or guide bars.
[II-165]The method to be employed to line an engine, or to discover if it is out of line, depends upon the design of the engine and its condition; thus an engine having a Corliss frame has the slides to receive the cross head made at a true right angle to the end face which meets the cylinder end; equidistant from the centre of the gland hole or axis of the piston rod, and the end of the frame fitting either the bore of the piston or the turned flange of the cylinder cover; hence the guide bars must be true if the frame is got up true, the fit of the frame end to the cylinder end insuring truth in the guide or cross-head slides, providing that the centre line of the frame, during the turning and planing operations, leads from the centre of the cylinder end of the frame to the centre of the crank-shaft brass; or, in other words, the planing and boring of the frame must be true with a line running from the centre of the cylinder end of frame to the centre of location for the crank shaft. This will not only cause the outside of the frame casting to stand at its proper level when the cylinder bore stands horizontally level; but it will insure that the crank-shaft bearing brasses both be of equal and of a proper thickness through the crown.
The engine being properly lined at first will not be liable to get out of line, excepting so far as affected by the wear of the crank-shaft bearing, which will cause the crank shaft to drop, as shown in Fig. 2525, where a a represents the true centre line of the cylinder and guide bars, which, when the crank is in the position shown in the cut, should be coincident with the centre line of the connecting rod and the crank, but the crank brass having worn below the centre line of the connecting rod and crank, the crank will get out of line as denoted by the line b b.
As a result, a portion of the piston movement and pressure which should be exerted on the crank after leaving the dead centre, will be exerted on it before it reaches the dead centre, thus causing a back pressure, involving a loss of power. Furthermore, the relative position of the eccentric to the valve gear will be altered, impairing the proper set of the valves; hence it follows that the wear of the crank bearing in this direction should be taken up (by raising the lower brass) before it becomes excessive. To find how much the bottom brass requires raising, or whether it requires raising or not, find the centre of the crank shaft, and from this centre strike the circle b, in Fig. 2526, whose diameter must equal that of the crank pin a, and place the edge of a spirit-level coincident with the perimeters of the crank pin and circle, as shown in the cut. When the bubble of the spirit-level stands in the same position as it does when the level is placed upon the bore of the cylinder or along the piston rod, the crank will be in line with the cylinder bore.
As a rule, the cylinder bore of a horizontal engine stands horizontally true, and the crank centre line should also stand so when the crank is on its dead centre, but if such is not the case the crank centre line must nevertheless stand true with the axial line of the cylinder, when the crank is on the dead centre.
If, instead of having a Corliss frame and fixed guide bars, the engine has a flat bed and adjustable guide bars, as shown in Fig. 2527, the operation is as follows:—
In setting up a new engine it is obvious that if the flanges of the cylinder are planed parallel with its bore and at the proper distance from its axial line, and the pillow block is made of the proper height, a line stretched axially true with the cylinder bore will pass through the centre of bore of pillow-block brasses, or be equal in height from the engine bed; but the length of the cylinder being only about one-fifth of the distance from the cylinder to the centre of pillow block, any error in the planing of the cylinder flange true to the cylinder bore becomes magnified five times at the pillow block; hence it is necessary to stretch a line through the cylinder bore and set the cylinder so that the line, being axially true with its bore, will pass the pillow block at the centre of the bore of its brasses. This is sometimes done by inserting thin pieces of sheet tin, metal, or even paper beneath the cylinder flanges and the bed, and in the requisite positions. The method of stretching the line is shown in Fig. 2527. f is a device for holding the line at that end. It consists of a frame in the form of a cross, with adjusting screws at the end of each arm, and a small hole at its centre to receive the line. The other end of the line a must be secured, under as much tension as the line will safely bear, to a piece of wood clamped to the engine frame at r. The adjustment of the line is made by measuring its distance from the walls of the bore of the cylinder at one end and of the bore of the gland hole at the other end, using a pair of inside calipers or a wire gauge. The latter should be bent in its length to admit of adjusting the same by straightening to increase, or still further bending to diminish, its length to suit the requirements.
The wire, when applied, should only just meet or touch the line and not bear the least hard, or it will spring the line, causing an error of adjustment that will be serious when multiplied by the length of the line to the pillow block as compared with the length of the cylinder bore.
If the pillow block is planed on its bottom face and has its brasses fitted, the latter may be marked off for boring from the line a, Fig. 2527, when stretched to set the cylinder, thus avoiding a second adjustment of the line a a.
Suppose now that it is required to line the brasses in the pillow blocks true to be bored (the pillow blocks being bolted in position). The distance of the face p, of the brass from the stretched line a, in Fig. 2527, must equal the distance from the centre of the length of the crank-pin journal, to the face of the large crank hub, and this distance may be shown by a line marked on the edge of the brass flange.
Place a straight-edge c, Fig. 2527, having a line d parallel with its edge e, so that this line will be in the centre of the width of the pillow-block jaws, and at a right angle to the line a. The line d will then represent the axial line of the crank shaft, and may be used as the centre from which to mark the lines on the brasses used to set them by for boring. To test if a and d are at a right angle, or to set d to a, a large square should be used. If the side face p p of the pillow block stands parallel to a, as it should do when it is true, it will serve to chuck the pillow block by, thus boring the brasses in their places in the pillow block, with the centre line of the bore at a right angle to p. If otherwise, two flat places should be filed on the brasses, as shown in Fig. 2528, in which c is the straight-edge, and a the stretched[II-166] line as before, h and i representing the flat places whose distance from a, as shown at j j, may be made to represent the thickness of the crank from its large hub face to the centre of length of crank-pin journal; hence the depth of the flat places will show how much to take off the face of the brass to leave it of the proper thickness.
A straight-edge placed across these flat places, or true to the lines h i, must stand at a right angle to the line d, so that by setting the brasses by the flat places they will be bored to stand at a right angle to a. To set the brasses the other way a circle is struck from d, as a centre, upon the faces of the brasses as in the end view, Fig. 2528, in which the straight-edge c is shown wedged in the bore of the brasses, which is the most convenient way when it can be done.
The line d is carried down on the end face of the straight-edge, and the latter is used as a support for the compass points while striking the circle m, which is defined more clearly by indenting it with fine centre-punch marks. The height of the centre for bore of brasses may be carried from the centre line of the cylinder a a to the end of the straight-edge c, by placing another straight-edge across the engine bed and measuring from the end of c to a.
Suppose now that the brasses are bored, and the position of the pillow block is to be set, and the process is the same, the line d being marked true from the bore of the brasses, and the pillow blocks adjusted until d is at a right angle to line a a.
Though in a new engine every part may be made as true as possible in the details of manufacture, yet when the parts come to be put together errors of alignment will generally be found to exist. These errors may be too minute for discovery in the separate piece, and yet form important defects in the finished engine.
In rough practice these defects are left to remove themselves by abrasion and wear, the process being to allow the parts to be somewhat loose (wherever possible) in their adjustment, and adjust them closer as the abrasion proceeds.
This is termed letting the parts wear down to a bearing. But the very process of wearing down to a bearing attests that the parts have not been properly fitted to a bearing, whereas to attain the best possible results the parts should be fitted to a bearing, because in wearing down to a bearing, undue abrasion, and to some extent or in some degree, roughness of the wearing surfaces, must ensue, because the strain intended to be distributed over the whole intended bearing area is limited to the actual bearing area. It is necessary, therefore, that, in putting an engine together, each part be properly fitted to its place, and that it be subsequently adjusted in its fit and position with relation to the other parts to which it is connected.
The fitting of the single piece is a test of its individual or disconnected truth; the subsequent or second adjustment is a test of its truth with relation to the others. Thus a pair of brasses may fit a journal perfectly, but that is no assurance that the brasses are so bored as to bring the rod holding them in proper line to enable connection at the other end without springing or bending the rod.
Furthermore, it often happens that the frame work of an engine does not form a base for the whole of the parts, thus in a large stationary engine, the end of the main shaft or crank shaft farthest from the crank (generally called the outboard bearing) is generally supported by a bearing having an independent foundation, and as this foundation does not exist until the engine comes to be permanently fixed for operation, its alignment must be performed when setting the engine. In an old engine this foundation may settle, or the wear itself may throw the engine out of line, so that the lining of an engine becomes periodically a necessity.
As a general rule a want of alignment induced by wear or incurred from repairs to the parts principally affects the main shaft, the cross head remaining more nearly true; and, with the exception of the crank pin, the same holds good with reference to a new engine.
Now while an error of alignment may exist in any direction, it is true, nevertheless, that an error in any direction will be discoverable if the parts be tested at four equidistant parts of the stroke or revolution, as, for instance, on the two dead centres of the crank and at the highest and lowest points of the path of rotation of the crank pin; hence attention may be confined to those four points.
Suppose then an engine already put together requires to be tested for being in line, and we have to test—
1st. The alignment of the main or crank shaft vertically.
2nd. The alignment of the main shaft horizontally.
3rd. The axial truth of the crank pin with the main or crank shaft.
4th. The adjustment of the crank shaft for vertical height, with relation to the cross-head journal.
Referring to this last, it may be necessary to remark that the axial line of the main shaft may be parallel when viewed either vertically or horizontally with the cross-head journal, and yet if a line be passed through the centre of the cylinder bore, and prolonged past the crank centre, the latter may fall above or below that line, but it will generally be below, because from the weight of the crank shaft its bottom bearings wear the most; and, further, to whatever extent those bearings wear after being in proper line, the crank shaft will fall too low.
We may now subdivide the errors of alignment of a crank shaft thus:—
1st. Its axial line, when viewed vertically, may form an acute angle to the axial line of the cross-head journal.
2nd. It may form an obtuse angle with the cross-head journal when so viewed.
3rd. It may, when viewed from the crank-pin end of the engine on about a horizontal position, be too high or too low at the crank-pin end only.
4th. It may be too high or too low at the outboard end only.
5th. It may be too high or too low at both ends, although parallel to the cross-head journals.
It will be found on consideration that with the exception of the[II-167] last-named case, the connecting rod forms the best test whereby to discover an error in any of these directions, because it magnifies the error and makes it more plainly discernible. It will further be found upon careful observation, that although a combination of these errors may exist, the connecting rod will serve to discover each error separately, as well as the collective error, because, although in some respects two distinct errors may have the same general result, yet the result will be different if taken in detail, and it follows, therefore, that the testing must be taken or made in detail first.
To test the parallelism of the axial line of the crank shaft with that of the cross-head journal, when viewed vertically: In Fig. 2529, let a a represent a line true axially with the bore of the cylinder, and b b a line at a right angle to a a, and passing through the centre of the pillow block or bearing spaces. If the engine were in line, b b would be coincident with the axial line of the crank. Suppose, however, that line b c represents the actual centre line of the crank, not then being at right angles to a, the end e of the connecting rod, if connected to the crank pin as shown, and made a good working fit so that there is no play of the pin in the brasses, will not come fair laterally with the bearing in the cross head. The amount of the error is the amount it is out of true in the length of the crank-pin journal, multiplied by the product of the length of the connecting rod (from centre to centre of the bores of the brasses) divided by the length of the crank-pin journal. It is apparent, however, that if the crank shaft be set to have its axial line at b b instead of at b c, the error at e d will be corrected, and thus we may employ the connecting rod to set the crank shaft in line.
It is, however, not sufficient to try the crank on one dead centre only (as will be seen presently), hence we place it on the other, and move the cross head to the other end of its stroke, and again try the end e of the connecting rod with the cross-head journal, and if it falls to one side, and on the same side as before, but to a less amount, it demonstrates that the axial line of the crank forms with the line a a an acute angle. If, however, instead of falling too much laterally towards the side f of the cross head, it fell too much towards d, but more so when tried with the crank on the dead centre nearest to the cylinder than when tried with the crank on the other dead centre, then it is proof that the axial line of the crank shaft forms with a a an obtuse angle.
The reason that the error will be more plainly shown with the crank on one dead centre than when on the other is shown in Fig. 2530, in which a a is a line coincident with the axial line of the cylinder bore, and b b the axial line of the crank shaft, from c to d is the plane of revolution of the crank pin, while g represents the crank centre. The points at c and f denote points central to the length and diameter of the crank-pin journal. Now, the centre line of the connecting rod for one dead centre is represented by e d, and for the other by f c, and it will be seen that the point at e is farther from a than is the point at f. It will be observed that the point d falls outside, while the point c falls inside of a a, and yet the centre line of the connecting rod stands, in both cases, at the same angle to the centre line a a of the engine, and in both cases throwing the end of the connecting rod, represented by the points at e f, outside the line a a.
If the connecting rod does not, when connected to the engine, as in Fig. 2529, fall true into the cross-head bearing, the error is the same in amount and comes on the outside of the cross-head journal with the crank placed on each respective dead centre, it is proof that either the flange of the crank-shaft brass (which is between the crank face and the frame) is too thick, or the inside flange of the connecting-rod on the crank pin is too thick, or else the crank is too thick, measured from the crank-pin journal to its inside hub face, the error being in the new crank or new brass, if one has been put in.
It may here be remarked that if the bore of the crank-pin brasses of the connecting rod is not at right angles to the centre line of the rod itself, the end e, Fig. 2529, might fall either inside or outside, laterally, of the cross-head bearing, but in this case the error will show more at one end of the stroke than at the other, for reasons which are explained with reference to Fig. 2530; hence it follows that the connecting-rod brasses should be properly fitted to their journals, and made to lead true before using the rod to line the engine by. In some cases it is more convenient to connect the rod at the cross-head end, and try the other end with the crank-pin journal, as shown in Fig. 2531. In this case, however, the connecting rod will (whenever the axial line of the crank shaft is out of square, forming an acute angle with the centre line a a, as in Figs. 2529 and 2530), fall laterally inside the crank-pin journal when on one dead centre, as in Fig. 2531, and outside when on the other dead centre, as in Fig. 2532, the respective amounts of error being in this case equal for the two positions. The reason for this is that the plane of revolution[II-168] of the crank pin falls outside of the centre line in one case, and inside for the other, as shown in Fig. 2530 at d c.
If the axis of the crank axle formed an obtuse angle to the engine centre line a a in Fig. 2529, the connecting-rod end tried with the crank pin, as shown in Fig. 2531, would fall outside of the crank-pin journal when the latter was on the dead centre nearest to the cylinder, as shown in Fig. 2534, and inside of the crank-pin journal when on the other dead centre, as in Fig. 2535.
Now, suppose either of the errors to exist, and the alignment be neglected, then if the brasses at each end be keyed up to fit their respective journals, then the body of the rod must be bent into a bow shape, and the strain of forcing or springing it into this shape will fall upon the journals, which will heat and pound in consequence.
It is now to be explained how to test if the axial line of the crank shaft is at a right angle to that of the cross-head journal, when viewed from the crank-shaft end and horizontally.
From a want of parallelism in this direction, heating of the crank pin and cross-head journals is sure, and a pound or thump is, to some extent, liable to occur, and the cause, if the error is slight, is difficult to discover, save by using the connecting rod to test it with.
When a thump occurs at the end of the stroke (when the crank is on a dead centre), it may arise from a ridge at the cylinder, or at the guide-bar end, or from the connecting-rod brasses being insufficiently keyed up; but when it occurs while the crank is at half stroke these causes are eliminated, and the cause must be looked for in either a crank pin not parallel to the crank shaft, or, as in the case now under consideration, because of one or the other of the crank-shaft journals being too low.
Assuming the crank pin and crank shaft to be axially true, one with the other, we may proceed to show separately the cause of the heating and that of the pounding, if the crank journal is too low at either end.
In Fig. 2536, let a represent the cross-head journal, and b b a line parallel to it. Let b c represent the axial line of the crank shaft (being out of parallel because the crank end is too high or the other end too low). Let f f represent the centre line of the crank pin when at the top, and g g when at the bottom of its path of rotation, and it will be observed that the vertical distance between the crank pin and the axial line of the cross-head journal[II-169] is less on one side than on the other; thus in the figure distance d is less than e. We have in this case measured these distances on a plane at a right angle to the cross-head journal, but it will make no difference if we measure them on a plane with the path of rotation of the crank pin, as will be seen in Fig. 2537, in which the distance from the centre of the crank pin at two opposite points in its path is represented by dots shown at e f, and from e to h measures less than from f to h, h representing the centre of the cross-head journal.
In Fig. 2537, let a represent the axial line of the cross-head journal, b a vertical line at a right angle to a; c representing the crank shaft extended by a dotted line, so as to enable comparison with a; d the crank, e and f the centre of the crank-pin journal, and g g a line at a right angle to cross-head journal a.
Now g, being at a right angle to a, represents what should be the plane of rotation of the crank pin, whereas c, being out of parallel with a, causes the path of rotation to be in the path from e to f, or as d compared to b; supposing then that the bores of the connecting-rod brasses to be axially parallel one to the other, and keyed up properly, and when at e one bore of those brasses will stand parallel to e while the other is parallel to a, or when at the bottom of the crank rotation, one bore will be parallel to f and the other parallel to a. Thus the rod will be twisted, and the strain due to this twist will cause the bearings to heat. That this twisting is continuous throughout the whole revolution may be seen by the want of parallelism of the dotted line (representing the crank pin when on the dead centre) with a (representing the cross-head journal).
It is now to be observed that if the plane of the crank rotation were at a right angle to the axis of the cross head, as it should be, the path of the centre of the crank-pin journal would be in the plane of g g, whereas it falls outside as at e, and inside as at f, while at h it is coincident; hence it appears that starting from a dead centre h, the rod bends, passing at that end outward to e (when the crank has made a quarter revolution), where it attains its maximum bend, thence diminishing until finally ceasing, when the crank reaches the other dead centre. As soon, however, as it passes the last dead centre a bend in the opposite direction takes place, attaining its maximum at f, and ceasing at h. This bending also causes undue friction and the consequent heating of the journals; furthermore, if there be any end play between the brasses and the journals, there will be a pound, as the brasses jump from one end of the journal to the other at different parts of the stroke. It is obvious that if the crank end of the crank shaft was too high instead of too low, as in our example, then the effects would be the same, but e would fall on the inside instead of the outside of g, while f would fall outside instead of inside.
To discover if the crank shaft is out of parallel in the direction here referred to, connect the connecting rod to the cross-head journal, setting the brasses up to a close working fit. At the other end of the connecting rod put the strap keys and brasses in their places, but not on the crank-pin journal. Place the crank in its highest position, and lower the end of the rod down to the crank-pin journal, as shown in Fig. 2538, and if the crank shaft is parallel (in the respect here referred to) to the cross-head journal, the brass flanges will just meet the faces of the crank-pin journal, as shown in Fig. 2539. If, however, the crank end of the crank shaft is too low, as in our example, the flanges of the brasses will fall to one side of the crank-pin journal, and that side will be toward b, Fig. 2540, when the crank pin is at the top, and toward c, Fig. 2541, when it is at the bottom of its path of rotation.
The effects will be precisely the same, and in the same direction with relation to the various parts of the crank’s revolution, if the crank-pin end of the shaft was of correct height; but the other end was too high, hence, in correcting the error, it is desirable to place the engine on the dead centre, so as to determine which end of the shaft to operate on—that is to say, whether to raise the crank-pin end or lower the other end. But suppose the error to be that the crank-pin end of the shaft was too high instead of too low, then, the testing being continued as before, the effects will be[II-170] of the same general character, but altered with relation to the specific parts of the revolution. Thus, when the crank is at the bottom, the rod would fall towards a, Fig. 2542, and when at the top, it would fall in the opposite direction—that is, towards d, Fig. 2542.
We now come to one of the most common errors in the alignment of the parts of an engine, and to the one that it is the most difficult to locate or discover, namely, a want of parallelism between the axial line of the crank pin and that of the crank shaft.
This generally arises from improper methods in the chucking of the crank to bore it, or from errors induced in fastening the crank to its shaft. The results are precisely alike in both cases, supposing, of course, the errors to exist in the same direction in the two cases.
The error in chucking usually consists in planing one surface of the crank, and bolting the planed surface against the chuck to bore both crank holes. In this case the crank holes will be out of true to twice the amount the lathe face plate may be out of true, and to whatever amount the crank may alter its form from having its surface metal removed.
To avoid these errors the large bore and its hub face should be turned at one chucking, and this hub face should be bolted to the face plate for the second chucking, the small end swinging free, except in so far as the ends of the plates may touch against it to steady it.
The error in putting the crank on may occur from the key springing the crank out of true, and if the crank is shrunk on from too great an allowance for shrinkage or improper heating for the shrinkage or contraction, as it is sometimes termed. Referring to the error in keying, it is more liable to occur when the crank bore and its seat upon the shaft are made taper, than when made parallel, because it is a difficult matter to insure accuracy in the fit of the taper, and the key pressure will spring the crank over on the side at which it is the easiest fit. In Fig. 2543 let a represent the end of the crank shaft; b the key, and c the crank shown partly in section: suppose the crank bore (whether made taper or parallel) has a slightly easier fit on the side d than on the side e, and the pressure of the key (supposing it to fit properly top and bottom) would spring the crank over in the direction shown in the figure, the axial line of the crank pin standing at the angle denoted by the line f, instead of parallel to the axial line of the shaft. Suppose the crank to be put on by hydraulic pressure, and the key to fit on the sides and not on the top and bottom, then its fit to its seat on the shaft would depend on the truth and smoothness of its bore and seat on the shaft, the amount allowed for the forcing fit and the amount of the error. If the latter amount was so small that the crank would fit at both ends, but simply fit tighter at e e than at d, the crank would remain true, but might possibly get loose in time. This would be especially liable to occur if the tool marks on the bore and seat were so deep that the contact was mainly at the tops of those marks or ridges which would be apt to compress. But if the surfaces were cylindrically true and smooth, and the amount allowed for forcing was sufficient as stated to give the bore and seat contact at d, with a key fitting sideways, the crank would probably remain tight and true.
Were the bore and its seat parallel the crank would remain true, no matter whether the key fitted on the sides or at the top and bottom, providing the key fitting top and bottom were bedded fairly from end to end.
When the surfaces are not smooth, but contain tool marks or ridges, an unequal pressure of the key at one end, as compared to the other, sets the crank over, as shown in the figure, because the key pressure compresses the ridges and lets the crank move over.
Supposing the strain of the key, or keys, to be depended upon to hold the crank, they must fit top and bottom, and their accurate fit becomes of the first importance; because not only is it necessary that they fit equally at each end, but they must also fit equally across the width of the key at each end. For example, in Fig. 2544 is a key binding most at the opposite corners, as denoted by the dotted surfaces a b, and the result will be that the key pressure would tend to twist the crank in the direction of d e, having c as a centre of motion, providing that the error was equal at a and b; but in proportion as the error was greatest and the fit tightest at a, or at b, would the centre of motion be moved nearer to either point.
Supposing now that the crank is to be shrunk, or contracted on, then the points of consideration are (supposing the crank to fit properly to its seat, whether the same be either parallel or taper) that the hub of the crank opposite to the throw is the weakest and[II-171] is likely to give most in the process of contraction, so that if one part (as f) of the crank be made hotter than another (as g) it will give way more, and this will twist the crank. This is specially liable to occur if an excessive amount of difference in the bore and seat diameters has been allowed for contraction.
It may not happen that a crank pin is out of truth in a direction in which the error will show plainest when the crank is on its dead centres, or at half-stroke; but if a crank pin, tested in those four positions, fails to show any error when tested by the connecting rod, it will be true enough for all practical purposes, and true enough to avoid heating and pounding, both of which evils accompany an untrue crank pin. Suppose, now, that a crank pin stands out of true in the direction shown in Fig. 2545, in which a a represents the axial line of the cylinder bore prolonged, and b b the axial line of the crank shaft (the two being parallel or in proper line). Let e e represent the centre line of the connecting rod when the crank is on one dead centre, the axial line of the crank pin being at c c. Then the brasses being keyed up to fit the crank pin, the centre or axial line of the connecting rod would stand as denoted by e e. But the brasses at the other end of the rod being keyed up to fit the cross-head journal, and their lines being at a right angle to the line a a, we have that the rod is at that end endeavored to be held parallel to a a; hence, keying up the connecting-rod brasses on the crank pin would tend to bind the rod, one end standing parallel to a a, and the other parallel to e e.
This would place great strain on the outer radial face of the cross-head journal, as well as on the cylindrical body of the journal.
When, however, the crank pin arrives at the opposite dead centre, as denoted by the dotted lines in Fig. 2545 (g g representing its axial line, and f f the centre line of the connecting rod at a right angle to g g), the want of truth in the pin throws the cross-head end of the connecting rod against the inside face of the cross-head journal. Hence, twice in each revolution is the connecting rod bent, and twice does it jam from side to side of the cross-head journal.
It may now be pointed out that if we take either dead centre singly, and connecting the rod at the crank-pin end, try it at the cross-head end, and it will be a difficult matter to determine whether any want of truth at the latter end is caused by the crank pin being out of axial truth, or whether it is the crank shaft itself that is out of line. But there is this difference between the two cases. When the error is due to want of alignment in the crank shaft, the connecting rod will show the error on the same side of the cross head, no matter on which dead centre the crank pin stands; but when it is due to the crank pin, the rod will fall inside the cross head on one dead centre, and outside when tried on the other dead centre, as is shown by the respective lines e and f, in Fig. 2545; e being at a right angle to c, and f at a right angle to g.
Again, it has been shown that when the shaft was out of line, a point on the crank-pin journal passed outside of the cylinder centre line at one dead centre and inside at the other; but when the pin is axially out of parallel, the path of a point on its journal will remain in the true plane, as is shown in Fig. 2546, the point being taken at the intersection of e and c c. a a represents the path of rotation of the same, which is parallel to the true face b of the crank.
From the angle of the axial line of the pin being in opposite directions, when on opposite dead centres to the axial line of the crank shaft, the bore of the brasses cannot wear to suit the error, which, therefore, only diminishes by the wear of the crank pin. Suppose the error to be 1⁄64 inch in a crank-pin journal 3 inches long, and that the connecting rod is 6 feet long, the error at the cross-head end of the rod will amount to 3⁄8 inch.
In Fig. 2546 the error is shown to exist in an opposite direction, throwing the rod to the other side of the cross-head journal. But, in this case, the crank, when on the dead centre nearest to the engine cylinder, throws the connecting-rod end against the inside face of the cross-head journal, as denoted by the line e, which is on the opposite side of a a to what it is in Fig. 2545. Again, when on the other dead centre, the line f f, in Fig. 2546, falls outside, while f f, in Fig. 2545, falls inside of a a, and it is by this difference that we are enabled to know in which direction the crank pin is out of true. To find the amount to which it is out of true in the length of its journal, place the crank on one dead centre, and with the connecting-rod brasses keyed up firmly home on the crank pin, and the other end of the connecting rod entirely disconnected from the cross head, mark on the latter a line coincident with the side face of the rod end, as at d, Fig. 2547. Then, with the crank pin placed on the other dead centre, mark another line on the cross head, coincident with the other side face of the rod, at c, Fig. 2547. Now, suppose that the line d shows the rod to fall 3⁄8 too much on that side, and line c shows it to fall (when on the other dead centre) 3⁄8 too much on the other side of the journal, and that the length of the rod is 6 feet, while that of the crank-pin journal is 3 inches, then the latter, divided into the former, gives 24, and this sum divided into the 3⁄8, the rod end falling out of true at c and d, Fig. 2547, gives us 1⁄64-inch as the amount the crank pin stands out of true in its length; hence, to correct the error, we may file on the crank pin a flat place at each end, as shown in Fig. 2548 by the lines c d, and then file on the top and the bottom of the crank pin a flat place b, 1⁄128-inch deep, and of equal depth all along the journal; by then filing the crank pin round and bringing the flat places just up to a circle, we shall have reduced the diameter of the crank pin by 1⁄64 inch, and have made it axially true with the cross-head journal. It is important, however, to bear in mind that, in this case, the crank pin is supposed to be out of true in the direction shown in Fig. 2545, and to stand axially true with the cross-head journal, when the crank is placed at half stroke, top and bottom, the crank shaft being in proper line.
[II-172]If the axial line of the cross-head journal stands truly horizontal, the flat places on the crank pin may be filed horizontally level, with the crank placed on the corresponding and respective dead centres. But as the length of the cross-head journal is so short, it is difficult to gauge, if it does stand axially exactly horizontal, hence it is better to try the rod, or follow the above directions; especially as the cross-head journal and crank shaft may be in line without being axially horizontal.
Suppose now that the axial line of the crank pin stands true with that of the cross-head journal when the crank is on either dead centre, but out of true when at the top and bottom half stroke. The connecting rod, connected as before, and tried with the cross head, will fall first to one and then to the other side of the cross-head journal, and the direction in which the crank is out of true may be known from the position of the crank pin when the error shows itself.
If the error exists to an extent that is practically measurable, a pound in the journals, as well as their heating, is the inevitable result. In Fig. 2549, for example, the rod end is shown in section, and it will be noted that the error being in the direction there shown, and the crank pin in the respective positions there shown, the brass bore only contacts with the journal at each end, and that the diameter of the bore of the brasses is greater than the diameter of the crank pin journal to twice the amount the crank pin is out of line. Now let us place the crank at the top of its revolution, as in Fig. 2550, and as its axial line then stands parallel to that of the cross-head journal, the brass bore is too large to fit the crank pin journal and there is lost motion.
From the time the crank pin passes the dead centre this lost motion increases in amount until it becomes sufficiently great to slam the rod over against the side of the cross-head journal, while at the same instant the crank pin pounds in the connecting-rod brasses. At what precise part of each quarter crank revolution this action will occur, depends upon the amount the crank pin is out of line; but the more it is out the nearer to the dead centre it will be, and, conversely, the nearer true it is the nearer the crank will approach its highest and lowest positions before the pound takes place. If it is attempted to key up the brasses so as to spring the rod and let them close along the journal, the brasses will heat in proportion to the amount of error; hence when the crank pin pounds with the brass properly adjusted, and heats while keyed up enough to stop the pound, the crank pin is out of true.
To test the alignment of an engine with stretched lines take out the piston and rod, and take off the connecting rod, then fasten a piece of iron at the open end of the cylinder so that it will hold a stretched line true with the axis of the cylinder bore. Provide at the crank end of the engine bed a fixed piece of wood to hold the other end of the line, and then with a piece of wire as a gauge set this line (tightly stretched) true with the cylinder bore. Then place the crank pin at the top of its path of rotation and drop a plumb line from the centre of its journal length, and this line should, if the crank shaft is horizontally level, just meet the stretched line. If it does not do so place a spirit level on a parallel part of the crank shaft, and if the shaft is not level it should be made so, and so adjusted that the line from the centre of the length of the crank pin journal just meets the stretched line from the cylinder bore.
To test if the axial line of the crank shaft is at a right angle to the cylinder bore axis move the crank pin nearly to its dead centre, and measure the distance from the middle of its length to the stretched line. Then move the crank pin over to nearly the opposite dead centre, and (by means of the plumb line) measure the distance of the plumb line from the stretched line. To be correct the plumb line from the crank pin will during this movement just touch the stretched line.
To test if the stretched line is fair with the centre of the crank shaft place a square on the end of that shaft and even with its centre, and the blade should then just meet the stretched line.
The edges of the guide bars may also be tested with the stretched line, and the top and bottom of the guide-bar flanges may be tested to prove if the bars are of the correct height.
To further test the bars place a spirit-level across them and lengthwise on them.
If the piston rod and connecting rod are in place the alignment may be tested as follows; Let the piston rod be as far out of the cylinder as possible, and stretch a line to one side of it, just far enough off to clear the guide bars, &c. Set this line as follows: Let it be in line with the rod as sighted by the eye when standing some few feet away from it but horizontally level with the centre of the rod, set it parallel to the rod with a rule or its equivalent. [II-173] Then the centre of the crank-pin journal should measure from the stretched line, the distance of the line from the piston rod added to half the diameter of that rod. This test, however, is not very accurate on account of the difficulty in setting the line, and because the piston rod may not have worn equally on each side.
Setting Slide-Valves—An engine slide-valve may be so set as to accomplish either one of three objects. First, to give equal lead for each stroke; second, to cause the live steam to be cut off and expansion to begin at an equal point in each stroke; and third, for the exhaust to begin at an equal point in each stroke.
If we, set the eccentric so that the exhaust will begin at corresponding points for the two strokes, the valve lead will not be equal, and the exhaust opening will be greater when the piston is at one end of the cylinder than it will be when the piston is at the other end.
If the eccentric be set to cut off the steam at corresponding points for the two strokes, then the lead, the admission, and the exhaust of the steam at one port will differ (with relation to the piston movement) from that at the other. It is generally preferred to set the eccentric so as to give equal lead for the two ports when the piston is at the respective ends of its stroke, which gives an equal amount of exhaust opening when the piston is at the respective ends of its stroke.
The only operations properly belonging to the setting of a slide-valve are those of finding the true dead centres of the crank pin, and setting the eccentric to give the valve the desired amount of lead. It is generally found, however, that the length of the eccentric rod requires a little correction, and as this must be done before the eccentric can be set, the setting operations should be conducted with a view to making the correction as early as possible.
In many of the instructions given by various writers it is directed to first square the valve, which is to attach the parts and move the engine crank, or fly-wheel, through one revolution, to ascertain if the valve moves an equal distance on each side of the centre of the cylinder ports, correcting the length of the eccentric rod until this is the case. This is an error, because on account of the angle of the eccentric rod the valve does not, when set to have equal lead at each end of the stroke, move an equal distance on each side of the cylinder ports, but travels farther over the port nearest than it does over that farthest from the crank.
When the travel of the valve is equal to twice the width of the steam port, added to twice the amount of steam lap, the valve does not fully open the farthest port from the crank. When the valve-travel is more than this amount both ports may open fully, but the error due to the unequal valve-travel from the angularity of the eccentric rod is increased. That the amount of error induced by squaring the valve is appreciable, may be seen from the fact that with 11⁄4 inch steam ports, 3⁄4 inch steam lap, and 41⁄2 inches of valve-travel, it amounts to about 1⁄8 inch with an eccentric rod 4 feet long. As the eccentric rod has (if a solid one, as in the case of a locomotive) to be operated upon by the blacksmith to alter its length, and requires some accurate setting for alignment after having its length corrected, it is obviously preferable to obtain its exact length at once. This may be done with less work than by the squaring process, which is entirely superfluous.
Assuming, then, that all the parts are properly connected and oiled, the valve is set as follows: Upon the face or edge of the fly-wheel an arc, true with the centre of the wheel, should be drawn, as at a b, in Fig. 2551, marking it on opposite sides of its diameter and opposite to the crank pin p. The engine should then be moved in the opposite direction to that in which it is to run, until the guide block i is very near its full travel. A straight-edge must then be placed to bear against, or be coincident with, the end face of block i, and held firmly while a line is drawn across the edge of the guide bars, as shown at c. There should then be fastened to the floor (which must be firm, and not give under the engineer’s weight), a piece of iron w, having a deep centre-punch mark, or its equivalent. A steel tram-rod t, pointed at each end, is then set in the centre-punch mark at w, and with the upper end d a line made across the wheel edge or face. The fly-wheel must then be moved so that the crank passes the dead centre, the guide block moves back and away from the line c, and then approaches it again. When the end of the guide block is again coincident with the line c, the tram should be set as before and a second line, f, marked on the fly-wheel rim, and from these two lines, d and f, the crank may be placed upon its true dead centre as follows:—
In Fig. 2552 a section of the fly-wheel rim is shown (enlarged for clearness of illustration); from the lines d, f the centre e is found, and marked with a centre punch dot to define it. It will be obvious, then, that if the fly-wheel be moved until this line and dot come fair with the upper edge of the tram t, the guide block will be at the exact end of its travel, and the crank, therefore, on its dead centre. By a similar operation performed with the guide block at the other end of the guide bars, and with lines on the other side of the wheel rim (as shown at b, j, k), the other centre l may be found. In obtaining these centres, however, a question arises as to the direction in which the wheel should be moved for bringing the guide block up to the lines at c, and for marking the[II-174] lines d f and j k, or for bringing e or l true with the tram point. If the fly-wheel be moved in the opposite direction to that in which the engine is to run, the cross-head journal and crank pin will bear against the boxes of their brasses in the direction in which they will have contact when the engine is running. Suppose, for example, that the top of the fly-wheel when the engine is in motion moves from the cylinder, then the cross-head and crank-pin journals, driven by the piston, will bear against the half-brass nearest to the cylinder, which, when the force-producing motion is applied to the fly-wheel instead of to the piston will be the case when the fly-wheel is moved in the opposite direction. By moving the fly-wheel in an opposite direction to that in which the engine is to run, the lost motion in the journals and bearings is therefore taken up in the proper direction so far as the connecting-rod brasses are concerned, and any lost motion between them and their journals will not impair the set of the valve, as would be the case were the fly-wheel moved in the direction in which it is to run.
But by moving the fly-wheel backwards the play in the eccentric and in all the joints between it and the valve spindle is up in the wrong direction, because the power to move the rods is being applied in the opposite direction to that in which it will be applied when the engine is running, and, therefore, the play motion of the jointed or working parts will cause a lost motion impairing the set of the valve.
Now there are generally more working parts between the eccentric and the valve than between the crank pin and the piston, and hence more liability for lost motion to exist, and it follows that in such case it is better to move the engine in the direction in which it is to run.
It may be remarked, however, that the play may be taken up in the proper direction in both cases, and the engine be brought upon its dead centre, by moving it in the opposite direction to that in which it is to run, and that in setting the eccentrics they be moved on the shaft in the direction in which the engine is to run, as forward for the forward eccentric, and backward for the backward one (assuming the engine to have a link motion, and, therefore, two eccentrics).
It is obvious that any other resting place may be used instead of the floor for the tram; thus in a locomotive the wheel guard may be used, the tram t being used to mark lines on the upper part of the wheel rim, instead of opposite the crank. To set the valve, place the fly-wheel on its dead centre, moving the fly-wheel as directed until one of the points (e or l, say e) comes fair with the point of the tram; then move the eccentric on the shaft until the steam port is open to the required amount of lead, and fasten the eccentric to the main shaft. Next move the fly-wheel around until on the opposite dead centre, and if the lead is the same in amount for both ports the valve is set. Suppose, however, that in this last case the lead is too great; then it shows that the eccentric rod is too long, and it must be shortened to an amount equal to half the difference in the lead. Or suppose that the lead when the wheel was tried on the last dead centre l, was less than for the other port; then the eccentric rod must be lengthened to half the amount of the difference. Assuming that the rod was too long by 1⁄32 of an inch, then it may very often be shortened by simply heating about six inches of its length to a low red heat, and quenching it in water. If the rod has a foot which bolts on a corresponding foot on the eccentric, then to lengthen it a liner of the requisite thickness may be placed between the two feet.
Suppose there is an equal amount of lead at each end but the amount is not sufficient or is too great: then the eccentric must be moved on the shaft until the proper amount of lead appears at the port. The lead must then be again tried at the other dead centre. In moving the eccentric, however, it must, under all conditions, be moved in the direction in which it will rotate, for reasons already given. The best method of measuring the lead where the lines on a rule cannot be seen is with a lead wedge p, as shown in Fig. 2553; this, if slightly forced in, will mark itself, showing how far it entered.
In some practice the position of the valve is transferred to the valve stem outside of the stuffing box or gland, as shown in Fig. 2554, sectional view. The valve stem being disconnected from the rod or arm that drives it, the valve is moved by hand to have the proper lead, as at a; a centre-punch mark is then made outside the stuffing box and a tram b rested thereon; with the other end of the tram a mark c is made on the valve stem. A similar mark is made on the stem when the crank is on the other dead centre, and the tram and marks, applied as shown, are employed instead of measuring the lead at the ports themselves. This involves extra work, but gives no more correct results. It involves marking lines on the valve stem, which is objectionable. If several trials have to be made there is a confusion of lines on the valve stem, and the wrong one is apt to be taken. On the other hand it affords a facility for setting the valve without having the steam chest open, which may in some cases be desirable. If this plan be adopted the lines on the valve rod should not be defined by centre-punch marks, for they will cut the packing in the stuffing box.
When the eccentrics are secured to the shaft by a set-screw only, and not by a feather, it is an excellent plan, after they are finally set, to mark their positions on the shaft, so that if they should move they may be set to these marks without moving the engine around.
For this purpose take a chisel with the cutting end ground to the form of a fiddle drill, one cutting edge being at a right angle to the other. The chisel must be held so that while one edge rests upon the axle, the other edge will bear against the radial face of the eccentric. A sharp blow with a hammer upon the chisel head will make a clean indented cut upon the axle and the eccentric, the two cuts exactly meeting in a point where the eccentric bore meets the axle circumference, so that when they coincide the eccentric is in its proper position.
If the eccentrics of a locomotive should slip when the engine is upon the road, and there are no marks whereby to readjust them, it may be done approximately as follows:—Put the reverse lever in the end notch of the forward gear, then place the crank as nearly on a dead centre as the eye will direct, and open both the cylinder cocks, then disconnect the slide-valve spindle from the rocker arm, and move the valve spindle until the opening of the port corresponding to the dead centre on which the crank stands will be shown by steam blowing through the cylinder cock, the throttle valve being opened a trifle. The position of the valve being thus determined, the eccentric must be moved upon the shaft until the valve spindle will connect with the rocker arm without being moved at all. The throttle valve should be very slightly opened, otherwise so much steam will be admitted into the cylinder that it will pass through any leak in the piston and blow through both cylinder cocks before there is time to ascertain which cock first gives exit to the steam.
Instead of finding when the crank pin is on the dead centre by means of the process shown in Fig. 2551, it may be found as in Fig. 2555, which is for a vertical engine. On the face of the crank and from the centre of the crank shaft as a centre, draw a circle b equal in diameter to the diameter of the crank pin. Then take a spirit-level c and apply it to the cylinder bore and note where its bubble stands. Then apply the spirit-level to the perimeter of the crank pin a and circle b, and move the crank until the spirit-level bubble stands in the same position as it occupies when applied to the cylinder bore. If the cylinder bore stands truly vertical the bubble will in both cases stand in the middle of the spirit tube; but in any event, the bubble must stand in the same position when[II-175] applied to the crank as when applied to the cylinder bore, in which case the crank will be on its dead centre whether the cylinder bore be horizontal, vertical, or at an angle, the dotted line e passing through the centre of the crank and the axis of the cylinder bore.
When an engine has two eccentrics, so as to enable the engine to run in either direction, as in the case of a locomotive, it is necessary to consider which eccentric is to be set for the forward, and which for the backward motion. In American locomotive practice it is usual to let the eccentric nearest to the wheel, and, therefore, the most difficult to get at, be for the backward motion, which is the least used, and therefore the least liable to get loose upon the axle.
The eccentric that connects to the top of the link is usually that for the forward motion, and hence that which connects with the eccentric farthest from the wheel.
In testing the lengths of the eccentric rods, work may be saved after the engine is first placed on its dead centre by putting the reverse-lever in the forward notch of the link, and adjusting the forward eccentric until the valve has the proper lead. Then set the reverse-lever in the back notch and move the backing eccentric (in both cases moving them in the direction in which they will run), until the proper amount of lead appears. The engine may then be placed on the other dead centre, and the lead both for forward and backward gear measured, so that if there are any errors both the rods may be corrected for length; but for the final trial the crank pin must be set on its dead centre for each direction of motion separately, so as to take up any lost motion in the connecting-rod brasses.
In the case of large marine engines it is not practicable to move or rotate the engines to set the valves, and the eccentrics are therefore adjusted to their positions on the crank shaft by lines before the crank shaft is put into its place or bearings. First, the throw of the crank is set to stand horizontally true by the following method: From the centre of the crank shaft strike a circle of the diameter of the crank pin, as shown in Fig. 2556, at a, and draw upon the face of the crank a line that shall just meet the two circles as denoted by the line b, using a straight-edge, one end of which rests upon the crank pin, while the other end is coincident with the perimeter of the circle a.
By means of the wedges shown at c d adjust the crank until the line b stands horizontally level, tested by a spirit-level. A straight-edge having straight and parallel edges is set horizontally level, beneath the eccentric, so that its edges will stand parallel with the throw line of the crank. On this straight-edge, and parallel to the edges, is marked the line a a, Fig. 2557. The first process is to mark on a a the centre of the crank shaft k, which is done as follows: Over k is placed the fine line b b, suspending the weights or plumb bobs at b b; coincident with this line and across a a, are marked two lines c d; midway between c d is marked e, which therefore stands directly beneath the shaft centre. From e the line f is drawn distant from e to the amount of lap added to the lead the valve is to have. From f as a centre two lines are drawn across a, their distance apart equalling the full diameter of the eccentric; the plumb line is then placed over the eccentric, and the latter is rotated on the shaft until the plumb lines come exactly fair with the lines g h.
It is obvious that instead of using plumb lines a square may be employed to mark the lines c d, and to set the eccentric to the lines g h, the square being applied as at s and s′, in Fig. 2558.
In this example it has been assumed that the direction of crank rotation was to be as denoted by the arrow; but, suppose the crank rotation required to be in the opposite direction, then the marks on the straight-edge would require to be located precisely the same, but the position of the eccentric throw-line would require to be as in Fig. 2559, the perimeter of the eccentric being set to the lines g h[II-176] as before. The eccentric rod being supposed to connect direct to the valve spindle, without the intervention of a rock shaft, for if there is no rock shaft the eccentric leads in the direction of rotation, while if the engine has a rock shaft the eccentric follows the crank-pin in the direction of rotation, and f must be marked on the crank-pin side of e, as in Fig. 2560.
If two eccentrics are used, as in a link motion, the lines for setting one eccentric are equally applicable to both; the lap and lead line f being located on the crank-pin side of e when there is a rock shaft, as is supposed to be the case in Fig. 2561; and on the other side of e when there is no rock shaft; and in this case the eccentric that is to operate the valve to make the engine run forward must have its throw-line following the crank pin, as at j, in Fig. 2561; the eccentric k operating the valve for running backward. Conversely, in the absence of a rock shaft, the throw-line of the forward eccentric leads, while that of the backward eccentric follows the crank pin.
When the line of connection of the eccentric rod is not parallel to the axial line of the cylinder bore, the crank must be placed horizontally level (or if it be a vertical engine, on the dead centre), but instead of the straight-edge being placed parallel to the throw-line of the crank, it must be placed at a right angle to the line of connection of the eccentric rod.
Thus in Fig. 2562 the engine is supposed to be a vertical one, and the crank is, therefore, placed on its dead centre, its throw-line being vertical instead of horizontal as in our previous examples (which were supposed to be for a horizontal engine). It is also supposed to have a rock shaft a; hence the straight-edge is set at a right angle to the line of connection of the eccentric rod which is denoted by b.
It is obvious that to set the crank throw-line vertical the circle b in Fig. 2509 may be used, the spirit-level being resorted to to discover when the crank stands vertical.
An example in the erection or setting of framed work is shown in Fig. 2563, which represents a side elevation of a frame put together in four parts, two side and two end frames. a and b are journal bearings requiring to stand parallel and true one to the other, b being capable for adjustment in distance from a by means of the adjusting screws g, h. The bearings c, d, e, f, are to be parallel one to the other and to a, b. Their proper relative distances apart, and the axes of all the shafts, are to stand at a right angle to the side frames.
Fig. 2564 represents an end view of the frame, the ends t being bolted to the side frames s and s′ at i, j, k, and l.
Now it is obvious that the ways for the bearings a, b, c, &c., may[II-177] be trued out, ready to have the brasses fitted before the framework is put together, and that from their positions they would have to be planed out at separate chuckings; supposing, of course, the frame to be too large to be within the capacity of the machine table. It would be difficult to cut all the surfaces of the bearing ways to stand in the same plane, unless there were some true plane to which all might be made common for parallelism.
Furthermore, unless the surfaces where t is fastened to s and s′ are properly bedded to fit each other, bolting them up would spring and bend the frames out of their normal planes. To meet these requirements, there are given to the side frames a slightly projecting surface where the feet of t meet them, and furthermore, the feet of t themselves project beyond the sides of t as shown. These projecting pieces may therefore be planed to a common plane without planing the sides of the respective frames; and this plane should be as nearly as can be parallel with the body of each frame surface. The surfaces of the bearing ways may then be planed parallel to those of the projections, and the jaw surfaces true to the side surfaces, and all the bearing ways will stand true if the frames be properly set—when put together with the bolts. But unless the bedding surfaces at i, j, k, l, be made to bed and fit properly, the whole truth of the bearing ways and their distances apart across the framework may be altered. Thus, supposing the feet of t at i and j to meet s as denoted by the dotted lines o r, and whether the fault lie with the feet of t or with the projections on s the result will be that the pressure of the bolts holding i j to s will bend s so that its plane will be a curve as denoted by the dotted line p p, and the distances apart of the journal ways b b and d d respectively will be wrong, being too wide on account of the bend outward of s.
But the feet may touch on the opposite corners, the surfaces of s′ or of t being out of true or out of full contact, as denoted by the dotted lines v w on k, l; in this case the frame s′ would be bent to the curve q q, and the journal ways would be too close together.
On the other hand, the want of fit between these surfaces may be in the direction of the length of the frame instead of the direction of its height, as has been supposed; or it may be in one direction on one foot and in another direction on another foot. But in whatever direction it does exist, it will inevitably bend and twist the frame.
It must not be taken for granted, that because these surfaces have been planed or milled, that therefore they are true; because frames of this class cannot, if large, be held without springing them to some extent from the pressure of the bolts or other devices necessary to hold them to be cut.
It is not uncommon to plane the surfaces as true as may be, and put the frames together, bolting them up tight, and then applying the straight-edge trammel and rule to test the truth, correcting any error that may be found by inserting pieces of paper, sheet tin or material of requisite thickness on one side of the surfaces, so as to offset the error in their fit and bring the framing true; but this is not the proper way, because it reduces the area of contact, and furthermore renders a new testing and adjustment necessary whenever the frames are taken apart. It is better therefore to apply a straight-edge to the surfaces and true them to it, testing them vertically as by placing the straight-edge across k l, and longitudinally across s′, at k and the corresponding projection at the other end of the frame, filing them until they appear true.
The holes through the frame may be drilled before filing these surfaces, so as to reduce the area to be filed. Since the end frames t do not in this example carry any journals or mechanism, the position of t is not so particular as it otherwise would be; hence, the holes in its feet may be marked off and drilled independently of the frame, the holes being drilled a little too small to allow for reaming with the holes in the frame. The framing will then be ready to put together (all machine work upon them being supposed to be done). The feet of all such frames should be planed true, so that the frame, when put together, may stand true and steady when placed upon a level floor or foundation, and in this case the distance and parallelism of the feet surfaces will be true with the ways or bearings, affording much assistance in holding the frame while putting it together. The height of the holes may be measured and marked from the feet surface, thus insuring truth as far as height is concerned. Lines may be drawn or marked on each side frame, at the proper distance from and parallel with the jaws of the ways a, b, thus completing on the side frames the marking of the location of the centres of the holes for bolting the end frames on.
If the frames were of a size to be sufficiently easily handled, the end frames might be put in their places, and the whole framework set true, so as to mark the holes in the end frames from those already drilled in the side frame. But if the use of a crane were necessary to lift them, it would be better to mark the holes on the end frames, and drill them before putting the framework together at all, leaving sufficient to ream out of the holes to bring them fair, notwithstanding any slight error in drilling them. In this case, a line denoted by the dotted line x in Fig. 2564, should be drawn across the frame, and the holes at i and j be made equidistant on each side of it, as well as the proper distance apart. x must be at a right angle to the trued foot surfaces at i j, so as to cause the side frames to stand vertical while their feet are horizontal.
Supposing now the holes to be drilled and the frames are to be bolted together, the whole frame may be held temporarily together by bolts passing through the side frames at each end, or a bolt may be passed through the holes f to steady it. Indeed, if these holes f have been accurately bored, a neatly fitting mandrel passed through them should hold the side frames true. The end frames t having been set to stand at a right angle to the side frames, and with their holes at i j, &c., as near fair as may be with the holes in the side frames, two feet, as i j, may have their holes reamed fair with the holes in the side frames, and tightly fitting bolts be driven in and screwed firmly home. Before reaming the other holes (as k l) of each end frame, the jaws to receive the bearing boxes should be tested for alignment one with the other. Truth, in this respect, being of the utmost consequence for the following reasons:
Suppose the bearing ways on one side frame to stand higher than those on the other, then, the shafts will not stand level in the frame unless (except in the case of the brasses or boxes in b) the lower brasses are made of unequal thickness through the crown, to an amount equal to that of the error. In the case of the brasses in a, c, d, e, the joint faces of all the brasses of one side frame would require to be made thinner beneath the journal than above it on the high frame, and thicker beneath than above on the low frame, This would entail much extra work in planing, marking, and boring the bearing boxes or brasses, and be an inferior job when done.
Again, the bores of all the brasses would not be parallel to the crown or bedding faces, and this error would entail the following extra work: 1. Ascertaining the amount of the error, and allowing for it in marking the brasses; 2. The setting of the ways of the brasses out of true with the ways when clinking them for boring; and, finally, extra fitting or filing the brass bores when fitted with the shafts in place. This extra fitting would be necessary for the following reasons:
When the surfaces of work are to be parallel, they can be measured with calipers. Surfaces to be at a right angle can be tested with a square; those to be in line can be tried with a straight-edge, and in each case the truth or alignment of the surfaces is tested by contact of the testing tool. But in the cases where surfaces at an angle are tested or measured the tools must be set to a line or lines, and the work must be measured or cut to lines, thus: Suppose it were found that the bedding surface of the brass b was a certain amount out of alignment with the corresponding bedding surface on the other side frame, and, by measurement, this amount determined to be 1⁄64 inch, then there is a liability to error in measuring this 1⁄64. The brasses must be marked (for boring the same 1⁄64 out of square, inducing another liability of error in marking that amount); this marking being done by lines, there is a liability to error in setting the work to the lines. From these liabilities to error, it is generally found that work not true in alignment requires, when it comes to be put together, to have each piece fitted to its place and corrected for alignment.
But, suppose the ways are made true and in proper alignment, then the brass bores are simply made of equal thickness at the crown, and on the sides at a right angle to the inside faces of the ways; and truth, in these respects, may be measured by actual contact, with the square or calipers, eliminating the chance of error.
In repairing the machine, or putting in new bearings or brasses;[II-178] the measurement and transferring of the error in the ways to the brasses has all to be gone through with again, and the parts fitted for alignment; whereas, if the ways are true, the brasses can be made true, and to go together, with but little, if any, adjustment when tried in their places.
The most accurate method of testing the adjustment of the ways is as follows: Fig. 2565 represents a plan view of the frame; n represents a straight-edge applied to the surfaces of the jaws a b. The method of applying this straight-edge is to place one end across a jaw, as a, while the other end is elevated above b; then, while pressing the end firmly against a, lower the other end to the face of b; if its edge at that end falls fair with b, so as just to touch it, the process may be reversed—one end being pressed to b, and the other lowered upon a. By this means, it will not only be discovered whether the jaws a and b stand square across the frame, but also whether the frame on either side is sprung. A square c may also be rested against n, and its blade d tested with the side face of the way, as shown. The same process of testing should be applied to the other jaw faces e, f.
Suppose, however, that the width between the jaws a, f was less than that between e, b, then the straight-edge, when pressed to a, would show a space between its edge and b; and also a space between its edge and e, when its other end was pressed to f; and, when these spaces were equal in amount, the frames would be set true in one direction. To test the truth in the other direction, the straight-edge should be applied after the same manner to the bottom surfaces g, h.
It will not answer to rest the straight-edge against the two surfaces and observe their coincidence with its edge, because any error cannot be sufficiently, readily, or accurately tested by this means. Nor will it answer to test by the bearing marks of a straight-edge applied with marking, unless the coat of marking be very fine and the straight-edge be moved without any vertical pressure on it; because, under such pressure, the straight-edge will bend.
The ways for all the bearings should be tested in this manner; so that, if from any error in the machine work, some of them will not come fair, the frames may be set to align those that it is of most importance to align truly; or if there is no choice in this respect, then those carrying the largest bearing should be set true; because, if it be decided to correct the error on the other bearing or bearings, there will be less area to file or operate upon. The setting being complete the holes may be reamed and the remaining bolts put in, the testing being repeated after the frame is finally bolted together. If this final test shows that bolting the frame up has altered the alignment by springing the frame, the bolts in one foot, as say i, Fig. 2564, may be slackened and the test repeated; and, if the frame is then found true, it is the bolting at i that causes the spring, on account of the bedding surfaces not fitting properly. If i is not found to be at fault, it may be bolted up again and j tested by loosening its bolts, and so on, until the location of the error is detected. Furthermore, when the frame is bolted up, the width of the bearings, as from a to b, should be tested; for in a job of this kind, it will pay to have the framework so true to the drawing that, if the other parts, as the shafts, bearing parts, &c., be also made to the drawings, the parts will go together, thus avoiding the necessity of varying all the other parts from the drawing to accommodate errors in the framework.
Among the jobs that the erector is often called upon to perform is that of patching or repairing pieces that have cracked or broken. Fig. 2566 represents a case of this kind, the fracture being at d. The principle to be observed in work of this kind is to cause the bolts to force the fractured pieces together, so that the irregularity or crookedness of the crack, as at d in the figure, may serve to lock the pieces together.
Suppose, for example, we were to put on a patch p, Fig. 2567, and there would be but little to prevent the crack from opening under severe strain, and the patch would stretch, permitting the crack to open and finally causing the bolts to break or sheer off. A preferable plan, therefore, is to put two patches on the sides in the following manner:—
The holes should be drilled through the beam and the plates held against the beam so that their holes may be marked by a scriber passed through the holes in the beam. The holes in the plates should be drilled closer together than those in the beam, so that when driven in they will serve as keys to close the two sides of the crack together, as shown in Fig. 2568, where it is seen that one side of the bolt bears against the holes in the patch and the other against the holes in the beam. To facilitate getting the bolts in place the plates may be heated so as to expand them.
In cases in which it would not be permissible to drill so many holes through the beam on account of weakening it, we may use patch bolts with countersunk heads, as in Fig. 2569. Two only of the bolts pass entirely through, and it is best to let them be taper, as at a in the figure, the head not meeting the patch. The hole in the beam, after being reamed taper, should be filed out on the side b, and that in the patch plates on the other side, as at c and d, so that the bolts will serve as keys. After these two bolts are in place[II-179] and their nuts firmly screwed home, the holes for the patch bolts may be drilled through the plates and into the beam. When the countersunk head bolts are fitted they should be turned down behind the head, so as to leave a part weaker than the bolt, and then screwed in until the required end breaks off. The taper bolts should be of steel, but those with countersunk heads may be of iron.
Erecting an Iron Planer.—If an iron planer be properly fitted and erected, the table will be quite solid in the V-ways in the bed, and will not rock or move even though a heavy vertical cut be taken at the extreme sides of the table, but any error of truth of alignment or fit either in the bed-ways or the table V’s will cause the table to lie improperly in the V’s and to be apt to rock as it traverses. The author has had planed upon a planer thirty years old, at the Freeland Tool Works, in New York City, a cast-iron surface 12 × 20 inches, the metal weighing about 60 lbs., and the surfaces were so truly planed that one would lift the other by reason of a partial vacuum between the two. These planed surfaces were exhibited by the author at the American Institute Exhibition in 1877, and were awarded a medal of superiority.
The manner in which this planer was fitted and erected, and the principles involved in such fitting and erecting, are as follows:
While it is essential that the foot or resting surface of a planer bed (whether it stands on legs or rests direct upon its foundation) be as true as it is practicable to plane it, still it is more essential that the V’s or ways be true, and as the casting will be apt to alter its form from having the surface metal removed, it is best to plane the side on which the ways are the last.
When the bed is placed upon the machine to have its resting surface planed, the casting being uneven, it will be necessary to place packing pieces of suitable thickness beneath the places where the clamping plates hold it, so that the pressure of those plates may not spring or bend the casting.
These packing pieces require to fill up solidly (without lifting the bed) the hollow places, and it is a good plan to place among them a piece of strong writing paper for reasons which will appear presently.
In planing the bed all the surfaces should be roughed out before any are finished. Before any finishing cuts are taken all the clamping bolts should be loosened and the pieces of paper tried by pulling them, so that if the casting has altered its form it will be made apparent by some one of the pieces of paper becoming loose.
In this case the packing must be readjusted, clamping both as lightly as will hold the work, and all as equally as possible, when the finishing cuts may be taken.
The best form of template to plane the ways to is that shown in Fig. 2570, in which b is a side and a an end view. A corresponding female template being shown at d to be used in planing the table V’s.
The length c of the V of the template must not be longer than from 4 to 6 inches, or it will be liable to spring or twist from its own weight. This template is not intended to be used in any sense as a straight-edge to test the truth of the length of the ways, but rather as one to test their width apart, and the correctness of the angles. The top surface a b should be quite true with the V’s, being equidistant from them, so that by testing that surface with a spirit-level it may be known whether the ways are level either crosswise or lengthwise.
The V’s of the template require to have red marking on them so as to mark the ways when the template is moved, and show that the ways accurately fit to the template, which is highly important.
In planing the table or platen it is essential to bear in mind that the area to be planed on the V side is always small in comparison with that to be planed on the other or work-holding side of the table, and as the planing of this latter surface is sure to cause the casting to alter its form, it is necessary to plane it first, so that the alteration of form may occur before and not after the V’s have been planed.
In chucking the table to plane its work-holding surface, the packing pieces must be used as described for the bed, and the bolts placed as there described.
Both bed and table being planed they require to be fitted together (no matter how expertly the planing has been done) if a really first-class job is to be made of them. In doing this it is essential that the bed be supported at the same points as it will be when the machine is put to work, for in large or long casting the deflection or bending from its own weight is sufficient to have an important practical effect. The same fact will also apply to the table and even to the cross slide, even though the latter be heavily ribbed and but, say, 5 feet long.
If, therefore, the bed is to be supported by legs, its guideways or V’s should be fitted after the legs are attached. The bed must be carefully levelled so that the ways may stand horizontally true, which may be tested by placing the template a b in Fig. 2570 in place and applying a spirit-level first across and then lengthwise of the upper surface of the template.
If the bed rests upon a foundation at several points in its length it should be rested at those points while being fitted and carefully levelled as before, the template and spirit-level being tried at every two or three feet of the bed length.
To test the width of the V’s and their widths apart in the fitting, the template a b, Fig. 2570, must be used in connection with red marking, but to true the lengths of the ways a surface plate about 4 feet long and slightly wider than the width of one side of the ways must be used, and if the template and the surface plate show the ways true they will be of the correct width, of correct angle and true planes. But this does not insure that the two ways are in line one with the other, and for this purpose separate test blocks are necessary, because the template is too narrow in width to give a good test, and cannot be made wider, because in that case its own weight would cause it to spring or deflect to suit any error in the work.
These test blocks are simply two pieces of metal, such as shown in Fig. 2571. The lengths of these blocks should be about 8 inches, and the best way to obtain them true and exactly alike is to make one block and then cut it into two. They possess an advantage[II-180] not possessed by a template that spans both ways, inasmuch as they may be turned end for end in each way and thus test the accuracy of the angles of each way.
Again, both may be placed in one way, and by various applications in connection with straight-edge, surface plate, and level they will test the truth of the ways, both individually and one with the other in a better manner than by any other method.
| VOL. II. | TESTING PLANER BEDS AND TABLES. | PLATE XI. | |
 |
|||
| Fig. 2572. | |||
 |
 |
||
| Fig. 2573. | Fig. 2574. | ||
 |
 |
||
| Fig. 2575. | Fig. 2576. | ||
 |
|||
| Fig. 2577. | |||
Fig. 2572 represents the various positions of the V blocks for the testing, a, b, c, d, e, f, g, h, representing the blocks; straight-edges may be placed as at i, at j, and at k, and if the ways are true the straight-edge, lightly coated with marking, should have contact clear across the upper surface of both V-blocks, and a spirit-level placed on the straight-edge (in each position of the same) should show them to be level.
The surface p, on which uprights or standards on that side of the plane, rest, being planed with the V-ways will be true with them, and the uprights may be erected thereon, their base surfaces being fitted to p until the standards stand truly vertical and parallel in their widths apart. In testing these uprights they should be bolted home as firmly as they will be when finally erected, as they will be liable to alter their set if bolted up more firmly than when tested. These front surfaces should be at a right angle to the length of the bed V-ways, and this may be tested by placing a straight-edge across their surfaces and testing it with a square rested against the edge of the planer table.
The method of erecting planers at the Pratt and Whitney Company’s shops is as follows:—
To test the V’s, a plate p, Fig. 2573, is applied as shown, its lugs a, a1 fitting to corresponding sides of the two Vs; as b, b. In Fig. 2573 the test is made by inserting thin pieces of tissue paper between a, a1 and the V-sides, the friction with which the paper is held showing the nature of the fit. Thus, if the paper will move easily at one end and is tight at the other end of either of the lugs a, a1 the fit is shown to be defective. When the fit on these sides is corrected, the plate p is turned around, as in Fig. 2574, and from a similar tissue-paper test, the other sides are corrected. Thus the outside angles of the two Vs are fitted to the same angle; inside angles are also fitted to the same angle. But it will be observed that it does not follow that the inside angles of the Vs are of the same degree of angle as are the outside halves or angles, unless the two lugs a, a1 of the plate p have equal angles. It is on this account that the test is made by tissue paper, rather than by the bearing marks produced by rubbing p along the Vs, since that might in time wear the angles a, a1 out of true. The same plate p may be used to true the male Vs on the work-holding table of the machine, as is shown in Figs. 2575 and 2576, where the table is seen upside down, as is necessary in order to apply the plate. Here, again, the outside angles or halves of the Vs are fitted from the same V (a1) of the plate, so that the fit of the table will be true to the bed, even though the angle on one side of the V-ways were not precisely correct, and there is less liability to error than would be the case were a male and female plate used instead of a single plate. The alignment next in importance is that of the uprights, standards, or side frames of a planing machine, and to enable the correct erection of these, the device a, Fig. 2577, is employed. It consists of a solid plate fitting into the V-ways of the planer-bed and having two steps, b and c, which receive the side frames to be erected. The width d is the width apart of the side frames, and the side surfaces of the steps (as g) are vertical to the centre line of the V-ways of the bed, so that the side frames may be rested against g on one side, and the corresponding surface on the other step. The surfaces e, f are at a right angle to the V-ways of the bed, so that when the side frames are against e, f they will be set square across the machine. The top face of the plate a is planed parallel to the Vs of the plate, so that in addition to resting each side frame against the surfaces (as f g) a square may be rested on plate a and applied to their trued surfaces, and thus may these side frames be set true and square, both one with the other, and with the ways in the bed, without the use of stretched lines and straight-edges, which secures greater accuracy and saves considerable labor.
All the smaller parts of the machine may then be erected true to the bed or the side frames, as may be required, and if it be a small planer, in which the bed rests upon feet, all that will be necessary in setting the machine in position to work is to set the surface of the work-table level. But in the case of a large heavy planer a solid foundation must be built for the bed, because it will spring, bend, and deflect from its own weight, and thus the side frames, as well as the bed, may be thrown out of true and alignment. Fig. 2578 is a side and plan view of the foundations for a planer, showing the bed-plate in position upon the same.
The stone blocks forming the base of the foundation require themselves to rest upon a solid base, and not upon a soil or gravel[II-181] that is liable to sink beneath them. The brickwork above them is best laid in cement, which should be properly set before the planer bed is placed in position. Near the centre of the bed, and directly beneath the cross-slide, is shown a screw jack, to take up any sag of the bed, and cause the Vs to have a good bearing directly beneath the cutting tool, which is essential to prevent the table from springing from the pressure of the tool cut.
Fitting up and Erecting a Lathe.—The first operation will be to true the bed or shears. If the lathe has raised Vs on the bed it will be sufficient to true them only, without truing the flat surfaces. The bed should during the fitting be supported at the same points as it will be when in use.
The method of aligning the lathe heads at the Pratt and Whitney Company’s workshops is as follows: Fig. 2579 is a side and an end view of a part of a lathe shears a, with the tailstock b thereon. To the bore of the tailstock there is closely fitted an arbor c, accurately turned in the lathe, and having at the end d and at e two short sections of enlarged diameter. A plate f is fitted to the inside Vs of the shears (upon which Vs the tailstock sits). This plate carries a stand g, and a second gauge or stand g. Stand g fits at its foot into a V provided in f, as shown, the object of which is to so hold g to f that its (g′s) face will stand parallel to arbor c. The stand is so adjusted that a piece i may be placed between c and g and just have contact with both, and it is obvious that if this is found to be the case with the tailstock and the stand placed at any position along the bed, the arbor c, and, therefore, the bore of the tailstock, must be true, sideways, to the inside Vs of the lathe shears. The testing, however, is made at the enlarged sections d and e, g of course being firmly bolted to f. To test the height of the arbor c from the Vs, and the parallelism in that direction, stand h is provided. It carries a pointer or feeler k, whose end is adjusted to just touch the enlarged sections d and e of c, it being obvious that when the degree of contact is equal at these two sections, with the tailstock and the plate f moved to various positions along the bed, the adjustment or alignment in that direction is also correct. The adjustment and corrections may then be made with the headstock of the lathe in place of the tailstock, the arbor fitting into the bored boxes of the lathe and extending from it, and having two sections of the same diameter, as sections e in the figure. Now, suppose that in the test thus made the bar c proves to stand true in some locations, but not in others, upon the bed; then it is proof that it is the Vs that require correction, while the tailstock is in error in all cases in which the error is constant, with the tailblock moved in various positions along the shears.
In some practice the heads are bored after being fitted to the ways, and in this case the boring bar may be supported by standards fitting to the lathe bed, running in bearings, and not on centres. There should be three of these bearings, one at one end of the head, and as close to it as convenient, another at the other end, as close as will permit the insertion of the cutters, and the third as far from the second as will permit the insertion on the bar and between them of a pulley to drive the bar, which must be splined to receive a feather in the pulley, so that the bar may be fed through its bearings and through the pulley to the cut. After the live head has been bored the tailstock or back-head may be bored from the other end of the bar, so that the standards will not require to be moved on the bed until the boring is completed. The bar may be fed by hand, or an automatic feed motion may be affixed to one of the standards. The heads being secured to the bed while being bored, there is no liability of error in their alignment, because, even if the holding bolts spring the heads in clamping them to the bed, the holes will be true when the heads are firmly home upon the bed, as they will be when in use, whereas under this condition such will not be the case if the holes for the spindles are bored before the seats are planed and fitted.
The feed screw must be placed quite parallel to the Vs or guides of the bed, or otherwise the pitches of threads cut in the lathe will be finer than they should be, and the screw will bind in the feed nut, causing undue wear to both.
The method employed to test the truth of lathe shears and heads in the David W. Pond Works, at Worcester, Massachusetts, is as follows:—
The planing, both of the lathe shears and of the heads, being done as accurately as possible, the heads are provided with a mandrel or arbor, to the end of which is secured the device shown in Fig. 2580, in which a is a hollow cylindrical piece having a threaded and split end, so that by means of a nut the bore may be closed to tightly fit the arbor referred to; b, b are two arms, a sliding fit in a, to enable their adjustment for the width of lathe Vs, and having a flat place on one side, as at c c, to receive the pressure of a locking device d, by means of which b, b may be fastened in their adjusted positions; e, e are cylindrical arms, a sliding fit in b, b, also having flat sides, and capable[II-182] of being secured in their adjusted positions by means of locking devices f, f.
Fig. 2581 is an end view of the device in position on a lathe tail stock, and Fig. 2582 is an enlarged view (being half full size) of the devices at the lower end of arms or rods e, e.
At the lower ends of e, e are provided two pieces g, g, which are capable of adjustment to fit the Vs h, h of the lathe, as follows:—
The middle pins i are fast in the arms j, but are pivoted in g, the end pins, as k, are pivoted in g, are flat where they pass through j, and threaded to receive the nuts, l, of which there are four, two to each piece g. By operating these nuts, g may be adjusted to bed fair on the angles on the lathe Vs h. At m are two fixed pins which afford a fulcrum, at n and o respectively, to four index needle arms. Two of these index arms only are seen in the cut, marked respectively p and q, which are pivoted at n. Two similar pointer or needle arms are on the other side of m, being behind p and q, these two being pivoted respectively at o. At the lower end of p is a point resting in the centre of the nut, and similarly the end of q rests in the centre of the nut on that side. Similarly the two needles not seen have pointed ends resting in the centre of the nuts marked respectively l. Between g and j are two springs placed back to back, which act to hold g away from j. But it will be seen that if either end of g be forced towards j, as by passing over a projection on the V h, then the pin k, will push nut l, and this will raise the end of the pointer or needle to a corresponding degree, and the pointer being pivoted (as at n), its upper end will move and denote on the graduated index r that there is an error in the lathe V, the amount of the error being shown multiplied on account of the leverage of the needle arms from the pivots.
The pieces g being adjusted to bed fairly on the lathe Vs, the heads of the lathe are moved along the lathe shears, and if the Vs are true to angle the upper ends of the needles will remain stationary, a projecting part of a V will, however, cause the needle point to move toward e, while a depression on a V would cause the springs k to move g in, keeping it in contact with the V, while the needle point would move away from e. To maintain the needle arms in contact with the nut heads l, springs s are employed. Variations in the widths apart of the Vs on either side of the shears would obviously be shown in the same manner, the defect being located by the needle movement. The corrections are made from the contact marks of the heads, caused by moving the heads along the Vs and by careful scraping.
Notwithstanding that every care and attention may be taken to make a lathe true in the process of manufacture, yet when the whole of the parts are assembled it is found essential to test the truth of the finished lathe, because, by the multiplication of minute errors the alignment of the lathe, as a whole, may be found to need correction. A special inspector is therefore employed to test finished machines before they leave the works, and in Fig. 2583 is represented the device employed for testing the alignment of the line of centres of lathes.
Upon the face of the face plate and near its perimeter there are turned up two steps, as denoted by b and c. The tail-spindle is provided with a stud s, which fits in the place of the dead centre, and carries what may be termed a double socket, one-half of which (as f) envelops the stud s, while the other half (a) envelops and carries a rod r. These two halves are in reality split sleeves, with set screws to close them and adjust the fit. By means of the screws e, the sleeve f may be made a tight working fit upon s, while, by means of screws g, sleeve a may be made to firmly grip the rod r, which may thus be securely held while still capable of being swung upon stud s. Upon the outer end of the rod r is another sleeve i, which is also split and secured to the rod r by means of screws corresponding to those shown at g. It also carries a pin, upon which a disk k is pivoted, and a lug through which the adjusting screw v is threaded. Upon k is a lug which has on one side of it the end of a spring t, and it is obvious that by operating v the disk k will be rotated upon its central pin. k carries two lugs, l and m, the latter being threaded and split. These two lugs receive a sleeve n, threaded into m, and a close plain fit in l. The small end of this sleeve is split and is threaded slightly taper, and is provided with the nut p. Through this sleeve passes a needle q q, one end of which is bent as shown, and it is obvious that by screwing nut p upon n the sleeve will be closed and will tightly grip the needle q q. Now, suppose that the head of n is operated, and it will move endwise through l and[II-183] m, carrying with it the needle q q, which will remain firmly clasped in the sleeve; or suppose that screw v is operated, and k will revolve, carrying with it the needle q q, which will still remain firmly gripped, and it follows that there is thus obtained a simple means of adjusting the needle without releasing it.
The application of the instrument is as follows: To test if the head and tailstocks are of equal height from the bed, the instrument is set and adjusted exactly as shown in the engraving, the needle being adjusted to just touch the diameter of the step at b. The rod r is then swung around so that the needle comes opposite to the same step b at the bottom of the face plate, and if the needle just touches there also the adjustment for tailstock height is correct. Similarly for testing if the tailstock is set true sideways the needle may be tried in the same manner and upon the same step, but upon the two opposite sides of the face plate, instead of at the top and bottom. It now remains to test if the tailstock is in line in a horizontal direction with the live spindle, and this is done by reversing the needle end for end in the sleeve n, and setting it to just touch the face c of the turned step on the face plate, and if it just touches at the top and bottom as well as at the two sides the tail-spindle is obviously in line. It may be observed, however, that if an error in any one direction is found, it is necessary to go through the whole series of tests in order to precisely locate the error. Suppose, for example, that the needle, being adjusted as in the engraving to just touch the step at b, does not touch it when tried at the bottom of the plate, then the error may be caused in three ways—thus, in the first place, the whole tailstock may be lower than the headstock; in the second place, the front end of the tailstock may be too low; or, in the third place, the back end of the tailstock may be too high. If the first was the cause, the test with the needle point tried with face c would show correct. If the second or third was the cause of the error, the needle point when tried to face c would touch when applied at the top, but would not touch when tried at the bottom of the face plate. Another case may be cited. For example, suppose the needle applied as shown touched at the bottom but not at the top of the step b, then the test with the needle reversed would show whether the whole tailstock was too high, or whether the front end only was too high, or the back end too low. There is one excellent feature in this device to which attention may be called, which is that the tests are made on as large a diameter of face plate as possible, which shows the errors magnified as much as possible.
The same device is used to test if the cross slide of the carriage or saddle is at a right angle to the lathe shears, the method of its application being as shown in Fig. 2584. The split sleeve a receives in this case a rod r, which is laid in the slideway s of the carriage or saddle, and a long rod h carries the needle-holding devices. The rod r is held fair against the slideway, and the face of the sleeve a is held against the edge of the carriage or[II-184] saddle. The needle q is then adjusted to just touch the edge d of the lathe bed. When this adjustment is made the rod h is swung over to the right and the coincidence of the needle point again tried with the edge of the lathe bed, the cross slideway being at a right angle when the needle point touches the edge d of the lathe bed when tried on the left hand, and also on the right hand, of the carriage. The stiffening rod u is brought under tension by a nut operated against a lug on x. To counterbalance the overhanging weight of the rod h and its attachments, a rod carrying a weight w is employed. It is obvious that the truth of the operation depends wholly upon the straightness and parallelism of the enlarged sections p of the rod r, upon keeping the end face of a in contact with the carriage at z, and upon the correct adjustment of the needle to the edge of the lathe bed.
Setting Line Shafting in Line.—The following method of adjusting line shafting or setting it in line, as it is termed, is that generally adopted in the best practice.
First prepare a number of rude wooden frames, such as shown in Fig. 2585. They are called targets, and are pieces of wood nailed together, with the outer edge face a planed true, and having a line marked parallel with the planed edge and about three-quarters of an inch inside of it. Upon this frame we hang a line suspending a weight and forming a plumb-line, and it follows that when the target is so held that the plumb-line falls exactly over and even all the way down with the scribed line, the planed face a, Fig. 2586, will stand vertical. To facilitate this adjustment, we cut a small V notch at the top of the scribed line, the bottom of the V falling exactly even with the scribed line, so that it will guide the top of the plumb-line even with the scribed line at the top; hence the eye need only be directed to causing the two lines to coincide at the bottom. To insure accuracy, the planed edge a should not be less than a foot in length. Then tightly stretch a strong closely-twisted and fine line of cord beside the line of shafting, as shown in Fig. 2587, placing it say six inches below and four inches on one side of the line of shafting, and equidistant at each end from the axial line of the same, adjusting it at the same time as nearly horizontally level as the eye will direct when standing[II-185] on the floor at some little distance off and sighting it with the line shaft.
In stretching and adjusting this line, however, we have the following considerations:—It must clear the largest pulley hub on the line of shafting, those pulleys having set-screws being moved to allow it to pass. If the whole line of shafting is parallel in diameter, we set the line equidistant from the shafting at each end. If one end of the shafting is of larger diameter, we set the line farther from the surface of the shafting, at the small end, to an amount equal to one-half of the difference in the two diameters; and since the line is sufficiently far from the shafting to clear the largest hub thereon, it makes, so far as stretching the line is concerned, no difference of what diameter the middle sections of shafting may be. The line should, however, be set true as indicated by a spirit-level.
We may now proceed to erect the targets as follows: The planed edge a in Fig. 2585 is brought true with the stretched line, and is adjusted so that the plumb-line b in Fig. 2586 will stand true with the line or mark b. When so adjusted, the target is nailed to the post carrying the shafting hanger. In performing this nailing, two nails may be slightly inserted so as to sustain the target, and the adjustment being made by tapping the target with the hammer, the nails may be driven home, the operator taking care that driving the nails does not alter the adjustment.
In Fig. 2588 a a represents the line of shafting, b, b two of the hanger posts, and c, c two of the adjusted targets.
We have now in the planed edges a of the targets a rigid substitute for the stretched line, forming a guide for the horizontal adjustment, and to provide a guide for the vertical adjustment we take a wooden straight-edge long enough to reach from one post to another. Then beginning at one end of the shafting, we place the flat side of the straight-edge against the planed edge of two targets at a distance of about 15 inches below the top of the shafting; and after levelling the straight-edge with a spirit-level, we mark (even with the edge of the straight-edge) a line on the planed edge of each target, and we then move the straight-edge to the next pair of targets, and place the edge even with the mark already made on the second target. We then level the straightedge with a spirit-level, and mark a line on the third target, continuing the process until we have marked a straight and horizontally level line across all the targets, the operation being shown in Fig. 2589, in which a represents the line of shafting, b the hangers, and c the targets. d represents the line on the first target, and e the line on second. f is the straightedge, levelled ready to form a guide whereby the line d may be carried forward, as at e, level and straight, to the third target, and so on across all the targets.
The line thus marked is the standard whereby the shafting is to be adjusted vertically; and for the purpose of this adjustment, we must take a piece of wood, or a square, such as is shown in Fig. 2590, the edges a and b being true and at a right angle to each other. The line d, in Fig. 2589, marked across the targets being 15 inches below the centre line of the shaft at the end from which it was started, we mark upon our piece of wood the line c in Fig. 2590, 15 inches from the edge a (as denoted by the dotted line); and it is evident that we have only to adjust our shaft for vertical height so that, the gauge being applied at each target in the manner shown in Fig. 2591, the shaft will be set exactly true, when the mark c on the piece of wood comes exactly fair with the lines d marked on the targets.
For horizontal adjustment, all we have to do is to place a straight-edge along the planed face of the target, and adjust the shaft equidistant from the straight-edge, as shown in Fig. 2592, in which a is the shaft, b the target, c the straight-edge referred to, and d a gauge or distance piece. If, then, we apply the straight-edge and wood gauge to every target, and to the adjustment, the whole line of shafting will be complete.
There are several points, however, during the latter part of the process at which consideration is required. Thus, after the horizontal line, marked on the targets by the straight-edge and used for the vertical adjustment, has been struck on all the targets, the distance from the centre of the shafting to that line should be measured at each end of the shafting, and if it is found to be equal, we may proceed with the adjustment; but if, on the other hand, it is not found to be equal, we must determine whether it will be well to lift one end of the shaft and lower the other, or make the whole adjustment at one end by lifting or lowering it, as the case may be. In coming to this determination we must bear in mind what effect it will have on the various belts, in making them too long or too short; and when a decision is reached, we must mark the line c, in Fig. 2590, on the gauge accordingly, and not at the distance represented in our example by the 15 inches.
The method of adjustment thus pursued possesses the advantage that it shows how much the whole line of shafting is out of true before any adjustment is made, and that without entailing any great trouble in ascertaining it; so that, in making the[II-186] adjustment, the operator acts intelligently and does not commence at one end utterly ignorant of where the adjustment is going to lead him to when he arrives at the other.
Then, again, it is a very correct method, nor does it make any difference if the shafting has sections of different diameters or not, for in that case we have but to measure the diameter of the shafting, and mark the adjusting line, represented in our example by c, in Fig. 2590, accordingly, and when the adjustment is complete, the centre line of the whole length of the line of shafting will be true and level. This is not necessarily the case, if the diameter of the shafting varies and a spirit-level is used directly upon the shafting itself.
In further explanation, however, it may be well to illustrate the method of applying the gauge shown in Fig. 2590, and the straight-edge c and gauge d shown in Fig. 2592, in cases where there are in the same line sections of shaftings of different diameters. Suppose, then, that the line of shafting in our example has a mid-section of 21⁄4 inches diameter, and is 2 inches at one, and 21⁄2 inches in diameter at the other end: all we have to do is to mark on the gauge, shown in Fig. 2590, two extra lines, denoted in figure by d and f. If the line c was at the proper distance from a for the section of 21⁄4 inches in diameter, then the line d will be at the proper distance for the section of 2 inches, and e at the proper distance for the section of 21⁄2 inches in diameter; the distance between c and d, and also between c and f, being 1⁄8 inch, in other words, half the amount of the difference in diameters.
In like manner for the horizontal adjustment, the gauge piece shown at d in Fig. 2592 would require when measuring the 21⁄4 inch section to be 1⁄8 inch shorter than for the 2 inch section, while for the 21⁄2 inch section would require to be 1⁄8 inch shorter than that used for the 21⁄4 inch section, the difference again being one-half the amount of the variation in the respective diameters. Thus the whole process is simple, easy of accomplishment, and very accurate.
If the line of shafting is suspended from the joists of a ceiling instead of from uprights, the method of procedure is the same, the forms of the targets being varied to suit the conditions. The process only requires that the faced edges of the targets shall all stand plumb and true with the stretched line. It will be noted that it is of no consequence how long the stretched line is, since its sag does not in any manner disturb the correct adjustment, but in cases where it is a very long one it may be necessary to place pins that will prevent it from swaying by reason of air currents or from jarring.
The same system may be employed for setting the shafting hangers, the bores of the boxes being used instead of the shafting itself.
Line shafting.—A line of shafting is one continuous run or length composed of lengths joined together by couplings. The main line of shafting is that which receives the power from the engine or other motor, and distributes it to other lines of shafting, or to the various machines to be driven. In some practice each line of shafting is driven by a separate engine or motor, so that it may be stopped without stopping the others. This same object may be obtained by providing a clutch for each line. It is obvious that in each line of shafting the length nearest to the driving motor transmits the whole of the power transmitted by the line, and that the diameter of the shafting may, therefore, be reduced as it proceeds from the engine in a proportion depending upon the degree to which the power it is required to transmit is reduced. It is desirable, therefore, so far as the shafting is concerned, to place the machines requiring the most power to drive as near as possible to that end of the shafting that receives power from the motor. Line shafting is supported in bearings provided in what are termed hangers, which are brackets to be bolted to either suitable framing, to walls, posts, or to the ceiling or floor of the building. The short lengths of shafting that are provided to effect changes of speed, and to enable the machine to be stopped or started at pleasure, are termed countershafts. When there is interposed a countershaft between the motor and the main line of shafting, it is sometimes termed a jack shaft.
Shafting is usually made cylindrically true either by special rolling processes as in what is known as “cold-rolled,” or “hot-rolled” shafting, or else it is turned up in the lathe. In either case it is termed bright shafting. What is known as black shafting is simply bars of iron rolled by the ordinary process and made cylindrically true only where it receives its couplings, and for its journal bearings, &c. The diameter of black shafting varies by a quarter of an inch, and is usually above its designated diameter by about 1⁄32 inch.
The main body of the shafting not being turned cylindrically true and parallel, the positions of the pulleys cannot be altered upon the shafts, nor can pulleys be added to the shaft as occasion may require without the sections being taken down and seatings turned for the required pulleys to be added. Furthermore black shafting does not run true, and is in this respect also objectionable. Nevertheless, black shafting is used for some special cases where extra pulleys are not likely to be required and the shafting is exposed to the weather, as in the case of yards for the manufacture of building bricks.
The diameters of bright or turned shafting (which is the ordinary form in which shafting is made, unless otherwise specified) vary by 1⁄4 inch up to about 31⁄2 inches in diameter; but the actual diameter is 1⁄16 inch less than the denominated commercial diameter, which is designated from the diameter of the round bar iron from which the shafting is turned; thus a length of what is known as 2-inch shafting will have an actual diameter of 115⁄16 inches, being parallel, or as nearly parallel as it is practicable to turn it in the ordinary lathe.
Cold-rolled shafting has its actual diameter agreeing with its designated or commercial diameter, and is parallel throughout its length.
In England the diameters of shafting vary by eighths of inches for diameters of an inch and less, and by quarters of an inch for diameters above an inch, the commercial and the actual diameters being alike.
The strains to which a line of shafting is subject are as follows: The torsional strain due to rotating the line of shafting, independent of the power transmitted; the torsional strain due to the amount of the power transmitted; and the transverse strain due to the unequal belt pressures and distances from the bearings of the driving or transmitting pulleys. The first and the last are, however, so intimately connected in practice that they may be considered as one: hence we have, 1st, the torsional strain due to driving the whole load, and, 2nd, the transverse strain due to the belt pressures being exerted more on one side than on another of the shaft, and to the belt pulleys being at unequal distances from the hanger bearings.
The first may be reduced to a minimum by so proportioning the strength of the line of shafting that it shall be capable of transmitting the required amount of power at the various sections of its length without suffering distortion of straightness beyond certain limits, and shall be at the same time as light as is consistent with this duty and a certain factor of safety.
Referring for a moment to the above limitation, the weight of the shaft itself will cause it to deflect between the hanger bearings, and the amount of this deflection will depend upon the distance apart of the points of support, or, in other words, of the distance apart of the hanger bearings.
The second may be reduced to a minimum by so regulating the distance apart of the hanger bearings that the deflection of the shaft from the belt pressures shall not be sufficient to produce sensible irregularities in the axis of rotation of the shaft; by so connecting the bearings to the hangers that they shall be rigidly held, and yet capable as far as possible of automatically adjusting their bores to be true with the shaft axis, notwithstanding its deflection from any cause; by placing the pulleys transmitting the most power as near to the hanger bearings as practicable; by so disposing the driving belts as to deliver the power as near as possible equally on all sides of the shaft; and by having the shafting and the pulleys balanced so as to run true, so that the strains on the pulleys shall be equal at each point in the shaft rotation. From this it appears that the distance apart of the shafting hangers may vary according to the amount of power transmitted by a shaft of a given diameter. The following table (given by Francis) gives the greatest admissible distances between the bearings of continuous shafts subject to no transverse strain except from their own weight, as would be the case were the power given off from the shaft equally on all sides, and at an equal distance from the hanger bearing.
| Diameter of shaft in inches. |
Distance between bearings, in feet. | |
| Wrought-iron shafts. | Steel shafts. | |
| 2 | 15.46 | 15.89 |
| 3 | 17.70 | 18.19 |
| 4 | 19.48 | 20.02 |
| 5 | 20.99 | 21.57 |
| 6 | 22.30 | 22.92 |
| 7 | 23.48 | 24.13 |
| 8 | 24.55 | 25.23 |
| 9 | 25.53 | 26.24 |
These conditions, however, do not usually obtain in the transmission of power by belts and pulleys, and the varying circumstances of each case render it impracticable to give any rule which would be of value for universal application.
For example, the theoretical requirements would demand that the bearings be nearer together on those sections of shafting where most power is delivered from the shaft, while considerations as to the location and desired contiguity of the driven machines may render it impracticable to separate the driving pulleys by the intervention of a hanger at the theoretically required location. The nearer together the bearings the less the deflection either from the shaft’s weight or from the belt stress, and since the friction of the shaft in its bearings is theoretically independent of the journal-bearing area, the closer the bearings the more perfect the theoretical conditions; but since[II-188] it is impracticable to maintain the true alignment of the shaft, and as the friction due to an error in alignment would increase with the nearer proximity of the bearings, they are usually placed from about 7 to 12 feet apart, according to the facilities afforded in the location in which they are to be erected.
It is to be observed, however, that the nearer together the bearings are the less the diameter, and, therefore, the lighter the shafting may be to transmit a given amount of power, and hence the less the amount of power consumed in rotating the shafting in its bearings.
Cold-rolled Shafting—This is shafting made cylindrically round and parallel by means of cold rolling, which leaves a smooth and bright surface. The effects of cold rolling upon the metal have been determined by Major Wm. Wade, U.S.A., Sir William Fairbairn, C.E., and Professor Thurston, of the Stevens Institute, as follows:—
The experiments were made upon samples of cold-rolled shafting submitted by Messrs. Jones and Laughlins, of Pittsburgh, Pennsylvania.
| Iron rolled while | Ratio of increase by cold rolling. |
Average rate per cent. of increase. |
|||||||||||
| Hot. | Cold. | ||||||||||||
| Transverse.—Bars supported at both ends; load applied in the middle; distance between the supports, 30 inches. Weight which gives a permanent set of one-tenth of an inch, viz. | - | 11⁄2 inch square bars | 3,100 | 10,700 | 3.451 | - | 162 | 1⁄2 | |||||
| Round bars, 2 | inch | diameter | 5,200 | 11,100 | 2.134 | ||||||||
| Round bars, 21⁄4 | „ | „ | 6,800 | 15,600 | 2.294 | ||||||||
| Torsion.—Weight which gives a permanent set of one degree, applied at 25 inches from centre of bars. Round bars, 13⁄4 inch diameter, and 9 inches between the clamps | 750 | 1,725 | 2.300 | 130 | |||||||||
| Compression.—Weight which gives a depression, and a permanent set of one-hundredth of an inch to columns 11⁄2 inches long and 5⁄8 inch diameter | 13,000 | 34,000 | 2.615 | 161 | 1⁄2 | ||||||||
| Weight which bends and gives a permanent set to columns 8 inches long and 3⁄4 inch diameter, viz. | - | Puddled iron | 21,000 | 31,000 | 1.476 | - | 64 | ||||||
| Charcoal bloom iron | 20,500 | 37,000 | 1.804 | ||||||||||
| Tension.—Weight per square inch, which caused rods 3⁄4 inch diameter to stretch and take a permanent set, viz. | - | Puddled iron | 37,250 | 68,427 | 1.837 | - | 95 | ||||||
| Charcoal bloom iron | 42,439 | 87,396 | 2.059 | ||||||||||
| Weight per square inch, at which the same rods broke, viz. | - | Puddled iron | 55,760 | 83,156 | 1.491 | - | 72 | ||||||
| Charcoal bloom iron | 50,927 | 99,293 | 1.950 | ||||||||||
| Hardness.—Weight required to produce equal indentations | 5,000 | 7,500 | 1.500 | 50 | |||||||||
| Note.—Indentations made by equal weights, in the centre, and near the edges of the fresh cut ends of the bars, were equal; showing that the iron was as hard in the centre of the bars as elsewhere. | |||||||||||||
| Condition of bar. | Breaking weight of bar in lbs. |
Breaking weight per square inch. |
Strength, the un- touched bar being unity. |
||
| In lbs. | In tons. | ||||
| 1 | Untouched (black) | 50,346 | 58.628 | 26.173 | 1.000 |
| 3 | Rolled cold | 69,295 | 88.230 | 39.388 | 1.505 |
| 4 | Turned | 47,710 | 60.746 | 27.119 | 1.036 |
| Note.—In the above summary it will be observed that the effect of consolidation by the process of cold rolling is to increase the tensile powers of resistance from 26.17 tons per square inch, to 39.38 tons, being in the ratio of 1:1.5, one-half increase of strength gained by the new process of cold rolling. | |||||
Extract from the general conclusions arrived at by Professor R. Thurston from experiments.
“The process of cold rolling produces a very marked change in the physical properties of the iron thus treated.
“It increases the tenacity from 25 to 40 per cent., and the resistance to transverse stress from 50 to 80 per cent.
“It elevates the elastic limit under torsional as well as tensile and transverse stresses, from 80 to 125 per cent....
“It gives the iron a smooth bright surface, absolutely free from the scale of black oxide unavoidably left when hot rolled.
“It is made exactly to gauge diameter, and for many purposes requires no further preparation.
“The cold-rolled metal resists stresses much more uniformly than does the untreated metal. Irregularities of resistance exhibited by the latter do not appear in the former; this is more particularly true for transverse stress.
“This treatment of iron produces a very important improvement in uniformity of structure, the cold-rolled iron excelling common iron in density from surface to centre, as well as in its uniformity of strength from outside to the middle of the bar.
“This great increase of strength, stiffness, elasticity, and resilience is obtained at the expense of some ductility, which diminishes as the tenacity increases. The modulus of ultimate resilience of the cold-rolled iron is, however, above 50 per cent. of that of the untreated iron.
“Cold-rolled iron thus greatly excels common iron in all cases where the metal is to sustain maximum loads without permanent set or distortion.”
From this it appears that cold-rolled iron is peculiarly adapted for line shafting. Suppose, for example, a given quantity of power to transmit, and that a length of cold-rolled and a length of hot-rolled iron be connected together to form the line. Then the diameters of the two being such as to have equal torsional strength, we have—
1st. That the weight of the cold rolled will be the least, and it will, therefore, produce less friction in the hanger bearings.
2nd. That the cold rolled will be harder, and will therefore suffer less from abrasion of the journals.
3rd. That being of smaller diameter the journals are more easily and perfectly lubricated.
The resistance to transverse stress (say) 50 per cent.; but the elastic limit under transverse stress is increased from 80 to 125 per cent., accepting the lesser amount we have in the case of the two shafts.
4th. That the resistance to permanent set or bend will be 30 per cent. more in the cold rolled.
5th. The accuracy to gauge diameter enables the employment of a coupling having a continuous sleeve, and gives an equal bearing along the entire coupling bore.
6th. The reduction of shaft diameter enables the employment of a smaller and lighter coupling; and
7th. The hubs of the pulleys may be made smaller and lighter, are easier to bore, and may be bored to gauge diameter with the assurance that they will fit the shaft.
[II-189]The friction between the journals of a line shafting and its bearings depends so intimately upon the distance apart of the bearings, upon the alignment of the same, upon the accurate bedding of the shaft journals to the bearings, and upon the amount of transverse strain; and this latter is so influenced by the amount of power that may be delivered from one side of the shaft more than from another, that the application of rules for determining the said friction under conditions of perfect alignment rigidity would be practically useless. The conditions found in actual practice are so widely divergent and so rarely alike, or even nearly alike, that the consideration of this part of the subject would, in the opinion of the author, be of no practical value. The reader, however, is referred to the remarks made with reference to the friction of journals.
To prevent end motion to a line of shafting it is necessary that there be fixed at some part of the line two shoulders, or collars, on relatively different sides of a bearing, or of the bearings, these collars meeting the side faces of the bearing. If shoulders are produced by reducing the diameter of the journal bearing of the shaft, the strength of the shafting is reduced to that at the reduced bearing, because the strength of the whole can be no greater than its strength at the weakest part. If collars are placed one on each end of the line of shafting, the difficulty is met that the collars will permit end motion to the shaft whenever the temperature of the shaft is greater than that which obtained at the time at which the collars were adjusted, which occurs on account of the increased expansion of the shaft. On the other hand the collars will bind against the side faces of the bearing boxes whenever the shaft is at a lower temperature than it was at the time of setting the shaft, because of the contraction of the shaft’s length, and this would cause undue friction, abrasion, and wear.
It is preferable, therefore, to place such collars one on each side of one bearing, so that the difference in contraction and expansion from varying temperatures shall be confined to the difference in expansion between the metal of which the bearing and shaft respectively are composed in the length of the bearing only, instead of being extended to the difference in expansion between the shaft throughout its whole length and that of the framework to which the hangers, or bearings, are bolted.
The collars may be shrunk on to the shaft so as to avoid the necessity of set-screws, or if set-screws are used they should be as short as is practicable so as to avoid the liability to catch against the lacings, &c., of belts, which, on slipping off the pulley may come into contact with the set-screw head. The Lane and Bodley Co., of Cincinnati, employ a collar (for loose pulleys, &c.) in which the radius of the collar for a width equal to the diameter of the set-screw head, is equal to that of the set-screw head thus projecting from the centre of the collar circumference, a slot in the ring affording access to the set-screw head, as shown in Fig. 2593. By this means the head of the set-screw is protected from contact with a belt, in case the latter should be off the pulley and resting upon the shaft.
As a rule it is preferable that the collars, to prevent end motion to the shaft, be placed at the bearing nearest to the engine or motor; and this is especially desirable where bevel-wheels are employed to drive the shaft, because in that case the pitch lines of the wheels are kept to coincide as nearly as practicable, and the teeth are prevented from getting too far into or out of gear.
Diameters of Line Shafting.—The necessary diameters of the various length of the shafts composing a line of shafting, should be proportioned to the quantity of power delivered by each respective length, and in this connection the position of the various pulleys upon the length and the amount of power given off by the pulley is an important consideration. Suppose, for example, that a piece of shafting delivers a certain amount of power, then it is obvious that the shaft will deflect or bend less if the pulley transmitting that power be placed close to a hanger or bearing than if it be placed midway between the two hangers or bearings.
The strength of a shaft to resist torsion is the cube of its diameter in inches, multiplied by the strength of the material of which the shaft is composed, per square inch of cross-sectional area, giving the strength in statical foot-pounds. The application of this rule is to find the necessary strength of the shaft to convey power irrespective of the distance from its centre at which it delivers such power.
But since the point at which the power to produce torsion is applied is at the rim of the pulley, the amount of torsion produced upon a shaft by a given stress must be obtained by multiplying the given amount of stress by the radius of the pulley in inches and parts of an inch. Example: the static stress upon a pulley, 24 inches diameter, is 100 lbs., what static torsion does it exert upon the shaft?
Here, stress 100 × 12 (radius of the pulley) = 1200 = static torsional stress.
In the following rules for finding the necessary diameters and strengths of shafts, the margin of extra diameter for strength necessary for safety is included, so that the given sizes are working diameters.
To find the necessary diameter of shaft from a given torsional stress.—Rule, divide the torsional stress expressed in statical foot lbs., by 57.2 for steel, by 27.7 for wrought iron, or by 18.5 for cast iron, and the cube root of the quotient is the required working diameter of shaft expressed in inches.
To find the maximum amount of horse-power capable, within good working limits, of being transmitted by a shaft of a given diameter.—Rule, multiply the cube of the diameter of the shaft, in inches, by its revolutions per minute and divide by 92 for steel, by 190 for wrought-iron, or by 285 for cast-iron shafts, and the quotient is the amount of horse-power.
Since, in this rule, the horse-power is a given quantity, the diameter of the pulley is of no consequence, since with a given stress it must have been taken into account in obtaining the horse-power.
To find the revolutions per minute a shaft will require to make to transmit a given amount of horse-power.—Rule, multiply the given amount of horse-power by 92 for steel, by 190 for wrought-iron, or by 285 for cast-iron shafts, and divide the product by the cube of the diameter of the shaft expressed in inches, and the quotient is the required revolutions per minute for the shaft.
The rule adopted by William Sellers and Co. to determine the size of shafts to transmit a given horse-power is:—Rule, divide the cube root of the horse-power by the revolutions per minute and multiply the quotient by 125, the product is the diameter of shaft required.
This gives a shaft strong enough to resist flexure, if the bearings are not too far apart. The distance apart that the bearings should be placed is an important consideration. Modern millwrights differ slightly in opinion in this respect: some construct their mills with beams 9 feet 6 inches apart, and put one hanger under each of the beams; others say 8 feet apart gives a better result. We are clearly of opinion that with 8 feet distance, and shafting lighter in proportion, the best result is obtained.
The following table (from “Machine Tools,” by Wm. Sellers and Co.) gives the strength of round wrought iron as given by Clark:—
| Dia- meter of shaft. |
Torsional Action. | Transverse Action. | |||||||||||||
| Ultimate resis- tance. |
Working stress. |
Work for one turn per minute. |
Horse Power at the rate of one turn per minute. |
Speed in turns per minute for one-horse power. |
Under the gross distributed weight. |
Under the net weight of shaft. |
|||||||||
| Distance of bearings for the limiting deflection. |
Gross weight for the span. |
Distance of bearings for the limiting deflection. |
|||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||
| Inches. | Stat’l. ft. tons. |
Stat’l ft. lbs. |
Ft. lbs. | H. P. | Turns. | Feet. | Lbs. | Feet. | |||||||
| 1 | .42 | 27 | .7 | 174 | .00526 | 190 | 6 | .6 | 30 | 7 | .9 | ||||
| 1 | 1⁄4 | .82 | 54 | .1 | 340 | .01028 | 97 | .3 | 7 | .7 | 55 | 9 | .2 | ||
| 1 | 1⁄2 | 1 | .42 | 93 | .5 | 587 | .01779 | 56 | .2 | 8 | .6 | 89 | 10 | .3 | |
| 1 | 5⁄8 | 1 | .80 | 118 | .9 | 746 | .02259 | 44 | .3 | 9 | .2 | 112 | 11 | .0 | |
| 1 | 3⁄4 | 2 | .25 | 148 | .4 | 932 | .02820 | 35 | .4 | 9 | .6 | 134 | 11 | .5 | |
| 1 | 7⁄8 | 2 | .77 | 182 | .6 | 1,147 | .03469 | 28 | .8 | 10 | .1 | 163 | 12 | .1 | |
| 2 | 3 | .36 | 221 | .6 | 1,391 | .04211 | 23 | .7 | 10 | .5 | 193 | 12 | .7 | ||
| 2 | 1⁄8 | 4 | .00 | 265 | .8 | 1,669 | .05062 | 19 | .8 | 11 | .0 | 227 | 13 | .2 | |
| 2 | 1⁄4 | 4 | .80 | 315 | .5 | 1,981 | .05995 | 16 | .7 | 11 | .4 | 264 | 13 | .7 | |
| 2 | 3⁄8 | 5 | .62 | 371 | .1 | 2,330 | .07051 | 14 | .2 | 11 | .8 | 305 | 14 | .2 | |
| 2 | 1⁄2 | 6 | .56 | 432 | .8 | 2,718 | .08224 | 12 | .2 | 12 | .5 | 359 | 15 | .0 | |
| 2 | 3⁄4 | 8 | .73 | 576 | .1 | 3,618 | .1094 | 9 | .14 | 13 | .0 | 450 | 15 | .6 | |
| 3 | 11 | .3 | 747 | .9 | 4,697 | .1421 | 7 | .04 | 13 | .7 | 566 | 16 | .5 | ||
| 3 | 1⁄4 | 14 | .4 | 951 | .0 | 5,972 | .1807 | 5 | .54 | 14 | .5 | 701 | 17 | .4 | |
| 3 | 1⁄2 | 18 | .0 | 1,188 | 7,458 | .2257 | 4 | .43 | 15 | .2 | 854 | 18 | .3 | ||
| 3 | 3⁄4 | 22 | .1 | 1,461 | 9,173 | .2775 | 3 | .60 | 16 | .0 | 1,029 | 19 | .2 | ||
| 4 | 26 | .9 | 1,773 | 11,136 | .3368 | 2 | .97 | 16 | .7 | 1,225 | 20 | .1 | |||
| 4 | 1⁄4 | 32 | .2 | 2,127 | 13,345 | .4040 | 2 | .48 | 17 | .4 | 1,439 | 20 | .9 | ||
| 4 | 1⁄2 | 38 | .2 | 2,524 | 15,851 | .4796 | 2 | .09 | 18 | .1 | 1,679 | 21 | .7 | ||
| 4 | 3⁄4 | 45 | .0 | 2,969 | 18,635 | .5642 | 1 | .77 | 18 | .8 | 1,943 | 22 | .6 | ||
| 5 | 52 | .5 | 3,463 | 21,750 | .6579 | 1 | .52 | 19 | .4 | 2,220 | 23 | .3 | |||
| 5 | 1⁄4 | 60 | .7 | 4,008 | 25,177 | .7616 | 1 | .31 | 20 | .0 | 2,525 | 24 | .0 | ||
| 5 | 1⁄2 | 69 | .8 | 4,609 | 28,936 | .8758 | 1 | .14 | 20 | .6 | 2,854 | 24 | .7 | ||
| 5 | 3⁄4 | 79 | .8 | 5,266 | 33,077 | 1 | .000 | 1 | .00 | 21 | .2 | 3,210 | 25 | .4 | |
| 6 | 90 | .6 | 5,983 | 37,584 | 1 | .137 | .880 | 21 | .6 | 3,600 | 26 | .2 | |||
| 6 | 1⁄2 | 117 | 7,606 | 47,780 | 1 | .445 | .692 | 22 | .9 | 4,421 | 27 | .5 | |||
| 7 | 144 | 9,501 | 59,682 | 1 | .805 | .554 | 24 | .2 | 5,426 | 29 | .0 | ||||
| 7 | 1⁄2 | 177 | 11,680 | 73,254 | 2 | .220 | .450 | 25 | .3 | 6,518 | 30 | .4 | |||
| 8 | 215 | 14,180 | 89,088 | 2 | .694 | .371 | 26 | .5 | 7,774 | 31 | .8 | ||||
| 8 | 1⁄2 | 258 | 17,010 | 106,836 | 3 | .232 | .309 | 27 | .6 | 9,133 | 33 | .1 | |||
| 9 | 306 | 20,190 | 126,846 | 3 | .837 | .261 | 28 | .7 | 10,650 | 34 | .4 | ||||
| 9 | 1⁄2 | 360 | 23,750 | 149,118 | 4 | .512 | .222 | 29 | .8 | 12,320 | 35 | .7 | |||
| 10 | 420 | 27,700 | 174,000 | 5 | .260 | .190 | 30 | .8 | 14,100 | 36 | .9 | ||||
| 11 | 559 | 36,870 | 231,594 | 7 | .005 | .143 | 32 | .8 | 18,180 | 39 | .4 | ||||
| 12 | 725 | 47,860 | 300,672 | 9 | .095 | .110 | 34 | .7 | 22,880 | 41 | .7 | ||||
| 13 | 922 | 60,860 | 382,278 | 11 | .83 | .0865 | 36 | .6 | 28,330 | 44 | .0 | ||||
| 14 | 1,152 | 76,010 | 477,456 | 14 | .44 | .0693 | 38 | .5 | 34,560 | 46 | .2 | ||||
| 15 | 1,417 | 93,490 | 587,250 | 17 | .76 | .0563 | 40 | .3 | 41,530 | 48 | .4 | ||||
| 16 | 1,720 | 113,500 | 712,704 | 21 | .56 | .0464 | 42 | .1 | 49,330 | 50 | .5 | ||||
| 17 | 2,062 | 136,100 | 854,862 | 25 | .86 | .0387 | 43 | .3 | 57,970 | 52 | .6 | ||||
| 18 | 2,447 | 161,500 | 1,014,768 | 30 | .69 | .0326 | 45 | .5 | 67,490 | 54 | .6 | ||||
| 19 | 2,880 | 190,000 | 1,193,466 | 36 | .10 | .0277 | 47 | .2 | 78,040 | 56 | .6 | ||||
| 20 | 3,360 | 221,600 | 1,392,000 | 42 | .11 | .0237 | 48 | .8 | 80,660 | 58 | .5 | ||||
| Note.—To find the corresponding values for shafts of
cast iron or steel, multiply the tabular values by the following multipliers: |
|||||||||||||||
| Cast iron |
2⁄5 | 2⁄3 | 2⁄3 | 2⁄3 | 1.5 | .86 | .81 | .86 | |||||||
| Steel | 1.2 | 2.06 | 2.06 | 2.06 | .48 | 1.05 | 1.07 | 1.05 | |||||||
“It is advantageous that the diameter of line shaft be kept as small as is possible with due regard to the duty, so as to avoid extra weight in the shafting hangers, pulley hubs and couplings, whose weights necessarily increase with the diameter of the shafting.
“Speeds For Shafting.—The speed at which shafting should run is determined within certain limits by the kind of machinery it is employed to drive. Shafting to drive wood-working machines may, for example, be made to rotate much faster than that employed to run metal-cutting machines, because the motions in the wood-working machines themselves are faster than those in metal-cutting machines. In a general sense, the rotation of shafting is greater in proportion as the movements of the machines driven require to run faster.
“This occurs because in proportion as the driving pulleys of the machines require to rotate faster than the line shaft, the diameters of the pulleys on the line shaft must be larger than the diameters of those on the machines; hence a great variation in speed would demand a corresponding increase of diameter of pulley on the line shaft, and the extra weight of this pulley would be so much added to the weight causing friction, as well as so much added to the cost. If small pulleys were used and countershafts employed to multiply the speed the cost would be increased, extra room would be taken up; indeed, this is so obvious as to require no discussion, further than to remark that the faster the shafting rotates the smaller may be its diameter to transmit a given horse-power. From deflection and weakness to resist transverse strains and other obvious causes it is not found in practice desirable to employ line shafts of less than about 11⁄4 inches in diameter, and the diameters of shafting employed are usually arrived at from a calculated speed of about 120 revolutions per minute for metal-cutting machines such as used in machine shops, 250 revolutions per minute for wood-working machines, and from 300 to 400 revolutions per minute for cotton and woollen mills, and the countershafts for the machines usually have pulleys of the requisite diameters to convert this speed of rotation into that required to run each respective machine. Tubular or hollow shafting has been made to run at 600 revolutions per minute, but this kind of shafting has been of very limited application because of its expensiveness.
“It is obvious that since the speed of a line shaft is used as a multiplier in the calculation of the horse-powers of shafts, a given diameter of shaft will transmit more power in proportion as its speed is increased. Thus a shaft capable of transmitting 20 horse-power when making 120 revolutions per minute will transmit 40 horse-power if making 240 revolutions per minute.
[II-191]“There are now running in some factories lines of shafting 1,000 feet long each. The power is generally applied to the shaft in the centre of the mill and the line extended each way from this. The head shaft being, say, 5 inches in diameter, the shafts extending each way are made smaller in proportion to the rate of distribution, so that from 5 inches they often taper down to 13⁄4.
“When very long lines of shafting are constructed of small or comparatively small diameter, such lines are liable to some irregularities in speed, owing to the torsion or twisting of the shaft as power is taken from it in more or less irregular manner. Shafts driving looms may at one time be under the strain of driving all the looms belted from them, but as some looms are stopped the strain on the shaft becomes relaxed, and the torsional strain drives some part of the line ahead, and again retards it when the looms are started up. This irregularity is in some cases a matter of serious consideration, as in the instance of driving weaving machinery. The looms are provided with delicate stop motion, whereby the breaking of a thread knocks off the belt shifter and stops the loom. An irregular driving motion is apt to cause the looms to knock off, as it is called, and hence the stopping of one or more may cause others near to them to stop also. This may in a measure be arrested by providing fly-wheels at intervals on the line shaft, so heavy in their rim as to act as a constant retardant and storer of power, which power is given back upon any reaction on the shaft, and thus the strain is equalized. We mention this, as at the present time it is occupying the thoughts of prominent millwrights, and the relative advantage and disadvantage of light and heavy fly-wheels are being discussed, and is influencing the proportions of shafting in mill construction.[36]”
[36] From “Machine Tools,” by William Sellers and Co.
Countershafts are separate sections of shafting (usually a short section) employed to increase or diminish belt speed, to alter the direction of belt motion, to carry a loose as well as a fast pulley (so that by moving the belt on to the loose pulley it may cease to communicate motion to the machine driven), and for all these purposes combined.
An excellent form of countershaft hanger is shown in Fig. 2594, the guide for the slide being adjustable along the arm, and fixed in its adjusted position by means of the set-screws. The bearing is self-adjusting horizontally for alignment. The countershaft is shown in Fig. 2595, a b being the bearings, c the cone pulley, d the fast and e the loose pulley, which is placed next to the bearing, so that it may be oiled without having to reach past the belt and fast pulley. By reducing the journal for the loose pulley no collar is needed, the shaft shoulder and the face of the bearing serving instead.
When the direction of rotation of the cone pulley on the countershaft requires to be occasionally reversed, there are two belts, an open one and a crossed one, from the line shaft to the countershaft, and there are three pulleys on the countershaft, their arrangement being as shown in Fig. 2596. l l′ are two loose pulleys, one receiving the open and the other the crossed belt, both these pulleys being a little more than twice the width of the belt; f is a fast pulley. By operating the belt skipper or shifter in the requisite direction either the open or the crossed belt is brought upon the fast pulley, the other belt merely moving across the width of its loose pulley, which must be twice that of the fast one. In the position of the belt shifter shown in the cut, both belts would be upon the loose pulleys l l′, hence the countershaft would remain at rest. If the direction of rotation of one pulley is required to be quicker than the other, two fast pulleys, each slightly more than twice the width of the belt, may be placed upon the line shaft, one of them being of enlarged diameter, to give the requisite increased velocity.
In Fig. 2597 Pratt’s patent friction clutch is shown applied to a countershaft requiring to rotate in both directions, but quicker in one direction than in the other; hence, one of the pulleys is of smaller diameter than the other. The pulleys are free to rotate upon the countershaft unless engaged by the clutch, which is constructed as follows:—
The inside surface of the pulley rim is bored and the end surface of the shoes is turned to correspond. The shoes are in the form of a bell crank, upon the exposed end of which is provided a small lug, clearly shown in the cut. To prevent end motion of the pulley a collar is placed on one side of it and secured to the countershaft, while, on the other, the sleeve to which the shoes are pivoted is also secured to the countershaft; upon the shaft between the two pulleys there is a sleeve, having at each end a conical hub. When this sleeve is moved to the right, its right-hand coned hub passes between the lugs on the exposed ends of the shoes, forcing these lugs apart and causing the shoes to grip the bore of the large pulley, which thereupon rotates the shaft through the medium of the sleeve upon which the shoes are pivoted. Similarly, if the engaging (and disengaging) sleeve be moved to the left it will pass between the lugs of the shoes on the left-hand pulley, which will, therefore, be caused to drive the shaft. In the position shown in the cut the engaging sleeve is clear of the ends of all the shoes, hence the pulleys would be caused to rotate (by their belts), but the shafts, &c., would remain stationary.
In yet another form the inner face of the pulley rim is coned, and in place of shoes a disk, whose circumference is coned to fit the pulley rim, is fast upon the shaft. The shaft is provided with a fixed collar, and from this collar, as a fulcrum, the pulley and disk are (by means of short levers attached to a sleeve upon the countershaft) brought into contact, the thrust on the other side of the pulley being sustained by a conical surface on the sleeve, fitting to a[II-192] similar cone on the hub of the pulley. Thus the pulley is gripped between two coned surfaces, one on each side, and is released by moving the sleeve laterally so as to relieve the grip, which it does noiselessly.
By this means motion to the shaft is communicated from the pulley without the sudden shock incidental to the impact of two fixed pieces, because the grip of the cones is gradual, and a certain amount of slip may occur until such time as the grip of the surfaces is sufficient to drive by friction.
Fig. 2598[37] represents a cone friction clutch pulley. The outer half is a working fit upon the shaft, but is secured against end motion by the collar d. The sliding half is coned and covered with leather as shown at c c, the outer half being coned to correspond. The sliding half is driven by a feather fast in its bore, and sliding in a feather-way or spline in the shaft.
[37] From The American Machinist.
The driving power of the device is obtained by means of the friction of the coned surfaces. The less the angle x of the cones the more power transmitted with a given pressure of the internal to the external cone.
On the other hand, however, this angle may be so little that the external cone will not release the internal one when the end pressure on the latter is removed.
The object is, therefore, to so proportion the angle x of the cones that their friction will be a maximum, while the internal cone may be moved endwise and unlocked from the external without undue effort or strain at the moving clutch bar e. If the angle be 30 degrees, the clutch will release itself when the lateral pressure is removed. If the angle be 25 degrees the internal cone will require a slight lateral pressure to release it. If the angle be 20 degrees, the internal cone cannot be released by end pressure applied by hand.
The transmitting capacity of the clutch depends upon the pressure applied to maintain the cones in contact, and therefore upon the leverage of the clutch bar, whose fork end is shown in section at e.
It is desirable that the end pressure be as small as possible, because of the friction between e and the hub of the sliding half of the pulley.
The hangers which carry the bearing boxes supporting shafting may be divided into four principal classes:—Those in which the bearing boxes are permitted to swivel, and to a certain extent to adjust themselves, to the axial line of the shafting, and having means to adjust the vertical height of the bolts.
Those in which the bearings are incapable of such adjustments.
Those in which the bearing boxes are supported on each side; and those in which the bearing is supported on one side only, so that the shafting may be taken down without disturbing the couplings.
The first named are desirable in that they eliminate to a certain extent the strains due to the extra journal bearing friction which occurs when the shafting is sprung out of its true alignment, and obviate to a great extent the labor involved in fitting the bore of the bearing boxes to the journals of the shafting, so as to hold the same with its axis in a straight line, while they permit of vertical movement to attain vertical alignment.
Fig. 2599 represents Wm. Sellers & Co.’s ball-and-socket hanger which has come into extensive use throughout the United States: a represents the frame of the hanger threaded to receive the cylindrical threaded plungers d e, which therefore by rotation advance or recede respectively from the centre of the bearing boxes b c.
The ends of these plungers are concave, and the top and bottom halves of the bearing boxes are provided with a spheroidal section fitting into the concaves of the plungers, so that when the plungers are adjusted to fit (a working fit) against the boxes, the latter are held in a ball-and-socket or universal joint, which permits motion in any direction, the centre of such motion being central to the spherical concaves on the ends of plungers e d.
To adjust the vertical height of the bearings or boxes, it is simply necessary to rotate the plungers d e, in the threaded holes in the frame. f is simply a dish to catch the lubricating oil after it has passed through the bearing.
It is obvious that if a shaft be aligned axially true, and held in a box of this design, the centre of a length of shaft on either side of the box may be sprung or deflected out of alignment, and that the box will adjust itself so that its bore will be parallel with the axis of the shaft thus deflected, hence the friction between the shaft journal and the bearing box will be at all times a minimum.
This feature of self-adjustment permits of the employment of longer bearings, which reduces the wear, as well as the friction, and by providing sufficient bearing and wearing area, enables the bearings to be composed of cast iron, which is the cheapest as well as the very best material of which a bearing can be made, provided that its area of bore is sufficiently large in proportion to[II-193] the duty, or load, to have a pressure of not more than about 60 lbs. per square inch of area.
Again, if the alignment of the shaft should require readjustment from the warping or sinking of beams, as is a very common occurrence where hangers are fixed to the joists of ceilings, the adjustment is readily and easily effected by means of the plungers, nor need the boxes be fitted to the shaft more than to see that when free from the hangers they bed firmly down until the crowns of their bore have contact with the shaft. The hangers themselves require no refinement of alignment, because that may be secured by means of the plungers, and the boxes require no fitting to the shafts after the hangers are erected.
In hangers in which the self-adjusting ball-and-socket feature is omitted, the bottom hangers must not only be accurately aligned, but the boxes must, to avoid friction and undue wear, all be fitted to the shaft, and the latter must, during such fitting, be tried in the boxes; the operation, if properly performed, costing far more in labor than is equivalent to the difference in the first cost of the ball-and-socket adjustable hangers and those solid or not self-adjustable, especially if the boxes be long ones, as about, or not less than, three times the diameter of the shaft, as they should be.
An external side elevation of this hanger is shown in Fig. 2600, it being obvious that the hanger is designed for bolting to timbers, or framing overhead.
Fig. 2601 represents a hanger of this class. In this the lower part carrying the bottom bearing is held to the upper by two bolts, as shown, the object being to enable the same to be placed in position on a line of shafting without disturbing the pulleys or the couplings. The lower section with the bottom bearing is removed and again put on after the hanger is set over the shaft.
Fig. 2602 represents an open-sided ball-and-socket hanger in which the plungers can be retired, the bearings removed, and the hanger erected on an existing line of shafting without removing the pulleys or couplings, or disturbing the line of shafting.
When the face of the framing to which the hangers are to be bolted stands vertical, the hangers are formed as in Fig. 2603, in which the ball-and-socket or swivelling feature is maintained as before.
Fig. 2604 represents a wall hanger, which is open in front[II-194] similar to the hanger shown in Fig. 2602, and for the same purpose.
The section of shafting receiving power from the engine or prime mover is usually supported in bearings or pillow blocks. Pillow blocks are also used for vertical shafts, and in cases where the foundation or framing is not liable to lose correct horizontal adjustment.
Fig. 2605 represents a pillow block, in which the ball-and-socket principle shown in Fig. 2602 is embodied. The bearings have each a ball section fitting into spherical recesses or cups provided in the body of the block, and in the cap, so that the bearings are capable of swivelling as already described with reference to the hanger Fig. 2599.
A sectional view of a pillow block having this adjustable feature is shown in Fig. 2606. To provide increased seating bearing, and also means of side adjustment to pillow blocks, they are sometimes bolted to base plates as in Fig. 2607, room being left in the bolt holes to permit of their being moved and adjusted upon the plate. The adjustment may be made by means of wedges, as at a, b in Fig. 2607. These base plates are usually employed when the pillow block is to be held against a wall.
An inverted pillow block of similar construction, but designed for the head line (as the length receiving power from the engine or motor is termed) of the shafting, is shown in Fig. 2608, but an improved form of the same has plungers so as to effect a vertical adjustment of the bearings.
When a pillow block requires to be enveloped by a wall it is provided with a wall box as shown in Fig. 2609, and within this box is set the pillow block as shown, space being sometimes left to adjust the pillow block laterally within the box by means of a wedge as shown.
In cases where the shafting requires to stand off from a wall to allow room for the pulleys, brackets or knees, such as shown in Fig. 2610, are employed.
Couplings for Line or Driving Shafts.—The couplings for connecting the ends of line shafts should accomplish the following objects:—
1. To hold the two shaft ends axially true one with the other.
2. To have an equal grip along the entire length of shaft enveloped by the coupling.
3. To have a fastening or locking device of such a nature that[II-195] it will not be liable to work loose from the torsional strains due to the flexure of the shaft, which is caused by the belts springing or straining the axial line of shafting out of the straight line.
4. To be capable of easy application and removal, so as to permit the erection or disconnection of the lengths of shafting with as little disarrangement of the hangers and bearings as possible, and to be light, run true, and be balanced.
To these requirements, however, may be added that, since it is well-nigh impracticable to obtain lengths of lathe-turned shafting of exactly equal diameter, couplings for such shafting require to fill the following further requirements:
5. The piece or pieces gripping the shaft ends must be capable of concentric and parallel closure along the entire area, enveloping the end of each shaft, and must do this at each end independently of the other, and the piece or pieces exerting the closing or compressing pressure must grip the closing piece or pieces, enveloping the shafting over the entire area.
If, for example, a sleeve be split at four equidistant parts of its circumference, and from each end nearly to the middle of its length, as in Fig. 2611, any pressure that may be applied to its circumference to cause it to grip the shaft it envelops will cause it to grip the shaft with greater force at one part than at another, according to the diameter of the shaft and the location of the external pressure. Thus, if the pressure be applied equally along the length a b, the weaker end b will close most readily, while at a the support afforded by the unsplit section offers a resistance to closure at the ends a of the split, hence the shaft, even though a working fit to the sleeve bore, will be gripped with least force at the end a. If the shaft were simply a close fit, as, say, just movable by hand on the sleeve bore, the form of the coupling bore would, when compressed upon the shaft, be as shown in Fig. 2612, the bend on the necks a, b, c, d, being magnified for clearness of illustration. If the compressing piece covered the compressed sleeve for a lesser distance, the grip would be more uniform, because there would be a greater length of the sleeve to afford the curves a, b, c, d, as shown in Fig. 2613. The grip may be more equalised by boring the sleeve of slightly smaller diameter than the shaft.
Fig. 2614 represents a sleeve carrying out this principle. It is composed of two halves, as shown, bored slightly smaller than the shaft diameter, and is to be compressed on the shaft, which, acting as a wedge, would spring open the sides of the bore until the crown of the bore bedded against the shaft. This, in the case of parallel shaft ends of equal diameter, would hold them with great force axially true, and with equal force and bearing, thus meeting all the requirements. If, however, the end of one shaft were of larger diameter than the end of the other (as has hitherto been supposed to be the case), the end accomplished by boring the sleeve of smaller diameter than the shaft is, that the end of the sleeve is afforded the extra elasticity due to the transverse spring of the sleeve, which permits the edges of each half of the sleeve to bear along a greater length of the shaft end than would otherwise be the case; but the bearing is in this case mainly at and near the edges of the split.
It will be perceived, then, that under this principle of construction, when applied to shaft ends of varying diameters, the metal is left to spring and conform itself to the shape of the parts to be connected, and that there is nothing outside of the condition of relative diameter of shaft to sleeve bore to determine what the direction of the spring or closure of sleeve shall be; but, on the other hand, the principle possesses excellence in that the sleeve being cylindrical and its closure taking place equally at similar points of contact the shafts will be held axially true, one with the other; or in other words, the movements of the metal while sleeve closure is progressing are equally radial to the axis of the sleeve, and there is no element tending to throw the shaft axis out of line one with the other.
If a sleeve have a single split, the manner in which it will grip a shaft smaller than the sleeve’s bore depends upon the manner in which the compression is effected.
In Fig. 2615, for example, is a ring supposed to be compressed by a pressure applied at a and at b, causing the ring to assume[II-196] the form shown by the dotted lines. The centre of the ring bore would therefore be moved from c to d. Now, suppose that the end of one section of shafting were to fit the sleeve bore, then compressing the sleeve upon it would not practically move the centre of the bore; but if the shaft at the other end of the sleeve were smaller than the sleeve bore, the compression of the sleeve to grip the shaft would move the centre of the bore, and, therefore, of the shaft towards d, hence the axial lines of the shafts would not be held true one with the other. To accomplish this latter object, the compression must be equal all round the sleeve, or it may be applied at the points e and f, Fig. 2616, although it is better to have the compression area embrace all the circumferential area possible of the sleeve, and to have the movement that effects the compression simultaneous and equal at all points on the circumference of the ring or sleeve, because if these movements are independent, more movement or compression may be given at one point than at another, and this alters the centre of the bore; thus, if more pressure were exerted at e than at f, in figure, the centre of the bore would be thrown towards f, or vice versâ. If the pressure be concentric, the single split ring or sleeve grips the shaft all round its circumference; hence it is only necessary in this case to maintain the circumference of the sleeve in line to insure that the shaft ends be held axially true one with the other; and if the pressure on the ring be applied equally from end to end its closure will also be parallel and equal, and the shaft will be held with equal force along that part of its length enveloped by the coupling. It is obvious, however, that the piece or sleeve gripping the end of one shaft must be independent of that gripping the other, so as to avoid the evils shown in Fig. 2612, while at the same time the casing or guide enveloping the two independent rings or sleeves must guide and hold them axially true, one with the other.
In Fig. 2617 is shown an excellent form of plate coupling, in which most of the requirements are obtained. a and b are the ends of the two lengths of shafting to be connected, c and d are the two halves of the coupling driven or forced on the ends of the shafting, and further secured by keys. The end of one half fits into a recess provided on the other half, so as to act as a guide to keep the shafts axially true one with the other, and also to keep the two halves true one with the other, while drilling the holes to receive the bolts e which bolt the coupling together. The objections to this form are, that it is costly to make, inasmuch as truth cannot be assured unless each half coupling is fitted and keyed to the shaft, and turned on the radial or joint faces afterwards. Furthermore, if the coupling were taken off in order to get a solid pulley on the shaft, the coupling is apt to be out of true when put together again, and, therefore, to spring the shaft out of true. Also, that the bearing, support, or hanger must be open-sided to admit the shaft, and that each coupling, being fitted and turned to its place, would be apt to run out of true if removed and applied to another shaft, whether the same be of equal diameter or not; but if each half coupling be provided with a feather instead of the usual key, the coupling may be readily removed and will remain true when put on again.
Fig. 2618 represents a plate coupling, in which one end of the shaft passes into the bore of the half coupling on the other length of shaft, which serves to keep the shafts in line one with the other.
Fig. 2619 represents a single cone coupling composed of an external sleeve having a conical bore and a split internal sleeve bored to receive the shaft, and turned on its outer diameter to the same cone as the bore of the outer or encasing sleeve. The bolts pass through the inner sleeve, the bolt head meeting the radial face of the inner sleeve while the nut meets the radial face of the outer sleeve, so that screwing up the nut forces the inner sleeve into the outer and closes the bore of the former upon the shaft. This coupling is open to the objection that it cannot grip the ends of the shafts equally unless both shafts be of exactly equal diameter, and the bearing on the smaller shaft will be mainly at the outer end only, as explained in Fig. 2611. As a result, the transverse strains on the shaft will cause the couplings to come loose in time.
Fig. 2620 represents a coupling composed of a cylindrical sleeve split longitudinally on one side, as at d; the bolts c pass through the split. Diametrally opposite is another split passing partly through as at b. A key is employed at right angles to the two splits as shown. Here, again, the pressure on a shaft that is smaller than the other, of the two shafts coupled, will be mainly at one end, but separation of the shaft ends is provided against by means of two cylindrical pins on the ends of the key fitting into corresponding holes drilled in the shaft, as shown in the side elevation in the figure.[II-197]
In Fig. 2621 is shown a coupling whose parts are shown in Fig. 2622. It consists of a cylindrical ring turned true on the outside and bored conical from each end to the middle of its length, as shown. The split cones are bored to receive the shaft and contain a keyway to receive a spline provided in the shaft ends, and are turned on the external diameter to fit the conical borings in the sleeve. Three square bolts pass through the split cones, which, being square, are prevented from rotating while their nuts are being screwed up.
To put the coupling together one split cone is passed over the end of one shaft and the other over that of the other. The sleeve is then put between the ends of the shaft, the position of the shaft adjusted for length and the split cones pushed up into the sleeve; the bolts are then passed through and screwed up. The forcing of the split cones into the conical borings of the sleeve causes the former (from being split) to close upon the shaft ends and grip them equally tight, notwithstanding any slight difference in the diameters of the shaft, there being left between the ends of the split cones sufficient space to allow them to pass through the conical borings sufficiently to close upon the respective ends of the shafts; the pressure being parallel and equal on each shaft end, because when the cone has gripped the largest shaft the whole movement due to screwing up the nuts is transferred to the cone enveloping the smaller shaft, and by reason of the cones fitting, the closure of the holes in the cones is parallel, giving an even grip along the shaft end and an equal amount of grip to each shaft end.
To remove the coupling the bolts are removed, and the sleeve being moved endways the cones open from their spring and relieve the grip upon the shaft.
It is evident that in their passage through the sleeve casing the cones will move with their axial lines true with the axial line of the casing; and it is equally evident that the taper on the cone accurately fitting the taper in the sleeve bore, the closure of the cone bores must be equal; while at the same time the pressure on the two cones upon the respective shaft ends must be equal, because it is the friction of the cone bores upon the shaft ends which equally resists the motion of both, while the pressure applied to the respective cones is derived from the same bolts, and hence is equal and simultaneous in its action.
To loosen this coupling for removal the bolts must be stacked back and a few blows on the exterior of the outer shell with a billet of wood may loosen the coupling; but if not, a wedge or a cold chisel may be driven in the splits of the cones to loosen them, but such wedge or chisel should not have contact with the sides of the split, either near the bore or near the perimeter, for fear of raising a burr.
In Fig. 2623 is shown a patent internal clamp coupling. It is formed of a cylindrical piece containing a pair of separate clamps, and between these clamps and the outer casing are four screws, two to each clamp; these screws are tapered so as to close the clamp when screwed up and release it when screwed outwards. The holes to receive the shaft ends are bored somewhat smaller than the shafts they are to fit, and the clamps opened to permit the easy insertion of the shaft ends by means of wedges a driven in the split b of each clamp, as shown in Fig. 2624.
The lower edge of the wedges should be slightly above the bore of the clamp to prevent the formation of a burr or projection of metal when the wedge is driven in. When placed upon the shaft ends and in proper position the wedges are removed and the clamp bore will have contact at and near the edges of the longitudinal split and on the opposite sides of the bore where the keyway is shown, but the pressure of the tape screws will spring the clamps on the side of the longitudinal splits, and increase the bearing area at those points.
The main features of this device are that though the bore be made a driving fit to the shaft, it can, by the employment of the wedges, be put on the shaft with the same ease as if it were an easy fit, while the clamps being separated by a transverse groove may open and close upon the shaft independently of each other, so as to conform separately to any variation in the diameters of the two shaft ends it couples. But it may be noted that since the circumference of each shaft end has a bearing along the line of the coupling bore diametrally opposite to the longitudinal splits, the shafts will not be held quite axially true one with the other unless there be as much difference in the diameters of the separate clamp bores as there is in the diameters of the shaft ends; because to hold two shafts of different diameters axially true one with the other the longitudinal planes of the two circumferences must not at any part of the circumferences form a straight line, as would be the case at that part of the coupling bore at and near the keyway.
It is to be noted, however, that this coupling is formed of one solid piece, and that the strain on the tightening bolts or screws is one of compression only, which tends to hold them firmly and prevent their coming loose.
If the workmanship of a plate coupling, such as in Fig. 2617, be accurately and well done, and the proportions of the same are of correct design, so that the strain placed on the same in keying and coupling it up does not distort it, the coupling and the shaft will run true, because the strain due to the key pressure will not be (if properly driven) sufficient to throw the coupling out of true. But the degree of accuracy in workmanship necessary to attain this end is greater than can be given to the work and compete in the market with work less accurately made, because the difference in the quality of the workmanship will not be discernible save to the most expert and experienced mechanic, and not to him even unless the pieces be taken apart for examination. If the bore of the coupling be true and smooth and of proper fit to the shaft the[II-198] key pressure, if the key fits on its top and bottom, will not, as stated, be sufficient to throw the coupling out of true. It is true, however, that such pressure is exerted on one half the bore of the coupling only, being the half bore opposite to the key. On the other diametral side of the coupling the strain due to the key is exerted on the top face of the key.
If, therefore, the key seats in the shaft and in the couplings are in line or parallel, and both therefore in the same plane, the strain due to the key may throw the coupling out of true to the amount that the key pressure may relieve the bore of the coupling (on the half circumference of the shaft of which the key is the centre) from contact or pressure with the shaft. As a result, the coupling may run to that extent out of true, but the shaft would run true nevertheless so long as the nature of the surfaces on the shaft and on the coupling bore was such that the key pressure caused no more compression or closer contact in the case of one half coupling than in the case of the other.
It is obvious that a plate coupling will require at least as much force to remove it from the shaft as it took to put it on, and sometimes, from rusting of the keys, &c., it requires more. If it be removed by blows it becomes damaged, and damage is likely to be also caused to the shaft, while the surfaces having to slide in contact under the pressure of the fit the surfaces abrade and compress, and the fit becomes impaired. But in couplings such as shown in Fig. 2621, the gripping pieces are relieved of pressure on the shaft by the removal of the bolts, and the removal of the coupling becomes comparatively easy.
The interchangeability of plate couplings is further destroyed by the fact already stated, that turned shafting is not, as a rule, of accurate gauge diameter, and the least variation in the pressure or fit of the coupling to its shaft is apt to cause a want of truth when the key bears on its top and bottom. The fit of the coupling to its shaft may be, it is true, relied on to do the main part of the driving duty, and the key fitting on the sides only may be a secondary consideration, but in proportion as the fit is relied on to drive, that fit must be tighter, and the difficulty of application and removal is increased.
Another and important disadvantage of the plate coupling in any form is that it necessitates the use of hangers open on one side to admit the shaft, because the couplings must be fitted upon the shaft before the same is erected and should not be removed after being fitted, as would be necessary to slide the end of the shaft through the bearing.
When plate couplings are constructed as in Fig. 2617, the removal of a section involves either the driving back of one-half of the coupling so that the other half will clear it, or else the moving endwise of the whole line to effect the same object.
With a plate coupling the half coupling on one end of the shaft must be removed when it is required to put an additional pulley on the shaft, unless, indeed, a split pulley be used, whereas with a clamp coupling, such as shown in Fig. 2621, the half coupling at each end may be slacked and moved back, one end of the shaft released, a solid pulley placed on the shaft and the coupling replaced, when it will run as true as before, and the pulley may be adjusted to its required position on the length of shafting.
It is to be remarked, however, that a well-made plate coupling, such as in Fig. 2618, makes a good and reliable permanent job that will not come loose under any ordinary or proper conditions.
In Fig. 2625 is shown a patent self-adjusting compression clamp, which is peculiarly adapted to connect shafting that is of proper gauge diameter. It consists of a sleeve a made in two halves, each embracing nearly one-half of the shaft circumference and being bored parallel and slightly smaller than the diameter of the shaft ends. Over this sleeve passes at each end a ring d e, bored conical and fitting a similar cone on the external diameter of the sleeve. On each end of the sleeve is the nut f g, which by forcing the cone ring up the taper of the sleeve causes the two halves of the latter to close upon and grip the shaft. For shafts less than two inches in diameter there are provided in the sleeve two pins to enter holes in the shaft ends in place of keys, but for sizes above that keys are employed. All parts of this coupling being cylindrical it is balanced. The separate parts of this coupling are shown in Fig. 2626.
In Figs. 2627 to 2630 are shown a side elevation and sectional view of another form of shaft coupling. a is the sleeve, b b nuts on the ends of the sleeve, and c c cones fitting taper holes in the sleeve. These cones are split, as shown in Fig. 2629, to permit them to close upon the shaft ends. The shaft ends themselves are matched with a half dovetail, as in Fig. 2630, which dispenses with the employment of a key.
In coupling shafts of different diameters it is usual to reduce the diameter of the end of the larger to that of the smaller shaft, and to employ a size of coupling suitable for the smaller shaft; but in this case it is necessary that the coupling be placed on the same side of the hanger or bearing as the smaller shaft, otherwise it is obvious that the strength of the larger would, between its bearings, be reduced to that of the smaller shaft.
The couplings for line shafting are usually placed as near to the bearings or hangers as will leave room for the removal of the couplings by sliding them along the shaft.
The couplings on the length of shaft receiving power from the motor are placed outside the bearings, hence on the succeeding lengths there will be one coupling between each pair of bearings, the couplings being in each case as close to each bearing as will allow the coupling to be moved towards the bearing sufficiently to[II-199] permit the length to be removed without disconnecting the adjacent length from its bearings.
Fig. 2631 represents a very superior form of coupling for line shafts. The ends of the line shaft are reduced to half diameters as shown, and lapped with a horizontal joint at an angle to the axis of the shaft as denoted by the dotted line, which prevents end motion; the ends of the shaft and their abutting surfaces are dovetailed, as shown a and b, and, therefore, perform driving duty. A sleeve envelops the whole joint and is secured by a key. This coupling accomplishes all that can be desired, but requires very accurate workmanship, and on this account is expensive to make.
Fig. 2632 represents a form of coupling suitable for light shafting. It consists of two halves a a, of cast iron, which are drawn together by the bolt c; the centre of the coupling is recessed to enable the coupling to take a better hold on the shaft, which is prevented turning by the pins d d. This coupling has no projections to catch clothes or belts, and is quickly applied or removed.
Fig. 2633[38] represents a form of coupling for heavy duty, the transmitting capacity only being limited by the strength of the projections a. If the shafts are not axially in line, this form of coupling accommodates the error, since the projections a may slide in their recesses, while if the axial lines of the shafts should vary from flexure of the bearings or foundations, as in steamships, clearance between the ends of a and the bottom of the recesses may be allowed, as shown at b.
[38] From Rankine’s “Machinery and Millwork.”
In Fig. 2634 is shown a coupling (commonly known as the universal joint coupling) which will transmit motion either in a straight line, or at any angle up to 45°.
It is formed of two double eyes, such as a, connected to a yoke or crosspiece b as shown at c. It is mainly used for connecting shafts or arms carrying tools of some kind, such as rubbers for polishing stone, tools for boring, or other similar purposes in which the tool requires to be rotated at varying angles with the driving shaft.
Pulleys for the transmission of power by belt may be divided into two principal classes, the solid and the split pulley. The former is either cast in one entire piece, or the hub and arms are in one casting, and the rim a wrought-iron band riveted on. The latter is cast in two halves so that they may be the more readily placed upon or removed from the shaft.
On account of the shrinkage strains in large pulley castings rendering them liable to break, it is usual to cast pulleys of more than about 6 feet in halves or parts which are bolted together to form the full pulley. On account of these same shrinkage strains it was formerly considered necessary to cast even small pulleys with curved arms, so that the strains might be accommodated or expended in bending or straightening the curves of the respective arms. It is found, however, that by properly proportioning the amount of metal in the hub, arms, and rim of the pulley, straight arm pulleys may be cast to be as strong as those with curved arms, and being lighter they are preferable, as causing less friction on the shafting journals, and, therefore, being easier to drive.
It is obvious that a pulley for a double belt requires to be stronger than is necessary for a single one, but the difference is not sufficiently great to give any practical advantage by making separate pulleys for single and double belts; hence all pulleys are made strong enough for double belts.
Pulleys are weaker in proportion to their duty as the speed at which they rotate is increased, because the centrifugal force generated by the rotation acts in a direction to burst the pulley asunder, so that if the speed of rotation be continuously increased a point will ultimately be reached at which the centrifugal force generated will be sufficient to cause the wheel to burst asunder. But the speed at which pulleys are usually run is so far within the limits of the pulley’s strength, that the element of centrifugal force is of no practical importance except in the case of very large pulleys, and even then may be disregarded provided that the pulleys be made in a sufficient number of pieces to avoid undue shrinkage strains in the castings, but if solid pulleys are rotated at high velocities the internal strains due to unequal cooling in the mould has been known to cause the wheels to fly asunder when under high speeds.
| VOL. II. | EXAMPLES OF PULLEYS. | PLATE XII. | |
 |
 |
||
| Fig. 2635. | Fig. 2636. | ||
 |
 |
||
| Fig. 2637. | Fig. 2638. | ||
 |
|||
| Fig. 2639. | |||
Fig. 2635 represents a solid pulley, the tapered arms meeting the rim in a slightly rounded corner or fillet, and the rim being thickened at and towards its centre. When the width of rim is excessive in proportion to one set of arms a double set is employed as in Fig. 2636.
In some forms of pulley the arms and hub are cast in one piece and the rim is formed of a band of wrought iron riveted to the arms. By this means shrinkage strains are eliminated and a strong and light pulley is obtained.
Fig. 2637 represents a split pulley in which the two halves are bolted together after being placed on the shaft.
Variable motion may be transmitted by means of an oval driving pulley, as in Fig. 2638, it being obvious that the belt velocity will vary according to the position of the major axis of the oval. Arrangements of this kind, however, are rarely met with in practice.
In Fig. 2639 is shown an expanding pulley largely employed on the drying cylinders of paper machinery, and in other similar situations where frequent small changes of revolution speed is required. Each arm of the wheel carries a segment of the rim, and is moved radially to increase or diminish the rim diameter by sliding in slots provided in the hub of the wheel, a radial screw operated by bevel gears receiving motion from the hand wheel and gear-wheels shown in the engraving. It is obvious that in this case the driving belt must be made long enough to embrace the pulley when expanded to its maximum diameter, the slack of the belt due to reduction of diameter being taken up by a belt tightener.
In Fig. 2640 is shown a wooden pulley having a continuous web or disk instead of arms. It is built up of segments, the web being secured to the shaft as follows. In Figs. 2641 and 2642 a, b are clamping plates, and c a split sleeve fitting easily to the shaft and passing through a, b, while receiving the nut e on the other side. The web of the pulley fits on the shoulder j, and the flange b fits on the shoulder k, so as to keep these parts true or concentric to a. The bore of a is taper to fit the taper of c; hence the nut e in drawing c through a, causes c to close upon and grip the shaft, while the flanges a, b grip the pulley and hold it to c.
In Figs. 2643 and 2644 are represented the Otis self-oiling loose pulley, designed to automatically oil itself upon its starting or stopping.
[II-201]The hub d is cored out in such manner as to form within it an annular chamber or cavity b b, entirely surrounding the bore, and serving as a reservoir to contain oil or other lubricating liquid.
This chamber or reservoir has no direct communication with the bore of the hub, but a communication is formed between it and the bore through one or more chambers c c, which are termed supply chambers, and which are partitioned off within the bore from the reservoir b, by coring the hub in a suitable manner.
These supply chambers have openings n n in their sides or ends communicating with the reservoir b, and also openings c c communicating with the bore of the pulley. These supply chambers are filled with wick or other fibrous or capillary material, which is also inserted into the openings n n, to draw the oil from the reservoir by capillary attraction and supply it in moderate quantities between the bore of the pulley and the shaft on which it runs. Three or more openings are provided in the outer shell of the hub for the introduction of oil into the reservoir b, which openings are closed by thumb-screws, plugs, or other stoppers e e. There being three of these openings, one will always be at or near the top when the pulley is at rest, and through this the oil may be introduced without difficulty. It is not intended that the reservoir should at any time contain more than one-third its capacity of oil, so that whenever the pulley is at rest the surface of the oil will be below the lowest point of the bore, thus preventing any waste of oil at such times.
When the pulley is in motion, the centrifugal force imparted to the oil in the reservoir throws it outwardly, causing it to be distributed in an even layer against the inner surface of the shell which encloses and forms the reservoir, thus preventing any possible waste when the pulley is in motion.
But when the pulley is either stopped or started, the oil is caused to change its position, and in so doing is brought into contact with the wicks protruding from the small openings n n, by which it is conveyed into the supply chamber, and thence to the shaft. By thus taking advantage of what is a necessity in all business establishments in which machinery is employed—to wit, the stopping and starting of the machinery at regular intervals—to insure the supplying, at such times, of a small quantity of oil to the bearings of the loose pulleys, the makers claim that a perfect and reliable means is obtained for guarding against any needless waste of the lubricant.
A crowning or crowned pulley is of largest diameter in the middle of its width or face, the object being to cause the belt to run on the middle of the pulley width. It would appear that this crowning would give to the belt a greater degree of tension at its centre than at its edges, but it is shown by experiment that if a piece of belt be clamped square across its width at each end and stretched, the centre as section b, in Fig. 2645, will stretch the most, and that if the piece be divided along its centre lengthwise, and both halves again stretched, they will again do so the most in the middle of their widths.
From this it appears that the crowning serves to produce a tension equal across the pulley width, because it will stretch the belt the most in the middle of its width, where it has the greatest capacity to stretch.
The amount of crowning employed in practice varies from about 3⁄16 to 3⁄8 inch per foot of width of pulley face, the minimum being employed where the belt requires to be moved or slipped laterally from one pulley to another of equal diameter, as from a fast to a loose pulley and vice versâ. To relieve the belt of strain when on a loose pulley the loose pulley is sometimes made of smallest diameter, and has a coned step up which the belt moves when pressed against it. During this passage of the belt, however, one edge is stretched more than the other, while in passing from the large to the smaller pulley the same edge is under tension, while the other is released from tension; hence, with the belt passing either to or from the large pulley there is a tendency to unduly stretch one of its edges. On the other hand, however, in cases where the belt requires to run for long periods on the loose pulley relieving it from tension is a great advantage.
In fixing pulleys so that they shall run true upon their shafts several difficulties are met with. First, it is difficult to turn the shafts quite parallel and to exact standard gauge diameter. Second, the bore of the pulley must be made a sufficiently easy fit to enable their being moved by hand along the shaft to the required location. As a result the set-screw pressure throws the pulley out of true, unless the mandrel on which the pulley is turned in the lathe be the same diameter as the pulley shaft, and the pulley be held upon the mandrel by the set-screw pressure, and not by driving the mandrel into the pulley bore. In this case two set-screws must be used one on each end of the pulley hub, so as to steady the pulley on the mandrel. A pulley thus trued will still run[II-202] out of true when on its shaft unless the shaft be of the same diameter as the mandrel.
One means of obviating this difficulty is to reduce the diameter of the shaft between the pulley seats sufficiently to allow the pulley to pass easily, and to make the pulley bores a driving fit to their seats. This, however, is only practicable in cases where the locations of the pulleys are permanently fixed, and no occasion arises for the addition of new pulleys.
To obviate this difficulty what is termed an internal clamp pulley has been constructed. This pulley is shown in Fig. 2646. The bore is made sufficiently smaller than the shaft diameter to be a forcing fit. A slot in the form of an arc of a circle is formed in the hub as shown, and a split runs from this arc into the bore. As a result a wedge driven between the walls of the split will spring open the bore and permit its easy passage along the shaft to its required location, when the removal of the wedge will permit the bore to close upon the shaft. To secure the pulley to the shaft four set-screws are employed, two of them being shown in the cut, and the other two being similarly located on the other side of the pulley.
By this means there will be less difference between the diameters of the pulley bore and of the shaft should the latter be slightly less than its standard diameter, and as a result the pulley will run more true.
Split pulleys are bored a tight fit to the shaft when the two halves are bolted firmly together. They may, however, be made to grip the shaft in two ways; first, if bored when bolted together the edges of the bore will meet the shaft and clip it so firmly as to require each half bore to spring open to permit it to pass on the shaft, but by inserting between the two halves of the hub two thicknesses of writing paper, and boring out the hole the thicknesses of the paper too large (which may be done by placing two pieces of the same paper beneath the calipers or gauge) the bore will be slightly oval when the paper is removed, and will grip the shaft at the crown of each half bore, but the grip thus obtained will not be so firm.
Pulleys of small diameter, as three feet or less in diameter, are usually held to their shafts by set-screws, the consideration of their shapes and position having been already treated of when referring to the applications of keys and set-screws. Pulleys of large diameters, and those which act as fly-wheels as well as pulleys, are usually held by keys.
Balancing Pulleys.—A pulley (more especially those running at high speed) should be balanced or in balance when rotating at the greatest speed at which it is intended to run. This is necessary, because if the centrifugal force generated by the pulley’s rotation be greater on one side than on another of the pulley, it will cause the pulley shaft to vibrate and shake whenever the amount of unbalanced centrifugal force becomes, on account of the speed of rotation, sufficient to bend the shaft or deflect the framing holding the shaft.
The balancing of a pulley will not be correct unless the centrifugal force is equal at all points on the perimeter in the same plane, as will appear presently. In practice two methods of testing the balance of a pulley are employed: first, the standing; and second, the running balance. A standing balance does not in any sense balance a pulley, but merely corrects the want of balance to a limited degree. A running balance correctly balances a pulley when running up to the speed at which the balance was made, but does not balance for greater speeds.
A standing balance is effected when the shaft being supported horizontally and with as little friction as possible, the pulley will remain at rest in any position in which it can be placed. Thus, in Fig. 2647 let c c represent the two centres of a lathe adjusted in their distance apart so as to sustain the shaft s with just sufficient force to prevent end movement or play of the shaft, and if the pulley p remains motionless when arrested at any point of rotation it is in standing balance. A common method of balancing is to set the pulley in slow rotation several times in succession, and if the same part of the pulley’s circumference comes to rest in each case at the bottom as at b then it is heaviest and its weight must be reduced, or weight must be added on the diametrically opposite side of the pulley. Another method is to rest the shaft horizontally on a pair of metallic strips as b b in Fig. 2648, the strips resting on a flat horizontal surface d, the testing being applied as before. Sometimes, however, cylindrical pieces are used in place of the strips or pieces b b.
A pulley that is in balance thus tested, may not, however, be in balance when rotated, or, as already stated, a standing balance may not be a running balance, for the following reasons: In Fig. 2649 is a pulley that if turned true inside and out would be of correct standing balance, because the weight is equal on each side of the shaft; thus the point a, though farther from the axis than b, would be counterbalanced by c, while b would be counterbalanced by d, but as soon as the pulley was put in rotation there[II-203] would be more centrifugal force generated at a than at b, and more at c than at d, because, though the weights would be equal, the velocities of a and c would be greatest.
Now, suppose that instead of a continuous wide pulley several pulleys were used, being out of true so as to be practically equal in shape to Fig. 2649, and it is apparent that the fact of pulley a b being out of balance is not removed by pulley c d being out in an opposite direction, and that each pulley will tend to bend the shaft in the direction of its excessive centrifugal force.
The effect of this inequality of centrifugal force will depend, in each case, upon the strength of the shaft in comparison with the amount of unbalanced centrifugal force. Suppose, for example, that the centrifugal force at a point a in Fig. 2650 were 10 lbs. greater than at b at a given velocity, and that the strength of the shaft be such that it will bend 1⁄32 inch under a weight of 10 lbs., then the effort of the point a will be to swing in a circle 1⁄16 inch larger than that due to its diameter. Suppose, then, the stand be so firmly fixed at c as to be motionless in a vertical direction under this effort, then the point a will swing in an oval, as denoted by the dotted lines, the shaft vibrating as denoted by the arrows.
Thus vibrations of the shaft, bearing, &c., occur whenever the excess of centrifugal motion on one side of a pulley is sufficient to spring the shaft, bearings, standard or foundation, as the case may be, and will occur most in the direction in which those parts will most easily succumb. From this it is evident that a pulley practically in balance, so far as being free from vibration at a certain speed, may be considerably out of balance at an increased speed. Thus, suppose a pulley p, in Fig. 2651, has a rim of equal thickness, but the distance of a from the axis of rotation is 6 inches, while the distance of b is 8 inches; then the centrifugal force at b will, at any speed of rotation, be one-quarter more than that at a, because the distance is one-quarter greater. Suppose, then, that its shaft, bearings, and foundation be capable of resisting 100 lbs. without sensible flexure, but that sensible flexure of those parts will occur under any pressure over 100 lbs.
The centrifugal force of 1 lb. at a and at b, respectively, may be calculated by the following rule:—
Rule.—Multiply the square of the number of revolutions per minute by the diameter of the circle of rotation in feet, and divide the product by 5,870. The quotient is the centrifugal force in terms of the weight of the body.
In the case of a the pulley making, say, 200 revolutions per minute, we have by the rule:
| 2002 × 1 | = 6.81 = the centrifugal force. |
| 5,870 |
Likewise, centrifugal force at b = (2002 × 1.25)/5,870 = 8.51 = the centrifugal force, 1 and 1.25 being diameters of circle of rotation of a and b in feet.
Now, suppose the revolutions to be 2,000 per minute, we have in the case of a 2,000 × 2,000 × 1 (= 4,000,000) ÷ 5,870 = 681 lbs. centrifugal force. Add one-quarter more, or 170 lbs., to obtain the centrifugal force at b = 851 lbs.; the unbalanced centrifugal force = 170 lbs.; and this being 70 lbs. more than the shaft, bearings, &c., are capable of resisting without flexure, a corresponding vibration will occur, whereas at 200 revolutions the unbalanced centrifugal force was: Centrifugal force at b = 8.51 lbs. less that at a = 6.81 = 1.70 lbs. unbalanced centrifugal force, and it becomes apparent that while at 200 revolutions the pulley would rotate without sensible vibration, at 2,000 revolutions (in the same time), sensible vibration would occur; hence, the sensible vibration of a pulley is in the proportion as the unbalanced centrifugal motion is to the resistance of the shaft, bearings, &c., to flexure, and further, as the unbalanced centrifugal motion increases with the velocity, so also does the sensible vibration increase with the velocity.
But there are two ways of increasing the velocity of a pulley: 1st, by increasing the revolutions of a given pulley; 2nd, by employing a pulley of a larger diameter, but making the same number of revolutions. In our example we increased the speed tenfold (from 200 revolutions to 2,000) but the centrifugal force was increased one hundredfold, according with the law that the centrifugal force increases with the square of the revolutions, and 10 × 10 = 100. But if the velocity had been increased by augmenting the diameter of the pulley, the centrifugal force would have increased in the same ratio as the pulley diameter was increased; hence it appears that under equal velocities larger pulleys generate less centrifugal force per unit of unbalanced weight than do smaller ones.
A device for testing the balance of pulleys is shown in Fig. 2652; it consists of a frame carrying a vertical spindle, which may be rotated by suitable bevel-wheels, and the hand wheel shown. In this case it would be preferable to balance the pulley at the greatest speed at which it would be convenient to run it by hand with the[II-204] wheel shown, because a pulley balanced at any given speed will be balanced at any lesser speed, although not at a greater one. But the pulley should not be driven by the arms, because the pressure against the same will affect the balance. It would be better therefore to let the spindle of the machine be small enough in diameter to fit the smallest bore of pulley to be balanced, to employ sleeves fitting the spindle and the bores of all larger bored pulleys, and to obtain the most correct results the pulley should be fastened to the sleeve by its set-screws, or keys of the pulley, as the case might be, so that whatever error there might be induced by tightening the same will be accounted for in the balancing. It is obvious also that the pulley bore should fit the sleeve with the same degree of tightness as it will fit the shaft to which it is to be fixed. The heaviest side of the pulley will rotate through a circle of larger diameter, and may be marked by a point, as a tool point moved up to it by a slide rest, or roughly by a piece of chalk steadily moved up to it by hand until it just touches the high side of the pulley.
The methods of correcting the balance are as follows: The heavy side of the pulley having been found, a weight is attached to the diametrically opposite side of the pulley; a convenient form of light weight for this purpose is shown in Fig. 2653; it consists of what may be termed a spring clamp, since it holds to the edge of the pulley rim, on which it is forced by hand, by reason of the spring of the jaws. There are numerous clamps of this form, each having a definite weight, as 2 ozs., 3 ozs., 4 ozs., &c.; but for weights above about 11⁄2 lb. a clamp with a set-screw is employed. For a running balance a set-screw is indispensable. It is obvious that pulleys will be more easily and correctly balanced when the inner side of their rim is turned up, as far as the arms will permit, in the lathe; but on account of the expense this is not usually done, except in the case of large pulleys.
In the best practice, however, the pulley is set in the lathe, so that the inside of the rim runs as true as possible. Remarks on this subject are given under the head of chucking pulleys.
When the balance is to be effected by adding weight to the pulley mushroom-shaped pieces of metal are made for the purpose, their weights varying by ounces; the stems are driven through holes drilled through the rim to receive them, and riveted on the face side. The stems are of wrought iron, while the heads may be of cast iron, but are better of lead, because in that case they may be set with a hammer to fit the inner surface of the pulley rim.
In some practice, protuberances, or a web in the middle of the pulley, are cast on the pulley, and the balance is effected by cutting this away to reduce the weight on the heavy side.
When pulleys are to revolve at very high speeds, as in the case of those for emery-wheel spindles, the shafts themselves require to be balanced, especially if of cast iron, because that part of the shaft uppermost in the mould will be of less density and weight than that at the bottom of the mould. The pulley should be balanced separately, and the whole again balanced after being put together, because the weight of the key or set-screw will be sufficient to destroy the balance under a sufficiently high speed of rotation.
The edges of pulley rims should be trued up in the lathe when the rim is turned so that the pulleys to receive a belt may be set in line by pressing a straight-edge, or setting a line to have contact with (as near as possible) diametrically opposite points of the edge of one pulley, and setting the other to have its corresponding edge in line.
Pulleys should run true so that the strain or tension of the belt shall be equal at all parts of the revolution, and the transmitting power shall be equal. The smoother and more polished the surface of the pulley the greater its driving power.
The transmitting power of a pulley may be increased by covering the pulley face with leather or rubber bands, but the thickness of these should be equal both across the width and all around the circumference so as to run true.
The amount of increase of driving power due to this covering is variously stated, but may be taken at about 20 to 30 per cent. A cement for fastening such pulley coverings may be made as follows: Take one ounce of caoutchouc (pure or native rubber) and cut it into thin slices, place it in a tinned sheet-iron vessel with six or seven ounces of sulphide of carbon; the vessel is then to be placed in a water tank previously heated to about 86° Fahr. To prevent the solution from becoming thick and unmanageable, mix with a solution consisting of spirits of turpentine, in which half an ounce of caoutchouc in shreds has been dissolved over a slow fire, and then a quarter of an ounce of powdered resin; from an ounce and a half to two ounces of turpentine being afterwards stirred in, to be added in small quantities. This cement must be kept in a large-mouthed bottle well corked, and in using clean the parts to be united thoroughly with benzine; apply two coats of cement, allowing each to dry before applying the next; when applying the last coat allow the cement to dry so as to become very sticky, then press the surfaces firmly together and allow to thoroughly dry. This is waterproof.
A pulley that imparts motion to the belt enveloping or partly enveloping it is termed a driving pulley or driver. A driven pulley is one that receives motion from, or is driven by, the belt; hence in every pair of pulleys connected by belt, one is termed the driver and the other the driven. The revolutions of two pulleys connected by belt will vary in the same proportion as their diameters, although their rim velocity will be equal.
Suppose, for example, that a pulley of 7 in. diameter drives one of 14 in. diameter, then if there is no slip on either pulley both pulleys will run at the same velocity as the belt, and this velocity must be equal to the velocity of the driver, because the belt is moved by the driver. Now, suppose the driver which is of 7 in. diameter makes one revolution in a minute, and as it is only one-half the diameter of the driven wheel, its circumference will also be half that of the driven, so that it must make two revolutions to carry around length of belt enough to pass once around the driven pulley. The revolutions of the two are, therefore, in the same proportions as are their diameters, which in this case is two to one. As the driven pulley is the largest diameter, it will make one revolution in the same time that the driver makes two. But suppose the driving pulley was 14 and the driven was 7 inches in diameter, then the proportion would still be two to one, and the driven would make two revolutions to every revolution of the driver.
If we are given the number of revolutions a driving pulley makes and the diameter or circumference of both pulleys, and require to find the number of revolutions the driven pulley will make to one or to any given number of the driver, we may consider as follows: Suppose the circumference of the driver to be 24 inches and that of the driven to be 18 inches, then in Fig. 2654 let circle a represent the driver, and circle b the driven pulley. If we divide the circumference of a into four equal divisions, as at 1, 2, 3, and 4, each of these divisions will equal 6 inches, because the whole circumference being 24 inches, one quarter of it will be 6. If we divide the circumference of b into six-inch divisions there will be but three of them as marked, because one-third of 18 (its circumference) is 6. Now three of the divisions at a will move a a full revolution, and the remaining division on a will move b through another one-third of a revolution, hence, each revolution of a equals 11⁄3 revolutions on b. The proportions of the circumference are, therefore, as 11⁄3 to 1, or as 133 is to 100, taking a as the driver, and, therefore, as the basis of the proportion. But suppose we take b as the basis of the proportion, and one revolution of b will cause a to make three quarters of a revolution, or during 100 revolutions of b, a will make[II-205] 75. But nevertheless during the period that a is making 100 revolutions b will have made one-third more, or 1331⁄3, because b makes 11⁄3 revolutions to cause a to make one revolution. From this it will be seen that the proportion is as the greater is to the lesser, and not as the lesser is to the greater, or, in other words, it is in this case as 24 is to 18, which is one and one-third times, for one-third of 18 is 6, and 18 + 6 = 24.
Suppose, now, we take the four divisions on a and the three on b to consider their proportions, and we may say 4 is 11⁄3 times 3, or we may with equal propriety say 3 is 3⁄4 of 4, hence 4 is not in the same proportion to 3 that 3 is to 4. Let it now be supposed that a driven pulley b is 18 inches in diameter, and requires to be driven one quarter faster than the driver, what then must be the diameter of that driver? As the revolutions require to be increased one-fourth the pulley diameter must be increased one-fourth. Thus one quarter of 18 = 41⁄2, and this added to 18 is 221⁄2, which is therefore the diameter of the driving pulley, as may be proved as follows: Suppose the circumferences instead of the pulley diameters to be 221⁄2 and 18 respectively, and that the largest pulley makes 100 revolutions, then it will pass 2,250 (221⁄2 × 100 = 2,250) inches of belt over its circumference, and every 18 inches of this belt will cause the small pulley to make one revolution; hence we divide 2,250 by 18, which gives us 125 as the revolutions made by the small pulley, while the large one makes 100. Thus it appears that we obtain the same result whether we take the circumferences or the diameters of the pulleys, because it is their relative proportions or relative revolutions that we are considering, and their actual diameters do not affect their proportions one to the other. Thus, if a 10-inch pulley drives a 30-inch one, the proportions being three to one, the revolutions will be three to one, and the driven being three times the largest, will make one revolution to every three of the driver. If the driver was 3 inches in diameter and the driven 9, the revolutions would be precisely the same as before, but with equal revolutions the velocities would be different, because in each revolution of the driver it will move a length of belt equal to its circumference; hence, the greater the circumference the greater length of belt it will move per revolution. To take the velocity into account, we must take into consideration the number of revolutions made in a given time by the driver. Suppose, for example, that the driver being 3 inches in diameter makes one revolution in a minute, then it will move in that minute a length of belt equal to its circumference, so that the circumference of the driver, multiplied by the number of its revolutions per minute, gives its velocity per minute. Thus, if a pulley has a circumference of 50 inches, and makes 120 revolutions per minute, then its velocity will be 6,000 inches per minute, because 50 × 120 = 6,000. The velocity of the belt, and therefore that of the driven wheel, will also be 6,000 inches per minute, as has already been shown. From this train of reasoning the following rules will be obvious:—
To find the diameter of the driving pulley when the diameter of the driven pulley and the revolutions per minute of each are given:
Rule.—Multiply the diameter of the driven by the number of its revolutions, and divide the product by the number of revolutions of the driver, and the quotient will be the diameter of the driver.
The diameter and revolutions of the driver in a given time being known, to find the diameter of a driven wheel that shall make a given number of revolutions in the same time:
Rule.—Multiply the diameter of the driver by its number of revolutions, and divide the product by the number of revolutions of the driven. The quotient will be the diameter of the driven.
To find the number of revolutions of a driven pulley in a given time, its diameter and the diameter and revolutions of the driver being given:
Rule.—Multiply the diameter of the driver by the number of its revolutions in the given time, and divide by the diameter of the driven, and the quotient will be the number of revolutions of the driven in the given time.
Suppose, however, that the speed of the shaft only is given, and we require to find the diameter of both pulleys, as, for example, suppose a shaft makes 150 revolutions per minute, and we require to drive the pulley on a machine 600 revolutions per minute. Here we have two considerations: first, the relative diameters of the two pulleys, and secondly, the diameter of pulley and width of belt necessary to transmit the amount of power necessary to drive the machine at the speed required. Leaving the second to be discussed hereafter in connection with the driving power of belts, we may proceed to determine the first as follows: The pulley on the machine must be as much smaller than that on the main shaft, as the speed of the pulley on the machine requires to run faster than does the main shaft, hence we divide the 600 by 150 and get four, which is the number of times smaller than the driver that the driven pulley must be. Suppose then the driver is made a 24-inch pulley, then the driven must be a 6-inch one, because 24 ÷ 4 = 6; or we may make the driver 36, and the driven 9, because 36 ÷ 4 = 9; or the driver being 48 inches in diameter, the driven must be 12, because 48 ÷ 4 = 12. To reverse the case, suppose the shaft to make 200 revolutions per minute, and the machine pulley to make 50, then since 200 ÷ 50 = 4, the driven (or machine pulley) must have a diameter four times that of the driver, and any two pulleys of which one is four times the diameter of the other may be used, as say: Pulley on line shaft 10 inches in diameter, pulley on machine 40 inches in diameter; or, pulley on line shaft 20 inches in diameter, pulley on machine 80 inches in diameter.
Now, in nearly all cases that are met with in practice, it would be inconvenient to have so large a pulley as 80 inches in diameter to drive a machine, and again in most cases a driving pulley of 10 inches in diameter would be too small. So likewise in cases where the machine pulley requires to run faster than the line shaft, a single pair of pulleys will be found to give, where great changes of revolution are required, too great a disproportion in the diameter of the pulleys; thus in the case of a shaft making 150, and the machine requiring to make 600, we may use the following pairs of pulleys:—
| On Main Shaft. | On Machine Shaft. | |||||
| First | 32 | inch | diameter | 8 | inch | diameter. |
| Second | 40 | „ | „ | 10 | „ | „ |
| Third | 48 | „ | „ | 12 | „ | „ |
| Fourth | 60 | „ | „ | 15 | „ | „ |
But the machine may require so much power to drive it, that with the width of belt it is desired to employ, a pulley larger than either of these is necessary, as, say, one 20 inches in diameter. Now, with a 20-inch driven pulley, the driver would require to be 80 inches in diameter, because 20 × 4 = 80. But there may not be room between the shaft and the ceiling for a pulley of so large a diameter, or such a large pulley may be too heavy to place on the shaft, or it may be too costly, and to avoid these evils, countershafts are used.
By the employment of a countershaft we simply obtain—with two pairs of pulleys and by means of small pulleys—that which could be obtained in a single pair, providing the great difference in their diameters (necessary to obtain great changes of rotation), were not objectionable; all that is necessary, therefore, is to accomplish part of the required change of rotation in one pair, and the remainder in the other. In doing this, however, while the velocity of each driver and driven will be equal (as was explained with reference to a single pair), notwithstanding the difference in their diameters, yet the velocity of one pair will necessarily differ from that of the other, so that the pulley on the machine will vary in its velocity as well as in its rotation from that of the first driver. The first driver is that on the main or driving shaft, and the pulley it drives is the first driven. The second driver is the second pulley on the countershaft, and the second driven is the one it drives or that on the machine. Suppose, then, a driving shaft makes 100 revolutions per minute, and the machine requires to make 600, then the speed of rotation requires to be increased six times. Now we may effect this change of six times in several ways; thus: Suppose we increase the rotations three times in the first pair, then the second pulley will make 300 rotations, or three times those of the main shaft, and all we have to do is to make the second driven one-half the diameter of the second driver, and its rotations will be double those of the second driver, which will give the required speed of 600 revolutions. Suppose, however, we change the speed four times in the first pair, and the 100 of the shaft becomes 400 on the countershaft, and to increase this to 600 on the second driven, all that is required is to make its diameter one-half less than that[II-206] of the second driver, because 600 is one-half more than 400. From this it will be perceived that the number of changes or amount of increase or decrease of speed being given, the proportion of diameters for both pairs of pulleys will be represented by any two numbers which, multiplied together, will give a sum equal to the number of increased revolutions required. Having found the proportions for each pair, it remains to determine their actual diameters, and they will be found to vary under different conditions.
Suppose, for example, we have the following conditions: Main shaft runs 100; machine must run 600. The pulley on the line shaft is 36 inches in diameter; required, the diameters for the other three pulleys.
To make three changes in the first pair, the first driven must be 1⁄3 the diameter of the first driver, which is 12 inches. Now the second pair we may make any diameters that are two to one; and since the second driver is to be the smallest, we may select as small a pulley as will answer for the machine, and make its driver twice its diameter.
But suppose it is the diameter of the pulley on the machine that is fixed, and the diameter of the other three require to be found. Let the diameter of the second driven be 12; then its driver on the countershaft must be 24. The other two must have diameters 3 to 1 as before, any suitable wheels being selected.
Yet another condition may occur. Thus, suppose the countershaft is on hand, and that it has on it two pulleys, as a 12 and a 24-inch; then a 36 on the inner shaft will be three times as large as the 12, and a 12-inch on the machine will be twice as small; or, what is the same, one half as large as the 24.
When the principle is clearly understood the calculations can be performed mentally with ease so far as the required diameters to attain the necessary speed is concerned, but there are other considerations that claim attention.
Thus, for example, to multiply the rotations 6 times we may proportion the first pair as follows: Driver 48, driven 16; second pair, driver 30, driven 15 inches in diameter.
Or we may proportion them as follows: First pair: driver 36, driven 12; second pair: driver 28, driven 14 inches in diameter.
In the second arrangement of diameters the drivers are each 2 inches, and the driven each 1 inch less in diameter than in the first; hence their cost would be diminished, as would also be the wear of the journals, on account of the reduced weight of the pulleys; hence, if the driving capacity of each pulley is equal to the requirements the second arrangement would be preferable.
In considering this part of the subject, first let it be shown that although the horse-power transmitted by the two belts is equal whatever be the proportions of the pulleys (provided, of course, that the belts do not slip), yet the strain or wear and tear of the belts varies, and the requirements for one belt are therefore different from those for the other.
In Fig. 2655 let a represent a 36-inch pulley on the driving shaft, b a 12-inch, and c a 24-inch pulley on a countershaft, and d a 12-inch pulley on a machine shaft. Let the main shaft make 100 revolutions per minute, and the machine requires a force to move it equal to 50 pounds applied to the perimeter of d. Now the rotations of d will, with these pulleys, be six to one of the main shaft or a, which gives d 600 revolutions per minute, thus: 100 × 6 = 600. The circumference of d is about 37.69 inches, which, multiplied by 600 (the number of its revolutions), gives 22,614 inches, or 1,884.5 feet as its speed per minute. This multiplied by the 50 pounds it takes to move the machine at the perimeter of d, gives 94,225 as the foot pounds per minute required to drive the machine 600 revolutions per minute, and this, therefore, is the amount of power transmitted by each belt. On the second belt this is shown to be composed of 50 pounds moving 1,8841⁄2 feet per minute, hence we may now find how it is composed on the first belt, as follows:—
The diameter of the first driver is 36 inches, and its circumference 113.09 inches, or 9.42 feet; this, multiplied by its revolutions per minute, will give its speed, thus: 9.42 × 100 = 942 feet per minute. To obtain the necessary amount of pull for this first belt, we must divide this speed into the number of foot pounds it takes to drive the machine, thus: 94,225 ÷ 942 = 100.02. The duties of the two belts are therefore as follows:—
| First belt, | weight of pull | 100.02 |
| „ | speed per minute | 942 feet. |
| Second belt, | weight of pull | 50.00 |
| „ | speed per minute | 1884.5 feet. |
The duty in foot pounds being equal, as may be shown by multiplying the feet per minute by the force or weight of the pull, leaving out the fractions, thus:—
| 942 | × | 100 | = | 94,200. |
| 1884 | × | 50 | = | 94,200. |
The difference in the requirements is, then, that the first belt must have as much more weight or force of pull than the second as its speed is less than that of the second.
It is obvious that in determining the proportions of the pulleys this difference in the requirements should be considered, and the manner in which this should be done depends entirely upon the conditions.
Thus, in the case we have considered, the speed was increased, but the object of the countershaft may be to decrease the speed, and in that case the conditions would be reversed, inasmuch as though the foot pounds transmitted by both belts would still be equal, yet the speed would be greatest and the strain or pull the most on the second belt instead of on the first.
It is obvious, then, that the proportions of the pulleys being determined the actual diameters must be large enough to transmit the required amount of power without unduly straining the belt.
The names of the various parts of a hide of leather as known to commerce are as follows:—
In Fig. 2656 the oblong portion between the two belly parts marked g g is known as the “butt,” and when split down the ridge, as shown by the dotted line down the centre, the two pieces are known as “bends;” the two pieces marked y are “belly offal;” d is known as “cheeks and faces.” The butt within the dotted line may extend in length from a to b, or from a to c; if cut off between b and c that portion is called the “range” or the whole from b to x may be cut in one piece and termed a “shoulder.”
Sometimes the range is cut off and the rest would be called a shoulder with “cheeks and faces” on; or, again, the range and shoulder may be in one nearly square piece. The manner of cutting this part depends upon the spread and size of the hide.
The part of the hide that is used to manufacture the best belting is shown in Fig. 2657, on which the characteristics of the various parts are marked. The piece enclosed by the dotted lines is that employed in the manufacture of the commonest belting, while that enclosed by the full lines b, c, d is that used for the best belting. The former includes the shoulder, which is more soft and spongy, while it contains numerous creases, as shown. These creases are plainly discernible in the belt when made up, and may be looked for near the belt points.
The centre of the length of the hide will stretch the least, and the outer edges on each side of the length of the hide the most. Hence it follows that the only strip of leather in the whole hide that will have an equal amount of stretch on each edge is that cut parallel to line a, and having that line as a centre of its width. All the remaining strips will have more stretch on one edge than on the other, and it follows that, to obtain the best results the leather should be stretched after it is cut into strips, and not as a whole in the hide, or in that part of it employed for the belt strips. It is found, indeed, that, even though stretched in strips, the leather is apt in time to curve. Thus a belt that is straight when rolled in the coil will, on being unrolled, be found to be curved. It is to be observed, also, that each time the width of the strips is reduced, this curving will subsequently take place; thus, if a belt 8 inches wide and quite straight, be cut into two belts of 4 inches wide, the latter will curve after a short time. The reason of this is almost obvious, because it is plain that the edge that was nearest the centre line of the hide offers the greatest resistance to stretching; hence, when the strip is stretched straight, and an equilibrium of tension is induced, reducing the width destroys to some extent this equilibrium, and the leather resumes, to some extent, its natural conformation. This, however, is not found to be of great practical importance, so long as the outer curve of one piece is on the same side as the outer curve of its neighbor, as shown on the left view in Fig. 2658, in which case the belt will run straight, notwithstanding its curve; but if the curves are reversed, as on the right in Fig. 2658, the belt will run crooked, wabbling from side to side on the pulley. To avoid this, small belts may be made continuous by cutting them from the hide, as shown in Fig. 2659; but in this case it is better that the belt be cut from the centre strip of the hide.
[II-208]If the leather is stretched in strips after being cut from the hide, the amount of the stretch is about 6 inches in a length of 41⁄2 feet of a belt, say, 4 inches wide, but the stretch will be greater in proportion as the width of the strip is reduced. But if stretched as a whole, the amount of stretch will be about 1 inch per foot of length, the shoulder end stretching one-third more.
If the leather has been properly stretched in strips the length of the belt may be cut to the length of an ordinary tape line drawn tightly over the pulleys, which allows the same stretch for the belt as there is on the tape line, added to the degree of tension due to cutting the belt too short to an amount equalling its thickness (as would be the case if the belt is cut of the same length as the tape line); or if the belt is a double one, the belt thus cut to length would be too short to an amount equal to twice the thickness of the strips of leather of which it is composed.
When the amount to which the leather has been stretched is an unknown quantity (as is commonly the case), the workman cuts the belt too short, to an amount dictated solely by judgment, following no fixed rule. If, as in the case of narrow belts, the stretching be done by hand, the belt is placed around the pulleys, stretched by hand, and cut too short to an amount dictated by judgment, but which may be stated as about 21⁄2 per cent. of its length.
But the stretch of a belt after it is put to work proceeds very much more rapidly if it has been stretched in the piece and not in the strip, hence it gets slack in the course of a few hours, or of a day or more, according to how much it has been stretched; whereas one properly stretched in the strip will last for weeks, and sometimes for months, without getting too slack.
| 2,000 | 1⁄4 | 3. | 2,050 | 3⁄16 | 3. | 1 | 2,150 | 3⁄16 | 3. | 2 | 2,175 | 1⁄4 | 3. | 3 | |
| 1,400 | 9⁄32 | 2. | 12 | 2,000 | 1⁄8 | 3. | 2,625 | 3⁄16 | 3. | 4 | 2,325 | 7⁄32 | 3. | 4 | |
| 2,000 | 1⁄4 | 2. | 11 | 2,075 | 3⁄16 | 3. | 1 | 2,375 | 7⁄32 | 3. | 4 | 2,175 | 7⁄32 | 3. | 5 |
| 2,075 | 1⁄4 | 2. | 12 | 2,700 | 7⁄32 | 3. | 3 | 2,600 | 7⁄32 | 3. | 4 | 2,275 | 5⁄32 | 3. | 7 |
| 2,450 | 1⁄4 | 2. | 13 | 3,025 | 9⁄32 | 3. | 7 | 2,575 | 11⁄32 | 3. | 8 | 2,225 | 7⁄32 | 3. | 10 |
| 2,475 | 1⁄4 | 3. | 2,975 | 5⁄16 | 3. | 6 | 3,200 | 9⁄32 | 3. | 10 | 2,175 | 3⁄8 | 3. | 10 | |
| 2,575 | 11⁄32 | 3. | 2 | 2,875 | 9⁄32 | 3. | 7 | 3,475 | 11⁄32 | 3. | 13 | 1,850 | 11⁄32 | 3. | 11 |
| 2,675 | 11⁄32 | 3. | 2 | 3,075 | 11⁄32 | 3. | 8 | 3,450 | 9⁄32 | 4. | 1,950 | 1⁄4 | 3. | 11 | |
| 2,650 | 3⁄8 | 3. | 2 | 2,900 | 9⁄32 | 3. | 6 | 3,150 | 3⁄16 | 3. | 15 | 2,225 | 1⁄4 | 3. | 10 |
| 2,800 | 1⁄4 | 3. | 1 | 3,050 | 5⁄16 | 3. | 6 | 2,850 | 1⁄4 | 3. | 13 | 2,275 | 3⁄16 | 3. | 7 |
| 2,700 | 1⁄4 | 3. | 3,150 | 7⁄32 | 3. | 5 | 3,000 | 3⁄16 | 3. | 10 | 2,600 | 1⁄4 | 3. | 5 | |
| 2,650 | 1⁄4 | 2. | 13 | 3,000 | 7⁄32 | 3. | 4 | 3,400 | 1⁄8 | 3. | 6 | 2,550 | 1⁄4 | 3. | 4 |
The results of some experiments made by Messrs. J. B. Hoyt & Co. on the strength of the various parts of a hide are given in Fig. 2660. One side of the part of the hide used for leather belting was divided off into 48 equal divisions, each piece being 113⁄4 inches long, and two inches wide, the results of each test being marked on the respective pieces. The first column is the strain under which the piece broke; the second column is the amount in parts of an inch that the piece stretched previous to breaking; and the third column is the weight of the piece in ounces and drachms.
From the table it appears that the centre of the hide which has the most equal stretch has the least textile strength, while in general that which has the most stretch has the greatest textile strength, but at the same time the variations are in many cases abrupt.
A single belt is one composed of a single thickness of leather put together, to form the necessary length, in pieces, riveted and cemented together at the joint, or sewed or pegged as hereafter described.
A double belt is similarly constructed, but is composed of two thicknesses of leather cemented and riveted, pegged, or sewed together throughout its whole length, as hereafter described. The object of a double belt is to increase the strength without increasing the width of the belt. Belts are usually made in long lengths coiled up for ease of transportation, the length of belt required being cut from the coil.
To find the length in a given coil that is closely rolled—Rule: the sum of the diameter of the roll and the eye in inches, multiplied by the number of turns made by the belt, and this product multiplied by the decimal .1309, will equal length of the belt in feet.
The grain or smooth side of the leather is the weakest, as may be readily found by chamfering it to a thin edge, when it will tear like paper, and a great deal more easily than will the flesh side under similar treatment. Again, it will crack much more readily: thus, take a piece of leather and double it close with the grain side outward, and it will crack, as shown in Fig. 2661 at c, whereas if doubled, however closely, on the flesh side no cracks will appear. If the edge of a clean-cut piece of leather be examined, there will be found extending from the grain side inward a layer of lighter color than the remainder of the belt; and this whole layer is less fibrous and much weaker than the body of the belt, the strongest part of which is on the flesh side. If the grain side is shaved off thin and stretched slightly with the fingers it will exhibit a perfect network of small holes showing where the hair had root. Here, then, we have weakness and excessive liability to crack on the grain side of the leather, and it is obvious[II-209] that if this side is the outside of the belt, as in Fig. 2662, at a, the tendency is to stretch and crack it, especially in the case of small pulleys, whereas if the grain side were next to the pulley the tendency would be to compress it, and therefore, rather to prevent either cracking or tearing. Furthermore, very little of the belt’s strength is lost by wearing away its weakest side.
Another and important consideration is, that the grain side will lie closest and have most contact over a given area with the pulley surface.
In making double belts of extra good quality, it is not uncommon to cut away or shave off the grain side of both belts, and place those surfaces together in making up the belts.
If the grain side of a belt is the outside when on the pulleys, and a crack should consequently start, the destruction of the belt proceeds rapidly, because the line of crack is the weakest part of the belt, and the belt has less elasticity as a continuous body, and more at the line of crack. Cracking may, to some extent, be provided against by oiling the belt, and for this purpose nothing is better than castor oil. In the manufacture of belts, extra pliability is induced by an application of fish oil and tallow, applied when the belt (after having been wetted), is in a certain stage of progress toward drying. The oil and tallow are supposed to enter the pores of the leather and supply the place of the evaporated water.
Length of Belts.—Since the stretch of a belt is variable in different belts of the same length, no rule can be given for the amount to which a belt should be cut shorter than the measured length around the pulleys, and it follows, therefore, that the length of a belt cannot be obtained precisely by calculation. In practice the necessary length for a belt to pass around pulleys already in their places upon the shaft is usually obtained by passing a tape line or cord around the pulleys, the stretch of the tape line being allowed as that necessary for the belt. Then when the belt is placed around the pulleys it is shortened if it should appear to require more tension. If, however, the belt length for pulleys not in position is required, it may be obtained as follows, the error being so slight as to be within the margin of difference of stretch in different belts, and therefore of no practical moment:—
For open belts let the distance between the shaft centres, as a b in Fig. 2663, be the base of a right angle triangle, and the difference between the semi-diameters, as b c, the perpendicular. Square the base and the perpendicular, and the square root of the sum of the two will give the hypothenuse, and this multiplied by 2 and added to one-half the circumference of each pulley is the required length for the belt. This will give a belt too long to the amount to be cut out of the belt to give it the necessary tension when on the pulleys.
Example.—Let the distance between centres in Fig. 2663 be 48 inches; diameter of large pulley 24 inches; diameter of small pulley 4 inches—
| Here distance | between | centres | 4 | 8 | ||||
| „ | „ | „ | 4 | 8 | ||||
| 38 | 4 | |||||||
| 192 | ||||||||
| 230 | 4 | |||||||
| Square of perpendicular | 10 | 0 | ||||||
| 240 | 4 | Square root of 2404 | = | 49.03 | ||||
| Multiply by 2 | 2 | |||||||
| 98.06 | ||||||||
| Half circumference of large pulley | 37.69 | 9 | ||||||
| 135.75 | 9 | |||||||
| Half circumference of small pulley | 6.28 | 3 | ||||||
| Length of belt | 142.04 | 2 | ||||||
A simpler rule which gives results sufficiently accurate for practical purposes is as follows:—
Rule.—Add the diameter of the two pulleys together, divide the result by 2, and multiply the quotient by 31⁄4, then add this product to twice the distance between the centres of the shafts, and you have the length required.
When the length of a crossed belt is required, and the pulleys are not erected upon the shafts, it is, on account of the abstruseness of a calculation for the purpose, preferred in workshop practice to mark off by lines the pulleys set at their proper distance apart (either full size or to scale), and measure the length of the side of the belt, supposing the belt to envelop one-half the circumference only of each pulley, and to add to this one-half the circumference of each pulley; or if there is a great difference between the relative diameters of the pulleys and the distance apart of the shafts is unusually small, the lengths of the straight sides of the belt are measured and the arcs of contact around the pulleys are stepped around by compasses, the set of the compasses being not more than about one-tenth the circumference of the pulleys. This gives a more near result than that obtained by calculation, because although it will give a belt shorter than by calculation, yet the belt will be too long on account of the stretch necessary to the tension required for ordinary conditions.
In narrow belts, as, say, three inches and less in width, the belt may be cut to the length of a tape line passed over the pulleys, and when placed over the pulleys it may be strained under a hand[II-210] pull and cut as much shorter as the tension under hand pressure indicates as being necessary.
But if the belt is a wide one a stretching clamp, such as shown in Fig. 2664, is employed, the screws being right hand at one end and left hand at the other, so that operating them draws the clamps, and therefore the ends of the belt, together.
The stretch of a belt not stretched in the piece proceeds slowly when the belt is at work, hence if laced at first to a proper degree of tension it will get slacker in a few hours or in a day or so, and must be tightened, or taken up as it is termed, by cutting a piece out. For this purpose a butt joint possesses the advantage that the piece to be taken out may be less, and still leave the end clear for new holes to be punched, than is the case with a lap joint, which occurs because the butt joint occupies a shorter length of the belt than is the case with a lap joint.
When a belt is under tension upon two pulleys and at rest, the friction or grip of the belt upon the respective pulleys (supposing them to be of the same diameter and therefore to have the same arc and area of contact) will depend upon the relative positions of the pulleys; thus suppose one pulley to be above the other as in Fig. 2665, the upper pulley p will have the grip due to the tension of the belt added to that due to the weight of the belt, whereas if placed horizontally, as in Fig. 2666, the weight of the belt will fall equally on the two pulleys, and for this reason vertical belts of a given width require to have a greater tension to transmit the same amount of power as the same belt would if placed horizontally. But as soon as motion was transmitted, by the belt, from one pulley to the other, the belt on one side of the pulley would be under greater tension then that on the other.
Suppose, for example, a belt to transmit motion and power from pulley a in Fig. 2667, to pulley b, then the side c of the belt is that which drives or pulls b, and it is therefore called the driving side of the belt, the resistance to rotation offered by b causing the driving side of the belt to be the most strained; and hence the straightest, whereas the side d will be free of the tension due to the resistance of b.
But if the direction of motion be reversed as in Fig. 2668, a still being the driving pulley, the side d will be the one most tightly strained, and therefore, the driving side of the belt; or, in other words, the driving side of a belt is always that side which approaches the driving pulley, and the slack side is always that which recedes from the driving pulley. In horizontal belts, however, the driving side of the belt is not a straight line, because of the belt sagging from its own weight no matter how tightly it may be strained, but the shorter the belt the less the sag.
It is always, therefore, desirable, so far as the driving power of the belt is concerned, to have the lower half (of belts running horizontally) the driving side, because in that case the sag of the belt causes it to envelop a greater arc of the pulley, which increases its driving power. If the circumstances will not permit this and the sag of the belt operates to practically incapacitate the belt for its duty, what is termed an idle wheel or idler may be employed as shown in Fig. 2669 at e, serving to prevent the sag and to cause the belt on the driving side to envelop a greater portion of the pulley’s circumference, and hence increase its friction on the pulley and therefore its driving power. In the example the two pulleys a and b are of equal diameters; hence the idle wheel is placed midway between them, but when such is not the case the idle wheel should be located according to the circumstances and the following considerations. The idle wheel requires a certain amount of power to drive it, and this amount will be greater as the idle wheel is nearer to the smallest wheel of the pair connected; but on the other hand, the closer the idle wheel to the small pulley (all other factors being equal) the greater the arc of small pulley surface enveloped by the belt, and hence the greater the belt’s driving power. When therefore a maximum increase of driving power is required, the idler must be placed near to the smallest pulley, the desired effect being paid for in the increased amount of motive power required to rotate the driving pulley.
But under equal conditions the larger the diameter of the idle wheel the less the power required to drive it, because the less its friction on its journal bearing. A belt tightener should whenever practicable be placed on the slack side of the belt.
Belt tighteners are sometimes used to give intermittent motion, as in the case of trip hammers; the belt being vertical is made long enough to run loose, until the tightening pulley closes the belt upon the pulley, taking up its slack and increasing the arc of contact.
When the direction of rotation of the driven pulley requires to be reversed from that of the driving pulley, the belt is crossed as in Fig. 2670. A crossed belt has a greater transmitting power than one uncrossed (or, as it is termed, than an “open belt”) because it envelops a greater arc of both pulleys’ circumference. This is often of great advantage where the two pulleys are of widely varying diameter, especially if the small pulley requires to transmit much power, and be of very small diameter.
But a crossed belt is open to the objection that the surfaces of the belt rub against each other at the point of crossing, which tends to rapidly wear out the laced joint of the belt. By crossing a vertical belt the lower pulley receives part of the weight of the belt.
When a belt connects two pulleys whose respective planes of revolution are at an angle one to the other, it is necessary that the centre line of the length of the belt shall approach the pulley in the plane of the pulley’s revolution, which is sufficient irrespective of the line of motion of the belt when receding from the pulley. This is shown in Fig. 2671, which represents what is known as a quarter twist; a, b are two pulleys having their planes of revolution at a right angle, the belt travelling as denoted by the arrows, then the centre line c of the belt being in the plane of rotation of a on the side on which it advances to a, the belt will continue to run upon the same section of a. If the pulley positions be reversed,[II-211] as in Fig. 2672, the same rule applies, and the side d in the figure being that which advances upon b must travel to b in the plane of b′s rotation, otherwise the belt would run off the pulley; hence it is obvious that the belt motion must occur in the one direction only.
Shafts at any angle one to another may have motion communicated from one to the other by a similar belt connection, providing that a line at a right angle to the axis of one shaft forms also a right angle with the axis of the other. Thus in Fig. 2673 the axis of shaft a may be set at any required angle to the plane of rotation of pulley b, provided that the axial line of a be made to lie at a right angle to the imaginary line l, which is at a right angle to the axis of the shaft of b, and that the side of the driving pulley which delivers the belt (as c, Fig. 2671) is in line with the centre line of the driven pulley, as denoted by the dotted line c.
But when this provision cannot be carried out, pulleys to guide the direction of motion of the belt must be employed; thus in Fig. 2674 are an elevation and plan[39] of an arrangement of these guide or mule pulleys; a b is the intersection of the middle planes e e and f f of the pulleys p and p′ to be connected by belt. Select any two points, a and b, on this line and draw tangents a c, b d to the principal pulleys. Then c a c and d b d are suitable directions for the belt. The guide pulleys must be placed with their middle planes coinciding with the planes c a c, d b d, and the belt will then run in either direction.
[39] From Unwin’s “Elements of Machine Design.”
In Fig. 2675 is an arrangement of guide pulleys by which two pulleys not in the same plane are connected, while the arc of contact of the smaller pulley c is increased by the idlers or guide pulleys a b, while either c or d may be driven running in either direction.
In Fig. 2676 is shown Cresson’s adjustable mule pulley stand, which is a device for carrying guide pulleys, and admitting of their adjustment in any direction. Thus the vertical post being cylindrical, the brackets can be swung around upon it and fastened in the required position by the set-screws shown. The brackets carrying the pulleys are also capable of being swung in a plane at a right angle to the axis of the guide pulleys, and between these two movements any desired pulley angle may be obtained. It is obvious that by moving the brackets along the cylindrical post their distance apart may be regulated.
When a belt is stretched upon two pulleys and remains at rest there will be an equal tension on all parts of the belt (that is to say, independent of its weight, which would cause increased tension as the points of support on the pulleys are approached from the centre of the belt between the two pulley shafts); but so[II-212] soon as motion begins and power is transmitted this equality ceases, for the following reasons:—
In the accompanying illustration, Fig. 2677, a is the driving and b the driven pulley, rotating as denoted by the arrows; hence c is the driving and d the slack side of the belt. Now let us examine how this slackness is induced. It is obvious that pulley a rotates pulley b through the medium of the side c only of the belt, and from the resistance offered by the load on b, the belt stretches on the side c. The elongation of the belt due to this stretch, pulley a takes up and transfers to side d, relieving it of tension and inducing its slackness. The belt therefore meets pulley b at the point of first contact, e, slack and unstretched, and leaves it at f, under the maximum of tension due to driving b. While, therefore, a point in the belt is travelling from e to f, it passes from a state of minimum to one of maximum tension. This tension proceeds by a regular increment, whose amount at any given point upon b is governed by the distance of that point from e. The increase of tension is, of course, accompanied by a corresponding degree of belt stretch, and therefore of belt length; and as a result, the velocity of that part of the belt on pulley b is greater than the velocity of any part on the slack side of the belt; hence the velocity of the pulley is also greater than that of the slack side of the belt. In the case of pulley a the belt meets it at g under a maximum of tension, and therefore of stretch, but leaves it at h under a minimum of tension and stretch, so that while passing from g to h the belt contracts, creeping or slipping back on the pulley, and therefore effecting a reduction of belt velocity below that of the pulley. To summarize, then, the velocity of the part of the belt enveloping a is less than that of a to the amount of the creep; hence the velocity of the slack side of the belt is that of a minus the belt creep on a. The velocity of the part of the belt on b is equal to that of the slack side of the belt plus the stretch of the belt while passing over b; and it follows that if the belt or slip creep on one pulley is equal in amount to the belt stretch on the other, the velocities of the two pulleys will be equal.
Now (supposing the elasticity of the belt to remain constant, so that no permanent stretch takes place) it is obvious that the belt-shortening which accompanies its release from tension can only equal the amount of elongation which occurs from the tension; hence, no matter what the size of the pulleys, the creep is always equal in amount to the stretch, and the velocity ratio of the driven pulley will (after the increase of belt length due to the stretch is once transferred to the slack side of the belt) always be equal to that of the driving pulley, no matter what the relative diameters of the pulleys may be. In Fig. 2678, for example, are two pulleys, a and b, the circumference of a being 10 inches, while that of b is 20; and suppose that the stretch of the belt is an inch in a revolution of a (a being the driving pulley). Suppose the revolutions of a to be one per minute, then the velocity of the belt where it envelops a and b, and on the sides c and d, will be as respectively marked.
Thus the creep being an inch per revolution of a, the belt velocity on the side c will be nine inches per minute, and its stretch on b being an inch, the velocity of b will be ten inches per minute, which is equal to the velocity of the driving pulley.
It is to be observed, however, that since a receives its motion independently of the belt, its motion is independent of the creep, which affects the belt velocity only: but in the case of b, which receives its motion from the belt, it remains to be seen if stretch is uniform in amount from the moment it meets this pulley until it leaves it, for unless this be the case, the belt will be moving faster than the pulley at some part of the arc of contact.
Thus suppose p, Fig. 2679, represents a driven pulley, whose load is 1,000 pounds, and that from a to b, from b to c, from c to d, and from d to e, represent equal arcs of contact between belt and pulley, then arc a b will have on it the amount of stretch due to a pull of 250 pounds at b, diminishing to nothing at a. Arc c b will have on it the amount of stretch due to a pull of 500 pounds at c and 250 at b; arc d c will have on it the amount of stretch due to a load of 750 at d, and 500 at c; and arc d e will have the tension due to a load of 1,000 pounds at e, and 750 pounds at d. Suppose, then, that the amount of belt stretch is greater between b and c than it is between d and e, then the belt will travel faster between b c than between d e to an amount equal to the difference in stretch, and will at b c slip over the pulley to that amount; or if the friction of the belt at b c is sufficient to move the pulley in accordance with the stretch, then the belt must move the pulley at a greater velocity than the belt motion from d to e.
But since the friction of the belt is greatest at d e, it will hold the pulley with the greatest force, and hence the velocity of the belt and pulley will be uniform, or at least the most uniform, at d e.
Here arises another consideration, in that the stretch of the leather is not uniform, and the section of belt at c b may stretch more or less under its load than section c d does under its load, in which event the velocities of the respective belt sections cannot be uniform, and to whatever amount belt slip ensues the velocity of the driven wheel will be less than that of the driver.
Attention has thus far been directed to the relative velocities of the pulleys while under continuous motion. But let us now examine the relative velocities when the two pulleys are first put in motion. Suppose, then, the belt and pulley to be at rest with an equal degree of tension (independently of the weight of the belt, as before) on both sides of the belt. On motion being imparted to the driving pulley, the amount of belt elongation due to the stress of the load on the driving pulley has first to be taken up and transferred to the slack side of the belt, and during such transfer[II-213] a creep is taking place on the arc of belt contact on the driving pulley.
Furthermore, let it be noted that while under continuous motion the belt first receives full stress at point f, Fig. 2677; at starting it first receives it at point e, and there will be a period of time during which the belt stretch will proceed from e towards f, the pulley remaining motionless. The length of duration of this period will, in a belt of a given width, and having a given arc of contact on the driven pulley, depend on the amount of the load. Thus, referring to Fig. 2680, if the amount of the load is such that the arc of contact between the top and the point b is sufficient to drive the pulley, the pulley will receive motion when the belt stretch has proceeded from a to b; but if the load on the pulley be increased the belt stretch will require to proceed farther towards c.
At the top the stretch will proceed simultaneously with that of the driving side of the belt, between the points f g, Fig. 2677; but from the friction between the belt and pulley, the stretch of the part enveloping the pulley will be subsequent and progressive from f towards e, Fig. 2677.
It follows, then, that the velocity of the driven wheel will be less than that of the driver at first starting than when in continuous motion.
As the length of the belt is increased, the gross amount of stretch, under any given condition, increases, and hence the longer the belt, the greater the variation of velocity at first starting between the driven pulley and the driver.
From what has been said, it follows that when a mathematically equal velocity ratio is essential, belts cannot be employed, but the elasticity that disturbs the velocity ratio possesses the quality of acting as a cushion, modifying on one pulley any shocks, sudden strains, or jars existing on the other, while the longer the belt and less strained within the limit of elasticity, the greater this power of modification; furthermore in case of a sudden or violent increase of load, the belt will slide on the pulley, and in most cases slip off it, thus preventing the breakage of parts of the driving gear or of the machine driven that would otherwise probably ensue. Furthermore, belt connections are lighter and cheaper than gear-wheel or other rigid and positive connections, and hence the wide application of leather belts for the transmission of power, notwithstanding the slight variations of pulley velocity ratio due to the unequal elasticity of the various parts of the leather composing the belt.
The ends of belts are joined by two principal methods, the butt and the lap joint. In butt joints the holes are pierced near the ends of the belts, and the ends of the belt are brought together by means of a leather lace threaded through these holes. If the duty is light a single row of holes is all that is necessary. An example of this kind is shown in Fig. 2681, in which there are five holes on one side, and four on the other of the joint, the extra hole coming in the middle of its end of the belt. The lace is drawn half-way through this extra hole, and laced each way to the side and back again to the middle, the ends being tied on the outside of the belt, which does not come in contact with the pulley surface. By this means the lacing is double through all the holes, and if the knot should slip the slackness will begin at the middle of the belt and extend gradually towards the edges; whereas, if the lacing terminated at one side, and the knot or fastening should slip, all the tension would be thrown on one edge of the belt, unduly stretching it, and rendering it liable to tear. By this method of lacing the lace is not crossed on either side of the belt, which is desirable, because it is found in practice that a crossed lace does not operate so well as an uncrossed one.
If the power to be transmitted is so much as to render it desirable to have the strength of the laced joint more nearly approach that of the solid belt than is obtainable with a single row of holes, a double row is provided, as shown in Fig. 2682.
For belts of about 3 inches wide and over, these holes are made as follows: a, b, and c, d, e, about an inch apart and 5⁄8 inch from the line of joint; f, g, h, and i, j, being about 1⁄2 inch behind a, b, and c, d, e, respectively.
For thinner belts the holes may be closer together, and to the edges of the belt the exact distances permissible being closer together as the duty is lighter; but however narrow the width of the belt, it should contain at least two holes on each side of the joint. The sizes of these holes are an important element, since the larger the hole the more the belt is weakened. The following are the sizes of holes employed in the best practice:—
| Width of Belt. | Size of Punched Hole. | |
| Up to 4 inches | 1⁄4 | inch. |
| From 4 to 8 inches | 5⁄16 | „ |
| From 8 inches upwards | 3⁄8 | „ |
The holes are usually made round, but from the pliability of the lace, which enables it to adapt itself to the form of the hole to a remarkable degree, it is not unusual to preserve the strength of a belt by making an oblong hole, as in Fig. 2683 at a, or a mere slit, as at b, which, from removing less material from the belt, leaves it to that extent stronger.
[II-214]The ends of the belt should be cut quite square, and at a right angle to the edges, so that when the two ends are drawn together by the lace the edges of the belt will remain straight, and not curved, as they would do if either end of the belt were not cut at a right angle. Suppose, for example, that the ends of a belt were cut aslant, as in Fig. 2684, when laced up the edge of the belt would come as in Fig. 2685.
The holes must be punched exactly opposite to each other, or lacing the belt will bring the edges out of fair, as shown in Fig. 2686, the tension of the lace drawing the holes opposite to each other, irrespective of where the edges of the belt will come. If some of the holes are opposite and others are not, the latter will throw the edges of the belt out of line to some extent, especially if the lace is first entered in the holes that are not opposite, because, in that case, drawing the lace tight at once throws the belt edges out, and the subsequent lacing has but a limited effect in correcting the error, unless, indeed, the majority of the holes are opposite, and but one or two are out of line.
The lace should be drawn sufficiently tight to bring the ends of the belt firmly together, and should be laced with an even tension throughout, and for a belt doing heavy duty should have its ends tied in a knot at the back, and in the middle of the belt.
The width of the lace is usually about as follows:—
| Width of Belt. | Width of Lace. | |
| 24 inches and over | 1⁄2 | inch |
| 6 to 24 inches | 3⁄8 | „ |
| 2 to 4 inches | 5⁄16 | „ |
| 2 inches and less | 1⁄4 | „ |
Since belts are tightened by cutting a piece off one end (preferably the end which shows the holes most stretched), it is obvious that a butt-joint possesses an advantage, because as less of the belt length is occupied by the holes they may be cut quite out and new ones punched, whereas, in some cases, the length of the belt occupied by the holes in a lap-joint is more than the length of belt required to be cut out to tighten it.
There are many different methods of lacing a belt, but those here described are generally preferred. Thus referring to Fig. 2687 the lace is first passed through holes g and d, the ends being of equal length from the belt and emerging on the side that is to be the outside of the belt, thence each end of the lace is laced towards the edge of the belt, the dotted lines in the cut showing the path of the lace. It is then laced back to the middle of the belt, the second inside lacing exactly overlaying the first, the laces never crossing; the outside appearing as in Fig. 2688. The ends are in some cases tied in a knot on the outside, and in others fastened as shown in Fig. 2689, in which case the ends are merely held by friction, which will serve very well unless for a belt that is tightly strained.
By this method of lacing all the crossing of the lace is on the outside of the belt, which is an advantage, because from the creep of the belt the lace undergoes considerable friction, which is apt to rapidly wear out the lace, especially if it be crossed on the side of the bed that meets the pulley surface.
Fig. 2690 shows a method of lacing in which the crossing of the lace is entirely avoided, the knot being on the outside at a a. The path of the lace on one side of the belt is shown in full lines, and on the other side in dotted lines.
The objections to lacing are that the lace lifts the belt from the pulley surface, which throws all the wear on the lace, causing it eventually to break, and which also reduces the area of belt (at the joint) in contact with the pulley surface and reduces the driving power of the belt at the time the joint is passing over the pulley. In fact, in running belts this reduction of transmitting capacity is not great, because of the rapidity with which the joint[II-215] passes over the pulley, but in slow moving belts slip is very apt to occur when the lace meets the pulley, especially if the power transmitted is great in proportion to the width of the belt.
There are considerable movement and friction between the lace and the belt, more especially when the latter passes over a pulley of small diameter, and this with the friction due to whatever amount of slip the belt may experience, wears away the lace so that in time it breaks. Sometimes a cover is employed as shown in Fig. 2691 at a, to protect the lace, the cover being riveted or cemented to the belt on the side that is to meet the pulley surface. A similar means is also sometimes employed to make a butt joint. Thus in Fig. 2692 a is the cover riveted or cemented to the two ends b c, of the belt so as to dispense with lacing.
Fig. 2693 represents an excellent method of joining very thin belts, the operation being as follows:—
Place the two ends of the belt together with the edges fair one with the other, and with an awl make a row of holes at a, through both ends; then take about half a yard of strong twine (in some cases a lace or gut is better) and draw half the length through the first hole, then pass each end of the twine through the second hole, one end to the right and the other to the left, and draw both tight at the same time, and so on until the last hole is reached, when one end only of the twine is passed through; the two ends of the twine are then knotted tight together and the excess cut off.
The middle sketch shows the joint when the belt is stretched. The lower sketch shows it passing over a small pulley, where it will be seen that in the act of bending over the curve there is no friction between the lace and the belt, and this is the reason of its superiority over other methods, where there is always more or less friction between the lace and the belt when bending over a curve. Another advantage is, that in this system the lace does not come into contact with the pulley, so that whatever friction or slipping may take place between the belt and the pulley, the lacing is perfectly unaffected by it.
A lap joint is one in which the two ends of the belt overlap, as in Fig. 2694. The overlap is cut down to a plain bevel so as to reduce the joint to nearly or quite the same thickness as the main body of the belt. The lap joint is employed to join together the strips of leather forming the belt, and to fasten the ends of the finished belt together. In making the belt the overlap is cemented and riveted, while in joining the ends it may be cemented, or riveted, or laced.
The advantage of rivets lies simply in that they are easily applied. Their disadvantages are that they grip but a small area of the belt, namely, that portion beneath the rivet head and washer surface; hence, when rivets are used the joint should always be cemented also. A more important defect is, however, that the heat generated by the compression of the rivet while riveting it is sufficiently great to burn the leather beneath the rivet-head. The reason that the leather under the head and not under the washer or burr at the riveted end of the rivet burns is, that although the heat due to riveting is most at the burr end of the rivet, its passage from the rivet to the washer is less rapid than it is through the body of the rivet, because in the one case it has to be transferred from one body to another (from the rivet to the burr), while in the other its passage is uninterrupted and continuous.
Rivets for lap joints are usually placed about, as in Fig. 2695, the rows a and c being about 1⁄2 inch from the edges b and d respectively, and the row f about 3⁄8 inch from the edge f of the lap, while the rivets are about 5⁄8 inch apart in the rows.
For comparatively narrow belts as, say, four inches wide, a single row g would be placed in the middle, additional middle rows should for wider belts be about 11⁄4 inches apart.
The rivet holes should be a close fit to the rivets, the latter being left just long enough to hold the washer or burr and sink with it, in the riveting, to the level surface of the belt.
The heads of the rivets should be on the side of the belt that is to run next to the pulley.
The strongest method of forming a belt is by means of small taper wooden pegs, such as are used in boot and shoe manufacture, the joint being cemented, and the pegs inserted. In this case the belt is merely pierced with an awl, hence none of the leather is removed.
[II-216]The arrangement of wooden pegs should be as in Fig. 2696, the rows a and b being respectively about 5⁄8 inch from the edges c d, the row e being about 1⁄4 inch from the edge of the joint, and h about 3⁄4 inch from that edge. The pegs are placed about 1⁄2 inch apart in the rows.
A cemented and pegged joint is the strongest made, and it preserves a more equal tension throughout the belt than any other, while the belt is strong, since the hole for the pegs may be pierced with an awl, which does not remove any leather from the belt, as is the case with punched holes.
The length of the lap in some of the best practice is as follows:
When the strips of leather are cut from the hide in such lengths that the part termed the shoulder of the hide is utilised, a uniform lap of 8 inches is employed for all widths of belt. When the strips do not contain the shoulder of the hide, the following are the respective lengths of lap:—
| Width of single belt. | Length of lap. | |||
| 1 to 41⁄2 inches | 4 | 1⁄4 | inches. | |
| 5 inches | 5 | „ | ||
| 6 to 8 inches | 6 | „ | ||
| 9 inches | 6 | 1⁄2 | „ | |
| 10 to 14 | inches | 7 | „ | |
| 15 to 24 | „ | 8 | „ | |
| All double belts are given a 6 inch lap. | ||||
Another and excellent method of joining a belt, or of fastening two thicknesses together to form a double belt, is to sew it together with lace leather, as shown in Fig. 2697. The lace is in this case about 1⁄4 inch wide, the holes being pierced so as to have the lace diagonal, as shown in the cut. Sometimes four rivets are added at the joint as shown in the cut.
Other methods of fastening the ends of leather belts are by means of metal hooks of various forms. Fig. 2698 represents a fastening of this kind, the appearance of both sides of the joint being shown in the figure. In this case considerable leather is removed from the belt, but this is to some extent compensated for, because the hook holds each end of the belt in two places; that is to say, in the crook of the hook as well as at the end. This, however, while it has the effect of increasing the grip of the hook on the belt, still leaves the belt as a whole weaker, by reason of the removal of leather to form the holes.
In Figs. 2699 and 2700 is shown a belt screw, intended to take the place of rivets, and thus avoid the burning of the leather which accompanies the use of rivets. It consists of two screws, one having a right and the other a left-hand thread. The former is of bronze, and has a coarse exterior thread cut conically, while it is hollow with a fine thread tapped inside. The latter is of steel, and has a conical shoulder underneath. The heads of both screws are slightly rounded and formed with circular grooves on the under side, to give them a firm grip on the leather. The conical screw is first run into the leather, and the steel screw is then introduced. The belt is run with the head of the latter on the inner side.
If the body of a narrow belt is riveted it contains two rows only of rivets; but as the width of the belt increases, other rows are introduced, all the rows running the entire length of the belt. In some cases two separate single belts running one over or outside the other are employed in place of an ordinary double belt, and the arrangement works well.
Two single belts applied in this manner are especially preferable to a double belt when used upon a small pulley, because they will bend to the curvature of the pulley more readily, being more pliable; whereas a double belt will from its resistance to bending not envelop as much of the circumference of the belt as is due to the relative sizes of the pulleys, and the distance apart of their axes.
Round leather belts are made in two forms, the solid and the twisted. The first consists of a simple leather cord, hence its diameter cannot exceed the thickness of the leather. The second consists of a strip of leather twisted into cylindrical form, the grain side of the leather being outside.
The ends of round belts are usually joined by means of cylindrical hooks and eyes, which are threaded so as to screw on to the end of the belt, but for twisted round belts it is better to place in the centre of the belt a small core of soft wood. The ends of the belt should be slightly tapered, and the hook and eye screwed firmly home. Sometimes from the smallness of the pulleys the inflexibility of the hook and eye becomes objectionable, and a simple hook is employed on solid round belting.
The length of twisted round belting may be altered by twisting[II-217] or untwisting it, which renders it unnecessary to cut the belt for a small amount of shortening.
Round belts should bear upon the sides, and not on the bottom of the pulley-groove, which increases their transmitting power. Thus, if the groove is a semicircle of the same radius as is the belt when new, the stretch of the belt as it wears decreasing its diameter, it will then touch only on the bottom of the groove. Furthermore, when the belt bears on the sides only of the groove it becomes wedged to a certain extent in the sides of the pulley groove.
V-belting is formed of strips of leather welted together, as shown in Figs. 2701 and 2702, the latter showing the joint or splice of the belt. The pulleys are V-grooved as shown. The tension of the belt causes it to grip the sides of the groove on the wedge principle, and the belt is flat at the apex of the V so that it shall not bottom in the groove, which would impair its wedging action. This class of belt is largely employed for connecting shafts at an angle, especially in cases where the distance between the shafts is small, in which case it will last much longer than a flat belt.
From the construction, the rivets joining the pieces forming the belt do not come into contact with the surfaces of the pulley, and from the tension of the belt causing it to wedge into the sides of the pulley groove, the driving power is greater than that simply due to the area of contact and the tension of the belt.
A belt will run to the largest diameter of a pulley, thus in Fig. 2703, the belt would, unless guided, gradually creep up to the side a of pulley p, and following this action would move to side c of pulley d.
If the pulleys are parallel, but the axis of their shafts are not in line, then the belt will run towards that side on which the axes are closest; thus in Fig. 2704 the belt would run towards the side p of the large pulley, because the belt b will meet the pulley surface at a, and if a point on the belt at b travelled coincident with the point on the pulley with which it took contact, its plane of rotation, while on the pulley, would be as denoted by the dotted line b.
But to follow this plane of rotation, the belt would require to bend edgeways, as denoted by the dotted line b, which it does to some extent, carrying the belt with it.
Changing or Slipping Belts on Pulleys.—To change a belt on a stepped cone, proceed as follows:—
Suppose the belt to be on the small step of the driving cone, and to require to run on the largest step. Throw the belt on the smallest step of the lower cone and place the palm of the hand on the inside face of the belt on the side on which it approaches that cone. Draw the belt tight enough (with the palm of the right hand) to take up the slack and cause the lower cone to rotate. When it is in full motion place the palm of the left hand against the inside face of the other side of the belt (while still keeping the pressure of the right hand against the slack side of the belt).
Release suddenly the pressure of the right hand and immediately with a quick and forcible lateral motion of the left hand force the belt towards the larger step of the upper cone, which will cause it to mount the next step, when the operation may be repeated for each succeeding step.
If the steps of the cone are too steep, or the belt is too long for this method, a wooden rod may be used, its end being applied to the side of the belt that runs on the upper cone and close to the cone. Then lift the belt with the rod, while the lower end of the rod is inclined away from the step the belt is to mount, when the belt will mount the step of the rotating cone.
In the case of broad heavy belts it is best to stop the running pulley and place the belt on it, then lift the belt edge on the stationary pulley at the point where the belt will first meet it when in motion, forcing the belt on by hand as far as possible. Take a strong cord, as, say 3⁄8 inch diameter, and double it, pass the loop between the pulley arms around the belt and over the pulley face. Pass the two free ends of the cord through the loop (formed by doubling the cord) and pull the free ends as tight as possible by hand. While standing on the side of the pulley opposite to that of the belt, communicate slow motion to the driving pulley and release the ends of the cords as soon as the belt is on. The belt, in travelling from the pulley, will then undo the cord of itself.
A belt may be taken off a pulley, either by pressing it in the required direction and as close to the pulley as possible, or by[II-218] holding the two sides of the belt together, which should be done as far from the running pulley as possible, or as far from the pulley the belt is required to come off as possible.
In Fig. 2705 is shown a device for automatically replacing a belt that has slipped off a pulley. a is the pulley and b the device, which has a curved projection which is of the full width of the device at one end, where it comes even with the perimeter of a, and tapers laterally towards the outside edge of the device. As a result the belt will easily pass on the broad end and cause the device to rotate, the belt running up the curved projection and therefore lifting clear of the pulley a, but on account of the taper of the projection the belt finally has contact with the projection on one edge only, and therefore tips over to the other side, and as a result falls on a, because it is under tension and naturally adjusts itself to be in line with the pulley at the other end of the belt. It would appear that the belt, if running, would move on the pulley, driving it, and this would be the case if sufficient time were allowed for it to do so, but the action of the device is too quick, and furthermore, when the belt is off one pulley and therefore loose its motion is apt to become greatly reduced, which retards its moving laterally on the pulley driving it.
It is obvious that the device must be applied to that side of the pulley on which the belt is found to run off, but it may be noted that belts are not apt to run off the loose pulley, but off the driving one, and only at times when from excessive resistance or duty the velocity of the pulley is reduced below that of the belt, or the velocity of the belt is less than that of the pulley driving it; hence the device must be applied on the outside of the fast or tight pulley.
The driving power of a belt is determined principally by the amount of its pull upon the pulley, and the speed at which it travels.
The amount of pull is determined by its tension, or in other words, the degree with which it grips the pulley and the closeness with which it lies to the pulley surface. The amount of tension a single belt is capable of withstanding with a due regard to its durability has been fixed by various experimenters at 662⁄3 lbs. per inch of its width. The pull of the belt under this degree of tension will vary as follows:—
It will be more with the grain or smooth side than it will with the flesh or fibrous side of the belt in contact with the pulley face, some authorities stating the amount of difference to be about 20 per cent. It will be more with a smooth and polished surface on the pulley than with one less smooth and polished. At high speeds it will be diminished by the interposition of air between the belt and pulley surface, and from the centrifugal force generated by the passage of the belt around the pulley. It will be more when the pulley is covered with leather rubber or other cushioning substance than when the pulley is bare, even though it be highly polished, some authorities stating this difference to be about 20 per cent.
It will be increased in proportion as the belt envelops a greater proportion of the pulley circumference, the part of the pulley enveloped by the belt when the pulley is at rest (or what is the same thing, at any point of time when it is in motion) being termed the arc of contact.
It is obvious that the arc of contact taken to calculate the belt power must be the least that exists on either the driving or the driven pulley, because when the belt slips it ceases to transmit the full amount of the power it receives, the remainder being expended in the friction caused by the belt slipping over the pulley.
The speed at which a belt may run is limited only by reason of the centrifugal force generated during its passage around the pulley, this force tending to diminish its pressure upon the pulley. The maximum of speed at which it is considered advisable to run a belt is about 6,000 feet per minute; but the amount of centrifugal force generated at this speed depends upon the diameter of the pulley, because the centrifugal force increases in direct proportion as the number of revolutions is increased, or in other words it increases in the same proportion as the velocity; but in a given circle it increases as the square of the velocity. Suppose, then, that it be required to double the velocity of a belt, and that the same pulley be used running at twice the velocity, this will increase fourfold the centrifugal force generated; but if the diameter of the pulley be doubled the centrifugal force generated will be simply doubled; hence it appears that the larger the pulley the less the centrifugal force of the belt in proportion to its velocity. This will be apparent when it is considered that the larger the pulley the nearer will the curve of its circumference approach to a straight line.
The following experiments on the transmission of power by belting were made Messrs. Wm. Sellers & Co.
[40]These experiments were undertaken with a view to determine, under actual working conditions, the internal resistances to be overcome, the percentage of slip, and the coefficient of friction on belt surface. They were conducted, during the spring of 1885, under the direction of Mr. J. Sellers Bancroft.
[40] From a paper read before the American Society of Mechanical Engineers by Wilfred Lewis.
These experiments seemed to show that the principal resistance to straight belts was journal friction, except at very high speeds, when the resistance of the air began to be felt. The resistance from stiffness of belt was not apparent, and no marked difference could be detected in the power required to run a wide double belt or a narrow light one for the same tension at moderate speeds. With crossed and quarter-twist belts the friction of the belt upon itself or upon the pulley in leaving it was frequently an item of more importance, as was shown by special experiments for that purpose.
In connection with the experiments upon internal resistances, some interesting points were noted. Changes in tension were made while the belt was running, commencing with a very slack belt and increasing by definite amounts to the working strength. As this point was approached, it was found necessary, to maintain a constant tension, that the tightening bolt should be constantly operated on account of stretch in the belt. Then, again, as the tension was reduced from this limit, it was found that at lower tensions the belt would begin to shrink and tighten for a fixed position of the sliding frame. This stretching and tightening would continue for a long time, the tightening being, of course, limited, but the stretching indefinite and unlimited.
The first series of experiments was made upon paper-coated pulleys 20′′ diameter, which carried an old 51⁄2′′ open belt 3⁄16′′ to 1⁄4′′ thick and 34 ft. long, weighing 16 lbs. The arc of contact on the pulleys has been calculated approximately from the tension on slack side, and for this purpose the width and length of the belt were taken. The percentage of slip must be considered as equally divided between the two pulleys, and from observations made it is easy to calculate the velocity of sliding when the speed is given.
Some of the most important results obtained with this belt are given in Table I. in which the experiments have been selected to avoid unnecessary repetition. In all cases the coefficient of friction is shown to increase with the percentage of slip. The adhesion on the paper-covered pulleys appears to be greater than on the cast-iron surfaces, but this difference may possibly have been due to some change in the condition of the belt surfaces.
After a fresh application of the belt dressing known as “Beltilene,” the results obtained are even higher on cast iron than on[II-219] paper surfaces, but after a time it was found that the adhesive property of this substance became sensibly less and less. Flakes of a tarry nature rolled up from the belt surface and deposited, themselves on the pulleys, or scaled off.
So much was found to depend upon the condition of the belt surface and the nature of the dressing used, that the necessity was felt for experiments upon some standard condition which could be easily realized and maintained. For this purpose a belt was taken from a planing machine when it had become perfectly dried by friction. The results of experiments upon this belt are given in Table II. When dry, as used on the planer, the coefficients for any given percentage of slip were much smaller than those given in Table I. This was naturally to be expected, and the experiments were continued to note the effect of a belt dressing in common use, known as “Sankey’s Life of Leather,” which was applied to the belt while running. At first, the adhesion was very much diminished, but it gradually increased as the lubricant became absorbed by the leather, and in a short time the coefficient of friction had reached the unprecedented figures of 1.44 and 1.37.
| No. of Exper- i’nt. |
Sum of Tensions T + t | [41] T - t Work- ing. |
[41] T |
[41] t |
[41] T ⁄ t |
Per- cent- age of Slip. |
Velocity of Slip in ft. per minute. |
Arc of con- tact. |
Coef- ficient of Friction. |
Remarks. | ||||||||
| Initial. | Work- ing. |
Final. | ||||||||||||||||
| 17 | 200 | 210 | 100 | 155 | 55 | 2 | .82 | .4 | 1 | .6 | 177 | ° | .336 | Paper-covered pulleys. |
||||
| 19 | 220 | 140 | 180 | 40 | 4 | .50 | .6 | 2 | .4 | 176 | .490 | |||||||
| 21 | 246 | 180 | 213 | 33 | 6 | .45 | 1 | .2 | 4 | .8 | 175 | .610 | ||||||
| 22 | 260 | 200 | 230 | 30 | 7 | .67 | 2 | .6 | 10 | .4 | 174 | .671 | ||||||
| 23 | 270 | 180 | 220 | 245 | 25 | 9 | .80 | 7 | .9 | 31 | .6 | 173 | .756 | |||||
| 24 | 300 | 316 | 200 | 258 | 58 | 4 | .45 | .7 | 2 | .8 | 177 | .483 | ||||||
| 27 | 344 | 260 | 302 | 42 | 7 | .20 | 1 | .0 | 4 | 176 | .643 | |||||||
| 28 | 350 | 280 | 315 | 35 | 9 | 1 | .8 | 7 | .2 | 175 | .719 | |||||||
| 29 | 364 | 300 | 332 | 32 | 10 | .4 | 2 | .8 | 11 | .2 | 175 | .784 | ||||||
| 30 | 380 | 260 | 320 | 350 | 30 | 11 | .7 | 5 | .5 | 22 | 175 | .805 | ||||||
| 31 | 400 | 422 | 200 | 211 | 111 | 1 | .90 | .5 | 2 | 179 | .205 | |||||||
| 33 | 440 | 280 | 360 | 80 | 4 | .50 | .8 | 3 | .2 | 178 | .484 | |||||||
| 35 | 470 | 360 | 415 | 55 | 7 | .54 | 1 | .1 | 4 | .4 | 177 | .654 | ||||||
| 36 | 506 | 400 | 453 | 53 | 8 | .54 | 2 | .1 | 8 | .4 | 177 | .694 | ||||||
| 37 | 520 | 380 | 420 | 470 | 50 | 9 | .40 | 5 | 20 | 177 | .725 | |||||||
| 60 | 200 | 205 | 80 | 147 | .5 | 67 | .5 | 2 | .18 | .5 | 2 | 178 | .251 | Cast-iron surfaces. | ||||
| 61 | 210 | 100 | 155 | 55 | 2 | .82 | .9 | 3 | .6 | 177 | .336 | |||||||
| 62 | 215 | 120 | 167 | .5 | 47 | .5 | 3 | .52 | 1 | .7 | 6 | .8 | 177 | .407 | ||||
| 63 | 220 | 140 | 180 | 40 | 4 | .50 | 3 | 12 | 176 | .490 | ||||||||
| 65 | 246 | 180 | 180 | 213 | 33 | 6 | .45 | 12 | 48 | 175 | .610 | |||||||
| 66 | 300 | 300 | 120 | 210 | 90 | 2 | .33 | .5 | 2 | 179 | .270 | |||||||
| 68 | 310 | 160 | 235 | 75 | 3 | .13 | .8 | 3 | .2 | 179 | .365 | |||||||
| 69 | 315 | 180 | 247 | .5 | 67 | .5 | 3 | .67 | 1 | 4 | 178 | .418 | ||||||
| 70 | 320 | 200 | 260 | 60 | 4 | .33 | 1 | .7 | 6 | .8 | 178 | .472 | ||||||
| 71 | 325 | 220 | 272 | .5 | 52 | .5 | 5 | .19 | 2 | .6 | 10 | .4 | 177 | .545 | ||||
| 72 | 340 | 240 | 290 | 50 | 5 | .80 | 3 | .8 | 15 | .2 | 177 | .569 | ||||||
| 73 | 350 | 260 | 305 | 45 | 6 | .77 | 5 | .5 | 22 | 176 | .623 | |||||||
| 74 | 360 | 280 | 320 | 40 | 8 | 8 | .6 | 34 | .4 | 176 | .677 | |||||||
| 75 | 375 | 300 | 337 | .5 | 37 | .5 | 9 | 15 | .2 | 60 | .8 | 175 | .719 | |||||
| 76 | 400 | 420 | 200 | 310 | 110 | 2 | .82 | .6 | 2 | .4 | 179 | .336 | Belt dressed with “Beltilene.” |
|||||
| 78 | 460 | 280 | 370 | 90 | 4 | .11 | 1 | 4 | 179 | .452 | ||||||||
| 81 | 480 | 340 | 410 | 70 | 5 | .86 | 1 | .5 | 6 | 178 | .569 | |||||||
| 84 | 510 | 400 | 455 | 55 | 8 | .27 | 2 | .2 | 8 | .8 | 177 | .684 | ||||||
| 86 | 535 | 440 | 487 | .5 | 47 | .5 | 10 | .2 | 4 | .5 | 18 | 177 | .760 | |||||
| 88 | 560 | 385 | 480 | 520 | 40 | 13 | 8 | .4 | 33 | .6 | 176 | .834 | ||||||
| 89 | 300 | 320 | 120 | 220 | 100 | 2 | .20 | .4 | 1 | .6 | 179 | .252 | ||||||
| 93 | 350 | 200 | 275 | 75 | 3 | .67 | .8 | 3 | .2 | 178 | .418 | |||||||
| 97 | 390 | 280 | 335 | 55 | 6 | 1 | .6 | 6 | .4 | 177 | .580 | |||||||
| 101 | 440 | 360 | 400 | 40 | 10 | 3 | .1 | 12 | .4 | 176 | .750 | |||||||
| 104 | 470 | 310 | 420 | 445 | 25 | 17 | .8 | 8 | .6 | 34 | .4 | 173 | .953 | |||||
[41] T represents the tension on the tight part, and t on the sag part of the belt.
An interesting feature of these and subsequent experiments is the progressive increase in the sum of the belt tensions during an increase in load. This is contrary to the generally accepted theory that the sum of the tensions is constant, but it may be accounted for to a large extent by the horizontal position of the belt, which permitted the tension on the slack side to be kept up by the sag. That this is only a partial explanation of the phenomenon, and that the sum of the tensions actually increases as their difference increases for even a vertical position of the belt, will be shown by a special set of experiments. If a belt be suspended vertically, and stretched by uniformly increasing weights, it will also be found that the extension is not uniform, but diminishes as the load is increased, or, as already stated, the stress increases faster than the extension. A little reflection will show that when this is the case the tensions must necessarily increase with the load transmitted.
| No. of Exper- i’nt. |
Sum of Tensions T + t | T - t Work- ing. |
T | t | T ⁄ t | Per- cent- age of Slip. |
Velocity of Slip in ft. per min. |
Arc of con- tact. |
Coef- ficient of Friction. |
Remarks. | |||||||||
| Initial. | Work- ing. |
Final. | |||||||||||||||||
| 105 | 100 | 104 | 40 | 72 | 32 | 2 | .25 | .3 | 1 | .2 | 177 | ° | .263 | ||||||
| 106 | 110 | 60 | 85 | 25 | 3 | .40 | .8 | 3 | .2 | 177 | .395 | ||||||||
| 107 | 122 | 80 | 101 | 21 | 4 | .81 | 1 | .7 | 6 | .8 | 176 | .511 | |||||||
| 108 | 138 | 100 | 119 | 19 | 6 | .26 | 4 | .3 | 17 | .2 | 175 | .600 | |||||||
| 109 | 200 | 208 | 80 | 144 | 64 | 2 | .25 | .4 | 1 | .6 | 179 | .260 | |||||||
| 110 | 212 | 100 | 156 | 56 | 2 | .81 | .7 | 2 | .8 | 179 | .331 | ||||||||
| 111 | 216 | 120 | 168 | 48 | 3 | .50 | 1 | 4 | 179 | .401 | |||||||||
| 112 | 220 | 140 | 180 | 40 | 4 | .50 | 1 | .8 | 7 | .2 | 178 | .484 | |||||||
| 113 | 230 | 160 | 195 | 35 | 5 | .57 | 4 | .4 | 17 | .6 | 178 | .553 | |||||||
| 114 | 300 | 308 | 120 | 214 | 94 | 2 | .28 | .4 | 1 | .6 | 180 | .262 | |||||||
| 116 | 316 | 160 | 238 | 78 | 3 | .05 | .8 | 3 | .2 | 180 | .355 | ||||||||
| 118 | 322 | 200 | 261 | 61 | 4 | .28 | 1 | .6 | 6 | .4 | 179 | .465 | |||||||
| 119 | 330 | 285 | 220 | 275 | 55 | 5 | 2 | .6 | 10 | .4 | 179 | .516 | |||||||
| 121 | 400 | 404 | 160 | 282 | 122 | 2 | .31 | .7 | 2 | .8 | 180 | .267 | |||||||
| 124 | 410 | 220 | 315 | 95 | 3 | .37 | 1 | .5 | 6 | 180 | .387 | ||||||||
| 125 | 412 | 240 | 326 | 86 | 3 | .79 | 2 | .3 | 9 | .2 | 180 | .424 | |||||||
| 126 | 414 | 260 | 338 | 78 | 4 | .33 | 3 | .7 | 14 | .8 | 179 | .469 | |||||||
| 127 | 416 | 370 | 280 | 348 | 68 | 5 | .12 | 10 | .1 | 40 | .4 | 179 | .523 | Belt almost slipped off. | |||||
| 128 | 500 | 516 | 200 | 358 | 158 | 2 | .27 | .5 | 2 | 180 | .261 | ||||||||
| 131 | 520 | 260 | 390 | 130 | 3 | 1 | .1 | 4 | .4 | 180 | .350 | ||||||||
| 133 | 525 | 300 | 412 | .5 | 112 | .5 | 3 | .67 | 1 | .8 | 7 | .2 | 180 | .414 | |||||
| 134 | 525 | 320 | 422 | .5 | 102 | .5 | 4 | .11 | 2 | .7 | 10 | .8 | 180 | .450 | |||||
| 135 | 525 | 460 | 340 | 432 | .5 | 92 | .5 | 4 | .67 | 5 | .1 | 20 | .4 | 180 | .490 | ||||
| 136 | 100 | 105 | 40 | 72 | .5 | 32 | .5 | 2 | .02 | .2 | .8 | 177 | .228 | Here the belt was coated with “Sankey’s Life of Leather,” and run until in good working condition before noting experiments. | |||||
| 137 | 110 | 60 | 85 | 25 | 3 | .40 | .4 | 1 | .6 | 177 | .396 | ||||||||
| 138 | 125 | 80 | 102 | .5 | 22 | .5 | 4 | .56 | .6 | 2 | .4 | 176 | .494 | ||||||
| 140 | 150 | 120 | 135 | 15 | 9 | 1 | .8 | 7 | .2 | 174 | .723 | ||||||||
| 141 | 164 | 140 | 152 | 12 | 12 | .7 | 2 | .8 | 10 | .8 | 172 | .779 | |||||||
| 142 | 180 | 160 | 170 | 10 | 17 | 5 | 20 | 170 | .954 | ||||||||||
| 144 | 215 | 200 | 207 | .5 | 7 | .5 | 27 | .7 | 7 | .3 | 29 | .2 | 166 | 1 | .15 | ||||
| 146 | 250 | 240 | 245 | 5 | 49 | 10 | .6 | 42 | .4 | 158 | 1 | .41 | |||||||
| 147 | 270 | 90 | 260 | 265 | 5 | 53 | 17 | .7 | 70 | .8 | 158 | 1 | .44 | ||||||
| 149 | 100 | 105 | 40 | 72 | .5 | 32 | .5 | 2 | .02 | .2 | .8 | 177 | .228 | Three days later without any additional dressing. | |||||
| 150 | 110 | 60 | 85 | 25 | 3 | .40 | .3 | 1 | .2 | 177 | .396 | ||||||||
| 151 | 120 | 80 | 100 | 20 | 5 | .4 | 1 | .6 | 176 | .524 | |||||||||
| 153 | 150 | 120 | 135 | 15 | 9 | .7 | 2 | .8 | 174 | .723 | |||||||||
| 155 | 182 | 160 | 171 | 11 | 15 | .5 | 1 | .2 | 4 | .8 | 172 | .913 | |||||||
| 156 | 202 | 180 | 191 | 11 | 17 | .3 | 3 | 12 | 172 | .950 | |||||||||
| 157 | 216 | 200 | 208 | 8 | 26 | 5 | .8 | 23 | .2 | 167 | 1 | .12 | |||||||
| 158 | 232 | 220 | 226 | 6 | 37 | .3 | 7 | 28 | 161 | 1 | .29 | ||||||||
| 159 | 252 | 240 | 246 | 6 | 41 | 9 | .8 | 39 | .2 | 161 | 1 | .32 | |||||||
| 161 | 292 | 280 | 286 | 6 | 47 | .7 | 13 | .7 | 54 | .8 | 161 | 1 | .37 | ||||||
A piece of belting 1 sq. in. in section and 92 ins. long was found by experiment to elongate 1⁄4 in. when the load was increased from 100 to 150 lbs., and only 1⁄8 in. when the load was increased from 450 to 500 lbs. The total elongation from 50 to 500 lbs. was 111⁄16′′, but this would vary with the time of suspension, and the measurements here given were taken as soon as possible after applying the loads. In a running belt the load is applied and removed alternately for short intervals of time, depending upon the length and speed of the belt, and the time for stretching would seldom be as great as that consumed in making the experiments just mentioned.
The differences between the initial and final tensions unloaded, as given in the tables, show the effect of extension or contraction during the course of the experiments made at a fixed position of the pulleys. The percentage of elongation which a belt undergoes in passing from its loose to its tight side, is the measure of the slip which must necessarily take place in the transmission of power. This is a direct loss, and within the assumed working strength of 500 lbs. per sq. in. for cemented belts without lacings, experiment indicates that it should not exceed 11⁄2 or 2 per cent. When, therefore, an experiment shows less than 2 per cent. of slip, the amount may be considered as allowable and proper, and the belt may be relied upon to work continuously at the figures given.
Table III. gives the results of experiments upon a soft and pliable rawhide belt made by the Springfield Glue and Emery Co. This belt had been used by the Midvale Steel Co. for a period of seven months, at its full capacity, and was sent in its usual working condition to be tested. It had been cleaned and dressed with[II-220] castor oil at intervals of three months, and was received three weeks after the last dressing. Commencing with the light initial tension of 50 lbs. on a side, it was found impossible with the power at command to reach a limit to the pulling power of the belt, and in order to do so the experiment was made of supporting the slack side of the belt upon a board to prevent sagging.
| No. of Exper- i’nt. |
Sum of Tensions T + t | T - t Work- ing. |
T | t | T ⁄ t | Per- cent- age of Slip. |
Velocity of Slip in ft. per min. |
Arc of con- tact. |
Coef- ficient of Friction. |
Dura- tion of run at time of experi- ment. |
Remarks. | ||||||||||
| Initial. | Work- ing. |
Final. | |||||||||||||||||||
| 171 | 100 | 118 | 40 | 79 | 39 | 2 | .03 | .2 | .8 | 177 | ° | .229 | |||||||||
| 173 | 140 | 80 | 110 | 30 | 3 | .67 | .4 | 1 | .6 | 176 | .423 | ||||||||||
| 175 | 168 | 120 | 144 | 24 | 6 | .6 | 2 | .4 | 174 | .590 | |||||||||||
| 177 | 202 | 160 | 181 | 21 | 8 | .62 | .8 | 3 | .2 | 172 | .661 | ||||||||||
| 179 | 232 | 200 | 216 | 16 | 13 | .5 | 1 | 170 | .897 | ||||||||||||
| 181 | 268 | 240 | 254 | 14 | 18 | .1 | 1 | .2 | 4 | .8 | 167 | .993 | |||||||||
| 183 | 302 | 280 | 291 | 11 | 26 | .5 | 1 | .4 | 5 | .6 | 163 | 1 | .15 | ||||||||
| 184 | 318 | 110 | 300 | 309 | 9 | 34 | .3 | 1 | .6 | 6 | .4 | 160 | 1 | .27 | |||||||
| 185 | 100 | 150 | 115 | 140 | 145 | 5 | 29 | 1 | .6 | 6 | .4 | 180 | 1 | .02 | Slack side of belt running on a board to prevent sagging. | ||||||
| 186 | 200 | 258 | 240 | 249 | 9 | 27 | .4 | 1 | .2 | 4 | .8 | 180 | 1 | .05 | |||||||
| 188 | 290 | 280 | 285 | 5 | 57 | 2 | .2 | 8 | .8 | 180 | 1 | .29 | |||||||||
| 189 | 300 | 412 | 400 | 406 | 6 | 67 | .7 | 1 | .7 | 6 | .8 | 180 | 1 | .34 | |||||||
| 190 | 428 | 420 | 424 | 4 | 106 | 1 | .8 | 7 | .2 | 180 | 1 | .48 | |||||||||
| 191 | 446 | 275 | 440 | 443 | 3 | 148 | 3 | .3 | 13 | .2 | 180 | 1 | .59 | ||||||||
| 192 | 400 | 570 | 360 | 560 | 565 | 5 | 113 | 2 | 180 | 1 | .47 | ||||||||||
| 329 | 100 | 110 | 40 | 75 | 35 | 2 | .14 | .3 | .6 | 177 | .246 | 10′′ cast-iron pulleys. | |||||||||
| 330 | 135 | 80 | 107 | .5 | 27 | .5 | 3 | .90 | .6 | 1 | .2 | 175 | .446 | ||||||||
| 331 | 198 | 160 | 179 | 19 | 9 | .42 | 1 | 171 | .751 | ||||||||||||
| 332 | 275 | 240 | 257 | .5 | 17 | .5 | 14 | .7 | 1 | .5 | 169 | .911 | |||||||||
| 334 | 345 | 320 | 232 | .5 | 12 | .5 | 18 | .6 | 2 | 165 | 1 | .01 | |||||||||
| 336 | 420 | 110 | 400 | 410 | 10 | 41 | 3 | .2 | 6 | .4 | 162 | 1 | .31 | ||||||||
| 339 | 200 | 230 | 160 | 195 | 35 | 5 | .86 | .8 | 1 | .6 | 176 | .576 | |||||||||
| 340 | 360 | 320 | 340 | 20 | 17 | 1 | .6 | 3 | .2 | 171 | .949 | ||||||||||
| 341 | 435 | 400 | 417 | .5 | 17 | .5 | 23 | .8 | 2 | 169 | 1 | .07 | |||||||||
| 342 | 505 | 480 | 492 | .5 | 12 | .5 | 39 | .4 | 2 | .7 | 5 | .4 | 165 | 1 | .28 | ||||||
| 343 | 590 | 200 | 560 | 575 | 15 | 38 | .3 | 5 | .0 | 168 | 1 | .24 | |||||||||
| 344 | 300 | 400 | 320 | 360 | 40 | 9 | 1 | .4 | 2 | .8 | 175 | .719 | |||||||||
| 345 | 450 | 400 | 425 | 25 | 17 | 1 | .7 | 3 | .4 | 173 | .938 | ||||||||||
| 346 | 520 | 480 | 500 | 20 | 25 | 2 | .1 | 4 | .2 | 171 | 1 | .08 | |||||||||
| 347 | 600 | 560 | 570 | 10 | 57 | 3 | 162 | 1 | .43 | 1 | min. | ||||||||||
| 348 | 600 | 280 | 560 | 570 | 10 | 57 | 3 | .4 | 6 | .8 | 162 | 1 | .43 | 5 | min. | ||||||
| 350 | 400 | 500 | 400 | 450 | 50 | 9 | 1 | .6 | 3 | .2 | 176 | .715 | |||||||||
| 352 | 605 | 560 | 577 | .5 | 17 | .5 | 21 | .3 | 2 | .3 | 4 | .6 | 169 | 1 | .04 | ||||||
| 353 | 680 | 640 | 660 | 20 | 33 | 3 | .2 | 6 | .4 | 171 | 1 | .17 | 1 | min. | |||||||
| 354 | 680 | 640 | 660 | 20 | 33 | 3 | .7 | 7 | .4 | 171 | 1 | .17 | 5 | min. | |||||||
| 355 | 680 | 640 | 660 | 20 | 33 | 4 | .1 | 8 | .2 | 171 | 1 | .17 | 10 | min. | [4 m. later. | ||||||
| 356 | 680 | 640 | 660 | 20 | 33 | 6 | .1 | 12 | .2 | 171 | 1 | .17 | 15 | min. | Belt slipped off | ||||||
| 357 | 600 | 560 | 580 | 20 | 29 | .0 | .0 | 171 | 1 | .13 | 20 | min. | Continuing. | ||||||||
| 358 | 600 | 560 | 580 | 20 | 29 | 17 | .2 | 34 | .4 | 171 | 1 | .13 | 25 | min. | |||||||
| 359 | 530 | 480 | 505 | 25 | 20 | .2 | 5 | .2 | 10 | .4 | 173 | .955 | 30 | min. | |||||||
| 360 | 530 | 350 | 480 | 505 | 25 | 20 | .2 | 2 | .8 | 5 | .6 | 173 | .955 | 35 | min. | ||||||
| 361 | 500 | 570 | 400 | 485 | 85 | 5 | .71 | 1 | .3 | 2 | .6 | 178 | .561 | ||||||||
| 364 | 700 | 640 | 670 | 30 | 22 | .3 | 2 | .3 | 4 | .6 | 174 | 1 | .02 | ||||||||
| 365 | 755 | 720 | 637 | .5 | 17 | .5 | 36 | .4 | 3 | .2 | 6 | .4 | 169 | 1 | .22 | ||||||
| 366 | 820 | 800 | 810 | 10 | 81 | 6 | .6 | 13 | .2 | 162 | 1 | .55 | Belt slipped off 2 m. later. | ||||||||
| 367 | 750 | 720 | 735 | 15 | 49 | 5 | .1 | 10 | .2 | 168 | 1 | .32 | 1 | min. | |||||||
| 368 | 750 | 720 | 735 | 15 | 49 | .1 | .2 | 168 | 1 | .32 | 5 | min. | |||||||||
| 369 | 690 | 640 | 665 | 25 | 26 | .6 | .2 | .4 | 173 | 1 | .09 | Belt slipped off 3 m. later. | |||||||||
| 370 | 610 | 560 | 585 | 25 | 23 | .4 | 14 | .4 | 28 | .8 | 173 | 1 | .05 | 1 | min. | ||||||
| 371 | 610 | 560 | 585 | 25 | 23 | .4 | .0 | .0 | 173 | 1 | .05 | 4 | min. | ||||||||
| 372 | 550 | 480 | 515 | 35 | 14 | .7 | 7 | .4 | 14 | .8 | 175 | .880 | 1 | min. | |||||||
| 373 | 550 | 410 | 480 | 515 | 35 | 14 | .7 | 2 | .3 | 4 | .6 | 175 | .880 | 5 | min. | ||||||
| 374 | 600 | 680 | 480 | 580 | 100 | 5 | .8 | 1 | .5 | 178 | .566 | ||||||||||
| 376 | 755 | 640 | 697 | .5 | 57 | .5 | 12 | .1 | 2 | .1 | 4 | .2 | 177 | .807 | |||||||
| 378 | 850 | 800 | 825 | 25 | 33 | 2 | .8 | 5 | .6 | 173 | 1 | .16 | 1 | min. | |||||||
| 379 | 850 | 800 | 825 | 25 | 33 | 3 | .5 | 173 | 1 | .16 | 5 | min. | Belt slipped off 5 m. later. | ||||||||
| 380 | 780 | 720 | 750 | 30 | 25 | 8 | .8 | 17 | .6 | 174 | 1 | .06 | 1 | min. | |||||||
| 381 | 680 | 560 | 620 | 60 | 10 | .3 | 11 | .2 | 22 | .4 | 177 | .755 | 5 | min. | |||||||
| 382 | 680 | 560 | 620 | 60 | 10 | .3 | 2 | 177 | .755 | After running 5 minutes at T - t = 560. | |||||||||||
| 383 | 730 | 640 | 685 | 45 | 15 | .2 | 2 | .5 | 176 | .886 | 1 | min. | |||||||||
| 384 | 730 | 640 | 685 | 45 | 15 | .2 | 2 | .4 | 4 | .8 | 176 | .886 | 5 | min. | |||||||
| 385 | 780 | 720 | 750 | 30 | 25 | 4 | .6 | 9 | .2 | 174 | 1 | .06 | 1 | min. | |||||||
| 388 | 780 | 550 | 720 | 750 | 30 | 25 | 8 | .8 | 17 | .6 | 174 | 1 | .06 | 5 | min. | ||||||
| 389 | 780 | 720 | 750 | 30 | 25 | 4 | 174 | 1 | .06 | 1 | min. | Belt scraped. | |||||||||
| 390 | 780 | 720 | 750 | 30 | 25 | 6 | .4 | 12 | .8 | 174 | 1 | .06 | 5 | min. | |||||||
| 391 | 730 | 640 | 685 | 45 | 15 | .2 | 3 | .7 | 7 | .4 | 176 | .886 | 1 | min. | Belt slipped off 2 m. later. | ||||||
| 392 | 730 | 550 | 640 | 685 | 45 | 15 | .2 | 3 | .9 | 7 | .8 | 176 | .886 | 5 | min. | ||||||
| 396 | 600 | 680 | 400 | 540 | 140 | 3 | .86 | 2 | .45 | 170 | .432 | 18 r. p. m. 10′′ cast-iron pulleys. | |||||||||
| 397 | 820 | 720 | 770 | 50 | 15 | .4 | 17 | .2 | 3 | .87 | 176 | .890 | |||||||||
| 398 | 750 | 640 | 695 | 55 | 12 | .6 | .5 | 3 | .37 | 177 | .874 | ||||||||||
| 399 | 700 | 560 | 630 | 70 | 9 | 9 | .4 | 2 | .17 | 177 | .711 | ||||||||||
| 400 | 670 | 480 | 575 | 95 | 6 | .05 | 4 | .5 | 1 | .12 | 178 | .579 | |||||||||
| 401 | 630 | 550 | 400 | 515 | 115 | 4 | .48 | 3 | .5 | .75 | 178 | .483 | |||||||||
| 402 | 830 | 720 | 775 | 55 | 14 | .1 | .6 | 5 | .85 | 177 | .856 | ||||||||||
| 403 | 630 | 320 | 475 | 155 | 3 | .06 | 1 | .5 | .30 | 179 | .358 | ||||||||||
| 404 | 610 | 60 | 335 | 275 | 1 | .22 | .7 | .16 | 180 | .063 | |||||||||||
| 408 | 600 | 610 | 120 | 365 | 245 | 1 | .49 | .2 | .09 | 180 | .127 | 20′′ cast-iron pulleys. 18 r. p. m. | |||||||||
| 413 | 660 | 400 | 530 | 130 | 4 | .08 | 1 | .45 | 179 | .450 | |||||||||||
| 415 | 710 | 560 | 635 | 75 | 8 | .46 | 1 | .9 | .86 | 177 | .691 | ||||||||||
| 416 | 750 | 640 | 695 | 55 | 12 | .6 | 3 | .2 | 1 | .44 | 177 | .820 | |||||||||
| 417 | 800 | 720 | 760 | 40 | 19 | 3 | .8 | 1 | .71 | 175 | .964 | ||||||||||
| 418 | 340 | 200 | 274 | 70 | 3 | .91 | .6 | .27 | 177 | .441 | |||||||||||
| 419 | 300 | 380 | 280 | 330 | 50 | 6 | .6 | 1 | .2 | .54 | 176 | .614 | |||||||||
| 421 | 450 | 400 | 425 | 25 | 17 | 3 | .2 | 1 | .44 | 173 | .938 | ||||||||||
| 423 | 515 | 480 | 497 | .5 | 17 | .5 | 28 | .4 | 4 | 1 | .8 | 169 | 1 | .13 | |||||||
| 425 | 580 | 560 | 570 | 10 | 57 | 5 | 2 | .25 | 162 | 1 | .43 | ||||||||||
| 427 | 695 | 680 | 687 | .5 | 7 | .5 | 91 | .7 | 7 | 3 | .15 | 155 | 1 | .67 | |||||||
These experiments, however, are subject to an error arising from the friction of the belt upon the board, the amount of which was not determined. All of the experiments, in fact, are subject to slight errors which were extremely difficult to eliminate or properly allow for, but an effort has been made throughout to obtain results which should approximate as closely as possible to the truth. The sum of the tensions, as determined by measuring scales, was subject only to errors in observation. This part of the apparatus was carefully tested by a horizontal pull of known amount and made to register correctly.
The difference of the tensions T - t, as computed from the reading of the scales, was measured by the force of an equivalent moment at 20′′ radius. This moment, divided by the radius of the pulley was taken to be the difference T - t.
In this calculation, it will be noticed that two slight corrections have been omitted which are opposite in effect and about equal in degree. One is the friction of the brake shaft in its bearings, which of course was not recorded on the scales, and the other is the thickness of the belt which naturally increases the effective radius of the pulley. Both of these errors are somewhat indefinite, but the correctness of the results obtained was tested in a number of cases by the sag of the belt, and the tension t, as calculated from the sag, was found to agree closely with the tension calculated by the adopted method.
As the limiting capacity of the belt was reached, the difficulty of obtaining simultaneous and accurate observations was increased by the vibrations of the scale beams. This was apparently due to irregularity in the slip, and it was only by the use of heavily loaded beams and a dash-pot that readings could then be taken at all. The dash-pot consisted of a large flat plate suspended freely in a bucket of water by a fine wire from the scale beam. This provision, however, was applied only to the scales on which the vibrations were more pronounced.
| No. of Exper- i’nt. |
Sum of Tensions T + t | T - t Work- ing. |
T | t | T ⁄ t | Per- cent- age of Slip. |
Velocity of Slip in ft. per min. |
Arc of con- tact. |
Coef- ficient of Friction. |
Dura- tion of run at time of experi- ment. |
Remarks. | ||||||||||
| Initial. | Work- ing. |
Final. | |||||||||||||||||||
| 209 | 120 | 120 | 48 | 84 | 36 | 2 | .33 | .4 | .8 | 176 | ° | .275 | |||||||||
| 210 | 140 | 80 | 110 | 30 | 3 | .67 | .6 | 1 | .2 | 175 | .426 | ||||||||||
| 211 | 168 | 120 | 144 | 24 | 6 | .9 | 1 | .8 | 174 | .590 | |||||||||||
| 212 | 198 | 160 | 179 | 19 | 9 | .42 | 1 | .6 | 3 | .2 | 170 | .756 | |||||||||
| 213 | 235 | 200 | 217 | .5 | 17 | .5 | 12 | .4 | 2 | .3 | 4 | .6 | 174 | .829 | |||||||
| 214 | 270 | 240 | 255 | 15 | 17 | 3 | .2 | 6 | .4 | 168 | .966 | [middle of belt. | |||||||||
| 215 | 310 | 280 | 295 | 15 | 19 | .7 | 5 | .1 | 10 | .2 | 168 | 1 | .02 | Sag 10′′ at | |||||||
| 216 | 345 | 122 | 320 | 332 | .5 | 12 | .5 | 25 | .8 | 9 | .4 | 18 | .8 | 164 | 1 | .13 | Finally slipped off. | ||||
| 217 | 200 | 200 | 48 | 124 | 76 | 1 | .63 | .4 | .8 | 179 | .156 | ||||||||||
| 219 | 240 | 160 | 200 | 40 | 5 | 1 | 2 | 176 | .524 | ||||||||||||
| 220 | 360 | 320 | 340 | 20 | 17 | 2 | .7 | 5 | .4 | 170 | .954 | ||||||||||
| 221 | 430 | 400 | 415 | 5 | 27 | .7 | 15 | 30 | 167 | 1 | .13 | ||||||||||
| 222 | 300 | 318 | 160 | 239 | 79 | 3 | .03 | .8 | 1 | .6 | 179 | .354 | |||||||||
| 223 | 350 | 240 | 295 | 55 | 5 | .36 | 1 | .2 | 2 | .4 | 177 | .543 | |||||||||
| 224 | 400 | 320 | 360 | 40 | 9 | 2 | 4 | 175 | .719 | ||||||||||||
| 225 | 470 | 440 | 455 | 15 | 30 | .3 | 8 | 1 | .6 | 167 | 1 | .17 | Belt finally slipped off. | ||||||||
| 226 | 450 | 400 | 425 | 25 | 17 | 4 | 8 | 172 | .943 | 1 | m. | ||||||||||
| 227 | 450 | 400 | 425 | 25 | 17 | 8 | 16 | 172 | .943 | 5 | m. | ||||||||||
| 228 | 450 | 400 | 425 | 25 | 17 | 17 | .3 | 34 | .6 | 172 | .943 | 10 | m. | Belt slip’d off. | |||||||
| 229 | 418 | 360 | 389 | 29 | 13 | .4 | 3 | 6 | 173 | .859 | 15 | m. | Continuing. | ||||||||
| 230 | 400 | 405 | 160 | 282 | .5 | 122 | .5 | 2 | .30 | .8 | 1 | .6 | 179 | .267 | |||||||
| 232 | 455 | 320 | 387 | .5 | 67 | .5 | 5 | .74 | 1 | .4 | 2 | .8 | 177 | .566 | |||||||
| 233 | 495 | 400 | 447 | .5 | 47 | .5 | 9 | .42 | 1 | .9 | 3 | .8 | 176 | .730 | 1 | m. | |||||
| 234 | 495 | 370 | 400 | 447 | .5 | 47 | .5 | 9 | .42 | 2 | .1 | 4 | .2 | 176 | .730 | 5 | m. | ||||
| 235 | 560 | 480 | 520 | 40 | 13 | 2 | .7 | 5 | .4 | 175 | .859 | Start. | |||||||||
| 236 | 560 | 480 | 520 | 40 | 13 | 4 | .5 | 9 | 175 | .859 | 5 | m. | |||||||||
| 237 | 560 | 480 | 520 | 40 | 13 | 7 | .5 | 15 | 175 | .859 | 10 | m. | |||||||||
| 238 | 550 | 380 | 480 | 465 | 85 | 5 | .47 | 20 | 40 | 178 | .547 | 15 | m. | ||||||||
| 239 | 400 | 560 | 480 | 520 | 40 | 13 | 3 | .4 | 6 | .8 | 175 | .859 | 1 | m. | After running 5 m. without load. | ||||||
| 240 | 500 | 610 | 480 | 545 | 65 | 8 | .38 | 2 | .1 | 4 | .2 | 177 | .688 | 1 | m. | ||||||
| 241 | 610 | 480 | 545 | 65 | 8 | .38 | 2 | .5 | 5 | 177 | .688 | 5 | m. | ||||||||
| 242 | 660 | 560 | 610 | 50 | 12 | .2 | 3 | .2 | 6 | .4 | 176 | .814 | 1 | m. | |||||||
| 243 | 655 | 560 | 607 | .5 | 47 | .5 | 12 | .8 | 8 | .4 | 16 | .8 | 176 | .830 | 5 | m. | Belt slipped off 2 m. later. | ||||
| 244 | 600 | 700 | 560 | 630 | 70 | 9 | 1 | .9 | 3 | .8 | 177 | .711 | 1 | m. | |||||||
| 245 | 700 | 560 | 630 | 70 | 9 | 2 | .1 | 4 | .2 | 177 | .711 | 5 | m. | ||||||||
| 246 | 690 | 550 | 560 | 625 | 65 | 9 | .69 | 2 | .3 | 4 | .6 | 177 | .735 | 10 | m. | ||||||
| 247[II-221] | 600 | 750 | 600 | 675 | 75 | 9 | 2 | .2 | 4 | .4 | 177 | .771 | 1 | m. | |||||||
| 248 | 740 | 585 | 600 | 670 | 70 | 9 | .57 | 2 | .4 | 4 | .8 | 177 | .731 | 5 | m. | ||||||
| 249 | 600 | 770 | 640 | 705 | 65 | 10 | .8 | 2 | .5 | 5 | 177 | .770 | 1 | m. | |||||||
| 250 | 765 | 640 | 702 | .5 | 62 | .5 | 11 | .2 | 3 | .5 | 7 | 177 | .782 | 5 | m. | ||||||
| 251 | 770 | 600 | 640 | 685 | 85 | 8 | .06 | 4 | .2 | 8 | .4 | 178 | .672 | 10 | m. | ||||||
| 252 | 600 | 790 | 680 | 735 | 55 | 13 | .4 | 4 | .3 | 8 | .6 | 176 | .845 | 1 | m. | [lat. Pul. warm. | |||||
| 253 | 790 | 680 | 735 | 55 | 13 | .4 | 6 | .3 | 12 | .6 | 176 | .845 | 5 | m. | Belt sl. off 2 m. | ||||||
| 254 | 100 | 100 | 44 | 72 | 28 | 2 | .57 | .6 | 1 | .2 | 176 | .307 | Belt scraped. | ||||||||
| 256 | 160 | 120 | 140 | 20 | 7 | 2 | .1 | 4 | .2 | 172 | .648 | ||||||||||
| 257 | 200 | 160 | 180 | 20 | 9 | 4 | 8 | 171 | .736 | ||||||||||||
| 258 | 230 | 200 | 215 | 15 | 14 | .3 | 6 | .6 | 13 | .2 | 168 | .907 | 1 | m. | |||||||
| 259 | 230 | 100 | 200 | 215 | 15 | 14 | .3 | 7 | .2 | 14 | .4 | 168 | .907 | 5 | m. | ||||||
| 261 | 100 | 100 | 44 | 72 | 28 | 2 | .57 | .6 | 1 | .2 | 176 | .307 | Belt dres’d with preparation recommend’d by maker. | ||||||||
| 263 | 160 | 120 | 140 | 20 | 7 | 2 | .8 | 5 | .6 | 172 | .648 | ||||||||||
| 264 | 200 | 160 | 180 | 20 | 9 | 5 | .1 | 10 | .2 | 171 | .736 | ||||||||||
| 265 | 230 | 200 | 215 | 15 | 14 | .3 | 7 | .3 | 14 | .6 | 168 | .907 | 1 | m. | |||||||
| 266 | 230 | 200 | 215 | 15 | 14 | .3 | 7 | .9 | 15 | .8 | 168 | .907 | 5 | m. | |||||||
| 267 | 270 | 240 | 255 | 15 | 17 | 10 | .7 | 21 | .4 | 168 | .966 | 1 | m. | Belt slipped off 3 m. later. | |||||||
| 268 | 300 | 350 | 240 | 295 | 55 | 5 | .36 | 1 | .4 | 2 | .8 | 177 | .544 | ||||||||
| 269 | 400 | 320 | 360 | 40 | 9 | 3 | 6 | 175 | .719 | ||||||||||||
| 270 | 450 | 400 | 425 | 25 | 17 | 6 | .8 | 13 | .6 | 172 | .943 | 1 | m. | Belt slipped off 3 m. later. | |||||||
| 271 | 418 | 360 | 389 | 29 | 13 | .4 | 8 | .8 | 17 | .6 | 173 | .859 | 1 | m. | |||||||
| 272 | 418 | 360 | 389 | 29 | 13 | .4 | 15 | .6 | 31 | .2 | 173 | .859 | 5 | m. | Belt slipped off 2 m. later. | ||||||
| 273 | 600 | 700 | 560 | 630 | 70 | 9 | 6 | .3 | 12 | .6 | 177 | .711 | |||||||||
| 274 | 650 | 480 | 565 | 85 | 6 | .65 | 3 | .1 | 6 | .2 | 178 | .610 | 1 | m. | |||||||
| 275 | 650 | 480 | 565 | 85 | 6 | .65 | 3 | .9 | 7 | .8 | 178 | .610 | 5 | m. | |||||||
| 276 | 650 | 480 | 565 | 85 | 6 | .65 | 4 | .4 | 8 | .8 | 178 | .610 | 10 | m. | |||||||
| 277 | 600 | 652 | 400 | 526 | 126 | 4 | .17 | 1 | .4 | 2 | .8 | 178 | .460 | One day later. | |||||||
| 279 | 715 | 560 | 637 | .5 | 77 | .5 | 8 | .23 | 2 | .4 | 4 | .8 | 177 | .682 | |||||||
| 280 | 705 | 560 | 632 | .5 | 72 | .5 | 8 | .72 | 2 | .8 | 5 | .6 | 177 | .701 | |||||||
| 281 | 700 | 560 | 560 | 630 | 70 | 9 | 3 | 6 | 177 | .711 | |||||||||||
| 282 | 560 | 750 | 640 | 695 | 55 | 12 | .6 | 4 | .1 | 8 | .2 | 176 | .824 | 1 | m. | ||||||
| 283 | 735 | 535 | 640 | 682 | .5 | 47 | .5 | 14 | .3 | 22 | 44 | 176 | .866 | 5 | m. | Belt slipp’d off. | |||||
| 284 | 770 | 640 | 705 | 65 | 10 | .7 | 5 | .4 | 10 | .8 | 177 | .767 | 1 | m. | After 3 min. intermission. | ||||||
| 285 | 300 | 350 | 240 | 295 | 55 | 5 | .36 | 1 | .2 | 2 | .4 | 177 | .543 | Temp. 52°. | |||||||
| 286 | 400 | 320 | 360 | 40 | 9 | 1 | .8 | 3 | .6 | 175 | .719 | ||||||||||
| 287 | 430 | 360 | 395 | 35 | 11 | .3 | 2 | .7 | 5 | .4 | 174 | .798 | |||||||||
| 289 | 465 | 400 | 432 | .5 | 32 | .5 | 13 | .3 | 5 | .3 | 10 | .6 | 174 | .852 | |||||||
| 290 | 455 | 400 | 427 | .5 | 27 | .5 | 15 | .5 | 7 | .3 | 14 | .6 | 173 | .907 | |||||||
| 291 | 460 | 400 | 430 | 30 | 14 | .3 | 11 | .6 | 23 | .2 | 173 | .881 | |||||||||
| 292 | 100 | 100 | 44 | 72 | 28 | 2 | .57 | .5 | 1 | 176 | .307 | ||||||||||
| 293 | 125 | 80 | 102 | .5 | 22 | .5 | 4 | .55 | .8 | 1 | .6 | 173 | .502 | ||||||||
| 294 | 165 | 120 | 142 | .5 | 22 | .5 | 6 | .33 | 1 | .2 | 2 | .4 | 173 | .611 | |||||||
| 295 | 200 | 160 | 180 | 20 | 9 | 2 | .1 | 4 | .2 | 171 | .736 | ||||||||||
| 296 | 230 | 200 | 215 | 15 | 14 | .3 | 3 | .4 | 6 | .8 | 168 | .907 | |||||||||
| 297 | 230 | 200 | 215 | 15 | 14 | .3 | 3 | .9 | 7 | .8 | 168 | .907 | |||||||||
| 298 | 100 | 270 | 240 | 225 | 15 | 17 | 5 | .7 | 11 | .4 | 168 | .966 | 1 | m. | |||||||
| 299 | 270 | 240 | 255 | 15 | 17 | 7 | .6 | 15 | .2 | 168 | .966 | 5 | m. | [4 m. later. | |||||||
| 300 | 270 | 240 | 255 | 15 | 17 | 9 | .3 | 18 | .6 | 168 | .966 | 10 | m. | Belt slipped off | |||||||
| 303 | 100 | 110 | 40 | 75 | 35 | 2 | .14 | .1 | .4 | 177 | .246 | 20 in. pulleys. | |||||||||
| 304 | 132 | 80 | 106 | 26 | 4 | .08 | .4 | 1 | .6 | 174 | .463 | ||||||||||
| 305 | 160 | 120 | 140 | 20 | 7 | 1 | 4 | 172 | .648 | ||||||||||||
| 306 | 195 | 160 | 177 | .5 | 17 | .5 | 10 | .1 | 1 | .9 | 7 | .6 | 169 | .814 | |||||||
| 307 | 230 | 200 | 215 | 15 | 14 | .3 | 3 | 12 | 168 | .907 | 1 | m. | |||||||||
| 308 | 230 | 90 | 200 | 215 | 15 | 14 | .3 | 3 | .5 | 14 | 168 | .907 | 5 | m. | |||||||
| 309 | 270 | 240 | 255 | 15 | 17 | 4 | .5 | 18 | 168 | .966 | 1 | m. | |||||||||
| 310 | 270 | 240 | 255 | 15 | 17 | 5 | .8 | 23 | .2 | 168 | .966 | 5 | m. | ||||||||
| 311 | 270 | 240 | 255 | 15 | 17 | 6 | .2 | 24 | .8 | 168 | .966 | 10 | m. | ||||||||
| 312 | 270 | 240 | 255 | 15 | 17 | 6 | .2 | 24 | .8 | 168 | .966 | 15 | m. | Temp. 56°. | |||||||
| 313 | 270 | 240 | 255 | 15 | 17 | 2 | 8 | 168 | .966 | 1 | m. | ||||||||||
| 314 | 270 | 240 | 255 | 15 | 17 | 2 | .1 | 8 | .4 | 168 | .966 | 5 | m. | Temp. 42°. | |||||||
| 315 | 305 | 280 | 292 | .5 | 12 | .5 | 23 | .4 | 3 | .4 | 13 | .6 | 165 | 1 | .09 | 1 | m. | ||||
| 316 | 305 | 100 | 280 | 292 | .5 | 12 | .5 | 23 | .4 | 3 | .5 | 14 | 165 | 1 | .09 | 5 | m. | ||||
| 317 | 100 | 335 | 320 | 327 | .5 | 7 | .5 | 43 | .7 | 5 | .2 | 20 | .8 | 152 | 1 | .42 | 1 | m. | |||
| 318 | 335 | 320 | 327 | .5 | 7 | .5 | 43 | .7 | 6 | .5 | 26 | 152 | 1 | .42 | 5 | m. | |||||
| 319 | 300 | 380 | 320 | 350 | 30 | 11 | .7 | 1 | .3 | 5 | .2 | 173 | .814 | 1 | m. | ||||||
| 320 | 380 | 320 | 350 | 30 | 11 | .7 | 1 | .4 | 5 | .6 | 173 | .814 | 5 | m. | |||||||
| 321 | 440 | 400 | 420 | 20 | 21 | 2 | .1 | 8 | .4 | 170 | 1 | .03 | 1 | m. | |||||||
| 322 | 440 | 260 | 400 | 420 | 20 | 21 | 2 | .4 | 9 | .6 | 170 | 1 | .03 | 5 | m. | ||||||
| 323 | 300 | 480 | 440 | 460 | 20 | 23 | 2 | .8 | 11 | .2 | 170 | 1 | .06 | 1 | m. | Temp. 46°. | |||||
| 324 | 480 | 285 | 440 | 460 | 20 | 23 | 3 | 12 | 170 | 1 | .06 | 5 | m. | ||||||||
| 325 | 510 | 480 | 495 | 15 | 33 | 3 | .2 | 12 | .8 | 167 | 1 | .20 | 1 | m. | [lat. Pul. warm. | ||||||
| 326 | 510 | 480 | 495 | 15 | 33 | 5 | 20 | 167 | 1 | .20 | 5 | m. | Belt sl. off 5 m. | ||||||||
A peculiar and important feature of Tables III. and IV. is the effect of time upon the percentage of slip. In previous experiments the percentage of slip was measured at once after the load was applied, but it was accidentally discovered that repeated measurements seldom agreed, and investigation showed that these discrepancies were principally due to the duration of the experiment. The continual slipping of the belt was found to cause a deposit of a thick black substance upon the surface of the pulley, which, acting as a lubricant, continued to increase the slip still further.
Upon removing the load on brake-wheel, this deposit would be again absorbed by the belt, and the original adhesion would be restored. The temperature was also found to affect the slipping, and, in general, the colder the weather the slower would this deposit take place.
Experiments 353 to 360 inclusive were made to determine the limit at which the belt would run continuously without increasing its percentage of slip. After the pulleys had become well coated and the slip had reached a high per cent., the load on the brake-wheel was gradually removed until a marked improvement was reached, as shown by experiments 359 and 360. The highest allowable coefficient of friction for this belt is therefore estimated to be somewhere between 1.13 and .995, or we may safely say 1. The highest coefficient obtained was 1.67, but, of course, this was temporary. The diameter of the pulley also appears to affect the coefficient of friction to some extent. This is especially to be noticed at the very slow speed of 18 revolutions per minute on 10 in. and 20 in. pulleys, where the adhesion on the 20 in. pulleys is decidedly greater; but, on the other hand, at 160 revolutions per minute the adhesion on the 10 in. pulleys is often as good, and sometimes better, than appears for the 20 in. at the same velocity of sliding.
It might be possible to determine the effect of pulley diameter upon adhesion for a perfectly dry belt, where the condition of its surface remains uniform, but for belts as ordinarily used it would be very difficult, on account of the ever-changing condition of surface produced by slip and temperature. It is generally admitted that the larger the diameter the greater the adhesion for any given tension, but no definite relation has ever been established, nor, indeed, does it seem possible to do so except by the most elaborate and extensive experiments.
It should be observed, however, that such a variation, if true, implies a corresponding variation in the coefficients of friction for different intensities of pressure upon the same pulleys, and that, consequently, our experiments should show higher coefficients under the lighter loads for the same velocity of sliding. Referring to Table II., where the condition of the belt is dry and uniform for a large range of tensions, we find that this inference is generally sustained, although there are some few exceptions.
Experiment 106 may be compared with 116, and 112 with 133, also 108, 113, and 135, all showing great reductions in the coefficients of friction for increments in tension. The exceptions are all to be found under the smallest velocities of sliding, and appear only in the third decimal place, so that the weight of their record against the probability of such a law is light. By a similar inference it should also follow that a wide belt would drive a little more at a given tension than a narrow one, on account of the reduction in pressure per square inch against the pulley. The mean intensity of pressure of a belt against its pulley may be considered as proportional to the sum of the tensions divided by the product of pulley diameter and width of belt, and an analysis of the experiments referred to will show the relation there existing between intensity of pressure and coefficient of friction.
If we let Ι = intensity of pressure, and φ = coefficient of friction, we shall find that φ is approximately proportional to Ι-.15, or, in other words that doubling the width of belt or diameter of pulley would apparently increase the coefficient of friction about 10 per cent. of its original value. This relation is not proved, of course, and it is given only as a suggestion toward the solution of the question. If the coefficient of friction does vary with the intensity of pressure, the problem of determining the driving power of a belt on strictly mathematical principles will indeed be complicated.
The coefficient of friction in the tables has been calculated by a well-known formula, developed upon the assumption of a uniform coefficient around the arc of contact, but this could no longer be considered as correct if the coefficient is known to vary with the pressure. Referring from Table II. to Table III., we shall find at once the proof and contradiction of the inferences drawn from Table II., and we are left as much in the dark as ever respecting the value of pressure intensity.
Practical millwrights all know, or think they know, that an increase of pulley diameter increases the drive, and it is a matter of common observation that when large and small pulleys are connected by a crossed belt, the smaller pulley will invariably slip first.
[II-222]On one side a great deal of testimony can be adduced to show that pressure intensity should be an important factor in the theory of belt transmission, and, on the other hand, we have strong evidence to the contrary. I may refer, in this connection, to the experiments of Mr. Holman in Journal of Franklin Institute for September, 1885, in which there is no indication that the coefficient of friction varies at all with the pressure. The coefficients obtained by Mr. Holman follow the variations in slip like our own, and it gives us pleasure to observe that our general results and conclusions are so strongly corroborative of each other. There is at the same time a great difference in the methods pursued in arriving at the same results. In his experiments, the velocity of sliding was the fixed condition upon which the coefficient of friction was determined, while, in ours, the conditions were those of actual practice in which the percentage of slip was measured. Our least amount of slip, with a dry belt running at the extremely slow speed of 90 feet per minute, was 1.08 inches, and ten times this would be perfectly proper and allowable. A great many of Mr. Holman’s experiments are taken at rates below 1′′ per minute, and the coefficients obtained are very much below the average practice, as himself seems to believe.
The velocity of sliding which may be assumed in selecting a proper coefficient is directly proportional to the belt speed, and may safely be estimated at .01 of that speed. For a pair of pulleys we should have .01 on each pulley, and therefore .02 for slip. Few belts run slower than 200 or 300 ft. per minute, and consequently a slip of less than 2 or 3 ft. per minute need seldom be considered. Another point of difference which may possibly affect the coefficients obtained, is that, in Mr. Holman’s case the same portion of belt surface was subject to continuous friction, while in ours, the friction was spread over the belt at successive portions as in actual work. This we consider a new and important feature of our experiments. As a matter of practical importance, care was taken to observe, as nearly as possible, the maximum slip which might safely take place before a belt would be thrown from its pulley. A number of observations taken throughout the experiments led to the final conclusion that 20 per cent. of slip was as much as could safely be admitted. This information has been found of value in cases where work is done intermittently by a fly-wheel and the belt has to restore the speed of the wheel. It cannot be said in regard to a maximum value of [phi] that any was determined or even indicated, although it is certain that the increase at high rates of slip becomes less rapid.
We have now seen that the driving power of a leather belt depends upon such a variety of conditions, that it would be manifestly impracticable if not impossible to correlate them all, and it is thought better to admit the difficulties at once than to involve the subject in a labyrinth of formulæ which life is too short to solve.
The relative value of pulley diameters may vary with different belts, and all that can be expected or desired is some general expression covering roughly the greatest number of cases. Our apparatus did not admit of extensive variations in this respect, and our attention was given principally to the question of slip.
The coefficients given in Table III. are remarkably high, and show a great superiority for the rawhide over tanned leather in point of adhesion. The belt in question was very soft and pliable, but a little twisted from use on a cone pulley where it had rubbed against one side. It is not desirable, on account of its soft and adhesive nature, to use this kind of belt where frequent shifting is required, and when used on cone pulleys it is liable to climb and stretch against the side of the cone; but for a plain straight connection, there seems to be little room for improvement. Table IV. contains the results of similar experiments upon an oak-tanned leather belt made by Chas. A. Shieren & Co. Here the coefficients are much smaller than those given in Table III., and there is quite a marked difference between the coefficients for 10 in. and 20 in. pulleys.
As before noticed, the outside temperature has its effect, and it is probable that much lower results would have been obtained had the experiments been made in the heat of midsummer. The high coefficients obtained, together with the rapid increase of tension, show that the pulling power of a long horizontal belt must, in many cases, be limited by its strength rather than by its adhesion.
Table V. gives the results of experiments upon a light planer belt at very slow and very high speeds. As would naturally be expected, much higher coefficients were found at the high speed on account of the greater velocity of sliding.
| No. of Exper- i’nt. |
Sum of Tensions T + t | T - t Work- ing. |
T | t | T ⁄ t | Per- cent- age of Slip. |
Velocity of Slip in ft. per min. |
Arc of con- tact. |
Coef- ficient of Friction. |
Dura- tion of run at time of experi- ment. |
Remarks. | ||||||||
| Initial. | Work- ing. |
Final. | |||||||||||||||||
| 429 | 100 | 110 | 40 | 75 | 35 | 2 | .14 | 1 | .2 | .54 | 179 | ° | .243 | 18 r.p.m. | |||||
| 430 | 115 | 60 | 87 | .5 | 27 | .5 | 3 | .18 | 6 | .1 | 2 | .75 | 178 | .372 | |||||
| 431 | 118 | 70 | 94 | 24 | 3 | .92 | 16 | .5 | 7 | .42 | 178 | .440 | |||||||
| 432 | 105 | 20 | 62 | .5 | 42 | .5 | 1 | .47 | .3 | .14 | 179 | .123 | |||||||
| 433 | 112 | 50 | 81 | 31 | 2 | .61 | 3 | .5 | 1 | .57 | 178 | .309 | |||||||
| 435 | 200 | 204 | 40 | 132 | 82 | 1 | .61 | .2 | .09 | 180 | .152 | ||||||||
| 436 | 206 | 60 | 133 | 73 | 1 | .82 | .7 | .32 | 180 | .191 | |||||||||
| 437 | 208 | 80 | 144 | 64 | 2 | .25 | 1 | .8 | .81 | 179 | .260 | ||||||||
| 438 | 210 | 100 | 155 | 55 | 2 | .82 | 3 | .7 | 1 | .66 | 179 | .332 | |||||||
| 439 | 212 | 120 | 166 | 40 | 3 | .61 | 7 | .7 | 3 | .47 | 179 | .411 | |||||||
| 440 | 215 | 140 | 177 | .5 | 37 | .5 | 4 | .73 | 18 | .4 | 8 | .28 | 179 | .497 | |||||
| 442 | 100 | 110 | 60 | 85 | 25 | 3 | .40 | .3 | 7 | .12 | 178 | .394 | 950 r.p.m. | ||||||
| 443 | 120 | 80 | 100 | 20 | 5 | .7 | 16 | .62 | 178 | .518 | |||||||||
| 445 | 125 | 90 | 107 | .5 | 17 | .5 | 6 | .14 | 3 | 71 | .25 | 177 | .587 | Start. | |||||
| 446 | 125 | 90 | 107 | .5 | 17 | .5 | 6 | .14 | 25 | 593 | .7 | 177 | .587 | min. | |||||
| 448 | 200 | 200 | 80 | 140 | 60 | 2 | .33 | .4 | 9 | .5 | 179 | .271 | |||||||
| 449 | 200 | 100 | 150 | 50 | 3 | .5 | 11 | .87 | 179 | .352 | |||||||||
| 450 | 195 | 175 | 120 | 157 | .5 | 37 | .5 | 4 | .20 | .8 | 19 | 179 | .459 | ||||||
| 451 | 150 | 175 | 120 | 147 | .5 | 27 | .5 | 5 | .36 | .9 | 21 | .38 | 178 | .540 | |||||
| 452 | 135 | 160 | 120 | 140 | 20 | 7 | 20 | 475 | 178 | .626 | |||||||||
It may here be mentioned that the sum of the tensions was the horizontal pressure of the belt against the pulleys, and that no allowance was necessary for the effect of the centrifugal force. At the speed here used, the tension indicated in the belt at rest was about 50 lbs. greater than when in motion.
| No. ex- per’ts in av’ge. |
Per- cent age of Slip. |
Veloc. of Sl. in ft. per m. |
Coeffi- cient of Fric- tion. |
Belt. | Pulleys. | Remarks. | |||||||
| 3 | 1 | .4 | 5 | .6 | .661 | 51⁄2′′ old belt. | Table | I | 20′′ diam. pap. cov’d | Belt in | nor. w’k’g | con. | |
| 2 | 1 | .7 | 6 | .8 | .44 | 51⁄2′′ old belt. | „ | I | 20′′ di. cast-iron sur. | „ | „ | „ | |
| 2 | 1 | .55 | 6 | .2 | .575 | 51⁄2′′ old belt. | „ | I | 20′′ di. cast-iron sur. | Belt dressed with “Beltiline.” |
|||
| 5 | 1 | .7 | 6 | .8 | .452 | 21⁄4′′ dbl. belt. | „ | II | 20′′ di. cast-iron sur. | B’t dry as us. on plan’r. |
|||
| 2 | 1 | .5 | 6 | .818 | 21⁄4′′ dbl. belt. | „ | II | 20′′ di. cast-iron sur. | Belt dressed with “Sankey’s Life of Leather.” |
||||
| 2 | 1 | .7 | 6 | .8 | 1 | .38 | 4′′ r’hide b. | „ | III | 20′′ di. cast-iron sur. | Belt in | nor. w’k’g | con. |
| 11 | 1 | .8 | 3 | .6 | .861 | 4′′ r’hide b. | „ | III | 10′′ diameter. | „ | „ | „ | |
| 1 | 2 | .45 | .432 | 4′′ r’hide b. | „ | III | 10′′ diameter. | „ | „ | „ | |||
| 1 | 1 | .9 | .86 | .691 | 4′′ r’hide b. | „ | III | 20′′ diameter. | „ | „ | „ | ||
| 7 | 1 | .94 | 3 | .88 | .617 | 4′′ o.tan’d b. | „ | IV | 10′′ diameter. | „ | „ | „ | |
| 4 | 1 | .85 | 7 | .40 | .906 | 4′′ o.tan’d b. | „ | IV | 20′′ diameter. | „ | „ | „ | |
| 2 | 1 | .5 | .67 | .251 | 2′′ o.tan’d b. | „ | V | 20′′ diameter. | B’t dry | as us. on | plan’r. | ||
| 2 | .8 | 38 | .529 | 2′′ o.tan’d b. | „ | V | 20′′ diameter. | „ | „ | „ | |||
The conclusion to be drawn from this series of experiments is the great importance of high speed in the economy of belt transmission. The friction of belts on pulleys is evidently dependent on the velocity of sliding, and, as a general rule, the greater the velocity the greater the friction. There are but few apparent exceptions to this rule, and investigation of them has led to the inference that in all such cases, the condition of the belt or pulley surface had undergone a change either by heating or by deposit from the belt on the pulley. The percentage of slip is the measure of the power lost in transmission by the belt itself, and the[II-223] higher the speed the less this becomes. There is a limit, however, to the power which may be transmitted as the speed is increased, and this limit is caused by the reduction in pressure against the pulley arising from the action of centrifugal force.
This point has been clearly demonstrated in a paper read before this Society by Mr. A. F. Nagle on the “Horse Power of Leather belts,”[43] and the formula there developed is written thus:
| HP = CVtw(S - .012 V2) ÷ 550, | (1.) |
in which C is a constant to be determined from the arc of contact and coefficient of friction as expressed in the equation:
| C = 1 - 10-.00758fα, | (2.) | ||||
| V | = | velocity of belt in feet per second. | |||
| t | = | thickness | of the belt | in inches. | |
| w | = | width | „ | „ | |
| S | = | working strength of leather in lbs. per square inch. | |||
| f | = | coefficient of friction. | |||
| α | = | arc of contact in degrees. | |||
[43] Transactions A. S. M. E., Vol. II., page 91. See also Mr. Nagle’s Tables I., II., and III., in Appendix VI. to this paper for values of C and H.P.
The velocity at which the maximum amount of power can be transmitted by any given belt is independent of its arc of contact and coefficient of friction, and depends only upon the working strength of the material and its specific gravity.
From equation (1.) we obtain for the maximum power of leather belts the condition:
| V = √(28S), | (3.) |
and for any other material whose specific gravity is y, we find
| V = 5 × √S/y, | (4.) |
The coefficient of friction .40, adopted by Mr. Nagle, appears from these experiments to be on the safe side for all working requirements, except in cases where dry belts are run at slow speeds.
If we assume 2 per cent. as the greatest allowable slip, and select within this limit the coefficient corresponding to the nearest approximations to it, we can form some idea of the coefficients which can be relied upon at different speeds.
Table VI. gives the average results obtained for this maximum allowance of slip, and shows an extreme variation in the coefficient of friction from .251 for a dry oak-tanned belt at the slow speed of 90 feet per minute to 1.38 for a rawhide belt at the moderate speed of 800 feet per minute.
For continuous working, it is probable that the coefficient 1.38 is too high, but still it is certain that a coefficient of 1.00 can be steadily maintained for an indefinite length of time, and we may say that in actual practice the coefficient of friction may vary from .25 to 1.00 under good working conditions. This extreme variation in the coefficient of friction does not give rise, as might at first be supposed, to such a great difference in the transmission of power. It will be seen by reference to formula (1.) that the power transmitted for any given working strength and speed is limited only by the value of C, which depends upon the arc of contact and the coefficient of friction.
For the usual arc of contact, 180°, the power transmitted when f = .25 is about 24 per cent. less than when f = .40, and when f = 1.00, the power transmitted is about 33 per cent. more, from which it appears that in extreme cases the power transmitted may be 1⁄4 less or 1⁄3 more than will be found from the use of Mr. Nagle’s coefficient of .40.
| No. of experi- m’nt. |
Ten- sion. T + t |
Moment in inch lbs. |
Dia- meter of pul- leys. |
Revo- lut’s per min. |
Width of Belt. |
Thick- ness of Belt. |
Manner of Driving. | Remarks. | |
| 1 | 100 | 20 | 20′′ | 160 | 6′′ | 7⁄32′′ | Straight open belt. | ||
| 3 | 300 | 25 | |||||||
| 5 | 500 | 30 | |||||||
| 7 | 700 | 35 | |||||||
| 10 | 1000 | 45 | |||||||
| 45 | 100 | 15 | |||||||
| 47 | 300 | 22 | .5 | ||||||
| 49 | 500 | 27 | .5 | ||||||
| 51 | 700 | 35 | |||||||
| 54 | 1000 | 50 | |||||||
| 163 | 100 | 17 | .5 | 20′′ | 160 | 4′′ | 9⁄32′′ | Straight open belt. | |
| 165 | 300 | 25 | |||||||
| 167 | 500 | 30 | |||||||
| 169 | 700 | 35 | |||||||
| 194 | 100 | 17 | .5 | 10′′ | 160 | 4′′ | 5⁄16′′ | Straight open belt. | |
| 196 | 300 | 27 | .5 | ||||||
| 198 | 500 | 40 | |||||||
| 200 | 700 | 55 | |||||||
| 202 | 900 | 70 | |||||||
| 203 | 1000 | 80 | |||||||
| 327 | 100 | 20 | 10′′ | 18 | 4′′ | 5⁄16′′ | Straight open belt. | ||
| 328 | 1000 | 80 | |||||||
| 393 | 100 | 20 | |||||||
| 394 | 1000 | 100 | |||||||
| 395 | 600 | 60 | |||||||
| 405 | 100 | 20 | 20′′ | 18 | 4′′ | 9⁄32′′ | Straight open belt. | ||
| 406 | 1000 | 160 | |||||||
| 407 | 600 | 100 | |||||||
| 428 | 100 | 20 | 20′′ | 18 | 2′′ | 9⁄32′′ | Straight open belt. | ||
| 434 | 200 | 25 | |||||||
| 441 | 100 | 25 | 20′′ | 950 | 2′′ | 3⁄16′′ | Straight open belt. | ||
| 447 | 200 | 30 | |||||||
| 453 | 100 | 25 | 20′′ | 160 | 6′′ | 7⁄32′′ | Crossed belt. | 14′ 6′′ between pulleys. | |
| 454 | 500 | 60 | |||||||
| 455 | 1000 | 110 | 14′ 6′′ bet. pul’ys. | ||||||
| 459 | 100 | 15 | 20′′ | 160 | 6′′ | 7⁄32′′ | Straight open belt. | 14′ 6′′ between pulleys. | |
| 460 | 500 | 25 | |||||||
| 461 | 1000 | 65 | |||||||
| 462 | 100 | 25 | 20′′ | 160 | 6′′ | 7⁄32′′ | Straight open belt. | With 8′′ tightener. | |
| 463 | 500 | 60 | |||||||
| 464 | 1000 | 110 | |||||||
| 465 | 100 | 45 | 20′′ | 160 | 6′′ | 7⁄32′′ | Crossed belt. | 8 feet between pulleys. | |
| 466 | 500 | 105 | |||||||
| 467 | 1000 | 180 | |||||||
| 470 | 100 | 25 | 20′′ | 160 | 6′′ | 7⁄32′′ | Quarter turn belt on 16′′ diameter mule pulleys. | ||
| 471 | 500 | 80 | |||||||
| 472 | 750 | 145 | |||||||
| 473 | 1000 | 250 | |||||||
| 474 | 750 | 170 | |||||||
| 475 | 500 | 110 | |||||||
| 476 | 1000 | 220 | |||||||
| 477 | 1000 | 140 | 20′′ | 160 | 6′′ | 7⁄32′′ | Quarter turn belt on 16′′ diameter mule pulleys. | Freshly oiled. | |
| 478 | 750 | 100 | |||||||
| 479 | 500 | 70 | |||||||
| 480 | 100 | 20 | |||||||
| 481 | 50 | 60 | 20′′ | 160 | 6′′ | 7⁄32′′ | Quarter turn on 16′′ mule pulleys. | Belt rub. against low. guide m. pul. | |
| 482 | 25 | 120 | |||||||
| 483 | 100 | 20 | 20′′ | 160 | 6′′ | 7⁄32′′ | Quarter turn on 16′′ mule pulleys. | Well oiled, after a run of 2 hrs. at T + t = 100. | |
| 484 | 500 | 50 | |||||||
| 485 | 750 | 70 | |||||||
| 486 | 1000 | 105 | |||||||
| 495 | 250 | 30 | 20′′ | 160 | 6′′ | 7⁄32′′ | Half turn belt on 16′′ mule pulleys. | ||
| 496 | 500 | 50 | |||||||
| 497 | 750 | 90 | |||||||
| 498 | 1000 | 170 | |||||||
| 503 | 1000 | 260 | 20′′ | 160 | 6′′ | 7⁄32′′ | Quarter twist. | 10 feet between pulleys. | |
| 504 | 750 | 190 | |||||||
| 505 | 500 | 130 | |||||||
| 506 | 250 | 80 | |||||||
| 507 | 100 | 30 | |||||||
| 513 | 100 | 50 | 20′′ | 160 | 6′′ | 7⁄32′′ | Quarter twist. | 7′ 6′′ between pulleys. | |
| 514 | 250 | 105 | |||||||
| 515 | 500 | 200 | |||||||
| 516 | 750 | 290 | |||||||
| 517 | 1000 | 380 | |||||||
| 523 | 100 | 25 | 20′′ | 160 | 4′′ | 1⁄4′′ | Quarter twist. | 10 feet between pulleys. | |
| 524 | 250 | 50 | |||||||
| 525 | 500 | 95 | |||||||
| 526 | 750 | 145 | |||||||
| 527 | 1000 | 210 | |||||||
| 528 | 100 | 65 | 20′′ | 160 | 4′′ | 1⁄4′′ | Quarter twist. | 6 feet between pulleys. | |
| 529 | 250 | 135 | |||||||
| 530 | 500 | 245 | |||||||
| 531 | 750 | 380 | |||||||
| 533 | 100 | 25 | 20′′ | 160 | 6′′ | 7⁄32′′ | Quarter twist. | 16′ 6′′ between pulleys. | |
| 534 | 250 | 40 | |||||||
| 535 | 500 | 75 | |||||||
| 536 | 750 | 105 | |||||||
| 537 | 1000 | 165 | |||||||
| 539[II-224] | 1000 | 130 | 20′′ | 160 | 6′′ | 7⁄32′′ | Quarter twist with 16′′ diameter carrying pulley. | 7′6′′ between pulleys. | |
| 540 | 750 | 110 | |||||||
| 541 | 500 | 90 | |||||||
| 542 | 250 | 60 | |||||||
| 543 | 100 | 40 | |||||||
| 544 | 100 | 30 | |||||||
| 545 | 250 | 55 | |||||||
| 546 | 500 | 90 | |||||||
| 547 | 750 | 120 | |||||||
| 548 | 1000 | 170 | |||||||
| 569 | 100 | 25 | 20′′ | 160 | 6′′ | 7⁄32′′ | Straight open belt. | ||
| 571 | 500 | 55 | |||||||
| 572 | 750 | 70 | |||||||
| 573 | 1000 | 90 | |||||||
The percentage of slip is the most important factor affecting the efficiency of belt transmission, but in addition to this we have journal friction, the resistance of the air, and with crossed belts the friction of the belt upon itself. These have been termed internal resistances, and their values for some of the most common arrangements of pulleys are given in Table VII. From this table it appears that the moment required to run a straight belt varies from 15 to 25 inch lbs. at 100 lbs. tension for all speeds. At 160 revolutions per minute and 1,000 lbs. tension, the required moment varied from 45 to 90 inch lbs., and at 18 revolutions per minute and at the same tension it varied from 80 to 150 inch lbs.
From the average of these quantities we find the moment of resistance to be expressed by the following formulæ for straight open belts between 2′′ journals:
At 160 r. p. m.:
| M = .053 S + 14.7, | (5.) |
At 18 r. p. m.:
| M = .11 S + 9, | (6.) |
in which
| M | = | moment of resistance in inch lbs. |
| S | = | sum of tensions. |
When a crossed belt does not rub upon itself, the resistance is the same as for an open belt.
The resistance offered by the introduction of carrying pulleys and tighteners is appreciable, and depends upon the pressure brought to bear against their journals. If the belt rubs against the flanges of the carrying pulleys, the resistance is very much increased, and this is often liable to occur in horizontal belts from a change of load. The friction on journals of carrying pulleys may be estimated by the formulæ already given if we substitute for S the pressure against their journals. In the experiments which were made upon internal resistances, the greatest resistance was offered by a quarter-twist belt 6 feet between journals on 20-inch pulleys.
The equation for this belt may be written:
| M = .35 S + 58, | (7.) |
but the introduction of a carrying pulley reduced the resistance to no more than what might be expected from the same number of journals with a straight belt.
With quarter-twist belts the resistance lies chiefly in slip, which occurs as the belt leaves the pulleys, and this naturally depends upon the distance between journals in terms of the diameters of the pulleys.
The effect of time upon the tension of the belt used in Table VIII. is plainly shown by experiments 588 to 613 inclusive, between which the pulleys remained at a fixed distance apart, and the belt slowly stretched from a tension of 380 to 280 lbs.
To estimate the efficiency of belt transmission for an average case, we may assume 40 in. lbs. as the moment of internal resistance for a belt whose tension is 500 lbs. and 40 in. lbs. statical moment = about 20 ft. lbs. per revolution. If the belt is transmitting 400 lbs. with two per cent. of slip on 20 in. pulleys, then .02 × 400 × 5 = 40 ft lbs. are lost per revolution in slip, making a total loss of 60 ft. lbs. per revolution.
| No. of experi- m’nt. |
Scales A. [44] |
Scales B. [44] |
Ten- sion T + t |
Ten- sion T - t |
T | t | Incre- m’nt of T + t |
Per- cen’e of Incre- ment. |
Date. | ||
| 578 | 93 | 101 | 194 | 16 | 105 | 89 | 0 | 5-15-1885. | |||
| 579 | 70 | 142 | 212 | 144 | 178 | 34 | 18 | ||||
| 580 | 67 | 170 | 237 | 206 | 221 | .5 | 15 | .5 | 43 | ||
| 581 | 66 | 180 | 246 | 228 | 237 | 9 | 52 | ||||
| 582 | 66 | 188 | 254 | 244 | 249 | 5 | 60 | .323 | |||
| 583 | 91 | 101 | 192 | 20 | 106 | 86 | -2 | ||||
| 584 | 202 | 210 | 412 | 16 | 214 | 214 | 0 | 5-15-1885. | |||
| 585 | 167 | 250 | 417 | 166 | 292 | .5 | 292 | .5 | 5 | ||
| 586 | 145 | 300 | 445 | 310 | 376 | .5 | 376 | .5 | 33 | .171 | |
| 587 | 185 | 195 | 380 | 20 | 200 | 200 | -32 | ||||
| 588 | 190 | 199 | 380 | 0 | 190 | 190 | 0 | 5-18-1885. | |||
| 589 | 133 | 250 | 393 | 214 | 303 | .5 | 89 | .5 | 13 | .033 | |
| 590 | 177 | 177 | 354 | 0 | 177 | 177 | 0 | 5-19-1885. | |||
| 591 | 156 | 203 | 359 | 94 | 226 | .5 | 132 | .5 | 5 | ||
| 592 | 138 | 235 | 373 | 194 | 283 | .5 | 89 | .5 | 19 | ||
| 593 | 135 | 250 | 385 | 230 | 307 | .5 | 77 | .5 | 31 | ||
| 594 | 128 | 275 | 403 | 294 | 348 | .5 | 34 | .5 | 49 | ||
| 595 | 125 | 300 | 425 | 350 | 387 | .5 | 37 | .5 | 71 | ||
| 596 | 123 | 325 | 448 | 404 | 426 | 22 | 94 | .333 | |||
| 597 | 168 | 168 | 336 | 0 | 168 | 168 | -18 | ||||
| 598 | 143 | 143 | 286 | 0 | 143 | 143 | 0 | 5-25-1885. | |||
| 599 | 140 | 148 | 288 | 16 | 152 | 136 | 2 | ||||
| 600 | 130 | 160 | 290 | 60 | 175 | 115 | 4 | ||||
| 601 | 122 | 170 | 292 | 196 | 194 | 98 | 6 | ||||
| 602 | 116 | 180 | 296 | 28 | 212 | 84 | 10 | ||||
| 603 | 112 | 190 | 302 | 156 | 229 | 73 | 16 | ||||
| 604 | 108 | 200 | 308 | 184 | 246 | 62 | 22 | ||||
| 605 | 105 | 210 | 315 | 210 | 262 | .5 | 52 | .5 | 29 | ||
| 606 | 102 | 220 | 322 | 236 | 279 | 43 | 36 | ||||
| 607 | 100 | 230 | 330 | 260 | 295 | 35 | 44 | ||||
| 608 | 99 | 240 | 339 | 282 | 310 | .5 | 28 | .5 | 53 | ||
| 609 | 98 | 250 | 348 | 304 | 326 | 22 | 62 | ||||
| 610 | 98 | 260 | 358 | 316 | 337 | 21 | 72 | ||||
| 611 | 99 | 270 | 369 | 342 | 355 | .5 | 13 | .5 | 83 | ||
| 612 | 100 | 280 | 380 | 360 | 370 | 10 | 94 | .357 | |||
| 613 | 140 | 140 | 280 | 0 | 140 | 140 | -6 | ||||
[44] Scales a recorded the reduction of the load on the testing device for vertical belts by the tension of the loose part of the belt (t.). Scales b, by that of the tight side of the belt (T).
The total power expended per revolution is about 2,000 ft. lbs., therefore .03 is lost.
Under light loads, the internal resistance, which is nearly constant in amount, may be a large percentage of the power transmitted, while under heavy loads the percentage of slip may become the principal loss.
It would be difficult to work out, or even to use, a general expression for the efficiency of belt transmission, but, from the foregoing, it would seem safe to assume that 97 per cent. can be obtained under good working conditions.
When a belt is too tight, there is a constant waste in journal friction, and when too loose, there may be a much greater loss in efficiency from slip. The allowance recommended of 2 per cent. for slip is rather more than experiment would indicate for any possible crawl or creep due to the elasticity of the belt, but in connection with this, there is probably always more or less actual slip, and we are inclined to think that in most cases this allowance may be divided into equal parts representing creep and slip proper. Under good working conditions, a belt is probably stretched about 1 per cent. on the tight side, which naturally gives 1 per cent. of creep, and to this we have added another per cent. for actual slip in fixing the limit proposed.
The indications and conclusions to be drawn from these experiments are:
1. That the coefficient of friction may vary under practical working conditions from 25 per cent. to 100 per cent.
2. That its value depends upon the nature and condition of the leather, the velocity of sliding, temperature, and pressure.
3. That an excessive amount of slip has a tendency to become greater and greater, until the belt finally leaves the pulley.
4. That a belt will seldom remain upon a pulley when the slip exceeds 20 per cent.
5. That excessive slipping dries out the leather and leads toward the condition of minimum adhesion.
6. That rawhide has much greater adhesion than tanned leather, giving a coefficient of 100 per cent. at the moderate slip of 5 ft. per minute.
[II-225]7. That a velocity of sliding equal to .01 of the belt speed is not excessive.
8. That the coefficients in general use are rather below the average results obtained.
9. That when suddenly forced to slip, the coefficient of friction becomes momentarily very high, but that it gradually decreases as the slip continues.
10. That the sum of the tensions is not constant, but increases with the load to the maximum extent of about 33 per cent. with vertical belts.
11. That, with horizontal belts, the sum of the tensions may increase indefinitely as far as the breaking strength of the belt.
12. That the economy of belt transmission depends principally upon journal friction and slip.
13. That it is important on this account to make the belt speed as high as possible within the limits of 5,000 or 6,000 ft. per minute.
14. That quarter-twist belts should be avoided.
15. That it is preferable in all cases, from considerations of economy in wear on belt and power consumed, to use an intermediate guide pulley, so placed that the belt may be run in either direction.
16. That the introduction of guide and carrying pulleys adds to the internal resistances an amount proportional to the friction of their journals.
17. That there is still need of more light on the subject.
Forging.—The operation of forging consists in beating or compressing metal into shape, and may be divided into five classes, viz., hand-forging, drop-forging, machine-forging, forging under trip or steam hammers, and hydraulic forging. In purely hand forging much work is shaped entirely by hand tools, but in large shops much work is roughed out under trip or steam hammers, and finished by hand, while some work is finished under these hammers. In drop forging the work is pressed into shape by dead blows, which compress it into shape in dies or moulds. In machine forging the work is either formed by successive quick blows rather than by a few heavy ones, or in some machines it is compressed by rolling. In hydraulic forging the metal is treated as a plastic material, and is forced into shape by means of great and continuous pressure.
In all forging the nature or quality of the iron is of primary importance; hence the following (which is taken from The English Mechanic), upon testing iron, may not be out of place.
“The English Admiralty and Lloyds’ surveyor’s tests for iron and steel are as follows:—
“Two strips are to be taken from each thickness of plate used for the internal parts of a boiler. One-half of these strips are to be bent cold over a bar, the diameter of which is equal to twice the thickness of the plate. The other half of the strips are to be heated to a cherry-red and cooled in water, and, when cold, bent over a bar with a diameter equal to three times the thickness of the plate—the angle to which they bend without fracture to be noted by the surveyor. Lloyds’ Circular on steel tests states that strips cut from the plate or beam are to be heated to a low cherry-red, and cooled in water at 82° Fahr. The pieces thus treated must stand bending double to a curve equal to not more than three times the thickness of the plate tested. This is severe treatment, and a plate containing a high enough percentage of carbon to cause any tempering is very unlikely to successfully stand the ordeal. Lloyds’ test is a copy of the Admiralty test, and in the Admiralty Circular it is stated that the strips are to be one and a half inches wide, cut in a planing machine with the sharp edges taken off. One and a half inches will generally be found a convenient width for the samples, and the length may be from six to ten inches, according to the thickness of the plate. If possible, the strips, and indeed all specimens for any kind of experimenting, should be planed from the plates, instead of being sheared or punched off. When, however, it is necessary to shear or punch, the piece should be cut large and dressed down to the desired size, so as to remove the injured edges. Strips with rounded edges will bend further without breaking than similar strips with sharp edges, the round edges preventing the appearance of the small initial cracks which generally exhibit themselves when bars with sharp edges are bent cold through any considerable angle. In a homogeneous material like steel these initial cracks are apt to extend and cause sudden fracture, hence the advantage of slightly rounding the corners of bending specimens.
“In heating the sample for tempering it is better to use a plate or bar furnace than a smith’s fire, and care should be taken to prevent unequal heating or burning. Any number of pieces may be placed together in a suitable furnace, and when at a proper heat plunged into a vessel containing water at the required temperature. When quite cold the specimens may be bent at the steam-hammer, or otherwise, and the results noted. The operation of bending may be performed in many different ways; perhaps the best plan, in the absence of any special apparatus for the purpose, is to employ the ordinary smithy steam-hammer. About half the length of the specimen is placed upon the anvil and the hammer-head pressed firmly down upon it, as in Fig. 2824. The exposed half may then be bent down by repeated blows from a fore-hammer, and if this is done with an ordinary amount of care it is quite possible to avoid producing a sharp corner.
“An improvement upon this is to place a cress on the anvil, as shown at Fig. 2825. The sample is laid upon the cress, and a round bar of a diameter to produce the required curve is pressed down upon it by the hammer-head.
“The further bending of the pieces thus treated is accomplished by placing them endwise upon the anvil-block, as shown in Fig. 2826. If the hammer is heavy enough to do it, the samples should be closed down by simple pressure, without any striking.
“Fig. 2827 is a sketch of a simple contrivance, by means of which a common punching machine may be converted temporarily into an efficient test-bending apparatus. The punch and bolster are removed, and the stepped cast-iron block a fixed in place of the bolster. When a sample is placed endwise upon one of the lower steps of the block a the descending stroke of the machine will bend the specimen sufficiently to allow of its being advanced to the next higher step, while the machine is at the top of its stroke. The next descent will effect still further bending, and so on till the desired curvature is attained. It would seem an easy matter, and well worth attention, to design some form of machine specially for making bending experiments; but with the exception of a small hydraulic machine, the use of which has, I believe, been abandoned on account of its slowness, nothing of the kind has come under the writer’s notice.
“The shape of a sample after it has been bent to pass Lloyds’ or the Admiralty test is that of a simple bend, the sides being brought parallel. While being bent the external surface becomes greatly elongated, especially at and about the point of the convex side,[II-227] where the extension is as much even as fifty per cent. This extreme elongation corresponds to the breaking elongation of a tensile sample, and can only take place with a very ductile material. While the stretching is going on at the external surface, the interior surface of the bend is being compressed, and the two strains extend into pieces till they meet in a neutral line, which will be nearer to the concave than to the convex curve with a soft specimen. When a sample breaks, the difference between the portions of the fracture which have been subject to tensile and compressive strains can easily be seen.
“Fig. 2828 shows a piece of plate folded close together; and this can generally be done with mild steel plates, when the thickness does not exceed half an inch.
“Common iron plates will not, of course, stand anything like the foregoing treatment. Lloyds’ test for iron mast-plates 1⁄2 inch thick, requires the plates to bend cold through an angle of 30° with the grain, and 8° across the grain; the plates to be bent over a slab, the corner of which should be rounded with a radius of 1⁄2 inch.
“When the sample of metal to be tested is of considerable thickness, as in the case of bars, it is often turned down in a lathe to the shape shown in Fig. 2829, so as to reduce its strength within the capacity of the machine. The part to be tested has usually a length between the shoulders of 8, 10, or 12 inches, and must be made exactly parallel with a cross-sectional area apportioned to the power of the machine and the strength of the material to be tested. When it is desired to investigate the elastic properties of materials, it is desirable to have the specimens of as great a length as the testing apparatus will accommodate.
“Many of the early experiments on the tensile strength of wrought iron were made with very short specimens, such as in Fig. 2830, which is a sketch of that used formerly in the royal arsenal at Woolwich. This had no parallel length for extension at all, its smallest diameter occurring at one only point. Mr. Kirkaldy, to whom is due in a great measure the honour of having raised ‘testing’ to an exact science, discovered that this form of specimen gave incorrect results. He found that experiments with such specimens, more especially when the metals were ductile, gave higher breaking strains than were obtained with specimens of equal cross-sectional area having the smallest diameter parallel for some inches of length. This was due to the form of the specimen resisting to some extent the ‘flow’ or alteration of shape which occurs in soft ductile materials previous to fracture. He accordingly commenced to use a specimen of the form shown in Fig. 2831, with a parallel portion for extension of several inches in length, and specimens like that in Fig. 2830 became a thing of the past.
“The specimens shown in the figures admit of being secured in the testing machine in many different ways. But whatever description of holder be employed, two absolute requirements must be kept in view. The holders must be stronger than the sample, and they must transmit the stress in a direction parallel to the axis of the sample without any bending or twisting tendency.
“Fig. 2832 gives two views of a very effective method of holding round specimens, used by Mr. Kirkaldy in his earlier experiments carried out for Messrs. Napier & Sons, of Glasgow. The enlarged ends of the samples are clasped in split sockets provided with eye-holes for attaching them to the shackles of the testing machine, the halves of the sockets being held together during the experiment by small bolts passing through the projecting lugs.
“Fig. 2833 explains the plan adopted for testing the strength of bolts and nuts in the same series of experiments.
“A good holder for lathe-turned samples is shown in Fig. 2834. Close fitting socket-pieces b b embrace each end of the specimen, and also the turned collar at the extremity of the shackle a. The halves of the socket are held together by a collar c, the interior of which and exterior of the socket rings are turned to an equal taper, so that the socket-pieces are held quite firmly when the collar c is simply slipped over them by hand. When the experiment is over, a few taps with the hammer will remove the collar c.
“Samples of plates for tensile testing are usually shaped like Fig. 2835. The parallel portion b is generally 8, 10, or 12 inches long, as in the case of the turned specimens. Two minor points in the preparation of specimens may be here alluded to. In the first place the holes a a must be made large enough to obviate any danger of the pins which are placed in these holes to secure the specimen being sheared in two before the specimen breaks. In the second place, enough material must be left around these pin or bolt holes to prevent the probability of the metal tearing away between the hole and the edge of the plate. The pin holes must be placed exactly in a line with the axis of the specimen, and the part b must be quite parallel in width, so that the strength (and the elongation during the testing) may be, as nearly as possible, equal throughout the length of b. The shoulders, as c, should be easy curves, so that sharp corners may be avoided. When a number of such specimens are required at the same time, the strips of plate may be clamped together and planed or slotted to the desired width as one piece, but the tool marks should be afterwards removed by careful draw-filing.
“When the plates are thin, small side pieces are riveted on the sides of the ends to be clamped, as shown in Fig. 2836. These stiffen those ends and afford a larger bearing for the securing pins. The connection with the shackles is made by means of steel pins passing through the end holes, and when specimens like 2835 are properly prepared, the direction of the stress on them must be in a line with their axis. Fig. 2837 shows another form of plate specimen in which the holes are dispensed with, the ends being held in the[II-228] machine by friction clips, as shown. These specimens are more easily prepared, and from the absence of holes may be made of a very narrow strip of plate.
“In Fig. 2837 the jaws or forked arms of the shackle are closed to form a rectangular ring, as shown in section in the figure. Two of the interior faces are tapered inwards to the same angle as the back of the wedges or clips a a′, which are perfectly smooth and free to slide upon the inclined or tapered surfaces of the shackles. The faces of the wedges, however, which come in contact with and grip the specimen to be tested, as b, are fluted or grooved, so that the friction of the edges against the specimen is much greater than against the inside surfaces of the shackles. The result of the arrangement is, that when the shackles are pulled, the wedges a a′ are tightened against the specimen with a degree of force proportionate to the load on the specimen, which is prevented from slipping through the clips by the ‘bite’ of their fluted faces. The grooves on the faces of the clips need not be deep—a depth of a little more than 1⁄16, with about the same distance apart, answering well for ordinary loads. With deep grooves and a wider pitch apart, the danger of the specimen breaking in the clips is increased. The inclination of the backs of the wedges a a′ to the faces may be at an angle of 5 or 6 degrees. When the taper is too small, the removal of the halves of the specimen after breaking is sometimes difficult, while on the other hand, when too great, the specimen is apt to slip between the wedges while being tested. The wedges exert a very considerable outward pressure, and the jaws of the shackles must be made strong enough to resist any strain likely, under extreme conditions, to fall on them, otherwise they will speedily become unfit for use. In securing a specimen care must be taken that its axis is in the direct line of strain, and the opposite clips should be driven in equally so that the stress may act fairly upon it. Parallel planed strips of metal, without any enlargement at the ends, may be tested in these friction clips, though, of course, there is a chance of the specimen breaking within them. Turned specimens may also be held by such clips; as also may rough, unturned round and square bars, an advantage when it is desired to immediately ascertain approximately the strength of metal samples.”
Open fires for hand forging purposes are mainly of two classes, those having a side and those with a bottom or vertical blast.
Fig. 2838 represents a side draft forge. f is the fireplace, usually from 3 to 5 feet long, t is the tuyère through which the blast enters the fire, b being the blast pipe. To prevent t from being burned away it is hollow as at s, and two pipes p and p′ connect to the water-tank w, thus maintaining a circulation of water through s; v is simply a valve or damper to shut off the supply of air from the tuyère; d is the opening to the chimney c.
The side blast, though not so much used as in former years, is still preferred by many skilful mechanics, on the ground that it will give a cleaner fire with less trouble. The method of accomplishing this is to dig out a hole in the fire bed and fill it in with coked coal, which will form a drain through which the slag or clinker may sink, instead of remaining in the active fire and obstructing the blast.
In cases where the fire requires to be built farther out from the chimney wall than the location of the tuyère permits, it may be built out as follows:—
A bar b, Fig. 2839, is placed in the tuyère hole and supported at the other end at p. The coal is well wetted and packed around and above the bar, which is then pulled out endwise, leaving a blast hole through the coal, as is shown in the end view Fig. 2840.
Fig. 2841 represents a patent tuyère of vertical or bottom draft, in which the blast passes through pipe a and circulates around b, finding egress at c into the fire. c is hollow and receives water from the tank f by the pipe d. The steam generated in the nozzle c is conveyed to the tanks by the pipe e.
Figs. 2842 and 2843 represent a blacksmith’s forge, for work up to and about 4 inches in diameter. It consists of a wind-box a, supported on brickwork which forms an ash-pit g beneath it. To this box is bolted the wind-pipe b, and at its bottom is the slide e. In an orifice at the top of a is a triangular and oval breaker d, connected to a rod operated by the handle c. This[II-229] rod is protected from the filling which is placed between the brickwork and the shell f of the forge by being encased in an iron pipe i. The blast passes up around the triangular oval piece d. The operation is as follows: when d is rotated, it breaks up the fire and the dirt falls down into the wind-box, cleaning the fire while the heat is on. At any time after a heat the slide e may be pulled out, letting the slag and dirt fall into the ash-pit beneath. It is a great advantage to be able to clean the fire while a heat is on without disturbing the heat.
Blacksmiths’ anvils are either of wrought iron steel faced, or of cast iron steel faced, the faces being hardened. It is sometimes fastened to the block by spikes driven in around the edges. A better plan, however, is to make the block the same size as the anvil, and secure the latter by two bands of iron and straps, as shown in Fig. 2844, because in this way the block will not come in the way of arms or projecting pieces that hang below the anvil. The square hole is for receiving the stems of swages, fullers, &c., and for placing work over to punch holes through it, and the round is used for punching small holes.
The proper shape for blacksmiths’ tongs depends upon whether they are to be used upon work of a uniform size and shape, or upon general work. In the first case, the tongs may be formed to exactly suit the special work. In the second case, they must be formed to suit as wide a range of work as convenient.
Suppose, for example, the tongs are for use on a special size and shape of metal only; then they should be formed so that the jaws will grip the work evenly all along, and therefore be straight along the gripping surface. It will be readily perceived, however, that if such tongs were put upon a piece of work of greater thickness, they would grip it at the inner end only, and it would be impossible to hold the work steady. The end of the work would act as a pivot, and the part on the anvil would move about. It is better, therefore, for general work to curve the jaws, putting the work sufficiently within the jaws to meet them at the back of the jaw, when the end will also grip the work. By putting the work more or less within the tongs, according to its thickness, contact at the end of the work and at the point of the tongs may be secured in one pair of tongs over a wider range of thickness of work than would otherwise be the case. This applies to tongs for round or other work equally as well as to flat or square work.
To maintain the jaw pressure of the tongs upon the work, a ring is employed, the tong ends being curved to prevent the ring from slipping off.
After a piece of work has left the fire it should, if there are scales adhering upon it, have them cleaned off before being forged, for which purpose the hammer head or an old file is used, otherwise the forging will not be smooth, and the scale will be hammered into the surface. This will render the forging very hard to operate upon by steel cutting tools, and cause them to dull rapidly. For the same reason it is proper to heat a finished forging to a low red heat and pass a file over its surface, which will leave the forging soft as well as free from scale. A forging should not be finally finished by being swaged or forged after it has become black hot, because it produces a surface tension that throws the work out of true as the metal is cut away in finishing it.
Work to be drawn out is treated according to the amount of elongation and reduction of diameter required. Thus, suppose a piece of square work to require to be drawn out, then it is hammered on its respective sides, being turned upon the anvil so that each successive side shall receive the hammer blows. It is essential, however, that the piece be forged square, or in other words, that during the forging the sides be kept at a right angle one to the other, or else the work will hammer hollow, as it is[II-230] termed; that is to say, the iron will split at the centre of the bar, which occurs from its being forged diamond-shaped instead of square. If a piece required to be forged diamond-shaped, it must be forged square until reduced to such dimensions as will leave sufficient to draw out while altering its form from the square to the diamond-shape.
In very small work, which is more apt to hammer hollow than large work, the end of the piece is left of enlarged size, as shown in the figure, the strength of the enlarged end serving to prevent the hammering hollow, which usually begins at the end of the piece; the end is in this case forged last. In the case of round work the same rule holds good, inasmuch as that a round bar may be forged smaller to some extent, either by hammer blows or by swaging, but if the forging by hammer blows be excessive, hammering hollow is liable to ensue.
The blacksmith’s set of chisels consists of a hot chisel for cutting off hot iron, a cold chisel for cutting cold metal, a hardy, which sets in the square hole in the anvil, C-chisels, which are curved somewhat like the carpenter’s gouge, and a cornering or V-chisel, in which the cutting edges are at a right angle one to the other.
The hot chisel has its edge well curved in its length, and is kept cool by lifting it from the work after each hammer blow, and by occasionally dipping it in water. Lifting it also prevents it from wedging in the work. The cold chisel is tempered to a blue, and answers virtually to the machinist’s chisel. The hardy is used for small work, which is laid upon it and struck with the hammer. The C-chisel is used, not only in curved corners, but also to cut off deep cuts, answering, like the cape or cross-cut chisel of the machinist, to relieve the corners of the hot chisel. The cornering chisel is used for square corners, situated so that the hot chisel cannot be used. The blacksmith’s punch is made well taper, so that it shall not wedge in the hole it produces.
For large holes a small punch is first used, and the hole enlarged in diameter by driving in punches of larger diameter. If this swells the work at the sides, it is forged down while the punch is in the hole.
The first blow given to the punch is a light one, so as to leave an indentation that will mark the location, and enable its easy correction if necessary. The blows delivered after the correct location is indented are quick and heavy; but a piece of soft coal is inserted and the punch placed on top of it, the gases formed by the combustion of the coal serving to prevent the punch from binding in the hole. Between the blows the blacksmith lifts the punch and moves the handle part of a lateral rotation, which prevents it from becoming fast in the hole. The punch should not be suffered to get red hot, but must be removed and cooled, a fresh piece of green soft coal being inserted in the hole just previous to the punch. If the punch is allowed to become as heated as the work, the end will “upset” or swell and become firmly locked. Should the punch lock in the hole a few blows will usually loosen it, but in extreme cases it is sometimes necessary to employ another punch from the opposite side of the work. Unless in very thin work, the hole is punched half way from each side, because by that means a short stout punch may be used.
It is obvious that when the hole requires to be bell-mouthed or of any other form, the punch must be made to correspond.
The tools employed by the blacksmith, other than tongs, hammers, chisels, and punches, are composed mainly of “fullers” and “swages” of various kinds. The fuller is essentially a spreading tool, while the swage may be termed essentially a shaping one.
In Fig. 2845, for example, let a represent an end view of an anvil, b the bottom, and c the top fuller, and the effects of blows upon c will be mainly to stretch the piece in the direction of its length without swelling it out sideways.
If the work requires to be swelled sideways we turn the fuller the other way around, as in Fig. 2846, in which it is supposed that one side of the work is to be kept flat, hence no bottom fuller is employed. The action of a fuller may be increased in the required direction by leaning in the direction in which we desire to drive the iron; thus, suppose we require to spread the end of a rectangular bar from the full lines to the dotted ones in Fig. 2847 and the first fuller across the piece as at a, Fig. 2848, and then spread out the end by fullering, as in Fig. 2849, inclining the fuller in the direction in which we desire to forge the iron.
It is the roundness of the face of the fuller that serves to control the direction in which it will drive the iron, since the curve acts somewhat on the principle of a wedge. Suppose, for example, that the faces were flat, as in Fig. 2850, and the iron would spread in both directions, the same as though the hammer were used direct, and if the work were intended to be kept parallel it would frequently require to be turned on edge to forge down the bulge that would form on the edge.
[II-231]Fullers are, however, also used as finishing tools for curves or corners, an example being given in Fig. 2851, which represents a fuller applied to finish the round corner of a collar.
For finishing plane surfaces the flatter shown in Fig. 2852 is employed, w representing the work. For inside surfaces the flatter requires to be offset, as in Fig. 2853, in which l represents a link whose face a may be flattened by the flatter f. There is a tendency in this case for the flatter to tip or cant; and to avoid this and regulate the flatter upon the work, a side foot is sometimes added, as at a in Fig. 2854.
Swages are shaped according to the kind of work they are to be used for.
Fig. 2855, for example, represents a top and bottom swage for rounding up iron. For general work the recesses or seats of such swages would be made considerably oval, as in Fig. 2856, the work being revolved slightly after each blow. This capacitates one swage for different sizes of iron. When, however, a swage is to be used for one particular size only, its cavity may be made more nearly a true half circle and may envelop one half the diameter of the work, so that when the top and bottom swages meet, the work will be known to be of the required diameter without measuring it. If the seat were made a true half circle it would lock upon the work, preventing the smith from revolving it and making it difficult to remove the swage.
If the conditions are such that a swage must be used to perform forging rather than finishing, its seat should be V-shaped and not curved. Suppose, for example, that a piece of iron, say, 6 inches in diameter, required a short section to be forged down to a diameter of 3 inches, then the swages should be formed as in Fig. 2857, because otherwise the effects of the blow will act to a certain extent to force the iron out sideways, for reasons which will be explained presently.
In some cases, for small work, the upper swage is guided by the lower one: thus, in Fig. 2858 is a swage for a cross piece, and the outside of its base is squared and fits easily within the upper part of the lower one shown in Fig. 2859. For very[II-232] small work, on which the hand hammer is sufficiently heavy to perform the swaging, a spring swage may be use: thus, in Fig. 2860 is a swage for pieces of 3⁄8, 5⁄16, and 1⁄4 inch in diameter, and having a square stem fitting into the square hole in the anvil. Fig. 2861 represents a spring swage for a pin having a collar, and it may be observed that the recess to form the collar must be tapered narrowest at the bottom, so that the top swage will readily release itself by the force of the spring, and so that the work may easily be revolved in the lower one. A similar tool is shown in Fig. 2862, designed for punching sheet metal cold, the die d being changeable for different sizes of punches p.
For large hand-made forgings the swage block, such as in Fig. 2863, is employed, s representing a stand for the block, whose dimensions are larger than the block, so that the latter may be rested on its face in the stand when the holes are to be used.
Fig. 2864 represents a swage block mounted on bearers, so that it may be revolved to bring the necessary cavity uppermost.
Swages for trip hammers or for small steam hammers are for work not exceeding about 4 inches in diameter, made as in Fig. 2865, the weight of the top swage being sufficient to keep the two closed as in the figure; for larger sizes the bottom swage fits to the anvil, and the top one is provided with a handle, as in Fig. 2866, b representing the anvil block, s′ the bottom, and s the top swage, having a handle h. The flange of the bottom swage is placed as in Fig. 2867, so as to prevent the swage from moving off the anvil block when the work is pushed through it endways. Obviously such swages are employed when the part to be swaged is less in length than the width of the hammer or of the anvil face.
| VOL. II. | EXAMPLES IN STEAM HAMMER WORK. | PLATE XV. | |||
 |
 |
 |
|||
| Fig. 2868. | Fig. 2869. | Fig. 2870. | |||
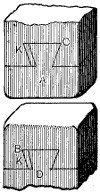 |
 |
 |
|||
| Fig. 2871. | Fig. 2872. | Fig. 2873. | |||
 |
 |
 |
|||
| Fig. 2874. | Fig. 2875. | Fig. 2876. | |||
 |
 |
||||
| Fig. 2877. | Fig. 2878. | ||||
If the hammer and anvil face is rounded as in Fig. 2868, or if dies thus shaped are placed in them, their action will be the same as that of the fuller, drawing the work out lengthways, with a minimum of effect in spreading it out sideways.
Detached fullers, such as shown in Figs. 2869 and 2870, are, however, used when the section to be acted upon is less in length than the hammer face.
In the case of trip hammers, steam hammers, &c., blocks fitted to the hammer and anvil block may take the place of detached swages and fullers. Thus, in Fig. 2871 is represented the hammer and anvil block for flat work, the corners being made rounded, because if left sharp they would leave marks on the work. The blocks or dies a and b are dovetailed into their places, and secured by keys k; hence they may be removed, and dies of other shapes substituted.
When the work is parallel it may be forged to its finished dimensions by forming in the lower die recesses whose depth equals the required dimensions. Thus, in Fig. 2872 the recess a in the lower die equals in depth the depth a of the work, while the depth of the recess b in the die equals the thickness of the bar; hence by passing the work successively from a to b, and turning it over a quarter turn, it will be made to finished size, when the faces c d of the dies meet.
For this class of work the recesses must obviously be made in the lower die, because it would be difficult to hold the work upon the lower die in the proper position to meet a recess cut in the upper one: and, furthermore, the recesses in the die should be wider than the work, to avoid the necessity of holding the work exactly straight in the recess, and keeping it against the shoulder or vertical face of the recess. If, however, the work is to be made taper, we may obviously make the recess taper, so as to produce smooth work, the die recess being made to be of the correct depth for the smallest end of the work.
When the shape of the work is such that it cannot be moved upon the die during the forging, the operation is termed stamping, or if the hammer or upper die falls of its own weight it is termed drop forging, and in this case the finishing dies are made the exact shape of the work, care being taken to let the work be[II-233] enveloped as much as possible by the bottom die, so that the top one shall not lift it out on its up stroke.
In forging large pieces from square to round we have several important considerations. In order to keep the middle of the work sound, it must be drawn square to as near as possible the required diameter before the finishing is begun. During this drawing-down process the blows are heavy and the tendency of the work is to spread out at the sides, as in Fig. 2873.
When the work is ready to be rounded up it is first drawn to an octagon, as shown in Fig. 2874, so as to bring it nearer the work, nearer to cylindrical form. The corners are then again hammered down, giving the work sixteen sides, the work during this part of the process being moved endways, as each corner is hammered down. The blows are during this part of the forging lighter, but still the tendency is to spread the work out sideways. The final finishing to cylindrical form is done with light blows, the work being revolved upon the anvil without being moved endways, so that a length equal to the width of the anvil is finished before the work is moved endways to finish a further part of the length. The tendency to spread sideways is here unchecked, because the iron is squeezed top and bottom only. We may check it to some extent, however, by employing a bottom swage block, as in Fig. 2875, in which case the contact of the swage and the work will extend further around the work circumference than would be the case with a flat anvil. If we were to use a top and a bottom swage, as in Fig. 2876, the circumferential surface receiving the force of the blow will be still further increased, but there will still be a tendency to spread at the sides, as at a b, in Fig. 2876. A better plan, therefore, is to use a V-block with the hammer, as in Fig. 2877, in which case the effects of the blow are felt at a, b, and c, and the points a b of resistance being brought higher up on the work, its tendency to spread is obviously diminished. By using a top and bottom V-block, as shown in Fig. 2878, the effect will be to drive the metal towards the centre, and, therefore, to keep it sound at the centre, it being found that if the metal is swaged much without means being taken to prevent spreading, it “hammers hollow,” as it is termed, or in other words, splits at its centre.
The points a b of resistance to the blow at c are higher and the tendency to spread sideways is better resisted. For cutting off under the steam hammer, the hack shown in Fig. 2879 is used, being simply a wedge with an iron handle.
Welding.—In the welding operations of the blacksmith there are points demanding special attention: first, to raise the temperature of the metal to a proper heat; second, to let the temperature be as nearly equal as practicable all through the mass; third, to have the surfaces to be welded as clean and free from oxidation as possible; fourth, have the parts to be welded of sufficient diameter or dimensions to permit of the welded joint being well forged.
The following remarks on the theory of welding are from a paper read by Alexander L. Holley before the American Institute of Mining Engineers:—
“The generally received theory of welding is that it is merely pressing the molecules of metal into contact, or rather into such proximity as they have in the other parts of the bar. Up to this point there can hardly be any difference of opinion, but here uncertainty begins. What impairs or prevents welding? Is it merely the interposition of foreign substances between the molecules of iron, or of iron and any other substance which will enter into molecular relations or vibrations with iron? Is it merely the mechanical preventing of contact between molecules, by the interposition of substances? This theory is based on such facts as the following:
“1. Not only iron but steel has been so perfectly united that the seam could not be discovered, and that the strength was as great as it was at any point, by accurately planing and thoroughly smoothing and cleaning the surfaces, binding the two pieces together, subjecting them to a welding heat, and pressing them together by a very few hammer blows. But when a thin film of oxide of iron was placed between similar smooth surfaces, a weld could not be effected.
“2. Heterogeneous steel scrap, having a much larger variation in composition than these irons have, when placed in a box composed of wrought-iron side and end pieces laid together, is (on a commercial scale) heated to the high temperature which the wrought-iron will stand, and then rolled into bars which are more homogeneous than ordinary wrought iron. The wrought-iron box so settles together as the heat increases that it nearly excludes the oxidizing atmosphere of the furnace, and no film of oxide of iron is interposed between the surfaces. At the same time the enclosed and more fusible steel is partially melted, so that the impurities are partly forced out and partly diffused throughout the mass by the rolling.
“The other theory is that the molecular motions of the iron are changed by the presence of certain impurities, such as copper and carbon, in such a manner that welding cannot occur, or is greatly impaired. In favor of this theory it may be claimed that, say, 2 per cent. of copper will almost prevent a weld, while, if the interposition theory were true, this copper could only weaken the weld 2 per cent., as it could only cover 2 per cent. of the surfaces of the molecules to be united. It is also stated that 1 per cent. of carbon greatly impairs welding power, while the mere interposition of carbon should only reduce it 1 per cent. On the other hand, it may be claimed that in the perfect welding due to the fusion of cast iron, the interposition of 10 or even 20 per cent. of impurities, such as carbon, silicon, and copper, does not affect the strength of the mass as much as 1 or 2 per cent. of carbon or copper affects the strength of a weld made at a plastic instead of a fluid heat. It is also true that high tool steel, containing 11⁄2 per cent. of carbon is much stronger throughout its mass, all of which has been welded by fusion, than it would be if it had less carbon. Hence copper and carbon cannot impair the welding power of iron in any greater degree than by their interposition, provided the welding has the benefit of that perfect mobility which is due to the fusion. The similar effect of partial fusion of steel in a wrought-iron box has already been mentioned. The inference is, that imperfect welding is not the result of a change in molecular motions due to impurities, but of imperfect mobility of the mass—of not giving the molecules a chance to get together.
“Should it be suggested that the temperature of fusion, as compared with that of plasticity, may so change chemical affinities as to account for the different degrees of welding power, it may be answered that the temperature of fusion in one kind of iron is lower than that of plasticity in another, and that as the welding and melting points of iron are largely due to the carbon they contain, such an impurity as copper, for instance, ought, on this theory, to impair welding in some cases and not to affect it in others.
“The obvious conclusions are: 1st. That any wrought iron, of whatever ordinary composition, may be welded to itself in an oxidizing atmosphere at a certain temperature, which may differ very largely from that one which is vaguely known as ‘a welding heat.’ 2nd. That in a non-oxidizing atmosphere heterogeneous irons, however impure, may be soundly welded at indefinitely high temperatures.
“The next inference would be that by increasing temperature we chiefly improve the quality of welding. If temperature is increased to fusion, welding is practically perfect; if to plasticity and mobility of surfaces, welding should be nearly perfect. Then how does it sometimes occur that the more irons are heated the worse they weld?
[II-234]“1. Not by reason of mere temperature, for a heat almost to dissociation will fuse wrought iron into a homogeneous mass.
“2. Probably by reason of oxidation, which, in a smith’s fire especially, necessarily increases as the temperature increases. Even in a gas furnace a very hot flame is usually an oxidizing flame. The oxide of iron forms a dividing film between the surfaces to be joined, while the slight interposition of the same oxide, when diffused throughout the mass by fusion or partial fusion, hardly affects welding. It is true that the contained slag, or the artificial flux, becomes more fluid as the temperature rises, and thus tends to wash away the oxide from the surfaces; but inasmuch as any iron with any welding flux can be oxidized till it scintillates, the value of a high heat in liquefying the slag is more than balanced by its damage in burning the iron.
“But it still remains to be explained why some irons weld at a higher temperature than others; notably, white irons high in carbon, or in some other impurities, can only be welded soundly by ordinary processes at low heats. It can only be said that these impurities, as far as we are aware, increase the fusibility of iron, and that in an oxidizing flame oxidation becomes more excessive as the point of fusion approaches. Welding demands a certain condition of plasticity of surface; if this condition is not reached, welding fails for want of contact due to mobility; if it is exceeded, welding fails for want of contact due to excessive oxidation. The temperature of this certain condition of plasticity varies with all the different compositions of irons. Hence, while it may be true that heterogeneous irons, which have different welding points, cannot be soundly welded to one another in an oxidizing flame, it is not yet proved, nor is it probable, that homogeneous irons cannot be welded together, whatever their composition, even in an oxidizing flame. A collateral proof of this is, that one smith can weld irons and steels which another smith cannot weld at all, by means of a skilful selection of fluxes and a nice variation of temperatures.
“To recapitulate. It is certain that perfect welds are made by means of perfect contact due to fusion, and that nearly perfect welds are made by means of such contact as may be got by partial fusion in a non-oxidizing atmosphere or by the mechanical fitting of surfaces, whatever the composition of the iron may be within all known limits. While high temperature is thus the first cause of that mobility which promotes welding, it is also the cause, in an oxidizing atmosphere, of that ‘burning’ which injures both the weld and the iron. Hence, welding in an oxidizing atmosphere must be done at a heat which gives a compromise between imperfect contact due to want of mobility on the one hand, and imperfect contact due to oxidation on the other hand. This heat varies with each different composition of irons. It varies because these compositions change the fusing points of irons, and hence their points of excessive oxidation. Hence, while ingredients such as carbon, phosphorus, copper, &c., positively do not prevent welding under fusion, or in a non-oxidizing atmosphere, it is probable that they impair it in an oxidizing atmosphere, not directly, but only by changing the susceptibility of the iron to oxidation.”
In welding steel to iron both are heated to as high a temperature as possible without burning, and a welding compound or flux of some kind is used.
In welding steel to steel the greatest care is necessary to obtain as great a heat as possible without burning, and to keep the surfaces clean.
An excellent welding compound is composed as follows: Copperas 2 ozs., salt 4 ozs., white sand 4 lbs., the whole to be mixed and thrown upon the heat, as is done when using white sand as described for welding iron. An equally good compound is made up of equal quantities of borax and pulverized glass, well wetted with alcohol, and heated to a red heat in a crucible. Pulverize when cool, and apply as in the case of sand only.
A welding compound for cast steel given by Mr. Rust in the Revue Industrielle is made up as follows: 61 parts of borax, 20 parts of sal-ammoniac, 163⁄4 parts of ferrocyanide, and 5 parts of colophonium. He states that with the acid of this compound cast steel may be welded at a yellow red heat, or at a temperature between the yellow, red, and white heats. The borax and sal-ammoniac are powdered, mixed, and slowly heated until they melt. The heating is continued until the strong odor of ammonia ceases almost entirely, a small quantity of water being added to make up for that lost by evaporation. The powdered ferrocyanide is then added, together with the colophonium, and the heating is continued until a slight smell of cyanogen is noticed. The mixture is allowed to cool by spreading it out in a thin layer.
The lap weld is formed as follows: Suppose it is required to weld together the ends of two cylindrical pieces, and the first operation is to pump or upset the ends to enlarge them, as shown in Fig. 2880, so as to allow some metal to be hammered down in making the weld without reducing the bar below its proper diameter. The next operation is to scarf the ends forming them, as shown in Fig. 2881, and in doing this it is necessary to make the scarf face somewhat rounding, so that when put together as in the figure contact will occur at the middle, and the weld will begin there and proceed as the joint comes together under the blows towards the outside edges. This squeezes out scale or dirt, and excludes the air, it being obvious that if the scarf touched at the edges first, air would be enclosed that would have to find its escape before the interior surfaces could come together.
It is obvious, that if the two pieces require to weld up to an exact length and be left parallel in diameter when finished an allowance for waste of iron must be made; and a good method of welding under these conditions is as follows:—
Let the length of the two pieces be longer than the finished length to an amount equal to the diameter. Then cut out a piece as at a, in Fig. 2882, the step measuring half the diameter of the bar as shown. The shoulder a is then thrown back with the hammer, and the piece denoted by the dotted line b is cut off, leaving the shaft as shown in Fig. 2883.
The faces of the scarf should be somewhat rounding, so that when the weld is put together contact will take place in the centre of the lapping areas. Then, as the surfaces come together, the air and any foreign substances will be forced out, whereas, were the surfaces hollow the air and any cinder or other foreign substances would be closed in the weld, impairing its soundness.
[II-235]The lap of the two pieces, when scarfed in this manner, is shown in Fig. 2884.
To take the welding heat the fire should be cleaned out and clear coked coal, and not gaseous coal, used. The main points in a welding heat are, to heat the iron equally all through, to obtain the proper degree of heat, and to keep the scarfed surfaces as free from oxidation, and at the same time as clean, as possible.
To accomplish these ends the iron must not be heated too quickly after it is at a good red heat, and the fire must be so made that the blast cannot meet it at any point until it has passed through the bed of the fire.
When the iron is getting near the welding heat it may be sprinkled with white sand, which will melt over it and form a flux that will prevent oxidation and cool the exterior, giving time to the interior to become equally heated. The sand should be thrown on the work while in the fire, as removing the work from the fire causes it to oxidize or scale rapidly. The work should be turned over and over in the fire, the scarf face being kept uppermost until the very last part of the heating, when the blast must be put on full, the bed of the fire kept full and clear so that there shall be sufficient bed to prevent the blast from meeting the heat until it has passed through the glowing coals.
When the heat is taken from the fire it should meet the anvil with a blow, the scarfed face being downwards, to jar off any dirt, cinder, &c., and the scarf should be cleaned by a stroke or two of a wire brush. But as every instant the iron is in the air it is both cooling and oxidizing, these operations must be performed as quickly as possible.
The two scarfs being laid together as shown in Fig. 2884, the first blows must be delivered lightly, so as not to cause the upper piece to move, and as quickly as possible, the force of the blows being increased regularly and gradually until the weld is sufficiently firm to hold well together, when it may be turned on edge and the edges of the scarf hammered to close and weld the seam. If this turning is done too soon, however, it may cause the two halves to separate. When the weld is firmly and completely made the enlarged diameter due to the scarfing may be forged down, working the iron as thoroughly as possible.
To form the scarf of a ring or collar, one end is bevelled, as at b in Fig. 2885 and after the piece is bent to a circle it is cut off and bevelled as at a. When a slight band is to be welded, and it is difficult to steady the ends to bring them together, a clamp may be used to hold them as in Fig. 2886.
Fig. 2887 represents a tongue weld, and it is obvious that to insure soundness the wedge piece should fit in the bottom of the split, which may be well closed upon it by the hammer blows.
Fig. 2888 represents an example of a V-weld applied to welding up a band that is to be square when finished, and as the lengths of the sides must be equal when finished, the side on which the weld is made should be made shorter, so that in stretching under the welding blows it will be brought to its proper length. The V form of weld is employed because it stretches less in welding than the lap weld. The V-piece to be welded in should bear at the bottom of the V, and the weld made by fullering.
Welds of this kind are obviously most suitable for cases in which the weld is required to influence the shape of the piece as little as possible. The figures above, which are taken from Mechanics, illustrate as an example the repairing of a broken strap for the beam of a river steamboat. The crack is at a, Fig. 2889, and is held together by a clamp as shown; a V-recess is cut out as in Fig. 2890, and this recess is fullered larger, as in Fig. 2891. A V-block is then welded in. The strap is then[II-236] turned over a second V-groove, cut out and fullered out, and a second V-piece welded in. By thus welding one side at a time the welding is taken in detail as it were, and the blows can be less heavy than if a larger weld were made at one heat, as would be the case if but one V block were used. A similar form of weld may be employed to form a square corner, as is shown in Fig. 2892, which is taken from “The Blacksmith and Wheelwright.” In this example the inside corner is shown to have a fillet, which greatly increases the difficulty of the job. The weld is made by first fullering the V-piece on the sides and on the rounded corner and then laying the piece on the anvil to forge down, the fullering leaving the finished job as in Fig. 2893.
When one piece has to be driven on to the other, the weld is called a pump-weld, for which the ends should be rounded as in Fig. 2894, so that they will meet at their centres, and will, when struck endways to make the weld, come to the shape shown in Fig. 2895.
It is obvious that in this case the interior of the iron comes together and is welded, and that dirt, &c., is effectually excluded; hence if the iron is properly heated the weld may be as sound as a lap weld, and is preferred by many as the sounder weld of the two. When a stem requires to be welded to a large flat surface, the pump weld is the only one possible, being formed as in Fig. 2896, in which the stem is supposed to be welded to a frame. The plate is cupped as shown, and the metal being driven up on the sides as much as possible, the stem overlaps well at c b, so that it may be fullered there. The stem should first meet its seat at a, so that dirt, &c., may squeeze out as the welding proceeds.
Figs. 2897 and 2898 represent an example of welding a collar on round iron. The bar is upset so as to enlarge it at a, where the collar is to be. The collar is left open at the joint, and while it is cold it is placed on the red-hot bar and swaged until the ends are closed. The welding of the whole may then be done at one heat, swaging the outside of the collar first. Unless the bar is upset there would be a crack in the neck b of the collar on both sides.
Welding Angle Iron.—Let it be required to form a piece of straight angle iron to a right angle.
The first operation is to cut out the frog, leaving the piece as shown in Fig. 2899; the width at the mouth a of the frog being 3⁄4 inch to every inch of breadth measured inside the flange as at b.
The edges of the frog are then scarfed and the piece bent to an acute angle; but in this operation it is necessary to keep the scarfs quite clean and not to bend them into position to weld until they are ready for the welding heat; otherwise scale will form where the scarfs overlap and the weld will not be sound.
The heat should be confined as closely as possible to the parts to be welded; otherwise the iron will scale and become reduced below its proper thickness.
The iron is then bent to the shape shown in Fig. 2900; and the angle to which it is bent is an important consideration. The object is to leave the overlapping scarf thicker than the rest of[II-237] the metal, and then the stretching which accompanies the welding will bring the two arms or wings to a right angle.
It is obvious, then, that the thickness of the metal at the weld determines the angle to which the arms must be bent before welding. The thicker the iron the more acute the angle. If the angle be made too acute for the thickness of the iron at the weld there is no alternative but to swage the flange down and thin it enough to bring the arms to a right angle. Hence it is advisable to leave the scarf too thick rather than too thin, because while it is easy to cut away the extra metal, if necessary, it is not so easy to weld a piece in to give more metal. In very thin angle irons, in which the wastage in the heating is greater in proportion to the whole body of metal, the width of the frog at a in Fig. 2901 may be less, as, say, 9⁄16 inch for every inch of angle-iron width measured as at b in the figure. For angles other than a right angle the process is the same, allowance being made in the scarf-joint and bend before welding for the stretching that will accompany the welding operation.
The welding blows should be light and quick, while during the scarfing the scale should be cleaned off as soon as the heat leaves the fire, so that it will not drive into the metal and prevent proper welding. The outside corner should not receive any blows at its apex; and as it will stretch on the outside and compress on the inside, the forging to bring the corner up square should be done after the welding.
The welding is done on the corner of an angle block, as in Fig. 2901, in which a is the angle iron and b the angle block.
To bend an angle iron into a circle, with the flange at the extreme diameter, the block and pins shown in Fig. 2902 are employed. The block is provided with the numerous holes shown for the reception of the pins. The pins marked 1 and 2 are first inserted and the iron bent by placing it between them and placed under strain in the necessary direction. Pins 3 and 4 are then added and the iron again bent, and so on; but when the holes do not fall in the right position, the length of the pin-heads vary in length to suit various curves.
To straighten the iron it is flattened on the surface a and swaged on the edge of the flange b, the bending and straightening being performed alternately.
When the flange of the angle iron is to be inside the circle, as in Fig. 2903, a special iron made thicker on the flange a is employed. The bending is accomplished, partly by the pins as before, and partly by forging thinner, and thus stretching the flange a while reducing it to its proper thickness.
To Forge a Bolt by Hand.—The blanks for bolts must be cut off sufficiently long to admit of one end being upset to form the head, the amount of this allowance, obviously, being determined by the size of the head.
Fig. 2904 is a side view, partly in section, and Fig. 2905 a top view of an anvil block for upsetting the ends of blanks to form the heads of bolts. The stem fits into the square hole of the anvil. The tongue is pivoted as shown in the top view to two lugs provided on the block; upon the tongue rests a steel pin whose length determines the height to which the blank will project above the top of the block, and, therefore, the amount or length of blank that will be upset to form the head, this amount being three times the diameter of the bolt for black heads.
The hole for the blank is made about 1⁄64 inch larger in diameter than the designated size of the bolt, to permit of the easy extraction of the blank after it is upset, this extraction being accomplished by striking the end of the tongue with the hammer. If the block is made of cast iron the upper end of the hole will become worn after forging five hundred or six hundred bolts, leaving the bolts with a rounded neck, as at c c in Fig. 2906; a steel block, however, will forge several thousand bolts without becoming enlarged.
[II-238]An excellent plan is to provide the block with removable dies, such as at d d in Fig. 2907, which are easily renewed, a number of such dies having different diameters of bore fitted to the same block.
When the bolt end is sufficiently reset or enlarged to form the head it is laid in a bottom swage, containing three of the six sides of the hexagon, and a hammer blow on the uppermost part of the end forges a flat side. After each blow the work is revolved one-sixth of a revolution, and as the angles of the swage are true they obviously true the angles of the bolt head. After the head has been roughed down it is necessary to flatten it again under the head and on the end, for which purpose it may be placed in the heading block shown in Fig. 2904, after which the sides of the head may be finished and the cupping tool for chamfering the head applied.
The bolt may require passing from the heading tool to the swage several times, as forging it in one direction spreads it in another.
In shops where bolt-making is of frequent occurrence a special bolt-making device is usually employed. It consists of an oliver or foot hammer, having two hammers and an anvil; in the square hole at one end of the anvil fits a hardy or bottom chisel, such as shown in Fig. 2908, for cutting up the bar or rod iron into bolt blanks; a is the anvil, h the hardy, and g a gauge to determine the length cut off the rod r to form a blank. An upsetting or heading device corresponding to that in Fig. 2907 is provided, and at the other end of the anvil is the swage for forming the bolt head.
The object of having two hammers is that one may be used for the upsetting of the blank and the other for the swage. The swaging hammer is provided with a hole and set-screw to receive top swages, and bolt hammers are adjustable for height so that they may be set so that their faces will meet the work fair.
Figs. 2909 to 2911 represent front, side, and top views of Pratt & Whitney’s portable bolt-forging device. It is provided with an elevating screw that permits the employment of a single bolster-pin for all lengths of bolt for a given diameter, instead of requiring a separate pin for each different length of bolt. In the figures, a is a frame carried upon wheels, and to which is pivoted at c c the jaw d. The bolt-gripping dies are shown at e f. A treadle g is pivoted at h, and acts upon the lower end of d, causing the die f to grip or release the bolts, as may be required. The bolster-pin rests upon the end of the screw i, which enters at its foot a split nut j, which is caused to grip and lock the screw by operating the nut of the bolt k that passes through the split of the nut. l is a spring that lifts the treadle when it is relieved of the pressure of the operator’s foot.
At m is a leather washer to protect the nut j from the scale that falls from the forging. The operation is as follows:—
The nut k is released and the screw i operated to suit the length of bolt required. Then j is caused to clamp the screw by operating the nut k. The blank for the bolt is placed in the dies resting on the bolster-pin, which in turn rests upon the end of the screw i. The treadle g is depressed, and the bolt blank clamped between e and f. The helper then with the sledge upsets the blank end to form the bolt head, and the blacksmith forges it to shape in the former bar b, which is provided with impressions for the form of head required, these impressions being of varying sizes, as shown. The device is so strongly proportioned as to be very solid, and is found to be a most useful addition to the blacksmith’s shop.
[II-239]To forge a turn buckle, such as in Fig. 2912, we bend two rings, such as in Fig. 2913, and weld into the open ends a piece as shown in Fig. 2914, on the opposite side a recess a, Fig. 2915, is cut out to receive a second piece, which being welded in the work appears as in Fig. 2916, and the end may be drawn taper. Two such pieces welded together obviously complete the job.
| VOL. II. | EXAMPLES IN HAND FORGING. | PLATE XVI. | |
 |
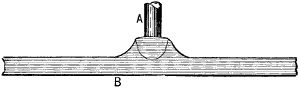 |
||
| Fig. 2917. | Fig. 2918. | ||
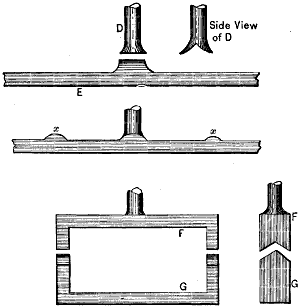 |
 |
||
| Fig. 2920. | |||
| Fig. 2919. | |||
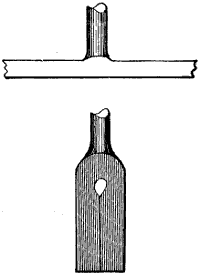 |
|||
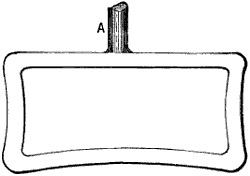 |
|||
| Fig. 2921. | Fig. 2922. | ||
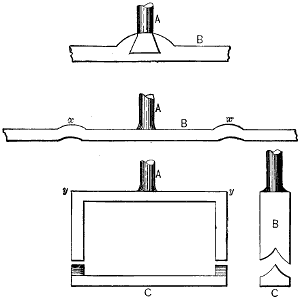 |
 |
||
| Fig. 2924. | |||
|
|
|||
| Fig. 2925. | |||
|
|
|||
| Fig. 2923. | Fig. 2926. | ||
Fig. 2917 represents a yoke for the slide valve of a steam engine or a locomotive, which may be forged by either of the following methods:
Fig. 2918 represents a stem a welded into the bar b, which may be bent to the required rectangle and welded at the ends.
A second method is to jump the stem d and split it open as in the side view in Fig. 2919. The bar e is forged with a projecting piece to go in the split of d, and after the weld is made, bar e is drawn to size as shown, leaving the two projections x where the corners are to come, which is necessary in order to have sufficient stock to bring the corners up square. The ends of e are split open as in the end view at f, and a piece g is then welded to f.
In a third method the end of the stem is rounded for the weld, as shown in Fig. 2920. The ends of the bar j are then split open and piece k welded on.
It is to be observed with reference to the two last methods that in hammering to forge the weld the frame is closed, so that after welding the swaging to finish may be carried on until the frame is brought to square, and any superfluous metal may be cut away; whereas if the kind of weld is such as to stretch the sides, it may happen that to get a sound weld will stretch the side welded too long and throw the frame out of shape.
Suppose, for example, that a scarf weld were made on the side of the yoke opposite to the stem, and if, in welding, the scarf is hammered too much, it would draw it out too much and throw the whole frame out of shape, as in Fig. 2921, so that the welded side would require to be jumped to bring it back to the proper length again.
A fourth method is to take a piece of iron and punch a hole in it, and then split it open up to the hole, as in Fig. 2922, and by opening out the split form the stem and part of the frame out of the solid, forging the remainder of the frame by the plan described for either the second or third methods.
A fifth method is to make the weld of the stem as in Fig. 2923, then forge out the bar b, leaving projections x x to bring the corners y y up square, and after bending to shape and squaring up to weld in a piece c.
A sixth method is to form the band first as in Fig. 2924, form the stem as in Fig. 2925, and weld as in Fig. 2926.
Figs. 2927, 2928, and 2929 represent a method of forging a fifth wheel for a vehicle. A rectangular piece of Norway iron is fullered to form the recess at c in Fig. 2927. Holes are then punched at h and splits are made to the dotted lines shown in the figure. The ends are then opened out, forming a piece such as in Fig. 2928. The letter a represents the same face of the work in all the figures, being the edge in Fig. 2927, and the top face after the ends are opened out. The four arms may then be dressed to shape, the two lower ones being drawn out and threaded before being finally closed to shape. A piece may then be welded on one end, as at b, to complete the circle.
[II-240]To forge a double eye, such as in Fig. 2930, we may take a piece of sufficient size and fuller at a a, Fig. 2931; a hole is then punched at b, and it is then split through to the dotted line in Fig. 2931, and opened out as in Fig. 2932, and then forged to shape.
Bending.—Fig. 2933 represents a tool for bending pieces of small diameter to a short curve, either when cold or heated. In bending hot iron it is advantageous to confine the heat as closely as possible to the part to be bent, as a more true bend may then be obtained.
As an example in bending, let it be required to bend a straight shaft into a crank shaft, and the following method (from “The Blacksmith and Wheelwright”) is pursued. The shaft is first bent as in Fig. 2934. The piece is next bent as in Fig. 2935, and finally as in Fig. 2936, the corners a a and b b corresponding in all the figures.
Blacksmith’s Bending Blocks.—In cases where a great number of pieces of the same size and shape are required to be bent during the forging process, a great deal of time may be saved and greater accuracy secured in the work by the employment of bending devices. Thus, in Fig. 2937 is shown at a a clip requiring to be bent to the shape at b. A pair of tongs is provided with a hole at c to receive the stem of the clip, and the jaw d is made of the necessary width to close the ends of the forging upon. It is obvious that the hole c being in the middle of the width of the tong jaw, the wings will be equidistant from the pin.
Figs. from 2938 to 2943 represent bending devices.
Figs. 2938, 2939, and 2940, represent a “former” for a stake pocket for freight cars. a is a cast-iron plate having a projection b, around which the stake pocket c is bent. d is fast upon a, and affords a pivoted joint for the bending levers e f. The work is placed in the former as shown in Fig. 2939, and levers e f are swung around to the position shown in Fig. 2938. To enable the work to be put in and taken out rapidly and yet keep it firmly against the end of b, a hand-piece g is used as in Fig. 2940, its form being more clearly shown in the enlarged Fig. 2941. Sufficient room is allowed between b and d to admit the work, and the end of the piece g, which is pressed in the direction denoted by the arrow in Fig. 2940, forcing the work against b. A number of the pieces are piled on the fire so as to heat them sufficiently fast to keep the former at work, and the bottom piece is the one taken out.
[II-241]The corners of the work are by this process brought up square and the faces are kept out of wind. The surface a forms a level bed. These advantages will be readily appreciated by all smiths who have had comparatively thin work to bend to a right angle in the ordinary way.
Figs. 2942 and 2943 represent a similar former for the step irons of freight cars. In Fig. 2942 the piece is thrown in place ready to be bent, its ends being fair with the lines j k on the bending levers e f. In Fig. 2943 the levers are shown closed and the work c therefore bent to shape. The bed plates a are mounted on a suitable frame to raise them to a convenient height for the blacksmith.
Forging a Stable-fork.—In the manufactories where stable and hay forks are made, the whole process of forging is done under the trip hammer, and is conducted as follows:—
To forge a four-tined fork, such as in Fig. 2944, a blank piece of steel is employed, its dimensions being 53⁄4 inches long, 73⁄4 inches wide, and 1⁄2 inch thick. The first operation is to swage down one end, as at a in Fig. 2945. A split is then cut down as at b in Fig. 2946. The split is then opened out as in Fig. 2947, and is fullered and drawn out at c. Two more splits are then made at d d, and the ends are bent open as in Fig. 2948, when the four tines e e and f f are drawn out and shaped out. The stem, a, Fig. 2945, is then finished for the handle.
The following example of forging under the hammer is derived from The Engineer, of London, England. Fig. 2950 shows the[II-242] piece to be forged. A block of iron, Fig. 2951, is drawn out as in the figure, the dimensions of a and b being considerably above the finished ones. A forked tool t, Fig. 2952, may be used to nick the two grooves shown in Fig. 2953, which marks the locations for the hub and forms a starting guide for the two fullering tools shown in Fig. 2954, one of which is held by the blacksmith and the other by the helper. After this fullering the forging will appear as in Fig. 2955. The ends e, f may then be drawn out, having the shape as in Fig. 2956. To shape the curve between the side of the hub and the body of the stem, grooves are formed as in Figs. 2957 and 2958, y and b being top and bottom half-round fullers, and these two grooves are subsequently made into one by means of larger half-round fullers, as in Fig. 2959. The object of making two small fullered grooves and then making them into one is to prevent the fullering from spreading the body of the stem by lessening the strain due to using a large fuller at once. The piece now appears as in Fig. 2960.
The next operation is to cut or punch away the metal between the ends of the hub and the body of the piece, which is accomplished as follows:
A top and bottom die and block are made to contain the work, as in Fig. 2961, a and b being the work ends. Through these dies are two holes for two punches which are driven through together as marked; the dies are held fair, one with the other, by four holes in the lower and four pins in the upper one, a section and top view of the dies being shown in Fig. 2962.
The piece is at this stage roughed out to shape all over, and may be finished between the pair of finishing dies shown in Fig. 2963, which also represents a plan and sectional view, a, b, c, d being the holes to receive guide pins in the upper die.
An excellent example of forgings in Siemens Martin steel is given[II-243] in the following figures, being the rope sockets for the Brooklyn Bridge.
Fig. 2964 represents two views of the forgings, and it will be readily perceived that they are very difficult to make on account of the taper hole, which is shown in dotted lines. The first operation was to take a bar of steel 61⁄2 inches square and punch a hole, as at a Fig. 2965.
Next the piece was fullered at b, c by the fuller a, Fig. 2966, and cut partly off as at d. The fullering at b was then extended by a spreading fuller, shaped as at b, and the end e was drawn out. Then the piece was cut off at d. Next the spreading fuller was applied to c, and the forging appeared as in Fig. 2967. The end f was then drawn out, and the appearance was as in Fig. 2968.
The next operation was to enlarge the hole a, Fig. 2965, by drawing taper mandrels through it, the mandrels being about 7 in. long, having 1⁄2-in. tapes on them, and being successively larger. With the last of these mandrels in the hole the hub was drawn out to length and diameter, leaving the forging roughly shaped, but having the form shown in Fig. 2969.
To finish the hole the forging was then placed in a block such as shown at g, in Fig. 2970, a finishing punch being shown at h in the figure.
The next operation was to let the steam hammer down upon the face of the punch and bring up the wings e f parallel, but not more than parallel, as then the mandrel could not be got out; the forging then appearing as in Fig. 2971.
The next process was to put in a bar mandrel such as shown in Fig. 2972 at i, the pieces j, k fitting on their sides to the mandrel and being curved outside to the circular and taper shape of the hole. The wings e f may then be closed on the mandrel to their proper width and the whole hub end being trimmed by hand, all the previous work having been done under the steam hammer. The[II-244] hub being finished the key m may be taken out and the washer l taken off, when i can be pulled out, leaving j k to be taken out separately. A pair of tongs are then put through the finished hub end, while the wings are punched and trimmed under the steam hammer, and subsequently finished by hand.
The forging of wrought-iron wheels for locomotives is an excellent example. The spokes are first forged in two pieces, as 1 and 2 in Fig. 2973, and then welded to form the complete spoke. Piece 1 is first forged in dies under the steam hammer to the form shown in Fig. 2974, the dimensions being correct when the faces of the dies meet. The stud c d is then drawn out to the required length and dimensions.
The upper half of the spoke is first blocked out under dies to the shape shown in Fig. 2975, and the block b spread so as to form a section of the wheel rim, as shown in Fig. 2976, in which d is a die, l a movable piece wedged up by the wedges w w, and removable to enable the extraction of the forging, and f is an end view of the fuller, the use of which is necessary to cause the metal to spread sufficiently in the direction of the dotted lines. The corners of the rim are then cut off, as shown in Fig. 2973, and the rim is bent in a block having its top face of the necessary curve, as in Fig. 2977, a being the block, and b a piece movable, to allow the extraction of the work, and fastened in place by the key or keys c. The two pieces are then welded together, their lengths, &c., being gauged by a sheet-iron template, formed as in Fig. 2978. The welding is usually performed with sledge-hammers, but as soon as the pieces will hold well together, the drawing down is done under a steam hammer.
The spokes thus forged are then put together, as in Fig. 2979, b representing a wrought-iron band, encircling the rim of the wheel and closed upon the same by the bolt and nut at n.
Two washers are then forged, to be placed and welded in as at w w, in Fig. 2980.
The welding together of the spokes and of the washers to the spokes proceeds simultaneously. The washers are heated to come to a welding heat at the same time as the wheel hub is at a welding heat, and the two are welded together under a steam hammer. During the heating of the wheel hub, however, the band b, Fig. 2979, is tightened up with the screw to bring the spokes into closer contact when heated to the welding point.
The seams between the spokes at the circumference of the hub are welded with bars as shown in Fig. 2981, in which r r are two bars of iron which are operated by hand as rams. The wedge shape of the washers on their inside faces performs important duty in spreading the metal as well as simply compressing it,[II-245] giving a much more sound weld than a flat washer or plain dish would.
The rim of the wheel is welded up as follows:
In Fig. 2982 are shown four spokes of the rim as they appear after the hub is welded. Into the V spaces, as a, b, c, d; wedges of metal, of the form shown at e, are welded, after which the surplus metal of e is cut away, and the rim is solid as at f. In this process, however, it is necessary to weld all the pieces on one side of the wheel, as at a b, &c., except one, which must be left unwelded until all the pieces save one on the other side are welded, and the wheel must be allowed to become quite cool before these last two pieces are welded. Otherwise the strain induced by the contraction of the wheel rim while cooling will often cause the rim to break with a report as loud as that of a rifle. In those cases in which this breakage does not occur the wheel will be very apt to break at some part of the rim, when subjected to heavy shocks or jars.
The Figs. 2983 to 2999 (which are taken from Mechanics), illustrate the method employed to forge the rudder frame of the steamship Pilgrim.
A side elevation of the rudder frame is shown in Fig. 2983.
The forging is made in eight separate pieces, which are so united as to make three pieces. These three pieces are finally joined by five welds. The whole length being 29 feet 113⁄4 inches, and the weight 6,500 pounds.
The work is commenced by piling and welding on the porter-bar at the point in the shaft marked a. The stubs b and c having been previously prepared, the pile on the porter-bar is heated and welded up and drawn, shown in Fig. 2984, and scarfed as shown in Fig. 2985; the piece, shown in Fig. 2986, is then laid in the scarf and welded; then the part from b to a is finished to size, the finished forging of the post being shown in Fig. 2984. The surplus stock to the right of b, Fig. 2984, is worked down into the post e, and the distance from b to f is thus made correct without loss of stock or time. The curve at d, Fig. 2983, was worked down somewhere near, and then another pile and weld carries the job to g. Here the same operations as at first are repeated, and the arm c is welded in. There is left a good lump of stock in front of c, and by another pile and weld enough is added to make the job to i, as shown in Fig. 2987. Holes are then punched at j and l, and the piece of stock m cut entirely out. A cut is made to l with a hack opening out the piece n from the shaft. A taper punch, with a 3-inch point and a 4-inch head, is then driven at l; to throw the piece n out into the position shown at n1, Fig. 2983; n1 is then finished, and the post from l to j brought to forging size; then, by the ordinary process of piling, welding and drawing, the shaft is finished from i to o. Next the porter-bar is cut off, so as to leave stock enough to make the lower part of the shaft, as shown in Fig. 2988. A hole was punched at q, and the stubs drawn out, as shown in Fig. 2989, which gives the post complete.
The pieces s and t, and the tiller v, having been forged, as shown[II-246] in Fig. 2991, the upper member of the frame is started on the porter-bar at w, Fig. 2983, and filed, welded and drawn to make the job as far as x1. Wooden templates, such as in Fig. 2992, are provided for the pieces of the frame, the first extending from w to x1 and x, and the second including the part from x1 to x2 and x3. After w, x1 has been drawn out with lumps left where the tiller and the arm s are to be joined, the scarf is made for the tiller and that is welded in, and the job finished to piece s. The scarf for s is then made, and s welded in. This makes the upper member of the frame. The lower member is made in the same way, starting at x3. These two members are shown complete in Fig. 2993. The post, Fig. 2989, was sent to the machine shop, and was turned, planed, bored, and slotted, as shown in Fig. 2990. The frame was now ready to be pieced up, by welds at w, x, x1, x2, and x3, Fig. 2983.
The several sections are now ready to be welded together for the complete frame, these welds being made as follows: The ends are upset as in Fig. 2994 to receive on each side a V-piece such as in Fig. 2995, which is heated on a porter-bar, and is of a more acute wedge than the ends to be welded, so that when laid in as in Fig. 2996 it will touch at the bottom first, and thus allow the air and whatever dirt there may be on the surfaces to squeeze out as the welding proceeds. The method of heating the frame for these welds is as follows: The V-block (which has the grain of the iron running in the same direction as that of the frame) being heated in the blacksmith’s forge, the frame is clamped together and counterbalanced by means of weights, so that it may be laid over a fire pot, constructed as in Fig. 2997. This fire pot is lined with brick, and has its blast supplied through a piece of flexible tube. The anvil is of cast iron, shaped as in Fig. 2998, and placed on the other side of the frame and opposite to the fire pot or portable forge, as shown in Fig. 2997, so that the frame, when the heat is ready, may be turned over upon the blocks on which it rests, and the part to be welded will come upon the anvil. After one side is welded the anvil and the portable forge change places, and the second side of the weld is made.
In the following figures (which are taken from Mechanics) is illustrated the method employed to build up the shaft shown in Fig. 3001, which was for the steamer Pilgrim. Forgings of such large dimensions are built up of pieces or slabs, called blooms, which are themselves forged from scrap iron, which is piled as in Fig. 3000. For the forging in question this scrap iron consisted of old horseshoes, boiler-plate clippings, boiler rivets and old bolts, and the first[II-247] step in the manufacture is to form this scrap into piles ready for the furnace.
These piles are made upon pieces of pine board 1⁄2 inch thick by 16 inches long by 10 inches wide. On these the scrap is piled about 14 inches high, each pile weighing about 270 pounds. After piling, the scrap goes into the furnace and is raised to a welding heat, the board retaining its form as a glowing coal almost to the last. The pile of scrap is heated so nearly to melting as to stick together enough so that it can be picked up in a long pair of tongs with peculiarly-shaped jaws, and, as these tongs are suspended by a chain from an overhead traveller running on an iron track, the bloom is easily transferred to the anvil of the steam hammer, where, after one or two blows, a small porter-bar with a crank end, such as shown in Fig. 3003, is welded on, and the pile is rapidly drawn out into a square bar. When completed the porter-bar is cut off, and the bar is laid aside to cool. The pile of scrap has now become a “bloom,” such as shown in Fig. 3002, and has been reduced in weight from 270 lbs. to 240 lbs. The bloom is about 30 inches by 5 inches by 5 inches in dimensions, and has rounded, ragged ends, and a surface full of lines marking welding of the individual pieces, and at the ends looking as though the scrap had united by melting rather than by any welding process.
These blooms are then taken to the large steam hammer and furnace by which the shaft is to be built up. The porter-bar, although merely a tool whereby to handle the mass, forms practically a base wherefrom to build up the shaft. The construction of the furnace is shown in Fig. 3004, the heat, after passing the work being used for the steam boiler that supplies steam to the steam hammer.
The porter-bar is held by a crane, the chain being placed in such position in the length of the porter-bar as to balance it. On the end of the porter-bar is a clamp, having arms by which the bar may be turned in the furnace and when under the hammer.
Fig. 3005 represents the bar in position in the furnace, the aperture through which it was admitted having been closed up by bricks luted with clay, one brick only being left loose, so that it may be removed to examine the heat of the bar. The end of the bar is flattened somewhat, and a slab is laid upon it as in Fig. 3006, the appearance after the first weld being shown in Fig. 3007. It is then turned upside down, and blooms are piled upon it as in Fig. 3008. After these are welded the end is shaped up round and to size. The extreme end is again flattened, or “broken down,” as it is termed, and first a slab, and after reheating, blooms are added, as already explained; when these are welded and forged enough to consolidate the mass the mass is rounded up again, thus increasing the length of finished shaft. The end is again broken down and a slab added, and so on, the shaft thus being forged continuously from one end, and being composed of alternating slabs and blooms.
To forge this shaft 118,000 lbs. of blooms, 185 tons of coal, and 360 days of labor were required, the time occupied being 34 working days.
The slabs are simply forged pieces of larger dimensions than the blooms, and more thoroughly worked, the difference between slabs and blooms being that there is more waste with the blooms than with slabs, because the blooms heat quicker than the forged part of the crank.
Between both the slabs and the blooms there are placed rectangular pieces to hold them apart, and let the furnace heat pass between them, the arrangement of these pieces being shown in Figs. 3009 and 3010.
Figs. 3011 to 3024 (which are taken from Mechanics), represent the method employed to forge the crank shaft of the United States steamship Alert.
| VOL. II. | FORGING UNDER THE HAMMER. | PLATE XVII. |
 |
 |
|
| Fig. 3011. | Fig. 3012. | |
 |
 |
 |
| Fig. 3013. | Fig. 3014. | Fig. 3015. |
 |
 |
 |
| Fig. 3016. | Fig. 3017. | Fig. 3018. |
 |
 |
 |
| Fig. 3020. | Fig. 3019. | Fig. 3021. |
 |
 |
 |
| Fig. 3022. | Fig. 3023. | Fig. 3024. |
Fig. 3011 represents the crank shaft, and Fig. 3012 an end[II-249] sectional view, showing how the throws were built up. The first operation was to forge the saddles shown in Fig. 3013, these being the pieces that are shown between the cap and the wrist.
These saddles were made in halves, each half appearing as in Fig. 3014. From a pile and weld of blooms on the porter-bar, enough to make the two halves, one half was cut off. The other half was then drawn down on the porter-bar, and the first half was then piled on the latter, as shown in Fig. 3015. The square cross bar goes clear across and projects about an inch at each side. The back pieces were short bits. The square cross bar makes the saddle less liable to split in welding it on to the square shaft. Two “caps” were also made before the forging of the shaft itself began. These are shown in Fig. 3016, and their position in the finished work is shown in Fig. 3012.
The shaft itself was piled, welded, and drawn on the porter-bar in the usual manner, until the location of a crank was reached. Then a part of the work some distance from the new end was squared, as shown in Fig. 3017, and on this square the saddle was piled to heat and weld, as shown in Fig. 3018. As will be seen, the saddle rested upon the outer lines of the angle. The first blow was struck square on the top of the saddle, and after three or four blows the job presented the appearance shown in Fig. 3019. The piece was now turned so as to lie as shown in Fig. 3020, and worked with blows on the sides to the shape shown in Fig. 3021. This opened the top of the juncture of the saddle and squared the shaft down to the point where the weld was good. The piece was then turned back to the position shown in Fig. 3019, and worked with blows which again closed the angle on top, and made the weld good all through. The piece was then returned to the furnace, and at the next heat the saddle was squared up and finished, and the cap was piled on top of the saddle, as shown in Fig. 3022. The cap was welded on at the next heat, and two cheeks, like that shown in Fig. 3023, were laid upon one flat of the crank and pinned with 15⁄8-inch round pins. One of these pins is shown in the figure. Bits of iron were put under these cheek pieces in the usual manner. As the cheeks were very much smaller in section than the crank body, it was necessary to turn them over away from the fire, or else the cheeks would be burned before the crank body was hot enough to weld. To prevent the cheeks from falling off in the furnace the pins were put in as described before heating. After two cheek pieces had been welded on one side, two more were added on the opposite side, and then the crank was finished, as shown in Fig. 3024.
As will be seen by inspection of Fig. 3012, the weld between the cap and the saddle comes about the middle of the wrist, and the cheek pieces support the cap sideways. By means of the piles and welds described, the grain of the iron was so disposed as to offer the most resistance to working strains. This method was devised by Mr. Farrell Dorrity, of the Morgan Iron Works.
Forging Large Crank Shafts.[45]—The following paper describes the method of forging marine crank shafts adopted at the Lancefield Forge, Glasgow. It will be better understood if a short account is first given of the ordinary methods in use for the same purpose.
[45] From a paper read at the Glasgow meeting of the Institution of Mechanical Engineers, by W. L. E. MacLean.
“First Method.—The most common method is technically termed by the forgeman, ‘finishing the piece before him.’ He begins with a staff or stave, as shown in Fig. 3025, suspended by a chain from the crane, and made round for the convenience of manipulating under the steam hammer; this stave is used over and over again for many forgings, as it is merely the “porter” to carry the piece and enable it to be worked. The forging is begun by two or three slabs being placed on the stave as at s s s, and then inserted in the furnace. These slabs are flat blocks made up of pieces of scrap iron, which have been piled and heated, and then welded together. After being brought to a welding heat in the furnace, the slabs are withdrawn, placed under the steam hammer, and beaten down solid. The piece is then turned upside down, and two or three similar slabs placed on the opposite side, as shown at s s. When sufficient iron has been thus added to form the collar of the shaft (assuming it is to have a collar), it is rounded under the hammer, as at c, Fig. 3026, and the body of the shaft next to the collar is roughly formed, as at d. More slabs, s s s, are added to bring out the body, and afterwards the crank itself is proceeded with, on the same plan. The piece will begin to assume the appearance of a, Fig. 3026. Then more slabs are welded on the top, as at s s s, till the depth of the crank is obtained, after which the forgeman proceeds to finish the collar and body of the shaft, as shown. The collar on being finished is cut all round, as shown at c d, Fig. 3027, so that it may be more easily detached from the stave when the shaft is completed, leaving only sufficient connection to carry it till then. The forgeman then cuts the gable of the crank as at e g, and rounds up the body and neck as at b n, Fig. 3027.
“This, it will be observed, is a speedy process, and would invariably be adopted if it were not attended with a very serious drawback; it is very hazardous to the solidity of the forging. For it will be easily understood that not above a third of the crank itself can be thus formed, because the iron at the neck n would not carry a greater mass; if the whole mass of the crank, or even the half of it, was formed before the body and neck of the shaft were finished, a proper heat could not be taken on the body and neck for finishing, without the neck giving way or rupturing. Indeed, as it is, the undue proportion often causes the shaft to be strained at this part, where most strength should be, so that it is rendered weak, and a flaw is developed which by-and-by causes it to be removed from the steamer as dangerous and useless, if indeed it does not break outright; so that the forgeman, if he adopts this method, must be very careful to proportion the amount of iron he has massed in the furnace to the size of the body he is finishing, otherwise the weakening above mentioned will take place. All marine engineers will easily recognise this defect, which frequently occurs, but the cause of which is probably not well understood. Such a flaw will present a similar appearance to that shown at f, Fig. 3033, taken from an actual example.
“This difficulty of proportioning the part of the crank first forged to the size of the neck, will be still better understood by the appearance of it in the furnace, as shown in Fig. 3028. Having reached this stage, with one end of the shaft completed, as also that portion of the crank itself which of necessity was completed before the collar was cut, in order that the neck might be finished, no more iron can be added on the top edge, as it is up to the full depth already; it must therefore be added on the flat, as in Fig. 3029, where the piece is shown on its flat side in the furnace, the finished portion being outside the furnace door. A number of slabs s s s are then placed side by side to bring out the width of the crank further; these being welded down, the piece is turned upside down, and the process repeated on the other side. Afterwards other slabs are similarly placed on both sides, as shown in Fig. 3030, of which one is the flat, and the other is the edge view of the crank at this[II-250] stage; and this is continued until sufficient iron has been massed to allow of the other gable of the crank being cut down, as at a, Fig. 3031, and sufficient also to allow of the other part of the body b being rounded and prepared for further piecing out.
“Now it will be observed that the first gable finished has the slabs all welded on the edge of the crank, and the hammering has all been on the edge; hence the subsequent hammering on the flat has a tendency to open up the weldings, if they have not been thoroughly made. A section taken at a b, Figs. 3028 and 3029, will show as in Fig. 3032, on the left, the weldings being across the web of the crank; the circle indicates the section which the crank pin would present if cut through there. But when the slabs are placed on the flat afterwards, some of the joinings of the ends of the slabs, or “scarf ends,” are certain to fall within the crank pin, as seen in Figs. 3028 and 3029; therefore the section through c d, Fig. 3030, will show somewhat like Fig. 3032 on the right, and the crank pin necessarily includes some of these flaws. The flaw thus produced, called ‘a scarf end in the pin,’ is readily recognizable by all marine engineers; at f, Fig. 3033, is a sketch from an actual occurrence.
“When the second gable is cut, and the other end is rounded, there is only the other collar to be put on (if a double-collared shaft), and the forging is completed.
This method is so speedy, compared with any other, that it is often resorted to even at the risk of making a bad forging; and too many broken shafts testify to the fact. Besides, it may be observed that in making a double crank shaft, while the one crank may be made in this way, the other must; for, the first crank, a, Fig. 3033, being completed, and the body, b, between the two cranks, also completed, the second crank, c, must of necessity be pieced off this body, even at the risk of the neck n being strained. This may account for the many instances in which one of the cranks of a double crank shaft gives way, rendering the shaft useless; and also for the plan, now almost universal, of making the two cranks separately and coupling them together; a further object being, no doubt, to have the means of replacing a defective half, if need be, without losing the whole shaft.
“At Lancefield, when a double crank shaft is to be made, the after crank, a, is first made by the method afterwards described, so as to insure that this crank, through which, as being next the propeller, all the power of the engine passes, is perfectly sound; and in piecing the other crank off the body, it is worked with slabs on the flat instead of on the edge, as afterwards described.
“The writer’s own opinion is that the crank is the most important part of the shaft, and, therefore, at all costs, should be made first. Others, no doubt, may take the same view, and, to avoid the risks just mentioned, may adopt the process described in the second method.
“Second Method.—This method builds the middle first, and is called “turning the shaft end for end.” The shaft is begun from a stave, by the addition of slabs, as shown in Figs. 3034 and 3035; Fig. 3034 shows it with iron added in slabs, till a butt is formed, as at b, to form the nucleus of the crank; slabs s s s are then piled on it to bring the crank up to the height.
“These are beaten down and welded, and more are added, as at s s s, Fig. 3035, till the full height of the crank is reached. Should the web (or edgeway of the crank) be thick, two slabs are frequently used to make up the breadth, placed edge to edge, as shown in Fig. 3035 on the right hand of the figure; the widths of these slabs are limited by that at which the shinglers can conveniently work and turn them under the steam hammer. The crank, however, is completed without any “side slabs,” for the beating down of the slabs on the edge will broaden out the mass, and give sufficient material to forge out the crank to the proper height by hammering on the flat. The crank is afterwards cut at the off gable at g, Fig. 3036, the body b pieced out and rounded, the collar welded on, and then a small stave s is drawn upon the end, to enable the forgeman to handle the piece when he “turns it end for end” to complete the other end of the shaft.
“This method, though better than the last, is also objectionable; for though there is not equal risk of ’scarf ends’ in the pin, yet the weldings are all on the edge, as in the lower view, in Fig. 3036, where the section of the crank pin is shown by the dotted circle; and the cheeks of the crank, o o, are thus liable to give way if a[II-251] heavy strain comes on the crank when at work. The defects arising from this cause are shown in Fig. 3037, and will be readily recognised by all engineers.
“Third Method.—Considerations such as these have led to the adoption of the third or Lancefield method.
“Fig. 3038 shows the piece begun from the stave in the usual way, with the slabs all welded, however, on the flat, till a basis is formed for the building up of the crank. A portion a is roughly rounded to form the one end of the shaft, and the butt of the crank will present the appearance of a slightly elongated square, as shown at b, Fig. 3039. The workman then “scarfs” or hollows it down at one edge all along the side, as indicated in the end view by the dotted line from c to d; it will then present the appearance shown by the end view, Fig. 3040, being somewhat bulged outward at the points e and f. Three long thin slabs, Fig. 3042, shaped for the purpose, are then placed on the hollowed part, the piece lying flat in the furnace. These slabs are tapered a little the broad way, not on the length, and little pieces of iron are interposed between them, to keep the surfaces apart, and allow the flame free access between them. The object of making them thin is that they may be all equally heated, which is not so readily achieved when the slabs are thick; and the object of the tapering is to allow the slag to flow out freely when the uppermost slab is struck by the steam hammer. The surfaces thus get solidly welded.
“Fig. 3041 represents the slabs thus placed in elevation, and the figure on the right, in section. The slabs are forged long enough to go right across the whole width of the crank, excepting about 6 inches; this margin is necessary to allow of the lengthening out of the slabs to the whole width under the process of forging. After these slabs are perfectly welded, the piece is turned upside down, and the process is repeated on the other side, as shown in Fig. 3042. When welded down the mass has increased in depth as well. Another scarfing takes place on the first side, and then another on the second side, as shown in the figure, and so on, till the full size is obtained; and it will be seen, as in the right-hand view in Fig. 3042, that by this process of “scarfing” equally from, both sides, the iron from the very middle of the body of the shaft is drawn up quite to the crank pin. The location of the pin is indicated by a a, and it will be seen that by no possibility can there be a “scarf end” in the crank pin, as the slabs in all cases go right across the crank, and also that the cheeks of the cranks have no edge weldings crossing them, as in the previous cases; for the tail of a slab may be at r, Fig. 3042, while the other end may be at s. The fibre is also developed by the continuous drawing up of the iron consequent upon the repeated flat scarfings across the whole width of the crank. When the crank has been thus massed sufficiently large, it is cut at the gable, with sufficient material left to piece out the other body of the shaft. This is now done, the coupling welded on, and a small stave drawn on the end to enable the forgeman to manipulate it, when it is turned end for end, to complete the other end.
“These proceedings occupy longer time than either of the other two methods, and consequently costs a little more; but the advantage is well worth all the difference, as greater confidence can be entertained that the forging is every way satisfactory. In brief, by making the crank first, is avoided the liability to weakness at the neck, characteristic of the forgeman’s making the shaft before him, as in the first method; by the repeated ‘side scarfing’ is avoided the liability to fracture across the cheeks, consequent upon the edge weldings of both first and second methods; while by having the slabs the whole length of the width of the crank, any ‘scarf end’ in the length way of the crank pin is impossible (such as may occur in the first method); and the welding of the mass of the crank being wholly on the flat must tend to form a more solid forging than if hammered otherwise. Thus, if the forging is well heated and properly hammered, the system promises to insure that no weak part will be found in the shaft after it is finished and put to work. The writer believes, from the success which has already followed in every case the adoption of this method, that it will eventually be found that almost more depends on the mode in which a crank shaft forging is constructed than on the material of which it is made.
“This leads him to some observations regarding the material for such shafts. It is of course well known that in the early days of engineering, before the time when steam navigation had received a great impetus by the invention of the screw propeller, the connecting rods, cranks, shafts, &c., of land engines were all formed of cast iron; except, indeed, where the connecting rods were made of wood, strapped with plates of wrought iron, as frequently was the case with pumping, winding and blowing engines. In fact, all the parts that could be made of cast iron were so made, and the piston rods, bolts, keys, straps, and other smaller parts were alone made of malleable iron, the smaller pieces being made from rolled bars direct, as at present, and the larger made of similar bars, but placed side by side and bound together or ‘fagoted,’ as they were called, from their resemblance to a bundle of fagots. These bars, thus fagoted, were either brought to a welding heat in a smith’s hearth and welded under the sledge-hammers of the men called ‘strikers,’ or hammermen; or else heated in a furnace, and welded under the tilt hammer worked by a steam engine. By-and-by it was found necessary to adopt the stronger material, wrought iron, for parts hitherto confined to cast iron, because the latter was found too deficient in cohesion to stand the strains due to the power of high-pressure steam, which was now almost universally superseding the use of low-pressure steam in the condensing engine. The system of fagoting, however, was still carried out, even far into the history of marine engineering; but when the rapid increase in the dimensions of engines, both stationary and marine, called forth the steam hammer, and so rendered the forging of heavy masses comparatively easy, the system of fagoting fell into disuse, for the following reason: In making up a fagot, say, of 18 inches or 20 inches square, it was found, that in the furnace the outside bars would reach a welding heat much sooner than those in the middle; consequently on welding this fagot under the steam hammer, though the blow might reach to the centre, yet the interior would not be welded, while the surface was; hence the shaft or other forging would not be welded throughout, and it was no uncommon thing for a shaft to break and expose the internal bars quite loose and separate from each other.
“When it was seen that malleable was so much superior to cast iron, and that the system of fagoting was so imperfect, the adoption of ‘scrap iron,’ which was then composed principally of parings of boiler plates, pieces of cuttings from smiths’ shops, old bolts, horseshoes, angle iron, &c., became general. These being piled together in suitable pieces, and in a pile of suitable size, for the convenience of working, were brought to a welding heat, and beaten out into a slab, or oblong-shaped piece, ready for the forgeman; who would[II-252] build two or three together, adding more when required, and so bring out his piece to a sufficient size to enable him to shape his forging out of it. Then it was that engineers, seeing what an increase of strength they obtained by these means, invariably specified on their drawings (as many of them still do), ‘These forgings are to be made of carefully selected scrap iron, free from flaws and defects.’
“To meet the requirements of their customers, therefore, forge-masters had now nothing to do but to select and use the best available scrap iron; but the universal adoption of iron hulls in place of wooden ones, conjoined with the rapid and unprecedented increase in steam navigation, soon introduced a class of scrap iron which did not possess the qualifications of good scrap, and also called for a very much greater supply of forgings than could be obtained in superior scrap iron. The consequence was that shafts of scrap iron, when turned and finished, became liable to exhibit streaks and seams, not due alone to imperfect welding in the forging, but likewise to the laminations and imperfections of the original scrap iron, which the process of piling and shingling into the slab was not sufficient to obliterate. So constantly does this yet occur that it causes a strong temptation to make such forgings of new iron puddled direct from the pig and then shingled into slabs or blooms, under the idea that these streaks and seams will thus be avoided, and that the iron will be improved almost to the condition of scrap iron, while being forged under the steam hammer. This, however, is found not to be the case. The forging is certainly free from the streaks of the scrap iron, but this is obtained at the expense of strength; for the material is too raw; it wants cohesion, and has not had the proper kind or amount of working to bring it to the condition of superior wrought iron. This method is still further tempting, inasmuch as it is far cheaper than the other; the material costs less than scrap iron, and, as it welds at a lower temperature, a forging can be much more quickly and easily made. Still, for whatever class of machinery it may be fitted, it should certainly be renewed in every case for a crank shaft or propeller shaft.
“From these considerations it has been the custom at Lancefield, in the preparation of the iron for crank shafts, to improve upon the ordinary condition of the scrap iron in the following manner: The pile is made up of carefully cleaned and selected scrap; it is brought to a welding heat, and then hammered under the steam hammer. But instead of being beaten into a flat slab for the forgeman, it is beaten into a square billet, which is afterwards rolled in the rolling-mill into a flat bar, as if for ‘best best’ merchant iron. By this additional heating, hammering and rolling, all the different qualities of the scrap iron composing the pile are merged into one homogeneous material, having the fibre given to it that was lost in the separated portions of the scrap iron; and this, when cut up into proper lengths, and again piled and shingled into the slab, results in a material possessing somewhat the closeness and density of steel, while retaining all the toughness and tenacity of superior malleable iron. The improved method of constructing the forging, previously detailed, is worthy the use of this superior material; and both having been adopted at Lancefield with results which have commended themselves so unmistakably to many engineers, that they now not only specify the material, but stipulate for the mode of manufacture, it is thought the system has only to be more widely known in order to be universally adopted. It is certain to give greater confidence in the endurance of such important parts of the machinery, although this confidence may have to be obtained by a small increase in the cost, due to the extra workmanship both on the material and on the forging.
“When we take into consideration the vastly accelerated speed of the marine engine in late years, and the many disastrous effects which follow the breaking of a shaft at sea—also that the tendency of the age is still towards much higher pressures, and further lengthening of stroke it is not surprising that improvement in such an important part as the crank shaft should be eagerly sought after; but it has hitherto been sought in the direction of the material alone. Cast steel has been advocated, and brought to some extent into use; but its expense renders such shafts costly out of all proportion to the other parts of the engine; while, in the event of their heating when at work (a very frequent casualty), and having the water-hose directed upon the crank pin or journals, it cannot be expected that the material will behave any better, or even so well, as tough wrought iron. What is termed puddled steel is liable to the same objection, and probably, from its mode of manufacture, in a still greater degree. The so-called mild steel is no doubt proving itself a superior material, and yielding good results when rolled into ship or boiler plates. But thus prepared it is more costly than ‘rolled scrap bar;’ and if not rolled, but cast into an ingot, then it possesses some of the crystalline characteristics of steel, with all the disadvantages attending its manipulation into a forging.
“For extra large crank shafts, the fear of unsoundness, arising from the ordinary mode of forging, has led some engineers to consider the propriety of building the shafts and cranks in separate pieces. This, with engineers generally, has not hitherto been looked upon with favor; as the fewer the pieces the more rigid the shaft. Moreover, the increased weight necessitated by this separate building is viewed as a disadvantage, even although it were not attended with greater cost, as undoubtedly it is.
“The material and mode of manufacture advocated in this paper may tend to dissipate some of these apprehensions. They will not obviate defective construction in the engines themselves, or faulty proportion of their parts, or neglectful supervision of their working, but they will reduce to a minimum the risk of breakage in such untoward circumstances. If any objection be taken on the score of extra size, the enterprise which a quarter of a century ago engaged in the making of the unusually large shafts necessary for the ‘Great Eastern’ may still be trusted to meet the advancing requirements of the present day.”
Fig. 3043 represents a foot-power hammer or Oliver. The hammer is upon a shaft in bearings, and is held in the position shown by an open coiled spring. On the shaft is a chain pulley, the other end of the chain being connected through a leather strap to the treadle. Means are provided to adjust the height to which the hammer will lift to bring the hammer face fair with the work and to give the required degree of tension to the spring.
Fig. 3044 represents a Standish’s foot-power hammer, in which the hammer and the anvil are provided with dovetail seats for receiving dies, swages, &c. The force of the blow is regulated by the height to which the hammer is raised, which may be adjusted by the nuts beneath the spiral springs. The handle on the hammer is for pulling the hammer down by hand when adjusting the lower die fair with the upper one.
What are known as power hammers are those driven by belt and pulley; while those known as trip hammers have their helve lifted through the medium of revolving lugs or cams. Steam hammers are those in which the hammer is lifted by a piston in a steam cylinder; while in hydraulic hammers, the hammer is moved by water pressure.
Fig. 3045 represents a Justice’s power hammer, in which the hammer is guided in a slideway and is operated by leather straps attached to the ends of a spring, at the crown of which is attached a connecting rod driven by a crank disk. The stroke is altered by means of placing the crank pin in the required position in the slot in the crank disk. By means of gibs the hammer may be set to match the dies. The pulley is provided with a friction clutch operated by the treadle, shown.
Fig. 3046 represents a Bradley’s Cushioned Hammer, in which motion is obtained by a belt passing over a pulley on a crank shaft, whose connecting rod r is capable of adjustment for length, so as to govern the distance to which the hammer shall fall, which obviously varies with different sizes of work. The hammer is lifted through the medium of a rubber cushion a, seated in a casting to one end of which is connected the rod r, while the other end is pivoted. The lever to which the hammer is affixed is raised against the compression of the rubber cushion b, and at the top of its stroke also meets the rubber cushion c; hence these two cushions accelerate its motion after the crank has passed its highest point of revolution. The cushion d prevents the rebound of the hammer after the blow is struck; hence as a result of these cushions, heavy or light blows may be struck with great rapidity and regularity. The weight w is on a lever that actuates a break upon the wheel shown at the side, so as to enable the stopping of the hammer quickly. The machine is put in motion by pressing the foot upon the treadle t, which [II-254]operates a belt tightener, the belt running loose when the treadle is released.
The hammer lever or helve is adjustable for height by means of the screw g and hand-wheel h, which raise or lower the bearings in which the helve journals are carried. This is necessary, because as the helve moves in the arc of a circle the faces of the upper and lower die, or of the hammer and the anvil, as the case may be, can only come fair at one particular point in the path of the hammer; hence in proportion as the blow terminates (by meeting the work surface) farther from the anvil face, the pivot or journal of the helve must be raised, so that the journal will be horizontally level (or as nearly so as possible) with the hammer face at the moment the blow is delivered.
By giving motion to the helve through the medium of cushions, a direct mechanical connection, and the destructive concussion that would accompany the same, is avoided; hence a high speed may be obtained without the frequent breakage that would otherwise ensue.
Fig. 3047 represents Corr’s power hammer, the construction being as follows: The semi-elliptic springs, shown on top and bottom of the beam, serve to balance the stroke, so that the hammer may run from 350 to 450 strokes per minute, with safety to the machinery. The hammer is adapted to almost any form or kind of forging. Large dies may be inserted for various kinds of forming and welding, such as making plough-shares and other articles, which require that the operation be commenced with a light tap, and increased to a heavy blow at the will of the operator.
The whole structure is mounted on a substantial iron bed v, 18 inches deep, 22 inches wide and 51⁄2 feet long. Attached to this bed v are two circular arms l; between them is pivoted near their top, at k, an oscillating frame h, having a longitudinal opening, in which is attached two semi-elliptic springs g g, and two plates i, with trunnions projecting laterally through the oscillating frame at k; the hammer beam f is inserted between the springs g g, and the trunnion plates i, which are bolted firmly to beam f at i; the ends of the trunnions and outsides of the oscillating frame h rest evenly against the inside of the circular arms l; at k a shaft is passed through the trunnions and beam f, and made rigid in them with its ends resting in boxing at k. Caps are provided to cover the ends of the boxing and shaft with set-screws projecting against the ends of the shaft, which secures it against end play.
By these mechanical arrangements the beam f and oscillator h are securely attached independently, vibrating on one common centre, allowing no side play of the hammer e, admitting f to the free action of the springs g g; in the lower end of the oscillating frame at n is a lateral opening 10 inches vertically by 6 inches longitudinally and 4 inches laterally, with flanges projecting longitudinally one inch into this opening from both sides. This makes the opening two inches smaller on the outside than the internal cavity; the rear and front internal walls are provided with steel plates, 4 by 10 inches, 1⁄4 thick, resting against the inner ends of four set-screws, not shown, provided to adjust these plates to or from the sliding box at n, to compensate for wear and prevent lost motion. These plates and flanges form slides and guides between which a loose box and eccentric is provided with shaft projecting laterally through boxing at n, which project upwards from an adjustable frame immediately under the oscillator h; this permanently locates the eccentric and shaft in the lateral opening in the oscillator h, at n. The adjustable frame mentioned rests on suitable bearings on the inside of the circular arms l, and is fastened down by four bolts passing through suitable slots in the adjustable frame, entering the bearings on the arms l. This frame is adjusted back or forth by set-screws s s; this adjustment is for the purpose of giving a greater or less distance between the anvil and hammer at d, as may be desired for large or small work, long or short dies, &c.
The anvil b, weighing about 500 lbs., sits down in the bed at r and rests on circular bearings (between r and b), which radiate to the centre of the top of the anvil at d, and is held rigidly in any position longitudinally desired by set-screws q q, with their inner ends resting on shoulders on the sides of the anvil b, which projects down about ten inches; between this lower projection and the internal wall of the bed is sufficient space to admit of any adjustment desired. This lateral adjustment is accomplished by set-screws r, passing through the sides of the bed v, with their inner ends resting against the anvil which holds it rigid at any lateral adjustment. By this arrangement the anvil is accommodated to all and any class of work or shape of dies.
The anvil is constructed in two parts. Four inches of the top c may be taken off, leaving a suitable place to insert large dies for various purposes, such as dies for welding plough-shares and dies for forging journals on large shafts. A counter-shaft, provided with suitable pulleys, is attached on the rear end of the bed; this shaft is kept constantly in speed and power by the vertical belt in the direction indicated by the arrow; the other end of the shaft is provided with a flanged pulley, corresponding to a flanged pulley m, on the eccentric shaft; around these pulleys is placed a loose belt, as shown; in contact with this is a press pulley t, adjustably attached by two arms to the projecting end of the treadle p at o. If the foot be placed on the treadle at u and it be pressed down, the break on the opposite side breaks contact with the balance wheel (not shown); the press pulley will at the same time tighten the loose belt on the flanged pulleys. This gives motion to the pulley m, in the direction indicated by the arrow. Its motion is increased by a heavier pressure until it attains the same speed as the other flanged pulley; this would be the full speed, which may[II-255] be diminished to any speed desired by lessening the pressure on the loose belt. By this means motion and power is given to the eccentric, which carries back and forth the lower end of the oscillating frame h; this gives vertical motion to the springs g g, and this imparts corresponding motion to the beam f. These springs accomplish a threefold object:
1st. They carry the hammer e up and down.
2nd. They cushion the hammer at the returning points and give off that power which was stored in them while cushioning.
3rd. By the power exerted in the machinery they follow up and impart still greater force to the blow.
It is found by this arrangement of eccentric loose box and oscillator that when the machinery is moved in the direction indicated by the arrow, that the downward stroke is one-sixth quicker than the up stroke; this is a natural result, for the down stroke is performed while the eccentric is revolving above the centre of its shaft and nearest the fulcrum of the operator h. With the present arrangement the downward stroke is performed with 5⁄12 of the revolution and the up stroke is performed with 7⁄12; the difference is 2⁄12, which equals one-sixth. The up stroke is performed while the eccentric is revolving below the centre of its shaft and in that part farthest from the fulcrum of the oscillator h, so if the machinery were reversed the quick stroke would be up and the slow stroke would be down.
In Fig. 3048 is shown a Kingsley’s trip hammer. The main bed or foundation plate a carries the bed plate or frame b, at one end of which are the pillar blocks c, which afford journal bearing to the casting carrying the hammer shaft e, being fastened thereto by the clamp d. These journals are the centre of motion of the hammer helve e.
At the other end of the bed plate b, are the pillar blocks f, affording journal bearing to the cam and fly-wheel shaft, a′′ is the tripping cam, which is provided with two toes or cam arms, which meet the tripping piece b′′, and this gives the hammer two strokes in a revolution of the fly-wheel shaft or cam shaft g. The stroke of the hammer may be altered by means of the set-screws c′′, which move the pillar blocks f, so that the cam toes a′′ have contact with the tripping piece b′′ through more or less of the revolution of a′′; the pillar blocks f being retained in their adjusted position by means of the set-screws shown below them in the bed piece b.
By the following means provision is made whereby the face of the hammer may be set out of parallel with that of the anvil block or lower die d′.
Fig. 3049 is a sectional view through the pillar blocks c, and casting and clamp d. The pillar blocks c c are carried in a semicircular frame a′, hence by unscrewing the bolts b′ and screwing up the pillar block on the other side, the journals are thrown out of parallel, and the plane of motion of the hammershaft is altered so that the face of the upper die does not meet that of the anvil die fair to an amount which may be varied at will by operating the screws b′. The object of this is to enable the forging taper (as in sword blades) with common dies, and thus to save the making of special dies for each degree of taper required.
Similar provision is made in the anvil block which is easier to set, providing the degree of taper is within the limit of its range, of movement, otherwise the hammer also may be set.
Fig. 3050 represents a drop hammer, and Fig. 3051 is a sectional view of the lifting mechanism.
This machine consists of a base or anvil, a hammer which moves up and down between two uprights, and a lifting device, which is secured to the top of the uprights.
A board secured to the hammer passes up between two friction rolls, which revolve in opposite directions. When the two rolls are moved towards each other, the friction on the board causes the hammer to rise; and when again separated the hammer will fall. The back roll is keyed to a shaft, on each end of which is a driving-pulley; and thus by the use of two pulleys on the same shaft, equal wear comes on the bearings in which it revolves. The front roll turns freely on its shaft, and is driven by the back roll being geared to it. To secure to the gears both strength and durability, they are made with wide faces, are geared at both ends, and the teeth are of peculiar shape.
The bearings to the shaft, on which the front roll revolves freely, are eccentric to the roll, and a partial revolution of the shaft moves the front towards the back roll, pinching the board. To an arm which is secured to the front shaft is fastened the upright rod, the upward movement of which opens the rolls, and whose[II-256] downward movement closes the same; the weight of the rod being sufficient to cause the hammer to rise. This arrangement, simple and yet substantial, dispenses with the two eccentric-armed bushings, and the spreading of the upright rod at the top to reach both bushings, which caused so much trouble in the old way. In place of the dog which is usually used to hold up the hammer, (which is limited in adjustment to holes located at fixed distances in one of the uprights, necessitating not only the removal of the dog to another hole, and connecting and disconnecting the same to the treadle, but also the most accurate adjustment of the collar on the upright rod to the dog holding the hammer), we use a pair of clamps, located on the lifter, under the rolls. These clamps, holding the hammer centrally, prevent the side blow against the upright, the inevitable result of the contact of hammer and dog, when the former is only held on one side, as it must be, by the use of the dog. The opening of the clamps by the foot-treadle allows the hammer to fall; and the clamps are so made that the hammer will ascend freely, whether the foot is on the treadle or not, and if the foot is off the treadle, will hold up the hammer at any point where it may be arrested in its upward movement. It will be readily seen that the only adjustment required is that of the collar on the upright rod, to any height of blow desired.
This machine has two treadles, one connected to the clamps, and the other to a lever which operates the upright rod.
To obtain repeated blows with one motion of the foot, place the foot upon the treadle connected to the clamps. If variable blows are wanted, place the foot upon the other treadle, and the hammer will follow the motion of the foot. This extra treadle is a late improvement, and is not shown in the cut. The operation required to obtain automatically any number of blows of the same height is described as follows:—
Pressure upon the treadle opens the clamps and allows the hammer to fall; just before the dies come together, the trip at the bottom which holds up the upright rod is released, and allows the rod to drop; this closes the rolls, causing the hammer to ascend. The hammer continues to rise until it strikes the collar on the upright rod, and, lifting the rod, opens the rolls, removing the pressure upon the board, and allows the trip at the bottom to go under to hold the rod up, and the hammer remains suspended, provided the foot is off the treadle. So long as pressure is kept[II-258] on the treadle, the blows of the hammer will be continuous; but upon removal of the pressure, the hammer will assume its original position.
To procure variable blows, the operation is as follows:—
Pressure upon the treadle connected to the lever which operates the upright rod communicates itself to the treadle that opens the clamps, and the hammer falls; a locking device (not shown in cut) keeps this treadle down, and on completion of the variable blows wanted, removal of the foot from the treadle disconnects the locking device, and the hammer goes up to its original position, and is there held by the clamps.
When the work is such that the operator requires an assistant, variable blows may be obtained by the use of the hand lever by this assistant.
A gentle pressure upon the treadle will allow the hammer to go down slowly, but it will stop and remain suspended at any point as soon as the pressure is removed. The hammer can also be arrested at any point on its way up, by bringing into action the hand lever, so that the next blow can be given from a state of rest at a less height than the collar is set for. The clamps in holding up the hammer keep the board from touching either roll, and prevent the same from being worn uneven when not in use.
The back roll is made adjustable to different thicknesses of lifting board, as are also the clamps.
Figures from 3052 to 3056 represent a steam hammer. The head a is set at an angle in the frame. The anvil or die c is oblong, as is also the anvil die d. The object of this arrangement is to enable the workman, after drawing out his work across the short way of the die, to turn it and finish it lengthwise without being inconvenienced by the frame. By this means skew and T-shaped dies can be dispensed with, and the full service of the ram utilised. The latter is moved between the guides e e, and held in place by the steel plate f, bolted through the frame b. The valve g is a plain cylinder of cast iron, enlarged at each end to work in the cylindrical seats h h, in which the ports i i are placed. Steam is admitted through the valve j, and circulates round the valve g, between the seats. The exhaust chamber k is below the cylinder, which therefore drains condensed steam into it at each stroke through the lower steam port. The exhaust above the piston passes down through the interior of the valve, as shown by the arrow on the drawing. The valve stem l is connected with the valves in the exhaust chamber. No stuffing box is therefore required, there being only atmospheric pressure on each side of it. This combination enables the valve to be so perfectly balanced that it will drop by its own weight while under steam.
The automatic motion is obtained by an inclined plane m upon the ram a, which actuates the rocker n, the outer arm of which is connected by a link to the valve stem, and thus gives motion to the valve. The valve is caused to rise in the up-stroke by means of the rocker n and its connections, through the inclined plane. The steam is thus admitted to the top, which drives down the[II-259] piston, while the valve and its connections follow by gravity, thus reducing considerably the friction and wear upon the valves. In very quick work the fall of the valves may be accelerated by the aid of a spring; or it may be retarded in heavy work by friction springs, so as to obtain a heavier blow by a fuller admission of steam. For general work, however, the arrangement shown is perfectly effective, and as the rocker n is hung upon the adjustment lever p, any required variation can be obtained by the movement of the lever. Single blows can be struck with any degree of force, or a rapid succession of constant or variable strokes may be given.
The anvil o rests upon a separate foundation, in order to reduce the effect of concussion upon the frame. The drawing illustrates the arrangement. The bed is long, extending beyond the hammer on each side so as to give plenty of area, and the ends are left open for convenient access in case the anvil should settle and require re-adjustment.
Other forms of hammers having the same general principles of construction are as follows:—
Fig. 3057 represents a double frame hammer, the weight of the hammer being supplemented by steam pressure. The spiral springs shown beneath the cylinder are to prevent the hammer from striking the cylinder and causing breakage from careless handling by the operator. The valve gear is arranged for operation either automatically or by hand.
Fig. 3058 represents a double frame steam drop hammer for stamping work out in formers or dies. The frames are bolted to the anvil base and the ram for the top die is guided by vertical slides on the inner face of the frame. Shoes are provided, whereby the wear of the ram and of the slides may be taken up, and the upper die kept properly matched with the lower one.
Fig. 3059 represents a double frame steam drop hammer for locomotive and car axles and truck bars. The frame is spread at the base to admit wide work, and the upper surface of the base[II-260] is provided with rollers supported by springs, these rollers supporting the work. The same may be operated automatically or by hand.
The hydraulic forging press at the Edgemore Iron Works of Wilmington, Delaware, consists of a piston operating in a cylinder, and having at its lower end a head guided by four cylindrical columns that secure the base plate, or anvil, as it may be termed, to the cylinder. To the above-mentioned head is secured the upper die, the lower one being secured to the base plate.
Fig. 3060 represents a female die, and Fig. 3061 plan of another female die, and Fig. 3062 plan of male die used in connection with the press to forge the eye bars for the Brooklyn Bridge, five pieces each an inch thick being welded to the bar and pressed into shape at one operation.
Figures from 3063 to 3066 represent a locomotive driving wheel ready to have its hub welded by hydraulic pressure. The spokes having been forged are held together by a band or hoop, as shown. The thickness of the hub or boss is made up by the rings or washers shown in the sectional view. The dies under which the welding is done are shown in Figs. 3064 and 3066.
Thin forgings are often made by compression between two rollers, the form of the surface of the rollers, or projections or depressions upon the same, pressing the forging to shape.
Thus, in Fig. 3068 are shown a pair of rolls a b, p representing a piece of work, and c d two cam pieces fast upon the roll surfaces; s is a fixed stop.
Suppose the work to be pushed through the rolls and to rest against the stop s, then when the cams c d meet it they will pull[II-261] it through and reduce its thickness by compression towards the workman. The rollers are obviously rotated by gear wheels; but they are sometimes provided with a certain amount of give or elasticity at their bearings, so that the reduction of work diameter may be obtained by several passages of the work through the rolls.
The shape of the cams, as c d, determines that of the work; thus in Fig. 3069 is shown a pair of rolls for forming knife blades, each cam having sunk in it a die equal in depth to half the thickness of the knife.
If the work is very short in comparison with the circumference of the rolls, two, three, or more cams may be arranged around the circumference, making an equal number of forgings or impressions, as the case may be, at each revolution of the rolls.
In Fig. 3067 is shown a nail-forging machine for producing, from strip iron, nails similar to hand-made, at rates varying from two to three hundred per minute, and lengths of from six to one inch, two nails being completed at each revolution of the driving shaft of the machine. The framing consists chiefly of a main casting, to which are fixed an upper frame, carriages for the driving shaft, and other details. The principal moving part is a heavy steel slide, deriving its motion from a crank pin with adjustable throw; this slide carries two shears, two gripping dies, and sundry indispensable appendages, to some of which it imparts motions for guiding the nails between the stages of cutting off and finishing.
The successive operations by which each nail is perfected are as follows:—
A piece of iron about six inches long, and of a width and thickness respectively of the finished nail, is inserted at a red heat to the feeder of the machine; a narrow strip is immediately cut off the lower side of the heated iron, and by the motion of the steel slide is carried to and pressed against a fixed die; while in this position another die rises at right angles and presses the partially formed nail against another fixed die. Thus the headless nail is firmly held on its four sides, and while in this position a lever, moved by a cam, and carrying a suitable tool, advances and forms the head, thus completing the nail. The return motion of the steel slide releases the nail, leaving it free to fall, but as its weight is not sufficient to insure this happening, a “knocker off” is provided, which at the right moment forcibly ejects the nail by way of a guiding shoot into a receptacle placed outside the machine. It is to be noted that the tools for shearing and gripping, and which have to be changed with each different size of nail, are made of a special mixture of cast iron. They are thus easy of preparation and renewal, while at the same time answering their intended purpose as well as or better than the finest cast steel, at less than half the cost. The whole of the machine is carried upon an open-top cast-iron water tank, serving as a receptacle for the tongs and tools heated in withdrawing the iron from the furnace.
Figs. 3070 and 3071 represent a machine for forging threads on rods and screws. As forgings, the threads are beautifully clean, and for the general work of coach screws much stronger than the cut threads. A perspective view of the machine is given in Fig. 3070, and a vertical of it shown in Fig. 3071. In the former figure, a b are the screw dies. The rod or bolt to be threaded is placed upon the lower die b, and fed forward while screwing it. The upper die is mounted on a slide c, which is actuated in the downward direction by an eccentric e on the main shaft and the toggle-bar d, the upward motion being obtained by an internal spiral spring f. The lower die b is carried in a slide g, and is adjusted at the proper distance from the upper die by means of wedge h, and the inclined plate i, beneath the slide g. The wedge h is operated by a pedal l, and secured in its highest position by a bolt j, received in a mortice made in the plate i, the bolt being operated by a pedal m. In order to release the wedge and return it to its lowest position, the bolt is raised by pressing down the pedal m, whereby the wedge is free to be returned by the counterweights k, in connection with pedal l; slide g, carrying the lower die, then descends by its own gravity, and so separates the two dies sufficiently to allow of the removal of the screw-bolt or rod therefrom. To compensate for the wear of the dies, and admit of their adjustment, another wedge o, with screw adjustment, is disposed below the inclined plate i.
Fig. 3072 represents a lag screw forged by the machine.
Fig. 3073 represents a finishing machine for horseshoes. The[II-263] bars of iron are rolled with the creases (for the nail heads of the finished shoe) in them. The blanks for the shoes are then cut to length and bent, and the nail holes punched. The shoes then pass to a machine, Fig. 3073, which consists of a frame a b, carrying the roll c, above the table d, and a second roll, not shown in the cut, but being directly beneath c, there being between these two rolls sufficient space to let the dies (which press the shoes into shape) pass.
These dies rest upon the table d, and are carried around upon it in a direction from left to right of the chain h, to the links of which the dies are attached. This chain is operated by the vertical shaft j, having a pulley for belt power at k.
As each die approaches the rollers, a shoe (cut to length, creased, and punched as already described) is placed on it, and on reaching the rolls the shoe is pressed into form on the die by the rolls, the bottom roll serving as a rolling bed so as to reduce the friction that would be due to a sliding motion on the bottom of the die. The top roll c, which presses the shoe into the die is driven by power.
A plan view of the machine is shown in Fig. 3074, and a view showing the shape of the dies is given in Fig. 3075.
The surface h forms the frog. To give the required concavity to the toe and sides of the shoe, the surface i is made convex, and tapered or inclined towards h. The tread e is deepest at the heel on both sides, and highest at the toe. It is obvious that by suitably shaping the surfaces h, i, and e, any required form may be given to the shoe. Fig. 3076 represents a shoe creased, punched, and bent ready to be passed to the machine.
Fig. 3077 represents a circular saw for cutting off hot iron; a is the frame of the machine, the arm b pivoted at c carrying the saw d; f is a spring bolted to the frame and serving to hold the saw in the position shown. The work e is gripped by the lever l, which is pushed over by hand. The lever l is adjusted to suit different sizes of work by the screw g, which raises or lowers the piece h, to which l is pivoted. The saw is brought into contact with the work, and fed to it by applying the foot to the lever or arm b at i, the screw j being made to contact with the foot of the machine by the time the saw has passed through the work, thus preventing the saw from moving too far forward after passing through the work.
Pattern-making.—Of the different kinds of wood serviceable to the pattern-maker, pine is, for many reasons, usually employed. It should be of the best quality, straight-grained, and free from knots; it is then easy to work in any direction, possessing at the same time sufficient strength for all but the most delicate kinds of work, and having besides the quality of cheapness to recommend it. Care taken in its selection at the lumber-yard will be amply repaid in the workshop. When it is straight-grained, the marks left by the saw will show an even roughness throughout the whole length of the plank; and the rougher the appearance, the softer the plank. That which is sawn comparatively smooth will be found hard and troublesome to work. If the plank has an uneven appearance—that is to say, if it is rough in some parts and smooth in others—the grain is crooked. Such timber is known to the trade as cat-faced. In planing it the grain tears up, and a nice smooth surface cannot be obtained. Before purchasing timber, it is well to note what convenience the yard possesses for storing. Lumber on the pile, though it be out in all weathers, does not deteriorate, but becomes seasoned; nevertheless its value is much increased if it has an extemporised roof to protect it from the sun and rain. But as it is not convenient to visit the pile for every customer, quantities are usually taken down to await sale, and for such a shelter must be provided, otherwise it will be impossible to insure that the lumber is dry, sound, and fit for pattern-making. It is obvious that the foregoing remarks on the storage of lumber apply to all woods.
The superiority of pine for pattern-making is not, however, maintained when we come to fine delicate patterns or patterns requiring great durability. When patterns for fine work, from which a great many castings are to be made, are required, a fine pattern wherefrom to cast an iron pattern is improvised, because, if pine were employed, it would not only become rapidly worn out, but would soon warp and become useless. It is true that a pine pattern will straighten more easily than one made of a hard wood; but its sphere of usefulness in fine patterns is, for the above reasons, somewhat limited. Iron patterns are very desirable on account of their durability, and because they leave the sand easily and cleanly, and because they not only do not warp but are also less liable than wooden ones to give way to the sand, while the latter is being rammed around them by the moulder, a defect that is often experienced with light patterns, especially if they are made of pine. Iron patterns, however, are expensive things to make, and therefore it is that mahogany is extensively employed for fine or durable pattern work. Other woods are sometimes employed, because they stand the rough usage of the moulding shop better and retain the sharp corners, which, if pine be used, in time become rounded impairing the appearance of the casting. Mahogany is not liable to warp, nor subject to decay; and it is exceedingly durable, and is for these reasons the most desirable of all woods employed in pattern-making, providing that first cost is not a primary consideration. There are various kinds of this beautiful wood: that known as South American mahogany is chiefly used for patterns.
Next to mahogany we may rank cherry, which is a very durable wood, but more liable to twist or warp than mahogany, and it is a little more harsh to the tool edge. If, however, it is stored in the workshop for a length of time before being used, reliable patterns may be made from it. In addition to these woods, walnut, beech, and teak are sometimes employed in pattern-making.
The one property in all timber to be specially guarded against is its tendency to warp, bend, expand, and contract, according to the amount of humidity in the atmosphere. Under ordinary conditions, we shall be right in supposing a moisture to be constantly given off from all the exposed surfaces of timber; therefore planks stored in the shop should be placed in a rack so contrived that they do not touch one another, so that the air may circulate between the planks, and dry all surfaces as nearly alike as possible. If a plank newly planed be lying on the bench on its flat side, the moisture will be given off freely from the upper surface, but will, on the under surface, be confined between the bench and the plank: the result being that a plank, planed straight, and left lying as described, will be found, even in an hour, to be curved, from the contraction of the upper surface due to its extra exposure; therefore it is obvious that lumber newly planed should be stored on end or placed on edge. Lumber expands and contracts with considerable force across the grain; hence if a piece, even of a dry plank, be rigidly held and confined at the edges, it will shrink and break in two, often with a loud report. There is no appreciable alteration lengthwise in timber from the above causes; and if two pieces be glued together so that the grain of one crosses that of the other, they can never safely be relied upon to hold. Hence they had better be screwed so that there will be a little liberty for the operation or play of the above forces, while the screws retain their hold. The shrinkage, expansion, and warping of timber may perhaps be better understood by the following considerations: The pores of wood run lengthwise, or with its grain, and hence the moisture contained in these passes off more readily endwise or from any surface on which the pores terminate.
The Shrinkage of Timber.—The direction in which timber shrinks in seasoning or drying is shown in the following figures, which are extracted from a lecture delivered by Dr. Anderson before the Society of Arts in London, England. The shrinkage of timber lengthwise of the grain is very slight, its shrinkage in a direction across or at a right angle to the length of the grain being much greater and depending upon the part of the log from which it is cut.
The shrinkage is greater on the outside than near the heart of the tree; thus if a log be cut into four quarters it will shrink as in Fig. 2706, from the full block outside to the inside or white outline; or if we cut out a square as in figure, one corner extending to the heart, it will shrink to the form shown in the figure. If we sever the log by the four parallel saw cuts it will shrink as shown by the[II-265] black outline, the shrinkage of the middle piece being more clearly shown in Fig. 2707.
It is evident, therefore, that to obtain a uniform degree of shrinkage throughout the length of a piece of timber, it should be sawn as near as possible parallel with the grain of the log. Thus in Figs. 2708 and 2709 we have a side and an end view of a log, the saw cuts at a being from logs that have been squared, the upper slab b being waste material, and the planks being parallel to the squared sides of the log.
The lines from a to c on the lower half of Fig. 2709 represent planks that are what is termed flitched, the saw cuts following the taper of the tree, and it is plain that the shrinkage would be more uniform; thus the outside plank is near the bark from end to end, while at the top of the figure the outside plank is near the outside at the small end only of the log, and would therefore shrink most at the right hand end. Furthermore as the planks at a cross the grain of the log at its large end, they are therefore weaker and more liable to split at that end.
Bending Timber.—By bending a piece of timber to bring it as near as possible the required shape the strength of the work is increased, because the grain of the wood runs parallel with the shape of the work, and, furthermore, the cutting tools act on this account to better advantage. In bending a piece of timber it is obvious that either the convex side must stretch, or the concave one compress, or if no extraneous pressure is brought to bear upon the piece, both of these actions may occur, and as the side of the piece that was nearest to the heart of the tree is the hardest and strongest, it will stretch less if made the convex side, or compress less if made the concave side of the timber, but the bent piece will maintain its shape better if the heart is the convex or outside of the curve.
The modern method of bending wood is to fasten on the outside, or convex side of the piece, a strap that will prevent it from stretching. And it is found that wood thus bent is stronger, stiffer, and heavier than before it was bent, because the fibres become interwoven, and it is found that the wood is harder to split than before.
Suppose we require to bend a piece to a half circle, and after it has been boiled, steamed, or heated with a dry heat it is placed in an iron strap, such as shown in Fig. 2710, having an eye at each end in which a hook may be inserted to hold the piece in shape (after it is bent) until it is dry again. The piece with this strap on its outside or uppermost surface is laid on the former or forming piece shown in Fig. 2711, which has a projection at a, fitting into the recess a of the bending block in Fig. 2712. On the outside of the piece is then placed the strap, shown in Fig. 2713, its blocks of wood fitting to the ends of the piece to be bent.
The winch of the bending block is provided with a rope, whose ends have two hooks which are engaged in the eyes of the straps, [II-266] shown in Fig. 2714, and by operating the winch the piece is bent to shape, as shown in Fig. 2714. While in this position a hook is placed through the eyes of the band that is around the bent piece of work, so that when removed from the forming block or stand it appears as in Fig. 2715.
When, however, the piece requires to be bent to more than one sweep or bend, the process requires to be changed somewhat. Thus, suppose the middle is to be bent circular and the two ends left straight, and the strap on the piece to be bent is provided with a piece, such as in Fig. 2716, the ends b engaging in eyes in the strap, and the screw a abutting against the end of the piece to bind the strap firmly upon the ends, as in Fig. 2717, in which the piece is shown within the strap. After it has been bent to the former it is held there by straps and wedges, as shown in Fig. 2718.
The next operation is to lock the curve, as shown in Fig. 2719, between an inside and outside former by means of straps a a and wedges c, when the ends d of the piece may be bent up to the dotted lines and locked to the ends of the top former by straps and wedges.
The length of time a piece should be boiled or steamed for the bending process depends upon the size of the piece and the kind of wood, hard wood requiring longer boiling or steaming. A piece of ash, say 2 by 4 inches in cross section, would require about six hours’ steaming with a low pressure of moist or wet steam, but it would not suffer damage if it were steamed for a day. Pieces not over half an inch thick may be bent after steaming them about half an hour.
[II-267]If the wood is steamed too much it loses its elasticity and will pucker on the inside surface of the bend when in the former or bending block.
The period during which the piece should be held to its bent shape before being released varies from twelve hours for thin pieces to twenty-four hours for thick ones, and it is found that pieces which have been bent in a strap so as to prevent the outside from stretching, will, in drying, increase their bend or curvature, while those not confined at their ends straighten out.
The cracks that are found in timber are termed shakes; thus in Fig. 2720 the black lines represent what are called heart shakes, while those in Fig. 2721, being wider, are termed star shakes. When the shakes are circular, as in Fig. 2722, they are called cup shakes.
Many of the tools used by the pattern-maker have been described in connection with hand turning, hand boring tools, lathe tools, &c., and therefore need no further reference.
Planes.—For roughing out the work the jack plane is employed, varying in size from 14 inches long with a cutter knife or blade 2 inches wide, to 27 long with a blade 21⁄4 inches wide, and as its purpose is to make a flat surface, it is preferable that it be as long as the work will conveniently permit. The jack plane is followed by the fore plane, the truing, or trying plane, which varies in size from about 18 inches long with a blade 21⁄8 inches wide, to 20 inches long with a cutter or blade 23⁄8 inches wide. When the fore plane is made longer, as for planing long joints, it is termed a jointer plane, the length being as much as 30 inches and the blade 25⁄8 inches wide.
The smoothing plane varies from about 5 inches long with a blade 11⁄2 inches wide, to 10 inches long with a blade 23⁄8 inches wide. Smoothing planes are, as the name implies, used to simply smoothen the work surface after it has been trued.
The angle of the plane blade to the sole of the plane is for ordinarily soft wood 45°, but 50° or 55° may be used for very hard woods.
To break the shaving the blade is attached to what is termed a cover, which is shown in Fig. 2723, b representing the blade and a the cover. The cover is curved to insure that it shall bed against the blade at its very end, and, therefore, as near to the cutting edge as a maximum distance 1⁄16 inch for rough and 1⁄32 inch for finishing cuts. The blade of a jack plane is most efficient when it is ground well away towards the corners, as at a b in Fig. 2724, thus producing an edge curved in its length.
When the blade is in position in the stock for cutting off the maximum of stuff, its blade should project nearly 1⁄16 through the sole of the stock, while the corners a b are about level with the face of the stock. The bevelled face should stand at about an angle of 25° to the flat face. In grinding it care should be taken to grind it as level as possible, rounding off the corners as shown above. The grindstone should be kept true and liberally supplied with water; the straight face should not be ground away, nor indeed touched upon the stone, except to remove the burr which will sometimes turn over. The pressure with which the blade is held against the grindstone should be slight at and toward the finishing part of the grinding process, so as not to leave a long ragged burr on the end of the blade, as is sure to be the case if much pressure is applied, and it will occur to a slight extent even with the greatest of care. The blade should not be held still upon the grindstone, no matter how true, flat, or smooth the latter may be; but it should be moved back and forth across the width of the stone, which will not only grind the blade bevel even and level, but will also tend to keep the grindstone in good order.
In oilstoning a plane blade, the straight face should be held quite level with the face of the oilstone, so that the cutting edge may not be bevelled off. Not much application to the oilstone is necessary to the straight face, because that face is not ground upon the grindstone, and it only requires to have the wire edge or burr removed, leaving an oilstone polish all along the cutting edge. The oilstoning should be performed alternately on the flat and bevelled faces, the blade being pressed very lightly on the oilstone toward the last part of the operation, so as to leave as fine a wire edge as possible. The wire is the edge or burr which bends or turns over at the extreme edge of the tool, in consequence of that extreme edge giving way to the pressure of the abrading tool, be it a grindstone or an oilstone. This wire edge is reduced to a minimum by the oilstone, and is then so fine that it is practically of but little account; to remove it, however, the plane blade or iron may be buffed backwards and forwards on the palm of the hand.
The blade being sharpened, we may screw the cover on, adjusting it so that its edge stands a shade below the corners of the iron, and then screwing it tight; the blade or iron and the cover must now be placed in the mouth of the plane stock, and adjusted in the following manner:—
The plane iron should be passed through the mouth of the stock until as much in depth of it is seen to protrude from the bottom face of the stock as is equal to the thickness of shaving it is intended to cut: to estimate which, place the back end of the plane upon the bench, holding the stock in the left hand with the thumb in the[II-268] plane mouth, so as to retain the iron and wedge in position, the wedge being turned towards the workman. A glance down the face of the stock will be sufficient to inform the operator how much or how little the cutting edge of the iron protrudes from the face of the plane stock, and hence how thick his shaving will be. When the distance is adjusted as nearly as possible, the wedge may then be tightened by a few light hammer blows. If, after tightening the wedge, the blade is found to protrude too much, a light blow on the fore end on the top face of the plane will cause it to retire; while a similar blow upon the back end will cause it to advance. In either case the wedge should be tightened by a light blow after it is finally adjusted.
In using a jack plane we commence each stroke by exerting a pressure mostly on the fore part of the plane, commencing at the end and towards the edge of the board, and taking off a shaving as long as the arms can conveniently reach. If the board is longer than can be reached without moving, we pass across the board, planing it all across at one standing; then we step sufficiently forward, and carry the planing forward, repeating this until the jack planing is completed. To try the level of the board, the edge or corner of the plane may be employed; and if the plane is moved back and forth on the corner or edge, it will indent and so point out the high places.
The fore plane (or truing plane, as it is sometimes called) is made large, so as to cover more surface, and therefore to cut more truly. It is ground and set in the same manner as the jack plane, with the exception that the corners of the iron or blade, for about one-eighth inch only, should be ground to a very little below the level of the rest of the cutting edge, the latter being made perfectly straight (or as near so as practically attainable) and square with the edge of the iron. If the end edge of the cover is made square with the side edge, and the iron is ground with the cover on, the latter will form a guide whereby to grind the iron edge true and square; but in such case the cover should be set back so that there will be no danger of the grindstone touching it. The oilstoning should be performed in the manner described for the jack plane, bearing in mind that the object to be aimed at is to be able to take as broad and fine a shaving as possible without the corners of the plane iron digging into the work. The plane iron should be so set that its cutting edge can only just be seen projecting evenly through the stock. In using the fore or truing plane, it is usual, on the back stroke, to twist the body of the plane so that it will slide along the board on its edge, there being no contact between the cutting edge of the plane iron and the face of the board, which is done to preserve the cutting edge of the plane iron from abrasion by the wood: as it is obvious that such abrasion would be much more destructive to the edge than the cutting duty performed during the front stroke would be, because the strain during the latter tends mainly to compress the metal, but, during the former, the whole action tends to abrade the cutting edge. The face of the fore plane must be kept perfectly flat on the underside, which should be square with the sides of the plane. If the under side be hollow, the plane iron edge will have to protrude farther through the plane face to compensate for the hollowness of the latter; and in that case it will be impossible to take fine shavings off thin stuff, because the blade or iron will protrude too much, and as a consequence there will be an unnecessary amount of labor incurred in setting and resetting the plane iron. The reason that the under surface should be square, that is to say, at a right angle to the sides of the body of the plane, is because the plane is sometimes used on its side on a shooting board.
When the under surface of the plane is worn out of true, let the iron be wedged in the plane mouth, but let the cutting edge of the iron be well below the surface of the plane stock. Then, with another fore plane, freshly sharpened and set very fine, true up the surface, and be sure the surface does not wind, which may be ascertained by the application of a pair of winding strips, the manner of applying which will be explained hereafter. If the mouth of a fore plane wears too wide, as it is apt in time to do, short little shavings, tightly curled up, will fall half in and half out of the mouth, and prevent the iron from cutting, and will cause it to leave scores in the work, entailing a great loss of time in removing them at every few strokes. The smoothing plane is used for smoothing rather than truing work, and is made shorter than the truing plane so as to be handier in using. It is sometimes impracticable to make a surface as smooth as desirable with a truing plane, because of the direction of the grain of the wood.
Fig. 2725 represents an ordinary compass plane, which is a necessary and very useful tool for planing the surfaces of hollow sweeps. This tool is sometimes made adjustable by means of a piece dovetailed in the front end of the plane, which, by being lowered, alters the sweep and finally converts it from a convex to a concave.
In Fig. 2726 is shown a much superior form of circular or compass plane. Its sole consists of a flexible steel blade, whose ends are attached to levers that are connected together by toothed segments. By means of the large hand-screw the levers are operated, causing the sole to bend to the required curvature, and by reason of the toothed segments the levers move equally, and therefore give the sole a uniform curve throughout its length.
Planes are also made with the sole and the cutting edge of the blade made to conform to the shape of the work. Thus Fig. 2727 represents a rabbeting plane, and Fig. 2728 a side rabbet plane. The latter is, however, very seldom used, but is especially useful in planing hard wood cogs fitted to iron wheels, or the teeth of wheel[II-269] patterns or other similar work. For ordinary use, it is sufficient to have two, a 3⁄4 and a 11⁄4 inch, and two or three having a flat sole for flat bottom grooves.
What is known as a core box plane has its sole at an angle of 90°, or a right angle; the principle of its action is that in a semicircle the angle is that of 90°.
In Fig. 2729, for example, it is seen that if a right angle be laid in a semicircle so that its sides meet the corners of the same when revolved, its corner will describe a true circle; hence at each plane stroke the plane may be slightly revolved, to put on the cut, which must be very light, as the core box plane is only suitable for finishing purposes. For planing across the end grain of wood, what are termed block planes are used, the angle of the blade to the sole being from 65 to 85 degrees, as shown in Fig. 2730, which represents the Stanley iron frame block plane. In block planes the bevel that is ground to sharpen the blade is placed in front and therefore meets the shaving instead of the flat face as in other planes.
Fig. 2731 represents the Stanley bull-nose rabbet plane for getting close into corners, and Fig. 2732, a block plane, in which the blade may be set in the usual position or at one end of the stock as denoted by the dotted lines.
For fine work planes having an iron body are much preferable to the wooden ones, and in the improved form of planes there is provided a screw mechanism, whereby the blade may be set much more accurately and easily than by hammer blows, such as are necessary with ordinary wedge-fastened blades. Thus Fig. 2733 represents Bailey’s patent adjustable planes, the handles only being of wood. The blade is secured by a simple lever movement, and is set by means of the thumb screw shown beneath and behind the blade. The metal stock possesses several advantages, such as that the sole keeps true, the mouth does not wear too large, as is the case with wooden planes. Planes are also made having a wooden body and an iron top, the latter containing the mechanism for locking the blade and setting it quickly. Fig. 2734 represents one of these planes.
Figs. 2735 to 2744 represent a combination plane. Fig. 2735 is a side, and Fig. 2736 a top view of the tool as a whole.
Pieces a and b form the body of the plane, between which the bits or all the tools are carried except the slitting knife, which is carried by a alone.
In the figures t is a beading tool shown in position, having a bearing or seat in both a and b so as to support it on both sides, and being locked in position by the thumb-screw c. At g is a depth gauge which is moved over into the hole at d, when that[II-270] position is most suitable for the kind of work in hand. Piece b is made adjustable in its distance from a so as to accommodate different widths of bits by sliding it on the arms m, securing it in its adjusted position by the set-screws s. Similarly the fence f slides on arms m, and is secured in its adjusted position by the set-screws h, thus enabling it to regulate the distance from the edge of the board at which the bits shall operate, and also guiding the bits true to the edge of the board or work. f is provided with an upper pair q, and a lower pair r of holes (as seen in Fig. 2737) so that it may be set on the arms m at two different heights as may best suit the nature of the work. In Fig. 2736 it is shown with arms m passing through the lower pair of holes. The points of the set-screws h meet the bores of both pairs of holes and therefore lock f to the arms, whether the upper or lower holes are upon the arms. For rabbeting and fillister work the upper holes q are used, while using ploughs the lower ones are brought into requisition.
At w, Fig. 2735, is a spur for cutting the end grain of the wood in advance of the bit, as is necessary in dado and other across grain work, the construction of the spur is seen more clearly in Fig. 2738. The pieces a and b are provided with a recess having four arms or branches, while the spur itself has but three, so that the spur may be set as in Fig. 2735 and be out of action, or its screw being loosened it may be given a half-turn, so that one of its arms will come below b as at x in Fig. 2738. The cutting edges of the spur come exactly flush with the outside faces of a and b, and the bits are so held in their seats that their edges also come flush with these outside faces, which therefore act as guide to the bit; thus Fig. 2739, shows a beading bit in position, and Fig. 2740 a section of work finished, a and b being in section. Fig. 2741 shows a plough in position on the work, a and b being shown in section. It is seen that their inner edges being bevelled, will in using a beading tool, act as a gauge regulating the thickness of shaving taken at each plane stroke, which will equal the depth to which the bit edge projects beyond the bevels of a and b. Similarly[II-271] in grooving or ploughing the amount to which the bits project below the lowest edges of a and b regulates the thickness of the shaving, and as a and b follow the bit into the work, the blade being once set requires no further attention, the depth gauge regulating the total depth of tool action.
This principle of the side pieces entering the work with the bits and being adjustable to suit various widths of bits, gives to the tool a wide range of capacity. Fig. 2742 represents the tool arranged for slitting thin stuff into parallel slips, the piece b being removed. The depth gauge is not shown in figure, because it would hide the slitting knife from view, but it is obvious that it would rest on the surface of the work and thus steady the plane. Fig. 2743 is an example of a number of operations performed by this one tool. For tonguing, the bit shown in Fig. 2744 is employed, the depth gauge g being adjustable in the groove by means of the slot shown.
Chisels.—The principal kinds of chisels are the paring chisel which is used entirely by hand, and the firmer chisel which is used with the mallet. The difference between the two lies in the shapes of their handles, and that the paring chisel is longest. A paring chisel worn to half its original length will serve for a firmer chisel, because when so worn it is long enough for the duty. A chisel should not, however, be used alternately as a paring and a firmer chisel, because the paring chisel requires to be kept in much better condition than the firmer chisel does. Mortice chisels are made thicker than either the paring or the firmer because of their being longer and requiring rougher usage. It is necessary to have several sizes of chisels, varying in width from an eighth of an inch to one and a half inches.
Fig. 2745 represents the form of handle for a paring chisel, its total length being 6 inches, and from a to b being 11⁄2 inches. The diameter at c is 11⁄2 inches, the hollow below d of 3⁄8 of an inch radius, the diameter at d 1 inch, and the length from b to e 11⁄2 inches. This form affords a firm grip to the hand, the end e being applied to the operator’s shoulder. The shape of handle for a firmer chisel is shown in Fig. 2746.
Chisels require great care both in grinding and oilstoning them, being held very lightly upon the grindstone when finishing the grinding so as to avoid as far as possible the formation of a long[II-272] feather edge. The flat face of the chisel should never be ground, as that would make it rounding in its length, hence there would be nothing to guide it in cutting straight and the value of the tool would be almost destroyed.
In oilstoning the chisel, great care is necessary in order to avoid forming a second facet at a different angle to that at which it was ground, because such a facet is too narrow to form any guide whereby to move the chisel in a straight line, and the consequence is that the edge is oilstoned rounding and cannot do good service. The whole length of the ground facet or bevel should rest on the oilstone, but the pressure should be directed mainly to the cutting end so that at that edge the oilstone will entirely remove the grinding marks, which will, however, remain at the back. If there is at hand a grindstone of sufficiently small diameter, the chisel may be made hollow on the bevel, as shown in Fig. 2745a, so that when laid on the oilstone the bevel will touch at the back and at the end only, and this will enable the chisel to be pressed evenly down on the stone, thus producing a very even and flat edge, while leaving but a small area to be oilstoned.
The motion of the hands should not for the oilstoning be simply back and forth, parallel with the oilstone length, but partly diagonal, which will assist in keeping the chisel level. The back of the chisel should be laid flat upon the oilstone and moved diagonally, under a light pressure, which will remove the wire edge, which may be further removed by lapping the chisel on the operator’s hand.
Chisels for turning work in the lathe are best if made short, and to enable the cutting edge to get up into a corner, the chisel is sometimes given two cutting edges, as at a, in Fig. 2747, the edges forming an angle, one to the other, of less than 90°. For finishing curves in the lathe the chisel shown at b in the figure is employed, or for deeper work, as in the bores of holes, handles are dispensed with, chisels being formed as at c and d in the figure.
Gouges, like chisels, are made “firmer and paring,” the distinction being precisely the same as in the case of chisels.
When the bevel is on the outside or convex side of the gouge it is termed an outside, while when the bevel is on the inside or concave side it is termed an inside gouge.
Fig. 2748 represents an outside firmer gouge. The inside gouge may be ground a little keener than the chisel, and requires great care in grinding, because it must be held on the corner of the grindstone, which is rarely of the desired curve. In oilstoning the concave side of a gouge an oilstone slip is employed, the gouge being held in the left hand and the slip in the right, the latter being supplied with clean oil.
The convex side of an outside gouge should be made level on the face of the oilstone, and while the gouge is moved to and fro its handle must be revolved so as to bring all parts of the curve in contact with the oilstone. The small amount of surface on the gouge in contact with the grindstone makes it very liable to have a long feather edge, hence it must be very lightly pressed to the stone, and the same remark applies to the oilstoning in order to reduce the wire edge.
Fig. 2749 represents a gouge for lathe work, its handle being made long enough to be held in both hands and used as described with reference to turning with hand tools.
Another tool, very useful to the pattern-maker, is the skew chisel, which is also described in connection with hand turning.
Saws.—There are two principal kinds of saws, the rip saw for cutting lengthwise of the grain of the wood, and the cross-cut saw for cutting across the grain. In shaping these saws the end to be obtained is to enable them to sever the fibre of the wood in advance of the effort to remove it from the main body.
| VOL. II. | THE ACTION OF SAW TEETH. | PLATE XIII. | |||
 |
 |
||||
| Fig. 2751. | Fig. 2752. | ||||
 |
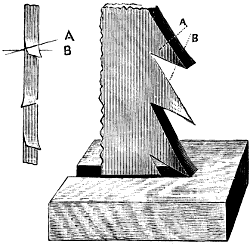 |
||||
| Fig. 2753. | Fig. 2754. | ||||
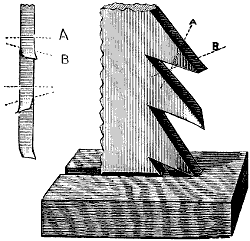 |
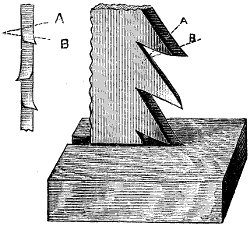 |
||||
| Fig. 2755. | Fig. 2756. | ||||
In Fig. 2750, for example, the grain of the wood runs lengthwise and the throat, or front face of each tooth, is hooking or hooked, so that the cutting edge will cut through the fibres at their ends before it is attempted to remove them from the main body of the wood. Suppose, for example, that the saw shown in Fig. 2750 was put into[II-273] a piece of timber and a tooth pressed hard enough on the wood to leave a mark, and this mark would appear as in Fig. 2751 at e, extending across a width equal to the full width of the saw tooth. It would do this because the front face or throat b and the back face a are both at a right angle to the saw length as is denoted by the dotted lines. As the grain is supposed in Fig. 2751 to run lengthways of the timber, clearly the fibre between the indentation e and the saw slot is severed and would be removed as the tooth passed farther down through the wood, the action of first severing the fibre at its end and then removing it being carried on by each tooth.
In Fig. 2752 is shown a cross-cut saw in action upon a piece of wood in which the grain or fibre runs across the timber, and in this case the teeth require to be shaped to cut on each side of the saw instead of directly in front of it, because in that way only can the ends of the wood fibre be severed before it is dislodged from its place.
To enable the cross-cut saw to accomplish this, one tooth cuts on one side of the saw slot and the next tooth on the other, as at a and b in Fig. 2751, from which it will be seen that as the grain runs lengthways of the timber, the fibres between the lines a and b will be severed at their ends by the extreme edges of the teeth before the thicker part of the tooth reaches them to remove them.
The necessity for this action may be plainly perceived if we apply the rip saw for cross-cutting and the cross-cut saw for ripping. Suppose, for example, we place the saw shown in Fig. 2750 to cut across the grain of the piece of timber, and as its tooth met the wood it would indent it as at g, Fig. 2751, and as this is in line with the grain, the tooth would wedge in the piece and the piece cut could not be dislodged without first tearing the fibres apart at each end. Or suppose we take the cross-cut saw and apply it for ripping (as cutting lengthways of the grain is called) and if we indented the surface with a single tooth it would leave a mark as at f, Fig. 2751, which is lengthways of the fibre, so that the tooth would here again wedge between the fibres and not cut them. The next tooth would make a mark parallel to f, but on the other side of the saw slot or kerf as it is called, still leaving the fibre unsevered at its ends where it should be severed first.
In order that the saw may not rub against the sides of the slot or kerf, and thus be hard to move or drive, it is necessary that the kerf be wider than the thickness of the saw blade, and to accomplish this the teeth are bent sideways, each alternate tooth being bent in an opposite direction, as shown in the front view of the teeth in Fig. 2753. This bending is called the set of the saw, and should be sufficient to make the kerf about two-thirds wider than the thickness of the saw blade.
While preserving the feature of severing the fibre before attempting to dislodge it from its place, we may at the same time give the teeth of rip saws more or less sharpness by fleaming their faces.
In Fig. 2754, for example, the throat face is filed square across or at a right angle to the length of the saw, but the back face a is at an angle, making the points of the teeth sharper, and therefore enabling them to cut more freely. The result of this fleam would be that the tooth, instead of cutting equal and level all the way across as in Fig. 2751 at e, would cut at the corner first and only across its full width as it entered deeper into the wood; we have, in fact, placed the leading part of the cutting edge more at the extreme point and less in front of the tooth.
In Fig. 2755 the throat or front face of the saw is given fleam, as shown by the line b, which is not at a right angle to the saw length, and as a result the cutting edge is carried still more advanced at the point and more towards the side of the tooth and we have, therefore, to a certain extent, qualified it as a cross-cut saw.
We might give the face b so much angle as to carry the leading part of the cutting edge to the side of the saw, thus giving it the characteristics of a cross cut.
In Fig. 2756, both the throat face b and the back face a are given fleam, making the points extremely sharp, and showing the leading part of the cutting edge towards the side, the corner leading still more.
In Fig. 2757 we have two saws r and s, the latter having fleam on the front and the former on the back face of the tooth, the amount or degree of fleam being equal.
In Fig. 2758 we have indentations of their teeth. The teeth of s would leave a mark as at e f, and r would leave a mark as at g h. The side cut f being more than the side cut g, and the front cut e being at a less angle to f than the front cut h to g, it follows that the saw s would be the best, provided the grain of the wood ran diagonally as shown, not only because it has more side and less front cut, but also because its cutting edge is keener on the side, as is seen on comparing the lines p and a in Fig. 2757.
If we give fleam to both faces we alter the indentation, as denoted in Fig. 2759, in which e f represents the line of tooth cut when one face has fleam, and g h the line of tooth cut when both faces are fleamed, the shape of the actual saw cut being shown at j.
Obviously the fleam makes the points weak, but this in coarse saws may be partially remedied by shaping the teeth as in Fig. 2760. Fleam on the front face or throat of the tooth has the effect of preserving its set, the pressure of the cut being as shown by the arrows in Fig. 2753.
It is evident that the finer the point of the tooth the sooner it will become dulled, and that the harder the timber the more quickly the tooth will become dull. So soon as this occurs the teeth refuse to cut freely, and the extra pressure on them acts to spring them upward and to take off the set. It is obvious that for[II-274] soft wood the teeth may be given fleam on both faces, and that the front face should have some fleam, even for the hardest of wood, whether the back face has fleam or not. Also, that in proportion as the grain of the wood runs more across the saw kerf than in line with it the teeth should be filed to cut on the side, and the hook of the front face may be lessened, while vice-versâ, in proportion as the grain of the wood runs parallel with the kerf, the tooth may have hook and fleam on the back face with a slight fleam on the front one.
Gauges.—Of gauges for marking on the work lines parallel to its edges there are several kinds, a common form being represented in Fig. 2761, in which the block that slides against the edge of the work is secured by a set-screw.
A better method, however, is to use a key set at a right angle to the stem, so that the head may be tightened or loosened by striking it, as if it were a hammer, against anything that may happen to lie on the bench, hence the gauge may be set and adjusted with one hand while the other is holding the work, as is often necessary when marking small work. The marking point should be a piece of steel wire fitted tightly in the stem, the protruding part being ground or tiled to a wedge, with the two facets slightly rounding, and whose broad faces stand at a right angle to the stem of the gauge, the point or edge only projecting sufficiently to produce a line clear enough to work by; otherwise it will not be suitable for accurate work.
The mortice gauge, Fig. 2762, is similar to the above as regards the stem and sliding piece, but it is provided with two marking points, their distance apart being adjustable. The head screw works in brass nuts.
For lines that are to be marked more than about ten inches from the edge of the work a broader base is necessary to the head or block, which may be shaped as shown in Fig. 2763.
The lines drawn upon pattern work require to be very fine, and for this purpose the cutting scriber, Fig. 2764, is employed. The end a is bevelled off on both sides like a skew chisel. The end b is ground to a fine point and both ends are oilstoned. The point end is for drawing lines with the grain, and the knife end for lines across the grain of the wood. The wooden handle is to afford a firm grip.
In Fig. 2765 we have the cutting gauge, in which a steel cutter takes the place of the marking point, being wedged in position. It is employed to cut thin strips of wood, that is to say, of thicknesses up to about a quarter of an inch. The cutter point should be tempered to a dark straw color.
The principal forms of joints employed by the pattern-maker are as follows:—
Fig. 2766 represents the mortice and tenon, the thickness of the tenon being one-third that at c, which leaves a thickness at e and d equal to that of the tenon. When the mortice is away from the end of the work the breadth b of the tenon is made less than the breadth f of the work so as to leave stuff at a to strengthen the mortised piece. To make this joint the two pieces, having been planed or otherwise made to size as required, are marked for the position and length of the mortice in one case, and for the length of the tenon in the other; both pieces are now gauged with a[II-275] mortice gauge, both being marked alike; and then from the face side we mark a tenon or mortice of the dimensions required.
If the stuff is broad two or more tenons and mortices may be given, as shown in Fig. 2767.
To lock the tenon in the mortice two methods may be employed. In the first and preferable one the mortice is tapered, as in Fig. 2768, and the two wedges are inserted and driven home. In the second the tenon is provided with saw cuts to receive the wedges.
A very superior method of jointing is the dovetail, shown in Fig. 2769, which is serviceable for connecting the ends and sides of a box, or any article in that form. The strength of the corner formed in this way is only limited by that of the material itself; therefore it should be preferred when available in making standard patterns, or for work too thin to admit nails or screws; the corner formed by this joint is not limited to 90° or a square, so called, but may form any angle. Nor is it imperative that the sides or ends of the box or other article be parallel. They may incline towards one another like a pyramid; a mill hopper is a familiar example of this. If it be required to dovetail a box together, get out four pieces for the sides and ends, to be of the full length and width respectively of the box outside. They are to be planed all over, not omitting the ends. The gauge, that is already set to the thickness of the stuff, must now be run along the ends, marking a line on both sides of each piece. Then mark and cut out the pins as on the piece a; the dovetail openings in b are traced from the pins in a. The pieces having been tried and found to go together are finally brought into contact and held in their places with glue.
Fig. 2770 is a mitre joint, the only one serviceable to mouldings, pipes, and other curved pieces. It is not a strong form of joint, and is only used where the preceding kinds are inapplicable. It is made with glue, the pieces having been previously sized; and as an additional precaution, if the work will admit, nails, brads, or screws are inserted at right angles to one another.
Fig. 2771 represents the half check joint, and it is obvious that the thickness at a must equal that at h, and be half that at b, which will give each half equal strength.
A gland for an engine piston rod forms a simple example of the different ways in which a pattern may be formed. Fig. 2772 represents the drawing for the gland.[46]
[46] From the “Pattern Maker’s Assistant.”
| VOL. II. | EXAMPLE IN PATTERN WORK. | PLATE XIV. | |||
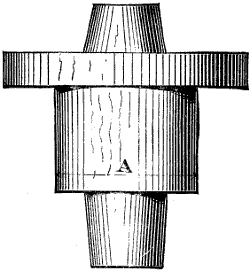 |
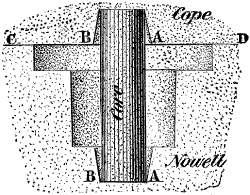 |
||||
| Fig. 2773. | Fig. 2774. | ||||
 |
 |
||||
| Fig. 2775. | Fig. 2776. | ||||
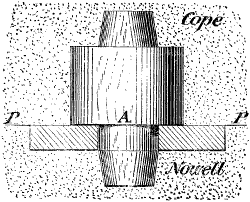 |
 |
||||
| Fig. 2777. | Fig. 2778. | ||||
 |
|||||
| Fig. 2779. | |||||
“Let us suppose the pattern-maker to be uninformed of the purpose the casting is to serve, or how it is to be treated: in such a case he is guided partly by his knowledge of the use of such patterns, and a consideration of being on the safe side. The form shown in Fig. 2773 would suggest itself as being a very ready method of making the pattern; by coring out the hole, it can be made parallel, which the drawing seems to require. The advantage of leaving the hole parallel is that less metal will require to be left for boring in case it should be necessary; because, if the hole is made taper, the largest end of the bore will require to have the proper amount of allowance to leave metal sufficient to allow the hole to be bored out true, and the smaller end would, therefore, have more than the necessary amount; while just the least taper given to the exterior would enable the moulder to withdraw the pattern from the mould. Made in this way, it would be moulded as shown in Fig. 2774, with the flange uppermost, because almost the whole of the pattern would be imbedded in the lower part of the flask, the top core print being all that would be contained in the cope; and even this may be omitted if[II-276] the hole requires to be bored, since the lower core print will hold the core sufficiently secure in small work, unless the core is required to be very true. The parting of the mould (at c d, Fig. 2774) being level with the top face of the flange, much taper should be given to the top print (as shown in Fig. 2773), so that the cope may be lifted off easily. Were this, however, the only reason, we might make the top print like the bottom one, providing we left it on loose, or made it part from the pattern and adjust to its place on the pattern by a taper pin; but another advantage is gained by well tapering the top print, in that it necessitates the tapering of the core print at that end; so that, when the two parts of the mould are being put together, that is to say, when the cope is being put in place, if the core has not been placed quite upright, its tapered end may still arrive and adjust itself in the conical impression, and thus correct any slight error of position of the core. The size of the core print should be, at the part next the pattern, the size of the core required; for if the extremities are made of the size of the core, and the taper or draft is in excess, there will be left a useless space around the core print, as shown at a b in Fig. 2774, into which space the metal will flow, producing on the casting, around the hole and projecting from the end face, a useless web, which is called a fin, which will of course require to be dressed off the casting.
“We will now suppose that our piece, when cast, is to be turned under the flange and along the outside of the hub or body, and that the hole also is to be bored. In this case the pattern made as above would still be good, but could be much more easily made and moulded if it has to leave its own core, its shape being as shown in Fig. 2775; because the trouble of making a core is obviated, and the core is sure to be in the centre of the casting, which it seldom is when a core is used. We must, however, allow more taper or draft to a hole in a pattern than is necessary on the outside; about one-sixteenth inch on the diameter for every inch of height on work of moderate size is sufficient. The allowance for boring should be one-sixteenth inch at the large end of the hole, provided the diameter of the hole is not more than five or six inches, slightly exceeding this amount as the diameter increases; whereas, if the pattern had been made with core prints, an allowance of one-eighth inch for small, and three-sixteenths inch for larger work would be required. These are the advantages due to making the pattern leave its own core. We have still to bear in mind, however, that, if the casting require a parallel hole, a core must be used; and furthermore, if the hole is a long one, we have the following considerations: The separate dry sand core is stronger, and therefore better adapted to cases where the length of the hole greatly exceeds the diameter. Then again, if the hole require to be bored parallel, it can be more readily done if the hole is cast parallel, because there will be less metal to cut out. The casting also will be lighter, entailing less cost, provided it has to be paid for by the pound, as is usually the case. The moulder is given more work by making the core; but the saving in metal, and in turning, more than compensates for this, provided the length of the hole is greater than the diameter of the bore.
“Let it now be required that the casting is to be finished all over. It would, in that case, be preferred that if the casting should contain any blow or air holes, they should not be on the outside face of the flange, and this will necessitate that the piece be moulded the reverse way to that shown in Fig. 2773: that is to say, it must be moulded as shown in Fig. 2776, with the flange downwards; for it may be here noted that the soundest part of a casting is always that at the bottom of the mould; and furthermore, the metal there is more dense, heavier, and stronger than it is at the top, for the reason that the air or gas, which does not escape from the mould, leaves holes in the top of the casting or as near to the top as they can, by reason of the shape of the casting, rise. The bottom metal also has the weight of the metal above it, compressing it, and making an appreciable difference in its density. It must, therefore, be remembered that faces requiring to be particularly sound should be cast downwards, or at least as near the bottom of the mould as they conveniently can. Following this principle, our gland will require to be moulded as shown in Fig. 2777, p p representing the line of the parting of the mould; so that, when the cope is lifted off, the loose hub a will rise with it, leaving the flange imbedded in the lower half of the mould. It is evident that in this case the pattern must be made, as shown in Fig. 2776, the body and core prints being in one piece and the flange in another, fitting easily on to a parallel part on one end, and adjoining the core print, as shown at a. For glands of moderate size, this method is usually adopted, and it answers very well for short pieces; but in cases where the length of the body approaches, say, three diameters, the horizontal position is the best, and the pattern should be made as shown in Figs. 2778, 2779, or 2780. Even in short pieces, when the internal diameter approaches that of the external, this plan is the best, because it is difficult for the moulder to tell when his core is accurately set in position.
“For a pattern to be moulded horizontally, Fig. 2780 shows the best style in which it can be made. Its diameters are turned parallel; the required draft is given by making the rim of the flange a little thinner than at the hub, and by making the end faces of the hub and the core prints slightly rounding. If the hub is very small, as, say, a half-inch or less, and the flange does not much exceed it, the pattern may be made solid, as shown in Fig. 2778; but if the hub be small and the flange large, it should be made as shown in Fig. 2776.
“To construct the pattern shown in Fig. 2773, we proceed as follows: From a piece of plank we saw off a piece of wood a little larger and thicker than the required flange, and turn it up between the lathe centres, using a pattern makers’ contraction rule, which has its measurements larger than the actual standard ones in the proportion of one-eighth inch per foot: so that a foot on the contraction rule is 121⁄8 standard inches, and an[II-277] inch is 11⁄96 standard inches. The reason for this is, that when the metal is poured into the mould, it is expanded by heat; and as it cools it contracts, and a casting is, therefore, when cold, always smaller than the size of the mould in which it was made. Brass castings are generally said to be smaller than the patterns in the proportion of one-eighth inch per foot, and cast-iron castings one-tenth inch per foot; and so, to avoid frequent calculations and possible errors, the contraction rule has the necessary allowance in every division of the foot and of the inch. It is not, however, to be supposed that the possession of such a rule renders it possible for the pattern-maker to discard all further considerations upon the contraction of the casting; because there are others continually stepping in. Such, for example, is the fact that the contraction will not be equal all over, but will be the greatest in those parts where the casting contains the greatest body of metal.
“In the smaller sizes of patterns, such as those of 6 inches and less in diameter, there is another and a more important matter requiring attention, which is, that after a moulder has imbedded the pattern in the sand, and has rammed the sand closely around it, it is held firmly by the sand and must be loosened before it can be extracted from the mould. To loosen it, the moulder drives into the exposed surface of the pattern a pointed piece of steel wire, which he then strikes on all sides, causing the pattern to compress the sand away from the sides of the pattern in all directions; and as a result, the mould is larger than the pattern. In many kinds of work, this fact may be and is disregarded, but where accuracy is concerned, it is of great importance, especially in the matter of our example (brasses for journals), for they can be chipped and filed to fit their places much more rapidly than they can be planed, and it is necessary to have the castings as nearly of the correct conformation as possible. In cases where it is necessary to have the castings of the correct size without any work done to them, the shake of the pattern in the sand is of the utmost importance. If it is required to cast a piece of iron 3 inches long and 1 inch square, supposing the pattern were made to correct measure by the contraction rule, the moulder, by rapping the pattern (as the loosening it in the mould is termed) would, by increasing the size of the mould above that of the pattern, cause the casting to be larger than the pattern; that is to say, it would be longer and broader, and therefore, in those two directions, considerably above the proper size, since even the pattern was too large to the amount allowed for contraction. The depth, however, would be of correct size, because the loosening process or rapping does not drive the pattern any deeper in the mould. It follows that, to obtain a casting of as nearly the correct size as possible, the pattern must be made less in width and in length than the proper size, to the amount of the rapping; and to insure that the moulder shall always put the pattern in the sand with the same side uppermost, the word “top” should be painted on the face intended to lie uppermost in the mould. The amount to be allowed for the rapping depends upon the size of the pattern, and somewhat upon the moulder, since some moulders rap the patterns more than others; hence, where a great number of castings of accurate size are required, it is best to have two or three castings made, and alter the pattern as the average casting indicates. For castings of about 1 inch in size, the patterns may be made 1⁄32 inch too narrow and the same amount too short; but for sizes above 6 inches, allowance for rapping may be disregarded.
“In patterns for small cast gears, the rapping is of the utmost consequence. Suppose, for instance, we have six rollers of 2 inches diameter requiring to be connected together by pinions, and to have contact one with the other all along the rollers; if we disregard the allowance for rapping, the pinions will be too thick, and we shall require to file them down, entailing a great deal of labor and time, besides the rapid destruction of files.
“Let it be required to cast a pillow block to contain a babbitt-metal bearing. In this case there requires to be a cavity to receive and hold the babbitt metal. This is provided by casting ridges of metal around the edges of the bearing, as shown in Fig. 2781, at d e and on each side at f, the pieces d e may be made solid with the pattern, but those for the sides must be removable, having dovetails as at c c to hold them in position while being moulded, or in place of the dovetails, wires as at f f may be employed, in either case the pattern would be extracted from the mould, leaving the side strips to be removed afterwards. If, instead of a pillow block, a bracket or frame, such as in Fig. 2782, were required, it must be moulded in the direction of the arrow, and in that event it would be desirable to core out the journal bearing. This would be accomplished by providing a core print to block up the whole opening b. A suitable core box for the bearing would be as in Fig. 2783. The core print must[II-278] project below the casting so as to form in the mould a core print for the core, and it is obvious that the core itself must be made of increased depth to the amount allowed for core print; hence the end piece b, Fig. 2783, is increased in thickness to the amount allowed for core print.”
Patterns for cylindrical bodies, especially those that are hollow and thin, are constructed in pieces by a process termed “building up.” The pieces are usually segments of circles, and the manner of marking them is as follows:—
Let it be required to make a pattern for a flanged pulley, such as shown in section in Fig. 2784. It would be constructed in two halves composed of a number of courses as from 1 to 8, and each course would be composed of segments of the form shown in Fig. 2785. The length of the arc of these segments must be such that it will require a certain number of these to complete the circle of that part of the cylinder which the segment is to form; and the manner of accomplishing this is shown in Fig. 2786, in which the circle c is of the diameter of the outside, while circle d is that of the outside of the pulley proper, circle e is of the diameter of the inside of the pulley rim. These circles are divided into as many equal divisions as there are to be segments in the circumference; hence the number of divisions determines the length of arc of the segments. Thus a would be a segment for the body of the pulley, and f a segment for the rim. A template is then made of each one of these segments, as at a and f. This template must be made slightly larger in every direction than the respective divisions, to allow for the stuff that will be turned off in truing the pattern in the lathe and in jointing the segments to one another during the building. The templates are employed to mark out on the board which should first be planed to the required thickness. This will be a trifle thicker than the course so as to allow for truing the surface of each finished course in the lathe. The courses are best built up on the chuck of the lathe on which they are to be turned, and a saving in time will be effected if there are two chucks, so that a course on one half of the pattern may be built up while the glue of another course on the other half is drying. On the lathe chuck, and directly beneath, where the joints of the segments will come, pieces of paper as at a, c, e, g, Fig. 2787, and if the segments are long ones, intermediate pieces of paper, as b, d, f, h, will be necessary. The radial edges of the segments are trimmed on what is termed a shooting board, which is a device such as shown in Fig. 2788, in which a is a piece of board on which is fastened the piece b. s is a piece projecting above b, and is provided to rest the segment s′ against, the flat surface of the latter lying on the board b. It is thus held in a fixed position, ready to have its edges e planed, the whole being laid upon the bench against the bench stop g. If, however, it is more convenient to rest the shooting board across the bench, a piece c may be fastened beneath a, so as to come against the edge of the bench as in Fig. 2789, in which t is the bench. The plane is laid with its side on a as in Fig. 2790, so that the surface of a acts as a guide, keeping the edge of the plane vertical, and thus planing the edges of the segment square. The plane is operated by hand in the usual manner (save that it lies on its side), taking its cut most off the outside or inside of the edge of the segment s′, according as the position of the latter is varied. In some of the shooting boards manufactured by tool makers, the height of b from a is adjustable, so that all parts of the plane blade edge may be used, which saves grinding, since only that part of the edge that is used dulls. Also there is provided means[II-279] whereby the required lateral position of the segment may be adjusted; such a device is shown at p, Fig. 2788, which is a plate having a slot through it, through which passes the thumb screw v, which screws into s. Hence the plate may be adjusted so that when one end of the segment rests against the end of s, and the other against the end of p, its edge e will be in the proper position to be planed to correct angle by the plane, whose line of action is in this case rendered positive by means of a slide on the plane, acting in a groove in the base a.
The first segment is glued to the pieces of paper on the chuck, as shown in Fig. 2787, s′ representing the segment. A second segment is then added, being set fair to the pencil circle o, and jointed and glued both to the chuck and to the ends of the first segments. Successive segments are added until the whole circle or course is completed, and when dry the radial face of this course is turned in the lathe so as to be true, flat, and of the required thickness, and the diameter is trued. The second course may then be added, but the joints at the ends of the segments should not come over those of the first course, but in the middle as shown by the dotted line. The ends of the segments should be made to bed properly against each other, and glue should be applied to the joint between the two courses and at the ends. By adding the successive courses the whole may be built up on the chuck ready to receive the arms. As each segment is added it should be clamped or weighted to press it firmly to its seat and press out the excess of glue.
If the pattern consists of two, or say three, courses, the glue will be sufficient to hold it to the chuck while turning, but if there are more courses a screw should be inserted through the chuck and into each segment of the first course. The cylinder must then be turned inside and out ready to receive the spokes. These are made of pieces equal in length to the internal diameter of the rim, or a trifle longer, so that the ends may be let into the rim. A line is then marked along the edge of the rim, dividing its thickness into two divisions, and in the centre of the length a recess should be cut out from the face to the line, the width of the recess equalling the width of the arm, so that one arm will let into the other, forming a cross, of which the flat surfaces lie in the same plane. This cross is let into the rim of the wheel and fixed temporarily with brads. The lathe may then be started and the centre of the arms (and therefore that of the cylinder or pulley) be found by a pencil point moved until it marks a point and not a circle when the lathe revolves. The arms may then be marked to shape and a recess turned at their centre to receive the hub. The arms being marked to their respective places and their outside faces being marked with a pencil so that they may be replaced in the same position in the wheel, they may be removed and shaped to the required dimensions and form, and then replaced and glued to the rim.
If the wheel is to have six arms they may be constructed as follows:—
Instead of taking two pieces of the diameter of the rim, as in the case of four arms, three pieces are necessary, and in this case the thickness of the edge of each piece is divided by two marked lines which will divide the thickness of the edge into three equal divisions, as shown by the dotted lines 1 and 2 in Fig. 2791, which will divide the thickness of the edge into three equal divisions of thickness. From the centre of the lengths of each of the three pieces we mark on the flat face a circle whose diameter will equal the width on the flat face of the pieces themselves.
With an angle square having its adjustable blade set to an angle of 60°, and set so that the back is fair with the edge of the piece, and one edge coincident with the perimeter of the circle, lines tangent to the circle and crossing each other are drawn on the pieces a c. On the piece b four of such tangent lines (two on each side) must be drawn. The piece a is recessed between one pair of tangent lines to the depth of the second lines on its edge, or, in other words, to a depth of two-thirds its thickness, and between the other pair to a depth of one-third, as shown, the two-thirds at d, the one-third at e. The piece d must be recessed between its tangents on each side to a depth of one-third its thickness, as denoted at f f, while on c the whole space between the tangent lines must be recessed to a depth equal to two-thirds its thickness, as shown at g. The pieces may then be put together so that the two diametrically opposite arms will be in one piece. If an odd number of arms is employed this form of construction cannot be followed; hence each spoke will be a separate piece, extending from the rim to the centre and jointed at the latter, as in Fig. 2792, which is for five arms.
For this construction draw a circle c, Fig. 2792, and divide it into as many equal points of division as there are to be arms in the wheel. From these points of division draw lines to the centre, and these lines will show the required bevel at the end of each spoke, as shown in the figure. The ends should be verified for bevel by striking from the common centre a second circle, as d; and measuring if the arms are equidistant, measured at the circle and from the edge of the arm to that of the next, finished along the full length. When fitted, corrected, glued and dry, the spokes may be let into the wheel and a recess turned into the centre to receive the hub.
The rim and all parts that can be got at may then be turned in the lathe, the pattern then being reversed in the lathe to turn the inside of the rim, or the other side of the spokes, when the job will be complete. When, however, the rim is to be a very thin[II-280] one, it may be necessary to fasten the segments together at the ends by other means as well as glue, hence a saw-cut may be made in each end, and a tongue inserted.
It is obvious that each half of the pattern is constructed by similar segments, the line of parting being through the centre of the arms, as at a b, in Fig. 2791. To keep the two halves coincident when in the mould, pins are inserted in the rim and arms of one half, fitting closely into holes provided in the other half.
To construct a pattern for a pipe, the pattern would be made in two halves, and constructed of what are termed staves, that is, pieces of wood running lengthways of the pipe. The number of these staves is optional, save that it must be even, so that each half pattern will contain an equal number.
Let it be required to make a pattern for a pipe 18 inches in diameter, and to be 1 inch thick. Draw the line a b, Fig. 2793, and from a point on it, as c, draw a semicircle a b, equal in diameter to the diameter of the outside of the pipe. Also the circle d e f, equal to the diameter of the inside of the pipe, and these will represent an end view of the pipe. Divide these semicircles into as many equal divisions as it is decided to have staves in the half pattern—as 1, 2, 3, 4, 5, 6; and from one of these divisions make a template as denoted by the oblique lines at 2, leaving it slightly larger than the division, to allow stuff to work on in fitting the staves, &c.
Now, when the staves are cut out it is necessary to have some kind of a frame or support to hold them while jointing them; hence, draw also from the points of division, as d, e, f, the lines a, b, c, d, e, f, and these will form the sides of a half-disk polygon, whose diameter is from d to f. A sufficient number of these polygonal half-disks are cut out to stand about two feet apart along the whole length of the pipe, as in Fig. 2794, and on these, temporarily fastened to the board b, the staves are jointed and fastened together by glue while each stave is held to its[II-281] place on each half-disk by a screw. The top stave may be put on first, as it will act as a stay to the half-disks. If the pipe is so long that it is composed of more than two pieces, the end pieces should be put on first, and the intervening space filled up last, which enables the ends to abut firmly. The second half may be added to the first one, putting a piece of paper between the edges of the two to prevent their sticking together.
If the pipe has a bend, it is built up separately, instead of being formed of staves, the process being as follows:—
In Fig. 2795 let b represent the centre of the bend curve, the line c representing one end, g the other end, h the inner and j the outer arc of the bend. Let it be determined to build up the bend in five pieces, as shown at 1, 2, 3, 4, 5, which represents an end view of the half pattern. Templates are then made for each of the pieces 1, 2, &c., being formed as denoted by the oblique lines, whose dimensions slightly exceed the half circle e of the pattern, to allow wood for dressing up. To find the curve for these pieces, set the compasses to a radius from b to the outer corner of piece 1, and draw the arc k. Set the compasses to the radius from b to the inner corner of piece 1, and draw the arc l, and the space between these two arcs, which space is marked 1 t, is a template for the curve of piece 1. By a similar process applied to pieces 2, 3, 4 and 5 similar templates for their respective curves are obtained; and selecting timber of a proper thickness, we mark out the respective curves from these templates, which may be of thin board or of stiff paper. In putting these pieces together the lower ones are set to lines forming a plan of the bend, being set a little outside the lines to allow wood for truing the pieces to shape after they are put together. The lower pieces are temporarily fixed to the board on which the plan is marked, and the upper ones fastened to the lower by glue, the joint surfaces of each line being planed true previous to being glued. It is a great assistance, however, to cut out two half circles, representing the ends of the pipe, and to place them on the board to build upon. When a bend of this kind occurs in a covering for a pipe that is exposed to view, it is necessary, for the sake of appearance, to have the pieces composing the bend to correspond with those on the straight part of the pipe, as shown in Fig. 2796. The part a would be got out in staves, as described for the pattern of a pipe. The bend b would be also got out as described for that figure for a bend, save that the number of staves for the bend would equal the number on the pipe. But in this case each stave should be fitted to its fellow by pins, or its edge fitting into dowels on the edge of its fellow; thus one edge of a stave would have the dowels and the other the pins; the whole, when finished, being bound together by metal bands, as shown in the figure.
The patterns for a globe valve, such as shown in section in Fig. 2797, would be made as follows (which is taken from “The Pattern Makers’ Assistant”):—
“The flanges vary in shape; but as a rule small valves are provided with hexagons and large ones with round flanges suitable for bolting to similar flanges to make joints. For small valves, say up to 2 inches, the pattern is usually made with the hexagons cut out of the solid, but for sizes above that, they should be made in separate pieces, as shown in Fig. 2798, and screwed to the pattern, so that in case of necessity they may be removed, and flanges substituted in their stead. In Fig. 2799, we have a perspective view of the finished pattern; and Fig. 2800 represents the pattern as prepared, ready to receive a flange or hexagon as may be required. A globe valve pattern should be made in halves, as shown in Fig. 2801, the parting line of the two halves being denoted by a b. To make this pattern, we first prepare two pieces of wood so large that, when pegged together, the ball[II-282] or body of the pattern can be turned out of them, and long enough not only to reach from p to p, in Fig. 2799, but also to allow an excess by means of which the two pieces may be glued or otherwise fixed together. These two pieces we plane to an equal thickness, and then peg them to retain them in a fixed position, taking care, however, that the pegs do not occur where the screws to hold the flanges will require to be. We also place two pegs within a short distance of what will be the ends of the pattern when the excess in length referred to is turned off. We next prepare, in the same way, two more pieces, to form the two halves of the branch, shown at b, in Fig. 2801, for which, however, one peg only will be necessary. These pieces must be somewhat wider than the size of the required hexagon across the corners, that is, supposing the hexagon is to be solid with the branch; otherwise we must make them a little wider than the diameter of the hub of the flange, or of the round part of the hexagonal pieces. Their lengths must be such as to afford a good portion to be let into the ball or body of the pattern (as shown by the dotted lines in Fig. 2800), which is necessary to give sufficient strength. The two pieces must be firmly fixed together, and then turned in the lathe.
“During the early stages of the turning, or, in other words, during the roughing out, we must occasionally stop the lathe and examine the flat places on the body; for unless these places disappear evenly, the work is not true, and one half will be thicker than the other, so that the joint of the pattern will not be in the middle. It was to insure this that the pieces were directed to be planed of equal thickness, since, if such is the case, and the flat sides disappear equally and simultaneously during the turning, the joint or parting of the pattern is sure to be central. If the lathe centres are not exactly true in the joint of the two pieces, they may be made so by tapping the work on the side having the narrowest flat place, the process being continued and the work being trued with the turning tool at each trial until the flat places become equal. By this means, we insure, without much trouble, two exact halves in the pattern, which is very important in a globe valve pattern on account of the branch and other parts, not to mention the moulding. Having turned the body of the pattern to the requisite outline, and made, while in the lathe, a fine line around the centre of the ball where the centre of the branch is to come, as shown in Fig. 2800 by the line a, we make a prick point (with a scriber) at each crossing of the line a and the joint or parting of the pattern. We then mount the body upon a lathe chuck, in the manner shown in Fig. 2802. A point centre should be placed in the lathe and should come exactly even with the line a. In Fig. 2802, v v are two V-blocks made to receive the core prints. These Vs are screwed to the lathe chuck, and the pattern is held to them by two thin straps of iron, placed over the core prints and fastened to the Vs by screws. If the chuck and centre point run true, the V-blocks are of equal height, and the core prints are equal in diameter, the prick point opposite to the one placed to the centre point will run quite true; and we may face off the ball or body to the required diameter of branch, and bore the recess to receive the same. We make the holes in the flanges of the same size as the core prints; but we should not check in the print, because, if a flange with a different length of hub were substituted, it would be a disadvantage. To obtain the half flanges, we take a chuck and face it off true in the lathe; then, with a fine scriber point, we mark the centre while the chuck is revolving. We then stop the lathe, and, placing a straight-edge to intersect the chuck centre, we draw a straight line across the chuck face. We then take two pieces suitable for the half flanges, and plane up one flat side and one edge of each piece. If the flanges are not large ones, they may be planed all at once in a long strip. We place the pieces in pairs, and mark on each pair a circle a little larger than the required finished size of flange. We then fix each pair to the chuck, with the planed faces against the chuck, and the planed edges placed in contact, their joint coming exactly even with the straight line marked on the chuck face, and we may then turn them as though they were made in one piece and to the requisite size.
“In Fig. 2803 we have a representation of one half of a suitable[II-283] core box, the other half being exactly the same, with the exception that the position of the internal partition is reversed. To get out this core box, we plane up two pieces of exactly the same size and length as the pattern, and of such width and thickness as will give sufficient strength around the sphere, allowing space for the third opening. After pegging these two pieces together, we gauge, on the joint face of each, lines representing the centres of the openings and the centre of the sphere. We then chuck them (separately) in the lathe, and turn out the half sphere. We next place the two halves together, and chuck the block so formed in the three positions necessary to bore out the openings; or if preferred, we may pare them out. The partition (a, in Fig. 2803) follows the roundness of the centre hole, and is on that account more difficult to extract from the core than if it were straight and vertical. When, however, the partitions are of this curved form, the pieces of which they are formed are composed of metal, brass being generally preferred. Patterns have in this case to be made wherefrom to cast these pieces, and they may be made as follows: First, two half pieces are turned; each is then cut away so as to leave the shape as shown at a in the same figure, and is then fitted into the spherical recess in the core box, letting each down until both are nearly but not quite level. The two wing pieces are then fastened on, and this pattern is complete. When the pieces are cast, they must be filed to fit the core box, and finished off level with its joint face, a small hole being drilled in the centre, and a pin being driven through the piece and into the box to steady the corners. We then saw the pieces in halves with a very fine saw.
“If the partition, instead of following the roundness of the valve seat, is made straight, the construction of the core box is much more simple. In this case, a zigzag mortice is made clear through each half of the box, its size and shape being that of the required partition. Fig. 2804 represents a half-core box of this kind. A piece of wood a is fixed, as shown, to the partition, to enable the core maker to draw it out before removing the core from the box. The mortice for the partition should be turned out before the half-spherical recess, the mortice being temporarily plugged with wood to render easy the operation of turning.
“In very large valves (say 10 or 12 inches) a half-core box is generally made to serve by fitting the two half partitions, shown at a, in Fig. 2803, to a half-core box, and keeping them in position by means of pegs, a half-core being made first with one and then one with the other in the core box. It is often necessary to form a raised seat in the body of an angle valve, such as shown in Fig. 2805, which represents a section of such a body. It is shown with flanged openings, though in small valves hexagons to receive a wrench would be substituted.
“Fig. 2806 is a plan of half the core box necessary for forming the raised seat. From this construction, it will be seen that the large core, though solid with the branch core, is not solid with that forming the hole in the seat and the part below it; therefore the core prints on the body pattern must be left extra long to give sufficient support in the mould for the overhanging cores. The loose round plug p, is made of the size of the outside of the seat and fitted to the box. The part outside the box is a roughly shaped handle to draw it out by. The diminished part d is a print, and into the impression left by it is inserted the core made in box shown in Fig. 2807. The print d is of the same diameter as the hole in the seat; and the print on the pattern is of the size of the increased diameter below the seat. Large angle valves are made with half a core box by making a branch opening in the box right and left, a semicircular plug being provided. Two half-cores are made with the plug, first in one and then in the other branch opening. The plug p should be in this case only half round.”
For finding the lengths of the sides of regular polygons, scales, such as shown in Figs. 2808 and 2809, may be used, the construction being as follows:—
[II-284] Draw a horizontal line o p, Fig. 2809, and at a right angle to it the line o b. Divide these two into inches and eighths of an inch, and draw lines meeting the corresponding divisions on o p, o b. From the point o draw the following lines: A line at 551⁄2 degrees from line o p, which is to serve for polygons having 9 sides; a line at 521⁄2 degrees to serve for polygons having 8 sides; a line at 49 degrees for polygons having 7 sides; a line at 45 degrees for 6 sides; a line at 40 degrees for polygons having 5 sides. It may be added, however, that additional lines may be drawn at the requisite angle for any other number of sides.
The application of the scale is as follows:—
The point o represents the centre of the polygon; hence from o to the requisite line of division on o b represents the radius of the work. From the line o b to the diagonal line (measured along the necessary horizontal line of division) is shown the length of a side of the polygon. From the point o, measured along the line having the requisite degrees of angle, to the horizontal line denoting the radius of the work, gives the diameter across corners of the polygon. The diameter across the flats of a square being given, its diameter across corners will be represented by the length of a line drawn from the necessary line of division on o b to the corresponding line of division on o p. A cylindrical body is to have six sides, its diameter being 2 inches, what will be the length of each side? Now, the radius of the 2-inch circle of the body is 1 inch; hence, find the figure 1 on line o b and measure along the corresponding horizontal line the distance from the 1 to the line of 45 degrees, as denoted by the thickened line.
A body has six sides, each side measuring an inch in length, what is its diameter across corners? Find a horizontal line that measures an inch from its intersection of the line o b to the line of 45 degrees, and along this latter to the point o is one-half the diameter across corners.
Example 3.—It is desired to find the diameter across corners of a square whose side is to measure 3 inches. Measure the distance from the 3 on line o p to the 3 on line o b, which will give the required diameter across corners.
This scale lacks, however, one element, in that the diameter across the flats of a regular polygon being given, it will not give the diameter across the corners. This, however, we may obtain by a somewhat similar construction. Thus, in Fig. 2808, draw the line o b, and divide it into inches and parts of an inch. From these points of division draw horizontal lines; from the point o draw the following lines and at the following angles from the horizontal line o p:—
| A line at | 75 | ° | for polygons having | 12 | sides. |
| „ | 72 | ° | „ | 10 | „ |
| „ | 67 | 1⁄2° | „ | 8 | „ |
| „ | 60 | ° | „ | 6 | „ |
From the point o to the numerals denoting the radius of the polygon is the radius across the flats, while from point o to the horizontal line drawn from those numerals is the radius across corners of the polygon.
A hexagon measures 2 inches across the flats, what is its diameter measured across the corners? Now, from point o to the horizontal line marked 1 inch, measured along the line of 60 degrees, is 15⁄32 inches; hence the hexagon measures twice that, or 25⁄16 inches across corners. The proof of the construction is shown in the figure, the hexagon and other polygons being marked for clearness of illustration.
Let it be required to make a pattern for a section of pipe such as shown in section and in plan in Fig. 2810, which is from “The Pattern Maker’s Assistant.” This pattern would be made to mould, as shown in the section, lying horizontally, and must therefore be made in two halves, the line of joint for the two halves being along a b in Fig. 2811.
“The body a and the branch b would be made separate from the flanges, and would be reduced in diameter at the ends to receive them. To form a, take two pieces of timber, say three inches longer than the length of a, including the core prints, and measuring a little more than half the diameter of the pipe one way, and a little larger than the full diameter of the pipe the other way, and glue them together at the ends for a distance of 11⁄2 inches, which will serve to hold them while turning them in the lathe.
“The pieces may then be turned in the lathe to the required diameter. During this turning, however, it is essential to insure that the joint of the two pieces be exactly in the centre, otherwise one half of the pattern will be (when the halves are separated) thicker than the other.
“The ends are then turned down to receive the flanges, the reduced diameter being necessary so as to leave a shoulder for the flanges to abut against to keep them true, or at a right angle to the axial line of the body. The branch is turned up in the same way, and the flanges are then turned and put on.
“The end of the branch may be cut to fit the circumference of the body as follows:—
“Set a bevel square to an angle of 45°. Take the halves of the branch apart, and rest the stock or back of the bevel against the end face, and let the blade lie on the joint face, and mark two lines a b in Fig. 2812, which lines must just meet in the centre of the branch at the end. Cut away the angular pieces c and d down to the lines a b. This performed on each half will leave[II-285] them when given a quarter turn as shown in Fig. 2812, and the curve shown by the junction of the horizontal with the vertical shading lines is the curve for the end; hence the surface covered with the horizontal lines requires to be cut away.
“When this is done on both halves the branch will fit to the body, as shown in Fig. 2813, in which a is the body and b c the two half branches. For a temporary pattern the branch may be fastened to the body with a few screws; but for a permanent pattern it should be glued also, which is done as follows:—
“Lay one half of the body a, Fig. 2813, on a board, with the flange overhanging to be out of the way, and clamp it there; lay the branch also on the board, and draw it firmly up to the body by clamps, while also clamping it flat down to the board, as shown in Fig. 2814. This will insure that the joint faces are true with one another, that is, lie in the same plane. Paper should, however, be placed between the joint faces and the board to prevent them from becoming glued to the board, and the edges, therefore, from breaking away. The second half can be put together as the first one, paper being put between the two to prevent them from being glued together; and to further strengthen the joint, let into each half a piece of hard wood p, Fig. 2815, and put in the screw shown at a.
“Suppose now that the diameter of the branch had been smaller than that of the body of the pattern, then the length of curve necessary on the branch end to let it abut fairly against the cylindrical pattern body may be found as follows:—
“Draw on a piece of board the line a b, Fig. 2816, and from any point c mark a semicircle equal in radius to that of the radius of the body of the pattern, draw the line e parallel to a b, and distant from it to an amount equal to the radius of the branch, then from the junction of e with the semicircle as at d, mark the line f at a right angle to a b. Let it now be noted that the semicircle a g represents half the pattern body, and e d f b the branch; hence from f to g is the length of the branch end that will require to be curved to fit the circumference of the body, while it is also the length to be added to the distance the branch requires to stand out from the body. To draw the curve on the end d f g of the branch the gauge or marking instrument, shown in Fig. 2817, is employed. The branch p is placed in V-blocks (Fig. 2818), resting upon a plane surface. The gauge consists of a stand e carrying a vertical bar a; upon a is the closely fitting cross-tube carrying the arm c, which in turn carries the marking pointer d, which is set distant from the centre of the bar a to the amount of the radius of the piece of work or the cylinder is to fit against.
“If the branch required to stand at an angle to the body, as in Fig. 2819, the marking may be performed by the same gauge and in the same manner, but the axial line of the branch must be set, when marking one side, at an acute angle to the axial line of a, and at an obtuse angle to a when turned over to mark the other side, which may be done in each case by raising one of the V-blocks until the branch lies in either case at the same angle to a as it will require to stand to the body on which it is to fit.
“When the body is much larger in diameter than the branch, a hole may be bored in the former to receive the end of the latter, by[II-286] giving to the branch end a stem, as in Fig. 2820, and then cutting in the body a recess for the branch end and its additional stem. This recess may be cut out in the lathe, chucking the body as in Fig. 2821.
“Should it occur that one end of the T is of larger diameter than the other, one chucking V must be deeper than the other, and we may find their respective depths by the following process:—
“Draw line a b, Fig. 2822, which line represents the chuck face. Let point c represent the centre of the lathe. Mark line c e and set a pair of compasses to the radius of the body of the pattern at the centre of the branch location. Then take a radius from c and about 1⁄16 inch up from line a b, and with this radius we mark on the line c e the point e. From this centre we mark the two arcs having radii corresponding to the unequal diameters of the pattern at the location where the chucking V’s are to be placed. We then draw tangent lines to each of these arcs, and thus obtain the correct depth of V necessary to hold the axial line of the pattern parallel to the lathe chuck.
“The core box would, unless the pattern were a small one, be built up in courses, as shown in Fig. 2823. The box would be drawn in plan, and end and side views drawn as shown, so as to draw in the half circle representing the bore of the half-core box and mark off the courses as from 1 to 6. These courses need not be of equal or of any particular thickness, but may suit that of any suitable timber at hand. Courses 1 and 2 should extend over the whole outline of the box, while the pieces 3 and 4 are made in width to suit the curvature of the core as shown, and to extend the full length of the box. The pieces 7, 8, 9, and 10 are of the length of the branch, and are made in width to suit the curvature of the branch core. If the branch core were a short one it could be cut out of the solid; but in any event, the grain of the wood should be as shown, and the holding pieces at g and h should be employed.”
The machines employed in wood working may be divided into 7 classes as follows:
1. Those driving circular saws.
2. Those driving ribbon or band saws.
3. Those driving boring or piercing tools.
4. Those employing knives having straight edges for surfacing purposes and cutting the work to thickness.
5. Those employing knives or cutters for producing irregular surfaces upon the edges of the work.
6. Those employed to produce irregular surfaces on the broad surface of work.
7. Those employed to finish surfaces after they have been acted upon by the ordinary steel cutting tools.
The thicknesses of circular saws is designated in terms of the Birmingham wire gauge, whose numbers and thicknesses are shown in Fig. 3078, where a Birmingham wire gauge is shown lying upon two circular saws, which show the various shapes of teeth employed upon saws used for different purposes.
The teeth numbered 1 are for large saws, as 36 inches in diameter, to be used on hard wood. Numbers 2 and 5 are for soft wood and a quick feed. Numbers 3 and 4 are for slabbing or converting round logs into square timber. Number 6 is for quick feeds in large log sawing. Numbers 7, 8, 9 and 10 are for bench saws, or, in other words, saws fed by hand or self-feeding saws. Number 8 is known as the “London Tooth,” because of being used in London, England, on hard and expensive woods. Number 9 is the regular rip-saw tooth for soft woods. Number 10 is the Scotch gullet tooth. Number 11 is for either cross-cutting or rip sawing by circular saws used on soft woods. Number 12, is for large cross-cut saws; the flat place at the bottom of the tooth prevents the teeth from being unnecessarily deep and weak. Number 13 is for cross-cutting purposes generally. Number 14 is for rip sawing on saws of small diameter. It is also used for tortoise-shell, having in that case a bevel or fleam on the front face, and no set to the teeth.
The following table gives the ordinary diameters and thicknesses of circular saws and the diameters of the mandrel hole:
| Diameter. | Thickness. | Size Mandrel Hole. |
|||
| 4 | inch. | 19 | gauge. | 3⁄4 | |
| 5 | „ | 19 | „ | 3⁄4 | |
| 6 | „ | 18 | „ | 3⁄4 | |
| 7 | „ | 18 | „ | 3⁄4 | |
| 8 | „ | 18 | „ | 7⁄8 | |
| 9 | „ | 17 | „ | 7⁄8 | |
| 10 | „ | 16 | „ | 1 | |
| 12 | „ | 15 | „ | 1 | |
| 14 | „ | 14 | „ | 1 | 1⁄8 |
| 16 | „ | 14 | „ | 1 | 1⁄8 |
| 18 | „ | 13 | „ | 1 | 1⁄4 |
| 20 | „ | 13 | „ | 1 | 5⁄16 |
| 22 | „ | 12 | „ | 1 | 5⁄16 |
| 24 | „ | 11 | „ | 1 | 3⁄8 |
| 26 | „ | 11 | „ | 1 | 3⁄8 |
| 28 | „ | 10 | „ | 1 | 1⁄2 |
| 30 | „ | 10 | „ | 1 | 1⁄2 |
| 32 | „ | 10 | „ | 1 | 5⁄8 |
| 34 | „ | 9 | „ | 1 | 5⁄8 |
| 36 | „ | 9 | „ | 1 | 5⁄8 |
| 38 | „ | 8 | „ | 1 | 5⁄8 |
| 40 | „ | 8 | „ | 2 | |
| 42 | „ | 8 | „ | 2 | |
| 44 | „ | 7 | „ | 2 | |
| 46 | „ | 7 | „ | 2 | |
| 48 | „ | 7 | „ | 2 | |
| 50 | „ | 7 | „ | 2 | |
| 52 | „ | 6 | „ | 2 | |
| 54 | „ | 6 | „ | 2 | |
| 56 | „ | 6 | „ | 2 | |
| 58 | „ | 6 | „ | 2 | |
| 60 | „ | 5 | „ | 2 | |
| 62 | „ | 5 | „ | 2 | |
| 64 | „ | 5 | „ | 2 | |
| 66 | „ | 5 | „ | 2 | |
| 68 | „ | 5 | „ | 2 | |
| 70 | „ | 4 | „ | 2 | |
| 72 | „ | 4 | „ | 2 | |
Circular saws are sometimes hollow ground or ground thinner at the eye than at the rim, to make them clear in the saw kerf or slot with as little set as possible, and therefore produce smooth work while diminishing the liability of the saw to become heated, which would impair its tension. They are also made thicker for a certain portion of the diameter and then bevelled off to the rim.
This is permissible when the work is thin enough to be easily opened from the log by means of a spreader or piece that opens out the sawn piece and prevents it binding against the saw.
The shingle saw, shown in Fig. 3079, is an example of this kind, the saw bolting to a disc or flange by means of countersink screws.
The concave saw shown in Fig. 3080, is employed for barrel heads. The three pieces for a barrel head are clamped together and fed in a circular path, so that the saw cuts out the head at the same time that it bevels the edge.
The advantage of the circular saw lies mainly in the rapidity of its action, whether used for ripping or cross-cutting purposes.[II-288] In order, however, that it may perform a maximum of duty, it is necessary that the teeth be of the proper shape for the work, that they have the proper amount of set, that they be kept sharp, and that the tension of the saw is uniform throughout when running at its working speed.
The centrifugal force created by the great speed of a circular saw is found to be sufficient to cause it to stretch and expand in diameter. This causes the saw to run unsteadily unless it is hammered in such a way as to have it rim bound when at rest, leaving the stretching caused by the centrifugal force to expand the saw and make its tension equal throughout. The saw obviously stretches least at the eye, and the most at its circumference, because the velocity of the circumference is the greatest, and the amount of stretch from the centrifugal force is therefore the greatest.
It is obvious that the amount of centrifugal force created will depend upon the speed of the saw, and it therefore follows that the hammering must be regulated to suit the speed at which the saw is to run when doing cutting duty, and in this the saw hammerer is guided solely by experience.
A circular saw may have its tension altered and impaired from several causes as follows:
1. From the saw becoming heated, which may occur from the arbor running hot in its bearings, or from the work not being fed in proper line with the saw.
2. From the reduction in diameter of the saw by frequent resharpening of the saw, this reduction diminishing the amount of centrifugal force generated by the saw, and therefore acting to cause the saw to become loose at the eye.
3. From the saw teeth being allowed to get too dull before being sharpened, which may cause the saw teeth to heat, and thus destroy the tension.
4. From stiffening the plate at the throats of the teeth when gumming the saw, an effect that is aggravated by using a dull punch.
5. From the saw teeth having insufficient set, and thus causing the saw to heat.
The methods of discovering the errors of tension in a saw, and the process of hammering to correct them, have already been explained with reference to the use of the hammer on pages from 68 to 70 of volume 2 of this work.
Before hanging a saw on a mandrel, it is necessary to know that the mandrel itself runs true in its bearings or boxes. In a new machine this may be assumed to be the case, but it is better to know that it is so, because if the mandrel does not run true several very improper conditions are set up. First, the saw will run out of true circumferentially, and therefore out of balance, and the high side of the saw will be called upon to do more cutting duty than the low side. Second, the centrifugal force will be greatest on the high side, and the saw will be stiffer, thus setting up an unequal degree of tension. Third, the saw will run out of true sideways, cutting a wider kerf than it should, thus wasting timber while requiring more power to drive.
The collar on the saw arbor should be slightly hollow, so that the saw will be gripped around the outer edge of the collar, and the arbor or mandrel should be level so that the saw will stand plumb. The boxes or bearings of the arbor should be an easy working fit to the journals, and there should be little, or what is better, no end play of the arbor in its bearings.
If a saw arbor becomes heated enough to impair the tension of the saw, it has been hot enough to impair its own truth, and should be examined and trued if necessary.
The most important point in this respect is that the face of the collar against which the saw is clamped should run true, bearing in mind that if it is one hundredth of an inch out of true in a diameter of, say 3 inches, it becomes twenty hundredths or one-fifth of an inch at the circumference of a saw that is 60 inches in diameter.
In cases of necessity, a saw that wabbles from the collar face of the mandrel running out of true, may be set true by means of the insertion of pieces of paper placed between the saw and the face of the collar.
The first thing to do in testing the saw is to take up the end motion of the saw arbor, or if this cannot be done, then a pointed piece of iron or wood should be pressed on the end of the mandrel so as to keep it from moving endways while the saw is being tested.
The saw should be revolved slowly, and a piece of chalk held in the cleft of a piece of wood should be slowly advanced until it meets some part of the face of the saw just below the bottom of the saw teeth.
As soon as the chalk has touched and the saw has made one or two revolutions the chalk should be moved a trifle farther on from the teeth, and another mark made, and then moved on again, and so on, care being taken to notice how much space there is between the high and low sides of the saw. It will be found, however, that the shorter the chalk marks are the more the saw is out of true.
A more correct method is to chalk the face of the saw and use a pointed piece of iron wire of about one-quarter inch in diameter, but in any case the saw should only be touched lightly.
The pieces of paper should be portions of rings or segments, and should extend an equal distance below the circumference of the collar, because the same thickness of paper will alter the saw more in proportion, as it is inserted farther in toward the eye of the saw.
[II-289]If it should happen that two thicknesses of paper are necessary to true the saw, one should be made about half the length of the other, and the long one may extend farther in toward the eye of the saw. Thus one ring of paper may be an inch deep and the other one-half inch deep.
If but one piece of thin paper is needed, it may be simply a straight piece inserted half way down the collar and trimmed off level with the collar. In placing the paper, the middle of its length should be on that side of the saw that is diametrically opposite to the marks left by the chalk on the face of the saw.
When the saw is trued and is started it will be loose on the outside, but as its speed increases it should stiffen up so as to run true and steadily when running at its working speed.
If the saw is to be tried by actual work, it must be borne in mind that the tension of the saw must be right for its speed when in actual use, and not when running idle. If the machine has belt power enough to maintain the same speed whether the saw is cutting at its usual rate of feed, or whether it is running idle, the tension will not be altered by putting on the feed, but if the saw has been hammered to run at the full speed of the machine when not cutting and the feed is heavy enough to slacken the speed, then the tension of the saw will not be correct for its working speed.
The eyes of small saws are either made to fit the mandrel an easy sliding fit, or else the mandrel is provided with cones to accommodate various sizes of holes, an ordinary construction being shown in Fig. 3081, in which a is the saw arbor, fast on which is the collar b, s representing a section of the saw, w a washer or loose collar, and n the nut for tightening up w. The cone c is screwed upon a and passed through the saw until it just fills the hole, and thus holds the saw true.
In putting on the saw, it should be passed up to the collar, and c screwed home until it binds in the saw eye with enough force to bring the threads of c fairly in contact with those on the mandrel a, but if screwed home too tightly it may spring the saw, especially if the saw is a very thin one.
As c must be removed from the arbor or mandrel every time the saw is changed, the wear on its thread is great, and in time it becomes loose, which impairs its accuracy.
This objection is overcome in the construction shown in Fig. 3082, which is that employed by the S. A. Woods Machine Company. It is seen in the figure that the cone c fits externally in a recess in the collar b, and at the coned end also upon the plain part e of the arbor. The cone is hollow and receives a spiral spring s, s. When the saw is put on it first meets c, and as nut n is screwed up, the saw s and cone are forced along arbor e until the saw meets the face of b, and the clamping takes place. The strength of the spring s is sufficient to hold the saw true, and as the motion of cone c is in this case but a very little, therefore its wear is but little, which makes this a durable and handy device, while the saw cannot be sprung from over-pressure of the cone. Circular saws of large diameter, as from 40 inches upwards, are made a fair sliding fit upon their arbors or mandrels, and are provided with two diametrically opposite pins that are fast in the arbor collar.
The pins should be on diametrically opposite sides of the arbor, and an easy sliding fit to the holes in the saw, but they should not bind tight. Both pins should bear against the holes in the saw, and if both the pins and the holes in the saw are properly located, the saw will pass up to the collar with either side against the arbor collar, or in other words, the saw may be turned around upon the arbor.
If the pins, or either of them, bind in the holes of the saw, and the latter is forced on the arbor, it will spring the saw out of true, and when this is the case care should be taken in making the correction to discover whether it is the pins or the holes in the saw that are wrongly located. If it is the pins, the error will show the same whichever side of the saw is placed next to the arbor collar, while if the error is in the holes, the error will show differently when the saw is reversed on the arbor.
When a saw becomes worn, and its teeth require sharpening, the first thing to do is to joint it, that is to say, bring down all its teeth to the same height, which may be done by holding an emery block or file against it while the saw is running, care being taken to hold the block or file firmly, and to continue the process until the tops of the teeth run true.
The next operation is to gum and sharpen the teeth. Gumming a saw is cutting out the throats, or gullets between the teeth, so as to maintain the height of the tooth, and it follows that on saws that have sharp gullets (or in other words, saws in which the back of one tooth and the face of the next tooth join in a sharp corner), the sharpening process with the file may be made to also perform the gumming.
In the case of teeth of coarse pitch, however, this would entail too much labor in filing, and furthermore, as the height of the teeth increases with the pitch or distance apart of the teeth of circular[II-290] saws, and as the higher the tooth the weaker it is, therefore coarse pitched teeth are given round gullets so as to strengthen them as much as possible. The gumming of a saw should always be performed before the sharpening, and the sharpening before the setting.
When the sharpening is to be done with the file, the cutting strokes of the file should be in the same direction as the teeth lean for the set, as this leaves a sharper cutting edge, and it follows that the proper plan is to file every other tooth first, going all around the saw, and to then turn the saw around in the vise, and file the remaining teeth.
The height of the teeth and the diameter of the saw will be best maintained by filing the front face of the tooth to bring it up to an edge, but in filing the front face the spacing of the teeth should be kept as even as possible.
If the front face has been filed until a tooth is as widely spaced as those already filed, and the edge is not brought up sharp, then the edge may be brought up by filing the back of the tooth.
A saw gumming, gulleting or chambering machine to be operated by hand, and constructed by Henry Disston & Sons, is illustrated in Fig. 3083. It consists of a frame spanning the saw, and having screws b b, b b, to adjust to the saw thickness; 4 and 5 are two saw teeth, and 6 the cutter, k is a wheel for the feed screw g, and c and d gauges for regulating position and depth of the gulleting.
The cutter 6 is driven or revolved by means of the handles h h, but an important point in the construction is, that a pawl and ratchet wheel is used to drive the cutter, so that if the handles h h were revolved in the wrong direction, the cutter would not be revolved. This saves the cutter teeth from breakage. The machine is operated as follows:
Run the cutter back by means of screw g as far as necessary, then place the machine on the saw, with the cutter close up in the chamber of the tooth to be gummed.
If the teeth are regular and the same distance apart, start the cutter in any chamber; but if they are irregular, make them even by commencing in the smallest space. After gumming the saw a few times the teeth must become regular. f is a set-screw to regulate the depth of gullet. Fasten the machine to the saw by means of the screws b b, and proceed to gum the first tooth, one of the points of the star being struck at each revolution by a projection on the handle, steadily feeding the cutter until arrested by set-screw f. Remove the machine to the next tooth towards you, after having run the cutter back, and proceed as before until the whole of the teeth are gummed.
The cutter is so arranged as to slide on its axis, and when one portion becomes dull, remove a washer from back to front, and thus present a new sharp cutting surface; and so continue changing the washers until the whole face of the cutter becomes dull.
Set is given to saw teeth in two ways: first, by what is called spring set, which is applied to thin saws and to cross-cut saws; and second, swage set, which is given to thick saws and to inserted teeth. Spring set consists of bending the teeth sideways so as to cause the saw to cut a passageway or kerf, as it is termed, wide enough to permit the saw to pass through the timber without rubbing on its sides.
Swage set consists of upsetting the point of the tooth with a swage, thus spreading it out equally on both sides of the body of the saw plate, as shown at a, Fig. 3084.
The set of the teeth, whether given by swaging or upsetting, or by spring set, should be equal throughout the saw, so that each tooth may have its proper share, and no more, of duty to perform.
If spring set is employed, it should not extend down more than half the depth of the teeth, and this point is one of considerable importance for the following reasons. The harder the saw is left in the tempering the easier the teeth will break, but the longer they will keep sharp. Now a tooth that is hard enough to break if it is attempted to carry the set down to the root or bottom, will set safely if the set is given to it for one-half its depth only.
If a saw is to be sharpened by filing, it should be made as hard as it can be to file properly, even at the expense of rapidly wearing out the file, because the difference in the amount of work the saw will do without getting dull enough to require resharpening is far more than enough to pay the extra cost of files.
Circular saws with inserted teeth are made of thicker plate than solid saws of corresponding diameters, which is necessary in order that they may securely hold the teeth. The principal difference in the various forms of inserted teeth lies in the method of locking or securing the teeth in the saw.
Figs. 3084 and 3085 represent the chisel tooth saws of r. Hoe and Company. The No. 2 tooth is that used on gang edging machines and for bench work. No. 3 tooth is that used in miscellaneous sawing, for hard woods and for frozen lumber. No. 4 is the shape used in the soft and pitchy woods of southern and tropical countries.
The method of inserting the teeth is shown in Fig. 3084 on the left, the pin wrench being shown in position to move the socket whose projection at c carries the tooth d home to its seat and locks it there.
The sockets for the numbers 3 and 4 tooth are, it is seen, provided with a split, which gives to them a certain amount of elasticity that prevents the sockets from getting loose.
Swing-frame saws are made in various forms, generally for cross-cutting purposes or cutting pieces to length.
Fig. 3086 represents a swing-frame saw that is mounted over a work bench, and can therefore be used without necessitating carrying the work from the bench. It consists essentially of a frame pivoted at the upper end to the pulley shaft and carrying[II-292] below a circular saw driven by belt over pulleys on the upper shaft and the saw arbor. In this machine the iron hubs carrying the frame have sockets fitting over the outer diameter of the hanger hubs, so that the frame hangs upon those hubs and not upon the pulley shaft. The advantage of this plan is that the frame joint is relieved of the wear which would ensue were it hung upon the revolving spindle, while at the same time the movement of the joint is so small as to induce a minimum of abrasion. To counterbalance the frame while it is placed out of the perpendicular, there is provided a compensating weight as shown in the engraving.
Fig. 3087 represents an example of that class of cutting-off saw bench in which the length of the work is determined by the width apart of the saws.
This machine is constructed by Trevor and Company, and is designed for cutting barrel staves to exact and uniform lengths.
The stave is laid upon the bars of the upright swing-frame (which is pivoted at its lower end), and the latter is vibrated by hand, which may obviously be done both easily and quickly on account of the lightness of the swing-frame and its vertical position. A dimension sawing machine, by G. Richards and Company, is shown in Fig. 3088. This machine is designed for general fine work, such as pattern making, and its general features are as follows:
It carries two saws (a cross-cut and a rip-saw), mounted on a frame that can be quickly revolved by a worm and worm wheel to bring either saw into position as may be required.
There is a fixed table and adjustable fence on one side of the saw, and a movable table and fence on the other.
| VOL II. | DIMENSION SAWING MACHINE. | PLATE XVIII. |
|
Large image (100 kB).  |
||
| Fig. 3089. | ||
The saws are ground thin at the centre, as shown in Fig. 3089, so that but little or no set need be given to the saw teeth; hence the cutting edges of the teeth are more substantial and true, and as a result the work is cut very smoothly, and if the machine is kept in thoroughly good order, the sandpaper may follow the saw.
In Fig. 3088, a is a substantial box frame, to which is bolted the fixed table t. t′ is the movable table which runs on rollers, and is guided by the ∧ slideway at e. This table the workman pushes to and fro by hand, the work being adjusted upon the table or to the fence, as the case may be. At w is the wheel for swinging the frame to bring the required saw into position.
In Fig. 3089 the worm gear for swinging the saws into position is shown, and also a sectional view of one saw arbor and of the movable table. a is the main frame, and f the disc frame carrying the two saw arbors. The disc d is turned to fit a seating formed in the base, while the other end of the disc frame fits through[II-293] a substantial bearing b; w′ is the worm wheel, and w′′ the worm for swinging the disc frame. The worm teeth fit closely to the worm wheel teeth, and backlash or play is prevented by means of the spring bearing shown at d, the spiral springs forcing the worm teeth into the worm wheel teeth. Thus a is the bearing for the worm carried in the box c, upon which is the spiral spring whose tension is regulated by the screw g.
The end of the worm is therefore held in a swivel joint that causes it to operate very easily.
Fence f, Fig. 3088 is for slitting, and is made to swing back for bevel cutting, while f′ is for cross cutting, and is adjustable for angle cutting. Fence f is fitted to a plate p, Fig. 3090, which rests on the table top, and also rests on the long slide g. This slide fits in a beveled way h, and contains a ⊥ groove. A tongue likewise beveled fits in the top of this groove, the tongue being permanently fast to the fence plate. The ⊥ bolt passes through the tongue and fence plate, having at its upper end a milled or knurled thumb wheel r, which when tightened up fastens the fence plate and the slide together.
Upon slacking the thumb wheel r, the fence plate and ⊥ bolt may be readily shifted, setting the fence as near to gauge as possible by hand, and the thumb wheel is then tightened, and the slide (which carries the fence bodily with it) is adjusted by means of the hand wheel h and its screw which threads into a lug from the table.
The fence f is pivoted to plate p at p, and the angling link which holds it in position is secured by a hand nut m.
The front journal of the saw arbor has a double cone, and by means of the nuts n n′, Fig. 3089, can be regulated for fit independently of the back bearing and journal, the latter being also coned and capable of independent adjustment by means of the adjustment nuts m m′.
The countershaft for driving the saw arbors is below the machine, so that the saw that is not in use remains stationary.
Examples of the work done on this machine are shown in Fig. 3091, the various sections shown being produced by the vertical movement of the saw through the table and the cross movement of the fence. For example, for cutting out a core box, such as shown at 6, small grooves are cut through to remove the bulk of the wood, and the saw marks at the bottom of each saw cut serve as gauge lines for the workman in finishing the circular bore with the gouge, etc.
An example in which the table is fixed to the frame and the saw[II-294] is adjusted for height above the table is shown in Fig. 3092. The saw arbor is here carried in a frame that is pivoted at one end to the main frame, while at the other end is a handle through which passes a locking screw for securing that end of the saw arbor frame to the arc slot shown on the main frame.
In a more expensive form of this machine an adjusting screw is used for regulating the height of the saw, and an iron table is employed instead of a wooden one.
A double saw machine constructed by P. Pryibil is shown in Fig. 3093. In this machine each saw is carried in separate frames, that are pivoted at one end to the main frame and secured at the other to segments, so that either saw may be elevated to the required distance above the work table.
[II-295]One saw is for ripping and the other for cross cutting, and the arbor of the latter is provided with an adjusting screw operated by the hand wheel shown on the right hand of the machine.
As the saws are on independent arbors, they can be speeded differently to suit different saw diameters, which is an advantage because, as machines of this class are for the lighter classes of work, the ripping saw will rarely be required for work of more than about 3 or 4 inches thick, and a rip saw of large diameter is not therefore necessary.
The cross cut saw however requires to be of larger diameter, as its work includes cross cutting up to 8 or 10 inches diameter, and the saw being larger does not require so high a speed of revolution.
Both saws are provided with ripping gauges and with right and left hand mitre fences, adapted to the application of either short or long work, and provided with length gauges.
Fig. 3094 illustrates the various gauges in place upon the table of a machine. The table is provided with a slideway, or slot, on each side of the saw, and parallel with it, and also with a slideway at one side of the table. In the figure, the mitre gauge, or gauge for sawing at an angle, is shown in two positions.
The gauge a a a is for cutting work to length, and for cropping the ends at the same time, an extension frame being used, as shown for unusually long work.
Fig. 3095 illustrates the method of employment of the mitre gauge. The pointer is set to the degree of angle the work is to be cut to, and is fastened to its adjusted position by the set screw h. The stop is set to the required length, and the work is held by hand against the face of the gauge, and at the same time endways against the stop, and the gauge is then moved along the slot, feeding the work to the saw. When the work is sawn and is to be withdrawn, care must be taken to keep the work fair, both against the gauge and against the stop.
[II-296]Figs. 3096 and 3097 show the application of the gauges for cropping off the ends of work and cutting it to exact length. There are two stops, s and t, each of which is secured in position by a set screw, and has a tongue that may be thrown over, as occasion may require—thus, suppose it is desired to merely crop off the end of the work—and both stops may be set for the work to rest against as in Fig. 3096, and the end of the work may be cut off or cropped to square it or remove a defective part. Stop s may then be thrown over as in Fig. 3097, and the squared or cropped end of the work rested against stop t, to gauge the length to which the work will be cut. This is a simple and convenient method of cropping and gauging.
Fig. 3098 represents a circular saw machine, constructed by the Egan Company, in which the table is carried on a vertical slide, and may be raised or lowered by means of the hand-wheel, bevel gears, and screw shown, and may be set at any required angle to the saw for cutting bevels.
The saw arbor or mandrel is carried by the main frame, and is therefore rigidly held.
The fences can be used on either side of the saw, which is very convenient when the table sets out of the level.
In this machine, which is shown in Figs. 3099, 3100, and 3101, the construction permits of the saw being set so as to revolve at other than a right angle to the work table, which is rigidly secured to the frame of the machine.
Fig. 3099 is a general view, while Figs. 3100 and 3101, are sectional views of the machine.
This machine is constructed by J. S. Graham & Company, and its action may be understood from the following:
The table is firmly bolted to the frame, and is fitted with the necessary groove slides and fences for rip sawing and cross cutting. [II-297] It is also provided with a removable piece, which allows the use of wabbling saws, dado heads, etc.
The sides of this machine a, a, Fig. 3099, are cast with an extension for countershaft. Referring now to Figs. 3100 and 3101,[II-298] the upright piece i, i, with arms b b, and g, g, is bolted to the frame as shown. The arbor frame m, m, is gibbed to t, t, by the circular piece u, and is moved to any angle by the hand wheel z, which operates the worm w, which in turn moves the arbor frame m, m. This arrangement does not require any locking device to hold the saw in position. As the centre upon which the arbor swings is in the intersection of the planes of the saw and table top, the opening in the table needs not be larger than for the ordinary saw. When cutting a mitre the saw takes the position j, Fig. 3101. When cutting at a right angle the saw takes the position j′ and the arbor takes the position p′ n′.
The saw arbor can be raised and lowered by the use of the hand wheel which operates the screw b (Fig. 3100.)
There is an accurate index located in front of the machine in sight of the operator, marked from 0 to 45°.
The iron table is of one piece 4 feet by 3 feet and fitted with the necessary groove slides for ripping and cross cutting gauges. It is also provided with removable piece e, Fig. 3101, allowing the use of dado head, etc. The table is provided with a bevel slitting gauge s′, and cross cut or mitering gauge x′, Fig. 3099, which in connection with the angular adjustment of the saw enables the operator to get every conceivable plain or double mitre ever required. The pulleys a′, b′, are made wide to allow the belt to travel as the saw is inclined. The pulley b′ takes up the slack of the belt. The countershaft and tightener are a part of the machine and can be run wherever a belt can be brought to them.
Figs. from 3102 to 3105 represent a roll feed circular saw, by J. Richards.
Fig. 3102 is a side elevation, Fig. 3103 a plan, and Fig. 3104 a cross-sectional view through the rolls.
In Fig. 3102, p is the saw-driving pulley, t a stand for carrying the saw guides a, b, c, d, which are adjustable for height by means of the arm whose set screw is shown at u; at w is the spreader for opening out the board after it has been cut by the saw, and thus prevent its binding against the saw and heating it.
The construction of the feed motion is shown in Figs. 3103, 3104, and 3105.
On the saw arbor is the feed cone c, Fig. 3103 having four steps so as to give four rates of feed. This cone connects by belt to feed cone d, whose shaft drives feed pulley e, which drives f by belt connection. f drives two worms shown by dotted lines at h and i, and these drive the worm wheels which drive the feed rolls, one of these worm wheels being shown at k, in the side view, Fig. 3102.
The feed roll l (Fig. 3103) is supplemented by a fence or gauge face p, which guides the work closer up to the saw than would be possible with a roll, and a supplemental roll is provided at m, thus affording a guiding surface for the work from m to the end of p. The stand for guide roll l fits in a slideway, and is adjustable along it by means of the screw s. Similarly the stand for roll n is fed along its slideway by screw r. There are three[II-299] separate sets of saw guides, all of which are shown in the plan view Fig. 3103, and of these the top ones, a, b, c, d, e, f, g, and h are adjustable by nuts. The front ones, l, m, n, o, p, q, and the back ones, i, j, k, and r, s, t, are adjustable by means of the wedges w. At z is a wedge for adjusting the spreader w so as to keep it close to the saw whatever the diameter of the latter may be.
Fig. 3105 is an end view of the machine showing the feed worms h and i, and the belt tightener v, which is carried on the arm u on whose shaft is the weight y, attached to which is the handle x.
A segmental circular saw is one in which the saw is composed of segments secured by screws to a disc, the construction being such as shown in Fig. 3106, in which a is the saw arbor, d the disc, and e, f, g, h, i, j, etc., the segments.
The segments are made of varying thicknesses at the cutting[II-301] edge, and are tapered for a distance for from 6 to 8 inches inwards from the teeth points. Thus in the figure there is shown at p an edge view of a segment, from a to b being parallel, and from b to c being ground off taper.
The segments are held to the disc by the two sets of screws, r, s, and are further secured at their edges by pieces of copper, as shown at w. Between the edges of the segments there is left a space or opening of about 1⁄16 inch, which is necessary to insure that the segments shall not bind together edgeways, as that might prevent their seating fairly against the face of the disc d.
The seats for these pieces of copper are shaped as shown in the face views at w, and in the edge views at w′, the mouth of the slot being widened on each side, so that riveting up the pieces of copper will prevent the segments from moving sideways.
In fitting in these pieces of copper, it is essential to take care that they do not completely fill the slots, but leave a small opening at each end of the slot, as at f and g in the figure, and in order to do this the copper must be left about 1⁄8 inch narrower than the width of the slot.
If the copper is, in riveting up, brought to bear against the end of the slot, it will twist the segments out of line one with the other, causing the saw to drag, cut roughly and produce bad work.
Figs. 3107 and 3108 represent portions of segmental saws for cutting veneering. In some of these saws the screw holes are so arranged that the segments can be moved out to maintain the diameter of the saw as it wears.
For dressing the edges of planks parallel and to width what are called gang edgers or gang edging machines are employed.
A gang edger consists of an arbor driving two or more circular saws, through which the boards to be edged are fed. Means are provided whereby the distance apart of the saws may be rapidly adjusted while the saws are in motion, so that if a board will not true up to a given width, the saws may be set to cut it to a less one without delay.
Fig. 3109 represents a self-feeding gang edger, constructed by J. A. Fay & Company, and in which the left-hand saw may be fixed at any required position on the left-hand half of the saw arbor, while the two right-hand ones may be adjusted independently along the arbor, while the machine is running.
At the back of the saw is a feed roll, and above it a pressure roll, whose pressure may be regulated by means of the weight and bar shown at the back of the machine. The object of placing the feed and pressure rolls at the back of the saws, is, that if a board is found to be too narrow for the adjustment of the saws, it may be withdrawn without stopping or reversing the machine, and the saws may be drawn together sufficiently to suit the case.
Fig. 3110 is a plan and Fig. 3111 an edge view of the work table, and show the means of adjusting the saws. a is the saw arbor, and 1, 2, 3, the circular saws. Saw 1 is carried by the sleeve b, which is secured in its adjusted position by the set screw c.
The mechanism for traversing saws 2 and 3 corresponds in design, and may be described as follows:
The arbor a has a spline s to drive the sleeves d, d′, which hold the saws and are carried by arms e, e′, which operate in slideways and have racks f, f′, into which gear pinions whose shafts g, g′, are operated by the hand wheels h, j.
It is obvious that by means of the hand wheels h, j, saws 2 and 3 may be regulated both in their distances apart or in their distances from saw 1, while the machine is in full motion, the bushes or sleeves d and d′ being carried by and revolving in the slide pieces or sliding bearings e and e′ respectively. Now suppose that e′ be moved to the left by hand wheel j, until it abuts against the end of d, at the slide end, and a further movement of d′ will also move d, causing it to operate its pinion and revolve the hand wheel h, hence d and d′ may be simultaneously moved without disturbing their distances apart by operating hand wheel j. On the yoke above the saws is a coarse-figured register plate to enable the setting of the saws to accurate widths apart.
This machine is employed for the purpose of reducing balks or logs into planks of any thickness required. The machine is fixed[II-302] on the floor of the saw mill, all the gearing being underneath the floor, so that the table may be set level with the floor, which is a great convenience when heavy logs are to be operated upon. The machine consists of a substantial bed plate or frame a, Fig. 3112, carrying the saw and the feed works. The carriage runs on rollers, some of which are fixed to the frame a, and others to the framing timbers b, which are long enough to support the carriage throughout its full length, when the carriage is at either end of its traverse.
| VOL. II. | RACK‑FEED SAW BENCH. | PLATE XIX. |
|
Large image (82 kB).  |
||
| Fig. 3112. | ||
The driving pulley for the saw arbor is shown at c, Fig. 3112, in dotted lines and in Fig. 3113 in full lines. Upon the saw arbor is a cone pulley d, Fig. 3113, for operating the carriage to the feed, the construction being as follows:
Referring to Figs. 3112 and 3113, cone pulley d connects by a crossed belt to cone pulley e, on whose shaft is a pulley e which drives the pulley f, on whose shaft is the pinion f, which drives the gear g. On the same shaft as g is a pinion g, which drives the gear wheel h, which engages the rack j, on the carriage, and feeds the carriage to the cut. The diameters of pulleys e, f, and of f, g, and g, are proportioned so as to reduce the speed of the cone pulley d, down to that desirable for the carriage feed. But, as there are four steps on the cones d, e, therefore there are four rates of cutting feed or forward carriage traverse, which varies from 15 to 30 feet per minute.
The speed of the saw varies in practice, some running it as slow as 9,000 feet per minute at the periphery of the saw, and others running it as high as 16,000 feet per minute. The latter speed however, is usually obtained when the saws are packed with fibrous packing, which will be explained presently.
The quick return motion for the carriage is obtained as follows:
Referring to Figs. 3113, and 3114, k is a fast and k′ a loose pulley on the shaft k, and receiving motion by belt from a countershaft.
The speed of the fast pulley k is such as to give a return[II-303] motion to the carriage of about 50 or 60 feet per minute, being about twice as fast as the carriage feed motion.
We have now to explain the methods of putting the respective carriage feed motions into and out of operation, and insuring that both shall not be in gear at the same time.
Referring therefore to Figs. 3113 and 3114, suppose the carriage to have completed a feed or cutting traverse, and the operator pushes with his knee the lever or handle h, Fig. 3114, which revolves shaft m, on which is an arm that moves the belt-shifting rod n, thus moving the belt from fast pulley f to loose pulley f′, thus throwing the feed gear out of engagement and causing the carriage to stop. He then presses down the foot lever l, Fig. 3113, which operates the belt-shifting rod p, Fig. 3114, and moves the belt from loose pulley k′, to fast pulley k, which having a crossed belt, operates the pulley f in the reverse direction and traverses the carriage backwards, or on the return motion.
Upon releasing the foot from the lever l, the weight w operates the foot lever l, and the belt is re-shifted from fast pulley k to loose pulley k′, and the carriage stops.
The carriage is formed of iron plates with an open space of about 1⁄2 inch between them, as shown in Fig. 3114, this space forming a race to permit the carriage to travel past the saw. The only connection between the two sections or parts of the table, is a wide plate at the rear end which secures them together, and causes the lighter portion of the table, which is merely driven by the friction of the rollers c, to always travel with the lower or under portion, which is driven by the rack j. In larger machines for the heaviest work, both sections are driven by a rack motion.
The guide motion for the carriage is constructed as follows:
a, a, are brackets placed at intervals along the whole frame work.
These brackets support rollers c, which have flanges on them to prevent any side motion of the carriage, the construction being most clearly seen in Fig. 3113; b being a bearing for the shaft v of the rollers. Each section of the carriage, it will be seen, has two ribs or ways which rest on the rollers, which are arranged four on each shaft v (i.e. two for each section of the carriage).
The fence or gauge against which the face of the work runs is very simply arranged as is shown in Figs. 3113, and 3114, being secured to the shaft q, by a long bolt t, threaded into the top of the fence, and at its lower end abutting against a shoe fitting partly around the top of the shaft q. It is squared at the top to receive a wrench or handle u, and it is obvious that unscrewing the handle releases the fence from shaft q, so that the fence may be moved rapidly by hand across the table to approximate the adjustment of the fence from the saw. The fence having been thus approximately adjusted, and locked to the shaft by means of the handle u, the final adjustment is made by means of the hexagon nut w, on the bed of the shaft nut x, serving as a lock nut, to hold q in its adjusted position.
Fibrous Packing.—The fibrous packing before referred to is composed of hemp, plaited in a four strand plait and inserted in an open-top trough, along the sides of the saw for a distance about two inches less than the radius of the smallest saw the machine uses.
[II-304]This packing steadies and stiffens the saw, and also affords a means of adjusting its tension, while the saw is running.
Suppose for example, that the saw is rim bound,[47] and the fibrous packing may be rammed tightly to the saw, as near to the saw rim as possible, and less tight as centre of the saw is approached.
[47] For the principles involved in hammering saws to equalize the tension see page 69 (Vol. II.) et seq.
This warms the saw, but makes it warmer at the circumference than at the centre, expanding the circumference, and by equalizing the tension, enables the saw to run straight.
When the packing is to be adjusted, the carriage is run out of the way, and the packing operation is performed by hand, with a caulking tool. The packing and its box, as applied to a rack saw bench is shown in Fig. 3115, by the dark rectangles. By thus packing the saw to guide it and keep it straight, thinner saws may be used, saws 52 inches in diameter, and having a thickness of but 7 or 8 gauge being commonly employed, and in some cases of 9 gauge.
Saws that are thus packed, produce much smoother work.
The packing, it may be observed, is kept well lubricated with oil, and the following is the method of adjusting it.
The side of the saw on which the operator stands is the last to[II-305] be packed, the packing on the other side being inserted so as bed fairly but lightly against the saw, so as not to spring it, which may be tried with a straight-edge. The packing on the other side is then inserted to also bed fairly against the saw, without springing it, and the saw is run until it gets as warm as it may, from the friction of the packing. If, then, the saw flops from side to side, the outside (circumference) is loose, and the packing is rammed together on both sides of the saw and near the saw arbor or mandrel, care being taken that in ramming the packing the saw is not unduly pressed on either side.
Expert sawyers generally change the packing when the saw is changed, and thus keep for each saw its own packing. The slot or pocket in which the packing lies is about 11⁄4 inches deep, and 1⁄2 inch wide.
In ordinary circular saw benches or machines the packing comes about up to the level of the table, as shown in Fig. 3116, in which a is a hand hole for putting in and lifting out the plate b, so as to put in or remove the wooden pieces c, d, upon which the packing rests.
| VOL. II. | PLANTATION SAW MILL. | PLATE XX. |
|
Large image (225 kB).  |
||
| Fig. 3117. | ||
Fig. 3117 represents a saw mill constructed by the Lane & Bodley Company. In this machine two circular saws are employed, the upper one being of small diameter and revolving in the same direction as the log feed. a is the driving pulley for the main saw arbor a, and b the driving pulley for the upper saw arbor b. The carriage feed is obtained by belt from cone pulley c to cone pulley d, on whose shaft is a friction pulley e, which, for the feed motion, is moved by lever e into driving contact with pulley f, whose shaft drives the pinion g, which gears with the rack of the carriage. The three steps on the cones c, d, give three rates of feed, and a quick return motion is given to the carriage by engaging the friction pulley with a wheel not shown in the engraving.
The log to be sawn rests upon the slideway s s’, and is secured thereon by the dogs j, j, which are capable of sliding up or down upon the heads h, h′. When the handles k are raised the slides carrying dogs j are free to be moved up and down h, h′, whereas when handles k are depressed the dogs j are locked and hold the log. The operation is to raise the dog slides to the top of h, h′, set the log up to the faces of h, h′, and then by raising handles k, let the dog slides fall, their weight forcing the dogs into the log, and the depression of k locks the dog slides upon h, h′, respectively.
The log feed is obtained from the lever l, which operates the ratchet wheel t, which drives bevel gears v and w, which operate the screws that slide the heads h, and h′, along the slideways s and s′.
Three rates of log feed are obtained by regulating the amount of motion that can be given to the lever l, the construction being as follows:
In the lever l is a slot in which a stop r can be secured at different heights, and the piece m has four notches. The limit to which l can be moved to the left is until it comes against the stop x, but the limit to which it can be moved to the right is governed by the height of the stop r in the slot in l. If stop r is set at its highest position in the slot, l can be moved to the right until the stop r meets the right hand step on the circumference of m, and a maximum of log feed is given.
Fig. 3118 represents a tubular saw machine. The saw runs in fixed bearings, the work feeding on the table b, running on ways on a. The work is here obviously sawn to a curve corresponding to that of the circumference of the saw.
In Figs. 3119 and 3120 is represented a machine constructed for either cross cutting or gaining, the gaining head shown on the machine being replaced by a cross-cut saw when cutting off is to be done.
[II-306]It consists of a vertical column or standard, upon the face of which a slideway a for the arm b, on which is a slideway c, along which the head for carrying the saw arbor traverses.
| VOL. II. | GAINING OR GROOVING MACHINE. | PLATE XXI. |
 |
||
| Fig. 3120. | ||
 |
||
| Fig. 3121. | ||
When the saw is to be used, the carriage or work table must be locked in position and adjusted so that the saw will come fair in the groove, provided in the table, but it is not necessary to dog or fasten the work to the table, because the saw itself draws the work over fair against the fence.
When the machine is used for gaining, the work must be dogged fast to the table, so that the work and table may be moved accurately together and the widths apart of the gains kept accurate.
Joshua Oldham’s combination saw for grooving or gaining is shown in Fig. 3121. It consists of two outside saws, such as shown at the top of the figure, and having spur teeth between the ordinary cutting teeth. The tops of the spur or cross-cutting teeth are a little higher than the other teeth, so that they sever the fiber before the ordinary teeth attempt to remove it, and thus produce very smooth work. The inside pieces, shown at the bottom of the figure, go between the two outside saws, if necessary, to make up the required width of gain. They are made 1⁄8 inch thick, with an odd one 1⁄16 inch thick, and will thus make gains advancing in widths by sixteenths of an inch.
The scroll sawing machine derives its name from the fact that it is particularly fitted for sawing scroll or curved work by reason of the saw (which is a ribbon of steel with the teeth cut on one edge) being very narrow.
The principal points in a scroll sawing machine are to have the saw held under as nearly equal tension as possible throughout the whole of the stroke; to render the machine readily adjustable for different lengths or sizes of saws, to provide it with means of taking up lost motion, and to avoid vibration when the machine is at work.
A scroll sawing machine constructed by the Egan Company is shown in Fig. 3122, a sectional view of the saw straining mechanism being shown in Fig. 3123. a, a, is a casting having slides for the head b, which is adjustable upon a to suit different lengths of saws, and is secured in its adjusted position by the bolt c and nut d. To the ends of the springs s, a strip or band of leather is secured, the other end passing around the small step f of a roller r, and being secured thereto. The roller r is so supported that it may rise and fall with the strokes of the saw. A second leather band g is secured at t, passes over the large step of r, and at its lower end hooks to the saw, which is strained by the springs s. This reduces the motion of the springs, and thus serves to equalize their pressure throughout the saw stroke.
The lower end of the saw is gripped in a slide or cross-head that is driven by the connecting rod and crank motion shown in the general view Fig. 3122. The lever shown at the foot of the machine moves the belt to the fast or loose pulley to start or stop the machine, and operates a brake to stop the machine quickly.
Fig. 3124 represents a scroll saw constructed by H. L. Beach. This machine is provided with a tilting table, which can be set[II-307] at any angle up to 39 degrees, either to the right or left, the exact angle being indicated by a graduated arc.
The straining device, including the springs, air pump, guide-ways, cross-head and steel bearing, are all attached to the vertical tubular shaft, which is secured to the heavy cast back support by the box e and eccentric lever f. By raising the lever f, the shaft, being balanced, is free to move up or down to suit any length of saw.
At the same time, the steel bearing l forms a support for the back and sides of the saw, and can be raised or lowered to suit any thickness of work.
The under guide-ways are so constructed that their expansion by tightening does not tighten the cross-head. Instead of the ordinary tight and loose pulleys, the crank shaft carries a friction pulley and combination brake by which the saw is stopped or started instantly, by a single motion of the foot.
This leaves the hands entirely free, and saves considerable time in stopping and starting.
The lower end of the saw is held by a steel clamp; when the saw breaks it can be used again by filing a notch. Both ends of the saw are arranged to take up lost motion and wear.
Any desired strain from 10 to 75 pounds can be given to the saw, and the strain is equal at all points of the stroke.
The simplest form of band sawing machine is that in which the work is fed to the saw by hand, a machine of this class, constructed by J. A. Fay & Co., being shown in Fig. 3125. It consists of a standard or frame a, carrying the saw-driving wheel b, and the upper wheel c, the saw being strained upon these two wheels. The lower wheel runs in fixed bearings, while the bearing of the upper wheel is carried in a slide provided in the frame, being operated in the slide by a screw, whose hand wheel is shown at e, so that it may be suited for different lengths of saws.
The bearing of the upper wheel is so arranged that the tension placed on the saw may be governed by a weighted lever f, which enables the upper bearing to lower slightly, so that if a chip should fall between the saw and the lower wheel, it may not overstrain, and therefore break the saw.
At j, is a bar carrying a guide g, which sustains the saw against the pressure of the cut, a similar guide being placed below the table t, at g′. This latter guide is fixed in position, whereas the upper one, g, is adjustable for height from the work table, so that it may be set close to the top of the work, let the height of the latter be what it may. g′′ is a guide and shield for the saw at the back of the machine, and h is a shield to prevent accident to the workman, in case the saw should break.
Band saws are ribbons of steel, brazed together at their ends and having their teeth provided on one edge. The widths of band saws vary from 1⁄16 inch to 8 inches, and their thicknesses from gauge 18 to 22 gauge, according to width.
The advantage of the band saw lies in that it may be run at high velocity, may be made thin, and its cutting action is continuous.
As a band saw is weak, it is desirable to have the teeth as short as possible and leave enough room for the sawdust, so that it shall not pack in the teeth.
In a circular saw, the centrifugal force acts to throw the sawdust out, while in a frame saw, the backward motion of the saw acts to clear the teeth of the dust, whereas in a band saw the dust is apt to pack in the teeth while they are passing through the work. The remedy is to space the teeth widely, thus giving room for the dust without having a deep tooth, an ordinary form of tooth being shown in Fig. 3126.
A stronger form of tooth is shown in Fig. 3127, the tooth gullets being well rounded out, and the teeth shallow at the back, while having ample room in front for the dust.
In determining the shapes of the teeth of band saws, we have the following considerations:
One of the principal objects is to have the back edge of the saw bear as little as possible upon the saw guide, and as the feed tends to force that edge against the guide, we must so shape the teeth as to relieve the back guide as much as the circumstances will permit. This may be done by giving to the front faces of the teeth as much rake as the nature of the work will permit. Thus, in Fig. 3128, it will be seen that from the front rake, or hook of the teeth, as it is commonly called, there is a tendency for the cut to pull the saw forward, this tendency being caused by the pressure, on the teeth in the direction of the arrows, and obviously acting to prevent the saw from being forced against the back guide.
For sawing soft woods, such as pine, the teeth may be given a maximum of front rake or hook, whereas for hard woods, the front faces must be made to stand at very nearly a right angle to the length of the blade, and the feed must therefore be lighter, in order to relieve the back edge of the saw from excessive contact[II-309] with the back guide, which would not only rapidly wear the guide, but acts to crystallize the edge of the saw and cause it to break.
The set of the teeth of band saws is given in two ways, i. e. by spring set, which consists of bending each alternate tooth sideways, as in Fig. 3129, or by swage set (upsetting or spreading the points of all the teeth), a plan that may be followed with advantage for all saws thicker than about 20 gauge.
Spring set is given either by bending, or by hammer blows, and swage set either by blows or by compression. In spring set, each tooth cuts on one side, and there is consequently a pressure tending to bend the tooth sideways, and break it at the root, whereas in spread set, the tooth cuts on both sides equally. As the front faces of band saw teeth are filed straight across, as in Fig. 3129, and are not given any fleam for any kind of woodwork, the set, whether spring or a spread, should be equal in amount for every tooth, and the pitch and depth of the teeth should be exactly alike, so that no one tooth will take more than its proper share of the cut.
The bend or set of the tooth in spring set saws, should not extend more than half way down the depth of the tooth, which will make the set more uniform and save tooth breakage, it being borne in mind, that a tooth hard enough to break if the set extends down to the root, will set easily if it extends half way down only, and that a saw may be soft enough to file, and of a proper temper, and yet break if the spring set is attempted to be carried too far down the tooth.
If as in the case of fine pitched teeth, the teeth are filed with a triangular or three square file but little front rake or hook can be given, without pitching the teeth widely. This is shown in Fig. 3130, in which s, is the section of a saw, and f, a section of a three square file. The front faces have no rake, and the file is shown as acting on both faces.
In Fig. 3131, we have the same pitch of teeth, but as the file is canted over, so as to give front rake or hook to the tooth, the tooth depth is reduced, and there is insufficient room for the sawdust. In order, therefore, to give to the teeth front rake, and maintain their depth while keeping the pitch fine, some other than a three square file must be used.
The principal defect of the band saw is its liability to break, especially in band saws of much width, as say 3 inches and over. A saw that is 6 inches wide will ordinarily break by the time it has worn down to a width of 4 inches. Now for heavy sawing it is necessary that wide saws be used, in order to get sufficient driving power without over-straining the saw.
The causes of this saw breakage are as follows:
In order that the saw may be regulated to run on the required part of the upper wheel, and lead true to the lower wheel, it is necessary that the upper wheel be canted out of the vertical, and band sawing machines are provided with means by which this may be done. If the upper wheel were set level, as in Fig. 3132, the saw itself would be held out of level, and the toothed edge would be more tightly strained than the back edge. Furthermore the middle of the saw cannot bed itself perfectly to the wheel. Furthermore, the velocity of the toothed edge would be greater than that of the back edge because of its running in a circle of larger diameter when passing over the wheels.
This is to some extent remedied by setting the wheel out of the vertical, as in Fig. 3133, in which case the two edges will be more equally strained, and have a more equal velocity while passing over the wheels.
There will still however, be an unequal strain or tension across[II-310] the saw width, and it is found that unless the saw is made what is known as loose,[48] it is liable to break, and will not produce good work. It is to be observed however, that the above may be to a great extent, and possibly altogether, overcome by means of having the rim face of the wheel, or of both wheels, curved or crowned in their widths, so that the saw will be in contact with the face of the wheel, nearly equally across the full saw width. This would also cause the saw to run in the middle of the wheel width, and thus enable the alignment of the saw to be made without requiring the upper wheel to be set out of level.
[48] See page 69, Vol. II., for what is technically known as looseness in a saw.
A re-sawing machine is one used to cut lumber (that has already been sawn) into thinner boards. Fig. 3134 represents a band saw machine, constructed by P. Pryibil, having a self-acting feed motion, consisting of four feed rolls, all of which are driven, and two small idle rolls, which are so arranged as to guide the last end of the stuff or work after it has left the driven rolls.
Four rates of feed are provided, and the upper wheel can be set at the required angle from a perpendicular while the machine is in motion.
The upper guide wheel, and the mechanism by which it is carried, is counterbalanced by a weight that hangs within the column or main frame, and is therefore out of sight.
The construction of the parts by means of which the upper wheel is adjusted in height to regulate the tension of the saw, and which also cants the wheel out of the vertical, is shown in Fig. 3135, which represents a portion of the main frame or column, on which is a slideway b, for the slide c, which carries the bearing for the upper wheel.
The method of moving the slide c for moving the upper wheel to adjust the saw tension is as follows:
By means of the handle h and the worm and worm wheel at w, the shaft s is revolved. The upper end of s is threaded into the nut n, which is capable of end motion in its bearing at e, and which abuts against the lever l, the latter abutting against the end of the screw m, and acting at its other end on the rubber cushion p. Now suppose that s be revolved in the direction denoted by the arrow, and the effect will be to raise the nut n. This effect will be transferred through the screw m to the slide c, which will rise up on b, carrying with it the upper wheel bearing and wheel.
When the upper wheel receives the strain of the saw, then the continued revolution of shaft s will cause the nut n to lift endways in its bearing e, the screw m acting as a fulcrum to cause the lever l to compress the rubber cushion p. The amount of tension on the saw is tested by springing it sideways with the hands. Now suppose the saw to be properly strained, and that a piece or chip of wood accidentally gets between the saw and the lower wheel, and the result will be that the slide c will (from the extra strain caused by the chip) move down on its slideway b, which it is capable of doing, because the long arm of the lever l can move down, compressing p, and this will prevent the saw from breaking.
To cant the wheel for leading the saw true to the lower wheel, the following means are provided:
The upper wheel bearing rests on the fulcrum at a, and is guided sideways by the screws c and d. At f is a stud threaded into the bottom half of the upper wheel bearing, the wheels g and h threading upon f. The weight of the upper saw wheel endeavors to lift the end j of the wheel bearing, and wheel h determines how much it shall do so, while wheel g acts as a check nut to lock the adjustment.
The feed rolls are carried in slides which are operated in slideways[II-311] by means of screws, and the two back rolls, or those nearest to the column are maintained vertical. The two front ones, however, are provided with means by which they may adjust themselves to bear along the full depth of the work, notwithstanding that it may be taper. The construction by means of which this is accomplished is shown in Figs. 3136 and 3137, in which a is front and b a back feed roll. The bearings of feed roll a abut against rubber cushions c, c, whose amount of compression is regulated by the set screws d, d.
The construction of the saw guides is shown in Fig. 3138, which is a plan view partly in section. s s are hardened steel plates set up to the saw by means of studs whose nuts are shown at n n. w is a friction wheel which supports the saw against the thrust caused by the work feeding to the saw. The adjustment of the wheel w to the saw is obtained by means of the wheel h.
The hand wheel h operates the screw r r, that adjusts the wheel w to the saw, the wheel j serving to lock the screw in its adjusted position.
| VOL. II. | BAND SAW WITH ADJUSTABLE FRAME. | PLATE XXII. |
 |
||
| Fig. 3139. | ||
Fig. 3139 represents Worssam’s band saw machine, in which the standard may be set at any required angle for cutting bevels.
When the work is heavy and not easily handled it is preferable to set the standard and saw at the required angle, rather than to set the table at an angle and have the saw remain vertical. In Worssam’s machine this is accomplished as follows:
a is the main frame carrying the work table t, and having circular guideways b, b′, which carry the standard c having guide c′ for working in the circular guideways b, b′.
The saw-driving wheel d, is carried in bearings provided in c, and, therefore moves when the standard c is moved.
At the upper end of c, is the slide e, which carries the bearing for the upper wheel f, this slide being adjusted to regulate the saw tension by the hand wheel o, whose screw threads into a nut in the slide e. h carries the front guide g, for the saw, the back guide g′ being carried by a bracket bolted to c. The back guide is fixed in position, but the front one is adjustable to suit the height of the work by raising or lowering it.
The means for setting the saw at the required angle to the work table are as follows:
At the back of the standard c is a rack j, whose pitch line is an arc of a circle of which the axis of the guideway c′ is the centre.
Into the rack j fits the worm wheel k, at the bottom of the shaft of which is a pair of bevel gear wheels l, which are operated by the hand wheel m.
| VOL. II. | BAND SAW MILL. | PLATE XXIII. |
|
Large image (130 kB).  |
||
| Fig. 3140. | ||
|
Large image (109 kB).  |
||
| Fig. 3141. | ||
|
Large image (130 kB). 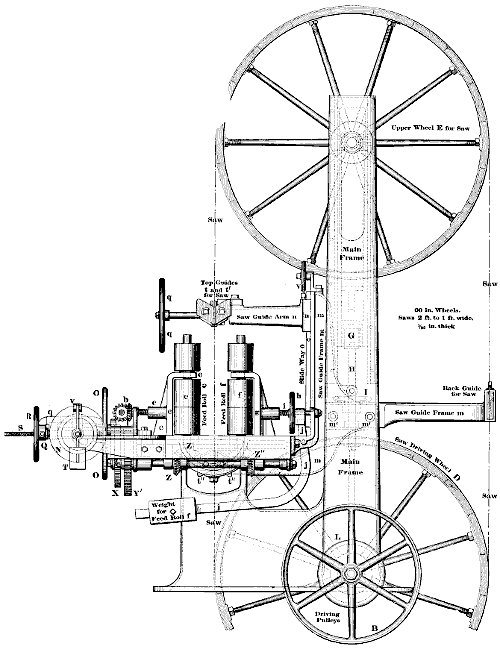 |
||
| Fig. 3142. | ||
A band saw machine constructed by Messrs. London, Berry & Orton, is shown by Figs. 3140, 3141 and 3142, in plate XXIII. The saw-driving wheel d, has wrought iron arms turned true and screwed into the wheel hub. The wooden segments have their grain lengthways of the rim, and between them are placed pieces of soft wood with the grain across the rim. This acts to keep the joints tight, notwithstanding the expansion and contraction of the wood.
The upper wheel is adjusted for straining the saw, and for leading the saw true, by the following construction. It is carried in a U-shaped frame f, which is pivoted at y to a slide that is gibbed to the main frame, and by operating the screw shown at x, the frame f is set to the required level.
To regulate the tension of the saw, the hand wheel k is operated, which drives the pair of bevel gears j and i, the latter of which operates the threaded shaft h, whose upper end g connects with the slide which carries f. Within g is a spring to act as a cushion to the slide, and thus prevent saw breakage should a chip pass between the saw and its driving wheel.
The saw guide frame is secured to the main frame at m′, m′. Upon the face of m, is a slideway for the saw guide arm n, which may thus be adjusted as closely to the upper face of the work as possible.
The weight of arm n is counterbalanced by a rope passing over the pulley v, and supporting the counterbalance weight w. The feed motion is constructed as follows:
On the same shaft as the main fast and loose pulleys a, b, is the feed pulley l, which by belt connection drives pulley m, which is on the shaft w, upon which is a friction disc n, by means of which the rate of feed is regulated. The feed disc n drives the wheel o; the degree of contact between these two (n and o) is regulated by means of the weight t, on the lever u.
On the same shaft as the friction wheel o, is a pinion driving the gear x, which is on the same shaft as the pinion y, which drives the two gears y′ and y′′.
Referring now to Fig. 3142, gear y′ drives the pair of bevel gears z and z′, for the feed roll e, and the pair of bevel gears shown at z′′, the feed roll f. The gear y′′ drives similar gearing for the feed rolls e′ and f′, seen in the plan Fig. 3140.
Referring now to the plan Fig. 3140, and the side elevation, Fig. 3142, the feed roll f is carried in a frame g, which is fitted on the slideway d, d, and receives a screw i, upon which is a hand wheel h; at the back of this wheel is the lever j, which is weighted as shown, so that the force with which feed roll f grips the work is determined by the weighted lever j, and may be varied to suit the nature of the work by moving the weight along j.
The construction of the gear for feed roll f′ is similar, as may be seen in the plan Fig. 3140, f′ being in a slide g′, which has a screw i′, and hand wheel h′, a weighted lever corresponding to j acting against wheel h′. In proportion as f and f′ are[II-312] opened out to admit thick stuff or work, the hand wheels h and h′, respectively are used to screw the screws i and i′ into their respective slides g and g′, and thus maintain the weighted levers in their requisite horizontal positions. The feed rolls e and e′ are carried in slides c and c′, and are adjusted to suit the thickness of the stuff or work by a hand gearing, which consists of the hand wheel a, seen in the plan and in the front elevation, Fig. 3141, which drives the pinions b and b′, which operate screws for the slides c and c′, the latter being a left hand screw. The front rolls e and e′ are therefore held in a fixed position, whereas the back ones f and f′ may open out under the pressure of the weighted levers j, and thus accommodate any variation in the thickness of the work.
The rate of feed is varied to suit the nature of the work by the following construction: The friction wheel o and the hand wheel r are connected by a yoke q, Fig. 3142, at the ends of which are the joints p, q, seen in the plan, Fig. 3140. Hand wheel r is threaded to receive the screw s, and it follows that by revolving r, the friction wheel o may be moved towards the centre of the friction disc n, which would reduce the velocity with which n would drive o, and therefore reduce the rate of feed. If the friction wheel o be moved from the position it occupies in the plan Fig. 3140, to any point on the other side of the centre of the friction disc n, the direction of feed motion would be reversed.
A band saw machine for the conversion of logs into timber, and constructed by Messrs. London, Berry & Orton, is shown in Fig. 3143. The logs are fixed to the carriage by dogs and the carriage traverses the log to the feed.
| VOL. II. | LOG CROSS‑CUTTING MACHINE. | PLATE XXIV. |
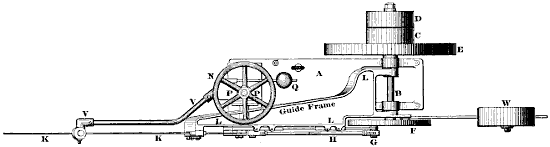 |
||
| Fig. 3144. | ||
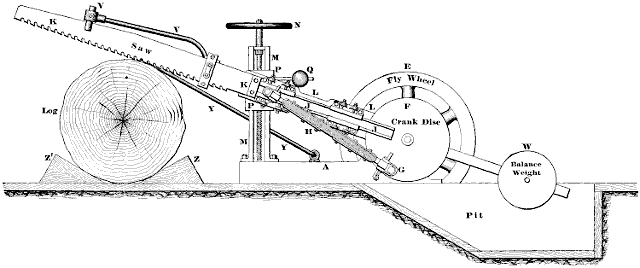 |
||
| Fig. 3145. | ||
Reciprocating Cross Cutting Saw For Logs.—The machine shown in Figs. 3144 and 3145 is designed for the purpose of cutting heavy and long logs into convenient lengths preparatory to cutting the logs up in other machines, and it is usually therefore placed at the entrance to the mill, where it is of immediate service as the lumber comes into the building.
The machine here shown is intended for logs up to 36 inches in diameter, is simple in construction, requires very little foundation, is easy to handle, and occupies but very little room.
The saw is here fed mechanically to its cut, whereas in some machines it is fed by its own weight, and therefore requires great care to be taken, when the saw is finishing its cut, in order to prevent it from falling after it has passed through the log.
Fig. 3145 is a side elevation and Fig. 3144 a plan of the machine, in which a is the frame of the machine on which are the bearings for the shaft b carrying the fast pulley c, loose pulley d and fly-wheel e at one end, and at the other, a crank disc f, whose pin is shown at g. This drives the saw k through the medium of the connecting rod h.
The saw is fast at the butt end to along slide j, j, which works in a long guide formed on the face of the swinging frame l, which pivots at one end on the shaft b and at the other is carried by a slide p, on the vertical slideway m, and is fed down the same to give the saw its cut by the screw whose hand wheel is shown at n.
v is a second guide for the saw, and being connected to the slide feeds down with the saw until it meets the log.
A counterweight w balances the weight of the slides and saw, so that there being a pit beneath the balance weight the saw and its guides may be raised so that the saw stands out of the way when not in use. y is a dog for holding the log, which is also blocked by the wedges z z′.
The construction of the main bearing is shown in Fig. 3146, in which it is seen that the hub or boss of the loose pulley is much longer than that of the fast one, thus providing a large amount of bearing surface, which is advantageous because the belt will remain longer at the loose pulley than it will on the tight one. The sleeves or bushes in which the shaft runs afford a simple means of renewal to restore the fit when the shaft has worn loose in its bearings.
It is obvious that as the guide frame l is pivoted to the shaft b, it carries the end of the saw (as it is fed down) in an arc of a circle of which the axis of b is the centre, whereas the slideway m is straight, and slide p therefore moves in a straight line instead of in the required arc. Provision however is made to accommodate these two motions as follows:
Fig. 3147 is a sectional view of the slides on the slideway m and Fig. 3148 a plan of the same. The hand wheel n corresponds to n in Fig. 3145. Upon the vertical slideway (in Fig. 3145) of the standard fits the slide p, which has a horizontal slideway for the slide r, which is free to slide automatically, having no screw or other device to restrain it, save the guide frame l, and therefore as this frame is lowered to feed the saw the slide r moves automatically to accommodate the arc of a circle in which the guide moves on account of being pivoted at b.
Horizontal Saw Frame.—This machine is designed for the more expensive woods, such as mahogany, and is finding much favor because it will cut at a very high speed, the saw travelling about 150 feet per minute.
The roughest shaped trunk may be easily fixed on the travelling table, and a thin saw may be used as it may be very tightly strained. This machine is used either for breaking down timber, or for converting it from the log to any desired thickness, the thickness of the boards being very readily and easily varied.
The machine consists essentially of a framework carrying either one or two very thin and tightly strained saws operating horizontally and cutting on both strokes, so that the feed is continuous, the construction being as follows:
| VOL. II. | HORIZONTAL SAW FRAME. | PLATE XXV. |
|
Large image (108 kB). 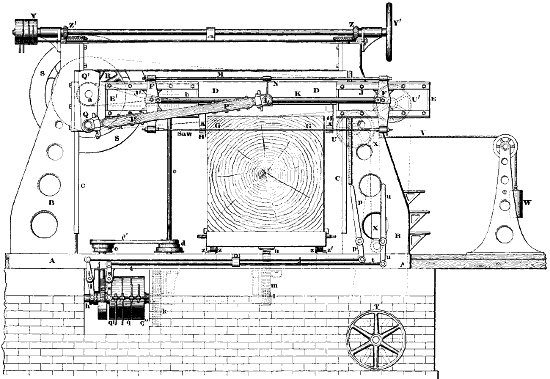 |
||
| Fig. 3149. | ||
Referring to Figs. 3149 and 3150, a is a base plate or bed carrying two uprights or standards b, b, having guideways c, c, for the cross-head d, which has slideways e, e′, for carrying the frame f, f, which carries the saw g, which is guided on each side of the work by the guides h, h′.
The frame f, f is connected to the slides j, j′, and has the rod k, to which the connecting rod pin l is attached, and the rod m, which acts as a stretcher. A connecting rod p, connects the pin l to the crank pin q, on the crank q′, which is driven by belt from the pulley t, a fly-wheel being provided at s.
It is obvious that as the crank revolves the saw reciprocates, its line of motion being determined by the guideways e, e′.
The construction of the saw is shown in Fig. 3151, and it is seen that for half its length, the teeth are formed to cut when the saw moves in one direction, while for the other half the teeth slope in the opposite direction, and are therefore arranged to cut when the saw is on the opposite or return stroke, and the construction whereby the saw is enabled to cut on both strokes is obtained as follows:
Referring to Fig. 3149, the two slides e, e′, on which the saw-carrying frame f f slides, are not in line or parallel one with the other, but each slide is at an angle of about 85 degrees to the line of feed, so that as frame f is reciprocated at each stroke,[II-315] one end of the saw advances towards the cut, and the other recedes from it, thus causing the saw to cut first on one half and then on the other of its length, one half cutting on the forward, and the other on the return stroke.
The studs or saw-buckles for attaching the saw to the frame are shown in Fig. 3151, in place on the ends of the saw, the part i, that fits in the frame f, Fig. 3149, being squared so that the saw cannot be twisted in tightening up the nuts of the saw-buckle.
The belt works for driving the saw are arranged as follows: at t are the fast and loose pulleys for driving pulley r, the belt passing from t over two pulleys (shown dotted in, Fig. 3149), u, u′, whence it stretches to the crank driving pulley r, whose bearing is provided on the cross-head, so that the two move together when the cross-head is altered in height from the work-table or carriage, to accommodate different thicknesses or diameters of logs.
It is obvious that in proportion as the cross-head is set nearer to the carriage, the belt from t to u, u′ would become slack; provision is made however, to prevent this as follows:
Pulley u, is carried on a frame or swing lever x, to which is attached by rope v the weight w, which therefore regulates the tension of the belt.
The cross-head d may be raised or lowered by belt power or by hand, as occasion may require, the usual course being to move it to nearly the required position by belt power, and then complete the adjustment by hand, a graduated scale being provided as shown, whereby the rack can be set to cut the required thickness of plank without measuring the timber.
The belt motion for raising or lowering the cross-head is obtained by the pulleys at y, the wheel for the hand adjustment being shown at y′. In either case the bevel gear wheels z, z′ operate, respectively, a vertical screw engaging a nut on the cross-head.
The log feed is obtained by a motion separate from the return motion, there being three rates of feed and a quick return motion, the construction being as follows:
Referring to Figs. 3149 and 3150, a is a belt pulley fast on the crank shaft, and driving pulley b, which is also shown dotted in. Pulley b drives the vertical shaft c, on which is the cone pulley d, having three steps, and which drives (by means of belt d′) cone pulley e, on which is a worm f, driving the worm wheel g, which runs idle on its shaft unless engaged therewith by means of the clutch h. The shaft of worm wheel g is omitted in Fig. 3149, so as to leave the belt-shifting mechanism for pulleys q, q′ exposed to view. On this shaft however is a pinion driving the gear wheel k, on whose shaft is a pinion l, driving the gear m, which engages the rack n, on the under side of the carriage.
The clutch h is engaged by the lever i, to the upper arm of which is attached the rod j, j, from the lever p, hence operating p (which is done by hand), back and forth, throws clutch h into and out of gear with the worm wheel g, and puts the carriage feed on or throws it out, according to the direction in which p is moved.
The upper end of shaft c is carried in a bearing on the cross-head, and is provided with a featherway or spline, so that as the cross-head is raised or lowered the upper end of c passes through its upper bearing, and the pulley b travels with the cross-head. The three rates of carriage feed are obviously obtained by means of the three steps on the cone pulleys d and e.
We have now to explain the construction of the mechanism for traversing the table back, and giving it a quick return motion, or in other words a quicker motion on the back than on the feed traverse, and this is arranged as follows:
q, is a fast and q′, q′′, are loose pulleys, one driven by an open belt r, Fig. 3150, and the other by a crossed belt r′, from a countershaft. The belt-shifting forks are operated by lever s, whose upper end engages with the rod t, which is operated by the lever u.
The loose pulleys q′ and q′′ are twice as wide as the fast pulley q.
Now suppose that lever u is moved to the right, and the belt would be moved from the loose pulley q′′ to the fast pulley q, while the other belt would merely be moved or shifted from one to the other side of loose pulley q′.
Similarly if lever u, be moved to the left, the belt on the loose pulley q′ will be moved on to the fast pulley q, and the belt on pulley q′′ would simply be moved across the face of the pulley, and as the countershaft pulleys for the two pulleys are of different diameters, therefore two rates of motion are obtained.
The shaft v, on which pulley q is fast, drives the pinion l, which drives m, the latter gearing with the rack beneath the carriage.
The carriage is guided by the wheels z, which are secured to it, and run on the iron guideways z′, the flanges of the wheels preventing side play, and causing the carriage traverse to be in a straight line.
The simplest form of planing machine for wood work, is the hand planer or buzz planer, as it is termed, an example of this class[II-316] of machine being shown in Fig. 3152, which has been designed and constructed by George Richards, for the use of pattern-makers.
It consists of a frame carrying a revolving shaft, which is by some called the cutter head, and by others the cutter bar, and to which the cutters or knives are attached.
The work is rested upon the work table, or else pressed against a guide or fence, and fed by hand over the revolving knives, whose cutting edges protrude above the surface of the table, to the amount of the depth of cut it is intended to take.
In this example, however, the table is made in two sections, the front one of which is below the cutter edges to an amount equal to the depth of the cut, and the back one level with the cutter edge, when the latter is at its highest point in its path of revolution, the construction being shown in Fig. 3153, in which j, j, represents the top part of the main frame of the machine, c the cutter head, b the front or feed table, a the back or delivery table, and w a piece of work being fed in the direction of the arrow.
Upon the upper surface of the frame j, j, and on the feed side of the cutter head is the carriage g, to which are pivoted two links l, l, which support the feed table b. At d is a hand wheel whose screw has journal bearing in a lug from the table, while the screw threads into a nut provided in the carriage. Obviously then by operating the hand wheel d, carriage g is moved along the top of the frame j, and the height of table b is adjusted. Thus if the carriage g is traversed to the left, the link l would fall more nearly to a horizontal position, and table b would lower. Or if g were moved to the right, links l would stand more nearly vertical, and table b would be raised, it being understood that table b is not permitted to move endways. Similarly by means of hand wheel c, carriage h may be moved to adjust the height of table a.
By this construction, the work can bed fairly on the delivery side, as well as on the feeding side of the cutter head, which is not the case when a single table is used.
It is obvious that the work must be fed in opposition to the pressure of the cut, which endeavors to push the work back from the cutter, and this limits the size of work that the machine can operate upon.
The work can be fed easier however, with a cutter skewed or set out of line with the axis of the cutter head. Thus in Fig. 3154, is the common form of cutter head, carrying two knives placed diametrally opposite, so that the weight of one counterbalances that of the other, and the head will therefore run steadily and smoothly. The knives k, k′ are here set parallel with the axis of the cutter head, hence the whole length of the cutting edge meets the work at the same instant, and a certain amount of time must pass after one cutting edge has left the work before the other cutter edge meets it.
This is remedied by the construction of cutter head shown in Fig. 3155, in which three cutters are used, and each cutter is set askew, or out of parallel with the axis of cutter head, so that the knife begins to cut at one end, and the cutting action gradually extends to the other, hence the cutting action is more continuous and uniform, and better work is produced, while less power is required to drive and feed the machine.
Fig. 3156 shows a cutter head with two skew cutters.
The cutter head is provided with a cover or guard, which is arranged as follows: In the table is cut a groove or slideway, in which a slide fits, and to this is attached a thin sheet-iron guard. To the slide is attached a weight, which draws the guard back to the fence after the work has passed over the cutter head. By this means the guard covers all the knife edge that protrudes beyond the work, no matter what the width or thickness of the work may be; the guard can however be fixed in position when a number of pieces of the same size are to be planed.
[II-317]The fence provides a guide surface for the work, and its face may be set at any required angle to the surface of the work table. Suppose, for example, that the sides or edges of a piece of work require to be at an angle of 100 degrees to the top and bottom surfaces, then the top surface may be planed first, and the fence being set at an angle of too degrees to the table surface, the top of the work may be pressed to the surface of the fence while fed across the cutter, and as a result, the side or edge will be planed at 100 degrees to the top.
Fig. 3157 represents a roll feed wood planing machine, designed and constructed by George Richards & Co., of Broadheath, near Manchester, England, the construction being more fully shown in the detailed figures following. The machine consists essentially of a framework, carrying a cutter head with two knives, and having a pair of feed rolls, in front and a pair behind it. The front pair feed the timber to the cutter head and the back pair deliver it from the cutter head.
Each pair of rolls is geared together, so that both the top and bottom rolls act to give a positive feed. Immediately in front of the cutter head and between it and the feed rolls (i. e. the front pair of rolls), is a pressure bar extending across the full width of the machine, and having at its lower extremity a steel spring which presses the work down to the table, and thus causes it to be planed of an equal thickness throughout its length. Immediately behind the cutter head and between it and the delivery rolls (i. e. the back pair of rolls), is a pressure bar that also extends across the machine and prevents the timber from rising up from the table after it has passed the cutters, all timber being found to have a tendency to rise after having been acted upon by the cutters. The arrangement of the feed rolls, delivery rolls and pressure bars is shown in Fig. 3158, in which t, t, t, represents three sections of the work table and w, w, a piece of work passing through the machine in the direction of the arrow. Feed roller f is fluted to increase its grip upon the work and insure a positive feed. The lower feed roller f′, and the lower delivery roller d′, are fixed in position, their upper surface projecting above the work table to about 1⁄100 inch. This is necessary to take the thrust of the upper rolls (f, d) and prevent them from forcing the work down upon the surface of the table with an undue amount of pressure, which would induce friction and consume an unnecessary amount of power in driving the rolls. The method of adjusting the lower rolls will be explained presently.
Between the cutter head c and the feed roll f is the pressure bar p, and behind the cutter head is the pressure bar b, both these bars being more clearly seen in Fig. 3159, in which the work w is shown entering the machine, and the lower rolls and work table are removed.
Pressure bar p has at its lower end a steel spring j, Fig. 3159, and is supported at each end by circular links y, projecting into grooves provided in the main frame of the machine, as shown in Figs. 3160 and 3161, in which c is the cutter spindle, y the circular link at the end of pressure bar p, and y the circular link at the end of pressure bar b, the two fitting into the one stepped groove.[II-318]
This groove is concentric with the cutter spindle c, so that the pressure bars keep at a positive or equal distance from the edges of the cutter, no matter what the thickness of the work or the depth of the cut may be.
In Fig. 3162, the work is shown passing beneath the two upper rollers, and the spring j (which extends the whole length of the pressure bar), is depressed from the weight of the bar. By this construction, the work is pressed to the table at a point as close as possible to the cutters. The pressure bar p cannot drop beyond a certain point, because of its tail piece y′, Fig. 3160, which rests on the top of the frame at y′′ when the bar p has fallen to its required limit.
The feed pressure bar p is bolted to its circular links, as shown in Fig. 3162, in which y is a part of the circular link which is bolted to the pressure bar p.
The delivery pressure bar b (Fig. 3160) is riveted to and forms part of its links y. It acts through the medium of spiral springs s, which are carried in cases or boxes s′, which overhang the end of the bar b. A set screw s′′ regulates the pressure of the spring, and a screw a (Fig. 3162) regulates the height of the pressure bar.
The adjustments of the feed and delivery rollers are made as follows:
The feed pressure is obtained through the medium of weights, shown at w, w′, in Fig. 3163, upon the bars a, a′, whose ends are pivoted to the lower ends of links m, n, the upper ends of which are pivoted to the side frame of the machine.
Bar a engages or rests at e, on a lug or projection on the link i, which fits in a recess provided in the side of the frame. This link i, extends up and has a bearing to receive the feed roller (f, Fig. 3160), whose driving gear is shown at o.
It is obvious therefore, that the amount of pressure on the feed roller f may be varied by moving the weight w along the bar a.
Similarly for the delivery pressure roller, the weight w′ is adjustable along the bar a′, which is pivoted to link n, and rests upon i at e′. The link i′ is guided in ways in the side frame of the machine, and at its upper end carries the delivery roller d, whose driving gear is shown at o′ (Fig. 3163).
It is obvious that there are bars a, a′, and links i, i′, on both sides of the machine, so as to adjust the feed rollers at both ends.
The work table and the two lower rollers are adjusted for different thicknesses of work as follows:
Between the two main side frames m and m′, Fig. 3164, are two[II-319] frames having corresponding inclines or slideways, of which the upper carries the work table and the lower rolls.
The lower incline sits on ways k, k, Fig. 3164, cast on the side frame, and is capable of being moved endwise by means of the hand wheel r, Figs. 3163 and 3164, which operates a screw threaded into the lower incline. When the lower incline is moved endways, the upper one, which carries the work table, is moved vertically, and as the lower feed rolls are carried by the upper incline, and the upper rolls are guided to move vertically only, the lower rolls maintain their position beneath the upper ones, or in other words, the table and lower rolls move together in a vertical direction only, when the lower incline is operated.
The lower rollers run in bearings formed in the links q, q, Fig. 3160, which are pivoted at their other ends to the upper incline. On the sides of the incline are lugs through which pass adjustment screws z, which by operating beneath the outer ends of the links q, q, adjust the heights, bearings of the lower rollers so that the uppermost point on the circumference stands about 1⁄100 inch above the level of the work table surface.
The upper surface of the lower incline is shown by the dotted line f, f, f, in Fig. 3163.
We may now consider the means employed to drive the rolls, first remarking that the upper rolls f and d, are given a motion slightly quicker than the lower ones, so as to cause them to clean themselves (from particles of wood that might otherwise cling to them), by a sort of rubbing action which is due to their velocity being greater than the lower rolls and the work. This rubbing action is due to the fact that the work has the slower motion of the lower rollers, resisting the quicker motion of the upper ones, and as a result there is a certain amount of slip between the upper rollers and the work.
Another and important feature, is that the upper delivery roller (d, Fig. 3160), is placed from 1⁄4 to 1⁄2 inch nearer to the cutter head than the bottom delivery roll, which assists in keeping the work down upon the table.
The mechanism for driving the feed rolls is shown in Figs. 3163, 3164 and 3165, in which l, l are the pulleys which receive motion from a countershaft, and drive the cutter head, being fast upon its shaft, as is also the pulley s, which connects by belt and drives pulley t, on whose shaft is the stepped pulley u, which connects by a crossed belt to pulley v, which drives the feed gear through the medium of the pinion a. The two steps on pulleys u and v, obviously give two rates of feed.
The pinions o and o′, both receive motion from the gear wheel e, this part of the gearing consisting of gears a, b, c, d and e, and as both pinions receive motion from the same gear, their revolutions are equal. The lower feed roll is driven by the pinion p, which gears with and is driven by wheel d, whose face is broad enough to meet p, which sits nearer to the frame than pinion o does, so that the teeth of p may escape those of o.
Now the velocities of all the wheels o, o′, e, d and p, will be equal at the pitch circles, because they constitute a simple train of gearing. Thus if d moves through a part of a revolution equal to the pitch e, then o and o′ will move through the same distance, because the wheels are in continuous gear. Now as d drives p, therefore the velocity of p must at the pitch circle be the same as d, let the numbers of teeth in the respective wheels be what it may, and it follows that the velocities of o, e, d and p are at the pitch circles equal. But by making the diameter of the upper roll[II-320] greater than the pitch circle of its gear o, and the diameter of the lower roll correspondingly less than the diameter of the pitch circle of its pinion p, the velocity of the circumference of the upper roll will be greater than that of the lower roll, and the rubbing action before referred to with reference to the upper roll will thus be induced.
Referring now to the lower delivery roll, its pinion x receives motion through gear w, which is also driven by gear e, which has a broad face so as to gear with x, which is behind and below gear o′. In this case the circumstances are the same, as will be seen from the following.
An inch of motion of the pitch circle of e will produce an inch of motion at the pitch circles of o′ and of w and x, hence the velocities of the pitch circles will be equal, and if the diameters of the upper and lower rolls are equal, or the same as the pitch circles, the velocities of the circumferences of the respective rolls will be equal, but by making the diameter of the upper delivery roll greater than that of the pitch circle of its pinion, and that of the lower roll less, a rubbing action is induced between the roll and the work, and this rubbing action will keep the roll clear of any dust, etc., that might otherwise cling to it.
The cutter head is formed triangular, as in Fig. 3166, carrying three knives. The knives are set at an angle to the axis of the cutter bar or cutter head. When the knives are at an angle, they take their cut gradually, and the cutting action is more continuous, which diminishes the vibration of the machine, and causes the finished surface to be smoother. Furthermore, the knives take a shearing cut, and therefore cut more easily and freely.
In some practice the knives are made spiral, but spiral knives are difficult to bed properly to the cutter head, and also difficult to grind. The cutter head is made of a solid mild centre steel forging, and runs in phosphor bronze journals, in which it has about 1⁄8 inch end play, which tends to distribute the oil along the bearing. It is driven by a pulley at each end, the pulleys seating on a cone.
The amount of skew is about 3⁄4 inch for a cutter head carrying a knife 30 inches long, and about 3⁄8 inch for a cutter head whose knives are 10 or 12 inches long.
[II-322]Figs. 3167 and 3168 represent a machine in which there are three feed rolls and one delivery roll, all being driven.
First there is the pair of feed rolls the bottom roll of which is set sufficiently above the surface of the table to relieve the work of friction upon the table.
The work next meets an upper feed roll that acts to force the work down to the table surface (there being in this case no lower feed roll).
After passing the knives, the work is carried out by a delivery roll that also acts to keep the work down to the table face.
All three upper rolls are provided with rubber springs in the casings h, h′.
p, p, are the pulleys for the cutter head and b, those for the feed works, which have two speeds. The feed is thrown in and out by the lever d, which moves the pinion d endways and engages or disengages it from its gear wheel.
[II-324]Figs. 3169, 3170, 3171 and 3172 represent a pony planer, by P. Pryibil.
Referring to the sectional view Fig. 3170, the work table slides in vertical slideways s, in the side frames, the elevating screw being operated by the bevel gears at g, which receive motion from the hand wheel m in Figs. 3170 and 3171. There are four upper rolls, marked 1, 2, 3 and 4 respectively, and of these the first two are fluted in the usual way. There are two lower rolls, marked respectively 5 and 6. The fluted feed rolls 1 and 2 are weighted, the weight lever acting on the rod r, which at its upper end connects to the cap y, which covers the bearings of feed rolls 1 and 2. By this construction the two rolls are acted upon by the same weights and levers, the rolls being of course weighted at each end, or in other words on both sides of the machine.
The delivery rolls 3 and 4 receive their pressure by the construction shown in Fig. 3172, the bearings of the rolls being held down by rubber cushions receiving pressure from the cap e, screwed down by the bolt and nut.
The rolls 5 and 6 are idle rolls, and are set to just relieve the work from undue pressure on the work table.
By this construction of feed mechanism the following ends are attained. First, sufficient feed power for heavy cuts is obtained without driving the lower rolls. Second the work is held to the table on both sides of the cutter head, hence there will not be left on the end of the work the step that is left when but two upper and two lower rolls are used, and which occurs because the work falls after leaving the feed rolls, whereas, in this machine the work is held to the table by rolls 2 and 3.
The cutter head h, Fig. 3170, has in front of it the pressure bar p, whose lever is shown at l and the weight at w. On the delivery side of the cutter head is a pressure bar r, which is acted upon by a spiral spring in the box c. In the engraving to the right of Fig. 3170 the knife k is shown in action on a piece of work, and it is seen that the end of the pressure bar p coming close to the edge of the knife prevents the pressure of the cut from splitting or splintering off the end of the work at a, and therefore acts as what is termed a chip break. Furthermore, the sides of the cutter head between the knives being hollowed out gives the shavings s room to curl in and prevent the work from splintering at the end when the cut is terminating.
Balancing Cutter Heads and Knives.—Planer knives must be balanced as accurately as possible, in order that they may run steadily and smoothly, and therefore produce smooth work.
The first requisite for proper balancing is that the cutter head itself be properly balanced, and in order that this may be the case the faces forming the knife seats must be equidistant from the axis of the cutter head, and the journals must run true, being best tested on dead centres. The holes for the cutter bolts should all be drilled to the same depth, and tapped equally deep. The faces or seats for the knives should be parallel one to the other, and this may be tested by a pair of straight edges, one pressed to each face and the width between them measured at each end, or if a long surface plate is at hand, one face of the head may be rested on the surface plate, and the straight edge ruled on the other face, and its distance measured from the surface plate at each end, with a pair of inside callipers delicately adjusted.
A straight edge rested lengthways along the knife seat of the head and projecting over the journal will show whether each knife seat is equidistant from the journal as it should be, the measurement being taken with a pair of inside callipers adjusted to just sensibly touch the journal and the straight edge. This measurement should be taken at each end of the head.
In all tests made with straight edges, the straight edge should be turned end for end and each measurement repeated, because, if the straight edge is true, turning it end for end will make no difference to the measurement, while if the straight edge is not true the measurement will vary when the straight edge is reversed.
If the cutter head is square, the straight edge tests may be applied to all four of its faces, and they may then be tested with a square, and if the head shows no error under these tests, and the[II-325] bolt holes or slots are of equal diameter and depths, the head will be correct as far as it can be tested without running it.
A cutter head may be roughly tested by placing it between the lathe centres, both centres being oiled and delicately adjusted so as to just prevent end motion of the head without perceptible friction when the head is revolved by hand.
The first thing to test is whether the journals run true, which may be tested by a pointer fastened in the slide seat, and moved up to just touch the journal. The pointer should be soft, and not a cutting tool, unless indeed it be set so high in the slide rest that it cannot cut.
If the journals do not run true, the next thing to test is whether the body of the head runs true to the centres, which may be done by first setting a pointer to just touch the extreme corners of the head at each end and in the middle of its length, and if there is an error in the same direction as the test at the journal shows, then the centres of the head are out of true, and must be corrected before a test of this kind can be proceeded with.
But the body of the head may show true at the corners while the journals do not run true, and if this is the case we may further test the body of the head as follows:
With the lathe slide rest at one end of the head we may set a pointer so that it will just pass on the flat of the cutter seat and make a mark when the slide rest is traversed along the lathe bed. We then move the slide rest so as to bring the pointer to the journal end of the head; give the head a half a revolution on the centres and try the pointer on the flat of the cutter seat, and if it makes a mark of equal strength, then two faces of the head are equidistant from the axis of the head.
The next thing to do is to make the same test at the other end of the head, and in order to do this without moving the pointer, and therefore without altering its adjustment, we must move the slide rest so as to bring the pointer opposite to the lathe centre, and out of the way of the body of the head, and take the cutter head out of the lathe and turn it end for end, and then repeat the test with the pointer, which will show whether both ends of those two flats are alike.
[II-326]This test we repeat on the other two faces of the head, and if they show true, then the head is true, except the journal, which must be made true with the head.
This testing will clearly show any want of truth in either the head or the journals, and in what direction correction needs to be made.
Now suppose the above tests do not disclose any error, either in the journals or in the head, and we may continue the tests by revolving the head by hand between the dead centres, and apply the pointer to the journals while the head is revolved as quickly as possible; as, however, the head cannot be revolved very fast in this way, we may adjust the lathe centres as before described, and revolve the head as rapidly as possible by hand, and letting it come to rest mark which side is at the bottom, and if on several tests the same side comes to the bottom of the plane of revolution at each test, that side is the heaviest and must be corrected. If it is found to be a flat side or cutter seat that comes to rest at the bottom, the correction can be made by deepening the bolt holes on that side, measuring to see which bolt hole is the shallowest, and making all as nearly as possible equally deep.
If the head has T slots instead of bolt holes, the slots may be cut or filed out to effect the balance, care being taken to make the slot equal in distance from the edges of the cutter seat face.
The next essential in order to have a properly balanced cutter head is that the bolts and nuts all weigh alike, and that the bolts be of the same length. The bolts should be turned to an equal diameter of equal length and threaded for an equal distance along the body of the bolt, and the nuts should be of equal depth and all fit accurately to the same wrench, and the weight of the bolts and nuts when put together may then be equalized by reducing the heads of the heavy ones.
We now come to the balancing of the knives, which must be made of equal thickness and width throughout, with the slots for the bolts of equal widths and depths.
The knives require to be as accurately balanced as it is possible to make them, for otherwise they will cause the head to jar and vibrate violently, thus producing rough work. The knives weighed individually may be of the same weight, and yet the head may run out of balance by reason of one end of a knife being heavier than the other end.
Fig. 3173 represents a machine constructed by J. A. Graham & Co., for balancing planer knives, moulding knives, cap screws, and knives in rotary cutter heads of all kinds.
Let it be supposed that the knives are the same specific weight, but that there is an excess of weight at one end; when revolving on the head, a violent jarring or throwing will be caused by reason of the excess. The knives could be reduced to the same specific weight by the aid of common grocers’ scales, but the ends could not be made the same proportional weight as on such balance.
In the cut s s is the base of the scale; l, m the standards for the support of the scale beams b b and k k.
d, d′ are two pivots of the scale beams.
d is the loop on which the pivot d works.
e is a joint in the loop.
d′, e′, and f show the loop and connection.
c is the sliding table which has the stop c′, and is adjustable for different lengths of knives.
a a is a knife in position for balancing endwise.
g is a slotted piece, and is held to the scale beam by the screw v. The slot in g is shown at g′, and limits the travel of the scale beams.
h is an angular piece fastened to the lower scale beam, and receives the screw j.
i is a small weight used for fine adjustment.
o, o are weights which slide along the scale beam k k, and are held in place by the thumb screws p, p.
n shows side view of weight, which is so constructed as to allow it to be easily removed. In using the machine the lightest cutter or knife of the set is first found and its two ends balanced, by turning it end for end on the scales, and reducing the weight of the heavier end. The other knife or knives are then balanced without disturbing the adjustment of the machine as made for the first knife.
This class of machine has a bed composed of slats which are connected together and driven by a chain.
Fig. 3174 represents an endless bed double surfacer constructed by the Egan Company. The upper cylinder may be raised or lowered to suit the thickness of the work. The front feed roll is in two sections, enabling two boards of unequal thickness to be planed simultaneously to an equal thickness. These rolls are held to the work by a leaf spring, as shown in the cut, the tension on the spring being adjusted by the screw at d, d serving as a check-nut.
A longitudinal section through the centre of the machine is shown in Fig. 3175. The spring s bears at each end on a block t, which carries the bearings for the feed roll. Feed roll m is held down by the screws e, e, acting on a rubber cushion or spring, and is provided with a scraper to clean it from dirt, etc.
The travelling bed is composed of slats s connected together by the chain shown, and resting upon slides a, a, supported by the girts b, b.
The chain is operated by the spur or sprocket wheel w, and is therefore pulled and not pushed, which tends to keep it under tension, and therefore rigid upon the top side.
The ends of the slide a, a are depressed so that the slats shall not tilt up at one corner above the level of the slide when in the positions denoted by s′.
The lower cutter head is carried in a sliding head or frame j, adjusted for height by the gears at h, which operate screw h, while the bed above it is adjusted by the gears at f. It is obvious that the bottom surface of this bed is set at the same height as the lowest point in the path of revolution of the cutting edges of the knives of the front cutter head or cylinder. The upper delivery roll n is provided with a scraper.
Planing and matching machines that are made narrow to suit the planing and matching of boards for flooring are sometimes called flooring machines, the distinctive feature of a flooring machine being that it is (unless in the case of a double machine) made narrow (because flooring boards are narrow), and this makes the machine very stiff and capable therefore of a high rate of feed and speed.
[II-328]Fig. 3176 is a general view, and 3177 a longitudinal section through a standard planing and matching machine of recent design, constructed by Messrs. J. S. Graham & Company. The plank passes through two pairs of rollers before meeting the front cutter head. The side heads then come into operation cutting (in the case of flooring) the tongue on one side of the plank and the groove on the other, the under side of the plank being dressed last.
The machine is built in three widths viz., 8′′, 14′′ and 26′′, each planing to 6′′ thick and matching as wide as it planes.
In place of matching heads, heads for beading, rabbeting, or fancy siding may then be used.
[II-329]The board r (Fig. 3177) is fed in over the grate m′ until it reaches the rolls e and f′, which are held in place by the boxes fitted to the roll stand n′, and brought to bear on the lumber by means of the screw a′, equalizing bar m and nuts p, p, together with the lever y y and the weight x.
After the lumber leaves the second pair of rolls, it runs over the bed plate w (Fig. 3178) and under the shoe l, the duty of which is to hold the board firmly against the bed plate, and also to break the chips on a heavy cut. After leaving the shoe it is operated on by the upper cutter head h, then it passes beneath the pressure bar g, which holds the lumber firmly while it is acted on by the matcher c.
It then passes beneath the cleaner e′′ (Fig. 3177) and under the delivering roll, which is held down by the weight u in connection with the lever v and screw a′, the top which is shown at c (Fig. 3179). The board then passes underneath the pressure bar q (Figs. 3177, 3180) and over the under cutter s, from which it passes finished.
The pressure bar q is moved up and down by turning the shaft a′′, the motion of which is given to the screw h′ by means of a pair of bevel gears. k′ is also a scraper that cleans the board before it passes under the pressure bar q. The under cutter is adjusted for depth of cut by turning hand wheel a′, which moves the screw u′. The rolls are raised and lowered by turning the shaft at p (Fig. 3176).
In feeding two boards through the machine, one thicker than the other, that end of the roll that passes over the thick board can raise up without taking the pressure off the thin one at the other end of the roll. This raising mechanism is shown in Fig. 3179. The bevel gear c works over a ball joint q′. The shoulder b′ on the screw a′ works on the under side of the ball q′. The shaft a passes through the tubular shell b to the opposite end of the roll. The cross tie j is bolted to the roll box k′′.
c, Fig. 3178, shows matcher hanger in position. It is gibbed to the bed plate z by the gib f, which is so constructed as to be free from dirt. The sliding gib f is adjustable for wear. One matcher hanger is moved by the screw e, the other by e′. The left hand matcher hanger is moved by the shaft l′ (Fig. 3177), which passes along the side of the machine until it reaches the shaft e, where its motion is imparted to the screw by means of a pair of spiral gears. An index at the rear of the machine enables the operator to set the matcher heads to any desired width. The right hand matcher hanger, together with the guide, can be moved across the machine by turning the screw e′ at the side of the machine (Fig. 3176).
The upright d which carries the pulley which drives the top cutter head, or cylinder as it is sometimes termed, is set at an angle so that the cylinder belt will always be of the same tension.
The top cylinder is raised by the shaft d (Fig. 3176) and screw b. It is held in place by the nut m (Fig. 3177). The bar i ties the cylinder boxes together. k is held down by the weight i, and yields with the pressure bar l.
The spindle of the matcher c′ (Fig. 3177) is driven by a belt which comes from the pulley h and passes over the guide pulley k, and then to the pulley b′.
The lower end of the matcher is held in place by being gibbed to the cross tie p′, Fig. 3177, which is adjusted and kept in position by the screw o′.
s′ sustains the matcher spindle by means of an adjustable step.
y′, Fig. 3176, is the feed shaft which drives the gearing that operates the rolls. The pulley that drives the feed shaft is shown at l′ (Fig. 3176). The belt passes over this pulley and under and over the tightener pulleys w′, w′, then to the pulley u′ which is on the feed shaft y′.
The apron m′ in front of the under cutter s (Fig. 3180) is easily dropped to m′′ by loosening the nut r′ and releasing the bolt t′ so as to allow the apron m′ to drop.
This enables the operator to have free access to the under cutter for sharpening knives, etc. z′ is the bed plate over which the lumber passes before it reaches the under cutter.
[II-330]A planing and matching machine designed and constructed by Messrs. London, Berry and Orton is represented in Fig. 3181. In this machine the upper surface of the board is surfaced first, and the matching second, the under surface being operated upon the last. The method of suspending the upper feed rolls of this machine is shown in Fig. 3182, in which a is an upper and b a lower feed roll. The upper roll a is suspended by the link c, which is supported by the link d, and also by link e, these three links forming a parallel motion which guides a in a vertical line.
At f (which is fast to e) is a bearing for the screw g, and the pair of bevel gears g that drives it. This screw threads into the nut h on the rod i, which receives the pressure of the bar j and weight k.
The lower feed rolls being larger in diameter gives them increased grip on the work, and gives it a better base, and also makes it enter and leave the rolls easier.
Each matcher bracket is fitted with a screw by which it can be moved at will across the machine, and by turning one other screw with the same wrench that moves the others, both brackets are firmly set to the slide and all screws held firmly. There are three changes of feed. The top cutter head is provided with improved pressure bars, which are set to or from the head by means of a double eccentric, which, while they can be set at any desired distance from the knives, limits their movement when moved towards them, rendering it impossible to get them into the cutters.
The term timber planer implies that plain knives only are used in the machine, which is therefore intended for producing plane surfaces. It also implies that the machine is designed for heavy or large work, such as is found in ship yards, bridge construction or car works, etc., etc.
In such work the cuts taken by the machine are sometimes very heavy, and as a result the feed works of the machine require to be very powerful and positive.
Fig. 3183 represents a timber planer designed and constructed by J. S. Graham & Co., to plane all four sides of the timber at one passage through the machine.
The timber passes through three pairs of feed rolls before reaching the first cutter head, which planes the bottom surface.
It then passes to the side heads, which dress both sides simultaneously, and then passes beneath the cutter head that finishes the upper surface, and is finally delivered from the machine by a pair of delivery rolls.
The work is passed over roller b, the fence or gauge being shown at b′. 1 and 2 are the first pair of feed rollers, a and b[II-331] being merely adjustable intermediate wheels, which by means of the pieces c′, b′, may be set so as to connect rollers 1 and 2 together, whatever their distance apart may be, or in other words whatever the thickness of the work may be.
From 1 and 2 the work passes to the second pair of feed rolls 3 and 4, c and d being the intermediates.
Similarly 5, 6, 7 and 8 are feed rolls, and e, f, g, h intermediates. The first head is shown at k′, the side heads at h, and the last head at i′, the latter being carried on a sliding head j, which is secured in its adjusted position by nuts i. On the side of the frame d on which j slides is a graduated index to denote the adjustment of the head i′.
The construction of the parts in immediate connection with the front cutter head is shown in Fig. 3184. n is the frame corresponding to n in Fig. 3183, the rolls 5 and 6 also corresponding in the two figures.
Upon n is a slide s having an arm g, carrying the roll g′, which holds the timber down to the cut of the cutter head k′. The pressure of roll g′ to the work is given through the medium of the rod a′, which receives the pressure of the equalizing bar x, Fig. 3183.
The bottom surface of the timber passes over the bed plate u, Fig. 3185, which raises and lowers with the lower feed rolls, being connected by the screw i, Fig. 3184, to the bearing box of feed roll 6.
All the lower feed rolls are operated simultaneously by means of the rod l, having for each lower feed roll a worm, driving a worm wheel l′ on a screw threaded into a hub m in each feed roll bearing; the crank for operating l is seen at p, Fig. 3183.
[II-332]The passage of the timber through the machine is continued in Fig. 3185, in which it is seen that after the lower surface of the timber has been planed it passes from the cutter head k′ to a bed plate v and is thus supported by a flat and true surface while the side cutter heads plane the two sides, one of these side heads being shown at h. The side heads are carried in hangers, one of which is shown at p′. It is gibbed to the under cutter frame u′ by the sliding gib x, the left hand head h being moved across the frame by the screw f′. The hanger is held at the bottom by the gib t and the cross tie t′. p is the pulley for the side head h, the end wear of whose shaft is taken up by the adjusting screw s′, r′ being a leather washer, and r the end of the shaft.
The top box h′ moves across the machine in the slideway b′′, Fig. 3186, a′′ being a part of the box h′.
Upon leaving the side heads the timber will have been planed on three sides and the side surfaces dressed to a right angle with the bottom surface.
It is then guided to the upper cylinder as follows:
The friction rolls k, k are to relieve the bed a′′ from the pressure due to the feed roll z′ and the roll j′, which holds the timber after it has left the cutter i′, and thus prevents it from vibrating. After leaving the pressure roll j′, the timber passes under the scraper d′, Fig. 3183, and thence to the delivery roll 7, which is held down by the weight l, in connection with the lever l′.
By means of this construction all the cutter heads act upon the timber within the short distance of 221⁄2 inches, while the side heads act within 81⁄2 inches of the under cutter. This is desirable, being conducive to the production of true work, which it is more difficult to produce in proportion as the cutter heads are wider apart. This machine will joint as narrow as 2 inches, and plane as thin as 3⁄4 inch.
The upper cylinder i′, Fig. 3183, is adjusted for height or thickness of cut by means of the screw f, and is locked in its adjusted position on d by the nut i.
The feed is started or stopped by operating the hand wheel o′.
The upper rolls are raised or lowered simultaneously by power, by means of the shaft s, and the bevel gears r, which operate the screw a′.
The upper cylinder is driven by belt from the pulley q, the under cylinder from q′ (both these cylinders being driven from both ends). p′ is the driving pulley for the feed belt, which passes to n′, which, through k′′ and y′, drives y, which drives the feed rolls.
The machine will feed from 25 to 60 feet per minute.
This class of machine is employed for the production of true surfaces, and is now used upon much of the work that was formerly assigned to the Daniels class of planing machine. In this machine, as in the case of the Daniels planing machine, the work is secured to the table, which travels to carry the work to the feed.
Fig. 3187 represents a machine by J. Richards, in which a cutter head with skew cutters is employed, and a pressure roll is placed in front and at the back of the cutter head, the construction being as follows:
| VOL. II. | TRYING‑UP MACHINE. | PLATE XXVI. |
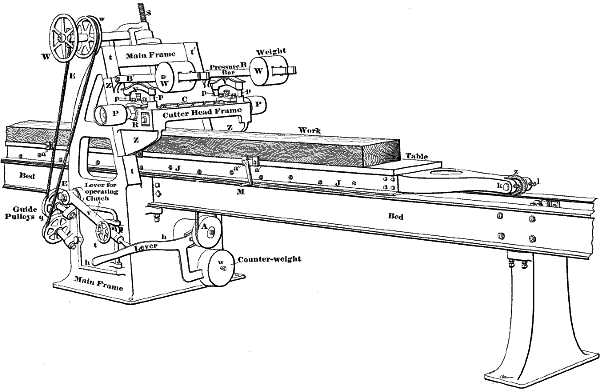 |
||
| Fig. 3187. | ||
Upon the main frame are the slideways t, t′, upon which the cross-head or cutter head frame z is carried, the elevating screw s raising or lowering the frame z, to suit the thickness of the work. The cutter head c, whose driving pulleys are shown at p, p, is carried in frame z, which also carries the pressure roll in front of the cutter (the bearing for this roll being shown at r), and a similar roll behind the cutter. To the frame z are pivoted the pressure bars b, b′, weighted with weights w. These bars rest on the cross-heads y, whose pins p act on the bearing boxes of the pressure rolls.
The cutter head frame may be raised or lowered, for varying thicknesses of work, either by hand or by power. The hand movement is obtained from the hand wheel w, Fig. 3188, which operates bevel gears b′′ and b′, the latter being threaded to receive the elevating screw.
The power or belt motion for raising or lowering the cutter head[II-333] frame is obtained from rope wheel w′, which receives motion from the guide pulleys shown in Fig. 3187. The wheel w′ drives its shaft by the friction cone of its bore, which is forced against the corresponding cone on the shaft by the hand nut l. The handle v, Fig. 3187, is for operating the upper guide pulley q, which acts as a belt-tightening pulley as well as a guide pulley, and the hand wheel t holds v in its adjusted position. When v is pushed downwards the rope (e) is loosened upon the pulleys, and both rope and pulleys remain idle.
The pulley that drives rope e is shown in Fig. 3189 at r.
The feed motions for the work table are shown in Fig. 3189, and the construction is such that for ordinary work the table has a quick return motion, while for heavy work the feed and return motions of the table are speeded alike.
The driving pulley b, Fig. 3189, for operating the feed mechanism, receives motion by belt connection from the countershaft, and drives the shaft on which are the bevel gears b and d, and from these gears the feed motion and quick return are derived, while from gear e and pulley r the cutter head may be raised and lowered by belt power as occasion may require. Beginning with the feed motion, the gear d drives gears e and f, which are a working fit on the shaft s. Between these two gears is the clutch r, r, which is operated by the handle shown in the perspective view, Fig. 3187, at v.
To operate the feed, clutch r is operated to engage gear e with the shaft s, upon which is the friction wheel m, which engages with the internal surface of the wheel or drum g, which drives the rope wheel a, which drives the rope for the work table traverse—wheel a and the rope being seen in the perspective view, Fig. 3187. The shaft n has bearing in a piece that is virtually a sleeve eccentric, because its bore is eccentric to its circumference; to this sleeve is attached a lug h′ to which the handle h, Fig. 3187, is bolted. Now suppose that handle h is depressed, and then g will partly revolve wheel g and cause it to engage with the friction wheel m, which will drive g, and therefore a.
Diametrally opposite to m is a friction wheel n, which is driven by the bevel gear c, and which is brought into or out of action with g by the eccentric action of sleeve g, it being obvious that when the sleeve g moves g in the direction of n, m is engaged and n disengaged from contact with g. Raising the handle h therefore places n in gear with g, which revolves it in the direction necessary to draw the work table on the back or return stroke.
The return motion of the table is more rapid than the feed motion because gear c is of smaller diameter than b, and n is larger than c and than m.
In the case of heavy work, however, the return motion may be made to have the same speed as the feed motion by simply moving the clutch r so as to engage wheel f with the shaft s.
The rope groove in the pulley a is waved as denoted by the dotted lines, and this prevents the rope from slipping, notwithstanding that the rope envelops but half the circumference of a. The wire rope from a operates a drum, in which are waved grooves for the table traversing rope which winds around this drum, and attaches to pins (k, Fig. 3187) carried in brackets at the ends of the table, and one of which is shown in Fig. 3187, at z.
The slack of the rope is readily taken up (as occasion may require) as follows:
[II-334]The pin k, to which the rope is fastened, has at one end a squared head to receive a wrench to revolve the pin and wind up the rope, set screw l locking the pin after the rope tension is adjusted.
We have now to explain the method of holding the work, which is as follows:
The side frames forming the bed are bolted to the main frame and form the ways on which the work table travels. The table frame j, Fig. 3187, is provided with rollers, which rest on the upper surface of the bed and reduce the friction.
The table is made in convenient sections bolted to the table frame j, and at their points of junction the work-holding dogs are placed, the construction being shown in Fig. 3190, in which t′ is the end of one, and t′′ the end of another section of the table. Referring now to Figs. 3187 and 3190, upon the edge of the table are the abutment pieces a′, a′′, against which the work is pulled by the dog, which is operated by the screw, which is squared at its outer end to receive the handle m, Fig. 3187.
The rate of work feed is 30 feet per minute and the quick return motion is 60 feet per minute.
In moulding machines for light work the feed rolls and cutter head overhang the frame, such machines being designated as outside moulding machines.
Fig. 3191 represents a machine of this class constructed by J. A. Fay & Company.
The table t slides on vertical ways on the main frame, being adjusted for height by the hand wheel w.
The work while fed over table t is pressed against the vertical face a by the four springs shown, whose pins swing to suit the width of the work.
[II-335]The two feed rolls are made up in sections or discs and the pressure bar is pivoted and has the weight shown to adjust its pressure to suit the work, and is combined with the bonnet whose shape throws the shavings outwards from the side of the machine. The particular machine here shown is constructed substantially enough to permit of its being used for light planing or work not exceeding 6 inches in width, a head with planing knives being shown in place on the machine. In a machine of this kind it is essential that the cutter head spindle and its bearings be rigid, and with ample journal bearings and free lubrication to prevent wear, and for these reasons the arbor is of steel running in self-oiling bearings of large diameter. The arbor frame is capable of lateral movement to enable an accurate adjustment of the cutters to the work.
The term sticker, as applied to a machine of this class, means that it is suitable for light work such as window sash and door stiles, blind slats, etc., etc.
Fig. 3192 represents a machine termed by its manufactures (the Egan Company) a “double head panel raiser and double sticker combined.” The term panel raiser means that the edges of the work may be dressed down so as to leave a raised panel. To fit the machine for such work the bed or table t is made wide.
The upper feed rolls are in sections, and the lower one extends nearly across the bed. The upper feed rolls are held down by a spring, whose tension may be regulated by a hand wheel with an adjustment at the back end to give a lead to both rolls. By this is meant that the plane of revolution of the feed rolls inclines toward the cutter head so that as the rolls feed they exert a pressure on the work, holding it securely against the face a.
A long spring extends from the front of the feed rolls past the back or bottom cutter head, passing as shown beneath the pressure bar, and is adjustable for height from the bed or table face t by having its ends pass through two studs in which they may be secured by set screws. This serves to keep the work down to the surface of t.
The cutter heads for panelling have three cutters set askew or at an angle to their plane of revolution so as to give a more continuous and a shearing cut, which is conducive to smooth work.
The bed above the lower cylinder is adjustable for height by means of the screw at h.
In the ordinary or common form of moulding cutter, the front face is flat and the lower end is bevelled off and filed to shape so as to give the required shape and keenness to the cutting edges, Fig. 3193 giving examples of such cutters.
Cutters of this class must be sharpened by filing the bevelled edge, which requires considerable skill in order to preserve the exact shape of the moulding.
In the solid milled cutter the bevelled surface at the cutting end of the cutter is a plane, and a curved, stepped or other shape is given to the cutting edge by cutting or milling suitably shaped recesses on the front face of the cutter as shown in Figs. 3194 and 3195, the former being a tongue cutter for cutting a groove, and the latter a grooved cutter for cutting a tongue.
Other examples for such cutters are given as follows:
Fig. 3196 represents a cove cutter and Fig. 3197 an ogee.[II-337] Fig. 3198, a double beading, and Fig. 3199 a bevel cutter, and it is obvious that by a suitable arrangement and shape of groove cutting edges of any of the ordinary forms may be produced.
The advantages of such cutters are that the plain bevelled face or facet of the cutter may be ground (to sharpen the cutter) on an ordinary emery wheel or grindstone, and the shape of the cutting edge will remain unaltered, providing that the cutter is always held to the grinding wheel or stone at the same angle, so that the length of the bevel remains the same.
A common practice is when making the cutter to so regulate the depth of the grooves or recesses in its face that the cutting edge will be of the required shape when the length of the bevelled facet is equal to three times the thickness of the cutter.
The method of finding the shape of cutter necessary to produce a given shape of moulding has been fully explained on pages 80 to 85, Vol. II.
Various forms of side heads are shown in the figures from 3200, to 3207. Fig. 3200 is a two-sided plain head, or in other words two diametrally opposite sides of the head are provided with bolt holes, for cutter fastening bolts. Fig. 3201 represents a four-sided slotted head, each side having T grooves, so that the cutter may be adjusted endways on the head. This enables the use of four narrow cutters, thus taking the cut in detail as it were.
The two-sided head shown in Fig. 3202 is provided with a set screw, by means of which a delicate adjustment of the height of the cutter may be made. Fig. 3203 represents a three-sided slotted head, or in other words T-shaped grooves, and not bolt holes are used.
This form of cutter head was invented by S. J. Shimer, and are generally known as Shimer cutter heads. The principle of construction is shown in Fig. 3204, which is for an ogee door pattern.
The cutters are circular in form and are seated at an angle to the flange to which they are bolted, this angle giving side clearance to the cutting edges.
The full amount of cut is taken in successive stages or increments; thus in the figure, the two upper cutters would produce one half the moulding, and the two lower ones the lower half. As the cutters are sharpened by grinding the front face, therefore they will maintain correct shape until they are worn out. Fig. 3205 represents a Shimer head for producing the tongue, and Fig. 3206 a similar head for producing the groove of matched boards.
[II-338]Fig. 3207 shows the action of the groove head, the cutter or bit d being shown in full lines and the second cutter being shown in dotted lines. Cutter d, it will be seen, operates on one half of the groove, and cutter c on the other half, each cutter having side clearance, because of being seated on a seat whose plane is not at a right angle to the axis of revolution of the head.
By thus taking the cut in detail, the head works steadily, while the side clearance makes the cutters cut clean and clear.
“Jointing” a piece of wood or timber, means producing a surface, so that the joint between two pieces that are to come together or be glued shall be close. In order to produce surfaces that shall be true enough for this purpose, it is necessary that the work be held in such a way that it is not sprung or deflected by the holding devices or feeding apparatus.
Fig. 3208, for example, represents a jointing machine, in which the work abuts against an inclined plate p at one end, while the other end is clamped down to the table, which is traversed past the revolving head h, to which are secured two gouge-shaped cutting tools, one of which is seen at t. By using tools of this class, the amount of cutting edge in action is small, and will not therefore spring the work, and if the cutter spindle is adjusted to have no end motion, the work will be true, notwithstanding any slight vibration of the head, because its plane of revolution coincides with the plane of the surface being surfaced or jointed.
In some jointing machines, knives are set on the face of a revolving disc, an example of this class of machine being shown in Fig. 3209, which is for facing the spokes of wheels and for finishing the mitre joint on them.
Three cutters are used, each being set at an angle to a radial line, so that the inner edge of the knife will meet the work first. This gives the knives a shearing cut, and prevents the whole of the cutting edge from striking the work at once. The spokes are placed against a stop on the table, and brought into contact with the cutters by the foot treadle.
The table has beneath it a spiral spring at each end, which returns the table as soon as the foot pressure is released from the treadle. The cutter head or disc is 10 inches in diameter, and should make 2,000 revolutions per minute.
Stroke jointers are machines (such as shown in Fig. 3210) in which a long plane e of the ordinary hand plane type is worked along a slide by a connecting rod c, operated by a crank motion. A machine of this class will do very accurate work, but is obviously suitable for thin work only.
A machine constructed by J. J. Spilker, for cutting mitre joints[II-339] by hand, is shown in Fig. 3211. The frame a carries a slideway for the slide to which the mitre cutting knife k is secured. The handle g operates a pinion gearing into a rack, which gives vertical motion to the slide and knife. At c is a fence or gauge against which the work is rested, and which is capable of a horizontal motion, so as to bring the work more or less under the knife. For heavy work, the fence c is set back, so that the first cut of the knife will leave the moulding, as shown at h, partly severed, and a second cut is necessary to sever it; for very fine work, a fine shaving may be taken off by a cut taken on the end of each piece separately, after the piece is severed. At d is a graduated scale or rule for cutting the work to exact dimensions, and as its lines are ruled parallel to the right hand edge of the knife k, the inside measurements of a mitre joint may be taken at the outer edge, and outside measurements at the inner end of each line, a set stop at e serving to gauge the pieces for length.
These are machines that cut mouldings on the edges of the work. The term friezing is applied by some, when the machine has but one cutter spindle, while by others these machines, whether having one or two spindles, are termed edge moulding machines. Still another term applied to this class of machine is that of variety moulders or variety moulding machines.
In machines of this class, it is of primary importance that lost motion or play in the bearings be avoided, because the cutter end of the spindle overhangs its bearings, and any side play of the spindle in its bearings is multiplied at the cutting edges of the cutters. Perfect lubrication of the spindle bearings, and ample bearing surface on the journals and bearings, are therefore of the first importance.
The work is rested on the upper surface of the table, and is fed to the cutters by hand.
[II-340]Figs. 3212 to 3215 represent a machine by J. S. Graham. The frame b, b, Fig. 3213, of this machine is cast in one piece cored out, and the base is wide, so as to give necessary solidity. The hollow column is fitted with a door w, and shelves v, v, forming a very complete case for the reception of tools, cutters, etc. The spindle boxes and slides c are one casting. They are planed on centres and held in the frame b′, Fig. 3215, by large gibs l, and sliding surfaces shown in c′, Fig. 3214. They are adjustable vertically by hand wheels k, in front of frame in connection with nut o, as shown in Fig. 3214, and require no lock to hold them at the proper height.
The cap o′ (Fig. 3213) has an oil chamber j and wick which feeds the oil to the upper bearing. The lower box is fitted with a patent self-oiling and adjustable step shown at a, b, c. The cap a, upon which the spindle d rests, has a small opening in the centre. The circular block b, under it, also has a hole in the centre. The bolt d has two holes in it, one horizontal and the other vertical.
The chamber surrounding this step and cup is filled with oil. The motion of the spindle d on the cap a causes the oil to flow from the chamber through the openings to the spindle. Thus the oil is kept in constant circulation. The end of this spindle d is by this arrangement kept always lubricated.
The spindles d are of 17⁄8 hammered tool steel accurately turned and fitted in the boxes, which are of extra length, and lined with the best genuine Babbitt metal. They are 30′′ from centre to[II-341] centre, and have independent screw tops, as shown at s, enabling the operator to use various sizes for large or small work, or clear the table of either spindle for special work.
h is the threaded part of the screw top, g is the nut, and f the fill-up collars.
The iron table a, a is 5 feet by 4 feet, planed and fitted with concentric rings e, e around the spindle, to suit the various sizes of heads and cutters. A heavy wooden table, made of narrow glued-up strips of hard wood, can be used if preferred.
This machine has been run up to 6,000 revolutions per minute, without perceptible jar, and cutter heads as large as 8′′ diameter may be used on it for heavy work.
Fig. 3216 represents an edge moulding machine by J. H. Blaisdell. In this machine the table is raised or lowered by the hand wheel upon the central column. The construction of the spindle and its bearings is shown in the sectional view, which also shows the square threaded screw by means of which the table is raised. The spindle has a coned hole for receiving the cutter sockets, which are therefore readily removable.
Figs. 3217 to 3220 represent examples of the shapes of cutters for use on edge moulding or friezing machines. Fig. 3217 represents a cutter for bevelling the edge of the work, the cutting edges being at a, b, or at c, d, according to the direction in which the cutter is revolved.
Fig. 3218 represents an ogee cutter, in position on the cutter spindle. As these cutters are made solid and accurately turned in the lathe, they are balanced so long as the cutting edges are kept diametrally opposite. The front faces only being ground to sharpen the cutting edges, the cutter always produces work of the same shape.
Fig. 3219 represents a cutter (in a chuck) for cutting a dove-tailed groove, and Fig. 3220 one for rounding an edge, it being obvious that a wide range of shapes may be given to such cutters, and that, as they may be sharpened on an emery wheel, they may be left comparatively hard, thus enhancing their durability.
To regulate the depth to which a cutter such as shown in Fig. 3220 will cut, a collar or washer is placed beneath it to act as a guide to the edge of the work.
Fig. 3221 represents a machine in which rotary cutters are used to produce all kinds of panel work, as well as edge moulding or friezing. In this case the cutter is above the table, the latter being adjustable for height to suit the thickness of the work. Examples of some of the work are shown at the foot of the machine.
The rapidity with which holes may be bored in wood enables the feed to be most expeditiously performed by hand or by foot motion. A foot motion leaves both the workman’s hands free to adjust and change the work, and is therefore suitable for light work or work having holes of a moderate depth.
The work tables of wood boring machines are provided with suitable fences for adjusting the work in position, and in some cases with stops to adjust the depth of hole.
Any of the augers or bits that are used in boring by hand may be used in a boring machine, but it is obvious that, as the bit or auger is forced to its feed by hand or foot, and as its revolution is very rapid, the screw point, which is intended as an aid in feeding when the bit is used by hand, is not necessary. On this account most augers for use in machines are provided with triangular points instead of screw points.
In Fig. 3222 is shown a wood boring machine by J. A. Fay & Co. The table is gibbed to a vertical slide on the face of the column, and is adjustable for height by the hand wheel a, which, through the medium of its shaft and a pair of bevel gears, operates the elevating screw b. The spindle c feeds through its bearings, the supporting rod d being pivoted at its lower end to permit c to feed in a straight line vertically. The feeding is done by the treadle f, which operates the rod e.
The table may be set at an angle of 30 degrees from the horizontal position.
The weight w counterbalances the treadle and brings it to its highest position when the workman’s foot pressure is removed.
The holes may all be gauged to an equal depth (when they are not to pass through the work) by so adjusting the height of the table that the hole is of the required depth when the treadle is depressed to its lowest point, or limit.
Fig. 3223 represents a horizontal boring machine such as used in furniture and piano factories. The spindle feeds through the driving cone, being operated by the treadle shown. The work table is adjustable for height by the hand wheel and elevating screw. The usual fences, stops, and clamping devices may be applied to the table, which is on compound slides to facilitate the adjustment of the work.
Fig. 3223a shows a double spindle horizontal boring machine, in[II-343] which the table and work are fed up to the boring tools by hand. The spindles are adjustable in their widths apart, and may also be set at an angle. The work table is adjustable for height, and the spindle carrying head is adjustable across the machine.
Fig. 3224 represents a machine by J. A. Fay & Co., for heavy work, rollers taking the place of the work table. The drill spindles are fed by hand from the stirrup handles shown, which are weighted to raise up the spindles as soon as they are released.
The mortising machine for wood work consists essentially of an ordinary auger, which bores the holes, and a chisel for cutting the corners so as to produce the square or rectangular mortise that is usually employed in wood work.
The chisel is reciprocated and its driving spindle is provided with means whereby the chisel may be reversed so as to cut on either the sides or the ends of the mortise. The chisel is fed gradually to its cut.
Fig. 3225 represents a mortising machine for the hubs of wheels.
The auger spindle is here fed vertically by a hand lever, the depth bored being regulated by a rod against which the hand lever comes when the hole is bored to the required depth.
Fig. 3226 represents a mortising machine in which the mortising tool consists of a hollow square chisel containing an auger, and having at its sides openings through which the cuttings escape.
The chisel is rectangular in cross section, but its cutting edges are highest at the corners, as may be clearly seen in the figure.
The work is firmly clamped to the work table and simultaneously to the fence, the upper hand wheel being operated to bring the work-holding clamp down to the work, and the lower one to clamp it so as to press it to both the table and the fence at the same time.
The chisel bar is mounted horizontally in a slide way on a substantial bed that is mounted on a vertical slideway, which enables the chisel bar to be set for height from the work table. It has a horizontal traverse motion or feed, the amount of this motion being governed by the horizontal rod with its nuts and check nuts as shown.
The auger runs continuously, and works slightly in advance of the cutting edge of the chisel, which is passive except when making the mortise.
The chisel bar and auger have a slow, reciprocating motion, and will complete a hole the size of the chisel used. An inch chisel will cut an inch-square hole, consequently a mortise 1′′ × 4′′ would only require four strokes forward to complete it. It has a capacity to work mortises from 3⁄4′′ to 3′′ square, and 5′′ in depth, and any length desired. The boring spindle is driven by an idler pulley, direct from the countershaft.
The bed upon which the timber is placed to be mortised is gibbed to a sliding frame, which allows it to be set to any position, with the chisel straight or at an angle. It is adjustable to and from the chisel bar, to suit the size of material, the under side of which always remains at one height. Adjustments are provided for moving the carriage forward, for regulating the depth of the mortise, the position of the chisel from the face of the material, and the adjustment of the chisel bar, controlling the mortises to be made in the timber.
Two treadles are used upon the side of the machine; the pressure upon one carrying the chisel bar attachment forward, completing the mortise, while the other will instantly force it back when it is desired to withdraw it from the wood, without allowing it to cut its full depth. Provision is made by stops for regulating the length of the stroke as well as the depth of the mortise.
In tenoning machines, the lengths of the pieces usually operated upon render it necessary that the work should lie horizontally upon the table, while the shortness of the tenon makes an automatic feed unnecessary.
The revolving heads carrying the cutters in tenoning machines are so constructed that the cutting edges of the cutters are askew to the sides of the heads, but so set as to produce work parallel to the axis of the cutter shaft.
This causes the cutting action to begin at one end of the cutter edge, and pass along it to the other, which enables a steady hand feed, and reduces the amount of power required to feed the work.
Fig. 3227 represents a cutter head for a tenoning machine, a, a and b, b being the cutters and c, c, d, d spurs which stand a little farther out than the cutter edges, so as to sever the fibre of the wood in advance of the cutter edges coming into action, and thus preserve a sharp shoulder to the tenon, and prevent the splitting out at the shoulder that would otherwise occur.
To bring the outer edge of the shoulder in very close contact with the mortised timber, the cutters are for some work followed by what is termed a cope head, which is a head carrying two cutters bent forward as in Fig. 3228, to make them cut very keenly, as is necessary in cutting the end grain of wood.
The cope head undercuts the shoulder, as shown at a, a, in Fig. 3229, which is a sectional view of a mortise and tenon.
Fig. 3230 represents a tenoning machine for heavy work, constructed by J. A. Fay & Co., adjusted for cutting a double tenon, the upper and lower heads revolving in a vertical plane, and the middle head in a horizontal plane.
a is a vertical slideway for the heads c, d, carrying the shafts for the cutter heads a, b. At b is the hand wheel for adjusting d, and at e that for adjusting c. The pulley d is for driving the cope heads, one of whose cutters is seen at c. The work carriage h is provided with rollers which run on the slide on k, and is supported by the arm i, which rises and falls to suit the cross motion of h. The fence g, for the work, is adjustable by means of the thumb nuts.
Sand-papering machines are of comparatively recent introduction in wood working establishments, but are found very efficient in finishing surfaces that were formerly finished by hand labor.
Fig. 3231 represents a sand-papering machine, by P. Pryibil, in which a spindle has three stepped cones on one end, and a parallel roller or cylinder at the other. The steps on the spindle are covered with a rubber sleeve, and the sand paper is cut to a template, and the edges brought together and joined by gluing a strip of tough paper under them. When this has become dry the paper is slightly dampened everywhere except at the joint, and is then slipped on the taper drums. In drying it shrinks and becomes tight and smooth upon the rubber covering with which the drums are provided. These are of different sizes to fit different curves in the work.
Flat work is done upon the table, which is hinged and provided with an adjusting screw to regulate its height, and it can be raised to give access to the drum.
When sand paper is applied in this way, every grain is brought into contact with the work, whereas at first only the larger grains cut when it is used on the faces of revolving discs, as in some machines of this class. Furthermore, when used on drums it is offered ample opportunity to clear itself of dust; it therefore does not become clogged, and, as a consequence, it lasts longer and does more and better work than when used on discs.
Fig. 3232 represents a similar machine, but having a spindle vertical also, so that one face of the work can be laid on the table, which acts as a guide to keep the work square, the table surface being at a right angle to the vertical spindle.
The vertical cylinder or drum is split on one side, and provided with internal cones, so, that by screwing down the nut shown the drum can be expanded to tightly grip the sand paper, which is glued and put on as already described.
Besides these rotary motions, these drums receive a slow vertical motion, the amount of which is variable at the operator’s pleasure. This provides for using the full face of the drum on narrow work, while it prevents the formation of ridges or grooves in the work.
For sand-papering true flat surfaces the flat table is provided, there being beneath it a parallel revolving drum, whose perimeter just protrudes through the upper surface of the table. The surface of the table thus serves as a guide to steady the work while the sand-papering is proceeding.
By using sand paper in this manner, every grain of the sand is brought into contact with the work; furthermore, a small area of sand paper is brought into contact with the work, and the wood fibre can fly off and not lodge in the sand paper; while at the same time the angles of the grains of sand or glass are presented more acutely to the work, and therefore cut more freely and easily. Hence the sand paper lasts much longer, because a given pressure is less liable to detach the sand from the paper.
The machine is constructed entirely of iron, and the drum is intended to revolve at about 800 revolutions per minute.
[II-348] Fig. 3233 represents a sand-papering machine in which a long parallel cylinder is employed, the work resting on the surface of the table and being fed by hand. In using a machine of this class the work should be distributed as evenly as possible along all parts of cylinder, or one end of the cylinder may become worn out while the other is yet sharp; this would incapacitate the machine for wide work unless a new covering of sand paper were applied.
Fig. 3234 represents a sand-papering machine constructed by J. A. Fay & Co., for finishing doors and similar work. The frame constitutes a universal joint enabling the sand paper disc to be moved anywhere about the door by hand. An exhaust fan on the top of the main column removes the dust from the work surface. The head carrying the disc is moved vertically in a slideway to suit different thicknesses of work.
| VOL. II. | SANDING MACHINES. | Plate XXVII. |
 |
||
| Fig. 3235. | ||
 |
||
| Fig. 3236. | ||
Fig. 3235 represents a self-feeding sand-papering machine constructed by J. A. Fay & Co. It is made in three sizes, to work material either 24′′, 30′′, or 36′′ wide by 4′′ thick and under; it has a powerful and continuous feed, and gives to the lumber a perfect surface by once passing it through the machine.
The feeding mechanism consists of six rollers, in three pairs, driven by a strong train of gearing. The upper feeding rollers, with the pressure rollers over the drum are lifted together in a perfect plane by the movement of four raising screws, operated by a chain and hand wheel. The lower feeding rollers always remain in perfect line with the drums.
It is supplied with two polishing cylinders, placed in the body of the machine, on which the upper frame rests, both having a vibratory lateral motion for removing lines made by irregularities in the sand paper. The finishing cylinder is placed so that the discharging rollers carry the lumber from it, thus running through and finishing one board, if desired, without another following, and these rollers are arranged for a vertical adjustment to suit the dressed reduction on the material to be worked. The roughing cylinder carries a coarse grade of sand paper, and the finishing one a finer grade. They may be driven in opposite or in the same direction, as may be necessary. The lower frame is hinged at each end to the upper frame, so that by removing a pin, either cylinder can be reached by raising the frame with the screw and worm gear, operated by a hand wheel at the end of the machine.
A brush attachment (not shown in the cut) is now placed at the end of the machine just beyond the finishing cylinder, which is a most complete device for brushing the material clean after it leaves the sand-papering cylinders.
Fig. 3236 represents a double wheel sanding machine by J. A. Fay & Co.
This machine is intended for accurately finishing the tread of the wheel ready for the tire, and is one of the most useful and labor-saving machines that can be placed in a wheel shop.
The frame is built entirely of iron, and has a heavy steel arbor running in long bearings, with tight and loose pulleys in the centre. On each end of the arbor is a large sand paper disc for polishing the tread of the rim.
The wheel to be finished is laid on a rotating carrying frame, having two upright drivers. These are attached to a jointed swinging frame, with flexible connections, adjustable to suit wheels of varying diameters.
The first section of the jointed frame is driven by a shaft and bevel gears, and swings upon it. The second one has the wheel-carrying frame, and swings upon the extreme end of the first one, and is driven from it by a chain connection.
A roller wheel is secured at the bottom of the leg, affording a[II-349] floor support; also a chain to regulate the proper distance of the wheel from the discs.
A wrought iron supporting frame is attached upon each side of the sand paper discs, adjustable for different sizes.
The wheel when placed in the machine is carried by the gearing against the sand paper discs, which finishes the tread in the most accurate and perfect manner.
Machines are made both single and double. The latter are the most desirable, as the operator has only to place a wheel in position on one side, when it feeds and takes care of itself.
By the time this is done, the wheel on the opposite side will be finished and ready to be removed, when a fresh one is put in, and the operation continued, the only care required being to put in and remove them. Its capacity is 150 set of wheels per day, and it will do the work better than can be done by hand.
The boiler for a steam engine requires the most careful usage and inspection, in the first case because a good boiler may be destroyed very rapidly by careless usage, and in the second case because the durability of a boiler depends to a great extent upon matters that are beyond ordinary control, and that in many cases do not make themselves known except in their results, which can only be discovered by careful and intelligent inspection. All that the working engineer is called upon to do is, to use the boiler properly, keep it clean, and examine it at such intervals as the nature of the conditions under which it is used may render necessary.
The periods at which a boiler should be cleaned and inspected depend upon the quality of the water, whether the feed water is purified or not, and to a certain extent upon the design of the boiler; hence these periods are variable under different circumstances.
The horse power of a boiler is estimated in various ways, and there is no uniform practice in this respect. Some makers estimate a boiler to have a horse power for every fifteen square feet of heating surface it possesses, while others allow but 12 square feet.
The heating surface of a boiler of any kind is the surface that is exposed to the action of the fire on one side, and has water on the other; hence the surface of the steam space is not reckoned as heating surface, even though it may be exposed to the action of the heat. The effectiveness of the heating surface of a boiler obviously, however, depends upon the efficiency of the fire, and this depends upon the amount of draught, hence the estimation of horse power from the amount of its heating surface, while affording to a certain extent a standard of measurement or comparison while the boiler is not in use, has no definite value when the boiler is erected and at work.
Thus whatever amount of steam a boiler may produce under a poor or moderate draught, it will obviously produce more under an increased draught; hence the efficiency of the same boiler depends to a certain extent upon the draught, or in other words upon the quantity of fuel that can be consumed upon its fire bars.
The amount of water required in steam boilers varies from 16 lbs. to 40 lbs., per horse power per hour, and it has been proposed to compute the horse power of boilers from the water evaporation, taking as a standard 30 lbs. of feed water at a temperature of 70 degrees, evaporated into steam at a temperature of 212 degrees, at which temperature the steam is assumed to equal the pressure of the atmosphere.
[49]“The strength of the shell of a cylindrical boiler to resist a pressure within it, is inversely proportional to its diameter and directly, to the thickness of the plate of which it is formed.
[49] From “Steam Boilers.”
“For instance, take three cylindrical boilers each made of 1⁄2 inch plate, the first one 2 feet 6 inches in diameter; the second twice that, or 5 feet in diameter; and the third twice that again, or 10 feet in diameter; and if the 2 foot 6 inch boiler is fit for a safe working pressure of 180 lbs. per square inch, then the 5 foot boiler will be fit for exactly one-half that amount, or 90 lbs. per square inch; and the ten foot boiler will be fit for half the working pressure of the five foot boiler, hence we have:
| Diameter of boiler shell. |
Thickness of plate. |
Relative working pressure. |
||||||||
| 2 | feet | 6 | inches. | 1⁄2 | inch. | 180 | lbs. | per | square | inch. |
| 5 | „ | „ | „ | 90 | „ | „ | „ | „ | ||
| 10 | „ | „ | „ | 45 | „ | „ | „ | „ | ||
“The reverse applies to the thickness of the plate. For instance, if we take two cylindrical boiler shells, each 5 feet in diameter, the first one made of plate 1⁄2 inch thick, and the second twice that, or 1 inch thick, and if the first is equal to a safe working pressure of 90 lbs. per square inch, then the second is equal to a safe working pressure of twice as much, or 180 lbs. per square inch, providing, of course, that the riveted seams are of equal strength in each case, and that both boilers are allowed the same margin for safety; hence we have:
| Diameter of boiler. |
Thickness of shell. |
Safe working pressure. | ||||||
| 5 | feet. | 1⁄2 | inch. | 90 | lbs. | per | square | inch. |
| 5 | „ | 1 | „ | 180 | „ | „ | „ | „ |
“These principles (namely, that the strength of a boiler is, all other things or elements being equal, inversely proportional to its diameter, and directly proportional to its thickness) afford us a groundwork upon which we may lay down rules for determining by calculation the strength of the solid part[50] of any boiler shell, and the bases of these calculations are as follows:
[50] In the case of the riveted joints or seams other considerations come in, as will be shown hereafter.
“If the shell plate of a cylindrical boiler is 1⁄2 inch thick, there is one inch section of metal to be broken before the boiler can be divided into two pieces, that is to say there is 1⁄2 inch on each side of the shell, as shown in Fig. 3237, and the two together will make 1 inch. If we take a ring an inch broad, as, say, at a in Fig. 3238, we shall obviously have a section of 1 square inch of metal to break before the ring can be broken into two pieces.
[II-351]“The next consideration is, what is the average strength of a plate of boiler iron? Now suppose we have a strip of boiler iron 2 inches wide and 1⁄2 inch thick, or, what is the same thing, a bar of boiler iron 1 inch square, and that we lay it horizontally and pull its ends apart until it breaks, how many lbs. will it bear before breaking? Now for our present purpose we may assume this to be 47,040 lbs., and if this number of lbs. be divided by the diameter of the boiler in inches, it will give the bursting pressure in lbs. for any square inch in the ring, or any other square inch in the cylindrical shell of the boiler.
“The reason for dividing by the diameter of the boiler is as follows:
“Of course the steam pressure presses equally on all parts of the interior surface of the shell, and may be taken as radiating from the centre of the boiler, as in Fig. 3239, which represents an end view of a strip an inch wide, of one half of a boiler. Now leaving the riveted seam out of the question, and supposing the shell to be truly cylindrical, and the metal to be of equal quality throughout, it will take just as much pressure to burst the shell apart in one direction as it will in another, hence we may suppose that the boiler is to be burst in the direction of arrow a, and it is the section of metal at b b that is resisting rupture in that direction.
“Now suppose we divide the surface against which the steam presses into six divisions, by lines radiating from the centre c, and to find the amount of area acting on each division to burst the shell in the direction of arrow a, we drop perpendicular lines, as line e, from the lines of division to the line b b, and the length of the line divided off (by the perpendicular) on the diameter represents the effectiveness of the area of that division to burst the boiler in the direction of arrow a; thus for that part of the boiler surface situate in the first division, or from b to line e, the area acting to burst the boiler in the direction of a is represented by the length of the line k, while the general direction of the pressure on this part of the shell is represented by arrow m.
“Similarly, for that part of the shell situate between vertical line e and vertical line f, the general direction of the steam pressure is denoted by the arrow l, while the proportion of this part that is acting to sever the boiler in the direction of a is represented by the distance n, or from the line e to line f measured on the line b b.
“By carrying out this process we shall perceive that, although the pressure acts upon the whole circumference, yet its effectiveness in bursting the boiler in any one direction is equal to the boiler diameter. Thus in Fig. 3240, the pressure acting in the direction of the arrows a (and to burst the boiler apart at b b) is represented by the diametral line b b, while the pressure actually exerted upon the whole boiler shell is represented by the circumference of the boiler.
“To proceed, then, it will now be clear that the ultimate strength of the boiler material, multiplied by twice the thickness of the boiler shell plate in inches or decimal parts of an inch, and this sum divided by the internal diameter of the boiler, in inches, gives the pressure (in lbs. per square inch) at which the boiler shell will burst.”
We have here only considered the strength of the solid plate of the shell, and may now consider the strength of the riveted joints, because, as the boiler cannot be any stronger as a whole than its weakest part is, and as the riveted joints are the weakest parts of a cylindrical boiler,[51] therefore the strength of the riveted joint determines the strength of the boiler.
[51] It may be here noted that the riveted joint of a flat plate is stronger than the flat surface of the plate, because at the joint the plate is doubled, or one plate overlaps the other.
[52]“The strains to which a riveted joint is subjected are as follows: That acting to shear the rivet across its diameter is called the shearing strain. But the same strain acts to tear the plate apart; hence, when spoken of with reference to the action on the plate, it is called the tearing strain.
[52] From “Steam Boilers.”
“The same strain also acts to crush and rupture the plate between the rivet hole and the edge of the plate, and in this connection it is called the crushing strain.
“Thus, Fig. 3241 represents a single riveted lap joint, in which the joint at rivets a, b, and c is intact, the metal outside of d has crushed, the rivets e, f have sheared, and the plate has torn at h, leaving a piece j on the rivets k l.
“It is obvious that, since it is the same strain that has caused these different kinds of rupture, the joint has, at each location, simply given way where it was the weakest.
“If a riveted joint was to give way by tearing only, the indication would be that the proportion of strength was greatest in the rivets, which might occur from the plate being of inferior metal to the rivets, or from the rivets being too closely spaced. If the rivets were to shear and the plate remain intact, it would indicate insufficient strength in the rivets, which might occur from faulty material in the rivets, from smallness of rivet diameter, or from the rivets being too widely spaced.
“The object then, in designing a riveted joint is to have its resistance[II-352] to tearing and shearing proportionately equal, whatever form of joint be employed.”
The English Board of Trade recommends that the rivet section should always be in excess of the plate section, whereas, in ordinary American practice, for stationary engine boilers, the plate and rivet percentages are made equal.
The forms of riveted joints employed in boiler work are as follows:
Fig. 3242 represents a single riveted lap joint. Fig. 3243 represents a double riveted lap joint, chain riveted; and Fig. 3244, a double riveted lap joint, with the rivets arranged zigzag.
Fig. 3245 represents a single and Fig. 3246 a double riveted butt joint, so called because the ends of the boiler plate abut together. The plates on each side of joint are called butt straps.
The advantages of the butt joint are, first, that the boiler shell is kept more truly cylindrical, and the joint is not liable to bend as it does in the lap joints, in the attempt of the boiler (when under pressure) to assume the form of a true circle, and second that the rivets are placed in double shear. That is to say, if in a lap joint the rivet was to shear between the plates, the joint would come apart, whereas, in a butt joint, the rivet must shear on each side of the plate, and therefore in two places.
Fig. 3247 represents a form of joint much used in locomotive practice in the United States. It is a lap joint, with a covering plate on the inside of the joint; rivets e and f are in single and rivets d in double shear.
[53]“When we have to deal with comparatively thin boiler plates, there is no difficulty in obtaining a sufficiently high percentage of strength in the joints, by using the ordinary double riveted joint, but when we have to deal with thick plates, as in the case of large marine boilers, as 1 inch or upwards, a more costly form of joint must be employed, in order to obtain the required percentage of strength at the joint; hence the ordinary double riveted joint is replaced by various other forms as follows:
[53] From “Steam Boilers.”
“First, a triple zigzag riveted lap joint, such as shown in Fig. 3248, or a chain riveted joint as in Fig. 3249, in both of which the third row of rivets enables the rivet pitch to be increased, thus increasing the plate percentage, while the third row of rivets also increases the rivet percentage.
“Second, by employing butt joints with butt straps, either double or treble riveted.[II-353]
“A double riveted butt joint with double straps is shown in Fig. 3250, and a treble with double straps in Figs. 3251 and 3252.
“Third. By various arrangements of the rivets in conjunction with butt joints and double straps, with which it is not necessary, at this point, to deal.
“One of the great advantages obtained by the use of the double strap is that of bringing the rivet into double shear (or in other words, the rivet must shear on each side of the plate, or in two places, instead of between the plates only, before the joint can give way by shearing), and thus obtaining an increased calculated strength of 13⁄4 times the ordinary or single shear, the rule being to find the rivet strength in the ordinary way (as before explained), and then multiply the result by 1.75.
“The Board of Trade rules for spacing the rivets of these joints are as follows:
“Dimension e is the distance from the edge of the plate to the centre of the rivet hole. Dimension v is the distance between the rows of rivets, dimension p is the pitch of the rivets, which is always measured from centre to centre of the rivets, and dimension pd is the diagonal pitch of the rivets.
“The rule for finding dimension e, whether the plates and rivets are either of steel or iron, is as follows:
“Multiply the diameter of the rivet by 3 and divide by 2, the formula being as follows:
| 3 × d | = e. |
| 2 |
“To find the distance v between the rows of rivets in chain riveted joints. This distance must not be less than twice the rivet diameter, and a more desirable rule is four times the rivet diameter plus 1 divided by 2, thus:
| 4d + 1 | = v. |
| 2 |
“To find the distance between the rows of zigzag riveted joints:
| √ (11p + 4d) × (p + 4d) | = v, |
| 10 |
that is, multiply 11 times the pitch plus 4 times the rivet diameter, by the pitch plus 4 times the rivet diameter, then extract the square root and divide by 10.
“To find diagonal pitch pd, multiply the pitch p by 6, then add 4 and divide by 10, thus:
| 6p + 4 | = pd.” |
| 10 |
Fig. 3253 represents a form of high percentage joint, used upon marine boilers of 10 to 14 feet diameter, and carrying from 100 to 190 lbs. pressure of steam. The rivets are what are termed unevenly pitched, or, that is to say, on each side of the joint, there[II-354] are three rows of rivets, of which the inner and outer rows are wider pitched than the middle row.
[54]“The advantage gained by this spacing is that the shear of the outer row of rivets is added to the plate section at the narrow pitch, that is to say, if the plate section broke through the line of rivet holes at the narrow pitch, it has yet to shear the outer row of rivets before the plate can separate.”
[54] From “Steam Boilers.”
Fig. 3254 represents a second example of joint with rivets unevenly pitched, this form finding much favor in recent practice. The four inner rows of rivets are spaced at narrow pitch and the two outer rows are wide pitched.
[55]“The strength percentage of this joint is calculated from three points of view, as follows:
[55] From “Steam Boilers.”
“First. The plate section at the wide pitched rivets.
“Second. The rivet section in one pitch.
“Third. The plate section at the narrow pitch plus half the double shear of the outer or wide pitched rivet.”
The steam pressures generally employed in the boilers of stationary engines range from about 60 to 100 lbs. per square inch, and as a result of these comparatively low pressures less perfect forms of construction are employed than would be permissible if higher pressures were used.
The strength of the shell plate of boilers of small diameter is always largely in excess of the requirements, and as a result the strength of the joints may bear a very low percentage to that of the solid plate, and yet give a sufficient factor of safety for the working pressure.
Take, for example, a boiler shell of 36 inches internal diameter with a shell plate 1⁄4 inch thick, and allowing the strength of the material to be 48,000 lbs. per inch of section, and with a factor of safety of 4, the working pressure will be 166 lbs. per square inch, thus:
| Strength of the material. |
Plate thickness × 2. |
||
| 48000 | × | (.25 × 2) | = 6662⁄3 lbs. = bursting pressure. |
| 36 | |||
| Diameter of boiler. |
|||
By dividing this 666 by the factor of safety 4 we get 1662⁄3 lbs. as the working pressure of the shell plate independent of the riveted joint. Usually, however, such a boiler would not be used for a pressure above about 60 lbs. per inch, and this leaves a wide margin for the reduction of strength caused by the riveted joints.
Suppose, for example, that a single riveted lap joint is used, and the strength of this joint is but 50 per cent. of that of the solid plate, and we have as follows:
| Strength of material. |
% strength of riveted joint. |
Twice the plate thickness. |
|||
| 48000 | × | .50 | × | (.25 × 2) | = 831⁄3 lbs. = W.P. |
| 36 | × | 4 | |||
| Internal diam. of boiler. |
Factor of safety. |
||||
Here then we find that the working pressure of the solid plate is double that of the riveted joint, and that the working pressure of the boiler is 83 lbs. per square inch, notwithstanding that the strength of the riveted joints is but 50 per cent. of that of the solid plate. Such a boiler would not, however, be used for a pressure of over 60 lbs. per square inch.
If the above-named boiler was double riveted so as to bring the percentage of joint strength up to say 70 per cent, of that of the solid plate, its working pressure would be 116 lbs. per square inch, thus:
| Strength of material. |
% strength of riveted joint. |
Twice plate thickness. |
|||
| 48000 | × | .70 | × | (.25 × 2) | = 1162⁄3 lbs. = W.P. |
| 36 | × | 4 | |||
| Internal diam. of boiler. |
Factor of safety. |
||||
But in practice such a boiler would not be used for pressures above about 75 lbs. per square inch, hence the shell plate thickness is still largely in excess of the requirements, and it may be remarked that plates less than 1⁄4 inch thick are not used on account of the difficulty of caulking them and keeping them steam tight.
On account therefore of the excessive strength of the shell plates in boilers of small diameter, butt straps are rarely used in stationary boilers, while punching the rivet holes and other inferior modes of construction are employed. We may now consider the circumferential seams of the boilers for stationary engines, such boilers sometimes being of great length in proportion to the diameter.
In proportion as the length of a boiler (in proportion to its diameter) is increased, the construction of the circumferential or transverse seams, as they are sometimes called, becomes of more importance.
The strength of the circumferential seams is so much greater than that of the longitudinal seams that it is often taken for granted that they are sufficiently strong if made with a lap joint and single riveted, but that such is not always the case will be shown presently.
In Fig. 3255 is represented a boiler composed of three strakes (i. e., three rings or sections), and it is clear that as the thickness of the shell is doubled at the circumferential seams where the ends of the middle strake pass within the end strakes, therefore the strength of the lapped joint of the shell to resist rupture in a transverse direction, as denoted by the arrows a, b, is actually increased by reason of the lap of the riveted joint. But suppose this boiler to be supported at the ends only, and the weight of the shell and of the water within it will be in a direction to cause the middle of the boiler to sag down, and therefore places a shearing strain on the rivets of the circumferential seams.[II-355]
Moreover, the temperature of the outside of the boiler cannot be made or maintained uniform, because the fire passing beneath the bottom of the boiler first will keep it hotter, causing it to expand more, and this expansion acts to shear the rivets of the circumferential seams. In proportion as the heat of the fire varies in intensity, the amount of the expansion will vary, and the consequence is that the circumferential seams may get leaky or the joint may work, especially in boilers that are long in proportion to their diameters. It is clear, therefore, that for the very best construction at least a double riveted circumferential joint should be employed.
Leaving these considerations out of the question, however, we may find the amount of stress on the circumferential seams by multiplying the area of the end of the boiler by the working pressure, and dividing by the cross-sectional area of all the rivets in one circumferential seam.
Suppose, for example, that the diameter of the boiler is 36 inches, the working pressure 60 lbs. per square inch, and that there are in each circumferential seam 50 rivets, each 3⁄4 inch in diameter, and we proceed as follows:
The area of a circle 36 inches in diameter = 1017.87 square inches.
The area of a rivet 3⁄4 inches in diameter = .4417 square inch.
Then
| Area of boiler end. |
Working pressure. |
||
| 1017.87 | × | 60 | = 2765 lbs. per cross-sectional square inch of rivet. |
| 50 | × | .4417 | |
| Number of rivets. |
Area of each rivet. |
By multiplying the area of the boiler end by the working pressure, we get the total steam pressure acting to shear the rivets, and by multiplying the number of rivets by the area of one rivet, we get the total area resisting the steam pressure, and then by dividing the one quantity into the other, we get the shearing stress per square inch of rivet section.
In the case of longitudinal seams, we have as follows, the pitch being say 21⁄8 and the rivets 3⁄4.
| Diameter of boiler in inches. |
Steam pressure. |
Pitch. | |||
| 36 | × | 60 | × | 2.125 | = 5196 lbs. per square inch of rivet area. |
| 2 | × | .4417 | |||
| Rivets in one pitch. |
Area of rivet. |
||||
It is seen, therefore, that the stress placed by the steam pressure on the transverse seam is about one-half of that it places on the longitudinal seam. But, as before remarked, the transverse seam is subject to racking strains, from which the longitudinal seams are exempt; thus, for example, the expansion of the boiler diameter, whether uniform or not, does not strain the longitudinal seam, whereas it may severely strain the transverse seam.
The English Board of Trade rules, in assigning values to the various constructions and qualities of workmanship, assign a certain value, in the form of an addition to the factor of safety, which takes into account the difference in the stress upon the transverse and longitudinal seams, the quantities in each case having been determined both from experiment and from experience. A comparison of the different values may be made as follows:
The rules take a boiler shell made of the best material, with all the rivet holes drilled after the strakes are rolled into shape and put together, with all the seams (both longitudinal and transverse) fitted with double butt straps each at least five-eighths of the thickness of the shell plates they cover, and with all the seams at least double riveted, with rivets having an allowance of not more than 75 per cent. over the single shear, and provided that the boilers have been open to the inspection of their surveyors during the whole period of construction, and say that such a boiler shell shall be allowed a factor of safety (divisor of seam strength) of 5.
But for every departure from this, which they deem the best mode of construction, a penalty in the shape of an addition to the factor of safety is made. These additions to the factors of safety with reference to the longitudinal as compared to the transverse seams, are given in the following table:
| Nature of the deviation in the construction or workmanship. | Addition to the factor 5 if the deviation is in the longitudinal seam. |
Addition to the factor 5 if the deviation is in the transverse seam. |
|
| The holes not fair and good | .75 | .2 | |
| Holes drilled out of place after bending | .15 | .1 | |
| Holes drilled before bending | .3 | .15 | |
| Holes punched after bending | .3 | .15 | |
| Holes punched before bending | .5 | .2 | |
| Joints lapped and double riveted instead of having double butt straps | .2 | .1 | |
| Joints double riveted but have single butt straps | .3 | .1 | |
| Joints single riveted and have a single butt strap | 1 | .0 | .2 |
| Joints lapped and single riveted | 1 | .0 | .2 |
An addition of .25 is also made to the factor of safety, when the strakes are not entirely under or over. In Fig. 3256 for example, strake b is within or under strake a at one end and strake c at the other end, hence b is entirely under; strake c is over b and d, and therefore entirely over; while strake d is under c, and over e, and therefore not entirely under nor entirely over.
When the rivet holes are punched they do not match properly, and unless the holes are punched somewhat smaller than the required size and reamed out afterwards, some rivets receive more stress than others, and may consequently shear in detail. It is customary, however, to punch the holes for ordinary stationary boilers, and it is with seams having punched holes therefore that we have at present to deal.
In the United States the rivet diameter and plate percentages are, in the boilers of stationary engines, usually made equal, and the reasons advanced both for and against this are as follows:
First, in favor of a greater plate percentage than rivet section, it is advanced that the plate gets thinner by wear, whereas the rivet does not, hence the wear reduces the plate section; that the plate is weakened by the punching process, and requires a greater percentage to make up its strength as compared to the rivet; that the rivets are usually of better material than the plates.
In favor of a greater rivet section than plate section, it is advanced that the shearing strength of iron is but about four-fifths of the tensile strength, and that with equal plate and rivet sections the rivet is therefore the weakest; that with punched holes the rivets may be sheared in detail, and that the rivets may be sheared gradually by the working of the joint from varying expansion and contraction.
From these premises the assumption is drawn that the weakening of the plate from being punched and from corrosion about offsets the excess of the tensile over the shearing strength, and that it is best therefore to employ such a pitch that the area of the rivet and of the metal left between the rivet holes shall be equal.
In order to do this the diameter of the rivet must be determined, and the following are the proportions given by the various authorities named:
| Thick- ness of Plate. |
Diameter of Rivets. | ||||||||||||
| Lloyds’ Rules. |
Liver- pool Rules. |
English Dock- yards. |
Fair- bairn. |
Unwin. | Wilson. | ||||||||
| in. | in. | in. | in. | in. | in. | in. | |||||||
| 5⁄16 | 5⁄8 | 5⁄8 | 1⁄2 | 5⁄8 | 11⁄16 | 5⁄8 | |||||||
| 3⁄8 | 5⁄8 | 5⁄8 | 5⁄8 | 3⁄4 | 3⁄4 | 11⁄16 | |||||||
| 7⁄16 | 5⁄8 | 3⁄4 | 3⁄4 | 21⁄32 | 13⁄16 | 3⁄4 | |||||||
| 1⁄2 | 3⁄4 | 13⁄16 | 3⁄4 | 3⁄4 | 7⁄8 | 3⁄4 | |||||||
| 9⁄16 | 3⁄4 | 13⁄16 | 7⁄8 | 27⁄32 | 7⁄8 | 7⁄8 | |||||||
| 5⁄8 | 3⁄4 | 7⁄8 | 7⁄8 | 15⁄16 | 15⁄16 | 7⁄8 | |||||||
| 11⁄16 | 7⁄8 | 7⁄8 | 7⁄8 | 1 | 1⁄32 | 1 | 7⁄8 | ||||||
| 3⁄4 | 7⁄8 | 15⁄16 | 1 | 1 | 1⁄8 | 1 | 1⁄16 | 1 | |||||
| 13⁄16 | 7⁄8 | 1 | 1 | 1 | 7⁄32 | 1 | 3⁄32 | 1 | |||||
| 7⁄8 | 1 | 1 | 1⁄8 | 1 | 1⁄8 | ... | 1 | 1⁄8 | 1 | ||||
| 15⁄16 | 1 | 1 | 3⁄16 | 1 | 1⁄8 | ... | 1 | 3⁄16 | 1 | 1⁄8 | |||
| 1 | 1 | 1 | 1⁄4 | 1 | 1⁄8 | ... | 1 | 1⁄4 | 1 | 1⁄8 | |||
From the above it is seen that with thin plates the diameter of rivet employed is about twice the thickness of the plate, whereas as the thickness of plate increases the proportion of rivet diameter decreases, and the reasons for this are, first, that with rivets twice the thickness of thick plates and pitched so as to equalize the rivet and plate sections the pitch would be too great to permit of the seams being caulked steam tight.
The diameter of the rivet having been determined, the rivet area and area of plate left between the rivet holes may be made equal by determining the pitch by the following rule:
Rule.—To the area of the rivet divided by the plate thickness add the diameter of the rivet, and the sum so obtained is the pitch. The correctness of this rule may be shown as follows:
Suppose the rivet diameter to be 7⁄8 inch = decimal equivalent .875, and its area will be .6013 square inch. Suppose the thickness of the plate to be 9⁄16 = decimal equivalent .5625, then by the rule:
| Rivet area. |
||
| Plate thickness = .5625 ) | .6013 | ( 1.0689 |
| 5625 | ||
| 388 | 00 | |
| 337 | 50 | |
| 50 | 500 | |
| 45 | 000 | |
| 5 | 5000 | |
| 5 | 0625 | |
To this 1.0689 we are to add the rivet diameter, thus:
| 1.0689 | |
| .8750 | = rivet diameter. |
| 1.9439 | = pitch of the rivets. |
We have thus found the required pitch to be 1.9439 inches, and as the joint is single riveted there are two half rivets or one whole one to one pitch, and if we subtract the diameter of the rivet from the pitch we shall get the width of the metal or plate left between the rivets, thus:
| 1.9439 | = pitch of rivets. |
| .8750 | = diameter of rivet. |
| 1.0689 | = distance in inches between the rivets. |
If now we multiply this distance between the rivets by the thickness of the plate, we shall get the area of the plate that is left between the rivet holes, thus:
| 1.0689 | = width of plate between rivets. | ||||||||
| .5625 | = thickness of plate. | ||||||||
| 53445 | |||||||||
| 21378 | |||||||||
| 64134 | |||||||||
| 53445 | |||||||||
| Area of plate between rivets = | .60125625 | ||||||||
Here then we find the area of plate left between the rivet holes to be 6.01 square inches, and as the area of the rivet is 6.01 square inches, the two are shown to be equal.
We may now place the various rivet diameters and the pitches that will make the rivet area and plate area in a single riveted joint equal in a table as follows:
| Thick- ness of Plate. |
Diameter of Rivet. |
Pitch. | |||
| 1⁄4 | 1⁄2 | 1 | 1⁄4 | ||
| 5⁄16 | 5⁄8 | 1 | 5⁄8 | ||
| 3⁄8 | 11⁄16 | 1 | 11⁄16 | ||
| 7⁄16 | 3⁄4 | 1 | 3⁄4 | ||
| 1⁄2 | 3⁄4 | 1 | 5⁄8 | ||
| 9⁄16 | 7⁄8 | 2 | |||
| 5⁄8 | 7⁄8 | 1 | 7⁄8 | ||
| 11⁄16 | 7⁄8 | 1 | 3⁄4 | ||
| 3⁄4 | 1 | .. | |||
| 13⁄16 | 1 | 2 | |||
| 7⁄8 | 1 | 1 | 1⁄8 | ||
| 15⁄16 | 1 | 1⁄8 | 2 | 1⁄8 | |
| 1 | 1 | 1⁄8 | 2 | 1⁄8 | |
| 1 | 1⁄16 | 1 | 1⁄8 | 2 | 1⁄8 |
| 1 | 1⁄8 | 1 | 3⁄16 | 2 | 1⁄4 |
| 1 | 1⁄4 | 1 | 3⁄16 | 2 | 1⁄8 |
The rivets in double riveted lap joints, and in butt strap joints having a single cover, are spaced alike, because in both cases there are two rivets in one pitch, and the rivets are in single shear.
As there are two rivets in one pitch (instead of only one as in a single riveted joint), therefore the percentage of rivet section is doubled, and the plate section must therefore be doubled if the plate and rivet sections are to be made equal, and the rule for finding the required pitch is as follows:
Rule.—To the amount of rivet area in one pitch, divided by the thickness of the plate, add the diameter of the rivet.
Example.—Let the plate thickness be as in the last example 9⁄16, decimal equivalent = .5625, and the rivet diameter be 7⁄8 inch = decimal equivalent .875, the area of one rivet being .6013 square inch, and the pitch is calculated as follows:
| .6013 | = area of one rivet. | |||
| 2 | = the rivets in one pitch. | |||
| Plate thickness = .5625 ) | 1.2026 | ( 2.1377 | ||
| 1.1250 | ||||
| 776 | 0 | 2.137 | ||
| 562 | 5 | .875 | = rivet diameter. | |
| 213 | 50 | 3.012 | = pitch. | |
| 168 | 75 | |||
| 43 | 750 | |||
| 39 | 375 | |||
| 4 | 3750 | |||
| 3 | 9375 | |||
| 4375 | ||||
We find, therefore, that the pitch is 3.012, or 3 inches (which is near enough for practical purposes), and we may now make it clear that this is correct.
In Fig. 3257 the joint is shown drawn one-half full size, and the length a of plate left between the rivet holes measures (as nearly as it is necessary to measure it) 25⁄32 inches, or 2.156, and if we[II-357] multiply this by the thickness of the plate = .5625 inch, we get 1.2 square inches as the area of the plate left between the rivet holes.
Now there are two rivets in a pitch (as one-half of b, one-half of c, and the whole of f), and as the area of each rivet is .6, therefore the area of the two will be 1.2, and the plate section and rivet section are shown to be equal.
The area at a is obviously the same as that at a, because the pitches of both rows of rivets are equal, this being an ordinary zigzag riveted joint.
We may now consider the diagonal pitch of the rivets, using the rule below.
| The pitch × 6, + 4 times the rivet diameter | = the diagonal pitch pd. |
| divided by 10 |
In this example the pitch has been found to be 3 inches, hence we have
| .875 | = diameter of rivet. | |
| 4 | = constant. | |
| 3.500 | ||
| 3 | = pitch of the rivets. | |
| 6 | = constant. | |
| 18 | ||
| 3 | .5 | = rivet diameter multiplied by 4. |
| 10 ) 21 | .5 | ( 2.15 = the diagonal pitch. |
| 20 | ||
| 1 | 5 | |
| 1 | 0 | |
| 50 | ||
The diagonal pitch, that is, the distance pd, Fig. 3257, is therefore found to be 2.15, or 21⁄8 inch full.
The amount of metal left between the rivets, measured on the diagonal pitch, is twice the dimension h multiplied by the thickness of the plate, and as this (with the diagonal pitch determined as above) always exceeds the pitch a or a, therefore if the plate fails, it will be along the line a, and not through the diagonal pitch.
We may now consider the total amount that the plates overlap in a double riveted lap joint zigzag riveted, this amount being twice the distance e, added to the distance v between the rows of rivets.
The distance e, Fig. 3257, is usually made one and a half times the diameter of the rivet, this being found to give sufficient strength to prevent the edge of the plate from tearing out and to prevent the rivet from shearing the plate out to the edge, rupture not being found to occur in either of these directions.
The rule for finding the distance v, when the diagonal pitch has been determined by the rules already explained, is as follows:
Rule.—To the pitch multiplied by 11, add 4 times the rivet diameter, then multiply by the pitch, plus 4 times the rivet diameter. Then extract the square root and divide by 10.
Placed in formula, the rule appears as follows, d representing the rivet diameter, and p the pitch.
| √(11p + 4d)(p + 4d) | = distance v between the rows of rivets. |
| 10 |
As this rule involves the extraction of the square root of the sum of quantities above the line, and as in determining the diagonal pitch, we have already determined the distance v, it is unnecessary to our purpose to carry out this latter calculation, as it is easier to find the diagonal pitch, and then, after drawing the joint, the distance between the rows of rivets can be measured if it is required, as it might be in finding the length of plate required to roll into a strake for a boiler of a given diameter and having a double riveted lap joint.
We may now consider chain riveted joints in comparison with zigzag riveted joints, which is especially necessary, because it has been assumed by some that the second row of rivets in a chain riveted joint added nothing to the strength of the joint.
Fig. 3258 represents a chain riveted joint, having the same thickness of plate, rivet diameter and pitch as the zigzag riveted joint in Fig. 3257, and it will be seen that the plate sections at a and at a are the same in the two figures, and as there are four half rivets, which are equal to two rivets, in one pitch, therefore the strength of the two joints is equal.
Each joint can be as efficiently caulked as the other, as the rivet spacing is the same and the edge of the plate is the same distance from the rivets in both cases.
The pitch of the rivets is obtained by the same rule as for zigzag riveted joints, and all we have now to consider is the distance apart of the two rows of rivets or distance v in the Fig. 3258, and for this there are two rules, the first being that it shall not be less than twice the diameter of the rivet, which would leave a dimension at h in the figure equal to the diameter of the rivet. The second rule is that a better proportion than the above is to multiply the diameter of the rivet by 3. This makes the dimension at h equal to twice the rivet diameter.
When the joints have double buttstraps, the rivets may be spaced as wide as the necessity for tight caulking will admit, because, on account of the rivets being in double shear, the rivet percentage exceeds the plate percentage.
[II-358]The allowance for the rivets being in double shear is 75 per cent., or in other words, a rivet in double shear is allowed 1.75 times the area of the same size rivet in single shear.
The simplest form of horizontal boiler is the plain cylinder boiler, an example of which is given in Fig. 3259, and which is largely used in iron works and coal mines.
Boilers of this class are easily cleaned, because the whole interior can be readily got at to clean.
As the bottom of this boiler gets thinned from wear, the boiler is turned upside down, thus prolonging its life.
Fig. 3260 represents an internally fired flue boiler, known as the Cornish or Lancashire boiler. The furnace is at one end of the flues, the fire passing through them to the chimney. There is here obviously more heating surface than in the plain cylinder boiler, but somewhat less facility for cleaning.
The Galloway boiler is of this class, but has vertical water tubes placed at intervals in the flues. These water tubes are wider at the top than at the bottom. They serve to break up the body of heat that passes through the flues, and increase the heating surface while extracting more of the heat and promoting the circulation of the water in the boiler.
A water tube is one in which the water is inside and the fire outside, as distinguished from a fire tube, in which the fire passes through the tube and the water is outside. A water tube is stronger than a fire tube, because the former is subject to bursting pressure and the latter to collapsing pressure.
Vertical boilers are internally fired, and in the ordinary forms have no return tubes or flues, examples of those used for small stationary engines being given as follows.
Fig. 3261 represents an ordinary form with vertical tubes. The upper ends of the tubes here pass through the steam space—a condition that under the moderate pressures and firing that this class of boiler is subjected to is of less importance than it is in boilers having higher chimneys and therefore a more rapid draught, and using higher pressures of steam. Furthermore, the small diameters and lengths or heights in which these boilers are made give them ample strength with shells and tubes of less thickness, while the condition of tube ends with steam on one side and fire on the other is permissible without the injurious effects that ensue under rapid combustion and high pressures.
The crown sheet of the fire boxes or furnaces of this class of boiler is very effective heating surface, first, because of the great depth[II-359] (and therefore weight) of water resting upon it insuring constant contact between the water and the plate, while there is no danger of the crown sheet burning from shortness of water.
A similar boiler, but with the upper ends of the tubes below the water level, is shown in Fig. 3262.
From the small diameters of these boilers, the flat surfaces are not stayed except to the extent that the holding power of the tubes serves that end.
A return flue vertical boiler is shown in Figs. 3263 and 3264. The whole of the surfaces having contact with the fire also have contact with the water, and the height of the crown sheet removes it from the intense heat of the fire. It is stayed to the top of the boiler. The fire box or combustion chamber being taper increases the effectiveness of its sides as heating surface, since the heat in its vertical passage impinges against it.
The products of combustion pass from the top of the combustion chamber through short horizontal flues, which enter an annular space surrounding the lower section of the boiler, and from this space vertical flues pass to a corresponding space at the bottom of the boiler.
The passage of the steam generated at the sides of the combustion chamber is facilitated by the taper of the chamber, which gives increased room for the steam as it gathers in ascending.
Vertical boilers for high pressures, as from 60 to 120 lbs. per inch, are represented in the figures from 3265 to 3269.
In boilers of this class, a majority contain water tubes, which, when properly arranged, promote rapid evaporation and circulation.
A boiler with Field tubes is shown in Fig. 3265. It consists of an outer shell and a cylindrical fire box, from the crown sheet of which a number of Field tubes are suspended in the fire box or combustion chamber.
Fig. 3266 is a sectional view of a Field tube, the construction being as follows:
The outer tube, which is expanded into the tube plate, is enclosed at its lower end, and has at its upper end in the water space of the boiler a perforated mouth piece, from which is suspended an inner tube that extends nearly to the bottom of the outer tube.
As the outer tube is bathed in the fire, steam is generated very rapidly, and a thorough and rapid circulation is kept up, the water passing down the inner and up the outer tubes, as denoted by the arrows.
The outer tube is spread out at the upper end to a slight cone, so that it cannot be forced out of the tube sheet by the pressure, and as it hangs free, there is no liability for it to loosen or get leaky from expansion and contraction.
From the great amount of heating surface obtained with these tubes, the fire box may be kept at a minimum diameter for the duty, while still leaving a wide space for the water leg, which facilitates the circulation.
[II-360]The damper, which is suspended in the uptake, spreads the fire sideways.
Fig. 3267 represents the arrangement of Field tubes in a boiler.
A boiler of this form may for a given capacity be made lighter and smaller than in any other of the ordinary forms, while the rapid circulation acts to keep the tubes clean.
The inner tubes may be thin, because they are under pressure both inside and out, while the outer tubes may be thin, because they are under a bursting strain, whereas a fire tube is under collapsing pressure.
A design of high rate boilers, in which the uptake does not come into contact with the water, and water tubes are employed, is shown in Fig. 3268. In the fire box is an inclined tube which promotes the circulation, and is very effective heating surface, and in the combustion chamber are a number of vertical water tubes.
Two manholes give access for cleaning purposes.
The efficiency of the heating surface in this class of boiler is increased from the fact that, as the heat does not pass direct through the boiler, it impinges against the surface. In Fig. 3269, for example, the exit from the spherical fire box is on one side of the boiler, and the uptake on the other, the heat passing from the fire box into a combustion chamber, and thence through the horizontal fire tubes to the uptake.
The crown sheet is here stayed by gusset stays, but if made spherical, as in Fig. 3270, the stays may be omitted.
| VOL. II. | BOILER FOR STATIONARY ENGINES. | PLATE XXVIII. |
|
Large image (86 kB). 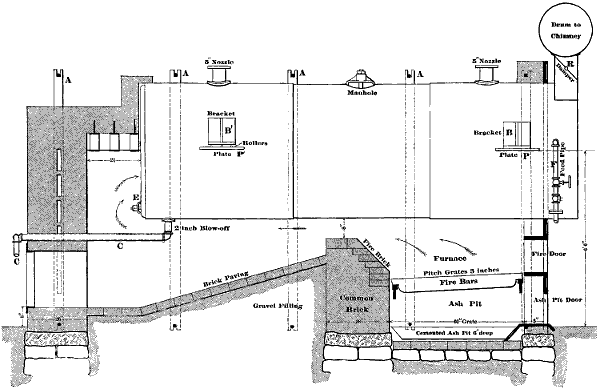 |
||
| Fig. 3271. | ||
Figs. 3271, 3272, and 3273 illustrate a 60-inch horizontal return tubular boiler constructed by the Hartford Steam Boiler Inspection and Insurance Company. This class of boiler has found much favor in the United States. It is an externally fired, return tube boiler, the fire passing beneath the boiler and returning through[II-361] the tubes to the front end of the boiler, whence it passes through the drum to the chimney.
The boiler is supported on the brackets b, b′, the front one, b, resting on an iron plate imbedded in the brickwork, and the back ones on rollers which rest on the plates p′ imbedded in the brickwork. This allows the boiler to expand[II-362] and contract endways under variations of temperature without racking the brickwork.
a, a, etc., are for holding the brickwork together. The blow-off pipe c is for emptying or blowing down the boiler. The feed-pipe f enters the front end of the boiler, passes along it, and then crosses over. A pipe h from the steam space of the boiler supplies steam to the steam gauge g, and to the upper end of the gauge glass, which is on the casting k. The lower end of the gauge glass receives water from a pipe which passes into the water space of the boiler; at j are the three gauge cocks for testing the height of the water in the boiler.
The manhole affords ingress into the boiler for inspecting and for scaling or cleaning it, the nozzles being for a safety valve. At e is a hand-hole for washing out and cleaning the boiler. p is a damper in the fire door for admitting air above the fire bars, and r is a damper for regulating the draught.
In the brick walls that support the boiler there are air spaces to prevent the conduction of the heat through and prevent cracking of the brickwork. The tubes are arranged in vertical and horizontal rows and are equally spaced throughout.
Fig. 3274 represents the front end, and Fig. 3275 a longitudinal sectional view of the front end of a boiler of this class. In this case, however, the pipes for the water gauge pass direct into the boiler.
In some practice the tubes are arranged as in Fig. 3276, being wider pitched or spaced in the middle of the boiler to increase the circulation of the water in the boiler.
Another arrangement is shown in Fig. 3277, the tubes being staggered or arranged zigzag. This permits of the employment of a greater number of tubes, but does not afford such free circulation of the water.
Fig. 3278 represents an arrangement where the tubes are in rows both vertically and horizontally.
Fig. 3279 represents a boiler by the Erie Iron Works, the details of the setting being as follows:
[II-365]Fig. 3280 is an end view of the setting with the brickwork in section.
Fig. 3281 side view of the boiler and setting.
Fig. 3282 a front end view of the boiler, and Fig. 3283 a ground plan of the brickwork. When the front plate of the boiler setting extends above the middle of the boiler, as in Fig. 3279, it is said to have a “full arch front.” Whereas when this plate or casting extends to the middle only of the boiler, it is said to have a half arch front.
Figs. 3284, 3285, 3286, and 3287 show the setting for a half arch front boiler, the dimensions of the settings of both these boilers being given in the following tables:
| No. | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | NO. OF FIRE BRICK. |
NO. COMMON BRICK ABOVE FLOOR LEVEL. |
|||
| Ft. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ft. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | |||||
| 1 | 7 | 32 | 12 | 20 | 16 | 45 | 44 | 7 | 32 | 64 | 85 | 26 | 19 | 11- | 6 | 20 | 40 | 12 | 16 | 36 | 34 | 4 | 600 | 6800 | ||
| 2 | 7 | 34 | 12 | 20 | 16 | 48 | 47 | 8 | 34 | 66 | 90 | 26 | 22 | 11- | 6 | 20 | 40 | 12 | 16 | 36 | 34 | 4 | 600 | 7500 | ||
| 3 | 8 | 36 | 12 | 20 | 16 | 48 | 47 | 8 | 36 | 68 | 92 | 26 | 22 | 12- | 6 | 24 | 40 | 12 | 16 | 36 | 34 | 4 | 650 | 7700 | ||
| 3 | 1⁄2 | 10 | 36 | 12 | 20 | 16 | 48 | 47 | 8 | 36 | 68 | 92 | 26 | 22 | 14- | 6 | 28 | 46 | 12 | 16 | 42 | 42 | 4 | 720 | 8500 | |
| 4 | 8 | 42 | 14 | 20 | 16 | 48 | 47 | 8 | 42 | 74 | 98 | 27 | 21 | 12- | 8 | 24 | 40 | 12 | 16 | 36 | 34 | 4 | 730 | 8500 | ||
| 5 | 10 | 42 | 14 | 20 | 16 | 48 | 47 | 8 | 42 | 74 | 98 | 27 | 21 | 14- | 8 | 28 | 46 | 12 | 16 | 42 | 42 | 4 | 770 | 9600 | ||
| 6 | 10 | 44 | 14 | 24 | 16 | 48 | 47 | 10 | 44 | 76 | 100 | 27 | 21 | 15- | 0 | 28 | 46 | 12 | 16 | 42 | 42 | 4 | 880 | 10500 | ||
| 7 | 12 | 44 | 14 | 24 | 16 | 48 | 46 | 1⁄2 | 10 | 44 | 76 | 100 | 27 | 21 | 17- | 0 | 32 | 52 | 12 | 16 | 48 | 49 | 4 | 940 | 10800 | |
| 7 | 1⁄2 | 14 | 44 | 14 | 24 | 16 | 47 | 45 | 1⁄2 | 10 | 44 | 76 | 99 | 26 | 21 | 19- | 0 | 36 | 58 | 12 | 16 | 54 | 84 | 4 | 1120 | 11500 |
| 8 | 12 | 48 | 16 | 24 | 16 | 47 | 45 | 1⁄2 | 10 | 48 | 88 | 103 | 26 | 21 | 17- | 2 | 32 | 52 | 12 | 20 | 48 | 49 | 4 | 1120 | 13600 | |
| 9 | 14 | 48 | 16 | 24 | 16 | 47 | 45 | 1⁄2 | 10 | 48 | 88 | 103 | 26 | 21 | 19- | 2 | 36 | 58 | 12 | 20 | 54 | 84 | 4 | 1140 | 15700 | |
| 10 | 12 | 54 | 16 | 24 | 20 | 50 | 48 | 1⁄2 | 10 | 54 | 94 | 112 | 26 | 24 | 17- | 6 | 32 | 52 | 12 | 20 | 48 | 49 | 4 | 1160 | 16200 | |
| 10 | 1⁄2 | 15 | 54 | 16 | 24 | 20 | 50 | 48 | 1⁄2 | 10 | 54 | 94 | 112 | 26 | 24 | 20- | 8 | 36 | 56 | 16 | 20 | 54 | 90 | 4 | 1270 | 17500 |
| 11 | 12 | 60 | 18 | 24 | 20 | 50 | 48 | 1⁄2 | 12 | 60 | 108 | 118 | 26 | 24 | 17- | 10 | 32 | 50 | 16 | 24 | 48 | 49 | 4 | 1400 | 20500 | |
| 12 | 14 | 60 | 18 | 24 | 20 | 50 | 48 | 1⁄2 | 12 | 60 | 108 | 118 | 26 | 24 | 19- | 10 | 36 | 56 | 16 | 24 | 54 | 84 | 4 | 1500 | 23000 | |
| 13 | 16 | 60 | 18 | 26 | 20 | 50 | 48 | 12 | 60 | 108 | 118 | 26 | 24 | 22- | 0 | 40 | 56 | 16 | 24 | 54 | 96 | 4 | 1540 | 25300 | ||
| 14 | 15 | 66 | 18 | 28 | 20 | 50 | 48 | 1⁄2 | 12 | 66 | 114 | 124 | 26 | 24 | 21- | 2 | 36 | 56 | 16 | 24 | 54 | 90 | 4 | 1590 | 26000 | |
| 15 | 16 | 66 | 18 | 28 | 20 | 50 | 48 | 12 | 66 | 114 | 124 | 26 | 24 | 22- | 2 | 40 | 56 | 16 | 24 | 54 | 96 | 4 | 1620 | 27000 | ||
| 16 | 16 | 72 | 20 | 30 | 20 | 50 | 48 | 12 | 72 | 120 | 130 | 26 | 24 | 22- | 6 | 40 | 56 | 16 | 24 | 54 | 96 | 4 | 1750 | 30000 | ||
| Note.—In setting “Standard” boilers, the side walls should be so built that the longitudinal seams of the shell will be protected from the fire. | ||||||||||||||||||||||||||
| No. | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | NO. OF FIRE BRICK. | NO. COMMON BRICK ABOVE FLOOR LEVEL. | ||||||||||
| Ft. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ft. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | Ins. | ||||||||||||
| 1 | 7 | 32 | 14 | 20 | 16 | 46 | 45 | 7 | 32 | 64 | 73 | 26 | 20 | 10- | 3 | 20 | 33 | 12 | 16 | 36 | 34 | 4 | 36 | 9 | 24 | 12 | 7 | 600 | 6150 | |||||||||
| 2 | 7 | 34 | 14 | 20 | 16 | 46 | 45 | 8 | 34 | 66 | 75 | 26 | 20 | 10- | 3 | 20 | 33 | 12 | 16 | 36 | 34 | 4 | 36 | 9 | 28 | 12 | 7 | 600 | 6200 | |||||||||
| 3 | 8 | 36 | 14 | 20 | 16 | 46 | 45 | 8 | 36 | 68 | 77 | 26 | 20 | 11- | 3 | 24 | 33 | 12 | 16 | 36 | 34 | 4 | 36 | 9 | 28 | 12 | 15 | 650 | 6700 | |||||||||
| 3 | 1⁄2 | 10 | 36 | 14 | 20 | 16 | 46 | 45 | 8 | 36 | 68 | 77 | 26 | 20 | 13- | 3 | 28 | 39 | 12 | 16 | 42 | 42 | 4 | 36 | 9 | 28 | 12 | 25 | 720 | 7050 | ||||||||
| 4 | 8 | 42 | 18 | 20 | 16 | 46 | 45 | 8 | 42 | 74 | 83 | 27 | 19 | 11- | 3 | 24 | 32 | 1⁄2 | 12 | 16 | 36 | 34 | 4 | 32 | 3⁄4 | 12 | 1⁄4 | 32 | 16 | 11 | 730 | 7700 | ||||||
| 5 | 10 | 42 | 18 | 20 | 16 | 46 | 45 | 8 | 42 | 74 | 83 | 27 | 19 | 13- | 3 | 28 | 38 | 1⁄2 | 12 | 16 | 42 | 42 | 4 | 32 | 3⁄4 | 12 | 1⁄4 | 32 | 16 | 25 | 770 | 8700 | ||||||
| 6 | 10 | 44 | 18 | 24 | 16 | 46 | 45 | 10 | 44 | 76 | 85 | 27 | 19 | 13- | 7 | 28 | 38 | 1⁄2 | 12 | 16 | 42 | 42 | 4 | 32 | 3⁄4 | 12 | 1⁄4 | 36 | 16 | 25 | 880 | 8800 | ||||||
| 7 | 12 | 44 | 18 | 24 | 16 | 46 | 44 | 1⁄2 | 10 | 44 | 76 | 85 | 27 | 19 | 15- | 7 | 32 | 44 | 1⁄2 | 12 | 16 | 48 | 49 | 4 | 32 | 1⁄4 | 12 | 1⁄4 | 36 | 20 | 35 | 940 | 9300 | |||||
| 7 | 1⁄2 | 14 | 44 | 18 | 24 | 16 | 46 | 44 | 1⁄2 | 10 | 44 | 76 | 85 | 27 | 19 | 17- | 7 | 36 | 50 | 1⁄2 | 12 | 16 | 54 | 84 | 4 | 32 | 1⁄4 | 12 | 1⁄4 | 36 | 24 | 45 | 1120 | 9500 | ||||
| 8 | 12 | 48 | 19 | 24 | 16 | 50 | 48 | 1⁄2 | 10 | 48 | 88 | 93 | 26 | 24 | 15- | 7 | 32 | 48 | 12 | 20 | 48 | 49 | 4 | 36 | 1⁄4 | 12 | 1⁄4 | 36 | 20 | 35 | 1120 | 11100 | ||||||
| 9 | 14 | 48 | 19 | 24 | 16 | 50 | 48 | 1⁄2 | 10 | 48 | 88 | 93 | 26 | 24 | 17- | 7 | 36 | 54 | 12 | 20 | 54 | 84 | 4 | 36 | 1⁄4 | 12 | 1⁄4 | 36 | 24 | 45 | 1140 | 12900 | ||||||
| 10 | 12 | 54 | 19 | 24 | 20 | 50 | 48 | 1⁄2 | 10 | 54 | 94 | 99 | 26 | 24 | 15- | 11 | 32 | 48 | 1⁄2 | 12 | 20 | 48 | 49 | 4 | 34 | 14 | 1⁄2 | 42 | 20 | 35 | 1160 | 13200 | ||||||
| 10 | 1⁄2 | 15 | 54 | 19 | 24 | 20 | 50 | 48 | 1⁄2 | 10 | 54 | 94 | 99 | 26 | 24 | 19- | 1 | 36 | 52 | 1⁄2 | 16 | 20 | 54 | 90 | 4 | 34 | 14 | 1⁄2 | 42 | 24 | 57 | 1270 | 14200 | |||||
| 11 | 12 | 60 | 21 | 24 | 20 | 46 | 3⁄4 | 45 | 1⁄2 | 12 | 60 | 108 | 101 | 3⁄4 | 26 | 20 | 3⁄4 | 16- | 1 | 32 | 47 | 16 | 24 | 48 | 49 | 4 | 31 | 14 | 1⁄2 | 48 | 20 | 37 | 1400 | 16700 | ||||
| 12 | 14 | 60 | 21 | 24 | 20 | 46 | 3⁄4 | 45 | 12 | 60 | 108 | 101 | 3⁄4 | 26 | 20 | 3⁄4 | 18- | 1 | 36 | 53 | 16 | 24 | 54 | 84 | 4 | 30 | 1⁄2 | 14 | 1⁄2 | 48 | 24 | 45 | 1500 | 19200 | ||||
| 13 | 16 | 60 | 21 | 26 | 20 | 46 | 3⁄4 | 45 | 12 | 60 | 108 | 101 | 3⁄4 | 26 | 20 | 3⁄4 | 20- | 3 | 40 | 53 | 16 | 24 | 54 | 96 | 4 | 30 | 1⁄2 | 14 | 1⁄2 | 48 | 24 | 65 | 1540 | 21500 | ||||
| 14 | 15 | 66 | 24 | 28 | 20 | 47 | 45 | 1⁄2 | 12 | 66 | 114 | 108 | 26 | 21 | 19- | 5 | 36 | 52 | 1⁄2 | 16 | 24 | 54 | 90 | 4 | 31 | 14 | 1⁄2 | 54 | 24 | 57 | 1590 | 22100 | ||||||
| 15 | 16 | 66 | 24 | 28 | 20 | 47 | 45 | 1⁄2 | 12 | 66 | 114 | 108 | 26 | 21 | 20- | 5 | 40 | 52 | 1⁄2 | 16 | 24 | 54 | 96 | 4 | 31 | 14 | 1⁄2 | 54 | 24 | 65 | 1620 | 23100 | ||||||
| 16 | 16 | 72 | 24 | 30 | 20 | 48 | 46 | 1⁄2 | 12 | 72 | 120 | 115 | 28 | 1⁄4 | 19 | 3⁄4 | 20- | 7 | 40 | 52 | 1⁄2 | 16 | 24 | 54 | 96 | 4 | 27 | 1⁄2 | 19 | 54 | 24 | 65 | 1750 | 26000 | ||||
| Note.—In setting “Standard” boilers, the side walls should be so built that the longitudinal seams of the shell will be protected from the fire. | ||||||||||||||||||||||||||||||||||||||
[56]“Many tests have been undertaken to ascertain the evaporative power of different classes of boilers in actual work; but few of these are of any value, owing to the unreliable means usually employed to measure the quantity of water evaporated. The easiest method, and consequently the one most frequently adopted, is to measure the quantity by the difference of its height in the water-gauge glass at the beginning and end of the trial, and also at intermediate stages. This method is very rude and uncertain, since there can be little doubt that in many boilers at work the surface of the water is not level, but is usually higher over the furnace, or where the greatest ebullition occurs. The difference in height at any moment will greatly depend upon the intensity of the ebullition, which is ever varying during the intervals between firing. With mechanical firing the difference of height is probably reduced to a minimum.
[56] From “A Treatise on Steam Boilers,” by Robert Wilson.
“The meters employed for measuring the water are sometimes not trustworthy. The only sure method of ascertaining the quantity of water evaporated is by actual measurement with a cistern or vessel whose cubic contents are accurately known. The quantity of water in the boiler before and after the trial should be measured at the same temperature, which should not exceed 212° to insure accuracy. But even when the amount of water introduced and the quantity passed off from the boiler are accurately ascertained, there yet remains a doubt as to how much has been actually evaporated, and how much may have passed off in priming, unless the trial has been conducted with the boiler open to the atmosphere, which appears to be the only condition under which accuracy can be insured, unless a suitable apparatus can be provided for accurately measuring the weight and temperature of all the steam and water given off, when the boiler is working above atmospheric pressure.
“There are very few boilers that do not prime more or less, and the quantity of water passed off in this manner is sometimes very considerable, and has led to the impossible results of 16 and 17 lbs. of water evaporated per lb. of ordinary coal in locomotive and water-tube boilers being seriously recorded. Externally fired boilers, that have given the moderate result of 5 lbs. of water per[II-367] lb. of coal at atmospheric pressure, have shown the unexpected result of 10 and 12 lbs. of water evaporated at 40 lbs. pressure. In fact, unless the amount of water passed over with the steam by priming or foaming, when working under pressure, can be accurately ascertained, the evaporative results are not to be relied upon, however careful in other respects the trial may have been conducted. It is customary to give the quantity of water evaporated from and at a temperature of 212°, or the boiling point at atmospheric pressure, to which the results of evaporation are reduced.”
The quantity corresponding to any temperature of feed water and working pressure can readily be found with the aid of the annexed table, taken from The Encyclopædia Britannica, wherein are presented the relations of the properties of steam, as now accepted by the best authorities.
| Total pres- sure per square inch mea- sured from a vacuum. lbs. |
Gauge pres- sure or pres- sure above atmo- sphere. lbs. |
Sensi- ble tempe- rature in Fahren- heit degrees. |
Total heat in degrees from zero of Fahren- heit. |
Weight of one cubic foot of steam. lbs. |
Rela- tive volume of steam compared with the water from which it was evapo- rated. |
|
| 1 | — | 102.1 | 1144.5 | .0030 | 20582 | |
| 2 | — | 126.3 | 1151.7 | .0058 | 10721 | |
| 3 | — | 141.6 | 1156.6 | .0085 | 7322 | |
| 4 | — | 153.1 | 1160.1 | .0112 | 5583 | |
| 5 | — | 162.3 | 1162.9 | .0138 | 4527 | |
| 6 | — | 170.2 | 1165.3 | .0163 | 3813 | |
| 7 | — | 176.9 | 1167.3 | .0189 | 3298 | |
| 8 | — | 182.9 | 1169.2 | .0214 | 2909 | |
| 9 | — | 188.3 | 1170.8 | .0239 | 2604 | |
| 10 | — | 193.3 | 1172.3 | .0264 | 2358 | |
| 11 | — | 197.8 | 1173.7 | .0289 | 2157 | |
| 12 | — | 202.0 | 1175.0 | .0314 | 1986 | |
| 13 | — | 205.9 | 1176.2 | .0338 | 1842 | |
| 14 | — | 209.6 | 1177.3 | .0362 | 1720 | |
| 14 | .7 | 0 | 212.0 | 1178.1 | .0380 | 1642 |
| 15 | .3 | 213.1 | 1178.4 | .0387 | 1610 | |
| 16 | 1.3 | 216.3 | 1179.4 | .0411 | 1515 | |
| 17 | 2.3 | 219.6 | 1180.3 | .0435 | 1431 | |
| 18 | 3.3 | 222.4 | 1181.2 | .0459 | 1357 | |
| 19 | 4.3 | 225.3 | 1182.1 | .0483 | 1290 | |
| 20 | 5.3 | 228.0 | 1182.9 | .0507 | 1229 | |
| 21 | 6.3 | 230.6 | 1183.7 | .0531 | 1174 | |
| 22 | 7.3 | 233.1 | 1184.5 | .0555 | 1123 | |
| 23 | 8.3 | 235.3 | 1185.2 | .0580 | 1075 | |
| 24 | 9.3 | 237.8 | 1185.9 | .0601 | 1036 | |
| 25 | 10.3 | 240.1 | 1186.6 | .0625 | 996 | |
| 26 | 11.3 | 242.3 | 1187.3 | .0650 | 958 | |
| 27 | 12.3 | 244.4 | 1187.8 | .0673 | 926 | |
| 28 | 13.3 | 246.4 | 1188.4 | .0696 | 895 | |
| 29 | 14.3 | 248.4 | 1189.1 | .0719 | 866 | |
| 30 | 15.3 | 250.4 | 1189.8 | .0743 | 838 | |
| 31 | 16.3 | 252.2 | 1190.4 | .0766 | 813 | |
| 32 | 17.3 | 254.1 | 1190.9 | .0779 | 789 | |
| 33 | 18.3 | 255.9 | 1191.5 | .0812 | 767 | |
| 34 | 19.3 | 257.6 | 1192.0 | .0835 | 746 | |
| 35 | 20.3 | 259.3 | 1192.5 | .0858 | 726 | |
| 36 | 21.3 | 260.9 | 1193.0 | .0881 | 707 | |
| 37 | 22.3 | 262.6 | 1193.5 | .0905 | 688 | |
| 38 | 23.3 | 264.2 | 1194.0 | .0929 | 671 | |
| 39 | 24.3 | 265.8 | 1194.5 | .0952 | 655 | |
| 40 | 25.3 | 267.3 | 1194.9 | .0974 | 640 | |
| 41 | 26.3 | 268.7 | 1195.4 | .0996 | 625 | |
| 42 | 27.3 | 270.2 | 1195.8 | .1020 | 611 | |
| 43 | 28.3 | 271.6 | 1196.2 | .1042 | 598 | |
| 44 | 29.3 | 273.0 | 1196.6 | .1065 | 595 | |
| 45 | 30.3 | 274.4 | 1197.1 | .1089 | 572 | |
| 46 | 31.3 | 275.8 | 1197.5 | .1111 | 561 | |
| 47 | 32.3 | 277.1 | 1197.9 | .1133 | 550 | |
| 48 | 33.3 | 278.4 | 1198.3 | .1156 | 539 | |
| 49 | 34.3 | 279.7 | 1198.7 | .1179 | 529 | |
| 50 | 35.3 | 281.0 | 1199.1 | .1202 | 518 | |
| 51 | 36.3 | 282.3 | 1199.5 | .1224 | 509 | |
| 52 | 37.3 | 283.5 | 1199.9 | .1246 | 500 | |
| 53 | 38.3 | 284.7 | 1200.3 | .1269 | 491 | |
| 54 | 39.3 | 285.9 | 1200.6 | .1291 | 482 | |
| 55 | 40.3 | 287.1 | 1201.0 | .1314 | 474 | |
| 56 | 41.3 | 288.2 | 1201.3 | .1336 | 466 | |
| 57 | 42.3 | 289.3 | 1201.7 | .1364 | 458 | |
| 58 | 43.3 | 290.4 | 1202.0 | .1380 | 451 | |
| 59 | 44.3 | 291.6 | 1202.4 | .1403 | 444 | |
| 60 | 45.3 | 292.7 | 1202.7 | .1425 | 437 | |
| 61 | 46.3 | 293.8 | 1203.1 | .1447 | 403 | |
| 62 | 47.3 | 294.8 | 1203.4 | .1469 | 424 | |
| 63 | 48.3 | 295.9 | 1203.7 | .1493 | 417 | |
| 64 | 49.3 | 296.9 | 1204.0 | .1516 | 411 | |
| 65 | 50.3 | 298.0 | 1204.3 | .1538 | 405 | |
| 66 | 51.3 | 299.0 | 1204.6 | .1560 | 399 | |
| 67 | 52.3 | 300.0 | 1204.9 | .1583 | 393 | |
| 68 | 53.3 | 300.9 | 1205.2 | .1605 | 388 | |
| 69 | 54.3 | 301.9 | 1205.5 | .1627 | 383 | |
| 70 | 55.3 | 302.9 | 1205.8 | .1648 | 378 | |
| 71 | 56.3 | 303.9 | 1206.1 | .1670 | 373 | |
| 72 | 57.3 | 304.8 | 1206.3 | .1692 | 368 | |
| 73 | 58.3 | 305.7 | 1206.6 | .1714 | 363 | |
| 74 | 59.3 | 306.6 | 1206.9 | .1736 | 359 | |
| 75 | 60.3 | 307.5 | 1207.2 | .1759 | 353 | |
| 76 | 61.3 | 308.4 | 1207.4 | .1782 | 349 | |
| 77 | 62.3 | 309.3 | 1207.7 | .1804 | 345 | |
| 78 | 63.3 | 310.2 | 1208.0 | .1826 | 341 | |
| 79 | 64.3 | 311.1 | 1208.3 | .1848 | 337 | |
| 80 | 65.3 | 312.0 | 1208.5 | .1869 | 333 | |
| 81 | 66.3 | 312.8 | 1208.8 | .1891 | 329 | |
| 82 | 67.3 | 313.6 | 1209.1 | .1913 | 325 | |
| 83 | 68.3 | 314.5 | 1209.4 | .1935 | 321 | |
| 84 | 69.3 | 315.3 | 1209.6 | .1957 | 318 | |
| 85 | 70.3 | 316.1 | 1209.9 | .1980 | 314 | |
| 86 | 71.3 | 316.9 | 1210.1 | .2002 | 311 | |
| 87 | 72.3 | 317.8 | 1210.4 | .2024 | 308 | |
| 88 | 73.3 | 318.6 | 1210.6 | .2044 | 305 | |
| 89 | 74.3 | 319.4 | 1210.9 | .2067 | 301 | |
| 90 | 75.3 | 320.2 | 1211.1 | .2089 | 298 | |
| 91 | 76.3 | 321.0 | 1211.3 | .2111 | 295 | |
| 92 | 77.3 | 321.7 | 1211.5 | .2133 | 292 | |
| 93 | 78.3 | 322.5 | 1211.8 | .2155 | 289 | |
| 94 | 79.3 | 323.3 | 1212.0 | .2176 | 286 | |
| 95 | 80.3 | 324.1 | 1212.3 | .2198 | 283 | |
| 96 | 81.3 | 324.8 | 1212.5 | .2219 | 281 | |
| 97 | 82.3 | 325.6 | 1212.8 | .2241 | 278 | |
| 98 | 83.3 | 326.3 | 1213.0 | .2263 | 275 | |
| 99 | 84.3 | 327.1 | 1213.2 | .2285 | 272 | |
| 100 | 85.3 | 327.9 | 1213.4 | .2307 | 270 | |
| 101 | 86.3 | 328.5 | 1213.6 | .2329 | 267 | |
| 102 | 87.3 | 329.1 | 1213.8 | .2351 | 265 | |
| 103 | 88.3 | 329.9 | 1214.0 | .2373 | 262 | |
| 104 | 89.3 | 330.6 | 1214.2 | .2393 | 260 | |
| 105 | 90.3 | 331.3 | 1214.4 | .2414 | 257 | |
| 106 | 91.3 | 331.9 | 1214.6 | .2435 | 255 | |
| 107 | 92.3 | 332.6 | 1214.8 | .2456 | 253 | |
| 108 | 93.3 | 333.3 | 1215.0 | .2477 | 251 | |
| 109 | 94.3 | 334.0 | 1215.3 | .2499 | 249 | |
| 110 | 95.3 | 334.6 | 1215.5 | .2521 | 247 | |
| 111 | 96.3 | 335.3 | 1215.7 | .2543 | 245 | |
| 112 | 97.3 | 336.0 | 1215.9 | .2564 | 243 | |
| 113 | 98.3 | 336.7 | 1216.1 | .2586 | 241 | |
| 114 | 99.3 | 337.4 | 1216.3 | .2607 | 239 | |
| 115 | 100.3 | 338.0 | 1216.5 | .2628 | 237 | |
| 116 | 101.3 | 338.6 | 1216.7 | .2649 | 235 | |
| 117 | 102.3 | 339.3 | 1216.9 | .2674 | 233 | |
| 118 | 103.3 | 339.9 | 1217.1 | .2696 | 231 | |
| 119 | 104.3 | 340.5 | 1217.3 | .2738 | 229 | |
| 120 | 105.3 | 341.1 | 1217.4 | .2759 | 227 | |
| 121 | 106.3 | 341.8 | 1217.6 | .2780 | 225 | |
| 122 | 107.3 | 342.4 | 1217.8 | .2801 | 224 | |
| 123 | 108.3 | 343.0 | 1218.0 | .2822 | 222 | |
| 124 | 109.3 | 343.6 | 1218.2 | .2845 | 221 | |
| 125 | 110.3 | 344.2 | 1218.4 | .2867 | 219 | |
| 126 | 111.3 | 344.8 | 1218.6 | .2889 | 217 | |
| 127 | 112.3 | 345.4 | 1218.8 | .2911 | 215 | |
| 128 | 113.3 | 346.0 | 1218.9 | .2933 | 214 | |
| 129 | 114.3 | 346.6 | 1219.1 | .2955 | 212 | |
| 130 | 115.3 | 347.2 | 1219.3 | .2977 | 211 | |
| 131 | 116.3 | 347.8 | 1219.5 | .2999 | 209 | |
| 132 | 117.3 | 348.3 | 1219.6 | .3020 | 208 | |
| 133 | 118.3 | 348.9 | 1219.8 | .3040 | 206 | |
| 134 | 119.3 | 349.5 | 1220.0 | .3060 | 205 | |
| 135 | 120.3 | 350.1 | 1220.2 | .3080 | 203 | |
| 136 | 121.3 | 350.6 | 1220.3 | .3101 | 202 | |
| 137 | 122.3 | 351.2 | 1220.5 | .3121 | 200 | |
| 138 | 123.3 | 351.8 | 1220.7 | .3142 | 199 | |
| 139 | 124.3 | 352.4 | 1220.9 | .3162 | 198 | |
| 140 | 125.3 | 352.9 | 1221.0 | .3184 | 197 | |
| 141 | 126.3 | 353.5 | 1221.2 | .3206 | 195 | |
| 142 | 127.3 | 354.0 | 1221.4 | .3228 | 194 | |
| 143 | 128.3 | 354.5 | 1221.6 | .3250 | 193 | |
| 144 | 129.3 | 355.0 | 1221.7 | .3273 | 192 | |
| 145 | 130.3 | 355.6 | 1221.9 | .3294 | 190 | |
| 146 | 131.3 | 356.1 | 1222.0 | .3315 | 189[II-368] | |
| 147 | 132.3 | 356.7 | 1222.2 | .3336 | 188 | |
| 148 | 133.3 | 357.2 | 1222.3 | .3357 | 187 | |
| 149 | 134.3 | 357.8 | 1222.5 | .3377 | 186 | |
| 150 | 135.3 | 358.3 | 1222.7 | .3397 | 184 | |
| 155 | 140.3 | 361.0 | 1223.5 | .3500 | 179 | |
| 160 | 145.3 | 363.4 | 1224.2 | .3607 | 174 | |
| 165 | 150.3 | 366.0 | 1224.9 | .3714 | 169 | |
| 170 | 155.3 | 368.2 | 1225.7 | .3821 | 164 | |
| 175 | 160.3 | 370.8 | 1226.4 | .3928 | 159 | |
| 180 | 165.3 | 372.9 | 1227.1 | .4035 | 155 | |
| 185 | 170.3 | 375.3 | 1227.8 | .4142 | 151 | |
| 190 | 175.3 | 377.5 | 1228.5 | .4250 | 148 | |
| 195 | 180.3 | 379.7 | 1229.2 | .4357 | 144 | |
| 200 | 185.3 | 381.7 | 1229.8 | .4464 | 141 | |
| 210 | 195.3 | 386.0 | 1231.1 | .4668 | 135 | |
| 220 | 205.3 | 389.9 | 1232.3 | .4872 | 129 | |
| 230 | 215.3 | 393.8 | 1233.5 | .5072 | 123 | |
| 240 | 225.3 | 397.5 | 1234.6 | .5270 | 119 | |
| 250 | 235.3 | 401.1 | 1235.7 | .5471 | 114 | |
| 260 | 245.3 | 404.5 | 1236.8 | .5670 | 110 | |
| 270 | 255.3 | 407.9 | 1237.8 | .5871 | 106 | |
| 280 | 265.3 | 411.2 | 1238.8 | .6070 | 102 | |
| 290 | 275.3 | 414.4 | 1239.8 | .6268 | 99 | |
| 300 | 285.3 | 417.5 | 1240.7 | .6469 | 96 | |
Here we see that at 212° the total quantity of heat in the steam is 1178.1°, which gives a difference of 966.1°. This heat, usually termed latent, is absorbed in performing the work of expanding the particles of water from the liquid to the gaseous state. Now, suppose the water is evaporated at 60 lbs. pressure, the steam will have a temperature of 307°, and a total heat of 1207°. If the feed has been introduced at 60°, it is evident that 1147° of heat have been imparted. As the amount evaporated is inversely proportional to the quantity of heat required, we have 1147 ÷ 966 = 1.2. Multiplying by this factor, the quantity evaporated at 60 lbs. pressure from 60°, we obtain the amount that would be evaporated at 212° by the same quantity of fuel.
By the same table can be ascertained the comparatively small increase of heat required to evaporate water at higher pressures. Suppose we take water evaporated at 45 lbs. pressure from a feed temperature of 60°, then each lb. of water will require 1202.7 - 60 = 1142.7 for its conversion into steam. If we take the pressure at 100 lbs., we shall have 1216.9 - 60 = 1156.9° as the quantity required. The difference between these two total quantities is only 14.2°, and is so small as to be scarcely worth considering. Leaving out of account the loss due to the slight reduction of the conducting power of the material, the increased amount of heat required for the higher pressure will be only 1⁄36 of the total heat required at 60 lbs. With an evaporation of 7 lbs. of water from 1 lb. of coal, it will be obtained by using 1⁄563 more fuel, or about 1 lb. in about 556 lbs., a quantity not appreciable to the ordinary modes of weighing coal. The economy is then manifest of using steam of high pressures when at the same time advantage is taken of the facilities it offers for working the steam more expansively to the engine cylinders.
The saving that may be effected by heating the feed water may be shown as follows:
If we take the normal temperature of the feed water at 60°, the temperature of the heated water at 212°, and the boiler pressure at 20 lbs., the total heat imparted to the steam in one case is
| 1192.5° | - | 60° | = | 1132.5° | |
| and in the other case | 1192.5° | - | 212° | = | 980.5° |
| the difference being 152°, or a saving of | 152° | ||||
| 1132.5° | |||||
which is 13.4 per cent. If the pressure be taken at 120 lbs., instead of 20 lbs., the saving will be 13.1 per cent, showing a slight diminution in the economy effected by heating the feed water when a high boiler pressure is employed.
The first thing to do in taking charge of a stationary engine boiler is to know from personal inspection that the safety fittings and the boiler-feeding apparatus are in good order.
The safety valve is the first thing to inspect, as it is liable to stick in its seat, especially in cases in which it is set at a greater pressure than is got up in the boiler, because in that case it is not lifted from the seat and in time sticks fast there.
In such cases it is proper to lift the valve at least once a day while steam is on. For this purpose a cord may be attached to the lever, passing over a pulley directly above the lever, and thence to some convenient place near the boiler, but where it is not liable to get caught and pulled accidentally.
Before lighting the fire, see that there is sufficient water in the boiler. If there is a gauge glass on the boiler, it should show three-quarters full, or three-quarters of a glass, as it is called.
The gauge glass may show a false water level, and to be sure that such is not the case, open the top gauge cock and the cock at the bottom of the gauge glass, letting the water run through the gauge glass. Open and close the cock below the gauge glass two or three times to see that the water comes to the same level each time.
If the steam pressure has been allowed to fall in the boiler without any of the cocks being opened, there will be a partial vacuum in the boiler, and air must be let in before the true water level will be shown either by the gauge glass or by the gauge cocks.
Opening the upper gauge cock will let in the air, and it should not be closed again until enough steam has been got up in the boiler to expel the air again, or in other words, until steam begins to issue from it.
The grate bars and ash pit should be cleaned of clinker, ashes, etc., and it should be seen that the tubes are clear of ashes, etc., before the fire is laid; if the grate is a shaking one, the lever should be applied to see that the grate will shake properly.
To light the Fire—In the case of anthracite or hard coal, as it is sometimes termed, first cover the bars with a thin layer of coal and then put in pieces of lighted greasy waste (if it is at hand) distributed about the furnace, taking especial care to light the fire at the fire-door end and in the corners, because the fire will spread from the front end towards the back easier than it will from the back end towards the front.
The fire should light from the bottom and not from the top, hence the thinnest pieces of the wood should be put in first.
If there is any soft coal at hand, a small quantity of it will accelerate lighting the fire, as it burns easier and quicker than hard coal.
Before putting on the coal the wood should be well lighted, the bottom portion of it having ceased flaming.
This causes the lighted wood to spread over the bars and the fire to light evenly.
Charge the coal lightly, first covering the places that have burned up the most.
Firing.—The fire door should be kept open as little as possible, as it admits cold air that is detrimental to the combustion, as well as to the draught, hence firing should be done quickly.
A good fireman will maintain as even a temperature as possible in the fire box by charging the coal lightly and quickly.
Some firemen will, after the fire is at its proper depth all over the grates, charge the fire in the front end, that is, at the fire-door end, and push it back as it burns up, to keep up the thickness of the fire at the back.
The thickness of the fire depends upon the size and kind of coal.
With small coal a fire from 4 to 6 inches deep will answer, while, if the lumps are five or six inches in diameter, a fire from a foot to 15 inches deep may be maintained, as is done in some locomotives.
The object is to have the fire thick enough to prevent it from burning through in spots or letting cold draughts of air pass through it.
The sides of the furnace require particular attention, not only because cold air is more likely to get through there, but also in boilers[II-369] having fire boxes the cool sides of the box keep the temperature of the fuel down, hence a thicker fire is necessary around the sides than in the middle of the furnace or fire box.
Three things are to be considered in cleaning a fire—first, that the boiler pressure will fall during, and for a short time after, the cleaning; second, that the depth of fire will be diminished by the cleaning; and third, that the temperature of the fire will fall during the cleaning.
When a furnace has shaking grate bars, the cleaning of the fire is greatly facilitated, and with bars that shake singly (and good coal) the fire is often not disturbed during the day, except to shake the bars occasionally, passing the poker through it and using the hoe to keep it evenly spread.
If the grate shakes in sections, more cleaning will be required to break up the clinker, while, if the bars do not shake, the cleaning assumes greater importance.
Before cleaning, therefore, see that there is sufficient water in the boiler, that it need not be fed while cleaning, nor just after cleaning the fire.
Prepare for cleaning by having a thick fire on the grate, so that after cleaning it will burn up quickly, and let the cleaning be done as quickly as possible.
The tools used for cleaning the fire are the slice bar, Fig. 3288, which is pushed along the top of the fire bars to loosen up the fire, and let the ashes fall through the bars.
The hoe, Fig. 3289, which is used to push the fire to the back of the furnace and to pull it forward. The poker, Fig. 3290, which dislodges any clinker that may be between the bars, and lets the ashes fall through.
The clinker hook or devil’s claw, Fig. 3291, which is used to haul clinker out of the fire, and the rake, Fig. 3292, which is used to spread the fire evenly over the bars after it is cleaned.
In cleaning a fire, first use the slice bar to loosen up the fire and let the ashes fall through, and also dislodge clinkers from the surface of the bars. Then push the fire to the back of the furnace. Next use the poker to clean out clinker from between the exposed part of the bars. Then with the hoe pull a part of the fire forward and pull out the clinker that may be in this part, doing so with the hoe as far as possible, as that will save time, but if it should be necessary, use the clinker hook.
Then pull forward a second portion of the fire, and spread it on the bars, removing the clinker as before. When all the fire has thus been cleaned, use the rake to spread it evenly over the bars, and put on a light charge of coal, covering the brightest parts of the fire first, and taking care that no part of the fire bars is left uncovered.
The cleaning should be done quickly.
Draught.—The draught should be decreased while the fire is being cleaned, but the damper should never be entirely closed, as this might cause an explosion in the fire box and tubes.
During a temporary interruption, as in the case of the engine stopping, partly close all the dampers, as it is wasteful to make steam and blow it off through the safety valve.
Combustion.—A blue flame is evidence of incomplete combustion, but there may be a blue flame and imperfect combustion at the back end of the furnace, and a white flame and perfect combustion at the other end.
This is likely to occur with heavy firing near the fire door, and a thin fire at the tube sheet end of the fire box. In this case the unconsumed gases produced near the fire door (as evidenced by the blue flame) are consumed in passing over the bright fire at the tube plate end of the furnace.
At Night.—Always leave plenty of water in the boiler when leaving it for the night, not only to allow for any leak, but also because it gives a fair start in the morning and more time to remedy any defect in the feed pump if it arise.
By plenty of water, very nearly a full gauge is meant, or if there is no gauge glass to the boiler, let the water stand above the second or middle cock.
The usual method of leaving the fire for the night is to bank it. There is an element of danger, however, in banking a fire, unless it is done to suit the circumstances, because steam may generate very rapidly, and perhaps more rapidly than the safety valve can carry it off.
A safe method is to clean the fire, leaving the clinker and ashes covering the front half of the grate and the fire piled up on the back half.
The damper and ash pit door should be closed tight, the fire door open, and the fire well covered with fresh coal, choosing small rather than large coal.
If this method is found not to keep up the fire sufficiently, the same plan may be employed, except that the ashes and clinker may be removed, and if this still leaves too cold a boiler, and too poor a fire in the morning, the fire may be left spread over the grate, but heavily covered with fresh coal, the draught being stopped as much as possible by closing the dampers and opening the furnace door.
To further insure safety, the weight on the safety valve lever should be pushed towards the valve, so as to cause the safety valve to blow off at a less pressure than during the day.
In the Morning.—In starting up a banked fire in the morning, first close the fire door and open the damper, so as to give the fire all the draught possible, and let it burn up a little; then, if it has been piled up at the back of the furnace, clean out the ashes by passing the T bar beneath the fire, and spread it over the grate, letting it burn up a little before making up a fire.
Boiler-Feed.—The fireman should endeavor, if possible, to so regulate the boiler feed that it is kept going as nearly continuously as possible while maintaining a uniform quantity of water in the boiler, and this, with uniform firing, will give the greatest economy.
When pumps are used to feed with, the amount of the lift of the valves can be regulated by a screw, so as to vary the amount of[II-370] water the pump will deliver, and in this case it is comparatively easy to set them so that the pump may be kept going without putting too much water in the boiler.
When injectors are used, however, the feed will be intermittent, and a uniform quantity of water in the boiler is best obtained by feeding at short intervals, stopping the feed when the fire door is opened much, as when cleaning the fire.
If the feed water is dirty, the gauge glass should be kept clean by first shutting off the upper cock and opening the lower one, so as to let the water blow through the lower cock, and then shutting off the lower cock from the boiler, and opening the upper one, which will let the steam blow all the water out of the glass. This should be done two or three times a day, so as to keep the holes in the boiler and those in the cocks from closing up with fur or scale.
If the water falls in the glass, or if the gauge cocks show the water to be falling, notwithstanding that the feed pump has been started, it is evident that the pump is not working.
This may occur from a stuck valve, a leak in the suction pipe, from the feed water being too hot, or from the pump failing to start in action from leaky or choked valves.
A stuck valve may generally be relieved by striking a few blows on the outside of the pump with a hammer and a block of wood, or if this does not answer, with the hammer only. Check valves are the ones most likely to stick.
If a pump fails to work by reason of the feed water being too hot, the remedy is to open the pet cock to let the steam out of the pump, but if this does not succeed, cold water may be poured on the outside of the pump, which will start it, after which, in most cases, the pump will keep going and the pet cock may be closed.
If the suction pipe has a joint, a leak there will impair the action of the pump, and, if the leak is great enough, will stop it; the remedy is to make the joint tight.
Plunger pumps sometimes fail to act because the plunger has worn so small in diameter that there is sufficient air between the plunger and the pump barrel to expand and compress without lifting the valve; the remedy is obviously a new plunger of as large diameter as the pump gland will admit of, boring the gland out to admit the new plunger.
All the impurities in the water are left in the boiler when the water has evaporated, and it is obvious these impurities must be blown off or they will form scale on the internal surface of the boiler and the external surface of the tubes or flues.
This scale obstructs the passage of the heat from the iron to the water, and if let get thick enough will cause the iron to rapidly burn out.
To prevent the formation of scale, two principal methods are employed, one being to purify the feed water, and the other to occasionally blow the impurities out of the boiler.
Feed-water heaters generally serve also as purifiers, and their effectiveness is increased in proportion as the water can pass quietly through them, and has a large area on which the impurities can settle. Horizontal heaters have the advantage that they have a large settling area, and a less distance for the impurities to fall through. The water-gauge glass and the lower gauge cock are usually set so as to have a margin of about three inches of water above the tubes or crown sheet of the fire box, hence if it is known that the water is but just below the bottom of the gauge glass or gauge cock, there is no positive danger, although it is improper to let it get so low.
If the water is out of sight, and it is not known exactly how low it is, then it is dangerously low, and every minute is of vital importance.
Should the water get dangerously low in the boiler, the most dangerous thing to do is to lift the safety valve or pump in cold water, especially if it is not known how much water there is in the boiler.
As quickly as possible cover the fire with ashes, coal, earth, sand, or anything that is at hand that will smother the fire, then close the draught to the fire, leaving the fire door and the chimney damper open.
Leave all the steam outlets just as they are, and also the feed.
Priming.—Priming, which is also called “foaming,” is that the steam carries up water into the steam space. This may arise from several causes, but it is well known that what will stop priming in some cases will cause it in others.
The known causes of priming are—first, too little room for the steam in the boiler, and it follows that a high water level may cause priming; second, it may be caused by a difference of temperature between the water and the steam in the boiler. Suppose, for example, that the pressure of the steam and water in the boiler is 160 lbs. by gauge, and its sensible temperature will be 370 degrees. Suppose then that enough steam is permitted to escape from the boiler to reduce the steam pressure to 140 lbs., and its temperature will be reduced to 361 degrees. But the water will remain at 270 degrees, and the result will be that it will pass into steam so rapidly that it will carry up the water and hold it in suspension among the steam. The water will pass with the steam into the engine cylinder, and the boiler will be said to “prime,” “foam,” or “work water.” The same thing may happen if the water is heated very rapidly.
Priming is wasteful because it rapidly empties the boiler of its water, and dangerous because it may cause the piston to knock out the cylinder head or cover.
When the safety valve blows off, priming may be induced, especially if the engine is at work, because in this case the boiler is being forced, or, in other words, is making steam more rapidly than it is designed to do, and the passage of so large a body of steam through the water is apt to lift it.
Muddy water will sometimes cause foaming or priming, as will also insufficient circulation of the water in the boiler or sometimes the presence of grease or oil.
Priming may be detected from the discharge of water with the steam when the gauge cock is opened, the steam looking white and fluttering as it escapes, and also by violent motion of the water in the gauge glass, or by a thump or pound at the ends of the piston stroke.
To stop priming, the steam from the boiler should be decreased by slackening the speed of the engine, or if necessary, by stopping it. The true water level can then be seen, and if there is too much water in the boiler some of it may be blown off, while if the quantity of water in the boiler will permit it, the feed may be put on.
If the boiler has a surface blow-off cock, or a mechanical boiler cleaner, it is best to blow off from that, as it carries off the scum at the same time as relieving the boiler.
To prevent priming, a steady and uniform rate of boiler feed, the use of pure water, a clean boiler, and steady firing are the best means, turning on the steam slowly so as not to violently disturb the water in the boiler.
The engine as well as the boiler requires attention when the boiler primes. Thus the cylinder cocks should be opened to let out the water from the cylinder and prevent breakage of the cylinder cover.
Scale in Boilers.—The steam leaves behind it all the impurities that the water contained, and these impurities deposit in form of mud and scale, which must be got rid of because it causes a loss of fuel, and if allowed to get thick enough will cause the boiler to burn.
The use of boiler compounds or scale preventatives may be resorted to with advantage, providing they are of a nature to suit the water, but mechanical cleaning must also be resorted to at periods determined by the nature of water.
Boilers are cleaned in two ways—first, by blowing off the impurities before they have formed into scale; and second, by removing at certain intervals whatever scale has formed.
Blowing down may be done in two ways—first, from the surface of the water by means of mechanical cleaners; and second, by blowing out from the bottom of the boiler.
The first draws off the impurities as they are thrown to the surface, the second draws them off after they have become more condensed and sink to the bottom.
How often a boiler should be blown down depends upon the kind of water fed to the boiler; where purifiers are used, less blowing down is obviously needed.
[II-371]It is best to blow off from the bottom of the boiler when no steam is being used, as during dinner time, letting the water blow down about a quarter of the glass, or from the upper to the middle gauge cock.
As no steam is being used, the feed can then be put on to restore the quantity of water without reducing the temperature of the boiler so much. The feed should be gradual and the fire regulated to keep the steam pressure even.
How often a boiler should be washed out and cleaned depends upon the quality of the water it uses, and varies from about once a week to once a month, according to whether bad and unpurified water or purified water is used.
The first thing to do is to draw the fire, leaving the chimney damper open and closing all the other dampers so that as little cold air as possible can get into the boiler, while the heat can pass away up the chimney.
Let the steam and water all remain in the boiler until there is a gauge pressure of about 5 lbs. in the boiler.
Then open the blow-off cock and let out the water. If the water is blown off under a high pressure, then after the waste is all out the iron is hot enough to dry up the scale, making it hard and very difficult to remove.
After all the water is blown off, take out all the mud plugs and the man-hole and hand-hole covers, and wash out the boiler under as much water pressure as can be had, directing the hose so to reach all parts of the boiler and tubes, and continuing the washing until the water leaves the boiler clean.
Then with a wooden hoe on a piece of gas-pipe of small diameter for a handle, and small enough to pass through the hand-hole, draw all the loose scale to the hand-hole and remove it, letting the water run slowly, so as to carry the small pieces of scale towards the hand-hole as fast as the hoe disturbs it.
Then get inside the boiler, and a few blows with a light ball-pened hammer will loosen the scale, and a steel scraper will remove more, which must be washed down and drawn out with a hoe.
After the cleaning and scaling are complete, the engineer, with lamp in hand, should carefully examine the interior of the boiler and of the fire box, paying especial attention to the stays to see that they are not broken.
The hammer test should also be applied. It consists of sounding the boiler by light blows given by a light ball-pened hand hammer, the sound indicating defective places.
The high pressure steam engine, in whatever form it exists, consists of a frame or bed plate carrying two distinct mechanisms, first, the driving or power-transmitting mechanism, and second, the valve gear or valve motion, and to these are added such other mechanisms as the nature of the duty the engine is to perform may require.
The most prominent of these additional mechanisms is a governor for regulating the speed at which the engine is to run; nearly all steam engines require a governor in some form or other, while for electric lighting and some other purposes it constitutes the main feature in the design of the engine.
In a locomotive the air brake and the sand box are elements not found in other engines.
In a jet condensing engine, the condenser and injection water, or condensing water mechanism, is a part of the engine.
In a surface condensing engine, the air pumps and circulating pumps are a part of the engine.
In marine engines there are mechanisms for turning the engine around when no steam is up; for moving the reversing gear quickly, and for varying the point of cut off, and therefore the amount of expansion, and various other and minor mechanisms.
Referring now to the simplest form of high pressure stationary steam engine, such as represented in Figs. 3293, 3294, and 3295, its valve gear or valve motion consists of the eccentric and its strap, the eccentric rod, the valve rod guide a, the valve rod or valve spindle, and the valve v, these parts controlling the admission of steam to one side of the piston, and the exhaust from the other.
The piston, piston rod, cross head, connecting rod, crank, crank shaft, main shaft or driving shaft, and the fly wheel constitute the driving or power-transmitting mechanism.
The steam side of the piston is that against which the steam is pressing, as side s in Fig. 3295. The exhaust side, e, of the piston is that on which the steam is passing out or exhausting.
The governor for a common D valve engine regulates the engine speed by varying the opening in the bore of the pipe through which the steam passes from the boiler to the steam chest, leaving a wider opening in proportion as the engine runs slower, and reducing the opening when the engine runs faster. Assuming the engine to be running at its slowest, or its load to be so great that a full supply of steam is required in order to keep the engine up to its proper speed, and the governor will be open at its widest, so that all the further action the governor can have is to reduce the steam pipe opening, and thus cause the pressure in the steam chest to be less than that in the steam pipe.
This action is called wire-drawing the steam, and the governor is called a throttling governor.
An engine bed or bed plate is a frame that is seated or bedded to its foundation along its whole length.
An engine frame is seated to its foundations at two or more places, but not continuously throughout its length.
Cylinders are secured to the engine frames in three principal ways, as follows: by bolting them down to the bed plate; by bolting them to one end of the bed plate, so that they may expand and contract without springing the bed plate; and in vertical engines, by bolting them to the top of the frames.
The bores of cylinders require to be parallel, so that the piston rings may fit to the bore without requiring to expand and contract in diameter at different parts of the stroke.
Cylinders are designated for size by the diameter of the cylinder bore and the length of the stroke; thus, a 10 × 12 cylinder has a piston of ten inches diameter and 12 inches stroke.
The wear of a cylinder bore is (if the engine is kept in proper line and the piston rings, or packing rings as they are sometimes termed, fit to the bore with an equal pressure throughout the stroke) greatest near the middle of the length and least at the ends of the stroke. But when the piston rings are set out by the steam pressure, and the point of cut off occurs early in the stroke, the wear may be greatest at the ends of the cylinder bore, because of the pressure of the steam diminishing during the expansion.
The counterbore of a cylinder is a short length at each end of the cylinder, that is made of larger diameter than the rest of the bore, so that the piston head may travel completely over the working bore, and thus prevent the formation of a shoulder at each end of the cylinder. Such a shoulder forms when there is a part of the bore over which the piston does not pass. The length of the counterbore should exceed the amount of the taper on the connecting rod key, so that as the connecting rod length alters from the wear, the piston shall not strike the cylinder head.
The clearance of a cylinder is the amount of space that exists between the face of the piston when it is at the end of its stroke and that of the valve when it covers the port, the piston being at the end of the stroke, and as this space exists at each end of the cylinder, the total clearance for a revolution is twice the above amount.
The clearance at the crank end of the cylinder is reduced by the piston rod passing through it.
The amount of clearance may be measured by the following method, which has been given by Professor John E. Sweet:
[II-373]See that the piston and valves are made tight, and the valves disconnected; arrange to fill the clearance spaces with water through the indicator holes, or holes drilled for the purpose. Turn the engine on the dead centre; make marks on the cross-head and guide that correspond; weigh a pail of water, and from it fill all the clearance space. Weigh the remaining water, so as to determine how much is used. Then weigh out exactly the same amount of water, turn the engine off the centre, pour in the second charge of water, and turn back until the water comes to the same point that it did in the first case. Make another mark on the cross-head, and the distance between these marks is exactly what you really wish to know; that is, it is just what piston travel equals the clearance. This gives the proportion that the clearance space bears to the space in the cylinder occupied by the steam at the end of the piston stroke. Thus, if it takes one pound of water to fill this space, and to admit the one pound of water the piston must be moved one inch, then the clearance bears the same relation to the capacity of the engine as one inch bears to the stroke of the piston. Thus, under these circumstances, in an engine of ten-inch stroke, it would be said the engine had ten per cent. clearance.
When a cylinder is to be rebored, the boring bar should be set true or central to the circumference of the counterbore, so that the bore of the cylinder may be brought to its original position with reference to the bore of the stuffing box.
Cylinders require lubricating, both to avoid friction and wear of the cylinder bore, as well as of the valve and valve seat. The amount of lubrication required depends upon the degree of tightness of the piston rings, upon the speed of the piston, upon the amount of pressure of the valve to its seat, and upon the method of operating the side valve.
Cylinders with releasing valve gears require freely lubricating, because the closure of the valve depends upon the dash pot, and undue friction retards the closing motion.
The less the movement of the valve at the moment of its release, the easier it is to move it, because the friction is less, and less lubrication is required.
Cylinders are lubricated by automatic oilers placed on the steam pipe of the engine, the oil being distributed over the surfaces by the steam.
Cylinder oilers sometimes have a pump to force the oil in, and in others the steam in the oiler condenses, and the water thus formed floats the oil over the top of a tube, or up to an orifice through which the oil gradually feeds as the condensation proceeds.
In other oil feeders, the feed is regulated by increasing or diminishing the opening through which the steam passes from the cup to the steam pipe.
Sight oil feeders are those in which there is a glass tube or body, in which the passage of the oil can be seen as it drops.
Cylinder cocks are employed at each end of the cylinder to let out the water that condenses from the steam when admitted to a cold or partly cooled cylinder. The two cocks are usually connected together by a rod, so that both may operate together.
Cylinder relief valves are valves at each end of the cylinder to relieve the cylinder from the charges of water that sometimes enter from the boiler with the live steam.
Steam ports give a quicker admission in proportion as their length is increased, and this reduces the amount of valve travel, and are sometimes given a length equal to the diameter of the cylinder bore.
The bottoms of the steam ports are sometimes so placed as to be below the level of the cylinder bore, so as to drain off the water of condensation of the steam.
Rule to find the required area of steam port.
Multiply the area in square inches of the piston, by the number opposite to the given piston speed in the following table:
| Speed of piston in feet per minute. |
Number by which to multiply the piston area. |
| 100 | 0.02 |
| 200 | 0.04 |
| 300 | 0.06 |
| 400 | 0.07 |
| 500 | 0.09 |
| 600 | 0.1 |
| 700 | 0.12 |
| 800 | 0.14 |
| 900 | 0.15 |
| 1,000 | 0.17 |
[II-374]The cylinder exhaust port must be open when the valve is at the end of its travel, to an amount equal to the width of the steam port, but what this width will be in any given case depends upon the width of the bridges, the amount of the steam lap and the travel of the valve, as will be explained with reference to the slide valve.
Jacketed cylinders are those in which there is a space around the cylinder that is filled with live steam.
The object of jacketing is to prevent the loss of heat from the steam within the cylinder by radiation. The steam in the jacket should be received direct from the boiler, and should not be drawn from the jacket into the steam chest because the jacket reduces its temperature and condenses it.
The water of condensation of a steam jacket should not be allowed to accumulate in any part of the jacket, but should drain off and pass back to the boiler. To render the jacket as effective as possible, it should extend from end to end of the cylinder, the exhaust steam pipe leading directly away, so as to have as little communication with both the cylinder and the jacket as possible.
The jacket should have open communication with the boiler at all times, so as to have the pressure in the jacket at the same pressure as that in the steam chest, while the cylinder being kept hot, it will be unnecessary to blow steam through in order to warm the cylinder when starting the engine. The steam should enter the jacket at the highest point, so as to prevent the accumulation of air in the jacket. Or, if the steam is admitted at some other point, it should be so arranged as to permit its thorough circulation in the jacket. When a jacket is used, the metal of the cylinder body should be as thin as possible, because the transmission of heat through the metal is, both in time and quantity, inversely as the distance or thickness passed through.
The steam in the jacket should be as dry as possible, so that all wet steam admitted during the live steam period may be evaporated by the heat received from the steam in the jacket. The outside of the jacket should be thoroughly protected from cooling by being lagged or clothed with felt or some other material that is a non-conductor of heat.
From experiments made by Mr. Charles A. Smith, of St. Louis, it was found that the amount of variation of temperature that occurred during the stroke in a locomotive cylinder was inversely proportional to the speed of engine revolution, which shows the advantages of jacketing cylinders and of lagging them, as well as the advantage of a high rotative speed.
A lagged cylinder is one clothed, which is sometimes done with wood or metal strips, leaving an air space around the cylinder, while in others this space is filled with felt or some non-conducting material.
Experiments made by Charles E. Emery gave the following general results: The thickness of the pipes and of the non-conducting materials was kept constant.
Hair felt was the best non-conducting material of all those tested, and the value of a thickness of two inches of hair felt was taken as unity and the maximum.
The value of two inches of mineral wool as a non-conductor was 0.832 of hair felt; two inches of mineral wool and tar was 0.715. Two inches of sawdust, 0.68; two inches of a cheaper grade of mineral wool, 0.676; charcoal, 0.632; two inches of pine wood, across the grain, 0.553; two inches of loam, 0.55. This was from the Jersey flats, and almost all vegetable fibre not yet become compact. Slaked lime from the gas works, expressed decimally, with hair felt as unity, 0.48; coal ashes, 0.345; coke, only 0.277, the same as used for fuel; two inches of air space, only 0.136, which dashes a great many people’s hopes, and is as interesting as any part of the data; two inches of asbestos, 0.363; two inches of Western coke, about the same as the other coke; two inches of gas house charcoal, 0.47.
These are very interesting, particularly so this matter of an air space. It has been supposed that an air space around a pipe is as good as anything we can have. The fact is, convection or circulation takes place; the air is cooled on one side of the space, descends, and rises on the other, and it is necessary to break up the air space, and that undoubtedly accounts for the efficiency of these different materials. It is the air probably that is the non-conductor; but it should be kept quiescent instead of being allowed to circulate. The air space itself is of very little value until the circulation is prevented.
In calculating the power of an engine it is the piston speed that is taken into account, and not the length of the stroke, the latter being used merely in order to obtain the piston speed.
Long strokes are usually employed upon engines running at moderate piston speeds, as from 300 to 500 feet per minute, and short strokes for piston speeds from 400 to 800 feet per minute.
The Porter Allen engine has been run noiselessly at 1,100 feet per minute.
In determining the stroke of an engine the nature of the valve-operating mechanism is taken into account.
In releasing mechanisms, or those in which connection between the eccentric rod and valve spindle is broken in order to permit the valve to close quickly, too high a speed of revolution may cause the tripping mechanism to fail to act, hence a high piston speed is obtained by means of employing a comparatively long stroke.
In positive valve gears, or those in which the valve is controlled throughout the whole of its movement by the eccentric, the valve mechanism may operate quicker without danger of missing, hence the piston speed may be greater.
When the stroke equals the diameter of the cylinder bore, the cylinder presents the least amount of exposed surface in proportion to its cubical contents.
To obtain the same amount of expansion in a short as in a long stroke engine, the steam must be expanded through an equal proportion of the stroke; thus, if the steam is cut off at half stroke in both cases, the amount of this expansion will be equal.
Pistons are made an easy fit to the cylinder bore, a steam-tight fit between the two being obtained by means of the piston rings.
Solid pistons are provided with snap piston rings.
A snap piston ring is one that is larger in diameter than the cylinder bore, and is closed in to get it into the cylinder, while it depends on its own spring outwards for its fit to the cylinder bore, having no supplementary rings or springs to force it out.
Piston rings that are expanded by supplementary springs should be tapering in thickness, the thickest part being opposite to the split, and the thinnest at the split. This causes the ring to conform itself to the cylinder bore, and makes it sit more evenly around its whole circumference. These rings are made larger in diameter than the cylinder bore, in proportion of about 1⁄8 inch per foot of diameter, the split being closed when the ring is sprung into place in the cylinder. But if made of brass, the split must be left open enough to allow for the expansion, or otherwise the ring expanding more than the cylinder will seize and cut single.
The split of a piston ring should be placed on the bottom of the piston (in a horizontal engine), so that the piston head, in resting on the cylinder bore, will cover up the opening of the ring.
When two or more rings are employed, the splits may be placed on the lower half of the cylinder, so as to cover up their splits as much as possible.
The follower of a piston is a plate or cover that is employed to hold the piston rings in place, and the piston rings should be so fitted that the follower should be bolted firmly up, or otherwise the bolts may come loose and work out, and getting between the piston and the cylinder cover, may cause the piston to knock the cylinder cover out.
Piston followers are necessary when the rings are set out by springs or other parts adjustable within the piston head. Snap piston rings, however, permit the use of a solid piston, dispensing with the need for a follower.
The effectiveness of a piston ring may be tested, when the construction of the engine will permit it, by disconnecting the valve for the head end, setting it so that it covers the port, and then taking off the cylinder cover at the head end and admitting[II-375] steam through the crank end steam port, when any leak in the piston rings will be seen by the escape of the steam.
Piston rods should be of slightly diminishing diameter at the ends, so that the wear shall not leave a shoulder at each end of the rod.
In determining the diameter of the piston rod, allowance is made for turning it occasionally in the lathe to restore its parallelism, the wear reducing its diameter more in the middle than at the ends. The diameter of a piston rod is found in practice to range between one-sixth and one-tenth the diameter of the cylinder bore.
Steel piston rods wear better than those of wrought iron, being free from scaly seams which are apt to cut the packing and cause the rod to wear in grooves.
The best method of securing a piston rod to a piston head and to the cross head is by a taper seat and a key, so that no nut is needed, and the cylinder cover need not have a recess to receive the nut when the piston is at the end of the stroke, and the amount of clearance is correspondingly reduced.
Piston head key ways are sometimes given so little clearance that the key completely fills the keyway when driven fully home. This prevents the edges of the keys from bulging into the clearance space in the keyway, which action is apt to cause the key to loosen in time. The key should have a safety pin at its small end.
When piston rods are threaded into the cross head, or into the piston, the threads are made an easy fit, and taper seats or split hubs secured by clamping screws are relied upon to keep the rod true to the cross head or piston, it being found that the screw alone cannot be relied upon for this purpose.
Piston rod packing, of fibrous or similar material, should be cut in rings that will not quite fully envelop the piston rod, and the first ring should be placed with its split upwards. After two or three rings have been inserted, each having its split at a different part of the bore, so as to “break joints,” the gland should be screwed up enough so as to carry the packing home to the back of the stuffing box. This process should be continued until the stuffing box is filled for about two-thirds of its depth, when the gland may be screwed home.
The gland should be screwed up quite evenly, so that the packing in the stuffing box shall be compressed equally all around the rod, and will not cause the gland to bind on the rod or in the stuffing box bore.
The wrench should be applied first to one nut, giving it a turn or two, and then to the other, and after the gland is firmly home the nuts should be eased back about two turns.
When a gland requires packing, it is proper to take out all the old packing that has become hard and set.
A leak in piston rod packing may sometimes be remedied by taking out three or four rings of the packing and reversing it.
If the packing is tightened up while the engine is running, it should be done very gently and evenly, as a very little screwing up may stop the leak, while excessive screwing produces undue friction.
Piston rods are in some of the most advanced practice packed with metallic packing, or packing composed of soft metal. In some forms of metallic packing the construction is such that the gland and packing do not attempt to restrain the line of motion of the piston rod, this duty being left to the guide blocks and guide bars, where it properly belongs.
In engines having Corliss frames, the cross head is provided with shoes and adjusting screws, to take up the wear.
When guide bars are shaped thus ![]() the cross head is provided
with gibs (usually of brass composition) to take up the wear.
the cross head is provided
with gibs (usually of brass composition) to take up the wear.
In either case care must be taken to make the adjustment correct, and thus keep the piston rod in line. The shoes or gibs should not bear hard upon the guides, but be an easy sliding fit without lost motion.
Cross head pins should be kept eased away on the two parts of their circumference which are within the connecting rod brasses or boxes and near the joint faces of the same. This is necessary because the wear is greatest on the crowns of the boxes, and the pins are apt to wear oval. In some engines, the surface of the pin is cut away, but if it is not, and the pin can be revolved in the cross head, it is a good plan to give it half a turn occasionally, which will keep it round.
The guide bars of an engine require to be set exactly in line with the axis of the cylinder bore, so that they may guide the piston to travel in a straight line. They should be an easy sliding fit to the cross-head guide.
The top bar is more difficult to lubricate than the bottom one, especially when it receives the most pressure, as is the case when the top of the fly-wheel runs towards the cylinder.
Cast iron guide bars wear better than either brass, iron, or steel ones, so long as they are properly lubricated. The face of each guide bar should be cut away, so that the ends of the cross head guides will travel past it. This will prevent a shoulder forming at the ends of the bar as the face wears away. Such shoulders are apt to cause a knock as the connecting rods are lined up, because in the lining the connecting rod is restored to its original length, and the path of the cross-head guides along the bars may be altered.
There are two principal kinds of connecting rods, the “strap ended” and the “solid ended.” The solid ended wear the best, but are more difficult to get on and off the engine.
Connecting rod straps are secured to the stub ends (as the ends of the rod are called), either by bolts or by one or two gibs, and the brasses are set up by a taper key or wedge.
The taper for connecting rod keys is about an inch per foot.
The angularity of a connecting rod is a term that applies to its path of motion, which is (during all parts of the stroke except on the dead centre) at an angle to the line of engine centres. The effect of this angularity is to cause the piston motion to be accelerated at one part of the stroke and retarded at another, thus causing the point of cut-off to occur at different points of the two strokes.
The direction of the variation is to cause the point of cut-off to occur later on the stroke when the piston is moving from the head end of the cylinder towards the crank.
The amount of variation caused in the two points of cut off by the connecting rod depends upon the proportion that exists between the length of the crank and that of the connecting rod, and is less in proportion as the length of the connecting rod is greater than that of the crank.
An ordinary length of connecting rod is six times the length of the crank, or six cranks, as it is commonly termed.
Fig. 3296 represents a cylinder, piston and rod, cross head, connecting rod, and crank.
The piston b is shown in the middle of the cylinder, the cross head at e, and the crank pin at b, instead of being at g′, as it would but for the connecting rod, or if the connecting rod was infinitely long.
Now take a pair of compasses and set it from b to e, and then try it from a to d, and from c to f, and it will be seen that the three cross head positions d, e, and f correspond correctly to the three piston positions a, b, c. Then take a pair of compasses and set them to the length of the connecting rod (from e to b) and try them from d to a, from b to e, and from c to f, and it will be seen that crank pin positions a, b, and c correspond to cross head positions d, e and f, and therefore that the crank is not at half[II-376] stroke when the piston is in the middle of the cylinder. Take these same compasses, and resting one point at (g′) mark the arc h, and that is where the cross head would be when the crank was at (g′). Now then we see that the connecting rod causes the piston to move slower while running from a to b than it does while running from b to c.
The various events which are governed by the D slide valve of a steam engine are as follows:
The live steam period is that during which the steam is admitted from the steam chest into the cylinder and the steam admitted during this period is termed live steam.
The point of cut off is that at which the valve closes the steam port, and the admission of steam into the cylinder is stopped, hence the point of cut off is at the end of the live steam period.
The period of expansion is that during which the steam is allowed to expand in the cylinder, and therefore begins at the point of cut off, and ends at the point of release.
The point of release is that at which the valve opens the port and permits the steam to escape.
The point of compression is that at which the exhaust port is closed, which occurs before the piston has reached the end of its stroke; the steam that has not passed out of the cylinder is therefore compressed, the compression continuing until the valve opens for the lead.
The lead of the valve is the amount the port is open to the live steam when the crank is on the dead centre.
The point of admission is that at which the port opens for the live steam to enter, and it follows that the lead and compression both act as a cushion, arresting the motion of the piston when it reaches the end of the stroke.
Cushioning begins, however, at the time the exhaust port is closed enough to arrest the escape of the steam, while compression begins when the valve has closed the exhaust port.
The construction of a common slide valve is shown in Fig. 3297, in which the valve is shown in its mid-position. p p are the cylinder steam ports (as the openings through which the steam passes from the steam chest to the cylinder are termed), and at x is the cylinder exhaust port, through which the steam escapes from the cylinder. z is the valve exhaust port or exhaust cavity.
The lip of a valve is the width of its flange face, or the distance l, which is measured from the steam edge a to the exhaust cavity z. At the other end of the valve, h is the lip extending from the steam edge b to the exhaust cavity.
Steam lap is the distance the steam ends (or the steam edges as they are called) a, b overlap the steam ports, this distance being shown on the ends of the valve at a c. If the valve had no steam lap, its steam edges would just cover the ports, as denoted by the dimension w.
Exhaust lap is the amount the exhaust cavity z overlaps the bridges q q′, as at p, r.
Unequal steam lap is given to cause the point of cut off to occur at equal points in the piston stroke; thus in the figure there is more steam lap at the head end than at the crank end of the valve. But unequal lap could also be given in order to greatly vary the points of cut off for the two piston strokes, if such was desired.
Unequal exhaust lap may be given to equalize the point of release, or to equalize the points of compression.
The head end of the valve (or of the cylinder) is that which is furthest from the crank shaft, the other end, or that nearest to the crank shaft, being termed the crank end.
The action of a common slide valve may be traced as follows:
Port a, open to the amount of the lead.
Port a, full open for the admission.
Port a, closed off for cut.
Valve opening port a, for the exhaust.
Port a, full open for the exhaust.
Suppose the port a to be at the head end of the cylinder and open to the amount of the lead with the crank on the corresponding dead centre, and if the valve travel be made equal to twice the lap and the lead, the various positions of the valve will be as marked in Figs. from 3298 to 3302; the event corresponding to each valve position being stated in the figures.
The term port applies strictly to the area of opening of the steam passage where it emerges upon the valve seat. The term steam passage includes the full length of the opening from the cylinder bore to the face upon which the valve is seated.
A double ported steam port is one in which there are two openings or steam ports, leading into one steam passage.
A double ported valve is one in which there are two ports at each end of the valve. These two ports in some cases admit steam to a single cylinder port, and in others to two steam ports, terminating in one steam passage.
A griddle valve is one that has two or more ports at each end upon a seat that has two or more ports for each steam passage.
Double ported valves are employed in some cases to increase the admission of live steam to the cylinder, and in others to increase the exhaust openings also. The effectiveness of a double ported valve is mainly valuable at the beginning of the stroke, and is especially valuable in cases when the travel of the valve is diminished to hasten the point of cut off, because in such cases the outer edges of the valve do not open the steam port to its full width, and a single port is apt to wire draw the steam. By the employment of more than one port, or several ports, a sufficient admission may be obtained with less valve travel.
The Allen double ported valve is one in which the second port increases the port opening for the admission only, as shown in Fig. 3303, in which the valve is moving in the direction of the arrow; the port k will receive steam through the opening at g, and from a port passing through the valve, the steam entering it as shown by the arrow. The second port forms part of the lap of the valve, and enables the travel to be short enough to be cut off at early points in the stroke, without employing so much steam lap as to widely distort the points of cut off, this latter being a defect of the D valve.
Webb’s patent slide valve is circular, and is so arranged as to be free to revolve in the hoop of the valve rod, the effect being that the valve moves around, or to and fro in the hoop, without any special mechanism to produce such movement, and the result is, that the valve and port facings wear smooth and even without any tendency to become grooved.
A balanced valve is one in which means are employed to relieve the back of the valve of the steam pressure, and thus prevent its being forced to its seat with unnecessary pressure.
In some of the most successful balanced valves this is accomplished by providing a cover plate, which may be set up to exclude the steam from the back of the valve which works (a sliding fit) between the valve face and the face of the cover plate. Such a method of balancing is sufficiently effective for all practical purposes, if the following conditions are observed: The valve rod must be accurately guided so as to avoid side strains; the valve must fit accurately to its seat and to the cover plate, and the adjustment so made that the valve slides freely at first, being steam tight, and yet allowing room for lubrication to enter. When the travel of a valve, balanced by a cover plate, is varied to alter the point of cut off, the construction must be such that the ends of the valve at the shortest stroke pass over the ends of the seat and cover plate faces, or otherwise the middle of the seat and cover plate faces will wear hollow.
The Buckeye, Porter-Allen, and Straight-Line Engines are examples of practically balanced valves. The first of these has a balancing device that follows up the wear; the second has an adjustment whereby the cover plate may be set up to take up the wear; and in the third the wear is reduced to a minimum, by accurately fitting and guiding the parts.
The construction of the valve in the Straight-Line Engine is shown in Fig. 3304, in which b represents the cylinder bore; the valve v rests on a parallel strip n, and on its top rests the parallel strip m, the pressure relieving plate p is set up firmly against the pieces m n, whose thicknesses are such as to leave the valve a working fit between the faces of r r and of p.
[II-378]Instead of the valve sliding on a flat face, it may work upon a shaft or spindle as a centre, its face moving in an arc of a circle, and its action will be the same as a flat valve having the same proportions. Fig. 3304a represents a valve v of this construction, whose shaft is at s, a being an arm fast on s, and driven by the eccentric rod r. To find the necessary amount of travel for such a valve, we draw lines, as f, g, from the inner edges of the steam ports, through the centre of the shaft s, and also draw an arc through the centre of the eye of arm a, and where lines f g cut the arc, as at d and e, are the extremes of motion of a.
A piston valve acts the same as a flat or plain (D) valve, having the same amount of lap lead and travel. In Fig. 3305 we have a cylinder with a flat valve on one side and a piston valve on the other, the head end ports being about to take steam, and it is seen that the eccentrics occupy the same positions for the two valves. The steam ports are, for the piston valve, annular grooves provided in the bore in which the valve fits. The piston valve is balanced because it receives its steam pressure on the ends, but it will not follow up its wear as the flat valve does, hence it is liable to leak.
Meyer’s cut off valve is constructed as shown in Fig. 3306, m being the main valve, and v v the two cut off valves, whose sole duty is to cut off the steam at an earlier point than the main valve would do. If the engine is to have a fixed point of cut off, or, in other words, if the cut off is always to occur at some one particular point in the stroke, the valves may be set to do so, and equalize the points of cut off.
Variable points of cut off with the Meyer’s valve may be obtained by shifting the position of the eccentric that operates the cut off valve, but it is usually done by means of moving the valve by a right and left hand screw, such as shown in Fig. 3306. The cut off eccentric is set ahead of the main eccentric, so that the cut off valve will close the ports before the main valve would do so; thus, in the figure the cut off valve is shown to have effected the cut off for port a by the time the main valve has fully opened port a, and is reversing its motion. If the engine requires to reverse its motion, the cut off eccentric is set exactly opposite to the crank, but otherwise, it may be set 8 or 10 degrees either ahead of or behind the crank, but if set too little ahead of the crank, the port may reopen after the cut off has been effected.
Gonzenback’s cut off valve is constructed as in Fig. 3307, the steam chest having two compartments. a, a are the cylinder steam ports, c the main valve, and e the cut off valve, whose ports (as g) are made wider than the ports f.
Reducing the travel delays the point of cut off in the Gonzenback valve, whereas in the common slide valve it gives an earlier cut off.
When a single eccentric is used, it is simply termed the eccentric. If a cut off valve (or two cut off valves) are used upon the engine, then the eccentric that works the main valve is called the main eccentric, while that which works the cut off valve or valves is called the cut off eccentric. The main valve is that which works on the cylinder face; the cut off valve is that which effects the cut off.
A shifting eccentric is one that is moved across the shaft so as to alter its amount of throw, and, therefore, the amount of valve travel, the effect being to vary the point of cut off.
In engines where a constant amount of lead is given, or in other words, when the eccentric position is intended to be fixed, the eccentric should be secured to the crank shaft by a feather or key sunk into the crank shaft so as to prevent the eccentric from moving, while enabling it to be taken off and replaced without requiring[II-379] any operations to adjust its position with relation to the crank.
The feather should fit tight on the sides, as well as on the top and bottom, and may have a slight taper on the sides, which will make it easier to fit the featherway or keyway to the feather, and easier to put the eccentric on or take it off.
By this means the eccentric cannot shift, and may be replaced after being taken off without having to set the whole valve motion over again.
When the amount of valve lead or of compression is varied to suit the speed at which the engine is to run, or to aid the counterbalancing of the engine, a feather cannot be used because it will not permit the eccentric to be moved to effect the adjustment.
Set screws possess disadvantages, inasmuch as that the point of the set screw may leave an indentation, which, if the eccentric is moved a trifle, may cause the set screw point to fall back into the old indentation, thus rendering it difficult to make a small adjustment of eccentric position.
An eccentric is the exact equivalent of a crank having the same amount of throw, as may be seen from Fig. 3308, in which the outer dotted circle represents the path of the crank and the inner one the path of the centre of the eccentric. A small crank is marked in, having the same throw as the eccentric has, and the motion given by this small crank is precisely the same as that given by the eccentric whose outer circumference is denoted by the full circle.
Considering the motion of both the crank and the eccentric, therefore, we may treat them precisely the same as two levers, placed a certain distance apart, revolving upon the same centre (the centre of the crank shaft), and represented by their throw-lines.
In Fig. 3309, let the full circle e e represent an eccentric upon a shaft whose centre is at c, and let the centre of the eccentric be at e. The path of revolution of the eccentric centre will be that of the dotted circle whose diameter is b, d. As the eccentric is in mid-position (e being equidistant from b and d), the valve will be in mid-position as denoted by the full lines at the bottom of the figure. Now suppose the eccentric to be revolved on the centre c, until its centre moves from e to v, its circumference being denoted by the dotted circle a a, and if we draw from v a vertical line cutting the line b, d at f, then from c to f will be the distance the eccentric would move the valve, which would then be in the position denoted by the dotted lines at the bottom of the figure. It becomes clear then that if we suppose the eccentric to have moved from mid-position to any other position, we may find how much it will have moved the valve by first drawing a circle representing the path of the centre of the eccentric, next drawing a line (as b d) through its centre, and then drawing a vertical line as (c e) through its mid-position and also a vertical line from the eccentric centre in its new position, the distance between these two vertical lines (as distance c f in the figure) being the amount the eccentric will have moved the valve.
It may have been noticed that the diameter of the eccentric does not affect the case, the distance b d, or the diameter of the circle described by the centre of the eccentric, being that which determines the amount of valve motion in all cases. This being the case, we may use the circle representing the path of the eccentric centre for tracing out the valve movement without drawing the full eccentric, and the diameter of that circle will of course equal the full travel of the valve.
[II-380]The position of an eccentric upon a shaft is often given in degrees of angle, which is very convenient in some cases. If a valve has no lap or lead, the eccentric will stand at a right angle or angle of 90 degrees when the crank is on the dead centre.
The division of a circle into degrees may be explained as follows:
Suppose we take a circle of any diameter whatever and divide its circumference into 360 equal divisions, then each of these divisions will be one degree. The number 360 has been taken as the standard, and this being the case, there are 360 degrees in a circle, in a quarter of a circle there will therefore be 90 degrees, because 90 is one quarter of 360. By means of dividing a circle in degrees therefore we have a means of measuring or defining any required portion of it.
In Fig. 3310 the degrees of a circle are applied for defining the relative positions of a crank and an eccentric. As the zero position of the crank is on a dead centre, it is so placed in the figure, while as the zero position of the eccentric (which is for a valve having no steam lap) is at 90 degrees from the crank, therefore the dotted circle representing the path of the eccentric centre has its o or zero point at 90 degrees from the crank. Now suppose the eccentric centre stood at v and the eccentric throw line at c v, and it will stand at 30 degrees from o, hence the angular advance of the eccentric is in this case 30 degrees, or in other words, it is 30 degrees in advance of its zero position, or the position it would occupy when the crank is on the dead centre and the valve has no lap and no lead.
If we measure the distance apart of the crank and the eccentric in degrees, we find it is 120 degrees, hence place the crank where we may, we can find the corresponding eccentric position because it is 120 degrees ahead of the crank. The sign for degrees is a small ° placed at the right hand of the figures and slightly above them; thus, thirty degrees would be written 30°.
Although not strictly within the line of duty of an engineer or engine driver, he is nevertheless sometimes called upon to find out how a valve of given proportions will dispose of the steam, or what proportions to give to a valve to accomplish certain results.
This is easy enough when either the travel of the valve or the amount of the lap and the width of the port are given, but if the width of the port alone is given, and all the other elements are to be found, it becomes a more difficult problem.
An engineer, however, is rarely called upon to solve the question from this stand-point, which properly belongs to the draughtsman or engine designer.
If the amount of valve travel is given, however, all the other elements may readily be found by the following construction:
Suppose that in Fig. 3311 a D valve is to be designed to cut off the steam when the piston has travelled from position b′ to r′, or at three-quarters of its stroke. Then to find the position the crank pin will be in when the cut off occurs, we draw a circle, b d, representing the path of the crank on the same scale that the length of the piston stroke is represented. The straight line from b to d will, therefore, represent the piston stroke without drawing the piston or cylinder at all (this being done in the figure to make the explanation clear). When the crank is on its dead centre, b, the piston, will be at b′, and the valve in the position shown (supposing it to have no lead). As soon as the crank and valves begin to move, the steam will enter steam port a, and to find where the crank will be when the piston is at three-quarters stroke, and is, therefore, in position r′, we mark a point at r three-quarters of the distance from b to d. Then, taking no account of the length of the connecting rod, we draw a vertical line y from r to the circle, and this line gives at h the position the crank will be in when the piston is at r. We have so far, therefore, that while the piston travels from b′ to r′, the crank will travel from b to h. Now, it will be found that if we set a pair of compasses from b to f, which is half-way from b to h, and then rest the compasses at d, and mark an arc v, then a line from v to the centre of the crank will give us the proper position of the eccentric. As the centre of the crank pin and also the centre of the eccentric both travel in a circle, we may, therefore, take a circle having a diameter equal to twice the throw of the eccentric, (or, what is the same thing, equal to the full travel of the valve), and let it represent the paths of both the eccentric centre and the crank pin centre, the latter being drawn to a scale that is found by dividing the length of the piston stroke by the travel of the valve; thus, if the travel is 3 inches and the stroke 30 inches, the diameter of a 3 inch circle will represent the valve travel full size, and the piston stroke one-tenth full size, because 30 ÷ 3 = 10. It has been shown on page 376 that the length of the connecting rod affects the motion of the piston by distorting it, and it is necessary to take this into account in constructing the actual diagram, which may be done as follows:
The valve travel and point of cut off being given, to find the required amount of lap, there being no lead, draw a circle equal in diameter to the travel of the valve, and draw the line of centres b d, Fig. 3312; mark on the line of centres a point r, representing the position the piston is to be in at the time the cut off is to take place.
Set a pair of compasses to represent the length of the connecting rod on the same scale as the circle b d represents the path of the crank; thus, if the connecting rod is three times the length[II-381] of the stroke, the compasses would be set to three times the diameter of the circle b d.
A straight line from b to d and passing through the centre c of the crank will represent the line of centres of the engine, which must be prolonged to the right sufficiently to rest the compasses on it and draw the arc y, which will give at h the position of the crank when the piston is at r, and the cut off is to occur.
We have thus found that the amount of circular path the crank will move through from the dead centre to the point of cut off is from b to h, and as the eccentric is fast upon the same shaft, it will, in the same time, of course, move through the same part of a circle.
One half of its motion will be to open and one half to close the port, so that we may by means of the arcs at f get the point f, which is midway between b and h, and with the compasses set from b to f, mark from d the two arcs v and v′ whose distance apart will obviously be the same as from b to h.
Then from v to v′ draw the line p, and from this line to the centre c of the crank shaft is the amount of steam lap necessary for the valve, while from this line (p) to d is the width of the steam port.
The proof of the diagram is as follows:
When the crank is on the dead centre, the centre of the eccentric is at v, its throw line being represented by the line from v to c, and the valve is about to open the port as shown in the figure.
While the eccentric is moving from v to d, the valve will move in the direction of the arrow and will fully open the port, while the crank pin will move from b to f.
Then, while the crank moves from f to h, the eccentric will have moved the valve to the position it occupies in the figure, having closed the port and effected the cut off.
We have here found the amount of lap and the position of the eccentric necessary for a given point of cut off when the latter is given in terms of the piston stroke. If, however, the point of cut off had been given in terms of the crank pin position, we might find the required amount of lap at once, by simply drawing a line from the centre b, the point to h where the crank pin is to be when the cut off occurs.
From this line we could then draw the dotted circle g, and just meeting the line p, which would give the eccentric position.
To find the piston position, the arc y would require to be drawn by the same means as before.
If the valve is to have lead, the diagram may be constructed as in[II-382] Fig. 3313, in which the circle has a diameter equal to the travel of the valve and the cut off is to occur when the piston is at r and the crank at h.
When the valve is at the end of its travel and has fully opened the port, the eccentric will be at d, hence from d we mark an arc g distant from d to an amount equal to the width of the steam port, drop the vertical m from g, and at its lower end v′ is the position of the eccentric centre at the point of cut off. Then draw a line p, distant from m equal to the lead, which will give at v the position of the eccentric when the crank is on the dead centre, and the valve is open to the amount of the lead. The lap is obviously the distance from the centre c of the crank shaft to the arc g.
We have here found all the points necessary except the point at which the valve will open the port for the lead, and this we may find by setting a pair of compasses to the radius b h (or to radius v v′, as both these radii are equal), and from v as a centre, mark at a an arc, which will give the crank pin position at the time the port first opens for the lead, or in other words it will give the position. The proof of the construction is, that if we set the compasses to the distance between the crank pin position on the dead centre and the point of cut off (or from b to h), we may apply the compasses to the points v, v′, which represent the eccentric position when the port is opened to the amount of the lead, and when the cut off occurs.
If the point of cut off only is to be found, we mark from c, Fig. 3314, an arc g representing the amount of valve lap and arc s representing the lead. A vertical p gives the eccentric position v when the crank is on the dead centre at b, and a vertical m from g gives at v′ the eccentric position at the point of cut off. Then with the compasses set to the points v v′, we may mark from b an arc, locating at h the position of the crank at the point of cut off, and from this with compasses set to represent the length of the connecting rod on the same scale as the circle represents the path of the crank, we may, from a point on the line of centres, mark an arc y giving at r the piston position at the point of cut off.
When, therefore, the lap is given, we mark it from the center c of the crank shaft, and find the other elements from it, whereas, when the lap is to be found, we mark the width of the port from the end d of the valve travel, and find the other elements from that.
A proof of all the constructions is given in Fig. 3314, in which the letters of reference correspond to those in the previous figures, and the positions of the parts are marked in degrees of angle.
To find the piston position at the point of cut off, measured in inches, of the piston stroke it must be borne in mind that as the circle b d represents the full travel of the valve, the diagram gives all the positions of the eccentric and valve full size, but that as it represents the crank path on a reduced scale, therefore we must multiply the measurement on the diagram by that scale.
Suppose, for example, that the piston stroke is 10 inches, and the valve travel 21⁄2 inches, and the circle being 21⁄2 inches in diameter, is, when considered with relation to the eccentric motion, full size, but when considered with relation to the piston or crank motion, it is only 1⁄4 the size, hence to find the piston position at the time of cut off, we must multiply the distance from b to r by 4.
The ordinary mechanism employed to enable a stationary engine to be reversed or run in either direction is the Stephenson link motion. Other forms of link motion have been devised, but the Stephenson form has become almost universal.
Fig. 3315 represents this link motion or reversing gear with the parts in position for the full gear of the forward motion, and Fig. 3316 represents it in full gear for the backward motion.
The meaning of the term full gear is that the parts are in the position in which the steam follows the piston throughout the longest or greatest part of the stroke. When in full gear the link motion operates the valve almost precisely the same as if the eccentric rod was attached direct to the valve spindle and no link motion was used.
Besides enabling the engine to run in both directions, however, the link motion provides a means of reducing the amount of valve travel and thus causes the live steam to be cut off earlier in the piston stroke, thus using the steam more expansively. This is done by moving the reversing lever more upright, the earliest point of cut off being obtained when it is upright and the latch is in the notch marked o on the sector in Fig. 3315. If with the engine standing still we move the link motion from full gear forward to full gear backward and watch the valve, we shall find that the valve lead increases as the reversing lever approaches the upright position, or mid gear as it is termed, and that after passing that point it gradually diminishes again, the valve being so set that the lead is the same for full gear forward as it is for full gear backward.
The reversing lever is used to move the link into the required position and to hold it there (the end of the latch fitting into the notches in the sector being the detaining or locking device); as the link is suspended by its saddle pin s and the link hanger, therefore its motion is to swing or partly rotate on the pin s, and at the same time ending in the arc of a circle whose centre of motion is in the pin at the upper end of the link hanger which is pivoted to the lower arm of the lifting shaft (which is sometimes termed the tumbling shaft). It will clearly be seen that with the position the parts occupy in Fig. 3315, and the crank motion being in the direction of the arrow, the forward eccentric will move the top of the link to the right and therefore the valve will move to the right, while the backward eccentric will move the bottom end of the link to the left.
In full gear, however, the bottom eccentric rod has but a very slight effect indeed on the motion of the valve because both the link hanger and the link block will permit the link to swing on centre of the link block pin as a pivot. If now we turn to Fig. 3316 for the full gear backward, we shall see that these conditions are reversed and the backward eccentric becomes the effective one, being in line with the valve spindle. By shifting the link from one gear to the other, therefore, we have merely changed the direction in which the link will move the valve, and, therefore, the direction in which the engine would run.
In Fig. 3315 for the full gear the parts are shown in position, with the piston at the crank end of the cylinder, and the crank pin on the dead centre, and the eccentrics must be set as shown in the cut, the eccentric rods being open and not crossed. When, however, the crank is on the other dead centre and the piston at the head end of the cylinder, the rods will cross each other, and it is necessary to remember that the rods should be open when the piston is at the crank end of the cylinder. If, however, the running gear contains a rock shaft, or rocker (as is the case in American locomotives), then these conditions are reversed, and the eccentric rods will cross when the piston is at the crank end of the cylinder.
In setting the slide valve of an engine having a link motion, there are two distinct operations. First, to put the crank on the respective dead centres, which will be fully described on page 394 and need not be repeated; and second, to set the eccentrics in their proper positions on the shaft, and correct, if necessary, the lengths of the eccentric rods. The crank being on the dead centre, with the piston at crank end of the cylinder, the eccentric should be moved around on the shaft by hand until there is the desired amount of lead at the crank end port, and temporarily fastened there, a set screw usually being provided (in the eccentric) for this purpose. The lead is best measured with a wedge, w, Fig. 3315. The crank is then put on its other dead centre, and the lead for the head end port is measured. If the lead is to be made equal for the two ports (as is usually the case in horizontal engines) and it is found to come so, the valve setting for the forward gear is complete. If the lead is not equal, the forward eccentric rod or else the valve spindle must be altered so as to make the lead equal. In some engines adjusting screws are provided for the purpose of regulating the length of either the eccentric rod or else of the slide spindle; it does not matter which is altered. The link motion is then put in full gear for the backward motion, and, with the[II-384] crank on the dead centre (it does not matter which dead centre), the eccentric is moved by hand upon the crank shaft until there is the required amount of valve lead. The eccentric is then fastened on the shaft and the crank put on the other dead centre, and the lead tried for the other port, and made equal by lengthening or shortening the backward eccentric rod. It is to be noted that altering the length of the eccentric rod or of the valve spindle makes it necessary to reset the eccentric, as it affects the amount of lead at both ports; hence, if any alteration of rod length is made, the whole process here described must be repeated after each alteration of rod length.
An isochronal governor is one in which the two opposing forces are equal throughout the whole range of governor action, or, in other words, equal, let the vertical height of the plane in which the balls revolve or swing be what it may.
A dancing governor is one that acts spasmodically. Such an action may occur from undue friction in the parts of the governor or of its throttle valve.
The friction offers a greater resistance to starting the parts in motion than it does to keep them in motion after being started; hence, the parts are apt to remain at rest too long, and to move too far after being put in motion.
Rule to find the number of revolutions a governor should make. Divide the constant number 375.36 by twice the square root of the height of the cone in inches. The quotient is the proper number of revolutions per minute.
Example.—A governor with arms 301⁄2 inches long, measuring from the centre of suspension to the centre of the ball, revolves, in the mean position of the arms, at an angle of about thirty degrees with a vertical spindle forming a cone of about 261⁄2 inches high. At what number of revolutions per minute should this governor be driven? Here the height of the cone being 26.5 inches, the square root of which is 5.14 and twice the square root 10.28, we divide 375.36 by 10.28, which give us 36.5 as the proper number of revolutions per minute at which the governor should be driven.
The construction of the Pickering governor is as follows:
In Fig. 3317 it is shown in its simplest form, and in Fig. 3318 with the driving pulley and speeder (or engine speed regulating device) attached. This speeder consists of a spiral spring whose tension may be adjusted to more or less resist the rise of the governor balls, and thus enable the engine to run at a greater speed for a given amount of rise of the governor balls, hence by increasing the tension the engine speed is increased.
The adjustment of the spring tension is made by a worm actuating a worm wheel on a rod passing through the spring, and to which one end of the spring is attached, the other acting on an arm that projects into a slot in the governor spindle. It is obvious that the speeder can be adjusted while the engine is running.
In Fig. 3319 the governor is shown with the speeder and Sawyer’s valve, the latter enabling the governor valve to be opened or closed without affecting the rise and fall of the governor balls, which is done by operating the arm shown on the right, whose ends are provided with loops, so that a cord may be attached, enabling the engineer to operate the governor from a distance.
The safety stop or stop motion is shown on the right, Fig. 3320.
It acts to close the governor valve and stop the engine in case the belt that drives the governor should get off the pulley or break. This stop motion consists of a pulley suspended by a rod, and riding on the belt which supports its weight. Should the governor belt break, this pulley falls and severs the connection between the valve and the governor, closing the valve, and holding it closed. Fig. 3321 shows the governor in section to expose the construction of the valve. The valve v is what is termed a poppet or poppet valve, which is balanced, because the steam entering at i, and taking the course denoted by the arrows, acts equally on both ends of the valve and does not press it in either direction, while as the steam surrounds the valve it is not pressed sideways.
At b is a gland or stuffing box to keep the spindle or rod steam-tight. At a is the slot for receiving the arm from the speeder and from the stop motion.
p is obviously the driving pulley, imparting motion to the bevel wheels g, which drive the outer spindle s, the inner spindle s′ being connected to a. The balls are upon ribbon springs d, which are secured at their lower ends to a link fast to the spindle s.
The centrifugal force generated by the balls causes them to move outwards, their upper ends pulling down the cap to which they are secured, and this cap operates the valve.
Governors of this class are sometimes termed fly-ball governors.
The method to be pursued before starting a plain slide-valve engine depends upon what the engineer knows about the condition of the engine.
If he knows the engine is in proper running order, all that is necessary is to first attend to the oil cups and start them feeding.
Then, if it is necessary, move the crank into the required position to start it easily; open the waste water cocks to relieve the cylinder of the water that will be condensed from the steam when it enters a cool cylinder, and turn on the steam; giving the throttle valve enough opening to start the engine slowly.
The best position for the crank pin to be in to enable its starting easily is midway between the horizontal and vertical position (or, in other words, at an angle of 45° to the line of centres) and inclining toward the cylinder, so that when the engine moves the piston will travel toward the crank shaft.
There are two reasons why this is the best position for starting.[II-385] The first applies to all engines because there is a greater piston area for the steam to act on when the piston is moving toward the crank than there is when it is moving away from it. This occurs because the piston rod excludes the steam from a part of the face of the piston. The second applies to all plain slide-valve engines whose slide valves have equal laps and both steam ports of equal widths, because the live steam follows further on the stroke when the piston is moving toward the crank than it does when it is moving away from it, and it follows that more piston power is developed, and the engine is less likely to stop when passing the dead centre.
When first taking charge of an engine, it is proper, before starting it, to ascertain that it is in fair working order.
A complete examination of an engine should include a test of the fit of the piston to the cylinder bore, of the cross head to the guide bars, of the connecting rod brasses to the crank pin and cross head journals, and of the crank shaft to its bearings. It would also include a testing of the alignment of the crank shaft and of the guide bars, as well as the set of the valves and the adjustment of the governor.
The least examination permissible with a due regard to safety would be to move the engine throughout at least one full revolution by hand, and to see that the connecting rod brasses and the main bearings do not fit too tight to their respective journals, and to then start the engine slowly by giving it only enough steam to move it, keeping the hand on the throttle valve so as to be able to shut off steam instantly should it become necessary.
A thorough examination should be made in the following order:
First, slightly loosen the nuts on the crank shaft bearings and also the connecting rod keys.
Then move the fly wheel around until the crank points straight to the cylinder, which will bring the piston up to the outer end of the cylinder bore.
Take off the cylinder cover and also the follower from the piston head, and see that the piston rings are set out to fit the cylinder bore but not to bind it tight. Then bolt the follower up firmly in place again.
Take off the connecting rod and move the piston until it touches the cylinder cover at the other or crank end of the cylinder, and then draw a line across the side face of the cross head guide and on the guide itself.
Put on the cylinder cover and push the piston back until it abuts against it, and then make another line on the cross head guide and the guide bar, and these two lines will show the extreme positions to which the piston can be moved when the connecting rod is disconnected.
Next put on the connecting rod, carefully adjust the keys or wedges, so that the bores of the brasses fit easily to the crank pin and cross head pin, seeing that the oil holes are clear, and that oil will feed properly to the journals.
In making this adjustment it is a good plan, if there is any end play of the brasses on the crank pin, to set up the key or wedge until the rod can just be moved by hand on the pin, by first pulling the rod to one end of the pin, and then pushing it to the other.
In putting on the rod, it will be necessary to move the piston a trifle towards the crank.
In making the adjustment of the crank pin fit to the rod brasses, it is a good plan to drive the key home until the brasses are known to bind the crank pin, and then mark a line across the side face of the key and fair with the top face of the connecting rod strap, to then slacken back the key enough to ease back the brasses to a proper fit, and then mark another line on the key.
The first line will form a guide as to how much to slacken back the brasses to adjust the fit, and the second one will form a guide as to how much the key is moved when making a second adjustment,[II-386] if one should be found necessary after the engine has been running.
Similarly in adjusting the main bearing boxes to the crank shaft, either the nuts, or what are called leads, may be taken to adjust the fit. Leads are necessary when the joint faces of the brasses do not meet, but are left open so that the wear can be taken up while the engine is running.
It is better, however, to let the brasses abut together, so that it may be known that the fit is correct when the nut is screwed firmly home.
The method of taking a lead is as follows: The top brass is loosened, and between the joint faces of the brasses or boxes on each side of the shaft a piece of lead wire is inserted. For a shaft of, say, four inches in diameter, the lead wire will be about 7⁄16 inch in diameter, or for a 10 inch shaft the wire should be 1⁄8 inch in diameter, and should be as long as the brass. The nuts are then screwed firmly home, and the wire will be squeezed between the brasses and thus flattened on two opposite sides, the thickness showing how far the joint faces of the brasses are apart when the bore grips the journal.
A liner, fit strip, distance piece, or shim (all these names meaning the same thing) is a strip of metal placed between the joint faces of the brasses to hold them the proper distance apart to make a working fit of the journal and brasses, when the latter are firmly bolted up.
The fit of the top brass therefore depends upon the fit strip being of the proper thickness from end to end.
Now the lead wire is the gauge for the thickness of the fit strip, the latter being made a trifle thicker than the flattened sides of the lead.
If the lead is thicker one end than the other, or if one lead is thicker than the other, the fit strips must be made so, and the leads must be marked so that it may be known which way they were placed between the brasses so that the proper fit strip may be on the proper side of the brass, and the proper end towards the crank.
Another method that is adopted in the case of large brasses is to screw down the nuts until the brasses bind the journal, and then make a mark on the nut and on the bolt thread. The nut is then slackened back as much as the judgment dictates, and a note made of how much this is, the marks forming a guide.
As the wear takes place, and the nuts screw farther down, a new mark is made on the nut, so that it may always be known how much to screw up or unscrew the nut, to make a light adjustment.
To avoid heating, it is a good plan to press some tallow into the bottom or in one corner of the oil cup, and then pour in the oil used for ordinary lubrication. So long as the bearing remains cool, the oil will feed and the tallow remain.
If the bearing heats, the tallow will melt, and, having a heavier body, will give a more suitable lubrication.
To find if the connecting rod is of the right length to give, as it should do, an equal amount of clearance (or space between the piston and the cylinder cover) at each end of the stroke, move the fly wheel a trifle in either direction, and then move it back until the crank is on the dead centre, and draw a line across the cross head guide and guide bar, and the distance between this line and that drawn when the connecting rod was disconnected, shows the amount of clearance at that end of the cylinder. Then move the crank pin over to its other dead centre, and mark a line across the cross head guide and the guide bar, and the distance between this line and that drawn before the connecting rod was put on will show the clearance at this end of the cylinder.
If the clearance is not equal for the two ends, it should be made so by putting liners behind the connecting rod brasses so as to lengthen or shorten the connecting rod (according as the case may require), and equalize the clearance, while at the same time bringing the connecting rod keys up to their proper heights.
To test the set of the valve, the steam-chest cover must be taken off, the crank placed alternately on each dead centre, and the lead measured for each port.
An unequal or an equal degree of valve lead may be given by suitably altering the length of the eccentric rod, but when the lead is equal for the two ports, its amount must be regulated by moving the position of the eccentric upon the crank shaft.
Squaring a Valve.—A method not uncommonly pursued in setting a valve is to what is called square it before trying it.
This squaring process consists in so adjusting the length of the eccentric rod that the valve travels an equal distance over or past the steam edge of each steam port; but since the valve does not, when set to give equal lead, travel equally past each port, therefore the work done in squaring a valve is all thrown away, and may result in altering the eccentric rod from its proper length to an improper one, necessitating that it be altered back again in order to set the lead right.
The proper method is to adjust both the length of the rod and the position of the eccentric, by testing the lead at once, lengthening the eccentric rod to increase the lead at the crank end, or vice versa.
Each alteration of eccentric position may render necessary an alteration of rod length, or vice versa, each alteration of rod length may render it necessary to alter the eccentric position, hence the lead should be tried at both ends of the cylinder after each alteration of either rod length or eccentric position.
In vertical engines the weight of the crank shaft causes it to wear the bottom brass or part of the bearing box the most, thus lowering its position, while the eccentric straps and pins wear most in the same direction; hence the wear increases the lead at the head end of the cylinder when the latter is above the crank, and at the crank end when the crank is above the cylinder.
When the cylinder is above the crank, the weight of the piston, cross head and connecting rod is counterbalanced at the end of the downward piston stroke by giving the crank end port more lead; but when the cylinder is below the crank, it is the head end port that must be given increased lead to prevent a pound or knock, or to allow for the wear downwards of the parts.
After an engine is started, the pet cocks should (if they are not automatic) be closed as soon as dry steam issues, and if this cannot be seen, it may be assumed to occur after the engine has made about 20 revolutions.
The parts that will then require particular attention are the crank pin, main bearings, cross head guides and the pump, if there is one. The former must be kept properly lubricated, so that they may not get hot and the cylinder lubricator (which is usually placed on the steam pipe) must be set to self feed properly.
If the crank shaft bearings should begin to heat, loosen the cap bolts and lubricate more freely, or, if it is at hand, some melted tallow may be applied with the oil, as a heavier lubricant may stop the heating.
The crank pin requires the most attention and is the most difficult to keep cool and to examine, because of its circular path rendering it difficult to feel it. This may be done, however, in two ways, first by standing at the end of the engine bed and gradually extending the hand, until the end of the rod meets it as it passes, and, second, by placing the hand on the connecting rod as near to the end of the guide bar as possible where its motion is diminished and moving the hand towards the crank pin, by which means the end of the crank pin may be approached gradually.
If the end of the rod is hot, the engine speed should be reduced or the engine should be stopped so that the connecting rod key or wedge may be eased back and the oil feed made more copious. Then, after the engine has been stopped for the night, the brasses should be taken out and any rough surface, either on the brasses or on the pin, smoothed down with a file.
Hot crank pins may occur from several causes, but by far the most common ones are from improper oiling, or from the engine being out of line.
A heavier oil will often stop, or at least modify, the heating, but its cause should always be discovered and remedied.
Engines that are used out of doors or are exposed to temperatures below the freezing point must be left so that steam leaks may not condense in any of the parts or pipes and burst them.
Leaky throttle valves may, for example, cause water to accumulate[II-387] in the steam chest and freeze, perhaps bursting the steam-chest cover.
To prevent this let the engine stand with the crank just past the dead centre, so that the steam port will be open, and open the waste water cocks on the cylinder, and also on the steam chest if there is any.
If the cylinder is jacketed all the drain cocks for the jacket should also be opened.
A leaky check valve may cause the steam to condense in the pump and freeze it up solid or burst it or the pipes. To avoid this, open the pump pet cock.
Open all the drain cocks on the heater and water pipes.
If the water is left in the boiler all night it is liable to freeze.
To prevent this leave a well banked fire.
In extreme weather remember that on exposed engines the oil, if of such quality as sperm or lard oil, may freeze and prevent feeding until the bearings get hot and melt the oil.
To prevent this use a lighter oil, as, for example, a mineral oil. Or, in case of freezing, melt the oil in the cups with a piece of wire made red hot while getting up steam in the morning.
A good plan to prevent oil from freezing and yet have a good quality of oil is to mix two parts of lard oil with one part of kerosene.
Portable engines should stand as nearly level as possible, so that the water will stand level above the tubes and crown sheet of the fire box.
When feed water is drawn from a natural supply, as from a stream, the strainer at the end of the suction pipe should be clear of the bottom of the stream, where it is liable to be choked.
When the exhaust steam is used to feed the boiler, do not open the valve that lets the exhaust steam into the feed-water tank until a little while after the engine has started, because the oil fed to the cylinder will otherwise pass into the feed tank and may cause priming.
In engines having plunger pumps for feeding the boiler it is essential to keep the plunger properly packed, as a leak there impairs or stops the pump from acting.
A gauge glass may be cleaned when the engine is cold by shutting off the cocks leading from the boiler and filling the glass with benzine, allowing it to stand two hours; the benzine must be let out at the bottom of the glass tube, and not allowed to enter the boiler.
In starting a new engine be careful to let the bearings be slightly loose.
At first give only enough steam to just keep the engine going, and keep the hand on the throttle valve ready to shut off steam instantly if occasion should require.
Pumps are divided into the following classes:
Lift pumps, in which the water flows freely away from the pump, which performs lifting duty only.
Force pumps, which deliver the water under pressure.
Plunger pumps, in which a “plunger,” or “ram,” as it is sometimes termed, is used.
Piston pumps have a piston instead of a plunger.
A double acting pump is one in which water enters into and is delivered from the pump at each stroke of its piston or plunger, or, in other words, one in which, while water is being drawn in at one end of the pump, it is also being forced out at the other.
A single acting pump is one in which the water enters the pump barrel during one piston or plunger stroke, and is expelled from the pump during the next stroke, hence the action of the suction and of the delivery is intermittent, although the pump is in continuous action.
For very heavy pressures plunger pumps are generally used, the plunger being termed a ram.
The advantage of the plunger or ram is that it gives a positive displacement, whereas in a piston pump a leaky piston permits the water from the suction side to pass through the leak in the piston, to the delivery side.
Piston pumps possess the advantage that there is less difference between the contents of the pump and the displacement than is the case in plunger pumps.
The displacement of a piston pump is found by multiplying the area of the pump bore by the length of the piston stroke.
The displacement of a plunger pump is less than the above, by reason of there being a certain amount of clearance or space between the circumference of the plunger and that of the cylinder bore.
It is desirable to keep the clearance space in all pumps as small as the conditions will allow, especially if the pump is liable to lose its water.
Losing the water means the falling of the suction water back into the source of supply, which may occur when the engine has to stop temporarily, and there is a leak in the suction valves.
Rotary pumps are those in which the piston revolves, an example of the most successful form of rotary pump being shown in Fig. 3322, which is that used by the Silsby fire engine.
The advantage possessed by a rotary pump is that it keeps the water passing through the suction in a continuous and uniform stream, as it has no valves.
It may therefore be run at a high velocity or attached direct to the engine shaft.
If a rotary pump leaks, the efficiency is not impaired so much as in a piston or plunger pump, all that is necessary being to run the pump at a high speed.
The principles of action of a pump may be understood from Fig. 3323, which represents a single acting plunger pump shown in section, and with the suction pipe in a tank of water, the pump being empty.
The surface of the water in the tank has the pressure of the atmosphere resting upon it, and as the pump is filled with air, the[II-388] surface of the water within the pipe is also under atmospheric pressure.
Now suppose the plunger to move to the right, and as no more air can get into the pump, that already within it will expand, and will therefore become lighter, hence there will be less pressure on the surface of the water within the suction pipe than there is on the outside of it, and as a result the water will rise up the pipe, not because the plunger draws it, but because the air outside the pipe presses it up within the pipe.
The water inside the pipe will rise above that outside in proportion to the amount to which it is relieved of the pressure of the air, so that if the first outward stroke of the plunger reduces the pressure within the pump from 15 lbs. to 14 lbs. per square inch (15 lbs. per square inch being assumed to be its normal pressure), the water will be forced up the suction pipe to a distance of about 21⁄4 feet, because a column of water an inch square and 21⁄4 feet high is equal to 1 lb. in weight. In Fig. 3324 the pump plunger is shown to have moved enough to have permitted the water to rise above the suction valve, and it will continue to rise and enter the pump barrel as long as the plunger moves to the right.
When the plunger stops, the suction valve will fall back to its seat and enclose the water in the pump; but as soon as the plunger moves back to the left hand and enters the barrel pump further, the delivery valve will rise, and the plunger will expel from the pump a body of air or water equal in volume to the cubical contents of the plunger, or rather of that part of it that is within the barrel, and displaces water.
If the plunger was at the end of its first stroke to the right and the pump half filled with air, then this air will be expelled from the pump before any water is; whereas if the pump was filled with water, the latter only will be delivered.
Now suppose the first plunger stroke reduces the air pressure from 15 to 14 lbs., and that the second drawing stroke of the plunger reduces the air pressure in the pipe to 13 pounds per inch, the water will rise up it another 21⁄4 feet, and so on until such time as the rise of a column of water within the pipe is sufficient to be equal in weight to the pressure of the air upon the surface of the water without; hence it is only necessary to determine the height of a column of water that will weigh 15 lbs. per square inch of area at the base of the column to ascertain how far a suction pump will cause water to rise, and this is found by calculation or measurement to be a column nearly 34 feet high.
It is clear then, that however high the pump may be above the level of the water, the water cannot rise more than 34 feet up the suction pipe, even though all the air be excluded from it and a perfect vacuum formed, because the propelling force, that is, the atmospheric pressure, can only raise a column of water equal in weight to itself, and it is found in practice to be an unusually good pump that will lift water thirty feet.
Fig. 3325 shows the plunger making a delivery stroke, the suction valve being closed, and the delivery valve open where it will remain until the plunger stops.
To regulate the quantity of water the pump will deliver in cases where it is necessary to restrict its capacity, as in the case of maintaining a constant boiler feed without pumping too much water in the boiler, the height to which the suction valves can lift must be restricted, so as to limit the amount of water that can enter the pump at each drawing stroke.
The delivery valve should lift no more than necessary to give a free discharge without causing the valve to seat with a blow; but if the pump has a positive motion, the delivery valve must open wide enough to let the water out, or pressure enough may be got up in the pump to break it.
A check valve is merely a second delivery valve placed close to the boiler and serving to enable the pump to be taken apart if occasion should arise, without letting the water out of the boiler.
The lift and fall of both valves act to impair the capacity of the pump. Thus, while the suction valve is falling to its seat, the water already in the pump passes back into the suction pipe, and similarly, while the delivery valve is closing, the delivery water passes back.
A foot valve is virtually a second suction valve placed at the bottom or foot of the suction pipe.
The capacity of a pump is from 70 to 85 per cent. of the displacement of the plunger or piston, and varies with the speed at which the plunger or piston runs.
If a pump runs too fast, the water has not sufficient time to follow the piston or plunger, especially if the suction pipe has bends in it, as these bends increase the friction of the water against the bore of the pipe.
The speed of the piston or plunger should not exceed such as will require the water to pass through the suction pipe at a speed not greater than 500 feet per minute, and better results will be obtained at 350 feet per minute.
An air chamber placed above the suction pipe of any pump causes a better supply of water to the pump by holding a body of water close to it, and by making the supply of water up the suction pipe more uniform and continuous. Air chambers should be made as long in the neck as convenient, so that the water in passing through the pump barrel to the delivery pipe could not be forced up into the chamber, as, if such be the case, the air in the chamber is soon absorbed by the water.
Belt pumps are more economical than independent steam pumps, because the power they utilize is more nearly the equivalent of the power it takes to drive them, whereas in steam pumps there is a certain amount of steam, and therefore of power, expended in tripping the valves and in filling the clearance spaces in the cylinder. Furthermore, the main engine uses the steam expansively, whereas the steam pump does not.
| VOL. II. | AMERICAN FREIGHT LOCOMOTIVE | PLATE XXIX. |
|
Large image (198 kB). 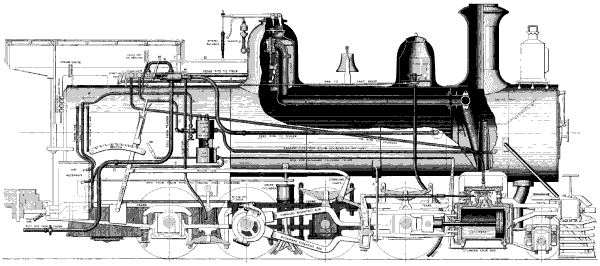 |
||
| Fig. 3326. | ||
In Fig. 3326 is shown a modern freight locomotive, the construction being as follows:
For generating the steam we have the boiler, which at the front end is firmly bolted to the engine cylinders, which are in turn bolted to the frames, while at the back end the boiler is suspended by the links b (one at each end of the fire box on each side of the engine).
The starting bar is shown in position to start the engine, and it is seen that the rod a and bell crank b are in such a position as to open the valve t, and thus admit steam from the dome to the pipe e, whence it passes through pipes f, g and r into the steam chest i, the slide valve v distributing the steam to the cylinder. The exhaust occurs through the exhaust port d, whence it passes up the exhaust pipe and out at the smoke stack.
The boiler is fed with water as follows:
The feed pipe from the tender supplies water to the injector, which is forced by the injector through the feed pipe to boiler and into the latter.
In the figure the parts are shown in position for the engine to go ahead, hence the reversing gear is in the extreme forward notch of the sector, and the valve gear is in full gear for the forward motion.
The lever m is for opening and closing the cylinder cocks, which are necessary to let the water of condensation out of the cylinder when the engine is first started and the cold cylinder condenses the steam.
To supply steam to the injectors (of which there are two, one on each side of the engine) and to the steam cylinder of the pump, there is a steam pipe leading from the dome to the steam drum, the pipe k supplying steam to the injector, and pipe j supplying steam to the steam cylinder of the air pump. The pipe for supplying oil to the slide valve and cylinder is furnished with a sight feed oil cup, the oil being carried by steam from the steam drum.
This pipe passes beneath the lagging until it reaches the smoke box, which is done to keep it warm and prevent the oil from freezing, while the steam pressure enables the oil to feed against the steam pressure in the steam chest.
The slide valve is balanced by means of strips let into its back, and bearing against a plate fixed to the steam chest cover.
The frame on the side of the engine shown in the engraving is shown broken away from the yoke a to the fire box, so as to expose the link motion to full view, the shaded portion of the frame being that on the other side of the engine.
The yoke or brace a carries one end of the guide bars. The safety valve s may be raised to see that it is in working order, or to regulate the steam pressure, by the lever o, which has a ratchet tongue engaging with the notches at l.
In addition to the safety valve with spring balance, however, a pop safety valve is employed on the part of the dome that is shown broken away, the construction of this pop valve being shown in the outside view, Fig. 3326a, and a sectional view, Fig. 3326b, the casing being removed from the latter. In the valve seat b is a recess a, and upon the circumference of the valve is a threaded ring c′. When the valve lifts, the steam is somewhat confined in the annular recess of the valve, and the extra valve area thus receiving pressure causes the valve to lift promptly and the steam to escape freely. The degree of this action is governed as follows:
The sleeve c′ is threaded upon the upper part of the valve, so that by screwing it up or down upon the valve the amount of opening between the annular recess a a, and the lower edge of the sleeve c′ c′, is increased or diminished at will; the less this opening, the more promptly the valve will rise after lifting from its seat.
To secure the sleeve or ring in its adjusted position, the ends of the screws l, l seat in notches cut in the upper edge of the sleeve. In many engines pop valves alone are used, and in some cases levers are provided by means of which the pop valve can be raised from its seat to test if it is in working order.
[II-390]Referring again to Fig. 3326, h is the handle for operating the injector, and w a rod for opening the injector overflow.
We now come to the automatic air brake; steam for the steam cylinder of which, is received from the steam drum through the pipe j, passing through the pump governor, or regulator g. The exhaust pipe for the steam cylinder of the air pump passes into the smoke box. The air cylinder receives its supply of air through the small holes at k, k, and delivers it through the pipe c into the air reservoir or tank, from which it passes through the tank pipe up to the threeway cock or engineer’s brake valve, whose handle is shown at m. The brakes are kept free from the wheels and out of action so long as there is air pressure in the air reservoir and in the train pipe, hence the normal position of the handle m is such as to let the air pass from the air reservoir up the pipe x and into the train pipe. When the brakes are to be applied, handle m is moved so that there is an open connection made between the train pipe and the pipe to open air, which releases the air pressure and then puts on the brakes not only on each car, but also on the engine, because the engine brake cylinders receive their air pressure from the pipe shown leading to the train pipe. From the tank pipe x a pipe h leads to the top of the pump governor g, whose action is to shut off the steam from the steam cylinder of the air pump whenever the pressure in the air reservoir or tank exceeds 70 lbs. per square inch. A small pipe leads up from pipe h to the air pressure gauge.
For regulating the draught of the fire there is a damper door at each end of the ash pan, and to increase the draught, a pipe leads from the steam drum into the smoke box, where it passes up alongside of the exhaust pipe, its end being shown at z. This is called the blower, and its pipe is on the other side of the engine. The plate shown at p, p in the smoke box checks the draught in the upper tubes, and therefore distributes it more through the lower ones.
There are two sand valves, both of which are operated by one rod, the construction being shown in Fig. 3327, which is a plan showing the bottom of the sand box broken away to expose the gear for moving the valves. The two valves v, v for the sand pipes are on raised seats e, e, and are fast on the same shafts as the segments s, s, but the valves are obviously above, while the segments are beneath the bottom of the sand box. The gear wheel w is pivoted to the under side of the bottom of the sand box, and the arm l is fixed to the wheel. At t are pieces of wire, which, being fast in the spindle, revolve with it and stir up the sand when the valves are moved. As shown in the figure, the two sand pipes a, a are open, but suppose the rod is moved endways and l will revolve w, which will move s, s and the valves v, v, causing the latter to move over and cover the pipes a, a, and shut off the sand from the pipes.
| VOL. II. | AMERICAN PASSENGER LOCOMOTIVE | PLATE XXX. |
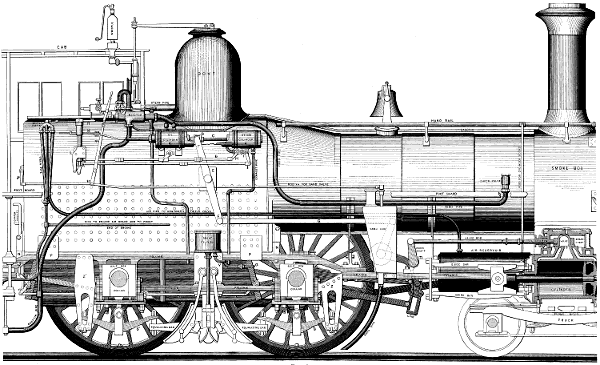 |
||
| Fig. 3328. | ||
Fig. 3328 represents an American passenger locomotive with a steam reversing gear, or in other words, a reversing gear that is operated by steam.
The link motion is substantially the same as that shown in Fig. 3326 for a freight locomotive, the eccentric rods in this case being straight, as there is no wheel axle in the way.
The injector for feeding the boiler is the same as that shown on the freight locomotive.
The ash pan is provided with two dampers, one at each end, and the front one is operated by the bell crank a c.
The sand boxes are here fastened to the frame, both sand valves being operated by the lever m, which at its lower end connects to a rod, u, which at its back end connects to an arm, p, on a shaft that extends across the fire box and connects to a rod corresponding to rod u, but situated on the other side of the engine and connecting with the other sand valve.
The steam pump for the automatic air brake is on the other side of the engine, and the air reservoirs, of which there are two, are horizontal and situated beneath the front end of the boiler. The air pipe to the triple valve here connects to the front pipe of the three beneath the triple valve, the middle pipe being that which is open to the atmosphere, which is the usual construction. The engine brake receives its air from a pipe on the other side of the engine which feeds the pipes g, v, for the brake cylinder shown in the figure. When the engine is running backwards, the train brakes are operated through the medium of the “pipe to air brake and to front end of engine” which is shown broken off.
The construction of the steam reversing gear is shown in Fig. 3328a. a is a steam cylinder and b a cylinder filled with oil or other liquid. Each of these cylinders has a piston, the two being connected together by their piston-rods c c′. These rods are also connected to a lever d e f, which works on a fulcrum e. The lower end of the lever is connected to the reverse rod f g, the front end of which is attached to the vertical arm of the lifting or reverse shaft. It will readily be seen that if the piston in b is free to move and steam is then admitted to either end of the steam cylinder a, the two pistons will be moved in a corresponding direction, and with them the lever d e f, and the other parts of the reversing gear. A valve, h, is provided, by which communication is opened between the cylinder a and the steam inlet pipe. Another valve, i, is placed between h and the cylinder a, by which the steam may be admitted either into the front or back end of the cylinder. It will be apparent, though, that if the piston in a is thus moved, and the reverse gear placed in any required position, some provision must be made to hold it there securely. This is accomplished by the oil cylinder and piston b. To it a valve, j, is provided, by which communication between the front and back ends of the cylinder may be opened or closed. It is evident that if the piston b is in any given position, and both ends of the cylinder are filled with liquid, the former will be held securely in that position if the liquid in one end cannot flow into the other. If, however, communication is opened between the two ends, then, if a pressure is exerted on the piston b, it will cause the liquid to flow from one end of the cylinder to the other, and thus permit b to move in whichever direction the pressure is exerted.
[II-391]r is the reverse lever, made in the form of a bell crank, the short end of which works in a slot c, in the upper end of a shaft or spindle d. This shaft is inclosed by a tubular shaft s, to which the fulcrum of r is fastened. The tubular shaft has an arm b. The reverse lever has two movements, the one to raise the end up, and the other to turn on the axis of the tubular shaft. The arm b on the latter is connected by a rod, f, with the valves j and h. The lower end of the shaft d is connected with a bell crank, f′, which, in turn, is connected by a rod, k l, with the valve i. Therefore, by turning the lever r so as to partly revolve the shaft s, the valves j and h may be opened or closed, and by moving the lever r up or down, the valve i is moved to admit steam to the front or back end of a. To reverse the engine, therefore, the lever r is turned so as to open the valves j and h. This opens communication between the opposite ends of b, and h admits steam to i. Now, by reversing the end of the reverse lever r, the valve i is moved so as to admit steam to either end of a, the pressure in which will move the reverse gear to the desired position. When this is done, the valves j and h are closed. This prevents the fluid in b from flowing from one end of the cylinder to the other, and thus securely locks the piston b in the position it may happen to be in, and at the same time the valve h shuts off steam from the cylinder a.
The bar k is graduated, as shown in the plan of r, k, to indicate to the locomotive runner the position of the reversing gear.
This apparatus enables the reversing gear to be handled with the utmost facility, and with almost no exertion on the part of the engineer. The engine can be reversed almost instantly, and it can be graduated with the most minute precision.
| VOL. II. | LOCOMOTIVE LINK MOTION. | PLATE XXXI. |
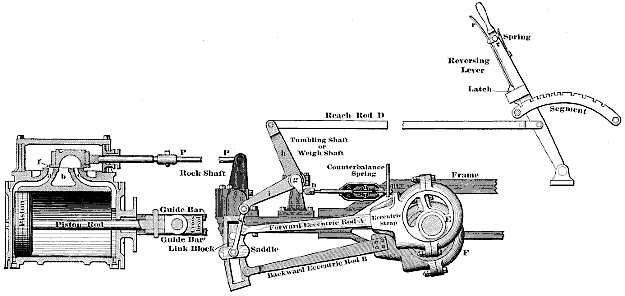 |
||
| Fig. 3329. | ||
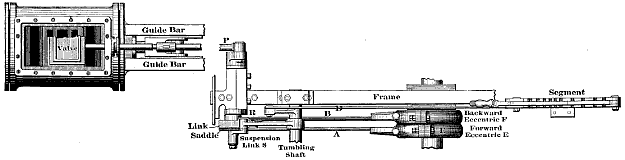 |
||
| Fig. 3330. | ||
The link motion of an American locomotive is shown in Figs. 3329 and 3330. In Fig. 3329 it is shown in full gear for the forward gear, or in other words, so as to place the engine in full power for going ahead.
[II-392]The meaning of the term full power is that, with the link motion in full gear, the steam follows the piston throughout very nearly the full stroke.
In Fig. 3331 the link motion is shown in mid gear, in which position the engine is at its least power, the cut off occurring at its earliest point, and in Fig. 3332 it is shown in full gear for the backward motion.
Referring to Fig. 3329 for the full gear forward, the reversing[II-393] gear proper consists of the reversing lever, the segment, the reach rod, the tumbling shaft, and its counterbalance rod and spring; while the link motion proper consists of the eccentrics and their rods, the link, the link block or die, the suspension link s, the rock shaft and the rod p p. These, however, are terms applied for shop purposes, so as to distribute the work in sections to different men, it being obvious that a complete link motion includes the reversing gear, the eccentrics, the link and its block, the rock shaft, the rod p p, and the valve and its spindle or stem. This mechanism, as a whole, may also be called, and is sometimes called, the valve gear, because it is the mechanism or gear that operates the slide valve.
The link motion may be moved from full gear forward to full gear backward or to any intermediate position, whether the engine is running or at rest, but is, when the engine is running, harder to move from full gear forward toward back gear, and easier to move from full gear backward toward mid and forward gears, which occurs because of the friction of the eccentrics in the straps, and it follows that this will be the case to a greater extent in proportion as the revolutions of the eccentrics are increased.
If in a properly constructed link motion we move the link from full gear forward to mid gear when the engine is standing still, and watch the valve, we shall find that the lead or opening at f gradually increases; and if we then move it from mid gear to full gear backward, the lead will gradually decrease and finally become the same as it was in full gear forward. The construction of the parts is as follows:
Referring to Fig. 3329 (full gear forward), the segment is fixed in position and the reversing lever is pivoted at its lower end. r r is a bell crank, which is pivoted to the reversing lever and to which the latch rod is pivoted at its upper end. The spring acts on the end of r r, and thus forces the tongue of the latch into the notches on the sector as soon as the tongue comes fair with the notch and r r is released from the hand pressure. As the reversing lever is moved over from full gear forward, the reach rod moves the tumbling shaft, whose lower arm i (through the medium of the suspension link s) lifts the link and brings the centre of the saddle pin nearer to the centre of the pin in the link block, which reduces the amount of motion given to the lower arm (b, Fig. 3331) of the rock shaft, and therefore reduces the amount of valve travel, thus causing the point of cut-off to occur earlier in the piston stroke.
The weight of the eccentric rods, the link, suspension link s, and the tumbling shaft arm i, is counterbalanced by the counterbalance spring in the box s s, whose rod attaches to the lug g on the tumbling shaft. To regulate the proper amount of counterbalancing, the nuts at m are provided, these nuts regulating the amount of tension on the spring s s.
The forward eccentric e is that which operates the valve when the link motion is in full gear forward, as in Fig. 3329, and the backward eccentric is that which moves the valve when the link motion is in back gear, as in Fig. 3332.
This occurs because it is the eccentric rod that is in line or nearest in line with the link block that has the most effect in moving the valve. When the link is in full gear, the motion of the valve is almost the same as though there was no link motion and the eccentric rod was attached direct to the rod p p, the difference being so slight as to have no practical importance. This will be seen by supposing that we were to loosen the backward eccentric f upon the shaft and revolve it around the shaft by hand, in which case it would swing the lower end of the link backward and forward with the centre of the link block as a pivot or centre of motion, the forward eccentric rod rising and falling a trifle only, and therefore moving the rock shaft to a very slight amount.
Let it now be noted that the suspension link not only sustains the weight of the link and eccentric rods, but also compels the centre of the saddle pin to swing (as the link is moved by the eccentrics) in an arc of a circle of which the centre is the upper end of the suspension link. Suppose, therefore, that the backward eccentric rod was to break, or was taken off and the engine could still run forward, but no motion would be given to the valve, if the link was placed in mid gear, because in that case the forward eccentric rod would simply swing the link on the centre of the link block as a pivot. Now, suppose the forward eccentric rod was to break or be taken off, and the engine may be made to go ahead by setting the backward eccentric fair with the forward eccentric and connecting its rod to the upper end of the link.
Similarly, if the engine was running with the smoke stack toward the train and the link motion in backward gear, and the backward eccentric rod was to break, we may take it off, shift the forward eccentric so that it comes fair or stands in line with the backward eccentric and connect its rod to the lower end of the eccentric and with the link motion in backward gear, the engine would still haul the train.
If the reach rod was to break, the tumbling shaft could be held in position by loosening the cap bolts of the tumbling shaft journal and putting between the cap and the tumbling shaft journal a piece of metal, which, on bolting up the cap screws again, would firmly grip the shaft and prevent it from moving.
[II-394]Setting the Slide Valves of a Locomotive.—The principles of designing, and the action of D valves, such as are used upon locomotives, have been so thoroughly explained with reference to stationary engines, that there is no need to repeat them in connection with the locomotive, and we may proceed to explain how to set the valves of a locomotive. In doing this, there are two distinct operations, one of which is to place the crank alternately exactly on its respective dead centres, and the other is to set the position of the eccentrics, and get the eccentric rod of the proper length. These two operations comprise all that require to be done to set the valves, under ordinary and workmanlike conditions; hence we may proceed at once to explain the operation.
The first thing to be done is to put the crank pin on a dead centre, and it does not matter which one.
In Fig. 3333 it is supposed that the piston is to be at the head end of the cylinder when the crank is on its corresponding dead centre.
The first thing to do is to put the reversing gear in full gear forward, so as to set the forward eccentric, and see if its rod is of proper length.
The next thing to do is to move the wheel so that the crank pin is nearly on the dead centre, and then take a tram (such as shown in the figure), pointed at each end, and mark on the splash plate, or any other convenient place, a centre punch dot in which the point b of the tram can rest. Next, from the centre of the axle as a centre, mark arcs or portions of circles a, a. This being done, point b of the tram is rested in the centre punch dot before referred to, and with the other end a line c is marked, a straight edge is then rested against the ends e e of the cross head, and a line d is marked on the guide bar, this line being exactly even or fair with the end e e of the cross head.
We then move the wheel in the direction of the arrow, and as soon as we begin to do so, the cross head will move to the left and away from the line d on the guide bar. But as soon as the crank pin has passed its dead centre, the cross head will begin to move to the right, and as soon as the end e e comes again exactly in line with the line d marked on the guide bar, we must stop moving the wheel, and again resting the point b of the tram in the centre punch mark before mentioned, we move its other end so as to mark a second line, which will be the line or arc f.
The next thing to do is to mark a fine centre punch dot, where c and f cross the arc or line a, and then find the point g midway between f and c, and mark a fine centre punch mark there. This being done, we must move the wheel back into the position it occupies in the figure, and then slowly move it in the direction of the arrow, until with the end b of the tram resting in the centre punch dot, the other end of the tram will fall dead into the centre punch dot at g, at which time the crank pin will be exactly on the dead centre.
During this part of the process we have nothing to do with anything except getting the crank pin on the dead centre, but there is one point that requires further explanation, as follows:
In this operation we have first put the crank on one side of the dead centre and then put it to the same amount on the other side of the dead centre, both being improper positions; but by finding the mean or mid position between the two, we have found the proper position. In doing so, however, we have moved the wheel, the wheel has moved the connecting rod, and the connecting rod has moved the piston. But in the actual running of the engine, this order of things will be reversed; for the steam will move the piston, the piston will move the connecting rod, and the connecting rod will move the crank and therefore the wheel.
The difference between the two operations is this: Suppose there is lost motion or play between the connecting rod brasses and the crank pin, or between the connecting rod brasses and the cross head pin, and then if we move the wheel in the direction denoted by the arrow, we take up this lost motion, so that if the tram was fair with the centre punch at g and steam was admitted to the piston, then there would be no lost motion to take up, and as soon as the piston moved the crank pin would move. But if we moved the wheel in the opposite direction to that denoted by the arrow, then we are placing any lost motion there may be in the opposite direction, and if steam were turned on, the piston and connecting rod might move before the crank and wheel moved.
In which direction the wheel should be moved while placing the crank on the dead centre depends upon the condition of the engine, as will be explained presently, the assumption being at present that the engine is in thorough good order, in which case the wheel should (while placing the crank on the dead centre) be moved in the direction of the arrow in the figure.
The object is under all conditions to bring the working surfaces to bear (while setting the valve) in the same way as they will bear when the engine is actually at work.
Having placed the crank on the dead centre, and thus completed the first operation in valve setting, we may turn our attention to the second, viz., correcting the lengths of the eccentric rods and setting the valve lead. Almost all writers who have dealt with this part of the subject have fallen into a very serious error, inasmuch as they began the operation by what they call squaring the valve. This means so adjusting the length of the eccentric rod that the valve will travel an equal distance each way from its mid position, so that if the engine wheel is revolved and the extreme positions of the valve marked by a line, these lines will measure equally from the edges of the steam ports, or, what is the same thing, from the centre of the cylinder exhaust port. This procedure is entirely erroneous, because, on account of the angularity[57] of the eccentric rod, the valve cannot, if equal lead is to be given to the valve, travel equally beyond the two steam ports, and if the eccentric rods are so adjusted for length as to square the valve, they are made wrong.
The valve lead, and the lead only, it is that determines the length of the eccentric rods. Suppose that, as is generally the case, the lead is to be equal, or, in other words, that there is to be as much valve lead when the piston is at one end of the cylinder as there is when it is at the other, and if we make the eccentric rods of such a length that the valve travels equally on each side of the steam port, there will be less lead at the head end port than there is at the crank end port. The proper method, therefore, is (as soon as the crank is on the dead centre and the link in full gear, as in Fig. 3334) to set the eccentric so as to give the desired amount of lead, and then give the wheel a half revolution, the lower end of the tram falling into the centre punch dot at s, when the crank pin will be on its other dead centre and ready for the lead to be measured again. If the lead is equal at each end, one eccentric rod is of the right length, and all we have to do is to set the eccentric so that the right amount of lead is given.
We now turn our attention to the backward eccentric and its rod, putting the reversing lever in full gear for the backward motion, and putting the crank on the respective dead centres, and testing the lead for both ports as before, and when the required amount of valve lead is given the valve setting is complete.
In some practice the wheel is blocked up on the pedestal guides while setting the valves, but a more correct method is to let the engine rest on the rails and push it back and forth with a crowbar to revolve the wheels when putting the crank pin on the dead centre. The best thing to measure the lead with is a wooden or leaden wedge having but a slight degree of taper, as say 3⁄16 or 1⁄4 inch in a length of four inches. We have in this example of valve setting supposed the parts to be of the proper dimensions, as they would be in a new engine or in an engine that had been running and merely had a new valve or a new eccentric put in.
But suppose the notches were not cut in the sector, and we have then to mark them off while setting the valves. All the difference that this makes to the operation is that we must clamp the reversing lever to the sector while setting the valve, taking care to so clamp it that there is the same space between the top end of the link block and the end of the link slot in the full forward gear as there is between the bottom end of the link block and the end of the link slot when the engine is in full backward gear. In this connection it is, however, to be remarked that when the link is in full gear, either forward or backward, and the crank is on the dead centre, the link block is not at the end of its motion toward the end of the link slot; hence it is a good plan to move the wheels around and to so regulate the length of the reach rod and the position of the reversing lever on the sector, that when the link block is at the highest point in the link slot for the forward gear and at the lowest point in the link slot for the backward gear, it comes an equal distance from the end of the link slot.
[II-395]The setting for an Allen valve is the same as that for an ordinary one, but in determining the amount of the lead it is to be borne in mind that it is virtually twice as much as it measures at the port because there are two openings for the steam. This will be seen from Fig. 3335, in which the valve is open to the amount of the lead at f. But the steam also enters at e, and passes through the port in the valve and into steam port a.
We have now to call attention to the fact, that the eccentric rods, when properly connected, are, in an American locomotive, crossed when the piston is at the crank end of the cylinder. In Fig. 3334, the piston is at the head end of the cylinder, and the rods are open. In Fig. 3336, however, the crank pin is supposed to be at b, and the eccentric rods are crossed, f being the forward and e the backward eccentric.
The injector shown in the general view of a freight locomotive, Fig. 3326, is that constructed by William Sellers & Co., and there are two, one on each side of the engine. The details of its construction are as follows:
| VOL. II. | INJECTOR AS APPLIED TO A LOCOMOTIVE. | PLATE XXXII. |
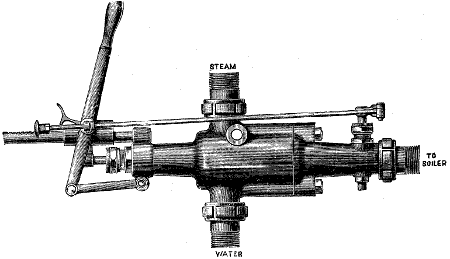 |
||
| Fig. 3337. | ||
|
Large image (67 kB). 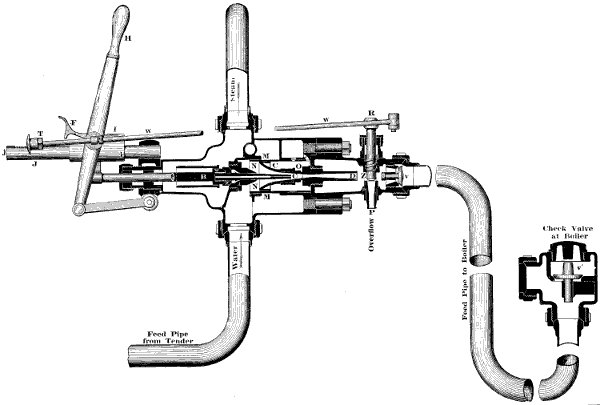 |
||
| Fig. 3338. | ||
Fig. 3337 is a side elevation, Fig. 3338 a section on a vertical plane, Fig. 3339 a section on a horizontal plane, Fig. 3340 an end view of the injector at the right-hand side of the engine, and Fig. 3341 a plan of the injector on the left-hand side of the engine.
This injector is self-contained, or in other words, it has both steam and check valves, so that it can be connected directly without other fittings, although, of course, it is generally desirable to place another stop valve in the steam pipe, and a check valve in the delivery pipe, so that the injector can be taken to pieces or disconnected at any time. Another important feature of this injector is, that it is operated by a single handle, and that the waste valve is only open at the instant of starting.
Referring to Fig. 3338, a is the receiving tube, which can be closed to the admission of steam by the valve x. A hollow spindle passing through the receiving tube into the combining tube is secured to the rod b, and the valve x is fitted to this spindle in such a way that the latter can be moved a slight distance (until the stop shown in the figure engages with valve x) without raising the valve x from its seat. A second valve w, secured to the rod b, has its seat in the upper side of the valve x, so that it can be opened (thus admitting the steam to the centre of the spindle) without raising the valve x from its seat, if the rod b is not drawn out any farther, after the stop on the hollow spindle comes in contact with the valve x. d is the delivery tube, o an overflow opening into space c, v the check valve in delivery pipe, and z the waste valve. The upper end of the combining tube has a piston n n attached to it, capable of moving freely in a cylindrical portion of the shell m, m, and the lower end of the combining tube slides in a cylindrical guide formed in the upper end of the delivery tube.
The rod b is connected to a cross head which is fitted over the guide rod j, and a lever h is secured to the cross head. A rod w, attached to a lever on the top end of the screw waste valve, passes through an eye that is secured to the lever h; and stops t, q control the motion of this rod, so that the waste valve is closed when the lever h has its extreme outward throw, and is opened when the lever is thrown in so as to close the steam valve x, while the lever can be moved between the positions of the stops t, q without affecting the waste valve. A latch f is thrown into action with teeth cut in the upper side of the guide rod j, when the lever h is drawn out to its full extent and then moved back; and this click is raised out of action as soon as it has been moved in far enough[II-396] to pass the last tooth on the rod j. An air vessel is arranged in the body of the instrument, as shown in the figure, for the purpose of securing a continuous jet when the injector and its connection are exposed to shocks, especially such as occur in the use of the instrument on locomotives.
The manipulation required to start the injector is exceedingly simple—much more so in practice, indeed, than it can be rendered in description. Moving the lever h until contact takes place between valve x and stop on hollow spindle, which can be felt by the hand upon the lever, steam is admitted to the centre of the spindle, and, expanding as it passes into the delivery tube d and waste orifice p, lifts the water through the supply pipe into the combining tube around the hollow spindle, acting after the manner of an ejector or steam siphon. As soon as solid water issues through the waste orifice p, the handle h may be drawn out to its full extent, opening the steam valve x and closing the waste valve, when the action of the injector will be continuous as long as steam and water are supplied to it.
To regulate the amount of water delivered, it is necessary only to move in the lever h until the click engages any of the teeth on the rod j, thus diminishing the steam supply, as the water supply is self-regulating. If too much water is delivered, some of it will escape through o into c, and, pressing on the piston n n, will move the combining tube away from the delivery tube, thus throttling the water supply; and, if sufficient water is not admitted, a partial vacuum will be formed in c, and the unbalanced pressure on the upper side of the piston n n will move the combining tube toward the delivery tube, thus enlarging the orifice for the admission of water. From this it is evident that the injector, once started, will continue to work without any further adjustment, delivering all its water to the boiler, the waste valve being kept shut. By placing the hand on the starting lever, it is easy to tell whether or not the injector is working; and, if desired, the waste valve can be opened momentarily by pushing the rod w, a knob on the end being provided for the purpose.
Figs. 3342, 3343 and 3344 represent the Westinghouse automatic air brake applied to an engine and tender, and in the following figures details of the construction of various parts are shown.
| VOL. II. | LOCOMOTIVE AIR BRAKES. | PLATE XXXIII. |
|
Large image (88 kB). 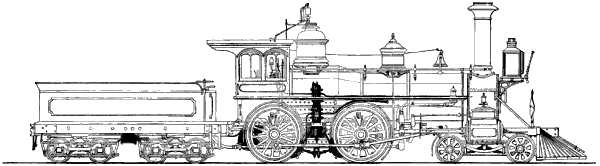 |
||
| Fig. 3342. | ||
|
Large image (Fig. 3343; 60 kB).  |
 |
|
| Fig. 3343. | Fig. 3344. | |
The pump governor, which is shown at g in Fig. 3326, of a modern freight locomotive, is shown in section in Fig. 3345.
The pump governor is employed for the purpose of cutting off the supply of steam to the pump when the air pressure in the train pipe exceeds a certain limit, say 70 lbs. per square inch.
Its operation is as follows:
When valve 10 is (by means of hand wheel 8) screwed home to its seat the steam is entirely shut off from the steam cylinder, but by operating wheel 8 to unscrew spindle 9, valve 10 is permitted to open and let the steam pass through a and b to the steam cylinder which operates, forcing air into the reservoir and thence into the train pipe. A pipe from the train pipe connects to the upper end of the pump governor, hence air from the train pipe passes around the stem 14 to the upper side of the thin diaphragm 18, which is held in its position by the spring 12 with a force sufficient to enable it to resist, without moving, a pressure of 70 lbs. per square inch. But when the pressure exceeds 70 lbs. per square inch it forces the diaphragm down, pushing down valve 13 and allowing the steam in a to pass up through valve 13 and out of the exhaust pipe 6. The steam pressure in a being thus reduced, that in b acts on the under side of the valve, causing it to rise and seat itself and thus cut off the supply of steam to the pump.
[II-399]When the pressure in the train pipe is diminished by the brakes being applied, the diaphragm is restored to the position it occupies in the figure by the action of the spring 16. Then valve 13 is seated by the spring 12, and the steam pressure accumulates on the upper end of valve 10, forcing it down and letting the steam from a into b and thence into the steam cylinder, starting it into action, which continues until the pressure in the train pipe exceeds 70 lbs. per square inch.
The use of this governor not only prevents the carrying of an excessive air pressure in the train pipe, which may result in entirely preventing the wheels from revolving and causing a flat place to wear on the wheel tire, but it also causes the accumulation of a surplus of air pressure in the main reservoir, while the brakes are applied, which insures the release of the brakes without delay. It also obviates the unnecessary working of the pump when the desired air pressure has been obtained.
A sectional view of the steam and air cylinders is shown in Fig. 3346, the construction being as follows:
Steam is distributed to the steam cylinder by means of a piston valve, composed of three pistons, marked 16, 14, and 20 respectively, the steam entering between pistons 16 and 14, and, in the positions in which the parts occupy in the figure, steam can pass through the bushing 18 and beneath the steam piston 7, propelling it upwards until the bottom of the hole in its piston rod strikes the end of rod 12, and raises it and valve 13. The chamber 23, in which valve 13 works, receives steam through a suitable port from the steam space between valves 14 and 16; and the steam from chamber 23, it is that (in the positions the parts occupy in the figure), acting on the area of the large valve piston 20, holds the valve down against the pressure on the bottom face of piston 14 of the valve. As soon, however, as the piston rod 7 strikes and raises rod 12 and valve 13, the steam is exhausted from the top of piston 20 of the valve, and the steam beneath piston 14 of the valve raises the valve, opening the lower port in the sleeve 18 for the exhaust, and piston 14 admits steam to the upper side of the steam piston 7. The construction of the air cylinder differs somewhat from that shown in the freight locomotive, Fig. 3326, this air pump corresponding with that shown on the engine and tender, Fig. 3342. A detail list of the parts may be given as follows:
| No. | |||
| 2. | Steam cylinder head (with reversing cylinder, piston, and valve bushes). | ||
| 3. | Steam cylinder (with main valve and bushes). | 23. | Reversing valve bush. |
| 4. | Centre piece. | 24. | Reversing valve cap. |
| 5. | Air cylinder (with lower discharge valve). | 25. | Piston rod nut. |
| 6. | Air cylinder head. | 26. | Piston packing gland. |
| 7. | Steam piston and rod. | 27. | Piston packing nuts. |
| 8. | Air piston. | 28. | Packing glands. |
| 9. | Piston rings. | 29. | Right Chamber cap. |
| 10. | Steam piston plate. | 30. | Left chamber cap. |
| 11. | Steam piston bolt. | 31. | Air valve bushing. |
| 12. | Reversing rod. | 32. | Air valve. |
| 13. | Reversing valve. | 33. | Air valve. |
| 14. | Piston valve. | 34. | Air valve. |
| 15. | Piston valve rings. | 35. | Delivery union. |
| 16. | Piston valve rings. | 36. | Exhaust steam outlet. |
| 17. | Upper valve bushing. | 40. | Steam cylinder gasket. |
| 18. | Lower valve bushing. | 42. | Top air-pump gasket. |
| 19. | Reversing piston casing. | 43. | Bottom air-pump gasket. |
| 20. | Reversing piston. | 44. | Waste water pipe. |
| 21. | Piston rings. | 46. | Exhaust union stud. |
| 22. | Reversing cylinder cap. | 49. | Air exhaust union stud. |
A side view of the driving wheel brakes is shown in Fig. 3347 and an end view in Fig. 3348. The brakes are, it is seen, suspended by links so that their weight tends to keep them from the[II-400] wheels. The brake piston rod carries at its end two links which attach to the arms attached to the brakes. The ends of these arms being curved roll together, the arrangement forming in effect a rolling toggle joint. The construction of the piston of the driving wheel brake is shown in Fig. 3349. The piston is made air tight by leather packing indicated by 11, held out by a spring 12. The piston rod packing, 7, is leather held in place by the cap 6 and the spring 8. The air for operating the brake enters below the piston.
The engineer’s duty in running a locomotive is more arduous and requires more watchfulness than any other engine running, because of the peculiarities attending it. In the first place, the jolts and jars to which the engine is subject are liable to cause nuts, pins, etc., to come loose, and some of the parts to become disconnected and cause a breakdown of the engine.
This renders necessary a careful examination of the engine, which should be made both before and after each trip.
In the second place, we have that the amount of load the engine has to pull varies with every varying grade in the railroad track, and the variation is so great that on some descending grades the engine may require no steam whatever, while on ascending grades the utmost power attainable from the engine may be required. In firing, feeding the pumps, oiling the parts, and determining the depth of water in the boiler, the grade and the length of each grade has an important bearing, and so has the weather, since it is clear that between the heat of summer and the blizzards of winter there is a wide range of the conditions under which the engine runs.
In former times, from the less perfect construction of locomotives, the engineer’s duties were greatly enhanced from breakdowns, which are comparatively rare with modern locomotives, and there is promise that from improved construction and safeguards they will become less frequent in the future.
It is as important for the locomotive engineer to be familiar with the track as it is to be with the engine, and there is no field of engine driving or running in which more scope is permitted to the engineer to exercise judgment and skill in his management, so as to effect economy in fuel consumption.
The quality and size of the coal is another element that requires attention and observation on the part of the engineer, in order that his train may keep its time and the fuel consumption be kept down.
The first thing to be done in getting ready for a trip is to see that there is sufficient water in the boiler, so that if there is not, there is time to supply the deficiency.
If the boiler is cold it may be that the condensation of the steam in cooling may have left a partial vacuum in the boiler, and it will be necessary in that case to open the top gauge cock and let in air so that the water will come to its proper level in the gauge glass. Similarly, in filling the boiler, it may be necessary to open a gauge cock to let the air out.
The lower cock of the gauge glass should be opened to let the steam blow through if there is pressure on the boiler, or to let a little water out if there is not.
The safety valve should next be examined and moved to see that it works properly and does not stick to its seat.
Before laying the fire the fire bars and ash pan should be cleared of ashes and clinkers, and the grate bars tried with the shaking levers to see that the grates will shake properly. It should be seen that the tubes, etc., are clear of ashes.
In laying a new fire an ample supply of lighting material should be used, disposing it so that the fire will light evenly and not in spots, and a good layer of wood should be evenly distributed over the bars, the thinnest pieces being at the bottom as they will light easiest, and it is necessary to light the fire at the bottom, so that the heat from the wood that is first lighted shall pass through that to be lighted.
The wood should be kept burning without coal until the lower[II-401] stratum has ceased to blaze and covers the bars, while there is an even layer of blazing wood above it.
The quantity of coal to be fed at a time, and the depth of fire to be kept, depends upon the size of the coal, because the larger the coal the less it obstructs the draught, and the thicker the layer required in order to prevent currents of air from passing through without entering into combination with the gases from the coal.
If the coal is mixed, containing large lumps, they should be broken.
The first layer of coal should be enough to cover the fire to a depth of about two inches, which will permit of a good draught. This will get well alight while the wood is still serviceable, and a second layer may be applied of another two inches. The third feeding should be given with a view to have a greater depth of fire at the sides than at the middle of the fire box, because the cool sides of the box prevent perfect combustion, and currents of cold air are more apt to find their way through the sides than in the middle of the fire box.
Banking a fire consists of piling it up at the back half of the fire box and covering it up with green coal, so that it may keep alight and keep the boiler hot without increasing the steam pressure.
The air passing through the uncovered half of the fire bars prevents rapid combustion and a dead fire is maintained.
In starting up a banked fire, the first thing to do is to clean it of ashes, clinker, etc., shaking up the bars to see that they will work properly. The fire is then spread evenly over the bars, and wood fed to enliven the fire and promote the draught.
The blower or blast pipe is then set going, and coal gradually fed a little at a time, evenly distributed, covering those parts the most where the fire burns through the most brightly.
A steady fire is better than one that is forced, because the combustion is more perfect and less clinker is formed, hence less cleaning will be necessary, and the fire door will not be kept open so long to let in cold air. This is important because a steady temperature in the fire box promotes its durability, as well as giving a uniform boiler pressure. The strains placed upon a fire box by a fierce fire suddenly cooled by a heavy charge of coal or of cold air from an open fire door are highly destructive.
Furthermore, the greatest economy of fuel is attained by keeping the boiler pressure up, and using the steam expansively by hooking up the links to shorten the point of cut-off.
A safety valve steadily blowing off steam, whether the engine is running or not, is a sign of bad firing and wastefulness.
It is the fireman’s duty to attend to the fire, but nevertheless a careful engineer will be as much interested in proper firing as in his own duties, and as the engineer has more experience than the fireman, he is warranted in exercising an ordinary supervision on the firing, which will be welcome to an earnest or ambitious fireman.
The engineer should examine, with a wrench in hand, the bolts and nuts about the trucks and axle boxes, as these are apt to become loose and come off on the road. A proper construction would remedy this defect almost entirely, and by a proper construction is meant the more frequent employment of split pins, cotters, and other similar safety appliances now omitted for the sake of economy of manufacture.
Nothing in the future of the locomotive is more certain than improvement in this respect, and nothing is more urgently needed, as any engineer will become satisfied if he will gather up along a mile of ordinary railroad the nuts and washers that lay along the track.
The eccentric straps and the pins in the link motion require an examination, which may be done while oiling the parts of the engine.
The oiling requires careful attention; first the cups themselves sometimes become loose, an argument in favor of having, wherever possible, the cups solid on the parts, as done in European practice.
Oil holes are apt to get choked by gumming, which is that the oil in time forms into a brown gummy substance that fills the oil hole. Perfect lubrication does not imply wasteful lubrication by any means, but a wasteful use of oil is probably less expensive than insufficient lubrication.
A thorough engineer will use no more oil than is necessary; he will leave nothing to conjecture or chance, but know from personal inspection that his engine is in complete working order, and to this end the lubrication of the working parts is a vital element.
After having oiled the eccentric straps, the link motion and the reversing gear beneath the engine, the reversing lever and the parts above the frame must be oiled, and the reversing lever moved back and forth several times, from end to end of the sector or quadrant, so as to distribute the oil throughout the joints and working surfaces.
The axle boxes require careful attention in oiling. In English practice, tallow is packed in the corners of the cavities of the top of the box, so that if the box should begin to heat the tallow will melt, and afford extra lubrication with a heavier lubricant than usual, which will often stop the heating.
The connecting and coupling rods then require attention, the cups being filled and the lubrication adjusted.
When steam is up the gauge glass should be blown through again, and it will be found that the water stands higher in the glass than it did before the boiler was under pressure.
The packing of the piston and of the pump glands, if the engine has pumps, should be known to be properly set up, bearing in mind that a leaky pump gland lets air into the pump and impairs its action.
The sand box should contain dry sand, as wet sand will not feed properly.
If steam is raising too rapidly, close the lower damper to reduce the consumption of fuel and save blowing off steam through the safety valve, which should always be avoided as much as possible.
Before starting the engine, open the cylinder cocks and keep[II-402] them open until the sound discloses that dry steam, and not steam and water, is issuing.
Open the throttle enough to start the engine easily and not with a jump, and be prepared to shut off steam instantly if a blow in any part of the engine should indicate an obstruction to its working.
In starting a train, the reversing lever is put in the end forward notch and the cylinder cocks opened. Then the throttle is opened a little at first, so as to avoid starting with a violent shock that might break the couplings.
If in starting (or in ascending gradients) the wheels are forced to slip, the sand lever should be operated, a slight sprinkling of sand serving better than a heavy one. If the sand is damp, it will fall in lumps and not distribute evenly as it should do, while at the same time a great deal more sand will be found necessary.
When the train is fairly under way, the aim should be to maintain full boiler pressure, so as to keep up the required speed with the links hooked up to work the steam as expansively as possible, bearing in mind that the higher up the links are hooked the more expansively the steam is used, and that therefore less steam is used to do the work and the boiler pressure can be kept up easier.
To understand this clearly, let it be supposed that the steam pressure in the boiler is 90 lbs. per square inch, and that the piston area is 400 inches, and the total pressure impelling the piston will be 36,000 lbs.; if this follows the piston for 22 inches, the power becomes 792,000 inch lbs. per stroke.
Now suppose the pressure is 150 lbs. per square inch, and this multiplied by the piston area (400) gives 60,000 lbs. impelling the piston, and this would require to follow the piston but 13.2 inches in order to give 792,000 inch lbs. In the one case we have 22 inches, and in the other 13.2 inches of the cylinder to fill with steam. Of course it will take more fuel under the heat of firing to keep the pressure up to the 150 lbs.; but on the other hand, when the steam is cut off in the cylinder there will be 160 lbs. per square inch in it, and all the work that this does in expanding is gained during the rest of the stroke, so that the required amount of power would be obtained by cutting off earlier than at 13 inches.
The water should, under ordinary conditions, be kept at an uniform level in the boiler. Steam can of course be made quicker with a small than with a large quantity of water, but the smaller the quantity of water the more the steam pressure is liable to fluctuate, and the closer the firing must be attended to.
Furthermore, the more water there is in the boiler, the greater the safety, because the longer the boiler can go without feeding, and, if the pumps or injectors, as the case may be, should act imperfectly, there is more time to get them working properly.
In testing the water level, the gauge glass alone is not to be entirely depended upon, hence the gauge cocks should be opened. The water should not be allowed to go below the middle gauge cock.
It is obvious that when the water is below a certain gauge cock, the gauge glass only can give any information as to how far it is below it, hence it must be used for this purpose.
When using it, it should be blown through by opening its lower cock, and if there is any doubt about its showing the proper water level it should be blown through two or three times, watching the level of the water in the glass at each trial.
A constant boiler feeding is the best, as it is more conducive to a uniform boiler pressure and temperature.
The fire should be fed in small charges, the fire door being kept open as little as possible, because a high temperature in the firebox is necessary to perfect combustion. If heavy charges of coal are given at once, then for some time the fire box will be cooled, and then, as the fire burns through, a fierce heat will be generated. This alternate heating and cooling is very destructive to the fire box and the tubes, as it causes an expansion and contraction that rack the joints and seams.
There are several ways of firing, each having its advocate. Upon the following points, however, there is no dispute. First, a slow combustion is the most perfect, because it produces less clinker, which saves fuel and also saves a large amount of fire cleaning and therefore of admission of cold air to the fire box. A high temperature is necessary to combustion, and the temperature of the fuel is most difficult to keep up at the sides of the fire box.
By light and frequent firing the bright fire will never be covered up, hence the temperature will be maintained. This favors an even distribution over a large surface of the fire of each shovelful of coal. But if at any point the draught is lifting the fire, and small bright pieces of fire are lifting up, it is an evidence that the fire is thinnest there or else that the bars are cleanest there. In either case, an extra amount of coal is required at that spot.
Some engineers will charge one side of the fire box lightly and then the other, this being done so as to keep up the temperature in the fire box. Others will fire first the front and then the back of the box, which answers the same purpose, but in no case should the charge be heavy.
A fireman may become so accustomed to the road and his engine, that under some conditions he may fire when he reaches certain points on the road, regulating it like clockwork.
On a trip from Philadelphia to Reading, on an engine having a Wooten fire box (whose special feature is a large fire box, which enables slow combustion), the firing was conducted as follows:
The fire was was not fed or touched until just before reaching Bridgeport, 18 miles from Philadelphia, when a thin layer of coal was spread evenly on the fire. Eleven miles were then made without opening the fire door, the next firing taking place just before reaching Phœnixville.
Ten miles were run before the next firing, which occurred just before arriving at Pottstown.
The next firing occurred at Bordenboro’, three miles from Pottstown. The remaining 8 miles were made without firing. The steam pressure did not vary more than 10 lbs. per square inch during the trip.
On a trip from New York to Philadelphia by the lightning express train the firing was conducted as follows:
The coal was anthracite and in lumps from 5 to 7 inches in diameter; at one end it reached up to the level of the fire door, while at the tube plate end of the fire box it was about 6 inches deep.
The grate bars were constructed to shake in three sections, and shaking the bars to clear out the fire caused it to feed forward of itself, and the combustion of the coal caused it to break up into lumps about 2 inches in diameter at the tube plate, where the fire was much brighter than at the fire door end. The steam pressure varied about 10 lbs. during the trip.
We now come to the best times to fire, to feed, and to oil the valves, and this depends on the level of the road.
On a level road these matters could be attended to with regularity, but as the engine has most work to do in ascending inclines, it is necessary to prepare for such emergencies: First, by having a good fire prepared, so that the fire door may be kept closed as much as possible while the engine is ascending; second, by having plenty of water in the boiler, so as to keep steam, without feeding any more than possible when the engine is calling for more steam, by reason of the reversing lever being put over towards full gear.
The speed is kept well up before reaching the incline, and the reversing lever moved forward a notch or two at a time to maintain the speed, while at the same time moving the sand lever to feed the sand as soon as the engine speed shows signs of reducing.
The accidents to which the locomotive is most liable when running upon the road, and the course to be pursued by the engineer to enable him to take the engine to the depot or complete the trip, are as follows:
Knocking out the Front Cylinder Head or Cover.—This arises from various causes, such as a breakage of a connecting rod strap, or of a piston rod or cross head. It is the practice of some locomotive builders to cut in the cylinder cover flange a small groove close to the part that fits the cylinder bore, so that the cover shall break out in the form of a disc, leaving the cover, flange, bolts, and nuts intact, and diminishing the liability to break the cylinder itself as well as the cover.
[II-403]The provisional remedy for this accident is to take off the connecting rod (on the side of the broken cover) and also the valve motion, either at the rock shaft arm or by taking down the eccentric rod straps. Then place the valve in the centre of its travel so that it shall cover and enclose both the cylinder steam ports and leave the exhaust port open. Then block the cross head firmly on the forward centre, and go ahead with the other cylinder.
Heating of Piston Rods.—This the engineer can often discover by sight, or by smelling it from the cab. The remedy is to stop the engine and slack back the gland until the steam from the engine cylinder leaks freely through the packing. Then apply a little extra lubrication or water while running slowly.
Breaking of a Piston Rod.—If the piston rod breaks, but does not knock out the cylinder head or cover, pursue the same course as directed for breaking the cylinder cover, taking the additional precaution to block the piston, which may be done by fitting pieces of wood between the guide bars, making the pieces long enough to fit between the cross head and guide yoke.
The cylinder or waste water cocks on the side of the accident must also be opened, to prevent any leakage of steam past the slide valve from getting into the cylinder and driving the piston against the cylinder cover, and breaking the cylinder cover or even the cylinder itself.
If the piston rod breaks from the cross head, it is safest to remove it from the cylinder, though this is unnecessary, if it be securely blocked against the cylinder head so that it cannot move, though steam may leak in on either side of it.
Breaking a Crank Pin.—This is a somewhat frequent accident, but seldom takes place on both sides of the engine at once.
The remedy is to take off all the parallel or coupling rods, and if it is the crank pin on the driving wheels which breaks, take off the connecting rod also, and securely block the cross head, disconnecting the valve motion as before directed, and opening the cylinder waste water cocks. In the case of this accident occurring, it is absolutely essential to take off the parallel rods on both sides of the engine, or otherwise the crank pins on the other side are apt to break.
Throwing Off a Wheel Tire.—In this case the best plan is to block the tireless wheel entirely clear of the track, which may be done by putting a block of wood into the oil cellar of the driving box, and then tow the engine to the repair shop; for if the engine is run to the shop, and the wheel touches the rail, it will impair its diameter for the proper size of tire.
Throwing Off a Driving Wheel.—This is not a common accident, but nevertheless it sometimes occurs; they break usually just outside of the driving axle box. In this case take out the driving box and fit in its place a block of wood affording journal bearing for the axle. Let this block rest on the pedestal cap, holding the axle up in the centre of the pedestal. Then secure the piston and disconnect the valve gearing and open the cylinder cocks as before, and the engine can be run slowly to the repair shop without danger of further accident, or, if convenient, it can be towed by another engine.
Breaking a Spring Or Spring Hanger.—Lift the engine with the jacks until the driving wheel axle box is about in the centre of the pedestal, and put any convenient piece of iron across the top of the driving axle box and between it and the engine frame, thus taking the weight of the engine on the frame instead of on the spring. Place also a block of iron between the end of the equalizing bar and the top of the engine frame, so as to prevent the movement of the equalizing bar, and to allow the spring at the other end of the equalizing bar to operate without moving the said bar. Every engineer should carry in his tool box pieces of metal suitable for this purpose, because this is a frequent accident. It does not, however, materially affect the working of the engine, and should not delay a train more than a few minutes.
Bursted Flues and Tubes.—These are usually plugged by tapering a piece of pine wood and driving it into the bursted tube by means of an iron bar. Taper iron plugs are often carried, and then driven into the end of the tube after the wooden one has been driven in. To enable this job to be done, it is necessary to thickly cover the fire with green coal, which operates to cool the tubes and prevent the loss of the water in the boiler. Sometimes careful engineers prepare for use pine plugs turned slightly taper, and a little slack, for the inside of the tube. In case of leak, this plug is inserted in the flue, and driven along it until it covers the fracture, the expansion due to its saturation causing it to become locked in the tube.
Slipping of Eccentrics.—Place the reverse lever in the forward notch of the sector. Place the crank on its forward dead centre, as near as can be judged by the eye, and loosen the set screw of the forward eccentric, that is to say, the eccentric which connects to the upper end of the link. Move that eccentric round upon the axle until the slide valve leaves the steam port at the front end of the cylinder open to the amount of required valve lead. In moving the eccentric round upon the shaft, move it in the direction in which it will rotate when the engine is running forward, so as to allow for and take up any lost motion there may be in the eccentric straps, in the eccentric rod eyes and bolts, and in the other working parts of the valve gear; for if the eccentric was moved backward, all such lost motion would operate to vitiate the set of the valve. The eccentric being placed as directed fastens its set screw securely.
If the backward eccentric is the loose one, throw the reverse lever to the backward notch of the sector, lifting the link up so that the eccentric connected to the lower end of the link may be approximately adjusted by moving it around upon the axle in the direction in which it will rotate when the engine is running backward, until the back cylinder port is open to the amount of the valve lead. Another very ready plan of temporarily adjusting the eccentrics is as follows: Place the reverse lever in the end notch forward, and place the engine crank or driving crank pin as near on a dead centre as the eye will direct, and open both the cylinder waste water cocks. Then disconnect the slide valve spindle from the rocker arm, and move the slide valve spindle until the opening of the cylinder steam port corresponding to the end of the cylinder at which the piston stands will be shown by steam blowing through the waste water cock at that end of the cylinder; the throttle valve being opened but a trifle, to allow a small steam supply to enter the steam chest and cylinder, for if much steam is admitted, it may pass through a leak in the piston and blow through both the waste water cylinder cocks.
The position of the valve being thus determined, the eccentric must be moved upon the driving axle until the valve spindle will connect with the rocker arm without being moved, or moving the valve at all.
Hot Axle Boxes.—If not convenient to reduce the speed of the engine, or if that and free lubrication do not cool the box, a plentiful supply of cold water should be administered, it being well to have at hand a small hose pipe, by means of which water from the tender tank can be used. If the brasses have Babbitt metal in them and it should melt, it is better, if possible, to cool the axle box while the engine is moving, which will injure the journal less than if the journal is stopped to cool the box, because in the latter case the brass or box is apt to become soldered to the journal of the axle, and when the engine is again started, the cutting or abrasion will recommence with extreme violence.
Breaking a Lifting Link Or the Saddle Pin That Connects The Slot Link To the Reverse Shaft.—Cut a piece of wood and tie it into the slot of the link, over the link block or die, making it of a length to keep the link in the position for hauling the train. Then fasten another piece of wood in the link slot beneath the sliding block or die, thus securing that die in the proper position for the engine to go ahead. In this case, the engineer must be careful in stopping, as he cannot reverse the engine on the crippled side.
Secondary accidents are almost sure to occur if a disconnected piston is not securely blocked in the cylinder, or from blocking the piston aright and attempting to let the slide valve run, or from attempting to run with the parallel rods on one side only disconnected. There are numerous accidents, which only common sense and a familiarity with the locomotive can provide a temporary remedy for, but those here enumerated are by far the most common.
When the wedges of the axle boxes are to be adjusted for fit to the pedestal shoes, the engine should be moved until the coupling rods on one side of the engine are in line with the piston rod, because in this position the rod will, to a certain extent, act as a guide in keeping the axles parallel to each other, and at a right angle to the line of engine centres.
Bear in mind that the distance from the centre to centre of axle boxes must be the same as the distance from centre to centre of the crank pins, and that when the coupling or side rods are in line with the piston rod, they act to resist the axle boxes from being set up too close together.
The importance of a proper adjustment of the axle boxes, coupling boxes, and connecting rods cannot be overestimated, and it is necessary therefore to explain it thoroughly. In Fig. 3350, then, s, s represent two wheel axles, whose boxes are between their wedges. At s, s′ are the screws for setting up the shoes or wedges w and w′ respectively. The axles are shown on the line of centres c, c of the engine, the piston being at the head end of the cylinder, and the crank pins on the line of centres as denoted by the small black circles. The wedges w and w′ are shorter than the leg of the pedestal, so that they may be set up by the set screws s and s′, and take up the wear.
In some engines the wedges v and v′ are also shorter for the same purpose. Now it is clear that setting up the screws s and s′ will move the axles s, s′ to the left, and this will alter the clearance between the piston when it is at the end of the stroke and the cylinder cover.
It is clear that the distance between the centres of the two axles must be the same as the distance between the centres of the two crank pins, or else the frame will be subjected to a great strain, tending to break the crank pins and the side rods.
In order to keep the clearance equal and to know when it is equal, it is necessary, at some time when the cylinder cover at the head end is off, to disconnect the connecting rod and push the piston clear up against the left hand cylinder cover, and from the cross head as a guide, make on the side of the guide a line l′. Then put on the cylinder cover at the head end and push the piston up against it and mark a line l. Then when the connecting rod is put on again, the wheels may be moved around if the engine is jacked up, or, if not, the engine may be moved along the rails with a pinch bar, and the clearance will be equal when the cross head (at the ends of the stroke) comes within an equal distance of the respective lines l′, l when the crank is on the dead centres, and it is well to adjust the wedges w w′ so that the cross head does travel within an equal distance, and mark on the guide bar two more lines, one at each end of the bar.
These lines are a permanent guide in setting up the shoes or wedges, and lining up the connecting rods, and coupling or side rods, because it is clear that from the method employed in marking them the distance between the end of the cross head, when at the end of its stroke, and the line l, and that between the face of the piston and the cylinder cover, will be equal.
A proper adjustment, therefore, should be made as follows: The piston should be at the end of its stroke, the crank pins being on the line of centres.
Screw s should be operated to set up the wedge w, taking up the wear of the sides of the box, and bringing the edge of the cross head the proper distance from the line l. The connecting rod brasses should then be set up to fit the pins, and the screw s′ operated to set up wedge w′ to have easy contact with the side of its axle box. If, however, there has been so much wear on the axle boxes that they are still too loose between the wedges, both wedges may be set up to take up this wear, since it is more important to have the axle boxes a proper fit between the wedges than it is to maintain an exactly equal amount of clearance at each end of the cylinder.
The engine will then be in proper tram on this side, or, in other words, the distance from the centre to centre of the crank pins will be the same as that from centre to centre of the axles.
On the other side of the engine the process is the same, the engine being moved until the crank pins are on the line of centres c c and the wedges set up according to the lines.
Power is distinguishable from force or pressure in that the term power means force or pressure in motion, and since this motion cannot occur without the expenditure of the force or pressure, power may, with propriety, be termed the expenditure of force or pressure.
If we suppose a piston to stand in a vertical cylinder sustaining a weight upon its surface and compressing the air within the cylinder, so long as there is no motion no work is done, as the term “work” is understood in a mechanical sense, and the weight merely produces a pressure. If, however, the weight be removed, the compressed air will force the piston upward, performing a certain quantity of work which may best be measured by the amount of power exercised or expended.
The mechanical value of a given amount of power cannot be either increased, diminished or destroyed by means of any mechanical device or appliance whatsoever through which it may be transmitted.
It may be concentrated, as it were, by decreasing the amount of its motion. It may be distended, as it were, by increasing the distance through which it moves, or it may be expended in giving or producing motion, but in either case the amount of duty or work done is the exact equivalent of the amount of power applied.
A gain or increase in speed is not, therefore, a loss of power, but merely a variation in the mode of using or utilizing such power.
For instance, 1 lb. moving through a distance of 12 inches in a given time represents an amount of power which may be employed either as 1 lb. moving a foot, 2 lbs. moving six inches, or 1⁄2 lb. moving through 24 inches, in the same space of time, the amount of the power or duty remaining the same in each case, the method of utilization merely having differed.
It is an inexorable law of nature that power is concentrated in proportion as the amount of its motion is diminished, or distended in precise proportion as such motion is increased.
Suppose, for example, that in Fig. 3351 l is a lever having its fulcrum at f, which is 4 inches from end a, and 8 inches from end b, and (leaving the weight of the lever out of the question) if we place an 8 lb. weight on a it will just balance 4 lbs. at b.
If the lever is moved, the amount of motion will be twice as much at end b as it is at end a.
If we apply the power at a, the lever has become a means of converting 8 lbs. moving a certain distance into 4 lbs. moving twice that distance, and nothing has been either gained or lost.
If we apply the power at b, the lever has merely been used as a means of converting 4 lbs. moving a certain distance into 8 lbs. moving one half that distance, and nothing has been gained or lost.
Suppose that end a was moved an inch, and the power at that end will be 8 inch pounds or 8 lbs. moving an inch, whereas at the end b the power is 4 lbs. moving 2 inches; we have, therefore, reduced the weight in the same proportion that we have increased the distance moved through.
Suppose now that the lever is moved to the position denoted by the dotted line m m, and the leverages will be altered; that at end a becoming that denoted by the distance from f to the vertical c, and that for end b being denoted by the distance from f to the vertical d.
This occurs because we are dealing with gravity, which always acts in a vertical line.
A crow bar is an excellent example of the application of the lever. In Fig. 3352, for example, we have a 1 lb. weight on the long end of the lever, and as we are dealing with a weight, the effective length of the long end of the lever is from the fulcrum f to w, which is divided into 10 equal divisions. The short end of the lever is from f to p, which is equal to one division, hence the 1 lb. is balanced by the 10 lbs.
A simple method of distending power is by means of pulleys or gear wheels. Suppose, for example, that in Fig. 3353, we have a weight of 12 lbs. suspended from a shaft or drum, whose radius a[II-406] is 10 inches, and that on the same shaft there is a pulley, whose radius b is 20 inches, and the two weights will balance each other.
In this case the falling of either weight would not effect the leverage, because the distance of both weights would remain the same from the centre of the shaft. The leverage of the 12 lbs. is denoted by the line a, and that of the 6 lbs. by b.
So far as the transmission of power is concerned, therefore, pulleys are in effect revolving levers, which may be employed to concentrate or to distend power, but do not vary its amount.
Suppose we have two shafts, on the first of which are two pulleys, b and c, Fig. 3354, while upon the second there are two pulleys d and e. A belt h, connecting c to d. Let the pulleys have the following dimensions:
If we take the first pair of wheels b and c, we have that the velocity will vary in the same ratio or degree as their diameters vary, notwithstanding that their revolutions are equal.
| Radius. | Diameter. | Circumference. | |||||
| B | = | 51⁄8 | inches. | 101⁄4 | inches. | 32.2 | inches. |
| C | = | 101⁄4 | „ | 201⁄2 | „ | 64.4 | „ |
| D | = | 75⁄8 | „ | 151⁄4 | „ | 47.9 | „ |
| E | = | 151⁄4 | „ | 301⁄2 | „ | 95.8 | „ |
The velocity is the space moved through in a unit of time, and as it is the circumference of the pulley that is considered, the velocity of the circumference is that taken; thus, if we make a mark on the circumferences of the two pulleys, b and c, Fig. 3354, the velocity of that on c will be twice that upon b, or in the same proportion as the diameters.
Let there be suspended from the circumference of b 10 lbs. weight, and let us see the degree to which this power will be distended by this arrangement of pulleys, supposing the weight to rotate b, and making no allowance for the friction of the shaft.
Suppose the weight to have fallen 32.2 inches, and we have 10 lbs. moving through 32.2 inches, this power it will have transmitted to pulley b.
To find what this becomes at the perimeter of c, we must reduce the number of lbs. in the same proportion that the perimeter of c moves faster than does that of b; hence we divide the circumference of one into the other, and with the sum so obtained divide the amount of the weight; thus, 64.4 (circumference of c) ÷ 32.2 (circumference of b), = 2; and 10 lbs. ÷ 2 = 5 lbs., which, as the circumference of c is twice that of b, will move twice as fast as the 10 lbs. at b, hence for c we have 5 lbs. moving through 64.4 inches.
Now c communicates this to d by means of the belt h, hence we have at d the same 5 lbs. moving through 64.4 inches.
Now e moves twice as fast as d, because its circumference is twice as great, and both are fast upon the same shaft, hence the 5 lbs. at d becomes 21⁄2 lbs. at e, but moves through a distance equal to twice 64.4, which is 128.8 inches. To recapitulate, then, we have as follows:
| The weight | gives | 10 | lbs. | moving | through | 32.2 | inches. | |||
| Pulley | b | „ | 10 | „ | „ | „ | 32.2 | „ | ||
| „ | c | „ | 5 | „ | „ | „ | 64.4 | „ | ||
| „ | d | „ | 5 | „ | „ | „ | 64.4 | „ | ||
| „ | e | „ | 2 | 1⁄2 | „ | „ | „ | 128.8 | „ | |
That the amount of power is equal in each case, may be shown as follows:
For c, 5 lbs. moving through 64.4 inches is an equal amount of power to 10 lbs. moving through 32.2 inches, because if we suppose the first pair of pulleys to be revolving levers, whose fulcrum is the centre of the shaft, it will be plain that one end of the lever being twice as long as the other, its motion will be twice as great, and the 5 at 101⁄4 inches just balances 10, at 51⁄8 inches from the fulcrum, as in the common lever.
In the case of d we have the same figures both for weight and motion as we have at c, because d simply receives the weight or force and the motion of c. In the case of e, we have the motion of the weight multiplied four times; for the distance e moves is 128.8 inches, which, divided by 4, gives 32.2 inches, which is the amount of motion of the weight, hence the 10 lbs. of the weight is decreased four times, thus 10 lbs. ÷ 4 = 21⁄2 lbs., hence the 21⁄2 lbs. moving through 128.8 inches is the same amount of power as 10 lbs. moving 32.2 inches, and we may concentrate or convert the one into the other, by dividing 128.8 by 4, and multiplying the 21⁄2 lbs. by 4, giving 10 lbs. moving 32.2 inches.
If, therefore, we make no allowance for friction, nothing has been lost and nothing gained.
Thus far, we have taken no account of the time in which the work was done, more than as one wheel is caused to move by the other, and all of them by the motion of the weight, they must all have begun and also have to move at the same time. Suppose, then, that the time occupied by the weight in falling the 32.2 inches was one minute, and the amount of power obtained may be found by multiplying the lbs. of the weight by the distance it moved through in the minute, thus 10 lbs. moving 32.2 inches in a minute gives 32.2 inch lbs. per minute, being the amount of power developed by the 10 lb. weight in falling the 32.2 inches.
We may now convert the power at each pulley perimeter or circumference into inch pounds by multiplying the respective lbs. by the distance moved through in inches, as per the following table:
| Distance moved. | ||||||||
| Lbs. | Inches. | Inch lbs. of power. | ||||||
| Weight | at | b | 10 | × | 32.2 | = | 322 | |
| „ | „ | c | 5 | × | 64.4 | = | 322 | |
| „ | „ | d | 5 | × | 64.4 | = | 322 | |
| „ | „ | e | 2 | 1⁄2 | × | 128.8 | = | 322 |
If we require to find the power in foot lbs. per minute, we divide by 12 (because there are 12 inches in a foot), thus 322 inch lbs. ÷ 12 = 26.83 foot lbs. per minute.
Now suppose that b was moved by a belt, with a pull of 10 lbs. at its perimeter, and made 100 revolutions in a minute instead of one, then the pull at the perimeters of c, d, and e would remain the same, but the motion would be 100 times as great, and the work done would therefore be increased one hundred fold. It will be apparent, then, that the time is as important an element as the weight.
The velocity and power of gear wheels are calculated at the pitch circle.
Now suppose the gear a in Fig. 3355 has 30, gear b 60, gear c 10 and gear e 80 teeth, and that 5 lbs. be applied at the pitch circle of a; to find what this 5 lbs. would become at the pitch circle of e, we multiply it by the number of teeth in b and divide it by the number of teeth in c, thus:
| Lbs. | |||
| At pitch of circle | a | 5 | |
| Number of teeth in | b | 60 | |
| Number of teeth in | c | 10 ) | 300 |
| 30 | |||
| Answer, 30 lbs. at the pitch circle of e. | |||
[II-407]Now suppose that on the shaft of a there is a pulley 20 inches in diameter, and that on this pulley there is a belt exerting a pull of 5 lbs., while on the shaft of e there is a pulley 16 inches in diameter, and to find how much this latter pulley would pull its belt, we proceed as follows:
| 2 ) | 20 | = | Diameter of pulley on a. | |||
| 10 | = | Radius of pulley on a. | ||||
| 5 | = | Pull on pulley a. | ||||
| Number of teeth in a | = | 30 ) | 50 | = | Pull at centre of shaft of a. | |
| 1.666 | ||||||
| 60 | = | Number of teeth on b. | ||||
| Number of teeth on c | = | 10 ) | 99.960 | = | Pull at axis of shaft of b. | |
| 9.996 | ||||||
| 80 | = | Number of teeth on e. | ||||
| Radius of pulley on shaft of e | 8 ) | 799.680 | Pull at axis of shaft e. | |||
| 99.96 | Pull at perimeter of last pulley. | |||||
We have in this case treated each pulley as a lever whose length equalled the radius of the pulley, while in the case of the wheel we have multiplied by the number of teeth when the power was transmitted from the circumference to the shaft, and divided by the number of teeth (the number of teeth representing the circumference) when the power was transmitted from the shaft to the teeth.
We thus find that power is composed of three things, first, the amount of impelling force; second, the distance that force moves through; and third, the time it takes to move that distance.
If we take a number of pulleys, say four, and arrange them one after another so that they drive by the friction of their circumferences, then the amount of power transmitted by each will be equal and the velocities will be equal, whereas, if we arrange them as in Fig. 3354, the power will be equal for each, but the velocities or space moved through in a given time will vary.
What is known as the unit of power is the foot lb., being the amount of power exerted in raising or lifting one lb. one foot, and from what has already been said, it will be perceived that this is the same amount of power as 12 lbs. moving a distance of one inch.
Watt determined that the power of a horse was equal to that necessary to raise 33,000 lbs. one foot high in a minute, and this is accepted, in English speaking countries, as being a horse power.
An engine or machine has as much horse power as it has capacity to lift 33,000 lbs. a foot high in a minute.
The horse-power of an engine may be calculated as follows:
Rule.—Multiply the area of the piston by the average steam pressure upon the piston throughout the stroke, and by the length of the stroke in inches, which gives the number of inch pounds received by the piston from the steam during one stroke.
As there are two piston strokes to one revolution of the engine, we multiply by two, and thus get the number of inch pounds received by the piston in one revolution.
By multiplying this by the number of revolutions the engine makes in a minute, we get the number of inch pounds of power received by the piston in a minute.
By dividing this by 12, we get the number of foot pounds the piston receives per minute, and dividing this by 33,000 lbs. we get the horse-power of the engine.
It has already been stated that Watt determined that a horse was capable of exerting a power equal to the raising of 33,000 lbs. one foot high in a minute, hence, having foot pounds of the engine per minute, dividing them by 33,000 gives the horse power.
This gives the amount of power received by the piston, but it is evident that the engine cannot exert so much power, because part of it is expended in overcoming the friction of the moving parts of the engine.
The amount of the piston power expended in overcoming the friction depends upon the fit of the parts, upon the lubrication and the amount of the load.
Thus, the friction of the cross head guides, of the cross head pin, of the crank pin and of the crank shaft bearings will increase with the amount of resistance offered to the piston motion.
The average pressure on the piston is a difficult thing to find, however, for several reasons.
First, because the pressure in the cylinder may, during the live steam period, vary from that in the steam chest because of the ports being too small or from the passages being choked from a defective casting.
Second, because the steam is wire drawn during the time that the slide valve is closing the port to effect the cut off.
Third, because the live steam in the port and passage at the time the cut off occurs gives out some power during the period of expansion.
Fourth, because there is some condensation of the steam in the cylinder after the point of cut off, and there is no means of finding by calculation how much loss there may be from this cause.
During the live steam period there is also loss from condensation in the cylinder, but this is made up for by steam from the steam chest.
Fifth, the loss from condensation after the cut off has occurred will vary with the speed of the engine, and is greater in proportion as the piston speed is less, because there is more time for the condensation to occur in.
Sixth, there is some pressure on the piston between the time that the exhaust begins and the piston ends its stroke.
Seventh, because the compression absorbs some of the piston power.
Assuming the average pressure on the piston to be known, however, we may calculate the horse power as follows:
Example.—What is the horse power of an engine whose piston is 20 inches in diameter, and stroke 30, the revolutions per minute being 120, and the average pressure on the piston 60 lbs. per square inch?
| Diameter of piston | 20 | |||
| Diameter of piston | 20 | |||
| Diameter of piston squared | 400 | |||
| .7854 | ||||
| 400 | ||||
| Area of piston = | 314.1600 | ( |
||
| 60 | average steam pressure. | |||
| lbs. pressure on piston | 18849.60 | ( |
||
| 30 | length of stroke in inches. | |||
| 565488.0 | inch lbs. per stroke. | |||
| 2 | two piston strokes per revolution. | |||
| 12 ) | 1130976 | inch lbs. per revolution. | ||
| 94248 | foot lbs. per revolution. | |||
| 120 | revolutions per minute. | |||
| 1884960 | ||||
| 94248 | ||||
| 11309760 | foot lbs. per minute. | |||
| 33000 ) 113097 | 60 ( 342.72 = horse power of engine. |
| 99000 | |
| 14097 | 6 |
| 13200 | 0 |
| 897 | 60 |
| 660 | 00 |
| 237 | 600 |
| 231 | 000 |
| 6 | 6000 |
| 6 | 6000 |
In working out the calculation, the ciphers that are decimals and are on the right hand are neglected or taken no account of, because they represent no value and may therefore be discarded.
Thus the area of the piston is 314.1600 inches, the two right hand ciphers having no value. Again the lbs. pressure on the piston is 18849.60 lbs., and the right hand cipher, having no value, is discarded. The inch lbs. per stroke is 565488.0, and the decimal cipher, representing nothing, is discarded when multiplying by the 2.
We have in this case taken no account of the fact that the piston rod prevents the steam from acting against a part of the piston area during one stroke; hence for correct results we must subtract from the area of the piston one half the area of the piston rod.
The horse power thus obtained is that which the engine receives from the steam, and is more than the engine is capable of exerting to drive machinery, because a part of this power is consumed in overcoming the friction of the working parts of the engine.
The useful horse power of a stationary engine may be readily and accurately obtained by means of a pair of scales, and a brake, as shown in Fig. 3356, which is constructed and used as follows:
On the crank shaft of the engine is a pulley enveloped by a friction brake, which consists of an iron band, to which wooden blocks are fastened.
The ends of the iron band do not meet, but are secured together by a bolt as shown.
By screwing up the bolt the wood blocks are brought to press against the circumference of the wheel.
This forms a friction brake that would revolve with the wheel, were it not for two arms that are secured to the brake, and rest at the other end upon a block placed upon a pair of scales.
The principle of action of this device is that the amount of friction between the brake and the wheel is weighed upon the scales, and this amount, multiplied by the velocity of the wheel at its circumference and divided by 33,000, is the horse-power of the engine.
It is necessary, in arranging this brake, to have its end rest upon the scale at the same height from the floor as the centre of the crank shaft, so that the line marked 5′ 3′′ (5 feet 3 inches), which represents the length of the lever, shall stand parallel with the surface of the platform of the scale.
To test the horse-power, we proceed as follows:
Suppose the pressure of the end of the lever on the scale is found by the weight on the scale beam to be 540 lbs., the diameter on which the brake blocks act being 3 feet, the length of the leverage being 5 feet 3 inches, as marked, and the engine making 150 revolutions per minute, and the calculation is as follows:
| 540 | lbs. on scale. | |||
| 5.25 | leverage in feet. | |||
| 2700 | ||||
| 1 | 080 | |||
| 27 | 00 | |||
| radius of pulley in feet 1.5 ) | 28 | 35.00 | ( 1890 lbs. at pulley perimeter. | |
| 15 | ||||
| 13 | 3 | |||
| 12 | 0 | |||
| 1 | 35 | |||
| 1 | 35 | |||
| . | ..0 | |||
Then
| 3.141 | 6 | ||
| 3 | diameter of pulley in feet. | ||
| 9.424 | 8 | circumference of pulley in feet. | |
| 1 | 50 | revolutions per minute. | |
| 4712 | 400 | ||
| 9424 | 8 | ||
| 1413.7 | 200 | velocity of pulley perimeter. | |
| 18 | 90 | pounds at pulley perimeter. | |
| 12723 | 480 | ||
| 113097 | 6 | ||
| 141372 | |||
| 267193 | 0.80 | foot lbs. per minute. | |
Then
| 33000 ) 267193 | 0.80 ( 80.9 |
| 264000 | |
| 3193 | 08 |
| 2970 | 00 |
| 223 | 080 |
| Answer, 809⁄10 horse power. | |
In this calculation we have nothing to do with the size of the cylinder or the steam pressure, because the scale beam tells us how many lbs. the brake exerts on the scale, and we treat the brake and brake pulley as levers. Thus by multiplying the lbs. on the scale by the leverage of the brake arm we get the number of lbs. exerted at the centre of the crank shaft, and by dividing this by the radius of the brake pulley we get the number of lbs. on the circumference, or, what is the same thing, the perimeter of the brake pulley.
By multiplying the circumference of the pulley in feet by the revolutions per minute, we get the speed at which the pounds travel, and by multiplying this speed by the number of lbs. we get[II-409] the foot lbs. per minute, which, divided by 33,000, gives us the effective horse power of the engine.
This effective horse power is correct, because in loading the engine by the brake the crank pin, the cross head guides, etc., are all placed under the same friction as they would be if it was a circular saw, or some other piece of machinery or machine that the engine was driving.
Among the most frequent questions asked in an engineer’s examination are those relating to the safety valves of boilers.
These questions may be easily answered from a study of the following:
The safety valve is a device for relieving the boiler of steam after it has reached a certain pressure.
This it accomplishes by letting the steam escape after it has reached the required pressure.
At what pressure the safety valve will blow off depends upon the position of the weight on the safety valve lever.
The calculations referring to this part of the subject are, finding how much weight will be required to be placed at a given point on the lever, in order, with a given sized valve, to blow off at a given pressure.
Finding the position on the lever of a given amount of weight, in order to blow off at a certain pressure.
Finding, with a given sized valve and a given weight, how to mark off the lever and where the notches must be cut for given pressures.
In each of these calculations there are three elements: first, the area of the valve and the steam pressure, which constitute the effect of acting to lift the valve; second, the amount of the weight and its position upon the lever, which acts to keep the valve closed; and third, the weight of the lever and of the valve, which act to keep the valve closed.
In Fig. 3357 we have a drawing of a safety valve shown in section, and if there was no weight upon the lever, the pressure of steam the valve would hold in the boiler would be that due to the weight of the valve and of the lever upon the valve.
To find out how much this would be, we would have to put the valve itself and the pin a on a pair of scales and weigh them.
Then put a piece of string through the hole at a in the lever, and see how much it weighed when suspended from that point.
Suppose the valve and pin to weigh 2 lbs. and the lever (suspended by the string) 10, and the total will be 12 lbs.
Next we find the area of the valve, and suppose this to be 8 square inches; then we may find how much pressure the valve would keep in the boiler, by dividing the area of the valve into the weight holding the valve down, thus:
| Lbs. | ||||||
| Weight | of | valve and pin, | 2 | |||
| „ | „ | lever, | 10 | |||
| Area of valve, | 8 ) | 12 | ||||
| Pressure the valve would hold, | 1 | .5 | lbs. | |||
The area of the valve is that part of its face receiving the steam pressure when the valve is seated, so that if the smallest part of the valve diameter is equal to the diameter of the seat bore, the diameter from which the valve area is to be calculated will be that denoted by d in the figure, and cannot in any case be less than this. But if the smallest end of the valve cone is of larger diameter than the smallest end of the seat cone (which should not, but might be the case), then it is the smallest diameter of valve cone that must be taken in calculating the area, because that is the area the steam will press against.
Now suppose we rest a 20 lb. weight on the top of the valve that is on the point denoted by i, and there will be 32 lbs. holding the valve down, thus, weight of valve 2 lbs., of lever 10, and weight added, 20 lbs., and to find how much pressure this would hold in the boiler, we divide it by the valve area, thus:
| Weight on valve. | ||||
| Valve area | = | 8 ) | 32 | |
| 4 | = pressure valve will hold. | |||
But suppose we put the weight on the lever, in the position shown in the figure, which is six times as far from the fulcrum f of the lever as the valve is, and its effect on the valve will be six times as great as it would if placed directly upon the valve, so that leaving the weight of the valve and of the lever out of the question (as is commonly done in engineers’ examinations), we may find out what pressure the valve will hold, as follows:
Rule.—Divide the length of the lever by the distance from the centre of the valve to the centre of the fulcrum. Multiply by the amount of the weight in lbs., and divide by the area of the valve.
Example.—The area of the valve is 8 inches, the distance from the centre of the fulcrum to the centre of the valve is 4 inches, and the distance from the fulcrum to the point of suspension of the weight 24 inches, the weight is 40 lbs., what pressure will the valve hold?
| Length of lever. | ||||
| From fulcrum to valve, | 4 ) | 24 | ||
| 6 | ||||
| 4 | 0 | amount of weight. | ||
| Area of valve, | 8 ) | 24 | 0 | |
| 3 | 0 | |||
| Lbs. per square inch the valve will hold = 30. | ||||
The philosophy of this is clear enough when we consider that as the weight is six times as far from the fulcrum as the valve is, and each 1 lb. of weight will press with a force of 6 lbs. on the valve, hence the 40 lbs. will press 240 lbs. on the valve, and as the valve has 8 square inches, the 240 becomes 30 lbs. for each inch of area.
Example.—The area of a safety valve is 8 inches, the distance from the fulcrum to the valve is 4 inches, and the weight is 40 lbs., how far must the weight be from the fulcrum to hold in the boiler a pressure of 30 lbs. per square inch?
| In lbs. | ||||
| From fulcrum to valve, | 4 ) | 4 | 0 | amount of weight. |
| 1 | 0 | |||
| Area of valve, | 8 | square inches. | ||
| Pressure required, | 3 | 0 | ||
| 10 ) | 24 | 0 | ||
| 2 | 4 | |||
| Answer = 24 inches from the fulcrum. | ||||
Example.—The diameter of a safety valve is 4 inches, the distance from the centre of the fulcrum to the valve is 3 inches, a 50 lb. weight is 30 inches from the fulcrum, what pressure will the valve hold?
| 3 | diameter of valve. |
| 3 | |
| 9 | |
| .7854 | |
| 36 | |
| 45 | |
| 72 | |
| 63 | |
| 7.0686 | = area of valve. |
| 3 ) | 30 | ||
| 10 | |||
| 50 | = weight | ||
| 10 | = leverage of weight. | ||
| Area of valve, 7.068 ) | 500 | .000 | ( 70.7 = lbs. pressure per sq. in. |
| 494 | 76 | ||
| 5 | 2400 | ||
| 4 | 9476 | ||
| 2924 | |||
The heat unit, or the unit whereby heat is measured, is the quantity of heat that is necessary to raise 1 lb. of water from its freezing temperature (which is 32° Fahrenheit) 1°, and this unit is sometimes termed a thermal unit.
The reason that some specific temperature, as 32° Fahrenheit, is taken, is because the quantity of heat required to heat a given quantity of water 1° increases with the temperature of the water; thus, it takes more heat to raise 1 lb. of water from 240° to 245° than it does to raise it from 235 to 240, although the temperature has been raised 5° in each case.
The whole quantity of heat in water or steam is not, however, sensible to the thermometer, or, in other words, is not shown by that instrument. The heat not so shown or indicated is termed latent heat.
Water obtains latent heat while passing from a solid to a liquid state, as from ice into water, and while passing from a liquid to a gaseous state, as while passing from water into steam, and the existence of latent heat in steam may be shown as follows:
If we take a body of water at a temperature above freezing, and insert therein a thermometer, the decrease in the temperature as the water becomes frozen will be shown by the thermometer. If, then, its temperature being say at zero, heat be continuously imparted to the ice, the thermometer will mark the rise in temperature until the ice begins to melt, when it will remain stationary at 32° so long as any ice remains unmelted, and it is obvious that all the heat that entered the water from the time the ice began to melt until it was all melted became latent, and neither sensible to the sense of feeling nor to the thermometer. Similarly, if the water, after the ice is all melted, be heated in the open air, the thermometer will mark the rise of temperature until the water boils, after which it will show no further rise of temperature, although the water still receives heat. The heat that enters the water from boiling until it is evaporated away is the latent heat of steam. The latent heat of water is 143° Fahrenheit, and that of steam when exposed to the pressure of the atmosphere, or under an atmospheric pressure of 15 lbs. (nearly), is 960°, which may be shown as follows:
If a given quantity of water, as say 1 lb., has imparted to it a continuously uniform degree of heat sufficient to cause it to boil in one hour, then it will take about 51⁄3 more hours to evaporate it all away, hence we find the latent heat by taking the difference in the amount of heat received by the water, and that shown by the thermometer thus:
| Degrees. | |||
| Temperature by thermometer at boiling point | 212 | ||
| Less the temperature of the water at first | 32 | ||
| Heat that entered the water in the first hour | 180 | ||
| Hours that the water was subsequently heated | 5 | 1⁄3 | |
| 900 | |||
| One-third of 180 | = | 60 | |
| Heat that entered the water during the 51⁄3 hours | 960 | degrees. | |
This, however, is not quite correct, as it would take slightly more than 51⁄3 hours to boil the water away, and the heat that entered the water after it commenced to boil would be about 966 degrees.
If the steam that arose from the water while it was boiling were preserved without increasing the pressure under which it boiled, and without losing any of its heat, it will have a temperature the same as that of the water from which it was boiled, which is a temperature of 212°, so that neither the steam nor the water account, by the thermometer, for the 966° of heat that entered the water after it boiled, hence the 966° became latent, constituting the latent heat of the steam when boiled from and at a temperature of 212°.
The total heat of steam is the sensible heat, or that shown by the thermometer, added to the latent heat; hence the heat necessary to evaporate water into steam at a temperature of 212° (which corresponds to a pressure of 14.7 lbs. per square inch) is 212° + 966°, which is 1178°, and these, therefore, are the number of degrees that must be imparted by the coal to the water, in order to form steam at a temperature of 212°.
Water is at its greatest density when at a temperature of 39.1° Fahrenheit, that is to say, it occupies its least space and weighs the most per given quantity (as per cubic inch) when at that temperature.
At a lower temperature water expands, its freezing point being 32° Fahrenheit, below which it forms ice. The weight of a cubic foot of water when at its maximum density (39.1) is 62.382 lbs. Water also expands as its temperature is increased above 39.1°; thus, while it is heated from 39.1 to 212°, its volume increases from 1 to 1.04332. The expansion for each degree of heat added to its temperature increases from 0 at 40° Fahrenheit to .0043 at 212°.
The rate of expansion of water at a temperature above 212° is unknown.
At every temperature above freezing point water passes from the liquid into a gaseous state, the gas being termed steam. While water is below its boiling point its evaporation occurs at its surface only; but when its mass is heated to boiling point, and additional heat is imparted to it, evaporation occurs from the water lying against the surface from which it receives the heat, and an ebullition is caused by the vaporized water passing through the mass, the ebullition being what is known as boiling.
The temperature at which water boils depends upon the pressure acting upon its surface, the boiling point being at a lower temperature in proportion as the pressure is reduced; thus water at the top of a mountain, where the pressure of the atmosphere is less than at the sea level, would boil at a lower temperature than 212°, which is the boiling point when the atmospheric pressure is 14.7 lbs., which it is assumed to be at the sea level. Conversely, the boiling point is raised in proportion as the pressure upon its surface is raised, whether that pressure consists of air or of steam. As, however, the pressure is increased, the boiling point is at a higher temperature. So long as the steam is in contact with the water both are at the same temperature, as denoted by the thermometer (although they do not contain the same quantity of heat, as will be show presently), and the steam is termed saturated steam.
The pressure of saturated steam cannot be either increased or diminished without either increasing or diminishing its temperature, hence there is a definite relation of pressure to temperature, which enables the pressure to be known from the temperature, or conversely, the temperature to be known from the pressure. But if the steam be separated from the water and heated, it may be what is termed superheated, which is that it may be surcharged with heat or contain more heat than saturated steam at the same pressure. Such additional heat, however, is latent.
The pressure of steam is the lbs. of force it exerts upon a given area, as upon a square inch. In non-condensing engines the effective pressure of the steam is its pressure above that of the atmosphere, because the exhaust side of the piston being exposed to the atmosphere receives the atmospheric pressure, which must be[II-411] overcome by a corresponding pressure of steam on the steam side of the piston, and this pressure is not, therefore, available for producing work or power in the engine.
In condensing engines, however, the exhaust side of the piston is (as nearly as practicable), relieved of the atmospheric pressure, and assuming a perfect vacuum to be formed, the whole of the steam pressure is exerted to propel the piston, in which case the steam pressure is termed the absolute pressure.
In considering the weight or density or the expansion of steam, its absolute and not its effective pressure must obviously be taken.
What is termed dry steam is saturated steam that does not contain what may be termed entrained water, which is water held in suspension in the steam, which may be caused by the surface of the water through which the steam is allowed to rise being too small in proportion to the volume of steam formed, in which case the rapid passage of the steam through the water causes it to carry up water with it and hold it in suspension, this action being termed foaming or priming.
Suppose, for example, that a boiler be filled with water up to the bottom of the steam dome, then all the steam formed would require to find exit from the water within the area of the dome, and the violence of the ebullition would cause foaming. Obviously, then, to obtain dry steam there must be provided a sufficient area of water surface for the steam to pass through.
But water so entrained is evaporated into steam, if the steam is wire drawn, that is, allowed to expand and reduce in pressure.
A cubic inch of water, when evaporated into steam at a pressure of 14.7 lbs. per square inch, occupies as steam a space or volume of 1644 cubic inches, and its weight will be equal to that of the water from which it was evaporated.
If additional heat be imparted (after its evaporation into steam), such additional heat becomes latent and does not cause an increase of sensible temperature or of pressure.
The weight of a given volume of steam, therefore, bears a definite and constant relation to the pressure and sensible temperature of the steam, so that the pressure or the sensible temperature being known, the weight of a given volume, as say a cubic foot, may be known therefrom. Or the weight of a cubic foot of steam being known, its sensible temperature and pressure may be known therefrom.
This would not be the case if steam expanded by heat. Suppose, for example, we have a cubic foot of steam at any absolute pressure, as say 15 pounds per square inch, a cubic foot weighing .0387 of a lb., and its sensible temperature will be 213°. Now it is evident that the weight will remain the same whatever the amount of heat that may be imparted to the steam. Now if the steam were maintained within the cubic foot of space, and was capable of expansion by the absorption of additional heat, its pressure would increase and its weight remaining the same, there would be no definite relation between the weight and the temperature and pressure.
But if the cubic foot of steam were allowed to expand so as to occupy more space, then additional heat is necessary to prevent its condensation.
The relation between the temperature, pressure, and weight of steam is not quite proportional to the volume, because steam is not a perfect gas, and does not, therefore, strictly follow Mariotte’s law.
A perfect gas is one that during expansion or compression follows the law laid down by Boyle and Mariotte, this law being that, if maintained at a constant temperature, the volume is inversely proportional to the pressure.
For example, the quantity of gas that, if confined in a cubic inch of space, would give a pressure of 80 lbs. per square inch, would give a pressure twice as great (or 160 lbs. per inch of area), if confined in one-half the space, that is, if compressed into one-half of a cubic inch. Conversely, if the cubic inch was allowed to expand until its pressure was 40 lbs., it would occupy 2 cubic inches of space, assuming, of course, that the temperature remains the same. Since, however, if a gas be compressed, its temperature is increased by reason of the friction of the particles moving one upon the other, the law of Mariotte may be better explained as follows:
Suppose we have three vessels, A, B, and C, filled with a fluid which is a perfect gas, the temperatures being equal. Let the pressure be: A 40, B 80, and C 160 lbs. per square inch, then 2 cubic inches of the fluid in B will weigh the same as 4 cubic inches in A, because that in B is at twice the pressure of that in A, and the 2 cubic inches in B will weigh the same as 1 cubic inch in C, because its pressure is one-half that of C, or, what is the same thing, whatever number of cubic inches of the fluid in C it takes to weigh a pound, it will take twice as many in B, and four times as many in A to weigh one pound.
But steam is not a perfect gas, as is evidenced by the fact that its volume does not increase in a ratio inverse to its pressure. For example, if a cubic inch of water be evaporated into steam at a pressure of 14.7 lbs. per square inch, its volume will be 1644 cubic inches, and its temperature 212° Fahrenheit.
But if the cubic inch of water be evaporated into steam at twice the pressure, which is 29.4 lbs per square inch, its volume will be 838 inches.
The volume then is not inversely as the pressure, although the actual quantity and weight remain the same, as is proven by the fact that if the steam at either pressure were condensed it would pass back into the cubic inch of water from which it was generated.
This may be accounted for in the difference in the boiling point of the water in the two pressures, or in other words, by the difference in the temperatures; thus the boiling point of the water at a pressure of 14.7 lbs. is 212°, while that for the pressure of 29.4 is increased about 38.4 degrees, and the steam is at the higher pressure expanded by these 38.4 degrees of heat, which adds to its pressure, although not affecting its actual quantity or weight.
The amount of this expansion may be estimated as follows:
Taking the 1644 cubic inches, and supposing the steam to be a perfect gas, we divide it by 2 to obtain half the volume, 1644 ÷ 2 = 822.
If then we subtract this 822, which is the volume of the steam if it acted as a perfect gas from the 838 it actually occupies, we get 16 (838 - 822 = 16), which is the number of cubic inches of expansion due to the increase in the boiling temperature.
When steam performs work a certain portion of the heat it contains is converted into work, the steam simply being a medium of conveying the heat into the cylinder in which the motion of the piston converts this proportion of heat into work. It has been proven that a given quantity of heat will pass into a given quantity of work, and conversely that a given quantity of work is convertible into a given quantity of heat, and it has also been proven that so much heat is convertible into so much work, independent of the temperature of the heat during its conversion into work, power, or energy, all three of these words being used to imply pressure, force, or weight in motion.
The accepted measurement of the conversion of heat into work is known as Joule’s equivalent; Joule having determined that the amount of power exerted in raising 772 lbs. one foot is the equivalent of the amount of heat that is required to raise the temperature of 1 lb. of water when at or near its freezing point (that is, at a temperature of 32°) one degree.
This is called the mechanical equivalent of heat, being merely the quantity of heat necessary to do a certain amount of work, but having no relation to the time in which that work was done.
The conversion of heat into work and of work into heat may be demonstrated as follows: Suppose a cylinder to be so situated that heat can neither be transferred to it or from it, and that saturated steam be admitted under the piston so as to fill one-half of the cylinder at a pressure of 50 lbs.
[II-412]Suppose then that we raise the piston from an independent application of power, the steam simply expanding to fill the space given by the piston, but not exerting its force to move the piston.
Now suppose the experiment is repeated, permitting the force of the steam to lift the piston, and the temperature of the steam will be less in the second than it was in the first, proving that in the second experiment a certain portion of the heat in the steam was converted into the work of raising the piston.
If we desire to reconvert the work into heat, we may force the piston back again to its original position, and its temperature will be restored to what it was before we allowed it to raise the piston. It is here, of course, assumed that there is no friction in moving the piston in the cylinder.
The apparent or external work performed by steam in expanding and moving a piston against a given resistance is measurable by multiplying the amount of the resistance against which the piston moved by the distance it moved through, thus:
Suppose a piston weighs 100 lbs. and had resting upon it a weight of 50 lbs., and that it be raised by the expansive action of steam a distance of a foot, then, since the total resistance it moved against would be (supposing it to move frictionless in the cylinder) 150 lbs., and since the amount of motion was 1 foot, the external or apparent amount of work performed by the steam will be 150 foot lbs., or 150 lbs. moved 1 foot.
But in expanding, the steam has performed a certain amount of what is called internal work, that is to say, its particles or atoms have done work in expanding, and this work has been done at the expense of some of the heat in the steam, so that the loss of heat due to the motion of the piston is the amount of heat converted into work in moving the piston against the piston resistance, added to that converted into the internal work due to the expansion of the steam.
It is because of this internal work that the steam in expanding does not strictly follow Mariotte’s law.
The mechanical theory of heat is, that the atoms of which bodies are composed are at absolute rest when at a temperature of 461.2° below the zero of Fahrenheit, which is supposed to be absolute cold, and at any degree of temperature above this the atoms are in motion; the extent and force of their motion determines what we know as the temperature of the body.
Atoms are capable of transmitting their motion to adjoining atoms of the same or of other bodies, losing, of course, the amount of motion they transmit, and it is in this way that heat is conveyed from one to another part of the same body, or from one body to another, this being known as the heat of conduction.
But heat may be conveyed by means of what is known as radiation, and also by convection.
Thus, the air surrounding a heated body becomes heated, and by reason of its expansion it then becomes lighter and rises, a fresh supply of cooler air taking its place, becoming in turn heated, and again giving place to cooler air; the heat thus conveyed away by the fluid or air is conveyed by what is termed convection.
Heat also passes from a body in straight lines or rays, which do not heat the air through which they pass to their own temperature, but do impart that temperature to a solid body, as iron or water; the heat that passes from a body in this manner is termed radiant heat, or the heat of radiation.
In the cylinder of a steam engine, therefore, the heat contained in the steam is disposed of as follows:
A certain portion of it is converted into work through the medium of the piston.
Another portion is conveyed away by the walls of the cylinder, this portion including the heat of convection and that of radiation.
Yet another portion is converted into internal work. Referring to the latter, suppose that steam is permitted to expand and its atoms will be in motion, which motion has been derived at the expense of or from the conversion of a certain quantity of heat.
The amount of the heat so converted obviously depends upon the amount of the motion. Suppose, for example, that steam is generated in a closed vessel as in a steam boiler, and that a certain pressure having been attained, the steam is permitted to pass off as fast as it is formed from the boiler, then the amount of atomic motion will remain constant, because the pressure remains constant; but suppose instead of the steam passing off, it be confined within the boiler, then the pressure will increase and there will be a greater resistance to the motion of the atoms, hence their motion will be less, and less of their heat will therefore be converted into atomic motion, and, as a consequence, more of it will exist in the form of sensible heat; hence while the pressure of steam continues to increase, its heat is increased, not only by reason of the heat it receives from the furnace, but also by reason of that abandoned by the steam, because it is prevented by the pressure, from expending it in atomic motion.
The indicator is an instrument which marks or draws a figure, or diagram as it is called, which shows the pressure there is in the cylinder at every point in the piston stroke, while it also shows the resistance offered by the same body of steam to the piston on its return stroke. From the form of this figure or diagram, the engineer is enabled to discover whether those parts of the engine whose operation regulates the admission of the steam to and its exhaust from the cylinder are correctly adjusted.
From the diagram the engineer may find the average or mean effective pressure of steam on the piston throughout the stroke, for use in calculating the power of the engine.
He may also locate the point of cut off, of release, the amount of back pressure, the degree of perfection of the vacuum in a condensing engine, and the amount of compression.
From the area of the diagram the engineer may also estimate the quantity of steam that is used, and supposing it to be dry steam, he may calculate the amount of water used to make the steam, and assuming one pound of coal to evaporate so much water, he may calculate the amount of coal used to produce the steam.
The indicators commonly used upon steam cylinders contain two principal mechanical movements; first, a drum revolving the piece of paper upon which the diagram is to be marked, and second, a piston and parallel motion for moving the pencil to mark the diagram upon the revolving paper.
The drum is given a motion that, to insure a correct diagram, is exactly timed with the piston motion.
The pencil is given a vertical movement; this movement must bear a constant and uniform relation to the pressure of the steam in the engine cylinder.
An indicator may be attached to each end of the cylinder or in the middle, with a pipe passing to each end of the cylinder, as in Fig. 3358, but an indicator of the usual construction and such as here referred to, can take a diagram, or card as it is sometimes called, from but one end of the cylinder at a time. The stop valves a and b are used, so that the communication between the indicator and one end of the cylinder may be shut off while a diagram is being taken from the other end, while both ends may be shut off when the indicator is not being used.
In the figure a piece of paper (or card, as it is commonly called) is shown in place upon the drum with a diagram upon it.
The Thompson Indicator is shown in Fig. 3359, and in section in Fig. 3360.
The Tabor Indicator is shown in Fig. 3361, and in section in Fig. 3362.
Both are made with the piston and parallel motion as light as possible, in order to enable the taking of diagrams at as high a speed of engine revolution as possible.
Each consists of a cylinder and piston, the bottom surface of the latter being in communication with the bore of the engine cylinder, so as to receive whatever steam pressure there may be in the cylinder.
This indicator piston receives, on its upper surface, the pressure of a spiral spring, which acts to resist the steam pressure.
The indicator piston rod actuates an arm or line on the end of which is a pencil, which, by means of a parallel motion, is caused to move in a straight line.
The paper or card being in place upon the drum, and steam let[II-414] into the indicator, the pencil lever is moved until the pencil touches the paper as lightly as possible, and as a result of the combined movements of the pencil and drum, the diagram is marked, its form being illustrated in Fig. 3363, which represents a diagram placed above a cylinder, and the engine piston in three positions; first at the beginning of the stroke; second, at the point of cut off (which is supposed to be at one-third of the stroke); and third, at the point of release where the valve first opens the port for the exhaust. For convenience, the diagram is shown as long as the cylinder, but the actual diagram usually measures about 21⁄2 inches high and 41⁄4 inches long.
Supposing the cylinder to be filled with air, and the engine piston in position 1, and the indicator piston would be at the corner a of the diagram; but if steam were admitted, the pencil would rise vertically, marking the line from a to b, which is therefore called the admission line, or by some, the induction line.
If on reaching b the pressure was enough to move the engine piston, that piston and the indicator drum would move simultaneously, and as long as live steam was admitted the line from b to c would be drawn, hence this is called the steam line, its length denoting the live steam period.
The cut off occurs when the engine piston is in position 2, and the indicator pencil at c.
From this point the pencil will fall, in proportion as the steam pressure falls from expansion until the exhaust begins, the piston then being in position 3, and the pencil at d.
The line from c to d is therefore called the expansion line or expansion curve, and the point d the point of release or point of exhaust.
We have now to explain that in reality the whole of the remainder of the line of the diagram is, in reality, the exhaust line, yet there is a difference between the part of the line from point d to the end e of the diagram, and that part from se to a, inasmuch as that during the period of exhaust from d to e, the pressure is helping to propel the piston, while after e is reached, whatever steam pressure there may remain in the cylinder acts to retard the piston.
The line from d to e is therefore the exhaust line, and that from e to a is the back pressure line or counter pressure line.
In this example it has been supposed that while the piston was moving from position 3 to the end of its stroke, and the pencil from d to e, the indicator piston would have a steam pressure on it equal to atmospheric pressure, hence the line from e to a, in this case, represents the atmospheric line, and also the back pressure line.
The atmospheric line is a line drawn when there is no steam admitted to the indicator, and represents a pressure above a perfect vacuum equal to the pressure of the atmosphere. Its use is to show the amount of back pressure, and in a condensing engine to show the degree of vacuum obtained.
It also forms a line wherefrom the line of perfect vacuum, or that of full boiler pressure, may be marked.
The steam pressure at any point in the stroke is denoted by the height of the diagram above the atmospheric line, but the steam pressure thus taken is obviously above atmospheric, and is thus the same as the pressure of a steam gauge, which is also above the atmospheric pressure, and therefore represents the pressure that produces useful effect in a non-condensing engine.
This is what may be called a theoretical diagram, because, first, it supposes the steam not to be admitted to the cylinder until the piston was at the end of its stroke, and to attain its full pressure in the cylinder before the piston lead begins to move, whereas, in order to attain a full steam pressure at the beginning of the stroke, the valve must have lead.
Second, it supposes the cut off to be effected simultaneously, whereas the valve must have time to move and close the port, and during this time the steam pressure will fall, and the curve c of the diagram will therefore be rounded more or less according to the rapidity with which the valve closed.
Third, it supposes the steam to have exhausted down to atmospheric pressure by the time the piston had reached the end of the stroke, whereas the piston will have moved some part of the[II-415] back or return stroke before the steam will have had time to exhaust down to atmospheric pressure; and,
Fourth, it supposes the steam to remain at atmospheric pressure until the piston arrives at the end of its return stroke, whereas the valve will begin to close the port and cause the steam remaining in the cylinder to compress before the piston has completed its return stroke.
In practice the diagram will, under favorable conditions, accord nearer to the shape shown in the lower part of Fig. 3363, in which the closure of the port for the cut off is shown by the curve at f. At the point denoted by g the valve began to close, and at the point denoted by h the cut off was completely effected, and the expansion curve began.
The curve beginning at d is caused by the gradual opening of the exhaust port.
The height of the line of back pressure above the atmospheric line shows the amount of back pressure.
At the point m, where the back pressure line rises into a curve, the valve had closed, shutting in the cylinder a portion of the exhaust steam, which is afterwards compressed by the piston.
This curve is therefore called the compression line or compression curve. The point at which it begins cannot be clearly seen when the exhaust port is closed slowly.
The compression curve ends at p, where it merges into the admission line, but the exact point where the compression ends and the admission begins cannot always be located, this being the case when the port is opened slowly or the compression extends through a large portion of the stroke.
The admission line is, however, in most cases nearly vertical when the valve has lead, because the valve opens the port quickly while the engine piston is moving at its slowest.
A diagram as drawn by the indicator does not account for all the steam that is used in the cylinder, however, as will be seen from Fig. 3363, because, as the paper drum of the indicator receives its motion from the engine cross head, its length represents the length of the piston stroke, whereas, there is a part of the cylinder bore between the piston (when it is at the end of the stroke) and the cylinder cover that is filled with steam as is also the steam passage.
This steam performs no useful work during the live steam period, but obviously expands during the expansion period, and therefore affects the expansion curve, and must be taken account of in calculating the consumption of steam, of water, or of coal from the diagram, or in marking in the true expansion curve.
In calculating the horse power, however, it may be neglected, as it does not enter into that subject.
But in any calculation involving the amount of steam used, the clearance must be marked in by a line at a right angle to the admission line and distant from the nearest point of the admission line to an amount that bears the same proportion to the whole length of the diagram as the clearance does to the whole contents of the cylinder.
The clearance line is shown at l, l′, in Fig. 3363, its distance from the admission line representing the amount of clearance which includes the contents of the steam port and passage, as well as that of the cylinder bore that is between the cylinder cover and the piston, when the latter is at the end of the stroke.
A method of measuring the amount of clearance has already been given with reference to stationary steam engines.
A diagram for a condensing engine is shown in Fig. 3364, which corresponds to Fig. 3363, except that the line of perfect vacuum or no pressure is marked in.
It represents a perfect vacuum, and must be marked on all diagrams from which the consumption of steam is to be calculated, because the quantity of steam used obviously includes that which is used in counter balancing the pressure of the atmosphere.
Learners often get confused on this point, hence it may be more fully explained as follows:
Suppose the engine piston to be blocked, in the middle of the cylinder, and has on one side of it a pressure of 20 lbs. of steam by steam gauge, and on the other the pressure of the atmosphere, and we might pump out the steam, thus leaving the cylinder empty on that side of the piston.
The atmosphere would then exert a pressure of about 141⁄2 lbs. per square inch on one side of the piston, and if we slowly admitted steam again, it would have to get up a pressure of 141⁄2 lbs. per square inch before the atmospheric pressure would be counterbalanced and the piston be in equilibrium.
But the steam gauge would at this time stand at zero, and not show that there was any steam in the cylinder, because the zero of the steam gauge is atmospheric pressure.
When, therefore, the steam gauge showed a pressure of 20 lbs. of steam in the cylinder, there would actually be a pressure of 341⁄2 lbs. of steam per square inch.
The clearance line and the vacuum line must both, therefore, be marked on the diagram when the quantity of steam used is to be computed from the diagram, and also when the proper or theoretical expansion curve is to be marked on the diagram.
This is clear, because in finding the expansion curve for a given volume of steam the whole of its volume must be taken into account, and this whole volume is represented by the area inclosed within the clearance line, the steam line, the expansion curve, the exhaust line, and the line of perfect vacuum, or line of no pressure.
The atmospheric line should be drawn after the diagram has been taken, and while the indicator is hot, as the expansion of the indicator affects the position of this line. It is drawn with the steam shut entirely off from the indicator, whose piston therefore has atmospheric pressure on both sides of it.
Whether the engine is condensing or non-condensing, the same amount of steam (all other things being equal) is used, the only difference being that in a condensing engine a greater portion of the steam is available for driving the piston.
If the condenser produced a perfect vacuum, the whole of the steam would be utilized in propelling the piston.
The “line of no pressure,” or of perfect vacuum, is marked as far below the atmospheric line as will represent the pressure of the atmosphere, which is, at the sea level, about 14.7 lbs. per square inch when the barometer stands at 29.99 inches.
A barometer is an instrument for denoting the pressure or weight of the atmosphere, which it does by means of a column of mercury inclosed in a tube, in which there is a vacuum, which may be produced as follows:
A tube having a parallel bore and closed at one end is filled with mercury and while the finger is placed over the open end of the tube, it is turned upside down and inverted in a cup of mercury that is open to receive the pressure of the atmosphere.
The finger is then removed from the end of the tube and the mercury will fall, leaving a vacuum at its upper end.
The pressure of the atmosphere on the surface of the mercury in the cup forces the mercury up the tube, because the surface of the mercury in the tube has no atmospheric pressure on it, the action being the same as that already described with reference to the principles of action of a pump.
The weight of the atmosphere is equal to the weight of that part of the column of mercury that is above the surface of the mercury in the cup, hence lines may be drawn at different heights representing the weight of the atmosphere, or of any other gas, when the column of mercury stands at the heights denoted by the respective lines.
[II-416]But as mercury expands by heat, a definite degree of temperature must be taken in marking a column, to represent the weight, this temperature being 32° Fahrenheit.
Similarly, as the weight of the atmosphere varies, according to the height at which it is taken from the surface of the earth, a definite height must be taken.
The sea level is that usually taken, the mean or average atmosphere (at that level) being 14.7 lbs. per square inch.
For higher altitudes, the mean atmospheric pressure in lbs. per square inch may be found by multiplying the altitude or height above sea level by .00053, and subtracting the product from 14.7.
Each pound on the square inch is represented by a height of 2.036 inches of mercury, hence the height of a column of mercury at a temperature of 32° that will balance the mean weight of the atmosphere is 29.92 inches, and to avoid fractions, it is usual (for purposes not requiring to be very exact) to say that the atmospheric pressure at sea level is represented by 30 inches of mercury.
The atmospheric pressure is also, to avoid using fractions, taken roughly at 15 lbs. per square inch at sea level.
Each 2 inches of mercury will, under these conditions, represent 1 lb. of pressure.
Vacuum gauges are based upon the same principles and subject to the same variations as to altitude as mercury gauges or the barometer.
To find the absolute pressure, or pressure above zero, or a perfect vacuum, we may add the pressure of the boiler steam gauge to that shown by the mercury gauge or barometer.
In Fig. 3364 the line of no pressure is marked at 15 lbs. per square inch below the atmospheric line of the diagram, the atmospheric pressure being for convenience taken as 15 lbs. above a perfect vacuum.
The line of no pressure serves as a guide in showing the effectiveness of the condenser, as well as for computing the volume of steam used, but is not necessary in computing the horse power of a non-condensing engine, because the gauge pressure has its zero marked to correspond with the atmospheric pressure.
In computing the consumption of steam or water from the diagram, therefore, both the clearance line and the line of no pressure must be marked on the diagram, and lines of the diagram extended so as to include them, thus accounting for all the steam that leaves the steam chest from the piston stroke.
Indicator springs are varied in strength to suit the pressure of steam they are to be used for.
The scale of the spring is the number of lbs. pressure per square inch represented by a vertical motion of the pencil; thus, a 40 lb. spring is one in which a pressure of steam of 40 lbs. per square inch would cause the piston to rise an inch above the atmospheric line of the diagram.
The strength or tension of the spring is so adjusted as to cause the diagram to be about 21⁄2 inches high, let the steam pressure be what it may. The following are the scales of springs of the Thompson and Tabor indicator.
THOMPSON INDICATOR. |
||||||
| Scale of spring. |
Used for pressure above atmosphere if not more than |
|||||
| 15 | lbs. | 21 | lbs. | per | square | inch. |
| 20 | „ | 38 | „ | „ | „ | „ |
| 30 | „ | 94 | „ | „ | „ | „ |
| 40 | „ | 90 | „ | „ | „ | „ |
| 60 | „ | 143 | „ | „ | „ | „ |
TABOR INDICATOR. |
||||||
| 10 | lbs. | 14 | „ | „ | „ | „ |
| 12 | „ | 20 | „ | „ | „ | „ |
| 16 | „ | 30 | „ | „ | „ | „ |
| 20 | „ | 40 | „ | „ | „ | „ |
| 24 | „ | 48 | „ | „ | „ | „ |
| 30 | „ | 60 | „ | „ | „ | „ |
| 32 | „ | 64 | „ | „ | „ | „ |
| 40 | „ | 80 | „ | „ | „ | „ |
| 48 | „ | 96 | „ | „ | „ | „ |
| 50 | „ | 100 | „ | „ | „ | „ |
| 60 | „ | 120 | „ | „ | „ | „ |
| 64 | „ | 128 | „ | „ | „ | „ |
| 80 | „ | 160 | „ | „ | „ | „ |
A spring that is strong enough for a given pressure may be used for any less pressure.
The height of the diagram will, however, be less, and accuracy is best secured by having the diagram up to the limit of about 21⁄2 inches, using a spring that is light enough to secure this result.
Diagrams of high speed engines, however, will have their lines
more regular in proportion as a stronger spring is used.
This occurs because the spring, being under more tension, is less liable to vibration.
An indicator requires careful cleaning and oiling with the best of oil, as the slightest undue friction seriously impairs the working of the instrument.
Instructions upon the care of the instrument, and how to take it apart, etc., are usually given by the makers of the indicator.
There are various methods of giving to the paper drum of the indicator a motion coincident with that of the engine piston, but few of them give correct results.
Reducing levers, such as shown in Fig. 3365, are constructed as follows:
Fig. 3365 represents a reducing lever with the indicators attached. a c is a strip of pine board three or four inches wide and about one and one-half times as long as the stroke of the engine. It is hung by a screw or small bolt to a wooden frame attached overhead. A link c one-third as long as the stroke is attached at one end to the lever, and at the other end to a stud screwed into the cross head, or to an iron clamped to the cross head by one of the nuts that adjust the gibs, or to any part of the cross head that may be conveniently used. The lever should stand in a vertical position when the piston is at the middle of the stroke. The connecting link c, when at that point, should be as far below a horizontal position as it is above it at either end of the stroke. The cords which drive the paper drums may be attached to a screw inserted in the lever near the point of suspension; but a better plan is to provide a segment, a, b, the centre of which coincides with the point of suspension, and allow the cord to pass around the circular edge. The distance from edge to centre should bear the same proportion to the length of the reducing lever as the desired length of diagram bears to the length of the stroke. On an engine having a stroke of 48 inches, the lever should be 72 inches, and the link c 16 inches in length, in which case, to obtain a diagram 4 inches long, the radius of the segment would be 6 inches. It is immaterial[II-417] what the actual length of the diagram is, except as it suits the operator’s fancy, but 4 inches is a length that is usually satisfactory. It may be reduced to advantage to 3 inches at very high speeds. The cords should leave the segment in a line parallel with the axis of the engine cylinder.
The pulleys over which they pass should incline from a vertical plane and point to the indicators wherever they may be located. If the indicators and the reducing lever can be placed so as to be in line with each other, the pulleys may be dispensed with and the cords carried directly from the segment to the instruments, a longer arc being provided for this purpose. The arm which holds the carrier pulleys on each indicator should be adjusted so as to point in the direction in which the cord is received.
In all arrangements of this kind the reduced motion is not mathematically exact, because the leverage is not constant at all points of the stroke.
Pantagraph motions have been devised for overcoming these defects. Two forms have been successfully used, which, if well made, well cared for, and properly handled, reproduce the motion on the reduced scale with perfect accuracy. They are shown in working position in Figs. 3366 and 3367.
Fig. 3366 represents the manner of attaching the pantagraph motion, or lazy tongs, as it is sometimes called, when the indicators are applied to the side of the cylinder. It works in a horizontal plane, the pivot end being supported by a post b erected in front of the guides, and the working end receiving motion from an iron attached to the cross head.
By adjusting the post to the proper height and at a proper distance in front of the cross head, the cords may be carried from the cord pin c to the indicators, without the intervention of carrier pulleys.
If the indicators are attached to the side of the cylinder, the simplest form of pantagraph shown in Fig. 3367 may be used. The working end a receives motion from the cross head, and the front piece b is attached to the floor. The cord pin d is fixed in line between the pivot and the working end, and the pulleys e, attached to the block c, guide the cords to the indicators.
The indicator rigging that gives the best results at high speeds is a plain reducing lever like that first described, provided at the lower end with a slot that receives a stud, screwed into the cross head. The length of the lever should be one and one-half times the engine stroke, as given on the preceding page.
Whatever plan is followed, it is desirable to avoid the use of long stretches of cord. If the motion must be carried a long distance, strips of wood may often be arranged in their place and operated with direct connections. Braided linen cord, a little in excess of one-sixteenth of an inch in diameter, is a suitable material for indicator work.
To take a diagram, a blank card is stretched smoothly upon the paper drum, the ends being held by the spring clips. The driving cord is attached and so adjusted that the motion of the drum is central.
For convenience two diagrams, one from each end of the cylinder, may be made on the same card, as shown in Fig. 3368.
The usual manner of testing the expansion curve of a diagram is to compare it with a curve representing Mariotte’s law for the expansion of a perfect gas.
A theoretic expansion curve that will accord with Mariotte’s law may be constructed on the diagram by the following method:
The diagram, as drawn by the indicator, will have the atmospheric line upon it, and from this as a basis we may mark in the line of no pressure or line of perfect vacuum.
To do this we draw, beneath the atmospheric line, a line as far beneath it as will represent the atmospheric line, on the same scale as the spring used, in the indicator, to draw the diagram.
Suppose, for example, that a 30 lb. spring was used, and assuming the atmospheric pressure to be 15 lbs. per inch, then the line of no pressure would be drawn half an inch below the atmospheric line, because 15 lbs. pull on the spring would cause it to distend half an inch.
The clearance line must then be drawn in, according to directions that have already been given.
The next thing to do is to divide the length of the diagram into any convenient number of equal parts, by vertical lines parallel to, and beginning at, the clearance line, as shown in Fig. 3369. These lines are numbered as shown, ten of them being used because that is a convenient number, but any other number would do.
We next decide at which part of the diagram its expansion curve and the test curve shall touch, and in this example we have chosen that it shall be at line 10.
We have now to find what pressure the length of line 10 represents on the scale of the indicator spring, which in this case we will suppose to be 25 lbs., the line measuring 25⁄30 of an inch, and a 30 lb. spring having been used to draw the diagram. Next multiply the pressure (25 lbs.) by the number of the line (10), and divide the product (250) by the number of each of the other lines in succession, and the quotient will be the pressures to be represented by the lines.
For example, for line 9 we have that 250 divided by 9 gives 27.7, hence line 9 must be long or high enough to represent a pressure of 27.7 lbs. above a perfect vacuum, or in this case 27.7⁄30 of an inch.
For line 8 we have that 250 divided by 8 gives 31.25 lbs., hence line 8 must be high enough to represent a pressure of 31.25 lbs. above a perfect vacuum.
The atmospheric line is, in this case, of no other service than to form a guide wherefrom to mark in the line of no pressure, or of perfect vacuum.
[II-418]Now take the case of line 5, and 250 divided by 5 gives 50, hence the height of line 5 must represent a pressure above vacuum of 50 lbs.
Having carried this out for all the lines from line 10 to line 1, we draw in the true expansion curve, which will touch the tops of all the lines.
Another method of drawing this curve is shown in Fig. 3370. Having drawn the clearance line b c, and vacuum line d c, as before and chosen where the curves shall touch (as at a), then draw from a a perpendicular a a.
Draw line a b, parallel to the vacuum line, and at any convenient height above or near the top of the diagram.
From a draw a c, and from a draw a b parallel to d c, then from its intersection with a c, erect the perpendicular b c, locating on a b, the theoretical point (c) of cut-off.
From a number of points on a b (which may be located without regard to equally spacing them), such as e, f, g and h, draw lines to c, and also drop perpendicular lines, as e e, f f, g g, h h.
From the intersection of e c with b c, draw a horizontal line to e. From the intersection of f c with b c, draw a horizontal line, and so on; and where these horizontals cut the verticals (as at e, f, g, h) are points in the curve, which begins at c, and passes through e, f, g, h, to a.
But this curve does not correctly represent the expansion of steam. It would do so if the steam remained or was maintained at a uniform temperature; hence it is called the isothermal curve, or curve of same temperature. But in fact steam and all other elastic fluids fall in temperature during their expansion, and rise during compression, and this change of temperature slightly affects the pressure.
A curve in which the combined effects of volume and resulting temperatures is represented is called the adiabatic curve, or curve of no transmission; since, if no heat is transmitted to or from the fluid during change of volume, its sensible temperature will change according to a fixed ratio, which will be the same for the same fluid in all cases.
A sufficiently close approximation to the adiabatic curve to enable the non-professional engineer to form an idea of the difference between the two may be produced by the following process:
Taking a similar diagram to that used for the foregoing illustrations, as in Fig. 3371. Fix on a point a near the terminal, where the total pressure is 25 pounds. As before, this point is chosen in order that the two curves may coincide there.
Any other point might have been chosen for the point of coincidence; but a point in that vicinity is generally chosen, so that the result will show the amount of power that should be obtained from the existing terminal. This point is 3.3 inches from the clearance line, and the volume of 25 pounds 996, that is, steam of that pressure has 996 times the bulk of water.
Now if we divide the distance of a from the clearance line by 996, and multiply the quotient by each of the volumes of the other pressures indicated by similar lines, the products will be the respective lengths of the lines measured from the clearance line; the desired curve passing through their other ends. Thus, the quotient of the first or 25 lb. pressure line divided by 996 is .003313; this, multiplied by 726, the volume of 35 lbs. pressure, gives 2.4, the length of the 35 lb. pressure line; and so on for all the rest.
The application of either of the above curves will show that some diagrams are much more accurate than others, even though taken from engines of the same design and quality of workmanship.
As a general rule, those from large engines will be more correct than from small ones, and those from high more correct than from low speeds, and in either case efficiently covering the steam pipes and jacketing the cylinder, to prevent condensation, will improve the diagram.
The character of the imperfection in the expansion curve, shown by the application of a test curve, is generally too high a terminal pressure for the point of cut off, the first part of the curve being generally the most correct, and nearly all the inaccuracy appearing in the last half.
The usual explanation of this is, that the steam admitted during the live steam period condenses because of having to heat the cylinder, and that this water of condensation re-evaporates during the latter part of the stroke when this water of condensation is at a higher temperature than the expanded steam, and thus increases the pressure.
A leaky admission valve may generally, however, be looked for (or else wet steam), if the expansion curve rises much during its lower half.
In calculating the horse power of an engine, the only assistance given by the indicator is, that it provides a means of obtaining the average pressure of the steam throughout the piston stroke.
There are two methods of doing this, one by means of a planimeter or averaging instrument, and the other by means of lines called ordinates.
The ordinates or lines are drawn at a right angle to the atmospheric[II-419] line, as shown in Fig. 3372, and each line is taken to represent the average height or length of one-half of the space between itself and the next lines.
Suppose, for example, that we require to get the area of that part of the diagram that lies between the dotted lines in the figure, and it is clear that the average height of this part of the diagram is represented by the height of the full line between them.
Any number of ordinates may be used, and the greater their number the greater the accuracy obtained. It is, however, usual to draw 10.
The end ordinates a and d, in the figure, should be only half the distance from the ends of the diagram that they are from the next ordinate, as will be seen when it is considered that the ordinate is in the middle of the space it represents.
The ordinates being drawn their lengths, are added together, and the sum so obtained is divided by the number of ordinates, which gives the average height of the ordinates.
Suppose, then, that the average height of the ordinate is two inches, and that the scale of the spring of the indicator that took the diagram was 30 lbs., then the average pressure, shown by the diagram, will be 60 lbs. per square inch. Or in other words, each inch in the height of the ordinate represents 30 lbs. pressure per square inch.
The mean effective pressure having been found, the indicated horse power (or I. H. P. as it is given in brief) is found by multiplying together the area of the piston (minus half the area of the piston rod when great accuracy is required) and the travel of the piston in feet per minute, and dividing the product by 33,000, an example having been already explained.
It is to be observed, however, that when great accuracy is required a diagram should be taken from each end of the cylinder, as the mean effective pressure at one end of the cylinder may vary considerably from that at the other.
This will be the case when a single valve is used with equal lap, because, in this case, the point of cut off will vary on one stroke as compared with the other, which occurs by reason of the angularity of the connecting rod.
When cut off valves or two admission valves are used, it may occur from improper adjustment of the valves. It occurs in all engines, because on one side of the piston the piston rod excludes the[II-420] steam from the piston face, unless, indeed, the piston rod passes through both covers, in which case the rod area must be subtracted from the piston area.
If the expansion curve in a diagram from a non-condensing engine should pass below the atmospheric line, then the mean effective pressure of that part of the card that is below the atmospheric line must be subtracted from the mean effective pressure of that part that is above the atmospheric line, because the part below represents back pressure or pressure resisting the piston motion.
The planimeter affords a much quicker and more accurate method of obtaining the average steam pressure from a diagram.
Coffin’s averaging instrument or planimeter is shown in Fig. 3373. The diagram is traced by the point o, and the register wheel gives the area of the diagram.
A quick method of approximating the mean effective pressure (or M. E. P. as it is called) of a diagram is to draw a line a b, in Fig. 3374, touching the expansion curve at a, and so inclined that the space e is, as near as the eye can judge, equal to the space d. Then the line f drawn in the middle of the diagram, and measured on the scale of the spring that was used to take the diagram, represents the mean effective pressure, or M. E. P. of the diagram.
The amount of water evaporated in the boiler is not accounted for by an indicator diagram or card, and the full reasons for this are not known.
It is obvious, however, that the loss, from the steam being unduly wet or containing water held in suspension, is not shown by the diagram, and this amount of loss will vary with the conditions.
Thus the loss from this cause will be less in proportion as the point of cut off occurs earlier in the stroke, because, as the water is at the same temperature as the steam, it will, as the temperature of the steam reduces from the expansion, evaporate more during the expansion period, doing so to a greater extent in proportion as the cut off is early, on account of there being a wider variation between the temperature of the steam at the point of cut off and at the end of the stroke. On the other hand, however, in proportion as the cut off is earlier, the proportionate loss from condensation during the live steam period is greater, because a greater length of the cylinder bore is cooled during the expansion period, and it has more time to cool in.
Whatever steam is saved by the compression, from the exhaust, must be credited to the engine in calculating the water consumption from the indicator card or diagram, since it fills, or partly fills, the clearance space.
In engines which vary the point of cut off, by varying the travel of the induction or admission valve, the amount of compression is variable with the point of cut off, and increases in proportion as the live steam period diminishes; hence to find the actual water or steam consumption per horse power per hour, diagrams would require to be taken continuously from both ends of the cylinder during the hour; assuming, however, that the point of cut off remains the same, that the amount of compression is constant, that the steam is saturated, and neither wet nor superheated, steam and the water consumption may be computed from the diagram as follows:
Water Consumption Calculations.—An engine driven by water instead of steam, at a pressure of 1 lb. per square inch, would require 859.375 lbs. per horse power per hour; the water being of such temperature and density that 1 cubic foot would weigh 621⁄2 lbs. If the mean pressure were more than 1 lb., the consumption would be proportionately less; and, if steam were used, the consumption would be as much less as the volume of steam used was greater than an equal weight of water. Hence, if we divide the number 859.375 by the mean effective pressure and by the volume of the terminal pressure, the result will be the theoretical rate of water consumption in pounds per I. H. P. per hour.
For the terminal pressure we may take the pressure at any convenient point in the expansion curve near the terminal, as at a, Fig. 3375, in which case the result found must be diminished in the proportion that the portion of stroke remaining to be made, a a, bears to the whole length of the stroke a b; and it may also be diminished by the proportion of stroke remaining to be made after the pressure at a has been reached in the compression curve at b. In other words, a b is the portion of the stroke a b, during which steam at the pressure at a is being consumed. Hence the result obtained by the above rule is multiplied by a b, and the product divided by a b.
To illustrate, suppose the mean effective pressure of the diagram to be 37.6 lbs., and the pressure at a, 25 lbs., of which the volume is 996.
Then 859.375/(37.6 × 996) = 22.94 pounds water per I. H. P. per hour, the rate that would be due to using an entire cylinder full of steam at 25 pounds pressure every stroke. But as the period of consumption is represented by b a (b a being the stroke), the following correction is required:
(22.94 × 3.03)/3.45′′ = 20.15; 3.03 inches being the portion b a, and 3.45 inches being the whole length b, a. This correction allows for the effects of clearance as well as compression, since, if more[II-421] clearance had existed, the pressure at a would not have been reached till later in the stroke, and the consumption line b a would have been longer.
But such a rate can never be realized in practice. Under the best attainable conditions, such as about the load indicated on the diagram, or more on a large engine with steam tight valves and piston, and well protected cylinder and pipes, the unindicated loss will seldom be less than 10 per cent., and it will be increased by departure from any of the above conditions to almost any extent. It will increase at an accelerating ratio as the load is diminished, so that such calculations applied to light load diagrams would be deceptive and misleading; in fact, they have but little practical value, except when made for comparison with tests of actual consumption for the purpose of determining the amount of loss under certain given conditions.
In seeking the causes that may produce a defective diagram, the following points should be remembered:
The indicator must be kept in perfect order, thoroughly clean and well lubricated, so that its parts will move freely. It should always be cleaned throughout after using.
The motion of the indicator drum should be an exact copy, on a reduced scale, of that of the piston at every point in the stroke.
The steam pipes from the cylinder to the indicator, if any are used, must be large enough to give a free and full pressure of steam, and care must be taken that the water of condensation does not obstruct them or enter the indicator.
The cord should be as strong as possible, or if long, fine wire should be substituted.
The pencil should be held to the card with just sufficient force to make a fine line with a sharp pencil.
The diagram should be as long as the atmospheric line, any difference in this respect showing unequal tension of the cord, probably from unequal pressure of the pencil to the paper or card.
A fall in the steam line could arise from too small a steam pipe, and this could be tested by a diagram taken from the steam chest. It could also occur from too small a steam port or an obstructed steam passage as well as from a leaky piston.
An expansion curve that is higher than it should be may arise from a leaky valve, letting in steam after the cut off had occurred, or if at the later point of expansion curve, it may be caused by the steam being wet or containing water, which evaporates as the temperature falls from the expansion.
An expansion curve that is lower than it should be may be caused by a leaky piston, by a valve that leaks on the exhaust side but not on the steam side, or if the exhaust valve is separate from the steam valve, it may leak while the steam valve is tight.
It may also be caused by the cylinder being unduly cooled, as from water accumulating in a steam jacket.
There are many defects in the adjustment of the valve gear, or of improper proportion in the parts, that may be clearly shown by a diagram, while there are defects which might exist and that would not be shown on the diagram.
It is possible, for example, that a steam valve and the engine piston may both leak to the same amount, and as a result the expansion curve may appear correct and not show the leak.
Insufficient valve lead would be shown by the piston moving a certain portion of its stroke before the steam line attained its greatest height in Fig. 3376, in which from a upwards, the admission line, instead of rising vertically, is at an angle to the right, showing that the piston had moved a certain portion of its stroke before full pressure of steam was admitted.
That too small a steam port or steam pipe did not cause this defect may be known from the following reasoning:
The port opened when the pencil was at a, which shows that the valve had lead. At this time the piston was near the dead centre and moving slower than it was when the pressure reached its highest point on the diagram, and since the steam line is fairly parallel with the atmospheric line, it shows that the port was large enough to maintain the pressure when the piston was travelling fast, and therefore ample when the piston was moving slow.
The remedy in this case is to set the eccentric back.
With less compression the point a would be lower.
Excessive lead is shown in Fig. 3377 by the loop at a, where the compression curve extends up to the steam line, and the lead carries the admission line above it, because of the piston moving against the incoming steam.
To mark in the theoretical compression curve, the vacuum line and the clearance line must be drawn in as in the figure, and ordinates must be drawn.
According to the diagram, in Fig. 3377, the compression is clearly defined to have begun at c, and at that time the space filled by steam is represented by the distance from c to the clearance line. The pressure above vacuum (or total pressure) of the steam in the cylinder when the compression began is represented by the length or height of the dotted line 1.
Now suppose the piston to have moved from the point c, where compression began, to line 2 (which is midway between line 1 and the clearance line), and as the compressed steam occupies one-half the space it did when the piston was at c, therefore the steam[II-422] pressure will be doubled, and line 2 may be drawn making it twice as high as line 1.
Line 2 is now the starting point for getting the next ordinate, and line 3, must be marked midway between line 2 and the clearance line, and twice as high as line 2, because at line 3 the steam will occupy half the space it did at line 2. Line 4 is obviously midway between line 3 and the clearance line.
Through the tops of these lines we may draw the theoretical compression curve, which is shown dotted in.
To find the amount of steam actually saved by the compression, we have to consider the compression curve only, beginning at the point of the diagram where it is considered that the compression actually began, and ending where the compression line joins the admission line, and the horizontal distance between these two points represents the length of the cylinder bore filled by the compression.
To find the average amount to which the steam is compressed, we must draw within this length of the diagram, and within the boundaries of the compression curve, and the line of no pressure ordinates corresponds to those given for finding the average shown pressure of a diagram, as explained with reference to that subject, taking care to have the end ordinates spaced half as wide as the intermediate ones, as explained with reference to Fig. 3372.
An automatic cut off engine is one in which the valve gear is so acted upon by the governor as to keep the speed of the engine uniform under variations of the load the engine drives, and notwithstanding variations in the boiler pressure. This it accomplishes by varying the point in the piston stroke at which the live steam is cut off. This is economical because it enables the engine to use the steam more expansively than is possible with engines having throttling governors, which govern the engine speed by wire drawing the steam.
There are two principal forms of automatic cut off engines, first, those in which the steam valve spindle or rod is released from the parts that move it to open for admission, while dash pots, weights, or springs close the valve to effect the cut off; and second, those in which the travel of the valve is varied so as to alter the point of cut off.
The first usually employ fly ball governors which actuate cams or stops to trip the valves for the steam cylinders. The second usually employ wheel governors or speed regulators, as they are sometimes termed.
The distinctive features in the action of the first, of which the Corliss engine is the most important, is that as two admission and two exhaust valves are used, therefore the amount of the valve lead, the point of exhaust and amount of the compression remain the same at whatever point in the piston stroke the cut off may occur; whereas in the second, the lead increases, the cut off occurs earlier, and the compression increases in proportion as the cut off occurs earlier in the piston stroke. In this class of engine the steam valve travels as quickly when opening the steam port for a short and early period of cut off as it does for a late one, hence the amount of steam port opening is as full, with reference to the piston motion, for an early as it is for a late point of cut off. In other words, there is the same amount of steam port opening for the first, second, third, and fourth inch of piston motion, let the point of cut off occur at whatever point in the piston motion it may. In engines which vary the point of cut off by reducing the travel of the slide valve, this is accomplished by using double ported valves or griddle valves.
Fig. 3378 represents the arrangement of the valves in a Corliss engine, v and v1 being the steam valves and v2 and v3 the exhaust valves. These valves, it will be seen, extend crossways of the cylinder and are circular. In the figure the valves are shown in the position they would occupy when the piston was at the crank end of the cylinder, as in the figure.
The principles of a Corliss valve gear will be understood from the following, which is derived from a book by the author of this work, and entitled Modern Steam Engines.
In 3379 and 3380 the valve gear (which is the distinctive feature of the engine) is represented with the parts in the position they occupy when the cut off occurs at half stroke, the piston having moved from the head end of the cylinder. In Figs. 3381 and 3382 the parts are shown in position with the crank on the dead centre and the piston at the crank end of the cylinder, valve v having opened its port to the amount of the lead.
| VOL. II. | THE CORLISS VALVE GEAR. | PLATE XXXIV. |
|
Large image (76 kB).  |
||
| Fig. 3381. | ||
Referring to Fig. 3379, motion from the eccentric is imparted by the rod m to the wrist plate y, to which are connected the rods c, c′, for operating the admission valves, whose shafts are seen at s, s′, and the rods f, f′, for operating the exhaust valves, whose shafts are seen at t, t′.
The mechanism for the steam or admission valves may be divided into three elements: first, that for operating the valve to open the port for admission; second, that for closing the valve to effect the cut off; and third, that which determines the point in the stroke at which the cut off shall occur.
The first consists of the rod m, wrist plate y, and the rods c and c′, which operate the bell cranks r r, r′ r′ which are fast on the valve shafts s, s′. Upon the ends of bell cranks r r, r′ r′, are pivoted latch links u, u′, which have in them a recess for the latch blocks, of which one is seen at e (the rod r′ and its connection with the valve stem being shown broken away to expose e to view). During the admission the latch block abuts against the end y of the recess w and is tripped therefrom by the cam n′. The ends of arms g of the latch links abut against the hub of the arms d, d′ upon which are cams n, n′, and at a, a′ are springs for keeping the ends g of latch links u, u′ against the hubs and cams of d, d′.
Referring now to the valve mechanism at the head end only, suppose the piston to be at the head end of the cylinder, and latch block e will be seated in the recess provided in a to receive it, and[II-424] as the bell crank moves, the latch block will be raised by the latch link, which is carried by a crank arm corresponding to that seen at x at the crank end of the cylinder, and as this crank arm is fast upon the valve spindle, the lifting of e will open the valve for admission. As soon, however, as the end g of the latch link meets the cam n′, the latch link will be moved so that the end y of its recess will leave contact with the latch block e and the dash pot will cause rod r′ to descend instantaneously and close the valve, thus effecting the cut off.
The period of admission, therefore, is determined by the amount of motion the latch link u′ is permitted to have before its end g meets the cam n′, which trips the latch link, and therefore frees e from the latch link recess.
The point at which the cut off will occur, therefore, is determined by the position of the cam n′, because if n′ is out of the way, the end g of the latch link will not meet it, the latch link will not disengage from the latch block e, and the cut off would be effected by the lap of the valve, and independently of the dash pot. As in Fig. 3379 the parts are shown in the positions they occupy at the instant the cut off is to occur, therefore the cam n′ has just tripped the latch link, and the end of e has just left contact with the end y of the recess w in the latch link u′.
The point in the stroke at which the tripping of u′ from e will occur and effect the cut off is determined by the governor, because d′ is connected to the governor through the rod g′. In proportion as the governor balls rise, d′ is moved from left to right, and the end of cam n′ meets g earlier, or, vice versa, in proportion as the governor balls fall, the arm d′ is moved to the left, g will meet the end of cam n′ later, and the point of cut off will be prolonged.
We now come to the means employed to close the valve quickly and without shock when the latch block is released from the latch link. Referring then to the crank end of the cylinder, the latch block for that valve is carried upon arm x, to which is attached the rod r from the dash pot piston (the arm corresponding to x, but at the head end being shown removed to expose the latch block to view). We may now turn again to the head end of the cylinder, rod r′ corresponding to rod r at the other end, and it is seen[II-425] that r′ connects to a dash pot piston p′ having a stepped diameter, the lower half fitting into bore h′, and the upper half fitting into a bore h. The piston p′ fits the bore h′ and fills it when the rod r′ is at the bottom of the stroke, hence as p′ is raised there is a vacuum in h that acts to cause p′, and therefore r′ and x, to fall quickly and close the valve the instant the latch block is released from the latch link. To prevent the descent of rod r′ and piston p′ from ending in a blow, a cushion of air is given in h by the following construction:
At s and s′ are valves, threaded to screw and unscrew, the ends forming a valve for a seat entering h.
As the rod r′ and its piston p′ descend, the air in h finds exit through a hole at h until that hole is closed by the piston p′ covering it, after which the remaining air in h can only find exit through the opening left by the end of the valve s′, and this amount of opening is so regulated by the adjustment of s′ that a certain amount of air cushion is given, which prevents p′ from coming to rest with a blow. The head of valve s′ is milled or knurled, and a spring t′ fits, at its end, into the milled indentation, thus holding it in its adjusted position. The under surface of the upper part of p′ is covered by a leather disc, while the part that fits in h′ is kept air-tight by a leather-cupped packing.
The connection of the cam arms d and d′ with the governor is shown in Figs. 3381 and 3382, in which the parts are shown in the position they would occupy when the crank is on the dead centre and the piston at the crank end of the cylinder. The rod g′ connects[II-426] the cam arm d′ with the upper end of lever a, which is connected to the governor and vibrates on its centre as the governor acts upon it.
Now suppose the speed to begin to diminish, and the governor balls to fall, and the direction in which a will move will be for its lower end to move to the right, thus moving d to the right and carrying its cam away from the end of the latch link, which will therefore continue to open the port for a longer period of admission. Or, referring to Fig. 3381, it is plain that, if the governor balls were to lower from a reduced governor speed, g′ would move to the left and cam n′ would be moved away from contact with the end g of the catch link, which, not being tripped, the admission would continue. On the other hand, suppose the governor balls to rise from an increase of governor speed, and d′ (Fig. 3379) would be moved to the right, and the cam n′ meeting g earlier, correspondingly hastening the cut off.
The governor is driven by a belt from a pulley on the crank shaft to the pulley w, Fig. 3381, whose shaft conveys motion to the governor spindle through the medium of a pair of bevel pinions in which v represents (referring again to Fig. 3378) the steam or admission valve for the crank end port, and v1 that for the head end port, while v2 is the exhaust valve for the crank end, and v2 that for the head end of the cylinder. All four valves are shown in the positions they would occupy when the crank was on the dead centre and the piston at the crank end of the cylinder, hence the valve positions shown correspond to the positions the parts of the valve motion occupy in Fig. 3381.
The faces of the valves are obviously arcs of circles of which the axes of the shafts s, s′ are the respective centres. Valve v has opened its port to the amount of the lead, which in this class of engine varies usually from 1⁄32 to about 1⁄16 inch. As separate exhaust valves are employed, the point of release, and (as the same valve edge that effects the release also effects the compression) therefore that of the compression, may be regulated at will by adjusting the lengths of the rods f, f′, Fig. 3379, which have at one end a right and at the other a left hand screw, so that by turning back the check nuts and then revolving the rods their lengths will be altered.
Similarly the amount of admission lead may be adjusted by an adjustment of the lengths of rods c, c′, which also have right and left hand screws. Referring now to the admission valve v, it is seen that its operating rod c is at a right angle to bell crank r, r, hence the amount of valve motion will not be diminished to any appreciable extent by reason of the wrist plate end of rod c moving in an arc of a circle, and the point of attachment of rod c to the wrist plate is such that, during the admission, the valve practically gives as quick an opening as though rod c continued at a right angle to r. But, if we turn to valve v′, which has closed its port and covers it to the amount of the lap, we find that bell crank r′ and its operating rod c′ are in such positions with relation to the wrist plate, that the motion of the latter will have but little effect in moving the bell crank r′. This is an especial feature of the Corliss valve motion and is of importance for the following reasons:
The lap of the valve (which corresponds to the lap of a plain D slide valve) is usually, in this class of engine, such as to cut off the steam at about 7⁄8 stroke, but the adjustment of the cam position is usually so made that, from the action of the governor, the latest point of cut off will occur when the piston has made 5⁄8 of its stroke, the range of cut off being from this to an admission equal to the amount of the lead.
As the eccentric is fixed upon the shaft, the speed at which the valve opens the port for the admission is the same for all corresponding[II-427] piston positions. Thus suppose the piston has moved an inch from the end of the stroke, and the valve speed will be the same, whether the cut off in that stroke is to occur at quarter stroke or half stroke, and as the valve continues to open the port until it is tripped, therefore, at the moment it is tripped, the direction of valve motion must be suddenly reversed.
As the duty of its reversal falls upon the dash pot, it is desirable to make this duty as light as possible, which is accomplished by the wrist motion, which acts to reduce the valve motion after the port is opened a certain amount for the admission.
We have, therefore, that during the earlier part of the admission, the port opening is quick because of the eccentric throw being a maximum, while during the later part of the port opening, this rapid motion is offset or modified by the wrist motion, thus lessening the duty of the dash pot and enabling it to promptly close the valve.
The range of governor action, so far as the governor itself is concerned, is obviously a constant amount, because a certain amount of rise and fall of the governor balls will move the cams a given amount. But the range of cut off may be varied as follows: At z, z′, are adjustment nuts, by means of which the lengths of rods g, g′ may be varied.
Lengthening rod g obviously moves arm d and its cam n further from the end of the latch link u, and therefore prolongs the admission period.
Shortening the rod g′ causes cam n′ to move around and away from the leg g of the latch link, and prolongs the admission.
The adjustment of the lengths of g and g′ may therefore be employed for two purposes; first, to prolong the point of cut off, and maintain the speed when the engine is overloaded, or to hasten the point of cut off for a given engine speed, and thus adjust the engine for a lighter load.
What are termed high speed engines are those whose pistons run at a velocity of more than about 600 feet per minute, some making as high as 800 or 900 feet in regular work. High speed engines are usually provided with an automatic cut off, and a majority of them vary the point of cut off, by means of shifting the eccentric across the shaft, so as to reduce the eccentric throw, and therefore the valve travel. This causes the valve to cut off the steam earlier.
The eccentric, instead of being fixed upon the crank shaft, has an elongated bore, and is hung on an arm that is pivoted at its other end after the manner of a pendulum. This arm is called the eccentric hanger.
A wheel governor is usually employed to shift the eccentric across the shaft. In some cases, however, two valves are employed, one effecting the admission, the release, and the compression, and the other the cut off.
When two valves are employed, the lead, the point of cut off, the point of release, and the point of compression may be maintained equal for all points of cut off; whereas, when a single valve is employed, the lead, the point of release, and the compression will vary with the point of cut off, or, in other words, will be different for every different point of cut off.
The general principles upon which a wheel governor is constructed is, that two weights or weighted levers in moving outwards from the engine shaft, from the action of centrifugal force, move or rather shift the eccentric across the shaft, reducing its throw, and therefore by reducing the travel of the valve hasten the point of cut off and reduce the power of the engine.
In the governor of the Buckeye engine, the centrifugal force may be varied by increasing or diminishing the distance of the weights from the pivots of the arms on which they swing.
This is shown in Fig. 3382a, in which it is seen that the weights a are adjustable along the arms a, a. The points of attachment d, d of the springs to the weight arms are also adjustable.
When reversing is done, by shifting the eccentric across the shaft, the lead cannot be kept equal, but will, if the eccentric is swung from a pivot that is on the line of centres, when the crank is on a dead centre, be greater at the head end than at the crank end of the cylinder. The discrepancy may, however, be equalized by swinging the eccentric from a pivot that is not on the line of centres at a time the crank is on a dead centre.
But this equalization will only exist at some one point in the[II-428] eccentric position, or in other words, if the eccentric is shifted across the crank shaft, simply to reverse the engine, and not to vary the point of cut-off, it will naturally be moved, in reversing the engine across the shaft, to a given and constant amount, and in this case, the pivot on which its hanger is hung may be so located with reference to the line of centres and the crank (the latter being on a dead centre when the point of suspension of the eccentric hanger is found) that the lead is equal for both the backward and forward gears.
But if the eccentric is shifted across the shaft to vary the point of cut off as well as to reverse the direction of engine revolution, the lead cannot be kept equal.
It is better, in this case, to so locate the point of eccentric hanger suspension as to let the lead be the most at the head end cylinder port, because the piston travels fastest at that end of the cylinder, and therefore requires more lead, in order to cushion the piston.
A construction for shifting the eccentric across the shaft is shown in Fig. 3383, in which d, d is a disc, having at b a pivot for the eccentric hanger. The amount the throw line of the eccentric must be shifted to reverse from full gear forwards to full gear backwards is from the line b x to line b x′, and the shifting is done by two racks f and j, having teeth at an angle of 45° to their lengths. f is fast to the eccentric, and j is carried in a sleeve that slides along the shaft, and sliding it moves the eccentric across the shaft by reason of the teeth of one rack being at a right angle to those of the other.
It is obvious that the eccentric may be moved around the shaft in place of across it, the distance its throw line requires to be moved being the same in either case.
To shift an eccentric so as to reverse the direction of engine revolution, all that is necessary is to place the crank on either dead centre and measure the amount of valve lead. Then loosen the eccentric from the crank shaft, and while the crank is stationary, move it around upon the shaft until it has opened the port full, and nearly closed it again, leaving it open to the same amount as it was before the eccentric was moved, or in other words, open to the amount of the lead.
Fig. 3384 represents a side elevation of a high speed wheel governor engine, designed and constructed by the Straight Line Engine Company of Syracuse, New York, the construction of the governor being shown in Fig. 3385, in which r is the eccentric rod, the eccentric being carried in a lever strap pivoted at a, and connected at b to two links c and d, the former of which connects to the spring e, and the latter to the weighted lever f. The centrifugal force generated by the weighted end of f endeavors to move the eccentric inwards, and thus reduce its throw, which reduces the valve travel and hastens the point of cut off.
On the other hand, the tension of the spring e acts to move the eccentric in the opposite direction, and maintain the full throw of the eccentric and maximum point of cut off. These two forces are so calculated in the design and proportion of the parts that under a maximum load the engine will run at its proper speed, while, if[II-429] the load decreases, the action of f will hasten the point of cut off enough to allow for the decreased engine load, and thus keep the engine still going at the same speed.
Other novel and interesting details in the construction of this engine are as follows:
The two arms forming the frame are cast with and run in straight lines from the cylinder to the two main bearings, and rest upon these self-adjusting points of support.
There are two fly wheels, both between the main bearings, and one of which carries the governor so that the centre of the valve is brought in line with the centre of the eccentric.
In order to simplify the explanation, the mechanism has been separated into three separate sections. Figs. 3386 and 3387 show such of the details of the parts between the cylinder and crank as are peculiar to this engine. The cross head is of the slipper guide style, and the illustration, Fig. 3386, shows the simple method adopted for adjusting the guide to the proper height to maintain the alignment. Another feature peculiar to the straight line not mentioned above, that of making the cross head pin fast in the connecting rod, is used in this engine also, but in a somewhat different form. As will be seen by Fig. 3387, the pin is made much larger, and this allows of its being made of “steel casting” and cast hollow with cross bars at each end for centring. These pins are held in the rod by a binding screw which catches in a groove that is milled around one-fourth of its circumference. After the pin is placed in the rod and the binding bolt is inserted, the pin is prevented from working out endwise, and the binding bolt prevents it from turning; but when the binding bolt is slackened, the pin can be rotated one-fourth of a revolution. The scheme is as follows: After running the engine for a while, the engineer is instructed to slack the binding bolt, give the pin a quarter turn and bind it fast. By repeating this, the pin can be kept more nearly round, probably, than by any other plan. By referring again to Fig. 3386, it will be seen that the plan for taking up the wear in the cross head pin bearings is simply that of setting up the common half box, and the endurance of the arrangement, with the hardened and ground steel pin[II-430] running in babbitt lined boxes of double the ordinary size and length, must be satisfactory.
The drop oil cups for lubricating the cross head pin are located so as to have the drop “picked” off just as the cross head completes its stroke at the cylinder end, and while it is travelling at its slowest speed. The oil, as it leaves the wearing surfaces of the pin, is conveyed to the lower slide.
Figs. 3388 and 3389 show the parts that connect the eccentric with the valve. The method of connecting the rod to the eccentric strap is convenient. The lower joint in the eccentric strap is set up tight, metal to metal, and the upper joint left open 1⁄8 of an inch.
In a steam fire engine the prime requisites are rapidity of getting up steam and efficiency with lightness, economy of fuel being a secondary consideration.
Fig. 3390 is a general view of a steam fire engine constructed by the Clapp & Jones Manufacturing Company.
| VOL. II. | STEAM FIRE ENGINE. | PLATE XXXV. |
|
Large image (125 kB). 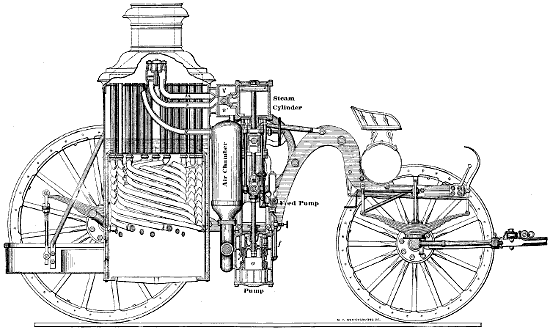 |
||
| Fig. 3390a. | ||
Fig. 3390a is a longitudinal section through the boiler and one steam cylinder and pump.
The construction of the boiler is shown in Figs. 3390a and 3391, the former being a vertical section of the engine and boiler bearing the steam pipe and exhaust pipe shown in place, and one of the draught tubes shown in section, and the latter a vertical central section.
The outside shell is represented at a′′, a′′. This shell extends the whole length of the boiler. The fire box sheet b′′, b is less in length, extending only to the lower tube sheet.
The lower tube sheet c′′ is perforated by all the tubes; the heavy lines showing the coil tubes in fire box, the others are smoke tubes. The upper tube sheet d has holes only for the smoke tubes. The smoke or draught tubes are shown at e′′, e′′, e′′; these also answer the important purposes of drying and superheating the steam.
f′′, f′′, f′′ are the sectional coil tubes, the main feature of this boiler. They are in the form of a spiral coil, the spiral bend being enough to leave room for five others of the same size between, so that there are six of these coils in each circular row. The number of rows is determined by the size of the boiler and the amount of steam required.
Each coil is connected with the lower tube sheet by screw joints, all right hand, that require no fibrous or elastic packing, an angle elbow being used to get the short bend at the end. The tubes then make about one turn around the fire box, and are joined to the side sheet of the same, with the same union used at its upper end, which makes a joint that never gets loose from any kind of work it may be subjected to. These unions or couplings are made of different kinds of metal, and put together so that no two pieces of iron come in contact to corrode and stick together; and should it, from any cause whatever, become necessary to take these coils out, it can be done, and the same tubes replaced without destroying any part of them, or damaging any piece so that it could not be used again.
g′′, g′′ is the ornamental dome or covering for the upper end; g′′, g′′ is the smoke bonnet and pipes for concentrating the hot escaping products of combustion for the purpose of making a draught of air through the fuel. h′′ are grate bars, and i′′ fire door. j′′, j′′ is the water line. The height has been determined by experiment, yet should be varied a little to get the best drying effect of the coal. A coal that makes a flame would call for a higher range of the water line, while coal that produces heat without the flame would call for a lower range; this the engineer will soon find. The working of the boiler is as follows: The fire being started in the fire box, as soon as the water in the coils begins to heat circulation commences from natural causes (nor is it at any time necessary to use a hand pump or any other artificial means for keeping it up), the heated water passing up in the steam drum, and the colder water from the leg and drum taking its place, as is shown by the arrows in the leg, till the whole is heated to the steam making temperature. At this point steam pressure begins to show, which goes up very fast, as the water is all so near the steam temperature. Of course, it is better to carry the water at about the height shown, as a uniform pressure of steam is easier maintained, which is always desirable; yet the limit of safety is not reached till the water is nearly all out, or so long as it is not below the connection[II-431] of the coils in the leg; and even at this point the only danger is in the damage to the coils from the heat when there is no water to protect them.
In Fig. 3391a, one engine and pump is shown in side elevation, and the other in section, the cranks being at a right angle, one to the other. A yoke from the piston rod spans the crank, so that the steam and pump pistons are in line and directly connected. From the lower end of this yoke, a rod connects to the crank shaft upon which are the two fly wheels and the eccentrics for the steam valves.
It will be seen in the longitudinal section, Fig. 3390a, that the steam valve face is a segment of a circle and therefore answers, so far as the distribution of the steam is concerned, to a simple D slide valve, which exhausts through the pipes m, p. The steam pipe n enters the bottom of the steam chest at n′.
The two main pumps a are made in one piece, entirely of composition; one of them is shown in section. The piston is a solid piece of brass, as well as the cylinder in which it works, but are made of different composition, one hard, the other soft, to prevent cutting. The valves are of India rubber; the discharge valve is a ring, one for each end of the pump, as shown at b, Fig. 3391a. One is shown open, while the other is closed. They are held in place by grooved rings of brass; these rings fit in grooves in the rubber, which, when they are put in the pump, and their set screws are in, with their points in the grooves in the brass rings spoken of above, the discharge valves are complete for work.
The suction valves are shown at k on Fig. 3391a, and will be easily understood. They are of a design for this special use and place, which is around the pump cylinder in a circular chamber. The water ways covered by these valves are long and narrow, one valve covering two of these openings, they being held in place by two studs that go through the centre part of the valve, a wire going through these studs, and close to the back of the valve which keeps it up to the seat, the only spring to either of these valves being the elasticity of the rubber. The opening and connection d, d is the inlet to the pump, and where the suction hose goes on, there being a pipe or chamber with branches for the two air chambers, and at each end is a discharge gate and a connection for the leading hose. The part d is the feed pump for the boiler supply, e is the air chamber on the pipe that leads to the boiler to ease off the shocks caused by the plunger striking the water, when the pump does not fill. It is drawn broken off to show the upper part of the pump barrel and stuffing box. The pipe f is the feed water pipe from the pump to boiler, shown from different points in Figs. 3390a and 3391a. g is what we call the suction pipe to the feed pump. It connects to the main pump in the discharge part of it.
A piece of hose pipe connects to the boiler at a point just above the water line, so that hot water or steam (according to the height of the water in the boiler) may be applied to any part that may have become frozen.
[II-432]Heaters are almost universally used in connection with steam fire engines to keep the water hot, and in many cases to keep a few pounds pressure to shorten the time of going to work should the fire be close at hand. This boiler has an advantage for this kind of heating; the circulation is so perfect and free that all the water in it is heated alike; so when the fire is lighted the steam starts[II-433] immediately up, instead of having to wait till some cold water has been heated that had not been reached by the very limited circulation in them, there being some parts that the circulation produced by the heater does not reach, leaving, of course, this water cold.
The arrows k′′ (Fig. 3391), show the direction of the circulation when working with fire in the fire box; those marked l′′ show the direction of it when on the heater which is directly opposite.
The outside pipe connected at about the water line is the outlet from the heater, and the inlet to the boiler, which carries the heated water over the crown sheet, where, as it gets cooler, it enters the coils, descends into the leg, and from there to the pipe near the bottom of the boiler; this pipe leads to the heater, so that the water is kept moving just in proportion to the heat given it; any kind of a heater can be used with the same result.
Marine engines are made in the following forms:
1. With a single or with two cylinders receiving live steam from the boilers, and exhausting into the atmosphere. These are termed high pressure engines, let the steam pressure be what it may. They are also, and more properly, termed non-condensing engines.
In the small sizes, such as are used for launch engines, it is simply a non-condensing engine, with a link motion for varying the point of cut off as well as for reversing purposes. Fig. 3392 represents an engine of this class constructed by Chas. P. Willard & Co.
The cylinder is what is called “inverted,” meaning that it is above the crank shaft.
The slide spindle or valve rod passes through a guide and connects direct to the link block or die, as it is sometimes called.
The thrust block is provided in the bearing of the crank shaft, and consists, as seen in the sectional view, of a series of collars on the crank shaft bearing.
2. The addition to each high pressure cylinder of a low pressure cylinder constitutes a compound engine, and if the engine has also a condenser, it is a compound condensing engine, an example being shown in Fig. 3392a, which represents an engine in which the link motions are employed to vary the points of cut off of both cylinders, as well as to reverse the engine. The engine being small, the power required to move the links is small enough to permit of their operation by hand, by means of the hand lever l, which is secured to its adjusted position on the sector t by the small lever nut shown on the side of the lever. The lever l operates a shaft d which shifts both link motions. The air and circulating pumps are at the back of the condenser, being operated from the beams b, b, each beam connecting to rods j which connect to rod c, which drives the air and circulating pumps.
The steam from the high pressure cylinder exhausts into a receiver or chamber between the two cylinders, and from which the low pressure cylinder receives its steam.
[II-436]The exhaust from the low pressure cylinder passes into the condenser, where it is condensed, leaving a partial vacuum on the exhaust side of the low pressure piston.
| VOL. II. | COMPOUND MARINE ENGINE. | PLATE XXXVI. | |||
|
Large image Fig. 3393 (124 kB), Fig. 3394 (147 kB).  |
 |
||||
| Fig. 3393. | Fig. 3394. | ||||
Figs. 3393 and 3394 show the arrangement of the pumps on a pair of compound engines for a dredger. The steam from the low pressure cylinder passes into the body of the condenser with which the air pump is in communication, as shown in the end elevation. At a is the foot valve of the condenser. The piston of the air pump has a similar valve, and at e is the delivery valve.
The circulating pump is shown in the back elevation (Fig. 3394), being a piston pump which forces the water through the tubes of the condenser.
There are two principal methods of compounding, in one of which the two cylinders are placed one above the other, with their axes in line, and both pistons connecting to the same crank, while in the other the cylinders are side by side, and each connects to its own crank, the two cranks usually being at a right angle.
When one cylinder is placed above the other, as in Fig. 3395, r being the high pressure and s the low pressure piston, no receiver is employed, the steam passing direct from the high pressure cylinder through the pipe p to the low pressure steam chest c. The high pressure steam valve v and the low pressure valve v are on the same stem, a cut off valve v′ being provided for the high pressure cylinder.
3. Triple expansion engines have three cylinders, a high pressure, an intermediate, and a low pressure cylinder.
In a triple expansion engine the intermediate cylinder receives the steam that is exhausted from the high pressure cylinder, and expands it further. The low pressure cylinder receives its steam from the exhaust of the intermediate cylinder, and exhausts into the condenser.
In the illustrations from Fig. 3396 to Fig. 3406 are represented the triple expansion engines of the steamship Matabele, constructed by Messrs. Hall, Russell & Company, of Aberdeen, Scotland. Fig. 3396 is a cross sectional view of the vessel showing the engine and its connections, and Fig. 3397 a similar view, showing the boilers. Fig. 3398 is a back elevation of the engine, showing the boilers also, and Fig. 3399 a plan of the same. Fig. 3400 is a sectional view, and Fig. 3401 an end view of the boilers. Fig. 3402 is a plan, Fig. 3403 an end elevation, and Fig. 3404 a front elevation, partly in section, of the engines. h p is the high pressure cylinder, i c the intermediate cylinder, and l p the low pressure cylinder. The high pressure cylinder has a piston valve, the steam chest being shown at a. The intermediate [II-438]cylinder is provided with a double ported flat valve as shown at b, and the low pressure cylinder is provided with a similar valve whose weight is counterbalanced by the small piston at e; at f are the relief valves for relieving the cylinders of water.
Each steam valve is provided with a link motion that may be used for varying the point of cut off (and therefore the expansion) as well as for reversing purposes.
The link motions are all shifted from one shaft, which may be operated by hand or by steam, the construction being as follows:
For shifting by hand, the wheel w is operated, its shaft having a worm driving the worm wheel g, Fig. 3403, which operates rod h, and through the lever j and rod k shifts the link l, one pair of eccentric rods being shown at n and p.
| VOL. II. | TRIPLE EXPANSION MARINE ENGINE. | PLATE XXXVII. |
|
Large image (278 kB).  |
||
| Fig. 3404. | ||
The shaft of the wheel w is, however, a crank shaft, and at m is a small engine, which may be connected or disconnected at will to shaft w. The lever j operates a shaft r in Fig. 3404, which connects (by a rod corresponding to rod k in Fig. 3403) to each link motion; hence all the links reverse together, and the ratio expansion of one cylinder to the other cannot be varied, or in other words, the point of cut off will be alike for each cylinder, let the link motion be shifted to whatever position it may.
The beam s, Fig. 3403, for working the air, circulating and feed pumps, is driven from the cross head of the intermediate cylinder.
The boilers are of the Scotch pattern that is usually employed for high pressures, as 160 or more lbs. per square inch, and have Fox corrugated furnaces and stay tubes.
Each cylinder requires a starting valve (which is sometimes called an auxiliary valve or a bye pass valve), which is used to warm the cylinder before starting the engine, and also (when there is no vacuum in the condenser) to admit high pressure steam when the high pressure piston is on the dead centre, in which case, there being no vacuum and no admission of steam to the low pressure[II-439] cylinder, the engine would not have sufficient power to start.
In some cases the high pressure cylinder has no starting valve, the reversing gear being used to admit steam to one end or the other of the high pressure piston, and the starting valve being used to admit enough live steam to the low pressure cylinder to compensate for the absence of the vacuum.
When the vacuum in the low pressure cylinder is maintained while the engine is standing still, its starting valve obviously need not be used, except for warming purposes, before starting the engine; as soon, however, as the engine has started, the starting valve must be closed.
Each cylinder is provided with a relief valve, both at the top and at the bottom, to relieve the cylinder from a heavy charge of water, such as may occur if the boiler primes heavily.
Each cylinder is also provided with drain cocks, to permit of the escape of the ordinary water of condensation in the cylinders when the engine is started, and also for use if the boiler primes.
The low pressure relief valve also prevents the accumulation of too great a pressure in the low pressure cylinder, which, from its large diameter, is not strong enough to withstand high pressure.
The oiling apparatus for the cylinders is arranged as follows:
In some cases pumps, and in others automatic or self-feeding devices are used. Oil is fed to the steam pipe of the high pressure[II-440] cylinder, and this lubricates both the valves and the cylinders, but in many cases it is also fed to the steam chest, so as to afford more perfect lubrication to the valve.
For the low pressure cylinder the oil is fed into the receiver, and usually at a point near the slide valves.
Large marine cylinders are usually constructed with a separate lining, which may be replaced when worn or otherwise required.
A surface condenser consists of a cast iron shell or chamber forming the back of the engine frame. At each end of this chamber is a short partition, so that the condenser is divided lengthways into what may be called three compartments, of which the middle one is the longest and contains a number of thin brass tubes about 5⁄8 or 3⁄4 inch in diameter, the ends of these tubes being held in the plates or tube sheets forming the partitions. The object of providing tubes of small diameter is to obtain a large area of cooling surface.
The exhaust steam from the engine generally passes into the shell or body of the condenser, filling the middle partition and surrounding the tubes.
The condensing or circulating water passes through the tubes, and by keeping them cool condenses the steam and forms a vacuum or partial vacuum in the condenser, which, having open communication with the low pressure cylinder, therefore gives a corresponding degree of vacuum on the exhaust side of the low pressure piston.
In some designs, however, the steam passes through the tubes and the circulating water fills the middle compartment of the condenser. As, however, there is no pressure to counterbalance the weight of the water, it is preferable to have the water inside the tubes, so that they are subjected to a bursting pressure, in which case they may, for a given strength, be made thinner, because the strength of the tube to resist bursting is greater than its strength to resist collapsing, hence the circulating water usually passes through the tubes. The chamber at the ends of the condenser permits the water to distribute through all the tubes.
In some cases the chamber at one end is divided horizontally into two compartments, so that the water is compelled to pass through one half and return through the other half of the tubes.
The water of condensation falls to the bottom of the condenser, from which it is removed by the air pump, which delivers it to the hot well.
The hot well is situated on the side of, and extends above, the pump, whose upper end it covers, thus water sealing the top of the air pump and preventing air from passing into it through a leaky valve or bucket.
The top of the hot well is provided with a vapor pipe, which permits the air and gases to pass overboard. This pipe emerges through the side of the ship above the water line, and as there is no valve between the hot well and the sea, no pressure can possibly accumulate in the hot well.
The boiler feed is taken from the hot well either by the feed pump or by injectors, as the case may be.
In case the boiler feed should stop working, however, the hot well is provided with a pipe of large diameter, and called the overboard discharge pipe, so that the water of condensation may not accumulate a pressure in the hot well if the boiler feed ceases.
This overboard discharge pipe is provided with a weighted valve (placed at the side of the ship), which is constructed after the manner of a safety valve, relieving the hot well of pressure if the water accumulates, and preventing the sea water from entering the hot well.
To prevent loss of fresh water, the exhaust steam from the various engines and pumps (if any) about the ship passes to the condenser and is pumped into the hot well.
In some cases, however, a separate and independent condenser is used for the smaller engines about the ship.
An independent condenser is one whose air pump and circulating pump are not worked from the main engine, and can therefore be operated when the main engine is standing still.
If the main condenser is independent, it may be started so as to form a vacuum before the main engine is started, and thus obviate the use of the starting valve on the low pressure cylinder except to warm the cylinder before starting.
Feed water for the boilers when the engine is standing is obtained by a pipe from the bottom of the condenser, so that the water of condensation of steam blown through the engine cylinders, and from the exhausts from the smaller engines about the ship, may be pumped or forced direct from the bottom of the condenser to the boiler.
This feed from the bottom of the condenser is necessary when the air pump is not working, and the water of condensation is not pumped into the hot well.
If the water thus obtained is not enough to keep the boilers supplied, an auxiliary or salt water feed admits extra water from the circulating water to the inside of the condenser to supply the deficiency.
This secondary suction pipe is provided with a valve because it must be shut off before the engine is started.
All the drain pipes from the cylinder pass into the condenser so as to save the fresh water.
The air pump is usually worked by a beam, receiving motion from the cross head of the low pressure cylinder.
The circulating pump is usually worked by the same beam as the air pump, or receives its motion from some other part of the main engine. In some cases, however, an independent circulating pump is employed.
It receives its water from a pipe leading to the sea, which is provided with an injection cock or Kingston valve, placed close to the side of the ship and well below the sea level. This valve is used to shut off the circulating water and prevent its flooding the ship in case of accident to the condenser or circulating pump.
The circulating water, after passing through the condenser, discharges overboard through the circulator discharge pipe.
This pipe is also provided with a valve placed close to the ship’s side, at or above the water level, so that the opening at the ship’s side may be closed, and sea water prevented from entering the ship in case of breakage to the condenser, etc.
To enable a surface condenser to be used as a jet condenser in case of accident to the circulating pump, a pipe leads from the injection cock of the circulating supply pump into the bottom of the exhaust pipe or column, where it enters the condenser.
This pipe is supplied with a spray or rose nozzle, which divides up the injection water and causes it to condense the steam as it enters the condenser.
An additional pipe is sometimes added to the suction side of the circulating pump, for use in pumping out the bilge by means of the circulating pump in case of emergency, and also for pumping out ballast tanks when the vessel is provided with such tanks.
An air valve is sometimes fitted to a reciprocating double acting circulating pump. It admits air to the water during the up stroke of the pump, and closes on the down stroke. The air thus admitted acts as a cushion to soften the shock of the water.
A snifting (or snifter valve, as it is sometimes called) is a valve fitted to the condenser and that opens upwards to permit of the discharge of the air and gases before the engine is started. It also serves to prevent any water from leaky condenser tubes from filling the condenser and flooding the engine cylinders. It is so loaded with dead weight that it opens automatically when the water in the condenser has reached a certain height and must be placed as low down on the condenser as possible, so as to receive the weight of the full height of the water in the condenser.
Condenser tubes are made water tight in the tube plates of the condenser by wooden or sometimes paper ferrules, which fit the tube and drive into the tube plate. In other cases, however, the tube ends project through the plates, and a rubber washer is placed on the end of each tube. A covering plate is then bolted over the whole of the tube ends, the holes in the covering plate being parallel for a short distance, and then reduced in diameter so as to form a shoulder. The rubber rings compress and make a joint, and the shoulders prevent the condenser tubes from working out endways from expansion and contraction. The tubes are usually about 3⁄64 inch thick.
A blow through valve is a valve attached to the casing or steam chest, and connecting by a pipe to condenser to blow out the air and gases that may have collected there when the engine is standing still, and that also connects to the exhaust port of the high pressure cylinder, so as to supply live steam to the low pressure[II-441] cylinder in case the high pressure cylinder should get disabled.
A bucket air pump is one in which there is a valve or valves in the pump piston, hence the pump is single acting, drawing on the lower side of the piston and delivering on the upper, hence the capacity of the pump per engine revolution is equal to the diameter of the bucket multiplied by the length of its stroke. The suction or foot valve is at the foot of the pump, and the delivery valve at the head.
A piston air pump is double acting, since it draws on each side alternately of the piston, one side delivering while the other is drawing, hence two suction and two delivery valves are required.
A plunger air pump is one in which a plunger is used in place of a piston, the delivery being due to the displacement of the plunger.
An air pump trunk is a hollow brass cylinder attached to or in one piece with the piston or bucket of the air pump. The rod which drives the piston passes through the trunk, and connects to a single eye at the bottom of the trunk.
A trunk air pump is necessary when the pump rod is driven direct from the crank shaft, and therefore has sufficient lateral motion to push the pump piston sideways, which would cause friction and excessive wear to the gland that keeps the trunk tight. The delivery capacity of the pump is obviously diminished to an amount equal to the displacement of that part of the plunger that passes through the gland and within the pump bore, whereas in a piston pump the delivery capacity is only diminished to an amount corresponding to the displacement of the pump piston rod.
A bucket pump may in some cases be worked without either a foot or a head valve, since the bucket valve will answer for both in cases when the delivery water cannot pass back into the pump on the down stroke of the bucket.
It will, however, be more efficient with the addition of either of them, and most efficient with both.
A bucket pump with a foot valve and no discharge valve would, however, suffer more from a leaky gland than if it had a discharge valve and no foot valve, because the air would, on the ascent of the bucket and the closing of the bucket valve, pass to the suction side of the bucket and impair the vacuum.
Let the delivery valves be where they may, the foot valve will always have some water above it, and the pump bucket will dip into this water, and on lifting produce a vacuum that will cause the pump to fill with water. Notwithstanding that the gland may leak air on the other side of the bucket, this air will in a single acting pump be expelled with the water, but in a double acting pump it will impair the vacuum, and therefore the suction, on the gland side of the piston.
Bucket air pumps are provided with a valve or pet cock on the top or delivery side of the bucket and above the bucket, when the latter is at the highest point of its stroke. This valve opens on the descent of the bucket, admitting air to act as a cushion between the surface of the water and the delivery valve, when the water is about to meet the latter. It obviously reduces the effectiveness of the pump, and in a double acting pump is inadmissible, because of its impairing the vacuum and the suction.
This valve also enables the engineer to know whether the air pump is working properly.
A pet cock is also supplied to the feed pumps for this same purpose.
A bilge injection is one in which the injection water is taken from the bilge, which may be done when the ship makes more water than the bilge pumps can get rid of.
The fittings necessary for a bilge injection are a cock or globe valve placed on the side of the condenser, and at or near the foot of the exhaust pipe, with a spray or rose inside that pipe. From the cock a pipe, usually lead, leads to the bilge, having at its end a strainer or strum, and care must be taken that this strum does not get choked and let the condenser get hot from the exhaust steam not being condensed.
The water in the hot well of a surface condenser is usually kept at a temperature of about 100° Fahrenheit. A higher temperature than 100° Fahrenheit injures the rubber valves of the air pump, while lower temperatures cool the engine cylinders too much and cause waste from cylinder condensation. Moreover, it is obvious that, since the boiler feed is taken from the hot well, it is desirable to keep it as hot as the valves and as the desired degree of vacuum will permit.
An air vessel or air chamber is a vessel fitted to the delivery and sometimes also to the suction side of a pump. Its office is to maintain a steady flow of water through the pipes.
Thus, in the case of the delivery air chamber, when the pump piston is travelling at a speed above its average for the stroke, the water accumulates in the air chamber, and the air is more compressed, while, when the pump is on the dead centre, or at the end of its stroke and the delivery valve closes, the air compressed in the air chamber continues the delivery or discharge, thus maintaining a more uniform flow.
Pumps sometimes have an air or vacuum chamber on the suction side, from which the air is exhausted when the pump starts, leaving a vacuum which causes a steady flow of water up the suction pipe.
Both these chambers are more effective as the speed of the pump increases. The chamber on the delivery side is apt to lose its air, which is gradually absorbed by the water, which should be let out when the pump is standing still.
Feed escape valves or feed relief valves are fitted to the feed pumps, so that in case all the feed water cannot pass into the boiler it may pass back to the hot well.
The construction of a feed escape valve is as follows:
It is an ordinary mitre valve held to its seat by the compression of a spiral spring, whose pressure upon the valve may be regulated by an adjusting screw, whose end abuts upon a stem provided for the purpose.
In proportion as the valve is relieved of the pressure of this spring, a greater proportion of the water delivered by the feed pump will pass back into the hot well, hence the amount of boiler feed may be regulated by the feed escape valve, which also acts as a safety valve, preventing undue pressure in the feed pipe.
When no feed escape valve is employed, the delivery water from the feed pump must pass unobstructed to the boiler, or the feed pipes may burst from over pressure, and it follows that the feed check valve on the side of the boiler must not be restrained in its amount of lift, hence it must not have a lift adjusting screw.
The amount of the boiler feed must, in this case, be regulated from the suction side of the pump, the suction pipe being fitted with a cock or valve whose amount of opening may be adjusted so as to regulate the amount of water drawn per pump stroke from the hot well.
If the feed valve on the suction side, or the escape valve on the delivery side of the pump, as the case may be, is adjusted to permit of a proper amount of boiler feed, and yet the feed is insufficient or ceases altogether, it may occur from the following causes:
1st. From the suction valve sticking or being choked, or from the delivery valve being choked and not seating itself, thus either letting the suction water pass back into the hot well, or the delivery water pass back into the pump.
2d. Through leaks in the joints of the pump or of the suction pipe.
3d. From the water in the hot well being too hot.
4th. Through the spring of the escape valve having become disarranged.
5th. If two or more boilers are connected, and one has less pressure in it than the other, it may take most of the feed water, or the water of the other may empty itself into it.
Bilge Injection. The injection water for a common or jet condenser may be obtained in one of two ways: first, direct from the sea, which is that for ordinary use; and secondly from the bilge, which is resorted to to assist the bilge pump in cases of emergency.
The necessary fittings for a bilge injection are, a pipe leading from the condenser to the bilge, with a cock at the condenser end and a strainer at the bilge end.
This pipe should be fitted with a check valve, which opens by lifting upwards so that no water can pass down it into the bilge, or otherwise, if the main and bilge injections should happen to be[II-442] left open together, the water from the main injection might pass down into the bilge. This check valve should be so constructed that its amount of lift can be regulated and as much of the bilge water used for injection as the circumstances may require.
In the case of surface condensers, the bilge water is drawn off by the circulating pump and used to supplement the main circulating water. The pipe from the bilge in this case leads to the suction side of the circulating pump, and requires a strainer at the bilge end, a cock at the circulating pump, and a check valve.
A ship’s side air pump discharge valve is an ordinary dead weight mitre valve that opens to let the water pass out into the sea, but seats itself and closes if the water attempts to pass inwards. It differs from a common stop valve in being weighted, and therefore self-acting. It requires to be lifted before starting the engine, as such valves are liable to stick in their seats.
The course of the main injection water of a jet condenser is as follows: From the rose plate or strainer, through the injection valve and pipe to the condenser, where it mingles with the exhaust steam and from which it is pumped with the products of condensation into the hot well. From the hot well it passes mainly overboard through the Kingston valve, but that part of it used for the boiler feed passes through the suction pipe and valve into the pump, and thence through the delivery valve, pipe and check valve into the boiler.
The course of the main circulating water of a surface condenser is through the Kingston valve (on the ship’s side or bottom), and the circulator inlet pipe, either direct to the condenser, from which it is drawn by the circulating pump, or else it passes through it, and is forced through the condenser. It circulates through the condenser twice or thrice according to the construction, and is forced overboard by the action of the circulating pump, passing through a valve on the ship’s side or bottom.
The advantages of surface condensation are, first, that the feed water is obtained at a higher temperature than if injection water was fed to the boiler. Second, the feed water is purer, and therefore less water requires to be blown out of the boiler in order to keep it clean. Third, the boiler does not scale so much, hence its heating surface is maintained more efficient; and fourth, the boiler suffers less from expansion and expansion strains when hot feed water is used.
Surface condensers foul from the grease with which the cylinders are lubricated and from the salt in the injection water. The condenser is cleaned by the admission of soda with the exhaust steam and by washing out.
A condensing engine has the following cocks and valves on the skin of the ship in the engine room: The main Kingston valve for the injection, or circulating water, the main delivery valve from the condenser, the bilge delivery valves, and the water service cocks for keeping the main bearings of the engine cool with streams of cold water.
A donkey engine is a small engine used to feed the boiler, and has the following connections: A steam pipe from the boiler to drive the donkey engine; and exhaust pipe into the condenser; a suction pipe from the hot well or from the sea, as the case may be; and a delivery pipe to the boiler; a suction pipe from the bilge, so that the donkey pump can assist in pumping the bilge out; a suction pipe to the condenser, to circulate the water when the main engines are stopped, and thus maintain the vacuum; and a suction pipe from the water ballast tanks, to pump them out when necessary.
The pipes that lead from, or go to, the sea are: Boiler blow off pipe, sea injection or circulator pipe, condenser discharge pipe, and, in some cases, donkey feed suction pipe.
The parts of an engine that are generally made of wrought iron are those in which strength with a minimum of weight and size is desired; for example, the piston rod, cross head, connecting rod, crank shaft, crank, eccentric rods, link motion, valve spindle pump rods, and all studs, bolts, and nuts.
The parts generally made of cast iron are those where strength and rigidity are required, and which are difficult to forge, while weight or size is of lesser importance, such as the bed plate, cylinders, pistons, condensers, and pumps.
The parts sometimes made of steel are those subject to great wear, and for which strength with a minimum of size is necessary, as piston springs, piston rods, connecting rods, cranks, crank pins, and valve rods.
The parts generally made of brass are those subject to abrasion or corrosion, as the connecting rod brasses, the bearings for the crank shaft, the pump plungers or pistons, and their rods, linings for the pump barrels or bores, the bores of the glands, the condenser tubes, and all cocks and valves.
White metal or babbitt metal is sometimes used in place of, or in connection with, brasses, serving as an anti-abrasion surface. It is easily renewed, as it is cast into its place, but will melt and run out at a temperature of about 600° Fahrenheit.
Muntz metal is used where iron or steel would suffer greatly from corrosion when in contact with salt water. It can be forged.
The difference in the composition of cast iron and steel has never been determined; the difference lies in the percentage of carbon they contain and the structure of the metal. Cast iron will not weld.
Cast iron is brittle, of granular structure, and always breaks short, having a very low elastic limit.
Wrought iron is tough and fibrous, will weld but will not harden, and is stronger than cast iron.
Steel is stronger than wrought iron, and will weld and harden and temper. The breaking strain of wrought iron varies from about 42,000 to 60,000 lbs. per square inch of section.
Steel is tempered by first being heated red hot and suddenly cooled (usually by plunging it into cold water), which hardens it. The surface is then brightened, and on being reheated the tempering colors appear, beginning at a pale yellow, and deepening into red, brown, purple, and blue, the latter gradually fading away as the metal is re-heated to a red heat. The higher the temperature to which the hardened steel is reheated the softer or lower it is tempered.
These colors merely indicate the temperature to which the piece is reheated, since they will appear on steel not hardened and upon iron.
Case hardening is a process that converts the surface of wrought iron into steel, which is accomplished by placing them in a box filled with bone dust, animal charcoal, or leather hoofs, etc. The box is sealed with clay, heated red hot for about 12 hours, and the pieces are quenched in water.
The parts usually case hardened are the link motion, and other light working parts that are of wrought iron.
The forgeable metals used in engine work are wrought iron, steel, copper, and Muntz metal. The brittle or short metals are cast iron and brass.
Welding is the joining of two pieces solidly together. Wrought iron, steel, and Muntz metal can be welded.
All the metals used in the construction of marine engines expand by heat, and this is allowed for in adjusting the lengths of the eccentric rods, or of the valve spindles when setting the valve lead. In the case of two marine boilers being connected together, the steam pipe is fitted with an expansion joint, one pipe end having an enlarged bore to receive the other. The joint is made by packing, which is squeezed up by a gland, whose bore fits on the outside of the pipe which moves through the gland bore, from the expansion and contraction.
The piston of a marine engine steam cylinder is a disc of cast iron, into which the piston rod is secured. Its body is cored out to lighten it. Around its circumference is a recess to receive the packing ring or rings, each of which is split across so that it may be expanded (to fit the bore of the cylinder) by means of the packing or of the springs. The split is closed in the centre by a tongue piece let into the ring, and fastened to one end of the ring.
To hold the piston rings or ring in place, a junk ring is employed, being an annular ring bolted to the piston. The piston rings are set out to fit the cylinder bore by suitable springs. The round plugs seen on the piston face merely fill the holes used to support the core in the mould and to extract it from the finished casting.
Cylinder drain cocks sometimes have a check valve upon them, so that while the water may pass out of the cylinder the air cannot pass in and destroy or impair the vacuum.
[II-443]Cylinder escape or relief valves are provided at the top and at the bottom of the cylinders, and consist of a spring loaded valve with an adjusting screw to regulate the pressure at which they shall act. They are most needed when the boiler primes heavily, and the water might knock out the cylinder heads or covers. They should be enclosed in a case with a pipe to lead the water away, thus preventing it from flying out and scalding the engineer.
A link motion is a valve gear by which the engine may be reversed (caused to run in either direction), or which may be used to vary the point of cut off. The advantage of the link motion is its simplicity and durability.
A link motion for a marine engine is usually of the Stephenson type, and consists of two eccentrics or eccentric sheaves fixed upon the crank shaft, and so set as to give more lead at the bottom than the top ports, because the wear of the journals, brasses, and pins gradually increases the lead at the upper, and correspondingly diminishes that at the lower port. In addition to this, however, more lead is required at the bottom port, to counterbalance the weight of the piston at the end of its descending stroke. The eccentric hoops or straps drive the rods which connect to the ends of the link.
The link may be a curved, solid, or a slotted bar, and in either case has fitted to it a block or die which connects to the valve spindle.
The link is pivoted at its centre to a swinging arm or suspension link,[58] and by this arm may be moved endways to bring the required end of the link beneath the valve rod or spindle. From the positions in which the eccentrics are set, one end of the link operates the valve to go ahead, while the other end operates it to go astern; hence all that is necessary (so far as the link motion is concerned) to reverse the engine is to move the link endwise to the requisite amount, which, for full gear, is so that the block is at or near the end of the link.
In proportion as the link block is (by moving the link endways) brought nearer to the middle of the link, the valve travel is reduced and the point of cut off is hastened, thus increasing the expansion.
When the link block is in the middle of the link, the latter is in mid gear, and the valve only opens the ports to the amount of the lead, and the link action is the same, whether the engine moves backwards or forwards.
The motion of the link is as follows:
The two ends are vibrated by the eccentrics from the central pin of the link hanger (or suspension link) as a centre of motion, while at the same time this end of the link hanger swings in an arc of which its other end is the centre of motion.
In small engines the link is sometimes used for varying the expansion as well as for reversing the direction of engine revolution.
In large engines it is used for reversing only, a separate expansion valve being used for varying the point of cut off.
In small engines the link is moved endwise for forward or backward gear by a simple arrangement of hand levers. In large engines these levers are supplemented by a worm and worm gear, and in still larger engines a steam reversing gear is used for shifting the links from forward to backward gear, or vice versa.
When there is no link motion, a Joy valve gear, a Marshall valve gear, or a loose eccentric may be used. A loose eccentric is one that can be moved around the shaft to reverse the engine. It may be moved around the shaft by mechanical means, or the eccentric rods may be disconnected, and the valve worked by hand, to cause the engine to run in the required direction, until a pin fast in the shaft meets a lug on the eccentric and drives it, there being two such lugs or shoulders spaced the requisite distance apart on the eccentric. This plan is obviously only suitable for small engines.
A separate expansion valve is a valve employed to effect the cut off and vary the expansion. It does not affect either the admission or exhaust of the steam to the cylinder.
It is used because by its means an early point of cut off and high rate of expansion may be obtained with a fixed point of exhaust, a fixed amount of compression, and a fixed amount of lead, whereas with the link motion alone the exhaust occurs earlier in the stroke, and the compression and the lead increase as the link is moved from full gear towards mid gear. The expansion valve should, when the engine is to be started, be set for the latest point of cut off. The eccentric for the expansion valve is set opposite to the crank, in order that its action may be the same, whether the engine runs backward or forward.
The small cylinders on top of the steam chests are for the purpose of guiding the upper ends of the valve spindles, and are fitted with pistons having steam beneath, the space above being in communication with the condenser. The steam pressure on the piston supports the weight of the valves and valve gear.
The friction of a slide valve may be relieved or reduced by excluding the steam from its back, which is done by various means, such as by a ring cast on its back and working steam tight against a plate held independently of the valve. The interior of the ring should be open to the exhaust.
The friction of a slide valve is caused by the steam pressing it to its seat, the amount of this pressure varying with the fit of the valve to its seat, and its position over the ports, or, in other words, upon how much of the valve area has steam pressing on one side only.
The travel of the eccentric rod is the distance it moves measured on a straight line. It is equal to twice the throw of the eccentric.
The throw of an eccentric is the distance between the axis of its bore and the centre or axis from which its circumference was turned in the lathe.
Double beat valves are composed of two discs or mitre valves, one above the other on the same stem, so that as the steam presses on the opposite faces of the two discs the valve is balanced. The objection to their use as safety valves is, that they are balanced and would not lift unless the area of the upper disc was made larger than that of the lower one, in which the objection would remain that the two discs do not expand equally, hence they are apt to leak. They are sometimes used instead of slide valves, but are objectionable because a separate admission and exhaust valve is required at each end of the cylinder, and because at quick speeds of revolution they fall to their seats with a shock or blow which wears out both the valve and the seat. When a high piston speed is obtained by great length of piston stroke, and not by high rotative speed, their use is less objectionable.
Expansion joints are joints which permit the parts they connect to expand and contract without straining them. They are necessary on the steam pipe connecting one boiler to another, and on the main steam pipe from the boilers to the engine. The working surfaces require to be of brass, so that they will not corrode.
They require the collar on the internal pipe of the joint (on which the gland fits) to be permanently fixed by soldering or brazing, and check nuts on the studs, so that the internal pipe shall not be blown out from the steam pressure.
This pipe is also sometimes fitted with chains or stops, in case the studs should break, or the nuts or collar strip.
An oil cup is either a cavity cast in the piece or a cup shaped vessel or hollow cylinder screwed in. It contains a pipe extending up about three-fourths of its height, and through this pipe the oil is fed to the surface required to be lubricated. A hinged lid or, in some cases, a screwed cap covers the oil cup to exclude dust, etc.
The syphon or worsted consists of a number of threads of worsted or lamp wick of equal lengths; a piece of lead or copper wire is laid across the middle of the worsted, the copper wire is doubled and twisted and is then pushed down the tube, carrying the doubled end of the worsted with it. The upper ends of the wire are bent over the end of the tube so as to hold the worsted, whose lower end should pass down below the level of the bottom of the oil cup. The oil feeds (on the syphon principle) through the medium of the wick or worsted, which should not fit the tube tight but quite easily, its upper ends hanging over the top of the tube to the bottom of the cup.
The worsted may be cleaned with scalding water, or by water thrown upon it from the boiler.
Tallow cups for high pressure cylinders must have two cocks, so that after the cup is filled the top cock may be closed and the bottom[II-444] one then opened. The top cock prevents the tallow or oil from being blown out of the cock by the steam. For the low pressure cylinder a cup with a single cock will answer, as the cock may be opened when the vacuum is at that end of the cylinder, and the air will force the oil or tallow in.
A steam lubricator or impermeator is an automatic oil feeding device placed on the steam pipe of the high pressure cylinder. Steam lubricators are made in various forms, some having a positive feed by a pumping arrangement, while in others the oil floats upon water in the body of the lubricator to which steam is admitted; the condensation of the steam increases the quantity of water and causes the floating oil to overflow and feed through a pipe leading into the steam pipe or steam chest, as the case may be. Cooling the impermeator causes more rapid condensation, and increases the amount of oil fed to the steam.
Cylinder escape or relief valves do not let all the water out of the cylinder because of the clearance,[59] hence the amount of water left in will equal the amount of clearance.
The small cylinders on top of the steam chest are for the purpose of guiding the upper ends of the valve spindles, and are fitted with pistons having steam beneath, the upper end being in communication with the condenser.
The effort of the piston to rise supports the weight of the valves and valve gear.
The valves of a marine engine that are worked by hand are, the stop valves for letting on steam from the boiler, the safety valve, which is lifted to see that it is in proper working order, the Kingston valve for letting in the circulating water, the blow through or starting valve for warming the cylinders and starting the engines. The valve for adjusting the rate of boiler feed has its lift adjusting screw operated by hand. The slide valve may also be operated by hand before the engine is started, or it may be operated by a steam reversing gear. The expansion valves are also set by hand to regulate the point of cut off or amount of expansion. The valves that are operated automatically, or from the motion of the parts, are the slide and expansion valves, the suction and delivery and check valves of all pumps, the air pump bucket valves, the snifting valves, and the ship’s side overboard discharge valves. When the engine is stopped and the steam shut off, close the dampers to check the draught and open the drain cocks on the high pressure cylinders.
If the engine is soon to start and the pressure in the boiler is at the blowing off point, start the boiler feed, if the height of the water in the boiler will permit it, and this is a good time to clean the fires. If the engine is to stop for any length of time, shut off the impermeator and the injection supply.
A vacuum gauge is an instrument for measuring the total or absolute pressure, or pressure above a perfect vacuum, and it is used to indicate the degree of vacuum that exists in the condenser, which, when the various joints about the cylinder and condenser are tight, averages about 27 inches of mercury when the temperature in the hot well is about 100° Fahrenheit.
In round numbers a column of mercury 32 inches high equals the weight of the atmosphere,[60] hence taking the weight of the atmosphere at sea level to be 15 lbs. per square inch, then each two inches of mercury represents an atmospheric pressure of 2 lbs. Suppose then that a bent U shaped tube, each leg of which is 30 inches high, is half filled with mercury, and that one end is in communication with the condenser, and the other end is open to the atmosphere, and if there was a perfect vacuum in the condenser, the pressure of the atmosphere in the open leg would force all the mercury into the leg that communicated with the condenser, hence there would be a column of 30 inches of mercury in one leg, and air in the other.
[60] See “Barometer,” Chapter XL.
If there was in the condenser a pressure of 11⁄2 pounds per square inch above a perfect vacuum, the mercury would stand 27 inches high in one leg, and 3 inches in the other, and so on, hence from the height of the column of mercury above its natural level the degree of vacuum in the condenser may be known. But the pressure of the atmosphere varies with its temperature, and the weight of mercury also varies with its temperature.
To find the total pressure in the condenser, therefore, we subtract height of the column of mercury given by the condenser from the height of the column in the barometer, and divide the remainder by 2.
Examples.—The barometer stands at 29.5 and the vacuum gauge at 26, what is the absolute pressure in the condenser?
Here,
29.5 - 26 = 3.5 ÷ 2 = 1.75
Answer, 175⁄100 lbs. per square inch.
A dial vacuum gauge of the Bourdon construction is similar to the Bourdon steam gauge, that is used upon the boiler, except that the inside of the elliptical tube is in communication with the condenser and the atmospheric pressure bends the tube into a curve of smaller radius (instead of to a larger one, as in the case of the steam gauge).
Obviously, therefore, the zero of the dial vacuum gauge is atmospheric pressure.
Suppose the dial vacuum gauge shows 10 lbs., the steam gauge 120 lbs., and the barometer 15 lbs., and we may find the total pressure or pressure above vacuum of the steam in the boiler is as follows:
| One-half Pressure by steam gauge = | 60 | lbs. |
| A perfect vacuum = | 15 | lbs. |
| Total pressure supposing condenser had a perfect vacuum = | 75 | lbs. |
To make the correction necessary because there is not a perfect vacuum in the condenser, we then proceed as follows:
| Barometer 30 inches of mercury = | 15 | lbs. | per | sq. | in. |
| Dial vacuum gauge = | 10 | „ | „ | „ | „ |
| Actual pressure in condenser = | 5 | „ | „ | „ | „ |
Then
| Total pressure supposing condenser had a perfect vacuum = | 75 |
| Actual pressure in condenser = | 5 |
| Actual pressure of the steam = | 70 |
Racing means a sudden acceleration of the engine speed, and occurs when the propeller is not fully immersed in the sea, as by reason of the pitching of the ship. Racing augments the strain on the working gear of the pumps, and is likely to lead to accident. It is obviated by the use of a governor or by partly shutting off the steam by hand.
A marine governor is a device for controlling the engine speed, by reducing the supply of steam to the engine cylinder whenever the engine begins to race. The governor is driven by band or rope on the crank shaft. Governors are made in various forms; thus, in one the shaft has a fly wheel and a friction clutch, one half of which is fast on the governor shaft, while between it and the other is a spiral spring which connects the two halves. If the speed accelerates, the sliding half of the clutch is moved along the governor shaft, and by means of links it closes the throttle valve of the main steam pipe, thus wire drawing the steam, reducing its pressure and thereby controlling the engine speed.
A common paddle wheel has a cast iron centre into which the wrought iron arms are set and secured by wrought iron bolts and nuts.
The bolts have hook heads to grip the back of the arm, and receive a nut and plate to secure the paddles.
Paddle wheels are sometimes provided with cast iron floats to act as counterweights to some unbalanced part of the engine. They are mostly required on side lever engines having a single crank; they are placed nearly opposite to the crank, but not quite, so that they may prevent it from stopping on the centre, and be difficult to start again.
Paddle wheels for engines having a single crank sometimes have their floats of varying breadths, so as to keep the speed of revolution as uniform as possible. This is accomplished by making some of the floats wider than the others. The broadest floats[II-445] are in action when the crank is at its points of greatest power, and the narrowest at the time the engine is on a dead centre, hence there are four general graduations of breadth in the circumference of the wheel.
A radial paddle wheel is one in which the floats are fixed to the paddle arms, and their ends are in a line radiating from the centre of the paddle shaft.
A feathering paddle float is pivoted at the centre of its ends, and so arranged that by a mechanical movement it will remain vertical when in the water, notwithstanding the circular path it revolves in.
The object of feathering is to cause the thrust of the float to be as nearly as possible in a horizontal line, and therefore more nearly parallel to the line of the ship’s motion, and thus utilize more of the paddle power to drive the ship.
The eccentric for feathering the floats is fixed to the ship’s side, and sometimes carries a plummer block or pillow block for the paddle shaft bearing. The centre of the eccentric sheave or wheel is placed ahead of and level with the paddle shaft axis. The working surfaces of a feathering wheel are of brass, and the bushes of the paddle arms of lignum vitæ.
The surfaces are lubricated by the water, but sometimes oil lubrication is provided for the eccentric sheave.
A disconnecting paddle engine is one in which the paddles may be driven separately or together. This is effected at the inner port bearing by a clutch wheel, which slides endways on the shaft and is driven by feathers seated in the shaft. This clutch wheel is operated by a lever so as to engage or disengage with the crank pin, which is fast in the outer crank.
Disconnecting paddle engines are always fitted with loose eccentrics, such engines being used for steam tugs and ferry boats, where quickness of turning and of reversing is of great importance.
The thread of a screw propeller is its length measured along the outer edge of the blade.
The angle of the thread is its angle to the axial line of the propeller shaft.
The length of the thread is the length of the outer or circumferential edge of the blade.
The area is the surface of one side of the blade.
The diameter is the distance apart of the two points on the edges that are diametrically opposite and furthest apart.
The pitch of a propeller is its degree of spirality, and is represented by the distance it would move forward if the water was a solid. It is measured by drawing a line representing the axis of the propeller shaft, and at a right angle to it a line representing in its length the circumference of the circle described by the tips of the blades; from the point of intersection of these two right angle lines a diagonal line is drawn representing the angle the blade at its outer edge stands at the propeller shaft axis. The greatest distance between the diagonal line and the line representing the propeller circumference is the pitch of the propeller.
A left handed propeller has a left hand thread or spiral, and revolves from left to right to move the ship ahead.
A right hand propeller has its blades inclined in the opposite direction, and of course revolves in the opposite direction to a left hand one.
The slip of a propeller is the difference between the distance the ship is moved by the propeller and the distance it would move if the water was solid. Slip is usually expressed in the percentage that the distance the ship actually travels bears to the distance she would have travelled if there had been no slip. From 10 to 20 per cent. is lost in slip.
A screw of increasing pitch is one in which the angle of the face of the propeller blade to the axis of the shaft increases as the thread recedes from the shaft, or from the centre to the circumference of the blade, or in both directions.
In a uniform pitch the angle of the blade to the propeller axis is the same at all distances from the axis.
An example of a screw of uniform pitch would be a piece of angle iron wound around a parallel shaft. If wound on a tape shaft, the largest diameter being nearest to the ship’s stern, it would have an increasing pitch. If wound around a parabola, the pitch would vary at every point in its diameter and thread.
A thrust bearing is a journal bearing provided with a number of corrugations or collars fitting with corresponding corrugations or recesses in the thrust block, the area thus provided serving to resist the end thrust placed by the propeller upon the shaft.
It must be freely lubricated by ways leading to each collar or corrugation, and so situated that it is accessible for examination. It is sometimes at the end of the first length of shaft aft of the engine.
A stern tube is a sleeve enveloping the aft end of the propeller shaft to protect it from the sea water, which would corrode it. At the aft end of the stern tube is a gland and stuffing box. At the inner end, which extends to the aft bulkhead, it has a flange which is bolted to the bulkhead.
The bearing area of the shaft and stern tube are lined with brass (about half an inch thick) to prevent their oxidation from the action of the sea water.
A lignum vitæ bearing is a wooden bearing generally fitted to the outer end of the stern tube in propeller engines, or to the outer ends of the paddle shaft of paddle engines. It consists of strips of lignum vitæ dovetailed into the bearing or bush, and running lengthways of it. These strips are prevented from working out by a check plate at each end of the bearing.
Screw propellers may be fastened to their shafts in several ways, as by a key or feather sunk in the shaft, and projecting into a keyway in the propeller bore, and a nut on the end of the shaft with a safety pin outside the nut, or by a key passing through the boss of the propeller, and a safety pin or plate upon the key.
The principal pipes of a marine engine and boiler, and the parts they connect, are, the main steam pipe, connecting the stop valve on the superheater to the steam chest of the engine cylinders; the waste steam pipe from the safety valve to the open air; the blow-off pipe, connecting the blow-off cocks on the bottom of the boiler with the blow-off Kingston cock on the ship’s side; cylinder jacket pipe from the stop cock on the boiler to the steam jacket.
The circulating suction pipe, connecting the main Kingston valve with the bottom of the circulating pump; the circulating delivery pipe, connecting the discharge compartment of the condenser with the main delivery valve on the ship’s skin; the air pump suction, connecting the body of the condenser with the suction side or bottom of the air pump; the main exhaust pipe, connecting the exhaust passage of the low pressure cylinder with the condenser; the feed water suction pipe, connecting the donkey feed pipe with the hot well; the feed water delivery pipe, connecting the donkey feed pump with the check valve on the boiler; the bilge suction pipe, connecting a strum box in the bilge with the bilge pump; a suction pipe from the strum in the bilge to the donkey pump; the bilge pump delivery pipe, connecting the bilge pumps with bilge delivery valves on the ship’s side.
A mud box is a rectangular box usually placed in the engine room, and serving to clear the bilge water from foreign substances, as small pieces of wood, coal, etc.; the construction is as follows: It is on the suction side of the bilge pumps, and is provided with a hinged lid that affords access to clean it out, and that must obviously close air tight, or the bilge pumps will not draw. The box is divided into two compartments by a loose division plate that stands vertical, and is perforated so as to act as a strainer.
The steam from the boiler passes through the superheater, main stop cock or valve, main steam pipe, separator, regulating and throttle valve, steam chest, steam port, steam passage into cylinder, returns through steam passage and port, exhaust cavity of valve into either the condenser or the low pressure cylinder, as the case may be, finally exhausting into condenser, whence the water of condensation is pumped by the air pump into the hot well. In the case of a jet condenser part only of the condensed steam goes back to the boiler, the rest going into the sea through the injection discharge pipe.
A steam jacket[61] is an outer casing to a steam cylinder, the space between it and the cylinder being filled with steam direct from the boiler, with the object of preventing condensation of the steam in the engine cylinder.
[II-446]A drain cock is supplied to the bottom of the jacket to pass off condensed water. Steam jackets should be lagged or felted to prevent condensation.
The parts of an engine that require to be felted or lagged are the cylinders and the steam pipes; the boilers also should be felted or otherwise covered to prevent loss of heat by radiation, and the uptake protected by means of thin plates, kept, by means of distance pieces and bolts, at a distance of two or three inches from the plates of the uptake.
Various non conducting substances are employed to prevent radiation, as, for example, felt, mineral wool, asbestos, and various kinds of cement.
The pieces of the engine through which the steam pressure is received and transmitted are as follows:
The piston, piston rod, cross head, cross head gudgeon, connecting rod, crank pin, crank shaft and couplings to the propeller shaft.
Trunk engines are generally used in war vessels where it is required to have the engines below the water line. The trunk passes through the cylinder and the piston is upon the trunk, the connecting rod passes down into the trunk and connects direct to the piston. A stuffing box and gland in each cylinder cover keeps the trunk steam tight. The trunk forms a guide to the piston in place of the ordinary cross head and guides, and thus saves the room required by those parts.
The cylinders for a right handed propeller should be on the starboard side of the vessel, so that the pressure on the piston, when the engine is going ahead, shall be in a direction to lift the trunk in the cylinder, and thus act to relieve the gland and cylinder bore of the weight of the trunk and piston.
An oscillating engine is one in which the cylinder is mounted on bearings called trunnions, so that the cylinder can swing and keep its bore and the piston pointing to the crank at all parts of the engine revolution. This enables the connecting rod and slide bars to be dispensed with. The trunnions are hollow, one containing the steam and the other the exhaust passage.
Oscillating engines are used for paddle steamers, because their construction permits of a good length of piston stroke, while still keeping the engine low down in the vessel.
The valve motion for an oscillating engine consists of an ordinary eccentric gear or motion, with the addition of various mechanical arrangements to accommodate the valve gear to the vibrating motion of the valve chest.
The stuffing box of an oscillating engine is made deeper than usual because the gland bore has more strain on it, and extra wearing surface is therefore required to prevent its wearing oval.
Geared engines are those with gear wheels to increase the revolutions of the shaft above those of the engine, and thus obtain a high propeller speed without a high piston speed.
The pressure that propels a vessel is taken by the thrust block in a screw propeller engine.
The pressure that drives a paddle steamer is applied to the hull at the shaft bearings and their holding beams, and to the bed plates. The amount of fuel required per horse power per hour, by modern compound engines, is from about 11⁄2 to 3 lbs., and by common condensing engines from 3 to 5 lbs. per horse power per hour.
The unit or measure of a horse power is the amount of power required to lift 33,000 lbs. one foot high in a minute.[62]
Nominal horse power is a term used to represent the commercial rating or power of an engine, and is usually based upon the area of the piston. It gives no measure of the engine power, however, because it does not take the piston speed into account.[63]
In a surface condensing engine the duty of the air pump is to merely pump the condensed steam and vapor from the condenser to the hot well, whereas in a jet condensing engine it has to also take the condensing water from the condenser, hence an air pump for a surface condenser may be made smaller than that for a jet condenser. As the air pump works against the pressure of the atmosphere, therefore the smaller it is the less of the engine power is absorbed in working it.
The injection cocks are regulated for opening by rods having handles attached. If the injection cocks are not open wide enough, the condenser will get hot and impair the vacuum, while if opened too wide, the water in the hot well will be cold and the boiler feed will be cold. These cocks should be so regulated as to keep the temperature in the hot well at about 100° Fahrenheit.
The parts of a marine engine that are exposed to danger in a cold climate are all pipes through which cold water circulates, and are liable to freeze.
The precautions necessary to prevent freezing in cold climates are to cover all pipes liable to freeze, to keep the water circulating through them, or to let it out of them if necessary, as in the case of the engine standing.
A marine engine may fail to start, or may be prevented from starting by the following causes:
1st. The H. P. slide valve may be off, or away from its seat, thus admitting the steam to both sides of the piston at the same time.
2d. The engineer may have forgotten to disengage the hand turning gear from the crank shaft.
3d. The propeller may be fouled with a piece of timber, or by a chain or rope (these causes sometimes occurring when the ship is in port), or there may be something wrong with the outer bearing of the propeller shaft.
4th. In the case of a propeller fitted with a banjo frame (for the purpose of raising the propeller) the propeller may be locked.
5th. An obstruction, as a block of wood, in the crank pit may prevent the crank from turning.
6th. The slide valve nut may have slackened back, thus loosening the slide valve.
7th. The slide valve spindle may have broken.
8th. When an engine has no auxiliary or starting, but an impulse valve that merely lets a puff of steam into the receiver, this impulse valve may leak, and if the escape or relief valve on the receiver is too much loaded, it may gag the H. P. piston by giving it high pressure steam on both sides, and this may throw the valve off its seat. Similarly, if the engine has an auxiliary or starting valve, and it leaks, high pressure steam may be admitted to both sides of the L. P. piston, thus gagging it and causing its slide valve to throw back and away from its seat.
9th. The cylinders may be choked with water, and the drain cocks choked up.
10th. The crank shaft bearings may be screwed up too tightly.
11th. The air or the circulating pump may be choked with water, either the air pump overflow valve or the circulating discharge valve being secured down.[64]
[64] The air pump overflow valve should never be permanently fastened down. More engines have been broken down from this than from almost any other neglectful cause, because, from great leaks in the condenser tubes and engines standing for a length of time, a larger quantity of water may require to be got rid of during the first few strokes of the pump than can pass through the small air or vapor pipe, which is usually fitted from the hot well either into the bilge or else overboard. Unless the valve in this overflow pipe is heavy enough of itself (which is very rarely the case), it should be loaded by a spring or weight, so that when the puff of the air pump causes it to lift, and the vessel is rolling, sea water may not pass into the hot well. To avoid this, some engineers erroneously fasten this valve down. An experienced engineer states that in his experience five engines have been broken down from this cause alone.
12th. From the engines being allowed to stand a long time in one position, and the glands being too tightly packed. An engine should be turned a little daily when not in use.
13th. From the piston rings being set out too tight to the cylinder bore.
14th. From the throttle or stop valve being shut, as from its spindle being broken.
15th. From the eccentric sheave, or wheel, having shifted on the shaft, some eccentrics having a key that is not sunk in the sheave, which is done so that the eccentric may shift rather than break if it should seize in its strap.
16th. From the H. P. piston leaking badly, or its ring being[II-447] broken, which will permit the cylinder to fill with steam and the slide valve to unseat.
17th. If the engine has been overhauled, the forward eccentric may have been connected to the wrong end of the link, thus giving an improper motion to the slide valve.
18th. The expansion may be set to cut off too early in the stroke.
19th. From the air pump rod, or from the circulating pump rod being broken, or from the valves being broken.
20th. From the cylinder casing or the receiver being cracked so as to admit steam to both sides of the piston at the same time.
A defective vacuum, or loss of vacuum, may occur from the following causes:
1st. From the glands of the low pressure cylinder leaking.
2d. From the pet cock of the air pump being left open.
3d. From the joints of the connections about the condenser leaking.[65]
[65] To discover a leak about a condenser, pass an exposed light, as a candle, about the joints, etc., and where there is a leak the flame will be drawn in towards the condenser.
4th. From the condenser being cracked, and therefore leaky.
5th. From the injection cock or valve being closed.
6th. From the condenser tubes being foul for lack of being cleaned. From the L. P. cylinder escape valves or cylinder cocks being leaky, and therefore letting in air.
7th. From the slide valve and piston of the L. P. cylinder leaking.
8th. From the air pump valve being leaky or broken. From the circulating pump being defective, as from having leaky valves.
9th. From the Kingston injection valve not being properly opened, or from its outside orifice being choked.
10th. The bilge injection may be so connected with the air pump or condenser as to impair the vacuum when its valve is accidentally stuck and its stop cock is left open.[66]
[66] It is obvious that a defective vacuum may or may not prevent an engine from starting, according to the degree of defectiveness.
The principal causes of heating are:
1st. The bearing caps being screwed down too tight.
2d. The bearings being left uncovered, thus allowing the brick dust used for cleaning the machinery, the dirt from coaling the ship, or the sand used for cleaning the decks, to get into the bearing.
3d. The oil grooves in the brasses being worn out or too shallow, or the brasses not being cleared at the sides.
4th. Improper fitting of the distance pieces or fit strips between the brasses.
5th. Bad oil or too light an oil.
6th. If the brasses are too slack and thump or pound, the back of the brass may be stretched by pening, causing the sides of the brass to close in upon and bind the crank journal or crank pin, and this will cause heating.
For other information concerning the engine see as follows:
| Page. | |
| Angularity of connecting rod | 375 |
| The slide valve | 376 |
| Double ported and griddle valves | 377 |
| Balanced valves | 377 |
| Piston valves | 378 |
| Separate cut off valves | 378 |
| Reversing gears | 383 |
| Finding the working results of a slide valve | 376 |
| Condensing engines | 442, 444 |
| Calculations on the mechanical powers | 405 |
| The unit of power | 407 |
| Calculating horse power | 407 |
| Calculations of safety valves | 409 |
| Heat, water, and steam | 410 |
| The expansion of steam | 411 |
| The conversion of heat into work | 411 |
| The indicator | 413 |
| Indicator diagrams | 414, 421 |
| The barometer | 415 |
| Calculating the horse power from indicator diagrams | 419 |
| Finding the steam of water consumption from an indicator | 421 |
Figs. 3405 and 3406 represent a triple expansion marine engine, the construction being as follows:
The high pressure cylinder has a piston valve and the intermediate and low pressure cylinders flat valves. Each cylinder has a link motion, and all three link motions are shifted from the same shaft, which is moved by a steam reversing gear. At a, Fig. 3405, are the eccentrics for the link b, for the high pressure cylinder; b′, b′ are those for link b′, for the intermediate cylinder; and c′ c′ are those for the link c′, for the low pressure cylinder. From each link are rods e, Fig. 3406, connected to arms on the shaft f f, to an arm on which is connected the rod g, from the worm wheel h, whose actuating worm i is on a crank shaft operated by the small steam cylinder j. The slide spindles d work in guides, and their cross heads c span the edges of the links, gibs being provided to take up the wear.
The gear for turning the engine when there is no steam in the main boilers is constructed as follows:
On the shaft of the wheel m, Fig. 3405, is a worm n operating a worm wheel p, on whose shaft is a worm which operates the large worm wheel shown on the main crank shaft.
Figs. 3407 and 3408 represent the compound engines of the steamship Poplar, concerning which The Engineer (from which the engravings are taken) says:
“Both the cylinders of these engines are fitted with piston valves, placed at the back of the cylinders and worked by the single eccentric valve gear, which has been so largely adopted and so successfully carried out by this firm in triple expansion as well as compound engines. It will be noticed that whilst this valve gear permits of the cylinders being close together, it allows of the crank shaft being made in two similar pieces, and affords exceptionally long main and crank pin bearings, of the former of which there are only three, instead of the usual four. In the case of the Poplar the cylinders are 29 in. and 55 in. in diameter and 33 in. stroke, and the crank pins are 11 in. long, whilst the centre main bearing, which does duty for both the engines, is 233⁄4 in. in length, each of the outer bearings being 18 in. in length, the diameter of the crank shaft being 91⁄2 in. Another very interesting feature about these compact little engines is the design of the front framework. Instead of the ordinary upright columns in front of each engine there is an arrangement which gives exceptional stiffness to the whole structure whilst affording the fullest possible accessibility to the main working parts, and which has the appearance of an arch, from the shoulders of which there are branches worked up to receive the feet of the cylinders, thus accommodating the close centres and providing for the support of the reversing wheel without in the least obstructing the gear below. The condenser is divided horizontally through the centre on a plan strongly advocated by the builders, the whole of the base of the engines being cast in one piece and made level on the under side, so as to enable it to receive support from, and be bolted to, the engine seating immediately beneath the crank shaft, as well as round the margin.”
Boilers for marine engines are, in England, made of special qualities of plate, the best being termed Yorkshire, and a nearly equal grade, Staffordshire. The plates for the shell, the furnace bottoms and the gusset stays are made of Staffordshire, while the tube plates, furnace tops, and such parts as require to be flanged and are subject to more intense heat, are made of Yorkshire plate, which has more ductility.
In the United States the grades of iron used for boilers are C H No. 1 S, or charcoal hammered No. 1 shell iron, for the shell, and C H No. 1 F, or charcoal No. 1 flange iron, which is used for the furnaces and such parts as require flanging.
In both countries steel is also used for boilers, except for the tubes, for which it is not entirely reliable if very high pressures are to be used.
Both the iron and steel plates are tested for tensile strength and ductility.
The breaking strain is that which is sufficient to cause rupture, while the proof strain is that which the metal is required to withstand with safety.
The safe working strain, or working pressure, W P, is the strain under which it is considered safe to work the boiler.
The strength of a boiler of a given diameter and thickness of plate varies according to the construction of the riveted seams or joints.
Boiler stays or braces are rods, ribs, or plates for supporting the weaker parts of the boiler. Thus the tube plates may be stayed by rods passing through both plates and screwed into them, or nuts and washers may be used on the stays one on each side of each tube plate.
Gusset stays are iron plates which are riveted to T irons or in some cases to L irons, which are riveted on the surfaces to be stayed.
Stay tubes are thick tubes (usually about 3⁄16 inch thick), which screw into the tube sheets and are riveted over at the ends. A superior construction, however, is to provide nuts and washers to the ends of the stay tubes, one on each side of each tube plate.
Boiler stays are usually made of such diameters that when new they will sustain a tensile strain of not more than 5,000 lbs. per square inch of cross section, this being the rule of the Board of Trade.
Stays are sometimes screwed into the tube plates and then riveted over at the outside ends. A better method, however, is to let the ends of the stays receive a nut on each side of each tube plate.
Boiler tubes are secured in their tube plates by being expanded in. This may be done by driving in a taper steel mandrel, and then clinching them over, or by using a tube expander. There are two principal kinds of tube expanders, in one of which small rolls travel around the bore of the tube and expand it, while in the other a number of segments, held together by a spring, are forced outwards by a mandrel driven in by hammer blows.
Too much expanding is apt to weaken the tube close to the inside face of the tube sheet.
Boiler tubes leak first at the end which receives the greatest heat from the fire, the leakage being caused by the expansion and contraction of the tube, which is obviously hotter than the water which causes the tube to expand more than the boiler shell. The remedy is to re-mandrel or expand the tube.
The scale that forms on the face of the tube sheet keeps the water away from contact with the plate, which with an undue thickness of scale will crack between the tube holes.
A tube that is split or that cannot be made steam tight by being re-mandrelled or expanded is plugged up at each end by means of either wooden or iron plugs. The best plan, however, is to use iron discs having a stepped diameter, so that one end will fit the bore of the tube, and the other will form a shoulder that will cover the end of the tube.
[II-453]Each disc has a hole through its centre, so that a wrought iron rod or bolt may be passed through the hole and receive a nut at each end. Beneath the flange of each disc, a grummet of spun yarn and white lead is placed, so as to make a steam tight joint when the nuts are screwed home. This stays the tube plates as well as stopping the leaky tube.
If wooden plugs are used, they are made a driving fit in the tube bore, and driven through until they have passed the split, and a second wooden plug is driven tightly from the same end of the tube.
The up take of a marine boiler is the casing or passage way through which the heat and gases pass after leaving the boiler. A dry up take is one which is outside of the boiler, as in Fig. 3409, which represents an outside view of a boiler such as shown in Figs. 3410 and 3411.
A wet up take is one which passes through the boiler, and therefore has fire on one side and steam on the other. It is therefore under a collapsing pressure.
The furnace of a marine boiler extends from the fire door to the combustion chamber (i. e., the box in which the heat of the furnace passes before returning through the tubes).
The superheater of a marine boiler is a cylindrical vessel receiving the steam from the boiler, and delivering it to the main steam pipe, whence the steam is delivered to the engines, etc. When it has no connection with the up take, it may, however, be more properly termed a steam driver, since it serves to separate the steam from entrained water, and does not superheat the steam.
In some cases, however, the superheater takes the form of a spherical ended cylinder standing in the up take.
The receiver of a marine boiler is a drum or cylinder that receives the steam from the boiler and from which the steam passes through the steam pipe to the engine. The receiver is by some called the steam chest of the boiler.
The fittings essential for a marine boiler are: The safety valves; the test cocks (or gauge cocks, as they are sometimes termed); the water gauge glass; the stop valves; the check valve for the boiler feed pipe, and the valves for letting on steam to the main engine and such other engine or engines as may take steam from the main boiler; the scum cocks; the blow off cocks; and a small cock to enable the drawing of water from the boiler to test its degree of saltness.
There are two kinds of safety valves, the dead weight and the spring loaded.
A dead weight safety valve is one in which the valve is held to its seat by dead weight, the objection to which is, that when the vessel rolls the effect of the weight or weights upon the valve is diminished; hence under heavy rolling the steam may blow off at a less pressure than the valve is set for.
A lock up safety valve is a dead weight safety valve, the top of whose spindle is provided with a cast iron cap or bonnet with two handles on. This cap is keyed to the spindle, and the keyway is so disposed that no extra weight can be added to the valve, while at the same time the valve can be lifted from its seat and turned around.
A spring loaded safety valve is one in which the valve is held down by the pressure of a spiral spring, and this pressure will obviously not vary, no matter how much the ship rolls.
In proportion as the valve lifts and the spring compresses, its resistance increases, and this tends to impair the accuracy of the valve. This, however, is offset from the fact that when the valve rises from its seat it presents a greater area for the steam to act against.
The area of safety valve required by the English Board of Trade is about 1⁄2 square inch of valve area per square foot of fire grate area.[67]
There are three test cocks, which are sometimes placed in a diagonal row on the front of the boiler, and sometimes on the fitting for the gauge glass. The top test cock shows highest level to which the water should rise in the boiler, and the lowest one the lowest level, the middle cock indicating the average. There is usually a vertical distance of about 4 inches between the test cocks, which gives a permissible range of 8 inches in the level of the water in the boiler.
Test cocks are prevented from choking with scale by passing a wire through the cock and clear into the boiler, a plug being provided, which, when removed by unscrewing, permits the insertion of the wire.
This cleaning must obviously be performed when there is no steam on the boiler.
A gauge glass is a glass tube whose bore is open to the boiler. It is fitted at each end to a brass socket that is screwed into the boiler, each socket having a cock that permits communication between the gauge glass and the boiler to be shut off in case the glass should break. The bottom socket is also fitted with a cock, which, on being opened, permits the water and steam to blow through the gauge glass and clean it of scum or dirt.
The gauge glass must be plainly in sight, and placed at such a height that when the desired quantity of water is in the boiler it will half fill the gauge glass.
Glass water gauges, instead of attaching to the boiler, are sometimes fitted to a fitting that connects to the top and bottom of the boiler, with the object of attaining, for the gauge glass, water free from the scum and impurities which collect at and near the surface of the water in the boiler. This fitting should have cocks in each pipe leading to the boiler, so that in case the gauge glass breaks, steam can be shut off from the boiler.
In some cases the test cocks are also attached to this fitting, and in this case the construction should be such that shutting off communication between the gauge glass and the boiler will not at the same time shut off communication between the test cocks and the boiler.
When the boiler is priming or steaming very fast, the gauge glass may show a false water level, hence reading should be compared with that of the test cocks.
If the water gets too low, the first parts of the boiler to be injured will be the top of the flame box, or the combustion chamber, and the top row of tubes, because they are the first surfaces that the water will fall below and leave exposed to the heat without having water on the other side.[68]
The pressure in the boiler is shown by a steam gauge, pressure gauge, or dial gauge as it is promiscuously called.
A Bourdon dial gauge or pressure gauge consists of a dial casing, containing a hollow thin brass hoop, oval in cross section, which receives steam from the boiler.
This hoop is fixed at one end, while the other end is closed and free to move. The free end is connected by a small link to a toothed sector, which gears or engages with a small pinion fast upon the spindle of the pointer or needle. When the steam is admitted into the hoop, it straightens out or expands in diameter to an amount that is proportionate to the amount of the pressure within the hoop, and thus causes the needle or index pointer to revolve, and denote from the markings or readings of a dial plate the amount of pressure within the hoop.
If the pressure within the hoop is released, it will move to its normal or zero position. In the course of time, however, the hoop is apt to get a slight permanent set and not indicate correctly. It may, however, be approximately tested for accuracy by testing its readings with that of the safety valve.
The working parts of the gauge, and its casings also, are made of brass, so that they shall not corrode, and to prevent the heat of the steam from permeating the gauge and impairing the action from expanding the parts, a small quantity of water interposes between the gauge and the steam, the construction being as follows:
Outside the gauge casing the steam pipe is bent into a loop forming an inverted syphon which is to contain the water.
At the lowest point in the bend of the syphon a small cock is inserted, which lets the water out of the leg of the syphon nearest to the boiler, because water in that leg would, from its weight, cause the gauge to show a pressure higher than that in the boiler.
The pressure shown by a steam gauge is that above atmosphere,[69] and not that above vacuum.
[II-454]The stop valve of a marine boiler is a valve that is opened to let the steam into the main steam pipe.
A blow off cock is a cock employed to blow off, or let all, or a part of, the water out of a boiler. There are generally two, one on the bottom of the boiler, and the other at the ship’s side, so that if the pipe was to break or get damaged, the cock at the vessel’s side can be closed to keep the sea water out, while that on the boiler may be closed to keep the water and steam in the boiler. These two ends cannot obviously be obtained if one blow off cock only was used.
Blow off cocks are opened and closed by a spanner or key that is removable from the cock, and to prevent the possibility of taking off the spanner or key, before the blow off cock is closed, a spanner guard is employed.
A spanner guard is a cap having a lug or tongue, which projects into the hole in the spanner guard, through which the spanner or key must pass before it can fit on the head of the blow off cock, and the key or spanner has a corresponding recess, so that the spanner or key can only be put on or taken off when the cock is closed.
Blowing off a boiler is emptying it entirely, as for examining the whole interior of the boiler.
Blowing down a boiler is letting out a portion of the water, so as to carry off the loose scale, mud, or sludge that may accumulate on the bottom of the boiler. The mud or sludge would form into scale if allowed to remain.
A scum cock is a cock employed to blow off a portion of the surface water in a boiler, and thus remove the scum, salt, and impurities which float or are thrown up to the surface.
Two scum cocks are employed, one on the side of the boiler, and one on the side of the ship. These two cocks are connected by a pipe. That on the boiler is placed a little below the working level, which is supposed to be (and is kept as nearly as possible) about 9 inches above the top row of tubes.
Sluice valves are doors sliding, water tight, in ways at the entrance to the bulkheads on both sides of the ship. They should be worked from above, in order that they may be shut when the depth of water in the bulk heads might prevent them from being worked from below. These valves should be operated occasionally to ensure that they slide easily and are in working order.
Scale in marine boilers using salt water is composed of sulphate of lime. It is most objectionable on the furnace tops, on the sides and tops of the combustion chamber, on the tubes and on the tube plates. It may be prevented to some extent from forming by a rapid circulation of the water in the boiler, by blowing down the boiler through the scum cocks, by the suspension in the boiler of zinc plates in contact with iron ones, by impregnating the water with chemical antidotes, which maintain the impurities in the form of mud or sludge, and by purifying the feed water. If surface condensers are used, scaling is obviously diminished by feeding as little salt water as possible, which may be done by not getting up a steam pressure high enough to cause the safety valve to blow off, and by preserving the water from the exhausts of the donkey or other engines about the ship.
A thin coating of scale, as say 1⁄32 inch thick, may serve as a protection against the chemical action of water that would act to corrode the surfaces, as in the case of harbors receiving the waste waters from chemical works or other impure waters. A thick coating of scale causes the plates to burn on the side receiving the furnace heat, and causes blisters to rise, while at the same time it decreases the value of the heating surface.
Scale on the tubes causes them to expand more, and therefore leak in the tube sheets.
This extra expansion sometimes breaks away the scale at the neck of the tube in the tube sheet and gives access to the water there, and the chemical action of water will in some cases cause the tube to be eaten through close to the tube plate.
Scale is removed mechanically by chisels, scrapers and chipping hammers, which are applied to all the surfaces that can be got at from the inside of the boiler (the man hole affording access to the boiler). After the scale has thus as far as possible been removed, it is washed out of the boiler. The efficiency with which scale may be removed from the tube sheets and tubes depends, to a great extent, upon the facilities the arrangement of the rows of tubes affords in giving access to the scaling chisels.
The salinometer. Salt water is heavier than fresh water, hence the amount of saltiness of water may be known from its density or weight. A salinometer is an instrument that determines from the density of the water the amount of salt contained in the water. It consists of a graduated stem at whose extremity is a weighted bulb which partially sinks the tube in the water; the depth to which the bulb sinks shows the density of the water.
The reading of a salinometer is taken at the water level, and is read on the tube, which is graduated as follows: The mark furthest from the bulb or highest up the stem is marked o, and if the zero line is level with the surface of the valve in which the salinometer floats, it indicates fresh water. If salt be added to the fresh water, the salinometer will rise in the water, and when the water contains 1 lb. of salt to 32 lbs. of water (which is the average degree of saltiness of sea water), the line marked 1⁄32 on the salinometer tube will be level with the surface of the water. If the saltiness of the water be increased, the salinometer will rise in the water until, at 2 lbs. of salt to 32 lbs. of water, a line (on the tube) marked 2⁄32 will be level with the surface of the water. The space between the 1⁄32 and 2⁄32 is divided into halves and quarters.
As the density of the water varies with its temperature, therefore the readings on the salinometer must agree with some specific temperature, which is usually 200° Fahrenheit, and the reading of the salinometer is correct only when the water is at that temperature. If, however, the water varies a few degrees from the standard of temperature for which the salinometer is marked, a correction of the reading may be made by adding 1⁄8 of 1⁄32 for each 10 degrees, that the water is hotter, or subtracting the same for each 10 degrees that it is cooler than the temperature at which the salinometer is correct.
The density or specific gravity of ordinary sea water is 1.027 (that of distilled water being unity or 1), and it contains about 4 oz. of salt per imperial gallon.
Tallow is sometimes forced into a boiler fed with salt water to stop priming, by means of a syringe that is screwed into a tallow cock provided upon the boiler below the water level. If the boiler is fed with fresh water, tallow is apt to cause priming.
Angle irons are used in boiler construction to be riveted to plates that require supporting or strengthening, or for gusset stays to be riveted to. Flanged plates are used in the construction of the furnaces, flame, boxes or combustion chambers, boiler ends and tube plates or tube sheets.
Division plates are fitted in some boilers to prevent the water from passing from one side of the boiler to the other when the vessel rolls heavily. This prevents some of the tubes from being left uncovered by water, and thereby getting injured from undue heat.
These division plates are neither steam nor water tight, and stand fore and aft of the ship. Similar division plates are sometimes used, however, to prevent the tops of the combustion boxes from getting overheated from the motion of the ship leaving them uncovered with water, their location being subserved to this end and varying with the position of the boiler.
The superheater of a marine boiler is provided with a safety valve, and sometimes with a pressure gauge to enable the comparing of the steam pressure with that in the boiler, and should also be provided with a gauge glass, to show when heavy priming is going on.
The main stop valve is upon the superheater, as is also the blast pipe.
Priming is a lifting, into the steam space of the boiler, of a part of the water, and may arise from heavy firing, from the safety valve blowing off, from too little steam space, and from other causes.
Priming[70] often occurs when the boiler feed is changed from salt water to fresh water, or from fresh to salt water.
[II-455]A separator or interceptor is a device fitted to either the superheater or to the steam receiver, for separating entrained water from the steam. It consists of a rectangular box or chamber with a partition plate extending from the top half down into the box.
The entering steam strikes the face of the partition plate against which the water collects, and from which it drops to the bottom of the box, while the steam passes under the partition and out at the other side to the engine.
The draught of a boiler is caused by the heat expanding the air and lightening it, thus causing it to ascend. It can be checked by stopping the exit of heated air up the funnel by means of a damper, by checking the flow of cold air into the furnace, by closing the dampers, by opening the furnace doors and letting cold air in the furnaces above the fires.[71]
A blast pipe is a small pipe leading from the superheater to the funnel, and provided with a stop cock.
It is used for letting a jet of steam up the funnel to promote the draught.
Flame seen at the top of the funnel is caused by the combustion of gases that would have been consumed in the furnace had there been sufficient air or sufficient room for complete combustion. It may be caused in a variety of ways, as insufficient openings between the fire bars, too narrow a space between the bridge wall and the boiler, or too deep a fire upon the bars. It is detrimental, because it obviously wastes fuel.
Dampers are used to regulate the draught in the furnace; they are fitted to the ash-pits or to the funnel, and should be fitted to both, because closing a damper in the funnel sets up a certain amount of pressure in the furnace by holding the heat, whereas dampers at the ash pit doors and none in the funnel lets the heat out and prevents cold air from getting in to promote combustion.
When there are no dampers the furnace doors are open instead, to check the draught; this is, however, highly injurious to the boilers.
The most rapid wasting of the plates of a marine boiler occurs alongside the fire bars, on the furnace tops, at the back of the flame box or combustion chamber, and in those plates generally that receive the most intense heat, and especially when they are heavily coated with scale and are not covered with water.
The scale that forms on the face of the tube sheet keeps the water away from contact with the plate, which, with an undue thickness of scale, will crack between the tube holes.
A tube that is split or that cannot be made steam tight by being re-mandrelled or expanded is plugged up at each end by means of either wooden or iron plugs. The best plan, however, is to use iron discs having a stepped diameter, so that one end will fit the bore of the tube, and the other will form a shoulder that will cover the end of the tube.
Each disc has a hole through its centre, so that a wrought iron rod or bolt may be passed through the hole and receive a nut at each end. Beneath the flange of each disc, a grummet of spun yarn and white lead is placed, so as to make a steam tight joint when the nuts are screwed home. This stays the tube plates as well as stopping the leaky tube.
If wooden plugs are used, they are made a driving fit in the tube bore, and driven through until they have passed the split, and a second wooden plug is driven tightly from the same end of the tube.
Black smoke is an evidence of incomplete or imperfect combustion, and may be, to a great extent, prevented by careful firing, as by feeding gradually and evenly, by the admission of the proper quantity of air, or by a jet of steam admitted above the dead plates.
The furnace bars are ordinarily of cast iron about 11⁄4 inches thick at the top, tapered towards the bottom, and with an air space of from 1⁄2 to 3⁄4 inch between them.
They require less air space for Welsh than for Newcastle coal, as the latter is the flaming or gaseous coal, and burns the fastest.
The quantity of coal burned in marine boiler furnaces is about 15 lbs. per square foot of fire grate area per hour; hence the quantity burnt per day with common average engines with 4 furnaces, 3 feet wide and 5 feet long, may be found by multiplying the area of the 4 furnaces (60 feet) by the number of lbs. (15) burned per foot of grate per hour, which will give the total lbs. weight burned per hour, which, divided by 112 lbs., will give the hundredweight burned per hour, and this, multiplied by the number of hours reckoned as constituting a day, gives the fuel consumption per day, based upon 15 lbs. coal per square foot of fire grate area.
The number of tons of steam coal burnt per day to drive an ordinary steamer of 40 feet beam 10 knots an hour by steam alone (or without sail), will depend upon the kind of engine used. Experience teaches us that with average vessels, the beam squared equals the consumption of coal for 40 days, in the case of an ordinary jet condenser engine; 50 days with a surface condensing engine; and 60 days with a compound engine; hence, in the present example, assuming the engine to be jet condensing, we may calculate the fuel consumption per day, for a vessel 40 feet beam giving 10 knots an hour, as follows:
The beam squared gives 1600 (40 × 40 = 1600), which divided by 40 (40 days) gives 40 tons per day. For surface condensing the 1600 would be divided by 50, giving 32 tons per day; and for a compound engine the 1600 would be divided by 60, giving 26 tons 131⁄3 cwt. per day.
It is obvious, however, that calculations of this kind, in which the ratio of expansion is not stated, are the merest approximations.
The number of tons of steam coal that will be burnt per day with a pair of average surface condensing engines having cylinders 50 inches in diameter will be, under average conditions, 16 tons per day, the calculations being based upon the common assumption that the diameter of one cylinder squared and divided by 100 gives the consumption of fuel in tons per day for condensing engines not compounded; thus, 40 × 40 = 1600 ÷ 100 = 16 tons of coal burned per day.
Here again, the ratio of expansion not being specified, the calculation has no real practical value.
If at sea and short of coal, bear in mind that the consumption of fuel per mile run is greater for fast than for slow speeds; hence the following points should be attended to:
Reduce the speed of the ship to say half the usual. Regulate the fire so as to keep up full boiler pressure without blowing off. This will allow the expansion or cut off valve to be set to cut off early in the stroke, and thus save steam. If, under these conditions, the steam should sometimes blow off at the safety valve, cover up part of the fire grate area.
Use a thin, rather than a thick, fire, but be careful that it is not so thin as to let currents of cold air pass through.
To Relieve the Boiler in Case of Emergency.—Suppose an engine breaks down at a time when the fires are heavy and going full, that the steam gauge shows blowing off pressure, but that the safety valve is stuck, or from some cause or other is prevented from blowing off, and cannot be eased or lifted, and the following is the course to be pursued:
1st. Close the ash pit dampers and open the smoke box door and fire door. If there are no ash pit doors, close the damper in the up take and open the fire and smoke box doors.
2d. Start the donkey engine to feed cold water into the boilers.
3d. Start the steam winches, and any other small engines that take steam from the main boilers.
4th. Slacken the escape valves, and open the drain cocks of the cylinders and receivers, and steam will blow through the H.P. cylinder escape valve and drain cock at once. The H. P. slide valve may then be worked by hand, back and forth, to let steam pass into the receiver and blow through its escape valves and drain cock.
5th. Open the scum or brine cocks and keep them open, also open all gauge or test cocks, etc., about the boiler.[72]
[72] It is not safe to draw the fire at a time when the pressure is at a dangerous point, especially if heavy, as disturbing it may temporarily increase the combustion and the danger of explosion.
[II-456]Figs. 3410 and 3411 represent an example of a steel marine boiler, designed for a working pressure of 160 lbs. per square inch, with a margin of safety of 5.
The dimensions are as follows:
| Diameter of shell | 12 feet | 6 | inches. | ||
| Shell plate | 1 | 1⁄8 | „ | thick. | |
| Front and back upper plates | 31⁄32 | „ | „ | ||
| Back rivet plates | 7⁄8 | „ | „ | ||
| Back lower plates | 7⁄8 | „ | „ | ||
| Front tube plate | 15⁄16 | „ | „ | ||
| Front lower plate | 13⁄16 | „ | „ | ||
| Furnaces | 17⁄32 | „ | „ | ||
| Inner tube plate | 3⁄4 | „ | „ | ||
| Combustion chamber back | 17⁄32 | „ | „ | ||
| Combustion chamber sides | 17⁄32 | „ | „ | ||
| Outer sides of wing combustion chambers | 9⁄16 | „ | „ | ||
| And bottom of centre one to be | 9⁄16 | „ | „ | ||
| Shell of receiver | 7⁄16 | „ | „ | ||
| Beds of receiver | 5⁄8 | „ | „ | ||
| Receiver connecting pipe | 3⁄4 | „ | „ | ||
The riveted joints have all holes drilled. The longitudinal seams are made with butt joints treble riveted, and with double butt straps.
The circumferential seams are lapped and treble riveted.
Fig. 3412 represents the “Martin” boiler for marine engines. In the return flue there are a number of vertical water tubes which are very effective in promoting circulation as well as in generating steam. These boilers are used largely in the United States navy for moderate pressures.
The following upon the testing and examining of a boiler of this class is from Modern Steam Boilers:
“Every new boiler should, when complete, be tested by water pressure to double the amount of the intended working pressure; for while the wisdom of applying as high a pressure as three times the working pressure, which is sometimes done, may be questionable, experience has shown that a test by hydraulic pressure will reveal defects that would otherwise be apt to pass unnoticed.
“For instance, when the top plate of a combustion box is stayed against the pressure by girder stays that are not stayed to the boiler shell, the girder stay merely acts to stiffen the top plate, and as a result the whole pressure on the area of the top plate falls on the walls of the combustion box. The back tube plate therefore springs down and transfers part of this pressure to the furnace,[II-457] causing it to become elliptical, as may generally be found by the application of rod gauges fitted to it before testing and tried while the pressure is on.
“This flattening under test naturally drew attention to the defectiveness of girder stays. Another instance may be given with reference to gusset stays, which, if fitted so as to support too large an area of back plate, in proportion to the area of combustion box it supports, may cause the combustion box to distort from its natural shape, pulling the tube sheet back and flattening the furnace. The amount of distortion may be only 1⁄16 inch in some cases, but that is sufficient to show the existence of unequal strains which require attention in boiler designing.
“This brings us to the important fact that in almost every instance where the furnaces of marine boilers collapse, they come down at the sides, notwithstanding that when collapse occurs from overheating, the crown of the furnace must have been left bare of[II-458] water first, and should therefore come down first, flattening the furnace at the top. This points to the conclusion, that the top of the furnace received some extraneous support.
“When a furnace collapses from corrosion, it naturally gives way at the most corroded part. An hydraulic test to twice the working pressures is recommended for new boilers only, unless it be small vertical cylindrical and steam launch boilers, which may always be subjected to the same test as new main boilers.
“In the case of old main boilers, however, and particularly rectangular ones, an hydraulic test of less than twice the working pressure may be employed, the amount being governed by the circumstances of the case. If, for instance, a boiler has undergone a thorough repair and received new furnaces, then every part of the boiler should have received proportionate consideration and an hydraulic test depending upon the judgment of the responsible engineer, but not less than one and one-half times the working pressure should be made, while one of one and three-quarter times could scarcely be objected to. This, however, is a subject upon which there is some controversy, especially in the case of old boilers having a good foundation of strength, but patched or local weak spots, such as combustion chamber backs and sides, these patches having been, perhaps, made with a view to a more extensive repair in the near future.
“In such a case as this an hydraulic test sufficient to prove the tightness of the seams and joints may, perhaps, be all that is absolutely essential.
“After a boiler has been tested by hydraulic pressure it should be examined internally, as it sometimes occurs that a stay may break under the test (especially if gusset stays are employed), and the extra strain thrown on the adjacent parts may cause them to fail, and thus cause the destruction of the boiler when under strain.
“When an examination is to be made inside and outside of a boiler, the boiler must be properly prepared for the same, which may be done as follows:
“The tubes should be swept; the furnace cleaned out; the fire bars should be taken out; the bridges in the furnace should be taken down; the up take smoke box and combustion box should be cleaned out and swept; every man hole and hand hole or peep hole door should be removed; the bottom of the boiler should be cleaned out and dried (in damp weather a little heat may be necessary for this purpose); all impediments, if any, should be removed in order to allow the bottom outside to be inspected; at the time of inspection a few mats, good lights, a hand hammer and small chipping hammer should be at hand. In the case of a boiler having any plates weakened by corrosion, a 5⁄8 inch tapping drill with a drilling brace should also be provided to test the thickness of such plates if considered necessary.
“The safety valves should invariably be taken out for examination, and it is a commendable feature sometimes followed to take out the feed valves, stop valves, blow off and brine cocks; at the same time, all the deposits that would prevent a thorough examination of the boiler should be removed. In some cases, however, there may not be time for the scaling before it is necessary for the repairs to be gone on with, and, in that case, a good examination may with care be made by an experienced man.
“To proceed, then, with the examination, the boiler should be entered through the man hole door beneath the furnaces, examining the boiler bottom and the bottom and sides of the furnaces all the way along, and on arriving at the end of the boiler the water space and stays at the backs of the combustion boxes can be examined as well as the midship combustion box stays and plates. In an old and corroded boiler it may be found necessary to use a chipping hammer very freely about the furnaces, particularly below the lap of the furnace.
“The most corroded part of a furnace will generally be found about on a line with the fire bars, but the furnaces may have suffered from some other cause than the corrosion due to ordinary wear, as, for example, from chemical or galvanic action, and in that case they may be found comparatively good at the sides but with the extreme bottoms in a dangerously corroded state, perhaps in the form of pit holes extending half through the plate and hidden by a coating of red scale, which requires to be chipped away before the pit holes are brought to light.
“Corrosion by galvanic action may have produced honey combing or a general attack over the surfaces, which have a dark or dark and sparkling appearance, the latter more particularly when corrosive action has been very active.
“Of these various classes of corrosion that which is the most deceiving is that which attacks the plates over the largest surface of the plate, leaving at the same time an apparently smooth exterior surface, for in this case the extent of the waste cannot be so clearly detected by the eye, and the only reliable way of testing the thickness is by drilling a hole through the plate.
“The flanges of the furnaces should always be examined in the bends, for flaws, for such defects, although not very common, do at times unexpectedly make their appearance, and might, if not detected, be the means of breaking the boiler down at sea. This part of the inspection being made, any drilling that is to be done to ascertain the thickness of suspected plates may be proceeded with before the rest of the inspection is made.
“It may, however, be well to remark that a very common defect is the wasting away of the combustion box plates around the necks of the stays or the internal surface of the plates, and it is a usual thing for deposits to accumulate around these necks, hence, unless these deposits have been removed (particularly in the case of boilers about three years old), the true condition of the boiler may not be known.
“The plate around the man hole door should next be examined, a great defect from waste at the surface that makes the water tight joint. Next comes the man hole door itself, which should have the rubber or other material used to make the joint cleaned off, for cases have occurred where the surface beneath was found apparently sound, whereas the application of a chisel showed that the iron was so corroded that but little iron was left in the flange, causing great surprise that the whole door had not blown out. This defect may generally be looked for in old boilers, and serves to emphasize the necessity for strong wrought iron doors.
“The outside surfaces of the end plate in the vicinity of the furnace fronts are a great source of trouble in some boilers, particularly where plane furnaces are fitted and flush rivets used for connecting them to the end shell plates.
“The insides of the furnaces and combustion boxes next require attention. The most common defects here are lamination of the furnace plate (if of iron), slight collapsing of furnaces, wasting of the furnace plates (particularly when anthracite coal has been used), and wasting when the fire bar bearers or bridges have rested against the plate.
“In the combustion box the buckling of flat plates may have occurred; plates may have wasted from leaks, distortion of the crown sheet from shortness of water may have occurred, or tubes may leak, and whenever, after sounding with the hammer, doubt exists as to the strength of the plate, a hole should be drilled through to test the thickness.
“The wing sides of the furnace may next be examined (through the usual peep holes or by having a boiler mounting taken off for the purpose), and the shell plating on the sides of the boiler, paying special attention to the plates where the feed water enters.
“We may next examine the outside of the bottom of the boiler, which should never be totally inaccessible to the eye, and should always be capable of being reached by a long-handled paint brush, for if kept well painted, the bottom of the boiler is, so far as the exterior is concerned, as durable as the other parts of the shell.
“If, however, the bottom is not kept painted and gets damp, and more particularly from bilge water, it will corrode rapidly, and the boiler must be lifted for examination. Under these circumstances a new boiler must at five years, at the very most, be lifted for examination, and if found comparatively good it should not be taken as an indication of the probable condition of any other boiler working under similar conditions, for the only means of avoiding a great risk in this matter is to rigidly inspect.
“In the case of flat bottomed boilers in small vessels a good result has obtained by placing them on a bed of cement, which if properly done excludes the bilge water from approaching the plate;[II-459] but even this precaution would scarcely be sufficient to justify an engineer in neglecting to lift the boiler at reasonable periods for examination of the bottom.
“The internal examination of the boiler is continued from the top by examining the stays in the steam space, the tube and tube plates, getting down between the nests of tubes and reaching the crowns of the furnaces. The surface of the shell plates should also be examined, more particularly if the boiler contains plates subject to heat on the outside and steam on the other (as in the case of wet up take boilers), for under these conditions a steel plate may become as weak and unreliable as a piece of cast iron.
“If the boiler is fitted with the superheater, the examination of the latter is of the utmost importance, as rapid destruction is here a common occurrence. In the case of a circular marine boiler of any size, nothing need be taken for granted, even though an hydraulic test be made up to twice the working pressure, because there is room for a thorough internal inspection which may disclose defects that would not be shown from the hydraulic test. The proper proportions of fire grate surface, heating surface, steam space, etc., in a marine boiler differ with the type of boiler and engine, and the steam pressure and degree of expansion employed.
“Upon the question of steam space, for example, it is asserted by many that marine boilers are not so liable to prime under the higher pressures, and as a result of this asserted fact the steam receiver is in some cases being dispensed with.
“It may be observed, however, that priming to any extent is so costly and detrimental that much consideration needs to be exercised before dispensing with the provisions ordinarily made to prevent it.
“For circular tubular boilers, having a working pressure of from 60 to 80 lbs. per square inch and to be used for compound engines, the following proportions represent current practice.
“1st. One square foot of fire grate area to every indicated horse power of the engine.
“2d. 28 square feet of heating surface[73] to 1 square foot of fire grate area.
[73] The heating surface here referred to includes the total interior surface of the tubes, the sides, backs, crowns and tube plates of the combustion boxes, and that part of the furnace that is above the level of the fire bars, but does not include the front tube plate (i. e., the tube plate in the smoke box).
“3d. 61⁄2 to 8 cubic feet of steam space to each square foot of fire grate area.
“4th. 8 to 10 square feet of tube surface to the total heating surface in single ended boilers.
“5th. 81⁄2 to 10 is about the ratio of tube surface to the total heating surface in double ended boilers.
“6th. The diameters of boiler tubes should be about one-half inch for each foot of length of tube. If less, the tube is liable to choke. About 14 cubic feet of steam (of from 60 to 80 lbs. pressure) should be made for each square foot of fire grate area.
“Each square foot of fire grate will burn from 13 to 18 lbs. of steam coal per hour. About 11⁄2 cubic feet of live steam (of the above pressure) is required for each indicated horse power.”
Hardening and tempering processes are performed upon steel for three purposes:
1st. To enable it to resist abrasion and wear.
2nd. To increase its elasticity.
3rd. To enable it to cut hard substances and increase the durability of the cutting edge.
Of these, the first is the simplest, because the precise degree of hardness imparted is not of vital importance.
The second is more difficult, because the quality of the steel employed for such purposes is variable, and hence the tempering process must be varied to suit the steel. The third is of the greatest importance, because the articles to be tempered are the most expensive to make, the duty obtained is of the greatest consequence to manufacturing pursuits, and the fine grade of steel employed renders it more liable to crack in the hardening process.
In those mechanical parts of machines which are hardened to resist abrasion and wear, the quality or grade of the steel is very often selected with a view to obtain strength in the parts and ease of mechanical manipulation in cutting them to the required shape, rather than to the capacity of the steel to harden. Hence, tougher and more fibrous grades of soft steel termed “Machine” steel, are employed, meaning that the steel is especially suitable for the working parts of machines. This class of steel is of a lower grade than that known as “tool” steel. It is softer, works, both on the anvil and in the lathe, more easily, and will bear heating to a higher temperature without deteriorating. It approaches more nearly to wrought iron, and is sometimes made of so low a grade as to be scarcely distinguishable therefrom.
The kinds of steel used where elasticity is desired are known as spring steel, blister steel, and shear or double-shear steel, although, for small springs, steel of the tool-steel class is often employed.
The word temper, as used by the manufacturer of steel, means the percentage of carbon it contains, the following being the most useful tempers of cast steel.
Razor Temper (11⁄2 per cent. carbon).—This steel is so easily burnt by being overheated that it can only be placed in the hands of a very skilful workman. When properly treated it will do twice the work of ordinary tool steel for turning chilled rolls, &c.
Saw-file Temper (13⁄8 per cent. carbon).—This steel requires careful treatment, and although it will stand more fire than the preceding temper should not be heated above a cherry red.
Tool Temper (11⁄4 per cent. carbon).—The most useful temper for turning tools, drills, and planing-machine tools in the hands of ordinary workmen. It is possible to weld cast steel of this temper, but not without care and skill.
Spindle Temper (11⁄8 per cent. carbon).—A very useful temper for mill picks, circular cutters, very large turning tools, taps, screwing dies, &c. This temper requires considerable care in welding.
Chisel Temper (1 per cent. carbon).—An extremely useful temper, combining, as it does, great toughness in the unhardened state, with the capacity of hardening at a low heat. It may also be welded without much difficulty. It is, consequently, well adapted for tools, where the unhardened part is required to stand the blow of a hammer without snipping, and where a hard cutting edge is required, such as cold chisels, hot salts, &c.
Set Temper (7⁄8 per cent. carbon).—This temper is adapted for tools where the chief punishment is on the unhardened part, such as cold sets, which have to stand the blows of a very heavy hammer.
Die Temper (3⁄4 per cent. carbon).—The most suitable temper for tools where the surface only is required to be hard, and where the capacity to withstand great pressure is of importance, such as stamping or pressing dies, boiler cups, &c. Both the last two tempers may be easily welded by a mechanic accustomed to weld cast steel.
The preference of an expert temperer for a particular brand of steel is, by no means, to be taken as proof of the superiority of that steel for the specific purpose. It may be that, under his conditions of manipulation, it is the best, but it may also be that, under a slight variation of treatment, other brands would be equal or even superior. It may be accepted as a rule that the reputation of a steel for a particular purpose is a sufficient guarantee of its adaptability to that purpose, and all that is necessary to a practical man is to be guided by the reputation of the brand of steel, and only change when he finds defects in the results, or ascertains that others are using a different steel with superior results.
Where large quantities of steel are used the steel manufacturers in many cases request customers to state for what particular purposes the steel is required, their experience teaching them what special grade of their make of steel is most suitable.
To harden steel it is heated to what is termed a “cherry red” and then dipped into water and held there until its temperature is reduced to that of the water.
Tempering steel as the blacksmith practises it consists in modifying, lowering, or tempering the degree of hardness obtained by hardening. The hardening of steel makes it brittle and weak in proportion as it is hardened, but this brittleness and weakness are removed and the steel recovers the strength and toughness due to its soft state in proportion as it is lowered or tempered.
When therefore a tool requires more strength than it possesses when hardened, it is strengthened by tempering it. Tempering proceeds in precise proportion as the temperature of the hardened steel is raised. When the steel is heated to redness the effects of the hardening are entirely removed, and the steel, if allowed to cool slowly, is softened or annealed. To distinguish maximum hardness from any lesser degree the terms to give the steel “all the water,” or to harden it “right out” are employed, both signifying that the steel was heated to at least a clear red, was cooled off in the water before being removed from the same, and was not subsequently tempered or modified in its hardness. If a piece of steel has its surface bright and is slowly heated, that surface will assume various colors, beginning with a pale straw color (which begins when the steel is heated to about 430°) and proceeds as in the following table:—
| Fahr. | ||
| Very pale yellow | 430 | ° |
| Straw yellow | 460 | |
| Brown yellow | 500 | |
| Light purple | 530 | |
| Dark purple | 550 | |
| Clear blue | 570 | |
| Pale blue | 610 | |
| Blue tinged with green | 630 | |
It happens that between the degree of hardness of hardened steel and the temper due to reheating it up to about 600° Fahr. lie all the degrees of hardness which experience has taught us are necessary for all steel-cutting tools. Hence we may use the appearance of colors as equivalent to a thermometer, and this is called color-tempering. The presence of these colors or of any one of the tints of color, however, is no guarantee that the steel has been tempered or possesses any degree of hardness above the normal condition, because they appear upon steel that is soft or has not been hardened. To obtain exact results by color tempering, therefore, the steel must first be thoroughly hardened, and this is known in practice by the whiteness of the hardened surface.
[II-461]Any number of pieces hardened so as to have a white surface may be tempered to an equal degree of color, or heated to an equal thermometrical temperature, with the assurance that they will possess a degree of hardness sufficiently uniform for all practical purposes; but if their hardened surfaces have dark patches, tempering to an equal tint of color is no guide as to their degree of temper. Successful tempering, therefore, must be preceded by proper hardening.
The muffle should therefore bear such a proportion in size that when heated to a blood red, and taken from the fire, its temperature will be reduced to nearly that of the steel when it has acquired its proper degree of temper.
The shape of the bore of the muffle should always conform to that of the article tempered; for round work, a round muffle; for square work, a square one; and so on. The muffle should be shorter than the work, so that the tempering of either end of the work may be retarded, if it is proceeding too fast, by allowing that end to protrude through the muffle.
Color tempering, it will be observed, gives us no guide or idea of any of the degrees of temper which occur while the hardened steel is being heated up to about 430° Fahr.; and thus it leaves us in the dark as to all the ranges of hardness existing in steel thoroughly hardened and tempered to any degree less than that due to about 430° degrees of reheating. How wide this range may be can be appreciated when it is remembered that in the color test there are only 200° of heat between the hardness known as straw color, which is hard enough for almost all cutting purposes, and blue, tinged with green, which is almost normal softness.
It is for this reason (among others) that where very exact results are to be obtained and a large number of pieces are to be tempered, fluxes, heated to the required temperature, are very often employed.
Color tempering is conducted in different ways. In a muffle, in heated sand, with hot pieces of flat iron, and in boxes heated to the requisite temperature in an oven, the temperature being indicated by a pyrometer or heat-gauge. The articles to be tempered remain in the oven a length of time determined by experiment or experience, these being influenced by the size and substance, or thickness, of the pieces.
A muffle is a tube or cylinder receiving its heat from the outside and open at the end or ends to receive the steel. Where tempering is carried on continuously the muffle is kept in the fire, although it is claimed by many that better results are obtained by removing it from the fire when heated. It is obvious that if the muffle is heated evenly the steel will temper most evenly by being held in the centre of the muffle, or the piece may be revolved and moved endways in the muffle in order that the steel may heat evenly. The tempering should always proceed slowly, otherwise the heat may not have time to penetrate the steel to the centre, the outside tempering more quickly, thus the tool will be weak because of the undue hardness of the interior metal. Furthermore, protruding edges, or slight sections of the steel, may reduce to the required temper before the main body of the steel, which induces either serious weakness of the insufficiently tempered part, or softness in the thin sections, providing that the steel is kept long enough in the muffle to temper the main body to the proper degree.
In heating steel to harden it, especial care is necessary, particularly when the tool is one finished to size, if its form is slight or irregular, or if it is a very long one, because unless the conditions both of heating and cooling be such that the temperature is raised and lowered uniformly throughout the mass, a change of form known as warping will ensue. If one part gets hotter than another it expands more, and the form of the steel undergoes the change necessary to accommodate this local expansion, and this alteration of shape becomes permanent. In work finished and fitted this is of very great consideration, and, in the case of tools, it often assumes sufficient importance to entirely destroy their value. If, then, an article has a thin side, it requires to be so manipulated in the fire that such side shall not become heated in advance of the rest of the body of the metal, or it will become locally distorted or warped, because, though there may exist but little difference in the temperature of the various parts, the more solid parts are too strong to give way to permit the expansion: hence the latter is accommodated at the expense of the form of the weakest part of the article.
Pieces, such as long taps, are very apt to warp both in the fire and in the water. In heating, they should rest upon an even bed of coked coal, and be revolved almost continuously while moved endways in the fire; or when the length is excessive, they may be rested in a heated tube, so that they may not bend of their own weight. So, likewise, spirals may be heated upon cylindrical pieces of iron or tubes to prevent their own weight from bending or disarranging the coils.
Experiments have demonstrated that the greater part of the hardness of steel depends upon the quickness with which its temperature is reduced from about 500° to a few degrees below 500°, and metal heated to 500° must be surrounded by a temperature which renders the existence of water under atmospheric pressure impossible; hence, so long as this temperature exists the steel cannot be in contact with the water, or, in other words, the heat from the steel vaporizes the immediately surrounding water. The vapour thus formed penetrates the surrounding water and is condensed, and from this action there is surrounding the steel a film of vapour separating the water from the steel, which continues so long as the heat from the steel is sufficiently great to maintain the film against the pressure of the water and the power of the water which rushes toward the steel to fill the spaces left vacant by the condensation of the vapour as it meets a cooler temperature and condenses. The thickness of the vapour film depends mainly upon the temperature of the steel; but here another consideration claims attention. As the heated steel enters the water the underneath side is constantly meeting water at its normal temperature, while the upper side is surrounded by water that the steel has passed by, and, to a certain extent, raised the temperature of. Hence, the vapour on the underneath side is the thinnest, because it is attacked with colder water and with greater force, because of the motion of the steel in dipping. For these reasons it is desirable, especially with thick pieces of steel, to inject the water in a full stream upon the article, as is done in the Brown & Sharpe hardening tanks.
In cases where a great many pieces are to be hardened and tempered to an even degree, the steel is heated for the hardening in a flue with the advantage that contact between the heated steel and the impurities (as sulphur or silicon) of ordinary fuels is avoided, and also that all the pieces may be heated, and therefore hardened, to a uniform degree. The capacity of this system is great, because a number of pieces can be heated without fear of any of them becoming overheated if not attended to immediately. Thus the Waltham Watch Co. heat their mainsprings for the hardening in a flux composed of melted salt and cyanide of potash, the latter serving to clean the surface of the steel; but as the latter wastes it requires to be added occasionally.
The Watch Company, however, find this mixture will not do for the hair springs, as it alters (to a very small degree, however) the nature of the steel; hence these springs are heated for hardening in melted glass.
The Pratt and Whitney Co. heat their taps, &c., for hardening in a composition of equal quantities of salt and cyanide of potash, adding the latter as it wastes, and temper them by the cold test.
The Morse Twist Drill Co. use a similar compound for heating to harden, and the following apparatus for dipping. In a large tank having a free water circulation, stand two pots of a capacity of about five gallons each, one of these contains cyanide of potash and salt, and another sperm oil. The heated work is dipped for an instant into the pot containing the potash and salt, which clean the surface of the steel, and then cooled in the main water tank; but if the work is, from its shape, liable to crack, it is at the final cooling dipped in the pot of sperm oil instead of in the water.
Before heating the steel it is dipped in soft soap to prevent oxidation, and on dipping it into the potash and salt pot it causes a cracking sound, the operator knowing from the sound if the mixture is proper, and how long to hold the steel therein.
This company first fill the heating pot with salt, and then add cyanide of potash until a trial of the tool gives quite satisfactory results, adding cyanide of potash as the work proceeds to make[II-462] up for the evaporation and keep the mixture of the compound correct.
In many cases it is considered an advantage to harden the outside of an article, keeping the inside as soft as possible so as to increase the strength. In such case the article may be heated in red-hot lead, the surface of which may be covered with charcoal. Under these conditions the outside of the article, especially if thick, will get red hot in advance of the inside.
Articles having thick and thin sections may be heated in fluxes to great advantage, the thick side being immersed first, and the article being lowered very slowly into the pot of lead. If the shape of the article is such as to render it liable to crack in the water because of containing holes or sharp corners in weak parts, these holes and sharp corners may be filled with fire-clay, the dipping water may be heated to about 50°, and salt (1 lb. per gallon of water) added to it.
The Monitor Sewing Machine Company harden and temper their spiral springs at one operation, by heating them to a blood-red heat and quenching them in a mixture of milk and water, which will give an excellent result, providing that the springs are heated to precise uniformity and the mixture of milk and water is correct. For a process of this kind (which is very expeditious, because the hardening and tempering is performed at one operation), the steel should be heated to a very uniform temperature, and a mixture of, say, two-thirds milk and one-third water tried at first, more milk being added to lower the temper, or more water to increase it if necessary.
Saws are hardened in compositions of animal oil, such as whale-oil, with which resin, pitch, and tallow are sometimes mixed.
Resin hardens but somewhat crystallises the metal, but it is used because, on common saws, the scale will not strike properly without it. Tallow gives body to the liquid and causes it to extract the heat quickly from the steel (and the hardening is solely due to the rapid extraction of the heat). In addition to this, the saws hardened in oil and tallow show a very fine grain if fractured, and are tough. The effect of pitch is much the same as that of resin. In place of tallow, bees-wax is sometimes used, giving an excellent result. A very little spirits of turpentine mixed with the oil every time it is used (that is, for every batch) is an excellent ingredient to cause the scale to strike, but being very inflammable, it is somewhat dangerous. If none of these ingredients are used, and the scale does not strike, it acts as a fine separating lining, preventing the contact between the metal and the liquid, and hence retarding the cooling, and therefore the hardening.
Let us suppose some thin saws of the finest grade of steel are to be tempered. The liquid would be about half a barrel of tallow to a barrel of whale-oil (which will harden as hard as glass). After the temperature of the saw is reduced to that of the bath, it is removed, the adhering oil is removed, and the surface dried by an application of sawdust, and the tempering process may be proceeded with.
There are three methods of drawing the temper. One is with the saw lying in the open furnace; a second, an English plan, is with the saw stretched in a frame, so as to prevent its warping, and in fact, to cause the tempering to aid in straightening the saw; and the third is to temper between flat dies.
In the first, the temper is determined by the appearance of the saw in the furnace. The saw absorbs some of the liquid in which it was quenched to harden it; and as it is reheated to temper it, this oil passes off as a cloud, or rather as a breath passes off the surface of a window-pane. This action takes place first on the lower surface of the saw, nearest to the furnace bottom, the oil exuding in a mist-like form. The length of time the saw must remain in the furnace after the cloud has passed off is determined by the thickness of the saw and the heat of the furnace, the operator being guided entirely by experience; but when the saw is taken from the furnace, it will have a very dark-red glimmer, and must be laid flat and allowed to cool off in the air, for if again dipped it would be too hard. When cool, the saw thus tempered will be of a sky-blue color, and will spring from point to butt without bend or break. This process requires skilful management and good judgment, but will give most excellent results. The main objection to it is, that it is expensive, since it gives no aid to the straightening processes.
The straightening frame, or English tempering system, is as follows: The plates of steel are made of a size that will cut into four saws. The furnace front is provided with a tramway extending to the floor of the furnace, and on this runs the stretcher-frame. The plates are stretched in the frame, which is run into the furnace so that the plate is heated under a tension, which operates to straighten them. As the temper lowers, the screws of the stretcher are turned, increasing the tension; when the tempering is done, the screws are made to stretch the plates very tight just previous to taking it from the fire, and the plates are allowed partly to cool off while kept in the frame. In this process the indications of the temper are determined as in the first process. In the third process, the saws are placed between a stationary and a movable die provided in the body of the furnace, the movable one descending and pressing the saw to the other die; thus the tempering is accompanied by a flattening process (the dies being operated by pressure). The degree of temper is regulated by the temperature to which the saws are heated, which is ascertained by a pyrometer. The furnace is kept at a constant temperature, and the length of time the saw remains between the dies is varied to suit the thickness of the saw. The gain due to this system is, that less straightening is required and a determinate temperature is secured. Some makers claim that in this system the vapour of oil that exudes from the saw has no means of escape, and that a chemical effect injurious to the steel ensues; and furthermore that the temperature of the dies will be greatest at or near their circumference, and hence the teeth and back and the ends of the saw will be softer than the middle of the width and length of the saw, and that if two saws, one above the other, be placed on the dies at once, the contacting surfaces of the saws will be the hardest, and those surfaces will be black by reason of the oil burning into the steel, instead of exuding, as in the open furnace process.
The floor of the tempering furnace should be flat and even; for if any part of the saw-plate lies suspended, it will sag when heated, greatly increasing the amount of straightening required. The furnace must be so constructed as to heat evenly all over, otherwise the temper of the saw will not be even. The air must be carefully excluded to prevent the steel from decarbonizing, which being thin, it is very apt to do. Thin saws warp proportionally as they are heated more, and if they are allowed to remain longer in the furnace and not heated too quickly, existing buckles or bends will partly straighten themselves in the furnace. Care must be taken to keep the tongs clear of the teeth, and in taking the saws from the furnace the length of the saw must stand at a right angle to the operator (two pairs of tongs being used), so that the saw’s own weight shall not cause it to bend. The saw must be transferred from the furnace to the bath very quickly, to prevent, as much as possible, its cooling in the air; for such cooling would take place unequally, causing the saw to warp, as well as impairing the temper. It should be dipped with the length horizontal, the teeth downward and the side faces vertical, and plunged quickly into the bath. On being dipped in the hardening liquid, they warp again, but the dipping may be manipulated to partly regulate the warping. From the moment the cold air strikes the plate a warping process sets in, hence quickness in transferring from the furnace to the bath is a great point. When the saw is hot enough to temper, the scale will begin to rise upon its surface, and if the furnace is unequally heated, the scale will arise first at the hottest part, instantly notifying the operator of the defect.
From the appearance of the surface of the saw after it comes from the hardening bath, the operator can see if it is properly hardened. If so, the scale will be what is termed “struck,” that is, it has come off, leaving the surface from a grey to a white color; while if the scale remains in dark patches, the saw is too soft in those parts.
After the saws are tempered they are allowed to cool in the open air, and then require to be straightened by the hammer, and in this process the tempering has been interfered with, inasmuch as that the elasticity due to the tempering has been[II-463] counterbalanced to some extent by the local condensation of the metal induced by the immediate effects of the hammer blows. The condensation of the metal has impaired the natural grain or fibre of the metal, and stiffens it so that if the saw be bent these stiffened hammer marks will cause it to remain set instead of springing back straight, as it should do. To remove this defect the saws are what is termed stiffened, that is, they are heated until the surface assumes a yellow color, when they are removed and allowed to cool. This causes the metal condensed by the hammer to assume its natural structural condition, and permits the tempering to spring the saw back straight, even though it be bent until the two ends touch, and the bend carried half way along the blade by carrying one end forward along the blade surface. The yellow color is subsequently removed by an application of a solution of muriatic acid.
The method employed by the Tomlinson Carriage Spring Company for carriage springs is as follows:—
The spring plates are heated to bend them to the former, which is a plate serving as a gauge whereby to bend the plate to its proper curve, which operation is performed quickly enough to leave the steel sufficiently hot for the hardening; hence the plates after bending are dipped edgeways and level into a tank of linseed oil which sets in a tank of circulating water, the latter serving to keep the oil at about a temperature of 70° when in constant use. About 3 inches from the bottom of the oil tank is a screw to prevent the plates from falling to the bottom among the refuse.
To draw the temper the hardened springs are placed in the furnace, which has the air-blast turned off, and when the scale begins to rise, showing that the adhering oil is about to take fire, they are turned end for end in the furnace so as to heat them equally all over. When the oil blazes and is freely blazed off, the springs are removed and allowed to cool in the open air, but if the heat of a plate, when dipped in the oil to harden is rather low, it is cooled, after blazing, in water. The cooling after blazing thus being employed to equalize any slight difference in the heat of the spring when hardened.
The furnace is about 10 inches wide and about 4 inches longer than the longest spring. The grate bars are arranged across the furnace with a distance of 3⁄8 inch between them. The coal used is egg anthracite. It is first placed at the back of the furnace, and raked forward as it becomes ignited and burns clearly. For shorter springs the coal is kept banked at the back of the furnace, so that the full length of the furnace is not operative, which, of course, saves fuel. By feeding the fire at the back end of the furnace, the gases formed before the coal burns clearly pass up the chimney without passing over the plates, which heat over a clear fire.
For commoner brands of steel, what is termed a water-chill temper is given. This process is not as good as oil-tempering, but serves excellently for the quality of steel on which it is employed. The process is as follows: The springs are heated and bent to shape on the former plate as before said; while at a clear red heat, and still held firmly to the former plate, water is poured from a dipper passed along the plate. The dipper is filled four or five times, according to the heat of the plate, which is cooled down to a low or very deep red. The cooling process on a plate 11⁄2 × 1⁄4 inches occupies about 6 seconds on an average, but longer if the steel was not at a clear red, and less if of a brighter red, when the cooling began. Some brands of steel of the Swede steel class will not temper by the water-chill process while yet other brands will not harden in oil, in which case water is used to dip the plates in for hardening, the tempering being blazing in oil as described. In all cases, however, steel that will not harden in oil will not temper by the water-chill process.
The Columbia Car Spring Company temper their springs as follows:—Using “Gregory crucible steel,” heating is performed in a furnace consuming gas coke, but the furnace has a number of return enclosed flues, and between these flues (one over the other), are ovens, the heat passing through the brick-work forming the flues into the ovens. To facilitate renewing the ovens (which of course also renews the flues), the floor of each oven (which forms the ceiling of the oven below), is built on iron supports, protected by the brick-work and suitable fire clay, the bricks all being made to pattern, thus involving very little labor in building. The furnace doors are at the ends, and are kept closed as much as possible. In this way the steel has no contact with the products of combustion of the fuel, and the air is excluded as far as practicable (two valuable features). The furnaces are long and narrow, and not being connected with the flue there is but little disposition for the cold air to rush in when the furnace doors are opened.
The hardening and tempering of springs whose coils are of thick cross-section is performed at one operation as follows: The springs are heated in the furnace or oven described, and are first immersed for a certain period in a tank containing fish oil (obtained from the fish “Moss Bunker,” and termed “straights”), and are then removed and cooled in a tank of water. The period of immersion in the oil is governed solely by the operator’s judgment, depending upon the thickness of the cross-section of the spring coil, or, in other words, the diameter of the round steel of which the spring is made.
The table below gives examples of the hardening and tempering in this way of springs of the following dimensions:—
| Number of coils in spring | 5 | 3⁄4 | |
| Length of the spring | 6 | inches. | |
| Outside diameter of coils | 4 | 3⁄4 | |
| Diameter of steel | 1 | ||
| Examples. | Time of Immersion in Oil. |
Number of Swings in Oil. |
| Seconds. | ||
| First | 28 | 35 |
| Second | 36 | 46 |
| Third | 27 | 36 |
| Fourth | 38 | 40 |
As will be seen, the spring in the first example was immersed in the oil and slowly swung back and forth for 28 seconds, having been given 35 swings during that time. Upon removal from the oil the spring took fire, was redipped for one second, and then put in the cold water tank to cool off.
The following are examples in hardening and tempering springs of the following dimensions:—
| Number of coils in the springs | 6 | ||
| Length of the springs | 9 | inches. | |
| Inside diameter of coils | 3 | 1⁄4 | |
| Size of steel | 1 × 1 | 1⁄2 | square. |
| Examples. | Time of Immersion in Oil. |
Number of Swings in Oil. |
| Seconds. | ||
| First | 9 | 12 |
| Second | 8 | 12 |
| Third | 8 | 12 |
| Fourth | 9 | 12 |
| Fifth | 9 | 12 |
| Sixth | 9 | 12 |
To keep the tempering oil cool and at an even temperature, the tank of fish oil was in a second or outer tank containing water, a circulation of the latter being maintained by a pump. The swinging of the coils causes a circulation of the oil, while at the same time it hastens the cooling of the spring. The water tank was kept cool by a constant stream and overflow. If a spring, upon being taken from the oil, took fire, it was again immersed as[II-464] in the first example. Resin and pitch are sometimes added to the oil to increase its hardening capacity, if necessary.
The test to which these springs were subjected was to compress them until the coils touched each other, measuring the height of the spring after each test, and continuing the operation until at two consecutive tests the spring came back to its height before the two respective compressions. The amount of set under these conditions is found to vary from 3⁄8 inch, in comparatively weak, to 7⁄8 inch for large stiff ones.
The New Haven Clock Company heat their springs in a furnace burning wood, the springs being kept in the flames only, and quenched in a composition of the following proportions:—“To a barrel of oil 10 quarts of resin and 12 quarts of tallow are added.”
If the springs “fly,” that is, break, more tallow is added, but if the fracture indicates brittleness or granulation of the steel, rather than excessive hardness, a ball of yellow beeswax, of about 6 inches in diameter, is added to the above.
These springs are tempered, singly, to a reddish purple by being placed on a frame having horizontally radiating arms like a “star,” which is attached at the end of a vertical rod. The spring is laid on the “star” and lowered into a pot of melted lead, being held there a length of time dictated by the judgment of the operator.
The star-shaped frame is termed a sinker, and if upon being lifted from the lead the colour of the spring is too high, a second immersion is given.
An efficient engineer must certainly be able to determine any practical question that may arise in the management, not only of his engine and boiler, but also in that of such shafting, pulleys, gear wheels, etc., as may constitute the driving gear connected with the engine.
A very moderate examination of an engineer (whether to test his suitability for employment or for promotion) should therefore include questions tending to determine his capability to give such directions as may be necessary when the engine or shafting breaks down, or when alterations are to be made and he is consulted with reference to them. The following questions have been framed with a view to include such information as a first-class engineer, and even an assistant or night engineer, may be expected to possess, and a large proportion of these questions have been taken from actual engineers’ examinations in various parts of the country.
In many cases engineers of manufactories are required to make, as far as possible, their own repairs and sometimes indeed also the repairs to the machinery the engine drives, but to give questions covering this ground would be to refer the reader to nearly every page in the two volumes, which is manifestly impracticable.
Matching gear wheels.—Suppose you were running a hoisting engine whose pinion had 15 teeth, driving a wheel with 150 teeth in it; if the pinion had teeth with radial flanks, what orders would you send to get another wheel that would work with the pair?—For answer, see Volume I., page 15.
Radial flanks.—If a pinion has radial flanks what information does that give to the engineer if at any time he requires to order another wheel to work with it? I. 15.
Teeth of gear wheels.—What is the difference between an epicycloidal tooth and an involute tooth of a gear wheel? I. 8, 13.
Ordering bevel gears.—Two lines of shafting are to be connected by a pair of bevel gears and one is to run twice as fast as the other; how would you find the bevel of the wheels so as to be able to tell the maker what was wanted, and what dimensions would you give, leaving the pitch and the shape of the teeth out of the question? I. 22.
Ordering taps.—Suppose you were ordering a set of taps for use in the engine room, what precautions would you be obliged to take as to the shape of the thread in order to get proper taps? I. 85.
Fitting a nut.—Will a nut having a United States standard thread fit a bolt having a common V thread, both threads having the same pitch and diameter, and how could you tell one bolt from the other? I. 85.
Curing a pounding cam.—Suppose some part of the machinery driven by an engine had a cam motion with a small roller which hammered and pounded on the cam, how would you cure the defect? I. 83.
Ordering a new spur wheel.—Suppose a spur wheel broke and you wanted to give the diameter for a new one, where would you measure the diameter of the old one? I. 1.
Comparing screw threads.—What is the difference between the common V thread and the United States standard thread? I. 85.
Using two set screws.—When two set screws are placed in a hub how should they be located? I. 127.
Best lathe tool.—What is the most useful turning tool for a hand lathe, such as is sometimes provided for an engineer to make repairs with? I. 331.
Fitting a crank pin.—How would you proceed to put in by a contraction fit a crank pin, the crank being on the engine? I. 366.
Increasing strength of teeth.—Suppose you had to order a new pair of wheels to replace a pair whose teeth frequently broke, what alterations in the dimensions of the wheels would you make so as to get stronger teeth in wheels of the same diameter? I. 65.
Wear of a cam roller.—If an engine had a valve motion worked by a parallel roller in a parallel cam groove, would the roller wear out quick, and why? I. 84.
Altering the speed of a shaft.—Do a pair of mitre wheels alter the speeds of the shaft they drive or not? I. 1.
Driving out a key.—In driving out a key is a quick or a slow hammer blow the most effective? II. 65.
Riveting a crank pin.—For riveting a crank pin what shape should the pene or pane of the hammer be? II. 73.
Face of a cold chisel.—What is the proper shape for the face of a cold chisel? II. 73.
Key bearing.—What is the effect upon a wheel if its key bears upon opposite corners? II. 107.
Fitting a key.—Should a key be driven lightly or not when fitting it, and why? II. 106.
Angle Of wrench jaws.—What angle should the jaws of a wrench be to its body in order to enable it to turn a nut in a corner with greatest advantage? I. 123.
Chucking a crank.—How should a crank be chucked in order to prevent the crank pin from being out of true, and the engine from beating and pounding? I. 247.
Chucking a cross-head.—How should a cross-head be chucked so as to have its piston rod and wrist pin at a true right angle? I. 252.
Length of drill edges.—Why should both edges of a drill be exactly equal in length and of equal angle? I. 277.
Boring bar edges.—Should a boring bar for an engine cylinder have one, two, three or four cutters? I. 289.
Spiral spring.—Give a method of making a spiral spring. I. 329.
Expansion fit.—What is meant by an expansion or a contraction fit, say for an engine crank pin? I. 366.
Fitting brasses.—Suppose the joint faces of a pair of brasses are not square with the sides of the box or strap in which the brasses fit, what will the effect be when the brasses are locked tight together by the key? II. 125.
Wear of brasses.—When an engineer is taking up the wear of connecting rod brasses, what must he do to keep the rod of the proper length? II. 124-127.
Case hardening.—Describe the simplest method of case hardening. II. 128.
Fitting pillar block brasses.—State the proper order of procedure in fitting in a new pair of main bearing or pillar block brasses for an engine. II. 130.
Driving brasses.—What will be the effect of driving a brass in and out with a hammer and without a block of wood to strike on? II. 72 and 132.
Originating a true plane.—How is a true plane or flat surface originated? II. 133.
Cover joint.—What is the best form of joint for an engine cylinder cover? II. 137.
Grinding a cover.—How must a cylinder cover be moved when grinding it? II. 137.
Appearance Of a joint.—What is the appearance of a finished ground joint? II. 137.
Grade of emery.—About what grade of emery would you use to make a ground joint? II. 137.
Best heat joint.—What is the best kind of joint to withstand great heat or flame? II. 138.
Best water joint.—What are the best kinds of joints for withstanding water pressure? II. 138.
Fitting a flange.—In fitting a flange to a boiler what part of the flange face should bed most? II. 140.
Rust joint.—- How are rust joints made? II. 140.
Leaky plug.—How would you test the fit of a leaky plug in a cock? II. 144.
Well-ground plug.—What is the appearance of a well-ground plug? II. 145.
Quick brass fitting.—Describe the quickest method of fitting a new brass or bearing box to its journal. II. 147.
Babbitt bearing.—What is the principal advantage of a Babbitted bearing? II. 156.[II-468]
Adjusting guide bars.—What two essential points are there in adjusting the bottom guide bars of an engine? II. 162.
Setting guide bars.—Describe roughly the method employed to set guide bars by means of a stretched line or cord? II. 163.
Pounding journals.—What are the two principal causes of the beating or pounding of the journals of an engine? II. 164.
Locating a pound.—How may the location of a pound be discovered? II. 164.
Cause of pounding.—What is the ordinary cause of beating and pounding in an engine? II. 164.
Wearing down.—What is the defect induced by letting the parts of an engine wear down to a bearing? II. 166.
Testing alignment.—What are the tests that should be made to find out what part of an engine is out of line? II. 166.
Best test for alignment.—What part of an engine can be used to form the best test of alignment to cure pounding? II. 167.
Connecting rod alignment.—State in a general way the method of using the connecting rod to place the engine in line, and thus prevent beating and pounding. II. 167 to 172.
Difficult alignment.—What error in the alignment of the parts of an engine is the most difficult to discover? II. 170.
Alignment of crank pin.—What is the general cause of a crank pin being out of line with the crank shaft? II. 170.
Pound at quarter stroke.—When a pound occurs in an engine at the time the crank pin is at quarter stroke, or thereabouts, where would you look for the cause? II. 170 to 172.
Setting a slide valve.—What are the three objects, either of which a slide valve may be so set as to accomplish? II. 173.
Essentials of slide valve setting.—What are the two operations essential to the setting of a slide valve? II. 173.
Squaring a valve.—Why is the common process of squaring the valve an improper proceeding? II. 173, 394.
Crank pin on dead centre.—How would you proceed to put an engine crank pin exactly on the dead centre for setting the valve? II. 173, 394.
Direction of movement.—What are the considerations that determine in which direction the engine should be moved when setting the valve? II. 173, 174, 394.
Setting eccentrics.—What tools are used to set eccentrics upon shafts before the shafts are upon the engine? II. 175.
Patching a break.—In patching a broken beam or frame, how may the bolts be made to serve to act as keys closing the crack? II. 178.
Erecting shafting.—Give a general or rough description of the method of adjusting or aligning or erecting shafting. II. 184 to 186.
Kinds of shafting.—What is the difference between bright and black shafting? II. 187.
Fitting a pulley.—If you had a pulley whose bore was 115⁄16 inches, what diameter of bright shafting would you order for it? II. 187.
Locating collars.—What is the best location for the collars that prevent end motion on a line shaft? II. 189.
Ball and socket hangers.—What are the advantages of hangers having a ball and socket adjustment? II. 192.
Shaft couplings.—What four objects should the couplings for line shafts accomplish? II. 194.
Universal joint.—What object does a universal joint accomplish? II. 199.
Crowning a pulley.—What is the object of crowning a pulley? II. 201.
Pulley balance.—Why should a pulley be balanced? What is a running and what a standing balance for a pulley? At what speed should a running balance be made? II. 202.
Size of pulleys.—If a shaft makes 150 revolutions per minute, and it is required to drive a pulley on a machine at 600 revolutions, what proportions must the diameter of the two pulleys have, and what determines the diameters of the pulleys? II. 205, 206.
Testing belts.—What appearance in leather belting indicates that it was cut from the spongy shoulder? II. 208.
Stronger side of belts.—Which is the stronger side of leather, the smooth or grain side or the rough or flesh side? II. 208.
Placing a belt tightener.—Should a belt tightener be placed on the tight or slack side of a belt? II. 210.
Crossed vs. open belt.—Which will transmit more power, an open or a crossed belt, and why? II. 210.
Crossed belt.—What are the objections to a crossed belt? II. 210.
Shortening a round belt.—Can a round twisted belt be shortened without removing either the hook or the eye and how? II. 216.
Wide belt.—How would you get a very wide belt on a pulley? II. 217.
Mending an eccentric rod.—Suppose an eccentric rod broke, and you were required to weld it again, what shape could you make the scarf for the weld? II. 234.
Butt weld.—What is a butt or pump weld? II. 236.
Scarf weld.—Describe roughly the means you would employ to make a scarf weld. II. 235.
Tongue weld.—What are the shapes of the two pieces that come together in a tongue weld? II. 235.
Strain on boiler joint.—How would you calculate the amount of stress there is upon the riveted joint of a boiler? II. 350.
Shearing strain.—What is meant by the terms, shearing, tearing and crushing strains of a steam boiler? II. 351.
Lapped and butt joints.—How does a lapped joint differ from a butt joint or seam in a boiler? II. 352.
Chain and zigzag riveting.—How does a chain riveted joint differ from a zigzag riveted joint? II. 352.
Butt joint.—What are the advantages of the butt joint? II. 352-353.
Margin for holes.—How would you find the proper distance the rivet holes should be from the edge of the plate in a boiler seam? II. 353.
Spacing rows Of rivets.—How would you find the distance apart for the rows of rivet holes in a double riveted joint? II. 353.
High percentage joint.—What is meant by a “high percentage” riveted joint? II. 353.
Single and double shear.—What is meant by a rivet being in single shear or double shear? II. 353.
Allowance for shear.—How much additional allowance is made in the shearing strength of a rivet in double shear over that of the same rivet if in single shear? II. 358.
Taking charge of a boiler.—What is the first thing you would do in taking charge of a boiler? II. 368, 400.
First inspection.—What part of the boiler would you inspect first? II. 368.
Safety valve defect.—To what defect is a safety valve most liable? II. 368, 400.
Water supply.—How much water should there be in the boiler when the fire is lit? II. 368.
Reliability of gauge glass.—Is a gauge glass always reliable for showing the height of the water in the boiler? II. 368, 402.
Testing gauge glass.—What would you do to find out if the gauge glass was showing the correct water level? II. 368.
Condensation in boiler.—What is likely to happen if the steam condenses in the boiler without any of the cocks being open? II. 368, 400.
Cleaning a boiler.—What parts of the boiler would you clean before lighting the fire? II. 368.
Laying a fire.—How would you lay the fire? II. 368.
Quick combustion.—Does bituminous (soft) or anthracite (hard) coal light more easily? II. 368.
First coal.—How soon would you put coal on after the fire is lit? How deep would you make the first layer of coal? II. 368, 401.
Amount of coal.—How much coal would you put on the fire at a time? II. 368, 401.
Even heat.—How can an even temperature be kept up in the fire box? Why is it necessary to keep an even temperature in the fire box? II. 368, 370.
Shaking grate.—What is the advantage possessed by shaking grate bars? II. 369.
Before cleaning a fire.—What preparations would you make before cleaning the fire? II. 369.
Fire tools and their uses.—What tools are used in cleaning a fire? And what is the use of each? II. 369.
Draught while firing.—How should the draught be regulated while the fire is being cleaned? II. 369.
Temporary interruption.—What should be done to prevent blowing off through the safety valve when the engine is stopped and no steam is being taken from the boiler? II. 369.
Blue flame.—What does blue flame in the fire box indicate? II. 369.
Water supply at night.—How much water would you have in a boiler when leaving it for all night? II. 369.
Fire at night.—How would you leave the fire for the night? II. 369.
Banking.—What is banking a fire? Give a safe method of banking a fire. II. 369, 401.
Dampers at night.—How should the dampers be left when the fire is banked? II. 369.[II-469]
Safety valve at night.—How would you set the safety valve for a banked fire? II. 369.
Opening a banked fire.—What is the first thing to do in starting up a banked fire? II. 369, 401.
Regulating boiler feed.—How would you regulate the boiler feed? II. 369.
Regulating a pump.—How can a pump be regulated so as to be kept pumping without surcharging the boiler? II. 369.
Even boiler injection.—Can a continuous feed be maintained if injectors are used? II. 370.
Stuck valve.—How may a stuck valve or a check valve be released? II. 370.
Hot feed water.—What would you do if the feed water got so hot that the pump worked imperfectly or not at all? II. 370.
Scale.—What causes scale to form in the boiler and what effect does scale have on the boiler? II. 370.
Preventing scale.—What are the principal methods employed to prevent the formation of scale in the boiler? II. 370.
Horizontal heater.—What advantage does a horizontal heater possess? II. 370.
Dirty gauge glass.—What should be done to the gauge glass if the feed water is dirty? How many times a day should the gauge be blown out? II. 370.
Priming.—What is the priming or foaming of the water in a boiler? What are the known causes of priming? Why is priming wasteful? Can blowing off at the safety valve cause priming? What are other causes of priming? How can priming be detected? What would you do to stop priming? What would you do to prevent priming? What parts of the engine would you attend to if the boiler primes? II. 370.
Low water.—What would you do if the water got dangerously low in the boiler? In such a case how would you regulate the dampers? What do you consider dangerously low? What is blowing down a boiler? II. 370.
Cleaning a boiler.—How often would you clean a boiler? II. 371.
Water falling.—What would you suppose was going wrong if the pump was kept going and the water still fell in the boiler? II. 370.
Empty pump.—What causes a pump to fail? II. 370.
Blowing down.—How much would you blow down a boiler? How low should the pressure get before the water is let out? What would be the result if the boiler was blown off under a high pressure? What would you do after the water is all out of the boiler? II. 371.
Special examination.—What parts would you pay special attention to in examining the boiler after cleaning it? II. 371.
Hammer test.—What does the “hammer test” consist of? II. 371.
Washing and scaling.—What determines the periods at which a boiler should be washed out and scaled? II. 371.
Regulating dampers.—How would you regulate the dampers when letting the fire out? II. 371.
Naming the parts.—Name all the parts of a simple or plain D slide-valve engine, beginning with the cylinder. II. 372.
Dividing the parts.—Into what three divisions may the parts of a plain slide-valve engine be divided? II. 372.
Defining clearance.—What is the meaning of the word “clearance” as applied to an engine cylinder? II. 372.
Finding equal clearance.—How would you proceed to find if the clearance in the cylinder was equal at each end? II. 372, 404.
Parts of valve motion.—What parts constitute the valve motion or valve gear? II. 372.
The driving parts.—What parts constitute the driving or power-transmitting mechanism? II. 372.
Lubricating attachments.—Name the attachments used upon an engine cylinder to lubricate the piston and valves. II. 373.
Pet cock.—What is the difference between a cylinder pet cock and a cylinder relief valve? II. 373.
Relief valves.—What are cylinder relief valves used for? II. 373.
Quick steam admission.—Which gives the quickest steam admission, a long and narrow or a wide and short steam port, both having the same area? II. 373.
Placing the piston-ring split.—At what part of the cylinder bore should the split of a piston ring be placed? II. 374.
Fitting a piston ring.—How tight should a piston ring fit to the cylinder bore? II. 374.
Testing steam tightness.—How would you test the steam tightness of a piston? II. 374.
Jacketed.—What is a jacketed cylinder? II. 374.
Valve gear.—What is a releasing valve gear? What is a positive valve gear? II. 374.
Packing a stuffing box.—About how full of packing would you fill a stuffing box for a piston gland? II. 375.
Connecting rods.—What are the two principal kinds of connecting rods? What is meant by the angularity of a connecting rod? II. 375.
Oiling guide bars.—Which guide-bar is the most difficult to oil, the top or the bottom one? II. 375.
Effect of angularity.—What effect does the angularity of the connecting rod have on the piston motion? Is this effect increased or diminished by shortening the connecting rod? II. 375.
Crank at full power.—When the crank is at its point of full power, is the piston in the middle of the cylinder? Is it nearer to the crank-end or the head-end of the cylinder? II. 375.
Piston motion irregular.—What causes the piston to have irregular motion? II. 375.
Live steam period.—What constitutes the live steam period of a position? II. 376.
Cut-off.—What is the point of cut-off? II. 375.—What is a separate cut-off valve, and what event does it control in the supply of the steam to the cylinder? How is the point of cut-off varied when a cut-off valve is used? II. 378.
Working expansively.—What causes the steam to be worked expansively in an engine cylinder? II. 402.
Follower.—- What is a piston follower? II. 374.
Valve lead.—What is the lead of valve? II. 376.
Valve lap.—What is the lap of a valve? II. 376.
Admission.—What is the point of admission? II. 376.
Cushioning.—At what point in the valve travel does cushioning begin? II. 376.
Release and compression.—What are the points of release and of compression? II. 376.
Double-ported valve.—What is a double-ported valve? II. 377.
Valves.—What is a griddle valve? What is a balanced valve? II. 377.—What is a piston valve? II. 378.
Slide and piston valves.—Is there any difference between the action of a plain slide valve and a piston valve if both have the same amount of lap, lead, and travel? II. 378.
Cut-off diagram.—Make a diagram to give the dimensions of a slide valve, to cut off at 3⁄4 stroke, the valve travel being 4 inches. II. 380.
Reversing an engine.—What is the ordinary means provided for reversing an engine? II. 383.
Full gear.—What is the meaning of the term full gear, with regard to a link motion? II. 383.
Third use Of link motion.—What does a link motion accomplish besides enabling the engine to run in either direction? II. 383.
Slide valve for link motion.—What are the two operations to be performed in setting the slide valve of an engine having a link motion? Describe these two operations. II. 383.
Governors.—What is a throttling governor? What is an isochronal governor? What is a dancing governor? II. 384.
Forward.—What is full gear forward? II. 383.
Backward.—What is full gear backward? II. 383.
Starting.—How would you proceed to start a plain slide valve? II. 384, 400.
Crank position.—What is the best position for the crank to be in to start the engine, and why is it the best position? II. 384.
Taking charge.—What is the first thing you would do in taking charge of an engine? II. 385.
Length of connecting rod.—How would you find out if the connecting rod was the right length to give an equal amount of clearance at each end of the cylinder? II. 385, 404.
Order of examination.—In what order should a thorough examination of the engine be made? II. 385.
Least examination.—What would constitute the least permissible examination of an engine, with a due regard to safety? II. 385.
Thorough examination.—What would constitute a complete examination of a plain slide-valve engine? In what order should such an examination be made? II. 385.
Quick examination.—What examination should an engineer make of a plain slide-valve engine, if called upon to start it as quickly as possible without knowing its condition? II. 385.
Taking a lead.—How would you take a lead for adjusting the fit of a bearing to its journal? II. 386.
Set of slide valve.—How would you test whether the slide valve was set properly? II. 386.
[II-470]Squaring a valve.—Is it proper to square a plain slide valve? II. 386.
Lead affected by wear.—How does the wear of the parts affect the lead in vertical engines? II. 386.
Heating of crank-shaft.—What would you do if the crank-shaft bearings began to heat? II. 386.
Hot crank-pins.—What are the principal causes of hot crank-pins? II. 386.
Heating.—What part of the engine is the most likely to get hot from the friction of the fit? II. 386.
Use of lead.—What is a lead used for in adjusting the fit of a brass to its journal? II. 386.
Fit of top brass.—When a liner is used between the two brasses, what does the fit of the top brass depend upon? II. 386.
Oiling.—In oiling the engine, what precaution would you take to prevent the journals from heating? II. 401.
Cold weather.—What is liable to happen to an engine that is used out of doors in cold weather? II. 386.
Leaky throttle valve.—What damage might a leaky throttle valve do, and how would you prevent it? II. 386.
Leaky check valve.—What damage may a leaky check valve do, and how would you prevent it? II. 387.
Freezing in the pump.—How would you prevent the water from freezing in the pump? II. 387.
Freezing oil.—How would you prevent the oil from freezing? II. 387.
Thawing oil.—How would you thaw frozen oil? II. 387.
Setting a portable engine.—How should a portable engine stand when it is at work, and why should it stand so? II. 387.
Natural supply of water.—What precaution would you take when feed water is drawn from a stream, or other natural source of supply? II. 387.
Pumps.—Into what classes may pumps be divided? What is a force pump? What is a piston pump? What is a single-acting pump? What is a double-acting pump? II. 387.
“Suction.”—What causes the flow of water up the suction pipe of a pump? How high can a pump lift water, or cause it to lift or rise? II. 388.
Regulating a pump.—How can the quantity of water a pump will deliver be regulated? II. 388.
Pump valves.—What is the check valve of a pump? What is the foot valve of a pump? II. 388.
Speed of pumping.—What is the highest speed at which a pump should run? What is the consequence if a pump runs too fast? II. 388.
Locating the air chamber.—When should the air chamber be placed on a pump, and what is its use? II. 388.
Belt pump.—What is the advantage possessed by a belt pump? II. 388.
Starting bar.—What is a starting bar, and what is it used for? II. 389.
Link sketch.—Make a rough sketch of a locomotive link motion. II. 392.
Link gear and eccentric.—Does a link motion when in full gear operate the valve much different to what a simple eccentric motion would do? II. 393.
Exchanging eccentric rods.—If the forward eccentric rod was to break, could the backward eccentric be utilized to run the engine forward? If so, how? II. 393.
Broken reach rod.—How would you hold the tumbling shaft if the reach rod broke? II. 393.
Eccentric and crank motions.—Does the acting eccentric lead or follow the crank when the link is in full gear? II. 393.
Setting a slide valve.—In what position would you place the link motion when the slide valve is to be set? II. 394.
Length of eccentric rod.—What determines the length of the eccentric rods when setting the slide valve? II. 394.
Setting an Allen valve.—What difference is there between setting a common slide valve and another (an Allen) valve? II. 395.
Injector.—What is an injector? II. 395.
Before firing.—What should be done before laying the fire? II. 400.
Kindling the fire.—How long should the wood burn before putting on coal? II. 400.
Oiling.—What points require examination when oiling the engine? II. 401.
After oiling.—What points would you move after having oiled the engine? II. 401.
Using tallow.—Where would you place tallow in oiling the engine, and for what purpose would you use it? II. 401.
Fire too hot.—What would you do if steam was rising too rapidly? II. 401.
Link position.—Where should the link be when starting the engine? II. 402.
Even steam pressure.—Why should the steam pressure be kept up, and what difference does it make in the consumption of the fuel? II. 402.
Quick steaming.—Can steam be made quickest with a large or with a small quantity of water in the boiler? II. 402.
Best boiler feed.—Which is better, a constant or an intermittent boiler feed? II. 402.
Best firing.—Which is better, heavy firing at long intervals or light and frequent firing, and why? II. 402.
Broken cylinder cover.—What would you do if the cylinder cover got knocked out while on the road? II. 402.
Hot piston rod.—What would you do if the piston rod got hot? II. 403.
Broken piston rod.—What if the piston rod broke? II. 403.
Broken crank-pin.—What if the crank-pin broke? II. 403.
Tire off.—What if a wheel tire came off? II. 403.
Driving wheel off.—What if a driving wheel came off? II. 403.
Broken lifting link.—What if a lifting link or saddle-pin broke? II. 403.
Slipping eccentric.—What if an eccentric slipped? II. 403.
Hot axle-box.—What if an axle-box got hot? II. 403.
Broken spring hanger.—What if a spring or spring hanger broke? II. 403.
Bursted tube.—What if a tube bursted? II. 403.
Fitting axle-box wedges.—In what position should the engine be placed when the axle-box wedges are to be adjusted for fit to the pedestals? II. 404.
Changing clearance.—What is it that, as the engine wears, tends to alter the amount of clearance? II. 404.
Crank-pin centres.—How would you get the distance from centre to centre of the crank-pins when adjusting the axle-boxes and the side rods, parallel rods, or coupling rods, as they are promiscuously termed? II. 404.
Adjusting Shoes.—In what position would you place the crank when adjusting the shoes or wedges of the axle-boxes? Why is this adjustment important? II. 404.
Force, pressure, and power.—What is the difference between force or pressure and power? II. 405.
Increase of power.—Can we increase a given amount of power by means of mechanical appliances? II. 405, 406.
Speed vs. power.—Is a gain in speed a loss in power? II. 405.
Lever.—Explain the principle of the lever. II. 405.
Elements of power.—What are the three elements composing power? II. 407.
Horse-power.—What is a horse-power as applied to steam-engine calculations? How would you calculate the horse-power of a steam engine? II. 407.—Give a method of testing the effective horse-power of an engine. II. 408.
Safety-valve problem.—A safety valve is three inches in diameter; the lever is twenty-eight inches long from the point of suspension of the weight to the pivoted end of the lever; the valve pin is four inches from the pivot; the weight is twenty pounds. What is the greatest pressure of steam the valve will hold, leaving the weight of the valve and of the lever out of the question? II. 409.
Thermal unit.—What is the heat unit or thermal unit? II. 410.
Latent heat.—Is all the heat in steam or water shown by a thermometer? What is the latent heat of water? What is the latent heat of steam? II. 410.
Sensible heat.—What is the sensible heat of steam? II. 410.
Total heat.—What is the total heat of steam? II. 410.
Heaviest water.—At what temperature is water at its greatest density? What is the weight of a cubic foot of water when at its maximum density? II. 410.
Heat of boiling water.—What determines the temperature at which water will boil? II. 410.
Heat of steam.—Can steam be made hotter than the water while they are in contact? What is superheated steam? II. 410.
Absolute pressure.—What is meant by the absolute pressure of steam? II. 411, 416.
Dry steam.—What is meant by dry steam? II. 411.
Weight of steam.—Is there any difference between the weight of water and that of the steam it will evaporate into? II. 411.
[II-471]A perfect gas.—What is Marriotte’s law, or Boyle’s law? Is steam a perfect gas? II. 411.
Joule’s equivalent.—What is meant by the conversion of heat into work? What is Joule’s equivalent? What is the mechanical equivalent of heat? II. 411.
Indicator.—What is a steam-engine indicator? II. 413.—How are indicators attached to an engine? II. 416.
Indicator diagram.—What are the names of the lines of a diagram? Why is a theoretical diagram not correct? II. 414.—What difference is there between the lines of a diagram of a condensing and those of a non-condensing engine? II. 415.—How is the expansion curve of a diagram tested? II. 417.
Barometer.—What is a barometer, and for what purpose is it used in connection with engine diagrams? II. 415.
Horse-power by diagram.—How do you calculate the horse-power of a steam engine from an indicator diagram? II. 418.
Diagram vs. diagram.—What difference is there between the diagram taken from one end and that taken from the other? II. 419.
Consumption of steam by diagram.—How would you calculate the consumption of steam or water of an engine from an indicator diagram? II. 420.
Steam line.—What would a fall in the steam line of a diagram indicate? II. 421.
Expansion curve.—If the expansion curve is above the true expansion curve, what defect in the engine does that indicate? If the expansion curve falls too low, what does it indicate? II. 421.
Valve lead by diagram.—How would insufficient valve lead be shown on a diagram? II. 421.
Excessive lead.—How is excessive lead shown on a diagram? II. 421.
Automatic cut-off.—What is an automatic cut-off engine? What are the principal forms of automatic cut-off engines? II. 423.
Releasing valve governor.—What kinds of governors do engines with releasing valves have? II. 423.
Corliss engine valves.—How many valves does a Corliss engine have? Explain the action of a Corliss valve gear. II. 423.
Crab claw.—What duty does the latch-link or crab-claw of a Corliss valve gear perform? II. 423.
Valve trip.—What means are employed in a Corliss engine to trip the admission valve? II. 423, 424.
Point of cut-off.—What determines the point of cut-off in a Corliss engine, and how does it do so? II. 424.
Valve closing.—What closes the valve in a Corliss engine? II. 424.
Dash-pot.—What is a dash-pot? What enables the dash-pot of a Corliss engine to work noiselessly? II. 424.—How is the amount of air cushion in the Corliss dash-pot regulated? II. 425.
Shape of Corliss valve.—What shape is a Corliss valve, and how far would its lap, as ordinarily constructed, carry the live steam period, leaving the cut-off mechanism out of the question? II. 426.
High-speed engines.—What is meant by the term high-speed engines? II. 427.
Adjusting for load.—What adjustments would you make if the engine had been running a very light load, and required to be adjusted for a heavy load? II. 427.
High-speed governor.—What class of governor is generally used upon high-speed engines? II. 427.
Varying the cut-off.—What is the usual method of varying the point of cut-off on high-speed engines? II. 427.
Wheel governor.—State, in a general way, what a wheel governor consists of. II. 427.
Even valve lead.—Can the valve lead be kept equal when the point of cut-off is varied by shifting the eccentric across the shaft or crank-axle? II. 427.
Marine engine.—What forms of engine are used for marine purposes? II. 434.
Inverted cylinder.—What is an inverted cylinder engine? II. 434.
Receiver.—What is a receiver? II. 434, 453.
Triple expansion.—What is a triple-expansion engine? II. 436.
Condensing engine.—What is a condensing engine? II. 434.
Compound engine.—What is a compound engine? II. 434.
Arranging compound cylinders.—What are the two methods of arranging compound cylinders? II. 436.
Condenser.—What is a surface condenser? II. 440.
Hot well.—What is a hot well? II. 440.
Steam condensation.—Describe the means by which the steam is condensed after it is exhausted from the cylinder in a surface condensing engine, and state what becomes of the water of condensation and the injection, circulating, or condensing water. II. 440.
Condenser tubes.—How are condenser tubes made tight? II. 440.
Blow-through valve.—What is a blow-through valve? II. 440.
Air pumps.—What is a bucket air pump, and is it single or double acting? What is a piston air pump? What is a plunger air pump? What is a trunk air pump? When is a trunk air pump necessary? II. 441.
Air-pump valves.—Are a foot valve and a head valve always necessary to an air pump? II. 441.
Pet cock.—Why are bucket pumps provided with a valve or pet cock? II. 441.
Bilge injection.—What is a bilge injection? What fittings are necessary for a bilge injection? II. 441.
Hot-well temperature.—At what temperature is the water in the hot well usually kept? II. 441.
Use of air chamber.—What is an air vessel or air chamber used on a pump for? II. 441.
Feed escape.—What is a feed relief, or feed escape valve? II. 441.
Checked boiler feed.—What causes may act to stop the boiler feed? II. 441.
Admitting the exhaust.—When the exhaust steam is condensed for boiler-feeding purposes, how soon after the engine has started would you let the exhaust into the feed tank? II. 441.
Ship’s side discharge.—What is a ship’s side air pump discharge valve? II. 442.
Course of water.—What is the course of the main injection water of a jet condenser? What is the course of the main circulating water of a surface condenser? II. 442.
Surface condensing.—What are the advantages of surface condensing? How are surface condensers cleaned out? II. 442.
Engine-room cocks and valves.—What cocks and valves are there in the engine room of a condensing engine? II. 442.
Donkey engine.—What is a donkey engine? What pipes connect to a donkey engine, and what are their uses? II. 442.
Pipes to the sea.—What are the pipes that lead from or go to the sea? II. 442.
Parts classified.—What parts of a marine engine are generally made of wrought iron, of cast iron, of brass, and what of steel? II. 442.
Use of Babbitt.—What is Babbitt metal or white metal used for? II. 442.
Use of Muntz.—What is Muntz metal used for? II. 442.
Breaking strain.—About what is the breaking strain of wrought iron per square inch of section? II. 442.
Tempering.—How is steel tempered? II. 442, 460-463.
Case-hardening.—What is case-hardening? What parts of an engine are usually case-hardened? II. 442.
Forging.—What are the forgeable metals used in engine construction? II. 442.
Welding.—What is welding? II. 442.
Metal expansion.—What metals used in engine construction expand by heat, and what allowances are made in the construction on this account? II. 442.
Composition of iron and steel.—What is the difference in the composition of cast iron and steel? II. 442.
Marine piston.—Describe a marine engine piston. II. 442.
Drain cocks.—What are cylinder drain cocks? II. 442.
Link motion.—What is a link motion? What is a link motion used for? II. 443.
Expansion valve.—What is a separate expansion valve? II. 443.
Top cylinders.—What are the small cylinders on top of the steam chests used for? II. 443.
The throw.—What is the throw of an eccentric? II. 443.
Double beat.—What is a double-beat valve? II. 443.
Expansion joint.—What is an expansion joint? II. 141, 443.
Oil cup.—What is an oil cup? II. 443.
Siphon.—What is a siphon or worsted? II. 443.
Impermeator.—What is a steam lubricator or impermeator? II. 444.
[II-472]Hand-worked valves.—What are the valves of a marine engine that are worked by hand? II. 444.
Vacuum gauge.—What is a vacuum gauge? What is a mercury vacuum gauge? II. 444.
Total condenser pressure.—How would you find the total pressure in a condenser? II. 444.
Racing.—What is meant by the racing of an engine? II. 444.
Uniform paddle-wheel revolution.—How may the speed of revolution of single crank paddle-wheels be made uniform? II. 444.
Paddle-wheel construction.—What is the construction of a common paddle wheel? What is a radial paddle wheel? What is a feathering paddle wheel? II. 445.
Disconnecting engine.—What is a disconnecting paddle engine? II. 445.
Propeller thread.—Where is the thread of a screw propeller measured? II. 445.
Propeller pitch.—What is the pitch of a propeller? II. 445.
L. H. propeller.—What is a left-hand propeller? II. 445.
Thrust bearing.—What is a thrust bearing? II. 445.
Propeller fastening.—How are screw propellers fastened to their shafts? II. 445.
Marine engine pipes.—What are the principal pipes of a marine engine and boiler? II. 445.
Mud box.—What is a mud box? II. 445.
Course of steam.—Describe the course of the steam from the boiler to the hot well. II. 445.
Exposure to cold.—What parts of an engine are exposed to danger in a cold climate? II. 446.
Preventing freezing.—What precautions are necessary to prevent the engine from freezing in cold climates? II. 446.
Failure to start.—Name all the reasons that may cause a marine engine to fail to start when it is expected to do so. II. 446.
Pressure pieces.—Name all the pieces of an engine through which the steam pressure is received and transmitted. II. 446.
Horse-power.—What is the unit or measure of horse-power? What is the meaning of nominal horse-power? II. 446.
Lost vacuum.—Name all the causes from which the vacuum may become defective or lost. II. 447.
Hot journals.—What are the principal causes of the heating of engine journals? II. 447.
Stays.—What is a boiler stay? What is a gusset stay? What is a tube stay or a stay tube? II. 452.
Stress per square inch.—How much stress is usually allowed per sectional square inch of boiler stay? II. 452.
Breaking of tubes.—What is the commonest cause of boiler tubes breaking? II. 452.
Split tube.—How is a split tube stopped up? II. 452.
Uptake.—What is the uptake of a marine boiler? What is a wet uptake? II. 453.
Superheater.—What is the superheater of a marine boiler? II. 453.
Fittings.—What fittings are essential to a marine boiler? II. 453.
Safety valves.—What is a dead-weight safety valve? What is a spring-loaded safety valve? What is a lock-up safety valve? II. 453.
Test cocks.—What do the three boiler test cocks show? How are boiler test cocks cleaned? II. 453.
Steam gauges.—What is a gauge glass or water-gauge glass? What is a Bourdon dial gauge? What pressure is shown by a boiler steam gauge? II. 453.
Scum cocks.—- How many scum cocks are used in a marine boiler? II. 454.
Sluice valves.—What are sluice valves in steamships? II. 454.
Removing scale.—How is scale removed in boilers? II. 454.
Salinometer.—What is a salinometer? II. 455.
Salt in sea water.—About how much salt does sea water contain? II. 454.
Division plates.—What are division plates in boilers? II. 455.
Intercepter.—What is the separator or intercepter of a marine boiler? II. 455.
Boiler draft.—What causes the draft in a boiler? II. 455.
Rapid wasting.—Where does the most rapid wasting occur in marine boilers? II. 455.
Coal consumption.—About how much coal is consumed per square foot of grate in marine boilers? II. 455.
Short of coal at sea.—If at sea and short of coal, what course would you pursue in order to save coal and get into port? II. 455.
Boiler relief in extreme danger.—How would you relieve a marine boiler in case of the safety valve being locked down from some accidental cause, the engine also being disabled? II. 455.
Pressure test.—At what pressure should a new boiler be tested? II. 456.
Boiler examination.—State what you would consider a proper examination, inside and out, of a marine boiler that had been in sufficient service to require examining. II. 458.
A
Addendum. That part of a gear wheel tooth that extends beyond or outwards from the pitch line.
Addendum-circle. The circle representing the full or greatest circumference of a gear wheel.
Adjustable reamer. A reamer whose teeth may be adjusted to the required diameter.
Angle-iron. A shape of wrought iron or steel having two flanges at a right angle; thus, L
Angle-plate. A plate having surfaces at a right angle, one to bolt to the machine work-table, the work being bolted to the other.
Angle-tooth. A gear wheel tooth that runs across the face of the wheel in a line that envelops part of the wheel circumference.
Angular cutters. Cutters, whose teeth are on a circumferential surface, that is, at an angle to the cutter axis, such angle not being that of 90° to either the side face nor to the axis of the cutter.
Angular-velocity. Velocity measured in degrees of angle.
Annular. In the form of a ring.
Apron. 1. The piece that carries the tool port or clamp on an iron planing machine. 2. The front plate of a lathe carriage.
Arbor. 1. A mandrel used to drive work upon. 2. A spindle or shaft of a machine.
Arc. A portion of a circle.
Archimedean drill (är-kĭ-m-ẹ-dē′an) A drilling device in which a nut moved endwise on a stock or handle causes the drill to revolve back and forth.
Arc of approach. That part in the revolution of a pair of gear wheels in which the teeth in contact approach the line of centres of the two wheels.
Arc of recess. That part in the revolution of a pair of gear wheels in which the teeth in contact recede from the line of centres of the two wheels.
Arc-pitch. The pitch of gear wheel teeth when measured around the pitch circle.
Attachment. A work-holding device that may be attached to a machine.
Auger. A wood-boring tool having two spiral plates and a pointed screw to feed it, the cutting edge being at the end of the tool.
Axle-box. The bearing in which an axle revolves.
B
Back-gear. The toothed wheels on the spindle of a lathe and at the back of the lathe-head, by means of which the speed of the lathe is reduced.
Back-geared lathe. A lathe having a back gear to reduce its motion.
Back-knife gauge-lathe. A lathe in which the work is finished and cut to size and shape by a knife at the back of the lathe.
Balanced pulley. A pulley whose weight is so equally distributed that it will run steadily and smoothly at the speed for which it is balanced.
Balanced valve. A valve so constructed as to move with equal force in either direction.
Ball and socket joint. A universal joint consisting of a ball on the end of a shaft and in a casing that envelops it and yet permits it to be moved in its casing.
Ball-cutter. A tool for finishing metal balls.
Ball-pene. A spherical pene of a hammer.
Band-saw. A continuous ribbon of steel having saw teeth on one of its edges.
Band-saw machine. A machine for operating a band-saw.
Bastard file. A file whose teeth are one degree or grade coarser than a second cut file and one degree finer than a coarse cut file.
Belt. A leather band employed to drive pulleys, for transmitting motion.
Belt-clamp. A clamp for pulling the ends of a belt together, to lace it, while the belt is upon the pulleys.
Belt-hook. A hook employed to fasten the ends of belts together.
Belt-pulley. A wheel that drives or is driven by a belt.
Belt-shipper. A device for moving a belt from one pulley to another.
Belt-tightener. A pulley employed to cause a belt to tighten upon another pulley to enable it to transmit motion periodically instead of continuously.
Bevel-sawing machine. A wood-working machine in which the saw or the work table may be set to cut a surface at other than a right angle to the face of the work that rests against the work table or the fence as the case may be.
Bevel-square. A square whose blade may be set to any required angle to the stock that holds it.
Bevel-wheel, or bevel-gear. A gear wheel with its teeth at an angle to its shaft.
Bit. 1. A boring tool. 2. A tool that is carried in a holder.
Blank. A piece of material roughly formed and ready to be formed into some definite shape.
Blast-pipe. 1. The pipe conveying the blast or air to a fire furnace or cupola. 2. A small pipe through which steam escapes up a locomotive chimney to increase the draught of the fires.
Blob. An extremely loose place in a plate or saw blade.
Block-plane. A short plane.
Boiler-shell. The outer casing of a steam-boiler.
Bolt. 1. A holding device having a head at one end and at the other a threaded stem to receive a nut. 2. A short piece of a round log.
Bolt-cutter. A machine for cutting screw threads upon bolts or similar work.
Boring-bar. A bar that carries boring tools.
Boring-machine. A machine for boring holes in metal or wood.
Boring-mill. A form of lathe used mainly for boring.
Boring-tool. A tool for cutting out and enlarging a bore or hole.
Boss. An enveloping piece on an axle or shaft and having upon it an arm, arms, or spokes.
Bottoming-tap. A tap having a full thread up to its very end so that it will cut a full thread to the bottom of a hole.
Box-chuck. A rectangular two-jawed chuck used by brass finishers.
Box-tool. A tool used in screw machines and turret heads, and which guides the work while it is being operated upon. A box tool in many cases carries more than one cutting tool.
Box-wrench. A wrench which fits over the head of the bolt and passes endways upon it.
Brace. 1. A rod, bar, or beam that braces or supports. 2. A device for revolving cutting tools.
Bracket. A projecting frame that is bolted to its supporting pieces or frame.
Brad-awl. An awl for piercing small holes in wood and having a wedge-shaped end.
Branch-pipe. A pipe leading out of another.
Brass-and-brass. A term used to denote that the two brasses or boxes of a bearing are locked together by the key, cap, or set-screw.
Brasses. Pieces fitted into a frame and intended to afford a bearing for a journal.
Break-lathe or gap-lathe. A lathe having a break or gap in the bed and beneath the face plate to let chucked work of large diameter pass.
Broach. A toothed tool for cutting the walls of a hole.
Broaching-press. A machine that forces a broach to its cut.
Bunter-dog. A work-gripping device for a planing machine, and consisting of a piece having a hook end to engage in the T-slot of the table, and a set-screw to bind the work.
Butt-joint. A riveted joint in which the ends of the plate abut fair, one against the other.
Butt-strap. A strip or band of iron employed to hold the joint together in a butt-joint.
Butt-weld. A weld in which the end of one piece merely abuts against the other when the two pieces are put together to weld.
Buzz-planer. A wood-planing machine in which the work is fed by hand.
C
Calender-roll. A roll for calendering paper.
Caliper-gauge. A gauge in the form of a solid caliper.
Calipers. A hinged tool for measuring work.
Cam. A revolving disc whose actuating surface is not a true circle.
Cam-motor. A cam together with the rod it actuates.
Cap. The plate or upper part of a bearing that holds the top half of the box or brasses in place.
Cape-chisel. A narrow machinist’s chisel.
Caps. The backward curves on the points of file teeth.
Cap-screw. A screw with a collar and a square head.
Carrier. A device for driving lathe work.
Case hardening. A process of hardening the surface of wrought iron, the hardening usually extending about 1⁄32 inch in depth.
Cat-head. A sleeve fastened by set-screws to slender lathe work and running in a bearing so as to steady the work.
Caulking-tool. A tool used for caulking riveted joints and in making rust-joints.
Centre-bit. A bit having a triangular conical point with its cutting edge on one-half of the end and a spur on the other half.
Centre-punch. A tool having a coned point for marking the centres to work.
Chamfer. A facet that removes the corner of a right angle.
Change-gears or change-wheels. The gear wheels employed to change the revolutions of a lead screw or feed motion.
Chaser. A toothed tool for cutting threads by hand in a lathe.
Check. A crack.
Check nut. A second nut screwed against the first to check it from slackening back.
Chip-break. A piece that rests upon the work of a wood-working machine and prevents the cutter from splitting out the wood as the cut leaves the surface.
Chipping-hammer. A machinist’s hand hammer.
Chips. 1. The cutting from a metal cutting machine tool. 2. The thick cuttings from a wedge-shaped wood-working tool, as from an axe or adz.
Chisel. A wedge-shaped tool.
Chisel-tooth saw. A saw having inserted teeth with a maximum of front rake.
Chop or hammer-sink. A mark left on a plate by a sawmaker’s or plate straightener’s hammer.
Chord-pitch. The pitch of gear wheel teeth measured in a straight line.
Chuck. A work-holding or tool-holding device.
Chucked. Held in a chuck.
Chucking-lathe. A lathe having a large face plate for chucking purposes, and usually a short bed.
Chuck-plate. A large face plate on which work may be chucked.
Circular saw. A saw having its teeth arranged around its circumference.
Clamp. A device for fastening or holding work together or to some other part.
Clearance. 1. The amount to which one piece clears or escapes another. 2. On a lathe tool, clearance is the amount to which the back face of the tool escapes the metal it is cutting.
Clements driver. A device for driving work in a lathe, and that places an equal strain on each end of the lathe dog or carrier.
Clutch. A device for engaging or disengaging so as to cause the motion of one piece to be communicated to another, or to stop such communication.
Cock. A device for opening or closing the bore of a pipe.
Cog. A wooden tooth for a gear wheel.
Collapsing-taps. A tap that is so formed that its teeth close inwards when the thread is cut so that the tap can be withdrawn without winding it backwards.
Collar. 1. A disc-shaped enlargement on a cylindrical piece. 2. A hollow cylindrical piece containing a set screw, to prevent a shaft from end motion.
Collet. A casing for holding tools or drawers in position.
Combination-chuck. A chuck in which the jaws may be moved simultaneously or independently.
Comparator. A machine for comparing measurements, for testing them and originating sub-divisions.
Compass-calipers. A pair of calipers having one bent leg and one leg with compass joint.
Compasses. A tool answering the same purpose as dividers, but with longer legs and a set screw to secure the position of the legs.
Compass-plane. A plane whose sole or bottom is curved in its length.
Compound gears. A train of gear wheels in which there are two wheels fixed on the same shaft but of different diameters so as to vary the velocity.
Compound slide-rest. A slide-rest having two slides, one above the other.
Cone-bearing. A bearing (for a journal) that contains a coned sleeve that may be moved endways to take up wear.
Cone-mandrel. A mandrel that holds hollow work by means of two cones.
Cone-plate. A device for steadying work in the lathe by supporting one end in a coned mouth.
Cone-pulley. A pulley having steps of different diameters.
Cone-shaft. The shaft for a cone-pulley.
Cook’s auger. An auger rounded at the end for cutting end-grain wood.
Cope-cutter. A cutter for under-cutting the shoulder of a tenon on wood-work.
Cope-head. A head for a cope-cutter in a tenoning machine.
Core. A body of sand that produces a hole or cavity in a casting.
Core-box. The box in which a core is made.
Cored. Containing a hole or recess.
[II-474]Cotter or cottar. A term applied to small keys that are very broad in proportion to their thickness.
Cotter-drill. A drill used in cutting out keyways in a machine.
Cotter-file. A file thin in proportion to its length, for filing out keyways or slots.
Counterbore. 1. A parallel recess at the mouth of a hole. 2. A tool for producing such a recess.
Countershaft. A shaft with pulleys upon it, employed to permit a machine to be started and stopped without stopping and starting the line shaft, also, to afford means for varying the speed of a machine.
Countersink. A tool for cutting a coned mouth to a hole.
Countersunk. Having a coned mouth.
Coupling. A piece used to connect two pieces together.
Covering-plate. A plate used to cover the seams of a boiler.
Cow-mouth chisel. A machinist’s chisel shaped at the cutting end like a carpenter’s gouge.
Crank. An arm that is fast to a shaft and is used as a lever wherewith to revolve the shaft.
Crank-shaft. A shaft having a crank.
Cross-cut. A narrow machinist’s chisel.
Cross-cut saw. A saw whose teeth are shaped to cut across the fibre or grain of wood.
Cross-face. A plate straightener’s or saw maker’s hammer, having one face at a right angle to the other.
Cross-feed. That feed of a lathe which runs across the bed.
Cross-filing. That class of filing in which the file is pushed in the line of its length.
Cross-head. That part of an engine that connects the piston rod to the connecting rod.
Cross-slide. A slide that stands across a work-table.
Crowning. Highest in the middle when tested by a straight edge.
Crown-wheel. A gear wheel having its teeth upon its side face.
Cup-chuck. A chuck having a coned or cupped mouth.
Cup-shape. A crack of circular form in a piece of timber or a log.
Cutter. A tool that is held or carried in a stock bar or mandrel.
Cutter-bar. The bar or shaft that carries the cutting knives in a wood-planing machine.
Cutter-grinder. A machine for grinding cutters.
Cutter-head. 1. A head that carries cutters. 2. The head that carries the cutters in a wood-moulding machine.
Cutting-off lathe. A lathe used for cutting up rods into required lengths, and having a hollow spindle through which the rod passes.
Cutting-off saw. A sawing machine designed for cropping the ends of work and cutting it to length.
Cutting-off tool. A tool for cutting up rods or bars, and used in the common lathe and in the cutting-off lathe.
Cycloid (si′kloid). A curve generated by a pencil fixed in the perimeter of a circle that is rolled upon another circle.
Cylinder. 1. That part of a steam-engine in which the steam is utilized to drive the piston. 2. The shaft that carries the knives in a wood-planing machine.
Cylinder-head, or cylinder-cover. A piece that encloses or seals the end of a cylinder.
D
Dead centre. The stationary centre of a lathe.
Dead-smooth file, or superfine file. The finest or smoothest cut of file.
Delivery-rolls. Rolls that remove the work from a machine or from its cutters or knives.
Describing-circle. The circle or cylinder containing the pencil for rolling a curve.
Diametral pitch. A system of designating the pitches of gear wheels.
Diamond-point. A machinist’s chisel, square in cross-section, having a diamond-shaped face at the end, and two cutting edges, one at a right angle to the other.
Die. 1. A tool for cutting threads upon external surfaces, such as bolts. 2. A chumpy sliding piece.
Differential screw. A screw having a coarse and a fine thread, the difference between the two pitches enabling a more powerful strain to be endured by the thread.
Dimension planer. A wood-planing machine, for planing accurately to size.
Disk or disc. A cylinder whose length is very short in proportion to its diameter.
Dividers. A tool having two legs with sharp points at their ends for measuring distances or drawing circles.
Dog. A work holding device.
Dog-chuck. A chuck containing independent dogs or jaws.
Dog-head. A hammer used in plate or saw straightening.
Double-eye or knuckle-joint. A joint in which one piece is forked at its end, to receive the other, and a pin passes through both.
Double-thread. A screw thread, having two spirals in the same bolt or body.
Dovetail. A groove that is wider at the bottom than at the top, or a projection thicker at the top than at the bottom.
Draw-filing. That class of filing in which the line of file motion is in the direction of the width of the file.
Drawn-down. Decreased in diameter, width or thickness, by forging or swaging.
Drawn-out. Increased in length, by forging or swaging.
Drift. A tool that cuts the walls of a hole while it is driven through by hammer blows.
Drift-pin. A taper pin that is used by boiler makers to drive through holes that do not come fair, or match properly.
Drill. A tool to pierce holes.
Drill-chuck. A chuck used to hold drills.
Drilling-machine. A machine for drilling holes in metal.
Driver. 1. A device for driving work in the lathe and sometimes called a dog or carrier. 2. A gear wheel which drives another.
Drop-hammer. A forging or stamping hammer which is lifted by power and let fall of its own weight.
Drunken thread. A screw thread that is not a true spiral, but is waved in its course.
Duplex slide-rest. A feed motion in which there are two slide-rests in one slide-way.
Dutchman. A piece let in to restore a worn part, or to hide a defect.
E
Edge-moulding machine. A machine for dressing the edges of wood-work to shape, and usually for forming a moulding thereon.
Emery grinder, or emery-grinding machine. A machine in which emery wheels are used to grind the work.
Emery wheel. A wheel composed of emery cemented together under pressure.
Endless screw. A short length of screw formed to drive the teeth of a worm wheel.
End-mill. A milling-machine cutter, having teeth on its end face.
Engine-lathe. A lathe having a feed motor for the cutting tool.
Epicycloid (ĕp-i-sī′-kloid). A cycloidal curve in which the rolling circle is rolled outside the fixed or base circle.
Equalizing-file. A file that is slightly thicker in the middle than it is at either end.
Expanding-chuck. A chuck that is capable of expanding to accommodate a slight variation of work-diameter and usually holding the work from its bore.
Expanding-mandrel. A mandrel whose diameter may be varied, usually by means of moving jaws or pieces.
Expansion-joint. A joint capable of permitting the parts it connects to expand and contract under variations of temperature.
Extension-bit. A bit in which a cutter can be set so as to bore different sizes of holes.
Extension-lathe. A lathe whose bed is in two longitudinal divisions so that the upper one may be moved endways and thus form a gap to let chucked work of large diameter pass.
F
Face. 1. The broadest surface of a piece, or that having the largest area. 2. The circumferential surface of a wheel or pulley. 3. A surface on a gear-wheel tooth.
Face-cam. A cam in which the actuating surface is on its side or sides.
Face-cutter. A milling cutter having its teeth upon its circumferential surface.
Face-plate. A plate or table having a plain or flat surface for holding work.
Facing-cutter. A cutter for levelling a face or surface.
Farrar planer. A wood-planing machine in which a travelling bed is used to feed the work to the cutter head.
Feather. A key that is fast in one piece of the work, and an easy fit to the other, so that the latter may be moved along the feather.
Feed-motor. That part of a machine that feeds either the work or the tool, so as to put on the cut.
Feed-rolls. Rolls that move the work to machines or to cutting tools.
Feed-screw. A screw that is used to feed the cutting tool in a machine.
Fence. A plate in a wood-working machine, against which the work is set or moved to hold it in proper position for the cutting operations.
Fiddle-drill. A drill that is revolved back and forth by a device similar to a fiddle-bow.
Fifth wheel. The circular slideway that enables the front axle of a vehicle to turn horizontally.
File. A hand tool for cutting metal, wood, ivory, bone and all other hard substances except stone.
File-card. A wire-brush for cleaning files.
Fillet. A curved piece for filling in a corner.
Fillister-head. A screw-head that is cylindrical and contains a screw slot.
Firmer-chisel. A stout carpenter’s chisel that is used for cutting out mortises and similar heavy work.
Fit-strip. A projection usually about an inch wide that is intended to be fitted to bed the piece properly and save bedding the whole surface of the piece.
Fixture. A device for holding work in an exact position, true with some one face, hole, or pin, as the case may be.
Flat-chisel. A wedge-shaped machinist’s chisel.
Flat-drill. A drill whose body is rectangular in cross-section.
Flatter. A swage for flat surfaces.
Fleam. Acuteness given to saw teeth by filing their front faces at an acute angle to the plane of the saw blade.
Flexible shaft. A shaft composed of wire, similar to a wire rope, for transmitting rotary motion, notwithstanding that the shaft may be an arc of a circle.
Flooring-machine. A machine for planing and matching at the same time, and generally used for floor boards.
Flute. A groove.
Fly-cutter. A cutting tool fastened in an arbor or spindle, and used for producing irregular shapes.
Follower. A gear wheel that receives motion from another gear wheel.
Follower-rest. A rest that steadies work on the lathe and travels with the slide rest.
Foot-block. A work-holding device containing a dead centre, used upon a milling machine.
Foot-lathe. A lathe operated by foot-power.
Fore-plane or jack-plane. A roughing out plane.
Forging. A piece or part that has been forged into shape.
Fork-centre. A centre used to drive woodwork in the lathe.
Fork-scriber. A double pointed tool used by boiler-makers to mark small circles.
Former. 1. A piece that acts as a guide to control the movement of a cutting tool. 2. A template or block on which a piece is bent or shaped.
Fox-lathe. A brass finisher’s lathe, having a turret head and spiral thread-cutting devices that obviate the use of a lead screw or change gears.
Friction-clutch. A clutch that operates by frictional contact.
Friction-gearing. Wheels that transmit motion by the frictional contact of their circumferences.
Friction-rollers. Rollers employed to reduce the friction of the parts.
Friction-wheel. A wheel that drives by the frictional contact of its surface.
Friezing-machine or edge-moulding-machine. A machine for cutting mouldings on the edge of wood work.
Front-tool. A tool having its cutting edge in front, and used for plain surfacing work.
Fuller. A blacksmith’s tool for spreading the metal in any particular direction.
G
Gang-drill. A drilling machine on which a number of drills may be used simultaneously.
Gang-edger or gang-edging machine. A machine in which a gang of saws are employed to trim the edges of boards or cut them to width.
Gang-mills. Milling machine cutters that are placed in gangs and side by side on the same arbor.
Gap-lathe or break-lathe. A lathe having a gap in its bed to enable the chucking of work that would not otherwise pass over the bed.
Gauge. 1. A standard of measurement. 2. A standard of shape.
Gear. A term applied to a piece of mechanism that accomplishes a single object: thus a valve-gear operates a valve; a steering-gear steers the vessel.
Geared. Placed in gear or connected together.
Gear-wheel. A wheel provided with teeth to engage with similar teeth upon another wheel.
Generating-circle. The circle that is supposed to move in the construction of cycloidal curves.
Gib. 1. A piece that may be set up to take up the wear. 2. A piece for holding a strap, and forming an abutting piece for a key.
Gimlet. A wood-boring hand tool, having a threaded conical end to pull it to its cut.
Gimlet-bit. A fluted gimlet having no thread at its end, but a spiral flute so shaped as to pull the bit forward to its cut.
Gland. A piece enveloping a stem and used to make a tight working joint.
Globe-valve. A valve, having a spherical body, used in pipe-work.
Goose-neck. A frame affording a fulcrum for a ratchet brace.
Gouge. A wood-cutting hand tool that is curved in its cross-section.
Gravis. A hand tool, rectangular in cross-section and having cutting edges at its end that are formed by grinding the end face at an acute angle to the body of the tool.
Groove-cam. A cam in which the actuating surface is in the form of a groove.
Ground joint. A joint that is finished by grinding the parts together, usually with oil and emery.
Guide-bar or slide-bar. A bar that forms a guide for the crosshead of an engine or other moving piece.
Gum. 1. The bottom of the space between saw teeth. 2. A rubber-like substance formed of oil that has dried.
H
Hack. A tool used for cutting iron in two under a steam hammer.
Hack-saw. A saw held in a frame and used by hand for cutting metal.
Half-check joint. A joint in which a piece is let into the other, so that the surfaces come level.
Half-round file. A file that is half round in cross-section.
Hand-file. A superior class of file that is parallel in width and thickest in the middle of its length.
Hand-hammer. A hammer that can be used in one hand.
Hand-lathe. A lathe with which hand cutting tools are used.
Hand-nut. A nut that may be screwed up by hand without the aid of a wrench.
Hand-planer. A wood-planing machine in which the work is fed by hand.
Hand-rest. The rest on which hand-turning tools are supported in a lathe.
Hand-tap. A tap that is used by hand.
Hand-vise. A small vise for use in the hand.
Hanger. A frame that is bolted to another frame or part, and carries another piece, usually a shaft of some kind.
Hardened. Hardened steel is that which has been made hard by heating to a cherry red and suddenly cooling it, usually by quenching it in water.
Hardy. A blacksmith’s chisel that fits into the anvil.
Heading-block. A block used in upsetting the heads of bolts or pins.
[II-475]Heart-shake. A split radiating from the centre of a log.
Heating-surface. That part of the surface of a steam-boiler that receives heat on one side and has water on the other.
Heel-tool. A hand turning tool having a projecting heel to cross the tool rest, and usually held in a wooden stock or handle.
Herring-bone tooth. A form of gear wheel tooth in which the tooth, instead of passing direct across the wheel face, curves partly around the circumference and then back again, so that the two ends of the tooth only are opposite to each other.
Hindley’s-screw. A short length of screw used to drive a worm wheel, and sometimes termed an endless screw.
Hob or hub. A tool for cutting the threads on screw cutting tools, such as chaser dies.
Hour-glass screw. A worm or tangent screw which is formed to envelop part of the arc of circumference of a worm wheel, and therefore assumes in outline the form of a sand hour-glass.
Hunting-tooth. An extra tooth put into a pair of gear wheels that would otherwise contain the same number of teeth, the object being to prevent the same teeth from always falling together.
Hypocycloid (hī-po-sī′kloid). A cycloidal curve in which the rolling circle is rolled within the fixed or base circle.
I
Idle pulley or guide pulley. A pulley employed to guide a belt.
Independent chuck. A chuck in which each jaw is operated separately.
Index-plate. A plate having holes or notches accurately dividing a circle into equal divisions.
Inserted-tooth cutter. A cutter in which the teeth are inserted in a disc or head.
Inside calipers. Calipers used to measure inside dimensions, as boxes, recesses, etc.
Intermediates. The wheels that are between the front driver and last follower of a train of gear wheels.
Involute. A curve generated by the path of a given point in a straight line, as the line is rolled upon a circle. (Vol. I. p. 31.)
J
Jack-plane. A plane employed to rough out the work.
Jig. A device for holding work and guiding the operating tool.
Jointing-machine. A machine for truing the surfaces of wood-work that are to form a joint.
Journal. That part of a shaft that runs in a bearing which guides or limits the motion of the shaft.
Jump or upset. To enlarge at the end by a forging process.
K
Kerf. The passageway or slot cut by a saw.
Key. A rectangular wedge for locking two pieces together.
Knife. The cutting tool used on a wood-planing or wood-splitting machine.
Knurling-tool or milling-tool. A tool used to press indentations into the edges or upon the surface of metal, in order to increase the hand grip of it.
L
Land. That part of a tap or a reamer that lies between its plates and carries the cutting edges or teeth.
Lantern. A primitive form of gear in which rungs are used instead of teeth.
Lap. A grinding device consisting of a lead or other soft metal surface, on which emery and oil is used.
Lap-joint. A joint in which one piece overlaps the other.
Lap-weld. A weld in which both pieces are beveled at the ends and one end overlaps the other where the two are put together to weld.
Lathe. A machine that revolves work to be operated by cutting tools.
Lathe-bed. The frame that carries the head and tail stock of a lathe, and that rests upon a solid foundation.
Lathe-carriage. The sliding piece that carries the tool rest of a lathe.
Lathe-centre. The piece or part of a lathe that enters the coned recess of lathe work that is held between centres.
Lathe-saddle. The sliding piece that carries the tool rest of a lathe.
Lathe-shears. The frame of a lathe that carries the head and tail stocks, and that rests on legs.
Lead-screw. A screw for a lathe that is used for screw cutting only.
Left-hand thread. A screw thread in which the nut must be revolved in a direction opposite to that in which the hands of a watch move, in order that the nut may screw upon the bolt.
Leg-vise. A machinist’s or blacksmith’s vise having legs.
Line of centres. A line, real or imaginary, passing from one centre to another.
Line out. To mark on work lines denoting the depth of surface that is to be cut away.
Liner. A piece of iron put behind or upon a piece to take up its wear.
Line-shaft. A shaft employed to transmit motion from an engine or motor to distant points.
Link. A piece having holes or pins at its end to connect two other pieces together.
Live centre. The centre of the live spindle of a lathe.
Live spindle. The revolving spindle of a lathe.
Loose. A term used to denote a part of a plate or saw that is not under tension.
Lost motion. Motion that is not transmitted on account of the looseness of the parts.
Lug. A small projection.
M
Machine-bolt. A bolt and nut of the sizes kept in stock by machinery dealers, the bolt usually being black or unturned.
Machine-screw. A small screw made to the Birmingham wire gauge.
Machine-tap. A long taper tap used in threading nuts in a machine.
Machine-tool. A machine that performs work by means of cutting tools.
Mandrel. 1. A cylindrical piece which is driven into hollow work and holds it while it is turned in the lathe. 2. A piece or bar on which work is driven or forced. 3. A shaft running in bearings.
Mangle-wheel. A gear wheel whose teeth are so arranged that the wheel is reciprocated back and forth on its centre, and does not make a full revolution.
Marking-gauge. A tool used by wood-workers to draw a line upon work.
Master-tap. A standard tap used for producing thread-cutting tools, or kept as a standard of size.
Matched. A board that has a tongue on one edge and a groove on the other so that the edges of the boards will match or be fitted together.
Matching-machine or matcher. A wood-working machine which cuts a groove on one edge and a tongue on the other edge of a board or piece of work.
Measuring-machine. A machine for determining the measurement of a piece.
Micrometer. (mī-krŏm′e-ter). A tool for measuring to minute fractions of an inch.
Mill-file. A single cut file used for filing sheet steel, saw teeth, etc.
Milling-cutter or mill. The cutter or cutting tool used in a milling-machine.
Milling-machine. A machine in which revolving cutters are used to dress the surfaces of metal and cut them to size and shape.
Mitre-cutting machine. A machine for cutting mitre joints.
Mitre-joint. A joint at an angle of 45 degrees to the plane of the pieces it joins.
Mitre-wheel. A bevel gear having its teeth at an angle of 45 degrees to its shaft.
Mortise. A recess slot usually square or rectangular, and employed to receive a tenon from another piece.
Moulding-cutters. The cutters employed to produce mouldings on wood.
Multiple-drilling machine. A drilling-machine in which more than one drilling-tool may be used, and separate and successive operations may be performed upon the work, carrying it from one drill-spindle to another.
Mute-pulley. A belt-guiding pulley that can be adjusted to various positions upon its stand.
N
Nail-bit. A boring tool for wood, used for cutting across the grain of wood.
Nut. A threaded piece for receiving a screw.
O
Odontograph (ō-dŏn′-to-grăf). An instrument employed in making or drawing gear-wheel teeth.
Oliver. A foot-power hammer used by blacksmiths, mainly for forging bolts or studs.
Outside-calipers. Calipers used to measure external surfaces.
P
Panelling-machine. A machine for cutting mouldings upon panels.
Parallel-file. A file whose thickness is equal from end to end.
Parallel-vise. A vise in which the gripping face of the movable jaw is maintained parallel to that of the fixed jaw.
Paring-chisel. A wood-worker’s chisel that is pushed to its cut by hand pressure.
Pattern-lathe. A lathe designed for the use of pattern-makers.
Pawl. A tongue that engages with a ratchet.
Pene (pēn) or pane. The lightest end of a hammer.
Pening (pēn′ing). The hammering of the surface of metal in order to stretch it and alter the shape of the piece.
Pillow-block, pillar-block or plumber-block. A piece that affords a bearing for a shaft and is bolted to a pillar or frame.
Pin-block. A wooden block used to steady small pins when filed in the vise.
Pinion. The smallest wheel in a pair of wheels or in a train of gearing.
Pin-wrench. A wrench having a pin to enter holes in the nut.
Pipe-cutter. A hand tool for cutting pipe into lengths.
Pipe-die. A tool for cutting threads on pipes.
Pipe-tongs. A hand tool for gripping pipes.
Piston. 1. That part of a steam-engine that moves under steam pressure. 2. A disc that fits a bore and slides therein.
Pitch. The distance apart of two pieces.
Pitch-circle. A circle drawn through these parts in a gear wheel where the face of the tooth meets the flank, this circle representing the diameter of the wheel for calculations involving its velocity.
Pitch-line. A part of a pitch circle.
Pitman. A name sometimes given to a connecting rod.
Planer-shaper. A metal-cutting machine in which the ram or slide carrying the tool is moved after the manner of a planing machine.
Planimeter (pla-nĭm′-e-ter). An instrument for finding the area of irregularly shaped plane surfaces.
Planing-machine. 1. For iron. A machine having a travelling work-table sliding in guideways, the tool being carried in a slideway that spans the table, two or more slide-rests are used in the larger-sized machines. 2. Wood-planing machine. A machine in which the work is fed to a revolving shaft or head carrying long planing knives.
Platen. 1. A work-holding table. 2. The plane surfaced plate which presses on the type in printing.
Play. Looseness of fit.
Plug. The interior piece of a cock.
Plug-and-collar gauge. A pair of gauges for the same size, the plug being sometimes termed the male and the collar the female gauge.
Plug-tap. A tap that follows the taper taps and has but two or three of its teeth eased off at the end.
Plumb-level. A levelling tool depending for its accuracy on a weighted line and an edge that is straight.
Plumb-rule. A straight edge containing a plumb-bob.
Pod-bit or nose-bit. A wood-boring tool, having a cutting lip at its end.
Point. The surface or the extremity of a gear-wheel tooth.
Polishing-lathe. A lathe that is used for polishing and therefore requires no tool-carrying devices.
Poppet-head. The main head of a lathe.
Porter-bar. A bar for handling heavy forgings, which is welded to the forging and afterwards cut off.
Pressure-bar. A bar or piece that presses the work to the table in a wood-planing machine.
Protractor. A tool having a blade which may be set to the degrees of a circle which are marked upon the back or stock of the protractor.
Pulley. A wheel that receives or drives a band, belt or rope.
Pulley or belt-pulley. A wheel that drives or is driven by a belt.
Q
Quadrant. 1. A piece forming one-fourth of a circle. 2. A piece forming the segment of a circle.
Quick return. A motion by means of which a head ram or work-table is moved faster during its return traverse than during its cutting traverse.
R
Rabbet. A step at the end of a piece of wood.
Rabbeting-plane. A plane for rabbeting.
Rack. A straight body, having on it, (1) teeth corresponding to the teeth in the wheel that drives it or that it drives; (2) notches to engage a pawl or ratchet.
Rack-feed. A feed motor in which the work-table has a rack driven by a gear-wheel.
Rake. The inclination of the front face of a cutting tool to the body of the steel of which it is made.
Ratchet. A pawl or tongue one end of which engages in notches in a rack or wheel.
Ratchet-brace. A hand-drilling device, in which a lever carries a pawl that engages with a ratchet-wheel, which drives the drill.
Rat-tail file. A taper round file of small diameter or less than one-fourth of an inch.
Reamer, rymer, or rimer. A tool for smoothing and enlarging bores or holes.
Recut-file. A file whose original teeth have been ground off and new teeth have been cut.
Red-marking. A mixture of Venetian red and common oil, used to put on a piece of work when trying its fit, and serving to denote the fit.
Return-cam. A secondary cam used to move a piece back, after the main cam has moved it forward.
Reverse-keys. An arrangement of keys or wedges, that releases two pieces that have been keyed together.
Rib. A projecting strip usually employed to strengthen a piece, as the arm of a wheel.
Right-hand thread. A screw thread in which, with the end of the bolt towards you, the top of the nut must revolve from left to right like the hands of a watch in order to cause it to screw upon the bolt.
Rip-saw. A saw whose teeth are shaped to cut lengthways of the grain of the wood.
Rod-feed. A feed motion that is operated by a rod.
Roll-feed. A feed motion in which the work is fed to the cutting tool by revolving rolls.
Rope-socket. A socket in which the ends of a wire rope are secured.
Rose-bit. A reamer that cuts at the end only.
Rotary planer. An iron planing machine in which a number of cutters are set in a revolving face plate that is fed to the cut by a head on a slide.
Round-nosed chisel. A machinist’s chisel whose cutting edge is shaped so as to cut a groove circular in cross-section.
Round-nosed tool. A tool whose cutting edge is circular in its course or length.
Routing-machine. A machine using a revolving cutter to cut away some parts of a surface and leave the rest in relief.
Rust-joint. A joint that is made by being filled with cast-iron cuttings mixed with sal-ammoniac and sulphur to cause the cuttings to rust and form a solid body.
S
Safe-edge file. A file having no teeth upon one of its edges.
Sanding or sand-papering machine. A machine in which sand-paper-covered rollers or wheels are used for finishing wood-work.
Saw-arbor. The arbor or mandrel on which a circular saw is driven.
[II-476]Saw-bench. A circular saw machine.
Saw-gummer. A machine for deepening the spaces between saw teeth.
Saw-packing. Plaited hemp that is packed on both sides of a circular saw to warm it and equalize its tension when it is running.
Scale. 1. A rule or measuring device having lines of division upon it. 2. Proportion of size.
Scarf. The bevel of a piece of metal that is to be lap welded.
Scraper. A hand tool that scrapes rather than cuts the metal.
Screw-cutting lathe. A lathe that has a screw feed with change gears to enable it to cut threads or screws upon the work.
Screw-cutting lathe with independent feed. A lathe that has a lead screw for cutting threads and a separate feed motion for ordinary tool traverse.
Screwing-machine. A machine used to cut screw threads.
Screw-machine. A form of lathe in which the spindle is hollow and a revolving head or turret is employed to carry the cutting tools.
Screw-plate. A tool for cutting external threads on small work.
Screw-thread. The thread upon a screw or other piece of work.
Screw-tool. Another name for a chaser.
Scribing-block or surface-gauge. A tool that carries a needle or scriber for marking on work lines denoting its finished size or the amount of metal that is to be cut off, and that is also used for setting work.
Second-cut file. A file whose teeth are coarser than a smooth file and finer than a bastard file.
Sector. A device used in connection with an index plate to denote the holes to be used in any particular division of a circle.
Segment. A piece having the shape of a segment of a circle, used for building up a hollow cylinder.
Segmental saw. A saw that is composed of parts secured to a frame or disc.
Self-acting lathe. A lathe having an automatic feed motion for the cutting tool.
Set. 1. The bend to one side of the body of the blade of the teeth of saws. 2. Adjustment or alignment. 3. Binding two pieces together.
Set-screw. A screw that binds or secures two pieces together by being screwed through one piece and against the other.
Shafting-rest. A slide rest carrying several cutting tools and usually employed for turning shafting in the lathe.
Shake. A crack in timber.
Shank-mill. A milling machine cutter that is provided with a shank or stem.
Shaper-centres. A chuck in which the work is held between centres.
Shaper or shaping-machine. 1. A machine for cutting such surfaces on iron work as can be cut by a tool travelling in a straight line. 2. A woodworking machine in which cutting tools are revolved on an upright spindle projecting above a work table.
Shavings. The cuttings from a paring tool.
Shell. 1. The body of a steam-boiler. 2. An outer casing.
Shell-reamer. A short reamer that is driven by fitting to a coned mandrel.
Shimer-heads. A form of cutter head for woodworking machines, in which circular cutters are used.
Shingle saw. A saw thick in the body and beveled off for about two or three inches of its outer diameter.
Shooting-board. A device upon which pieces are held when required to have their ends dressed to exact shape or angle.
Shrinkage-fit or contraction-fit. A means of securing two pieces together by leaving the hole of one too small to receive the other, and then expanding the piece containing the hole so that it will go on and bind fast as it cools and contracts.
Side-chisel. A machinist’s chisel shaped to cut on the sides of slots or keyways, and having its cutting edge on one side of the end facet.
Side-tool. A tool used to cut the ends of lathe work that is held between the lathe centres.
Single-geared lathe. A lathe in which there is no back gear.
Single-riveted joint. A joint having but one row of rivets in a lap joint and one row of rivets on each side of the plate joint in a butt joint.
Single-thread. A screw thread having a single spiral.
Skew-bevel. A bevel gear wheel in which the teeth sides do not form lines radiating from the wheel centre, but point to one side of it.
Skew-chisel. A carpenter’s chisel in which the cutting edge is not at a right angle to the body of the tool.
Skew-cutter. A cutter in which the cutting edge does not stand parallel to the axis of the shaft that drives it.
Slab. 1. A rough square piece of iron forged from scrap. 2. The first piece cut from the side of a log of wood.
Sleeve. An enveloping piece that is usually cylindrical and too long to be termed a ring.
Slide-valve. The valve that governs the admission of steam into and its exhaust out of a cylinder.
Slot. A rectangular passage or hole passing entirely through the material.
Slotting-machine. A machine having a vertical bar or ram that carries the cutting tool on its lower end and has a vertical reciprocating motion.
Smooth-file. The finest cut of file that is made for ordinary use.
Smoothing-plane. A carpenter’s short plane for producing a smooth surface.
Socket. A piece that is hollow and receives another.
Socket-wrench. A wrench that envelops the whole of the head of a bolt.
Solid milled cutters. Cutters for woodwork, in which an irregular shaped cutting edge is obtained by recesses cut in the flat face of the cutter.
Space or spaces. The opening between the teeth of gear wheels.
Spanner. A form of wrench.
Spindle. A shaft that is used to transmit purely rotary motion, and that is usually of small diameter in proportion to its length.
Spiral cutter. A milling cutter having its teeth cut spirally and not parallel to the axis of its bore.
Spiral head. A device for holding work and revolving it in a milling machine.
Spirit-level. An instrument in which an air-space or bubble is utilized to disclose whether the surface upon which the spirit level is laid is horizontal.
Spline. A long feather-way.
Split-pin. A pin that is split so that its end can be opened out to prevent its coming out of place.
Spoke. The arm that connects the hub of a wheel to its rim or felloe.
Spoon-bit. A wood-boring tool that is shaped somewhat like a gouge.
Spring. 1. A piece of elastic metal. 2. The movement or deflection of a piece of metal on a tool, by its own weight or from the strain placed on it.
Spring-tool. A tool so formed as to have a slight give or spring to it.
Spur. A sharp cutting edge placed on some kind of wood-cutting tools to sever the fibre before the cutting edge removes the wood cuttings.
Spur-wheel. A gear-wheel having its teeth upon its circumferential surface.
Square-centre. A lathe centre having four cutting edges at its coned end.
Square thread. A screw-thread that is rectangular in cross-section.
Stanchion (stăn′shun). A vertical frame.
Standard. An upright piece.
Standing-bolt. A bolt that screws into the work, and does not therefore require a nut.
Stave. 1. A piece that forms part of a hollow wooden casing. 2. A pin on a gear-wheel that has pins instead of teeth.
Steady-rest or back-rest. A device for steadying work in the lathe.
Steam-boiler. A boiler used to generate steam and hold it at a pressure above that of the atmosphere.
Steam-hammer. A forging machine in which the hammer is raised or lifted by steam, and is sometimes also forced downwards by steam.
Steam-space. That part of the boiler that is above the level of the water.
Sticker. A machine that operates on wood of small cross-sectional area in proportion to its length, such as picture frame moulding.
Stock. Material.
Stocks-and-dies. Tools for cutting external threads by hand.
Stop. 1. A piece that arrests the motion of another piece. 2. A part of a gauge, against which the work abuts.
Stop-motion. A device for preventing the overwinding of clocks and watches.
Straddle-mills. Milling-machine cutters that are used in pairs and straddle the work, both cutters being of the same diameter.
Straight edge. A piece or strip having one or both edges made straight to use as a guide in testing work.
Stub end. The end of a connecting rod.
Stud. 1. A bolt that screws into the work at one end and receives a nut at the other. 2. A piece that screws into the work at one end.
Stuffing-box. The box in which a gland fits.
Surface-plate. A plate having a true flat surface to test the flatness of work by.
Swage. A blacksmith’s tool for smoothing and shaping surfaces.
Swing-frame. A frame having a movable stud for carrying the change gears of a lathe.
Swing-saw. A saw that is suspended in a swinging frame.
Swivel-vise. A vise that may be swiveled or revolved upon its base plate.
T
T or tee. A pipe fitting having two bores at a right angle, one to the other.
Tailstock or tailblock. That part of a lathe that carries the dead centre.
Tangent-wheel. A wheel whose teeth are formed to work with a screw or worm.
Tap. 1. A tool for cutting threads in holes or bores. 2. A device for shutting off or turning on the flow of water through a pipe.
Taper-tap. A tap that has part of the thread turned off in order that it may enter the hole easily and start to cut the thread. It is sometimes termed the first tap.
Tapped. 1. Threaded internally. 2. Having a connection that branches from the main pipe or flow.
Target. A frame used in setting shafting in line.
Temper. 1. The degree of hardness that has been imparted to steel by heating and suddenly cooling it. 2. A term employed by steel makers with reference to the percentage of carbon contained in steel.
Tempering. Tempering consists in reheating hardened steel and thus modifying or reducing its degree of hardness.
Template or Templet. A piece of metal made to shape, to serve as a pattern for one or more of the work surfaces.
Thread-gauge. A threaded cylinder or bore that serves as a standard of reference for the shape and diameter of a screw thread.
Threading-tool. A tool for cutting screws in the lathe.
Throw-line. The travel of a piece, moved by an eccentric.
Thumb-nut. A nut so shaped that it may be screwed up or unscrewed by hand.
Tight. A term used to denote those parts of a plate or saw that are under undue tension, and prevent the other parts of the plate from lying flat.
Timber-planer. A wood-planing machine for thick work, usually having side heads as well as cutter bars.
Tire. The iron band surrounding a wheel rim.
Tit-drill. A drill having a point or teat, and employed to cut flat-bottomed holes.
Tool-post. The device employed in a slide-rest to grip the cutting tool.
Train. An arrangement of gear wheels in which there are more than two gear wheels employed.
Trammels or tram. A device for measuring distances too great to be measured by ordinary compasses.
Trip-hammer. A forging machine in which the helve or hammer holding beam is tripped by a revolving cam.
Trundle. A gear-wheel having rungs in place of teeth.
Trying-up. A term usually employed to indicate that the work is accurately done or fitted.
Try-square. A tool having a rectangular back, and a blade whose edges are a right angle to the edges of the back.
T Slot. A slot or groove, shaped to receive a bolt head and prevent it from turning when the nut is screwed up.
Turnbuckle. A socket that receives and holds the ends of two rods and permits either to be revolved independently of the other or the socket to be revolved without revolving either rod.
Turret-lathe. A lathe in which a revolving head or turret carries the cutting tools.
Tuyère (twē′ar). The nozzle through which air is forced into a blacksmith’s fire, a furnace or a cupola.
Twin-mills. Milling cutters that are used in pairs, and have teeth on their side faces as well as upon the circumference.
Twist-drill. A drill having a spiral flute along it.
Twist-hammer. A sawmaker’s hammer having its two faces parallel, so that by turning it over in the hand its marks will be in opposite directions.
Two-jawed chuck. A chuck having two jaws.
U
Universal chuck. A chuck in which the jaws move simultaneously.
Universal joint. A joint or connection that permits a piece to be moved about in any required direction.
Universal milling-machine. A milling-machine that is capable of cutting spirals, and is provided with an index head.
Upright. A vertical post or frame.
U. S. standard thread. A V-shaped thread having a flat place at the top and bottom.
V
Vernier (vër′ni-er). A measuring device in which two sets of lines of division are employed, one set being narrower spaced than the other, but so spaced that in a certain number of divisions the two end lines of each piece measure exactly alike: this provides a means of making a minute measurement.
Vise. A work-holding device in which one jaw is movable and the other stationary.
Vise-clamp. A piece of metal placed on the vise jaw and passing between it and the work to prevent the jaw teeth from indenting the work.
V-thread. A V-shaped thread, sharp at the top and bottom.
W
Warding file. A thin file suitable for filing out the wards of the keys of door locks, etc.
Washer. A perforated disc of metal, usually forming a seating for some other piece as a rest or a pin.
Wheel lathe. A lathe for turning wheels.
Whitworth’s quick-return motion. A mechanism employed to move a cutting tool faster on its return than on its cutting stroke.
Whitworth’s thread. A screw thread designed by Sir Joseph Whitworth, and having a rounded top and bottom.
Winding strips. A pair of straight edges, used to detect any wind or twist in surfaces that ought to be parallel.
Wing-nut. A nut having wings so that it may be screwed up with the fingers.
Wire-gauge. A gauge having notches in it that are standards of size for wire, for the thickness of sheet metal, for screws, etc., etc.
Worm-wheel. A wheel whose teeth are formed to work with a worm or screw.
Wrench. A tool for turning nuts, etc.
Y
Yoke. A piece that embraces two other pieces to hold them together, or adjust their distance apart.
A
Absolute steam pressure, ii, 411.
Accidents to locomotives, ii, 402.
Accurate standards, i, 341.
Admission of steam to indicator, ii, 414.
point of, ii, 376.
Adjustable centre rest, ii, 14.
chucks for true work, i, 235.
cutters, i, 448.
with half-round bit, i, 281.
die stock, i, 448.
drivers for bolt-heads, i, 224.
end measurement gauges, i, 377.
or jamb dies, i, 98.
planes, ii, 269.
reamers, i, 189, 284,
ii, 99.
shell reamers, i, 284.
tap wrenches, i, 110.
taps, i, 104.
wrenches, various forms of, i, 125.
Adjusting connecting rod brasses, ii, 385.
length of connecting rods, ii, 126.
main bearings, ii, 386.
parts of a locomotive, ii, 404.
Adjustment of band saws, ii, 309.
by differential screw, i, 119.
Advantages of face cutters, i, 108.
of involute gear teeth, i, 34.
Air brake for locomotives, ii, 398.
Air pumps, ii, 441.
Aligning connecting rods, ii, 119, 124.
Alignment in crank pins, errors, ii, 169.
of cranks, testing the, ii, 167.
of lathe tail stocks, i, 145.
Allen valve, ii, 377.
Allowance, for contraction fits, i, 366.
for hydraulic fits, i, 365.
Alteration of shape of threads from the wear of tools, i, 89.
Angle irons, welding of, ii, 236.
of clearance in lathe tools, i, 257.
plate chucking, examples of, i, 251.
plates for planer tables, i, 418.
valve patterns, ii, 283, 284.
Angles for the facets of scrapers, ii, 97.
of cutting edges of chisels, ii, 74.
of thread cutting tools, i, 91.
Angular advance of eccentrics, ii, 380.
cutters, ii, 19.
cutters for groove cutting, ii, 27.
of helical teeth, i, 69.
teeth, and thrust of, i, 69.
herring-bone, i, 69.
velocity of gear-wheels, i, 6.
Angularity of connecting rods, ii, 375.
Annular emery wheels, ii, 47.
wheels, i, 1.
compared with spur, i, 32.
Anvils, ii, 230.
Apparatus for oiling, ii, 439, 440.
Appliances for bending timber, ii, 265.
for tapping standard work, i, 111.
Aprons, lathe, feed motion for, i, 168.
Apron tools for planers, i, 411.
Arbors, adjustable, i, 227.
cutter, ii, 25.
emery wheel, construction of, i, 198.
expanding, i, 227.
for eccentric work, i, 229.
shell reamers, i, 283.
threaded work, i, 228.
lathe, i, 227.
Arc of approach of gear-wheels, i, 13, 16.
of contact of gear-wheels, i, 17, 25.
of recess of gear-wheels, i, 13,
16, 20.
Area of the indicator diagram, ii, 419.
Arms for pulleys, ii, 279.
pivoted, for tooth templates, i, 44.
Atmosphere, influence of, on oils, ii, 153.
Auger bit, i, 453.
Augers for end-grain wood, i, 454.
Augers for wood boring, ii, 342.
Automatic air brake, ii, 398.
cut-off engines, ii, 423.
engine, high speed, ii, 427.
engine, straight line, ii, 428.
wheel governors, ii, 427.
feed motions, i, 408; ii, 8.
gear cutter, ii, 54.
nut tapping machine socket, ii, 475.
grindstone traversing device, ii, 53.
Auxiliary valve, ii, 438, 439.
Ax handle lathes, i, 210.
Axle boxes, hot, ii, 403.
locomotive, ii, 148.
brasses, testing, i, 366.
Axles, crank, lathes for turning, i, 152.
forging, ii, 259.
B
Babbitting boxes, methods of, ii, 155.
Babbitt metal-lined boxes, ii, 155.
Back-gear of lathe, i, 135, 145.
throwing in and out, i, 165.
treble, i, 143.
Back-knife gauge lathe, i, 211.
Back rest, i, 233.
Balanced valves, ii, 377.
Balancing cutter heads, ii, 324, 326.
emery wheels, ii, 39.
pulleys, ii, 202.
Ball turning, i, 325.
Banking fires, ii, 401.
Band saw machines, ii, 308, 311, 312.
Band saw guides, ii, 311.
teeth, ii, 308-310.
pitch of, ii, 309.
tension, ii, 310, 311.
Bar cutters, boring, i, 289.
the shapes of, i, 291.
Bar iron, straightening, i, 305.
Barometer, graduation of, ii, 416.
construction of, ii, 415.
Bars, boring, i, 289.
boring, with fixed heads, i, 290.
Bar steel, forms of, for chisels, ii, 73.
Bearings, adjusting, ii, 386.
for lead screw, i, 139.
of engine lathes, i, 134.
of line shafting, ii, 166.
surfaces of keys, i, 126.
thrust of, ii, 445.
various forms of, ii, 147.
wear of, i, 158.
Beating and pounding, causes of, ii, 168.
Bedding brasses in their boxes, ii, 132.
Beds, planer, flat guideways for, i, 414.
planer, oiling devices for, i, 415.
Belt stretching clamps, ii, 210.
lacings, covers for, ii, 215.
forms of, ii, 214.
Belt pumps, ii, 388.
shifting mechanism, i, 406, 407.
Belts, bevelled joints for, ii, 215.
changing or shipping, ii, 217.
driving power of, ii, 208-225.
friction, coefficient of, ii, 222.
grain side, weak, ii, 208.
to pulley, ii, 209.
guide pulleys for, ii, 211.
lap joints for, ii, 215.
length of, ii, 209.
line of motion of, ii, 217.
parts of hide used for, ii, 207.
pegged, ii, 215.
single and double, ii, 208.
stretch of, parts of hide, ii, 208.
the creep of, ii, 222.
length of, ii, 209.
sag of, ii, 210.
tension of, ii, 211, 224.
torsional moment, ii, 223.
V or angular, ii, 217.
Bench lathes, i, 130.
Bending appliances, ii, 226, 265.
block for wood, ii, 265, 266.
iron, ii, 226, 240.
timber, ii, 265, 266.
wood, modern methods, ii, 265.
Bent files, use of, ii, 93.
Bevel gear teeth, originating, i, 22.
pinion, drawings for, i, 59.
protractors, i, 380.
squares, i, 380.
wheel, body pattern, i, 59.
Bevel wheels, i, 1, 21, 61.
formation of the teeth of, i, 22.
testing the angle of, i, 60.
Bilge injection marine engines, ii, 441.
Billiard cues, steady rest for, i, 233.
Birmingham wire gauge for gold and silver, i, 387.
Bit, half round, i, 281.
Bits for wood working, ii, 342.
Blacksmith’s anvils, ii, 230.
drilling levers, i, 456.
fire, side blast for, ii, 228.
forges, ii, 228, 229.
swages, ii, 230, 231.
temper, ii, 460.
tools, ii, 229, 230.
work, swaging, ii, 232.
Blade, form of, necessary to produce a given shape of moulding, ii, 77.
Block planes, ii, 269.
Blocks for filing pins, ii, 104.
pillow for shafting, ii, 194.
or pillar, patterns for, ii, 277.
swage, ii, 232.
Blotting paper, oil test, ii, 154.
Blowing down boilers, ii, 370.
Blows upon plates, effects of, ii, 69.
Blow through valve, ii, 440.
Boiler fitting joints, ii, 140.
Boilermakers, drilling machine, i, 435.
drilling machine, feed motion, i, 436.
Boilermakers’ turning machine, i, 435.
Boiler, blowing down, ii, 370.
cleaning, ii, 370.
evaporative efficiency of, ii, 366.
examining, ii, 458.
factors of safety of, ii, 355.
feed water, ii, 370.
feeding, instruction upon, ii, 370.
fire cleaning, ii, 369.
cleaning tools, ii, 369.
for stationary engine, ii, 350.
gauge cocks, ii, 368.
grate bars, ii, 369.
bars, shaking, ii, 369.
horizontal, return tubes, ii, 361.
lighting the fire under, ii, 368.
internally fired, ii, 358.
plate, the strength of, ii, 351.
settings, ii, 364-366.
seams, diameter of rivets, ii, 356.
treble riveted, ii, 353.
shells, drilling machines for, i, 436.
the strains on, ii, 351.
the strength of, ii, 350.
strains on, ii, 355.
the care and management of, ii, 368.
tubes, for fire engines, ii, 431.
vertical, ii, 359.
external uptakes, ii, 361.
water gauge glass of, ii, 368.
with Field tubes, ii, 359.
Boilers, low water in, ii, 370.
of marine engines, ii, 436, 437.
of steam fire engines, ii, 431.
priming in, ii, 370.
Bolt-cutting machine, head of, i, 466.
dies, i, 473.
rapid, i, 467.
the construction of dies for, i, 473.
with automatic stop motion, i, 466.
back gear, i, 467.
Bolt-forging, ii, 238.
Bolt-threading machinery, i, 468.
capacity of, i, 471.
construction of, i, 468-472.
Bolted connecting-rod straps, ii, 116.
Bolt-heads, adjustable drivers for, i, 224.
bedding, i, 117.
filing, ii, 105.
Bolt-holes, classification of, i, 112.
Bolts and nuts, table for, i, 114.
Bolts, classification of, i, 112.
countersunk, i, 112.
devices for forging, ii, 238.
for foundations, forms of, i, 113.
planer tables, forms of, i, 417.
quick removal, i, 116.
forms of drivers for, i, 224.
hook, i, 113.
not passing through the work, i, 117.
rapid construction of, i, 468.
removing corroded, i, 122.
self-locking, i, 117.
Bore gauge, i, 387.
Boring and turning mill or lathe, i, 211.
bar, centres for, i, 293.
cutters, i, 289.
cutters, shapes of, i, 291.
bars, i, 289.
for taper work, forms of, i, 292.
three or four cutters for, i, 290.
with fixed heads, i, 290.
with sliding heads, i, 290.
double-coned work, i, 293.
end grain wood, augers for, i, 453.
head with nut feed, i, 291.
heads, i, 288.
lathe for engine cylinders, i, 219.
with double heads, i, 220.
with traversing spindle, i, 218.
mill, i, 211.
purposes, chucking lathe for, i, 152.
tool holders, i, 287.
tools for brass, lathe, and small work, i, 285-287.
octagon, holders for, i, 175.
the spring of, i, 286.
Boring-machine, i, 431.
for car wheels, i, 438.
wood, ii, 342.
horizontal, i, 433.
pulley, i, 438.
the feed motion of, i, 432.
Box wrenches, i, 124.
body chucks, i, 237.
tools for screw machines, i, 208.
Brace drill, i, 455.
with multiplying gear, i, 456.
ratchet motion, i, 456.
Brad awl, i, 452.
Brake for lathe pulley, i, 149.
for pattern lathe, i, 149.
lathe, i, 151.
Branch pipe core boxes, ii, 286.
Brasses, fitting to their journals, ii, 145.
Brasses, for connecting rods, adjusting, ii, 120-127,
130-132.
lead lined, ii, 148.
oil cavities for, ii, 150.
open, ii, 149.
various forms of, ii, 127, 147.
Brass work, boring tools for, i, 286.
front tools for, i, 264.
hand tool for roughing out, i, 332.
side tools for, i, 264.
special lathes for, i, 217.
Breast drill with double gear, i, 456.
Broaches, construction of, i, 479.
Broaching press, i, 478.
Broken frames, repairing, ii, 178.
Brush wheels, for polishing, ii, 50.
speed of, ii, 50.
Built-up gearwheels, i, 61.
Burnishing lathe work, i, 311.
Butt joints, boiler, ii, 352.
Butt welds, ii, 236.
Buzz planer, ii, 315.
By-pass valve, ii, 438.
C
Calculating the horse power of engines, ii, 407, 419.
revolutions of, and power transmitted by, gear wheels, i, 5.
speeds of pulleys, ii, 204.
strength of gear teeth, i, 65.
strength of riveted seams, ii, 354.
horse power by indicator diagrams, ii, 418, 419.
Calculations, safety-valve, ii, 409.
Calendar roll lathe, i, 195, 215.
Caliper, the micrometer, i, 354.
Calipers, compass, i, 378.
holding and using, i, 361, 362.
inside, i, 360.
spring, i, 360.
with locking devices, i, 360.
Cam chuck for irregular work, i, 328.
motion for an engine slide-valve without steam lap, i, 83.
motions, applications of, i, 327.
for engines, i, 83.
return or backing, i, 82.
Cams, finding the pitch line of, i, 80.
finding the working face of, i, 80.
originating in the lathe, i, 326.
return, finding the shapes of, i, 82.
Capacity of pumps, ii, 388.
of thread cutting machine, i, 471.
Cape chisels or cross-cut chisels, ii, 74.
Car axle lathe, i, 147.
the feed motions of, i, 148.
Carpenter’s chisel, ii, 77.
Carriages, lathe, testing, ii, 182.
for lathes, i, 137, 145.
Carriers, lathe, i, 222.
Car wheels, boring machine for, i, 438.
Case-hardening, ii, 128, 442.
finished work, ii, 129.
preparing work for, ii, 129.
Casting pillow blocks, ii, 277.
Cast gear, contact of the teeth of, i, 67.
iron, internal strains, i, 306.
teeth, contact of, i, 67.
scale for curves of, i, 51.
side clearance, i, 53.
Cat head, i, 233.
steady rest, i, 233.
Caulking tools, ii, 141.
Cement chuck, i, 242.
Cements used in the manufacture of emery wheels, ii, 38.
Centre bit, i, 454.
dead, methods of removing, i, 159.
drill and countersink, i, 300.
chuck, i, 302.
drilling lathe attachment, i, 300.
chucks for, i, 303.
machine, i, 300.
live, removing, i, 159.
of rough work, i, 301.
planer, i, 408.
punch, i, 300.
guide, i, 301.
Centres for boring bars, i, 293.
for hollow work, i, 226.
lathe, i, 296.
shaping machines, i, 397.
taper work, i, 226.
live, tapers for, i, 159.
Centring devices for crank axles, i, 230.
square, i, 300.
work with the scribing block, i, 301.
Chain riveted joints, ii, 352.
Chambering or gumming, ii, 290.
Change gears, arrangement of, i, 319.
gears, compounded, i, 321.
table for finding, for screw cutting, i, 180.
hanging, i, 158.[II-478]
wheels, pitches of teeth, i, 182, 321.
Changing or slipping belts, ii, 217.
Chasers, errors in applying, i, 336.
forms of, i, 268.
holders, i, 268.
improved form of, i, 90.
outside and inside, i, 335.
setting, i, 268.
Check valves, ii, 388.
Chisels, angle of presentation, ii, 77.
angles of cutting edges, ii, 74.
blacksmith’s, ii, 230.
cape or cross-cut, ii, 74.
carpenter’s, ii, 77.
cow-mouthed, ii, 75.
curved or oil groove, ii, 76.
cutting ends of, ii, 74.
diamond point, ii, 76.
dimensions of, ii, 74.
for wood, ii, 271.
handles for, ii, 271.
holders, ii, 74.
machinist’s application of, ii, 76.
round-nosed, ii, 76.
shapes of cutting edges, ii, 74.
the use of, ii, 76.
Chucking device for pulleys, i, 318.
devices for planer tables, i, 408.
errors in, i, 250.
lathe for boring purposes, i, 152.
machine beds, on a planer, i, 421.
on angle plates, i, 251.
reamers, for true work, i, 283.
the halves of large pulleys on a planer, i, 422.
Chucks and chucking, i, 234.
Chucks, box body, i, 237.
cement, i, 242.
combination, i, 237.
cone, i, 232.
contracting, for lathes, i, 188.
drill, i, 446.
drill-holding, construction of, ii, 41.
expanding, i, 188.
for centre-drilling and countersinking, i, 303.
large planing machines, i, 422.
milling machines, ii, 31.
screw machine, i, 205.
straightening wire, i, 305.
true work, adjustable, i, 235.
wood-working lathes, i, 242.
independent, i, 238.
planer, for curved work, i, 420.
planer, for grooved work, i, 419.
reversible jawed, i, 237.
special forms of, i, 234-241.
swivelling, i, 395.
tailstock for drilled work, i, 279.
the wear of, i, 240.
three and four-jawed, i, 237.
two-jawed, i, 236.
universal, i, 238.
various forms of, i, 394.
vise, for vise work, i, 396.
vise, holding taper work in, i, 394.
vise, rapid motion, i, 396.
Circle, dividing the, i, 348.
rolling, for change gears, i, 16.
Circular cutters, i, 272; ii, 22.
cutters, tool holders for, i, 272.
cutting tools, i, 267.
plane, ii, 268.
saw gauges, ii, 287.
inserting teeth, ii, 290, 291.
machine, roll feed, ii, 298, 300.
mandrel hole, size of, ii, 287.
segmental, ii, 300.
stretching by heat, ii, 288.
tension, ii, 288.
Circular slide valves, ii, 377.
Circulating pumps, ii, 440.
Circumferential seam strength, ii, 356.
grindstone speed, ii, 52.
Clamp couplings, ii, 197.
Clamping work on face plates, i, 245.
Clamps, belt, ii, 210.
chucking, i, 245.
for steady rests, i, 233.
polishing for lathe-work, i, 311.
steady rest, i, 233.
vise, various forms of, ii, 64.
Classification of bolts, i, 112.
of bolt heads, i, 112.
of lathes, i, 129.
of measuring tools, i, 354.
Cleaning boilers, ii, 370.
files, ii, 94.
Clearance in cast gear teeth, i, 53.
of front tools, i, 254.
of planer tools, i, 424.
of taps, i, 102.
of tools for square threads, i, 269.
of twist drills, i, 274, 275.
on cutter, ii, 35.
Clements driver, i, 223.
Clinker hook, ii, 369.
Clip-ended connecting-rod, ii, 115.
Clock wheels, i, 21.
Clutches, friction, ii, 192.
Cocks and plugs, grinding, ii, 144.
leaky, ii, 145.
Cogged gear-wheels, i, 63.
Cogs, durability of, i, 66.
strength of, i, 66.
thickness of, i, 66.
methods of fastening, i, 63.
Cold-rolled shafting, ii, 187.
Collapsing tap, screw machine, i, 107.
taps, tapping machine, i, 107.
Collar gauges and standard plug, i, 356.
for threads, i, 91.
testing, i, 356.
Collars for shafting, ii, 189.
Color tempering, ii, 460.
Combination chucks, i, 237.
Combination planes, ii, 269, 270.
Combined centre-drill and countersink, i, 300.
cutting off tools and holders, i, 273.
drilling machine and lathe, i, 433.
Compasses, i, 377.
Compound engines, ii, 434, 435.
slide rest, i, 140.
tool holders for, i, 174.
Compounded gears, i, 320.
Compounds for welding, ii, 234.
Compression curve of engines, ii, 422.
Compression curve, ii, 415.
line, ii, 415.
the point of, ii, 376.
Condenser, total pressure in, ii, 444.
Condensing engine diagram, ii, 415.
Cone chuck, i, 232.
Connecting-rods, adjusting the length of, ii, 126.
angularity of, ii, 375.
brasses, adjusting, ii, 385.
joint faces of, ii, 122.
lining up, ii, 126.
double gibbed, ii, 116.
ends, tapered, ii, 117.
fitting up, ii, 118.
keys, ii, 375.
keyways, filing out, ii, 120.
locomotive, ii, 115.
length of, ii, 123.
marine engine, ii, 116.
marking length of, ii, 123.
repairing, ii, 125.
setting up keys of, ii, 126.
solid-ended, ii, 114.
strap-ended, ii, 115.
straps, ii, 120.
bolted, ii, 116.
stepped, ii, 117.
trammelling the length of, ii, 122.
various forms of, ii, 117.
welding up stub ends of, ii, 119.
Construction of gland patterns, ii, 276.
of groove cams, i, 84.
of lathe carriages, i, 137.
of emery wheel arbors, i, 198.
of tailstock of engine lathe, i, 135.
of reciprocating cross-cut saw, ii, 312.
of scroll sawing machines, ii, 306, 307.
of the barometer, ii, 415.
Contact of cast teeth, i, 67.
Contracting chucks for lathes, i, 188.
Contraction or shrinking fits, i, 366.
Convection, ii, 412.
Conversion of heat into work, ii, 411.
Cope cutters, ii, 344.
Core boxes for branch pipes, ii, 286.
Core box plane, i, 269.
Cored work, drivers for, i, 225.
Corliss engine, ii, 423, 424.
valve, lap of, ii, 426, 427.
valve gear, ii, 424, 425.
Correcting the errors of thread pitch caused by hardening, i, 109.
Corroded bolts, removing, i, 122.
nuts, removing, i, 122.
Cotter or keyway drilling machine, i, 438.
drills, i, 446.
Counterbore and drill, i, 449.
Countershafts, ii, 191.
Countersink cutters, i, 449.
Countersink, for hardened work, i, 303.
for lathe work, i, 302.
with adjustable drill, i, 300.
Countersinking, chucks for, i, 303.
Countersinks, i, 285.
Countersunk bolt heads, i, 112.
Coupling for light shafting, ii, 198.
plate, ii, 196.
universal, ii, 199.
Couplings, clamp, ii, 197.
for line shafting, ii, 194.
for split sleeves, ii, 195.
self-adjusting, ii, 196.
Covers for belt lacings, ii, 215.
Cow mouthed chisel, ii, 75.
Crank, application of slide-rest, i, 152.
axles, centring devices, i, 230.
axles, lathe for turning, i, 152.
drill, i, 457.
lathe for turning, i, 154.
motion for shaping machines, i, 401.
simple, i, 13.
placing at right angles, ii, 156.
Crank-pin aligning, errors, ii, 158, 170.
remedying errors of, ii, 171.
riveting, ii, 73.
Crank-pins, hot, ii, 386.
Crank position, engine starting, ii, 384.
Crank-shaft, forging, ii, 248, 249.
setting eccentrics on, ii, 174.
Cranks, placing at right angles, ii, 156.
special lathe chuck for, i, 248.
testing the alignment of, ii, 167.
Creep of belts, ii, 211.
Cropping gauge, ii, 296.
Cross-bar, construction of, i, 409.
Cross-cut, or cape chisels, ii, 74.
saws, ii, 272, 273, 312.
Cross-cutting or gaining machine, ii, 305.
Cross-feed motion, construction of, i, 138.
Cross-files, ii, 91.
Cross-head chucking, i, 251, 253.
Cross-heads of steam engines, ii, 375.
Crowding of cutters, to avoid, ii, 27.
Crowned pulleys, ii, 200.
Crowns of brasses, shapes of, ii, 127.
Crown wheels, i, 1.
Curve of expansion of indicator diagrams, ii, 414.
of gear wheel teeth, variation of, i, 12.
Curved or oil groove chisel, ii, 76.
work, planer chuck for, i, 410.
work, turning, i, 314, 315.
Curves, compression, ii, 415.
marking, by hand, i, 45.
of gear teeth for bevel gear, i, 22.
templates for, i, 384.
Cushioned hammers, ii, 252, 253.
Cut, and kinds of rasps, ii, 87.
of files, ii, 86.
gear-wheel teeth, strength of, i, 65.
Cut-off engines, ii, 423.
the point of, ii, 376.
valves, ii, 378.
Cutter, adjustable, i, 448.
adjustable on half-round bit, i, 281.
angle for worm wheels, i, 43.
angle of, for spiral grooves, ii, 29.
arbors, ii, 25.
boring-bar, the shapes of, i, 291.
clearance of, ii, 35.
grinding taper, thin edge, ii, 33.
heads, ii, 337.
heads for planing machines, ii, 320.
revolving, for gear teeth, i, 37.
Cutters, angular, ii, 18.
angular, grooving, setting of, ii, 28.
circular, ii, 22.
countersink, i, 449.
crowding, to avoid, ii, 27.
face, ii, 17.
fly, ii, 21.
for drilling machines, i, 442.
edge moulding, ii, 341.
friezing machines, ii, 340.
moulding machines, ii, 340.
mouldings, ii, 336, 337.
standard shapes, i, 111.
gang or composite, ii, 23.
holders for fly, ii, 22.
matched, ii, 73.
milling, ii, 16.
milling, errors in grinding, ii, 32.
parallel, fixture for grinding, ii, 32.
right and left-hand, ii, 18.
rotary, for all kinds of work, ii, 341.
shank, ii, 19.
sizes of, ii, 17.
slide of gear-cutter, operating, ii, 55.
spiral, grinding teeth of, ii, 36.
tube-plate, i, 448.
twin, ii, 18.
with inserted teeth, ii, 24.
with spiral teeth, ii, 17.
Cutting cams in the lathe, i, 326.
coarse pitch square threads, i, 269.
double threads, i, 322.
edge of chisels, angles of, ii, 74.
of chisels, shapes of, ii, 74.
on drills, clearance, ii, 43, 44.
edges for dies, number of, i, 471.
for taps, number of, i, 105.
ends of chisels, ii, 74.
feeds for wrought iron, i, 294.
files, ii, 101.
gauge, ii, 274.
grooves in cylindrical work, ii, 27.
helical teeth in the lathe, i, 69.
iron when hot, ii, 263.
keyways by hand, ii, 108.
left-hand threads, i, 322.
out keyways by drifts, ii, 109.
steam ports, jigs for, i, 441.
right and left-hand grooves, ii, 29.
right or left-hand thread, single, double, or treble, with same dies, i, 99.
screws by the metric system, i, 322.
screw thread by hand, i, 62.
speeds, examples of, i, 295.
for threading dies, i, 474.
for wrought iron, i, 294.
taper threads, i, 338.
threads, multiple, i, 322.
on taper work, i, 324.
tools, circular, i, 267.
producing gauges for, i, 92.
power required to drive, i, 273.
the utmost duty of, i, 258.
wheels, angle of cutter for, i, 43.
wood slips, ii, 271.
worm-wheel teeth in the lathe, i, 42.
Cutting-off machine, i, 193.
tool for screw machines, i, 208.
tools, i, 262, 273.
Cycloidal curves for gear teeth, i, 8.
Cylinder boring lathe with facing slide rests, i, 219.
cover joints, ii, 137.
cover, turning a, i, 318.
ends, scraping out, ii, 161.
Cylinder heads, knocking out, ii, 402.
Cylinders, bores of, ii, 372.
clearance in, ii, 372.
counterbore of, ii, 372.
for steam engines, ii, 372.
jacketed, ii, 374.
lagging, ii, 374.
lubricating, ii, 373.
reboring in place, ii, 160.
relief valves for, ii, 373.
steam, ports of, ii, 373.
waste water cocks of, ii, 373.
wear of, ii, 372.
Cylindrical work, cutting grooves, ii, 27.
D
Dancing governors, ii, 384.
Dead-centre, finding the, ii, 174.
methods of removing, i, 159.
of the crank, finding the, ii, 172.
Deflection of surface plates, ii, 135.
Depth of gear wheel teeth, i, 42.
Designing slide valves, ii, 380.
Detachable slide rest, i, 143.
Determining the pitches of the teeth for change wheels, i, 182.
Diagram, theoretical, ii, 414.
the uses of, ii, 413.
Diagrams for condensing engine, ii, 415.
indicator, ii, 414.
defective, ii, 421.
Diameter at the roots of threads, i, 269.
of circle for generating curves of gear teeth, i, 10.
of the pitch circle of wheels, i, 1.
Diameters of line shafting, ii, 189.
Diametral clearance of twist drills, i, 274.
Diamond point chisel, ii, 76.
Diamond pointed tool for lathe work, i, 254.
Dictionary of work-shop terms, ii, 473.
Die stock for pipe-threading by hand, i, 463.
by power, i, 463.
Dies, adjustable, i, 98.
for finishing square threads, i, 269.
for forging eye-bars, ii, 260.
for gas and steam pipes, i, 101.
or chasers in the heads of bolt-cutting machines, i, 463.
the wear of, i, 89.
with four cutting edges, i, 100.
Differential threads for locking, i, 119.
Displacement of pumps, ii, 387.
Distance between bearings of line-shafting, ii, 186.
Dividers, i, 377.
Dividing device for circle, i, 352.
engine, i, 349.
mechanism for gear cutting, ii, 57.
Division of the circle, i, 348.
Dog-head hammer, ii, 69.
Dogs, lathe, various kinds of, i, 222.
movable for face-plate work, i, 250.
Donkey engines, ii, 442.
Double beat valves, ii, 443.
eye, filing up a, ii, 103.
forging of, ii, 240.
eyes, fitting pins in, i, 121.
gibbed connecting rod, ii, 115.
head panel raiser and sticker, ii, 335.
heads for planing machines, i, 404.
ported side valves, ii, 377.
rapid bolt threading machine, i, 467.
riveted lap joint, ii, 352.
saw machine, ii, 294, 295.
spindle milling machine, ii, 16.
threads, cutting, i, 322.
tool holder for slide rest, i, 169.
wheel sanding machines, ii, 348.
Double-coned work, boring, i, 293.
Dovetail joint, ii, 275.
Draught of keys, i, 127.
Draw filing, ii, 93.
Drawing the temper, ii, 462.
Drawings for bevel pinion, i, 59.
for gear wheels, i, 59.
Drifts, forms of, ii, 109.
methods of using, ii, 160.
Drill, and counter-bore, i, 449.
brace, i, 445.
universal joint for, i, 456.
with multiplying gear, i, 456.
with ratchet motion, i, 456.
chucks, i, 446; ii, 41.
cranks, i, 457.
for stone, i, 454.
for wood work, i, 449.
grinding, varied for diameter, ii, 41.
conditions for all diameters, ii, 41.
holders, flat, for lathe work, i, 281.
holders, twist, i, 274.
machine, grinding, ii, 41.
position, for all drills, ii, 41.
shanks, i, 445.
shank, improved form of, i, 446.
sockets, i, 445.
with cord, i, 455.
with spring motion, i, 455.
Drilled work, tailstock chucks for, i, 279.
Drilling and boring machine, i, 431.
feed motion of, i, 432.
device for lock work, i, 459.
engine cylinders, jigs for, i, 440, 441.
hard metal, i, 445.
[II-479]Drilling
holes true to location with flat drills, i, 442.
levers for blacksmith, i, 457.
square holes, device for, i, 450.
taper holes, i, 451.
and turning machine for boiler makers, i, 435.
machine, and lathe combined, i, 433.
cotter or keyway, i, 438.
feed motion of, i, 432.
feed motions of, i, 436.
for boiler shells, i, 436.
four-spindle, i, 434.
hand, i, 459.
lever feed, i, 428.
power, i, 428.
three-spindle, i, 434.
with automatic motions, i, 428.
with quick return, i, 428.
machines, counterbores for, i, 449.
cutters for, i, 447.
drills for, i, 442.
fixtures for, i, 439.
flat drills for, i, 442.
jigs for, i, 439.
radial, i, 430, 431.
stocks for, i, 447.
Drills and cutters, i, 442, 447.
cotter or keyway, i, 446.
flat, errors in grinding, i, 443.
flat, for drilling machines, i, 442.
flat, for lathe work, i, 280.
for wood work, i, 279.
square-shanked, i, 446.
disadvantages of, i, 446.
stock, with spiral grooves, i, 445.
twist, diametral clearance of, i, 274.
fluting, ii, 29.
front rake of, i, 275; ii, 44.
grinding by hand, i, 279.
large, grinding, ii, 41.
speeds and feeds for, i, 277.
Driver, and face plate, i, 223.
Drivers, equalizing, i, 223.
for bolt heads, i, 224.
coned work, i, 225.
lathe mandrels or arbors, i, 227.
steady rest work, i, 22.
threaded work, i, 225.
wood, i, 225.
lathe, i, 222.
the elements, i, 223.
Driving cones, steps of, i, 159-164.
drills, flexible shaft for, i, 458.
gear of universal milling machine, ii, 15.
gear table, i, 404.
Duration of a hammer blow, experiments on, ii, 65, 66.
Duplex slide-rests, i, 143.
E
Eccentrics, fixed and shifting, ii, 378.
slipping, ii, 403.
turning in the lathe, i, 317.
Eccentric work, lathe mandrels for, i, 229.
Edge tools, oilstoning, ii, 54.
Effects of hammer blows, ii, 69.
of speed of a hammer blow, ii, 65.
Elevating slide rests, i, 168.
Elliptical gears, tooth curves of, i, 73.
gear wheels, i, 70.
gears, the pitch lines of, i, 70.
taps, in cross section, i, 109.
Emery belt grinding machine, ii, 47.
grinder for car axle boxes, ii, 45.
for engine guide bars, ii, 45.
machine knives, ii, 46.
rough work, ii, 46.
true surfaces, ii, 45.
with revolving emery wheel, ii, 40.
machines, grinding, ii, 40.
charging, polishing wheels, ii, 50.
paper, use on lathe work, i, 308.
wheel arbors, i, 198.
arbors, positions of, ii, 35.
swing frame for dressing large castings, ii, 46.
wheels, annular, ii, 48.
balancing, ii, 39.
cements used in the manufacture of, ii, 38.
clearance of, ii, 39.
coarseness and fineness of, ii, 38.
positions of, i, 282; ii, 36,
37.
presenting to work, ii, 47.
qualifications of, ii, 38.
recessed, ii, 47.
speeds of, ii, 39.
wear of, ii, 48.
End, face and twin milling, ii, 25.
grain wood boring, i, 453.
measurements of lathe work, i, 376.
milling, advantages of, ii, 25.
thrust of angular teeth, i, 69.
Endless screw thread, cutting, i, 62.
Engine, alignment, errors in, ii, 166.
calculating the power of, ii, 407.
connecting rods, ii, 375.
crank turning, i, 247.
crossheads, ii, 375.
crosshead turning, i, 252.
cylinder covers, turning, i, 318.
cylinders, bores of, ii, 372.
boring lathe for, i, 219.
clearance in, ii, 372-404.
counterbore of, ii, 372.
fitting, ii, 158.
jacketed, ii, 374.
lagging, ii, 374.
lubricating, ii, 373.
relief valves for, ii, 373.
steam ports, ii, 373.
waste water cocks of, ii, 373.
wear of, ii, 372.
eccentrics, ii, 378.
turning a cover, i, 318.
gear cutting, ii, 56.
glands, turning, i, 316.
guide bars, ii, 375.
setting, ii, 162.
spring of, ii, 162.
testing, ii, 163.
lathe, i, 129, 147.
construction of carriage, i, 137.
of the back gear, i, 135.
of the bearings, i, 134.
of the head stock, i, 134.
general construction of, i, 133.
lead screw and change wheels of, i, 139.
shears of, i, 134.
link motion, designing, ii, 389.
plain slide valve, starting, ii, 384.
valves, ii, 376-378.
balanced, ii, 377.
circular, ii, 377.
cut-off, ii, 378.
double ported, ii, 377.
exhaust lap of, ii, 376.
lead of, ii, 376.
point of admission, ii, 376.
slide and piston, ii, 378.
slide, designing, ii, 380.
testing horse power of, ii, 408.
the Allen, ii, 377.
the D, ii, 376.
tracing the action of, ii, 376.
Webb’s, ii, 377.
Engines, compound, ii, 434, 435.
donkey, ii, 442.
heating and knocking of, ii, 164.
subject to freezing, ii, 386.
Engineers, test questions for, ii, 467.
Engraver’s plates, polishing, ii, 51.
Epicycloidal gear teeth, curves, i, 8.
teeth, the strength of, i, 64.
filleting the roots of, i, 53.
Equalizing drivers for lathe work, i, 223.
Erecting, ii, 137.
a lathe, ii, 181.
an iron planer, ii, 179.
pipe-work, ii, 143.
the framework of machinery, ii, 176.
Errors in alignment, determining, ii, 158-167.
in chucking, i, 250.
crank pin alignment, ii, 169.
cutting threads on taper work, i, 324.
cutting up inside chasers, i, 337.
drill-grinding machines, ii, 41.
grinding flat drills, i, 443.
grinding milling cutters, ii, 32.
jigs, limits of, i, 439.
shafting couplings, ii, 196.
Evaporative efficiency of boilers, ii, 366.
Examining a boiler, ii, 368.
a locomotive, ii, 401.
Excessive lead of engines, ii, 421.
Exhaust lap, ii, 376.
Expanding bit, i, 454.
chucks for lathes, i, 188.
for ring work, i, 241.
for large work, i, 228.
laps, i, 311.
mandrels, i, 227.
taps, i, 107.
Expansion, ii, 376.
curve of indicator, ii, 417, 418.
testing of indicator, ii, 417, 418.
joint, ii, 141.
line of diagrams, ii, 414, 415.
of steam, ii, 411.
pulleys, ii, 200.
valves, separate, ii, 443.
Experiments on duration of a blow, ii, 65, 66.
on the strength of the parts of a hide, ii, 208.
Extension lathe, i, 151.
Eye-bar dyes, ii, 260.
Eyes, hammer, shapes of, ii, 66.
F
Face and taper cutters, fixture, ii, 34.
cutters, ii, 17.
advantages of, ii, 18.
disadvantages of, ii, 18.
fixtures for, ii, 34.
milling, advantages of, ii, 26.
length of feed, ii, 26.
plate, clamping work on, i, 245.
clamps, i, 245.
errors in, and their effects, i, 243.
for wood-work, i, 247.
work, examples of, i, 249.
work, movable dogs for, i, 250.
Facets of scrapers, angles for, ii, 97.
Facing and countersink cutters, i, 449.
cutters, i, 449.
rests, boring lathe with, i, 220.
tool with reamer-pin, i, 449.
Facing tools or knife tools, i, 262.
Factors of safety, boiler seams, ii, 355.
Fastening cogs, i, 63.
pulleys to their shafts, ii, 201.
Featheredge, removing, ii, 54.
Feathers and their applications, i, 127.
methods of securing, ii, 102.
sinking into shafts, ii, 101.
Feed, direction, for shank cutters, ii, 20.
for spiral grooves, ii, 27.
escape valve, ii, 441.
gear, i, 197.
for screw machine, i, 205.
in cutting spiral grooves, ii, 28.
length, in face milling, ii, 26.
motions, automatic, i, 408.
construction of, i, 390.
examples of, i, 170.
for boiler-maker’s drilling and turning machine, i, 436.
for boring machine, i, 432.
boring mills, i, 215.
cam turning, i, 326.
car-axle lathe, i, 148.
carriage or saddle, i, 137.
chucking lathe, i, 150.
drilling machine, i, 432.
grinding lathe, i, 200.
lathe aprons, i, 168.
milling machine, ii, 13.
planer heads, i, 413.
reversing traverse, i, 168.
special lathe, i, 146.
weighted slide rest, i, 168.
wood-working, i, 209.
friction wheels for, i, 78.
nut, position of, i, 177.
ratchet, i, 173.
regulators for screw cutting, i, 171.
spindle bearings, i, 139.
spindle for lathe, i, 139.
spindle, giving motion to, i, 135.
water, heating, ii, 370.
Feeds, cutting, for wrought iron, i, 294.
for roughing cuts, i, 306.
for twist drills, i, 277.
Feed-water, ii, 370.
from natural supply, ii, 387.
Fiddle drill with feeding device, i, 455.
Field tube for boilers, ii, 359.
Fifth wheel, forging of, ii, 239.
File cutters’ hammers, ii, 71.
cutting, ii, 101.
teeth, shapes of, ii, 85.
Files, ii, 85.
bent, using, ii, 93.
cleaning of, ii, 94.
cross, ii, 91.
cut of, ii, 86.
flat sizes and kinds, ii, 86, 87.
for soft metals, ii, 95.
Groubet, ii, 87.
half-round, ii, 90.
instruction on holding, ii, 92.
knife, ii, 91.
names of, ii, 88.
putting handles on, ii, 92.
reaper, ii, 91.
resharpening, ii, 95.
round, ii, 90.
selection of, ii, 91.
thin, ii, 93.
three square, ii, 90.
tumbler, ii, 91.
warping, ii, 93.
Filing bolt heads, ii, 105.
cross, ii, 93.
draw, ii, 93.
fixture for lathes, i, 189.
lathe work, i, 308.
nuts, ii, 105.
out connecting rod keyways, ii, 120.
out round corners, ii, 95.
pins, ii, 105.
pins, blocks for, ii, 104.
the link slot, template for, ii, 127.
the teeth of band saws, ii, 309.
Filleting the roots of gear teeth, i, 53.
Finishing cast iron with water, i, 307.
cast iron work, specks in, i, 307.
cuts, rates of feeds for, i, 307.
horseshoes, machines for, ii, 262.
internal work, laps for, i, 311.
lathe work, scrapers for, i, 307.
Fire cleaning, ii, 369.
cleaning tools, ii, 369.
engine boiler tubes, ii, 431.
engine heaters, ii, 432, 433.
engines, steering gear for, i, 75.
Firing boilers, ii, 368.
methods of, ii, 402.
Firmer chisels, ii, 272.
Fits, shrinkage or contraction, i, 366.
Fitting brasses to connecting rod straps, ii, 121.
brasses to journals, ii, 146.
engine cylinders, ii, 158.
keys, ii, 107.
keys, examples of, ii, 107.
straps, ii, 120.
taper pins, i, 122.
taper work, i, 313.
the keys and gibs, ii, 120.
up connecting rods, ii, 118.
a double eye, ii, 103.
a fork end connecting rod, ii, 123.
a lathe, ii, 181.
a link motion, ii, 127.
Fixed pins, i, 122.
Fixture for grinding cutters, ii, 32, 33.
for grinding taper work, ii, 33.
Fixtures for drilling machines, ii, 439.
Flank contact of gear teeth, i, 28.
Flat drill holders, i, 281.
drills, drilling with, i, 444.
errors in grinding, i, 443, 444.
for lathe work, i, 280.
files, sizes and kinds, ii, 86, 87.
guideways for planer beds, i, 414.
side lathe shears, i, 183.
Flexible shaft for driving drills, i, 458.
Flue boiler, ii, 358.
Flutes, shapes of taps, i, 105.
the number of, i, 107.
Fluting twist drills, ii, 29.
Fluxes, heating in, ii, 462.
Fly ball governors, ii, 384.
cutters, ii, 21.
holders for, ii, 22.
making, ii, 21.
methods of originating, ii, 21.
Follower rests, i, 234.
Foot lathe, i, 130.
Foot-power hammers, ii, 252, 253.
Foot valves, ii, 388.
Forges for blacksmiths, ii, 228, 229.
side blast for, ii, 228.
Forging bolts, ii, 238.
crank shafts, ii, 248, 249.
hydraulic, ii, 260.
machine thread, ii, 261.
nails by machinery, ii, 261.
of bolts, ii, 238.
press, ii, 260.
rope sockets, ii, 243, 244.
rudder frames, ii, 245, 246.
steel forks, ii, 241.
threads on rods, ii, 261, 262.
turn buckles, ii, 239, 240.
under the hammer, ii, 242, 243.
under a steam hammer, ii, 241.
wheels, ii, 244, 245.
Fork end connecting rod, fitting, ii, 123.
aligning, ii, 124.
Fork forging, ii, 241.
Former of Corliss bevel gear-wheel engine, i, 45.
Form of lead screw threads, i, 177.
worm to give a period of rest, i, 74.
Forms of lathe shears, i, 183.
of outside calipers, i, 360.
pin wrenches, i, 126.
riveted joint, ii, 352.
taps, i, 102.
templates for gear teeth, i, 44.
wrenches, i, 125.
Foundations for an iron planer, ii, 179.
Four-jawed chucks, i, 237.
Four-spindle drilling machine, i, 434.
Fractional pitch change gears, i, 34.
Frames for rudders, forging, ii, 245, 246.
of machinery, erecting, ii, 176.
Freezing, preventing an engine from, ii, 386.
French gear-cutting machine, ii, 56-61.
Friction clutches, ii, 192.
experiments on, ii, 154.
of jamb dies, i, 98.
plane surfaces, ii, 135.
slide valves, ii, 443.
taper taps, i, 103.
tap threads, i, 108.
wheels, i, 77.
for feed motion, i, 78.
materials for, i, 77.
paper, i, 78.
to reduce journal strain, i, 79.
Friezing machines, cutters for, ii, 340.
or moulding machines, ii, 334, 339.
Front rake of twist drills, ii, 44.
tools for brass work, i, 264.
rake and clearance of, i, 254.
Fullers, blacksmith’s, ii, 230.
Furnaces for scrap iron, ii, 247.
G
Galvanized iron, gauge for, i, 387.
Gang edging machines, ii, 301.
Gang or composite cutters, ii, 23.
Gap, or break lathe, i, 151.
Gas pipe, dies for, i, 101.
Gauge cocks for boiler, ii, 368.
Gauges, i, 356-359.
adjustable, i, 377.
cropping, use of, ii, 296.
cutting, ii, 274.
for American sheet zinc, i, 387.
circular saws, ii, 287.
cutting tools, i, 92.
galvanized iron, i, 387.
lathe work, i, 359.
marking wood, ii, 274.
music wire, i, 386.
planer tools, i, 423.
planing V-guideways, i, 421.
Russian sheet iron, i, 387.
setting over taper work, i, 313.
shrinkage fits, i, 367.
threading tools, i, 266.
woodworking machine, ii, 295.
forms of laps for, i, 310.
hexagon, i, 381.
instrument, standard, i, 96.
mitre, use of, ii, 294.
mortise, ii, 274.
[II-480]notch
wire, i, 384.
plug and collar, comparing, i, 356.
screw thread, producing, i, 92.
standard for taper work, i, 316.
standard, comparing, i, 356.
surface, i, 378.
vacuum, i, 444.
wire, i, 387.
Gauging the pitch of threads, after hardening, i, 108.
Gear cutter, automatic, ii, 55.
cutting engine, vertical spindle, ii, 56.
machine, half-automatic, ii, 56.
machine, French, ii, 56-61.
table of index holes for, i, 417.
racks, i, 77.
Gear-teeth, i, 73.
arc of approaching contact, i, 16.
of receding contact, i, 16.
pitch of, i, 2.
calculating strength of, i, 65.
chord pitch of, i, 2.
curve of, for bevel gear, i, 22.
curves, templates for rolling, i, 43.
cutting by hand, i, 62.
cutting templates for, i, 35.
elliptical, i, 70.
depth or height of, i, 1.
errors produced by wear, i, 18.
faces of, i, 1.
factors of safety for, i, 64.
flank contact of, i, 18.
depth or height, i, 1.
flanks of, i, 1.
forms of template for, i, 44.
generating involute curves, i, 31.
helical, i, 69.
line of centres of, i, 2.
pitch line of, i, 2.
point of, i, 2.
requirements of curves, i, 7.
revolving cutters for, i, 37.
rolling and sliding motion of, i, 16.
curves for, i, 43.
strength of, i, 65.
table of cutters for, i, 41.
variation of curve, i, 12.
of shape, i, 16.
Gear-wheels, i, 1.
angular velocity of, i, 6.
bevel, i, 21.
drawing for built-up, i, 61.
pinion, drawings for, i, 59.
calculating revolutions of, i, 5.
chord pitch, i, 3.
cogged, i, 63.
cogs, i, 67.
durability of, i, 66.
diameters of pitch circles of, i, 4.
drawings for, i, 59.
driver and follower, i, 3.
for rapid increase of motion, i, 75.
reciprocating motion, i, 77.
reversing motion, i, 75.
steering steam fire engines, i, 75.
variable motion, i, 74.
generating curves for, i, 11.
hunting tooth in, i, 7.
interchangeable gearing, i, 16.
internal, compared with spur, i, 25.
or annular, i, 23 to 27.
making cogs for, i, 63.
mortised, i, 63.
motion at a right angle, i, 69.
patterns, i, 54-61.
power of, ii, 406.
transmitted by, i, 5.
skew bevel, i, 61.
spacing teeth on, i, 58.
stop motion of, i, 7.
strength of, i, 66.
table of pitches, i, 3.
table giving strength of, i, 67.
thickness of, i, 66.
tracing path of contact, i, 13.
value of cutters, table, i, 41.
various applications of, i, 74.
velocity of, uniform, i, 16.
with dovetail teeth, i, 60.
involute teeth, i, 31-34.
stepped teeth, i, 69.
Gear-worm or endless screw, i, 62.
Gears, for screw cutting, i, 320.
Generating the involute curve, i, 31.
German bit, i, 452.
Gibbed elevating slide-rest, i, 169.
Gimlet bit, i, 452.
Gland patterns, ii, 275.
Globe valve patterns, ii, 281, 282.
Gonzenback’s cut-off valve, ii, 378.
Gouge for wood, ii, 272.
use of, i, 338.
Governors, dancing, ii, 384.
fly ball or throttling, ii, 384.
for automatic engines, ii, 427, 428.
for stationary engines, ii, 425, 426.
isochronal, ii, 384.
Sawyer’s valve for, ii, 384.
speed of, ii, 384.
speeders for, ii, 384.
spring, adjustment of, ii, 386.
Grate bars, cleaning, ii, 368.
Grades of emery wheels, ii, 38.
Graduations of planer heads, i, 412.
Grain side of leather, weakness of, ii, 208.
Graver, i, 330.
Grinder, emery, for axle boxes, ii, 45.
for engine guide bars, ii, 45.
Grinder for planing machine cutters, ii, 46.
for rough work, ii, 46.
for true surfaces, ii, 45.
Grinding clamps for lathe work, i, 311.
cocks and plugs, ii, 145.
operations, ii, 38.
taper cutters, ii, 33.
taper work, i, 313.
teeth of reamers, i, 282.
teeth of spiral cutters, ii, 36.
thin cutters, ii, 33.
twist drills by hand, i, 279.
universal, i, 195.
with elevating rest, i, 194.
with traversing wheel, ii, 46.
Grinding-lathes, i, 193.
for calendar rolls, i, 199.
construction of tailstock, i, 200.
special chuck for, i, 196.
Grinding-machine, drill, ii, 41.
emery belt, ii, 47.
for milling cutters, ii, 32.
errors in construction, ii, 41.
Grindstones and tool grinding, ii, 51.
application of work to, ii, 53.
for saws or iron plates, ii, 52.
wood-working tools, ii, 52.
hacking, ii, 53.
speeds of, ii, 52.
traversing device for, ii, 53.
truing device for, ii, 53.
various kinds of, ii, 51, 52.
Gripping devices, ii, 227.
Groove cams, i, 84.
proper construction of, i, 84.
wear of, i, 84.
with double roller, i, 84.
Groove cutting, angular cutters, ii, 27.
Grooved friction wheels, wear of, i, 79.
Grooves, producing different shapes with same cutter, ii, 29, 30.
right and left-hand, ii, 29.
Groubet files, ii, 87.
Ground joint, ii, 137.
Guide-bars, ii, 375.
setting by stretched lines, ii, 163.
Guide pulleys for belts, ii, 211.
Guide for centre punches, i, 301.
Guideways, flat, i, 414.
planing, i, 422.
Guides for band saws, ii, 311.
Gumming or gulleting, ii, 290.
H
Hacking grindstones, ii, 53.
Hack saw, ii, 97.
Half-round bit for true work, i, 281.
for wrought iron or steel, i, 281.
or pod auger, i, 281.
reamers, ii, 99.
with adjustable cutter, i, 281.
Hammer, ii, 64.
blow, effects of, ii, 65, 69.
coopers’, ii, 71, 72.
cushioned, ii, 252.
dog-head, ii, 69.
drop, ii, 255.
eyes, shapes of, ii, 66.
foot power, ii, 252.
forging, methods, ii, 242.
file cutters’, ii, 71.
handles, putting in, ii, 67.
machinists’ hand, ii, 66.
paning or pening, ii, 68.
plate and saw makers’, ii, 68.
power, ii, 252.
riveters’, ii, 71.
sledge, machinists’, ii, 71.
steam, ii, 256-259.
trip, ii, 254.
Hand bolt threading machine, i, 97.
device to straighten lathe work, i, 305.
drilling machine, i, 459.
finishing tool, i, 331.
hammers, machinists’, ii, 66.
lathe, i, 130.
watch manufacturers’, i, 191.
milling machine, ii, 1.
planer, i, 391.
reamers, ii, 98.
shaping machine, i, 392.
side tools, i, 331.
tools for brass-work, i, 332.
round nosed, for iron, i, 331.
screw cutting, i, 96.
threading machine, head, i, 465.
turning, i, 330.
vise, ii, 104.
work, swages for, ii, 230.
Handles for chisels, ii, 271.
of files, putting on, ii, 92.
of hammers, putting in, ii, 67.
Hangers, shafting, forms of, ii, 192.
wall, ii, 194.
Hardening, case, ii, 128, 442.
outside, ii, 462.
saws, ii, 462.
to resist wear, ii, 460.
increase elasticity, ii, 460.
provide a cutting edge, ii, 460.
Hard metal, drilling, i, 444.
Head boring, i, 288.
with nut feed, i, 291.
Heads, construction of, i, 408.
double for planing machines, i, 404.
Heads for match board grooves, ii, 337, 338.
for tenoning machines, ii, 345.
of the rapid machines, i, 468.
planer, feed motions for, i, 414.
safety devices for, i, 413.
V-guideways for, i, 414.
Headstock lathe, construction, i, 153.
of engine lathes, i, 134.
grinding lathes, i, 200.
special lathe, i, 144.
Heat, ii, 410.
conversion of, into work, ii, 411.
latent, ii, 410.
radiation of, ii, 412.
Heaters for fire engines, ii, 432, 433.
Heating and knocking, ii, 164.
feed-water, ii, 370.
showing the causes of, ii, 168.
Heavy oil for hot bearings, ii, 386.
Heel tool, i, 330.
Height of lathe tools, ii, 260.
of vise jaws, i, 62.
Helical teeth, cutting in the lathe, i, 69.
Herring-bone gear-teeth, i, 69.
Hexagon gauge, i, 381.
Hide, parts of, used for belting, ii, 208.
High pressure steam engine, ii, 372.
High speed automatic engines, ii, 427.
Hobbing dies, methods of, i, 473.
Hob for threading dies, i, 474.
Hobs and their uses, i, 335.
for cutting up dies, i, 99.
threading dies, i, 474.
Hoe, ii, 369.
Holders, for chasers, i, 268.
for fly cutters, ii, 22.
octagon boring tools, i, 175.
Holding chisels, ii, 74.
Hollow work, centres for, i, 226.
Hook bolts, i, 113.
Hooks, belt, ii, 216.
Horizontal boring machine, i, 433.
Horse-power, from diagram, ii, 418.
of an engine, calculating, ii, 407, 419.
testing, ii, 408.
Horseshoes, finishing, machine for, ii, 262, 263.
Horizontal tubular boiler, ii, 361-366.
saw frame, ii, 312.
Hydraulic fits, allowance for, i, 365.
parallel holes and taper plugs for, i, 365.
forging, ii, 260.
press, ii, 260.
pressure, i, 366.
Hypocycloidal curves, i, 8.
I
Inclination of skew bevel teeth, i, 61.
Index plate of milling machine, ii, 7.
Index wheel, originating, i, 342, 353.
Indicator, ii, 413.
attachment of, to engine, ii, 416.
diagram, area of the, ii, 419.
diagrams, ii, 414.
defective, ii, 421.
expansion curve, ii, 417, 418.
springs, ii, 416.
vacuum line, ii, 415.
Injector, feed, ii, 370.
for locomotives, ii, 395.
Inside calipers, i, 360.
chasers, i, 335.
errors in cutting up, i, 337.
Interchangeable gearing, i, 16.
Intermediate gears, i, 3.
wheels, i, 319.
rolling circle, i, 24.
Internal gear wheels, i, 23-27.
strains in cast iron work, i, 306.
threading tools, i, 264.
wheels, i, 23.
Involute curves for gear teeth, i, 8.
teeth, advantages of, i, 34.
Iron and steel welding, ii, 234.
bending, ii, 240.
devices, ii, 240.
galvanized, gauge for, i, 387.
planer, erecting an, ii, 179.
foundation for, ii, 180.
plates, grindstones for, ii, 52.
testing, ii, 226.
Irregular forms, lathes for, i, 210.
motion, cams for, i, 80.
work, turning, i, 326.
Isochronal governors, ii, 384.
J
Jacketed cylinders, ii, 374.
Jam dies, i, 98.
nuts, i, 119.
Jeweller’s rests for lathes, i, 189.
Jigs, designing, i, 440.
errors in, limit of, i, 439.
for cutting out steam ports, i, 441.
drilling engine cylinders, i, 440.
drilling machines, i, 439.
simple work, i, 440.
Jointing machines, ii, 338.
Joints, boiler fitting, ii, 140.
butt, boiler, ii, 352.
cylinder cover, ii, 137.
dovetail, ii, 275.
easily removable, ii, 141.
expansion, ii, 140.
for boiler work, ii, 352.
rough surfaces, ii, 138.
gauze, ii, 138.
ground, ii, 137.
half check, ii, 275.
lap, boiler, ii, 352.
mitre, ii, 275.
mortise, ii, 274.
open, for wear, ii, 121.
riveted, proportioning, ii, 355, 356.
rubber, ii, 139.
rust or caulked, ii, 141.
scraped, ii, 137.
tenon, ii, 274.
thimble, ii, 141.
to withstand great heat, ii, 138.
water, ii, 138.
Joule’s equivalent, ii, 411.
K
Key seats, cutting, ii, 101.
Keys and gibs, fitting, ii, 120.
bearing surfaces of, i, 126.
draught of, i, 127.
forms of, i, 126.
for parallel rods, i, 128.
seating rule, i, 378; ii, 101.
with set-screws, i, 127.
Keyway calipers, i, 363.
Keyways, cutting by hand, ii, 101, 108.
cutting out by drifts, ii, 109.
Knife blade rolls, ii, 261.
files, ii, 91.
Knives for balanced heads, ii, 324-326.
for jointing machines, ii, 338.
moulding machines, ii, 336-340.
moulding, scale for shapes of, ii, 83.
Knurling tool, improved forms of, i, 328.
L
Lap joint, boiler, ii, 352.
of Corliss engine valve, ii, 426.
Latent heat, ii, 410.
Lathe, advantages of, i, 129.
apron, i, 138.
feed motion for, i, 168.
back gear, i, 144.
bench, i, 130.
boring devices for, i, 288.
tools, shapes of, i, 285.
break, i, 151.
capacity, i, 130.
carriage, i, 145.
feed motion for, i, 37.
testing, ii, 182.
carriers, i, 222.
centre drilling attachment, i, 300.
centres, i, 290.
removing, i, 159.
shapes of, i, 299.
testing, i, 298.
change wheels for, i, 139.
chucks for, i, 188.
chucking for boring purposes, i, 152.
clamps, i, 223.
classification of, i, 129.
cutting fractional threads on, i, 181.
helical teeth in the, i, 69.
screws in the, i, 319.
cutting-off machine, i, 193.
cylinder boring, i, 219.
dogs, various kinds of simple, i, 222.
drivers, i, 222.
English chucking, i, 149, 150.
erecting a, ii, 180.
extension, i, 151.
face-plates, i, 243.
chucking, i, 246.
clamps for, i, 245.
errors in, i, 143.
for wood work, i, 247.
feed-motions, i, 144.
feed-screw, i, 175.
feed, spindle for, i, 139.
filing, fixtures for, i, 189.
fit of the live spindle of a, i, 157.
fitting up, ii, 180.
foot, i, 130.
for axe handles, i, 210.
engine cylinders, i, 219.
irregular forms, i, 210.
taper turning, i, 142.
turning crank shafts, i, 152, 154.
turning wheel hubs, i, 221.
gap, i, 151.
grinding, i, 193.
universal, i, 195.
with elevating rest, i, 194.
hand, i, 130.
headstock, construction of, i, 153.
importance and advantages of, i, 129.
jewellers’, rest for, i, 189.
locking spindles of, i, 186.
lead-screw, i, 175.
bearings for, i, 139.
nuts for, i, 140.
supporting long, i, 176.
mandrels, drivers for, i, 227.
expanding, i, 227.
for eccentric work, i, 229.
nuts, i, 229.
threaded work, i, 228.
tubular work, i, 227.
forms of, i, 229.
[II-481]with
expanding cones, i, 278.
with expanding pieces, i, 228.
motions for turning cams, i, 326.
open spindle, tailstocks for, i, 189.
pattern makers’, i, 148.
pulley, i, 150.
screws, errors of pitch, i, 79.
screw slotting, i, 192.
self-acting, English, i, 148.
shears, the legs of, i, 184.
various forms of, i, 183.
methods of ribbing, i, 184.
or beds, i, 182.
with flat slides, i, 183.
V and flat slides, i, 183.
V slides, i, 183.
sizes of, i, 130.
slide-rest for, i, 131, 145.
lost motion of, i, 133.
special chucks for, i, 190.
swing frames, i, 158.
tailblock, i, 185.
setting over, for tapers, i, 136.
various methods of testing, i, 187.
wear of the spindles of, i, 185.
with rapid spindle motion, i, 185.
releasing devices, i, 185.
testing, i, 186.
instruments for, ii, 182.
tool-holders for outside work, i, 270.
with clamp, i, 271.
tools, angle of clearance of, i, 257.
height of, i, 260.
shapes of, i, 254.
watchmakers’, i, 188.
with compound slide-rest, i, 140-143.
elevating rest, i, 194.
flat chucking surface, i, 143.
rapid spindle motion, i, 185.
sliding heads, i, 290.
variable speed, i, 192.
wooden bed, i, 149.
work, boring tools for, i, 285.
burnishing, i, 311.
chisels for, i, 339.
countersinks for, i, 302.
end measurements of, i, 376.
filing, i, 308.
flat drills for, i, 280.
holders for, i, 281.
forms of countersink for, i, 302.
gauge for, i, 359.
grinding clamps for, i, 311.
holding straps for, i, 244.
mandrels or arbors for, i, 227.
method of polishing, i, 308.
polishing clamps for, i, 311.
side tools for, i, 261.
technical terms used in, i, 296.
use of emery paper on, i, 308.
Lead-lined brasses, ii, 149, 386.
Lead of a valve, adjusting the, ii, 386.
Lead of slide valves, ii, 376.
Lead-screw, bearings for, i, 139.
conveying motion to the, i, 147.
nuts, i, 180.
for lathes, i, 175.
forms of threads of, i, 177.
long supporting, i, 176.
swing frame for, i, 139.
with three threads per inch, i, 177.
five threads per inch, i, 178.
Leather, grain side, weak, ii, 208.
Left-hand threads, cutting, i, 322.
Leg vise with parallel motion, ii, 63.
Lever feed drilling machine, i, 428.
drilling, for blacksmiths, i, 457.
principles of, ii, 405.
Lift and force pumps, ii, 387.
Line of contact of skew bevel gear wheels, i, 61.
Line shafts, couplings for, ii, 194.
Line shafting, diameters of, ii, 189.
ordinary, ii, 186.
setting in line, ii, 184, 185.
sizes of, ii, 186.
the strength of, ii, 189.
Lined boxes, babbitt metal, ii, 155.
Lining connecting rod brasses, ii, 126.
Link-motion, gear, ii, 383.
fitting up, ii, 127.
for expansion engines, ii, 438.
for marine engines, ii, 443.
quick return shaper, i, 399.
setting the valves for, ii, 383.
the action of, ii, 383.
Link slot, templates for filing, ii, 127.
Lip drill, i, 443.
Live centres, tapers for, i, 159.
spindle, end adjustment of, i, 158.
wear of bearings, i, 158.
with coned journals, i, 157.
Locking, differential threads for, i, 119.
Lock work, drilling device for, i, 459.
Locomotive ash pan, ii, 390.
automatic air brake, ii, 390, 398.
axle boxes, ii, 147.
blower, ii, 390.
boiler and frames, ii, 389.
connecting-rod, ii, 116.
freight engine, ii, 389-404.
injector, ii, 395.
link motion, ii, 391-393.
passenger engine, ii, 390.
reversing gear, ii, 391.
sand valves, ii, 390.
safety and pop valves, ii, 389.
Locomotive wheel forging, ii, 244.
yoke and guide bars, ii, 389.
Longevity of lubricants, ii, 153.
Lost motion in valve setting, ii, 174.
Low water in boilers, ii, 370.
Lubricants, longevity of, ii, 153.
qualities of, ii, 152.
testing, ii, 152.
Lubricators, steam, ii, 444.
M
Machine centre drilling, i, 300.
cross cutting or gaining, ii, 305, 306.
for cutting mitre joint, ii, 338.
finishing horseshoes, ii, 262.
forging threads, ii, 261, 262.
gang edging, ii, 301.
gumming or gulleting, ii, 290.
horizontal saw frame, ii, 313.
moulding, ii, 334.
scroll sawing, ii, 306.
Machinery for wood working, ii, 287.
Machinists’ chisels, applications, ii, 76.
hand hammers, ii, 66.
sledge hammer, ii, 71.
Main bearings, adjusting, ii, 386.
Mallet, ii, 72.
Mandrels, expanding, i, 227.
for threaded work, i, 228.
lathe, i, 227.
expanding, i, 228.
for eccentric work, i, 229.
for nuts, forms of, i, 229.
with expanding cones, i, 228.
with expanding pieces, i, 228.
or arbors for lathe work, i, 227.
Mangle gearing, various forms of, i, 76.
Manufacturers’ temper, ii, 460.
Marine-engine boilers, ii, 436, 437.
connecting-rod, ii, 116.
link motion, ii, 443.
pumps, ii, 436.
valves, ii, 444.
Marine engines, pipes of, ii, 445.
various, ii, 434.
Marriotte’s law, ii, 411.
Matched cutters, ii, 23.
Matching and planing machines, ii, 326.
Mean effective steam pressure, ii, 420.
Measurements, the standards of, in various countries, i, 341.
Measuring by sight, and feeling, i, 341.
machine for sheet metal, i, 348.
special, i, 342-346.
tools, classification of, i, 354.
valve lead, ii, 173.
Mechanical equivalent of heat, ii, 411.
powers, ii, 405.
Metal, soft, files for, ii, 95.
Metric pitch screws, i, 322.
Meyer’s cut-off valve, ii, 378.
Micrometer caliper, i, 354.
gauge for thread angles, i, 91.
Mill boring, i, 211.
turning, i, 211.
Milling-cutters, grinding, ii, 32.
or mills, ii, 16.
with inserted teeth, ii, 24.
Milling-machine, ii, 1-16.
advantages of, ii, 1.
chucks for, ii, 31.
cam cutting attachment, ii, 12.
cutters, ii, 17-31.
double-spindle, ii, 16.
fixtures for, ii, 10.
hand, i, 410.
head for spiral cutting, ii, 12.
holding work on, ii, 30.
power, ii, 2.
rotary vise for, ii, 10.
universal, ii, 2, 4, 12,
15.
head and back centre, ii, 10.
head for gear cutting, ii, 11.
vertical, ii, 31.
Milling or knurling tools, i, 328.
Milling taper work, ii, 30.
Mitre gauge, use of, ii, 295.
joint, ii, 275.
machine, ii, 338.
wheels, i, 1.
Monkey wrench, i, 125.
Mortise gauge, ii, 274.
Mortised gear-wheels, i, 63.
Mortising machines, ii, 344.
Moulding knives, scale for marking out the necessary shapes of, ii, 83.
Moulding-machines, ii, 334, 339.
cutters for, ii, 336, 337,
341.
Muffle, ii, 461.
Mule pulleys for belts, ii, 211.
Music wire, gauge for, i, 386.
N
Nail bit, i, 452.
Nail forging machines, ii, 261.
Non-condensing engine, ii, 372.
Nose bit, i, 453.
Notch wire gauges, i, 384.
Number of cutters used for a train of wheels, i, 41.
of cutters on boring bars, i, 290.
of cutting edges on taps, i, 105.
of cutting edges on reamers, i, 282.
Nut-tapping-machine, i, 475.
automatic socket for, i, 475.
rotary, i, 475.
three-spindle, i, 475.
Nuts, filing, ii, 105.
jam, i, 119.
lock, i, 119.
lost motion in, i, 120.
removing corroded, i, 122.
securing by cotters, i, 121.
by notched plates, i, 121.
by taper pins, i, 121.
devices, i, 120.
steam tight, the forms of, i, 118.
taking up the wear of, i, 120.
O
Odontograph, using, i, 47, 49.
Oil and lubrication, ii, 151.
cavities for brasses, ii, 150.
groove or curved chisel, ii, 76.
for brasses, ii, 150.
heavy, for hot bearings, ii, 386.
stones, truing, ii, 54.
various kinds of, ii, 54.
test, Swiss, ii, 153.
Oiling apparatus, ii, 439, 440.
devices for planer beds, i, 416.
true surfaces, ii, 135.
Oils, testing for acids, ii, 153.
testing for salts, ii, 153.
Oilstoning edge tools, ii, 54.
Open brasses, ii, 149.
sided shafting hangers, ii, 193.
spindle lathes, tailstocks for, i, 187.
Originating angles for screw threads, i, 92.
cams, i, 326.
fly cutters, ii, 21.
gear teeth, i, chaps. I, II,
III.
index wheels, i, 345.
surface plates, ii, 135.
templates for screw threads, i, 92.
Outside and inside chasers, i, 335.
calipers, making, ii, 105.
the various forms of, i, 360.
threads, starting, i, 338.
P
Paning or pening, ii, 72.
hammers, ii, 68.
Pantagraph engine for dressing the cutters for gear teeth, i, 38.
motions, ii, 417.
Paper friction wheel, i, 78.
Parallel cutters, grinding, ii, 32.
holes and taper plugs for hydraulic fits, i, 365.
rods, keys for, i, 128.
Paring chisels, ii, 271.
Patching broken frames, ii, 178.
Path of gear tooth contact, i, 13, 16.
Pattern lathe, brake for, i, 149.
slide-rest for, i, 149.
with wooden bed, i, 149.
Pattern-makers’ lathe, i, 148.
pipe gauge, i, 379.
Pattern-making, woods for, ii, 264.
Patterns, building up, ii, 278.
brasses, proper shape for, ii, 132.
choice of wood for, ii, 264, 265.
for angle pipe, ii, 284, 285.
glands, ii, 275.
globe valves, ii, 281, 282.
pillow blocks, ii, 277.
pipes, ii, 280, 281.
pulleys, ii, 278, 279.
spacing gear-wheel teeth on, i, 58.
Pattern-wheel scale, i, 51.
Pening or paning, ii, 72.
Piaté gear cutting machine, ii, 56-61.
Pillow-block casting, ii, 277.
fitting brasses to, ii, 131.
for shafting, ii, 194.
patterns, ii, 277.
Pinion bevel, drawings for, i, 59.
with dovetail teeth, i, 60.
Pins, securing, for adjustment, i, 121.
filing, ii, 103.
fitting in double eyes, i, 121.
fixed, i, 122.
taper, i, 128.
working, i, 122.
wrench, i, 126.
Pipe cutters, ii, 142.
gauge, pattern-makers’, i, 379.
patterns, ii, 280, 281.
threads, taper for, i, 95.
tongs, ii, 143.
vises, ii, 142.
work, erecting, ii, 144.
Pipe-threading by hand, i, 463.
by power, i, 463.
machine, i, 475-477.
machines, construction of, i, 463.
Piston valves, ii, 378.
Pitch, alteration in hardening, i, 108.
circle, the diameter of, i, 1.
correcting the errors of, i, 109.
gauging the, after hardening, i, 108.
line of cams, i, 80.
lines of elliptical gear-teeth, i, 70.
number of teeth, and pitch diameter, i, 68.
of screw threads, i, 85.
Pitch of teeth for band saws, ii, 305.
Pivoted arms for tooth templates, i, 44.
Plane blades, ii, 77.
blades, finding shapes of, for mouldings, ii, 78-83.
Planer beds, flat guideways for, i, 414.
beds, oiling devices for, i, 416.
centres, i, 408.
chuck, for curved work, i, 420.
chucking halves of pulleys on, i, 423.
chucks, i, 419.
for spiral grooved work, i, 419.
for timber, ii, 330, 331.
head slides, wear of, i, 410.
or iron planing machine, i, 402.
shapers, reversing, i, 398, 399.
swivel heads for, i, 411.
swivelling tool holder, i, 411.
tool, aprons for, i, 411.
heads, feed motions for, i, 414.
graduations of, i, 390.
safety devices for, i, 413.
V-guideways for, i, 414.
tables, angle plates for, i, 418.
chucking devices for, i, 422.
chucking machine beds on, i, 421.
forms of bolts for, i, 417.
supplementary tables for, i, 417.
tool-holder, applications of, i, 425.
with tool post, i, 425.
examples of application of, i, 426.
simple form of, i, 426.
tools for coarse finishing feeds, i, 423.
for slotted work, i, 424.
clearance of, i, 424.
shapes of, i, 423.
gauge for, i, 423.
Planes, ii, 267-270.
circular, ii, 268.
combination, ii, 269.
compass, ii, 268.
core-box, ii, 269.
for pattern making, ii, 268, 269.
fore, ii, 268.
grinding of, ii, 267.
jack, ii, 267.
oilstoning of, ii, 267.
rabetting, ii, 268.
Plane surfaces, friction of, ii, 135.
Planet motion, i, 75.
Planimeter, ii, 420.
Planing and matching machine, ii, 326.
curved work, i, 420.
guideways, i, 421.
Planing-machine, i, 406-426.
gear, ii, 56.
large, chucks for, i, 423.
motions of, i, 402, 403.
tables, i, 414.
tables, slots and holes in, i, 415.
with double heads, i, 404.
wood, ii, 326.
Plate couplings, ii, 196.
straightener’s hammers, ii, 68.
Plates, angle, for planer tables, i, 418.
iron, grindstones for, ii, 52.
saw, grindstones for, ii, 52.
straightening, ii, 69.
Plug and collar gauges, i, 357.
Plug gauges for threads, i, 91.
Plumb level, ii, 136.
rule, ii, 136.
Point of compression, ii, 376.
cut off, ii, 376.
release, ii, 376.
Poker, ii, 369.
Polishing clamps, i, 311.
device for engraver’s plates, ii, 51.
materials, for brush wheels, ii, 50.
for polishing wheels, ii, 50.
for rag wheels, ii, 51.
wheels, ii, 49-51.
construction of, ii, 49.
emery charging, ii, 50.
for brass work, ii, 50.
lapping leather on, ii, 49.
large, keeping true, ii, 50.
materials for, ii, 50.
rag, ii, 51.
speed of, ii, 50.
Polygons, measuring sides, ii, 283.
Pony planer, ii, 323.
Position of emery wheel, ii, 35-37.
of dies in bolt cutting, i, 473.
of taper pins for locking, i, 128.
Positive feed, gear cutter, ii, 55.
Pounding, the causes of, ii, 168.
Power drilling machine, i, 428.
hammer, ii, 252.
lathes, i, 130.
milling machine, i, 470.
of an engine, testing, ii, 408.
threading machine, i, 465.
Powers, mechanical, ii, 405.
Preserving wood, ii, 264.
Press for forging, ii, 260.
Pressure and volume of steam, ii, 411.
Priming, its causes and prevention, ii, 370.
Profiling machine, ii, 31, 32.
Protractors, bevel, i, 380.
Propeller, screw, ii, 445.
Pulley arms, ii, 280.
Pulley balancing, device for, ii, 203.
boring machine, i, 438.
considered as a lever, ii, 405.
diameter, change for grindstone speed, ii, 52.
[II-482]crowned,
ii, 201.
expansion, ii, 200.
lathe, i, 150.
patterns for, ii, 278.
self-oiling, ii, 200.
solid and split, ii, 200.
calculating speeds of, ii, 204.
transmitting power of, ii, 204.
turning, i, 318.
turning, special lathe for, i, 211.
wood, ii, 200.
Pump air chambers, ii, 388.
capacity of, ii, 388.
displacement, ii, 387.
plunger, ii, 387.
principles of action of, ii, 387.
Pumps belt, ii, 388.
for circulating, ii, 440.
double acting, ii, 387.
lift and force, ii, 387.
for marine engines, ii, 436.
regulating, ii, 388.
rotary, ii, 387.
single acting, ii, 387.
Q
Quartering machine, i, 434.
Questions for Engineers, ii, 467.
Quick removal, bolts for, i, 116.
Quick-return motion, Whitworth’s, i, 401.
shapers, link motion for, i, 399.
R
Rabbet planes, ii, 269.
Rack and pinion wheel, i, 1.
Rack feed saw bench, ii, 301.
Radial drilling machines, i, 430, 431.
Radiation of heat, ii, 412.
Rag polishing wheels, ii, 51.
wheel, polishing materials for, ii, 51.
Raised V-guideways, lathes with, i, 182.
Rake, ii, 369.
Ramsden’s dividing engine, i, 349.
Rasps, kinds and cut of, ii, 87.
Ratchet brace, i, 457.
feeds, i, 173.
Rates of feed for finishing cuts, i, 307.
Reamers, adjustable, ii, 99.
chucking, i, 280.
chucking for true work, i, 283.
for framing, ii, 99.
grinding the teeth of, i, 282.
half-round, ii, 99.
hand, ii, 98.
number of teeth for, i, 282.
rose-bit or rose, i, 283.
shell, i, 283.
shell rose, i, 284.
spacing the teeth of, i, 282.
spiral teeth for, i, 282.
square, ii, 99.
taper, ii, 99.
Reamer-pin, with facing tool, i, 449.
Reamer-teeth, odd or even, i, 282.
spacing of, i, 282.
Reaper-files, ii, 91.
Reboring cylinders in place, ii, 160.
Recentring turned work, i, 304.
Recessed emery wheels, ii, 47.
Reciprocating motion, gear for, i, 77.
Red marking for vise work, ii, 96.
Reducing knife, i, 209.
Reduction of temper, ii, 461.
Refitting leaky cocks and plugs, ii, 144.
Regulating pumps, ii, 388.
Release, the point of, ii, 376.
Releasing devices, tailblock with, i, 185.
Relief feed valve, ii, 441.
Removing corroded bolts, i, 122.
corroded nuts, i, 122.
featheredge, ii, 54.
Repairing broken frames, ii, 178.
connecting rods, ii, 124.
Resharpening files, ii, 95.
Rests, follower, i, 234.
Return cams, designing, i, 82.
motions compared, i, 401.
Reversible jawed chucks, i, 237.
Revolving cutters for gear teeth, i, 37.
Ribbing lathe shears, i, 184.
Right and left angular cutters, ii, 18.
and left hand cutters, ii, 18.
Ring work, expanding chucks for, i, 241.
Rings, welding, ii, 235.
Rivet diameters, ii, 356.
Riveter’s hammer, ii, 71.
Riveting crank pins, ii, 73.
Riveted-joints, forms of, ii, 352.
proportioning, ii, 354-356.
strength of, ii, 354.
unevenly spaced rivets, ii, 353.
Rivets, diagonal pitch of, ii, 353.
spacing of, ii, 353.
Rod-feed for screw machines, i, 206.
Roll-feed circular saw, ii, 298-300.
wood planing machine, ii, 317.
Rolling motion of gear teeth, i, 16, 27.
Rolling-circles, by using two, the pinion may contain but one tooth less than the wheel, i, 26.
circles for internal gearing, i, 25.
curves for gear teeth, i, 43.
Roll-turning lathe, i, 215.
lathe, tools for, i, 216.
calender, method of driving, i, 200.
Rolls for knife blades, ii, 261.
Rope socket, forging, ii, 243.
Rose-bit or rose reamers, i, 283.
Rotary nut tapping machine, i, 475.
planing machine, i, 395.
pumps, ii, 387.
Roughing cuts, feeds for, i, 306.
Rough surfaces, joints for, ii, 138.
Round corners, filing out, ii, 95.
files, using of, ii, 95.
half-round, three-square files, ii, 90.
Round-nosed chisels, ii, 75.
tools, i, 258.
Rudder frame, forging, ii, 245.
Rule for finding horse-power, ii, 418.
for locating pitch line of worm, i, 29.
for finding the chord pitch, diametral pitch, and arc pitch, i, 3.
for proportioning the steps of the driving cone, i, 159, 161.
Russian sheet iron, gauge for, i, 387.
Rust or caulked joints, ii, 140.
S
Safety devices for planer heads, i, 413.
Safety-valve, the inspection of, ii, 368.
calculations for, ii, 409.
Sag of belts, ii, 210.
Salts and acids, testing oils for, ii, 153.
Sand blast process, ii, 96.
Sand-papering machines, ii, 347-349.
Saturated steam, ii, 410.
Saw bench, rack feed, ii, 301.
frame, horizontal, ii, 312.
hack, ii, 97.
hammering, ii, 70, 71.
machine, tubular, ii, 305.
machines, re-sawing band, ii, 310.
maker’s hammer, ii, 68.
plates, grindstones for, ii, 52.
straightening, ii, 70, 71.
teeth, shapes of, ii, 273, 287.
Sawing hot iron, ii, 263.
Saws, chisel teeth for, ii, 290.
concave, ii, 287, 288.
cross-cut, ii, 272, 273.
for swing frame, ii, 292.
grindstones for, ii, 52.
hardening, ii, 462.
heating of circular, ii, 288.
insertion of teeth in, ii, 290.
rip, ii, 272, 273.
sharpening the teeth of, ii, 290.
shingle, ii, 287, 288.
stiffening, ii, 463.
tension of, ii, 288.
truth of circular, ii, 288.
Sawyer’s valve for governors, ii, 384.
Scale for moulding knives, ii, 83.
of tooth proportions, i, 54.
Scraped joint making, ii, 137.
Scrapers, angles for facets of, ii, 97.
applications of, i, 332.
for finishing, i, 307.
for true surfaces, ii, 97.
various forms of, ii, 97.
Scraping out cylinder heads, ii, 160.
Scrap iron, furnaces, ii, 247.
welding, ii, 247.
Screw-cutting, driver for, i, 223.
face plate for, i, 223.
feed regulators for, i, 171.
hand tools, i, 96.
pitches, metric system, i, 322.
reversing tool traverse in, i, 168.
with hand tools, i, 334.
Screw-driver, and shape, ii, 97.
Screw-machine, box tools for, i, 208.
chuck for, i, 205.
cross-slide for, i, 205.
feed gear for, i, 205.
cutting off tool for, i, 208.
examples of use of, i, 203.
for heavy work, i, 201.
light work, i, 203, 204.
or screw making lathe, i, 200.
stop motion for, i, 206.
threading tool for, i, 208.
tool holders and tools for, i, 202.
turret of, i, 205.
with special wire feed, i, 206.
Screw-propeller, ii, 445.
Screw-slotting lathe, i, 192.
Screw-thread angles, gauge for, i, 91.
cutting tools, the wear of, i, 89.
standard forms of, i, 85, 86.
Screw-threads, alteration of shape, i, 89.
pitch of, i, 85.
requirements of, i, 86.
self-locking, i, 85.
tools for cutting, i, 87.
variation of pitch, i, 87.
Screws, i, 115.
belt, ii, 216.
set, i, 127.
variation of pitch, i, 87.
Scroll chucks, i, 238.
chuck threads, wear of, i, 238.
sawing machine, ii, 306.
Seams for boilers, forms of, ii, 352.
Securing feathers, methods of, i, 120.
devices, nut, i, 120.
pins for exact adjustments, i, 121.
Segmental circular saws, ii, 300.
Segments, for patterns, ii, 278, 279.
saw, fastening to discs, ii, 301.
Self-acting lathe, English form of, i, 148.
locking bolts, i, 117.
nuts, i, 85.
screw threads, i, 85.
Self-adjusting couplings, ii, 198.
Self-oiling pulleys, ii, 201.
Set-screws, i, 115.
application to hubs, i, 127.
Setting angular grooving cutters, ii, 28.
brasses to pillow-blocks or axle-boxes, ii, 131.
double eccentric by lines, ii, 175.
connecting-rod brasses, ii, 125.
eccentrics on crank shafts, ii, 174.
engine cylinders, ii, 159.
engine guide bars, ii, 162.
guide-bars by stretched line, ii, 163.
line shafting in line, ii, 184, 185.
locomotive slide valves, ii, 394.
numbers and tabular values for odontograph, i, 50.
over tailstock to turn tapers, i, 312.
slide valves, ii, 173.
threading tools, i, 266.
up or aligning new engines, ii, 165.
up axle box wedges, ii, 404.
up keys of connecting rods, ii, 127.
work after case hardening, ii, 129.
Settings for boilers, ii, 364.
Shaft, flexible, for driving drills, i, 459.
forging, ii, 249-252.
Shafting, collars for, ii, 189.
couplings, errors in, ii, 196.
pillow blocks for, ii, 194.
speeds for, ii, 190.
tests of, ii, 188.
turning, three-tool slide-rest, i, 143.
hangers, open-sided, ii, 193.
various forms of, ii, 192.
Shafts, sinking feathers in, ii, 101.
welding to exact lengths, ii, 234.
Shaking grate bars, ii, 369.
Shank cutters, ii, 19.
cutters, applications of, ii, 20.
feed for, ii, 20.
sizes of, ii, 21.
drill, improved form of, i, 446.
Shanks, drill, i, 445.
Shapes of boring bar cutters, i, 291.
of centres for large work, i, 299.
crowns of brasses, ii, 127.
cutting edges of chisels, ii, 74.
file teeth, ii, 85.
hammer eyes, ii, 66.
lathe boring tools, i, 285.
lathe tools, i, 254.
planer tools, i, 423.
Shaping-machine, centres for, i, 397.
crank motions for, i, 401.
general description of, i, 389.
or planer shaper, with tappet motion for reversing, i, 399.
quick return link motion, i, 399.
with traveling head, i, 397.
Shears, lathe, i, 182.
Sheet iron, gauge for, i, 387.
metal, measuring, machine for, i, 348.
zinc, gauge for, i, 387.
Shell reamers, i, 283.
reamers, arbor for, i, 283.
rose reamers, i, 284.
Shimer heads, ii, 337.
Shrinkage fits, i, 366.
gauge for, i, 367.
of iron, i, 368, 374.
system at the royal gun factory at Woolwich, i, 367.
Shrinking work, to refit it, i, 374.
Side rake in lathe tools, i, 256.
tools for lathe work, i, 261.
Siphon, ii, 443.
Size of mandrel holes for saws, ii, 287.
Sizes of lathes, i, 130.
Skew bevel gear-wheels, i, 61.
cutters, ii, 316.
knives, ii, 316.
Sledge hammer, machinist’s, ii, 71.
Slice bar, ii, 369.
Slide, construction of, i, 390.
Slide-rest, American form of, i, 132.
application of, to a crank, i, 155.
compound tool-holder for, i, 174.
detachable, i, 143.
double tool-holder for, i, 169.
English form of, i, 132.
for lathe crank turning, i, 154.
lathes, i, 131.
pattern lathe, i, 149.
special lathe, i, 145.
spherical-work, i, 133.
gibbed, elevating, i, 169.
various forms of, i, 132.
Slides of planers, construction of, i, 410.
of planer heads, wear of, i, 410.
Sliding motion of gear teeth, i, 16, 27.
motion of worm-wheel teeth, i, 28.
Slide-valve, exhaust lap of, ii, 376.
lead adjusting, ii, 386.
setting a, ii, 386, 394.
squaring, ii, 386.
the Allen, ii, 377.
the D, ii, 376.
Webb’s, ii, 377.
Slide-valves, balanced, ii, 377.
circular, ii, 377.
designing, ii, 380.
double ported, ii, 377.
Slide-valves, steam lap of, ii, 376.
the lead of, ii, 376.
Slots and holes in planing-machine tables, i, 417.
Slotted work, tools for, i, 424.
Slotting-machine, i, 459.
sectional view of, i, 460.
tool-holders, i, 460, 461.
tools, i, 461.
Snifting valve, ii, 440.
Socket forging, ii, 243, 244.
wrench, i, 125.
Sockets, drill, i, 445.
Solid and split pulleys, ii, 200.
ended connecting rods, ii, 114.
leather wheels, ii, 51.
tap wrenches, i, 110.
Spacing gear-wheel teeth, i, 57, 58.
reamer teeth, i, 282, ii, 98.
rivets in boiler seams, ii, 353.
Special chucks for watchmakers’ lathes, i, 190.
index plate for gear cutting, ii, 7.
forms of chucks, i, 241.
lathe for pulley turning, i, 211.
for wood working, i, 208.
for brass work, i, 216.
Specks in cast-iron work, i, 307.
Speeders for governors, ii, 384.
Speed of a hammer blow, effects of, ii, 65.
of automatic engines, ii, 427.
brush-wheels, ii, 50.
cutter heads or discs, ii, 338.
emery-wheels, ii, 39.
governors, ii, 384.
grindstones, ii, 52.
pulleys, calculating, ii, 204.
polishing wheels, ii, 50.
shafting, ii, 190.
Speeds and feeds for twist drills, i, 277.
for cutting wrought iron, i, 294.
Spherical work, slide-rest for, i, 133.
Spindles live, with coned journals, i, 157.
various methods of locking, i, 186.
Spiral cutters, grinding teeth of, ii, 36.
feed in cutting, ii, 27.
grooves, drill stock with, i, 445.
planer chucks for, i, 419.
springs, winding in the lathe, i, 329.
teeth for reamers, i, 282.
Spirit levels, ii, 136.
Spoon bit, i, 452.
Spring adjustment of governors, ii, 384.
calipers, i, 360.
of engine guide-bars, ii, 162.
swages for blacksmiths, ii, 231.
tools, i, 263.
Springs for indicators, ii, 416.
Spur-wheel, annular, i, 23.
compared with annular, i, 32.
construction of pattern for, i, 54.
Square work, steady rest for, i, 233.
centre, advantage of, i, 303.
various forms of, i, 303.
centring, i, 300.
holes, device for drilling, i, 450.
reamers, ii, 99.
bevel, i, 380.
shanked drills, i, 446.
the T, i, 379.
the try, i, 379.
Squaring a valve, ii, 386.
Square-threads, clearance of tools, i, 269.
cutting, i, 269.
dies for finishing, i, 270.
worms to work with, i, 29.
Stable fork, forging of, ii, 241.
Standard-cutters, ii, 17.
Standard bar for the United States standard of measurement, i, 341.
gauges, diameter of work limits the application of, i, 363.
for taper work, i, 316.
for wire, etc., i, 384.
plug and collar gauges, i, 91.
screw threads, i, 91.
sizes of washers, i, 123.
taps, i, 104.
variations in, i, 341.
Starting a slide valve engine, ii, 384.
a locomotive, ii, 400.
Stationary engine boilers, ii, 350-371.
Steady-rest, cat-head, i, 233.
clamps, i, 233.
for square and taper work, i, 232.
improved form of, i, 233.
or back rest, i, 231.
work, drivers for, i, 225.
Steam, ii, 410.
admitted to indicator, ii, 414.
amount of, used in engines, ii, 420.
engine high pressure, ii, 372.
expansion of, ii, 411.
fire engine, ii, 430, 431.
hammer forging, examples in, ii, 241.
hammers, ii, 252-259.
laps of slide valves, ii, 376.
lubricators, ii, 444.
pipe thread, tapping machine, i, 477.
pipes, dies for, i, 101.
ports, jigs for cutting out, i, 431.
pressure absolute, ii, 411.
reversing gear, locomotive, ii, 390.
saturated, ii, 410.
superheated, ii, 410.
tight nuts, i, 118.
volume and pressure of, ii, 411.
[II-483]weight
of, ii, 411.
Steaming, wood for bending, ii, 266, 267.
Steel and iron welding, ii, 233, 234.
plates, engraver’s, polishing, ii, 51.
Steering gear for fire engines, i, 75.
Stepped connecting-rod straps, ii, 117.
reamers for taper work, i, 285.
Stiffening saws, ii, 463.
Stock, adjustable, i, 448.
Stocks and dies, i, 97, 101.
for drilling machines, i, 449.
forms of, i, 101.
Stone drill, i, 454.
Stop motion for gear-wheels, i, 7.
for screw machines, i, 206.
Straight-edge and applications, i, 381.
Straightening saws, ii, 70, 71.
lathe work, device for, i, 305.
machine for bar iron, i, 304.
plates, ii, 69.
wire, check for, i, 305.
work by pening, ii, 72.
Straight-line-engine, automatic, ii, 428.
important details of, ii, 429, 430.
Strains on boiler shells, ii, 351.
Strap ended connecting rod, ii, 116.
Straps, connecting rod, ii, 115.
connecting rod, fitting, ii, 120.
Strength of boiler plate, ii, 350.
boiler shells, ii, 350.
gear-wheel cogs, i, 66.
gear-wheel teeth, i, 64.
line shafting, ii, 190.
wire, experiments on the, i, 387.
Stroke jointers, ii, 338, 339.
Studs, i, 115.
Sun-and-planet motion, i, 75.
Superheated steam, ii, 410.
Supplementary planer tables, i, 417.
Surface condensers, ii, 440, 442.
condensing engine valves, ii, 442.
Surface gauge, i, 378.
Surface plates, originating, i, 383; ii, 132.
Surfaces, rough, joints for, ii, 138.
true, scrapers for, ii, 97.
Swage blocks, ii, 232.
Swages, spring, ii, 232.
for blacksmiths, ii, 230, 231.
Swaging, blacksmiths’ work, ii, 232, 233.
Swing-frame, i, 158.
attaching, i, 166.
for lead screw, i, 139.
saws, ii, 290, 291.
Swing machine with fixed table, ii, 294.
Swing machine bevel or mitre, ii, 296.
Swiveled tool-holding devices, i, 411.
Swiveling vise chucks, i, 395.
vises, ii, 63.
Swivel-heads, construction of, i, 389.
for planers, i, 411.
Swiveling tool-rest, i, 174.
T
Table of arc and diametral pitches, i, 3.
change wheels, screw cutting, i, 180.
circular saw diameters, ii, 287.
feeds for twist-drills, i, 277.
index holes for gear cutting, ii, 7.
natural sines, i, 3.
of wrought iron tubes, i, 95.
pitch-diameter, pitch, and number of teeth in gear-wheels, i, 68.
pressure, temperature and volume of steam, ii, 367.
screw threads, i, 95, 96,
107.
sizes of, bolts and nuts, i, 114.
milling-machine cutters, ii, 17.
tapping drills, i, 445.
twist drills and shanks, i, 442.
speeds for twist drills, i, 277.
spring for indicators, ii, 416.
standard for the V-thread, i, 95.
Tabular values and setting numbers for odontograph, i, 51.
Tail-block lathe, i, 185.
Tailstock, adjustments of, i, 245.
chucks, i, 135, 145.
construction of, i, 209.
for drilled work, i, 279.
engine lathe, i, 135.
open spindle lathes, i, 189.
securing and releasing, i, 136.
Tangent screw, i, 1.
Tap-wrenches, adjustable, i, 110.
Taper bolts, standards, i, 359.
cutters, fixtures for, ii, 34.
for pipe threads, i, 95.
grinding, ii, 33.
holes, device for drilling, i, 451.
milling, ii, 30.
pins, fitting, i, 128.
position for locking, i, 128.
plugs for hydraulic fits, i, 365.
reamers, ii, 99.
taps for blacksmiths, i, 106.
threads, cutting, i, 338.
turning attachments, i, 143.
lathe, i, 142.
Tapered connecting-rod ends, ii, 117.
Taper-work, centres for, i, 226.
chucking, i, 394.
fitting, i, 313.
fixture for grinding, ii, 33.
gauge for setting over, i, 313.
grinding, i, 313.
plug and collar gauges for, i, 357.
standard gauges for, i, 316.
Taper-work, steady rest for, i, 233.
stepped reamers for, i, 285.
turning, i, 312, 313.
wear of lathe centres in, i, 312.
Tapers for live centres, i, 159.
Tapping, i, 111.
drills, table of sizes of, i, 445.
machine for steam pipe thread, i, 477.
Taps, clearance on, i, 102.
collapsing, machine, i, 107.
for lead, i, 109.
for very straight holes, i, 109.
form of, i, 103, 104.
improved forms of, i, 103.
number of cutting edges, i, 106, 471.
taper, for blacksmiths, i, 106.
taper, the friction of, i, 102.
wear of, i, 89.
Technical terms in lathe work, i, 296.
Tees, patterns for, ii, 284.
Teeth, angular, end thrust of, i, 69.
angular or herring bone, i, 69.
band saw, ii, 308, 309.
cast, the contact of, i, 67.
curves of elliptical, i, 73.
file, shapes of, ii, 85.
gear-wheel, factors of safety, i, 64.
for variable motion, i, 74.
requirements of curves, i, 7.
helical, i, 69.
reamer, number of, i, 282.
spacing of, ii, 98.
saw, ii, 273, 287.
Temper, blacksmiths’, ii, 460.
drawing, the, ii, 462.
manufacturers’, ii, 460.
reduction of, ii, 461.
Tempering, ii, 460-464.
color, ii, 460.
heating in fluxes, ii, 462.
methods of, special, ii, 461-464.
outside, ii, 462.
using a muffle, ii, 461.
warping in, ii, 461.
Template, ii, 110-112.
of Corliss bevel-gear-engine, i, 45.
for curves, i, 384.
marking division lines on the face of a gear wheel, i, 59.
filing a link slot, ii, 129.
gear-teeth, i, 43, 44.
involute curves, i, 32.
planing teeth to shape, i, 54.
rolling gear-tooth curves, i, 43.
gauges for end measurements, i, 376.
Tenoning machines, ii, 344.
Tenon joints, ii, 274.
Tension of band saws, ii, 310, 311.
belts, ii, 211.
circular saws, ii, 288.
Testing angle of bevel wheels while in the lathe, i, 60.
boilers, strength of, ii, 456.
engine alignment, ii, 166-172.
engine guide-bars, ii, 163.
indicator expansion curves, ii, 417.
iron, ii, 226-228.
lathe carriages, ii, 182.
lathe tailblock, i, 187.
lathes, i, 180, 181.
lubricants, ii, 152.
machines for iron, ii, 227, 228.
oils, ii, 153, 154.
shafting, ii, 188.
squares, various methods of, i, 379.
the power of an engine, ii, 408.
various methods of, i, 187.
Theoretical compression curve, ii, 421.
diagram, ii, 415.
expansion curve, ii, 417, 418.
Thimble joints, ii, 141.
Thinning twist-drill points, ii, 44.
Thread angles, gauge for, i, 91.
cutting, i, 111.
avoiding friction in, i, 474.
dies, i, 97.
taps, i, 102.
tools, angles of, i, 91.
wear of, i, 88.
pitch varied by hardening, i, 87.
screw, forms of, i, 85.
Threaded work, drivers for, i, 225.
Threading dies, cutting speeds for, i, 474.
dies, hob for, i, 474.
machine, hand bolt, i, 464.
hand, revolving head, i, 465.
pipe, i, 463, 475-477.
power, i, 466.
tools, circular, i, 264, 267.
for gauges, i, 266.
screw machine, i, 203.
holders, i, 267.
internal, i, 264.
setting, i, 266.
the level of, i, 265.
Threads, diameter at the roots of, i, 269.
left-hand cutting, i, 322.
square, clearance of tools for, i, 269.
Three and four-jawed chucks, i, 237.
Three-spindle drilling machine, i, 434.
nut tapping machine, i, 475.
Three-tool slide-rest for shafting, i, 143.
Three or four boring bar cutters, i, 290.
Throttle valves leaky, ii, 386.
Throttling governors, ii, 384.
Thrust bearings, ii, 445.
Thrust on wheel shafts, i, 16.
Timber, bending, ii, 265, 266.
Timber, shakes or cracks in, ii, 264.
shrinkage of, ii, 264.
steaming to bend it, ii, 266.
Tit drill, i, 443.
Tongs, blacksmith’s, ii, 229.
Tool aprons for planers, i, 411.
edge, oilstoning, ii, 54.
front for lathe work, i, 254.
facing with reamer pin, i, 449.
grinding and grindstones, ii, 51.
holders, boring, i, 287.
combined, i, 273.
for compound slide-rests, i, 174.
circular cutters, i, 272.
octagon boring tools, i, 175.
screw machine, i, 202.
lathe for outside work, i, 270.
planer, i, 426.
slotting machine, i, 460, 461.
swiveled, i, 273.
threading, i, 267.
holding devices, i, 173.
swiveled for planers, i, 411.
rest, swiveling, i, 174.
taps, improved, i, 103.
Tools, caulking, ii, 141.
bolt heading, ii, 237.
box for screw machine, i, 208.
circular cutting, i, 267.
cutting-off or grooving, i, 262.
cutting, the utmost duty of, i, 258.
diamond-pointed, i, 254.
facing or knife, i, 262.
for blacksmiths, ii, 229, 230.
cutting rods in pieces, i, 305.
screw threads, i, 87.
wood slips, ii, 271.
a worm in a lathe, i, 62.
mortising machines, ii, 344.
roll turning, i, 215.
screw machine, i, 202.
standard shapes, i, 111.
testing lathe centres, i, 298.
planer, clearance of, i, 424.
for coarse finishing feeds, i, 423.
slotted work, i, 424.
gauge for, i, 423.
shapes of, i, 423.
round-nosed, i, 258.
spring, i, 263.
square-nosed, i, 260.
thread-cutting, i, 97.
threading for screw machine, i, 264.
wood working, grindstones for, ii, 52.
with side rake, i, 256.
Tooth form, variation of, i, 15.
proportions, scale of, i, 54.
templates, pivoted arms for, i, 44.
Trammeling connecting rods, ii, 122.
Trams or trammels, i, 377.
Traversing grindstones, automatic, ii, 53.
spindle lathe, i, 218.
Triple riveted joints, ii, 353.
Triple-expansion-engine, ii, 436.
link motions of, ii, 438.
valves of, ii, 438, 439.
Trip-hammers, ii, 254.
swages for, ii, 231.
Trying-up machines, ii, 332.
Try-squares, i, 379.
True surfaces, scrapers for, ii, 97.
surfaces, oiling, ii, 135.
plane, originating, ii, 132.
Truing grindstones, ii, 53.
lathe centres, devices for, i, 297.
oilstones, ii, 54.
Trundle-wheels, i, 1.
T-squares, i, 379.
Tube plate cutters, i, 448.
Tubular saw machine, ii, 305.
Tubular work, lathe mandrels for, i, 227.
Tubes, boiler, arrangement of, ii, 364.
bursted, ii, 403.
Tumbler-files, ii, 91.
Turn-buckle, forging, ii, 239.
Turned work, recentring, i, 304.
Turning a cylinder cover, i, 318.
calendar rolls, i, 215.
crank axles, lathe for, i, 152.
crank, lathe for, i, 154.
irregular shapes, i, 210.
machine, feed motions of, i, 436.
for boiler makers, i, 435.
mill, i, 211.
outside threads, i, 338.
pulleys, i, 318.
shafting, three tool slide rest, i, 143.
tapers, i, 136, 312.
Turret for screw machine, i, 205.
Twin cutters, ii, 18.
milling, advantages, ii, 25.
Twist-drills, i, 274.
clearance of, i, 274; ii,
41-44.
effect of improper grinding, i, 276.
fluting, ii, 29.
feeds and speeds for, i, 277.
front rake of, i, 275; ii, 44.
grinding, i, 276.
large, thinning the points of, ii, 44.
table of sizes of, i, 442.
Two-jawed chucks, i, 236.
U
United States standard for gas pipe, i, 93.
for finished bolts and nuts, i, 113.
rough bolts and nuts, i, 114.
United States standard for screw thread, i, 86.
Universal chucks, i, 238.
coupling, ii, 199.
grinding lathes, i, 195.
joint for drill brace, i, 456.
milling-machines, ii, 2-15.
for heavy work, ii, 15.
V
Vacuum gauge, ii, 444.
line of indicator diagram, ii, 415.
Valve, cut off, ii, 378.
expansion, ii, 443.
for marine engines, ii, 444.
for triple expansion engines, ii, 439.
gear, principles of the Corliss, ii, 424.
globe, pattern for, ii, 281.
Kingston, ii, 440.
lead adjusting, ii, 386.
measuring, ii, 173.
motion, designing, ii, 381.
of surface condensing engines, ii, 442.
snifting, ii, 440.
squaring a, ii, 386.
throttle freezing, ii, 386, 387.
Velocity, uniform for gear wheels, i, 16.
Vertical boilers, ii, 359, 361.
milling machine, ii, 31.
water tube boiler, ii, 360.
V-guideways for planer heads, i, 414.
Vise, ii, 62, 63.
chucks for vise work, i, 396.
construction of, i, 393.
chucking work in, i, 393.
holding taper work in, i, 394.
rapid motion, i, 396.
swiveling, i, 395.
various forms of, i, 394.
clamps, various forms of, ii, 64.
hand, ii, 104.
jaws, heights of, ii, 62.
leg, with parallel motion, ii, 63.
wood workers’, ii, 62.
work, classification of, ii, 62.
examples in, ii, 102-135.
red marking for, ii, 96.
Vises, swiveling, ii, 63.
Volume and pressure of steam, ii, 411.
V-slide lathe shears, i, 182.
V-thread standard, i, 93.
V-tool for starting threads, i, 337.
W
Wall hangers, ii, 193.
Warping, ii, 461.
Warping of files, ii, 93.
Washers, i, 123.
standard sizes of, i, 123.
Watchmakers’ lathes, i, 188.
Watch manufacturers’ hand lathe, i, 191.
lathe, details of, i, 190.
Water, ii, 410.
evaporation, calculation of, ii, 420.
gauge glass, ii, 368.
joints, ii, 139.
tube boiler, vertical, ii, 360.
Wear of dies, i, 89.
of back bearings, i, 158.
emery wheels, ii, 48.
groove cams, i, 84.
nuts, i, 120.
planer head slides, i, 410.
scroll chuck threads, i, 238.
spindles of lathe tailblock, i, 185.
taps, i, 89.
worm and worm-wheel, i, 28.
upon grooved friction wheels, i, 79.
Weight of steam, ii, 411.
Weighted elevated slide rest, i, 168.
slide-rest, feed motion for, i, 168.
Weld, butt, ii, 234.
lap, ii, 234.
split, ii, 235.
Welded connecting rods, aligning, ii, 118.
Welding iron and steel, ii, 233, 234.
scrap iron, ii, 247.
stub ends of connecting rods, ii, 118.
theory of, ii, 233.
Wheel, emery, position of, ii, 35.
forging of fifth, ii, 239.
hubs, lathe for turning, i, 221.
lathe, i, 151.
rack and pinion, i, 1.
rim, spacing the teeth on, i, 56, 58.
shafts thrust on, i, 16.
tire, throwing off, ii, 403.
worm, i, 1.
Wheels, bevel line of faces, i, 22.
brush, for polishing, ii, 50.
speed of, ii, 50.
clock, i, 21.
considered as levers, ii, 405.
emery, annular, ii, 47.
balancing, ii, 39.
grades of, ii, 39.
presenting, to work, ii, 47.
qualifications of, ii, 38.
recessed, ii, 47.
swing frame, large work, ii, 46.
speeds of, ii, 39.
wear of, ii, 48.
work suitable for, ii, 39.
friction, i, 77.
material for, i, 77.
for transmitting motion, i, 21.
gear drawings for, i, 59.
[II-484]intermediate,
i, 319.
locomotive, forging, ii, 244.
number of cutters for a train of, i, 39.
paddle, ii, 444.
polishing, construction of, ii, 49.
charging with emery, ii, 50.
for brass work, ii, 50.
large, method of truing, ii, 50.
polishing materials for, ii, 50.
rag, ii, 51.
speed of, ii, 50.
solid leather, ii, 51.
trundle, i, 1.
White-metal lined boxes, ii, 155.
Width and thickness of chisels, ii, 74.
Winding spiral springs, i, 329.
strips and their use, i, 382.
Wire-feed for screw machines, i, 206.
gauge, i, 387.
Wire, strength of, experiments on, i, 387.
Wood bending block, ii, 265, 266.
boring machines, ii, 343.
for patterns, ii, 264.
gouges, ii, 272.
moulding machines, knives of, ii, 84.
planing machine, ii, 317-341.
pulleys, ii, 200.
steaming, ii, 266.
turning, hand tools for, i, 338.
work, chisels for, ii, 271.
counterbore for, i, 449.
drill for, i, 449.
drivers for, i, 225.
forms of joints for, ii, 275.
lathe, face plates for, i, 247.
on swing frame machine, ii, 292.
twist drills for, i, 279.
worker’s vise, ii, 62.
Wood-working, circular-saw gauges for, ii, 295.
lathes, chucks for, i, 242.
machinery, ii, 287-349.
special lathe for, i, 208.
tools, grindstones for, ii, 52.
Woods for patterns, ii, 264.
Work, cored, drivers for, i, 225.
face plate, examples of, i, 249.
holding straps, i, 244.
hollow centres for, i, 226.
shrinking, to refit, i, 374.
Worm and worm-wheel, i, 28.
gears, i, 62.
wheel, application of, i, 30.
cutting teeth of, i, 42.
enveloping teeth, i, 28.
number of teeth in, i, 29.
teeth, sliding motion of, i, 28.
Worm to work with a square thread, i, 29.
Wrench, adjustable, i, 125.
for carriage bolts, i, 125.
jaws, angle for, i, 123.
monkey, i, 125.
pin, i, 126.
sockets, i, 125.
various forms of, i, 125.
Wrought iron, cutting speeds for, i, 294.
Y
Yoke and guide-bars, ii, 389.
Z
Zigzag riveted seams, ii, 352.
Zinc gauge, the American sheet, i, 387.
gauge, the Belgian sheet, i, 387.
Transcriber’s Notes.
Text:
Tables:
Illustrations:
Changes made to original:
| Page | Original work | Changes made |
| Volume I | ||
| page xi | Machine 309 | Machine 300 |
| page 7 | under wear | undue wear |
| page 30 | Hindleys’ | Hindley’s |
| page 35, Fig. 102: o added, o′ moved, lines added | ||
| page 37 | Fig. 106 | Fig. 109 |
| page 40 | (for 97 bears... | (for 96 bears... |
| page 47, table in fig. 135, row 16 teeth, 2nd last value | 191 | 119 |
| page 49 | 1⁄2 = 500 | 1⁄2 = .500 |
| page 67 | After very few blows | After every few blows |
| page 84 | cannot be maintained a close fit | cannot be maintained in a close fit |
| page 87, second reference to Fig. 258 | Fig. 258 | Fig. 259 |
| page 94, Fig. 288: triangle redrawn, original was too crooked | ||
| page 95 | apt to have a waver | apt to have a wave |
| page 95 | a single operation. | a single operation”. |
| page 95 | November,—December, 1886 | November-December, 1886 |
| page 96, Whitworth table, Hydraulic Piping, 1′′ ID, row 2 | 13⁄8 | 15⁄8 |
| page 107, table | 512⁄16 | 513⁄16 |
| page 127 | .937/100 | 937/1000 |
| page 136 | in figure: | in Fig. 498: |
| page 142: reference to Fig. 588, which shows something else, therefore reference not linked to figure. | ||
| page 162, table, column 1, row ending in 0.00 | .05 4 | .0594 |
| page 162, table: column 2 moved to between columns 1 and 3 | ||
| page 162, table, column 33, row ending in 0.72 | 1.22 0 | 1.2200 |
| page 162, table, column 31, row ending in 0.96 | .8 94 | .8994 |
| page 186 | gibbs | gibs |
| page 234 | out if true | out of true |
| page 274 (table) | 1⁄6 | 1⁄8 |
| page 307 | Fig. 1029 | Fig. 1209 |
| page 312 | smoothes | smooths |
| page 321 | 66 ÷ 36 = 23⁄4 | 99 ÷ 36 = 23⁄4 |
| page 322 | as at J in Fig. 1241 | as at I in Fig. 1241 |
| page 335 | Fig. 1334 | Fig. 1324 |
| page 344 | Fig. 1532 | Fig. 1352 |
| page 356 | Lloyd’s | Lloyds’ (as elsewhere) |
| page 366 | if it is found possible | if it is found impossible |
| page 367 | will expend | will expand |
| page 369, Fig. 1429: decimal point added to 74 | ||
| page 370, Fig. 1430 | ” | ′′ (inches) |
| x | × (for consistency) | |
| page 371, Fig. 1431 | 74 | .74 |
| page 388 | reamless | seamless |
| page 388, table, row 2′′ column 3 | 1⁄5 | 1⁄8 |
| page 404, Fig. 1560: S flipped over | ||
| page 406 | Fig. 1669 | Fig. 1569 |
| page 442 first table, row 11⁄16, column 2 | 81⁄4 | 91⁄4 |
| Volume II | ||
| page x | Mariotte’s law | Marriotte’s law (as in text; usual spelling is Mariotte) |
| page 7 table, row 25 teeth, column 3 | 12⁄0 | 12⁄20 |
| page 17 | a length of 3 inches | a length of 3 feet |
| page 53, Plate V, Fig. 2064 top | F | E |
| page 88 | Figs. 2211, 2212 and 2213 | Figs. 2210, 2211 and 2212 |
| page 132, footnote 33 | p. 162 | p. 68 |
| page 151 | Figs. 2405 and 2500 | Figs. 2495 and 2500 |
| page 154, first table, row Smooth metal surfaces, occasionally greased, second column | 4 to 11⁄2 | 4 to 41⁄2 (as in Bourne’s book, Rose’s source, at archive.org) |
| page 208, table in illustration, row 7, column 5 | 9.32 | 9⁄32 |
| page 208, table in illustration | all fractions x-y | x⁄y |
| page 208, table in illustration | enlarged table added underneath illustration | |
| page 224, second formula | 11. | .11 |
| page 243, Fig. 2962 | punche | punches |
| page 265, Fig. 2709 | B | C |
| page 311 | Ortow | Orton (as elsewhere) |
| page 319 | Fig. 3260 | Fig. 3160 |
| page 348 | 4′ (feet) | 4′′ (inches) |
| page 354, first formula | by 2 | 2 |
| page 354, formula resulting in 1162⁄3 lbs. | + | × |
| page 367 | found the required pitch to | found the required pitch to be |
| page 367 table row Total pressure 33, column 3 | 225.2 | 252.2 |
| page 367 table row Total pressure 44, column 6 | 595 | 585 |
| page 367 table row Total pressure 61, column 6 | 403 | 430 |
| page 401 | colters | cotters |
| page 407, first calculation | line added under 5 (third row) | |
| page 471 | Marriott’s | Marriotte’s |
| page 476 | Tuyere | Tuyère (as in text) |
| page 476 | Verneer | Vernier (as in text) |
| page 479 | featheredge | feather-edge (as in text) |
| page 480 | Gimblet | Gimlet (as in text) |
| doghead | dog-head (as in text) | |
| Guideways | Guide-ways (as in text) | |
| page 481 | Marriott’s | Marriotte’s |
| rabbetting | rabetting (as in text) | |
| Piaté | Piat’s as in Table of Contents (word does not occur in text) | |
| page 482 | featheredge | feather-edge (as in text) |
End of the Project Gutenberg EBook of Modern Machine-Shop Practice, Vol. I
(of 2), by Joshua Rose
*** END OF THIS PROJECT GUTENBERG EBOOK MODERN MACHINE-SHOP PRACTICE, VOL 1 ***
***** This file should be named 39225-h.htm or 39225-h.zip *****
This and all associated files of various formats will be found in:
http://www.gutenberg.org/3/9/2/2/39225/
Produced by Ben Beasley, Harry Lamé and the Online
Distributed Proofreading Team at http://www.pgdp.net
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
http://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need are critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at http://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
http://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at http://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit http://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including checks, online payments and credit card donations.
To donate, please visit: http://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart is the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
http://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.