
Migration of Birds
Museum of Natural History
Volume 3, No. 2, pp. 361-472, 47 figures in text
June 29, 1951
University of Kansas
LAWRENCE
1951
Editors: E. Raymond Hall, Chairman; A. Byron Leonard,
Edward H. Taylor, Robert W. Wilson
UNIVERSITY OF KANSAS
Lawrence, Kansas
PRINTED BY
FERD VOILAND, JR., STATE PRINTER
TOPEKA, KANSAS
1951
23-1020
The nocturnal migration of birds is a phenomenon that long has intrigued zoologists the world over. Yet, despite this universal interest, most of the fundamental aspects of the problem remain shrouded in uncertainty and conjecture.
Bird migration for the most part, whether it be by day or by night, is an unseen movement. That night migrations occur at all is a conclusion derived from evidence that is more often circumstantial than it is direct. During one day in the field we may discover hundreds of transients, whereas, on the succeeding day, in the same situation, we may find few or none of the same species present. On cloudy nights we hear the call notes of birds, presumably passing overhead in the seasonal direction of migration. And on stormy nights birds strike lighthouses, towers, and other tall obstructions. Facts such as these are indisputable evidences that migration is taking place, but they provide little basis for evaluating the flights in terms of magnitude or direction.
Many of the resulting uncertainties surrounding the nocturnal migration of birds have a quantitative aspect; their resolution hinges on how many birds do one thing and how many do another. If we knew, for instance, how many birds are usually flying between 2 and 3 A. M. and how this number compares with other one-hour intervals in the night, we would be in a position to judge to what extent night flight is sustained from dusk to dawn. If we could measure the number of birds passing selected points of observation, we could find out whether such migration in general proceeds more or less uniformly on a broad front or whether it follows certain favored channels or flyways. This in turn might give us a clearer insight into the nature of the orienting mechanism and the extent to which it depends on visual clues. And, if we had some valid way of estimating the number of birds on the wing under varying weather conditions, we might be able to understand better the nature and development of migration waves so familiar to field ornithologists. These are just random examples suggesting some of the results that may be achieved in a broad field of inquiry that is still virtually untouched—the quantitative study of migratory flights.
This paper is a venture into that field. It seeks to evaluate on a more factual basis the traditional ideas regarding these and similar problems, that have been developed largely from circumstantial [Pg_366] criteria. It is primarily, therefore, a study of comparative quantities or volumes of migration—or what may be conveniently called flight densities, if this term be understood to mean simply the number of birds passing through a given space in a given interval of time.
In the present study, the basic data permitting the numerical expression of such migration rates from many localities under many different sets of circumstances were obtained by a simple method. When a small telescope, mounted on a tripod, is focused on the moon, the birds that pass before the moon's disc may be seen and counted, and their apparent pathways recorded in terms of coördinates. In bare outline, this approach to the problem is by no means new. Ornithologists and astronomers alike have recorded the numbers of birds seen against the moon in stated periods of time (Scott, 1881a and 1881b; Chapman, 1888; Libby, 1889; West, 1896; Very, 1897; Winkenwerder, 1902a and 1902b; Stebbins, 1906; Carpenter, 1906). Unfortunately, as interesting as these observations are, they furnish almost no basis for important generalizations. Most of them lack entirely the standardization of method and the continuity that would make meaningful comparisons possible. Of all these men, Winkenwerder appears to have been the only one to follow up an initial one or two nights of observation with anything approaching an organized program, capable of leading to broad conclusions. And even he was content merely to reproduce most of his original data without correlation or comment and without making clear whether he fully grasped the technical difficulties that must be overcome in order to estimate the important flight direction factor accurately.
The present study was begun in 1945, and early results obtained were used briefly in a paper dealing with the trans-Gulf migration of birds (Lowery, 1946). Since that time the volume of field data, as well as the methods by which they can be analyzed, has been greatly expanded. In the spring of 1948, through the cooperation and collaboration of a large number of ornithologists and astronomers, the work was placed on a continent-wide basis. At more than thirty stations (Figure 34, page 437) on the North American continent, from Yucatán to Ontario, and from California to South Carolina, observers trained telescopes simultaneously on the moon and counted the birds they saw passing before its disc.
Most of the stations were in operation for several nights in the full moon periods of March, April, and May, keeping the moon under constant watch from twilight to dawn when conditions permitted. They have provided counts representing more than one thousand [Pg_367] hours of observation, at many places in an area of more than a million square miles. But, as impressive as the figures on the record sheets are, they, like the published observations referred to above, have dubious meaning as they stand. Were we to compare them directly, station for station, or hour for hour, we would be almost certain to fall into serious errors. The reasons for this are not simple, and the measures that must be taken to obtain true comparisons are even less so. When I first presented this problem to my colleague, Professor William A. Rense, of the Department of Physics and Astronomy at Louisiana State University, I was told that mathematical means exist for reducing the data and for ascertaining the desired facts. Rense's scholarly insight into the mathematics of the problem resulted in his derivation of formulae that have enabled me to analyze on a comparable basis data obtained from different stations on the same night, and from the same station at different hours and on different nights. Astronomical and technical aspects of the problem are covered by Rense in his paper (1946), but the underlying principles are discussed at somewhat greater length in this paper.
Part I of the present paper, dealing with the means by which the data were obtained and processed, will explore the general nature of the problem and show by specific example how a set of observations is prepared for analysis. Part II will deal with the results obtained and their interpretation.
In the pursuit of this research I have received a tremendous amount of help from my colleagues, students, and other friends. In the first place, in order to obtain much of the data on which the study was based, it was necessary to enlist the aid of many persons in various parts of the country and to draw heavily on their time and patience to get all-night telescopic counts of migrating birds. Secondly, the processing of the primary data and its subsequent analysis demanded that I delve into the fields of astronomy and mathematics. Here, from the outset, I have enjoyed the constant and untiring help of Professor W. A. Rense of the Department of Physics and Astronomy at Louisiana State University. Without his collaboration, I would not have been able to do this work, for he not only supplied formulae whereby I was able to make desired computations, but time and again he maneuvered me through my difficulties in the mathematical procedures. Moreover, Professor Rense has manifested a great interest in the ornithological aspect of the problem, and his trenchant advice has been of inestimable value to me. No less am I indebted to my associate, Robert J. Newman, with whom I have spent untold hours discussing the various aspects of the problem. Indeed, most of the concepts that have evolved in the course of this study have grown out of discussions [Pg_368] over a four-year period with both Rense and Newman. Whatever merit this work may have may be attributable in no small part to the help these two men have given me. In the preparation of many of the illustrations, I am further obligated to Newman for his excellent creative ideas as well as draftsmanship, and to Miss Helen Behrnes and A. Lowell Wood for their assistance.
The mathematical computations required in this study have been laborious and time-consuming. It is estimated that more than two thousand man-hours have gone into this phase of the work alone. Whereas I have necessarily done most of this work, I have received a tremendous amount of help from A. Lowell Wood. Further assistance in this regard came from Herman Fox, Donald Norwood, and Lewis Kelly.
The recording of the original field data in the spring of 1948 from the thirty-odd stations in North America involved the participation of more than 200 ornithologists and astronomers. This collaboration attests to the splendid cooperative spirit that exists among scientists. Many of these persons stayed at the telescope, either as observer or as recorder, hours on end in order to get sets of data extending through a whole night.
The following were responsible for much of the field data herein used: J. R. Andrews, S. A. Arny, M. Dale Arvey, H. V. Autrey, Charles C. Ayres, Mr. and Mrs. Roy Bailey, Irwin L. Baird, Maurice F. Baker, Rollin H. Baker, Bedortha and Edna Baldwin, Mrs. A. Marguerite Baumgartner, T. A. Becket, Paul Bellington, Donald Bird, Carl Black, Jr., Lea Black, Lytle Blankenship, Mr. and Mrs. J. Stewart Boswell, Bruce Boudreaux, Frank Bray, Mr. and Mrs. Leonard Brecher, Homer Brewer, Mrs. Harvey Broome, Heyward Brown, Floyd Browning, Cyril Broussard, Paul Buress, Ralph M. Burress, Robert Cain, Don Carlos, Mrs. Reba Campbell, Mr. and Mrs. E. Burnham Chamberlain, Laura Chaney, Van B. Chaney, Jr., Edward Clebsch, Mr. and Mrs. Ben B. Coffey, William Cook, Dr. Jack Craven, Hugh C. and William Davis, Katherine Davis, Richard Davis, Richard DeArment, Robert E. Delphia, J. C. Dickinson, Mr. and Mrs. Otto Dietrich, John Dietrich, Clara Dixon, Nina Driven, John J. Duffy, Mr. and Mrs. R. J. Dunbar, Betty Dupre, Bernard E. Eble, Jr., Robert G. Eble, Dr. and Mrs. William H. Elder, C. C. Emory, Davis Emory, Alice H. Farnsworth, James Fielding, William R. Fish, Mr. and Mrs. Myron Ford, W. G. Fuller, Louis Gainey, Dr. Mary E. Gaulden, Mr. and Mrs. John J. Giudice, Lt. L. E. Goodnight, Earl R. Greene, Max Grilkey, W. W. H. Gunn, Noel Maxwell Hall, Jr., A. J. Hanna, Paul Hansen, Harold W. Harry, Joseph Healy, Dorothy Helmer, Mr. and Mrs. John H. Helmer, Philip E. Hoberecht, William D. Hogan, Dr. and Mrs. Joseph C. Howell, E. J. Huggins, Mrs. Walter Huxford, Hugh Iltis, W. S. Jennings, William M. Johnson, William Kasler, Luther F. Keeton, Lawrence C. Kent, W. H. Kiel, L. P. Kindler, Mr. and Mrs. Joseph E. King, Harriet Kirby, E. J. Koestner, Roy Komarek, Ann Knight, Mr. and Mrs. N. B. Langworthy, Mr. and Mrs. C. F. Lard, Prentiss D. Lewis, Ernest Liner, Dr. and Mrs. R. W. Lockwood, Dr. Harvey B. Lovell, William J. Lueck, Don Luethy, James Major, Mr. and Mrs. Russell L. Mannette, Mrs. John B. Mannix, Donald Mary, Dale E. McCollum, Stewart McConnell, Mr. and Mrs. M. L. McCroe, Robert L. McDaniel, Mr. and Mrs. Frank McGill, Thomas Merimer, Mr. and Mrs. I. S. H. Metcalf, Ann Michener, John Michener, T. H. Milby, D. S. Miller, Burt Monroe, Jr., Burt Monroe, Sr., Mrs. R. A. Monroe, Gordon Montague, Duryea Morton, James Mosimonn, Don L. Moyle, Grant Murphy, [Pg_369] John T. Murphy, Mrs. H. F. Murphy, Mrs. Hill Myers, Mr. and Mrs. Robert J. Newman, William Nichols, R. A. Norris, Floyd Oaks, Eugene P. Odum, Mrs. E. E. Overton, Lennie E. Pate, Kenneth Patterson, Ralph Paxton, Louis Peiper, Marie Peiper, Mr. and Mrs. Harold S. Peters, Mary Peters, Mr. and Mrs. D. W. Pfitzer, Betty Plice, Max Plice, Lestar Porter, D. R. Power, Kenneth Price, George Rabb, Marge Reese, Wayne L. Reeve, C. L. Riecke, R. D. Ritchie, V. E. Robinson, Beverly J. Rose, Mary Jane Runyon, Roger Rusk, Bernd Safinsley, Mr. and Mrs. Glen C. Sanderson, Lewis L. Sandidge, John Sather, J. Benton Schaub, Evelyn Schneider, Henry W. Setzer, Mr. and Mrs. Walter Shackleton, Mr. and Mrs. Francis P. Shannon, Mr. and Mrs. Charles Shaw, Paul H. Shepard, Jr., Alan C. Sheppard, Mabel Slack, Alice Smith, R. Demett Smith, Jr., Nat Smith, Major and Mrs. Charles H. Snyder, Albert Springs, Dr. and Mrs. Fred W. Stamm, J. S. Steiner, Mrs. Paul Stephenson, Herbert Stern, Jr., Herbert Stoddard, Mr. and Mrs. F. W. Stomm, Charles Strull, Harold P. Strull, Mrs. Fan B. Tabler, Dr. and Mrs. James T. Tanner, S. M. H. Tate, David Taylor, Hall Tennin, Scott Terry, Mr. and Mrs. S. Charles Thacher, Olive Thomas, G. A. Thompson, Jr., Dr. and Mrs. S. R. Tipton, Robert Tucker, Tom Uzzel, Mr. and Mrs. M. G. Vaiden, Richard Vaught, Edward Violante, Brother I. Vincent, Marilyn L. Walker, Mr. and Mrs. Willis Weaver, Mr. and Mrs. W. L. Webb, Margaret M. L. Wehking, W. A. Welshans, Jr., Mrs. J. F. Wernicke, Francis M. Weston, Miss G. W. Weston, Dr. James W. White, John A. White, A. F. Wicke, Jr., Oren Williams, J. L. Wilson III, W. B. Wilson, Dr. and Mrs. Leonard Wing, Sherry Woo, Rodney Wuthnow, Grace Wyatt, Mr. and Mrs. Malcom Young, Mr. and Mrs. A. J. Zimmerman. To the scores of other people who assisted in making these observations I extend my hearty thanks.
Drs. E. R. Hall, Edward H. Taylor, and H. B. Hungerford of the University of Kansas have read the manuscript and have made valuable suggestions, as have also Dr. W. H. Gates of Louisiana State University and Dr. Donald S. Farner of the State College of Washington. Dr. Farner has also been of great help, together with Drs. Ernst Mayr, J. Van Tyne, and Ernst Schüz, in suggesting source material bearing on the subject in foreign literature. Dr. N. Wyaman Storer, of the University of Kansas, pointed out a short-cut in the method for determining the altitude and azimuth of the moon, which resulted in much time being saved. For supplying climatological data and for guidance in the interpretation thereof, I am grateful to Dr. Richard Joel Russell, Louisiana State University; Commander F. W. Reichelderfer, Chief of the U. S. Weather Bureau, Washington, D. C.; Mr. Merrill Bernard, Chief of the Climatological and Hydrologic Services; and Mr. Ralph Sanders, U. S. Weather Bureau at New Orleans, Louisiana.
Acknowledgment is made to Bausch and Lomb Optical Company for the loan of six telescopes for use in this project. Messrs. G. V. Cutler and George Duff of Smith and Johnson Steamship Company, operators of the Yucatan Line, are to be thanked for granting me free passage on the "S. S. Bertha Brřvig" to Progreso, Yucatán, where I made observations in 1945 and 1948. I am also indebted to the Louisiana State University Committee on Faulty Research for a grant-in-aid.
[Pg_370]
The subject matter of this paper is wholly ornithological. It is written for the zoologist interested in the activities of birds. But its bases, the principles that make it possible, lie in other fields, including such rather advanced branches of mathematics as analytical geometry, spherical geometry, and differential calculus. No exhaustive exposition of the problem is practicable, that does not take for granted some previous knowledge of these disciplines on the part of all readers.
There are, however, several levels of understanding. It is possible to appreciate what is being done without knowing how to do it; and it is possible to learn how to carry out the successive steps of a procedure without entirely comprehending why. Some familiarity with the concepts underlying the method is essential to a full understanding of the results achieved, and details of procedure must be made generally available if the full possibilities of the telescopic approach are to be realized. Without going into proof of underlying propositions or actual derivation of formulae, I shall accordingly present a discussion of the general nature of the problem, conveyed as much as possible in terms of physical visualization. The development begins with the impressions of the student when he first attempts to investigate the movements of birds by means of the moon.
Watched through a 20-power telescope on a cloudless night, the full moon shines like a giant plaster hemisphere caught in the full glare of a floodlight. Inequalities of surface, the rims of its craters, the tips of its peaks, gleam with an almost incandescent whiteness; and even the darker areas, the so-called lunar seas, pale to a clear, glowing gray.
Against this brilliant background, most birds passing in focus appear as coal-black miniatures, only 1/10 to 1/30 the apparent diameter of the moon. Small as these silhouettes are, details of form are often beautifully defined—the proportions of the body, the shape of the tail, the beat of the wings. Even when the images are so far away that they are pin-pointed as mere flecks of black against the illuminated area, the normal eye can follow their progress easily. [Pg_371] In most cases the birds are invisible until the moment they "enter," or pass opposite, the rim of the moon and vanish the instant they reach the other side. The interval between is likely to be inestimably brief. Some birds seem fairly to flash by; others, to drift; yet seldom can their passing be counted in seconds, or even in measureable fractions of seconds. During these short glimpses, the flight paths tend to lie along straight lines, though occasionally a bird may be seen to undulate or even to veer off course.
Now and again, in contrast to this typical picture, more eerie effects may be noted. Some of them are quite startling—a minute, inanimate-looking object drifting passively by like a corpuscle seen in the field of a microscope; a gigantic wing brushing across half the moon; a ghost-like suggestion of a bird so transparent it seems scarcely more than a product of the imagination; a bird that pauses in mid-flight to hang suspended in the sky; another that beats its way ineffectually forward while it moves steadily to the side; and flight paths that sweep across the vision in astonishingly geometric curves. All of these things have an explanation. The "corpuscle" is possibly a physical entity of some sort floating in the fluid of the observer's eye and projected into visibility against the whiteness of the moon. The winged transparency may be an insect unconsciously picked up by the unemployed eye and transferred by the camera lucida principle to the field of the telescope. It may be a bird flying very close, so drastically out of focus that the observer sees right through it, as he would through a pencil held against his nose. The same cause, operating less effectively, gives a characteristic gray appearance with hazy edges to silhouettes passing just beneath the limits of sharp focus. Focal distortions doubtless also account for the precise curvature of some flight paths, for this peculiarity is seldom associated with distinct images. Suspended flight and contradictory directions of drift may sometimes be attributable to head winds or cross winds but more often are simply illusions growing out of a two-dimensional impression of a three-dimensional reality.
Somewhat more commonplace are the changes that accompany clouds. The moon can be seen through a light haze and at times remains so clearly visible that the overcast appears to be behind, instead of in front of, it. Under these circumstances, birds can still be readily discerned. Light reflected from the clouds may cause the silhouettes to fade somewhat, but they retain sufficient definition to distinguish them from out-of-focus images. On occasion, when white [Pg_372] cloud banks lie at a favorable level, they themselves provide a backdrop against which birds can be followed all the way across the field of the telescope, whether or not they directly traverse the main area of illumination.
The nature of the observations just described imposes certain limitations on the studies that can be made by means of the moon. The speed of the birds, for instance, is utterly beyond computation in any manner yet devised. Not only is the interval of visibility extremely short, but the rapidity with which the birds go by depends less on their real rate of motion than on their proximity to the observer. The identification of species taking part in the migration might appear to offer more promise, especially since some of the early students of the problem frequently attempted it, but there are so many deceptive elements to contend with that the results cannot be relied upon in any significant number of cases. Shorn of their bills by the diminution of image, foreshortened into unfamiliar shape by varying angles of perspective, and glimpsed for an instant only, large species at distant heights may closely resemble small species a few hundred feet away. A sandpiper may appear as large as a duck; or a hawk, as small as a sparrow. A goatsucker may be confused with a swallow, and a swallow may pass as a tern. Bats, however, can be consistently recognized, if clearly seen, by their tailless appearance and the forward tilt of their wings, as well as by their erratic flight. And separations of nocturnal migrants into broad categories, such as seabirds and passerine birds, are often both useful and feasible.
It would be a wonderful convenience to be able to clock the speed of night-flying birds accurately and to classify them specifically, but neither of these things is indispensable to the general study of nocturnal migration, nor as important as the three kinds of basic data that are provided by telescopes directed at the moon. These concern:—(1) the direction in which the birds are traveling; (2) their altitude above the earth; (3) the number per unit of space passing the observation station.
Unfortunately none of these things can be perceived directly, except in a very haphazard manner. Direction is seen by the observer in terms of the slant of a bird's pathway across the face of the moon, and may be so recorded. But the meaning of every such slant in terms of its corresponding compass direction on the plane of [Pg_373] the earth constantly changes with the position of the moon. Altitude is only vaguely revealed through a single telescope by the size and definition of images whose identity and consequent real dimensions are subject to serious misinterpretation, for reasons already explained. The number of birds per unit of space, seemingly the easiest of all the features of migration to ascertain, is actually the most difficult, requiring a prior knowledge of both direction and altitude. To understand why this is so, it will be necessary to consider carefully the true nature of the field of observation.
Most of the observations used in this study were made in the week centering on the time of the full moon. During this period the lunar disc progresses from nearly round to round and back again with little change in essential aspect or apparent size. To the man behind the telescope, the passage of birds looks like a performance in two dimensions taking place in this area of seemingly constant diameter—not unlike the movement of insects scooting over a circle of paper on the ground. Actually, as an instant's reflection serves to show, the two situations are not at all the same. The insects are all moving in one plane. The birds only appear to do so. They may be flying at elevations of 500, 1000, or 2000 feet; and, though they give the illusion of crossing the same illuminated area, the actual breadth of the visible space is much greater at the higher, than at the lower, level. For this reason, other things being equal, birds nearby cross the moon much more swiftly than distant ones. The field of observation is not an area in the sky but a volume in space, bounded by the diverging field lines of the observer's vision. Specifically, it is an inverted cone with its base at the moon and its vertex at the telescope.
Since the distance from the moon to the earth does not vary a great deal, the full dimensions of the Great Cone determined by the diameter of the moon and a point on the earth remain at all times fairly constant. Just what they are does not concern us here, except as regards the angle of the apex (roughly ½°), because obviously the effective field of observation is limited to that portion of the Great Cone below the maximum ceiling at which birds fly, a much smaller cone, which I shall refer to as the Cone of Observation (Figure 1).
[Pg_374]
[Pg_375]
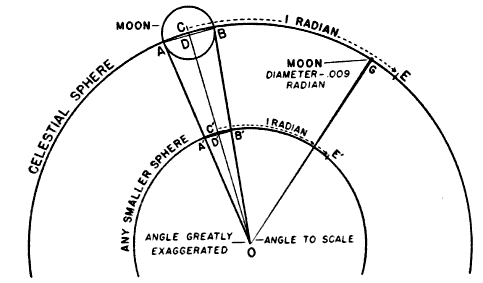

The problem of expressing the number of passing birds in terms of a definite quantity of space is fundamentally one of finding out the critical dimensions of this smaller cone. The diameter at any distance from the observer may be determined with enough accuracy for our purposes simply by multiplying the distance by .009, a convenient approximation of the diameter of the moon, expressed in radians (see Figure 2). One hundred feet away, it is approximately 11 inches; 1000 feet away, nine feet; at one mile, 48 feet; at two miles, 95 feet. Estimating the effective length of the field of observation presents more formidable difficulties, aggravated by the fact that the lunar base of the Great Cone does not remain stationary. The moon rises in the general direction of east and sets somewhere in the west, the exact points where it appears and disappears on the horizon varying somewhat throughout the year. As it drifts across the sky it carries the cone of observation with it like the slim beam of an immense searchlight slowly probing space. This situation is ideal for the purpose of obtaining a random sample of the number of birds flying out in the darkness, yet it involves great complications; for the size of the sample is never at two consecutive instants the same. The nearer the ever-moving great cone of the moon moves toward a vertical position, the nearer its intersection with the flight ceiling approaches the observer, shortening, therefore, the cone of observation (Figure 3). The effect on the number of [Pg_376] birds seen is profound. In extreme instances it may completely reverse the meaning of counts. Under the conditions visualized in Figure 3, the field of observation at midnight is only one-fourth as large as the field of observation earlier in the evening. Thus the twenty-four birds seen from 7 to 8 P. M., represent not twice as many birds actually flying per unit of space as the twelve observed from 11:30 to 12:30 A. M., but only half the amount. Figure 4, based on observations [Pg_377] at Ottumwa, Iowa, on the night of May 22-23, shows a similar effect graphically. Curve A represents the actual numbers of birds per hour seen; Curve B shows the same figures expressed as flight densities, that is, corrected to take into account the changing size of the field of observation. It will be noted that the trends are almost exactly opposite. While A descends, B rises, and vice-versa. In this case, inferences drawn from the unprocessed data lead to a complete misinterpretation of the real situation.

Nor does the moon suit our convenience by behaving night after night in the same way. On one date we may find it high in the sky between 9 and 10 P. M.; on another date, during the same interval of time, it may be near the horizon. Consequently, the size of the cone is different in each case, and the direct comparison of flights in the same hour on different dates is no more dependable than the misleading comparisons discussed in the preceding paragraph.
The changes in the size of the cone have been illustrated in Figure 3 as though the moon were traveling in a plane vertical to the earth's surface, as though it reached a point directly over the observer's head. In practice this least complicated condition seldom obtains in the regions concerned in this study. In most of the northern [Pg_378] hemisphere, the path of the moon lies south of the observer so that the cone is tilted away from the vertical plane erected on the parallel of latitude where the observer is standing. In other words it never reaches the zenith, a point directly overhead. The farther north we go, the lower the moon drops toward the horizon and the more, therefore, the cone of observation leans away from us. Hence, at the same moment, stationed on the same meridian, two observers, one in the north and one in the south, will be looking into different effective volumes of space (Figure 5).

As a further result of its inclination, the cone of observation, seldom affords an equal opportunity of recording birds that are flying in two different directions. This may be most easily understood by [Pg_379] considering what happens on a single flight level. The plane parallel to the earth representing any such flight level intersects the slanting cone, not in a circle, but in an ellipse. The proportions of this ellipse are very variable. When the moon is high, the intersection on the plane is nearly circular; when the moon is low, the ellipse becomes greatly elongated. Often the long axis may be more than twice the length of the short axis. It follows that, if the long axis happens to lie athwart the northward direction of flight and the short axis across the eastward direction, we will get on the average over twice as large a sample of birds flying toward the north as of birds flying toward the east.
In summary, whether we wish to compare different stations, different hours of the night, or different directions during the same hour of the night, no conclusions regarding even the relative numbers of birds migrating are warranted, unless they take into account the ever-varying dimensions of the field of observation. Otherwise we are attempting to measure migration with a unit that is constantly expanding or contracting. Otherwise we may expect the same kind of meaningless results that we might obtain by combining measurements in millimeters with measurements in inches. Some method must be found by which we can reduce all data to a standard basis for comparison.
In seeking this end, we must immediately reject the simple logic of sampling that may be applied to density studies of animals on land. We must not assume that, since the field of observation is a volume in space, the number of birds therein can be directly expressed in terms of some standard volume—a cubic mile, let us say. Four birds counted in a cone of observation computed as 1/500 of a cubic mile are not the equivalent of 500 × 4, or 2000, birds per cubic mile. Nor do four birds flying over a sample 1/100 of a square mile mathematically represent 400 birds passing over the square mile. The reason is that we are not dealing with static bodies fixed in space but with moving objects, and the objects that pass through a cubic mile are not the sum of the objects moving through each of its 500 parts. If this fact is not immediately apparent, consider the circumstances in Figures 6 and 7, illustrating the principle as it applies to areas. The relative capacity of the sample and the whole to intercept bodies in motion is more closely expressed by the ratio of their perimeters in the case of areas and the ratio of their surface areas in the case of volumes. But even these ratios lead to inaccurate results [Pg_380] unless the objects are moving in all directions equally (see Figure 8). Since bird migration exhibits strong directional tendencies, I have come to the conclusion that no sampling procedure that can be applied to it is sufficiently reliable short of handling each directional trend separately.

For this reason, the success of the whole quantitative study of migration depends upon our ability to make directional analyses of primary data. As I have already pointed out, the flight directions of birds may be recorded with convenience and a fair degree of objectivity by noting the slant of their apparent pathways across the disc of the moon. But these apparent pathways are seldom the real pathways. Usually they involve the transfer of the flight line from a horizontal plane of flight to a tilted plane represented by the face of the moon, and so take on the nature of a projection. They are [Pg_381] clues to directions, but they are not the directions themselves. For each compass direction of birds flying horizontally above the earth, there is one, and only one, slant of the pathway across the moon at a given time. It is possible, therefore, knowing the path of a bird in relation to the lunar disc and the time of the observation, to compute the direction of its path in relation to the earth. The formula employed is not a complicated one, but, since the meaning of the lunar coördinates in terms of their corresponding flight paths parallel to the earth is constantly changing with the position of the moon, the calculation of each bird's flight separately would require a tremendous amount of time and effort.


Whatever we do, computed individual flight directions must be frankly recognized as approximations. Their anticipated inaccuracies are not the result of defects in the mathematical procedure employed. This is rigorous. The difficulty lies in the impossibility of reading the slants of the pathways on the moon precisely and in the three-dimensional nature of movement through space. The observed coördinates of birds' pathways across the moon are the projected product of two component angles—the compass direction of the flight and its slope off the horizontal, or gradient. These two factors cannot be dissociated by any technique yet developed. All we can do is to compute what a bird's course would be, if it were flying horizontal to the earth during the interval it passes before the moon. We cannot reasonably assume, of course, that all nocturnal migration takes place on level planes, even though the local distractions so often associated with sloping flight during the day are minimized in the case of migrating birds proceeding toward a distant destination in darkness. We may more safely suppose, however, that deviations from the horizontal are random in nature, that it is mainly a matter of chance whether the observer happens to see an ascending segment of flight or a descending one. Over a series of observations, we may expect a fairly even distribution of ups and downs. It follows that, although departures from the horizontal may distort individual directions, they tend to average out in the computed trend of the mean. The working of this principle applied to the undulating flight of the Goldfinch (Spinus) is illustrated in Figure 9.

[Pg_384] Since individually computed directions are not very reliable in any event, little is to be lost by treating the observed pathways in groups. Consequently, the courses of all the birds seen in a one-hour period may be computed according to the position of the moon at the middle of the interval and expressed in terms of their general positions on the compass, rather than their exact headings. For this latter purpose, the compass has been divided into twelve fixed sectors, 22½ degrees wide. The trends of the flight paths are identified by the mid-direction of the sector into which they fall. The sectoring method is described in detail in the section on procedures.

The problem remains of converting the number of birds involved in each directional trend to a fixed standard of measurement. Figure 7A contains the partial elements of a solution. All of the west-east flight paths that cross the large square also cross one of its mile-long sides and suggest the practicability of expressing the amount of migration [Pg_385] in any certain direction in terms of the assumed quantity passing over a one-mile line in a given interval of time. However, many lines of that length can be included within the same set of flight paths (Figure 10); and the number of birds intercepted depends in part upon the orientation of the line. The 90° line is the only one that fully measures the amount of flight per linear unit of front; and so I have chosen as a standard an imaginary mile on the earth's surface lying at right angles to the direction in which the birds are traveling.
When the count of birds in the cone of observation is used as a sample to determine the theoretical number in a sector passing over such a mile line, the resulting quantity represents what I shall call a Sector Density. It is one of several expressions of the more general concept of Flight Density, which may be defined as the passage of migration past an observation station stated in terms of the theoretical number of birds flying over a one-mile line on the earth's surface in a given interval of time. Note that a flight density is primarily a theoretical number, a statistical expression, a rate of passage. It states merely that birds were moving through the effective field of observation at the rate of so many per mile per unit of time. It may or may not closely express the amount of migration occurring over an actual mile or series of miles. The extent to which it does so is to be decided by other general criteria and by the circumstances surrounding a given instance. Its basic function is to take counts of birds made at different times and at different places, in fields of observation of different sizes, and to put them on the statistically equal footing that is the first requisite of any sound comparison.
The idea of a one-mile line as a standard spacial measurement is an integral part of the basic concept, as herein propounded. But, within these limitations, flight density may be expressed in many different ways, distinguished chiefly by the directions included and the orientation of the one-mile line with respect to them. Three such kinds of density have been found extremely useful in subsequent analyses and are extensively employed in this paper: Sector, Net Trend, and Station Density, or Station Magnitude.
Sector Density has already been referred to. It may be defined as the flight density within a 22½° directional spread, or sector, measured across a one-mile line lying at right angles to the mid-direction of the sector. It is the basic type of density from the point [Pg_386] of view of the computer, the others being derived from it. In analysis it provides a means of comparing directional trends at the same station and of studying variation in directional fanning.
Net Trend Density represents the maximum net flow of migration over a one-mile line. It is found by plotting the sector densities directionally as lines of thrust, proportioned according to the density in each sector, and using vector analysis to obtain a vector resultant, representing the density and direction of the net trend. The mile line defining the spacial limits lies at right angles to this vector resultant, but the density figure includes all of the birds crossing the line, not just those that do so at a specified angle. Much of the directional spread exhibited by sector densities undoubtedly has no basis in reality but results from inaccuracies in coördinate readings and from practical difficulties inherent in the method of computation. By reducing all directions to one major trend, net trend density has the advantage of balancing errors one against the other and may often give the truer index to the way in which the birds are actually going. On the other hand, if the basic directions are too widely spread or if the major sector vectors are widely separated with little or no representation between, the net trend density may become an abstraction, expressing the idea of a mean direction but pointing down an avenue along which no migrants are traveling. In such instances, little of importance can be learned from it. In others, it gives an idea of general trends indispensable in comparing station with station to test the existence of flyways and in mapping the continental distribution of flight on a given night to study the influence of weather factors.
Station Density, or Station Magnitude, represents all of the migration activity in an hour in the vicinity of the observation point, regardless of direction. It expresses the sum of all sector densities. It includes, therefore, the birds flying at right angles over several one-mile lines. One way of picturing its physical meaning is to imagine a circle one-mile in diameter lying on the earth with the observation point in the center. Then all of the birds that fly over this circle in an hour's time constitute the hourly station density. While its visualization thus suggests the idea of an area, it is derived from linear expressions of density; and, while it involves no limitation with respect to direction, it could not be computed without taking every component direction into consideration. Station density is adapted to studies involving the total migration activity at various stations. So far it has been the most profitable of all the density [Pg_387] concepts, throwing important light on nocturnal rhythm, seasonal increases in migration, and the vexing problem of the distribution of migrating birds in the region of the Gulf of Mexico.
Details of procedure in arriving at these three types of flight density will be explained in Section B of this discussion. For the moment, it will suffice to review and amplify somewhat the general idea involved.
A flight density, as we have seen, may be defined as the number of birds passing over a line one mile long; and it may be calculated from the number of birds crossing the segment of that line included in an elliptical cross-section of the cone of observation. It may be thought of with equal correctness, without in any way contradicting the accuracy of the original definition, as the number of birds passing through a vertical plane one mile long whose upper limits are its intersection with the flight ceiling and whose base coincides with the one mile line of the previous visualization. From the second point of view, the sample becomes an area bounded by the triangular projection of the cone of observation on the density plane. The dimensions of two triangles thus determined from any two cones of observation stand in the same ratio as the dimensions of their elliptical sections on any one plane; so both approaches lead ultimately to the same result. The advantage of this alternative way of looking at things is that it enables us to consider the vertical aspects of migration—to comprehend the relation of altitude to bird density.
If the field of observation were cylindrical in shape, if it had parallel sides, if its projection were a rectangle or a parallelogram, the height at which birds are flying would not be a factor in finding out their number. Then the sample would be of equal breadth throughout, with an equally wide representation of the flight at all levels. Since the field of observation is actually an inverted cone, triangular in section, with diverging sides, the opportunity to detect birds increases with their distance from the observer. The chances of seeing the birds passing below an elevation midway to the flight ceiling are only one-third as great as of seeing those passing above that elevation, simply because the area of that part of the triangle below the mid-elevation is only one-third as great as the area of that part above the mid-elevation. If we assume that the ratio of the visible number of birds to the number passing through the density plane is the same as the ratio of the triangular section of the cone [Pg_388] to the total area of the plane, we are in effect assuming that the density plane is made up of a series of triangles the size of the sample, each intercepting approximately the same number of birds. We are assuming that the same number of birds pass through the inverted triangular sample as through the erect and uninvestigable triangle beside it (as in Figure 11, Diagram II). In reality, the assumption is sound only if the altitudinal distribution of migrants is uniform.

The definite data on this subject are meagre. Nearly half a century ago, Stebbins worked out a way of measuring the altitude of [Pg_369] migrating birds by the principle of parallax. In this method, the distance of a bird from the observers is calculated from its apparent displacement on the moon as seen through two telescopes. Stebbins and his colleague, Carpenter, published the results of two nights of observation at Urbana, Illinois (Stebbins, 1906; Carpenter, 1906); and then the idea was dropped until 1945, when Rense and I briefly applied an adaptation of it to migration studies at Baton Rouge. Results have been inconclusive. This is partly because sufficient work has not been done, partly because of limitations in the method itself. If the two telescopes are widely spaced, few birds are seen by both observers, and hence few parallaxes are obtained. If the instruments are brought close together, the displacement of the images is so reduced that extremely fine readings of their positions are required, and the margin of error is greatly increased. Neither alternative can provide an accurate representative sample of the altitudinal distribution of migrants at a station on a single night. New approaches currently under consideration have not yet been perfected.
Meanwhile the idea of uniform vertical distribution of migrants must be dismissed from serious consideration on logical grounds. We know that bird flight cannot extend endlessly upward into the sky, and the notion that there might be a point to which bird density extends in considerable magnitude and then abruptly drops off to nothing is absurd. It is far more likely that the migrants gradually dwindle in number through the upper limits at which they fly, and the parallax observations we have seem to support this view.
Under these conditions, there would be a lighter incidence of birds in the sample triangle than in the upright triangle beside it (Figure 11, Diagram III). Compensation can be made by deliberately scaling down the computed size of the sample area below its actual size. A procedure for doing this is explained in Figure 11. If it were applied to present altitudinal data, it would place the computational flight ceiling somewhere below 4000 feet. In arriving at the flight densities used in this paper, however, I have used an assumed ceiling of one mile. When the altitude factor is thus assigned a value of 1, it disappears from the formula, simplifying computations. Until the true situation with respect to the vertical distribution of flight is better understood, it seems hardly worthwhile to sacrifice the convenience of this approximation to a rigorous interpretation of scanty data. This particular uncertainty, however, does not necessarily impair the analytical value of the [Pg_390] computations. Provided that the vertical pattern of migration is more or less constant, flight densities still afford a sound basis for comparisons, wherever we assume the upper flight limits to be. Raising or lowering the flight ceiling merely increases or reduces all sample cones or triangles proportionately.
A more serious possibility is that the altitudinal pattern may vary according to time or place. This might upset comparisons. If the divergencies were severe enough and frequent enough, they could throw the study of flight densities into utter confusion.
This consideration of possible variation in the altitudinal pattern combines with accidents of sampling and the concessions to perfect accuracy, explained on pages 379-385, to give to small quantities of data an equivocal quality. As large-scale as the present survey is from one point of view, it is only a beginning. Years of intensive work and development leading to a vast accumulation of data must elapse before the preliminary indications yet discernible assume the status of proved principles. As a result, much of the discussion in Part II of this paper is speculative in intent, and most of the conclusions suggested are of a provisional nature. Yet, compared with similar procedures in its field, flight density study is a highly objective method, and a relatively reliable one. In no other type of bird census has there ever been so near a certainty of recording all of the individuals in a specified space, so nearly independently of the subjective interpretations of the observer. The best assurance of the essential soundness of the flight density computations lies in the coherent results and the orderly patterns that already emerge from the analyses presented in Part II.
At least two people are required to operate an observation station—one to observe, the other to record the results. They should exchange duties every hour to avoid undue eye fatigue. Additional personnel are desirable so that the night can be divided into shifts.
Essential materials and equipment include: (1) a small telescope; (2) a tripod with pan-tilt or turret head and a mounting cradle; (3) data sheets similar to the one illustrated in Figure 12. Bausch and Lomb or Argus spotting scopes (19.5 ×) and astronomical telescopes up to 30- or 40-power are ideal. Instruments of higher magnification are subject to vibration, unless very firmly mounted, and lead to difficulties in following the progress of the moon, unless powered by clockwork. Cradles usually have to be devised. An [Pg_391] adjustable lawn chair is an important factor in comfort in latitudes where the moon reaches a point high overhead.

Click here to see a transcription.
As much detail as possible should be entered in the space provided at the top of the data sheet. Information on the weather should include temperature, description of cloud cover, if any, and the [Pg_392] direction and apparent speed of surface winds. Care should be taken to specify whether the telescope used has an erect or inverted image. The entry under "Remarks" in the heading should describe the location of the observation station with respect to watercourses, habitations, and prominent terrain features.
The starting time is noted at the top of the "Time" column, and the observer begins the watch for birds. He must keep the disc of the moon under unrelenting scrutiny all the while he is at the telescope. When interruptions do occur as a result of changing positions with the recorder, re-adjustments of the telescope, or the disappearance of the moon behind clouds, the exact duration of the "time out" must be set down.


Whenever a bird is seen, the exact time must be noted, together with its apparent pathway on the moon. These apparent pathways can be designated in a simple manner. The observer envisions the disc of the moon as the face of a clock, with twelve equally spaced points on the circumference marking the hours (Figure 13). He calls the bottommost point 6 o'clock and the topmost, 12. The intervals in between are numbered accordingly. As this lunar clockface moves across the sky, it remains oriented in such a way that 6 o'clock continues [Pg_393] to be the point nearest the horizon, unless the moon reaches a position directly overhead. Then, all points along the circumference are equidistant from the horizon, and the previous definition of clock values ceases to have meaning. This situation is rarely encountered in the northern hemisphere during the seasons of migration, except [Pg_394] in extreme southern latitudes. It is one that has never actually been dealt with in the course of this study. But, should the problem arise, it would probably be feasible to orient the clock during this interval with respect to the points of the compass, calling the south point 6 o'clock.
When a bird appears in front of the moon, the observer identifies its entry and departure points along the rim of the moon with respect to the nearest half hour on the imaginary clock and informs the recorder. In the case of the bird shown in Figure 13, he would simply call out, "5 to 10:30." The recorder would enter "5" in the "In" column on the data sheet (see Figure 12) and 10:30 in the "Out" column. Other comment, offered by the observer and added in the remarks column, may concern the size of the image, its speed, distinctness, and possible identity. Any deviation of the pathway from a straight line should be described. This information has no bearing on subsequent mathematical procedure, except as it helps to eliminate objects other than birds from computation.
The first step in processing a set of data so obtained is to blue-pencil all entries that, judged by the accompanying remarks, relate to extraneous objects such as insects or bats. Next, horizontal lines are drawn across the data sheets marking the beginning and the end of each even hour of observation, as 8 P. M.-9 P. M., 9 P. M.-10 P. M., etc. The coördinates of the birds in each one-hour interval may now be plotted on separate diagrammatic clockfaces, just as they appeared on the moon. Tick marks are added to each line to indicate the number of birds occurring along the same coördinate. The slant of the tick marks distinguishes the points of departure from the points of entry. Figure 14 shows the plot for the 11 P. M.-12 P. M. observations reproduced in Table 1. The standard form, illustrated in Figure 15, includes four such diagrams.
Applying the self-evident principle that all pathways with the same slant represent the same direction, we may further consolidate the plots by shifting all coördinates to the corresponding lines passing through the center of the circle, as in Figure 15. To illustrate, the 6 to 8, 5 to 9, 3 to 11, and 2 to 12 pathways all combine on the 4 to 10 line. Experienced computers eliminate a step by directly plotting the pathways through center, using a transparent plastic straightedge ruled off in parallel lines.

============================= =============================
Time In Out Time In Out
----------------------------- -----------------------------
10:37-10:41 Time out 11:15 8 9:30
10:45 5:30 10 11:16 4 11
6 9 5 9
5:30 10 11:17 5 11:30
10:46 6 8 11:18 5 12
3:30 11 6 11:30
5 12 11:19 5:30 11:30
10:47 3:15 1 11:20 6 10
6 8:30 3 12
5:45 11:45 5 12
5 10 11:21 5:45 11
10:48 6 9:45 5 11
10:50 5:30 11 11:23 5 12
10:51 4 11 11:25 5 10:30
10:52 4 2 6 11
5:30 11 6 12
10:53 5:30 11:30 11:27 6 10
5 11 11:28 6 11:30
10:55 5 12 5:30 12:30
5 11 11:29 6 11:30
10:56 6 10 4 12
10:58 4:30 11:30 6:30 10:30
5:45 11:45 6 11
10:59 6:30 10:30 11:30 3 10
11:00 3:30 12 (2 birds at once)
6:30 11 11:31 5 10:30
(2 birds at once) 5:30 10:30
11:03 6 11 11:32 6 11:30
11:04 3 12 11:33 7:30 9:30
5 12 4 10:30
11:05 6 10 6 11:30
5 11 8 9:30
11:06 6 10:30 11:35 7 10
11:07 3 10 4:30 1
11:08 6 11 11:38 6:30 11
11:10 7 9:30 11:40 5:30 12
11:11 5 9:15 11:42 4 2
11:13 5 12 5 12
11:14 6:30 10 6 10
5:30 1 4 2
4 12 5 12
============================= =============================
Time In Out Time In Out
----------------------------- -----------------------------
11:44 8 9:30 8 10:15
7 11 12:16 3:30 1:30
6 10 8 11
11:45 5 12 12:23 7 1:30
6 10:30 6 12:30
5:45 11 12:36 8 11
4 12 12:37 7:30 1
11:46 7 11 12:38 7 12:30
6 12 12:40 8 1
11:47 8 10 12:45 7:30 1
11:48 6 10 12:47 5:30 1
11:49 6:30 10:30 12:48 7 1
11:51 8 10 12:52 5:30 1:30
8 10 12:54-12:55 Time out
8 10 12:56 8 10:45
8 10 12:58 5:30 1:30
6 10 7 1:30
8 10 7 2
6 11 12:59 5 3
7 12 1:00-1:30 Time out
11:52 5 1 1:37 8 12
11:54 7 11 1:38 8 12
6 12:30 1:48 7 1
11:55 5 12 7 1
11:56 7 10 1:51 5:30 11
5 12 1:57 8 1
11:58 8 11 2:07 7 2
11:59 5:30 12 2:09 9 12
12:00-12:03 Time out 2:10 8 1
12:03 5:30 11:30 2:17 9 12
12:04 8 11 2:21 6 2
12:07 6 12:30 2:30 5:30 3:15
7:30 1 2:32 8 2
12:08 5 10:30 2:46 7 1
12:09 5:30 1 3:36 9 2
7:30 2 3:39 8:30 2
12:10 6:30 12:45 3:45 6 4
12:13 8 11 3:55 9 2
12:14 7 1 4:00 8 3
12:15 7 12:30 4:03 9 2
7:15 1:30 4:30 Closed station
----------------------------- -----------------------------
We now have a concise picture of the apparent pathways of all the birds recorded in each hour of observation. But the coördinates do not have the same meaning as readings of a horizontal clock on the earth's surface, placed in relation to the points of the compass. They are merely projections of the birds' courses. An equation is available for reversing the effect of projection and discovering the true directions of flight. This formula, requiring thirty-five separate computations for the pathways reproduced in Figure 12 alone, is far too-consuming for the handling of large quantities of data. A simpler procedure is to divide the compass into sectors and, with the aid of a reverse equation, to draw in the projected boundaries of these divisions on the circular diagrams of the moon. A standardized set of sectors, each 22½° wide and bounded by points of the compass, has been evolved for this purpose. They are identified as shown in Figure 16. The zones north of the east-west line are known as the North, or N, Sectors, as N1, N2, N3, etc. Each zone south of the east-west line bears the same number as the sector opposite, but is distinguished by the designation S.

Several methods may be used to find the projection of the sector boundaries on the plot diagrams of Figure 15. Time may be saved by reference to graphic tables, too lengthy for reproduction here, showing the projected reading in degrees for every boundary, at every position of the moon; and a mechanical device, designed by [Pg_399] C. M. Arney, duplicating the conditions of the original projection, speeds up the work even further. Both methods are based on the principle of the following formula:
| tan θ = tan (η - ψ) / cos Z0 | (1) |

The symbols have these meanings:
θ is the position angle of the sector boundary on the lunar clock, with positive values measured counterclockwise from 12 o'clock, negative angles clockwise (Figure 17A).
η is the compass direction of the sector boundary expressed in degrees reckoned west from the south point (Figure 17B).
[Pg_400] Z0 is the zenith distance of the moon's center midway through the hour of observation, that is, at the half hour. It represents the number of degrees of arc between the center of the moon and a point directly over the observer's head (Figure 17C).
ψ is the azimuth of the moon midway through the hour of observation, measured from the south point, positive values to the west, negative values to the east (Figure 17D).

[Pg_401] The angle η for any sector boundary can be found immediately by measuring its position in the diagram (Figure 16). The form (Figure 18) for the "Computation of Zenith Distance and Azimuth of the Moon" illustrates the steps in calculating the values of Z0 and ψ0. From the American Air Almanac (Anonymous, 1945-1948), issued annually by the U. S. Naval Observatory in three volumes, each covering four months of the year, the Greenwich Hour Angle (GHA) and the declination of the moon may be obtained for any ten-minute interval of the date in question. The Local Hour Angle (LHA) of the observation station is determined by subtracting the longitude of the station from the GHA. Reference is then made to the "Tables of Computed Altitude and Azimuth," published by the U. S. Navy Department, Hydrographic Office (Anonymous, 1936-1941), and better known as the "H.O. 214," to locate the altitude and azimuth of the moon at the particular station for the middle of the hour during which the observations were made. The tables employ three variables—the latitude of the locality measured to the nearest degree, the LHA as determined above, and the declination of the moon measured to the nearest 30 minutes of arc. Interpolations can be made, but this exactness is not required. When the latitude of the observation station is in the northern hemisphere, the H.O. 214 tables entitled "Declinations Contrary Name to Latitude" are used with south declinations of the moon, and the tables "Declinations Same Name as Latitude," with north declinations. In the sample shown in Figure 15, the declination of the moon at 11:30 P. M., midway through the 11 to 12 o'clock interval, was S 20° 22´. Since the latitude of Progreso, Yucatán is N 21° 17´, the "Contrary Name" tables apply to this hour.
Because the H.O. 214 expresses the vertical position of the moon in terms of its altitude, instead of its zenith distance, a conversion is required. The former is the number of arc degrees from the horizon to the moon's center; therefore Z0 is readily obtained by subtracting the altitude from 90°. Moreover, the azimuth given in the H.O. 214 is measured on a 360° scale from the north point, whereas the azimuth used here (ψ0) is measured 180° in either direction from the south point, negative values to the east, positive values to the west. I have designated the azimuth of the tables as Azn and obtained the desired azimuth (ψ0) by subtracting 180° from Azn. The sign of ψ0 may be either positive or negative, depending on whether or not the moon has reached its zenith and hence the meridian of the observer. When the GHA is greater than the local longitude [Pg_402] (that is, the longitude of the observation station), the azimuth is positive. When the GHA is less than the local longitude, the azimuth is negative.
Locating the position of a particular sector boundary now becomes a mere matter of substituting the values in the equation (1) and reducing. The computation of the north point for 11 to 12 P. M. in the sample set of data will serve as an example. Since the north point reckoned west from the south point is 180°, its η has a value of 180°.

| tan θNpt. = | tan (180° - ψ0) |
| cos Z0 |
Substituting values of ψ0 found on the form (Figure 18):
| tan θNpt. = | tan [180° - (-35°)] | = | tan 215° | = | .700 | = 1.09 |
| cos 50° | cos 50° | .643 |

Four angles, one in each quadrant, have the same tangent value. [Pg_404] Since, in processing spring data, we are dealing mainly with north sectors, it is convenient to choose the acute angle, in this instance 47°28´. In doubtful cases, the value of the numerator of the equation (here 215°) applied as an angular measure from 6 o'clock will tell in which quadrant the projected boundary must fall. The fact that projection always draws the boundary closer to the 3-9 line serves as a further check on the computation.

In the same manner, the projected position angles of all the pertinent sector boundaries for a given hour may be calculated and plotted in red pencil with a protractor on the circular diagrams of Figure 15. To avoid confusion in lines, the zones are not portrayed in the black and white reproduction of the sample plot form. They are shown, however, in the shaded enlargement (Figure 19) of the 11 to 12 P. M. diagram. The number of birds recorded for each sector may be ascertained by counting the number of tally marks between each pair of boundary lines and the information may be entered in the columns provided in the plot form (Figure 15). [Pg_405]
We are now prepared to turn to the form for "Computations of Sector Densities" (Figure 20), which systematizes the solution of the following equation:
![D = (220*(60/T)(No. of Birds)(cos^2 Z_{0}))/(1 - sin^2 Z_{0} cos^2 [alpha])^0.5 Complex Formula](images/formula_2.png) |
(2) |


Some of the symbols and factors, appearing here for the first time, require brief explanation. D stands for Sector Density. The constant, 220, is the reciprocal of the quotient of the angular diameter of the moon divided by 2. T is Time In, arrived at by subtracting the total number of minutes of time out, as noted for each hour on the original data sheets, from 60. "No. of Birds" is the number for the sector and hour in question as just determined on the plot form. The symbol represents the angle between the mid-line of the sector and the azimuth line of the moon. The quantity is found by the equation:
| α = 180° - η + ψ0 | (3) |
The symbol η here represents the position of the mid-line of the sector expressed in terms of its 360° compass reading. This equation is illustrated in Figure 21. The values of η for various zones are given in the upper right-hand corner of the form (Figure 20). The subsequent reductions of the equations, as they appear in the figure for four zones, are self-explanatory. The end result, representing the sector density, is entered in the rectangular box provided.
After all the sector densities have been computed, they are tabulated on a form for the "Summary of Sector Densities" (Figure 22). By totaling each vertical column, sums are obtained, expressing the Station Density or Station Magnitude for each hour.

An informative way of depicting the densities in each zone is to plot them as lines of thrust, as in Figure 23. Each sector is represented by the directional slant of its mid-line drawn to a length expressing the flight density per zone on some chosen scale, such as 100 birds per millimeter. Standard methods of vector analysis are then applied to find the vector resultant. This is done by considering the first two thrust lines as two sides of an imaginary parallelogram and using a drawing compass to draw intersecting arcs locating the position of the missing corner. In the same way, the third vector [Pg_408] is combined with the invisible resultant whose distal end is represented by the intersection of the first two arcs. The process is repeated successively with each vector until all have been taken into consideration. The final intersection of arcs defines the length and slant of the Vector Resultant, whose magnitude expresses the Net Trend Density in terms of the original scale.
The final step in the processing of a set of observations is to plot on graph paper the nightly station density curve as illustrated by Figure 24.
Present day concepts of the whole broad problem of bird migration are made up of a few facts and many guesses. The evolutionary origin of migration, the modern necessities that preserve its biologic utility, the physiological processes associated with it, the sensory mechanisms that make it possible, the speed at which it is achieved, and the routes followed, all have been the subject of some investigation and much conjecture. All, to a greater or less extent, remain matters of current controversy. All must be considered unknowns in every logical equation into which they enter. Since all aspects of the subject are intimately interrelated, since all have a bearing on the probabilities relating to any one, and since new conjectures must be judged largely in the light of old conjectures rather than against a background of ample facts, the whole field is one in which many alternative explanations of the established phenomena remain equally tenable. Projected into this uncertain atmosphere, any statistical approach such as determinations of flight density will require the accumulation of great masses of data before it is capable of yielding truly definitive answers to those questions that it is suited to solve. Yet, even in their initial applications, density analyses can do much to bring old hypotheses regarding nocturnal migration into sharper definition and to suggest new ones.
The number of birds recorded through the telescope at a particular station at a particular time is the product of many potential variables. Some of these—like the changing size of the field of observation and the elevation of flight—pertain solely to the capacity of the observer to see what is taking place. It is the function of the density and direction formulae to eliminate the influences of these two variables insofar as is possible, so that the realities of the situation take shape in a nearly statistically true form. There remain to be considered those influences potentially responsible for [Pg_409] variations in the real volume of migration at different times and places—things like the advance of season, geographic location, disposition of terrain features, hourly activity rhythm, wind currents, and other climatological causes. The situation represented by any set of observations probably is the end result of the interaction of several such factors. It is the task of the discussions that follow to analyze flight densities in the light of the circumstances surrounding them and by statistical insight to isolate the effects of single factors. When this has been done, we shall be brought closer to an understanding of these influences themselves as they apply to the seasonal movements of birds. Out of data that is essentially quantitative, conclusions of a qualitative nature will begin to take form. It should be constantly borne in mind, however, that such conclusions relate to the movement of birds en masse and that caution must be used in applying these conclusions to any one species.
Since the dispersal of migrants in the night sky has a fundamental bearing on the sampling procedure itself, and therefore on the reliability of figures on flight density, consideration can well be given first to the horizontal distribution of birds on narrow fronts.
Bird migration, as we know it in daytime, is characterized by spurts and uneven spatial patterns. Widely separated V's of geese go honking by. Blackbirds pass in dense recurrent clouds, now on one side of the observer, now on the other. Hawks ride along in narrow file down the thermal currents of the ridges. Herons, in companies of five to fifty, beat their way slowly along the line of the surf. And an unending stream of swallows courses low along the levees. Everywhere the impression is one of birds in bunches, with vast spaces of empty sky between.
Such a situation is ill-suited to the sort of sampling procedure on which flight density computations are based. If birds always traveled in widely separated flocks, many such flocks might pass near the cone of observation and still, by simple chance, fail to enter the sliver of space where they could be seen. Chance would be the dominating factor in the number of birds recorded, obscuring the effects of other influences. Birds would seldom be seen, but, when they did appear, a great many would be observed simultaneously or in rapid succession. [Pg_410] When these telescopic studies were first undertaken at Baton Rouge in 1945, some assurance already existed, however, that night migrants might be so generally dispersed horizontally in the darkness above that the number passing through the small segment of sky where they could be counted would furnish a nearly proportionate sample of the total number passing in the neighborhood of the observation station. This assurance was provided by the very interesting account of Stone (1906: 249-252), who enjoyed the unique experience of viewing a nocturnal flight as a whole. On the night of March 27, 1906, a great conflagration occurred in Philadelphia, illuminating the sky for a great distance and causing the birds overhead to stand out clearly as their bodies reflected the light. Early in the night few birds were seen in the sky, but thereafter they began to come in numbers, passing steadily from the southwest to the northeast. At ten o'clock the flight was at its height. The observer stated that two hundred birds were in sight at any given moment as he faced the direction from which they came. This unparalleled observation is of such great importance that I quote it in part, as follows: "They [the birds] flew in a great scattered, wide-spread host, never in clusters, each bird advancing in a somewhat zigzag manner…. Far off in front of me I could see them coming as mere specks…gradually growing larger as they approached…. Over the illuminated area, and doubtless for great distances beyond, they seemed about evenly distributed…. I am inclined to think that the migrants were not influenced by the fire, so far as their flight was concerned, as those far to the right were not coming toward the blaze but keeping steadily on their way…. Up to eleven o'clock, when my observations ceased, it [the flight] continued apparently without abatement, and I am informed that it was still in progress at midnight."
Similarly, in rather rare instances in the course of the present study, the combination of special cloud formations and certain atmospheric conditions has made it possible to see birds across the entire field of the telescope, whether they actually passed before the moon or not. In such cases the area of the sky under observation is greatly increased, and a large segment of the migratory movement can be studied. In my own experience of this sort, I have been forcibly impressed by the apparent uniformity and evenness of the procession of migrants passing in review and the infrequence with which birds appeared in close proximity.
As striking as these broader optical views of nocturnal migration are, they have been too few to provide an incontestable basis for [Pg_411] generalizations. A better test of the prevailing horizontal distribution of night migrants lies in the analysis of the telescopic data themselves.

The distribution in time of birds seen by a single observer may be studied profitably in this connection. Since the cone of observation is in constant motion, swinging across the front of birds migrating from south to north, each interval of time actually represents a different position in space. This is evident from the map of the progress of the field of observation across the terrain at Tampico, Tamaulipas, on April 21-22, 1948 (Figure 25). At this station on this night, a total of 259 birds were counted between 7:45 P. M. and 3:45 [Pg_412] A. M. The number seen in a single hour ranged from three to seventy-three, as the density overhead mounted to a peak and then declined. The number of birds seen per minute was not kept with stop watch accuracy; consequently, analysis of the number of birds that passed before the moon in short intervals of time is not justified. It appears significant, however, that in the ninety minutes of heaviest flight, birds were counted at a remarkably uniform rate per fifteen minute interval, notwithstanding the fact that early in the period the flight rate overhead had reached a peak and had begun to decline. The number of birds seen in successive fifteen-minute periods was twenty-six, twenty-five, nineteen, eighteen, fifteen, and fifteen.
Also, despite the heavy volume of migration at this station on this particular night, the flight was sufficiently dispersed horizontally so that only twice in the course of eight hours of continuous observation did more than one bird simultaneously appear before the moon. These were "a flock of six birds in formation" seen at 12:09 A. M. and "a flock of seven, medium-sized and distant," seen at 2:07 A. M. In the latter instance, as generally is the case when more than one bird is seen at a time, the moon had reached a rather low altitude, and consequently the cone of observation was approaching its maximum dimensions.
The comparative frequency with which two or more birds simultaneously cross before the moon would appear to indicate whether or not there is a tendency for migrants to fly in flocks. It is significant, therefore, that in the spring of 1948, when no less than 7,432 observations were made of birds passing before the moon, in only seventy-nine instances, or 1.1 percent of the cases, was more than one seen at a time. In sixty percent of these instances, only two birds were involved. In one instance, however, again when the moon was low and the cone of observation near its maximum size, a flock estimated at twenty-five was recorded.
The soundest approach of all to the study of horizontal distribution at night, and one which may be employed any month, anywhere, permitting the accumulation of statistically significant quantities of data, is to set up two telescopes in close proximity. Provided the flight overhead is evenly dispersed, each observer should count approximately the same number of birds in a given interval of time. Some data of this type are already available. On May 19-20, at Urbana, Illinois, while stationed twenty feet apart making parallax studies with two telescopes to determine the height above [Pg_413] the earth of the migratory birds, Carpenter and Stebbins (loci cit.) saw seventy-eight birds in two and one-half hours. Eleven were seen by both observers, thirty-three by Stebbins only, and thirty-four by Carpenter only. On October 10, 1905, at the same place, in two hours, fifty-seven birds were counted, eleven being visible through both telescopes. Of the remainder, Stebbins saw seventeen and Carpenter, twenty-nine. On September 12, 1945, at Baton Rouge, Louisiana, in an interval of one hour and forty minutes, two independent observers each counted six birds. Again, on October 17, 1945, two observers each saw eleven birds in twenty-two minutes. On April 10, 1946, in one hour and five minutes, twenty-four birds were seen through one scope and twenty-six through the other. Likewise on May 12, 1946, in a single hour, seventy-three birds were counted by each of two observers. The Baton Rouge observations were made with telescopes six to twelve feet apart. These results show a remarkable conformity, though the exceptional October observation of Carpenter and Stebbins indicates the desirability of continuing these studies, particularly in the fall.
On the whole, the available evidence points to the conclusion that night migration differs materially from the kind of daytime migration with which we are generally familiar. Birds are apparently evenly spread throughout the sky, with little tendency to fly in flocks. It must be remembered, however, that only in the case of night migration have objective and truly quantitative studies been made of horizontal distribution. There is a possibility that our impressions of diurnal migration are unduly influenced by the fact that the species accustomed to flying in flocks are the ones that attract the most attention.
These conclusions relate to the uniformity of migration in terms of short distances only, in the immediate vicinity of an observation station. The extent to which they may be applied to broader fronts is a question that may be more appropriately considered later, in connection with continental aspects of the problem.
There are few aspects of nocturnal migration about which there is less understanding than the matter of when the night flight begins, at what rate it progresses, and for what duration it continues. One would think, however, that this aspect of the problem, above most others, would have been thoroughly explored by some means of objective study. Yet, this is not the case. Indeed, I find not a [Pg_414] single paper in the American literature wherein the subject is discussed, although some attention has been given the matter by European ornithologists. Siivonen (1936) recorded in Finland the frequency of call notes of night migrating species of Turdus and from these data plotted a time curve showing a peak near midnight. Bergman (1941) and Putkonen (1942), also in Finland, studied the night flights of certain ducks (Clangula hyemalis and Oidemia fusca and O. nigra) and a goose (Branta bernicla) and likewise demonstrated a peak near midnight. However, these studies were made at northern latitudes and in seasons characterized by evenings of long twilight, with complete darkness limited to a period of short duration around midnight. Van Oordt (1943: 34) states that in many cases migration lasts all night; yet, according to him, most European investigators are of the opinion that, in general, only a part of the night is used, that is, the evening and early morning hours. The consensus of American ornithologists seems to be that migratory birds begin their flights in twilight or soon thereafter and that they remain on the wing until dawn. Where this idea has been challenged at all, the implication seems to have been that the flights are sustained even longer, often being a continuation far into the night of movements begun in the daytime. The telescopic method fails to support either of these latter concepts.

When the nightly curves of density at the various stations are plotted as a function of time, a salient fact emerges—that the flow [Pg_415] of birds is in no instance sustained throughout the night. The majority of the curves rise smoothly from near zero at the time of twilight to a single peak and then decline more or less symmetrically to near the base line before dawn. The high point is reached in or around the eleven to twelve o'clock interval more often than at any other time.

Figure 26, representing the average hourly densities for all stations on all nights of observation, demonstrates the over-all effect of these tendencies. Here the highest density is reached in the hour before midnight with indications of flights of great magnitude also in the hour preceding and the hour following the peak interval. The curve ascends somewhat more rapidly than it declines, which fact may or may not be significant. Since there is a great disproportion in the total volume of migration at different localities, the thought might be entertained that a few high magnitude stations, such as Tampico and Progreso, have imposed their own characteristics on the final graph. Fortunately, this idea may be tested by subjecting the data to a second treatment. If hourly densities are expressed as a percentage of the nightly peak, each set of observations, regardless of the number of birds involved, carries an equal weight in determining the character of the over-all curve. Figure 27 shows that percentage analysis produces a curve almost identical with the preceding one. To be sure, all of the individual curves do not conform with the composite, either in shape or incidence of [Pg_416] peak. The extent of this departure in the latter respect is evident from Figure 28, showing the number of individual nightly station curves reaching a maximum peak in each hour interval. Even this graph demonstrates that maximum densities near midnight represent the typical condition.

The remarkable smoothness and consistency of the curves shown in Figures 26 and 27 seem to lead directly to the conclusion that the volume of night migration varies as a function of time. Admittedly other factors are potentially capable of influencing the number of birds passing a given station in a given hour. Among these are weather conditions, ecological patterns, and specific topographical features that might conceivably serve as preferred avenues of flight. However, if any of these considerations were alone responsible for changes in the numbers of birds seen in successive intervals, the distribution of the peak in time could be expected to be haphazard. For example, there is no reason to suppose that the cone of observation would come to lie over favored terrain at precisely the hour between eleven and twelve o'clock at so many widely separated stations. Neither could the topographical hypothesis explain the consistently ascending and descending pattern of the ordinates in Figure 28. This is not to say that other factors are without effect; they no doubt explain the divergencies in the time pattern exhibited by Figure 28. Nevertheless, the underlying circumstances are such that when many sets of data are merged these other influences are subordinated to the rise and fall of an evident time pattern. [Pg_417] Stated in concrete terms, the time frequencies shown in the graphs suggest the following conclusions: first, nocturnal migrations are not a continuation of daytime flights; second, nearly all night migrants come to earth well before dawn; and, third, in each hour of the night up until eleven or twelve o'clock there is typically a progressive increase in the number of birds that have taken wing and in each of the hours thereafter there is a gradual decrease. Taken at its face value, the evidence seems to indicate that birds do not begin their night migrations en masse and remain on the wing until dawn and that in all probability most of them utilize less than half of the night.
Interestingly enough, the fact that the plot points in Figure 26 lie nearly in line tempts one to a further conclusion. The curve behaves as an arithmetic progression, indicating that approximately the same number of birds are leaving the ground in each hour interval up to a point and that afterwards approximately the same number are descending within each hour. However, some of the components making up this curve, as later shown, are so aberrant in this regard that serious doubt is cast on the validity of this generalization.
Because the results of these time studies are unexpected and startling, I have sought to explore other alternative explanations and none appears to be tenable. For example, the notion that the varying flight speeds of birds might operate in some way to produce a cumulative effect as the night progresses must be rejected on close analysis. If birds of varying flight speeds are continuously and evenly distributed in space, a continuous and even flow would result all along their line of flight. If they are haphazardly distributed in space, a correspondingly haphazard density pattern would be expected.
Another explanation might be sought in the purely mathematical effects of the method itself. The computational procedure assumes that the effective area of the sample is extremely large when the moon is low, a condition that usually obtains in the early hours of the evening in the days surrounding the full moon. Actually no tests have yet been conducted to ascertain how far away a silhouette of a small bird can be seen as it passes before the moon. Consequently, it is possible that some birds are missed under these conditions and that the effective field of visibility is considerably smaller than the computed field of visibility. The tendency, therefore, may be to minimize the densities in such situations more than is justified. [Pg_418] However, in many, if not most, cases, the plotting of the actual number of birds seen, devoid of any mathematical procedures, results in an ascending and descending curve.

A third hypothesis proposes that all birds take wing at nearly the same time, gradually increase altitude until they reach the mid-point of their night's journey, and then begin a similarly slow descent. Since the field of observation of the telescope is conical, it is assumed that the higher the birds arise into the sky the more they increase their chances of being seen. According to this view, the changes [Pg_419] in the density curve represent changes in the opportunity to see birds rather than an increase or decrease in the actual number of migrants in the air. Although measurements of flight altitude at various hours of the night have not been made in sufficient number to subject this idea to direct test, it is hardly worthy of serious consideration. The fallacy in the hypothesis is that the cone of observation itself would be rising with the rising birds so that actually the greatest proportion of birds flying would still be seen when the field of observation is in the supine position of early evening.
It cannot be too strongly emphasized that the over-all time curves just discussed have been derived from a series of individual curves, some of which differ radically from the composite pattern. In Figure 29, six dissimilar types are shown. This variation is not surprising in view of the fact that many other causative factors aside from time operate on the flow of birds from hour to hour. Figure 29A illustrates how closely some individual patterns conform with the average. Figure 29B is an example of a random type of fluctuation with no pronounced time character. It is an effect rarely observed, occurring only in the cases where the number of birds observed is so small that pure chance has a pronounced effect on the computed densities; its vacillations are explicable on that account alone. Errors of sampling may similarly account for some, though not all, of the curves of the bimodal type shown in Figure 29C. Some variation in the curves might be ascribed to the variations in kinds of species comprising the individual flights at different times at different places, provided that it could be demonstrated that different species of birds show dissimilar temporal patterns. The other atypical patterns are not so easily dismissed and will be the subject of inquiry in the discussions that follow. It is significant that in spite of the variety of the curves depicted, which represent every condition encountered, in not a single instance is the density sustained at a high level throughout the night. Moreover, these dissident patterns merge into a remarkably harmonious, almost normal, average curve.
When, at some future date, suitable data are available, it would be highly desirable to study the average monthly time patterns to ascertain to what extent they may deviate from the over-all average. At present this is not justifiable because there are not yet enough sets of data in any two months representing the same selection of stations.
It is especially interesting to note that the data pertaining to this problem derived from other methods of inquiry fit the conclusions adduced by the telescopic method. Overing (1938), who for several years kept records of birds striking the Washington Monument, stated that the record number of 576 individuals killed on the night of September 12, 1937, all came down between 10:30 P. M. and midnight. His report of the mortality on other nights fails to mention the time factor, but I am recently informed by Frederick C. Lincoln (in litt.) that it is typical for birds to strike the monument in greatest numbers between ten and twelve o'clock at night. At the latter time the lights illuminating the shaft are extinguished, thus resulting in few or no casualties after midnight. The recent report by Spofford (1949) of over 300 birds killed or incapacitated at the Nashville airport on the night of September 9-10, 1948, after flying into the light beam from a ceilometer, is of interest in this connection even though the cause of the fatality is shrouded in mystery. It may be noted, however, that "most of the birds fell in the first hour," which, according to the account, was between 12:30 A. M. and 1:30 A. M. Furthermore, birds killed at the Empire State Building in New York on the night of September 10-11, 1948, began to strike the tower "shortly after midnight" (Pough, 1948). Also it will be recalled that the observations of Stone (loc. cit.), already referred to in this paper (page 410), show a situation where the flight in the early part of the night was negligible but mounted to a peak between ten and eleven o'clock, with continuing activity at least until midnight.
All of these observations are of significance in connection with the conclusions herein advanced, but by far the most striking correlation between these present results and other evidences is found in the highly important work of various European investigators studying the activity of caged migratory birds. This work was recently reviewed and extended by Palmgren (1944) in the most comprehensive treatise on the subject yet published. Palmgren recorded, by an electrically operated apparatus, the seasonal, daily, and hourly activity patterns in caged examples of two typical European migrants, Turdus ericetorum philomelos Brehm and Erithacus rubecula (Linnaeus). Four rather distinct seasonal phases in activity of the birds were discerned: winter non-migratory, spring migratory, summer non-migratory, and autumn migratory. The first of these is distinguished by morning and evening maxima [Pg_421] of activity, the latter being better developed but the former being more prolonged. Toward the beginning of migration, these two periods of activity decline somewhat. The second, or spring migratory phase, which is of special interest in connection with the present problem, is characterized by what Palmgren describes as nightly migratory restlessness (Zugunruhe). The morning maximum, when present, is weaker and the evening maximum often disappears altogether. Although variations are described, the migratory restlessness begins ordinarily after a period of sleep ("sleeping pause") in the evening and reaches a maximum and declines before midnight.
This pattern agrees closely with the rhythm of activity indicated by the time curves emerging from the present research. Combining the two studies, we may postulate that most migrants go to sleep for a period following twilight, thereby accounting for the low densities in the early part of the night. On awakening later, they begin to exhibit migratory restlessness. The first hour finds a certain number of birds sufficiently stimulated so that they rise forthwith into the air. In the next hour still others respond to this urge and they too mount into the air. This continues until the "restlessness" begins to abate, after which fewer and fewer birds take wing. By this time, the birds that began to fly early are commencing to descend, and since their place is not being filled by others leaving the ground, the density curve starts its decline. Farner (1947) has called attention to the basic importance of the work by Palmgren and the many experimental problems it suggests. Of particular interest would be studies comparing the activity of caged American migrant species and the nightly variations in the flight rates.
As already stated, the present study was initiated at Baton Rouge, Louisiana, in 1945, and from the outset a very peculiar density time pattern was manifest. I soon found that birds virtually disappeared from the sky after midnight. Within an hour after the termination of twilight, the density would start to ascend toward a peak which was usually reached before ten o'clock, and then would begin, surprisingly enough, a rapid decline, reaching a point where the migratory flow was negligible. In Figure 30 the density curves are shown for five nights that demonstrate this characteristically early decline in the volume of migration at this station. Since, in the early stages of the work, coördinates of apparent pathways of all the birds seen were not recorded, I am unable now to ascertain the direction of flight and thereby arrive at a density figure based on the dimension of the cone and the length of the front presented to birds flying in certain directions. It is feasible, nevertheless, to compute what I have termed a "plus or minus" flight density figure stating the rate of passage of birds in terms of the maximum and minimum corrections which all possible directions of flight would impose. In other words, density is here computed, first, as if all the birds were flying perpendicular to the long axis of the ellipse, and, secondly, as if all the birds were flying across the short axis of the ellipse. Since the actual directions of flight were somewhere between these two extremes, the "plus or minus" density figure is highly useful.

[Pg_423] The well-marked decline before midnight in the migration rates at Baton Rouge may be regarded as one of the outstanding results emerging from this study. Many years of ornithological investigation in this general region failed to suggest even remotely that a situation of this sort obtained. Now, in the light of this new fact, it is possible for the first time to rationalize certain previously incongruous data. Ornithologists in this area long have noted that local storms and cold-front phenomena at night in spring sometimes precipitate great numbers of birds, whereupon the woods are filled the following day with migrants. On other occasions, sudden storms at night have produced no visible results in terms of bird densities the following day. For every situation such as described by Gates (1933) in which hordes of birds were forced down at night by inclement weather, there are just as many instances, even at the height of spring migration, when similar weather conditions yielded no birds on the ground. However, the explanation of these facts is simple; for we discover that storms that produced birds occurred before midnight and those that failed to produce birds occurred after that time (the storm described by Gates occurred between 8:30 and 9:00 P. M.).
The early hour decline in density at Baton Rouge at first did not seem surprising in view of the small amount of land area between this station and the Gulf of Mexico. Since the majority of the birds destined to pass Baton Rouge on a certain night come in general from the area to the south of that place, and since the distances to various points on the coast are slight, we inferred that a three-hour flight from even the more remote points would probably take the bulk of the birds northward past Baton Rouge. In short, the coastal plain would be emptied well before midnight of its migrant bird life, or at least that part of the population destined to migrate on any particular night in question. Although data [Pg_424] in quantity are not available from stations on the coastal plain other than Baton Rouge, it may be pointed out that such observations as we do have, from Lafayette and New Orleans, Louisiana, and from Thomasville, Georgia, are in agreement with this hypothesis.
A hundred and seventy miles northward in the Mississippi Valley, at Oak Grove, Louisiana, a somewhat more normal density pattern is manifested. There, in four nights of careful observation, a pronounced early peak resulted on the night of May 21-22 (Figure 29E), but on the other three nights significant densities held up until near twelve o'clock, thereby demonstrating the probable effect of the increased amount of land to the south of the station.
Subsequent studies, revealing the evident existence of an underlying density time pattern, cast serious doubt on the explanations just advanced of the early decline in the volume of migration at Baton Rouge. It has as yet been impossible to reconcile the early drop-off at this station with the idea that birds are still mounting into the air at eleven o'clock, as is implied by the ideal time curves.
To this point we have considered the horizontal distribution of birds in the sky only on a very narrow scale and mainly in terms of the chance element in observations. Various considerations have supported the premise that the spread of nocturnal migration is rather even, at least within restricted spacial limits and short intervals of time. This means that in general the flow of birds from hour to hour at a single station exhibits a smooth continuity. It does not mean that it is a uniform flow in the sense that approximately the same numbers of birds are passing at all hours, or at all localities, or even on all one-mile fronts in the same locality. On the contrary, there is evidence of a pronounced but orderly change through the night in the intensity of the flight, corresponding to a basic and definitely timed cycle of activity. Other influences may interfere with the direct expression of this temporal rhythm as it is exhibited by observations at a particular geographical location. Among these, as we have just seen, is the disposition of the areas that offer suitable resting places for transient birds and hence contribute directly and immediately to the flight overhead. A second possible geographical effect is linked with the question of the tendency of night migrants to follow topographical features.
That many diurnal migrants tend to fly along shorelines, rivers, [Pg_425] and mountain ridges is well known, but this fact provides no assurance that night migrants do the same thing. Many of the obvious advantages of specialized routes in daylight, such as feeding opportunities, the lift provided by thermal updrafts, and the possible aid of certain landmarks in navigation, assume less importance after night falls. Therefore, it would not be safe to conclude that all nocturnal migrants operate as do some diurnal migrants. For instance, the passage of great numbers of certain species of birds along the Texas coast in daylight hours cannot be regarded as certain proof that the larger part of the nocturnal flight uses the same route. Neither can we assume that birds follow the Mississippi River at night simply because we frequently find migrants concentrated along its course in the day. Fortunately we shall not need to speculate indefinitely on this problem; for the telescopic method offers a means of study based on what night migrants are doing at night. Two lines of attack may be pursued. First we may compare flight densities obtained when the field of the telescope lies over some outstanding topographical feature, such as a river, with the recorded volume of flight when the cone of observation is directed away from that feature. Secondly, we may inquire how the major flight directions at a certain station are oriented with respect to the terrain. If the flight is concentrated along a river, for instance, the flight density curve should climb upward as the cone of observation swings over the river, regardless of the hour at which it does so. The effect should be most pronounced if the observer were situated on the river bank, so that the cone would eventually come to a position directly along the watercourse. Though in that event birds coming up the river route would be flying across the short axis of an elliptical section of the cone, the fact that the whole field of observation would be in their path should insure their being seen in maximum proportions. If, on the other hand, the telescope were set up some distance away from the river so that the cone merely moved across its course, only a section of the observation field would be interposed on the main flight lane.
The interaction of these possibilities with the activity rhythm should have a variety of effects on the flight density curves. If the cone comes to lie over the favored topographical feature in the hour of greatest migrational activity, the results would be a simple sharp peak of doubtful meaning. However, since the moon rises at a different time each evening, the cone likewise would reach the immediate [Pg_426] vicinity of the terrain feature at a different time each night. As a result, the terrain peak would move away from its position of coincidence with the time peak on successive dates, producing first, perhaps, a sustention of peak and later a definitely bimodal curve. Since other hypotheses explain double peaks equally well, their mere existence does not necessarily imply that migrants actually do travel along narrow topographical lanes. Real proof requires that we demonstrate a moving peak, based on properly corrected density computations, corresponding always with the position of the cone over the most favored terrain, and that the flight vectors be consistent with the picture thus engendered.
To date, none of the evidence in favor of the topographical hypothesis completely fills these requirements. Winkenwerder (loc. cit.), in analyzing the results of telescopic counts of birds at Madison and Beloit, Wisconsin, Detroit and Ann Arbor, Michigan, and at Lake Forest, Illinois, between 1898 and 1900, plotted the number of birds seen at fifteen-minute intervals as a function of the time of the night. He believed that the high points in the resulting frequency histograms represented intervals when the field of the telescope was moving over certain topographically determined flight lanes, though he did not specify in all cases just what he assumed the critical physiographic features to be. Especially convincing to him were results obtained at Beloit, where the telescope was situated on the east bank of the Rock River, on the south side of the city. Immediately below Beloit the river turns southwestward and continues in this direction about five miles before turning again to flow in a southeastward course for approximately another five miles. In this setting, on two consecutive nights of observation in May, the number of birds observed increased tremendously in the 2 to 3 A. M. interval, when, according to Winkenwerder's interpretation of the data (he did not make the original observations at Beloit himself), the telescope was pointing directly down the course of the river. This conclusion is weakened, however, by notable inconsistencies. Since the moon rises later each evening, it could not have reached the same position over the Rock River at the same time on both May 12-13 and May 13-14, and therefore, if the peaks in the graph were really due to a greater volume of migration along the watercourse, they should not have so nearly coincided. As a matter of fact the incidence of the peak on May 12-13 should have preceded that of [Pg_427] the peak on May 13-14; whereas his figure shows the reverse to have been true. Singularly enough, Winkenwerder recognized this difficulty in his treatment of the data from Madison, Wisconsin. Unable to correlate the peak period with the Madison terrain by the approach used for Beloit, he plotted the observations in terms of hours after moonrise instead of standard time. This procedure was entirely correct; the moon does reach approximately the same position at each hour after its rise on successive nights. The surprising thing is that Winkenwerder did not seem to realize the incompatibility of his two approaches or to realize that he was simply choosing the method to suit the desired results.
Furthermore, as shown in Part I of this paper, the number of birds seen through the telescope often has only an indirect connection with the actual number of birds passing over. My computations reveal that the highest counts of birds at Beloit on May 12-13 were recorded when the moon was at an altitude of only 8° to 15° and, that when appropriate allowance is made for the immense size of the field of observation at this time, the partially corrected flight density for the period is not materially greater than at some other intervals in the night when the telescope was not directed over the course of the Rock River. These allowances do not take the direction factor into consideration. Had the birds been flying at right angles to the short axis of an elliptical section of the cone throughout the night, the flight density in the period Winkenwerder considered the peak would have been about twice as high as in any previous interval. On the other hand, if they had been flying across the long axis at all times, the supposed peak would be decidedly inferior to the flight density at 10 to 11:00 P. M., before the cone came near the river.
Admittedly, these considerations contain a tremendous element of uncertainty. They are of value only because they expose the equal uncertainty in Winkenwerder's basic evidence. Since the coördinates of the birds' apparent pathways at Beloit were given, I at first entertained the hope of computing the flight densities rigorously, by the method herein employed. Unfortunately, Winkenwerder was apparently dealing with telescopes that gave inverted images, and he used a system for recording coördinates so ambiguously described that I am not certain I have deciphered its true meaning. When, however, his birds are plotted according to the instructions as he stated them, the prevailing direction of flight indicated by the projection formula falls close to west-northwest, not along the course of the Rock River, but at direct right angles to it.


I am in a position to establish more exact correlations between flight density and terrain features in the case of current sets of observations. Some of these data seem at first glance to fit the idea of narrow topographically-oriented flight lanes rather nicely. At Tampico, where six excellent sets of observations were made in March and April, 1948, the telescope was set up on the beach within a few yards of the Gulf of Mexico. As can be seen from Figure 25 (ante), the slant of the coastline at this point is definitely west of north, as is also the general trend of the entire coast from southern Veracruz to southern Tamaulipas (see Figure 34, beyond). The [Pg_429] over-all vector resultant of all bird flights at this station was N 11° W, and, as will be seen from Figure 31, none of the nightly vector resultants in April deviates more than one degree from this average. Thus the prevailing direction of flight, as computed, agrees with the trend of the coast at the precise point of the observations, at least to the extent that both are west of north. To be sure, the individual sector vectors indicate that not all birds were following this course; indeed, some appear to have been flying east of north, heading for a landfall in the region of Brownsville, Texas, and a very few to have been traveling northeastward toward the central Gulf coast. But it must be remembered that a certain amount of computational deviation and of localized zigzagging in flight must be anticipated. Perhaps none of these eastward vectors represents an actual extended flight path. The nightly vector resultants, on the other hand, are so consistent that they have the appearance of remarkable accuracy and tempt one to draw close correlations with the terrain. When this is done, it is found that, while the prevailing flight direction is 11° west of north, the exact slant of the coastline at the location of the station is about 30° west of north, a difference of around 19°. It appears, therefore, that the birds were not following the shoreline precisely but cutting a chord about ten miles long across an indentation of the coast. If it be argued that the method of calculation is not accurate enough to make a 19° difference significant, and that most of the birds might have been traveling along the beach after all, it can be pointed out with equal justification that, if this be so, the 11° divergence from north does not mean anything either and that perhaps the majority of the birds were [Pg_430] going due north. We are obliged to conclude either that the main avenue of flight paralleled the disposition of the major topographical features only in a general way or that the angle between the line of the coast and true north is not great enough to warrant any inference at all.
Consideration of the Tampico density curves leads to similarly ambiguous results. On the night of April 21-22, as is evident from a comparison of Figures 25 and 32, the highest flight density occurred when the projection of the cone on the terrain was wholly included within the beach. This is very nearly the case on the night of April 23-24 also, the positions of the cone during the peak period of density being only about 16° apart. (On the intervening date, clouds prevented continuous observation during the critical part of the night.) These correlations would seem to be good evidence that most of these night migrants were following the coastline of the Gulf of Mexico. However, the problem is much more complicated. The estimated point of maximum flight density fell at 10:45 P. M. on April 21-22 and 11:00 P. M. on April 23-24, both less than an hour from the peak in the ideal time curve (Figure 26, ante). We cannot be sure, therefore, that the increase in density coinciding with the position of the moon over the beach is not an increase which would have occurred anyway. Observations conducted several nights before or after the second quarter, when the moon is not on or near its zenith at the time of the predictable peak in the density curve, would be of considerable value in the study of this particular problem.
The situation at Tampico has been dealt with at length because, among all the locations for which data are available, it is the one that most strongly supports the topographical hypothesis. In none of the other cases have I been able to find a definite relation between the direction of migration and the features of the terrain. Studies of data from some of these stations disclose directional patterns that vary from night to night only slightly more than does the flight at Tampico. In three nights of observation at Lawrence, Kansas, marked by very high densities, the directional trend was north by north-northeast with a variation of less than 8°, yet Lawrence is so situated that there seems to be no feature of the landscape locally or in the whole of eastern Kansas or of western Missouri that coincides with this heading. At Mansfield, Louisiana, in twelve nights of observation, the strong east by northeast trend varied less than 15°, but again there appears to be no correlation over a wide area [Pg_431] between this direction and any landmarks. And, at Progreso, Yucatán, where the vector resultants were 21° and 27° on successive nights, most of the birds seen had left the land and were beginning their flight northward over the trackless waters of the Gulf of Mexico. Furthermore, as I have elsewhere pointed out (1946: 205), the whole northern part of the Yucatán Peninsula itself is a flat terrain, unmarked by rivers, mountains, or any other strong physiographic features that conceivably might be followed by birds.

In Figure 33 I have shown the directional patterns at certain stations where, unlike the cases noted above, there is considerable change on successive nights. Each vector shown is the vector resultant for one particular night. The lengths of the vectors have been determined by their respective percentages of the total computed density, or total station magnitude, for all the nights in question. In other words, the lengths of the individual vectors denote the percentile rôle that each night played in the total density. From the directional spread at these stations it becomes apparent that if most of the birds were traveling along a certain topographic feature on one [Pg_432] night, they could not have been traveling along the same feature on other nights.
The possibility should be borne in mind, however, that there may be more than one potential topographic feature for birds to follow at some stations. Moreover, it is conceivable that certain species might follow one feature that would lead them in the direction of their ultimate goal, whereas other species, wishing to go in an entirely different direction, might follow another feature that would lead them toward their respective destination. It would seem unlikely, however, that the species composition of the nocturnal flights would change materially from night to night, although there is a strong likelihood that it might do so from week to week and certainly from month to month.
By amassing such data as records of flight direction along the same coast from points where the local slant of the shoreline is materially different, and comparisons of the volume of migration at night along specialized routes favored during the day with the flight densities at progressive distances from the critical terrain feature involved, we shall eventually be able to decide definitely the rôle topography plays in bird migration. We cannot say on the basis of the present ambiguous evidence that it is not a factor in determining which way birds fly, but, if I had to hazard a guess one way or the other, I would be inclined to discount the likelihood of its proving a major factor.
A study of the total nightly or seasonal densities at the various stations brings forth some extremely interesting factors, many of which, however, cannot be fully interpreted at this time. A complete picture of the magnitude of migration at a given station cannot be obtained from the number of birds that pass the station on only a few nights in one spring. Many years of study may be required before hard and fast principles are justifiable. Nevertheless, certain salient features stand out in the continental density pattern in the spring of 1948. (The general results are summarized in Tables 2-5; the location of the stations is shown in Figure 34.) These features will be discussed now on a geographical basis.
| Observation Station | Nights of observation | Hours of observation | Season density |
||||||
| March | April | May | Total | March | April | May | Total | ||
| Canada | |||||||||
| Pt. Pelee | 1 | 1 | 6 | 6 | 2,500 | ||||
| Mexico | |||||||||
| S. L. P.: Ebano | 1 | 1 | 3 | 3 | 1,300 | ||||
| Tamps.: Tampico | 3 | 3 | 6 | 20 | 20 | 40 | 140,300 | ||
| Yuc.: Progreso | 3 | 3 | 18 | 18 | 60,500 | ||||
| United States | |||||||||
| Fla.: Pensacola | 2 | 2 | 4 | 8 | 7 | 15 | 1,500 | ||
| Winter Park | 5 | 6 | 11 | 39 | 38 | 77 | 21,700 | ||
| Ga.: Athens | 2 | 2 | 10 | 10 | 4,000 | ||||
| Thomasville | 1 | 1 | 2 | 8 | 8 | 16 | 4,700 | ||
| Iowa: Ottumwa | 5 | 5 | 10 | 16 | 28 | 44 | 134,400 | ||
| Kans.: Lawrence | 2 | 1 | 3 | 16 | 4 | 20 | 68,700 | ||
| Ky.: Louisville | 3 | 2 | 5 | 20 | 14 | 34 | 49,300 | ||
| Murray | 2 | 2 | 13 | 13 | 26,200 | ||||
| La.: Baton Rouge | 3 | 3 | 15 | 15 | 11,000 | ||||
| Lafayette | 1 | 1 | 5 | 5 | 2,800 | ||||
| Mansfield | 1 | 5 | 4 | 10 | 2 | 16 | 22 | 40 | 22,400 |
| New Orleans | 1 | 1 | 2 | 5 | 2 | 7 | 1,900 | ||
| Oak Grove | 2 | 2 | 4 | 16 | 15 | 31 | 33,900 | ||
| Mich.: Albion | 1 | 1 | 3 | 3 | 1,100 | ||||
| Minn.: Hopkins | 1 | 1 | 4 | 4 | 2,000 | ||||
| Miss.: Rosedale | 1 | 1 | 2 | 6 | 8 | 14 | 12,600 | ||
| Mo.: Columbia | 2 | 1 | 3 | 8 | 6 | 14 | 13,100 | ||
| Liberty | 1 | 1 | 2 | 7 | 7 | 14 | 4,800 | ||
| Okla.: Stillwater | 1 | 2 | 1 | 4 | 5 | 11 | 3 | 19 | 8,400 |
| S. Car.: Charleston | 1 | 1 | 1 | 3 | 5 | 8 | 9 | 22 | 3,000 |
| Tenn.: Knoxville | 2 | 2 | 4 | 18 | 14 | 32 | 35,400 | ||
| Memphis | 2 | 3 | 2 | 7 | 13 | 20 | 12 | 45 | 29,700 |
| Tex.: College Station | 3 | 1 | 4 | 19 | 8 | 27 | 32,200 | ||
| Rockport | 1 | 1 | 4 | 4 | 6,200 | ||||
| Observation Station | March | April | May | Season |
| Canada | ||||
| Pt. Pelee | 400 | 400 | ||
| Mexico | ||||
| S. L. P.: Ebano | 400 | 400 | ||
| Tamps.: Tampico | 700 | 6,300 | 3,500 | |
| Yuc.: Progreso | 2,800 | 2,800 | ||
| United States | ||||
| Fla.: Pensacola | 0+ | 200 | 100 | |
| Winter Park | 300 | 200 | 300 | |
| Ga.: Athens | 400 | 400 | ||
| Thomasville | 500 | 100 | 300 | |
| Iowa: Ottumwa | 1,700 | 3,800 | 3,100 | |
| Kans.: Lawrence | 4,000 | 1,400 | 3,400 | |
| Ky.: Louisville | 2,000 | 700 | 1,500 | |
| Murray | 2,000 | 2,000 | ||
| La.: Baton Rouge | 700 | 700 | ||
| Lafayette | 600 | 600 | ||
| Mansfield | 0 | 700 | 800 | 600 |
| New Orleans | 60 | 800 | 300 | |
| Oak Grove | 1,400 | 800 | 1,100 | |
| Mich.: Albion | 400 | 400 | ||
| Minn.: Hopkins | 500 | 500 | ||
| Miss.: Rosedale | 1,100 | 700 | 900 | |
| Mo.: Columbia | 400 | 1,700 | 900 | |
| Liberty | 500 | 200 | 300 | |
| Okla.: Stillwater | 500 | 200 | 1,000 | 400 |
| S. Car.: Charleston | 200 | 200 | 0+ | 100 |
| Tenn.: Knoxville | 1,300 | 800 | 1,100 | |
| Memphis | 300 | 800 | 900 | 700 |
| Tex.: College Station | 1,100 | 1,500 | 1,200 | |
| Rockport | 1,600 | 1,600 |
| Observation Station | March | April | May |
| Canada | |||
| Pt. Pelee | 1,400 | ||
| Mexico | |||
| S. L. P.: Ebano | 600 | ||
| Tamps.: Tampico | 3,100 | 21,200 | |
| Yuc.: Progreso | 11,900 | ||
| United States | |||
| Fla.: Pensacola | 100 | 700 | |
| Winter Park | 2,300 | 1,000 | |
| Ga.: Athens | 900 | ||
| Thomasville | 1,500 | 200 | |
| Iowa: Ottumwa | 3,800 | 12,500 | |
| Kans.: Lawrence | 14,500 | 2,200 | |
| Ky.: Louisville | 5,000 | 1,400 | |
| Murray | 3,700 | ||
| La.: Baton Rouge | 3,400 | ||
| Lafayette | 1,800 | ||
| Mansfield | 2,100 | 1,600 | |
| New Orleans | 200 | 1,100 | |
| Oak Grove | 2,700 | 2,500 | |
| Mich.: Albion | 700 | ||
| Minn.: Hopkins | 1,100 | ||
| Miss.: Rosedale | 2,200 | 1,400 | |
| Mo.: Columbia | 800 | 3,400 | |
| Liberty | 800 | 800 | |
| Okla.: Stillwater | 900 | 700 | 1,400 |
| S. Car.: Charleston | 400 | 600 | 200 |
| Tenn.: Knoxville | 5,800 | 1,900 | |
| Memphis | 1,200 | 3,400 | 2,100 |
| Tex.: College Station | 3,400 | 3,100 | |
| Rockport | 2,400 |
| Observation Station | March | April | May |
| Mexico | |||
| Tamps.: Tampico | 5,500 | 63,600 | |
| Yuc.: Progreso | 31,600 | ||
| United States | |||
| Fla.: Winter Park | 6,200 | ||
| Ga.: Athens | 2,600 | ||
| Thomasville | 3,900 | ||
| Iowa: Ottumwa | 15,300 | 54,600 | |
| Kans.: Lawrence | 51,600 | 5,400 | |
| Ky.: Louisville | 17,000 | 8,400 | |
| Murray | 16,400 | ||
| La.: Baton Rouge | 6,200 | ||
| Mansfield | 4,900 | 5,200 | |
| Oak Grove | 13,600 | 5,800 | |
| Miss.: Rosedale | 6,800 | 5,800 | |
| Mo.: Columbia | 1,400 | 10,300 | |
| Okla.: Stillwater | 2,700 | 1,900 | 3,000 |
| Tenn.: Knoxville | 15,200 | 9,000 | |
| Memphis | 3,600 | 7,900 | 7,000 |
| Tex.: College Station | 6,200 | 13,200 |

In view of the controversy in recent years pertaining to migration routes in the region of the Gulf of Mexico (Williams, 1945 and 1947; Lowery, 1945 and 1946), the bearing of the new data on the problem is of especial interest. While recent investigations have lent further support to many of the ideas expressed in my previous papers on the subject, they have suggested alternative explanations in the case of others. In the three years that have elapsed since my last paper dealing with Gulf migration, some confusion seems to have arisen regarding the concepts therein set forth. Therefore, I shall briefly re-state them.
It was my opinion that evidence then available proved conclusively that birds traverse the Gulf frequently and intentionally; that the same evidence suggested trans-Gulf flights of sufficient magnitude to come within the meaning of migration; that great numbers of birds move overland around the eastern and western edges of the Gulf; that it was too early to say whether the coastal or trans-Gulf route was the more important, but that enough birds cross the water from Yucatán to account for transient migration in the extreme lower Mississippi Valley; and, that, in fair weather, most trans-Gulf migrants continue on inland for some distance before coming to land, creating an area of "hiatus" that is usually devoid of transient species. I tried to make it emphatically clear that I realized that many birds come into Texas from Mexico overland, that I did not think the hordes of migrants normally seen on the Texas coast in spring were by any means all trans-Gulf migrants. I stated (1946: 206): "Proving that birds migrate in numbers across the Gulf does not prove that others do not make the journey by the coastal routes. But that is exactly the point. No one has ever pretended that it does." Although some ornithologists seem to have gained the impression that I endorse only the trans-Gulf route, this is far from the truth. I have long held that the migrations overland through eastern Mexico and southern Texas on one hand, and the over-water flights on the other, are each part of the broad movement of transients northward into the United States. There are three avenues of approach by which birds making up the tremendous concentrations on the Texas coast may have reached there: by a continental pathway from a wintering ground in eastern and southern Mexico; by the over-water route from Yucatán and points to the southward; and, finally, by an overland route from Central America via the western edge of the Gulf. As a result of Louisiana State University's four-year study of the avifauna in [Pg_439] eastern Mexico, I know that migrants reach Texas from the first source. As a consequence of my studies in Yucatán of nocturnal flight densities and their directional trends, I strongly believe that migrants reach Texas from this second source. As for the third source, I have never expressed an opinion. I am not prepared to do so now, for the reason that today, as three years ago, there is no dependable evidence on which to base a judgment one way or another.
Among the present flight density data bearing on the above issues, are the six sets of observations from the vicinity of Tampico, Tamaulipas, already referred to. These were secured in the spring of 1948 by a telescope set up on the Gulf beach just north of the Miramar pavilion and only a hundred feet from the surf (see Figure 25, ante). The beach here is approximately 400 feet wide and is backed by scrub-covered dunes, which rapidly give way toward the west to a rather dense growth of low shrubs and trees. One might have expected that station densities at Tampico in March would be rather high. Actually, though they are the second highest recorded for the month, they are not impressive and afford a striking contrast with the record flights there in April (Table 6). Unfortunately, only
| Date | Average hour of observation | ||||||||
| 8:30 | 9:30 | 10:30 | 11:30 | 12:30 | 1:30 | 2:30 | 3:30 | 4:30 | |
| 22-23 March | 600 | 700 | 1,000 | 800 | 100 | 100 | 0 | 100 | .. |
| 23-24 March | 0 | 400 | 1,200 | 3,100 | 800 | .. | .. | .. | .. |
| 24-25 March | 300 | 700 | 800 | 1,600 | 1,100 | .. | .. | .. | .. |
| 21-22 April | 1,100 | 7,000 | 14,900 | 12,900 | 8,100 | 3,800 | 3,500 | 200 | .. |
| 22-23 April | 700 | 2,900 | 7,500 | .. | .. | .. | .. | .. | .. |
| 23-24 April | 600 | 4,700 | 19,100 | 21,200 | 5,500 | 5,900 | 4,000 | 2,000 | 200 |
a few stations were operating in March and thus adequate comparisons are impossible; but the indications are that, in March, migration activity on the western edges of the Gulf is slight. It fails even to approach the volume that may be observed elsewhere at the same time, as for example, in eastern Kansas where, however, the migration is not necessarily correlated with the migration in the [Pg_440] lower Gulf area. Strangely enough, on the night of March 22-23, at Tampico, approximately 85 per cent of the birds were flying from north of an east-west line to south of it, opposite to the normal trend of spring migration. This phenomenon, inexplicable in the present instance, will be discussed below. On the other two nights in March, the directional trend at Tampico was northward with few or no aberrant components. Observations made approximately thirty-five miles inland from the Gulf, at Ebano, San Luis Potosí, on the night of March 25-26, show lower station densities than the poorest night at Tampico, but since they cover only a three-hour watch, they reveal little or nothing concerning the breadth of the so-called coastal flyway.
April flight densities at Tampico are the highest recorded in the course of this study. The maximum hourly density of 21,200 birds is 46 per cent higher than the maximum hourly density anywhere else. The average hourly density of 6,300 in April is more than twice as great as the next highest average for that month. These figures would seem to satisfy certain hypotheses regarding a coastwise flight of birds around the western edge of the Gulf. Other aspects of the observations made at that time do not satisfy these hypotheses. Texas ornithologists have found that in periods of heavy spring migration, great numbers of birds are invariably precipitated by rainy weather. On April 23, in the midst of the record-breaking telescopic studies at Tampico, Mr. Robert J. Newman made a daytime census immediately following four hours of rain. He made an intensive search of a small area of brush and low growth back of the beach for traces of North American migrants. In his best hour, only thirteen individual birds out of seventy-five seen were of species that do not breed there. The transient species were the Ruby-throated Hummingbird (1), Scissor-tailed Flycatcher (1), Western Wood Pewee (1), Black-throated Green Warbler (2) Orchard Oriole (7), and Baltimore Oriole (1), all of which winter extensively in southern Mexico. Perhaps, however, the apparent scarcity of transients on this occasion is not surprising in the light of the analysis of flight density in terms of bird density on the ground which I shall develop beyond. My only point here is to demonstrate that rain along the coast does not always produce birds.
As large as the nocturnal flights at Tampico have so far proved to be, they are not commensurate with the idea that nearly all birds follow a narrow coastwise route around the Gulf. To establish the [Pg_441] latter idea, one must be prepared to show that the migrant species returning to the United States pass along two flyways a few miles wide in the immense volume necessary to account for their later abundance on a 1500-mile front extending across eastern North America. One might expect at least ten to twenty fold the number observable at any point in the interior of the United States. In actuality, the highest nightly density of 63,600 birds at Tampico is barely sufficient to account for the highest nightly density of 54,600 at Ottumwa, Iowa, alone.
Of course, there is no way of knowing how closely a ratio of anywhere from ten to one through twenty to one, employed in this comparison, expresses the true situation. It may be too high. It could be too low, particularly considering that preliminary studies of flight density in Florida indicate that the western shores of the Gulf of Mexico must carry the major part of the traffic if migratory flights back to the United States in spring take place only along coastwise routes. Consideration of the data obtained in Florida in 1948 will serve to emphasize the point.
At Winter Park, Florida, seventy-seven hours were spent at the telescope in April and May. This was 71 per cent more hours of actual observation than at the next highest station. Nevertheless, the total seasonal density amounted to only 21,700 birds. The average hourly density was only 300 birds, with the maximum for any one hour being 2,300 birds. In contrast, forty-five hours of observation at Tampico, Tamaulipas, in March and April, yielded a total station density of 140,300 birds. At the latter place, on the night of April 23-24, almost as many birds passed in a single hour as passed Winter Park in all of its seventy-seven hours of observation.
Should future telescopic studies at Florida stations fail to produce densities appreciably higher than did Winter Park in 1948, the currently-held ideas that the Florida Peninsula is a major flyway will be seriously shaken. But one consideration must be kept in mind regarding the present picture. No observations were made at Winter Park in March, when it is conceivable that densities may have been materially higher. We know, for instance, that many of the early migrants to the southern United States are species whose winter homes are in the West Indies. Numbers of Vireonidae and Parulidae (notably the genera Vireo, Parula, Protonotaria, Mniotilta, Seiurus, Geothlypis, Setophaga, and certain Dendroica and Vermivora) winter extensively in this region and are among the first [Pg_442] birds to return to the southern states in the spring. Many of them often reach Louisiana and other states on the Gulf coastal plain by mid-March. In the same connection, it may be mentioned that many of the outstanding instances of birds striking lighthouses in southern Florida occurred in March and early April (Howell, 1932).
I have long felt that the answers to many of the questions which beset us in our study of Gulf migration are to be found on the open waters of the Gulf of Mexico itself or on the northern tip of the Yucatán Peninsula. Accordingly, in the spring of 1945 I crossed the Gulf by slow freighter for the purpose of determining how many and what kinds of birds might be seen between the mouth of the Mississippi River and the Yucatán Peninsula in fair weather, when it could not be argued that the birds had been blown there by inclement weather. To my own observations I was able to add those of other ornithologists who likewise had been aboard ship in the Gulf.
The summary of results proved that birds of many species cross the Gulf and do so frequently. It failed to demonstrate beyond all doubt that they do so in large numbers. Nor had I expected it to do so. The consensus of Gulf coast ornithologists seemed to be that transient migration in their respective regions is often performed at too high an elevation to be detected unless the birds are forced to earth by bad weather. I saw no reason to anticipate that the results would be otherwise over the waters of the Gulf of Mexico.
The application of the telescopic method held promise of supplying definite data on the numbers of trans-Gulf migrants, however high their flight levels. The roll and vibration of the ship had prevented me in 1945 from making telescopic observations at sea. Since no immediate solution to the technical difficulties involved presented itself, I undertook to reach one of the small cays in Alacrán Reef, lying seventy-five miles north of Yucatán and in line with the coast of southern Louisiana. Because of transportation difficulties, my plans to place a telescopic station in this strategic location failed. Consequently, I returned in 1948 by freighter to Progreso, Yucatán, where telescopic counts were made for three nights, one of which was rendered almost valueless by the cloud cover.

The observation station at Progreso was situated on the northern end of the new wharf which projects northward from the beach to a point one mile over the Gulf. As will be seen from Figure 35, the entire cone of observation lay at nearly all times over the intervening ing water between the telescope on the end of the wharf and the beach. Therefore, nearly all of the birds seen were actually observed leaving the coast and passing out over the open waters of the Gulf. The hourly station densities are shown in Table 7 and Figures 24 and 36. In the seventeen hours of observation on the nights of April 23-24 and April 24-25, a total computed density of 59,200 birds passed within one-half mile of each side of Progreso. This is the third highest density recorded in the course of this study. The [Pg_444] maximum for one hour was a computed density of 11,900 birds. This is the fourth highest hourly density recorded in 1948.

| Date | Average hour of observation | ||||||||
| 8:30 | 9:30 | 10:30 | 11:30 | 12:30 | 1:30 | 2:30 | 3:30 | 4:30 | |
| 23-24 April | 400 | 3,000 | 5,100 | 10,000 | 9,000 | 2,800 | 900 | 400 | .... |
| 24-25 April | 0 | 500 | 3,700 | 11,900 | 7,900 | 1,900 | 1,100 | 400 | 200 |
It is not my contention that this many birds leave the northern coast of Yucatán every night in spring. Indeed, further studies may show negligible flight densities on some nights and even greater densities on others. As a matter of fact several hours of observation on the night of April 25-26, at Mérida, Yucatán, approximately twenty-five miles inland from Progreso, indicated that on this night the density overhead was notably low, a condition possibly accounted for by a north wind of 10 mph blowing at 2,000 feet. I merely submit [Pg_445] that on the nights of April 23-24 and 24-25, birds were leaving the coast of Yucatán at Progreso at the rate indicated. But, as I have emphasized in this paper and elsewhere (1946: 205-206), the northern part of the Yucatán Peninsula is notably unmarked by streams or any other physiographic features which birds might follow. The uniformity of the topography for many miles on either side of Progreso, if not indeed for the entire breadth of the Peninsula, makes it probable that Progreso is not a particularly favored spot for observing migration, and that it is not the only point along the northern coast of Yucatán where high flight densities can be recorded. This probability must be considered when comparisons are made between Progreso densities and those at Tampico. The argument could be advanced that the present densities from Tampico do not sufficiently exceed those at Progreso to establish the coastal route as the main avenue of traffic in spring, since there is every reason to suspect topography of exerting some influence to produce a channeling effect in eastern Mexico. Here the coast parallels the directional trend of the migratory movement for more than 600 miles. Likewise the Sierra Madre Oriental of eastern Mexico, situated approximately 100 miles inland (sometimes less), lies roughly parallel to the coast. Because of the slant of the Mexican land mass, many winter residents in southern Mexico, by short northward movements, would sooner or later filter into the coastal plain. Once birds are shunted into this lowland area, it would seem unlikely that they would again ascend to the top of the Sierra Madre to the west. In this way the great north-south cordillera of mountains may act as a western barrier to the horizontal dispersion of transients bound for eastern North America. Similarly, the Gulf itself may serve as an eastern barrier; for, as long as migrants may progress northward in the seasonal direction of migration and still remain over land, I believe they would do so.
To put the matter in a slightly different way, the idea of a very narrow flight lane is inherent in the idea of coastwise migration. For, as soon as we begin to visualize flights of great volume over fronts extending back more than fifty miles from the shore line, we are approaching, if indeed we have not already passed, the point where the phenomenon is no longer coastwise in essence, but merely overland (as indeed my own unprocessed, telescopic data for 1949 indicate may be the case). In actuality, those who have reported on the migration along the western edge of the Gulf of Mexico have never estimated the width of the main flight at more than fifty miles [Pg_446] and have intimated that under some circumstances it may be as narrow as two miles. No evidence of such restrictions can be discerned in the case of the trans-Gulf flights. If it cannot be said that they may be assumed to be as wide as the Gulf itself, they at least have the potential breadth of the whole 260-mile northern coast of the Yucatán Peninsula. On these premises, to be merely equal in total magnitude, the coastwise flights must exhibit, depending on the particular situation, from five to 130 times the concentrations observable among trans-Gulf migrants. This point seems almost too elementary to mention, but I have yet to find anyone who, in comparing the two situations, takes it into consideration.
Judged in this light, the average hourly density of 2,800 birds at Progreso in April would appear to be indicative of many more migrants on the entire potential front than the 6,300 birds representing the average hourly density for the same month at Tampico.
That the Progreso birds were actually beginning a trans-Gulf flight seems inevitable. The Yucatán Peninsula projects 200 miles or more northward into the vast open expanses of the Gulf of Mexico and the Caribbean Sea, with wide stretches of water on either side. The great majority of the birds were observed after they had proceeded beyond the northern edge of this land mass. Had they later veered either to the east or the west, they would have been obliged to travel several hundred miles before again reaching land, almost as far as the distance straight across the Gulf. Had they turned southward, some individuals should have been detected flying in that direction. As can be seen from Figures 23, 42, and 44, not one bird observed was heading south of east or south of west on either night. No other single piece of evidence so conclusively demonstrates that birds cross the Gulf of Mexico in spring in considerable numbers as do flight density data recorded from Progreso in 1948.
Unfortunately only a few data on flight density are available from critical localities on the northern shores of the Gulf in spring. As the density curves in Figure 30 demonstrate, several sets of observation, including some phenomenal flights, have been recorded at Baton Rouge. This locality, however, lies sixty-four miles from the closest point on the Gulf coast, and the point due southward on the coast is eighty-four miles distant. Since all of the birds seen at Baton Rouge on any one night may have come from the heavily forested area between Baton Rouge and the coast of the Gulf, we cannot use data from Baton Rouge as certainly representative of [Pg_447] incoming trans-Gulf flights. Data from repeated observations at stations on the coast itself are needed to judge the degree of trans-Gulf migration northward. On the few nights of observation at such localities (Cameron and Grand Isle, Louisiana, and Pensacola, Florida), flight densities have been zero or negligible. To be sure, negative results have been obtained at stations in the interior of the United States, and flights of low density have been recorded on occasion at stations where the flight densities are otherwise high. Nevertheless, in view of the volume of migration departing from Progreso, Yucatán, it would appear, upon first consideration, that we should at times record on the coast of Louisiana enough birds arriving in a night of continuous observation to yield a high density figure.
Upon further consideration, however, there are factors mitigating against heavy densities of birds in northern flight on the northern coast of the Gulf. In the first place, presuming the main trans-Gulf flight to originate from northern Yucatán, and that there is a directional fanning to the northward, the birds leave on a 260-mile front, and arrive on a front 400 miles or more wide. Consequently, other factors remaining the same, there would be only approximately half the number of birds on the coast of arrival, at a given time and place, as there was on the coast of departure. Secondly, we may now presume on the basis of the telescopic studies at Progreso, that most migrants leaving northern Yucatán do so in the few hours centering about midnight. The varying speeds of the birds making the 580-mile flight across the Gulf distribute them still more sparsely on the north coast of the Gulf both in time and in space. Also we can see only that segment of the flight, which arrives in that part of a twenty-four hour period when the moon is up. This circumstance further reduces the interceptive potential because the hours after dark, to which the present telescopic studies have been restricted, comprise the period in which the fewest migrants arrive from over the water. To illustrate: it is a mathematical certainty that none of the birds leaving Yucatán in the hours of heaviest flight, before 12 P. M., and flying on a straight course at a speed of approximately 33 mph will reach the northern Gulf coast after nightfall; they arrive in the daytime. It will be useful to devise a technique for employing the sun as a background for telescopic observation of birds, thereby making observations possible on a twenty-four hour basis, so as to test these inferences by objective data.
When a whole night's observation (1949 data not yet processed) at Port Aransas, on the southern coast of Texas, on the great overland route from eastern Mexico, yields in one night in April only seven birds, the recording of no birds at a station near the mouth of the Mississippi River becomes less significant.
As I have previously remarked in this paper, the new data obtained since 1946, when I last wrote on the subject of migration in the region of Gulf of Mexico, requires that I alter materially some of my previously held views. As more and more facts come to light, I may be compelled to alter them still further. For one thing, I have come to doubt seriously the rigidity of the coastal hiatus as I envisioned it in 1945. I believe instead that the scarcity of records of transient migrants on the Gulf coastal plain in fair weather is to a very large extent the result of a wide dispersion of birds in the dense cover that characterizes this general region. I now question if appreciable bird densities on the ground ever materialize anywhere except when the sparseness of suitable habitat for resting or feeding tends to concentrate birds in one place, or when certain meteorological conditions erect a barrier in the path of an oncoming migratory flight, precipitating many birds in one place.
This retrenchment of ideas is a direct consequence of the present study, for time and again, as discussed in the case of Tampico densities, maximal nightly flights have failed to produce a visible abundance of transients on land the following day. A simple example may serve to illustrate why. The highest one-hour density recorded in the course of this study is 21,200 birds. That means that this many birds crossed a line one mile long on the earth's surface and at right angles to the direction of flight. Let us further assume that the average flight speed of all birds comprising this flight was 30 mph. Had the entire flight descended simultaneously, it would have been dispersed over an area one mile wide and thirty miles long, and the precipitated density on the ground would have been only 1.1 birds per acre. Moreover, if as many as ten species had been involved in the flight, this would have meant an average per species of less than one bird per nine acres. This would have failed, of course, to show appreciable concentrations to the observer in the field the following day. If, however, on the other hand, the same flight of 21,200 birds had encountered at one point a weather barrier, such as a cold-front storm, all 21,200 birds might have been precipitated in one place and the field observer would have recorded an "inundation of migrants." This would be especially true if the [Pg_449] locality were one with a high percentage of open fields or prairies and if the flight were mainly of woodland dwelling species, or conversely, if the locality were densely forested with few open situations and the flight consisted mainly of open-country birds. As explained on page 389, the density formula may be too conservative in its expression of actual bird densities. Even if the densities computed for birds in the air are only half as high as the actual densities in the air, the corresponding ground density of 2.2 birds per acre that results if all the birds descended simultaneously would hardly be any more impressive than the 1.1 bird per acre.
This consideration is doubtless highly modified by local circumstances, but, in general, it seems to suggest a working hypothesis that provides an explanation for many of the facts that we now have. For example, on the coast of Texas there are great expanses of terrain unattractive to such birds as warblers, vireos, tanagers, and thrushes. The precipitation there by bad weather of even a mediocre nightly flight composed of birds of the kinds mentioned would surely produce an overwhelming concentration of birds in the scattered woods and shrubs.
In spite of all that has been written about the great concentrations of transient migrants on the coast of Texas in spring, I am not convinced that they are of a different order of magnitude than those concentrations that sometimes occur along the cheniers and coastal islands of Louisiana and Mississippi. I have read over and over the highly informative accounts of Professor Williams (loci cit.) and the seasonal summaries by Davis (1936-1940) and Williams (1941-1945). I have conversed at length with Mrs. Jack Hagar, whom I regard as one of the leading authorities on the bird life of the Texas coast, and she has even permitted me access to her voluminous records covering a period of fifteen years residence at Rockport. Finally, I have spent a limited amount of time myself on the Texas coast studying first-hand the situation that obtains there in order that I might be in a position to compare it with what I have learned from observations elsewhere in the region of the Gulf of Mexico, Louisiana, Florida, Yucatán, and eastern Mexico.
Although the concentrations of birds on some days near the mouth of the Mississippi River are almost incalculable, the fact remains that in Texas the densities of transient species on the ground are more consistently high from day to day. The reason for this may be simple. As birds move up daily from Mexico overland, a certain percentage would be destined to come down at all points along the [Pg_450] route but so dispersed in the inland forest that they might pass unnoticed. However, that part of the same flight settling down in coastal areas, where trees are scarce, would produce visible concentrations of woodland species. With the advent of a cold-front storm, two diametrically opposite effects of the same meteorological phenomenon would tend to pile up great concentrations of migrants of two classes—the overland and the trans-Gulf flights. During the prepolar-front weather the strong southerly (from the south) and southeasterly winds would tend to displace much of the trans-Gulf segment to the western part of the Gulf. With the shift of the winds to the north and northwest, which always occurs as the front passes, the overland flight still in the air would tend to be banked up against the coast, and the incoming trans-Gulf flight would be confronted with a barrier, resulting in the precipitation of birds on the first available land.
These postulated conditions are duplicated in part in autumn along the Atlantic coast of the eastern United States. There, as a result of the excellent work of Allen and Peterson (1936) and Stone (1937), a similar effect has been demonstrated when northwest winds shove the south-bound flights up against the coast of New Jersey and concentrate large aggregations of migrants there.
Attention has been drawn already to the nature of the nightly flights at stations immediately inland from the Gulf coast, where densities decline abruptly well before midnight. I have suggested that this early drop-off is mainly a result of the small amount of terrain south of these stations from which birds may be contributed to a night's flight. At Oak Grove, Louisiana, the flight exhibited a strong directional trend with no significant aberrant components. Therefore, one may infer that a considerable part of the flight was derived from regions to the south of the station.
At Mansfield, Louisiana, thirty-eight hours of observation in April and May resulted in flight densities that are surprisingly low—much lower, in fact, than at Oak Grove. In eleven of the hours of observation no birds at all were seen. A possible explanation for these low densities lies in the fact that eastern Texas and western Louisiana, where, probably, the Mansfield flights originated, is not an especially attractive region to migrants because of the great amount of deforested and second growth pine land. Oak Grove, in contrast, is in the great Tensas-Mississippi River flood plain, characterized by an almost solid stand of deciduous forest extending over thousands of square miles in the lower Mississippi valley.

In further contrast to the considerable flight densities and pronounced directional trend at Oak Grove, we have the results from Rosedale, Mississippi, only seventy miles to the north and slightly to the east. At Rosedale the densities were mediocre and the flight directions were extremely divergent. Many of the nights of observation at this locality were seriously interrupted by clouds, but such counts as were made on those dates indicated little migration taking place. On two nights, however, April 21-22 and May 20-21, visibility was almost continuous and densities were moderately high. In Figure 37 I have shown the flight directions for these two nights. The lengths of the individual sector vectors are plotted as a percentage of the total station density for each of the two nights (5,800 and 6,800 birds, respectively). Although the vector resultants show a net movement of birds to the northeast, there are important divergent components of the flights. This "round-the-compass" pattern is characteristic of stations on the edge of meteorological disturbances, as was Rosedale on April 21-22, but not on the night of May 20-21. If bats are presumed to have played a rôle in these latter observations, their random flights would tend to cancel [Pg_452] out and the vector resultant would emerge as a graphic representation of the actual net trend density of the birds and its prevailing direction of flow. Although I do not believe that bats are the real reason for the diverse directional patterns at Rosedale, I can offer no alternative explanation consistent with data from other stations.
Moving northward in the valley of the Mississippi and its tributaries, we find a number of stations that yielded significantly high densities on most nights when weather conditions were favorable for migration. Louisville and Murray, Kentucky, and Knoxville, Tennessee, each show several nights with many birds flying, but only Lawrence, Kansas, and Ottumwa, Iowa, had migrations that approach in magnitude the record station densities at Tampico. Indeed, these were the only two stations in the United States that produced flights exceeding the densities at Progreso, Yucatán. The densities at Lawrence are unique in one respect, in that they were extremely high in the month of March. Since there were very few stations in operation then, these high densities would be of little significance were it not for the fact that at no time in the course of this study from 1945 to the present have comparable densities been obtained this early in the migration period. Examination of the "Remarks" section of the original data sheets from Lawrence show frequent mention of "duck-like" birds passing before the moon. We may infer from these notations that a considerable part of the overhead flight was composed of ducks and other aquatic birds that normally leave the southern United States before the main body of transient species reach there. The heavy flight densities at Lawrence may likewise have contained certain Fringillidae, Motacillidae, Sylviidae, and other passerine birds that winter mainly in the southern United States and which are known to begin their return northward in March or even earlier. Observations in 1948 at Lawrence in April were hindered by clouds, and in May no studies were attempted. However, we do have at hand two excellent sets of data recorded at Lawrence on the nights of May 3-4 and May 5-6, 1947, when the density was also extremely high.
At Ottumwa, Iowa, where a splendid cooperative effort on the part of the local ornithologists resulted in forty-four hours of observation in April and May, densities were near the maximum for all stations. Considering this fact along with results at Lawrence and other mid-western stations where cloud cover did not interfere at the critical periods of observation, we have here evidence supporting the generally held thesis that eastern Kansas, Missouri, and Iowa lie on a principal migratory flyway.
[Pg_453]Stations in Minnesota, Illinois, Michigan, Massachusetts, and Ontario were either operated for only parts of one or two nights, or else clouds seriously interfered with observations, resulting in discontinuous counts. It may be hoped that future studies will include an adequate representation of stations in these states and that observations will be extensive enough to permit conclusions regarding the density and direction of migration.
Charleston, South Carolina, which does not conveniently fall in any of the geographic regions so far discussed, had, to me, a surprisingly low flight density; twenty-two hours of observation there in March, April, and May yielded a total flight density of only 3,000 birds. This is less, for example, than the number of birds computed to have passed Lawrence, Kansas, in one hour, or to have passed Progreso, Yucatán, in one twenty-minute interval! Possibly observations at Charleston merely chanced to fall on nights of inexplicably low densities; further observations will be required to clear up this uncertainty.
The belief that winds affect the migration of birds is an old one. The extent to which winds do so, and the precise manner in which they operate, have not until rather recently been the subject of real investigation. With modern advances in aerodynamics and the development of the pressure-pattern system of flying in aviation, attention of ornithologists has been directed anew to the part that air currents may play in the normal migrations of birds. In America, a brief article by Bagg (1948), correlating the observed abundance of migrants in New England with the pressure pattern obtaining at the time, has been supplemented by the unpublished work of Winnifred Smith. Also Landsberg (1948) has pointed out the close correspondence between the routes of certain long-distance migrants and prevailing wind trajectories. All of this is basis for the hypothesis that most birds travel along definite air currents, riding with the wind. Since the flow of the air moves clockwise around a high pressure area and counterclockwise around a low pressure area, the birds are directed away from the "high" and toward the center of the "low." The arrival of birds in a particular area can be predicted from a study of the surrounding meteorological conditions, and the evidence in support of the hypothesis rests mainly upon the success of these predictions in terms of observations in the field.
From some points of view, this hypothesis is an attractive one. It explains how long distances involved in many migrations may be [Pg_454] accomplished with a minimum of effort. But the ways in which winds affect migration need analysis on a broader scale than can be made from purely local vantage points. Studies of the problem must be implemented by data accumulated from a study of the process in action, not merely from evidence inferred from the visible results that follow it. Although several hundred stations operating simultaneously would surely yield more definite results, the telescopic observations in 1948 offer a splendid opportunity to test the theory on a continental scale.
The approach employed has been to plot on maps sector vectors and vector resultants that express the directional trends of migration in the eastern United States and the Gulf region, and to compare the data on these maps with data supplied by the U. S. Weather Bureau regarding the directions and velocities of the winds, the location of high and low pressure areas, the movement of cold and warm fronts, and the disposition of isobars or lines of equal pressure. It should be borne in mind when interpreting these vectors that they are intended to represent the directions of flight only at the proximal ends, or junction points, of the arrows. The tendency of the eye to follow a vector to its distal extremity should not be allowed to create the misapprehension that the actual flight is supposed to have continued on in a straight line to the map location occupied by the arrowhead.
A fundamental difficulty in the pressure-pattern theory of migration has no doubt already suggested itself to the reader. The difficulty to which I refer is made clear by asking two questions. How can the birds ever get where they are going if they are dependent upon the whim of the winds? How can pressure-pattern flying be reconciled with the precision birds are supposed to show in returning year after year to the same nesting area? The answer is, in part, that, if the wind is a major controlling influence on the routes birds follow, there must be a rather stable pattern of air currents prevailing from year to year. Such a situation does in fact exist. There are maps showing wind roses at 750 and 1,500 meters above mean sea level during April and May (Stevens, 1933, figs. 13-14, 17-18). Similarly, the "Airway Meteorological Atlas for the United States" (Anonymous, 1941) gives surface wind roses for April (Chart 6) and upper wind roses at 500 and 1,000 meters above mean sea level for the combined months of March, April, and May (Charts 81 and 82). The same publication shows wind resultants at 500 and 1,000 meters above mean sea level (Charts 108 and 109). Further information permitting a description in general terms of conditions prevailing in April and May is found in the "Monthly Weather Review" covering these months (cf. Anonymous, 1948 a, Charts 6 and 8; 1948 b, Charts 6 and 8).

[Pg_456]

[Pg_457] First, however, it is helpful as a starting point to consider the over-all picture created by the flight trends computed from this study. In Figure 38, the individual sector vectors are mapped for the season for all stations with sufficient data. The length of each sector vector is determined as follows: the over-all seasonal density for the station is regarded as 100 percent, and the total for the season of the densities in each individual sector is then expressed as a percentage. The results show the directional spread at each station. In Figure 39, the direction of the over-all vector resultant, obtained from the sector vectors on the preceding map, is plotted to show the net trend at each station.
As is evident from the latter figure, the direction of the net trend at Progreso, Yucatán, is decidedly west of north (N 26° W). At Tampico this trend is west of north (N 11° W), but not nearly so much so as at Progreso. In Texas, Louisiana, Georgia, Tennessee, and Kentucky, it is decidedly east of north. In the upper Mississippi Valley and in the eastern part of the Great Plains, the flow appears to be northward or slightly west of north. At Winter Park, Florida, migration follows in general the slant of the Florida Peninsula, but, the meager data from Thomasville, Georgia, do not indicate a continuation of this trend.
It might appear, on the basis of the foregoing data, that birds migrate along or parallel to the southeast-northwest extension of the land masses of Central America and southern Mexico. This would carry many of them west of the meridian of their ultimate goal, obliging them to turn back eastward along the lines of net trend in the Gulf states and beyond. This curved trajectory is undoubtedly one of the factors—but certainly not the only factor—contributing to the effect known as the "coastal hiatus." The question arises as to whether this northwestward trend in the southern part of the hemisphere is a consequence of birds following the land masses or whether instead it is the result of some other natural cause such as a response to prevailing winds. I am inclined to the opinion that both factors are important. Facts pertinent to this opinion are given below.
In April and May a high pressure area prevails over the region of the Gulf of Mexico. As the season progresses, fewer and fewer [Pg_458] cold-front storms reach the Gulf area, and as a result the high pressure area over the Gulf is more stable. Since the winds move clockwise around a "high," this gives a general northwesterly trajectory to the air currents in the vicinity of the Yucatán Peninsula. In the western area of the Gulf, the movement of the air mass is in general only slightly west of north, but in the central Gulf states and lower Mississippi Valley the trend is on the average northeasterly. In the eastern part of the Great Plains, however, the average circulation veers again slightly west of north. The over-all vector resultants of bird migration at stations in 1948, as mapped in Figure 39, correspond closely to this general pattern.
Meteorological data are available for drawing a visual comparison between the weather pattern and the fight pattern on individual nights. I have plotted the directional results of four nights of observation on the Daily Weather Maps for those dates, showing surface conditions (Figures 40, 42, 44 and 46). Each sector vector is drawn in proportion to its percentage of the corresponding nightly station density; hence the vectors at each station are on an independent scale. The vector resultants, distinguished by the large arrowheads, are all assigned the same length, but the nightly and average hourly station densities are tabulated in the legends under each figure. For each map showing the directions of flight, there is on the facing page another map showing the directions of winds aloft at 2,000 and 4,000 feet above mean sea level on the same date (see Figures 41-47). The maps of the wind direction show also the velocities.
Unfortunately, since there is no way of analyzing the sector trends in terms of the elevations of the birds involved, we have no certain way of deciding whether to compare a given trend with the winds at 2,000, 1,000, or 0 feet. Nor do we know exactly what wind corresponds to the average or median flight level, which would otherwise be a good altitude at which to study the net trend or vector resultant. Furthermore, the Daily Weather Map illustrates conditions that obtained at 12:30 A. M. (CST); the winds aloft are based on observations made at 10:00 P. M. (CST); and the data on birds covers in most cases the better part of the whole night. Add to all this the fact that the flight vectors, their resultants, and the wind representations themselves are all approximations, and it becomes apparent that only the roughest sort of correlations are to be expected.
However, as will be seen from a study of the accompanying maps (Figures 40-47), the shifts in wind direction from the surface up to 4,000 feet above sea level are not pronounced in most of the instances [Pg_459] at issue, and such variations as do occur are usually in a clockwise direction. All in all, except for regions where frontal activity is occurring, the weather maps give a workable approximation to the average meteorological conditions on a given night.
The maps (Figures 40-47) permit, first, study of the number of instances in which the main trend of flight, as shown by the vector resultant, parallels the direction of wind at a reasonable potential mean flight elevation, and, second, comparison of the larger individual sector vectors and the wind currents at any elevation below the tenable flight ceiling—one mile.
On the whole, inspection of the trend of bird-flight and wind direction on specific nights supports the principle that the flow of migration is in general coincident with the flow of air. It might be argued that when the flow of air is toward the north, and when birds in spring are proceeding normally in that direction, no significance can be attached to the agreement of the two trends. However, the same coincidence of wind directions and bird flights seems to be maintained when the wind currents deviate markedly from a northward trajectory. Figures 46 and 47, particularly in regard to the unusual slants of the flight vectors at Ottumwa, Knoxville, and Memphis, illustrate that this coincidence holds even when the wind is proceeding obliquely eastward or westward. On the night of May 22-23, when a high pressure area prevailed from southern Iowa to the Atlantic coast, and the trajectory of the winds was northward, migration activity at Knoxville and Ottumwa was greatly increased and the flow of birds was again northward in the normal seasonal direction of migration.
Further study of the data shows fairly conclusively that maximum migration activity occurs in the regions of high barometric pressure and that the volume of migration is either low or negligible in regions of low pressure. The passage of a cold-front storm may almost halt migration in spring. This was demonstrated first to me by the telescopic method at Baton Rouge, on April 12, 1946, following a strong cold front that pushed southeastward across the Gulf coastal plain and over the eastern Gulf of Mexico. The winds, as usual, shifted and became strong northerly. On this night, following the shift of the wind, only three birds were seen in seven hours of continuous observation. Three nights later, however, on April 15, when the warm air of the Gulf was again flowing from the south, I saw 104 birds through the telescope in two hours. Apropos of this consideration in the 1948 data are the nights of May 21-22 and 22-23.

|


|


|


|

[Pg_468] On the first night, following the passage of a cold front, migration at Ottumwa was comparatively low (6,900 birds in five hours). On the following night, when the trajectory of the winds was toward the north, the volume of migration was roughly twice as high (22,300 birds in eight hours). At Louisville, on May 21-22, the nightly station density was only 1,500 birds in seven hours, whereas on the following night, it was 8,400 birds in the same length of time, or about six times greater.
The evidence adduced from the present study gives support to the hypothesis that the continental pattern of spring migration in eastern North America is regulated by the movement of air masses. The clockwise circulation of warm air around an area of high pressure provides, on its western edge, tail winds which are apparently favorable to northward migration. High pressure areas exhibit a centrifugal force outward from the center, which may tend to disperse the migratory flight originating at any given point. In contrast, the circulation of air in the vicinity of a low pressure area is counterclockwise with the force tending to be directed inward toward the center. Since the general movement of the air is from the high pressure area toward a low pressure area, birds starting their migrations with favorable tail winds, are often ultimately carried to a region where conditions are decidedly less favorable. In the vicinity of an area of low pressure the greater turbulence and high wind velocities, combined with the possibly slightly less buoyant property of the air, cause birds to descend. Since low pressure areas in spring generally precede cold fronts, with an attending shift of the wind to the north, an additional barrier to the northward migration of birds is imposed. The extreme manifestation of low pressure conditions and the manner in which they operate against bird flight, are associated with tropical hurricanes. There, the centripetal force of the wind is so great that it appears to draw birds into the "eye" of the hurricane. A classic example of this effect is seen in the case of the birds that came aboard the "West Quechee" when this vessel passed through the "eye" of a hurricane in the Gulf of Mexico in August, 1927. I have already discussed the details of this incident in a previous paper (1946:192). There is also the interesting observation of Mayhew (1949), in which a similar observation was made of large numbers of birds aboard a ship passing through one of these intense low-pressure areas.
Although the forces associated with an ordinary low-pressure area are by no means as intense as those associated with a tropical hurricane, [Pg_469] the forces operating are much the same. Consequently birds conceivably might tend to be drawn toward a focal point near the center of the low, where the other factors already mentioned would tend to precipitate the entire overhead flight. Visible evidence of migration would then manifest itself to the field ornithologists.
| 1. | Telescopic counts of birds passing before the moon may be used to determine reliable statistical expressions of the volume of migration in terms of direction and of definite units of time and space. |
| 2. | Night migrants fly singly more often than in flocks, creating a remarkably uniform dispersion on a local scale throughout the sky, quite unlike the scattered distributions observable in the daytime. |
| 3. | The nocturnal migration of birds is apparently preceded by a resting or feeding pause during which there are few migrants in the air. It is not to an important degree a non-stop continuation of flights begun in the daylight. |
| 4. | Nightly migrational activity in North America varies from hour to hour according to a definite temporal pattern, corresponding to the Zugunruhe of caged European birds, and expressed by increasingly heavy flights up until the hour before midnight, followed by a pronounced decline. |
| 5. | The visible effects of the time pattern are subject to modification at a particular station by its location with respect to the resting areas from which the night's flight originates. |
| 6. | Quantitative and directional studies have so far failed to prove that nocturnal migrants favor narrow, topographically-determined flight lanes to an important degree. |
| 7. | Flight densities on the east coast of Mexico, though of first magnitude, have not yet been demonstrated in the volume demanded by the premise that almost all migrants returning to the United States from regions to the south do so by coastal routes. |
| 8. | Heavy flights have been recorded from the northern coast of Yucatán under circumstances leading inevitably to the conclusion that birds migrate across the Gulf of Mexico in considerable numbers. |
| 9. | There is reason to believe that the importance of the Florida Peninsula as an April and May flyway has been over-estimated, as regards the numbers of birds using it in comparison with the numbers of birds using the Mexican and Gulf routes. |
| 10. | The amount of migration is apparently seldom sufficient to produce [Pg_470] heavy densities of transient species on the ground without the operation of concentrative factors such as ecological patterns and meteorological forces. |
| 11. | The absence or scarcity of transients in some areas in fine weather may be explained by this consideration. |
| 12. | A striking correlation exists between air currents and the directional flight trends of birds, suggesting that most night migrants travel by a system of pressure-pattern flying. |
Transmitted June 1, 1949.
The University of Kansas Publications, Museum of Natural History, are offered in exchange for the publications of learned societies and institutions, universities and libraries. For exchanges and information, address the Exchange Desk, University of Kansas Library, Lawrence, Kansas, U. S. A.
Museum Of Natural History.—E. Raymond Hall, Chairman, Editorial Committee.Cited as Univ. Kans. Publ., Mus. Nat. Hist.
| Vol. 1. | (Complete) Nos. 1-26. Pp. 1-638. August 15, 1946-January 20, 1951. | |
| Vol. 2. | (Complete) Mammals of Washington. By Walter W. Dalquest. Pp. 1-444, 140 figures in text. April 9, 1948. | |
| Vol. 3. | 1. | The avifauna of Micronesia, its origin, evolution, and distribution. By Rollin H. Baker. Pp. 1-359, 16 figures in text. June 12, 1951. |
| 2. | A quantitative study of the nocturnal migration of birds. By George H. Lowery, Jr. Pp. 361-472, 47 figures in text. June 29, 1951. | |
With the exception of the typographical corrections detailed below and some minor corrections for missing periods or extra punctuation (item 28 in List of Figures), the text presented here is that contained in the original printed version. A transcription of the Data presented in Figure 12 was added (see below) to illustrate the information contained on that sheet. Some text was moved to rejoin paragraphs.
There are two notes in the original text indicating that the images for Figures 41 and 45 were transposed. The correct images have been placed with the captions and the two notes were removed. Lastly, the cover image was compiled from a copy of the original cover with two of the graphics contained in the article added and the list of UK pulications was moved to the end of the document.
| Page | Correction |
| 385 | flght ⇒ flight |
| 394 | diargrams ⇒ diagrams |
| 404 | Determinaton ⇒ Determination |
| 411 | obsever ⇒ observer |
| 419 | Morover ⇒ Moreover |
| 425 | Mississippii ⇒ Mississippi |
| 425 | a ⇒ as |
| 430 | at ⇒ and |
| 431 | inserted "a" ("…traveling along a certain topographic feature…") |
| 442 | concensus ⇒ consensus |
| 472 | Stephens, Loyd A. ⇒ Stevens, Lloyd A. |
|
Transcription of the Data in Figure 12
ORIGINAL DATA SHEET
DATE 24-25 April 1948 LOCALITY Progreso, Yucatán
OBSERVERS Harold Harry; George H. Lowery
WEATHER Moderate to strong "trade" winds along coast, slightly N of E.
Moon emerged above low cloud bank at 8:26.
INSTRUMENT B. & L. 19.5 Spotting Scope; image erect
REMARKS Observation station located 1 mile from land, over Gulf of
Mexico, at end of new Progreso wharf
-----------+------+-------+--------------------------------------------
TIME | IN | OUT | REMARKS
-----------+------+-------+--------------------------------------------
C.S.T | | |
8:26 | -- | -- | observations begin; H.H. observing
50 | 4:30 | 9 | slow; small
56 | 3 | 10 | medium size
9:00 | 2 | 10:30 | very small
11 | 5 | 9:30 | moderately fast
25 | 5 | 10 | very small; rather slow
26 | 3 | 11 | " "
36 | 5 | 10 | medium size
40 | 3 | 10 | " "
43 | 5:30 | 9 | " "
46 | 3:30 | 10 | small
56 | 4:30 | 10 | medium size
9:58-10:00 | -- | -- | time out to change observers; G.L. at scope
10:05 | 4:30 | 11:30 | small
06 | 3 | 11 |
12 | 5 | 8 | very small
25 | 5 | 12 | very fast; small
30 | 4 | 10 | small
32 | 4 | 11 | "
32 | 2 | 11 | "
33 | 5 | 11 | "
33 | 4 | 1 | "
33 | 5:30 | 11 | "
35 | 4:30 | 10 | swallow-like
36 | 5 | 1:30 |
|