 Fanciful Portrait of Pythagoras
Calandri's Arithmetic, 1491
Fanciful Portrait of Pythagoras
Calandri's Arithmetic, 1491
Project Gutenberg's The Teaching of Geometry, by David Eugene Smith This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: The Teaching of Geometry Author: David Eugene Smith Release Date: October 10, 2011 [EBook #37681] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK THE TEACHING OF GEOMETRY *** Produced by Juliet Sutherland, Anna Hall and the Online Distributed Proofreading Team at http://www.pgdp.net
BY
DAVID EUGENE SMITH
GINN AND COMPANY
BOSTON · NEW YORK · CHICAGO · LONDON
COPYRIGHT, 1911, BY DAVID EUGENE SMITH
ALL RIGHTS RESERVED
911.6
The Athenæum Press
PREFACE
A book upon the teaching of geometry may be planned in divers ways. It may be written to exploit a new theory of geometry, or a new method of presenting the science as we already have it. On the other hand, it may be ultraconservative, making a plea for the ancient teaching and the ancient geometry. It may be prepared for the purpose of setting forth the work as it now is, or with the tempting but dangerous idea of prophecy. It may appeal to the iconoclast by its spirit of destruction, or to the disciples of laissez faire by its spirit of conserving what the past has bequeathed. It may be written for the few who always lead, or think they lead, or for the many who are ranked by the few as followers. And in view of these varied pathways into the joint domain of geometry and education, a writer may well afford to pause before he sets his pen to paper, and to decide with care the route that he will take.
At present in America we have a fairly well-defined body of matter in geometry, and this occupies a fairly well-defined place in the curriculum. There are not wanting many earnest teachers who would change both the matter and the place in a very radical fashion. There are not wanting others, also many in number, who are content with things as they find them. But by far the largest part of the teaching body is of a mind to welcome the natural and gradual evolution of geometry toward better things, contributing to this evolution as[Pg iv] much as it can, glad to know the best that others have to offer, receptive of ideas that make for better teaching, but out of sympathy with either the extreme of revolution or the extreme of stagnation.
It is for this larger class, the great body of progressive teachers, that this book is written. It stands for vitalizing geometry in every legitimate way; for improving the subject matter in such manner as not to destroy the pupil's interest; for so teaching geometry as to make it appeal to pupils as strongly as any other subject in the curriculum; but for the recognition of geometry for geometry's sake and not for the sake of a fancied utility that hardly exists. Expressing full appreciation of the desirability of establishing a motive for all studies, so as to have the work proceed with interest and vigor, it does not hesitate to express doubt as to certain motives that have been exploited, nor to stand for such a genuine, thought-compelling development of the science as is in harmony with the mental powers of the pupils in the American high school.
For this class of teachers the author hopes that the book will prove of service, and that through its perusal they will come to admire the subject more and more, and to teach it with greater interest. It offers no panacea, it champions no single method, but it seeks to set forth plainly the reasons for teaching a geometry of the kind that we have inherited, and for hoping for a gradual but definite improvement in the science and in the methods of its presentation.
DAVID EUGENE SMITH
[Pg v]
| CHAPTER | PAGE | |
| I. | Certain Questions now at Issue | 1 |
| II. | Why Geometry is Studied | 7 |
| III. | A Brief History of Geometry | 26 |
| IV. | Development of the Teaching of Geometry | 40 |
| V. | Euclid | 47 |
| VI. | Efforts at Improving Euclid | 57 |
| VII. | The Textbook in Geometry | 70 |
| VIII. | The Relation of Algebra to Geometry | 84 |
| IX. | The Introduction to Geometry | 93 |
| X. | The Conduct of a Class in Geometry | 108 |
| XI. | The Axioms and Postulates | 116 |
| XII. | The Definitions of Geometry | 132 |
| XIII. | How to attack the Exercises | 160 |
| XIV. | Book I and its Propositions | 165 |
| XV. | The Leading Propositions of Book II | 201 |
| XVI. | The Leading Propositions of Book III | 227 |
| XVII. | The Leading Propositions of Book IV | 252 |
| XVIII. | The Leading Propositions of Book V | 269 |
| XIX. | The Leading Propositions of Book VI | 289 |
| XX. | The Leading Propositions of Book VII | 303 |
| XXI. | The Leading Propositions of Book VIII | 321 |
| INDEX | 335 |
It is commonly said at the present time that the opening of the twentieth century is a period of unusual advancement in all that has to do with the school. It would be pleasant to feel that we are living in such an age, but it is doubtful if the future historian of education will find this to be the case, or that biographers will rank the leaders of our generation relatively as high as many who have passed away, or that any great movements of the present will be found that measure up to certain ones that the world now recognizes as epoch-making. Every generation since the invention of printing has been a period of agitation in educational matters, but out of all the noise and self-assertion, out of all the pretense of the chronic revolutionist, out of all the sham that leads to dogmatism, so little is remembered that we are apt to feel that the past had no problems and was content simply to accept its inheritance. In one sense it is not a misfortune thus to be blinded by the dust of present agitation and to be deafened by the noisy clamor of the agitator, since it stirs us to action at finding ourselves in the midst of the skirmish; but in another sense it is detrimental to our progress,[Pg 2] since we thereby tend to lose the idea of perspective, and the coin comes to appear to our vision as large as the moon.
In considering a question like the teaching of geometry, we at once find ourselves in the midst of a skirmish of this nature. If we join thoughtlessly in the noise, we may easily persuade ourselves that we are waging a mighty battle, fighting for some stupendous principle, doing deeds of great valor and of personal sacrifice. If, on the other hand, we stand aloof and think of the present movement as merely a chronic effervescence, fostered by the professional educator at the expense of the practical teacher, we are equally shortsighted. Sir Conan Doyle expressed this sentiment most delightfully in these words:
The dead are such good company that one may come to think too little of the living. It is a real and pressing danger with many of us that we should never find our own thoughts and our own souls, but be ever obsessed by the dead.
In every generation it behooves the open-minded, earnest, progressive teacher to seek for the best in the way of improvement, to endeavor to sift the few grains of gold out of the common dust, to weigh the values of proposed reforms, and to put forth his efforts to know and to use the best that the science of education has to offer. This has been the attitude of mind of the real leaders in the school life of the past, and it will be that of the leaders of the future.
With these remarks to guide us, it is now proposed to take up the issues of the present day in the teaching of geometry, in order that we may consider them calmly and dispassionately, and may see where the opportunities for improvement lie.[Pg 3]
At the present time, in the educational circles of the United States, questions of the following type are causing the chief discussion among teachers of geometry:
1. Shall geometry continue to be taught as an application of logic, or shall it be treated solely with reference to its applications?
2. If the latter is the purpose in view, shall the propositions of geometry be limited to those that offer an opportunity for real application, thus contracting the whole subject to very narrow dimensions?
3. Shall a subject called geometry be extended over several years, as is the case in Europe,[1] or shall the name be applied only to serious demonstrative geometry[2] as given in the second year of the four-year high school course in the United States at present?
4. Shall geometry be taught by itself, or shall it be either mixed with algebra (say a day of one subject followed by a day of the other) or fused with it in the form of a combined mathematics?
5. Shall a textbook be used in which the basal propositions are proved in full, the exercises furnishing the opportunity for original work and being looked upon as the most important feature, or shall one be employed in which the pupil is expected to invent the proofs for the basal propositions as well as for the exercises?
6. Shall the terminology and the spirit of a modified Euclid and Legendre prevail in the future as they have
in the past, or shall there be a revolution in the use of terms and in the general statements of the propositions?
7. Shall geometry be made a strong elective subject, to be taken only by those whose minds are capable of serious work? Shall it be a required subject, diluted to the comprehension of the weakest minds? Or is it now, by proper teaching, as suitable for all pupils as is any other required subject in the school curriculum? And in any case, will the various distinct types of high schools now arising call for distinct types of geometry?
This brief list might easily be amplified, but it is sufficiently extended to set forth the trend of thought at the present time, and to show that the questions before the teachers of geometry are neither particularly novel nor particularly serious. These questions and others of similar nature are really side issues of two larger questions of far greater significance: (1) Are the reasons for teaching demonstrative geometry such that it should be a required subject, or at least a subject that is strongly recommended to all, whatever the type of high school? (2) If so, how can it be made interesting?
The present work is written with these two larger questions in mind, although it considers from time to time the minor ones already mentioned, together with others of a similar nature. It recognizes that the recent growth in popular education has brought into the high school a less carefully selected type of mind than was formerly the case, and that for this type a different kind of mathematical training will naturally be developed. It proceeds upon the theory, however, that for the normal mind,—for the boy or girl who is preparing to win out in the long run,—geometry will continue to be taught as demonstrative geometry, as a vigorous thought-compelling[Pg 5] subject, and along the general lines that the experience of the world has shown to be the best. Soft mathematics is not interesting to this normal mind, and a sham treatment will never appeal to the pupil; and this book is written for teachers who believe in this principle, who believe in geometry for the sake of geometry, and who earnestly seek to make the subject so interesting that pupils will wish to study it whether it is required or elective. The work stands for the great basal propositions that have come down to us, as logically arranged and as scientifically proved as the powers of the pupils in the American high school will permit; and it seeks to tell the story of these propositions and to show their possible and their probable applications in such a way as to furnish teachers with a fund of interesting material with which to supplement the book work of their classes.
After all, the problem of teaching any subject comes down to this: Get a subject worth teaching and then make every minute of it interesting. Pupils do not object to work if they like a subject, but they do object to aimless and uninteresting tasks. Geometry is particularly fortunate in that the feeling of accomplishment comes with every proposition proved; and, given a class of fair intelligence, a teacher must be lacking in knowledge and enthusiasm who cannot foster an interest that will make geometry stand forth as the subject that brings the most pleasure, and that seems the most profitable of all that are studied in the first years of the high school.
Continually to advance, continually to attempt to make mathematics fascinating, always to conserve the best of the old and to sift out and use the best of the new, to believe that "mankind is better served by[Pg 6] nature's quiet and progressive changes than by earthquakes,"[3] to believe that geometry as geometry is so valuable and so interesting that the normal mind may rightly demand it,—this is to ally ourselves with progress. Continually to destroy, continually to follow strange gods, always to decry the best of the old, and to have no well-considered aim in the teaching of a subject,—this is to join the forces of reaction, to waste our time, to be recreant to our trust, to blind ourselves to the failures of the past, and to confess our weakness as teachers. It is with the desire to aid in the progressive movement, to assist those who believe that real geometry should be recommended to all, and to show that geometry is both attractive and valuable that this book is written.
With geometry, as with other subjects, it is easier to set forth what are not the reasons for studying it than to proceed positively and enumerate the advantages. Although such a negative course is not satisfying to the mind as a finality, it possesses definite advantages in the beginning of such a discussion as this. Whenever false prophets arise, and with an attitude of pained superiority proclaim unworthy aims in human life, it is well to show the fallacy of their position before proceeding to a constructive philosophy. Taking for a moment this negative course, let us inquire as to what are not the reasons for studying geometry, or, to be more emphatic, as to what are not the worthy reasons.
In view of a periodic activity in favor of the utilities of geometry, it is well to understand, in the first place, that geometry is not studied, and never has been studied, because of its positive utility in commercial life or even in the workshop. In America we commonly allow at least a year to plane geometry and a half year to solid geometry; but all of the facts that a skilled mechanic or an engineer would ever need could be taught in a few lessons. All the rest is either obvious or is commercially and technically useless. We prove, for example, that the angles opposite the equal sides of a triangle are equal, a fact that is probably quite as obvious as the postulate that but one line can be drawn[Pg 8] through a given point parallel to a given line. We then prove, sometimes by the unsatisfactory process of reductio ad absurdum, the converse of this proposition,—a fact that is as obvious as most other facts that come to our consciousness, at least after the preceding proposition has been proved. And these two theorems are perfectly fair types of upwards of one hundred sixty or seventy propositions comprising Euclid's books on plane geometry. They are generally not useful in daily life, and they were never intended to be so. There is an oft-repeated but not well-authenticated story of Euclid that illustrates the feeling of the founders of geometry as well as of its most worthy teachers. A Greek writer, Stobæus, relates the story in these words:
Some one who had begun to read geometry with Euclid, when he had learned the first theorem, asked, "But what shall I get by learning these things?" Euclid called his slave and said, "Give him three obols, since he must make gain out of what he learns."
Whether true or not, the story expresses the sentiment that runs through Euclid's work, and not improbably we have here a bit of real biography,—practically all of the personal Euclid that has come down to us from the world's first great textbook maker. It is well that we read the story occasionally, and also such words as the following, recently uttered[4] by Sir Conan Doyle,—words bearing the same lesson, although upon a different theme:
In the present utilitarian age one frequently hears the question asked, "What is the use of it all?" as if every noble deed was not its own justification. As if every action which makes for[Pg 9] self-denial, for hardihood, and for endurance was not in itself a most precious lesson to mankind. That people can be found to ask such a question shows how far materialism has gone, and how needful it is that we insist upon the value of all that is nobler and higher in life.
An American statesman and jurist, speaking upon a similar occasion[5], gave utterance to the same sentiments in these words:
When the time comes that knowledge will not be sought for its own sake, and men will not press forward simply in a desire of achievement, without hope of gain, to extend the limits of human knowledge and information, then, indeed, will the race enter upon its decadence.
There have not been wanting, however, in every age, those whose zeal is in inverse proportion to their experience, who were possessed with the idea that it is the duty of the schools to make geometry practical. We have them to-day, and the world had them yesterday, and the future shall see them as active as ever.
These people do good to the world, and their labors should always be welcome, for out of the myriad of suggestions that they make a few have value, and these are helpful both to the mathematician and the artisan. Not infrequently they have contributed material that serves to make geometry somewhat more interesting, but it must be confessed that most of their work is merely the threshing of old straw, like the work of those who follow the will-o'-the-wisp of the circle squarers. The medieval astrologers wished to make geometry more practical, and so they carried to a considerable length the study of the star polygon, a figure that they could use in their profession. The cathedral builders, as their
art progressed, found that architectural drawings were more exact if made with a single opening of the compasses, and it is probable that their influence led to the development of this phase of geometry in the Middle Ages as a practical application of the science. Later, and about the beginning of the sixteenth century, the revival of art, and particularly the great development of painting, led to the practical application of geometry to the study of perspective and of those curves[6] that occur most frequently in the graphic arts. The sixteenth and seventeenth centuries witnessed the publication of a large number of treatises on practical geometry, usually relating to the measuring of distances and partly answering the purposes of our present trigonometry. Such were the well-known treatises of Belli (1569), Cataneo (1567), and Bartoli (1589).[7]
The period of two centuries from about 1600 to about 1800 was quite as much given to experiments in the creation of a practical geometry as is the present time, and it was no doubt as much by way of protest against this false idea of the subject as a desire to improve upon Euclid that led the great French mathematician, Legendre, to publish his geometry in 1794,—a work that soon replaced Euclid in the schools of America.
It thus appears that the effort to make geometry practical is by no means new. Euclid knew of it, the Middle Ages contributed to it, that period vaguely styled the Renaissance joined in the movement, and the first three centuries of printing contributed a large literature to the
subject. Out of all this effort some genuine good remains, but relatively not very much.[8] And so it will be with the present movement; it will serve its greatest purpose in making teachers think and read, and in adding to their interest and enthusiasm and to the interest of their pupils; but it will not greatly change geometry, because no serious person ever believed that geometry was taught chiefly for practical purposes, or was made more interesting or valuable through such a pretense. Changes in sequence, in definitions, and in proofs will come little by little; but that there will be any such radical change in these matters in the immediate future, as some writers have anticipated, is not probable.[9]
A recent writer of much acumen[10] has summed up this thought in these words:
Not one tenth of the graduates of our high schools ever enter professions in which their algebra and geometry are applied to concrete realities; not one day in three hundred sixty-five is a high school graduate called upon to "apply," as it is called, an algebraic or a geometrical proposition.... Why, then, do we teach these subjects, if this alone is the sense of the word "practical"!... To me the solution of this paradox consists in boldly confronting the dilemma, and in saying that our conception of the practical utility of those studies must be readjusted, and that we have frankly to face the truth that the "practical" ends we seek are in a sense ideal practical ends, yet such as have, after all, an eminently utilitarian value in the intellectual sphere.
He quotes from C. S. Jackson, a progressive contemporary teacher of mechanics in England, who speaks of pupils confusing millimeters and centimeters in some simple computation, and who adds:
There is the enemy! The real enemy we have to fight against, whatever we teach, is carelessness, inaccuracy, forgetfulness, and slovenliness. That battle has been fought and won with diverse weapons. It has, for instance, been fought with Latin grammar before now, and won. I say that because we must be very careful to guard against the notion that there is any one panacea for this sort of thing. It borders on quackery to say that elementary physics will cure everything.
And of course the same thing may be said for mathematics. Nevertheless it is doubtful if we have any other subject that does so much to bring to the front this danger of carelessness, of slovenly reasoning, of inaccuracy, and of forgetfulness as this science of geometry, which has been so polished and perfected as the centuries have gone on.
There have been those who did not proclaim the utilitarian value of geometry, but who fell into as serious an error, namely, the advocating of geometry as a means of training the memory. In times not so very far past, and to some extent to-day, the memorizing of proofs has been justified on this ground. This error has, however, been fully exposed by our modern psychologists. They have shown that the person who memorizes the propositions of Euclid by number is no more capable of memorizing other facts than he was before, and that the learning of proofs verbatim is of no assistance whatever in retaining matter that is helpful in other lines of work. Geometry, therefore, as a training of the memory is of no more value than any other subject in the curriculum.
If geometry is not studied chiefly because it is practical, or because it trains the memory, what reasons can[Pg 13] be adduced for its presence in the courses of study of every civilized country? Is it not, after all, a mere fetish, and are not those virulent writers correct who see nothing good in the subject save only its utilities?[11] Of this type one of the most entertaining is William J. Locke,[12] whose words upon the subject are well worth reading:
... I earned my living at school slavery, teaching to children the most useless, the most disastrous, the most soul-cramping branch of knowledge wherewith pedagogues in their insensate folly have crippled the minds and blasted the lives of thousands of their fellow creatures—elementary mathematics. There is no more reason for any human being on God's earth to be acquainted with the binomial theorem or the solution of triangles, unless he is a professional scientist,—when he can begin to specialize in mathematics at the same age as the lawyer begins to specialize in law or the surgeon in anatomy,—than for him to be expert in Choctaw, the Cabala, or the Book of Mormon. I look back with feelings of shame and degradation to the days when, for a crust of bread, I prostituted my intelligence to wasting the precious hours of impressionable childhood, which could have been filled with so many beautiful and meaningful things, over this utterly futile and inhuman subject. It trains the mind,—it teaches boys to think, they say. It doesn't. In reality it is a cut-and-dried subject, easy to fit into a school curriculum. Its sacrosanctity saves educationalists an enormous amount of trouble, and its chief use is to enable mindless young men from the universities to make a dishonest living by teaching it to others, who in their turn may teach it to a future generation.
To be fair we must face just such attacks, and we must recognize that they set forth the feelings of many
honest people. One is tempted to inquire if Mr. Locke could have written in such an incisive style if he had not, as was the case, graduated with honors in mathematics at one of the great universities. But he might reply that if his mind had not been warped by mathematics, he would have written more temperately, so the honors in the argument would be even. Much more to the point is the fact that Mr. Locke taught mathematics in the schools of England, and that these schools do not seem to the rest of the world to furnish a good type of the teaching of elementary mathematics. No country goes to England for its model in this particular branch of education, although the work is rapidly changing there, and Mr. Locke pictures a local condition in teaching rather than a general condition in mathematics. Few visitors to the schools of England would care to teach mathematics as they see it taught there, in spite of their recognition of the thoroughness of the work and the earnestness of many of the teachers. It is also of interest to note that the greatest protests against formal mathematics have come from England, as witness the utterances of such men as Sir William Hamilton and Professors Perry, Minchin, Henrici, and Alfred Lodge. It may therefore be questioned whether these scholars are not unconsciously protesting against the English methods and curriculum rather than against the subject itself. When Professor Minchin says that he had been through the six books of Euclid without really understanding an angle, it is Euclid's text and his own teacher that are at fault, and not geometry.
Before considering directly the question as to why geometry should be taught, let us turn for a moment to the other subjects in the secondary curriculum. Why,[Pg 15] for example, do we study literature? "It does not lower the price of bread," as Malherbe remarked in speaking of the commentary of Bachet on the great work of Diophantus. Is it for the purpose of making authors? Not one person out of ten thousand who study literature ever writes for publication. And why do we allow pupils to waste their time in physical education? It uses valuable hours, it wastes money, and it is dangerous to life and limb. Would it not be better to set pupils at sawing wood? And why do we study music? To give pleasure by our performances? How many who attempt to play the piano or to sing give much pleasure to any but themselves, and possibly their parents? The study of grammar does not make an accurate writer, nor the study of rhetoric an orator, nor the study of meter a poet, nor the study of pedagogy a teacher. The study of geography in the school does not make travel particularly easier, nor does the study of biology tend to populate the earth. So we might pass in review the various subjects that we study and ought to study, and in no case would we find utility the moving cause, and in every case would we find it difficult to state the one great reason for the pursuit of the subject in question,—and so it is with geometry.
What positive reasons can now be adduced for the study of a subject that occupies upwards of a year in the school course, and that is, perhaps unwisely, required of all pupils? Probably the primary reason, if we do not attempt to deceive ourselves, is pleasure. We study music because music gives us pleasure, not necessarily our own music, but good music, whether ours, or, as is more probable, that of others. We study literature because we derive pleasure from books; the better the[Pg 16] book the more subtle and lasting the pleasure. We study art because we receive pleasure from the great works of the masters, and probably we appreciate them the more because we have dabbled a little in pigments or in clay. We do not expect to be composers, or poets, or sculptors, but we wish to appreciate music and letters and the fine arts, and to derive pleasure from them and to be uplifted by them. At any rate, these are the nobler reasons for their study.
So it is with geometry. We study it because we derive pleasure from contact with a great and an ancient body of learning that has occupied the attention of master minds during the thousands of years in which it has been perfected, and we are uplifted by it. To deny that our pupils derive this pleasure from the study is to confess ourselves poor teachers, for most pupils do have positive enjoyment in the pursuit of geometry, in spite of the tradition that leads them to proclaim a general dislike for all study. This enjoyment is partly that of the game,—the playing of a game that can always be won, but that cannot be won too easily. It is partly that of the æsthetic, the pleasure of symmetry of form, the delight of fitting things together. But probably it lies chiefly in the mental uplift that geometry brings, the contact with absolute truth, and the approach that one makes to the Infinite. We are not quite sure of any one thing in biology; our knowledge of geology is relatively very slight, and the economic laws of society are uncertain to every one except some individual who attempts to set them forth; but before the world was fashioned the square on the hypotenuse was equal to the sum of the squares on the other two sides of a right triangle, and it will be so after this world is dead; and the inhabitant of[Pg 17] Mars, if he exists, probably knows its truth as we know it. The uplift of this contact with absolute truth, with truth eternal, gives pleasure to humanity to a greater or less degree, depending upon the mental equipment of the particular individual; but it probably gives an appreciable amount of pleasure to every student of geometry who has a teacher worthy of the name. First, then, and foremost as a reason for studying geometry has always stood, and will always stand, the pleasure and the mental uplift that comes from contact with such a great body of human learning, and particularly with the exact truth that it contains. The teacher who is imbued with this feeling is on the road to success, whatever method of presentation he may use; the one who is not imbued with it is on the road to failure, however logical his presentation or however large his supply of practical applications.
Subordinate to these reasons for studying geometry are many others, exactly as with all other subjects of the curriculum. Geometry, for example, offers the best developed application of logic that we have, or are likely to have, in the school course. This does not mean that it always exemplifies perfect logic, for it does not; but to the pupil who is not ready for logic, per se, it offers an example of close reasoning such as his other subjects do not offer. We may say, and possibly with truth, that one who studies geometry will not reason more clearly on a financial proposition than one who does not; but in spite of the results of the very meager experiments of the psychologists, it is probable that the man who has had some drill in syllogisms, and who has learned to select the essentials and to neglect the nonessentials in reaching his conclusions, has acquired habits in reasoning that will help him in every line of work. As part of this[Pg 18] equipment there is also a terseness of statement and a clearness in arrangement of points in an argument that has been the subject of comment by many writers.
Upon this same topic an English writer, in one of the sanest of recent monographs upon the subject,[13] has expressed his views in the following words:
The statement that a given individual has received a sound geometrical training implies that he has segregated from the whole of his sense impressions a certain set of these impressions, that he has then eliminated from their consideration all irrelevant impressions (in other words, acquired a subjective command of these impressions), that he has developed on the basis of these impressions an ordered and continuous system of logical deduction, and finally that he is capable of expressing the nature of these impressions and his deductions therefrom in terms simple and free from ambiguity. Now the slightest consideration will convince any one not already conversant with the idea, that the same sequence of mental processes underlies the whole career of any individual in any walk of life if only he is not concerned entirely with manual labor; consequently a full training in the performance of such sequences must be regarded as forming an essential part of any education worthy of the name. Moreover, the full appreciation of such processes has a higher value than is contained in the mental training involved, great though this be, for it induces an appreciation of intellectual unity and beauty which plays for the mind that part which the appreciation of schemes of shape and color plays for the artistic faculties; or, again, that part which the appreciation of a body of religious doctrine plays for the ethical aspirations. Now geometry is not the sole possible basis for inculcating this appreciation. Logic is an alternative for adults, provided that the individual is possessed of sufficient wide, though rough, experience on which to base his reasoning. Geometry is, however, highly desirable in that the objective bases are so simple and precise that they can be grasped at an early age, that the amount of training for the imagination is very large, that the deductive processes are not beyond the scope of[Pg 19] ordinary boys, and finally that it affords a better basis for exercise in the art of simple and exact expression than any other possible subject of a school course.
Are these results really secured by teachers, however, or are they merely imagined by the pedagogue as a justification for his existence? Do teachers have any such appreciation of geometry as has been suggested, and even if they have it, do they impart it to their pupils? In reply it may be said, probably with perfect safety, that teachers of geometry appreciate their subject and lead their pupils to appreciate it to quite as great a degree as obtains in any other branch of education. What teacher appreciates fully the beauties of "In Memoriam," or of "Hamlet," or of "Paradise Lost," and what one inspires his pupils with all the nobility of these world classics? What teacher sees in biology all the grandeur of the evolution of the race, or imparts to his pupils the noble lessons of life that the study of this subject should suggest? What teacher of Latin brings his pupils to read the ancient letters with full appreciation of the dignity of style and the nobility of thought that they contain? And what teacher of French succeeds in bringing a pupil to carry on a conversation, to read a French magazine, to see the history imbedded in the words that are used, to realize the charm and power of the language, or to appreciate to the full a single classic? In other words, none of us fully appreciates his subject, and none of us can hope to bring his pupils to the ideal attitude toward any part of it. But it is probable that the teacher of geometry succeeds relatively better than the teacher of other subjects, because the science has reached a relatively higher state of perfection. The body of truth in geometry has been more clearly marked out, it has been[Pg 20] more successfully fitted together, its lesson is more patent, and the experience of centuries has brought it into a shape that is more usable in the school. While, therefore, we have all kinds of teaching in all kinds of subjects, the very nature of the case leads to the belief that the class in geometry receives quite as much from the teacher and the subject as the class in any other branch in the school curriculum.
But is this not mere conjecture? What are the results of scientific investigation of the teaching of geometry? Unfortunately there is little hope from the results of such an inquiry, either here or in other fields. We cannot first weigh a pupil in an intellectual or moral balance, then feed him geometry, and then weigh him again, and then set back his clock of time and begin all over again with the same individual. There is no "before taking" and "after taking" of a subject that extends over a year or two of a pupil's life. We can weigh utilities roughly, we can estimate the pleasure of a subject relatively, but we cannot say that geometry is worth so many dollars, and history so many, and so on through the curriculum. The best we can do is to ask ourselves what the various subjects, with teachers of fairly equal merit, have done for us, and to inquire what has been the experience of other persons. Such an investigation results in showing that, with few exceptions, people who have studied geometry received as much of pleasure, of inspiration, of satisfaction, of what they call training from geometry as from any other subject of study,—given teachers of equal merit,—and that they would not willingly give up the something which geometry brought to them. If this were not the feeling, and if humanity believed that geometry is what Mr. Locke's words would seem to[Pg 21] indicate, it would long ago have banished it from the schools, since upon this ground rather than upon the ground of utility the subject has always stood.
These seem to be the great reasons for the study of geometry, and to search for others would tend to weaken the argument. At first sight they may not seem to justify the expenditure of time that geometry demands, and they may seem unduly to neglect the argument that geometry is a stepping-stone to higher mathematics. Each of these points, however, has been neglected purposely. A pupil has a number of school years at his disposal; to what shall they be devoted? To literature? What claim has letters that is such as to justify the exclusion of geometry? To music, or natural science, or language? These are all valuable, and all should be studied by one seeking a liberal education; but for the same reason geometry should have its place. What subject, in fine, can supply exactly what geometry does? And if none, then how can the pupil's time be better expended than in the study of this science?[14] As to the second point, that a claim should be set forth that geometry is a sine qua non to higher mathematics, this belief is considerably exaggerated because there are relatively few who proceed from geometry to a higher branch of mathematics. This argument would justify its status as an elective rather than as a required subject.
Let us then stand upon the ground already marked out, holding that the pleasure, the culture, the mental poise, the habits of exact reasoning that geometry brings,
and the general experience of mankind upon the subject are sufficient to justify us in demanding for it a reasonable amount of time in the framing of a curriculum. Let us be fair in our appreciation of all other branches, but let us urge that every student may have an opportunity to know of real geometry, say for a single year, thereafter pursuing it or not, according as we succeed in making its value apparent, or fail in our attempt to present worthily an ancient and noble science to the mind confided to our instruction.
The shortsightedness of a narrow education, of an education that teaches only machines to a prospective mechanic, and agriculture to a prospective farmer, and cooking and dressmaking to the girl, and that would exclude all mathematics that is not utilitarian in the narrow sense, cannot endure.
The community has found out that such schemes may be well fitted to give the children a good time in school, but lead them to a bad time afterward. Life is hard work, and if they have never learned in school to give their concentrated attention to that which does not appeal to them and which does not interest them immediately, they have missed the most valuable lesson of their school years. The little practical information they could have learned at any time; the energy of attention and concentration can no longer be learned if the early years are wasted. However narrow and commercial the standpoint which is chosen may be, it can always be found that it is the general education which pays best, and the more the period of cultural work can be expanded the more efficient will be the services of the school for the practical services of the nation.[15]
Of course no one should construe these remarks as opposing in the slightest degree the laudable efforts that are constantly being put forth to make geometry more
interesting and to vitalize it by establishing as strong motives as possible for its study. Let the home, the workshop, physics, art, play,—all contribute their quota of motive to geometry as to all mathematics and all other branches. But let us never forget that geometry has a raison d'être beyond all this, and that these applications are sought primarily for the sake of geometry, and that geometry is not taught primarily for the sake of these applications.
When we consider how often geometry is attacked by those who profess to be its friends, and how teachers who have been trained in mathematics occasionally seem to make of the subject little besides a mongrel course in drawing and measuring, all the time insisting that they are progressive while the champions of real geometry are reactionary, it is well to read some of the opinions of the masters. The following quotations may be given occasionally in geometry classes as showing the esteem in which the subject has been held in various ages, and at any rate they should serve to inspire the teacher to greater love for his subject.
The enemies of geometry, those who know it only imperfectly, look upon the theoretical problems, which constitute the most difficult part of the subject, as mental games which consume time and energy that might better be employed in other ways. Such a belief is false, and it would block the progress of science if it were credible. But aside from the fact that the speculative problems, which at first sight seem barren, can often be applied to useful purposes, they always stand as among the best means to develop and to express all the forces of the human intelligence.—Abbé Bossut.
The sailor whom an exact observation of longitude saves from shipwreck owes his life to a theory developed two thousand years ago by men who had in mind merely the speculations of abstract geometry.—Condorcet.
If mathematical heights are hard to climb, the fundamental principles lie at every threshold, and this fact allows them to be comprehended by that common sense which Descartes declared was "apportioned equally among all men."—Collet.
It may seem strange that geometry is unable to define the terms which it uses most frequently, since it defines neither movement, nor number, nor space,—-the three things with which it is chiefly concerned. But we shall not be surprised if we stop to consider that this admirable science concerns only the most simple things, and the very quality that renders these things worthy of study renders them incapable of being defined. Thus the very lack of definition is rather an evidence of perfection than a defect, since it comes not from the obscurity of the terms, but from the fact that they are so very well known.—Pascal.
God eternally geometrizes.—Plato.
God is a circle of which the center is everywhere and the circumference nowhere.—Rabelais.
Without mathematics no one can fathom the depths of philosophy. Without philosophy no one can fathom the depths of mathematics. Without the two no one can fathom the depths of anything.—Bordas-Demoulin.
We may look upon geometry as a practical logic, for the truths which it studies, being the most simple and most clearly understood of all truths, are on this account the most susceptible of ready application in reasoning.—D'Alembert.
The advance and the perfecting of mathematics are closely joined to the prosperity of the nation.—Napoleon.
Hold nothing as certain save what can be demonstrated.—Newton.
To measure is to know.—Kepler.
The method of making no mistake is sought by every one. The logicians profess to show the way, but the geometers alone ever reach it, and aside from their science there is no genuine demonstration.—Pascal.
The taste for exactness, the impossibility of contenting one's self with vague notions or of leaning upon mere hypotheses, the necessity for perceiving clearly the connection between certain propositions and the object in view,—these are the most precious fruits of the study of mathematics.—Lacroix.
Bibliography. Smith, The Teaching of Elementary Mathematics, p. 234, New York, 1900; Henrici, Presidential Address before the British Association, Nature, Vol. XXVIII, p. 497; Hill, Educational Value of Mathematics, Educational Review, Vol. IX, p. 349; Young, The Teaching of Mathematics, p. 9, New York, 1907. The closing quotations are from Rebière, Mathématiques et Mathématiciens, Paris, 1893.
The geometry of very ancient peoples was largely the mensuration of simple areas and solids, such as is taught to children in elementary arithmetic to-day. They early learned how to find the area of a rectangle, and in the oldest mathematical records that have come down to us there is some discussion of the area of triangles and the volume of solids.
The earliest documents that we have relating to geometry come to us from Babylon and Egypt. Those from Babylon are written on small clay tablets, some of them about the size of the hand, these tablets afterwards having been baked in the sun. They show that the Babylonians of that period knew something of land measures, and perhaps had advanced far enough to compute the area of a trapezoid. For the mensuration of the circle they later used, as did the early Hebrews, the value π = 3. A tablet in the British Museum shows that they also used such geometric forms as triangles and circular segments in astrology or as talismans.
The Egyptians must have had a fair knowledge of practical geometry long before the date of any mathematical treatise that has come down to us, for the building of the pyramids, between 3000 and 2400 B.C., required the application of several geometric principles. Some knowledge of surveying must also have been necessary[Pg 27] to carry out the extensive plans for irrigation that were executed under Amenemhat III, about 2200 B.C.
The first definite knowledge that we have of Egyptian mathematics comes to us from a manuscript copied on papyrus, a kind of paper used about the Mediterranean in early times. This copy was made by one Aah-mesu (The Moon-born), commonly called Ahmes, who probably flourished about 1700 B.C. The original from which he copied, written about 2300 B.C., has been lost, but the papyrus of Ahmes, written nearly four thousand years ago, is still preserved, and is now in the British Museum. In this manuscript, which is devoted chiefly to fractions and to a crude algebra, is found some work on mensuration. Among the curious rules are the incorrect ones that the area of an isosceles triangle equals half the product of the base and one of the equal sides; and that the area of a trapezoid having bases b, b', and the nonparallel sides each equal to a, is ½a(b + b'). One noteworthy advance appears, however. Ahmes gives a rule for finding the area of a circle, substantially as follows: Multiply the square on the radius by (16/9)2, which is equivalent to taking for π the value 3.1605. This papyrus also contains some treatment of the mensuration of solids, particularly with reference to the capacity of granaries. There is also some slight mention of similar figures, and an extensive treatment of unit fractions,—fractions that were quite universal among the ancients. In the line of algebra it contains a brief treatment of the equation of the first degree with one unknown, and of progressions.[16]
Herodotus tells us that Sesostris, king of Egypt,[17] divided the land among his people and marked out the boundaries after the overflow of the Nile, so that surveying must have been well known in his day. Indeed, the harpedonaptæ, or rope stretchers, acquired their name because they stretched cords, in which were knots, so as to make the right triangle 3, 4, 5, when they wished to erect a perpendicular. This is a plan occasionally used by surveyors to-day, and it shows that the practical application of the Pythagorean Theorem was known long before Pythagoras gave what seems to have been the first general proof of the proposition.
From Egypt, and possibly from Babylon, geometry passed to the shores of Asia Minor and Greece. The scientific study of the subject begins with Thales, one of the Seven Wise Men of the Grecian civilization. Born at Miletus, not far from Smyrna and Ephesus, about 640 B.C., he died at Athens in 548 B.C. He spent his early manhood as a merchant, accumulating the wealth that enabled him to spend his later years in study. He visited Egypt, and is said to have learned such elements of geometry as were known there. He founded a school of mathematics and philosophy at Miletus, known from the country as the Ionic School. How elementary the knowledge of geometry then was may be understood from the fact that tradition attributes only about four propositions to Thales,—(1) that vertical angles are equal, (2) that equal angles lie opposite the equal sides of an isosceles triangle, (3) that a triangle is determined by two angles and the included side, (4) that a diameter bisects the circle, and possibly the propositions about the
angle-sum of a triangle for special cases, and the angle inscribed in a semicircle.[18]
The greatest pupil of Thales, and one of the most remarkable men of antiquity, was Pythagoras. Born probably on the island of Samos, just off the coast of Asia Minor, about the year 580 B.C., Pythagoras set forth as a young man to travel. He went to Miletus and studied under Thales, probably spent several years in Egypt, very likely went to Babylon, and possibly went even to India, since tradition asserts this and the nature of his work in mathematics suggests it. In later life he went to a Greek colony in southern Italy, and at Crotona, in the southeastern part of the peninsula, he founded a school and established a secret society to propagate his doctrines. In geometry he is said to have been the first to demonstrate the proposition that the square on the hypotenuse is equal to the sum of the squares upon the other two sides of a right triangle. The proposition was known in India and Egypt before his time, at any rate for special cases, but he seems to have been the first to prove it. To him or to his school seems also to have been due the construction of the regular pentagon and of the five regular polyhedrons. The construction of the regular pentagon requires the dividing of a line into extreme and mean ratio, and this problem is commonly assigned to the Pythagoreans, although it played an important part in Plato's school. Pythagoras is also said to have known that six equilateral triangles, three [Pg 30]regular hexagons, or four squares, can be placed about a point so as just to fill the 360°, but that no other regular polygons can be so placed. To his school is also due the proof for the general case that the sum of the angles of a triangle equals two right angles, the first knowledge of the size of each angle of a regular polygon, and the construction of at least one star-polygon, the star-pentagon, which became the badge of his fraternity. The brotherhood founded by Pythagoras proved so offensive to the government that it was dispersed before the death of the master. Pythagoras fled to Megapontum, a seaport lying to the north of Crotona, and there he died about 501 B.C.[19]
For two centuries after Pythagoras geometry passed through a period of discovery of propositions. The state [Pg 31] of the science may be seen from the fact that Œnopides of Chios, who flourished about 465 B.C., and who had studied in Egypt, was celebrated because he showed how to let fall a perpendicular to a line, and how to make an angle equal to a given angle. A few years later, about 440 B.C., Hippocrates of Chios wrote the first Greek textbook on mathematics. He knew that the areas of circles are proportional to the squares on their radii, but was ignorant of the fact that equal central angles or equal inscribed angles intercept equal arcs.
Antiphon and Bryson, two Greek scholars, flourished about 430 B.C. The former attempted to find the area of a circle by doubling the number of sides of a regular inscribed polygon, and the latter by doing the same for both inscribed and circumscribed polygons. They thus approximately exhausted the area between the polygon and the circle, and hence this method is known as the method of exhaustions.
About 420 B.C. Hippias of Elis invented a certain curve called the quadratrix, by means of which he could square the circle and trisect any angle. This curve cannot be constructed by the unmarked straightedge and the compasses, and when we say that it is impossible to square the circle or to trisect any angle, we mean that it is impossible by the help of these two instruments alone.
During this period the great philosophic school of Plato (429-348 B.C.) flourished at Athens, and to this school is due the first systematic attempt to create exact definitions, axioms, and postulates, and to distinguish between elementary and higher geometry. It was at this time that elementary geometry became limited to the use of the compasses and the unmarked straightedge,[Pg 32] which took from this domain the possibility of constructing a square equivalent to a given circle ("squaring the circle"), of trisecting any given angle, and of constructing a cube that should have twice the volume of a given cube ("duplicating the cube"), these being the three famous problems of antiquity. Plato and his school interested themselves with the so-called Pythagorean numbers, that is, with numbers that would represent the three sides of a right triangle and hence fulfill the condition that a2 + b2 = c2. Pythagoras had already given a rule that would be expressed in modern form, as ¼(m2 + 1)2 = m2 + ¼(m2 - 1)2. The school of Plato found that ((½m)2 + 1)2 = m2 + ((½m)2 - 1)2. By giving various values to m, different Pythagorean numbers may be found. Plato's nephew, Speusippus (about 350 B.C.), wrote upon this subject. Such numbers were known, however, both in India and in Egypt, long before this time.
One of Plato's pupils was Philippus of Mende, in Egypt, who flourished about 380 B.C. It is said that he discovered the proposition relating to the exterior angle of a triangle. His interest, however, was chiefly in astronomy.
Another of Plato's pupils was Eudoxus of Cnidus (408-355 B.C.). He elaborated the theory of proportion, placing it upon a thoroughly scientific foundation. It is probable that Book V of Euclid, which is devoted to proportion, is essentially the work of Eudoxus. By means of the method of exhaustions of Antiphon and Bryson he proved that the pyramid is one third of a prism, and the cone is one third of a cylinder, each of the same base and the same altitude. He wrote the first textbook known on solid geometry.[Pg 33]
The subject of conic sections starts with another pupil of Plato's, Menæchmus, who lived about 350 B.C. He cut the three forms of conics (the ellipse, parabola, and hyperbola) out of three different forms of cone,—the acute-angled, right-angled, and obtuse-angled,—not noticing that he could have obtained all three from any form of right circular cone. It is interesting to see the far-reaching influence of Plato. While primarily interested in philosophy, he laid the first scientific foundations for a system of mathematics, and his pupils were the leaders in this science in the generation following his greatest activity.
The great successor of Plato at Athens was Aristotle, the teacher of Alexander the Great. He also was more interested in philosophy than in mathematics, but in natural rather than mental philosophy. With him comes the first application of mathematics to physics in the hands of a great man, and with noteworthy results. He seems to have been the first to represent an unknown quantity by letters. He set forth the theory of the parallelogram of forces, using only rectangular components, however. To one of his pupils, Eudemus of Rhodes, we are indebted for a history of ancient geometry, some fragments of which have come down to us.
The first great textbook on geometry, and the greatest one that has ever appeared, was written by Euclid, who taught mathematics in the great university at Alexandria, Egypt, about 300 B.C. Alexandria was then practically a Greek city, having been named in honor of Alexander the Great, and being ruled by the Greeks.
In his work Euclid placed all of the leading propositions of plane geometry then known, and arranged them[Pg 34] in a logical order. Most geometries of any importance written since his time have been based upon Euclid, improving the sequence, symbols, and wording as occasion demanded. He also wrote upon other branches of mathematics besides elementary geometry, including a work on optics. He was not a great creator of mathematics, but was rather a compiler of the work of others, an office quite as difficult to fill and quite as honorable.
Euclid did not give much solid geometry because not much was known then. It was to Archimedes (287-212 B.C.), a famous mathematician of Syracuse, on the island of Sicily, that some of the most important propositions of solid geometry are due, particularly those relating to the sphere and cylinder. He also showed how to find the approximate value of π by a method similar to the one we teach to-day, proving that the real value lay between 3-1/7 and 3-10/71. The story goes that the sphere and cylinder were engraved upon his tomb, and Cicero, visiting Syracuse many years after his death, found the tomb by looking for these symbols. Archimedes was the greatest mathematical physicist of ancient times.
The Greeks contributed little more to elementary geometry, although Apollonius of Perga, who taught at Alexandria between 250 and 200 B.C., wrote extensively on conic sections, and Hypsicles of Alexandria, about 190 B.C., wrote on regular polyhedrons. Hypsicles was the first Greek writer who is known to have used sexagesimal fractions,—the degrees, minutes, and seconds of our angle measure. Zenodorus (180 B.C.) wrote on isoperimetric figures, and his contemporary, Nicomedes of Gerasa, invented a curve known as the conchoid, by means of which he could trisect any angle. Another contemporary, Diocles, invented the cissoid, or ivy-shaped[Pg 35] curve, by means of which he solved the famous problem of duplicating the cube, that is, constructing a cube that should have twice the volume of a given cube.
The greatest of the Greek astronomers, Hipparchus (180-125 B.C.), lived about this period, and with him begins spherical trigonometry as a definite science. A kind of plane trigonometry had been known to the ancient Egyptians. The Greeks usually employed the chord of an angle instead of the half chord (sine), the latter having been preferred by the later Arab writers.
The most celebrated of the later Greek physicists was Heron of Alexandria, formerly supposed to have lived about 100 B.C., but now assigned to the first century A.D. His contribution to geometry was the formula for the area of a triangle in terms of its sides a, b, and c, with s standing for the semiperimeter ½(a + b + c). The formula is
Probably nearly contemporary with Heron was Menelaus of Alexandria, who wrote a spherical trigonometry. He gave an interesting proposition relating to plane and spherical triangles, their sides being cut by a transversal. For the plane triangle ABC, the sides a, b, and c being cut respectively in X, Y, and Z, the theorem asserts substantially that
(AZ/BZ) · (BX/CX) · (CY/AY) = 1.
The most popular writer on astronomy among the Greeks was Ptolemy (Claudius Ptolemaeus, 87-165 A.D.), who lived at Alexandria. He wrote a work entitled "Megale Syntaxis" (The Great Collection), which his followers designated as Megistos (greatest), on which account the Arab translators gave it the name "Almagest"[Pg 36] (al meaning "the"). He advanced the science of trigonometry, but did not contribute to geometry.
At the close of the third century Pappus of Alexandria (295 A.D.) wrote on geometry, and one of his theorems, a generalized form of the Pythagorean proposition, is mentioned in Chapter XVI of this work. Only two other Greek writers on geometry need be mentioned. Theon of Alexandria (370 A.D.), the father of the Hypatia who is the heroine of Charles Kingsley's well-known novel, wrote a commentary on Euclid to which we are indebted for some historical information. Proclus (410-485 A.D.) also wrote a commentary on Euclid, and much of our information concerning the first Book of Euclid is due to him.
The East did little for geometry, although contributing considerably to algebra. The first great Hindu writer was Aryabhatta, who was born in 476 A.D. He gave the very close approximation for π, expressed in modern notation as 3.1416. He also gave rules for finding the volume of the pyramid and sphere, but they were incorrect, showing that the Greek mathematics had not yet reached the Ganges. Another Hindu writer, Brahmagupta (born in 598 A.D.), wrote an encyclopedia of mathematics. He gave a rule for finding Pythagorean numbers, expressed in modern symbols as follows:
He also generalized Heron's formula by asserting that the area of an inscribed quadrilateral of sides a, b, c, d, and semiperimeter s, is
The Arabs, about the time of the "Arabian Nights Tales" (800 A.D.), did much for mathematics, translating[Pg 37] the Greek authors into their language and also bringing learning from India. Indeed, it is to them that modern Europe owed its first knowledge of Euclid. They contributed nothing of importance to elementary geometry, however.
The greatest of the Arab writers was Mohammed ibn Musa al-Khowarazmi (820 A.D.). He lived at Bagdad and Damascus. Although chiefly interested in astronomy, he wrote the first book bearing the name "algebra" ("Al-jabr wa'l-muqābalah," Restoration and Equation), composed an arithmetic using the Hindu numerals,[20] and paid much attention to geometry and trigonometry.
Euclid was translated from the Arabic into Latin in the twelfth century, Greek manuscripts not being then at hand, or being neglected because of ignorance of the language. The leading translators were Athelhard of Bath (1120), an English monk; Gherard of Cremona (1160), an Italian monk; and Johannes Campanus (1250), chaplain to Pope Urban IV.
The greatest European mathematician of the Middle Ages was Leonardo of Pisa[21] (ca. 1170-1250). He was very influential in making the Hindu-Arabic numerals known in Europe, wrote extensively on algebra, and was the author of one book on geometry. He contributed nothing to the elementary theory, however. The first edition of Euclid was printed in Latin in 1482, the first one in English appearing in 1570.
Our symbols are modern, + and - first appearing in a German work in 1489; = in Recorde's "Whetstone of Witte" in 1557; > and < in the works of Harriot (1560-1621); and × in a publication by Oughtred (1574-1660).
The most noteworthy advance in geometry in modern times was made by the great French philosopher Descartes, who published a small work entitled "La Géométrie" in 1637. From this springs the modern analytic geometry, a subject that has revolutionized the methods of all mathematics. Most of the subsequent discoveries in mathematics have been in higher branches. To the great Swiss mathematician Euler (1707-1783) is due, however, one proposition that has found its way into elementary geometry, the one showing the relation between the number of edges, vertices, and faces of a polyhedron.
There has of late arisen a modern elementary geometry devoted chiefly to special points and lines relating to the triangle and the circle, and many interesting propositions have been discovered. The subject is so extensive that it cannot find any place in our crowded curriculum, and must necessarily be left to the specialist.[22] Some idea of the nature of the work may be obtained from a mention of a few propositions:
The medians of a triangle are concurrent in the centroid, or center of gravity of the triangle.
The bisectors of the various interior and exterior angles of a triangle are concurrent by threes in the incenter or in one of the three excenters of the triangle.
The common chord of two intersecting circles is a special case of their radical axis, and tangents to the circles from any point on the radical axis are equal.
If O is the orthocenter of the triangle ABC, and X, Y, Z are the feet of the perpendiculars from A, B, C respectively, and P, Q, R are the mid-points of a, b, c respectively, and L, M, N are the mid-points of OA, OB, OC respectively; then the points L, M, N; P, Q, R; X, Y, Z all lie on a circle, the "nine points circle."
In the teaching of geometry it adds a human interest to the subject to mention occasionally some of the historical facts connected with it. For this reason this brief sketch will be supplemented by many notes upon the various important propositions as they occur in the several books described in the later chapters of this work.[Pg 40]
We know little of the teaching of geometry in very ancient times, but we can infer its nature from the teaching that is still seen in the native schools of the East. Here a man, learned in any science, will have a group of voluntary students sitting about him, and to them he will expound the truth. Such schools may still be seen in India, Persia, and China, the master sitting on a mat placed on the ground or on the floor of a veranda, and the pupils reading aloud or listening to his words of exposition.
In Egypt geometry seems to have been in early times mere mensuration, confined largely to the priestly caste. It was taught to novices who gave promise of success in this subject, and not to others, the idea of general culture, of training in logic, of the cultivation of exact expression, and of coming in contact with truth being wholly wanting.
In Greece it was taught in the schools of philosophy, often as a general preparation for philosophic study. Thus Thales introduced it into his Ionic school, Pythagoras made it very prominent in his great school at Crotona in southern Italy (Magna Græcia), and Plato placed above the door of his Academia the words, "Let no one ignorant of geometry enter here,"—a kind of entrance examination for his school of philosophy. In[Pg 41] these gatherings of students it is probable that geometry was taught in much the way already mentioned for the schools of the East, a small group of students being instructed by a master. Printing was unknown, papyrus was dear, parchment was only in process of invention. Paper such as we know had not yet appeared, so that instruction was largely oral, and geometric figures were drawn by a pointed stick on a board covered with fine sand, or on a tablet of wax.
But with these crude materials there went an abundance of time, so that a number of great results were accomplished in spite of the difficulties attending the study of the subject. It is said that Hippocrates of Chios (ca. 440 B.C.) wrote the first elementary textbook on mathematics and invented the method of geometric reduction, the replacing of a proposition to be proved by another which, when proved, allows the first one to be demonstrated. A little later Eudoxus of Cnidus (ca. 375 B.C.), a pupil of Plato's, used the reductio ad absurdum, and Plato is said to have invented the method of proof by analysis, an elaboration of the plan used by Hippocrates. Thus these early philosophers taught their pupils not facts alone, but methods of proof, giving them power as well as knowledge. Furthermore, they taught them how to discuss their problems, investigating the conditions under which they are capable of solution. This feature of the work they called the diorismus, and it seems to have started with Leon, a follower of Plato.
Between the time of Plato (ca. 400 B.C.) and Euclid (ca. 300 B.C.) several attempts were made to arrange the accumulated material of elementary geometry in a textbook. Plato had laid the foundations for the science, in the form of axioms, postulates, and definitions, and he[Pg 42] had limited the instruments to the straightedge and the compasses. Aristotle (ca. 350 B.C.) had paid special attention to the history of the subject, thus finding out what had already been accomplished, and had also made much of the applications of geometry. The world was therefore ready for a good teacher who should gather the material and arrange it scientifically. After several attempts to find the man for such a task, he was discovered in Euclid, and to his work the next chapter is devoted.
After Euclid, Archimedes (ca. 250 B.C.) made his great contributions. He was not a teacher like his illustrious predecessor, but he was a great discoverer. He has left us, however, a statement of his methods of investigation which is helpful to those who teach. These methods were largely experimental, even extending to the weighing of geometric forms to discover certain relations, the proof being given later. Here was born, perhaps, what has been called the laboratory method of the present.
Of the other Greek teachers we have but little information as to methods of imparting instruction. It is not until the Middle Ages that there is much known in this line. Whatever of geometry was taught seems to have been imparted by word of mouth in the way of expounding Euclid, and this was done in the ancient fashion.
The early Church leaders usually paid no attention to geometry, but as time progressed the quadrivium, or four sciences of arithmetic, music, geometry, and astronomy, came to rank with the trivium (grammar, rhetoric, dialectics), the two making up the "seven liberal arts." All that there was of geometry in the first thousand years of Christianity, however, at least in the great[Pg 43] majority of Church schools, was summed up in a few definitions and rules of mensuration. Gerbert, who became Pope Sylvester II in 999 A.D., gave a new impetus to geometry by discovering a manuscript of the old Roman surveyors and a copy of the geometry of Boethius, who paraphrased Euclid about 500 A.D. He thereupon wrote a brief geometry, and his elevation to the papal chair tended to bring the study of mathematics again into prominence.
Geometry now began to have some place in the Church schools, naturally the only schools of high rank in the Middle Ages. The study of the subject, however, seems to have been merely a matter of memorizing. Geometry received another impetus in the book written by Leonardo of Pisa in 1220, the "Practica Geometriae." Euclid was also translated into Latin about this time (strangely enough, as already stated, from the Arabic instead of the Greek), and thus the treasury of elementary geometry was opened to scholars in Europe. From now on, until the invention of printing (ca. 1450), numerous writers on geometry appear, but, so far as we know, the method of instruction remained much as it had always been. The universities began to appear about the thirteenth century, and Sacrobosco, a well-known medieval mathematician, taught mathematics about 1250 in the University of Paris. In 1336 this university decreed that mathematics should be required for a degree. In the thirteenth century Oxford required six books of Euclid for one who was to teach, but this amount of work seems to have been merely nominal, for in 1450 only two books were actually read. The universities of Prague (founded in 1350) and Vienna (statutes of 1389) required most of plane geometry for the teacher's[Pg 44] license, although Vienna demanded but one book for the bachelor's degree. So, in general, the universities of the thirteenth, fourteenth, and fifteenth centuries required less for the degree of master of arts than we now require from a pupil in our American high schools. On the other hand, the university students were younger than now, and were really doing only high school work.
The invention of printing made possible the study of geometry in a new fashion. It now became possible for any one to study from a book, whereas before this time instruction was chiefly by word of mouth, consisting of an explanation of Euclid. The first Euclid was printed in 1482, at Venice, and new editions and variations of this text came out frequently in the next century. Practical geometries became very popular, and the reaction against the idea of mental discipline threatened to abolish the old style of text. It was argued that geometry was uninteresting, that it was not sufficient in itself, that boys needed to see the practical uses of the subject, that only those propositions that were capable of application should be retained, that there must be a fusion between the demands of culture and the demands of business, and that every man who stood for mathematical ideals represented an obsolete type. Such writers as Finæus (1556), Bartoli (1589), Belli (1569), and Cataneo (1567), in the sixteenth century, and Capra (1678), Gargiolli (1655), and many others in the seventeenth century, either directly or inferentially, took this attitude towards the subject,—exactly the attitude that is being taken at the present time by a number of teachers in the United States. As is always the case, to such an extreme did this movement lead that there was a reaction that brought the Euclid type of book[Pg 45] again to the front, and it has maintained its prominence even to the present.
The study of geometry in the high schools is relatively recent. The Gymnasium (classical school preparatory to the university) at Nürnberg, founded in 1526, and the Cathedral school at Württemberg (as shown by the curriculum of 1556) seem to have had no geometry before 1600, although the Gymnasium at Strassburg included some of this branch of mathematics in 1578, and an elective course in geometry was offered at Zwickau, in Saxony, in 1521. In the seventeenth century geometry is found in a considerable number of secondary schools, as at Coburg (1605), Kurfalz (1615, elective), Erfurt (1643), Gotha (1605), Giessen (1605), and numerous other places in Germany, although it appeared but rarely in the secondary schools of France before the eighteenth century. In Germany the Realschulen—schools with more science and less classics than are found in the Gymnasium—came into being in the eighteenth century, and considerable effort was made to construct a course in geometry that should be more practical than that of the modified Euclid. At the opening of the nineteenth century the Prussian schools were reorganized, and from that time on geometry has had a firm position in the secondary schools of all Germany. In the eighteenth century some excellent textbooks on geometry appeared in France, among the best being that of Legendre (1794), which influenced in such a marked degree the geometries of America. Soon after the opening of the nineteenth century the lycées of France became strong institutions, and geometry, chiefly based on Legendre, was well taught in the mathematical divisions. A worthy rival of Legendre's geometry was the[Pg 46] work of Lacroix, who called attention continually to the analogy between the theorems of plane and solid geometry, and even went so far as to suggest treating the related propositions together in certain cases.
In England the preparatory schools, such as Rugby, Harrow, and Eton, did not commonly teach geometry until quite recently, leaving this work for the universities. In Christ's Hospital, London, however, geometry was taught as early as 1681, from a work written by several teachers of prominence. The highest class at Harrow studied "Euclid and vulgar fractions" one period a week in 1829, but geometry was not seriously studied before 1837. In the Edinburgh Academy as early as 1885, and in Rugby by 1839, plane geometry was completed.
Not until 1844 did Harvard require any plane geometry for entrance. In 1855 Yale required only two books of Euclid. It was therefore from 1850 to 1875 that plane geometry took a definite place in the American high school. Solid geometry has not been generally required for entrance to any eastern college, although in the West this is not the case. The East teaches plane geometry more thoroughly, but allows a pupil to enter college or to go into business with no solid geometry. Given a year to the subject, it is possible to do little more than cover plane geometry; with a year and a half the solid geometry ought easily to be covered also.
Bibliography. Stamper, A History of the Teaching of Elementary Geometry, New York, 1909, with a very full bibliography of the subject; Cajori, The Teaching of Mathematics in the United States, Washington, 1890; Cantor, Geschichte der Mathematik, Vol. IV, p. 321, Leipzig, 1908; Schotten, Inhalt und Methode des planimetrischen Unterrichts, Leipzig, 1890.
It is fitting that a chapter in a book upon the teaching of this subject should be devoted to the life and labors of the greatest of all textbook writers, Euclid,—a man whose name has been, for more than two thousand years, a synonym for elementary plane geometry wherever the subject has been studied. And yet when an effort is made to pick up the scattered fragments of his biography, we are surprised to find how little is known of one whose fame is so universal. Although more editions of his work have been printed than of any other book save the Bible,[23] we do not know when he was born, or in what city, or even in what country, nor do we know his race, his parentage, or the time of his death. We should not feel that we knew much of the life of a man who lived when the Magna Charta was wrested from King John, if our first and only source of information was a paragraph in the works of some historian of to-day; and yet this is about the situation in respect to Euclid. Proclus of Alexandria, philosopher, teacher, and mathematician, lived from 410 to 485 A.D., and wrote a commentary on the works of Euclid. In his writings, which seem to set forth in amplified form his lectures to the students in the Neoplatonist School
of Alexandria, Proclus makes this statement, and of Euclid's life we have little else:
Not much younger than these[24] is Euclid, who put together the "Elements," collecting many of the theorems of Eudoxus, perfecting many of those of Theætetus, and also demonstrating with perfect certainty what his predecessors had but insufficiently proved. He flourished in the time of the first Ptolemy, for Archimedes, who closely followed this ruler,[25] speaks of Euclid. Furthermore it is related that Ptolemy one time demanded of him if there was in geometry no shorter way than that of the "Elements," to whom he replied that there was no royal road to geometry.[26] He was therefore younger than the pupils of Plato, but older than Eratosthenes and Archimedes; for the latter were contemporary with one another, as Eratosthenes somewhere says.[27]
Thus we have in a few lines, from one who lived perhaps seven or eight hundred years after Euclid, nearly all that is known of the most famous teacher of geometry that ever lived. Nevertheless, even this little tells us about when he flourished, for Hermotimus and Philippus were pupils of Plato, who died in 347 B.C., whereas Archimedes was born about 287 B.C. and was writing about 250 B.C. Furthermore, since Ptolemy I reigned from 306 to 283 B.C., Euclid must have been teaching about 300 B.C., and this is the date that is generally assigned to him.
Euclid probably studied at Athens, for until he himself assisted in transferring the center of mathematical
culture to Alexandria, it had long been in the Grecian capital, indeed since the time of Pythagoras. Moreover, numerous attempts had been made at Athens to do exactly what Euclid succeeded in doing,—to construct a logical sequence of propositions; in other words, to write a textbook on plane geometry. It was at Athens, therefore, that he could best have received the inspiration to compose his "Elements."[28] After finishing his education at Athens it is quite probable that he, like other savants of the period, was called to Alexandria by Ptolemy Soter, the king, to assist in establishing the great school which made that city the center of the world's learning for several centuries. In this school he taught, and here he wrote the "Elements" and numerous other works, perhaps ten in all.
Although the Greek writers who may have known something of the life of Euclid have little to say of him, the Arab writers, who could have known nothing save from Greek sources, have allowed their imaginations the usual latitude in speaking of him and of his labors. Thus Al-Qifṫī, who wrote in the thirteenth century, has this to say in his biographical treatise "Ta'rīkh al-Ḥukamā":
Euclid, son of Naucrates, grandson of Zenarchus, called the author of geometry, a Greek by nationality, domiciled at Damascus, born at Tyre, most learned in the science of geometry, published a most excellent and most useful work entitled "The Foundation or Elements of Geometry," a subject in which no more general treatise existed before among the Greeks; nay, there was no one even of later date who did not walk in his footsteps and frankly profess his doctrine.
This is rather a specimen of the Arab tendency to manufacture history than a serious contribution to the biography of Euclid, of whose personal history we have only the information given by Proclus.
Euclid's works at once took high rank, and they are mentioned by various classical authors. Cicero knew of them, and Capella (ca. 470 A.D.), Cassiodorius (ca. 515 A.D.), and Boethius (ca. 480-524 A.D.) were all more[Pg 51] or less familiar with the "Elements." With the advance of the Dark Ages, however, learning was held in less and less esteem, so that Euclid was finally forgotten, and manuscripts of his works were either destroyed or buried in some remote cloister. The Arabs, however, whose civilization assumed prominence from about 750 A.D. to about 1500, translated the most important treatises of the Greeks, and Euclid's "Elements" among the rest. One of these Arabic editions an English monk of the twelfth century, one Athelhard (Æthelhard) of Bath, found and translated into Latin (ca. 1120 A.D.). A little later Gherard of Cremona (1114-1187) made a new translation from the Arabic, differing in essential features from that of Athelhard, and about 1260 Johannes Campanus made still a third translation, also from Arabic into Latin.[29] There is reason to believe that Athelhard, Campanus, and Gherard may all have had access to an earlier Latin translation, since all are quite alike in some particulars while diverging noticeably in others. Indeed, there is an old English verse that relates:
If this be true, Euclid was known in England as early as 924-940 A.D.
Without going into particulars further, it suffices to say that the modern knowledge of Euclid came first through the Arabic into the Latin, and the first printed
edition of the "Elements" (Venice, 1482) was the Campanus translation. Greek manuscripts now began to appear, and at the present time several are known. There is a manuscript of the ninth century in the Bodleian library at Oxford, one of the tenth century in the Vatican, another of the tenth century in Florence, one of the eleventh century at Bologna, and two of the twelfth century at Paris. There are also fragments containing bits of Euclid in Greek, and going back as far as the second and third century A.D. The first modern translation from the Greek into the Latin was made by Zamberti (or Zamberto),[30] and was printed at Venice in 1513. The first translation into English was made by Sir Henry Billingsley and was printed in 1570, sixteen years before he became Lord Mayor of London.
Proclus, in his commentary upon Euclid's work, remarks:
In the whole of geometry there are certain leading theorems, bearing to those which follow the relation of a principle, all-pervading, and furnishing proofs of many properties. Such theorems are called by the name of elements, and their function may be compared to that of the letters of the alphabet in relation to language, letters being indeed called by the same name in Greek [στοιχεια, stoicheia].[31]
This characterizes the work of Euclid, a collection of the basic propositions of geometry, and chiefly of plane geometry, arranged in logical sequence, the proof of each depending upon some preceding proposition, definition, or assumption (axiom or postulate). The number
of the propositions of plane geometry included in the "Elements" is not entirely certain, owing to some disagreement in the manuscripts, but it was between one hundred sixty and one hundred seventy-five. It is possible to reduce this number by about thirty or forty, because Euclid included a certain amount of geometric algebra; but beyond this we cannot safely go in the way of elimination, since from the very nature of the "Elements" these propositions are basic. The efforts at revising Euclid have been generally confined, therefore, to rearranging his material, to rendering more modern his phraseology, and to making a book that is more usable with beginners if not more logical in its presentation of the subject. While there has been an improvement upon Euclid in the art of bookmaking, and in minor matters of phraseology and sequence, the educational gain has not been commensurate with the effort put forth. With a little modification of Euclid's semi-algebraic Book II and of his treatment of proportion, with some scattering of the definitions and the inclusion of well-graded exercises at proper places, and with attention to the modern science of bookmaking, the "Elements" would answer quite as well for a textbook to-day as most of our modern substitutes, and much better than some of them. It would, moreover, have the advantage of being a classic,—somewhat the same advantage that comes from reading Homer in the original instead of from Pope's metrical translation. This is not a plea for a return to the Euclid text, but for a recognition of the excellence of Euclid's work.
The distinctive feature of Euclid's "Elements," compared with the modern American textbook, is perhaps this: Euclid begins a book with what seems to him the[Pg 54] easiest proposition, be it theorem or problem; upon this he builds another; upon these a third, and so on, concerning himself but little with the classification of propositions. Furthermore, he arranges his propositions so as to construct his figures before using them. We, on the other hand, make some little attempt to classify our propositions within each book, and we make no attempt to construct our figures before using them, or at least to prove that the constructions are correct. Indeed, we go so far as to study the properties of figures that we cannot construct, as when we ask for the size of the angle of a regular heptagon. Thus Euclid begins Book I by a problem, to construct an equilateral triangle on a given line. His object is to follow this by problems on drawing a straight line equal to a given straight line, and cutting off from the greater of two straight lines a line equal to the less. He now introduces a theorem, which might equally well have been his first proposition, namely, the case of the congruence of two triangles, having given two sides and the included angle. By means of his third and fourth propositions he is now able to prove the pons asinorum, that the angles at the base of an isosceles triangle are equal. We, on the other hand, seek to group our propositions where this can conveniently be done, putting the congruent propositions together, those about inequalities by themselves, and the propositions about parallels in one set. The results of the two arrangements are not radically different, and the effect of either upon the pupil's mind does not seem particularly better than that of the other. Teachers who have used both plans quite commonly feel that, apart from Books II and V, Euclid is nearly as easily understood as our modern texts, if presented in as satisfactory dress.[Pg 55]
The topics treated and the number of propositions in
the plane geometry of the "Elements" are as follows:
| Book I. | Rectilinear figures | 48 |
| Book II. | Geometric algebra | 14 |
| Book III. | Circles | 37 |
| Book IV. | Problems about circles | 16 |
| Book V. | Proportion | 25 |
| Book VI. | Applications of proportion | 33 |
| —— | ||
| 173 | ||
Of these we now omit Euclid's Book II, because we have an algebraic symbolism that was unknown in his time, although he would not have used it in geometry even had it been known. Thus his first proposition in Book II is as follows:
If there be two straight lines, and one of them be cut into any number of segments whatever, the rectangle contained by the two straight lines is equal to the rectangles contained by the uncut straight line and each of the segments.
This amounts to saying that if x = p + q + r + ···, then ax = ap + aq + ar + ···. We also materially simplify Euclid's Book V. He, for example, proves that "If four magnitudes be proportional, they will also be proportional alternately." This he proves generally for any kind of magnitude, while we merely prove it for numbers having a common measure. We say that we may substitute for the older form of proportion, namely,
a : b = c : d,
the fractional form a/b = c/d.
From this we have ad = bc.
Whence a/c = b/d.
[Pg 56]
In this work we assume that we may multiply equals by b and d. But suppose b and d are cubes, of which, indeed, we do not even know the approximate numerical measure; what shall we do? To Euclid the multiplication by a cube or a polygon or a sphere would have been entirely meaningless, as it always is from the standpoint of pure geometry. Hence it is that our treatment of proportion has no serious standing in geometry as compared with Euclid's, and our only justification for it lies in the fact that it is easier. Euclid's treatment is much more rigorous than ours, but it is adapted to the comprehension of only advanced students, while ours is merely a confession, and it should be a frank confession, of the weakness of our pupils, and possibly, at times, of ourselves.
If we should take Euclid's Books II and V for granted, or as sufficiently evident from our study of algebra, we should have remaining only one hundred thirty-four propositions, most of which may be designated as basal propositions of plane geometry. Revise Euclid as we will, we shall not be able to eliminate any large number of his fundamental truths, while we might do much worse than to adopt these one hundred thirty-four propositions in toto as the bases, and indeed as the definition, of elementary plane geometry.
Bibliography. Heath, The Thirteen Books of Euclid's Elements, 3 vols., Cambridge, 1908; Frankland, The First Book of Euclid, Cambridge, 1906; Smith, Dictionary of Greek and Roman Biography, article Eukleides; Simon, Euclid und die sechs planimetrischen Bücher, Leipzig, 1901; Gow, History of Greek Mathematics, Cambridge, 1884, and any of the standard histories of mathematics. Both Heath and Simon give extensive bibliographies. The latest standard Greek and Latin texts are Heiberg's, published by Teubner of Leipzig.
From time to time an effort is made by some teacher, or association of teachers, animated by a serious desire to improve the instruction in geometry, to prepare a new syllabus that shall mark out some "royal road," and it therefore becomes those who are interested in teaching to consider with care the results of similar efforts in recent years. There are many questions which such an attempt suggests: What is the real purpose of the movement? What will the teaching world say of the result? Shall a reckless, ill-considered radicalism dominate the effort, bringing in a distasteful terminology and symbolism merely for its novelty, insisting upon an ultralogical treatment that is beyond the powers of the learner, rearranging the subject matter to fit some narrow notion of the projectors, seeking to emasculate mathematics by looking only to the applications, riding some little hobby in the way of some particular class of exercises, and cutting the number of propositions to a minimum that will satisfy the mere demands of the artisan? Such are some of the questions that naturally arise in the mind of every one who wishes well for the ancient science of geometry.
It is not proposed in this chapter to attempt to answer these questions, but rather to assist in understanding the problem by considering the results of similar attempts.[Pg 58] If it shall be found that syllabi have been prepared under circumstances quite as favorable as those that obtain at present, and if these syllabi have had little or no real influence, then it becomes our duty to see if new plans may be worked out so as to be more successful than their predecessors. If the older attempts have led to some good, it is well to know what is the nature of this good, to the end that new efforts may also result in something of benefit to the schools.
It is proposed in this chapter to call attention to four important syllabi, setting forth briefly their distinguishing features and drawing some conclusions that may be helpful in other efforts of this nature.
In England two noteworthy attempts have been made within a century, looking to a more satisfactory sequence and selection of propositions than is found in Euclid. Each began with a list of propositions arranged in proper sequence, and each was thereafter elaborated into a textbook. Neither accomplished fully the purpose intended, but each was instrumental in provoking healthy discussion and in improving the texts from which geometry is studied.
The first of these attempts was made by Professor Augustus de Morgan, under the auspices of the Society for the Diffusion of Useful Knowledge, and it resulted in a textbook, including "plane, solid, and spherical" geometry, in six books. According to De Morgan's plan, plane geometry consisted of three books, the number of propositions being as follows:
| Book I. | Rectilinear figures | 60 |
| Book II. | Ratio, proportion, applications | 69 |
| Book III. | The circle | 65 |
| —— | ||
| Total for plane geometry | 194 | |
Of the 194 propositions De Morgan selected 114 with their corollaries as necessary for a beginner who is teaching himself.
In solid geometry the plan was as follows:
| Book IV. | Lines in different planes, solids contained by planes | 52 |
| Book V. | Cylinder, cone, sphere | 25 |
| Book VI. | Figures on a sphere | 42 |
| —— | ||
| Total for solid geometry | 119 | |
Of these 119 propositions De Morgan selected 76 with their corollaries as necessary for a beginner, thus making 190 necessary propositions out of 305 desirable ones, besides the corollaries in plane and solid geometry. In other words, of the desirable propositions he considered that about two thirds are absolutely necessary.
It is interesting to note, however, that he summed up the results of his labors by saying:
It will be found that the course just laid down, excepting the sixth book of it only, is not of much greater extent, nor very different in point of matter from that of Euclid, whose "Elements" have at all times been justly esteemed a model not only of easy and progressive instruction in geometry, but of accuracy and perspicuity in reasoning.
De Morgan's effort, essentially that of a syllabus-maker rather than a textbook writer, although it was published under the patronage of a prominent society with which were associated the names of men like Henry Hallam, Rowland Hill, Lord John Russell, and George Peacock, had no apparent influence on geometry either in England or abroad. Nevertheless the syllabus was in many respects excellent; it rearranged the matter, it classified the propositions, it improved some of the terminology, and it reduced the number of essential propositions; it had the assistance of De Morgan's enthusiasm and of the society[Pg 60] with which he was so prominently connected, and it was circulated with considerable generosity throughout the English-speaking world; but in spite of all this it is to-day practically unknown.
A second noteworthy attempt in England was made about a quarter of a century ago by a society that was organized practically for this very purpose, the Association for the Improvement of Geometrical Teaching. This society was composed of many of the most progressive teachers in England, and it included in its membership men of high standing in mathematics in the universities. As a result of their labors a syllabus was prepared, which was elaborated into a textbook, and in 1889 a revised syllabus was issued.
As to the arrangement of matter, the syllabus departs from Euclid chiefly by separating the problems from the theorems, as is the case in our American textbooks, and in improving the phraseology. The course is preceded by some simple exercises in the use of the compasses and ruler, a valuable plan that is followed by many of the best teachers everywhere. Considerable attention is paid to logical processes before beginning the work, such terms as "contrapositive" and "obverse," and such rules as the "rule of conversion" and the "rule of identity" being introduced before any propositions are considered.
The arrangement of the work and the number of propositions in plane geometry are as follows:
| Book I. | The straight line | 51 |
| Book II. | Equality of areas | 19 |
| Book III. | The circle | 42 |
| Book IV. | Ratio and proportion | 32 |
| Book V. | Proportion | 24 |
| —— | ||
| Total for plane geometry | 168 | |
Here, then, is the result of several years of labor by a somewhat radical organization, fostered by excellent mathematicians, and carried on in a country where elementary geometry is held in highest esteem, and where Euclid was thought unsuited to the needs of the beginner. The number of propositions remains substantially the same as in Euclid, and the introduction of some unusable logic tends to counterbalance the improvement in sequence of the propositions. The report provoked thought; it shook the Euclid stronghold; it was probably instrumental in bringing about the present upheaval in geometry in England, but as a working syllabus it has not appealed to the world as the great improvement upon Euclid's "Elements" that was hoped by many of its early advocates.
The same association published later, and republished in 1905, a "Report on the Teaching of Geometry," in which it returned to Euclid, modifying the "Elements" by omitting certain propositions, changing the order and proof of others, and introducing a few new theorems. It seems to reduce the propositions to be proved in plane geometry to about one hundred fifteen, and it recommends the omission of the incommensurable case. This number is, however, somewhat misleading, for Euclid frequently puts in one proposition what we in America, for educational reasons, find it better to treat in two, or even three, propositions. This report, therefore, reaches about the same conclusion as to the geometric facts to be mastered as is reached by our later textbook writers in America. It is not extreme, and it stands for good mathematics.
In the United States the influence of our early wars with England, and the sympathy of France at that time,[Pg 62] turned the attention of our scholars of a century ago from Cambridge to Paris as a mathematical center. The influx of French mathematics brought with it such works as Legendre's geometry (1794) and Bourdon's algebra, and made known the texts of Lacroix, Bertrand, and Bezout. Legendre's geometry was the result of the efforts of a great mathematician at syllabus-making, a natural thing in a country that had early broken away from Euclid. Legendre changed the Greek sequence, sought to select only propositions that are necessary to a good understanding of the subject, and added a good course in solid geometry. His arrangement, with the number of propositions as given in the Davies translation, is as follows:
| Book I. | Rectilinear figures | 31 |
| Book II. | Ratio and proportion | 14 |
| Book III. | The circle | 48 |
| Book IV. | Proportions of figures and areas | 51 |
| Book V. | Polygons and circles | 17 |
| —— | ||
| Total for plane geometry | 161 | |
Legendre made, therefore, practically no reduction in the number of Euclid's propositions, and his improvement on Euclid consisted chiefly in his separation of problems and theorems, and in a less rigorous treatment of proportion which boys and girls could comprehend. D'Alembert had demanded that the sequence of propositions should be determined by the order in which they had been discovered, but Legendre wisely ignored such an extreme and gave the world a very usable book.
The principal effect of Legendre's geometry in America was to make every textbook writer his own syllabus-maker, and to put solid geometry on a more satisfactory footing. The minute we depart from a standard text[Pg 63] like Euclid's, and have no recognized examining body, every one is free to set up his own standard, always within the somewhat uncertain boundary prescribed by public opinion and by the colleges. The efforts of the past few years at syllabus-making have been merely attempts to define this boundary more clearly.
Of these attempts two are especially worthy of consideration as having been very carefully planned and having brought forth such definite results as to appeal to a large number of teachers. Other syllabi have been made and are familiar to many teachers, but in point of clearness of purpose, conciseness of expression, and form of publication they have not been such as to compare with the two in question.
The first of these is the Harvard syllabus, which is placed in the hands of students for reference when trying the entrance examinations of that university, a plan not followed elsewhere. It sets forth the basal propositions that should form the essential part of the student's preparation, and that are necessary and sufficient for proving any "original proposition" (to take the common expression) that may be set on the examination. The propositions are arranged by books as follows:
| Book I. | Angles, triangles, parallels | 25 |
| Book II. | The circle, angle measure | 18 |
| Book III. | Similar polygons | 10 |
| Book IV. | Area of polygons | 8 |
| Book V. | Polygons and circle measure | 11 |
| Constructions | 21 | |
| Ratio and proportion | 6 | |
| —— | ||
| Total for plane geometry | 99 | |
The total for solid geometry is 79 propositions, or 178 for both plane and solid geometry. This is perhaps the[Pg 64] most successful attempt that has been made at reaching a minimum number of propositions. It might well be further reduced, since it includes the proposition about two adjacent angles formed by one line meeting another, and the one about the circle as the limit of the inscribed and circumscribed regular polygons. The first of these leads a beginner to doubt the value of geometry, and the second is beyond the powers of the majority of students. As compared with the syllabus reported by a Wisconsin committee in 1904, for example, here are 99 propositions against 132. On the other hand, a committee appointed by the Central Association of Science and Mathematics Teachers reported in 1909 a syllabus with what seems at first sight to be a list of only 59 propositions in plane geometry. This number is fictitious, however, for the reason that numerous converses are indicated with the propositions, and are not included in the count, and directions are given to include "related theorems" and "problems dealing with the length and area of a circle," so that in some cases one proposition is evidently intended to cover several others. This syllabus is therefore lacking in definiteness, so that the Harvard list stands out as perhaps the best of its type.
The second noteworthy recent attempt in America is that made by a committee of the Association of Mathematical Teachers in New England. This committee was organized in 1904. It held sixteen meetings and carried on a great deal of correspondence. As a result, it prepared a syllabus arranged by topics, the propositions of solid geometry being grouped immediately after the corresponding ones of plane geometry. For example, the nine propositions on congruence in a plane are followed[Pg 65] by nine on congruence in space. As a result, the following summarizes the work in plane geometry:
| Congruence in a plane | 9 |
| Equivalence | 3 |
| Parallels and perpendiculars | 9 |
| Symmetry | 20 |
| Angles | 15 |
| Tangents | 4 |
| Similar figures | 18 |
| Inequalities | 8 |
| Lengths and areas | 17 |
| Loci | 2 |
| Concurrent lines | 5 |
| —— | |
| Total for plane geometry | 110 |
Not so conventional in arrangement as the Harvard syllabus, and with a few propositions that are evidently not basal to the same extent as the rest, the list is nevertheless a very satisfactory one, and the parallelism shown between plane and solid geometry is suggestive to both student and teacher.
On the whole, however, the Harvard selection of basal propositions is perhaps as satisfactory as any that has been made, even though it appears to lack a "factor of safety," and it is probable that any further reduction would be unwise.
What, now, has been the effect of all these efforts? What teacher or school would be content to follow any one of these syllabi exactly? What textbook writer would feel it safe to limit his regular propositions to those in any one syllabus? These questions suggest their own answers, and the effect of all this effort seems at first thought to have been so slight as to be entirely out of proportion to the end in view. This depends, however, on what this end is conceived to be. If the[Pg 66] purpose has been to cut out a very large number of the propositions that are found in Euclid's plane geometry, the effort has not been successful. We may reduce this number to about one hundred thirty, but in general, whatever a syllabus may give as a minimum, teachers will favor a larger number than is suggested by the Harvard list, for the purpose of exercise in the reading of mathematics if for no other reason. The French geometer, Lacroix, who wrote more than a century ago, proposed to limit the propositions to those needed to prove other important ones, and those needed in practical mathematics. If to this we should add those that are used in treating a considerable range of exercises, we should have a list of about one hundred thirty.
But this is not the real purpose of these syllabi, or at most it seems like a relatively unimportant one. The purpose that has been attained is to stop the indefinite increase in the number of propositions that would follow from the recent developments in the geometry of the triangle and circle, and of similar modern topics, if some such counter-movement as this did not take place. If the result is, as it probably will be, to let the basal propositions of Euclid remain about as they always have been, as the standards for beginners, the syllabi will have accomplished a worthy achievement. If, in addition, they furnish an irreducible minimum of propositions to which a student may have access if he desires it, on an examination, as was intended in the case of the Harvard and the New England Association syllabi, the achievement may possibly be still more worthy.
In preparing a syllabus, therefore, no one should hope to bring the teaching world at once to agree to any great reduction in the number of basal propositions, nor to[Pg 67] agree to any radical change of terminology, symbolism, or sequence. Rather should it be the purpose to show that we have enough topics in geometry at present, and that the number of propositions is really greater than is absolutely necessary, so that teachers shall not be led to introduce any considerable number of propositions out of the large amount of new material that has recently been accumulating. Such a syllabus will always accomplish a good purpose, for at least it will provoke thought and arouse interest, but any other kind is bound to be ephemeral.[32]
Besides the evolutionary attempts at rearranging and reducing in number the propositions of Euclid, there have been very many revolutionary efforts to change his treatment of geometry entirely. The great French mathematician, D'Alembert, for example, in the eighteenth century, wished to divide geometry into three branches: (1) that dealing with straight lines and circles, apparently not limited to a plane; (2) that dealing with surfaces; and (3) that dealing with solids. So Méray in France and De Paolis[33] in Italy have attempted to fuse plane and solid geometry, but have not produced a system that has been particularly successful. More recently Bourlet, Grévy, Borel, and others in France have produced several works on the elements of mathematics that may lead to something of value. They place intuition to the front, favor as much applied mathematics as is reasonable, to all of which American teachers would generally agree,
but they claim that the basis of elementary geometry in the future must be the "investigation of the group of motions." It is, of course, possible that certain of the notions of the higher mathematical thought of the nineteenth century may be so simplified as to be within the comprehension of the tyro in geometry, and we should be ready to receive all efforts of this kind with open mind. These writers have not however produced the ideal work, and it may seriously be questioned whether a work based upon their ideas will prove to be educationally any more sound and usable than the labors of such excellent writers as Henrici and Treutlein, and H. Müller, and Schlegel a few years ago in Germany, and of Veronese in Italy. All such efforts, however, should be welcomed and tried out, although so far as at present appears there is nothing in sight to replace a well-arranged, vitalized, simplified textbook based upon the labors of Euclid and Legendre.
The most broad-minded of the great mathematicians who have recently given attention to secondary problems is Professor Klein of Göttingen. He has had the good sense to look at something besides the mere question of good mathematics.[34] Thus he insists upon the psychologic point of view, to the end that the geometry shall be adapted to the mental development of the pupil,—a thing that is apparently ignored by Méray (at least for the average pupil), and, it is to be feared, by the other recent French writers. He then demands a careful selection of the subject matter, which in our American schools would mean the elimination of propositions that are not basal, that is, that are not used for most of the
exercises that one naturally meets in elementary geometry and in applied work. He further insists upon a reasonable correlation with practical work to which every teacher will agree so long as the work is really or even potentially practical. And finally he asks that we look with favor upon the union of plane and solid geometry, and of algebra and geometry. He does not make any plea for extreme fusion, but presumably he asks that to which every one of open mind would agree, namely, that whenever the opportunity offers in teaching plane geometry, to open the vision to a generalization in space, or to the measurement of well-known solids, or to the use of the algebra that the pupil has learned, the opportunity should be seized.[Pg 70]
In considering the nature of the textbook in geometry we need to bear in mind the fact that the subject is being taught to-day in America to a class of pupils that is not composed like the classes found in other countries or in earlier generations. In general, in other countries, geometry is not taught to mixed classes of boys and girls. Furthermore, it is generally taught to a more select group of pupils than in a country where the high school and college are so popular with people in all the walks of life. In America it is not alone the boy who is interested in education in general, or in mathematics in particular, who studies geometry, and who joins with others of like tastes in this pursuit, but it is often the boy and the girl who are not compelled to go out and work, and who fill the years of youth with a not over-strenuous school life. It is therefore clear that we cannot hold the interest of such pupils by the study of Euclid alone. Geometry must, for them, be less formal than it was half a century ago. We cannot expect to make our classes enthusiastic merely over a logical sequence of proved propositions. It becomes necessary to make the work more concrete, and to give a much larger number of simple exercises in order to create the interest that comes from independent work, from a feeling of conquest, and from a desire to do something[Pg 71] original. If we would "cast a glamor over the multiplication table," as an admirer of Macaulay has said that the latter could do, we must have the facilities for so doing.
It therefore becomes necessary in weighing the merits of a textbook to consider: (1) if the number of proved propositions is reduced to a safe minimum; (2) if there is reasonable opportunity to apply the theory, the actual applications coming best, however, from the teacher as an outside interest; (3) if there is an abundance of material in the way of simple exercises, since such material is not so readily given by the teacher as the seemingly local applications of the propositions to outdoor measurements; (4) if the book gives a reasonable amount of introductory work in the use of simple and inexpensive instruments, not at that time emphasizing the formal side of the subject; (5) if there is afforded some opportunity to see the recreative side of the subject, and to know a little of the story of geometry as it has developed from ancient to modern times.
But this does not mean that there is to be a geometric cataclysm. It means that we must have the same safe, conservative evolution in geometry that we have in other subjects. Geometry is not going to degenerate into mere measuring, nor is the ancient sequence going to become a mere hodge-podge without system and with no incentive to strenuous effort. It is now about fifteen hundred years since Proclus laid down what he considered the essential features of a good textbook, and in all of our efforts at reform we cannot improve very much upon his statement. "It is essential," he says, "that such a treatise should be rid of everything superfluous, for the superfluous is an obstacle to the acquisition of knowledge; it should select everything that embraces the subject and[Pg 72] brings it to a focus, for this is of the highest service to science; it must have great regard both to clearness and to conciseness, for their opposites trouble our understanding; it must aim to generalize its theorems, for the division of knowledge into small elements renders it difficult of comprehension."
It being prefaced that we must make the book more concrete in its applications, either directly or by suggesting seemingly practical outdoor work; that we must increase the number of simple exercises calling for original work; that we must reasonably reduce the number of proved propositions; and that we must not allow the good of the ancient geometry to depart, let us consider in detail some of the features of a good, practical, common-sense textbook.
The early textbooks in geometry contained only the propositions, with the proofs in full, preceded by lists of definitions and assumptions (axioms and postulates). There were no exercises, and the proofs were given in essay form. Then came treatises with exercises, these exercises being grouped at the end of the work or at the close of the respective books. The next step was to the unit page, arranged in steps to aid the eye, one proposition to a page whenever this was possible. Some effort was made in this direction in France about two hundred years ago, but with no success. The arrangement has so much to commend it, however, the proof being so much more easily followed by the eye than was the case in the old-style works, that it has of late been revived. In this respect the Wentworth geometry was a pioneer in America, and so successful was the effort that this type of page has been adopted, as far as the various writers were able to adopt it, in all successful geometries that have[Pg 73] appeared of late years in this country. As a result, the American textbooks on this subject are more helpful and pleasing to the eye than those found elsewhere.
The latest improvements in textbook-making have removed most of the blemishes of arrangement that remained, scattering the exercises through the book, grading them with greater care, and making them more modern in character. But the best of the latest works do more than this. They reduce the number of proved theorems and increase the number of exercises, and they simplify the proofs whenever possible and eliminate the most difficult of the exercises of twenty-five years ago. It would be possible to carry this change too far by putting in only half as many, or a quarter as many, regular propositions, but it should not be the object to see how the work can be cut down, but to see how it can be improved.
What should be the basis of selection of propositions and exercises? Evidently the selection must include the great basal propositions that are needed in mensuration and in later mathematics, together with others that are necessary to prove them. Euclid's one hundred seventy-three propositions of plane geometry were really upwards of one hundred eighty, because he several times combined two or more in one. These we may reduce to about one hundred thirty with perfect safety, or less than one a day for a school year, but to reduce still further is undesirable as well as unnecessary. It would not be difficult to dispense with a few more; indeed, we might dispense with thirty more if we should set about it, although we must never forget that a goodly number in addition to those needed for the logical sequence are necessary for the wide range of exercises that are offered.[Pg 74] But let it be clear that if we teach 100 instead of 130, our results are liable to be about 100/130 as satisfactory. We may theorize on pedagogy as we please, but geometry will pay us about in proportion to what we give.
And as to the exercises, what is the basis of selection? In general, let it be said that any exercise that pretends to be real should be so, and that words taken from science or measurements do not necessarily make the problem genuine. To take a proposition and apply it in a manner that the world never sanctions is to indulge in deceit. On the other hand, wholly to neglect the common applications of geometry to handwork of various kinds is to miss one of our great opportunities to make the subject vital to the pupil, to arouse new interest, and to give a meaning to it that is otherwise wanting. It should always be remembered that mental discipline, whatever the phrase may mean, can as readily be obtained from a genuine application of a theorem as from a mere geometric puzzle. On the other hand, it is evident that not more than 25 per cent of propositions have any genuine applications outside of geometry, and that if we are to attempt any applications at all, these must be sought mainly in the field of pure geometry. In the exercises, therefore, we seek to-day a sane and a balanced book, giving equal weight to theory and to practice, to the demands of the artisan and to those of the mathematician, to the applications of concrete science and to those of pure geometry, thus making a fusion of pure and applied mathematics, with the latter as prominent as the supply of genuine problems permits. The old is not all bad and the new is not all good, and a textbook is a success in so far as it selects boldly the good that is in the old and rejects with equal boldness the bad that is in the new.[Pg 75]
Lest the nature of the exercises of geometry may be misunderstood, it is well that we consider for a moment what constitutes a genuine application of the subject. It is the ephemeral fashion just at present in America to call these genuine applications by the name of "real problems." The name is an unfortunate importation, but that is not a matter of serious moment. The important thing is that we should know what makes a problem "real" to the pupil of geometry, especially as the whole thing is coming rapidly into disrepute through the mistaken zeal of some of its supporters.
A real problem is a problem that the average citizen may sometime be called upon to solve; that, if so called upon, he will solve in the manner indicated; and that is expressed in terms that are familiar to the pupil.
This definition, which seems fairly to state the conditions under which a problem can be called "real" in the schoolroom, involves three points: (1) people must be liable to meet such a problem; (2) in that case they will solve it in the way suggested by the book; (3) it must be clothed in language familiar to the pupil. For example, let the problem be to find the dimensions of a rectangular field, the data being the area of the field and the area of a road four rods wide that is cut from three sides of the field. As a real problem this is ridiculous, since no one would ever meet such a case outside the puzzle department of a schoolroom. Again, if by any stretch of a vigorous imagination any human being should care to find the area of a piece of glass, bounded by the arcs of circles, in a Gothic window in York Minster, it is fairly certain that he would not go about it in the way suggested in some of the earnest attempts that have been made by several successful teachers to add interest to[Pg 76] geometry. And for the third point, a problem is not real to a pupil simply because it relates to moments of inertia or the tensile strength of a steel bar. Indeed, it is unreal precisely because it does talk of these things at a time when they are unfamiliar, and properly so, to the pupil.
It must not be thought that puzzle problems, and unreal problems generally, have no value. All that is insisted upon is that such problems as the above are not "real," and that about 90 per cent of problems that go by this name are equally lacking in the elements that make for reality in this sense of the word. For the other 10 per cent of such problems we should be thankful, and we should endeavor to add to the number. As for the great mass, however, they are no better than those that have stood the test of generations, and by their pretense they are distinctly worse.
It is proper, however, to consider whether a teacher is not justified in relating his work to those geometric forms that are found in art, let us say in floor patterns, in domes of buildings, in oilcloth designs, and the like, for the purpose of arousing interest, if for no other reason. The answer is apparent to any teacher: It is certainly justifiable to arouse the pupil's interest in his subject, and to call his attention to the fact that geometric design plays an important part in art; but we must see to it that our efforts accomplish this purpose. To make a course in geometry one on oilcloth design would be absurd, and nothing more unprofitable or depressing could be imagined in connection with this subject. Of course no one would advocate such an extreme, but it sometimes seems as if we are getting painfully near it in certain schools.
A pupil has a passing interest in geometric design. He should learn to use the instruments of geometry, and[Pg 77] he learns this most easily by drawing a few such patterns. But to keep him week after week on questions relating to such designs of however great variety, and especially to keep him upon designs relating to only one or two types, is neither sound educational policy nor even common sense. That this enthusiastic teacher or that one succeeds by such a plan is of no significance; it is the enthusiasm that succeeds, not the plan.
The experience of the world is that pupils of geometry like to use the subject practically, but that they are more interested in the pure theory than in any fictitious applications, and this is why pure geometry has endured, while the great mass of applied geometry that was brought forward some three hundred years ago has long since been forgotten. The question of the real applications of the subject is considered in subsequent chapters.
In Chapter VI we considered the question of the number of regular propositions to be expected in the text, and we have just considered the nature of the exercises which should follow those propositions. It is well to turn our attention next to the nature of the proofs of the basal theorems. Shall they appear in full? Shall they be merely suggested demonstrations? Shall they be only a series of questions that lead to the proof? Shall the proofs be omitted entirely? Or shall there be some combination of these plans?
The natural temptation in the nervous atmosphere of America is to listen to the voice of the mob and to proceed at once to lynch Euclid and every one who stands for that for which the "Elements" has stood these two thousand years. This is what some who wish to be considered as educators tend to do; in the language of the mob, to "smash things"; to call reactionary that which[Pg 78] does not conform to their ephemeral views. It is so easy to be an iconoclast, to think that cui bono is a conclusive argument, to say so glibly that Raphael was not a great painter,—to do anything but construct. A few years ago every one must take up with the heuristic method developed in Germany half a century back and containing much that was commendable. A little later one who did not believe that the Culture Epoch Theory was vital in education was looked upon with pity by a considerable number of serious educators. A little later the man who did not think that the principle of Concentration in education was a regula aurea was thought to be hopeless. A little later it may have been that Correlation was the saving factor, to be looked upon in geometry teaching as a guiding beacon, even as the fusion of all mathematics is the temporary view of a few enthusiasts to-day.[35]
And just now it is vocational training that is the catch phrase, and to many this phrase seems to sound the funeral knell of the standard textbook in geometry. But does it do so? Does this present cry of the pedagogical circle really mean that we are no longer to have geometry for geometry's sake? Does it mean that a panacea has been found for the ills of memorizing without understanding a proof in the class of a teacher who is so inefficient as to allow this kind of work to go on? Does it mean that a teacher who does not see the human side of
geometry, who does not know the real uses of geometry, and who has no faculty of making pupils enthusiastic over geometry,—that this teacher is to succeed with some scrappy, weak, pretending apology for a real work on the subject?
No one believes in stupid teaching, in memorizing a textbook, in having a book that does all the work for a pupil, or in any of the other ills of inefficient instruction. On the other hand, no fair-minded person can condemn a type of book that has stood for generations until something besides the mere transient experiments of the moment has been suggested to replace it. Let us, for example, consider the question of having the basal propositions proved in full, a feature that is so easy to condemn as leading to memorizing.
The argument in favor of a book with every basal proposition proved in full, or with most of them so proved, the rest having only suggestions for the proof, is that the pupil has before him standard forms exhibiting the best, most succinct, most clearly stated demonstrations that geometry contains. The demonstrations stand for the same thing that the type problems stand for in algebra, and are generally given in full in the same way. The argument against the plan is that it takes away the pupil's originality by doing all the work for him, allowing him to merely memorize the work. Now if all there is to geometry were in the basal propositions, this argument might hold, just as it would hold in algebra in case there were only those exercises that are solved in full. But just as this is not the case in algebra, the solved exercises standing as types or as bases for the pupil's real work, so the demonstrated proposition forms a relatively small part of geometry, standing as a type,[Pg 80] a basis for the more important part of the work. Moreover, a pupil who uses a syllabus is exposed to a danger that should be considered, namely, that of dishonesty. Any textbook in geometry will furnish the proofs of most of the propositions in a syllabus, whatever changes there may be in the sequence, and it is not a healthy condition of mind that is induced by getting the proofs surreptitiously. Unless a teacher has more time for the course than is usually allowed, he cannot develop the new work as much as is necessary with only a syllabus, and the result is that a pupil gets more of his work from other books and has less time for exercises. The question therefore comes to this: Is it better to use a book containing standard forms of proof for the basal propositions, and have time for solving a large number of original exercises and for seeking the applications of geometry? Or is it better to use a book that requires more time on the basal propositions, with the danger of dishonesty, and allows less time for solving originals? To these questions the great majority of teachers answer in favor of the textbook with most of the basal propositions fully demonstrated. In general, therefore, it is a good rule to use the proofs of the basal propositions as models, and to get the original work from the exercises. Unless we preserve these model proofs, or unless we supply them with a syllabus, the habit of correct, succinct self-expression, which is one of the chief assets of geometry, will tend to become atrophied. So important is this habit that "no system of education in which its performance is neglected can hope or profess to evolve men and women who are competent in the full sense of the word. So long as teachers of geometry neglect the possibilities of the subject in this respect, so long will the time devoted[Pg 81] to it be in large part wasted, and so long will their pupils continue to imbibe the vicious idea that it is much more important to be able to do a thing than to say how it can be done."[36]
It is here that the chief danger of syllabus-teaching lies, and it is because of this patent fact that a syllabus without a carefully selected set of model proofs, or without the unnecessary expenditure of time by the class, is a dangerous kind of textbook.
What shall then be said of those books that merely suggest the proofs, or that give a series of questions that lead to the demonstrations? There is a certain plausibility about such a plan at first sight. But it is easily seen to have only a fictitious claim to educational value. In the first place, it is merely an attempt on the part of the book to take the place of the teacher and to "develop" every lesson by the heuristic method. The questions are so framed as to admit, in most cases, of only a single answer, so that this answer might just as well be given instead of the question. The pupil has therefore a proof requiring no more effort than is the case in the standard form of textbook, but not given in the clear language of a careful writer. Furthermore, the pupil is losing here, as when he uses only a syllabus, one of the very things that he should be acquiring, namely, the habit of reading mathematics. If he met only syllabi without proofs, or "suggestive" geometries, or books that endeavored to question every proof out of him, he would be in a sorry plight when he tried to read higher mathematics, or even other elementary treatises. It is for reasons such as these that the heuristic textbook has never succeeded for any great length of time or in any wide territory.
And finally, upon this point, shall the demonstrations be omitted entirely, leaving only the list of propositions,—in other words, a pure syllabus? This has been sufficiently answered above. But there is a modification of the pure syllabus that has much to commend itself to teachers of exceptional strength and with more confidence in themselves than is usually found. This is an arrangement that begins like the ordinary textbook and, after the pupil has acquired the form of proof, gradually merges into a syllabus, so that there is no temptation to go surreptitiously to other books for help. Such a book, if worked out with skill, would appeal to an enthusiastic teacher, and would accomplish the results claimed for the cruder forms of manual already described. It would not be in general as safe a book as the standard form, but with the right teacher it would bring good results.
In conclusion, there are two types of textbook that have any hope of success. The first is the one with all or a large part of the basal propositions demonstrated in full, and with these propositions not unduly reduced in number. Such a book should give a large number of simple exercises scattered through the work, with a relatively small number of difficult ones. It should be modern in its spirit, with figures systematically lettered, with each page a unit as far as possible, and with every proof a model of clearness of statement and neatness of form. Above all, it should not yield to the demand of a few who are always looking merely for something to change, nor should it in a reactionary spirit return to the old essay form of proof, which hinders the pupil at this stage.
The second type is the semisyllabus, otherwise with all the spirit of the first type. In both there should be an honest fusion of pure and applied geometry, with no[Pg 83] exercises that pretend to be practical without being so, with no forced applications that lead the pupil to measure things in a way that would appeal to no practical man, with no merely narrow range of applications, and with no array of difficult terms from physics and engineering that submerge all thought of mathematics in the slough of despond of an unknown technical vocabulary. Outdoor exercises, even if somewhat primitive, may be introduced, but it should be perfectly understood that such exercises are given for the purpose of increasing the interest in geometry, and they should be abandoned if they fail of this purpose.
Bibliography. For a list of standard textbooks issued prior to the present generation, consult the bibliography in Stamper, History of the Teaching of Geometry, New York, 1908.
From the standpoint of theory there is or need be no relation whatever between algebra and geometry. Algebra was originally the science of the equation, as its name[37] indicates. This means that it was the science of finding the value of an unknown quantity in a statement of equality. Later it came to mean much more than this, and Newton spoke of it as universal arithmetic, and wrote an algebra with this title. At present the term is applied to the elements of a science in which numbers are represented by letters and in which certain functions are studied, functions which it is not necessary to specify at this time. The work relates chiefly to functions involving the idea of number. In geometry, on the other hand, the work relates chiefly to form. Indeed, in pure geometry number plays practically no part, while in pure algebra form plays practically no part.
In 1687 the great French philosopher, Descartes, wishing to picture certain algebraic functions, wrote a work of about a hundred pages, entitled "La Géométrie," and in this he showed a correspondence between the numbers of algebra (which may be expressed by letters) and the concepts of geometry. This was the first great step in the analytic geometry that finally gave us the graph
in algebra. Since then there have been brought out from time to time other analogies between algebra and geometry, always to the advantage of each science. This has led to a desire on the part of some teachers to unite algebra and geometry into one science, having simply a class in mathematics without these special names.
It is well to consider the advantages and the disadvantages of such a plan, and to decide as to the rational attitude to be taken by teachers concerning the question at issue. On the side of advantages it is claimed that there is economy of time and of energy. If a pupil is studying formulas, let the formulas of geometry be studied; if he is taking up ratio and proportion; let him do so for algebra and geometry at the same time; if he is solving quadratics, let him apply them at once to certain propositions concerning secants; and if he is proving that (a + b)2 equals a2 + 2ab + b2, let him do so by algebra and by geometry simultaneously. It is claimed that not only is there economy in this arrangement, but that the pupil sees mathematics as a whole, and thus acquires more of a mastery than comes by our present "tandem arrangement."
On the side of disadvantages it may be asked if the same arguments would not lead us to teach Latin and Greek together, or Latin and French, or all three simultaneously? If pupils should decline nouns in all three languages at the same time, learn to count in all at the same time, and begin to translate in all simultaneously, would there not be an economy of time and effort, and would there not be developed a much broader view of language? Now the fusionist of algebra and geometry does not like this argument, and he says that the cases are not parallel, and he tries to tell why they are not.[Pg 86] He demands that his opponent abandon argument by analogy and advance some positive reason why algebra and geometry should not be fused. Then his opponent says that it is not for him to advance any reason for what already exists, the teaching of the two separately; that he has only to refute the fusionist's arguments, and that he has done so. He asserts that algebra and geometry are as distinct as chemistry and biology; that they have a few common points, but not enough to require teaching them together. He claims that to begin Latin and Greek at the same time has always proved to be confusing, and that the same is true of algebra and geometry. He grants that unified knowledge is desirable, but he argues that when the fine arts of music and color work fuse, and when the natural sciences of chemistry and physics are taught in the same class, and when we follow the declension of a German noun by that of a French noun and a Latin noun, and when we teach drawing and penmanship together, then it is well to talk of mixing algebra and geometry.
It is well, before deciding such a question for ourselves (for evidently we cannot decide it for the world), to consider what has been the result of experience. Algebra and geometry were always taught together in early times, as were trigonometry and astronomy. The Ahmes papyrus contains both primitive algebra and primitive geometry. Euclid's "Elements" contains not only pure geometry, but also a geometric algebra and the theory of numbers. The early works of the Hindus often fused geometry and arithmetic, or geometry and algebra. Even the first great printed compendium of mathematics, the "Sūma" of Paciuolo (1494) contained all of the branches of mathematics. Much of this later attempt was not,[Pg 87] however, an example of perfect fusion, but rather of assigning one set of chapters to algebra, another to geometry, and another to arithmetic. So fusion, more or less perfect, has been tried over long periods, and abandoned as each subject grew more complete in itself, with its own language and its peculiar symbols.
But it is asserted that fusion is being carried on successfully to-day by more than one enthusiastic teacher, and that this proves the contention that the plan is a good one. Books are cited to show that the arrangement is feasible, and classes are indicated where the work is progressing along this line.
What, then, is the conclusion? That is a question for the teacher to settle, but it is one upon which a writer on the teaching of mathematics should not fear to express his candid opinion.
It is a fact that the Greek and Latin fusion is a fair analogy. There are reasons for it, but there are many more against it, the chief one being the confusion of beginning two languages at once, and the learning simultaneously of two vocabularies that must be kept separate. It is also a fact that algebra and geometry are fully as distinct as physics and chemistry, or chemistry and biology. Life may be electricity, and a brief cessation of oxidization in the lungs brings death, but these facts are no reasons for fusing the sciences of physics, biology, and chemistry. Algebra is primarily a theory of certain elementary functions, a generalized arithmetic, while geometry is primarily a theory of form with a highly refined logic to be used in its mastery. They have a few things in common, as many other subjects have, but they have very many more features that are peculiar to the one or the other. The experience of the world has led[Pg 88] it away from a simultaneous treatment, and the contrary experience of a few enthusiastic teachers of to-day proves only their own powers to succeed with any method. It is easy to teach logarithms in the seventh school year, but it is not good policy to do so under present conditions. So the experience of the world is against the plan of strict fusion, and no arguments have as yet been advanced that are likely to change the world's view. No one has written a book combining algebra and geometry in this fashion that has helped the cause of fusion a particle; on the contrary, every such work that has appeared has damaged that cause by showing how unscientific a result has come from the labor of an enthusiastic supporter of the movement.
But there is one feature that has not been considered above, and that is a serious handicap to any effort at combining the two sciences in the high school, and this is the question of relative difficulty. It is sometimes said, in a doctrinaire fashion, that geometry is easier than algebra, since form is easier to grasp than function, and that therefore geometry should precede algebra. But every teacher of mathematics knows better than this. He knows that the simplest form is easier to grasp than the simplest function, but nevertheless that plane geometry, as we understand the term to-day, is much more difficult than elementary algebra for a pupil of fourteen. The child studies form in the kindergarten before he studies number, and this is sound educational policy. He studies form, in mensuration, throughout his course in arithmetic, and this, too, is good educational policy. This kind of geometry very properly precedes algebra. But the demonstrations of geometry, the study by pupils of fourteen years of a geometry that was written for[Pg 89] college students and always studied by them until about fifty years ago,—that is by no means as easy as the study of a simple algebraic symbolism and its application to easy equations. If geometry is to be taught for the same reasons as at present, it cannot advantageously be taught earlier than now without much simplification, and it cannot successfully be fused with algebra save by some teacher who is willing to sacrifice an undue amount of energy to no really worthy purpose. When great mathematicians like Professor Klein speak of the fusion of all mathematics, they speak from the standpoint of advanced students, not for the teacher of elementary geometry.
It is therefore probable that simple mensuration will continue, as a part of arithmetic, to precede algebra, as at present; and that algebra into or through quadratics will precede geometry,[38] drawing upon the mensuration of arithmetic as may be needed; and that geometry will follow this part of algebra, using its principles as far as possible to assist in the demonstrations and to express and manipulate its formulas. Plane geometry, or else a year of plane and solid geometry, will probably, in this country, be followed by algebra, completing quadratics and studying progressions; and by solid geometry, or a supplementary course in plane and solid geometry, this work being elective in many, if not all, schools.[39] It is also probable that a general review of mathematics, where the fusion idea may be carried out, will prove to be a feature of the last year of the high school, and one
that will grow in popularity as time goes on. Such a plan will keep algebra and geometry separate, but it will allow each to use all of the other that has preceded it, and will encourage every effort in this direction. It will accomplish all that a more complete fusion really hopes to accomplish, and it will give encouragement to all who seek to modernize the spirit of each of these great branches of mathematics.
There is, however, a chance for fusion in two classes of school, neither of which is as yet well developed in this country. The first is the technical high school that is at present coming into some prominence. It is not probable even here that the best results can be secured by eliminating all mathematics save only what is applicable in the shop, but if this view should prevail for a time, there would be so little left of either algebra or geometry that each could readily be joined to the other. The actual amount of algebra needed by a foreman in a machine shop can be taught in about four lessons, and the geometry or mensuration that he needs can be taught in eight lessons at the most. The necessary trigonometry may take eight more, so that it is entirely feasible to unite these three subjects. The boy who takes such a course would know as much about mathematics as a child who had read ten pages in a primer would know about literature, but he would have enough for his immediate needs, even though he had no appreciation of mathematics as a science. If any one asks if this is not all that the school should give him, it might be well to ask if the school should give only the ability to read, without the knowledge of any good literature; if it should give only the ability to sing, without the knowledge of good music; if it should give only the ability to speak, without any training in the use[Pg 91] of good language; and if it should give a knowledge of home geography, without any intimation that the world is round,—an atom in the unfathomable universe about us.
The second opportunity for fusion is possibly (for it is by no means certain) to be found in a type of school in which the only required courses are the initial ones. These schools have some strong advocates, it being claimed that every pupil should be introduced to the large branches of knowledge and then allowed to elect the ones in which he finds himself the most interested. Whether or not this is sound educational policy need not be discussed at this time; but if such a plan were developed, it might be well to offer a somewhat superficial (in the sense of abridged) course that should embody a little of algebra, a little of geometry, and a little of trigonometry. This would unconsciously become a bait for students, and the result would probably be some good teaching in the class in question. It is to be hoped that we may have some strong, well-considered textbooks upon this phase of the work.
As to the fusion of trigonometry and plane geometry little need be said, because the subject is in the doctrinaire stage. Trigonometry naturally follows the chapter on similar triangles, but to put it there means, in our crowded curriculum, to eliminate something from geometry. Which, then, is better,—to give up the latter portion of geometry, or part of it at least, or to give up trigonometry? Some advocates have entered a plea for two or three lessons in trigonometry at this point, and this is a feature that any teacher may introduce as a bit of interest, as is suggested in Chapter XVI, just as he may give a popular talk to his class upon the fourth dimension or the non-Euclidean geometry. The lasting[Pg 92] impression upon the pupil will be exactly the same as that of four lessons in Sanskrit while he is studying Latin. He might remember each with pleasure, Latin being related, as it is, to Sanskrit, and trigonometry being an outcome of the theory of similar triangles. But that either of these departures from the regular sequence is of any serious mathematical or linguistic significance no one would feel like asserting. Each is allowable on the score of interest, but neither will add to the pupil's power in any essential feature.
Each of these subjects is better taught by itself, each using the other as far as possible and being followed by a review that shall make use of all. It is not improbable that we may in due time have high schools that give less extended courses in algebra and geometry, adding brief practical courses in trigonometry and the elements of the calculus; but even in such schools it is likely to be found that geometry is best taught by itself, making use of all the mathematics that has preceded it.
It will of course be understood that the fusion of algebra and geometry as here understood has nothing to do with the question of teaching the two subjects simultaneously, say two days in the week for one and three days for the other. This plan has many advocates, although on the whole it has not been well received in this country. But what is meant here is the actual fusing of algebra and geometry day after day,—a plan that has as yet met with only a sporadic success, but which may be developed for beginning classes in due time.[Pg 93]
There are two difficult crises in the geometry course, both for the pupil and for the teacher. These crises are met at the beginning of the subject and at the beginning of solid geometry. Once a class has fairly got into Book I, if the interest in the subject can be maintained, there are only the incidental difficulties of logical advance throughout the plane geometry. When the pupil who has been seeing figures in one plane for a year attempts to visualize solids from a flat drawing, the second difficult place is reached. Teachers going over solid geometry from year to year often forget this difficulty, but most of them can easily place themselves in the pupil's position by looking at the working drawings of any artisan,—usually simple cases in the so-called descriptive geometry. They will then realize how difficult it is to visualize a solid from an unfamiliar kind of picture. The trouble is usually avoided by the help of a couple of pieces of heavy cardboard or box board, and a few knitting needles with which to represent lines in space. If these are judiciously used in class for a few days, until the figures are understood, the second crisis is easily passed. The continued use of such material, however, or the daily use of either models or photographs, weakens the pupil, even as a child is weakened by being kept too long in a perambulator. Such devices have their place; they are useful[Pg 94] when needed, but they are pernicious when unnecessary. Just as the mechanic must be able to make and to visualize his working drawings, so the student of solid geometry must be able to get on with pencil and paper, representing his solid figures in the flat.
But the introduction to plane geometry is not so easily disposed of. The pupil at that time is entering a field that is entirely unfamiliar. He is only fourteen or fifteen years of age, and his thoughts are distinctly not on geometry. Of logic he knows little and cares less. He is not interested in a subject of which he knows nothing, not even the meaning of its name. He asks, naturally and properly, what it all signifies, what possible use there is for studying geometry, and why he should have to prove what seems to him evident without proof. To pass him successfully through this stage has taxed the ingenuity of every real teacher from the time of Euclid to the present; and just as Euclid remarked to King Ptolemy, his patron, that there is no royal road to geometry, so we may affirm that there is no royal road to the teaching of geometry.
Nevertheless the experience of teachers counts for a great deal, and this experience has shown that, aside from the matter of technic in handling the class, certain suggestions are of value, and a few of these will now be set forth.
First, as to why geometry is studied, it is manifestly impossible successfully to explain to a boy of fourteen or fifteen the larger reasons for studying anything whatever. When we confess ourselves honestly we find that these reasons, whether in mathematics, the natural sciences, handwork, letters, the vocations, or the fine arts, are none too clear in our own minds, in spite of any pretentious language that we may use. It is therefore most satisfactory to anticipate the question at once, and to set[Pg 95] the pupils, for a few days, at using the compasses and ruler in the drawing of geometric designs and of the most common figures that they will use. This serves several purposes: it excites their interest, it guards against the slovenly figures that so often lead them to erroneous conclusions, it has a genuine value for the future artisan, and it shows that geometry is something besides mere theory. Whether the textbook provides for it or not, the teacher will find a few days of such work well spent, it being a simple matter to supplement the book in this respect. There was a time when some form of mechanical drawing was generally taught in the schools, but this has given place to more genuine art work, leaving it to the teacher of geometry to impart such knowledge of drawing as is a necessary preliminary to the regular study of the subject.
Such work in drawing should go so far, and only so far, as to arouse an interest in geometric form without becoming wearisome, and to familiarize the pupil with the use of the instruments. He should be counseled about making fine lines, about being careful in setting the point of his compasses on the exact center that he wishes to use, and about representing a point by a very fine dot, or, preferably at first, by two crossed lines. Unless these details are carefully considered, the pupil will soon find that the lines of his drawings do not fit together, and that the result is not pleasing to the eye. The figures here given are good ones upon which to begin, the dotted construction lines being erased after the work is completed. They may be constructed with the compasses and ruler alone, or the draftsman's T-square, triangle, and protractor may be used, although these latter instruments are not necessary. We should[Pg 96] constantly remember that there is a danger in the slavish use of instruments and of such helps as squared paper.
Just as Euclid rode roughshod over the growing intellects of boys and girls, so may instruments ride roughshod over their growing perceptions by interfering with natural and healthy intuitions, and making them the subject of laborious measurement.[40]
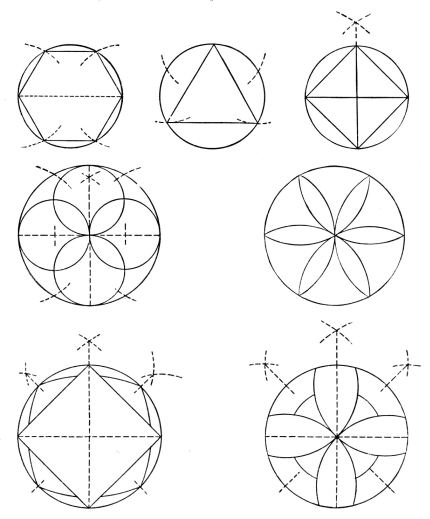
The pupil who cannot see the equality of vertical angles intuitively better than by the use of the protractor is abnormal. Nevertheless it is the pupil's interest that is at stake, together with his ability to use the instruments of daily life. If, therefore, he can readily be
supplied with draftsmen's materials, and is not compelled to use them in a foolish manner, so much the better. They will not hurt his geometry if the teacher does not interfere, and they will help his practical drawing; but for obvious reasons we cannot demand that the pupil purchase what is not really essential to his study of the subject. The most valuable single instrument of the three just mentioned is the protractor, and since a paper one costs only a few cents and is often helpful in the drawing of figures, it should be recommended to pupils.
There is also another line of work that often arouses a good deal of interest, namely, the simple field measures that can easily be made about the school grounds. Guarding against the ever-present danger of doing too much of such work, of doing work that has no interest for the pupil, of requiring it done in a way that seems unreal to a class, and of neglecting the essence of geometry by a line of work that involves no new principles,—such outdoor exercises in measurement have a positive value, and a plentiful supply of suggestions in this line is given in the subsequent chapters. The object is chiefly to furnish a motive for geometry, and for many pupils this is quite unnecessary. For some, however, and particularly for the energetic, restless boy, such work has been successfully offered by various teachers as an alternative to some of the book work. Because of this value a considerable amount of such work will be suggested for teachers who may care to use it, the textbook being manifestly not the place for occasional topics of this nature.
For the purposes of an introduction only a tape line need be purchased. Wooden pins and a plumb line can[Pg 98] easily be made. Even before he comes to the propositions in mensuration in geometry the pupil knows, from his arithmetic, how to find ordinary areas and volumes, and he may therefore be set at work to find the area of the school ground, or of a field, or of a city block. The following are among the simple exercises for a beginner:
1. Drive stakes at two corners, A and B, of the school grounds, putting a cross on top of each; or make the crosses on the sidewalk, so as to get two points between which to measure. Measure from A to B by holding the tape taut and level, dropping perpendiculars when necessary by means of the plumb line, as shown in the figure. Check the work by measuring from B back to A in the same way. Pupils will find that their work should always be checked, and they will be surprised to see how the results will vary in such a simple measurement as this, unless very great care is taken. If they learn the lesson of accuracy thus early, they will have gained much.

2. Take two stakes, X, Y, in a field, preferably two or three hundred feet apart, always marked on top with crosses so as to have exact points from which to work. Let it then be required to stake out or "range" the line from X to Y by placing stakes at specified distances. One boy stands at Y and another at X, each with a plumb line. A third one takes a plumb line and stands at P, the observer at X motioning to him to move his plumb line to the right or the left until it is exactly in line with X and Y. A stake is then driven at P, and the pupil at X moves on to the stake P. Then[Pg 99] Q is located in the same way, and then R, and so on. The work is checked by ranging back from Y to X. In some of the simple exercises suggested later it is necessary to range a line so that this work is useful in making measurements. The geometric principle involved is that two points determine a straight line.
3. To test a perpendicular or to draw one line perpendicular to another in a field, we may take a stout cord twelve feet long, having a knot at the end of every foot. If this is laid along four feet, the ends of this part being fixed, and it is stretched as here shown, so that the next vertex is five feet from one of these ends and three feet from the other end, a right angle will be formed. A right angle can also be run by making a simple instrument, such as is described in Chapter XV. Still another plan of drawing a line perpendicular to another line AB, from a point P, consists in swinging a tape from P, cutting AB at X and Y, and then bisecting XY by doubling the tape. This fixes the foot of the perpendicular.
4. It is now possible to find the area of a field of irregular shape by dividing it into triangles and trapezoids, as shown in the figure. Pupils know from their work in arithmetic how to find the area of a triangle or a trapezoid, so that the area of the field is easily found. The work may be checked by comparing[Pg 100] the results of different groups of pupils, or by drawing another diagonal and dividing the field into other triangles and trapezoids.
These are about as many types of field work as there is any advantage in undertaking for the purpose of securing the interest of pupils as a preliminary to the work in geometry. Whether any of it is necessary, and for what pupils it is necessary, and how much it should trespass upon the time of scientific geometry are matters that can be decided only by the teacher of a particular class.
A second difficulty of the pupil is seen in his attitude of mind towards proofs in general. He does not see why vertical angles should be proved equal when he knows that they are so by looking at the figure. This difficulty should also be anticipated by giving him some opportunity to know the weakness of his judgment, and for this purpose figures like the following should be placed before him. He should be asked which of these lines is longer, AB or XY. Two equal lines should then be arranged in the form of a letter T, as here shown, and he should be asked which is the longer, AB or CD. A figure that is very deceptive, particularly if drawn larger and with heavy cross lines, is this one in which AB and CD are really parallel, but do not seem to be so. Other interesting deceptions have to do with producing lines, as in these figures, where it is quite difficult in advance to tell whether AB and CD are in the same line, and similarly for WX and YZ. Equally[Pg 101] deceptive is this figure, in which it is difficult to tell which line AB will lie along when produced. In the next figure AB appears to be curved when in reality it is straight, and CD appears straight when in reality it is curved. The first of the following circles seems to be slightly flattened at the points P, Q, R, S, and in the second one the distance BD seems greater than the distance AC. There are many equally deceptive figures, and a few of them will convince the beginner that the proofs are necessary features of geometry.
It is interesting, in connection with the tendency to feel that a statement is apparent without proof, to recall an anecdote related by the French mathematician, Biot, concerning the great scientist, Laplace:
Once Laplace, having been asked about a certain point in his "Celestial Mechanics," spent nearly an hour in trying to recall the chain of reasoning which he had carelessly concealed by the words "It is easy to see."
A third difficulty lies in the necessity for putting a considerable number of definitions at the beginning of geometry, in order to get a working vocabulary. Although practically all writers scatter the definitions as much as[Pg 102] possible, there must necessarily be some vocabulary at the beginning. In order to minimize the difficulty of remembering so many new terms, it is helpful to mingle with them a considerable number of exercises in which these terms are employed, so that they may become fixed in mind through actual use. Thus it is of value to have a class find the complements of 27°, 32° 20', 41° 32' 48", 26.75°, 33-1/3°, and 0°. It is true that into the pure geometry of Euclid the measuring of angles in degrees does not enter, but it has place in the practical applications, and it serves at this juncture to fix the meaning of a new term like "complement."
The teacher who thus anticipates the question as to the reason for studying geometry, the mental opposition to proving statements, and the forgetfulness of the meaning of common terms will find that much of the initial difficulty is avoided. If, now, great care is given to the first half dozen propositions, the pupil will be well on his way in geometry. As to these propositions, two plans of selection are employed. The first takes a few preliminary propositions, easily demonstrated, and seeks thus to introduce the pupil to the nature of a proof. This has the advantage of inspiring confidence and the disadvantage of appearing to prove the obvious. The second plan discards all such apparently obvious propositions as those about the equality of right angles, and the sum of two adjacent angles formed by one line meeting another, and begins at once on things that seem to the pupil as worth the proving. In this latter plan the introduction is usually made with the proposition concerning vertical angles, and the two simplest cases of congruent triangles.
Whichever plan of selection is taken, it is important to introduce a considerable number of one-step exercises[Pg 103] immediately, that is, exercises that require only one significant step in the proof. In this way the pupil acquires confidence in his own powers, he finds that geometry is not mere memorizing, and he sees that each proposition makes him the master of a large field. To delay the exercises to the end of each book, or even to delay them for several lessons, is to sow seeds that will result in the attempt to master geometry by the sheer process of memorizing.
As to the nature of these exercises, however, the mistake must not be made of feeling that only those have any value that relate to football or the laying out of a tennis court. Such exercises are valuable, but such exercises alone are one-sided. Moreover, any one who examines the hundreds of suggested exercises that are constantly appearing in various journals, or who, in the preparation of teachers, looks through the thousands of exercises that come to him in the papers of his students, comes very soon to see how hollow is the pretense of most of them. As has already been said, there are relatively few propositions in geometry that have any practical applications, applications that are even honest in their pretense. The principle that the writer has so often laid down in other works, that whatever pretends to be practical should really be so, applies with much force to these exercises. When we can find the genuine application, if it is within reasonable grasp of the pupil, by all means let us use it. But to put before a class of girls some technicality of the steam engine that only a skilled mechanic would be expected to know is not education,—it is mere sham. There is a noble dignity to geometry, a dignity that a large majority of any class comes to appreciate when guided by an earnest teacher; but the[Pg 104] best way to destroy this dignity, to take away the appreciation of pure mathematics, and to furnish weaker candidates than now for advance in this field is to deceive our pupils and ourselves into believing that the ultimate purpose of mathematics is to measure things in a way in which no one else measures them or has ever measured them.
In the proof of the early propositions of plane geometry, and again at the beginning of solid geometry, there is a little advantage in using colored crayon to bring out more distinctly the equal parts of two figures, or the lines outside the plane, or to differentiate one plane from another. This device, however, like that of models in solid geometry, can easily be abused, and hence should be used sparingly, and only until the purpose is accomplished. The student of mathematics must learn to grasp the meaning of a figure drawn in black on white paper, or, more rarely, in white on a blackboard, and the sooner he is able to do this the better for him. The same thing may be said of the constructing of models for any considerable number of figures in solid geometry; enough work of this kind to enable a pupil clearly to visualize the solids is valuable, but thereafter the value is usually more than offset by the time consumed and the weakened power to grasp the meaning of a geometric drawing.
There is often a tendency on the part of teachers in their first years of work to overestimate the logical powers of their pupils and to introduce forms of reasoning and technical terms that experience has proved to be unsuited to one who is beginning geometry. Usually but little harm is done, because the enthusiasm of any teacher who would use this work would carry the pupils over the difficulties without much waste of energy on their[Pg 105] part. In the long run, however, the attempt is usually abandoned as not worth the effort. Such a term as "contrapositive," such distinctions as that between the logical and the geometric converse, or between perfect and partial geometric conversion, and such pronounced formalism as the "syllogistic method,"—all these are happily unknown to most teachers and might profitably be unknown to all pupils. The modern American textbook in geometry does not begin to be as good a piece of logic as Euclid's "Elements," and yet it is to be observed that none of these terms is found in this classic work, so that they cannot be thought to be necessary to a logical treatment of the subject. We need the word "converse," and some reference to the law of converse is therefore permissible; the meaning of the reductio ad absurdum, of a necessary and sufficient condition, and of the terms "synthesis" and "analysis" may properly form part of the pupil's equipment because of their universal use; but any extended incursion into the domain of logic will be found unprofitable, and it is liable to be positively harmful to a beginner in geometry.
A word should be said as to the lettering of the figures in the early stages of geometry. In general, it is a great aid to the eye if this is carried out with some system, and the following suggestions are given as in accord with the best authors who have given any attention to the subject:
1. In general, letter a figure counterclockwise, for the reason that we read angles in this way in higher mathematics, and it is as easy to form this habit now as to form one that may have to be changed. Where two triangles are congruent, however, but have their sides arranged in opposite order, it is better to letter them so[Pg 106] that their corresponding parts appear in the same order, although this makes one read clockwise.
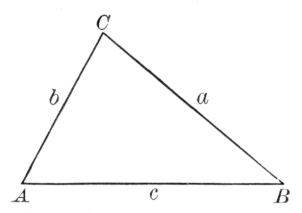
2. For the same reason, read angles counterclockwise. Thus ∠A is read "BAC," the reflex angle on the outside of the triangle being read "CAB." Of course this is not vital, and many authors pay no attention to it; but it is convenient, and if the teacher habitually does it, the pupils will also tend to do it. It is helpful in trigonometry, and it saves confusion in the case of a reflex angle in a polygon. Designate an angle by a single letter if this can conveniently be done.
3. Designate the sides opposite angles A, B, C, in a triangle, by a, b, c, and use these letters in writing proofs.
4. In the case of two congruent triangles use the letters A, B, C and A', B', C', or X, Y, Z, instead of letters chosen at random, like D, K, L. It is easier to follow a proof where some system is shown in lettering the figures. Some teachers insist that a pupil at the blackboard should not use the letters given in the textbook, hoping thereby to avoid memorizing. While the danger is probably exaggerated, it is easy to change with some system, using P, Q, R and P', Q', R', for example.
5. Use small letters for lines, as above stated, and also place them within angles, it being easier to speak of and to see ∠m than ∠DEF. The Germans have a convenient system that some American teachers follow to advantage, but that a textbook has no right to require. They use, as in the following figure, A for the point, a for the opposite side, and the Greek letter α (alpha) for the angle. The learning of the first three Greek letters,[Pg 107] alpha (α), beta (β), and gamma (γ), is not a hardship, and they are worth using, although Greek is so little known in this country to-day that the alphabet cannot be demanded of teachers who do not care to use it.
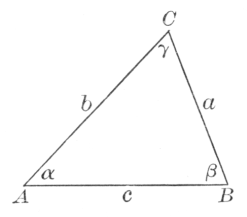
6. Also use small letters to represent numerical values. For example, write c = 2πr instead of C = 2πR. This is in accord with the usage in algebra to which the pupil is accustomed.
7. Use initial letters whenever convenient, as in the case of a for area, b for base, c for circumference, d for diameter, h for height (altitude), and so on.
Many of these suggestions seem of slight importance in themselves, and some teachers will be disposed to object to any attempt at lettering a figure with any regard to system. If, however, they will notice how a class struggles to follow a demonstration given with reference to a figure on the blackboard, they will see how helpful it is to have some simple standards of lettering. It is hardly necessary to add that in demonstrating from a figure on a blackboard it is usually better to say "this line," or "the red line," than to say, without pointing to it, "the line AB." It is by such simplicity of statement and by such efforts to help the class to follow demonstrations that pupils are led through many of the initial discouragements of the subject.[Pg 108]
No definite rules can be given for the detailed conduct of a class in any subject. If it were possible to formulate such rules, all the personal magnetism of the teacher, all the enthusiasm, all the originality, all the spirit of the class, would depart, and we should have a dull, dry mechanism. There is no one best method of teaching geometry or anything else. The experience of the schools has shown that a few great principles stand out as generally accepted, but as to the carrying out of these principles there can be no definite rules.
Let us first consider the general question of the employment of time in a recitation in geometry. We might all agree on certain general principles, and yet no two teachers ever would or ever should divide the period even approximately in the same way. First, a class should have an opportunity to ask questions. A teacher here shows his power at its best, listening sympathetically to any good question, quickly seeing the essential point, and either answering it or restating it in such a way that the pupil can answer it for himself. Certain questions should be answered by the teacher; he is there for that purpose. Others can at once be put in such a light that the pupil can himself answer them. Others may better be answered by the class. Occasionally, but more rarely, a pupil may be told to "look that up for[Pg 109] to-morrow," a plan that is commonly considered by students as a confession of weakness on the part of the teacher, as it probably is. Of course a class will waste time in questioning a weak teacher, but a strong one need have no fear on this account. Five minutes given at the opening of a recitation to brisk, pointed questions by the class, with the same credit given to a good question as to a good answer, will do a great deal to create a spirit of comradeship, of frankness, and of honesty, and will reveal to a sympathetic teacher the difficulties of a class much better than the same amount of time devoted to blackboard work. But there must be no dawdling, and the class must feel that it has only a limited time, say five minutes at the most, to get the help it needs.
Next in order of the division of the time may be the teacher's report on any papers that the class has handed in. It is impossible to tell how much of this paper work should be demanded. The local school conditions, the mental condition of the class, and the time at the disposal of the teacher are all factors in the case. In general, it may be said that enough of this kind of work is necessary to see that pupils are neat and accurate in setting down their demonstrations. On the other hand, paper work gives an opportunity for dishonesty, and it consumes a great deal of the teacher's time that might better be given to reading good books on the subject that he is teaching. If, however, any papers have been submitted, about five minutes may well be given to a rapid review of the failures and the successes. In general, it is good educational policy to speak of the errors and failures impersonally, but occasionally to mention by name any one who has done a piece of work that is worthy of special comment. Pupils may better be praised in public[Pg 110] and blamed in private. There is such a thing, however, as praising too much, when nothing worthy of note has been done, just as there is danger of blaming too much, resulting in mere "nagging."
The third division of the recitation period may profitably go to assigning the advance lesson. The class questions and the teacher's report on written work have shown the mental status of the pupils, so that the teacher now knows what he may expect for the next lesson. If he assigns his lesson at the beginning of the period, he does not have this information. If he waits to the end, he may be too hurried to give any "development" that the new lesson may require. There can be no rule as to how to assign a new lesson; it all depends upon what the lesson is, upon the mental state of the class, and not a little upon the idiosyncrasy of the teacher. The German educator, Herbart, laid down certain formal steps in developing a new lesson, and his successors have elaborated these somewhat as follows:
1. Aim. Always take a class into your confidence. Tell the members at the outset the goal. No one likes to be led blindfolded.
2. Preparation. A few brief questions to bring the class to think of what is to be considered.
3. Presentation of the new. Preferably this is done by questions, the answers leading the members of the class to discover the new truth for themselves.
4. Apperception. Calling attention to the fact that this new fact was known before, in part, and that it relates to a number of things already in the mind. The more the new can be tied up to the old the more tenaciously it will be held.
5. Generalization and application.[Pg 111]
It is evident at once that a great deal of time may be wasted in always following such a plan, perhaps in ever following it consciously. But, on the other hand, probably every good teacher, whether he has heard of Herbart or not, naturally covers these points in substantially this order. For an inexperienced teacher it is helpful to be familiar with them, that he may call to mind the steps, arranged in a psychological sequence, that he would do well to follow. It must always be remembered that there is quite as much danger in "developing" too much as in taking the opposite extreme. A mechanical teacher may develop a new lesson where there is need for only a question or two or a mere suggestion. It should also be recognized that students need to learn to read mathematics for themselves, and that always to take away every difficulty by explanations given in advance is weakening to any one.
Therefore, in assigning the new lesson we may say "Take the next two pages," and thus discourage most of the class. On the other hand, we may spend an unnecessary amount of time and overdevelop the work of those same pages, and have the whole lesson lose all its zest. It is here that the genius of the teacher comes forth to find the happy mean.
The fourth division of the hour should be reached, in general, in about ten minutes. This includes the recitation proper. But as to the nature of this work no definite instructions should be attempted. To a good teacher they would be unnecessary, to a poor one they would be harmful. Part of the class may go to the board, and as they are working, the rest may be reciting. Those at the board should be limited as to time, for otherwise a premium is placed on mere dawdling. They should be so[Pg 112] arranged as to prevent copying, but the teacher's eye is the best preventive of this annoying feature. Those at their seats may be called upon one at a time to demonstrate at the blackboard, the rest being called upon for quick responses, as occasion demands. The European plan of having small blackboards is in many respects better than ours, since pupils cannot so easily waste time. They have to work rapidly and talk rapidly, or else take their seats.
What should be put on the board, whether the figure alone, or the figure and the proof, depends upon the proposition. In general, there should be a certain number of figures put on the board for the sake of rapid work and as a basis for the proofs of the day. There should also be a certain amount of written work for the sake of commending or of criticizing adversely the proof used. There are some figures that are so complicated as to warrant being put upon sheets of paper and hung before the class. Thus there is no rule upon the subject, and the teacher must use his judgment according to the circumstances and the propositions.
If the early "originals" are one-step exercises, and a pupil is required to recite rapidly, a habit of quick expression is easily acquired that leads to close attention on the part of all the class. Students as a rule recite slower than they need to, from mere habit. Phlegmatic as we think the German is, and nervous as is the American temperament, a student in geometry in a German school will usually recite more quickly and with more vigor than one with us. Our extensive blackboards have something to do with this, allowing so many pupils to be working at the board that a teacher cannot attend to them all. The result is a habit of wasting the minutes[Pg 113] that can only be overcome by the teacher setting a definite but reasonable time limit, and holding the pupil responsible if the work is not done in the time specified. If this matter is taken in hand the first day, and special effort made in the early weeks of the year, much of the difficulty can be overcome.
As to the nature of the recitation to be expected from the pupil, no definite rule can be laid down, since it varies so much with the work of the day. In general, however, a pupil should state the theorem quickly, state exactly what is given and what is to be proved, with respect to the figure, and then give the proof. At first it is desirable that he should give the authorities in full, and later give only the essential part in a few words. It is better to avoid the expression "by previous proposition," for it soon comes to be abused, and of course the learning of section numbers in a book is a barbarism. It is only by continually stating the propositions used that a pupil comes to have well fixed in his memory the basal theorems of geometry, and without these he cannot make progress in his subsequent mathematics. In general, it is better to allow a pupil to finish his proof before asking him any questions, the constant interruptions indulged in by some teachers being the cause of no little confusion and hesitancy on the part of pupils. Sometimes it is well to have a figure drawn differently from the one in the book, or lettered differently, so as to make sure that the pupil has not memorized the proof, but in general such devices are unnecessary, for a teacher can easily discover whether the proof is thoroughly understood, either by the manner of the pupil or by some slight questioning. A good textbook has the figures systematically lettered in some helpful way that is easily followed by the class[Pg 114] that is listening to the recitation, and it is not advisable to abandon this for a random set of letters arranged in no proper order.
It is good educational policy for the teacher to commend at least as often as he finds fault when criticizing a recitation at the blackboard and when discussing the pupils' papers. Optimism, encouragement, sympathy, the genuine desire to help, the putting of one's self in the pupil's place, the doing to the pupil as the teacher would that he should do in return,—these are educational policies that make for better geometry as they make for better life.
The prime failure in teaching geometry lies unquestionably in the lack of interest on the part of the pupil, and this has been brought about by the ancient plan of simply reading and memorizing proofs. It is to get away from this that teachers resort to some such development of the lesson in advance, as has been suggested above. It is usually a good plan to give the easier propositions as exercises before they are reached in the text, where this can be done. An English writer has recently contributed this further idea:
It might be more stimulating to encourage investigation than to demand proofs of stated facts; that is to say, "Here is a figure drawn in this way, find out anything you can about it." Some such exercises having been performed jointly by teachers and pupils, the lust of investigation and healthy competition which is present in every normal boy or girl might be awakened so far as to make such little researches really attractive; moreover, the training thus given is of far more value than that obtained by proving facts which are stated in advance, for it is seldom, if ever, that the problems of adult life present themselves in this manner. The spirit of the question, "What is true?" is positive and constructive, but that involved in "Is this true?" is negative and destructive.[41]
When the question is asked, "How shall I teach?" or "What is the Method?" there is no answer such as the questioner expects. A Japanese writer, Motowori, a great authority upon the Shinto faith of his people, once wrote these words: "To have learned that there is no way to be learned and practiced is really to have learned the way of the gods."[Pg 116]
The interest as well as the value of geometry lies chiefly in the fact that from a small number of assumptions it is possible to deduce an unlimited number of conclusions. With the truth of these assumptions we are not so much concerned as with the reasoning by which we draw the conclusions, although it is manifestly desirable that the assumptions should not be false, and that they should be as few as possible.
It would be natural, and in some respects desirable, to call these foundations of geometry by the name "assumptions," since they are simply statements that are assumed to be true. The real foundation principles cannot be proved; they are the means by which we prove other statements. But as with most names of men or things, they have received certain titles that are time-honored, and that it is not worth the while to attempt to change. In English we call them axioms and postulates, and there is no more reason for attempting to change these terms than there is for attempting to change the names of geometry[42] and of algebra.[43]
Since these terms are likely to continue, it is necessary to distinguish between them more carefully than is often done, and to consider what assumptions we are justified in including under each. In the first place, these names do not go back to Euclid, as is ordinarily supposed, although the ideas and the statements are his. "Postulate" is a Latin form of the Greek αιτημα (aitema), and appears only in late translations. Euclid stated in substance, "Let the following be assumed." "Axiom" (αξίωμα, axioma) dates perhaps only from Proclus (fifth century A.D.), Euclid using the words "common notions" (κοιναὶ εννοιαι, koinai ennoiai) for "axioms," as Aristotle before him had used "common things," "common principles," and "common opinions."
The distinction between axiom and postulate was not clearly made by ancient writers. Probably what was in Euclid's mind was the Aristotelian distinction that an axiom was a principle common to all sciences, self-evident but incapable of proof, while the postulates were the assumptions necessary for building up the particular science under consideration, in this case geometry.[44]
We thus come to the modern distinction between axiom and postulate, and say that a general statement admitted to be true without proof is an axiom, while a postulate in geometry is a geometric statement admitted to be true, without proof. For example, when we say "If equals are added to equals, the sums are equal," we state an assumption that is taken also as true in arithmetic, in algebra, and in elementary mathematics in general. This is therefore an axiom. At one time such a
statement was defined as "a self-evident truth," but this has in recent years been abandoned, since what is evident to one person is not necessarily evident to another, and since all such statements are mere matters of assumption in any case. On the other hand, when we say, "A circle may be described with any given point as a center and any given line as a radius," we state a special assumption of geometry, and this assumption is therefore a geometric postulate. Some few writers have sought to distinguish between axiom and postulate by saying that the former was an assumed theorem and the latter an assumed problem, but there is no standard authority for such a distinction, and indeed the difference between a theorem and a problem is very slight. If we say, "A circle may be passed through three points not in the same straight line," we state a theorem; but if we say, "Required to pass a circle through three points," we state a problem. The mental process of handling the two propositions is, however, practically the same in spite of the minor detail of wording. So with the statement, "A straight line may be produced to any required length." This is stated in the form of a theorem, but it might equally well be stated thus: "To produce a straight line to any required length." It is unreasonable to call this an axiom in one case and a postulate in the other. However stated, it is a geometric postulate and should be so classed.
What, now, are the axioms and postulates that we are justified in assuming, and what determines their number and character? It seems reasonable to agree that they should be as few as possible, and that for educational purposes they should be so clear as to be intelligible to beginners. But here we encounter two conflicting ideas.[Pg 119] To get the "irreducible minimum" of assumptions is to get a set of statements quite unintelligible to students beginning geometry or any other branch of elementary mathematics. Such an effort is laudable when the results are intended for advanced students in the university, but it is merely suggestive to teachers rather than usable with pupils when it touches upon the primary steps of any science. In recent years several such attempts have been made. In particular, Professor Hilbert has given a system[45] of congruence postulates, but they are rather for the scientist than for the student of elementary geometry.
In view of these efforts it is well to go back to Euclid and see what this great teacher of university men[46] had to suggest. The following are the five "common notions" that Euclid deemed sufficient for the purposes of elementary geometry.
1. Things equal to the same thing are also equal to each other. This axiom has persisted in all elementary textbooks. Of course it is a simple matter to attempt criticism,—to say that -2 is the square root of 4, and +2 is also the square root of 4, whence -2 = +2; but it is evident that the argument is not sound, and that it does not invalidate the axiom. Proclus tells us that Apollonius attempted to prove the axiom by saying, "Let a equal b, and b equal c. I say that a equals c. For, since a equals b, a occupies the same space as b. Therefore a occupies
the same space as c. Therefore a equals c." The proof is of no value, however, save as a curiosity.
2. And if to equals equals are added, the wholes are equal.
3. If equals are subtracted from equals, the remainders are equal.
Axioms 2 and 3 are older than Euclid's time, and are the only ones given by him relating to the solution of the equation. Certain other axioms were added by later writers, as, "Things which are double of the same thing are equal to one another," and "Things which are halves of the same thing are equal to one another." These two illustrate the ancient use of duplatio (doubling) and mediatio (halving), the primitive forms of multiplication and division. Euclid would not admit the multiplication axiom, since to him this meant merely repeated addition. The partition (halving) axiom he did not need, and if needed, he would have inferred its truth. There are also the axioms, "If equals are added to unequals, the wholes are unequal," and "If equals are subtracted from unequals, the remainders are unequal," neither of which Euclid would have used because he did not define "unequals." The modern arrangement of axioms, covering addition, subtraction, multiplication, division, powers, and roots, sometimes of unequals as well as equals, comes from the development of algebra. They are not all needed for geometry, but in so far as they show the relation of arithmetic, algebra, and geometry, they serve a useful purpose. There are also other axioms concerning unequals that are of advantage to beginners, even though unnecessary from the standpoint of strict logic.
4. Things that coincide with one another are equal to one another. This is no longer included in the list of axioms. It is rather a definition of "equal," or of "congruent,"[Pg 121] to take the modern term. If not a definition, it is certainly a postulate rather than an axiom, being purely geometric in character. It is probable that Euclid included it to show that superposition is to be considered a legitimate form of proof, but why it was not placed among the postulates is not easily seen. At any rate it is unfortunately worded, and modern writers generally insert the postulate of motion instead,—that a figure may be moved about in space without altering its size or shape. The German philosopher, Schopenhauer (1844), criticized Euclid's axiom as follows: "Coincidence is either mere tautology or something entirely empirical, which belongs not to pure intuition but to external sensuous experience. It presupposes, in fact, the mobility of figures."
5. The whole is greater than the part. To this Clavius (1574) added, "The whole is equal to the sum of its parts," which may be taken to be a definition of "whole," but which is helpful to beginners, even if not logically necessary. Some writers doubt the genuineness of this axiom.
Having considered the axioms of Euclid, we shall now consider the axioms that are needed in the study of elementary geometry. The following are suggested, not from the standpoint of pure logic, but from that of the needs of the teacher and pupil.
1. If equals are added to equals, the sums are equal. Instead of this axiom, the one numbered 8 below is often given first. For convenience in memorizing, however, it is better to give the axioms in the following order: (1) addition, (2) subtraction, (3) multiplication, (4) division, (5) powers and roots,—all of equal quantities.
2. If equals are subtracted from equals, the remainders are equal.[Pg 122]
3. If equals are multiplied by equals, the products are equal.
4. If equals are divided by equals, the quotients are equal.
5. Like powers or like positive roots of equals are equal. Formerly students of geometry knew nothing of algebra, and in particular nothing of negative quantities. Now, however, in American schools a pupil usually studies algebra a year before he studies demonstrative geometry. It is therefore better, in speaking of roots, to limit them to positive numbers, since the two square roots of 4 (+2 and -2), for example, are not equal. If the pupil had studied complex numbers before he began geometry, it would have been advisable to limit the roots still further to real roots, since the four fourth roots of 1 (+1, -1, +√(-1), -√(-1)), for example, are not equal save in absolute value. It is well, however, to eliminate these fine distinctions as far as possible, since their presence only clouds the vision of the beginner.
It should also be noted that these five axioms might be combined in one, namely, If equals are operated on by equals in the same way, the results are equal. In Axiom 1 this operation is addition, in Axiom 2 it is subtraction, and so on. Indeed, in order to reduce the number of axioms two are already combined in Axiom 5. But there is a good reason for not combining the first four with the fifth, and there is also a good reason for combining two in Axiom 5. The reason is that these are the axioms continually used in equations, and to combine them all in one would be to encourage laxness of thought on the part of the pupil. He would always say "by Axiom 1" whatever he did to an equation, and the teacher would not be certain whether the pupil was thinking definitely of dividing equals by equals, or had[Pg 123] a hazy idea that he was manipulating an equation in some other way that led to an answer. On the other hand, Axiom 5 is not used as often as the preceding four, and the interchange of integral and fractional exponents is relatively common, so that the joining of these two axioms in one for the purpose of reducing the total number is justifiable.
6. If unequals are operated on by positive equals in the same way, the results are unequal in the same order. This includes in a single statement the six operations mentioned in the preceding axioms; that is, if a > b and if x = y, then a + x > b + y, a - x > b - y, ax > by, etc. The reason for thus combining six axioms in one in the case of inequalities is apparent. They are rarely used in geometry, and if a teacher is in doubt as to the pupil's knowledge, he can easily inquire in the few cases that arise, whereas it would consume a great deal of time to do this for the many equations that are met. The axiom is stated in such a way as to exclude multiplying or dividing by negative numbers, this case not being needed.
7. If unequals are added to unequals in the same order, the sums are unequal in the same order; if unequals are subtracted from equals, the remainders are unequal in the reverse order. These are the only cases in which unequals are necessarily combined with unequals, or operate upon equals in geometry, and the axiom is easily explained to the class by the use of numbers.
8. Quantities that are equal to the same quantity or to equal quantities are equal to each other. In this axiom the word "quantity" is used, in the common manner of the present time, to include number and all geometric magnitudes (length, area, volume).[Pg 124]
9. A quantity may be substituted for its equal in an equation or in an inequality. This axiom is tacitly assumed by all writers, and is very useful in the proofs of geometry. It is really the basis of several other axioms, and if we were seeking the "irreducible minimum," it would replace them. Since, however, we are seeking only a reasonably abridged list of convenient assumptions that beginners will understand and use, this axiom has much to commend it. If we consider the equations (1) a = x and (2) b = x, we see that for x in equation (1) we may substitute b from equation (2) and have a = b; in other words, that Axiom 8 is included in Axiom 9. Furthermore, if (1) a = b and (2) x = y, then since a + x is the same as a + x, we may, by substituting, say that a + x = a + x = b + x = b + y. In other words, Axiom 1 is included in Axiom 9. Thus an axiom that includes others has a legitimate place, because a beginner would be too much confused by seeing its entire scope, and because he will make frequent use of it in his mathematical work.
10. If the first of three quantities is greater than the second, and the second is greater than the third, then the first is greater than the third. This axiom is needed several times in geometry. The case in which a > b and b = c, therefore a > c, is provided for in Axiom 9.
11. The whole is greater than any of its parts and is equal to the sum of all its parts. The latter part of this axiom is really only the definition of "whole," and it would be legitimate to state a definition accordingly and refer to it where the word is employed. Where, however, we wish to speak of a polygon, for example, and wish to say that the area is equal to the combined areas of the triangles composing it, it is more satisfactory to[Pg 125] have this axiom to which to refer. It will be noticed that two related axioms are here combined in one, for a reason similar to the one stated under Axiom 5.
In the case of the postulates we are met by a problem similar to the one confronting us in connection with the axioms,—the problem of the "irreducible minimum" as related to the question of teaching. Manifestly Euclid used postulates that he did not state, and proved some statements that he might have postulated.[47]
The postulates given by Euclid under the name αἰτήματα (aitemata) were requests made by the teacher to his pupil that certain things be conceded. They were five in number, as follows:
1. Let the following be conceded: to draw a straight line from any point to any point.
Strictly speaking, Euclid might have been required to postulate that points and straight lines exist, but he evidently considered this statement sufficient. Aristotle had, however, already called attention to the fact that a mere definition was sufficient only to show what a concept is, and that this must be followed by a proof that the thing exists. We might, for example, define x as a line that bisects an angle without meeting the vertex, but this would not show that an x exists, and indeed it does not exist. Euclid evidently intended the postulate to assert that this line joining two points is unique, which is only another way of saying that two points determine a straight line, and really includes the idea
that two straight lines cannot inclose space. For purposes of instruction, the postulate would be clearer if it read, One straight line, and only one, can be drawn through two given points.
2. To produce a finite straight line continuously in a straight line.
In this postulate Euclid practically assumes that a straight line can be produced only in a straight line; in other words, that two different straight lines cannot have a common segment. Several attempts have been made to prove this fact, but without any marked success.
3. To describe a circle with any center and radius.
4. That all right angles are equal to one another.
While this postulate asserts the essential truth that a right angle is a determinate magnitude so that it really serves as an invariable standard by which other (acute and obtuse) angles may be measured, much more than this is implied, as will easily be seen from the following consideration. If the statement is to be proved, it can only be proved by the method of applying one pair of right angles to another and so arguing their equality. But this method would not be valid unless on the assumption of the invariability of figures, which would have to be asserted as an antecedent postulate. Euclid preferred to assert as a postulate, directly, the fact that all right angles are equal; and hence his postulate must be taken as equivalent to the principle of invariability of figures, or its equivalent, the homogeneity of space.[48]
It is better educational policy, however, to assert this fact more definitely, and to state the additional assumption that figures may be moved about in space without deformation. The fourth of Euclid's postulates is often given as an axiom, following the idea of the Greek philosopher Geminus (who flourished in the first century B.C.), but this is because Euclid's distinction between
axiom and postulate is not always understood. Proclus (410-485 A.D.) endeavored to prove the postulate, and a later and more scientific effort was made by the Italian geometrician Saccheri (1667-1733). It is very commonly taken as a postulate that all straight angles are equal, this being more evident to the senses, and the equality of right angles is deduced as a corollary. This method of procedure has the sanction of many of our best modern scholars.
5. That, if a straight line falling on two straight lines make the interior angle on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
This famous postulate, long since abandoned in teaching the beginner in geometry, is a remarkable evidence of the clear vision of Euclid. For two thousand years mathematicians sought to prove it, only to demonstrate the wisdom of its author in placing it among the assumptions.[49] Every proof adduced contains some assumption that practically conceals the postulate itself. Thus the great English mathematician John Wallis (1616-1703) gave a proof based upon the assumption that "given a figure, another figure is possible which is similar to the given one, and of any size whatever." Legendre (1752-1833) did substantially the same at one time, and offered several other proofs, each depending upon some equally unprovable assumption. The definite proof that the postulate cannot be demonstrated is due to the Italian Beltrami (1868).
Of the alternative forms of the postulate, that of Proclus is generally considered the best suited to beginners. As stated by Playfair (1795), this is, "Through a given point only one parallel can be drawn to a given straight line"; and as stated by Proclus, "If a straight line intersect one of two parallels, it will intersect the other also." Playfair's form is now the common "postulate of parallels," and is the one that seems destined to endure.
Posidonius and Geminus, both Stoics of the first century B.C., gave as their alternative, "There exist straight lines everywhere equidistant from one another." One of Legendre's alternatives is, "There exists a triangle in which the sum of the three angles is equal to two right angles." One of the latest attempts to suggest a substitute is that of the Italian Ingrami (1904), "Two parallel straight lines intercept, on every transversal which passes through the mid-point of a segment included between them, another segment the mid-point of which is the mid-point of the first."
Of course it is entirely possible to assume that through a point more than one line can be drawn parallel to a given straight line, in which case another type of geometry can be built up, equally rigorous with Euclid's. This was done at the close of the first quarter of the nineteenth century by Lobachevsky (1793-1856) and Bolyai (1802-1860), resulting in the first of several "non-Euclidean" geometries.[50]
Taking the problem to be that of stating a reasonably small number of geometric assumptions that may form a basis to supplement the general axioms, that shall cover the most important matters to which the student must refer, and that shall be so simple as easily to be understood by a beginner, the following are recommended:
1. One straight line, and only one, can be drawn through two given points. This should also be stated for convenience in the form, Two points determine a straight line. From it may also be drawn this corollary, Two straight lines can intersect in only one point, since two points would determine a straight line. Such obvious restatements of or corollaries to a postulate are to be commended, since a beginner is often discouraged by having to prove what is so obvious that a demonstration fails to commend itself to his mind.
2. A straight line may be produced to any required length. This, like Postulate 1, requires the use of a straightedge for drawing the physical figure. The required length is attained by using the compasses to measure the distance. The straightedge and the compasses are the only two drawing instruments recognized in elementary geometry.[51] While this involves more than Euclid's postulate, it is a better working assumption for beginners.
3. A straight line is the shortest path between two points. This is easily proved by the method of Euclid[52] for the case where the paths are broken lines, but it is needed as a postulate for the case of curve paths. It is a better statement than the common one that a straight line is the shortest distance between two points; for distance is
measured on a line, but it is not itself a line. Furthermore, there are scientific objections to using the word "distance" any more than is necessary.
4. A circle may be described with any given point as a center and any given line as a radius. This involves the use of the second of the two geometric instruments, the compasses.
5. Any figure may be moved from one place to another without altering the size or shape. This is the postulate of the homogeneity of space, and asserts that space is such that we may move a figure as we please without deformation of any kind. It is the basis of all cases of superposition.
6. All straight angles are equal. It is possible to prove this, and therefore, from the standpoint of strict logic, it is unnecessary as a postulate. On the other hand, it is poor educational policy for a beginner to attempt to prove a thing that is so obvious. The attempt leads to a loss of interest in the subject, the proposition being (to state a paradox) hard because it is so easy. It is, of course, possible to postulate that straight angles are equal, and to draw the conclusion that their halves (right angles) are equal; or to proceed in the opposite direction, and postulate that all right angles are equal, and draw the conclusion that their doubles (straight angles) are equal. Of the two the former has the advantage, since it is probably more obvious that all straight angles are equal. It is well to state the following definite corollaries to this postulate: (1) All right angles are equal; (2) From a point in a line only one perpendicular can be drawn to the line, since two perpendiculars would make the whole (right angle) equal to its part; (3) Equal angles have equal complements, equal supplements, and equal[Pg 131] conjugates; (4) The greater of two angles has the less complement, the less supplement, and the less conjugate. All of these four might appear as propositions, but, as already stated, they are so obvious as to be more harmful than useful to beginners when given in such form.
The postulate of parallels may properly appear in connection with that topic in Book I, and it is accordingly treated in Chapter XIV.
There is also another assumption that some writers are now trying to formulate in a simple fashion. We take, for example, a line segment AB, and describe circles with A and B respectively as centers, and with a radius AB. We say that the circles will intersect as at C and D. But how do we know that they intersect? We assume it, just as we assume that an indefinite straight line drawn from a point inclosed by a circle will, if produced far enough, cut the circle twice. Of course a pupil would not think of this if his attention was not called to it, and the harm outweighs the good in doing this with one who is beginning the study of geometry.
With axioms and with postulates, therefore, the conclusion is the same: from the standpoint of scientific geometry there is an irreducible minimum of assumptions, but from the standpoint of practical teaching this list should give place to a working set of axioms and postulates that meet the needs of the beginner.
Bibliography. Smith, Teaching of Elementary Mathematics, New York, 1900; Young, The Teaching of Mathematics, New York, 1901; Moore, On the Foundations of Mathematics, Bulletin of the American Mathematical Society, 1903, p. 402; Betz, Intuition and Logic in Geometry, The Mathematics Teacher, Vol. II, p. 3; Hilbert, The Foundations of Geometry, Chicago, 1902; Veblen, A System of Axioms for Geometry, Transactions of the American Mathematical Society, 1904, p. 343.
When we consider the nature of geometry it is evident that more attention must be paid to accuracy of definitions than is the case in most of the other sciences. The essence of all geometry worthy of serious study is not the knowledge of some fact, but the proof of that fact; and this proof is always based upon preceding proofs, assumptions (axioms or postulates), or definitions. If we are to prove that one line is perpendicular to another, it is essential that we have an exact definition of "perpendicular," else we shall not know when we have reached the conclusion of the proof.
The essential features of a definition are that the term defined shall be described in terms that are simpler than, or at least better known than, the thing itself; that this shall be done in such a way as to limit the term to the thing defined; and that the description shall not be redundant. It would not be a good definition to say that a right angle is one fourth of a perigon and one half of a straight angle, because the concept "perigon" is not so simple, and the term "perigon" is not so well known, as the term and the concept "right angle," and because the definition is redundant, containing more than is necessary.
It is evident that satisfactory definitions are not always possible; for since the number of terms is limited, there must be at least one that is at least as simple as any[Pg 133] other, and this cannot be described in terms simpler than itself. Such, for example, is the term "angle." We can easily explain the meaning of this word, and we can make the concept clear, but this must be done by a certain amount of circumlocution and explanation, not by a concise and perfect definition. Unless a beginner in geometry knows what an angle is before he reads the definition in a textbook, he will not know from the definition. This fact of the impossibility of defining some of the fundamental concepts will be evident when we come to consider certain attempts that have been made in this direction.
It should also be understood in this connection that a definition makes no assertion as to the existence of the thing defined. If we say that a tangent to a circle is an unlimited straight line that touches the circle in one point, and only one, we do not assert that it is possible to have such a line; that is a matter for proof. Not in all cases, however, can this proof be given, as in the existence of the simplest concepts. We cannot, for example, prove that a point or a straight line exists after we have defined these concepts. We therefore tacitly or explicitly assume (postulate) the existence of these fundamentals of geometry. On the other hand, we can prove that a tangent exists, and this may properly be considered a legitimate proposition or corollary of elementary geometry. In relation to geometric proof it is necessary to bear in mind, therefore, that we are permitted to define any term we please; for example, "a seven-edged polyhedron" or Leibnitz's "ten-faced regular polyhedron," neither of which exists; but, strictly speaking, we have no right to make use of a definition in a proof until we have shown or postulated that the thing defined[Pg 134] has an existence. This is one of the strong features of Euclid's textbook. Not being able to prove that a point, a straight line, and a circle exists, he practically postulates these facts; but he uses no other definition in a proof without showing that the thing defined exists, and this is his reason for mingling his problems with his theorems. At the present time we confessedly sacrifice his logic in this respect for the reason that we teach geometry to pupils who are too young to appreciate that logic.
It was pointed out by Aristotle, long before Euclid, that it is not a satisfactory procedure to define a thing by means of terms that are strictly not prior to it, as when we attempt to define something by means of its opposite. Thus to define a curve as "a line, no part of which is straight," would be a bad definition unless "straight" had already been explicitly defined; and to define "bad" as "not good" is unsatisfactory for the reason that "bad" and "good" are concepts that are evolved simultaneously. But all this is only a detail under the general principle that a definition must employ terms that are better understood than the one defined.
It should be understood that some definitions are much more important than others, considered from the point of view of the logic of geometry. Those that enter into geometric proofs are basal; those that form part of the conversational language of geometry are not. Euclid gave twenty-three definitions in Book I, and did not make use of even all of these terms. Other terms, those not employed in his proofs, he assumed to be known, just as he assumed a knowledge of any other words in his language. Such procedure would not be satisfactory under modern conditions, but it is of great importance[Pg 135] that the teacher should recognize that certain definitions are basal, while others are merely informational.
It is now proposed to consider the basal definitions of geometry, first, that the teacher may know what ones are to be emphasized and learned; and second, that he may know that the idea that the standard definitions can easily be improved is incorrect. It is hoped that the result will be the bringing into prominence of the basal concepts, and the discouraging of attempts to change in unimportant respects the definitions in the textbook used by the pupil.
In order to have a systematic basis for work, the definitions of two books of Euclid will first be considered.[53]
1. Point. A point is that which has no part. This was incorrectly translated by Capella in the fifth century, "Punctum est cuius pars nihil est" (a point is that of which a part is nothing), which is as much as to say that the point itself is nothing. It generally appears, however, as in the Campanus edition,[54] "Punctus est cuius pars non est," which is substantially Euclid's wording. Aristotle tells of the definitions of point, line, and surface that prevailed in his time, saying that they all defined the prior by means of the posterior.[55] Thus a point was defined as "an extremity of a line," a line as "the extremity of a surface," and a surface as "the extremity of
a solid,"—definitions still in use and not without their value. For it must not be assumed that scientific priority is necessarily priority in fact; a child knows of "solid" before he knows of "point," so that it may be a very good way to explain, if not to define, by beginning with solid, passing thence to surface, thence to line, and thence to point.
The first definition of point of which Proclus could learn is attributed by him to the Pythagoreans, namely, "a monad having position," the early form of our present popular definition of a point as "position without magnitude." Plato defined it as "the beginning of a line," thus presupposing the definition of "line"; and, strangely enough, he anticipated by two thousand years Cavalieri, the Italian geometer, by speaking of points as "indivisible lines." To Aristotle, who protested against Plato's definitions, is due the definition of a point as "something indivisible but having position."
Euclid's definition is essentially that of Aristotle, and is followed by most modern textbook writers, except as to its omission of the reference to position. It has been criticized as being negative, "which has no part"; but it is generally admitted that a negative definition is admissible in the case of the most elementary concepts. For example, "blind" must be defined in terms of a negation.
At present not much attention is given to the definition of "point," since the term is not used as the basis of a proof, but every effort is made to have the concept clear. It is the custom to start from a small solid, conceive it to decrease in size, and think of the point as the limit to which it is approaching, using these terms in their usual sense without further explanation.[Pg 137]
2. Line. A line is breadthless length. This is usually modified in modern textbooks by saying that "a line is that which has length without breadth or thickness," a statement that is better understood by beginners. Euclid's definition is thought to be due to Plato, and is only one of many definitions that have been suggested. The Pythagoreans having spoken of the point as a monad naturally were led to speak of the line as dyadic, or related to two. Proclus speaks of another definition, "magnitude in one dimension," and he gives an excellent illustration of line as "the edge of a shadow," thus making it real but not material. Aristotle speaks of a line as a magnitude "divisible in one way only," as contrasted with a surface which is divisible in two ways, and with a solid which is divisible in three ways. Proclus also gives another definition as the "flux of a point," which is sometimes rendered as the path of a moving point. Aristotle had suggested the idea when he wrote, "They say that a line by its motion produces a surface, and a point by its motion a line."
Euclid did not deem it necessary to attempt a classification of lines, contenting himself with defining only a straight line and a circle, and these are really the only lines needed in elementary geometry. His commentators, however, made the attempt. For example. Heron (first century A.D.) probably followed his definition of line by this classification:
| Straight | ||||
| Lines | Circular circumferences | |||
| Not straight | Spiral shaped | |||
| Curved (generally) |
Proclus relates that both Plato and Aristotle divided lines into "straight," "circular," and "a mixture of the[Pg 138] two," a statement which is not quite exact, but which shows the origin of a classification not infrequently found in recent textbooks. Geminus (ca. 50 B.C.) is said by Proclus to have given two classifications, of which one will suffice for our purposes:
| Composite (broken line forming an angle) | ||||
| Lines | Forming a figure, or determinate. (Circle, ellipse, cissoid.) | |||
| Incomposite | Not forming a figure, or indeterminate and extending without a limit. (Straight line, parabola, hyperbola, conchoid.) |
Of course his view of the cissoid, the curve represented by the equation y2(a + x) = (a - x)3, is not the modern view.
3. The extremities of a line are points. This is not a definition in the sense of its two predecessors. A modern writer would put it as a note under the definition of line. Euclid did not wish to define a point as the extremity of a line, for Aristotle had asserted that this was not scientific; so he defined point and line, and then added this statement to show the relation of one to the other. Aristotle had improved upon this by stating that the "division" of a line, as well as an extremity, is a point, as is also the intersection of two lines. These statements, if they had been made by Euclid, would have avoided the objection made by Proclus, that some lines have no extremities, as, for example, a circle, and also a straight line extending infinitely in both directions.
4. Straight Line. A straight line is that which lies evenly with respect to the points on itself. This is the least satisfactory of all of the definitions of Euclid, and emphasizes the fact that the straight line is the most difficult to define of the elementary concepts of geometry.[Pg 139] What is meant by "lies evenly"? Who would know what a straight line is, from this definition, if he did not know in advance?
The ancients suggested many definitions of straight line, and it is well to consider a few in order to appreciate the difficulties involved. Plato spoke of it as "that of which the middle covers the ends," meaning that if looked at endways, the middle would make it impossible to see the remote end. This is often modified to read that "a straight line when looked at endways appears as a point,"—an idea that involves the postulate that our line of sight is straight. Archimedes made the statement that "of all the lines which have the same extremities, the straight line is the least," and this has been modified by later writers into the statement that "a straight line is the shortest distance between two points." This is open to two objections as a definition: (1) a line is not distance, but distance is the length of a line,—it is measured on a line; (2) it is merely stating a property of a straight line to say that "a straight line is the shortest path between two points,"—a proper postulate but not a good definition. Equally objectionable is one of the definitions suggested by both Heron and Proclus, that "a straight line is a line that is stretched to its uttermost"; for even then it is reasonable to think of it as a catenary, although Proclus doubtless had in mind the Archimedes statement. He also stated that "a straight line is a line such that if any part of it is in a plane, the whole of it is in the plane,"—a definition that runs in a circle, since plane is defined by means of straight line. Proclus also defines it as "a uniform line, capable of sliding along itself," but this is also true of a circle.[Pg 140]
Of the various definitions two of the best go back to Heron, about the beginning of our era. Proclus gives one of them in this form, "That line which, when its ends remain fixed, itself remains fixed." Heron proposed to add, "when it is, as it were, turned round in the same plane." This has been modified into "that which does not change its position when it is turned about its extremities as poles," and appears in substantially this form in the works of Leibnitz and Gauss. The definition of a straight line as "such a line as, with another straight line, does not inclose space," is only a modification of this one. The other definition of Heron states that in a straight line "all its parts fit on all in all ways," and this in its modern form is perhaps the most satisfactory of all. In this modern form it may be stated, "A line such that any part, placed with its ends on any other part, must lie wholly in the line, is called a straight line," in which the force of the word "must" should be noted. This whole historical discussion goes to show how futile it is to attempt to define a straight line. What is needed is that we should explain what is meant by a straight line, that we should illustrate it, and that pupils should then read the definition understandingly.
5. Surface. A surface is that which has length and breadth. This is substantially the common definition of our modern textbooks. As with line, so with surface, the definition is not entirely satisfactory, and the chief consideration is that the meaning of the term should be made clear by explanations and illustrations. The shadow cast on a table top is a good illustration, since all idea of thickness is wanting. It adds to the understanding of the concept to introduce Aristotle's statement that a surface is generated by a moving line, modified by saying[Pg 141] that it may be so generated, since the line might slide along its own trace, or, as is commonly said in mathematics, along itself.
6. The extremities of a surface are lines. This is open to the same explanation and objection as definition 3, and is not usually given in modern textbooks. Proclus calls attention to the fact that the statement is hardly true for a complete spherical surface.
7. Plane. A plane surface is a surface which lies evenly with the straight lines on itself. Euclid here follows his definition of straight line, with a result that is equally unsatisfactory. For teaching purposes the translation from the Greek is not clear to a beginner, since "lies evenly" is a term not simpler than the one defined. As with the definition of a straight line, so with that of a plane, numerous efforts at improvement have been made. Proclus, following a hint of Heron's, defines it as "the surface which is stretched to the utmost," and also, this time influenced by Archimedes's assumption concerning a straight line, as "the least surface among all those which have the same extremities." Heron gave one of the best definitions, "A surface all the parts of which have the property of fitting on [each other]." The definition that has met with the widest acceptance, however, is a modification of one due to Proclus, "A surface such that a straight line fits on all parts of it." Proclus elsewhere says, "[A plane surface is] such that the straight line fits on it all ways," and Heron gives it in this form, "[A plane surface is] such that, if a straight line pass through two points on it, the line coincides with it at every spot, all ways." In modern form this appears as follows: "A surface such that a straight line joining any two of its points lies wholly in the surface is called a[Pg 142] plane," and for teaching purposes we have no better definition. It is often known as Simson's definition, having been given by Robert Simson in 1756.
The French mathematician, Fourier, proposed to define a plane as formed by the aggregate of all the straight lines which, passing through one point on a straight line in space, are perpendicular to that line. This is clear, but it is not so usable for beginners as Simson's definition. It appears as a theorem in many recent geometries. The German mathematician, Crelle, defined a plane as a surface containing all the straight lines (throughout their whole length) passing through a fixed point and also intersecting a straight line in space, but of course this intersected straight line must not pass through the fixed point. Crelle's definition is occasionally seen in modern textbooks, but it is not so clear to the pupil as Simson's. Of the various ultrascientific definitions of a plane that have been suggested of late it is hardly of use to speak in a book concerned primarily with practical teaching. No one of them is adapted to the needs and the comprehension of the beginner, and it seems that we are not likely to improve upon the so-called Simson form.
8. Plane Angle. A plane angle is the inclination to each other of two lines in a plane which meet each other and do not lie in a straight line. This definition, it will be noticed, includes curvilinear angles, and the expression "and do not lie in a straight line" states that the lines must not be continuous one with the other, that is, that zero and straight angles are excluded. Since Euclid does not use the curvilinear angle, and it is only the rectilinear angle with which we are concerned, we will pass to the next definition and consider this one in connection therewith.[Pg 143]
9. Rectilinear Angle. When the lines containing the angle are straight, the angle is called rectilinear. This definition, taken with the preceding one, has always been a subject of criticism. In the first place it expressly excludes the straight angle, and, indeed, the angles of Euclid are always less than 180°, contrary to our modern concept. In the second place it defines angle by means of the word "inclination," which is itself as difficult to define as angle. To remedy these defects many substitutes have been proposed. Apollonius defined angle as "a contracting of a surface or a solid at one point under a broken line or surface." Another of the Greeks defined it as "a quantity, namely, a distance between the lines or surfaces containing it." Schotten[56] says that the definitions of angle generally fall into three groups:
a. An angle is the difference of direction between two lines that meet. This is no better than Euclid's, since "difference of direction" is as difficult to define as "inclination."
b. An angle is the amount of turning necessary to bring one side to the position of the other side.
c. An angle is the portion of the plane included between its sides.
Of these, b is given by way of explanation in most modern textbooks. Indeed, we cannot do better than simply to define an angle as the opening between two lines which meet, and then explain what is meant by size, through the bringing in of the idea of rotation. This is a simple presentation, it is easily understood, and it is sufficiently accurate for the real purpose in
mind, namely, the grasping of the concept. We should frankly acknowledge that the concept of angle is such a simple one that a satisfactory definition is impossible, and we should therefore confine our attention to having the concept understood.
10. When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands. We at present separate these definitions and simplify the language.
11. An obtuse angle is an angle greater than a right angle.
12. An acute angle is an angle less than a right angle.
The question sometimes asked as to whether an angle of 200° is obtuse, and whether a negative angle, say -90°, is acute, is answered by saying that Euclid did not conceive of angles equal to or greater than 180° and had no notion of negative quantities. Generally to-day we define an obtuse angle as "greater than one and less than two right angles." An acute angle is defined as "an angle less than a right angle," and is considered as positive under the general understanding that all geometric magnitudes are positive unless the contrary is stated.
13. A boundary is that which is an extremity of anything. The definition is not exactly satisfactory, for a circle is the boundary of the space inclosed, but we hardly consider it as the extremity of that space. Euclid wishes the definition before No. 14.
14. A figure is that which is contained by any boundary or boundaries. The definition is not satisfactory, since it excludes the unlimited straight line, the angle, an[Pg 145] assemblage of points, and other combinations of lines and points which we should now consider as figures.
15. A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another.
16. And the point is called the center of the circle.
Some commentators add after "one line," definition 15, the words "which is called the circumference," but these are not in the oldest manuscripts. The Greek idea of a circle was usually that of part of a plane which is bounded by a line called in modern times the circumference, although Aristotle used "circle" as synonymous with "the bounding line." With the growth of modern mathematics, however, and particularly as a result of the development of analytic geometry, the word "circle" has come to mean the bounding line, as it did with Aristotle, a century before Euclid's time. This has grown out of the equations of the various curves, x2 + y2 = r2 representing the circle-line, a2y2 + b2x2 = a2b2 representing the ellipse-line, and so on. It is natural, therefore, that circle, ellipse, parabola, and hyperbola should all be looked upon as lines. Since this is the modern use of "circle" in English, it has naturally found its way into elementary geometry, in order that students should not have to form an entirely different idea of circle on beginning analytic geometry. The general body of American teachers, therefore, at present favors using "circle" to mean the bounding line and "circumference" to mean the length of that line. This requires redefining "area of a circle," and this is done by saying that it is the area of the plane space inclosed. The matter is not of greatest consequence, but teachers will probably prefer to join in the modern American usage of the term.[Pg 146]
17. Diameter. A diameter of the circle is any straight line drawn through the center and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle. The word "diameter" is from two Greek words meaning a "through measurer," and it was also used by Euclid for the diagonal of a square, and more generally for the diagonal of any parallelogram. The word "diagonal" is a later term and means the "through angle." It will be noticed that Euclid adds to the usual definition the statement that a diameter bisects the circle. He does this apparently to justify his definition (18), of a semicircle (a half circle).
Thales is said to have been the first to prove that a diameter bisects the circle, this being one of three or four propositions definitely attributed to him, and it is sometimes given as a proposition to be proved. As a proposition, however, it is unsatisfactory, since the proof of what is so evident usually instills more doubt than certainty in the minds of beginners.
18. Semicircle. A semicircle is the figure contained by the diameter and the circumference cut off by it. And the center of the semicircle is the same as that of the circle. Proclus remarked that the semicircle is the only plane figure that has its center on its perimeter. Some writers object to defining a circle as a line and then speaking of the area of a circle, showing minds that have at least one characteristic of that of Proclus. The modern definition of semicircle is "half of a circle," that is, an arc of 180°, although the term is commonly used to mean both the arc and the segment.
19. Rectilinear Figures. Rectilinear figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained[Pg 147] by four, and multilateral those contained by more than four, straight lines.
20. Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.
21. Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute.
These three definitions may properly be considered together. "Rectilinear" is from the Latin translation of the Greek euthygrammos, and means "right-lined," or "straight-lined." Euclid's idea of such a figure is that of the space inclosed, while the modern idea is tending to become that of the inclosing lines. In elementary geometry, however, the Euclidean idea is still held. "Trilateral" is from the Latin translation of the Greek tripleuros (three-sided). In elementary geometry the word "triangle" is more commonly used, although "quadrilateral" is more common than "quadrangle." The use of these two different forms is eccentric and is merely a matter of fashion. Thus we speak of a pentagon but not of a tetragon or a trigon, although both words are correct in form. The word "multilateral" (many-sided) is a translation of the Greek polypleuros. Fashion has changed this to "polygonal" (many-angled), the word "multilateral" rarely being seen.
Of the triangles, "equilateral" means "equal-sided"; "isosceles" is from the Greek isoskeles, meaning "with equal legs," and "scalene" from skalenos, possibly from skazo (to limp), or from skolios (crooked). Euclid's limitation of isosceles to a triangle with two, and only two,[Pg 148] equal sides would not now be accepted. We are at present more given to generalizing than he was, and when we have proved a proposition relating to the isosceles triangle, we wish to say that we have thereby proved it for the equilateral triangle. We therefore say that an isosceles triangle has two sides equal, leaving it possible that all three sides should be equal. The expression "equal legs" is now being discarded on the score of inelegance. In place of "right-angled triangle" modern writers speak of "right triangle," and so for the obtuse and acute triangles. The terms are briefer and are as readily understood. It may add a little interest to the subject to know that Plutarch tells us that the ancients thought that "the power of the triangle is expressive of the nature of Pluto, Bacchus, and Mars." He also states that the Pythagoreans called "the equilateral triangle the head-born Minerva and Tritogeneia (born of Triton) because it may be equally divided by the perpendicular lines drawn from each of its angles."
22. Of quadrilateral figures a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral and not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another, but is neither equilateral nor right-angled. And let all quadrilaterals other than these be called trapezia. In this definition Euclid also specializes in a manner not now generally approved. Thus we are more apt to-day to omit the oblong and rhomboid as unnecessary, and to define "rhombus" in such a manner as to include a square. We use "parallelogram" to cover "rhomboid," "rhombus," "oblong," and "square." For "oblong" we use "rectangle," letting it include square. Euclid's definition of "square"[Pg 149] illustrates his freedom in stating more attributes than are necessary, in order to make sure that the concept is clear; for he might have said that it "is that which is equilateral and has one right angle." We may profit by his method, sacrificing logic to educational necessity. Euclid does not use "oblong," "rhombus," "rhomboid," and "trapezium" (plural, "trapezia") in his proofs, so that he might well have omitted the definitions, as we often do.
23. Parallels. Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction. This definition of parallels, simplified in its language, is the one commonly used to-day. Other definitions have been suggested, but none has been so generally used. Proclus states that Posidonius gave the definition based upon the lines always being at the same distance apart. Geminus has the same idea in his definition. There are, as Schotten has pointed out, three general types of definitions of parallels, namely:
a. They have no point in common. This may be expressed by saying that (1) they do not intersect, (2) they meet at infinity.
b. They are equidistant from one another.
c. They have the same direction.
Of these, the first is Euclid's, the idea of the point at infinity being suggested by Kepler (1604). The second part of this definition is, of course, unusable for beginners. Dr. (now Sir Thomas) Heath says, "It seems best, therefore, to leave to higher geometry the conception of infinitely distant points on a line and of two straight lines meeting at infinity, like imaginary points of intersection, and, for the purposes of elementary geometry, to rely on the plain distinction between 'parallel'[Pg 150] and 'cutting,' which average human intelligence can readily grasp."
The direction definition seems to have originated with Leibnitz. It is open to the serious objection that "direction" is not easy of definition, and that it is used very loosely. If two people on different meridians travel due north, do they travel in the same direction? on parallel lines? The definition is as objectionable as that of angle as the "difference of direction" of two intersecting lines.
From these definitions of the first book of Euclid we see (1) what a small number Euclid considered as basal; (2) what a change has taken place in the generalization of concepts; (3) how the language has varied. Nevertheless we are not to be commended if we adhere to Euclid's small number, because geometry is now taught to pupils whose vocabulary is limited. It is necessary to define more terms, and to scatter the definitions through the work for use as they are needed, instead of massing them at the beginning, as in a dictionary. The most important lesson to be learned from Euclid's definitions is that only the basal ones, relatively few in number, need to be learned, and these because they are used as the foundations upon which proofs are built. It should also be noticed that Euclid explains nothing in these definitions; they are hard statements of fact, massed at the beginning of his treatise. Not always as statements, and not at all in their arrangement, are they suited to the needs of our boys and girls at present.
Having considered Euclid's definitions of Book I, it is proper to turn to some of those terms that have been added from time to time to his list, and are now usually incorporated in American textbooks. It will be seen that[Pg 151] most of these were assumed by Euclid to be known by his mature readers. They need to be defined for young people, but most of them are not basal, that is, they are not used in the proofs of propositions. Some of these terms, such as magnitudes, curve line, broken line, curvilinear figure, bisector, adjacent angles, reflex angles, oblique angles and lines, and vertical angles, need merely a word of explanation so that they may be used intelligently. If they were numerous enough to make it worth the while, they could be classified in our textbooks as of minor importance, but such a course would cause more trouble than it is worth.
Other terms have come into use in modern times that are not common expressions with which students are familiar. Such a term is "straight angle," a concept not used by Euclid, but one that adds so materially to the interest and value of geometry as now to be generally recognized. There is also the word "perigon," meaning the whole angular space about a point. This was excluded by the Greeks because their idea of angle required it to be less than a straight angle. The word means "around angle," and is the best one that has been coined for the purpose. "Flat angle" and "whole angle" are among the names suggested for these two modern concepts. The terms "complement," "supplement," and "conjugate," meaning the difference between a given angle and a right angle, straight angle, and perigon respectively, have also entered our vocabulary and need defining.
There are also certain terms expressing relationship which Euclid does not define, and which have been so changed in recent times as to require careful definition at present. Chief among these are the words "equal," "congruent," and "equivalent." Euclid used the single word[Pg 152] "equal" for all three concepts, although some of his recent editors have changed it to "identically equal" in the case of congruence. In modern speech we use the word "equal" commonly to mean "like-valued," "having the same measure," as when we say the circumference of a circle "equals" a straight line whose length is 2πr, although it could not coincide with it. Of late, therefore, in Europe and America, and wherever European influence reaches, the word "congruent" is coming into use to mean "identically equal" in the sense of superposable. We therefore speak of congruent triangles and congruent parallelograms as being those that are superposable.
It is a little unfortunate that "equal" has come to be so loosely used in ordinary conversation that we cannot keep it to mean "congruent"; but our language will not permit it, and we are forced to use the newer word. Whenever it can be used without misunderstanding, however, it should be retained, as in the case of "equal straight lines," "equal angles," and "equal arcs of the same circle." The mathematical and educational world will never consent to use "congruent straight lines," or "congruent angles," for the reason that the terms are unnecessarily long, no misunderstanding being possible when "equal" is used.
The word "equivalent" was introduced by Legendre at the close of the eighteenth century to indicate equality of length, or of area, or of volume. Euclid had said, "Parallelograms which are on the same base and in the same parallels are equal to one another," while Legendre and his followers would modify the wording somewhat and introduce "equivalent" for "equal." This usage has been retained. Congruent polygons are therefore[Pg 153] necessarily equivalent, but equivalent polygons are not in general congruent. Congruent polygons have mutually equal sides and mutually equal angles, while equivalent polygons have no equality save that of area.
In general, as already stated, these and other terms should be defined just before they are used instead of at the beginning of geometry. The reason for this, from the educational standpoint and considering the present position of geometry in the curriculum, is apparent.
We shall now consider the definitions of Euclid's Book III, which is usually taken as Book II in America.
1. Equal Circles. Equal circles are those the diameters of which are equal, or the radii of which are equal.
Manifestly this is a theorem, for it asserts that if the radii of two circles are equal, the circles may be made to coincide. In some textbooks a proof is given by superposition, and the proof is legitimate, but Euclid usually avoided superposition if possible. Nevertheless he might as well have proved this as that two triangles are congruent if two sides and the included angle of the one are respectively equal to the corresponding parts of the other, and he might as well have postulated the latter as to have substantially postulated this fact. For in reality this definition is a postulate, and it was so considered by the great Italian mathematician Tartaglia (ca. 1500-ca. 1557). The plan usually followed in America to-day is to consider this as one of many unproved propositions, too evident, indeed, for proof, accepted by intuition. The result is a loss in the logic of Euclid, but the method is thought to be better adapted to the mind of the youthful learner. It is interesting to note in this connection that the Greeks had no word for "radius," and were therefore compelled to use some such phrase as[Pg 154] "the straight line from the center," or, briefly, "the from the center," as if "from the center" were one word.
2. Tangent. A straight line is said to touch a circle which, meeting the circle and being produced, does not cut the circle.
Teachers who prefer to use "circumference" instead of "circle" for the line should notice how often such phrases as "cut the circle" and "intersecting circle" are used,—phrases that signify nothing unless "circle" is taken to mean the line. So Aristotle uses an expression meaning that the locus of a certain point is a circle, and he speaks of a circle as passing through "all the angles." Our word "touch" is from the Latin tangere, from which comes "tangent," and also "tag," an old touching game.
3. Tangent Circles. Circles are said to touch one another which, meeting one another, do not cut one another.
The definition has not been looked upon as entirely satisfactory, even aside from its unfortunate phraseology. It is not certain, for instance, whether Euclid meant that the circles could not cut at some other point than that of tangency. Furthermore, no distinction is made between external and internal contact, although both forms are used in the propositions. Modern textbook makers find it convenient to define tangent circles as those that are tangent to the same straight line at the same point, and to define external and internal tangency by reference to their position with respect to the line, although this may be characterized as open to about the same objection as Euclid's.
4. Distance. In a circle straight lines are said to be equally distant from the center, when the perpendiculars drawn to them from the center are equal.[Pg 155]
It is now customary to define "distance" from a point to a line as the length of the perpendicular from the point to the line, and to do this in Book I. In higher mathematics it is found that distance is not a satisfactory term to use, but the objections to it have no particular significance in elementary geometry.
5. Greater Distance. And that straight line is said to be at a greater distance on which the greater perpendicular falls.
Such a definition is not thought essential at the present time.
6. Segment. A segment of a circle is the figure contained by a straight line and the circumference of a circle.
The word "segment" is from the Latin root sect, meaning "cut." So we have "sector" (a cutter), "section" (a cut), "intersect," and so on. The word is not limited to a circle; we have long spoken of a spherical segment, and it is common to-day to speak of a line segment, to which some would apply a new name "sect." There is little confusion in the matter, however, for the context shows what kind of a segment is to be understood, so that the word "sect" is rather pedantic than important. It will be noticed that Euclid here uses "circumference" to mean "arc."
7. Angle of a Segment. An angle of a segment is that contained by a straight line and a circumference of a circle.
This term has entirely dropped out of geometry, and few teachers would know what it meant if they should hear it used. Proclus called such angles "mixed."
8. Angle in a Segment. An angle in a segment is the angle which, when a point is taken on the circumference of the segment and straight lines are joined from it to[Pg 156] the extremities of the straight line which is the base of the segment, is contained by the straight lines so joined.
Such an involved definition would not be usable to-day. Moreover, the words "circumference of the segment" would not be used.
9. And when the straight lines containing the angle cut off a circumference, the angle is said to stand upon that circumference.
10. Sector. A sector of a circle is the figure which, when an angle is constructed at the center of the circle, is contained by the straight lines containing the angle and the circumference cut off by them.
There is no reason for such an extended definition, our modern phraseology being both more exact (as seen in the above use of "circumference" for "arc") and more intelligible. The Greek word for "sector" is "knife" (tomeus), "sector" being the Latin translation. A sector is supposed to resemble a shoemaker's knife, and hence the significance of the term. Euclid followed this by a definition of similar sectors, a term now generally abandoned as unnecessary.
It will be noticed that Euclid did not use or define the word "polygon." He uses "rectilinear figure" instead. Polygon may be defined to be a bounding line, as a circle is now defined, or as the space inclosed by a broken line, or as a figure formed by a broken line, thus including both the limited plane and its boundary. It is not of any great consequence geometrically which of these ideas is adopted, so that the usual definition of a portion of a plane bounded by a broken line may be taken as sufficient for elementary purposes. It is proper to call attention, however, to the fact that we may have cross polygons of various types, and that the line that "bounds" the[Pg 157] polygon must be continuous, as the definition states. That is, in the second of these figures the shaded portion is not considered a polygon. Such special cases are not liable to arise, but if questions relating to them are suggested, the teacher should be prepared to answer them. If suggested to a class, a note of this kind should come out only incidentally as a bit of interest, and should not occupy much time nor be unduly emphasized.
It may also be mentioned to a class at some convenient time that the old idea of a polygon was that of a convex figure, and that the modern idea, which is met in higher mathematics, leads to a modification of earlier concepts. For example, here is a quadrilateral with one of its diagonals, BD, outside the figure. Furthermore, if we consider a quadrilateral as a figure formed by four intersecting lines, AC, CF, BE, and EA, it is apparent that this general quadrilateral has six vertices, A, B, C, D, E, F, and three diagonals, AD, BF, and CE. Such broader ideas of geometry form the basis of what is called modern elementary geometry.
The other definitions of plane geometry need not be discussed, since all that have any historical interest have been considered. On the whole it may be said that our definitions to-day are not in general so carefully considered as those of Euclid, who weighed each word with[Pg 158] greatest skill, but they are more teachable to beginners, and are, on the whole, more satisfactory from the educational standpoint. The greatest lesson to be learned from this discussion is that the number of basal definitions to be learned for subsequent use is very small.
Since teachers are occasionally disturbed over the form in which definitions are stated, it is well to say a few words upon this subject. There are several standard types that may be used. (1) We may use the dictionary form, putting the word defined first, thus: "Right triangle. A triangle that has one of its angles a right angle." This is scientifically correct, but it is not a complete sentence, and hence it is not easily repeated when it has to be quoted as an authority. (2) We may put the word defined at the end, thus: "A triangle that has one of its angles a right angle is called a right triangle." This is more satisfactory. (3) We may combine (1) and (2), thus: "Right triangle. A triangle that has one of its angles a right angle is called a right triangle." This is still better, for it has the catchword at the beginning of the paragraph.
There is occasionally some mental agitation over the trivial things of a definition, such as the use of the words "is called." It would not be a very serious matter if they were omitted, but it is better to have them there. The reason is that they mark the statement at once as a definition. For example, suppose we say that "a triangle that has one of its angles a right angle is a right triangle." We have also the fact that "a triangle whose base is the diameter of a semicircle and whose vertex lies on the semicircle is a right triangle." The style of statement is the same, and we have nothing in the phraseology to show that the first is a definition and the second[Pg 159] a theorem. This may happen with most of the definitions, and hence the most careful writers have not consented to omit the distinctive words in question.
Apropos of the definitions of geometry, the great French philosopher and mathematician, Pascal, set forth certain rules relating to this subject, as also to the axioms employed, and these may properly sum up this chapter.
1. Do not attempt to define terms so well known in themselves that there are no simpler terms by which to express them.
2. Admit no obscure or equivocal terms without defining them.
3. Use in the definitions only terms that are perfectly understood or are there explained.
4. Omit no necessary principles without general agreement, however clear and evident they may be.
5. Set forth in the axioms only those things that are in themselves perfectly evident.
6. Do not attempt to demonstrate anything that is so evident in itself that there is nothing more simple by which to prove it.
7. Prove whatever is in the least obscure, using in the demonstration only axioms that are perfectly evident in themselves, or propositions already demonstrated or allowed.
8. In case of any uncertainty arising from a term employed, always substitute mentally the definition for the term itself.
Bibliography. Heath, Euclid, as cited; Frankland, The First Book of Euclid, as cited; Smith, Teaching of Elementary Mathematics, p. 257, New York, 1900; Young, Teaching of Mathematics, p. 189, New York, 1907; Veblen, On Definitions, in the Monist, 1903, p. 303.
The old geometry, say of a century ago, usually consisted, as has been stated, of a series of theorems fully proved and of problems fully solved. During the nineteenth century exercises were gradually introduced, thus developing geometry from a science in which one learned by seeing things done, into one in which he gained power by actually doing things. Of the nature of these exercises ("originals," "riders"), and of their gradual change in the past few years, mention has been made in Chapter VII. It now remains to consider the methods of attacking these exercises.
It is evident that there is no single method, and this is a fortunate fact, since if it were not so, the attack would be too mechanical to be interesting. There is no one rule for solving every problem nor even for seeing how to begin. On the other hand, a pupil is saved some time by having his attention called to a few rather definite lines of attack, and he will undoubtedly fare the better by not wasting his energies over attempts that are in advance doomed to failure.
There are two general questions to be considered: first, as to the discovery of new truths, and second, as to the proof. With the first the pupil will have little to do, not having as yet arrived at this stage in his progress. A bright student may take a little interest in seeing what[Pg 161] he can find out that is new (at least to him), and if so, he may be told that many new propositions have been discovered by the accurate drawing of figures; that some have been found by actually weighing pieces of sheet metal of certain sizes; and that still others have made themselves known through paper folding. In all of these cases, however, the supposed proposition must be proved before it can be accepted.
As to the proof, the pupil usually wanders about more or less until he strikes the right line, and then he follows this to the conclusion. He should not be blamed for doing this, for he is pursuing the method that the world followed in the earliest times, and one that has always been common and always will be. This is the synthetic method, the building up of the proof from propositions previously proved. If the proposition is a theorem, it is usually not difficult to recall propositions that may lead to the demonstration, and to select the ones that are really needed. If it is a problem, it is usually easy to look ahead and see what is necessary for the solution and to select the preceding propositions accordingly.
But pupils should be told that if they do not rather easily find the necessary propositions for the construction or the proof, they should not delay in resorting to another and more systematic method. This is known as the method of analysis, and it is applicable both to theorems and to problems. It has several forms, but it is of little service to a pupil to have these differentiated, and it suffices that he be given the essential feature of all these forms, a feature that goes back to Plato and his school in the fifth century B.C.
For a theorem, the method of analysis consists in reasoning as follows: "I can prove this proposition if I[Pg 162] can prove this thing; I can prove this thing if I can prove that; I can prove that if I can prove a third thing," and so the reasoning runs until the pupil comes to the point where he is able to add, "but I can prove that." This does not prove the proposition, but it enables him to reverse the process, beginning with the thing he can prove and going back, step by step, to the thing that he is to prove. Analysis is, therefore, his method of discovery of the way in which he may arrange his synthetic proof. Pupils often wonder how any one ever came to know how to arrange the proofs of geometry, and this answers the question. Some one guessed that a statement was true; he applied analysis and found that he could prove it; he then applied synthesis and did prove it.
For a problem, the method of analysis is much the same as in the case of a theorem. Two things are involved, however, instead of one, for here we must make the construction and then prove that this construction is correct. The pupil, therefore, first supposes the problem solved, and sees what results follow. He then reverses the process and sees if he can attain these results and thus effect the required construction. If so, he states the process and gives the resulting proof. For example:
In a triangle ABC, to draw PQ parallel to the base AB, cutting the sides in P and Q, so that PQ shall equal AP + BQ.
Analysis. Assume the problem solved.
Then AP must equal some part of PQ as PX, and BQ must equal QX.
But if AP = PX, what must ∠PXA equal?
∵ PQ is || AB, what does ∠PXA equal?
Then why must ∠BAX = ∠XAP?
Similarly, what about ∠QBX and ∠XBA?
Construction. Now reverse the process. What may we do to ⦞A and B in order to fix X? Then how shall PQ be drawn? Now give the proof.
The third general method of attack applies chiefly to problems where some point is to be determined. This is the method of the intersection of loci. Thus, to locate an electric light at a point eighteen feet from the point of intersection of two streets and equidistant from them, evidently one locus is a circle with a radius eighteen feet and the center at the vertex of the angle made by the streets, and the other locus is the bisector of the angle. The method is also occasionally applicable to theorems. For example, to prove that the perpendicular bisectors of the sides of a triangle are concurrent. Here the locus of points equidistant from A and B is PP', and the locus of points equidistant from B and C is QQ'. These can easily be shown to intersect, as at O. Then O, being equidistant from A, B, and C, is also on the perpendicular bisector of AC. Therefore these bisectors are concurrent in O.
These are the chief methods of attack, and are all that should be given to an average class for practical use.
Besides the methods of attack, there are a few general directions that should be given to pupils.
1. In attacking either a theorem or a problem, take the most general figure possible. Thus, if a proposition relates to a quadrilateral, take one with unequal sides and unequal angles rather than a square or even a rectangle. The simpler figures often deceive a pupil into feeling that he has a proof, when in reality he has one only for a special case.[Pg 164]
2. Set forth very exactly the thing that is given, using letters relating to the figure that has been drawn. Then set forth with the same exactness the thing that is to be proved. The neglect to do this is the cause of a large per cent of the failures. The knowing of exactly what we have to do and exactly what we have with which to do it is half the battle.
3. If the proposition seems hazy, the difficulty is probably with the wording. In this case try substituting the definition for the name of the thing defined. Thus instead of thinking too long about proving that the median to the base of an isosceles triangle is perpendicular to the base, draw the figure and think that there is given
AC = BC,
AD = BD,
and that there is to be proved that
∠CDA = ∠BDC.
Here we have replaced "median," "isosceles," and "perpendicular" by statements that express the same idea in simpler language.
Bibliography. Petersen, Methods and Theories for the Solution of Geometric Problems of Construction, Copenhagen, 1879, a curious piece of English and an extreme view of the subject, but well worth consulting; Alexandroff, Problèmes de géométrie élémentaire, Paris, 1899, with a German translation in 1903; Loomis, Original Investigation; or, How to attack an Exercise in Geometry, Boston, 1901; Sauvage, Les Lieux géométriques en géométrie élémentaire, Paris, 1893; Hadamard, Leçons de géométrie, p. 261, Paris, 1898; Duhamel, Des Méthodes dans les sciences de raisonnement, 3e éd., Paris, 1885; Henrici and Treutlein, Lehrbuch der Elementar-Geometrie, Leipzig, 3. Aufl., 1897; Henrici, Congruent Figures, London, 1879.
Having considered the nature of the geometry that we have inherited, and some of the opportunities for improving upon the methods of presenting it, the next question that arises is the all-important one of the subject matter, What shall geometry be in detail? Shall it be the text or the sequence of Euclid? Few teachers have any such idea at the present time. Shall it be a mere dabbling with forms that are seen in mechanics or architecture, with no serious logical sequence? This is an equally dangerous extreme. Shall it be an entirely new style of geometry based upon groups of motions? This may sometime be developed, but as yet it exists in the future if it exists at all, since the recent efforts in this respect are generally quite as ill suited to a young pupil as is Euclid's "Elements" itself.
No one can deny the truth of M. Bourlet's recent assertion that "Industry, daughter of the science of the nineteenth century, reigns to-day the mistress of the world; she has transformed all ancient methods, and she has absorbed in herself almost all human activity."[57] Neither can one deny the justice of his comparison of Euclid with a noble piece of Gothic architecture and of his assertion that as modern life demands another type of building, so it demands another type of geometry.
But what does this mean? That geometry is to exist merely as it touches industry, or that bad architecture is to replace the good? By no means. A building should to-day have steam heat and elevators and electric lights, but it should be constructed of just as enduring materials as the Parthenon, and it should have lines as pleasing as those of a Gothic façade. Architecture should still be artistic and construction should still be substantial, else a building can never endure. So geometry must still exemplify good logic and must still bring to the pupil a feeling of exaltation, or it will perish and become a mere relic in the museum of human culture.
What, then, shall the propositions of geometry be, and in what manner shall they answer to the challenge of the industrial epoch in which we live? In reply, they must be better adapted to young minds and to all young minds than Euclid ever intended his own propositions to be. Furthermore, they must have a richness of application to pure geometry, in the way of carefully chosen exercises, that Euclid never attempted. And finally, they must have application to this same life of industry of which we have spoken, whenever this can really be found, but there must be no sham and pretense about it, else the very honesty that permeated the ancient geometry will seem to the pupil to be wanting in the whole subject.[58]
Until some geometry on a radically different basis shall appear, and of this there is no very hopeful sign at present, the propositions will be the essential ones of Euclid, excluding those that may be considered merely intuitive, and excluding all that are too difficult for the pupil who
to-day takes up their study. The number will be limited in a reasonable way, and every genuine type of application will be placed before the teacher to be used as necessity requires. But a fair amount of logic will be retained, and the effort to make of geometry an empty bauble of a listless mind will be rejected by every worthy teacher. What the propositions should be is a matter upon which opinions may justly differ; but in this chapter there is set forth a reasonable list for Book I, arranged in a workable sequence, and this list may fairly be taken as typical of what the American school will probably use for many years to come. With the list is given a set of typical applications, and some of the general information that will add to the interest in the work and that should form part of the equipment of the teacher.
An ancient treatise was usually written on a kind of paper called papyrus, made from the pith of a large reed formerly common in Egypt, but now growing luxuriantly only above Khartum in Upper Egypt, and near Syracuse in Sicily; or else it was written on parchment, so called from Pergamos in Asia Minor, where skins were first prepared in parchment form; or occasionally they were written on ordinary leather. In any case they were generally written on long strips of the material used, and these were rolled up and tied. Hence we have such an expression as "keeping the roll" in school, and such a word as "volume," which has in it the same root as "involve" (to roll in), and "evolve" (to roll out). Several of these rolls were often necessary for a single treatise, in which case each was tied, and all were kept together in a receptacle resembling a pail, or in a compartment on a shelf. The Greeks called each of the separate parts of a treatise biblion (βιβλίον), a word meaning "book."[Pg 168] Hence we have the books of the Bible, the books of Homer, and the books of Euclid. From the same root, indeed, comes Bible, bibliophile (booklover), bibliography (list of books), and kindred words. Thus the books of geometry are the large chapters of the subject, "chapter" being from the Latin caput (head), a section under a new heading. There have been efforts to change "books" to "chapters," but they have not succeeded, and there is no reason why they should succeed, for the term is clear and has the sanction of long usage.
Theorem. If two lines intersect, the vertical angles are equal.
This was Euclid's Proposition 15, being put so late because he based the proof upon his Proposition 13, now thought to be best taken without proof, namely, "If a straight line set upon a straight line makes angles, it will make either two right angles or angles equal to two right angles." It is found to be better pedagogy to assume that this follows from the definition of straight angle, with reference, if necessary, to the meaning of the sum of two angles. This proposition on vertical angles is probably the best one with which to begin geometry, since it is not so evident as to seem to need no proof, although some prefer to rank it as semiobvious, while the proof is so simple as easily to be understood. Eudemus, a Greek who wrote not long before Euclid, attributed the discovery of this proposition to Thales of Miletus (ca. 640-548 B.C.), one of the Seven Wise Men of Greece, of whom Proclus wrote: "Thales it was who visited Egypt and first transferred to Hellenic soil this theory of geometry. He himself, indeed, discovered much, but still more did he introduce to his successors the principles of the science."[Pg 169]
The proposition is the only basal one relating to the intersection of two lines, and hence there are no others with which it is necessarily grouped. This is the reason for placing it by itself, followed by the congruence theorems.
There are many familiar illustrations of this theorem. Indeed, any two crossed lines, as in a pair of shears or the legs of a camp stool, bring it to mind. The word "straight" is here omitted before "lines" in accordance with the modern convention that the word "line" unmodified means a straight line. Of course in cases of special emphasis the adjective should be used.
Theorem. Two triangles are congruent if two sides and the included angle of the one are equal respectively to two sides and the included angle of the other.
This is Euclid's Proposition 4, his first three propositions being problems of construction. This would therefore have been his first proposition if he had placed his problems later, as we do to-day. The words "congruent" and "equal" are not used as in Euclid, for reasons already set forth on page 151. There have been many attempts to rearrange the propositions of Book I, putting in separate groups those concerning angles, those concerning triangles, and those concerning parallels, but they have all failed, and for the cogent reason that such a scheme destroys the logical sequence. This proposition may properly follow the one on vertical angles simply because the latter is easier and does not involve superposition.
As far as possible, Euclid and all other good geometers avoid the proof by superposition. As a practical test superposition is valuable, but as a theoretical one it is open to numerous objections. As Peletier pointed out in his (1557) edition of Euclid, if the superposition of[Pg 170] lines and figures could freely be assumed as a method of demonstration, geometry would be full of such proofs. There would be no reason, for example, why an angle should not be constructed equal to a given angle by superposing the given angle on another part of the plane. Indeed, it is possible that we might then assume to bisect an angle by imagining the plane folded like a piece of paper. Heath (1908) has pointed out a subtle defect in Euclid's proof, in that it is said that because two lines are equal, they can be made to coincide. Euclid says, practically, that if two lines can be made to coincide, they are equal, but he does not say that if two straight lines are equal, they can be made to coincide. For the purposes of elementary geometry the matter is hardly worth bringing to the attention of a pupil, but it shows that even Euclid did not cover every point.
Applications of this proposition are easily found, but they are all very much alike. There are dozens of measurements that can be made by simply constructing a triangle that shall be congruent to another triangle. It seems hardly worth the while at this time to do more than mention one typical case,[59] leaving it to teachers who may find it desirable to suggest others to their pupils.
Wishing to measure the distance across a river, some boys sighted from A to a point P. They then turned and measured AB at right angles to AP. They placed a stake at O, halfway from A to B, and drew a perpendicular to AB at B. They placed a stake at C, on this perpendicular, and in line with O and P. They then found the width by measuring BC. Prove that they were right.
This involves the ranging of a line, and the running of a line at right angles to a given line, both of which have been described in Chapter IX. It is also fairly accurate to run a line at any angle to a given line by sighting along two pins stuck in a protractor.
Theorem. Two triangles are congruent if two angles and the included side of the one are equal respectively to two angles and the included side of the other.
Euclid combines this with his Proposition 26:
If two triangles have the two angles equal to two angles respectively, and one side equal to one side, namely, either the side adjoining the equal angles, or that subtending one of the equal angles, they will also have the remaining sides equal to the remaining sides, and the remaining angle to the remaining angle.
He proves this cumbersome statement without superposition, desiring to avoid this method, as already stated, whenever possible. The proof by superposition is old, however, for Al-Nairīzī[60] gives it and ascribes it to some earlier author whose name he did not know. Proclus tells us that "Eudemus in his geometrical history refers this theorem to Thales. For he says that in the method by which they say that Thales proved the distance of ships in the sea, it was necessary to make use of this theorem." How Thales did this is purely a matter of conjecture, but he might have stood on the top of a tower rising from the level shore, or of such headlands as abound near Miletus, and by some simple instrument sighted to the ship. Then, turning, he might have sighted along the shore to a point having the same angle of declination, and then have measured the distance from the tower [Pg 172]to this point. This seems more reasonable than any of the various plans suggested, and it is found in so many practical geometries of the first century of printing that it seems to have long been a common expedient. The stone astrolabe from Mesopotamia, now preserved in the British Museum, shows that such instruments for the measuring of angles are very old, and for the purposes of Thales even a pair of large compasses would have answered very well. An illustration of the method is seen in Belli's work of 1569, as here shown. At the top of the picture a man is getting the angle by means of the visor of his cap; at the bottom of the picture a man is using a ruler screwed to a staff.[61] The story goes that [Pg 173]one of Napoleon's engineers won the imperial favor by quickly measuring the width of a stream that blocked the progress of the army, using this very method.
This proposition is the reciprocal or dual of the preceding one. The relation between the two may be seen from the following arrangement:
Two triangles are congruent if two sides and the included angle of the one are equal respectively to two sides and the included angle of the other.
Two triangles are congruent if two angles and the included side of the one are equal respectively to two angles and the included side of the other.
In general, to every proposition involving points and lines there is a reciprocal proposition involving lines and points respectively that is often true,—indeed, that is always true in a certain line of propositions. This relation is known as the Principle of Reciprocity or of Duality. Instead of points and lines we have here angles (suggested by the vertex points) and lines. It is interesting to a class to have attention called to such relations, but it is not of sufficient importance in elementary geometry to justify more than a reference here and there. There are other dual features that are seen in geometry besides those given above.
Theorem. In an isosceles triangle the angles opposite the equal sides are equal.
This is Euclid's Proposition 5, the second of his theorems, but he adds, "and if the equal straight lines be produced further, the angles under the base will be equal to one another." Since, however, he does not use this second part, its genuineness is doubted. He would not admit the common proof of to-day of supposing the vertical angle bisected, because the problem about bisecting an angle does not precede this proposition, and therefore[Pg 174] his proof is much more involved than ours. He makes CX = CY, and proves ⧌XBC and YAC congruent,[62] and also ⧌XBA and YAB congruent. Then from ∠YAC he takes ∠YAB, leaving ∠BAC, and so on the other side, leaving ∠CBA, these therefore being equal.
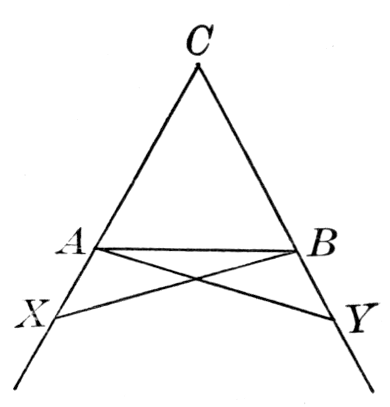
This proposition has long been called the pons asinorum, or bridge of asses, but no one knows where or when the name arose. It is usually stated that it came from the fact that fools could not cross this bridge, and it is a fact that in the Middle Ages this was often the limit of the student's progress in geometry. It has however been suggested that the name came from Euclid's figure, which resembles the simplest type of a wooden truss bridge. The name is applied by the French to the Pythagorean Theorem.
Proclus attributes the discovery of this proposition to Thales. He also says that Pappus (third century A.D.), a Greek commentator on Euclid, proved the proposition as follows:
Let ABC be the triangle, with AB = AC. Conceive of this as two triangles; then AB = AC, AC = AB, and ∠A is common; hence the ⧌ABC and ACB are congruent, and ∠B of the one equals ∠C of the other.
This is a better plan than that followed by some textbook writers of imagining ⧍ABC taken up and laid down on itself. Even to lay it down on its "trace" is more objectionable than the plan of Pappus.
Theorem. If two angles of a triangle are equal, the sides opposite the equal angles are equal, and the triangle is isosceles.
The statement is, of course, tautological, the last five words being unnecessary from the mathematical standpoint, but of value at this stage of the student's progress as emphasizing the nature of the triangle. Euclid stated the proposition thus, "If in a triangle two angles be equal to one another, the sides which subtend the equal angles will also be equal to one another." He did not define "subtend," supposing such words to be already understood. This is the first case of a converse proposition in geometry. Heath distinguishes the logical from the geometric converse. The logical converse of Euclid I, 5, would be that "some triangles with two angles equal are isosceles," while the geometric converse is the proposition as stated. Proclus called attention to two forms of converse (and in the course of the work, but not at this time, the teacher may have to do the same): (1) the complete converse, in which that which is given in one becomes that which is to be proved in the other, and vice versa, as in this and the preceding proposition; (2) the partial converse, in which two (or even more) things may be given, and a certain thing is to be proved, the converse being that one (or more) of the preceding things is now given, together with what was to be proved, and the other given thing is now to be proved. Symbolically, if it is given that a = b and c = d, to prove that x = y, the partial converse would have given a = b and x = y, to prove that c = d.
Several proofs for the proposition have been suggested, but a careful examination of all of them shows that the one given below is, all things considered, the best one for pupils beginning geometry and following the[Pg 176] sequence laid down in this chapter. It has the sanction of some of the most eminent mathematicians, and while not as satisfactory in some respects as the reductio ad absurdum, mentioned below, it is more satisfactory in most particulars. The proof is as follows:
 Given the triangle ABC, with the angle A equal to the angle B.
Given the triangle ABC, with the angle A equal to the angle B.
To prove that AC = BC.
Proof. Suppose the second triangle A'B'C' to be an exact reproduction of the given triangle ABC.
Turn the triangle A'B'C' over and place it upon ABC so that B' shall fall on A and A' shall fall on B.
Then B'A' will coincide with AB.
Since ∠A' = ∠B', Given
and ∠A = ∠A', Hyp.
∴∠A = ∠B'.
∴B'C' will lie along AC.
Similarly, A'C' will lie along BC.
Therefore C' will fall on both AC and BC, and hence at their intersection.
∴B'C' = AC.
But B'C' was made equal to BC.
∴AC = BC. Q.E.D.
If the proposition should be postponed until after the one on the sum of the angles of a triangle, the proof would be simpler, but it is advantageous to couple it with its immediate predecessor. This simpler proof consists[Pg 177] in bisecting the vertical angle, and then proving the two triangles congruent. Among the other proofs is that of the reductio ad absurdum, which the student might now meet, but which may better be postponed. The phrase reductio ad absurdum seems likely to continue in spite of the efforts to find another one that is simpler. Such a proof is also called an indirect proof, but this term is not altogether satisfactory. Probably both names should be used, the Latin to explain the nature of the English. The Latin name is merely a translation of one of several Greek names used by Aristotle, a second being in English "proof by the impossible," and a third being "proof leading to the impossible." If teachers desire to introduce this form of proof here, it must be borne in mind that only one supposition can be made if such a proof is to be valid, for if two are made, then an absurd conclusion simply shows that either or both must be false, but we do not know which is false, or if only one is false.
Theorem. Two triangles are congruent if the three sides of the one are equal respectively to the three sides of the other.
It would be desirable to place this after the fourth proposition mentioned in this list if it could be done, so as to get the triangles in a group, but we need the fourth one for proving this, so that the arrangement cannot be made, at least with this method of proof.
This proposition is a "partial converse" of the second proposition in this list; for if the triangles are ABC and A'B'C', with sides a, b, c and a', b', c', then the second proposition asserts that if b = b', c = c', and ∠A = ∠A', then a = a' and the triangles are congruent, while this proposition asserts that if a = a', b = b', and c = c', then ∠A = ∠A' and the triangles are congruent.
The proposition was known at least as early as Aristotle's time. Euclid proved it by inserting a preliminary[Pg 178] proposition to the effect that it is impossible to have on the same base AB and the same side of it two different triangles ABC and ABC', with AC = AC', and BC = BC'. The proof ordinarily given to-day, wherein the two triangles are constructed on opposite sides of the base, is due to Philo of Byzantium, who lived after Euclid's time but before the Christian era, and it is also given by Proclus. There are really three cases, if one wishes to be overparticular, corresponding to the three pairs of equal sides. But if we are allowed to take the longest side for the common base, only one case need be considered.
Of the applications of the proposition one of the most important relates to making a figure rigid by means of diagonals. For example, how many diagonals must be drawn in order to make a quadrilateral rigid? to make a pentagon rigid? a hexagon? a polygon of n sides. In particular, the following questions may be asked of a class:
1. Three iron rods are hinged at the extremities, as shown in this figure. Is the figure rigid? Why?
2. Four iron rods are hinged, as shown in this figure. Is the figure rigid? If not, where would you put in the fifth rod to make it rigid? Prove that this would accomplish the result.
Another interesting application relates to the most ancient form of leveling instrument known to us. This kind of level is pictured on very ancient monuments, and it is still used in many parts of the world. Pupils in manual training may make such an instrument, and indeed one is easily made out of cardboard.[Pg 179] If the plumb line passes through the mid-point of the base, the two triangles are congruent and the plumb line is then perpendicular to the base. In other words, the base is level. With such simple primitive instruments, easily made by pupils, a good deal of practical mathematical work can be performed. The interesting old illustration here given shows how this form of level was used three hundred years ago.
Teachers who seek for geometric figures in practical mechanics will find this proposition illustrated in the ordinary hoisting apparatus of the kind here shown. From the study of such forms and of simple roof and bridge trusses, a number of the usual properties of the isosceles triangle may be derived.[Pg 180]
Theorem. The sum of two lines drawn from a given point to the extremities of a given line is greater than the sum of two other lines similarly drawn, but included by them.
It should be noted that the words "the extremities of" are necessary, for it is possible to draw from a certain point within a certain triangle two lines to the base such that their sum is greater than the sum of the other two sides.
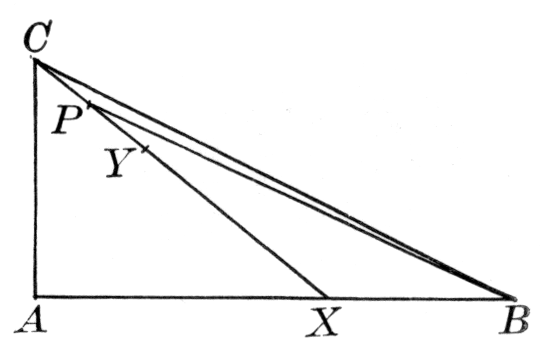
Thus, in the right triangle ABC draw any line CX from C to the base. Make XY = AC, and CP = PY. Then it is easily shown that PB + PX > CB + CA.
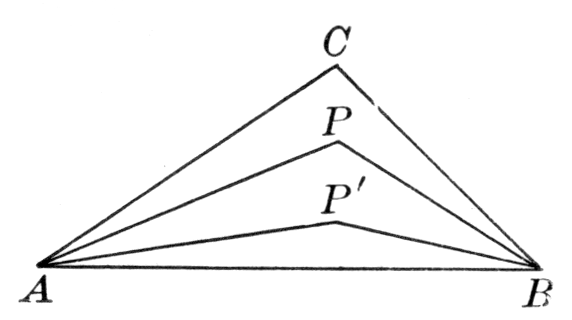
It is interesting to a class to have a teacher point out that, in this figure, AP + PB < AC + CB, and AP' + P'B < AP + PB, and that the nearer P gets to AB, the shorter AP + PB becomes, the limit being the line AB. From this we may infer (although we have not proved) that "a straight line (AB) is the shortest path between two points."
Theorem. Only one perpendicular can be drawn to a given line from a given external point.
Theorem. Two lines drawn from a point in a perpendicular to a given line, cutting off on the given line equal segments from the foot of the perpendicular, are equal and make equal angles with the perpendicular.
Theorem. Of two lines drawn from the same point in a perpendicular to a given line, cutting off on the line unequal segments from the foot of the perpendicular, the more remote is the greater.
Theorem. The perpendicular is the shortest line that can be drawn to a straight line from a given external point.[Pg 181]
These four propositions, while known to the ancients and incidentally used, are not explicitly stated by Euclid. The reason seems to be that he interspersed his problems with his theorems, and in his Propositions 11 and 12, which treat of drawing a perpendicular to a line, the essential features of these theorems are proved. Further mention will be made of them when we come to consider the problems in question. Many textbook writers put the second and third of the four before the first, forgetting that the first is assumed in the other two, and hence should precede them.
Theorem. Two right triangles are congruent if the hypotenuse and a side of the one are equal respectively to the hypotenuse and a side of the other.
Theorem. Two right triangles are congruent if the hypotenuse and an adjacent angle of the one are equal respectively to the hypotenuse and an adjacent angle of the other.
As stated in the notes on the third proposition in this sequence, Euclid's cumbersome Proposition 26 covers several cases, and these two among them. Of course this present proposition could more easily be proved after the one concerning the sum of the angles of a triangle, but the proof is so simple that it is better to leave the proposition here in connection with others concerning triangles.
Theorem. Two lines in the same plane perpendicular to the same line cannot meet, however far they are produced.
This proposition is not in Euclid, and it is introduced for educational rather than for mathematical reasons. Euclid introduced the subject by the proposition that, if alternate angles are equal, the lines are parallel. It is, however, simpler to begin with this proposition, and there is some advantage in stating it in such a way as to[Pg 182] prove that parallels exist before they are defined. The proposition is properly followed by the definition of parallels and by the postulate that has been discussed on page 127.
A good application of this proposition is the one concerning a method of drawing parallel lines by the use of a carpenter's square. Here two lines are drawn perpendicular to the edge of a board or a ruler, and these are parallel.
Theorem. If a line is perpendicular to one of two parallel lines, it is perpendicular to the other also.
This, like the preceding proposition, is a special case under a later theorem. It simplifies the treatment of parallels, however, and the beginner finds it easier to approach the difficulties gradually, through these two cases of perpendiculars. It should be noticed that this is an example of a partial converse, as explained on page 175. The preceding proposition may be stated thus: If a is ⊥ to x and b is ⊥ to x, then a is || to b. This proposition may be stated thus: If a is ⊥ to x and a is || to b, then b is ⊥ to x. This is, therefore, a partial converse.
These two propositions having been proved, the usual definitions of the angles made by a transversal of two parallels may be given. It is unfortunate that we have no name for each of the two groups of four equal angles, and the name of "transverse angles" has been suggested. This would simplify the statements of certain other propositions; thus: "If two parallel lines are cut by a transversal, the transverse angles are equal," and this includes two propositions as usually given. There is not as yet, however, any general sanction for the term.
Theorem. If two parallel lines are cut by a transversal, the alternate-interior angles are equal.[Pg 183]
Euclid gave this as half of his Proposition 29. Indeed, he gives only four theorems on parallels, as against five propositions and several corollaries in most of our American textbooks. The reason for increasing the number is that each proposition may be less involved. Thus, instead of having one proposition for both exterior and interior angles, modern authors usually have one for the exterior and one for the interior, so as to make the difficult subject of parallels easier for beginners.
Theorem. When two straight lines in the same plane are cut by a transversal, if the alternate-interior angles are equal, the two straight lines are parallel.
This is the converse of the preceding theorem, and is half of Euclid I, 28, his theorem being divided for the reason above stated. There are several typical pairs of equal or supplemental angles that would lead to parallel lines, of which Euclid uses only part, leaving the other cases to be inferred. This accounts for the number of corollaries in this connection in later textbooks.
Surveyors make use of this proposition when they wish, without using a transit instrument, to run one line parallel to another.
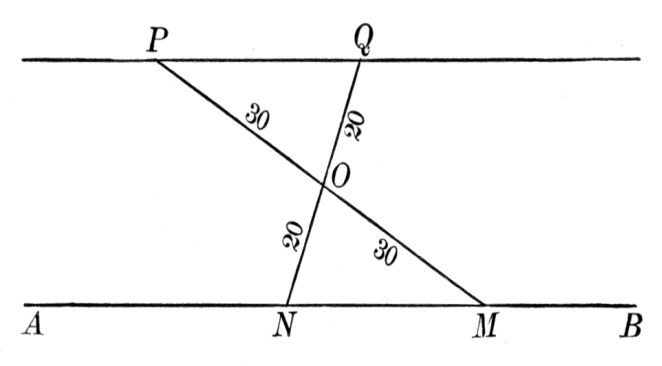
For example, suppose two boys are laying out a tennis court and they wish to run a line through P parallel to AB. Take a 60-foot tape and swing it around P until the other end rests on AB, as at M. Put a stake at O, 30 feet from P and M. Then take any convenient point N on AB, and measure ON. Suppose it equals 20 feet. Then sight from N through O, and put a stake at Q just 20 feet from O. Then P and Q determine the parallel, according to the proposition just mentioned.
Theorem. If two parallel lines are cut by a transversal, the exterior-interior angles are equal.
This is also a part of Euclid I, 29. It is usually followed by several corollaries, covering the minor and obvious cases omitted by the older writers. While it would be possible to dispense with these corollaries, they are helpful for definite reference in later propositions.
Theorem. The sum of the three angles of a triangle is equal to two right angles.
Euclid stated this as follows: "In any triangle, if one of the sides be produced, the exterior angle is equal to the two interior and opposite angles, and the three interior angles of the triangle are equal to two right angles." This states more than is necessary for the basal fact of the proposition, which is the constancy of the sum of the angles.
The theorem is one of the three most important propositions in plane geometry, the other two being the so-called Pythagorean Theorem, and a proposition relating to the proportionality of the sides of two triangles. These three form the foundation of trigonometry and of the mensuration of plane figures.
The history of the proposition is extensive. Eutocius (ca. 510 A.D.), in his commentary on Apollonius, says that Geminus (first century B.C.) testified that "the ancients investigated the theorem of the two right angles in each individual species of triangle, first in the equilateral, again in the isosceles, and afterwards in the scalene triangle." This, indeed, was the ancient plan, to proceed from the particular to the general. It is the natural order, it is the world's order, and it is well to follow it in all cases of difficulty in the classroom.
Proclus (410-485 A.D.) tells us that Eudemus, who lived just before Euclid (or probably about 325 B.C.),[Pg 185] affirmed that the theorem was due to the Pythagoreans, although this does not necessarily mean to the actual pupils of Pythagoras. The proof as he gives it consists in showing that a = a´, b = b´, and a´ + c + b´ = two right angles. Since the proposition about the exterior angle of a triangle is attributed to Philippus of Mende (ca. 380 B.C.), the figure given by Eudemus is probably the one used by the Pythagoreans.

There is also some reason for believing that Thales (ca. 600 B.C.) knew the theorem, for Diogenes Laertius (ca. 200 A.D.) quotes Pamphilius (first century A.D.) as saying that "he, having learned geometry from the Egyptians, was the first to inscribe a right triangle in a circle, and sacrificed an ox." The proof of this proposition requires the knowledge that the sum of the angles, at least in a right triangle, is two right angles. The proposition is frequently referred to by Aristotle.
There have been numerous attempts to prove the proposition without the use of parallel lines. Of these a German one, first given by Thibaut in the early part of the eighteenth century, is among the most interesting. This, in simplified form, is as follows:
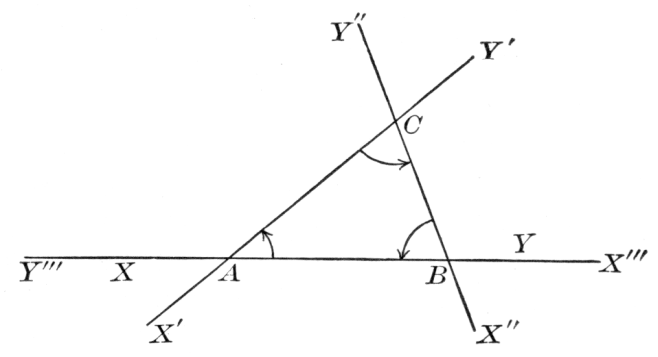
Suppose an indefinite line XY to lie on AB. Let it swing about A, counterclockwise, through ∠A, so as to lie on AC, as X'Y'. Then let it swing about C, through ∠C, so as to lie on CB, as X''Y''. Then let it swing about B, through ∠B, so as to lie on BA, as X'''Y'''. It now lies on AB,[Pg 186] but it is turned over, X''' being where Y was, and Y''' where X was. In turning through ⦞A, B, and C it has therefore turned through two right angles.
One trouble with the proof is that the rotation has not been about the same point, so that it has never been looked upon as other than an interesting illustration.
Proclus tried to prove the theorem by saying that, if we have two perpendiculars to the same line, and suppose them to revolve about their feet so as to make a triangle, then the amount taken from the right angles is added to the vertical angle of the triangle, and therefore the sum of the angles continues to be two right angles. But, of course, to prove his statement requires a perpendicular to be drawn from the vertex to the base, and the theorem of parallels to be applied.
Pupils will find it interesting to cut off the corners of a paper triangle and fit the angles together so as to make a straight angle.
This theorem furnishes an opportunity for many interesting exercises, and in particular for determining the third angle when two angles of a triangle are given, or the second acute angle of a right triangle when one acute angle is given.
Of the simple outdoor applications of the proposition, one of the best is illustrated in this figure.
To ascertain the height of a tree or of the school building, fold a piece of paper so as to make an angle of 45°. Then walk back from the tree until the top is seen at an angle of 45° with the ground (being therefore careful to have the base of the triangle level). Then the height AC will equal the base AB, since ABC is isosceles. A paper protractor may be used for the same purpose.
Distances can easily be measured by constructing a large equilateral triangle of heavy pasteboard, and standing pins at the vertices for the purpose of sighting.
To measure PC, stand at some convenient point A and sight along APC and also along AB. Then walk along AB until a point B is reached from which BC makes with BA an angle of the triangle (60°). Then AC = AB, and since AP can be measured, we can find PC.
Another simple method of measuring a distance AC across a stream is shown in this figure.
Measure the angle CAX, either in degrees, with a protractor, or by sighting along a piece of paper and marking down the angle. Then go along XA produced until a point B is reached from which BC makes with A an angle equal to half of angle CAX. Then it is easily shown that AB = AC.
A navigator uses the same principle when he "doubles the angle on the bow" to find his distance from a lighthouse or other object.
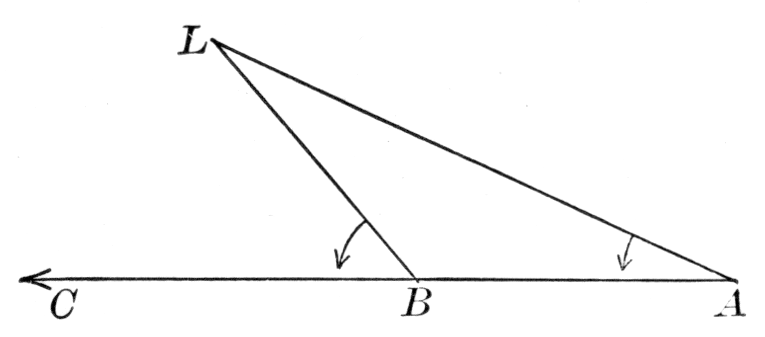
If he is sailing on the course ABC and notes a lighthouse L when he is at A, and takes the angle A, and if he notices when the angle that the lighthouse makes with his course is just twice the angle noted at A, then BL = AB. He has AB from his log (an instrument that tells how far a ship goes in a given time), so he knows BL. He has "doubled the angle on the bow" to get this distance.
[Pg 188] It would have been possible for Thales, if he knew this proposition, to have measured the distance of the ship at sea by some such device as this:
Make a large isosceles triangle out of wood, and, standing at T, sight to the ship and along the shore on a line TA, using the vertical angle of the triangle. Then go along TA until a point P is reached, from which T and S can be seen along the sides of a base angle of the triangle. Then TP = TS. By measuring TB, BS can then be found.
Theorem. The sum of two sides of a triangle is greater than the third side, and their difference is less than the third side.
If the postulate is assumed that a straight line is the shortest path between two points, then the first part of this theorem requires no further proof, and the second part follows at once from the axiom of inequalities. This seems the better plan for beginners, and the proposition may be considered as semiobvious. Euclid proved the first part, not having assumed the postulate. Proclus tells us that the Epicureans (the followers of Epicurus, the Greek philosopher, 342-270 B.C.) used to ridicule this theorem, saying that even an ass knew it, for if he wished to get food, he walked in a straight line and not along two sides of a triangle. Proclus replied that it was one thing to know the truth and another thing to prove it, meaning that the value of geometry lay in the proof rather than in the mere facts, a thing that all who seek to reform the teaching of geometry would do well to keep in mind. The theorem might simply appear as a corollary under the postulate if it were of any importance to reduce the number of propositions one more.[Pg 189]
If the proposition is postponed until after those concerning the inequalities of angles and sides of a triangle, there are several good proofs.
For example, produce AC to X,
making
CX = CB.
Then ∠X = ∠XBC.
∴ ∠XBA > ∠X.
∴ AX > AB.
∴ AC + CB > AB.
The above proof is due to Euclid. Heron of Alexandria (first century A.D.) is said by Proclus to have given the following:
Let CX bisect ∠C.
Then ∠BXC > ∠ACX.
∴∠BXC > ∠XCB.
∴CB > XB.
Similarly, AC > AX.
Adding, AC + CB > AB.
Theorem. If two sides of a triangle are unequal, the angles opposite these sides are unequal, and the angle opposite the greater side is the greater.
Euclid stated this more briefly by saying, "In any triangle the greater side subtends the greater angle." This is not so satisfactory, for there may be no greater side.
Theorem. If two angles of a triangle are unequal, the sides opposite these angles are unequal, and the side opposite the greater angle is the greater.
Euclid also stated this more briefly, but less satisfactorily, thus, "In any triangle the greater angle is subtended by the greater side." Students should have their attention called to the fact that these two theorems[Pg 190] are reciprocal or dual theorems, the words "sides" and "angles" of the one corresponding to the words "angles" and "sides" respectively of the other.
It may also be noticed that the proof of this proposition involves what is known as the Law of Converse; for
(1) if b = c, then ∠B = ∠C;
(2) if b > c, then ∠B > ∠C;
(3) if b < c, then ∠B < ∠C;
therefore the converses must necessarily be true as a matter of logic; for
if ∠B = ∠C, then b cannot be greater than c without violating (2), and b cannot be less than c without violating (3), therefore b = c;
and if ∠B > ∠C, then b cannot equal c without violating (1), and b cannot be less than c without violating (3), therefore b > c;
similarly, if ∠B < ∠C, then b < c.
This Law of Converse may readily be taught to pupils, and it has several applications in geometry.
Theorem. If two triangles have two sides of the one equal respectively to two sides of the other, but the included angle of the first triangle greater than the included angle of the second, then the third side of the first is greater than the third side of the second, and conversely.
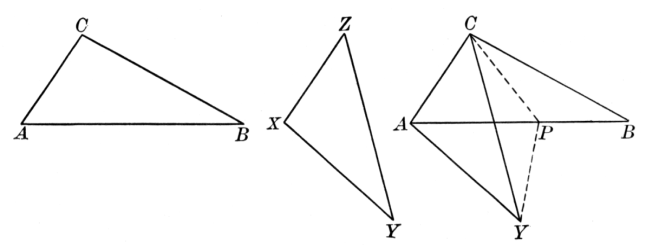
In this proposition there are three possible cases: the point Y may fall below AB, as here shown, or on[Pg 191] AB, or above AB. As an exercise for pupils all three may be considered if desired. Following Euclid and most early writers, however, only one case really need be proved, provided that is the most difficult one, and is typical. Proclus gave the proofs of the other two cases, and it is interesting to pupils to work them out for themselves. In such work it constantly appears that every proposition suggests abundant opportunity for originality, and that the complete form of proof in a textbook is not a bar to independent thought.
The Law of Converse, mentioned on page 190, may be applied to the converse case if desired.
Theorem. Two angles whose sides are parallel, each to each, are either equal or supplementary.
This is not an ancient proposition, although the Greeks were well aware of the principle. It may be stated so as to include the case of the sides being perpendicular, each to each, but this is better left as an exercise. It is possible, by some circumlocution, to so state the theorem as to tell in what cases the angles are equal and in what cases supplementary. It cannot be tersely stated, however, and it seems better to leave this point as a subject for questioning by the teacher.
Theorem. The opposite sides of a parallelogram are equal.
Theorem. If the opposite sides of a quadrilateral are equal, the figure is a parallelogram.
This proposition is a very simple test for a parallelogram. It is the principle involved in the case of the common folding parallel ruler, an instrument that has long been[Pg 192] recognized as one of the valuable tools of practical geometry. It will be of some interest to teachers to see one of the early forms of this parallel ruler, as shown in the illustration.[63] If such an instrument is not available in the school, one suitable for illustrative purposes can easily be made from cardboard.
 Parallel Ruler of the Seventeenth Century
Parallel Ruler of the Seventeenth CenturyA somewhat more complicated form of this instrument may also be made by pupils in manual training, as is shown in this illustration from Bion's great treatise. The principle involved may be taken up in class, even if the instrument is not used. It is evident that, unless the workmanship is unusually good, this form of parallel ruler is not as accurate as the common one illustrated above. The principle is sometimes used in iron gates.
 Parallel Ruler of the Eighteenth Century
Parallel Ruler of the Eighteenth CenturyTheorem. Two parallelograms are congruent if two sides and the included angle of the one are equal respectively to two sides and the included angle of the other.
This proposition is discussed in connection with the one that follows.
Theorem. If three or more parallels intercept equal segments on one transversal, they intercept equal segments on every transversal.
These two propositions are not given in Euclid, although generally required by American syllabi of the present time. The last one is particularly useful in subsequent work. Neither one offers any difficulty, and neither has any interesting history. There are, however, numerous interesting applications to the last one. One that is used in mechanical drawing is here illustrated.
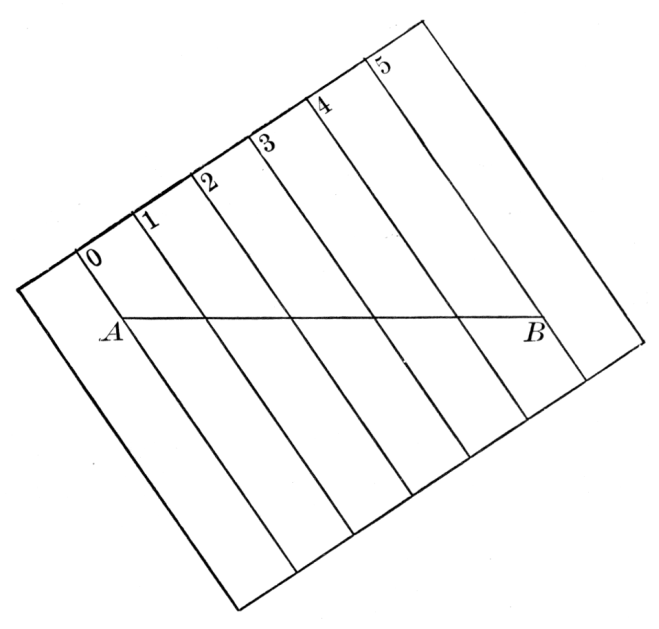
If it is desired to divide a line AB into five equal parts, we may take a piece of ruled tracing paper and lay it over the given line so that line 0 passes through A, and line 5 through B. We may then prick through the paper and thus determine the points on AB. Similarly, we may divide AB into any other number of equal parts.
Among the applications of these propositions is an interesting one due to the Arab Al-Nairīzī (ca. 900 A.D.). The problem is to divide a line into any number of equal parts, and he begins with the case of trisecting AB. It may be given as a case of practical drawing even before the problems are reached, particularly if some preliminary work with the compasses and straightedge has been given.[Pg 194]
Make BQ and AQ' perpendicular to AB, and make BP = PQ = AP' = P'Q'. Then ⧍XYZ is congruent to ⧍YBP, and also to ⧍XAP'. Therefore AX = XY = YB. In the same way we might continue to produce BQ until it is made up of n - 1 lengths BP, and so for AQ', and by properly joining points we could divide AB into n equal parts. In particular, if we join P and P', we bisect the line AB.
Theorem. If two sides of a quadrilateral are equal and parallel, then the other two sides are equal and parallel, and the figure is a parallelogram.
This was Euclid's first proposition on parallelograms, and Proclus speaks of it as the connecting link between the theory of parallels and that of parallelograms. The ancients, writing for mature students, did not add the words "and the figure is a parallelogram," because that follows at once from the first part and from the definition of "parallelogram," but it is helpful to younger students because it emphasizes the fact that here is a test for this kind of figure.
Theorem. The diagonals of a parallelogram bisect each other.
This proposition was not given in Euclid, but it is usually required in American syllabi. There is often given in connection with it the exercise in which it is proved that the diagonals of a rectangle are equal. When this is taken, it is well to state to the class that carpenters and builders find this one of the best checks in laying out floors and other rectangles. It is frequently applied also in laying out tennis courts. If the class is doing any work in mensuration, such as finding the area of the school grounds, it is a good plan to check a few rectangles by this method.[Pg 195]
An interesting outdoor application of the theory of parallelograms is the following:
Suppose you are on the side of this stream opposite to XY, and wish to measure the length of XY. Run a line AB along the bank. Then take a carpenter's square, or even a large book, and walk along AB until you reach P, a point from which you can just see X and B along two sides of the square. Do the same for Y, thus fixing P and Q. Using the tape, bisect PQ at M. Then walk along YM produced until you reach a point Y' that is exactly in line with M and Y, and also with P and X. Then walk along XM produced until you reach a point X' that is exactly in line with M and X, and also with Q and Y. Then measure Y'X' and you have the length of XY. For since YX' is ⊥ to PQ, and XY' is also ⊥ to PQ, YX' is || to XY'. And since PM = MQ, therefore XM = MX' and Y'M = MY. Therefore Y'X'YX is a parallelogram.
The properties of the parallelogram are often applied to proving figures of various kinds congruent, or to constructing them so that they will be congruent.
For example, if we draw A'B' equal and parallel to AB, B'C' equal and parallel to BC, and so on, it is easily proved that ABCD and A'B'C'D' are congruent. This may be done by ordinary superposition, or by sliding ABCD along the dotted parallels.
There are many applications of this principle of parallel translation in practical construction work. The principle is more far-reaching than here intimated, however, and a few words as to its significance will now be in place.[Pg 196]
The efforts usually made to improve the spirit of Euclid are trivial. They ordinarily relate to some commonplace change of sequence, to some slight change in language, or to some narrow line of applications. Such attempts require no particular thought and yield no very noticeable result. But there is a possibility, remote though it may be at present, that a geometry will be developed that will be as serious as Euclid's and as effective in the education of the thinking individual. If so, it seems probable that it will not be based upon the congruence of triangles, by which so many propositions of Euclid are proved, but upon certain postulates of motion, of which one is involved in the above illustration,—the postulate of parallel translation. If to this we join the two postulates of rotation about an axis,[64] leading to axial symmetry; and rotation about a point,[65] leading to symmetry with respect to a center, we have a group of three motions upon which it is possible to base an extensive and rigid geometry.[66] It will be through some such effort as this, rather than through the weakening of the Euclid-Legendre style of geometry, that any improvement is likely to come. At present, in America, the important work for teachers is to vitalize the geometry they have,—an effort in which there are great possibilities,—seeing to it that geometry is not reduced to mere froth, and recognizing the possibility of another geometry that may sometime replace it,—a geometry
as rigid, as thought-compelling, as logical, and as truly educational.
Theorem. The sum of the interior angles of a polygon is equal to two right angles, taken as many times less two as the figure has sides.
This interesting generalization of the proposition about the sum of the angles of a triangle is given by Proclus. There are several proofs, but all are based upon the possibility of dissecting the polygon into triangles. The point from which lines are drawn to the vertices is usually taken at a vertex, so that there are n - 2 triangles. It may however be taken within the figure, making n triangles, from the sum of the angles of which the four right angles about the point must be subtracted. The point may even be taken on one side, or outside the polygon, but the proof is not so simple. Teachers who desire to do so may suggest to particularly good students the proving of the theorem for a concave polygon, or even for a cross polygon, although the latter requires negative angles.
Some schools have transit instruments for the use of their classes in trigonometry. In such a case it is a good plan to measure the angles in some piece of land so as to verify the proposition, as well as show the care that must be taken in reading angles. In the absence of this exercise it is well to take any irregular polygon and measure the angles by the help of a protractor, and thus accomplish the same results.
Theorem. The sum of the exterior angles of a polygon, made by producing each of its sides in succession, is equal to four right angles.
This is also a proposition not given by the ancient writers. We have, however, no more valuable theorem for the purpose of showing the nature and significance[Pg 198] of the negative angle; and teachers may arouse a great deal of interest in the negative quantity by showing to a class that when an interior angle becomes 180° the exterior angle becomes 0, and when the polygon becomes concave the exterior angle becomes negative, the theorem holding for all these cases. We have few better illustrations of the significance of the negative quantity, and few better opportunities to use the knowledge of this kind of quantity already acquired in algebra.
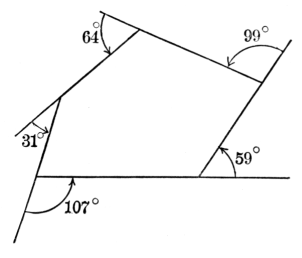
In the hilly and mountainous parts of America, where irregular-shaped fields are more common than in the more level portions, a common test for a survey is that of finding the exterior angles when the transit instrument is set at the corners. In this field these angles are given, and it will be seen that the sum is 360°. In the absence of any outdoor work a protractor may be used to measure the exterior angles of a polygon drawn on paper. If there is an irregular piece of land near the school, the exterior angles can be fairly well measured by an ordinary paper protractor.
The idea of locus is usually introduced at the end of Book I. It is too abstract to be introduced successfully any earlier, although authors repeat the attempt from time to time, unmindful of the fact that all experience is opposed to it. The loci propositions are not ancient. The Greeks used the word "locus" (in Greek, topos), however. Proclus, for example, says, "I call those locus theorems in which the same property is found to exist on the whole of some locus." Teachers should be careful to have the pupils recognize the necessity for proving[Pg 199] two things with respect to any locus: (1) that any point on the supposed locus satisfies the condition; (2) that any point outside the supposed locus does not satisfy the given condition. The first of these is called the "sufficient condition," and the second the "necessary condition." Thus in the case of the locus of points in a plane equidistant from two given points, it is sufficient that the point be on the perpendicular bisector of the line joining the given points, and this is the first part of the proof; it is also necessary that it be on this line, i.e. it cannot be outside this line, and this is the second part of the proof. The proof of loci cases, therefore, involves a consideration of "the necessary and sufficient condition" that is so often spoken of in higher mathematics. This expression might well be incorporated into elementary geometry, and when it becomes better understood by teachers, it probably will be more often used.
In teaching loci it is helpful to call attention to loci in space (meaning thereby the space of three dimensions), without stopping to prove the proposition involved. Indeed, it is desirable all through plane geometry to refer incidentally to solid geometry. In the mensuration of plane figures, which may be boundaries of solid figures, this is particularly true.
It is a great defect in most school courses in geometry that they are entirely confined to two dimensions. Even if solid geometry in the usual sense is not attempted, every occasion should be taken to liberate boys' minds from what becomes the tyranny of paper. Thus the questions: "What is the locus of a point equidistant from two given points; at a constant distance from a given straight line or from a given point?" should be extended to space.[67]
The two loci problems usually given at this time, referring to a point equidistant from the extremities of a given line, and to a point equidistant from two intersecting lines, both permit of an interesting extension to three dimensions without any formal proof. It is possible to give other loci at this point, but it is preferable merely to introduce the subject in Book I, reserving the further discussion until after the circle has been studied.
It is well, in speaking of loci, to remember that it is entirely proper to speak of the "locus of a point" or the "locus of points." Thus the locus of a point so moving in a plane as constantly to be at a given distance from a fixed point in the plane is a circle. In analytic geometry we usually speak of the locus of a point, thinking of the point as being anywhere on the locus. Some teachers of elementary geometry, however, prefer to speak of the locus of points, or the locus of all points, thus tending to make the language of elementary geometry differ from that of analytic geometry. Since it is a trivial matter of phraseology, it is better to recognize both forms of expression and to let pupils use the two interchangeably.[Pg 201]
Having taken up all of the propositions usually given in Book I, it seems unnecessary to consider as specifically all those in subsequent books. It is therefore proposed to select certain ones that have some special interest, either from the standpoint of mathematics or from that of history or application, and to discuss them as fully as the circumstances seem to warrant.
Theorems. In the same circle or in equal circles equal central angles intercept equal arcs; and of two unequal central angles the greater intercepts the greater arc, and conversely for both of these cases.
Euclid made these the twenty-sixth and twenty-seventh propositions of his Book III, but he limited them as follows: "In equal circles equal angles stand on equal circumferences, whether they stand at the centers or at the circumferences, and conversely." He therefore included two of our present theorems in one, thus making the proposition doubly hard for a beginner. After these two propositions the Law of Converse, already mentioned on page 190, may properly be introduced.
Theorems. In the same circle or in equal circles, if two arcs are equal, they are subtended by equal chords; and if two arcs are unequal, the greater is subtended by the greater chord, and conversely.
Euclid dismisses all this with the simple theorem, "In equal circles equal circumferences are subtended by[Pg 202] equal straight lines." It will therefore be noticed that he has no special word for "chord" and none for "arc," and that the word "circumference," which some teachers are so anxious to retain, is used to mean both the whole circle and any arc. It cannot be doubted that later writers have greatly improved the language of geometry by the use of these modern terms. The word "arc" is the same, etymologically, as "arch," each being derived from the Latin arcus (a bow). "Chord" is from the Greek, meaning "the string of a musical instrument." "Subtend" is from the Latin sub (under), and tendere (to stretch).
It should be noticed that Euclid speaks of "equal circles," while we speak of "the same circle or equal circles," confining our proofs to the latter, on the supposition that this sufficiently covers the former.
Theorem. A line through the center of a circle perpendicular to a chord bisects the chord and the arcs subtended by it.
This is an improvement on Euclid, III, 3: "If in a circle a straight line through the center bisects a straight line not through the center, it also cuts it at right angles; and if it cuts it at right angles, it also bisects it." It is a very important proposition, theoretically and practically, for it enables us to find the center of a circle if we know any part of its arc. A civil engineer, for example, who wishes to find the center of the circle of which some curve (like that on a running track, on a railroad, or in a park) is an arc, takes two chords, say of one hundred feet each, and erects perpendicular bisectors. It is well to ask a class why, in practice, it is better to take these chords some distance apart. Engineers often check their work by taking three chords, the perpendicular bisectors[Pg 203] of the three passing through a single point. Illustrations of this kind of work are given later in this chapter.
Theorem. In the same circle or in equal circles equal chords are equidistant from the center, and chords equidistant from the center are equal.
This proposition is practically used by engineers in locating points on an arc of a circle that is too large to be described by a tape, or that cannot easily be reached from the center on account of obstructions.
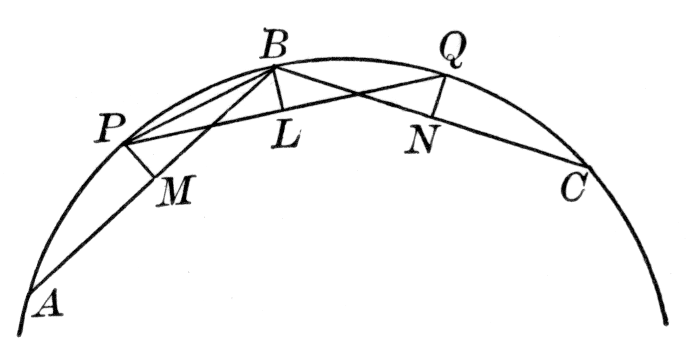
If part of the curve APB is known, take P as the mid-point. Then stretch the tape from A to B and draw PM perpendicular to it. Then swing the length AM about P, and PM about B, until they meet at L, and stretch the length AB along PL to Q. This fixes the point Q. In the same way fix the point C. Points on the curve can thus be fixed as near together as we wish. The chords AB, PQ, BC, and so on, are equal and are equally distant from the center.
Theorem. A line perpendicular to a radius at its extremity is tangent to the circle.
The enunciation of this proposition by Euclid is very interesting. It is as follows:
The straight line drawn at right angles to the diameter of a circle at its extremity will fall outside the circle, and into the space between the straight line and the circumference another straight line cannot be interposed; further, the angle of the semicircle is greater and the remaining angle less than any acute rectilineal angle.
The first assertion is practically that of tangency,—"will fall outside the circle." The second one states, substantially, that there is only one such tangent, or, as we say in modern mathematics, the tangent is unique. The third statement relates to the angle formed by the diameter[Pg 204] and the circumference,—a mixed angle, as Proclus called it, and a kind of angle no longer used in elementary geometry. The fourth statement practically asserts that the angle between the tangent and circumference is less than any assignable quantity. This gives rise to a difficulty that seems to have puzzled many of Euclid's commentators, and that will interest a pupil: As the circle diminishes this angle apparently increases, while as the circle increases the angle decreases, and yet the angle is always stated to be zero. Vieta (1540-1603), who did much to improve the science of algebra, attempted to explain away the difficulty by adopting a notion of circle that was prevalent in his time. He said that a circle was a polygon of an infinite number of sides (which it cannot be, by definition), and that, a tangent simply coincided with one of the sides, and therefore made no angle with it; and this view was also held by Galileo (1564-1642), the great physicist and mathematician who first stated the law of the pendulum.
Theorem. Parallel lines intercept equal arcs on a circle.
The converse of this proposition has an interesting application in outdoor work.
Suppose we wish to run a line through P parallel to a given line AB. With any convenient point O as a center, and OP as a radius, describe a circle cutting AB in X and Y. Draw PX. Then with Y as a center and PX as a radius draw an arc cutting the circle in Q. Then run the line from P to Q. PQ is parallel to AB by the converse of the above theorem, which is easily shown to be true for this figure.
Theorem. If two circles are tangent to each other, the line of centers passes through the point of contact.
There are many illustrations of this theorem in practical work, as in the case of cogwheels. An interesting application to engineering is seen in the case of two parallel streets or lines of track which are to be connected by a "reversed curve."
If the lines are AB and CD, and the connection is to be made, as shown, from B to C, we may proceed as follows: Draw BC and bisect it at M. Erect PO, the perpendicular bisector of BM; and BO, perpendicular to AB. Then O is one center of curvature. In the same way fix O'. Then to check the work apply this theorem, M being in the line of centers OO'. The curves may now be drawn, and they will be tangent to AB, to CD, and to each other.
At this point in the American textbooks it is the custom to insert a brief treatment of measurement, explaining what is meant by ratio, commensurable and incommensurable quantities, constant and variable, and limit, and introducing one or more propositions relating to limits. The object of this departure from the ancient sequence, which postponed this subject to the book on ratio and proportion, is to treat the circle more completely in Book III. It must be confessed that the treatment is not as scientific as that of Euclid, as will be explained under Book III, but it is far better suited to the mind of a boy or girl.
It begins by defining measurement in a practical way, as the finding of the number of times a quantity of any kind contains a known quantity of the same kind. Of[Pg 206] course this gives a number, but this number may be a surd, like √2. In other words, the magnitude measured may be incommensurable with the unit of measure, a seeming paradox. With this difficulty, however, the pupil should not be called upon to contend at this stage in his progress. The whole subject of incommensurables might safely be postponed, although it may be treated in an elementary fashion at this time. The fact that the measure of the diagonal of a square, of which a side is unity, is √2, and that this measure is an incommensurable number, is not so paradoxical as it seems, the paradox being verbal rather than actual.
It is then customary to define ratio as the quotient of the numerical measures of two quantities in terms of a common unit. This brings all ratios to the basis of numerical fractions, and while it is not scientifically so satisfactory as the ancient concept which considered the terms as lines, surfaces, angles, or solids, it is more practical, and it suffices for the needs of elementary pupils.
"Commensurable," "incommensurable," "constant," and "variable" are then defined, and these definitions are followed by a brief discussion of limit. It simplifies the treatment of this subject to state at once that there are two classes of limits,—those which the variable actually reaches, and those which it can only approach indefinitely near. We find the one as frequently as we find the other, although it is the latter that is referred to in geometry. For example, the superior limit of a chord is a diameter, and this limit the chord may reach. The inferior limit is zero, but we do not consider the chord as reaching this limit. It is also well to call the attention of pupils to the fact that a quantity may decrease towards its limit as well as increase towards it.[Pg 207]
Such further definitions as are needed in the theory of limits are now introduced. Among these is "area of a circle." It might occur to some pupil that since a circle is a line (as used in modern mathematics), it can have no area. This is, however, a mere quibble over words. It is not pretended that the line has area, but that "area of a circle" is merely a shortened form of the expression "area inclosed by a circle."
The Principle of Limits is now usually given as follows: "If, while approaching their respective limits, two variables are always equal, their limits are equal." This was expressed by D'Alembert in the eighteenth century as "Magnitudes which are the limits of equal magnitudes are equal," or this in substance. It would easily be possible to elaborate this theory, proving, for example, that if x approaches y as its limit, then ax approaches ay as its limit, and x/a approaches y/a as its limit, and so on. Very much of this theory, however, wearies a pupil so that the entire meaning of the subject is lost, and at best the treatment in elementary geometry is not rigorous. It is another case of having to sacrifice a strictly scientific treatment to the educational abilities of the pupil. Teachers wishing to find a scientific treatment of the subject should consult a good work on the calculus.
Theorem. In the same circle or in equal circles two central angles have the same ratio as their intercepted arcs.
This is usually proved first for the commensurable case and then for the incommensurable one. The latter is rarely understood by all of the class, and it may very properly be required only of those who show some aptitude in geometry. It is better to have the others understand fully the commensurable case and see the nature[Pg 208] of its applications, possibly reading the incommensurable proof with the teacher, than to stumble about in the darkness of the incommensurable case and never reach the goal. In Euclid there was no distinction between the two because his definition of ratio covered both; but, as we shall see in Book III, this definition is too difficult for our pupils. Theon of Alexandria (fourth century A.D.), the father of the Hypatia who is the heroine of Kingsley's well-known novel, wrote a commentary on Euclid, and he adds that sectors also have the same ratio as the arcs, a fact very easily proved. In propositions of this type, referring to the same circle or to equal circles, it is not worth while to ask pupils to take up both cases, the proof for either being obviously a proof for the other.
Many writers state this proposition so that it reads that "central angles are measured by their intercepted arcs." This, of course, is not literally true, since we can measure anything only by some thing, of the same kind. Thus we measure a volume by finding how many times it contains another volume which we take as a unit, and we measure a length by taking some other length as a unit; but we cannot measure a given length in quarts nor a given weight in feet, and it is equally impossible to measure an arc by an angle, and vice versa. Nevertheless it is often found convenient to define some brief expression that has no meaning if taken literally, in such way that it shall acquire a meaning. Thus we define "area of a circle," even when we use "circle" to mean a line; and so we may define the expression "central angles are measured by their intercepted arcs" to mean that central angles have the same numerical measure as these arcs. This is done by most writers, and is legitimate as explaining an abbreviated expression.[Pg 209]
Theorem. An inscribed angle is measured by half the intercepted arc.
In Euclid this proposition is combined with the preceding one in his Book VI, Proposition 33. Such a procedure is not adapted to the needs of students to-day. Euclid gave in Book III, however, the proposition (No. 20) that a central angle is twice an inscribed angle standing on the same arc. Since Euclid never considered an angle greater than 180°, his inscribed angle was necessarily less than a right angle. The first one who is known to have given the general case, taking the central angle as being also greater than 180°, was Heron of Alexandria, probably of the first century A.D.[68] In this he was followed by various later commentators, including Tartaglia and Clavius in the sixteenth century.
One of the many interesting exercises that may be derived from this theorem is seen in the case of the "horizontal danger angle" observed by ships.
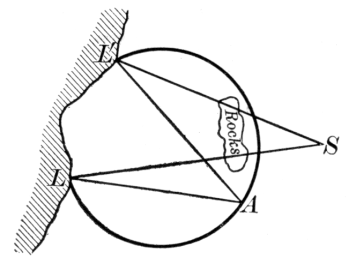
If some dangerous rocks lie off the shore, and L and L' are two lighthouses, the angle A is determined by observation, so that A will lie on a circle inclosing the dangerous area. Angle A is called the "horizontal danger angle." Ships passing in sight of the two lighthouses L and L' must keep out far enough so that the angle L'SL shall be less than angle A.
To this proposition there are several important corollaries, including the following:
1. An angle inscribed in a semicircle is a right angle. This corollary is mentioned by Aristotle and is attributed
to Thales, being one of the few propositions with which his name is connected. It enables us to describe a circle by letting the arms of a carpenter's square slide along two nails driven in a board, a pencil being held at the vertex.
A more practical use for it is made by machinists to determine whether a casting is a true semicircle. Taking a carpenter's square as here shown, if the vertex touches the curve at every point as the square slides around, it is a true semicircle. By a similar method a circle may be described by sliding a draftsman's triangle so that two sides touch two tacks driven in a board.

Another interesting application of this corollary may be seen by taking an ordinary paper protractor ACB, and fastening a plumb line at B. If the protractor is so held that the plumb line cuts the semicircle at C, then AC is level because it is perpendicular to the vertical line BC. Thus, if a class wishes to determine the horizontal line AC, while sighting up a hill in the direction AB, this is easily determined without a spirit level.
It follows from this corollary, as the pupil has already found, that the mid-point of the hypotenuse of a right triangle is equidistant from the three vertices. This is useful in outdoor measuring, forming the basis of one of the best methods of letting fall a perpendicular from an external point to a line.[Pg 211]
Suppose XY to be the edge of a sidewalk, and P a point in the street from which we wish to lay a gas pipe perpendicular to the walk. From P swing a cord or tape, say 60 feet long, until it meets XY at A. Then take M, the mid-point of PA, and swing MP about M, to meet XY at B. Then B is the foot of the perpendicular, since ∠PBA can be inscribed in a semicircle.
2. Angles inscribed in the same segment are equal.
By driving two nails in a board, at A and B, and taking an angle P made of rigid material (in particular, as already stated, a carpenter's square), a pencil placed at P will generate an arc of a circle if the arms slide along A and B. This is an interesting exercise for pupils.
Theorem. An angle formed by two chords intersecting within the circle is measured by half the sum of the intercepted arcs.
Theorem. An angle formed by a tangent and a chord drawn from the point of tangency is measured by half the intercepted arc.
Theorem. An angle formed by two secants, a secant and a tangent, or two tangents, drawn to a circle from an external point, is measured by half the difference of the intercepted arcs.
These three theorems are all special cases of the general proposition that the angle included between two lines that cut (or touch) a circle is measured by half the sum of the intercepted arcs. If the point passes from within the circle to the circle itself, one arc becomes zero and the angle becomes an inscribed angle. If the point passes outside the circle, the smaller arc becomes negative, having passed through zero. The point may even "go to[Pg 212] infinity," as is said in higher mathematics, the lines then becoming parallel, and the angle becoming zero, being measured by half the sum of one arc and a negative arc of the same absolute value. This is one of the best illustrations of the Principle of Continuity to be found in geometry.
Problem. To let fall a perpendicular upon a given line from a given external point.
This is the first problem that a student meets in most American geometries. The reason for treating the problems by themselves instead of mingling them with the theorems has already been discussed.[69] The student now has a sufficient body of theorems, by which he can prove that his constructions are correct, and the advantage of treating these constructions together is greater than that of following Euclid's plan of introducing them whenever needed.
Proclus tells us that "this problem was first investigated by Œnopides,[70] who thought it useful for astronomy." Proclus speaks of such a line as a gnomon, a common name for the perpendicular on a sundial, which casts the shadow by which the time of day is known. He also speaks of two kinds of perpendiculars, the plane and solid, the former being a line perpendicular to a line, and the latter a line perpendicular to a plane.
It is interesting to notice that the solution tacitly assumes that a certain arc is going to cut the given line in two points, and only two. Strictly speaking, why may it not cut it in only one point, or even in three points? We really assume that if a straight line is drawn through[Pg 213]a point within a circle, this line must get out of the circle on each of two sides of the given point, and in getting out it must cut the circle twice. Proclus noticed this assumption and endeavored to prove it. It is better, however, not to raise the question with beginners, since it seems to them like hair-splitting to no purpose.
The problem is of much value in surveying, and teachers would do well to ask a class to let fall a perpendicular to the edge of a sidewalk from a point 20 feet from the walk, using an ordinary 66-foot or 50-foot tape. Practically, the best plan is to swing 30 feet of the tape about the point and mark the two points of intersection with the edge of the walk. Then measure the distance between the points and take half of this distance, thus fixing the foot of the perpendicular.
Problem. At a given point in a line, to erect a perpendicular to that line.
This might be postponed until after the problem to bisect an angle, since it merely requires the bisection of a straight angle; but considering the immaturity of the average pupil, it is better given independently. The usual case considers the point not at the extremity of the line, and the solution is essentially that of Euclid. In practice, however, as for example in surveying, the point may be at the extremity, and it may not be convenient to produce the line.
Surveyors sometimes measure PB = 3 ft., and then take 9 ft. of tape, the ends being held at B and P, and the tape being stretched to A, so that PA = 4 ft. and AB = 5 ft. Then P is a right angle by the Pythagorean Theorem. This theorem not having yet been proved, it cannot be used at this time.
A solution for the problem of erecting a perpendicular from the extremity of a line that cannot be produced, depending, however, on the problem of bisecting an angle, and therefore to be given after that problem, is attributed by Al-Nairīzī (tenth century A.D.) to Heron of Alexandria. It is also given by Proclus.
Required to draw from P a perpendicular to AP. Take X anywhere on the line and erect XY ⊥ to AP in the usual manner. Bisect ∠PXY by the line XM. On XY take XN = XP, and draw NM ⊥ to XY. Then draw PM. The proof is evident.
These may at the proper time be given as interesting variants of the usual solution.
Problem. To bisect a given line.
Euclid said "finite straight line," but this wording is not commonly followed, because it will be inferred that the line is finite if it is to be bisected, and we use "line" alone to mean a straight line. Euclid's plan was to construct an equilateral triangle (by his Proposition 1 of Book I) on the line as a base, and then to bisect the vertical angle. Proclus tells us that Apollonius of Perga, who wrote the first great work on conic sections, used a plan which is substantially that which is commonly found in textbooks to-day,—constructing two isosceles triangles upon the line as a common base, and connecting their vertices.
Problem. To bisect a given angle.
It should be noticed that in the usual solution two arcs intersect, and the point thus determined is connected with the vertex. Now these two arcs intersect twice, and since one of the points of intersection may be the vertex[Pg 215] itself, the other point of intersection must be taken. It is not, however, worth while to make much of this matter with pupils. Proclus calls attention to the possible suggestion that the point of intersection may be imagined to lie outside the angle, and he proceeds to show the absurdity; but here, again, the subject is not one of value to beginners. He also contributes to the history of the trisection of an angle. Any angle is easily trisected by means of certain higher curves, such as the conchoid of Nicomedes (ca. 180 B.C.), the quadratrix of Hippias of Elis (ca. 420 B.C.), or the spiral of Archimedes (ca. 250 B.C.). But since this problem, stated algebraically, requires the solution of a cubic equation, and this involves, geometrically, finding three points, we cannot solve the problem by means of straight lines and circles alone. In other words, the trisection of any angle, by the use of the straightedge and compasses alone, is impossible. Special angles may however be trisected. Thus, to trisect an angle of 90° we need only to construct an angle of 60°, and this can be done by constructing an equilateral triangle. But while we cannot trisect the angle, we may easily approximate trisection. For since, in the infinite geometric series 1/2 + 1/8 + 1/32 + 1/128 + ..., s = a ÷ (1 - r), we have s = 1/2 ÷ 3/4 = 2/3. In other words, if we add 1/2 of the angle, 1/8 of the angle, 1/32 of the angle, and so on, we approach as a limit 2/3 of the angle; but all of these fractions can be obtained by repeated bisections, and hence by bisections we may approximate the trisection.
The approximate bisection (or any other division) of an angle may of course be effected by the help of the protractor and a straightedge. The geometric method is, however, usually more accurate, and it is advantageous[Pg 216] to have the pupils try both plans, say for bisecting an angle of about 49-1/2°.
Applications of this problem are numerous. It may be desired, for example, to set a lamp-post on a line bisecting the angle formed by two streets that come together a little unsymmetrically, as here shown, in which case the bisecting line can easily be run by the use of a measuring tape, or even of a stout cord.
A more interesting illustration is, however, the following:
Let the pupils set a stake, say about 5 feet high, at a point N on the school grounds about 9 A.M., and carefully measure the length of the shadow, NW, placing a small wooden pin at W. Then about 3 P.M. let them watch until the shadow NE is exactly the same length that it was when W was fixed, and then place a small wooden pin at E. If the work has been very carefully done, and they take the tape and bisect the line WE, thus fixing the line NS, they will have a north and south line. If this is marked out for a short distance from N, then when the shadow falls on NS, it will be noon by sun time (not standard time) at the school.
Problem. From a given point in a given line, to draw a line making an angle equal to a given angle.
Proclus says that Eudemus attributed to Œnopides the discovery of the solution which Euclid gave, and which is substantially the one now commonly seen in textbooks. The problem was probably solved in some fashion before the time of Œnopides, however. The object of the problem is primarily to enable us to draw a line parallel to a given line.[Pg 217]
Practically, the drawing of one line parallel to another is usually effected by means of a parallel ruler (see page 191), or by the use of draftsmen's triangles, as here shown, or even more commonly by the use of a T-square, such as is here seen. This illustration shows two T-squares used for drawing lines parallel to the sides of a board upon which the drawing paper is fastened.[71]
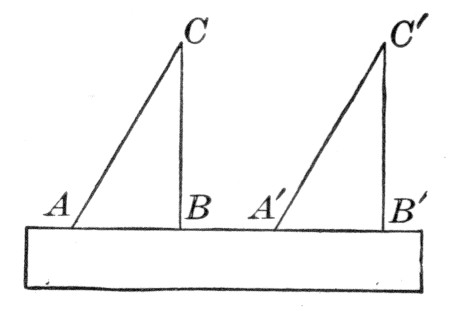
An ingenious instrument described by Baron Dupin is illustrated below.
To the bar A is fastened the sliding check B. A movable check D may be fastened by a screw C. A sharp point is fixed in B, so that as D slides along the edge of a board, the point marks a line parallel to the edge. Moreover, F and G are two brass arms of equal length joined by a pointed screw H that marks a line midway between B and D. Furthermore, it is evident that H will draw a line bisecting any irregular board if the checks B and D are kept in contact with the irregular edges.
Book II offers two general lines of application that may be introduced to advantage, preferably as additions to the textbook work. One of these has reference to topographical drawing and related subjects, and the other to geometric design. As long as these can be introduced
to the pupil with an air of reality, they serve a good purpose, but if made a part of textbook work, they soon come to have less interest than the exercises of a more abstract character. If a teacher can relate the problems in topographical drawing to the pupil's home town, and can occasionally set some outdoor work of the nature here suggested, the results are usually salutary; but if he reiterates only a half-dozen simple propositions time after time, with only slight changes in the nature of the application, then the results will not lead to a cultivation of power in geometry,—a point which the writers on applied geometry usually fail to recognize.
One of the simple applications of this book relates to the rounding of corners in laying out streets in some of our modern towns where there is a desire to depart from the conventional square corner. It is also used in laying out park walks and drives.
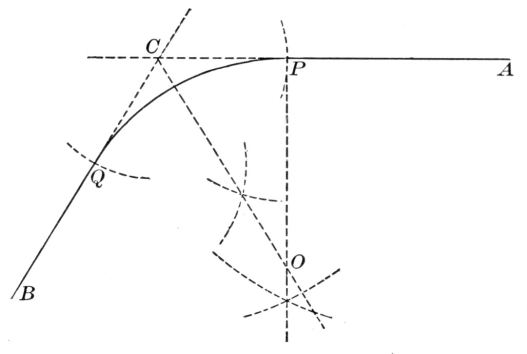
The figure in the middle of the page represents two streets, AP and BQ, that would, if prolonged, intersect at C. It is required to construct an arc so that they shall begin to curve at P and Q, where CP = CQ, and hence the "center of curvature" O must be found.[Pg 219]
The problem is a common one in railroad work, only here AP is usually oblique to BQ if they are produced to meet at C, as in the second figure on page 218. It is required to construct an arc so that the tracks shall begin to curve at P and Q, where CP = CQ.
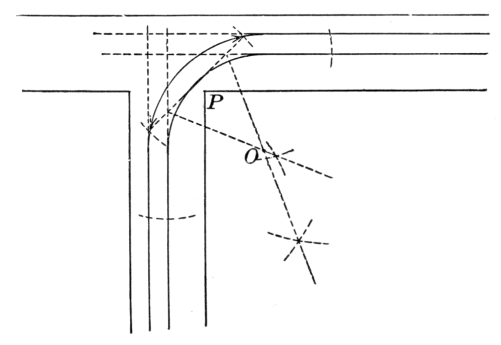
The problem becomes a little more complicated, and correspondingly more interesting, when we have to find the center of curvature for a street railway track that must turn a corner in such a way as to allow, say, exactly 5 feet from the point P, on account of a sidewalk.
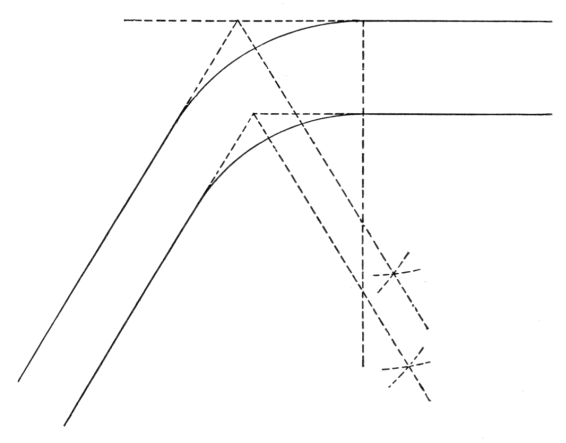
The problem becomes still more difficult if we have two roads of different widths that we wish to join on a curve. Here the two centers of curvature are not the same, and the one road narrows to the other on the curve. The solutions will be understood from a study of the figures.
The number of problems of this kind that can easily be made is limitless, and it is well to avoid the danger[Pg 220] of hobby riding on this or any similar topic. Therefore a single one will suffice to close this group.
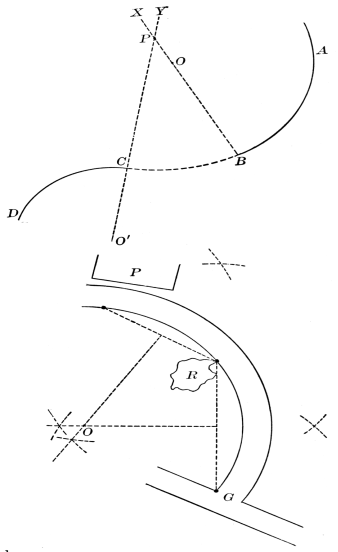
If a road AB on an arc described about O, is to be joined to road CD, described about O', the arc BC should evidently be internally tangent to AB and externally tangent to CD. Hence the center is on BOX and O'CY, and is therefore at P. The problem becomes more real if we give some width to the roads in making the drawing, and imagine them in a park that is being laid out with drives.
It will be noticed that the above problems require the erecting of perpendiculars, the bisecting of angles, and the application of the propositions on tangents.
A somewhat different line of problems is that relating to the passing of a circle through three given points. It is very easy to manufacture problems of this kind that have a semblance of reality.
For example, let it be required to plan a driveway from the gate G to the porch P so as to avoid a mass of rocks R, an arc[Pg 221] of a circle to be taken. Of course, if we allow pupils to use the Pythagorean Theorem at this time (and for metrical purposes this is entirely proper, because they have long been familiar with it), then we may ask not only for the drawing, but we may, for example, give the length from G to the point on R (which we may also call R), and the angle RGO as 60°, to find the radius.
A second general line of exercises adapted to Book II is a continuation of the geometric drawing recommended as a preliminary to the work in demonstrative geometry. The copying or the making of designs requiring the describing of circles, their inscription in or circumscription about triangles, and their construction in various positions of tangency, has some value as applying the various problems studied in this book. For a number of years past, several enthusiastic teachers have made much of the designs found in Gothic windows, having their pupils make the outline drawings by the help of compasses and straightedge. While such work has its value, it is liable soon to degenerate into purposeless formalism, and hence to lose interest by taking the vigorous mind of youth from the strong study of geometry to the weak manipulation of instruments. Nevertheless its value should be appreciated and conserved, and a few illustrations of these forms are given in order that the teacher may have examples from which to select. The best way of using this material is to offer it as supplementary work, using much or little, as may seem best, thus giving to it a freshness and interest that some have trouble in imparting to the regular book work.
The best plan is to sketch rapidly the outline of a window on the blackboard, asking the pupils to make a rough drawing, and to bring in a mathematical drawing on the following day.[Pg 222]
It might be said, for example, that in planning a Gothic window this drawing is needed. The arc BC is drawn with A as a center and AB as a radius. The small arches are described with A, D, and B as centers and AD as a radius. The center _P_ is found by taking A and B as centers and AE as a radius. How may the points D, E, and F be found? Draw the figure. From the study of the rectilinear figures suggested by such a simple pattern the properties of the equilateral triangle may be inferred.
The Gothic window also offers some interesting possibilities in connection with the study of the square. For example, the illustration given on page 223 shows a number of traceries involving the construction of a square, the bisecting of angles, and the describing of circles.[72]

The properties of the square, a figure now easily constructed by the pupils, are not numerous. What few there are may be brought out through the study of art forms, if desired. In case these forms are shown to a class, it is important that they should be selected from good designs. We have enough poor art in the world, so that geometry should not contribute any more. This illustration is a type of the best medieval Gothic parquetry.[73]
Even simple designs of a semipuzzling nature have their advantage in this connection. In the following example the inner square contains all of the triangles, the letters showing where they may be fitted.[74]
Still more elaborate designs, based chiefly upon the square and circle, are shown in the window traceries on page 225, and others will be given in connection with the study of the regular polygons.
Designs like the figure below are typical of the simple forms, based on the square and circle, that pupils may profitably incorporate in any work in art design that they may be doing at the time they are studying the circle and the problems relating to perpendiculars and squares.
Among the applications of the problem to draw a tangent to a given circle is the case of the common tangents to two given circles. Some authors give this as a basal problem, although it is more commonly given as an exercise or a corollary. One of the most obvious applications of the idea is that relating to the transmission of circular motion by means of a band over two wheels,[75] A and B, as shown on page 226.
The band may either not be crossed (the case of the two exterior tangents), or be crossed (the interior tangents), the latter allowing the wheels to turn in opposite directions. In case the band is liable to change its length, on account of stretching or variation in heat or moisture, a third wheel, D, is used. We then have the case of tangents to three pairs of circles. Illustrations of this nature make the exercise on the drawing of common tangents to two circles assume an appearance of genuine reality that is of advantage to the work.
In the American textbooks Book III is usually assigned to proportion. It is therefore necessary at the beginning of this discussion to consider what is meant by ratio and proportion, and to compare the ancient and the modern theories. The subject is treated by Euclid in his Book V, and an anonymous commentator has told us that it "is the discovery of Eudoxus, the teacher of Plato." Now proportion had been known long before the time of Eudoxus (408-355 B.C.), but it was numerical proportion, and as such it had been studied by the Pythagoreans. They were also the first to study seriously the incommensurable number, and with this study the treatment of proportion from the standpoint of rational numbers lost its scientific position with respect to geometry. It was because of this that Eudoxus worked out a theory of geometric proportion that was independent of number as an expression of ratio.
The following four definitions from Euclid are the basal ones of the ancient theory:
A ratio is a sort of relation in respect of size between two magnitudes of the same kind.
Magnitudes are said to have a ratio to one another which are capable, when multiplied, of exceeding one another.
Magnitudes are said to be in the same ratio, the first to the second and the third to the fourth, when, if any equimultiples whatever be taken of the first and third, and any equimultiples[Pg 228] whatever of the second and fourth, the former equimultiples alike exceed, are alike equal to, or alike fall short of, the latter equimultiples respectively taken in corresponding order.
Let magnitudes which have the same ratio be called proportional.[76]
Of these, the first is so loose in statement as often to have been thought to be an interpolation of some later writer. It was probably, however, put into the original for the sake of completeness, to have some kind of statement concerning ratio as a preliminary to the important definition of quantities in the same ratio. Like the definition of "straight line," it was not intended to be taken seriously as a mathematical statement.
The second definition is intended to exclude zero and infinite magnitudes, and to show that incommensurable magnitudes are included.
The third definition is the essential one of the ancient theory. It defines what is meant by saying that magnitudes are in the same ratio; in other words, it defines a proportion. Into the merits of the definition it is not proposed to enter, for the reason that it is no longer met in teaching in America, and is practically abandoned even where the rest of Euclid's work is in use. It should be said, however, that it is scientifically correct, that it covers the case of incommensurable magnitudes as well as that of commensurable ones, and that it is the Greek forerunner of the modern theories of irrational numbers.
As compared with the above treatment, the one now given in textbooks is unscientific. We define ratio as "the quotient of the numerical measures of two quantities of the same kind," and proportion as "an equality of ratios."
But what do we mean by the quotient, say of √2 by √3? And when we multiply a ratio by √5, what is the meaning of this operation? If we say that √2 : √3 means a quotient, what meaning shall we assign to "quotient"? If it is the number that shows how many times one number is contained in another, how many times is √3 contained in √2? If to multiply is to take a number a certain number of times, how many times do we take it when we multiply by √5? We certainly take it more than 2 times and less than 3 times, but what meaning can we assign to √5 times? It will thus be seen that our treatment of proportion assumes that we already know the theory of irrationals and can apply it to geometric magnitudes, while the ancient treatment is independent of this theory.
Educationally, however, we are forced to proceed as we do. Just as Dedekind's theory of numbers is a simple one for college students, so is the ancient theory of proportion; but as the former is not suited to pupils in the high school, so the latter must be relegated to the college classes. And in this we merely harmonize educational progress with world progress, for the numerical theory of proportion long preceded the theory of Eudoxus.
The ancients made much of such terms as duplicate, triplicate, alternate, and inverse ratio, and also such as composition, separation, and conversion of ratio. These entered into such propositions as, "If four magnitudes are proportional, they will also be proportional alternately." In later works they appear in the form of "proportion by composition," "by division," and "by composition and division." None of these is to-day of much importance, since modern symbolism has greatly simplified the ancient expressions, and in particular the[Pg 230] proposition concerning "composition and division" is no longer a basal theorem in geometry. Indeed, if our course of study were properly arranged, we might well relegate the whole theory of proportion to algebra, allowing this to precede the work in geometry.
We shall now consider a few of the principal propositions of Book III.
Theorem. If a line is drawn through two sides of a triangle parallel to the third side, it divides those sides proportionally.
In addition to the usual proof it is instructive to consider in class the cases in which the parallel is drawn through the two sides produced, either below the base or above the vertex, and also in which the parallel is drawn through the vertex.
Theorem. The bisector of an angle of a triangle divides the opposite side into segments which are proportional to the adjacent sides.
The proposition relating to the bisector of an exterior angle may be considered as a part of this one, but it is usually treated separately in order that the proof shall appear less involved, although the two are discussed together at this time. The proposition relating to the exterior angle was recognized by Pappus of Alexandria.
If ABC is the given triangle, and CP_1, CP_2 are respectively the internal and external bisectors, then AB is divided harmonically by P1 and P2.
∴AP1 : P1B = AP2 : P2B.
∴AP2 : P2B = AP2 - P1P2 : P1P2 - P2B,
and this is the criterion for the harmonic progression still seen in many algebras. For, letting AP2 = a, P1P2 = b, P2B = c, we have
a/c = (a - b)/(b - c),
[Pg 231]
which is also derived from taking the reciprocals of a, b, c, and placing them in an arithmetical progression, thus:
1/b - 1/a = 1/c - 1/b,
whence (a - b)/ab = (b - c)/bc,
or (a - b)/(b - c) = ab/bc = a/c.
This is the reason why the line AB is said to be divided harmonically. The line P1P2 is also called the harmonic mean between AP2 and P2B, and the points A, P1, B, P2 are said to form an harmonic range.
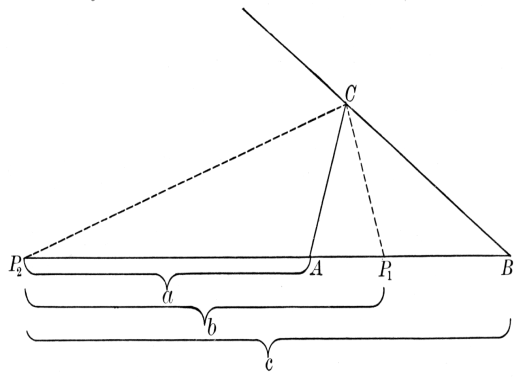
It may be noted that ∠P2CP1, being made up of halves of two supplementary angles, is a right angle. Furthermore, if the ratio CA : CB is given, and AB is given, then P1 and P2 are both fixed. Hence C must lie on a semicircle with P1P2 as a diameter, and therefore the locus of a point such that its distances from two given points are in a given ratio is a circle. This fact, Pappus tells us, was known to Apollonius.
At this point it is customary to define similar polygons as such as have their corresponding angles equal and their corresponding sides proportional. Aristotle gave substantially this definition, saying that such figures have "their sides proportional and their angles[Pg 232] equal." Euclid improved upon this by saying that they must "have their angles severally equal and the sides about the equal angles proportional." Our present phraseology seems clearer. Instead of "corresponding angles" we may say "homologous angles," but there seems to be no reason for using the less familiar word.
It is more general to proceed by first considering similar figures instead of similar polygons, thus including the most obviously similar of all figures,—two circles; but such a procedure is felt to be too difficult by many teachers. By this plan we first define similar sets of points, A1, A2, A3, ..., and B1, B2, B3, ..., as such that A1A2, B1B2, C1C2, ... are concurrent in O, and A1O : A2O = B1O : B2O = C1O : C2O = ... Here the constant ratio A1O : A2O is called the ratio of similitude, and O is called the center of similitude. Having defined similar sets of points, we then define similar figures as those figures whose points form similar sets. Then the two circles, the four triangles, and the three quadrilaterals[Pg 233] respectively are similar figures. If the ratio of similitude is 1, the similar figures become symmetric figures, and they are therefore congruent. All of the propositions relating to similar figures can be proved from this definition, but it is customary to use the Greek one instead.
Among the interesting applications of similarity is the case of a shadow, as here shown, where the light is the center of similitude. It is also well known to most high school pupils that in a camera the lens reverses the image. The mathematical arrangement is here shown, the lens inclosing the center of similitude. The proposition may also be applied to the enlargement of maps and working drawings.
The propositions concerning similar figures have no particularly interesting history, nor do they present any difficulties that call for discussion. In schools where there is a little time for trigonometry, teachers sometimes find it helpful to begin such work at this time, since all of the trigonometric functions depend upon the properties of similar triangles, and a brief explanation of the simplest trigonometric functions may add a little interest to the work. In the present state of our curriculum we cannot do more than mention the matter as a topic of general interest in this connection.[Pg 234]
It is a mistaken idea that geometry is a prerequisite to trigonometry. We can get along very well in teaching trigonometry if we have three propositions: (1) the one about the sum of the angles of a triangle; (2) the Pythagorean Theorem; (3) the one that asserts that two right triangles are similar if an acute angle of the one equals an acute angle of the other. For teachers who may care to make a little digression at this time, the following brief statement of a few of the facts of trigonometry may be of value:
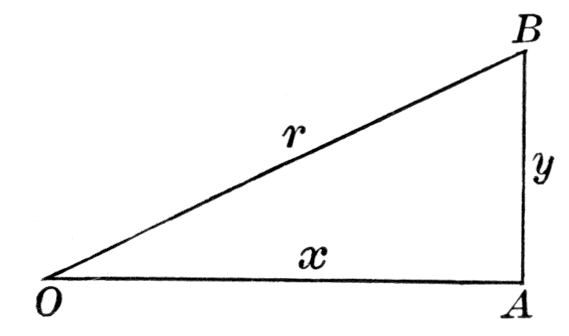
In the right triangle OAB we shall let AB = y, OA = x, OB = r, thus adopting the letters of higher mathematics. Then, so long as ∠O remains the same, such ratios as y/x, y/r, etc., will remain the same, whatever is the size of the triangle. Some of these ratios have special names. For example, we call
y/r the sine of O, and we write sin O = y/r;
x/r the cosine of O, and we write cos O = x/r;
y/x the tangent of O, and we write tan O = y/x.
Now because
sin O = y/r, therefore r sin O = y;
and because cos O = x/r, therefore r cos O = x;
and because tan O = y/x, therefore x tan O = y.
Hence, if we knew the values of sin O, cos O, and tan O for the various angles, we could find x, y, or r if we knew any one of them.
Now the values of the sine, cosine, and tangent (functions of the angles, as they are called) have been computed for the various angles, and some interest may be developed by obtaining them[Pg 235] by actual measurement, using the protractor and squared paper. Some of those needed for such angles as a pupil in geometry is likely to use are as follows:
| Angle | Sine | Cosine | Tangent | Angle | Sine | Cosine | Tangent |
| 5° | .087 | .996 | .087 | 50° | .766 | .643 | 1.192 |
| 10° | .174 | .985 | .176 | 55° | .819 | .574 | 1.428 |
| 15° | .259 | .966 | .268 | 60° | .866 | .500 | 1.732 |
| 20° | .342 | .940 | .364 | 65° | .906 | .423 | 2.145 |
| 25° | .423 | .906 | .466 | 70° | .940 | .342 | 2.748 |
| 30° | .500 | .866 | .577 | 75° | .966 | .259 | 3.732 |
| 35° | .574 | .819 | .700 | 80° | .985 | .174 | 5.671 |
| 40° | .643 | .766 | .839 | 85° | .996 | .087 | 11.430 |
| 45° | .707 | .707 | 1.000 | 90° | 1.000 | .000 | ∞ |
It will of course be understood that the values are correct only to the nearest thousandth. Thus the cosine of 5° is 0.99619, and the sine of 85° is 0.99619. The entire table can be copied by a class in five minutes if a teacher wishes to introduce this phase of the work, and the author has frequently assigned the computing of a simpler table as a class exercise.
Referring to the figure, if we know that r = 30 and ∠O = 40°, then since y = r sin O, we have y = 30 × 0.643 = 19.29. If we know that x = 60 and ∠O = 35°, then since y = x tan O, we have y = 60 × 0.7 = 42. We may also find r, for cos O = x/r, whence r = x/(cos O) = 60/0.819 = 73.26.
Therefore, if we could easily measure ∠O and could measure the distance x, we could find the height of a[Pg 236] building y. In trigonometry we use a transit for measuring angles, but it is easy to measure them with sufficient accuracy for illustrative purposes by placing an ordinary paper protractor upon something level, so that the center comes at the edge, and then sighting along a ruler held against it, so as to find the angle of elevation of a building. We may then measure the distance to the building and apply the formula y = x tan O.
It should always be understood that expensive apparatus is not necessary for such illustrative work. The telescope used on the transit is only three hundred years[Pg 237] old, and the world got along very well with its trigonometry before that was invented. So a little ingenuity will enable any one to make from cheap protractors about as satisfactory instruments as the world used before 1600. In order that this may be the more fully appreciated, a few illustrations are here given, showing the old instruments and methods used in practical surveying before the eighteenth century.
The illustration on page 236 shows a simple form of the quadrant, an instrument easily made by a pupil who[Pg 238] may be interested in outdoor work. It was the common surveying instrument of the early days. A more elaborate example is seen in the illustration, on page 237, of a seventeenth-century brass specimen in the author's collection.[77]
Another type, easily made by pupils, is shown in the above illustration from Bartoli, 1689. Such instruments were usually made of wood, brass, or ivory.[78]
Instruments for the running of lines perpendicular to other lines were formerly common, and are easily made. They suffice, as the following illustration shows, for surveying an ordinary field.
 Surveying Instrument of the Eighteenth Century
Surveying Instrument of the Eighteenth CenturyThe quadrant was practically used for all sorts of outdoor measuring. For example, the illustration from Finaeus, on this page, shows how it was used for altitudes, and the one reproduced on page 240 shows how it was used for measuring depths.
A similar instrument from the work of Bettinus is given on page 241, the distance of a ship being found by constructing an isosceles triangle. A more elaborate form, with a pendulum attachment, is seen in the illustration from De Judaeis, which also appears on page 241.[Pg 240]
 The Quadrant Used for Distances
The Quadrant Used for Distances[Pg 242] The quadrant finally developed into the octant, as shown in the following illustration from Hoffmann, and this in turn developed into the sextant, which is now used by all navigators.
In connection with this general subject the use of the speculum (mirror) in measuring heights should be mentioned. The illustration given on page 243 shows how in early days a simple device was used for this purpose. Two similar triangles are formed in this way, and we have only to measure the height of the eye above the ground, and the distances of the mirror from the tower and the observer, to have three terms of a proportion.
All of these instruments are easily made. The mirror is always at hand, and a paper protractor on a[Pg 243] piece of board, with a plumb line attached, serves as a quadrant. For a few cents, and by the expenditure of an hour or so, a school can have almost as good instruments as the ordinary surveyor had before the nineteenth century.
A well-known method of measuring the distance across a stream is illustrated in the figure below, where the distance from A to some point P is required.
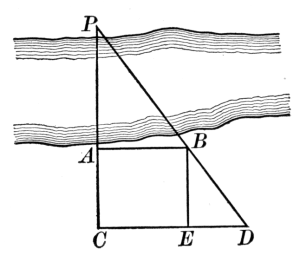
Run a line from A to C by standing at C in line with A and P. Then run two perpendiculars from A and C by any of the methods already given,—sighting on a protractor or along the edge of a book if no better means are at hand. Then sight from some point D, on CD, to P, putting a stake at B. Then run the perpendicular BE. Since DE : EB = BA : AP, and since we can measure DE, EB, and BA with the tape, we can compute the distance AP.
There are many variations of this scheme of measuring distances by means of similar triangles, and pupils may be encouraged to try some of them. Other figures are suggested on page 244, and the triangles need not be confined to those having a right angle.[Pg 244]
A very simple illustration of the use of similar triangles is found in one of the stories told of Thales. It is related that he found the height of the pyramids by measuring their shadow at the instant when his own shadow just equaled his height. He thus had the case of two similar isosceles triangles. This is an interesting exercise which may be tried about the time that pupils are leaving school in the afternoon.
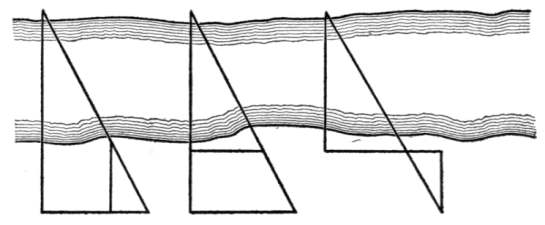
Another application of the same principle is seen in a method often taken for measuring the height of a tree.
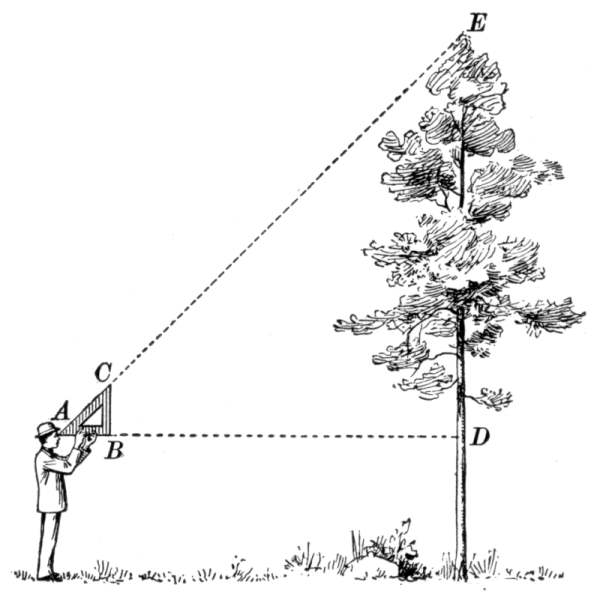
The observer has a large right triangle made of wood. Such a triangle is shown in the picture, in which AB = BC. He holds AB level and walks toward the tree until he just sees the top along AC. Then because
AB = BC,
and AB : BC = AD : DE,
the height above D will equal the distance AD.
Questions like the following may be given to the class:
1. What is the height of the tree in the picture if the triangle is 5 ft. 4 in. from the ground, and AD is 23 ft. 8 in.?
2. Suppose a triangle is used which has AB = twice BC. What is the height if AD = 75 ft.?
There are many variations of this principle. One consists in measuring the shadows of a tree and a staff at the same time. The height of the staff being known, the height of the tree is found by proportion. Another consists in sighting from the ground, across a mark on an upright staff, to the top of the tree. The height of the mark being known, and the distances from the eye to the staff and to the tree being measured, the height of the tree is found.
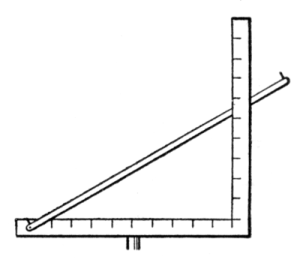
An instrument sold by dealers for the measuring of heights is known as the hypsometer. It is made of brass, and is of the form here shown. The base is graduated in equal divisions, say 50, and the upright bar is similarly divided. At the ends of the hinged radius are two sights. If the observer stands 50 feet from a tree and sights at the top, so that the hinged radius cuts the upright bar at 27, then he knows at once that the tree is 27 feet high. It is easy for a class to make a fairly good instrument of this kind out of stiff pasteboard.
An interesting application of the theorem relating to similar triangles is this: Extend your arm and point to a distant object, closing your left eye and sighting across your finger tip with your right eye. Now keep the finger in the same position and sight with your left eye. The finger will then seem to be pointing to an object some distance to the right of the one at which you were pointing. If you can estimate the distance between these two objects, which can often be done with a fair degree of accuracy when there are houses intervening, then you will be able to tell approximately your distance from the[Pg 246] objects, for it will be ten times the estimated distance between them. The finding of the reason for this by measuring the distance between the pupils of the two eyes, and the distance from the eye to the finger tip, and then drawing the figure, is an interesting exercise.
Perhaps some pupil who has read Thoreau's descriptions of outdoor life may be interested in what he says of his crude mathematics. He writes, "I borrowed the plane and square, level and dividers, of a carpenter, and with a shingle contrived a rude sort of a quadrant, with pins for sights and pivots." With this he measured the heights of a cliff on the Massachusetts coast, and with similar home-made or school-made instruments a pupil in geometry can measure most of the heights and distances in which he is interested.
Theorem. If in a right triangle a perpendicular is drawn from the vertex of the right angle to the hypotenuse:
1. The triangles thus formed are similar to the given triangle, and are similar to each other.
2. The perpendicular is the mean proportional between the segments of the hypotenuse.
3. Each of the other sides is the mean proportional between the hypotenuse and the segment of the hypotenuse adjacent to that side.
To this important proposition there is one corollary of particular interest, namely, The perpendicular from any point on a circle to a diameter is the mean proportional between the segments of the diameter. By means of this corollary we can easily construct a line whose numerical value is the square root of any number we please.
Thus we may make AD = 2 in., DB = 3 in., and erect DC ⊥ to AB. Then the length of DC will be √6 in., and we may find √6 approximately by measuring DC.
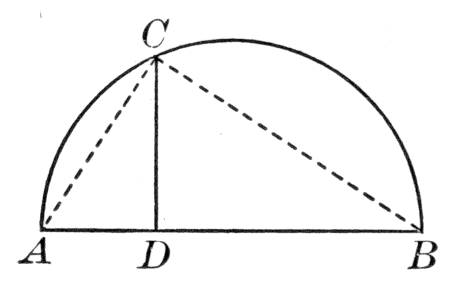
Furthermore, if we introduce negative magnitudes into geometry, and let DB = +3 and DA = -2, then DC will equal √(-6). In other words, we have a justification for representing imaginary quantities by lines perpendicular to the line on which we represent real quantities, as is done in the graphic treatment of imaginaries in algebra.
It is an interesting exercise to have a class find, to one decimal place, by measuring as above, the value of √2, √3, √5, and √9, the last being integral. If, as is not usually the case, the class has studied the complex number, the absolute value of √(-6), √(-7), ..., may be found in the same way.
A practical illustration of the value of the above theorem is seen in a method for finding distances that is frequently described in early printed books. It seems to have come from the Roman surveyors.
If a carpenter's square is put on top of an upright stick, as here shown, and an observer sights along the arms to a distant point B and a point A near the stick, then the two triangles are similar. Hence AD : DC = DC : DB. Hence, if AD and DC are measured, DB can be found. The experiment is an interesting and instructive one for a class, especially as the square can easily be made out of heavy pasteboard.
Theorem. If two chords intersect within a circle, the product of the segments of the one is equal to the product of the segments of the other.
Theorem. If from a point without a circle a secant and a tangent are drawn, the tangent is the mean proportional between the secant and its external segment.[Pg 248]
Corollary. If from a point without a circle a secant is drawn, the product of the secant and its external segment is constant in whatever direction the secant is drawn.
These two propositions and the corollary are all parts of one general proposition: If through a point a line is drawn cutting a circle, the product of the segments of the line is constant.
If P is within the circle, then xx' = yy'; if P is on the circle, then x and y become 0, and 0 · x' = 0 · y' = 0; if P is at P3, then x and y, having passed through 0, may be considered negative if we wish, although the two negative signs would cancel out in the equation; if P is at P4, then y = y' and we have xx' = y2, or x : y = y : x', as stated in the proposition.
We thus have an excellent example of the Principle of Continuity, and classes are always interested to consider the result of letting P assume various positions. Among the possible cases is the one of two tangents from an external point, and the one where P is at the center of the circle.
Students should frequently be questioned as to the meaning of "product of lines." The Greeks always used "rectangle of lines," but it is entirely legitimate to speak of "product of lines," provided we define the expression consistently. Most writers do this, saying that by the product of lines is meant the product of their numerical values, a subject already discussed at the beginning of this chapter.
Theorem. The square on the bisector of an angle of a triangle is equal to the product of the sides of this angle[Pg 249] diminished by the product of the segments made by the bisector upon the third side of the triangle.
This proposition enables us to compute the length of a bisector of a triangle if the lengths of the sides are known.
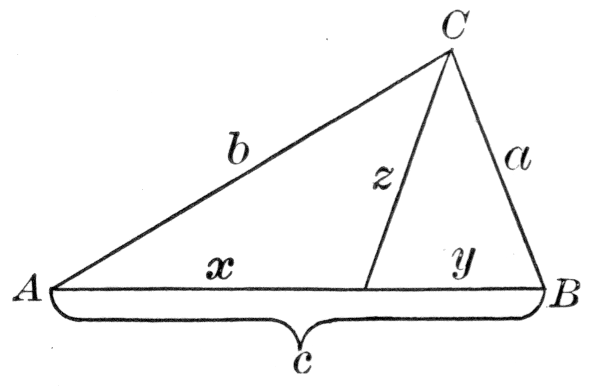
For, in this figure, let a = 3, b = 5, and c = 6.
Then ∵ x : y = b : a, and y = 6 - x,
we have x/(6 - x) = 5/3.
∴ 3x = 30 - 5x.
∴ x = 3 3/4, y = 2 1/4.
By the theorem, z2 = ab - xy
= 15 - (8 7/16) = 6 9/16.
∴ z = √(6 9/16) = 1/4 √105 = 2.5+.
Theorem. In any triangle the product of two sides is equal to the product of the diameter of the circumscribed circle by the altitude upon the third side.
This enables us, after the Pythagorean Theorem has been studied, to compute the length of the diameter of the circumscribed circle in terms of the three sides.
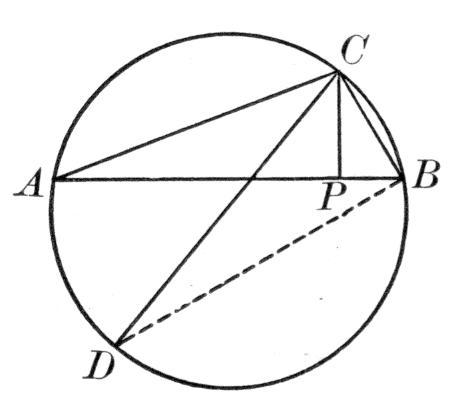
For if we designate the sides by a, b, and c, as usual, and let CD = d and PB = x, then
(CP)2 = a2 - x2
= b2 - (c - x)2.
∴ a2 - x2 = b2 - c2 + 2cx - x2.
∴ x = (a2 - b2 + c2) / 2c.
∴ (CP)2 = a2 - ((a2 - b2 + c2) / 2c)2.
But CP · d = ab.
∴ d = 2abc / √(4a2c2 - (a2 - b2 + c2)2).
This is not available at this time, however, because the Pythagorean Theorem has not been proved.
These two propositions are merely special cases of the following general theorem, which may be given as an interesting exercise:
If ABC is an inscribed triangle, and through C there are drawn two straight lines CD, meeting AB in D, and CP, meeting the circle in P, with angles ACD and PCB equal, then AC × BC will equal CD × CP.
Fig. 1 is the general case where D falls between A and B. If CP is a diameter, it reduces to the second figure given on page 249. If CP bisects ∠ACB, we have Fig. 3, from which may be proved the proposition given at the foot of page 248. If D lies on BA produced, we have Fig. 2. If D lies on AB produced, we have Fig. 4.
This general proposition is proved by showing that ⧌ADC and PBC are similar, exactly as in the second proposition given on page 249.
These theorems are usually followed by problems of construction, of which only one has great interest, namely, To divide a given line in extreme and mean ratio.
The purpose of this problem is to prepare for the construction of the regular decagon and pentagon. The division of a line in extreme and mean ratio is called "the golden section," and is probably "the section" mentioned by Proclus when he says that Eudoxus "greatly added to the number of the theorems which[Pg 251] Plato originated regarding the section." The expression "golden section" is not old, however, and its origin is uncertain.
If a line AB is divided in golden section at P, we have
AB × PB = (AP)2.
Therefore, if AB = a, and AP = x, we have
a(a - x) = x2,
or x2 + ax - a2 = 0;
whence x = - a/2 ± a/2√5
= a(1.118 - 0.5)
= 0.618a,
the other root representing the external point.
That is, x = about 0.6a, and a - x = about 0.4a, and a is therefore divided in about the ratio of 2 : 3.
There has been a great deal written upon the æsthetic features of the golden section. It is claimed that a line is most harmoniously divided when it is either bisected or divided in extreme and mean ratio. A painting has the strong feature in the center, or more often at a point about 0.4 of the distance from one side, that is, at the golden section of the width of the picture. It is said that in nature this same harmony is found, as in the division of the veins of such leaves as the ivy and fern.[Pg 252]
Book IV treats of the area of polygons, and offers a large number of practical applications. Since the number of applications to the measuring of areas of various kinds of polygons is unlimited, while in the first three books these applications are not so obvious, less effort is made in this chapter to suggest practical problems to the teachers. The survey of the school grounds or of vacant lots in the vicinity offers all the outdoor work that is needed to make Book IV seem very important.
Theorem. Two rectangles having equal altitudes are to each other as their bases.
Euclid's statement (Book VI, Proposition 1) was as follows: Triangles and parallelograms which are under the same height are to one another as their bases. Our plan of treating the two figures separately is manifestly better from the educational standpoint.
In the modern treatment by limits the proof is divided into two parts: first, for commensurable bases; and second, for incommensurable ones. Of these the second may well be omitted, or merely be read over by the teacher and class and the reasons explained. In general, it is doubtful if the majority of an American class in geometry get much out of the incommensurable case. Of course, with a bright class a teacher may well afford to take it as it is given in the textbook, but the important[Pg 253] thing is that the commensurable case should be proved and the incommensurable one recognized.
Euclid's treatment of proportion was so rigorous that no special treatment of the incommensurable was necessary. The French geometer, Legendre, gave a rigorous proof by reductio ad absurdum. In America the pupils are hardly ready for these proofs, and so our treatment by limits is less rigorous than these earlier ones.
Theorem. The area of a rectangle is equal to the product of its base by its altitude.
The easiest way to introduce this is to mark a rectangle, with commensurable sides, on squared paper, and count up the squares; or, what is more convenient, to draw the rectangle and mark the area off in squares.
It is interesting and valuable to a class to have its attention called to the fact that the perimeter of a rectangle is no criterion as to the area. Thus, if a rectangle has an area of 1 square foot and is only 1/440 of an inch high, the perimeter is over 2 miles. The story of how Indians were induced to sell their land by measuring the perimeter is a very old one. Proclus speaks of travelers who described the size of cities by the perimeters, and of men who cheated others by pretending to give them as much land as they themselves had, when really they made only the perimeters equal. Thucydides estimated the size of Sicily by the time it took to sail round it. Pupils will be interested to know in this connection that of polygons having the same perimeter and the same number of sides, the one having equal sides and equal angles is the greatest, and that of plane figures having the same perimeter, the circle is the greatest. These facts were known to the Greek writers, Zenodorus (ca. 150 B.C.) and Proclus (410-485 A.D.).[Pg 254]
The surfaces of rectangular solids may now be found, there being an advantage in thus incidentally connecting plane and solid geometry wherever it is natural to do so.
Theorem. The area of a parallelogram is equal to the product of its base by its altitude.
The best way to introduce this theorem is to cut a parallelogram from paper, and then, with the class, separate it into two parts by a cut perpendicular to the base. The two parts may then be fitted together to make a rectangle. In particular, if we cut off a triangle from one end and fit it on the other, we have the basis for the proof of the textbooks. The use of squared paper for such a proposition is not wise, since it makes the measurement appear to be merely an approximation. The cutting of the paper is in every way more satisfactory.
Theorem. The area of a triangle is equal to half the product of its base by its altitude.
Of course, the Greeks would never have used the wording of either of these two propositions. Euclid, for example, gives this one as follows: If a parallelogram have the same base with a triangle and be in the same parallels, the parallelogram is double of the triangle. As to the parallelogram, he simply says it is equal to a parallelogram of equal base and "in the same parallels," which makes it equal to a rectangle of the same base and the same altitude.
The number of applications of these two theorems is so great that the teacher will not be at a loss to find genuine ones that appeal to the class. Teachers may now introduce pyramids, requiring the areas of the triangular faces to be found.
The Ahmes papyrus (ca. 1700 B.C.) gives the area of an isosceles triangle as ½ bs, where s is one of the equal[Pg 255] sides, thus taking s for the altitude. This shows the primitive state of geometry at that time.
Theorem. The area of a trapezoid is equal to half the sum of its bases multiplied by the altitude.
An interesting variation of the ordinary proof is made by placing a trapezoid T', congruent to T, in the position here shown. The parallelogram formed equals a(b + b'), and therefore
T = a · (b + b')/2.
The proposition should be discussed for the case b = b', when it reduces to the one about the area of a parallelogram. If b'= 0, the trapezoid reduces to a triangle, and T = a · b/2.
This proposition is the basis of the theory of land surveying, a piece of land being, for purposes of measurement, divided into trapezoids and triangles, the latter being, as we have seen, a kind of special trapezoid.
The proposition is not in Euclid, but is given by Proclus in the fifth century.
The term "isosceles trapezoid" is used to mean a trapezoid with two opposite sides equal, but not parallel. The area of such a figure was incorrectly given by the Ahmes papyrus as ½(b + b')s, where s is one of the equal sides. This amounts to taking s = a.
The proposition is particularly important in the surveying of an irregular field such as is found in hilly districts. It is customary to consider the field as a polygon, and to draw a meridian line, letting fall perpendiculars upon it from the vertices, thus forming triangles and trapezoids that can easily be measured. An older plan, but one better suited to the use of pupils who may be working only with the tape, is given on page 99.[Pg 256]
Theorem. The areas of two triangles which have an angle of the one equal to an angle of the other are to each other as the products of the sides including the equal angles.
This proposition may be omitted as far as its use in plane geometry is concerned, for we can prove the next proposition here given without using it. In solid geometry it is used only in a proposition relating to the volumes of two triangular pyramids having a common trihedral angle, and this is usually omitted. But the theorem is so simple that it takes but little time, and it adds greatly to the student's appreciation of similar triangles. It not only simplifies the next one here given, but teachers can at once deduce the latter from it as a special case by asking to what it reduces if a second angle of one triangle is also equal to a second angle of the other triangle.
It is helpful to give numerical values to the sides of a few triangles having such equal angles, and to find the numerical ratio of the areas.
Theorem. The areas of two similar triangles are to each other as the squares on any two corresponding sides.
This may be proved independently of the preceding proposition by drawing the altitudes p and p'. Then
⧍ABC/⧍A'B'C' = cp/c'p'.
But c/c' = p/p',
by similar triangles.
∴ ⧍ABC/⧍A'B'C' = c2/c'2,
and so for other sides.
This proof is unnecessarily long, however, because of the introduction of the altitudes.
In this and several other propositions in Book IV occurs the expression "the square on a line." We have, in our departure from Euclid, treated a line either as a geometric figure or as a number (the length of the line), as was the more convenient. Of course if we are speaking of a line, the preferable expression is "square on the line," whereas if we speak of a number, we say "square of the number." In the case of a rectangle of two lines we have come to speak of the "product of the lines," meaning the product of their numerical values. We are therefore not as accurate in our phraseology as Euclid, and we do not pretend to be, for reasons already given. But when it comes to "square on a line" or "square of a line," the former is the one demanding no explanation or apology, and it is even better understood than the latter.
Theorem. The areas of two similar polygons are to each other as the squares on any two corresponding sides.
This is a proposition of great importance, and in due time the pupil sees that it applies to circles, with the necessary change of the word "sides" to "lines." It is well to ask a few questions like the following: If one square is twice as high as another, how do the areas compare? If the side of one equilateral triangle is three times as long as that of another, how do the perimeters compare? how do the areas compare? If the area of one square is twenty-five times the area of another square, the side of the first is how many times as long as the side of the second? If a photograph is enlarged so that a tree is four times as high as it was before, what is the ratio of corresponding dimensions? The area of the enlarged photograph is how many times as great as the area of the original?[Pg 258]
Theorem. The square on the hypotenuse of a right triangle is equivalent to the sum of the squares on the other two sides.
Of all the propositions of geometry this is the most famous and perhaps the most valuable. Trigonometry is based chiefly upon two facts of plane geometry: (1) in similar triangles the corresponding sides are proportional, and (2) this proposition. In mensuration, in general, this proposition enters more often than any others, except those on the measuring of the rectangle and triangle. It is proposed, therefore, to devote considerable space to speaking of the history of the theorem, and to certain proofs that may profitably be suggested from time to time to different classes for the purpose of adding interest to the work.
Proclus, the old Greek commentator on Euclid, has this to say of the history: "If we listen to those who wish to recount ancient history, we may find some of them referring this theorem to Pythagoras and saying that he sacrificed an ox in honor of his discovery. But for my part, while I admire those who first observed the truth of this theorem, I marvel more at the writer of the 'Elements' (Euclid), not only because he made it fast by a most lucid demonstration, but because he compelled assent to the still more general theorem by the irrefragable arguments of science in Book VI. For in that book he proves, generally, that in right triangles the figure on the side subtending the right angle is equal to the similar and similarly placed figures described on the sides about the right angle." Now it appears from this that Proclus, in the fifth century A.D., thought that Pythagoras discovered the proposition in the sixth century B.C., that the usual proof, as given in most of our[Pg 259] American textbooks, was due to Euclid, and that the generalized form was also due to the latter. For it should be made known to students that the proposition is true not only for squares, but for any similar figures, such as equilateral triangles, parallelograms, semicircles, and irregular figures, provided they are similarly placed on the three sides of the right triangle.
Besides Proclus, Plutarch testifies to the fact that Pythagoras was the discoverer, saying that "Pythagoras sacrificed an ox on the strength of his proposition as Apollodotus says," but saying that there were two possible propositions to which this refers. This Apollodotus was probably Apollodorus, surnamed Logisticus (the Calculator), whose date is quite uncertain, and who speaks in some verses of a "famous proposition" discovered by Pythagoras, and all tradition makes this the one. Cicero, who comments upon these verses, does not question the discovery, but doubts the story of the sacrifice of the ox. Of other early writers, Diogenes Laertius, whose date is entirely uncertain (perhaps the second century A.D.), and Athenæus (third century A.D.) may be mentioned as attributing the theorem to Pythagoras, while Heron (first century A.D.) says that he gave a rule for forming right triangles with rational integers for the sides, like 3, 4, 5, where 32 + 42 = 52. It should be said, however, that the Pythagorean origin has been doubted, notably in an article by H. Vogt, published in the Bibliotheca Mathematica in 1908 (Vol. IX (3), p. 15), entitled "Die Geometrie des Pythagoras," and by G. Junge, in his work entitled "Wann haben die Griechen das Irrationale entdeckt?" (Halle, 1907). These writers claim that all the authorities attributing the proposition to Pythagoras are centuries later than[Pg 260] his time, and are open to grave suspicion. Nevertheless it is hardly possible that such a general tradition, and one so universally accepted, should have arisen without good foundation. The evidence has been carefully studied by Heath in his "Euclid," who concludes with these words: "On the whole, therefore, I see no sufficient reason to question the tradition that, so far as Greek geometry is concerned ..., Pythagoras was the first to introduce the theorem ... and to give a general proof of it." That the fact was known earlier, probably without the general proof, is recognized by all modern writers.
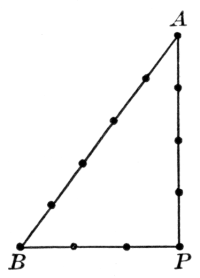
Pythagoras had studied in Egypt and possibly in the East before he established his school at Crotona, in southern Italy. In Egypt, at any rate, he could easily have found that a triangle with the sides 3, 4, 5, is a right triangle, and Vitruvius (first century B.C.) tells us that he taught this fact. The Egyptian harpedonaptae (rope stretchers) stretched ropes about pegs so as to make such a triangle for the purpose of laying out a right angle in their surveying, just as our surveyors do to-day. The great pyramids have an angle of slope such as is given by this triangle. Indeed, a papyrus of the twelfth dynasty, lately discovered at Kahun, in Egypt, refers to four of these triangles, such as 12 + (3/4)2 = (1-1/4)2. This property seems to have been a matter of common knowledge long before Pythagoras, even as far east as China. He was, therefore, naturally led to attempt to prove the general property which had already been recognized for special cases, and in particular for the isosceles right triangle.[Pg 261]
How Pythagoras proved the proposition is not known. It has been thought that he used a proof by proportion, because Proclus says that Euclid gave a new style of proof, and Euclid does not use proportion for this purpose, while the subject, in incomplete form, was highly esteemed by the Pythagoreans. Heath suggests that this is among the possibilities:
⧌ABC and APC are similar.
∴ AB × AP = (AC)2.
Similarly, AB × PB = (BC)2.
∴ AB(AP + PB) = (AC)2 + (BC)2,
or (AB)2 = (AC)2 + (BC)2.
Others have thought that Pythagoras derived his proof from dissecting a square and showing that the square on the hypotenuse must equal the sum of the squares on the other two sides, in some such manner as this:
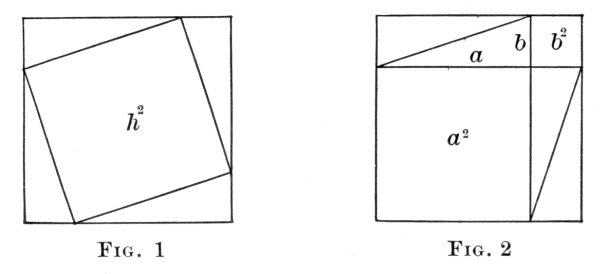
Here Fig. 1 is evidently h2 + 4 ⧌.
Fig. 2 is evidently a2 + b2 + 4 ⧌.
∴ h2 + 4 ⧌ = a2 + b2 + 4 ⧌, the ⧌ all being congruent.
∴ h2 = a2 + b2.
The great Hindu mathematician, Bhaskara (born 1114 A.D.), proceeds in a somewhat similar manner. He draws this figure, but gives no proof. It is evident that he had in mind this relation:
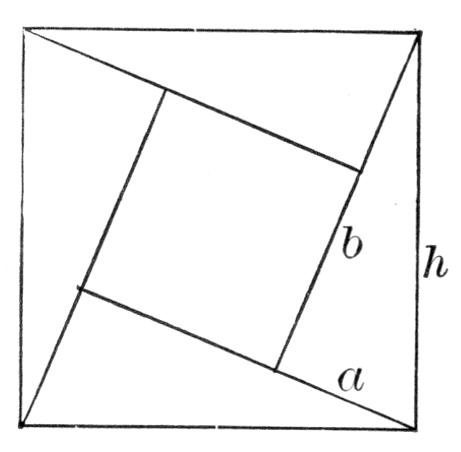
h2 = 4 · ab/2 + (b - a)2 = a2 + b2.
A somewhat similar proof can be based upon the following figure:
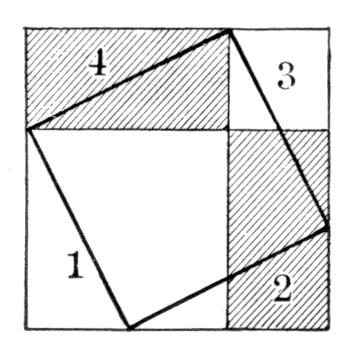
If the four triangles, 1 + 2 + 3 + 4, are taken away, there remains the square on the hypotenuse. But if we take away the two shaded rectangles, which equal the four triangles, there remain the squares on the two sides. Therefore the square on the hypotenuse must equal the sum of these two squares.
It has long been thought that the truth of the proposition was first observed by seeing the tiles on the floors of ancient temples. If they were arranged as here shown, the proposition would be evident for the special case of an isosceles right triangle.
The Hindus knew the proposition long before Bhaskara, however, and possibly before Pythagoras. It is referred to in the old religious poems of the Brahmans, the "Sulvasutras," but the date of these poems is so uncertain that it is impossible to state that they preceded the sixth century B.C.,[79] in which Pythagoras lived. The "Sulvasutra" of Apastamba has
a collection of rules, without proofs, for constructing various figures. Among these is one for constructing right angles by stretching cords of the following lengths: 3, 4, 5; 12, 16, 20; 15, 20, 25 (the two latter being multiples of the first); 5, 12, 13; 15, 36, 39; 8, 15, 17; 12, 35, 37. Whatever the date of these "Sulvasutras," there is no evidence that the Indians had a definite proof of the theorem, even though they, like the early Egyptians, recognized the general fact.
It is always interesting to a class to see more than one proof of a famous theorem, and many teachers find it profitable to ask their pupils to work out proofs that are (to them) original, often suggesting the figure. Two of the best known historic proofs are here given.
The first makes the Pythagorean Theorem a special case of a proposition due to Pappus (fourth century A.D.), relating to any kind of a triangle.
Somewhat simplified, this proposition asserts that if ABC is any kind of triangle, and MC, NC are parallelograms on AC, BC, the opposite sides being produced to meet at P; and if PC is produced making QR = PC; and if the parallelogram AT is constructed, then AT = MC + NC.
For MC = AP = AR, having equal bases and equal altitudes.
Similarly, NC = QT.
Adding, MC + NC = AT.
If, now, ABC is a right triangle, and if MC and NC are squares, it is easy to show that AT is a square, and the proposition reduces to the Pythagorean Theorem.
The Arab writer, Al-Nairīzī (died about 922 A.D.), attributes to Thābit ben Qurra (826-901 A.D.) a proof substantially as follows:
The four triangles T can be proved congruent. Then if we take from the whole figure T and T', we have left the squares on the two sides of the right angle. If we take away the other two triangles instead, we have left the square on the hypotenuse. Therefore the former is equivalent to the latter.
A proof attributed to the great artist, Leonardo da Vinci (1452-1519), is as follows:
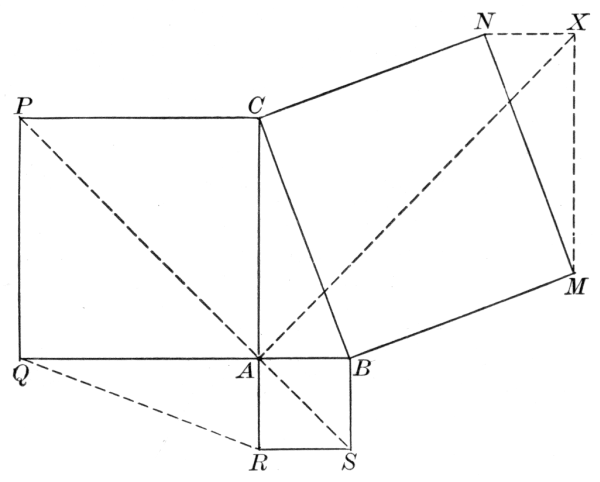
The construction of the following figure is evident. It is easily shown that the four quadrilaterals ABMX, XNCA, SBCP, and SRQP are congruent.
∴ ABMXNCA equals SBCPQRS but is not congruent to it, the congruent quadrilaterals being differently arranged.
Subtract the congruent triangles MXN, ABC, RAQ, and the proposition is proved.[80]
The following is an interesting proof of the proposition:
Let ABC be the original triangle, with AB < BC. Turn the triangle about B, through 90°, until it comes into the position A'BC'. Then because it has been turned through 90°, C'A'P will be perpendicular to AC. Then
1/2(AB)2 = ⧍ABA',
and 1/2(BC')2 = ⧍BC'C,
because BC = BC'.
∴ 1/2((AB)2 + (BC)2) = ⧍ABA' + ⧍BC'C.
∴ 1/2((AB)2 + (BC)2)
= ⧍AC'A' + ⧍A'C'C
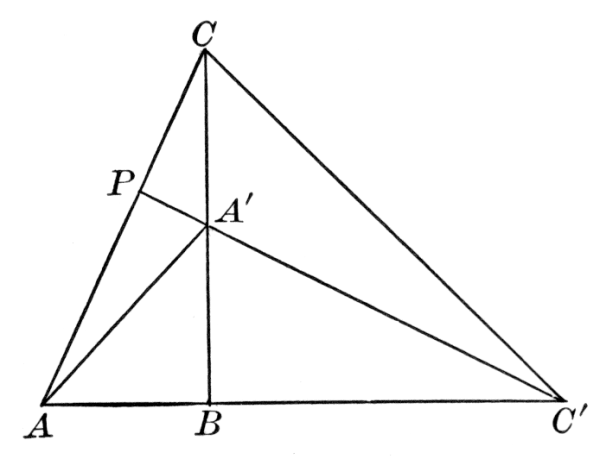
(For ⧍ABA' + ⧍BC'A' + ⧍A'C'C is the second member of both equations.)
= 1/2A'C' · AP
+ 1/2A'C' · PC
= 1/2A'C' · AC
= 1/2(AC)2.
∴ (AB)2 + (BC)2 = (AC)2.
The Pythagorean Theorem, as it is generally called, has had other names. It is not uncommonly called the pons asinorum (see page 174) in France. The Arab writers called it the Figure of the Bride, although the reason for this name is unknown; possibly two being joined in one has something to do with it. It has also been called the Bride's Chair, and the shape of the Euclid figure is not unlike the chair that a slave carries on his back, in which the Eastern bride is sometimes transported to the wedding ceremony. Schopenhauer, the German philosopher, referring to the figure, speaks of it as "a proof walking on stilts," and as "a mouse-trap proof."
An interesting theory suggested by the proposition is that of computing the sides of right triangles so that they shall be represented by rational numbers. Pythagoras seems to have been the first to take up this theory, although such numbers were applied to the right triangle[Pg 266] before his time, and Proclus tells us that Plato also contributed to it. The rule of Pythagoras, put in modern symbols, was as follows:
n2 + ((n2 - 1)/2)2 = ((n2 + 1)/2)2,
the sides being n, (n2 - 1)/2, and (n2 + 1)/2. If for n we put 3, we have 3, 4, 5. If we take the various odd numbers, we have
n = 1, 3, 5, 7, 9, ···,
(n2 - 1)/2 = 0, 4, 12, 24, 40, ···,
(n2 + 1)/2 = 1, 5, 13, 25, 41, ···.
Of course n may be even, giving fractional values. Thus, for n = 2 we have for the three sides, 2, 1-1/2, 2-1/2. Other formulas are also known. Plato's, for example, is as follows:
(2n)2 + (n2 - 1)2 = (n2 + 1)2.
If 2n = 2, 4, 6, 8, 10, ···,
then n2 - 1 = 0, 3, 8, 15, 24, ···,
and n2 + 1 = 2, 5, 10, 17, 26, ···.
This formula evidently comes from that of Pythagoras by doubling the sides of the squares.[81]
Theorem. In any triangle the square of the side opposite an acute angle is equal to the sum of the squares of the other two sides diminished by twice the product of one of those sides by the projection of the other upon that side.
Theorem. A similar statement for the obtuse triangle.
These two propositions are usually proved by the help of the Pythagorean Theorem. Some writers, however, actually construct the squares and give a proof similar to the one in that proposition. This plan goes back at least to Gregoire de St. Vincent (1647).
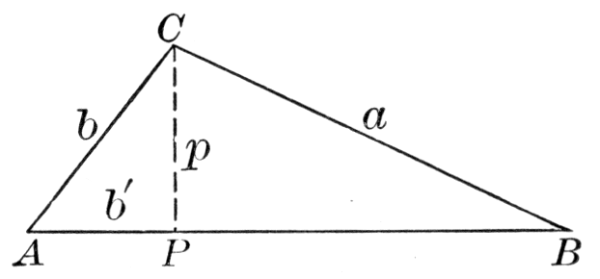
It should be observed that
a2 = b2 + c2 - 2b'c.
If ∠A = 90°, then b' = 0, and this becomes
a2 = b2 + c2.
If ∠A is obtuse, then b' passes through 0 and becomes negative, and a2 = b2 + c2 + 2b'c.
Thus we have three propositions in one.
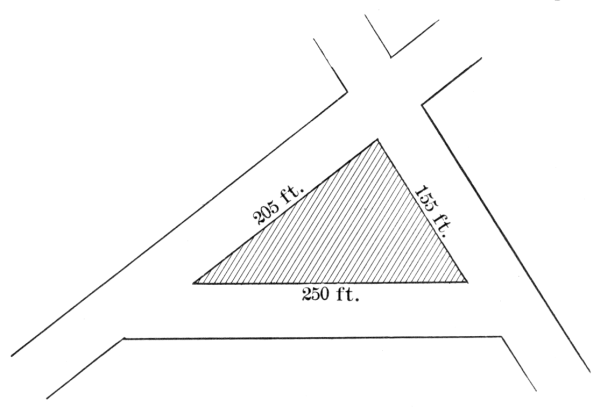
At the close of Book IV many geometries give as an exercise, and some give as a regular proposition, the celebrated problem that bears the name of Heron of Alexandria, namely, to compute the area of a triangle in terms of its sides. The result is the important formula
Area = √(s(s - a)(s - b)(s - c)),
where a, b, and c are the sides, and s is the semiperimeter ½(a + b + c). As a practical application the class may be able to find a triangular piece of land, as here shown, and to measure the sides. If the piece is clear, the result may be checked by measuring the altitude and applying the formula a = ½bh.
It may be stated to the class that Heron's formula is only a special case of the more general one developed[Pg 268] about 640 A.D., by a famous Hindu mathematician, Brahmagupta. This formula gives the area of an inscribed quadrilateral as √((s - a)(s - b)(s - c)(s - d)), where a, b, c, and d are the sides and s is the semiperimeter. If d = 0, the quadrilateral becomes a triangle and we have Heron's formula.[82]
At the close of Book IV, also, the geometric equivalents of the algebraic formulas for (a + b)2, (a - b)2, and (a + b)(a - b) are given. The class may like to know that Euclid had no algebra and was compelled to prove such relations as these by geometry, while we do it now much more easily by algebraic multiplication.

Book V treats of regular polygons and circles, and includes the computation of the approximate value of π. It opens with a definition of a regular polygon as one that is both equilateral and equiangular. While in elementary geometry the only regular polygons studied are convex, it is interesting to a class to see that there are also regular cross polygons. Indeed, the regular cross pentagon was the badge of the Pythagoreans, as Lucian (ca. 100 B.C.) and an unknown commentator on Aristophanes (ca. 400 B.C.) tell us. At the vertices of this polygon the Pythagoreans placed the Greek letters signifying "health."
Euclid was not interested in the measure of the circle, and there is nothing in his "Elements" on the value of π. Indeed, he expressly avoided numerical measures of all kinds in his geometry, wishing the science to be kept distinct from that form of arithmetic known to the Greeks as logistic, or calculation. His Book IV is devoted to the construction of certain regular polygons, and his propositions on this subject are now embodied in Book V as it is usually taught in America.
If we consider Book V as a whole, we are struck by three features. Of these the first is the pure geometry involved, and this is the essential feature to be emphasized. The second is the mensuration of the circle, a relatively unimportant piece of theory in view of the[Pg 270] fact that the pupil is not ready for incommensurables, and a feature that imparts no information that the pupil did not find in arithmetic. The third is the somewhat interesting but mathematically unimportant application of the regular polygons to geometric design.
As to the mensuration of the circle it is well for us to take a broad view before coming down to details. There are only four leading propositions necessary for the mensuration of the circle and the determination of the value of π. These are as follows: (1) The inscribing of a regular hexagon, or any other regular polygon of which the side is easily computed in terms of the radius. We may start with a square, for example, but this is not so good as the hexagon because its side is incommensurable with the radius, and its perimeter is not as near the circumference. (2) The perimeters of similar regular polygons are proportional to their radii, and their areas to the squares of the radii. It is now necessary to state, in the form of a postulate if desired, that the circle is the limit of regular inscribed and circumscribed polygons as the number of sides increases indefinitely, and hence that (2) holds for circles. (3) The proposition relating to the area of a regular polygon, and the resulting proposition relating to the circle. (4) Given the side of a regular inscribed polygon, to find the side of a regular inscribed polygon of double the number of sides. It will thus be seen that if we were merely desirous of approximating the value of π, and of finding the two formulas c = 2πr and a = πr2, we should need only four propositions in this book upon which to base our work. It is also apparent that even if the incommensurable cases are generally omitted, the notion of limit is needed at this time, and that it must briefly be reviewed before proceeding further.[Pg 271]
There is, however, a much more worthy interest than the mere mensuration of the circle, namely, the construction of such polygons as can readily be formed by the use of compasses and straightedge alone. The pleasure of constructing such figures and of proving that the construction is correct is of itself sufficient justification for the work. As to the use of such figures in geometric design, some discussion will be offered at the close of this chapter.
The first few propositions include those that lead up to the mensuration of the circle. After they are proved it is assumed that the circle is the limit of the regular inscribed and circumscribed polygons as the number of sides increases indefinitely. This may often be proved with some approach to rigor by a few members of an elementary class, but it is the experience of teachers that the proof is too difficult for most beginners, and so the assumption is usually made in the form of an unproved theorem.
The following are some of the leading propositions of this book:
Theorem. Two circumferences have the same ratio as their radii.
This leads to defining the ratio of the circumference to the diameter as π. Although this is a Greek letter, it was not used by the Greeks to represent this ratio. Indeed, it was not until 1706 that an English writer, William Jones, in his "Synopsis Palmariorum Matheseos," used it in this way, it being the initial letter of the Greek word for "periphery." After establishing the properties that c = 2πr, and a = πr2, the textbooks follow the Greek custom and proceed to show how to inscribe and circumscribe various regular polygons, the purpose being to use these in computing the approximate[Pg 272] numerical value of π. Of these regular polygons two are of special interest, and these will now be considered.
Problem. To inscribe a regular hexagon in a circle.
That the side of a regular inscribed hexagon equals the radius must have been recognized very early. The common divisions of the circle in ancient art are into four, six, and eight equal parts. No draftsman could have worked with a pair of compasses without quickly learning how to effect these divisions, and that compasses were early used is attested by the specimens of these instruments often seen in museums. There is a tradition that the ancient Babylonians considered the circle of the year as made up of 360 days, whence they took the circle as composed of 360 steps or grades (degrees). This tradition is without historic foundation, however, there being no authority in the inscriptions for this assumption of the 360-division by the Babylonians, who seem rather to have preferred 8, 12, 120, 240, and 480 as their division numbers. The story of 360° in the Babylonian circle seems to start with Achilles Tatius, an Alexandrian grammarian of the second or third century A.D. It is possible, however, that the Babylonians got their favorite number 60 (as in 60 seconds make a minute, 60 minutes make an hour or degree) from the hexagon in a circle (1/6 of 360° = 60°), although the probabilities seem to be that there is no such connection.[83]
The applications of this problem to mensuration are numerous. The fact that we may use for tiles on a floor three regular polygons—the triangle, square, and hexagon—is noteworthy, a fact that Proclus tells us was recognized by Pythagoras. The measurement of
the regular hexagon, given one side, may be used in computing sections of hexagonal columns, in finding areas of flower beds, and in other similar cases.
This review of the names of the polygons offers an opportunity to impress their etymology again on the mind. In this case, for example, we have "hexagon" from the Greek words for "six" and "angle."
Problem. To inscribe a regular decagon in a given circle.
Euclid states the problem thus: To construct an isosceles triangle having each of the angles at the base double of the remaining one. This makes each base angle 72° and the vertical angle 36°, the latter being the central angle of a regular decagon,—essentially our present method.
This proposition seems undoubtedly due to the Pythagoreans, as tradition has always asserted. Proclus tells us that Pythagoras discovered "the construction of the cosmic figures," or the five regular polyhedrons, and one of these (the dodecahedron) involves the construction of the regular pentagon.
Iamblichus (ca. 325 A.D.) tells us that Hippasus, a Pythagorean, was said to have been drowned for daring to claim credit for the construction of the regular dodecahedron, when by the rules of the brotherhood all credit should have been assigned to Pythagoras.
If a regular polygon of s sides can be inscribed, we may bisect the central angles, and therefore inscribe one of 2s sides, and then of 4s sides, and then of 8s sides, and in general of 2ns sides. This includes the case of s = 2 and n = 0, for we can inscribe a regular polygon of two sides, the angles being, by the usual formula, 2(2-2)/2 = 0, although, of course, we never think of two equal and coincident lines as forming what we might call a digon.[Pg 274]
We therefore have the following regular polygons:
From the equilateral triangle, regular polygons of 2n · 3 sides;
From the square, regular polygons of 2n sides;
From the regular pentagon, regular polygons of 2n · 5 sides;
From the regular pentedecagon, regular polygons of 2n · 15 sides.
This gives us, for successive values of n, the following regular polygons of less than 100 sides:
From 2n · 3, 3, 6, 12, 24, 48, 96;
From 2n, 2, 4, 8, 16, 32, 64;
From 2n · 5, 5, 10, 20, 40, 80;
From 2n · 15, 15, 30, 60.
Gauss (1777-1855), a celebrated German mathematician, proved (in 1796) that it is possible also to inscribe a regular polygon of 17 sides, and hence polygons of 2n · 17 sides, or 17, 34, 68, ..., sides, and also 3 · 17 = 51 and 5 · 17 = 85 sides, by the use of the compasses and straightedge, but the proof is not adapted to elementary geometry. In connection with the study of the regular polygons some interest attaches to the reference to various forms of decorative design. The mosaic floor, parquetry, Gothic windows, and patterns of various kinds often involve the regular figures. If the teacher[Pg 275] uses such material, care should be taken to exemplify good art. For example, the equilateral triangle and its relation to the regular hexagon is shown in the picture of an ancient Roman mosaic floor on page 274.[84] In the next illustration some characteristic Moorish mosaic work appears, in which it will be seen that the basal figure is the square, although at first sight this would not seem to be the case.[85] This is followed by a beautiful Byzantine mosaic, the original of which was in five colors of marble. Here it will be seen that the equilateral triangle and the regular hexagon are the basal figures, and a few of the properties of these polygons might be derived from the study of such a design. In the Arabic pattern on page 276 the dodecagon appears as the basis, and the remarkable powers of the Arab designer are shown in the use of symmetry without employing regular figures.
Problem. Given the side and the radius of a regular inscribed polygon, to find the side of the regular inscribed polygon of double the number of sides.
The object of this proposition is, of course, to prepare the way for finding the perimeter of a polygon of 2n sides, knowing that of n sides. The Greek plan was generally to use both an inscribed and a circumscribed polygon, thus approaching the circle as a limit both from without and within. This is more conclusive from the ultrascientific point of view, but it is, if anything, less conclusive to a beginner, because he does not so readily follow the proof. The plan of using the two polygons was carried out by Archimedes of Syracuse (287-212 B.C.) in his famous method of approximating the value of π, although before him Antiphon (fifth century B.C.) had inscribed a square (or equilateral triangle) as a basis for the work, and Bryson (his contemporary) had attacked the problem by circumscribing as well as inscribing a regular polygon.
Problem. To find the numerical value of the ratio of the circumference of a circle to its diameter.
As already stated, the usual plan of the textbooks is in part the method followed by Archimedes. It is possible to start with any regular polygon of which the side can conveniently be found in terms of the radius. In particular we might begin with an inscribed[Pg 277] square instead of a regular hexagon. In this case we should have
| Length of Side | Perimeter | |
| s4 = 1.414... | = 1.41 | 5.66 |
| s8 = √(2-√(4-1.4142)) | = 0.72 | 5.76 |
and so on.
It is a little easier to start with the hexagon, however, for we are already nearer the circle, and the side and perimeter are both commensurable with the radius. It is not, of course, intended that pupils should make the long numerical calculations. They may be required to compute s12 and possibly s24, but aside from this they are expected merely to know the process.
If it were possible to find the value of π exactly, we could find the circumference exactly in terms of the radius, since c = 2πr. If we could find the circumference exactly, we could find the area exactly, since a = πr2. If we could find the area exactly in this form, π times a square, we should have a rectangle, and it is easy to construct a square equivalent to any rectangle. Therefore, if we could find the value of π exactly, we could construct a square with area equivalent to the area of the circle; in other words, we could "square the circle." We could also, as already stated, construct a straight line equivalent to the circumference; in other words, we could "rectify the circumference." These two problems have attracted the attention of the world for over two thousand years, but on account of their interrelation they are usually spoken of as a single problem, "to square the circle."
Since we can construct √a by means of the straightedge and compasses, it would be possible for us to square the circle if we could express π by a finite number of square roots. Conversely, every geometric construction[Pg 278] reduces to the intersection of two straight lines, of a straight line and a circle, or of two circles, and is therefore equivalent to a rational operation or to the extracting of a square root. Hence a geometric construction cannot be effected by the straightedge and compasses unless it is equivalent to a series of rational operations or to the extracting of a finite number of square roots. It was proved by a German professor, Lindemann, in 1882, that π cannot be expressed as an algebraic number, that is, as the root of an equation with rational coefficients, and hence it cannot be found by the above operations, and, furthermore, that the solution of this famous problem is impossible by elementary geometry.[86]
It should also be pointed out to the student that for many practical purposes one of the limits of π stated by Archimedes, namely, 3-1/7, is sufficient. For more accurate work 3.1416 is usually a satisfactory approximation. Indeed, the late Professor Newcomb stated that "ten decimal places are sufficient to give the circumference of the earth to the fraction of an inch, and thirty decimal places would give the circumference of the whole visible universe to a quantity imperceptible with the most powerful microscope."
Probably the earliest approximation of the value of π was 3. This appears very commonly in antiquity, as in I Kings vii, 23, and 2 Chronicles iv, 2. In the Ahmes papyrus (ca. 1700 B.C.) there is a rule for finding the area of the circle, expressed in modern symbols as (8/9)2d2, which makes π = 256/81 or 3.1604....
Archimedes, using a plan somewhat similar to ours, found that π lay between 3-1/7 and 3-10/71. Ptolemy, the great Greek astronomer, expressed the value as 3-17/120, or 3.14166.... The fact that Ptolemy divided his diameter into 120 units and his circumference into 360 units probably shows, however, the influence of the ancient value 3.
In India an approximate value appears in a certain poem written before the Christian era, but the date is uncertain. About 500 A.D. Aryabhatta (or possibly a later writer of the same name) gave the value 62832/20000, or 3.1416. Brahmagupta, another Hindu (born 598 A.D.), gave √(10), and this also appears in the writings of the Chinese mathematician Chang Hêng (78-139 A.D.). A little later in China, Wang Fan (229-267) gave 142 ÷ 45, or 3.1555...; and one of his contemporaries, Lui Hui, gave 157 ÷ 50, or 3.14. In the fifth century Ch'ung-chih gave as the limits of π, 3.1415927 and 3.1415926, from which he inferred that 22/7 and 355/113 were good approximations, although he does not state how he came to this conclusion.
In the Middle Ages the greatest mathematician of Italy, Leonardo Fibonacci, or Leonardo of Pisa (about 1200 A.D.), found as limits 3.1427... and 3.1410.... About 1600 the Chinese value 355/113 was rediscovered by Adriaen Anthonisz (1527-1607), being published by his son, who is known as Metius (1571-1635), in the year 1625. About the same period the French mathematician Vieta (1540-1603) found the value of π to 9 decimal places, and Adriaen van Rooman (1561-1615) carried it to 17 decimal places, and Ludolph van Ceulen (1540-1610) to 35 decimal places. It was carried to 140 decimal places by Georg Vega (died in 1793), to 200 by Zacharias Dase (died in 1844), to 500 by Richter (died in 1854), and more recently by Shanks to 707 decimal places.[Pg 280]
There have been many interesting formulas for π, among them being the following:
π/2 = 2/1 · 2/3 · 4/3 · 4/5 · 6/5 · 6/7 · 8/7 · 8/9 · .... (Wallis, 1616-1703)
4/π = 1 + 1/2
+ 9/2
+ 25/2
+ 49/2
+ .... (Brouncker, 1620-1684)
π/4 = 1 - 1/3 + 1/5 - 1/7 + .... (Gregory, 1638-1675)
π/6 = √(1/3) · (1 - 1/(3 · 3) + 1/(32 · 5) - 1/(33 · 7) + ...).
π/2 = (log i) / i. (Bernoulli)
π/(2√(3)) = 1 - 1/5 + 1/7 - 1/11 + 1/13 - 1/17 + 1/19...,
thus connecting the primes.
π2 / 16 = 1 - 1/22 - 1/32 + 1/42 - 1/52 + 1/62 - 1/72 - 1/82 + 1/92 + ....
π/2 = x/2 + sin x + (sin2 x) / 2 + (sin3 x) / 3 + .... (0 < x < 2π)
π/4 = 3/4 + 1/(2 · 3 · 4) - 1/(4 · 5 · 6) + 1/(6 · 7 · 8) - ....
2π2/3 = 7 - (1/(1 · 3) + 1/(3 · 6) + 1/(6 · 10) + ...).
π = 2n√(2 - √(2 + √(2 + √(2 + √(2...))))).
Students of elementary geometry are not prepared to appreciate it, but teachers will be interested in the remarkable formula discovered by Euler (1707-1783), the great Swiss mathematician, namely, 1 + eiπ = 0. In this relation are included the five most interesting quantities in mathematics,—zero, the unit, the base of the so-called Napierian logarithms, i = √(-1), and π. It was by means of this relation that the transcendence of[Pg 281] e was proved by the French mathematician Hermite, and the transcendence of π by the German Lindemann.

There should be introduced at this time, if it has not already been done, the proposition of the lunes of Hippocrates (ca. 470 B.C.), who proved a theorem that asserts, in somewhat more general form, that if three semicircles be described on the sides of a right triangle as diameters, as shown, the lunes L + L' are together equivalent to the triangle T.
In the use of the circle in design one of the simplest forms suggested by Book V is the trefoil (three-leaf), as here shown, with the necessary construction lines. This is a very common ornament in architecture, both with rounded ends and with the ends slightly pointed.
The trefoil is closely connected with hexagonal designs, since the regular hexagon is formed from the inscribed equilateral triangle by doubling the number of sides. The following are designs that are easily made:
It is not very profitable, because it is manifestly unreal, to measure the parts of such figures, but it offers plenty of practice in numerical work.[Pg 282]
In the illustrations of the Gothic windows given in Chapter XV only the square and circle were generally involved. Teachers who feel it necessary or advisable to go outside the regular work of geometry for the purpose of increasing the pupil's interest or of training his hand in the drawing of figures will find plenty of designs given in any pictures of Gothic cathedrals. For example, this picture of the noble window in the choir of Lincoln Cathedral shows the use of the square, hexagon, and pentagon. In the porch of the same cathedral, shown in the next illustration, the architect has made use of the triangle, square, and pentagon in planning his ornamental stonework. It is possible to add to the work in pure geometry some work in the mensuration of the curvilinear figures shown in these designs. This form of mensuration is not of much value, however, since it[Pg 283] places before the pupil a problem that he sees at once is fictitious, and that has no human interest.
The designs given on page 283 involve chiefly the square as a basis, but it will be seen from one of the[Pg 285] figures that the equilateral triangle and the hexagon also enter. The possibilities of endless variation of a single design are shown in the illustration on page 284, the basis[Pg 286] in this case being the square. The variations in the use of the triangle and hexagon have been the object of study of many designers of Gothic windows, and some[Pg 287] examples of these forms are shown on page 285. In more simple form this ringing of the changes on elementary figures is shown on page 286. Some teachers have used color work with such designs for the purpose of increasing the interest of their pupils, but the danger of thus using the time with no serious end in view will be apparent.
In the matter of the mensuration of the circle the annexed design has some interest. The figure is not uncommon in decoration, and it is interesting to show, as a matter of pure geometry, that the area of the circle is divided into three equal portions by means of the four interior semicircles.
An important application of the formula a = πr2 is seen in the area of the annulus, or ring, the formula being a = πr2 - πr'2 = π(r2 - r'2) = π(r + r') (r - r'). It is used in finding the area of the cross section of pipes, and this is needed when we wish to compute the volume of the iron used.
Another excellent application is that of finding the area of the surface of a cylinder, there being no reason why such simple cases from solid geometry should not furnish working material for plane geometry, particularly as they have already been met by the pupils in arithmetic.
A little problem that always has some interest for pupils is one that Napoleon is said to have suggested to his staff on his voyage to Egypt: To divide a circle into four equal parts by the use of circles alone.[Pg 288]
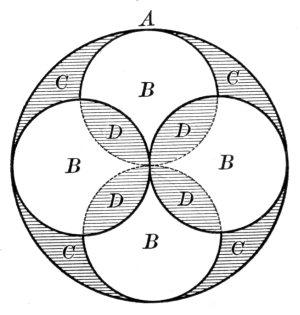
Here the circles B are tangent to the circle A at the points of division. Furthermore, considering areas, and taking r as the radius of A, we have A = πr2, and B = π(r/2)2. Hence B = 1/4A, or the sum of the areas of the four circles B equals the area of A. Hence the four D's must equal the four C's, and D = C. The rest of the argument is evident. The problem has some interest to pupils aside from the original question suggested by Napoleon.
At the close of plane geometry teachers may find it helpful to have the class make a list of the propositions that are actually used in proving other propositions, and to have it appear what ones are proved by them. This forms a kind of genealogical tree that serves to fix the parent propositions in mind. Such a work may also be carried on at the close of each book, if desired. It should be understood, however, that certain propositions are used in the exercises, even though they are not referred to in subsequent propositions, so that their omission must not be construed to mean that they are not important.
An exercise of distinctly less value is the classification of the definitions. For example, the classification of polygons or of quadrilaterals, once so popular in textbook making, has generally been abandoned as tending to create or perpetuate unnecessary terms. Such work is therefore not recommended.[Pg 289]
There have been numerous suggestions with respect to solid geometry, to the effect that it should be more closely connected with plane geometry. The attempt has been made, notably by Méray in France and de Paolis in Italy, to treat the corresponding propositions of plane and solid geometry together; as, for example, those relating to parallelograms and parallelepipeds, and those relating to plane and spherical triangles. Whatever the merits of this plan, it is not feasible in America at present, partly because of the nature of the college-entrance requirements. While it is true that to a boy or girl a solid is more concrete than a plane, it is not true that a geometric solid is more concrete than a geometric plane. Just as the world developed its solid geometry, as a science, long after it had developed its plane geometry, so the human mind grasps the ideas of plane figures earlier than those of the geometric solid.
There is, however, every reason for referring to the corresponding proposition of plane geometry when any given proposition of solid geometry is under consideration, and frequent references of this kind will be made in speaking of the propositions in this and the two succeeding chapters. Such reference has value in the apperception of the various laws of solid geometry, and it also adds an interest to the subject and creates some[Pg 290] approach to power in the discovery of new facts in relation to figures of three dimensions.
The introduction to solid geometry should be made slowly. The pupil has been accustomed to seeing only plane figures, and therefore the drawing of a solid figure in the flat is confusing. The best way for the teacher to anticipate this difficulty is to have a few pieces of cardboard, a few knitting needles filed to sharp points, a pine board about a foot square, and some small corks. With the cardboard he can illustrate planes, whether alone, intersecting obliquely or at right angles, or parallel, and he can easily illustrate the figures given in the textbook in use. There are models of this kind for sale, but the simple ones made in a few seconds by the teacher or the pupil have much more meaning. The knitting needles may be stuck in the board to illustrate perpendicular or oblique lines, and if two or more are to meet in a point, they may be held together by sticking them in one of the small corks. Such homely apparatus, costing almost nothing, to be put together in class, seems much more real and is much more satisfactory than the German models.[87]
An extensive use of models is, however, unwise. The pupil must learn very early how to visualize a solid from the flat outline picture, just as a builder or a mechanic learns to read his working drawings. To have a model for each proposition, or even to have a photograph or a stereoscopic picture, is a very poor educational policy. A textbook may properly illustrate a few propositions by photographic aids, but after that the pupil should use
the kind of figures that he must meet in his mathematical work. A child should not be kept in a perambulator all his life,—he must learn to walk if he is to be strong and grow to maturity; and it is so with a pupil in the use of models in solid geometry.[88]
The case is somewhat similar with respect to colored crayons. They have their value and their proper place, but they also have their strict limitations. It is difficult to keep their use within bounds; pupils come to use them to make pleasing pictures, and teachers unconsciously fall into the same habit. The value of colored crayons is two-fold: (1) they sometimes make two planes stand out more clearly, or they serve to differentiate some line that is under consideration from others that are not; (2) they enable a class to follow a demonstration more easily by hearing of "the red plane perpendicular to the blue one," instead of "the plane MN perpendicular to the plane PQ." But it should always be borne in mind that in practical work we do not have colored ink or colored pencils commonly at hand, nor do we generally have colored crayons. Pupils should therefore become accustomed to the pencil and the white crayon as the regulation tools, and in general they should use them. The figures may not be as striking, but they are more quickly made and they are more practical.
The definition of "plane" has already been discussed in Chapter XII, and the other definitions of Book VI are not of enough interest to call for special remark. The axioms are the same as in plane geometry, but there is
at least one postulate that needs to be added, although it would be possible to state various analogues of the postulates of plane geometry if we cared unnecessarily to enlarge the number.
The most important postulate of solid geometry is as follows: One plane, and only one, can be passed through two intersecting straight lines. This is easily illustrated, as in most textbooks, as also are three important corollaries derived from it:
1. A straight line and a point not in the line determine a plane. Of course this may be made the postulate, as may also the next one, the postulate being placed among the corollaries, but the arrangement here adopted is probably the most satisfactory for educational purposes.
2. Three points not in a straight line determine a plane. The common question as to why a three-legged stool stands firmly, while a four-legged table often does not, will add some interest at this point.
3. Two parallel lines determine a plane. This requires a slight but informal proof to show that it properly follows as a corollary from the postulate, but a single sentence suffices.
While studying this book questions of the following nature may arise with an advanced class, or may be suggested to those who have had higher algebra:
How many straight lines are in general (that is, at the most) determined by n points in space? Two points determine 1 line, a third point adds (in general, in all these cases) 2 more, a fourth point adds 3 more, and an nth point n - 1 more. Hence the maximum is 1 + 2 + 3 + ... + (n - 1), or n(n-1)/2, which the pupil will understand if he has studied arithmetical progression.[Pg 293] The maximum number of intersection points of n straight lines in the same plane is also n(n - 1)/2.
How many straight lines are in general determined by n planes? The answer is the same, n(n - 1)/2.
How many planes are in general determined by n points in space? Here the answer is 1 + 3 + 6 + 10 + ... + (n - 2)(n - 1)/2, or n(n - 1)(n - 2)/(1 × 2 × 3). The same number of points is determined by n planes.
Theorem. If two planes cut each other, their intersection is a straight line.
Among the simple illustrations are the back edges of the pages of a book, the corners of the room, and the simple test as to whether the edge of a card is straight by testing it on a plane. It is well to call attention to the fact that if two intersecting straight lines move parallel to their original position, and so that their intersection rests on a straight line not in the plane of those lines, the figure generated will be that of this proposition. In general, if we cut through any figure of solid geometry in some particular way, we are liable to get the figure of a proposition in plane geometry, as will frequently be seen.
Theorem. If a straight line is perpendicular to each of two other straight lines at their point of intersection, it is perpendicular to the plane of the two lines.
If students have trouble in visualizing the figure in three dimensions, some knitting needles through a piece of cardboard will make it clear. Teachers should call attention to the simple device for determining if a rod is perpendicular to a board (or a pipe to a floor, ceiling, or[Pg 294] wall), by testing it twice, only, with a carpenter's square. Similarly, it may be asked of a class, How shall we test to see if the corner (line) of a room is perpendicular to the floor, or if the edge of a box is perpendicular to one of the sides?
In some elementary and in most higher geometries the perpendicular is called a normal to the plane.
Theorem. All the perpendiculars that can be drawn to a straight line at a given point lie in a plane which is perpendicular to the line at the given point.
Thus the hands of a clock pass through a plane as the hands revolve, if they are, as is usual, perpendicular to the axis; and the same is true of the spokes of a wheel, and of a string with a stone attached, swung as rapidly as possible about a boy's arm as an axis. A clock pendulum too swings in a plane, as does the lever in a pair of scales.
Theorem. Through a given point within or without a plane there can be one perpendicular to a given plane, and only one.
This theorem is better stated to a class as two theorems.
Thus a plumb line hanging from a point in the ceiling, without swinging, determines one definite point in the floor; and, conversely, if it touches a given point in the floor, it must hang from one definite point in the ceiling. It should be noticed that if we cut through this figure, on the perpendicular line, we shall have the figure of the corresponding proposition in plane geometry, namely, that there can be, under similar circumstances, only one perpendicular to a line.
Theorem. Oblique lines drawn from a point to a plane, meeting the plane at equal distances from the foot of the perpendicular, are equal, etc.[Pg 295]
There is no objection to speaking of a right circular cone in connection with this proposition, and saying that the slant height is thus proved to be constant. The usual corollary, that if the obliques are equal they meet the plane in a circle, offers a new plan of drawing a circle. A plumb line that is a little too long to reach the floor will, if swung so as just to touch the floor, describe a circle. A 10-foot pole standing in a 9-foot room will, if it moves so as to touch constantly a fixed point on either the floor or the ceiling, describe a circle on the ceiling or floor respectively.
One of the corollaries states that the locus of points in space equidistant from the extremities of a straight line is the plane perpendicular to this line at its middle point. This has been taken by some writers as the definition of a plane, but it is too abstract to be usable. It is advisable to cut through the figure along the given straight line, and see that we come back to the corresponding proposition in plane geometry.
A good many ships have been saved from being wrecked by the principle involved in this proposition.
If a dangerous shoal A is near a headland H, the angle HAX is measured and is put down upon the charts as the "vertical danger angle." Ships coming near the headland are careful to keep far enough away, say at S, so that the angle HSX shall be less than this danger angle. They are then sure that they will avoid the dangerous shoal.
Related to this proposition is the problem of supporting a tall iron smokestack by wire stays. Evidently[Pg 296] three stays are needed, and they are preferably placed at the vertices of an equilateral triangle, the smokestack being in the center. The practical problem may be given of locating the vertices of the triangle and of finding the length of each stay.
Theorem. Two straight lines perpendicular to the same plane are parallel.
Here again we may cut through the figure by the plane of the two parallels, and we get the figure of plane geometry relating to lines that are perpendicular to the same line. The proposition shows that the opposite corners of a room are parallel, and that therefore they lie in the same plane, or are coplanar, as is said in higher geometry.
It is interesting to a class to have attention called to the corollary that if two straight lines are parallel to a third straight line, they are parallel to each other; and to have the question asked why it is necessary to prove this when the same thing was proved in plane geometry. In case the reason is not clear, let some student try to apply the proof used in plane geometry.
Theorem. Two planes perpendicular to the same straight line are parallel.
Besides calling attention to the corresponding proposition of plane geometry, it is well now to speak of the fact that in propositions involving planes and lines we may often interchange these words. For example, using "line" for "straight line," for brevity, we have:
| One line does not determine a plane. | One plane does not determine a line. |
| Two intersecting lines determine a plane. | Two intersecting planes determine a line. |
| Two lines perpendicular to a plane are parallel. | Two planes perpendicular to a line are parallel. |
| If one of two parallel lines is perpendicular to a plane, the other is also perpendicular to the plane. | If one of two parallel planes is perpendicular to a line, the other is also perpendicular to the line. |
| If two lines are parallel, every plane containing one of the lines is parallel to the other line. | If two planes are parallel, every line in one of the planes is parallel to the other plane. |
Theorem. The intersections of two parallel planes by a third plane are parallel lines.
Thus one of the edges of a box is parallel to the next succeeding edge if the opposite faces are parallel, and in sawing diagonally through an ordinary board (with rectangular cross section) the section is a parallelogram.
Theorem. A straight line perpendicular to one of two parallel planes is perpendicular to the other also.
Notice (1) the corresponding proposition in plane geometry; (2) the proposition that results from interchanging "plane" and (straight) "line."
Theorem. If two intersecting straight lines are each parallel to a plane, the plane of these lines is parallel to that plane.
Interchanging "plane" and (straight) "line," we have: If two intersecting planes are each parallel to a line, the line of (intersection of) these planes is parallel to that line. Is this true?
Theorem. If two angles not in the same plane have their sides respectively parallel and lying on the same side of the straight line joining their vertices, they are equal and their planes are parallel.
Questions like the following may be asked in connection with the proposition: What is the corresponding proposition in plane geometry? Why do we need another proof here? Try the plane-geometry proof here.[Pg 298]
Theorem. If two straight lines are cut by three parallel planes, their corresponding segments are proportional.
Here, again, it is desirable to ask for the corresponding proposition of plane geometry, and to ask why the proof of that proposition will not suffice for this one. The usual figure may be varied in an interesting manner by having the two lines meet on one of the planes, or outside the planes, or by having them parallel, in which cases the proof of the plane-geometry proposition holds here. This proposition is not of great importance from the practical standpoint, and it is omitted from some of the standard syllabi at present, although included in certain others. It is easy, however, to frame some interesting questions depending upon it for their answers, such as the following: In a gymnasium swimming tank the water is 4 feet deep and the ceiling is 8 feet above the surface of the water. A pole 15 feet long touches the ceiling and the bottom of the tank. Required to know what length of the pole is in the water.
At this point in Book VI it is customary to introduce the dihedral angle. The word "dihedral" is from the Greek, di- meaning "two," and hedra meaning "seat." We have the root hedra also in "trihedral" (three-seated), "polyhedral" (many-seated), and "cathedral" (a church having a bishop's seat). The word is also, but less properly, spelled without the h, "diedral," a spelling not favored by modern usage. It is not necessary to dwell at length upon the dihedral angle, except to show the analogy between it and the plane angle. A few illustrations, as of an open book, the wall and floor of a room, and a swinging door, serve to make the concept clear, while a plane at right angles to the edge shows the measuring plane angle. So manifest is this[Pg 299] relationship between the dihedral angle and its measuring plane angle that some teachers omit the proposition that two dihedral angles have the same ratio as their plane angles.
Theorem. If two planes are perpendicular to each other, a straight line drawn in one of them perpendicular to their intersection is perpendicular to the other.
This and the related propositions allow of numerous illustrations taken from the schoolroom, as of door edges being perpendicular to the floor. The pretended applications of these propositions are usually fictitious, and the propositions are of value chiefly for their own interest and because they are needed in subsequent proofs.
Theorem. The locus of a point equidistant from the faces of a dihedral angle is the plane bisecting the angle.
By changing "plane" to "line," and by making other obvious changes to correspond, this reduces to the analogous proposition of plane geometry. The figure formed by the plane perpendicular to the edge is also the figure of that analogous proposition. This at once suggests that there are two planes in the locus, provided the planes of the dihedral angle are taken as indefinite in extent, and that these planes are perpendicular to each other. It may interest some of the pupils to draw this general figure, analogous to the one in plane geometry.
Theorem. The projection of a straight line not perpendicular to a plane upon that plane is a straight line.
In higher mathematics it would simply be said that the projection is a straight line, the special case of the projection of a perpendicular being considered as a line-segment of zero length. There is no advantage, however, of bringing in zero and infinity in the course in elementary geometry. The legitimate reason for the[Pg 300] modern use of these terms is seldom understood by beginners.
This subject of projection (Latin pro-, "forth," and jacere, "to throw") is extensively used in modern mathematics and also in the elementary work of the draftsman, and it will be referred to a little later. At this time, however, it is well to call attention to the fact that the projection of a straight line on a plane is a straight line or a point; the projection of a curve may be a curve or it may be straight; the projection of a point is a point; and the projection of a plane (which is easily understood without defining it) may be a surface or it may be a straight line. An artisan represents a solid by drawing its projection upon two planes at right angles to each other, and a map maker (cartographer) represents the surface of the earth by projecting it upon a plane. A photograph of the class is merely the projection of the class upon a photographic plate (plane), and when we draw a figure in solid geometry, we merely project the solid upon the plane of the paper.
There are other projections than those formed by lines that are perpendicular to the plane. The lines may be oblique to the plane, and this is the case with most projections. A photograph, for example, is not formed by lines perpendicular to a plane, for they all converge in the camera. If the lines of projection are all perpendicular to the plane, the projection is said to be orthographic, from the Greek ortho- (straight) and graphein (to draw). A good example of orthographic projection may be seen in the shadow cast by an object upon a piece of paper that is held perpendicular to the sun's rays. A good example of oblique projection is a shadow on the floor of the schoolroom.[Pg 301]
Theorem. Between two straight lines not in the same plane there can be one common perpendicular, and only one.
The usual corollary states that this perpendicular is the shortest line joining them. It is interesting to compare this with the case of two lines in the same plane. If they are parallel, there may be any number of common perpendiculars. If they intersect, there is still a common perpendicular, but this can hardly be said to be between them, except for its zero segment.
There are many simple illustrations of this case. For example, what is the shortest line between any given edge of the ceiling and the various edges of the floor of the schoolroom? If two galleries in a mine are to be connected by an air shaft, how shall it be planned so as to save labor? Make a drawing of the plan.
At this point the polyhedral angle is introduced. The word is from the Greek polys (many) and hedra (seat). Students have more difficulty in grasping the meaning of the size of a polyhedral angle than is the case with dihedral and plane angles. For this reason it is not good policy to dwell much upon this subject unless the question arises, since it is better understood when the relation of the polyhedral angle and the spherical polygon is met. Teachers will naturally see that just as we may measure the plane angle by taking the ratio of an arc to the whole circle, and of a dihedral angle by taking the ratio of that part of the cylindric surface that is cut out by the planes to the whole surface, so we may measure a polyhedral angle by taking the ratio of the spherical polygon to the whole spherical surface. It should also be observed that just as we may have cross polygons in a plane, so we may have spherical polygons[Pg 302] that are similarly tangled, and that to these will correspond polyhedral angles that are also cross, their representation by drawings being too complicated for class use.
The idea of symmetric solids may be illustrated by a pair of gloves, all their parts being mutually equal but arranged in opposite order. Our hands, feet, and ears afford other illustrations of symmetric solids.
Theorem. The sum of the face angles of any convex polyhedral angle is less than four right angles.
There are several interesting points of discussion in connection with this proposition. For example, suppose the vertex V to approach the plane that cuts the edges in A, B, C, D, ..., the edges continuing to pass through these as fixed points. The sum of the angles about V approaches what limit? On the other hand, suppose V recedes indefinitely; then the sum approaches what limit? Then what are the two limits of this sum? Suppose the polyhedral angle were concave, why would the proof not hold?[Pg 303]
Book VII relates to polyhedrons, cylinders, and cones. It opens with the necessary definitions relating to polyhedrons, the etymology of the terms often proving interesting and valuable when brought into the work incidentally by the teacher. "Polyhedron" is from the Greek polys (many) and hedra (seat). The Greek plural, polyhedra, is used in early English works, but "polyhedrons" is the form now more commonly seen in America. "Prism" is from the Greek prisma (something sawed, like a piece of wood sawed from a beam). "Lateral" is from the Latin latus (side). "Parallelepiped" is from the Greek parallelos (parallel) and epipedon (a plane surface), from epi (on) and pedon (ground). By analogy to "parallelogram" the word is often spelled "parallelopiped," but the best mathematical works now adopt the etymological spelling above given. "Truncate" is from the Latin truncare (to cut off).
A few of the leading propositions are now considered.
Theorem. The lateral area of a prism is equal to the product of a lateral edge by the perimeter of the right section.
It should be noted that although some syllabi do not give the proposition that parallel sections are congruent, this is necessary for this proposition, because it shows[Pg 304] that the right sections are all congruent and hence that any one of them may be taken.
It is, of course, possible to construct a prism so oblique and so low that a right section, that is, a section cutting all the lateral edges at right angles, is impossible. In this case the lateral faces must be extended, thus forming what is called a prismatic space. This term may or may not be introduced, depending upon the nature of the class.
This proposition is one of the most important in Book VII, because it is the basis of the mensuration of the cylinder as well as the prism. Practical applications are easily suggested in connection with beams, corridors, and prismatic columns, such as are often seen in school buildings. Most geometries supply sufficient material in this line, however.
Theorem. An oblique prism is equivalent to a right prism whose base is equal to a right section of the oblique prism, and whose altitude is equal to a lateral edge of the oblique prism.
This is a fundamental theorem leading up to the mensuration of the prism. Attention should be called to the analogous proposition in plane geometry relating to the area of the parallelogram and rectangle, and to the fact that if we cut through the solid figure by a plane parallel to one of the lateral edges, the resulting figure will be that of the proposition mentioned. As in the preceding proposition, so in this case, there may be a question raised that will make it helpful to introduce the idea of prismatic space.
Theorem. The opposite lateral faces of a parallelepiped are congruent and parallel.
It is desirable to refer to the corresponding case in plane geometry, and to note again that the figure is[Pg 305] obtained by passing a plane through the parallelepiped parallel to a lateral edge. The same may be said for the proposition about the diagonal plane of a parallelepiped. These two propositions are fundamental in the mensuration of the prism.
Theorem. Two rectangular parallelepipeds are to each other as the products of their three dimensions.
This leads at once to the corollary that the volume of a rectangular parallelepiped equals the product of its three dimensions, the fundamental law in the mensuration of all solids. It is preceded by the proposition asserting that rectangular parallelepipeds having congruent bases are proportional to their altitudes. This includes the incommensurable case, but this case may be omitted.
The number of simple applications of this proposition is practically unlimited. In all such cases it is advisable to take a considerable number of numerical exercises in order to fix in mind the real nature of the proposition. Any good geometry furnishes a certain number of these exercises.
The following is an interesting property of the rectangular parallelepiped, often called the rectangular solid:
If the edges are a, b, and c, and the diagonal is d, then (a/d)2 + (b/d)2 + (c/d)2 = 1. This property is easily proved by the Pythagorean Theorem, for d2 = a2 + b2 + c2, whence (a2 + b2 + c2) / d2 = 1.
In case c = 0, this reduces to the Pythagorean Theorem. The property is the fundamental one of solid analytic geometry.
Theorem. The volume of any parallelepiped is equal to the product of its base by its altitude.
This is one of the few propositions in Book VII where a model is of any advantage. It is easy to make one[Pg 306] out of pasteboard, or to cut one from wood. If a wooden one is made, it is advisable to take an oblique parallelepiped and, by properly sawing it, to transform it into a rectangular one instead of using three different solids.
On account of its awkward form, this figure is sometimes called the Devil's Coffin, but it is a name that it would be well not to perpetuate.
Theorem. The volume of any prism is equal to the product of its base by its altitude.
This is also one of the basal propositions of solid geometry, and it has many applications in practical mensuration. A first-class textbook will give a sufficient list of problems involving numerical measurement, to fix the law in mind. For outdoor work, involving measurements near the school or within the knowledge of the pupils, the following problem is a type:
If this represents the cross section of a railway embankment that is l feet long, h feet high, b feet wide at the bottom, and b´ feet wide at the top, find the number of cubic feet in the embankment. Find the volume if l = 300, h = 8, b = 60, and b´ = 28.
The mensuration of the volume of the prism, including the rectangular parallelepiped and cube, was known to the ancients. Euclid was not concerned with practical measurement, so that none of this part of geometry appears in his "Elements." We find, however, in the papyrus of Ahmes, directions for the measuring of bins, and the Egyptian builders, long before his time, must have known the mensuration of the rectangular parallelepiped. Among the Hindus, long before the Christian era, rules were known for the construction of altars, and among the Greeks the problem of constructing a cube with twice the volume of a given[Pg 307] cube (the "duplication of the cube") was attacked by many mathematicians. The solution of this problem is impossible by elementary geometry.
If e equals the edge of the given cube, then e3 is its volume and 2e3 is the volume of the required cube. Therefore the edge of the required cube is e∛2. Now if e is given, it is not possible with the straightedge and compasses to construct a line equal to e∛2, although it is easy to construct one equal to e√2.
The study of the pyramid begins at this point. In practical measurement we usually meet the regular pyramid. It is, however, a simple matter to consider the oblique pyramid as well, and in measuring volumes we sometimes find these forms.
Theorem. The lateral area of a regular pyramid is equal to half the product of its slant height by the perimeter of its base.
This leads to the corollary concerning the lateral area of the frustum of a regular pyramid. It should be noticed that the regular pyramid may be considered as a frustum with the upper base zero, and the proposition as a special case under the corollary. It is also possible, if we choose, to let the upper base of the frustum pass through the vertex and cut the lateral edges above that point, although this is too complicated for most pupils. If this case is considered, it is well to bring in the general idea of pyramidal space, the infinite space bounded on several sides by the lateral faces, of the pyramid. This pyramidal space is double, extending on two sides of the vertex.
Theorem. If a pyramid is cut by a plane parallel to the base:
1. The edges and altitude are divided proportionally.
2. The section is a polygon similar to the base.
[Pg 308]
To get the analogous proposition of plane geometry, pass a plane through the vertex so as to cut the base. We shall then have the sides and altitude of the triangle divided proportionally, and of course the section will merely be a line-segment, and therefore it is similar to the base line.
The cutting plane may pass through the vertex, or it may cut the pyramidal space above the vertex. In either case the proof is essentially the same.
Theorem. The volume of a triangular pyramid is equal to one third of the product of its base by its altitude, and this is also true of any pyramid.
This is stated as two theorems in all textbooks, and properly so. It is explained to children who are studying arithmetic by means of a hollow pyramid and a hollow prism of equal base and equal altitude. The pyramid is filled with sand or grain, and the contents is poured into the prism. This is repeated, and again repeated, showing that the volume of the prism is three times the volume of the pyramid. It sometimes varies the work to show this to a class in geometry.
This proposition was first proved, so Archimedes asserts, by Eudoxus of Cnidus, famous as an astronomer, geometer, physician, and lawgiver, born in humble circumstances about 407 B.C. He studied at Athens and in Egypt, and founded a famous school of geometry at Cyzicus. His discovery also extended to the volume of the cone, and it was his work that gave the beginning to the science of stereometry, the mensuration part of solid geometry.
Theorem. The volume of the frustum of any pyramid is equal to the sum of the volumes of three pyramids whose common altitude is the altitude of the frustum, and whose[Pg 309] bases are the lower base, the upper base, and the mean proportional between the bases of the frustum.
Attention should be called to the fact that this formula v = 1/3 a(b + b' + √(bb')) applies to the pyramid by letting b' = 0, to the prism by letting b = b', and also to the parallelepiped and cube, these being special forms of the prism. This formula is, therefore, a very general one, relating to all the polyhedrons that are commonly met in mensuration.
Theorem. There cannot be more than five regular convex polyhedrons.
Eudemus of Rhodes, one of the principal pupils of Aristotle, in his history of geometry of which Proclus preserves some fragments, tells us that Pythagoras discovered the construction of the "mundane figures," meaning the five regular polyhedrons. Iamblichus speaks of the discovery of the dodecahedron in these words:
As to Hippasus, who was a Pythagorean, they say that he perished in the sea on account of his impiety, inasmuch as he boasted that he first divulged the knowledge of the sphere with the twelve pentagons. Hippasus assumed the glory of the discovery to himself, whereas everything belongs to Him, for thus they designate Pythagoras, and do not call Him by name.
Iamblichus here refers to the dodecahedron inscribed in the sphere. The Pythagoreans looked upon these five solids as fundamental forms in the structure of the universe. In particular Plato tells us that they asserted that the four elements of the real world were the tetrahedron, octahedron, icosahedron, and cube, and Plutarch ascribes this doctrine to Pythagoras himself. Philolaus, who lived in the fifth century B.C., held that the elementary nature of bodies depended on their form. The tetrahedron was assigned to fire, the octahedron to air, the icosahedron to water, and the cube to earth, it being[Pg 310] asserted that the smallest constituent part of each of these substances had the form here assigned to it. Although Eudemus attributes all five to Pythagoras, it is certain that the tetrahedron, cube, and octahedron were known to the Egyptians, since they appear in their architectural decorations. These solids were studied so extensively in the school of Plato that Proclus also speaks of them as the Platonic bodies, saying that Euclid "proposed to himself the construction of the so-called Platonic bodies as the final aim of his arrangement of the 'Elements.'" Aristæus, probably a little older than Euclid, wrote a book upon these solids.
As an interesting amplification of this proposition, the centers of the faces (squares) of a cube may be connected, an inscribed octahedron being thereby formed. Furthermore, if the vertices of the cube are A, B, C, D, A', B', C', D', then by drawing AC, CD', D'A, D'B', B'A, and B'C, a regular tetrahedron will be formed. Since the construction of the cube is a simple matter, this shows how three of the five regular solids may be constructed. The actual construction of the solids is not suited to elementary geometry.[89]
It is not difficult for a class to find the relative areas of the cube and the inscribed tetrahedron and octahedron. If s is the side of the cube, these areas are 6s2, (1/2)s2√3, and s2√3; that is, the area of the octahedron is twice that of the tetrahedron inscribed in the cube.
Somewhat related to the preceding paragraph is the fact that the edges of the five regular solids are incommensurable with the radius of the circumscribed sphere. This fact seems to have been known to the Greeks, perhaps
to Theætetus (ca. 400 B.C.) and Aristæus (ca. 300 B.C.), both of whom wrote on incommensurables.
Just as we may produce the sides of a regular polygon and form a regular cross polygon or stellar polygon, so we may have stellar polyhedrons. Kepler, the great astronomer, constructed some of these solids in 1619, and Poinsot, a French mathematician, carried the constructions so far in 1801 that several of these stellar polyhedrons are known as Poinsot solids. There is a very extensive literature upon this subject.
The following table may be of some service in assigning problems in mensuration in connection with the regular polyhedrons, although some of the formulas are too difficult for beginners to prove. In the table e = edge of the polyhedron, r = radius of circumscribed sphere, r' = radius of inscribed sphere, a = total area, v = volume.
| Number of Faces | 4 | 6 | 8 | 12 | 20 |
| r | e√(3/8) | (e/2)√3 | e√(1/2) | (e/4)√3(√5 + 1) | e√((5 + √5)/8) |
| r' | e√(1/24) | e/2 | e√(1/6) | (e/2)√((25 + 11√5)/10) | (e√3)/12(√5 + 3) |
| a | e2√3 | 6e2 | 2e2√3 | 3e2√(5(5 + 2√5)) | (5e2)√3 |
| v | (e3/12)√2 | e3 | (e3/3)√2 | ((e3)/4)(15 + 7√5) | ((5e3)/12)(√5 + 3) |
Some interest is added to the study of polyhedrons by calling attention to their occurrence in nature, in the form of crystals. The computation of the surfaces and volumes of these forms offers an opportunity for applying[Pg 312] the rules of mensuration, and the construction of the solids by paper folding or by the cutting of crayon or some other substance often arouses a considerable interest. The following are forms of crystals that are occasionally found:
They show how the cube is modified by having its corners cut off. A cube may be inscribed in an octahedron, its vertices being at the centers of the faces of the octahedron. If we think of the cube as expanding, the faces of the octahedron will cut off the corners of the cube as seen in the first figure, leaving the cube as shown in the second figure. If the corners are cut off still more, we have the third figure.
Similarly, an octahedron may be inscribed in a cube, and by letting it expand a little, the faces of the cube will cut off the corners of the octahedron. This is seen in the following figures:
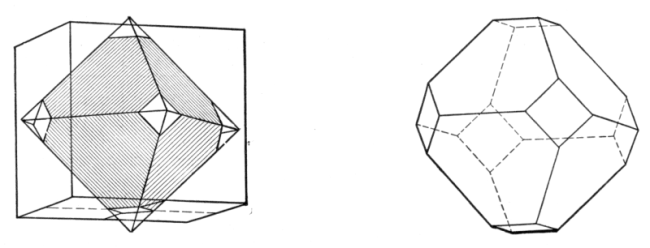
This is a form that is found in crystals, and the computation of the surface and volume is an interesting[Pg 313] exercise. The quartz crystal, an hexagonal pyramid on an hexagonal prism, is found in many parts of the country, or is to be seen in the school museum, and this also forms an interesting object of study in this connection.
The properties of the cylinder are next studied. The word is from the Greek kylindros, from kyliein (to roll). In ancient mathematics circular cylinders were the only ones studied, but since some of the properties are as easily proved for the case of a noncircular directrix, it is not now customary to limit them in this way. It is convenient to begin by a study of the cylindric surface, and a piece of paper may be curved or rolled up to illustrate this concept. If the paper is brought around so that the edges meet, whatever curve may form a cross section the surface is said to inclose a cylindric space. This concept is sometimes convenient, but it need be introduced only as necessity for using it arises. The other definitions concerning the cylinder are so simple as to require no comment.
The mensuration of the volume of a cylinder depends upon the assumption that the cylinder is the limit of a certain inscribed or circumscribed prism as the number of sides of the base is indefinitely increased. It is possible to give a fairly satisfactory and simple proof of this fact, but for pupils of the age of beginners in geometry in America it is better to make the assumption outright. This is one of several cases in geometry where a proof is less convincing than the assumed statement.
Theorem. The lateral area of a circular cylinder is equal to the product of the perimeter of a right section of the cylinder by an element.[Pg 314]
For practical purposes the cylinder of revolution (right circular cylinder) is the one most frequently used, and the important formula is therefore l = 2πrh where l = the lateral area, r = the radius, and h = the altitude. Applications of this formula are easily found.
Theorem. The volume of a circular cylinder is equal to the product of its base by its altitude.
Here again the important case is that of the cylinder of revolution, where v = πr2h.
The number of applications of this proposition is, of course, very great. In architecture and in mechanics the cylinder is constantly seen, and the mensuration of the surface and the volume is important. A single illustration of this type of problem will suffice.
A machinist is making a crank pin (a kind of bolt) for an engine, according to this drawing. He considers it as weighing the same as three steel cylinders having the diameters and lengths in inches as here shown, where 7-3/4" means 7-3/4 inches. He has this formula for the weight (w) of a steel cylinder where d is the diameter and l is the length: w = 0.07πd2l. Taking π = 3-1/7, find the weight of the pin.
The most elaborate study of the cylinder, cone, and sphere (the "three round bodies") in the Greek literature is that of Archimedes of Syracuse (on the island of Sicily), who lived in the third century B.C. Archimedes tells us, however, that Eudoxus (born ca. 407 B.C.) discovered that any cone is one third of a cylinder of the same base and the same altitude. Tradition says that Archimedes requested that a sphere and a cylinder be carved upon his tomb, and that this was done. Cicero relates that he discovered the tomb by means of these symbols. The tomb now shown to visitors in ancient Syracuse as[Pg 315] that of Archimedes cannot be his, for it bears no such figures, and is not "outside the gate of Agrigentum," as Cicero describes.
The cone is now introduced. A conic surface is easily illustrated to a class by taking a piece of paper and rolling it up into a cornucopia, the space inclosed being a conic space, a term that is sometimes convenient. The generation of a conic surface may be shown by taking a blackboard pointer and swinging it around by its tip so that the other end moves in a curve. If we consider a straight line as the limit of a curve, then the pointer may swing in a plane, and so a plane is the limit of a conic surface. If we swing the pointer about a point in the middle, we shall generate the two nappes of the cone, the conic space now being double.
In practice the right circular cone, or cone of revolution, is the important type, and special attention should be given to this form.
Theorem. Every section of a cone made by a plane passing through its vertex is a triangle.
At this time, or in speaking of the preliminary definitions, reference should be made to the conic sections. Of these there are three great types: (1) the ellipse, where the cutting plane intersects all the elements on one side of the vertex; a circle is a special form of the ellipse; (2) the parabola, where the plane is parallel to an element; (3) the hyperbola, where the plane cuts some of the elements on one side of the vertex, and the rest on the other side; that is, where it cuts both nappes. It is to be observed that the ellipse may vary greatly in shape, from a circle to a very long ellipse, as the cutting plane changes from being perpendicular to the axis to being nearly parallel to an element. The instant it[Pg 316] becomes parallel to an element the ellipse changes suddenly to a parabola. If the plane tips the slightest amount more, the section becomes an hyperbola.
While these conic sections are not studied in elementary geometry, the terms should be known for general information, particularly the ellipse and parabola. The study of the conic sections forms a large part of the work of analytic geometry, a subject in which the figures resemble the graphic work in algebra, this having been taken from "analytics," as the higher subject is commonly called. The planets move about the sun in elliptic orbits, and Halley's comet that returned to view in 1909-1910 has for its path an enormous ellipse. Most comets seem to move in parabolas, and a body thrown into the air would take a parabolic path if it were not for the resistance of the atmosphere. Two of the sides of the triangle in this proposition constitute a special form of the hyperbola.
The study of conic sections was brought to a high state by the Greeks. They were not known to the Pythagoreans, but were discovered by Menæchmus in the fourth century B.C. This discovery is mentioned by Proclus, who says, "Further, as to these sections, the conics were conceived by Menæchmus."
Since if the cutting plane is perpendicular to the axis the section is a circle, and if oblique it is an ellipse, a parabola, or an hyperbola, it follows that if light proceeds from a point, the shadow of a circle is a circle, an ellipse, a parabola, or an hyperbola, depending on the position of the plane on which the shadow falls. It is interesting and instructive to a class to see these shadows, but of course not much time can be allowed for such work. At this point the chief thing is to have[Pg 317] the names "ellipse" and "parabola," so often met in reading, understood.
It is also of interest to pupils to see at this time the method of drawing an ellipse by means of a pencil stretching a string band that moves about two pins fastened in the paper. This is a practical method, and is familiar to all teachers who have studied analytic geometry. In designing elliptic arches, however, three circular arcs are often joined, as here shown, the result being approximately an elliptic arc.
Here O is the center of arc BC, M of arc AB, and N of arc CD. Since XY is perpendicular to BM and BO, it is tangent to arcs AB and BC, so there is no abrupt turning at B, and similarly for C.[90]
Theorem. The volume of a circular cone is equal to one third the product of its base by its altitude.
It is easy to prove this for noncircular cones as well, but since they are not met commonly in practice, they may be omitted in elementary geometry. The important formula at this time is v = 1/3πr2h. As already stated, this proposition was discovered by Eudoxus of Cnidus (born ca. 407 B.C., died ca. 354 B.C.), a man who, as already stated, was born poor, but who became one of the most illustrious and most highly esteemed of all the Greeks of his time.
Theorem. The lateral area of a frustum of a cone of revolution is equal to half the sum of the circumferences of its bases multiplied by the slant height.
An interesting case for a class to notice is that in which the upper base becomes zero and the frustum becomes a cone, the proposition being still true. If the upper base is equal to the lower base, the frustum becomes a cylinder, and still the proposition remains true. The proposition thus offers an excellent illustration of the elementary Principle of Continuity.
Then follows, in most textbooks, a theorem relating to the volume of a frustum.
In the case of a cone of revolution v = (1/3)πh(r2 + r'2 + rr'). Here if r' = 0, we have v = (1/3)πr2h, the volume of a cone. If r' = r, we have v = (1/3)πh(r2 + r2 + r2) = πhr2, the volume of a cylinder.
If one needs examples in mensuration beyond those given in a first-class textbook, they are easily found. The monument to Sir Christopher Wren, the professor of geometry in Cambridge University, who became the great architect of St. Paul's Cathedral in London, has a Latin inscription which means, "Reader, if you would see his monument, look about you." So it is with practical examples in Book VII.
Appended to this Book, or more often to the course in solid geometry, is frequently found a proposition known as Euler's Theorem. This is often considered too difficult for the average pupil and is therefore omitted. On account of its importance, however, in the theory of polyhedrons, some reference to it at this time may be helpful to the teacher. The theorem asserts that in any convex polyhedron the number of edges increased by two is equal to the number of vertices increased by the number of faces. In other words, that e + 2 = v + f. On account of its importance a proof will be given that differs from the one ordinarily found in textbooks.[Pg 319]
Let s1, s2, ···, sn be the number of sides of the various faces, and f the number of faces. Now since the sum of the angles of a polygon of s sides is (s - 2)180°, therefore the sum of the angles of all the faces is (s1 + s2 + s3 + ··· + sn - 2f)180°.
But s1 + s2 + s3 + ··· + sn is twice the number of edges, because each edge belongs to two faces.
∴ the sum of the angles of all the faces is
(2e - 2f)180°, or (e - f)360°.
Since the polyhedron is convex, it is possible to find some outside point of view, P, from which some face, as ABCDE, covers up the whole figure, as in this illustration. If we think of all the vertices projected on ABCDE, by lines through P, the sum of the angles of all the faces will be the same as the sum of the angles of all their projections on ABCDE. Calling ABCDE s1, and thinking of the projections as traced by dotted lines on the opposite side of s1, this sum is evidently equal to
(1) the sum of the angles in s1, or (s1 - 2) 180°, plus
(2) the sum of the angles on the other side of s1, or (s1 - 2)180°, plus
(3) the sum of the angles about the various points shown as inside of s1, of which there are v - s1 points, about each of which the sum of the angles is 360°, making (v - s1)360° in all.
Adding, we have
(s1 - 2)180° + (s1 - 2)180° + (v - s1)360° = ((s1 - 2) + (v - s1))360°
= (v - 2)360°.
Equating the two sums already found, we have
(e - f)360° = (v - 2)360°,
or e - f = v - 2,
or e + 2 = v + f.
This proof is too abstract for most pupils in the high school, but it is more scientific than those found in any of the elementary textbooks, and teachers will find it of service in relieving their own minds of any question as to the legitimacy of the theorem.
Although this proposition is generally attributed to Euler, and was, indeed, rediscovered by him and published in 1752, it was known to the great French geometer Descartes, a fact that Leibnitz mentions.[91]
This theorem has a very practical application in the study of crystals, since it offers a convenient check on the count of faces, edges, and vertices. Some use of crystals, or even of polyhedrons cut from a piece of crayon, is desirable when studying Euler's proposition. The following illustrations of common forms of crystals may be used in this connection:
The first represents two truncated pyramids placed base to base. Here e = 20, f = 10, v = 12, so that e + 2 = f + v. The second represents a crystal formed by replacing each edge of a cube by a plane, with the result that e = 40, f = 18, and v = 24. The third represents a crystal formed by replacing each edge of an octahedron by a plane, it being easy to see that Euler's law still holds true.
Book VIII treats of the sphere. Just as the circle may be defined either as a plane surface or as the bounding line which is the locus of a point in a plane at a given distance from a fixed point, so a sphere may be defined either as a solid or as the bounding surface which is the locus of a point in space at a given distance from a fixed point. In higher mathematics the circle is defined as the bounding line and the sphere as the bounding surface; that is, each is defined as a locus. This view of the circle as a line is becoming quite general in elementary geometry, it being the desire that students may not have to change definitions in passing from elementary to higher mathematics. The sphere is less frequently looked upon in geometry as a surface, and in popular usage it is always taken as a solid.
Analogous to the postulate that a circle may be described with any given point as a center and any given line as a radius, is the postulate for constructing a sphere with any given center and any given radius. This postulate is not so essential, however, as the one about the circle, because we are not so concerned with constructions here as we are in plane geometry.
A good opportunity is offered for illustrating several of the definitions connected with the study of the sphere, such as great circle, axis, small circle, and pole,[Pg 322] by referring to geography. Indeed, the first three propositions usually given in Book VIII have a direct bearing upon the study of the earth.
Theorem. A plane perpendicular to a radius at its extremity is tangent to the sphere.
The student should always have his attention called to the analogue in plane geometry, where there is one. If here we pass a plane through the radius in question, the figure formed on the plane will be that of a line tangent to a circle. If we revolve this about the line of the radius in question, as an axis, the circle will generate the sphere again, and the tangent line will generate the tangent plane.
Theorem. A sphere may be inscribed in any given tetrahedron.
Here again we may form a corresponding proposition of plane geometry by passing a plane through any three points of contact of the sphere and the tetrahedron. We shall then form the figure of a circle inscribed in a triangle. And just as in the case of the triangle we may have escribed circles by producing the sides, so in the case of the tetrahedron we may have escribed spheres by producing the planes indefinitely and proceeding in the same way as for the inscribed sphere. The figure is difficult to draw, but it is not difficult to understand, particularly if we construct the tetrahedron out of pasteboard.
Theorem. A sphere may be circumscribed about any given tetrahedron.
By producing one of the faces indefinitely it will cut the sphere in a circle, and the resulting figure, on the plane, will be that of the analogous proposition of plane geometry, the circle circumscribed about a triangle. It[Pg 323] is easily proved from the proposition that the four perpendiculars erected at the centers of the faces of a tetrahedron meet in a point (are concurrent), the analogue of the proposition about the perpendicular bisectors of the sides of a triangle.
Theorem. The intersection of two spherical surfaces is a circle whose plane is perpendicular to the line joining the centers of the surfaces and whose center is in that line.
The figure suggests the case of two circles in plane geometry. In the case of two circles that do not intersect or touch, one not being within the other, there are four common tangents. If the circles touch, two close up into one. If one circle is wholly within the other, this last tangent disappears. The same thing exists in relation to two spheres, and the analogous cases are formed by revolving the circles and tangents about the line through their centers.
In plane geometry it is easily proved that if two circles intersect, the tangents from any point on their common chord produced are equal. For if the common chord is AB and the point P is taken on AB produced, then the square on any tangent from P is equal to PB × PA. The line PBA is sometimes called the radical axis.
Similarly in this proposition concerning spheres, if from any point in the plane of the circle formed by the intersection of the two spherical surfaces lines are drawn tangent to either sphere, these tangents are equal. For it is easily proved that all tangents to the same sphere from an external point are equal, and it can be proved as in plane geometry that two tangents to the two spheres are equal.
Among the interesting analogies between plane and solid geometry is the one relating to the four common[Pg 324] tangents to two circles. If the figure be revolved about the line of centers, the circles generate spheres and the tangents generate conical surfaces. To study this case for various sizes and positions of the two spheres is one of the most interesting generalizations of solid geometry.
An application of the proposition is seen in the case of an eclipse, where the sphere O' represents the moon, O the earth, and S the sun. It is also seen in the case of the full moon, when S is on the other side of the earth. In this case the part MIN is fully illuminated by the moon, but the zone ABNM is only partly illuminated, as the figure shows.[92]
Theorem. The sum of the sides of a spherical polygon is less than 360°.
In all such cases the relation to the polyhedral angle should be made clear. This is done in the proofs usually given in the textbooks. It is easily seen that this is true only with the limitation set forth in most textbooks, that the spherical polygons considered are convex. Thus we might have a spherical triangle that is concave, with its base 359°, and its other two sides each 90°, the sum of the sides being 539°.
Theorem. The sum of the angles of a spherical triangle is greater than 180° and less than 540°.
It is for the purpose of proving this important fact that polar triangles are introduced. This proposition shows the relation of the spherical to the plane triangle. If our planes were in reality slightly curved, being small portions of enormous spherical surfaces, then the sum of the angles of a triangle would not be exactly 180°, but would exceed 180° by some amount depending on the curvature of the surface. Just as a being may be imagined as having only two dimensions, and living always on a plane surface (in a space of two dimensions), and having no conception of a space of three dimensions, so we may think of ourselves as living in a space of three dimensions but surrounded by a space of four dimensions. The flat being could not point to a third dimension because he could not get out of his plane, and we cannot point to the fourth dimension because we cannot get out of our space. Now what the flat being thinks is his plane may be the surface of an enormous sphere in our three dimensions; in other words, the space he lives in may curve through some higher space without his being conscious of it. So our space may also curve through some higher space without our being conscious of it. If our planes have really some curvature, then the sum of the angles of our triangles has a slight excess over 180°. All this is mere speculation, but it may interest some student to know that the idea of fourth and higher dimensions enters largely into mathematical investigation to-day.
Theorem. Two symmetric spherical triangles are equivalent.
While it is not a subject that has any place in a school, save perhaps for incidental conversation with some group of enthusiastic students, it may interest the teacher to consider this proposition in connection with the fourth[Pg 326] dimension just mentioned. Consider these triangles, where ∠A = ∠A', AB = A'B', AC = A'C'. We prove them congruent by superposition, turning one over and placing it upon the other. But suppose we were beings in Flatland, beings with only two dimensions and without the power to point in any direction except in the plane we lived in. We should then be unable to turn ⧍A'B'C' over so that it could coincide with ⧍ABC, and we should have to prove these triangles equivalent in some other way, probably by dividing them into isosceles triangles that could be superposed.
Now it is the same thing with symmetric spherical triangles; we cannot superpose them. But might it not be possible to do so if we could turn them through the fourth dimension exactly as we turn the Flatlander's triangle through our third dimension? It is interesting to think about this possibility even though we carry it no further, and in these side lights on mathematics lies much of the fascination of the subject.
Theorem. The shortest line that can be drawn on the surface of a sphere between two points is the minor arc of a great circle joining the two points.
It is always interesting to a class to apply this practically. By taking a terrestrial globe and drawing a great circle between the southern point of Ireland and New York City, we represent the shortest route for ships[Pg 327] crossing to England. Now if we notice where this great-circle arc cuts the various meridians and mark this on an ordinary Mercator's projection map, such as is found in any schoolroom, we shall find that the path of the ship does not make a straight line. Passengers at sea often do not understand why the ship's course on the map is not a straight line; but the chief reason is that the ship is taking a great-circle arc, and this is not, in general, a straight line on a Mercator projection. The small circles of latitude are straight lines, and so are the meridians and the equator, but other great circles are represented by curved lines.
Theorem. The area of the surface of a sphere is equal to the product of its diameter by the circumference of a great circle.
This leads to the remarkable formula, a = 4πr2. That the area of the sphere, a curved surface, should exactly equal the sum of the areas of four great circles, plane surfaces, is the remarkable feature. This was one of the greatest discoveries of Archimedes (ca. 287-212 B.C.), who gives it as the thirty-fifth proposition of his treatise on the "Sphere and the Cylinder," and who mentions it specially in a letter to his friend Dositheus, a mathematician of some prominence. Archimedes also states that the surface of a sphere is two thirds that of the circumscribed cylinder, or the same as the curved surface of this cylinder. This is evident, since the cylindric surface of the cylinder is 2πr × 2r, or 4πr2, and the two bases have an area πr2 + πr2, making the total area 6πr2.
Theorem. The area of a spherical triangle is equal to the area of a lune whose angle is half the triangle's spherical excess.[Pg 328]
This theorem, so important in finding areas on the earth's surface, should be followed by a considerable amount of computation of triangular areas, else it will be rather meaningless. Students tend to memorize a proof of this character, and in order to have the proposition mean what it should to them, they should at once apply it. The same is true of the following proposition on the area of a spherical polygon. It is probable that neither of these propositions is very old; at any rate, they do not seem to have been known to the writers on elementary mathematics among the Greeks.
Theorem. The volume of a sphere is equal to the product of the area of its surface by one third of its radius.
This gives the formula v = (4/3)πr3. This is one of the greatest discoveries of Archimedes. He also found as a result that the volume of a sphere is two thirds the volume of the circumscribed cylinder. This is easily seen, since the volume of the cylinder is πr2 × 2r, or 2πr3, and (4/3)πr3 is 2/3 of 2πr3. It was because of these discoveries on the sphere and cylinder that Archimedes wished these figures engraved upon his tomb, as has already been stated. The Roman general Marcellus conquered Syracuse in 212 B.C., and at the sack of the city Archimedes was killed by an ignorant soldier. Marcellus carried out the wishes of Archimedes with respect to the figures on his tomb.
The volume of a sphere can also be very elegantly found by means of a proposition known as Cavalieri's Theorem. This asserts that if two solids lie between parallel planes, and are such that the two sections made by any plane parallel to the given planes are equal in area, the solids are themselves equal in volume. Thus, if these solids have the same altitude, a, and if S and S'[Pg 329] are equal sections made by a plane parallel to MN, then the solids have the same volume. The proof is simple, since prisms of the same altitude, say a/n, and on the bases S and S' are equivalent, and the sums of n such prisms are the given solids; and as n increases, the sums of the prisms approach the solids as their limits; hence the volumes are equal.
This proposition, which will now be applied to finding the volume of the sphere, was discovered by Bonaventura Cavalieri (1591 or 1598-1647). He was a Jesuit professor in the University of Bologna, and his best known work is his "Geometria Indivisilibus," which he wrote in 1626, at least in part, and published in 1635 (second edition, 1647). By means of the proposition it is also possible to prove several other theorems, as that the volumes of triangular pyramids of equivalent bases and equal altitudes are equal.
To find the volume of a sphere, take the quadrant OPQ, in the square OPRQ. Then if this figure is revolved about OP, OPQ will generate a hemisphere, OPR will generate a cone of volume (1/3)πr3, and OPRQ will generate a cylinder of volume πr3. Hence the figure generated by ORQ will have a volume πr3 - (1/3)πr3, or (2/3)πr3, which we will call x.
Now OA = AB, and OC = AD; also (OC)2 - (OA)2 = (AC)2, so that
(AD)2 - (AB)2 = (AC)2,
and π(AD)2 - π(AB)2 = π(AC)2.
[Pg 330]
But π(AD)2 - π(AB)2 is the area of the ring generated by BD, a section of x, and π(AC)2 is the corresponding section of the hemisphere. Hence, by Cavalieri's Theorem,
(2/3)πr3 = the volume of the hemisphere.
∴ (4/3)πr3 = the volume of the sphere.
In connection with the sphere some easy work in quadratics may be introduced even if the class has had only a year in algebra.
For example, suppose a cube is inscribed in a hemisphere of radius r and we wish to find its edge, and thereby its surface and its volume.
If x = the edge of the cube, the diagonal of the base must be x√2, and the projection of r (drawn from the center of the base to one of the vertices) on the base is half of this diagonal, or (x√2)/2.
Hence, by the Pythagorean Theorem,
r2 = x2 + ((x√2)/2)2 = (3/2)x2
∴ x = r√(2/3),
and the total surface is 6x2 = 4r2,
and the volume is x3 = (2/3)r3√(2/3).
In the Valley of Youth, through which all wayfarers must pass on their journey from the Land of Mystery to the Land of the Infinite, there is a village where the pilgrim rests and indulges in various excursions for which the valley is celebrated. There also gather many guides in this spot, some of whom show the stranger all the various points of common interest, and others of whom take visitors to special points from which the views are of peculiar significance. As time has gone on new paths have opened, and new resting places have been made from which these views are best obtained. Some of the mountain peaks have been neglected in the past, but of late they too have been scaled, and paths have been hewn out that approach the summits, and many pilgrims ascend them and find that the result is abundantly worth the effort and the time.
The effect of these several improvements has been a natural and usually friendly rivalry in the body of guides that show the way. The mountains have not changed, and the views are what they have always been. But there are not wanting those who say, "My mountain may not be as lofty as yours, but it is easier to ascend"; or "There are quarries on my peak, and points of view from which a building may be seen in process of erection, or a mill in operation, or a canal, while your mountain shows only a stretch of hills and valleys, and thus you will see that mine is the more profitable to visit."[Pg 332] Then there are guides who are themselves often weak of limb, and who are attached to numerous sand dunes, and these say to the weaker pilgrims, "Why tire yourselves climbing a rocky mountain when here are peaks whose summits you can reach with ease and from which the view is just as good as that from the most famous precipice?" The result is not wholly disadvantageous, for many who pass through the valley are able to approach the summits of the sand dunes only, and would make progress with greatest difficulty should they attempt to scale a real mountain, although even for them it would be better to climb a little way where it is really worth the effort instead of spending all their efforts on the dunes.
Then, too, there have of late come guides who have shown much ingenuity by digging tunnels into some of the greatest mountains. These they have paved with smooth concrete, and have arranged for rubber-tired cars that run without jar to the heart of some mountain. Arrived there the pilgrim has a glance, as the car swiftly turns in a blaze of electric light, at a roughly painted panorama of the view from the summit, and he is assured by the guide that he has accomplished all that he would have done, had he laboriously climbed the peak itself.
In the midst of all the advocacy of sand-dune climbing, and of rubber-tired cars to see a painted view, the great body of guides still climb their mountains with their little groups of followers, and the vigor of the ascent and the magnificence of the view still attract all who are strong and earnest, during their sojourn in the Valley of Youth. Among the mountains that have for ages attracted the pilgrims is Mons Latinus, usually called in the valley by the more pleasing name Latina.[Pg 333] Mathematica, and Rhetorica, and Grammatica are also among the best known. A group known as Montes Naturales comprises Physica, Biologica, and Chemica, and one great peak with minor peaks about it is called by the people Philosophia. There are those who claim that these great masses of rock are too old to be climbed, as if that affected the view; while others claim that the ascent is too difficult and that all who do not favor the sand dunes are reactionary. But this affects only a few who belong to the real mountains, and the others labor diligently to improve the paths and to lessen unnecessary toil, but they seek not to tear off the summits nor do they attend to the amusing attempts of those who sit by the hillocks and throw pebbles at the rocky sides of the mountains upon which they work.
Geometry is a mountain. Vigor is needed for its ascent. The views all along the paths are magnificent. The effort of climbing is stimulating. A guide who points out the beauties, the grandeur, and the special places of interest commands the admiration of his group of pilgrims. One who fails to do this, who does not know the paths, who puts unnecessary burdens upon the pilgrim, or who blindfolds him in his progress, is unworthy of his position. The pretended guide who says that the painted panorama, seen from the rubber-tired car, is as good as the view from the summit is simply a fakir and is generally recognized as such. The mountain will stand; it will not be used as a mere commercial quarry for building stone; it will not be affected by pellets thrown from the little hillocks about; but its paths will be freed from unnecessary flints, they will be[Pg 334] straightened where this can advantageously be done, and new paths on entirely novel plans will be made as time goes on, but these paths will be hewed out of rock, not made out of the dreams of a day. Every worthy guide will assist in all these efforts at betterment, and will urge the pilgrim at least to ascend a little way because of the fact that the same view cannot be obtained from other peaks; but he will not take seriously the efforts of the fakir, nor will he listen with more than passing interest to him who proclaims the sand heap to be a Matterhorn.[Pg 335]
| List price | |
| Allen: Civics and Health | $1.25 |
| Brigham: Geographic Influences in American History | 1.25 |
| Channing and Hart: Guide to the Study of American History | 2.00 |
| Hall: Aspects of Child Life and Education | 1.50 |
| Hodge: Nature Study and Life | 1.50 |
| Johnson: Education by Plays and Games | .90 |
| Johnson: What to Do at Recess | .25 |
| Kern: Among Country Schools | 1.25 |
| Mace: Method in History | 1.00 |
| MacVicar: The Principles of Education | .60 |
| Moral Training in the Public Schools | 1.25 |
| Prince: Courses of Studies and Methods of Teaching | .75 |
| Scott: Social Education | 1.25 |
| Tompkins: Philosophy of School Management | .75 |
| Tompkins: Philosophy of Teaching | .75 |
| Wiltse: Place of the Story in Early Education, and Other Essays. | |
| A Manual for Teachers | .50 |
| Comings: Complete Record--Attendance and Scholarship | |
| Graded-School Edition | .30 |
| High-School Edition | .30 |
| Ginn and Company: Teacher's Class Books | |
| No. I | .30 |
| No. II | .40 |
| Twenty Weeks' Class Book | .30 |
By WILLIAM H. ALLEN, Secretary of the Bureau of Municipal Research, New York City. With an Introduction by Professor William T. Sedgwick, Professor of Biology in the Massachusetts Institute of Technology
List price, $1.25
Adopted by the Teachers' Reading Circles of
Maryland, Kentucky, North Dakota, South Dakota, Oklahoma,
New Mexico, South Carolina, Alabama, Arizona, Illinois,
Michigan, Colorado, Texas, Virginia, Iowa, Arkansas,
Wyoming, Missouri, Indiana, Nebraska, and Washington
For Dr. Allen prevention is a text and the making of sound citizens a sermon. In "Civics and Health" he sounds a slogan which should awaken every community in this country to its opportunities in municipal reform. Every teacher who reads this book will gain a new sense of duty in matters of hygiene and sanitation.
Civics and Health is enthrallingly interesting. It is humanized sociology. Cleaning up children by scientific illumination will appeal to every father and mother, every child lover who has any patriotism or desire to learn how we as a people are to make moral-reform agitations fruitful through health of American children, and so establish health of national life.—Boston Transcript.
This is one of the books we wish the law required every citizen to have in his house and to know by heart. Then, indeed, mankind would have made an immense stride forward.—Chicago Medical Recorder.
The book is alive from cover to cover. It breathes reform but not of the platform variety. It abounds in ugly facts but superabounds in the statement of best methods of getting rid of this ugliness. As claimed by the publishers, it is preëminently a book on "getting things done."—Hygiene and Physical Education, Springfield, Mass.
[1] And really, though not nominally, in the United States, where the first concepts are found in the kindergarten, and where an excellent course in mensuration is given in any of our better class of arithmetics. That we are wise in not attempting serious demonstrative geometry much earlier seems to be generally conceded.
[2] The third stage of geometry as defined in the recent circular (No. 711) of the British Board of Education, London, 1909.
[3] The closing words of a sensible review of the British Board of Education circular (No. 711), on "The Teaching of Geometry" (London, 1909), by H. S. Hall in the School World, 1909, p. 222.
[4] In an address in London, June 15, 1909, at a dinner to Sir Ernest Shackelton.
[5] Governor Hughes, now Justice Hughes, of New York, at the Peary testimonial on February 8, 1910, at New York City.
[6] The first work upon this subject, and indeed the first printed treatise on curves in general, was written by the famous artist of Nürnberg, Albrecht Dürer.
[7] Several of these writers are mentioned in Chapter IV.
[8] If any reader chances upon George Birkbeck's English translation of Charles Dupin's "Mathematics Practically Applied," Halifax, 1854, he will find that Dupin gave more good applications of geometry than all of our American advocates of practical geometry combined.
[9] See, for example, Henrici's "Congruent Figures," London, 1879, and the review of Borel's "Elements of Mathematics," by Professor Sisam in the Bulletin of the American Mathematical Society, July, 1910, a matter discussed later in this work.
[10] T. J. McCormack, "Why do we study Mathematics: a Philosophical and Historical Retrospect," p. 9, Cedar Rapids, Iowa, 1910.
[11] Of the fair and candid arguments against the culture value of mathematics, one of the best of the recent ones is that by G. F. Swain, in the Atti del IV Congresso Internazionale dei Matematici, Rome, 1909, Vol. III, p. 361. The literature of this school is quite extensive, but Perry's "England's Neglect of Science," London, 1900, and "Discussion on the Teaching of Mathematics," London, 1901, are typical.
[12] In his novel, "The Morals of Marcus Ordeyne."
[13] G. W. L. Carson, "The Functions of Geometry as a Subject of Education," p. 3, Tonbridge, 1910.
[14] It may well be, however, that the growing curriculum may justify some reduction in the time formerly assigned to geometry, and any reasonable proposition of this nature should be fairly met by teachers of mathematics.
[15] Professor Münsterberg, in the Metropolitan Magazine for July, 1910.
[16] It was published in German translation by A. Eisenlohr, "Ein mathematisches Handbuch der alten Aegypter," Leipzig, 1877, and in facsimile by the British Museum, under the title, "The Rhind Papyrus," in 1898.
[17] Generally known as Rameses II. He reigned in Egypt about 1350 B.C.
[18] Two excellent works on Thales and his successors, and indeed the best in English, are the following: G. J. Allman, "Greek Geometry from Thales to Euclid," Dublin, 1889; J. Gow, "A History of Greek Mathematics," Cambridge, 1884. On all mathematical subjects the best general history is that of M. Cantor, "Geschichte der Mathematik," 4 vols, Leipzig, 1880-1908.
[19] Another good work on Greek geometry, with considerable material on Pythagoras, is by C. A. Bretschneider, "Die Geometrie und die Geometer vor Eukleides," Leipzig, 1870.
[20] Smith and Karpinski, "The Hindu-Arabic Numerals," Boston, 1911.
[21] For a sketch of his life see Smith and Karpinski, loc. cit.
[22] Those who care for a brief description of this phase of the subject may consult J. Casey, "A Sequel to Euclid," Dublin, fifth edition, 1888; W. J. M'Clelland, "A Treatise on the Geometry of the Circle," New York, 1891; M. Simon, "Über die Entwicklung der Elementar-Geometrie im XIX. Jahrhundert," Leipzig, 1906.
[23] Riccardi, Saggio di una bibliografia Euclidea, Part I, p. 3, Bologna, 1887. Riccardi lists well towards two thousand editions.
[24] Hermotimus of Colophon and Philippus of Mende.
[25] Literally, "Who closely followed the first," i.e. the first Ptolemy.
[26] Menæchmus is said to have replied to a similar question of Alexander the Great: "O King, through the country there are royal roads and roads for common citizens, but in geometry there is one road for all."
[27] This is also shown in a letter from Archimedes to Eratosthenes, recently discovered by Heiberg.
[28] On this phase of the subject, and indeed upon Euclid and his propositions and works in general, consult T. L. Heath, "The Thirteen Books of Euclid's Elements," 3 vols., Cambridge, 1908, a masterly treatise of which frequent use has been made in preparing this work.
[29] A contemporary copy of this translation is now in the library of George A. Plimpton, Esq., of New York. See the author's "Rara Arithmetica," p. 433, Boston, 1909.
[30] A beautiful vellum manuscript of this translation is in the library of George A. Plimpton, Esq., of New York. See the author's "Rara Arithmetica," p. 481, Boston, 1909.
[31] Heath, loc. cit., Vol. I, p. 114.
[32] The author is a member of a committee that has for more than a year been considering a syllabus in geometry. This committee will probably report sometime during the year 1911. At the present writing it seems disposed to recommend about the usual list of basal propositions.
[33] "Elementi di Geometria," Milan, 1884.
[34] See his "Elementarmathematik vom höheren Standpunkt aus," Part II, Leipzig, 1909.
[35] For some classes of schools and under certain circumstances courses in combined mathematics are very desirable. All that is here insisted upon is that any general fusion all along the line would result in weak, insipid, and uninteresting mathematics. A beginning, inspirational course in combined mathematics has a good reason for being in many high schools in spite of its manifest disadvantages, and such a course may be developed to cover all of the required mathematics given in certain schools.
[36] Carson, loc. cit., p. 15.
[37] Al-jabr wa'l-muqābalah: "restoration and equation" is a fairly good translation of the Arabic.
[38] Or be carried along at the same time as a distinct topic.
[39] With a single year for required geometry it would be better from every point of view to cut the plane geometry enough to admit a fair course in solid geometry.
[40] Carson, loc. cit., p. 13.
[41] Carson, loc. cit., p. 12.
[42] From the Greek γη, ge (earth), + μετρειν metrein (to measure), although the science has not had to do directly with the measure of the earth for over two thousand years.
[43] From the Arabic al (the) + jabr (restoration), referring to taking a quantity from one side of an equation and then restoring the balance by taking it from the other side (see page 37).
[44] One of the clearest discussions of the subject is in W. B. Frankland, "The First Book of Euclid's 'Elements,'" p. 26, Cambridge, 1905.
[45] "Grundlagen der Geometrie," Leipzig, 1899. See Heath's "Euclid," Vol. I, p. 229, for an English version; also D. E. Smith, "Teaching of Elementary Mathematics," p. 266, New York, 1900.
[46] We need frequently to recall the fact that Euclid's "Elements" was intended for advanced students who went to Alexandria as young men now go to college, and that the book was used only in university instruction in the Middle Ages and indeed until recent times.
[47] For example, he moves figures without deformation, but states no postulate on the subject; and he proves that one side of a triangle is less than the sum of the other two sides, when he might have postulated that a straight line is the shortest path between two points. Indeed, his followers were laughed at for proving a fact so obvious as this one concerning the triangle.
[48] T. L. Heath, "Euclid," Vol. I, p. 200.
[49] For a résumé of the best known attempts to prove this postulate, see Heath, "Euclid," Vol. I, p. 202; W. B. Frankland, "Theories of Parallelism," Cambridge, 1910.
[50] For the early history of this movement see Engel and Stäckel, "Die Theorie der Parallellinien von Euklid bis auf Gauss," Leipzig, 1895; Bonola, Sulla teoria delle parallele e sulle geometrie non-euclidee, in his "Questioni riguardanti la geometria elementare," 1900; Karagiannides, "Die nichteuklidische Geometrie vom Alterthum bis zur Gegenwart," Berlin, 1893.
[51] This limitation upon elementary geometry was placed by Plato (died 347 B.C.), as already stated.
[52] Book I, Proposition 20.
[53] Free use has been made of W. B. Frankland, "The First Book of Euclid's 'Elements,'" Cambridge, 1905; T. L. Heath, "The Thirteen Books of Euclid's 'Elements,'" Cambridge, 1908; H. Schotten, "Inhalt und Methode des planimetrischen Unterrichts," Leipzig, 1893; M. Simon, "Euclid und die sechs planimetrischen Bücher," Leipzig, 1901.
[54] For a facsimile of a thirteenth-century MS. containing this definition, see the author's "Rara Arithmetica," Plate IV, Boston, 1909.
[55] Our slang expression "The cart before the horse" is suggestive of this procedure.
[56] Loc. cit., Vol. II, p. 94.
[57] Address at Brussels, August, 1910.
[58] For a recent discussion of this general subject, see Professor Hobson on "The Tendencies of Modern Mathematics," in the Educational Review, New York, 1910, Vol. XL, p. 524.
[59] A more extended list of applications is given later in this work.
[60] Abū'l-'Abbās al-Fadl ibn Hātim al-Nairīzī, so called from his birthplace, Nairīz, was a well-known Arab writer. He died about 922 A.D. He wrote a commentary on Euclid.
[61] This illustration, taken from a book in the author's library, appeared in a valuable monograph by W. E. Stark, "Measuring Instruments of Long Ago," published in School Science and Mathematics, Vol. X, pp. 48, 126. With others of the same nature it is here reproduced by the courtesy of Principal Stark and of the editors of the journal in which it appeared.
[62] In speaking of two congruent triangles it is somewhat easier to follow the congruence if the two are read in the same order, even though the relatively unimportant counterclockwise reading is neglected. No one should be a slave to such a formalism, but should follow the plan when convenient.
[63] Stark, loc. cit.
[64] Of which so much was made by Professor Olaus Henrici in his "Congruent Figures," London, 1879,—a book that every teacher of geometry should own.
[65] Much is made of this in the excellent work by Henrici and Treutlein, "Lehrbuch der Geometrie," Leipzig, 1881.
[66] Méray did much for this movement in France, and the recent works of Bourlet and Borel have brought it to the front in that country.
[67] W. N. Bruce, "Teaching of Geometry and Graphic Algebra in Secondary Schools," Board of Education circular (No. 711), p. 8, London, 1909.
[68] This is the latest opinion. He is usually assigned to the first century B.C.
[70] A Greek philosopher and mathematician of the fifth century B.C.
[71] This illustration and the following two are from C. Dupin, "Mathematics Practically Applied," translated from the French by G. Birkbeck, Halifax, 1854. This is probably the most scholarly attempt ever made at constructing a "practical geometry."
[72] This illustration and others of the same type used in this work are from the excellent drawings by R. W. Billings, in "The Infinity of Geometric Design Exemplified," London, 1849.
[73] From H. Kolb, "Der Ornamentenschatz ... aus allen Kunst-Epochen," Stuttgart, 1883. The original is in the Church of Saint Anastasia in Verona.
[74] From J. Bennett, "The Arcanum ... A Concise Theory of Practicable Geometry," London, 1838, one of the many books that have assumed to revolutionize geometry by making it practical.
[75] The figures are from Dupin, loc. cit.
[76] For a very full discussion of these four definitions see Heath's "Euclid," Vol. II, p. 116, and authorities there cited.
[77] These two and several which follow are from Stark, loc. cit.
[78] The author has a beautiful ivory specimen of the Sixteenth century.
[79] See, for example, G. B. Kaye, "The Source of Hindu Mathematics," in the Journal of the Royal Asiatic Society, July, 1910.
[80] An interesting Japanese proof of this general character may be seen in Y. Mikami, "Mathematical Papers from the Far East," p. 127, Leipzig, 1910.
[81] Special recognition of indebtedness to H. A. Naber's "Das Theorem des Pythagoras" (Haarlem, 1908), Heath's "Euclid," Gow's "History of Greek Mathematics," and Cantor's "Geschichte" is due in connection with the Pythagorean Theorem.
[82] The rule was so ill understood that Bhaskara (twelfth century) said that Brahmagupta was a "blundering devil" for giving it ("Lilavati," § 172).
[83] Bosanquet and Sayre, "The Babylonian Astronomy," Monthly Notices of the Royal Asiatic Society, Vol. XL, p. 108.
[84] This and the three illustrations following are from Kolb, loc. cit.
[85] This was in five colors of marble.
[86] The proof is too involved to be given here. The writer has set it forth in a chapter on the transcendency of π in a work soon to be published by Professor Young of The University of Chicago.
[87] These may be purchased through the Leipziger Lehrmittelanstalt, Leipzig, Germany, which will send catalogues to intending buyers.
[88] An excellent set of stereoscopic views of the figures of solid geometry, prepared by E. M. Langley of Bedford, England, is published by Underwood & Underwood, New York. Such a set may properly have place in a school library or in a classroom in geometry, to be used when it seems advantageous.
[89] The actual construction of these solids is given by Pappus. See his "Mathematicae Collectiones," p. 48, Bologna, 1660.
[90] The illustration is from Dupin, loc. cit.
[91] For the historical bibliography consult G. Holzmüller, Elemente der Stereometrie, Vol. I, p. 181, Leipzig, 1900.
[92] The illustration is from Dupin, loc. cit.
Transcribers notes
On page 30 Megapontum has been left as printed, though the author probably meant Metapontum.
On page 269 100 B.C. has been left as it was printed, though it is
probably a typo for 100 A.D.
End of Project Gutenberg's The Teaching of Geometry, by David Eugene Smith
*** END OF THIS PROJECT GUTENBERG EBOOK THE TEACHING OF GEOMETRY ***
***** This file should be named 37681-h.htm or 37681-h.zip *****
This and all associated files of various formats will be found in:
http://www.gutenberg.org/3/7/6/8/37681/
Produced by Juliet Sutherland, Anna Hall and the Online
Distributed Proofreading Team at http://www.pgdp.net
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
http://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need, are critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at http://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
http://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at http://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit http://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including checks, online payments and credit card donations.
To donate, please visit: http://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart is the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
http://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.