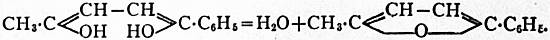The Project Gutenberg EBook of Encyclopaedia Britannica, 11th Edition,
Volume 11, Slice 3, by Various
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
Title: Encyclopaedia Britannica, 11th Edition, Volume 11, Slice 3
"Frost" to "Fyzabad"
Author: Various
Release Date: August 13, 2011 [EBook #37064]
Language: English
Character set encoding: ISO-8859-1
*** START OF THIS PROJECT GUTENBERG EBOOK ENCYC. BRITANNICA, VOL 11, SL 3 ***
Produced by Marius Masi, Don Kretz and the Online
Distributed Proofreading Team at https://www.pgdp.net
|
Transcriber’s note:
|
A few typographical errors have been corrected. They
appear in the text like this, and the
explanation will appear when the mouse pointer is moved over the marked
passage. Sections in Greek will yield a transliteration
when the pointer is moved over them, and words using diacritic characters in the
Latin Extended Additional block, which may not display in some fonts or browsers, will
display an unaccented version.
Links to other EB articles: Links to articles residing in other EB volumes will
be made available when the respective volumes are introduced online.
|
THE ENCYCLOPÆDIA BRITANNICA
A DICTIONARY OF ARTS, SCIENCES, LITERATURE AND GENERAL INFORMATION
ELEVENTH EDITION
VOLUME XI SLICE III
Frost to Fyzabad
Articles in This Slice
| FROST | FULMAR |
| FROSTBITE | FULMINIC ACID |
| FROSTBURG | FULTON, ROBERT |
| FROTHINGHAM, OCTAVIUS BROOKS | FULTON (Missouri, U.S.A.) |
| FROUDE, JAMES ANTHONY | FULTON (New York, U.S.A.) |
| FRUCTOSE | FUM |
| FRUGONI, CARLO INNOCENZIO MARIA | FUMARIC AND MALEIC ACIDS |
| FRUIT | FUMAROLE |
| FRUIT AND FLOWER FARMING | FUMIGATION |
| FRUMENTIUS | FUMITORY |
| FRUNDSBERG, GEORG VON | FUNCHAL |
| FRUSTUM | FUNCTION |
| FRUYTIERS, PHILIP | FUNDY, BAY OF |
| FRY | FUNERAL RITES |
| FRY, SIR EDWARD | FUNGI |
| FRY, ELIZABETH | FUNJ |
| FRYXELL, ANDERS | FUNKIA |
| FUAD PASHA | FUNNEL |
| FUCHOW | FUR |
| FUCHS, JOHANN NEPOMUK VON | FURAZANES |
| FUCHS, LEONHARD | FURETIÈRE, ANTOINE |
| FUCHSIA | FURFOOZ |
| FUCHSINE | FURFURANE |
| FUCINO, LAGO DI | FURIES |
| FUEL | FURLONG |
| FUENTE OVEJUNA | FURNACE |
| FUENTERRABIA | FURNEAUX, TOBIAS |
| FUERO | FURNES |
| FUERTEVENTURA | FURNESS, HORACE HOWARD |
| FUGGER | FURNESS |
| FUGITIVE SLAVE LAWS | FURNISS, HARRY |
| FUGLEMAN | FURNITURE |
| FUGUE | FURNIVALL, FREDERICK JAMES |
| FÜHRICH, JOSEPH VON | FURSE, CHARLES WELLINGTON |
| FUJI | FÜRST, JULIUS |
| FU-KIEN | FÜRSTENBERG |
| FUKUI | FÜRSTENWALDE |
| FUKUOKA | FÜRTH |
| FULA | FURTWÄNGLER, ADOLF |
| FULCHER OF CHARTRES | FURZE |
| FULDA | FUSARO, LAGO |
| FULGENTIUS, FABIUS PLANCIADES | FUSELI, HENRY |
| FULGINIAE | FUSEL OIL |
| FULGURITE | FUSIBLE METAL |
| FULHAM | FUSILIER |
| FULK (king of Jerusalem) | FUSION |
| FULK (archbishop of Reims) | FÜSSEN |
| FULKE, WILLIAM | FUST, JOHANN |
| FULK NERRA | FUSTEL DE COULANGES, NUMA DENIS |
| FÜLLEBORN, GEORG GUSTAV | FUSTIAN |
| FULLER, ANDREW | FUSTIC |
| FULLER, GEORGE | FUTURES |
| FULLER, MARGARET | FUX, JOHANN JOSEPH |
| FULLER, MELVILLE WESTON | FUZE |
| FULLER, THOMAS | FYNE, LOCH |
| FULLER, WILLIAM | FYRD |
| FULLER'S EARTH | FYT, JOHANNES |
| FULLERTON, LADY GEORGIANA CHARLOTTE | FYZABAD |
251
FROST (a common Teutonic word, cf. Dutch, vorst, Ger. Frost,
from the common Teutonic verb meaning “to freeze,” Dutch,
vriezen, Ger. frieren; the Indo-European root is seen in Lat.
pruina, hoar-frost, cf. prurire, to itch, burn, pruna, burning coal,
Sansk. plush, to burn), in meteorology, the act, or agent of the
process, of freezing; hence the terms “hoar-frost” and “white-frost”
applied to visible frozen vapour formed on exposed surfaces.
A frost can only occur when the surface temperature falls below
32° F., the freezing-point of water; if the temperature be
between 28° and 32° it is a “light frost,” if below 28° it is a
“heavy,” “killing” or “black frost”; the term “black frost”
is also used when no hoar-frost is present. The number of
degrees below freezing-point is termed “degrees of frost.” As
soon as a mass of air is cooled to its dew-point, water begins to
be precipitated in the form of rain, dew, snow or hail. Hoarfrost
is only formed at the immediate surface of the land if the
latter be at a temperature below 32°, and this may occur even
when the temperature of the air a few feet above the ground is
12°-16° above the freezing-point. The heaviest hoar-frosts are
formed under weather conditions similar to those under which
the heaviest summer dews occur, namely, clear and calm nights,
when there is no cloud to impede the radiation of heat from the
surface of the land, which thereby becomes rapidly and completely
cooled. The danger of frost is minimized when the soil
is very moist, as for example after 10-12 mm. of rain; and it
is a practice in America to flood fields on the receipt of a frost
warning, radiation being checked by the light fog sheets which
develop over moist soils, just as a cloud-layer in the upper
atmosphere impedes radiation on a grand scale. A layer of
smoke will also impede radiation locally, and to this end smoky
fires are sometimes lit in such positions that the smoke may
drift over planted ground which it is desirable to preserve from
frost. Similarly, frost may occur in open country when a town,
protected by its smoke-cloud above, is free of it. In a valley
with fairly high and steep flanks frost sometimes occurs locally
at the bottom, because the layer of air cooled by contact with
the cold surface of the higher ground is heavier than that not so
cooled, and therefore tends to flow or settle downwards along the
slope of the land. When meteorological considerations point
to a frost, an estimate of the night temperature may be obtained
by multiplying the difference between the readings of the wet
and dry bulb thermometer by 2.5 and subtracting the result
from the dry bulb temperature. This rule applies when the
evening air is at about 50° and 30.1 in. pressure, the sky being
clear. An instrument has been devised in France for the prediction
of frost. It consists of a wet bulb and a dry bulb thermometer,
mounted on a board on which is also a scale of lines
corresponding to degrees of the dry bulb, and a pointer traversing
a scale graduated according to degrees of the wet bulb. Observations
for the night are taken about half an hour before sunset.
By means of the pointer and scale, the point may be found at
which the line of the dry-bulb reading meets the pointer set to
the reading of the wet bulb. The scale is further divided by
colours so that the observed point may fall within one of three
zones, indicating certain frost, probable frost or no probability
of frost.
FROSTBITE, a form of mortification (q.v.), due to the action
of extreme cold in cutting off the blood-supply from the fingers,
toes, nose, ears, &c. In comparatively trifling forms it occurs
as “chaps” and “chilblains,” but the term frostbite is usually
applied only to more severe cases, where the part affected
becomes in danger of gangrene. An immediate application of
snow, or ice-water, will restore the circulation; the application
of heat would cause inflammation. But if the mortification has
gone too far for the circulation to be restored, the part will be
lost, and surgical treatment may be necessary.
FROSTBURG, a town of Allegany county, Maryland, U.S.A.,
11 m. W. of Cumberland. Pop. (1890) 3804; (1900) 5274
(578 foreign-born and 236 negroes); (1910) 6028. It is served
by the Cumberland & Pennsylvania railway and the Cumberland
& Westernport electric railway. The town is about 2000 ft.
above sea-level on a plateau between the Great Savage and Dans
mountains, and its delightful scenery and air have made it
attractive as a summer resort. It is the seat of the second state
normal school, opened in 1904. Frostburg is in the midst of the
coal region of the state, and is itself almost completely undermined;
it has planing mills and manufactures large quantities
of fire-brick. The municipality owns and operates its waterworks.
Natural gas is piped to Frostburg from the West Virginia
fields, 120 m. away. Frostburg was first settled in 1812; was
called Mount Pleasant until about 1830, when the present name
was substituted in honour of Meshech Frost, one of the town’s
founders; and was incorporated in 1870.
FROTHINGHAM, OCTAVIUS BROOKS (1822-1895), American
clergyman and author, was born in Boston on the 26th of
November 1822, son of Nathaniel Langdon Frothingham (1793-1870),
a prominent Unitarian preacher of Boston, and through
his mother’s family related to Phillips Brooks. He graduated
from Harvard College in 1843 and from the Divinity School in
1846. He was pastor of the North Unitarian church of Salem,
Massachusetts, in 1847-1855. From 1855 to 1860 he was pastor
of a new Unitarian society in Jersey City, where he gave up the
Lord’s Supper, thinking that it ministered to self-satisfaction;
and it was as a radical Unitarian that he became pastor of another
young church in New York City in 1860. Indeed in 1864 he was
recognized as leader of the radicals after his reply to Dr Hedge’s
address to the graduating students of the Divinity School on
Anti-Supernaturalism in the Pulpit. In 1865, when he had
practically given up “transcendentalism,” his church building
was sold and his congregation began to worship in Lyric Hall
under the name of the Independent Liberal Church; in 1875
they removed to the Masonic Temple, but four years later ill-health
compelled Frothingham’s resignation, and the church
dissolved. Paralysis threatened him and he never fully recovered
his health; in 1881 he returned to Boston, where he died on the
27th of November 1895. To this later period of his life belongs
his best literary work. While he was in New York he was for a
time art critic of the Tribune. Always himself on the unpopular
side and an able but thoroughly fair critic of the majority, he
habitually under-estimated his own worth; he was not only an
anti-slavery leader when abolition was not popular even in New
England, and a radical and rationalist when it was impossible
for him to stay conveniently in the Unitarian Church, but he
252
was the first president of the National Free Religious Association
(1867) and an early and ardent disciple of Darwin and Spencer.
To his radical views he was always faithful. It is a mistake to
say that he grew more conservative in later years; but his
judgment grew more generous and catholic. He was a greater
orator than man of letters, and his sermons in New York were
delivered to large audiences, averaging one thousand at the
Masonic Temple, and were printed each week; in eloquence and
in the charm of his spoken word he was probably surpassed in
his day by none save George William Curtis. Personally he
seemed cold and distant, partly because of his impressive appearance,
and partly because of his own modesty, which made him
backward in seeking friendships.
His principal published works are: Stories from the Life of the
Teacher (1863), A Child’s Book of Religion (1866), and other works
of religious teaching for children; several volumes of sermons;
Beliefs of Unbelievers (1876), The Cradle of the Christ: a Study in
Primitive Christianity (1877), The Spirit of New Faith (1877),
The Rising and the Setting Faith (1878), and other expositions of
the “new faith” he preached; Life of Theodore Parker (1874),
Transcendentalism in New England (1876), which is largely biographical,
Gerrit Smith, a Biography (1878), George Ripley (1882),
in the “American Men of Letters” series, Memoir of William
Henry Channing (1886), Boston Unitarianism, 1820-1850 (1890),
really a biography of his father; and Recollections and Impressions,
1822-1890 (1891).
FROUDE, JAMES ANTHONY (1818-1894), English historian,
son of R.H. Froude, archdeacon of Totnes, was born at
Dartington, Devon, on the 23rd of April 1818. He was educated
at Westminster and Oriel College, Oxford, then the centre of the
ecclesiastical revival. He obtained a second class and the
chancellor’s English essay prize, and was elected a fellow of
Exeter College (1842). His elder brother, Richard Hurrell
Froude (1803-1836), had been one of the leaders of the High
Church movement at Oxford. Froude joined that party and
helped J.H. Newman, afterwards cardinal, in his Lives of the
English Saints. He was ordained deacon in 1845. By that time
his religious opinions had begun to change, he grew dissatisfied
with the views of the High Church party, and came under the
influence of Carlyle’s teaching. Signs of this change first appeared
publicly in his Shadows of the Clouds, a volume containing two
stories of a religious sort, which he published in 1847 under the
pseudonym of “Zeta,” and his complete desertion of his party
was declared a year later in his Nemesis of Faith, an heretical
and unpleasant book, of which the earlier part seems to be
autobiographical.
On the demand of the college he resigned his fellowship at
Oxford, and mainly at least supported himself by writing,
contributing largely to Fraser’s Magazine and the Westminster
Review. The excellence of his style was soon generally recognized.
The first two volumes of his History of England
from the Fall of Wolsey to the Defeat of the Spanish Armada
appeared in 1856, and the work was completed in 1870. As an
historian he is chiefly remarkable for literary excellence, for the
art with which he represents his conception of the past. He
condemns a scientific treatment of history and disregards its
philosophy. He held that its office was simply to record human
actions and that it should be written as a drama. Accordingly
he gives prominence to the personal element in history. His
presentations of character and motives, whether truthful or not,
are undeniably fine; but his doctrine that there should be “no
theorizing” about history tended to narrow his survey, and
consequently he sometimes, as in his remarks on the foreign
policy of Elizabeth, seems to misapprehend the tendencies of a
period on which he is writing.
Froude’s work is often marred by prejudice and incorrect
statements. He wrote with a purpose. The keynote of his
History is contained in his assertion that the Reformation was
“the root and source of the expansive force which has spread
the Anglo-Saxon race over the globe.” Hence he overpraises
Henry VIII. and others who forwarded the movement, and
speaks too harshly of some of its opponents. So too, in his
English in Ireland (1872-1874), which was written to show the
futility of attempts to conciliate the Irish, he aggravates all
that can be said against the Irish, touches too lightly on English
atrocities, and writes unjustly of the influence of Roman Catholicism.
A strong anti-clerical prejudice is manifest in his historical
work generally, and is doubtless the result of the change in his
views on Church matters and his abandonment of the clerical
profession. Carlyle’s influence on him may be traced both in
his admiration for strong rulers and strong government, which
led him to write as though tyranny and brutality were excusable,
and in his independent treatment of character. His rehabilitation
of Henry VIII. was a useful protest against the idea that
the king was a mere sanguinary profligate, but his representation
of him as the self-denying minister of his people’s will is erroneous,
and is founded on the false theory that the preambles of the acts
of Henry’s parliaments represented the opinions of the educated
laymen of England. As an advocate he occasionally forgets
that sobriety of judgment and expression become an historian.
He was not a judge of evidence, and seems to have been unwilling
to admit the force of any argument or the authority of any
statement which militated against his case. In his Divorce of
Catherine of Aragon (1891) he made an unfortunate attempt to
show that certain fresh evidence on the subject, brought forward
by Dr Gairdner, Dr Friedmann and others, was not inconsistent
with the views which he has expressed in his History nearly
forty years before. He worked diligently at original manuscript
authorities at Simancas, the Record Office and Hatfield House;
but he used his materials carelessly, and evidently brought to his
investigation of them a mind already made up as to their significance.
His Life of Caesar (1879), a glorification of imperialism,
betrays an imperfect acquaintance with Roman politics and the
life of Cicero; and of his two pleasant books of travel, The
English in the West Indies (1888) shows that he made little effort
to master his subject, and Oceana (1886), the record of a tour in
Australia and New Zealand, among a multitude of other blunders,
notes the prosperity of the working-classes in Adelaide at the
date of his visit, when, in fact, owing to a failure in the wheat-crop,
hundreds were then living on charity. He was constitutionally
inaccurate, and seems to have been unable to represent the
exact sense of a document which lay before him, or even to
copy from it correctly. Historical scholars ridiculed his mistakes,
and Freeman, the most violent of his critics, never let slip a
chance of hitting at him in the Saturday Review. Froude’s
temperament was sensitive, and he suffered from these attacks,
which were often unjust and always too savage in tone. The
literary quarrel between him and Freeman excited general
interest when it blazed out in a series of articles which Freeman
wrote in the Contemporary Review (1878-1879) on Froude’s
Short Study of Thomas Becket.
Notwithstanding its defects, Froude’s History is a great
achievement; it presents an important and powerful account
of the Reformation period in England, and lays before us a
picture of the past magnificently conceived, and painted in
colours which will never lose their freshness and beauty. As
with Froude’s work generally, its literary merit is remarkable;
it is a well-balanced and orderly narrative, coherent in design
and symmetrical in execution. Though it is perhaps needlessly
long, the thread of the story is never lost amid a crowd of details;
every incident is made subordinate to the general idea, appears
in its appropriate place, and contributes its share to the perfection
of the whole. The excellence of its form is matched by the beauty
of its style, for Froude was a master of English prose. The most
notable characteristic of his style is its graceful simplicity; it is
never affected or laboured; his sentences are short and easy,
and follow one another naturally. He is always lucid. He was
never in doubt as to his own meaning, and never at a loss for the
most appropriate words in which to express it. Simple as his
language is, it is dignified and worthy of its subject. Nowhere
perhaps does his style appear to more advantage than in his four
series of essays entitled Short Studies on Great Subjects (1867-1882),
for it is seen there unfettered by the obligations of narrative.
Yet his narrative is admirably told. For the most part flowing
easily along, it rises on fit occasions to splendour, picturesque
beauty or pathos. Few more brilliant pieces of historical
253
writing exist than his description of the coronation procession
of Anne Boleyn through the streets of London, few more full of
picturesque power than that in which he relates how the spire
of St Paul’s was struck by lightning; and to have once read is
to remember for ever the touching and stately words in which
he compares the monks of the London Charterhouse preparing
for death with the Spartans at Thermopylae. Proofs of his
power in the sustained narration of stirring events are abundant;
his treatment of the Pilgrimage of Grace, of the sea fight at
St Helens and the repulse of the French invasion, and of the
murder of Rizzio, are among the most conspicuous examples of
it. Nor is he less successful when recording pathetic events,
for his stories of certain martyrdoms, and of the execution of
Mary queen of Scots, are told with exquisite feeling and in
language of well-restrained emotion. And his characters are
alive. We may not always agree with his portraiture, but the
men and women whom he saw exist for us instinct with the life
with which he endows them and animated by the motives which
he attributes to them. His successes must be set against his
failures. At the least he wrote a great history, one which can
never be disregarded by future writers on his period, be their
opinions what they may; which attracts and delights a multitude
of readers, and is a splendid example of literary form and grace
in historical composition.
The merits of his work met with full recognition. Each
instalment of his History, in common with almost everything
which he wrote, was widely read, and in spite of some adverse
criticisms was received with eager applause. In 1868 he was
elected rector of St Andrews University, defeating Disraeli
by a majority of fourteen. He was warmly welcomed in the
United States, which he visited in 1872, but the lectures on
Ireland which he delivered there caused much dissatisfaction.
On the death of his adversary Freeman in 1892, he was appointed,
on the recommendation of Lord Salisbury, to succeed him as
regius professor of modern history at Oxford. Except to a
few Oxford men, who considered that historical scholarship
should have been held to be a necessary qualification for the
office, his appointment gave general satisfaction. His lectures
on Erasmus and other 16th-century subjects were largely
attended. With some allowance for the purpose for which
they were originally written, they present much the same
characteristics as his earlier historical books. His health gave
way in the summer of 1894, and he died on the 20th of
October.
His long life was full of literary work. Besides his labours as
an author, he was for fourteen years editor of Fraser’s Magazine.
He was one of Carlyle’s literary executors, and brought some
sharp criticism upon himself by publishing Carlyle’s Reminiscences
and the Memorials of Jane Welsh Carlyle, for they
exhibited the domestic life and character of his old friend in an
unpleasant light. Carlyle had given the manuscripts to him,
telling him that he might publish them if he thought it well
to do so, and at the close of his life agreed to their publication.
Froude therefore declared that in giving them to the world he
was carrying out his friend’s wish by enabling him to make a
posthumous confession of his faults. Besides publishing these
manuscripts he wrote a Life of Carlyle. His earlier study of
Irish history afforded him suggestions for a historical novel
entitled The Two Chiefs of Dunboy (1889). In spite of one or
two stirring scenes it is a tedious book, and its personages are
little more than machines for the enunciation of the author’s
opinions and sentiments. Though Froude had some intimate
friends he was generally reserved. When he cared to please,
his manners and conversation were charming. Those who
knew him well formed a high estimate of his ability in practical
affairs. In 1874 Lord Carnarvon, then colonial secretary, sent
Froude to South Africa to report on the best means of promoting
a confederation of its colonies and states, and in 1875 he was
again sent to the Cape as a member of a proposed conference to
further confederation. Froude’s speeches in South Africa were
rather injudicious, and his mission was a failure (see South
Africa: History). He was twice married. His first wife, a
daughter of Pascoe Grenfell and sister of Mrs Charles Kingsley,
died in 1860; his second, a daughter of John Warre, M.P. for
Taunton, died in 1874.
Froude’s Life, by Herbert Paul, was published in 1905.
(W. Hu.)
FRUCTOSE, Laevulose, or Fruit-Sugar, a carbohydrate
of the formula C6H12O6. It is closely related to ordinary d-glucose,
with which it occurs in many fruits, starches and also
in honey. It is a hydrolytic product of inulin, from which it
may be prepared; but it is more usual to obtain it from “invert
sugar,” the mixture obtained by hydrolysing cane sugar with
sulphuric acid. Cane sugar then yields a syrupy mixture of
glucose and fructose, which, having been freed from the acid
and concentrated, is mixed with water, cooled in ice and calcium
hydroxide added. The fructose is precipitated as a saccharate,
which is filtered, suspended in water and decomposed by carbon
dioxide. The liquid is filtered, the filtrate concentrated, and
the syrup so obtained washed with cold alcohol. On cooling the
fructose separates. It may be obtained as a syrup, as fine,
silky needles, a white crystalline powder, or as a granular
crystalline, somewhat hygroscopic mass. When anhydrous it
melts at about 95° C. It is readily soluble in water and in dilute
alcohol, but insoluble in absolute alcohol. It is sweeter than
cane sugar and is more easily assimilated. It has been employed
under the name diabetin as a sweetening agent for diabetics,
since it does not increase the sugar-content of the urine; other
medicinal applications are in phthisis (mixed with quassia or
other bitter), and for children suffering from tuberculosis or
scrofula in place of cane sugar or milk-sugar.
Chemically, fructose is an oxyketone or ketose, its structural
formula being CH2OH·(CH·OH)3·CO·CH2OH; this result followed
from its conversion by H. Kiliani into methylbutylacetic
acid. The form described above is laevo-rotatory, but it is
termed d-fructose, since it is related to d-glucose. Solutions
exhibit mutarotation, fresh solutions having a specific rotation
of −104.0°, which gradually diminishes to −92°. It was
synthesized by Emil Fischer, who found the synthetic sugar
which he named α-acrose to be (d + l)-fructose, and by splitting
this mixture he obtained both the d and l forms. Fructose
resembles d-glucose in being fermentable by yeast (it is the one
ketose which exhibits this property), and also in its power of
reducing alkaline copper and silver solutions; this latter
property is assigned to the readiness with which hydroxyl and
ketone groups in close proximity suffer oxidation. For the
structural (stereochemical) relations of fructose see Sugar.
FRUGONI, CARLO INNOCENZIO MARIA (1692-1768),
Italian poet, was born at Genoa on the 21st of November 1692.
He was originally destined for the church and at the age of
fifteen, in opposition to his strong wishes, was shut up in a
convent; but although in the following year he was induced to
pronounce monastic vows, he had no liking for this life. He
acquired considerable reputation as an elegant writer both of
Latin and Italian prose and verse; and from 1716 to 1724 he
filled the chairs of rhetoric at Brescia, Rome, Genoa, Bologna
and Modena successively, attracting by his brilliant fluency a
large number of students at each university. Through Cardinal
Bentivoglio he was recommended to Antonio Farnese, duke of
Parma, who appointed him his poet laureate; and he remained
at the court of Parma until the death of Antonio, after which
he returned to Genoa. Shortly afterwards, through the intercession
of Bentivoglio, he obtained from the pope the remission
of his monastic vows, and ultimately succeeded in recovering
a portion of his paternal inheritance. After the peace of Aix-la-Chapelle
he returned to the court of Parma, and there devoted
the later years of his life chiefly to poetical composition. He
died on the 20th of December 1768. As a poet Frugoni was
one of the best of the school of the Arcadian Academy, and
his lyrics and pastorals had great facility and elegance.
His collected works were published at Parma in 10 vols. in 1799,
and a more complete edition appeared at Lucca in the same year in
15 vols. A selection from his works was published at Brescia in
1782, in 4 vols.
254
FRUIT (through the French from the Lat. fructus; frui, to
enjoy), in its widest sense, any product of the soil that can be
enjoyed by man or animals; the word is so used constantly
in the Bible, and extended, as a Hebraism, to offspring or
progeny of man and of animals, in such expressions as “the
fruit of the body,” “of the womb,” “fruit of thy cattle” (Deut.
xxviii. 4), &c., and generally to the product of any action or
effort. Between this wide and frequently figurative use of the
word and its application in the strict botanical sense treated
below, there is a popular meaning, regarding the objects denoted
by the word entirely from the standpoint of edibility, and
differentiating them roughly from those other products of the
soil, which, regarded similarly, are known as vegetables. In
this sense “fruit” is applied to such seed-envelopes of plants
as are edible, either raw or cooked, and are usually sweet, juicy
or of a refreshing flavour. But applications of the word in this
sense are apt to be loose and shifting according to the fashion
of the time.
Fruit, in the botanical sense, is developed from the flower
as the result of fertilization of the ovule. After fertilization
various changes take place in the parts of the flower. Those
more immediately concerned in the process, the anther and
stigma, rapidly wither and decay, while the filaments and style
often remain for some time; the floral envelopes become dry,
the petals fall, and the sepals are either deciduous, or remain
persistent in an altered form; the ovary becomes enlarged,
forming the pericarp; and the ovules are developed as the
seeds, containing the embryo-plant. The term fruit is strictly
applied to the mature pistil or ovary, with the seeds in its interior;
but it often includes other parts of the flower, such as the bracts
and floral envelopes. Thus the fruit of the hazel and oak consists
of the ovary enveloped by the bracts; that of the apple and pear,
of the ovary and floral receptacle; and that of the pine-apple,
of the whole inflorescence. Such fruits are sometimes distinguished
as pseudocarps. In popular language, the fruit includes
all those parts which exhibit a striking change as the result of
fertilization. In general, the fruit is not ripened unless fertilization
has been effected; but cases occur as the result of cultivation
in which the fruit swells and becomes to all appearance perfect,
while no seeds are produced. Thus, there are seedless oranges,
grapes and pineapples. When the ovules are unfertilized, it is
common to find that the ovary withers and does not come to
maturity; but in the case of bananas, plantains and bread-fruit,
the non-development of seeds seems to lead to a larger growth
and a greater succulence of fruit.
The fruit, like the ovary, may be formed of a single carpel or of
several. It may have one cell or cavity, being unilocular; or many,
multilocular, &c. The number and nature of the divisions depend
on the number of carpels and the extent to which their edges are
folded inwards. The appearances presented by the ovary do not
always remain permanent in the fruit. Great changes are observed
to take place, not merely as regards the increased size of the ovary,
its softening or hardening, but also in its internal structure, owing
to the suppression, additional formation or enlargement of parts.
Thus, in the ash (fig. 1) an ovary with two cells, each containing an
ovule attached to a central placenta, is changed into a unilocular
fruit with one seed; one ovule becomes abortive, while the other, g,
gradually enlarging until the septum is pushed to one side, unites
with the walls of the cell, and the placenta appears to be parietal.
In the oak and hazel, an ovary with three and two cells respectively,
and two ovules in each, produces a one-celled fruit with one seed.
In the coco-nut, a trilocular and triovular ovary produces a one-celled,
one-seeded fruit. This abortion may depend on the pressure
caused by the development of certain ovules, or it may proceed from
non-fertilization of all the ovules and consequent non-enlargement
of the carpels. Again, by the growth of the placenta, or the folding
inwards of parts of the carpels, divisions occur in the fruit which
did not exist in the ovary. In Cathartocarpus Fistula a one-celled
ovary is changed into a fruit having each of its seeds in a separate
cell, in consequence of spurious dissepiments being produced horizontal
from the inner wall of the ovary. In flax (Linum) by the
folding inwards of the back of the carpels a five-celled ovary becomes
a ten-celled fruit. In Astragalus the folding inwards of the dorsal
suture converts a one-celled ovary into a two-celled fruit; and in
Oxytropis the folding of the ventral suture gives rise to a similar
change. The development of cellular or pulpy matter, and the
enlargement of parts not forming whorls of the flower, frequently
alter the appearance of the fruit, and render it difficult to discover
its formation. In the gooseberry (fig. 29), grape, guava, tomato
and pomegranate, the seeds nestle in pulp formed by the placentas.
In the orange the pulpy matter surrounding the seeds is formed
by succulent cells, which are produced from the inner partitioned
lining of the pericarp. In the strawberry the receptacle becomes
succulent, and bears the mature carpels on its convex surface (fig. 2);
in the rose there is a fleshy hollow receptacle which bears the carpels
on its concave surface (fig. 3). In the juniper the scaly bracts grow
up round the seeds and become succulent, and in the fig (fig. 4) the
receptacle becomes succulent and encloses an inflorescence.
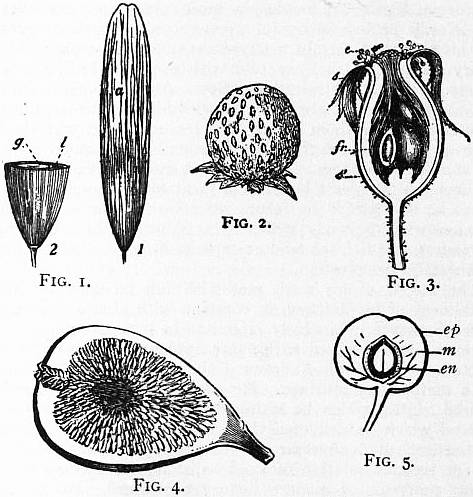
Fig. 1.—Samara or winged fruit of Ash (Fraxinus). 1, Entire,
with its wing a; 2, lower portion cut transversely, to show that it
consists of two cells; one of which, l, is abortive, and is reduced to
a very small cavity, while the other is much enlarged and filled
with a seed g.
Fig. 2.—Fruit of the Strawberry (Fragaria vesca), consisting of
an enlarged succulent receptacle, bearing on its surface the small
dry seed-like fruits (achenes). (After Duchartre.)
From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer.
Fig. 3.—Fruit of the Rose cut vertically. s’, Fleshy hollowed
receptacle; s, persistent sepals; fr, ripe carpels; e, stamens,
withered.
Fig. 4.—Peduncle of Fig (Ficus Carica), ending in a hollow
receptacle enclosing numerous male and female flowers.
Fig. 5.—Fruit of Cherry (Prunus Cerasus) in longitudinal section.
ep, Epicarp; m, mesocarp; en, endocarp.
From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer.
The pericarp consists usually of three layers, the external, or
epicarp (fig. 5, ep); the middle, or mesocarp, m; and the internal,
or endocarp, en. These layers are well seen in such a fruit as the
peach, plum or cherry, where they are separable one from the
other; in them the epicarp forms what is commonly called the
skin; the mesocarp, much developed, forms the flesh or pulp,
and hence has sometimes been called sarcocarp; while the endocarp,
hardened by the production of woody cells, forms the stone or
putamen immediately covering the kernel or seed. The pulpy
matter found in the interior of fruits, such as the gooseberry, grape
and others, is formed from the placentas, and must not be confounded
with the sarcocarp. In some fruits, as in the nut, the
three layers become blended together and are indistinguishable.
In bladder senna (Colutea arborescens) the pericarp retains its leaf-like
appearance, but in most cases it becomes altered both in consistence
and in colour. Thus in the date the epicarp is the outer
brownish skin, the pulpy matter is the mesocarp or sarcocarp, and
the thin papery-like lining is the endocarp covering the hard seed.
In the medlar the endocarp becomes of a stony hardness. In the
melon the epicarp and endocarp are very thin, while the mesocarp
forms the bulk of the fruit, differing in texture and taste in its external
and internal parts. The rind of the orange consists of epicarp
and mesocarp, while the endocarp forms partitions in the interior,
filled with pulpy cells. The part of the pericarp attached to the
peduncle is the base, and the point where the style or stigma existed
is the apex. This latter is not always the apparent apex, as in the
case of the ovary; it may be lateral or even basilar. The style
sometimes remains in a hardened form, rendering the fruit apiculate;
at other times it falls off, leaving only traces of its existence. The
presence of the style or stigma serves to distinguish certain single-seeded
pericarps from seeds.
255
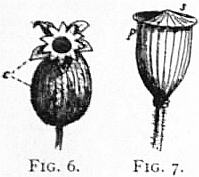 |
| Fig. 6.—Seed-vessel or capsule
of Campion, opening by ten
teeth at the apex. The calyx c
is seen surrounding the seed-vessel. |
| Fig. 7.—Capsule of Poppy,
opening by pores p, under the
radiating peltate stigma s. |
When the fruit is mature and the seeds are ripe, the carpels
usually give way either at the ventral or dorsal suture or at both,
and so allow the seeds to escape. The fruit in this case
is dehiscent. But some fruits are indehiscent, falling to
Dehiscence of fruits.
the ground entire, and the seeds eventually reaching the
soil by their decay. By dehiscence the pericarp becomes divided
into different pieces, or valves, the fruit being univalvular, bivalvular
or multivalvular, &c., according as there are one, two or many
valves. The splitting extends the whole length of the fruit, or is
partial, the valves forming teeth
at the apex, as in the order Caryophyllaceae
(fig. 6). Sometimes
the valves are detached only at
certain points, and thus dehiscence
takes place by pores at the apex,
as in poppy (fig. 7), or at the base,
as in Campanula. Indehiscent
fruits are either dry, as the nut,
or fleshy, as the cherry and apple.
They are formed of one or several
carpels. In the former case they
usually contain only a single seed,
which may become so incorporated
with the pericarp as to appear to
be naked, as in the grain of wheat
and generally in grasses. In such
cases the presence of the remains
of style or stigma determines
their true nature.
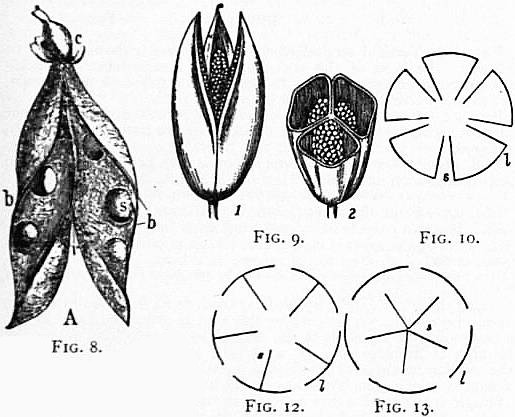
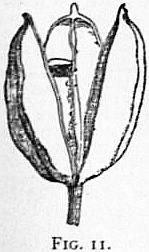 |
Fig. 8.—Dry dehiscent fruit. The pod
(legume) of the Pea; r, the dorsal suture;
b, the ventral; c, calyx; s, seeds.
From Vines’ Students’ Text-Book of Botany, by permission
of Swan Sonnenschein & Co.
Fig. 9.—(1) Fruit or capsule of Meadow
Saffron (Colchicum autumnale), dehiscing along
the septa (septicidally); (2) same cut across,
showing the three chambers with the seeds
attached along the middle line (axile placentation).
Fig. 10.—Diagram to illustrate the septicidal
dehiscence in a pentalocular capsule.
The loculaments l correspond to the number of the carpels, which
separate by splitting through the septa, s.
Fig. 11.—The seed vessel (capsule) of the Flower-de-Luce (Iris),
opening in a loculicidal manner. The three valves bear the septa
in the centre, and the opening takes place through the back of the
loculaments. Each valve is formed by the halves of contiguous
carpels.
Fig. 12.—Diagram to illustrate loculicidal dehiscence. The loculaments
l, split at the back, and the valves separate, bearing the
septa s on their centres.
Fig. 13.—Diagram to illustrate septifragal dehiscence, in which
the dehiscence takes place through the back of the loculaments l,
and the valves separate from the septa s, which are left attached to
the placentas in the centre.
Dehiscent fruits, when composed
of single carpels, may open
by the ventral suture only, as in the paeony, hellebore, Aquilegia (fig.
28) and Caltha; by the dorsal suture only, as in magnolias and some
Proteaceae, or by both together, as in the pea (fig. 8) and bean;
in these cases the dehiscence is sutural. When composed of several
united carpels, two types of dehiscence occur—a longitudinal and a
transverse. In the longitudinal the separation may take place by
the dissepiments throughout their length, so that the fruit is resolved
into its original carpels, and each valve represents a carpel, as in
rhododendron, Colchicum, &c.; this dehiscence, in consequence of
taking place through the septum, is called septicidal (figs. 9, 10).
The valves separate from their commissure, or central line of union,
carrying the placentas with them, or they leave the latter in the
centre, so as to form with the axis a column of a cylindrical, conical
or prismatic shape. Dehiscence is loculicidal when the union
between the edges of the carpels is persistent, and they dehisce by
the dorsal suture, or through the back of the loculaments, as in the
lily and iris (figs. 11, 12). In these cases each valve consists of a
half of each of two contiguous carpels. The placentas either remain
united to the axis, or they separate from it, being attached to the
septa on the valves. When the outer walls of the carpels break off
from the septa, leaving them attached to the central column, the
dehiscence is said to be septifragal (fig. 13), and where, as in Linum
catharticum and Calluna, the splitting takes place first of all in a
septicidal manner, the fruit is described as septicidally septifragal;
while in other cases, as in thorn apple (Datura Stramonium), where
the splitting is at first loculicidal, the dehiscence is loculicidally
septifragal. In all those forms the separation of the valves takes
place either from above downwards or from below upwards. In
Saxifraga a splitting for a short distance of the ventral sutures of
the carpels takes place, so that a large apical pore is formed. In
the fruit of Cruciferae, as wallflower (fig. 14), the valves separate
from the base of the fruit, leaving a central replum, or frame, which
supports the false septum formed by a prolongation from the parietal
placentas on opposite sides of the fruit, extending between the
ventral sutures of the carpels. In Orchidaceae (fig. 15) the pericarp,
when ripe, separates into three valves in a loculicidal manner,
but the midribs of the carpels, to which the placentas are attached,
often remain adherent to the axis both at the apex and base after
the valves bearing the seeds have fallen. The other type of dehiscence
is transverse, or circumscissile, when the upper part of the
united carpels falls off in the form of a lid or operculum, as in Anagallis
and in henbane (Hyoscyamus) (fig. 16).
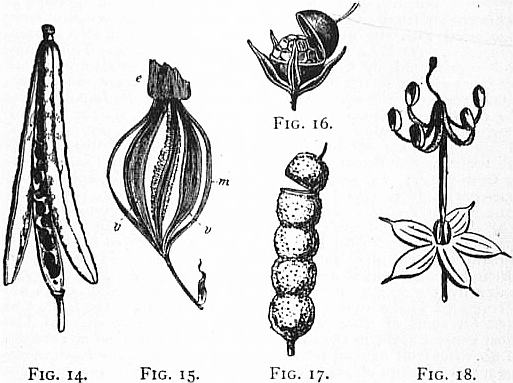
Fig. 14.—Siliqua or seed-vessel of Wallflower (Cheiranthus Cheiri),
opening by two valves, which separate from the base upwards,
leaving the seeds attached to the dissepiment which is supported by
the replum.
From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer.
Fig. 15.—Capsule of an Orchid (Xylobium). v, valve.
Fig. 16.—Seed-vessel of Anagallisarvensis, opening by circumscissile
dehiscence.
From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer.
Fig. 17.—Lomentum of Hedysarum which, when ripe, separates
transversely into single-seeded portions or mericarps.
Fig. 18.—Fruit of Geranium pratense, after splitting.
Sometimes the axis is prolonged beyond the base of the carpels,
as in the mallow and castor-oil plant, the carpels being united to it
throughout their length by their faces, and separating from it without
opening. In the Umbelliferae the two carpels separate from the
lower part of the axis, and remain attached by their apices to a
prolongation of it, called a carpophore or podocarp, which splits
into two (fig. 25) and suspends them; hence the fruit is termed a
cremocarp, which divides into two mericarps. The general term
schizocarp is applied to all dry fruits, which break up into two or
more one-seeded indehiscent mericarps, as in Hedysarum (fig. 17).
In the order Geraniaceae the styles remain attached to a central
column, and the mericarps separate from below upwards, before
dehiscing by their ventral suture (fig. 18). Carpels which separate
one from another in this manner are called cocci. They are well
256
seen in the order Euphorbiaceae, where there are usually three such
carpels, and the fruit is termed tricoccus. In many of them, as
Hura crepitans, the cocci separate with great force and elasticity.
In many leguminous plants, such as Ornithopus, Hedysarum (fig. 17),
Entada, Coronilla and the gum-arabic plant (Acacia arabica), the
fruit becomes a schizocarp by the formation of transverse partitions
from the folding in of the sides of the pericarp, and distinct separations
taking place at these partitions.
Fruits are formed by one flower, or are the product of several
flowers combined. In the former case they are either apocarpous,
of one mature carpel or of several separate free carpels; or syncarpous,
of several carpels, more or less completely united. When
the fruit is composed of the ovaries of several flowers united, it is
usual to find the bracts and floral envelopes also joined with them,
so as to form one mass; hence such fruits are known as multiple,
confluent or anthocarpous. The term simple is applied to fruits
which are formed by the ovary of a single flower, whether they are
composed of one or several carpels, and whether these carpels are
separate or combined.
From Vines’ Students’ Text-Book of Botany, by
permission of Swan Sonnenschein & Co.
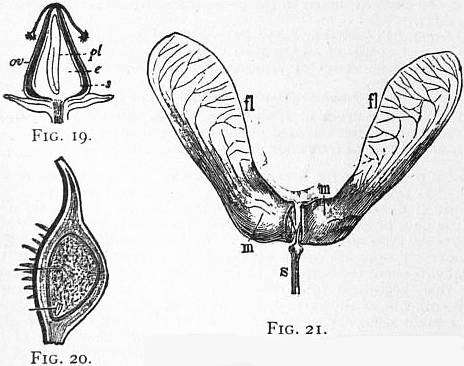
Fig. 19.—Dry one-seeded fruit of dock (Rumex) cut vertically.
ov, Pericarp formed from ovary wall; s, seed; e, endosperm; pl,
embryo with radicle pointing upwards and cotyledons downwards—enlarged.
Fig. 20.—Achene of Ranunculus arvensis in longitudinal section;
e, endosperm; pl, embryo. (After Baillon, enlarged.)
From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer.
Fig. 21.—Fruit of Common Sycamore (Acer Pseudoplatanus),
dividing into two mericarps m; s, pedicel; fl, wings (nat. size).
The object of the fruit in the economy of the plant is the protection
and nursing of the developing seed and the dispersion of the ripe
seeds. Hence, generally, one-seeded fruits are indehiscent,
while fruits containing more than one seed open to allow
Dispersal of fruit or seed.
of the dispersal of the seeds over as wide an area as
possible. The form, colour, structure and method of
dehiscence of fruits and the form of the contained seeds are intimately
associated with the means of dispersal, which fall into several
categories. (1) By a mechanism residing in the fruit. Thus many
fruits open suddenly when they are dry, and the seeds are ejected
by the twisting or curving of the valves, or in some other way;
e.g. in gorse, by the spiral curving of the valves; in Impatiens, by
the twisting of the cocci; in squirting cucumber, by the pressure
exerted on the pulpy contents by the walls of the pericarp. (2)
By aid of various external agencies such as water. Fruits or seeds
are sometimes sufficiently buoyant to float for a long time on sea- or
fresh-water; e.g. coco-nut, by means of its thick, fibrous coat
(mesocarp), is carried hundreds of miles in the sea, the tough,
leathery outer coat (epicarp) preventing it from becoming water-soaked.
Fruits and seeds of West Indian plants are thrown up on
the coasts of north-west Europe, having been carried by the Gulf
Stream, and will often germinate; many are rendered buoyant by
air-containing cavities, and the embryo is protected from the seawater
by the tough coat of fruit or seed. Water-lily seeds are
surrounded with a spongy tissue when set free from the fruit, and
float for some distance before dropping to the bottom. (3) The
most general agent in the dispersal of seeds is the wind or currents
of air—the fruit or seed being rendered buoyant by wing-developments
as in fruits of ash (fig. 1) or maple (fig. 21), seeds of pines
and firs, or many members of the order Bignoniaceae; or hair-developments
as in fruits of clematis, where the style forms a feathery
appendage, fruits of many Compositae (dandelion, thistle, &c.),
which are crowned by a plumose pappus, or seeds of willow and
poplar, or Asclepias (fig. 36), which bear tufts of silky hairs; to
this category belong bladder-like fruits, such as bladder-senna,
which are easily rolled by the wind, or cases like the so-called rose
of Jericho, a small cruciferous plant (Anastatica hierocuntica), where
the plant dries up after developing its fruits and becomes detached
from the ground; the branches curl inwards, and the whole plant is
rolled over the dry ground by the wind. The wind also aids the
dispersal of the seeds in the case of fruits which open by small teeth
(many Caryophyllaceae [fig. 6]) or pores (poppy [fig. 7], Campanula,
&c.); the seeds are in these cases small and numerous, and are jerked
through the pores when the capsules, which are generally borne on
long, dry stems or stalks, are shaken by the wind. (4) In other cases
members of the animal world aid in seed-dispersal. Fruits often
bear stiff hairs or small hooks, which cling to the coat of an animal
or the feathers of a bird; such are fruits of cleavers (Galium Aparine),
a common hedge-row plant, Ranunculus arvensis (fig. 20), carrot,
Geum, &c.; or the fruit or seed has an often bright-coloured, fleshy
covering, which is sought by birds as food, as in stone-fruits such as
plum, cherry (fig. 5), &c., where the seed is protected from injury
in the mouth or stomach of the animal by the hard endocarp; or
the hips of the rose (fig. 3), where the succulent scarlet “fruit”
(the swollen receptacle) envelops a number of small dry true fruits
(achenes), which cling by means of stiff hairs to the beak of the bird.
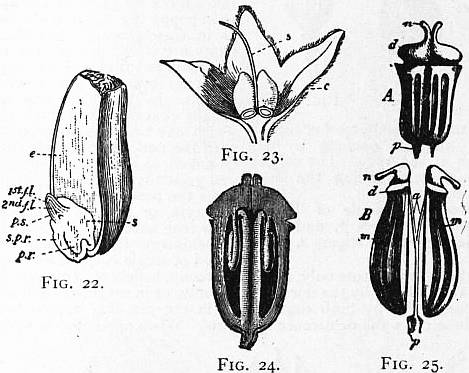
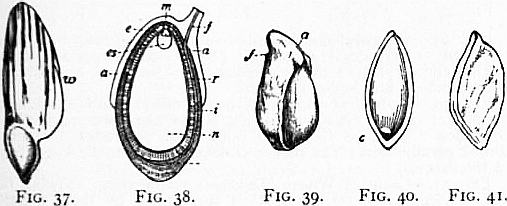
Fig. 22.—Vertical section of a grain of wheat, showing embryo
below at the base of the endosperm e; s, scutellum separating
embryo from endosperm; f.l, foliage leaf; p.s, sheath of plumule;
p.r, primary root; s.p.r, sheath of primary root.
Fig. 23.—Fruit of Comfrey (Symphytum) surrounded by persistent
calyx, c. The style s appears to arise from the base of the carpels,
enlarged.
Fig. 24.—Ovary of Foeniculum officinale with pendulous ovules, in
longitudinal section. (After Berg and Schmidt, magnified.)
From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer.
Fig. 25.—Fruit of Carum Carui. A, Ovary of the flower; B, ripe
fruit. The two carpels have separated so as to form two mericarps
(m). Part of the septum constitutes the carpophore (a). p, Top of
flower-stalk; d, disk on top of ovary; n, stigma.
From Vines’ Students’ Text-Book of Botany, by permission of Swan Sonnenschein
& Co.
Simple fruits have either a dry or succulent pericarp. The achene
is a dry, one-seeded, indehiscent fruit, the pericarp of which is closely
applied to the seed, but separable from it. It is solitary,
forming a single fruit, as in the dock (fig. 19) and in the
Forms of fruit.
cashew, where it is supported on a fleshy peduncle; or
aggregate, as in Ranunculus (fig. 20), where several achenes are
placed on a common elevated receptacle. In the strawberry the
achenes (fig. 2) are aggregated on a convex succulent receptacle.
In the rose they are supported on a concave receptacle (fig. 3), and
in the fig the succulent receptacle completely encloses the achenes
(fig. 4). In Dorstenia the achenes are situated on a flat or slightly
concave receptacle. Hence what in common language are called the
seeds of the strawberry, rose and fig, are in reality ripe carpels.
The styles occasionally remain attached to the achenes in the form
of feathery appendages, as in Clematis. In Compositae, the fruit
is an inferior achene (cypsela), to which the pappus (modified calyx)
remains adherent. Such is also the nature of the fruit in
Dipsacaceae (e.g. scabious). When the pericarp is thin, and
appears like a bladder surrounding the seed, the achene is termed
a utricle, as in Amarantaceae. When the pericarp is extended in
the form of a winged appendage, a samara or samaroid achene is
produced, as in the ash (fig. 1) and common sycamore (fig. 21).
In these cases there are usually two achenes united, one of which,
however, as in Fraxinus (fig. 1), may be abortive. The wing surrounds
the fruit longitudinally in the elm. When the pericarp becomes
so incorporated with the seed as to be inseparable from it,
as in grains of wheat (fig. 22), maize, oats and other grasses, then the
name caryopsis is given. The one-seeded portions (mericarps) of
schizocarps often take the form of achenes, e.g. the mericarps of the
257
mallows or of umbellifers (figs. 24, 25). In Labiatae and Boraginaceae
(e.g. comfrey, fig. 23), where the bicarpellary ovary becomes
our one-seeded portions in the fruit, the partial fruits are of the
nature of achenes or nutlets according to the texture (leathery or
hard) of the pericarp.
 |
| From Strasburger’s Lehrbuch der Botanik,
by permission of Gustav Fischer. |
| Fig. 26.—Cupule of Quercus
Aegilops. cp, cupule; gl, fruit.
(After Duchartre.) |
The nut or glans is a dry one-celled indehiscent fruit with a
hardened pericarp, often surrounded by bracts at the base, and,
when mature, containing only
one seed. In the young state
the ovary often contains two
or more ovules, but only one
comes to maturity. It is illustrated
by the fruits of the hazel
and chestnut, which are covered
by leafy bracts, in the form of
a husk, and by the acorn, in
which the bracts and receptacle
form a cupula or cup (fig. 26).
The parts of the pericarp of the
nut are united so as to appear
one. In common language the
term nut is very vaguely
applied both to fruit and seeds.
The drupe is a succulent
usually one-seeded indehiscent
fruit, with a pericarp easily
distinguishable into epicarp,
mesocarp and endocarp. This
term is applied to such fruits
as the cherry (fig. 5), peach,
plum, apricot or mango. The
endocarp is usually hard, forming
the stone (putamen) of the fruit, which encloses the kernel
or seed. The mesocarp is generally pulpy and succulent, so as to be
truly a sarcocarp, as in the peach, but it is sometimes of a tough
texture, as in the almond, and at other times is more or less fibrous,
as in the coco-nut. In the almond there are often two ovules
formed, only one of which comes to perfection. In the raspberry
and bramble several small drupes or drupels are aggregated so as to
constitute an etaerio.
The follicle is a dry unilocular many-seeded fruit, formed from
one carpel and dehiscing by the ventral suture. It is rare to meet
with a solitary follicle forming the fruit. There are usually several
aggregated together, either in a whorl on a shortened receptacle,
as in hellebore, aconite, larkspur, columbine (figs. 27, 28) or the order
Crassulaceae, or in a spiral manner on an elongated receptacle, as
in Magnolia and Banksia. Occasionally, follicles dehisce by the
dorsal suture, as in Magnolia grandiflora and Banksia.
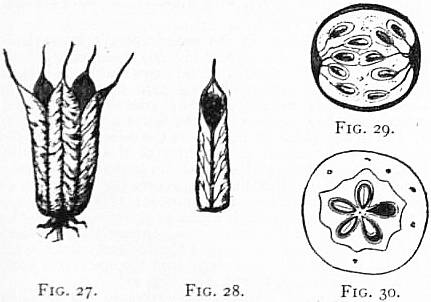
Fig. 27.—Fruit of Columbine (Aquilegia), formed of five follicles.
Fig. 28.—Single follicle, showing dehiscence by the ventral suture.
Fig. 29.—Transverse section of berry of Gooseberry, showing the
seeds attached to the parietal placentas and immersed in pulp,
which is formed partly from the endocarp, partly from the seed-coat.
Fig. 30.—Section of the fruit of the Apple (Pyrus Malus), or pome,
consisting of a fleshy covering formed by the floral receptacle and
the true fruit or core with five cavities with seeds.
The legume or pod is a dry monocarpellary unilocular many-seeded
fruit, formed from one carpel, dehiscing both by the ventral and the
dorsal suture. It characterizes leguminous plants, as the bean and
pea (fig. 8). In the bladder-senna it forms an inflated legume. In
some Leguminosae, as Arachis, Cathartocarpus Fistula and the
tamarind, the fruit must be considered a legume, although it does
not dehisce. The first of these plants produces its fruit underground,
and is called earth-nut; the second has a partitioned
legume and is schizocarpic; and both the second and third have
pulpy matter surrounding the seeds. Some legumes are schizocarpic
by the formation of constrictions externally. Such a form is the
lomentum or lomentaceous legume of Hedysarum (fig. 17), Coronilla,
Ornithopus, Entada and of some Acacias. In Medicago the legume
is twisted like a snail, and in Caesalpinia coriaria, or Divi-divi, it is
vermiform or curved like a worm. Sometimes the number of seeds
is reduced, as in Erythrina monosperma and Geoffroya superba,
which are one-seeded, and in Pterocarpus and Dalbergia, which are
two-seeded.
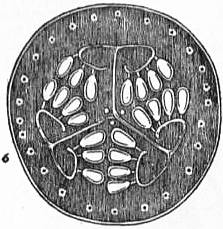 |
| Fig. 31.—Transverse section
of the fruit of the Melon
(Cucumis Melo), showing the
placentas with the seeds attached
to them. The three carpels
forming the pepo are separated
by partitions. From the centre
processes pass outwards, ending
in the curved placenta. |
The berry (bacca) is a term applied generally to all fruits with
seeds immersed in pulp, and includes fruits of very various origin.
In Actaea (baneberry) or Berberis
(barberry) it is derived from a
single free carpel; generally, however,
it is the product of a syncarpous
ovary, which is superior,
as in grape or potato, or inferior,
as in gooseberry (fig. 29) or currant.
In the pomegranate there is a
peculiar baccate many-celled
inferior fruit, having a tough rind,
enclosing two rows of carpels
placed one above the other. The
seeds are immersed in pulp, and
are attached irregularly to the
wall, base and centre of the loculi.
In the baobab there is a multilocular
syncarpous fruit, in which
the seeds are immersed in pulp.
The pepo, another indehiscent
syncarpous fruit, is illustrated by
the fruit of the gourd, melon (fig.
31) and other Cucurbitaceae. It
is formed of three carpels, surmounted
by the calyx; the rind
is thick and fleshy, and there are
three or more seed-bearing parietal placentas, either surrounding a
central cavity or prolonged inwards into it. The fruit of the papaw
resembles the pepo, but the calyx is not superior.
The hesperidium is the name given to such indehiscent fleshy
syncarpous fruits as the orange, lemon and shaddock, in which the
epicarp and mesocarp form a separable rind, and the endocarp
sends prolongations inwards, forming triangular divisions, to the
inner angle of which the seeds are attached, pulpy cells being developed
around them from the wall. Both pepo and hesperidium may
be considered as modifications of the berry.
The pome (fig. 30), seen in the apple, pear, quince, medlar and
hawthorn, is a fleshy indehiscent syncarpous fruit, in the formation
of which the receptacle takes part. The outer succulent part is the
swollen receptacle, the horny core being the true fruit developed
from the usually five carpels and enclosing the seeds. In the medlar
the core (or true pericarp) is of a stony hardness, while the outer
succulent covering is open at the summit. The pome somewhat
resembles the fruit of the rose (fig. 3), where the succulent receptacle
surrounds a number of separate achenes.
The name capsule is applied generally to all dry syncarpous fruits,
which dehisce by valves. It may thus be unilocular or multilocular,
one- or many-seeded. The true valvular capsule is observed in
Colchicum (fig. 9), lily and iris (fig. 11). The porose capsule is seen
in the poppy (fig. 7), Antirrhinum and Campanula. In Campanula
the pores occur at the base of the capsule, which becomes inverted
when ripe. When the capsule opens by a lid, or by circumscissile
dehiscence, it is called a pyxidium, as in pimpernel (Anagallis
arvensis) (fig. 16), henbane and monkey-pot (Lecythis). The capsule
assumes a screw-like form in Helicteres, and a star-like form in star-anise
(Illicium anisatum). In certain instances the cells of the
capsule separate from each other, and open with elasticity to scatter
the seeds. This kind of capsule is met with in the sandbox tree
(Hura crepitans) and other Euphorbiaceae, where the cocci, containing
each a single seed, burst asunder with force; and in Geraniaceae,
where the cocci, each containing, when mature, usually one
seed, separate from the carpophore, become curved upwards by their
adherent styles, and open by the ventral suture (fig. 18).
The siliqua is a dry syncarpous bilocular many-seeded fruit, formed
from two carpels, with a false septum, dehiscing by two valves
from below upwards, the valves separating from the placentas and
leaving them united by the septum (fig. 32). The seeds are attached
on both sides of the septum, either in one row or in two. When
the fruit is long and narrow it is a siliqua (fig. 14); when broad
and short, silicula (fig. 33). It occurs in cruciferous plants, as wallflower,
cabbage and cress. In Glaucium and Eschscholtzia (Papaveraceae)
the dissepiment is of a spongy nature. It may become
transversely constricted (lomentaceous), as in radish (Raphanus)
and sea-kale, and it may be reduced, as in woad (Isatis), to a
one-seeded
condition.
It sometimes happens that the ovaries of two flowers unite so as
to form a double fruit (syncarp). This may be seen in many species
of honeysuckle. But the fruits which are now to be considered
consist usually of the floral envelopes, as well as the ovaries of
several flowers united into one, and are called multiple or confluent.
The term anthocarpous has also been applied as indicating that the
floral envelopes as well as the carpels are concerned in the formation
of the fruit.
The sorosis is a succulent multiple fruit formed by the confluence
258
of a spike of flowers, as in the fruit of the pine-apple (fig. 34), the
bread-fruit and jack-fruit. Similarly the fruit of the mulberry
represents a catkin-like inflorescence.
The syconus is an anthocarpous fruit, in which the receptacle
completely encloses numerous flowers and becomes succulent. The
fig (fig. 4) is of this nature, and what are called its seeds are the
achenes of the numerous flowers scattered over the succulent hollowed
receptacle. In Dorstenia the axis is less deeply hollowed, and of a
harder texture, the fruit exhibiting often very anomalous forms.
The strobilus, or cone, is a seed-bearing spike, more or less elongated,
covered with scales, each of which may be regarded as representing
a separate flower, and has often two seeds at its base; the
seeds are naked, no ovary being present. This fruit is seen in the
cones of firs, spruces, larches and cedars, which have received the
name of Coniferae, or cone-bearers, on this account. Cone-like
fruit is also seen in most Cycadaceae. The scales of the strobilus
are sometimes thick and closely united, so as to form a more or less
angular and rounded mass, as in the cypress; while in the juniper
they become fleshy, and are so incorporated as to form a globular
fruit like a berry. The dry fruit of the cypress and the succulent
fruit of the juniper have received the name of galbulus. In the hop
the fruit is called also a strobilus, but in it the scales are thin and
membranous, and the seeds are not naked but are contained in
pericarps.
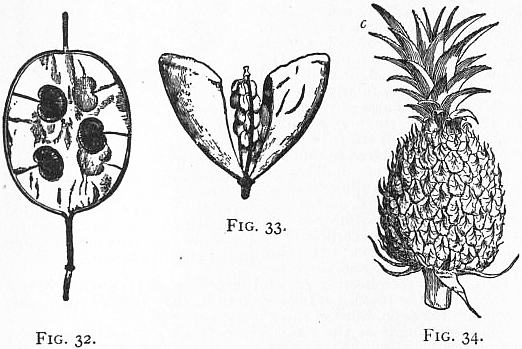
Fig. 32.—Honesty (Lunaria biennis), showing the septum after
the carpels have fallen away.
From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer.
Fig. 33.—Silicula or pouch of shepherd’s purse (Capsella), opening
by two folded valves, which separate from above downwards. The
partition is narrow, hence the silicula is angustiseptal.
From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer.
Fig. 34.—Fruit of the pine-apple (Ananassa sativa), developed
from a spike of numerous flowers with bracts, united so as to
form a collective or anthocarpous fruit. The crown of the pine-apple,
c, consists of a series of empty bracts prolonged beyond the fruit.
The same causes which produce alterations in the other parts of
the flower give rise to anomalous appearances in the fruit. The
carpels, in place of bearing seeds, are sometimes changed into leaves,
with lobes at their margins. Leaves are sometimes produced from
the upper part of the fruit. In the genus Citrus, to which the orange
and lemon belong, it is very common to meet with a separation of
the carpels, so as to produce what are called horned oranges and
fingered citrons. In this case a syncarpous fruit has a tendency to
become apocarpous. In the orange we occasionally find a supernumerary
row of carpels produced, giving rise to the appearance of
small and imperfect oranges enclosed within the original one; the
navel orange is of this nature. It sometimes happens that, by the
union of flowers, double fruits are produced. Occasionally a double
fruit is produced, not by the incorporation of two flowers, but by
the abnormal development of a second carpel in the flower.
Arrangement of Fruits.
A. True fruits—developed from the ovary alone.
1. Pericarp not fleshy or fibrous.
i. Indehiscent—not opening to allow the escape of the
seeds—generally one-seeded. Achene; caryopsis;
cypsela; nut; schizocarp.
ii. Dehiscent—the pericarp splits to allow the escape
of the seeds—generally many-seeded. Follicle;
legume; siliqua; capsule.
2. Pericarp generally differentiated into distinct layers, one
of which is succulent or fibrous. Drupe; berry.
B. Pseudocarps—the development extends beyond the ovary.
Pome; syconus; sorosis.
The Seed.—The seed is formed from the ovule as the result of
fertilization. It is contained in a seed-vessel formed from the ovary
in the plants called angiospermous; while in gymnospermous plants,
such as Coniferae and Cycadaceae, it is naked, or, in other words,
has no true pericarp. It sometimes happens in Angiosperms, that
the seed-vessel is ruptured at an early period of growth, so that
the seeds become more or less exposed during their development;
this occurs in mignonette, where the capsule opens at the apex,
and in Cuphea, where the placenta bursts through the ovary and
floral envelopes, and appears as an erect process bearing the young
seeds. After fertilization the ovule is greatly changed, in connexion
with the formation of the embryo. In the embryo-sac of most
Angiosperms (q.v.) there is a development of cellular tissue, the
endosperm, more or less filling the embryo-sac. In Gymnosperms
(q.v.) the endosperm is formed preparatory to fertilization. The
fertilized egg enlarges and becomes multicellular, forming the
embryo. The embryo-sac enlarges greatly, displacing gradually
the surrounding nucellus, which eventually forms merely a thin layer
around the sac, or completely disappears. The remainder of the
nucellus and the integuments of the ovules form the seed-coats.
In some cases (fig. 35) a delicate inner coat or tegmen can be distinguished
from a tougher outer coat or testa; often, however, the
layers are not thus separable. The consistency of the seed-coat,
its thickness, the character of its surface, &c., vary widely, the
variations being often closely associated with the environment or
with the means of seed-dispersal. An account of the development
of the seed from the ovule will be found in the article Angiosperms.
When the pericarp is dehiscent the seed-covering is of a strong and
often rough character; but when the pericarp is indehiscent and
encloses the seed for a long period, the outer seed-coat is thin and
soft. The cells of the testa are often coloured, and have projections
and appendages of various kinds. Thus in Abrus precatorius and
Adenanthera pavonina it is of a bright red colour; in French beans
it is beautifully mottled; in the almond it is veined; in the tulip
and primrose it is rough; in the snapdragon it is marked with
depressions; in cotton and Asclepias (fig. 36) it has hairs attached to
it; and in mahogany, Bignonia, and the pines and firs it is expanded
in the form of wing-like appendages (fig. 37). In Collomia, Acanthodium,
Cobaea scandens and other seeds, it contains spiral cells, from
which, when moistened with water, the fibres uncoil in a beautiful
manner; and in flax (Linum) and others the cells are converted into
mucilage. These structural peculiarities of the testa in different
plants have relation to the scattering of the seed and its germination
upon a suitable nidus. But in some plants the pericarps assume
structures which subserve the same purpose; this especially occurs
in small pericarps enclosing single seeds, as achenes, caryopsides, &c.
Thus in Compositae and valerian, the pappose limb of the calyx
forms a parachute to the pericarp; in Labiatae and some Compositae
spiral cells are formed in the epicarp; and the epicarp is prolonged
as a wing in Fraxinus (fig. 1) and Acer (fig. 21).
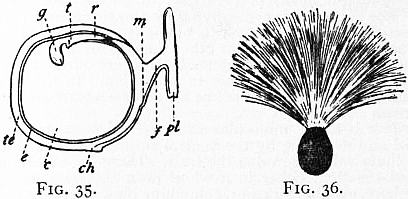
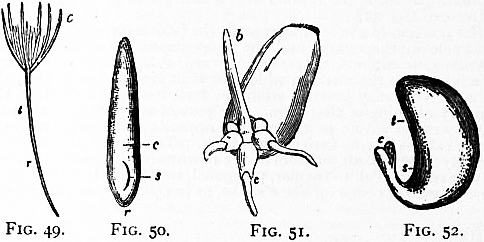
Fig. 35.—Seed of Pea (Pisum) with one cotyledon removed. c,
Remaining cotyledon; ch, chalaza-point at which the nourishing
vessels enter; e, tegmen or inner coat; f, funicle or stalk; g,
plumule of embryo; m, micropyle; pl, placenta; r, radicle of
embryo; t, tigellum or stalk between root and plumule; te, testa.
Fig. 36.—Seed of Asclepias, with a cluster of hairs arising from
the edges of the micropyle.
Sometimes there is an additional covering to the seed, formed
after fertilization, to which the name arillus has been given (fig. 38).
This is seen in the passion-flower, where the covering arises from the
placenta or extremity of the funicle at the base of the ovule and
passes upwards towards the apex, leaving the micropyle uncovered.
In the nutmeg and spindle tree this additional coat is formed from
above downwards, constituting in the former case a laciniated
scarlet covering called mace. In such instances it has been called
an arillode (fig. 39). This arillode, after growing downwards, may
be reflected upwards so as to cover the micropyle. The fleshy
scarlet covering formed around the naked seed in the yew is by
some considered of the nature of an aril. On the testa, at various
points, there are produced at times other cellular bodies, to which
the name of strophioles, or caruncles, has been given, the seeds being
strophiolate or carunculate. These tumours may occur near the
base of the seed, as in Polygala, or at the apex, as in Castor-oil
plant (Ricinus); or they may occur in the course of the raphe, as in
blood-root (Sanguinaria) and Asarabacca. The funicles of the ovules
frequently attain a great length in the seed, and in some magnolias,
when the fruit dehisces, they appear as long scarlet cords suspending
the seeds outside. The hilum or umbilicus of the seed is usually
259
well marked, as a scar of varying size; in the calabar bean and in
some species of Mucuna and Dolichos it extends along a large
portion of the edge of the seed; it frequently exhibits marked
colours, being black in the bean, white in many species of Phaseolus,
&c. The micropyle (fig. 35, m) of the seed may be recognizable by
the naked eye, as in the pea and bean tribe, Iris, &c., or it may be
very minute or microscopic. It indicates the true apex of the seed,
and is important as marking the point to which the root of the embryo
is directed. At the micropyle in the bean is observed a small
process of integument, which, when the young plant sprouts, is
pushed up like a lid; it is called the embryotega. The chalaza (fig.
38, ch) is often of a different colour from the rest of the seed. In the
orange (fig. 40) it is of a reddish-brown colour, and is easily recognized
at one end of the seed when the integuments are carefully removed.
In anatropal seeds the raphe forms a distinct ridge along one side
of the seed (fig. 41).
The position of the seed as regards the pericarp resembles that of
the ovule in the ovary, and the same terms are applied—erect,
ascending, pendulous, suspended, curved, &c. These terms have
no reference to the mode in which the fruit is attached to the axis.
Thus the seed may be erect while the fruit itself is pendent, in the
ordinary meaning of that term. The part of the seed next the axis
or the ventral suture is its face, the opposite side being the back.
Seeds exhibit great varieties of form. They may be flattened
laterally (compressed), or from above downwards (depressed). They
may be round, oval, triangular, polygonal, rolled up like a snail, as in
Physostemon, or coiled up like a snake, as in Ophiocaryon paradoxum.
Fig. 37.—Seed of Pine (Pinus), with a membranous appendage
w to the testa, called a wing.
Fig. 38.—Young anatropal seed of the white Water-lily (Nymphaea
alba), cut vertically. It is attached to the placenta by the funicle f,
cellular prolongations from which form an aril a a. The vessels of
the cord are prolonged to the base of the nucellus n by means of
the raphe r. The base of the nucellus is indicated by the chalaza ch,
while the apex is at the micropyle m. The covering of the seed is
marked i. n is the nucellus or perisperm, enclosing the embryo-sac es,
in which the endosperm is formed. The embryo e, with its suspensor,
is contained in the sac, the radicle pointing to the micropyle m.
Fig. 39.—Arillode a, or false aril, of the Spindle-tree (Euonymus),
arising from the micropyle f.
Fig. 40.—Anatropal seed of the Orange (Citrus Aurantium)
opened to show the chalaza c, which forms a brown spot at one end.
Fig. 41.—Entire anatropal seed of the Orange (Citrus Aurantium),
with its rugose or wrinkled testa, and the raphe r ramifying in the
thickness of the testa on one side.
The endosperm formed in the embryo-sac of angiosperms after
fertilization, and found previous to it in gymnosperms, consists of
cells containing nitrogenous and starchy or fatty matter, destined
for the nutriment of the embryo. It occupies the whole cavity of
the embryo-sac, or is formed only at certain portions of it, at the
apex, as in Rhinanthus, at the base, as in Vaccinium, or in the middle,
as in Veronica. As the endosperm increases in size along with the
embryo-sac and the embryo, the substance of the original nucellus
of the ovule is gradually absorbed. Sometimes, however, as in
Musaceae, Cannaceae, Zingiberaceae, no endosperm is formed;
the cells of the original nucellus, becoming filled with food-materials
for the embryo, are not absorbed, but remain surrounding the
embryo-sac with the embryo, and constitute the perisperm. Again,
in other plants, as Nymphaeaceae (fig. 38) and Piperaceae, both
endosperm and perisperm are present. It was from observations
on cases such as these that old authors, imagining a resemblance
betwixt the plant-ovule and the animal ovum, applied the name
albumen to the outer nutrient mass or perisperm, and designated
the endosperm as vitellus. The term albumen is very generally
used as including all the nutrient matter stored up in the seed, but
it would be advisable to discard the name as implying a definite
chemical substance. There is a large class of plants in which
although at first after fertilization a mass of endosperm is formed,
yet, as the embryo increases in size, the nutrient matter from the
endospermic cells passes out from them, and is absorbed by the
cells of the embryo plant. In the mature seed, in such cases, there
is no separate mass of tissue containing nutrient food-material
apart from the embryo itself. Such a seed is said to be exalbuminous,
as in Compositae, Cruciferae and most Leguminosae (e.g. pea, fig. 35).
When either endosperm or perisperm or both are present the seed
is said to be albuminous.
 |
| Fig. 42.—The dicotyledonous
embryo of the Pea laid open.
c, c, The two fleshy cotyledons,
or seed-lobes, which remain under
ground when the plant sprouts;
r, the radicular extremity of the
axis whence the root arises; t,
the axis (hypocotyl) bearing the
young stalk and leaves g (plumule),
which lie in a depression of
the cotyledons f. |
The albumen varies much in its nature and consistence, and
furnishes important characters. It may be farinaceous or mealy,
consisting chiefly of cells filled with starch, as in cereal grains,
where it is abundant; fleshy or cartilaginous, consisting of thicker
cells which are still soft, as in the coco-nut, and which sometimes
contain oil, as in the oily albumen of Croton, Ricinus and poppy;
horny, when the cell-walls are slightly thickened and capable of
distension, as in date and coffee; the cell-walls sometimes become
greatly thickened, filling up the testa as a hard mass, as in vegetable
ivory (Phytelephas). The albumen may be uniform throughout, or
it may present a mottled appearance,
as in the nutmeg, the seeds of
Anonaceae and some Palms, where
it is called ruminated. This
mottled appearance is due to a
protrusion of a dark lamella of
the integument between folded
protuberances of albumen. A
cavity is sometimes left in the
centre which is usually filled with
fluid, as in the coco-nut. The
relative size of the embryo and of
the endosperm varies much. In
Monocotyledons the embryo is
usually small, and the endosperm
large, and the same is true in the
case of coffee and many other
plants amongst Dicotyledons.
The opposite is the case in other
plants, as in the Labiatae, Plumbaginaceae,
&c.
The embryo consists of an axis bearing the cotyledons (fig. 42, c),
or the first leaves of the plant. To that part of this axis immediately
beneath the cotyledons the terms hypocotyl, caulicle or tigellum (t)
have been applied, and continuous backwards with it is the young
root or radicle (r), the descending axis, their point of union being
the collar or neck. The terminal growing bud of the axis is called
the plumule or gemmule (g), and represents the ascending axis. The
radicular extremity points towards the micropyle, while the cotyledonary
extremity is pointed towards the base of the ovule or the
chalaza. Hence, by ascertaining the position of the micropyle and
chalaza, the two extremities of the embryo can in general be discovered.
It is in many cases difficult to recognize the parts in an
embryo; thus in Cuscuta, the embryo appears as an elongated
axis without divisions; and in Caryocar the mass of the embryo is
made up by the radicular extremity and hypocotyl, in a groove of
which the cotyledonary extremity lies embedded (fig. 52). In some
monocotyledonous embryos, as in Orchidaceae, the embryo is a
cellular mass showing no parts. In parasitic plants also which form
no chlorophyll, as Orobanche, Monotropa, &c., the embryo remains
without differentiation, consisting merely of a mass of cells until the
ripening of the seed. When the embryo is surrounded by the endosperm
on all sides except its radicular extremity it is internal (see
figs. 19, 20); when lying outside the endosperm, and only coming
into contact with it at certain points, it is external, as in grasses (e.g.
wheat, fig. 22). When the embryo follows the direction of the axis
of the seed, it is axile or axial (fig. 43); when it is not in the direction
of the axis, it becomes abaxile or abaxial. In campylotropal seeds
the embryo is curved, and in place of being embedded in endosperm,
is frequently external to it, following the concavity of the seed (fig.
44), and becoming peripherical, with the chalaza situated in the
curvature of the embryo, as in Caryophyllaceae.
It has been already stated that the radicle of the embryo is
directed to the micropyle, and the cotyledons to the chalaza. In
some cases, by the growth of the integuments, the former is turned
round so as not to correspond with the apex of the nucellus, and then
the embryo has the radicle directed to one side, and is called excentric,
as is seen in Primulaceae, Plantaginaceae and many palms, especially
the date. The position of the embryo in different kinds of seeds
varies. In an orthotropal seed the embryo is inverted or antitropal,
the radicle pointing to the apex of the seed, or to the part opposite
the hilum. Again, in an anatropal seed the embryo is erect or
homotropal (fig. 43), the radicle being directed to the base of the
seed. In curved or campylotropal seeds the embryo is folded so
that its radicular and cotyledonary extremities are approximated,
and it becomes amphitropal (fig. 44). In this instance the seed
may be exalbuminous, and the embryo may be folded on itself;
or albuminous, the embryo surrounding more or less completely the
endosperm and being peripherical. According to the mode in
which the seed is attached to the pericarp, the radicle may be
directed upwards or downwards, or laterally, as regards the ovary.
In an orthotropal seed attached to the base of the pericarp it is
superior, as also in a suspended anatropal seed. In other anatropal
seeds the radicle is inferior. When the seed is horizontal as regards
the pericarp, the radicle is either centrifugal, when it points to the
outer wall of the ovary; or centripetal, when it points to the axis
or inner wall of the ovary. These characters are of value for purposes
of classification, as they are often constant in large groups of genera.
260
Plants in which there are two cotyledons produced in the embryo
are dicotyledonous. The two cotyledons thus formed are opposite
to each other (figs. 42 and 45), but are not always of the same size.
Thus, in Abronia and other members of the order Nyctaginaceae, one
of them is smaller than the other (often very small), and in Carapa
guianensis there appears to be only one, in consequence of the
intimate union which takes place between the two. The union
between the cotyledonary leaves may continue after the young plant
begins to germinate. Such embryos have been called pseudomonocotyledonous.
The texture of the cotyledons varies. They may be
thick, as in the pea (fig. 42), exhibiting no traces of venation, with
their flat internal surfaces in contact, and their backs more or less
convex; or they may be in the form of thin and delicate laminae,
flattened on both sides, and having distinct venation, as in Ricinus,
Jatropha, Euonymus, &c. The cotyledons usually form the greater
part of the mature embryo, and this is remarkably well seen in such
exalbuminous seeds as the bean and pea.
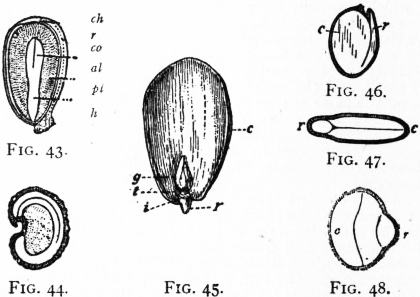
Fig. 43.—Seed of Pansy (Viola tricolor) cut vertically. The embryo
pl is axial, in the midst of fleshy endosperm al. The seed is
anatropal, and the embryo is homotropal; the cotyledons co point
to the base of the nucellus or chalaza ch, while the radicle, or the
other extremity of the embryo, points to the micropyle, close to the
hilum h. The hilum or base of the seed, and the chalaza or base of
the nucellus are united by means of the raphe r.
Fig. 44.—Seed of the Red Campion (Lychnis), cut vertically,
showing the peripheral embryo, with its two cotyledons and its
radicle. The embryo is curved round the albumen, so that its
cotyledons and radicle both come near the hilum (amphitropal).
Fig. 45.—Mature dicotyledonous embryo of the Almond, with
one of the cotyledons removed. r, Radicle; t, young stem or
caulicle; c, one of the cotyledons left; i, line of insertion of the
cotyledon which has been removed; g, plumule.
Fig. 46.—Exalbuminous seed of Wallflower (Cheiranthus) cut
vertically. The radicle r is folded on the edges of the cotyledons c
which are accumbent.
Fig. 47.—Transverse section of the seed of the Wallflower (Cheiranthus),
showing the radicle r folded on the edges of the accumbent
cotyledons c.
Fig. 48.—Transverse section of the seed of the Dame’s Violet
(Hesperis). The radicle r is folded on the back of the cotyledons c,
which are said to be incumbent.
Cotyledons are usually entire and sessile. But they occasionally
become lobed, as in the walnut and the lime; or petiolate, as in
Geranium molle; or auriculate, as in the ash. Like leaves in the
bud, cotyledons may be either applied directly to each other, or
may be folded in various ways. In geranium the cotyledons are
twisted and doubled; in convolvulus they are corrugated; and in
the potato and in Bunias, they are spiral,—the same terms being
applied as to the foliage leaves. The radicle and cotyledons are
either straight or variously curved. Thus, in some cruciferous
plants, as the wallflower, the cotyledons are applied by their faces,
and the radicle (figs. 46, 47) is folded on their edges, so as to be
lateral; the cotyledons are here accumbent. In others, as Hesperis,
the cotyledons (fig. 48) are applied to each other by their faces,
and the radicle, r, is folded on their back, so as to be dorsal, and
the cotyledons are incumbent. Again, the cotyledons are conduplicate
when the radicle is dorsal, and enclosed between their folds.
In other divisions the radicle is folded in a spiral manner, and the
cotyledons follow the same course.
In many gymnosperms more than two cotyledons are present,
and they are arranged in a whorl. This occurs in Coniferae, especially
in the pine, fir (fig. 49), spruce and larch, in which six, nine,
twelve and even fifteen have been observed. They are linear, and
resemble in their form and mode of development the clustered or
fasciculated leaves of the larch. Plants having numerous cotyledons
are termed polycotyledonous. In species of Streptocarpus the
cotyledons are permanent, and act the part of leaves. One of them
is frequently largely developed, while the other is small or abortive.
Fig. 49.—Polycotylodonous embryo of the Pine (Pinus) beginning
to sprout. t, Hypocotyl; r, radicle. The cotyledons c are numerous.
Within the cotyledons the primordial leaves are seen, constituting
the plumule or first bud of the plant.
Fig. 50.—Embryo of a species of Arrow-grass (Triglochin), showing
a uniform conical mass, with a slit s near the lower part. The
cotyledon c envelops the young bud, which protrudes at the slit
during germination. The radicle is developed from the lower part
of the axis r.
Fig. 51.—Grain of wheat (Triticum) germinating, showing (b)
the cotyledon and (c) the rootlets surrounded by their sheaths
(coleorrhizae).
Fig. 52.—Embryo of Caryocar. t, Thick hypocotyl, forming nearly
the whole mass, becoming narrowed and curved at its extremity,
and applied to the groove s. In the figure this narrowed portion is
slightly separated from the groove; c, two rudimentary cotyledons.
In those plants in which there is only a single cotyledon in the
embryo, hence called monocotyledonous, the embryo usually has a
cylindrical form more or less rounded at the extremities, or elongated
and fusiform, often oblique. The axis is usually very short compared
with the cotyledon, which in general encloses the plumule
by its lower portion, and exhibits on one side a small slit which indicates
the union of the edges of the vaginal or sheathing portion of
the leaf (fig. 50). In grasses, by the enlargement of the embryo in a
particular direction, the endosperm is pushed on one side, and thus
the embryo comes to lie outside at the base of the endosperm (figs. 22,
51). The lamina of the cotyledon is not developed. Upon the side
of the embryo next the endosperm and enveloping it is a large
shield-shaped body, termed the scutellum. This is an outgrowth
from the base of the cotyledon, enveloping more or less the cotyledon
and plumule, in some cases, as in maize, completely investing it;
in other cases, as in rice, merely sending small prolongations over its
anterior face at the apex. By others this scutellum is considered
as the true cotyledon, and the sheathing structure covering the
plumule is regarded as a ligule or axillary stipule (see Grasses).
In many aquatic monocotyledons (e.g. Potamogeton, Ruppia and
others) there is a much-developed hypocotyl, which forms the
greater part of the embryo and acts as a store of nutriment in
germination; these are known as macropodous embryos. A similar
case is that of Caryocar among Dicotyledons, where the swollen
hypocotyl occupies most of the embryo (fig. 52). In some grasses,
as oats and rice, a projection of cellular tissue is seen upon the side
of the embryo opposite to the scutellum, that is, on the anterior
side. This has been termed the epiblast. It is very large in rice.
This by some was considered the rudimentary second cotyledon;
but is now generally regarded as an outgrowth of the sheath of the
true cotyledon.
(A. B. R.)
FRUIT AND FLOWER FARMING. The different sorts of
fruits and flowers are dealt with in articles under their own
headings, to which reference may be made; and these give
the substantial facts as to their cultivation. See also the article
Horticulture.
Great Britain
Table I.—Extent of Orchards in Great Britain in each Year,
1887 to 1901.
| Year. | Acres. | Year. | Acres. | Year. | Acres. |
| 1887 | 202,234 | 1892 | 208,950 | 1897 | 224,116 |
| 1888 | 199,178 | 1893 | 211,664 | 1898 | 226,059 |
| 1889 | 199,897 | 1894 | 214,187 | 1899 | 228,603 |
| 1890 | 202,305 | 1895 | 218,428 | 1900 | 232,129 |
| 1891 | 209,996 | 1896 | 221,254 | 1901 | 234,660 |
Table II.—Areas under Orchards in England, Wales and
Scotland—Acres.
| Year. | England. | Wales. | Scotland. | Great Britain. |
| 1896 | 215,642 | 3677 | 1935 | 221,254 |
| 1897 | 218,261 | 3707 | 2148 | 224,116 |
| 1898 | 220,220 | 3690 | 2149 | 226,059 |
| 1899 | 222,712 | 3666 | 2225 | 228,603 |
| 1900 | 226,164 | 3695 | 2270 | 232,129 |
| 1901 | 228,580 | 3767 | 2313 | 234,660 |
| 1908 | 244,430 | 3577 | 2290 | 250,297 |
The extent of the fruit industry may be gathered from the
figures for the acreage of land under cultivation in orchards
and small fruit plantations. The Board of Agriculture returns
concerning the orchard areas of Great Britain showed a continuous
expansion year by year from 199,178 acres in 1888 to 234,660
acres in 1901, as will be learnt from Table I. There was, it is
true, an exception in 1892, but the decline in that year is explained
by the circumstance that since 1891 the agricultural
returns have been collected only from holdings of more than
one acre, whereas they were previously obtained from all holdings
of a quarter of an acre or more. As there are many holdings
of less than an acre in extent upon which fruit is grown, and as
fruit is largely raised also in suburban and other gardens which
261
do not come into the returns, it may be taken for granted that
the actual extent of land devoted to fruit culture exceeds that
which is indicated by the official figures. In the Board of
Agriculture returns up to June 1908, 308,000 acres are stated
to be devoted to fruit cultivation of all kinds in Great Britain.
Table II. shows that the expansion of the orchard area of Great
Britain is mainly confined to England, for it has slightly decreased
in Wales and Scotland. The acreage officially returned
as under orchards is that of arable or grass land which is also
used for fruit trees of any kind. Conditions of soil and climate
determine the irregular distribution of orchards in Great Britain.
The dozen counties which possess the largest extent of orchard
land all lie in the south or west of the island. According to the
returns for 1908 (excluding small fruit areas) they were the
following:—
| County. | Acres. | County. | Acres. | County. | Acres. |
| Kent | 32,751 | Worcester | 23,653 | Salop | 4685 |
| Devon | 27,200 | Gloucester | 20,424 | Dorset | 4464 |
| Hereford | 28,316 | Cornwall | 5,415 | Monmouth | 3914 |
| Somerset | 25,279 | Middlesex | 5,300 | Wilts | 3630 |
Leaving out of consideration the county of Kent, which grows
a greater variety of fruit than any of the others, the counties
of Devon, Hereford, Somerset, Worcester and Gloucester have
an aggregate orchard area of 124,872 acres. These five counties
of the west and south-west of England—constituting in one
continuous area what is essentially the cider country of Great
Britain—embrace therefore rather less than half of the entire
orchard area of the island, while Salop, Monmouth and Wilts
have about 300 less than they had a few years ago. Five English
counties have less than 1000 acres each of orchards, namely,
the county of London, and the northern counties of Cumberland,
Westmorland, Northumberland and Durham. Rutland has
just over 100 acres. The largest orchard areas in Wales are in
the two counties adjoining Hereford—Brecon with 1136 acres
and Radnor with 727 acres; at the other extreme is Anglesey,
with a decreasing orchard area of only 22 acres. Of the Scottish
counties, Lanark takes the lead with 1285 acres, Perth, Stirling
and Haddington following with 684 and 129 acres respectively.
Ayr and Midlothian are the only other counties possessing 100
acres or more of orchards, whilst Kincardine, Orkney and
Shetland return no orchard area, and Banff, Bute, Kinross,
Nairn, Peebles, Sutherland and Wigtown return less than 10
acres each. It may be added that in 1908 Jersey returned 1090
acres of orchards, Guernsey, &c., 144 acres, and the Isle of Man,
121 acres; the two last-named places showing a decline as
compared with eight years previously.
Outside the cider counties proper of England, the counties in
which orchards for commercial fruit-growing have increased
considerably in recent years include Berks, Buckingham,
Cambridge, Essex, Lincoln, Middlesex, Monmouth, Norfolk,
Oxford, Salop, Sussex, Warwick and Wilts. Apples are the
principal fruit grown in the western and south-western counties,
pears also being fairly common. In parts of Gloucestershire,
however, and in the Evesham and Pershore districts of Worcestershire,
plum orchards exist. Plums are almost as largely grown
as apples in Cambridgeshire. Large quantities of apples, plums,
damsons, cherries, and a fair quantity of pears are grown for the
market in Kent, whilst apples, plums and pears predominate in
Middlesex. In many counties damsons are cultivated around
fruit plantations to shelter the latter from the wind.
Of small fruit (currants, gooseberries, strawberries, raspberries,
&c.) no return was made of the acreage previous to 1888, in
which year it was given as 36,724 acres for Great Britain. In
1889 it rose to 41,933 acres.
Later figures are shown in Table III. It will be observed that,
owing to corrections made in the enumeration in 1897, a considerable
reduction in the area is recorded for that year, and presumably
the error then discovered existed in all the preceding
returns. The returns for 1907 gave the acreage of small fruit
as 82,175 acres, and in 1908 at 84,880 acres—an area more than
double that of 1889.
Table III.—Areas of Small Fruit in Great Britain.
| Year. | Acres. | Year. | Acres. | Year. | Acres. |
| 1890 | 46,234 | 1894 | 68,415 | 1898 | 69,753 |
| 1891 | 58,704 | 1895 | 74,547 | 1899 | 71,526 |
| 1892 | 62,148 | 1896 | 76,245 | 1900 | 73,780 |
| 1893 | 65,487 | 1897 | 69,792 | 1901 | 74,999 |
Table IV.—Areas under Small Fruit in England, Wales and
Scotland—Acres.
| Year. | England. | Wales. | Scotland. | Great Britain. |
| 1898 | 63,438 | 1044 | 5271 | 69,753 |
| 1899 | 64,867 | 1106 | 5553 | 71,526 |
| 1900 | 66,749 | 1109 | 5922 | 73,780 |
| 1901 | 67,828 | 1092 | 6079 | 74,999 |
| 1908 | 75,750 | 1200 | 7930 | 84,880 |
There has undoubtedly been a considerable expansion, rather
than a contraction, of small fruit plantations since 1896. The
acreage of small fruit in Great Britain is about one-third that of
the orchards. As may be seen in Table IV., it is mainly confined
to England, though Scotland has over 4000 more acres of small
fruit than of orchards. About one-third of the area of small
fruit in England belongs to Kent alone, that county having
returned 24,137 acres in 1908. Cambridge now ranks next with
6878 acres, followed by Norfolk with 5876 acres, Worcestershire
with 4852 acres, Middlesex with 4163 acres, Hants with 3320
acres and Essex with 2150 acres. It should be remarked that
between 1900 and 1908 Cambridgeshire had almost doubled
its area of small fruits, from 3740 to 6878 acres; whilst both
Norfolk and Worcestershire in 1908 had larger areas devoted
to small fruits than Middlesex—in which county there had
been a decrease of about 400 acres during the same period.
The largest county area of small fruit in Wales is 806 acres
in Denbighshire, and in Scotland 2791 acres in Perthshire,
2259 acres in Lanarkshire, followed by 412 acres in Forfarshire.
The only counties in Great Britain which make no return under
the head of small fruit are Orkney and Shetland; and Sutherland
only gives 2½ acres. It is hardly necessary to say that considerable
areas of small fruit, in kitchen gardens and elsewhere, find
no place in the official returns, which, however, include small
fruit grown between and under orchard trees.
Gooseberries are largely grown in most small fruit districts.
Currants are less widely cultivated, but the red currant is more
extensively grown than the black, the latter having suffered
seriously from the ravages of the black currant mite. Kent is
the great centre for raspberries and for strawberries, though,
in addition, the latter fruit is largely grown in Cambridgeshire
(2411 acres), Hampshire (2327 acres), Norfolk (2067 acres)
and Worcestershire (1273 acres). Essex, Lincolnshire, Cheshire,
262
Cornwall and Middlesex each has more than 500 acres devoted
to strawberry cultivation.
The following statement from returns for 1908 shows the
area under different kinds of fruit in 1907 and 1908 in Great
Britain, and also whether there had been an increase or decrease:
| | 1907. | 1908. | Increase or
Decrease. |
| | Acres. | Acres. | Acres. |
| Small Fruit— | | | |
| Strawberries | 27,827 | 28,815 | + 988 |
| Raspberries | 8,878 | 9,323 | + 445 |
| Currants and Gooseberries | 25,590 | 26,241 | + 651 |
| Other kinds | 19,880 | 20,501 | + 621 |
| | 82,175 | 84,880 | +2705 |
| Orchards— | | | |
| Apples | 172,643 | 172,751 | + 108 |
| Pears | 8,911 | 9,604 | + 693 |
| Cherries | 12,027 | 11,868 | − 159 |
| Plums | 14,901 | 15,683 | + 782 |
| Other kinds | 41,694 | 40,391 | −1303 |
| | 250,176 | 250,297 | + 121 |
It appears from the Board of Agriculture returns that 27,433
acres of small fruit was grown in orchards, so that the total
extent of land under fruit cultivation in Great Britain at the end
of 1908 was about 308,000 acres.
There are no official returns as to the acreage devoted to
orchard cultivation in Ireland. The figures relating to small fruit,
moreover, extend back only to 1899, when the area under this
head was returned as 4809 acres, which became 4359 acres in
1900 and 4877 acres in 1901. In most parts of the country
there are districts favourable to the culture of small fruits,
such as strawberries, raspberries, gooseberries and currants,
and of top fruits, such as apples, pears, plums and damsons.
The only localities largely identified with fruit culture as an
industry are the Drogheda district and the Armagh district.
In the former all the kinds named are grown except strawberries,
the speciality being raspberries, which are marketed in Dublin,
Belfast and Liverpool. In the Armagh district, again, all the
kinds named are grown, but in this case strawberries are the
speciality, the markets utilized being Richhill, Belfast, and those
in Scotland. In the Drogheda district the grower bears the
cost of picking, packing and shipping, but he cannot estimate
his net returns until his fruit is on the market. Around Armagh
the Scottish system prevails—that is, the fruit is sold while
growing, the buyer being responsible for the picking and
marketing.
The amount of fruit imported into the United Kingdom has
such an important bearing on the possibilities of the industry
that the following figures also may be useful:
The quantities of apples, pears, plums, cherries and grapes
imported in the raw condition into the United Kingdom in each
year, 1892 to 1901, are shown in Table V. Previous to 1892 apples
only were separately enumerated. Up to 1899 inclusive the quantities
were given in bushels, but in 1900 a change was made to hundred-weights.
This renders the quantities in that and subsequent years
not directly comparable with those in earlier years, but the comparison
of the values, which are also given in the table, continues
to hold good. The figures for 1908 have been added to show the
increase that had taken place. In some years the value of imported
apples exceeds the aggregate value of the pears, plums, cherries
and grapes imported. The extreme values for apples shown in the
table are £844,000 in 1893 and £2,079,000 in 1908. Grapes rank next
to apples in point of value, and over the seventeen years the amount
ranged between £394,000 in 1892 and £728,000 in 1908. On the
average, the annual outlay on imported pears is slightly in excess
of that on plums. The extremes shown are £167,000 in 1895 and
£515,000 in 1908. In the case of plums, the smallest outlay tabulated
is £166,000 in 1895, whilst the largest is £498,000 in 1897. The
amounts expended upon imported cherries varied between £96,000
in 1895 and £308,000 in 1900. In 1900 apricots and peaches, imported
raw, previously included with raw plums, were for the first
time separately enumerated, the import into the United Kingdom
for that year amounting to 13,689 cwt., valued at £25,846; in 1901
the quantity was 13,463 cwt. and the value £32,350. The latter
rose in 1908 to £60,000. In 1900, also, currants, gooseberries and
strawberries, hitherto included in unenumerated raw fruit, were
likewise for the first time separately returned. Of raw currants
the import was 64,462 cwt., valued at £87,170 (1908, £121,850);
of raw gooseberries 26,045 cwt., valued at £14,626 (1908, £25,520);
and of raw strawberries, 52,225 cwt., valued at £85,949. In 1907
only 44,000 cwt. of strawberries were imported. In 1901 the
quantities and values were respectively—currants, 70,402 cwt.,
£75,308; gooseberries, 21,735 cwt., £11,420; strawberries, 38,604
cwt., £51,290. Up to 1899 the imports of tomatoes were included
amongst unenumerated raw vegetables, so that the quantity was
not separately ascertainable. For 1900 the import of tomatoes
was 833,032 cwt., valued at £792,339, which is equivalent to a
fraction under 2½d. per ℔. For 1901 the quantity was 793,991 cwt.,
and the value £734,051; for 1906, there were 1,124,700 cwt., valued
at £953,475; for 1907, 1,135,499 cwt., valued at £1,020,805; and
for 1908, 1,160,283 cwt., valued at £955,983.
Table V.—Imports of Raw Apples, Pears, Plums, Cherries and
Grapes into the United Kingdom, 1892 to 1901. Quantities in
Thousands of Bushels (thousands of cwt. in 1900 and 1901).
Values in Thousands of Pounds Sterling.
| Year. | Quantities. |
| Apples. | Pears. | Plums. | Cherries. | Grapes. |
| 1892 | 4515 | 637 | 413 | 217 | 762 |
| 1893 | 3460 | 915 | 777 | 346 | 979 |
| 1894 | 4969 | 1310 | 777 | 311 | 833 |
| 1895 | 3292 | 407 | 401 | 196 | 865 |
| 1896 | 6177 | 483 | 560 | 219 | 883 |
| 1897 | 4200 | 1052 | 1044 | 312 | 994 |
| 1898 | 3459 | 492 | 922 | 402 | 1136 |
| 1899 | 3861 | 572 | 558 | 281 | 1158 |
| 1900 | 2129* | 477* | 423* | 243* | 593* |
| 1901 | 1830* | 349* | 264* | 213* | 680* |
| Values. |
| 1892 | 1354 | 297 | 200 | 135 | 394 |
| 1893 | 844 | 347 | 332 | 195 | 530 |
| 1894 | 1389 | 411 | 302 | 167 | 470 |
| 1895 | 960 | 167 | 166 | 96 | 487 |
| 1896 | 1582 | 207 | 242 | 106 | 443 |
| 1897 | 1187 | 378 | 498 | 178 | 495 |
| 1898 | 1108 | 222 | 435 | 231 | 550 |
| 1899 | 1186 | 266 | 294 | 154 | 588 |
| 1900 | 1225 | 367 | 393 | 308 | 595 |
| 1901 | 1183 | 296 | 244 | 214 | 695 |
| 1908 | 2079 | 515 | 428 | 235 | 728 |
| * Thousands of cwts. |
In 1908 the outlay of the United Kingdom upon imported raw
fruits, such as can easily be produced at home, was £4,195,654,
made up as follows:
| Apples | £2,079,703 | Plums | £428,966 |
| Grapes | 728,026 | Currants | 121,852 |
| Pears | 515,914 | Apricots and peaches | 60,141 |
| Cherries | 235,523 | Gooseberries | 25,529 |
In addition about £280,000 was spent upon “unenumerated” raw
fruit, and £560,000 on nuts other than almonds “used as fruit,”
which would include walnuts and filberts, both produced at home.
It is certain, therefore, that the expenditure on imported fruits,
such as are grown within the limits of the United Kingdom, exceeds
four millions sterling per annum. The remainder of the outlay on
imported fruit in 1908, amounting to over £5,000,000, was made
up of £2,269,651 for oranges, £471,713 for lemons, £1,769,249 for
bananas, and £560,301 for almond-nuts; these cannot be grown on
an industrial scale in the British Isles.
It may be interesting to note the source of some of these imported
fruits. The United States and Canada send most of the apples,
the quantity for 1907 being 1,413,000 cwt. and 1,588,000 cwt.
respectively, while Australia contributes 280,000 cwt. Plums
come chiefly from France (200,000 cwt.), followed with 38,000 cwt.
from Germany and 28,000 cwt. from the Netherlands. Pears are
imported chiefly from France (204,000 cwt.) and Belgium (176,000);
but the Netherlands send 52,000 cwt., and the United States 24,000
cwt. The great bulk of imported tomatoes comes from the Canary
Islands, the quantity in 1907 being 604,692 cwt. The Channel
Islands also sent 223,800 cwt., France 115,500 cwt., Spain 169,000
cwt., and Portugal a long way behind with 11,700 cwt. Most of
the strawberries imported come from France (33,800 cwt.) and the
Netherlands (10,300 cwt.).
Fruit-growing in Kent.—Kent is by far the largest fruit-growing
county in England. For centuries that county has been famous
for its fruit, and appears to have been the centre for the distribution
of trees and grafts throughout the country. The cultivation
263
of fruit land upon farms in many parts of Kent has always been
an important feature in its agriculture. An excellent description
of this noteworthy characteristic of Kentish farming is contained
in a comprehensive paper on the agriculture of Kent by Mr
Charles Whitehead,1 whose remarks, with various additions and
modifications, are here reproduced.
Where the conditions are favourable, especially in East and Mid
Kent, there is a considerable acreage of fruit land attached to each
farm, planted with cherry, apple, pear, plum and damson trees,
and with bush fruits, or soft fruits as they are sometimes called,
including gooseberries, currants, raspberries, either with or without
standard trees, and strawberries, and filberts and cob-nuts in Mid
Kent. This acreage has largely increased, and will no doubt continue
to increase, as, on the whole, fruit-growing has been profitable
and has materially benefited those fortunate enough to have fruit
land on their farms. There are also cultivators who grow nothing
but fruit. These are principally in the district of East Kent, between
Rochester and Canterbury, and in the district of Mid Kent near
London, and they manage their fruit land, as a rule, better than
farmers, as they give their undivided attention to it and have more
technical knowledge. But there has been great improvement of
late in the management of fruit land, especially of cherry and apple
orchards, the grass of which is fed off by animals having corn or
cake, or the land is well manured. Apple trees are grease-banded
and sprayed systematically by advanced fruit-growers to prevent
or check the attacks of destructive insects. Far more attention is
being paid to the selection of varieties of apples and pears having
colour, size, flavour, keeping qualities, and other attributes to meet
the tastes of the public, and to compete with the beautiful fruit that
comes from the United States and Canada.
Of the various kinds of apples at present grown in Kent mention
should be made of Mr Gladstone, Beauty of Bath, Devonshire
Quarrenden, Lady Sudely, Yellow Ingestre and Worcester Pearmain.
These are dessert apples ready to pick in August and September,
and are not stored. For storing, King of the Pippins, Cox’s Orange
Pippin (the best dessert apple in existence), Cox’s Pomona, Duchess,
Favourite, Gascoyne’s Scarlet Seedling, Court Pendu Plat, Baumann’s
Red Reinette, Allington Pippin, Duke of Devonshire and Blenheim
Orange. Among kitchen apples for selling straight from the trees
the most usually planted are Lord Grosvenor, Lord Suffield, Keswick
Codlin, Early Julian, Eclinville Seedling, Pott’s Seedling, Early
Rivers, Grenadier, Golden Spire, Stirling Castle and Domino. For
storing, the cooking sorts favoured now are Stone’s or Loddington,
Warner’s King, Wellington, Lord Derby, Queen Caroline, Tower of
Glamis, Winter Queening, Lucombe’s Seedling, Bismarck, Bramley’s
Seedling, Golden Noble and Lane’s Prince Albert. Almost all these
will flourish equally as standards, pyramids and bushes. Among
pears are Hessle, Clapp’s Favourite, William’s Bon Chrétien, Beurré
de Capiaumont, Fertility, Beurré Riche, Chissel, Beurré Clairgeau,
Louise Bonne of Jersey, Doyenne du Comice and Vicar of Winkfield.
Among plums, Rivers’s Early Prolific, Tsar, Belgian Purple, Black
Diamond, Kentish Bush Plum, Pond’s Seedling, Magnum Bonum
and Victoria are mainly cultivated. The damson known as Farleigh
Prolific, or Crittenden’s, is most extensively grown throughout the
county, and usually yields large crops, which make good prices.
As a case in point, purchasers were offering to contract for quantities
of this damson at £20 per ton in May of 1899, as the prospects of the
yield were unsatisfactory. On the other hand, in one year recently
when the crop was abnormally abundant, some of the fruit barely
paid the expenses of sending to market. The varieties of cherries
most frequently grown are Governor Wood, Knight’s Early Black,
Frogmore Blackheart, Black Eagle, Waterloo, Amberheart, Bigarreau,
Napoleon Bigarreau and Turk. A variety of cherry known as the
Kentish cherry, of a light red colour and fine subacid flavour, is
much grown in Kent for drying and cooking purposes. Another
cherry, similar in colour and quality, which comes rather late, known
as the Flemish, is also extensively cultivated, as well as the very
dark red large Morello, used for making cherry brandy. These three
varieties are grown extensively as pyramids, and the last-named
also on walls and sides of buildings. Sometimes the cherry crop is
sold by auction to dealers, who pick, pack and consign the fruit to
market. Large prices are often made, as much as £80 per acre being
not uncommon. The crop on a large cherry orchard in Mid Kent
has been sold for more than £100 per acre.
Where old standard trees have been long neglected and have
become overgrown by mosses and lichens, the attempts made to
improve them seldom succeed. The introduction of bush fruit trees
dwarfed by grafting on the Paradise stock has been of much advantage
to fruit cultivators, as they come into bearing in two or three years,
and are more easily cultivated, pruned, sprayed and picked than
standards. Many plantations of these bush trees have been formed in
Kent of apples, pears and plums. Half standards and pyramids have
also been planted of these fruits, as well as of cherries. Bushes of
gooseberries and currants, and clumps or stools of raspberry canes,
have been planted to a great extent in many parts of the East and
Mid divisions of Kent, but not much in the Weald, where apples are
principally grown. Sometimes fruit bushes are put in alternate rows
with bush of standard trees of apple, pear, plum or damson, or they
are planted by themselves. The distances apart for planting are generally
for cherry and apple trees on grass 30 ft. by 30 ft.; for standard
apples and pear trees from 20 ft. to 24 ft. upon arable land, with bush
fruit, as gooseberries and currants, under them. These are set 6 ft. by
6 ft. apart, and 5 ft. by 2 ft. for raspberries, and strawberries 2 ft. 6 in.
to 3 ft. by 1 ft. 6 in. to 1 ft. 3 in. apart. On some fruit farms bush
or dwarf trees—apples, pears, plums—are planted alone, at distances
varying from 8 ft. to 10 ft. apart, giving from 485 to 680 bush trees
per acre, nothing being grown between them except perhaps strawberries
or vegetables during the first two or three years. It is believed
that this is the best way of ensuring fruit of high quality and colour.
Another arrangement consists in putting standard apple or pear
trees 30 ft. apart (48 trees per acre), and setting bush trees of apples
or pears 15 ft. apart between them; these latter come quickly into
bearing, and are removed when the standards are fully grown.
Occasionally gooseberry or currant bushes, or raspberry canes or
strawberry plants, are set between the bush trees, and taken away
directly they interfere with the growth of these. Half standard
apple or plum trees are set triangularly 15 ft. apart, and strawberry
plants at a distance of 1½ ft. from plant to plant and 2½ ft. from row
to row. Or currant or gooseberry bushes are set between the half
standards, and strawberry plants between these.
These systems involve high farming. The manures used are
London manure, where hops are not grown, and bone meal, super-phosphate,
rags, shoddy, wool-waste, fish refuse, nitrate of soda,
kainit and sulphate of ammonia. Where hops are grown the London
manure is wanted for them. Fruit plantations are always dug by
hand with the Kent spud. Fruit land is never ploughed, as in the
United States and Canada. The soil is levelled down with the
“Canterbury” hoe, and then the plantations are kept free from
weeds with the ordinary draw or “plate” hoe. The best fruit
farmers spray fruit trees regularly in the early spring, and continue
until the blossoms come out, with quassia and soft soap and paraffin
emulsions, and a very few with Paris green only, where there is no
under fruit, in order to prevent and check the constant attacks of
the various caterpillars and other insect pests. This is a costly and
laborious process, but it pays well, as a rule. The fallacy that fruit
trees on grass land require no manure, and that the grass may be
allowed to grow up to their trunks without any harm, is exploding,
and many fruit farmers are well manuring their grass orchards and
removing the grass for some distance round the stems, particularly
where the trees are young.
Strawberries are produced in enormous quantities in the northern
part of the Mid Kent district round the Crays, and from thence to
Orpington; also near Sandwich, and to some extent near Maidstone.
Raspberry canes have been extensively put in during the last few
years, and in some seasons yield good profits. There is a very great
and growing demand for all soft fruits for jam-making, and prices
are fairly good, taking an average of years, notwithstanding the
heavy importations from France, Belgium, Holland, Spain and Italy.
The extraordinary increase in the national demand for jam and other
fruit preserves has been of great benefit to Kent fruit producers.
The cheapness of duty-free sugar, as compared with sugar paying
duty in the United States and other large fruit-producing countries,
afforded one of the very few advantages possessed by British
cultivators, but the reimposition of the sugar duty in the United
Kingdom in 1901 has modified the position in this respect. Jam
factories were established in several parts of Kent about 1889 or
1890, but most of them collapsed either from want of capital or from
bad management. There are still a few remaining, principally in
connexion with large fruit farms. One of these is at Swanley, whose
energetic owners farm nearly 2000 acres of fruit land in Kent. The
fruit grown by them that will not make satisfactory prices in a fresh
raw state is made into jam, or if time presses it is first made into
pulp, and kept until the opportunity comes for making it into jam.
In this factory there are fifteen steam-jacketed vats in one row, and
six others for candied peel. A season’s output on a recent occasion
comprised about 3500 tons of jam, 850 tons of candied peel and
750 gross (108,000 bottles) of bottled fruit. A great deal of the fruit
preserved is purchased, whilst much of that grown on the farms is
sold. A strigging machine is employed, which does as much work
as fifty women in taking currants off their strigs or stalks. Black
currant pulp is stored in casks till winter, when there is time to
convert it into jam. Strawberries cannot be pulped to advantage,
but it is otherwise with raspberries, the pulp of which is largely made.
Apricots for jam are obtained chiefly from France and Spain. There
is another flourishing factory near Sittingbourne worked on the
same lines. It is very advantageous to fruit farmers to have jam
factories in connexion with their farms or to have them near, as
they can thoroughly grade their fruit, and send only the best to market,
thus ensuring a high reputation for its quality. Carriage is saved,
which is a serious charge, though railway rates from Kent to the great
manufacturing towns and to Scotland are very much less proportionally
than those to London, and consequently Kent growers send
increasing quantities to these distant markets, where prices are
better, not being so directly interfered with by imported fruit,
which generally finds its way to London.
Kentish fruit-growers are becoming more particular in picking,
264
grading, packing and storing fruit, as well as in marketing it. A
larger quantity of fruit is now carefully stored, and sent to selected
markets as it ripens, or when there is an ascertained demand, as it
is found that if it is consigned to market direct from the trees there
must frequently be forced sales and competition with foreign fruit
that is fully matured and in good order. It was customary formerly
for Kentish growers to consign all their fruit to the London markets;
now a good deal of it is sent to Manchester, Birmingham, Liverpool,
Sheffield, Newcastle and other large cities. Some is sent even to
Edinburgh and Glasgow. Many large growers send no fruit to
London now. It is by no means uncommon for growers to sell
their fruit crops on the trees or bushes by auction or private treaty,
or to contract to supply a stipulated quantity of specified fruit, say
of currants, raspberries or strawberries, to jam manufacturers. There
is a considerable quantity of fruit, such as grapes, peaches, nectarines,
grown under glass, and this kind of culture tends to increase.
Filberts and cob-nuts are a special product of Kent, in the neighbourhood
of Maidstone principally, and upon the Ragstone soils, certain
conditions of soil and situation being essential for their profitable
production. A part of the filbert and cob-nut crop is picked green
in September, as they do well for dessert, though their kernels are
not large or firm, and it pays to sell them green, as they weigh more
heavily. One grower in Mid Kent has 100 acres of nuts, and has
grown 100 tons in a good year. The average price of late years has
been about 5d. per ℔, which would make the gross return of the
100 acres amount to £4660. Kentish filberts have long been proverbial
for their excellence. Cobs are larger and look better for
dessert, though their flavour is not so fine. They are better croppers,
and are now usually planted. This cultivation is not much extending,
as it is very long before the trees come into full bearing. The London
market is supplied entirely with these nuts from Kent, and there is
some demand in America for them. Filbert and cob trees are most
closely pruned. All the year’s growth is cut away except the very
finest young wood, which the trained eye of the tree-cutter sees at
a glance is blossom-bearing. The trees are kept from 5½ to 7 ft.
high upon stems from 1½ to 2 ft. high, and are trained so as to form
a cup of from 7 to 8 ft. in diameter.
There seems no reason to expect any decrease in the acreage of
fruit land in Kent, and if the improvement in the selection of varieties
and in the general management continues it will yet pay. A hundred
years ago every one was grubbing fruit land in order that hops might
be planted, and for this many acres of splendid cherry orchards were
sacrificed. Now the disposition is to grub hop plants and substitute
apples, plums, or small fruit or cherry trees.
Fruit-growing in other Districts.—The large fruit plantations in
the vicinity of London are to be found mostly in the valley of the
Thames, around such centres as Brentford, Isleworth, Twickenham,
Heston, Hounslow, Cranford and Southall. All varieties of orchard
trees, but mostly apples, pears, and plums and small fruit, are grown
in these districts, the nearness of which to the metropolitan fruit
market at Covent Garden is of course an advantage. Some of the
orchards are old, and are not managed on modern principles. They
contain, moreover, varieties of fruit many of which are out of date
and would not be employed in establishing new plantations. In
the better-managed grounds the antiquated varieties have been
removed, and their places taken by newer and more approved types.
In addition to apples, pears, plums, damsons, cherries and quinces
as top fruit, currants, gooseberries and raspberries are grown as
bottom fruit. Strawberries are extensively grown in some of the
localities, and in favourable seasons outdoor tomatoes are ripened and
marketed.
Fruit is extensively grown in Cambridgeshire and adjacent counties
in the east of England. A leading centre is Cottenham, where the
Lower Greensand crops out and furnishes one of the best of soils for
fruit-culture. In Cottenham about a thousand acres are devoted
to fruit, and nearly the same acreage to asparagus, which is, however,
giving place to fruit. Currants, gooseberries and strawberries are the
most largely grown, apples, plums and raspberries following. Of
varieties of plums the Victoria is first in favour, and then Rivers’s
Early Prolific, Tsar and Gisborne. London is the chief market,
as it receives about half the fruit sent away, whilst a considerable
quantity goes to Manchester, and some is sent to a neighbouring jam
factory at Histon, where also a moderate acreage of fruit is grown.
Another fruit-growing centre in Cambridgeshire is at Willingham,
where—besides plums, gooseberries and raspberries—outdoor
tomatoes are a feature. Greengages are largely grown near Cambridge.
Wisbech is the centre of an extensive fruit district,
situated partly in Cambridgeshire and partly in Norfolk. Gooseberries,
strawberries and raspberries are largely grown, and as many
as 80 tons of the first-named fruit have been sent away from Wisbech
station in a single day. In the fruit-growing localities of Huntingdonshire
apples, plums and gooseberries are the most extensively grown,
but pears, greengages, cherries, currants, strawberries and raspberries
are also cultivated. As illustrating variations in price, it may be
mentioned that about the year 1880 the lowest price for gooseberries
was £10 per ton, whereas it has since been down to £4. Huntingdonshire
fruit is sent chiefly to Yorkshire, Scotland and South Wales,
but railway freights are high.
Essex affords a good example of successful fruit-farming at Tiptree
Heath, near Kelvedon, where under one management about 260
acres out of a total of 360 are under fruit. The soil, a stiff loam,
grows strawberries to perfection, and 165 acres are allotted to this
fruit. The other principal crops are 43 acres of raspberries and 30
acres of black currants, besides which there are small areas of red
currants, gooseberries, plums, damsons, greengages, cherries, apples,
quinces and blackberries. The variety of strawberry known as the
Small Scarlet is a speciality here, and it occupies 55 acres, as it
makes the best of jam. The Paxton, Royal Sovereign and Noble
varieties are also grown. Strawberries stand for six or seven years
on this farm, and begin to yield well when two years old. A jam
factory is worked in conjunction with the fruit farm. Pulp is not
made except when there is a glut of fruit. Perishable fruit intended
for whole-fruit preserves is never held over after it is gathered.
The picking of strawberries begins at 4 A.M., and the first lot is made
into jam by 6 A.M.
Hampshire, like Cambridgeshire and Norfolk, are the only counties
in which the area of small fruit exceeds that of orchards. The returns
for 1908 show that Hampshire had 3320 acres of small fruit to 2236
acres of orchards; Cambridge had 6878 acres of small fruit to 5221
of orchards; and Norfolk had 5876 acres of small fruit against
5188 acres of orchards. Compared with twenty years previously,
the acreage of small fruit had trebled. This is largely due in Hampshire
to the extension of strawberry culture in the Southampton
district, where the industry is in the hands of many small growers,
few of whom cultivate more than 20 acres each. Sarisbury and
Botley are the leading parishes in which the business is carried on.
Most of the strawberry holdings are from half an acre to 5 acres in
extent, a few are from 5 to 10 acres, fewer still from 10 to 20 acres
and only half-a-dozen over that limit. Runners from one-year plants
are used for planting, being found more fruitful than those from
older plants. Peat-moss manure from London stables is much
used, but artificial manures are also employed with good results.
Shortly after flowering the plants are bedded down with straw at
the rate of about 25 cwt. per acre. Picking begins some ten days
earlier than in Kent, at a date between 1st June and 15th June.
The first week’s gathering is sent mostly to London, but subsequently
the greater part of the fruit goes to the Midlands and to Scotland and
Ireland.
In recent years fruit-growing has much increased in South
Worcestershire, in the vicinity of Evesham and Pershore. Hand-lights
are freely used in the market gardens of this district for the
protection of cucumbers and vegetable marrows, besides which
tomatoes are extensively grown out of doors. At one time the egg
plum and the Worcester damson were the chief fruit crops, apples and
cherries ranking next, pears being grown to only a moderate extent.
According to the 1908 returns, however, apples come first, plums
second, pears third and cherries fourth. In a prolific season a single
tree of the Damascene or Worcester damson will yield from 400 to
500 ℔ of fruit. There is a tendency to grow plum trees in the bush
shape, as they are less liable than standards to injury from wind.
The manures used include soot, fish guano, blood manure and
phosphates—basic slag amongst the last-named. In the Pershore
district, where there is a jam factory, plums are the chief tree fruit,
whilst most of the orchard apples and pears are grown for cider and
perry. Gooseberries are a feature, as are also strawberries, red and
black currants and a few white, but raspberries are little grown.
The soil, a strong or medium loam of fair depth, resting on clay, is so
well adapted to plums that trees live for fifty years. In order to check
the ravages of the winter moth, plum and apple trees are grease-banded
at the beginning of October and again at the end of March.
The trees are also sprayed when necessary with insecticidal solutions.
Pruning is done in the autumn. An approved distance apart at
which to grow plum trees is 12 ft. by 12 ft. In the Earl of Coventry’s
fruit plantation, 40 acres in extent, at Croome Court, plums and
apples are planted alternately, the bottom fruit being black currants,
which are less liable to injury from birds than are red currants or
gooseberries. Details concerning the methods of cultivation of
fruit and flowers in various parts of England, the varieties commonly
grown, the expenditure involved, and allied matters, will be found in
Mr W.E. Bear’s papers in the Journal of the Royal Agricultural
Society in 1898 and 1899.
Apart altogether from market gardening and commercial fruit-growing,
it must be borne in mind that an enormous business is
done in the raising of young fruit-trees every year. Hundreds of
thousands of apples, pears, plums, cherries, peaches, nectarines and
apricots are budded or grafted each year on suitable stocks. They
are trained in various ways, and are usually fit for sale the third
year. These young trees replace old ones in private and commercial
gardens, and are also used to establish new plantations in different
parts of the kingdom.
The Woburn Experimental Fruit Farm.—The establishment in
1894 of the experimental fruit farm at Ridgmont, near Woburn,
Beds, has exercised a healthy influence upon the progress and
development of fruit-farming in England. The farm was founded
and carried on by the public-spirited enterprise of the Duke of
Bedford and Mr Spencer U. Pickering, the latter acting as director.
The main object of the experimental station was “to ascertain facts
relative to the culture of fruit, and to increase our knowledge of, and
to improve our practice in, this industry.” The farm is 20 acres in
extent, and occupies a field which up to June 1894 had been used as
265
arable land for the ordinary rotation of farm crops. The soil is a
sandy loam 9 or 10 in. deep, resting on a bed of Oxford Clay. Although
it contains a large proportion of sand, the land would generally be
termed very heavy, and the water often used to stand on it in places
for weeks together in a wet season. The tillage to which the ground
was subjected for the purposes of the fruit farm much improved its
character, and in dry weather it presents as good a tilth as could be
desired. Chemical analyses of the soil from different parts of the field
show such wide differences that it is admitted to be by no means an
ideal one for experimental purposes. Without entering upon further
details, it may be useful to give a summary of the chief results
obtained.
Apples have been grown and treated in a variety of ways, but of
the different methods of treatment careless planting, coupled with
subsequent neglect, has given the most adverse results, the crop
of fruit being not 5% of that from trees grown normally. Of the
separate deleterious items constituting total neglect, by far the most
effective was the growth of weeds on the surface; careless planting,
absence of manure, and the omission of trenching all had comparatively
little influence on the results. A set of trees that had been
carelessly planted and neglected, but subsequently tended in the
early part of 1896, were in the autumn of that year only 10%
behind their normally-treated neighbours, thus demonstrating that
the response to proper attention is prompt. The growth of grass
around young apple trees produced a very striking effect, the injury
being much greater than that due to weeds. It is possible, however,
that in wet years the ill-effects of both grass and weeds would be
less than in dry seasons. Nevertheless, the grass-grown trees, after
five years, were scarcely bigger than when planted, and the actual
increase in weight which they showed during that time was about
eighteen times smaller than in the case of similar trees in tilled
ground. It is believed that one of the main causes of the ill-effects
is the large increase in the evaporation of water from the soil which
is known to be produced by grass, the trees being thereby made to
suffer from drought, with constant deprivation of other nourishment
as well. That grass growing round young apple trees is deleterious
was a circumstance known to many horticulturists, but the extent to
which it interferes with the development of the trees had never before
been realized. Thousands of pounds are annually thrown away in England
through want of knowledge of this fact. Yet trees will flourish
in grass under certain conditions. Whether the dominant factor is
the age (or size) of the tree has been investigated by grassing over
trees which have hitherto been in the open ground, and the results
appear to indicate that the grass is as deleterious to the older trees as
it was to the younger ones. Again, it appears to have been demonstrated
that young apple trees, at all events in certain soils, require
but little or no manure in the early stages of their existence, so
that in this case also large sums must be annually wasted upon
manurial dressings which produce no effects. The experiments
have dealt with dwarf trees of Bramley, Cox and Potts, six trees
of each variety constituting one investigation. Some of the experiments
were repeated with Stirling Castle, and others with standard
trees of Bramley, Cox and Lane’s Prince Albert. All were planted
in 1894-1895, the dwarfs being then three years old and the standards
four. In each experiment the “normal” treatment is altered in
some one particular, this normal treatment consisting of planting
the trees carefully in trenched ground, and subsequently keeping
the surface clean; cutting back after planting, pruning moderately
in autumn, and shortening the growths when it appeared necessary
in summer; giving in autumn a dressing of mixed mineral manures,
and in February one of nitrate of soda, this dressing being probably
equivalent to one of 12 tons of dung per acre. In the experiments
on branch treatment, the bad effects of omitting to cut the trees back
on planting, or to prune them subsequently, is evident chiefly in
the straggling and bad shape of the resulting trees, but such trees also
are not so vigorous as they should be. The quantity of fruit borne,
however, is in excess of the average. The check on the vigour and
growth of a tree by cutting or injuring its roots is in marked contrast
with the effects of a similar interference with the branches. Trees
which had been root-pruned each year were in 1898 little more than
half as big as the normal trees, whilst those root-pruned every second
year were about two-thirds as big as the normal. The crops borne
by these trees were nevertheless heavy in proportion to the size of
the trees. Such frequent root-pruning is not, of course, a practice
which should be adopted. It was found that trees which had been
carefully lifted every other year and replanted at once experienced
no ill-effects from the operation; but in a case where the trees after
being lifted had been left in a shed for three days before replanting—which
would reproduce to a certain extent the conditions experienced
when trees are sent out from a nursery—material injury was suffered,
these trees after four years being 28% smaller than similar ones
which had not been replanted. Sets of trees planted respectively
in November, January and March have, on the whole, shown
nothing in favour of any of these different times for planting
purposes. Some doubt is thrown on the accepted view that there
is a tendency, at any rate with young apple and pear trees, to fruit
in alternate seasons.
Strawberries of eighty-five different varieties have been experimented
with, each variety being represented in 1900 by plants of
five different ages, from one to five years. In 1896 and 1898 the
crops of fruit were about twice as heavy as in 1897 and 1899, but
it has not been found possible to correlate these variations with the
meteorological records of the several seasons. Taking the average of all
the varieties, the relative weights of crop per plant, when these are
compared with the two-year-old plants in the same season, are, for
the five ages of one to five years, 31, 100, 122, 121 and 134, apparently
showing that the bearing power increases rapidly up to two years,
less rapidly up to three years, after which age it remains practically
constant. The relative average size of the berries shows a deterioration
with the age of the plant. The comparative sizes from plants of
one to five years old were 115, 100, 96, 91 and 82 respectively. If
the money value of the crop is taken to be directly dependent on its
total weight, and also on the size of the fruits, the relative values
of the crop for the different ages would be 34, 100, 117, 111 and 110,
so that, on the Ridgmont ground, strawberry plants could be profitably
retained up to five years and probably longer. As regards
what may be termed the order of merit of different varieties of
strawberries, it appears that even small differences in position and
treatment cause large variations, not only in the features of the
crop generally, but also in the relative behaviour of the different
varieties. The relative cropping power of the varieties under
apparently similar conditions may often be expressed by a number
five or tenfold as great in one case as in the other. A comparison
of the relative behaviour of the same varieties in different seasons
is attended by similar variations. The varying sensitiveness of
different varieties of strawberry plants to small and undefinable
differences in circumstances is indeed one of the most important
facts brought to light in the experiments.
Fruit Culture in Ireland.—The following figures have been kindly
supplied by the Irish Board of Agriculture, and deal with the acreage
under fruit culture in Ireland up to the end of the year 1907.
| 1. Orchard Fruit— | Statute Acres. |
| Apples | 5829 |
| Pears | 224 |
| Plums | 223 |
| Damsons | 138 |
| Other kinds | 129 |
| | —— |
| | Total 6543 |
| 2. Small Fruit— | |
| Currants, black | 234 |
| Currants, red and white | 159 |
| Gooseberries | 675 |
| Raspberries | 374 |
| Strawberries | 994 |
| Mixed fruit | 2470 |
| | —— |
| | Total 4906 |
It therefore appears that while Ireland grows only about one-thirty-third
the quantity of apples that England does, it is nevertheless
nearly 5000 acres ahead of Scotland and about 2000 acres ahead of
Wales. It grows 41 times fewer pears than England, but still is
ahead of Scotland and a long way ahead of Wales in this fruit.
There are 70 times fewer plums grown in Ireland than in England,
and about the same in Scotland, while Wales does very little indeed.
In small fruit Ireland is a long way behind Scotland in the culture
of strawberries and raspberries, although with currants and gooseberries
it is very close. Considering the climate, and the fact that
there are, according to the latest available returns, over 62,000
holdings above 1 acre but not exceeding 5 acres (having a total of
224,000 acres), it is possible fruit culture may become more prevalent
than it has been in the past.
The Flower-growing Industry.—During the last two or three
decades of the 19th century a very marked increase in flower
production occurred in England. Notably was this the case in
the neighbourhood of London, where, within a radius of 15 or
20 m., the fruit crops, which had largely taken the place of garden
vegetables, were themselves ousted in turn to satisfy the increasing
demand for land for flower cultivation. No flower has entered
more largely into the development of the industry than the
narcissus or daffodil, of which there are now some 600 varieties.
Comparatively few of these, however, are grown for market
purposes, although all are charming from the amateur point of
view. On some flower farms a dozen or more acres are devoted
to narcissi alone, the production of bulbs for sale as well as of
flowers for market being the object of the growers.
In the London district the country in the Thames valley west
of the metropolis is as largely occupied by flower farms as it is
by fruit farms—in fact, the cultivation of flowers is commonly
associated with that of fruit. In the vicinity of Richmond
narcissi are extensively grown, as they also are more to the west
in the Long Ditton district, and likewise around Twickenham,
Isleworth, Hounslow, Feltham and Hampton. Roses come more
into evidence in the neighbourhood of Hounslow, Cranford,
266
Hillingdon and Uxbridge, and in some gardens daffodils and
roses occupy alternate rows. In this district also such flowers
as herbaceous paeonies, Spanish irises, German irises, Christmas
roses, lilies of the valley, chrysanthemums, foxgloves, hollyhocks,
wallflowers, carnations, &c., are extensively grown in
many market gardens. South of London is the Mitcham country,
long noted for its production of lavender. The incessant growth
of the lavender plant upon the same land, however, has led to
the decline of this industry, which has been largely transferred
to districts in the counties of Bedford, Essex and Hertford. At
Mitcham, nevertheless, mixed flowers are very largely grown
for the supply of the metropolis, and one farm alone has nearly
100 acres under flowers and glass-houses. Chrysanthemums,
asters, Iceland poppies, gaillardias, pansies, bedding calceolarias,
zonal pelargoniums and other plants are cultivated in immense
quantities. At Swanley and Eynsford, in Kent, flowers are
extensively cultivated in association with fruit and vegetables.
Narcissi, chrysanthemums, violets, carnations, campanulas,
roses, pansies, irises, sweet peas, and many other flowers are here
raised, and disposed of in the form both of cut flowers and of
plants.
The Scilly Isles are important as providing the main source
of supply of narcissi to the English markets in the early months
of the year. This trade arose almost by accident, for it was
about the year 1865 that a box of narcissi sent to Covent Garden
Market, London, realized £1; and the knowledge of this fact
getting abroad, the farmers of the isles began collecting wild
bulbs from the fields in order to cultivate them and increase their
stocks. Some ten years, however, elapsed before the industry
promised to become remunerative. In 1885 a Bulb and Flower
Association was established to promote the industrial growth
of flowers. The exports of flowers in that year reached 65 tons,
and they steadily increased until 1893, when they amounted
to 450 tons. A slight decline followed, but in 1896 the quantity
exported was no less than 514 tons. This would represent
upwards of 3½ million bunches of flowers, chiefly narcissi and
anemones. Rather more than 500 acres are devoted to flower-growing
in the isles, by far the greater part of this area being
assigned to narcissi, whilst anemones, gladioli, marguerites,
arum lilies, Spanish irises, pinks and wallflowers are cultivated
on a much smaller scale. The great advantage enjoyed by the
Scilly flower-growers is earliness of production, due to climatic
causes; the soil, moreover, is well suited to flower culture and
there is an abundance of sunshine. The long journey to London
is somewhat of a drawback, in regard to both time and freight,
but the earliness of the flowers more than compensates for this.
Open-air narcissi are usually ready at the beginning of January,
and the supply is maintained in different varieties up to the
middle or end of May. The narcissus bulbs are usually planted
in October, 4 in. by 3 in. apart for the smaller sorts and 6 in.
by 4 to 6 in. for the larger. A compost of farmyard manure,
seaweed, earth and road scrapings is the usual dressing, but
nitrate of soda, guano and bones are also occasionally employed.
A better plan, perhaps, is to manure heavily the previous crop,
frequently potatoes, no direct manuring then being needed for
the bulbs, these not being left in the ground more than two or
three years. The expenses of cultivation are heavy, the cost
of bulbs alone—of which it requires nearly a quarter of a million
of the smaller varieties, or half as many of the largest, to plant
an acre—being considerable. The polyanthus varieties of
narcissus are likely to continue the most remunerative to the
flower-growers of Scilly, as they flourish better in these isles
than on the mainland.
In the district around the Wash, in the vicinity of such towns
as Wisbech, Spalding and Boston, the industrial culture of bulbs
and flowers underwent great expansion in the period between
1880 and 1909. At Wisbech one concern alone has a farm of
some 900 acres, devoted chiefly to flowers and fruit, the soil
being a deep fine alluvium. Roses are grown here, one field
containing upwards of 100,000 trees. Nearly 20 acres are
devoted to narcissi, which are grown for the bulbs and also,
together with tulips, for cut flowers. Carnations are cultivated
both in the field and in pots. Cut flowers are sent out in large
quantities, neatly and effectively packed, the parcel post being
mainly employed as a means of distribution. In the neighbourhood
of Spalding crocuses and snowdrops are less extensively
grown than used to be the case. On one farm, however, upwards
of 20 acres are devoted to narcissi alone, whilst gladioli, lilies
and irises are grown on a smaller scale. Around Boston narcissi
are also extensively grown for the market, both bulbs and cut
blooms being sold. The bulbs are planted 3 in. apart in rows, the
latter being 9 in. apart, and are allowed to stand from two to
four years.
The imports of fresh flowers into the United Kingdom were not
separately shown prior to 1900. In that year, however, their value
amounted to £200,585, in 1901 to £225,011, in 1906 to £233,884, in
1907 to £233,641, and in 1908 to £229,802, so that the trade showed
a fairly steady condition. From the monthly totals quoted in
Table VI. it would appear that the trade sinks to its minimum
dimensions in the four months July to October inclusive, and that
after September the business continually expands up to April,
subsequent to which contraction again sets in. About one-half of
the trade belongs practically to the three months of February,
March and April.
Table VI.—Values of Fresh Flowers imported into the United
Kingdom.
| Month. | 1906. | 1907. | 1908. |
| January | £31,035 | £18,545 | £29,180 |
| February | 34,647 | 25,541 | 30,541 |
| March | 50,232 | 42,611 | 35,185 |
| April | 30,809 | 50,418 | 42,681 |
| May | 22,980 | 21,767 | 23,129 |
| June | 17,641 | 18,358 | 16,904 |
| July | 3,386 | 4,509 | 3,467 |
| August | 1,646 | 1,539 | 1,081 |
| September | 852 | 736 | 953 |
| October | 4,481 | 3,180 | 4,504 |
| November | 17,506 | 15,763 | 15,097 |
| December | 18,669 | 30,674 | 27,080 |
| Total | £233,884 | £233,641 | £229,802 |
Hothouse Culture of Fruit and Flowers.—The cultivation
of fruit and flowers under glass has increased enormously
since about the year 1880, especially in the neighbourhood
of London, where large sums of money have been sunk in the
erection and equipment of hothouses. In the parish of Cheshunt,
Herts, alone there are upwards of 130 acres covered with glass,
and between that place on the north and London on the south
extensive areas of land are similarly utilized. In Middlesex,
in the north, in the districts of Edmonton, Enfield, Ponders End
and Finchley, and in the west from Isleworth to Hampton,
Feltham, Hillingdon, Sipson and Uxbridge, many crops are now
cultivated under glass. At Erith, Swanley, and other places in
Kent, as also at Worthing, in Sussex, glass-house culture has
much extended. A careful estimate puts the area of industrial
hothouses in England at about 1200 acres, but it is probably
much more than this. Most of the greenhouses are fixtures,
but in some parts of the kingdom structures that move on rails
and wheels are used, to enable the ground to be prepared in the
open for one crop while another is maturing under glass. The
leading products are grapes, tomatoes and cucumbers, the last-named
two being true fruits from the botanist’s point of view,
though commercially included with vegetables. To these may
be added on the same ground dwarf or French beans, and runner
or climbing beans. Peaches, nectarines and strawberries are
largely grown under glass, and, in private hothouses—from
which the produce is used mainly for household consumption,
and which are not taken into consideration here—pineapples,
figs and other fruit. Conservative estimates indicate the average
annual yield of hothouse grapes to be about 12 tons per acre and
of tomatoes 20 tons. The greater part of the space in the hothouses
is assigned to fruit, but whilst some houses are devoted
exclusively to flowers, in others, where fruit is the main
object, flowers are forced in considerable quantities in winter
and early spring. The flowers grown under glass include tulips,
hyacinths, primulas, cyclamens, spiraeas, mignonettes, fuchsias,
267
calceolarias, roses, chrysanthemums, daffodils, arum lilies or
callas, liliums, azaleas, eucharises, camellias, stephanotis,
tuberoses, bouvardias, gardenias, heaths or ericas, poinsettias,
lilies of the valley, zonal pelargoniums, tuberous and fibrous rooted
begonias, and many others. There is an increasing demand for
foliage hothouse plants, such as ferns, palms, crotons, aspidistras,
araucarias, dracaenas, India-rubber plants, aralias, grevilleas,
&c. Berried plants like solanums and aucubas also find a ready
sale, while the ornamental kinds of asparagus such as sprengeri
and plumosus nanus, are ever in demand for trailing decorations,
as well as myrsiphyilum. Special mention must be made of the
winter or perpetual flowering carnations which are now grown
by hundreds of thousands in all parts of the kingdom for
decorative work during the winter season. The converse of
forcing plants into early blossom is adopted with such an important
crop as lily of the valley. During the summer season the
crowns are placed in refrigerators with about 2 degrees of frost,
and quantities are taken out as required every week and transferred
to the greenhouse to develop. Tomatoes are grown
largely in houses exclusively occupied by them, in which case two
and sometimes three crops can be gathered in the year. In the
Channel Islands, where potatoes grown under glass are lifted
in April and May, in order to secure the high prices of the early
markets, tomato seedlings are planted out from boxes into the
ground as quickly as the potatoes are removed, the tomato
planter working only a few rows behind the potato digger.
The trade in imported tomatoes is so considerable that home
growers are well justified in their endeavours to meet the demand
more fully with native produce, whether raised under glass or
in the open. Tomatoes were not separately enumerated in the
imports previous to 1900. It has already been stated that in
1900 the raw tomatoes imported amounted to 833,032 cwt.,
valued at £792,339, and in 1901 to 793,991 cwt., valued at
£734,051. From the monthly quantities given in Table VII.,
it would appear that the imports are largest in June, July and
August, about one-half of the year’s total arriving during those
three months. It is too early in June and July for home-grown
outdoor tomatoes to enter into competition with the imported
product, but home-grown hothouse tomatoes should be qualified
to challenge this trade.
Table VII.—Quantities of Tomatoes imported into the United
Kingdom.
| Month. | 1906. | 1907. | 1908. |
| January | 61,940 | 56,022 | 73,409 |
| February | 58,187 | 58,289 | 69,350 |
| March | 106,458 | 98,028 | 86,928 |
| April | 103,273 | 109,057 | 74,917 |
| May | 67,933 | 114,041 | 88,901 |
| June | 62,906 | 144,379 | 127,793 |
| July | 238,362 | 150,907 | 171,978 |
| August | 180,046 | 102,600 | 124,757 |
| September | 114,860 | 101,198 | 119,224 |
| October | 52,678 | 67,860 | 75,722 |
| November | 41,513 | 66,522 | 74,292 |
| December | 36,316 | 66,591 | 73,012 |
| Total | 1,124,472 | 1,135,494 | 1,160,283 |
| Value | £953,475 | £1,135,499 | £1,160,283 |
An important feature of modern flower growing is the production
and cultivation of what are known as “hardy herbaceous
perennials.” Some 2000 or 3000 different species and varieties
of these are now raised in special nurseries; and during the
spring, summer and autumn seasons magnificent displays are
to be seen not only in the markets but at the exhibitions in
London and at the great provincial shows held throughout the
kingdom. The production of many of these perennials is so
easy that amateurs in several instances have taken it up as a
business hobby; and in some cases, chiefly through advertising
in the horticultural press, very lucrative concerns have been
established.
Ornamental flowering trees and shrubs constitute another
feature of modern gardening. These are grown and imported
by thousands chiefly for their sprays of blossom or foliage, and
for planting in large or small gardens, public parks, &c., for
landscape effect. Indeed there is scarcely an easily grown plant
from the northern or southern temperate zones that does not now
find a place in the nursery or garden, provided it is sufficiently
attractive to sell for its flowers, foliage or appearance.
Conditions of the Fruit and Flower growing Industries.—As
regards open-air fruit-growing, the outlook for new ventures is
perhaps brighter than in the hothouse industry, not—as Mr
Bear has pointed out—because the area of fruit land in England
is too small, but because the level of efficiency, from the selection
of varieties to the packing and marketing of the produce, is very
much lower in the former than in the latter branch of enterprise.
In other words, whereas the practice of the majority of hothouse
nurserymen is so skilled, so up-to-date, and so entirely under high
pressure that a new competitor, however well trained, will find
it difficult to rise above mediocrity, the converse is true of open-air
fruit-growers. Many, and an increasing proportion, of the
latter are thoroughly efficient in all branches of their business,
and are in possession of plantations of the best market varieties
of fruit, well cultivated, pruned and otherwise managed. But
the extent of fruit plantations completely up to the mark in
relation to varieties and treatment of trees and bushes, and in
connexion with which the packing and marketing of the produce
are equally satisfactory, is small in proportion to the total fruit
area of the country. Information concerning the best treatment
of fruit trees has spread widely in recent years, and old plantations,
as a rule, suffer from the neglect or errors of the past,
however skilful their present holders may be. Although the
majority of professional market fruit-growers may be well up
to the standard in skill, there are numerous contributors to
the fruit supply who are either ignorant of the best methods
of cultivation and marketing or careless in their application.
The bad condition of the great majority of farm orchards is
notorious, and many landowners, farmers and amateur gardeners
who have planted fruit on a more or less extensive scale have
mismanaged their undertakings. For these reasons new growers
of open-air fruit for market have opportunities of succeeding by
means of superiority to the majority of those with whom they
will compete, provided that they possess the requisite knowledge,
energy and capital. It has been asserted on sound authority
that there is no chance of success for fruit-growers except in
districts favourable as regards soil, climate and nearness to a
railway or a good market; and, even under these conditions,
only for men who have had experience in the industry and are
prepared to devote their unremitting attention to it. Most
important is it to a beginner that he should ascertain the varieties
of fruit that flourish best in his particular district. Certain kinds
seem to do well or fairly well in all parts of the country; others,
whilst heavy croppers in some localities, are often unsatisfactory
in others.
As has been intimated, there is probably in England less room
for expansion of fruit culture under glass than in the open.
The large increase of glass-houses in modern times appears to
have brought the supply of hothouse produce, even at greatly
reduced prices, at least up to the level of the demand; and as
most nurserymen continue to extend their expanse of glass,
the prospect for new competitors is not a bright one. Moreover,
the vast scale upon which some of the growers conduct the
hothouse industry puts small producers at a great disadvantage,
not only because the extensive producers can grow grapes and
other fruit more economically than small growers—with the
possible exception of those who do all or nearly all their own
work—but also, and still more, because the former have greater
advantages in transporting and marketing their fruit. There has,
in recent years, been a much greater fall in the prices of hothouse
than of open-air fruit, especially under the existing system of
distribution, which involves the payment by consumers of 50
to 100% more in prices than growers receive. The best openings
for new nurseries are probably not where they are now to be
found in large groups, and especially not in the neighbourhood
268
of London, but in suitable spots near the great centres of population
in the Midlands and the North, or big towns elsewhere not
already well supplied with nurseries. By such a selection of a
locality the beginner may build up a retail trade in hothouse
fruit, or at least a trade with local fruiterers and grocers, thus
avoiding railway charges and salesmen’s commissions to a great
extent, though it may often be advantageous to send certain
kinds of produce to a distant market. Above all, a man who has
no knowledge of the hothouse industry should avoid embarking
his capital in it, trusting himself in the hands of a foreman, as
experience shows that such a venture usually leads to disaster.
Some years of training in different nurseries are desirable for
any young man who is desirous of becoming a grower of hothouse
fruits or flowers.
There can be no doubt that flower-growing is greatly extending
in England, and that competition among home growers is becoming
more severe. Foreign supplies of flowers have increased,
but not nearly as greatly in proportion as home supplies, and it
seems clear that home growers have gained ground in relation
to their foreign rivals, except with respect to flowers for the
growth of which foreigners have extraordinary natural advantages.
There seems some danger of the home culture of the narcissus
being over-done, and the florists’ chrysanthemum appears to
be produced in excess of the demand. Again, in the production
of violets the warm and sunny South of France has an advantage
not possessed by England, whilst Holland, likewise for climatic
reasons, maintains her hold upon the hyacinth and tulip trade.
Whether the production of flowers as a whole is gaining ground
upon the demand or not is a difficult question to answer. It is
true that the prices of flowers have fallen generally; but production,
at any rate under glass, has been cheapened, and if a fair
profit can be obtained, the fall in prices, without which the
existing consumption of flowers would be impossible, does not
necessarily imply over-production. There is some difference of
opinion among growers upon this point; but nearly all agree
that profits are now so small that production on a large scale is
necessary to provide a fair income. Industrial flower-growing
affords such a wide scope for the exercise of superior skill,
industry and alertness, that it is not surprising to find some
who are engaged in it doing remarkably well to all appearance,
while others are struggling on and hardly paying their way.
That a man with only a little capital, starting in a small way,
has many disadvantages is certain; also, that his chance of
saving money and extending his business quickly is much
smaller than it was. To the casual looker-on, who knows
nothing of the drudgery of the industry, flower-growing seems a
delightful method of getting a living. That it is an entrancing
pursuit there is no doubt; but it is equally true that it is a very
arduous one, requiring careful forethought, ceaseless attention
and abundant energy. Fortunately for those who might be
tempted, without any knowledge of the industry, to embark
capital in it, flower-growing, if at all comprehensive in scope, so
obviously requires a varied and extensive technical knowledge,
combined with good commercial ability, that any one can see
that a thorough training is necessary to a man who intends to
adopt it as a business, especially if hothouse flowers are to be
produced.
The market for fruit, and more especially for flowers, is a fickle
one, and there is nearly always some uncertainty as to the course
of prices. The perishable nature of soft fruit and cut flowers renders
the markets very sensitive to anything in the nature of a glut, the
occurrence of which is usually attended with disastrous results to
producers. Foreign competition, moreover, has constantly to be
faced, and it is likely to increase rather than diminish. French
growers have a great advantage over the open-air cultivators of
England, for the climate enables them to get their produce into the
markets early in the season, when the highest prices are obtainable.
The geographical advantage which France enjoys in being so near
to England is, however, considerably discounted by the increasing
facilities for cold storage in transit, both by rail and sea. The development
of such facilities permits of the retail sale in England of luscious
fruit as fresh and attractive as when it was gathered beneath the
sunny skies of California. In the case of flowers, fashion is an
element not to be ignored. Flowers much in request in one season
may meet with very little demand in another, and it is difficult
for the producer to anticipate the changes which caprice may dictate.
Even for the same kind of flower the requirements are very uncertain,
and the white blossom which is all the rage in one season may be
discarded in favour of one of another colour in the next. The sale
of fresh flowers for church decoration at Christmas and Easter has
reached enormous dimensions. The irregularity in the date of the
festival, however, causes some inconvenience to growers. If it falls
very early the great bulk of suitable flowers may not be sufficiently
forward for sale, whilst a late Easter may find the season too far
advanced. The trade in cut flowers, therefore, is generally attended
by uncertainty, and often by anxiety.
(W. Fr.; J. Ws.)
United States
In the United States horticulture and market gardening have
now assumed immense proportions. In a country of over
3,000,000 sq. m., stretching from the Atlantic to the Pacific
on the one hand, and from the Gulf of Mexico to the great
northern lakes and the Dominion of Canada on the other, a
great variation of climatic conditions is not unnatural. From a
horticultural point of view there are practically two well-defined
regions: (1) that to the east of the Rocky Mountains across
to the Atlantic, where the climate is more like that of eastern
Asia than of western Europe so far as rainfall, temperature and
seasonable conditions are concerned; (2) that to the west of the
Rockies, known as the Pacific coast region, where the climate
is somewhat similar to that of western Europe. It may be added
that in the northern states—in Washington, Montana, North
Dakota, Minnesota, Wisconsin, &c.—the winters are often very
severe, while the southern states practically enjoy a temperature
somewhat similar to that of the Riviera. Indeed the range of
temperature between the extreme northern states and the
extreme southern may vary as much as 120° F. The great aim
of American gardeners, therefore, has been to find out or to
produce the kinds of fruits, flowers and vegetables that are
likely to flourish in different parts of this immense country.
Fruit Culture.—There is probably no country in the world
where so many different kinds of fruit can be grown with advantage
to the nation as in the United States. In the temperate
regions apples, pears and plums are largely grown, and orchards
of these are chiefly to be found in the states of New York,
Massachusetts, Pennsylvania, Michigan, Missouri, Colorado,
and also in northern Texas, Arkansas and N. California. To
these may be added cranberries and quinces, which are chiefly
grown in the New England states. The quinces are not a crop
of first-rate importance, but as much as 800,000 bushels of
cranberries are grown each year. The peach orchards are
assuming great proportions, and are chiefly to be found in
Georgia and Texas, while grapes are grown throughout the
Republic from east to west in all favourable localities. Oranges,
lemons and citrons are more or less extensively grown in Florida
and California, and in these regions what are known as Japanese
or “Kelsey” plums (forms of Prunus triflora) are also grown
as marketable crops. Pomegranates are not yet largely grown,
but it is possible their culture will develop in southern Texas
and Louisiana, where the climate is tempered by the waters of
the Gulf of Mexico. Tomatoes are grown in most parts of the
country so easily that there is frequently a glut; while the
strawberry region extends from Florida to Virginia, Pennsylvania
and other states—thus securing a natural succession from south
to north for the various great market centres.
Of the fruits mentioned apples are undoubtedly the most
important. Not only are the American people themselves
supplied with fresh fruit, but immense quantities are exported
to Europe—Great Britain alone absorbing as much as 1,430,000
cwt. in 1908. The varieties originally grown were of course
those taken or introduced from Europe by the early settlers.
Since the middle of the 19th century great changes have been
brought about, and the varieties mostly cultivated now are
distinctly American. They have been raised by crossing and
intercrossing the most suitable European forms with others
since imported from Russia. In the extreme northern states
indeed, where it is essential to have apple trees that will stand
the severest winters, the Russian varieties crossed with the
berry crab of eastern Europe (Pyrus baccata) have produced
269
a race eminently suited to that particular region. The individual
fruits are not very large, but the trees are remarkably hardy.
Farther south larger fruited varieties are grown, and among
these may be noted Baldwins, Newton pippins, Spitzenbergs
and Rhode Island greening. Apple orchards are numerous
in the State of New York, where it is estimated that over 100,000
acres are devoted to them. In the hilly regions of Missouri,
Arkansas and Colorado there are also great plantations of apples.
The trees, however, are grown on different principles from those
in New York State. In the latter state apple trees with ordinary
care live to more than 100 years of age and produce great crops;
in the other states, however, an apple tree is said to be middle-aged
at 20, decrepit at 30 and practically useless at 40 years of
age. They possess the advantage, however, of bearing early and
heavily.
Until the introduction of the cold-storage system, about the
year 1880, America could hardly be regarded as a commercial
fruit-growing country. Since then, however, owing to the
great improvements made in railway refrigerating vans and
storage houses, immense quantities of fruit can be despatched
in good condition to any part of the world; or they can be kept
at home in safety until such time as the markets of Chicago,
New York, Boston, Baltimore, Philadelphia, &c., are considered
favourable for their reception.
Apple trees are planted at distances varying from 25 ft. to
30 ft. apart in the middle western states, to 40 ft. to 50 ft. apart
in New York State. Here and there, however, in some of the
very best orchards the trees are planted 60 ft. apart every way.
Each tree thus has a chance to develop to its utmost limits, and
as air and light reach it better, a far larger fruit-bearing surface
is secured. Actual experience has shown that trees planted at
60 ft. apart—about 28 to the acre—produce more fruit by 43
bushels than trees at 30 ft. apart—i.e. about 48 to the acre.
Until recent years pruning as known to English and French
gardeners was practically unknown. There was indeed no great
necessity for it, as the trees, not being cramped for space, threw
their branches outwards and upwards, and thus rarely become
overcrowded. When practised, however, the operation could
scarcely be called pruning; lopping or trimming would be more
accurate descriptions.
Apple orchards are not immune from insect pests and fungoid
diseases, and an enormous business is now done in spraying
machines and various insecticides. It pays to spray the trees,
and figures have been given to show that orchards that have
been sprayed four times have produced an average income of
£211 per acre against £103 per acre from unsprayed orchards.
The spring frosts are also troublesome, and in the Colorado
and other orchards the process known as “smudging” is now
adopted to save the crops. This consists in placing 20 or 30,
or even more, iron or tin pots to an acre, each pot containing
wooden chips soaked in tar (or pitch) mixed with kerosene.
Whenever the thermometer shows 3 or 4 degrees of frost the
smudge-pots are lighted. A dense white smoke then arises and
is diffused throughout the orchards, enveloping the blossoming
heads of the trees in a dense cloud. This prevents the frost
from killing the tender pistils in the blossoms, and when several
smudge-pots are alight at the same time the temperature of the
orchard is raised two or three degrees. This work has generally
to be done between 3 and 5 A.M., and the growers naturally
have an anxious time until all danger is over. The failure to
attend to smudging, even on one occasion, may result in the
loss of the entire crop of plums, apples or pears.
Next to apples perhaps peaches are the most important fruit
crop. The industry is chiefly carried on in Georgia, Texas
and S. Carolina, and on a smaller scale in some of the adjoining
states. Peaches thus flourish in regions that are quite unsuitable
for apples or pears. In many orchards in Georgia,
where over 3,000,000 acres have been planted, there are as
many as 100,000 peach trees; while some of the large fruit
companies grow as many as 365,000. In one place in West
Virginia there is, however, a peach orchard containing 175,000
trees, and in Missouri another company has 3 sq. m. devoted
to peach culture. As a rule the crops do well. Sometimes,
however, a disease known as the “yellows” makes sad havoc
amongst them, and scarcely a fruit is picked in an orchard which
early in the season gave promise of a magnificent crop.
Plums are an important crop in many states. Besides the
European varieties and those that have been raised by crossing
with American forms, there is now a growing trade done in
Japanese plums. The largest of these is popularly known as
“Kelseys,” named after John Kelsey, who raised the first fruit
in 1876 from trees brought to California in 1870. Sometimes the
fruits are 3 in. in diameter, and like most of the Japanese
varieties are more heart-shaped and pointed than plums of
European origin. One apparent drawback to the Kelsey plum
is its irregularity in ripening. It has been known in some years
to be quite ripe in June, while in others the fruits are still green
in October.
Pears are much grown in such states as Massachusetts, New
York, Pennsylvania, Missouri and California; while bush fruits
like currants, gooseberries and raspberries find large spaces
devoted in most of the middle and northern states. Naturally a
good deal of crossing and intercrossing has taken place amongst
the European and American forms of these fruits, but so far as
gooseberries are concerned no great advance seems to have been
made in securing varieties capable of resisting the devastating
gooseberry mildew.
Other fruits of more or less commercial value are oranges,
lemons and citrons, chiefly in Florida. Lemons are practically a
necessity to the American people, owing to the heat of the
summers, when cool and refreshing drinks with an agreeable
acidulous taste are in great demand. The pomelo (grape-fruit)
is a kind of lemon with a thicker rind and a more acid flavour.
At one time its culture was confined to Florida, but of recent
years it has found its way into Californian orchards. Notwithstanding
the prevailing mildness of the climate in both California
and Florida, the crops of oranges, lemons, citrons, &c., are
sometimes severely injured by frosts when in blossom.
Other fruits likely to be heard of in the future are the kaki
or persimmon, the loquat, which is already grown in Louisiana,
as well as the pomegranate.
Great aid and encouragement are given by the government to
the progress of American fruit-growing, and by the experiments
that are being constantly carried out and tabulated at Cornell
University and by the U.S.A. department of agriculture.
Flower Culture.—So far as flowers are concerned there appears
to be little difference between the kinds of plants grown in the
United States and in England, France, Belgium, Germany,
Holland, &c. Indeed there is a great interchange of new varieties
of plants between Europe and America, and modifications in
systems of culture are being gradually introduced from one side
of the Atlantic to the other. The building of greenhouses for
commercial purposes is perhaps on a somewhat different scale
from that in England, but there are probably no extensive
areas of glass such as are to be seen north of London from
Enfield Highway to Broxburne. Hot water apparatus differs
merely in detail, although most of the boilers used resemble
those on the continent of Europe rather than in England. Great
business is done in bulbs—mostly imported from Holland—stove
and greenhouse plants, hardy perennials, orchids, ferns of the
“fancy” and “dagger” types of Nephrolepis, and in carnations
and roses. Amongst the latter thousands of such varieties as
Beauty, Liberty, Killarney, Richmond and Bride are grown,
and realize good prices as a rule in the markets. Carnations
of the winter-flowering or “perpetual” type have long been
grown in America, and enormous prices have been given for
individual plants on certain occasions, rivalling the fancy prices
paid in England for certain orchids. The American system of
carnation-growing has quite captivated English cultivators,
and new varieties are being constantly raised in both countries.
Chrysanthemums are another great feature of American florists,
and sometimes during the winter season a speculative grower
will send a living specimen to one of the London exhibitions in
the hope of booking large orders for cuttings of it later on. Sweet
270
peas, dahlias, lilies of the valley, arum lilies and indeed every
flower that is popular in England is equally popular in America,
and consequently is largely grown.
Vegetables.—So far as these are concerned, potatoes, cabbages,
cauliflowers, beans of all kinds, cucumbers, tomatoes (already
referred to under fruits), musk-melons, lettuces, radishes, endives,
carrots, &c.; are naturally grown in great quantities, not only in the
open air, but also under glass. The French system of intensive
cultivation as practised on hot beds of manure round Paris is practically
unknown at present. In the southern states there would be
no necessity to practise it, but in the northern ones it is likely to
attract attention.
(J. Ws.)
1 Jour. Roy. Agric. Soc., 1899.
FRUMENTIUS (c. 300-c. 360), the founder of the Abyssinian
church, traditionally identified in Abyssinian literature with
Abba Salama or Father of Peace (but see Ethiopia), was a
native of Phoenicia. According to the 4th-century historian
Rufinus (x. 9), who gives Aedesius himself as his authority, a
certain Tyrian, Meropius, accompanied by his kinsmen Frumentius
and Aedesius, set out on an expedition to “India,”
but fell into the hands of Ethiopians on the shore of the Red Sea
and, with his ship’s crew, was put to death. The two young men
were taken to the king at Axum, where they were well treated
and in time obtained great influence. With the help of Christian
merchants who visited the country Frumentius gave Christianity
a firm footing, which was strengthened when in 326 he was
consecrated bishop by Athanasius of Alexandria, who in his
Epistola ad Constantinum mentions the consecration, and gives
some details of the history of Frumentius’s mission. Later
witnesses speak of his fidelity to the homoousian during the
Arian controversies. Aedesius returned to Tyre, where he was
ordained presbyter.
FRUNDSBERG, GEORG VON (1473-1528), German soldier,
was born at Mindelheim on the 24th of September 1473. He
fought for the German king Maximilian I. against the Swiss
in 1499, and in the same year was among the imperial troops
sent to assist Ludovico Sforza, duke of Milan, against the French.
Still serving Maximilian, he took part in 1504 in the war over
the succession to the duchy of Bavaria-Landshut, and afterwards
fought in the Netherlands. Convinced of the necessity
of a native body of trained infantry Frundsberg assisted Maximilian
to organize the Landsknechte (q.v.), and subsequently at
the head of bands of these formidable troops he was of great
service to the Empire and the Habsburgs. In 1509 he shared in
the war against Venice, winning fame for himself and his men;
and after a short visit to Germany returned to Italy, where
in 1513 and 1514 he gained fresh laurels by his enterprises
against the Venetians and the French. Peace being made, he
returned to Germany, and at the head of the infantry of the
Swabian league assisted to drive Ulrich of Württemberg from
his duchy in 1519. At the diet of Worms in 1521 he spoke words
of encouragement to Luther, and when the struggle between
France and the Empire was renewed he took part in the invasion
of Picardy, and then proceeding to Italy brought the greater
part of Lombardy under the influence of Charles V. through his
victory at Bicocca in April 1522. He was partly responsible for
the great victory over the French at Pavia in February 1525, and,
returning to Germany, he assisted to suppress the Peasant revolt,
using on this occasion, however, diplomacy as well as force.
When the war in Italy was renewed Frundsberg raised an army
at his own expense, and skilfully surmounting many difficulties,
joined the constable de Bourbon near Piacenza and marched
towards Rome. Before he reached the city, however, his unpaid
troops showed signs of mutiny, and their leader, stricken with
illness and unable to pacify them, gave up his command.
Returning to Germany, he died at Mindelheim on the 20th of
August 1528. He was a capable and chivalrous soldier, and a
devoted servant of the Habsburgs. His son Caspar (1500-1536)
and his grandson Georg (d. 1586) were both soldiers of some
distinction. With the latter’s death the family became extinct.
See Adam Reissner, Historia Herrn Georgs und Herrn Kaspars
von Frundsberg (Frankfort, 1568). A German translation of this
work was published at Frankfort in 1572. F.W. Barthold, Georg
von Frundsberg (Hamburg, 1833); J. Heilmann, Kriegsgeschichte
von Bayern, Franken, Pfalz und Schwaben (Munich, 1868).
FRUSTUM (Latin for a “piece broken off”), a term in geometry
for the part of a solid figure, such as a cone or pyramid,
cut off by a plane parallel to the base, or lying between two
parallel planes; and hence in architecture a name given to the
drum of a column.
FRUYTIERS, PHILIP (1627-1666), Flemish painter and
engraver, was a pupil of the Jesuits’ college at Antwerp in 1627,
and entered the Antwerp gild of painters without a fee in 1631.
He is described in the register of that institution as “illuminator,
painter and engraver.” The current account of his life is “that
he worked exclusively in water colours, yet was so remarkable
in this branch of his art for arrangement, drawing, and especially
for force and clearness of colour, as to excite the admiration of
Rubens, whom he portrayed with all his family.” The truth
is that he was an artist of the most versatile talents, as may be
judged from the fact that in 1646 he executed an Assumption
with figures of life size, and four smaller pictures in oil, for the
church of St Jacques at Antwerp, for which he received the
considerable sum of 1150 florins. Unhappily no undoubted
production of his hand has been preserved. All that we can
point to with certainty is a series of etched plates, chiefly portraits,
which are acknowledged to have been powerfully and
skilfully handled. If, however, we search the portfolios of art
collections on the European continent, we sometimes stumble
upon miniatures on vellum, drawn with great talent and
coloured with extraordinary brilliancy. In form they quite
recall the works of Rubens, and these, it may be, are the work
of Philip Fruytiers.
FRY, the name of a well-known English Quaker family,
originally living in Wiltshire. About the middle of the 18th
century Joseph Fry (1728-1787), a doctor, settled in Bristol,
where he acquired a large practice, but eventually abandoned
medicine for commerce. He became interested in china-making,
soap-boiling and type-founding businesses in Bristol, and in a
chemical works at Battersea, all of which ventures proved very
profitable. The type-founding business was subsequently removed
to London and conducted by his son Edmund. Joseph
Fry, however, is best remembered as the founder of the great
Bristol firm of J.S. Fry & Sons, chocolate manufacturers.
He purchased the chocolate-making patent of William Churchman
and on it laid the foundations of the present large business.
After his death the Bristol chocolate factory was carried on with
increasing success by his widow and by his son, Joseph Storrs
Fry (1767-1835).
In 1795 a new and larger factory was built in Union Street,
Bristol, which still forms the centre of the firm’s premises, and
in 1798 a Watt’s steam-engine was purchased and the cocoa-beans
ground by steam. On the death of Joseph Storrs Fry his
three sons, Joseph (1795-1879), Francis, and Richard (1807-1878)
became partners in the firm, the control being mainly in the
hands of Francis Fry (1803-1886). Francis Fry was in every
way a remarkable character. The development of the business
to its modern enormous proportion was chiefly his work, but
this did not exhaust his activities. He took a principal part in
the introduction of railways to the west of England, and in 1852
drew up a scheme for a general English railway parcel service.
He was an ardent bibliographer, taking a special interest in
early English Bibles, of which he made in the course of a long
life a large and striking collection, and of the most celebrated
of which he published facsimiles with bibliographical notes.
Francis Fry died in 1886, and his son Francis J. Fry and nephew
Joseph Storrs Fry carried on the business, which in 1896 was
for family reasons converted into a private limited company,
Joseph Storrs Fry being chairman and all the directors members
of the Fry family.
FRY, SIR EDWARD (1827- ), English judge, second son
of Joseph Fry (1795-1879), was born at Bristol on the 4th of
November 1827, and educated at University College, London,
and London University. He was called to the bar in 1854 and
was made a Q.C. in 1869, practising in the rolls court and becoming
recognized as a leading equity lawyer. In 1877 he was raised
to the bench and knighted. As chancery judge he will be
271
remembered for his careful interpretations and elucidations of
the Judicature Acts, then first coming into operation. In 1883
he was made a lord justice of appeal, but resigned in 1892; and
subsequently his knowledge of equity and talents for arbitration
were utilized by the British government from time to time in
various special directions, particularly as chairman of many
commissions. He was also one of the British representatives
at the Paris North Sea Inquiry Commission (1905), and was
appointed a member of the Hague Permanent Arbitration Court.
He wrote A Treatise on the Specific Performance of Public Contracts
(London, 1858, and many subsequent editions).
FRY, ELIZABETH (1780-1845), English philanthropist, and,
after Howard, the chief promoter of prison reform in Europe,
was born in Norwich on the 21st of May 1780. Her father,
John Gurney, afterwards of Earlham Hall, a wealthy merchant
and banker, represented an old family which for some generations
had belonged to the Society of Friends. While still a girl she
gave many indications of the benevolence of disposition, clearness
and independence of judgment, and strength of purpose, for which
she was afterwards so distinguished; but it was not until after
she had entered her eighteenth year that her religion assumed
a decided character, and that she was induced, under the preaching
of the American Quaker, William Savery, to become an earnest
and enthusiastic though never fanatical “Friend.” In August
1800 she became the wife of Joseph Fry, a London merchant.
Amid increasing family cares she was unwearied in her attention
to the poor and the neglected of her neighbourhood; and in
1811 she was acknowledged by her co-religionists as a “minister,”
an honour and responsibility for which she was undoubtedly
qualified, not only by vigour of intelligence and warmth of heart,
but also by an altogether unusual faculty of clear, fluent and
persuasive speech. Although she had made several visits to
Newgate prison as early as February 1813, it was not until
nearly four years afterwards that the great public work of her
life may be said to have begun. The association for the Improvement
of the Female Prisoners in Newgate was formed in April
1817. Its aim was the much-needed establishment of some of
what are now regarded as the first principles of prison discipline,
such as entire separation of the sexes, classification of criminals,
female supervision for the women, and adequate provision for
their religious and secular instruction, as also for their useful
employment. The ameliorations effected by this association,
and largely by the personal exertions of Mrs Fry, soon became
obvious, and led to a rapid extension of similar methods to other
places. In 1818 she, along with her brother, visited the prisons
of Scotland and the north of England; and the publication
(1819) of the notes of this tour, as also the cordial recognition
of the value of her work by the House of Commons committee
on the prisons of the metropolis, led to a great increase of her
correspondence, which now extended to Italy, Denmark and
Russia, as well as to all parts of the United Kingdom. Through
a visit to Ireland, which she made in 1827, she was led to direct
her attention to other houses of detention besides prisons; and
her observations resulted in many important improvements
in the British hospital system, and in the treatment of the insane.
In 1838 she visited France, and besides conferring with many
of the leading prison officials, she personally visited most of the
houses of detention in Paris, as well as in Rouen, Caen and some
other places. In the following year she obtained an official
permission to visit all the prisons in that country; and her tour,
which extended from Boulogne and Abbeville to Toulouse and
Marseilles, resulted in a report which was presented to the
minister of the interior and the prefect of police. Before returning
to England she had included Geneva, Zürich, Stuttgart and
Frankfort-on-Main in her inspection. The summer of 1840
found her travelling through Belgium, Holland and Prussia
on the same mission; and in 1841 she also visited Copenhagen.
In 1842, through failing health, Mrs Fry was compelled to forgo
her plans for a still more widely extended activity, but had the
satisfaction of hearing from almost every quarter of Europe
that the authorities were giving increased practical effect to her
suggestions. In 1844 she was seized with a lingering illness, of
which she died on the 12th of October 1845. She was survived
by a numerous family, the youngest of whom was born in 1822.
Two interesting volumes of Memoirs, with Extracts from her
Journals and Letters, edited by two of her daughters, were published
in 1847. See also Elizabeth Fry, by G. King Lewis (1910).
FRYXELL, ANDERS (1795-1881), Swedish historian, was
born at Hesselskog, Dalsland, Sweden, on the 7th of February
1795. He was educated at Upsala, took holy orders in 1820,
was made a doctor of philosophy in 1821, and in 1823 began to
publish the great work of his life, the Stories from Swedish
History. He did not bring this labour to a close until, fifty-six
years later, he published the forty-sixth and crowning volume
of his vast enterprise. Fryxell, as a historian, appealed to every
class by the picturesqueness of his style and the breadth of his
research; he had the gift of awakening to an extraordinary
degree the national sense in his readers. In 1824 he published
his Swedish Grammar, which was long without a rival. In 1833
he received the title of professor, and in 1835 he was appointed
to the incumbency of Sunne, in the diocese of Karlstad, where
he resided for the remainder of his life. In 1840 he was elected
to the Swedish Academy in succession to the poet Wallin (1779-1839).
In 1847 Fryxell received from his bishop permission to
withdraw from all the services of the Church, that he might devote
himself without interruption to historical investigation. Among
his numerous minor writings are prominent his Characteristics
of Sweden between 1592 and 1600 (1830), his Origins of the Inaccuracy
with which the History of Sweden in Catholic Times has
been Treated (1847), and his Contributions to the Literary History
of Sweden. It is now beginning to be seen that the abundant
labours of Fryxell were rather of a popular than of a scientific
order, and although their influence during his lifetime was
unbounded, it is only fair to later and exacter historians to
admit that they threaten to become obsolete in more than one
direction. On the 21st of March 1881 Anders Fryxell died at
Stockholm, and in 1884 his daughter Eva Fryxell (born 1829)
published from his MS. an interesting History of My History,
which was really a literary autobiography and displays the
persistency and tirelessness of his industry.
(E. G.)
FUAD PASHA (1815-1869), Turkish statesman, was the son
of the distinguished poet Kechéji-zadé Izzet Molla. He was
educated at the medical school and was at first an army surgeon.
About 1836 he entered the civil service as an official of the
foreign ministry. He became secretary of the embassy in
London; was employed on special missions in the principalities
and at St Petersburg (1848), and was sent to Egypt as special
commissioner in 1851. In that year he became minister for
foreign affairs, a post to which he was appointed also on four
subsequent occasions and which he held at the time of his death.
During the Crimean War he commanded the troops on the
Greek frontier and distinguished himself by his bravery. He
was Turkish delegate at the Paris conference of 1856; was
charged with a mission to Syria in 1860; grand vizier in 1860
and 1861, and also minister of war. He accompanied the
sultan Abd-ul-Aziz on his journey to Egypt and Europe, when
the freedom of the city of London was conferred on him. He
died at Nice (whither he had been ordered for his health) in
1869. Fuad was renowned for his boldness and promptness
of decision, as well as for his ready wit and his many bons mots.
Generally regarded as the partisan of a pro-English policy,
he rendered most valuable service to his country by his
able management of the foreign relations of Turkey, and not
least by his efficacious settlement of affairs in Syria after the
massacres of 1860.
FUCHOW, Fu-Chau, Foochow, a city of China, capital of
the province of Fu-kien, and one of the principal ports open to
foreign commerce. In the local dialect it is called Hokchiu.
It is situated on the river Min, about 35 m. from the sea, in
26° 5′ N. and 119º 20′ E., 140 m. N. of Amoy and 280 S. of
Hang-chow. The city proper, lying nearly 3 m. from the north
bank of the river, is surrounded by a wall about 30 ft. high and
12 ft. thick, which makes a circuit of upwards of 5 m. and is pierced
by seven gateways surrounded by tall fantastic watch-towers.
272
The whole district between the city and the river, the island of
Nantai, and the southern banks of the Min are occupied by
extensive suburbs; and the river itself bears a large floating
population. Communication from bank to bank is afforded
by a long stone bridge supported by forty solid stone piers in its
northern section and by nine in its southern. The most remarkable
establishment of Fuchow is the arsenal situated about
3 m. down the stream at Pagoda Island, where the sea-going
vessels usually anchor. It was founded in 1867, and is conducted
under the direction of French engineers according to European
methods. In 1870 it employed about 1000 workmen besides
fifty European superintendents, and between that date and
1880 it turned out about 20 or 30 small gunboats. In 1884 it
was partially destroyed by the French fleet, and for a number of
years the workshops and machinery were allowed to stand idle
and go to decay. On the 1st of August 1895 an attack was
made on the English mission near the city of Ku-chang, 120 m.
west of Fuchow, on which occasion nine missionaries, of whom
eight were ladies, were massacred. The port was opened to
European commerce in 1842; and in 1853 the firm of Russell
and Co. shipped the first cargoes of tea from Fuchow to Europe
and America. The total trade in foreign vessels in 1876 was
imports to the value of £1,531,617, and exports to the value
of £3,330,489. In 1904 the imports amounted to £1,440,351,
and the exports to £1,034,436. The number of vessels that
entered in 1876 was 275, and of these 211 were British, 27
German, 11 Danish and 9 American. While in 1904, 480
vessels entered the port, 216 of which were British. A large
trade is carried on by the native merchants in timber, paper,
woollen and cotton goods, oranges and olives; but the foreign
houses mainly confine themselves to opium and tea. Commercial
intercourse with Australia and New Zealand is on the increase.
The principal imports, besides opium, are shirtings, T-cloths,
lead and tin, medicines, rice, tobacco, and beans and peas.
Two steamboat lines afford regular communication with Hong-Kong
twice a month. The town is the seat of several important
missions, of which the first was founded in 1846. That supported
by the American board had in 1876 issued 1,3000,000 copies of
Chinese books and tracts.
FUCHS, JOHANN NEPOMUK VON (1774-1856), German
chemist and mineralogist, was born at Mattenzell, near Brennberg
in the Bavarian Forest, on the 15th of May 1774. In 1807 he
became professor of chemistry and mineralogy at the university
of Landshut, and in 1823 conservator of the mineralogical
collections at Munich, where he was appointed professor of
mineralogy three years later, on the removal thither of the
university of Landshut. He retired in 1852, was ennobled by
the king of Bavaria in 1854, and died at Munich on the 5th of
March 1856. His name is chiefly known for his mineralogical
observations and for his work on soluble glass.
His collected works, including Über den Einfluss der Chemie und
Mineralogie (1824), Die Naturgeschichte des Mineralreichs (1842),
Über die Theorien der Erde (1844), were published at Munich in 1856.
FUCHS, LEONHARD (1501-1566), German physician and
botanist, was born at Wembdingen in Bavaria on the 17th
of January 1501. He attended school at Heilbronn and Erfurt,
and in 1521 graduated at the university of Ingolstadt. About
the same time he espoused the doctrines of the Reformation.
Having in 1524 received his diploma as doctor of medicine, he
practised for two years in Munich. He became in 1526 professor
of medicine at Ingolstadt, and in 1528 physician to the margrave
of Anspach. In Anspach he was the means of saving the lives
of many during the epidemic locally known as the “English
sweating-sickness.” By the duke of Württemberg he was, in
1535, appointed to the professorship of medicine at the university
of Tübingen, a post held by him till his death on the 10th of May
1566. Fuchs was an advocate of the Galenic school of medicine,
and published several Latin translations of treatises by its
founder and by Hippocrates. But his most important publication
was De historia stirpium commentarii insignes (Basel, 1542),
a work illustrated with more than five hundred excellent outline
illustrations, including figures of the common foxglove and of
another species of the genus Digitalis, which was so named by
him.
 |
| Fuchsia coccinea. |
| 1, Flower cut open after removal of
sepals; 2, fruit; 3, floral diagram. |
FUCHSIA, so named by Plumier in honour of the botanist
Leonhard Fuchs, a genus of plants of the natural order Onagraceae,
characterized by entire, usually opposite leaves, pendent flowers,
a funnel-shaped, brightly coloured, quadripartite, deciduous
calyx, 4 petals, alternating with the calycine segments, 8, rarely
10, exserted stamens, a long filiform style, an inferior ovary,
and fruit, a fleshy ovoid many-seeded berry. All the members
of the genus, with the exception of the New Zealand species,
F. excorticata, F. Colensoi and F. procumbens, are natives of
Central and South America—occurring in the interior of forests
or in damp and shady mountainous situations. The various
species differ not a little in size as well as in other characters;
some, as F. verrucosa, being dwarf shrubs; others, as F. arborescens
and F. apetala, attaining a height of 12 to 16 ft., and having
stems several inches in diameter. Plumier, in his Nova plantarum
Americanarum genera (p. 14, tab. 14, Paris, 1703), gave
a description of a species of fuchsia, the first known, under the
name of Fuchsia triphylla, flore coccineo, and a somewhat conventional
outline figure
of the same plant was
published at Amsterdam
in 1757 by Burmann.
In the Histoire
des plantes médicinales
of the South American
traveller Feuillée (p. 64,
pl. XLVII.), written in
1709-1711, and published
by him with his
Journal, Paris, 1725,
the name Thilco is
applied to a species of
fuchsia from Chile,
which is described,
though not evidently
so figured, as having
a pentamerous calyx.
The F. coccinea of Alton
(fig.) (see J.D. Hooker,
in Journal Linnean Soc.,
Botany, vol. x. p. 458,
1867), the first species
of fuchsia cultivated in
England, where it was
long confined to the
greenhouse, was brought
from South America by
Captain Firth in 1788 and placed in Kew Gardens. Of this
species Mr Lee, a nurseryman at Hammersmith, soon afterwards
obtained an example, and procured from it by means
of cuttings several hundred plants, which he sold at a guinea
each. In 1823 F. macrostemma and F. gracilis, and during
the next two or three years several other species, were introduced
into England; but it was not until about 1837, or
soon after florists had acquired F. fulgens, that varieties of
interest began to make their appearance. The numerous
hybrid forms now existing are the result chiefly of the
intercrossing of that or other long-flowered with globose-flowered
plants. F. Venus-victrix, raised by Mr Gulliver,
gardener to the Rev. S. Marriott of Horsemonden, Kent, and sold
in 1822 to Messrs Cripps, was the earliest white-sepalled fuchsia.
The first fuchsia with a white corolla was produced about 1853
by Mr Storey. In some varieties the blossoms are variegated,
and in others they are double. There appears to be very little
limit to the number of forms to be obtained by careful cultivation
and selection. To hybridize, the flower as soon as it opens is
emasculated, and it is then fertilized with pollen from some
different flower.
Ripe seed is sown either in autumn or about February or March
in light, rich, well-drained mould, and is thinly covered with
273
sandy soil and watered. A temperature of 70° to 75° Fahr. has
been found suitable for raising. The seedlings are pricked off
into shallow pots or pans, and when 3 in. in height are transferred
to 3-in. pots, and are then treated the same as plants from
cuttings. Fuchsias may be grafted as readily as camellias,
preferably by the splice or whip method, the apex of a young
shoot being employed as a scion; but the easiest and most usual
method of propagation is by cuttings. The most expeditious
way to procure these is to put plants in heat in January, and to
take their shoots when 3 in. in length. For summer flowering
in England they are best made about the end of August, and
should be selected from the shortest-jointed young wood. They
root readily in a compost of loam and silver-sand if kept close
and sprinkled for a short time. In from two to three weeks they
may be put into 3-in. pots containing a compost of equal parts of
rich loam, silver-sand and leaf-mould. They are subsequently
moved from the frame or bed, first to a warm and shady, and
then to a more airy part of the greenhouse. In January a little
artificial heat may be given, to be gradually increased as the
days lengthen. The side-shoots are generally pruned when they
have made three or four joints, and for bushy plants the leader is
stopped soon after the first potting. Care is taken to keep the
plants as near the glass as possible, and shaded from bright
sunshine, also to provide them plentifully with water, except
at the time of shifting, when the roots should be tolerably dry.
For the second potting a suitable soil is a mixture of well-rotted
cow-dung or old hotbed mould with leaf-mould and sandy peat,
and to promote drainage a little peat-moss may be placed
immediately over the crocks in the lower part of the pot. Weak
liquid manure greatly promotes the advance of the plants, and
should be regularly supplied twice or thrice a week during the
flowering season. After this, water is gradually withheld from
them, and they may be placed in the open air to ripen their wood.
Among the more hardy or half-hardy plants for inside borders
are varieties of the Chilean species, F. macrostemma (or F.
magellanica), a shrub 6 to 12 ft. high with a scarlet calyx, such
as F. m. globosa, F. m. gracilis; one of the most graceful and
hardy of these, a hybrid F. riccartoni, was raised at Riccarton,
near Edinburgh, in 1830. For inside culture may be mentioned
F. boliviana (Bolivia), 2 to 4 ft. high, with rich crimson flowers
with a trumpet-shaped tube; F. corymbiflora (Peru), 4 to 6 ft.
high, with scarlet flowers nearly 2 in. long in long terminal
clusters; F. fulgens (Mexico), 4 to 6 ft., with drooping apical
clusters of scarlet flowers; F. microphylla (Central America),
with small leaves and small scarlet funnel-shaped flowers, the
petals deep red; F. procumbens (New Zealand), a pretty little
creeper, the small flowers of which are succeeded by oval magenta-crimson
berries which remain on for months; and F. splendens
(Mexico), 6 ft. high, with very showy scarlet and green flowers.
But these cannot compare in beauty or freedom of blossom with
the numerous varieties raised by gardeners. The nectar of
fuchsia flowers has been shown to contain nearly 78% of cane
sugar, the remainder being fruit sugar. The berries of some
fuchsias are subacid or sweet and edible. From certain species
a dye is obtainable. The so-called “native fuchsias” of southern
and eastern Australia are plants of the genus Correa, natural
order Rutaceae.
FUCHSINE, or Magenta, a red dye-stuff consisting of a mixture
of the hydrochlorides or acetates of pararosaniline and rosaniline.
It was obtained in 1856 by J. Natanson (Ann., 1856, 98, p. 297)
by the action of ethylene chloride on aniline, and by A.W.
Hofmann in 1858 from aniline and carbon tetrachloride. It
is prepared by oxidizing “aniline for red” (a mixture of aniline
and ortho- and para-toluidine) with arsenic acid (H. Medlock,
Dingler’s Poly. Jour., 1860, 158, p. 146); by heating aniline
for red with nitrobenzene, concentrated hydrochloric acid and
iron (Coupier, Ber., 1873, 6, p. 423); or by condensing formaldehyde
with aniline and ortho-toluidine and oxidizing the mixture.
It forms small crystals, showing a brilliant green reflex, and is
soluble in water and alcohol with formation of a deep red solution.
It dyes silk, wool and leather direct, and cotton after mordanting
with tannin and tartar emetic (see Dyeing). An aqueous solution
of fuchsine is decolorized on the addition of sulphurous
acid, the easily soluble fuchsine sulphurous acid being formed.
This solution is frequently used as a test reagent for the detection
of aldehydes, giving, in most cases, a red coloration on the
addition of a small quantity of the aldehyde.
The constitution of the fuchsine bases (pararosaniline and rosaniline)
was determined by E. and O. Fischer in 1878 (Ann., 1878,
194, p. 242); A.W. Hofmann having previously shown that oxidation
of pure aniline alone or of pure toluidine yielded no fuchsine,
whilst oxidation of a mixture of aniline and para-toluidine gave
rise to the fine red dye-stuff para-fuchsine (pararosaniline hydrochloride)
| CH3·C6H4NH2 + 2C6H5NH2 + 3O = HO·C(C6H4NH2)3 + 2H2O. |
| Colour base (pararosaniline). |
| HO·C(C6H4NH2)3·HCl = H2O + (H2N·C6H4)2C : C6H4 : NH2Cl. |
| Pararosaniline hydrochloride. |
A. Rosenstiehl (Jahres., 1869, p. 693) found also that different rosanilines
were obtained according to whether ortho- or para-toluidine
was oxidized with aniline; and he gave the name rosaniline to the
one obtained from aniline and ortho-toluidine, reserving the term
pararosaniline for the other. E. and O. Fischer showed that these
compounds were derivatives of triphenylmethane and tolyldiphenylmethane
respectively. Pararosaniline was reduced to the
corresponding leuco compound (paraleucaniline), from which by
diazotization and boiling with alcohol, the parent hydrocarbon was
obtained
| (H2N·C5H4)2C : C6H4:NH2Cl → | HC(C6H4NH2·HCl)3 → | HC(C6H4N2Cl3)
→ | HC(C6H5)3. |
| Pararosaniline hydrochloride. | Paraleucaniline. | | Triphenylmethane. |
The reverse series of operations was also carried out by the Fischers,
triphenylmethane being nitrated, and the nitro compound then
reduced to triaminotriphenylmethane or paraleucaniline, which on
careful oxidation is converted into the dye-stuff. A similar series of
reactions was carried out with rosaniline, which was shown to be
the corresponding derivative of tolyldiphenylmethane.
The free pararosaniline, C19H19N3O, and rosaniline,
C20H21N3O,
may be obtained by precipitating solutions of their salts with a
caustic alkali, colourless precipitates being obtained, which crystallize
from hot water in the form of needles or plates. The position
of the amino groups in pararosaniline was determined by the work
of H. Caro and C. Graebe (Ber., 1878, II, p. 1348) and of E. and O.
Fischer (Ber., 1880, 13, p. 2204) as follows: Nitrous acid converts
pararosaniline into aurin, which when superheated with water yields
para-dioxybenzophenone. As the hydroxyl groups in aurin correspond
to the amino groups in pararosaniline, two of these in the latter
compound must be in the para position. The third is also in the
para position; for if benzaldehyde be condensed with aniline,
condensation occurs in the para position, for the compound formed
may be converted into para-dioxybenzophenone,
| C6H5CHO → C6H5CH(C6H4NH2)2 → C6H5CH(C6H4OH)2
→ CO(C6H4OH)2; |
but if para-nitrobenzaldehyde be used in the above reaction and the
resulting nitro compound NO2.C6H4.CH(C6H4NH2)2 be reduced,
then pararosaniline is the final product, and consequently the third
amino group occupies the para position. Many derivatives of pararosaniline
and rosaniline are known, in which the hydrogen atoms of
the amino groups are replaced by alkyl groups; this has the effect
of producing a blue or violet shade, which becomes deeper as the
number of groups increases (see Dyeing).
FUCINO, LAGO DI [Lat. Lacus Fucinus], a lake bed of the
Abruzzi, Italy, in the province of Aquila, 2 m. E. of the town of
Avezzano. The lake was 37 m. in circumference and 65 ft. deep.
From the lack of an outlet, the level of the lake was subject to
great variations, often fraught with disastrous consequences.
As early as A.D. 52 the emperor Claudius, realizing a project of
Julius Caesar, constructed a tunnel 3½ m. long, with 40 shafts at
intervals, by which the surplus waters found an outlet to the
Liris (or Garigliano). No less than 30,000 workmen were employed
for eleven years in driving this tunnel. In the following
reign the tunnel was allowed to fall into disrepair, but was
repaired by Trajan. When, however, it finally went out of use is
uncertain. The various attempts made to reopen it from 1240
onwards were unsuccessful. By 1852 the lake had gradually
risen until it was 30 ft. above its original level, and had become a
source of danger to the surrounding countryside. A company
undertook to drain it on condition of becoming proprietors of the
site when dry; in 1854, however, the rights and privileges were
purchased by Prince Giulio Torlonia (d. 1886), the great Roman
banker, who carried on the work at his own expense until, in 1876,
the lake was finally drained at the cost of some £1,700,000. The
274
reclaimed area is 12½ m. long, 7 m. broad, and is cultivated by
families from the Torlonia estates. The outlet by which it was
drained is 4 m. long and 24 sq. yds. in section.
See A. Brisse and L. de Rotron, Le Desséchement du lac Fucin,
exécuté par S.E. le Prince A. Torlonia (Rome, 1876).
(T. As.)
FUEL (O. Fr. feuaile, popular Lat. focalia, from focus, hearth,
fire), a term applicable to all substances that can be usefully
employed for the production of heat by combustion. Any
element or combination of elements susceptible of oxidation may
under appropriate conditions be made to burn; but only those
that ignite at a moderate initial temperature and burn with comparative
rapidity, and, what is practically of more importance,
are obtainable in quantity at moderate prices, can fairly be
regarded as fuels. The elementary substances that can be so
classed are primarily hydrogen, carbon and sulphur, while others
finding more special applications are silicon, phosphorus, and the
more readily oxidizable metals, such as iron, manganese, aluminium
and magnesium. More important, however, than the
elements are the carbohydrates or compounds of carbon, oxygen
and hydrogen, which form the bulk of the natural fuels, wood,
peat and coal, as well as of their liquid and gaseous derivatives—coal-gas,
coal-tar, pitch, oil, &c., which have high values as fuel.
Carbon in the elementary form has its nearest representative in
the carbonized fuels, charcoal from wood and coke from coal.
Solid Fuels.
Wood may be considered as having the following average
composition when in the air-dried state: Carbon, 39.6; hydrogen,
4.8; oxygen, 34.8; ash, 1.0; water, 20%.
When it is freshly felled, the water may be from 18 to
Wood.
50%. Air-dried or even green wood ignites readily when a considerable
surface is exposed to the kindling flame, but in large
masses with regular or smooth surfaces it is often difficult to get
it to burn. When previously torrefied or scorched by heating to
a temperature of about 200°, at which incipient charring is set up,
it is exceedingly inflammable. The ends of imperfectly charred
boughs from the charcoal heaps in this condition are used in Paris
and other large towns in France for kindling purposes, under the
name of fumerons. The inflammability, however, varies with
the density,—the so-called hard woods, oak, beech and maple,
taking fire less readily than the softer, and, more especially,
the coniferous varieties rich in resin. The calorific power of
absolutely dry woods may as an average be taken at about 4000
units, and when air-dried, i.e. containing 25% of water, at 2800
to 3000 units. Their evaporative values, i.e. the quantities of
water evaporated by unit weight, are 3.68 and 4.44.
Wood being essentially a flaming fuel is admirably adapted for
use with heat-receiving surfaces of large extent, such as locomotive
and marine boilers, and is also very clean in use. The
absence of all cohesion in the cinders or unburnt carbonized
residue causes a large amount of ignited particles to be projected
from the chimney, when a rapid draught is used, unless special
spark-catchers of wire gauze or some analogous contrivance are
used. When burnt in open fireplaces the volatile products given
off in the apartment on the first heating have an acrid penetrating
odour, which is, however, very generally considered to be
agreeable. Owing to the large amount of water present, no very
high temperatures can be obtained by the direct combustion of
wood, and to produce these for metallurgical purposes it is
necessary to convert it previously either into charcoal or into
inflammable gas.
Peat includes a great number of substances of very unequal
fuel value, the most recently formed spongy light brown kind
approximating in composition to wood, while the
dense pitchy brown compact substance, obtained from
Peat.
the bottom of bogs of ancient formation, may be compared with
lignite or even in some instances with coal. Unlike wood, however,
it contains incombustible matter in variable but large
quantity, from 5 to 15% or even more. Much of this, when the
amount is large, is often due to sand mechanically intermixed;
when air-dried the proportion of water is from 8 to 20%. When
these constituents are deducted the average composition may
be stated to be—carbon, 52 to 66; hydrogen, 4.7 to 7.4; oxygen,
28 to 39; and nitrogen, 1.5 to 3%. Average air-dried peat may
be taken as having a calorific value of 3000 to 3500 units, and when
dried at 100° C., and with a minimum of ash (4 to 5%), at about
5200 units, or from a quarter to one-third more than that of an
equal weight of wood. The lighter and more spongy varieties of
peat when air-dried are exceedingly inflammable, firing at a
temperature of 200° C.; the denser pulpy kinds ignite less readily
when in the natural state, and often require a still higher temperature
when prepared by pulping and compression or partial
carbonization. Most kinds burn with a red smoky flame, developing
a very strong odour, which, however, has its admirers in the
same way that wood smoke has. This arises from the destructive
distillation of imperfectly carbonized organic matter. The ash,
like that of wood, is light and powdery, except when much sand
is present, when it is of a denser character.
Peat is principally found in high latitudes, on exposed high
tablelands and treeless areas in more temperate climates, and
in the valleys of slow-flowing rivers,—as in Ireland, the west of
Scotland, the tableland of Bavaria, the North German plain,
and parts of the valleys of the Somme, Oise and a few other
rivers in northern France. A principal objection to its use is its
extreme bulk, which for equal evaporative effect is from 8 to 18
times that of coal. Various methods have been proposed, and
adopted more or less successfully, for the purpose of increasing
the density of raw peat by compression, either with or without
pulping; the latter process gives the heaviest products, but the
improvement is scarcely sufficient to compensate for the cost.
Lignite or brown coal is of intermediate character between
peat and coal proper. The best kinds are undistinguishable in
quality from free-burning coals, and the lowest earthy
kinds are not equal to average peat. When freshly
Lignite.
raised, the proportion of water may be from 45 to 50% and
even more, which is reduced from 28 to 20% by exposure to
dry air. Most varieties, however, when fully dried, break up
into powder, which considerably diminishes their utility as fuel,
as they cannot be consolidated by coking. Lignite dust may,
however, be compacted into serviceable blocks for burning, by
pressure in machines similar to those used for brickmaking,
either in the wet state as raised from the mines or when kiln-dried
at 200° C. This method was adopted to a very large extent
in Prussian Saxony. The calorific value varies between 3500
and 5000 units, and the evaporative factor from 2.16 when freshly
raised to 5.84 for the best kinds of lignite when perfectly dried.
Of the other natural fuels, apart from coal (q.v.), the most
important is so-called vegetable refuse, such as cotton stalks,
brushwood, straw, and the woody residue of sugar-cane
after the extraction of the saccharine juice known as
Other natural fuels.
megasse or cane trash. These are extensively used in
countries where wood and coal are scarce, usually for
providing steam in the manufactures where they arise, e.g.
straw for thrashing, cotton stalks for ploughing, irrigating, or
working presses, and cane trash for boiling down sugar or driving
the cane mill. According to J. Head (Proc. Inst. of Civil Engineers,
vol. xlviii. p. 75), the evaporative values of 1 ℔ of these
different articles when burnt in a tubular boiler are—coal, 8 ℔;
dry peat, 4 ℔; dry wood, 3.58-3.52 ℔; cotton stalks or
megasse, 3.2-2.7 ℔; straw, 2.46-2.30 ℔. Owing to the
siliceous nature of the ash of straw, it is desirable to have a
means of clearing the grate bars from slags and clinkers at short
intervals, and to use a steam jet to clear the tubes from similar
deposits.
The common fuel of India and Egypt is derived from the
dung of camels and oxen, moulded into thin cakes, and dried
in the sun. It has a very low heating power, and in burning
gives off acrid ammoniacal smoke and vapour.
Somewhat similar are the tan cakes made from spent tanners’
bark, which are used to some extent in eastern France and in
Germany. They are made by moulding the spent bark into cakes,
which are then slowly dried by exposure to the air. Their effect
is about equivalent to 80 and 30% of equal weights of wood and
coal respectively.
275
Sulphur, phosphorus and silicon, the other principal combustible
elements, are only of limited application as fuels. The
first is used in the liquidation of sulphur-bearing rocks. The ore
is piled into large heaps, which are ignited at the bottom, a
certain proportion, from one-fourth to one-third, of the sulphur
content being sacrificed, in order to raise the mass to a sufficient
temperature to allow the remainder to melt and
run down to the collecting basin. Another application
is in the so-called “pyritic smelting,” where
ores of copper (q.v.) containing iron pyrites, FeS2,
are smelted with appropriate fluxes in a hot blast,
without preliminary roasting, the sulphur and iron
of the pyrites giving sufficient heat by oxidation to
liquefy both slag and metal. Phosphorus, which is
of value from its low igniting point, receives its only
application in the manufacture of lucifer matches.
The high temperature produced by burning phosphorus is in
part due to the product of combustion (phosphoric acid) being
solid, and therefore there is less heat absorbed than would be the
case with a gaseous product. The same effect is observed in a
still more striking manner with silicon, which in the only special
case of its application to the production of heat, namely, in the
Bessemer process of steel-making, gives rise to an enormous
increase of temperature in the metal, sufficient indeed to keep
the iron melted. The absolute calorific value of silicon is lower
than that of carbon, but the product of combustion (silica)
being non-volatile at all furnace temperatures, the whole of
the heat developed is available for heating the molten iron,
instead of a considerable part being consumed in the work of
volatilization, as is the case with carbonic oxide, which burns
to waste in the air.
Assay and Valuation of Carbonaceous Fuels.—The utility or value
of a fuel depends upon two principal factors, namely, its calorific
power and its calorific intensity or pyrometric effect, that
is, the sensible temperature of the products of combustion.
Calorific power.
The first of these is constant for any particular product of
combustion independently of the method by which the burning is
effected, whether by oxygen, air or a reducible metallic oxide. It
is most conveniently determined in the laboratory by measuring
the heat evolved during the combustion of a given weight of the fuel.
The method of Lewis Thompson is one of the most useful. The
calorimeter consists of a copper cylinder in which a weighed quantity
of coal intimately mixed with 10-12 parts of a mixture of 3 parts
of potassium chlorate and 1 of potassium nitrate is deflagrated
under a copper case like a diving-bell, placed at the bottom of a deep
glass jar filled with a known weight of water. The mixture is fired
by a fuse of lamp-cotton previously soaked in a nitre solution and
dried. The gases produced by the combustion rising through the
water are cooled, with a corresponding increase of temperature in
the latter, so that the difference between the temperature observed
before and after the experiment measures the heat evolved. The
instrument is so constructed that 30 grains (2 grammes) of coal are
burnt in 29,010 grains of water, or in the proportion of 1 to 937,
these numbers being selected that the observed rise of temperature
in Fahrenheit degrees corresponds to the required evaporative value
in pounds, subject only to a correction for the amount of heat
absorbed by the mass of the instrument, for which a special coefficient
is required and must be experimentally determined. The ordinary
bomb calorimeter is also used. An approximate method is based
upon the reduction of lead oxide by the carbon and hydrogen of the
coal, the amount of lead reduced affording a measure of the oxygen
expended, whence the heating power may be calculated, 1 part of
pure carbon being capable of producing 34½ times its weight of lead.
The operation is performed by mixing the weighed sample with a
large excess of litharge in a crucible, and exposing it to a bright
red heat for a short time. After cooling, the crucible is broken and
the reduced button of lead is cleaned and weighed. The results
obtained by this method are less accurate with coals containing
much disposable hydrogen and iron pyrites than with those approximating
to anthracite, as the heat equivalent of the hydrogen in
excess of that required to form water with the oxygen of the coal
is calculated as carbon, while it is really about four times as great.
Sulphur in iron pyrites also acts as a reducing agent upon litharge,
and increases the apparent effect in a similar manner.
The evaporative power of a coal found by the above methods,
and also by calculating the separate calorific factors of the components
as determined by the chemical analysis, is always considerably
above that obtained by actual combustion under a steam boiler,
as in the latter case numerous sources of loss, such as imperfect
combustion of gases, loss of unburnt coal in cinders, &c., come into
play, which cannot be allowed for in laboratory experiments. It is
usual, therefore, to determine the value of a coal by the combustion
of a weighed quantity in the furnace of a boiler, and measuring the
amount of water evaporated by the heat developed.
In a research upon the heating power and other properties of coal
for naval use, carried out by the German admiralty, the results
tabulated below were obtained with coals from different localities.
| | Slag left
in Grate. | Ashes in
Ashpit. | Soot in
Flues. | Water
evaporated by
1 ℔ of Coal |
| Westphalian gas coals | 0.33-6.42 | 2.83-6.53 | 0.32-0.46 | 6.60-7.45 ℔ |
| Do. bituminous coals | 0.98-9.10 | 1.97-9.63 | 0.24-0.88 | 7.30-8.66 |
| Do. dry coals | 1.93-5.70 | 4.37-10.63 | 0.24-0.48 | 7.03-8.51 |
| Silesian coals | 0.92-1.30 | 3.15-3.50 | 0.24-0.30 | 6.73-7.10 |
| Welsh steam coals | 1.20-4.07 | 4.07 | 0.32 | 8.41 |
| Newcastle coals | 1.92 | 2.57 | 0.35 | 7.28 |
The heats of combustion of elements and compounds will be
found in most of the larger works on physical and chemical constants;
a convenient series is given in the Annuaire du Bureau des Longitudes,
appearing in alternate years. The following figures for the principal
fuel elements are taken from the issue for 1908; they are expressed
in gramme “calories” or heat units, signifying the weight of water
in grammes that can be raised 1° C. in temperature by the combustion
of 1 gramme of the substance, when it is oxidized to the condition
shown in the second column:
| Element. | Product of Combustion. | Calories. |
| Hydrogen | Water, H2O, condensed to liquid | 34,500 |
| ” as vapour | 29,650 |
| Carbon— | | |
| Diamond | Carbon Dioxide, CO2 | 7,868 |
| Graphite | ” ” | 7,900 |
| Amorphous | ” ” | 8,133 |
| Silicon— | | |
| Amorphous | Silicon Dioxide, SiO2 | 6,414 |
| Crystallized | ” ” | 6,570 |
| Phosphorus | Phosphoric pentoxide, P2O5 | 5,958 |
| Sulphur | Sulphur dioxide, SO2, gaseous | 2,165 |
The results may also be expressed in terms of the atomic equivalent
of the combustible by multiplying the above values by the atomic
weight of the substance, 12 for carbon, 28 for silicon, &c.
In all fuels containing hydrogen the calorific value as found by
the calorimeter is higher than that obtainable under working conditions
by an amount equal to the latent heat of volatilization of
water which reappears as heat when the vapour is condensed,
though under ordinary conditions of use the vapour passes away uncondensed.
This gives rise to the distinction of higher and lower
calorific values for such substances, the latter being those generally
used in practice. The differences for the more important compound
gaseous fuels are as follows:—
| | Calorific Value. |
| | Higher. | Lower. |
| Acetylene, C2H2 | 11,920 | 11,500 |
| Ethylene, C2H4 | 11,880 | 11,120 |
| Methane, CH4 | 13,240 | 11,910 |
| Carbon monoxide, CO | 2,440 | 2,440 |
The calorific intensity or pyrometric effect of any particular fuel
depends upon so many variable elements that it cannot be determined
except by actual experiment. The older method
was to multiply the weight of the products of combustion
Caloric intensity.
by their specific heats, but this gave untrustworthy
results as a rule, on account of two circumstances—the great increase
in specific heat at high temperatures in compound gases such as
water and carbon dioxide, and their instability when heated to
1800° or 2000°. At such temperatures dissociation to a notable
extent takes place, especially with the latter substance, which is also
readily reduced to carbon monoxide when brought in contact with
carbon at a red heat—a change which is attended with a large
heat absorption. This effect is higher with soft kinds of carbon,
such as charcoal or soft coke, than with dense coke, gas retort
carbon or graphite. These latter substances, therefore, are used
when an intense local heat is required, as for example, in the Deville
furnace, to which air is supplied under pressure. Such a method is,
however, only of very special application, the ordinary method being
to supply air to the fire in excess of that required to burn the fuel
to prevent the reduction of the carbon dioxide. The volume of
flame, however, is increased by inert gas, and there is a proportionate
diminution of the heating effect. Under the most favourable conditions,
when the air employed has been previously raised to a high
temperature and pressure, the highest attainable flame temperature
from carbonaceous fuel seems to be about 2100°-2300° C.; this is
realized in the bright spots or “eyes” of the tuyeres of blast furnaces.
Very much higher temperatures may be reached when the products
of combustion are not volatile, and the operation can be effected
by using the fuel and oxidizing agent in the proportions exactly
276
required for perfect combustion and intimately mixed. These
conditions are met in the “Thermit” process of Goldschmidt,
where finely divided aluminium is oxidized by the oxide of some
similar metal, such as iron, manganese or chromium, the reaction
being started by a primer of magnesium and barium peroxide.
The reaction is so rapidly effected that there is an enormous rise in
temperature, estimated to be 5400° F. (3000° C.), which is sufficient
to melt the most refractory metals, such as chromium. The slag
consists of alumina which crystallizes in the forms of corundum and
ruby, and is utilized as an abrasive under the name of corubin.
The chemical examination includes the determination of (1)
moisture, (2) ash, (3) coke, (4) volatile matter, (5) fixed carbon in
coke, (6) sulphur, (7) chlorine, (8) phosphorus. Moisture is determined
by noting the loss in weight when a sample is heated at 100°
for about one hour. The ash is determined by heating a sample
in a muffle furnace until all the combustible matter has been burnt
off. The ash, which generally contains silica, oxides of the alkaline
earths, ferric oxide (which gives the ash a red colour), sulphur, &c.,
is analysed by the ordinary gravimetric methods. The determination
of coke is very important on account of the conclusions concerning
the nature of the coal which it permits to be drawn. A sample is
finely powdered and placed in a covered porcelain crucible, which
is surrounded by an outer one, the space between them being packed
with small coke. The crucibles are heated in a wind furnace for
1 to 1½ hours, then allowed to cool, the inner crucible removed,
and the coke weighed. The coke may be (1) pulverulent, (2)
slightly fritted, (3) spongy and swelled, (4) compact. Pulverulent
cokes indicate a non-caking bituminous coal, rich in oxygen if the
amount be below 60%, but if the amount be very much less it
generally indicates a lignite; if the amount be above 80% it indicates
an anthracite containing little oxygen or hydrogen. A fritted
coke indicates a slightly coking coal, while the spongy appearance
points to a highly coking coal which has been partly fused in the
furnace. A compact coke is yielded by good coking coals, and is
usually large in amount. The volatile matters are determined as the
loss of weight on coking less the amount of moisture. The “fixed
carbon” is the carbon retained in the coke, which contains in addition
the ash already determined. The fixed carbon is therefore the difference
between the coke and the ash, and may be determined from
these figures; or it may be determined directly by burning off the
coke in a muffle and noting the loss in weight. Sulphur may be
present as (1) organic sulphur, (2) as iron pyrites or other sulphides,
(3) as the sulphates of calcium, aluminium and other metals; but
the amount is generally so small that only the total sulphur is
determined. This is effected by heating a mixture of the fuel
with lime and sodium carbonate in a porcelain dish to redness in a
muffle until all the carbonaceous matter has been burnt off. The
residue, which contains the sulphur as calcium sulphate, is transferred
to a beaker containing water to which a little bromine has
been added. Hydrochloric acid is carefully added, the liquid
filtered and the residue washed. To the filtrate ammonia is added,
and then barium chloride, which precipitates the sulphur as barium
sulphate. Sulphur existing in the form of sulphates may be removed
by washing a sample with boiling water and determining the sulphuric
acid in the solution. The washed sample is then fused in the usual
way to determine the proportion of sulphur existing as iron pyrites.
The distinction between sulphur present as sulphate and sulphide
is of importance in the examination of coals intended for iron
smelting, as the sulphates of the earthy metals are reduced by the
gases of the furnace to sulphides, which pass into the slag without
affecting the quality of the iron produced, while the sulphur of the
metallic sulphides in the ash acts prejudicially upon the metal.
Coals for gas-making should contain little sulphur, as the gases
produced in the combustion are noxious and have very corrosive
properties. Chlorine is rarely determined, but when present in
quantity it corrodes copper and brass boiler tubes, with which consequently
chlorine-bearing coals cannot be used. The element is
determined by fusing with soda lime in a muffle, dissolving the residue
in water and precipitating with silver nitrate. Phosphorus is
determined in the ash by fusing it with a mixture of sodium and
potassium carbonates, extracting the residue with hydrochloric acid,
and twice evaporating to dryness with the same acid. The residue
is dissolved in hydrochloric acid, a few drops of ferric chloride added,
and then ammonia in excess. The precipitate of ferric phosphate
is then treated as in the ordinary estimation of phosphates. If it be
necessary to determine the absolute amount of carbon and hydrogen in
a fuel, the dried sample is treated with copper oxide as in the ordinary
estimation of these elements in organic compounds.
(H. B.)
Liquid Fuel.
Vegetable oil is not used for fuel except for laboratory purposes,
partly because its constituent parts are less adaptable
for combustion under the conditions necessary for steam-raising,
but chiefly because of the commercial difficulty of producing it
with sufficient economy to compete with mineral fuel either solid
or liquid.
The use of petroleum as fuel had long been recognized as a
scientific possibility, and some attempts had been made to adopt
it in practice upon a commercial scale, but the insufficiency,
and still more the irregularity, of the supplies prevented it from
coming into practical use to any important extent until about
1898, when discoveries of oil specially adapted by chemical
composition for fuel purposes changed the aspect of the situation.
These discoveries of special oil were made first in Borneo and
later in Texas, and experience in treating the oils from both
localities has shown that while not less adapted to produce
kerosene or illuminating oil, they are better adapted to produce
fuel oil than either the Russian or the Pennsylvanian products.
Texas oil did not hold its place in the market for long, because
the influx of water into the wells lowered their yield, but discoveries
of fuel oil in Mexico have come later and will help to
maintain the balance of the world’s supply, although this is still
a mere fraction of the assured supply of coal.
With regard to the chemical properties of petroleum, it is not
necessary to say more in the present place than that the lighter
and more volatile constituents, known commercially as naphtha
and benzene, must be removed by distillation in order to leave
a residue composed principally of hydrocarbons which, while
containing the necessary carbon for combustion, shall be sufficiently
free from volatile qualities to avoid premature ignition
and consequent danger of explosion. Attempts have been made
to use crude oil for fuel purposes, and these have had some
success in the neighbourhood of the oil wells and under boilers
of unusually good ventilation both as regards their chimneys
and the surroundings of their stokeholds; but for reasons both
of commerce and of safety it is not desirable to use crude oil
where some distillation is possible. The more complete the
process of distillation, and the consequent removal of the volatile
constituents, the higher the flash-point, and the more turgid
and viscous is the fuel resulting; and if the process is carried to
an extreme, the residue or fuel becomes difficult to ignite by the
ordinary process of spraying or atomizing mechanically at the
moment immediately preceding combustion. The proportions
which have been found to work efficiently in practice are as
follows:—
| Carbon | 88.00 % |
| Hydrogen | 10.75 % |
| Oxygen | 1.25 % |
| | ——— |
| Total | 100 |
The standards of safety for liquid fuel as determined by
flash-point are not yet finally settled, and are changing from time
to time. The British admiralty require a flash-point of 270° F.,
and to this high standard, and the consequent viscosity of the
fuel used by vessels in the British fleet, may partly be attributed
the low rate of combustion that was at first found possible in
them. The German admiralty have fixed a flash-point of 187° F.,
and have used oil of this standard with perfect safety, and at the
same time with much higher measure of evaporative duty than
has been attained in British war-vessels. In the British mercantile
marine Lloyd’s Register has permitted fuel with a flash-point
as low as 150° F. as a minimum, and no harm has resulted.
The British Board of Trade, the department of the government
which controls the safety of passenger vessels, has fixed a higher
standard upon the basis of a minimum of 185°. In the case of
locomotives the flash-point as a standard of safety is of less
importance than in the case of stationary or marine boilers,
because the storage is more open, and the ventilation, both of the
storage tanks and the boilers during combustion, much more
perfect than in any other class of steam-boilers.
The process of refining by distillation is also necessary to
reduce two impurities which greatly retard storage and combustion,
i.e. water and sulphur. Water is found in all crude
petroleum as it issues from the wells, and sulphur exists in
important quantities in oil from the Texas wells. Its removal
was at first found very expensive, but there no longer exists
difficulty in this respect, and large quantities of petroleum fuel
practically free from sulphur are now regularly exported from
Texas to New York and to Europe.
277
Water mixed with fuel is in intimate mechanical relation, and
frequently so remains in considerable quantities even after the
process of distillation. It is in fact so thoroughly mixed as to
form an emulsion. The effect of feeding such a mixture into a
furnace is extremely injurious, because the water must be decomposed
chemically into its constituents, hydrogen and oxygen,
thus absorbing a large quantity of heat which would otherwise
be utilized for evaporation. Water also directly delays combustion
by producing from the jet a long, dull, red flame instead
of a short bright, white flame, and the process of combustion,
which should take place by vaporization of the oil near the
furnace mouth, is postponed and transferred to the upper part of
the combustion-box, the tubes, and even the base of the chimney,
producing loss of heat and injury to the boiler structure. The
most effective means of ridding the fuel of this dangerous
impurity is by heat and settlement. The coefficients of expansion
of water and oil by heat are substantially different, and a
moderate rise of temperature therefore separates the particles
and precipitates the water, which is easily drawn off—leaving
the oil available for use. The heating and precipitation are
usually performed upon a patented system of settling tanks
and heating apparatus known as the Flannery-Boyd system,
which has proved itself indispensable for the successful use at
sea of petroleum fuel containing any large proportion of water.
The laboratory and mechanical use of petroleum for fuel has
already been referred to, but it was not until the year 1870 that
petroleum was applied upon a wider and commercial
scale. In the course of distillation of Russian crude
Progress of liquid fuel.
petroleum for the production of kerosene or lamp oil,
large quantities of refuse were produced—known by
the Russian name of astatki—and these were found an incumbrance
and useless for any commercial purpose. To a Russian
oil-refiner gifted with mechanical instinct and the genius for
invention occurred the idea of utilizing the waste product as
fuel by spraying or atomizing it with steam, so that, the thick
and sluggish fluid being broken up into particles, the air
necessary for combustion could have free access to it. The
earliest apparatus for this
purpose was a simple piece
of gas-tube, into which the
thick oil was fed; by
another connexion steam
at high pressure was admitted
to an inner and
smaller tube, and, the end
of the tube nearest to the
furnace being open, the
pressure of the steam blew
the oil into the furnace,
and by its velocity broke
it up into spray. The apparatus
worked with
success from the first. Experience
pointed out the
proper proportionate sizes
for the inlets of steam and
oil, the proper pressure for
the steam, and the proportionate
sizes for the orifices
of admission to the furnaces,
as well as the sizes of
air-openings and best arrangements of fire-bricks in the furnaces
themselves; and what had been a waste product now became
a by-product of great value. Practically all the steam power
in South Russia, both for factories and navigation of the inland
seas and rivers, is now raised from astatki fuel.
In the Far East, including Burma and parts of China and
Japan, the use of liquid fuel spread rapidly during the years
1899, 1900 and 1901, owing entirely to the development of the
Borneo oil-fields by the enterprise of Sir Marcus Samuel and the
large British corporation known as the Shell Transport and
Trading Company, of which he is the head. This corporation
has since amalgamated with the Royal Dutch Petroleum Company
controlling the extensive wells in Dutch Borneo, and
together they supply large quantities of liquid fuel for use in the
Far East. In the United States of America liquid fuel is not
only used for practically the whole of the manufacturing and
locomotive purposes of the state of Texas, but factories in New
York, and a still larger number in California, are now discarding
the use of coal and adopting petroleum, because it is more
economical in its consumption and also more easily handled in
transit, and saves nearly all the labour of stoking. So far the
supplies for China and Japan have been exported from Borneo,
but the discoveries of new oil-fields in California, of a character
specially adapted for fuel, have encouraged the belief that it may
be possible to supply Chile and Peru and other South American
countries, where coal is extremely expensive, with Californian
fuel; and it has also found its way across the Pacific to Japan.
There are believed to be large deposits in West Africa, but in the
meantime the only sources of supply to those parts of Africa
where manufacture is progressing, i.e. South Africa and Egypt,
are the oil-fields of Borneo and Texas, from which the import
has well begun, from Texas to Alexandria via the Mediterranean,
and from Borneo to Cape Town via Singapore.
In England, notwithstanding the fact that there exist the
finest coal-fields in the world, there has been a surprising development
of the use of petroleum as fuel. The Great Eastern railway
adapted 120 locomotive engines to its use, and these ran with
regularity and success both on express passenger and goods
trains until the increase in price due to short supply compelled
a return to coal fuel. The London, Brighton & South Coast
railway also began the adaptation of some of their locomotive
engines, but discontinued the use of liquid fuel from the same
cause. Several large firms of contractors and cement manufacturers,
chiefly on the banks of the Thames, made the same
adaptations which proved mechanically successful, but were
not continued when the price of liquid fuel increased with the
increased demand.
 |
| Fig. 1.—Holden Burner. |
The chief factors of economy are the greater calorific value
of oil than coal (about 16 ℔ of water per ℔ of oil fuel evaporated
from a temperature of 212° F.), not only in laboratory practice,
but in actual use on a large scale, and the saving of labour both
Economy of liquid fuel.
in transit from the source of supply to the place of use and in
the act of stoking the furnaces. The use of cranes,
hand labour with shovels, wagons and locomotives,
horses and carts, is unavoidable for the transit of
coal; and labour to trim the coal, to stoke it when
under combustion, and to handle the residual ashes, are all
indispensable to steam-raising by coal. On the other hand, a
system of pipes and pumps, and a limited quantity of skilled
278
labour to manage them, is all that is necessary for the transit
and combustion of petroleum fuel; and it is certain that even
in England will be found places which, from topographical
and other circumstances, will use petroleum more economically
than coal as fuel for manufacturing purposes under reasonable
conditions of price for the fuel.
 |
| Fig. 2.—Rusden and Eeles Burner. |
The theoretical calorific value of oil fuel is more nearly realized
in practice than the theoretical calorific value of coal, because
the facilities for complete combustion, due to the artificial
admixture of the air by the atomizing process, are greater in
the case of oil than coal, and for this reason, among others, the
practical evaporative results are proportionately higher with
liquid fuel. In some cases the work done in a steam-engine by
2 tons of coal has been performed by 1 ton of oil fuel, but in
others the proportions have been as 3 to 2, and these latter can be
safely relied on in practice as a minimum. This saving, combined
with the savings of labour and transit already explained, will
in the near future make the use of liquid fuel compulsory, except
in places so near to coal-fields that the cost of coal becomes
sufficiently low to counterbalance the savings in weight of fuel
consumed and in labour in handling it. In some locomotives
on the Great Eastern railway the consumption of oil and coal
for the same development of horse-power was as 17 ℔ oil is
to 35 ℔ coal; all, however, did not realize so high a result.
The mechanical apparatus for applying petroleum to steam-raising
in locomotives is very simple. The space in the tender
usually occupied by coal is closed up by steel-plating closely
riveted and tested, so as to form a storage tank. From this tank
Liquid fuel in locomotives.
a feed-pipe is led to a burner of the combined steam-and-oil
type already indicated, and this burner is so arranged
as to enter a short distance inside the furnace
mouth. The ordinary fire-bars are covered with a thin
layer of coal, which starts the ignition in the first
place, and the whole apparatus is ready for work. The burner
best adapted for locomotive practice is the Holden Burner
(fig. 1), which was used on the Great Eastern railway. The
steam-pipe is connected at A, the oil-pipe at B, and the hand-wheels
C and D are for the adjustment of the
internal orifices according to the rate of combustion
required. The nozzle E is directed
towards the furnace, and the external ring
FF, supplied by the small pipe G and the
by-pass valve H, projects a series of steam
jets into the furnace, independent of the
injections of atomized fuel, and so induces an
artificial inrush of air for the promotion of
combustion. This type of burner has also
been tried on stationary boilers and on board
ship. It works well, although the great consumption
of steam by the supplementary ring
is a difficulty at sea, where the water lost by
the consumption of steam cannot easily be
made up.
Although the application of the new fuel
for land and locomotive boilers has already
been large, the practice at sea has
been far more extensive. The reason
is chiefly to be found in the fact that
although the sources of supply are at a distance
Liquid fuel at sea.
from Great Britain, yet they are in
countries to whose neighbourhood British
steamships regularly trade, and in which
British naval squadrons are regularly stationed,
so that the advantages of adopting liquid fuel
have been more immediate and the economy
more direct. The certainty of continuous supply of the fuel and
the wide distribution of storage stations have so altered the
conditions that the general adoption of the new fuel for marine
purposes becomes a matter of urgency for the statesman, the
merchant and the engineer. None of these can afford to neglect
the new conditions, lest they be noted and acted upon by their
competitors. Storage for supply now exists at a number of sea
ports: London, Barrow, Southampton, Amsterdam, Copenhagen,
New Orleans, Savannah, New York, Philadelphia,
Singapore, Hong Kong, Madras, Colombo, Suez, Hamburg,
Port Arthur, Rangoon, Calcutta, Bombay, Alexandria,
Bangkok, Saigon, Penang, Batavia, Surabaya, Amoy, Swatow,
Fuchow, Shanghai, Hankow, Sydney, Melbourne, Adelaide,
Zanzibar, Mombasa, Yokohama, Kobe and Nagasaki; also
in South African and South American ports.
 |
| Fig. 3.—Storage of Liquid Fuel on Oil-carrying Steamers
(Flannery-Boyd System). |
The British admiralty have undertaken experiments with
liquid fuel at sea, and at the same time investigations of the
279
possibility of supply from sources within the regions of the
British empire. There is an enormous supply of shale under the
north-eastern counties of England, but no oil that can be pumped—still
less oil with a pressure above it so as to “gush” like the
wells in America—and the only sources of liquid supply under the
British flag appear to be in Burma and Trinidad. The Borneo
fields are not under British control, although developed
entirely by British capital. The Italian admiralty have fitted
several large warships with boiler apparatus to burn petroleum.
The German admiralty are regularly using liquid fuel on the
China station. The Dutch navy have fitted coal fuel and liquid
fuel furnaces in combination, so that the smaller powers required
may be developed by coal alone, and the larger powers by
supplementing coal fuel with oil fuel. The speeds of some
vessels of the destroyer type have by this means been accelerated
nearly two knots.
 |
| Fig. 4.—Installation on ss. “Trochas.” |
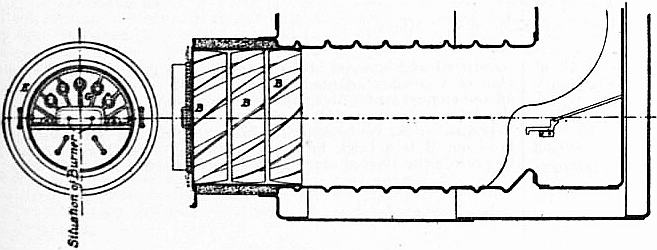 |
| Fig. 5.—Details of Furnace, Meyer System. |
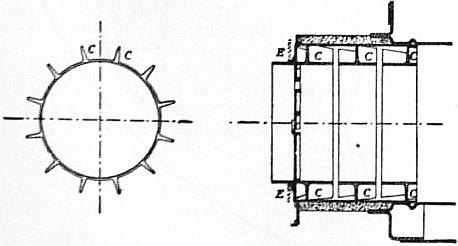 |
| Fig. 6.—Details of Exterior Elongation of Furnace, Meyer System. |
The questions which govern the use of fuel in warships are
more largely those of strategy and fighting efficiency than
economy of evaporation. Indeed, the cost of constructing
and maintaining in fighting efficiency a modern
Advantages in warships.
warship is so great that the utmost use strategically
must be obtained from the vessel, and in this comparison
the cost of fuel is relatively so small an item that its increase
or decrease may be considered almost a negligible quantity.
The desideratum in a warship is to obtain the greatest fighting
efficiency based on the thickest armour, the heaviest and most
numerous guns, the highest maximum speed, and, last and not
least, the greatest range of effective action based upon the
maximum supplies of fuel, provisions and other consumable
stores that the ship can carry. Now, if by changing the type
of fuel it be possible to reduce its weight by 30%, and to abolish
the stokers, who are usually more than half the ship’s
company, the weight saved will be represented not
merely by the fuel, but by the consumable stores
otherwise necessary for the stokers. Conversely, the
radius of effective action of the ship will be doubled
as regards consumable stores if the crew be halved, and
will be increased by 50% if the same weight of fuel be
carried in the form of liquid instead of coal. In space
the gain by using oil fuel is still greater, and 36 cubic
feet of oil as stored are equal in practical calorific value
to 67 cubic feet of coal according to the allowance usual
for ship’s bunkering. On the other hand, coal has
been relied upon, when placed in the side bunkers of
unarmoured ships, as a protection against shot and
shell, and this advantage, if it really exists, could not
be claimed in regard to liquid fuel.
Recent experiments in coaling warships at sea have
not been very successful, as the least bad weather has
prevented the safe transmission of coal bags from the collier to
the ship. The same difficulty does not exist for oil fuel, which
has been pumped through flexible tubing from one ship to the
other even in comparatively rough weather. Smokelessness,
so important a feature of sea strategy, has not always been
attained by liquid fuel, but where the combustion is complete,
by reason of suitable furnace arrangements and
careful management, there is no smoke. The
great drawback, however, to the use of liquid
fuel in fast small vessels is the confined space
allotted to the boilers, such confinement being
unavoidable in view of the high power concentrated
in a small hull. The British admiralty’s
experiments, however, have gone far
to solve the problem, and the quantity of oil
which can be consumed by forced draught in
confined boilers now more nearly equals the
quantity of coal consumed under similar conditions.
All recent vessels built for the British
navy are so constructed that the spaces between
their double bottoms are oil-tight and capable
of storing liquid fuel in the tanks so formed. Most recent battleships
and cruisers have also liquid fuel furnace fittings, and in
1910 it already appeared probable that the use of oil fuel in warships
would rapidly develop.
In view of recent accusations of insufficiency of coal storage in
foreign naval depots, by reason of the allegation that coal so
stored quickly perishes, it is interesting to note that liquid fuel
may be stored in tanks for an indefinite time without any
deterioration whatever.
In the case of merchant steamers large progress has also been
made. The Shell Transport and Trading Company have twenty-one
vessels successfully navigating in all parts of the
world and using liquid fuel. The Hamburg-American
Advantages in merchant ships.
Steamship Company have four large vessels similarly
fitted for oil fuel, which, however, differ in furnace
arrangements, as will be hereafter described, although using
coal when the fluctuation of the market renders that the more
economical fuel. One of the large American transatlantic
lines is adopting liquid fuel, and French, German, Danish and
American mercantile vessels are also beginning to use it in
considerable amounts.
In the case of very large passenger steamers, such as those
of 20 knots and upwards in the Atlantic trade, the saving in cost
of fuel is trifling compared with the advantage arising from the
greater weight and space available for freight. Adopting a basis
of 3 to 2 as between coal consumption and oil consumption,
there is an increase of 1000 tons of dead weight cargo in even a
280
medium-sized Atlantic steamer, and a collateral gain of about
100,000 cub. ft. of measurement cargo, by reason of the ordinary
bunkers being left quite free, and the oil being stored in the double
bottom spaces hitherto unutilized except for the purpose of
water ballast. The cleanliness and saving of time from bunkering
by the use of oil fuel is also an important factor in passenger
ships, whilst considerable additional speed
is obtainable. The cost of the installation,
however, is very considerable, as
it includes not only burners and pipes for
the furnaces, but also the construction of
oil-tight tanks, with pumps and numerous
valves and pipe connexions.
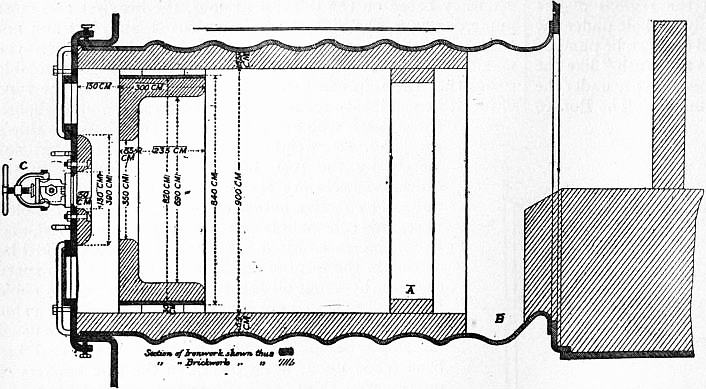 |
| Fig. 7.—Furnace on ss. “Ferdinand Laeisz.” A, it is proposed to do away with this ring
of brickwork as being useless; B, it is proposed to fill this space up, thus continuing lining
of furnace to combustion chamber, and also to fit protection bricks in way of saddle plate. |
 |
| Fig. 8.—Fuel Tanks, &c., of ss. “Murex.” |
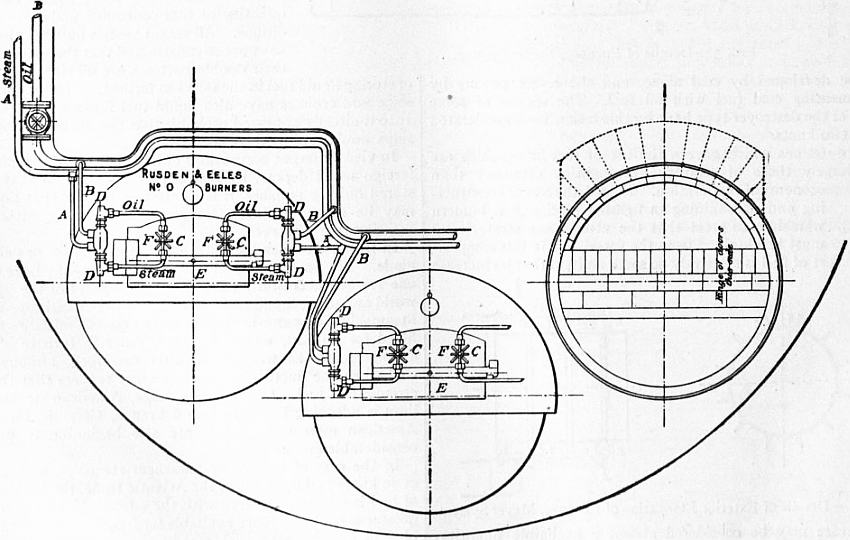 |
| Fig. 9.—Furnace Gear of ss. “Murex.” |
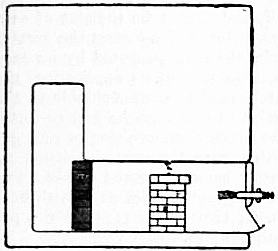 |
| Fig. 10.—Section through Furnace
of ss. “Murex.” |
Fig. 2 shows a burner of Rusden and
Eeles’ patent as generally used on board
ships for the purpose of injecting the oil.
A is a movable cap holding the packing B,
which renders the annular spindle M oil and
steam tight. E is the outer casing containing
the steam jacket from which the steam,
after being fed through the steam-supply
pipe G, passes into the annular space surrounding
the spindle P. It will be seen that
if the spindle P be travelled inwards by
turning the handle N, the orifice at the
nozzle RR will be opened so as to allow
the steam to flow out radially. If at the
same time the annular spindle M be drawn
inwards by revolving the handle L, the oil
which passes through the supply pipe F will
also have emission at RR, and, coming in
contact with the outflowing steam, will be
pulverized and sprayed into the furnace. Fig. 3 is a profile and
plan of a steamer adapted for carrying oil in bulk, and showing
all the storage arrangements for handling liquid fuel. Fig. 4 shows
the interior arrangement of the boiler furnace of the steamship
“Trocas.” A is broken fire-brick resting on the ordinary
fire-bars, B is a brick bridge, C a casing of fire-brick intended
to protect the riveted seam immediately above it from the direct
281
impact of the flame, and D is a lining of fire-brick at the back of the
combustion-box, also intended to protect the plating from the direct
impact of the petroleum flame. The arrangement of the furnace on
the Meyer system is shown in fig. 5, where E is an annular projection
built at the mouth of the furnace, and BB are spiral passages
for heating the air before it passes into the furnace. Fig. 6 shows
the rings CC and details of the casting which forms the projection
or exterior elongation of the furnace. The brickwork arrangement
adopted for the double-ended boilers on the Hamburg-American
Steamship Company’s “Ferdinand Laeisz” is represented in fig. 7.
The whole furnace is lined with fire-brick, and the burner is mounted
upon a circular disk plate which covers the mouth of the furnace.
The oil is injected not by steam pulverization, but by pressure due
to a steam-pump. The oil is heated to about 60°C. before entering
the pump, and further heated to 90°C. after leaving the pump. It
is then filtered, and passes
to the furnace injector C at
about 30-℔ pressure; and
its passage through this injector
and the spiral passages
of which it consists
pulverizes the oil into spray,
in which form it readily
ignites on reaching the
interior of the furnace. The
injector is on the Körting
principle, that is, it atomizes
by fracture of the liquid oil
arising from its own momentum
under pressure.
The advantage of this
system as compared with
the steam-jet system is the
saving of fresh water, the
abstraction of which is so
injurious to the boiler by the formation of scale.
The general arrangement of the fuel tanks and filling pipes on the
ss. “Murex” is shown in fig. 8; and fig. 9 represents the furnace
gear of the same vessel, A being the steam-pipe, B the oil-pipe,
C the injector, D the swivel upon which the injector is hung so that
it may be swung clear of the furnace, E the fire-door, and F the
handle for adjusting the injector. In fig. 10, which represents a
section of the furnace, H is a fire-brick pier and K a fire-brick
baffling bridge.
It is found in practice that to leave out the fire-bars ordinarily
used for coal produces a better result with liquid fuel than the
alternative system of keeping them in place and protecting them
by a layer of broken fire-brick.
Boilers fitted upon all the above systems have been run for
thousands of miles without trouble. In new construction it is
desirable to give larger combustion chambers and longer and narrower
boiler tubes than in the case of boilers intended for the combustion
of coal alone.
(F. F.*)
Gaseous Fuel.
Strictly speaking, much, and sometimes even most, of the
heating effected by solid or liquid fuel is actually performed by
the gases given off during the combustion. We speak, however,
of gaseous fuel only in those cases where we supply a combustible
gas from the outset, or where we produce from ordinary solid
(or liquid) fuel in one place a stream of combustible gas which
is burned in another place, more or less distant from that where
it has been generated.
The various descriptions of gaseous fuel employed in practice
may be classified under the following heads:
I. Natural Gas.
II. Combustible Gases obtained as by-products in various
technical operations.
III. Coal Gas (Illuminating Gas).
IV. Combustible Gases obtained by the partial combustion of
coal, &c.
I. Natural Gas.—From time immemorial it has been known
that in some parts of the Caucasus and of China large quantities
of gases issue from the soil, sometimes under water, which can
be lighted and burn with a luminous flame. The “eternal
fires” of Baku belong to this class. In coal-mines frequently
similar streams of gas issue from the coal; these are called
“blowers,” and when they are of somewhat regular occurrence
are sometimes conducted away in pipes and used for underground
lighting. As a regular source of heating power, however, natural
gas is employed only in some parts of the United States, especially
in Pennsylvania, Kansas, Ohio and West Virginia, where it
always occurs in the neighbourhood of coal and petroleum
fields. The first public mention of it was made in 1775, but it was
not till 1821 that it was turned to use at Fredonia, N.Y. In
Pennsylvania natural gas was discovered in 1859, but at first
very little use was made of it. Its industrial employment dates
only from 1874, and became of great importance about ten
years later. Nobody ever doubted that the gas found in these
localities was an accumulation of many ages and that, being
tapped by thousands of bore-holes, it must rapidly come to an
end. This assumption was strengthened by the fact that the
“gas-wells,” which at first gave out the gas at a pressure of 700
or 800, sometimes even of 1400 ℔ per sq. in., gradually showed
a more and more diminishing pressure and many of them ceased
to work altogether. About the year 1890 the belief was fairly
general that the stock of natural gas would soon be entirely
exhausted. Indeed, the value of the annual production of natural
gas in the United States, computed as its equivalent of coal,
was then estimated at twenty-one million dollars, in 1895 at
twelve millions, in 1899 at eleven and a half millions. But the
output rose again to a value of twenty-seven millions in 1901,
and to fifty million dollars in 1907. Mostly the gas, derived
from upwards of 10,000 gas-wells, is now artificially compressed
to a pressure of 300 or 400 ℔ per sq. in. by means of steam-power
or gas motors, fed by the gas itself, and is conveyed over
great distances in iron pipes, from 9 or 10 to 36 in. in diameter.
In 1904 nearly 30,000 m. of pipe lines were in operation. In
1907 the quantity of natural gas consumed in the United States
(nearly half of which was in Pennsylvania) was 400,000 million
cub. ft., or nearly 3 cub. m. Canada (Ontario) also produces
some natural gas, reaching a maximum of about $746,000 in
1907.
The principal constituent of natural gas is always methane,
CH4, of which it contains from 68.4 to 94.0% by volume. Those
gases which contain less methane contain all the more hydrogen,
viz. 2.9 to 29.8%. There is also some ethylene, ethane and
carbon monoxide, rarely exceeding 2 or 3%. The quantity
of incombustible gases—oxygen, carbon dioxide, nitrogen—ranges
from mere traces to about 5%. The density is from
0.45 to 0.55. The heating power of 1000 cub. ft. of natural gas
is equal to from 80 to 120 ℔, on the average 100 ℔, of good
coal, but it is really worth much more than this proportion
would indicate, as it burns completely, without smoke or ashes,
and without requiring any manual labour. It is employed for
all domestic and for most industrial purposes.
The origin of natural gas is not properly understood, even
now. The most natural assumption is, of course, that its formation
is connected with that of the petroleum always found in
the same neighbourhood, the latter principally consisting of the
higher-boiling aliphatic hydrocarbons of the methane series.
But whence do they both come? Some bring them into connexion
with the formation of coal, others with the decomposition
of animal remains, others with that of diatomaceae, &c., and
even an inorganic origin of both petroleum and natural gas has
been assumed by chemists of the rank of D.I. Mendeléeff and
H. Moissan.
II. Gases obtained as By-products.—There are two important
cases in which gaseous by-products are utilized as fuel; both
are intimately connected with the manufacture of iron, but in
a very different way, and the gases are of very different
composition.
(a) Blast-furnace Gases.—The gases issuing from the mouths
of blast-furnaces (see Iron and Steel) were first utilized in
1837 by Faber du Faur, at Wasseralfingen. Their use became
more extensive after 1860, and practically universal after 1870.
The volume of gas given off per ton of iron made is about 158,000
cub. ft. Its percentage composition by volume is:
| Carbon monoxide | 21.6 | to | 29.0, | mostly | about | 26 | % |
| Hydrogen | 1.8 | ” | 6.3, | ” | ” | 3 | % |
| Methane | 0.1 | ” | 0.8, | ” | ” | 0.5 | % |
| Carbon dioxide | 6 | ” | 12, | ” | ” | 9.5 | % |
| Nitrogen | 51 | ” | 60, | ” | ” | 56 | % |
| Steam | 5 | ” | 12, | ” | ” | 5 | % |
| | ——— |
| | 100 | % |
There is always a large amount of mechanically suspended
282
flue-dust in this gas. It is practically equal to a poor producer-gas
(see below), and is everywhere used, first for heating the blast
in Cowper stoves or similar apparatus, and secondly for raising
all the steam required for the operation of the blast-furnace,
that is, for driving the blowing-engines, hoisting the materials,
&c. Where the iron ore is roasted previously to being fed into
the furnace, this can also be done by this gas, but in some cases
the waste in using it is so great that there is not enough left for
the last purpose. The calorific power of this gas per cubic foot
is from 80 to 120 B.Th.U.
Since about 1900 a great advance has been made in this field.
Instead of burning the blast-furnace gas under steam boilers
and employing the steam for producing mechanical energy, the
gas is directly burned in gas-motors on the explosion principle.
Thus upwards of three times the mechanical energy is obtained
in comparison with the indirect way through the steam boiler.
After all the power required for the operations of the blast-furnace
has been supplied, there is a surplus of from 10 to
20 h.p. for each ton of pig-iron made, which may be applied
to any other purpose.
(b) Coke-oven Gases.—Where the coking of coal is performed
in the old beehive ovens or similar apparatus the gas issuing
at the mouth of the ovens is lost. The attempts at utilizing the
gases in such cases have not been very successful. It is quite
different where coke is manufactured in the same way as illuminating
gas, viz. by the destructive distillation
of coal in closed apparatus
(retorts), heated from the outside.
This industry, which is described in
detail in G. Lunge’s Coal-Tar and
Ammonia (4th ed., 1909), originated
in France, but has spread far
more in Germany, where more than
half of the coke produced is made
by it; in the United Kingdom and the
United States its progress has been
much slower, but there also it has long
been recognized as the only proper
method. The output of coke is
increased by about 15% in comparison with the beehive ovens,
as the heat required for the process of distillation is not produced
by burning part of the coal itself (as in the beehive ovens), but
by burning part of the gas. The quality of the coke for iron-making
is quite as good as that of beehive coke, although it
differs from it in appearance. Moreover, the gases can be made
to yield their ammonia, their tar, and even their benzene vapours,
the value of which products sometimes exceeds that of the coke
itself. And after all this there is still an excess of gas available
for any other purpose.
As the principle of distilling the coal is just the same, whether
the object is the manufacture of coal gas proper or of coke as the
main product, although there is much difference in the details
of the manufacture, it follows that the quality of the gas is very
similar in both cases, so far as its heating value is concerned.
Of course this heating value is less where the benzene has been
extracted from coke-oven gas, since this compound is the richest
heat-producer in the gas. This is, however, of minor importance
in the present case, as there is only about 1% benzene in these
gases.
The composition of coke-oven gases, after the extraction of
the ammonia and tar, is about 53% hydrogen, 36% methane,
6% carbon monoxide, 2% ethylene and benzene, 0.5% sulphuretted
hydrogen, 1.5% carbon dioxide, 1% nitrogen.
III. Coal Gas (Illuminating Gas).—Although ordinary coal gas
is primarily manufactured for illuminating purposes, it is also
extensively used for cooking, frequently also for heating domestic
rooms, baths, &c., and to some extent also for industrial operations
on a small scale, where cleanliness and exact regulation of
the work are of particular importance. In chemical laboratories
it is preferred to every other kind of fuel wherever it is available.
The manufacture of coal gas being described elsewhere in this
work (see Gas, § Manufacture), we need here only point out that
it is obtained by heating bituminous coal in fireclay retorts and
purifying the products of this destructive distillation by cooling,
washing and other operations. The residual gas, the ordinary
composition of which is given in the table below, amounts to
about 10,000 cub. ft. for a ton of coal, and represents about
21% of its original heating value, 56.5% being left in the coke,
5.5% in the tar and 17% being lost. As we must deduct from
the coke that quantity which is required for the heating of the
retorts, and which, even when good gas producers are employed,
amounts to 12% of the weight of the coal, or 10% of its heat
value, the total loss of heat rises to 27%. Taking, further, into
account the cost of labour, the wear and tear, and the capital
interest on the plant, coal gas must always be an expensive fuel
in comparison with coal itself, and cannot be thought of as a
general substitute for the latter. But in many cases the greater
expense of the coal gas is more than compensated by its easy
distribution, the facility and cleanliness of its application, the
general freedom from the mechanical loss, unavoidable in the
case of coal fires, the prevention of black smoke and so forth.
The following table shows the average composition of coal gas
by volume and weight, together with the heat developed by
its single constituents, the latter being expressed in kilogram-calories
per cub. metre (0.252 kilogram-calories = 1 British heat
unit; 1 cub. metre = 35.3 cub. ft.; therefore 0.1123 calories per
cub. metre = 1 British heat unit per cub. foot).
| Constituents. | Volume
per cent. | Weight
per cent. | Heat-value
per Cubic
Metre
Calories.
| Heat-value
per Quantity
contained in
1 Cub. Met. | Heat-value
per cent.
of Total. |
| Hydrogen, H2 | 47 | 7.4 | 2,582 | 1213 | 22.8 |
| Methane, CH4 | 34 | 42.8 | 8,524 | 2898 | 54.5 |
| Carbon monoxide, CO | 9 | 19.9 | 3,043 | 273 | 5.1 |
| Benzene vapour, C6H6 | 1.2 | 7.4 | 33,815 | 405 | 7.7 |
| Ethylene, C2H4 | 3.8 | 8.4 | 13,960 | 530 | 9.9 |
| Carbon dioxide, CO2 | 2.5 | 8.6 | .. | .. | .. |
| Nitrogen, N2 | 2.5 | 5.5 | .. | .. | .. |
| Total | 100.0 | 100.0 | .. | 5319 | 100.0 |
One cubic metre of such gas weighs 568 grammes. Rich gas,
or gas made by the destructive distillation of certain bituminous
schists, of oil, &c., contains much more of the heavy hydrocarbons,
and its heat-value is therefore much higher than the above.
The carburetted water gas, very generally made in America, and
sometimes employed in England for mixing with coal gas, is
of varying composition; its heat-value is generally rather less
than that of coal gas (see below).
IV. Combustible Gases produced by the Partial Combustion of
Coal, &c.—These form by far the most important kind of gaseous
fuel. When coal is submitted to destructive distillation to
produce the illuminating gas described in the preceding paragraph,
only a comparatively small proportion of the heating
value of the coal (say, a sixth or at most a fifth part) is obtained
in the shape of gaseous fuel, by far the greater proportion remaining
behind in the shape of coke.
An entirely different class of gaseous fuels comprises those
produced by the incomplete combustion of the total carbon
contained in the raw material, where the result is a mixture of
gases which, being capable of combining with more oxygen, can
be burnt and employed for heating purposes. Apart from some
descriptions of waste gases belonging to this class (of which the
most notable are those from blast-furnaces), we must distinguish
two ways of producing such gaseous fuels entirely different in
principle, though sometimes combined in one operation. The
incomplete combustion of carbon may be brought about by
means of atmospheric oxygen, by means of water, or by a
simultaneous combination of these two actions. In the first
case the chemical reaction is
C + O = CO
(a);
the nitrogen accompanying the oxygen in the atmospheric air
necessarily remains mixed with carbon monoxide, and the resulting
gases, which always contain some carbon dioxide, some
283
products of the destructive distillation of the coal, &c., are known
as producer gas or Siemens gas. In the second case the chemical
reaction is mainly
C + H2O = CO + H2
(b);
that is to say, the carbon is converted into monoxide and the
hydrogen is set free. As both of these substances can combine
with oxygen, and as there is no atmospheric nitrogen to deal
with, the resulting gas (water gas) is, apart from a few impurities,
entirely combustible. Another kind of water gas is formed by
the reaction
C + 2H2O = CO2 + 2H2
(c),
but this reaction, which converts all the carbon into the incombustible
form of CO2, is considered as an unwelcome, although
never entirely avoidable, concomitant of (b).
The reaction by which water gas is produced being endothermic
(as we shall see), this gas cannot be obtained except by introducing
the balance of energy in another manner. This might be done
by heating the apparatus from without, but as this method would
be uneconomical, the process is carried out by alternating the
endothermic production of water gas with the exothermic
combustion of carbon by atmospheric air. Pure water gas is
not, therefore, made by a continuous process, but alternates
with the production of other gases, combustible or not. But
instead of constantly interrupting the process in this way, a
continuous operation may be secured by simultaneously carrying
on both the reactions (a) and (b) in such proportions that the heat
generated by (a) at least equals the heat absorbed by (b). For
this purpose the apparatus is fed at the same time with atmospheric
air and with a certain quantity of steam, preferably
in a superheated state. Gaseous mixtures of this kind have been
made, more or less intentionally, for a long time past. One of
the best known of them, intended less for the purpose of serving
as ordinary fuel than for that of driving machinery, is the
Dowson gas.
An advantage common to all kinds of gaseous fuel, which
indeed forms the principal reason why it is intentionally produced
from solid fuel, in spite of inevitable losses in the course
of the operation, is the following. The combustion of solid fuel
(coal, &c.) cannot be carried on with the theoretically necessary
quantity of atmospheric air, but requires a considerable excess
of the latter, at least 50%, sometimes 100% and more. This is
best seen from the analyses of smoke gases. If all the oxygen
of the air were converted into CO2 and H2O, the amount of CO2
in the smoke gases should be in the case of pure carbon nearly
21 volumes %, as carbon dioxide occupies the same volume as
oxygen; while ordinary coal, where the hydrogen takes up a
certain quantity of oxygen as well, should show about 18.5%
CO2. But the best smoke gases of steam boilers show only 12
or 13%, much more frequently only 10% CO2, and gases from
reverberatory furnaces often show less than 5%. This means
that the volume of the smoke gases escaping into the air is
from 1½ to 2 times (in the case of high-temperature operations
often 4 times) greater than the theoretical minimum; and as
these gases always carry off a considerable quantity of heat,
the loss of heat is all the greater the less complete is the utilization
of the oxygen and the higher the temperature of the operation.
This explains why, in the case of the best-constructed steam-boiler
fires provided with heat economizers, where the smoke
gases are deprived of most of their heat, the proportion of the
heat value of the fuel actually utilized may rise to 70 or even 75%,
while in some metallurgical operations, in glass-making and
similar cases, it may be below 5%.
One way of overcoming this difficulty to a certain extent is
to reduce the solid fuel to a very fine powder, which can be
intimately mixed with the air so that the consumption of the
latter is only very slightly in excess of the theoretical quantity;
but this process, which has been only recently introduced on a
somewhat extended scale, involves much additional expense and
trouble, and cannot as yet be considered a real success. Generally,
too, it is far less easily applied than gaseous fuel. The latter
can be readily and intimately mixed with the exact quantity of
air that is required and distributed in any suitable way, and
much of the waste heat can be utilized for a preliminary heating
of the air and the gas to be burned by means of “recuperators.”
We shall now describe the principal classes of gaseous fuel,
produced by the partial combustion of coal.
A. Producer Gas, Siemens Gas.—As we have seen above, this
gas is made by the incomplete combustion of fuel. The materials
generally employed for its production are anthracite, coke or
other fuels which are not liable to cake during the operation,
and thus stop the draught or otherwise disturb the process, but
by special measures also bituminous coal, lignite, peat and other
fuel may be utilized for gas producers. The fuel is arranged in
a deep layer, generally from 4 ft. up to 10 ft., and the air is
introduced from below, either by natural draught or by means of
a blast, and either by a grate or only by a slit in the wall of the
“gas producer.” Even if the primary action taking place at
the entrance of the air consisted in the complete combustion of
the carbon to dioxide, CO2, the latter, in rising through the high
column of incandescent fuel, must be reduced to monoxide:
CO2 + C = 2CO. But as the temperature in the producer rises
rather high, and as in ordinary circumstances the action of
oxygen on carbon above 1000° C. consists almost entirely in
the direct formation of CO, we may regard this compound as
primarily formed in the hotter parts of the gas-producer. It is
true that ordinary producer gas always contains more or less
CO2, but this may be formed higher up by air entering through
leakages in the apparatus. If we ignore the hydrogen contained
in the fuel, the theoretical composition of producer gas would
be 33.3% CO and 66.7% N, both by volume and weight. Its
weight per cubic metre is 1.251 grammes, and its heat value 1013
calories per cubic metre, or less than one-fifth of the heat-value
of coal gas. Practically, however, producer gas contains a small
percentage of gases, increasing its heat-value, like hydrogen,
methane, &c., but on the other hand it is never free from carbon
dioxide to the extent of from 2 to 8%. Its heat-value may
therefore range between 800 and 1100 calories per cubic metre.
Even when taking as the basis of our calculation a theoretical gas
of 33.3% CO, we find that there is a great loss of heat-value in
the manufacture of this gas. Thermochemistry teaches us that
the reaction C + O develops 29.5% of the heat produced by the
complete oxidation of C to CO2, thus leaving only 70.5% for
the stage CO + O = CO2. If, therefore, the gas given off in the
producer is allowed to cool down to ordinary temperature,
nearly 30% of the heat-value of the coal is lost by radiation.
If, however, the gas producer is built in close proximity to the
place where the combustion takes place, so that the gas does not
lose very much of its heat, the loss is correspondingly less. Even
then there is no reason why this mode of burning the fuel, i.e.
first with “primary air” in the producer (C + O = CO), then with
“secondary air” in the furnace (CO + O =CO2), should be
preferred to the direct complete burning of the fuel on a grate,
unless the above-mentioned advantage is secured, viz. reduction
of the smoke gases to a minimum by confining the supply of air
as nearly as possible to that required for the formation of CO2,
which is only possible by producing an intimate mixture of the
producer gas with the secondary air. The advantage in question
is not very great where the heat of the smoke gases can be very
fully utilized, e.g. in well-constructed steam boilers, salt-pans
and the like, and as a matter of fact gas producers have not
found much use in such cases. But a very great advantage is
attained in high-temperature operations, where the smoke
gases escape very hot, and where it is on that account all-important
to confine their quantity to a minimum.
It is precisely in these cases that another requirement frequently
comes in, viz. the production at a given point of a higher temperature
than is easily attained by ordinary fires. Gas-firing lends
itself very well to this end, as it is easily combined with a preliminary
heating up of the air, and even of the gas itself, by
means of “recuperators.” The original and best-known form
of these, due to Siemens Brothers, consists of two brick chambers
filled with loosely stacked fire-bricks in such manner that any
gases passed through the chambers must seek their way through
the interstices left between the bricks, by which means a thorough
284
interchange of temperature takes place. The smoke gases,
instead of escaping directly into the atmosphere, are made to
pass through one of these chambers, giving up part of their
heat to the brickwork. After a certain time the draught is
changed by means of valves, the smoke gases are passed through
another chamber, and the cold air intended to feed the combustion
is made to pass through the first chamber, where it
takes up heat from the white-hot bricks, and is thus heated up
to a bright red heat until the chamber is cooled down too far,
when the draughts are again reversed. Sometimes the producer
gas itself is heated up in this manner (especially when it has
been cooled down by travelling a long distance); in that case
four recuperator chambers must be provided instead of two.
Another class of recuperators is not founded on the alternating
system, but acts continuously; the smoke gases travel always
in the same direction in flues contiguous to other flues or pipes
in which the air flows in the opposite direction, an interchange
of heat taking place through the walls of the flues or pipes. Here
the surface of contact must be made very large if a good effect
is to be produced. In both cases not merely is a saving effected
of all the calories which are abstracted by the cold air from the
recuperator, but as less fuel has to be burned to get a given
effect, the quantity of smoke gas is reduced. For details and
other producer gases, see Gas, II. For Fuel and Power.
Gas-firing in the manner just described can be brought about
by very simple means, viz. by lowering the fire-grate of an
ordinary fire-place to at least 4 ft. below the fire-bridge, and by
introducing the air partly below the grate and partly behind
the fire-place, at or near the point where the greatest heat
is required. Usually, however, more elaborate apparatus is
employed, some of which we shall describe below. Gas-firing
has now become universal in some of the most important industries
and nearly so in others. The present extension of
steel-making and other branches of metallurgy is intimately
connected with this system, as is the modern method of glass-making,
of heating coal gas retorts and so forth.
The composition of producer gas differs considerably, principally
according to the material from which it is made. Analyses
of ordinary producer gas (not such as falls under the heading of
“semi-water gas,” see sub C) by volume show 22 to 33% CO,
1 to 7% CO2, 0.5 to 2% H2, 0.5 to 3% hydrocarbons, and
64 to 68% N2.
B. Water Gas.—The reaction of steam on highly heated
carbonaceous matter was first observed by Felice Fontana in
1780. This was four years before Henry Cavendish isolated
hydrogen from water, and thirteen years before William Murdoch
made illuminating gas by the distillation of coal, so that it was
no wonder that Fontana’s laboratory work was soon forgotten.
Nor had the use of carburetted water gas, as introduced by
Donovan in 1830 for illuminating purposes, more than a very
short life. More important is the fact that during nine years
the illumination of the town of Narbonne was carried on by
incandescent platinum wire, heated by water gas, where also
internally heated generators were for the first time regularly
employed. The Narbonne process was abandoned in 1865, and
for some time no real progress was made in this field in Europe.
But in America, T.S.C. Lowe, Strong, Tessié du Motay and others
took up the matter, the first permanent success being obtained
by the introduction (1873) of Lowe’s system at Phoenixville, Pa.
In the United States the abundance of anthracite, as well as of
petroleum naphtha, adapted for carburetting the gas, secures a
great commercial advantage to this kind of illuminant over coal
gas, so that now three-fourths of all American gas-works employ
carburetted water gas. In Europe the progress of this industry
was naturally much less rapid, but here also since 1882, when
the apparatus of Lowe and Dwight was introduced in the town
of Essen, great improvements have been worked out, principally
by E. Blass, and by these improvements water gas obtained a
firm footing also for certain heating purposes. The American
process for making carburetted water gas, as an auxiliary to
ordinary coal gas, was first introduced by the London Gas Light
and Coke Company on a large scale in 1890.
Water gas in its original state is called “blue gas,” because it
burns with a blue, non-luminous flame, which produces a very
high temperature. According to the equation C + H2O = CO + H2,
this gas consists theoretically of equal volumes of carbon
monoxide and hydrogen. We shall presently see why it is
impossible to avoid the presence of a little carbon dioxide and
other gases, but we shall for the moment treat of water gas as
if it were composed according to the above equation. The
reaction C + H2O = CO + H2 is endothermic, that is, its thermal
value is negative. One gram-molecule of carbon produces 97
great calories (1 great calorie or kilogram-calorie = 1000 gram-calories)
when burning to CO2, and this is of course the maximum
effect obtainable from this source. If the same gram-molecule
of carbon is used for making water gas, that is, CO + H2, the
heat produced by the combustion of the product is 68.4 +
57.6 = 126 great calories, an apparent surplus of 29 calories,
which cannot be got out of nothing. This is made evident by
another consideration. In the above reaction C is not burned
to CO2, but to CO, a reaction which produces 28.6 calories per
gram-molecule. But as the oxygen is furnished from water,
which must first be decomposed by the expenditure of energy,
we must introduce this amount, 68.5 calories in the case of
liquid water, or 57.6 calories in the case of steam, as a negative
quantity, and the difference, viz. + 28.6 − 57.6 = 29 great calories,
represents the amount of heat to be expended from another
source in order to bring about the reaction of one gram-molecule
of carbon on one gram-molecule of H2O in the shape of steam.
This explains why steam directed upon incandescent coal will
produce water gas only for a very short time: even a large
mass of coal will quickly be cooled down so much that at first a
gas of different composition is formed and soon the process will
cease altogether. We can avoid this result by carrying on the
process in a retort heated from without by an ordinary coal fire,
and all the early water gas apparatus was constructed in this
way; but such a method is very uneconomical, and was long ago
replaced by a process first patented by J. and T.N. Kirkham
in 1854, and very much improved by successive inventors. This
process consists in conducting the operation in an upright brick
shaft, charged with anthracite, coke or other suitable fuel. This
shaft resembles an ordinary gas producer, but it differs in being
worked, not in a continuous manner, which, as shown above,
would be impossible, but by alternately blowing air and steam
through the coal for periods of a few minutes each. During the
first phase, when carbon is burned by atmospheric oxygen, and
thereby heat is produced, this heat, or rather that part of it
which is not carried away by radiation and by the products
of combustion on leaving the apparatus, is employed in raising
the temperature of the remaining mass of fuel, and is thus
available for the second phase, in which the reaction (b)
C + H2O = CO + H2 goes on with the abstraction of a corresponding
amount of heat from the incandescent fuel, so that the latter
rapidly cools down, and the process must be reversed by blowing
in air and so forth. The formation of exactly equal volumes
of carbon monoxide and hydrogen goes on only at temperatures
over 1200° C., that is, for a very few minutes. Even at 1100° C.
a little CO2 can be proved to exist in the gas, and at 900° its
proportion becomes too high to allow the process to go on.
About 650° C. the CO has fallen to a minimum, and the reaction
is now essentially (c) C + 2H2O = CO2 + 2H2; soon after the
temperature of the mass will have fallen to such a low point
that the steam passes through it without any perceptible action.
The gas produced by reaction (c) contains only two-thirds of
combustible matter, and is on that account less valuable than
proper water gas formed by reaction (b); moreover, it requires
the generation of twice the amount of steam, and its presence is
all the less desirable since it must soon lead to a total cessation
of the process. In ordinary circumstances it is evident that the
more steam is blown in during a unit of time, the sooner reaction
(c) will set in; on the other hand, the more heat has been
accumulated in the producer the longer can the blowing-in of
steam be continued.
The process of making water gas consequently comprises
285
two alternating operations, viz. first “blowing-up” by means
of a current of air, by which the heat of the mass of fuel is raised
to about 1200° C.; and, secondly “steaming,” by injecting a
current of (preferably superheated) steam until the temperature
of the fuel had fallen to about 900° C., and too much carbon
dioxide appears in the product. During the steaming the gas
is carried off by a special conduit into a scrubber, where the dust
mechanically carried away in the current is washed out, and the
gas is at the same time cooled down nearly to the ordinary
temperature. It is generally stored in a gas-holder, from which
it is conducted away as required. It is never quite free from
nitrogen, as the producer at the beginning of steaming contains
much of this gas, together with CO or CO2. The proportion of
hydrogen may exceed 50%, in consequence of reaction (c)
setting in at the close of the steaming. Ordinary “blue” water
gas, if, as usual, made from coke or anthracite, contains 48-52%
H2, 40-41% CO, 1-5% CO2, 4-5% N2, and traces of hydrocarbons,
especially methane. If made from bituminous coal,
it contains more of the latter. If “carburetted” (a process
which increases its volume 50% and more) by the vapours from
superheated petroleum naphtha, the proportion of CO ranges
about 25%, with about as much methane, and from 10 to 15%
of “illuminants” (heavy hydrocarbons). The latter, of course,
greatly enhance the fuel-value of the gas. Pure water gas would
possess the following fuel-value per cubic metre:
| 0.5 | cub. met. | H2 | = 1291 | calories |
| 0.5 | ” ” | CO | = 1522 | ” |
| | 2813 | ” |
Ordinary “blue” water gas has a fuel-value of at least 2500
calories. Carburetted water gas, which varies very much in
its percentage of hydrocarbons, sometimes reaches nearly the
heat-value of coal gas, but such gas is only in exceptional cases
used for heating purposes.
We must now turn to the “blowing-up” stage of the process.
Until recently it was assumed that during this stage the combustion
of carbon cannot be carried on beyond the formation of
carbon monoxide, for as the gas-producer must necessarily
contain a deep layer of fuel (generally about 6 to 10 ft.), any CO2
formed at first would be reduced to CO; and it was further
assumed that hardly any CO2 would be formed from the outset,
as the temperature of the apparatus is too high for this reaction
to take place. But as the combustion of C to CO produces only
about 30% of the heat produced when C is burned into CO2,
the quantity of fuel consumed for “blowing-up” is very large,
and in fact considerably exceeds that consumed in “steaming.”
There is, of course, a further loss by radiation and minor sources,
and the result is that 1 kilogram of carbon yields only about
1.2 cub. met. of water gas. Each period of blowing-up generally
occupies from 8 to 12 minutes, that of steaming only 4 or 5
minutes. This low yield of water gas until quite recently appeared
to be unavoidable, and the only question seemed to be whether
and to what extent the gas formed during blowing-up, which
is in fact identical with ordinary producer gas (Siemens gas),
could be utilized. In America, where the water gas is mostly
employed for illuminating purposes, at least part of the blowing-up
gas is utilized for heating the apparatus in which the naphtha
is volatilized and the vapours are “fixed” by superheating.
This process, however, never utilizes anything like the whole
of the blowing-up gas, nor can this be effected by raising and
superheating the steam necessary for the second operation;
indeed, the employment of this gas for raising steam is not very
easy, owing to the irregularities of and constant interruptions
in the supply. In some systems the gas made during the blowing-up
stage is passed through chambers, loosely filled with bricks,
like Siemens recuperators, where it is burned by “secondary”
air: the heat thus imparted to the brickwork is utilized by passing
through the recuperator, and thus superheating, the steam
required for the next steaming operation. In many cases,
principally where no carburetting is practised, the blowing-up
gas is simply burned at the mouth of the producer, and is thus
altogether lost; and in no case can it be utilized without great
waste. A very important improvement in this respect was
effected by C. Dellwik and E. Fleischer. They found that the
view that it is unavoidable to burn the carbon to monoxide
during the blowing-up holds good only for the pressure of blast
formerly applied. This did not much exceed that which is
required for overcoming the frictional resistance within the
producer. If, however, the pressure is considerably increased,
and the height of the column of fuel reduced, both of these
conditions being strictly regulated in accordance with the result
desired, it is easy to attain a combustion of the carbon to dioxide,
with only traces of monoxide, in spite of the high temperature.
Evidently the excess of oxygen coming into contact with each
particle of carbon in a given unit of time produces other conditions
of chemical equilibrium than those existing at lower pressures. At
any rate, experience has shown that by this process, in which the
full heat-value of carbon is utilized during the blowing-up stage,
the time of heating-up can be reduced from 10 to 1½ or 2 minutes,
and the steaming can be prolonged from 4 or 5 to 8 or 10 minutes,
with the result that twice the quantity of water gas is obtained,
viz. upwards of 2 cub. metres from 1 kilogram of carbon.
The application of water gas as a fuel mainly depends upon
the high temperatures which it is possible to attain by its aid,
and these are principally due to the circumstance that it forms
a much smaller flame than coal gas, not to speak of Siemens gas,
which contains at most 33% of combustible matter against
90% or more in water gas. The latter circumstance also allows
the gas to be conducted and distributed in pipes of moderate
dimensions. Its application, apart from its use as an illuminant
(with which we are not concerned here), was formerly retarded
by its high cost in comparison with Siemens gas and other
sources of heat, but as this state of affairs has been changed by
the modern improvements, its use is rapidly extending, especially
for metallurgical purposes.
C. Mixed Gas (Semi-Water Gas).—This class is sometimes
called Dowson gas, irrespective of its method of production,
although it was made and extensively used a long time before
J.E. Dowson constructed his apparatus for generating such a
gas principally for driving gas-engines. By a combination of
the processes for generating Siemens gas and water gas, it is
produced by injecting into a gas-producer at the same time a
certain quantity of air and a corresponding quantity of steam,
the latter never exceeding the amount which can be decomposed
by the heat-absorbing reaction, C + H2O = CO + H2, at the expense
of the heat generated by the action of the air in the
reaction C + O = CO. Such gas used to be frequently obtained in
an accidental way by introducing liquid water or steam into
an ordinary gas-producer for the purpose of facilitating its
working by avoiding an excessive temperature, such as might
cause the rapid destruction of the brickwork and the fusion of
the ashes of the fuel into troublesome cakes. It was soon found
that by proceeding in this way a certain advantage could be
gained in regard to the consumption of fuel, as the heat abstracted
by the steam from the brickwork and the fuel itself was usefully
employed for decomposing water, its energy thus reappearing
in the shape of a combustible gas. It is hardly necessary to
mention explicitly that the total heat obtained by any such
process from a given quantity of carbon (or hydrogen) can in
no case exceed that which is generated by direct combustion;
some inventors, however, whether inadvertently or intentionally,
have actually represented this to be possible, in manifest violation
of the law of the conservation of energy.
Roughly speaking, this gas may be said to be produced by
the combination of the reactions, described sub A and B, to the
joint reaction: 2C + O + H2O = 2CO + H2. The decomposition
of H2O (applied in the shape of steam) absorbs 57.6 gram calories,
the formation of 2CO produces 59 gram calories; hence there is
a small positive excess of 1.4 calories at disposal. This in reality
would not be sufficient to cover the loss by radiation, &c.;
hence rather more free oxygen (i.e. atmospheric air) must be
employed than is represented by the above equation. All this
free oxygen is, of course, accompanied by nearly four times
its volume of nitrogen.
286
The mixed gas thus obtained differs very much in composition,
but is always much richer in hydrogen (of which it contains
sometimes as much as 20%) and poorer in carbon monoxide
(sometimes down to 20%) than Siemens gas; generally it
contains more of CO2 than the latter. The proportion of nitrogen
is always less, about 50%. It is therefore a more concentrated
fuel than Siemens gas, and better adapted to the driving of gas-engines.
It scarcely costs more to make than ordinary Siemens
gas, except where the steam is generated and superheated in
special apparatus, as is done in the Dowson producer, which,
on the other hand, yields a correspondingly better gas. As is
natural, its properties are some way between those of Siemens
gas and of water gas; but they approach more nearly the
former, both as to costs and as to fuel-value, and also as to the
temperatures reached in combustion. This is easily understood
if we consider that gas of just the same description can be
obtained by mixing one volume of real water gas with the four
volumes of Siemens gas made during the blowing-up stage—an
operation which is certainly too expensive for practical use.
A modification of this gas is the Mond gas, which is made,
according to Mond’s patent, by means of such an excess of steam
that most of the nitrogen of the coke is converted into ammonia
(Grouven’s reaction). Of course much of this steam passes on
undecomposed, and the quantity of the gas is greatly increased
by the reaction C + 2H2O = CO2 + 2H2; hence the fuel-value
of this gas is less than that of semi-water gas made in other ways.
Against this loss must be set the gain of ammonia which is
recovered by means of an arrangement of coolers and scrubbers,
and, except at very low prices of ammonia, the profit thus made
is probably more than sufficient to cover the extra cost. But
as the process requires very large and expensive plant, and its
profits would vanish in the case of the value of ammonia becoming
much lower (a result which would very probably follow if it were
somewhat generally introduced), it cannot be expected to supplant
the other descriptions of gaseous fuel to more than a
limited extent.
Semi-water gas is especially adapted for the purpose of driving
gas-engines on the explosive principle (gas-motors). Ordinary
producer-gas is too poor for this purpose in respect of heating
power; moreover, owing to the prevalence of carbon monoxide,
it does not light quickly enough. These defects are sufficiently
overcome in semi-water gas by the larger proportion of hydrogen
contained in it. For the purpose in question the gas should be
purified from tar and ashes, and should also be cooled down before
entering the gas-engine. The Dowson apparatus and others
are constructed on this principle.
Air Gas.—By forcing air over or through volatile inflammable
liquids a gaseous mixture can be obtained which burns with a
bright flame and which can be used for illumination. Its employment
for heating purposes is quite exceptional, e.g. in chemical
laboratories, and we abstain, therefore, from describing any of the
numerous appliances, some of them bearing very fanciful names,
which have been devised for its manufacture.
(G. L.)
FUENTE OVEJUNA [Fuenteovejuna], a town of Spain, in the
province of Cordova; near the sources of the river Guadiato,
and on the Fuente del Arco-Belmez-Cordova railway. Pop.
(1900) 11,777. Fuente Ovejuna is built on a hill, in a well-irrigated
district, which, besides producing an abundance of
wheat, wine, fruit and honey, also contains argentiferous lead
mines and stone quarries. Cattle-breeding is an important
local industry, and leather, preserved meat, soap and flour
are manufactured. The parish church formerly belonged to
the knights of Calatrava (c. 1163-1486).
FUENTERRABIA (formerly sometimes written Fontarabia;
Lat. Fons Rapidus), a town of northern Spain, in the province
of Guipúzcoa; on the San Sebastian-Bayonne railway; near
the Bay of Biscay and on the French frontier. Pop. (1870)
about 750; (1900) 4345. Fuenterrabia stands on the slope of a
hill on the left bank of the river Bidassoa, and near the point
where its estuary begins. Towards the close of the 19th century
the town became popular as a summer resort for visitors from
the interior of Spain, and, in consequence, its appearance underwent
many changes and much of its early prosperity returned.
Hotels and villas were built in the new part of the town that
sprang up outside the picturesque walled fortress, and there is
quite a contrast between the part inside the heavy, half-ruined
ramparts, with its narrow, steep streets and curious gable-roofed
houses, its fine old church and castle and its massive town hall,
and the new suburbs and fishermen’s quarter facing the estuary
of the Bidassoa. Many industries flourish on the outskirts of
the town, including rope and net manufactures, flour mills, saw
mills, mining railways, paper mills.
Fuenterrabia formerly possessed considerable strategic importance,
and it has frequently been taken and retaken in
wars between France and Spain. The rout of Charlemagne in
778, which has been associated with Fontarabia, by Milton
(Paradise Lost, i. 587), is generally understood to have taken
place not here but at Roncesvalles (q.v.), which is nearly 40 m.
E.S.E. Unsuccessful attempts to seize Fuenterrabia were
made by the French troops in 1476 and again in 1503. In a
subsequent campaign (1521) these were more successful, but the
fortress was retaken in 1524. The prince of Condé sustained a
severe repulse under its walls in 1638, and it was on this occasion
that the town received from Philip IV. the rank of city (muy
noble, muy leal, y muy valerosa ciudad, “most noble, most loyal,
and most valiant city”), a privilege which involved some
measure of autonomy. After a severe siege, Fuenterrabia
surrendered to the duke of Berwick and his French troops in
1719; and in 1794 it again fell into the hands of the French,
who so dismantled it that it has never since been reckoned by
the Spaniards among their fortified places. It was by the ford
opposite Fuenterrabia that the duke of Wellington, on the 8th of
October 1813, successfully forced a passage into France in the
face of an opposing army commanded by Marshal Soult. Severe
fighting also took place here during the Carlist War in 1837.
FUERO, a Spanish term, derived from the Latin forum. The
Castillan use of the word in the sense of a right, privilege or
charter is most probably to be traced to the Roman conventus
juridici, otherwise known as jurisdictiones or fora, which in
Pliny’s time were already numerous in the Iberian peninsula. In
each of these provincial fora the Roman magistrate, as is well
known, was accustomed to pay all possible deference to the
previously established common law of the district; and it was
the privilege of every free subject to demand that he should be
judged in accordance with the customs and usages of his proper
forum. This was especially true in the case of the inhabitants of
those towns which were in possession of the jus italicum. It is
not, indeed, demonstrable, but there are many presumptions,
besides some fragments of direct evidence, which make it more
than probable that the old administrative arrangements both of
the provinces and of the towns, but especially of the latter,
remained practically undisturbed at the period of the Gothic
occupation of Spain.1 The Theodosian Code and the Breviary
of Alaric alike seem to imply a continuance of the municipal
system which had been established by the Romans; nor does the
later Lex Visigothorum, though avowedly designed in some
points to supersede the Roman law, appear to have contemplated
any marked interference with the former fora, which were still to
a large extent left to be regulated in the administration of justice
by unwritten, immemorial, local custom. Little is known of the
condition of the subject populations of the peninsula during the
Arab occupation; but we are informed that the Christians were,
sometimes at least, judged according to their own laws in
separate tribunals presided over by Christian judges;2 and the
mere fact of the preservation of the name alcalde, an official
whose functions corresponded so closely to those of the judex or
defensor civitatis, is fitted to suggest that the old municipal fora,
if much impaired, were not even then in all cases wholly destroyed.
At all events when the word forum3 begins to appear for the first
time in documents of the 10th century in the sense of a liberty or
287
privilege, it is generally implied that the thing so named is
nothing new. The earliest extant written fuero is probably that
which was granted to the province and town of Leon by Alphonso
V. in 1020. It emanated from the king in a general council of the
kingdom of Leon and Castile, and consisted of two separate
parts; in the first 19 chapters were contained a series of statutes
which were to be valid for the kingdom at large, while the rest of
the document was simply a municipal charter.4 But in neither
portion does it in any sense mark a new legislative departure,
unless in so far as it marks the beginning of the era of written
charters for towns. The “fuero general” does not profess to
supersede the consuetudines antiquorum jurium or Chindaswint’s
codification of these in the Lex Visigothorum; the “fuero
municipal” is really for the most part but a resuscitation of
usages formerly established, a recognition and definition of
liberties and privileges that had long before been conceded or
taken for granted. The right of the burgesses to self-government
and self-taxation is acknowledged and confirmed, they, on the
other hand, being held bound to a constitutional obedience and
subjection to the sovereign, particularly to the payment of
definite imperial taxes, and the rendering of a certain amount of
military service (as the ancient municipia had been). Almost
contemporaneous with this fuero of Leon was that granted to
Najera (Naxera) by Sancho el Mayor of Navarre (ob. 1035), and
confirmed, in 1076, by Alphonso VI.5 Traces of others of perhaps
even an earlier date are occasionally to be met with. In the fuero
of Cardeña, for example, granted by Ferdinand I. in 1039,
reference is made to a previous forum Burgense (Burgos), which,
however, has not been preserved, if, indeed, it ever had been
reduced to writing at all. The phraseology of that of Sepulveda
(1076) in like manner points back to an indefinitely remote
antiquity.6 Among the later fueros of the 11th century, the
most important are those of Jaca (1064) and of Logroño (1095).
The former of these, which was distinguished by the unusual
largeness of its concessions, and by the careful minuteness of its
details, rapidly extended to many places in the neighbourhood,
while the latter charter was given also to Miranda by Alphonso
VI., and was further extended in 1181 by Sancho el Sabio of
Navarre to Vitoria, thus constituting one of the earliest written
fora of the “Provincias Vascongadas.” In the course of the 12th
and 13th centuries the number of such documents increased very
rapidly; that of Toledo especially, granted to the Mozarabic
population in 1101, but greatly enlarged and extended by
Alphonso VII. (1118) and succeeding sovereigns, was used as a
basis for many other Castilian fueros. Latterly the word fuero
came to be used in Castile in a wider sense than before, as meaning
a general code of laws; thus about the time of Saint Ferdinand
the old Lex Visigothorum, then translated for the first
time into the vernacular, was called the Fuero Juzgo, a name
which was soon retranslated into the barbarous Latin of the period
as Forum Judicum;7 and among the compilations of Alphonso
the Learned in like manner were an Espejo de Fueros and also the
Fuero de las leyes, better known perhaps as the Fuero Real. The
famous code known as the Ordenamiento Real de Alcalá, or Fuero
Viejo de Castilla, dates from a still later period. As the power of
the Spanish crown was gradually concentrated and consolidated,
royal pragmaticas began to take the place of constitutional laws;
the local fueros of the various districts slowly yielded before the
superior force of imperialism; and only those of Navarre and the
Basque provinces (see Basques) have had sufficient vitality to
enable them to survive to comparatively modern times. While
actually owning the lordship of the Castilian crown since about the
middle of the 14th century, these provinces rigidly insisted upon
compliance with their consuetudinary law, and especially with
that which provided that the señor, before assuming the government,
should personally appear before the assembly and swear
to maintain the ancient constitutions. Each of the provinces
mentioned had distinct sets of fueros, codified at different periods,
and varying considerably as to details; the main features, however,
were the same in all. Their rights, after having been recognized
by successive Spanish sovereigns from Ferdinand the
Catholic to Ferdinand VII., were, at the death of the latter in
1833, set aside by the government of Castaños. The result was a
civil war, which terminated in a renewed acknowledgment of the
fueros by Isabel II. (1839). The provisional government of 1868
also promised to respect them, and similar pledges were given
by the governments which succeeded. In consequence, however,
of the Carlist rising of 1873-1876, the Basque fueros were finally
extinguished in 1876. The history of the Foraes of the Portuguese
towns, and of the Fors du Béarn, is precisely analogous to
that of the fueros of Castile.
Among the numerous works that more or less expressly deal with
this subject, that of Marina (Ensayo historico-critico sobre la antigua
legislacion y principales cuerpos legales de los reynos de Leon y
Castilla) still continues to hold a high place. Reference may also
be made to Colmeiro’s Curso de derecho político según la historia de
Leon y de Castilla (Madrid, 1873); to Schäfer’s Geschichte von
Spanien, ii. 418-428, iii. 293 seq.; and to Hallam’s Middle Ages,
c. iv.
1 The nature of the evidence may be gathered from Savigny, Gesch.
d. röm. Rechts. See especially i. pp. 154, 259 seq.
2 Compare Lembke u. Schäfer, Geschichte von Spanien, i. 314; ii. 117.
3 Or rather forus. See Ducange, s.v.
4 Cap. xx. begins: “Constituimus etiam ut Legionensis civitas,
quae depopulata fuit a Sarracenis in diebus patris mei Veremundi
regis, repopulatur per hos foros subscriptos.”
5 “Mando et concedo et confirmo ut ista civitas cum sua plebe et
cum omnibus suis pertinentiis sub tali lege et sub tali foro maneat
per saecula cuncta. Amen. Isti sunt fueros quae habuerunt in
Naxera in diebus Sanctii regis et Gartiani regis.”
6 “Ego Aldefonsus rex et uxor mea Agnes confirmamus ad Septempublica
suo foro quod habuit in tempore antiquo de avolo meo et in
tempore comitum Ferrando Gonzalez et comite Garcia Ferdinandez
et comite Domno Santio.”
7 This Latin is later even than that of Ferdinand, whose words are:
“Statuo et mando quod Liber Judicum, quo ego misi Cordubam,
translatetur in vulgarem et vocetur forum de Corduba ... et quod
per saecula cuncta sit pro foro et nullus sit ausus istud forum aliter
appellare nisi forum de Corduba, et jubeo et mando quod omnis
morator et populator ... veniet ad judicium et ad forum de
Corduba.”
FUERTEVENTURA, an island in the Atlantic Ocean, forming
part of the Spanish archipelago of the Canary Islands (q.v.).
Pop. (1900) 11,669; area 665 sq. m. Fuerteventura lies between
Lanzarote and Grand Canary. It has a length of 52 m., and an
average width of 12 m. Though less mountainous than the other
islands, its aspect is barren. There are only two springs of fresh
water, and these are confined to one valley. Lava streams and
other signs of volcanic action abound, but there has been no
igneous activity since the Spaniards took possession. At each
extremity of the island are high mountains, which send off
branches along the coast so as to enclose a large arid plain.
The highest peak reaches 2500 ft. In external appearance,
climate and productions, Fuerteventura greatly resembles
Lanzarote. An interval of three years without rain has been
known. Oliva (pop. 1900, 2464) is the largest town. A smaller
place in the centre of the island named Betancuria (586) is the
administrative capital. Cabras (1000) on the eastern coast is
the chief port. Dromedaries are bred here.
FUGGER, the name of a famous German family of merchants
and bankers. The founder of the family was Johann Fugger,
a weaver at Graben, near Augsburg, whose son, Johann, settled
in Augsburg probably in 1367. The younger Johann added the
business of a merchant to that of a weaver, and through his
marriage with Clara Widolph became a citizen of Augsburg.
After a successful career he died in 1408, leaving two sons,
Andreas and Jakob, who greatly extended the business which
they inherited from their father. Andreas, called the “rich
Fugger,” had several sons, among them being Lukas, who was
very prominent in the municipal politics of Augsburg and who
was very wealthy until he was ruined by the repudiation by the
town of Louvain of a great debt owing to him, and Jakob, who
was granted the right to bear arms in 1452, and who founded the
family of Fugger vom Reh—so called from the first arms of the
Fuggers, a roe (Reh) or on a field azure—which became extinct
on the death of his great-grandson, Ulrich, in 1583. Johann
Fugger’s son, Jakob, died in 1469, and three of his seven sons,
Ulrich (1441-1510), Georg (1453-1506) and Jakob (1459-1525),
men of great resource and industry, inherited the family business
and added enormously to the family wealth. In 1473 Ulrich
obtained from the emperor Frederick III. the right to bear arms
for himself and his brothers, and about the same time he began
288
to act as the banker of the Habsburgs, a connexion destined to
bring fame and fortune to his house. Under the lead of Jakob,
who had been trained for business in Venice, the Fuggers were
interested in silver mines in Tirol and copper mines in Hungary,
while their trade in spices, wool and silk extended to almost
all parts of Europe. Their wealth enabled them to make large
loans to the German king, Maximilian I., who pledged to them
the county of Kirchberg, the lordship of Weissenhorn and other
lands, and bestowed various privileges upon them. Jakob
built the castle of Fuggerau in Tirol, and erected the Fuggerei
at Augsburg, a collection of 106 dwellings, which were let at low
rents to poor people and which still exist. Jakob Fugger and
his two nephews, Ulrich (d. 1525) and Hieronymus (d. 1536),
the sons of Ulrich, died without direct heirs, and the family was
continued by Georg’s sons, Raimund (1489-1535) and Anton
(1493-1560), under whom the Fuggers attained the summit of
their wealth and influence.
Jakob Fugger’s florins had contributed largely to the election
of Charles V. to the imperial throne in 1519, and his nephews
and heirs maintained close and friendly relations with the great
emperor. In addition to lending him large sums of money, they
farmed his valuable quicksilver mines at Almaden, his silver
mines at Guadalcanal, the great estates of the military orders
which had passed into his hands, and other parts of his revenue
as king of Spain; receiving in return several tokens of the
emperor’s favour. In 1530 Raimund and Anton were granted
the imperial dignity of counts of Kirchberg and Weissenhorn,
and obtained full possession of these mortgaged properties;
in 1534 they were given the right of coining money; and in 1541
received rights of jurisdiction over their lands. During the diet
of Augsburg in 1530 Charles V. was the guest of Anton Fugger
at his house in the Weinmarkt, and the story relates how the
merchant astonished the emperor by lighting a fire of cinnamon
with an imperial bond for money due to him. This incident
forms the subject of a picture by Carl Becker which is in the
National Gallery at Berlin. Continuing their mercantile career,
the Fuggers brought the new world within the sphere of their
operations, and also carried on an extensive and lucrative
business in farming indulgences. Moreover, both brothers
found time to acquire landed property, and were munificent
patrons of literature and art. When Anton died he is said to
have been worth 6,000,000 florins, besides a vast amount of
property in Europe, Asia and America; and before this time
the total wealth of the family had been estimated at 63,000,000
florins. The Fuggers were devotedly attached to the Roman
Catholic Church, which benefited from their liberality. Jakob
had been made a count palatine (Pfalzgraf) and had received
other marks of favour from Pope Leo X., and several members
of the family had entered the church; one, Raimund’s son,
Sigmund, becoming bishop of Regensburg.
In addition to the bishop, three of Raimund Fugger’s sons
attained some degree of celebrity. Johann Jakob (1516-1575),
was the author of Wahrhaftigen Beschreibung des österreichischen
und habsburgischen Nahmens, which was largely used by S. von
Bircken in his Spiegel der Ehren des Erzhauses Österreich (Nuremberg,
1668), and of a Geheim Ernbuch des Fuggerischen Geschlechtes.
He was also a patron of art, and a distinguished counsellor of
Duke Albert IV. of Bavaria. After the death of his son Konstantin,
in 1627, this branch of the family was divided into three
lines, which became extinct in 1738, 1795 and 1846 respectively.
Another of Raimund’s sons was Ulrich (1526-1584), who, after
serving Pope Paul III. at Rome, became a Protestant. Hated
on this account by the other members of his family, he took
refuge in the Rhenish Palatinate; greatly interested in the
Greek classics, he occupied himself in collecting valuable manuscripts,
which he bequeathed to the university of Heidelberg.
Raimund’s other son was Georg (d. 1579), who inherited the
countships of Kirchberg and Weissenhorn, and founded a branch
of the family which still exists, its present head being Georg,
Count Fugger of Kirchberg and Weissenhorn (b. 1850).
Anton Fugger left three sons, Marcus (1529-1597), Johann
(d. 1598) and Jakob (d. 1598), all of whom left male issue.
Marcus was the author of a book on horse-breeding, Wie und
wo man ein Gestüt von guten edeln Kriegsrossen aufrichten soll
(1578), and of a German translation of the Historia ecclesiastica
of Nicephorus Callistus. He founded the Nordendorf branch
of the family, which became extinct on the death of his grandson,
Nicolaus, in 1676. Another grandson of Marcus was Franz
Fugger (1612-1664), who served under Wallenstein during the
Thirty Years’ War, and was afterwards governor of Ingolstadt.
He was killed at the battle of St Gotthard on the 1st of August
1664.
Johann Fugger had three sons, Christoph (d. 1615) and
Marcus (d. 1614), who founded the families of Fugger-Glött and
Fugger-Kirchheim respectively, and Jakob, bishop of Constance
from 1604 until his death in 1626. Christoph’s son, Otto Heinrich
(1592-1644), was a soldier of some distinction and a knight
of the order of the Golden Fleece. He was one of the most
active of the Bavarian generals during the Thirty Years’ War,
and acted as governor of Augsburg, where his rule aroused
much discontent. The family of Kirchheim died out in 1672.
That of Glött was divided into several branches by the sons
of Otto Heinrich and of his brother Johann Ernst (d. 1628).
These lines, however, have gradually become extinct except the
eldest line, represented in 1909 by Karl Ernst, Count Fugger of
Glött (b. 1859). Anton Fugger’s third son Jakob, the founder of
the family of Wellenburg, had two sons who left issue, but in 1777
the possessions of this branch of the family were again united by
Anselm Joseph (d. 1793), Count Fugger of Babenhausen. In
1803 Anselm’s son, Anselm Maria (d. 1821), was made a prince of
the Holy Roman Empire, the title of Prince Fugger of Babenhausen
being borne by his direct descendant Karl (b. 1861). On
the fall of the empire in 1806 the lands of the Fuggers, which
were held directly of the empire, were mediatized under Bavaria
and Württemberg. The heads of the three existing branches
of the Fuggers are all hereditary members of the Bavarian
Upper House.
Augsburg has many interesting mementoes of the Fuggers,
including the family burial-chapel in the church of St Anna;
the Fugger chapel in the church of St Ulrich and St Afra; the
Fuggerhaus, still in the possession of one branch of the family;
and a statue of Johann Jakob Fugger.
In 1593 a collection of portraits of the Fuggers, engraved by
Dominique Custos of Antwerp, was issued at Augsburg. Editions
with 127 portraits appeared in 1618 and 1620, the former accompanied
by a genealogy in Latin, the latter by one in German. Another
edition of this Pinacotheca Fuggerorum, published at Vienna in 1754,
includes 139 portraits. See Chronik der Familie Fugger vom Jahre
1599, edited by C. Meyer (Munich, 1902); A. Geiger, Jakob Fugger,
1459-1525 (Regensburg, 1895); A. Schulte, Die Fugger in Rom,
1495-1523 (Leipzig, 1904); R. Ehrenberg, Das Zeitalter der Fugger
(Jena, 1896); K. Häbler, Die Geschichte der Fuggerschen Handlung
in Spanien (Weimar, 1897); A. Stauber, Das Haus Fugger (Augsburg,
1900); and M. Jansen, Die Anfänge der Fugger (Leipzig,
1907).
FUGITIVE SLAVE LAWS, a term applied in the United
States to the Statutes passed by Congress in 1793 and 1850 to
provide for the return of negro slaves who escaped from one
state into another or into a public territory. A fugitive slave
clause was inserted in the Articles of Confederation of the New
England Confederation of 1643, providing for the return of the
fugitive upon the certificate of one magistrate in the jurisdiction
out of which the said servant fled—no trial by jury being provided
for. This seems to have been the only instance of an inter-colonial
provision for the return of fugitive slaves; there were,
indeed, not infrequent escapes by slaves from one colony to
another, but it was not until after the growth of anti-slavery
sentiment and the acquisition of western territory, that it
became necessary to adopt a uniform method for the return of
fugitive slaves. Such provision was made in the Ordinance of
1787 (for the Northwest Territory), which in Article VI. provided
that in the case of “any person escaping into the same [the
Northwest Territory] from whom labor or service is lawfully
claimed in any one of the original states, such fugitive may be
lawfully reclaimed and conveyed to the person claiming his or
her labor or service as aforesaid.” An agreement of the sort was
289
necessary to persuade the slave-holding states to union, and in
the Federal Constitution, Article IV., Section II., it is provided
that “no person held to service or labor in one state, under the
laws thereof, escaping into another, shall, in consequence of any
law or regulation therein, be discharged from such service or
labor, but shall be delivered up on claim of the party to whom
such service or labour may be due.”
The first specific legislation on the subject was enacted on the
12th of February 1793, and like the Ordinance for the Northwest
Territory and the section of the Constitution quoted above, did
not contain the word “slave”; by its provisions any Federal
district or circuit judge or any state magistrate was authorized
to decide finally and without a jury trial the status of an alleged
fugitive. The measure soon met with strong opposition in the
northern states, and Personal Liberty Laws were passed to hamper
officials in the execution of the law; Indiana in 1824 and Connecticut
in 1828 providing jury trial for fugitives who appealed
from an original decision against them. In 1840 New York and
Vermont extended the right of trial by jury to fugitives and
provided them with attorneys. As early as the first decade of
the 19th century individual dissatisfaction with the law of 1793
had taken the form of systematic assistance rendered to negroes
escaping from the South to Canada or New England—the
so-called “Underground Railroad.”1 The decision of the
Supreme Court of the United States in the case of Prigg v.
Pennsylvania in 1842 (16 Peters 539), that state authorities
could not be forced to act in fugitive slave cases, but that
national authorities must carry out the national law, was
followed by legislation in Massachusetts (1843), Vermont (1843),
Pennsylvania (1847) and Rhode Island (1848), forbidding state
officials to help enforce the law and refusing the use of state
gaols for fugitive slaves. The demand from the South for more
effective Federal legislation was voiced in the second fugitive slave
law, drafted by Senator J.M. Mason of Virginia, and enacted on
the 18th of September 1850 as a part of the Compromise Measures
of that year. Special commissioners were to have concurrent
jurisdiction with the U.S. circuit and district courts and the
inferior courts of Territories in enforcing the law; fugitives could
not testify in their own behalf; no trial by jury was provided;
penalties were imposed upon marshals who refused to enforce the
law or from whom a fugitive should escape, and upon individuals
who aided negroes to escape; the marshal might raise a posse
comitatus; a fee of $10 was paid to the commissioner when his
decision favoured the claimant and only $5 when it favoured the
fugitive; and both the fact of the escape and the identity of the
fugitive were to be determined on purely ex parte testimony.
The severity of this measure led to gross abuses and defeated its
purpose; the number of abolitionists increased, the operations
of the Underground Railroad became more efficient, and new
Personal Liberty Laws were enacted in Vermont (1850), Connecticut
(1854), Rhode Island (1854), Massachusetts (1855),
Michigan (1855), Maine (1855 and 1857), Kansas (1858) and
Wisconsin (1858). These Personal Liberty Laws forbade justices
and judges to take cognizance of claims, extended the habeas
corpus act and the privilege of jury trial to fugitives, and
punished false testimony severely. The supreme court of
Wisconsin went so far (1859) as to declare the Fugitive Slave Law
unconstitutional. These state laws were one of the grievances
officially referred to by South Carolina (in Dec. 1860) as justifying
her secession from the Union. Attempts to carry into effect the
law of 1850 aroused much bitterness. The arrests of Sims and
of Shadrach in Boston in 1851; of “Jerry” M’Henry, in
Syracuse, New York, in the same year; of Anthony Burns in
1854, in Boston; and of the two Garner families in 1856, in
Cincinnati, with other cases arising under the Fugitive Slave
Law of 1850, probably had as much to do with bringing on the
Civil War as did the controversy over slavery in the Territories.
With the beginning of the Civil War the legal status of the
slave was changed by his master’s being in arms. General B.F.
Butler, in May 1861, declared negro slaves contraband of war.
A confiscation bill was passed in August 1861 discharging from
his service or labour any slave employed in aiding or promoting
any insurrection against the government of the United States.
By an act of the 17th of July 1862 any slave of a disloyal master
who was in territory occupied by northern troops was declared
ipso facto free. But for some time the Fugitive Slave Law was
considered still to hold in the case of fugitives from masters in
the border states who were loyal to the Union government, and
it was not until the 28th of June 1864 that the Act of 1850 was
repealed.
See J.F. Rhodes, History of the United States from the Compromise
of 1850, vols. i. and ii. (New York, 1893); and M.G. M’Dougall,
Fugitive Slaves, 1619-1865 (Boston, 1891).
1 The precise amount of organization in the Underground Railroad
cannot be definitely ascertained because of the exaggerated use of
the figure of railroading in the documents of the “presidents” of
the road, Robert Purvis and Levi Coffin, and of its many “conductors,”
and their discussion of the “packages” and “freight”
shipped by them. The system reached from Kentucky and Virginia
across Ohio, and from Maryland across Pennsylvania and New
York, to New England and Canada, and as early as 1817 a group of
anti-slavery men in southern Ohio had helped to Canada as many as
1000 slaves. The Quakers of Pennsylvania possibly began the
work of the mysterious Underground Railroad; the best known of
them was Thomas Garrett (1789-1871), a native of Pennsylvania,
who, in 1822, removed to Wilmington, Delaware, where he was
convicted in 1848 on four counts under the Fugitive Slave Law and
was fined $8000; he is said to have helped 2700 slaves to freedom.
The most picturesque figure of the Underground Railroad was
Harriet Tubman (c. 1820), called by her friend, John Brown,
“General” Tubman, and by her fellow negroes “Moses.” She
made about a score of trips into the South, bringing out with her
300 negroes altogether. At one time a reward of $40,000 was offered
for her capture. She was a mystic, with remarkable clairvoyant
powers, and did great service as a nurse, a spy and a scout in the
Civil War. Levi Coffin (1798-1877), a native of North Carolina
(whose cousin, Vestal Coffin, had established before 1819 a “station”
of the Underground near what is now Guilford College, North Carolina),
in 1826 settled in Wayne County, Ohio; his home at New
Garden (now Fountain City) was the meeting point of three “lines”
from Kentucky; and in 1847 he removed to Cincinnati, where his
labours in bringing slaves out of the South were even more successful.
It has been argued that the Underground Railroad delayed the final
decision of the slavery question, inasmuch as it was a “safety
valve”; for, without it, the more intelligent and capable of the
negro slaves would, it is asserted, have become the leaders of insurrections
in the South, and would not have been removed from
the places where they could have done most damage. Consult
William Still, The Underground Railroad (Philadelphia, 1872), a collection
of anecdotes by a negro agent of the Pennsylvania Anti-Slavery
Society, and of the Philadelphia branch of the Railroad; and the
important and scholarly work of Wilbur H. Siebert, The Underground
Railroad from Slavery to Freedom (New York, 1898).
FUGLEMAN (from the Ger. Flügelmann, the man on the
Flügel or wing), properly a military term for a soldier who is
selected to act as “guide,” and posted generally on the flanks
with the duty of directing the march in the required line, or of
giving the time, &c., to the remainder of the unit, which conforms
to his movements, in any military exercise. The word is then
applied to a ringleader or one who takes the lead in any movement
or concerted movement.
FUGUE (Lat. fuga, flight), in music, the mutual “pursuit”
of voices or parts. It was, up to the end of the 16th century,
if not later, the name applied to two art-forms. (A) Fuga
ligata was the exact reproduction by one or more voices of the
statement of a leading part. The reproducing voice (comes)
was seldom if ever written out, for all differences between it
and the dux were rigidly systematic; e.g. it was an exact inversion,
or exactly twice as slow, or to be sung backwards, &c. &c.
Hence, a rule or canon was given, often in enigmatic form, by
which the comes was deduced from the dux: and so the term
canon became the appropriate name for the form itself, and is
still retained. (B) A composition in which the canonic style
was cultivated without canonic restriction was, in the 16th
century, called fuga ricercata or simply a ricercare, a term which
is still used by Bach as a title for the fugues in Das musikalische
Opfer.
The whole conception of fugue, rightly understood, is one of
the most important in music, and the reasons why some contrapuntal
compositions are called fugues, while others are not,
are so trivial, technically as well as aesthetically, that we have
290
preferred to treat the subject separately under the general
heading of Contrapuntal Forms, reserving only technical
terms for definition here.
(i.) If in the beginning or “exposition” the material with which
the opening voice accompanies the answer is faithfully reproduced
as the accompaniment to subsequent entries of the subject, it
is called a countersubject (see Counterpoint, under sub-heading
Double Counterpoint). Obviously the process may be carried
further, the first countersubject going on to a second when the
subject enters in the third part and so on. The term is also
applied to new subjects appearing later in the fugue in combination
(immediate or destined) with the original subject. Cherubini,
holding the doctrine that a fugue cannot have more than one
subject, insists on applying the term to the less prominent of
the subjects of what are commonly called double fugues, i.e.
fugues which begin with two parts and two subjects simultaneously,
and so also with triple and quadruple fugues.
(ii.) Episodes are passages separating the entries of the subject.1
Episodes are usually developed from the material of the subject
and countersubjects; they are very rarely independent, but
then conspicuously so.
(iii.) Stretto, the overlapping of subject and answer, is a resource
the possibilities of which may be exemplified by the setting of
the words omnes generationes in Bach’s Magnificat (see Bach).
(iv.) The distinction between real and tonal fugue, which is
still sometimes treated as a thing of great historical and technical
importance, is really a mere detail resulting from the fact that
a violent oscillation between the keys of tonic and dominant
is no part of the function of a fugal exposition, so that the answer
is (especially in its first notes and in points that tend to shift the
key) not so much a transposition of the subject to the key of
the dominant as an adaptation of it from the tonic part to the
dominant part of the scale, or vice versa; in short, the answer
is as far as possible on the dominant, not in the dominant. The
modifications this principle produces in the answer (which have
been happily described as resembling “fore-shortening”) are
the only distinctive marks of tonal fugue; and the text-books
are half filled with the attempt to reduce them from matters
of ear to rules of thumb, which rules, however, have the merit
(unusual in those of the academic fugue) of being founded on
observation of the practice of great masters. But the same
principle as often as not produces answers that are exact transpositions
of the subject; and so the only kind of real fugue
(i.e. fugue with an exact answer) that could rightly be contrasted
with tonal fugue would be that in which the answer ought to
be tonal but is not. It must be admitted that tonal answers are
rare in the modal music of the 16th century, though their melodic
principles are of yet earlier date; still, though tonal fugue does
not become usual until well on in the 17th century, the idea
that it is a separate species is manifestly absurd, unless the term
simply means “fugue in modern tonality or key,” whatever the
answer may be.
The term “answer” is usually reserved for those entries of
the subject that are placed in what may be called the “complementary”
position of the scale, whether they are “tonally”
modified or not. Thus the order of entries in the exposition of
the first fugue of the Wohltemp. Klav. is subject, answer, answer,
subject; a departure from the usual rule according to which
subject and answer are strictly alternate in the exposition.
In conclusion we may remind the reader of the most accurate
as well as the most vivid description ever given of the essentials
of a fugue, in the famous lines in Paradise Lost, book xi.
“His volant touch,
Instinct through all proportions, low and high,
Fled and pursued transverse the resonant fugue.”
|
It is hard to realize that this description of organ-music was
written in no classical period of instrumental polyphony, but
just half-way between the death of Frescobaldi and the birth
of Bach. Every word is a definition, both retrospective and
prophetic; and in “transverse” we see all that Sir Frederick
Gore Ouseley expresses in his popular distinction between the
“perpendicular” or homophonic style in which harmony is
built up in chords, and the “horizontal” or polyphonic style in
which it is woven in threads of independent melody.
(D. F. T.)
1 An episode occurring during the exposition is sometimes called
codetta, a distinction the uselessness of which at once appears on
an analysis of Bach’s 2nd fugue in the Wohltemp. Klav. (the term
codetta is more correctly applied to notes filling in a gap between
subject and its first answer, but such a gap is rare in good examples).
FÜHRICH, JOSEPH VON (1800-1876), Austrian painter, was
born at Kratzau in Bohemia on the 9th of February 1800. Deeply
impressed as a boy by rude pictures adorning the wayside chapels
of his native country, his first attempt at composition was a
sketch of the Nativity for the festival of Christmas in his father’s
house. He lived to see the day when, becoming celebrated as
a composer of scriptural episodes, his sacred subjects were
transferred in numberless repetitions to the roadside churches of
the Austrian state, where humble peasants thus learnt to admire
modern art reviving the models of earlier ages. Führich has
been fairly described as a “Nazarene,” a romantic religious artist
whose pencil did more than any other to restore the old spirit
of Dürer and give new shape to countless incidents of the gospel
and scriptural legends. Without the power of Cornelius or the
grace of Overbeck, he composed with great skill, especially in
outline. His mastery of distribution, form, movement and
expression was considerable. In its peculiar way his drapery
was perfectly cast. Essentially creative as a landscape
draughtsman, he had still no feeling for colour; and when
he produced monumental pictures he was not nearly so
successful as when designing subjects for woodcuts. Führich’s
fame extended far beyond the walls of the Austrian capital,
and his illustrations to Tieck’s Genofeva, the Lord’s Prayer,
the Triumph of Christ, the Road to Bethlehem, the Succession
of Christ according to Thomas à Kempis, the Prodigal
Son, and the verses of the Psalter, became well known. His
Prodigal Son, especially, is remarkable for the fancy with which
the spirit of evil is embodied in a figure constantly recurring,
and like that of Mephistopheles exhibiting temptation in a human
yet demoniacal shape. Führich became a pupil at the Academy
of Prague in 1816. His first inspiration was derived from the
prints of Dürer and the Faust of Cornelius, and the first fruit of
this turn of study was the Genofeva series. In 1826 he went to
Rome, where he added three frescoes to those executed by
Cornelius and Overbeck in the Palazzo Massimi. His subjects
were taken from the life of Tasso, and are almost solitary examples
of his talent in this class of composition. In 1831 he finished
the Triumph of Christ now in the Raczynski palace at Berlin.
In 1834 he was made custos and in 1841 professor of composition
in the Academy of Vienna. After this he completed the monumental
pictures of the church of St Nepomuk, and in 1854-1861
the vast series of wall paintings which cover the inside of the
Lerchenfeld church at Vienna. In 1872 he was pensioned and
made a knight of the order of Franz Joseph; 1875 is the date of his
illustrations to the Psalms. He died on the 13th of March 1876.
His autobiography was published in 1875, and a memoir by his
son Lucas in 1886.
FUJI (Fuji-san, Fujiyama, Fusiyama), a celebrated mountain
of Japan, standing W.S.W. of Tokyo, its base being about 70 m.
by rail from that city. It rises to a height of 12,395 ft. and its
southern slopes reach the shore of Suruga Bay. It is a cone of
beautifully simple form, the more striking to view because it
stands isolated; but its summit is not conical, being broken by
a crater some 2000 ft. in diameter, for Fuji is a quiescent volcano.
Small outbursts of steam are still to be observed at some points.
An eruption is recorded so lately as the first decade of the 18th
century. The mountain is the resort of great numbers of pilgrims
(see also Japan).
FU-KIEN (formerly Min), a south-eastern province of China,
bounded N. by the province of Cheh-kiang, S. by that of Kwang-tung,
W. by that of Kiang-si and E. by the sea. It occupies an
area of 53,480 sq. m. and its population is estimated at 20,000,000.
The provincial capital is Fuchow Fu, and it is divided into eleven
prefectures, besides that ruled over by the prefect of the capital
city. Fu-kien is generally mountainous, being overspread by the
Nan-shan ranges, which run a general course of N.E. and S.W.
291
The principal river is the Min, which is formed by the junction,
in the neighbourhood of the city of Yen-p’ing Fu, of three rivers,
namely, the Nui-si, which takes its rise in the mountains on the
western frontier in the prefecture of Kien-ning Fu, the Fuh-tun
Ki, the source of which is found in the district of Kwang-tsih in
the north-west of the province, and the Ta-shi-ki (Shao Ki), which
rises in the mountains in the western district of Ning-hwa. From
Yen-p’ing Fu the river takes a south-easterly course, and after
passing along the south face of the city of Fuchow Fu, empties
itself into the sea about 30 m. below that town. Its upper course
is narrow and rocky and abounds in rapids, but as it approaches
Fuchow Fu the channel widens and the current becomes slow
and even. Its depth is very irregular, and it is navigable only by
native boats of a small class. Two other rivers flow into the sea
near Amoy, neither of which, however, is navigable for any
distance from its mouth owing to the shallows and rapids with
which they abound. Thirty-five miles inland from Amoy stands
the city of Chang Chow, famous for the bridge which there spans
the Kin-lung river. This bridge is 800 ft. long, and consists of
granite monoliths stretching from one abutment to another. The
soil of the province is, as its name, “Happy Establishment,”
indicates, very productive, and the scenery is of a rich and varied
character. Most of the hills are covered with verdure, and the
less rugged are laid out in terraces. The principal products of
the province are tea, of which the best kind is that known as
Bohea, which takes its name, by a mispronunciation, from the
Wu-e Mountains, in the prefecture of Kien-ning Fu, where it is
grown; grains of various kinds, oranges, plantins, lichis, bamboo,
ginger, gold, silver, lead, tin, iron, salt (both marine and rock),
deers’ horns, beeswax, sugar, fish, birds’ nests, medicine, paper,
cloth, timber, &c. Fu-kien has three open ports, Fuchow Fu
opened in 1842, Amoy opened to trade in the same year and
Funing. The latter port was only opened to foreign trade in
1898, but in 1904 it imported and exported goods to the value of
£7668 and £278,160 respectively.
FUKUI, a town of Japan in the province of Echizen, Nippon,
near the west coast, 20 m. N. by E. of Wakasa Bay. It lies in
a volcanic district much exposed to earthquakes, and suffered
severely during the disturbances of 1891-1892, when a chasm over
40 m. long was opened across the Neo valley from Fukui to
Katabira. But Fukui subsequently revived, and is now in a
flourishing condition, with several local industries, especially the
manufacture of paper, and an increasing population exceeding
50,000. Fukui has railway communication. There are ruins of
a castle of the Daimios of Echizen.
FUKUOKA, a town on the north-west coast of the island of
Kiushiu, Japan, in the province of Chikuzen, 90 m. N.N.E. of
Nagasaki by rail. Pop. about 72,000. With Hakata, on the
opposite side of a small coast stream, it forms a large centre of
population, with an increasing export trade and several local
industries. Of these the most important is silk-weaving, and
Hakata especially is noted for its durable silk fabrics. Fukuoka
was formerly the residence of the powerful daimio of Chikuzen,
and played a conspicuous part in the medieval history of Japan;
the renowned temple of Yeiyas in the district was destroyed by
fire during the revolution of 1868. There are several other places
of this name in Japan, the most important being Fukuoka in the
province of Mutsu, North Nippon, a railway station on the main
line from Tokyo to Aimori Ura Bay. Pop. about 5000.
FULA (Fulbe, Fellatah or Peuls), a numerous and powerful
African people, spread over an immense region from Senegal
nearly to Darfur. Strictly they have no country of their own, and
nowhere form the whole of the population, though nearly always
the dominant native race. They are most numerous in Upper
Senegal and in the countries under French sway immediately
south of Senegambia, notably Futa Jallon. Farther east they
rule, subject to the control of the French, Segu and Massena,
countries on both banks of the upper Niger, to the south-west of
Timbuktu. The districts within the great bend of the Niger
have a large Fula population. East of that river Sokoto and its
tributary emirates are ruled by Fula princes, subject to the
control of the British Nigerian administration. Fula are settled
in Bornu, Bagirmi, Wadai and the upper Nile Valley,1 but have
no political power in those countries. Their most southerly
emirate is Adamawa, the country on both sides of the upper
Benue. In this vast region of distribution the Fula populations
are most dense towards the west and north, most scattered
towards the east and south. Originally herdsmen in the western
and central Sudan, they extended their sway east of the Niger,
under the leadership of Othman Dan Fodio, during the early
years of the 19th century, and having subdued the Hausa states,
founded the empire of Sokoto with the vassal emirates of Kano,
Gando, Nupe, Adamawa, &c.
The question of the ethnic affinities of the Fula has given rise
to an enormous amount of speculation, but the most reasonable
theory is that they are a mixture of Berber and Negro. This is
now the most generally accepted theory. Certainly there is no
reason to connect them with the ancient Egyptians. In the
district of Senegal known as Fuladugu or “Fula Land,” where
the purest types of the race are found, the people are of a reddish
brown or light chestnut colour, with oval faces, ringlety or even
smooth hair, never woolly, straight and even aquiline noses,
delicately shaped lips and regular features quite differentiating
them from the Negro type. Like most conquering races the
Fula are, however, not of uniform physique, in many districts
approximating to the local type. They nevertheless maintain
throughout their widespread territory a certain national solidarity,
thanks to common speech, traditions and usages. The
ruling caste of the Fula differs widely in character from the
herdsmen of the western Sudan. The latter are peaceable,
inoffensive and abstemious. They are mainly monogamous,
and by rigidly abstaining from foreign marriages have preserved
racial purity. The ruling caste in Nigeria, on the other hand,
despise their pastoral brethren, and through generations of
polygamy with the conquered tribes have become more Negroid
in type, black, burly and coarse featured. Love of luxury,
pomp and finery is their chief characteristic. Taken as a whole,
the Fula race is distinguished by great intelligence, frankness of
disposition and strength of character. As soldiers they are
renowned almost exclusively as cavalry; and the race has
produced several leaders possessed of much strategical skill.
Besides the ordinary Negro weapons, they use iron spears with
leatherbound handles and swords. They are generally excellent
rulers, stern but patient and just. The Nigerian emirs acquired,
however, an evil reputation during the 19th century as slave
raiders. They have long been devout Mahommedans, and
mosques and schools exist in almost all their towns. Tradition
says that of old every Fula boy and girl was a scholar; but
during the decadence of their power towards the close of the 19th
century education was not highly valued. Power seems to have
somewhat spoilt this virile race, but such authorities as Sir
Frederick Lugard believe them still capable of a great future.
The Fula language has as yet found no place in any African
linguistic family. In its rudiments it is akin to the Hamito-Semitic
group. It possesses two grammatical genders, not
masculine and feminine, but the human and the non-human;
the adjective agrees in assonance with its noun, and euphony
plays a great part in verbal and nominal inflections. In some
ways resembling the Negro dialects, it betrays non-Negroid
influences in the use of suffixes. The name of the people has many
variations. Fulbe or Fula (sing. Pullo, Peul) is the Mandingan
name, Follani the Hausa, Fellatah the Kanuri, Fullan the
Arab, and Fulde on the Benue. Like the name Abate, “white,”
given them in Kororofa, all these seem to refer to their light
reddish hue.
See F. Ratzel, History of Mankind (English ed., London, 1896-1898);
Sir F. Lugard, “Northern Nigeria,” in Geographical Journal
(July 1904); Grimai de Guirodon, Les Puls (1887); E.A. Brackenbury,
A Short Vocabulary of the Fulani Language (Zungeru, 1907);
the articles Nigeria and Sokoto and authorities there cited.
1 Sir Wm. Wallace in a report on Northern Nigeria (“Colonial
Office” series, No. 551, 1907) calls attention to the exodus “of
thousands of Fulani of all sorts, but mostly Mellawa, from the
French Middle Niger,” and states that the majority of the emigrants
are settling in the Nile valley.
292
FULCHER (or Foucher) OF CHARTRES (1058-c. 1130),
French chronicler, was a priest who was present at the council
of Clermont in 1095, and accompanied Robert II., duke of
Normandy, on the first crusade in 1096. Having spent some
time in Italy and taken part in the fighting on the way to the
Holy Land, he became chaplain to Baldwin, who was chosen
king of Jerusalem in 1100, and lived with Baldwin at Edessa
and then at Jerusalem. He accompanied this king on several
warlike expeditions, but won more lasting fame by writing his
Historia Hierosolymitana or Gesta Francorum Jerusalem expugnantium,
one of the most trustworthy sources for the history
of the first crusade. In its final form it is divided into three
books, and covers the period between the council of Clermont
and 1127, and the author only gives details of events which he
himself had witnessed. It was used by William of Tyre. Fulcher
died after 1127, probably at Jerusalem. He has been confused
with Foucher of Mongervillier (d. 1171), abbot of St-Père-en-Vallée
at Chartres, and also with another person of the same
name who distinguished himself at the siege of Antioch in
1098.
The Historia, but in an incomplete form, was first published by
J. Bongars in the Gesta Dei per Francos (Hanover, 1611). The best
edition is in tome iii. of the Recueil des historiens des croisades,
Historiens occidentaux (Paris, 1866); and there is a French translation
in tome xxiv. of Guizot’s Collection des mémoires relatifs à
l’histoire de France (Paris, 1823-1835).
See H. von Sybel, Geschichte des ersten Kreuzzuges (Leipzig, 1881);
and A. Molinier, Les Sources de l’histoire de France, tome ii. (Paris,
1902).
FULDA, a town and episcopal see of Germany, in the Prussian
province of Hesse-Nassau, between the Rhön and the Vogel-Gebirge,
69 m. N.E. from Frankfort-on-Main on the railway
to Bebra. Although irregularly built the town is pleasantly
situated, and contains two fine squares, on one of which stands a
fine statue of St Boniface. The present cathedral was built
at the beginning of the 18th century on the model of St Peter’s
at Rome, but it has an ancient crypt, which contains the bones
of St Boniface and was restored in 1892. Opposite the cathedral
is the former monastery of St Michael, now the episcopal palace.
The Michaelskirche, attached to it, is a small round church built,
in imitation of the Holy Sepulchre, in 822 and restored in 1853.
Of other buildings may be mentioned the Library, with upwards
of 80,000 printed books and many valuable MSS., the stately
palace with its gardens and orangery, the former Benedictine
nunnery (founded 1625, and now used as a seminary), and the
Minorite friary (1238) now used as a furniture warehouse. Among
the secular buildings are the fine Schloss, the Bibliothek, the
town hall and the post office. There are several schools, a hospital
founded in the 13th century, and some new artillery barracks.
Many industries are carried on in Fulda. These include weaving
and dyeing, the manufacture of linen, plush and other textiles
and brewing. There are also railway works in the town. A
large trade is done in cattle and grain, many markets being held
here. Fine views are obtained from several hills in the neighbourhood,
among these being the Frauenberg, the Petersberg and
the Kalvarienberg.
Fulda owes its existence to its famous abbey. It became a
town in 1208, and during the middle ages there were many
struggles between the abbots and the townsfolk. During the
Peasants’ War it was captured by the rebels and during the
Seven Years’ War by the Hanoverians. It came finally into the
possession of Prussia in 1866. From 1734 to 1804 Fulda was
the seat of a university, and latterly many assemblies of German
bishops have been held in the town.
The great Benedictine abbey of Fulda occupies the place in
the ecclesiastical history of Germany which Monte Cassino holds
in Italy, St Gall in South Germany, Corvey in Saxony, Tours
in France and Iona in Scotland. Founded in 744 at the instigation
of St Boniface by his pupil Sturm, who was the first abbot,
it became the centre of a great missionary work. It was liberally
endowed with land by the princes of the Carolingian house and
others, and soon became one of the most famous and wealthy
establishments of its kind. About 968 the pope declared that
its abbot was primate of all the abbots in Germany and Gaul,
and later he became a prince of the Empire. Fulda was specially
famous for its school, which was the centre of the theological
learning of the early middle ages. Among the teachers here
were Alcuin, Hrabanus Maurus, who was abbot from 822 to 842,
and Walafrid Strabo. Early in the 10th century the monastery
was reformed by introducing monks from Scotland, who were
responsible for restoring in its old strictness the Benedictine rule.
Later the abbey lost some of its lands and also its high position,
and some time before the Reformation the days of its glory
were over. Johann von Henneberg, who was abbot from 1529
to 1541, showed some sympathy with the teaching of the reformers,
but the Counter-Reformation made great progress here
under Abbot Balthasar von Dernbach. Gustavus Adolphus
gave the abbey as a principality to William, landgrave of Hesse,
but William’s rule only lasted for ten years. In 1752 the abbot
was raised to the rank of a bishop, and Fulda ranked as a
prince-bishopric. This was secularized in 1802, and in quick succession
it belonged to the prince of Orange, the king of France and the
grand-duchy of Frankfort. In 1816 the greater part of the
principality was ceded by Prussia to Hesse-Cassel, a smaller
portion being united with Bavaria. Sharing the fate of Hesse-Cassel,
this larger portion was annexed by Prussia in 1866. In
1829 a new bishopric was founded at Fulda.
For the town see A. Hartmann, Zeitgeschichte von Fulda (Fulda,
1895); J. Schneider, Führer durch die Stadt Fulda (Fulda, 1899);
and Chronik von Fulda und dessen Umgebungen (1839). For the
history of the abbey see Gegenbaur, Das Kloster Fulda im Karolinger
Zeitalter (Fulda, 1871-1874); Arndt, Geschichte des Hochstifts Fulda
(Fulda, 1860); and the Fuldaer Geschichtsblätter (1902 fol.).
FULGENTIUS, FABIUS PLANCIADES, Latin grammarian,
a native of Africa, flourished in the first half of the 6th (or the
last part of the 5th) century A.D. He is to be distinguished
from Fulgentius, bishop of Ruspe (468-533), to whom he was
probably related, and also from the bishop’s pupil and biographer,
Fulgentius Ferrandus. Four extant works are attributed to
him. (1) Mythologiarum libri iii., dedicated to a certain
Catus, a presbyter of Carthage, containing 75 myths briefly told,
and then explained in the mystical and allegorical manner of
the Stoics and Neoplatonists. For this purpose the author
generally invokes the aid of etymologies which, borrowed from
the philosophers, are highly absurd. As a Christian, Fulgentius
sometimes (but less frequently than might have been expected)
quotes the Bible by the side of the philosophers, to give a
Christian colouring to the moral lesson. (2) Expositio Vergilianae
continentiae (continentia = contents), a sort of appendix to (1),
dedicated to Catus. The poet himself appears to the author and
explains the twelve books of the Aeneid as a picture of human
life. The three words arma (= virtus), vir (= sapientia), primus
(= princeps) in the first line represent respectively substantia
corporalis, sensualis, ornans. Book i. symbolizes the birth and
early childhood of man (the shipwreck of Aeneas denotes the
peril of birth), book vi. the plunge into the depths of wisdom.
(3) Expositio sermonum antiquorum, explanations of 63 rare and
obsolete words, supported by quotations (sometimes from authors
and works that never existed). It is much inferior to the similar
work of Nonius, with which it is often edited. (4) Liber absque
litteris de aetatibus mundi et hominis. In the MS. heading of this
work, the name of the author is given as Fabius Claudius
Gordianus Fulgentius (Claudius is the name of the father, and
Gordianus that of the grandfather of the bishop, to whom some
attribute the work). The title Absque litteris indicates that one
letter of the alphabet is wholly omitted in each successive book
(A in bk. i., B in bk. ii.). Only 14 books are preserved. The
matter is chiefly taken from sacred history. In addition to these,
Fulgentius speaks of early poetical attempts after the manner of
Anacreon, and of a work called Physiologus, dealing with medical
questions, and including a discussion of the mystical signification
of the numbers 7 and 9. Fulgentius is a representative of the
so-called late African style, taking for his models Apuleius,
Tertullian and Martianus Capella. His language is bombastic,
affected and incorrect, while the lengthy and elaborate periods
make it difficult to understand his meaning.
293
See the edition of the four works by R. Helm (1898, Teubner
series); also M. Zink, Der Mytholog Fulgentius (1867); E. Jungmann,
“De Fulgentii aetate et scriptis,” in Acta Societatis Philologae
Lipsiensis, i. (1871); A. Ebert, Allgemeine Geschichte der Litt. des
Mittelalters, i.; article “Fulgentius” by C.F. Böhr in Ersch and
Gruber’s Allgemeine Encyklopädie; Teuffel-Schwabe, History of
Roman Literature (Eng. trans.).
FULGINIAE (mod. Foligno), an ancient town of Umbria,
Italy, on the later line of the Via Flaminia, 15 m. S. of Nuceria.
It appears to have been of comparatively late origin, inasmuch
as it had no city walls, but, in imperial times especially, owing
to its position on the new line of the Via Flaminia, it must have
increased in importance as being the point of departure of roads
to Perusia and to Picenum over the pass of Plestia. It appears
to have had an amphitheatre, and three bridges over the Topino
are attributed to the Roman period. Three miles to the N. lies
the independent community of Forum Flaminii, the site of
which is marked by the church of S. Giovanni Profiamma, at
or near which the newer line of the Via Flaminia rejoined the
older. It was no doubt founded by the builder of the road,
C. Flaminius, consul in 220 B.C. (See Foligno and Flaminia,
Via.)
(T. As.)
FULGURITE (from Lat. fulgur, lightning), in petrology, the
name given to rocks which have been fused on the surface by
lightning, and to the characteristic holes in rocks formed by the
same agency. When lightning strikes the naked surfaces of
rocks, the sudden rise of temperature may produce a certain
amount of fusion, especially when the rocks are dry and the
electricity is not readily conducted away. Instances of this
have been observed on Ararat and on several mountains in the
Alps, Pyrenees, &c. A thin glassy crust, resembling a coat of
varnish, is formed; its thickness is usually not more than one-eighth
of an inch, and it may be colourless, white or yellow. When
examined under the microscope, it usually shows no crystallization,
and contains minute bubbles due to the expansion of air
or other gases in the fused pellicle. Occasionally small microliths
may appear, but this is uncommon because so thin a film would
cool with extreme rapidity. The minerals of the rock beneath
are in some cases partly fused, but the more refractory often
appear quite unaffected. The glass has arisen from the melting
of the most fusible ingredients alone.
Another type of fulgurite is commonest in dry sands and
takes the shape of vertical tubes which may be nearly half an
inch in diameter. Generally they are elliptical in cross section,
or flattened by the pressure exerted by the surrounding sand on
the fulgurite at a time when it was still very hot and plastic.
These tubes are often vertical and may run downwards for
several feet through the sand, branching and lessening as they
descend. Tubular perforations in hard rocks have been noted
also, but these are short and probably follow original cracks.
The glassy material contains grains of sand and many small
round or elliptical cavities, the long axes of which are radial.
Minerals like felspar and mica are fused more readily than
quartz, but analysis shows that some fulgurite glasses are very
rich in silica, which perhaps was dissolved in the glass rather
than simply fused. The central cavity of the tube and the
bubbles in its walls point to the expansion of the gases
(air, water, &c.) in the sand by sudden and extreme heating.
Very fine threads of glass project from the surface of the tube
as if fused droplets had been projected outwards with considerable
force. Where the quartz grains have been greatly
heated but not melted they become white and semi-opaque,
but where they are in contact with the glass they usually show
partial solution. Occasionally crystallization has begun before
the glass solidified, and small microliths, the nature of which is
undeterminable, occur in streams and wisps in the clear hyaline
matrix.
(J. S. F.)
FULHAM, a western metropolitan borough of London,
England, bounded N.W. by Hammersmith, N.E. by Kensington,
E. by Chelsea, and S.E., S. and S.W. by the river Thames.
Pop. (1901) 137,289. The principal thoroughfares are Fulham
Palace Road running S. from Hammersmith, Fulham Road
and King’s Road, W. from Chelsea, converging and leading to
Putney Bridge over the Thames; North End Road between
Hammersmith and Fulham Roads; Lillie Road between South
Kensington and Fulham Palace Road; and Wandsworth Bridge
Road leading S. from New King’s Road to Wandsworth Bridge.
In the north Fulham includes the residential district known as
West Kensington, and farther south that of Walham Green.
The manor house or palace of the bishops of London stands in
grounds, beautifully planted and surrounded by a moat, believed
to be a Danish work, near the river west of Putney Bridge. Its
oldest portion is the picturesque western quadrangle, built by
Bishop Fitzjames (1506-1522). The parish church of All
Saints, between the bridge and the grounds, was erected in
1881 from designs by Sir Arthur Blomfield. The fine old monuments
from the former building, dating from the 16th to the
18th centuries, are mostly preserved, and in the churchyard are
the memorials of several bishops of London and of Theodore Hook
(1841). The public recreation grounds include the embankment
and gardens between the river and the palace grounds, and
there are also two well-known enclosures used for sports within
the borough. Of these Hurlingham Park is the headquarters
of the Hurlingham Polo Club and a fashionable resort; and
Queen’s Club, West Kensington, has tennis and other courts
for the use of members, and is also the scene of important
football matches, and of the athletic meetings between Oxford
and Cambridge Universities, and those between the English
and American Universities held in England. In Seagrave Road
is the Western fever hospital. The parliamentary borough of
Fulham returns one member. The borough council consists of
a mayor, 6 aldermen and 36 councillors. Area, 1703.5 acres.
Fulham, or in its earliest form Fullanham, is uncertainly
stated to signify “the place” either “of fowls” or “of dirt.”
The manor is said to have been given to Bishop Erkenwald
about the year 691 for himself and his successors in the see of
London, and Holinshed relates that the Bishop of London was
lodging in his manor place in 1141 when Geoffrey de Mandeville,
riding out from the Tower of London, took him prisoner. At
the Commonwealth the manor was temporarily out of the
bishops’ hands, being sold to Colonel Edmund Harvey. There
is no record of the first erection of a parish church, but the first
known rector was appointed in 1242, and a church probably
existed a century before this. The earliest part of the church
demolished in 1881, however, did not date farther back than
the 15th century. In 879 Danish invaders, sailing up the
Thames, wintered at Fulham and Hammersmith. Near the
former wooden Putney Bridge, built in 1729 and replaced in
1886, the earl of Essex threw a bridge of boats across the river
in 1642 in order to march his army in pursuit of Charles I., who
thereupon fell back on Oxford. Margravine Road recalls the
existence of Bradenburg House, a riverside mansion built by
Sir Nicholas Crispe in the time of Charles I., used as the headquarters
of General Fairfax in 1647 during the civil wars, and
occupied in 1792 by the margrave of Bradenburg-Anspach
and Bayreuth and his wife, and in 1820 by Caroline, consort of
George IV.
FULK, king of Jerusalem (b. 1092), was the son of Fulk IV.,
count of Anjou, and his wife Bertrada (who ultimately deserted
her husband and became the mistress of Philip I. of France).
He became count of Anjou in 1109, and considerably added to
the prestige of his house. In particular he showed himself a
doughty opponent to Henry I. of England, against whom he
continually supported Louis VI. of France, until in 1127 Henry
won him over by betrothing his daughter Matilda to Fulk’s son
Geoffrey Plantagenet. Already in 1120 Fulk had visited the
Holy Land, and become a close friend of the Templars. On his
return he assigned to the order of the Templars an annual subsidy,
while he also maintained two knights in the Holy Land
for a year. In 1128 he was preparing to return to the East,
when he received an embassy from Baldwin II., king of Jerusalem,
who had no male heir to succeed him, offering his daughter
Melisinda in marriage, with the right of eventual succession to
the kingdom. Fulk readily accepted the offer; and in 1129
he came and was married to Melisinda, receiving the towns of
294
Acre and Tyre as her dower. In 1131, at the age of thirty-nine,
he became king of Jerusalem. His reign is not marked by any
considerable events: the kingdom which had reached its zenith
under Baldwin II., and did not begin to decline till the capture
of Edessa in the reign of Baldwin III., was quietly prosperous
under his rule. In the beginning of his reign he had to act as
regent of Antioch, and to provide a husband, Raymund of
Poitou, for the infant heiress Constance. But the great problem
with which he had to deal was the progress of the atabeg Zengi
of Mosul. In 1137 he was beaten near Barin, and escaping into
the fort was surrounded and forced to capitulate. A little
later, however, he greatly improved his position by strengthening
his alliance with the vizier of Damascus, who also had to fear
the progress of Zengi (1140); and in this way he was able to
capture the fort of Banias, to the N. of Lake Tiberias. Fulk
also strengthened the kingdom on the south; while his butler,
Paganus, planted the fortress of Krak to the south of the Dead
Sea, and helped to give the kingdom an access towards the
Red Sea, he himself constructed Blanche Garde and other forts
on the S.W. to overawe the garrison of Ascalon, which was still
held by the Mahommedans, and to clear the road towards Egypt.
Twice in Fulk’s reign the eastern emperor, John Comnenus,
appeared in northern Syria (1137 and 1142); but his coming
did not affect the king, who was able to decline politely a visit
which the emperor proposed to make to Jerusalem. In 1143 he
died, leaving two sons, who both became kings, as Baldwin III.
and Amalric I.
Fulk continued the tradition of good statesmanship and
sound churchmanship which Baldwin I. and Baldwin II. had
begun. William of Tyre speaks of him as a fine soldier, an able
politician, and a good son of the church, and only blames him
for partiality to his friends, and a forgetfulness of names and
faces, which placed him at a disadvantage and made him too
dependent on his immediate intimates. Little, perhaps, need
be made of these censures: the real fault of Fulk was his neglect
to envisage the needs of the northern principalities, and to
head a combined resistance to the rising power of Zengi of
Mosul.
His reign in Jerusalem is narrated by R. Röhricht (Geschichte des
Königreichs Jerusalem, Innsbruck, 1898), and has been made the
subject of a monograph by G. Dodu (De Fulconis Hierosolymitani
regno, Paris, 1894).
(E. Br.)
FULK (d. 900), archbishop of Reims, and partisan of Charles
the Simple in his struggle with Odo, count of Paris, was elected
to the see as archbishop in 883 upon the death of Hincmar.
In 887 he was engaged in a struggle with the Normans who
invaded his territories. Upon the deposition of Charles the Fat
he sided with Charles the Simple in his contest for the West
Frankish dominions against Count Odo of Paris, and crowned
him king in his own metropolitan church at Reims after most
of the nobles had gone over to Odo (893). Upon the death of
Odo he succeeded in having Charles recognized as king by a
majority of the West Frankish nobility. In 892 he obtained
special privileges for his province from Pope Formosus, who
promised that thereafter, when the archbishopric became
vacant, the revenues should not be enjoyed by anyone while
the vacancy existed, but should be reserved for the new incumbent,
provided the election took place within the canonical
limit of three months. From 898 until his death he held the
office of chancellor, which for some time afterwards was regularly
filled by the archbishop of Reims. In his efforts to keep the
wealthy abbeys and benefices of the church out of the hands
of the nobles, he incurred the hatred of Baldwin, count
of Flanders, who secured his assassination on the 17th of
June 900, a crime which the weak Carolingian monarch left
unpunished.
Fulk left some letters, which are collected in Migne, Patrologia
Latina, vol. cxxxi. 11-14.
FULKE, WILLIAM (1538-1589), Puritan divine, was born
in London and educated at Cambridge. After studying law for
six years, he became a fellow at St John’s College, Cambridge,
in 1564. He took a leading part in the “vestiarian” controversy,
and persuaded the college to discard the surplice. In consequence
he was expelled from St. John’s for a time, but in 1567 he became
Hebrew lecturer and preacher there. After standing unsuccessfully
for the headship of the college in 1569, he became chaplain
to the earl of Leicester, and received from him the livings of
Warley, in Essex, and Dennington in Suffolk. In 1578 he was
elected master of Pembroke Hall, Cambridge. As a Puritan
controversialist he was remarkably active; in 1580 the bishop
of Ely appointed him to defend puritanism against the Roman
Catholics, Thomas Watson, ex-bishop of Lincoln (1513-1584),
and John Feckenham, formerly abbot of Westminster, and in
1581 he was one of the disputants with the Jesuit, Edmund
Campion, while in 1582 he was among the clergy selected
by the privy council to argue against any papist. His
numerous polemical writings include A Defense of the sincere
true Translations of the holie Scriptures into the English
tong (London, 1583), and confutations of Thomas Stapleton
(1535-1598), Cardinal Allen and other Roman Catholic
controversialists.
FULK NERRA (c. 970-1040), count of Anjou, eldest son of
Count Geoffrey I., “Grisegonelle” (Grey Tunic) and Adela of
Vermandois, was born about 970 and succeeded his father in
the countship of Anjou on the 21st of July 987. He was successful
in repelling the attacks of the count of Rennes and laying the
foundations of the conquest of Touraine (see Anjou). In this
connexion he built a great number of strong castles, which has
led in modern times to his being called “the great builder.”
He also founded several religious houses, among them the abbeys
of Beaulieu, near Loches (c. 1007), of Saint-Nicholas at Angers
(1020) and of Ronceray at Angers (1028), and, in order to expiate
his crimes of violence, made three pilgrimages to the Holy Land
(in 1002-1003, c. 1008 and in 1039). On his return from the
third of these journeys he died at Metz in Lorraine on the 21st of
June 1040. By his first marriage, with Elizabeth, daughter of
Bouchard le Vénérable, count of Vendôme, he had a daughter,
Adela, who married Boon of Nevers and transmitted to her
children the countship of Vendôme. Elizabeth having died in
1000, Fulk married Hildegarde of Lorraine, by whom he had a
son, Geoffrey Martel (q.v.), and a daughter Ermengarde, who
married Geoffrey, count of Gâtinais, and was the mother of
Geoffrey “le Barbu” (the Bearded) and of Fulk “le Réchin”
(see Anjou).
See Louis Halphen, Le Comté d’Anjou au XIe siècle (Paris, 1906).
The biography of Fulk Nerra by Alexandre de Salies, Histoire de
Foulques Nerra (Angers, 1874) is confused and uncritical. A very
summary biography is given by Célestin Port, Dictionnaire historique,
géographique et biographique de Maine-et-Loire (3 vols., Paris-Angers,
1874-1878), vol. ii. pp. 189-192, and there is also a sketch in Kate
Norgate, England under the Angevin Kings (2 vols., London, 1887),
vol. i. ch. iii.
(L. H.*)
FÜLLEBORN, GEORG GUSTAV (1769-1803), German philosopher,
philologist and miscellaneous writer, was born at Glogau,
Silesia, on the 2nd of March 1769, and died at Breslau on the
6th of February 1803. He was educated at the University of
Halle, and was made doctor of philosophy in recognition of his
thesis De Xenophane, Zenone et Gorgia. He took diaconal orders
in 1791, but almost immediately became professor of classics at
Breslau. His philosophical works include annotations to Garve’s
translation of the Politics of Aristotle (1799-1800), and a large
share in the Beiträge zur Geschichte der Philosophie (published in
twelve parts between 1791 and 1799), in which he collaborated
with Forberg, Reinhold and Niethammer. In philology he
wrote Encyclopaedia philologica sive primae lineae Isagoges in
antiquorum studia (1798; 2nd ed., 1805); Kurze Theorie des
lateinischen Stils (1793); Leitfaden der Rhetorik (1802); and an
annotated edition of the Satires of Persius. Under the pseudonym
“Edelwald Justus” he published several collections of popular
tales—Bunte Blätter (1795); Kleine Schriften zur Unterhaltung
(1798); Nebenstunden (1799). After his death were published
Taschenbuch für Brunnengäste (1806) and Kanzelreden (1807).
He was a frequent contributor to the press, where his writings
were very popular.
See Schummel, Gedächtnisrede (1803) and Garve und Fülleborn;
Meusel, Gelehrtes Teutschland, vol. ii.
295
FULLER, ANDREW (1754-1815), English Baptist divine, was
born on the 6th of February 1754, at Wicken in Cambridgeshire.
In his boyhood and youth he worked on his father’s farm. In his
seventeenth year he became a member of the Baptist church at
Soham, and his gifts as an exhorter met with so much approval
that, in the spring of 1775, he was called and ordained as pastor
of that congregation. In 1782 he removed to Kettering in
Northamptonshire, where he became friendly with some of the
most eminent ministers of the denomination. Before leaving
Soham he had written the substance of a treatise in which he had
sought to counteract the prevailing Baptist hyper-Calvinism
which, “admitting nothing spiritually good to be the duty
of the unregenerate, and nothing to be addressed to them
in a way of exhortation excepting what related to external
obedience,” had long perplexed his own mind. This work he
published, under the title The Gospel worthy of all Acceptation,
soon after his settlement in Kettering; and although it immediately
involved him in a somewhat bitter controversy which lasted
for nearly twenty years, it was ultimately successful in considerably
modifying the views prevalent among English dissenters.
In 1793 he published a treatise, The Calvinistic and Socinian
systems examined and compared as to their moral tendency, in which
he rebutted the accusation of antinomianism levelled by the
Socinians against those who over-emphasized the doctrines of
free grace. This work, along with another against Deism,
entitled The Gospel its own Witness, is regarded as the production
on which his reputation as a theologian mainly rests. Fuller
also published an admirable Memoir of the Rev. Samuel Pearce,
of Birmingham, and a volume of Expository Lectures in Genesis,
besides a considerable number of smaller pieces, chiefly sermons
and pamphlets, which were issued in a collected form after his
death. He was a man of forceful character, more prominent on
the practical side of religion than on the devotional, and accordingly
not pre-eminently successful in his local ministry. His
great work was done in connexion with the Baptist Missionary
Society, formed at Kettering in 1792, of which he was secretary
until his death on the 7th of May 1815. Both Princeton and
Yale, U.S.A., conferred on him the degree of D. D., but he never
used it.
Several editions of his collected works have appeared, and a
Memoir, principally compiled from his own papers, was published
about a year after his decease by Dr Ryland, his most intimate
friend and coadjutor in the affairs of the Baptist mission. There
is also a biography by the Rev. J.W. Morris (1816); and his son
prefixed a memoir to an edition of his chief works in Bohn’s Standard
Library (1852).
FULLER, GEORGE (1822-1884), American figure and portrait
painter, was born at Deerfield, Massachusetts, in 1822. At the
age of twenty he entered the studio of the sculptor H.K. Brown,
at Albany, New York, where he drew from the cast and modelled
heads. Having attained some proficiency he went about the
country painting portraits, settling at length in Boston, where he
studied the works of the earlier Americans, Stuart, Copley and
Allston. After three years in that city, and twelve in New York,
where in 1857 he was elected a member of the National Academy
of Design, he went to Europe for a brief visit and for study.
During all this time his work had received little recognition and
practically no financial encouragement, and on his return he
settled on the family farm at Deerfield, where he continued to
work in his own way with no thought of the outside world. In
1876, however, he was forced by pressing needs to dispose of
his work, and he sent some pictures to a dealer in Boston, where
he met with immediate success, financial and artistic, and for the
remaining eight years of his life he never lacked patrons. He
died in Boston on the 21st of March 1884. He was a poetic
painter, and a dreamer of delicate fancies and quaint, intangible
phases of nature, his canvases being usually enveloped in a brown
mist that renders the outlines vague. Among his noteworthy
canvases are: “The Turkey Pasture,” “Romany Girl,” “And
she was a Witch,” “Nydia,” “Winifred Dysart” and “The
Quadroon.”
FULLER, MARGARET, Marchioness Ossoli (1810-1850),
American authoress, eldest child of Timothy Fuller (1778-1835),
a lawyer and politician of some eminence, was born at Cambridgeport,
Massachusetts, on the 23rd of May 1810. Her education
was conducted by her father, who, she states, made the mistake
of thinking to “gain time by bringing forward the intellect as
early as possible,” the consequence being “a premature development
of brain that made her a youthful prodigy by day, and by
night a victim of spectral illusions, nightmare and somnambulism.”
At six years she began to read Latin, and at a very early
age she had selected as her favourite authors Shakespeare,
Cervantes and Molière. Soon the great amount of study
exacted of her ceased to be a burden, and reading became
a habit and a passion. Having made herself familiar with the
masterpieces of French, Italian and Spanish literature, she in
1833 began the study of German, and within the year had
read some of the masterpieces of Goethe, Körner, Novalis
and Schiller.
After her father’s death in 1835 she went to Boston to teach
languages, and in 1837 she was chosen principal teacher in the
Green Street school, Providence, Rhode Island, where she
remained till 1839. From this year until 1844 she stayed at
different places in the immediate neighbourhood of Boston,
forming an intimate acquaintance with the colonists of Brook
Farm, and numbering among her closest friends R.W. Emerson,
Nathaniel Hawthorne and W.H. Channing. In 1839 she
published a translation of Eckermann’s Conversations with
Goethe, which was followed in 1842 by a translation of the correspondence
between Karoline von Günderode and Bettina von
Arnim, entitled Günderode. Aided by R.W. Emerson and
George Ripley, she in 1840 started The Dial, a poetical and
philosophical magazine representing the opinions and aims of
the New England Transcendentalists. This journal she continued
to edit for two years, and while in Boston she also conducted
conversation classes for ladies in which philosophical and
social subjects were discussed with a somewhat over-accentuated
earnestness. These meetings may be regarded as perhaps the
beginning of the modern movement in behalf of women’s rights.
R.W. Emerson, who had met her as early as 1836, thus describes
her appearance: “She was then twenty-six years old. She had
a face and frame that would indicate fulness and tenacity of life.
She was rather under the middle height; her complexion was
fair, with strong fair hair. She was then, as always, carefully and
becomingly dressed, and of ladylike self-possession. For the
rest her appearance had nothing prepossessing. Her extreme
plainness, a trick of incessantly opening and shutting her eyelids,
the nasal tone of her voice, all repelled; and I said to myself we
shall never get far.” On better acquaintance this unprepossessing
exterior seemed, however, to melt away, and her inordinate self-esteem
to be lost in the depth and universality of her sympathy.
She possessed an almost irresistible power of winning the intellectual
and moral confidence of those with whom she came in
contact, and “applied herself to her companion as the sponge
applies itself to water.” She obtained from each the best they
had to give. It was indeed more as a conversationalist than as a
writer that she earned the title of the Priestess of Transcendentalism.
It was her intimate friends who admired her most.
Smart and pungent though she is as a writer, the apparent
originality of her views depends more on eccentricity than either
intellectual depth or imaginative vigour. In 1844 she removed
to New York at the desire of Horace Greeley to write literary
criticism for The Tribune, and in 1846 she published a selection
from her articles on contemporary authors in Europe and
America, under the title Papers on Literature and Art. The same
year she paid a visit to Europe, passing some time in England
and France, and finally taking up her residence in Italy. There
she was married in December 1847 to the marquis Giovanni
Angelo Ossoli, a friend of Mazzini. During 1848-1849 she was
present with her husband in Rome, and when the city was
besieged she, at the request of Mazzini, took charge of one
of the two hospitals while her husband fought on the walls.
In May 1850, along with her husband and infant son, she
embarked at Leghorn for America, but when they had all
but reached their destination the vessel was wrecked on Fire
296
Island beach on the 16th of June, and the Ossolis were among
the passengers who perished.
Life Without and Life Within (Boston, 1860) is a collection of
essays, poems, &c., supplementary to her Collected Works, printed
in 1855. See the Autobiography of Margaret Fuller Ossoli, with
additional memoirs by J.F. Clarke, R.W. Emerson and W.H.
Channing (2 vols., Boston, 1852); also Margaret Fuller (Marchesa
Ossoli), by Julia Ward Howe (1883), in the “Eminent Women”
series; Margaret Fuller Ossoli (Boston, 1884), by Thomas Wentworth
Higginson in the “American Men of Letters” series, which is
based largely on unedited material; and The Love Letters of Margaret
Fuller, 1845-1846 (London and New York, 1903), with an introduction
by Julia Ward Howe.
FULLER, MELVILLE WESTON (1833-1910), American jurist,
chief justice of the Supreme Court of the United States, was born
at Augusta, Maine, on the 11th of February 1833. After graduating
at Bowdoin College in 1853 he spent a year at the Harvard
Law School, and in 1855 began the practice of law at Augusta,
where he was an associate-editor of a Democratic paper, The
Age, and served in the city council and as city attorney. In
1856 he removed to Chicago, Illinois, where he continued to
practise until 1888, rising to a high position at the bar of the
Northwest. For some years he was active in Democratic politics,
being a member of the Illinois Constitutional Convention in
1862 and of the State House of Representatives from 1863 to
1865. He was a delegate to various National conventions of
his party, and in that of 1876 placed Thomas A. Hendricks in
nomination for the presidency. In 1888, by President Cleveland’s
appointment, he succeeded Morrison R. Waite as chief-justice
of the Supreme Court of the United States. In 1899 he was
appointed by President McKinley a member of the arbitration
commission at Paris to settle the Venezuela-British Guiana
boundary dispute.
FULLER, THOMAS (1608-1661), English divine and historian,
eldest son of Thomas Fuller, rector of Aldwincle St Peter’s,
Northamptonshire, was born at his father’s rectory and was
baptized on the 19th of June 1608. Dr John Davenant, bishop
of Salisbury, was his uncle and godfather. According to Aubrey,
Fuller was “a boy of pregnant wit.” At thirteen he was admitted
to Queens’ College, Cambridge, then presided over by Dr John
Davenant. His cousin, Edward Davenant, was a tutor in the
same college. He was apt and quick in study; and in Lent
1624-1625 he became B.A. and in July 1628 M.A. Being overlooked
in an election of fellows of his college, he was removed
by Bishop Davenant to Sidney Sussex College, November 1628.
In 1630 he received from Corpus Christi College the curacy of
St Benet’s, Cambridge.
Fuller’s quaint and humorous oratory soon attracted attention.
He published in 1631 a poem on the subject of David and
Bathsheba, entitled David’s Hainous Sinne, Heartie Repentance,
Heavie Punishment. In June of the same year his uncle gave him
a prebend in Salisbury, where his father, who died in the following
year, held a canonry. The rectory of Broadwindsor, Dorsetshire,
then in the diocese of Bristol, was his next preferment
(1634); and on the 11th of June 1635 he proceeded B.D. At
Broadwindsor he compiled The Historie of the Holy Warre (1639),
a history of the crusades, and The Holy State and the Prophane
State (1642). This work describes the holy state as existing in
the family and in public life, gives rules of conduct, model
“characters” for the various professions and profane biographies.
It was perhaps the most popular of all his writings.
He was in 1640 elected proctor for Bristol in the memorable
convocation of Canterbury, which assembled with the Short
Parliament. On the sudden dissolution of the latter he joined
those who urged that convocation should likewise dissolve as
usual. That opinion was overruled; and the assembly continued
to sit by virtue of a royal writ. Fuller has left in his Church
History a valuable account of the proceedings of this synod,
for sitting in which he was fined £200, which, however, was never
exacted. His first published volume of sermons appeared in
1640 under the title of Joseph’s party-coloured Coat, which contains
many of his quaint utterances and odd conceits. His grosser
mannerisms of style, derived from the divines of the former
generation, disappeared for the most part in his subsequent
discourses.
About 1640 he had married Eleanor, daughter of Hugh
Grove of Chisenbury, Wiltshire. She died in 1641. Their eldest
child, John, baptized at Broadwindsor by his father, 6th
June 1641, was afterwards rector of Sidney Sussex College, edited
the Worthies of England, 1662, and became rector of Great
Wakering, Essex, where he died in 1687.
At Broadwindsor, early in the year 1641, Thomas Fuller, his
curate Henry Sanders, the church wardens, and others, nine
persons altogether, certified that their parish, represented by
242 grown-up male persons, had taken the Protestation ordered
by the speaker of the Long Parliament. Fuller was not formally
dispossessed of his living and prebend on the triumph of the
Presbyterian party, but he relinquished both preferments about
this time. For a short time he preached with success at the Inns
of Court, and thence removed, at the invitation of the master
of the Savoy (Dr Balcanqual) and the brotherhood of that
foundation, to be lecturer at their chapel of St Mary Savoy.
Some of the best discourses of the witty preacher were delivered
at the Savoy to audiences which extended into the chapel-yard.
In one he set forth with searching and truthful minuteness the
hindrances to peace, and urged the signing of petitions to the
king at Oxford, and to the parliament, to continue their care in
advancing an accommodation. In his Appeal of Injured Innocence
Fuller says that he was once deputed to carry a petition to the
king at Oxford. This has been identified with a petition entrusted
to Sir Edward Wardour, clerk of the pells, Dr Dukeson, “Dr
Fuller,” and four or five others from the city of Westminster
and the parishes contiguous to the Savoy. A pass was granted
by the House of Lords, on the 2nd of January 1643, for an
equipage of two coaches, four or six horses and eight or ten
attendants. On the arrival of the deputation at Uxbridge, on
the 4th of January, officers of the Parliamentary army stopped
the coaches and searched the gentlemen; and they found upon
the latter “two scandalous books arraigning the proceedings
of the House,” and letters with ciphers to Lord Viscount Falkland
and the Lord Spencer. Ultimately a joint order of both Houses
remanded the party; and Fuller and his friends suffered a
brief imprisonment. The Westminster Petition, notwithstanding,
reached the king’s hands; and it was published with the royal
reply (see J.E. Bailey, Life of Thomas Fuller, pp. 245 et seq.).
When it was expected, three months later, that a favourable
result would attend the negotiations at Oxford, Fuller preached
a sermon at Westminster Abbey, on the 27th of March 1643, on
the anniversary of Charles I.’s accession, on the text, “Yea, let
him take all, so my Lord the King return in peace.” On
Wednesday, the 26th of July, he preached on church reformation,
satirizing the religious reformers, and maintaining that only the
Supreme Power could initiate reforms.
He was now obliged to leave London, and in August 1643 he
joined the king at Oxford. He lived in a hired chamber at
Lincoln College for 17 weeks. Thence he put forth a witty and
effective reply to John Saltmarsh, who had attacked his views
on ecclesiastical reform. Fuller subsequently published by
royal request a sermon preached on the 10th of May 1644, at
St Mary’s, Oxford, before the king and Prince Charles, called
Jacob’s Vow.
The spirit of Fuller’s preaching, always characterized by calmness
and moderation, gave offence to the high royalists, who
charged him with lukewarmness in their cause. To silence
unjust censures he became chaplain to the regiment of Sir
Ralph Hopton. For the first five years of the war, as he said,
when excusing the non-appearance of his Church History, “I
had little list or leisure to write, fearing to be made a history, and
shifting daily for my safety. All that time I could not live to
study, who did only study to live.” After the defeat of Hopton
at Cheriton Down, Fuller retreated to Basing House. He took
an active part in its defence, and his life with the troops caused
him to be afterwards regarded as one of “the great cavalier
parsons.” In his marches with his regiment round about Oxford
and in the west, he devoted much time to the collection of details,
297
from churches, old buildings, and the conversation of ancient
gossips, for his Church-History and Worthies of England. He
compiled in 1645 a small volume of prayers and meditations,—the
Good Thoughts in Bad Times,—which, set up and printed in
the besieged city of Exeter, whither he had retired, was called
by himself “the first fruits of Exeter press.” It was inscribed to
Lady Dalkeith, governess to the infant princess, Henrietta Anne
(b. 1644), to whose household he was attached as chaplain. The
corporation gave him the Bodleian lectureship on the 21st of
March 1645/6, and he held it until the 17th of June following,
soon after the surrender of the city to the parliament. The Fear
of losing the Old Light (1646) was his farewell discourse to his
Exeter friends. Under the Articles of Surrender Fuller made his
composition with the government at London, his “delinquency”
being that he had been present in the king’s garrisons. In
Andronicus, or the Unfortunate Politician (1646), partly authentic
and partly fictitious, he satirized the leaders of the Revolution;
and for the comfort of sufferers by the war he issued (1647) a
second devotional manual, entitled Good Thoughts in Worse
Times, abounding in fervent aspirations, and drawing moral
lessons in beautiful language out of the events of his life or the
circumstances of the time. In grief over his losses, which included
his library and manuscripts (his “upper and nether millstone”),
and over the calamities of the country, he wrote his work on
the Cause and Cure of a Wounded Conscience (1647). It was
prepared at Boughton House in his native county, where he and
his son were entertained by Edward Lord Montagu, who had
been one of his contemporaries at the university and had taken
the side of the parliament.
For the next few years of his life Fuller was mainly dependent
upon his dealings with booksellers, of whom he asserted that
none had ever lost by him. He made considerable progress in
an English translation from the MS. of the Annales of his friend
Archbishop Ussher. Amongst his benefactors it is curious to
find Sir John Danvers of Chelsea, the regicide. Fuller in 1647
began to preach at St Clement’s, Eastcheap, and elsewhere
in the capacity of lecturer. While at St Clement’s he was
suspended; but speedily recovering his freedom, he preached
wherever he was invited. At Chelsea, where also he occasionally
officiated, he covertly preached a sermon on the death of Charles
I., but he did not break with his Roundhead patrons. James
Hay, 2nd earl of Carlisle, made him his chaplain, and presented
him in 1648 or 1649 to the curacy of Waltham Abbey. His
possession of the living was in jeopardy on the appointment of
Cromwell’s “Tryers”; but he evaded their inquisitorial questions
by his ready wit. He was not disturbed at Waltham in
1655, when the Protector’s edict prohibited the adherents of
the late king from preaching. Lionel, 3rd earl of Middlesex,
who lived at Copt Hall, near Waltham, gave him what remained
of the books of the lord treasurer his father; and through the
good offices of the marchioness of Hertford, part of his own
pillaged library was restored to him. Fuller was thus able to
prosecute his literary labours, producing successively his descriptive
geography of the Holy Land, called A Pisgah-Sight of
Palestine (1650), and his Church-History of Britain (1655), from
the birth of Jesus Christ until the year 1648. With the Church-History
was printed The History of the University of Cambridge
since the Conquest and The History of Waltham Abbey. These
works were furthered in no slight degree by his connexion with
Sion College, London, where he had a chamber, as well for
the convenience of the press as of his city lectureships. The
Church-History was angrily attacked by Dr P. Heylyn, who, in
the spirit of High-Churchmanship, wished, as he said, to vindicate
the truth, the church and the injured clergy. About 1652
Fuller married his second wife, Mary Roper, youngest sister of
Thomas, Viscount Baltinglass, by whom he had several children.
At the Oxford Act of 1657, Robert South, who was Terrae filius,
lampooned Fuller, whom he described in this Oratio as living
in London, ever scribbling and each year bringing forth new
folia like a tree. At length, continues South, the Church-History
came forth with its 166 dedications to wealthy and noble friends;
and with this huge volume under one arm, and his wife (said to
be little of stature) on the other, he ran up and down the streets
of London, seeking at the houses of his patrons invitations to
dinner, to be repaid by his dull jests at table.
His last and best patron was George Berkeley, 1st Earl Berkeley
(1628-1698), of Cranford House, Middlesex, whose chaplain he
was, and who gave him Cranford rectory (1658). To this nobleman
Fuller’s reply to Heylyn’s Examen Historicum, called The
Appeal of Injured Innocence (1659), was inscribed. At the end
of the Appeal is an epistle “to my loving friend Dr Peter Heylyn,”
conceived in the admirable Christian spirit which characterized
all Fuller’s dealings with controversialists. “Why should
Peter,” he asked, “fall out with Thomas, both being disciples
to the same Lord and Master? I assure you, sir, whatever you
conceive to the contrary, I am cordial to the cause of the English
Church, and my hoary hairs will go down to the grave in sorrow
for her sufferings.”
In An Alarum to the Counties of England and Wales (1660)
Fuller argued for a free and full parliament—free from force,
as he expressed it, as well as from abjurations or previous
engagements. Mixt Contemplations in Better Times (1660),
dedicated to Lady Monk, tendered advice in the spirit of its
motto, “Let your moderation be known to all men: the Lord
is at hand.” There is good reason to suppose that Fuller was at
the Hague immediately before the Restoration, in the retinue
of Lord Berkeley, one of the commissioners of the House of
Lords, whose last service to his friend was to interest himself in
obtaining him a bishopric. A Panegyrick to His Majesty on his
Happy Return was the last of Fuller’s verse-efforts. On the
2nd of August, by royal letters, he was admitted D.D. at Cambridge.
He resumed his lectures at the Savoy, where Samuel
Pepys heard him preach; but he preferred his conversation or
his books to his sermons. Fuller’s last promotion was that of
chaplain in extraordinary to Charles II. In the summer of 1661
he visited the west in connexion with the business of his prebend,
which had been restored to him. On Sunday, the 12th of August,
while preaching at the Savoy, he was seized with typhus fever,
and died at his new lodgings in Covent Garden on the 16th of
August. He was buried in Cranford church, where a mural
tablet was afterwards set up on the north side of the chancel,
with an epitaph which contains a conceit worthy of his own pen,
to the effect that while he was endeavouring (viz. in The Worthies)
to give immortality to others, he himself attained it.
Fuller’s wit and vivacious good-humour made him a favourite
with men of both sides, and his sense of humour kept him from
extremes. Probably Heylyn and South had some excuse for
their attitude towards his very moderate politics. “By his
particular temper and management,” said Echard (Hist. of
England, iii. 71), “he weathered the late great storm with more
success than many other great men.” He was known as “a
perfect walking library.” The strength of his memory was
proverbial, and some amusing anecdotes are connected with it.
His writings were the product of a highly original mind. He
had a fertile imagination and a happy faculty of illustration.
Antithetic and axiomatic sentences abound in his pages, embodying
literally the wisdom of the many in the wit of one. He was
“quaint,” and something more. “Wit,” said Coleridge, in a
well-known eulogy, “was the stuff and substance of Fuller’s
intellect. It was the element, the earthen base, the material
which he worked in; and this very circumstance has defrauded
him of his due praise for the practical wisdom of the thoughts,
for the beauty and variety of the truths, into which he shaped
the stuff. Fuller was incomparably the most sensible, the least
prejudiced, great man of an age that boasted a galaxy of great
men” (Literary Remains, vol. ii. (1836), pp. 389-390). This
opinion was formed after the perusal of the Church-History.
That work and The History of the Worthies of England are
unquestionably Fuller’s greatest efforts. They embody the
collections of an entire life; and since his day they have been
the delight of many readers. The Holy State has taken rank
amongst the best books of “characters.” Charles Lamb made
some selections from Fuller, and had a profound admiration for
the “golden works” of the “dear, fine, silly old angel.” Since
298
Lamb’s time, mainly through the appreciative criticisms of
S.T. Coleridge, Robert Southey and others, Fuller’s works have
received much attention.
There is an elaborate account of the life and writings of Fuller
by William Oldys in the Biographia Britannica, vol. iii. (1750), based
on Fuller’s own works and the anonymous Life of ... Dr Thomas
Fuller (1661; reprinted in a volume of selections by A.L.J. Gosset,
1893). The completest account of him is The Life of Thomas Fuller,
with Notices of his Books, his Kinsmen and his Friends (1874), by
J.E. Bailey, who gives a detailed bibliography (pp. 713-762) of his
works. The Worthies of England was reprinted by John Nichols
(1811) and by P.A. Nuttall (1840). His Collected Sermons were
edited by J.E. Bailey and W.E.A. Axon in 1891. Fuller’s quaint
wit lends itself to selection, and there are several modern volumes of
extracts from his works.
FULLER, WILLIAM (1670-c. 1717), English impostor, was
born at Milton in Kent on the 20th of September 1670. His
paternity is doubtful, but he was related to the family of Herbert.
After 1688 he served James II.’s queen, Mary of Modena, and
the Jacobites, seeking at the same time to gain favour with
William III.; and after associating with Titus Oates, being
imprisoned for debt and pretending to reveal Jacobite plots, the
House of Commons in 1692 declared he was an “imposter,
cheat and false accuser.” Having stood in the pillory he was
again imprisoned until 1695, when he was released; and at this
time he took the opportunity to revive the old and familiar
story that Mary of Modena was not the mother of the prince of
Wales. In 1701 he published his autobiographical Life of
William Fuller and some Original Letters of the late King James.
Unable to prove the assertions made in his writings he was put
in the pillory, whipped and fined. He died, probably in prison,
about 1717. Fuller’s other writings are Mr William Fuller’s
trip to Bridewell, with a full account of his barbarous usage in the
pillory; The sincere and hearty confession of Mr William Fuller
(1704); and An humble appeal to the impartial judgment of all
parties in Great Britain (1716).
He must be distinguished from William Fuller (1608-1675),
dean of St Patrick’s (1660), bishop of Limerick (1663), and bishop of
Lincoln (1667), the friend of Samuel Pepys; and also from William
Fuller (c. 1580-1659), dean of Ely and later dean of Durham.
FULLER’S EARTH (Ger. Walkererde, Fr. terre à foulon, argile
smectique)—so named from its use by fullers as an absorbent of
the grease and oil of cloth,—a clay-like substance, which from
its variability is somewhat difficult to define. In colour it is
most often greenish, olive-green or greenish-grey; on weathering
it changes to a brown tint or it may bleach. As a rule it falls
to pieces when placed in water and is not markedly plastic;
when dry it adheres strongly to the tongue; since, however,
these properties are possessed by many clays that do not exhibit
detergent qualities, the only test of value lies in the capacity
to absorb grease or clarify oil. Fuller’s earth has a specific gravity
of 1.7-2.4, and a shining streak; it is usually unctuous to the
touch. Microscopically, it consists of minute irregular-shaped
particles of a mineral that appears to be the result of a chloritic
or talcose alteration of a felspar. The small size of most of the
grains, less than .07 mm., makes their determination almost
impossible. Chemical analysis shows that the peculiar properties
of this earth are due to its physical rather than its chemical
nature.
The following analyses of the weathered and unweathered condition
of the earth from Nutfield, Surrey, represent the composition
of one of the best known varieties:—
Blue Earth (dried at 100° C.).
| Insoluble residue | 69.96 | Insoluble residue— | |
| Fe2O3 | 2.48 | SiO2 | 62.81 |
| Al2O3 | 3.46 | Al2O3 | 3.46 |
| CaO | 5.87 | Fe2O3 | 1.30 |
| MgO | 1.41 | CaO | 1.53 |
| P2O5 | 0.27 | MgO | 0.86 |
| SO3 | 0.05 | | ——— |
| NaCl | 0.05 | | 69.96 |
| K2O | 0.74 | | ——— |
| H2O (combined) | 15.57 | |
| | ——— | |
| | 99.86 | |
| | ——— | |
Yellow Earth (dried at 100° C.).
| Insoluble residue | 76.13 | Insoluble residue— | |
| Fe2O3 | 2.41 | SiO2 | 59.37 |
| Al2O3 | 1.77 | Al2O3 | 10.05 |
| CaO | 4.31 | Fe2O3 | 3.86 |
| MgO | 1.05 | CaO | 1.86 |
| P2O5 | 0.14 | MgO | 1.04 |
| SO3 | 0.07 | | ——— |
| NaCl | 0.14 | | 76.18 |
| K2O | 0.84 | | ——— |
| H2O (combined) | 13.19 | |
| | ——— | |
| | 100.05 | |
| | ——— | |
(Analysis by P.G. Sanford, Geol. Mag., 1889, 6, pp. 456, 526.)
Of other published analyses, not a few show a lower silica content
(44%, 50%), along with a higher proportion of alumina (11%, 23%).
Fuller’s earth may occur on any geological horizon; at Nutfield
in Surrey, England, it is in the Cretaceous formations; at Midford
near Bath it is of Jurassic age; at Bala, North Wales, it occurs in
Ordovician strata; in Saxony it appears to be the decomposition
product of a diabasic rock. In America it is found in California
in rocks ranging from Cretaceous to Pleistocene age; in S.
Dakota, Custer county and elsewhere a yellow, gritty earth of
Jurassic age is worked; in Florida and Georgia occurs a brittle,
whitish earth of Oligocene age. Other deposits are worked in
Arkansas, Texas, Colorado, Massachusetts and South Carolina.
Fuller’s earth is either mined or dug in the open according to
local circumstances. It is then dried in the sun or by artificial
heat and transported in small lumps in sacks. In other cases it
is ground to a fine powder after being dried; or it is first roughly
ground and made into a slurry with water, which is allowed to
carry off the finer from the coarser particles and deposit them in a
creamy state in suitable tanks. After consolidation this fine
material is dried artificially on drying floors, broken into lumps,
and packed for transport. The use of fuller’s earth for cleansing
wool and cloth has greatly decreased, but the demand for the
material is as great or greater than it ever was. It is now used
very largely in the filtration of mineral oils, and also for decolourizing
certain vegetable oils. It is employed in the formation of
certain soaps and cleansing preparations.
The term “Fuller’s Earth” has a special significance in
geology, for it was applied by W. Smith in 1799 to certain clays
in the neighbourhood of Bath, and the use of the expression is
still retained by English geologists, either in this form or in the
generalized “Fullonian.” The Fullonian lies at the base of the
Great Oolite or Bathonian series, but its palaeontological
characters place it between that series and the underlying
Inferior Oolite. The zonal fossils are Perisphinctes arbustigerus
and Macrocephalus subcontractus with Ostrea acuminata,
Rhynchonella concinna and Goniomya angulifera. The formation
is in part the equivalent of the “Vesulien” of J. Marcou (Vesoul
in Haute-Saône). In Dorsetshire and Somersetshire, where it
is best developed, it is represented by an Upper Fuller’s Earth
Clay, the Fuller’s Earth Rock (an impersistent earthy limestone,
usually fossiliferous), and the Lower Fuller’s Earth Clay. Commercial
fuller’s earth has been obtained only from the Upper
Clay. In eastern Gloucestershire and northern Oxfordshire
the Fuller’s Earth passes downwards without break into the
Inferior Oolite; northward it dies out about Chipping Norton
in Oxfordshire and passes laterally into the Stonesfield Slates
series; in the midland counties it may perhaps be represented
by the “Upper Estuarine Series.” In parts of Dorsetshire the
clays have been used for brickmaking and the limestone (rock)
for local buildings.
See H.B. Woodward, “Jurassic Rocks of Great Britain,” vol.
iv. (1894), Mem. Geol. Survey (London).
[J. A. H.]
FULLERTON, LADY GEORGIANA CHARLOTTE (1812-1885),
English novelist and philanthropist, youngest daughter of the
1st Earl Granville, was born at Tixall Hall in Staffordshire on
the 23rd of September 1812. In 1833 she married Alexander
George Fullerton, then an Irish officer in the guards. After
living in Paris for some eight years she and her husband accompanied
Lord Granville to Cannes and thence to Rome. In 1843
299
her husband entered the Roman Catholic church, and in the
following year Lady Georgiana Fullerton published her first novel,
Ellen Middleton, which attracted W.E. Gladstone’s attention
in the English Review. In 1846 she entered the Roman Catholic
church. The death of her only son in 1854 plunged her in grief,
and she continued to wear mourning until the end of her life.
In 1856 she became one of the third order of St Francis, and
thenceforward devoted herself to charitable work. In conjunction
with Miss Taylor she founded the religious community
known as “The Poor Servants of the Mother of God Incarnate,”
and she also took an active part in bringing to England the
sisters of St Vincent of Paul. Her philanthropic work is described
in Mrs Augustus Craven’s work Lady Georgiana Fullerton, sa
vie et ses œuvres (Paris, 1888), which was translated into English
by Henry James Coleridge. She died at Bournemouth on the 19th
of January 1885. Among her other novels were Grantley Manor
(1847), Lady Bird (1852), and Too Strange not to be True (1864).
FULMAR, from the Gaelic Fulmaire, the Fulmarus glacialis of
modern ornithologists, one of the largest of the petrels (Procellariidae)
of the northern hemisphere, being about the size of the
common gull (Larus canus) and not unlike it in general coloration,
except that its primaries are grey instead of black. This bird,
which ranges over the North Atlantic, is seldom seen on the
European side below lat. 53° N., but on the American side comes
habitually to lat. 45° or even lower. In the Pacific it is represented
by a scarcely separable form, F. glupischa. It has been commonly
believed to have two breeding-places in the British Islands,
namely, St Kilda and South Barra; but, according to Robert
Gray (Birds of the West of Scotland, p. 499), it has abandoned
the latter since 1844, though still breeding in Skye. Northward
it established itself about 1838 on Myggenaes Holm, one of the
Faeroes, while it has several stations off the coast of Iceland and
Spitsbergen, as well as at Bear Island. Its range towards the
pole seems to be only bounded by open water, and it is the constant
attendant upon all who are employed in the whale and
seal fisheries, showing the greatest boldness in approaching boats
and ships, and feeding on the offal obtained from them. By
British seamen it is commonly called the “molly mawk”1
(corrupted from Mallemuck), and is extremely well known to them,
its flight, as it skims over the waves, first with a few beats of
the wings and then gliding for a long way, being very peculiar.
It only visits the land to deposit its single white egg, which is
laid on a rocky ledge, where a shallow nest is made in the turf
and lined with a little dried grass. Many of its breeding-places
are a most valuable property to those who live near them and
take the eggs and young, which, from the nature of the locality,
are only to be had at a hazardous risk of life. In St Kilda a
large number of the young are killed in one week of August, the
only time when, by the custom of the community, they are
allowed to be taken. These, after the oil is extracted from them,
serve the islanders with food for the winter. The oil has been
chemically analysed and found to be a fish-oil, and to possess
nearly all the qualities of that obtained from the liver of the cod,
with a lighter specific gravity. It, however, has an extremely
strong scent, which is said by those who have visited St Kilda
to pervade every thing and person on the island, and is certainly
retained by an egg or skin of the bird for many years. Whenever
a live example is seized in the hand it ejects a considerable
quantity of this oil from its mouth.
1 A name misapplied in the southern hemisphere to Diomedea
melanophrys, one of the albatrosses.
FULMINIC ACID, HCNO or H2C2N2O2, an organic acid
isomeric with cyanic and cyanuric acids; its salts, termed
fulminates, are very explosive and are much employed as detonators.
The free acid, which is obtained by treating the salts
with acids, is an oily liquid smelling like prussic acid; it is very
explosive, and the vapour is poisonous to about the same degree
as that of prussic acid. The first fulminate prepared was the
“fulminating silver” of L.G. Brugnatelli, who found in 1798
that if silver be dissolved in nitric acid and the solution added
to spirits of wine, a white, highly explosive powder was obtained.
This substance is to be distinguished from the black “fulminating
silver” obtained by C.L. Berthollet in 1788 by acting with
ammonia on precipitated silver oxide. The next salt to be
obtained was the mercuric salt, which was prepared in 1799 by
Edward Charles Howard, who substituted mercury for silver in
Brugnatelli’s process. A similar method is that of J. von Liebig
(1823), who heated a mixture of alcohol, nitric acid and mercuric
nitrate; the salt is largely manufactured by processes closely
resembling the last. A laboratory method is to mix solutions
of sodium nitromethane, CH2 : NO(ONa), and mercuric chloride,
a yellow basic salt being formed at the same time. Mercuric
fulminate is less explosive than the silver salt, and forms white
needles (with ½H2O) which are tolerably soluble in water. The
use of mercuric fulminate as a detonator dates from about 1814,
when the explosive cap was invented. It is still the commonest
detonator, but it is now usually mixed with other substances;
the British service uses for percussion caps 6 parts of fulminate,
6 of potassium chlorate and 4 of antimony sulphide, and for
time fuses 4 parts of fulminate, 6 of potassium chlorate and 4
of antimony sulphide, the mixture being damped with a shellac
varnish; for use in blasting, a home office order of 1897 prescribes
a mixture of 4 parts of fulminate and 1 of potassium chlorate.
In 1900 Bielefeldt found that a fulminate placed on top of an
aromatic nitro compound, such as trinitrotoluene, formed a
useful detonator; this discovery has been especially taken
advantage of in Germany, in which country detonators of this
nature are being largely employed. Tetranitromethylaniline
(tetryl) has also been employed (Brit. Pat. 13340 of 1905).
It has been proposed to replace fulminate by silver azoimide
(Wöhler & Matter, Brit. Pat. 4468 of 1908), and by lead azoimide
(Hyronimus, Brit. Pat. 1819 of 1908).
The constitution of fulminic acid has been investigated by many
experimenters, but apparently without definitive results. The
researches of Liebig (1823), Liebig and Gay-Lussac (1824), and of
Liebig again in 1838 showed the acid to be isomeric with cyanic acid,
and probably (HCNO)2, since it gave mixed and acid salts. Kekulé,
in 1858, concluded that it was nitroacetonitrile, NO2·CH2·CN, a
view opposed by Steiner (1883), E. Divers and M. Kawakita (1884),
R. Scholl (1890), and by J.U. Nef (1894), who proposed the formulae:
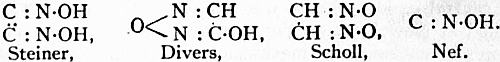
The formulae of Kekulé, Divers and Armstrong have been discarded,
and it remains to be shown whether Nef’s carbonyloxime formula
(or the bimolecular formula of Steiner) or Scholl’s glyoxime peroxide
formula is correct. There is some doubt as to the molecular formula
of fulminic acid. The existence of double salts, and the observations
of L. Wöhler and K. Theodorovits (Ber., 1905, 38, p. 345), that only
compounds containing two carbon atoms yielded fulminates, points
to (HCNO)2; on the other hand, Wöhler (loc. cit. p. 1351) found
that cryoscopic and electric conductivity measurements showed
sodium fulminate to be NaCNO. Nef based his formula, which
involves bivalent carbon, on many reactions; in particular, that
silver fulminate with hydrochloric acid gave salts of formylchloridoxime,
which with water gave hydroxylamine and formic acid, thus
and also on the production from sodium nitromethane and mercuric
chloride, thus CH2 : NO·Ohg → H2O + C : NOhg(hg = ½Hg). H.
Wieland and F.C. Palazzo (1907) support this formula, finding that
methyl nitrolic acid, NO2·CH : N·OH, yielded under certain conditions
fulminic acid, and vice versa (Palazzo, 1907). M.Z. Jowitschitsch
(Ann., 1906, 347, p. 233) inclines to Scholl’s formula; he
found that the synthetic silver salt of glyoxime peroxide resembled
silver fulminate in yielding hydroxylamine with hydrochloric acid,
but differed in being less explosive, and in being soluble in nitric
acid. H. Wieland and his collaborators regard “glyoxime peroxide”
as an oxide of furazane (q.v.), and have shown that a close relationship
exists between the nitrile oxides, furoxane, and fulminic acid (see
Ann. Rep., London Chem. Soc., 1909, p. 84). Fulminuric acid,
(HCNO)3, obtained by Liebig by boiling mercuric fulminate with
water, was synthesized in 1905 by C. Ulpiani and L. Bernardini
(Gazetta, iii. 35, p. 7), who regard it as NO2·CH(CN)·CO·NH2. It
deflagrates at 145°, and forms a characteristic cuprammonium salt.
The early history of mercuric fulminate and a critical account of its
application as a detonator is given in The Rise and Progress of the
British Explosives Industry (International Congress of Applied
Chemistry, 1909). The manufacture and modern aspects are treated
in Oscar Guttmann, The Manufacture of Explosives, and Manufacture
of Explosives, Twenty Years’ Progress (1909).
300
FULTON, ROBERT (1765-1815), American engineer, was born
in 1765 in Little Britain (now Fulton, Lancaster county), Pa.
His parents were Irish, and so poor that they could afford him
only a very scanty education. At an early age he was bound
apprentice to a jeweller in Philadelphia, but subsequently
adopted portrait and landscape painting as his profession. In
his twenty-second year, with the object of studying with his
countryman, Benjamin West, he went to England, and there
became acquainted with the duke of Bridgewater, Earl Stanhope
and James Watt. Partly by their influence he was led to devote
his attention to engineering, especially in connexion with canal
construction; he obtained an English patent in 1794 for superseding
canal locks by inclined planes, and in 1796 he published
a Treatise on the Improvement of Canal Navigation. He then took
up his residence in Paris, where he projected the first panorama
ever exhibited in that city, and constructed a submarine boat,
the “Nautilus,” which was tried in Brest harbour in 1801 before
a commission appointed by Napoleon I., and by the aid of which
he was enabled to blow up a small vessel with a torpedo. It
was at Paris also in 1803 that he first succeeded in propelling a
boat by steam-power, thus realizing a design which he had
conceived ten years previously. Returning to America he
continued his experiments with submarine explosives, but failed
to convince either the English, French or United States governments
of the adequacy of his methods. With steam navigation
he had more success. In association with Robert R. Livingston
(q.v.), who in 1798 had been granted the exclusive right to
navigate the waters of New York state with steam-vessels, he
constructed the “Clermont,” which, engined by Boulton &
Watt of Birmingham, began to ply on the Hudson between
New York and Albany in 1807. The privilege obtained by
Livingston in 1798 was granted jointly to Fulton and Livingston
in 1803, and by an act passed in 1808 the monopoly was
secured to them and their associates for a period depending on
the number of steamers constructed, but limited to a maximum
of thirty years. In 1814-1815, on behalf of the United States
government, he constructed the “Fulton,” a vessel of 38 tons
with central paddle-wheels, which was the first steam warship.
He died at New York on the 24th of February 1815. Among
Fulton’s inventions were machines for spinning flax, for making
ropes, and for sawing and polishing marble.
See C.D. Colden, Life of Robert Fulton (New York, 1817); Robert
H. Thurston, History of the Growth of the Steam-Engine (New York,
1878); George H. Preble, Chronological History of Steam Navigation
(Philadelphia, 1883); and Mrs A.C. Sutcliffe, Robert Fulton and the
Clermont (New York, 1909).
FULTON, a city and the county-seat of Callaway county,
Missouri, U.S.A., 25 m. N.E. of Jefferson City. Pop. (1890)
4314; (1900) 4883 (1167 negroes); (1910) 5228. It is served by
the Chicago & Alton railway. The city has an important stock
market and manufactures fire-brick and pottery. At Fulton
are the Westminster College (Presbyterian, founded in 1853),
the Synodical College for Young Women (Pres., founded in
1871), the William Woods College for Girls (Christian Church,
1890), and the Missouri school for the deaf (1851). Here, too,
is a state hospital for the insane (1847), the first institution
of the kind in Missouri. The place was laid out as a town in
1825 and named Volney, but in honour of Robert Fulton the
present name was adopted a little later. Fulton was incorporated
in 1859.
FULTON, a city of Oswego county, New York, U.S.A., on the
right bank of the Oswego river, about 10 m. S. by E. of Oswego.
Pop. (1900) 5281; (1905, state census) 8847; (1910) 10,480.
Fulton is served by the Delaware, Lackawanna & Western, the
New York Central & Hudson River, and the New York, Ontario
& Western railways, by electric railway to Oswego and Syracuse
and by the Oswego Canal. The city has a Carnegie library.
Ample water-power is furnished by the Oswego river, which here
flows in a series of rapids, and the manufactures are many in
kind. On the 3rd of July 1756, on an island (afterward called
Battle Island) 4 m. N. of the present city of Fulton, a British
force of about 300 under Captain John Bradstreet (1711-1774)
defeated an attacking force of French and Indians (numbering
about 700) under De Villiers. Soon after this, Bradstreet built
a fort within the present limits of Fulton. The first civilian
settler came in 1793, and the first survey (which included only
a part of the subsequent village) was made in 1815. Fulton
was incorporated as a village in 1835, and in April 1902 was
combined with the village of Oswego Falls (pop. in 1900, 2925)
and was chartered as a city.
FUM, or Funj Hwang, one of the four symbolical creatures
which in Chinese mythology are believed to keep watch and ward
over the Celestial Empire. It was begotten by fire, was born in
the Hill of the Sun’s Halo, and its body bears inscribed on it
the five cardinal virtues. It has the breast of a goose, the hindquarters
of a stag, a snake’s neck, a fish’s tail, a fowl’s forehead,
a duck’s down, the marks of a dragon, the back of a tortoise,
the face of a swallow, the beak of a cock, is about six cubits high,
and perches only on the woo-tung tree. The appearance of Fum
heralds an age of universal virtue. Its figure is that which is
embroidered on the dresses of some mandarins.
FUMARIC AND MALEIC ACIDS, two isomeric unsaturated
acids of composition C4H4O4. Fumaric acid is found in fumitory
(Fumaria officinalis), in various fungi (Agaricus piperatus, &c.),
and in Iceland moss. It is obtained by heating malic acid alone
to 150° C., or by heating it with hydrochloric acid (V. Dessaignes,
Jahresb., 1856, p. 463) or with a large quantity of hydrobromic
acids (A. Kekulé, Ann., 1864, 130, p. 21). It may also be obtained
by boiling monobromsuccinic acid with water; by the action of
dichloracetic acid and water on silver malonate (T. Komnenos,
Ann., 1883, 218, p. 169); by the cyanide synthesis from acetylene
di-iodide; and by heating maleic acid to 210° C. (Z. Skraup,
Monats. f. Chemie, 1891, 12, p. 112). It crystallizes in small
prisms or needles, and is practically insoluble in cold water. It
sublimes to some extent at about 200° C., being partially converted
into maleic anhydride and water, the reaction becoming
practically quantitative if dehydrating agents be used. Reducing
agents (zinc and caustic alkali, hydriodic acid, sodium amalgam,
&c.) convert it into succinic acid. Bromine converts it into
dibromsuccinic acid. Potassium permanganate oxidizes it to
racemic acid (A. Kekulé and R. Anschutz, Ber., 1881, 14,
p. 713). By long-continued heating with caustic soda at 100° C.
it is converted into inactive malic acid.
Maleic acid is obtained by distilling malic or fumaric acids;
by heating fumaric acid with acetyl chloride to 100° C; or by
the hydrolysis of trichlorphenomalic acid (β-trichloraceto-acrylic
acid) [A. Kekulé, Ann., 1884, 223, p. 185]. It crystallizes
in monoclinic prisms, which are easily soluble in water, melt
at 130° C., and boil at 160° C., decomposing into water and
maleic anhydride. When heated with concentrated hydrobromic
or hydriodic acids, it is converted into fumaric acid. It yields
an anilide; oxidation converts it into mesotartaric acid. Maleic
anhydride is obtained by distilling fumaric acid with phosphorus
pentoxide. It forms triclinic crystals which melt at 60° C. and
boil at 196° C.
Both acids are readily esterified by the action of alkyl halides on
their silver salts, and the maleic ester is readily transformed into the
fumaric ester by warming with iodine, the same result being obtained
by esterification of maleic acid in alcoholic solution by means of
hydrochloric acid. Both acids yield acetylene by the electrolysis
of aqueous solutions of their alkali salts, and on reduction both
yield succinic acid, whilst by the addition of hydrobromic acid they
both yield monobromsuccinic acid (R. Fittig, Ann., 1877, 188, p. 98).
From these results it follows that the two acids are structurally
identical, and the isomerism has consequently to be explained on
other grounds. This was accomplished by W. Wislicenus [ӆber
die räumliche Anordnung der Atome,” &c., Trans, of the Saxon Acad.
of Sciences (Math. Phys. Section), 1887, p. 14] by an extension of
the van’t Hoff hypothesis (see Stereo-Isomerism). The formulae
of the acids are written thus:
These account for maleic acid readily yielding an anhydride, whereas
fumaric acid does not, and for the behaviour of the acids towards
bromine, fumaric acid yielding ordinary dibromsuccinic acid, and
maleic acid the isomeric isodibromsuccinic acid.
FUMAROLE, a vent from which volcanic vapours issue,
named indirectly from the Lat. fumariolum, a smoke-hole.
301
The vapours from fumaroles were studied first by R.W. Bunsen,
on his visit to Iceland, and afterwards by H. Sainte-Claire Deville
and other chemists and geologists in France, who examined the
vapours from Santorin, Etna, &c. The hottest vapours issue
from dry fumaroles, at temperatures of at least 500° C., and
consist chiefly of anhydrous chlorides, notably sodium chloride.
The acid fumaroles yield vapours of lower temperature (300° to
400°) containing much water vapour, with hydrogen chloride
and sulphur dioxide. The alkaline fumaroles are still cooler,
though above 100°, and evolve ammonium chloride with other
vapours. Cold fumaroles, below 100°, discharge principally
aqueous vapour, with carbon dioxide, and perhaps hydrogen
sulphide. The fumaroles of Mont Pelé in Martinique during the
eruption of 1902 were examined by A. Lacroix, and the vapours
analysed by H. Moissan, who found that they consisted chiefly
of water vapour, with hydrogen chloride, sulphur, carbon dioxide,
carbon monoxide, methane, hydrogen, nitrogen, oxygen and
argon. These vapours issued at a temperature of about 400°.
Armand Gautier has pointed out that these gases are practically
of the same composition as those which he obtained on heating
granite and certain other rocks. (See Volcano).
FUMIGATION (from Lat. fumigare, to smoke), the process
of producing smoke or fumes, as by burning sulphur, frankincense,
tobacco, &c., whether as a ceremony of incantation, or
for perfuming a room, or for purposes of disinfection or destruction
of vermin. In medicine the term has been used of the exposure
of the body, or a portion of it, to fumes such as those of
nitre, sal-ammoniac, mercury, &c.; fumigation, by the injection
of tobacco smoke into the great bowel, was a recognized procedure
in the 18th century for the resuscitation of the apparently
drowned. “Fumigated” or “fumed” oak is oak which has
been darkened by exposure to ammonia vapour.
FUMITORY, in botany, the popular name for the British
species of Fumaria, a genus of small, branched, often climbing
annual herbs with much-divided leaves and racemes of small
flowers. The flowers are tubular with a spurred base, and in the
British species are pink to purplish in colour. They are weeds of
cultivation growing in fields and waste places. F. capreolata
climbs by means of twisting petioles. In past times fumitory
was in esteem for its reputed cholagogue and other medicinal
properties; and in England, boiled in water, milk or whey, it
was used as a cosmetic. The root of the allied species (Corydalis
cava or tuberosa) is known as radix aristolochia, and has been used
medicinally for various cutaneous and other disorders, in doses
of 10 to 30 grains. Some eleven alkaloids have been isolated
from it. The herbage of Fumaria officinalis and F. racemosa is
used in China under the name of Tsze-hwa-ti-ting as an application
for glandular swellings, carbuncles and abscesses, and was
formerly valued in jaundice, and in cases of accidental swallowing
of the beard of grain (see F. Porter Smith, Contrib. towards the
Mat. Medica ... of China, p. 99, 1871). The name fumitory,
Latin fumus terrae, has been supposed to be derived from the
fact that its juice irritates the eyes like smoke (see Fuchs, De
historia stirpium, p. 338, 1542); but The Grete Herball, cap.
clxix., 1529, fol., following the De simplici medicina of Platearius,
fo. xciii. (see in Nicolai Praepositi dispensatorium ad aromatarios,
1536), says: “It is called Fumus terre fume or smoke of the
erthe bycause it is engendred of a cours fumosyte rysynge frome
the erthe in grete quantyte lyke smoke: this grosse or cours
fumosyte of the erthe wyndeth and wryeth out: and by workynge
of the ayre and sonne it turneth into this herbe.”
FUNCHAL, the capital of the Portuguese archipelago of the
Madeiras; on the south coast of Madeira, in 32° 37′ N. and
16° 54′ W. Pop. (1900) 20,850. Funchal is the see of a bishop,
in the archiepiscopal province of Lisbon; it is also the administrative
centre of the archipelago, and the residence of the
governor and foreign consuls. The city has an attractive
appearance from the sea. Its whitewashed houses, in their
gardens full of tropical plants, are built along the curving shore
of Funchal Bay, and on the lower slopes of an amphitheatre of
mountains, which form a background 4000 ft. high. Numerous
country houses (quintas), with terraced gardens, vineyards and
sugar-cane plantations occupy the surrounding heights. Three
mountain streams traverse the city through deep channels,
which in summer are dry, owing to the diversion of the water
for irrigation. A small fort, on an isolated rock off shore,
guards the entrance to the bay, and a larger and more powerfully
armed fort crowns an eminence inland. The chief buildings
include the cathedral, Anglican and Presbyterian churches,
hospitals, opera-house, museum and casino. There are small
public gardens and a meteorological observatory. In the steep
and narrow streets, which are lighted by electricity, wheeled
traffic is impossible; sledges drawn by oxen, and other primitive
conveyances are used instead (see Madeira). In winter the fine
climate and scenery attract numerous invalids and other visitors,
for whose accommodation there are good hotels; many foreigners
engaged in the coal and wine trades also reside here permanently.
The majority of these belong to the British community, which
was first established here in the 18th century. Funchal is the
headquarters of Madeiran industry and commerce (see Madeira).
It has no docks and no facilities for landing passengers or goods;
vessels are obliged to anchor in the roadstead, which, however,
is sheltered from every wind except the south. Funchal is
connected by cable with Carcavellos (for Lisbon), Porthcurnow
(for Falmouth, England) and St Vincent in the Cape Verde
Islands (for Pernambuco, Brazil).
FUNCTION,1 in mathematics, a variable number the value
of which depends upon the values of one or more other variable
numbers. The theory of functions is conveniently divided into
(I.) Functions of Real Variables, wherein real, and only real,
numbers are involved, and (II.) Functions of Complex Variables,
wherein complex or imaginary numbers are involved.
I. Functions of Real Variables
1. Historical.—The word function, defined in the above sense,
was introduced by Leibnitz in a short note of date 1694 concerning
the construction of what we now call an “envelope”
(Leibnizens mathematische Schriften, edited by C.I. Gerhardt,
Bd. v. p. 306), and was there used to denote a variable length
related in a defined way to a variable point of a curve. In 1698
James Bernoulli used the word in a special sense in connexion with
some isoperimetric problems (Joh. Bernoulli, Opera, t. i. p. 255).
He said that when it is a question of selecting from an infinite set
of like curves that one which best fulfils some function, then of
two curves whose intersection determines the thing sought one
is always the “line of the function” (Linea functionis). In 1718
John Bernoulli (Opera, t. ii. p. 241) defined a “function of a
variable magnitude” as a quantity made up in any way of this
variable magnitude and constants; and in 1730 (Opera, t. iii.
p. 174) he noted a distinction between “algebraic” and “transcendental”
functions. By the latter he meant integrals of
algebraic functions. The notation ƒ(x) for a function of a variable
x was introduced by Leonhard Euler in 1734 (Comm. Acad.
Petropol. t. vii. p. 186), in connexion with the theorem of the
interchange of the order of differentiations. The notion of
functionality or functional relation of two magnitudes was thus
of geometrical origin; but a function soon came to be regarded
as an analytical expression, not necessarily an algebraic expression,
containing the variable or variables. Thus we may have
rational integral algebraic functions such as ax² + bx + c, or
rational algebraic functions which are not integral, such as
| a1xn + a2xn−1 + ... + an |
, |
| b1xm + b2xm−1 + ... + bm |
or irrational algebraic functions, such as √x, or, more generally
the algebraic functions that are determined implicitly by an
algebraic equation, as, for instance,
ƒn(x, y) + ƒn−1(x, y) + ... + ƒ0 = 0
302
where ƒn(x, y), ... mean homogeneous expressions in x and y
having constant coefficients, and having the degrees indicated
by the suffixes, and ƒ0 is a constant. Or again we may have
trigonometrical functions, such as sin x and tan x, or inverse
trigonometrical functions, such as sin−1x, or exponential functions,
such as ex and ax, or logarithmic functions, such as log x and log
(1 + x). We may have these functional symbols combined in
various ways, and thus there arises a great number of functions.
Further we may have functions of more than one variable, as, for
instance, the expression xy/(x² + y²), in which both x and y are
regarded as variable. Such functions were introduced into
analysis somewhat unsystematically as the need for them arose,
and the later developments of analysis led to the introduction
of other classes of functions.
2. Graphic Representation.—In the case of a function of one
variable x, any value of x and the corresponding value y of the
function can be the co-ordinates of a point in a plane. To any
value of x there corresponds a point N on the axis of x, in accordance
with the rule that x is the abscissa of N. The corresponding
value of y determines a point P in accordance with the rule that
x is the abscissa and y the ordinate of P. The ordinate y gives
the value of the function which corresponds to that value of
the variable x which is specified by N; and it may be described
as “the value of the function at N.” Since there is a one-to-one
correspondence of the points N and the numbers x, we may also
describe the ordinate as “the value of the function at x.” In
simple cases the aggregate of the points P which are determined
by any particular function (of one variable) is a curve, called
the “graph of the function” (see § 14). In like manner a function
of two variables defines a surface.
3. The Variable.—Graphic methods of representation, such
as those just described, enabled mathematicians to deal with
irrational values of functions and variables at the time when there
was no theory of irrational numbers other than Euclid’s theory
of incommensurables. In that theory an irrational number was
the ratio of two incommensurable geometric magnitudes. In
the modern theory of number irrational numbers are defined in
a purely arithmetical manner, independent of the measurement
of any quantities or magnitudes, whether geometric or of any
other kind. The definition is effected by means of the system
of ordinal numbers (see Number). When this formal system is
established, the theory of measurement may be founded upon it;
and, in particular, the co-ordinates of a point are defined as
numbers (not lengths), which are assigned in accordance with a
rule. This rule involves the measurement of lengths. The theory
of functions can be developed without any reference to graphs, or
co-ordinates or lengths. The process by which analysis has been
freed from any consideration of measurable quantities has been
called the “arithmetization of analysis.” In the theory so
developed, the variable upon which a function depends is always
to be regarded as a number, and the corresponding value of the
function is also a number. Any reference to points or co-ordinates
is to be regarded as a picturesque mode of expression,
pointing to a possible application of the theory to geometry.
The development of “arithmetized analysis” in the 19th century
is associated with the name of Karl Weierstrass.
All possible values of a variable are numbers. In what
follows we shall confine our attention to the case where the
numbers are real. When complex numbers are introduced,
instead of real ones, the theory of functions receives a wide
extension, which is accompanied by appropriate limitations
(see below, II. Functions of Complex Variables). The set of all
real numbers forms a continuum. In fact the notion of a one-dimensional
continuum first becomes precise in virtue of the
establishment of the system of real numbers.
4. Domain of a Variable.—Theory of Aggregates.—The notion
of a “variable” is that of a number to which we may assign
at pleasure any one of the values that belong to some chosen set,
or aggregate, of numbers; and this set, or aggregate, is called
the “domain of the variable.” This domain may be an
“interval,” that is to say it may consist of two terminal numbers,
all the numbers between them and no others. When this is
the case the number is said to be “continuously variable.”
When the domain consists of all real numbers, the variable is
said to be “unrestricted.” A domain which consists of all the
real numbers which exceed some fixed number may be described
as an “interval unlimited towards the right”; similarly we
may have an interval “unlimited towards the left.”
In more complicated cases we must have some rule or process for
assigning the aggregate of numbers which constitute the domain of
a variable. The methods of definition of particular types of aggregates,
and the theorems relating to them, form a branch of analysis
called the “theory of aggregates” (Mengenlehre, Théorie des ensembles,
Theory of sets of points). The notion of an “aggregate” in general
underlies the system of ordinal numbers. An aggregate is said to
be “infinite” when it is possible to effect a one-to-one correspondence
of all its elements to some of its elements. For example, we
may make all the integers correspond to the even integers, by making
1 correspond to 2, 2 to 4, and generally n to 2n. The aggregate of
positive integers is an infinite aggregate. The aggregates of all
rational numbers and of all real numbers and of points on a line are
other examples of infinite aggregates. An aggregate whose elements
are real numbers is said to “extend to infinite values” if, after any
number N, however great, is specified, it is possible to find in the
aggregate numbers which exceed N in absolute value. Such an
aggregate is always infinite. The “neighbourhood of a number
(or point) a for a positive number h” is the aggregate of all numbers
(or points) x for which the absolute value of x − a denoted by
|x − a|, does not exceed h.
5. General Notion of Functionality.—A function of one variable
was for a long time commonly regarded as the ordinate of a
curve; and the two notions (1) that which is determined by a
curve supposed drawn, and (2) that which is determined by an
analytical expression supposed written down, were not for a
long time clearly distinguished. It was for this reason that
Fourier’s discovery that a single analytical expression is capable
of representing (in different parts of an interval) what would
in his time have been called different functions so profoundly
struck mathematicians (§ 23). The analysts who, in the middle
of the 19th century, occupied themselves with the theory of the
convergence of Fourier’s series were led to impose a restriction
on the character of a function in order that it should admit of
such representation, and thus the door was opened for the
introduction of the general notion of functional dependence.
This notion may be expressed as follows: We have a variable
number, y, and another variable number, x, a domain of the
variable x, and a rule for assigning one or more definite values
to y when x is any point in the domain; then y is said to be a
“function” of the variable x, and x is called the “argument”
of the function. According to this notion a function is, as it
were, an indefinitely extended table, like a table of logarithms;
to each point in the domain of the argument there correspond
values for the function, but it remains arbitrary what values the
function is to have at any such point.
For the specification of any particular function two things are
requisite: (1) a statement of the values of the variable, or of the
aggregate of points, to which values of the function are to be made
to correspond, i.e. of the “domain of the argument”; (2) a rule
for assigning the value or values of the function that correspond to
any point in this domain. We may refer to the second of these two
essentials as “the rule of calculation.” The relation of functions
to analytical expressions may then be stated in the form that the
rule of calculation is: “Give the function the value of the expression
at any point at which the expression has a determinate value,” or
again more generally, “Give the function the value of the expression
at all points of a definite aggregate included in the domain of the
argument.” The former of these is the rule of those among the
earlier analysts who regarded an analytical expression and a function
as the same thing, and their usage may be retained without causing
confusion and with the advantage of brevity, the analytical expression
serving to specify the domain of the argument as well as the
rule of calculation, e.g. we may speak of “the function 1/x.” This
function is defined by the analytical expression 1/x at all points
except the point x = 0. But in complicated cases separate statements
of the domain of the argument and the rule of calculation
cannot be dispensed with. In general, when the rule of calculation
is determined as above by an analytical expression at any aggregate
of points, the function is said to be “represented” by the expression
at those points.
When the rule of calculation assigns a single definite value for a
function at each point in the domain of the argument the function
is “uniform” or “one-valued.” In what follows it is to be understood
that all the functions considered are one-valued, and the values
303
assigned by the rule of calculation real. In the most important
cases the domain of the argument of a function of one variable is an
interval, with the possible exception of isolated points.
6. Limits.—Let ƒ(x) be a function of a variable number x;
and let a be a point such that there are points of the domain
of the argument x in the neighbourhood of a for any number
h, however small. If there is a number L which has the property
that, after any positive number ε, however small, has been
specified, it is possible to find a positive number h, so that
|L − ƒ(x)| < ε for all points x of the domain (other than a) for
which |x − a| < h, then L is the “limit of ƒ(x) at the point a.”
The condition for the existence of L is that, after the positive
number ε has been specified, it must be possible to find a positive
number h, so that |ƒ(x′) − ƒ(x)| < ε for all points x and x′ of
the domain (other than a) for which |x − a| < h and |x′ − a| < h.
It is a fundamental theorem that, when this condition is
satisfied, there exists a perfectly definite number L which is the
limit of ƒ(x) at the point a as defined above. The limit of ƒ(x)
at the point a is denoted by Ltx=aƒ(x), or by
limx=aƒ(x).
If ƒ(x) is a function of one variable x in a domain which extends
to infinite values, and if, after ε has been specified, it is possible to
find a number N, so that |ƒ(x′) − ƒ(x)| < ε for all values of x and x′
which are in the domain and exceed N, then there is a number L
which has the property that |ƒ(x) − L| < ε for all such values of x.
In this case ƒ(x) has a limit L at x = ∞. In like manner ƒ(x) may
have a limit at x = −∞. This statement includes the case where
the domain of the argument consists exclusively of positive integers.
The values of the function then form a “sequence,” u1, u2, ...
un, ..., and this sequence can have a limit at n = ∞.
The principle common to the above definitions and theorems is
called, after P. du Bois Reymond, “the general principle of convergence
to a limit.”
It must be understood that the phrase “x = ∞” does not mean
that x takes some particular value which is infinite. There is no
such value. The phrase always refers to a limiting process in which,
as the process is carried out, the variable number x increases without
limit: it may, as in the above example of a sequence, increase by
taking successively the values of all the integral numbers; in other
cases it may increase by taking the values that belong to any domain
which “extends to infinite values.”
A very important type of limits is furnished by infinite series.
When a sequence of numbers u1, u2, ... un, ... is given, we may
form a new sequence s1, s2, ... sn, ... from it by the rules s1 = u1,
s2 = u1 + u2, ... sn = u1 + u2 + ... + un or by the equivalent rules
s1 = u, sn − sn−1 = un(n = 2, 3, ...). If the new sequence has a limit
at n = ∞, this limit is called the “sum of the infinite series”
u1 + u2 + ..., and the series is said to be “convergent” (see
Series).
A function which has not a limit at a point a may be such that,
if a certain aggregate of points is chosen out of the domain of the
argument, and the points x in the neighbourhood of a are restricted
to belong to this aggregate, then the function has a limit at a. For
example, sin(1/x) has limit zero at 0 if x is restricted to the
aggregate 1/π, 1/2π, ... 1/nπ, ... or to the aggregate 1/2π,
2/5π, ... n/(n2 + 1)π, ..., but if x takes all values in the neighbourhood
of 0, sin (1/x) has not a limit at 0. Again, there may be a limit
at a if the points x in the neighbourhood of a are restricted by the
condition that x − a is positive; then we have a “limit on the
right” at a; similarly we may have a “limit on the left” at a
point. Any such limit is described as a “limit for a restricted
domain.” The limits on the left and on the right are denoted by
ƒ(a − 0) and ƒ(a + 0).
The limit L of ƒ(x) at a stands in no necessary relation to the value
of ƒ(x) at a. If the point a is in the domain of the argument, the
value of ƒ(x) at a is assigned by the rule of calculation, and may be
different from L. In case ƒ(a) = L the limit is said to be “attained.”
If the point a is not in the domain of the argument, there is no value
for ƒ(x) at a. In the case where ƒ(x) is defined for all points in an
interval containing a, except the point a, and has a limit L at a,
we may arbitrarily annex the point a to the domain of the argument
and assign to ƒ(a) the value L; the function may then be said to
be “extrinsically defined.” The so-called “indeterminate forms”
(see Infinitesimal Calculus) are examples.
7. Superior and Inferior Limits; Infinities.—The value of a
function at every point in the domain of its argument is finite,
since, by definition, the value can be assigned, but this does not
necessarily imply that there is a number N which exceeds all
the values (or is less than all the values). It may happen that,
however great a number N we take, there are among the values
of the function numbers which exceed N (or are less than −N).
If a number can be found which is greater than every value
of the function, then either (α) there is one value of the function
which exceeds all the others, or (β) there is a number S which
exceeds every value of the function but is such that, however
small a positive number ε we take, there are values of the function
which exceed S − ε. In the case (α) the function has a greatest
value; in case (β) the function has a “superior limit” S, and
then there must be a point a which has the property that there
are points of the domain of the argument, in the neighbourhood
of a for any h, at which the values of the function differ from
S by less than ε. Thus S is the limit of the function at a, either
for the domain of the argument or for some more restricted
domain. If a is in the domain of the argument, and if, after
omission of a, there is a superior limit S which is in this way the
limit of the function at a, if further ƒ(a) = S, then S is the greatest
value of the function: in this case the greatest value is a limit
(at any rate for a restricted domain) which is attained; it may
be called a “superior limit which is attained.” In like manner
we may have a “smallest value” or an “inferior limit,” and a
smallest value may be an “inferior limit which is attained.”
All that has been said here may be adapted to the description of
greatest values, superior limits, &c., of a function in a restricted
domain contained in the domain of the argument. In particular,
the domain of the argument may contain an interval; and therein
the function may have a superior limit, or an inferior limit, which
is attained. Such a limit is a maximum value or a minimum value
of the function.
Again, if, after any number N, however great, has been specified,
it is possible to find points of the domain of the argument at which
the value of the function exceeds N, the values of the function are
said to have an “infinite superior limit,” and then there must be
a point a which has the property that there are points of the domain,
in the neighbourhood of a for any h, at which the value of the function
exceeds N. If the point a is in the domain of the argument the
function is said to “tend to become infinite” at a; it has of course
a finite value at a. If the point a is not in the domain of the argument
the function is said to “become infinite” at a; it has of
course no value at a. In like manner we may have a (negatively)
infinite inferior limit. Again, after any number N, however great,
has been specified and a number h found, so that all the values of
the function, at points in the neighbourhood of a for h, exceed N in
absolute value, all these values may have the same sign; the function
is then said to become, or to tend to become, “determinately
(positively or negatively) infinite”; otherwise it is said to become
or to tend to become, “indeterminately infinite.”
All the infinities that occur in the theory of functions are of the
nature of variable finite numbers, with the single exception of the
infinity of an infinite aggregate. The latter is described as an
“actual infinity,” the former as “improper infinities.” There is no
“actual infinitely small” corresponding to the actual infinity.
The only “infinitely small” is zero. All “infinite values” are of
the nature of superior and inferior limits which are not attained.
8. Increasing and Decreasing Functions.—A function ƒ(x) of one
variable x, defined in the interval between a and b, is “increasing
throughout the interval” if, whenever x and x′ are two numbers
in the interval and x′ > x, then ƒ(x′) > ƒ(x); the function “never
decreases throughout the interval” if, x′ and x being as before,
ƒ(x′) > ƒ(x). Similarly for decreasing functions, and for functions
which never increase throughout an interval. A function which
either never increases or never diminishes throughout an interval
is said to be “monotonous throughout” the interval. If we take
in the above definition b > a, the definition may apply to a function
under the restriction that x′ is not b and x is not a; such a
function is “monotonous within” the interval. In this case we
have the theorem that the function (if it never decreases) has
a limit on the left at b and a limit on the right at a, and these are
the superior and inferior limits of its values at all points within
the interval (the ends excluded); the like holds mutatis mutandis
if the function never increases. If the function is monotonous
throughout the interval, ƒ(b) is the greatest (or least) value
of ƒ(x) in the interval; and if ƒ(b) is the limit of ƒ(x) on the left
at b, such a greatest (or least) value is an example of a superior
(or inferior) limit which is attained. In these cases the function
tends continually to its limit.
These theorems and definitions can be extended, with obvious
modifications, to the cases of a domain which is not an interval, or
extends to infinite values. By means of them we arrive at sufficient,
but not necessary, criteria for the existence of a limit; and these
are frequently easier to apply than the general principle of convergence
to a limit (§ 6), of which principle they are particular cases.
For example, the function represented by x log (1/x) continually
304
diminishes when 1/e > x > 0 and x diminishes towards zero, and it
never becomes negative. It therefore has a limit on the right at
x = 0. This limit is zero. The function represented by x sin (1/x)
does not continually diminish towards zero as x diminishes towards
zero, but is sometimes greater than zero and sometimes less than
zero in any neighbourhood of x = 0, however small. Nevertheless,
the function has the limit zero at x = 0.
9. Continuity of Functions.—A function ƒ(x) of one variable x
is said to be continuous at a point a if (1) ƒ(x) is defined in an
interval containing a; (2) ƒ(x) has a limit at a; (3) ƒ(a) is
equal to this limit. The limit in question must be a limit for
continuous variation, not for a restricted domain. If ƒ(x) has
a limit on the left at a and ƒ(a) is equal to this limit, the function
may be said to be “continuous to the left” at a; similarly the
function may be “continuous to the right” at a.
A function is said to be “continuous throughout an interval”
when it is continuous at every point of the interval. This implies
continuity to the right at the smaller end-value and continuity
to the left at the greater end-value. When these conditions at the
ends are not satisfied the function is said to be continuous
“within” the interval. By a “continuous function” of one
variable we always mean a function which is continuous throughout
an interval.
The principal properties of a continuous function are:
1. The function is practically constant throughout sufficiently small
intervals. This means that, after any point a of the interval has been
chosen, and any positive number ε, however small, has been
specified, it is possible to find a number h, so that the difference
between any two values of the function in the interval between a − h and
a + h is less than ε. There is an obvious modification if a is an
end-point of the interval.
2. The continuity of the function is “uniform.” This means that the
number h which corresponds to any ε as in (1) may be the same at
all points of the interval, or, in other words, that the numbers h which
correspond to ε for different values of a have a positive
inferior limit.
3. The function has a greatest value and a least value in the interval,
and these are superior and inferior limits which are attained.
4. There is at least one point of the interval at which the function
takes any value between its greatest and least values in the interval.
5. If the interval is unlimited towards the right (or towards the left),
the function has a limit at ∞ (or at −∞).
10. Discontinuity of Functions.—The discontinuities of a
function of one variable, defined in an interval with the possible
exception of isolated points, may be classified as follows:
(1) The function may become infinite, or tend to become
infinite, at a point.
(2) The function may be undefined at a point.
(3) The function may have a limit on the left and a limit on
the right at the same point; these may be different from each
other, and at least one of them must be different from the value
of the function at the point.
(4) The function may have no limit at a point, or no limit on
the left, or no limit on the right, at a point.
In case a function ƒ(x), defined as above, has no limit at a point a,
there are four limiting values which come into consideration. Whatever
positive number h we take, the values of the function at points
between a and a + h (a excluded) have a superior limit (or a greatest
value), and an inferior limit (or a least value); further, as h decreases,
the former never increases and the latter never decreases; accordingly
each of them tends to a limit. We have in this way two limits on
the right—the inferior limit of the superior limits in diminishing
neighbourhoods, and the superior limit of the inferior limits in
diminishing neighbourhoods. These are denoted by ƒ(a + 0) and
ƒ(a + 0), and they are called the “limits of indefiniteness” on the
right. Similar limits on the left are denoted by ƒ(a − 0) and ƒ(a − 0).
Unless ƒ(x) becomes, or tends to become, infinite at a, all these must
exist, any two of them may be equal, and at least one of them must
be different from ƒ(a), if ƒ(a) exists. If the first two are equal there
is a limit on the right denoted by ƒ(a + 0); if the second two are
equal, there is a limit on the left denoted by ƒ(a − 0). In case the
function becomes, or tends to become, infinite at a, one or more of
these limits is infinite in the sense explained in § 7; and now it is
to be noted that, e.g. the superior limit of the inferior limits in
diminishing neighbourhoods on the right of a may be negatively
infinite; this happens if, after any number N, however great, has
been specified, it is possible to find a positive number h, so that all
the values of the function in the interval between a and a + h (a
excluded) are less than −N; in such a case ƒ(x) tends to become
negatively infinite when x decreases towards a; other modes of
tending to infinite limits may be described in similar terms.
11. Oscillation of Functions.—The difference between the
greatest and least of the numbers ƒ(a), ƒ(a + 0), ƒ(a + 0), ƒ(a − 0),
ƒ(a − 0), when they are all finite, is called the “oscillation” or
“fluctuation” of the function ƒ(x) at the point a. This difference
is the limit for h = 0 of the difference between the superior and
inferior limits of the values of the function at points in the
interval between a − h and a + h. The corresponding difference
for points in a finite interval is called the “oscillation of the
function in the interval.” When any of the four limits of
indefiniteness is infinite the oscillation is infinite in the sense
explained in § 7.
For the further classification of functions we divide the domain
of the argument into partial intervals by means of points between
the end-points. Suppose that the domain is the interval between a
and b. Let intermediate points x1, x2 ... xn−1, be taken so that
b > xn−1 > xn−2 ... > x1 > a. We may devise a rule by which, as n
increases indefinitely, all the differences
b − xn−1, xn−1 − xn−2, ... x1 − a
tend to zero as a limit. The interval is then said to be divided
into “indefinitely small partial intervals.”
A function defined in an interval with the possible exception of
isolated points may be such that the interval can be divided into a
set of finite partial intervals within each of which the function is
monotonous (§ 8). When this is the case the sum of the oscillations
of the function in those partial intervals is finite, provided the
function does not tend to become infinite. Further, in such a case
the sum of the oscillations will remain below a fixed number for any
mode of dividing the interval into indefinitely small partial intervals.
A class of functions may be defined by the condition that the sum
of the oscillations has this property, and such functions are said
to have “restricted oscillation.” Sometimes the phrase “limited
fluctuation” is used. It can be proved that any function with
restricted oscillation is capable of being expressed as the sum of
two monotonous functions, of which one never increases and the other
never diminishes throughout the interval. Such a function has a
limit on the right and a limit on the left at every point of the interval.
This class of functions includes all those which have a finite number
of maxima and minima in a finite-interval, and some which have an
infinite number. It is to be noted that the class does not include all
continuous functions.
12. Differentiable Function.—The idea of the differentiation
of a continuous function is that of a process for measuring the
rate of growth; the increment of the function is compared with
the increment of the variable. If ƒ(x) is defined in an interval
containing the point a, and a − k and a + k are points of the
interval, the expression
(1)
represents a function of h, which we may call φ(h), defined at all
points of an interval for h between −k and k except the point 0.
Thus the four limits φ(+0), φ(+0), φ(−0), φ(−0) exist, and two
or more of them may be equal. When the first two are equal
either of them is the “progressive differential coefficient” of
ƒ(x) at the point a; when the last two are equal either of them
is the “regressive differential coefficient” of ƒ(x) at a; when all
four are equal the function is said to be “differentiable” at a,
and either of them is the “differential coefficient” of ƒ(x) at a,
or the “first derived function” of ƒ(x) at a. It is denoted by
dƒ(x) / dx or by ƒ′(x). In this case φ(h) has a definite limit at h = 0,
or is determinately infinite at h = 0 (§ 7). The four limits here in
question are called, after Dini, the “four derivates” of ƒ(x) at a.
In accordance with the notation for derived functions they may
be denoted by
ƒ′ + (a), ƒ′ + (a), ƒ′ − (a), ƒ′ − (a).
A function which has a finite differential coefficient at all points
of an interval is continuous throughout the interval, but if the
differential coefficient becomes infinite at a point of the interval
the function may or may not be continuous throughout the interval;
on the other hand a function may be continuous without being
differentiable. This result, comparable in importance, from the
point of view of the general theory of functions, with the discovery
of Fourier’s theorem, is due to G.F.B. Riemann; but the failure
of an attempt made by Ampère to prove that every continuous
function must be differentiable may be regarded as the first step in
the theory. Examples of analytical expressions which represent
continuous functions that are not differentiable have been given by
Riemann, Weierstrass, Darboux and Dini (see § 24). The most
important theorem in regard to differentiable functions is the
“theorem of intermediate value.” (See Infinitesimal Calculus.)
305
13. Analytic Function.—If ƒ(x) and its first n differential
coefficients, denoted byƒ′(x), ƒ″(x), ... ƒ(n) (x), are continuous
in the interval between a and a + h, then
| ƒ(a + h) = ƒ(a) + hƒ′(a) + | h² |
ƒ″(a) + ... + | hn−1 |
ƒ(n−1)(a) + Rn, |
| 2! | (n − 1)! |
where Rn may have various forms, some of which are given in
the article Infinitesimal Calculus. This result is known as
“Taylor’s theorem.”
When Taylor's theorem leads to a representation of the
function by means of an infinite series, the function is said to be
“analytic” (cf. § 21).
14. Ordinary Function.—The idea of a curve representing a
continuous function in an interval is that of a line which has the
following properties: (1) the co-ordinates of a point of the curve
are a value x of the argument and the corresponding value y of
the function; (2) at every point the curve has a definite tangent;
(3) the interval can be divided into a finite number of partial
intervals within each of which the function is monotonous;
(4) the property of monotony within partial intervals is retained
after interchange of the axes of co-ordinates x and y. According
to condition (2) y is a continuous and differentiable function
of x, but this condition does not include conditions (3) and (4):
there are continuous partially monotonous functions which are
not differentiable, there are continuous differentiable functions
which are not monotonous in any interval however small; and
there are continuous, differentiable and monotonous functions
which do not satisfy condition (4) (cf. § 24). A function which
can be represented by a curve, in the sense explained above, is
said to be “ordinary,” and the curve is the graph of the function
(§2). All analytic functions are ordinary, but not all ordinary
functions are analytic.
15. Integrable Function.—The idea of integration is twofold.
We may seek the function which has a given function as its
differential coefficient, or we may generalize the question of
finding the area of a curve. The first inquiry leads directly to the
indefinite integral, the second directly to the definite integral.
Following the second method we define “the definite integral
of the function ƒ(x) through the interval between a and b” to be
the limit of the sum
Σn1 ƒ(x′r) (xr − xr−1)
when the interval is divided into ultimately indefinitely small
partial intervals by points x1, x2, ... xn−1. Here x′r denotes
any point in the rth partial interval, x0 is put for a, and xn for b.
It can be shown that the limit in question is finite and independent
of the mode of division into partial intervals, and of the
choice of the points such as x′r, provided (1) the function is
defined for all points of the interval, and does not tend to become
infinite at any of them; (2) for any one mode of division of the
interval into ultimately indefinitely small partial intervals, the
sum of the products of the oscillation of the function in each
partial interval and the difference of the end-values of that
partial interval has limit zero when n is increased indefinitely.
When these conditions are satisfied the function is said to be
“integrable” in the interval. The numbers a and b which limit
the interval are usually called the “lower and upper limits.”
We shall call them the “nearer and further end-values.” The
above definition of integration was introduced by Riemann in
his memoir on trigonometric series (1854). A still more general
definition has been given by Lebesgue. As the more general
definition cannot be made intelligible without the introduction
of some rather recondite notions belonging to the theory of
aggregates, we shall, in what follows, adhere to Riemann’s
definition.
We have the following theorems:—
1. Any continuous function is integrable.
2. Any function with restricted oscillation is integrable.
3. A discontinuous function is integrable if it does not tend to
become infinite, and if the points at which the oscillation of the
function exceeds a given number σ, however small, can be enclosed
in partial intervals the sum of whose breadths can be diminished
indefinitely.
These partial intervals must be a set chosen out of some complete
set obtained by the process used in the definition of integration.
4. The sum or product of two integrable functions is integrable.
As regards integrable functions we have the following theorems:
1. If S and I are the superior and inferior limits (or greatest and
least values) of ƒ(x) in the interval between a and b, ∫ ba ƒ(x)dx is
intermediate between S(b − a) and I(b − a).
2. The integral is a continuous function of each of the end-values.
3. If the further end-value b is variable, and if ∫ xa ƒ(x)dx = F(x),
then if ƒ(x) is continuous at b, F(x) is differentiable at b, and
F′(b) = ƒ(b).
4. In case ƒ(x) is continuous throughout the interval F(x) is continuous
and differentiable throughout the interval, and F′(x) = ƒ(x)
throughout the interval.
5. In case ƒ′(x) is continuous throughout the interval between a
and b,
∫ ba ƒ′(x)dx = ƒ(b) − ƒ(a).
6. In case ƒ(x) is discontinuous at one or more points of the interval
between a and b, in which it is integrable,
∫ xa ƒ(x)dx
is a function of x, of which the four derivates at any point of the
interval are equal to the limits of indefiniteness of ƒ(x) at the point.
7. It may be that there exist functions which are differentiable
throughout an interval in which their differential coefficients are
not integrable; if, however, F(x) is a function whose differential
coefficient, F′(x), is integrable in an interval, then
F(x) = ∫ xa F′(x)dx + const.,
where a is a fixed point, and x a variable point, of the interval.
Similarly, if any one of the four derivates of a function is integrable
in an interval, all are integrable, and the integral of either differs from
the original function by a constant only.
The theorems (4), (6), (7) show that there is some discrepancy
between the indefinite integral considered as the function which has
a given function as its differential coefficient, and as a definite
integral with a variable end-value.
We have also two theorems concerning the integral of the product
of two integrable functions ƒ(x) and φ(x); these are known as “the
first and second theorems of the mean.” The first theorem of the
mean is that, if φ(x) is one-signed throughout the interval between
a and b, there is a number M intermediate between the superior
and inferior limits, or greatest and least values, of ƒ(x) in the interval,
which has the property expressed by the equation
M ∫ ba φ(x)dx = ∫ ba ƒ(x)φ(x)dx
The second theorem of the mean is that, if ƒ(x) is monotonous
throughout the interval, there is a number ξ between a and b which
has the property expressed by the equation
∫ ba ƒ(x) φ(x)dx = ƒ(a) ∫ ξa φ(x)dx + ƒ(b) ∫ bξ φ(x)dx.
(See Fourier’s Series.)
16. Improper Definite Integrals.—We may extend the idea of
integration to cases of functions which are not defined at some
point, or which tend to become infinite in the neighbourhood of
some point, and to cases where the domain of the argument
extends to infinite values. If c is a point in the interval between
a and b at which ƒ(x) is not defined, we impose a restriction on
the points x′r of the definition: none of them is to be the point c.
This comes to the same thing as defining ∫ ba ƒ(x)dx to be
Lt ε=0∫ c−εa ƒ(x)dx + Lt ε′=0∫ bc+ε′ ƒ(x)dx,
(1)
where, to fix ideas, b is taken > a, and ε and ε′ are positive. The
same definition applies to the case where ƒ(x) becomes infinite, or
tends to become infinite, at c, provided both the limits exist.
This definition may be otherwise expressed by saying that a
partial interval containing the point c is omitted from the
interval of integration, and a limit taken by diminishing the
breadth of this partial interval indefinitely; in this form it
applies to the cases where c is a or b.
Again, when the interval of integration is unlimited to the
right, or extends to positively infinite values, we have as a
definition
∫ ∞a ƒ(x)dx = Lt h=∞∫ ha ƒ(x)dx,
306
provided this limit exists. Similar definitions apply to
∫ −∞a ƒ(x)dx, and to ∫ ∞−∞ ƒ(x)dx.
All such definite integrals as the above are said to be “improper.”
For example, ∫ ∞0 sin x / x dx is improper in two ways. It means
Lt h=∞ Lt ε=0 ∫ hε sinx/x dx,
in which the positive number ε is first diminished indefinitely,
and the positive number h is afterwards increased indefinitely.
The “theorems of the mean” (§ 15) require modification when
the integrals are improper (see Fourier’s Series).
When the improper definite integral of a function which
becomes, or tends to become, infinite, exists, the integral is said
to be “convergent.” If ƒ(x) tends to become infinite at a point
c in the interval between a and b, and the expression (1) does not
exist, then the expression ∫ ba ƒ(x)dx, which has no value, is called
a “divergent integral, “and it may happen that there is a definite
value for
Lt { ∫ c−εa ƒ(x) dx + ∫ bc+ε′ ƒ(x) dx }
provided that ε and ε′ are connected by some definite relation,
and both, remaining positive, tend to limit zero. The value of
the above limit is then called a “principal value” of the divergent
integral. Cauchy’s principal value is obtained by making ε′ = ε,
i.e. by taking the omitted interval so that the infinity is at
its middle point. A divergent integral which has one or more
principal values is sometimes described as “semi-convergent.”
17. Domain of a Set of Variables.—The numerical continuum
of n dimensions (Cn) is the aggregate that is arrived at by attributing
simultaneous values to each of n variables x1, x2, ... xn,
these values being any real numbers. The elements of such an
aggregate are called “points,” and the numbers x1, x2 ... xn
the “co-ordinates” of a point. Denoting in general the points
(x1, x2, ... xn) and (x′1, x′2 ... x′n) by x and x′, the sum of
the differences |x1 − x′1| + |x2 − x′2| + ... + |xn − x′n| may
be denoted by |x − x′| and called the “difference of the two
points.” We can in various ways choose out of the continuum
an aggregate of points, which may be an infinite aggregate, and
any such aggregate can be the “domain” of a “variable point.”
The domain is said to “extend to an infinite distance” if, after
any number N, however great, has been specified, it is possible
to find in the domain points of which one or more co-ordinates
exceed N in absolute value. The “neighbourhood” of a point
a for a (positive) number h is the aggregate constituted of all the
points x, which are such that the “difference” denoted by
|x − a| < h. If an infinite aggregate of points does not extend
to an infinite distance, there must be at least one point a, which
has the property that the points of the aggregate which are in
the neighbourhood of a for any number h, however small, themselves
constitute an infinite aggregate, and then the point a is
called a “limiting point” of the aggregate; it may or may not
be a point of the aggregate. An aggregate of points is “perfect”
when all its points are limiting points of it, and all its limiting
points are points of it; it is “connected” when, after taking
any two points a, b of it, and choosing any positive number ε,
however small, a number m and points x′, x″, ... x(m) of the
aggregate can be found so that all the differences denoted by
|x′ − a|, |x″ − x′|, ... |b − x(m)| are less than ε. A perfect connected
aggregate is a continuum. This is G. Cantor’s definition.
The definition of a continuum in Cn leaves open the question of
the number of dimensions of the continuum, and a further explanation
is necessary in order to define arithmetically what is meant by a
“homogeneous part” Hn of Cn. Such a part would correspond to
an interval in C1, or to an area bounded by a simple closed contour
in C2; and, besides being perfect and connected, it would have the
following properties: (1) There are points of Cn, which are not points
of Hn; these form a complementary aggregate H′n. (2) There are
points “within” Hn; this means that for any such point there is
a neighbourhood consisting exclusively of points of Hn. (3) The
points of Hn which do not lie “within” Hn are limiting points of
H′n; they are not points of H′n, but the neighbourhood of any such
point for any number h, however small, contains points within Hn
and points of H′n: the aggregate of these points is called the
“boundary” of Hn. (4) When any two points a, b within Hn are
taken, it is possible to find a number ε and a corresponding number
m, and to choose points x′, x″, ... x(m), so that the neighbourhood
of a for ε contains x′, and consists exclusively of points within Hn,
and similarly for x′ and x″, x″ and x″′, ... x(m) and b. Condition
(3) would exclude such an aggregate as that of the points within and
upon two circles external to each other and a line joining a point on
one to a point on the other, and condition (4) would exclude such
an aggregate as that of the points within and upon two circles which
touch externally.
18. Functions of Several Variables.—A function of several
variables differs from a function of one variable in that the
argument of the function consists of a set of variables, or is a
variable point in a Cn when there are n variables. The function
is definable by means of the domain of the argument and the
rule of calculation. In the most important cases the domain of
the argument is a homogeneous part Hn of Cn with the possible
exception of isolated points, and the rule of calculation is that
the value of the function in any assigned part of the domain
of the argument is that value which is assumed at the point by
an assigned analytical expression. The limit of a function at a
point a is defined in the same way as in the case of a function of
one variable.
We take a positive fraction ε and consider the neighbourhood of a
for h, and from this neighbourhood we exclude the point a, and we
also exclude any point which is not in the domain of the argument.
Then we take x and x′ to be any two of the retained points in the
neighbourhood. The function ƒ has a limit at a if for any positive ε,
however small, there is a corresponding h which has the property
that |ƒ(x′) − ƒ(x)| < ε, whatever points x, x′ in the neighbourhood
of a for h we take (a excluded). For example, when there are two
variables x1, x2, and both are unrestricted, the domain of the argument
is represented by a plane, and the values of the function are
correlated with the points of the plane. The function has a limit
at a point a, if we can mark out on the plane a region containing
the point a within it, and such that the difference of the values of
the function which correspond to any two points of the region
(neither of the points being a) can be made as small as we please
in absolute value by contracting all the linear dimensions of the
region sufficiently. When the domain of the argument of a function
of n variables extends to an infinite distance, there is a “limit at
an infinite distance” if, after any number ε, however small, has been
specified, a number N can be found which is such that |ƒ(x′) − ƒ(x)| < ε,
for all points x and x′ (of the domain) of which one or more co-ordinates
exceed N in absolute value. In the case of functions of
several variables great importance attaches to limits for a restricted
domain. The definition of such a limit is verbally the same as the
corresponding definition in the case of functions of one variable
(§ 6). For example, a function of x1 and x2 may have a limit at
(x1 = 0, x2 = 0) if we first diminish x1 without limit, keeping x2 constant,
and afterwards diminish x2 without limit. Expressed in
geometrical language, this process amounts to approaching the
origin along the axis of x2. The definitions of superior and inferior
limits, and of maxima and minima, and the explanations of what
is meant by saying that a function of several variables becomes
infinite, or tends to become infinite, at a point, are almost identical
verbally with the corresponding definitions and explanations in the
case of a function of one variable (§ 7). The definition of a continuous
function (§ 9) admits of immediate extension; but it is very important
to observe that a function of two or more variables may be
a continuous function of each of the variables, when the rest are kept
constant, without being a continuous function of its argument.
For example, a function of x and y may be defined by the conditions
that when x = 0 it is zero whatever value y may have, and when
x ≠ 0 it has the value of sin {4 tan−1 (y/x)}. When y has any particular
value this function is a continuous function of x, and, when x has
any particular value this function is a continuous function of y;
but the function of x and y is discontinuous at (x = 0, y = 0).
19. Differentiation and Integration.—The definition of partial
differentiation of a function of several variables presents no
difficulty. The most important theorems concerning differentiable
functions are the “theorem of the total differential,”
the theorem of the interchangeability of the order of partial
differentiations, and the extension of Taylor’s theorem (see
Infinitesimal Calculus).
With a view to the establishment of the notion of integration
through a domain, we must define the “extent” of the domain.
Take first a domain consisting of the point a and all the points x
for which |x − a| < ½h, where h is a chosen positive number;
the extent of this domain is hn, n being the number of variables;
such a domain may be described as “square,” and the number h
may be called its “breadth”; it is a homogeneous part of the
307
numerical continuum of n dimensions, and its boundary consists
of all the points for which |x − a| = ½h. Now the points of
any domain, which does not extend to an infinite distance, may
be assigned to a finite number m of square domains of finite
breadths, so that every point of the domain is either within one
of these square domains or on its boundary, and so that no point
is within two of the square domains; also we may devise a rule
by which, as the number m increases indefinitely, the breadths
of all the square domains are diminished indefinitely. When
this process is applied to a homogeneous part, H, of the numerical
continuum Cn, then, at any stage of the process, there will be
some square domains of which all the points belong to H, and
there will generally be others of which some, but not all, of the
points belong to H. As the number m is increased indefinitely
the sums of the extents of both these categories of square
domains will tend to definite limits, which cannot be negative;
when the second of these limits is zero the domain H is said to
be “measurable,” and the first of these limits is its “extent”;
it is independent of the rule adopted for constructing the square
domains and contracting their breadths. The notion thus introduced
may be adapted by suitable modifications to continua of
lower dimensions in Cn.
The integral of a function ƒ(x) through a measurable domain H,
which is a homogeneous part of the numerical continuum of n
dimensions, is defined in just the same way as the integral through
an interval, the extent of a square domain taking the place of the
difference of the end-values of a partial interval; and the condition
of integrability takes the same form as in the simple case. In particular,
the condition is satisfied when the function is continuous
throughout the domain. The definition of an integral through a
domain may be adapted to any domain of measurable extent. The
extensions to “improper” definite integrals may be made in the
same way as for a function of one variable; in the particular case
of a function which tends to become infinite at a point in the domain
of integration, the point is enclosed in a partial domain which is
omitted from the integration, and a limit is taken when the extent
of the omitted partial domain is diminished indefinitely; a divergent
integral may have different (principal) values for different modes
of contracting the extent of the omitted partial domain. In applications
to mathematical physics great importance attaches to convergent
integrals and to principal values of divergent integrals.
For example, any component of magnetic force at a point within a
magnet, and the corresponding component of magnetic induction
at the same point are expressed by different principal values of the
same divergent integral. Delicate questions arise as to the possibility
of representing the integral of a function of n variables through a
domain Hn, as a repeated integral, of evaluating it by successive
integrations with respect to the variables one at a time and of interchanging
the order of such integrations. These questions have been
discussed very completely by C. Jordan, and we may quote the
result that all the transformations in question are valid when the
function is continuous throughout the domain.
20. Representation of Functions in General.—We have seen
that the notion of a function is wider than the notion of an
analytical expression, and that the same function may be
“represented” by one expression in one part of the domain of
the argument and by some other expression in another part of
the domain (§ 5). Thus there arises the general problem of the
representation of functions. The function may be given by
specifying the domain of the argument and the rule of calculation,
or else the function may have to be determined in accordance
with certain conditions; for example, it may have to
satisfy in a prescribed domain an assigned differential equation.
In either case the problem is to determine, when possible, a
single analytical expression which shall have the same value as
the function at all points in the domain of the argument. For
the representation of most functions for which the problem can
be solved recourse must be had to limiting processes. Thus we
may utilize infinite series, or infinite products, or definite integrals;
or again we may represent a function of one variable
as the limit of an expression containing two variables in a domain
in which one variable remains constant and another varies.
An example of this process is afforded by the expression
Lty = ∞xy / (x²y + 1), which represents a function of x vanishing at
x = 0 and at all other values of x having the value of 1/x. The
method of series falls under this more general process (cf. § 6).
When the terms u1, u2, ... of a series are functions of a variable
x, the sum sn of the first n terms of the series is a function of x
and n; and, when the series is convergent, its sum, which is
Ltn = ∞ sn, can represent a function of x. In most cases the series
converges for some values of x and not for others, and the values
for which it converges form the “domain of convergence.”
The sum of the series represents a function in this domain.
The apparently more general method of representation of a
function of one variable as the limit of a function of two variables
has been shown by R. Baire to be identical in scope with the method
of series, and it has been developed by him so as to give a very
complete account of the possibility of representing functions by
analytical expressions. For example, he has shown that Riemann’s
totally discontinuous function, which is equal to 1 when x is rational
and to 0 when x is irrational, can be represented by an analytical
expression. An infinite process of a different kind has been adapted
to the problem of the representation of a continuous function by
T. Brodén. He begins with a function having a graph in the form
of a regular polygon, and interpolates additional angular points in
an ordered sequence without limit. The representation of a function
by means of an infinite product falls clearly under Baire’s method,
while the representation by means of a definite integral is analogous
to Brodén’s method. As an example of these two latter processes
we may cite the Gamma function [Γ(x)] defined for positive values
of x by the definite integral
∫ ∞0 e−t tx−1 dt,
or by the infinite product
| Ltn=∞ nx/x(1 + x)(1 + ½x) ... ( 1 + | x |
). |
| n − 1 |
The second of these expressions avails for the representation of the
function at all points at which x is not a negative integer.
21. Power Series.—Taylor’s theorem leads in certain cases
to a representation of a function by an infinite series. We have
under certain conditions (§ 13)
| ƒ(x) = ƒ(a) + Σn−1r=1 | (x − a)r |
ƒ(r)(a) + Rn; |
| r! |
and this becomes
| ƒ(x) = ƒ(a) + Σ∞r=1 | (x − a)r |
ƒ(r)(a), |
| r! |
provided that (α) a positive number k can be found so that at
all points in the interval between a and a + k (except these points)
ƒ(x) has continuous differential coefficients of all finite orders,
and at a has progressive differential coefficients of all finite
orders; (β) Cauchy’s form of the remainder Rn, viz.
[(x − a) / (n − 1)!] (1 − θ)n−1 ƒn {a + θ(x − a)}, has the limit zero when n increases
indefinitely, for all values of θ between 0 and 1, and for
all values of x in the interval between a and a + k, except possibly
a + k. When these conditions are satisfied, the series (1) represents
the function at all points of the interval between a and a + k,
except possibly a + k, and the function is “analytic” (§ 13) in
this domain. Obvious modifications admit of extension to an
interval between a and a − k, or between a − k and a + k. When
a series of the form (1) represents a function it is called “the
Taylor’s series for the function.”
Taylor’s series is a power series, i.e. a series of the form
Σ∞n=0 an (x − a)n.
As regards power series we have the following theorems:
1. If the power series converges at any point except a there is a
number k which has the property that the series converges absolutely
in the interval between a − k and a + k, with the possible exception
of one or both end-points.
2. The power series represents a continuous function in its domain
of convergence (the end-points may have to be excluded).
3. This function is analytic in the domain, and the power series
representing it is the Taylor’s series for the function.
The theory of power series has been developed chiefly from the
point of view of the theory of functions of complex variables.
22. Uniform Convergence.—We shall suppose that the domain
of convergence of an infinite series of functions is an interval with
the possible exception of isolated points. Let ƒ(x) be the sum
of the series at any point x of the domain, and ƒn(x) the sum of
the first n + 1 terms. The condition of convergence at a point
a is that, after any positive number ε, however small, has been
specified, it must be possible to find a number n so that
|ƒm(a) − ƒp(a)| < ε for all values of m and p which exceed n.
The sum, ƒ(a), is the limit of the sequence of numbers ƒn(a) at
308
n = ∞. The convergence is said to be “uniform” in an interval
if, after specification of ε, the same number n suffices at all
points of the interval to make |ƒ(x) − ƒm(x)| < ε for all values of
m which exceed n. The numbers n corresponding to any ε,
however small, are all finite, but, when ε is less than some fixed
finite number, they may have an infinite superior limit (§ 7);
when this is the case there must be at least one point, a, of the
interval which has the property that, whatever number N we
take, ε can be taken so small that, at some point in the neighbourhood
of a, n must be taken > N to make |ƒ(x) − fm(x)| < ε
when m > n; then the series does not converge uniformly in the
neighbourhood of a. The distinction may be otherwise expressed
thus: Choose a first and ε afterwards, then the number n is
finite; choose ε first and allow a to vary, then the number n
becomes a function of a, which may tend to become infinite, or
may remain below a fixed number; if such a fixed number
exists, however small ε may be, the convergence is uniform.
For example, the series sin x − ½ sin 2x + 1⁄3 sin 3x − ... is convergent
for all real values of x, and, when π > x > −π its sum is ½x;
but, when x is but a little less than π, the number of terms which
must be taken in order to bring the sum at all near to the value of
½x is very large, and this number tends to increase indefinitely as
x approaches π. This series does not converge uniformly in the
neighbourhood of x = π. Another example is afforded by the series
| Σ∞n=0 | nx |
− | (n + 1)x |
, |
| n²x² + 1 | (n + 1)²x² + 1 |
of which the remainder after n terms
is nx/(n²x² + 1). If we put x = 1/n, for any value of n, however
great, the remainder is ½; and the number of terms required to be
taken to make the remainder tend to zero depends upon the value of
x when x is near to zero—it must, in fact, be large compared with
1/x. The series does not converge uniformly in the neighbourhood
of x = 0.
As regards series whose terms represent continuous functions
we have the following theorems:
(1) If the series converges uniformly in an interval it represents
a function which is continuous throughout the interval.
(2) If the series represents a function which is discontinuous
in an interval it cannot converge uniformly in the interval.
(3) A series which does not converge uniformly in an interval
may nevertheless represent a function which is continuous
throughout the interval.
(4) A power series converges uniformly in any interval contained
within its domain of convergence, the end-points being
excluded.
(5) If Σ∞r=0 ƒr(x) = ƒ(x) converges uniformly in the interval
between a and b
∫ ba ƒ(x)dx = Σbr=0 ∫ ba ƒr(x)dx,
or a series which converges uniformly may be integrated term by
term.
(6) If Σ∞r=0 ƒ′r(x) converges uniformly in an interval, then
Σ∞r=0 ƒr(x) converges in the interval, and represents a continuous
differentiable function, φ(x); in fact we have
φ′(x) = Σ∞r=0 ƒ′r(x),
or a series can be differentiated term by term if the series of
derived functions converges uniformly.
A series whose terms represent functions which are not continuous
throughout an interval may converge uniformly in the
interval. If Σ∞r=0 ƒr(x) = ƒ(x), is such a series, and if all the
functions ƒr(x) have limits at a, then ƒ(x) has a limit at a, which
is Σ∞r=0 Lt x=a ƒr(x). A similar theorem holds for limits on the left
or on the right.
23. Fourier’s Series.—An extensive class of functions admit
of being represented by series of the form
| a0 + Σ∞n=1 ( an cos | nπx |
+ bn sin | nπx |
), |
| c | c |
and the rule for determining the coefficients an, bn of such a
series, in order that it may represent a given function ƒ(x) in
the interval between −c and c, was given by Fourier, viz. we
have
| a0 = | 1 |
∫ c−c ƒ(x)dx, an= | 1 |
∫ c−c ƒ(x)cos | nπx |
dx, bn= | 1 |
∫ c−c sin | nπx |
dx. |
| 2c | c |
c | c | c |
The interval between −c and c may be called the “periodic
interval,” and we may replace it by any other interval, e.g. that
between 0 and 1, without any restriction of generality. When
this is done the sum of the series takes the form
Lt n=∞ ∫ 10 Σr = nr = −n ƒ(z) cos {2rπ(z − x)}dz,
and this is
| Lt n=∞ ∫ 10 ƒ(z) | sin {(2n + 1) (z − x)π} |
dz. |
| sin {(z − x)π} |
(ii.)
Fourier’s theorem is that, if the periodic interval can be divided
into a finite number of partial intervals within each of which the
function is ordinary (§ 14), the series represents the function
within each of those partial intervals. In Fourier’s time a
function of this character was regarded as completely arbitrary.
By a discussion of the integral (ii.) based on the Second Theorem
of the Mean (§ 15) it can be shown that, if ƒ(x) has restricted oscillation
in the interval (§ 11), the sum of the series is equal to ½{ƒ(x + 0) + ƒ(x − 0)}
at any point x within the interval, and that it is equal to
½ {ƒ(+0) + ƒ(1 − 0} at each end of the interval. (See the article
Fourier’s Series.) It therefore represents the function at any
point of the periodic interval at which the function is continuous
(except possibly the end-points), and has a definite value at each
point of discontinuity. The condition of restricted oscillation
includes all the functions contemplated in the statement of the
theorem and some others. Further, it can be shown that, in any
partial interval throughout which ƒ(x) is continuous, the series
converges uniformly, and that no series of the form (i), with coefficients
other than those determined by Fourier’s rule, can represent
the function at all points, except points of discontinuity, in the same
periodic interval. The result can be extended to a function ƒ(x)
which tends to become infinite at a finite number of points a of the
interval, provided (1) ƒ(x) tends to become determinately infinite
at each of the points a, (2) the improper definite integral of ƒ(x)
through the interval is convergent, (3) ƒ(x) has not an infinite number
of discontinuities or of maxima or minima in the interval.
24. Representation of Continuous Functions by Series.—If the
series for ƒ(x) formed by Fourier’s rule converges at the point
a of the periodic interval, and if ƒ(x) is continuous at a, the
sum of the series is ƒ(a); but it has been proved by P. du Bois
Reymond that the function may be continuous at a, and yet the
series formed by Fourier’s rule may be divergent at a. Thus
some continuous functions do not admit of representation by
Fourier’s series. All continuous functions, however, admit of
being represented with arbitrarily close approximation in either
of two forms, which may be described as “terminated Fourier’s
series” and “terminated power series,” according to the two
following theorems:
(1) If ƒ(x) is continuous throughout the interval between 0 and
2π, and if any positive number ε however small is specified,
it is possible to find an integer n, so that the difference between
the value of ƒ(x) and the sum of the first n terms of the series
for ƒ(x), formed by Fourier’s rule with periodic interval from
0 to 2π, shall be less than ε at all points of the interval. This
result can be extended to a function which is continuous in any
given interval.
(2) If ƒ(x) is continuous throughout an interval, and any
positive number ε however small is specified, it is possible to
find an integer n and a polynomial in x of the nth degree, so
that the difference between the value of ƒ(x) and the value of the
polynomial shall be less than ε at all points of the interval.
Again it can be proved that, if ƒ(x) is continuous throughout
a given interval, polynomials in x of finite degrees can be found,
so as to form an infinite series of polynomials whose sum is equal
to ƒ(x) at all points of the interval. Methods of representation
of continuous functions by infinite series of rational fractional
functions have also been devised.
Particular interest attaches to continuous functions which are
not differentiable. Weierstrass gave as an example the function
represented by the series Σ ∞0 an cos (bn xπ), where a is positive and less
than unity, and b is an odd integer exceeding (1 + 3⁄2π)/a. It can be
shown that this series is uniformly convergent in every interval,
309
and that the continuous function ƒ(x) represented by it has the
property that there is, in the neighbourhood of any point x0, an
infinite aggregate of points x′, having x0 as a limiting point, for
which {ƒ(x′) − ƒ(x0)} / (x′ − x0) tends to become infinite with one
sign when x′ − x0 approaches zero through positive values, and
infinite with the opposite sign when x′ − x0 approaches zero through
negative values. Accordingly the function is not differentiable at
any point. The definite integral of such a function ƒ(x) through the
interval between a fixed point and a variable point x, is a continuous
differentiable function F(x), for which F′(x) = ƒ(x); and, if ƒ(x) is
one-signed throughout any interval F(x) is monotonous throughout
that interval, but yet F(x) cannot be represented by a curve. In
any interval, however small, the tangent would have to take the
same direction for infinitely many points, and yet there is no interval
in which the tangent has everywhere the same direction. Further,
it can be shown that all functions which are everywhere continuous
and nowhere differentiable are capable of representation by series of
the form Σanφn(x), where Σan is an absolutely convergent series of
numbers, and φn(x) is an analytic function whose absolute value
never exceeds unity.
25. Calculations with Divergent Series.—When the series
described in (1) and (2) of § 24 diverge, they may, nevertheless,
be used for the approximate numerical calculation of the values
of the function, provided the calculation is not carried beyond a
certain number of terms. Expansions in series which have the
property of representing a function approximately when the
expansion is not carried too far are called “asymptotic expansions.”
Sometimes they are called “semi-convergent series”;
but this term is avoided in the best modern usage, because
it is often used to describe series whose convergence depends
upon the order of the terms, such as the series 1 − ½ + 1⁄3 − ...
In general, let ƒ0(x) + ƒ1(x) + ... be a series of functions which
does not converge in a certain domain. It may happen that, if any
number ε, however small, is first specified, a number n can afterwards
be found so that, at a point a of the domain, the value ƒ(a) of
a certain function ƒ(x) is connected with the sum of the first n + 1
terms of the series by the relation |ƒ(a) − Σ nr = 0 ƒr(a)| < ε. It must
also happen that, if any number N, however great, is specified, a
number n′(>n) can be found so that, for all values of m which exceed
n′, |Σ mr = 0 ƒr(a)| > N. The divergent series ƒ0(x) + ƒ1(x) + ... is then an
asymptotic expansion for the function f(x) in the domain.
The best known example of an asymptotic expansion is Stirling’s
formula for n! when n is large, viz.
n! = √(2π) ½nn + ½ e−n + θ/12n,
where θ is some number lying between 0 and 1. This formula is
included in the asymptotic expansion for the Gamma function.
We have in fact
log {Γ(x)} = (x − ½) log x − x + ½ log 2π + ω(x),
where ω(x) is the function defined by the definite integral
ω(x) = ∫ ∞0 {(1 − e−t)−1 − t−1 − ½} t−1 e−tx dt.
The multiplier of e−tx under the sign of integration can be expanded
in the power series
| B1 |
− | B2 |
t2 + | B3 |
t4 − ..., |
| 2! | 4! | 6! |
where B1, B2, ... are “Bernoulli’s numbers” given by the formula
Bm = 2.2m! (2π)−2m Σ ∞r = 1 (r−2m).
When the series is integrated term by term, the right-hand member
of the equation for ω(x) takes the form
| B1 |
| 1 |
− | B2 |
| 1 |
+ | B3 |
| 1 |
− ..., |
| 1·2 | x |
3·4 | x3 |
5·6 | x5 |
This series is divergent; but, if it is stopped at any term, the difference
between the sum of the series so terminated and the value of ω(x) is
less than the last of the retained terms. Stirling’s formula is obtained
by retaining the first term only. Other well-known examples of asymptotic
expansions are afforded by the descending series for Bessel’s
functions. Methods of obtaining such expansions for the solutions of
linear differential equations of the second order were investigated by
G.G. Stokes (Math. and Phys. Papers, vol. ii. p. 329), and a general
theory of asymptotic expansions has been developed by H. Poincaré.
A still more general theory of divergent series, and of the conditions
in which they can be used, as above, for the purposes of approximate
calculation has been worked out by É. Borel. The great merit of
asymptotic expansions is that they admit of addition, subtraction,
multiplication and division, term by term, in the same way as
absolutely convergent series, and they admit also of integration
term by term; that is to say, the results of such operations are
asymptotic expansions for the sum, difference, product, quotient,
or integral, as the case may be.
26. Interchange of the Order of Limiting Operations.—When
we require to perform any limiting operation upon a function
which is itself represented by the result of a limiting process,
the question of the possibility of interchanging the order of the
two processes always arises. In the more elementary problems
of analysis it generally happens that such an interchange is
possible; but in general it is not possible. In other words, the
performance of the two processes in different orders may lead
to two different results; or the performance of them in one of the
two orders may lead to no result. The fact that the interchange
is possible under suitable restrictions for a particular class of
operations is a theorem to be proved.
Among examples of such interchanges we have the differentiation
and integration of an infinite series term by term (§ 22), and the
differentiation and integration of a definite integral with respect to
a parameter by performing the like processes upon the subject of
integration (§ 19). As a last example we may take the limit of the
sum of an infinite series of functions at a point in the domain of
convergence. Suppose that the series Σ ∞0 ƒr(x) represents a function
(ƒx) in an interval containing a point a, and that each of the functions
ƒr(x) has a limit at a. If we first put x=a, and then sum the series,
we have the value ƒ(a); if we first sum the series for any x, and
afterwards take the limit of the sum at x = a, we have the limit of
ƒ(x) at a; if we first replace each function ƒr(x) by its limit at a, and
then sum the series, we may arrive at a value different from either
of the foregoing. If the function ƒ(x) is continuous at a, the first and
second results are equal; if the functions ƒr(x) are all continuous at
a, the first and third results are equal; if the series is uniformly
convergent, the second and third results are equal. This last case
is an example of the interchange of the order of two limiting operations,
and a sufficient, though not always a necessary, condition,
for the validity of such an interchange will usually be found in some
suitable extension of the notion of uniform convergence.
Authorities.—Among the more important treatises and memoirs
connected with the subject are: R. Baire, Fonctions discontinues
(Paris, 1905); O. Biermann, Analytische Functionen (Leipzig, 1887);
É. Borel, Théorie des fonctions (Paris, 1898) (containing an introductory
account of the Theory of Aggregates), and Séries divergentes
(Paris, 1901), also Fonctions de variables réelles (Paris, 1905); T.J.
I’A. Bromwich, Introduction to the Theory of Infinite Series (London,
1908); H.S. Carslaw, Introduction to the Theory of Fourier’s Series
and Integrals (London, 1906); U. Dini, Functionen e. reellen Grösse
(Leipzig, 1892), and Serie di Fourier (Pisa, 1880); A. Genocchi
u. G. Peano, Diff.- u. Int.-Rechnung (Leipzig, 1899); J. Harkness
and F. Morley, Introduction to the Theory of Analytic Functions
(London, 1898); A. Harnack, Diff. and Int. Calculus (London, 1891);
E.W. Hobson, The Theory of Functions of a real Variable and the
Theory of Fourier’s Series (Cambridge, 1907); C. Jordan, Cours
d’analyse (Paris, 1893-1896); L. Kronecker, Theorie d. einfachen
u. vielfachen Integrale (Leipzig, 1894); H. Lebesgue, Leçons sur
l’intégration (Paris, 1904); M. Pasch, Diff.- u. Int.-Rechnung
(Leipzig, 1882); E. Picard, Traité d’analyse (Paris, 1891); O.
Stolz, Allgemeine Arithmetik (Leipzig, 1885), and Diff.- u. Int.-Rechnung
(Leipzig, 1893-1899); J. Tannery, Théorie des fonctions
(Paris, 1886); W.H. and G.C. Young, The Theory of Sets of Points
(Cambridge, 1906); Brodén, “Stetige Functionen e. reellen Veränderlichen,”
Crelle, Bd. cxviii.; G. Cantor, A series of memoirs on the
“Theory of Aggregates” and on “Trigonometric series” in Acta
Math. tt. ii., vii., and Math. Ann. Bde. iv.-xxiii.; Darboux, “Fonctions
discontinues,” Ann. Sci. École normale sup. (2), t. iv.; Dedekind,
Was sind u. was sollen d. Zahlen? (Brunswick, 1887), and Stetigkeit
u. irrationale Zahlen (Brunswick, 1872); Dirichlet, “Convergence
des séries trigonométriques,” Crelle, Bd. iv.; P. Du Bois Reymond,
Allgemeine Functionentheorie (Tübingen, 1882), and many memoirs
in Crelle and in Math. Ann.; Heine, “Functionenlehre,” Crelle,
Bd. lxxiv.; J. Pierpont, The Theory of Functions of a real Variable
(Boston, 1905); F. Klein, “Allgemeine Functionsbegriff,” Math.
Ann. Bd. xxii.; W.F. Osgood, “On Uniform Convergence,” Amer.
J. of Math. vol. xix.; Pincherle, “Funzioni analitiche secondo
Weierstrass,” Giorn. di mat. t. xviii.; Pringsheim, “Bedingungen
d. Taylorschen Lehrsatzes,” Math. Ann. Bd. xliv.; Riemann,
“Trigonometrische Reihe,” Ges. Werke (Leipzig, 1876); Schoenflies,
“Entwickelung d. Lehre v. d. Punktmannigfaltigkeiten,” Jahresber.
d. deutschen Math.-Vereinigung, Bd. viii.; Study, Memoir on
“Functions with Restricted Oscillation,” Math. Ann. Bd. xlvii.;
Weierstrass, Memoir on “Continuous Functions that are not Differentiable,”
Ges. math. Werke, Bd. ii. p. 71 (Berlin, 1895), and on the
“Representation of Arbitrary Functions,” ibid. Bd. iii. p. 1; W.H.
Young, “On Uniform and Non-uniform Convergence,” Proc. London
Math. Soc. (Ser. 2) t. 6. Further information and very full references
will be found in the articles by Pringsheim, Schoenflies and Voss in
the Encyclopädie der math. Wissenschaften, Bde. i., ii. (Leipzig, 1898,
1899).
(A. E. H. L.)
310
II—Functions of Complex Variables
In the preceding section the doctrine of functionality is discussed
with respect to real quantities; in this section the theory
when complex or imaginary quantities are involved receives
treatment. The following abstract explains the arrangement
of the subject matter: (§ 1), Complex numbers, states what a
complex number is; (§ 2), Plotting of simple expressions involving
complex numbers, illustrates the meaning in some simple cases,
introducing the notion of conformal representation and proving
that an algebraic equation has complex, if not real, roots; (§ 3),
Limiting operations, defines certain simple functions of a complex
variable which are obtained by passing to a limit, in particular
the exponential function, and the generalized logarithm, here
denoted by λ(z); (§ 4), Functions of a complex variable in general,
after explaining briefly what is to be understood by a region of
the complex plane and by a path, and expounding a logical
principle of some importance, gives the accepted definition of a
function of a complex variable, establishes the existence of a
complex integral, and proves Cauchy’s theorem relating thereto;
(§ 5), Applications, considers the differentiation and integration
of series of functions of a complex variable, proves Laurent’s
theorem, and establishes the expansion of a function of a complex
variable as a power series, leading, in (§ 6), Singular points, to
a definition of the region of existence and singular points of a
function of a complex variable, and thence, in (§ 7), Monogenic
Functions, to what the writer believes to be the simplest definition
of a function of a complex variable, that of Weierstrass; (§ 8),
Some elementary properties of single valued functions, first discusses
the meaning of a pole, proves that a single valued function with
only poles is rational, gives Mittag-Leffler’s theorem, and Weierstrass’s
theorem for the primary factors of an integral function,
stating generalized forms for these, leading to the theorem of
(§ 9), The construction of a monogenic function with a given region of
existence, with which is connected (§10), Expression of a monogenic
function by rational functions in a given region, of which the
method is applied in (§ 11), Expression of (1 − z)−1 by polynomials,
to a definite example, used here to obtain (§ 12), An expansion
of an arbitrary function by means of a series of polynomials, over
a star region, also obtained in the original manner of Mittag-Leffler;
(§ 13), Application of Cauchy’s theorem to the determination
of definite integrals, gives two examples of this method; (§ 14),
Doubly Periodic Functions, is introduced at this stage as furnishing
an excellent example of the preceding principles. The
reader who wishes to approach the matter from the point of view
of Integral Calculus should first consult the section (§ 20) below,
dealing with Elliptic Integrals; (§ 15), Potential Functions,
Conformal representation in general, gives a sketch of the connexion
of the theory of potential functions with the theory of
conformal representation, enunciating the Schwarz-Christoffel
theorem for the representation of a polygon, with the application
to the case of an equilateral triangle; (§ 16), Multiple-valued
Functions, Algebraic Functions, deals for the most part with
algebraic functions, proving the residue theorem, and establishing
that an algebraic function has a definite Order; (§ 17), Integrals
of Algebraic Functions, enunciating Abel’s theorem; (§ 18),
Indeterminateness of Algebraic Integrals, deals with the periods
associated with an algebraic integral, establishing that for an
elliptic integral the number of these is two; (§ 19), Reversion of
an algebraic integral, mentions a problem considered below in
detail for an elliptic integral; (§ 20), Elliptic Integrals, considers
the algebraic reduction of any elliptic integral to one of three
standard forms, and proves that the function obtained by
reversion is single-valued; (§ 21), Modular Functions, gives a
statement of some of the more elementary properties of some
functions of great importance, with a definition of Automorphic
Functions, and a hint of the connexion with the theory of linear
differential equations; (§ 22), A property of integral functions,
deduced from the theory of modular functions, proves that there
cannot be more than one value not assumed by an integral
function, and gives the basis of the well-known expression of
the modulus of the elliptic functions in terms of the ratio of the
periods; (§ 23), Geometrical applications of Elliptic Functions,
shows that any plane curve of deficiency unity can be expressed
by elliptic functions, and gives a geometrical proof of the addition
theorem for the function ℜ(u); (§ 24), Integrals of Algebraic
Functions in connexion with the theory of plane curves, discusses
the generalization to curves of any deficiency; (§ 25), Monogenic
Functions of several independent variables, describes briefly the
beginnings of this theory, with a mention of some fundamental
theorems: (§ 26), Multiply-Periodic Functions and the Theory
of Surfaces, attempts to show the nature of some problems now
being actively pursued.
Beside the brevity necessarily attaching to the account here
given of advanced parts of the subject, some of the more elementary
results are stated only, without proof, as, for instance:
the monogeneity of an algebraic function, no reference being
made, moreover, to the cases of differential equations whose
integrals are monogenic; that a function possessing an algebraic
addition theorem is necessarily an elliptic function (or a particular
case of such); that any area can be conformally represented on
a half plane, a theorem requiring further much more detailed
consideration of the meaning of area than we have given; while
the character and properties, including the connectivity, of a
Riemann surface have not been referred to. The theta functions
are referred to only once, and the principles of the theory of
Abelian Functions have been illustrated only by the developments
given for elliptic functions.
§ 1. Complex Numbers.—Complex numbers are numbers of
the form x + iy, where x, y are ordinary real numbers, and i is a
symbol imagined capable of combination with itself and the
ordinary real numbers, by way of addition, subtraction, multiplication
and division, according to the ordinary commutative,
associative and distributive laws; the symbol i is further such
that i² = −1.
Taking in a plane two rectangular axes Ox, Oy, we assume that
every point of the plane is definitely associated with two real numbers
x, y (its co-ordinates) and conversely; thus any point of the plane is
associated with a single complex number; in particular, for every
point of the axis Ox, for which y = O, the associated number is an
ordinary real number; the complex numbers thus include the real
numbers. The axis Ox is often called the real axis, and the axis Oy
the imaginary axis. If P be the point associated with the complex
variable z = x + iy, the distance OP be called r, and the positive
angle less than 2π between Ox and OP be called θ, we may write
z = r (cos θ + i sin θ); then r is called the modulus or absolute value
of z and often denoted by |z| and θ is called the phase or amplitude
of z, and often denoted by ph (z); strictly the phase is ambiguous
by additive multiples of 2π. If z′ = x′ + iy′ be represented by P′,
the complex argument z′ + z is represented by a point P″ obtained
by drawing from P′ a line equal to and parallel to OP; the geometrical
representation involves for its validity certain properties
of the plane; as, for instance, the equation z′ + z = z + z′ involves
the possibility of constructing a parallelogram (with OP″ as diagonal).
It is important constantly to bear in mind, what is capable of easy
algebraic proof (and geometrically is Euclid’s proposition III. 7),
that the modulus of a sum or difference of two complex numbers is
generally less than (and is never greater than) the sum of their
moduli, and is greater than (or equal to) the difference of their
moduli; the former statement thus holds for the sum of any number
of complex numbers. We shall write E(iθ) for cos θ + i sin θ; it is
at once verified that E(iα). E(iβ) = E[i(α + β)], so that the phase of a
product of complex quantities is obtained by addition of their
respective phases.
§ 2. Plotting and Properties of Simple Expressions involving
a Complex Number.—If we put ζ = (z-i)/(z + i), and, putting
ζ = ξ + iη, take a new plane upon which ξ, η are rectangular
co-ordinates, the equations ξ= (x² + y²− 1)/[x² + (y + 1)²],
η = −2xy/[x² + (y + i)²] will determine, corresponding to any
point of the first plane, a point of the second plane. There is
the one exception of z = −i, that is, x = 0, y = −1, of which the
corresponding point is at infinity. It can now be easily proved
that as z describes the real axis in its plane the point ζ describes
once a circle of radius unity, with centre at ζ = 0, and that there
is a definite correspondence of point to point between points
in the z-plane which are above the real axis and points of the
ζ-plane which are interior to this circle; in particular z = i
corresponds to ζ = 0.
Moreover, ζ being a rational function of z, both ξ and η are continuous
differentiable functions of x and y, save when ζ is infinite;
311
writing ζ = ƒ(x, y) = ƒ(z − iy, y), the fact that this is really independent
of y leads at once to ∂f/∂x + i∂ƒ/∂y = 0, and hence to
| ∂ξ |
= | ∂η |
, | ∂ξ |
= − | ∂η |
, | ∂²ξ |
+ | ∂²ξ |
= 0; |
| ∂x | ∂x′ |
∂y | ∂x′ |
∂x² | ∂y² |
so that ξ is not any arbitrary function of x, y, and when ξ is known
η is determinate save for an additive constant. Also, in virtue of
these equations, if ζ, ζ′ be the values of ζ corresponding to two
near values of z, say z and z′, the ratio (ζ′ − ζ)/(z′ − z) has a definite
limit when z′ = z, independent of the ultimate phase of z′ − z, this
limit being therefore equal to ∂ζ/∂x, that is, ∂ξ/∂x + i∂η)/∂x. Geometrically
this fact is interpreted by saying that if two curves in the
z-plane intersect at a point P, at which both the differential coefficients
∂ξ/∂x, ∂η/∂x are not zero, and P′, P″ be two points near
to P on these curves respectively, and the corresponding points of the
ζ-plane be Q, Q′, Q″, then (1) the ratios PP″/PP′, QQ″/QQ′ are
ultimately equal, (2) the angle P′PP″ is equal to Q′QQ″, (3) the
rotation from PP′ to PP″ is in the same sense as from QQ′ to QQ″,
it being understood that the axes of ξ, η in the one plane are related
as are the axes of x, y. Thus any diagram of the z-plane becomes a
diagram of the ζ-plane with the same angles; the magnification,
however, which is equal to [(∂ξ/∂x)² + (∂ξ/∂y)² ]1/2 varies from point to
point. Conversely, it appears subsequently that the expression
of any copy of a diagram (say, a map) which preserves angles requires
the intervention of the complex variable.
As another illustration consider the case when ζ is a polynomial
in z,
ζ = p0zn + p1zn−1 + ... + pn;
H being an arbitrary real positive number, it can be shown that a
radius R can be found such for every |z| > R we have |ζ| > H;
consider the lower limit of |ζ| for |z| < R; as ξ² + η² is a real
continuous function of x, y for |z| < R, there is a point (x, y),
say (x0, y0), at which |ζ| is least, say equal to ρ, and therefore
within a circle in the ζ-plane whose centre is the origin, of radius ρ,
there are no points ζ representing values corresponding to |z| < R.
But if ζ0 be the value of ζ corresponding to (x0, y0), and the expression
of ζ − ζ0 near z0 = x0 + iy0, in terms of z − z0, be A(z − z0)m +
B(z − z0)m + 1 + ..., where A is not zero, to two points near to (x0, y0),
say (x1, y1) or z1 and
z2 = z0 + (z1 − z0) (cos π/m + i sin π/m), will correspond
two points near to ζ0, say ζ1, and 2ζ0 − ζ′1, situated so that ζ0
is between them. One of these must be within the circle (ρ). We
infer then that ρ = 0, and have proved that every polynomial in
z vanishes for some value of z, and can therefore be written as a
product of factors of the form z − α, where α denotes a complex
number. This proposition alone suffices to suggest the importance
of complex numbers.
§ 3. Limiting Operations.—In order that a complex number
ζ = ξ + iη may have a limit it is necessary and sufficient that each
of ξ and η has a limit. Thus an infinite series w0 + w1 + w2 + ...,
whose terms are complex numbers, is convergent if the real
series formed by taking the real parts of its terms and that
formed by the imaginary terms are both convergent. The
series is also convergent if the real series formed by the moduli
of its terms is convergent; in that case the series is said to be
absolutely convergent, and it can be shown that its sum is
unaltered by taking the terms in any other order. Generally
the necessary and sufficient condition of convergence is that,
for a given real positive ε, a number m exists such that for every
n > m, and every positive p, the batch of terms wn + wn+1 +
... + wn+p is less than ε in absolute value. If the terms depend
upon a complex variable z, the convergence is called uniform
for a range of values of z, when the inequality holds, for the
same ε and m, for all the points z of this range.
The infinite series of most importance are those of which the
general term is anzn, wherein an is a constant, and z is regarded as
variable, n = 0, 1, 2, 3, ... Such a series is called a power series,
if a real and positive number M exists such that for z = z0 and every
n, |anz0n| < M, a condition which is satisfied, for instance, if the
series converges for z = z0, then it is at once proved that the series
converges absolutely for every z for which |z| < |z0|, and converges
uniformly over every range |z| < r′ for which r′ < |z0|.
To every power series there belongs then a circle of convergence
within which it converges absolutely and uniformly; the function
of z represented by it is thus continuous within the circle (this being
the result of a general property of uniformly convergent series of
continuous functions); the sum for an interior point z is, however,
continuous with the sum for a point z0 on the circumference, as z
approaches to z0 provided the series converges for z = z0, as can be
shown without much difficulty. Within a common circle of convergence
two power series Σ anzn, Σ bnzn can be multiplied together
according to the ordinary rule, this being a consequence of a theorem
for absolutely convergent series. If r1 be less than the radius of
convergence of a series Σ an zn and for |z| = r1, the sum of the series
be in absolute value less than a real positive quantity M, it can be
shown that for |z| = r1 every term is also less than M in absolute value,
namely, |an| < Mr1−n. If in every arbitrarily small neighbourhood of
z=0 there be a point for which two converging power series Σan zn,
Σbnzn agree in value, then the series are identical, or an = bn; thus also
if Σanzn vanish at z = 0 there is a circle of finite radius about z = 0 as
centre within which no other points are found for which the sum of
the series is zero. Considering a power series ƒ(z) = Σanzn of radius of
convergence R, if |z0| < R and we put z = z0 + t with |t| < R-|z0|,
the resulting series Σan(z0 + t)n may be regarded as a double series
in z0 and t, which, since |z0| + t < R, is absolutely convergent;
it may then be arranged according to powers of t. Thus we may
write ƒ(z) = Σ Antn; hence A0 = ƒ(z0), and we have [ƒ(z0 + t) − ƒ(z0)]/t =
Σn=1 Antn−l, wherein the continuous series on the right reduces to A1
for t = 0; thus the ratio on the left has a definite limit when t = 0,
equal namely to A1 or Σnanz0n − 1. In other words, the original series
may legitimately be differentiated at any interior point z0 of its circle
of convergence. Repeating this process we find ƒ(z0 + t) = Σtnƒ(n)(z0)/n!,
where ƒ(n)(z0) is the nth differential coefficient. Repeating for this
power series, in t, the argument applied about z = 0 for Σanzn, we
infer that for the series ƒ(z) every point which reduces it to zero is
an isolated point, and of such points only a finite number lie within
a circle which is within the circle of convergence of ƒ(z).
Perhaps the simplest possible power series is ez = exp(z) = 1 + z2/2! +
z3/3! + ... of which the radius of convergence is infinite. By
multiplication we have exp(z)·exp(z1) = exp(z + z1). In particular
when x, y are real, and z = x + iy, exp(z) = exp(x)exp(iy). Now the
functions
U0 = sin y, V0 = 1 − cos y, U1 = y − sin y,
V1 = 1⁄2y² − 1 + cos y, U2 = 1⁄6y³ − y + sin y, V2 = 1⁄24y4 − 1⁄2y2 + 1 − cos y, ...
all vanish for y = 0, and the differential coefficient of any one after
the first is the preceding one; as a function (of a real variable) is
increasing when its differential coefficient is positive, we infer, for
y positive, that each of these functions is positive; proceeding to a
limit we hence infer that
cos y = 1 − 1⁄2y² + 1⁄24y4 − ..., sin y = y − 1⁄6y³ + 1⁄120y5 − ...,
for positive, and hence, for all values of y. We thus have exp(iy) =
cos y + i sin y, and exp (z) = exp (x)·(cos y + i sin y). In other words,
the modulus of exp (z) is exp (x) and the phase is y. Hence also
exp(z + 2πi) = exp(x) [cos (y + 2π) + i sin(y + 2π)],
which we express by saying that exp (z) has the period 2πi,
and hence also the period 2kπi, where k is an arbitrary integer.
From the fact that the constantly increasing function exp (x) can
vanish only for x = 0, we at once prove that exp (z) has no other
periods.
Taking in the plane of z an infinite strip lying between the lines
y = 0, y = 2π and plotting the function ζ = exp (z) upon a new plane,
it follows at once from what has been said that every complex value
of ζ arises when z takes in turn all positions in this strip, and that
no value arises twice over. The equation ζ = exp(z) thus defines z,
regarded as depending upon ζ, with only an additive ambiguity
2kπi, where k is an integer. We write z = λ(ζ); when ζ is real this
becomes the logarithm of ζ; in general λ(ζ) = log |ζ| + i ph (ζ) +
2kπi, where k is an integer; and when ζ describes a closed circuit
surrounding the origin the phase of ζ increases by 2π, or k increases
by unity. Differentiating the series for ζ we have dζ/dz = ζ, so
that z, regarded as depending upon ζ, is also differentiable, with
dz/dζ = ζ− 1. On the other hand, consider the series ζ − 1 − ½(ζ− 1)2 +
1⁄3(ζ − 1)3 − ...; it converges when ζ = 2 and hence converges for
|ζ − 1| < 1; its differential coefficient is, however, 1 − (ζ − 1) +
(ζ − 1)2 − ..., that is, (1 + ζ − 1)− 1. Wherefore if φ(ζ) denote this
series, for |ζ − 1| < 1, the difference λ(ζ) − φ(ζ), regarded as a
function of ξ and η, has vanishing differential coefficients; if we
take the value of λ(ζ) which vanishes when ζ = 1 we infer thence
that for |ζ − 1| < 1, λ(ζ) = Σn=1 [(−1)(n−1)/n (ζ − 1)n. It is to be remarked
that it is impossible for ζ while subject to |ζ − 1| < 1 to make a
circuit about the origin. For values of ζ for which |ζ − 1| ≮ 1, we
can also calculate λ(ζ) with the help of infinite series, utilizing the
fact that λ(ζζ′) = λ(ζ) + λ(ζ′).
The function λ(ζ) is required to define ζa when ζ and a are complex
numbers; this is defined as exp [aλ(ζ)], that is as Σn=0 an [λ(ζ)]n/n!.
When a is a real integer the ambiguity of λ(ζ) is immaterial here,
since exp [aλ(ζ) + 2kaπi] = exp [aλ(ζ)]; when a is of the form 1/q,
where q is a positive integer, there are q values possible for ζ1/q, of
the form exp [1/q λ(ζ)] exp (2kπi/q), with k = 0, 1, ... q − 1, all other
values of k leading to one of these; the qth power of any one of
these values is ζ; when a = p/q, where p, q are integers without
common factor, q being positive, we have ζp/q = (ζ1/q)p. The
definition of the symbol ζa is thus a generalization of the ordinary
definition of a power, when the numbers are real. As an example,
let it be required to find the meaning of ii; the number i is of
modulus unity and phase ½π; thus λ(i) = i (½π + 2kπ); thus
ii = exp (−½π − 2kπ) = exp (−½π) exp (−2kπ),
is always real, but has an infinite number of values.
312
The function exp (z) is used also to define a generalized form of
the cosine and sine functions when z is complex; we write, namely,
cos z = ½[exp (iz) + exp (−iz)] and sin z = −½i [exp (iz) − exp(−iz)].
It will be found that these obey the ordinary relations holding when
z is real, except that their moduli are not inferior to unity. For
example, cos i = 1 + 1/2! + 1/4! + ... is obviously greater than unity.
§4. Of Functions of a Complex Variable in General.—We have
in what precedes shown how to generalize the ordinary rational,
algebraic and logarithmic functions, and considered more
general cases, of functions expressible by power series in z.
With the suggestions furnished by these cases we can frame a
general definition. So far our use of the plane upon which z is
represented has been only illustrative, the results being capable
of analytical statement. In what follows this representation is
vital to the mode of expression we adopt; as then the properties
of numbers cannot be ultimately based upon spatial intuitions,
it is necessary to indicate what are the geometrical ideas requiring
elucidation.
Consider a square of side a, to whose perimeter is attached a
definite direction of description, which we take to be counter-clockwise;
another square, also of side a, may be added to this, so
that there is a side common; this common side being erased we
have a composite region with a definite direction of perimeter;
to this a third square of the same size may be attached, so
that there is a side common to it and one of the former squares,
and this common side may be erased. If this process be continued
any number of times we obtain a region of the plane bounded by one
or more polygonal closed lines, no two of which intersect; and at
each portion of the perimeter there is a definite direction of description,
which is such that the region is on the left of the describing
point. Similarly we may construct a region by piecing together
triangles, so that every consecutive two have a side in common,
it being understood that there is assigned an upper limit for the
greatest side of a triangle, and a lower limit for the smallest angle.
In the former method, each square may be divided into four others
by lines through its centre parallel to its sides; in the latter method
each triangle may be divided into four others by lines joining the
middle points of its sides; this halves the sides and preserves the
angles. When we speak of a region of the plane in general, unless
the contrary is stated, we shall suppose it capable of being generated
in this latter way by means of a finite number of triangles, there
being an upper limit to the length of a side of the triangle and a
lower limit to the size of an angle of the triangle. We shall also
require to speak of a path in the plane; this is to be understood as
capable of arising as a limit of a polygonal path of finite length,
there being a definite direction or sense of description at every point
of the path, which therefore never meets itself. From this the
meaning of a closed path is clear. The boundary points of a region
form one or more closed paths, but, in general, it is only in a limiting
sense that the interior points of a closed path are a region.
There is a logical principle also which must be referred to. We
frequently have cases where, about every interior or boundary,
point z0 of a certain region a circle can be put, say of radius r0, such
that for all points z of the region which are interior to this circle,
for which, that is, |z − z0| < r0, a certain property holds. Assuming
that to r0 is given the value which is the upper limit for z0, of the
possible values, we may call the points |z − z0| < r0, the neighbourhood
belonging to or proper to z0, and may speak of the property
as the property (z, z0). The value of r0 will in general vary with z0;
what is in most cases of importance is the question whether the
lower limit of r0 for all positions is zero or greater than zero. (A)
This lower limit is certainly greater than zero provided the property
(z, z0) is of a kind which we may call extensive; such, namely, that
if it holds, for some position of z0 and all positions of z, within a certain
region, then the property (z, z1) holds within a circle of radius R
about any interior point z1 of this region for all points z for which
the circle |z − z1| = R is within the region. Also in this case r0
varies continuously with z0. (B) Whether the property is of this
extensive character or not we can prove that the region can be divided
into a finite number of sub-regions such that, for every one of these,
the property holds, (1) for some point z0 within or upon the boundary
of the sub-region, (2) for every point z within or upon the boundary
of the sub-region.
We prove these statements (A), (B) in reverse order. To prove
(B) let a region for which the property (z, z0) holds for all points z and
some point z0 of the region, be called suitable: if each of the triangles
of which the region is built up be suitable, what is desired is proved;
if not let an unsuitable triangle be subdivided into four, as before
explained; if one of these subdivisions is unsuitable let it be again
subdivided; and so on. Either the process terminates and then
what is required is proved; or else we obtain an indefinitely continued
sequence of unsuitable triangles, each contained in the
preceding, which converge to a point, say ζ; after a certain stage
all these will be interior to the proper region of ζ; this, however, is
contrary to the supposition that they are all unsuitable.
We now make some applications of this result (B). Suppose a
definite finite real value attached to every interior or boundary
point of the region, say ƒ(x, y). It may have a finite upper limit H
for the region, so that no point (x, y) exists for which ƒ(x, y) > H,
but points (x, y) exist for which ƒ(x, y) > H − ε, however small ε may
be; if not we say that its upper limit is infinite. There is then at
least one point of the region such that, for points of the region within
a circle about this point, the upper limit of ƒ(x, y) is H, however
small the radius of the circle be taken; for if not we can put about
every point of the region a circle within which the upper limit of
ƒ(x, y) is less than H; then by the result (B) above the region
consists of a finite number of sub-regions within each of which the
upper limit is less than H; this is inconsistent with the hypothesis
that the upper limit for the whole region is H. A similar statement
holds for the lower limit. A case of such a function ƒ(x, y) is the
radius r0 of the neighbourhood proper to any point z0, spoken of
above. We can hence prove the statement (A) above.
Suppose the property (z, z0) extensive, and, if possible, that the
lower limit of r0 is zero. Let then ζ be a point such that the lower
limit of r0 is zero for points z0 within a circle about ζ however small;
let r be the radius of the neighbourhood proper to ζ; take z0 so
that |z0-ζ| < ½r; the property (z, z0), being extensive, holds
within a circle, centre z0, of radius r − |z0 − ζ|, which is greater
than |z0 − ζ|, and increases to r as |z0 − ζ| diminishes; this being
true for all points z0 near ζ, the lower limit of r0 is not zero for the
neighbourhood of ζ, contrary to what was supposed. This proves
(A). Also, as is here shown that r0 ⋝ r − |z0 − ζ|, may similarly be
shown that r ⋝ r0 − |z0 − ζ|. Thus r0 differs arbitrarily little from
r when |z0 − ζ| is sufficiently small; that is, r0 varies continuously
with z0. Next suppose the function ƒ(x, y), which has a
definite finite value at every point of the region considered, to be
continuous but not necessarily real, so that about every point z0,
within or upon the boundary of the region, η being an arbitrary real
positive quantity assigned beforehand, a circle is possible, so that
for all points z of the region interior to this circle, we have
|ƒ(x, y) −ƒ(x0, y0)| < ½η, and therefore (x′, y′) being any other point
interior to this circle, |ƒ(x′, y′) − ƒ(x, y)| < η. We can then apply
the result (A) obtained above, taking for the neighbourhood proper
to any point z0 the circular area within which, for any two points
(x, y), (x′, y′), we have |ƒ(x′, x′) − ƒ(x, y)| < η. This is clearly an
extensive property. Thus, a number r is assignable, greater than
zero, such that, for any two points (x, y), (x′, y′) within a circle
|z − z0| = r about any point z0, we have |ƒ(x′, y′) − ƒ(x, y)| < η,
and, in particular, |ƒ(x, y) −ƒ(x0, y0)| < η, where η is an arbitrary
real positive quantity agreed upon beforehand.
Take now any path in the region, whose extreme points are z0, z,
and let z1, ... zn−1 be intermediate points of the path, in order;
denote the continuous function ƒ(x, y) by ƒ(z), and let ƒr denote any
quantity such that |ƒr − ƒ(zr)| ⋜ |ƒ(zr+1) − ƒ(zr)|; consider the sum
(z1 − z0)ƒ0 + (z2 − z1)ƒ1 + ... + (z − zn−1)ƒn−1.
By the definition of a path we can suppose, n being large enough,
that the intermediate points z1, ... zn − 1 are so taken that if zi,
zi + 1 be any two points intermediate, in order, to zr and zr + 1, we have
|zi + i-zi| < |zr+1 − zr|; we can thus suppose |z1 − z0|, |z2 − z1|, ...
|z − zn−1|all to converge constantly to zero. This being so, we can
show that the sum above has a definite limit. For this it is sufficient,
as in the case of an integral of a function of one real variable, to
prove this to be so when the convergence is obtained by taking new
points of division intermediate to the former ones. If, however,
zr, 1, zr, 2, ... zr, m−1 be intermediate in order to zr and zr+1, and
|ƒr, i − ƒ(zr, i)| < |ƒ(zr, i+1) − ƒ(zr, i)|, the difference between Σ(zr+1 − zr)ƒr
and
Σ { (zr, 1-zr)ƒr, 0 + (zr, 2 − zr, 1)ƒr, 1 + ... + (zr+1 − zr, m−1)ƒr, m−1 },
which is equal to
Σr Σi (zr, i+1 − zr, i) (ƒr, i − ƒr),
is, when |zr+1 − zr| is small enough, to ensure |ƒ(zr+1) − ƒ(zr)| < η,
less in absolute value than
Σ2η Σ |zr, i+1 − zr, i|,
which, if S be the upper limit of the perimeter of the polygon from
which the path is generated, is < 2ηS, and is therefore arbitrarily
small.
The limit in question is called ∫ zz0 ƒ(z)dz. In particular when
ƒ(z) = 1, it is obvious from the definition that its value is z − z0;
when ƒ(z) = z, by taking ƒr = ½(zr+1 − zr), it is equally clear that its
value is ½(z² − z0²); these results will be applied immediately.
Suppose now that to every interior and boundary point z0 of a
certain region there belong two definite finite numbers ƒ(z0), F(z0),
such that, whatever real positive quantity η may be, a real positive
number ε exists for which the condition
| | | ƒ(z) − ƒ(z0) |
− F(z0) | < η, |
| z − z0 |
which we describe as the condition (z, z0), is satisfied for every point z,
within or upon the boundary of the region, satisfying the limitation
|z − z0| < ε. Then ƒ(z0) is called a differentiable function of the
complex variable z0 over this region, its differential coefficient being
F(z0). The function ƒ(z0) is thus a continuous function of the real
313
variables x0, y0, where z0 = x0 + iy0, over the region; it will appear
that F(z0) is also continuous and in fact also a differentiable function
of z0.
Supposing η to be retained the same for all points z0 of the region,
and σ0 to be the upper limit of the possible values of ε for the point z0,
it is to be presumed that σ0 will vary with z0, and it is not obvious
as yet that the lower limit of the values of σ0 as z0 varies over the
region may not be zero. We can, however, show that the region
can be divided into a finite number of sub-regions for each of which
the condition (z, z0), above, is satisfied for all points z, within or upon
the boundary of this sub-region, for an appropriate position of z0,
within or upon the boundary of this sub-region. This is proved
above as result (B).
Hence it can be proved that, for a differentiable function ƒ(z),
the integral ∫ zz1 ƒ(z)dz has the same value by whatever path within
the region we pass from z1 to z. This we prove by showing that when
taken round a closed path in the region the integral ∫ƒ(z)dz vanishes.
Consider first a triangle over which the condition (z, z0) holds, for
some position of z0 and every position of z, within or upon the
boundary of the triangle. Then as
ƒ(z) = ƒ(z0) + (z − z0) F(z0) + ηθ(z − z0), where |θ| < 1,
we have
∫ƒ(z)dz = [ƒ(z0) − z0 F(z0)] ∫dz + F(z0) ∫zdz + η∫θ(z − z0)dz,
which, as the path is closed, is η ∫θ(z − z0)dz. Now, from the theorem
that the absolute value of a sum is less than the sum of the absolute
values of the terms, this last is less, in absolute value, than ηap,
where a is the greatest side of the triangle and p is its perimeter; if
Δ be the area of the triangle, we have Δ = ½ab sin C > (α/π) ba, where
α is the least angle of the triangle, and hence a(a + b + c) < 2a(b + c)
< 4πΔ/α; the integral ∫ƒ(z)dz round the perimeter of the triangle
is thus < 4πηΔ/α. Now consider any region made up of triangles,
as before explained, in each of which the condition (z, z0) holds, as
in the triangle just taken. The integral ∫ƒ(z)dz round the boundary
of the region is equal to the sum of the values of the integral round
the component triangles, and thus less in absolute value than
4πηK/α, where K is the whole area of the region, and α is the smallest
angle of the component triangles. However small η be taken,
such a division of the region into a finite number of component
triangles has been shown possible; the integral round the perimeter
of the region is thus arbitrarily small. Thus it is actually zero,
which it was desired to prove. Two remarks should be added:
(1) The theorem is proved only on condition that the closed path of
integration belongs to the region at every point of which the conditions
are satisfied. (2) The theorem, though proved only when
the region consists of triangles, holds also when the boundary points
of the region consist of one or more closed paths, no two of which
meet.
Hence we can deduce the remarkable result that the value of ƒ(z)
at any interior point of a region is expressible in terms of the value
of ƒ(z) at the boundary points. For consider in the original region
the function ƒ(z)/(z − z0), where z0 is an interior point: this satisfies
the same conditions as ƒ(z) except in the immediate neighbourhood
of z0. Taking out then from the original region a small regular
polygonal region with z0 as centre, the theorem holds for the remaining
portion. Proceeding to the limit when the polygon becomes a
circle, it appears that the integral ∫ dzƒ(z)/(z − z0) round the boundary of
the original region is equal to the same integral taken counter-clockwise
round a small circle having z0 as centre; on this circle,
however, if z − z0 = rE(iθ), dz/(z − z0) = idθ, and ƒ(z) differs arbitrarily
little from f(z0) if r is sufficiently small; the value of the integral
round this circle is therefore, ultimately, when r vanishes, equal to
2πiƒ(z0). Hence ƒ(z0) = 1/2πi ∫ (dtƒ(t)/(t − z0), where this integral is round the
boundary of the original region. From this it appears that
| F(z0) = lim. | ƒ(z) − ƒ(z0) |
= | 1 |
∫ | dtƒ(t) |
| z − z0 | 2πi |
(t − z0)² |
also round the boundary of the original region. This form shows,
however, that F(z0) is a continuous, finite, differentiable function of z0
over the whole interior of the original region.
§ 5. Applications.—The previous results have manifold applications.
(1) If an infinite series of differentiable functions of z be
uniformly convergent along a certain path lying with the region
of definition of the functions, so that S(2) = u0(z) + u1(z) + ... +
un−1(z) + Rn(z), where |Rn(z)| < ε for all points of the path, we have
|
∫ zz0 S(z)dz = ∫ zz0 u0(z)dz + ∫ zz0 u1(z)dz + ... + ∫ zz0 un−1(z)dz + ∫ zz0 Rn(z)dz,
|
wherein, in absolute value, ∫ zz0 Rn(z)dz < εL, if L be the length of the
path. Thus the series may be integrated, and the resulting series
is also uniformly convergent.
(2) If ƒ(x, y) be definite, finite and continuous at every point of a
region, and over any closed path in the region ∫ƒ(x, y)dz = 0, then
ψ(z) = ∫ zz0 ƒ(x, y)dz, for interior points z0, z, is a differentiable function
of z, having for its differential coefficient the function ƒ(x, y), which
is therefore also a differentiable function of z at interior points.
(3) Hence if the series u0(z) + u1(z) + ... to ∞ be uniformly convergent
over a region, its terms being differentiable functions of z,
then its sum S(z) is a differentiable function of z, whose differential
coefficient, given by (1/2πi) ∫ 2πi/(t − z)², is obtainable by differentiating the
series. This theorem, unlike (1), does not hold for functions of a
real variable.
(4) If the region of definition of a differentiable function ƒ(z)
include the region bounded by two concentric circles of radii r, R,
with centre at the origin, and z0 be an interior point of this region,
| ƒ(z0) = | 1 |
∫ | ƒ(t)dt |
− | 1 |
∫ | ƒ(t)dt |
, |
| 2πi | Rt − z0 |
2πi | rt − z0 |
where the integrals are both counter-clockwise
round the two circumferences respectively; putting in the
first (t − z0)−1 = Σn=0 z0n/tn+1, and in the second (t − z0)−1 = − Σn=0 tn/z0n+1,
we find ƒ(z0) = Σ ∞−∞ Anz0n, wherein An = (1/2πi) ∫ [ƒ(t)/tn+1] dt, taken round any
circle, centre the origin, of radius intermediate between r and R.
Particular cases are: (α) when the region of definition of the
function includes the whole interior of the outer circle; then we
may take r = 0, the coefficients An for which n < 0 all vanish, and
the function ƒ(z0) is expressed for the whole interior |z0| < R by a
power series Σ ∞0 Anz0n. In other words, about every interior point c of
the region of definition a differentiable function of z is expressible by a
power series in z − c; a very important result.
(β) If the region of definition, though not including the origin,
extends to within arbitrary nearness of this on all sides, and at the
same time the product zmƒ(z) has a finite limit when |z| diminishes
to zero, all the coefficients An for which n < −m vanish, and we have
f(z0) = A−mz0−m + A−m+1z0−m+1 + ... + A−1z0−1 + A0 + A1z0 ... to ∞.
Such a case occurs, for instance, when ƒ(z) = cosec z, the number m
being unity.
§ 6. Singular Points.—The region of existence of a differentiable
function of z is an unclosed aggregate of points, each of which
is an interior point of a neighbourhood consisting wholly of
points of the aggregate, at every point of which the function is
definite and finite and possesses a unique finite differential
coefficient. Every point of the plane, not belonging to the
aggregate, which is a limiting point of points of the aggregate,
such, that is, that points of the aggregate lie in every neighbourhood
of this, is called a singular point of the function.
About every interior point z0 of the region of existence the function
may be represented by a power series in z − z0, and the series converges
and represents the function over any circle centre at z0
which contains no singular point in its interior. This has been
proved above. And it can be similarly proved, putting z = 1/ζ,
that if the region of existence of the function contains all points of
the plane for which |z| > R, then the function is representable for
all such points by a power series in z− 1 or ζ; in such case we say
that the region of existence of the function contains the point z = ∞.
A series in z− 1 has a finite limit when |z| = ∞; a series in z cannot
remain finite for all points z for which |z| > R; for if, for |z| = R,
the sum of a power series Σanzn in z is in absolute value less than M,
we have |an| < Mr−n, and therefore, if M remains finite for all values
of r however great, an = 0. Thus the region of existence of a function
if it contains all finite points of the plane cannot contain the point
z = ∞; such is, for instance, the case of the function exp (z) = Σzn/n!.
This may be regarded as a particular case of a well-known result
(§ 7), that the circumference of convergence of any power series
representing the function contains at least one singular point. As
an extreme case functions exist whose region of existence is circular,
there being a singular point in every arc of the circumference,
however small; for instance, this is the case for the functions represented
for |z| < 1 by the series Σ n=0 zm, where m = n², the series Σ n=0zm
where m = n!, and the series Σ n=1 zm/(m + 1)(m + 2) where m = an,
a being a positive integer, although in the last case the series actually
converges for every point of the circle of convergence |z| = 1. If z
be a point interior to the circle of convergence of a series representing
the function, the series may be rearranged in powers of z − z0; as z0
approaches to a singular point of the function, lying on the circle
of convergence, the radii of convergence of these derived series in
z − z0 diminish to zero; when, however, a circle can be put about z0,
not containing any singular point of the function, but containing
points outside the circle of convergence of the original series, then
the series in z − z0 gives the value of the function for these external
points. If the function be supposed to be given only for the interior
of the original circle, by the original power series, the series in z − z0
converging beyond the original circle gives what is known as an
analytical continuation of the function. It appears from what has
314
been proved that the value of the function at all points of its region
of existence can be obtained from its value, supposed given by a
series in one original circle, by a succession of such processes of
analytical continuation.
§ 7. Monogenic Functions.—This suggests an entirely different
way of formulating the fundamental parts of the theory of
functions of a complex variable, which appears to be preferable
to that so far followed here.
Starting with a convergent power series, say in powers of z, this
series can be arranged in powers of z − z0, about any point z0 interior
to its circle of convergence, and the new series converges certainly for
|z − z0| < r − |z0|, if r be the original radius of convergence. If for
every position of z0 this is the greatest radius of convergence of the
derived series, then the original series represents a function existing
only within its circle of convergence. If for some position of z0
the derived series converges for |z − z0| < r − |z0| + D, then it can be
shown that for points z, interior to the original circle, lying in the
annulus r − |z0| < |z − z0| < r − |z0| + D, the value represented by the
derived series agrees with that represented by the original series.
If for another point z1 interior to the original circle the derived series
converges for |z − z1| < r − |z1| + E, and the two circles |z − z0| =
r − |z0| + D, |z − z1| = r − |z1| + E have interior points common, lying
beyond |z| = r, then it can be shown that the values represented by
these series at these common points agree. Either series then can
be used to furnish an analytical continuation of the function as
originally defined. Continuing this process of continuation as far
as possible, we arrive at the conception of the function as defined
by an aggregate of power series of which every one has points of
convergence common with some one or more others; the whole
aggregate of points of the plane which can be so reached constitutes
the region of existence of the function; the limiting points of this
region are the points in whose neighbourhood the derived series have
radii of convergence diminishing indefinitely to zero; these are the
singular points. The circle of convergence of any of the series has
at least one such singular point upon its circumference. So regarded
the function is called a monogenic function, the epithet having reference
to the single origin, by one power series, of the expressions
representing the function; it is also sometimes called a monogenic
analytical function, or simply an analytical function; all that is
necessary to define it is the value of the function and of all its
differential coefficients, at some one point of the plane; in the method
previously followed here it was necessary to suppose the function
differentiable at every point of its region of existence. The theory
of the integration of a monogenic function, and Cauchy’s theorem,
that ∫ƒ(z)dz = 0 over a closed path, are at once deducible from the
corresponding results applied to a single power series for the interior
of its circle of convergence. There is another advantage belonging
to the theory of monogenic functions: the theory as originally given
here applies in the first instance only to single valued functions; a
monogenic function is by no means necessarily single valued—it may
quite well happen that starting from a particular power series,
converging over a certain circle, and applying the process of analytical
continuation over a closed path back to an interior point of this circle,
the value obtained does not agree with the initial value. The
notion of basing the theory of functions on the theory of power
series is, after Newton, largely due to Lagrange, who has some
interesting remarks in this regard at the beginning of his Théorie
des fonctions analytiques. He applies the idea, however, primarily
to functions of a real variable for which the expression by power
series is only of very limited validity; for functions of a complex
variable probably the systematization of the theory owes most to
Weierstrass, whose use of the word monogenic is that adopted above.
In what follows we generally suppose this point of view to be regarded
as fundamental.
§ 8. Some Elementary Properties of Single Valued Functions.—A
pole is a singular point of the function ƒ(z) which is not a
singularity of the function 1/ƒ(z); this latter function is therefore,
by the definition, capable of representation about this point,
z0, by a series [ƒ(z)]−1 = Σan(z − z0)n. If herein a0 is not zero we
can hence derive a representation for ƒ(z) as a power series about
z0, contrary to the hypothesis that z0 is a singular point for this
function. Hence a0 = 0; suppose also a1 = 0, a2 = 0, ... am−1 = 0,
but am ± 0. Then [ƒ(z)]−1 = (z − z0)m[am + am+1 (z − z0) + ...], and
hence (z − z0)mƒ(z) = am−1 + Σbn (z − z0)n, namely, the expression of
ƒ(z) about z = z0 contains a finite number of negative powers
of z − z0 and a (finite or) infinite number of positive powers.
Thus a pole is always an isolated singularity.
The integral ∫ƒ(z)dz taken by a closed circuit about the pole not
containing any other singularity is at once seen to be 2πiA1, where
A1 is the coefficient of (z − z0)−1 in the expansion of ƒ(z) at the pole;
this coefficient has therefore a certain uniqueness, and it is called
the residue of ƒ(z) at the pole. Considering a region in which there
are no other singularities than poles, all these being interior points,
the integral (1/2πi) ∫ ƒ(z)dz round the boundary of this region is equal to
the sum of the residues at the included poles, a very important result.
Any singular point of a function which is not a pole is called an
essential singularity; if it be isolated the function is capable, in the
neighbourhood of this point, of approaching arbitrarily near to any
assigned value. For, the point being isolated, the function can be
represented, in its neighbourhood, as we have proved, by a series
Σ ∞−∞ an(z − z0)n; it thus cannot remain finite in the immediate neighbourhood
of the point. The point is necessarily an isolated essential
singularity also of the function {ƒ(z) − A}−1 for if this were expressible
by a power series about the point, so would also the function ƒ(z)
be; as {ƒ(z) − A}− 1 approaches infinity, so does ƒ(z) approach the
arbitrary value A. Similar remarks apply to the point z = ∞, the
function being regarded as a function of ζ = z−1. In the neighbourhood
of an essential singularity, which is a limiting point also of
poles, the function clearly becomes infinite. For an essential singularity
which is not isolated the same result does not necessarily
hold.
A single valued function is said to be an integral function
when it has no singular points except z = ∞. Such is, for
instance, an integral polynomial, which has z = ∞ for a pole, and
the functions exp (z) which has z = ∞ as an essential singularity.
A function which has no singular points for finite values of
z other than poles is called a meromorphic function. If it also
have a pole at z = ∞ it is a rational function; for then, if
a1, ... as be its finite poles, of orders m1; m2, ... ms, the
product (z − a1)m1 ... (z − as) msƒ(z) is an integral function with
a pole at infinity, capable therefore, for large values of z, of an
expression (z−1)−m Σ r=0 ar(z−1)r; thus (z − a1)m1 ... (z − as)msƒ(z)
is capable of a form Σ r=0 brzr, but z−m Σ r=0 brzr remains finite for
z = ∞. Therefore br+1 = br+2 = ... = 0, andƒ(z) is a rational
function.
If for a single valued function F(z) every singular point in the
finite part of the plane is isolated there can only be a finite
number of these in any finite part of the plane, and they can be
taken to be a1, a2, a3, ... with |a1| ⋜ |a2| ⋜ |a3| ... and limit
|an| = ∞. About as the function is expressible as Σ ∞−∞ An(z − as)n;
let ƒs(z) = Σ 1−∞ An(z − as)n be the sum of the negative powers in this
expansion. Assuming z = 0 not to be a singular point, let ƒs(z) be
expanded in powers of z, in the form Σ n=0 Cnzn, and μs be chosen so
that Fs(z) = ƒs(z) − Σ μs−11 Cnzn = Σ ∞μs Cnzn is, for |z| < rs < |as|, less in absolute
value than the general term εs of a fore-agreed convergent series of
real positive terms. Then the series φ(z) = Σ ∞s=1 Fs(z) converges uniformly
in any finite region of the plane, other than at the points as,
and is expressible about any point by a power series, and near
as, φ(z) − fs(z) is expressible by a power series in z − as. Thus
F(z) − φ(z) is an integral function. In particular when all the finite
singularities of F(z) are poles, F(z) is hereby expressed as the sum
of an integral function and a series of rational functions. The
condition |Fs(z)| < εs is imposed only to render the series ΣFs(z)
uniformly convergent; this condition may in particular cases be
satisfied by a series Σ Gs(z) where Gs(z) = ƒs(z) − Σ νs−11 Cnzn and νs < μs.
An example of the theorem is the function π cot πz − z− 1 for which,
taking at first only half the poles, ƒs(z) = 1/(z − s); in this case the
series Σ Fs(z) where Fs(z) = (z − s)−1 + s−1 is uniformly convergent;
thus π cot πz − z−1 − Σ ∞−∞ [(z − s)−1 + s−1], where s = 0 is excluded from
the summation, is an integral function. It can be proved that this
integral function vanishes.
Considering an integral function ƒ(z), if there be no finite positions
of z for which this function vanishes, the function λ[ƒ(z)] is at once
seen to be an integral function, φ(z), or ƒ(z) = exp[φ(z)]; if however
great R may be there be only a finite number of values of z for which
ƒ(z) vanishes, say z = a1, ... am, then it is at once seen that ƒ(z) =
exp [φ(z)]. (z − a1)h1...(z − am)hm, where φ(z) is an integral function,
and h1, ... hm are positive integers. If, however, ƒ(z) vanish for z = a1,
a2 ... where |a1| ⋜ |a2| ⋜ ... and limit |an| = ∞, and if for simplicity
we assume that z − 0 is not a zero and all the zeros a1, a2, ... are
of the first order, we find, by applying the preceding theorem to
the function [1 / ƒ(z)] [dƒ(z) / dz], that ƒ(z) = exp [φ(z)] Π ∞n=1 {(1 − z/an) exp φn(z)},
where φ(z) is an integral function, and φn(z) is an integral polynomial
of the form φn(z) = z/an + z2/2an2 + ... + zs/sans. The number s may be the
same for all values of n, or it may increase indefinitely with n; it is
sufficient in any case to take s = n. In particular for the function
315
sinπx/πx, we have
| sin πx |
= Π ∞−∞ { (1 − | x |
) exp ( | x |
) }, |
| πx | n |
n |
where n = 0 is excluded from the product. Or again we have
| 1 |
= xeCx Π ∞n=1 { (1 + | x |
) exp ( − | x |
) }, |
| Γ(x) | n |
n |
where C is a constant, and Γ(x) is a function expressible when x is
real and positive by the integral ∫ ∞0 e−t tx−1dt.
There exist interesting investigations as to the connexion of the
value of s above, the law of increase of the modulus of the integral
function ƒ(z), and the law of increase of the coefficients in the series
ƒ(z) = Σ anzn as n increases (see the bibliography below under Integral
Functions). It can be shown, moreover, that an integral function
actually assumes every finite complex value, save, in exceptional
cases, one value at most. For instance, the function exp (z) assumes
every finite value except zero (see below under § 21, Modular
Functions).
The two theorems given above, the one, known as Mittag-Leffler’s
theorem, relating to the expression as a sum of simpler
functions of a function whose singular points have the point
z = ∞ as their only limiting point, the other, Weierstrass’s
factor theorem, giving the expression of an integral function as
a product of factors each with only one zero in the finite part of
the plane, may be respectively generalized as follows:—
I. If a1, a2, a3, ... be an infinite series of isolated points having
the points of the aggregate (c) as their limiting points, so that in
any neighbourhood of a point of (c) there exists an infinite number
of the points a1, a2, ..., and with every point ai there be associated
a polynomial in (z − ai)−1, say gi; then there exists a single valued
function whose region of existence excludes only the points (a) and
the points (c), having in a point ai a pole whereat the expansion
consists of the terms gi, together with a power series in z − ai;
the function is expressible as an infinite series of terms gi − γi,
where γi is also a rational function.
II. With a similar aggregate (a), with limiting points (c), suppose
with every point ai there is associated a positive integer ri. Then
there exists a single valued function whose region of existence
excludes only the points (c), vanishing to order ri at the point ai,
but not elsewhere, expressible in the form
| Π ∞n=1 ( 1 − | an − cn |
) r n exp (gn), |
| z − cn |
where with every point an is associated a proper point cn of (c), and
| gn = rn Σ μ ns=1 | 1 |
( | an − cn |
) s, |
| s | z − cn |
μn being a properly chosen positive integer.
If it should happen that the points (c) determine a path dividing
the plane into separated regions, as, for instance, if an = R(1 − n−1) exp (iπ √2·n),
when (c) consists of the points of the circle |z| = R, the
product expression above denotes different monogenic functions in
the different regions, not continuable into one another.
§ 9. Construction of a Monogenic Function with a given Region
of Existence.—A series of isolated points interior to a given
region can be constructed in infinitely many ways whose limiting
points are the boundary points of the region, or are boundary
points of the region of such denseness that one of them is found
in the neighbourhood of every point of the boundary, however
small. Then the application of the last enunciated theorem
gives rise to a function having no singularities in the interior of
the region, but having a singularity in a boundary point in every
small neighbourhood of every boundary point; this function
has the given region as region of existence.
§ 10. Expression of a Monogenic Function by means of Rational
Functions in a given Region.—Suppose that we have a region R0
of the plane, as previously explained, for all the interior or
boundary points of which z is finite, and let its boundary points,
consisting of one or more closed polygonal paths, no two of
which have a point in common, be called C0. Further suppose
that all the points of this region, including the boundary points,
are interior points of another region R, whose boundary is
denoted by C. Let z be restricted to be within or upon the
boundary of C0; let a, b, ... be finite points upon C or outside
R. Then when b is near enough to a, the fraction (a − b)/(z − b)
is arbitrarily small for all positions of z; say
| | | a − b |
| < ε, for |a − b| < η; |
| z − b |
the rational function of the complex variable t,
| 1 |
[ 1 − ( | a − b |
)n ], |
| t − a | t − a |
in which n is a positive integer, is not infinite at t = a, but has a
pole at t = b. By taking n large enough, the value of this function,
for all positions z of t belonging to R0, differs as little as may be
desired from (t − a)−1. By taking a sum of terms such as
| F = Σ Ap { | 1 |
[ 1 − ( | a − b |
) n ] } p, |
| t − a | t − b |
we can thus build a rational function differing, in value, in
R0, as little as may be desired from a given rational function
ƒ = Σ Ap(t − a)−p,
and differing, outside R or upon the boundary of R, from ƒ,
in the fact that while ƒ is infinite at t = a, F is infinite only at
t = b. By a succession of steps of this kind we thus have the
theorem that, given a rational function of t whose poles are
outside R or upon the boundary of R, and an arbitrary point c
outside R or upon the boundary of R, which can be reached by a
finite continuous path outside R from all the poles of the rational
function, we can build another rational function differing in R0
arbitrarily little from the former, whose poles are all at the
point c.
Now any monogenic function ƒ(t) whose region of definition includes
C and the interior of R can be represented at all points z in R0 by
| ƒ(z) = | 1 |
∫ | ƒ(t)dt |
, |
| 2πi | t − z |
where the path of integration is C. This integral is the limit of a
sum
| S = | 1 |
Σ | ƒ(ti) (ti+1 − ti) |
, |
| 2πi | ti − z |
where the points ti are upon C; and the proof we have given of the
existence of the limit shows that the sum S converges to ƒ(z) uniformly
in regard to z, when z is in R0, so that we can suppose, when
the subdivision of C into intervals ti+1 − ti, has been carried sufficiently
far, that
|S − ƒ(z)| < ε,
for all points z of R0, where ε is arbitrary and agreed upon beforehand.
The function S is, however, a rational function of z with poles upon C,
that is external to R0. We can thus find a rational function differing
arbitrarily little from S, and therefore arbitrarily little from ƒ(z),
for all points z of R0, with poles at arbitrary positions outside R0
which can be reached by finite continuous curves lying outside R
from the points of C.
In particular, to take the simplest case, if C0, C be simple closed
polygons, and Γ be a path to which C approximates by taking the
number of sides of C continually greater, we can find a rational
function differing arbitrarily little from ƒ(z) for all points of R0 whose
poles are at one finite point c external to Γ. By a transformation
of the form t − c = r−1, with the appropriate change in the rational
function, we can suppose this point c to be at infinity, in which case
the rational function becomes a polynomial. Suppose ε1, ε2, ...
to be an indefinitely continued sequence of real positive numbers,
converging to zero, and Pr to be the polynomial such that, within
C0, |Pr − ƒ(z)| < εr; then the infinite series of polynomials
P1(z) + {P2(z) − P1(z)} + {P3(z) − P2(z)} + ...,
whose sum to n terms is Pn(z), converges for all finite values of z and
represents ƒ(z) within C0.
When C consists of a series of disconnected polygons, some of
which may include others, and, by increasing indefinitely the number
of sides of the polygons C, the points C become the boundary points
Γ of a region, we can suppose the poles of the rational function,
constructed to approximate to ƒ(z) within R0, to be at points of Γ.
A series of rational functions of the form
H1(z) + {H2(z) − H1(z)} + {H3(z) − H2(z)} + ...
then, as before, represents ƒ(z) within R0. And R0 may be taken to
coincide as nearly as desired with the interior of the region bounded
by Γ.
§ 11. Expression of (1 − z)−1 by means of Polynomials. Applications.—We
pursue the ideas just cursorily explained in some
further detail.
Let c be an arbitrary real positive quantity; putting the complex
variable ζ = ξ + iη, enclose the points ζ = l, ζ = 1 + c by means
of (i.) the straight lines η = ±a, from ξ = l to ξ = 1 + c, (ii.) a semicircle
convex to ζ = 0 of equation (ξ − 1)2 + η2 = a2, (iii.) a semicircle
concave to ζ = 0 of equation (ξ − 1 − c)2 + η2 = a2. The quantities
c and a are to remain fixed. Take a positive integer r so that
1/r (c/a) is less than unity, and put σ = 1/r (c/a). Now take
c1 = 1 + c/r, c2 = 1 + 2c/r, ... cr = 1 + c;
316
if n1, n2, ... nr, be positive integers, the rational function
| 1 |
{ 1 − ( | c1 − 1 |
) n1 } |
| 1 − ζ | c1 − ζ |
is finite at ζ = 1, and has a pole of order n1 at ζ = c1; the rational
function
| 1 |
{ 1 − ( | c1 − 1 |
) n1 } { 1 − ( | c2 − c1 |
) n2 } n1 |
| 1 − ζ | c1 − ζ |
c2 − ζ |
is thus finite except for ζ = c2, where it has a pole of order n1n2;
finally, writing
| xs = ( | cs − cs−1 |
) ns, |
| cs − ζ |
the rational function
|
U = (1 − ζ)−1 (1 − x1) (1 − x2)n1 (1 − x3)n1n2 ... (1 − xr)n1n2 ... nr − 1
|
has a pole only at ζ = 1 + c, of order n1n2 ... nr.
The difference (1 − ζ)−1 − U is of the form (1 − ζ)−1P, where P, of
the form
1 − (1 − ρ1) (1 − ρ2)...(1 − ρk),
in which there are equalities among ρ1, ρ2, ... ρk, is of the form
Σρ1 − Σρ1ρ2 + Σρ1ρ2ρ3 − ...;
therefore, if |ri| = |ρi|, we have
|
|P| < Σ r1 + Σ r1r2 + Σ r1r2r3 + ... < (1 + r1) (1 + r2)...(1 + rk) − 1;
|
now, so long as ζ is without the closed curve above described round
ζ = 1, ζ = 1 + c, we have
| | | 1 |
| < | 1 |
, | | cm − cm−1 |
| < | c/r |
< σ, |
| 1 − ζ | a |
cm − ζ | a |
and hence
|
|(1 − ζ)−1 − U| < a−1 {(1 + σn1) (1 + σn2)n1 (1 + σn3)n1n2 ... (1 + σnr)n1n2 ... nr−1 − 1}.
|
Take an arbitrary real positive ε, and μ, a positive number, so that
εmu − 1 < εa, then a value of n1 such that σn1 < μ/(1 + μ) and therefore
σn1/(1 − σn1 < μ, and values for n2, n3 ... such that σn2 < 1/n1 σ2n1,
σn3 < 1/n1n2 σ3n1, ... σnr < 1/(n1 ... nr−1) σnr n1; then, as 1 + x < ex, we have
|
|(−ζ)−1 − U| < a−1 {exp (σn1 + n1σn2 + n1n2σn3 + ... + n1n2 ... nr−1σnr) − 1},
|
and therefore less than
a−1 {exp (σn1 + σ2n1 + ... + σnr n1) − 1},
which is less than
| 1 |
[ exp ( | σn1 |
) − 1 ] |
| a | 1 − σn1 |
and therefore less than ε.
The rational function U, with a pole at ζ = 1 + c, differs therefore
from (1 − ζ)−1, for all points outside the closed region put about
ζ = 1, ζ = l + c, by a quantity numerically less than ε. So long as
a remains the same, r and σ will remain the same, and a less value
of ε will require at most an increase of the numbers n1, n2, ... nr; but
if a be taken smaller it may be necessary to increase r, and with this
the complexity of the function U.
Now put
| z = | cζ |
, ζ = | (c + 1)z |
; |
| c + 1 − ζ | c + z |
thereby the points ζ = 0, 1, 1 + c become the points z = 0, 1, ∞, the
function (1 − z)−1 being given by (1 − z)−1 = c(c + 1)−1 (1 − ζ)−1 + (c + 1)−1;
the function U becomes a rational function of z with a pole only at
z = ∞, that is, it becomes a polynomial in z, say [(c + 1)/c] H − 1/c, where H
is also a polynomial in z, and
| 1 |
− H = | c |
[ | 1 |
− U ]; |
| 1 − z | c + 1 |
1 − ζ |
the lines η = ±a become the two circles expressed, if z = x + iy, by
| (x + c)² + y² = ± | c(c + 1) |
y, |
| a |
the points (η = 0, ξ = 1 − a), (η = 0, ξ = 1 + c + a) become respectively
the points (y = 0, x = c(1 − a)/(c + a), (y = 0, x = −c(l + c + a)/a), whose
limiting positions for a = 0 are respectively (y = 0, x = 1), (y = 0,
x = −∞). The circle (x + c)² + y² = c(c + 1)y/a can be written
| y = | (x + c)² |
+ | (x + c)4 |
{μ + √[μ² − (x + c)²]}−2, |
| 2μ | 2μ |
where μ = ½c(c + 1)/a; its ordinate y, for a given value of x, can
therefore be supposed arbitrarily small by taking a sufficiently small.
We have thus proved the following result; taking in the plane of z
any finite region of which every interior and boundary point is at a
finite distance, however short, from the points of the real axis for
which 1 ⋜ x ⋜ ∞, we can take a quantity a, and hence, with an
arbitrary c, determine a number r; then corresponding to an arbitrary
εs, we can determine a polynomial Ps, such that, for all points
interior to the region, we have
|(1 − z−1) − Ps| < εs;
thus the series of polynomials
P1 + (P2 − P1) + (P3 − P2) + ...,
constructed with an arbitrary aggregate of real positive numbers
ε1, ε2, ε3, ... with zero as their limit, converges uniformly and
represents (1 − z)−1 for the whole region considered.
§ 12. Expansion of a Monogenic Function in Polynomials, over a
Star Region.—Now consider any monogenic function ƒ(z) of which
the origin is not a singular point; joining the origin to any singular
point by a straight line, let the part of this straight line, produced
beyond the singular point, lying between the singular point and z = ∞,
be regarded as a barrier in the plane, the portion of this straight line
from the origin to the singular point being erased. Consider next
any finite region of the plane, whose boundary points constitute a
path of integration, in a sense previously explained, of which every
point is at a finite distance greater than zero from each of the barriers
before explained; we suppose this region to be such that any line
joining the origin to a boundary point, when produced, does not
meet the boundary again. For every point x in this region R we
can then write
| 2πiƒ(x) = ∫ | ƒ(t) |
| ƒ(t) |
, |
| t | 1 − xt−1 |
where ƒ(x) represents a monogenic branch of the function, in case it
be not everywhere single valued, and t is on the boundary of the
region. Describe now another region R0 lying entirely within R,
and let x be restricted to be within R0 or upon its boundary; then
for any point t on the boundary of R, the points z of the plane for
which zt− 1 is real and positive and equal to or greater than 1, being
points for which |z| = |t| or |z| > |t|, are without the region R0, and
not infinitely near to its boundary points. Taking then an arbitrary
real positive ε we can determine a polynomial in xt− 1, say P(xt−1),
such that for all points x in R0 we have
|(1 − xt−1)−1 − P(xt−1)| < ε;
the form of this polynomial may be taken the same for all points t
on the boundary of R, and hence, if E be a proper variable quantity
of modulus not greater than ε,
| | 2πiƒ(x) − ∫ | dt |
ƒ(t)P(xt−1) | = | ∫ | dt |
ƒ(t)E | ⋜ εLM, |
| t | t |
where L is the length of the path of integration, the boundary of R,
and M is a real positive quantity such that upon this boundary
|t−1 ƒ(t)| < M. If now
P (xt−1) = c0 + c1xt−1 + ... + cm xm t−m,
and
| 1 |
∫ t−r−1 ƒ(t)dt = μr, |
| 2πi |
this gives
|ƒ(x) − {c0μ0 + c1μ1x + ... + cmμmxm}| ⋜ εLM/2π,
where the quantities μ0, μ1, μ2, ... are the coefficients in the expansion
of ƒ(x) about the origin.
If then an arbitrary finite region be constructed of the kind
explained, excluding the barriers joining the singular points of ƒ(x)
to x = ∞, it is possible, corresponding to an arbitrary real positive
number σ, to determine a number m, and a polynomial Q(x), of
order m, such that for all interior points of this region
|ƒ(x) − Q(x)| < σ.
Hence as before, within this region ƒ(x) can be represented by a
series of polynomials, converging uniformly; when ƒ(x) is not a
single valued function the series represents one branch of the function.
The same result can be obtained without the use of Cauchy’s
integral. We explain briefly the character of the proof. If a
monogenic function of t, φ(t) be capable of expression as a power
series in t − x about a point x, for |t − x| ⋜ ρ, and for all points of this
circle |φ(t)| < g, we know that |φ(n)(x)| < gρ−n(n!). Hence, taking
|z| < 1⁄3ρ, and, for any assigned positive integer μ, taking m so that
for n > m we have (μ + n)μ < (3⁄2)n, we have
| | | φ(μ + n)(x)·zn |
| < | φ(μ + n)(x) |
(μ + n)μ |z|n < | g |
( | 3 |
) n ( | ρ |
) n < | g |
, |
| n! |
(μ + n)! | ρμ + n |
2 | 3 | ρμ 2n |
and therefore
| φμ (x + z) = Σ mn=0 | φ(μ + n) (x) |
zn + εμ, |
| n! |
where
| |εμ| < | g |
Σ ∞n=m+1 | 1 |
< | g |
. |
| ρμ | 2n |
ρμ 2m |
Now draw barriers as before, directed from the origin, joining the
singular point of φ(z) to z = ∞, take a finite region excluding all
these barriers, let ρ be a quantity less than the radii of convergence
of all the power series developments of φ(z) about interior points of
this region, so chosen moreover that no circle of radius ρ with centre
at an interior point of the region includes any singular point of φ(z),
let g be such that |φ(z)| < g for all circles of radius ρ whose centres are
interior points of the region, and, x being any interior point of the
region, choose the positive integer n so that 1/n |x| < 1⁄3ρ; then take the
points a1 = x/n, a2 = 2x/n, a3 = 3x/n, ... an = x; it is supposed that
the region is so taken that, whatever x may be, all these are interior
points of the region. Then by what has been said, replacing x, z
respectively by 0 and x/n, we have
317
| φ(μ) (a1) = Σ m1λ1=0 | φ(μ + λ1) (0) |
( | x |
) λ1 + αμ |
| λ1! |
n |
with
αμ < g/ρμ 2m1,
provided (μ + m1 + 1)μ < (2⁄3)m1 + 1; in fact for μ ⋜ 2n2n−2 it is sufficient
to take m1 = n2n; by another application of the same inequality,
replacing x, z respectively by a1 and x/n, we have
| φ(μ) (a2) = Σ m2λ2=0 |
φ(μ + λ2) (a1) |
( | x |
) λ2 + β′μ , |
| λ2! | n |
where
|β′μ| < g / ρμ 2m2
provided (μ + m2 + 1)μ < (3⁄2)m2 + 1; we take m2 = n2n − 2, supposing
μ < 2n2n−4. So long as λ2 ⋜ m2 ⋜ n2n−2 and μ < 2n2n−4 we have
μ + λ2 < 2n2n−2, and we can use the previous inequality to substitute
here for φ(μ + λ2) (a1). When this is done we find
| φ(μ) (a2) =
Σ m2λ2=0
Σ m1λ1=0 |
φ(μ + λ1 + λ2) (0) |
( | x |
) λ1 + λ2 + βμ , |
| λ1! λ2! | n |
where |βμ| < 2g/ρμ 2m2, the numbers m1, m2 being respectively n2n
and n2n−2.
Applying then the original inequality to φ(μ) (a3) = φ(μ) (a2 + x/n),
and then using the series just obtained, we find a series for φ(μ) (a3).
This process being continued, we finally obtain
| φ(x) =
Σ m1λ1=0
Σ m2λ2=0 ...
Σ mnλn=0 |
φh (0) |
( | x |
) h + ε , |
| K | n |
where h = λ1 + λ2 + ... + λn, K = λ1! λ2! ... λn!,
m1 = n2n, m2 = n2n−2, ..., mn= n², |ε| < 2g/2mn.
By this formula φ(x) is represented, with any required degree of
accuracy, by a polynomial, within the region in question; and
thence can be expressed as before by a series of polynomials converging
uniformly (and absolutely) within this region.
§ 13. Application of Cauchy’s Theorem to the Determination of
Definite Integrals.—Some reference must be made to a method
whereby real definite integrals may frequently be evaluated by
use of the theorem of the vanishing of the integral of a function
of a complex variable round a contour within which the function
is single valued and non singular.
We are to evaluate an integral ∫ ba ƒ(x)dx; we form a closed contour
of which the portion of the real axis from x = a to x = b forms a part,
and consider the integral ∫ƒ(z)dz round this contour, supposing
that the value of this integral can be determined along the curve
forming the completion of the contour. The contour being supposed
such that, within it, ƒ(z) is a single valued and finite function of the
complex variable z save at a finite number of isolated interior points,
the contour integral is equal to the sum of the values of ∫ƒ(z)dz taken
round these points. Two instances will suffice to explain the
method. (1) The integral ∫ ∞0 [(tan x)/x] dx is convergent if it be understood
to mean the limit when ε, ζ, σ, ... all vanish of the sum of the
integrals
| ∫ 1/2π−ε0 | tan x |
dx, ∫ 3/2π−ζ1/2π+ε | tan x |
dx, ∫ 5/2π−σ3/2π+ζ | tan x |
dx, ... |
| x | x |
x |
Now draw a contour consisting in part of the whole of the positive
and negative real axis from x = −nπ to x = +nπ, where n is a positive
integer, broken by semicircles of small radius whose centres are the
points x = ±½π, x = ±¾π, ... , the contour containing also the lines
x = nπ and x = −nπ for values of y between 0 and nπ tan α, where α
is a small fixed angle, the contour being completed by the portion
of a semicircle of radius nπ sec α which lies in the upper half of the
plane and is terminated at the points x = ±nπ, y = nπ tan α. Round
this contour the integral ∫ [(tan z / z)] dz has the value zero. The contributions
to this contour integral arising from the semicircles of centres
−½(2s − 1)π, + ½(2s − 1)π, supposed of the same radius, are at once
seen to have a sum which ultimately vanishes when the radius of the
semicircles diminishes to zero. The part of the contour lying on
the real axis gives what is meant by 2 ∫ nπ0 [(tan x / x)] dx. The contribution
to the contour integral from the two straight portions at
x = ±nπ is
| ∫ nπ tan α0 idy ( | tan iy |
− | tan iy |
) |
| nπ + iy | −nπ + iy |
where i tan iy, = −[exp(y) − exp(−y)]/[exp(y) + exp(−y)], is a real
quantity which is numerically less than unity, so that the contribution
in question is numerically less than
| ∫ nπ tan α0 dy | 2nπ |
, that is than 2α. |
| n²π² + y² |
Finally, for the remaining part of the contour, for which, with
R = nπ sec α, we have z = R(cos θ + i sin θ) = RE(iθ), we have
| dz |
= idθ, i tan z = | exp(−R sin θ) E(iR cos θ) − exp(R sin θ) E(−iR cos θ) |
; |
| z | exp(−R sin θ) E(iR cos θ) + exp(R sin θ) E(−iR cos θ) |
when n and therefore R is very large, the limit of this contribution
to the contour integral is thus
− ∫ π−αα dθ = − (π − 2α).
Making n very large the result obtained for the whole contour is
| 2 ∫ ∞0 | tan x |
dx − (π − 2α) − 2αε = 0, |
| x |
where ε is numerically less than unity. Now supposing α to diminish
to zero we finally obtain
(2) For another case, to illustrate a different point, we may take the
integral
wherein a is real quantity such that 0 < a < 1, and the contour consists
of a small circle, z = rE(iθ), terminated at the points x = r cos α,
y = ± r sin α, where α is small, of the two lines y = ± r sin α for
r cos α ⋜ x ⋜ R cos β, where R sin β = r sin α, and finally of a large
circle z = RE(iφ), terminated at the points x = R cos β, y = ±R sin β.
We suppose α and β both zero, and that the phase of z is zero for
r cos a ⋜ x ⋜ R cos β, y = r sin α = R sin β. Then on r cos α ⋜ x ⋜ R cos β,
y = −r sin α, the phase of z will be 2π, and zα − 1 will be equal to
xα − 1 exp [2πi(a − 1)], where x is real and positive. The two straight
portions of the contour will thus together give a contribution
| [1 − exp(2πiα)] ∫ R cos βr cos α | xa−1 |
dx. |
| 1 + x |
It can easily be shown that if the limit of zƒ(z) for z = 0 is zero, the
integral ∫ƒ(z)dz taken round an arc, of given angle, of a small circle
enclosing the origin is ultimately zero when the radius of the circle
diminishes to zero, and if the limit of zƒ(z) for z = ∞ is zero, the same
integral taken round an arc, of given angle, of a large circle whose
centre is the origin is ultimately zero when the radius of the circle
increases indefinitely; in our case with ƒ(z) = zα−1/(1 + z), we have
zƒ(z) = za/(1 + z), which, for 0 < a < 1, diminishes to zero both for z = 0
and for z = ∞. Thus, finally the limit of the contour integral when
r = 0, R = ∞ is
| [1 − exp(2πiα)] ∫ ∞0 | xα−1 |
dx. |
| 1 + x |
Within the contour ƒ(z) is single valued, and has a pole at z = 1; at
this point the phase of z is π and za−1 is exp [iπ(a − 1)] or − exp(iπa);
this is then the residue of ƒ(z) at z = −1; we thus have
| [1 − exp (2πia)] ∫ ∞0 | xa−1 |
dx = −2πi exp(iπa), |
| 1 + x |
that is
| ∫ ∞0 | xa−1 |
dx = π cosec (aπ). |
| 1 + x |
§ 14. Doubly Periodic Functions.—An excellent illustration
of the preceding principles is furnished by the theory of single
valued functions having in the finite part of the plane no
singularities but poles, which have two periods.
Before passing to this it may be convenient to make here a few
remarks as to the periodicity of (single valued) monogenic functions.
To say that ƒ(z) is periodic is to say that there exists a constant ω
such that for every point z of the interior of the region of existence
of ƒ(z) we have ƒ(z + ω) = ƒ(z). This involves, considering all existing
periods ω = ρ + iσ, that there exists a lower limit of ρ² + σ² other than
zero; for otherwise all the differential coefficients of ƒ(z) would be
zero, and ƒ(z) a constant; we can then suppose that not both ρ
and σ are numerically less than ε, where ε > σ. Hence, if g be any
real quantity, since the range (−g, ... g) contains only a finite
number of intervals of length ε, and there cannot be two periods
ω = ρ + iσ such that με ⋜ ρ < (μ + 1)ε, νε ⋜ σ < (ν + 1)ε, where μ, ν are
integers, it follows that there is only a finite number of periods
for which both ρ and σ are in the interval (−g ... g). Considering
then all the periods of the function which are real multiples of one
period ω, and in particular those periods λω wherein 0 < λ ⋜ 1, there is
a lower limit for λ, greater than zero, and therefore, since there is
only a finite number of such periods for which the real and imaginary
parts both lie between −g and g, a least value of λ, say λ0. If
Ω = λ0ω and λ = Mλ0 + λ′, where M is an integer and 0 ⋜ λ′ < λ0, any
period λω is of the form MΩ + λ′ω; since, however, Ω, MΩ and λω
are periods, so also is λ′ω, and hence, by the construction of λ0,
we have λ′ = 0; thus all periods which are real multiples of ω are
expressible in the form MΩ where M is an integer, and Ω a period.
If beside ω the functions have a period ω′ which is not a real
multiple of ω, consider all existing periods of the form μω + νω′
wherein μ, ν are real, and of these those for which 0 ⋜ μ ⋜ 1, 0 < ν ⋜ 1;
318
as before there is a least value for ν, actually occurring in one or
more periods, say in the period Ω′ = μ0ω + ν0ω′; now take, if μω + νω′
be a period, ν = N′ν0 + ν′, where N′ is an integer, and 0 ⋜ ν′ < ν0;
thence μω + νω′ = μω + N′(Ω′ − μ0ω) + ν′ω′; take then μ − Nμ0 = Nλ0 + λ′,
where N is an integer and λ0 is as above, and 0 ⋜ λ′ < λ0; we
thus have a period NΩ + N′Ω′ + λ′ω + ν′ω′, and hence a period
λ′ω + ν′ω′, wherein λ′ < λ0, ν′ < ν0; hence ν′ = 0 and λ′ = 0. All
periods of the form μω + νω′ are thus expressible in the form
NΩ + N′Ω′, where Ω, Ω′ are periods and N, N′ are integers. But
in fact any complex quantity, P + iQ, and in particular any other
possible period of the function, is expressible, with μ, ν real, in the
form μω + νω′; for if ω = ρ + iσ, ω′ = ρ′ + iσ′, this requires only
P = μρ + νρ′, Q = μσ + νσ′, equations which, since ω′/ω is not real,
always give finite values for μ and ν.
It thus appears that if a single valued monogenic function of z
be periodic, either all its periods are real multiples of one of them,
and then all are of the form MΩ, where Ω is a period and M is an
integer, or else, if the function have two periods whose ratio is not
real, then all its periods are expressible in the form NΩ + N′Ω′,
where Ω, Ω′ are periods, and N, N′ are integers. In the former case,
putting ζ = 2πiz/Ω, and the function ƒ(z) = φ(ζ), the function φ(ζ)
has, like exp (ζ), the period 2πi, and if we take t = exp (ζ) or ζ = λ(t)
the function is a single valued function of t. If then in particular ƒ(z)
is an integral function, regarded as a function of t, it has singularities
only for t = 0 and t = ∞, and may be expanded in the form Σ ∞−∞ an tn.
Taking the case when the single valued monogenic function has
two periods ω, ω′ whose ratio is not real, we can form a network
of parallelograms covering the plane of z whose angular points are
the points c + mω + m′ω′, wherein c is some constant and m, m′ are
all possible positive and negative integers; choosing arbitrarily
one of these parallelograms, and calling it the primary parallelogram,
all the values of which the function is at all capable occur for points
of this primary parallelogram, any point, z′, of the plane being,
as it is called, congruent to a definite point, z, of the primary parallelogram,
z′ − z being of the form mω + m′ω′, where m, m′ are integers.
Such a function cannot be an integral function, since then, if, in the
primary parallelogram |ƒ(z)| < M, it would also be the case, on a circle
of centre the origin and radius R, that |ƒ(z)| < M, and therefore, if
Σan zn be the expansion of the function, which is valid for an integral
function for all finite values of z, we should have |an| < MR−n, which
can be made arbitrarily small by taking R large enough. The
function must then have singularities for finite values of z.
We consider only functions for which these are poles. Of these
there cannot be an infinite number in the primary parallelogram,
since then those of these poles which are sufficiently near to one
of the necessarily existing limiting points of the poles would be
arbitrarily near to one another, contrary to the character of a pole.
Supposing the constant c used in naming the corners of the parallelograms
so chosen that no pole falls on the perimeter of a parallelogram,
it is clear that the integral 1/(2πi) ∫ƒ(z) dz round the perimeter of the
primary parallelogram vanishes; for the elements of the integral
corresponding to two such opposite perimeter points as z, z + ω
(or as z, z + ω′) are mutually destructive. This integral is, however,
equal to the sum of the residues of ƒ(z) at the poles interior to the
parallelogram. Which sum is therefore zero. There cannot therefore
be such a function having only one pole of the first order in
any parallelogram; we shall see that there can be such a function
with two poles only in any parallelogram, each of the first order,
with residues whose sum is zero, and that there can be such a function
with one pole of the second order, having an expansion near this pole
of the form (z-a)−2 + (power series in z − a).
Considering next the function φ(z) = [ƒ(z)]−1 dƒ(z)/dz, it is easily seen
that an ordinary point of ƒ(z) is an ordinary point of φ(z), that a
zero of order m for ƒ(z) in the neighbourhood of which ƒ(z) has a form,
(z − a)m multiplied by a power series, is a pole of φ(z) of residue m,
and that a pole of ƒ(z) of order n is a pole of φ(z) of residue −n;
manifestly φ(z) has the two periods of ƒ(z). We thus infer, since the
sum of the residues of φ(z) is zero, that for the function ƒ(z), the
sum of the orders of its vanishing at points belonging to one parallelogram,
Σm, is equal to the sum of the orders of its poles, Σn; which is
briefly expressed by saying that the number of its zeros is equal to
the number of its poles. Applying this theorem to the function
ƒ(z) − A, where A is an arbitrary constant, we have the result, that
the function ƒ(z) assumes the value A in one of the parallelograms
as many times as it becomes infinite. Thus, by what is proved above,
every conceivable complex value does arise as a value for the doubly
periodic function ƒ(z) in any one of its parallelograms, and in fact
at least twice. The number of times it arises is called the order of the
function; the result suggests a property of rational functions.
Consider further the integral ∫ z [ƒ′(z)/ƒ(z)] dz, where ƒ′(z) = dƒ(z)/dz taken
round the perimeter of the primary parallelogram; the contribution
to this arising from two opposite perimeter points such as z and z + ω
is of the form −ω ∫ z [ƒ′(z)/ƒ(z)] dz, which, as z increases from z0 to z0 + ω′, gives,
if λ denote the generalized logarithm, − ω {λ [ƒ(z0 + ω′)] − λ[ƒ(z0)]}, that
is, since ƒ(z0 + ω′) = ƒ(z0), gives 2πiNω, where N is an integer; similarly
the result of the integration along the other two opposite sides is of
the form 2πiN′ω′, where N′ is an integer. The integral, however,
is equal to 2πi times the sum of the residues of zƒ′(z) / ƒ(z) at the poles
interior to the parallelogram. For a zero, of order m, of ƒ(z) at z = a,
the contribution to this sum is 2πima, for a pole of order n at z = b
the contribution is −2πinb; we thus infer that Σma − Σnb = Nω + N′ω′;
this we express in words by saying that the sum of the values of z
where ƒ(z) = 0 within any parallelogram is equal to the sum of the
values of z where ƒ(z) = ∞ save for integral multiples of the periods.
By considering similarly the function ƒ(z) − A where A is an arbitrary
constant, we prove that each of these sums is equal to the sum of
the values of z where the function takes the value A in the parallelogram.
We pass now to the construction of a function having two
arbitrary periods ω, ω′ of unreal ratio, which has a single pole
of the second order in any one of its parallelograms.
For this consider first the network of parallelograms whose corners
are the points Ω = mω + m′ω′, where m, m′ take all positive and
negative integer values; putting a small circle about each corner
of this network, let P be a point outside all these circles; this will
be interior to a parallelogram whose corners in order may be denoted
by z0, z0 + ω, z0 + ω + ω′, z0 + ω′; we shall denote z0, z0 + ω by A0, B0;
this parallelogram Π0 is surrounded by eight other parallelograms,
forming with Π0 a larger parallelogram Π1, of which one side, for
instance, contains the points z0 − ω − ω′, z0 − ω′, z0 − ω′ + ω, z0 − ω′ + 2ω,
which we shall denote by A1, B1, C1, D1. This parallelogram Π1 is
surrounded by sixteen of the original parallelograms, forming with
Π1 a still larger parallelogram Π2 of which one side, for instance,
contains the points z0 − 2ω − 2ω′, z0 − ω − 2ω′, z0 − 2ω′, z0 + ω − 2ω′,
z0 + 2ω − 2ω′, z0 + 3ω − 2ω′, which we shall denote by A2, B2, C2, D2,
E2, F2. And so on. Now consider the sum of the inverse cubes of
the distances of the point P from the corners of all the original
parallelograms. The sum will contain the terms
| S0 = | 1 |
+ ( | 1 |
+ | 1 |
+ | 1 |
) + ( | 1 |
+ | 1 |
+ ... + | 1 |
) + ... |
| PA03 | PA13 |
PB13 | PC13 |
PA23 | PB23 |
PE23 |
and three other sets of terms, each infinite in number, formed in a
similar way. If the perpendiculars from P to the sides A0B0,
A1B1C1, A2B2C2D2E2, and so on, be p, p + q, p + 2q and so on, the
sum S0 is at most equal to
| 1 |
+ | 3 |
+ | 5 |
+ ... + | 2n + 1 |
+ ... |
| p3 | (p + q)3 |
(p + 2q)3 | (p + nq)3 |
of which the general term is ultimately, when n is large, in a ratio of
equality with 2q−3 n−2, so that the series S0 is convergent, as we know
the sum Σn−2 to be; this assumes that p ≠ 0; if P be on A0B0
the proof for the convergence of S0 − 1/PA03, is the same. Taking
the three other sums analogous to S0 we thus reach the result that
the series
φ(z) = −2Σ (z − Ω)−3,
where Ω is mω + m′ω′, and m, m′ are to take all positive and negative
integer values, and z is any point outside small circles described with
the points Ω as centres, is absolutely convergent. Its sum is therefore
independent of the order of its terms. By the nature of the proof,
which holds for all positions of z outside the small circles spoken of,
the series is also clearly uniformly convergent outside these circles.
Each term of the series being a monogenic function of z, the series may
therefore be differentiated and integrated outside these circles, and
represents a monogenic function. It is clearly periodic with the
periods ω, ω′; for φ(z + ω) is the same sum as φ(z) with the terms
in a slightly different order. Thus φ(z + ω) = φ(z) and φ(z + ω′) = φ(z).
Consider now the function
| ƒ(z) = | 1 |
+ ∫ z0 { φ(z) + | 2 |
} dz, |
| z2 | z3 |
where, for the subject of integration, the area of uniform convergence
clearly includes the point z = 0; this gives
and
| ƒ(z) = | 1 |
+ Σ′ { | 1 |
− | 1 |
} , |
| z2 | (z − Ω)2 |
Ω2 |
wherein Σ′ is a sum excluding the term for which m = 0 and m′ = 0.
Hence ƒ(z + ω) − ƒ(z) and ƒ(z + ω′) − ƒ(z) are both independent of z.
Noticing, however, that, by its form, ƒ(z) is an even function of z,
and putting z = −½ω, z = −½ω′ respectively, we infer that also ƒ(z)
has the two periods ω and ω′. In the primary parallelogram Π0,
however, ƒ(z) is only infinite at z = 0 in the neighbourhood of which
its expansion is of the form z−2 + (power series in z). Thus ƒ(z) is
such a doubly periodic function as was to be constructed, having in
any parallelogram of periods only one pole, of the second order.
It can be shown that any single valued meromorphic function
of z with ω and ω′ as periods can be expressed rationally in terms
of ƒ(z) and φ(z), and that [φ(z)]2 is of the form 4[ƒ(z)]3 + Aƒ(z) + B,
where A, B are constants.
319
To prove the last of these results, we write, for |z| < |Ω|,
| 1 |
− | 1 |
= | 2z |
+ | 3z² |
+ ..., |
| (z − Ω)² | Ω² |
Ω³ | Ω4 |
and hence, if Σ′Ω−2n = σn, since Σ′Ω−(2n−1) = 0, we have, for sufficiently
small z greater than zero,
ƒ(z) = z−2 + 3σ2·z2 + 5σ3·z4 + ...
and
φ(z) = −2z−3 + 6σ2·z + 20σ3·z3 + ...;
using these series we find that the function
F(z) = [φ(z)]² − 4[ƒ(z)]³ + 60σ2ƒ(z) + 140σ3
contains no negative powers of z, being equal to a power series in z²
beginning with a term in z². The function F(z) is, however, doubly
periodic, with periods ω, ω′, and can only be infinite when either
ƒ(z) or φ(z) is infinite; this follows from its form in ƒ(z) and φ(z);
thus in one parallelogram of periods it can be infinite only when
z = 0; we have proved, however, that it is not infinite, but, on the
contrary, vanishes, when z = 0. Being, therefore, never infinite for
finite values of z it is a constant, and therefore necessarily always
zero. Putting therefore ƒ(z) = ζ and φ(z) = dζ/dz we see that
| dz |
= (4ζ³ − 60σ2ζ − 140σ3)−1/2. |
| dζ |
Historically it was in the discussion of integrals such as
∫ dζ (4ζ³ − 60σ2·ζ − 140σ3)−1/2,
regarded as a branch of Integral Calculus, that the doubly periodic
functions arose. As in the familiar case
z = ∫ ζ0 (1 − ζ²)−1/2 dζ,
where ζ = sin z, it has proved finally to be simpler to regard ζ as a
function of z. We shall come to the other point of view below,
under § 20, Elliptic Integrals.
To prove that any doubly periodic function F(z) with periods
ω, ω′, having poles at the points z = a1, ... z = am of a parallelogram,
these being, for simplicity of explanation, supposed to be
all of the first order, is rationally expressible in terms of φ(z)
and ƒ(z), and we proceed as follows:—
Consider the expression
| Φ(z) = | (ζ, 1)m + η(ζ, 1)m−2 |
| (ζ − A1) (ζ − A2)...(ζ − Am) |
where As = ƒ(as), ζ is an abbreviation for ƒ(z) and η for φ(z), and
(ζ, 1)m, (ζ, 1)m−2, denote integral polynomials in ζ, of respective orders
m and m − 2, so that there are 2m unspecified, homogeneously
entering, constants in the numerator. It is supposed that no one
of the points a1, ... am is one of the points mω + m′ω′ where f(z) = ∞.
The function Φ(z) is a monogenic function of z with the periods ω, ω′,
becoming infinite (and having singularities) only when (1) ζ = ∞ or
(2) one of the factors ζ-As is zero. In a period parallelogram
including z = 0 the first arises only for z = 0; since for ζ = ∞, η is in
a finite ratio to ζ3/2; the function Φ(z) for ζ = ∞ is not infinite
provided the coefficient of ζm in (ζ, 1)m is not zero; thus Φ(z) is
regular about z = 0. When ζ − As = 0, that is ƒ(z) = f(as), we have
z = ±as + mω + m′ω′, and no other values of z, m and m′ being
integers; suppose the unspecified coefficients in the numerator so
taken that the numerator vanished to the first order in each of the
m points −a1, −a2, ... −am; that is, if φ(as) = Bs, and therefore
φ(−as) = −Bs, so that we have the m relations
(As, 1)m − Bs(As, 1)m−2 = 0;
then the function Φ(z) will only have the m poles a1, ... am. Denoting
further the m zeros of F(z) by a1′, ... am′, putting ƒ(as′) = As′,
φ(as′) = Bs′, suppose the coefficients of the numerator of Φ(z) to
satisfy the further m − 1 conditions
(As′, 1)m + Bs′ (As′, 1)m−2 = 0
for s = 1, 2, ... (m − 1). The ratios of the 2m coefficients in the
numerator of Φ(z) can always be chosen so that the m + (m − 1) linear
conditions are all satisfied. Consider then the ratio
F(z) / Φ(z);
it is a doubly periodic function with no singularity other than the
one pole am′. It is therefore a constant, the numerator of Φ(z)
vanishing spontaneously in am′. We have
F(z) = AΦ(z),
where A is a constant; by which F(z) is expressed rationally in
terms of ƒ(z) and φ(z), as was desired.
When z = 0 is a pole of F(z), say of order r, the other poles, each of
the first order, being a1, ... am, similar reasoning can be applied to
a function
| (ζ, 1)h + η(ζ, 1)k |
, |
| (ζ − A1) ... (ζ − Am) |
where h, k are such that the greater of 2h − 2m, 2k + 3 − 2m is equal
to r; the case where some of the poles a1, ... am are multiple is
to be met by introducing corresponding multiple factors in the denominator
and taking a corresponding numerator. We give a
solution of the general problem below, of a different form.
One important application of the result is the theorem that the
functions ƒ(z + t), φ(z + t), which are such doubly periodic function of
z as have been discussed, can each be expressed, so far as they depend
on z, rationally in terms of ƒ(z) and φ(z), and therefore, so far as they
depend on z and t, rationally in terms of ƒ(z), ƒ(t), φ(z) and φ(t).
It can in fact be shown, by reasoning analogous to that given above,
that
| ƒ(z + t) + ƒ(z) + ƒ(t) = ¼ [ | φ(z) − φ(t) |
] 2. |
| ƒ(z) − ƒ(t) |
This shows that if F(z) be any single valued monogenic function
which is doubly periodic and of meromorphic character, then
F(z + t) is an algebraic function of F(z) and F(t). Conversely any
single valued monogenic function of meromorphic character, F(z),
which is such that F(z + t) is an algebraic function of F(z) and F(t),
can be shown to be a doubly periodic function, or a function obtained
from such by degeneration (in virtue of special relations connecting
the fundamental constants).
The functions ƒ(z), φ(z) above are usually denoted by ℜ(z), ℜ′(z);
further the fundamental differential equation is usually written
(ℜ′z)² = 4(ℜz)³ − g2ℜz − g3,
and the roots of the cubic on the right are denoted by e1, e2, e3;
for the odd function, ℜ′z, we have, for the congruent arguments
−½ωand ½ω, ℜ′ (½ω) = −ℜ′ (−½ω) = −ℜ′ (½ω), and hence ℜ′ (½ω) = 0;
hence we can take e1 = ℜ (½ω), e2 = ℜ (½ω + ½ω′), e3 = ℜ (½ω). It can
then be proved that [ℜ(z) − e1] [ℜ (z + ½ω) − e1] = (e1 − e2) (e1 − e3), with
similar equations for the other half periods. Consider more particularly
the function ℜ(z) − e1; like ℜ(z) it has a pole of the second
order at z = 0, its expansion in its neighbourhood being of the form
z−2 (1 − e1z2 + Az4 + ...); having no other pole, it has therefore either
two zeros, or a double zero in a period parallelogram (ω, ω′). In fact
near its zero ½ω its expansion is (x − ½ω) ℜ′ (½ω) + ½(z − ½ω)² ℜ″ (½ω) +
...; we have seen that ℜ′ (½ω) = 0; thus it has a zero of the second
order wherever it vanishes. Thus it appears that the square root
[ℜ(z) − e1]1/2, if we attach a definite sign to it for some particular value
of z, is a single valued function of z; for it can at most have two
values, and the only small circuits in the plane which could lead
to an interchange of these values are those about either a pole or a
zero, neither of which, as we have seen, has this effect; the function
is therefore single valued for any circuit. Denoting the function,
for a moment, by ƒ1(z), we have ƒ1(z + ω) = ±ƒ1(z), ƒ1(z + ω′) = ±ƒ1(z);
it can be seen by considerations of continuity that the right sign
in either of these equations does not vary with z; not both these
signs can be positive, since the function has only one pole, of the first
order, in a parallelogram (ω, ω′); from the expansion of ƒ1(z) about
z = 0, namely z− 1 (1 − ½e1z² + ...), it follows that ƒ1(z) is an odd
function, and hence ƒ1 (−½ω′) = −ƒ1 (½ω′), which is not zero since
[ƒ1 (½ω′)]² = e3 − e1, so that we have ƒ1 (z + ω′) = −ƒ1(z); an equation
f1(z + ω) = −ƒ1(z) would then give ƒ1(z + ω + ω′) = ƒ1(z), and hence
ƒ1(½ω + ½ω′) = ƒ1(−½ω − ½ω′), of which the latter is −ƒ1(½ω + ½ω′); this
would give ƒ1(½ω + ½ω′) = 0, while [ƒ1(½ω + ½ω′)]² = e2 − e1. We thus
infer that ƒ1(z + ω) = ƒ1(z), ƒ1(z + ω′) = −ƒ1(z), ƒ1(z + ω + ω′) = −ƒ1(z).
The function ƒ1(z) is thus doubly periodic with the periods ω and
2ω′; in a parallelogram of which two sides are ω and 2ω′ it has
poles at z = 0, z = ω′ each of the first order, and zeros of the first
order at z = ½ω, z = ½ω + ω′; it is thus a doubly periodic function
of the second order with two different poles of the first order in its
parallelogram (ω, 2ω′). We may similarly consider the functions
ƒ2(z) = [ℜ(z) − e2]1/2, ƒ3(z) = [ℜ(z) − e3]1/2; they give
| ƒ2(z + ω + ω′) = ƒ2(z), ƒ2(z + ω) = −ƒ2(z), ƒ2(z + ω′) = −ƒ2(z), |
ƒ3(z + ω′) = ƒ3z, ƒ3(z + ω) = −ƒ3(z), ƒ3(z + ω + ω′) = −ƒ3(z). |
Taking u = z (e1 − e3)1/2, with a definite determination of the constant
(e1 − e3)1/2, it is usual, taking the preliminary signs so that for z = 0
each of zƒ1(z), zƒ2(z), zƒ3(z) is equal to +1, to put
| sn(u) = | (e1 − e3)1/2 |
, cn(u) = | ƒ1(z) |
, dn(u) = | f2(z) |
, |
| ƒ3(z) | ƒ3(z) |
ƒ3(z) |
| k² = (e2 − e3) / (e1 − e3), K = ½ω (e1 − e3)1/2, iK′ = ½ω′ (e1 − e3)1/2; |
thus sn(u) is an odd doubly periodic function of the second order
with the periods 4K, 2iK, having poles of the first order at u = iK′,
u = 2K + iK′, and zeros of the first order at u = 0, u = 2K; similarly
cn(u), dn(u) are even doubly periodic functions whose periods can be
written down, and sn²(u) + cn²(u) = 1, k²sn²(u) + dn²(u) = 1; if x = sn(u)
we at once find, from the relations given here, that
| du |
= [(1 − x²) (1 − k²x²)]−1/2; |
| dx |
if we put x = sinφ we have
| du |
= [1 − k²sin²φ]−1/2, |
| dφ |
and if we call φ the amplitude of u, we may write φ = am(u), x = sin·am(u),
which explains the origin of the notation sn(u). Similarly
cn(u) is an abbreviation of cos·am(u), and dn(u) of Δam(u), where
Δ(φ) meant (1 − k²sin²φ)1/2. The addition equation for each of the
functions ƒ1(z), ƒ2(z), ƒ3(z) is very simple, being
| ƒ(z + t) = ½ ( | ∂ |
+ | ∂ |
) log | ƒ(z) + ƒ(t) |
= | ƒ(z)ƒ′(t) − ƒ(t)ƒ′(z) |
, |
| ∂z | ∂i |
ƒ(z) − ƒ(t) | ƒ²(z) − ƒ²(t) |
where f1′(z) means dƒ1(z)/dz, which is equal to −ƒ2(z)·ƒ3(z), and ƒ²(z)
320
means [ƒ(z)]2. This may be verified directly by showing, if R denote
the right side of the equation, that ∂R/∂z = ∂R/∂t; this will require
the use of the differential equation
[ƒ1′(z)]2 = [ƒ12(z) + e1 − e2] [ƒ12(z) + e1 − e3],
and in fact we find
| ( | ∂2 |
− | ∂2 |
) log [ƒ(z) + ƒ(t)] = ƒ2(z) − ƒ2(t) = ( | ∂2 |
− | ∂2 |
) log [ƒ(z) − ƒ(t)]; |
| ∂z2 | dt2 |
∂z2 | dt2 |
hence it will follow that R is a function of z + t, and R is at once seen
to reduce to ƒ(z) when t = 0. From this the addition equation for
each of the functions sn(u), cn(u), dn(u) can be deduced at once;
if s1, c1, d1, s2, c2, d2 denote respectively sn(u1), cn(u1), dn(u1), sn(u2),
cn(u2), dn(u2), they can be put into the forms
| sn(u1 + u2) = (s1c2d2 + s2c1d1) / D, |
cn(u1 + u2) = (c1c2 − s1s2d1d2) / D, |
dn(u1 + u2) = (d1d2 − k2s1s2c1c2) / D, |
where
D = 1 − k2s12s22.
The introduction of the function ƒ1(z) is equivalent to the introduction
of the function ℜ(z; ω, 2ω′) constructed from the periods
ω, 2ω′ as was ℜ(z) from ω and ω′; denoting this function by ℜ1(z)
and its differential coefficient by ℜ′1(z), we have in fact
| ƒ1(z) = ½ | ℜ′1(z) |
| ℜ1(ω′) − ℜ1(z) |
as we see at once by considering the zeros and poles and the limit of
zƒ1(z) when z = 0. In terms of the function ℜ1(z) the original function
ℜ(z) is expressed by
ℜ(z) = ℜ1(z) + ℜ1(z + ω′) − ℜ1(ω′),
as a consideration of the poles and expansion near z = 0 will show.
A function having ω, ω′ for periods, with poles at two arbitrary
points a, b and zeros at a′, b′, where a′ + b′ = a + b save for an expression
mω + m′ω′, in which m, m′ are integers, is a constant multiple of
| {ℜ [z − ½(a′ + b′)] − ℜ [a′ − ½(a′ + b′)]} / {ℜ [z − ½(a + b)] − ℜ [a − ½(a + b)]}; |
if the expansion of this function near z = a be
λ(z − a)−1 + μ + Σ n=1 μn (z − a)n,
the expansion near z = b is
−λ (z − b)− 1 + μ + Σ n=1 (−1)n μn (z − b)n,
as we see by remarking that if z′ − b = −(z − a) the function has the
same value at z and z′; hence the differential equation satisfied
by the function is easily calculated in terms of the coefficients in
the expansions.
From the function ℜ(z) we can obtain another function, termed the
Zeta-function; it is usually denoted by ζ(z), and defined by
| ζ(z) − | 1 |
= ∫ π0 [ | 1 |
− ℜ(z) ] dz = Σ′ ( | 1 |
+ | 1 |
+ | z |
), |
| z | z2 |
z − Ω | Ω |
Ω2 |
for which as before we have equations
| ζ(z + ω) = ζ(z) + 2πiη, ζ(z + ω′) = ζ(z) + 2πiη′, |
where 2η, 2η′ are certain constants, which in this case do not both
vanish, since else ζ(z) would be a doubly periodic function with only
one pole of the first order. By considering the integral
∫ ζ(z)dz
round the perimeter of a parallelogram of sides ω, ω′ containing
z = 0 in its interior, we find ηω′ − η′ω = 1, so that neither of η, η′
is zero. We have ζ′(z) =−ℜ(z). From ζ(z) by means of the equation
| σ(z) |
= exp { ∫ z0 [ ζ(x) − | 1 |
] dz } = Π′ [ ( 1 − | z |
) exp ( | z |
+ | z2 |
) ], |
| z | z |
Ω | Ω |
2Ω2 |
we determine an integral function σ(z), termed the Sigma-function,
having a zero of the first order at each of the points z = Ω; it can be
seen to satisfy the equations
| σ(z + ω) |
= −exp [2πiη(z + ½ω)], | σ(z + ω′) |
= −exp [2πiη′ (z + ½ω′)]. |
| σ(z) | σ(z) |
By means of these equations, if a1 + a2 + ... + am = a′1 + a′2 + ...
+ a′m, it is readily shown that
| σ(z − a′1) σ(z − a′2) ... σ(z − a′m) |
| σ(z − a1) σ(z − a2) ... σ(z − am) |
is a doubly periodic function having a1, ... am as its simple poles,
and a′1, ... a′m as its simple zeros. Thus the function σ(z) has the
important property of enabling us to write any meromorphic doubly
periodic function as a product of factors each having one zero in the
parallelogram of periods; these form a generalization of the simple
factors, z − a, which have the same utility for rational functions of z.
We have ζ(z) = σ′(z)/σ(z).
The functions ζ(z), ℜ(z) may be used to write any meromorphic
doubly periodic function F(z) as a sum of terms having each only one
pole; for if in the expansion of F(z) near a pole z = a the terms with
negative powers of z − a be
A1(z − a)−1 + A2(z − a)−2 + ... + Am+1(z − a)−(m+1),
then the difference
| F(z) − A1ζ (z − a) − A2ℜ (z − a) − ... + | Am+1 |
(−1)m ℜm−1 (z − a) |
| m! |
will not be infinite at z = a. Adding to this a sum of further terms
of the same form, one for each of the poles in a parallelogram of
periods, we obtain, since the sum of the residues A is zero, a doubly
periodic function without poles, that is, a constant; this gives the
expression of F(z) referred to. The indefinite integral ∫F(z)dz can
then be expressed in terms of z, functions ℜ(z − a) and their differential
coefficients, functions ζ(z − a) and functions logσ(z − a).
§ 15. Potential Functions. Conformal Representation in
General.—Consider a circle of radius a lying within the region
of existence of a single valued monogenic function, u + iv, of
the complex variable z, = x + iy, the origin z = 0 being the centre
of this circle. If z = rE(iφ) = r(cosφ + i sinφ) be an internal point
of this circle we have
| u + iv = | 1 |
∫ | (U + iV) |
dt, |
| 2πi | t − z |
where U + iV is the value of the function at a point of the circumference
and t = aE(iθ); this is the same as
| u + iv = | 1 |
∫ | (U + iV) [1 − (r/a) E (iθ − iφ)] |
dθ. |
| 2π | 1 + (r/a)² − 2(r/a) cos (θ − φ) |
If in the above formula we replace z by the external point
(a²/r) E(iφ) the corresponding contour integral will vanish, so that
also
| 0 = | 1 |
∫ | (U + iV) [(r/a)² − (r/a) E (iθ − iφ)] |
dθ; |
| 2π | 1 + (r/a)² − 2(r/a) cos (θ − φ) |
hence by subtraction we have
| u = | 1 |
∫ | U(a² − r²) |
dθ, |
| 2π | a² + r² − 2ar cos (θ − φ) |
and a corresponding formula for v in terms of V. If O be the
centre of the circle, Q be the interior point z, P the point aE(iθ)
of the circumference, and ω the angle which QP makes with OQ
produced, this integral is at once found to be the same as
| u = | 1 |
∫ Udω − | 1 |
∫ Udθ |
| π | 2π |
of which the second part does not depend upon the position of z,
and the equivalence of the integrals holds for every arc of
integration.
Conversely, let U be any continuous real function on the circumference,
U0 being the value of it at a point P0 of the circumference,
and describe a small circle with centre at P0 cutting the given circle in
A and B, so that for all points P of the arc AP0B we have |U − U0| < ε,
where ε is a given small real quantity. Describe a further circle,
centre P0 within the former, cutting the given circle in A′ and B′,
and let Q be restricted to lie in the small space bounded by the arc
A′P0B′ and this second circle; then for all positions of P upon the
greater arc AB of the original circle QP² is greater than a definite
finite quantity which is not zero, say QP² > D². Consider now the
integral
| u′ = | 1 |
∫ U | (a² − r²) |
dθ = | 1 |
∫ Udω − | 1 |
∫ Udθ, |
| 2π | a² + r² − 2ar cos (θ − φ) |
π | 2π |
which we evaluate as the sum of two, respectively along the small arc
AP0B and the greater arc AB. It is easy to verify that, for the
whole circumference,
| U0 = | 1 |
∫ U0 | a² − r² |
dθ = | 1 |
∫ U0 dω − | 1 |
∫ U0 dθ. |
| 2π | a² + r² − 2ar cos (θ − φ) |
π | 2π |
Hence we can write
| u′ − U0 = | 1 |
∫ AP0B (U − U0)dω − | 1 |
∫ AP0B (U − U0)dθ + | 1 |
∫ AB (U − U0) | (a² − r²) |
dθ. |
| 2π | 2π |
2π | QP² |
If the finite angle between QA and QB be called Φ and the finite
angle AOB be called Θ, the sum of the first two components is
numerically less than
If the greatest value of |(U − U0)| on the greater arc AB be called H,
the last component is numerically less than
of which, when the circle, of centre P0, passing through A′B′ is
sufficiently small, the factor a² − r² is arbitrarily small. Thus it
appears that u′ is a function of the position of Q whose limit, when Q,
interior to the original circle, approaches indefinitely near to P0, is
U0. From the form
| u′ = | 1 |
∫ Udω − | 1 |
∫ Udθ, |
| π | 2π |
since the inclination of QP to a fixed direction is, when Q varies, P
remaining fixed, a solution of the differential equation
where z, = x + iy, is the point Q, we infer that u′ is a differentiable
321
function satisfying this equation; indeed, when r < a, we can write
| 1 |
∫ U | (a² − r²) |
dθ = | 1 |
∫ U [ 1 + 2 | r |
cos (θ − φ) + 2 | r² |
cos 2(θ − φ) + ... ] dθ |
| 2π | a² + r² − 2ar cos (θ − φ) |
2π | a |
a² |
= a0 + a1x + b1y + a2 (x² − y²) + 2b2xy + ...,
where
| a0 = | 1 |
∫ Udθ, a1 = | 1 |
∫ | U cosθ |
dθ, b1 = | 1 |
∫ | U sinθ |
dθ, |
| 2π | π |
a | π |
a |
| a2 = | 1 |
∫ | U cos 2θ |
dθ, b2 = | 1 |
∫ | U sin 2θ |
dθ. |
| π | a² |
π | a² |
In this series the terms of order n are sums, with real coefficients,
of the various integral polynomials of dimension n which satisfy
the equation ∂²ψ/∂x² + ∂²ψ/∂y²; the series is thus the real part of
a power series in z, and is capable of differentiation and integration
within its region of convergence.
Conversely we may suppose a function, P, defined for the interior
of a finite region R of the plane of the real variables x, y, capable
of expression about any interior point x0, y0 of this region by a power
series in x − x0, y − y0, with real coefficients, these various series being
obtainable from one of them by continuation. For any region R0
interior to the region specified, the radii of convergence of these
power series will then have a lower limit greater than zero, and
hence a finite number of these power series suffice to specify the
function for all points interior to R0. Each of these series, and
therefore the function, will be differentiable; suppose that at all
points of R0 the function satisfies the equation
we then call it a monogenic potential function. From this, save
for an additive constant, there is defined another potential function
by means of the equation
| Q = ∫ (x, y) ( | ∂P |
dy − | ∂P |
dx ). |
| ∂x | ∂y |
The functions P, Q, being given by a finite number of power series,
will be single valued in R0, and P + iQ will be a monogenic function of
z within R0· In drawing this inference it is supposed that the region
R0 is such that every closed path drawn in it is capable of being
deformed continuously to a point lying within R0, that is, is simply
connected.
Suppose in particular, c being any point interior to R0, that P
approaches continuously, as z approaches to the boundary of R,
to the value log r, where r is the distance of c to the points of the
perimeter of R. Then the function of z expressed by
ζ = (z − c) exp (−P − iQ)
will be developable by a power series in (z − z0) about every point z0
interior to R0, and will vanish at z = c; while on the boundary of R
it will be of constant modulus unity. Thus if it be plotted upon a
plane of ζ the boundary of R will become a circle of radius unity
with centre at ζ=0, this latter point corresponding to z=c. A
closed path within R0, passing once round z=c, will lead to a closed
path passing once about ζ = 0. Thus every point of the interior of
R will give rise to one point of the interior of the circle. The converse
is also true, but is more difficult to prove; in fact, the differential
coefficient dζ/dz does not vanish for any point interior to R.
This being assumed, we obtain a conformal representation of the
interior of the region R upon the interior of a circle, in which the
arbitrary interior point c of R corresponds to the centre of the circle,
and, by utilizing the arbitrary constant arising in determining the
function Q, an arbitrary point of the boundary of R corresponds to
an arbitrary point of the circumference of the circle.
There thus arises the problem of the determination of a real monogenic
potential function, single valued and finite within a given
arbitrary region, with an assigned continuous value at all points
of the boundary of the region. When the region is circular this
problem is solved by the integral 1/π ∫ Udω − 1/π ∫ Udθ previously
given. When the region is bounded by the outermost portions
of the circumferences of two overlapping circles, it can hence be
proved that the problem also has a solution; more generally, consider
a finite simply connected region, whose boundary we suppose
to consist of a single closed path in the sense previously explained,
ABCD; joining A to C by two non-intersecting paths AEC, AFC
lying within the region, so that the original region may be supposed
to be generated by the overlapping regions AECD, CFAB, of which
the common part is AECF; suppose now the problem of determining
a single valued finite monogenic potential function for the region
AECD with a given continuous boundary value can be solved, and
also the same problem for the region CFAB; then it can be shown
that the same problem can be solved for the original area. Taking
indeed the values assigned for the original perimeter ABCD, assume
arbitrarily values for the path AEC, continuous with one another
and with the values at A and C; then determine the potential function
for the interior of AECD; this will prescribe values for the path
CFA which will be continuous at A and C with the values originally
proposed for ABC; we can then determine a function for the interior
of CFAB with the boundary values so prescribed. This in its turn
will give values for the path AEC, so that we can determine a new
function for the interior of AECD. With the values which this
assumes along CFA we can then again determine a new function for
the interior of CFAB. And so on. It can be shown that these
functions, so alternately determined, have a limit representing
such a potential function as is desired for the interior of the original
region ABCD. There cannot be two functions with the given
perimeter values, since their difference would be a monogenic
potential function with boundary value zero, which can easily be
shown to be everywhere zero. At least two other methods have
been proposed for the solution of the same problem.
A particular case of the problem is that of the conformal representation
of the interior of a closed polygon upon the upper half
of the plane of a complex variable t. It can be shown without much
difficulty that if a, b, c, ... be real values of t, and α, β, γ, ... be n
real numbers, whose sum is n − 2, the integral
z = ∫ (t − a)α−1 (t − b)β−1 ... dt,
as t describes the real axis, describes in the plane of z a polygon of n
sides with internal angles equal to απ, βπ, ..., and, a proper sign
being given to the integral, points of the upper half of the plane of t
give rise to interior points of the polygon. Herein the points a, b, ...
of the real axis give rise to the corners of the polygon; the condition
Σα = n − 2 ensures merely that the point t = ∞ does not correspond
to a corner; if this condition be not regarded, an additional corner
and side is introduced in the polygon. Conversely it can be shown
that the conformal representation of a polygon upon the half plane
can be effected in this way; for a polygon of given position of more
than three sides it is necessary for this to determine the positions
of all but three of a, b, c, ...; three of them may always be supposed
to be at arbitrary positions, such as t = 0, t = 1, t = ∞.
As an illustration consider in the plane of z = x + iy, the portion
of the imaginary axis from the origin to z = ih, where h is positive
and less than unity; let C be this point z = ih; let BA be of length
unity along the positive real axis, B being the origin and A the
point z = 1; let DE be of length unity along the negative real axis,
D being also the origin and E the point z = − 1; let EFA be a
semicircle of radius unity, F being the point z = i. If we put
ζ = [(z² + h²)/(1 + h²z²)]1/2, with ζ = 1 when z = 1, the function is single
valued within the semicircle, in the plane of z, which is slit along the
imaginary axis from the origin to z = ih; if we plot the value of ζ
upon another plane, as z describes the continuous curve ABCDE,
ζ will describe the real axis from ζ = 1 to ζ = − 1, the point C giving
ζ = 0, and the points B, D giving the points ζ = ±h. Near z = 0
the expansion of ζ is ζ − h = z² (1 − h4 / 2h) + ..., or ζ + h = −z² (1 − h4 / 2h) + ...;
in either case an increase of ½π in the phase of z gives an increase
of π in the phase of ζ − h or ζ + h. Near z = ih the expansion of ζ is
ζ = (z − ih)1/2 [2ih/(1 − h4)]1/2 + ..., and an increase of 2π in the phase of
z − ih also leads to an increase of π in the phase of ζ. Then as z
describes the semicircle EFA, ζ also describes a semicircle of radius
unity, the point z = i becoming ζ = i. There is thus a conformal
representation of the interior of the slit semicircle in the z-plane,
upon the interior of the whole semicircle in the ζ-plane, the function
z = [(ζ² − h²) / (1 − h²ζ²)]1/2
being single valued in the latter semicircle. By means of a transformation
t = (ζ + 1)² / (ζ − 1)², the semicircle in the plane of ζ can
further be conformably represented upon the upper half of the whole
plane of t.
As another illustration we may take the conformal representation
of an equilateral triangle upon a half plane. Taking the elliptic
function ℜ(u) for which ℜ′²(u) = 4ℜ³(u) − 4, so that, with ε = exp (2⁄3πi),
we have e1 = 1, e2 = ε², e3 = ε, the half periods may be taken to be
| ½ω = ∫ ∞1 | dt |
, ½ω′ = ∫ ∞e3 | dt |
= ½εω; |
| 2(t³ − 1)1/2 | 2(t³ − 1)1/2 |
drawing the equilateral triangle whose vertices are O, of argument O,
A of argument ω, and B of argument ω + ω′ = −ε²ω, and the equilateral
triangle whose angular points are O, B and C, of argument ω′,
let E, of argument 1⁄3(2ω + ω′), and D, of argument 1⁄3(ω + 2ω′), be the
centroids of these triangles respectively, and let BE, OE, AE cut
OA, AB, BO in K, L, H respectively, and BD, OD, CD cut OC, BC,
OB in F, G, H respectively; then if u = ξ + iη be any point of the
interior of the triangle OEH and v = εu0 = ε(ξ − iη) be any point of the
interior of the triangle OHD, the points respectively of the ten
triangles OEK, EKA, EAL, ELB, EBH, DHB, DBG, DGC, DCF,
DFO are at once seen to be given by −εv, ω + εu, ω − η²v, ω + ω′ + ε²u,
ω + ω′ − v, ω + ω′ − u, ω + ω′ + εv, ω′ − εu, ω′ + ε²v, −ε²u. Further, when
u is real, since the term − 2(u + mω + m′ε²ω)−3, which is the conjugate
complex of −2(u + mω + m′ε²ω)3, arises in the infinite sum
which expresses ℜ′(u), namely as −2(u + μω + μ′εω)−3, where
μ = m − m′, μ′ = −m′, it follows that ℜ′(u) is real; in a similar
way we prove that ℜ′(u) is pure imaginary when u is pure imaginary,
and that ℜ′(u) = ℜ′(εu) = ℜ′(ε²u), as also that for v = εu0, ℜ′(v) is the
conjugate complex of ℜ′(u). Hence it follows that the variable
t = ½ iℜ′(u)
322
takes each real value once as u passes along the perimeter of the
triangle ODE, being as can be shown respectively ∞, 1, 0, − 1 at O,
D, H, E, and takes every complex value of imaginary part positive
once in the interior of this triangle. This leads to
u = 1⁄3 i ∫ ∞t (t2 − 1)−2/3dt
in accordance with the general theory.
It can be deduced that τ = t2 represents the triangle ODH on the
upper half plane of τ, and ζ = (i − τ−1)1/2 represents similarly the
triangle OBD.
§ 16. Multiple valued Functions. Algebraic Functions.—The
explanations and definitions of a monogenic function hitherto
given have been framed for the most part with a view to single
valued functions. But starting from a power series, say in
z − c, which represents a single value at all points of its circle
of convergence, suppose that, by means of a derived series in
z − c′, where c′ is interior to the circle of convergence, we can
continue the function beyond this, and then by means of a series
derived from the first derived series we can make a further
continuation, and so on; it may well be that when, after a
closed circuit, we again consider points in the first circle of
convergence, the value represented may not agree with the
original value. One example is the case z1/2, for which two values
exist for any value of z; another is the generalized logarithm
λ(z), for which there is an infinite number of values. In such
cases, as before, the region of existence of the function consists
of all points which can be reached by such continuations with
power series, and the singular points, which are the limiting
points of the point-aggregate constituting the region of existence,
are those points in whose neighbourhood the radii of convergence
of derived series have zero for limit. In this description the
point z = ∞ does not occupy an exceptional position, a power
series in z − c being transformed to a series in 1/z when z is near
enough to c by means of z − c = c(1 − cz−1) [1 − (1 − cz−1)]−1, and a
series in 1/z to a series in z − c, when z is near enough to c, by
means of 1/z = 1/c [1 + (z − c / c)]−1.
The commonest case of the occurrence of multiple valued functions
is that in which the function s satisfies an algebraic equation ƒ(s, z) =
p0sn + p1sn−1 + ... + pn = 0, wherein p0, p1, ... pn are integral polynomials
in z. Assuming ƒ(s, z) incapable of being written as a product
of polynomials rational in s and z, and excepting values of z for
which the polynomial coefficient of sn vanishes, as also the values
of z for which beside ƒ(s, z) = 0 we have also ∂f(s, z)/∂s = 0, and also
in general the point z = ∞, the roots of this equation about any point
z=c are given by n power series in z − c. About a finite point z = c
for which the equation ∂f(s, z)/∂s = 0 is satisfied by one or more of the
roots s of ƒ(s, z) = 0, the n roots break up into a certain number of
cycles, the r roots of a cycle being given by a set of power series in
a radical (z − c)1/r, these series of the cycle being obtainable from
one another by replacing (z − c)1/r by ω(z − r)1/r, where ω, equal to
exp (2πih/r), is one of the rth roots of unity. Putting then z − c = tr
we may say that the r roots of a cycle are given by a single power
series in t, an increase of 2π in the phase of t giving an increase of
2πr in the phase of z − c. This single series in t, giving the values of
s belonging to one cycle in the neighbourhood of z = c when the phase
of z − c varies through 2πr, is to be looked upon as defining a single
place among the aggregate of values of z and s which satisfy ƒ(s, z) = 0;
two such places may be at the same point (z = c, s = d) without
coinciding, the corresponding power series for the neighbouring
points being different. Thus for an ordinary value of z, z = c, there
are n places for which the neighbouring values of s are given by n
power series in z − c; for a value of z for which ∂f(s, z)/∂s = 0 there
are less than n places. Similar remarks hold for the neighbourhood
of z = ∞; there may be n places whose neighbourhood is given by n
power series in z− 1 or fewer, one of these being associated with a
series in t, where t = (z−1)1/r; the sum of the values of r which thus
arise is always n. In general, then, we may say, with t of one of
the forms (z − c), (z − c)1/r, z−1, (z−1)1/r. that the neighbourhood of
any place (c, d) for which ƒ(c, d) = 0 is given by a pair of expressions
z = c + P(t), s = d + Q(t), where P(t) is a (particular case of a) power
series vanishing for t = 0, and Q(t) is a power series vanishing for
t = 0, and t vanishes at (c, d), the expression z − c being replaced by
z−1 when c is infinite, and similarly the expression s − d by s−1 when
d is infinite. The last case arises when we consider the finite values
of z for which the polynomial coefficient of sn vanishes. Of such a
pair of expressions we may obtain a continuation by writing t = t0 +
λ1τ + λ2τ² + ..., where τ is a new variable and λ1 is not zero;
in particular for an ordinary finite place this equation simply becomes
t = t0 + τ. It can be shown that all the pairs of power series z = c +
P(t), s = d + Q(t) which are necessary to represent all pairs of values
of z, s satisfying the equation ƒ(s, z) = 0 can be obtained from one
of them by this process of continuation, a fact which we express by
saying that the equation ƒ(s, z) = 0 defines a monogenic algebraic
construct. With less accuracy we may say that an irreducible
algebraic equation ƒ(s, z) = 0 determines a single monogenic function
s of z.
Any rational function of z and s, where ƒ(s, z) = 0, may be considered
in the neighbourhood of any place (c, d) by substituting therein
z = c + P(t), s = d + Q(t); the result is necessarily of the form tmH(t),
where H(t) is a power series in t not vanishing for t=0 and m is an
integer. If this integer is positive, the function is said to vanish
to order m at the place; if this integer is negative, = −μ, the function
is infinite to order μ at the place. More generally, if A be an
arbitrary constant, and, near (c, d), R(s, z) −A is of the form tmH(t),
where m is positive, we say that R(s, z) becomes m times equal to A
at the place; if R(s, z) is infinite of order μ at the place, so also is
R(s, z) − A. It can be shown that the sum of the values of m at all
the places, including the places z = ∞, where R(s, z) vanishes, which
we call the number of zeros of R(s, z) on the algebraic construct, is
finite, and equal to the sum of the values of μ where R(s, z) is infinite,
and more generally equal to the sum of the values of m where
R(s, z) = A; this we express by saying that a rational function
R(s, z) takes any value (including ∞) the same number of times on
the algebraic construct; this number is called the order of the
rational function.
That the total number of zeros of R(s, z) is finite is at once obvious,
these values being obtainable by rational elimination of s between
ƒ(s, z) = 0, R(s, z) = 0. That the number is equal to the total number
of infinities is best deduced by means of a theorem which is also of
more general utility. Let R(s, z) be any rational function of s, z,
which are connected by ƒ(s, z) = 0; about any place (c, d) for which
z = c + P(t), s = d + Q(t), expand the product
in powers of t and pick out the coefficient of t−1. There is only a
finite number of places of this kind. The theorem is that the sum
of these coefficients of t−1 is zero. This we express by
| [ R(s, z) | dz |
]t−1 = 0. |
| dt |
The theorem holds for the case n=1, that is, for rational functions
of one variable z; in that case, about any finite point we have
z − c = t, and about z = ∞ we have z−1 = t, and therefore dz/dt = −t−2;
in that case, then, the theorem is that in any rational function of z,
| Σ ( | A1 |
+ | A2 |
+ ... + | Am |
) + Pzh + Qzh−1 + ... + R, |
| z − a | (z − a)² |
(z − a)m |
the sum ΣA1 of the sum of the residues at the finite poles is equal
to the coefficient of 1/z in the expansion, in ascending powers of 1/z,
about z = ∞; an obvious result. In general, if for a finite place
of the algebraic construct associated with ƒ(s, z) = 0, whose neighbourhood
is given by z = c + tr, s = d + Q(t), there be a coefficient of t−1 in
R(s, z) dz/dt, this will be r times the coefficient of t−r in R(s, z) or
R[d + Q(t), c + tr], namely will be the coefficient of t−r in the sum of
the r series obtainable from R [d + Q(t), c + tr] by replacing t by ωt,
where ω is an rth root of unity; thus the sum of the coefficients of
t−1 in R(s, z) dz/dt for all the places which arise for z = c, and the corresponding
values of s, is equal to the coefficient of (z − c)−1 in R(s1, z) +
R(s2z) + ... + R(sn, z), where s1, ... sn are the n values of s for a
value of z near to z = c; this latter sum Σ R(si, z) is, however, a
rational function of z only. Similarly, near z = ∞, for a place given
by z−1=tr, s = d + Q(t), or s−1 = Q(t), the coefficient of t−1 in R(s, z) dz/dt
is equal to −r times the coefficient of tr in R[d + Q(t), t−r], that is
equal to the negative coefficient of z−l in the sum of the r series
R[d + Q(ωt), t−r], so that, as before, the sum of the coefficients of
t−1 in R(s, z) dz/dt at the various places which arise for z = ∞ is equal
to the negative coefficient of z− 1 in the same rational function of z,
Σ R(si, z). Thus, from the corresponding theorem for rational functions
of one variable, the general theorem now being proved is seen to
follow.
Apply this theorem now to the rational function of s and z,
at a zero of R(s, z) near which R(s, z) = tmH(t), we have
| 1 |
| dR(s, z) |
| dz |
= | d |
{λ [R(s, z)] }, |
| R(s, z) | dz |
dt | dt |
where λ denotes the generalized logarithmic function, that is equal
to
mt−1 + power series in t;
similarly at a place for which R(s, z) = t−μK(t); the theorem
| [ | 1 |
| dR(s, z) |
| dz |
]t−1 = 0 |
| R(s, z) | dz |
dt |
thus gives Σm = Σμ, or, in words, the total number of zeros of R(s, z)
on the algebraic construct is equal to the total number of its poles.
The same is therefore true of the function R(s, z) − A, where A is an
arbitrary constant; thus the number in question, being equal to the
number of poles of R(s, z) − A, is equal also to the number of times
that R(s, z) = A on the algebraic construct.
323
We have seen above that all single valued doubly periodic meromorphic
functions, with the same periods, are rational functions of
two variables s, z connected by an equation of the form s² = 4z³ +
Az + B. Taking account of the relation connecting these variables s, z
with the argument of the doubly periodic functions (which was above
denoted by z), it can then easily be seen that the theorem now proved
is a generalization of the theorem proved previously establishing for
a doubly periodic function a definite order. There exists a generalization
of another theorem also proved above for doubly periodic
functions, namely, that the sum of the values of the argument in one
parallelogram of periods for which a doubly periodic function takes
a given value is independent of that value; this generalization,
known as Abel’s Theorem, is given § 17 below.
§ 17. Integrals of Algebraic Functions.—In treatises on Integral
Calculus it is proved that if R(z) denote any rational function,
an indefinite integral ∫R(z)dz can be evaluated in terms of
rational and logarithmic functions, including the inverse trigonometrical
functions. In generalization of this it was long ago
discovered that if s² = az² + bz + c and R(s, z) be any rational
function of s, z any integral ∫R(s, z)dz can be evaluated in terms
of rational functions of s, z and logarithms of such functions;
the simplest case is ∫s− 1dz or ∫(az² + bz + c) −1/2dz. More generally
if f(s, z) = 0 be such a relation connecting s, z that when θ is an
appropriate rational function of s and z both s and z are rationally
expressible, in virtue of ƒ(s, z) = 0 in terms of θ, the integral
∫R(s, z)dz is reducible to a form ∫H(θ)dθ, where H(θ) is rational
in θ, and can therefore also be evaluated by rational functions
and logarithms of rational functions of s and z. It was natural
to inquire whether a similar theorem holds for integrals
∫R(s, z)dz wherein s² is a cubic polynomial in z. The answer is
in the negative. For instance, no one of the three integrals
| ∫ | dz |
, ∫ | zdz |
, ∫ | dz |
| s | s |
(z − c)s |
can be expressed by rational and logarithms of rational functions
of s and z; but it can be shown that every integral ∫R(s, z)dz
can be expressed by means of integrals of these three types
together with rational and logarithms of rational functions of
s and z (see below under § 20, Elliptic Integrals). A similar
theorem is true when s² = quartic polynomial in z; in fact when
s² = A(z − a) (z − b) (z − c) (z − d), putting y = s(z − a)−2, x = (z − a)−1,
we obtain y2 = cubic polynomial in x. Much less is the theorem
true when the fundamental relation ƒ(s, z) = 0 is of more general
type. There exists then, however, a very general theorem,
known as Abel’s Theorem, which may be enunciated as follows:
Beside the rational function R(s, z) occurring in the integral
∫R(s, z)dz, consider another rational function H(s, z); let
(a1), ... (am) denote the places of the construct associated
with the fundamental equation ƒ(s, z) = 0, for which H(s, z) is
equal to one value A, each taken with its proper multiplicity,
and let (b1), ... (bm) denote the places for which H(s, z) = B,
where B is another value; then the sum of the m integrals
∫ (bi)(ai) R(s, z)dz is equal to the sum of the coefficients of t−1 in the
expansions of the function
| R(s, z) | dz |
λ ( | H(s, z) − B |
), |
| dt | H(s, z) − A |
where λ denotes the generalized logarithmic function, at the
various places where the expansion of R(s, z)dz/dt contains
negative powers of t. This fact may be obtained at once from
the equation
| [ | 1 |
R(s, z) | dz |
]t−1 = 0, |
| H(s, z) − μ | dt |
wherein μ is a constant. (For illustrations see below, under
§ 20, Elliptic Integrals.)
§ 18. Indeterminateness of Algebraic Integrals.—The theorem
that the integral ∫ xa ƒ(z)dz is independent of the path from a to
z, holds only on the hypothesis that any two such paths are
equivalent, that is, taken together from the complete boundary
of a region of the plane within which ƒ(z) is finite and single
valued, besides being differentiable. Suppose that these conditions
fail only at a finite number of isolated points in the finite
part of the plane. Then any path from a to z is equivalent,
in the sense explained, to any other path together with closed
paths beginning and ending at the arbitrary point a each enclosing
one or more of the exceptional points, these closed paths being
chosen, when ƒ(z) is not a single valued function, so that the final
value of ƒ(z) at a is equal to its initial value. It is necessary for
the statement that this condition may be capable of being
satisfied.
For instance, the integral ∫ z1 z−1dz is liable to an additive indeterminateness
equal to the value obtained by a closed path about z = 0,
which is equal to 2πi; if we put u = ∫ z1 z−1dz and consider z as a
function of u, then we must regard this function as unaffected by
the addition of 2πi to its argument u; we know in fact that
z = exp (u) and is a single valued function of u, with the period 2πi.
Or again the integral ∫ z0 (1 + z²)−1dz is liable to an additive indeterminateness
equal to the value obtained by a closed path about
either of the points z = ±i; thus if we put u = ∫ z0 (1 + z²)−1dz, the
function z of u is periodic with period π, this being the function
tan (u). Next we take the integral u = ∫ (z)(0) (1 − z²)−1/2dz, agreeing that
the upper and lower limits refer not only to definite values of z, but
to definite values of z each associated with a definite determination
of the sign of the associated radical (1 − z²)−1/2. We suppose 1 + z,
1 − z each to have phase zero for z = 0; then a single closed circuit
of z = −1 will lead back to z = 0 with (l − z²)1/2 = −1; the additive
indeterminateness of the integral, obtained by a closed path which
restores the initial value of the subject of integration, may be
obtained by a closed circuit containing both the points ±1 in its
interior; this gives, since the integral taken about a vanishing
circle whose centre is either of the points z = ±1 has ultimately
the value zero, the sum
| ∫ −10 | dz |
+ ∫ 0−1 | dz |
+ ∫ 10 | dz |
+ ∫ 01 | dz |
, |
| (1 − z²)1/2 | −(1 − z²)1/2 |
−(1 − z²)1/2 | (1 − z²)1/2 |
where, in each case, (1 − z²)1/2 is real and positive; that is, it gives
or 2π. Thus the additive indeterminateness of the integral is of the
form 2kπ, where k is an integer, and the function z of u, which is
sin (u), has 2π for period. Take now the case
| u = ∫ (z)(z0) | dz |
, |
| √{ (z − a) (z − b) (z − c) (z − d) } |
adopting a definite determination for the phase of each of the
factors z − a, z − b, z − c, z − d at the arbitrary point z0, and supposing
the upper limit to refer, not only to a definite value of z, but also
to a definite determination of the radical under the sign of integration.
From z0 describe a closed loop about the point z = a, consisting,
suppose, of a straight path from z0 to a, followed by a vanishing
circle whose centre is at a, completed by the straight path from a
to z0. Let similar loops be imagined for each of the points b, c, d,
no two of these having a point in common. Let A denote the value
obtained by the positive circuit of the first loop; this will be in fact
equal to twice the integral taken from z0 along the straight path
to a; for the contribution due to the vanishing circle is ultimately
zero, and the effect of the circuit of this circle is to change the sign
of the subject of integration. After the circuit about a, we arrive
back at z0 with the subject of integration changed in sign; let
B, C, D denote the values of the integral taken by the loops enclosing
respectively b, c and d when in each case the initial determination
of the subject of integration is that adopted in calculating
A. If then we take a circuit from z0 enclosing both a and b but
not either c or d, the value obtained will be A − B, and on returning
to z0 the subject of integration will have its initial value. It appears
thus that the integral is subject to an additive indeterminateness
equal to any one of the six differences such as A − B. Of these
there are only two linearly independent; for clearly only A − B,
A − C, A − D are linearly independent, and in fact, as we see by
taking a closed circuit enclosing all of a, b, c, d, we have A − B +
C − D = 0; for there is no other point in the plane beside a, b, c, d
about which the subject of integration suffers a change of sign, and a
circuit enclosing all of a, b, c, d may by putting z = 1/ζ be reduced to a
circuit about ζ = 0 about which the value of the integral is zero.
The general value of the integral for any position of z and the associated
sign of the radical, when we start with a definite determination
of the subject of integration, is thus seen to be of the form
u0 + m(A − B) + n(A − C), where m and n are integers. The value of
A − B is independent of the position of z0, being obtainable by a single
closed positive circuit about a and b only; it is thus equal to twice the
integral taken once from a to b, with a proper initial determination
of the radical under the sign of integration. Similar remarks to the
above apply to any integral ∫ H(z)dz, in which H(z) is an algebraic
function of z; in any such case H(z) is a rational function of z and a
quantity s connected therewith by an irreducible rational algebraic
324
equation ƒ(s, z) = 0. Such an integral ƒK(z, s)dz is called an Abelian
Integral.
§ 19. Reversion of an Algebraic Integral.—In a limited number of
cases the equation u = ∫ [z0 to z] H(z)dz, in which H(z) is an algebraic function
of z, defines z as a single valued function of u. Several cases of this
have been mentioned in the previous section; from what was
previously proved under § 14, Doubly Periodic Functions, it appears
that it is necessary for this that the integral should have at most
two linearly independent additive constants of indeterminateness;
for instance, for an integral
u = ∫ zz0 [(z − a) (z − b) (z − c) (z − d) (z − e) (z − f) ]−1/2dz,
there are three such constants, of the form A − B, A − C, A − D,
which are not connected by any linear equation with integral coefficients,
and z is not a single valued function of u.
§ 20. Elliptic Integrals.—An integral of the form ∫ R(z, s)dz,
where s denotes the square root of a quartic polynomial in z,
which may reduce to a cubic polynomial, and R denotes a
rational function of z and s, is called an elliptic integral.
To each value of z belong two values of s, of opposite sign; starting,
for some particular value of z, with a definite one of these two
values, the sign to be attached to s for any other value of z will be
determined by the path of integration for z. When z is in the neighbourhood
of any finite value z0 for which the radical s is not zero,
if we put z − z0 = t, we can find s − s0 = a power series in t, say
s=s0 + Q(t); when z is in the neighbourhood of a value, a, for which
s vanishes, if we put z = a + t², we shall obtain s = tQ(t), where Q(t) is a
power series in t; when z is very large and s² is a quartic polynomial
in z, if we put z−1 = t, we shall find s−1 = t²Q(t); when z is very large
and s² is a cubic polynomial in z, if we put z−1 = t², we shall find
s−l = t³Q(t). By means of substitutions of these forms the character
of the integral ∫ R(z, s)dz may be investigated for any position of z;
in any case it takes a form ∫ [Ht−m + Kt−m+1 + ... + Pt−1 + R + St + ... ]dt
involving only a finite number of negative powers of t in the subject
of integration. Consider first the particular case ∫ s−1dz; it is easily
seen that neither for any finite nor for infinite values of z can negative
powers of t enter; the integral is everywhere finite, and is said to be
of the first kind; it can, moreover, be shown without difficulty that
no integral ∫ R(z, s)dz, save a constant multiple of ∫ s−1dz, has this
property. Consider next, s² being of the form a0z4 + 4a1z³ + ...,
wherein a0 may be zero, the integral ∫ (a0z² + 2a1z) s−1dz; for any finite
value of z this integral is easily proved to be everywhere finite;
but for infinite values of z its value is of the form At−1 + Q(t), where
Q(t) is a power series; denoting by √a0 a particular square root of a0
when a0 is not zero, the integral becomes infinite for z = ∞ for both
signs of s, the value of A being + √a0 or − √a0 according as s is
√a0·z² (1 + [2a1/a0] z−1 + ... ) or is the negative of this; hence the integral
J1 = ∫ ( [a0z² + 2a1z]/s + √a0) dz becomes infinite when z is infinite, for
the former sign of s, its infinite term being 2√a0·t−1 or 2a0·z,
but does not become infinite for z infinite for the other sign of s.
When a0 = 0 the signs of s for z = ∞ are not separated, being obtained
one from the other by a circuit of z about an infinitely large circle,
and the form obtained represents an integral becoming infinite as
before for z = ∞, its infinite part being 2√a1·t−1 or 2√a1·√z. Similarly
if z0 be any finite value of z which is not a root of the polynomial
ƒ(z) to which s² is equal, and s0 denotes a particular one of the determinations
of s for z=z0, the integral
| J2 = ∫ { | s²0 + ½(z − z0) ƒ′(z0) |
+ | s0 |
} dz, |
| (z − z0)² s | (z − z0)² |
wherein ƒ′(z) = dƒ(z)/dz, becomes infinite for z = z0, s = s0, but not for
z = z0, s = −s0. its infinite term in the former case being the negative of
2s0(z − z0). For no other finite or infinite value of z is the integral
infinite. If z = θ be a root of ƒ(z), in which case the corresponding
value of s is zero, the integral
| J3 = ½ƒ′(θ) ∫ | dz |
| (z − θ) s |
becomes infinite for z=0, its infinite part being, if z − θ = t², equal to
−[ƒ′(θ)]½ t−1: and this integral is not elsewhere infinite. In each
of these cases, of the integrals J1, J2, J3, the subject of integration
has been chosen so that when the integral is written near its point of
infinity in the form ∫[At−2 + Bt−1 + Q(t)] dt, the coefficient B is zero,
so that the infinity is of algebraic kind, and so that, when there are
two signs distinguishable for the critical value of z, the integral
becomes infinite for only one of these. An integral having only
algebraic infinities, for finite or infinite values of z, is called an
integral of the second kind, and it appears that such an integral
can be formed with only one such infinity, that is, for an infinity
arising only for one particular, and arbitrary, pair of values (s, z)
satisfying the equation s² = ƒ(z), this infinity being of the first order.
A function having an algebraic infinity of the mth order (m > 1),
only for one sign of s when these signs are separable, at (1) z = ∞,
(2) z = z0, (3) z = a, is given respectively by (s d/dz)m−1 J1, (s d/dz)m−1 J2,
(s d/dz)m−1 J3, as we easily see. If then we have any elliptic integral
having algebraic infinities we can, by subtraction from it of an
appropriate sum of constant multiples of J1, J2, J3 and their differential
coefficients just written down, obtain, as the result, an integral
without algebraic infinities. But, in fact, if J, J1 denote any two
of the three integrals J1, J2, J3, there exists an equation AJ + BJ′ +
Cƒs−1dz = rational function of s, z, where A, B, C are properly chosen
constants. For the rational function
is at once found to become infinite for (z0, s0), not for (z0, −s0), its
infinite part for the first point being 2s/(z − z0), and to become
infinite for z infinitely large, and one sign of s only when these are
separable, its infinite part there being 2z √a0 or 2 √a1 √z when a0 = 0.
It does not become infinite for any other pair (z, s) satisfying the
relation s2 = ƒ(z); this is in accordance with the easily verified
equation
| s + s0 |
+ z √a0 − J1 + J2 + (a0z02 + 2a1z0) ∫ | dz |
= 0; |
| z − z0 | s |
and there exists the analogous equation
| s |
+ z √a0 − J1 + J3 + (a0θ2 + 2a1θ) ∫ | dz |
. |
| z − θ | s |
Consider now the integral
| P = ∫ ( | s + s0 |
+ z √a0 ) | dz |
; |
| z − z0 | 2s |
this is at once found to be infinite, for finite values of z, only for
(z0, s0), its infinite part being log (z − z0), and for z = ∞, for one sign
of s only when these are separable, its infinite part being −log t,
that is −log z when a0 ≠ 0, and −log (z1/2) when a0 = 0. And, if
ƒ(θ) = 0, the integral
| P1 = ∫ ( | s |
+ z √a0 ) | dz |
| z − θ | 2s |
is infinite at z = θ, s = 0 with an infinite part log t, that is log (z − θ)1/2,
is not infinite for any other finite value of z, and is infinite like P for
z = ∞. An integral possessing such logarithmic infinities is said
to be of the third kind.
Hence it appears that any elliptic integral, by subtraction from
it of an appropriate sum formed with constant multiples of the
integral J3 and the rational functions of the form (s d/dz)m−1 J1
with constant multiples of integrals such as P or P1, with constant
multiples of the integral u = ∫s−1dz, and with rational functions,
can be reduced to an integral H becoming infinite only for z = ∞,
for one sign of s only when these are separable, its infinite part being
of the form A log t, that is, A log z or A log (z1/2). Such an integral
H = ∫R(z, s)dz does not exist, however, as we at once find by writing
R(z, s) = P(z) + sQ(z), where P(z), Q(z) are rational functions of z,
and examining the forms possible for these in order that the integral
may have only the specified infinity. An analogous theorem holds
for rational functions of z and s; there exists no rational function
which is finite for finite values of z and is infinite only for z = ∞
for one sign of s and to the first order only; but there exists a
rational function infinite in all to the first order for each of two or
more pairs (z, s), however they may be situated, or infinite to the
second order for an arbitrary pair (z, s); and any rational function
may be formed by a sum of constant multiples of functions such as
| s + s0 |
+ z √a0 or | s |
+ z √a0 |
| z − z0 | z − θ |
and their differential coefficients.
The consideration of elliptic integrals is therefore reducible to
that of the three
| u = ∫ | dz |
, J = ∫ ( | a0z2 + 2a1z |
+ z √a0 ) dz, P = ∫ ( | s + s0 |
+ z √a0 ) | dz |
| s | s |
z − z0 | 2s |
respectively of the first, second and third kind. Now the equation
s2 = a0z4 + ... = a0 (z − θ) (z − φ) (z − ψ) (z − χ), by putting
y = 2s (z − θ)−2 [a0 (θ − φ) (θ − ψ) (θ − χ) ]−1/2
| x = | 1 |
+ | 1 |
( | 1 |
+ | 1 |
+ | 1 |
) |
| z − θ | 3 |
θ − φ | θ − ψ |
θ − χ |
is at once reduced to the form y2 = 4x3 − g2x − g3 = 4(x − e1) (x − e2) (x − e3),
say; and these equations enable us to express s and z rationally
in terms of x and y. It is therefore sufficient to consider three
elliptic integrals
| u = ∫ | dx |
, J = ∫ | xdx |
, P = ∫ | y + y0 |
| dx |
. |
| y | y |
x − x0 | 2y |
Of these consider the first, putting
where the limits involve not only a value for x, but a definite sign
for the radical y. When x is very large, if we put x−1 = t2, y−1 =
2t3 (1 − ¼ g2t4 − ¼ g3t6)−1/2, we have
u = ∫ t0 (1 + 1⁄8 g2t4 + ... ) dt = t + 1⁄40 g2t5 + ...,
325
whereby a definite power series in u, valid for sufficiently small value
of u, is found for t, and hence a definite power series for x, of the form
x = u−2 + 1⁄20 g2u2 + ...
Let this expression be valid for 0 < |u| < R, and the function defined
thereby, which has a pole of the second order for u=0, be denoted
by φ(u). In the range in question it is single valued and satisfies the
differential equation
[φ′(u)]2 = 4[φ(u)]3 − g2φ(u) − g3;
in terms of it we can write x = φ(u), y = − φ′(u), and, φ′(u) being an
odd function, the sign attached to y in the original integral for x = ∞
is immaterial. Now for any two values u, v in the range in question
consider the function
| F(u, v) = ¼ [ | φ′(u) − φ′(v) |
]2 − φ(u) − φ(v); |
| φ(u) − φ(v) |
it is at once seen, from the differential equation, to be such that
∂F/∂u = ∂F/∂v; it is therefore a function of u + v; supposing
|u + v| < R we infer therefore, by putting v = 0, that
| φ(u + v) = ¼ [ | φ′(u) − φ′(v) |
]2 − φ(u) − φ(v). |
| φ(u) − φ(v) |
By repetition of this equation we infer that if u1, ... un be any arguments
each of which is in absolute value less than R, whose sum is also
in absolute value less than R, then φ(u1 + ... + un) is a rational
function of the 2n functions φ(us), φ′(us); and hence, if |u| < R,
that
| φ(u) = H [ φ ( | u |
), φ′ ( | u |
) ], |
| n | n |
where H is some rational function of the arguments φ(u/n), φ′(u/n).
In fact, however, so long as |u/n| < R, each of the functions φ(u/n),
φ′(u/n) is single valued and without singularity save for the pole at
u=0; and a rational function of single valued functions, each of
which has no singularities other than poles in a certain region, is
also a single valued function without singularities other than poles in
this region. We infer, therefore, that the function of u expressed by
H [φ(u/n), φ′(u/n)] is single valued and without singularities other
than poles so long as |u| < nR; it agrees with φ(u) when |u| < R, and
hence furnishes a continuation of this function over the extended
range |u| < nR. Moreover, from the method of its derivation, it
satisfies the differential equation [φ′(u)]2 = 4[φ(u)]3 − g2φ(u) − g3. This
equation has therefore one solution which is a single valued monogenic
function with no singularities other than poles for any finite
part of the plane, having in particular for u = 0, a pole of the second
order; and the method adopted for obtaining this near u=0 shows
that the differential equation has no other such solution. This,
however, is not the only solution which is a single valued meromorphic
function, a the functions φ(u + α), wherein α is arbitrary,
being such. Taking now any range of values of u, from u = 0,
and putting for any value of u, x = φ(u), y = −φ′(u), so that
y2=4x3-g2x-g3, we clearly have
conversely if x0 = φ(u0), y0 = −φ′(u0) and ξ, η be any values satisfying
η2 = 4ξ2 − g2ξ − g3, which are sufficiently near respectively to x0, y0,
while v is defined by
| v − u0 = − ∫ (ξ, η)(x0, y0) | dξ |
, |
| η |
then ξ, η are respectively φ(v) and −φ′(v); for this equation leads
to an expansion for ξ − x0 in terms of v = u0 and only one such expansion,
and this is obtained by the same work as would be necessary
to expand φ(v) when v is near to u0; the function φ(u) can therefore
be continued by the help of this equation, from v = u0, provided
the lower limit of |ξ − x0| necessary for the expansions is not zero
in the neighbourhood of any value (x0, y0). In fact the function φ(u)
can have only a finite number of poles in any finite part of the plane
of u; each of these can be surrounded by a small circle, and in the
portion of the finite part of the plane of u which is outside these
circles, the lower limit of the radii of convergence of the expansions
of φ(u) is greater than zero; the same will therefore be the case
for the lower limit of the radii |ξ − x0| necessary for the continuations
spoken of above provided that the values of (ξ, η) considered do not
lead to infinitely increasing values of v; there does not exist, however,
any definite point (ξ0, η0) in the neighbourhood of which the
integral ∫ (ξ, η)(x0, y0) dξ/η increases indefinitely, it is only by a path of infinite
length that the integral can so increase. We infer therefore that
if (ξ, η) be any point, where η2 = 4ξ3 − g2ξ − g3, and v be defined by
then ξ = φ(v) and η = −φ′(v). Thus this equation determines (ξ, η)
without ambiguity. In particular the additive indeterminatenesses
of the integral obtained by closed circuits of the point of integration
are periods of the function φ(u); by considerations advanced above
it appears that these periods are sums of integral multiples of two
which may be taken to be
| ω = 2 ∫ ∞e1 | dx |
, ω′ = 2 ∫ ∞e3 | dx |
; |
| y | y |
these quantities cannot therefore have a real ratio, for else, being
periods of a monogenic function, they would, as we have previously
seen, be each integral multiples of another period; there would
then be a closed path for (x, y), starting from an arbitrary point
(x0, y0), other than one enclosing two of the points (e1, 0), (e2, 0),
(e3, 0), (∞, ∞), which leads back to the initial point (x0, y0), which is
impossible. On the whole, therefore, it appears that the function
φ(u) agrees with the function ℜ(u) previously discussed, and the
discussion of the elliptic integrals can be continued in the manner
given under § 14, Doubly Periodic Functions.
§ 21. Modular Functions.—One result of the previous theory
is the remarkable fact that if
| ω = 2 ∫ ∞e1 | dx |
, ω′ = 2 ∫ ∞e3 | dx |
; |
| y | y |
where y2 = 4(x − e1) (x − e2) (x − e3), then we have
e1 = (½ω)−2 + Σ′ {[(m + ½) ω + m′ω′]−2 − [mω + m′ω′]−2},
and a similar equation for e3, where the summation refers to
all integer values of m and m′ other than the one pair m = 0,
m′ = 0. This, with similar results, has led to the consideration
of functions of the complex ratio ω′/ω.
It is easy to see that the series for ℜ(u), u−2 + Σ′[(u + mω + m′ω′)2 −
(mω + m′ω′)2], is unaffected by replacing ω, ω′ by two quantities Ω, Ω′
equal respectively to pω + qω′, p′ω′ + q′ω′, where p, q, p′, q′ are any
integers for which pq′ − p′q = ±1; further it can be proved that all
substitutions with integer coefficients Ω = pω + qω′, Ω′ = p′ω + q′ω′,
wherein pq′ − p′q = 1, can be built up by repetitions of the two particular
substitutions (Ω = −ω′, Ω′ = ω), (Ω = ω, Ω′ = ω + ω′). Consider
the function of the ratio ω′/ω expressed by
h = −ℜ (½ω′) / ℜ(½ω);
it is at once seen from the properties of the function ℜ(u) that by
the two particular substitutions referred to we obtain the corresponding
substitutions for h expressed by
h′ = 1/h, h′ = 1 − h;
thus, by all the integer substitutions Ω = pω + qω′, Ω′ = p′ω + q′ω′, in
which pq′ − p′q = 1, the function h can only take one of the six values
h, 1/h, 1 − h, 1/(1 − h), h/(h − 1), (h − 1)/h, which are the roots of an
equation in θ,
| (1 − θ + θ2)3 |
= | (1 − h + h2)3 |
; |
| θ2(1 − θ)2 | h2(1 − h)2 |
the function of τ, = ω′/ω, expressed by the right side, is thus
unaltered by every one of the substitutions τ′ = (p′ + q′τ / p + qτ), wherein
p, q, p′, q′ are integers having pq′ − p′q = 1. If the imaginary part
σ, of τ, which we may write τ = ρ + iσ, is positive, the imaginary part
of τ′, which is equal to σ(pq′ − p′q)/[(p + qρ)2 + q2σ2], is also positive;
suppose σ to be positive; it can be shown that the upper half of the
infinite plane of the complex variable τ can be divided into regions,
all bounded by arcs of circles (or straight lines), no two of these
regions overlapping, such that any substitution of the kind under
consideration, τ′ = (p′ + q′τ)/(p + qτ) leads from an arbitrary point τ,
of one of these regions, to a point τ′ of another; taking τ = ρ + iσ,
one of these regions may be taken to be that for which −½ < ρ < ½,
ρ2 + σ2 > 1, together with the points for which ρ is negative on the
curves limiting this region; then every other region is obtained
from this so-called fundamental region by one and only one of the
substitutions τ = (p′ + q′τ)/(p + qτ), and hence by a definite combination
of the substitutions τ′ = −1/τ, τ′ = 1 + τ. Upon the infinite half
plane of τ, the function considered above,
| z(τ) = 4⁄27 | [ℜ2 (½ω) + ℜ (z(½ω) ℜ (½ω′) + ℜ2 (½ω′)]3 |
|
| ℜ2 (½ω) ℜ2 (½ω′) [ℜ (½ω) + ℜ (½ω′]2 |
is a single valued monogenic function, whose only essential singularities
are the points τ′ = (p′ + q′τ)/(p + qτ) for which τ = ∞, namely
those for which τ′ is any real rational value; the real axis is thus a
line over which the function z(τ) cannot be continued, having an
essential singularity in every arc of it, however short; in the fundamental
region, z(τ) has thus only the single essential singularity,
r = ρ + iσ, where σ = ∞; in this fundamental region z(τ) takes any
assigned complex value just once, the relation z(τ′) = z(τ) requiring,
as can be shown, that τ′ is of the form (p′ + q′τ)/(p + qτ), in which
p, q, p′, q′ are integers with pq′ − p′q = 1; the function z(τ) has thus
a similar behaviour in every other of the regions. The division of
the plane into regions is analogous to the division of the plane,
in the case of doubly periodic functions, into parallelograms; in that
case we considered only functions without essential singularities,
and in each of the regions the function assumed every complex value
twice, at least. Putting, as another function of τ, J(τ) = z(τ) [z(τ) − 1],
it can be shown that J(τ) = 0 for τ = exp (2⁄3πi), that J(τ) = 1 for τ = i,
these being values of τ on the boundary of the fundamental region;
like z(τ) it has an essential singularity for τ = ρ + iσ, σ = + ∞. In the
326
theory of linear differential equations it is important to consider the
inverse function τ(J); this is infinitely many valued, having a cycle
of three values for circulation of J about J = 0 (the circuit of this
point leading to a linear substitution for τ of period 3, such as
τ′ = −(1 + τ)−1), having a cycle of two values about J = 1 (the circuit
leading to a linear substitution for τ of period 2, such as τ′ = −τ−1),
and having a cycle of infinitely many values about J = ∞ (the circuit
leading to a linear substitution for τ which is not periodic, such as
τ′ = 1 + τ). These are the only singularities for the function τ(J).
Each of the functions
| [J(τ)]1/3, [J(τ) − 1]1/2, [ − | ℜ (½ω) + 2ℜ (½ω′) |
]1/8, |
| ℜ (½ω) − ℜ (½)ω′) |
beside many others (see below), is a single valued function of τ,
and is expressible without ambiguity in terms of the single valued
function of τ,
| η(τ) = exp ( | iπτ |
) Π ∞n=1 [1 − exp (2iπnτ)] = exp ( | iπτ |
) Σ ∞m=−∞ (−1)m exp [(3m2 + m) iπτ]. |
| 12 | 12 |
It should be remarked, however, that η(τ) is not unaltered by all
the substitutions we have considered; in fact
η(−τ−1) = (−iτ) ½η (τ), η(1 + τ) = exp (1⁄12 iπ) η(τ).
The aggregate of the substitutions τ′ = (p′ + q′τ)/(p + qτ), wherein
p, q, p′, q′ are integers with pq′ − p′q = 1, represents a Group; the
function J(τ), unaltered by all these substitutions, is called a Modular
Function. More generally any function unaltered by all the substitutions
of a group of linear substitutions of its variable is called an
Automorphic Function. A rational function, of its variable h, of this
character, is the function (1 − h + h2)3 h−2(1 − h)−2 presenting itself
incidentally above; and there are other rational functions with a
similar property, the group of substitutions belonging to any one
of these being, what is a very curious fact, associable with that of
the rotations of one of the regular solids, about an axis through its
centre, which bring the solid into coincidence with itself. Other
automorphic functions are the double periodic functions already
discussed; these, as we have seen, enable us to solve the algebraic
equation y2 = 4x3 − g2x − g3 (and in fact many other algebraic equations,
see below, under § 23, Geometrical Applications of Elliptic
Functions) in terms of single valued functions x = ℜ(u), y = −ℜ′(u).
A similar utility, of a more extended kind, belongs to automorphic
functions in general; but it can be shown that such functions
necessarily have an infinite number of essential singularities except
for the simplest cases.
The modular function J(τ) considered above, unaltered by the
group of linear substitutions τ′ = (p′ + q′τ) / (p + qτ), where p, q, p′, q′
are integers with pq′ − p′q = 1, may be taken as the independent
variable x of a differential equation of the third order, of the form
| s″′ |
− | 3 |
( | s″ |
)2 = | 1 − α2 |
+ | 1 − β2 |
+ | α2 + β2 − γ2 − 1 |
, |
| s′ | 2 |
s′ | 2(x − 1)2 |
2x2 | 2x (x − 1) |
where s′ = ds/dx, &c., of which the dependent variable s is equal to τ.
A differential equation of this form is satisfied by the quotient of
two independent integrals of the linear differential equation of the
second order satisfied by the hypergeometric functions. If the
solution of the differential equation for s be written s(α,β,γ, x),
we have in fact τ = s(½, 1⁄3, 0, J). If we introduce also the function
of τ given by
| λ = | 2ℜ (½ω′) + ℜ (½ω) |
, |
| ℜ (½ω′) − ℜ (½ω) |
we similarly have τ = s(0, 0, 0, λ); this function λ is a single valued
function of τ, which is also a modular function, being unaltered by a
group of integral substitutions also of the form τ′ = (p′ + q′τ)/(p + qτ),
with pq′ − p′q = 1, but with the restriction that p′ and q are even
integers, and therefore p and q′ are odd integers. This group is
thus a subgroup of the general modular group, and is in fact of the
kind called a self-conjugate subgroup. As in the general case this
subgroup is associated with a subdivision of the plane into regions
of which any one is obtained from a particular region, called the
fundamental region, by a particular one of the substitutions of the
subgroup. This fundamental region, putting τ = ρ + iσ, may be
taken to be that given by −1 < ρ < 1, (ρ + ½)2 + σ2 > ¼, (ρ − ½)2 + σ2 > ¼,
and is built up of six of the regions which arose for the general
modular group associated with J(τ). Within this fundamental
region, λ takes every complex value just once, except the values
λ = 0, 1, ∞, which arise only at the angular points τ = 0, τ = ∞, τ = − 1
and the equivalent point τ = 1; these angular points are essential
singularities for the function λ(τ). For λ(τ) as for J(τ), the region of
existence is the upper half plane of τ, there being an essential singularity
in every length of the real axis, however short.
If, beside the plane of τ, we take a plane to represent the values of
λ, the function τ = s(0, 0, 0, λ) being considered thereon, the values of
τ belonging to the interior of the fundamental region of the τ-plane
considered above, will require the consideration of the whole of the
λ-plane taken once with the exception of the portions of the real
axis lying between −∞ and 0 and between 1 and +∞, the two
sides of the first portion corresponding to the circumferences of the
τ-plane expressed by (ρ + ½)2 + σ2 = ¼, (ρ − ½)2 + σ2 = ¼, while the two
sides of the latter portion, for which λ is real and > 1, correspond
to the lines of the τ-plane expressed by ρ = ±1. The line for
which λ is real, positive and less than unity corresponds to the
imaginary axis of the τ-plane, lying in the interior of the fundamental
region. All the values of τ = s(0, 0, 0, λ) may then be derived
from those belonging to the fundamental region of the τ-plane by
making λ describe a proper succession of circuits about the points
λ = 0, λ = 1; any such circuit subjects τ to a linear substitution
of the subgroup of τ considered, and corresponds to a change of τ
from a point of the fundamental region to a corresponding point
of one of the other regions.
§ 22. A Property of Integral Functions deduced from the Theory
of Modular Functions.—Consider now the function exp(z),
for finite values of z; for such values of z, exp(z) never vanishes,
and it is impossible to assign a closed circuit for z in the finite
part of the plane of z which will make the function λ = exp(z)
pass through a closed succession of values in the plane of λ
having λ = 0 in its interior; the function s[0, 0, 0, exp(z)],
however z vary in the finite part of the plane, will therefore never
be subjected to those linear substitutions imposed upon
s(0, 0, 0, λ) by a circuit of λ about λ = 0; more generally, if
φ(z) be an integral function of z, never becoming either zero or
unity for finite values of z, the function λ = φ(z), however z vary
in the finite part of the plane, will never make, in the plane of λ,
a circuit about either λ = 0 or λ = 1, and s(0, 0, 0, λ), that is
s[0, 0, 0, φ(z)], will be single valued for all finite values of z;
it will moreover remain finite, and be monogenic. In other
words, s[0, 0, 0, φ(z)] is also an integral function—whose imaginary
part, moreover, by the property of s(0, 0, 0, λ), remains positive
for all finite values of z. In that case, however, exp {is[0, 0, 0, φ(z)]}
would also be an integral function of z with modulus less than
unity for all finite values of z. If, however, we describe a circle
of radius R in the z plane, and consider the greatest value of the
modulus of an integral function upon this circle, this certainly
increases indefinitely as R increases. We can infer therefore
that an integral function φ(z) which does not vanish for any finite
value of z, takes the value unity and hence (by considering the
function A−1φ(z)) takes every other value for some definite value
of z; or, an integral function for which both the equations
φ(z) = A, φ(z) = B are unsatisfied by definite values of z, does not
exist, A and B being arbitrary constants.
A similar theorem can be proved in regard to the values assumed
by the function φ(z) for points z of modulus greater than R, however
great R may be, also with the help of modular functions. In general
terms it may be stated that it is a very exceptional thing for an
integral function not to assume every complex value an infinite
number of times.
Another application of modular functions is to prove that the
function s(α, β, γ, λ) is a single valued function of τ = s(0, 0, 0, λ);
for, putting τ′ = (τ − i)/(τ + i), the values of τ′ which correspond to the
singular points λ = 0, 1, ∞ of s(α, β, γ, λ), though infinite in number,
all lie on the circumference of the circle |τ′| = 1, within which therefore
s(α, β, γ, x) is expressible in a form Σ ∞n=0 anτ′n. More generally any
monogenic function of λ which is single valued save for circuits of
the points λ = 0, 1, ∞, is a single valued function of τ = s(0, 0, 0, λ).
Identifying λ with the square of the modulus in Legendre’s form of
the elliptical integral, we have τ = iK′/K, where
| K = ∫ 10 | dt |
, K′ = ∫ 10 | dt |
; |
| √[1 − t2] [1 − λt2] | √[1 − t2] [1 − (1 − λ) t2] |
functions such as λ1/4, (1 − λ)1/4, [λ(1 − λ)]1/4, which have only λ = 0, 1, ∞
as singular points, were expressed by Jacobi as power series in q = eiπτ,
and therefore, at least for a limited range of values of τ, as single
valued functions of τ; it follows by the theorem given that any
product of a root of λ and a root of 1 − λ is a single valued function
of τ. More generally the differential equation
| x(1 − x) | d2y |
+ [γ − (α + β + 1)x] | dy |
− αβγ = 0 |
| dx2 | dx |
may be solved by expressing both the independent and dependent
variables as single valued functions of a single variable τ, the expression
for the independent variable being x = λ(τ).
§ 23. Geometrical Applications of Elliptic Functions.—Consider
any irreducible algebraic equation rational in x, y, f(x, y) = 0, of
such a form that the equation represents a plane curve of order
n with ½n(n − 3) double points; taking upon this curve n− 3
arbitrary fixed points, draw through these and the double
points the most general curve of order n − 2; this will intersect
327
ƒ in n(n − 2) − n(n − 3) − (n − 3) = 3 other points, and will contain
homogeneously at least ½(n − 1)n − ½n(n − 3) −(n − 3) = 3 arbitrary
constants, and so will be of the form λφ + λ1φ1 + λ2φ2 +
... = 0, wherein λ3, λ4, ... are in general zero. Put now
ξ = φ1/φ, η = φ2/φ and eliminate x, y between these equations and
ƒ(x, y) = 0, so obtaining a rational irreducible equation F(ξ, η) = 0,
representing a further plane curve. To any point (x, y) of ƒ will
then correspond a definite point (ξ, η) of F.
For a general position of (x, y) upon ƒ the equations
φ1(x′, x′)/φ(x′, x′) = φ1(x, y)/φ(x, y), φ2(x′, x′)/φ(x′, x′) = φ2(x, y)/φ(x, y),
subject to ƒ(x′, x′) = 0, will have the same number of solutions (x′, x′);
if their only solution is x′ = x, x′ = y, then to any position (ξ, η) of F
will conversely correspond only one position (x, y) of ƒ. If these
equations have another solution beside (x, y), then any curve
λφ + λ1φ1 + λ2φ2 = 0 which passes (through the double points of ƒ
and) through the n − 2 points of ƒ constituted by the fixed n− 3
points and a point (x0, y0), will necessarily pass through a further
point, say (x0′, y0′), and will have only one further intersection with
ƒ; such a curve, with the n − 2 assigned points, beside the double
points, of ƒ, will be of the form μψ + μ1ψ1 + ... = 0, where μ2, μ3, ...
are generally zero; considering the curves ψ + tψ1 = 0, for variable t,
one of these passes through a further arbitrary point of ƒ, by choosing
t properly, and conversely an arbitrary value of t determines a single
further point of ƒ; the co-ordinates of the points of ƒ are thus
rational functions of a parameter t, which is itself expressible rationally
by the co-ordinates of the point; it can be shown algebraically
that such a curve has not ½(n − 3)n but ½(n − 3)n + 1 double points.
We may therefore assume that to every point of F corresponds
only one point of ƒ, and there is a birational transformation between
these curves; the coefficients in this transformation will involve
rationally the co-ordinates of the n− 3 fixed points taken upon ƒ,
that is, at the least, by taking these to be consecutive points, will
involve the co-ordinates of one point of ƒ, and will not be rational
in the coefficients of ƒ unless we can specify a point of ƒ whose co-ordinates
are rational in these. The curve F is intersected by a
straight line aξ + bη + c = 0 in as many points as the number of
unspecified intersections of ƒ with aφ + bφ1 + cφ2 = 0, that is, 3; or F
will be a cubic curve, without double points.
Such a cubic curve has at least one point of inflection Y, and if a
variable line YPQ be drawn through Y to cut the curve again in P
and Q, the locus of a point R such that YR is the harmonic mean of
YP and YQ, is easily proved to be a straight line. Take now a
triangle of reference for homogeneous co-ordinates XYZ, of which
this straight line is Y = 0, and the inflexional tangent at Y is Z = 0;
the equation of the cubic curve will then be of the form
ZY² = aX³ + bX²Z + cXZ² + dZ³;
by putting X equal to λX + μZ, that is, choosing a suitable line
through Y to be X = 0, and choosing λ properly, this is reduced to
the form
ZY² = 4X³ − g2XZ² − g3Z³,
of which a representation is given, valid for every point, in terms of
the elliptic functions ℜ(u), ℜ′(u), by taking X = Zℜ(u), Y = Zℜ′(u).
The value of u belonging to any point is definite save for sums of
integral multiples of the periods of the elliptic functions, being
given by
| u = ∫ (x)(∞) | ZdX − XdZ |
, |
| ZY |
where (∞) denotes the point of inflection.
It thus appears that the co-ordinates of any point of a plane curve,
ƒ, of order n with ½(n − 3)n double points are expressible as elliptic
functions, there being, save for periods, a definite value of the argument
u belonging to every point of the curve. It can then be shown
that if a variable curve, φ, of order m be drawn, passing through
the double points of the curve, the values of the argument u at the
remaining intersections of φ with ƒ, have a sum which is unaffected
by variation of the coefficients of φ, save for additive aggregates
of the periods. In virtue of the birational transformation this
theorem can be deduced from the theorem that if any straight line
cut the cubic y² = 4x³ − g2x − g3, in points (u1), (u2), (u3), the sum
u1 + u2 + u3 is zero, or a period; or the general theorem is a corollary
from Abel’s theorem proved under § 17, Integrals of Algebraic
Functions. To prove the result directly for the cubic we remark
that the variation of one of the intersections (x, y) of the cubic
with the straight line y = mx + n, due to a variation δm, δn in m
and n, is obtained by differentiation of the equation for the three
abscissae, namely the equation
F(x) = 4x³ − g2x − g3 − (mx + n)² = 0,
and is thus given by
and the sum of three such fractions as that on the right for the three
roots of F(x) = 0 is zero; hence u1 + u2 + u3 is independent of the
straight line considered; if in particular this become the inflexional
tangent each of u1, u2, u3 vanishes. It may be remarked in passing
that x1 + x2 + x3 = ¼m², and hence is ¼ {(y1 − y2)/(x1 − x2)}²; so that we
have another proof of the addition equation for the function ℜ(u).
From this theorem for the cubic curve many of its geometrical
properties, as for example those of its inflections, the properties of
inscribed polygons, of the three kinds of corresponding points, and
the theory of residuation, are at once obvious. And similar results
hold for the curve of order n with ½(n − 3)n double points.
§ 24. Integrals of Algebraic Functions in Connexion with the
Theory of Plane Curves.—The developments which have been
explained in connexion with elliptic functions may enable the
reader to appreciate the vastly more extensive theory similarly
arising for any algebraical irrationality, ƒ(x, y) = o.
The algebraical integrals ∫ R(x, y)dx associated with this may as
before be divided into those of the first kind, which have no infinities,
those of the second kind, possessing only algebraical infinities,
and those of the third kind, for which logarithmic infinities enter.
Here there is a certain number, p, greater than unity, of linearly
independent integrals of the first kind; and this number p is unaltered
by any birational transformation of the fundamental equation
ƒ(x, y) = 0; a rational function can be constructed with poles of the
first order at p + 1 arbitrary positions (x, y), satisfying ƒ(x, y) = 0,
but not with a fewer number unless their positions are chosen
properly, a property we found for the case p = 1; and p is the number
of linearly independent curves of order n − 3 passing through the
double points of the curve of order n expressed by ƒ(x, y) = 0. Again
any integral of the second kind can be expressed as a sum of p
integrals of this kind, with poles of the first order at arbitrary
positions, together with rational functions and integrals of the first
kind; and an integral of the second kind can be found with one
pole of the first order of arbitrary position, and an integral of the
third kind with two logarithmic infinities, also of arbitrary position;
the corresponding properties for p = 1 are proved above.
There is, however, a difference of essential kind in regard to the
inversion of integrals of the first kind; if u = ∫R(x, y)dx be such an
integral, it can be shown, in common with all algebraic integrals
associated with ƒ(x, y) = 0, to have 2p linearly independent additive
constants of indeterminateness; the upper limit of the integral
cannot therefore, as we have shown, be a single valued function
of the value of the integral. The corresponding theorem, if ∫Ri(x, y)dx
denote one of the integrals of the first kind, is that the p equations
∫ Ri (x1, y1)dx1 + ... + ∫ Ri (xp, yp)dxp = ui,
determine the rational symmetric functions of the p positions (x1, y1),
... (xp, yp) as single valued functions of the p variables, u1, ... up.
It is thus necessary to enter into the theory of functions of several
independent variables; and the equation ƒ(x, y) = 0 is thus not,
in this way, capable of solution by single valued functions of one
variable. That solution in fact is to be sought with the help of
automorphic functions, which, however, as has been remarked,
have, for p > 1, an infinite number of essential singularities.
§ 25. Monogenic Functions of Several Independent Variables.—A
monogenic function of several independent complex variables
ui, ... up is to be regarded as given by an aggregate of power
series all obtainable by continuation from any one of them in a
manner analogous to that before explained in the case of one
independent variable. The singular points, defined as the
limiting points of the range over which such continuation is
possible, may either be poles, or polar points of indetermination,
or essential singularities.
A pole is a point (u(0)1, ... u(0)p) in the neighbourhood of which the
function is expressible as a quotient of converging power series in
u1 − u(0)1 ... up − u(0)p; of these the denominator series D must
vanish at (u(0)1, ... u(0)p), since else the fraction is expressible as a
power series and the point is not a singular point, but the numerator
series N must not also vanish at (u(0)1, ... u(0)p), or if it does, it must
be possible to write D = MD0, N = MN0, where M is a converging
power series vanishing at (u(0)1, ...u(0)p), and N0 is a converging power
series, in (u1 − u(0)1 ... up − u(0)p), not so vanishing. A polar point
of indetermination is a point about which the function can be
expressed as a quotient of two converging power series, both of
which vanish at the point. As in such a simple case as (Ax + By)/
(ax + by), about x = 0, y = 0, it can be proved that then the function
can be made to approach to any arbitrarily assigned value by
making the variables u1, ... up approach to u(0)1, ... u(0)p by a proper
path. It is the necessary existence of such polar points of indetermination,
which in case p > 2 are not merely isolated points,
which renders the theory essentially more difficult than that of
functions of one variable. An essential singularity is any which
does not come under one of the two former descriptions and includes
very various possibilities. A point at infinity in this theory is one
for which any one of the variables u1, ... up is indefinitely great;
such points are brought under the preceding definitions by means
328
of the convention that for u(0)i = ∞, the difference ui − u(0)i is to be
understood to stand for u−1i. This being so, a single valued function
of u1, ... up without essential singularities for infinite or finite values
of the variables can be shown, by induction, to be, as in the case of
p = 1, necessarily a rational function of the variables. A function
having no singularities for finite values of all the variables is as before
called an integral function; it is expressible by a power series
converging for all finite values of the variables; a single valued
function having for finite values of the variables no singularities
other than poles or polar points of indetermination is called a
meromorphic function; as for p = 1 such a function can be expressed
as a quotient of two integral functions having no common zero
point other than the points of indetermination of the function;
but the proof of this theorem is difficult.
The single valued functions which occur, as explained above, in
the inversion of algebraic integrals of the first kind, for p > 1, are
meromorphic. They must also be periodic, unaffected that is when
the variables u1, ... up are simultaneously increased each by a
proper constant, these being the additive constants of indeterminateness
for the p integrals ∫ Ri(x, y)dx arising when (x, y) makes a closed
circuit, the same for each integral. The theory of such single valued
meromorphic periodic functions is simpler than that of meromorphic
functions of several variables in general, as it is sufficient to consider
only finite values of the variables; it is the natural extension of
the theory of doubly periodic functions previously discussed. It
can be shown to reduce, though the proof of this requires considerable
developments of which we cannot speak, to the theory of a single
integral function of u1, ... up, called the Theta Function. This is
expressible as a series of positive and negative integral powers of
quantities exp (c1u1), exp (c2u2), ... exp (cpup), wherein c1, ... cp are
proper constants; for p = 1 this theta function is essentially the
same as that above given under a different form (see § 14, Doubly
Periodic Functions), the function σ(u). In the case of p = 1, all
meromorphic functions periodic with the same two periods have
been shown to be rational functions of two of them connected by a
single algebraic equation; in the same way all meromorphic functions
of p variables, periodic with the same sets of simultaneous periods,
2p sets in all, can be shown to be expressible rationally in terms of
p + 1 such periodic functions connected by a single algebraic equation.
Let x1, ... xp, y denote p + 1 such functions; then each of the partial
derivatives dxi/∂ui will equally be a meromorphic function of the
same periods, and so expressible rationally in terms of x1, ... xp, y;
thus there will exist p equations of the form
dxi = R1du1 + ... + Rpdup,
and hence p equations of the form
dui = Hi, 1dx1 + ... + Hi, pdxp,
wherein Hi, j are rational functions of x1, ... xp, y, these being connected
by a fundamental algebraic (rational) equation, say ƒ(x1, ... xp, y)
= 0. This then is the generalized form of the corresponding equation
for p = 1.
§ 26. Multiply-Periodic Functions and the Theory of Surfaces.—The
theory of algebraic integrals ∫ R(x, y)dx, wherein x, y are
connected by a rational equation ƒ(x, y) = 0, has developed
concurrently with the theory of algebraic curves; in particular
the existence of the number p invariant by all birational transformations
is one result of an extensive theory in which curves
capable of birational correspondence are regarded as equivalent;
this point of view has made possible a general theory of what
might otherwise have remained a collection of isolated theorems.
In recent years developments have been made which point to
a similar unity of conception as possible for surfaces, or indeed for
algebraic constructs of any number of dimensions. These developments
have been in two directions, at first followed independently,
but now happily brought into the most intimate connexion. On the
analytical side, E. Picard has considered the possibility of classifying
integrals of the form ∫(Rds + Sdy), belonging to a surface ƒ(x, y, z)
= 0, wherein R and S are rational functions of x, y, z, according as
they are (1) everywhere finite, (2) have poles, which then lie along
curves upon the surface, or (3) have logarithmic infinities, also then
lying along curves, and has brought the theory to a high degree
of perfection. On the geometrical side A. Clebsch and M.
Noether, and more recently the Italian school, have considered the
geometrical characteristics of a surface which are unaltered by birational
transformation. It was first remarked that for surfaces of
order n there are associated surfaces of order n − 4, having properties
in relation thereto analogous to those of curves of order n − 3 for a
plane curve of order n; if such a surface ƒ(x, y, z) = 0 have a double
curve with triple points triple also for the surface, and φ(x, y, z) = 0
be a surface of order n − 4 passing through the double curve, the
double integral
is everywhere finite; and, the most general everywhere finite
integral of this form remains invariant in a birational transformation
of the surface ƒ, the theorem being capable of generalization to
algebraic constructs of any number of dimensions. The number of
linearly independent surfaces of order n − 4, possessing the requisite
particularity in regard to the singular lines and points of the surface,
is thus a number invariant by birational transformation, and
the equality of these numbers for two surfaces is a necessary condition
of their being capable of such transformation. The number
of surfaces of order m having the assigned particularity in regard to
the singular points and lines of the fundamental surface can be given
by a formula for a surface of given singularity; but the value of this
formula for m = n − 4 is not in all cases equal to the actual number
of surfaces of order n − 4 with the assigned particularity, and for a
cone (or ruled surface) is in fact negative, being the negative of the
deficiency of the plane section of the cone. Nevertheless this
number for m = n − 4 is also found to be invariant for birational
transformation. This number, now denoted by pa, is then a second
invariant of birational transformation. The former number, of
actual surfaces of order n − 4 with the assigned particularity in regard
to the singularities of the surface, is now denoted by pg. The
difference pg − pa, which is never negative, is a most important
characteristic of a surface. When it is zero, as in the case of the
general surface of order n, and in a vast number of other ordinary
cases, the surface is called regular.
On a plane algebraical curve we may consider linear series of sets
of points, obtained by the intersection with it of curves λφ + λ1φ1 +
... = 0, wherein λ, λ1, ... are variable coefficients; such a series
consists of the sets of points where a rational function of given poles,
belonging to the construct ƒ(x, y) = 0, has constant values. And we
may consider series of sets of points determined by variable curves
whose coefficients are algebraical functions, not necessarily rational
functions, of parameters. Similarly on a surface we may consider
linear systems of curves, obtained by the intersection with the
given surface of variable surfaces λφ + λ1φ1 + ... = 0, and may
consider algebraic systems, of which the individual curve is given
by variable surfaces whose coefficients are algebraical, not necessarily
rational, functions of parameters. Of a linear series upon a plane
curve there are two numbers manifestly invariant in birational
transformation, the order, which is the number of points forming a
set of the series, and the dimension, which is the number of parameters
λ1/λ, λ2/λ, ... entering linearly in the equation of the series.
The series is complete when it is not contained in a series of the same
order but of higher dimension. So for a linear system of curves
upon a surface, we have three invariants for birational transformation;
the order, being in the number of variable intersections of two
curves of the system, the dimension, being the number of linear
parameters λ1/λ, λ2/λ, ... in the equation for the system, and the
deficiency of the individual curves of the system. Upon any curve
of the linear system the other curves of the system define a linear
series, called the characteristic series; but even when the linear
system is complete, that is, not contained in another linear system
of the same order and higher dimension, it does not follow that the
characteristic series is complete; it may be contained in a series whose
dimension is greater by pg − pa than its own dimension. When this
is so it can be shown that the linear system of curves is contained
in an algebraic system whose dimension is greater by pg − pa than the
dimension of the linear system. The extra p = pg − pa variable parameters
so entering may be regarded as the independent co-ordinates
of an algebraic construct ƒ(y, x1, ... xp) = 0; this construct has the
property that its co-ordinates are single valued meromorphic
functions of p variables, which are periodic, possessing 2p systems
of periods; the p variables are expressible in the forms
ui = ∫ R1(x, y) dx1 + ... + Rp(x, y) dxp,
wherein Ri(x, y) denotes a rational function of x1, ... xp and y.
The original surface has correspondingly p integrals of the form
∫(R dx + S dy), wherein R, S are rational in x, y, z, which are everywhere
finite; and it can be shown that it has no other such integrals.
From this point of view, then, the number p, = pg − pa is, for a surface,
analogous to the deficiency of a plane curve; another analogy
arises in the comparison of the theorems: for a plane curve of zero
deficiency there exists no algebraic series of sets of points which
does not consist of sets belonging to a linear series; for a surface for
which pg − pa = 0 there exists no algebraic system of curves not
contained in a linear system.
But whereas for a plane curve of deficiency zero, the co-ordinates
of the points of the curve are rational functions of a single parameter,
it is not necessarily the case that for a surface having pg − pa = 0 the
co-ordinates of the points are rational functions of two parameters;
it is necessary that pg − pa = 0, but this is not sufficient. For surfaces,
beside the pg linearly independent surfaces of order n − 4
having a definite particularity at the singularities of the surface, it is
useful to consider surfaces of order k(n − 4), also having each a
definite particularity at the singularities, the number of these, not
containing the original surface as component, which are linearly
independent, is denoted by Pk. It can then be stated that a sufficient
condition for a surface to be rational consists of the two conditions
pa = 0, P2 = 0. More generally it becomes a problem to classify
surfaces according to the values of the various numbers which are
invariant under birational transformation, and to determine for
each the simplest form of surface to which it is birationally equivalent.
Thus, for example, the hyperelliptic surface discussed by Humbert,
329
of which the co-ordinates are meromorphic functions of two variables
of the simplest kind, with four sets of periods, is characterized by
pg = 1, pa = −1; or again, any surface possessing a linear system of
curves of which the order exceeds twice the deficiency of the individual
curves diminished by two, is reducible by birational transformation
to a ruled surface or is a rational surface. But beyond
the general statement that much progress has already been made
in this direction, of great interest to the student of the theory of
functions, nothing further can be added here.
Bibliography.—The learner will find a lucid introduction to the
theory in E. Goursat, Cours d’analyse mathématique, t. ii. (Paris,
1905), or, with much greater detail, in A.R. Forsyth, Theory of
Functions of a Complex Variable (2nd ed., Cambridge, 1900); for
logical rigour in the more difficult theorems, he should consult
W.F. Osgood, Lehrbuch der Functionentheorie, Bd. i. (Leipzig, 1906-1907);
for greater precision in regard to the necessary quasi-geometrical
axioms, beside the indications attempted here, he should
consult W.H. Young, The Theory of Sets of Points (Cambridge,
1906), chs. viii.-xiii., and C. Jordan, Cours d’analyse, t. i. (Paris,
1893), chs. i., ii.; a comprehensive account of the Theory of Functions
of Real Variables is by E.W. Hobson (Cambridge, 1907). Of the
theory regarded as based after Weierstrass upon the theory of power
series, there is J. Harkness and F. Morley, Introduction to the Theory
of Analytic Functions (London, 1898), an elementary treatise;
for the theory of the convergence of series there is also T.J. I’A.
Bromwich, An Introduction to the Theory of Infinite Series (London,
1908); but the student should consult the collected works of Weierstrass
(Berlin, 1894 ff.), and the writings of Mittag-Leffler in the early
volumes of the Acta mathematica; earlier expositions of the theory
of functions on the basis of power series are in C. Méray, Leçons
nouvelles sur l’analyse infinitésimale (Paris, 1894), and in Lagrange’s
books on the Theory of Functions. An account of the theory of
potential in its applications to the present theory is found in most
treatises; in particular consult E. Picard, Traité d’analyse, t. ii.
(Paris, 1893). For elliptic functions there is an introductory book,
P. Appell and E. Lacour, Principes de la théorie des fonctions elliptiques
et applications (Paris, 1897), beside the treatises of G.H. Halphen,
Traité des fonctions elliptiques et de leurs applications (three parts,
Paris, 1886 ff.), and J. Tannery et J. Molk, Éléments de la théorie
des fonctions elliptiques (Paris, 1893 ff.); a book, A.G. Greenhill,
The Applications of Elliptic Functions (London, 1892), shows how
the functions enter in problems of many kinds. For modular
functions there is an extensive treatise, F. Klein and R. Fricke,
Theorie der elliptischen Modulfunctionen (Leipzig, 1890); see also
the most interesting smaller volume, F. Klein, Über das Ikosaeder
(Leipzig, 1884) (also obtainable in English). For the theory of
Riemann’s surface, and algebraic integrals, an interesting introduction
is P. Appeil and E. Goursat, Théorie des fonctions algébriques
et de leurs intégrales; for Abelian functions see also H. Stahl, Theorie
der Abel’schen Functionen (Leipzig, 1896), and H.F. Baker, An
Introduction to the Theory of Multiply Periodic Functions (Cambridge,
1907), and H.F. Baker, Abel’s Theorem and the Allied Theory, including
the Theory of the Theta Functions (Cambridge, 1897); for
theta functions of one variable a standard work is C.G. Jacobi,
Fundamenta nova, &c. (Königsberg, 1828); for the general theory
of theta functions, consult W. Wirtinger, Untersuchungen über Theta-Functionen
(Leipzig, 1895). For a history of the theory of algebraic
functions consult A. Brill and M. Noether, Die Entwicklung der
Theorie der algebraischen Functionen in älterer und neuerer Zeit,
Bericht der deutschen Mathematiker-Vereinigung (1894); and for a
special theory of algebraic functions, K. Hensel and G. Landsberg,
Theorie der algebraischen Function u.s.w. (Leipzig, 1902). The
student will, of course, consult also Riemann’s and Weierstrass’s
Ges. Werke. For the applications to geometry in general an important
contribution, of permanent value, is E. Picard and G. Simart,
Théorie des fonctions algébriques de deux variables indépendantes
(Paris, 1897-1906). This work contains, as Note v. t. ii. p. 485, a
valuable summary by MM. Castelnuovo and Enriques, Sur quelques
résultats nouveaux dans la théorie des surfaces algébriques, containing
many references to the numerous memoirs to be found, for the most
part, in the transactions of scientific societies and the mathematical
journals of Italy.
Beside the books above enumerated there exists an unlimited
number of individual memoirs, often of permanent importance
and only imperfectly, or too elaborately, reproduced in the pages
of the volumes in which the student will find references to them.
The German Encyclopaedia of Mathematics, and the Royal Society’s
Reference Catalogue of Current Scientific Literature, Pure Mathematics,
published yearly, should also be consulted.
(H. F. Ba.)
1 The word “function” (from Lat. fungi, to perform) has many
uses, with the fundamental sense of an activity special or proper
to an office, business or profession, or to an organ of an animal or
plant, the definite work for which the organ is an apparatus. From
the use of the word, as in the Italian funzione, for a ceremony of
the Roman Church, “function” is often employed for a public
ceremony of any kind, and loosely of a social entertainment or
gathering.
FUNDY, BAY OF, an inlet of the North Atlantic, separating
New Brunswick from Nova Scotia. It is 145 m. long and 48 m.
wide at the mouth, but gradually narrows towards the head,
where it divides into Chignecto Bay to the north, which subdivides
into Shepody Bay and Cumberland Basin (the French
Beaubassin), and Minas Channel, leading into Minas Basin, to
the east and south. Off its western shore opens Passamaquoddy
Bay, a magnificent sheet of deep water with good anchorage,
receiving the waters of the St Croix river and forming part of
the boundary between New Brunswick and the state of Maine,
The Bay of Fundy is remarkable for the great rise and fall of
the tide, which at the head of the bay has been known to reach
62 ft. In Passamaquoddy Bay the rise and fall is about 25 ft.,
which gradually increases toward the narrow upper reaches.
At spring tides the water in the Bay of Fundy is 19 ft. higher
than it is in Bay Verte, in Northumberland Strait, only 15 m.
distant. Though the bay is deep, navigation is rendered
dangerous by the violence and rapidity of the tide, and in summer
by frequent fogs. At low tide, at such points as Moncton or
Amherst, only an expanse of red mud can be seen, and the tide
rushes in a bore or crest from 3 to 6 ft. in height. Large areas
of fertile marshes are situated at the head of the bay, and the
remains of a submerged forest show that the land has subsided
in the latest geological period at least 40 ft. The bay receives
the waters of the St Croix and St John rivers, and has numerous
harbours, of which the chief are St Andrews (on Passamaquoddy
Bay) and St John in New Brunswick, and Digby and Annapolis
(on an inlet known as Annapolis Basin) in Nova Scotia. It was
first explored by the Sieur de Monts (d. c. 1628) in 1604 and
named by him La Baye Française.
FUNERAL RITES, the ceremonies associated with different
methods of disposing of the dead. (See also Burial and Burial
Acts; Cemetery; and Cremation.) In general we have little
record, except in their tombs, of races which, in a past measured
not merely by hundreds but by thousands of years, occupied
the earth; and exploration of these often furnishes our only
clue to the religions, opinions, customs, institutions and arts of
long vanished societies. In the case of the great culture folks
of antiquity, the Babylonians, Egyptians, Hindus, Persians,
Greeks and Romans, we have, besides their monuments, the
evidence of their literatures, and so can know nearly as much of
their rites as we do of our own. The rites of modern savages
not only help us to interpret prehistoric monuments, but explain
peculiarities in our own rituals and in those of the culture folks
of the past of which the significance was lost or buried under
etiological myths. We must not then confine ourselves to the
rites of a few leading races, neglecting their less fortunate
brethren who have never achieved civilization. It is better to
try to classify the rites of all races alike according as they embody
certain leading conceptions of death, certain fears, hopes, beliefs
entertained about the dead, about their future, and their relations
with the living.
The main ideas, then, underlying funeral rites may roughly be
enumerated as follows:
1. The pollution or taboo attaching to a corpse.
2. Mourning.
3. The continued life of the dead as evinced in the housing and
equipment of the dead, in the furnishing of food for them, and in the
orientation and posture assigned to the body.
4. Communion with the dead in a funeral feast and otherwise.
5. Sacrifice for the dead and expiation of their sins.
6. Death witchery.
7. Protection of the dead from ghouls.
8. Fear of ghosts.
1. A dead body is unclean, and the uncleanness extends
to things and persons which touch it. Hence the Jewish law
(Num. v. 2) enacted that “whoever is unclean by the dead
shall be put outside the camp, that they defile not the camp
in the midst whereof the Lord dwells.” Such persons were
unclean until the even, and might not eat of the holy things
unless they bathed their flesh in water. A high priest might on
no account “go in to any dead body” (Lev. xxi. 11). Why
a corpse is so widely tabooed is not certain; but it is natural to
see one reason in the corruption which in warm climates soon
sets in. The common experience that where one has died
another is likely to do so may also have contributed, though, of
course, there was no scientific idea of infection. The old Persian
scriptures are full of this taboo. He who has touched a corpse is
“powerless in mind, tongue and hand” (Zend Avesta in Sacred
Books of the East, pt. i. p. 120), and the paralysis is inflicted by
the innumerable drugs or evil spirits which invest a corpse.
Fire and earth, being alike creations of the good and pure god
330
Ahuramazda, a body must not be burned or buried; and so the
ancient Persians and their descendants the Parsees build Dakmas
or “towers of silence” on hill-tops far from human habitations.
Inside these the corpses are laid on a flagged terrace which
drains into a central pit. Twice a year the bones, picked clean
by dogs and birds of prey, are collected in the pit, and when it
is full another tower is built. In ancient times perhaps the
bodies of the magi or priests alone were exposed at such expense;
the common folk were covered with wax and laid in the earth,
the wax saving the earth from pollution. In Rome and Greece
the corpse was buried by night, lest it should pollute the sunlight;
and a trough of water was set at the door of the house of death
that men might purify themselves when they came out, before
mixing in general society. Priests and magistrates in Rome
might not meet or look on a corpse, for they were thereby
rendered unclean and incapable of fulfilling their official duties
without undergoing troublesome rites of purification. At a
Roman funeral, when the remains had been laid in the tomb,
all present were sprinkled with lustral water from a branch of
olive or laurel called aspergillum; and when they had gone
home they were asperged afresh and stepped over a fire. The
house was also swept out with a broom, probably lest the ghost
of the dead should be lying about the floor. Many races, to
avoid pollution, destroy the house and property of the deceased.
Thus the Navahos pull down the hut in which he died, leaving its
ruins on the ground; but if it be an expensive hut, a shanty
is extemporized alongside, into which the dying man is transferred
before death. No one will use the timbers of a hut so
ruined. A burial custom of the Solomon Islands, noted by
R.H. Codrington (The Melanesians, p. 255), may be dictated
by the same scruple. There “the mourners having hung up a
dead man’s arms on his house make great lamentations; all
remains afterwards untouched, the house goes to ruin, mantled,
as time goes on, with the vines of the growing yams, a picturesque
and indeed, perhaps, a touching sight; for these things are not
set up that they may in a ghostly manner accompany their
former owner.” H. Oldenberg (Religion des Veda, p. 426) describes
how Hindus shave themselves and cut off their nails after a
death, at the same time that they wash, renew the hearth fire,
and furnish themselves with new vessels. For the hair and
nails may harbour pollution, just as the medieval Greeks believed
that evil spirits could lurk in a man’s beard (Leo Allatius, De
opinionibus quorundam Graecorum). The dead man’s body
is shorn and the nails cut for a kindred reason; for it must be
purified as much as can be before it is burned as an offering on
the pyre and before he enters on a new sphere of existence.
2. We are accustomed to regard mourning costume as primarily
an outward sign of our grief. Originally, however, the special
garb seems to have been intended to warn the general public
that persons so attired were unclean. In ancient Rome mourners
stayed at home and avoided all feasts and amusements; laying
aside gold, purple and jewels, they wore black dresses called
lugubria or even skins. They cut neither hair nor beard, nor
lighted fire. Under the emperors women began to wear white.
On the west coast of Africa negroes wear white, on the Gold
Coast red. The Chinese wear hemp, which is cheap, for mourning
dress must as a rule be destroyed when the season of grief is
past to get rid of the taboo. Among the Aruntas of Australia
the wives of a dead man smear themselves with white pipe-clay
until the last ceremonies are finished, sometimes adding ashes—this
not to conceal themselves from the ghost (which may partly
be the aim of some mourning costumes), but to show the ghost
that they are duly sorrowing for their loss. These widows must
not talk except on their hands for a whole year. “Among the
Maoris,” says Frazer (Golden Bough, i. 323), “anyone who had
handled a corpse, helped to convey it to the grave, or touched a
dead man’s bones; was cut off from all intercourse and almost
all communication with mankind. He could not enter any
house, or come into contact with any person or thing, without
utterly bedevilling them. He might not even touch food with
his hands, which had become so frightfully tabooed or unclean
as to be quite useless. Food would be set for him on the ground,
and he would then sit or kneel down, and, with his hands carefully
held behind his back, would gnaw at it as best he could.” Often
a degraded outcast was kept in a village to feed mourners. Such
a taboo is strictly similar to those which surround a sacred chief
or his property, a menstruous woman or a homicide, rendering
them dangerous to themselves and to all who approach them.
3. Primitive folk cannot conceive of a man’s soul surviving
apart from his body, nor of another life as differing from this,
and the dead must continue to enjoy what they had here.
Accordingly the Patagonians kill horses at the grave that the
dead may ride to Alhuemapu, or country of the dead. After a
year they collect a chief’s bones, arrange them, tie them together
and dress them in his best garments with beads and feathers.
Then they lay him with his weapons in a square pit, round
which dead horses are placed set upright on their feet by stakes.
As late as 1781 in Poland F. Casimir’s horse was slain and buried
with him. In the Caucasus a Christian lady’s jewels are buried
with her. The Hindus used to burn a man’s widow on his pyre,
because he could not do without her; and St Boniface commends
the self-sacrifice of the Wend widows who in his day burned
themselves alive on their husbands’ pyres.
The tumuli met with all over the north of Europe (in the
Orkneys alone 2000 remain) are regular houses of the dead,
models of those they occupied in life. The greater the dignity
of the deceased, the loftier was his barrow. Silbury hill is
170 ft. high; the tomb of Alyattes, father of Croesus, was a
fourth of a league round; the Pyramids are still the largest
buildings in existence; at Oberea in Tahiti is a barrow 267 ft.
long, 87 wide and 44 high. Some Eskimo just leave a dead
man’s body in his house, and shut it up, often leaving by his
side a dog’s head to guide him on his last journey, along with
his tools and kayak. The Sea Dyaks set a chief adrift in his war
canoe with his weapons. So in Norse story Hake “was laid
wounded on a ship with the dead men and arms; the ship was
taken out to sea and set on fire.” The Viking was regularly
buried in his ship or boat under a great mound. He sailed
after death to Valhalla. In the ship was laid a stone as anchor
and the tools, clothes, weapons and treasures of the dead. The
Egyptians, whose land was the gift of the river Nile, equally
believed that the dead crossed over water, and fashioned the
hearse in the form of a boat. Hence perhaps was derived the
Greek myth of Charon and the Styx, and the custom, which still
survives in parts of Europe, of placing a coin in the mouth of the
dead with which to pay the ferryman. The Egyptians placed
in the tomb books of a kind to guide the dead to the next world.
The Copts in a later age did the same, and to this custom we owe
the recovery in Egypt of much ancient literature. The Armenians
till lately buried with a priest his missal or gospel.
In Egyptian entombments of the XIIth to the XIVth dynasties
were added above the sepulchres what Professor Petrie terms soul-houses,
viz. small models of houses furnished with couch and
table, &c., for the use of the ka or double whenever it might wish
to come above ground and partake of meats and drinks. They
recall, in point of size, the hut-urns of the Etruscans, but the
latter had another use, for they contain incinerated remains.
Etruscan tombs, like those of Egypt and Asia Minor, were made
to resemble the dwelling-houses of the living, and furnished with
coffered ceilings, panelled walls, couches, stools, easy chairs with
footstools attached, all hewn out of the living rock (Dennis,
Cities and Cemeteries of Etruria, vol i. p. lxx.).
Of the old Peruvian mummies in the Kircherian Museum at
Rome, several are of women with babies in their arms, whence
it is evident that a mother had her suckling buried with her;
it would console her in the next world and could hardly survive
her in this. The practice of burying ornaments, tools and
weapons with the dead characterizes the inhumations of the
Quaternary epoch, as if in that dim and remote age death was
already regarded as the portal of another life closely resembling
this. The cups, tools, weapons, ornaments and other articles
deposited with the dead are often carefully broken or turned
upside down and inside out; for the soul or manes of objects is
liberated by such fracture or inversion and so passes into the
331
dead man’s use and possession. For the same reason where the
dead are burned, their properties are committed to the flames.
The ghost of the warrior has a ghostly sword and buckler to
fight with and a ghostly cup to drink from, and he is also nourished
by the impalpable odour and reek of the animal victims sacrificed
over his grave. Instead of valuable objects cheap images and
models are often substituted; and why not, if the mere ghosts
of the things are all that the wraith can enjoy? Thus Marco
Polo (ii. 76) describes how in the land of Kinsay (Hang-chau)
“the friends and relations make a great mourning for the
deceased, and clothe themselves in hempen garments, and follow
the corpse, playing on a variety of instruments and singing
hymns to their idols. And when they come to the burning place
they take representations of things cut out of parchment, such
as caparisoned horses, male and female slaves, camels, armour,
suits of cloth of gold (and money), in great quantities, and these
things they put on the fire along with the corpse so that they
are all burned with it. And they tell you that the dead man
shall have all these slaves and animals of which the effigies are
burned, alive in flesh and blood, and the money in gold, at his
disposal in the next world; and that the instruments which
they have caused to be played at his funeral, and the idol hymns
that have been chaunted shall also be produced again to welcome
him in the next world.” The manufacture of such paper simulacra
for consumption at funerals is still an important industry
in Chinese cities. The ancient Egyptians, assured that a man’s
ka or double shall revivify his body, took pains to guard the
flesh from corruption, steeping the corpse in natron and stuffing
it with spices. A body so prepared is called a mummy (q.v.),
and the custom was already of a hoary antiquity in 3200 B.C.,
when the oldest dated mummy we have was made. The bowels,
removed in the process, were placed in jars over the corpse in the
tomb, together with writing tablets, books, musical instruments,
&c., of the dead. Cemeteries also remain full of mummies of
crocodiles, cats, fish, cows and other sacred animals. The
Greeks settled in Egypt learned to mummify their dead, but
the custom was abhorrent to the Jews, although the Christian
belief in the resurrection of the flesh must have been formed to
a large extent under Egyptian influence. Half the superiority of
the Jewish to other ancient religions lay in this, that it prescribed
no funeral rites other than the simplest inhumation.
The dead all over the world and from remote antiquity have
been laid not anyhow in the earth, but with the feet and face
towards the region in which their future will be spent; the
Samoans and Fijians towards the far west whither their souls
have preceded them; the Guarayos with head turned eastwards
because their god Tamoi has in that quarter “his happy hunting
grounds where the dead will meet again” (Tylor, Prim. Cult.
ii. 422). The legend is that Christ was buried with His head to
the west, and the church follows the custom, more ancient than
itself, of laying the dead looking to the East, because that is
the attitude of prayer, and because at the last trump they will
hurry eastwards. So in Eusebius (Hist. Eccl. 430.19) a martyr
explains to his pagan judge that the heavenly Jerusalem, the
fatherland of the pious, lay exactly in the east at the rising place
of the sun. Where the body is laid out straight it is difficult to
discern the presence of any other idea than that it is at rest. In
Scandinavian barrows, e.g. in the one opened at Goldhavn in
1830, the skeletons have been found seated on a low stone bench
round the wall of the grave chamber facing its opening, which
always looks south or east, never north. Here the dead were
continuing the drinking bouts they enjoyed on earth.
The Peruvians mummified their dead and placed them jointed
and huddled up with knees to chin, looking toward the sunset,
with the hands held before the face. In the oldest prehistoric
tombs along the Nile the bodies are doubled up in the same
position. It would seem as if in these and numerous other
similar cases the dead were deliberately given in their graves
the attitude of a foetus in the womb, and, as Dr Budge remarks
(Egyptian Ideas of the Future Life, London, 1899, p. 162), “we
may perhaps be justified in seeing in this custom the symbol
of a hope that, as the child is born from this position into the
world, so might the deceased be born into the life beyond the
grave.” The late Quaternary skeletons of the Mentone cave
were laid in a layer of ferrugineous earth specially laid down for
them, and have contracted a red colour therefrom. Many other
prehistoric skeletons found in Italy have a reddish colour, perhaps
for the same reason, or because, as often to-day, the bones were
stripped of flesh and painted. Ambrose relates that the skeletons
of the martyrs Gervasius and Protasius, which he found and
deposited A.D. 386 under the altar of his new basilica in Milan,
were mirae magnitudinis ut prisca aetas ferebat, and were also
coloured red. He imagined the red to be the remains of the
martyrs’ blood! Hic sanguis clamat coloris indicio. Salomon
Reinach has rightly divined that what Ambrose really hit upon
was a prehistoric tomb. Red earth was probably chosen as a
medium in which to lay a corpse because demons flee from red.
Sacred trees and stones are painted red, and for the most solemn
of their rites savages bedaub themselves with red clay. It is
a favourite taboo colour.
4. A feast is an essential feature of every primitive funeral,
and in the Irish “wake” it still survives. A dead man’s soul
or double has to be fed at the tomb itself, perhaps to keep it
from prowling about the homes of the survivors in search of
victuals; and such food must also be supplied to the dead at
stated intervals for months or years. Many races leave a
narrow passage or tube open down to the cavity in which the
corpse lies, and through it pour down drinks for the dead.
Traces of such tubes are visible in the prehistoric tombs of the
British Isles. However, such provision of food is not properly
a funeral feast unless the survivors participate. In the Eastern
churches and in Russia the departed are thus fed on the ninth,
twelfth and fortieth days from death. “Ye appease the shades
of the dead with wine and meals,” was the charge levelled at
the Catholics by the 4th-century Manichaeans, and it has hardly
ceased to be true even now after the lapse of sixteen centuries.
The funeral feast proper, however, is either a meal of communion
with or in the dead, which accompanies interment, or a banquet
off the flesh of victims slain in atonement of the dead man’s
sins. Some anthropologists see in the common meal held at the
grave “the pledge and witness of the unity of the kin, the chief
means, if not of making, at least of repairing and renewing it.”1
The flesh provided at these banquets is occasionally that of the
dead man himself; Herodotus and Strabo in antiquity relate
this of several half-civilized races in the East and West, and a
similar story is told by Marco Polo of certain Tatars. Nor
among modern savages are funeral feasts off the flesh of the dead
unknown, and they seem to be intended to effect and renew a
sacramental union or kinship of the living with the dead. The
Uaupes in the Amazons incinerate a corpse a month after death,
pound up the ashes, and mix them with their fermented drink.
They believe that the virtues of the dead will thus be passed on
to his survivors. The life of the tribe is kept inside the tribe
and not lost. Such cannibal sacraments, however, are rare, and,
except in a very few cases, the evidence for them weak. The
slaying and eating of animal victims, however, at the tomb is universal
and bears several meanings, separately or all at once. The
animals may be slain in order that their ghosts may accompany
the deceased in his new life. This significance we have already
dwelt upon. Or it is believed that the shade feeds upon them,
as the shades came up from Hades and lapped up out of a trench
the blood of the animals slain by Ulysses. The survivors by
eating the flesh of a victim, whose blood and soul the dead thus
consume, sacramentally confirm the mystic tie of blood kinship
with the dead. Or lastly, the victim may be offered for the sins
of the dead. His sins are even supposed to be transferred into
it and eaten by the priest. Such expiatory sacrifices of animals
for the dead survive in the Christian churches of Armenia, Syria
and of the East generally. Their vicarious character is emphasized
in the prayers which accompany them, but the popular understanding
of them probably combines all the meanings above
enumerated. It has been suggested by Robertson Smith
(Religion of the Semites, 336) that the world-wide customs of
332
tearing the hair, rending the garments, and cutting and wounding
the body were originally intended to establish a life-bond between
the dead and the living. The survivors, he argues, in leaving
portions of their hair and garments, and yet more by causing
their own blood to stream over the corpse from self-inflicted
wounds, by cutting off a finger and throwing it into the grave,
leave what is eminently their own with the dead, so drawing
closer their tie with him. Conversely, many savages daub themselves
with the blood and other effluences of their dead kinsmen,
and explain their custom by saying that in this way a portion
of the dead is incorporated in themselves. Often the survivors,
especially the widows, attach the bones or part of them to their
persons and wear them, or at least keep them in their houses.
The retention of the locks of the deceased and of parts of his
dress is equally common. There is also another side to such
customs. Having in their possession bits of the dead, and being
so far in communion with him, the survivors are surer of his
friendship. They have ensured themselves against ghosts who
are apt to be by nature envious and mischievous. But whatever
their original significance, the tearing of cheeks and hair and
garments and cutting with knives are mostly expressions of real
sorrow, and, as Robertson Smith remarks, of deprecation and
supplication to an angry god or spirit. It must not be supposed
that the savage or ancient man feels less than ourselves the
poignancy of loss.
6. Death-witchery has close parallels in the witch and heretic
hunts of the Christians, but, happily for us, only flourishes
to-day among savages. Sixty % of the deaths which occur in
West Africa are, according to Miss Mary Kingsley—a credible
witness—believed to be due to witchcraft and sorcery. The
blacks regard old age or effusion of blood as the sole legitimate
causes of death. All ordinary diseases are in their opinion due
to private magic on the part of neighbours, just as a widespread
epidemic marks the active hatred “of some great outraged nature
spirit, not of a mere human dabbler in devils.”2 Similarly in
Christian countries an epidemic is set down to the wrath of a God
offended by the presence of Jews, Arians and other heretics.
The duty of an African witch-doctor is to find out who bewitched
the deceased, just as it was of an inquisitor to discover the
heretic. Every African post-mortem accordingly involves the
murder of the person or persons who bewitched the dead man
and caused him to die. The death-rate by these means is nearly
doubled; but, since the use of poison against an obnoxious
neighbour is common, the right person is occasionally executed.
It is also well for neighbours not to quarrel, for, if they do and
one of them dies of smallpox, the other is likely to be slain as
a witch, and his lungs, liver and spleen impaled on a pole at the
entrance of the village. It is the same case with the Australian
blacks: “no such thing as natural death is realized by the
native; a man who dies has of necessity been killed by some
other man, or perhaps even by a woman, and sooner or
later that man or woman will be attacked. In the normal
condition of the tribe every death meant the killing of another
individual.”3
7. Lastly, a primitive interment guards against the double
risk of the ghost haunting the living and of ghouls or vampires
taking possession of the corpse. The latter end is likely to be
achieved if the body is cremated, for then there is no nidus to
harbour the demon; but whether, in the remote antiquity to
which belong many barrows containing incinerated remains,
this motive worked, cannot be ascertained. The Indo-European
race seems to have cremated at an early epoch, perhaps before
the several races of East and West separated. In Christian
funeral rites many prayers are for the protection of the body
from violation by vampires, and it would seem as if such a motive
dictated the architectural solidity of some ancient tombs.
Christian graves were for protection regularly sealed with the
cross; and the following is a characteristic prayer from the old
Armenian rite for the burial of a layman:
“Preserve, Almighty Lord, this man’s spirit with all saints and
with all lovers of Thy holy name. And do Thou seal and guard the
sepulchre of Thy servant, Thou who shuttest up the depths and
sealest them with Thy almighty right hand ... so let the seal of
Thy Lordship abide unmoved upon this man’s dwelling-place and
upon the shrine which guards Thy servant. And let not any filthy
and unclean devil dare to approach him, such as assail the body and
souls of the heathen, who possess not the birth of the holy font, and
have not the dread seal laid upon their graves.”
A terrible and revolting picture of the superstitious belief in
ghouls which violate Christian tombs is given by Leo Allatius
(who held it) in his tract De opinionibus quorundam Graecorum
(Paris, 1646). It was probably the fear of such demonic assaults
on the dead that inspired the insanitary custom of burying the
dead under the floors of churches, and as near as possible to the
altar. In the Greek Church this practice was happily forbidden
by the code of Justinian as well as by the older law in the case of
churches consecrated with Encaenia and deposition of relics.
In the Armenian Church the same rule holds, and Ephrem Syrus
in his testament particularly forbade his body to be laid within
a church. Such prohibitions, however, are a witness to the
tendency in question.
The custom of lighting candles round a dead body and watching
at its side all night was originally due to the belief that a corpse,
like a person asleep, is specially liable to the assaults of demons.
The practice of tolling a bell at death must have had a similar
origin, for it was a common medieval belief that the sound of a
consecrated bell drives off the demons which when a man dies
gather near in the air to waylay his fleeting soul. For a like
reason the consecrated bread of the Eucharist was often buried
with believers, and St Basil is said to have specially consecrated
a Host to be placed in his coffin.
8. Some of the rites described under the previous heads may be
really inspired by the fear of the dead haunting the living, but
it must be kept in mind that the taboo attaching to a dead body
is one thing and fear of a ghost another. A corpse is buried or
burned, or scaffolded on a tree, a tower or a house-top, in order
to get it out of the way and shield society from the dangerous
infection of its taboo; but ghosts quâ ghosts need not be feared
and a kinsman’s ghost usually is not. On the contrary, it is fed
and consoled with everything it needs, is asked not to go away
but to stay, is in a thousand ways assured of the sorrow and
sympathy of the survivors. Even if the body be eaten, it is
merely to keep the soul of the deceased inside the circle of
kinsmen, and Strabo asserts that the ancient Irish and Massagetae
regarded it as a high honour to be so consumed by relatives.
In Santa Cruz in Melanesia they keep the bones for arrow heads
and store a skull in a box and set food before it “saying that
this is the man himself” (R.H. Codrington, The Melanesians,
p. 264), or the skull and jaw bone are kept and “are
called mangite, which are saka, hot with spiritual power, and by
means of which the help of the lio’a, the powerful ghost of the
man whose relics these are, can be obtained” (ibid. p. 262).
Here we have the savage analogue to Christian relics. So the
Australian natives make pointing sticks out of the small bones of
the arm, with which to bewitch enemies.
We may conclude then that in the most primitive societies,
where blood-kinship is the only social tie and root of social custom
it is the shades, not of kinsmen, but of strangers, who as such
are enemies, that are dangerous and uncanny. In more developed
societies, however, all ghosts alike are held to be so; and if a
ghost walks it is because its body has not been properly interred
or because its owner was a malefactor. Still, even allowing for
this, it remains true that for a friendly ghost the proper place is
the grave and not the homes of the living, and accordingly the
Aruntas with cries of Wah! Wah! with wearing of fantastic
head-dresses, wild dancing and beating of the air with hands and
weapons “drive the spirit away from the old camp which it is
supposed to haunt,” and which has been set fire to, and hunt
it at a run into the grave prepared, and there stamp it down into
the earth. “The loud shouting of the men and women shows him
that they do not wish to be frightened by him in his present
state, and that they will be angry with him if he does not rest.”
333
(Spencer and Gillen, Native Tribes of Central Australia, p. 508).
In Mesopotamia cemeteries have been discovered where the
sepulchral jars were set upside down, clearly by way of hindering
the ghosts from escaping into the upper world. In the Dublin
museum we see specimens of ancient Celtic tombs showing the
same peculiarity. For a like reason perhaps the name of the
dead must among the Aruntas not be uttered, nor the grave
approached, by certain classes of kinsmen. The same repugnance
to naming the dead exists all over the world, and leads survivors
who share the dead man’s name to adopt another, at least for a
time. If the dead man’s name was that of a plant, tree, animal
or stream, that too is changed. Here is a potent cause of linguistic
change, that also renders any historical tradition impossible.
The survivors seem to fear that the ghost will come when he
hears his name called; but it also hangs together with the taboo
which hedges round the dead as it does kings, chieftains and
priests.
Authorities.—B. Spencer and F.J. Gillen, The Native Tribes
of Central Australia (London, 1899); F.B. Jevons, Introduction to
History of Religion (London, 1896); E.S. Hartland, The Legend of
Perseus, vol. ii.; J.G. Frazer, The Golden Bough (London, 1900);
L.W. Faraday, “Custom and Belief in the Icelandic Sagas,” in
Folk-lore, vol. xvii. No. 4; E.B. Tylor, Primitive Culture (London,
1903); E.A. W. Budge, The Mummy (Cambridge, 1893); C. Royer,
“Les Rites funéraires aux époques préhistoriques,” Revue d’anthropologie
(1876); Forrer, Über die Totenbestattung bei den Pfahlbauern
(Ausland, 1885); J. Lubbock, Origin of Civilization (London, 1875)
and Prehistoric Times (London, 1865); L.A. Muratori, “De antiquis
Christianorum sepulchris,” Anecd. Graeca (Padua, 1709); Onaphr.
Panvinius, De ritu sepeliendi mortuos apua veteres Christianos, reprinted
in Volbeding’s Thesaurus (Leipzig, 1841).
(F. C. C.)
1 E.S. Hartland, Legend of Perseus (1895), ii. 278.
2 Mary Kingsley, West African Studies (1901), p. 178.
3 B. Spencer and F.J. Gillen, The Native Tribes of Central Australia
(1899), p. 48.
FUNGI (pl. of Lat. fungus, a mushroom), the botanical name
covering in the broad sense all the lower cellular Cryptogams
devoid of chlorophyll, which arise from spores, and the thallus
of which is either unicellular or composed of branched or unbranched
tubes or cell-filaments (hyphae) with apical growth,
or of more or less complex wefted sheets or tissue-like masses
of such (mycelium). The latter may in certain cases attain large
dimensions, and even undergo cell-divisions in their interior,
resulting in the development of true tissues. The spores, which
may be uni- or multicellular, are either abstricted free from
the ends of hyphae (acrogenous), or formed from segments in
their course (chlamydospores) or from protoplasm in their interior
(endogenous). The want of chlorophyll restricts their mode of
life—which is rarely aquatic—since they are therefore unable
to decompose the carbon dioxide of the atmosphere, and renders
them dependent on other plants or (rarely) animals for their
carbonaceous food-materials. These they obtain usually in the
form of carbohydrates from the dead remains of other organisms,
or in this or other forms from the living cells of their hosts;
in the former case they are termed saprophytes, in the latter
parasites. While some moulds (Penicillium, Aspergillus) can
utilize almost any organic food-materials, other fungi are more
restricted in their choice—e.g. insect-parasites, horn- and
feather-destroying fungi and parasites generally. It was
formerly the custom to include with the Fungi the Schizomycetes
or Bacteria, and the Myxomycetes or Mycetozoa; but the
peculiar mode of growth and division, the cilia, spores and other
peculiarities of the former, and the emission of naked amoeboid
masses of protoplasm, which creep and fuse to streaming plasmodia,
with special modes of nutrition and spore-formation of
the latter, have led to their separation as groups of organisms
independent of the true Fungi. On the other hand, lichens,
previously regarded as autonomous plants, are now known to
be dual organisms—fungi symbiotic with algae.
The number of species in 1889 was estimated by Saccardo at
about 32,000, but of these 8500 were so-called Fungi imperfecti—i.e.
forms of which we only know certain stages, such as conidia,
pycnidia, &c., and which there are reasons for regarding as merely
the corresponding stages of higher forms. Saccardo also included
about 400 species of Myxomycetes and 650 of Schizomycetes.
Allowing for these and for the cases, undoubtedly not few,
where one and the same fungus has been described under different
names, we obtain Schroeter’s estimate (in 1892) of 20,000 species.
In illustration of the very different estimates that have been
made, however, may be mentioned that of De Bary in 1872 of
150,000 species, and that of Cooke in 1895 of 40,000, and Massee
in 1899 of over 50,000 species, the fact being that no sufficient
data are as yet to hand for any accurate census. As regards their
geographical distribution, fungi, like flowering plants, have no
doubt their centres of origin and of dispersal; but we must not
forget that every exchange of wood, wheat, fruits, plants,
animals, or other commodities involves transmission of fungi
from one country to another; while the migrations of birds and
other animals, currents of air and water, and so forth, are particularly
efficacious in transmitting these minute organisms. Against
this, of course, it may be argued that parasitic forms can only go
where their hosts grow, as is proved to be the case by records
concerning the introduction of Puccinia malvacearum, Peronospora
viticola, Hemileia vastatrix, &c. Some fungi—e.g. moulds
and yeasts—appear to be distributed all over the earth. That
the north temperate regions appear richest in fungi may be due
only to the fact that North America and Europe have been
much more thoroughly investigated than other countries; it is
certain that the tropics are the home of very numerous species.
Again, the accuracy of the statement that the fleshy Agaricini,
Polyporei, Pezizae, &c., are relatively rarer in the tropics may
depend on the fact that they are more difficult to collect and
remit for identification than the abundantly recorded woody
and coriaceous forms of these regions. When we remember
that many parts of the world are practically unexplored as
regards fungi, and that new species are constantly being discovered
in the United States, Australia and northern Europe—the
best explored of all—it is clear that no very accurate census
of fungi can as yet be made, and no generalizations of value as
to their geographical distribution are possible.
The existence of fossil fungi is undoubted, though very few
of the identifications can be relied on as regards species or genera.
They extend back beyond the Carboniferous, where they occur
as hyphae, &c., preserved in the fossil woods, but the best specimens
are probably those in amber and in siliceous petrifactions
of more recent origin.
 |
| Fig. 1.—1, Peronospora parasitica (De Bary). Mycelium with
haustoria (h); 2, Erysiphe; A and B, mycelium (m), with haustoria
(h). (After De Bary.) |
Organs.—Individual hyphae or their branches often exhibit
specializations of form. In many Basidiomycetes minute branches
arise below the septa; their tips curve over the outside of the latter,
and fuse with the cell above just beyond it, forming a clamp-connexion.
Many parasitic hyphae put out minute lateral branches,
which pierce the cell-wall of the host and form a peg-like (Trichosphaeria),
sessile (Cystopus), or stalked (Hemileia), knot-like, or a
more or less branched (Peronospora) or coiled (Protomyces) haustorium.
In Rhizopus certain hyphae creep horizontally on the surface of the
substratum, and then anchor their tips to it by means of a tuft of
short branches (appressorium), the walls of which soften and gum
334
themselves to it, then another branch shoots out from the tuft and
repeats the process, like a strawberry-runner. Appressoria are
also formed by some parasitic fungi, as a minute flattening of the tip
of a very short branch (Erysiphe), or the swollen end of any hypha
which comes in contact with the surface of the host (Piptocephalis,
Syncephalis), haustoria piercing in each case the cell-wall below.
In Botrytis the appressoria assume the form of dense tassels of short
branches. In Arthrobotrys side-branches of the mycelium sling themselves
around the host (Tylenchus) much as tendrils round a support.
Many fungi (Phallus, Agaricus, Fumago, &c.) when strongly
growing put out ribbon-like or cylindrical cords, or sheet-like
mycelial plates of numerous parallel hyphae, all growing together
equally, and fusing by anastomoses, and in this way extend long
distances in the soil, or over the surfaces of leaves, branches, &c.
These mycelial strands may be white and tender, or the outer
hyphae may be hard and black, and very often the resemblance of
the subterranean forms to a root is so marked that they are termed
rhizomorphs. The outermost hyphae may even put forth thinner
hyphae, radiating into the soil like root-hairs, and the convergent
tips may be closely appressed and so divided by septa as to resemble
the root-apex of a higher plant (Armillaria mellea).
Sclerotia.—Fungi, like other plants, are often found to store up
large quantities of reserve materials (oil, glycogen, carbohydrates,
&c.) in special parts of their vegetative tissues, where they lie
accumulated between a period of active assimilation and one of
renewed activity, forming reserves to be consumed particularly
during the formation of large fructifications. These reserve stores
may be packed away in single hyphae or in swollen cells, but the
hyphae containing them are often gathered into thick cords or
mycelial strands (Phallus, mushroom, &c.), or flattened and anastomosing
ribbons and plates, often containing several kinds of hyphae
(Merulius lacrymans). In other cases the strands undergo differentiation
into an outer layer with blackened, hardened cell-walls
and a core of ordinary hyphae, and are then termed rhizomorphs
(Armillaria mellea), capable not only of extending the fungus in
the soil, like roots, but also of lying dormant, protected by the
outer casing. Such aggregations of hyphae frequently become
knotted up into dense masses of interwoven and closely packed
hyphae, varying in size from that of a pin’s head or a pea (Peziza,
Coprinus) to that of a man’s fist or head, and weighing 10 to 25 ℔
or more (Polyporus Mylittae, P. tumulosus, Lentinus Woermanni,
P. Sapurema, &c.). The interwoven hyphae fuse and branch
copiously, filling up all interstices. They also undergo cutting
up by numerous septa into short cells, and these often divide again
in all planes, so that a pseudoparenchyma results, the walls of
which may be thickened and swollen internally, or hardened and
black on the exterior. In many cases the swollen cell-walls serve
as reserves, and sometimes the substance is so thickly deposited in
strata as to obliterate the lumen, and the hyphae become nodular
(Polyporus sacer, P. rhinoceros, Lentinus Woermanni). The various
sclerotia, if kept moist, give rise to the fructifications of the fungi
concerned, much as a potato tuber does to a potato plant, and in
the same way the reserve materials are consumed. They are
principally Polyporei, Agaricini, Pezizae; none are known among
the Phycomycetes, Uredineae or Ustilagineae. The functions of
mycelial strands, rhizomorphs and sclerotia are not only to collect
and store materials, but also to extend the fungus, and in many
cases similar strands act as organs of attack. The same functions
of storage in advance of fructification are also exercised by the
stromata so common in Ascomycetes.
Tissue Differentiations.—The simpler mycelia consist of hyphae
all alike and thin-walled, or merely differing in the diameter of the
branches of various orders, or in their relations to the environment,
some plunging into the substratum like roots, others remaining on
its surface, and others (aerial hyphae) rising into the air. Such
hyphae may be multicellular, or they may consist of simple tubes
with numerous nuclei and no septa (Phycomycetes), and are then
non-cellular. In the more complex tissue-bodies of higher fungi,
however, we find considerable differences in the various layers or
strands of hyphae.
An epidermis-like or cortical protective outer layer is very common,
and is usually characterized by the close septation of the densely
interwoven hyphae and the thickening and dark colour of their
outer walls (sclerotia, Xylaria, &c.). Fibre-like hyphae with
the lumen almost obliterated by the thick walls occur in mycelial
cords (Merulius). Latex-tubes abound in the tissues of Lactarius,
Stereum, Mycena, Fistulina, filled with white or coloured milky
fluids, and Istvanffvi has shown that similar tubes with fluid or
oily contents are widely spread in other Hymenomycetes. Sometimes
fatty oil or watery sap is found in swollen hyphal ends, or
such tubes contain coloured sap. Cystidia and paraphyses may be
also classed here. In Merulius lacrymans Hartig has observed
thin-walled hyphae with large lumina, the septa of which are perforated
like those of sieve-tubes.
As regards its composition, the cell-wall of fungi exhibits variations
of the same kind as those met with in higher plants. While
the fundamental constituent is a cellulose in many Mucorini and
other Phycomycetes, in others bodies like pectose, callose, &c.,
commonly occur, and Wisselingh’s researches show that chitin, a
gluco-proteid common in animals, forms the main constituent in
many cases, and is probably deposited directly as such, though, like
the other substances, it may be mixed with cellulose. As in other
cell-walls, so here the older membranes may be altered by deposits
of various substances, such as resin, calcium oxalate, colouring
matters; or more profoundly altered throughout, or in definite
layers, by lignification, suberization (Trametes, Daedalea), or swelling
to a gelatinous mucilage (Tremella, Gymnosporangium), while cutinization
of the outer layers is common. One of the most striking
alterations of cell-walls is that termed carbonization, in which the
substance gradually turns black, hard and brittle, as if charred—e.g.
Xylaria, Ustulina, some sclerotia. At the other extreme the
cell-walls of many lichen-fungi are soft and colourless, but turn
blue in iodine, as does starch. The young cell-wall is always tenuous
and flexible, and may remain so throughout, but in many cases
thickenings and structural differentiations, as well as the changes
referred to above, alter the primary wall considerably. Such
thickening may be localized, and pits (e.g. Uredospores, septa of
Basidiomycetes), spirals, reticulations, rings, &c. (capillitium fibres
of Podaxon, Calostoma, Battarrea), occur as in the vessels of higher
plants, while sculptured networks, pittings and so forth are as
common on fungus-spores as they are on pollen grains.
Cell-Contents.—The cells of fungi, in addition to protoplasm,
nuclei and sap-vacuoles, like other vegetable cells, contain formed
and amorphous bodies of various kinds. Among those directly
visible to the microscope are oil drops, often coloured (Uredineae)
crystals of calcium oxalate (Phallus, Russula), proteid crystals
(Mucor, Pilobolus, &c.) and resin (Polyporei). The oidia of Erysipheae
contain fibrosin bodies and the hyphae of Saprolegnieae
cellulin bodies, but starch apparently never occurs. Invisible to the
microscope, but rendered visible by reagents, are glycogen, Mucor,
Ascomycetes, yeast, &c. In addition to these cell-contents we
have good indirect evidence of the existence of large series of other
bodies, such as proteids, carbohydrates, organic acids, alkaloids,
enzymes, &c. These must not be confounded with the numerous
substances obtained by chemical analysis of masses of the fungus,
as there is often no proof of the manner of occurrence of such bodies,
though we may conclude with a good show of probability that
some of them also exist preformed in the living cell. Such are
sugars (glucose, mannite, &c.), acids (acetic, citric and a whole series
of lichen-acids), ethereal oils and resinous bodies, often combined
with the intense colours of fungi and lichens, and a number of
powerful alkaloid poisons, such as muscarin (Amanita), ergotin
(Claviceps), &c.
Among the enzymes already extracted from fungi are invertases
(yeasts, moulds, &c.), which split cane-sugar and other complex
sugars with hydrolysis into simpler sugars such as dextrose and
levulose; diastases, which convert starches into sugars (Aspergillus,
&c.); cytases, which dissolve cellulose similarly (Botrytis, &c.);
peptases, using the term as a general one for all enzymes which
convert proteids into peptones and other bodies (Penicillium, &c.);
lipases, which break up fatty oils (Empusa, Phycomyces, &c.);
oxydases, which bring about the oxidations and changes of colour
observed in Boletus, and zymase, extracted by Buchner from yeast,
which brings about the conversion of sugar into alcohol and carbon-dioxide.
That such enzymes are formed in the protoplasm is
evident from the behaviour of hyphae, which have been observed
to pierce cell-membranes, the chitinous coats of insects, artificial
collodion films and layers of wax, &c. That a fungus can secrete
more than one enzyme, according to the materials its hyphae
have to attack, has been shown by the extraction of diastase,
inulase, trehalase, invertase, maltase, raffinase, malizitase, emulsin,
trypsin and lipase from Aspergillus by Bourquelot, and similar
events occur in other fungi. The same fact is indicated by the wide
range of organic substances which can be utilized by Penicillium
and other moulds, and by the behaviour of parasitic fungi which
destroy various cell-contents and tissues. Many of the coloured
pigments of fungi are fixed in the cell-walls or excreted to the outside
(Peziza aeruginosa). Matruchot has used them for staining
the living protoplasm of other fungi by growing the two together.
Striking instances of coloured mycella are afforded by Corticium
sanguineum, blood-red; Elaphomyces Leveillei, yellow-green;
Chlorosplenium aeruginosum, verdigris green; and the Dematei,
brown or black.
Nuclei.—Although many fungi have been regarded as devoid of
nuclei, and all have not as yet been proved to contain them, the
numerous investigations of recent years have revealed them in the
cells of all forms thoroughly examined, and we are justified in
concluding that the nucleus is as essential to the cell of a fungus
as to that of other organisms. The hyphae of many contain
numerous, even hundreds of nuclei (Phycomycetes); those of others
have several (Aspergillus) in each segment, or only two (Exoascus)
or one (Erysiphe) in each cell. Even the isolated cells of the yeast
plant have each one nucleus. As a rule the nuclei of the mycelium
are very minute (1.5-2 μ in Phycomyces), but those of many asci
and spores are large and easily rendered visible. As with other
plants, so in fungi the essential process of fertilization consists in the
fusion of two nuclei, but owing to the absence of well-marked sexual
organs from many fungi, a peculiar interest attaches to certain
nuclear fusions in the vegetative cells or in young spores of many
forms. Thus in Ustilagineae the chlamydospores, and in Uredineae
335
the teleutospores, each contain two nuclei when young, which
fuse as the spores mature. In young asci a similar fusion of two
nuclei occurs, and also in basidia, in each case the nucleus of the
ascus or of the basidium resulting from the fusion subsequently
giving rise by division to the nuclei of the ascospores and basidiospores
respectively. The significance of these fusions will be discussed
under the various groups. Nuclear division is usually
accompanied by all the essential features of karyokinesis.
Spores.—No agreement has ever been arrived at regarding the
consistent use of the term spore. This is apparently owing to the
facts that too much has been attempted in the definition, and that
differences arise according as we aim at a morphological or a physiological
definition. Physiologically, any cell or group of cells separated
off from a hypha or unicellular fungus, and capable of itself
growing out—germinating—to reproduce the fungus, is a spore; but
it is evident that so wide a definition does not exclude the ordinary
vegetative cells of sprouting fungi, such as yeasts, or small sclerotium
like cell-aggregates of forms like Coniothecium. Morphologically
considered, spores are marked by peculiarities of form, size, colour,
place of origin, definiteness in number, mode of preparation, and so
forth, such that they can be distinguished more or less sharply from
the hyphae which produce them. The only physiological peculiarity
exhibited in common by all spores is that they germinate and
initiate the production of a new fungus-plant. Whether a spore
results from the sexual union of two similar gametes (zygospore)
or from the fertilization of an egg-cell by the protoplasm of a
male organ (oospore); or is developed asexually as a motile
(zoospore) or a quiescent body cut off from a hypha (conidium) or
developed along its course (oidium or chlamydospore), or in its
protoplasm (endospore), are matters of importance which have their
uses in the classification and terminology of spores, though in many
respects they are largely of academic interest.
 |
| Fig. 2.—Peronospora parasitica
(De Bary). Conidiophore
with conidia. |
Klebs has attempted to divide spores into three categories as
follows: (1) kinospores, arising by relatively simple cell-divisions
and subserving rapid dissemination and propagation, e.g. zoospores,
conidia, endogonidia, stylospores, &c.; (2) paulospores, due to
simple rearrangement of cell-contents, and subserving the persistence
of the fungus through periods of exigency, e.g. gemmae, chlamydospores,
resting-cells, cysts, &c.; (3) carpospores, produced by a
more or less complex formative process, often in special fructifications,
and subserving either or both multiplication and persistence,
e.g. zygospores, oospores, brand-spores, aecidiospores, ascospores,
basidiospores, &c. Little or nothing is gained by these definitions,
however, which are especially physiological. In practice these
various kinds of spores of fungi receive further special names in the
separate groups, and names, moreover,
which will appear, to those
unacquainted with the history,
to have been given without any
consistency or regard to general
principles; nevertheless, for ordinary
purposes these names are far
more useful in most cases, owing
to their descriptive character, than
the proposed new names, which
have been only partially accepted.
Sporophores.—In some of the
simpler fungi the spores are not
borne on or in hyphae which can
be distinguished from the vegetative
parts or mycelium, but in
the vast majority of cases the
sporogenous hyphae either ascend
free into the air or radiate into
the surrounding water as distinct
branches, or are grouped into
special columns, cushions, layers
or complex masses obviously
different in colour, consistency,
shape and other characters from
the parts which gather up and
assimilate the food-materials. The
term “receptacle” sometimes
applied to these spore-bearing
hyphae is better replaced by sporophore.
The sporophore is obsolete
when the spore-bearing hyphae
are not sharply distinct from the
mycelium, simple when the constituent
hyphae are isolated, and
compound when the latter are
conjoined. The chief distinctive characters of the sporogenous
hyphae are their orientation, usually vertical; their limited apical
growth; their peculiar branching, form, colour, contents, consistency;
and their spore-production. According to the characters
of the last, we might theoretically divide them into conidiophores,
sporangiophores, gametophores, oidiophores, &c.; but since the two
latter rarely occur, and more than one kind of spore or spore-case
may occur on a sporophore, it is impossible to carry such a scheme
fully into practice.
A simple sporophore may be merely a single short hypha, the end
of which stops growing and becomes cut off as a conidium by the
formation of a septum, which then splits and allows the conidium
to fall. More generally the hypha below the septum grows forwards
again, and repeats this process several times before the terminal
conidium falls, and so a chain of conidia results, the oldest of which
terminates the series (Erysiphe); when the primary branch has
thus formed a basipetal series, branches may arise from below and
again repeat this process, thus forming a tuft (Penicillium). Or the
primary hypha may first swell at its apex, and put forth a series of
short peg-like branches (sterigmata) from the increased surface thus
provided, each of which develops a similar basipetal chain of conidia
(Aspergillus), and various combinations of these processes result in
the development of numerous varieties of exquisitely branched
sporophores of this type (Botrytis, Botryosporium, Verticillium, &c.).
 |
| Fig. 3.—Cystopus candidus. |
|
A. a, Conidia.
b, Conidiophores.
c, Conidium emitting zoospores.
d, Free zoospore.
B.og, Oogonium. |
os, Oosphere.
an, Antheridium.
C. Formation of zoospores by oospores.
z, Free zoospores.
(After De Bary.) |
A second type is developed as follows: the primary hypha forms
a septum below its apex as before, and the terminal conidium, thus
abstricted, puts out a branch at its apex, which starts as a mere
point and rapidly swells to a second conidium; this repeats the
process, and so on, so that we now have a chain of conidia developed
in acropetal succession, the oldest being below, and, as in Penicillium,
&c., branches put forth lower down may repeat the process (Hormodendron).
In all these cases we may speak of simple conidiophores.
The simple sporophore does not necessarily terminate in conidia,
however. In Mucor, for example, the end of the primary hypha
swells into a spheroidal head (sporangium), the protoplasm of which
undergoes segmentation into more or less numerous globular masses,
each of which secretes an enveloping cell-wall and becomes a spore
(endospore), and branched systems of sporangia may arise as before
(Thamnidium). Such may be termed sporangiophores. In Sporodinia
the branches give rise also to short branches, which meet and
fuse their contents to form zygospores. In Peronospora, Saprolegnia,
&c., the ends of the branches swell up into sporangia, which develop
zoospores in their interior (zoosporangia), or their contents become
oospheres, which may be fertilized by the contents of other branches
(antheridia) and so form egg-cases (oogonia). Since in such cases
the sporophore bears sexual cells, they may be conveniently termed
gametophores.
Compound sporophores arise when any of the branched or unbranched
types of spore-bearing hyphae described above ascend
into the air in consort, and are more or less crowded into definite
layers, cushions, columns or other complex masses. The same laws
apply to the individual hyphae and their branches as to simple
sporophores, and as long as the conidia, sporangia, gametes, &c.,
are borne on their external surfaces, it is quite consistent to speak
of these as compound sporophores, &c., in the sense described, however
complex they may become. Among the simplest cases are
the sheet-like aggregates of sporogenous hyphae in Puccinia, Uromyces,
&c., or of basidia in Exobasidium, Corticium, &c., or of asci in
Exoascus, Ascocorticium, &c. In the former, where the layer is small,
it is often termed a sorus, but where, as in the latter, the sporogenous
layer is extensive, and spread out more or less sheet-like on
the supporting tissues, it is more frequently termed a hymenium.
Another simple case is that of the columnar aggregates of sporogenous
hyphae in forms like Stilbum, Coremium, &c. These lead
336
us to cases where the main mass of the sporophore forms a supporting
tissue of closely crowded or interwoven hyphae, the sporogenous
terminal parts of the hyphae being found at the periphery or apical
regions only. Here we have the cushion-like type (stroma) of
Nectria and many Pyrenomycetes, the clavate “receptacle” of
Clavaria, &c., passing into the complex forms met with in Sparassis,
Xylaria, Polyporei, and Agaricini, &c. In these cases the compound
sporophore is often termed the hymenophore, and its various parts
demand special names (pileus, stipes, gills, pores, &c.) to denote
peculiarities of distribution of the hymenium over the surface.
Other series of modifications arise in which the tissues corresponding
to the stroma invest the sporogenous hyphal ends, and thus
enclose the spores, asci, basidia, &c., in a cavity. In the simplest
case the stroma, after bearing its crop of conidia or oidia, develops
ascogenous branches in the loosened meshes of its interior (e.g.
Onygena). Another simple case is where the plane or slightly convex
surface of the stroma rises at its margins and overgrows the sporogenous
hyphal ends, so that the spores, asci, &c., come to lie in the
depression of a cavity—e.g. Solenia, Cyphella—and even simpler
cases are met with in Mortierella, where the zygospore is invested by
the overgrowth of a dense mat of closely branching hyphae, and in
Gymnoascus, where a loose mat of similarly barren hyphae covers
in the tufts of asci as they develop.
In such examples as the above we may regard the hymenium
(Solenia, Cyphella), zygospores, or asci as truly invested by later
growth, but in the vast majority of cases the processes which result
in the enclosure of the spores, asci, &c., in a “fructification” are
much more involved, inasmuch as the latter is developed in the
interior of hyphal tissues, which are by no means obviously homologous
with a stroma. Thus in Penicillium, Eurotium, Erysiphe,
&c., hyphal ends which are the initials of ascogenous branches, are
invested by closely packed branches at an early stage of development,
and the asci develop inside what has by that time become
a complete investment. Whether a true sexual process precedes
these processes or not does not affect the present question, the
point being that the resulting spheroidal “fructification” (cleistocarp,
perithecium) has a definite wall of its own not directly comparable
with a stroma. In other cases (Hypomyces, Nectria) the
perithecia arise on an already mature stroma, while yet more numerous
examples can be given (Poronia, Hypoxylon, Claviceps, &c.)
where the perithecia originate below the surface of a stroma formed
long before. Similarly with the various types of conidial or oidial
“fructifications,” termed pycnidia, spermogonia, aecidia, &c. In
the simplest of these cases—e.g. Fumago—a single mycelial cell
divides by septa in all three planes until a more or less solid clump
results. Then a hollow appears in the centre owing to the more
rapid extension of the outer parts, and into this hollow the cells
lining it put forth short sporogenous branches, from the tips of
which the spores (stylospores, conidia, spermatia) are abstricted. In
a similar way are developed the pycnidia of Cicinnobolus, Pleospora,
Cucurbitaria, Leptosphaeria and others. In other cases (Diplodia,
Aecidium, &c.) conidial or oidial “fructifications” arise by a number
of hyphae interweaving themselves into a knot, as if they were
forming a Sclerotium. The outer parts of the mass then differentiate
as a wall or investment, and the interior becomes a hollow, into
which hyphal ends grow and abstrict the spores. Much more
complicated are the processes in a large series of “fructifications,”
where the mycelium first develops a densely packed mass of hyphae,
all alike, in which labyrinths of cavities subsequently form by
separation of hyphae in the previously homogeneous mass, and the
hymenium covers the walls of these cavities and passages as with a
lining layer. Meanwhile differences in consistency appear in various
strata, and a dense outer protective layer (peridium), soft gelatinous
layers, and so on are formed, the whole eventually attaining great
complexity—e.g. puff-balls, earth-stars and various Phalloideae.
Spore-Distribution.—Ordinary conidia and similarly abstricted
dry spores are so minute, light and numerous that their dispersal
is ensured by any current of air or water, and we also know that
rats and other burrowing animals often carry them on their fur;
similarly with birds, insects, slugs, worms, &c., on claws, feathers,
proboscides, &c., or merely adherent to the slimy body. In addition
to these accidental modes of dispersal, however, there is a series of
interesting adaptations on the part of the fungus itself. Passing
over the locomotor activity of zoospores (Pythium, Peronospora,
Saprolegnia) we often find spores held under tension in sporangia
(Pilobolus) or in asci (Peziza) until ripe, and then forcibly shot out
by the sudden rupture of the sporangial wall under the pressure of
liquid behind—mechanism comparable to that of a pop-gun, if we
suppose air replaced by watery sap. Even a single conidium, held
tense to the last moment by the elastic cell-wall, may be thus shot
forward by a spurt of liquid under pressure in the hypha abstricting
it (e.g. Empusa), and similarly with basidiospores (Coprinus,
Agaricus, &c.). A more complicated case is illustrated by Sphaerobolus,
where the entire mass of spores, enclosed in its own peridium,
is suddenly shot up into the air like a bomb from a mortar by the
elastic retroversion of a peculiar layer which, up to the last moment,
surrounded the bomb, and then suddenly splits above, turns inside
out, and drives the former as a projectile from a gun. Gelatinous
or mucilaginous degenerations of cell-walls are frequently employed
in the interests of spore dispersal. The mucilage surrounding
endospores of Mucor, conidia of Empusa, &c., serves to gum the spore
to animals. Such gums are formed abundantly in pycnidia, and,
absorbing water, swell and carry out the spores in long tendrils,
which emerge for days and dry as they reach the air, the glued spores
gradually being set free by rain, wind, &c. In oidial chains (Sclerotinia)
a minute double wedge of wall-substance arises in the middle
lamella between each pair of contiguous oidia, and by its enlargement
splits the separating lamella. These disjunctors serve as points of
application for the elastic push of the swelling spore-ends, and as
the connecting outer lamella of cell-wall suddenly gives way, the
spores are jerked asunder. In many cases the slimy masses of
spermatia (Uredineae), conidia (Claviceps), basidiospores (Phallus,
Coprinus), &c., emit more or less powerful odours, which attract
flies or other insects, and it has been shown that bees carry the
fragrant oidia of Sclerotinia to the stigma of Vaccinium and infect
it, and that flies carry away the foetid spores of Phallus, just as
pollen is dispersed by such insects. Whether the strong odour of
trimethylamine evolved by the spores of Tilletia attracts insects is
not known.
The recent observations and exceedingly ingenious experiments of
Falck have shown that the sporophores of the Basidiomycetes—especially
the large sporophores of such forms as Boletus, Polyporus—contain
quantities of reserve combustible material which are burnt
up by the active metabolism occurring when the fruit-body is ripe.
By this means the temperature of the sporophore is raised and the
difference between it and the surrounding air may be one of several
degrees. As a result convection currents are produced in the air
which are sufficient to catch the basidiospores in their fall and carry
them, away from the regions of comparative atmospheric stillness
near the ground, to the upper air where more powerful air-currents
can bring about their wide distribution.
Classification.—It has been accepted for some time now that
the majority of the fungi proper fall into three main groups,
the Phycomycetes, Ascomycetes and Basidiomycetes, the
Schizomycetes and Myxomycetes (Mycetozoa) being considered
as independent groups not coming under the true fungi.
The chief schemes of classification put forward in detail have
been those of P.A. Saccardo (1882-1892), of Oskar Brefeld and
Von Tavel (1892), of P.E.L. Van Tieghem (1893) and of J.
Schroeter (1892). The scheme of Brefeld, which was based on
the view that the Ascomycetes and Basidiomycetes were completely
asexual and that these two groups had been derived
from one division (Zygomycetes) of the Phycomycetes, has been
very widely accepted. The recent work of the last twelve years
has shown, however, that the two higher groups of fungi exhibit
distinct sexuality, of either a normal or reduced type, and has
also rendered very doubtful the view of the origin of these two
groups from the Phycomycetes. The real difficulty of classification
of the fungi lies in the polyphyletic nature of the group.
There is very little doubt that the primitive fungi have been
derived by degradation from the lower algae. It appears,
however, that such a degradation has occurred not only once
in evolution but on several occasions, so that we have in the
Phycomycetes not a series of naturally related forms, but groups
which have arisen perfectly independently of one another from
various groups of the algae. It is also possible in the absence
of satisfactory intermediate forms that the Ascomycetes and
Basidiomycetes have also been derived from the algae independently
of the Phycomycetes, and perhaps of one another.
A natural classification on these lines would obviously be very
complicated, so that in the present state of our knowledge it
will be best to retain the three main groups mentioned above,
bearing in mind that the Phycomycetes especially are far from
being a natural group. The following gives a tabular survey of
the scheme adopted in the present article:
A. Phycomycetes. Alga-like fungi with unicellular thallus
and well-marked sexual organs.
Class I.—Oomycetes. Mycelium usually well developed, but
sometimes poor or absent. Sexual reproduction by oogonia
and antheridia; asexual reproduction by zoospores or
conidia.
1. Monoblepharidineae. Mycelium present, antheridia with
antherozoids, oogonium with single oosphere: Monoblepharidaceae.
2. Peronosporineae. Mycelium present; antheridia but no
antherozoids; oogonia with one or more oospheres:
Peronosporaceae, Saprolegniaceae.
3. Chytridineae. Mycelium poorly developed or absent;
oogonia and antheridia (without antherozoids) known in
some cases; zoospores common: Chytridiaceae. Ancylistaceae.
337
Class II.—Zygomycetes. Mycelium well developed; sexual reproduction
by zygospores; asexual reproduction by sporangia
and conidia.
1. Mucorineae. Sexual reproduction as above, asexual by
sporangia or conidia or both: Mucoraceae. Mortierellaceae,
Chaetocladiaceae, Piptocephalidaceae.
2. Entomophthorineae. Sexual reproduction typical but
with sometimes inequality of the fusing gametes (gametangia ?):
Entomophthoraceae.
B. Higher Fungi. Fungi with segmental thallus; sexual
reproduction sometimes with typical antheridia and oogonia
(ascogonia) but usually much reduced.
Class I.—Ustilaginales. Forms with septate thallus, and reproduction
by chlamydospores which on germination produce
sporidia; sexuality doubtful.
Class II.—Ascomycetes. Thallus septate; spores developed
in special type of sporangium, the ascus, the number of spores
being usually eight. Sexual reproduction sometimes typical,
usually reduced.
Exoascineae, Saccharomycetineae, Perisporinea, Discomycetes,
Pyrenomycetes, Tuberineae, Laboulbeniineae.
Class III.—Basidiales. Thallus septate. Conidia (basidiospores)
borne in fours on a special conidiophore, the basidium.
Sexual reproduction always much reduced.
1. Uredineae. Life-history in some cases very complex and
with well-marked sexual process and alternation of generations,
in others much reduced; basidium (promycelium)
derived usually from a thick-walled spore (teleutospore).
2. Basidiomycetes. Life-history always very simple, no well-marked
alternation of generations; basidium borne
directly on the mycelium.
(A) Protobasidiomycetes. Basidia septate.
Auriculariaceae, Pilacreaceae, Tremellinaceae.
(B) Autobasidiomycetes. Basidia non-septate.
Hymenomycetes, Gasteromycetes.
A. Phycomycetes.—Most of the recent work of importance
in this group deals with the cytology of sexual reproduction and
of spore-formation, and the effect of external conditions on the
production of reproductive organs.
Monoblepharidaceae consists of a very small group of aquatic
forms living on fallen twigs in ponds and ditches. Only one genus,
Monoblepharis, can certainly be placed here, though a somewhat
similar genus, Myrioblepharis, with a peculiar multiciliate zoospore
like that of Vaucheria, is provisionally placed in the same group.
Monoblepharis was first described by Cornu in 1871, but from that
time until 1895 when Roland Thaxter described several species
from America the genus was completely lost sight of. Monoblepharis
has oogonia with single oospheres and antheridia developing a few
amoeboid uniciliate antherozoids; these creep to the opening of the
oogonium and then swim in. The resemblance between this genus
and Oedogonium among the algae is very striking, as is also that of
Myrioblepharis and Vaucheria.
Peronosporaceae are a group of endophytic parasites—about 100
species—of great importance as comprising the agents of “damping
off” disease (Pythium), vine-mildew (Plasmopara), potato disease
(Phytophthora), onion-mildew (Peronospora). Pythium is a semi-aquatic
form attacking seedlings which are too plentifully supplied
with water; its hyphae penetrate the cell-walls and rapidly destroy
the watery tissues of the living plant; then the fungus lives in the
dead remains. When the free ends of the hyphae emerge again into
the air they swell up into spherical bodies which may either fall
off and behave as conidia, each putting out a germ-tube and infecting
the host; or the germ-tube itself swells up into a zoosporangium
which develops a number of zoospores. In the rotting tissues
branches of the older mycelium similarly swell up and form antheridia
and oogonia (fig. 4). The contents of the antheridium are not set
free, but that organ penetrates the oogonium by means of a narrow
outgrowth, the fertilizing tube, and a male nucleus then passes over
into the single oosphere, which at first multinucleate becomes uninucleate
before fertilization. Pythium is of interest as illustrating
the dependence of zoospore-formation on conditions and the indeterminate
nature of conidia. The other genera are more purely
parasitic; the mycelium usually sends haustoria into the cells of
the host and puts out branched, aerial conidiophores through the
stomata, the branches of which abstrict numerous “conidia”;
these either germinate directly or their contents break up into
zoospores (fig. 5). The development of the “conidia” as true
conidial spores or as zoosporangia may occur in one and the same
species (Cystopus candidus, Phytophthora infestans) as in Pythium
described above; in other cases the direct conidial germination is
characteristic of genera—e.g. Peronospora; while others emit
zoospores—e.g. Plasmopara, &c. In Cystopus (Albugo) the “conidia”
are abstricted in basipetal chain-like series from the ends of hyphae
which come to the surface in tufts and break through the epidermis
as white pustules. Each “conidium” contains numerous nuclei
and is really a zoosporangium, as after dispersal it breaks up into a
number of zoospores. The Peronosporaceae reproduce themselves
sexually by means of antheridia and oogonia as described in Pythium.
In Cystopus Bliti the oosphere contains numerous nuclei, and all
the male nuclei from the antheridium pass into it, the male and
female nuclei then fusing in pairs. We thus have a process of
“multiple fertilization”; the oosphere really represents a large
number of undifferentiated gametes and has been termed a coenogamete.
Between Cystopus Bliti on the one hand and Pythium de
Baryanum on the other a number of cytologically intermediate
forms are known. The oospore on germination usually gives origin
to a zoosporangium, but may form directly a germ tube which infects
the host.
 |
| From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer. |
| Fig. 4.—Fertilization of the Peronosporeae. After Wager. |
|
1, Peronospora parasitica. Young
multinucleate oogonium (og)
and antheridium (an).
2, Albugo candida. Oogonium
with the central uninucleate
oosphere and the fertilizing
tube (a) of the antheridium
which introduces the male
nucleus. |
3, The same. Fertilized egg-cell
(o) surrounded by the
periplasm (p). |
 |
| Fig. 5.—Phytophthora infestans. Fungus of Potato Disease. |
|
A, B, Section of Leaf of Potato
with sporangiophores of Phytophthora
infestans passing
through the stomata D, on
the under surface of the leaf.
E, Sporangia.
F, G, H, J, Further development
of the sporangia. |
K, Germination of the zoospores
formed in the sporangia.
L, M, N, Fertilization of the
oogonium and development of
the oospore in Peronospora. |
Saprolegniaceae are aquatic forms found growing usually on dead
insects lying in water but occasionally on living fish (e.g. the salmon
disease associated with Saprolegnia ferax). The chief genera are
338
Saprolegnia, Achlya, Pythiopsis, Dictyuchus, Aplanes. Motile zoospores
which escape from the zoosporangium are present except in Aplanes.
The sexual reproduction shows all transitions between forms which
are normally sexual, like the Peronosporaceae, to forms in which
no antheridium is developed and the oospheres develop parthenogenetically.
The oogonia, unlike the Peronosporaceae, contain more
than one oosphere. Klebs has shown that the development of
zoosporangia or of oogonia and pollinodia respectively in Saprolegnia
is dependent on the external conditions; so long as a continued
stream of suitable food-material is ensured the mycelium grows on
without forming reproductive organs, but directly the supplies of
nitrogenous and carbonaceous food fall below a certain degree of
concentration sporangia are developed. Further reduction of the
supplies of food effects the formation of oogonia. This explains the
sequence of events in the case of a Saprolegnia-mycelium radiating
from a dead fly in water. Those parts nearest the fly and best
supplied develop barren hyphae only; in a zone at the periphery,
where the products of putrefaction dissolved in the water form a
dilute but easily accessible supply, the zoosporangia are developed
in abundance; oogonia, however, are only formed in the depths of
this radiating mycelium, where the supplies of available food
materials are least abundant.
Chytridineae.—These parasitic and minute, chiefly aquatic, forms
may be looked upon as degenerate Oomycetes, since a sexual process
and feeble unicellular mycelium occur in some; or they may be
regarded as series of primitive forms leading up to higher members.
There is no means of deciding the question. They are usually
included in Oomycetes, but their simple structure, minute size,
usually uniciliate zoospores, and their negative characters would
justify their retention as a separate group. It contains less than
200 species, chiefly parasitic on or in algae and other water-plants
or animals, of various kinds, or in other fungi, seedlings, pollen and
higher plants. They are often devoid of hyphae, or put forth fine
protoplasmic filaments into the cells of their hosts. After absorbing
the cell-contents of the latter, which it does in a few hours or days,
the fungus puts out a sporangium, the contents of which break up
into numerous minute swarm-spores, usually one-ciliate, rarely
two-ciliate. Any one of these soon comes to rest on a host-cell,
and either pierces it and empties its contents into its cavity, where
the further development occurs (Olpidium), or merely sends in
delicate protoplasmic filaments (Rhizophydium) or a short hyphal
tube of, at most, two or three cells, which acts as a haustorium,
the further development taking place outside the cell-wall of the
host (Chytridium). In some cases resting spores are formed inside
the host (Chytridium), and give rise to zoosporangia on germination.
In a few species a sexual process is described, consisting in
the conjugation of similar cells (Zygochytrium) or the union of
two dissimilar ones (Polyphagus). In the development of distinct
antheridial and oogonial cells the allied Ancylistineae show
close alliances to Pythium and the Oomycetes. On the other hand,
the uniciliate zoospores of Polyphagus have slightly amoeboid
movements, and in this and the pseudopodium-like nature of the
protoplasmic processes, such forms suggest resemblances to the
Myxomycetes. Opinions differ as to whether the Chytridineae are degraded
or primitive forms, and the group still needs critical revision.
Many new forms will doubtless be discovered, as they are rarely
collected on account of their minuteness. Some forms cause damping
off of seedlings—e.g. Olpidium Brassicae; others discoloured spots
and even tumour-like swellings—e.g. Synchytium Scabiosae, S.
Succisae, Urophlyctis, &c., on higher plants. Analogies have been
pointed out between Chytridiaceae and unicellular algae, such as
Chlorosphaeraceae, Protococcaceae, “Palmellaceae,” &c., some of
which are parasitic, and suggestions may be entertained as to
possible origin from such algae.
The Zygomycetes, of which about 200 species are described, are
especially important from a theoretical standpoint, since they furnished
the series whence Brefeld derived the vast majority of the
fungi. They are characterized especially by the zygospores, but
the asexual organs (sporangia) exhibit interesting series of changes,
beginning with the typical sporangium of Mucor containing numerous
endospores, passing to cases where, as in Thamnidium, these are
accompanied with more numerous small sporangia (sporangioles)
containing few spores, and thence to Chaetocladium and Piptocephalis,
where the sporangioles form but one spore and fall and germinate
as a whole; that is to say, the monosporous sporangium has become
a conidium, and Brefeld regarded these and similar series of changes
as explaining the relation of ascus to conidium in higher fungi.
According to his view, the ascus is in effect the sporangium with
several spores, the conidium the sporangiole with but one spore,
and that not loose but fused with the sporangiole wall. On this
basis, with other interesting morphological comparisons, Brefeld
erected his hypothesis, now untenable, that the Ascomycetes and
Basidiomycetes diverge from the Zygomycetes, the former having
particularly specialized the ascus (sporangial) mode of reproduction,
the latter having specialized the conidial (indehiscent one-spored
sporangiole) mode. In addition to sporangia and the conidial spores
referred to, some Mucorini show a peculiar mode of vegetative
reproduction by means of gemmae or chlamydospores—i.e. short
segments of the hyphae become stored with fatty reserves and act
as spores. The gemmae formed on submerged Mucors may bud like
a yeast, and even bring about alcoholic fermentation in a saccharine
solution.
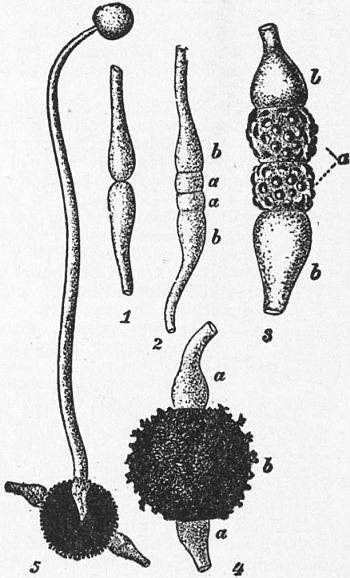 |
| From Strasburger’s Lehrbuch der Botanik, by
permission of Gustav Fischer. |
| Fig. 6.—Mucor Mucedo. Different
stages in the formation and germination
of the zygospore. (After Brefeld,
1-4. 5 from v. Tavel, Pilze.) |
|
1, Two conjugating branches in contact.
2, Septation of the conjugating cells (a)
from the suspensors (b).
3, More advanced stage, the conjugating
cells (a) are still distinct from
one another; the warty thickenings
of their walls have commenced to
form.
4, Ripe zygospore (b) between the suspensors
(a).
5, Germinating zygospore with a germ-tube
bearing a sporangium. |
The segments of the hyphae in this group usually contain several
nuclei. At the time of sporangial formation the protoplasm with
numerous nuclei streams into the swollen end of the sporangiophore
and there becomes cut off by a cell-wall to form the sporangium.
The protoplasm then becomes cut up by a series of clefts into a
number of smaller and smaller pieces which are unicellular in
Pilobolus, multicellular in Sporodinia. These then become surrounded
by a cell-wall and form the spores. This mode of spore-formation
is totally different from that in the ascus; hence one of
the difficulties of the acceptance of Brefeld’s view of the homology
of ascus and sporangium. The cytology of zygospore-formation is
not known in detail;
the so-called gametes
which fuse are multinucleate
and are no doubt
of the nature of gametangia.
The fate of these
nuclei is doubtful, probably
they fuse in pairs
(fig. 6).
Blakeslee has lately
made some very important
observations of the
Zygomycetes. It is well
known that while in some
forms, e.g. Spordinia,
zygospores are easily obtained,
in others, e.g. most
species of Mucor, they
are very erratic in their
appearance. This has now
been explained by
Blakeslee, who finds that
the Mucorinae can be
divided into two groups,
termed homothallic and
heterothallic respectively.
In the first group zygospores
can arise by the
union of branches from
the same mycelium and
so can be produced by the
growth from a single spore;
this group includes Spordinia
grandis, Spinellus
fusiger, some species of
Mucor, &c. The majority
of forms, however, fall
into the heterothallic
group, in which the association
of branches from
two mycelia different in
nature is necessary for the
formation of zygospores.
These structures cannot
then be produced from the
product of a single spore
nor even from the thalli
derived from any two
spores. The two kinds of
thalli Blakeslee considers
to have a differentiation
of the nature of sex and
he distinguishes them as (+) and (−) forms; the former being
usually distinguished by a somewhat greater luxuriance of growth.
The classification of the Mucorini depends on the prevalence and
characters of the conidia, and of the sporangia and zygospores—e.g.
the presence or absence of a columella in the former, the formation
of an investment round the latter. Most genera are saprophytes,
but some—Chaetocladium, Piptocephalis—are parasites on other
Mucorini, and one or two are associated casually with the rotting
of tomatoes and other fruits, bulbs, &c., the fleshy parts of which
are rapidly destroyed if once the hyphae gain entrance. Even more
important is the question of mycosis in man and other animals,
referred to species of Mucor, and investigated by Lucet and Costantin.
Klebs has concluded that transpiration is the important
factor in determining the formation of sporangia, while zygote-development
depends on totally different conditions; these results
have been called in question by Falck.
The Entomophthoraceae contain three genera, Empusa, Entomophthora
and Basidiobolus. The two first genera consist of forms
which are parasitic on insects. Empusa Muscae causes the well-known
epidemic in house-flies during the autumn; the dead, affected
flies are often found attached to the window surrounded by a white
halo of conidia. B. ranarum is found in the alimentary canal of the
frog and growing on its excrement. In these three genera the conidia
are cast off with a jerk somewhat in the same way as the sporangium
of Pilobolus.
339
B. Higher Fungi.—Now that Brefeld’s view of the origin
of these forms from the Zygomycetes has been overthrown,
the relationship of the higher and lower forms of fungi is left
in obscurity. The term Eumycetes is sometimes applied to this
group to distinguish them from the Phycomycetes, but as the
same name is also applied to the fungi as a whole to differentiate
them from the Mycetozoa and Bacteria, the term had best be
dropped. The Higher Fungi fall into three groups: the Ustilaginales,
of doubtful position, and the two very sharply marked
groups Basidiales and Ascomycetes.
 |
| From Vine’s Students’ Text Book of
Botany, by permission of Swan Sonnenschein
& Co. |
| Fig. 7.—Germinating resting-gonidia.
A, of Ustilago
receptaculorum; B, of Tilletia
Caries. |
|
sp, The gonidium.
pm, The promycelium.
d, The sporidia: in B the
sporidia have coalesced
in pairs at v. |
I. Ustilaginales.—This includes two families Ustilaginaceae
(smuts) and Tilletiaceae (bunts). The bunts and smuts which
damage our grain and fodder plants comprise about 400 species of
internal parasites, found in all countries on herbaceous plants, and
especially on Monocotyledons. They are remarkable for their dark
spores developed in gall-like excrescences on the leaves, stems, &c.,
or in the fruits of the host. The discovery of the yeast-conidia of
these fungi, and their thorough investigation by Brefeld, have
thrown new lights on the group, as also have the results elucidating
the nature of the ordinary dark spores—smuts, bunt, &c.—which by
their mode of origin and development are chlamydospores. When
the latter germinate a slender “promycelium” is put out; in
Ustilago and its allies this is transversely septate, and bears lateral
conidia (sporidia); in Tilletia and its allies non-septate, and bears
a terminal tuft of conidia (sporidia) (fig. 7). Brefeld regarded the
promycelium as a kind of basidium, bearing lateral or terminal
conidia (comparable to basidiospores),
but since the number of
basidiospores is not fixed, and the
basidium has not yet assumed very
definite morphological characters,
Brefeld termed the group Hemibasidii,
and regarded them as a half-way
stage in the evolution of the
true Basidiomycetes from Phycomycetes,
the Tilletia type leading
to the true basidium (Autobasidium),
the Ustilago type to the protobasidium,
with lateral spores; but this
view is based on very poor evidence,
so that it is best to place these forms
as a separate group, the Ustilaginales.
The yeast-conidia, which bud off
from the conidia or their resulting
mycelium when sown in nutrient
solutions, are developed in successive
crops by budding exactly as
in the yeast plant, but they cannot
ferment sugar solutions. It is the
rapid spread of these yeast-conidia
in manure and soil waters which
makes it so difficult to get rid of
smuts, &c., in the fields, and they,
like the ordinary conidia, readily
infect the seedling wheat, oats,
barley or other cereals. Infection
in these cases occurs in the seedling
at the place where root and shoot
meet, and the infecting hypha having entered the plant goes on living
in it and growing up with it as if it had no parasitic action at all. When
the flowers form, however, the mycelium sends hyphae into the young
ovaries and rapidly replaces the stores of sugar and starch, &c.,
which would have gone to make the grain, by the soot-like mass of
spores so well known as smut, &c. These spores adhere to the grain,
and unless destroyed, by “steeping” or other treatment, are sown
with it, and again produce sporidia and yeast-conidia which infect
the seedlings. In other species the infection occurs through the
style of the flower, but the fungus after reaching the ovule develops
no further during that year but remains dormant in the embryo
of the seed. On germination, however, the fungus behaves in the
same way as one which has entered in the seedling stage. The
cytology of these forms is very little known; Dangeard states that
there is a fusion of two nuclei in the chlamydospore, but this requires
confirmation. Apart from this observation there is no other trace
of sexuality in the group.
II. Ascomycetes.—This, except in the case of a few of the simpler
forms, is a very sharply marked group characterized by a special
type of sporangium, the ascus. In the development of the ascus we
find two nuclei at the base which fuse together to form the single
nucleus of the young ascus. The single nucleus divides by three
successive divisions to form eight nuclei lying free in the protoplasm
of the ascus. Then by a special method, described first by Harper,
a mass of protoplasm is cut out round each nucleus; thus eight
uninucleate ascospores are formed by free-cell formation. The
protoplasm remaining over is termed epiplasm and often contains
glycogen (fig. 8). In some cases nuclear division is carried further
before spore-formation occurs, and the number of spores is then 16,
32 and 64, &c.; in a few cases the number of spores is less than
eight by abortion of some of the eight nuclei. The ascus is thus one
of the most sharply characterized structures among the fungi.
 |
| From Strasburger’s Lehrbuch der
Botanik, by permission of Gustav
Fischer. |
| Fig. 8.—Development of the
Ascus. |
|
A-C, Pyronema confluens.
(After Harper.)
D, Young ascus of Boudiera
with eight spores.
(After Claussen.) |
In some forms we find definite male and female sexual organs
(Sphaerotheca, Pyronema, &c.), in others the antheridium is abortive
or absent, but the ascogonium (oogonium) is still present and the
female nuclei fuse in pairs (Lachnea
stercorea, Humaria granulata, Ascobolus
furfuraceus); while in other
forms ascogonium and antheridium
are both absent and fusion occurs
between vegetative nuclei (Humaria
rutilans, and probably the majority
of other forms). In other cases the
sexual fusion is apparently absent
altogether, as in Exoascus. In the first
case (fig. 9) we have a true sexual
process, while in the second and third
cases we have a reduced sexual process
in which the fusion of other nuclei
has replaced the fusion of the normal
male and female nuclei. It is to be
noted that all the forms exhibit the
fusion of nuclei in the ascus, so that
those with the normal or reduced
sexual process described above have
two nuclear fusions in their life-history.
The advantage or significance
of the second (ascus) fusion is
not clearly understood.
The group of the Hemiasci was
founded by Brefeld to include forms
which were supposed to be a connecting
link between Phycomycetes and
Ascomycetes. As mentioned before,
the connexion between these two groups is very doubtful, and the derivation
of the ascus from an ordinary sporangium of the Zygomycetes
cannot be accepted. The majority of the forms which were formerly
included in this group have been shown to be either true Phycomycetes
(like Ascoidea) or true Ascomycetes (like Thelebolus). Eremascus and
Dipodascus, which are often placed among the Hemiasci, possibly do
not belong to the Ascomycetes series at all.
 |
| From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer. |
| Fig. 9.—Sphaerotheca Castagnei. Fertilization and Development
of the Perithecium. (After Harper.) |
|
1, Oogonium (og) with the antheridial
branch (az) applied to its surface
2, Separation of antheridium
(an).
3, Passage of the antheridial
nucleus towards that of the
oogonium. |
4, Union of the nuclei.
5, Fertilized oogonium surrounded
by two layers of
hyphae derived from the
stalk-cell (st).
6, The multicellular ascogonium
derived by division from the
oogonium; the terminal cell
with the two nuclei (as)
gives rise to the ascus. |
Exoascaceae are a small group of doubtful extent here used to
include Exoascus, Taphrina, Ascorticium and Endomyces. The
mycelium is very much reduced in extent. The asci are borne
directly on the mycelium and are therefore fully exposed, being
devoid from the beginning of any investment. The Taphrineae,
which include Exoascus and Taphrina, are important parasites—e.g.
pocket-plums and witches’ brooms on birches, &c., are due to
their action (fig. 10). Exoascus and Ascorticium present interesting
parallels to Exobasidium and Corticium among the Basidiomycetes.
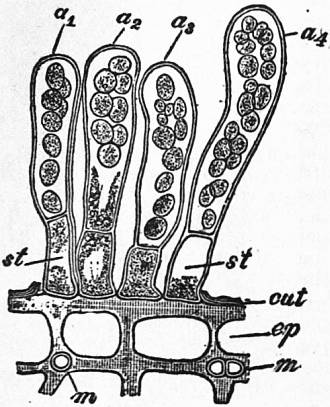 |
| From Strasburger’s Lehrbuch der
Botanik, by permission of Gustav Fischer. |
| Fig. 10.—Taphrina Pruni.
Transverse section through the
epidermis of an infected plum.
Four ripe asci, a1, a2, with eight
spores, a3, a4, with yeast-like
conidia abstricted from the spores.
After Sadebeck. |
st, Stalk-cells of the asci.
m, Filaments of the mycelium cut transversely.
cut, Cuticle.
sp, Epidermis. |
Saccharomycetaceae include the well-known yeasts which belong
mainly to the genus Saccharomyces. They are characterized by
their unicellular nature, their power of rapid budding, their capacity
for fermenting various sugars, and their power of forming endogenous
340
spores. The sporangium with its endogenous spores has been
compared with an ascus, and on these grounds the group is placed
among the Ascomycetes—a very doubtful association. The group
has attained an importance of late even beyond that to which it was
brought by Pasteur’s researches on alcoholic fermentation, chiefly
owing to the exact results of the investigations of Hansen, who
first applied the methods of pure cultures to the study of these
organisms, and showed that many of the inconsistencies hitherto
existing in the literature were
due to the coexistence in the
cultures of several species or
races of yeasts morphologically
almost indistinguishable, but
physiologically very different.
About fifty species of Saccharomyces
are described more or less
completely, but since many of
these cannot be distinguished
by the microscope, and some
have been found to develop
physiological races or varieties
under special conditions of
growth, the limits are still far
too ill-defined for complete
botanical treatment of the genus.
A typical yeast is able to develop
new cells by budding when submerged
in a saccharine solution,
and to ferment the sugar—i.e.
so to break up its molecules that,
apart from small quantities used
for its own substance, masses of
it out of all proportion to the
mass of yeast used become
resolved into other bodies, such
as carbon dioxide and alcohol,
the process requiring little or
no oxygen. Brefeld regards the
budding process as the formation
of conidia. Under other
conditions, of which the temperature
is an important one, the
nucleus in the yeast-cell divides,
and each daughter-nucleus again,
and four spores are formed in the mother cell, a process obviously comparable
to the typical development of ascospores in an ascus. Under
yet other conditions the quiescent yeast-cells floating on the surface
of the fermented liquor grow out into elongated sausage-shaped or
cylindrical cells and branching cell-series, which mat together into
mycelium-like veils. At the bottom of the fermented liquor the
cells often obtain fatty contents and thick walls, and behave as
resting cells (chlamydospores). The characters employed by experts
for determining a species of yeast are the sum of its peculiarities as
regards form and size: the shapes, colours, consistency, &c., of
the colonies grown on certain definite media; the optimum temperature
for spore-formation, and for the development of the
“veils”; and the behaviour as regards the various sugars.
The following summary of some of the principal characteristics
of half-a-dozen species will serve to show how such peculiarities can
be utilized for systematic purposes:
| Species. | Optimum Temperature for | Characters of | Sugars Fermented and
Products, &c. |
| Spores. | Veils. | Fermentation. | Cells. | Spores. |
| S. cereviseae I. | 30° | 20°-28° | High | Rounded | Globoid | Inverts maltose and saccharose
and form alcohol 4-6 vol. %. |
| S. Pastorianus I | 27°-5° | 26°-28° | Low | Rounded | Globoid |
| S. ellipsoideus | 25° | 33°-34° | Low | Rounded | Globoid |
| S. anomalus | 28°-31° | ? | High | Elliptical | Hat-shaped | Ditto, and evolves a fragrant ether. |
| S. Ludwigii | 30°-31° | ? | ? | Elongated | Globoid | Will not invert maltose. |
| S. membranaefaciens | 30° | ? | High | Elongated | Globoid | Inverts neither maltose nor saccharose. |
Two questions of great theoretical importance have been raised
over and over again in connexion with yeasts, namely, (1) the
morphological one as to whether yeasts are merely degraded forms
of higher fungi, as would seem implied by their tendency to form
elongated, hypha-like cells in the veils, and their development
of “ascospores” as well as by the wide occurrence of yeast-like
“sprouting forms” in other fungi (e.g. Mucor, Exoasci, Ustilagineae,
higher Ascomycetes and Basidiomycetes); and (2) the question as
to the physiological nature and meaning of fermentation. With
regard to the first question no satisfactory proof has as yet been
given that Saccharomycetes are derivable by culture from any
higher form, the recent statements to that effect not having been
confirmed. At the same time there are strong grounds for insisting
on the resemblances between Endomyces, a hyphal fungus bearing
yeast-like asci, and such a form as Saccharomyces anomalus. Concerning
the second question, the recent investigations of Buchner
and others have shown that a ferment (zymase) can be extracted
from yeast-cells which causes sugar to break up into carbon dioxide
and alcohol. It has since been shown by Buchner and Albert that
yeast-cells which have been killed by alcohol and ether, or with
acetone, still retain the enzyme. Such material is far more active
than the zymase obtained originally by Buchner from the expressed
juice of yeast-cells. Thus alcoholic fermentation is brought into line
with the other fermentations.
Schizosaccharomyces includes a few species in which the cells do
not “bud” but become elongated and then divide transversely.
In the formation of sporangia two cells fuse together by means of
outgrowths, in a manner very similar to that of Spirogyra; sometimes,
however, the wall between two cells merely breaks down. The
fused cell becomes a sporangium, and in it eight spores are developed.
In certain cases single cells develop parthenogenetically, without
fusion, each cell producing, however, only four spores. In Zygosaccharomyces
described by Barker (1901) we have a form of the
usual sprouting type, but here again there is a fusion of two cells to
form a sporangium.
Cytology.—The study of the nucleus of yeast-cells is rendered
difficult by the presence of other deeply staining granules termed by
Guillermond metachromatic granules. These have often been mistaken
for nuclei and have to be carefully distinguished by differential
stains. In the process of budding the nucleus divides apparently
by a process of direct division. In the formation of spores the nucleus
of the cell divides, the protoplasm collects round the nuclei to form
the spores by free-cell formation; the protoplasm (epiplasm) not
used in this process becomes disorganized. A fusion of nuclei was
originally described by Jansens and Leblanc, but it was observed
neither by Wager nor Guillermond and is probably absent. In
Schizosaccharomyces and Zygosaccharomyces, however, we have a
fusion of nuclei in connexion with the conjugation of cells which
precedes sporangium-formation. The theory may be put forward
that the ordinary forms have been derived from sexual forms like
Schizosaccharomyces and Zygosaccharomyces by a loss of sexuality,
the sporangium being formed parthenogenetically without any
nuclear fusion. This suggests a possible relationship to Eremascus,
which can only doubtfully be placed in the Ascomycetes (vide supra).
Carpoascomycetes.—The other divisions of the Ascomycetes may
be distinguished as Carpoascomycetes because they do not bear
the asci free on the mycelium but enclosed in definite fruit bodies
or ascocarps. The ascocarps can be distinguished into two portions,
a mass of sterile or vegetative hyphae forming the main mass of the
fruit body, and surrounding the fertile ascogenous hyphae which
bear at their ends the asci. When the ascogonium (female organ)
is present the ascogenous hyphae arise from it, with or without its
previous fusion with an antheridium. In other cases the ascogenous
hyphae arise directly from the vegetative hyphae. In connexion
with this condition of reduction a fusion of nuclei has been observed
in Humaria rutilans and is probably of frequent occurrence. The
asci may be derived from the terminal cell of the branches of the
ascogenous hyphae, but usually they are derived from the penultimate
cell, the tip curving over to form the so-called crozier. By
this means the ascus cell is brought uppermost, and after the fusion
of the two nuclei it develops enormously and produces the ascospores.
The ascospores escape from the asci in various ways, sometimes by
a special ejaculation-mechanism. The Ascomycetes, at least the
Carpoascomycetes, exhibit a well-marked alternation of sexual and
asexual generations. The ordinary mycelium is the gametophyte
since it bears the ascogonia and antheridia when present; the
ascogenous hyphae with their asci represent the sporophyte since
they are derived from the fertilized ascogonium. The matter is
complicated by the apogamous transition from gametophyte to
sporophyte in the absence of the ascogonium; also by the fact that
there are normally two fusions in the life-history as mentioned
earlier. If there are two fusions one would expect two reductions,
and Harper has suggested that the division of the nuclei into eight
in the ascus, instead of into four spores as in most reduction processes,
is associated with a double reduction process in the ascus.
Miss Fraser in Humaria rutilans finds two reductions: a normal
synaptic reduction in the first nuclear division of the ascus, and a
peculiar reduction division termed brachymeiosis in the third ascus
division.
Various types of ascocarp are characteristic of the different
divisions of the Carpoascomycetes: the cleistothecium, apothecium
and perithecium.
341
Perisporineae.—This includes two chief families, Erysiphaceae
and Perisporiaceae. They are characterized by an ascocarp without
any opening to the exterior, the ascospores being set free by the
decay or rupture of the ascocarp wall; such a fruit-body is termed
a cleistothecium (cleistocarp). The Erysiphaceae are a sharply
marked group of forms which live as parasites. They form a superficial
mycelium on the surface of the plant, the hyphae not usually
penetrating the tissues but merely sending haustoria into the epidermal
cells. Only in rare cases is the mycelium intercellular.
Owing to their appearance they go by the popular name of mildews.
Sphaerotheca Humuli is the well known hop-mildew, Sphaerotheca
Mors-Uvae is the gooseberry mildew, the recent advent of which
has led to special legislation in Great Britain to prevent its spreading,
as when rampant it makes the culture of gooseberries impossible.
Erysiphe, Uncinula and Phyllactinia are other well-known genera.
The form of the fruit body, the difference and the nature of special
outgrowths upon it—the appendages—are characteristic of the
various genera. Besides peritheca the members of the Erysiphaceae
possess conidia borne in simple chains. De Bary brought forward
very strong evidence for the origin of the ascocarp in Sphaerotheca
and Erysiphe by a sexual process, but Harper in 1895 was the first
to prove conclusively, by the observation of the nuclear fusion, that
there was a definite fertilization in Sphaerotheca Humuli by the
fusion of a male (antheridial) nucleus with a female, ascogonial
(oogonial) nucleus. Since then Harper has shown that the same
process occurs in Erysiphe and Phyllactinia.
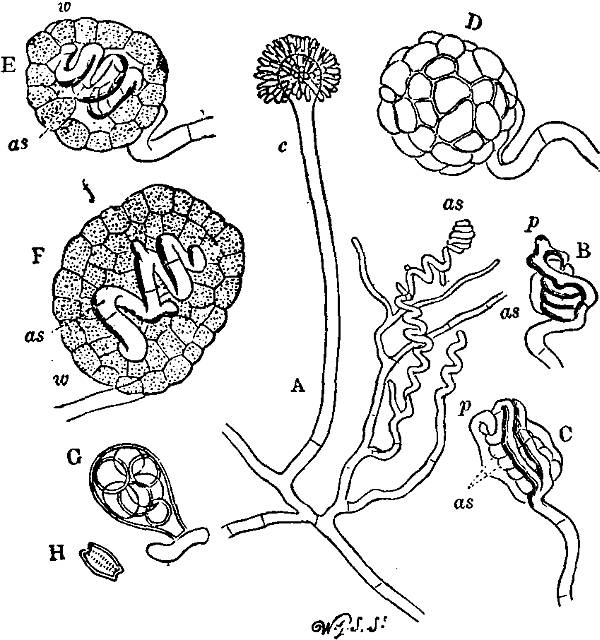 |
| Fig. 11.—Development of Eurotium repens. (After De Bary.) |
|
A, Small portion of mycelium
with conidiophore (c), and
archicarp (as).
B, The spiral archicarp (as),
with the antheridium (p).
D, The same, beginning to be
surrounded by the hyphae
forming the perithecium wall.
D, The perithecium. |
E, F, Sections of young perithecia.
w, Parietal cells.
f, Pseudo-parenchyma.
as, Ascogonium.
G, An ascus.
H, An ascospore. |
The Perisporiaceae are saprophytic forms, the two chief genera
being Aspergillus and Penicillium. The blue-green mould P.
crustaceum and the green mould A. herbariorium (= Eurotium
herbariorum) are extraordinarily widely distributed, moulds being
found on almost any food-material which is exposed to the air.
They have characteristic conidiophores bearing numerous conidia,
and also cleistothecia which are spherical in form and yellowish in
colour. The latter arise from the crown of a spirally coiled archicarp
(bearing an ascogonium at its end) and a straight antheridium.
Vegetative hyphae then grow up and surround these and enclose
them in a continuous sheath of plectenchyma (fig. 11). It has lately
been shown by Fraser and Chambers that in Eurotium both
ascogonium and antheridium contain a number of nuclei (i.e. are
coenogametes), but that the antheridium disorganizes without
passing its contents into the ascogonium. There is apparently a
reduced sexual process by the fusion of the ascogonial (female)
nuclei in pairs. Aspergillus Oryzae plays an important part in
saccharifying the starch of rice, maize, &c., by means of the abundant
diastase it secretes, and, in symbiosis with a yeast which ferments
the sugar formed, has long been used by the Japanese for the preparation
of the alcoholic liquor saké. The process has now been
successfully introduced into European commerce.
 |
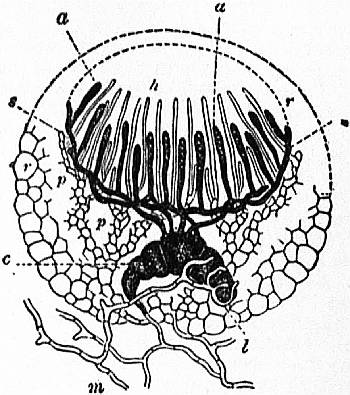 |
| From Strasburger’s Lehrbuch
der Botanik, by permission
of Gustav Fischer. |
Fig. 13.—Ascobolus furfuraceus.
Diagrammatic section of the fructification.
(After Janczewski.) |
| Fig. 12.—Peziza aurantiaca.
(After Krombholz,
nat. size.) |
m, Mycelium.
c, Archicarp.
l, Pollinodium.
s, Ascogenous filaments.
a, Asri.
r, p, The sterile tissue from which the paraphyses h spring. |
Discomycetes.—Used in its widest sense this includes the
Hysteriaceae, Phacidiaceae, Helvellaceae, &c. The group is
characterized in general by the possession of an ascocarp which,
though usually a completely closed structure during the earlier
stages of development, at maturity opens out to form a bowl or
saucer-shaped organ, thus completely exposing the layer of asci
which forms the hymenium. Such an ascocarp goes by the name of
apothecium. Owing to the shape of the fruit-body many of these
forms are known as cup-fungi, the cup or apothecium often attaining
a large size, sometimes several inches across (fig. 12). Functional
male and female organs have been shown to exist in Pyronema and
Boudiera; in Lachnea stercorea
both ascogonia and antheridia
are present, but the antheridium
is non-functional, the ascogonial
(female) nuclei fusing in pairs;
this is also the case in Humaria
granulata and Ascobolus furfuraceus,
where the antheridium is
entirely absent. In H. rutilans,
however, both sexual organs are
absent and the ascogenous
hyphae arise apogamously from
the ordinary hyphae of the mycelim.
In all these cases the
ascogonium and antheridium contain numerous nuclei; they are
to be looked upon as gametangia in which there is no differentiation
of gametes, and since they act as single gametes they are termed
coenogametes. In some forms as in Ascobolus the ascogonium is
multicellular, the various cells
communicating by pores in
the transverse walls (fig. 13).
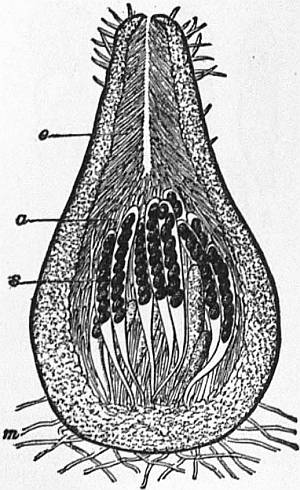 |
| From Strasburger’s Lehrbuch der Botanik,
by permission of Gustav Fischer. |
| Fig. 14.—Perithecium of Podospora
fimiseda in longitudinal section. After v. Tavel. |
|
s, Asci.
a, Paraphyses.
e, Periphyses.
m, Mycelial hyphae. |
In the Helvellaceae there is
no apothecium but a large
irregular fruit body which at
maturity bears the asci on its
surface. The development is
only slightly known, but there
is some evidence for believing
that the fruit-body is closed in
its very early stages.
The genus Peziza (in its
widest sense) may be taken as
the type of the group. Most
of them grow on living plants
or on dead vegetable remains,
very often on fallen wood; a
number, however, are found
growing on earth which is rich
in humus. The genus Sclerotinia
may be mentioned here;
a number of forms have been
investigated by Woronin. The
conidia are fragrant and are
carried by bees to the stigma
of the bilberry; here they
germinate with the pollen and
the hyphae pass with the pollen
tubes down the style; the
former infect the ovules and
produce sclerotia, therein reducing
the fruits to a mummified
condition. From the
sclerotia later the apothecium
develops. One species, S.
heteroica, is heteroecious; the
ascospores infecting the leaves of Vaccinium uliginosum, while the
conidia which then arise infect only Ledum palustre. This is the
only case of heteroecism known in the vegetable kingdom outside
the Uredineae.
Pyrenomycetes.—This is an extraordinarily large and varied group
of forms which mostly live parasitically or saprophytically on
vegetable tissue, but a few are parasitic on insect-larvae. The group
342
is characterized by a special type of ascocarp, the perithecium.
This is typically of a flask-shaped form opening with a small pore at
the top. The asci live at the bottom often mixed with paraphyses,
while the upper “neck” of the flask is lined with special hyphae,
the periphyses, which aid in the ejection of the spores (fig. 14).
The simpler forms bear the perithecia directly on the mycelium, but
the more highly developed forms often bear them on a special
mycelial development—the stroma, which is often of large size and
special shape and colour, and of dense consistence. The cytological
details of development of the perithecia are not well known; most
of them appear to develop their ascogenous hyphae in an apogamous
way without any connexion with an ascogonium. Besides the
special ascocarps, accessory reproductive organs are known in the
majority of cases in the form of conidia.
Tuberineae.—These are a small group of fungi including the well-known
truffles. They are found living saprophytically (in part
parasitically) underground in forests. The asci are developed in
the large dense fruit bodies (cleistothecia) and the spores escape by
the decay of the wall. The fruit-body is of complicated structure,
but its early stages of development are not known. Many of the
fruit-bodies have a pleasant flavour and are eaten under the name of
truffles (Tuber brumale and other species). The exact life-history
of the truffle is not known.
 |
| From Strasburger’s Lehrbuch der Botanik,
by permission of Gustav Fischer. |
| Fig. 15.—Armillaria mellea. (After
Ruhland.) |
|
A, Young basidium with the two
primary nuclei.
B, After fusion of the two nuclei.
Hypholoma appendiculatum.
C, A basidium before the four
nuclei derived from the secondary
nucleus of the basidium
have passed into the four
basidiospores.
D, Passage of a nucleus through
the sterigma into the basidiospore. |
Laboulbeniineae are a group of about 150 species of fungi found
on insects, especially beetles, and principally known from the researches
of Thaxter in America. The plant is a small, dark brown,
erect structure (receptacle) of a few cells, and 1-10 mm. high, attached
to the insect by the lowermost end (foot), and easily mistaken for a
hair or similar appendage of the insect. The receptacle ends above
in appendages, each consisting of one or a few cells, some of which
are the male organs, others the female organs, and others again may
be barren hairs. The male organ (antheridium) consists of a few
cells, the terminal one of which either abstricts from its end, or emits
from its interior the non-motile spermatia, reminding us of those
of the Florideae. The female organ is essentially a flask-shaped
structure; the neck of the flask growing out as the trichogyne, and
the belly composed of an axial carpogenic cell surrounded by investing
cells, and with one cell (trichophoric) between it and the trichogyne.
These three elements—trichogyne, trichophoric cell, and
carpogenic cell—are regarded as the procarp. The spermatia have
been shown by Thaxter to fuse with the trichogyne, after which the
axial cell below (carpogenic cell) undergoes divisions, and ultimately
forms asci containing ascospores, while cells investing this form a
perithecium, the whole structure reminding us essentially of the
fructification of a Pyrenomycete. Many modifications in details
occur, and the plants may be
dioecious. No injury is done to
the infested insects. It has lately
been shown that there is a fusion
of nuclei in connexion with ascus
formation, so that there can be
no doubt of the position of this
extraordinary group of plants
among the Ascomycetes. The
various cells of these organisms
are connected by large pits
which are traversed by thick
protoplasmic threads connecting
one cell with the next. In this
point and in their method of
fertilization the Laboulbeniineae
suggest a possible relationship
of Ascomycetes and the Red
Algae.
Basidiales.—This very large
group of plants is characterized
by the possession of a special
type of conidiophore—the basidium,
which gives its name to
the group. The basidium is
a unicellular or multicellular
structure from which four basidiospores
arise as outgrowths;
it starts as a binucleate structure,
but soon, like the ascus, becomes
uninucleate by the fusion of the
two nuclei. Then two successive
nuclear divisions occur resulting
in the formation of four nuclei
which later migrate respectively into the four basidiospores (fig. 15).
The Basidiales are further characterized by the complete loss of
normal sexuality, but at some time or other in the life-history
there takes place an association of two nuclei in a cell; the two
nuclei are derived from separate cells or possibly in some cases are
sister nuclei of the same cell. The two nuclei when once associated
are termed “conjugate” nuclei, and they always divide at the same
time, a half of each passing into each cell. This conjugate condition
is finally brought to a close by the nuclear fusion in the basidium.
Between the nuclear association and the nuclear fusion in the
basidium many thousands of cell generations may be intercalated.
This nuclear association of equivalent nuclei apparently represents
a reduced sexual process (like the fusion of female nuclei in Humaria
granulata and of vegetative nuclei in H. rutilans, among the Ascomycetes)
in which, however, the actual fusion (normally, in a sexual
process, occurring immediately after association) is delayed until
the formation of the basidium. During the tetrad division in the
basidium nuclear reduction occurs. There is thus in all the Basidiales
an alternation of generations, obscured, however, by the apogamous
transition from the gametophyte to sporophyte. The sporophyte
may be considered to begin at the stage of nuclear association and
end with the nuclear reduction in the basidium.
 |
| Fig. 16.—Puccinia graminis. |
|
A, Mass of teleutospores (t) on a
leaf of couch-grass.
e, Epidermis ruptured.
b, Sub-epidermal fibres. (After
De Bary.) |
B, Part of vertical section
through leaf of Berberis
vulgaris, with a, aecidium
fruits, p, peridium, and sp,
spermogonia. (After Sachs.)
C, Mass of uredospores (ur),
with one teleutospore (t).
sh, Sub-hymenial hyphae. (After
De Bary.) |
Uredineae.—This is a large group of about 2000 forms. They are
all intercellular parasites living mostly on the leaves of higher
plants. Owing to the presence of oily globules of an orange-yellow
or rusty-red colour in their hyphae and spores they are termed
Rust-Fungi. They are distinguished from the other fungi and the
rest of the Basidiales by the great variety of the spores and the
great elaboration of the life-history to be found in many cases.
Five different kinds of spores may be present—teleutospores,
sporidia (= basidiospores), aecidiospores, spermatia and uredospores
(fig. 16). The teleutospore, with the sporidia which arise from it,
is always present, and the division into genera is based chiefly on
its characters. The teleutospore puts forth on germination a four-celled
structure, the promycelium or basidium, and this bears later
four sporidia or basidiospores, one on each cell. When the sporidia
infect a plant the mycelium so produced gives origin to aecidiospores
and spermatia; the aecidiospores on infection produce a mycelium
which bears uredospores and later teleutospores. This is the life-history
of the most complicated forms, of the so-called eu forms.
In the opsis forms the uredospores are absent, the mycelium from the
aecidiospores producing directly the teleutospores. In brachy and
hemi the aecidiospores are absent, the mycelium from the sporidia
giving origin directly to the uredospores; the former possess spermatia,
in the latter they are absent. In lepto and micro forms both
aecidiospores and uredospores are absent, the sporidia producing a
mycelium which gives rise directly to teleutospores; in the lepto
forms the teleutospores can germinate directly, in the micro forms
only after a period of rest. We have thus a series showing a progressive
reduction in the complexity of the life-history, the lepto and
micro forms having a life-history like that of the Basidiomycetes.
The eu and opsis forms may exhibit the remarkable phenomenon
of heteroecism, i.e. the dependence of the fungus on two distinct
host-plants for the completion of the life-history. Heteroecism
is very common in this group and is now known in over one hundred
and fifty species. In all cases of heteroecism the sporidia infect
one host leading to the production of aecidiospores and spermatia
(if present), while the aecidiospores are only able to infect another
343
host on which the uredospores (if present) and the teleutospores
are developed. A few examples are appended:
| Species. | Teleutospores on | Aecidiospores on |
| Coleosporium Senecionis | Pinus | Senecio |
| Melampsora Rostrupi | Populus | Mecurialis |
| Pucciniastrum Goeppertiana | Vaccinium | Abies |
| Gymnosporangium Sabinae | Juniperus | Pyrus |
| Uromyces Pisi | Pisum, &c. | Euphorbia |
| Puccinia graminis | Triticum, &c. | Berberis |
| P. dispersa | Secale, &c. | Anchusa |
| P. coronata | Agrostis | Rhamnus |
| P. Ari-Phalaridis | Phalaris | Arum |
| P. Caricis | Carex | Urtica |
| Cronartium Ribicola | Ribes | Pinus |
| Chrysomyxa Rhododendri | Rhododendron | Picea |
Some of the Uredineae also exhibit the peculiarity of the development
of biologic forms within a single morphological species, sometimes
termed specialization of parasitism; this will be dealt with
later under the section Physiology.
 |
| From Strasburger’s Lehrbuch der Botanik,
by permission of Gustav Fischer. |
| Fig. 17.—Phragmidium Violaceum.
(After Blackman.) |
|
A, Portion of a young aecidium.
st, Sterile cell.
a, Fertile cells; at a2 the
passage of a nucleus from
the adjoining cell is seen.
B, Formation of the first spore-mother-cell
(sm), from the
basal cell (a) of one of the
rows of spores.
C, A further stage in which
from sm1 the first aecidiospore
(a) and the intercalary
cell (z) have arisen.
sm2, The second spore-mother-cell.
D, Ripe aecidiospore |
Cytology of Uredineae.—The study of the nuclear behaviour of
the cells of the Uredineae has thrown great light on the question of
sexuality. This group like the rest of the Basidiales exhibits an
association of nuclei at some
point in its life-history, but
unlike the case of the Basidiomycetes
the point of association
in the Uredineae is very well
defined in all those forms which
possess aecidiospores. We find
thus that in the eu and opsis
forms the association of nuclei
takes place at the base of the
aecidium which produces the
aecidiospores. There we find
an association of nuclei either
by the fusion of two similar cells
as described by Christmann or
by the migration of the nucleus
of a vegetative cell into a special
cell of the aecidium. After this
association the nuclei continue
in the conjugate condition so
that the aecidiospores, the uredospore-bearing
mycelium, the
uredospores and the young
teleutospores all contain two
paired nuclei in their cells (fig.
17). Before the teleutospore
reaches maturity the nuclei fuse,
and the uninucleate condition
then continues again until aecidium
formation. In the hemi,
brachy, micro and lepto forms,
which possess no aecidium, we
find that the association takes
place at various points in the
ordinary mycelium but always
before the formation of the
uredospores in the hemi and
brachy forms, and before the
formation of teleutospores in
micro and lepto form. Whether
the association of nuclei in the
ordinary mycelium takes place
by the migration of a nucleus
from one cell to another or
whether two daughter nuclei
become conjugate in one cell,
is not yet clear. The most
reasonable interpretation of the
spermatia is that they are
abortive male cells. They have
never been found to cause infection,
and they have not the characters of conidia; the large
size of their nuclei, the reduction of their cytoplasm and the
absence of reserve material and their thin cell wall all point to their
being male gametes. Although in the forms without aecidia the
two generations are not sharply marked off from one another, we
may look up the generation with single nuclei in the cells as the
gametophyte and that with conjugate nuclei as the sporophyte.
The subjoined diagram will indicate the relationship of the forms.
Basidiomycetes.—This group is characterized by its greatly reduced
life-history as compared with that of the eu forms among the Uredineae.
All the forms have the same life-history as the lepto forms
of that group, so that there is no longer any trace of sexual organs.
There is also a further reduction in that the basidium is not derived
from a teleutospore but is borne directly on the mycelium. Formerly,
before the relationship of promycelium and basidium were understood,
the Uredineae were considered as quite independent of the
Basidiomycetes. Later, however, these Uredineae were placed as a
mere subdivision of the Basidiomycetes. Although the Uredineae
clearly lead on to the Basidiomycetes, yet owing to their retaining
in many cases definite traces of sexual organs they are clearly a more
primitive group. Their marked parasitic habit also separates them
off, so that they are best included with the Basidiomycetes in a larger
cohort which may
be called Basidiales.
Most of
Basidiomycetes
are characterized
by the large sporophore
on which the
basidia with its
basidiospores are
borne.
 |
| From Annals of Botany, by permission of the Clarendon Press. |
| Fig. 18. |
It must be
clearly borne in
mind that though
the Basidiomycetes
show no
traces of differentiated
sexual
organs yet, like
the micro and lepto
forms of the Uredineae,
they still
show (in the association
of nuclei
and later fusion of
nuclei in the basidium),
a reduced
fertilization which denotes their derivation, through the Uredineae,
from more typically sexual forms. No one has yet made out in any
form the exact way in which the association of nuclei takes place in the
group. The mycelium is always found to contain conjugate nuclei
before the formation of basidia, but the point at which the conjugate
condition arises seems very variable. Miss Nichols finds that it
occurs very soon after the germination of the spore in Coprinus, but
no fusion of cells or migration of nuclei was to be observed.
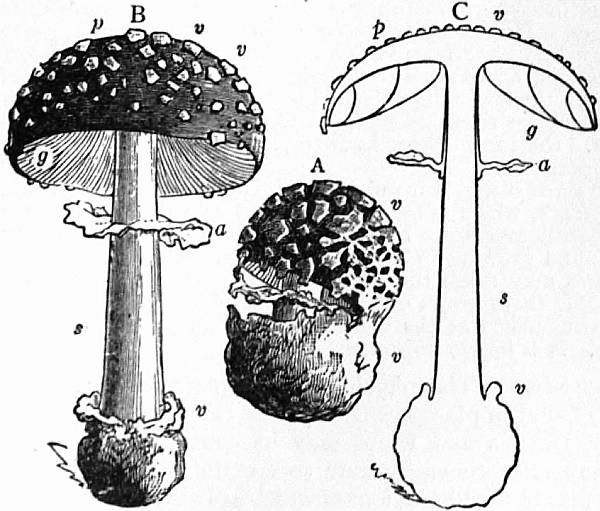 |
| Fig. 19.—Amanita muscaria. |
|
A, The young plant.
B, The mature plant.
C, Longitudinal section of mature plant.
p, The pileus. |
g, The gills.
a, The annulus, or remnant of velum partiale,
v, Remains of volva or velum universale.
s, The stalk. |
Protobasidiomycetes.—This, by far the smaller division of Basidiomycetes,
includes those forms which have a septate basidium. There
are three families—Auriculariaceae, Pilacreaceae and Tremellinaceae.
The first named contains a small number of forms with the basidium
divided like the promycelium of the Uredineae. They are characterized
by their gelatinous consistence and large size of their sporophore.
Hirneola (Auricularia) Auricula-Judae is the well-known
Jew’s Ear, so named from the resemblance of the sporophore to a
human ear.
The Pilacreaceae are a family found by Brefeld to contain the genus
Pilacre. P. Petersii has a transversely divided basidium as in
Auriculariaceae, but the basidia are surrounded with a peridium-like
sheath. The Tremellinaceae are characterized by the possession of
basidia which are divided by two vertical walls at right angles to
one another. From each of the four segments in the case of Tremella
a long outgrowth arises which reaches to the surface of the hymenium
344
and bears the basidiospores. In Dacryomyces only two outgrowths
and two spores are produced.
Autobasidiomycetes.—In this by far the larger division of the
Basidiomycetes the basidia are undivided and the four basidiospores
are borne on short sterigmata nearly always at the apex of the
basidium. The group may be divided into two main divisions,
Hymenomycetes and Gasteromycetes.
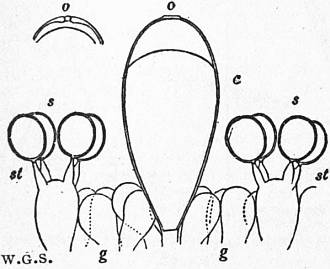 |
| Fig. 20.—Agaricus mucidus. Portion
of hymenium. s, Sporidia; st, sterigmata;
g, sterile cells; c, cystidium, with operculum
o. |
Hymenomycetes are a very large group containing over 11,000
species, most of which live in soil rich in humus or on fallen wood
or stems, a few only being parasites. In the simplest forms (e.g.
Exobasidium) the basidia are borne directly on the ordinary
mycelium, but in the majority of cases the basidia are found developed
in layers (hymenium) on special sporophores of characteristic
form in the various groups. In these sporophores (such
as the well-known toadstools and mushrooms where the ordinary
vegetative mycelium is underground) we have structures specially
developed for bearing the basidiospores and protecting them from
rain, &c., and for the distribution of the spores—see earlier part of
article on distribution of spores (figs. 19 and 20). The underground
mycelium in many cases
spreads wider and wider
each year, often in a
circular manner, and the
sporophores springing
from it appear in the
form of a ring—the so-called
fairy rings. Armillaria
melleus and
Polyporus annosus are
examples of parasitic
forms which attack and
destroy living trees,
while Merulius lacrymans is the well-known
“dry rot” fungus.
Gasteromycetes are
characterized by having
closed sporophores or
fruit-bodies which only
open after the spores are
ripe and then often merely by a small pore. The fruit-bodies are of
very various shapes, showing a differentiation into an outer peridium
and an inner spore-bearing mass, the gleba. The gleba is usually
differentiated into a number of chambers which are lined directly
by the hymenium (basidial layer), or else the chambers contain an
interwoven mass of hyphae, the branches of which bear the basidia.
By the breaking down of the inner tissues the spores often come
to lie as a loose powdery mass in the interior of the hollow fruit-body,
mixed sometimes with a capillitium. The best-known genera
are Bovista, Lycoperdon (puff-ball) Scleroderma, Geaster (earth-star,
q.v.). In the last-named genus the peridium is double and the outer
layer becomes ruptured and spreads out in the form of star-shaped
pieces; the inner layer, however, merely opens at the apex by a
small pore.
The most complex members of the Gasteromycetes belong to the
Phalloideae, which is sometimes placed as a distinct division of the
Autobasidiomycetes. Phallus impudicus, the stink-horn, is occasionally
found growing in woods in Britain. The fruit-body before it
ruptures may reach the size of a hen’s egg and is white in colour;
from this there grows out a hollow cylindrical structure which can
be distinguished at the distance of several yards by its disgusting
odour. It is highly poisonous.
Physiology.—The physiology of the fungi comes under the
head of that of plants generally, and the works of Pfeffer, Sachs,
Vines, Darwin and Klebs may be consulted for details. But
we may refer generally here to certain phenomena peculiar to
these plants, the life-actions of which are restricted and specialized
by their peculiar dependence on organic supplies of carbon and
nitrogen, so that most fungi resemble the colourless cells of higher
plants in their nutrition. Like these they require water, small
but indispensable quantities of salts of potassium, magnesium,
sulphur and phosphorus, and supplies of carbonaceous and
nitrogenous materials in different stages of complexity in the
different cases. Like these, also, they respire oxygen, and are
independent of light; and their various powers of growth,
secretion, and general metabolism, irritability, and response to
external factors show similar specific variations in both cases.
It is quite a mistake to suppose that, apart from the chlorophyll
function, the physiology of the fungus-cell is fundamentally
different from that of ordinary plant-cells. Nevertheless,
certain biological phenomena in fungi are especially pronounced,
and of these the following require particular notice.
Parasitism. —Some fungi, though able to live as saprophytes,
occasionally enter the body of living plants, and are thus termed
facultative parasites. The occasion may be a wound (e.g. Nectria,
Dasyscypha, &c.), or the enfeeblement of the tissues of the host, or
invigoration of the fungus, the mycelium of which then becomes
strong enough to overcome the host’s resistance (Botrytis). Many
fungi, however, cannot complete their life-history apart from the
host-plant. Such obligate parasites may be epiphytic (Erysipheae),
the mycelium remaining on the outside and at most merely sending
haustoria into the epidermal cells, or endophytic (Uredineae,
Ustilagineae, &c.), when the mycelium is entirely inside the organs
of the host. An epiphytic fungus is not necessarily a parasite,
however, as many saprophytes (moulds, &c.) germinate and develop
a loose mycelium on living leaves, but only enter and destroy the
tissues after the leaf has fallen; in some cases, however, these
saprophytic epiphytes can do harm by intercepting light and air
from the leaf (Fumago, &c.), and such cases make it difficult to
draw the line between saprophytism and parasitism. Endophytic
parasites may be intracellular, when the fungus or its mycelium
plunges into the cells and destroys their contents directly (Olpidium,
Lagenidium, Sclerotinia, &c.), but they are far more frequently
intercellular, at any rate while young, the mycelium growing in the
lacunae between the cells (Peronospora, Uredineae) into which it
may send short (Cystopus), or long and branched (Peronospora
Calotheca) haustoria, or it extends in the middle lamella (Ustilago),
or even in the solid substance of the cell-wall (Botrytis). No sharp
lines can be drawn, however, since many mycelia are intercellular at
first and subsequently become intracellular (Ustilagineae), and the
various stages doubtless depend on the degrees of resistance which
the host tissues are able to offer. Similar gradations are observed
in the direct effect of the parasite on the host, which may be local
(Hemileia) when the mycelium never extends far from the point of
infection, or general (Phytophthora) when it runs throughout the
plant. Destructive parasites rapidly ruin the whole plant-body
(Pythium), whereas restrained parasites only tax the host slightly,
and ill effects may not be visible for a long time, or only when the
fungus is epidemic (Rhytisma). A parasite may be restricted during
a long incubation-period, however, and rampant and destructive
later (Ustilago). The latter fact, as well as the extraordinary
fastidiousness, so to speak, of parasites in their choice of hosts or of
organs for attack, point to reactions on the part of the host-plant,
as well as capacities on that of the parasite, which may be partly
explained in the light of what we now know regarding enzymes and
chemotropism. Some parasites attack many hosts and almost any
tissue or organ (Botrytis cinerea), others are restricted to one family
(Cystopus Candidus) or genus (Phytophthora infestans) or even
species (Pucciniastrum Padi), and it is customary to speak of root-parasites,
leaf-parasites, &c., in expression of the fact that a given
parasite occurs only on such organs—e.g. Dematophora necatrix on
roots, Calyptospora Goeppertiana on stems, Ustilago Scabiosae in
anthers, Claviceps purpurea in ovaries, &c. Associated with these
relations are the specializations which parasites show in regard to
the age of the host. Many parasites can enter a seedling, but are
unable to attack the same host when older—e.g. Pythium, Phytophthora
omnivora.
Chemotropism.—Taken in conjunction with Pfeffer’s beautiful discovery
that certain chemicals exert a distinct attractive influence
on fungus hyphae (chemotropism), and the results of Miyoshi’s
experimental application of it, the phenomena of enzyme-secretion
throw considerable light on the processes of infection and parasitism
of fungi. Pfeffer showed that certain substances in definite concentrations
cause the tips of hyphae to turn towards them; other
substances, though not innutritious, repel them, as also do nutritious
bodies if too highly concentrated. Marshall Ward showed that the
hyphae of Botrytis pierce the cell-walls of a lily by secreting a cytase
and dissolving a hole through the membrane. Miyoshi then demonstrated
that if Botrytis is sown in a lamella of gelatine, and this
lamella is superposed on another similar one to which a chemotropic
substance is added, the tips of the hyphae at once turn from the
former and enter the latter. If a thin cellulose membrane is interposed
between the lamellae, the hyphae nevertheless turn chemotropically
from the one lamella to the other and pierce the cellulose
membrane in the process. The hyphae will also dissolve their way
through a lamella of collodion, paraffin, parchment paper, elder-pith,
or even cork or the wing of a fly, to do which it must excrete very
different enzymes. If the membrane is of some impermeable
substance, like gold leaf, the hyphae cannot dissolve its way through,
but the tip finds the most minute pore and traverses the barrier
by means of it, as it does a stoma on a leaf We may hence conclude
that a parasitic hyphae pierces some plants or their stomata and
refuses to enter others, because in the former case there are chemotropically
attractive substances present which are absent from the
latter, or are there replaced by repellent poisonous or protective
substances such as enzymes or antitoxins.
Specialization of Parasitism.—The careful investigations of recent
years have shown that in several groups of fungi we cannot be
content to distinguish as units morphologically different species,
but we are compelled to go deeper and analyse further the species.
It has been shown especially in the Uredineae and Erysiphaceae that
many forms which can hardly be distinguished morphologically,
or which cannot be differentiated at all by structural characters, are
not really homogeneous but consist of a number of forms which are
345
sharply distinguishable by their infecting power. Eriksson found,
for example, that the well-known species Puccinia graminis could be
split up into a number of forms which though morphologically
similar were physiologically distinct. He found that the species
really consisted of six distinct races, each having a more or less
narrow range of grasses on which it can live. The six races he named
P. graminis Secalis, Tritici, Avenae, Airae, Agrostis, Poae. The
first named will grow on rye and barley but not on wheat or oat.
The form Tritici is the least sharply marked and will grow on wheat,
barley, rye and oat but not on the other grasses. The form Avenae
will grow on oat and many grasses but not on the other three cereals
mentioned. The last three forms grow only on the genera Aira,
Agrostis and Poa respectively. All these forms have of course their
aecidium-stage on the barberry. The terms biologic forms, biological
species, physiological species, physiological races, specialized forms
have all been applied to these; perhaps the term biologic forms is
the most satisfactory. A similar specialization has been observed
by Marshall Ward in the Puccinia parasitic on species of Bromus,
and by Neger, Marchal and especially Salmon in the Erysiphaceae.
In the last-named family the single morphological species Erysiphe
graminis is found growing on the cereals, barley, oat, wheat, rye
and a number of wild grasses (such as Poa, Bromus, Dactylis). On
each of these host-plants the fungus has become specialized so that
the form on barley cannot infect the other three cereals or the wild
grasses and so on. Just as the uredospores and aecidiospores both
show these specialized characters in the case of Puccinia graminis
so we find that both the conidia and ascospores of E. graminis show
this phenomenon. Salmon has further shown in investigating the
relation of E. graminis to various species of the genus, Bromus, that
certain species may act as “bridging species,” enabling the transfer
of a biologic form to a host-plant which it cannot normally infect.
Thus the biologic form on B. racemosus cannot infect B. commutatus.
If, however, conidia from B. racemosus are sown on B. hordaceus,
the conidia which develop on that plant are now able to infect
B. commutatus; thus B. hordaceus acts as a bridging species. Salmon
also found that injury of a leaf by mechanical means, by heat, by
anaesthetics, &c., would affect the immunity of the plant and allow
infection by conidia which was not able to enter a normal leaf. The
effect of the abnormal conditions is probably to stop the production
of, or weaken or destroy the protective enzymes or antitoxins, the
presence of which normally confers immunity on the leaf.
Symbiosis.—The remarkable case of life in common first observed
in lichens, where a fungus and an alga unite to form a compound
organism—the lichen—totally different from either, has now been
proved to be universal in these plants, and lichens are in all cases
merely algae enmeshed in the interwoven hyphae of fungi (see
LICHENS). This dualism, where the one constituent (alga) furnishes
carbohydrates, and the other (fungus) ensures a supply of mineral
matters, shade and moisture, has been termed symbiosis. Since
then numerous other cases of symbiosis have been demonstrated.
Many trees are found to have their smaller roots invaded by fungi
and deformed by their action, but so far from these being injurious,
experiments go to show that this mycorhiza (fungus-root) is
necessary for the well-being of the tree. This is also the case with
numerous other plants of moors and woodlands—e.g. Ericaceae,
Pyrolaceae, Gentianaceae, Orchidaceae, ferns, &c. Recent
experiments have shown that the difficulties of getting orchid
seeds to germinate are due to the absence of the necessary fungus,
which must be in readiness to infect the young seedling immediately after
it emerges from the seed. The well-known failures with rhododendrons,
heaths, &c., in ordinary garden soils are also explained by
the need of the fungus-infected peat for their roots. The rôle of the
fungus appears to be to supply materials from the leaf-mould around,
in forms which ordinary root-hairs are incapable of providing for
the plant; in return the latter supports the fungus at slight expense
from its abundant stores of reserve materials. Numerous other
cases of symbiosis have been discovered among the fungi of fermentation,
of which those between Aspergillus and yeast in saké
manufacture, and between yeasts and bacteria in kephir and in the
ginger-beer plant are best worked out. For cases of symbiosis see
Bacteriology.
Authorities.—General: Engler and Prantl, Die natürlichen
Pflanzenfamilien, i. Teil (1892 onwards); Zopf, Die Pilze (Breslau,
1890); De Bary, Comparative Morphology of Fungi, &c. (Oxford,
1887); von Tafel, Vergleichende Morphologie der Pilze (Jena, 1892);
Brefeld, Unters. aus dem Gesamtgebiete der Mykologie, Heft i. 13
(1872-1905); Lotsy, Vorträge über botanische Stammesgeschichte
(Jena, 1907). Distribution, &c.: Cooke, Introduction to the Study
of Fungi (London, 1895); Felix in Zeitschr. d. deutsch. geologisch.
Gesellsch. (1894-1896); Staub, Sitzungsber. d. bot. Sec. d. Kgl.
ungarischen naturwiss. Gesellsch. zu Budapest (1897). Anatomy,
&c.: Bommer, “Sclerotes et cordons mycéliens,” Mém. de l’Acad.
Roy. de Belg. (1894); Mangin, “Observ. sur la membrane des
mucorinées,” Journ. de Bot. (1899); Zimmermann, Die Morph.
und Physiologie des Pflanzenzellkernes (Jena, 1896); Wisselingh,
“Microchem. Unters. über die Zellwände d. Fungi,” Pringsh.
Jahrb. B. 31, p. 619 (1898); Istvanffvi, “Unters. über die phys.
Anat. der Pilze,” Prings. Jahrb. (1896). Spore Distribution: Fulton,
“Dispersal of the Spores of Fungi by Insects,” Ann. Bot. (1889);
Falck, “Die Sporenverbreitung bei den Basidiomyceten,” Beitr.
zur Biol. d. Pflanzen, ix. (1904). Spores and Sporophores: Zopf,
Die Pilze; also the works of von Tafel and Brefeld. Classification:
van Tieghem, Journ. de bot. p. 77 (1893), and the works of Brefeld,
Engler and Prantl, von Tafel, Saccardo and Lotsy already cited,
Oomycetes: Wager, “On the Fertilization of Peronospora parasitica,”
Ann. Bot. vol. xiv. (1900); Stevens, “The Compound
Oosphere of Albugo Bliti,” Bot. Gaz. vol. 28 (1899); “Gametogenesis
and Fertilization in Albugo,” ibid. vol. 32 (1901);
Miyake, “The Fertilization of Pythium de Baryanum,” Ann. of Bot.
vol. xv. (1901); Trow, “On Fertilization in the Saprolegnieae,”
Ann. of Bot. vol. xviii. (1904); Thaxter, “New and Peculiar Aquatic
Fungi,” Bot. Gaz. vol. 20 (1895); Lagerheim, “Unters. über die
Monoblepharideae,” Bih. Svenska Vet. Acad. Handlingar, 25.
Afd. iii. (1900); Woronin, “Beitrag zur Kenntnis der Monoblepharideen,”
Mém. de l’Acad. Imp. d. Sc. de St-Pétersbourg, 8 sér.
vol. 16 (1902). Zygomycetes: Harper, “Cell-division in Sporangia
and Asci,” Ann. Bot. vol. xiii. (1899); Klebs, Die Bedingungen der
Fortpflanzung, &c. (Jena, 1896), and “Zur Physiologie der Fortpflanzung”
Prings. Jahr. (1898 and 1899), “Über Sporodinia
grandis,” Bot. Zeit. (1902); Falck, “Die Bedingungen der Zygotenbildung
bei Sporodinia grandis,” Cohn’s Beitr. z. Biol. d. Pflanzen,
Bd. 8 (1902); Gruber “Verhalten der Zellkerne in den Zygosporen
von Sporodinia grandis,” Ber. d. deutschen bot. Ges. Bd. 19 (1901);
Blakeslee, “Sexual Reproduction in the Mucorineae,” Proc. Am.
Acad. (1904); “Zygospore germination in the Mucorineae,” Annales
mycologici (1906). Ustilagineae: Plowright, British Uredineae and
Ustilagineae (London, 1889); Massee, British Fungi (Phycomycetes
and Ustilagineae) (London, 1891); Brefeld, Unters. aus dem
Gesamtgeb. der Mykol. Hefte xi. and xii.; and Falck, “Die Bluteninfektion
bei den Brandpilzen,” ibid. Heft xiii. 1905; Dangeard, “La
Reproduction sexuelle des Ustilaginées,” C.R., Oct. 9, 1893;
Maire, “Recherches cytologiques et taxonomiques sur les Basidiomyceten,”
Annexé au Bull. de la Soc. Mycol. de France (1902).
Saccharomycetaceae: Jorgensen, The Micro-organisms of Fermentation
(1899); Barker, Ann. of Bot. vol. xiv. (1901); “On Spore-formation
among the Saccharomycetes,” Journ. of the Fed. Institute
of Brewing, vol. 8 (1902); Guillermond, Recherches cytologiques
sur lés levures (Paris, 1902); Hansen, Centralbl. f. Bakt. u. Parasitenp.
Abt. ii. Bd. 12 (1904). Exoascaceae: Giesenhagen, “Taphrina,
Exoascus, Magnusiella” (complete literature given), Bot.
Zeit. Bd. 7 (1901). Erysiphaceae: Harper, “Die Entwicklung des
Perithecium bei Sphaerotheca castagnei,” Ber. d. deut bot Ges. (1896);
“Sexual Reproduction and the Organization of the Nucleus in certain
Mildews,” Publ. Carnegie Institution (Washington, 1906); Blackman
& Fraser, “Fertilization in Sphaerotheca,” Ann. of Bot. (1905).
Perisporiaceae: Brefeld, Untersuchungen aus dem Gesamtgeb. der
Mykol. Heft 10 (1891); Fraser and Chamber, Annales mycologici
(1907). Discomycetes: Harper, “Über das Verhalten der Kerne bei
Ascomyceten,” Jahr. f. wiss. Bot. Bd. 29 (1890); “Sexual Reproduction
in Pyronema confluens,” Ann. of Bot. 14 (1900); Claussen,
“Zur Entw. der Ascomyceten,” Boudiera, Bot. Zeit. Bd. 63 (1905);
Dangeard, “Sur le Pyronema confluens,” Le Botaniste, 9 série (1903)
(and numerous papers in same journal earlier and later); Ramlow,
“Zur Entwick. von Thelebolus stercoren,” Bot. Zeit. (1906); Woronin,
“Über die Sclerotienkrankheit der Vaccineen Beeren,” Mem. de
l’Acad. Imp. des Sciences de St-Pétersbourg, 7 série, 36 (1888);
Dittrich, “Zur Entwickelungsgeschichte der Helvellineen,” Cohn’s
Beitr. z. Biol. d. Pflanzen (1892). Pyrenomycetes: Fisch, “Beitr.
z. Entwickelungsgeschichte einiger Ascomyceten,” Bot. Zeit.
(1882); Frank, “Über einige neue u. weniger bekannte Pflanzkrankh.,”
Landw. Jahrb. Bd. 12 (1883); Ward, “Onygena
equina, a horn-destroying fungus,” Phil. Trans., vol. 191
(1899); Dawson, “On the Biology of Poroniapunctata,” Ann. of
Bot. 14 (1900). Tuberineae: Buchholtz, “Zur Morphologie u.
Systematik der Fungi hypogaei,” Ann. Mycol. Bd. 1 (1903);
Fischer in Engler and Prantl, Die natürlichen Pflanzenfamilien
(1896). Laboulbeniineae: Thaxter, “Monograph of the Laboulbeniaceae,”
Mem. Amer. Acad. of Arts and Sciences, vol. 12 (1895).
Uredineae: Eriksson and Henning, Die Getreideroste (Stockholm,
1896); Eriksson, Botan. Gaz. vol. 25 (1896); “On the Vegetative
Life of some Uredineae,” Ann. of Bot. (1905); Klebahn, Die wirtwechselnden
Rostpilze (Berlin, 1904); Sapin-Trouffy, “Recherches
histologiques sur la famille des Urédinées,” Le Botaniste (1896-1897);
Blackman, “On the Fertilization, Alternation of Generations and
General Cytology of the Uredineae,” Ann. of Bot. vol. 18 (1904);
Blackman and Fraser, “Further Studies on the Sexuality of Uredineae,”
Ann. of Bot. vol. 20 (1906); Christman, “Sexual Reproduction
of Rusts,” Ann. of Bot. vol. 20 (1906); Ward, “The
Brooms and their Rust Fungus,” Ann. of Bot. vol. 15 (1901).
Basidiomycetes: Dangeard, “La Reprod. sexuelle des Basidiomycètes,”
Le Botaniste (1894 and 1900); Maire, “Recherches
cytologiques et taxonomiques sur les Basidiomycètes,” Annexe du
Bull. de la Soc. Mycol. de France (1902); Möller, “Protobasidiomyceten,”
Schimper’s Mitt. aus den Tropen, Heft 8 (Jena, 1895);
Nichols, “The Nature and Origin of the Binucleated Cells in certain
Basidiomycetes,” Trans. Wisconsin Acad. of Sciences, vol. 15
(1905); Wager, “The Sexuality of the Fungi,” Ann. of Bot. 13
(1899); Woronin, “Exobasidium Vaccinii,” Verh. Naturf. Ges. zu
Freiburg, Bd. 4 (1867). Fermentation: Buchner, “Gährung ohne Hefezellen,”
Bot. Zeit. Bd. 18 (1898); Albert, Cent. f. Bakt. Bd. 17 (1901);
346
Green, The Soluble Ferments and Fermentation (Cambridge, 1899).
Parasitism: “On some Relations between Host and Parasite,”
Proc. Roy. Soc. vol. 47 (1890); “A Lily Disease,” Ann. of Botany,
vol. 2 (1888); Eriksson & Hennings, Die Getreideroste (vide supra);
Ward, “On the Question of Predisposition and Immunity in Plants,”
Proc. Cambridge Phil. Soc. vol. 11 (1902); also Annals of Bot.
vol. 16 (1902) and vol. 19 (1905); Neger, “Beitr. z. Biol. d.
Erysipheen” Flora, Bde. 88 and 90 (1901-1902); Salmon, “Cultural
Experiments with ‘Biologic Forms’ of the Erysiphaceae,” Phil.
Trans. (1904); “On Erysiphe graminis and its adaptative parasitism
within the genus, Bromus,” Ann. Mycol. vol. 11 (1904), also Ann.
of Bot. vol. 19 (1905). Symbiosis: Ward, “The Ginger-Beer
Plant,” Phil. Trans. Roy. Soc. (1892); “Symbiosis,” Ann. of Bot. 13
(1899); Shalk, “Der Sinn der Mykorrhizenbildung,” Jahrb. f.
wiss. Bot. Bd. 34 (1900); Bernard, “On some Different Cases of
Germination,” Gardener’s Chronicle (1900); Pierce, Publ. Univ.
California (1900).
(H. M. W.; V. H. B.)
FUNJ (Funniyeh, Fung, Fungha), a very mixed negroid
race, occupying parts of Sennar and the hilly country to the
south between the White and Blue Niles. They traditionally
come from west of the White Nile and are affiliated by some to
the Kordofan Nubas, by others, more justifiably, to the negro
Shilluks. These Funj, who became the dominant race in Sennar
in the 15th century, almost everywhere assimilated the speech,
religion and habits of the Arabs settled in that region. Until
the 19th century they were one of the most powerful of African
peoples in the eastern Sudan. About the end of the 15th century
they overthrew the kingdom of Aloa, between the two Niles,
and conquered the neighbouring peoples of the Sudan, Nubia
and even Kordofan. The Funj had mixed much with the Arabs
before their conquests, and had been converted to Islam. But
they were still in many ways savages, for James Bruce (who
traversed the district in 1772) says that their most famous
king, Malek-el-Gahman, preferred human liver to any other
food, and the Belgian traveller E. Pruyssenaere (1826-1864)
found them still performing pagan rites on their sacred Mount
Gula. Ernst Marno declared that as late as 1870 the most
southern branch of the race, the Boruns, a non-Arabic speaking
tribe, were cannibals. The Funj kings were content with
levying tribute on their neighbours, and in this loose way Shendi,
Berber and Dongola were once tributary. The Arab viziers
gradually absorbed all power, the Funj sovereignty becoming
nominal; and in 1821 the Egyptians easily destroyed the Funj
domination. To-day the Funj are few, and represent no real
type. They are a bright, hospitable folk. Many of them are
skilful surgeons and go far afield in their work. The fellahin,
indeed, call surgeons “Senaari” (men of Sennar). See further
Sennar and Sudan (Anglo-Egyptian).
FUNKIA, in botany, a genus of rather handsome, hardy,
herbaceous plants belonging to the natural order Liliaceae,
and natives of China and Japan. They are tuberous, with
broadly ovate or heart-shaped leaves and racemes of white or
pale lilac, drooping, funnel-shaped flowers. They are useful
for the borders of a shrubbery, the lawn or rock-work, or may
be grown in pots for the greenhouse. The plants are propagated
by dividing the crowns in autumn or when growth begins in
spring.
FUNNEL (through an O. Fr. founil, found in Breton, from
Lat. infundibulum, that through which anything is poured,
from fundere, to pour), a vessel shaped like a cone having a small
tube at the apex through which powder, liquid, &c., may be
easily passed into another vessel with a small opening. The
term is used in metal-casting of the hole through which the
metal is poured into a mould, and in anatomy and zoology of an
infundibulum or funnel-shaped organ. The word is thus used
generally of any shaft or passage to convey light, air or smoke,
as of the chimney of an engine or a steam-boat, or the flue of an
ordinary chimney. It is also used of a shaft or channel in rocks,
and in the decoying of wild-fowl is applied to the cone-shaped
passage leading from a pond and covered with a net, a “funnel-net,”
into which the birds are decoyed.
FUR (connected with O. Fr. forre, a sheath or case; so “an
outer covering”), the name specially given to the covering of
the skin in certain animals which are natives of the colder
climates, lying alongside of another and longer covering, called
the overhair. The fur differs from the overhair, in that it is
soft, silky, curly, downy and barbed lengthwise, while the
overhair is straight, smooth and comparatively rigid. These
properties of fur constitute its essential value for felting purposes,
and mark its difference from wool and silk; the first, after some
slight preparation by the aid of hot water, readily unites its
fibres into a strong and compact mass; the others can best be
managed by spinning and weaving.
On the living animal the overhair keeps the fur filaments
apart, prevents their tendency to felt, and protects them from
injury—thus securing to the animal an immunity from cold and
storm; while, as a matter of fact, this very overhair, though of
an humbler name, is most generally the beauty and pride of the
pelt, and marks its chief value with the furrier. We arrive
thus at two distinct and opposite uses and values of fur. Regarded
as useful for felt it is denominated staple fur, while with
respect to its use with and on the pelt it is called fancy fur.
History.—The manufacture of fur into a felt is of comparatively
modern origin, while the use of fur pelts as a covering for the
body, for the couch, or for the tent is coeval with the earliest
history of all northern tribes and nations. Their use was not
simply a barbarous expedient to defend man from the rigours
of an arctic winter; woven wool alone cannot, in its most perfect
form, accomplish this. The pelt or skin is requisite to keep out
the piercing wind and driving storm, while the fur and overhair
ward off the cold; and “furs” are as much a necessity to-day
among more northern peoples as they ever were in the days of
barbarism. With them the providing of this necessary covering
became the first purpose of their toil; subsequently it grew
into an object of barter and traffic, at first among themselves,
and afterwards with their neighbours of more temperate climes;
and with the latter it naturally became an article of fashion,
of ornament and of luxury. This, in brief, has been the history
of its use in China, Tatary, Russia, Siberia and North America,
and at present the employment of fancy furs among civilized
nations has grown to be more extensive than at any former period.
The supply of this demand in earlier times led to such severe
competition as to terminate in tribal pillages and even national
wars; and in modern times it has led to commercial ventures
on the part of individuals and companies, the account of which,
told in its plainest form, reads like the pages of romance. Furs
have constituted the price of redemption for royal captives,
the gifts of emperors and kings, and the peculiar badge of state
functionaries. At the present day they vie with precious gems
and gold as ornaments and garniture for wealth and fashion;
but by their abundance, and the cheapness of some varieties,
they have recently come within the reach of men of moderate
incomes. The history of furs can be read in Marco Polo, as
he grows eloquent with the description of the rich skins of the
khan of Tatary; in the early fathers of the church, who lament
their introduction into Rome and Byzantium as an evidence of
barbaric and debasing luxury; in the political history of Russia,
stretching out a powerful arm over Siberia to secure her rich
treasures; in the story of the French occupation of Canada,
and the ascent of the St Lawrence to Lake Superior, and the
subsequent contest to retain possession against England; in
the history of early settlements of New England, New York
and Virginia; in Irving’s Astoria; in the records of the Hudson’s
Bay Company; and in the annals of the fairs held at Nizhniy
Novgorod and Leipzig. Here it may suffice to give some account
of the present condition of the trade in fancy furs. The collection
of skins is now chiefly a matter of private enterprise. Few, if
any, monopolies exist.
Natural Supplies.—We are dependent upon the Carnivora,
Rodentia, Ungulata and Marsupialia for our supplies of furs,
the first two classes being by far of the greatest importance. The
Carnivora include bears, wolverines, wolves, raccoons, foxes,
sables, martens, skunks, kolinskis, fitch, fishers, ermines, cats,
sea otters, fur seals, hair seals, lions, tigers, leopards, lynxes,
jackals, &c. The Rodentia include beavers, nutrias, musk-rats
or musquash, marmots, hamsters, chinchillas, hares, rabbits,
squirrels, &c. The Ungulata include Persian, Astrachan, Crimean,
347
Chinese and Tibet lambs, mouflon, guanaco, goats, ponies, &c.
The Marsupialia include opossums, wallabies and kangaroos.
These, of course, could be subdivided, but for general purposes
of the fur trade the above is deemed sufficient.
The question frequently arises, not only for those interested
in the production of fur apparel, but for those who derive so
much comfort and pleasure from its use, whether the supply of
fur-bearing animals is likely to be exhausted. Although it is
a fact that the demand is ever increasing, and that some of the
rarer animals are decreasing in numbers, yet on the other hand
some kinds of furs are occasionally neglected through vagaries of
fashion, which give nature an opportunity to replenish their
source. These respites are, however, becoming fewer every day,
and what were formerly the most neglected kinds of furs are
becoming more and more sought after. The supply of some of
the most valuable, such as sable, silver and natural black fox,
sea otter and ermine, which are all taken from animals of a more
or less shy nature, does very gradually decrease with persistent
hunting and the encroachment of man upon the districts where
they live, but the climate of these vast regions is so cold and
inhospitable that the probabilities of man ever permanently
inhabiting them in numbers sufficient to scare away or exterminate
the fur-bearing wild animals is unlikely. Besides these
there are many useful, though commonplace, fur-bearing animals
like mink, musquash, skunk, raccoon, opossum, hamster, rabbit,
hares and moles, that thrive by depredations upon cultivated
land. Some of these are reared upon extensive wild farms.
In addition there are domestic fur-bearing animals, such as
Persian, Astrachan and Chinese lambs, and goats, easily bred
and available.
With regard to the rearing of the Persian lamb, there is a
prevalent idea that the skins of the unborn lamb are frequently
used; this, however, is a mistake. A few such skins have been
taken, but they are too delicate to be of any service. The youngest,
known as “broadtails,” are killed when a few days old, but for
the well-developed curly fur, the lambs must be six or seven weeks
old. During these weeks their bodies are covered with leather
so that the fur may develop in close, light and clean curls. The
experiment has been tried of rearing rare, wild, fur-bearing
animals in captivity, and although climatic conditions and food
have been precisely as in their natural environment, the fur has
been poor in quality and bad in colour, totally unlike that taken
from animals in the wild state. The sensation of fear or the restriction
of movement and the obtaining of food without exertion
evidently prevent the normal development of the creature.
In mountainous districts in the more temperate zones some
good supplies are found. Chinchillas and nutrias are obtained
from South America, whence come also civet cats, jaguars,
ocelots and pumas. Opossums and wallabies, good useful furs,
come from Australia and New Zealand. The martens, foxes
and otters imported from southern Europe and southern Asia,
are very mixed in quality, and the majority are poor compared
with those of Canada and the north.
Certain characteristics In the skin reveal to the expert from
what section of territory they come, but in classifying them it
is considered sufficient to mention territories only.
Some of the poorer sorts of furs, such as hamster, marmot,
Chinese goats and lambs, Tatar ponies, weasels, kaluga, various
monkeys, antelopes, foxes, otters, jackals and others from the
warmer zones, which until recently were neglected on account
of their inferior quality of colour, by the better class of the trade,
are now being deftly dressed or dyed in Europe and America,
and good effects are produced, although the lack of quality when
compared with the better furs from colder climates which possess
full top hair, close underwool and supple leathers, is readily
manifest. It is only the pressure of increasing demand that makes
marketable hard pelts with harsh brittle hair of nondescript
hue, and these would, naturally, be the last to attract the notice
of dealers.
As it is impossible that we shall ever discover any new fur-bearing
animals other than those we know, it behoves responsible
authorities to enforce close seasons and restrictions, as to the
sex and age, in the killing for the purpose of equalizing the
numbers of the catches. As evidence of indiscriminate slaughter
the case of the American buffaloes may be cited. At one time
thousands of buffalo skins were obtainable and provided material
for most useful coats and rugs for rough wear in cold regions,
but to-day only a herd or so of the animals remain, and in
captivity.
The majority of animals taken for their fur are trapped or
snared, the gun being avoided as much as possible in order that
the coat may be quite undamaged. Many weary hours are
spent in setting baits, traps and wires, and, frequently, when
the hunter retraces his steps to collect the quarry it is only to
find it gone, devoured by some large animal that has visited
his traps before him. After the skins have been carefully
removed—the sooner after death the better for the subsequent
condition of the fur—they are lightly tacked out, pelt outwards,
and, without being exposed to the sun or close contact with a
fire, allowed to dry in a hut or shady place where there is some
warmth or movement of air. With the exception of sealskins,
which are pickled in brine, all raw skins come to the various
trade markets simply dried like this.
Quality and Colour.—The best fur is obtained by killing
animals when the winter is at its height and the colder the season
the better its quality and colour. Fur skins taken out of season
are indifferent, and the hair is liable to shed itself freely; a
good furrier will, however, reject such faulty specimens in the
manufacturing. The finest furs are obtained from the Arctic
and northern regions, and the lower the latitude the less full and
silky the fur, till, at the torrid zone, fur gives place to harsh hair
without any underwool. The finest and closest wools are
possessed by the amphibious Carnivora and Rodentia, viz. seals,
otters, beavers, nutrias and musquash, the beauty of which is
not seen until after the stiff water or top hairs are pulled out
or otherwise removed. In this class of animal the underneath
wool of the belly is thicker than that of the back, while the
opposite is true of those found on the land. The sea otter, one
of the richest and rarest of furs, especially for men’s wear, is an
exception to this unhairing process, which it does not require,
the hair being of the same length as the wool, silky and bright,
quite the reverse of the case of other aquatic animals.
Of sealskins there are two distinct classes, the fur seals and the
hair seals. The latter have no growth of fur under the stiff top
hair and are killed, with few exceptions (generally of the marbled
seals), on account of the oil and leather they yield. The best
fur seals are found off the Alaska coast and down as far south
as San Francisco.
It is found that in densely wooded districts furs are darker in
colour than in exposed regions, and that the quality of wool and
hair is softer and more silky than those from bare tracts of country,
where nature exacts from its creatures greater efforts to secure
food, thereby developing stronger limbs and a consequently
coarser body covering.
As regards density of colour the skunk or black marten has
the blackest fur, and some cats of the domestic kind, specially
reared for their fur, are nearly black. Black bears have occasionally
very black coats, but the majority have a brownish underwool.
The natural black fox is a member of the silver fox
family and is very rare, the skins bringing a high price. Most
silver foxes have dark necks and in some the dark shade runs a
quarter, half-way, or three-quarters, or even the whole length
of the skin, but it is rather of a brownish hue. Some Russian
sables are of a very dense bluish brown almost a black, which is
the origin undoubtedly of the term “sables,” while some, from
one district in particular, have a quantity of silver hairs, evenly
interspersed in the fur, a peculiarity which has nothing to do
with age. The best sea otters have very dark coats which are
highly esteemed, a few with silver hairs in parts; where these
are equally and evenly spread the skins are very valuable. Otters
and beavers that run dark in the hair or wool are more valuable
than the paler ones, the wools of which are frequently touched
with a chemical to produce a golden shade. This is also done
with nutrias after unhairing. The darker sorts of mink,
348
musquash, raccoon and wolverine are more valuable than the
paler skins.
Collective Supplies and Sales.—There are ten large American
and Canadian companies with extensive systems for gathering
the annual hauls of skins from the far-scattered trappers. These
are the Hudson’s Bay Co., Russian Fur Co., Alaska Commercial
Co., North American Commercial Co., Russian Sealskin Co.,
Harmony Fur Co., Royal Greenland Fur Co., American Fur Co.,
Missouri Co. and Pacific Co. Most of the raw skins are forwarded
to about half-a-dozen brokers in London, who roughly sort them
in convenient lots, issuing catalogues to the traders of the world,
and after due time for examination of the goods by intending
purchasers, the lots are sold by public auction. The principal
sales of general furs are held in London in January and March,
smaller offerings being made in June and October; while the
bulk of fur sealskins is sold separately in December. The
Hudson’s Bay Co.’s sales take place before the others, and, as
no reserves are placed on any lot, the results are taken as exactly
indicating current values. While many buyers from America
and Russia are personally in attendance at the sales, many more
are represented by London and Leipzig agents who buy for them
upon commission. In addition to the fur skins coming from
North America vast numbers from Russia, Siberia, China, Japan,
Australia and South America are offered during the same periods
at public auction. Fairs are also held in Siberia, Russia and
Germany for the distribution of fur skins as follows:—
| January: | Frankfort-on-the-Oder | Small collection of provincial produce,
such as otter, fox, fitch and marten. |
| February: | Irbit, Siberia | General Russian furs. |
| Easter: | Leipzig, Germany | General furs. |
| August: | Nizhniy Novgorod, Russia | Persian lamb and general furs. |
| August: | Kiakhta, Siberia | Chinese furs and ermine. |
| December: | Ishim, Siberia | Chiefly squirrels. |
Of course there are many transactions, generally in the cheaper
and coarser kinds of furs, used only in central Europe, Russia
and Asia which in no way interest the London market, and there
are many direct consignments of skins from collectors in America
and Russia to London, New York and Leipzig merchants. But
the bulk of the fine furs of the world is sold at the large public
trade auction sales in London. The chief exceptions are the
Persian and Astrachan lambs, which are bought at the Russian
fairs, and are dressed and dyed in Leipzig, and the ermine and
Russian squirrels, which are dressed and manufactured into
linings either in Russia or Germany before offered for sale to the
wholesale merchants or manufacturers.
The annual collection of fur skins varies considerably in
quantity according to the demand and to the good or bad climatic
conditions of the season; and it is impossible to give a complete
record, as many skins are used in the country of their origin or
exported direct to merchants. But a fairly exact statement of
the numbers sold in the great public trade auction sales in
London during the year 1905-1906 is herewith set out.
| Year ending 31st of March 1906. | Total Number
of Skins. |
| Badger | 28,634 |
| Badger, Japanese | 6,026 |
| Bear | 18,576 |
| Beaver | 80,514 |
| Cat, Civet | 157,915 |
| Cat, House | 126,703 |
| Cat, Wild | 32,253 |
| Chinchilla (La Plata), known also as Bastard | 43,578 |
| Chinchilla Peruvian finest | 5,603 |
| Deer, Chinese | 124,355 |
| Ermine | 40,641 |
| Fisher | 5,949 |
| Fitch | 77,578 |
| Fox, Blue | 1,893 |
| Fox, Cross | 10,276 |
| Fox, Grey | 59,561 |
| Fox, Japanese | 81,429 |
| Fox, Kit | 4,023 |
| Fox, Red | 158,961 |
| Fox, Silver | 2,510 |
| Fox, White | 27,463 |
| Goats, Chinese | 261,190 |
| Hares | 41,256 |
| Kangaroo | 7,115 |
| Kid, Chinese linings and skins equal to | 5,080,047 |
| Kolinsky | 114,251 |
| Lamb, Mongolian linings and skins equal to | 214,072 |
| Lamb, Slink linings and skins equal to | 167,372 |
| Lamb, Tibet linings and skins equal to | 794,130 |
| Leopard | 3,574 |
| Lynx | 88,822 |
| Marmot, linings and skins equal to | 1,600,600 |
| Marten, Baum | 4,573 |
| Marten, Japanese | 16,461 |
| Marten, Stone | 12,939 |
| Mink, Canadian and American | 299,254 |
| Mink, Japanese | 360,373 |
| Mouflon | 23,594 |
| Musk-rat or Musquash, Brown | 5,126,339 |
| Musk-rat or Musquash, Black | 41,788 |
| Nutria | 82,474 |
| Opossum, American | 902,065 |
| Opossum, Australian | 4,161,685 |
| Otter, River | 21,235 |
| Otter, Sea | 522 |
| Raccoon | 310,712 |
| Sable, Canadian and American | 97,282 |
| Sable, Japanese | 556 |
| Sable, Russian | 26,399 |
| Seals, Fur | 77,000 |
| Seals, Hair | 31,943 |
| Skunk | 1,068,408 |
| Squirrel | 194,596 |
| Squirrel Linings each averaging 126 skins | 1,982,736 |
| Tiger | 392 |
| Wallaby | 60,956 |
| Wolf | 56,642 |
| Wolverine | 1,726 |
| Wombat | 193,625 |
A brief account of the different qualities of the pelts, with
some general remarks as to their customary uses, follows. The
prices quoted are subject to constant fluctuation and represent
purely trade prices for bulk, and it should be explained that the
very great variations are due to different sizes, qualities and
colours, and moreover are only first cost, before skins are dressed
and prepared. These preparations are in some cases expensive,
and there is generally a considerable percentage of waste. The
prices cannot be taken as a guide to the wholesale price of a
single and finished skin, but simply as relative value.
The fullest and darkest skins of each kind are the most valuable,
and, in cases of bluish grey or white, the fuller, clearer and
brighter are the more expensive. A few albinos are found in
every species, but whatever their value to a museum, they are of
little commercial importance. Some odd lots of skins arrive
designated simply as “sundries,” so no classification is possible,
and this will account for the absence of a few names of skins of
which the imports are insignificant in quantity, or are received
direct by the wholesale merchants.
Names, Qualities and Uses of Pelts.1
Astrachan.—See Lambs, below.
Badger.—Size 2 × 1 ft. American sorts have coarse thick underwool
of a pale fawn or stone colour with a growth of longer black
and white hairs, 3 or 4 in. long; a very durable but clumsy fur.
The best skins are exported to France, Spain and Italy, and used for
carriage rugs and military purposes. Asiatic, including Japanese,
skins are more woolly. Russian and Prussian kinds are coarser and
darker, and used mostly for brush trade. Value 6d. to 19s.
Bear, Australian.—See Wombat, below.
Bear, Black.—Size 6 × 3 ft. Fine dark brown underwool with
bright black and flowing top hair 4 in. long. Cubs are nearly as long
in the hair although only about half the size and not only softer and
better, but have the advantage of being very much lighter in pelt.
Widely distributed in North America, the best come from Canada,
are costly and are used for military caps, boas, muffs, trimmings,
carriage rugs and coachmen’s capes, and the fur wears exceedingly
well. Value 17s. 6d. to 86s. Those from East India and warm
climates are harsh, poor and only fit for floor rugs.
Bear, Brown.—Size 6 × 3 ft. Similar in quality to the black,
but far more limited in number; the colours range from light yellow
to a rich dark brown. The best come from Hudson Bay territory
and are valuable. Used for muffs, trimmings, boas, and carriage
349
rugs. Inferior sorts, almost grizzly in effect and some very pale,
are found in Europe and Asia and are mostly used locally. In India
there is a species called Isabelline bear, which was formerly imported
to Great Britain, but does not now arrive in any quantity worth
mentioning. Value 10s. 6d. to 60s., Isabelline sort 10s. 6d. to 78s.
Bear, Grizzly.—Size 8 × 4 ft. Coarse hair, heavy pelt, mostly
dark yellowish and brown colours, only found in western parts of
United States, Russia and Siberia. Used as carriage rugs and floor
rugs, most durable for latter purpose and of fine effect. They are
about half the value of brown bear. Value 15s. to 54s.
Bear, Isabelline.—See Bear, Brown, above.
Bear, White.—Size 10 × 5 ft. The largest of all bears. Short
close hair except on flanks, colour white to yellow. An inhabitant
of the Arctic circle, best from Greenland. Used for floor rugs, very
durable; and very white specimens are valuable. Value 20s. to 520s.
Beaver. Size 3 × 2 ft. The largest of rodents, it possesses a
close underwool of bluish-brown hue, nearly an inch in depth, with
coarse, bright, black or reddish-brown top hair, 3 in. long. Found
widely in North America. After being unhaired the darkest wools
are the most valuable, although many people prefer the bright,
lighter brown tones. Used for collars, cuffs, boas, muffs, trimmings,
coat linings and carriage aprons, and is of a most durable nature, in
addition to having a rich and good appearance. Value 10s. to
39s. 6d.
Broadtail.—See Lambs, below.
Caracal.—A small lynx from India, the fur very poor, seldom
imported.
Caracul.—See Goats and Lambs, below.
Cat, Civet.—Size 9 × 4½ in., short, thick and dark underwool
with silky black top hair with irregular and unique white markings.
It is similar to skunk, but is much lighter in weight, softer and less
full, without any disagreeable odour. Used for coat linings it is
very warm and durable. A few come from China, but the fur is
yellowish-grey, slightly spotted and worth little. Value 1s. 1d.
to 1s. 11d.
Cat, House, &c.—18 × 9 in., mostly black and dark brown,
imported from Holland, Bavaria, America and Russia, where they
are reared for their coats. The best, from Holland, are used for coat
linings. Although in colour, weight and warmth they are excellent,
the fur is apt to become loose and to fall off with friction of wear.
The black are known as genet, although the true genet is a spotted
wild cat. Wild sorts of the tabby order are coarser, and not so good
and silky in effect as when domestically reared. Value of the
black sorts 2d. to 3s. Wild 9d. to 14s. Some small wild cats, very
poor flat fur of a pale fawn colour with yellow spots, are imported
from Australia and used for linings. Value 5½d. to 1s. 1d.
Cheetah.—Size of a small leopard and similar in colour, but has
black spots in lieu of rings. Only a few are now imported, which are
used for mats. Value 2s. 6d. to 18s.
Chinchilla, Peruvian and Bolivian.—Size 12 × 7 in., fur 1 to
1¼ in. deep. Delicate blue-grey with black shadings, one of nature’s
most beautiful productions, though not a durable one. Used for
ladies’ coats, stoles, muffs, hats and trimmings. Yearly becoming
scarcer and most costly. Value 8s. 6d. to 56s. 8d.
Chinchilla, La Plata, incorrectly named and known in the trade
as “bastard chinchilla,” size 9 × 4 in., in a similar species, but owing
to lower altitudes and warmer climatic conditions of habitation
is smaller, with shorter and less beautiful fur, the underwool colour
being darker and the top colour less pure. Used exactly as the
better kind, and the picked skins are most effective. As with the
best sort it is not serviceable for constant wear. Value 4s. 2d. to
27s. 6d.
Chinchillone.—Size 13 × 8 in., obtained also from South America.
Fur is longer and weaker and poorer and yellower than chinchilla.
Probably a crossbred animal, very limited importation. Value
3s. 6d. to 16s. 8d.
Deer, Chinese and East Indian.—Small, light, pelted skins,
the majority of which are used for mats. Reindeer and other
varieties are of little interest for use other than trophy mats.
Thousands are taken for the leather trade. Value of Chinese 1s. 2d.
to 1s. 6d. each.
Dog.—The only dogs that are used in the fur trade in civilized
countries are those imported from China, which are heavy and
coarse, and only used in the cheaper trade, chiefly for rugs. Value
6d. to 1s.
Dog Wolf.—See Wolf, below.
Ermine.—Size 12 × 2½ in. Underwool short and even, with a shade
longer top hair. Pelt light and close in texture, and durable. In
the height of winter the colour is pure white with exception of the
tip of tail, which is quite black. Supplies are obtained from Siberia
and America. Best are from Ishim in Siberia. Used for cloak
linings, stoles, muffs and trimmings, also for embellishment of
British state, parliamentary and legal robes. When this fur is
symmetrically spotted with black lamb pieces it is styled miniver,
in which form it is used at the grand coronation functions of British
sovereigns. Value 1s. 3d. to 8s. 6d.
Fisher.—Size 30 × 12 in., tail 12 to 18 in. long, the largest of the
martens; has a dark shaded deep underwool with fine, glossy, dark
and strong top hair 2 in. or more long. Best obtained from British
America. The tails are almost black and make up most handsomely
into trimmings, muffs, &c. Tails worked separately in these forms are
as rich and fine and more durable than any other fur suitable for a
like purpose. The fur of the skin itself is something like a dark
silky raccoon, but is not as attractive as the tails. Value 12s. to 46s.
Fitch.—Size 12 × 3 in., of the marten species, also known as the
pole cat. Yellow underwool 1/3 in. deep, black top hair, 1½ to 1¾ in.
long, very fine and open in growth, and not close as in martens.
Largest skins come from Denmark, Holland and Germany. The
Russian are smaller, but more silky and, as now dyed, make a cheap
and fair substitute for sable. They are excellent for linings of
ladies’ coats, being of light weight and fairly strong in the pelt.
English mayors’ and civic officials’ robes are frequently trimmed
with this fur in lieu of sable. Value of the German variety 2s. to
5s. 6d. and of the Russian 7d. to 1s. 4d.
Fox, Blue.—Size 24 × 8 in. Underwool thick and long. Top
hair fine and not so plentiful as in other foxes. Found in Alaska,
Hudson Bay territory, Archangel and Greenland. Although called
blue, the colour is a slaty or drab tone. Those from Archangel are
more silky and of a smoky bluish colour and are the most valuable.
These are scarce and consequently dear. The white foxes that are
dyed smoke and celestial blue are brilliant and totally unlike the
browner shades of this fox. Value 34s. to 195s.
Fox, Common.—The variation of size and quality is considerable,
and the colour is anything from grey to red. In Great Britain the
animal is now only regarded for the sport it provides. On the
European continent, however, some hundreds of thousands of skins,
principally German, Russian and Norwegian, are sold annually,
for home use, and for dyeing and exportation, chiefly to the United
States. The qualities do not compare with those species found in
North America and the Arctic circle. The Asiatic, African and
South American varieties are, with the exception of those taken in
the mountains, poorly furred and usually brittle and therefore of no
great service. No commercial value can be quoted.
Fox, Cross.—Size 20 × 7 in., are about as large as the silver and
generally have a pale yellowish or orange tone with some silvery
points and a darkish cross marking on the shoulders. Some are very
similar to the pale red fox from the North-West of America and a
few are exceptionally large. The darkest and best come from
Labrador and Hudson Bay, and the ordinary sorts from the north-west
of the United States and, as with silver and other kinds, the
quality is inferior when taken from warmer latitudes. Value 10s. 6d.
to 60s.
Fox, grey.—Size 27 × 10 in. Has a close dark drab underwool
with yellowish grizzly, grey, regular and coarse top hair. The
majority used for the trade come from Virginia and the southern
and western parts of the United States. Those from the west are
larger than the average, with more fur of a brighter tone. The fur
is fairly serviceable for carriage rugs, the leather being stout, but its
harshness of quality and nondescript colour does not contribute to
make it a favourite. Value 9d. to 4s. 9d.
Fox, Japanese.—See Fox, Red, and Raccoon, below.
Fox, Kit.—Size 20 × 6 in. The underwool is short and soft, as
is also the top hair, which is of very pale grey mixed with some
yellowish-white hair. It is the smallest of foxes, and is found in
Canada and the northern section of the United States. It is similar
in colour and quality to the prairie fox and to many kinds from the
warmer zones, such as from Turkey, eastern Asia and elsewhere.
Value 1s. 3d. to 5s. 6d.
Fox, Red.—Size 24 × 8 in., though a few kinds are much larger.
The underwool is long and soft and the hair plentiful and strong.
It is found widely in the northern parts of America and in smaller
numbers south of the United States, also in China, Japan and
Australia. The colours vary from pale yellowish to a dark red,
some being very brilliant. Those of Kamschatka are rich and fine in
quality. Farther north, especially near the sea, the fur is coarse.
Where the best coloured skins are not used for carriage rugs they are
extensively dyed, and badger and other white hairs are inserted
to resemble silver fox. They are also dyed a sable colour. The
skins, being the strongest of foxes’, both in the fur and pelt, are
serviceable. The preparations in imitation of the natural black and
silver sorts are very good and attractive. Value 1s. to 41s.
Fox, Silver. Size 30 × 10 in. Underwool close and fine. Top
hair black to silvery, 3 in. long. The fur upon the necks usually
runs dark, almost black, and in some cases the fur is black half-way
down the length of the skin, in rarer cases three-quarters of the
length and, in the most exceptional instances, the whole length,
and when this is the case they are known as “Natural Black Foxes”
and fetch enormous prices. The even silvery sorts are highly
esteemed, and the fur is one of the most effective and precious.
The finest are taken in Labrador. The farther south they are found,
the poorer and coarser the fur. The brush has invariably a white
tip. Value £1 to £320.
Fox, White.—Size 20 × 7 in. Animals of this species are generally
small in size and inhabit the extreme northern sections of Hudson
Bay, Newfoundland, Greenland, Labrador and Siberia. The
Canadian are silky in nature and inclined to a creamy colour, while
the Siberian are more woolly and rather whiter. Those taken in
central Asia near or in Chinese territory are poorer and yellowish.
The underwool in all sorts is generally of a bluish-grey tone, but the
top hair in the depth of winter is usually full enough in quantity to
350
hide any such variation. Those skins in which the underwool is
quite white are rare and much more expensive. In summer specimens
of this species, as with other white furred animals, have slightly
discoloured coats. The skins that are not perfectly white are dyed
jet black, dark or light smoke, violet-blue, blue-grey, and also in
imitation of the drab shades of the natural blue. Value 18s. to 66s.
Genet.—Size 10 × 4 in. The genet proper is a small white spotted
cat found in Europe, but the quantity is too small to be of commercial
interest. The name has been adopted for the black cats used so
much in the trade. (See Cats, above.) Value 1s. to 6s. 6d.
Goats.—Size varies greatly. The European, Arabian and East
Indian kinds are seldom used for rugs, the skins are chiefly dressed
as leather for books and furniture, and the kids for boots and gloves,
and the finer wool and hair are woven into various materials. Many
from Russia are dyed black for floor and carriage rugs; the hair is
brittle, with poor underwool and not very durable; the cost, however,
is small. The Chinese export thousands of similar skins in black,
grey and white, usually ready dressed and made into rugs of two
skins each. A great many are dyed black and brown, in imitation
of bear, and are used largely in the western parts of the United
States and Canada for sleigh and carriage rugs. Many are used for
their leather. Thousands of the kids are also dyed black and worked
into cross-shaped pieces, in which shape they are largely exported
to Germany, France, Great Britain and America, and sold by the
retail as caracal, kid or caracul. The grey ones are in good demand
for motor coats. The word caracul has been adopted from the
Turkish and signifies black-eared. See also Lambs, caracul. Value
of Chinese white 3s. 6d. to 6s. 6d.: grey, 4s. to 6s. 9d.
The Angora from the heights of central Asia Minor has curly,
fleecy, silky, white wool, 4 to 7 in. long. The fur is not used in Great
Britain, as formerly, and the greater quantity, known as mohair,
is now imported for purposes of weaving. This species of goat was
some years since introduced into Cape Colony, but its wool is not
so good as the Asiatic breed. Good business, however, is done with
the product, but chiefly for leather. Value 4s. to 12s. 6d.
The Mongolian goat has a very soft silk underwool, and after the
long top hair is removed it is dressed and imported and erroneously
named mouflon. The colour is a light fawn, but it is so pale that it
lends itself to be dyed any colour. It was popular some years since
in the cheaper trade, but it is not now much seen in England. Value
2s. to 6s.
The Tibet goat is similar to the Angora in the fineness of its wool,
and many are used in the making of cashmere shawls. The Tibet
lamb so largely imported and used for children’s wear is often miscalled
Tibet goat. Value 3s. to 7s. 6d.
Guanaco.—Size 30 × 15 in. Is a species of goat found in Patagonia
and other parts of South America. It has a very long neck and
exceedingly soft woolly fur of a light reddish-fawn colour with very
white flanks. It is usually imported in small quantities, native
dressed, and ready made into rugs. The dressing is hard and
brittle. If the skins are dressed in Europe they afford a very comfortable
rug, though a very marked one in effect. They have a
similar wool to the vicuna, but coarser and redder; both are largely
used in South America. Value 1s. to 4s. 6d.
Hamster.—Size 8 × 3½ in. A destructive rodent, is found in
great numbers in Russia and Germany. The fur is very flat and poor,
of a yellowish pale brown with a little marking of black. Being
of a light weight it is used for linings. Value 3d. to 1s.
Hare.—Size 24 × 9 in. The common hare of Europe does not
much interest the furrier, the fur being chiefly used by makers of
hatters’ felt. The white hares, however, of Russia, Siberia and other
regions in the Arctic circle are very largely used in the cheaper trade
of Europe, America and the British colonies. The fur is of the
whitest when killed in winter, and that upon the flanks of the animal
is very much longer than that upon its back. The flanks are usually
cut off and made into muffs and stoles. The hair is, however, brittle
and is not at all durable. This fur is dyed jet black and various
shades of brown and grey, and manufactured into articles for the
small drapers and for exportation. The North American hares
are also dyed black and brown and used in the same way. Value
of white 2d. to 5d.
Jackal.—Size 2 to 3 ft. long. Is found in India and north and
south Africa. Indian are light brown and reddish, those from the
Cape are dark grey and rather silvery. Few are imported. Fur
generally poor and harsh, only suitable for carriage rugs. Value
1s. to 3s. 6d.
Jaguar.—Size 7 to 10 ft. long. Is found in Mexico and British
Honduras. The markings are an irregular ring formation with a
spot in the centre. Leopards have rings only and cheetahs solid
spots. Suitable only for hearth-rugs. Supply very limited. Value
5s. to 45s.
Kaluga.—See Souslik, below.
Kangaroo.—The sizes vary considerably, some being huge,
others quite small. The larger varieties, viz. the red and the great,
do not usually interest furriers, the fur being harsh and poor without
underwool. They are tanned for the leather trade. The sorts used
for carriage aprons, coat linings and the outside of motor coats
include: blue kangaroo, bush kangaroo, bridled kangaroo, wallaroo,
yellow kangaroo, rock wallaby, swamp wallaby and short-tailed
wallaby. Many of the swamp sort are dyed to imitate skunk and
look well. Generally the colours are yellowish or brown. Some are
dark brown as in the swamp, which being strong are suitable for
motor coats. The rock wallabies are soft and woolly and often of a
pretty bluish tone, and make moderately useful carriage rugs and
perambulator aprons. The redder and browner sorts are also good
for rugs as they are thick in the pelt. On the European continent
many of these are dyed. The best of the lighter weights are frequently
insufficiently strong in the hair to stand the friction of wear
in a coat lining. Value, kangaroo 9d. to 3s., wallaby 1½ d. to 5s. 3d.,
wallaroo 1s. to 5s. 6d.
Kids.—See Goats, above.
Kolinsky.—Size 12 × 2½ in. Is one of the marten tribe. The
underwool is short and rather weak, but regular, as is also the top
hair; the colour is usually yellow. They have been successfully
dyed and used as a substitute for sable. They are found in Siberia,
Amoor, China and Japan, but the best are from Siberia. They are
light in weight and therefore suitable for linings of coats. The tails
are used for artists’ “sable” brushes. The fur has often been
designated as red or Tatar sable. Value 1s. 6d. to 4s. 6d.
Lambs.—The sorts that primarily interest the fur trade in Europe
and America are those from south Russia, Persia and Afghanistan,
which are included under the following wholesale or retail commercial
terms: Persian lamb, broadtail, astrachan, Shiraz, Bokharan
and caracul lamb. With the public the general term astrachan is an
old one, embracing all the above curly sorts; the flatter kinds, as broadtail
and caracul lamb, have always been named separately. The
Persian lambs, size 18 × 9 in., are the finest and the best of them.
When dressed and dyed they should have regular, close and bright
curl, varying from a small to a very large one, and if of equal size,
regularity, tightness and brightness, the value is comparatively a
matter of fancy. Those that are dull and loose, or very coarse and
flat in the curl, are of far less market value.
All the above enumerated lambs are naturally a rusty black or
brown, and with very few exceptions are dyed a jet black. Lustre,
however, cannot be imparted unless the wool was originally of a
silky nature. Broadtails, size 10 × 5 in., are the very young of the
Persian sheep, and are killed before the wool has time to develop
beyond the flat wavy state which can be best compared to a piece
of moiré silk. They are naturally exceedingly light in weight, and
those that are of an even pattern, possessing a lustrous sheen, are
costly. There is, notwithstanding, a great demand for these from
the fashionable world, as not only are they very effective, but being
so flat in the wool the figure of the wearer can be shown as perfectly
as in a garment made of silk. It cannot be regarded as an economical
fur, as the pelt is too delicate to resist hard wear.
| Persian Lamb | price 12s. 6d. | to 25s. |
| Broadtail | price 10s. | to 35s. |
Astrachan, Shiraz and Bokharan lambs, size 22 by 9 in., are of a
coarser, looser curl, and chiefly used for coat linings, while the
Persians are used for outside of garments, collars, cuffs, stoles, muffs,
hats and trimmings and gloves. The so-called caracul lambs, size
12 × 6 in., are the very young of the astrachan sheep, and the pick
of them are almost as effective as broadtails, although less fine in the
texture. See also remarks as to caracul kid under Goats, above.
| Astrachan | price 1s. | to 5s. 6d. |
| Caracul Lamb | price 2s. 6d | to 10s. 6d. |
| Shiraz | price 4s. 6d | to 10s. |
| Bokharan | price 1s. 6d | to 3s. 6d. |
Grey lambs, size 24 × 10 in., are obtained from the Crimea and known
in the trade as “crimmers.” They are of a similar nature to the
caracul lambs, but looser in curl, ranging from a very light to a
dark grey. The best are the pale bluish greys, and are chiefly used
for ladies’ coats, stoles, muffs and hats. Price 2s. to 6s. Mongolian
lambs, size 24 × 15 in., are of a short wavy loose curl, creamy white
colour, and are usually exported from China dressed, the majority
being ready-made into cross-shaped coats or linings. They are used
principally for linings of good evening wraps for ladies. Price 1s.
to 2s. 6d. Slink lambs come from South America and China. The
former are very small and generally those that are stillborn. They
have a particularly thin pelt with very close wool of minute curl.
The China sorts are much larger. The smallest are used for glove
linings and the others for opera cloak linings. Price 1s. to 6s. 6d.
Leopard.—Size 3 to 6 ft. long. There are several kinds, the chief
being the snow or ounce, Chinese, Bengal, Persian, East Indian and
African. The first variety inhabit the Himalayas and are beautifully
covered with a deep soft fur quite long compared to the flat harsh
hair of the Bengal sort. The colours are pale orange and white with
very dark markings, a strong contrast making a fine effect. Most
artists prize these skins above all others. The Chinese are of a
medium orange brown colour, but full in fur. The East Indian are
less full and not so dark. The Bengal are dark and medium in colour,
short and hard hair, but useful for floor rugs, as they do not hold the
dust like the fuller and softer hair of the kinds previously named.
They are also used for drummers’ aprons and saddle cloths in the
Indian army. The African are small with pale lemon colour grounds
very closely marked with black spots on the skin, the strong contrast
making a pleasing effect. Occasionally, where something very
marked is wanted, skating jackets and carriage aprons are made
351
from the softest and flattest of skins, but usually they are made into
settee covers, floor rugs and foot muffs. Value 2s. to 40s.
Lion.—Size 5 to 6 ft. long. These skins are found in Africa,
Arabia and part of India, and are every year becoming scarcer.
They are only used for floor rugs, and the males are more highly
esteemed on account of the set-off of the mane. Value, lions’ £10
to £100; lionesses’ £5 to £25.
Lynx.—Size 45 × 20 in. The underwool is thinner than fox, but
the top hair is fine, silky and flowing, 4 in. long, of a pale grey,
slightly mottled with fine streaks and dark spots. The fur upon the
flanks is longer and white with very pronounced markings of dark
spots, and this part of the skin is generally worked separately from
the rest and is very effective for gown trimmings. Where the colour
is of a sandy and reddish hue the value is far less than where it is
of a bluish tone. They inhabit North America as far south as
California, also Norway and Sweden. Those from the Hudson Bay
district and Sweden are the best and are very similar. Those taken
in Central Asia are mostly used locally. For attire the skins manufactured
in Europe are generally dyed black or brown, in which
state it has a similar appearance to dyed fox, but having less thick
underwool and finer hair flows freely. The finest skins when dyed
black are used very largely in America in place of the dyed black
fox so fashionable for mourning wear in Great Britain and France.
The British Hussar busbies are made of the dark brown lynx, and it
is the free silky easy movement of the fur with the least disturbance
in the atmosphere that gives it such a pleasing effect. It is used
for rugs in its natural state and also in Turkey as trimmings for
garments. Value 13s. 6d. to 56s.
Lynx Cat or Bay Lynx.—Is about half the size and depth of fur
of a lynx proper, and inhabits the central United States. It is a
flat and reddish fur compared to the lynx and is suitable for cheap
carriage aprons. A few come from Canada and are of better quality.
Value 5s. to 15s.
Marmot.—Size 18 × 12 in. Is a rodent and is found in considerable
numbers in the south of Prussia. The fur is a yellowish brown and
rather harsh and brittle and has no underwool. Since, however,
the value of all good furs has advanced, dyers and manufacturers
have made very successful efforts with this fur. The Viennese have
been particularly successful, and their method has been to dye the
skins a good brown and then not put in the dark stripes, which
exist in sable and mink, until the garment or article is finished, thus
obtaining as perfectly symmetrical effects as if the articles were
made of small skins instead of large ones. Marmots are also found
in North America, Canada and China; the best, however, come from
Russia. It should always be a cheap fur, having so few good qualities
to recommend it. Value 9d. to 2s. 6d.
Marten, American.—See Sable, below.
Marten, Baum.—Size 16 × 5 in. Is sometimes called the pine
marten, and is found in quantity in the wooded and mountainous
districts of Russia, Norway, Germany and Switzerland. It possesses
a thick underwool with strong top hair, and ranges from a pale to a
dark bluish brown. The best, from Norway, are very durable and
of good appearance and an excellent substitute for American sable.
The tails when split into two or three, with small strips of narrow
tape so as to separate the otherwise dense fur, formerly made very
handsome sets of trimmings, ties and muffs, and the probabilities
are, as with other fashions, such use will have its period of revival.
Value 6s. to 85s.
Marten, Black.—See Skunk, below.
Marten, Japanese.—Size 16 × 5 in. Is of a woolly nature with
rather coarse top hair and quite yellow in colour. It is dyed for
the cheap trade for boas and muffs, but it is not an attractive fur
at the best of times. It lacks a silky, bright and fresh appearance,
and therefore is unlikely to be in great demand, except where economy
is an object. Value 6s. 6d. to 18s. 6d.
Marten, Stone.—Size and quality similar to the baum; the
colour, however, of the underwool is a stony white and the top hair
is very dark, almost black. They live in rocky and stony districts.
Skins of a pale bluish tone are generally used in their natural state
for stoles, boas and muffs, but the less clear coloured skins are dyed
in beautiful shades similar in density to the dark and valuable sables
from Russia, and are the most effective skins that can be purchased
at a reasonable price. The tails have also been worked, in the
manner explained with regard to the baum marten, as sets of trimmings
and in other forms. Stone martens are found in Russia,
Bosnia, Turkey, Greece, Germany, the Alps and France. The
Bosnian and the French are the best in colour. The Asiatic sorts are
less woolly, but being silky are useful when dyed. There are many
from Afghanistan and India which are too poor to interest the
European markets. Value 7s. 6d. to 26s.
Mink.—Size 16 × 5 in. Is of the amphibious class and is found
throughout North America and in Russia, China and Japan. The
underwool is short, close and even, as is also the top hair, which is
very strong. The best skins are very dark and are obtained from
Nova Scotia. In the central states of America the colour is a good
brown, but in the north-west and south-west the fur is coarse and
generally pale. It is very durable for linings, and is an economical
substitute for sable for coats, capes, boas and trimmings. Values
have greatly increased, and the fur possessing good qualities as to
colour and durability will doubtless always be in good request.
The Russian species is dark but flat and poor in quality, and the
Chinese and Japanese are so pale that they are invariably dyed.
These, however, are of very inferior nature. Value of American
3s. 3d. to 40s., Japanese 3d. to 2s. 3d.
Mole.—Size 3½ × 2½ in. Moles are plentiful in the British Isles
and Europe, and owing to their lovely velvety coats of exquisite
blue shade and to the dearness of other furs are much in demand.
Though the fur is cheap in itself, the expense of dressing and working
up these little skins is considerable, and they possess the unique
charm of an exceptional colour with little weight of pelt; the quality
of resistance to friction is, however, so slight as to make them expensive
in wear. The best are the dark blue from the Fen district of
Cambridgeshire in England. Value ½d. to 2d.
Mongolian Lambs.—See Lambs, above.
Monkey, Black.—Size 18 × 10 in. Among the species of monkeys
only one interests to any extent the fur trade, and that is the black
monkey taken on the west coast of Africa (Colobus satanas). The
hair is very long, very black and bright with no underwool, and the
white pelt of the base of the hair, by reason of the great contrast of
colour, is very noticeable. The skins were in 1850 very fashionable
in England for stoles, muffs and trimmings, and in America also as
recently as 1890. They are now mostly bought for Germany and
the continent. Value 6d. to 1s. 6d.
Mouflon.—Size 30 × 15 in. Is a sheep found in Russia and
Corsica and now very little in demand, and but few are imported
into Great Britain. Many Mongolian goats with the long hairs
pulled out are sold as mouflon. Value 4s. to 10s. 6d.
Musk-Ox.—Size 6 × 3 ft. These animals have a dense coat of
fine, long brown wool, with very long dark brown hair on the head,
flanks and tail, and, in the centre, a peculiar pale oval marking.
There is no other fur that is so thick, and it is eminently suitable
for sleighing rugs, for which purpose it is highly prized in Canada.
The musk-ox inhabits the north part of Greenland and part of
Canada, but in very limited numbers. Value 10s. to 130s.
Musquash or Musk-Rat, Brown and Black Russian.—Size
12 × 8 in. A very prolific rodent of the amphibious class obtained
from Canada and the United States, similar in habit to the English
vole, with a fairly thick and even brown underwool and rather
strong top dark hair of medium density. It is a very useful fur for
men’s coat linings and ladies’ driving or motoring coats, being
warm, durable and not too heavy. If the colour were less motley
and the joins between the skins could be made less noticeable, it
would be largely in demand for stoles, ties and muffs. As it is, this
fur is only used for these smaller articles for the cheaper trade. It
has, however, of later years been “unhaired,” the underwool clipped
very even and then dyed seal colour, in which way very useful and
attractive garments are supplied at less than half the cost of the
cheaper sealskins. They do not wear as well, however, as the pelt
and the wool are not of a strength comparable to those of sealskin.
With care, however, such a garment lasts sufficiently long to warrant
the present outlay. Value 5½d. to 1s. 9d.
There is a so-called black variety found in Delaware and New
Jersey, but the number is very small compared to the brown species.
They are excellent for men’s coat linings and the outside of ladies’
coats, for stoles, muffs, collars and cuffs. Value 10d. to 3s. 7d.
The Russian musquash is very small, 7 × 4 in., and is limited in
numbers compared to the brown. Only a few thousands are imported
to London. It is of a very pretty silvery-blue shade of even
wool with very little silky top hair, having silvery-white sides and
altogether a very marked effect. The odour, however, even after
dressing is rather pungent of musk, which is generally an objection.
Value 4s. to 6s. 6d.
Nutria.—Size 20 × 12 in. Is a rodent known in natural history
as the coypu, about half the size of a beaver, and when unhaired has
not more than half, generally less, the depth of fur, which is also
not so close. Formerly the fur was only used for hatters’ felt, but
with the rise in prices of furs these skins have been more carefully
removed and—with improved dressing, unhairing and silvering
processes—the best provides a very effective and suitable fur for
ladies’ coats, capes, stoles, muffs, hats and gloves, while the lower
qualities make very useful, light-weighted and inexpensive linings
for men’s or women’s driving coats. It is also dyed sealskin colour,
but its woolly nature renders it less effective than the more silky
musquash. They are obtained from the northern part of South
America. Value is. 6d. to 6s. 6d.
Ocelot.—Size 36 × 13 in. Is of the nature of a leopard and
prettily marked with stripes and oblong spots. Only a few are now
imported from South America for carriage aprons or mats. The
numbers are very limited. Value 1s. to 2s. 6d.
Opossum, American.—Size 18 × 10 in. Is a marsupial, a class
with this exception not met with out of Australia. The underwool
is of a very close frizzy nature, and nearly white, with long bluish
grey mixed with some black top hair. It is only found in the central
sections of the United States. About 1870 in England it was dyed
dark brown or black and used for boas, muffs and trimmings, but
until recently has been neglected on the continent. With, however,
recent experiments in brown and skunk coloured dyes, it bids fair
to become a popular fur. Value 2½d. to 5s. 6d.
Opossum, Australian.—Size 16 × 8 in. Is a totally different
nature of fur to the American. Although it has wool and top hair,
352
the latter is so sparse and fine that the coat may be considered as
one of close even wool. The colour varies according to the district
of origin, from a blue grey to yellow with reddish tones. Those
from the neighbourhood of Sydney are light clear blue, while those
from Victoria are dark iron grey and stronger in the wool. These
animals are most prolific and evidently increasing in numbers.
Their fur is pretty, warm and as yet inexpensive, and is useful for
rugs, coat linings, stoles, muffs, trimmings and perambulator aprons.
The worst coloured ones are frequently dyed black and brown.
The most pleasing natural grey come from Adelaide. The reddest
are the cheapest. Value 3¾d. to 3s. 6d.
Opossum, Ringtailed.—Size 7 × 4 in. Has a very short close and
dark grey wool, some being almost black. There are but a few
thousands imported, and being so flat they are only of use for coat
linings, but they are very warm and light in weight. Value 6d.
to 10d.
Opossum, Tasmanian (grey and black).—Size 20 × 10 in. Is of a
similar description, but darker and stronger in the wool and larger.
Besides these there are some very rich brown skins which were
formerly in such request in Europe, especially Russia, that undue
killing occurred until 1899, when the government stopped for a time
the taking of any of this class. They are excellent for carriage
aprons, being not only very light in weight and warm, but handsome.
Value 2s. 6d. to 8s. 6d.
Otter, River.—The size varies considerably, as does the underwool
and the top hair, according to the country of origin. There
are few rivers in the world where they do not live. But it is in the
colder northern regions that they are found in the greatest numbers
and with the best fur or underwool, the top hair, which, with the
exception of the scarce and very rich dark brown specimens they
have in common with most aquatic animals, is pulled out before the
skins are manufactured. Most of the best river otter comes from
Canada and the United States and averages 36 × 18 in. in size. Skins
from Germany and China are smaller, and shorter in the wool. The
colours of the under wools of river otters vary, some being very
dark, others almost yellow. Both as a fur and as a pelt it is extremely
strong, but owing to its short and close wool it is usually made up
for the linings, collars and cuffs of men’s coats. A large number of
skins, after unhairing, is dyed seal colour and used in America.
Those from hot climates are very poor in quality. Value 28s. to 118s.
Otter, Sea.—Size 50 × 25 in. Possesses one of the most beautiful
of coats. Unlike other aquatic animals the skin undergoes no process
of unhairing, the fur being of a rich dense silky wool with the softest
and shortest of water hairs. The colours vary from pale grey brown
to a rich black, and many have even or uneven sprinkling of white
or silvery-white hairs. The blacker the wool and the more regular
the silver points, the more valuable the skin. Sea otters are, unfortunately,
decreasing in numbers, while the demand is increasing.
The fur is most highly esteemed in Russia and China; in the latter
country it is used to trim mandarins’ state robes. In Europe and
America it is much used for collar, long facings and cuffs of a gentleman’s
coat; such a set may cost from £200 to £600, and in all probability
will soon cost more. Taking into consideration the size,
it is not so costly as the natural black fox, or the darkest Russian
sable, which is now the most expensive of all. The smaller and young
sea otters of a grey or brown colour are of small value compared to
the large dark and silvery ones. Value £10 to £220. A single skin
has been known to fetch £400.
Ounce.—See Leopard, above.
Persian Lambs.—See Lambs, above.
Platypus.—Size 12 × 8 in. One of the most singular of fur-bearing
animals, being the link between bird and beast. It has fur
similar to otter, is of aquatic habits, being web-footed with spurs of
a cock and the bill of a duck. The skins are not obtained in any
numbers, but being brought over by travellers as curiosities and
used for muffs, collars and cuffs, &c., they are included here for
reference. Value 2s. to 3s. 6d.
Pony or Tatar Foal.—Size 36 × 20 in. These skins are of
comparatively recent importation to the civilized world. They are
obtained from the young of the numerous herds of wild horses that
roam over the plains of Turkestan. The coat is usually a shade of
brown, sometimes greyish, fairly bright and with a suggestion of
waviness. Useful for motor coats. Value 3s. to 10s. 6d.
Puma.—Size 4½ × 3 ft. Is a native of South America, similar to
a lion in habits and colour of coat. The hair and pelt is, however, of
less strength, and only a few are now used for floor rugs. Value
5s. to 10s.
Raccoon.—Size 20 × 12 in. Is an animal varying considerably
in size and in quality and colour of fur, according to the part of
North America in which it is found. In common parlance, it may
be described as a species of wild dog with close affinity to the bear.
The underwool is 1 to 1½ in. deep, pale brown, with long top hairs
of a dark and silvery-grey mixture of a grizzly type, the best having
a bluish tone and the cheapest a yellowish or reddish-brown. A
limited number of very dark and black sorts exist and are highly
valued for trimmings. The very finest skins are chiefly used for
stoles and muffs, and the general run for coachmen’s capes and
carriage rugs, which are very handsome when the tails, which are
marked with rings of dark and light fur alternately, are left on.
Raccoons are used in enormous quantities in Canada for men’s
coats, the fur outside. The poorer qualities are extensively bought
and made up in a similar way for Austria-Hungary and Germany.
These make excellent linings for coats or footsacks for open driving
in very cold climates. The worst coloured skins are dyed black or
brown and are used for British military busbies, or caps, stoles,
boas, muffs and coachmen’s capes. The best skins come from the
northern parts of the United States. A smaller and poorer species
inhabits South America, and a very few are found in the north of
India, but these do not interest the European trade. From Japan
a similar animal is obtained in smaller quantities with very good
but longer fur, of yellowish motley light-brown shades. It is more
often imported and sold as Japanese fox, but its resemblance to
the fur of the American raccoon is so marked as to surely identify
it. When dyed dark blue or skunk colour it is good-looking and is
sold widely in Europe. Raccoon skins are also frequently unhaired,
and if the underwool is of good quality the effect is similar to beaver.
It is the most useful fur for use in America or Russia, having a full
quantity of fur which will retain heat. Value 10d. to 26s.
Sable, American and Canadian.—Size 17 × 5 in. The skins are
sold in the trade sale as martens, but as there are many that are of a
very dark colour and the majority are almost as silky as the Russian
sable, the retail trade has for generations back applied the term of
sable to this fur. The prevailing colour is a medium brown, and
many are quite yellow. The dyeing of these very pale skins has
been for so long well executed that it has been possible to make
very good useful and effective articles of them at a moderate price
compared to Russian sable. The finest skins are found in the East
Main and the Esquimaux Bay, in the Hudson’s Bay Company’s
districts, and the poorest in Alaska. They are not found very far
south of the northern boundary of the United States. The best
skins are excellent in quality, colour and effect, and wear well.
Value 27s. 3d. to 290s.
Sable, Chinese and Japanese.—Size 14 × 4½ in. These are
similar to the Amur skins previously referred to, but of much poorer
quality and generally only suitable for linings. The very palest
skins are dyed and made by the Chinese into mandarins’ coats, in
which form they are found in the London trade sales, but being
overdressed they are inclined to be loose in the hair and the colour
of the dye is not good. The Japanese kind are imported raw, but
are few in numbers, very pale and require dyeing. Value 15s. to
150s.
Sable, Russian.—Size 15 × 5 in. These skins belong to a species
of marten, very similar to the European and American, but much
more silky in the nature of their fur. They have long been known
as “sables,” doubtless owing to the density of colour to which
many of them attain, and they have always been held in the highest
esteem by connoisseurs as possessing a combination of rare qualities.
The underwool is close, fine and very soft, the top hair is regular,
fine, silky and flowing, varying from 1½ to 2½ in. in depth. In
colour they range from a pale stony or yellowish shade to a rich dark
brown, almost black with a bluish tone. The pelts are exceedingly
fine and close in texture and, although of little weight, are very
durable, and articles made of them produce a sensation of warmth
immediately they are put upon the body.
The Yakutsk, Okhotsk and Kamschatka sorts are good, the last
being the largest and fullest furred, but of less density of colour than
the others. Many from other districts are pale or yellowish brown,
and those from Saghalien are poor in quality. The most valuable
are the darkest from Yakutsk in Siberia, particularly those that have
silvery hairs evenly distributed over the skin. These however are
exceedingly scarce, and when a number are required to match for
a large garment, considerable time may be necessary to collect them.
This class of skin is the most expensive fur in the world, reckoning
values by a square foot unit.
The Amur skins are paler, but often of a pretty bluish stony tone
with many frequently interspersed silvery hairs. The quality
too is lower, that is, the fur is not so close or deep, but they are very
effective, particularly for close-fitting garments, as they possess the
least appearance of bulk. The paler skins from all districts in Siberia
are now cleverly coloured or “topped,” that is, just the tips of the
hair are stained dark, and it is only an expert who can detect them
from perfectly natural shades. If this colouring process is properly
executed it remains fairly fast. Notwithstanding the reported
rights of the Russian imperial authorities over some regions with
respect to these and other valuable fur-bearing animals, there are in
addition to the numbers regularly sent to the trade auction sales
in London many good parcels of raw skins to be easily bought direct,
provided price is not the first consideration. Value 25s. to 980s.
Seal, Fur.—Sizes range from 24 × 15 in. to 55 × 25 in., the width
being taken at the widest part of the skin after preparation. The
centre of the skin between the fins is very narrow and the skins taper
at each end, particularly at the tail. The very small pups are of a
beautiful quality, but too tiny to make into garments, and, as the aim
of a good furrier is to avoid all lateral or cross seams, skins are
selected that are the length of the garment that is to be made. The
most useful skins for coats are the large pups 42 in. long, and the
quality is very good and uniform. The largest skins, known in the
trade as “wigs,” which range up to 8 ft. in length, are uneven and
weak in the fur, and hunters do not seek to obtain them. The supply
of the best sort is chiefly from the North Pacific, viz. Pribilof
353
Islands, Alaska, north-west coast of America, Copper Island of the
Aleutian group near to Kamschatka, Robben Island and Japan.
Other kinds are taken from the South Pacific and South Atlantic
Oceans, around Cape Horn, the Falkland Islands up to Lobos
Islands at the entrance of the La Plata river, off the Cape of Good
Hope and Crozet Isles. With, however, the exception of the pick
of the Lobos Island seals the fur of the southern sea seals is very
poor and only suitable for the cheapest market. Formerly many
skins were obtained from New Zealand and Australia, but the
importation is now small and the quality not good. The preparation
of seal skin occupies a longer time than any other fur skin, but its
fine rich effect when finished and its many properties of warmth
and durability well repay it. Value 10s. to 232s.
Seal, Hair.—There are several varieties of these seals in the seas
stretching north from Scotland, around Newfoundland, Greenland
and the north-west coast of America, and they are far more numerous
than fur seals. Generally they have coarse rigid hair and none
possess any underwool. They are taken principally for the oil and
leather they yield. Some of the better haired sorts are dyed black
and brown and used for men’s motor coats when quite a waterproof
garment is wanted, and they are used also for this quality in China.
The young of the Greenland seals are called whitecoats on account
of the early growth being of a yellowish white colour; the hair is
¾ to 1 in. long, and at this early stage of their life is soft compared to
that of the older seals. These fur skins are dyed black or dark brown
and are used for military caps and hearth-rugs. Value 2s. to 15s.
There are fewer hair seals in the southern than in the northern seas.
Sheep.—Vary much in size and in quality of wool. Many of the
domestic kind in central and northern Europe and Canada are used
for drivers’ and peasants’ coat linings, &c. In Great Britain many
coats of the home-reared sheep, having wools two and a half to five
inches long, are dyed various colours and used as floor rugs. Skins
with very short wool are dyed black and used for military saddle-cloths.
The bulk, however, is used in the wool trade. The Hungarian
peasants are very fond of their natural brown sheep coats,
the leather side of which is not lined, but embellished by a very close
fancy embroidery, worked upon the leather itself; these garments
are reversible, the fur being worn inside when the weather is cold.
Chinese sheep are largely used for cheap rugs. Value of English
sheep from 3s. to 10s.
Skunk or Black Marten.—Size 15 × 8 in. The underwool is
full and fairly close with glossy, flowing top hair about 2½ in. long.
The majority have two stripes of white hair, extending the whole
length of the skin, but these are cut out by the manufacturing
furrier and sold to the dealers in pieces for exportation. The animals
are found widely spread throughout North and South America.
The skins which are of the greatest interest to the European trade
are those from North America, the South American species being
small, coarse and generally brown. The best skins come from Ohio
and New York. If it were not for its disagreeable odour, skunk
would be worth much more than the usual market value, as it is
naturally the blackest fur, silky in appearance and most durable.
The improved dressing processes have to a large extent removed the
naturally pungent scent. The fur is excellent for stoles, boas,
collars, cuffs, muffs and trimmings. Value 1s. 6d. to 11s.
Souslik.—Size 7 in. × 2¼. Is a small rodent found in the south
of Russia and also in parts of America. It has very short hair and is
a poor fur even for the cheapest linings, which is the only use to
which the skin could be put. It is known as kaluga when imported
in ready-made linings from Russia where the skins are dressed and
worked in an inferior way. Value 1d. to 3d.
Squirrel.—Size 10 × 5 in. This measurement refers to the
Russian and Siberian sorts, which are the only kind imported for
the fur. The numerous other species are too poor in their coats
to attract notice from fur dealers. The back of the Russian squirrel
has an even close fur varying from a clear bluish-grey to a reddish-brown,
the bellies in the former being of a flat quality and white,
in the latter yellowish. The backs are worked into linings separately,
as are the bellies or “locks.” The pelts, although very light, are
tough and durable, hence their good reputation for linings for
ladies’ walking or driving coats. The best skins also provide excellent
material for coats, capes, stoles, ties, collars, cuffs, gloves, muffs,
hoods and light-weight carriage aprons. The tails are dark and very
small, and when required for ends of boas three or four are made as
one. Value per skin from 2½d. to 1s. 1d.
Tibet Lamb.—Size 27 × 13 in. These pretty animals have a long,
very fine, silky and curly fleece of a creamy white. The majority
are consigned to the trade auction sales in London ready dressed
and worked into cross-shaped coats, and the remainder, a fourth of
the total, come as dressed skins. They are excellent for trimmings
of evening mantles and for children’s ties, muffs and perambulator
aprons. The fur is too long and bulky for linings. Value per skin
from 4s. 6d. to 8s. 6d.
Tiger.—Size varies considerably, largest about 10 ft. from nose
to root of tail. Tigers are found throughout India, Turkestan,
China, Mongolia and the East Indies. The coats of the Bengal kind
are short and of a dark orange brown with black stripes, those
from east or further India are similar in colour, but longer in the hair,
while those from north of the Himalayas and the mountains of China
are not only huge in size, but have a very long soft hair of delicate
orange brown with very white flanks, and marked generally with the
blackest of stripes. The last are of a noble appearance and exceedingly
scarce. They all make handsome floor rugs.
| Value of the Indian | from £3 to £15. |
| Value of the Chinese | from £10 to £65. |
Vicuna is a species of long-necked sheep native to South America,
bearing some resemblance to the guanaco, but the fur is shorter,
closer and much finer. The colour is a pale golden-brown and the
fur is held in great repute in South America for carriage rugs. The
supply is evidently small as the prices are high. There is scarcely
a commercial quotation in London, few coming in except from
private sources. 2s. 6d. to 5s. 6d. may be considered as the average
value.
Wallaby.—See Kangaroo, above.
Wallaroo.—See Kangaroo, above.
Wolf.—Size 50 × 25 in. Is closely allied to the dog tribe and,
like the jackals, is found through a wide range of the world,—North
and South America, Europe and Asia. Good supplies are available
from North America and Siberia and a very few from China. The
best are the full furred ones of a very pale bluish-grey with fine
flowing black top hair, which are obtained from the Hudson Bay
district. Those from the United States and Asia are harsher in
quality and browner. A few black American specimens come into
the market, but usually the quality is poor compared to the lighter
furred animal. The Siberian is smaller than the North American
and the Russian still smaller. Besides the wolf proper a large number
of prairie or dog wolves from America and Asia are used for cheaper
rugs. In size they are less than half that of a large wolf and are of
a motley sandy colour. Numbers of the Russian are retained for
home use. The finest wolves are very light weighted and most
suitable for carriage aprons, in fact, ideal for the purpose, though
lacking the strength of some other furs.
| Wolves | value 2s. 6d. | to 64s. |
| Dog wolves | value 1s. | to 2s. 6d. |
Wolverine.—Size 16 × 18 in. Is native to America, Siberia,
Russia and Scandinavia and generally partakes of the nature of a
bear. The underwool is full and thick with strong and bright top
hair about 2½ in. long. The colour is of two or three shades of brown
in one skin, the centre being an oval dark saddle, edged as it were
with quite a pale tone and merging to a darker one towards the
flanks. This peculiar character alone stamps it as a distinguished
fur, in addition to which it has the excellent advantage of being the
most durable fur for carriage aprons, as well as the richest in colour.
It is not prolific, added to which it is very difficult to match a number
of skins in quality as well as colour. Hence it is an expensive fur,
but its excellent qualities make it valuable. The darkest of the
least coarse skins are worth the most. Prices from 6s. to 37s.
Wombat, Koala or Australian Bear.—Size 20 × 12 in. Has
light grey or brown close thick wool half an inch deep without any top
hair, with a rather thick spongy pelt. It is quite inexpensive and
only suitable for cheap rough coats, carriage rugs, perambulator
aprons and linings for footbags. The coats are largely used in
western America and Canada. Value 3d. to 1s. 8½d.
Preparing and Dressing.—A furrier or skin merchant must
possess a good eye for colour to be successful, the difference in
value on this subtle matter solely (in the rarer precious sorts,
especially sables, natural black, silver and blue fox, sea otters,
chinchillas, fine mink, &c.) being so considerable that not only a
practised but an intuitive sense of colour is necessary to accurately
determine the exact merits of every skin. In addition to
this a knowledge is required of what the condition of a pelt
should be; a good judge knows by experience whether a skin
will turn out soft and strong, after dressing, and whether the
hair is in the best condition of strength and beauty. The dressing
of the pelt or skin that is to be preserved for fur is totally different
to the making of leather; in the latter tannic acid is used, but
never should be with a fur skin, as is so often done by natives of
districts where a regular fur trade is not carried on. The results
of applying tannic acid are to harden the pelt and discolour
and weaken the fur. The best methods for dressing fur skins
are those of a tawer or currier, the aim being to retain all the
natural oil in the pelt, in order to preserve the natural colour
of the fur, and to render the pelt as supple as possible. Generally
the skins are placed in an alkali bath, then by hand with a blunt
wooden instrument the moisture of the pelt is worked out and
it is drawn carefully to and fro over a straight, dull-edged knife
to remove any superfluous flesh and unevenness. Special grease
is then rubbed in and the skin placed in a machine which softly
and continuously beats in the softening mixture, after which it
is put into a slowly revolving drum, fitted with wooden paddles,
partly filled with various kinds of fine hard sawdust according
to the nature of the furs dealt with. This process with a moderate
degree of heat thoroughly cleans it of external greasy matter,
354
and all that is necessary before manufacturing is to gently tap
the fur upon a leather cushion stuffed with horsehair with smooth
canes of a flexibility suited to the strength of the fur. After
dressing most skins alter in shape and decrease in size.
With regard to the merits of European dressing, it may be
fairly taken that English, German and French dressers have
specialities of excellence. In England, for instance, the dressing
of sables, martens, foxes, otters, seals, bears, lions, tigers and
leopards is first rate; while with skunk, mink, musquash,
chinchillas, beavers, lambs and squirrels, the Germans show
better results, particularly in the last. The pelt after the German
dressing is dry, soft and white, which is due to a finishing process
where meal is used, thus they compare favourably with the
moister and consequently heavier English finish. In France they
do well with cheaper skins, such as musquash, rabbit and hare,
which they dye in addition to dressing. Russian dressing is
seldom reliable; not only is there an unpleasant odour, but in
damp weather the pelts often become clammy, which is due to
the saline matter in the dressing mixture. Chinese dressing is
white and supple, but contains much powder, which is disagreeable
and difficult to get rid of, and in many instances the skin
is rendered so thin that the roots of the fur are weakened, which
means that it is liable to shed itself freely, when subject to
ordinary friction in handling or wearing. American and Canadian
dressing is gradually improving, but hitherto their results have
been inferior to the older European methods.
In the case of seal and beaver skins the process is a much more
difficult one, as the water or hard top hairs have to be removed
by hand after the pelt has been carefully rendered moist and
warm. With seal skins the process is longer than with any other
fur preparation and the series of processes engage many
specialists, each man being constantly kept upon one section of
the work. The skins arrive simply salted. After being purchased
at the auction sales they are washed, then stretched upon a
hoop, when all blubber and unnecessary flesh is removed, and
the pelt is reduced to an equal thickness, but not so thin as it is
finally rendered. Subsequently the hard top hairs are taken out
as in the case of otters and beavers and the whole thoroughly
cleaned in the revolving drums. The close underwool, which is
of a slightly wavy nature and mostly of a pale drab colour, is
then dyed by repeated applications of a rich dark brown colour,
one coat after another, each being allowed to thoroughly dry
before the next is put on, till the effect is almost a lustrous black
on the top. The whole is again put through the cleaning process
and evenly reduced in thickness by revolving emery wheels,
and eventually finished off in the palest buff colour.
The English dye for seals is to-day undoubtedly the best; its
constituents are more or less of a trade secret, but the principal ingredients
comprise gall nuts, copper dust, camphor and antimony,
and it would appear after years of careful watching that the
atmosphere and particularly the water of London are partly
responsible for good and lasting results. The Paris dyers do
excellent work in this direction, but the colour is not so durable,
probably owing to a less pure water. In America of late, strides
have been made in seal dyeing, but preference is still given to
London work. In Paris, too, they obtain beautiful results in the
“topping” or colouring Russian sables and the Germans are
particularly successful in dyeing Persian lambs black and foxes
in all blue, grey, black and smoke colours and in the insertion of
white hairs in imitation of the real silver fox. Small quantities
of good beaver are dyed in Russia occasionally, and white hairs
put in so well that an effect similar to sea otter is obtained.
The process of inserting white hairs is called in the trade
“pointing, “and is either done by stitching them in with a needle
or by adhesive caoutchouc.
The Viennese are successful in dyeing marmot well, and their
cleverness in colouring it with a series of stripes to represent the
natural markings of sable which has been done after the garments
have been made, so as to obtain symmetry of lines, has secured
for them a large trade among the dealers of cheap furs in England
and the continent.
Manufacturing Methods and Specialities.—In the olden times
the Skinners’ Company of the city of London was an association
of furriers and skin dressers established under royal charter
granted by Edward III. At that period the chief concern of
the body was to prevent buyers from being imposed upon by
sellers who were much given to offering old furs as new; a century
later the Skinners’ Company received other charters empowering
them to inspect not only warehouses and open markets, but
workrooms. In 1667 they were given power to scrutinize the
preparing of rabbit or cony wool for the wool trade and the
registration of the then customary seven years’ apprenticeship.
To-day all these privileges and powers are in abeyance, and the
interest that they took in the fur trade has been gradually
transferred to the leather-dressing craft.
The work done by English furriers was generally good, but
since about 1865 has considerably improved on account of the
influx of German workmen, who have long been celebrated
for excellent fur work, being In their own country obliged to
satisfy officially appointed experts and to obtain a certificate
of capacity before they can be there employed. The French
influence upon the trade has been, and still is, primarily one of
style and combination of colour, bad judgment in which will mar
the beauty of the most valuable furs. It is a recognized law
among high-class furriers that furs should be simply arranged,
that is, that an article should consist of one fur or of two furs
of a suitable contrast, to which lace may be in some cases added
with advantage. As illustrative of this, it may be explained that
any brown tone of fur such as sable, marten, mink, black marten,
beaver, nutria, &c., will go well upon black or very dark-brown
furs, while those of a white or grey nature, such as ermine, white
lamb, chinchilla, blue fox, silver fox, opossum, grey squirrel, grey
lamb, will set well upon seal or black furs, as Persian lamb,
broadtail, astrachan, caracul lamb, &c. White is also permissible
upon some light browns and greys, but brown motley colours
and greys should never be in contrast. One neutralizes the other
and the effect is bad. The qualities, too have to be considered—the
fulness of one, the flatness of the other, or the coarseness or
fineness of the furs. The introduction of a third fur in the same
garment or indiscriminate selection of colours of silk linings,
braids, buttons, &c., often spoils an otherwise good article.
With regard to the natural colours of furs, the browns that
command the highest prices are those that are of a bluish rather
than a reddish tendency. With greys it is those that are bluish,
not yellow, and with white those that are purest, and with black
the most dense, that are most esteemed and that are the rarest.
Perhaps for ingenuity and the latest methods of manipulating
skins in the manufacturing of furs the Americans lead the way,
but as fur cutters are more or less of a roving and cosmopolitan
character the larger fur businesses in London, Berlin, Vienna,
St Petersburg, Paris and New York are guided by the same
thorough and comparatively advanced principles.
During the period just mentioned the tailors’ methods of
scientific pattern cutting have been adopted by the leading
furriers in place of the old chance methods of fur cutters, so that
to-day a fur garment may be as accurately and gracefully fitted
as plush or velvet, and with all good houses a material pattern
is fitted and approved before the skins are cut.
Through the advent of German and American fur sewing-machines
since about 1890 fur work has been done better and
cheaper. There are, however, certain parts of a garment, such as
the putting in of sleeves and placing on of collars, &c., that can
only be sewn by hand. For straight seams the machines are
excellent, making as neat a seam as is found in glove work, unless,
of course, the pelts are especially heavy, such as bears and sheep
rugs.
A very great feature of German and Russian work is the fur
linings called rotondes, sacques or plates, which are made for
their home use and exportation chiefly to Great Britain, America
and France.
In Weissenfels, near Leipzig, the dressing of Russian grey
squirrel and the making it into linings is a gigantic industry, and
is the principal support of the place. After the dressing process
the backs of the squirrels are made up separately from the under
355
and thinner white and grey parts, the first being known as squirrel-back
and the other as squirrel-lock linings. A few linings are
made from entire skins and others are made from the quite white
pieces, which in some instances are spotted with the black ear
tips of the animals to resemble ermine. The smaller and uneven
pieces of heads and legs are made up into linings, so there is
absolutely no waste. Similar work is done in Russia on almost
as extensive a scale, but neither the dressing nor the work is
so good as the German.
The majority of heads, gills or throats, sides or flanks, paws
and pieces of skins cut up in the fur workshops of Great Britain,
America and France, weighing many tons, are chiefly exported
to Leipzig, and made up in neighbouring countries and Greece,
where labour can be obtained at an alarmingly low rate. Although
the sewing, which is necessarily done by hand, the sections
being of so unequal and tortuous a character, is rather roughly
executed, the matching of colours and qualities is excellent.
The enormous quantities of pieces admit of good selection and
where odd colours prevail in a lining it is dyed. Many squirrel-lock
linings are dyed blue and brown and used for the outside
of cheap garments. They are of little weight, warm and effective,
but not of great durability.
The principal linings are as follows: Sable sides, sable heads
and paws, sable gills, mink sides, heads and gills, marten sides,
heads and gills, Persian lamb pieces and paws, caracul lamb
pieces or paws, musquash sides and heads, nutria sides, genet
pieces, raccoon sides or flanks, fox sides, kolinski whole skins, and
small rodents as kaluga and hamster. The white stripes cut out
of skunks are made into rugs.
Another great source of inexpensive furs is China, and for
many years past enormous quantities of dressed furs, many of
which are made up in the form of linings and Chinese loose-shaped
garments, have been imported by England, Germany
and France for the lower class of business; the garments are only
regarded as so much fur and are reworked. With, however, the
exception of the best white Tibet lambs, the majority of Chinese
furs can only be regarded as inferior material. While the work
is often cleverly done as to matching and manipulation of the
pelt which is very soft, there are great objections in the odour
and the brittleness or weakness of the fur. One of the most
remarkable results of the European intervention in the Boxer
rising in China (1900) was the absurd price paid for so-called
“loot” of furs, particularly in mandarins’ coats of dyed and
natural fox skins and pieces, and natural ermine, poor in quality
and yellowish in colour; from three to ten times their value
was paid for them when at the same time huge parcels of similar
quality were warehoused in the London docks, because purchasers
could not be found for them.
With regard to Japanese furs, there is little to commend them.
The best are a species of raccoon usually sold as fox, and, being
of close long quality of fur, they are serviceable for boas, collars,
muffs and carriage aprons. The sables, martens, minks and
otters are poor in quality, and all of a very yellow colour and
they are generally dyed for the cheap trade. A small number
of very pretty guanaco and vicuna carriage rugs are imported
into Europe, and many come through travellers and private
sources, but generally they are so badly dressed that they are
quite brittle upon the leather side. Similar remarks are applicable
to opossum rugs made in Australia. From South
Africa a quantity of jackal, hyena, fox, leopard and sheep
karosses, i.e. a peculiarly shaped rug or covering used by native
chiefs, is privately brought over. The skins are invariably tanned
and beautifully sewn, the furs are generally flat in quality and
not very strong in the hair, and are retained’ more as curiosities
than for use as a warm covering.
Hatters’ Furs and Cloths and Shawls.—The hat trade is largely
interested in the fur piece trade, the best felt hats being made
from beaver and musquash wool and the cheaper sorts from nutria,
hare and rabbit wools. For weaving, the most valuable pieces
are mohair taken from the angora and vicuna. They are limited
in quantity and costly, and the trade depends upon various
sorts of other sheep and goat wools for the bulk of its productions.
Frauds and Imitations.—The opportunities for cheating in
the fur trade are very considerable, and most serious frauds
have been perpetrated in the selling of sables that have been
coloured or “topped”; that is, just the tips of the hairs stained
dark to represent more expensive skins. It is only by years of
experience that some of these colourings can be detected. Where
the skins are heavily dyed it is comparatively easy to see the
difference between a natural and a dyed colour, as the underwool
and top hair become almost alike and the leather is also dark,
whereas in natural skins the base of the underwool is much
paler than the top, or of a different colour, and the leather Is
white unless finished in a pale reddish tone as is sometimes
the case when mahogany sawdust is used in the final cleaning.
As has been explained, sable is a term applied for centuries past
to the darker sorts of the Russian Siberian martens, and for years
past the same term has been bestowed by the retail trade upon
the American and Canadian martens. The baum and stone
martens caught in France, the north of Turkey and Norway
are of the same family, but coarser in underwool and the top
hair is less in quantity and not so silky. The kolinski, or as it
is sometimes styled Tatar sable, is the animal, the tail of which
supplies hair for artists’ brushes. This is also of the marten
species and has been frequently offered, when dyed dark, as have
baum and stone martens, as Russian sables. Hares, too, are
dyed a sable colour and advertised as sable. The fur, apart
from a clumsy appearance, is so brittle, however, as to be of
scarcely any service whatever.
Among the principal imitations of other furs is musquash,
out of which the top hair has been pulled and the undergrowth
of wool clipped and dyed exactly the same colour as is used for
seal, which is then offered as seal or red river seal. Its durability,
however, is far less than that of seal. Rabbit is prepared and
dyed and frequently offered as “electric sealskin.” Nutria also
is prepared to represent sealskin, and in its natural colour, after
the long hairs are plucked out, it is sold as otter or beaver. The
wool is, however, poor compared to the otter and beaver, and the
pelt thin and in no way comparable to them in strength. White
hares are frequently sold as white fox, but the fur is weak, brittle
and exceedingly poor compared to fox and possesses no thick
underwool. Foxes, too, and badger are dyed a brownish black,
and white hairs inserted to imitate silver fox, but the white hairs
are too coarse and the colour too dense to mislead any one who
knows the real article. But if sold upon its own merits, pointed
fox is a durable fur.
Garments made of sealskin pieces and Persian lamb pieces
are frequently sold as if they were made of solid skins, the term
“pieces” being simply suppressed. The London Chamber of
Commerce have issued to the British trade a notice that any
misleading term in advertising and all attempts at deception are
illegal, and offenders are liable under the Merchandise Marks
Act 1887.
The most usual misnaming of manufactured furs is as follow:—
| Musquash, pulled and dyed | Sold as seal. |
| Nutria, pulled and dyed | Sold as seal. |
| Nutria, pulled and natural | Sold as beaver. |
| Rabbit, sheared and dyed | Sold as seal or electric seal. |
| Otter, pulled and dyed | Sold as seal. |
| Marmot, dyed | Sold as mink or sable. |
| Fitch, dyed | Sold as sable. |
| Rabbit, dyed | Sold as sable or French sable. |
| Hare, dyed | Sold as sable, or fox, or lynx. |
| Musquash, dyed | Sold as mink or sable. |
| Wallaby, dyed | Sold as skunk. |
| White Rabbit | Sold as ermine. |
| White Rabbit, dyed | Sold as chinchilla. |
| White Hare, dyed or natural | Sold as fox, foxaline, and other similar names. |
| Goat, dyed | Sold as bear, leopard, &c. |
| Dyed manufactured articles of all kinds | Sold as “natural.” |
| White hairs inserted in foxes and sables | Sold as real or natural furs. |
| Kids | Sold as lamb or broadtails. |
| American sable | Sold as real Russian sable. |
| Mink | Sold as sable. |
The Preservation of Furs.—For many years raw sealskins
356
have been preserved in cold storage, but it is only within a
recent period, owing to the difficulty there was in obtaining
the necessary perfectly dry atmosphere, that dressed and made-up
furs have been preserved by freezing. Furs kept in such a condition
are not only immune from the ravages of the larvae of
moth, but all the natural oils in the pelt and fur are conserved,
so that its colour and life are prolonged, and the natural deterioration
is arrested. Sunlight has a tendency to bleach furs and to
encourage the development of moth eggs, therefore continued
exposure is to be avoided. When furs are wetted by rain they
should be well shaken and allowed to dry in a current of air
without exposure to sun or open fire.
Where a freezing store for furs is not accessible, furs should be
well shaken and afterwards packed in linen and kept in a perfectly
cool dry place, and examined in the summer at periods of
not less than five weeks. Naphthalene and the usual malodorous
powders are not only very disagreeable, but quite useless. Any
chemical that is strong enough to destroy the life in a moth egg
would also be sufficiently potent to injure the fur itself. In
England moth life is practically continuous all the year round,
that is, as regards those moths that attack furs, though the
destructive element exists to a far greater extent during spring
and summer.
Comparative Durability of Various Furs and Weight of Unlined
Skins per Square Foot.
The following estimates of durability refer to the use of fur when
made up “hair outside” in garments or stoles, not as a lining.
The durability of fur used as linings, which is affected by other
conditions, is set forth separately. Otter, with its water hairs
removed, the strongest of furs for external use, is, in this table, taken
as the standard at 100 and other furs marked accordingly:—
The Precious Furs.
| | Points of
Durability. | 2 Weight
in oz. per
sq. ft. |
| Sable | 60 | 2½ |
| Sea | 75 | 3 |
| Fox, Silver or Black | 40 | 3 |
| Fox, White | 20 | 3 |
| Ermine | 25 | 1¼ |
| Chinchilla | 15 | 1½ |
| Sea-otter (for stoles or collars) | 100 | 4¼ |
The Less Valuable Furs.
| | Points of
Durability. | Weight
in oz. per
sq. ft. |
| Sable “topped,” i.e. top hairs coloured | 55 | 2½ |
| Sable tinted, i.e. fur all coloured. | 50 | 2½ |
| Baum Marten, natural | 65 | 2¾ |
| Baum Marten, tinted | 45 | 2¾ |
| Stone Marten | 40 | 2¾ |
| Nutria | 27 | 3¼ |
| Musquash, natural | 37 | 3¼ |
| Musquash, water hairs removed, sheared and seal finished. | 33 | 3¼ |
| Skunk | 70 | 2¾ |
| Mink | 70 | 3¼ |
| Lynx, natural | 25 | 2¾ |
| Lynx, tinted black | 20 | 2¾ |
| Marmot, tinted | 10 | 3 |
| Fox, tinted black | 25 | 3 |
| Fox, tinted blue | 20 | 3 |
| Opossum | 37 | 3 |
| Otter (with water hairs) | 100 | 4 |
| Otter (water hairs removed) | 95 | 315⁄16 |
| Beaver (water hairs cut level with fur) | 90 | 4 |
| Beaver (water hairs removed) | 85 | 315⁄16 |
| Moleskin | 7 | 1¾ |
| Persian Lamb | 65 | 3¼ |
| Grey Lamb | 30 | 3¼ |
| Broadtail | 15 | 2¼ |
| Caracul Kid | 10 | 3¼ |
| Caracul Lamb | 15 | 3¼ |
| Squirrel | 25 | 1¾ |
| Hare | 5 | 1¾ |
| Rabbit | 5 | 2¼ |
Quantities of Fur needed, in Square Feet.
The “Paris Model” figure is the basis of these estimates for
ladies’ garments, the standard measurements being height 5 ft.
6 in., waist 23 in., bust 38 in.
| | Sq. Ft.
(approximate). |
| Straight stole ½ length (just below the waist line) | 2¾ |
| Straight stole ¾ length (just below the knee) | 3¾ |
| Stole, broad enough at the neck to cover the top of arm ¾ length | 5 |
| The same, full length (to hem of skirt) | 6 |
| Eton jacket, without collar | 13 |
| Plain cape, 15 in. long | 6½ |
| Deep cape, 30 in. long | 15 |
| Full cape with broad stole front, ¾ length | 15 |
| Inverness cape (to knee) | 25 |
| Double-breasted, straight, semi-fitting coat, covering hips | 16 |
| Double-breasted sacque jacket, 36 in. long, full sleeves | 20 |
| Same, 30 in. long | 18 |
| Same, 22 in. long | 15 |
| Long, full, shawl cape with points at back and front, well below knee | 15 |
| Shorter shawl cape | 16 |
| Motoring or driving coat, ¾ length | 22 |
| Motoring or driving coat, full length | 27 |
Weight and Durability of Furs for Men’s Coat Linings.
Otter with the water hairs removed, the strongest fur suited for
linings, is here taken as the standard.
| | Points of
Durability. | Weight
in oz. per
sq. ft. |
| Otter (the water hairs removed) | 100 | 315⁄16 |
| Beaver (the water hairs removed) | 90 | 315⁄16 |
| Mink | 90 | 3¼ |
| Sealskin | 75 | 3 |
| Raccoon | 75 | 4½ |
| Persian lamb or astrachan | 70 | 3¼ |
| Sable | 65 | 2½ |
| Musquash | 55 | 3½ |
| Nutria | 40 | 3¼ |
| Grey Opossum | 40 | 3 |
| Wallaby | 30 | 3¾ |
| Squirrel | 30 | 1¾ |
| Hamster | 15 | 1¼ |
| Rabbit | 10 | 2¼ |
Durability and Weight of Linings for Ladies’ Coats or Wraps.
Sable gills, the strongest fur suited for ladies’ linings, is taken as
the standard.
| | Points of
Durability. | Weight
in oz. per
sq. ft. |
| Sable gills | 100 | 27⁄8 |
| Sable | 85 | 2½ |
| Sable paws | 64 | 15⁄8 |
| Ermine | 57 | 1¼ |
| Squirrel back | 50 | 1¾ |
| Squirrel heads | 36 | 2½ |
| Squirrel lock | 21 | 13⁄16 |
| Hamster | 10 | 1¼ |
| Rabbit | 7 | 2¼ |
Durability and Weight of Motoring Furs made up with Fur outside.
Otter with the water hairs, the strongest fur suited for motoring
garments, is taken as the standard.
| | Points of
Durability. | Weight
in oz. per
sq. ft. |
| Otter (with water hairs) | 100 | 4 |
| Sealskin, marble | 80 | 3 |
| ”Hair Sealskin” (tinted) with water hairs (a special variety of seal) | 75 | 3¼ |
| Raccoon | 65 | 4½ |
| Russian Pony | 35 | 25⁄8 |
357
Durability and Weight of Furs for Rugs and Foot-sacks.
| | Points of
Durability. | Weight
in oz. per
sq. ft. |
| Wolverine | 100 | 6 |
| Bear (black or brown natural) | 94 | 7 |
| Bear (tinted black) | 88 | 7½ |
| Beaver | 88 | 4 |
| Raccoon | 77 | 4½ |
| Opossum | 61 | 3 |
| Wolf | 50 | 6½ |
| Jackal | 27 | 4½ |
| Australian Bear | 16 | 6 |
| Goat | 11 | 41⁄6 |
Wolverine, the strongest fur suited for rugs and foot-sacks, is
taken as the standard.
For a rug about 20 to 25 sq. ft. of fur are needed, for a foot-sack
14½.
(W. S. P.)
1 The measurements given are from nose to root of tail of average
large sizes after the dressing process, which has a shrinking tendency.
The depths of fur quoted are the greatest, but there are plenty of
good useful skins possessing a lesser depth.
2 Stout, old-fashioned boxcloth is almost the only cloth that
(after a soft, heavy lining has been added to it) affords even two-thirds
as much protection against cold as does fur. It weighs
4.273 oz. per sq. ft. more than the heaviest of coat-furs, and is so
rigid as to be uncomfortable, while the subtileness of fur makes it
“kind” to the body.
FURAZANES (furo—a.a′—diazoles), organic compounds obtained
by heating the glyoximes (dioximes of ortho-diketones)
with alkalis or ammonia. Dimethylfurazane is prepared by
heating dimethylglyoxime with excess of ammonia for six hours
at 165° C. (L. Wolff, Ber., 1895, 28, p. 70). It is a liquid (at
ordinary temperature) which boils at 156° C. (744 mm.).
Potassium permanganate oxidizes it first to methylfurazane-carboxylic
acid and then to furazanedicarboxylic acid. Methyl-ethylfurazane
and diphenylfurazane are also known. By
warming oxyfurazane acetic acid with excess of potassium permanganate
to 100° C. oxyfurazanecarboxylic acid is obtained
(A. Hantzsch and J. Urbahn, Ber., 1895, 28, p. 764). It crystallizes
in prisms, which melt at 175° C. Furazanecarboxylic
acid is prepared by the action of a large excess of potassium
permanganate on a hot solution of furazanepropionic acid.
It melts at 107º C, and dissolves in caustic soda, with a deep
yellow colour and formation of nitrosocyanacetic acid (L. Wolff
and P.F. Ganz, Ber., 1891, 24, p. 1167). Furoxane is an oxide
of furazane, considered by H. Wieland to be identical with
glyoxime peroxide; Kekulés dibromnitroacetonitrile is dibromfuroxane.
The formulae of the compounds above mentioned are:
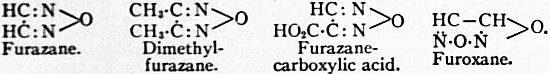
FURETIÈRE, ANTOINE (1619-1688), French scholar and
miscellaneous writer, was born in Paris on the 28th of December
1619. He first studied law, and practised for a time as an
advocate, but eventually took orders and after various preferments
became abbé of Chalivoy in the diocese of Bourges in
1662. In his leisure moments he devoted himself to letters, and
in virtue of his satires—Nouvelle Allégorique, ou histoire des
derniers troubles arrivés au royaume d’éloquence (1658); Voyage de
Mercure (1653)—he was admitted a member of the French
Academy in 1662. That learned body had long promised a
complete dictionary of the French tongue; and when they
heard that Furetière was on the point of issuing a work of a
similar nature, they interfered, alleging that he had purloined
from their stores, and that they possessed the exclusive privilege
of publishing such a book. After much bitter recrimination
on both sides the offender was expelled in 1685; but for this
act of injustice he took a severe revenge in his satire, Couches
de l’académie (Amsterdam, 1687). His Dictionnaire universel
was posthumously published in 1690 (Rotterdam, 2 vols.).
It was afterwards revised and improved by the Protestant
jurist, Henri Basnage de Beauval (1656-1710), who published his
edition (3 vols.) in 1701; and it was only superseded by the
compilation known as the Dictionnaire de Trévoux (Paris, 3 vols.,
1704; 7th ed., 8 vols., 1771), which was in fact little more than a
reimpression of Basnage’s edition. Furetière is perhaps even
better known as the author of Le Roman bourgeois (1666). It
cast ridicule on the fashionable romances of Mlle de Scudéry
and of La Calprenède, and is of interest as descriptive of the
everyday life of his times. There is no element of burlesque,
as in Scarron’s Roman comique, but the author contents himself
with stringing together a number of episodes and portraits,
obviously drawn from life, without much attempt at sequence.
The book was edited in 1854 by Edward Fournier and Charles
Asselineau and by P. Jannet.
The Fureteriana, which appeared in Paris eight years after
Furetière’s death, which took place on the 14th of May 1688, is a
collection of but little value.
FURFOOZ, a village some 10 m. from Dinant in the Ardennes,
Belgium. Three caves containing prehistoric remains were here
excavated in 1872. Of these the Trou de Frontal is the most
famous. In it were found human skeletons with brachycephalic
skulls, associated with animal bones, those of the reindeer being
particularly plentiful. Among the skeletons was discovered
an oval vase of pottery. The Furfooz type of mankind is believed
to date from the close of the Quaternary age. G. de Mortillet
dates the type in the Robenhausen epoch of the Neolithic
period. His theory is that the bones are those of men of that
period buried in what had been a cave-dwelling of the Madelenian
epoch.
FURFURANE, or Furane, C4H4O, a colourless liquid boiling
at 32° C., found in the distillation products of pine wood. It
was first synthetically prepared by H. Limpricht (Ann., 1873,
165, p. 281) by distilling barium mucate with soda lime, pyromucic
acid C4H3O·CO2H being formed, which, on further loss
of carbon dioxide, yielded furfurane. A. Henniger (Ann. chim.
phys., 1886 [2], 7, p. 220), by distilling erthyrite with formic
acid, obtained a dihydrofurfurane
C4H6(OH)4 + 2H2CO2 = C4H6O + CO + CO2 + 4H2O,
which, on treatment with phosphorus pentachloride, yielded
furfurane. Furfurane is insoluble in water and possesses a
characteristic smell. It does not react with sodium or with
phenylhydrazine, but yields dye-stuffs with isatin and phenanthrenequinone.
It reacts violently with hydrochloric acid,
producing a brown amorphous substance. Methyl and phenyl
derivatives have been prepared by C. Paal (Ber., 1884, 17, p.
915). Paal prepared acetonyl acetophenone by condensing
sodium acetoacetate with phenacylbromide, and this substance
on dehydration yields αα′-phenylmethylfurfurane, the acetonyl
acetophenone probably reacting in the tautomeric “enolic” form,
| CH3·CO·CHNa·COOR + C6H5·CO·CH2Br =
CH3·CO·CH(CH2COC6H5)·COOR. |
This ester readily hydrolyses, and the acid formed yields acetonyl
acetophenone (by loss of carbon dioxide), which then on dehydration
yields the furfurane derivative, thus
L. Knorr (Ber., 1889, 22, p. 158) obtained diacetosuccinic ester
by condensing sodium acetoacetate with iodine, and by dehydrating
the ester he prepared αα′-dimethylfurfurane ββ′-dicarboxylic
acid (carbopyrotritaric acid), which on distillation
yields αα′-dimethylfurfurane as a liquid boiling at 94° C. Paal
also obtained this compound by using monochloracetone in the
place of phenacylbromide. By the distillation of mucic acid
or isosaccharic acid, furfurane-α-carboxylic acid (pyromucic
acid), C4H3O·CO2H, is obtained; it crystallizes in needles or
leaflets, and melts at 134° C.
Furfurol (furol), C4H3O·CHO, is the aldehyde of pyromucic
acid, and is formed on distilling bran, sugar, wood and most
carbohydrates with dilute sulphuric acid, or by distilling
the pentoses with hydrochloric acid. It is a colourless liquid
which boils at 162° C., and is moderately soluble in water;
it turns brown on exposure to air and has a characteristic
aromatic smell. It shows all the usual properties of an aldehyde,
forming a bisulphite compound, an oxime and a hydrazone;
whilst it can be reduced to the corresponding furfuryl alcohol by
means of sodium amalgam, and oxidized to pyromucic acid by
means of silver oxide. It also shows all the condensation reactions
of benzaldehyde (q.v.); condensing with aldehydes
and ketones in the presence of caustic soda to form more
complex aldehydes and ketones with unsaturated side chains,
358
such as furfuracrolein, C4H3O·CH:CH·CHO, and furfuracetone,
C4H3O·CH:CH·CO·CH3. With alcoholic potassium cyanide
It changes to furoin, C4H3O·CHOH·CO·C4H3O, which can be
oxidized to furil, C4H3O·CO·CO·C4H3O, whilst alcoholic potash
converts it into furfuryl alcohol. With fatty acids and acid
anhydrides it gives the “Perkin” reaction (see Cinnamic Acid).
Furfurol is shown to have its aldehydic group in the a position,
by conversion into furfurpropionic acid, C4H3O·CH2·CH2·CO2H,
which on oxidation by bromine water and subsequent reduction
of the oxidized product is converted into n-pimelic acid,
HO2C(CH2)5CO2H. Furfurol in minute quantities can be
detected by the red colour it forms with a solution of aniline
acetate.
Furfurane—αα′-dicarboxylic acid or dehydromucic acid,
C4H2O(CO2H)2, is formed when mucic acid is heated with hydrochloric
acid at 100° C. On being heated, it loses carbon dioxide
and gives pyromucic acid. By digesting acetoacetic ester with
sodium succinate and acetic anhydride, methronic acid, C8H8O5,
is obtained; for the constitution of this acid, see L. Knorr, Ber.,
1889, 22, p. 152, and R. Fittig, Ann., 1889, 259, p. 166.
Di- and tetrahydrofurfurane compounds are also known (see
A. Lipp, Ber., 1889, 22, p. 1196; W.H. Perkin, junr. Journ. Chem.
Soc., 1899, 57, p. 944; and S. Ruhemann, ibid., 1896, 69, p. 1383).
FURIES (Lat. Furiae, also called Dirae), in Roman mythology
an adaptation of the Greek Erinyes (q.v.), with whom they
are generally identical. A special aspect of them in Virgil is
that of agents employed by the higher gods to stir up mischief,
strife and hatred upon earth. Mention may here be made of
an old Italian deity Furina (or Furrina), whose worship fell
early into disuse, and who was almost forgotten in the time of
Varro. By the mythologists of Cicero’s time the name was
connected with the verb furere and the noun furia, which in the
plural (not being used in the singular in this sense) was accepted
as the equivalent of the Greek Erinyes. But it is more probably
related to furvus, fuscus, and signifies one of the spirits of darkness,
who watched over men’s lives and haunted their abodes.
This goddess had her own special priest, a grove across the Tiber
where Gaius Gracchus was slain, and a festival on the 25th of
July. Authorities differ as to the existence of more than one
goddess called Furina, and their identity with the Forinae
mentioned in two inscriptions found at Rome (C.I.L. vi.
422 and 10,200).
FURLONG (from the O. Eng. furlang, i.e. “furrow-long”),
a measure of length, originally the length of a furrow in the
“common field” system. As the field in this system was
generally taken to be a square, 10 acres in extent, and as the
acre varied in different districts and at different times, the
“furlong” also varied. The side of a square containing 10
statute acres is 220 yds. or 40 poles, which was the usually
accepted length of the furlong. This is also the length of 1⁄8th of
the statute mile. “Furlong” was as early as the 9th century
used to translate the Latin stadium, 1⁄8th of the Roman mile.
FURNACE, a contrivance for the production and utilization
of heat by the combustion of fuel. The word is common to all
the Romance tongues, appearing in more or less modified forms
of the Latin fornax. But in all those languages the word has a
more extended meaning than in English, as it covers every
variety of heating apparatus; while here, in addition to furnaces
proper, we distinguish other varieties as ovens, stoves and kilns.
The first of these, in the form Ofen, is used in German as a general
term like the French four; but in English it has been restricted
to those apparatus in which only a moderate temperature,
usually below a red heat, is produced in a close chamber. Our
bakers’ ovens, hot-air ovens or stoves, annealing ovens for glass
or metal, &c., would all be called fours in French and Öfen in
German, in common with furnaces of all kinds. Stove, an
equivalent of oven, is from the German Stube, i.e. a heated room,
and is commonly so understood; but is also applied to open
fire-places, which appears to be somewhat of a departure from
the original signification.
Furnaces are constructed according to many different patterns
with varying degrees of complexity in arrangement; but all
may be considered as combining three essential parts, namely,
the fire-place in which the fuel is consumed, the heated chamber,
laboratory, hearth or working bed, as it is variously called,
where the heat is applied to the special work for which the furnace
is designed, and the apparatus for producing rapid combustion
by the supply of air under pressure to the fire. In the simplest
cases the functions of two or more of these parts may be combined
into one, as in the smith’s forge, where the fire-place and heating
chamber are united, the iron being placed among the coals, only
the air for burning being supplied under pressure from a blowing
engine by a second special contrivance, the tuyere, tuiron,
twyer or blast-pipe; but in the more refined modern furnaces,
where great economy of fuel is an object, the different functions
are distributed over separate and distinct apparatus, the fuel
being converted into gas in one, dried in another, and heated
in a third, before arriving at the point of combustion in the
working chamber of the furnace proper.
Furnaces may be classified according as the products of combustion
are employed (1) only for heating purposes, or (2) both for
heating and bringing about some chemical change. The furnaces
employed for steam-raising or for heating buildings are invariably
of the first type (see Boiler and Heating), while those employed
in metallurgy are generally of the second. The essential difference
in construction is that in the first class the substances heated do
not come into contact with either the fuel or the furnace gases,
whereas in the second they do. Metallurgical furnaces of the first
class are termed crucible, muffle or retort furnaces, and of the
second shaft and reverberatory furnaces. The following is a detailed
subdivision:—
(1) Fuel and substance in contact.
(a) Height of furnace greater than diameter = shaft furnaces.
(α) No blast = kilns.
(β) With blast = blast furnaces.
(b) Height not much greater than diameter = hearth furnaces.
(2) Substance heated by products of combustion = reverberatory
furnaces.
(a) Charge not melted = roasting or calcining furnaces.
(b) Charge melted = melting furnaces.
(3) Substance is not directly heated by the fuel or by the products
of combustion.
(a) Heating chamber fixed and forming part of furnace =
muffle furnaces.
(b) Crucible furnaces.
(c) Retort furnaces.
Another classification may be based upon the nature of the heating
agent, according as it is coal (or some similar combustible) oil, gas
or electricity. In this article the general principles of metallurgical
furnaces will be treated; the subject of gas- and oil-heated furnaces
is treated in the article Fuel, and of the electric furnace in the
article Electrometallurgy. For special furnaces reference should
be made to the articles on the industry concerned, e.g. Glass, Gas,
§ Manufacture, &c.
Shaft, Blast and Hearth Furnaces.—The blast furnace in its
simplest form is among the oldest, if not the oldest, of metallurgical
contrivances. In the old copper-smelting district of
Arabia Petraea, clay blast-pipes dating back to the earlier
dynasties of ancient Egypt have been found buried in slag heaps;
and in India the native smiths and iron-workers continue to use
furnaces of similar types. These, when reduced to their most
simple expression, are mere basin-shaped hollows in the ground,
containing ignited charcoal and the substances to be heated,
the fire being urged by a blast of air blown in through one or
more nozzles from a bellows at or near the top. They are
essentially the same as the smith’s forge. This class of furnace
is usually known as an open fire or hearth, and is represented in
a more advanced stage of development by the Catalan, German
and Walloon forges formerly used in the production of malleable
iron.
 |
| Fig. 1.—Elevation of Catalan
Forge. |
Fig. 1 represents a Catalan forge. The cavity in the ground is
represented by a pit of square or rectangular section lined with
brick or stone of a kind not readily acted on by heat, about 1½ or
2 ft. deep, usually somewhat larger above than below, with a tuyere
or blast-pipe of copper penetrating one of the walls near the top,
with a considerable downward inclination, so that the air meets
the fuel some way down. In iron-smelting the ore is laid in a heap
upon the fuel (charcoal) filling up the hearth, and is gradually brought
to the metallic state by the reducing action of the carbon monoxide
formed at the tuyere. The metal sinks through the ignited fuel,
forming, in the hearth, a spongy mass or ball, which is lifted out by
the smelters at the end of each operation, and carried to the forge
hammer. The earthy matters form a fusible glass or slag melt, and
359
collect at the lowest point of the hearth, whence they are removed
by opening a hole pierced through the front wall at the bottom.
The active portion of such a furnace is essentially that above the
blast-pipe, the function of the lower part being merely the collection
of the reduced metal; the fire may therefore be regarded as burning
in an unconfined space, with the waste of a large amount of its
heating power. By continuing the walls of the hearth above the
tuyere, into a shaft or stack either
of the same or some other section,
we obtain a furnace of increased
capacity, but with no greater
power of consuming fuel, in which
the material to be treated can be
heated up gradually by loading it
into the stack, alternately with
layers of fuel, the charge descending
regularly to the point of combustion,
and absorbing a proportion
of the heat of the flame
that went to waste in the open
fire. This principle is capable of
very wide extension, the blast
furnace being mainly limited in
height by the strength the column
of materials or “burden” has to
resist crushing, under the weight due to the head adopted, and the
power of the blowing engine to supply blast of sufficient density
to overcome the resistance of the closely packed materials to the
free passage of the spent gases. The consuming power of the
furnace or the rate at which it can burn the fuel supplied is measured
by the number of tuyeres and their section.
The development of blast furnaces is practically the development
of iron-smelting. The profile has been very much varied
at different times. The earliest examples were square or rectangular
in horizontal section, but the general tendency of modern
practice is to substitute round sections, their construction being
facilitated by the use of specially moulded bricks which have
entirely superseded the sandstone blocks formerly used. The
vertical section, on the other hand, is subject to considerable
variation according to the work to which the furnace is applied.
Where the operation is simply one of fusion, as in the iron-founder’s
cupola, in which there is no very great change in volume
in the materials on their descent to the tuyeres, the stack is nearly
or quite straight-sided; but when, as is the case with the smelting
of iron ores with limestone flux, a large proportion of volatile
matter has to be removed in the process, a wall of varying
inclination is used, so that the body of the furnace is formed of
two dissimilar truncated cones, joined by their bases, the lower
one passing downwards into a short, nearly cylindrical,
position. For further consideration of this subject see Iron
and Steel.
Hearth furnaces are employed in certain metallurgical operations,
e.g. in the air-reduction process for smelting lead ores.
The principle is essentially that of the Catalan forge. Such
furnaces are very wasteful, and have little to recommend them
(see Schnabel, Metallurgy, 1905, vol. 1. p. 409).
Reverberatory Furnaces.—Blast furnaces are, from the intimate
contact between the burden to be smelted and the fuel, the least
wasteful of heat; but their use supposes the possibility of obtaining
fuel of good quality and free from sulphur or other substances
likely to deteriorate the metal produced. In all cases, therefore,
where it is desired to do the work out of contact with the solid
fuel, the operation of burning or heat-producing must be performed
in a special fire-place or combustion chamber, the body
of flame and heated gas being afterwards made to act upon the
surface of the material exposed in a broad thin layer in the
working bed or laboratory of the furnace by reverberation from
the low vaulted roof covering the bed. Such furnaces are known
by the general name of reverberatory or reverbatory furnaces,
also as air or wind furnaces, to distinguish them from those
worked with compressed air or blast.
Originally the term cupola was used for the reverberatory
furnace, but in the course of time it has changed its meaning,
and is now given to a small blast furnace such as that used by
iron-founders—reverberatory smelting furnaces in the same
trade being called air furnaces.
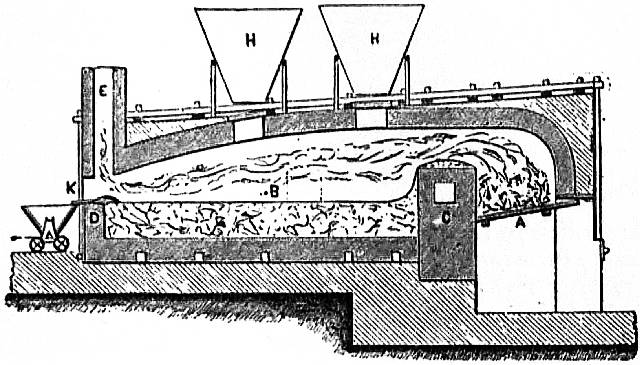 |
| Fig. 2.—Longitudinal section of Reverberatory Furnace. |
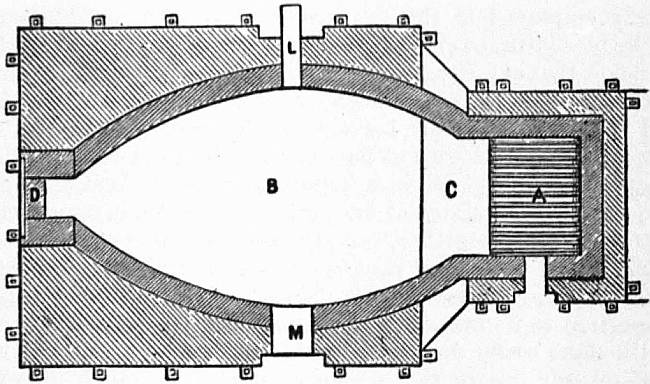 |
| Fig. 3.—Reverberatory Furnace (horizontal section). |
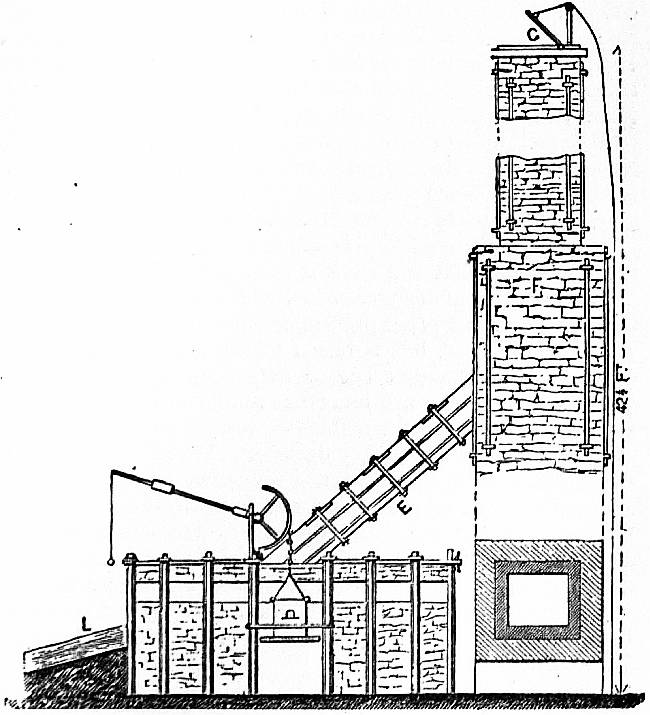 |
| Fig. 4.—Reverberatory Furnace (elevation at flue end). |
Figs. 2, 3 and 4 represent a reverberatory furnace such as is used
for the fusion of copper ores for regulus, and may be taken as generally
representing its class. The fire-place A is divided from the
working bed B by a low wall C known as the fire bridge, and at the
opposite end there is sometimes, though not invariably, a second
bridge of less height called the flue bridge D. A short diagonal flue
or up-take E conveys the current of spent flame to the chimney
F, which is of square section, diminishing by steps at two or three
different heights, and provided at the top with a covering plate or
damper G, which may be raised or lowered by a chain reaching to
the ground, and serves for regulating the speed of the exhaust gases,
and thereby the draught of air through the fire. Where several
furnaces are connected with the same chimney stack, the damper
takes the form of a sliding plate in the mouth of the connecting flue,
so that the draught in one may be modified without affecting the
others. The fire bridge is partially protected against the intense
360
heat of the body of flame issuing through the fire arch by a passage
to which the air has free access. The material to be melted is
introduced into the furnace from the hoppers HH through the
charging holes in the roof. When melted the products separate on
the bed (which is made of closely packed sand or other infusible
substances), according to their density; the lighter earthy matters
forming an upper layer of slag are drawn out by the slag hole K at
the flue end into an iron wagon or bogie, while the metal subsides
to the bottom of the bed, and at the termination of the operation
is run out by the tap hole L into moulds or granulated into water.
The opposite opening M is the working door, through which the tool
for stirring the charge is introduced. It is covered by a plate
suspended to a lever, similar to that seen in the end elevation (fig. 4)
in front of the slag hole.
According to the purposes to which they are applied, reverberatory
furnaces may be classed into two groups, namely, fusion
or melting furnaces, and calcining or wasting furnaces, also
called calciners. The former have a very extended application
in many branches of industry, being used by both founders and
smelters in the fusion of metals; in the concentration of poor
metallic compounds by fusion into regulus; in the reduction
of lead and tin ores; for refining copper and silver; and for
making malleable iron by the puddling processes and welding.
Calcining furnaces have a less extended application, being
chiefly employed in the conversion of metallic sulphides into
oxides by continued exposure to the action of air at a temperature
far below that of fusion, or into chlorides by roasting with common
salt. As some of these substances (for example, lead sulphide
and copper pyrites) are readily fusible when first heated, but
become more refractory as part of the sulphur is dissipated and
oxygen takes its place, it is important that the heat should be
very carefully regulated at first, otherwise the mass may become
clotted or fritted together, and the oxidizing effect of the air soon
ceases unless the fritted masses be broken small again. This is
generally done by making the bed of the furnace very long in
proportion to its breadth and to the fire-grate area, which may
be the more easily done as a not inconsiderable amount of heat
is given out during the oxidation of the ore—such increased
length being often obtained by placing two or even three working
beds one above the other, and allowing the flame to pass over them
in order from below upwards. Such calciners are used especially
in roasting zinc blende into zinc oxide, and in the conversion of
copper sulphides into chlorides in the wet extraction process. In
some processes of lead-smelting, where the minerals treated
contain sand, the long calciner is provided with a melting bottom
close to the fire-place, so that the desulphurized ore leaves the
furnace as a glassy slag or silicate, which is subsequently reduced
to the metallic state by fusion with fluxes in blast furnaces.
Reverberatory furnaces play an important part in the manufacture
of sodium carbonate; descriptions and illustrations are
given in the article Alkali Manufacture.
Muffle, Crucible and Retort Furnaces.—A third class of furnaces
is so arranged that the work is done by indirect heating; that
is, the material under treatment, whether subjected to calcination,
fusion or any other process, is not brought in contact either
with fuel or flame, but is raised to the proper temperature by
exposure in a chamber heated externally by the products of
combustion. These are known as muffle or chamber furnaces;
and by supposing the crucibles or retorts to represent similar
chambers of only temporary duration, the ordinary pot melting
air furnaces, and those for the reduction of zinc ores or the
manufacture of coal gas, may be included in the same category.
These are almost invariably air furnaces, though sometimes air
under pressure is used, as, for example, in the combustion of
small anthracitic coal, where a current of air from a fan-blower
is sometimes blown under the grate to promote combustion.
Types of muffle furnaces are figured in the article Annealing,
Hardening and Tempering.
Furnace Materials.—The materials used in the construction
of furnaces are divisible into two classes, namely, ordinary and
refractory or fire-resisting. The former are used principally as
casing, walls, pillars or other supporting parts of the structure,
and includes ordinary red or yellow bricks, clay-slate, granite
and most building stones; the latter are reserved for the parts
immediately in contact with the fuel and flame, such as the
lining of the fire-place, the arches, roof and flues, the lower part
if not the whole of the chimney lining in reverberatory furnaces,
and the whole of the internal walls of blast furnaces. Among
such substances are fireclay and firebricks, certain sandstones,
silica in the form of ganister, and Dinas stone and bricks, ferric
oxide and alumina, carbon (as coke and graphite), magnesia,
lime and chromium oxide—their relative importance being
indicated by their order, the last two or three indeed being only
of limited use.
The most essential point in good fireclays, or in the bricks
or other objects made from them, is the power of resisting
fusion at the highest heat to which they may be exposed. This
supposes them to be free from metallic oxides forming easily
fusible compounds with silica, such as lime or iron, the presence
of the former even in comparatively small proportion being very
detrimental. As clays they must be sufficiently plastic to be
readily moulded, but at the same time possess sufficient stiffness
not to contract too strongly in drying, whereby the objects
produced would be liable to be warped or cracked before firing.
In most cases, however, the latter tendency is guarded against,
in making up the paste for moulding, by adding to the fresh
clay a certain proportion of burnt material of the same kind,
such as old bricks or potsherds, ground to a coarse powder.
Coke dust or graphite is used for the same purpose in crucible
making (see Firebrick).
The most highly valued fireclays are derived from the Coal
Measures. Among the chief localities are the neighbourhood of
Stourbridge in Worcestershire and Stannington near Sheffield,
which supply most of the materials for crucibles used in steel and
brass melting, and the pots for glass houses; Newcastle-on-Tyne
and Glenboig near Glasgow, where heavy blast furnace and other
firebricks, gas retorts, &c., are made in large quantities. Coarse-grained
but very strong firebricks are also made of the waste of
china clay works.
In Belgium the clay raised at Andenne is very largely used for
making retorts for zinc furnaces. The principal French fireclays
are derived from the Tertiary strata in the south, and more nearly
resemble porcelain clays than those of the Coal Measures. They
give wares of remarkably fine texture and surface, combined with
high refractory character.
In Germany, Ips and Passau on the Danube, and Gross Almerode
in Hesse, are the best known localities producing fireclay goods, the
crucibles from the last-mentioned place, known as Hessian crucibles,
going all over the world. These, though not showing a great resistance
to extreme heat, are very slightly affected by sudden alternations
in heating, as they may be plunged cold into a strongly heated
furnace without cracking, a treatment to which French and Stourbridge
pots cannot be subjected with safety.
Plumbago or graphite is largely used in the production of
crucibles, not in the pure state but in admixture with fireclay;
the proportion of the former varies with the quality from 25 to
nearly 50%. These are the most enduring of all crucibles, the
best lasting out 70 or 80 meltings in brass foundries, about 50
with bronze, and 8 to 10 in steel-melting.
Silica is used in furnace-building in the forms of sand, ganister,
a finely ground sandstone from the Coal Measures of Yorkshire,
and the analogous substance known as Dinas clay, which is
really nearly pure silica, containing at most about 2½% of bases.
Dinas clay is found at various places in the Vale of Neath in
South Wales, in the form of a loose disintegrated sandstone,
which is crushed between rollers, mixed with about 1% of lime,
and moulded into bricks that are fired in kilns at a very high
temperature. These bricks are specially used for the roof, fire
arches, and other parts subjected to intense heat in reverberatory
steel-melting furnaces, and, although infusible under
ordinary conditions, are often fairly melted by the heat without
fluxing or corrosion after a certain amount of exposure. Ganister,
a slightly plastic siliceous sand, is similarly used for the lining
of Bessemer steel converters; it is found in the neighbourhood
of Sheffield.
Alumina as a refractory material is chiefly used in the form
of bauxite, but its applications are somewhat special. It has
been found to stand well for the linings of rotatory puddling
furnaces, where, under long-continued heating, it changes into
a substance as hard and infusible as natural emery. In the
361
Paris Exhibition of 1878 bricks very hard and dense in character,
said to be of pure alumina, were exhibited by Muller & Co. of
Paris, as well as bricks of magnesia, the latter being specially
remarkable for their great weight. They are intended for use
at the extreme temperatures obtainable in steel furnaces, or
for the melting of platinum before the oxy-hydrogen blowpipe.
For the latter purpose, however, lime is generally used; but as
this substance has only small stability, it is usually bedded in a
casing of firebrick. Oxide of chromium and chrome iron ore
have been proposed as refractory crucible materials. The former
may be used as a bed for melting platinum in the same way as
lime or magnesia, without affecting the quality of the metal.
Ferric oxide, though not strictly infusible, is largely used as a
protecting lining for furnaces in which malleable iron is made,
a portion of the ore being reduced and recovered in the process.
In an oxidizing atmosphere it is indifferent to silica, and therefore
siliceous bricks containing a considerable proportion of ferric
oxide, when used in flues of boilers, brewers’ coppers, &c. and
similar situations, are perfectly fire-resisting so long as the heated
gas contains a large proportion of unconsumed air. The red
firebricks known as Windsor bricks, which are practically
similar in composition to soft red sandstone, are of this character.
The electric furnace has led to the discovery of several
important materials, which have been employed as furnace
linings. Carborundum (q.v.) was applied by Engels in 1899,
firebricks being washed with carborundum paste and then baked.
Siloxicon, a compound of carbon, silicon and oxygen, formed
from carbon and silica in the electric furnace, was patented by
E.G. Acheson in 1903. It is very refractory, and is applied by
mixing with water and some bond, such as sodium silicate or
gas-tar. An amorphous, soft silicon carbide, also formed in the
electric furnace, was patented by B. Talbot in 1899. For basic
linings, magnesia crystallized in the electric furnace is being
extensively used, replacing dolomite to some extent (see E.
Kilburn Scott, “Refractory Materials for Furnace Linings,”
Faraday Soc., 1906, p. 289).
Furnace Construction.—In the construction of furnaces provision
has to be made for the unequal expansion of the different parts under
the effect of heat. This is especially necessary in the case of reverberatory
furnaces, which are essentially weak structures, and
therefore require to be bound together by complicated systems of
tie rods and uprights or buck staves. The latter are very commonly
made of old flat bottom rails, laid with the flat of the flange against
the wall. Puddling furnaces are usually entirely cased with iron
plates, and blast furnaces with hoops round each course of the stack,
or in those of thinner constructions the firebrick work is entirely
enclosed in a wrought iron casing or jacket. Such parts as may be
subjected to extreme heat and the fretting action of molten material,
as the tuyere and slag breasts of blast furnaces, and the fire bridges
and bed plates of reverberatory furnaces, are often made in cast
iron with double walls, a current of water or air being kept circulating
through the intermediate space. In this way the metal, owing to
its high conductivity and low specific heat as compared to that of
water, is kept at a temperature far below its melting point if the
water is renewed quickly enough. It is of course necessary in such
cases that the circulation shall be perfectly free, in order to prevent
the accumulation of steam under pressure in the interior of the
casting. This method has received considerable extension, notably
in furnace-smelting of iron ores containing manganese, where the
entire hearth is often completely water-cased, and in some lead
furnaces where no firebrick lining is used, the lower part of the
furnace stack being a mere double iron box cooled by water sufficiently
to keep a coating of slag adhering to the inner shell which
prevents the metal from being acted upon.
Mechanical Furnaces.—The introduction and withdrawal of the
charges in fusion furnaces is effected by gravitation, the solid masses
of raw ore, fuel and flux being thrown in at the top, and flowing
out of the furnace at the taphole or slag run at the bottom. Vertical
kilns, such as those used for burning limestone, are worked in a
similar manner—the raw stone going in at the top, and the burnt
product falling through holes in the bottom when allowed to do so.
With reverberatory calciners, however, where the work is done
upon a horizontal bed, a considerable amount of hand labour is
expended in raking out the charge when finished, and in drawing
slags from fusion furnaces; and more particularly in the puddling
process of refining iron the amount of manual exertion required is
very much greater. To diminish the item of expenditure on this
head, various kinds of mechanical furnaces have been adopted, all
of which can be classified under three heads of gravitating furnaces,
mechanical stirrers and revolving furnaces.
1. In gravitating furnaces the bed is laid at a slope just within the
angle of repose of the charge, which is introduced at the upper end,
and is pushed down the slope by fresh material, when necessary,
in the contrary direction to the flame which enters at the lower end.
Gerstenhofer’s pyrites burner is a furnace of this class. It has a tall
vertical chamber heated from below, and traversed by numerous
narrow horizontal cross bars at different heights. The ore in fine
powder is fed in at the top, through a hopper, in a regular thin
stream, by a pair of rollers, and in falling lodges on the flats of the
bars, forming a talus upon each of the height corresponding to the
angle of rest of the material, which is, however, at short intervals
removed to lower levels by the arrival of fresh ore from above. In
this way a very large surface is exposed to the heat, and the ore, if
containing sufficient sulphur to maintain the combustion, is perfectly
burned when it arrives at the bottom; if, however, it is imperfectly
sized or damp, or if it contains much earthy matter, the result is
not very satisfactory. There are many other furnaces in which the
same principle is utilized.
2. Mechanical stirrers constitute a second division of mechanical
furnaces, in which the labour of rabbling or stirring the charges is
performed by combinations of levers and wheel-work taking motion
from a rotating shaft, and more or less perfectly imitating the action
of hand labour. They are almost entirely confined to puddling
furnaces.
3. Revolving furnaces, the third and most important division of
mechanical furnaces, are of two kinds. The first of these resemble
an ordinary reverberatory furnace by having a flat bed which,
however, has the form of a circular disk mounted on a central shaft,
and receives a slow movement of rotation from a water-wheel or
other motor, so that every part of the surface is brought successively
under the action of the fire, the charge being stirred and ultimately
removed by passing under a series of fixed scraper arms placed above
the surface at various points. Brunton’s calciner, used in the “burning”
of the pyritic minerals associated with tin ore, is a familiar
example of this type. The hearth may either rotate on an inclined
axis, so that the path of its surface is oblique to that of the flame,
or the working part may be a hollow cylinder, between the fireplace
and flue, with its axis horizontal or nearly so, whose inner surface
represents the working bed, mounted upon friction rollers, and
receiving motion from a special steam-engine by means of a central
belt of spur gearing. Furnaces of the second kind were first used in
alkali works for the conversion of sulphate into carbonate of sodium
in the process known as black ash fusion, but have since been applied
to other processes. As calciners they are used in tin mines and for
the chlorination of silver ores. Mechanical furnaces are figured in
the article Alkali Manufacture.
Use of Heated Air.—The calorific intensity of fuel is found to be
very considerably enhanced, if the combustion be effected with air
previously heated to any temperature between that of boiling water
and a dull red heat, the same effect being observed both with solid
and gaseous fuel. The latter, especially when brought to the burning
point at a high temperature, produces a heat that can be resisted
by the most refractory substances only, such as silica, alumina and
magnesia. This is attained in the regenerative furnace of Siemens,
detailed consideration of which belongs more properly to the subject
of iron.
Economy of Waste Heat.—In every system of artificial heating, the
amount of heat usefully applied is but a small proportion of that
developed by combustion. Even under the most advantageous
application, that of evaporation of water in a steam boiler where the
gases of the fire have to travel through a great length of flues bounded
by thin iron surfaces of great heat-absorbing capacity, the temperature
of the current at the chimney is generally much above that
required to maintain an active draught in the fireplace; and other
tubes containing water, often in considerable numbers, forming the
so-called fuel economizers, may often be interposed between the
boiler and the chimney with marked advantage as regards saving
of fuel. In reverberatory and air furnaces used in the different
operations of iron manufacture, where an extremely high temperature
has to be maintained in spaces of comparatively small extent, such
as the beds of puddling, welding and steel-melting furnaces, the
temperature of the exhaust gases is exceedingly high, and if allowed
to pass directly into the chimney they appear as a great body of
flame at the top. It is now general to save a portion of this heat by
passing the flame through flues of steam boilers, air-heating apparatus,
or both—so that the steam required for the necessary operations
of the forge and heated blast for the furnace itself may be obtained
without further expenditure of fuel. The most perfect method of
utilizing the waste heat hitherto applied is that of the Siemens regenerator,
in which the spent gases are made to travel through
chambers, known as regenerators or recuperators of heat, containing
a quantity of thin firebricks piled into a cellular mass so as to offer
a very large heat-absorbing surface, whereby their temperature is
very considerably reduced, and they arrive at the chimney at a heat
not exceeding 300 or 400 degrees. As soon as the bricks have become
red hot, the current is diverted to an adjacent chamber or pair of
chambers, and the acquired heat is removed by a current of cool
gas or air passing towards the furnace, where it arrives at a temperature
sufficiently high to ensure the greatest possible heating
effect in combustion.
362
In iron-smelting blast furnaces the waste gases are of considerable
fuel value, and may render important services if properly applied.
Owing to the conditions of the work, which require the maintenance
of a sensibly reducing atmosphere, they contain a very notable
proportion of carbonic oxide, and are drawn off by large wrought iron
tubes near the top of the furnace and conveyed by branch pipes
to the different boilers and air-heating apparatus, which are now
entirely heated by the combustion of such gases, or mixed with air
and exploded in gas engines. Formerly they were allowed to burn
to waste at the mouth of a short chimney place above the furnace
top, forming a huge body of flame, which was one of the most
striking features of the Black Country landscape at night.
Laboratory and Portable Furnaces.—Small air-furnaces with hot
plates or sand bath flues were formerly much employed in chemical
laboratories, as well as small blast furnaces for crucibles heated with
charcoal or coke. The use of such furnaces has very considerably
diminished, owing to the general introduction of coal-gas for heating
purposes in laboratories, which has been rendered possible by the
invention of the Bunsen burner, in which the mixture of air and gas
giving the least luminous but most powerfully heating flame is
effected automatically by the effluent gas. These burners, or
modifications of them, have also been applied to muffle furnaces,
which are convenient when only a few assays have to be made—the
furnace being a mere clay shell and soon brought to a working
temperature; but the fuel is too expensive to allow of their being
used habitually or on a large scale. Petroleum, or rather the heavy
oils obtained in tar refineries, having an equal or superior heating
power to coal-gas, may also be used in laboratories for producing
high temperatures. The oil is introduced in a thin stream upon a
series of inclined and channelled bars, where it is almost immediately
volatilized and burnt by air flowing in through parallel orifices.
Furnaces of this kind may be used for melting cast iron or bronze
in small quantities, and were employed by H. Sainte Claire Deville
in experiments in the metallurgy of the platinum group of metals.
Sefstrom’s blast furnace, used in Sweden for the assay of iron ores,
is a convenient form of portable furnace applied to melting in
crucibles. It consists of a sheet-iron cylinder about 8 or 9 in. in
diameter, within which is fixed one of smaller size lined with fireclay.
The space between the two cylinders serves as a heater and
distributor for the blast, which is introduced through the nozzle at
the bottom, and enters the furnace through a series of several small
tuyeres arranged round the inner lining. Charcoal is the fuel used,
and the crucibles stand upon the bottom of the clay lining. When
a large body of fuel is required, the cylinder can be lengthened by
an iron hoop which fits over the top ring. Deville’s portable blast
furnace is very similar in principle to the above, but the body of the
furnace is formed of a single cast iron cylinder lined with fireclay,
closed below by a cast iron plate perforated by a ring of small holes—a
hemispherical basin below forming the air-heating chamber.
FURNEAUX, TOBIAS (1735-1781), English navigator, was
born at Swilly near Plymouth on the 21st of August 1735. He
entered the royal navy, and was employed on the French and
African coasts and in the West Indies during the latter part of the
Seven Years’ War (1760-1763). He served as second lieutenant
of the “Dolphin” under Captain Samuel Wallis on the latter’s
voyage round the globe (August 1766-May 1768); was made
a commander in November 1771; and commanded the “Adventure”
which accompanied Captain Cook (in the “Resolution”)
in Cook’s second voyage. On this expedition Furneaux
was twice separated from his leader (February 8-May 19, 1773;
October 22, 1773-July 14, 1774, the date of his return to
England). On the former occasion he explored a great part of
the south and east coasts of Tasmania, and made the earliest
British chart of the same. Most of his names here survive;
Cook, visiting this shore-line on his third voyage, confirmed
Furneaux’s account and delineation of it (with certain minor
criticisms and emendations), and named after him the islands
in Banks Straits, opening into Bass’s Straits, and the group now
known as the Low Archipelago. After the “Adventure” was
finally separated from the “Resolution” off New Zealand in
October 1773, Furneaux returned home alone, bringing with him
Omai of Ulaietea. This first South Sea Islander seen in the
British Isles returned to his home with Cook in 1776-1777.
Furneaux was made a captain in 1775, and commanded the
“Syren” in the British attack of the 28th of June 1776 upon
Charleston, South Carolina. His successful efforts to introduce
domestic animals and potatoes into the South Sea Islands are
worthy of note. He died at Swilly on the 19th of September
1781.
See Hawkesworth’s Narrative of Wallis’ Voyage; Captain Cook’s
Narrative of his Second Voyage; also T. Furneaux’s life by Rev.
Henry Furneaux in the Dictionary of National Biography.
FURNES (Flem. Veurne), an old-fashioned little town amid
the dunes near the coast in West Flanders, Belgium, about
26 m. S.W. of Bruges. Pop. (1904) 6099. It is the centre of a
considerable area extending to the French frontier, and its
market is an important one for the disposal of corn, stock, hops
and dairy produce. During the Norman raids Furnes was
destroyed, and the present town was built by Baldwin Bras de
Fer, first count of Flanders, about the year 870. At the height
of the prosperity of the Flemish communes in the 14th century
there were dependent on the barony of Furnes not fewer than
fifty-two rich villages, but these have all disappeared, partly
no doubt as the consequence of repeated French invasions down
to the end of the 18th century, but chiefly through the encroachment
of the sea followed by the accumulation of sand along the
whole of this portion of the coast. Furnes contains many
curious old houses and the church of St Walburga, which is a
fine survival of the 13th century with some older portions. The
old church and buildings, grouped round the Grand Place, which
is the scene of the weekly market, present a quaint picture
which is perhaps not to be equalled in the country. Near Furnes
on the seashore is the fashionable bathing place called La Panne.
Furnes one day a year becomes a centre of attraction to all
the people of Flanders. This is the last Sunday in July, when the
fête of Calvary and the Crucifixion is celebrated. Of all popular
festivities in Belgium this is the nearest approach to the old
Passion Play. The whole story of Christ is told with great
precision by means of succeeding groups which typify the different
phases of the subject. The people of Furnes pose as Roman
soldiers or Jewish priests, as the apostles or mere spectators,
while the women put on long black veils so that they may figure
in the procession as the just women.
FURNESS, HORACE HOWARD (1833- ), American
Shakespearian scholar, was born in Philadelphia on the 2nd of
November 1833, being the son of William Henry Furness (1802-1896)
minister of the First Unitarian church in that city, a
powerful preacher and writer. He graduated at Harvard in
1854, and was admitted to the bar in 1859, but soon devoted
himself to the study of Shakespeare. He accumulated a collection
of illustrative material of great richness and extent, and brought
out in 1871 the first volume of a new Variorum edition, designed
to represent and summarize the conclusions of the best authorities
in all languages—textual, critical and annotative. The volumes
appeared as follows: Romeo and Juliet (1871); Macbeth (1873)
(revised edition, 1903); Hamlet (2 vols., 1877); King Lear
(1880); Othello (1886); The Merchant of Venice (1888); As You
Like It (1890); The Tempest (1892); A Midsummer Night’s
Dream (1895); The Winter’s Tale (1898); Much Ado about
Nothing (1899); Twelfth Night (1901); Love’s Labour’s Lost
(1904). The edition has been generally accepted as a thorough
and scholarly piece of work; its chief fault is that, beginning
with Othello (1858), the editor used the First Folio text as his
basis, while in others he makes the text of the Cambridge (Globe)
editors his foundation. His wife, Helen Kate Furness (1837-1883),
compiled A Concordance to the Poems of Shakespeare (1872).
FURNESS, a district of Lancashire, England, separated from
the major portion of the county by Morecambe Bay. It is
bounded S.E. by this inlet of the Irish Sea, S.W. by the sea,
W. by the Duddon estuary and Cumberland, and N. and E. by
Westmorland. Its area is about 250 sq. m. It forms the greater
part of the North Lonsdale parliamentary division of Lancashire,
and contains the parliamentary borough of Barrow-in-Furness.
The surface is almost entirely hilly. The northern half is included
in the celebrated Lake District, and contains such eminences
as the Old Man of Coniston and Wetherlam. Apart from the
Duddon, which forms part of the western boundary, the principal
rivers are the Leven and Crake, flowing southward into a common
estuary in Morecambe Bay. The Leven drains Windermere
and the Crake Coniston Lake. The usage of the term “Lake
District,” however, tends to limit the name of Furness in common
thought to the district south of the Lakes, where several of the
place-names are suffixed with that of the district, as Barrow-in-Farness,
Dalton-in-Furness, Broughton-in-Furness. Between
363
the Duddon and Morecambe Bay lies Walney Island, 8 m. in
length, and in the shallow strait between it and the mainland
are several smaller islands. That part of Furness which forms a
peninsula between the Leven estuary and Morecambe Bay, and
the Duddon estuary, is rich in hematite iron ore, which has been
worked from very early times. It was known and smelted by
British and Romans, and by the monks of Furness Abbey and
Conishead Priory, both in the district. It was owing to the
existence of this ore that the town of Barrow grew up in the 19th
century; at first as a port from which the ore was exported to
South Wales, while later furnaces were established on the spot,
and acquired additional importance on the introduction of the
Bessemer process, which requires a non-phosphoric ore such as
is found here. The hematite is also worked at Ulverston, Askam,
Dalton and elsewhere, but the furnaces now depend in part
upon ore imported from Spain. The supposed extension of the
ore under the sands of the Duddon estuary led to the construction
of a sea wall to facilitate the working. The district is served
by the main line of the Furness railway, from Carnforth (junction
with the London & North-Western railway), passing the pleasant
watering-place of Grange, and approximately following the
coast by Ulverston, Dalton and Barrow, with branches to Lake
Side, Windermere, and to Coniston.
Apart from its industrial importance and scenic attractions,
Furness has an especial interest on account of its famous abbey.
The ruins of this, beautifully situated in a wooded
valley, are extensive, and mainly of fine transitional
Furness Abbey.
Norman and Early English date, acquiring additional
picturesqueness from the warm colour of the red sandstone
of which they are built. The abbey of Furness, otherwise
Furdenesia or the further nese (promontory), which was dedicated
to St Mary, was founded in 1127 by a small body of monks
belonging to the Benedictine order of Savigny. In 1124 they
had settled at Tulketh, near Preston, but migrated in 1127 to
Furness under the auspices of Stephen, count of Boulogne,
afterwards king, at that time lord of the liberty of Furness.
In 1148 the brotherhood joined the Cistercian order. Stephen
granted to the monks the lordship of Furness, and his charter
was confirmed by Henry I., Henry II. and subsequent kings.
The abbot’s power throughout the lordship was almost absolute;
he had a market and fair at Dalton, was free from service to the
county and wapentake, and held a sheriff’s tourn. By a succession
of gifts the abbey became one of the richest in England
and was the largest Cistercian foundation in the kingdom. At
the Dissolution its revenues amounted to between £750 and
£800 a year, exclusive of meadows, pastures, fisheries, mines,
mills and salt works, and the wealth of the monks enabled them
to practise a regal hospitality. The abbot was one of the twenty
Cistercian abbots summoned to the parliament of 1264, but was
not cited after 1330, as he did not hold of the king in capite per
baroniam. The abbey founded several offshoot houses, one of
the most important being Rushen Abbey in the Isle of Man. In
1535 the royal commissioners visited the abbey and reported
four of its inmates, including the abbot, for incontinence. In
1536 the abbot was charged with complicity in the Pilgrimage
of Grace, and on the 7th of April 1537, under compulsion,
surrendered the abbey to the king. A few monks were granted
pensions, and the abbot was endowed with the profits of the
rectory of Dalton, valued at £33, 6s. 8d. per annum. In 1540
the estates and revenues were annexed by act of parliament to
the Duchy of Lancaster. About James I.’s reign the site and
territories were alienated to the Prestons of Preston-Patrick,
from whom they descended to the dukes of Devonshire.
Conishead Priory, near Ulverston, an Augustinian foundation
of the reign of Henry II., has left no remains, but of the priory
of Cartmel (1188) the fine church is still in use. It is a cruciform
structure of transitional Norman and later dates, its central
tower having the upper storey set diagonally upon the lower.
The chancel contains some superb Jacobean carved oak screens,
with stalls of earlier date.
FURNISS, HARRY (1854- ), British caricaturist and
illustrator, was born at Wexford, Ireland, of English and Scottish
parents. He was educated in Dublin, and in his schooldays
edited a Schoolboy’s Punch in close imitation of the original.
He came to London when he was nineteen, and began to draw
for the illustrated papers, being for some years a regular contributor
to the Illustrated London News. His first drawing in Punch
appeared in 1880, and he joined its staff in 1884. He illustrated
Lucy’s “Diary of Toby, M.P.,” in Punch, where his political
caricatures became a popular feature. Among his other successes
were a series of “Puzzle Heads,” and his annual “Royal
Academy guy’d.” In Royal Academy Antics (1890) he published
a volume of caricatures of the work of leading artists. He
resigned from the staff of Punch in 1894, produced for a short
time a weekly comic paper Lika Joko, and in 1898 began a
humorous monthly, Fair Game; but these were short-lived.
Among the numerous books he illustrated were James Payn’s
Talk of the Town, Lewis Carroll’s Sylvie and Bruno, Gilbert à
Beckett’s Comic Blackstone, G.E. Farrow’s Wallypug Book,
and his own novel, Poverty Bay (1905). Our Joe, his great Fight
(1903), was a collection of original cartoons. His volume of
reminiscences, Confessions of a Caricaturist (1901), was followed
by Harry Furniss at Home (1904). In 1905 he published How to
draw in Pen and Ink, and produced the first number of Harry
Furniss’s Christmas Annual.
FURNITURE (from “furnish,” Fr. fournir), a general term
of obscure origin, used to describe the chattels and fittings required
to adapt houses and other buildings for use. Wood,
ivory, precious stones, bronze, silver and gold have been used
from the most ancient times in the construction or for the
decoration of furniture. The kinds of objects required for
furniture have varied according to the changes of manners and
customs, as well as with reference to the materials at the command
of the workman, in different climates and countries.
Of really ancient furniture there are very few surviving examples,
partly by reason of the perishable materials of which it was usually
constructed; and partly because, however great may have been
the splendour of Egypt, however consummate the taste of Greece,
however luxurious the life of Rome, the number of household
appliances was very limited. The chair, the couch, the table,
the bed, were virtually the entire furniture of early peoples,
whatever the degree of their civilization, and so they remained
until the close of what are known in European history as the
middle ages. During the long empire-strewn centuries which
intervened between the lapse of Egypt and the obliteration of
Babylon, the extinction of Greece and the dismemberment of
Rome and the great awakening of the Renaissance, household
comfort developed but little. The Ptolemies were as well lodged
as the Plantagenets, and peoples who spent their lives in the
open air, going to bed in the early hours of darkness, and rising
as soon as it was light, needed but little household furniture.
Indoor life and the growth of sedentary habits exercised a
powerful influence upon the development of furniture. From
being splendid, or at least massive, and exceedingly sparse and
costly, it gradually became light, plentiful and cheap. In the
ancient civilizations, as in the periods when our own was slowly
growing, household plenishings, save in the rudest and most
elementary forms, were the privilege of the great—no person
of mean degree could have obtained, or would have dared to
use if he could, what is now the commonest object in every
house, the chair (q.v.). Sparse examples of the furniture of
Egypt, Nineveh, Greece and Rome are to be found in museums;
but our chief sources of information are mural and sepulchral
paintings and sculptures. The Egyptians used wooden furniture
carved and gilded, covered with splendid textiles, and supported
upon the legs of wild animals; they employed chests and coffers
as receptacles for clothes, valuables and small objects generally.
Wild animals and beasts of the chase were carved upon the
furniture of Nineveh also; the lion, the bull and the ram were
especially characteristic. The Assyrians were magnificent in
their household appointments; their tables and couches were
inlaid with ivory and precious metals. Cedar and ebony were
much used by these great Eastern peoples, and it is probable that
they were familiar with rosewood, walnut and teak. Solomon’s
364
bed was of cedar of Lebanon. Greek furniture was essentially
Oriental in form; the more sumptuous varieties were of bronze,
damascened with gold and silver. The Romans employed Greek
artists and workmen and absorbed or adapted many of their
mobiliary fashions, especially in chairs and couches. The Roman
tables were of splendid marbles or rare woods. In the later
ages of the empire, in Rome and afterwards in Constantinople,
gold and silver were plentifully used in furniture; such indeed
was the abundance of these precious metals that even cooking
utensils and common domestic vessels were made of them.
The architectural features so prominent in much of the
medieval furniture begin in these Byzantine and late Roman
thrones and other seats. These features became paramount as
Pointed architecture became general in Europe, and scarcely
less so during the Renaissance. Most of the medieval furniture,
chests, seats, trays, &c., of Italian make were richly gilt and
painted. In northern Europe carved oak was more generally
used. State seats in feudal halls were benches with ends carved
in tracery, backs panelled or hung with cloths (called cloths of
estate), and canopies projecting above. Bedsteads were square
frames, the testers of panelled wood, resting on carved posts.
Chests of oak carved with panels of tracery, or of Italian cypress
(when they could be imported), were used to hold and to carry
clothes, tapestries, &c., to distant castles and manor houses;
for house furniture, owing to its scarcity and cost, had to be
moved from place to place. Copes and other ecclesiastical
vestments were kept in chests with ornamental lock plates and
iron hinges. The splendour of most feudal houses depended
on pictorial tapestries which could be packed and carried from
place to place. Wardrobes were rooms fitted for the reception
of dresses, as well as for spices and other valuable stores. Excellent
carving in relief was executed on caskets, which were of
wood or of ivory, with painting and gilding, and decorated with
delicate hinge and lock metal-work. The general subjects of
sculpture were taken from legends of the saints or from metrical
romances. Renaissance art made a great change in architecture,
and this change was exemplified in furniture. Cabinets (q.v.) and
panelling took the outlines of palaces and temples. In Florence,
Rome, Venice, Milan and other capitals of Italy, sumptuous
cabinets, tables, chairs, chests, &c., were made to the orders
of the native princes. Vasari (Lives of Painters) speaks of
scientific diagrams and mathematical problems illustrated in
costly materials, by the best artists of the day, on furniture made
for the Medici family. The great extent of the rule of Charles V.
helped to give a uniform training to artists from various countries
resorting to Italy, so that cabinets, &c., which were made in
vast numbers in Spain, Flanders and Germany, can hardly be
distinguished from those executed in Italy. Francis I. and
Henry VIII. encouraged the revived arts in their respective
dominions. Pietra dura, or inlay of hard pebbles, agate, lapis
lazuli, and other stones, ivory carved and inlaid, carved and gilt
wood, marquetry or veneering with thin woods, tortoise-shell,
brass, &c., were used in making sumptuous furniture during the
first period of the Renaissance. Subjects of carving or relief
were generally drawn from the theological and cardinal virtues,
from classical mythology, from the seasons, months, &c. Carved
altarpieces and woodwork in churches partook of the change in
style.
The great period of furniture in almost every country was,
however, unquestionably the 18th century. That century saw
many extravagances in this, as in other forms of art, but on the
whole it saw the richest floraison of taste, and the widest sense
of invention. This is the more remarkable since the furniture
of the 17th century has often been criticized as heavy and coarse.
The criticism is only partly justified. Throughout the first three-quarters
of the period between the accession of James I. and
that of Queen Anne, massiveness and solidity were the distinguishing
characteristics of all work. Towards the reign of
James II., however, there came in one of the most pleasing and
elegant styles ever known in England. Nearly a generation
before then Boulle was developing in France the splendid and
palatial method of inlay which, although he did not invent it,
is inseparably associated with his name. We owe it perhaps to
the fact that France, as the neighbour of Italy, was touched
more immediately by the Renaissance than England that the
reign of heaviness came earlier to an end in that country than on
the other side of the Channel. But there is a heaviness which is
pleasing as well as one which is forbidding, and much of the
furniture made in England any time after the middle of the
17th century was highly attractive. If English furniture of
the Stuart period be not sought after to the same extent as that
of a hundred years later, it is yet highly prized and exceedingly
decorative. Angularity it often still possessed, but generally
speaking its elegance of form and richness of upholstering lent
it an attraction which not long before had been entirely lacking.
Alike in France and in England, the most attractive achievements
of the cabinetmaker belong to the 18th century—English Queen
Anne and early Georgian work is universally charming; the
regency and the reigns of Louis XV. and XVI. formed a period
of the greatest artistic splendour. The inspiration of much of
the work of the great English school was derived from France,
although the gropings after the Chinese taste and the earlier
Gothic manner were mainly indigenous. The French styles of the
century, which began with excessive flamboyance, closed before
the Revolution with a chaste perfection of detail which is perhaps
more delightful than anything that has ever been done in
furniture. In the achievements of Riesener, David Röntgen,
Gouthière, Oeben and Rousseau de la Rottière we have the high-water
mark of craftsmanship. The marquetry of the period,
although not always beautiful in itself, was executed with
extraordinary smoothness and finish; the mounts of gilded
bronze, which were the leading characteristic of most of the work
of the century, were finished with a minute delicacy of touch
which was until then unknown, and has never been rivalled since.
If the periods of Francis I. and Henry II., of Louis XIV. and
the regency produced much that was sumptuous and even elegant,
that of Louis XVI., while men’s minds were as yet undisturbed
by violent political convulsions, stands out as, on the whole,
the one consummate era in the annals of furniture. Times of
great achievement are almost invariably followed directly by
those in which no tall thistles grow and in which every little
shrub is magnified to the dimensions of a forest tree; and the
so-called “empire style” which had begun even while the last
monarch of the ancien régime still reigned, lacked alike the graceful
conception and the superb execution of the preceding style.
Heavy and usually uninspired, it was nurtured in tragedy and
perished amid disaster. Yet it is a profoundly interesting style,
both by reason of the classical roots from which it sprang and
the attempt, which it finally reflected, to establish new ideas in
every department of life. Founded upon the wreck of a lingering
feudalism it reached back to Rome and Greece, and even to
Egypt. If it is rarely charming, it is often impressive by its
severity. Mahogany, satinwood and other rich timbers were
characteristic of the style of the end of the 18th century;
rosewood was most commonly employed for the choicer work
of the beginning of the 19th. Bronze mounts were in high
favour, although their artistic character varied materially.
Previously to the middle of the 18th century the only cabinetmaker
who gained sufficient personal distinction to have had
his name preserved was André Charles Boulle; beginning with
that period France and England produced many men whose
renown is hardly less than that of artists in other media. With
Chippendale there arose a marvellously brilliant school of English
cabinetmakers, in which the most outstanding names are those
of Sheraton, Heppelwhite, Shearer and the Adams. But if the
school was splendid it was lamentably short-lived, and the 19th
century produced no single name in the least worthy to be
placed beside these giants. Whether, in an age of machinery,
much room is left for fine individual execution may be doubted,
and the manufacture of furniture now, to a great extent, takes
place in large factories both in England and on the continent.
Owing to the necessary subdivision of labour in these
establishments, each piece of furniture passes through numerous
distinct workshops. The master and a few artificers formerly
365
superintended each piece of work, which, therefore, was never
far removed from the designer’s eye. Though accomplished
artists are retained by the manufacturers of London, Paris and
other capitals, there can no longer be the same relation between
the designer and his work. Many operations in these modern
factories are carried on by machinery. This, though an economy
of labour, entails loss of artistic effect. The chisel and the knife
are no longer in such cases guided and controlled by the sensitive
touch of the human hand.
Plate I.
 |
 |
 |
 |
| Fig. 1.—Venetian Folding Chair of
carved and gilt walnut, leather
back and seat; about 1530. |
Fig. 2.—Oak Arm-chair. English,
17th century. |
Fig. 3.—Arm-chair, solid seat, cane
back; about 1660. |
Fig. 4.—Arm-chair, stuffed back and
seat; about 1650. | |
 |
 |
 |
| Fig. 5.—Painted and carved High-Back
Chair; about 1660. |
Fig. 6.—Carved Walnut Chairs. English, early 18th century.
The arm-chair is inlaid. |
Fig. 7.—Walnut Chair; about 1710. | |
 |
 |
 |
 |
| Fig. 8.—Carved Mahogany Chair
in the style of Chippendale; 2nd
half of 18th century. |
Fig. 9.—Carved Mahogany Arm-chair,
in the style of Chippendale, with
ribbon pattern. |
Fig. 10.—Carved and Inlaid Mahogany
Chair, in the style of Hepplewhite;
late 18th century. |
Fig. 11.—Mahogany Chair in the
style of Sheraton; about 1780. | |
 |
 |
 |
 |
| Fig. 12.—Painted and gilt Arm-chair
with cane seat, in the style of
Adam; about 1790. |
Fig. 13.—Arm-chair of carved and gilt
wood with stuffed back, seat and
arms. French, Louis XV. style. |
Fig. 14.—Mahogany Arm-chair. Empire
style, early 19th century, said to have
belonged to the Bonaparte family. |
Fig. 15.—Painted and gilt Beech Chair.
English, about 1800. | |
Plate II.
 |
 |
| Fig. 1.—Front of Oak Coffer with wrought iron bands.
French, 2nd half of 13th century. |
Fig. 2.—English Oak Chest, dated 1637. | |
 |
 |
| Fig. 3.—Italian (Florentine) Coffer of Wood with gilt arabesque
stucco ornament, about 1480. |
Fig. 4.—Italian “Cassone” or Marriage Coffer, 13th century.
Carved and gilt wood with painted front and ends. | |
 |
 |
| Fig. 5.—Walnut Table with expanding leaves. Swiss, 17th century. |
Fig. 6.—Oak Gate-Legged Table. English,
17th century. | |
 |
 |
| Fig. 7.—Writing Table. French, end of Louis XV. period.
Riesener marquetry, ormolu mounts and Sèvres plaques. |
Fig. 8.—Painted Satin-Wood Tables, in the style of Sheraton,
about 1790. |
| (The above are in the Victoria and Albert Museum, except Fig. 8, which were in the Bethnal Green Exhibition, 1892.) | |
Plate III.
 |
 |
| 1. CARVED OAK SIDEBOARD. English, 17th century. Victoria and Albert
Museum. |
2. CARVED OAK COURT CUPBOARD. English, early 17th
century. Victoria and Albert Museum. | |
 |
 |
| 3. EBONY CARVED CABINET. The interior
decorated with inlaid ivory and coloured
woods; French or Dutch, middle of 17th
century. Victoria and Albert Museum. |
4. VENEERED CHEST OF DRAWERS. About
1690. Lent to Bethnal Green Exhibition by
Sir Spencer Ponsonby-Fane, G.C.B. | |
 |
 |
| 5. EBONY ARMOIRE. With tortoise-shell
panels inlaid with brass and other
metals, and ormolu mountings. Designed
by Bérain, and executed by André
Boulle. French, Louis XIV. period.
Victoria and Albert Museum. |
6. GLASS-FRONTED BOOKCASE AND CABINET. Of
mahogany. In the style of Sheraton, about 1790. Lent
to the Bethnal Green Exhibition by the late Vincent J. Robinson,
C.I.E. | |
Plate IV.
 |
 |
| 1. COMMODE OF PINE. With marquetry of brass, ebony, tortoise-shell,
mother-of-pearl, ivory, and green-stained bone. “Boulle” work with
designs in the style of Bérain. French, late period of Louis XIV. |
2. COMMODE. With panels of Japanese lacquer and ormolu mountings,
in the style of Caffieri. French, Louis XV. period. | |
 |
 |
| 3. TABLE OF KING AND TULIP WOODS. With ormolu mountings.
Louis XV. period. |
4. ESCRITOIRE À TOILETTE. Formerly belonging to Marie Antoinette.
Of tulip and sycamore woods inlaid with other coloured woods, ormolu
mounts. Louis XV. period. | |
 |
 |
| 5. FOUR-POST BEDSTEAD. Of oak inlaid
with bog-oak and holly, from the “Inlaid Room”
at Sizergh Castle, Westmorland. Latter half of
sixteenth century. |
6. CARVED AND GILT BEDSTEAD. With
blue silk damask coverings and hangings.
French, late 18th century. Louis XVI. period. |
| From the Victoria and Albert Museum, S. Kensington. | |
Plate V.
 |
 |
| Photo, Mansell & Co. |
| THE “BUREAU DU ROI,” MADE FOR LOUIS XV., NOW IN THE LOUVRE. For description, see Desk. |
A decided, if not always intelligent, effort to devise a new
style in furniture began during the last few years of the 19th
century, which gained the name of “l’art nouveau.” Its pioneers
professed to be free from all old traditions and to seek inspiration
from nature alone. Happily nature is less forbidding than many
of these interpretations of it, and much of the “new art” is a
remarkable exemplification of the impossibility of altogether
ignoring traditional forms. The style was not long in degenerating
into extreme extravagance. Perhaps the most striking consequence
of this effort has been, especially in England, the
revival of the use of oak. Lightly polished, or waxed, the cheap
foreign oaks often produce very agreeable results, especially
when there is applied to them a simple inlay of boxwood and
stained holly, or a modern form of pewter. The simplicity of
these English forms is in remarkable contrast to the tortured
and ungainly outlines of continental seekers after a conscious
and unpleasing “originality.”
Until a very recent period the most famous collections of
historic furniture were to be found in such French museums as
the Louvre, Cluny and the Garde Meuble. Now, however, they
are rivalled, if not surpassed, by the magnificent collections of
the Victoria and Albert Museum at South Kensington, and the
Wallace collection at Hertford House, London. The latter, in
conjunction with the Jones bequest at South Kensington, forms
the finest of all gatherings of French furniture of the great
periods, notwithstanding that in the Bureau du Roi the Louvre
possesses the most magnificent individual example in existence.
In America there are a number of admirable collections representative
of the graceful and homely “colonial furniture”
made in England and the United States during the Queen Anne
and Georgian periods.
See also the separate articles in this work on particular forms of
furniture. The literature of the subject has become very extensive,
and it is needless to multiply here the references to books. Perrot
and Chipiez, in their great Histoire de l’art dans l’antiquité (1882
et seq.) deal with ancient times, and A. de Champeaux, in Le Meuble
(1885), with the middle ages and later period; English furniture is
admirably treated by Percy Macquoid in his History of English
Furniture (1905); and Lady Dilke’s French Furniture in the 18th
Century (1901), and Luke Vincent Lockwood’s Colonial Furniture in
America (1901), should also be consulted.
(J. P. B.)
FURNIVALL, FREDERICK JAMES (1825-1910), English
philologist and editor, was born at Egham, Surrey, on the 4th
of February 1825, the son of a surgeon. He was called to the bar
in 1849, but his attention was soon diverted to philological
studies and social problems. He gave Frederick Denison Maurice
valuable assistance in the Christian Socialist movement, and was
one of the founders of the Working Men’s College. For half a
century he indefatigably promoted the study of early English
literature, partly by his own work as editor, and still more
efficaciously by the agency of the numerous learned societies
of which he was both founder and director, especially the Early
English Text Society (1864), which has been of inestimable
service in promoting the study of early and middle English.
He also established and conducted the Chaucer, Ballad, New
Shakespeare and Wyclif Societies, and at a later period societies
for the special study of Browning and Shelley. He edited texts
for the Early English Text Society, for the Roxburghe Club
and the Rolls Series; but his most important labours were
devoted to Chaucer, whose study he as an editor greatly assisted
by his “Six-Text” edition of the Canterbury Tales, and other
publications of the Chaucer Society. He was the honorary
secretary of the Philological Society, and was one of the original
promoters of the Oxford New English Dictionary. He co-operated
with its first editor, Herbert Coleridge, and after his death
was for some time principal editor during the preliminary period
of the collection of material. The completion of his half-century
of labour was acknowledged in 1900 by a handsome testimonial,
including the preparation by his friends of a volume of philological
essays specially dedicated to him, An English Miscellany
(Oxford, 1901), and a considerable donation to the Early English
Text Society. Dr Furnivall was always an enthusiastic oarsman,
and till the end kept up his interest in rowing; with John
Beesley in 1845 he introduced the new type of narrow sculling
boat, and in 1886 started races on the Thames for sculling fours
and sculling eights. He died on the 2nd of July 1910.
FURSE, CHARLES WELLINGTON (1868-1904), English
painter, born at Staines, the son of the Rev. C.W. Furse, archdeacon
of Westminster, was descended collaterally from Sir
Joshua Reynolds, and in his short span of life achieved such
rare excellence as a portrait and figure painter that he forms an
important link in the chain of British portraiture which extends
from the time when Van Dyck was called to the court of Charles I.
to our own day. His talent was precocious; at the age of seven
he gave indications of it in a number of drawings illustrating
Scott’s novels. He entered the Slade school in 1884, winning the
Slade scholarship in the following year, and completed his education
at Julian’s atelier in Paris. Hard worker as he was, his
activity was frequently interrupted by spells of illness, for he had
developed signs of consumption when he was still attending the
Slade school. An important canvas called “Cain” was his first
contribution (1888) to the Royal Academy, to the associateship
of which he was elected in the year of his death. For some years
before he had been a staunch supporter of the New English Art
Club, to the exhibitions of which he was a regular contributor.
He was married in October 1900 to Katherine, daughter of John
Addington Symonds. His fondness for sport and of an open-air
life found expression in his art and introduced a new, fresh and
vigorous note into portraiture. There is never a suggestion of
the studio or of the fatiguing pose in his portraits. The sitters
appear unconscious of being painted, and are generally seen in
the pursuit of their favourite outdoor sport or pastime, in the
full enjoyment of life. Such are the “Diana of the Uplands,”
the “Lord Roberts” and “The Return from the Ride” at the
Tate Gallery; the four children in the “Cubbing with the York
and Ainsty,” “The Lilac Gown,” “Mr and Mrs Oliver Fishing”
and the portrait of Lord Charles Beresford. Most of these
pictures, and indeed nearly all the work completed in the few
years of Furse’s activity, show a pronounced decorative tendency.
His sense of space, composition and decorative design can best
be judged by his admirable mural decorations for Liverpool
town hall, executed between 1899 and 1902. A memorial exhibition
of Furse’s paintings and sketches was held at the Burlington
Fine Arts Club in 1906.
FÜRST, JULIUS (1805-1873), German Orientalist, was born
of Jewish parents at Zerkowo in Posen, on the 12th of May 1805.
He studied philosophy and philology at Berlin, and oriental
literature at Posen, Breslau and Halle. In 1857 he was appointed
to a lectureship at the university of Leipzig, and he was promoted
to a professorship in 1864, which he held until his death at Leipzig
on the 9th of February 1873. Among his writings may be
mentioned Lehrgebäude der aramäischen Idiome (Leipzig, 1835);
Librorum sacrorum Veteris Testamenti concordantiae Hebraicae
atque Chaldaicae (Leipzig, 1837-1840); Hebräisches und chaldäisches
Wörterbuch (1851, English translation by S. Davidson 1867);
Kultur und Literaturgeschichte der Juden in Asien (1849). Fürst
also edited a valuable Bibliotheca Judaica (Leipzig, 1849-1863),
and was the author of some other works of minor importance.
From 1840 to 1851 he was editor of Der Orient, a journal devoted
to the language, literature, history and antiquities of the Jews.
FÜRSTENBERG, the name of two noble houses of Germany.
1. The more important is in possession of a mediatized principality
in the district of the Black Forest and the Upper Danube,
which comprises the countship of Heiligenberg, about 7 m. to
the N. of the Lake of Constance, the landgraviates of Stühlingen
and Baar, and the lordships of Jungnau, Trochtelfingen, Hausen
366
and Möskirch or Messkirch. The territory is discontinuous;
and as it lies partly in Baden, partly in Württemberg, and partly
in the Prussian province of Sigmaringen, the head of the family
is an hereditary member of the first chamber of Baden and of
the chamber of peers in Württemberg and in Prussia. The
relations of the principality with Baden are defined by the treaty
of May 1825, and its relations with Württemberg by the royal
declaration of 1839. The Stammort or ancestral seat of the
family is Fürstenberg in the Black Forest, about 13 m. N. of
Schaffhausen, but the principal residence of the present representatives
of the main line is at Donaueschingen.
The family of Fürstenberg claims descent from a certain
Count Unruoch, a contemporary of Charlemagne, but their
authentic pedigree is only traceable to Egino II., count of
Urach, who died before 1136. In 1218 his successors inherited
the possessions of the house of Zähringen in the Baar district
of the Black Forest, where they built the town and castle of
Fürstenberg. Of the two sons of Egino V. of Urach, Conrad,
the elder, inherited the Breisgau and founded the line of the
counts of Freiburg, while the younger, Heinrich (1215-1284),
received the territories lying in the Kinzigthal and Baar, and
from 1250 onward styled himself first lord, then count, of
Fürstenberg. His territories were subsequently divided among
several branches of his descendants, though temporarily reunited
under Count Friedrich III., whose wife, Anna, heiress
of the last count of Wardenberg, brought him the countship of
Heiligenberg and lordships of Jungnau and Trochtelfingen in
1534. On Friedrich’s death (1559) his territories were divided
between his two sons, Joachim and Christof I. Of these the
former founded the line of Heiligenberg, the latter that of
Kinzigthal. The Kinzigthal branch was again subdivided in
the 17th century between the two sons of Christof II. (d. 1614),
the elder, Wratislaw II. (d. 1642), founding the line of Mösskirch,
the younger, Friedrich Rudolf (d. 1655), that of Stühlingen.
The Heiligenberg branch received an accession of dignity by the
elevation of Count Hermann Egon (d. 1674) to the rank of prince
of the Empire in 1664, but his line became extinct with the
death of his son Prince Anton Egon, favourite of King Augustus
the Strong and regent of Saxony, in 1716. The heads of both
the Mösskirch and Stühlingen lines were now raised to the
dignity of princes of the Empire (1716). The Mösskirch branch
died out with Prince Karl Friedrich (d. 1744); the territories
of the Stühlingen branch had been divided on the death of
Count Prosper Ferdinand (1662-1704) between his two sons,
Joseph Wilhelm Ernst (1699-1762) and Ludwig August Egon
(1705-1759). The first of these was created prince of the Empire
on the 10th of December 1716, and founded the princely line
of the Swabian Fürstenbergs; in 1772 he obtained from the
emperor Francis I. for all his legitimate sons and their descendants
the right to bear, instead of the style of landgrave, that of
prince, which had so far been confined to the reigning head of
the family. Ludwig, on the other hand, founded the family of
the landgraves of Fürstenberg, who, since their territories lay
in Austria and Moravia, were known as the “cadet line in
Austria.” The princely line became extinct with the death
of Karl Joachim in 1804, and the inheritance passed to the
Bohemian branch of the Austrian cadet line in the person of
Karl Egon II. (see below). Two years later the principality
was mediatized.
In 1909 there were two branches of the princely house of
Fürstenberg: (1) the main branch, that of Fürstenberg-Donaueschingen,
the head of which was Prince Maximilian Egon (b.
1863), who succeeded his cousin Karl Egon III. in 1896; (2)
that of Fürstenberg-Königshof, in Bohemia, the head of which
was Prince Emil Egon (b. 1876), chamberlain and secretary of
legation to the Austro-Hungarian embassy in London (1907).
The cadet line of the landgraves of Fürstenberg is now extinct,
its last representative having been the landgrave Joseph Friedrich
Ernst of Fürstenberg-Weitra (1860-1896), son of the
landgrave Ernst (1816-1889) by a morganatic marriage. He
was not recognized as ebenbürtig by the family. The landgraves
of Fürstenberg were in 1909 represented only by the landgravines
Theresa (b. 1839) and Gabrielle (b. 1844), daughters of the
landgrave Johann Egon (1802-1879).
From the days of Heinrich of Urach, a relative and notable
supporter of Rudolph of Habsburg, the Fürstenbergs have
played a stirring part in German history as statesmen, ecclesiastics
and notably soldiers. There was a popular saying that
“the emperor fights no great battle but a Fürstenberg falls.”
In the Heiligenberg line the following may be more particularly
noticed.
Franz Egon (1625-1682), bishop of Strassburg, was the elder
son of Egon VII., count of Fürstenberg (1588-1635), who served
with distinction as a Bavarian general in the Thirty Years’ War.
He began life as a soldier in the imperial service, but on the
elevation of his friend Maximilian Henry of Bavaria to the
electorate of Cologne in 1650, he went to his court and embraced
the ecclesiastical career. He soon gained a complete ascendancy
over the weak-minded elector, and, with his brother William
Egon (see below), was mainly instrumental in making him the
tool of the aggressive policy of Louis XIV. of France. Ecclesiastical
preferments were heaped upon him. As a child he had
been appointed to a canonry of Cologne; to these he added
others at Strassburg, Liége, Hildesheim and Spires; he became
also suffragan bishop and dean of Cologne and provost of Hildesheim,
and in 1663 bishop of Strassburg. Later he was also
prince-abbot of Lüders and Murbach and abbot of Stablo and
Malmedy. On the conclusion of a treaty between the emperor
and the elector of Cologne, on the 11th of May 1674, Franz was
deprived of all his preferments in Germany, and was compelled
to take refuge in France. He was, however, amnestied with his
brother William by a special article of the treaty of Nijmwegen
(1679), whereupon he returned to Cologne. After the French
occupation of Strassburg (1681) he took up his residence there
and died on the 1st of April 1682.
His brother William Egon (1629-1704), bishop of Strassburg,
began his career as a soldier in the French service. He went to
the court of the elector of Cologne at the same time as Franz
Egon, whose zeal for the cause of Louis XIV. of France he shared.
In 1672 the intrigues of the two Fürstenbergs had resulted in a
treaty of offensive alliance between the French monarchy and
the electorate of Cologne, and, the brothers being regarded by
the Imperialists as the main cause of this disaster, William was
seized by imperial soldiers in the monastery of St Pantaleon at
Cologne, hurried off to Vienna and there tried for his life. He
was saved by the intervention of the papal nuncio, but was kept
in prison till the signature of the treaty of Nijmwegen (1679).
As a reward for his services Louis XIV. appointed him bishop
of Strassburg in succession to his brother in 1682, in 1686 obtained
for him from Pope Innocent XI. the cardinal’s hat, and in 1688
succeeded in obtaining his election as coadjutor-archbishop of
Cologne and successor to the elector Maximilian Henry. At the
instance of the emperor, however, the pope interposed his veto;
the canons followed the papal lead, and, the progress of the
Allies against Louis XIV. depriving him of all prospect of
success, William Egon retired to France. Here he took up his
abode at his abbey of St Germain des Près near Paris, where he
died on the 10th of April 1704.
In the Stühlingen line the most notable was Karl Egon
(1796-1854), prince of Fürstenberg, the son of Prince Karl
Alois of Fürstenberg, a general in the Austrian service, who was
killed at the battle of Loptingen on the 25th of March 1799.
In 1804 he inherited the Swabian principality of Fürstenberg
and all the possessions of the family except the Moravian estates.
He studied at Freiburg and Würzburg, and in 1815 accompanied
Prince Schwarzenberg to Paris as staff-officer. In 1817 he came
of age, and in the following year married the princess Amalie
of Baden. By the mediatization of his principality in 1806 the
greater part of his vast estates had fallen under the sovereignty
of the grand-duke of Baden, and Prince Fürstenberg took a
conspicuous part in the upper house of the grand-duchy. In
politics he distinguished himself by a liberalism rare in a great
German noble, carrying through by his personal influence with
his peers the abolition of tithes and feudal dues and stanchly
367
advocating the freedom of the press. He was not less distinguished
by his large charities: among other foundations he
established a hospital at Donaueschingen. For the industrial
development of the country, too, he did much, and proved himself
also a notable patron of the arts. His palace of Donaueschingen,
with its collections of paintings, engravings and coins, was a
centre of culture, where poets, painters and musicians met with
princely entertainment. He died on the 14th of September
1869, and was succeeded by his son Karl Egon II. (1820-1892),
with the death of whose son, Karl Egon III., in 1896, the title
and estates passed to Prince Maximilian Egon, head of the cadet
line of Fürstenberg-Pürglitz.
See Münch, Gesch. des Hauses und des Landes Fürstenberg, 4 vols.
(Aix-la-Chapelle, 1829-1847); S. Riezler, Gesch. des fürstlichen
Hauses Fürstenberg bis 1507 (Tübingen, 1883); Fürstenbergisches
Urkundenbuch, edited by S. Riezler and F.L. Baumann, vols. i.-vii.
(Tübingen, 1877-1891), continued s. tit. Mitteilungen aus dem
fürstlich. Fürstenbergischem Archiv by Baumann and G. Tumbült,
2 vols. (ib. 1899-1902); Stokvis, Manuel d’histoire (Leiden, 1890-1893);
Almanach de Gotha; Allgemeine deutsche Biographie.
2. The second Fürstenberg family has its possessions in
Westphalia and the country of the Rhine, and takes its name
from the castle of Fürstenberg on the Ruhr. The two most
remarkable men whom it has produced are Franz Friedrich
Wilhelm, freiherr von Fürstenberg, and Franz Egon, count von
Fürstenberg-Stammheim. The former (1728-1810) became
ultimately vicar-general of the prince-bishop of Münster, and
effected a great number of important reforms in the administration
of the country, besides doing much for its educational
and industrial development. The latter (1797-1859) was an
enthusiastic patron of art, who zealously advocated the completion
of the Cologne cathedral, and erected the beautiful church
of St Apollinaris near Remagen on the Rhine. He was a member
of the Prussian Upper House in 1849, collaborated in founding
the Preussisches Wochenblatt, and was an ardent defender of
Catholic interests. His son, Count Gisbert von Fürstenberg-Stammheim
(b. 1836), was in 1909 head of the Rhenish line of
the house of Fürstenberg.
FÜRSTENWALDE, a town of Germany, in the Prussian
province of Brandenburg, on the right bank of the Spree, and
on the railway from Berlin to Frankfort-on-Oder, 28 m. E. of
the former city. Pop. (1905) 20,498. Its beautiful cathedral
church contains several old monuments. The industries are
important, including, besides brewing and malting, manufactures
of starch, vinegar, electric lamps and gas-fittings, stoves, &c.,
iron-founding and wool-weaving. Fürstenwalde is one of the
oldest towns of Brandenburg. From 1385 it was the seat of
the bishop of Lebus, whose bishopric was incorporated with
the electorate of Brunswick in 1595.
FÜRTH, a manufacturing town of Germany, in the kingdom
of Bavaria, at the confluence of the Pegnitz with the Regnitz,
5 m. N.W. from Nuremberg by rail, at the junction of lines to
Hof and Würzburg. Pop. (1885) 35,455; (1905) 60,638. It is
a modern town in appearance, with broad streets and palatial
business houses. Of its four Evangelical churches, the old St
Michaeliskirche is a handsome structure; but its chief edifices
are the new town hall, with a tower 175 ft. high and the
magnificent synagogue. The Jews have also a high school,
which enjoys a great reputation. There are besides a classical,
a wood-carving and an agricultural school and a library. Fürth
is the seat of several important industries; particularly, the
production of chromolithographs and picture-books, the manufacture
of mirrors and mirror-frames, bronze and gold-leaf wares,
pencils, toys, haberdashery, optical instruments, silver work,
turnery, chicory, machinery, fancy boxes and cases, and an
extensive trade is carried on in these goods as also in hops,
metals, wool, groceries and coal. A large annual fair is held
at Michaelmas and lasts for eleven days. The earliest railway
in Germany was that between Nuremberg and Fürth (opened
on the 7th of December 1835).
Fürth was founded, according to tradition, by Charlemagne,
who erected a chapel there. It was for a time a Vogtei (advocateship)
under the burgraves of Nuremberg, but about 1314 it was
bequeathed to the see of Bamberg, and in 1806 it came into
the possession of Bavaria. In 1632 Gustavus Adolphus besieged
it in vain, and in 1634 it was pillaged and burnt by the Croats.
It owes its rise to prosperity to the tolerance it meted out to the
Jews, who found here an asylum from the oppression under
which they suffered in Nuremberg.
See Fronmüller, Chronik der Stadt Fürth (1887).
FURTWÄNGLER, ADOLF (1853-1907), German archaeologist,
was born at Freiburg im Breisgau, and was educated there,
at Leipzig and at Munich, where he was a pupil of H. Brunn,
whose comparative method in art-criticism he much developed.
He took part in the excavations at Olympia in 1878, became
an assistant in the Berlin Museum in 1880, and professor at
Berlin (1884) and later at Munich. His latest excavation work
was at Aegina. He was a prolific writer, with a prodigious
knowledge and memory, and a most ingenious and confident
critic; and his work not only dominated the field of archaeological
criticism but also raised its standing both at home and abroad.
Among his numerous publications the most important were a
volume on the bronzes found at Olympia, vast works on ancient
gems and Greek vases, and the invaluable Masterpieces of
Greek Sculpture (English translation by Eugénie Strong). He
died at Athens on the 10th of October 1907.
FURZE, Gorse or Whin; botanical name Ulex (Ger.
Stechginster, Fr. ajonc), a genus of thorny papilionaceous
shrubs, of few species, confined to west and central Europe and
north-west Africa. Common furze, U. europaeus, is found on
heaths and commons in western Europe from Denmark to Italy
and Greece, and in the Canaries and Azores, and is abundant
in nearly all parts of the British Isles. It grows to a height
of 2-6 ft.; it has hairy stems, and the smaller branches end each
in a spine; the leaves, sometimes lanceolate on the lowermost
branches, are mostly represented by spines from 2 to 6 lines long,
and branching at their base; and the flowers, about three-quarters
of an inch in length, have a shaggy, yellowish-olive calyx, with two
small ovate bracts at its base, and appear in early spring and
late autumn. They are yellow and sweet-scented and visited by
bees. The pods are few-seeded; their crackling as they burst
may often be heard in hot weather. This species comprises the
varieties vulgaris, or U. europaeus proper, which has spreading
branches, and strong, many-ridged spines, and strictus (Irish
furze), with erect branches, and slender 4-edged spines. The
other British species of furze is U. nanus, dwarf furze, a native
of Belgium, Spain and the west of France; it is a procumbent
plant, less hairy than U. europaeus, with smaller and more
orange-coloured flowers, which spring from the primary spines,
and have a nearly smooth calyx, with minute basal bracts.
Furze, or gorse, is sometimes employed for fences.
Notwithstanding its formidable spines, the young shoots
yield a palatable and nutritious winter forage for horses and
cattle. To fit it for this purpose it must be chopped and bruised
to destroy the spines. This is sometimes done in a primitive
and laborious way by laying the gorse upon a block of wood and
beating it with a mallet, flat at one end and armed with crossed
knife-edges at the other, by the alternate use of which it is
bruised and chopped. There are now a variety of machines
by which this is done rapidly and efficiently, and which are in
use where this kind of forage is used to any extent. The agricultural
value of this plant has often been over-rated by theoretical
writers. In the case of very poor, dry soils it does, however,
yield much valuable food at a season when green forage is not
otherwise to be had. It is on this account of importance to
dairymen; and to them it has this further recommendation,
that cows fed upon it give much rich milk, which is free from
any unpleasant flavour. To turn it to good account, it
must be sown in drills, kept clean by hoeing, and treated
as a regular green crop. If sown in March, on land fitly prepared
and afterwards duly cared for, it is ready for use in the
autumn of the following year. A succession of cuttings of
proper age is obtained for several years from the same field.
It is cut by a short stout scythe, and must be brought
from the field daily; for when put in a heap after being
368
chopped and bruised it heats rapidly. It is given to horses and
cows in combination with chopped hay or straw. An acre will
produce about 2000 faggots of green two-year-old gorse, weighing
20 ℔ each.
This plant is invaluable in mountain sheep-walks. The
rounded form of the furze bushes that are met with in such
situations shows how diligently the annual growth, as far as it
is accessible, is nibbled by the sheep. The food and shelter
afforded to them in snowstorms by clusters of such bushes is
of such importance that the wonder is our sheep farmers do not
bestow more pains to have it in adequate quantity. Young
plants of whin are so kept down by the sheep that they can
seldom attain to a profitable size unless protected by a fence
for a few years. In various parts of England it is cut for fuel.
The ashes contain a large proportion of alkali, and are a good
manure, especially for peaty land.
FUSARO, LAGO, a lake of Campania, Italy, ½ m. W. of Baia,
and 1 m. S. of the acropolis of Cumae. It is the ancient Acherusia
palus, separated from the sea on the W. by a line of sandhills.
It may have been the harbour of Cumae in early antiquity.
In the 1st century A.D. an artificial outlet was dug for it at its
S. end, with a tunnel, lined with opus reticulatum and brick,
under the hill of Torregaveta. This hill is covered with the
remains of a large villa, which is almost certainly that of Servilius
Vatia, described by Seneca (Epist. 55). There are remains of
other villas on the shores of the lake. Oyster cultivation is
carried on there.
See J. Beloch, Campanien (2nd ed., Breslau, 1890), 188.
(T. As.)
FUSELI, HENRY (1741-1825), English painter and writer on
art, of German-Swiss family, was born at Zürich in Switzerland
on the 7th of February 1741; he himself asserted in 1745, but
this appears to have been a mere whim. He was the second
child in a family of eighteen. His father was John Caspar
Füssli, of some note as a painter of portraits and landscapes,
and author of Lives of the Helvetic Painters. This parent
destined his son for the church, and with this view sent him to
the Caroline college of his native town, where he received an
excellent classical education. One of his schoolmates there
was Lavater, with whom he formed an intimate friendship.
After taking orders in 1761 Fuseli was obliged to leave his
country for a while in consequence of having aided Lavater to
expose an unjust magistrate, whose family was still powerful
enough to make its vengeance felt. He first travelled through
Germany, and then, in 1765, visited England, where he supported
himself for some time by miscellaneous writing: there was a
sort of project of promoting through his means a regular literary
communication between England and Germany. He became
in course of time acquainted with Sir Joshua Reynolds, to whom
he showed his drawings. By Sir Joshua’s advice he then devoted
himself wholly to art. In 1770 he made an art-pilgrimage to
Italy, where he remained till 1778, changing his name from
Füssli to Fuseli, as more Italian-sounding. Early in 1779 he
returned to England, taking Zürich on his way. He found a
commission awaiting him from Alderman Boydell, who was then
organizing his celebrated Shakespeare gallery. Fuseli painted
a number of pieces for this patron, and about this time published
an English edition of Lavater’s work on physiognomy. He likewise
gave Cowper some valuable assistance in preparing the
translation of Homer. In 1788 Fuseli married Miss Sophia
Rawlins (who it appears was originally one of his models, and who
proved an affectionate wife), and he soon after became an
associate of the Royal Academy. Two years later he was promoted
to the grade of Academician. In 1799 he exhibited a
series of paintings from subjects furnished by the works of
Milton, with a view to forming a Milton gallery corresponding
to Boydell’s Shakespeare gallery. The number of the Milton
paintings was forty-seven, many of them very large; they were
executed at intervals within nine years. This exhibition, which
closed in 1800, proved a failure as regards profit. In 1799 also
he was appointed professor of painting to the Academy. Four
years afterwards he was chosen keeper, and resigned his professorship;
but he resumed it in 1810, and continued to hold
both offices till his death. In 1805 he brought out an edition of
Pilkington’s Lives of the Painters, which, however, did not add
much to his reputation. Canova, when on his visit to England,
was much taken with Fuseli’s works, and on returning to Rome
in 1817 caused him to be elected a member of the first class in
the Academy of St Luke. Fuseli, after a life of uninterrupted
good health, died at Putney Hill on the 16th of April 1825,
at the advanced age of eighty-four, and was buried in the crypt
of St Paul’s cathedral. He was comparatively rich at his death,
though his professional gains had always appeared to be meagre.
As a painter, Fuseli had a daring invention, was original,
fertile in resource, and ever aspiring after the highest forms
of excellence. His mind was capable of grasping and realizing
the loftiest conceptions, which, however, he often spoiled on the
canvas by exaggerating the due proportions of the parts, and
throwing his figures into attitudes of fantastic and over-strained
contortion. He delighted to select from the region of the supernatural,
and pitched everything upon an ideal scale, believing
a certain amount of exaggeration necessary in the higher branches
of historical painting. “Damn Nature! she always puts me
out,” was his characteristic exclamation. In this theory he was
confirmed by the study of Michelangelo’s works and the marble
statues of the Monte Cavallo, which, when at Rome, he used
often to contemplate in the evening, relieved against a murky
sky or illuminated by lightning. But this idea was by him
carried out to an excess, not only in the forms, but also in the
attitudes of his figures; and the violent and intemperate action
which he often displays destroys the grand effect which many
of his pieces would otherwise produce. A striking illustration
of this occurs in his famous picture of “Hamlet breaking from
his Attendants to follow the Ghost”: Hamlet, it has been said,
looks as though he would burst his clothes with convulsive
cramps in all his muscles. This intemperance is the grand defect
of nearly all Fuseli’s compositions. On the other hand, his
paintings are never either languid or cold. His figures are full
of life and earnestness, and seem to have an object in view
which they follow with rigid intensity. Like Rubens he excelled
in the art of setting his figures in motion. Though the lofty and
terrible was his proper sphere, Fuseli had a fine perception of the
ludicrous. The grotesque humour of his fairy scenes, especially
those taken from A Midsummer-Night’s Dream, is in its way not
less remarkable than the poetic power of his more ambitious
works. As a colourist Fuseli has but small claims to distinction.
He scorned to set a palette as most artists do; he merely dashed
his tints recklessly over it. Not unfrequently he used his paints
in the form of a dry powder, which he rubbed up with his pencil
with oil, or turpentine, or gold size, regardless of the quantity,
and depending for accident on the general effect. This recklessness
may perhaps be explained by the fact that he did not paint
in oil till he was twenty-five years of age. Despite these drawbacks
he possessed the elements of a great painter.
Fuseli painted more than 200 pictures, but he exhibited only
a minority of them. His earliest painting represented “Joseph
interpreting the Dreams of the Baker and Butler”; the first
to excite particular attention was the “Nightmare,” exhibited
in 1782. He produced only two portraits. His sketches or
designs numbered about 800; they have admirable qualities of
invention and design, and are frequently superior to his paintings.
His general powers of mind were large. He was a thorough
master of French, Italian, English and German, and could write
in all these tongues with equal facility and vigour, though he
preferred German as the vehicle of his thoughts. His writings
contain passages of the best art-criticism that English literature
can show. The principal work is his series of Lectures in the
Royal Academy, twelve in number, commenced in 1801.
Many interesting anecdotes of Fuseli, and his relations to contemporary
artists, are given in his Life by John Knowles, who also
edited his works in 3 vols. 8vo, London, 1831.
(W. M. R.)
FUSEL OIL (from the Ger. Fusel, bad spirits), the name applied
to the volatile oily liquids, of a nauseous fiery taste and smell,
which are obtained in the rectification of spirituous liquors made
by the fermentation of grain, potatoes, the marc of grapes, and
369
other material, and which, as they are of higher boiling point
than ethyl alcohol, occur in largest quantity in the last portions
of the distillate. Besides ethyl or ordinary alcohol, and amyl
alcohol, which are present in them all, there have been found in
fusel oil several other bodies of the CnH2n+1·OH series, also
certain ethers, and members of the CnH2n+1·CO2H series of
fatty acids. Normal propyl alcohol is contained in the fusel
oil of the marc brandy of the south of France, and isoprimary
butyl alcohol in that of beet-root molasses. The chief constituent
of the fusel oil procured in the manufacture of alcohol from
potatoes and grain, usually known as fusel oil and potato-spirit,
is isoprimary amyl alcohol, or isobutylcarbinol. Ordinary fusel
oil yields also an isomeric amyl alcohol (active amyl alcohol)
boiling at about 128°. Variable quantities of fusel oil, less or
greater according to the stage of ripening, exist in commercial
spirits (see Spirits).
Fusel oil and its chief constituent, amyl alcohol, are direct
nerve poisons. In small doses it causes only thirst and headache,
with furred tongue and some excitement. In large doses it is
a convulsent poison. Impure beverages induce all the graver
neurotic and visceral disorders in alcoholism; and, like fusel
oil, furfurol and the essence of absinthe, are convulsent poisons.
Pure ethyl alcohol intoxication, indeed, is rarely seen, being
modified in the case of spirits by the higher alcohols contained
in fusel oil. According to Rabuteau the toxic properties of the
higher alcohols increase with their molecular weight and boiling
point. Richet considers that the fusel oil contained in spirits
constitutes the chief danger in the consumption of alcoholic
beverages. The expert can immediately detect the peculiarly
virulent characters of the mixed intoxication due to the consumption
of spirits containing a large percentage of fusel oil.
FUSIBLE METAL, a term applied to certain alloys, generally
composed of bismuth, lead and tin, which possess the property of
melting at comparatively low temperatures. Newton’s fusible
metal (named after Sir Isaac Newton) contains 50 parts of
bismuth, 31.25 of lead and 18.75 of tin; that of Jean Darcet
(1725-1801), 50 parts of bismuth with 25 each of lead and tin;
and that of Valentin Rose the elder, 50 of bismuth with 28.1 of
lead and 24.1 of tin. These melt between 91° and 95° C. The
addition of cadmium gives still greater fusibility; in Wood’s
metal, for instance, which is Darcet’s metal with half the tin
replaced by cadmium, the melting point is lowered to 66°-71° C.;
while another described by Lipowitz and containing 15 parts of
bismuth, 8 of lead, 4 of tin and 3 of cadmium, softens at about
55° and is completely liquid a little above 60°. By the addition
of mercury to Darcet’s metal the melting point may be reduced
so low as 45°. These fusible metals have the peculiarity of expanding
as they cool; Rose’s metal, for instance, remains pasty
for a considerable range of temperature below its fusing point,
contracts somewhat rapidly from 80° to 55°, expands from 55°
to 35°, and contracts again from 35° to 0°. For this reason they
may be used for taking casts of anatomical specimens or making
clichés from wood-blocks, the expansion on cooling securing
sharp impressions. By suitable modification in the proportions
of the components, a series of alloys can be made which melt
at various temperatures above the boiling point of water; for
example, with 8 parts of bismuth, 8 of lead and 3 of tin the
melting point is 123°, and with 8 of bismuth, 30 of lead and 24 of
tin it is 172°. With tin and lead only in equal proportions it is
241°. Such alloys are used for making the fusible plugs inserted
in the furnace-crowns of steam boilers, as a safeguard in the event
of the water-level being allowed to fall too low. When this
happens the plug being no longer covered with water is heated
to such a temperature that it melts and allows the contents of
the boiler to escape into the furnace. In automatic fire-sprinklers
the orifices of the pipes are closed with fusible metal, which melts
and liberates the water when, owing to an outbreak of fire in
the room, the temperature rises above a predetermined limit.
FUSILIER, originally (in French about 1670, in English about
1680) the name of a soldier armed with a light flintlock musket
called the fusil; now a regimental designation. Various forms
of flintlock small arms had been used in warfare since the middle
of the 16th century. At the time of the English civil war (1642-1652)
the term “firelock” was usually employed to distinguish
these weapons from the more common matchlock musket. The
special value of the firelock in armies of the 17th century lay
in the fact that the artillery of the time used open powder barrels
for the service of the guns, making it unsafe to allow lighted
matches in the muskets of the escort. Further, a military escort
was required, not only for the protection, but also for the
surveillance of the artillerymen of those days. Companies of
“firelocks” were therefore organized for these duties, and out of
these companies grew the “fusiliers” who were employed in
the same way in the wars of Louis XIV. In the latter part of
the Thirty Years’ War (1643) fusiliers were simply mounted
troops armed with the fusil, as carabiniers were with the carbine.
But the escort companies of artillery came to be known by the
name shortly afterwards, and the regiment of French Royal
Fusiliers, organized in 1671 by Vauban, was considered the model
for Europe. The general adoption of the flintlock musket and
the suppression of the pike in the armies of Europe put an end
to the original special duties of fusiliers, and they were subsequently
employed to a large extent in light infantry work,
perhaps on account of the greater individual aptitude for
detached duties naturally shown by soldiers who had never been
restricted to a fixed and unchangeable place in the line of battle.
The senior fusilier regiment in the British service, the (7th)
Royal Fusiliers (City of London Regiment), was formed on the
French model in 1685; the 5th foot (now Northumberland
Fusiliers), senior to the 7th in the army, was not at that time
a fusilier regiment. The distinctive head-dress of fusiliers in the
British service is a fur cap, generally resembling, but smaller
than and different in details from, that of the Foot Guards.
In Germany the name “fusilier” is borne by certain infantry
regiments and by one battalion in each grenadier regiment.
FUSION, the term generally applied to the melting of a solid
substance, or the change of state of aggregation from the solid
to the liquid. The term “liquefaction” is frequently employed
in the same sense, but is often restricted to the condensation
of a gas or vapour. The converse process of freezing or solidification,
the change from the liquid to the solid state, is subject to
the same laws, and must be considered together with fusion.
The solution of a solid in a foreign liquid, and the deposition or
crystallization of a solid from a solution, are so closely related
to the fusion of a pure substance, that it will also be necessary
to consider some of the analogies which they present.
1. General Phenomena.—There are two chief varieties of the
process of fusion, namely, crystalline and amorphous, which are
in many ways distinct, although it is possible to find intermediate
cases which partake of the characteristics of both. The melting
of ice may be taken as a typical case of crystalline fusion. The
passage from rigid solid to mobile liquid occurs at a definite
surface without any intermediate stage or plastic condition.
The change takes place at a definite temperature, the fusing or
freezing point (abbreviated F.P.), and requires the addition
of a definite quantity of heat to the solid, which is called the
latent heat of fusion. There is also in general a considerable
change of volume during fusion, which amounts in the case of
ice to a contraction of 9%. Typical cases of amorphous solidification
are those of silica, glass, plastic sulphur, pitch, alcohol and
many organic liquids. In this type the liquid gradually becomes
more and more viscous as the temperature falls, and ultimately
attains the rigidity characteristic of a solid, without any definite
freezing point or latent heat. The condition of the substance
remains uniform throughout, if its temperature is uniform;
there is no separation into the two distinct phases of solid
and liquid, and there is no sudden change of volume at any
temperature.
A change or transition from one crystalline form to another
may occur in the solid state with evolution or absorption of
heat at a definite temperature, and is analogous to the change
from solid to liquid, but usually takes place more slowly owing
to the small molecular mobility of the solid state. Thus
rhombic sulphur when heated passes slowly at 95.6° C. into the
370
monosymmetric form which melts at 120°, but if heated rapidly
the rhombic form melts at 114.5. The two forms, rhombic and
monosymmetric, can exist in equilibrium at 95.6°, the transition
point at which they have the same vapour pressure. Similarly
a solid solution of carbon in iron, when cooled slowly, passes
at about 700° C., with considerable evolution of heat, into the
form of “pearlite,” which is soft when cold, but if rapidly chilled
the carbon remains in solution and the steel is very hard (see
also Alloys).
In the case of crystalline fusion it is necessary to distinguish
two cases, the homogeneous and the heterogeneous. In the first
case the composition of the solid and liquid phases are the same,
and the temperature remains constant during the whole process
of fusion. In the second case the solid and liquid phases differ
in composition; that of the liquid phase changes continuously,
and the temperature does not remain constant during the fusion.
The first case comprises the fusion of pure substances, and
that of eutectics, or cryohydrates; the second is the general
case of an alloy or a solution. These have been very fully
studied and their phenomena greatly elucidated in recent
years.
There is also a sub-variety of amorphous fusion, which may
be styled colloid or gelatinous, and may be illustrated by the
behaviour of solutions of water in gelatin. Many of these jellies
melt at a fairly definite temperature on heating, and coagulate or
set at a definite temperature on cooling. But in some cases the
process is not reversible, and there is generally marked hysteresis,
the temperature of setting and other phenomena depending on
the rate of cooling. This case has not yet been fully worked out;
but it appears probable that in many cases the jelly possesses
a spongy framework of solid, holding liquid in its meshes or
interstices. It might be regarded as a case of “heterogeneous”
amorphous fusion, in which the liquid separates into two phases
of different composition, one of which solidifies before the other.
The two phases cannot, as a rule, be distinguished optically,
but it is generally possible to squeeze out some of the liquid
phase when the jelly has set, which proves that the substance
is not really homogeneous. In very complicated mixtures, such
as acid lavas or slags containing a large proportion of silica,
amorphous and crystalline solidification may occur together.
In this case the crystals separate first during the process of
cooling, the mother liquor increases gradually in viscosity, and
finally sets as an amorphous ground-mass or matrix, in which
crystals of different kinds and sizes, formed at different stages
of the cooling, remain embedded. The formation of crystals
in an amorphous solid after it has set is also of frequent
occurrence. It is termed devitrification, but is a very slow
process unless the solid is in a plastic state.
2. Homogeneous Crystalline Fusion.—The fusion of a solid of
this type is characterized most clearly by the perfect constancy
of temperature during the process. In fact, the law of constant
temperature, which is generally stated as the first of the so-called
“laws of fusion,” does not strictly apply except to this case.
The constancy of the F.P. of a pure substance is so characteristic
that change of the F.P. is often one of the most convenient tests
of the presence of foreign material. In the case of substances
like ice, which melt at a low temperature and are easily obtained
in large quantities in a state of purity, the point of fusion may
be very accurately determined by observing the temperature
of an intimate mixture of the solid and liquid while slowly
melting as it absorbs heat from surrounding bodies. But in the
majority of cases it is more convenient to observe the freezing
point as the liquid is cooled. By this method it is possible to
ensure perfect uniformity of temperature throughout the mass
by stirring the liquid continuously during the process of freezing,
whereas it is difficult to ensure uniformity of temperature in
melting a solid, however gradually the heat is supplied, unless
the solid can be mixed with the liquid. It is also possible to
observe the F.P. in other ways, as by noting the temperature
at the moment of the breaking of a wire, of the stoppage of a
stirrer, or of the maximum rate of change of volume, but these
methods are generally less certain in their indications than the
point of greatest constancy of temperature in the case of homogeneous
crystalline solids.
Fusing Points of Common Metals
| Mercury | −38.8° | Antimony | 630° |
| Potassium | 62.5° | Aluminium | 655° |
| Sodium | 95.6° | Silver | 962° |
| Tin | 231.9° | Gold | 1064° |
| Bismuth | 269.2° | Copper | 1082° |
| Cadmium | 320.7° | Nickel | 1427° |
| Lead | 327.7° | Palladium | 1535° |
| Zinc | 419.0° | Platinum | 1710° |
The above table contains some of the most recent values of
fusing points of metals determined (except the first three and
the last three) with platinum thermometers. The last three
values are those obtained by extrapolation with platinum-rhodium
and platinum-iridium couples. (See Harker, Proc.
Roy. Soc. A 76, p. 235, 1905.) Some doubt has recently been
raised with regard to the value for platinum, which is much
lower than that previously accepted, namely 1775°.
3. Superfusion, Supersaturation.—It is generally possible to
cool a liquid several degrees below its normal freezing point
without a separation of crystals, especially if it is protected
from agitation, which would assist the molecules to rearrange
themselves. A liquid in this state is said to be “undercooled”
or “superfused.” The phenomenon is even more familiar in
the case of solutions (e.g. sodium sulphate or acetate) which may
remain in the “metastable” condition for an indefinite time
if protected from dust, &c. The introduction into the liquid
under this condition of the smallest fragment of the crystal,
with respect to which the solution is supersaturated, will produce
immediate crystallization, which will continue until the
temperature is raised to the saturation point by the liberation
of the latent heat of fusion. The constancy of temperature at
the normal freezing point is due to the equilibrium of exchange
existing between the liquid and solid. Unless both solid and
liquid are present, there is no condition of equilibrium, and the
temperature is indeterminate.
It has been shown by H.A. Miers (Jour. Chem. Soc., 1906, 89,
p. 413) that for a supersaturated solution in metastable equilibrium
there is an inferior limit of temperature, at which it passes
into the “labile” state, i.e. spontaneous crystallization occurs
throughout the mass in a fine shower. This seems to be analogous
to the fine misty condensation which occurs in a supersaturated
vapour in the absence of nuclei (see Vaporization) when the
supersaturation exceeds a certain limit.
4. Effect of Pressure on the F.P.—The effect of pressure on the
fusing-point depends on the change of volume during fusion. Substances
which expand on freezing, like ice, have their freezing points
lowered by increase of pressure; substances which expand on
fusing, like wax, have their melting points raised by pressure.
In each case the effect of pressure is to retard increase of volume.
This effect was first predicted by James Thomson on the analogy
of the effect of pressure on the boiling point, and was numerically
verified by Lord Kelvin in the case of ice, and later by Bunsen in
the case of paraffin and spermaceti. The equation by which the
change of the F.P. is calculated may be proved by a simple application
of the Carnot cycle, exactly as in the case of vapour and liquid.
(See Thermodynamics.) If L be the latent heat of fusion in
mechanical units, v′ the volume of unit mass of the solid, and v″
that of the liquid, the work done in an elementary Carnot cycle of
range dθ will be dp(v″ − v′), if dp is the increase of pressure required
to produce a change dθ in the F.P. Since the ratio of the work-difference
or cycle-area to the heat-transferred L must be equal to
dθ/θ, we have the relation
dθ/dp = θ (v″ − v′)/L.
(1)
The sign of dθ, the change of the F.P., is the same as that of the
change of volume (v″ − v′). Since the change of volume seldom
exceeds 0.1 c.c. per gramme, the change of the F.P. per atmosphere
is so small that it is not as a rule necessary to take account of variations
of atmospheric pressure in observing a freezing point. A
variation of 1 cm. in the height of the barometer would correspond
to a change of .0001° C. only in the F.P. of ice. This is far beyond the
limits of accuracy of most observations. Although the effect of
pressure is so small, it produces, as is well known, remarkable
results in the motion of glaciers, the moulding and regelation of
ice, and many other phenomena. It has also been employed to
explain the apparent inversion of the order of crystallization in
rocks like granite, in which the arrangement of the crystals indicates
that the quartz matrix solidified subsequently to the crystals of
371
felspar, mica or hornblende embedded in it, although the quartz
has a higher melting point. It is contended that under enormous
pressure the freezing points of the more fusible constituents might
be raised above that of the quartz, if the latter is less affected by
pressure. Thus Bunsen found the F.P. of paraffin wax 1.4° C.
below that of spermaceti at atmospheric pressure. At 100 atmospheres
the two melted at the same temperature. At higher pressures
the paraffin would solidify first. The effect of pressure on the
silicates, however, is much smaller, and it is not so easy to explain
a change of several hundred degrees in the F.P. It seems more
likely in this particular case that the order of crystallization depends
on the action of superheated water or steam at high temperatures
and pressures, which is well known to exert a highly solvent and
metamorphic action on silicates.
5. Variation of Latent Heat.—C.C. Person in 1847 endeavoured to
show by the application of the first law of thermodynamics that
the increase of the latent heat per degree should be equal to the
difference (s″ − s′) between the specific heats of the liquid and solid.
If, for instance, water at 0° C. were first frozen and then cooled to
−t° C., the heat abstracted per gramme would be (L′ + s′t) calories.
But if the water were first cooled to −t° C., and then frozen at −t°C.,
by abstracting heat L″, the heat abstracted would be L″ + s″t.
Assuming that the heat abstracted should be the same in the two
cases, we evidently obtain L′ − L″ = (s″ − s′)t. This theory has been
approximately verified by Petterson, by observing the freezing of a
liquid cooled below its normal F.P. (Jour. Chem. Soc. 24, p. 151).
But his method does not represent the true variation of the latent
heat with temperature, since the freezing, in the case of a superfused
liquid, really takes place at the normal freezing point. A quantity
of heat s″t is abstracted in cooling to −t, (L″ − s″t) in raising to 0°
and freezing at 0°, and s’t in cooling the ice to -t. The latent heat
L″ at −t does not really enter into the experiment. In order to
make the liquid freeze at a different temperature, it is necessary to
subject it to pressure, and the effect of the pressure on the latent
heat cannot be neglected. The entropy of a liquid φ″ at its F.P.
reckoned from any convenient zero φ0 in the solid state may be
represented by the expression
φ″ − φ0 = ∫ s′dθ/θ + L/θ.
(2)
Since θdφ″/dθ = s″, we obtain by differentiation the relation
dL/dθ = s″ − s′ + L/θ,
(3)
which is exactly similar to the equation for the specific heat of a
vapour maintained in the saturated condition. If we suppose that
the specific heats s′ and s″ of the solid and liquid at equilibrium
pressure are nearly the same as those ordinarily observed at constant
pressure, the relation (3) differs from that of Person only by
the addition of the term L/θ. Since s″ is greater than s′ in all cases
hitherto investigated, and L/θ is necessarily positive, it is clear that
the latent heat of fusion must increase with rise of temperature, or
diminish with fall of temperature. It is possible to imagine the F.P.
so lowered by pressure (positive or negative) that the latent heat
should vanish, in which case we should probably obtain a continuous
passage from the liquid to the solid state similar to that which
occurs in the case of amorphous substances. According to equation
(3), the rate of change of the latent heat of water is approximately
0.80 calorie per degree at 0° C. (as compared with 0.50, Person),
if we assume s″ = 1, and s′ = 0.5. Putting (s″ − s′) = 0.5 in equation
(2), we find L = 0 at −160° C. approximately, but no stress can be
laid on this estimate, as the variation of (s″ − s′) is so uncertain.
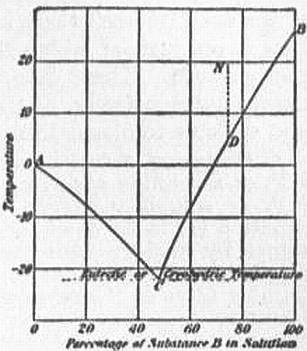 |
| Fig. 1.—F.P. or Solubility
Curve: simple case. |
6. Freezing of Solutions and Alloys.—The phenomena of
freezing of heterogeneous crystalline mixtures may be illustrated
by the case of aqueous solutions and of metallic solutions or
alloys, which have been most widely studied. The usual effect
of an impurity, such as salt or sugar in solution in water, is to
lower the freezing point, so that no crystallization occurs until
the temperature has fallen below the normal F.P. of the pure
solvent, the depression of F.P. being nearly proportional to the
concentration of the solution. When freezing begins, the solvent
generally separates out from the solution in the pure state. This
separation of the solvent involves an increase in the strength
of the remaining solution, so that the temperature does not
remain constant during the freezing, but continues to fall as
more of the solvent is separated. There is a perfectly definite
relation between temperature and concentration at each stage
of the process, which may be represented in the form of a curve
as AC in fig. 1, called the freezing point curve. The equilibrium
temperature, at the surface of contact between the solid and
liquid, depends only on the composition of the liquid phase and
not at all on the quantity of solid present. The abscissa of the
F.P. curve represents the composition of that portion of the
original solution which remains liquid at any temperature. If
instead of starting with a dilute solution we start with a strong
solution represented by a point N, and cool it as shown by the
vertical line ND, a point D is generally reached at which the
solution becomes “saturated.” The dissolved substance or
“solute” then separates out as the solution is further cooled,
and the concentration diminishes with fall of temperature in
a definite relation, as indicated by the curve CB, which is called
the solubility curve. Though often called by different names,
the two curves AC and CB are
essentially of a similar nature.
To take the case of an aqueous
solution of salt as an example,
along CB the solution is saturated
with respect to salt, along
AC the solution is saturated with
respect to ice. When the point
C is reached along either curve,
the solution is saturated with
respect to both salt and ice.
The concentration cannot vary
further, and the temperature
remains constant, while the salt
and ice crystallize out together,
maintaining the exact proportions
in which they exist in the solution. The resulting solid was
termed a cryohydrate by F. Guthrie, but it is really an intimate
mixture of two kinds of crystals, and not a chemical compound
or hydrate containing the constituents in chemically equivalent
proportions. The lowest temperature attainable by means of a
freezing mixture is the temperature of the F.P. of the corresponding
cryohydrate. In a mixture of salt and ice with the least
trace of water a saturated brine is quickly formed, which dissolves
the ice and falls rapidly in temperature, owing to the absorption
of the latent heat of fusion. So long as both ice and salt are
present, if the mixture is well stirred, the solution must necessarily
become saturated with respect to both ice and salt, and this can
only occur at the cryohydric temperature, at which the two
curves of solubility intersect.
The curves in fig. 1 also illustrate the simplest type of freezing
point curve in the case of alloys of two metals A and B which
do not form mixed crystals or chemical compounds. The alloy
corresponding to the cryohydrate, possessing the lowest melting
point, is called the eutectic alloy, as it is most easily cast and
worked. It generally possesses a very fine-grained structure,
and is not a chemical compound. (See Alloys.)
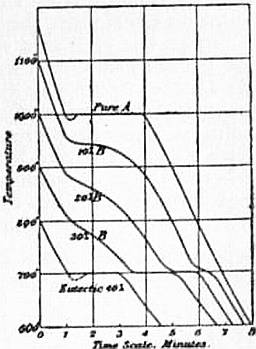 |
| Fig. 2.—Cooling Curves
of Alloys: typical case. |
To obtain a complete F.P. curve even for a binary alloy is a
laborious and complicated process, but the information contained
in such a curve is often very valuable. It is necessary to operate
with a number of different alloys of suitably chosen composition,
and to observe the freezing points of each separately. Each alloy
should also be analysed after the process if there is any risk of
its composition having been altered by oxidation or otherwise.
The freezing points are generally best
determined by observing the gradual
cooling of a considerable mass, which
is well stirred so long as it remains
liquid. The curve of cooling may most
conveniently be recorded, either photographically,
using a thermocouple and
galvanometer, as in the method of Sir
W. Roberts-Austen, or with pen and
ink, if a platinum thermometer is available,
according to the method put in
practice by C.T. Heycock and F.H.
Neville. A typical set of curves obtained
in this manner is shown in fig. 2. When
the pure metal A in cooling reaches its
F.P. the temperature suddenly becomes
stationary, and remains accurately constant for a considerable
period. Often it falls slightly below the F.P. owing to super-fusion,
but rises to the F.P. and remains constant as soon as
freezing begins. The second curve shows the cooling of A with
10% of another metal B added. The freezing begins at a lower
temperature with the separation of pure A. The temperature
372
no longer remains constant during freezing, but falls more and
more rapidly as the proportion of B in the liquid increases.
When the eutectic temperature is reached there is a second
F.P. or arrest at which the whole of the remaining liquid solidifies.
With 20% of B the first F.P. is further lowered, and the temperature
falls faster. The eutectic F.P. is of longer duration, but
still at the same temperature. For an alloy of the composition
of the eutectic itself there is no arrest until the eutectic temperature
is reached, at which the whole solidifies without change of
temperature. There is a great advantage in recording these
curves automatically, as the primary arrest is often very slight,
and difficult to observe in any other way.
7. Change of Solubility with Temperature.—The lowering of the
F.P. of a solution with increase of concentration, as shown by the
F.P. or solubility curves, may be explained and calculated by
equation (1) in terms of the osmotic pressure of the dissolved substance
by analogy with the effect of mechanical pressure. It is
possible in salt solutions to strain out the salt mechanically by a
suitable filter or “semi-permeable membrane,” which permits the
water to pass, but retains the salt. To separate 1 gramme of
salt requires the performance of work PV against the osmotic
pressure P, where V is the corresponding diminution in the volume
of the solution. In dilute solutions, to which alone the following
calculation can be applied, the volume V is the reciprocal of the
concentration C of the solution in grammes per unit volume, and
the osmotic pressure P is equal to that of an equal number of molecules
of gas in the same space, and may be deduced from the usual
equation of a gas,
P = Rθ / VM = RθC / M,
(4)
where M is the molecular weight of the salt in solution, θ the absolute
temperature, and R a constant which has the value 8.32 joules,
or nearly 2 calories, per degree C. It is necessary to consider
two cases, corresponding to the curves CB and AB in fig. 1, in
which the solution is saturated with respect to salt and water
respectively. To facilitate description we take the case of a salt
dissolved in water, but similar results apply to solutions in other
liquids and alloys of metals.
(a) If unit mass of salt is separated in the solid state from a saturated
solution of salt (curve CB) by forcing out through a semi-permeable
membrane against the osmotic pressure P the corresponding
volume of water V in which it is dissolved, the heat evolved
is the latent heat of saturated solution of the salt Q together with
the work done PV. Writing (Q + PV) for L, and V for (v″ − v′) in
equation (1), and substituting P for p, we obtain
Q + PV = VθdP / dθ,
(5)
which is equivalent to equation (1), and may be established by
similar reasoning. Substituting for P and V in terms of C from
equation (4), if Q is measured in calories, R = 2, and we obtain
QC = 2θ²dC / dθ,
(6)
which may be integrated, assuming Q constant, with the result
2logeC″ / C′ = Q / θ′ − Q / θ″,
(7)
where C′, C″ are the concentrations of the saturated solution corresponding
to the temperatures θ′ and θ″. This equation may be
employed to calculate the latent heat of solution Q from two observations
of the solubility. It follows from these equations that
Q is of the same sign as dC/dθ, that is to say, the solubility increases
with rise of temperature if heat is absorbed in the formation of the
saturated solution, which is the usual case. If, on the other hand,
heat is liberated on solution, as in the case of caustic potash or
sulphate of calcium, the solubility diminishes with rise of temperature.
(b) In the case of a solution saturated with respect to ice (curve
AC), if one gramme of water having a volume v is separated by freezing,
we obtain a precisely similar equation to (5), but with L the latent
heat of fusion of water instead of Q, and v instead of V. If the
solution is dilute, we may neglect the external work Pv in comparison
with L, and also the heat of dilution, and may write P/t for dP/dθ,
where t is the depression of the F.P. below that of the pure solvent.
Substituting for P in terms of V from equation (4), we obtain
t = 2θ²v / LVM = 2θ²w / LWM,
(8)
where W is the weight of water and w that of salt in a given volume
of solution. If M grammes of salt are dissolved in 100 of water,
w = M and W = 100. The depression of the F.P. in this case is
called by van ‘t Hoff the “Molecular Depression of the F.P.” and
is given by the simple formula
t = .02θ² / L.
(9)
Equation (8) may be used to calculate L or M, if either is known,
from observations of t, θ and w/W. The results obtained are
sufficiently approximate to be of use in many cases in spite of the
rather liberal assumptions and approximations effected in the
course of the reasoning. In any case the equations give a simple
theoretical basis with which to compare experimental data in order
to estimate the order of error involved in the assumptions. We
may thus estimate the variation of the osmotic pressure from the
value given by the gaseous equation, as the concentration of the
solution or the molecular dissociation changes. The most uncertain
factor in the formula is the molecular weight M, since the
molecule in solution may be quite different from that denoted by
the chemical formula of the solid. In many cases the molecule of
a metal in dilute solution in another metal is either monatomic, or
forms a compound molecule with the solvent containing one atom
of the dissolved metal, in which case the molecular depression is
given by putting the atomic weight for M. In other cases, as
Cu, Hg, Zn, in solution in cadmium, the depression of the F.P.
per atom, according to Heycock and Neville, is only half as great,
which would imply a diatomic molecule. Similarly As and Au in
Cd appear to be triatomic, and Sn in Pb tetratomic. Intermediate
cases may occur in which different molecules exist together in
equilibrium in proportions which vary according to the temperature
and concentration. The most familiar case is that of an electrolyte,
in which the molecule of the dissolved substance is partly dissociated
into ions. In such cases the degree of dissociation may be estimated
by observing the depression of the F.P., but the results obtained
cannot always be reconciled with those deduced by other methods,
such as measurement of electrical conductivity, and there are many
difficulties which await satisfactory interpretation.
Exactly similar relations to (8) and (9) apply to changes of boiling
point or vapour pressure produced by substances in solution (see
Vaporization), the laws of which are very closely connected with
the corresponding phenomena of fusion; but the consideration of
the vapour phase may generally be omitted in dealing with the fusion
of mixtures where the vapour pressure of either constituent is small.
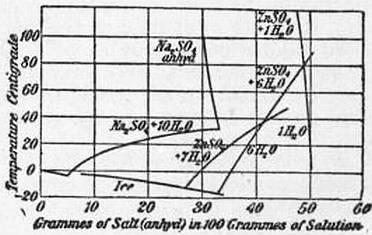 |
| Fig. 3.—Solubility Curves of
Hydrates. |
8. Hydrates.—The simple case of a freezing point curve,
illustrated in fig. 1, is generally modified by the occurrence
of compounds of a character analogous to hydrates of soluble
salts, in which the dissolved substance combines with one or
more molecules of the solvent. These hydrates may exist as
compound molecules in the solution, but their composition
cannot be demonstrated unless they can be separated in the solid
state. Corresponding to each crystalline hydrate there is generally
a separate branch of the solubility curve along which the
crystals of the hydrate are in equilibrium with the saturated
solution. At any given temperature the hydrate possessing the
least solubility is the most stable. If two are present in contact
with the same solution, the more soluble will dissolve, and the
less soluble will be formed at its expense until the conversion
is complete. The two hydrates cannot be in equilibrium with the
same solution except at the temperature at which their solubilities
are equal, i.e. at the point where the corresponding curves
of solubility intersect. This temperature is called the “Transition
Point.” In the case of ZnSO4, as shown in fig. 3, the heptahydrate,
with seven molecules of water, is the least soluble
hydrate at ordinary temperatures,
and is generally
deposited from saturated
solutions. Above 39° C.,
however, the hexahydrate,
with six molecules, is less
soluble, and a rapid conversion
of the hepta- into the
hexahydrate occurs if the
former is heated above the
transition point. The solubility
of the hexahydrate is
greater than that of the heptahydrate below 39°, but increases
more slowly with rise of temperature. At about 80° C.
the hexahydrate gives place to the monohydrate, which
dissolves in water with evolution of heat, and diminishes in
solubility with rise of temperature. Intermediate hydrates
exist, but they are more soluble, and cannot be readily isolated.
Both the mono- and hexahydrates are capable of existing in
equilibrium with saturated solutions at temperatures far below
their transition points, provided that the less soluble hydrate
is not present in the crystalline form. The solubility curves can
therefore be traced, as in fig. 3, over an extended range of temperature.
The equilibrium of each hydrate with the solvent,
considered separately, would present a diagram of two branches
similar to fig. 1, but as a rule only a small portion of each curve
can be realized, and the complete solubility curve, as experimentally
determined, is composed of a number of separate
pieces corresponding to the ranges of minimum solubility of
different hydrates. Failure to recognize this, coupled with the
373
fact that in strong and viscous solutions the state of equilibrium
is but slowly attained, is the probable explanation of the remarkable
discrepancies existing in many recorded data of solubility.
Transition Points of Hydrates.
| Na2CrO4·10H2O | 19.9° |
NaBr·2H20 | 50.7° |
| Na2SO4·10H2O | 32.4° |
MnCl2·4H2O | 57.8° |
| Na2CO3·10H2O | 35.1° |
Na3PO4·12H2O | 73.4° |
| Na2S2O3·5H2O | 48.0° |
Ba(OH)2·8H2O | 77.9° |
The transition points of the hydrates given in the above list
(Richards, Proc. Amer. Acad., 1899, 34, p. 277) afford well-marked
constant temperatures which can be utilized as fixed
points for experimental purposes.
9. Formation of Mixed Crystals.—An important exception
to the general type already described, in which the addition of a
dissolved substance lowers the F.P. of the solvent, is presented
by the formation of mixed crystals, or “solid solutions,” in
which the solvent and solute occur mixed in varying proportions.
This isomorphous replacement of one substance by another, in
the same crystal with little or no change of form, has long been
known and studied in the case of minerals and salts, but the
relations between composition and melting-point have seldom
been investigated, and much still remains obscure. In this case
the process of freezing does not necessitate the performance of
work of separation of the constituents of the solution, the F.P.
is not necessarily depressed, and the effect cannot be calculated
by the usual formula for dilute solutions. One of the simplest
types of F.P. curve which may result from the occurrence of
mixed crystals is illustrated by the case of alloys of gold and
silver, or gold and platinum, in which the F.P. curve is nearly
a straight line joining the freezing-points of the constituents.
The equilibrium between the solid and liquid, in both of which
the two metals are capable of mixing in all proportions, bears in
this case an obvious and close analogy to the equilibrium between
a mixed liquid (e.g. alcohol and water) and its vapour. In the
latter case, as is well known, the vapour will contain a larger
proportion of the more volatile constituent. Similarly in the case
of the formation of mixed crystals, the liquid should contain
a larger proportion of the more fusible constituent than the solid
with which it is in equilibrium. The composition of the crystals
which are being deposited at any moment will, therefore,
necessarily change as solidification proceeds, following the
change in the composition of the liquid, and the temperature
will fall until the last portions of the liquid to solidify will consist
chiefly of the more fusible constituent, at the F.P. of which the
solidification will be complete. If, however, as seems to be
frequently the case, the composition of the solid and liquid phases
do not greatly differ from each other, the greater part of the
solidification will occur within a comparatively small range of
temperature, and the initial F.P. of the alloy will be well marked.
It is possible in this case to draw a second curve representing
the composition of the solid phase which is in equilibrium with
the liquid at any temperature. This curve will not represent the
average composition of the crystals, but that of the outer coating
only which is in equilibrium with the liquid at the moment.
H.W.B. Roozeboom (Zeit. Phys. Chem. xxx. p. 385) has
attempted to classify some of the possible cases which may
occur in the formation of mixed crystals on the basis of J.W.
Gibbs’s thermodynamic potential, the general properties of which
may be qualitatively deduced from a consideration of observed
phenomena. But although this method may enable us to classify
different types, and even to predict results in a qualitative
manner, it does not admit of numerical calculation similar to
equation (8), as the Gibbs’s function itself is of a purely abstract
nature and its form is unknown. There is no doubt that the
formation of mixed crystals may explain many apparent
anomalies in the study of F.P. curves. The whole subject has
been most fruitful of results in recent years, and appears full of
promise for the future.
For further details in this particular branch the reader may consult
a report by Neville (Brit. Assoc. Rep., 1900), which contains numerous
references to original papers by Roberts-Austen, Le Chatelier,
Roozeboom and others. For the properties of solutions see Solution.
(H. L. C.)
FÜSSEN, a town of Germany, in the kingdom of Bavaria, at
the foot of the Alps (Tirol), on the Lech, 2500 ft. above the sea,
with a branch line to Oberdorf on the railway to Augsburg. Pop.
4000. It has six Roman Catholic churches, a Franciscan monastery
and a castle. Rope-making is an important industry.
The castle, lying on a rocky eminence, is remarkable for the
peace signed here on the 22nd of April 1745 between the elector
Maximilian III., Joseph of Bavaria and Maria Theresa. Two
miles to the S.E., immediately on the Austrian frontier, romantically
situated on a rock overlooking the Schwanensee, is the
magnificent castle of Hohenschwangau, and a little to the north,
on the site of an old castle, that of Neuschwanstein, built by
Louis II. of Bavaria.
See H. Feistle, Füssen und Umgebung (1898).
FUST, JOHANN ( ?-1466), early German printer, belonged
to a rich and respectable burgher family of Mainz, which is known
to have flourished from 1423, and to have held many civil and
religious offices. The name was always written Fust, but in
1506 Johann Schöffer, in dedicating the German translation of
Livy to the emperor Maximilian, called his grandfather Faust,
and thenceforward the family assumed this name, and the Fausts
of Aschaffenburg, an old and quite distinct family, placed
Johann Fust in their pedigree. Johann’s brother Jacob, a
goldsmith, was one of the burgomasters in 1462, when Mainz
was stormed and sacked by the troops of Count Adolf of Nassau,
on which occasion he seems to have perished (see a document,
dated May 8, 1463, published by Wyss in Quartalbl. des hist.
Vereins für Hessen, 1879, p. 24). There is no evidence that, as
is commonly asserted, Johann Fust was a goldsmith, but he
appears to have been a money-lender or banker. On account of
his connexion with Gutenberg (q.v.), he has been represented
by some as the inventor of printing, and the instructor as well as
the partner of Gutenberg, by others as his patron and benefactor,
who saw the value of his discovery and supplied him with means
to carry it out, whereas others paint him as a greedy and
crafty speculator, who took advantage of Gutenberg’s necessity
and robbed him of the fruits of his invention. However this may
be, the Helmasperger document of November 6, 1455, shows
that Fust advanced money to Gutenberg (apparently 800
guilders in 1450, and another 800 in 1452) for carrying on his
work, and that Fust, in 1455, brought a suit against Gutenberg
to recover the money he had lent, claiming 2020 (more correctly
2026) guilders for principal and interest. It appears that he had
not paid in the 300 guilders a year which he had undertaken to
furnish for expenses, wages, &c., and, according to Gutenberg,
had said that he had no intention of claiming interest. The suit
was apparently decided in Fust’s favour, November 6, 1455,
in the refectory of the Barefooted Friars of Mainz, when Fust
made oath that he himself had borrowed 1550 guilders and
given them to Gutenberg. There is no evidence that Fust, as
is usually supposed, removed the portion of the printing materials
covered by his mortgage to his own house, and carried on printing
there with the aid of Peter Schöffer, of Gernsheim (who is known
to have been a scriptor at Paris in 1449), to whom, probably
about 1455,1 he gave his only daughter Dyna or Christina in
marriage. Their first publication was the Psalter, August 14,
1457, a folio of 350 pages, the first printed book with a complete
date, and remarkable for the beauty of the large initials printed
each in two colours, red and blue, from types made in two
pieces.2 The Psalter was reprinted with the same types, 1459
(August 29), 1490, 1502 (Schöffer’s last publication) and 1516.
Fust and Schöffer’s other works are given below.3 In 1464 Adolf
374
of Nassau appointed for the parish of St Quintin three Baumeisters
(master-builders) who were to choose twelve chief parishioners
as assistants for life. One of the first of these “Vervaren,”
who were named on May-day 1464, was Johannes Fust, and in
1467 Adam von Hochheim was chosen instead of “the late”
(selig) Johannes Fust. Fust is said to have gone to Paris in 1466
and to have died of the plague, which raged there in August and
September. He certainly was in Paris on the 4th of July, when
he gave Louis de Lavernade of the province of Forez, then
chancellor of the duke of Bourbon and first president of the
parliament of Toulouse, a copy of his second edition of Cicero,
as appears from a note in Lavernade’s own hand at the end of
the book, which is now in the library of Geneva. But nothing
further is known than that on the 30th of October, probably
in 1471, an annual mass was instituted for him by Peter Schöffer,
Conrad Henlif (for Henekes, or Henckis, Schöffer’s partner?
who married Fust’s widow about 14684) and Johann Fust (the
son), in the abbey-church of St Victor of Paris, where he was
buried; and that Peter Schöffer founded a similar memorial
service for Fust in 1473 in the church of the Dominicans at
Mainz (Bockenheimer, Gesch. der Stadt Mainz, iv. 15).
Fust was formerly often confused with the famous magician
Dr Johann Faust, who, though an historical figure, had nothing
to do with him (see Faust).
(J. H. H.)
1 This date is uncertain; some place the marriage in 1453 or soon
after, others about 1464. It is probable that Fust alluded to this
relationship when he spoke of Schöffer as pueri mei in the colophons
of Cicero’s De officiis of 1465 and 1466.
2 This method was patented in England by Solomon Henry in
1780, and by Sir William Congreve in 1819.
3 (3) Durandus, Rationale divinorum officiorum (1459), folio, 160
leaves; (4) the Clementine Constitutions, with the gloss of Johannes
Andreae (1460), 51 leaves; (5) Biblia Sacra Latina (1462), folio,
2 vols., 242 and 239 leaves, 48 lines to a full page; (6) the Sixth
Book of Decretals, with Andreae’s gloss, 17th December 1465, folio,
141 leaves; (7) Cicero, De officiis (1465). 4to, 88 leaves, the first
edition of a Latin classic and the first book containing Greek characters,
while in the colophon Fust for the first time calls Schöffer
“puerum suum”; (8) the same, 4th February 1466; (9) Grammatica
rhytmica (1466), folio, 11 leaves. They also printed in 1461-1462
several papal bulls, proclamations of Adolf of Nassau, &c. Nothing
is known to have appeared for three years after the storming and
capture of Mainz in 1462.
4 Some confusion in the history of the Fust family has arisen
since the publication of Bernard’s Orig. de l’imprimerie (1853).
On p. 262, vol. i. he gave an extract from the correspondence between
Oberlin and Bodmann (now preserved in the Paris Nat. Library),
from which it would appear that Peter Schöffer was the son-in-law,
not of Johann Fust, but of a brother of his, Conrad Fust. Of the
latter, however, no other trace has been found, and he is no doubt
a fiction of F.J. Bodmann, who, partly basing himself on the
“Conrad” (Henlif, or Henckis) mentioned above, added the rest
to gratify Oberlin (see Wyss in Quartalblätter des hist. Vereins für
Hessen, 1879, p. 17).
FUSTEL DE COULANGES, NUMA DENIS (1830-1889), French
historian, was born in Paris on the 18th of March 1830, of Breton
descent. After studying at the École Normale Supérieure he
was sent to the French school at Athens in 1853, directed some
excavations in Chios, and wrote an historical account of the
island. After his return he filled various educational offices,
and took his doctor’s degree with two theses, Quid Vestae cultus
in institutis veterum privatis publicisque valuerit and Polybe,
ou la Grèce conquise par les Romains (1858). In these works
his distinctive qualities were already revealed. His minute
knowledge of the language of the Greek and Roman institutions,
coupled with his low estimate of the conclusions of contemporary
scholars, led him to go direct to the original texts, which he read
without political or religious bias. When, however, he had
succeeded in extracting from the sources a general idea that
seemed to him clear and simple, he attached himself to it as if to
the truth itself, employing dialectic of the most penetrating,
subtle and even paradoxical character in his deduction of the
logical consequences. From 1860 to 1870 he was professor of
history at the faculty of letters at Strassburg, where he had a
brilliant career as a teacher, but never yielded to the influence
exercised by the German universities in the field of classical and
Germanic antiquities.
It was at Strassburg that he published his remarkable volume
La Cité antique (1864), in which he showed forcibly the part
played by religion in the political and social evolution of Greece
and Rome. Although his making religion the sole factor of this
evolution was a perversion of the historical facts, the book was
so consistent throughout, so full of ingenious ideas, and written
in so striking a style, that it ranks as one of the masterpieces of
the French language in the 19th century. By this literary
merit Fustel set little store, but he clung tenaciously to his
theories. When he revised the book in 1875, his modifications
were very slight, and it is conceivable that, had he recast it,
as he often expressed the desire to do in the last years of his life,
he would not have abandoned any part of his fundamental
thesis. The work is now largely superseded.
Fustel de Coulanges was the most conscientious of men, the
most systematic and uncompromising of historians. Appointed
to a lectureship at the École Normale Supérieure in February
1870, to a professorship at the Paris faculty of letters in 1875,
and to the chair of medieval history created for him at the
Sorbonne in 1878, he applied himself to the study of the political
institutions of ancient France. The invasion of France by
the German armies during the war of 1870-71 attracted his
attention to the Germanic invasions under the Roman Empire.
Pursuing the theory of J.B. Dubos, but singularly transforming
it, he maintained that those invasions were not marked by the
violent and destructive character usually attributed to them;
that the penetration of the German barbarians into Gaul was a
slow process; that the Germans submitted to the imperial
administration; that the political institutions of the Merovingians
had their origins in the Roman laws at least as much as, if not
more than, in German usages; and, consequently, that there was
no conquest of Gaul by the Germans. This thesis he sustained
brilliantly in his Histoire des institutions politiques de l’ancienne
France, the first volume of which appeared in 1874. It was the
author’s original intention to complete this work in four volumes,
but as the first volume was keenly attacked in Germany as well
as in France, Fustel was forced in self-defence to recast the book
entirely. With admirable conscientiousness he re-examined
all the texts and wrote a number of dissertations, of which,
though several (e.g. those on the Germanic mark and on the
allodium and beneficium) were models of learning and sagacity,
all were dominated by his general idea and characterized by a
total disregard for the results of such historical disciplines as
diplomatic. From this crucible issued an entirely new work,
less well arranged than the original, but richer in facts and
critical comments. The first volume was expanded into three
volumes, La Gaule romaine (1891), L’Invasion germanique et
la fin de l’empire (1891) and La Monarchie franque (1888), followed
by three other volumes, L’Alleu et le domaine rural pendant
l’époque mérovingienne (1889), Les Origines du système féodal:
le bénéfice et le patronat ... (1890) and Les Transformations de
la royauté pendant l’époque carolingienne (1892). Thus, in six
volumes, he had carried the work no farther than the Carolingian
period. The result of this enormous labour, albeit worthy of a
great historian, clearly showed that the author lacked all sense
of historical proportion. He was a diligent seeker after the truth,
and was perfectly sincere when he informed a critic of the exact
number of “truths” he had discovered, and when he remarked
to one of his pupils a few days before his death, “Rest assured
that what I have written in my book is the truth.” Such superb
self-confidence can accomplish much, and it undoubtedly helped
to form Fustel’s talent and to give to his style that admirable
concision which subjugates even when it fails to convince;
but a student instinctively distrusts an historian who settles the
most controverted problems with such impassioned assurance.
The dissertations not embodied in his great work were collected
by himself and (after his death) by his pupil, Camille Jullian,
and published as volumes of miscellanies: Recherches sur
quelques problèmes d’histoire (1885), dealing with the Roman
colonate, the land system in Normandy, the Germanic mark, and
the judiciary organization in the kingdom of the Franks;
Nouvelles recherches sur quelques problèmes d’histoire (1891);
and Questions historiques (1893), which contains his paper on
Chios and his thesis on Polybius.
His life was devoted almost entirely to his teaching and his
books. In 1875 he was elected member of the Académie des
Sciences Morales, and in 1880 reluctantly accepted the post
of director of the École Normale. Without intervening personally
in French politics, he took a keen interest in the questions of
administration and social reorganization arising from the fall
of the imperialist régime and the disasters of the war. He wished
375
the institutions of the present to approximate more closely to
those of the past, and devised for the new French constitution a
body of reforms which reflected the opinions he had formed
upon the democracy at Rome and in ancient France. But these
were dreams which did not hold him long, and he would have
been scandalized had he known that his name was subsequently
used as the emblem of a political and religious party. He died
at Massy (Seine-et-Oise) on the 12th of September 1889. Throughout
his historical career—at the École Normale and the Sorbonne
and in his lectures delivered to the empress Eugénie—his sole
aim was to ascertain the truth, and in the defence of truth his
polemics against what he imagined to be the blindness and
insincerity of his critics sometimes assumed a character of harshness
and injustice. But, in France at least, these critics were
the first to render justice to his learning, his talents and his
disinterestedness.
See Paul Guiraud, Fustel de Coulanges (1896); H. d’Arbois de
Jubainville, Deux Manières d’écrire l’histoire: critique de Bossuet,
d’Augustin Thierry et de Fustel de Coulanges (1896); and Gabriel
Monod, Portraits et souvenirs (1897).
(C. B.*)
FUSTIAN, a term which includes a variety of heavy woven
cotton fabrics, chiefly prepared for men’s wear. It embraces
plain twilled cloth called jean, and cut fabrics similar to velvet,
known as velveteen, moleskin, corduroy, &c. The term was
once applied to a coarse cloth made of cotton and flax; now,
fustians are usually of cotton and dyed various colours. In the
reign of Edward III. the name was given to a woollen fabric.
The name is said to be derived from El-Fustat, a suburb of Cairo,
where it was first made; and certainly a kind of cloth has long
been known under that name. In a petition to parliament,
temp. Philip and Mary, “fustian of Naples” is mentioned. In
the 13th and 14th centuries priests’ robes and women’s dresses
were made of fustian, but though dresses are still made from
some kinds the chief use is for labourers’ clothes.
FUSTIC (Fr. fustoc, from Arab. fustuq, Gr. πιστάκη, pistachio)
Yellow Wood or Old Fustic, a dye-stuff consisting of the
wood of Chlorophora tinctoria, a large tree of the natural order
Moraceae, growing in the West Indies and tropical America.
Fustic occurs in commerce in blocks, which are brown without,
and of a brownish-yellow within. It is sometimes employed for
inlaid work. The dye-stuff termed young fustic or Zante fustic,
and also Venetian sumach, is the wood of Rhus cotinus (fustet,
or smoke tree), a southern European and Asiatic shrub of the
natural order Anacardiaceae, called by Gerarde “red sumach,”
and apparently the “coccygia” and “cotinus” of Pliny (Nat.
Hist. xiii. 41, xvi. 30). Its colouring matter is fisetin, C15H10O6,
which was synthesized by S. von Kostanecki (Ber., 1904, 37,
p. 384). (See Dyeing.)
FUTURES, a term used in the produce markets for purchases
or sales of commodities to be completed at a future date, as
opposed to cash or “spot” transactions, which are settled
immediately. See Market, and (for a detailed discussion of
the question as affecting cotton) Cotton: Marketing and Supply.
FUX, JOHANN JOSEPH (1660-1741), Austrian musician,
was born at Hirtenfeld (Styria) in 1660. Of his youth and
early training nothing is known. In 1696 he was organist at one
of the principal churches of Vienna, and in 1698 was appointed
by the emperor Leopold I. as his “imperial court-composer,”
with a salary of about £6 a month. At the court of Leopold and
of his successors Joseph I. and Charles VI., Fux remained for
the rest of his life. To his various court dignities that of organist
at St Stephen’s cathedral was added in 1704. He married the
daughter of the government secretary Schnitzbaum. As a
proof of the high favour in which he was held by the art-loving
Charles VI., it is told that at the coronation of that emperor
as king of Bohemia in 1723 an opera, La Constanza e la Fortezza,
especially composed by Fux for the occasion, was given at
Prague in an open-air theatre. Fux at the time was suffering
from gout, but the emperor had him carried in a litter all the
way from Vienna, and gave him a seat in the imperial box.
Fux died at Vienna on the 13th of February 1741. His life,
although passed in the great world, was eventless, and his only
troubles arose from the intrigues of his Italian rivals at court.
Of the numerous operas which Fux wrote it is unnecessary to
speak. They do not essentially differ from the style of the
Italian opera seria of the time. Of greater importance are his
sacred compositions, psalms, motets, oratorios and masses,
the celebrated Missa Canonica amongst the latter. It is an all
but unparalleled tour de force of learned musicianship, being
written entirely in that most difficult of contrapuntal devices—the
canon. As a contrapuntist and musical scholar generally,
Fux was unsurpassed by any of his contemporaries, and his
great theoretical work, the Gradus ad Parnassum, long
remained by far the most thorough treatment of counterpoint
and its various developments. The title of the original
Latin edition is Gradus ad Parnassum sive manuductio ad
compositionem musicae regularem, methoda nova ac certa nondum
ante tam exacta ordine in lucem edita, elaborata a Joanne Josepho
Fux (Vienna, 1715). It was translated into most European
languages during the 18th century, and is still studied by
musicians interested in the history of their art. The expenses
of the publication were defrayed by the emperor Charles VI.
Fux’s biography was published by Ludwig von Köchel (Vienna,
1871). It is based on minute original research and contains, amongst
other valuable materials, a complete catalogue of the composer’s
numerous works.
FUZE or Fuse, an appliance for firing explosives in blasting
operations, military shells, &c. (see Blasting and Ammunition,
§ Shell). The spelling is not governed by authority, but modern
convenience has dictated the adoption of the “z” by military
engineers as a general rule, in order to distinguish this sense
from that of melting by heat (see below). The word, according
to the New English Dictionary, is one of the forms in which the
Lat. fusus, spindle, has been adapted through Romanic into
English, the ordinary fuze taking the shape of a spindle-like
tube. Similarly the term “fusee” (Fr. fusée, spindle full of tow,
Late Lat. fusata) is applied to a coned spindle sometimes used in
the wheel train of watches and spring clocks to equalize the action
of the mainspring (see Watch); and the application of the same
term to a special kind of match may also be due to its resemblance
to a spindle. Again, in heraldry, another form, “fusil,” derived
through the French from a Late Lat. diminutive (fusillus or
fusellus) of this same fusus, is used of a bearing, an elongated
lozenge. According to other etymological authorities, however
(see Skeat, Etym. Dict., 1898), “fuze” or “fuse,” and “fusee”
in the sense of match, are all forms derived through the Fr. fusil,
from Late Lat. focile, steel for striking fire from a flint, from Lat.
focus, hearth. The Fr. fusil and English “fusil” were thus
transferred to the “firelock,” i.e. the light musket of the 17th
century (see Fusilier).
In electrical engineering a “fuse” (always so spelled) is a
safety device, commonly consisting of a strip or wire of easily
fusible metal, which melts and thus interrupts the circuit of
which it forms part, whenever that circuit, through some accident
or derangement, is caused to carry a current larger than that
for which it is intended. In this sense the word must be connected
with fusus, the past participle of Lat. fundere, to pour,
whence comes the verb “fuse,” to melt by heat, often used
figuratively in the sense of blend, mix.
FYNE, LOCH, an inlet of the sea, Argyllshire, Scotland.
From the head, 6 m. above Inveraray, to the mouth on the Sound
of Bute, it has a south-westerly and then southerly trend and
is 44 m. long, its width varying from ¼ m. to 6 m. It receives the
Fyne, Shira, Aray and many other streams, and, on the western
side, gives off Lochs Shira, Gair, Gilp (with Ardrishaig, the
Crinan Canal and Lochgilphead) and East Tarbert (with Tarbert
village). The glens debouching on the lake are Fyne, Shira,
Aray, Kinglas and Hell’s Glen. The coast generally is picturesque
and in many parts well wooded. All vessels using the Crinan
Canal navigate the loch to and from Ardrishaig, and there are
daily excursions during the season, as far up as Inveraray.
There are ferries at St Catherine’s and Otter, and piers at Tarbert,
Ardrishaig, Kilmory, Crarae, Furnace, Inveraray, Strachur and
elsewhere. The industries comprise granite quarrying at Furnace
376
and Crarae, distilling at Ardrishaig, gunpowder-making at
Furnace and Kilfinan, and, above all, fishing. Haddock, whiting
and codling are taken, and the famous “Loch Fyne herrings”
command the highest price in the market.
FYRD, the name given to the English army, or militia, during
the Anglo-Saxon period (see Army, 60). It is first mentioned
in the Anglo-Saxon Chronicle under the date 605. The ealdorman,
or sheriff, of the shire was probably charged with the duty of
calling out and leading the fyrd, which appears always to have
retained a local character, as during the time of the Danish
invasions we read of the fyrd of Kent, of Somerset and of
Devon. As attendance at the fyrd was included in the trinoda
necessitas it was compulsory on all holders of land; but that
it was not confined to them is shown by the following extract
from the laws of Ine, king of the West Saxons, dated about
690, which prescribes the penalty for the serious offence of
neglecting the fyrd: “If a gesithcund man owning land neglect
the fyrd, let him pay 120 shillings, and forfeit his land; one not
owning land 60 shillings; a ceorlish man 30 shillings as fyrdwite.”
The fyrd was gradually superseded by the gathering of the
thegns and their retainers, but it was occasionally called out for
defensive purposes even after the Norman Conquest.
FYT, JOHANNES (1609-1661), Belgian animal painter, was
born at Antwerp and christened on the 19th of August 1609.
He was registered apprentice to Hans van den Berghe in 1621.
Professionally van den Berghe was a restorer of old pictures
rather than a painter of new ones. At twenty Johannes Fyt
entered the gild of St Luke as a master, and from that time
till his death in 1661 he produced a vast number of pictures
in which the bold facility of Snyders is united to the powerful
effects of Rembrandt, and harmonies of gorgeous tone are not
less conspicuous than freedom of touch and a true semblance
of nature. There never was such a master of technical processes
as Fyt in the rendering of animal life in its most varied forms.
He may have been less correct in outline, less bold in action
than Snyders, but he was much more skilful and more true in
the reproduction of the coat of deer, dogs, greyhounds, hares
and monkeys, whilst in realizing the plumage of peacocks,
woodcocks, ducks, hawks, and cocks and hens, he had not his
equal, nor was any artist even of the Dutch school more effective
in relieving his compositions with accessories of tinted cloth,
porcelain ware, vases and fruit. He was not clever at figures,
and he sometimes trusted for these to the co-operation of Cornelius
Schut or Willeborts, whilst his architectural backgrounds
were sometimes executed by Quellyn. “Silenus amongst
Fruit and Flowers,” in the Harrach collection at Vienna, “Diana
and her Nymphs with the Produce of the Chase,” in the Belvedere
at Vienna, and “Dead Game and Fruit in front of a Triumphal
Arch,” belonging to Baron von Rothschild at Vienna, are
specimens of the co-operation respectively of Schut, Willeborts
and Quellyn. They are also Fyt’s masterpieces. The earliest
dated work of the master is a cat grabbing at a piece of dead
poultry near a hare and birds, belonging to Baron Cetto at
Munich, and executed in 1644. The latest is a “Dead Snipe
with Ducks,” of 1660, sold with the Jäger collection at Cologne
in 1871. Great power is shown in the bear and boar hunts at
Munich and Ravensworth castle. A “Hunted Roedeer with
Dogs in the Water,” in the Berlin Museum, has some of the life
and more of the roughness of Snyders, but lacks variety of tint
and finish. A splendid specimen is the Page and Parrot near a
table covered with game, guarded by a dog staring at a monkey,
in the Wallace collection. With the needle and the brush
Fyt was equally clever. He etched 16 plates, and those representing
dogs are of their kind unique.
FYZABAD, or Faizabad, a city, district and division of
British India in the United Provinces. The city stands on the
left bank of the river Gogra, 78 m. by rail E. of Lucknow. Pop.
(1901) 75,085. To the E. of Fyzabad, and now forming a
suburb, is the ancient site of Ajodhya(q.v.). Fyzabad was
founded about 1730 by Sa’adat Ali Khan, the first nawab
wazir of Oudh, who built a hunting-lodge here. It received its
present name in the reign of his successor; and Shuja-ud-daula,
the third nawab, laid out a large town and fortified it, and here
he was buried. It was afterwards the residence of the Begums
of Oudh, famous in connexion with the impeachment of Warren
Hastings. When the court of Oudh was removed to Lucknow
in 1775 all the leading merchants and bankers abandoned the
place. At the census of 1869 Fyzabad contained only 37,804
inhabitants; but it is now again advancing in prosperity and
population. On the outbreak of the Mutiny in 1857, the cantonment
contained two regiments of infantry, a squadron of cavalry,
and a light field battery of artillery—all natives. Owing to
their threatening demeanour after the Meerut massacre, many
of the European women and children were sheltered by one of
the great landholders of Oudh, and others were sent to less
disturbed parts of the country. The troops rose, as was anticipated,
and although they at first permitted their officers to take
boats and proceed towards Dinapur, a message was afterwards
sent to a rebel force lower down the river to intercept the fugitives.
Of four boats, one, having passed the rebels unnoticed, succeeded
in reaching Dinapur safely. Of those in the other three boats,
one alone escaped. Fyzabad is now a station for European
as well as for native troops. It is the headquarters of a brigade
in the 8th division of the northern army. There is a government
college. Sugar-refining and trade in agricultural produce are
important.
The District of Fyzabad, lying between the two great rivers
Gogra and Gumti, has an area of 1740 sq. m. It is entirely
alluvial and well wooded, and has a good climate. Pop. (1901)
1,225,374, an increase of .7% in the decade. The district is
traversed throughout its length by the Oudh and Rohilkhand
railway from Lucknow to Benares, with a branch to Allahabad.
Tanda, with a population in 1901 of 19,853, has the largest
production of cotton goods in Oudh.
The Division of Fyzabad has an area of 12,113 sq. m., and
comprises the six districts of Fyzabad, Gonda, Bahraich,
Sultanpur, Partabgarh and Bara Banki. Pop. (1901) 6,855,991,
an increase of 2% in the decade.
End of the Project Gutenberg EBook of Encyclopaedia Britannica, 11th
Edition, Volume 11, Slice 3, by Various
*** END OF THIS PROJECT GUTENBERG EBOOK ENCYC. BRITANNICA, VOL 11, SL 3 ***
***** This file should be named 37064-h.htm or 37064-h.zip *****
This and all associated files of various formats will be found in:
https://www.gutenberg.org/3/7/0/6/37064/
Produced by Marius Masi, Don Kretz and the Online
Distributed Proofreading Team at https://www.pgdp.net
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
https://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need are critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at https://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
https://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at https://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit https://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including including checks, online payments and credit card
donations. To donate, please visit: https://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart was the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
https://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.